Le document aborde des concepts mathématiques fondamentaux, notamment les opérations sur les fractions, les polynômes du second degré et les équations quadratiques. Il détaille les étapes pour résoudre des équations et des inéquations, ainsi que l'application des discriminants. De plus, il inclut des instructions de factorisation et des illustrations, offrant une approche méthodique pour l'apprentissage des mathématiques.

1. Séquence 1
Activités numériques
Sommaire
1. Formulaire p.6
2. Le second degré p.9
3. Systèmes d’équations linéaires p.16
4. Inéquations linéaires - Programmation linéaire p.21
5. Corrigés des exercices p.30
Séquence 1 5
Cned – Académie en ligne

2. 1 Formulaire
A Fractions - Racines carrées - Puissances
Attention
Fractions Racines carrées
̈ On ne peut addition-
ner que des frac- a a ×c a ÷c a ×b = a × b
tions qui ont même = =
b b ×c b ÷c ( a ≥ 0 et b ≥ 0 )
dénominateur.
a ac a b a +b a a
̈ = + = = ( a ≥ 0 et b > 0 )
b b d d d b b
c
a c a ×c
a × = a n = ( a )n
b = a b d b ×d
̈ ( a ≥ 0 et n entier )
c bc
a c a d a ×d a si a ≥ 0
: = × = a2 = =a
b d b c b ×c −a si a ≤ 0
Attention
Puissances
̈ Ne pas confondre
Soit a et b deux réels non nuls.
2−3 et −23 Soit m et n deux entiers relatifs.
1 1
2−3 = 3 =
2 8 a −n =
1 ( ab )n = an × bn ( am )n = amn
n
et −23 = −8 a
̈ 00 n’existe pas. am × an = am + n ⎛a⎞
n
an am
= = am –n
⎜b⎟
⎝ ⎠ n
bn a
Cas particuliers
a 0 = 1 (a ≠ 0 ) 0n = 0 (n ≠ 0 ) 1n = 1−n = 1
6 Séquence 1
Cned – Académie en ligne

3. B Calculs algébriques - Identités remarquables
développer Calculs algébriques Identités remarquables
a (b + c ) = ab + ac
a(b + c ) = ab + ac (a + b )2 = a2 + 2ab + b2
factoriser Produit en croix (bd ≠ 0 ) (a − b )2 = a2 – 2ab + b2
a c Ne pas oublier le dou-
̈ a 2 + b 2 ne se factorise pas. = ⇔ ad = bc
b d
ble produit 2ab.
ab = 0 ⇔ a = 0 ou b = 0 (a − b )(a + b ) = a2 − b2
C Ordre dans ‫ - ޒ‬Valeur absolue
a ≤b ⇔a −b ≤0 Ordre dans ‫ޒ‬
a ≤b ⇔b −a ≥0
Pour tout c réel : a ≤ b ⇔ a + c ≤ b + c
Addition ⎧a ≤ b
Point méthode Si ⎨ alors a + c ≤ b + d
⎩c ≤ d
Pour comparer 2
nombres on peut étu- si c > 0 alors ac ≤ bc
Si a ≤ b et
dier le signe de leur Multiplica- si c < 0 alors ac ≥ bc
différence (ce n’est tion ⎧0 ≤ a ≤ x ≤ b
pas la seule métho- Si ⎨ alors 0 ≤ ac ≤ xy ≤ bd
de…) ⎪0 ≤ c ≤ y ≤ d
⎩
Carrés
Si 0 ≤ a et 0 ≤ b alors a ≤ b ⇔ a2 ≤ b2
2 2
Si a ≤ 0 et b ≤ 0 alors a ≤ b ⇔ a ≥ b
x3 x2 1 1
Si 0 < a et 0 < b alors a ≤ b ⇔ ≤
b a
Inverses
1 1
Si a < 0 et b < 0 alors a ≤ b ⇔ ≤
x b a
1
Racines
carrées Si 0 ≤ a et 0 ≤ b alors a ≤ b ⇔ a ≤ b
illustration
Comparai- 3 2
son de a, Si 0 < a < 1 alors a < a < a < 1
graphique
a2 et a3
O 1 (a > 0 ) Si 1 < a alors 1 < a < a2 < a3
Séquence 1 7
Cned – Académie en ligne

4. Valeur absolue
x si x ≥ 0 Soit r ≥ 0
x =
− x si x ≤ 0 x = r ⇔ x = r ou x = −r
x ≥ 0 et − x = x
x ≤r ⇔ x ∈ [ −r ; r ]
x x
xy = x × y ; = (y ≠ 0)
y y x ≥ r ⇔ x ≤ −r ou x ≥ r
xn = x
n
(n entier ) x − c ≤ r ⇔ x ∈ [c − r ; c + r ]
x = y ⇔ x = y ou x = −y x − c ≥ r ⇔ x ≤ c − r ou x ≥ c + r
Représentation graphique.
x Յr x–c Յ r
x уr x–c у r
–r O r c–r c c+r
8 Séquence 1
Cned – Académie en ligne

5. 2 Le second degré
A Polynômes du second degré
Note 1. Définitions
On parle souvent, par ̈ Un polynôme P du second degré (on dit le plus sou-
abus de langage, du vent trinôme) peut s’écrire, pour tout x réel, sous la
trinôme ax 2 + bx + c . forme P ( x ) = ax 2 + bx + c avec a, b, c réels et a ≠ 0.
̈ Les racines du trinôme ax 2 + bx + c sont, si elles exis-
2
tent, les solutions de l’équation ax + bx + c = 0.
2
̈ Le discriminant du trinôme ax + bx + c est le nom-
Attention 2
bre réel, noté Δ, défini par Δ = b – 4ac.
Le coefficient a de x2 ̈ Tout trinôme P ( x ) = ax 2 + bx + c peut s’écrire sous
est toujours non nul. forme canonique :
b
P ( x ) = a( x − α )2 + β avec α = − et β = P ( α )
2a
Exemple 1 Soit P(x) = –2x2 – 3x + 5
Calculer le discriminant du trinôme P ( x ).
a Solution P ( x ) est un trinôme où a = −2, b = −3, c = 5.
Δ = b2 − 4ac = ( −3)2 − 4( −2)(5) = 9 + 40.
Δ = 49
2. Équation ax 2 + bx +c = 0 (avec a ≠ 0).
Factorisation
Δ = b 2 – 4ac Δ>0 Δ=0 Δ<0
Solutions (ou racines) 2 solutions distinctes 1 racine double pas de racine
de ax 2 + bx + c = 0 −b − Δ α=−
b
x1 =
2a 2a
(on a posé α = x1 = x2)
−b + Δ
x2 =
2a
2
Factorisation de 2 ⎛ b⎞ pas de
a( x − x1 )( x − x2 ) a( x − α ) = a ⎜ x + ⎟
ax 2 + bx + c ⎝ 2a ⎠ factorisation
Séquence 1 9
Cned – Académie en ligne

6. Exemple 2
−x2 + x + 6 = 0 1 x 2 − 2x + 3 = 0
̈ ̈ 2x 2 + 2x + = 0 ̈
2
Δ = 12 − 4( −1)( 6 ) = 25 ⎛ 1⎞
Δ = 22 − 4(2)⎜ ⎟ = 0 Δ = ( −2)2 − 4(1)( 3) = −8
−1 − 5 ⎝ 2⎠
x1 = =3 Δ < 0, pas de racine
−2 2 1
α=− =−
−1 + 5 4 2
x2 = = −2
−2 ⎧ 1⎫
᏿ = ⎨− ⎬
⎩ 2⎭ ᏿ =∅
᏿ = { −2 ; 3}
2
1 ⎛ 1⎞
̈ − x 2 + x + 6 = −( x − 3 )( x + 2 ) ̈ 2x 2 + 2x + = 2⎜ x + ⎟ ̈ Pas de factorisation
2 ⎝ 2⎠
3. Représentation graphique
d’une fonction trinôme
La courbe représentative de la fonction trinôme f défi-
nie par f(x) = ax 2 + bx + c (avec a ≠ 0 ) est une parabo-
b
le ᏼ de sommet S(α ; β ) avec α = − et β = f ( α )
2a
(pour l’allure de la parabole voir le paragraphe suivant).
B Signe du trinôme P(x) = ax2 + bx + c
avec a ≠ 0
Δ>0 Δ=0 Δ<0
Position de
la parabole
par rapport
à l’axe des
abscisses.
x1 x2 α
x x x
Signe de a > 0 P(x) + 0 – 0 + P(x) + 0 + P(x) +
P(x).
signe
de
–a
signe de a signe de a signe de a
10 Séquence 1
Cned – Académie en ligne

7. Δ>0 Δ=0 Δ<0
Position
de la pa-
rabole par
rapport à
l’axe des x1 x2 α
abscisses.
x x x
P(x) – 0 + 0 – P(x) – 0 – P(x) –
Signe de a <0
P(x).
signe
de
–a
signe de a signe de a signe de a
Exemple 3 Résoudre dans ‫ ޒ‬l’inéquation :
1
3x 2 + x − 1 < 0.
2
2 2
a Solution ⎛ 1⎞ 1 49 ⎛ 7⎞
Δ = ⎜ ⎟ − 4( 3)( −1) = + 12 = d’où Δ = ⎜ ⎟ .
⎝ 2⎠ 4 4 ⎝ 2⎠
1 7 1 7
− − − +
2 2 = − 8 = −2 1
x1 = et x2 = 2 2 = .
6 12 3 6 2
2 1
Allure de la parabole d’équation y = 3x + x − 1.
2
⎤ 2 1⎡
1 ᏿ = ⎥− ; ⎢
2
3 2 ⎦ 3 2⎣
2
y Exemple 4 Soit ᏼ la parabole d’équation y = x − x − 2 et Ᏸ la
4 B droite d’équation y = x + 1.
ᏼ
Étudier les positions relatives des deux courbes.
3
a Solution On cherche à situer la parabole par rapport à la droite
2
(au-dessus ; en dessous). Pour cela on étudie le si-
1
gne de la différence d ( x ) = x 2 − x − 2 − ( x + 1).
A x
On a donc d ( x ) = x 2 − 2x − 3.
–1 O 1 2 3
Ᏸ
Séquence 1 11
Cned – Académie en ligne

8. 2− 4 2+ 4
Δ = 4 + 12 = 16. x1 = = −1 et x2 = = 3.
–1 3 2 2
Allure de la parabole d’équation y = x 2 − 2x − 3.
Conclusion
• ᏼ est au-dessus de Ᏸ sur ] − ∞ ; − 1[ et sur ]3 ; + ∞[ ;
• ᏼ est en dessous de Ᏸ sur ]− 1 ; 3[ ;
• ᏼ coupe Ᏸ aux points A( −1 ; 0 ) et B( 3 ; 4 ).
C Équations où le calcul de Δ
n’est pas nécessaire
Exemple 5 Équation produit
Résoudre dans ‫ ޒ‬l’équation ( −2x + 3)(5 + x ) = 0.
a Solution −2x + 3 = 0 ou 5 + x = 0
3
Ne pas développer (on obtien- x= ou x = −5.
drait : −2x 2 − 7x + 15 = 0 2
et Δ = 169 ) ⎧ 3⎫
᏿ = ⎨−5 ; ⎬
⎩ 2⎭
Exemple 6 Équation incomplète ax2 + bx = 0
2
Résoudre dans ‫ ޒ‬l’équation 3x − 5x = 0.
a Solution x ( 3x − 5) = 0 d’où x = 0 ou 3x − 5 = 0.
⎧ 5⎫
On met x en facteur. ᏿ = ⎨0 ; ⎬
⎩ 3⎭
Exemple 7 Équation incomplète ax2 + c = 0
Résoudre dans ‫ ޒ‬les deux équations suivantes :
(E 1 ) x 2 − 5 = 0 ; (E 2 ) 2x 2 + 1 = 0.
a Solution (E 1 ) est une différence (E 2 ) est une somme de
Rappel de deux carrés. deux carrés.
2
x − 5 = ( x − 5 )( x + 5 ). On a donc, pour tout x
a 2 − b 2 = (a − b )(a + b ) réel, 2x 2 + 1 > 0.
2
x − 5 = 0 ⇔ x − 5 = 0 L’équation 2x 2 + 1 = 0
Si a et c sont de même signe, ou x + 5 = 0. n’a pas de solution.
alors ax + c = 0 n’a pas de so-
2
᏿ =∅
lution.
᏿ = { − 5 ; 5 }.
12 Séquence 1
Cned – Académie en ligne

9. Exemple 8 Le trinôme est un carré parfait
Résoudre dans ‫ ޒ‬les deux équations suivantes :
1
(E 3 ) x 2 + x + = 0 ; (E 4 ) 4 x 2 − 12x + 9 = 0.
4
1
a Solution (E 3 ) x 2 + x + = (E 4 ) 4 x 2 − 12x + 9 =
4
⎛
2 (2x − 3)2
1⎞
⎜ x + 2⎟
⎝ ⎠ 3
(2x − 3)2 = 0 ⇔ x = .
2 2
⎛ 1⎞ 1
⎜ x + 2⎟ = 0 ⇔ x = − 2 .
⎝ ⎠
⎧ 1⎫ ⎧3 ⎫
᏿ = ⎨− ⎬ ᏿ =⎨ ⎬
⎩ 2⎭ ⎩2⎭
D Situations du second degré
Exemple 9 Résolution d’une équation « bicarrée »
Résoudre dans ‫ ޒ‬l’équation (E ) 4 x 4 − 17x 2 − 15 = 0.
Solution
a En posant x 2 = X l’équation (E ) s’écrit sous la forme
Une équation bicarrée est de la
4 X 2 − 17X − 15 = 0, avec X ≥ 0.
f o r m e : ax 4 + bx 2 + c = 0 a v e c
a ≠ 0. Δ = ( −17 )2 − 4( 4 )( −15) = 529 et Δ = 232.
17 − 23 6 3 17 + 23
X1 = = − = − et X2 = = 5.
Point méthode 8 8 4 8
3
Pour résoudre une • x 2 = − est impossible.
4
équation bicarrée on 2
pose x 2 = X . • x = 5 ⇔ x = − 5 ou x = 5.
᏿ = {− 5 ; 5 }
Exemple 10 Étude d’une situation concrète
Plusieurs amis décident de partir ensemble en
voyage.
Le séjour coûte en tout 3 600 €. En amenant trois
personnes supplémentaires, la part de chacun serait
diminuée de 60 €.
Déterminer le nombre d’amis au départ et calculer
alors la part initiale de chacun d’eux.
Séquence 1 13
Cned – Académie en ligne

10. a Solution Désignons par x le nombre d’amis prévus au départ.
On peut présenter la situation dans un tableau.
Nombre de Part de chacun,
personnes en €
3 600
Situation initiale x La part ini-
x tiale est di-
Si 3 personnes minuée de
x +3 3 600 3 600
supplémentaires = − 60 60 €
x +3 x
Résolvons 3 600 = 3 600 − 60 qui s’écrit aussi :
x +3 x
3 600 3 600 − 60x
= .
x +3 x
Le produit en croix nous donne :
3 600x = ( x + 3)( 3 600 − 60x ).
Attention En simplifiant par 60 on obtient : 60x = ( x + 3)( 60 − x ).
2 2
Dans une situation D’où x + 3x − 180 = 0. Δ = 9 + 720 = 729 et 729 = 27 .
concrète il arrive que −3 − 27 −3 + 27
toutes les solutions x1 = = −15 ; x2 = = 12.
2 2
possibles ne convien-
nent pas. Seule la racine positive x2 convient.
3 600 3 600
Pour x = 12 on a = = 300.
x 12
Au départ il y a 12 amis, la part initiale étant égale
à 300 €.
E Exercices d’application
a À vous de jouer…
Exercice 1 On considère les trinômes P, Q et R définis par :
1
P ( x ) = x 2 + 12x + 35 ; Q( x ) = − x 2 + 2x − ;
2
R ( x ) = 2x 2 − 4 x + 3.
ᕡ Résoudre dans ‫ ޒ‬les trois équations suivantes :
P ( x ) = 0 ; Q( x ) = 0 ; R ( x ) = 0.
ᕢ Mettre, si possible, les trinômes P, Q, R sous forme
d’un produit de facteurs du premier degré.
14 Séquence 1
Cned – Académie en ligne

11. Exercice 2 Sans calculer Δ, résoudre dans ‫ ޒ‬les équations sui-
vantes :
(E 1 ) ( x − 2 008 )(1 789x + 1) = 0 ;
(E 2 ) 121x 2 − 143x = 0 ;
(E 3 ) 25x2 + 20x + 4 = 0 ;
(E 4 ) (2x − 3)2 − 5 = 0.
Exercice 3 Résoudre dans ‫ ޒ‬les trois inéquations suivantes :
(I1 ) x 2 + 12x + 35 ≥ 0 ; (I2 ) − x 2 + 3x − 5 < 0 ;
(I3 ) (2x − 3)( 4 − x ) > 0.
Exercice 4 Résoudre dans ‫ ޒ‬les deux équations bicarrées sui-
vantes :
(B1 ) x 4 + 7x 2 + 10 = 0 ; (B2 ) x 4 − 11x 2 + 18 = 0.
Exercice 5 Soit ᏼ la parabole représentant la fonction trinôme
définie sur ‫ ޒ‬par f ( x ) = − x 2 − 4 x + 3.
ᕡ Déterminer les coordonnées du sommet S de la pa-
rabole ᏼ.
ᕢ Déterminer les coordonnées des points où ᏼ cou-
pe l’axe des abscisses et situer ᏼ par rapport à cet
axe.
ᕣ Situer ᏼ par rapport à la droite Ᏸ d’équation
y = −2x .
Séquence 1 15
Cned – Académie en ligne

12. 3 Systèmes d’équations
linéaires
A Systèmes de deux équations à deux
inconnues (dit "2 ϫ 2")
1. Résolution algébrique - Méthode
dite de « substitution »
Exemple 11 Résoudre, par la méthode de substitu-
tion, le système (S) suivant :
⎧−2x + 3y − 9 = 0 L1
⎪
(S ) ⎨
⎪ 6x + 8y − 7 = 0 L2
⎩
2
a Solution En isolant y dans L1 on obtient : y = x + 3.
3
⎧ 2 ⎧ 2
⎪y = x + 3 ⎪y = x + 3
Point méthode ⎪ 3 ⎪ 3
(S ) ⇔ ⎨ ⇔⎨
⎛2 ⎞ 34
On isole l’une des in- ⎪6x + 8 x + 3 − 7 = 0 ⎪ x + 17 = 0
⎪ ⎜3 ⎟ ⎪3
connues (soit x, soit y) ⎩ ⎝ ⎠ ⎩
dans l’une des équa-
⎧ 2
tions et on la rempla-
⎪y = x + 3 ⎧ 3
ce dans l’autre. ⎪ 3 ⎪x = −
(S ) ⇔ ⎨ ⇔⎨ 2
⎪ x = − 3 × 17 = − 3 ⎪y = 2
⎪ ⎩
⎩ 34 2
Le système ( S ) possède un couple solution unique.
⎧⎛ 3
⎪ ⎞⎫⎪
᏿ = ⎨⎜ − ; 2⎟ ⎬
⎪⎝ 2 ⎠ ⎪
⎩ ⎭
2. Résolution algébrique - Méthode
des combinaisons linéaires
On reprend le même exemple 11.
16 Séquence 1
Cned – Académie en ligne

13. a Solution
Coefficients
multiplicateurs
Point méthode
En multipliant L1 par ⎧−2x + 3y − 9 = 0
⎪ –8 3
–8, L2 par 3 et en (S ) ⎨
faisant la somme, les
⎪ 6x + 8y − 7 = 0
⎩ 3 1
« termes en y » s’an-
nulent. ⎧16x − 24y + 72 = 0
⎪ ⎧−6 x + 9y − 27 = 0
⎪
Pour éliminer x, on (S ) ⎨ (S ) ⎨
choisit 3 et 1. ⎩18x + 24 y − 21 = 0
⎪ ⎩ 6x + 8y − 7 = 0
⎪
34 x + 51 = 0 17y − 34 = 0
On obtient un nouveau système :
⎧−8 L1 + 3 L2
⎪
(S ') ⎨ ⎧ 3
⎩3 L1 + 1 L2
⎪ ⎧34 x + 51 = 0 ⎪ x = −
( S ') ⎨ ⇔⎨ 2
⎪17y − 34 = 0 ⎪
⎩
⎩y = 2
⎧⎛ 3
⎪ ⎞⎪⎫
᏿ = ⎨⎜ − ; 2⎟ ⎬
⎪⎝ 2 ⎠ ⎪
⎩ ⎭
3. Résolution graphique
On reprend encore le même exemple 11.
a Solution ̈ −2x + 3y − 9 = 0 est l’équation cartésienne d’une
droite (d1 ).
̈ 6x + 8y − 7 = 0 est l’équation cartésienne d’une
Mémo
droite (d2 ).
Toute droite (d) a
une équation carté-
sienne de la forme Déterminons les équations réduites de (d1 ) et (d2 ).
ax + by + c = 0 2
−2x + 3y − 9 = 0 ⇔ 3y = 2x + 9 ⇔ y = x + 3.
avec (a ; b ) ≠ (0 ; 0). 3
̈ Si b ≠ 0 ,alors (d) 3 7
6x + 8y − 7 = 0 ⇔ 8y = −6x + 7 ⇔ y = − x + .
n’est pas parallèle à 4 8
l’axe des ordonnées
Traçons (d1 ) et (d2 ) dans un repère du plan.
et son équation ré-
duite est y = mx + p. x –3 0 3 x –1,5 0,5 2,5
̈ Si b = 0 , alors (d) (d1) (d2)
y 1 3 5 y 2 0,5 –1
est parallèle à l’axe
des ordonnées et
a pour équation
x = k. Voir le graphique en page suivante.
Séquence 1 17
Cned – Académie en ligne

14. Parallélisme y
̈ Équations réduites
5 (d1)
La droite (d) d’équation
y = mx + p a pour coefficient point
b 4
directeur m = − . solution
a
(d ) y = mx + p 3
(d ') y = m ' x + p '
K 3
2
(d ) //(d ') ⇔ m = m '
1
̈ Équations cartésiennes
(d ) ax + by + c = 0 x
(d ') a ' x + b ' y + c ' = 0 –3 –2 3 –1 O 1 2 3
–
2
(d ) //(d ') ⇔ ab '− a ' b = 0 –1
(d2)
Attention Résoudre le système ( S ) revient à chercher les coor-
données du point d’intersection, s’il existe, des droi-
Un graphique ne per-
tes (d ) et (d2 ).
1
met pas de connaître
avec certitude les ⎛ 3 ⎞
coordonnées d’un Les droites (d1 ) et (d2 ) se coupent en K ⎜ − ; 2⎟ .
⎝ 2 ⎠
point d’intersection. ⎧⎛ 3 ⎞⎫
⎪ ⎪
᏿ = ⎨⎜ − ; 2⎟ ⎬ .
⎪⎝ 2 ⎠ ⎪
⎩ ⎭
̈ Remarque
En calculant ab '− a 'b = ( −2)( 8 ) − ( 6 )( 3) = −34 on peut
affirmer que (d1) et (d2) ne sont pas parallèles : elles
sont donc sécantes et le système possède une solution
unique.
B Systèmes de trois équations à trois
inconnues (dit « 3 ϫ 3 »)
Exemple 12 Résoudre le système :
Point méthode
La résolution d’un ⎧ x − y + 2z = 6 [E ]
1
système « 3 ϫ 3 » ⎪
⎪
( S ) ⎨4 x + 2y − z = −3 [E 2 ]
peut se ramener à
⎪
celle d’un système ⎪3x + 3y − 2z = −7 [E 3 ]
⎩
« 2 ϫ 2 ».
18 Séquence 1
Cned – Académie en ligne

15. a Solution On va résoudre ( S ) en utilisant deux méthodes :
̈ Méthode par substitution ;
̈ Méthode par combinaisons.
Méthode par substitution Méthode par combinaisons
Étape 1 Étape 1
On exprime l’une des inconnues en fonc- On élimine l’une des inconnues (par exem-
tion des deux autres. ple z) pour obtenir un système 2 × 2 où les
inconnues sont x et y .
[E 1 ] x = y − 2z + 6
⎧ x − y + 2z = 6 1 1
Étape 2 ⎪
On remplace, dans les deux autres équa- ⎨4 x + 2y − z = −3 2
⎪3x + 3y − 2z = −7 1
tions, l’inconnue par son expression en ⎩
fonction des deux autres. x − y + 2z = 6 x − y + 2z = 6
[E 2 ] 4( y − 2z + 6 ) + 2y − z = −3 + +
3x + 3y − 2z = −7 8x + 4y − 2z = −6
6y − 9z = −27 ⇔ 2y − 3z = −9 4 x + 2y = −1 9x + 3y = 0
[E 3 ] 3( y − 2z + 6 ) + 3y − 2z = −7
6y − 8z = −25 Étape 2
Étape 3 On résout par combinaisons le nouveau
système ( S '') obtenu.
On résout le nouveau système ( S ') obtenu.
⎧
⎪4 x + 2y = −1 1 3
⎧ 3z − 9 ( S '') ⎨
⎪y= ⎩3x + y = 0
⎪ −2 −4
⎧2y − 3z = −9
⎪ ⎪ 2
( S ') ⎨ ⇔⎨
4 x + 2y = −1 12x + 6y = −3
⎩6y − 8z = −25 ⎪6 ⎛ 3z − 9 ⎞ − 8z = −25 +
⎪ +
⎪ ⎝⎜ 2 ⎟ ⎠ −6x − 2y = 0 −12x − 4y = 0
⎩
⎧ 3z − 9 ⎧ 3 −2x = −1 2y = −3
⎪y = ⎪y = −
⇔⎨ 2 ⇔⎨ 2 1 3
⎪z = 2 ⎪z = 2 d’où x = ; y =−
⎩ ⎩ 2 2
3 1 dans [E 2 ] z = 4 x + 2y + 3 = 2.
On obtient x = − − 4 + 6 = .
2 2
Étape 4
Étape 3
On vérifie la solution obtenue On vérifie la solution obtenue.
1 3 1 3
[E 1 ] + + 4 = 6 vrai [E 1 ] + + 4 = 6 vrai
2 2 2 2
[E 2 ] 2 − 3 − 2 = −3 vrai
[E 2 ] 2 − 3 − 2 = −3 vrai
3 9
[E 3 ] − − 4 = −7 vrai 3 9
2 2 [E 3 ] − − 4 = −7 vrai
2 2
Étape 5 Conclusion
Étape 4 Conclusion
Le système ( S ) admet un triplet solution.
Le système ( S ) admet un triplet solution.
⎧⎛ 1
⎪ 3 ⎞⎫⎪
᏿ = ⎨⎜ ; − ; 2⎟ ⎬ ⎧⎛ 1 ⎞⎫
⎪⎝ 2 2 ⎠⎪ ⎪ 3 ⎪
⎩ ⎭ ᏿ = ⎨⎜ ; − ; 2⎟ ⎬
⎪⎝ 2
⎩ 2 ⎠⎪ ⎭
Séquence 1 19
Cned – Académie en ligne

16. C Exercices d’application
a À vous de jouer…
Exercice 6 Résoudre les systèmes suivants et interpréter graphi-
quement les résultats :
Calculer d’abord ab '− a ' b. ⎧ ⎧−3x + 5y = −3
⎪−3x + 5y = −3 ⎪
( S1 ) ⎨ ( S2 ) ⎨ 1 5
⎩ x + 3y = 5
⎪ ⎪ x − y =1
⎩2 6
⎧4 x − y = 3
⎪
( S3 ) ⎨ 2 1 1
⎪ x− y =
⎩3 6 2
Exercice 7 Le plan étant muni d’un repère, on considère les trois
points A( −3 ; − 1), B( 0 ; 3), C (2 ; − 2).
Faire une figure et déterminer une équation de cha-
cune des droites ( AB ),(BC ),( AC ).
Exercice 8 Résoudre les systèmes :
⎧1 2
Pour (S 2 ) on posera : ⎧ x − y = 10
⎪ ⎪ − y = −4
⎪
1 ( S1 ) ⎨
2 2
( S2 ) ⎨ x
= X et y 2 = Y . ⎩ x − y = 40
⎪ ⎪ 2 + 3y 2 = 2
x
⎪
⎩x
Exercice 9 Résoudre les systèmes suivants :
̈ Résoudre (S1) par combinaisons.
⎧2x − y + z = 0 ⎧x y z
̈ Pour (S 2 ) on pose : ⎪ ⎪ = =
( S1 ) ⎨− x + 4y + 2z = −1 ( S2 ) ⎨ 3 4 5
x y z ⎪3x − 4y + 6z = −4 ⎪5x − 4y + 3z = 7
= = =t ⎩
3 4 5 ⎩
et on détermine d’abord t.
20 Séquence 1
Cned – Académie en ligne

17. Inéquations linéaires
4 Programmation linéaire
A Inéquations linéaires à deux inconnues
Exemple 13 Résoudre graphiquement les deux inéqua-
tions suivantes :
(I1 ) x − 3y − 6 ≥ 0 ; (I2 ) 3x + 2y − 7 ≥ 0.
( I1 ) x − 3 y − 6 ≥ 0 ( I2 ) 3 x + 2 y − 7 ≥ 0
Étape 1 1 3 7
On isole l’inconnue y. y ≤ x −2 y ≥− x+
3 2 2
Étape 2 1 3 7
On trace la droite (d) (d1) a pour équation y = 3 x − 2 (d2) a pour équation y = − x +
2 2
d’équation y = mx + p. x 0 2 3 x –1 1 3
Il est conseillé de choi-
4
sir 3 points pour tracer y –2 − –1 y 5 2 –1
une droite. 3
Étape 3 y y
On détermine le demi-
plan qui convient. 5 5
y > mx + p
4 4
y = mx + p demi-plan
solution
3 3
y < mx + p
2 2
On colorie le demi-plan 1 1
solution.
x x
–1 O 1 2 3 –1 O 1 2 3
–1 –1
–2 –2 (d2)
(d1) demi-plan
solution
Séquence 1 21
Cned – Académie en ligne

18. Étape 4 Tout point M( x ; y ) situé en dessous Tout point M( x ; y ) situé au-des-
Conclusion. de (ou sur) (d1 ) a des coordonnées sus de (ou sur) (d2 ) a des coordon-
vérifiant l’inéquation (I1 ). nées vérifiant l’inéquation (I2 ).
Cet ensemble est colorié sur le gra- Cet ensemble est colorié sur le gra-
phique (frontière incluse). phique (frontière incluse).
B Systèmes d’inéquations linéaires
à deux inconnues
Exemple 14 Résoudre graphiquement le système :
⎧ x − 3y − 6 ≥ 0
⎪
(S ) ⎨
⎪3x + 2y − 7 ≥ 0
⎩
a Solution Le système ( S ) est formé des deux inéquations de
l’exemple 13.
Point méthode Il suffit de faire un seul graphique sur lequel on indi-
quera la région solution.
On résout séparé- y
ment chacune des
inéquations du sys- 5
tème.
4
Étape 1
On trace :
(d 1) x − 3y − 6 = 0 3
(d 2 ) 3x + 2y − 7 = 0
2
Étape 2
On détermine chaque demi-plan
solution. 1
Étape 3
6
On détermine la région solution. 5 x
–1 O 1 2 3 4
Étape 4
Ne pas oublier de faire une phra- –1
se de conclusion. région
qui
–2
convient
(d1)
Par convention on hachure ce (d2)
qui ne convient pas.
Conclusion
Tout point M( x ; y ) situé dans la région coloriée a des coordonnées vérifiant le sys-
tème (frontières incluses).
22 Séquence 1
Cned – Académie en ligne

19. C Programmation linéaire
Exemple 15 Une couturière fabrique des pantalons suivant deux
modèles A et B. Elle dispose de 15 m de tissu par se-
La programmation linéaire est maine et travaille 40 heures par semaine.
la recherche du maximum ou du Le modèle A nécessite 1 m de tissu et 4 h de travail.
minimum d’une fonction économi- Le modèle B nécessite 1,5 m de tissu et 2 h de travail.
que, compte tenu de certaines On note x le nombre de pantalons du modèle A et y
contraintes représentées par des le nombre de pantalons du modèle B fabriqués par
équations ou des inéquations. semaine.
ᕡ Montrer que les productions hebdomadaires de la
couturière sont soumises aux contraintes suivantes :
⎧ x ≥ 0 et y ≥ 0 ( x et y entiers )
⎪
⎨2x + 3y ≤ 30
⎪2x + y ≤ 20
⎩
ᕢ Représenter graphiquement les contraintes de pro-
duction dans un repère orthonormal (O ; i , j ). On
choisira 1 cm comme unité graphique.
ᕣ Sur un pantalon du modèle A la couturière fait un
bénéfice de 60 € et sur un pantalon du modèle
B un bénéfice de 40 €. On suppose qu’elle vend
toute sa production.
a) Exprimer, en fonction de x et y, le bénéfice heb-
domadaire b qu’elle peut réaliser.
b) Représenter sur le graphique précédent les cou-
ples ( x ; y ) qui permettent de réaliser un béné-
fice de 240 €.
c) Déterminer graphiquement le nombre de panta-
lons de chaque modèle à fabriquer par semaine
pour que le bénéfice soit le plus grand possible.
Quel est alors le bénéfice réalisé ?
a Solution ᕡ La couturière fabrique un nombre entier de panta-
lons ce qui implique x ∈» et y ∈». D’où x ≥ 0 et
y ≥ 0.
̈ Contrainte tissu : x + 1,5y ≤ 15, soit 2x + 3y ≤ 30.
̈ Contrainte horaire : 4 x + 2y ≤ 40, soit 2x + y ≤ 20.
Voici le système d’inéquations traduisant toutes les
contraintes.
⎧ x ≥ 0 et y ≥ 0 ( x et y entiers )
⎪
⎨2x + 3y ≤ 30
⎪2x + y ≤ 20
⎩
Séquence 1 23
Cned – Académie en ligne

20. ᕢ Soit Ᏸ la droite d’équation 2x + 3y = 30, ou en-
1
2
core y = − x + 10.
3
Soit Ᏸ 2 la droite d’équation 2x + y = 20, ou en-
core y = −2x + 20.
On choisit, si possible, des coor- x 0 3 6 x 5 6 10
données entières. Ᏸ1 Ᏸ2
y 10 8 6 y 10 8 0
̈ x ≥0 est y
vérifié pour
tout point M droite Δ’ de
situé à droite bénéfice maximal
de l’axe des 10
y = – 3 x + 16
ordonnées. 2
̈ y ≥ 0 est vé-
rifié pour tout
point M situé
au-dessus de
l’axe des abs-
cisses. cette
6 région
̈ point
convient solution
2x + 3y ≤ 30 ⇔ I K (8 ; 4)
2
y ≤ − x + 10
3
4
Tout point M K
situé en des-
3
sous de Ᏸ 1 Ᏸ1
convient. y=– 3x+6
2
̈
2x + y ≤ 20 ⇔
1
y ≤ −2x + 20 Ᏸ2
Tout point M x
O 1 2 4 8 10 Δ’
situé en des-
Δ
sous de Ᏸ 1
convient.
̈ La région coloriée est appelée
« polygone des contraintes ». Conclusion
̈ Ᏸ 1 et Ᏸ 2 se coupent en
I (7,5 ; 5). Tout point M( x ; y ) ayant des coordonnées en-
L’abscisse de I n’est pas un nom- tières et situé dans la région coloriée a des coor-
bre entier.
données vérifiant le système des contraintes
̈ C’est en K (8 ; 4) que le béné- (frontières incluses).
fice est maximal.
24 Séquence 1
Cned – Académie en ligne

21. ᕣ a) Le bénéfice b est tel que b = 60 x + 40y
b) Soit Δ la droite d’équation 240 = 60x + 40y , soit
3
encore 3x + 2y = 12 ou y = − x + 6.
2
Δ passe par les points ( 0 ; 6 ) et ( 4 ; 0 ).
Sur cette droite il n’y a que 3 points à coordonnées
entières.
Les 3 couples qui permettent de réaliser un béné-
fice de 240 € sont :
( 0 ; 6 ) ( 2 ; 3 ) ( 4 ; 0 ).
̈ Les droites Δ b sont toutes paral- c) Soit Δb la droite d’équation b = 60x + 40y , ou en-
lèles entre elles, et donc à Δ 240, 3 b
core y = − x + .
car elles ont toutes pour coeffi- 2 40
3 b
cient directeur − . Le bénéfice b est maximal lorsque est maximal,
2 40
̈ Pour trouver Δ ' on fait « glis- c’est-à-dire lorsque l’ordonnée à l’origine de Δb est
ser », avec une règle, la droite maximale. On cherche donc la droite Δb ayant une
Δ parallèlement à elle-même. ordonnée à l’origine maximale et qui coupe le poly-
gone des contraintes en au moins un point de coor-
données entières. La droite Δb qui convient est celle
passant par le point K ( 8 ; 4 ).
On calcule bmax = 60 × 8 + 40 × 4 = 640.
La couturière réalise un bénéfice maximal de 640 €
pour la vente de 8 pantalons du modèle A et de 4 pan-
talons du modèle B.
Exemple 16 Le patron d’un restaurant prévoit l’achat de mobilier
de jardin en vue d’aménager un parc pour ses clients.
Il choisit deux modèles, l’un en bois, l’autre en métal.
Pour le modèle en bois, le lot comprend une table,
trois chaises, quatre fauteuils, le tout pour 2 400
euros.
Pour le modèle en métal, le lot comprend une ta-
ble, neuf chaises, deux fauteuils, le tout pour 1 600
euros.
Le projet est de disposer d’au moins 63 chaises et 30
fauteuils.
ᕡ Soit x le nombre de lots en bois et y le nombre de
lots en métal achetés par le restaurateur.
Écrire le système des contraintes correspondant
au problème.
ᕢ Déterminer graphiquement l’ensemble des points
M du plan dont les coordonnées vérifient le systè-
me des contraintes (unité graphique : 0,5 cm).
Séquence 1 25
Cned – Académie en ligne

22. ᕣ Exprimer en fonction de x et y la dépense d cor-
respondant à l’achat de x lots en bois et y lots en
métal.
ᕤ Déterminer une équation de la droite Δ correspon-
dant à une dépense de 24 000 euros et tracer Δ.
ᕥ Le restaurateur veut minimiser sa dépense. Com-
bien doit-il acheter alors de lots en bois et de lots
en métal ? Donner le montant de cette dépense
minimale.
a Solution ᕡ Le nombre x de lots en bois et le nombre y de lots
en métal sont des entiers positifs.
D’où x ≥ 0, y ≥ 0, avec x et y entiers.
̈ Contrainte chaises : 3x + 9y ≥ 63, soit
x + 3y ≥ 21.
̈ Contrainte fauteuils : 4 x + 2y ≥ 30, soit
2x + y ≥ 15.
Voici le système d’inéquations traduisant toutes
les contraintes.
⎧ x ≥ 0 et y ≥ 0 ( x et y entiers )
⎪
⎨ x + 3y ≥ 21
⎪2x + y ≥ 15
⎩
ᕢ Soit D la droite d’équation x + 3y = 21, ou encore
1
1
y = − x + 7.
3
Soit D2 la droite d’équation 2x + y = 15, ou encore
y = −2x + 15.
x 0 3 6 x 0 3 6
D1 D2
y 7 6 5 y 15 9 3
u Voir le graphique en page suivante.
ᕣ La dépense d est telle que d = 2 400 x + 1600y
ᕤ La droite Δ correspondant à une dépense de 24 000
euros a pour équation 24 000 = 2 400x + 1 600y ,
soit encore :
3
y = − x + 15.
2
Cette droite Δ passe par les points :
( 0 ; 15) et (10 ; 0 ).
26 Séquence 1
Cned – Académie en ligne

23. y
̈
x + 3y ≥ 21 ⇔ droite Δ’ de
1 dépense minimale
y ≥ − x +7 15
3 y = – 3 x + 13
Tout point M 2
13
situé au-des-
sus de D1
convient.
cette
̈
9 région
2x + y ≥ 15 ⇔ convient
point
y ≥ −2x + 15 K solution
Tout point M 7 K (4 ; 7)
situé au-des-
sus de D2 5 I
convient.
̈ Dans cet
exemple la ré-
1
gion coloriée D1 x
est infinie. y = – 3 x + 15
O 1 2 3 4 5 6 10 Δ 2 21
D2
Δ’
̈ Un calcul nous montre que Conclusion
D 1 et D sont sécantes en Tout point M( x ; y ) ayant des coordonnées en-
2
I (4, 8 ; 5, 4). Les coordonnées tières et situé dans la région coloriée a des coor-
de I ne sont pas entières. données vérifiant le système des contraintes
(frontières incluses).
̈ Les droites Δd sont toutes pa- ᕥ Soit Δ la droite d’équation d = 2 400x + 1 600y
d
rallèles à Δ 24000 (même coeffi- 3 d
ou encore y = − x + .
3 2 1 600
cient directeur − ). d
2 La dépense d est minimale lorsque est mi-
1 600
x 3 4 5 nimal, c’est-à-dire lorsque l’ordonnée à l’origine
y 9 7 6 de Δd est minimale. On cherche donc la droite
d 21 600 20 800 21 600 Δd ayant une ordonnée à l’origine minimale et qui
Ȇ coupe la région coloriée en au moins un point de
Min coordonnées entières. La droite Δd qui convient
semble être celle passant par le point K ( 4 ; 7 ).
Pour en être certain on peut effectuer quelques
calculs pour des points voisins de K .
On calcule dmin = 2 400 × 4 + 1 600 × 7 = 20 800.
La dépense minimale de 20 800 euros est obtenue
pour l’achat de 4 lots en bois et 7 lots en métal.
Séquence 1 27
Cned – Académie en ligne

24. D Exercices d’application
a À vous de jouer…
Exercice 10 Déterminer un système d’inéquations caractérisant
tout point M( x ; y ) situé à l’intérieur (ou sur les cô-
tés) du triangle ABC défini dans l’exercice 7.
Exercice 11 Résoudre graphiquement les systèmes suivants :
⎧x + y ≥ 0 ⎧ x ≥ 0 et y ≥ 0
⎪ ⎪
( S1 ) ⎨y ≤ 3 ( S2 ) ⎨2x + y − 6 ≤ 0
⎪x − y − 1 ≤ 0 ⎪x + y − 4 ≤ 0
⎩ ⎩
Exercice 12 Un promoteur étudie la construction d’une résiden-
ce composée de studios et de petits appartements.
Il prévoit pour un studio une surface habitable de
30 m2, une fenêtre et espère le vendre 60 000 euros.
Pour un petit appartement, il prévoit une surface
habitable de 50 m2, 3 fenêtres et espère le vendre
120 000 euros.
̈ Il veut que la résidence ait au moins 20 logements.
̈ Il dispose de 1 160 m2 de surface habitable et de
60 fenêtres.
̈ Par ailleurs, il ne peut pas vendre plus de 15 stu-
dios.
Le but de l’exercice est de déterminer le nombre x de
studios et le nombre y de petits appartements que le
promoteur doit construire pour réaliser un chiffre d’af-
faires maximal.
ᕡ Déterminer un système d’inéquations portant sur x
et y traduisant les contraintes du problème.
ᕢ Déterminer graphiquement l’ensemble des points
M dont les coordonnées ( x ; y ) vérifient toutes les
contraintes précédentes. On choisira un repère or-
thonormal ayant pour unité graphique 0,5 cm.
ᕣ a) Exprimer en fonction de x et y le chiffre d’affaires
C , exprimé en euros, correspondant à la vente
de x studios et de y petits appartements.
b) Écrire l’équation de la droite ΔC correspondant à
un chiffre d’affaires C sous la forme y = ax + b. Tra-
cer la droite ΔC dans le cas où C = 1 920 000.
28 Séquence 1
Cned – Académie en ligne

25. Déterminer graphiquement tous les couples ( x ; y )
qui permettent de réaliser un chiffre d’affaires de
1 920 000 euros.
ᕤ Déterminer à l’aide du graphique le nombre x de
studios et le nombre y de petits appartements à
construire pour permettre au promoteur de réaliser
un chiffre d’affaires maximal. Calculer ce chiffre
d’affaires maximal.
Séquence 1 29
Cned – Académie en ligne

26. 5 Corrigés des exercices
Exercice 1 ᕡ ̈ P ( x ) = x 2 + 12x + 35 = 0.
Δ = 122 − 4(1)( 35) = 4. Il y a deux solutions dis-
Les trois équations sont de la tinctes.
forme ax + bx + c = 0.
2
−12 − 2 −12 + 2
x1 = = −7 et x2 = = −5.
a b c 2 2
P (x ) S = { −7 ; − 5}
1 12 35
1
1 ̈ Q( x ) = − x 2 + 2x − = 0.
Q (x ) −1 2 − 2
2 1
Δ = ( 2 )2 − 4( −1)( − ) = 2 − 2 = 0. Il y a une ra-
cine double. 2
R (x ) 2 −4 3
b 2 2
x1 = x2 = − =− = .
2a −2 2
⎧ 2⎫
⎪ ⎪
S=⎨ ⎬
⎪ 2 ⎪
⎩ ⎭
̈ R ( x ) = 2x 2 − 4 x + 3 = 0.
Δ = ( −4 )2 − 4(2)( 3) = −8.
Δ < 0 et l’équation n’a pas de solution.
S =∅
ᕢ ̈ P ( x ) = x 2 + 12x + 35. Comme Δ > 0, on peut fac-
toriser P ( x ).
a = 1 ; x1 = −7 ; x2 = −5. P(x) = ( x + 7)( x + 5).
1
̈ Q( x ) = − x 2 + 2x − . Comme Δ = 0, on peut fac-
2
toriser Q(x).
2
a = −1 ; x1 = x2 =
2
2
⎛ 2⎞
Q(x) = − ⎜ x − ⎟
⎝ 2 ⎠
̈ R ( x ) = 2x 2 − 4 x + 3. Δ < 0.
R ( x ) ne se factorise pas.
30 Séquence 1
Cned – Académie en ligne

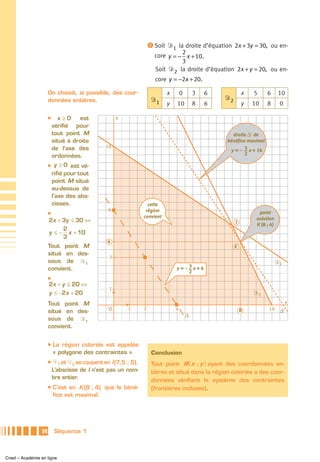
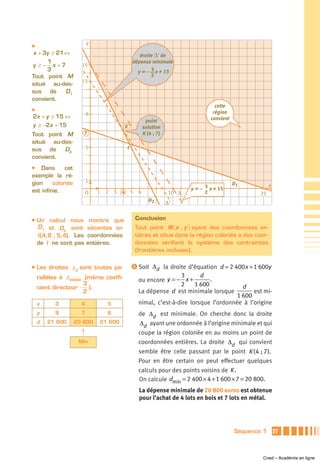
27. Exercice 2 ̈ (E 1 ) ( x − 2 008 )(1 789x + 1) = 0
Surtout ne pas développer. x − 2 008 = 0 ou 1 789x + 1 = 0.
On aurait Δ = 3 592 3132 . 1
x = 2 008 ou x = − .
1 789
⎧ 1 ⎫
S = ⎨− ; 2 008 ⎬
⎩ 1 789 ⎭
̈ (E 2 ) 121x 2 − 143x = 0.
On factorise le trinôme :
121x 2 − 143x = 11x (11x − 13).
x = 0 ou 11x − 13 = 0.
13
x = 0 ou x = .
11
⎧ 13 ⎫
S = ⎨0 ; ⎬
⎩ 11 ⎭
̈ (E 3 ) 25x 2 + 20x + 4 = 0.
La solution est une solution On reconnaît une identité remarquable.
double.
25x 2 + 20x + 4 = (5x + 2)2 .
2
(5x + 2)2 = 0 d'où x = − .
5
⎧ 2⎫
S = ⎨− ⎬
⎩ 5⎭
̈ (E 4 ) (2x − 3)2 − 5 = 0.
On reconnaît une différence de 2 carrés :
(2x − 3)2 − ( 5 )2 = 0.
[(2x − 3) − 5 ][(2x − 3) + 5 ] = 0.
2x − 3 − 5 = 0 ou 2x − 3 + 5 = 0.
3+ 5 3− 5
x= ou x =
2 2
⎧3 − 5 3 + 5 ⎫
⎪ ⎪
S=⎨ ; ⎬
⎩ 2
⎪ 2 ⎭⎪
Séquence 1 31
Cned – Académie en ligne

28. Exercice 3 ̈ (I1 ) x 2 + 12x + 35 ≥ 0.
Méthode 2 Dans l’exercice 1 on a trouvé les racines du trinôme
Allure de la parabole d’équation P ( x ) = x 2 + 12x + 35. Ces racines sont −7 et −5.
y = x 2 + 12x + 35.
Méthode 1
Comme a > 0 (ici a = 1 ) le trinôme est positif à
l’extérieur des racines.
–7 –5 S = ] − ∞ ; − 7] ∪ [ −5 ; + ∞[
̈ (I2 ) − x 2 + 3x − 5 < 0.
Autre méthode
Allure de la parabole d’équation Δ = 32 − 4( −1)( −5) = 9 − 20 = −11.
y = − x 2 + 3x − 5. Comme Δ < 0, le trinôme n’admet pas de racine.
Comme a < 0 (ici a = −1 ) le trinôme est toujours
négatif et l’inéquation toujours vérifiée.
S = » = ] − ∞ ; + ∞[
̈ ( I3 ) (2x − 3)( 4 − x ) > 0.
Le trinôme est déjà factorisé : Le trinôme (2x − 3)( 4 − x ) a deux racines qui sont
ne pas développer. 3
x1 = et x2 = 4.
2 2
(2x − 3)(4 − x ) = −2x 2 + … Le coefficient de x du trinôme (2x − 3)( 4 − x ) est
égal à −2.
La parabole d’équation y = (2x − 3)( 4 − x ) a ses
branches orientées vers le bas.
⎤3 ⎡
S = ⎥ ; 4⎢ 3 4
⎦ 2 ⎣ 2
Exercice 4 ̈ (B1 ) x 4 + 7x 2 + 10 = 0.
2
Posons x = X .
2
(B1 ) s’écrit alors : X + 7X + 10 = 0.
Point méthode Δ = 49 − 40 = 9. L’équation en X admet deux so-
Équation bicarrée :
lutions.
−7 − 3 −7 + 3
ax 4 + bx 2 + c = 0. X1 = = −5 et X2 = = −2.
2 2
On pose x = X .
2
2
• x = −5 est impossible.
• x 2 = −2 est impossible.
L’équation en x n’admet pas de racine.
S =∅ .
32 Séquence 1
Cned – Académie en ligne

29. ̈ (B2 ) x 4 − 11x 2 + 18 = 0.
2
Posons x = X .
2
(B2 ) s’écrit alors : X − 11X + 18 = 0.
Rappel 2nde Δ = ( −11)2 − 4(1)(18 ) = 121 − 72 = 49.
Résolution de L’équation en X admet deux solutions.
x = a, avec a > 0.
11 − 7 11 + 7
X1 = = 2 et X2 = = 9.
2
2 2
x 2 = a ⇔ x = − a ou
2
x = a. • x = 2 ⇔ x = − 2 ou x = 2.
2
• x = 9 ⇔ x = −3 ou x = 3.
L’équation en x admet quatre solutions.
S = { −3 ; − 2 ; 2 ; 3}
Exercice 5 ᕡ La parabole ᏼ a pour équation
y = f ( x ) = − x 2 − 4 x + 3.
Sommet S(α ; β) On calcule l’abscisse α du sommet S .
⎧ b −4
⎪α = − α=− = −2.
⎨ 2a −2
⎪β = f (α) L’ordonnée β du sommet S est :
⎩
β = f ( −2) = −4 + 8 + 3 = 7.
Les coordonnées du sommet S sont (−2 ; 7 )
ᕢ ̈ Les abscisses des points d’intersection de la pa-
rabole ᏼ avec l’axe des abscisses sont les solu-
tions, si elles existent, de l’équation f ( x ) = 0.
Point méthode
Résolvons − x 2 − 4 x + 3 = 0.
Situer une courbe Ꮿ
y = f (x ) Δ = ( −4 )2 − 4( −1)( 3) = 28. D’où Δ = 4 × 7 = 2 7.
d’équation
par rapport à l’axe 4−2 7 4+2 7
des abscisses revient x1 = = −2 + 7 et x2 = = −2 − 7 .
−2 −2
à étudier le signe de
f (x ). ᏼ coupe l’axe des abscisses en
f (x ) > 0, Ꮿ au-dessus A( −2 − 7 ; 0 ) et en B ( −2 + 7 ; 0 )
de l’axe.
f (x ) < 0, Ꮿ en des- ̈ Situer ᏼ par rapport à l’axe des abscisses revient à
sous de l’axe. chercher le signe de f ( x ).
f (x ) = 0, Ꮿ coupe Comme a < 0 (ici a = −1 ) le trinôme est négatif à
l’axe. l’extérieur des racines.
On peut conclure par un tableau.
Séquence 1 33
Cned – Académie en ligne

30. Illustration graphique
x −∞ −2 − 7 −2 + 7 +∞
y
f (x ) – 0 + 0 –
Ᏸ
S position ᏼ au-
7 ᏼ en ᏼ en
dessus
dessous dessous
E 6 de l’axe ᏼ coupe de l’axe ᏼ coupe de l’axe
5 l’axe l’axe
4
ᕣ Pour situer ᏼ par rapport à la droite Ᏸ d’équation
3 y = −2x on étudie le signe de la différence.
ᏼ 2
d ( x ) = − x 2 − 4 x + 3 − ( −2x ) = − x 2 − 2x + 3.
1
x Δ = 4 + 12 = 16 et Δ = 4.
–3 –2 O 1
2+ 4 2− 4
x1 = = −3 et x2 = = 1.
–2 F −2 −2
2
Allure de la parabole d’équation y = − x − 2x + 3.
–3 1
Conclusion
• ᏼ est au-dessus de Ᏸ sur] – 3 ; 1 [ ;
ᏼ
au-dessus • ᏼ est en dessous de Ᏸ sur ]– ∞ ; – 3 [ et sur
] 1 ; + ∞[ ;
de Ᏸ
• ᏼ coupe Ᏸ aux deux points E (– 3 ; 6) et
F (1 ; – 2).
Exercice 6 Calculons le nombre ab' – a'b pour chacun des sys-
tèmes.
Illustration graphique
droites 1 seule
( S1 ) ab '− a 'b = −14
d1 sécantes solution
d2
( S2 ) ab '− a 'b = 0 0 solution
droites ou une
ab '− a ' b ≠ 0 parallèles « droite
( S3 ) ab '− a 'b = 0 solution »
Droites sécan-
tes.
1 seule solu-
⎧−3x + 5y = −3 1 −3
⎪
̈( S1 ) ⎨
tion. ⎪ x + 3y = 5 3 5
⎩
−3x + 5y = −3 9x − 15y = 9
3x + 9y = 15 5x + 15y = 25 ⎧⎛ 17 6 ⎞ ⎫
⎪ ⎪
᏿ = ⎨⎜ ; ⎟⎬
14y = 12 14 x = 34 ⎪⎝ 7 7 ⎠ ⎪
⎩ ⎭
34 Séquence 1
Cned – Académie en ligne

31. Illustration graphique Interprétation graphique : les droites (d1 ) et (d2 )
d1 d’équations respectives −3x + 5y = −3 et x + 3y = 5
d2 ⎛ 17 6 ⎞
sont sécantes au point I ⎜ ; ⎟ .
⎝ 7 7⎠
⎧−3x + 5y = −3 1
Droites parallè- ⎪
̈ (S ) ⎨ 1 5
2
les et distinctes. ⎪ x − y = 1 −6
0 solution. ⎩2 6
⎧−3x + 5y = −3
⎪
( S2 ) ⇔ ⎨ Comme −3 ≠ −6 ᏿ = ∅
ab '− a ' b = 0 OU ⎩−3x + 5y = −6
⎪
d1 d2 Interprétation graphique : les droites (d1 ) et
(d2 ) d’équations respectives −3x + 5y = −3 et
Droites confon-
dues. 1 infinité −3x + 5y = −6 n’ont aucun point commun.
de solutions ⎧4 x − y = 3 1 ᏿ est l’ensem-
(1 « droite solu- ⎪
̈ (S ) ⎨ 2 1 1 ble des couples
3
tion ») ⎪ x− y = 6 (x ; 4x – 3)
⎩3 6 2
⎧4 x − y = 3
⎪
( S3 ) ⇔ ⎨ ⇔ 4x − y = 3
⎩4 x − y = 3
⎪
Interprétation graphique : les droites (d1 ) et (d2 )
2 1 1
d’équations respectives 4 x − y = 3 et x − y =
3 6 2
sont confondues. Il y a une infinité de solutions.
Exercice 7 y
Mémo 3 B
̈ Soit (AB ) est une
droite d’équation 2
y = mx + p.
yB − y A 1
m= .
̈ xB − x A
x
B
–3 –2 –1 O 1 2
m = –5
2 –1
5 A
–2
2
C C
B
4
m=4
̈ Pour ( AB ) lecture graphique : m =et p = 3.
3 4 3
5
̈ Pour (BC ) lecture graphique : m = − et p = 3.
A 2
3
1 1
̈ Pour ( AC ) m = − . y = − x + p .
5 5
Séquence 1 35
Cned – Académie en ligne

32. 2 8
En C : −2 = − + p d’où p = − .
5 5
4 5 1 8
( AB ) y = x + 3( BC ) y = − x + 3 ( AC ) y = − x −
3 2 5 5
⎧ x − y = 10
⎪ ⎧ x − y = 10
⎪
Exercice 8 ̈ ( S1 ) ⎨ ⇔⎨ ⇔
⎪ x − y = 40 ⎩( x − y )( x + y ) = 40
2 2 ⎪
⎩
⎧
⎪ x − y = 10 1 −1
⎨
⎪x + y = 4 1 1
⎩
2x = 14 et 2y = −6 ᏿ = {( 7 ; − 3 )}
⎧1 2
⎪ − y = −4
⎪x 1
̈ (S ) ⎨
2 Posons = X et y 2 = Y .
⎪ 2 + 3y 2 = 2 x
⎪
⎩x
⎧ X − Y = −4 3 −2
( S2 ) ⇔ ⎨
⎩2X + 3Y = 2 1 1
5X = −10 et 5Y = 10, ce qui donne X = −2 et Y = 2.
1 1
• = −2 d’où x = − .
x 2
• y 2 = 2 d’où y = − 2 ou y = 2.
⎧⎛ 1
⎪ ⎞ ⎛ 1 ⎞⎫⎪
᏿ = ⎨⎜ − ; − 2 ⎟ ; ⎜ − ; 2⎟ ⎬
⎩⎝ 2
⎪ ⎠ ⎝ 2 ⎠⎭⎪
⎧2x − y + z = 0 4
⎪
Exercice 9 ̈ ( S ) ⎨ − x + 4y + 2z = −1 1 1
1
⎪3x − 4y + 6z = −4 1
⎩
⎧2x + 8z = −5 3 7
( S '1 ) ⎨
On choisit d’éliminer y. ⎩7x + 6z = −1 −4 −2
On aurait pu éliminer soit x, 1 3
−22x = −11 et 44z = −33 x = et z = − .
soit z. 2 4
1
On obtient, dans la première équation, y = 2x + z = .
4
⎧⎛ 1 1
⎪ 3⎞ ⎫
⎪
On vérifie que la solution ᏿ = ⎨⎜ ; ; − ⎟ ⎬
⎛1 1 3 ⎞ convient. ⎩⎝ 2 4
⎪ 4⎠ ⎭
⎪
⎜ ; 4 ; − 4⎟
⎝2 ⎠ ⎧x y z
⎪ = = L1 x y z
̈ (S ) ⎨ 3 4 5 Posons = = = t .
2
⎪5x − 4y + 3z = 7 L 3 4 5
⎩ 2
D’où x = 3t , y = 4t , z = 5t .
7 1
Dans L2 : 15t − 16t + 15t = 7 soit t = = .
14 2
3 5 ⎧⎛ 3
⎪ 5⎞ ⎫
⎪
Ainsi x = , y = 2, z = . ᏿ = ⎨⎜ ; 2 ; ⎟ ⎬
2 2 ⎪⎝ 2
⎩ 2⎠ ⎪
⎭
36 Séquence 1
Cned – Académie en ligne

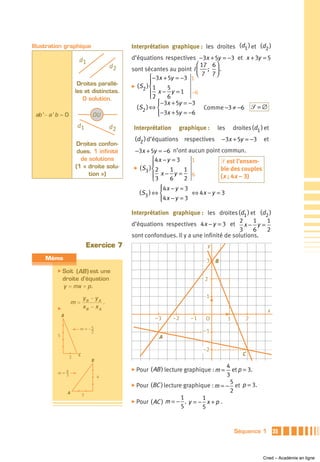
33. Exercice 10 Un point M est à l’intérieur du triangle s’il est situé en
dessous de ( AB ), en dessous de (BC ) et au-dessus
de ( AC ).
On obtient donc :
4 5 1 8
y < x +3 ; y < − x +3 ; y > − x − .
3 2 5 5
Comme M peut être sur les ⎧ 4 x − 3y + 9 ≥ 0
⎪
côtés on écrit des inégalités D’où le système ⎨5 x + 2y − 6 ≤ 0
« larges ». ⎪ x + 5y + 8 ≥ 0
⎩
⎧x + y ≥ 0 [I1 ]
⎪
Exercice 11 ̈ ( S1 ) ⎨y ≤ 3 [I2 ]
⎪x − y − 1 ≤ 0
⎩ [I3 ]
Droite et équation d1 x +y =0 d2 y =3 d3 x − y −1= 0
2 points (1 ; − 1) et ( −1 ; 1) ( 0 ; 3) et ( 3 ; 3) (1 ; 0 ) et (0 ; –1)
Calcul en un point
K (1 ; 1) x + y = 2 O( 0 ; 0 ) y=0 O( 0 ; 0 ) x − y − 1 = −1
particulier
Signe en ce point x +y ≥0 y = 0 donc y ≤ 3 x −y −1≤ 0
Le demi-plan de Le demi-plan de fron- Le demi-plan de fron-
Conclusion frontière d1, conte- tière d2 , contenant tière d3 , contenant O
nant K convient. O convient. convient.
Point méthode y
d2
Soit (d ) : ax + by + c = 0 3
A C
La droite (d) partage
le plan en deux demi-
2
plans ouverts :
• dans l’un ax+by+c > 0 K
• dans l’autre ax+by+c< 0 1
On cherche donc le si-
gne de ax + by + c en x
un seul point non situé –3 –2 –1 O 1 2 3 4
sur la droite. –1 B
Si (d) ne passe pas par
l’origine O on cherche
d3 –2 d1
le signe au point O.
Conclusion
Tout point M (x ; y) situé à l’intérieur du triangle ABC (ou sur les côtés) a des coor-
données vérifiant le système.
Séquence 1 37
Cned – Académie en ligne

34. x ≥ 0 et y ≥ 0 définissent le ⎧ x ≥ 0 et y ≥ 0
quart de plan situé au-dessus de ⎪
̈ ( S ) ⎨2x + y − 6 ≤ 0
l’axe des abscisses et à droite 2
⎪x + y − 4 ≤ 0
de l’axe des ordonnées (axes ⎩
compris).
La droite D1 d’équation 2x + y − 6 = 0 passe par les
points ( 0 ; 6 ) et ( 3 ; 0 ).En O( 0 ; 0 ) on a 2x + y − 6 = −6
x>o et −6 < 0. C’est le demi-plan de frontière D1 conte-
et nant 0 qui convient.
y>o
La droite D2 d’équation x + y − 4 = 0 passe par les
points ( 0 ; 4 ) et ( 4 ; 0 ). En O( 0 ; 0 ) on a x + y − 4 = −4
1er quadrant et −4 < 0. C’est le demi-plan de frontière D2 conte-
nant le point 0 qui convient.
O y Soit A (3 ; 0)
B (0 ; 4)
6
K (2 ; 2)
c’est le cas
dans les 5
exercices
polygone
concrets
B des
4
contraintes
3
K
Conclusion 2
Tout point M (x ; y) situé à
l’intérieur du polygone des 1
contraintes OAKB (ou sur les x
A
côtés) a des coordonnées vé- O 1 2 3 4
rifiant le système. D1 D2
Exercice 12 ᕡ On peut présenter les contraintes sous forme de
tableau.
Nombre Surface habitable Fenêtre
x studios x 30 x x 0 ≤ x ≤ 15
y petits appartements y 50 y 3y 0≤y
Contraintes x + y ≥ 20 30x + 50y ≥ 1 160 x + 3y ≥ 60
Le système d’inéquations vérifiant toutes les contrain-
tes est le suivant :
38 Séquence 1
Cned – Académie en ligne

35. ⎪
⎧0 ≤ x ≤ 15 ( x entier ) ⎪
⎪ ⎪0 ≤ x ≤ 15 ( x entier )
⎪0 ≤ y ( y entier ) ⎪0 ≤ y ( y entier )
⎪ ⎪
⎨ x + y ≥ 20 ⇔ ⎨y ≥ − x + 20
⎪3 x + 5y ≤ 116 ⎪ 3 116
⎪ ⎪y ≤ − x +
⎪ x + 3y ≤ 60
⎩ ⎪ 5 5
⎪ 1
ᕢ ⎪y ≤ − x + 20
⎩ 3
Droite D1 D2 D3
Équation cartésienne x + y = 20 3x + 5y = 116 x + 3y = 60
y = − x + 20 3 116 1
Équation réduite y =− x+ y = − x + 20
5 5 3
( 0 ; 20 ), (5 ; 15), (2 ; 22), ( 7 ; 19 ) ( 0 ; 20 ), ( 6 ; 18 ),
3 points
(10 ; 10 ) (12 ; 16 ) (12 ; 16 )
y
Attention droite
de C.A. x=15
Ici x ≤ 15 maximal
20
point
Tout point M situé : solution
I (12 ; 16)
• à droite de l’axe des ordon- I
nées, 16
D3
• à gauche de la droite d’équa- polygone
tion x = 15, des
contraintes D2
• au-dessus de D 1,
• en dessous de D 2 et D 3 , 12
convient. y = – 1 x + 16
11 2
10
9
Δ
D1
Conclusion
Tout point M (x ; y) situé à
l’intérieur du polygone des
1
contraintes (ou sur les côtés) x
convient. O 1 8 10 12 14 15
Séquence 1 39
Cned – Académie en ligne

36. ᕣ a) Le chiffre d’affaires est C = 60 000 x + 120 000 y
1 C
b) Équation réduite de ΔC : y =− x+
2 120 000
1
Posons Δ1 920 000 = Δ Pour C = 1 920 000 on obtient : y = − x + 16
2
La droite Δ passe par les points ( 0 ; 16 ), ( 8 ; 12),
(12 ; 10 ).
Le graphique nous montre que la droite Δ coupe le
polygone des contraintes en 4 points de coordonnées
entières.
Les couples ( x ; y ) permettant de réaliser un chiffre
d’affaires de 1 920 000 euros sont :
( 8 ; 12 ), ( 10 ; 11), ( 12 ; 10 ), ( 14 ; 9 ).
C
Les droites ΔC sont toutes paral- ᕤ Le chiffre d’affaires C est maximal lorsque
120 000
lèles à Δ (même coefficient direc- est maximal. On cherche donc la droite ΔC ayant une
1 ordonnée à l’origine maximale et coupant le polygone
teur − ).
2
des contraintes en au moins un point.
La droite ΔC qui convient est celle qui passe par le
point I intersection de D2 et D3 .
I a pour coordonnées x = 12 et y = 16.
On a C max = 60 000 × 12 + 120 000 × 16 = 2 640 000
Pour réaliser un chiffre d’affaires maximal de
2 640 000 euros le promoteur devra construire (et
vendre…) 12 studios et 16 petits appartements.
̈ Remarque
Dans ce cas la contrainte « nombre de logements »
sera largement dépassée car le promoteur pourra
construire 28 logements, soit 8 de plus que le mini-
mum imposé.
40 Séquence 1
Cned – Académie en ligne