Ce chapitre discute de la résolution des équations algébriques polynomiales, en précisant que pour les degrés supérieurs à 4, on doit recourir à des méthodes numériques. Il présente plusieurs techniques telles que la méthode de dichotomie, la méthode de la sécante, la méthode du point fixe et la méthode de Newton, en soulignant l'importance de la convergence et de la rapidité de ces méthodes. Enfin, il explique comment séparer les racines graphiquement ou par balayage avant d'appliquer ces méthodes.

1. Chapitre IV
16/03/2013 INTTIC 1

2. Résolution de f(x)=0
 Les méthodes analytiques de résolution des équations
algébriques polynômiales sont limitées à certaines formes
de faible degré telles que les équations quadratiques,
cubiques, quartiques et des formes particulières du type:
2n n
P ( x) ax bx
n
c 0
 Pour les degrés > 4 il n’existe pas de méthodes exactes
pour la résolution  utiliser les méthodes numériques
pour trouver les racines approchées.
 Les méthodes présentées dans ce chapitre servent à
approximer la racine de la fonction.
 Pour trouver toutes les racines il faut les séparer d’abord
pour pouvoir appliquer ces méthodes.
16/03/2013 INTTIC 2

3. Résolution de f(x)=0
 En étudiant les méthodes de résolution de f(x)=0, on
pose souvent deux questions:
1. La méthode converge-t-elle vers la solution cherchée
x*? (la suite x(1), x(2), …, x(n) converge-t-elle vers x*?)
2. Dans le cas affirmatif, quelle est sa rapidité?
 La rapidité de convergence nous permet de comparer
les méthodes entre elles.
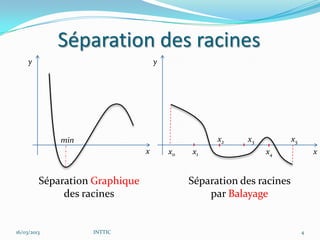
 Pour séparer les racines, on peut:
1. Étudier la fonction graphiquement
2. Utiliser la méthode de balayage: examiner un certain
nombre de domaines [xi, xi+1] jusqu’à obtenir le
changement de signe attendu.
16/03/2013 INTTIC 3

4. Séparation des racines
y y
min x2 x3 x5
x x0 x1 x4 x
Séparation Graphique Séparation des racines
des racines par Balayage
16/03/2013 INTTIC 4

5. Résolution de f(x)=0
 Plusieurs méthodes existent
 Méthode de dichotomie (bi-section)
 Méthode de la sécante
 Méthode du point fixe
 Méthode de Newton
 Problèmes ?
 Convergence
 Complexité
16/03/2013 INTTIC 5

6. Méthode dichotomique
a b
f (a ) f (b) 0 c
2
si f (c) f(b)
alors on a trouvé la solution : c
sinon si f (a ) f (c) 0
alors a c
sinon si f (b) f (c) 0
alors b c
Théorème : a c=(a+b)/2
b
soit pn n N la suite générée par
l' algorithme de recherche par dichotomie, f(c)
soit p la solution du problème : f ( p ) 0
Alors pn n N converge vers p avec :
b a f(a)
pn p n
n 1
2
On peut prendre c à l’intersection de la sécante et de l’axe des x
16/03/2013 INTTIC 6

7. Méthode de la sécante
 Cette méthode est appelée aussi méthode de la corde,
des fausses positions (régula falsi) ou aussi méthode
de Lagrange.
 Soient f(a)<0 et f(b)>0.
 Relions par une droite les points A(a, f(a)) et B(b, f(b)).
 Prenons comme approximation l’abscisse x1 du point
d’intersection de la droite AB et l’axe Ox.
 Cette valeur est donnée par: (b a) f (a)
x1 a f (b) f (a)
16/03/2013 INTTIC 7

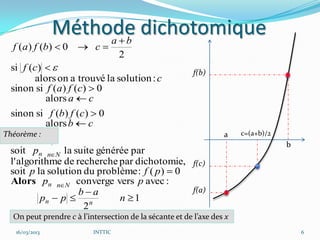
8. Méthode de la sécante
 Si f(x1)<0 alors le nouveau segment est [x1, b].
 De la même façon, on a: (b x1 ) f ( x1 )
x x2 1
f (b) f ( x1 )
(b xn ) f ( xn )
 Il vient que: x n 1 x n
f (b) f ( xn )
y
B B est fixe
a x1 x2
O c b x
A1
A
16/03/2013 INTTIC 8

9. Méthode de la sécante
 Si f(x1)>0 alors le nouveau segment est [a, x1].
 La formule de récurrence devient:
( xn a ) f ( a )
x n 1
a
f ( xn ) f ( a )
y
B1 B A est fixe
ac
O x2 x1 b x
A
16/03/2013 INTTIC 9

10. Méthode de la sécante
Test d’arrêt
 Le calcul continu jusqu’à ce que les décimales qu’on
veut conserver cessent de varier.
 On peut prendre comme test d’arrêt:
x x
n n 1
e
Où e est la borne d’erreur absolue donnée.
16/03/2013 INTTIC 10

11. Méthode de la sécante
Convergence
 L’avantage est d’opérer dans un
intervalle qui entoure toujours y
la racine qui se réduit à chaque
itération. La convergence est
donc assurée.
 Le taux de convergence peut a x1
b x
s’avérer faible dans certains
cas.
 Si la fonction est fortement
convexe (concave), la
convergence est lente.
16/03/2013 INTTIC 11

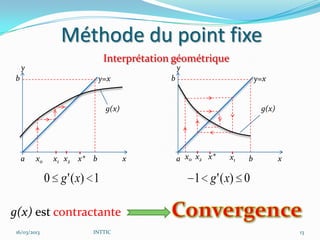
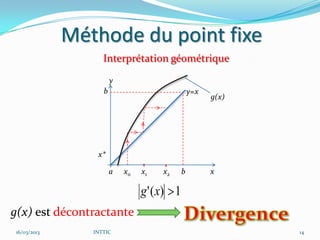
12. Méthode du point fixe
Principe
 Si l’équation donnée est mise sous la forme x=g(x),
avec g(x) est une fonction continue sur [a, b] et
|g’(x)|≤L<1 (contractante) pour tout x de [a, b] sur
lequel l’équation n’a qu’une seule racine alors:
 En partant d’une valeur initiale x0∈[a, b], on peut
construire la suite: x1 g ( x0), x2 g ( x1),..., xn 1 g ( xn)
 La limite de cette suite est la racine unique de f(x)=0
 On arrête les opération si: xn xn 1
16/03/2013 INTTIC 12

13. Méthode du point fixe
Interprétation géométrique
y y
b y=x b y=x
g(x) g(x)
a x0 x1 x2 x* b x a x0 x2 x* x1 b x
0 g ' ( x) 1 1 g ' ( x) 0
g(x) est contractante
16/03/2013 INTTIC 13

14. Méthode du point fixe
Interprétation géométrique
y
b y=x
g(x)
x*
a x0 x1 x2 b x
g ' ( x) 1
g(x) est décontractante
16/03/2013 INTTIC 14

15. Méthode de Newton
Principe
 Remplacer l’arc de courbe (AB) par la droite tangente à
la courbe aux points A ou B. L’intersection avec Ox
détermine le prochain élément (x1). On forme la suite
(xi) par itérations.
y
 Formule de récurrence:
f ( xn )
x n 1 x n
f ' ( xn ) n 0,1, 2, ...
x*
x 0
[ a, b]
x2 x1 x0 x
 If faut que f’(xn)≠0 au voisinage
de x*.
16/03/2013 INTTIC 15

16. Méthode de Newton
Principe
 Déterminer un intervalle [a, b] sur lequel il y a convergence de
Newton n’est pas toujours facile. Il existe cependant un théorème
qui donne une condition suffisante.
Théorème (convergence globale de la méthode de Newton)
Si la fonction f(x) définie sur [a, b] vérifie:
1. f (a) f (b) 0
2. x [a, b] f ' ( x) 0 (strictemonotonie de f )
3. x [a, b] f ' ' ( x) 0 (concativité de f dans le même sens)
Alors en choisissant x0 de [a, b] tel que f(x0)f’’(x0)>0, les
itérations de Newton convergent vers l’unique solution x* de
f(x)=0 dans [a, b]. De plus, la convergence est quadratique.
16/03/2013 INTTIC 16