Le document traite des méthodes de dérivation et d'intégration numériques pour les fonctions définies sur un intervalle. Il présente des formules de différences pour la dérivation numérique et plusieurs méthodes d'intégration, y compris les méthodes des rectangles, des trapèzes, et de Simpson, en comparant leurs précisions. Des exemples d'applications illustrent ces méthodes, démontrant que la subdivision des intervalles améliore la précision des résultats.

1. Analyse numérique
Jaouad DABOUNOU
Département de Mathématiques et Informatique
Dérivation et Intégration numériques
Année universitaire2014/2015
Université Hassan Premier
Faculté des Sciences et Techniques
Settat

2. Dérivation et Intégration numériques
- Soit f une fonction définie et dérivable sur [a , b]
- Soit x]a , b[, la dérivée de f en x est donnée par :
- Soit f une fonction définie et continue sur [a , b]
- L’intégrale de f sur [a , b] est donnée par :
Le calcul analytique des dérivées ou des intégrales est souvent difficile ou
couteux.
h
xfhxf
xf
h
)()(
lim)('
0










1
0
)(lim)(
n
in
b
a n
ab
iaf
n
ab
dxxf
Dérivation et Intégration numériques

3. Dérivation numérique
Formule de différences progressives
Soit x]a , b[ et h > 0 tel que x+h ]a , b[, on a :
x x+h
(x , f(x))
(x+h , f(x+h))
Pente de f en x à
l’ordre 1 près
x
y
h
xfhxf
xf
)()(
)('

 avec )("
2
)( cf
h
xe  c] x , x+h[,
On a ici une approximation d'ordre 1 de f '(x)
Pente de f en x

4. Dérivation numérique
Formule de différences centrales
Soit x]a , b[ et h > 0 tel que x-h ]a , b[ et x+h ]a , b[, on a :
h
hxfhxf
xf
2
)()(
)('

 avec ),(
!3
)( )3(
2
cf
h
xe  c] x-h , x+h[,
On a ici une approximation d'ordre 1 de f '(x)
x x+h
(x+h , f(x+h))
Pente de f en x à
l’ordre 2 près
x
y
x-h
(x-h , f(x-h))
Pente
de f en x

5. Intégration numérique
Soit f une fonction définie et continue sur [a , b].
L’intégrale de f sur [a , b] est donnée par :
On approche f sur [a , b] par un polynôme P, ensuite, on considère
que :

6. Intégration numérique
Estimation de l’erreur d’intégration
On approche f par P, le polynôme d’interpolation de f en x0, x1,… , xn.
L’erreur d’interpolation est donnée par
En plus, on a
Donc

7. 7
Méthode des rectangles
Polynôme d’interpolation : P0(x) = f(a). On a
[a , b]

8. 8
Méthode des trapèzes
Polynôme d’interpolation en x0=a et x1=b: P1(x) = f[a] + (x – a) f[a,b]. On a
[a , b]

9. 9
Méthode de Simpson
P2(x) Polynôme d’interpolation en x0=a, x1=m= et x2=b. On a
[a , b]

10. 10
Intégration numérique
Exemple d'application
Soit f(x) = 2(x –1) + cos(x) esin(x)
Une primitive de f est donnée par : F(x) = x2 - 2x + esin(x)

11. 11
Intégration numérique
Exemple d'application
On a
Tableau de l'intégrale obtenue pour chacune des méthodes présentées
La méthode de Simpson donne le meilleur résultat
Méthode Intégrale
Rectangles 1,2534
Trapèzes 1,1101
Simpson 1,1646

12. 12
Subdivision de l'intervalle d'intégration
Subdivision de [a , b] en des sous-intervalles d'intégration.
Ainsi, pour deux sous-intervalles [a , m] et sur [m , b] avec
La méthode des rectangles donne
[a , b]
On voit que l’erreur est divisée par 2.

13. 13
Subdivision de l'intervalle d'intégration
Exemple:
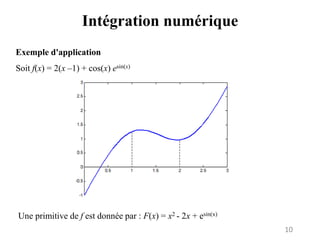
On reprend la fonction : f(x) = 2(x –1) + cos(x) esin(x)
Tableau des résultats avec et sans subdivision de [1 , 2].
On rappelle que la solution analytique est
On voit que la précision est améliorée par la subdivision de l'intervalle pour chacune
des méthodes utilisées est divisée par 2.
Méthode
Intégration sur
[1 , 2]
Intégration sur
[1 , 1.5] et [1.5 , 2]
Rectangles 1,2534 1,2226
Trapèzes 1,1101 1,1510
Simpson 1,1646 1,16288