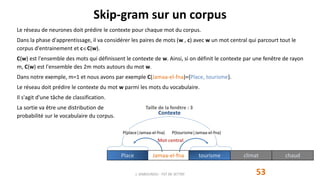
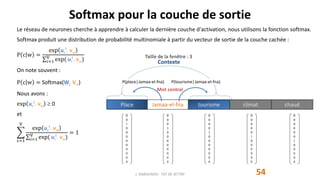
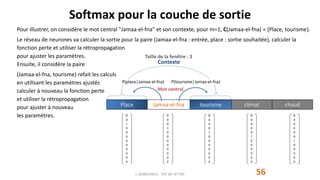
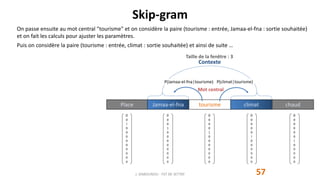
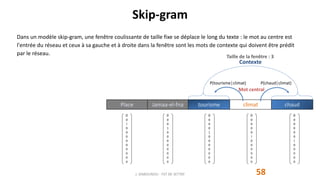
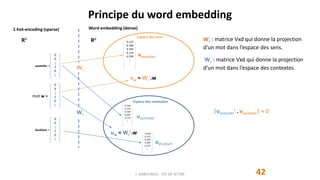
Le document présente le concept de word embedding en traitement automatique du langage naturel, en détaillant les méthodes comme le one hot encoding et l'algorithme word2vec. Il explique comment ces techniques génèrent des représentations vectorielles des mots, permettant de capturer les relations sémantiques et d'effectuer des opérations arithmétiques sur ces vecteurs. De plus, il aborde la notion d'hypothèse distributionnelle et l'utilisation de ces vecteurs dans diverses tâches de traitement de texte.

1. Traitement automatique du langage naturel
(TALN)
NATURAL LANGUAGE PROCESSING
(NLP)
juillet 2020
JAOUAD DABOUNOU
FST de Settat
Université Hassan 1er
Centre CLIK

2. Objectif du Word embedding
Objectifs :
• Générer des représentations vectorielles des mots qui portent des significations sémantiques et traduisent les
similarités ou relations entre les sens des mots.
• Chaque mot vecteur peut avoir plusieurs centaines de dimensions
• Représentation vectorielle (mathématique) qui est, en même temps cohérente avec la sémantique.
• Permettre des opérations arithmétiques cohérentes avec la sémantique et des règles de la langue
J. DABOUNOU - FST DE SETTAT 31

3. One hot encoding
Représenter les mots contenus dans un texte par des nombres que les machines savent interpréter.
L’approche la plus simple : le one hot encoding.
Corpus :
• « Marrakech est connue par sa place jamaa-el-fna et son climat chaud et sec »
• « Le numérique est en train de transformer le monde »
Chaque mot du corpus est représenté par un vecteur de longueur V de la forme : (0,…,0,1,0,…,0). V étant la
longueur du vocabulaire du corpus.
On considère pour simplifier, à partir du corpus présenté, le vocabulaire V suivant :
V = {Marrakech, est, connue, par, sa, place, jamaa-el-fna, et, son, climat, chaud, sec, le, numérique, en, train, de,
transformer, monde}
V représente à la fois le vocabulaire et le nombre entier ici V=19 qui désigne sa longueur.
J. DABOUNOU - FST DE SETTAT 32

4. One hot encoding
On peut écrire:
Marrakech : (1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0)
est : (0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0)
connue : (0,0,1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0)
…
jamaa-el-fna : (0,0,0,0,0,0,1,0,0,0,0,0,0,0,0,0,0,0,0)
monde : (0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1)
Les mots sont ainsi plongés dans un espace de dimension RV
.
Ici, on a V=19, mais sur la figure on visualise seulement un espace de 3 dimensions.
Les phrases du corpus sont représentées par l’ensemble des vecteurs qui codent les mots qui les composent.
Marrakech connue
jamaa-el-fna
J. DABOUNOU - FST DE SETTAT 33

5. Problèmes avec one hot encoding
Le one hot encoding présente plusieurs problèmes.
1. Voir tous les mots comme des unités discrètes n'est pas idéal et le premier problème auquel nous serions
confrontés lors de l'utilisation de représentations one-hot est un problème de parcimonie.
2. Ne préserve pas les proximités possibles entre les mots. Normalement la proximité de deux vecteurs se traduit
par le produit scalaire entre ces deux vecteurs. Dans le cas de 1-hot encoding, l’angle est toujours de 90° pour
n’importe quel couple de vecteurs et la longueur (ou norme) de chaque vecteur est égale à 1.
3. Lorsque V est très grand, la dimensionnalité des vecteurs obtenus sera du même ordre (RV
). Ainsi, Google
propose dans un dataset un vocabulaire de 3 millions de mots. Le traitement des mots sera alors très couteux
en temps de calcul comme en mémoire allouée.
4. Cette approche qui privilégie une représentation atomique des mots produit un espace des sémantiques
discret. Il suffit de considérer les couleurs pour se rendre compte que cette représentation contredit
l’intuition. Entre le noir et le blanc on a un continuum de niveaux de gris.
J. DABOUNOU - FST DE SETTAT 34

6. Word2vec
35
Algorithme proposé en 2013 chez Google par Mikolov et son équipe.
Se base sur un réseau de neurones pour effectuer du word embedding à partir d’un corpus.
Un mot central wt est fortement corrélé aux mots qui constituent son contexte; ici ceux qui se trouvent entre wt-m
et wt et puis entre wt et wt+m, pour un entier m fixé au départ appelé rayon.
m est un hyper-paramètre de l’algorithme qui caractérise la longueur fixe de la fenêtre qui définit le contexte.
On choisit généralement m entre 4 et 12.
Les mots partageant le même contexte se trouvent représentés par des vecteurs proches.
J. DABOUNOU - FST DE SETTAT
wt-4 wt-3 wt-2 wt-1 wt wt+1 wt+2 wt+3 wt+4
Taille de la fenêtre : 9
Contexte
Mot central

7. Illustration du Word2vec
36
Considérons la phrase que l’on a un peu prétraitée :
Marrakech connue place Jamaa-el-fna climat chaud sec
où m=2 (ou taille de la fenêtre égale à 5).
On a alors Mot: climat et Contexte: {place, Jamaa-el-fna, chaud, sec}
Le word embedding permet de représenter chaque mot du corpus par un
vecteur à valeur dense.
Les distances entre ces vecteurs et la comparaison de leurs directions permettraient alors une représentation des
sémantiques des mots et de leur contenu conceptuel.
Word embedding comme prétraitement pour diverses tâches NLP : Classification de documents, reconnaissance
d'entités nommées, analyse des sentiments...
Ces tâches NLP exploitent les informations sémantiques contenues dans les vecteurs obtenus par Word
embedding.
J. DABOUNOU - FST DE SETTAT
wtwt-1wt-2 wt+2wt+1
Jamaa-el-fna
chaud
sec
numérique
Marrakech
climat
place
Illustration du word embedding en 3D

8. Hypothèse distributionnelle
37
Le Word2vec adopte la notion de linguistique distributionnelle. Celle-ci émet l’hypothèse selon laquelle
les mots qui apparaissent dans des contextes similaires tendent à avoir des sens similaires.
Exemple:
L'étudiant essaie de comprendre des notions mathématiques
L'étudiant essaie d’assimiler des notions mathématiques
On utilise cette hypothèse pour définir la proximité sémantique de deux mots en fonction des contextes
communs qu’ils partagent.
Ainsi, les mots qui apparaissent dans des contextes similaires auront des vecteurs similaires, reflétant la
grande corrélation de leurs usages.
J. DABOUNOU - FST DE SETTAT

9. Hypothèse distributionnelle
38
Développement de modèles de sémantique distributionnelle grâce à :
• Disponibilité de corpus électroniques de taille importantes : wikipédia, EuroParlement, TOEFL 2000
• Apparition des ordinateurs puissants
Contextes contribuant à déterminer le sens du verbe « assimiler »:
• On doit suivre la conférence pour assimiler des concepts théoriques difficiles
• L'étudiant essaie d’assimiler des notions mathématiques
• Tous les élèves se doivent d'assimiler le socle commun de compétences
• La ville a pu assimiler les traditions et valeurs des populations qui la composent
J. DABOUNOU - FST DE SETTAT

10. Encodage des analogies
39
Dans les algorithmes Word2vec un mot du corpus peut jouer deux rôles:
1. Porter un sens, quand il s’agit d’un mot central
2. Contribuer à construire le contexte pour un mot central
Les vecteurs de mots ont tendance à obéir aux lois de l'analogie et à encoder des informations
sémantiques et syntactiques. Par exemple, considérons l'analogie. Ainsi, on a :
vqueen− vwoman + vman ≈ vking
vqueen, vwoman, vman et vking correspondent respectivement aux mots queen, woman, man et king
J. DABOUNOU - FST DE SETTAT
WALKING
WALK
DRIVING
DRIVE
SPEAKING
SPEAK
QUEENS
KINGS
QUEEN
KING
WOMAN
MAN
WOMAN
UNCLE
QUEEN
KING

11. Espace des sens, espace des contextes
40
Espace dense de dimension d pour représenter les sens à l’aide de vecteurs (espace des
sémantiques).
d étant un hyper-paramètre de l’algorithme. d souvent entre 100 et 300.
d << V.
Exemple :
assimiler =
Représentation distribuée des mots, c’est-à-dire que le sens d’un mot est distribué entre les d
composantes.
J. DABOUNOU - FST DE SETTAT
0.125
-0.380
0.760
0.123
-0.590
⸽

12. Espace des sens, espace des contextes
41
Les mots qui constituent les contextes sont aussi représentés par des vecteurs de dimension d.
Exemple :
assimiler =
Le mot contexte « étudiant » peut avoir la représentation suivante :
étudiant =
J. DABOUNOU - FST DE SETTAT
0.360
0.150
-0.560
-0.685
0.110
⸽
0.030
-0.255
0.490
0.085
-0.205
⸽

13. Principe du word embedding
42J. DABOUNOU - FST DE SETTAT
RV Rd
0
0
⸽
1
0
⸽
assimiler =
0
0
⸽
1
0
⸽
étudiant =
Espace des sens
Espace des contextes
Ws
Wc
1-hot-encoding (sparse) Word embedding (dense)
0
0
⸽
1
0
⸽
mot w =
vw = Ws
t.w
uw = Wc
t.w
Ws : matrice Vxd qui donne la projection
d’un mot dans l’espace des sens.
Wc : matrice Vxd qui donne la projection
d’un mot dans l’espace des contextes.
vassimiler
uassimiler
uétudiant
|uassimiler
t . vassimiler|  0

14. Algorithmes Word2vec
43J. DABOUNOU - FST DE SETTAT
Il y a essentiellement deux variantes du word2vec que nous allons présenter par la suite :
Skip-gram : ce modèle apprend à prédire le contexte d'un mot en fonction de la donnée du mot central.
CBOW : ce modèle apprend à prédire le mot central à partir de la donnée du contexte.
wt
wt-1
wt-2
wt+2
wt+1
CBOW
SortieCouche
cachée
Entrée
wt
wt-1
wt-2
wt+2
wt+1
Skip-gram
SortieCouche
cachée
Entrée

15. Skip-gram
44J. DABOUNOU - FST DE SETTAT
Il s'agit d'un apprentissage non supervisé appliqué à un réseau de neurones pour réaliser un word embedding.
L’apprentissage se fait sur un grand corpus de données textuelles comme Wikipédia.
L'entrée est un mot central et la sortie prédit les mots de contexte, étant donné le mot central. Si, par exemple, on
utilise une fenêtre de longueur 2, on peut avoir :
Corpus Mot central Contexte
Marrakech connue place Jamaa-el-fna climat chaud sec connue connue
Marrakech connue place Jamaa-el-fna climat chaud sec connue Marrakech, place
Marrakech connue place Jamaa-el-fna climat chaud sec place connue, Jamaa-el-fna
Marrakech connue place Jamaa-el-fna climat chaud sec Jamaa-el-fna place, climat
Marrakech connue place Jamaa-el-fna climat chaud sec climat Jamaa-el-fna, chaud
Marrakech connue place Jamaa-el-fna climat chaud sec chaud climat, sec
Marrakech connue place Jamaa-el-fna climat chaud sec connue chaud

16. Illustration du Word2vec
45
Considérons le corpus d'entrainement Ctrain :
Marrakech connue place Jamaa-el-fna tourisme climat chaud
Conférence climat palais congrès Marrakech
Jardins climat congrès favorisent tourisme Marrakech
Tourisme Marrakech climat chaud jardins
V={Marrakech, connue, place, Jamaa-el-fna, tourisme, climat, chaud, conférence, palais , congrès, jardins, favorisent}
On utilise un 1-hot-encoding pour représenter les mots de V. Ces vecteurs sont dans RV = R12.
On considère le mot "climat" et on utilise un contexte de rayon 1. On a alors l'ensemble des contextes
C(climat)={(tourisme, chaud),(Conférence, palais),(Jardins, congrès),(Marrakech, chaud)}
Nous disposons ainsi d'un corpus de mots w et leurs contextes C(w). Dans word2vec, on construit un réseau de neurones qui
apprend à prendre en entrée un mot w et à prédire son contexte C(w).
J. DABOUNOU - FST DE SETTAT
1
0
0
0
0
0
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
0
0
0
0
0
1

17. 0
0
0
0
0
1
0
0
0
0
0
0
chaud
0
0
0
0
0
0
1
0
0
0
0
0
marrakech
connue
place
jamaa-el-fna
tourisme
climat
chaud
conférence
palais
congrès
jardins
favorisent
marrakech
connue
place
jamaa-el-fna
tourisme
climat
chaud
conférence
palais
congrès
jardins
favorisent
tourisme
0
0
0
0
1
0
0
0
0
0
0
0
climat
Skip-gram
Réseau de neurones que l’on souhaite créer pour le modèle Skip-gram.
En entrée un mot w du corpus d’entrainement
et en sortie le contexte C(w).

18. La couche cachée est obtenue par une transformation linéaire de matrice Ws.
La couche de sortie est obtenue par une transformation
linéaire de matrice Wc suivie par une softmax.
Paramètres du modèle : éléments de Ws et Wc.
J. DABOUNOU - FST DE SETTAT
0
0
0
0
0
1
0
0
0
0
0
0
chaud
0
0
0
0
0
0
1
0
0
0
0
0
marrakech
connue
place
jamaa-el-fna
tourisme
climat
chaud
conférence
palais
congrès
jardins
favorisent
marrakech
connue
place
jamaa-el-fna
tourisme
climat
chaud
conférence
palais
congrès
jardins
favorisent
tourisme
0
0
0
0
1
0
0
0
0
0
0
0
Ws
Wc
Wc
climat
Paramètres du modèle

19. Skip-gram FeedForward
48J. DABOUNOU - FST DE SETTAT
w Ws
1.1 0.5 0.2 -0.2 0.3
0.4 0.6 -1.0 -1.1 -0.3
0.8 -0.2 0.3 -0.5 -0.3
0.8 0.2 -0.1 -1.0 0.1
-0.2 -0.3 -0.2 -0.5 -0.5
0.1 -1.1 -0.3 -1.0 0.1
-0.6 0.2 -0.1 -0.9 -0.3
-0.2 0.2 0.2 0.7 -0.3
0.1 0.1 -1.1 0.1 0.8
0.3 -0.2 0.7 0.6 0.1
0.1 0.2 0.7 0.6 0.3
-0.2 1.0 -0.3 0.7 -1.1
Détails du modèle Skip-gram à travers un exemple. Un mot w en entrée, par exemple
le mot "climat", one-hot-encoded. Le vecteur obtenu par transformation linéaire de
matrice Ws
t est vw = Ws
t w. vw est tout simplement la ligne correspondant à w dans Ws.
0
0
0
0
0
1
0
0
0
0
0
0
0.1
-1.1
-0.3
-1.0
0.1
vw = Ws
t w
climat
wt
wt-1
wt+1
Skip-gram avec m=1
SortieCouche
cachée
Entrée
Ws
Wc
Wc
Modèle utilisé pour illustration
On note ainsi vi les lignes de la matrice Ws. Les vi sont de ce fait des paramètres du modèle.

20. Skip-gram FeedForward
49J. DABOUNOU - FST DE SETTAT
w Ws
1.1 0.5 0.2 -0.2 0.3
0.4 0.6 -1.0 -1.1 -0.3
0.8 -0.2 0.3 -0.5 -0.3
0.8 0.2 -0.1 -1.0 0.1
-0.2 -0.3 -0.2 -0.5 -0.5
0.1 -1.1 -0.3 -1.0 0.1
-0.6 0.2 -0.1 -0.9 -0.3
-0.2 0.2 0.2 0.7 -0.3
0.1 0.1 -1.1 0.1 0.8
0.3 -0.2 0.7 0.6 0.1
0.1 0.2 0.7 0.6 0.3
-0.2 1.0 -0.3 0.7 -1.1
La couche de sortie est obtenue par une transformation linéaire de matrice Wc suivie par une softmax.
0
0
0
0
0
1
0
0
0
0
0
0
0.1
-1.1
-0.3
-1.0
0.1
vw = Ws
t w
climat
-0.2 0.1 -1.1 0.3 0.1
-0.3 -0.7 -1.0 0.4 0.7
0.1 -1.1 0.1 0.8 0.2
0.1 0.7 0.2 0.7 -1.0
0.2 0.7 -1.1 -0.3 0.3
-0.8 -0.2 0.3 0.4 0.5
0.1 -1.1 -0.3 -1.0 0.1
-0.5 -0.3 -0.7 -0.5 -0.5
0.4 -0.3 -0.2 -0.7 0.1
-1.0 0.1 0.8 0.2 0.7
0.1 0.2 0.7 -1.1 -0.3
0.7 0.1 0.2 0.7 0.2
-0.1
0.7
0.4
-1.6
-0.1
-0.3
2.3
0.9
1.1
-0.6
0.7
-0.8
0.036
0.081
0.060
0.008
0.036
0.030
0.405
0.102
0.125
0.022
0.076
0.018
0.036
0.081
0.060
0.008
0.036
0.030
0.405
0.102
0.125
0.022
0.076
0.018
Wc vwWc
Softmax(Wc vw)
P(tourisme│climat) = 0.036
P(chaud│climat) = 0.405

21. Skip-gram FeedForward
50J. DABOUNOU - FST DE SETTAT
w Ws
1.1 0.5 0.2 -0.2 0.3
0.4 0.6 -1.0 -1.1 -0.3
0.8 -0.2 0.3 -0.5 -0.3
0.8 0.2 -0.1 -1.0 0.1
-0.2 -0.3 -0.2 -0.5 -0.5
0.1 -1.1 -0.3 -1.0 0.1
-0.6 0.2 -0.1 -0.9 -0.3
-0.2 0.2 0.2 0.7 -0.3
0.1 0.1 -1.1 0.1 0.8
0.3 -0.2 0.7 0.6 0.1
0.1 0.2 0.7 0.6 0.3
-0.2 1.0 -0.3 0.7 -1.1
Détails du modèle Skip-gram à travers un exemple
0
0
0
0
0
1
0
0
0
0
0
0
0.1
-1.1
-0.3
-1.0
0.1
vw = Ws
t w
climat
-0.2 0.1 -1.1 0.3 0.1
-0.3 -0.7 -1.0 0.4 0.7
0.1 -1.1 0.1 0.8 0.2
0.1 0.7 0.2 0.7 -1.0
0.2 0.7 -1.1 -0.3 0.3
-0.8 -0.2 0.3 0.4 0.5
0.1 -1.1 -0.3 -1.0 0.1
-0.5 -0.3 -0.7 -0.5 -0.5
0.4 -0.3 -0.2 -0.7 0.1
-1.0 0.1 0.8 0.2 0.7
0.1 0.2 0.7 -1.1 -0.3
0.7 0.1 0.2 0.7 0.2
-0.1
0.7
0.4
-1.6
-0.1
-0.3
2.3
0.9
1.1
-0.6
0.7
-0.8
0.036
0.081
0.060
0.008
0.036
0.030
0.405
0.102
0.125
0.022
0.076
0.018
0.036
0.081
0.060
0.008
0.036
0.030
0.405
0.102
0.125
0.022
0.076
0.018
P c w =
exp uc
t
. vw
𝑖=1
V
exp( ui
t
. vw)
Wc vw
0.036
0.081
0.060
0.008
0.036
0.030
0.405
0.102
0.125
0.022
0.076
0.018
Wc
Softmax(Wc vw)
marrakech
connue
place
jamaa-el-fna
tourisme
climat
chaud
conférence
palais
congrès
jardins
favorisent
La probabilité de trouver le mot "palais" dans le contexte
du mot "climat" sélectionné aléatoirement est égale à 0.125.

22. Skip-gram FeedForward
51J. DABOUNOU - FST DE SETTAT
w Ws
1.1 0.5 0.2 -0.2 0.3
0.4 0.6 -1.0 -1.1 -0.3
0.8 -0.2 0.3 -0.5 -0.3
0.8 0.2 -0.1 -1.0 0.1
-0.2 -0.3 -0.2 -0.5 -0.5
0.1 -1.1 -0.3 -1.0 0.1
-0.6 0.2 -0.1 -0.9 -0.3
-0.2 0.2 0.2 0.7 -0.3
0.1 0.1 -1.1 0.1 0.8
0.3 -0.2 0.7 0.6 0.1
0.1 0.2 0.7 0.6 0.3
-0.2 1.0 -0.3 0.7 -1.1
Détails du modèle Skip-gram à travers un exemple
0
0
0
0
0
1
0
0
0
0
0
0
0.1
-1.1
-0.3
-1.0
0.1
vw = Ws
t w
0
0
0
0
1
0
0
0
0
0
0
0
tourisme
0
0
0
0
0
0
1
0
0
0
0
0
chaud
climat
-0.2 0.1 -1.1 0.3 0.1
-0.3 -0.7 -1.0 0.4 0.7
0.1 -1.1 0.1 0.8 0.2
0.1 0.7 0.2 0.7 -1.0
0.2 0.7 -1.1 -0.3 0.3
-0.8 -0.2 0.3 0.4 0.5
0.1 -1.1 -0.3 -1.0 0.1
-0.5 -0.3 -0.7 -0.5 -0.5
0.4 -0.3 -0.2 -0.7 0.1
-1.0 0.1 0.8 0.2 0.7
0.1 0.2 0.7 -1.1 -0.3
0.7 0.1 0.2 0.7 0.2
-0.1
0.7
0.4
-1.6
-0.1
-0.3
2.3
0.9
1.1
-0.6
0.7
-0.8
0.036
0.081
0.060
0.008
0.036
0.030
0.405
0.102
0.125
0.022
0.076
0.018
0.036
0.081
0.060
0.008
0.036
0.030
0.405
0.102
0.125
0.022
0.076
0.018
P c w =
exp uc
t
. vw
𝑖=1
V
exp( ui
t
. vw)
Wc vw
0.036
0.081
0.060
0.008
0.036
0.030
0.405
0.102
0.125
0.022
0.076
0.018
Wc
Softmax(Wc vw)
marrakech
connue
place
jamaa-el-fna
tourisme
climat
chaud
conférence
palais
congrès
jardins
favorisent
P(tourisme│climat) = 0.036
P(chaud│climat) = 0.405
P chaud climat =
exp uchaud
t
. vclimat
𝑖=1
V
exp( ui
t
. vclimat)
P tourisme climat =
exp utourisme
t
. vclimat
𝑖=1
V
exp( ui
t
. vclimat)

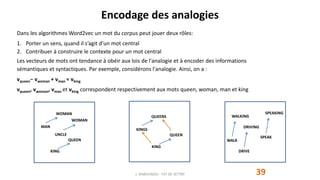
23. Skip-gram Paramètres
52J. DABOUNOU - FST DE SETTAT
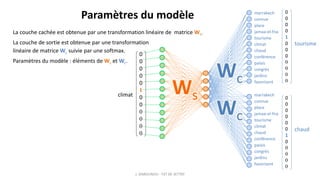
Ws
t = [v1, v2, … , vV] et Wc
t = [u1, u2, … , uV] et  = {v1, v2, … , vV, u1, u2, … , uV} constitue l'ensemble des paramètres du
modèle.
Pour k=1,V on a vk est le vecteur qui représente le mot wk dans l'espace des sens et uk est le vecteur qui représente le
mot wk dans l'espace des contextes.
1.1 0.5 0.2 -0.2 0.3
0.4 0.6 -1.0 -1.1 -0.3
0.8 -0.2 0.3 -0.5 -0.3
0.8 0.2 -0.1 -1.0 0.1
-0.2 -0.3 -0.2 -0.5 -0.5
0.1 -1.1 -0.3 -1.0 0.1
-0.6 0.2 -0.1 -0.9 -0.3
-0.2 0.2 0.2 0.7 -0.3
0.1 0.1 -1.1 0.1 0.8
0.3 -0.2 0.7 0.6 0.1
0.1 0.2 0.7 0.6 0.3
-0.2 1.0 -0.3 0.7 -1.1
-0.2 0.1 -1.1 0.3 0.1
-0.3 -0.7 -1.0 0.4 0.7
0.1 -1.1 0.1 0.8 0.2
0.1 0.7 0.2 0.7 -1.0
0.2 0.7 -1.1 -0.3 0.3
-0.8 -0.2 0.3 0.4 0.5
0.1 -1.1 -0.3 -1.0 0.1
-0.5 -0.3 -0.7 -0.5 -0.5
0.4 -0.3 -0.2 -0.7 0.1
-1.0 0.1 0.8 0.2 0.7
0.1 0.2 0.7 -1.1 -0.3
0.7 0.1 0.2 0.7 0.2
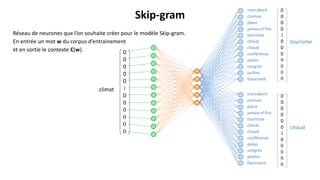
marrakech
connue
place
jamaa-el-fna
tourisme
climat
chaud
conférence
palais
congrès
jardins
favorisent
marrakech
connue
place
jamaa-el-fna
tourisme
climat
chaud
conférence
palais
congrès
jardins
favorisent
Espace des sens Espace des contextes
v6 = vclimat =
0.1
-1.1
-0.3
-1.0
0.1
u5 = utourisme =
0.2
0.7
-1.1
-0.3
0.3
v7 = vchaud =
-0.6
0.2
-0.1
-0.9
-0.3
u6 = uclimat =
-0.8
-0.2
0.3
0.4
0.5
u7 = uchaud =
0.1
-1.1
-0.3
-1.0
0.1
Le produit scalaire : uchaud
t
. vclimat caractérise la similarité entre les vecteurs uchaud et vclimat. Globalement, plus il est positif
et grand, plus cela signifie que cos(uchaud
t
, vclimat) est proche de 1, et donc que les vecteurs "vont dans le même sens".
Le modèle va être entrainé pour maximiser le produit scalaire uc
t
. vw lorsque le mot c apparait dans le contexte du mot w.

24. Le réseau de neurones doit prédire le contexte pour chaque mot du corpus.
Dans la phase d'apprentissage, il va considérer les paires de mots (w , c) avec w un mot central qui parcourt tout le
corpus d'entrainement et cC(w).
C(w) est l'ensemble des mots qui définissent le contexte de w. Ainsi, si on définit le contexte par une fenêtre de rayon
m, C(w) est l'ensemble des 2m mots autours du mot w.
Dans notre exemple, m=1 et nous avons par exemple C(Jamaa-el-fna)={Place, tourisme}.
Le réseau doit prédire le contexte du mot w parmi les mots du vocabulaire.
Il s'agit d'une tâche de classification.
La sortie va être une distribution de
probabilité sur le vocabulaire du corpus.
Skip-gram sur un corpus
53J. DABOUNOU - FST DE SETTAT
Place Jamaa-el-fna tourisme climat chaud
Taille de la fenêtre : 3
Contexte
Mot central
P(place│Jamaa-el-fna) P(tourisme│Jamaa-el-fna)

25. Softmax pour la couche de sortie
54J. DABOUNOU - FST DE SETTAT
Place Jamaa-el-fna tourisme climat chaud
Taille de la fenêtre : 3
Contexte
Mot central
0
0
0
1
0
0
0
0
0
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
0
0
P(place│Jamaa-el-fna) P(tourisme│Jamaa-el-fna)
Le réseau de neurones cherche à apprendre à calculer la dernière couche d'activation, nous utilisons la fonction softmax.
Softmax produit une distribution de probabilité multinomiale à partir du vecteur de sortie de la couche cachée :
P c w =
exp uc
t
. vw
𝑖=1
V
exp( ui
t
. vw)
On note souvent :
P c w = Softmax(Wc Vw)
Nous avons :
exp uc
t
. vw  0
et
c=1
V
exp uc
t
. vw
𝑖=1
V
exp( ui
t
. vw)
= 1

26. Avec une fenêtre de rayon m, m constitue d'ailleurs un hyperparamètre du modèle, on note wt le mot central en cours.
Le contexte de wt sera: C(wt) = {wt-m, wt-m+1,…wt-1,wt+1, …, wt+m-1, wt+m}
Pour j=m, le réseau de neurones va calculer la sortie :
pour la paire (wt : entrée, wt-j : sortie souhaitée), calculer la fonction perte et utiliser la rétropropagation pour ajuster les
paramètres. Ensuite, on considère j=m-1,…,1,-1,…,-m+1,-m et on refait les mêmes calculs pour la paire
(wt : entrée, wt-j : sortie souhaitée), ce qui correspond au reste des mots contexte de wt, on calcule la fonction perte et
on utilise la rétropropagation pour ajuster les paramètres.
Ensuite, on considère wt+1 comme mot central et le contexte C(wt+1) et on refait tous les calculs comme ci-dessus.
Softmax pour la couche de sortie
55J. DABOUNOU - FST DE SETTAT
… wt-m-1 wt-m wt-m+1 … wt-1 wt wt+1 … wt+m-1 wt+m wt+m+1 …
Taille de la fenêtre : m
Contexte
Mot central
P(wt+1│wt)
P(wt+m│wt)
P(wt+m-1│wt)
P(wt-1│wt)
P(wt-m│wt)
P(wt-m+1│wt)
P wt−j wt =
exp uwt−jt
. vwt
𝑖=1
V
exp( ui
t
. vwt
)

27. Pour illustrer, on considère le mot central "Jamaa-el-fna" et son contexte, pour m=1, C(Jamaa-el-fna) = {Place, tourisme}.
Le réseau de neurones va calculer la sortie pour la paire (Jamaa-el-fna : entrée, place : sortie souhaitée), calculer la
fonction perte et utiliser la rétropropagation
pour ajuster les paramètres.
Ensuite, il considère la paire
(Jamaa-el-fna, tourisme) refait les calculs
en utilisant les paramètres ajustés
calculer à nouveau la fonction perte
et utiliser la rétropropagation
pour ajuster à nouveau
les paramètres.
Softmax pour la couche de sortie
56J. DABOUNOU - FST DE SETTAT
Place Jamaa-el-fna tourisme climat chaud
Taille de la fenêtre : 3
Contexte
Mot central
0
0
0
1
0
0
0
0
0
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
0
0
P(place│Jamaa-el-fna) P(tourisme│Jamaa-el-fna)

28. Skip-gram
57J. DABOUNOU - FST DE SETTAT
Place Jamaa-el-fna tourisme climat chaud
Taille de la fenêtre : 3
Contexte
Mot central
0
0
0
1
0
0
0
0
0
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
0
0
P(Jamaa-el-fna│tourisme) P(climat│tourisme)
On passe ensuite au mot central "tourisme" et on considère la paire (tourisme : entrée, Jamaa-el-fna : sortie souhaitée)
et on fait les calculs pour ajuster les paramètres.
Puis on considère la paire (tourisme : entrée, climat : sortie souhaitée) et ainsi de suite …

29. Skip-gram
58J. DABOUNOU - FST DE SETTAT
Place Jamaa-el-fna tourisme climat chaud
Taille de la fenêtre : 3
Contexte
Mot central
0
0
0
1
0
0
0
0
0
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
0
0
0
0
0
1
0
0
0
0
0
P(tourisme│climat) P(chaud│climat)
Dans un modèle skip-gram, une fenêtre coulissante de taille fixe se déplace le long du texte : le mot au centre est
l'entrée du réseau et ceux à sa gauche et à droite dans la fenêtre sont les mots de contexte qui doivent être prédit
par le réseau.
0
0
1
0
0
0
0
0
0
0
0
0

30. Skip-gram FeedForward
59J. DABOUNOU - FST DE SETTAT
w Ws
1.1 0.5 0.2 -0.2 0.3
0.4 0.6 -1.0 -1.1 -0.3
0.8 -0.2 0.3 -0.5 -0.3
0.8 0.2 -0.1 -1.0 0.1
-0.2 -0.3 -0.2 -0.5 -0.5
0.1 -1.1 -0.3 -1.0 0.1
-0.6 0.2 -0.1 -0.9 -0.3
-0.2 0.2 0.2 0.7 -0.3
0.1 0.1 -1.1 0.1 0.8
0.3 -0.2 0.7 0.6 0.1
0.1 0.2 0.7 0.6 0.3
-0.2 1.0 -0.3 0.7 -1.1
0
0
0
0
0
1
0
0
0
0
0
0
0.1
-1.1
-0.3
-1.0
0.1
Vw = Ws
t w
0
0
0
0
1
0
0
0
0
0
0
0
tourisme
0
0
0
0
0
0
1
0
0
0
0
0
chaud
climat
-0.2 0.1 -1.1 0.3 0.1
-0.3 -0.7 -1.0 0.4 0.7
0.1 -1.1 0.1 0.8 0.2
0.1 0.7 0.2 0.7 -1.0
0.2 0.7 -1.1 -0.3 0.3
-0.8 -0.2 0.3 0.4 0.5
0.1 -1.1 -0.3 -1.0 0.1
-0.5 -0.3 -0.7 -0.5 -0.5
0.4 -0.3 -0.2 -0.7 0.1
-1.0 0.1 0.8 0.2 0.7
0.1 0.2 0.7 -1.1 -0.3
0.7 0.1 0.2 0.7 0.2
-0.1
0.7
0.4
-1.6
-0.1
-0.3
2.3
0.9
1.1
-0.6
0.7
-0.8
0.036
0.081
0.060
0.008
0.036
0.030
0.405
0.102
0.125
0.022
0.076
0.018
0.036
0.081
0.060
0.008
0.036
0.030
0.405
0.102
0.125
0.022
0.076
0.018
P c w =
exp uc
t
. vw
𝑖=1
V
exp( ui
t
. vw)
Wc Vw
0.036
0.081
0.060
0.008
0.036
0.030
0.405
0.102
0.125
0.022
0.076
0.018
Wc
Softmax(Wc Vw)
marrakech
connue
place
jamaa-el-fna
tourisme
climat
chaud
conférence
palais
congrès
jardins
favorisent
P(tourisme│climat) = 0.036
P(chaud│climat) = 0.405
P chaud climat =
exp uchaud
t
. vclimat
𝑖=1
V
exp( ui
t
. vclimat)
P tourisme climat =
exp utourisme
t
. vclimat
𝑖=1
V
exp( ui
t
. vclimat)

31. Pour ajuster les paramètres, Skip-gram maximise la vraisemblance
L θ =
w∈Ctrain
c∈𝐂(w)
P(c|w; θ)
C(w) étant le contexte du mot w et  les paramètres du modèle.
Cela donne aussi (la log-vraisemblance ) :
LL(θ) =
w∈Ctrain
𝐜∈𝐂(w)
log(P c w; θ )
On cherche donc à minimiser la fonction de perte :
J(θ) = −
1
Ctrain
LL(θ) = −
1
Ctrain
w∈Ctrain
c∈𝐂(w)
log(P c w; θ )
0
0
0
0
0
1
0
0
0
0
0
0
marrakech
connue
place
jamaa-el-fna
tourisme
climat
chaud
conférence
palais
congrès
jardins
favorisent
marrakech
connue
place
jamaa-el-fna
tourisme
climat
chaud
conférence
palais
congrès
jardins
favorisent
c1
Ws
Wc
Wc
w
c2
0
0
0
0
0
0
1
0
0
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0 C(w)
60J. DABOUNOU - FST DE SETTAT
Vraisemblance

32. Souvent, dans la phase d′apprentissage, on considère à chaque fois un seul mot de Ctrain, comme cela a été expliqué plus
haut, (ou un batch) et on itère sur tous les mots de Ctrain. Pour cela, on considère :
J(θ; w) = −
c∈𝐂(w)
log(P c w; θ )
Or on a :
P c w; θ =
exp uc
t
. vw
𝑖=1
V
exp( ui
t
. vw)
Donc
J(θ; w) = −
c∈𝐂 w
log
exp uc
t
. vw
𝑖=1
V
exp( ui
t
. vw)
= −
c∈𝐂 w
log (exp uc
t
. vw ) +
c∈𝐂 w
log
𝑖=1
V
exp( ui
t
. vw)
En développant, on trouve :
J(θ; w) = −
c∈𝐂 w
uc
t
. vw + 2m log
𝑖=1
V
exp( ui
t
. vw)
Vraisemblance pour un exemple
d'entrainement
Terme indépendant des
mots contexte

33. J(θ) = −
1
Ctrain
w∈Ctrain
c∈𝐂 w
log P c w; θ = −
1
Ctrain
w∈Ctrain
c∈𝐂 w
log
exp uc
t
. vw
𝑖=1
V
exp( ui
t
. vw)
Et ainsi :
J(θ) = −
1
Ctrain
w∈Ctrain
c∈𝐂 w
log(exp uc
t
. vw ) +
1
Ctrain
w∈Ctrain
c∈𝐂 w
log
𝑖=1
V
exp( ui
t
. vw)
Et finalement
J(θ) = −
1
Ctrain
w∈Ctrain
c∈𝐂 w
uc
t
. vw +
2m
Ctrain
w∈Ctrain
log
𝑖=1
V
exp( ui
t
. vw)
Les paramètres qui maximisent la vraisemblance sont :
θ = arg min
θ
J(θ) = arg min
θ
−
1
Ctrain
w∈Ctrain
c∈𝐂 w
uc
t
. vw +
2m
Ctrain
w∈Ctrain
log
𝑖=1
V
exp( ui
t
. vw)
Fonction de perte sur le corpus d'entrainement

34. On calcule la dérivée de la fonction de perte par rapport à uc :
𝜕J(θ)
𝜕vw
= −
1
Ctrain
w′∈Ctrain
c∈𝐂 w′
𝜕 (uc
t
. vw′)
𝜕vw
+
2m
Ctrain
w′∈Ctrain
𝜕 log 𝑖=1
V
exp( ui
t
. vw′)
𝜕vw
𝜕 (uc
t
. vw)
𝜕vw
= uc et
𝜕 (uc
t
. vw′)
𝜕vw
= 0 si w′w.
𝜕 log 𝑖=1
V
exp( ui
t
. vw)
𝜕vw
=
1
𝑖=1
V
exp( ui
t
. vw)
𝜕 𝑖=1
V
exp( ui
t
. vw)
𝜕vw
=
1
𝑖=1
V
exp( ui
t
. vw)
𝑖=1
V
𝜕 exp(ui
t
. vw)
𝜕vw
=
1
𝑖=1
V
exp( ui
t
. vw)
𝑖=1
V
exp(ui
t
. vw)
𝜕 ui
t
. vw
𝜕vw
=
𝑖=1
V
exp(ui
t
. vw)
k=1
V
exp( uk
t
. vw)
ui =
𝑖=1
V
P ui w ui
A noter que si w′
 w alors
𝜕 log i=1
V
exp( ui
t
. vw′)
𝜕vw
= 0.
𝜕J(θ)
𝜕vw
= −
2m
Ctrain
w′∈Ctrain ,w′= w
(uc −
𝑖=1
V
P ui w ui)
Calcul du gradient

35. On calcule la dérivée de la fonction de perte par rapport à uc :
𝜕J(θ)
𝜕uc
= −
1
Ctrain
w∈Ctrain
c∈𝐂 w
𝜕 (uc
t
. vw)
𝜕uc
+
2m
Ctrain
w∈Ctrain
𝜕 log 𝑖=1
V
exp( ui
t
. vw)
𝜕uc
𝜕 (uc
t
. vw)
𝜕uc
= vw
𝜕 log 𝑖=1
V
exp( ui
t
. vw)
𝜕uc
=
1
𝑖=1
V
exp( ui
t
. vw)
𝜕 𝑖=1
V
exp( ui
t
. vw)
𝜕uc
=
1
𝑖=1
V
exp( ui
t
. vw)
𝑖=1
V
𝜕 exp(ui
t
. vw)
𝜕uc
=
1
𝑖=1
V
exp( ui
t
. vw)
𝑖=1
V
exp(ui
t
. vw)
𝜕 ui
t
. vw
𝜕uc
=
exp(uc
t
. vw)
𝑖=1
V
exp( ui
t
. vw)
vw = P uc w vw
𝜕J(θ)
𝜕uc
= −
2m
Ctrain
w∈Ctrain
(1 − P uc w ) vw
Calcul du gradient

36. Les paramètres qui maximisent la vraisemblance sont :
θ = arg min
θ
J(θ) = arg min
θ
−
1
Ctrain
w∈Ctrain
c∈𝐂 w
uc
t
. vw +
2m
Ctrain
w∈Ctrain
log
𝑖=1
V
exp( ui
t
. vw)
La rétropropagation implique le calcul des erreurs de prédiction et la mise à jour de la matrice de poids (θ) pour
optimiser la représentation vectorielle des mots.
θk+1 = θk −  J(θk)
Si maintenant on choisit de faire une descente de gradient stochastique, on aura les équations générales de mise à
jour suivantes pour la matrice de poids (θ):
θk+1 = θk −  J(θk, w)
Mise à jour des paramètres

37. Illustration du Word2vec
66
Considérons le corpus d'entrainement Ctrain :
Marrakech connue place Jamaa-el-fna tourisme climat chaud
Conférence climat palais congrès Marrakech
Jardins climat congrès favorisent tourisme Marrakech
Tourisme Marrakech climat chaud jardins
V={Marrakech, connue, place, Jamaa-el-fna, tourisme, climat, chaud, conférence, palais , congrès, jardins, favorisent}
On a V = 12 et |Ctrain|=23.
On utilise un contexte de rayon m=1.
C(climat)={(tourisme, chaud),(Conférence, palais),(Jardins, congrès),(Marrakech, chaud)}
J. DABOUNOU - FST DE SETTAT
1
0
0
0
0
0
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
0
0
0
0
0
1

38. Ajuster les paramètres
67J. DABOUNOU - FST DE SETTAT
w Ws
1.1 0.5 0.2 -0.2 0.3
0.4 0.6 -1.0 -1.1 -0.3
0.8 -0.2 0.3 -0.5 -0.3
0.8 0.2 -0.1 -1.0 0.1
-0.2 -0.3 -0.2 -0.5 -0.5
0.1 -1.1 -0.3 -1.0 0.1
-0.6 0.2 -0.1 -0.9 -0.3
-0.2 0.2 0.2 0.7 -0.3
0.1 0.1 -1.1 0.1 0.8
0.3 -0.2 0.7 0.6 0.1
0.1 0.2 0.7 0.6 0.3
-0.2 1.0 -0.3 0.7 -1.1
0
0
0
0
0
1
0
0
0
0
0
0
0.1
-1.1
-0.3
-1.0
0.1
Vw = Ws
t w
0
0
0
0
1
0
0
0
0
0
0
0
tourisme
0
0
0
0
0
0
1
0
0
0
0
0
chaud
climat
-0.2 0.1 -1.1 0.3 0.1
-0.3 -0.7 -1.0 0.4 0.7
0.1 -1.1 0.1 0.8 0.2
0.1 0.7 0.2 0.7 -1.0
0.2 0.7 -1.1 -0.3 0.3
-0.8 -0.2 0.3 0.4 0.5
0.1 -1.1 -0.3 -1.0 0.1
-0.5 -0.3 -0.7 -0.5 -0.5
0.4 -0.3 -0.2 -0.7 0.1
-1.0 0.1 0.8 0.2 0.7
0.1 0.2 0.7 -1.1 -0.3
0.7 0.1 0.2 0.7 0.2
-0.1
0.7
0.4
-1.6
-0.1
-0.3
2.3
0.9
1.1
-0.6
0.7
-0.8
0.036
0.081
0.060
0.008
0.036
0.030
0.405
0.102
0.125
0.022
0.076
0.018
0.036
0.081
0.060
0.008
0.036
0.030
0.405
0.102
0.125
0.022
0.076
0.018
Wc VwWc
Softmax(Wc Vw)
marrakech
connue
place
jamaa-el-fna
tourisme
climat
chaud
conférence
palais
congrès
jardins
favorisent
On adopte une optimisation stochastique :
𝜕J(θ; w)
𝜕vw
= −uc +
i=1
V
P ui w ui = − + =
𝜕J(θ; w)
𝜕uc
= − 1 − P uc w vw
Pour w="climat" et c="tourisme", on a
𝐯w
new
= vw − 
𝜕J(θ;w)
𝜕vw
= − 0.05 =
𝜕J(θ; w)
𝜕uc
= − 1 − P uc w vw = − 1 − 0.036 =
𝐮c
new
= uc − 
𝜕J(θ;w)
𝜕uc
= − 0.05 =
-0.204
-1.289
0.812
-0.212
-0.211
0.2
0.7
-1.1
-0.3
0.3
-0.004
-0.589
-0.288
-0.512
0.089
0.1
-1.1
-0.3
-1.0
0.1
-0.096
1.060
0.289
0.964
-0.096
0.1
-1.1
-0.3
-1.0
0.1
-0.096
1.060
0.289
0.964
-0.096
0.110
-1.036
-0.341
-0.989
0.111
0.2
0.7
-1.1
-0.3
0.3
-0.096
1.060
0.289
0.964
-0.096
0.205
0.647
-1.114
-0.348
0.305
Les paramètres à ajuster sont les d composantes de vw et
les Vxd éléments de la matrice Wc.

39. Interpréter : Ajuster les paramètres
68J. DABOUNOU - FST DE SETTAT
w Ws
1.1 0.5 0.2 -0.2 0.3
0.4 0.6 -1.0 -1.1 -0.3
0.8 -0.2 0.3 -0.5 -0.3
0.8 0.2 -0.1 -1.0 0.1
-0.2 -0.3 -0.2 -0.5 -0.5
0.1 -1.1 -0.3 -1.0 0.1
-0.6 0.2 -0.1 -0.9 -0.3
-0.2 0.2 0.2 0.7 -0.3
0.1 0.1 -1.1 0.1 0.8
0.3 -0.2 0.7 0.6 0.1
0.1 0.2 0.7 0.6 0.3
-0.2 1.0 -0.3 0.7 -1.1
0
0
0
0
0
1
0
0
0
0
0
0
0.1
-1.1
-0.3
-1.0
0.1
Vw = Ws
t w
0
0
0
0
1
0
0
0
0
0
0
0
tourismeclimat
-0.2 0.1 -1.1 0.3 0.1
-0.3 -0.7 -1.0 0.4 0.7
0.1 -1.1 0.1 0.8 0.2
0.1 0.7 0.2 0.7 -1.0
0.2 0.7 -1.1 -0.3 0.3
-0.8 -0.2 0.3 0.4 0.5
0.1 -1.1 -0.3 -1.0 0.1
-0.5 -0.3 -0.7 -0.5 -0.5
0.4 -0.3 -0.2 -0.7 0.1
-1.0 0.1 0.8 0.2 0.7
0.1 0.2 0.7 -1.1 -0.3
0.7 0.1 0.2 0.7 0.2
-0.1
0.7
0.4
-1.6
-0.1
-0.3
2.3
0.9
1.1
-0.6
0.7
-0.8
0.036
0.081
0.060
0.008
0.036
0.030
0.405
0.102
0.125
0.022
0.076
0.018
Wc VwWc Softmax(Wc Vw)
marrakech
connue
place
jamaa-el-fna
tourisme
climat
chaud
conférence
palais
congrès
jardins
favorisent
On adopte une optimisation stochastique :
𝜕J(θ; w)
𝜕vw
= −uc +
i=1
V
P ui w ui
𝜕J(θ; w)
𝜕uc
= − 1 − P uc w vw
et on a
𝐯w
new
= vw − 
𝜕J(θ;w)
𝜕vw
= vw +  (uc −
i=1
V
P ui w ui)
𝐮c
new
= uc − 
𝜕J(θ;w)
𝜕uc
= uc +  1 − P uc w vw
Pour deux vecteurs initialisés aléatoirement avec certaines valeurs,
si on ajoute juste un tout petit peu d'un vecteur à l'autre, les
vecteurs se rapprochent l'un de l'autre et donc la similitude
cosinus augmente. si on retranche un tout petit peu d'un vecteur à
l'autre, les vecteurs s'éloignent l'un de l'autre et donc la similitude
cosinus diminue. vw + uc
vw
ui
−P ui w ui
vw
uc
uc
la similitude cosinus augmente la similitude cosinus diminue
vw − P ui w ui)