Le document traite des algorithmes d'approximation, notamment dans la recherche des points fixes d'une fonction. Il présente également diverses méthodes pour calculer des valeurs approchées de constantes mathématiques comme pi et e, ainsi que des techniques pour estimer des aires sous des courbes à l'aide de méthodes de rectangles et de trapèzes. Des exemples de programmes en Pascal illustrent ces algorithmes d'approximation.

1. Chapitre : les algorithmes d’approximation Enseignant : Mohamed SAYARI
4ème
SI 1
LES ALGORITHMES D’APPROXIMATION
I. Introduction
Les problèmes d’optimisation forment un ensemble très riche de possibilités : de la possibilité
d’approcher avec une précision arbitraire, à l’impossibilité de toute garantié sur la qualité de
l’approximation.
II. RecheRche du point fixe d’une fonction
1) Présentation
 En mathématiques, pour une application f d’un ensemble E dans lui-même, un élément x de E est
un point fixe de f si f(x) = x
 Dans le plan, la symétrie par rapport à un point A admet un unique point fixe : A
 l’application inverse (définie sur l’ensemble des réels non nuls) admet deux points fixes : -1 et 1
 Graphiquement, les points fixes d’une fonction f (où la variable est réelle) s’obtiennent en traçant la
droite d’équation y = x : tous les points d’intersection de la courbe représentative de f avec cette
droite sont alors les points fixes de f.
 Toutes les fonctions n’ont pas nécessairement de point fixe ; par exemple, la fonction
n’en possède pas, car il n’existe aucun nombre réel x égal à x+1.
2) Activité
On désire écrire un programme en Pascal qui permet de résoudre l’équation sin(x)=1-x
a) Décomposer le problème en modules
b) Ecrire les analyses des modules, en déduire les algorithmes
c) Traduire en pascal la solution obtenue
 Sin(x)= 1-x  x= 1-sin(x)

2. Chapitre : les algorithmes d’approximation Enseignant : Mohamed SAYARI
4ème
SI 2
Tableaux de valeurs :
X 0 0.111111 0.222222 0.333333 0.444444 0.555556 0.666667 0.777778 0.888889
F(x)=1-sin(x) 1 0.889117 0.779602 0.672805 0.570044 0.472585 0.38163 0.298302 0.223628
X 0.5 0.511111 0.522222 0.533333 0.544444 0.555556 0.566667 0.577778 0.588889
F(x)=1-sin(x) 0.520574 0.510853 0.501193 0.491593 0.482057 0.472585 0.463177 0.453836 0.444563
a) Analyse du programme principal :
2) Résultat= Ecrire ("le point fixe est : ", x1, "trouvé après ", i, "itérations")
1) (Pfixe,i)= [i  0, x1 1] Répéter
i  i+1
x2  x1
x1  F(x1)
Jusqu’à (ABS(x1-x2) <epsilon)

3. Chapitre : les algorithmes d’approximation Enseignant : Mohamed SAYARI
4ème
SI 3
b) Algorithme du programme principal
0) Début Point_fixe
1) i  0
x1 1
Répéter
i  i+1
x2  x1
x1  F(x1)
Jusqu’à (ABS(x1-x2) <epsilon)
2) Ecrire ("le point fixe est : ", x1, "trouvé après ", i, "itérations")
3) Fin Point_Fixe
TDOG
Objet Type/Nature
i entier
X1, x2 Réel
epsilon Constante = 10-5
F Fonction
c) Analyse de la fonction F
1) Résultat= f  1- sin(x)
d) Algorithme de la fonction f
0) Fonction F (x : réel) : Réel
1) F 1- sin(x)
2) fin F
TDOL
Objet Type/Nature
X Réel
e) Traduction en Pascal

4. Chapitre : les algorithmes d’approximation Enseignant : Mohamed SAYARI
4ème
SI 4
III.Calcul de valeurs approchées de constantes connus
1) Activité
Il existe plusieurs constantes numériques :
 e (nombre de Neper) ≈ 2,718…
 (nombre Pi) ≈ 3,1616…
 ≈ 9.8066
Dans ce qui suit, nous allons présenter des algorithmes permettant de calculer des valeurs approchées pour les
constantes et e
2) Valeur approchée de
 Il est impossible de connaître la valeur exacte de . En effet, il a été démontré par deux
mathématiciens de la fin du XVIIIème
siècle, Lambert et Legendre, qu'il ne peut exister aucune fraction
[de deux entiers] égale à .
 Les hommes de science - Euler, Gauss, Leibniz, Machin, Newton, Viète - ont recherché toutes sortes
de formules permettant de calculer une approximation de plus ou moins précise.
a) Valeur approchée par la formule d’Euler
Ecrire une analyse, un algorithme et la traduction en Pascal d’un programme intitulé Pi_Euler, qui
permet de calculer et d’afficher une valeur approchée de Pi en utilisant la formule d’Euler :
Cela signifie que :
Cela signifie que :
 Analyse :
2) Résultat= Ecrire ("la valeur approchée de Pi est ", RacineCarrée(6 * S2))
1) S2= [S2 1, i2] Répéter
S1  S2
S2  S1+1/carrée(i)
i  i + 1
jusqu’à (RacineCarée(6*S2) – RacineCarrée(6*S1)) < epsilon
TDO
Objet Type/Nature
i Entier long
S1, S2 Réel

5. Chapitre : les algorithmes d’approximation Enseignant : Mohamed SAYARI
4ème
SI 5
epsilon Constante = 10-5
 Algorithme
0) Début Pi_Euler
1) S2 1,
i2
Répéter
S1  S2
S2  S1+1/carrée(i)
i  i + 1
jusqu’à (RacineCarée(6*S2) – RacineCarrée(6*S1)) < epsilon
2) Ecrire ("la valeur approchée de Pi est ", RacineCarrée(6 * S2))
3) Fin Pi_Euler
 Traduction en PASCAL
b) Valeur approchée par la formule de Wallis
Ecrire une analyse, un algorithme et la traduction en Pascal d’un programme intitulé Pi_Wallis, qui permet
de calculer et d’afficher une valeur approchée de Pi en utilisant la formule de Wallis :
Cela signifie que :
Cela signifie que :

6. Chapitre : les algorithmes d’approximation Enseignant : Mohamed SAYARI
4ème
SI 6
 Analyse
2) Résultat= Ecrire ("la valeur approchée de Pi est ", 2* p2)
1) P2= [i 1, P21] Répéter
P1  P2
P2  p1*((2*i)/(2*i-1))*((2*i)/(2*i+1))
i  i + 1
Jusqu’à (abs ((2*p2)-(2*p1)) <epsilon)
TDO
Objet Type/Nature
i Entier long
P1, P2 Réel
epsilon Constante = 10-5
 Algorithme
0) Début Pi_Wallis
1) i 1,
P21
Répéter
P1  P2
P2  p1*((2*i)/ (2*i-1))*((2*i)/ (2*i+1))
i  i + 1
Jusqu’à (abs ((2*p2)-(2*p1)) <epsilon)
2) Ecrire ("la valeur approchée de Pi est ", 2* p2)
3) Fin Pi_Wallis
 Traduction en PASCAL

7. Chapitre : les algorithmes d’approximation Enseignant : Mohamed SAYARI
4ème
SI 7
3) Valeur approchée de e
Ecrire une analyse, un algorithme et la traduction en Pascal d’un programme intitulé e, qui permet de
calculer et d’afficher une valeur approchée de e (nombre d’Euler, ou nombre Népérien) en utilisant la
formule suivante:
* Analyse du programme principal
2) Résultat= Ecrire ("la valeur approchée de e est : ", S2)
1) S2= [S21, i1] Répéter
S1  S2
S2  S1 + 1/Fact(i)
i  i + 1
Jusqu’à (s2-s1<epsilon)
TDOG
Objet Type/Nature
i entier
S1, S2 Réel
epsilon Constante = 10-5
Fact Fonction
* Algorithme du programme principal
0) Début e
1) S21
i1
Répéter
S1  S2
S2  S1 + 1/Fact(i)
i  i + 1
Jusqu’à (s2-s1<epsilon)
2) Ecrire ("la valeur approchée de e est : ", S2)
3) Fin e
* Analyse de la fonction Fact
Résultat= Fact
1) Fact = [ ] Si a=0 alors Fact 1
Sinon Fact  a* Fact(a-1)
Fin Si
 Algorithme de la fonction Fact
0) Fonction Fact (a : entier) : entier long
1) Si a=0 alors Fact 1
Sinon Fact  a* Fact(a-1)
Fin Si
2) Fin Fact

8. Chapitre : les algorithmes d’approximation Enseignant : Mohamed SAYARI
4ème
SI 8
 Traduction en PASCAL
IV.calcul d’aiRes
1) Introduction
Soit une fonction f continue sur l’intervalle [a, b].
Signifie l'aire sous la courbe de la fonction entre a et b.
2) Méthodes de rectangles
a) Principe
Consiste à partager l'intervalle d'intégration en intervalles de même amplitude à partir desquels on construit des
rectangles dont on calcule la somme des aires.
On peut prouver que quand le nombre d'intervalles tend vers l'infini, la somme des aires tend vers l'intégrale de la
fonction.
Méthode des rectangles à gauche Méthode des rectangles à droite
= =

9. Chapitre : les algorithmes d’approximation Enseignant : Mohamed SAYARI
4ème
SI 9
Méthode du point milieux
=
b) Application
On se propose de calculer l’aire résultante de la courbe de la fonction f : x  en utilisant la
méthode de rectangles
 Analyses
 Analyse du programme principal
2) Résultat = Ecrire ("une valeur approchée de l’intégrale est = ", FN CALCUL (a, b, n))
1) (a,b,n) = Proc saisir (a, b, n)
TDOG
Objet Type/Nature
n entier
a, b Réel
calcul Fonction
saisir procédure
 Analyse de la procédure saisir
Résultat= a,b , n
2) b= [ ] Répéter
b= donnée ("b=")
Jusqu’à (b >a)
1) a= donnée ("a=")
3) n= [ ] Répéter
n= donnée ("n=")
Jusqu’à (n >0)

10. Chapitre : les algorithmes d’approximation Enseignant : Mohamed SAYARI
4ème
SI 10
 Analyse de la fonction calcul
3) Résultat = calcul  somme * h
1) h  (b-a)/n
2) somme [somme  0, x a+h/2] Pour i de 1 à N Faire
somme  somme + f(x)
x  x+h
Fin Pour
 Analyse de la fonction F
1) Résultat = F  carré (x) / (1 + carrée (x))
 Algorithmes
 Algorithme du programme principal
0) Début Rectangles
1) Proc saisir (a, b, n)
2) Ecrire ("une valeur approchée de l’intégrale est = ", FN CALCUL (a, b, n))
3) Fin Rectangles
 Algorithme de la procédure saisir
0) Procédure saisir (var a,b : Réel ; var n :entier)
1) Ecrire ("a="), lire (a)
2) Répéter
Ecrire ("b=")
Lire (b)
Jusqu’à (b>a)
3) Répéter
Ecrire ("n=")
Lire (n)
Jusqu’à (n>0)
4) Fin saisir
 Algorithme de la fonction calcul
0. Fonction CALCUL (a,b : réel ; n :entier) : Réel
1. h  (b-a)/n
2. somme  0
x a+h/2
Pour i de 1 à N Faire
somme  somme + f(x)
x  x+h
Fin Pour
3. calcul  somme * h
4. Fin CALCUL
 Algorithme de la fonction f
0) Fonction f (x :réel) : réel
1) F  carré(x) / (1+ carré(x))
2) Fin f

11. Chapitre : les algorithmes d’approximation Enseignant : Mohamed SAYARI
4ème
SI 11
 Traduction en PASCAL
Méthode de milieu

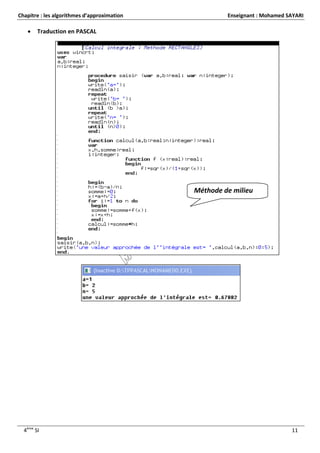
12. Chapitre : les algorithmes d’approximation Enseignant : Mohamed SAYARI
4ème
SI 12
3) Méthode de trapèze
On se propose de calculer l’aire résultante de la courbe de la fonction f : x  en utilisant la méthode de
trapèzes.
NB : Même démarche que la méthode précédente, on s’intéresse à écrire l’analyse et l’algorithme de la fonction
CALCUL.
 Analyse de la fonction calcul
3) Résultat = calcul  somme * h
1) h  (b-a)/n
2) somme [somme  (f(a) + f(a+h))/2, x a] Pour i de 1 à N-1 Faire
x  x+h
somme  somme + (f(x) + f(x+h))/2
Fin Pour
 Algorithme de la fonction calcul
0) Fonction CALCUL (a,b : réel ; n :entier) : Réel
1) h  (b-a)/n
2) somme  (f(a) + f(a+h))/2
x a
Pour i de 1 à N-1 Faire
x  x+h
somme  somme + (f(x) + f(x+h))/2
Fin Pour
3) calcul  somme * h
4) Fin CALCUL

13. Chapitre : les algorithmes d’approximation Enseignant : Mohamed SAYARI
4ème
SI 13
 Traduction en PASCAL