Le chapitre aborde la définition et les propriétés de l'intégration, incluant des concepts géométriques, la notion de primitive, et des règles pour le calcul d'aires et de volumes. Il explique également l'intégration de fonctions continues et fournit des exemples d'applications pratiques. Enfin, des théorèmes sont présentés, notamment ceux relatifs à la linéarité et à l'inégalité de la moyenne.

1. CHAPITRE 7 INTÉGRATION
1 Définition et approche géométrique
1. Définition
Soit f une fonction continue et positive sur un intervalle [ a, b ].
On considère le domaine délimité par la courbe représentant f, l’axe des
abscisses et les droites d’équations x = a et x = b.
b
L’aire de ce domaine, en unités d’aire, est le nombre réel noté
appelé intégrale de a à b de la fonction f.
∫
a
f ( x ) dx et
2. Approche géométrique
La fonction f peut être encadrée par deux fonctions en escalier, l’une majo-
rant f et l’autre la minorant.
L’aire du domaine sous la courbe est donc encadrée par deux suites adja-
centes d’aires de rectangles associés à une subdivision de [ a, b ]. Si on sub-
divise de plus en plus finement, ces deux suites convergent vers un même
nombre, ce nombre est l’aire sous la courbe f .
y
f
O a b x
3. Généralisation
Si f est continue et négative sur un intervalle [ a, b ], l’opposée de cette
fonction est positive et on peut revenir à la définition précédente.
b b
Si f 0, alors ∫
a
f ( x ) dx 0 et ∫
a
f ( x ) dx représente une aire.
b b
Si f 0, alors ∫
a
f ( x ) dx 0 et ∫
a
f ( x ) dx représente l’opposé d’une aire.
218

2. cours savoir-faire exercices corrigés
exemple d’application
On considère la fonction f : x x 2 sur [ 0 ; 1 ] .
1
1
On subdivise l’intervalle [ 0 ; 1 ] en segments d’amplitude -- . Calculer
n
-
∫ 0
f ( x ) dx
en utilisant la définition.
corrigé commenté
1
Sur 0 ; -- , l’aire sous la courbe
-
n 1
est encadrée par celle d’un rectan-
gle d’aire nulle associée à x 0 et
par celle d’un rectangle d’aire égale
1 1 2 1 2
à -- ×  --  associé à x  --  .
- - -
n  n  n
Et ainsi de suite jusqu’au dernier
n–1
intervalle ------------ ; 1 , où l’aire
n
sous la courbe est encadrée par
1
l’aire du rectangle de largeur -- et -
n 1 2 n–1
2 0 --
- --
- ------------ 1
n–1
de longueur  ------------ associée à n n n
 n 
n–1 2 1
x  ------------ et l’aire du rectangle de largeur -- et de longueur 1 associée à x
- 1.
 n  n
Donc l’aire sous la courbe représentant f sur [ 0 ; 1 ] est telle que :
1 1 n–1 2 1 1
1 1 2 2 1 1
0 + ----- × -- + … +  ------------ × -- ----- × -- +  --  × -- + … + -- × 1
n
- -
2 n  n  n
-
∫ 0
f ( x ) dx
n
- -
2 n  n
-
n
-
n
-
1
1 1
soit ----- [ 1 + 2 2 + … + ( n – 1 ) 2 ]
n3
-
∫ 0
f ( x ) dx ----- ( 1 + 2 2 + … + n 2 ).
n3
-
Indication : On rappelle que la somme des carrés des n premiers nombres entiers
n ( n + 1 ) ( 2n + 1 )
naturels est ------------------------------------------- .
-
6
1
1 1
Donc --------- ( n – 1 ) ( n ) ( 2n – 1 )
6n 3
-
∫ 0
f ( x ) dx --------- n ( n + 1 ) ( 2n + 1 ),
6n 3
-
1
1 1 1 1 1 1
soit -- – ------ + ---------
-
3 2n 6n 2
- -
∫ 0
f ( x ) dx -- + ------ + --------- ;
-
3 2n 6n 2
- -
lim  -- – ------ + --------- = lim  -- + ------ + --------- = -- ,
1 1 1 1 1 1 1
or - - - - - - -
n → + ∞ 3 2n 6n 2 n → + ∞ 3 2 n 6 n 2 3
1
1
d’où
∫ 0
f ( x ) dx = -- .
3
-
219

3. CHAPITRE 7 INTÉGRATION
2 Propriétés des intégrales
1. Propriétés
Soit f et g deux fonctions définies et continues sur [ a, b ].
a b a
• ∫
a
f ( x ) dx = 0 ; ∫ a
f ( x ) dx = – ∫ b
f ( x ) dx.
b c b
• Relation de Chasles : ∫ a
f ( x ) dx = ∫ a
f ( x ) dx + ∫
c
f ( x ) dx.
• Linéarité de l’intégrale : ( ∀α ∈ ) ( ∀β ∈ )
b b b
∫ a
( αf + βg ) ( x ) dx = α ∫ a
f ( x ) dx + β ∫ a
g ( x ) dx .
a a
• Si f est paire, alors ∫ –a
f ( x ) dx = 2 ∫0
f ( x ) dx.
a
• Si f est impaire, alors ∫–a
f ( x ) dx = 0.
a+T T
• Si f est périodique de période T, alors ∫ a
f ( x ) dx = ∫ 0
f ( x ) dx.
2. Intégrales et inégalités
Soit f et g deux fonctions définies et continues sur [ a, b ].
b
• Si pour tout réel x ∈ [ a, b ] , on a f ( x ) 0, alors ∫ a
f ( x ) dx 0.
Conséquence : Si pour tout x de [ a, b ] on a f ( x ) g ( x ),
b b
alors ∫a
f ( x ) dx ∫a
g ( x ) dx.
• Inégalité de la moyenne
La fonction f étant continue sur [ a, b ] il existe deux réels m et M tels que,
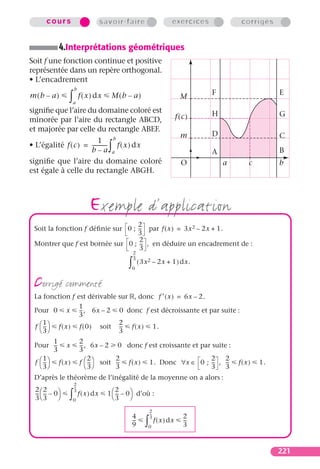
pour tout réel x ∈ [ a, b ], on ait m f ( x ) M et alors :
b
m(b – a) ∫ a
f ( x ) dx M(b – a)
3. Théorème de la moyenne
Pour toute fonction f définie et continue sur l’intervalle [ a, b ], il existe au
b
1
moins un réel c de [ a, b ] tel que f ( c ) = ----------- f ( x ) dx.
b–a a
-
∫
Le réel f ( c ) est appelé valeur moyenne de f sur [ a, b ].
220

4. cours savoir-faire exercices corrigés
4.Interprétations géométriques
Soit f une fonction continue et positive
représentée dans un repère orthogonal.
• L’encadrement
b
∫
m(b – a) f ( x ) dx M(b – a) F E
M
a
signifie que l’aire du domaine coloré est H G
minorée par l’aire du rectangle ABCD, f(c)
et majorée par celle du rectangle ABEF.
m D C
1 b
b–a a ∫
• L’égalité f ( c ) = ----------- f ( x ) dx
-
A B
signifie que l’aire du domaine coloré O a c b
est égale à celle du rectangle ABGH.
exemple d’application
2
Soit la fonction f définie sur 0 ; -- par f ( x ) = 3x 2 – 2x + 1.
-
3
2
Montrer que f est bornée sur 0 ; -- , en déduire un encadrement de :
-
3
2
--
-
∫
3
( 3x 2 – 2x + 1 ) dx.
0
corrigé commenté
La fonction f est dérivable sur , donc f ′ ( x ) = 6x – 2.
1
Pour 0 x -- , 6x – 2 0 donc f est décroissante et par suite :
-
3
1 2
f  --  f ( x ) f ( 0 ) soit -- f ( x ) 1.
- -
 3 3
1 2
Pour -- x- -- , 6x – 2
- 0 donc f est croissante et par suite :
3 3
1 2 2 2 2
f  --  f ( x )
- f  --  soit
- --
- f(x) 1. Donc ∀x ∈ 0 ; -- , --
- - f(x) 1.
 3  3 3 3 3
D’après le théorème de l’inégalité de la moyenne on a alors :
2
--
-
22
-- -- – 0 1  -- – 0 d’où :
2
∫
3
- - f ( x ) dx -
33  0
3 
2
--
-
4 2
∫
3
--
- f ( x ) dx --
-
9 0 3
221

5. CHAPITRE 7 INTÉGRATION
3 Intégration et dérivation
1. Notion de primitive
Soit une fonction f définie et continue sur un intervalle I et a un réel de I,
x
la fonction F telle que F ( x ) = ∫a
f ( t ) dt est l’unique primitive de f sur I qui
s’annule en a.
2. Définition d’une intégrale à l’aide de primitives
Soit f une fonction définie et continue sur un intervalle [ a, b ], F une pri-
mitive quelconque de f.
Le nombre réel F ( b ) – F ( a ) est indépendant de la primitive F choisie, on
l’appelle intégrale de f sur [ a, b ].
b b
On note ∫ a
f ( x ) dx = F ( b ) – F ( a ) = F ( x )
a
.
Remarque : La lettre choisie pour la variable est une variable muette ce qui signi-
b b b
fie que : ∫
a
f ( x ) dx = ∫ a
f ( t ) dt = ∫
a
f ( u ) du = F ( b ) – F ( a ).
3. Intégration par parties
Si u et v sont deux fonctions définies et deux fois dérivables sur [ a, b ] :
b b b
∫ a
u ( x )v′ ( x ) dx = u ( x )v ( x )
a
– ∫
a
u′ ( x )v ( x ) dx.
4
exemples d’application
³ Calculer ∫ ln x dx.
1
corrigé commenté
On ne connaît pas de primitive de la fonction logarithme, on utilise une intégra-
 1
 f ( x ) = ln x  f ′ ( x ) = --
-
tion par parties en posant  d’où  x
 g′ ( x ) = 1  g ( x ) = x.

222

6. cours savoir-faire exercices corrigés
Les fonctions f, g sont dérivables et f ′ et g′ sont continues sur [ 1 ; 4 ] donc :
4 4 4
1
∫ 1
ln x dx = x ln x
1
–
∫ 1
-- × x dx
x
-
4 4 4 4
∫ 1
ln x dx = x ln x
1
–
∫ 1
dx = x ln x – x
1
.
4 4
Remarque :
∫ 1
ln x dx = x ln x – x
1
traduit le fait que x x ln x – x est une
primitive de x ln x.
4 4
∫ 1
ln x dx = 4 ln 4 – 4 – ln 1 + 1 d’où
∫ 1
ln x dx = 4 ln 4 – 3.
3
· Calculer le réel I tel que I =
∫ x – 2 dx.
0
corrigé commenté
On commence par écrire x – 2 sans barre de valeur absolue sur [ 0 ; 3 ] .
Sur [ 0 ; 2 ] , x–2 = –x+2;
Sur [ 2 ; 3 ] , x – 2 = x – 2.
2 3
Donc I =
∫ 0
( 2 – x ) dx +
∫ 2
( x – 2 ) dx
soit :
2 3
x2 x2 9 5
I = 2x – ----- + ----- – 2x = 4 – 2 + -- – 6 – 2 + 4 d’où
- I = -- .
-
2 0 2 2 2 2
» Écrire à l’aide d’une intégrale, ln x pour x réel strictement positif.
Retrouver grâce à cette écriture qui est aussi la définition de la fonction ln, les
variations de f sur ]0 ; +∞[.
corrigé commenté
La fonction ln est la primitive sur ]0 ; +∞[ de la fonction inverse qui s’annule en
1, donc :
x
dt
ln x = ----- .
1 t
-
∫
1
Par définition d’une primitive d’une fonction, ln′ ( x ) = -- .
-
x
1
Or sur ]0 ; +∞[, -- 0 donc la fonction ln est strictement croissante sur ]0 ; +•[.
-
x
223

7. CHAPITRE 7 INTÉGRATION
4 Calculs d’aires et de volumes
1. Calcul d’aire
Soit f et g deux fonctions continues sur
le segment [ a, b ], telles que pour tout g
x de [ a, b ], on ait f ( x ) g ( x ). L’aire
du domaine D coloré, délimité par les
courbes f , g et les droites d’équa- D
tions x = a et x = b, est égale au réel
b
∫
tel que = [ g ( x ) – f ( x ) ] dx. Ce j f
a
0 a b
réel est exprimé en unités d’aire noté i
u.a.
2. Calcul de volume
L’espace est rapporté à un repère orthogonal ( O ; i , j , k ) .
Soit V le volume d’un solide délimité par une surface latérale Σ et deux
plans P1 et P2 parallèles à ( O ; i , j ) et de cotes respectives a et b.
Soit le plan P parallèle à P1 et P2 de cote z.
Le plan P coupe le solide selon une surface S dont l’aire ( z ) est telle que
b
z ( z ) soit continue sur [ a, b ] et alors V = ∫ a
( z ) dz.
Le volume V est exprimé en unités de volume noté u.v.
z
b
P2
P
a P1
k
i j y
x
224

8. cours savoir-faire exercices corrigés
exemples d’application
³ Calculer le volume V de la boule de centre O et de rayon R, en cm3, dans un
repère orthonormé ( O ; i , j , k ) d’unités graphiques 1 cm.
z
O′ A
z
k
O j y
i
x
La section de la boule par le plan P de cote z ( – R z R ) est un disque de rayon O′A.
Le triangle OO′A est rectangle en O′ donc O′A 2 = OA 2 – O′O 2 = R 2 – z 2 .
Soit ( z ) l’aire de ce disque.
( z ) = ( R 2 – z 2 )π donc, en centimètres cubes :
R R R
V = π
∫ –R
( R 2 – z 2 ) dz = πR 2
∫ –R
dz – π
∫ –R
z 2 dz
R R
z3 2R 3
V = πR 2 z – π ----
- = πR 2 ( 2R ) – π  --------- 
-
–R 3 –R
 3 
4
V = -- πR 3 cm 3 .
-
3
· Soit la représentation graphique de x e x dans un repère ( O ; i , j ) .
Sur [ 0 ; + ∞ [, la courbe subit une révolution d’axe (Ox).
Quel est le volume du solide déterminé par les plans d’équations x = 0, x = 1
et engendré par la courbe ?
corrigé commenté
La section du solide par un plan perpendiculaire à (Ox) est un disque dont l’aire
S(x) est telle que S ( x ) = π ( e x ) 2 soit S ( x ) = πe 2x .
La fonction S est continue sur [0 ; 1], donc le volume V en u.v du solide est tel que :
1 1
1 1
π
V =
∫ 0
S ( x ) dx = π
∫ 0
e 2x dx = π -- e 2x
2
-
0
= -- ( e 2 – 1 ),
2
-
π
d’où V = -- ( e 2 – 1 )
-
2
225