Le document contient des corrigés d'exercices sur différents sujets mathématiques tels que la logique, l'algèbre, l'optimisation, la dérivation et l'intégration. Chaque chapitre aborde des notions spécifiques accompagnées d'exemples et de démonstrations. Les exercices sont structurés par thème et incluant des résolutions détaillées.

1. CORRIGÉS
DES EXERCICES
1. Logique et théorie des ensembles 3
2. Algèbre 5
3. La résolution d’équations 18
4. Les fonctions d’une variable 23
5. Les propriétés des fonctions 36
6. La dérivation 44
7. Les dérivées en action 56
8. Fonctions concaves et convexes 73
9. Optimisation 79
10. Intégration 91
11. Mathématiques financières et modèles dynamiques 108
12. Algèbre des matrices 119
13. Déterminants, matrices inverses et formes quadratiques 132
14. Les fonctions de plusieurs variables 151
15. Les dérivées partielles en action 164
16. Les intégrales multiples 182
17. Optimisation sans contraintes d’égalité 183
18. Optimisation sans contraintes d’égalité 200
19. Programmation linéaire 215
20. Programmation non linéaire 225

3. CORRIGÉS
DES EXERCICES
Chapitre 1 / Logique et théorie des ensembles
1.1
1. (a) 5 ∈ 𝐶, 𝐷 ⊆ 𝐶 et 𝐵 = 𝐶 sont vrais. Les trois autres sont faux.
(b) 𝐴 ∩ 𝐵 = {2}, 𝐴 ∪ 𝐵 = {2, 3, 4, 5, 6}, 𝐴 𝐵 = {3, 4}, 𝐵 𝐴 = {5, 6},
(𝐴 ∪ 𝐵) (𝐴 ∩ 𝐵) = {3, 4, 5, 6}, 𝐴 ∪ 𝐵 ∪ 𝐶 ∪ 𝐷 = {2, 3, 4, 5, 6}, 𝐴 ∩ 𝐵 ∩ 𝐶 = {2} et
𝐴 ∩ 𝐵 ∩ 𝐶 ∩ 𝐷 = ∅.
2. Les 23 = 8 sous-ensembles de {𝑎, 𝑏, 𝑐} sont l’ensemble lui-même, l’ensemble vide, ainsi
que les six sous-ensembles {𝑎}, {𝑏}, {𝑐}, {𝑎, 𝑏}, {𝑎, 𝑐} et {𝑏, 𝑐}. Les 24 = 16 sous-
ensembles de {𝑎, 𝑏, 𝑐, 𝑑} sont les huit ensembles précédents avec huit ensembles de plus
incluant 𝑑 : {𝑑}, {𝑎, 𝑑}, {𝑏, 𝑑}, {𝑐, 𝑑}, {𝑎, 𝑏, 𝑑}, {𝑎, 𝑐, 𝑑}, {𝑏, 𝑐, 𝑑} et {𝑎, 𝑏, 𝑐, 𝑑}.
Outre {𝑎, 𝑏, 𝑐, 𝑑} et l’ensemble vide, il y a 14 sous-ensembles.
3. (b) est vraie car 𝐴 ∩ (𝐵 ∪ 𝐶) = (𝐴 ∩ 𝐵) ∪ (𝐴 ∩ 𝐶) ⊆ (𝐴 ∩ 𝐵) ∪ 𝐶 ; les trois autres sont
en général fausses. En effet, (a) 𝐴 𝐵 ≠ 𝐵 𝐴 dès que 𝐵 ⊆ 𝐴 avec ∅ ≠ 𝐵 ≠ 𝐴; (c) est
vraie si et seulement si 𝐴 ⊆ 𝐶 ; (d) est fausse par exemple pour 𝐴 = {1, 2}, 𝐵 = {1} et
𝐶 = {1, 3}.
1.2
1. 2𝑥 − 4 = 2 ⇒ 𝑥 = 3
(a) 𝑥 = 3 ⇒ 2𝑥 − 4 = 2
(b)
𝑥 = 1 ⇒ 𝑥2 − 2𝑥 + 1 = 0
(c) 𝑥2 > 4 ⇔ |𝑥| > 2
(d)
2. (a), (b) et (e) sont vraies; (e) correspond en fait à la définition courante de l’égalité de deux
ensembles. Pour (c), supposons par exemple que 𝐴 = {𝑥}, 𝐵 = {𝑦} et {𝑧}, avec 𝑥, 𝑦, 𝑧

4. 4 CORRIGÉS DES EXERCICES
tous différents. Alors 𝐴 ∩ 𝐵 = 𝐴 ∩ 𝐶 = ∅, ce qui contredit 𝐵 ≠ 𝐶. Pour (d), supposons
par exemple que 𝐴 = {𝑥, 𝑦, 𝑧}, 𝐵 = {𝑦} et 𝐶 = {𝑧}, où 𝑥, 𝑦, 𝑧 sont tous différents. Alors
𝐴 ∪ 𝐵 = 𝐴 ∪ 𝐶 = 𝐴, ce qui contredit 𝐵 ≠ 𝐶.
3. (a) ⇒ vraie, ⇐ vraie. (b) ⇒ vraie, ⇐ fausse. (c) ⇒ fausse, ⇐ vraie. (d) ⇒ vraie,
⇐ fausse (en fait, 𝑥 et 𝑦 sont tous deux nuls). (e) ⇒ et ⇐ vraies toutes les deux.
(f) ⇒ fausse (0 × 5 = 0 × 4, mais 5 ≠ 4), ⇐ vraie.
4. On a 2𝑥 + 5 ⩾ 13 ⇔ 𝑥 ⩾ 4, donc : (a) 𝑥 ⩾ 0 est nécessaire, mais pas suffisante;
(b) 𝑥 ⩾ 50 est suffisante, mais pas nécessaire; (c) 𝑥 ⩾ 4 est nécessaire et suffisante.
5. (a) 𝑥 < 0 ou 𝑦 < 0. (b) Il existe un 𝑥 tel que 𝑥 < 𝑎. (c) 𝑥 < 5 ou 𝑦 < 5, ou les deux.
(d) Il existe un 𝜀 > 0 tel que 𝐵 n’est pas satisfaite quel que soit 𝛿 > 0. (e) Il existe
quelqu’un qui n’aime pas les chats. (f) Il existe quelqu’un qui n’aime jamais personne.
1.3
1. (b), (d) et (e) expriment tous la même condition. (a) et (c) sont différents.
2. Si 𝑥 et 𝑦 ne sont pas tous les deux impairs, au moins un des deux est pair. Si, par exemple,
𝑥 = 2𝑛, avec 𝑛 entier, alors 𝑥𝑦 = 2𝑛𝑦 est aussi pair. De même si 𝑦 = 2𝑚 avec 𝑚 un entier.
1.4
1. Pour 𝑛 = 1, les deux membres valent 1. On suppose (∗) vrai pour 𝑛 = 𝑘. Alors
1 + 2 + 3 + · · · + 𝑘 + (𝑘 + 1) = 1
2 𝑘(𝑘 + 1) + (𝑘 + 1) = 1
2 (𝑘 + 1) (𝑘 + 2)
qui est (∗) pour 𝑛 = 𝑘 + 1. Donc par induction, (∗) est vrai pour tout entier naturel 𝑛.
2. Pour 𝑛 = 1, les deux membres valent 1
2 . On suppose (∗∗) vraie pour 𝑛 = 𝑘. Alors
1
1 × 2
+ · · · +
1
𝑘(𝑘 + 1)
+
1
(𝑘 + 1)(𝑘 + 2)
=
𝑘
𝑘 + 1
+
1
(𝑘 + 1)(𝑘 + 2)
=
𝑘(𝑘 + 2) + 1
(𝑘 + 1)(𝑘 + 2)
.
Mais 𝑘(𝑘 + 2) + 1 = 𝑘2 + 2𝑘 + 1 = (𝑘 + 1)2. La dernière fraction se simplifie donc en
(𝑘 + 1)/(𝑘 + 2). Ainsi, (∗∗) est aussi vraie pour 𝑛 = 𝑘 + 1. Il s’ensuit par induction que
(∗∗) est vraie pour tout entier naturel 𝑛.
3. L’affirmation est vraie pour 𝑛 = 1. Par hypothèse, on suppose que 𝑘3 + (𝑘 + 1)3 + (𝑘 + 2)3
est divisible par 9. Notez que
(𝑘 + 1)3
+ (𝑘 + 2)3
+ (𝑘 + 3)3
= (𝑘 + 1)3
+ (𝑘 + 2)3
+ 𝑘3
+ 9𝑘2
+ 27𝑘 + 27
= 𝑘3
+ (𝑘 + 1)3
+ (𝑘 + 2)3
+ 9 (𝑘2
+ 3𝑘 + 3).
Sous cette forme, la divisibilité par 9 devient évidente, en tant que somme de deux termes
divisibles par 9.

5. Chapitre 2 / Algèbre 5
Exercices récapitulatifs du chapitre 1
1. 𝐴∩𝐵 = {1, 4} ; 𝐴∪𝐵 = {1, 3, 4, 6} ; 𝐴𝐵 = {3} ; 𝐵 𝐴 = {6} ; (𝐴∪𝐵)(𝐴∩𝐵) = {3, 6} ;
𝐴 ∪ 𝐵 ∪ 𝐶 ∪ 𝐷 = {1, 2, 3, 4, 5, 6} ; 𝐴 ∩ 𝐵 ∩ 𝐶 = {4} et 𝐴 ∩ 𝐵 ∩ 𝐶 ∩ 𝐷 = ∅.
2. (a) ⇒ vraie, ⇐ fausse car 𝑥 = 𝑦 = 1 résout aussi 𝑥 + 𝑦 = 2.
(b) ⇒ fausse (car 𝑥2 = 16 a aussi comme solution 𝑥 = −4), ⇐ vraie, car, si 𝑥 = 4, alors
𝑥2 = 16.
(c) ⇒ vraie, car (𝑥−3)2 ⩾ 0; ⇐ fausse, car avec 𝑦 > −2 et 𝑥 = 3 on a (𝑥−3)2 (𝑦+2) = 0.
(d) ⇒ et ⇐ toutes les deux vraies, car l’équation 𝑥3 = 8 a comme solution 𝑥 = 2 et
aucune autre(1).
3. On démontre le résultat par induction sur 𝑛 avec 𝑥 ⩾ −1 fixé. De manière évidente,
(1 + 𝑥)𝑛 ⩾ 1 + 𝑛𝑥 est vraie avec égalité pour 𝑛 = 1. Posons l’hypothèse (1 + 𝑥)𝑘 ⩾ 1 + 𝑘𝑥
pour un entier naturel quelconque 𝑘. Alors, comme 1 + 𝑥 ⩾ 0, on a
(1 + 𝑥)𝑘+1
= (1 + 𝑥)𝑘
(1 + 𝑥) ⩾ (1 + 𝑘𝑥)(1 + 𝑥).
Or (1 + 𝑘𝑥)(1 + 𝑥) = 1 + (𝑘 + 1)𝑥 + 𝑘𝑥2 ⩾ 1 + (𝑘 + 1)𝑥, d’où (1 + 𝑥)𝑘+1 ⩾ 1 + (𝑘 + 1)𝑥,
ce qui achève la démonstration par récurrence
Chapitre 2 / Algèbre
2.1
1. (a) Vrai. (b) Faux, −5 étant inférieur à −3, il est à gauche de −3 sur la droite des
nombres. (c) Faux, −13 est un entier, mais pas un entier naturel car tous les entiers
naturels sont positifs. (d) Vrai.Tout entier naturel est rationnel. Par exemple, 5 = 5/1.
(e) Faux, car 3,1415 = 31 415/10 000, le quotient de deux entiers (3,1415 n’est qu’une
approximation de 𝜋). (f) Faux. Contre-exemple :
√
2 + (−
√
2) = 0. (g) Vrai.
(h) Vrai.
2. Dans le nombre 1,01001000100001000001 . . ., un 0 supplémentaire est ajouté entre
deux 1 successifs : il n’y a de toute évidence pas de suite finie dont les chiffres se répètent
indéfiniment.
2.2
1. 103 = 10 × 10 × 10 = 1000
(a) (−0,3)2 = 0,09
(b)
4−2 = 1/16
(c) (0,1)−1 = 1/0,1 = 10
(d)
2. (a) 4 = 22 (b) 1 = 20 (c) 64 = 26 (d) 1/16 = 2−4
(1) Dans les termes de la section 6.3, la fonction 𝑓 (𝑥) = 𝑥3 est strictement croissante. Voir exercice 6.3.3 et
figure 4.3.7.

6. 6 CORRIGÉS DES EXERCICES
3. (a) 153 (b) −1
3
3
(c) 10−1 (d) 10−7 (e) 𝑡6 (f) (𝑎 − 𝑏)3
(g) 𝑎2𝑏4 (h) (−𝑎)3
4. 25 × 25 = 25+5 = 210
(a) 38 × 3−2 × 3−3 = 38−2−3 = 33
(b)
(2𝑥)3 = 23𝑥3 = 8𝑥3
(c) (−3𝑥𝑦2)3 = (−3)3𝑥3 (𝑦2)3 = −27𝑥3𝑦6
(d)
𝑝24 𝑝3
𝑝4 𝑝
= 𝑝24+3−4−1
= 𝑝22
(e)
𝑎4𝑏−3
(𝑎2𝑏−3)2
=
𝑎4𝑏−3
𝑎4𝑏−6
=𝑎4−4
𝑏−3−(−6)
=𝑏3
(f)
34 (32)6
(−3)1537
=
34312
−31537
= −3−6
(g)
𝑝𝛾 (𝑝𝑞)𝜎
𝑝2𝛾+𝜎𝑞𝜎−2
= 𝑝−𝛾
𝑞2
(h)
5. (a) 26 = 64 (b) 64/27 (c) 8/3 (d) 𝑥9 (e) 𝑦12 (f) 8𝑥3𝑦3 (g) *(2) 10−2 = 1/100
(h) 𝑘4 (i) (𝑥 + 1)2
6. (a) Comme 4𝜋(3𝑟)2 = 4𝜋32𝑟2 = 9 (4𝜋𝑟2), la surface de la sphère est amplifiée d’un
facteur 9.
(b) Quand le rayon𝑟 augmente de 16 %, cela veut dire que𝑟 est multiplié par le facteur 1,16
et 𝑟2 par le facteur (1,16)2 = 1,3456. La surface augmente de 34,56 %.
7. (a) Faux. 𝑎0 = 1. (b) Vrai. 𝑐−𝑛 = 1/𝑐𝑛 pour tout 𝑐 ≠ 0.
(c) Vrai. 𝑎𝑚 × 𝑎𝑚 = 𝑎𝑚+𝑚 = 𝑎2𝑚. (d) Faux (sauf si 𝑚 = 0 ou 𝑎𝑏 = 1). 𝑎𝑚𝑏𝑚 = (𝑎𝑏)𝑚.
(e) Faux (sauf si 𝑚 = 1). Par exemple, (𝑎 + 𝑏)2 est égal à 𝑎2 + 2𝑎𝑏 + 𝑏2, qui ne se réduit
pas à 𝑎2 + 𝑏2 puisque 𝑎𝑏 0. (f) Faux (sauf si 𝑎𝑚𝑏𝑛 = 1). Par exemple, 𝑎2𝑏3 n’est
pas égal à (𝑎𝑏)2+3 = (𝑎𝑏)5 = 𝑎5𝑏5.
8. 𝑥3𝑦3 = (𝑥𝑦)3 = 33 = 27
(a) (𝑎𝑏)4 = (−2)4 = 16
(b)
(𝑎8)0 = 1 pour tout 𝑎 ≠ 0.
(c) (−1)2𝑛 = [(−1)2]𝑛 = 1𝑛 = 1
(d)
9. 150 × 0,13 = 19,5
(a) 2 400 × 0,06 = 144
(b) 200 × 0,055 = 11
(c)
10. (a) Un investissement initial de 50 e s’il est placé à un taux d’intérêt de 11% l’an, pendant
8 années, devient 50 × (1,11)8 ≈ 115,23 e.
(b) Un investissement initial de 10 000 e placés à 12 % l’an, pendant 20 ans, devient
10 000 × (1,12)20 ≈ 96 462,93 e.
(c) 5 000× (1,07)−10 ≈ 2 541,75 e est le montant que vous auriez dû investir il y a 10 ans
pour avoir 5 000 e aujourd’hui, si le taux d’intérêt est resté constant à 7 %.
11. 1,50 meilleur marché, ce qui est 15 % de 10.
12. (a) 12 000 × (1,04)15 ≈ 21 611,32 (b) 50 000 × (1,06)−5 ≈ 37 362,91
13. 𝑝 ≈ 95,3%, puisque (1,25)3 = 1,9531.
2.3
1. (a) 1 (b) 6 (c) −18 (d) −18 (e) 3𝑥 + 12 (f) 45𝑥 − 27𝑦 (g) 3 (h) 0 (i) −1
2. (a) 3𝑎2 − 5𝑏 (b) −2𝑥2 + 3𝑥 + 4𝑦 (c) 𝑡 (d) 2𝑟3 − 6𝑟2𝑠 + 2𝑠3

7. Chapitre 2 / Algèbre 7
3. (a) −3𝑛2 + 6𝑛 − 9 (b) 𝑥5 + 𝑥2 (c) 4𝑛2 − 11𝑛 + 6 (d) −18𝑎3𝑏3 + 30𝑎3𝑏2
(e) 𝑎3𝑏 − 𝑎𝑏3 (f) 𝑥3 − 6𝑥2𝑦 + 11𝑥𝑦2 − 6𝑦3 (g) 𝑎𝑐𝑥2 + (𝑎𝑑 + 𝑏𝑐) 𝑥 + 𝑏𝑑
(h) 4 − 𝑡4 (i) [(𝑢 − 𝑣) (𝑢 + 𝑣)]2 = (𝑢2 − 𝑣2)2 = 𝑢4 − 2𝑢2𝑣2 + 𝑣4
4. (a) (2𝑡 − 1) (𝑡2
− 2𝑡 + 1) = 2𝑡 (𝑡2
− 2𝑡 + 1) − (𝑡2
− 2𝑡 + 1)
= 2𝑡3
− 4𝑡2
+ 2𝑡 − 𝑡2
+ 2𝑡 − 1 = 2𝑡3
− 5𝑡2
+ 4𝑡 − 1
(b) (𝑎 +1)2 + (𝑎 −1)2 −2 (𝑎 +1) (𝑎 −1) = 𝑎2 +2𝑎 +1+𝑎2 −2𝑎 +1−2𝑎2 +2 = 4. Sinon, on
applique l’identité du deuxième degré 𝑥2 + 𝑦2 −2𝑥𝑦 = (𝑥 − 𝑦)2 avec 𝑥 = 𝑎 +1 et 𝑦 = 𝑎 −1
et on obtient (𝑎 + 1)2 + (𝑎 − 1)2 − 2 (𝑎 + 1) (𝑎 − 1) = [(𝑎 + 1) − (𝑎 − 1)]2 = 22 = 4.
(c) (𝑥 + 𝑦 + 𝑧)2
= (𝑥 + 𝑦 + 𝑧) (𝑥 + 𝑦 + 𝑧) = 𝑥 (𝑥 + 𝑦 + 𝑧) + 𝑦 (𝑥 + 𝑦 + 𝑧) + 𝑧 (𝑥 + 𝑦 + 𝑧)
= 𝑥2
+ 𝑥𝑦 + 𝑥𝑧 + 𝑦𝑥 + 𝑦2
+ 𝑦𝑧 + 𝑧𝑥 + 𝑧𝑦 + 𝑧2
= 𝑥2
+ 𝑦2
+ 𝑧2
+ 2𝑥𝑦 + 2𝑥𝑧 + 2𝑦𝑧
(d) Avec 𝑎 = 𝑥 + 𝑦 + 𝑧 et 𝑏 = 𝑥 − 𝑦 − 𝑧,
(𝑥 + 𝑦 + 𝑧)2
− (𝑥 − 𝑦 − 𝑧)2
= 𝑎2
− 𝑏2
= (𝑎 + 𝑏) (𝑎 − 𝑏) = 2𝑥 (2𝑦 + 2𝑧) = 4𝑥 (𝑦 + 𝑧).
5. (a) 𝑥2 + 4𝑥𝑦 + 4𝑦2 (b) 1/𝑥2
− 2 + 𝑥2
(c) 9𝑢2 − 30𝑢𝑣 + 25𝑣2 (d) 4𝑧2 − 25𝑤2
6. (a) 2012 − 1992 = (201 + 199) (201 − 199) = 400 × 2 = 800
(b) Si 𝑢2 − 4𝑢 + 4 = (𝑢 − 2)2 = 1 alors 𝑢 − 2 = ±1, donc 𝑢 = 1 ou 𝑢 = 3.
(c)
(𝑎 + 1)2 − (𝑎 − 1)2
(𝑏 + 1)2 − (𝑏 − 1)2
=
𝑎2 + 2𝑎 + 1 − (𝑎2 − 2𝑎 + 1)
𝑏2 + 2𝑏 + 1 − (𝑏2 − 2𝑏 + 1)
=
4𝑎
4𝑏
=
𝑎
𝑏
7.
1 0002
(2522 − 2482)
=
1 0002
(252 + 248) (252 − 248)
=
1 0002
500 × 4
= 500
8. (a) (𝑎 + 𝑏)3 = (𝑎 + 𝑏)2 (𝑎 + 𝑏) = (𝑎2 + 2𝑎𝑏 + 𝑏2) (𝑎 + 𝑏) = 𝑎3 + 3𝑎2𝑏 + 3𝑎𝑏2 + 𝑏3
(b) (𝑎 − 𝑏)3 = (𝑎 − 𝑏)2 (𝑎 − 𝑏) = (𝑎2 − 2𝑎𝑏 + 𝑏2) (𝑎 − 𝑏) = 𝑎3 − 3𝑎2𝑏 + 3𝑎𝑏2 − 𝑏3
(c) et (d) : développer les membres de droite.
9. (a) 3 × 7 × 𝑥𝑥𝑦𝑦𝑦 (b) 3 (𝑥 − 3𝑦 + 9𝑧) (c) 𝑎𝑎 (𝑎 − 𝑏) (d) 2 × 2 × 2𝑥𝑦 (𝑥𝑦 − 2)
(e) 2 × 2 × 7𝑎𝑎𝑏𝑏𝑏 (f) 2 × 2 (𝑥 + 2𝑦 − 6𝑧) (g) 2𝑥 (𝑥 − 3𝑦) (h) 2𝑎𝑎𝑏𝑏 (3𝑎 + 2𝑏)
(i) 7𝑥 (𝑥 − 7𝑦) (j) 5𝑥𝑦𝑦 (1 − 3𝑥) (1 + 3𝑥) (k) (4 + 𝑏) (4 − 𝑏) (l) 3 (𝑥 + 2) (𝑥 − 2)
10. (a) 𝑎2 + 4𝑎𝑏 + 4𝑏2 = (𝑎 + 2𝑏)2 par l’identité du second degré.
(b) 𝐾𝐿(𝐾 − 𝐿) (c) 𝐾−5(𝐾 − 𝐿)
(d) 9𝑧2 − 16𝑤2 = (3𝑧 − 4𝑤) (3𝑧 + 4𝑤), selon la formule de la différence de deux carrés.
(e) −1
5 𝑥2 + 2𝑥𝑦 − 5𝑦2 = −1
5 (𝑥2 − 10𝑥𝑦 + 25𝑦2) = −1
5 (𝑥 − 5𝑦)2
(f) 𝑎4 − 𝑏4 = (𝑎2 − 𝑏2) (𝑎2 + 𝑏2), grâce à la formule de la différence de deux carrés.
Comme 𝑎2 − 𝑏2 = (𝑎 − 𝑏) (𝑎 + 𝑏), 𝑎4 − 𝑏4 = (𝑎 − 𝑏) (𝑎 + 𝑏) (𝑎2 + 𝑏2).
11. (a) (𝑥 − 2) (𝑥 − 2) (b) 2 × 2𝑡𝑠 (𝑡 − 2𝑠) (c) 2 × 2 (2𝑎 + 𝑏) (2𝑎 + 𝑏)
(d) 5𝑥 (𝑥 +
√
2𝑦) (𝑥 −
√
2𝑦) (e) (5 + 𝑎) (𝑥 + 𝑦)
(f) 𝑢2 − 𝑣2 + 3 (𝑢 + 𝑣) = (𝑢 + 𝑣) (𝑢 − 𝑣) + 3 (𝑢 + 𝑣) = (𝑢 + 𝑣) (𝑢 − 𝑣 + 3)
(g) (𝑃 + 𝑄) (𝑃2 + 𝑄2) (h) 𝐾𝐾 (𝐾 − 𝐿) (i) 𝐾𝐿(𝐿2 + 1) (j) (𝐿 + 𝐾) (𝐿 − 𝐾)
(k) (𝐾 − 𝐿) (𝐾 − 𝐿) (l) 𝐾𝐿 (𝐾 − 2𝐿) (𝐾 − 2𝐿)

8. 8 CORRIGÉS DES EXERCICES
2.4
1. (a) 2/7 (b) 13/12 (c) 5/24 (d) 2/25 (e) 9/5 (f) 1/2 (g) 1/2 (h) 11/27
2. (a) 3𝑥/2 (b) 3𝑎/5 (c) 1/5 (d) 1
12 (−5𝑥 + 11) (e) −1/(6𝑏) (f) 1/𝑏
3. (a)
5 × 5 × 13
5 × 5 × 5 × 5
=
13
25
(b)
𝑎𝑏2
8𝑐2
(c)
2
3
(𝑎 − 𝑏) (d)
𝑃(𝑃 + 𝑄) (𝑃 − 𝑄)
(𝑃 + 𝑄)2
=
𝑃(𝑃 − 𝑄)
𝑃 + 𝑄
4. (a) 1/2 (b) 6 (c) 5/7 (d) 9/2
5. (a)
1
𝑥 − 2
−
1
𝑥 + 2
=
𝑥 + 2
(𝑥 − 2) (𝑥 + 2)
−
𝑥 − 2
(𝑥 + 2) (𝑥 − 2)
=
𝑥 + 2 − 𝑥 + 2
(𝑥 − 2) (𝑥 + 2)
=
4
𝑥2 − 4
(b) Comme 4𝑥 + 2 = 2 (2𝑥 + 1) et 4𝑥2 − 1 = (2𝑥 + 1) (2𝑥 − 1), le plus petit dénominateur
commun est 2 (2𝑥 + 1) (2𝑥 − 1). Ensuite,
6𝑥 + 25
4𝑥 + 2
−
6𝑥2 + 𝑥 − 2
4𝑥2 − 1
=
(6𝑥 + 25) (2𝑥 − 1) − 2 (6𝑥2 + 𝑥 − 2)
2 (2𝑥 + 1) (2𝑥 − 1)
=
42𝑥 − 21
2 (2𝑥 + 1) (2𝑥 − 1)
=
21
2 (2𝑥 + 1)
.
(c)
18𝑏2
𝑎2 − 9𝑏2
−
𝑎
𝑎 + 3𝑏
+ 2 =
18𝑏2 − 𝑎 (𝑎 − 3𝑏) + 2 (𝑎2 − 9𝑏2)
(𝑎 + 3𝑏) (𝑎 − 3𝑏)
=
𝑎 (𝑎 + 3𝑏)
(𝑎 + 3𝑏) (𝑎 − 3𝑏)
=
𝑎
𝑎 − 3𝑏
(d)
1
8𝑎𝑏
−
1
8𝑏 (𝑎 + 2)
=
(𝑎 + 2) − 𝑎
8𝑎𝑏 (𝑎 + 2)
=
2
8𝑎𝑏 (𝑎 + 2)
=
1
4𝑎𝑏 (𝑎 + 2)
(e)
2𝑡 − 𝑡2
𝑡 + 2
×
5𝑡
𝑡 − 2
−
2𝑡
𝑡 − 2
=
𝑡 (2 − 𝑡)
𝑡 + 2
×
3𝑡
𝑡 − 2
=
−𝑡 (𝑡 − 2)
𝑡 + 2
×
3𝑡
𝑡 − 2
=
−3𝑡2
𝑡 + 2
(f)
𝑎
1 − 1
2𝑎
0,25
=
𝑎 − 1
2
1
4
= 4𝑎−2, d’où2 −
𝑎
1 − 1
2𝑎
0,25
= 2 − (4𝑎 − 2) = 4 − 4𝑎 = 4 (1 − 𝑎).
6. (a)
2
𝑥
+
1
𝑥 + 1
− 3 =
2 (𝑥 + 1) + 𝑥 − 3𝑥 (𝑥 + 1)
𝑥 (𝑥 + 1)
=
2 − 3𝑥2
𝑥 (𝑥 + 1)
(b)
𝑡
2𝑡 + 1
−
𝑡
2𝑡 − 1
=
𝑡 (2𝑡 − 1) − 𝑡 (2𝑡 + 1)
(2𝑡 + 1) (2𝑡 − 1)
=
−2𝑡
4𝑡2 − 1
(c)
3𝑥
𝑥 + 2
−
4𝑥
2 − 𝑥
−
2𝑥 − 1
(𝑥 − 2) (𝑥 + 2)
=
3𝑥 (𝑥 − 2) + 4𝑥 (𝑥 + 2) − (2𝑥 − 1)
(𝑥 − 2) (𝑥 + 2)
=
7𝑥2 + 1
𝑥2 − 4
(d)
1
𝑥
+
1
𝑦
1
𝑥𝑦
=
1
𝑥
+
1
𝑦
𝑥𝑦
1
𝑥𝑦
× 𝑥𝑦
=
𝑦 + 𝑥
1
= 𝑥 + 𝑦
(e)
1
𝑥2
−
1
𝑦2
1
𝑥2
+
1
𝑦2
=
1
𝑥2
−
1
𝑦2
× 𝑥2𝑦2
1
𝑥2
+
1
𝑦2
× 𝑥2𝑦2
=
𝑦2 − 𝑥2
𝑦2 + 𝑥2
(f) Réduire les fractions du numérateur et du dénominateur au dénominateur commun 𝑥𝑦,
puis simplifier.
𝑎 (𝑦 − 𝑥)
𝑎 (𝑦 + 𝑥)
=
𝑦 − 𝑥
𝑦 + 𝑥

9. Chapitre 2 / Algèbre 9
7.
−8𝑥
𝑥2 + 2𝑥𝑦 − 3𝑦2
8. (a) 1
4 − 1
5 = 5
20 − 4
20 = 1
20 . De là, 1
4 − 1
5
−2
= 1
20
−2
= 202 = 400.
(b) 𝑛 −
𝑛
1 −
1
𝑛
= 𝑛 −
𝑛 × 𝑛
1 −
1
𝑛
× 𝑛
= 𝑛 −
𝑛2
𝑛 − 1
=
𝑛 (𝑛 − 1) − 𝑛2
𝑛 − 1
=
−𝑛
𝑛 − 1
(c) On pose 𝑢 = 𝑥𝑝−𝑞. Alors
1
1 + 𝑥𝑝−𝑞
+
1
1 + 𝑥𝑞−𝑝
=
1
1 + 𝑢
+
1
1 + 1/𝑢
=
1
1 + 𝑢
+
𝑢
1 + 𝑢
= 1.
(d) En utilisant 𝑥2 − 1 = (𝑥 − 1)(𝑥 + 1), on a
1
𝑥 − 1
+
1
𝑥2 − 1
(𝑥2 − 1)
𝑥 −
2
𝑥 + 1
(𝑥2
− 1)
=
(𝑥 + 1) + 1
𝑥3 − 𝑥 − 2𝑥 + 2
=
𝑥 + 2
(𝑥 + 2) (𝑥2 − 2𝑥 + 1)
=
1
(𝑥 − 1)2
.
(e)
1
(𝑥 + ℎ)2
−
1
𝑥2
=
𝑥2 − (𝑥 + ℎ)2
𝑥2 (𝑥 + ℎ)2
=
−2𝑥ℎ − ℎ2
𝑥2 (𝑥 + ℎ)2
, d’où
1
(𝑥 + ℎ)2
−
1
𝑥2
ℎ
=
−2𝑥 − ℎ
𝑥2 (𝑥 + ℎ)2
.
(f) En multipliant numérateur et dénominateur par 𝑥2 − 1 = (𝑥 + 1) (𝑥 − 1), il vient
10𝑥2
5𝑥 (𝑥 − 1)
=
2𝑥
𝑥 − 1
.
2.5
1. (a) 3 (b) 40 (c) 10 (d) 5 (e) 1/6 (f) 0,7 (g) 0,1 (h) 1/5
2. (a) =. (Les deux expressions sont égales à 20.)
(b) ≠. En fait,
√
25 + 16 =
√
41 ≠ 9 =
√
25 +
√
16. (c) ≠. (Posez 𝑎 = 𝑏 = 1.)
(d) =. En fait, (
√
𝑎 + 𝑏 )−1 = [(𝑎 + 𝑏)1/2]−1 = (𝑎 + 𝑏)−1/2.
3. (a) 81 (b) 4 (c) 623 (d) 15 (e) −1 (f) 2𝑥 − 2𝑥−1 = 2𝑥−1(2 − 1) = 2𝑥−1 = 4 pour
𝑥 = 3.
4. (a) 6
7
√
7 (b) 4 (c) 1
8
√
6 (d) 1 (e) 1
6
√
6 (f)
2
p
2𝑦
𝑦
(g)
√
2𝑥
2
(h) 𝑥 +
p
𝑥
5. (a) Multiplier numérateur et dénominateur par
√
7 −
√
5. Réponse : 1
2
√
7 −
√
5
.
(b) Multiplier numérateur et dénominateur par
√
5 −
√
3. Réponse : 4 −
√
15.
(c) Multiplier numérateur et dénominateur par
√
3 + 2. Réponse : −𝑥
√
3 + 2
.
(d) Multiplier numérateur et dénominateur par 𝑥
√
𝑦 − 𝑦
√
𝑥. Réponse :
√
𝑥 −
√
𝑦
2
𝑥 − 𝑦
.
(e) Multiplier numérateur et dénominateur par
√
𝑥 + ℎ +
√
𝑥. Réponse :
√
𝑥 + ℎ +
√
𝑥.
(f) Multiplier numérateur et dénominateur par 1 −
√
𝑥 + 1. Réponse :
1
𝑥
2
√
𝑥 + 1 − 𝑥 − 2
.

10. 10 CORRIGÉS DES EXERCICES
6. (a)
3
√
125 = 5, car 53 = 125. (b) (243)1/5 = 3, car 35 = 243. (c) −2
(d) 3
√
0,008 = 0,2 car (0,2)3 = 0,008. (e) 9 (f) 1/4
(g) 16−2,25 = 16−9/4 =
4
√
16
−9
= 2−9 = 1/512 (h) (1/3−2)−2 = 1/34 = 1/81
7. 40 (1 + 𝑝/100)12 = 60 donne (1 + 𝑝/100)12 = 1,5 et donc 1 + 𝑝/100 = (1,5)1/12. En
résolvant par rapport à 𝑝, 𝑝 = 100 [(1,5)1/12 − 1] ≈ 3,44.
8. (a) 3𝑥𝑝 𝑦2𝑞𝑧4𝑟 (b) (𝑥 + 15)4/3−5/6 = (𝑥 + 15)1/2 =
√
𝑥 + 15
(c)
8𝑥2/3𝑦1/4𝑧−1/2
−2𝑥1/3𝑦5/2𝑧1/2
= −4𝑥1/3
𝑦−9/4
𝑧−1
9. (a) 𝑎
1
2
2
3
3
4
4
5 = 𝑎1/5 (b) 𝑎
1
2 + 2
3 + 3
4 + 4
5 = 𝑎163/60 (c) 9𝑎7/2 (d) 𝑎1/4
10. 𝑉 = (4/3)𝜋𝑟3 donc 𝑟3 = 3𝑉/4𝜋 et 𝑟 = (3𝑉/4𝜋)1/3.
Ainsi, 𝑆 = 4𝜋𝑟2 = 4𝜋 3𝑉/4𝜋
2/3
=
3
√
36𝜋 𝑉2/3.
11. (a) (2𝑥)2 = 22𝑥 = 2𝑥2
si et seulement si 2𝑥 = 𝑥2, ou si et seulement si 𝑥 = 0 ou 𝑥 = 2.
(b) Correct, car 𝑎𝑝−𝑞 = 𝑎𝑝/𝑎𝑞.
(c) Correct, car 𝑎−𝑝 = 1/𝑎𝑝.
(d) 51/𝑥 = 1/5𝑥 = 5−𝑥 si et seulement si 1/𝑥 = −𝑥 ou −𝑥2 = 1, de sorte qu’il n’y a pas de
nombre réel 𝑥 qui vérifie l’équation.
(e) En posant 𝑢 = 𝑎𝑥 et 𝑣 = 𝑎𝑦, l’équation se réduit à 𝑢𝑣 = 𝑢 + 𝑣 ou
0 = 𝑢𝑣 − 𝑢 − 𝑣 = (𝑢 − 1) (𝑣 − 1) − 1.
Ce n’est valable que dans des cas particuliers de 𝑢 et 𝑣 et donc dans des cas particuliers
de 𝑥 et 𝑦. En particulier, l’équation est fausse quand 𝑥 = 𝑦 = 1.
(f) En posant 𝑢 =
√
𝑥 et 𝑣 =
√
𝑦, l’équation se réduit à 2𝑢 × 2𝑣 = 2𝑢𝑣, qui est correct si et
seulement si 𝑢𝑣 = 𝑢 + 𝑣, comme en (e) ci-dessus.
12. 𝑥 4. (Si 𝑥 0, alors 32𝑥3/2 4𝑥3 si et seulement si 8𝑥3/2 𝑥3, ce qui est équivalent à
8 𝑥3/2 et donc 𝑥 82/3 = 4.)
2.6
1. (a), (b), (d), (f) et (h) sont vraies, (c), (e) et (g) ne sont pas vraies.
2. (a) 𝑥 ⩾ −8 (b) 𝑥 −9 (c) Tout 𝑥. (d) 𝑥 ⩽ 25/2 (e) 𝑥 ⩽ 19/7 (f) 𝑡 −17/12
3. (a) −41/6 𝑥 ⩽ 2/3 (b) 𝑥 −1/5
4. (a) 𝑥(𝑥 + 3) 0 pour 𝑥 dans ] − 3, 0[, donc ⇒. (b) 𝑥2 9 pour 𝑥 dans ] − 3, 3[,
donc ⇒. (c) ⇐ . (d) 𝑦2 ⩾ 0, donc ⇒.
5. (a) Oui. (b) Non, prenez 𝑥 = 1
2 , par exemple. (c) Non, pas pour 𝑥 ⩽ 0.
(d) Oui, car l’inégalité est équivalente à 𝑥2 − 2𝑥𝑦 + 𝑦2 ⩾ 0, ou (𝑥 − 𝑦)2 ⩾ 0, qui est
satisfaite pour tout 𝑥 et 𝑦.

11. Chapitre 2 / Algèbre 11
6. Pour tout 𝑘 = 1, 2, . . ., soit 𝑠𝑘 la somme 𝑎1 +𝑎2 +· · ·+𝑎𝑘 et 𝑝𝑘 le produit 𝑎1 𝑎2 · · · 𝑎𝑘. On
a 𝑠2 et 𝑝2 strictement positifs d’après (2.6.1). Prenons comme hypothèse de récurrence
𝑠𝑘 et 𝑝𝑘 tous deux strictement positifs. Comme 𝑠𝑘+1 = 𝑠𝑘 + 𝑎𝑘+1 et 𝑝𝑘+1 = 𝑝𝑘 × 𝑎𝑘+1,
d’après (2.6.1), 𝑠𝑘+1 et 𝑝𝑘+1 sont tous deux strictement positifs. Le résultat suit par
récurrence.
7.
√
𝑎 −
√
𝑏
2
= 𝑎 − 2
√
𝑎𝑏 + 𝑏 ⩾ 0 fournit 𝑎 + 𝑏 ⩾ 2
√
𝑎𝑏 ; en divisant par 2, 𝑚𝐴 ⩾ 𝑚𝐺.
Comme
√
𝑎 −
√
𝑏
2
= 0 est équivalent à 𝑎 = 𝑏, on a aussi 𝑚𝐴 𝑚𝐺 sauf si 𝑎 = 𝑏.
L’inégalité 𝑚𝐺 ⩾ 𝑚𝐻 découle aisément de la suggestion.
2.7
1. (a) |2 × 0 − 3| = 3, |2 × 1
2 − 3| = 2, |2 × 7
2 − 3| = 4
(b) |2𝑥 − 3| = 0 ⇔ 2𝑥 − 3 = 0, donc 𝑥 = 3/2.
(c) |2𝑥 − 3| = 2𝑥 − 3 pour 𝑥 ⩾ 3/2, et 3 − 2𝑥 pour 𝑥 3/2
2. (a) |5 − 3 (−1)| = 8, |5 − 3 × 2| = 1, |5 − 3 × 4| = 7
(b) |5 − 3𝑥| = 5 ↔ 5 − 3𝑥 = ±5, donc 𝑥 = 0 ou 10/3.
(c) |5 − 3𝑥| = 5 − 3𝑥 quand 𝑥 ⩽ 5/3, |5 − 3𝑥| = 3𝑥 − 5 quand 𝑥 5/3.
3. (a) 𝑥 = −1 et 𝑥 = 4. (b) −2 ⩽ 𝑥 ⩽ 2 (c) 1 ⩽ 𝑥 ⩽ 3 (d) −1/4 ⩽ 𝑥 ⩽ 1
(e) 𝑥
√
2 ou 𝑥 −
√
2. (f) 1 ⩽ 𝑥2 ⩽ 3, c’est-à-dire 1 ⩽ 𝑥 ⩽
√
3 ou −
√
3 ⩽ 𝑥 ⩽ −1.
2.8
1. (a) 2
3𝑥 + 1
2𝑥 + 4
a les mêmes solutions que
3𝑥 + 1
2𝑥 + 4
− 2 0 ou
3𝑥 + 1 − 2 (2𝑥 + 4)
2𝑥 + 4
0 ou encore
−𝑥 − 7
2𝑥 + 4
0.
Un tableau de signes révèle que l’inégalité est satisfaite pour −7 𝑥 −2. Ce serait une
grave erreur de multiplier l’inégalité par 2𝑥 + 4 sans faire attention au signe de 2𝑥 + 4. Si
2𝑥 + 4 0, multiplier par ce nombre inverse l’inégalité(2).
(b) L’inégalité est équivalente à
120
𝑛
⩽ 0,75 ou
480 − 3𝑛
4𝑛
⩽ 0.
Un tableau de signes révèle que l’inégalité est vraie pour 𝑛 0 et pour 𝑛 ⩾ 160(3).
(c) Facile : 𝑔(𝑔 − 2) ⩽ 0, d’où 0 ⩽ 𝑔 ⩽ 2.
(d) Notez que 𝑝2 − 4𝑝 + 4 = (𝑝 − 2)2 et que l’inégalité se réduit à
𝑝 + 1
(𝑝 − 2)2
⩾ 0.
La fraction n’a pas de sens quand 𝑝 = 2. La conclusion est donc 𝑝 ⩾ −1 et 𝑝 ≠ 2.
(2) Ce serait une bonne idée de tester l’inégalité pour quelques valeurs de 𝑥. Par exemple, pour 𝑥 = 0 elle n’est pas
vraie. Et en 𝑥 = −5?
(3) Notez que pour 𝑛 = 0 l’inégalité n’a pas de sens. Pour 𝑛 = 160, on a l’égalité.

12. 12 CORRIGÉS DES EXERCICES
(e) L’inégalité est équivalente à
−𝑛 − 2
𝑛 + 4
− 2 0 c’est-à-dire
−𝑛 − 2 − 2𝑛 − 8
𝑛 + 4
0 ou
−3𝑛 − 10
𝑛 + 4
0
et finalement −4 𝑛 −10/3.
(f) 𝑥4 − 𝑥2 = 𝑥2(𝑥2 − 1) 0 ⇔ 𝑥 ≠ 0 et 𝑥2 1 ⇔ −1 𝑥 0 ou 0 𝑥 1.
2. (a) −2 𝑥 1 (b) 𝑥 −4 ou 𝑥 3. (c) −5 ⩽ 𝑎 ⩽ 5 (d) 𝑥 −4 ou 𝑥 1.
(e) 𝑥 −4 et 𝑥 ≠ 1. (f) 1 ⩽ 𝑥 ⩽ 2 (g) 𝑥 1 et 𝑥 ≠ 1/5. (h) 1/5 𝑥 1
(i) 𝑥 0 (j) −3 𝑥 −2 ou 𝑥 0 (k) 𝑥 ≠ 2 (l) 𝑥 ⩽ 0
3. −1 𝑥 0
2.9
1. (a) 1 + 2 + 3 + · · · + 10 = 55
(b) (5 × 30 − 2) + (5 × 31 − 3) + (5 × 32 − 4) + (5 × 33 − 5) + (5 × 34 − 6) = 585
(c) 1 + 3 + 5 + 7 + 9 + 11 = 36 (d) 220
+ 221
+ 222
= 21 + 22 + 24 = 22
(e) 2 × 10 = 20 (f) 2/1 + 3/2 + 4/3 + 5/4 = 73/12
2. (a) 2
√
0 + 2
√
1 + 2
√
2 + 2
√
3 + 2
√
4 = 2 (3 +
√
2 +
√
3)
(b) (𝑥 + 0)2 + (𝑥 + 2)2 + (𝑥 + 4)2 + (𝑥 + 6)2 = 4 (𝑥2 + 6𝑥 + 14)
(c) 𝑎1𝑖𝑏2 + 𝑎2𝑖𝑏3 + 𝑎3𝑖𝑏4 + · · · + 𝑎𝑛𝑖𝑏𝑛+1
(d) 𝑓 (𝑥0)Δ𝑥0 + 𝑓 (𝑥1)Δ𝑥1 + 𝑓 (𝑥2)Δ𝑥2 + · · · + 𝑓 (𝑥𝑚)Δ𝑥𝑚
3. (a)-(d) : dans chaque cas, regardez le dernier terme de la somme et remplacez 𝑛 par 𝑘
pour obtenir une expression du 𝑘-ième terme. Notez-le 𝑠𝑘. Dans (a), (b) et (d), la somme
s’écrit
Í𝑛
𝑘=1 𝑠𝑘 ; dans (c), elle s’écrit
Í𝑛
𝑘=0 𝑠𝑘.
(a)
𝑛
Õ
𝑘=1
4𝑘 (b)
𝑛
Õ
𝑘=1
𝑘3
(c)
𝑛
Õ
𝑘=0
(−1)𝑘 1
2𝑘 + 1
(d)
𝑛
Õ
𝑘=1
𝑎𝑖𝑘 𝑏𝑘 𝑗
(e) Les coefficients sont les puissances de 3 pour 𝑛 = 1, 2, 3, 4, 5. Le terme général est
donc 3𝑛𝑥𝑛.
(f)
𝑝
Õ
𝑗=3
𝑎
𝑗
𝑖 𝑏𝑖+ 𝑗 (g)
𝑝
Õ
𝑘=0
𝑎𝑘+3
𝑖+𝑘 𝑏𝑖+𝑘+3
(h) L’astuce est de voir que chaque terme a 198 unités de plus que le précédent,
3
Õ
𝑘=0
(81 297 + 198𝑘).
4. (a)
10
Õ
𝑘=1
(𝑘 − 2)𝑡𝑘
=
8
Õ
𝑚=−1
𝑚𝑡𝑚+2
(b)
𝑁
Õ
𝑛=0
2𝑛+5
=
𝑁 +1
Õ
𝑗=1
32 × 2𝑗−1
(car 32 = 25)
5. (a) Le nombre total de travailleurs issus du pays 𝑖 qui ont transféré leur lieu de travail.
(b) Le nombre total de travailleurs qui ont transféré leur lieu de travail vers le pays 𝑗.
6. (a), (c), (d) et (e) sont toujours vraies; (b) et (f) ne sont généralement pas vraies.

13. Chapitre 2 / Algèbre 13
2.10
1. On démontre ici seulement (2.10.6). La démonstration de (2.10.5) est très similaire,
quoiqu’un peu plus facile. Comme la dernière égalité dans (2.10.6) se déduit directement
de (2.10.4), on se concentre sur la démonstration de l’égalité
13
+ 23
+ 33
+ · · · + 𝑛3
=
1
2 𝑛(𝑛 + 1)
2
(∗)
Pour 𝑛 = 1, les membres de gauches et de droite de (∗) sont tous deux égaux à 1. Comme
hypothèse de récurrence (ou induction), supposons que (∗) est vraie pour 𝑛 = 𝑘. Alors
𝑘+1
Õ
𝑖=1
𝑖3
=
𝑘
Õ
𝑖=1
𝑖3
+ (𝑘 + 1)3
= [ 1
2 𝑘(𝑘 + 1)]2 + (𝑘 + 1)3 = (𝑘 + 1)2( 1
4 𝑘2 + 𝑘 + 1).
Mais cette dernière expression est égale à
1
4
(𝑘 + 1)2
(𝑘2
+ 4𝑘 + 4) = [
1
2
(𝑘 + 1)(𝑘 + 2)]2
,
ce qui montre que (∗) est vraie pour 𝑛 = 𝑘 + 1. On a donc démontré (∗) par induction.
2.
𝑛
Õ
𝑘=1
(𝑘2
+ 3𝑘 + 2) =
𝑛
Õ
𝑘=1
𝑘2
+ 3
𝑛
Õ
𝑘=1
𝑘 +
𝑛
Õ
𝑘=1
2
=
1
6
𝑛 (𝑛 + 1) (2𝑛 + 1) + 3
1
2
𝑛 (𝑛 + 1)
+ 2𝑛 =
1
3
𝑛 (𝑛2
+ 6𝑛 + 11)
3.
𝑛−1
Õ
𝑖=0
(𝑎 + 𝑖𝑑) =
𝑛−1
Õ
𝑖=0
𝑎 + 𝑑
𝑛−1
Õ
𝑖=0
𝑖 = 𝑛𝑎 + 𝑑 1
2 [1 + (𝑛 − 1)](𝑛 − 1) = 𝑛𝑎 + 1
2 𝑛 (𝑛 − 1) 𝑑.
(On peut aussi se passer du signe de sommation, en écrivant la somme sous la forme
𝑎 + (𝑎 + 𝑑) + (𝑎 + 2𝑑) + · · · + (𝑎 + (𝑛 − 1)𝑑). Il y a 𝑛 termes. La somme de tous les 𝑎 fait
𝑛𝑎. Le reste est 𝑑(1 + 2 + · · · + (𝑛 − 1)). Puis on utilise (2.10.4).)
2.11
1. (𝑎 + 𝑏)6 = 𝑎6 +6𝑎5𝑏 +15𝑎4𝑏2 +20𝑎3𝑏3 +15𝑎2𝑏4 +6𝑎𝑏5 + 𝑏6. (Les coefficients sont ceux
de la septième ligne du triangle de Pascal.)
2. (a)
8
3
= 56 et
8
8 − 3
=
8
5
= 56 ;
8
3
+
8
3 + 1
= 56+70 = 126;
8 + 1
3 + 1
=
9
4
= 126.
(b)
𝑚
𝑘
=
𝑚!
(𝑚 − 𝑘)!𝑘!
=
𝑚
𝑚 − 𝑘
;
𝑚
𝑘
+
𝑚
𝑘 + 1
=
𝑚!
(𝑚 − 𝑘)!𝑘!
+
𝑚!
(𝑚 − 𝑘 − 1)!(𝑘 + 1)!
=
𝑚!(𝑘 + 1 + 𝑚 − 𝑘)
(𝑚 − 𝑘)!(𝑘 + 1)!
=
(𝑚 + 1)!
(𝑚 − 𝑘)!(𝑘 + 1)!
=
𝑚 + 1
𝑘 + 1
.
3.
𝑚
Õ
𝑘=0
𝑚
𝑘
=
𝑚
Õ
𝑘=0
𝑚
𝑘
1𝑘
1𝑚−𝑘
= (1 + 1)𝑚
= 2𝑚
.

14. 14 CORRIGÉS DES EXERCICES
2.12
1. (a)
3
Õ
𝑖=1
4
Õ
𝑗=1
𝑖 × 3𝑗
=
3
Õ
𝑖=1
(𝑖 × 3 + 𝑖 × 9 + 𝑖 × 27 + 𝑖 × 81) =
3
Õ
𝑖=1
120𝑖 = 720
(b) Notons tout d’abord que
𝑟𝑠
𝑟 + 𝑠
2
= 0 lorsque 𝑠 = 0. Ainsi,
2
Õ
𝑠=0
4
Õ
𝑟=2
𝑟𝑠
𝑟 + 𝑠
2
se
simplifie en
2
Õ
𝑠=1
2𝑠
2 + 𝑠
2
+
3𝑠
3 + 𝑠
2
+
4𝑠
4 + 𝑠
2
#
=
2
3
2
+
3
4
2
+
4
5
2
+
4
4
2
+
6
5
2
+
8
6
2
qui est égal à
4
9
+
9
16
+
16
25
+ 1 +
36
25
+
16
9
=
(4 + 16) · 400 + 9 · 225 + (16 + 36) · 144
3 600
+ 1
ou
8 000 + 2 025 + 7488
3 600
+ 1 =
17 513
3 600
+ 1 = 5 +
3 113
3 600
.
(c) Comme
𝑚
Õ
𝑖=1
𝑛
Õ
𝑗=1
(𝑖 + 𝑗2
) =
𝑛
Õ
𝑗=1
𝑚
Õ
𝑖=1
𝑖
+
𝑚
Õ
𝑖=1
𝑛
Õ
𝑗=1
𝑗2
.
on peut utiliser les formules (2.10.4) et (2.10.5) avec l’égalité
Í𝑝
𝑘=1 𝑎 = 𝑝𝑎 pour écrire
cette somme sous la forme
𝑛
Õ
𝑗=1
1
2 𝑚(𝑚 + 1) +
𝑚
Õ
𝑖=1
1
6 𝑛 (𝑛 + 1) (2𝑛 + 1) = 𝑛1
2 𝑚(𝑚 + 1) + 𝑚
1
6
𝑛 (𝑛 + 1) (2𝑛 + 1)
= 1
6 𝑚𝑛 (2𝑛2
+ 3𝑛 + 3𝑚 + 4).
(d) En utilisant de nouveau (2.10.4) et (2.10.5), on obtient
𝑚
Õ
𝑖=1
2
Õ
𝑗=1
𝑖𝑗
=
𝑚
Õ
𝑖=1
(𝑖 + 𝑖2
) =
𝑚
Õ
𝑖=1
𝑖 +
𝑚
Õ
𝑖=1
𝑖2
= 1
2 𝑚 (𝑚 + 1) + 1
6 𝑚 (𝑚 + 1) (2𝑚 + 1) = 1
3 𝑚 (𝑚 + 1) (𝑚 + 2)
2. (a) Le nombre total d’unités du bien 𝑖.
(b) Le nombre total d’unités de tous les biens détenus par la personne 𝑗.
(c) Le nombre total d’unités de tous les biens détenus par le groupe tout entier.
3.
Í𝑖
𝑗=1 𝑎𝑖 𝑗 est la somme des 𝑖 éléments de la 𝑖ème ligne, chacune de ces 𝑚 sommes étant
à additionner, c’est la première double somme.
Í𝑚
𝑖=𝑗 𝑎𝑖 𝑗 est la somme des 𝑚 − 𝑗 + 1
éléments de la 𝑗ème colonne, chacune de ces 𝑚 colonnes étant à additionner, c’est la
deuxième double somme.
4. ¯
𝑎 est la moyenne des moyennes des colonnes ¯
𝑎𝑗 puisque
1
𝑛
𝑛
Õ
𝑗=1
¯
𝑎𝑗 =
1
𝑛
𝑛
Õ
𝑗=1
1
𝑚
𝑚
Õ
𝑟=1
𝑎𝑟 𝑗
=
1
𝑚𝑛
𝑚
Õ
𝑟=1
𝑛
Õ
𝑗=1
𝑎𝑟 𝑗 = ¯
𝑎.

15. Chapitre 2 / Algèbre 15
Pour démontrer (∗), on note que, par le fait que 𝑎𝑟 𝑗 − ¯
𝑎 est indépendant de l’indice de
sommation 𝑠, il est un facteur commun quand on somme sur 𝑠. Par conséquent,
𝑚
Õ
𝑠=1
(𝑎𝑟 𝑗 − ¯
𝑎)(𝑎𝑠 𝑗 − ¯
𝑎) = (𝑎𝑟 𝑗 − ¯
𝑎)
𝑚
Õ
𝑠=1
(𝑎𝑠 𝑗 − ¯
𝑎)
pour chaque 𝑟. Ensuite, en sommant sur 𝑟, on obtient
𝑚
Õ
𝑟=1
𝑚
Õ
𝑠=1
(𝑎𝑟 𝑗 − ¯
𝑎) (𝑎𝑠 𝑗 − ¯
𝑎) =
𝑚
Õ
𝑟=1
(𝑎𝑟 𝑗 − ¯
𝑎)
𝑚
Õ
𝑠=1
(𝑎𝑠 𝑗 − ¯
𝑎)
(∗∗)
car
Í𝑚
𝑠=1(𝑎𝑟 𝑗 − ¯
𝑎) est un facteur commun quand on somme sur 𝑟. Grâce aux propriétés
des sommes et à la définition de ¯
𝑎𝑗, on a
𝑚
Õ
𝑟=1
(𝑎𝑟 𝑗 − ¯
𝑎) =
𝑚
Õ
𝑟=1
𝑎𝑟 𝑗 −
𝑚
Õ
𝑟=1
¯
𝑎 = 𝑚 ¯
𝑎𝑗 − 𝑚 ¯
𝑎 = 𝑚( ¯
𝑎𝑗 − ¯
𝑎).
De même, en remplaçant 𝑟 par 𝑠 comme indice de sommation, on a aussi
𝑚
Õ
𝑠=1
(𝑎𝑠 𝑗 − ¯
𝑎) = 𝑚( ¯
𝑎𝑗 − ¯
𝑎).
Par substitution de ces valeurs dans (∗∗), on a confirmation de (∗).
Exercices récapitulatifs du chapitre 2
1. (a) 53 = 5 × 5 × 5 = 125 (b) 10−3 = 1/103 = 1/1 000 = 0,001 (c) 1/3−3 = 33 = 27
(d) −1 000 (e) 3 (f) (3−2)−3 = 36 = 729 (g) −1
(h)
−
1
2
−3
=
1
(−
1
2
)3
=
1
−
1
8
= −8
2. (a) 1 (b) Non défini. (c) 1 (d) 1
3. (a) 2−6 = 1/64 (b) 3
2 − 3
4 = 3
4 (c) −45/4 (d) 1
4. (a) (2𝑥)4 = 24𝑥4 = 16𝑥4
(b) 2−1 − 4−1 = 1
2 − 1
4 = 1
4 , de sorte que (2−1 − 4−1)−1 = 4.
(c) Éliminer le facteur commun 4𝑥2𝑦𝑧2. On obtient 6𝑥𝑦𝑧.
(d) −(−𝑎𝑏3)−3 = −(−1)−3𝑎−3𝑏−9 = 𝑎−3𝑏−9, de sorte que
[−(−𝑎𝑏3
)−3
(𝑎6
𝑏6
)2
]3
= [𝑎−3
𝑏−9
𝑎12
𝑏12
]3
= [𝑎9
𝑏3
]3
= 𝑎27
𝑏9
.
(e)
𝑎5𝑎3𝑎−2
𝑎−3𝑎6
=
𝑎6
𝑎3
= 𝑎3
(f)
𝑥
2
3
×
8
𝑥−2
−3
=
𝑥3
8
×
8
𝑥−2
−3
=
𝑥3
𝑥−2
−3
= (𝑥5
)−3
= 𝑥−15

16. 16 CORRIGÉS DES EXERCICES
5. (a) 𝑥3𝑦3 = (𝑥−1𝑦−1)−3 = 3−3 = 1/27
(b) (𝑥−3)6 (𝑥2)2 = 𝑥−18𝑥4 = 𝑥−14 = (𝑥7)−2 = 2−2 = 1/4
(c) (𝑧/𝑥𝑦)6 = (𝑥𝑦/𝑧)−6 = [(𝑥𝑦/𝑧)−2]3 = 33 = 27
(d) (𝑎𝑏𝑐)4 = (𝑎−1𝑏−1𝑐−1)−4 = (1/4)−4 = 44 = 256
6. (a) Si on a un taux d’intérêt de 1 % par an, dans 8 ans, un investissement de 100 millions
d’euros aura augmenté de 100 × (1,01)8 ≈ 108, 3 millions d’euros.
(b) Au taux d’intérêt annuel fixé de 15 %, un investissement initial de 50 000 £ sera
devenu après 10 ans 50 000 × (1,15)10 ≈ 202 277 £.
(c) 6 000 × (1,03)−8 ≈ 4 736 $ est la somme que vous auriez dû déposer il y a 8 ans pour
avoir aujourd’hui 6 000 $, au taux de 3 %.
7. (a) 100 000 (1,08)10 ≈ 215 892 (b) 25 000 (1,08)−6 ≈ 15 754
8. (a) 𝑎2 − 𝑎 (b) 𝑥2 + 4𝑥 − 21
(c) −
√
3
√
3 −
√
6
= −3 +
√
3
√
6 = −3 +
√
3
√
3
√
2 = −3 + 3
√
2 (d) 3 − 2
√
2
(e) 𝑥3 − 3𝑥2 + 3𝑥 − 1 (f) 1 − 𝑏4
(g) (1 + 𝑥 + 𝑥2 + 𝑥3) (1 − 𝑥) = (1 + 𝑥 + 𝑥2 + 𝑥3) − (1 + 𝑥 + 𝑥2 + 𝑥3) 𝑥 = 1 − 𝑥4
(h) (1 + 𝑥)4 = (1 + 𝑥)2 (1 + 𝑥)2 = (1 + 2𝑥 + 𝑥2) (1 + 2𝑥 + 𝑥2) = 𝑥4 + 4𝑥3 + 6𝑥2 + 4𝑥 + 1
9. (a) 5 (5𝑥 − 1) (b) 𝑥𝑥 (3 − 𝑥𝑦) (c) (
√
50 − 𝑥) (
√
50 + 𝑥) (d) 𝑎 (𝑎 − 2𝑏)2
10. (a) (5 + 𝑎) (𝑥 + 2𝑦) (b) (𝑎 + 𝑏) (𝑐 − 𝑑)
(c) 𝑎𝑥 + 𝑎𝑦 + 2𝑥 + 2𝑦 = 𝑎 (𝑥 + 𝑦) + 2 (𝑥 + 𝑦) = (𝑎 + 2) (𝑥 + 𝑦)
(d) 2𝑥2
− 5𝑦𝑧 + 10𝑥𝑧 − 𝑥𝑦 = 2𝑥2
+ 10𝑥𝑧 − (𝑥𝑦 + 5𝑦𝑧) = 2𝑥 (𝑥 + 5𝑧) − 𝑦 (𝑥 + 5𝑧)
= (2𝑥 − 𝑦) (𝑥 + 5𝑧)
(e) 𝑝2 − 𝑞2 + 𝑝 − 𝑞 = (𝑝 − 𝑞) (𝑝 + 𝑞) + (𝑝 − 𝑞) = (𝑝 − 𝑞) (𝑝 + 𝑞 + 1)
(f) 𝑢3
+ 𝑣3
− 𝑢2
𝑣 − 𝑣2
𝑢 = 𝑢2
(𝑢 − 𝑣) + 𝑣2
(𝑣 − 𝑢) = (𝑢2
− 𝑣2
) (𝑢 − 𝑣)
= (𝑢 + 𝑣) (𝑢 − 𝑣) (𝑢 − 𝑣) = (𝑢 + 𝑣) (𝑢 − 𝑣)2
11. (a) 161/4 =
4
√
16 = 2 (b) 243−1/5 = 1/
5
√
243 = 1/3
(c) 51/7 × 56/7 = 51/7+6/7 = 51 = 5 (d) 4−3/2 = 1/8
(e) 641/3 +
3
√
125 = 4 + 5 = 9 (f) (−8/27)2/3 = ( 3
p
−8/27 )2 = (−2/3)2 = 4/9
(g) (−1/8)−2/3 + (1/27)−2/3 = ( 3
p
−1/8 )−2 + ( 3
p
1/27 )−2 = (−1/2)−2 + (1/3)−2 = 4 + 9 = 13
(h)
1 000−2/3
3
√
5−3
=
(
3
√
1 000 )−2
5−1
=
10−2
5−1
=
1
20
12. (a) 8 = 23, de sorte que 𝑥 = 3/2.
(b) 1/81 = 3−4, de sorte que 3𝑥 + 1 = −4 ou 𝑥 = −5/3.
(c) 𝑥2 − 2𝑥 + 2 = 2, de sorte que 𝑥 = 0 ou 𝑥 = 2.
13. (a) 5 + 𝑥 = 3, de sorte que 𝑥 = −2.
(b) 3𝑥 − 3𝑥−2 = 3𝑥−2(32 − 1) = 3𝑥−2 × 8, de sorte que 3𝑥−2 = 3 et donc 𝑥 = 3.
(c) 3𝑥 × 3𝑥−1 = 32𝑥−1 = 81 = 34 à condition que 𝑥 = 2,5.

17. Chapitre 2 / Algèbre 17
(d) 35 + 35 + 35 = 3 × 35 = 36 de sorte que 𝑥 = 6.
(e) 4−6 + 4−6 + 4−6 + 4−6 = 4 × 4−6 = 4−5 de sorte que 𝑥 = −5.
(f)
226 − 223
226 + 223
=
223(23 − 1)
223(23 + 1)
=
7
9
de sorte que 𝑥 = 7.
14. (a)
𝑠
2𝑠 − 1
−
𝑠
2𝑠 + 1
=
𝑠(2𝑠 + 1) − 𝑠(2𝑠 − 1)
(2𝑠 − 1) (2𝑠 + 1)
=
2𝑠
4𝑠2 − 1
(b)
𝑥
3 − 𝑥
−
1 − 𝑥
𝑥 + 3
−
24
𝑥2 − 9
=
−𝑥 (𝑥 + 3) − (1 − 𝑥) (𝑥 − 3) − 24
(𝑥 − 3) (𝑥 + 3)
=
−7 (𝑥 + 3)
(𝑥 − 3) (𝑥 + 3)
=
−7
𝑥 − 3
(c) En multipliant numérateur et dénominateur par 𝑥2𝑦2, il vient
𝑦 − 𝑥
𝑦2 − 𝑥2
=
𝑦 − 𝑥
(𝑦 − 𝑥) (𝑦 + 𝑥)
=
1
𝑥 + 𝑦
.
15. (a) Simplifier par le facteur 25𝑎𝑏.
(b) 𝑥2 − 𝑦2 = (𝑥 + 𝑦) (𝑥 − 𝑦). Simplifier par 𝑥 + 𝑦.
(c) La fraction peut être écrite
(2𝑎 − 3𝑏)2
(2𝑎 − 3𝑏) (2𝑎 + 3𝑏)
=
2𝑎 − 3𝑏
2𝑎 + 3𝑏
.
(d)
4𝑥 − 𝑥3
4 − 4𝑥 + 𝑥2
=
𝑥 (2 − 𝑥) (2 + 𝑥)
(2 − 𝑥)2
=
𝑥 (2 + 𝑥)
2 − 𝑥
16. (a) 𝑥 13/2 (b) 𝑦 ⩾ −3 (c) Valable pour tout 𝑥. (d) 𝑥 29/14
(e) −1 ⩽ 𝑥 ⩽ 13/3 (f) −
√
6 ⩽ 𝑥 ⩽ −
√
2 ou
√
2 ⩽ 𝑥 ⩽
√
6.
17. (a) 30 + 0,16𝑥 (b) Au minimum 7,5 heures. Au maximum 10 heures.
18. 2𝜋(𝑟 + 1) − 2𝜋𝑟 = 2𝜋, où 𝑟 est le rayon de la Terre (supposée sphérique). Le supplément
de corde est seulement de 6,28 m!
19. (a) Poser 𝑝/100 = 𝑟. Alors l’expression donnée devient 𝑎 + 𝑎𝑟 − (𝑎 + 𝑎𝑟)𝑟 = 𝑎 (1 − 𝑟2),
comme demandé. (b) 2 000 × 1,05 × 0,95 = 1 995 e. (c) Le résultat est exac-
tement celui de la formule (a). (d) Avec la notation utilisée en (a), cela s’écrit
𝑎 − 𝑎𝑟 + (𝑎 − 𝑎𝑟)𝑟 = 𝑎 (1 − 𝑟2), ce qui est la même expression qu’en (a).
20. (a) Non, par exemple, −1 −2, mais (−1)2 (−2)2.
(b) On suppose 𝑎 𝑏 ou 𝑎 − 𝑏 0. Si 𝑎 + 𝑏 0, alors 𝑎2 − 𝑏2 = (𝑎 + 𝑏) (𝑎 − 𝑏) 0, de
sorte que 𝑎2 𝑏2.
21. (a) 2 1 et 1/2 1/1. Aussi, −1 −2 et 1/(−1) −1/2. Par ailleurs, 2 −1 et
1/2 1/(−1).
(b) Si 𝑎𝑏 0 et 𝑎 𝑏, alors 1/𝑏 − 1/𝑎 = (𝑎 − 𝑏)/𝑎𝑏 0, de sorte que 1/𝑏 1/𝑎.
(Aussi, si 𝑎𝑏 0 et 𝑎 𝑏, alors 1/𝑏 − 1/𝑎 = (𝑎 − 𝑏)/𝑎𝑏 0 de sorte que 1/𝑏 1/𝑎.)
22. (a) Quel que soit 𝑐, |𝑐| =
√
𝑐2. Ensuite |𝑎𝑏| =
p
(𝑎𝑏)2 =
√
𝑎2𝑏2 =
√
𝑎2
√
𝑏2 = |𝑎||𝑏|.
(b) De deux choses l’une, ou 𝑎 = |𝑎|, ou 𝑎 = −|𝑎|, de sorte que −|𝑎| ⩽ 𝑎 ⩽ |𝑎|.
De même, −|𝑏| ⩽ 𝑏 ⩽ |𝑏|. L’addition de ces inégalités conduit à
−|𝑎| − |𝑏| ⩽ 𝑎 + 𝑏 ⩽ |𝑎| + |𝑏|
et donc |𝑎 + 𝑏| ⩽ |𝑎| + |𝑏|.

18. 18 CORRIGÉS DES EXERCICES
23. (a)
Õ4
𝑖=1
1
𝑖(𝑖 + 2)
=
1
1 × 3
+
1
2 × 4
+
1
3 × 5
+
1
4 × 6
=
17
30
(b)
Õ9
𝑗=5
(2𝑗 − 8)2
= 22
+ 42
+ 62
+ 82
+ 102
= 220
(c)
Õ5
𝑘=1
𝑘 − 1
𝑘 + 1
=
5
Õ
𝑘=1
1 −
2
𝑘 + 1
= 5 −
2
2
−
2
3
−
2
4
−
2
5
−
2
6
=
21
10
(d)
Õ5
𝑛=2
(𝑛 − 1)2
(𝑛 + 2) = 12
× 4 + 22
× 5 + 32
× 6 + 42
× 7 = 4 + 20 + 54 + 112 = 190
(e)
Õ5
𝑘=1
1
𝑘
−
1
𝑘 + 1
= 1 −
1
6
=
5
6
(f)
Õ3
𝑖=−2
(𝑖 + 3)𝑖
= 1−2
+ 2−1
+ 30
+ 41
+ 52
+ 63
= 1 + 1/2 + 1 + 4 + 25 + 216 =
495
2
24. (a) 3 + 5 + 7 + · · · + 199 + 201 =
Õ100
𝑖=1
(1 + 2𝑖) (b)
2
1
+
3
2
+
4
3
+ · · · +
97
96
=
Õ96
𝑖=1
1 + 𝑖
𝑖
(c) 4 × 6 + 5 × 7 + 6 × 8 + · · · + 38 × 40 =
38
Õ
𝑖=4
𝑖(𝑖 + 2) (d)
1
𝑥
+
1
𝑥2
+ · · · +
1
𝑥𝑛
=
Õ𝑛
𝑖=1
𝑥−𝑖
(e) 1 +
𝑥2
3
+
𝑥4
5
+
𝑥6
7
+ · · · +
𝑥32
33
=
Õ16
𝑖=0
𝑥2𝑖
1 + 2𝑖
(f) 1 −
1
2
+
1
3
−
1
4
+ · · · −
1
80
+
1
81
=
Õ81
𝑖=1
(−1)𝑖−1 1
𝑖
25. (a) et (c) sont vraies. (b) est fausse sauf s’il se trouve que la différence entre les membres
de gauche et de droite, 2
Í𝑛
𝑖=1 𝑎𝑖𝑏𝑖, est nulle. (d) est aussi fausse.
26. (a) En utilisant l’astuce qui a mené à l’équation (2.10.4), on a
𝑅 = 3 + 5 + 7 + · · · + 197 + 199 + 201
𝑅 = 201 + 199 + 197 + · · · + 7 + 5 + 3.
On additionne terme à terme
2𝑅 = 204 + 204 + 204 + · · · + 204 + 204 + 204 = 100 × 204 = 20 400.
D’où 𝑅 = 10 200.
(b) 𝑆 = 1 001 + 2 002 + 3 003 + · · · + 8 008 + 9 009 + 10 010
= 1 001 (1 + 2 + 3 + · · · + 8 + 9 + 10) = 1 001 × 55 = 55 055
Chapitre 3 / La résolution d’équations
3.1
1. (a) 𝑥 = 3 (b) 𝑥 = 6 (c) N’importe quelle valeur de 𝑥 est une solution.
(d) 𝑥 = 1 (e) 𝑥 = −5. (Suggestion : 𝑥2 + 10𝑥 + 25 = (𝑥 + 5)2.) (f) 𝑥 = −1
2. (a) 𝑥 = −28/11 (b) 𝑥 = 5/11 (c) 𝑥 = 1 (d) 𝑥 = 121

19. Chapitre 3 / La résolution d’équations 19
3. (a) On remarque d’abord que l’équation n’a pas de sens pour 𝑥 = −3 et 𝑥 = −4.
En multipliant l’équation par le dénominateur commun (𝑥 + 3) (𝑥 + 4), on obtient
(𝑥 − 3) (𝑥 + 4) = (𝑥 + 3) (𝑥 − 4), c’est-à-dire 𝑥2 + 𝑥 − 12 = 𝑥2 − 𝑥 − 12, d’où 𝑥 = 0.
(b) En multipliant l’équation par le dénominateur commun (𝑥 − 3) (𝑥 + 3), on obtient
3 (𝑥 + 3) − 2 (𝑥 − 3) = 9, d’où 𝑥 = −6.
(c) En multipliant l’équation par le dénominateur commun 15𝑥 (en supposant 𝑥 ≠ 0), on
obtient 18𝑥2 − 75 = 10𝑥2 − 15𝑥 + 8𝑥2, d’où 𝑥 = 5.
4. (a) Avec 𝑥 le plus petit possible, 𝑥 + (𝑥 + 1) + (𝑥 + 2) = 10 + 2𝑥, de sorte que 𝑥 = 7 et les
nombres sont 7, 8 et 9.
(b) Si 𝑥 est le salaire horaire normal de Claudia, alors 38𝑥 + (48−38) 2𝑥 = 812. Solution :
𝑥 = 812/58 = 14.
(c) 1 500 + 12𝑥/100 = 2 100, donc 12𝑥 = 60 000, d’où 𝑥 = 5 000.
(d) 2
3 𝑥 + 1
4 𝑥 + 100 000 = 𝑥. Solution : 𝑥 = 1 200 000.
5. (a) En multipliant l’équation par le dénominateur commun 12, on obtient
9𝑦 − 3 − 4 + 4𝑦 + 24 = 36𝑦 et ainsi 𝑦 = 17/23.
(b) En multipliant l’équation par le dénominateur commun 2𝑥 (𝑥 + 2), on obtient
8 (𝑥 + 2) + 6𝑥 = 2 (2𝑥 + 2) + 7𝑥, d’où 𝑥 = −4.
(c) En multipliant les numérateur et dénominateur de la première fraction par 1 − 𝑧,
2 − 2𝑧 − 𝑧
(1 − 𝑧) (1 + 𝑧)
=
6
2𝑧 + 1
.
En multipliant chaque membre par (1−𝑧2) (2𝑧 +1), on obtient (2−3𝑧) (2𝑧 +1) = 6−6𝑧2,
et ainsi 𝑧 = 4.
(d) On effectue les produits,
𝑝
4
−
3
8
−
1
4
+
𝑝
12
−
1
3
+
𝑝
3
= −
1
3
puis on multiplie par le dénominateur commun 24. On obtient 6𝑝−9−6+2𝑝−8+8𝑝 = −8,
dont la solution est 𝑝 = 15/16.
3.2
1. (a) On multiplie les deux membres par 𝑎𝑏𝑥 pour obtenir 𝑏 + 𝑎 = 2𝑎𝑏𝑥. De là,
𝑥 =
𝑏 + 𝑎
2𝑎𝑏
=
𝑏
2𝑎𝑏
+
𝑎
2𝑎𝑏
=
1
2
1
𝑎
+
1
𝑏
.
(b) On multiplie l’équation par 𝑐𝑥 + 𝑑 pour obtenir 𝑎𝑥 + 𝑏 = 𝑐𝐴𝑥 + d𝐴, qui s’écrit aussi
(𝑎 − 𝑐𝐴) 𝑥 = d𝐴 − 𝑏 et donc 𝑥 = (d𝐴 − 𝑏)/(𝑎 − 𝑐𝐴).
(c) On multiplie l’équation par 𝑥1/2 pour obtenir 1
2 𝑝 = 𝑤𝑥1/2, d’où 𝑥1/2 = 𝑝/2𝑤. En
élevant chaque membre au carré, 𝑥 = 𝑝2/4𝑤2.
(d) On multiplie chaque membre par
√
1 + 𝑥 pour obtenir 1 + 𝑥 + 𝑎𝑥 = 0, de sorte que
𝑥 = −1/(1 + 𝑎).

20. 20 CORRIGÉS DES EXERCICES
(e) 𝑥2 = 𝑏2/𝑎2, de sorte que 𝑥 = ±
𝑏
𝑎
à condition que 𝑎 ≠ 0.
(f) On voit immédiatement que 𝑥 = 0.
2. (a) 𝑝 = 20𝑞/3 − 14/15 (b) 𝑃 = (𝑆 − 𝛼)/𝛽 (c) 𝑏 = 2𝐴/ℎ (d) 𝑟 = (3𝑉/4𝜋)1/3
(e) 𝐿 = (𝑌0 𝐴−1𝐾−𝛼)1/𝛽
3. (a) 𝛼𝑥 − 𝑎 = 𝛽𝑥 − 𝑏 si et seulement si (𝛼 − 𝛽) 𝑥 = 𝑎 − 𝑏 de sorte que 𝑥 = (𝑎 − 𝑏)/(𝛼 − 𝛽).
(b) 𝑌 = 94 + 0,2 (𝑌 − (20 + 0,5𝑌)) = 94 + 0,2𝑌 − 4 − 0,1𝑌, de sorte que 0,9𝑌 = 90, soit
𝑌 = 100.
(c) En élevant chaque membre de
√
𝑝𝑞 = 3𝑞 + 5 au carré, on a 𝑝𝑞 = (3𝑞 + 5)2, de sorte
que 𝑝 = (3𝑞 + 5)2/𝑞.
(d) On élève chaque membre à la puissance quatrième
𝐾2 𝑟
2𝑤
𝐾 = 𝑄4
de sorte que 𝐾3
= 2𝑤𝑄4
/𝑟 et, de là, 𝐾 = 2𝑤𝑄4
/𝑟
1/3
.
(e) En multipliant numérateur et dénominateur dans la fraction du membre de gauche par
4𝐾1/2𝐿3/4, on obtient 2𝐿/𝐾 = 𝑟/𝑤, d’où on tire 𝐿 = 𝑟𝐾/2𝑤.
(f) On élève chaque membre à la puissance quatrième, 1
16 𝑝4𝐾−1 (𝑟/2𝑤) = 𝑟4. Il s’ensuit
que 𝐾−1 = 32𝑟3𝑤/𝑝4, puis 𝐾 = 1
32 𝑝4𝑟−3𝑤−1.
4. (a) 𝑠 =
𝑡𝑇
𝑇 − 𝑡
(b) 𝑀 = (𝐵 + 𝛼𝐿)2/𝐾𝐿 (c) 𝑧 = (4𝑥𝑦 − 𝑥 + 2𝑦)/(𝑥 + 4𝑦)
(d) 𝑇 = 𝑁(1 − 𝑉/𝐶)
3.3
1. (a) 𝑥 (15 − 𝑥) = 0, les solutions sont donc 𝑥 = 0 et 𝑥 = 15.
(b) 𝑝 = ±4 (c) 𝑞 = 3 et 𝑞 = −4. (d) Pas de solution. (e) 𝑥 = 0 et 𝑥 = 3.
(f) 𝑥 = 2. (Notez que 𝑥2 − 4𝑥 + 4 = (𝑥 − 2)2.)
2. (a) 𝑥2 −5𝑥+6 = (𝑥−2) (𝑥−3) = 0 pour 𝑥 = 2 et pour 𝑥 = 3. (Avec 𝑥2 −5𝑥 = −6, compléter
le carré donne 𝑥2 − 5𝑥 + (5/2)2 = (5/2)2 − 6 = 25/4 − 6 = 1/4 ou (𝑥 − 5/2)2 = 1/4. De
là, 𝑥 − 5/2 = ±1/2.)
(b) 𝑦2 − 𝑦 − 12 = (𝑦 − 4) (𝑦 + 3) = 0 pour 𝑦 = 4 et pour 𝑦 = −3.
(c) Pas de solution et donc pas de factorisation.
(d) −1
4 𝑥2 + 1
2 𝑥 + 1
2 = −1
4
𝑥 − 1 +
√
3
𝑥 − 1 −
√
3
= 0 pour 𝑥 = 1 ±
√
3.
(e) 𝑚2 − 5𝑚 − 3 =
𝑚 − 1
2 5 +
√
37
𝑚 − 1
2 5 −
√
37
= 0 pour 𝑚 = 1
2 5 ±
√
37
.
(f) 0,1𝑝2 + 𝑝 − 2,4 = 0,1 (𝑝 − 2) (𝑝 + 12) = 0 pour 𝑝 = 2 et 𝑝 = −12.
3. (a) 𝑟 = −13, 𝑟 = 2 (b) 𝑝 = −16, 𝑝 = 1 (c) 𝐾 = 100, 𝐾 = 200 (d) 𝑟 = −
√
3,
𝑟 =
√
2 (e) 𝑥 = −0,5, 𝑥 = 0,8 (f) 𝑝 = −1/6, 𝑝 = 1/4
4. 𝑥 = 1, 𝑥 = 2
(a) 𝑡 = 1
10 1 ±
√
61
(b) 𝑥 = 1
4 3 ±
√
13
(c)
𝑥 = 1
3 −7 ±
√
5
(d) 𝑥 = −300, 𝑥 = 100
(e) 𝑥 = 1
6 5 ±
√
13
(f)

21. Chapitre 3 / La résolution d’équations 21
5. (a) Si les côtés sont de longueur 𝑥 et 𝑦, le périmètre a pour longueur 2𝑥 +2𝑦 = 40 et l’aire
𝑥𝑦 = 75. Ainsi, 𝑥 et 𝑦 sont les racines de l’équation 𝑧2 − 20𝑧 + 75 = 0. Les côtés ont donc
pour longueur 5 et 15.
(b) Si les deux nombres sont 𝑛 et 𝑛 + 1, alors 𝑛2 + (𝑛 + 1)2 = 13. Cette équation se réduit
à 2𝑛2 + 2𝑛 − 12 = 0, dont les solutions sont 𝑛1 = −3 et 𝑛2 = 2. Mais 𝑛 doit être positif,
donc la seule possibilité est 𝑛 = 2. Les deux nombres recherchés sont donc 2 et 3(4).
(c) Si le côté le plus court est désigné par 𝑥, l’autre est 𝑥 + 14. D’après le théorème de
Pythagore, 𝑥2 + (𝑥 + 14)2 = 342, ou 𝑥2 + 14𝑥 − 480 = 0. La seule solution positive est
𝑥 = 16 et, de là, 𝑥 + 14 = 30. Les longueurs sont donc de 16 cm et 30 cm.
(d) Si la vitesse habituelle est 𝑥 km/h et le temps habituel 𝑡 heures, alors 𝑥𝑡 = 80. Une
période de 16 minutes représente 16/60 = 4/15 d’heure. Rouler à la vitesse 𝑥+10 pendant
𝑡 −4/15 d’heure donne (𝑥+10) (𝑡 −4/15) = 80. De la première équation, on tire 𝑡 = 80/𝑥.
On substitue dans la seconde équation, (𝑥 + 10) (80/𝑥 − 4/15) = 80. Après remise en
ordre et simplification, on obtient 𝑥2 + 10𝑥 − 3 000 = 0, dont une solution positive est
𝑥 = 50. Sa vitesse habituelle est 50 km/h.
6. (a) 𝑥 = −2, 𝑥 = 0, 𝑥 = 2, car 𝑥 (𝑥2 − 4) = 0 ou 𝑥 (𝑥 + 2) (𝑥 − 2) = 0.
(b) 𝑥 = −2, 𝑥 = −1, 𝑥 = 1, 𝑥 = 2. (Posez 𝑥2 = 𝑢.)
(c) 𝑧 = −1/3, 𝑧 = 1/5. (Posez 𝑧−1 = 𝑢.)
3.4
1. (a) 𝑥 = 1, 𝑦 = −1 (b) 𝑥 = −4, 𝑦 = 7 (c) 𝑥 = −7/2, 𝑦 = 10/3
2. (a) 𝑝 = 2, 𝑞 = 3 (b) 𝑟 = 2,1, 𝑠 = 0,1
3. (a) 39 et 13. (b) 120 e pour une table et 60 e pour une chaise. (c) 450 de qualité B
et 300 de qualité P. (d) 2 000 e au taux d’intérêt de 5 % et 8 000 e au taux de 7,2 %.
Exercices récapitulatifs du chapitre 3
1. (a) 𝑥 = 12 (b) 𝑥 = 3 (c) 𝑥 = −3/2 (d) 𝑥 = −19 (e) 𝑥 = 11/7 (f) 𝑥 = 39
2. (a) En supposant 𝑥 ≠ ±4, on multiplie par le dénominateur commun (𝑥 − 4) (𝑥 + 4). Cela
réduit l’équation à 𝑥 = −𝑥, de sorte que 𝑥 = 0.
(b) L’équation donnée n’a de sens que si 𝑥 ≠ ±3. Si on multiplie par le dénominateur
commun (𝑥 + 3) (𝑥 − 3), on obtient 3 (𝑥 + 3)2 − 2 (𝑥2 − 9) = 9𝑥 + 27 ou 𝑥2 + 9𝑥 + 18 = 0,
avec comme solutions 𝑥 = −6 et 𝑥 = −3. La seule solution est donc 𝑥 = −6.
(c) En soustrayant 2𝑥/3 à chaque membre, l’équation se simplifie en 0 = −1 + 5/𝑥, dont
la seule solution est 𝑥 = 5.
(4) Bien sûr, pour de si petits nombres, il est encore plus facile de procéder par essai/erreur, en commençant par les
plus petits nombres. 12 + 22 = 5, qui est trop petit, mais 22 + 32 = 13, ce qui correspond à ce qu’on cherche. Si on
continue, les nombres deviennent trop grands : la réponse est donc 2 et 3.

22. 22 CORRIGÉS DES EXERCICES
(d) À condition que 𝑥 ≠ 0 et 𝑥 ≠ ±5, on multiplie par le dénominateur commun
𝑥 (𝑥 − 5) (𝑥 + 5) pour obtenir 𝑥 (𝑥 − 5)2 − 𝑥 (𝑥2 − 25) = 𝑥2 − 25 − (11𝑥 + 20) (𝑥 + 5). Le
développement des deux membres conduit à
𝑥3
− 10𝑥2
+ 25𝑥 − 𝑥3
+ 25𝑥 = 𝑥2
− 25 − 11𝑥2
− 75𝑥 − 100
et après simplification 50𝑥 = −125 − 75𝑥, dont la solution est 𝑥 = −1.
3. (a) 𝑥 = 2
3 (𝑦 − 3) + 𝑦 = 2
3 𝑦 − 2 + 𝑦 = 5
3 𝑦 − 2 ou 5
3 𝑦 = 𝑥 + 2, de sorte que 𝑦 = 3
5 (𝑥 + 2).
(b) 𝑎𝑥 − 𝑐𝑥 = 𝑏 + 𝑑, ou (𝑎 − 𝑐) 𝑥 = 𝑏 + 𝑑, de sorte que 𝑥 = (𝑏 + 𝑑)/(𝑎 − 𝑐).
(c)
√
𝐿 = 𝑌0/𝐴𝐾, de sorte qu’en élevant les deux membres au carré, 𝐿 = (𝑌0/𝐴𝐾)2.
(d) 𝑞𝑦 = 𝑚 − 𝑝𝑥, de sorte que 𝑦 = (𝑚 − 𝑝𝑥)/𝑞.
(e) On pose 𝑠 = 1/(1 + 𝑟). Alors 𝑠 = (𝑎 + 𝑏𝑐)/(1 − 𝑐), de sorte que
𝑟 = (1/𝑠) − 1 = [(1 − 𝑎) − 𝑐(1 + 𝑏)]/(𝑎 + 𝑏𝑐).
(f) En multipliant par (𝑃𝑥 + 𝑄)1/3, on obtient 𝑃𝑥 + 𝑃𝑥 + 𝑄 = 0, de sorte que
𝑥 = −𝑄/2𝑃.
4. (a) Multiplier l’équation par 5𝐾1/2 pour obtenir 15𝐿1/3 = 𝐾1/2. Élever les deux membres
au carré, 𝐾 = 225𝐿2/3.
(b) Élever chaque membre à la puissance 1/𝑡 pour obtenir 1 + 𝑟/100 = 21/𝑡 et ainsi
𝑟 = 100 (21/𝑡 − 1).
(c) 𝑎𝑏𝑥𝑏−1
0 = 𝑝, d’où 𝑥𝑏−1
0 = 𝑝/𝑎𝑏. Élever chaque membre à la puissance 1/(𝑏 − 1).
(d) Élever chaque membre à la puissance −𝜌 pour obtenir (1 − 𝜆) 𝑎−𝜌 + 𝜆𝑏−𝜌 = 𝑐−𝜌 ou
𝑏−𝜌 = 𝜆−1(𝑐−𝜌 − (1 − 𝜆) 𝑎−𝜌). Enfin, élever à la puissance −1/𝜌.
5. 𝑧 = 0 ou 𝑧 = 8.
(a) 𝑥 = −7 ou 𝑥 = 5.
(b) 𝑝 = −7 ou 𝑝 = 2.
(c)
𝑝 = 1/4 ou 𝑝 = 1/3.
(d) 𝑦 = 4 ±
√
31
(e) 𝑥 = −7 ou 𝑥 = 6.
(f)
6. (a) Des deuxième et troisième équations du modèle, on tire 𝐶 = 𝑏 (𝑌 − 𝑡𝑌) = 𝑏 (1 − 𝑡)𝑌.
On introduit cette expression dans la première équation et on résout par rapport à 𝑌,
𝑌 =
¯
𝐼 + 𝐺
1 − 𝑏 (1 − 𝑡)
d’où 𝐶 =
𝑏 (1 − 𝑡) ( ¯
𝐼 + 𝐺)
1 − 𝑏 (1 − 𝑡)
.
(b) Notez que 0 𝑏 (1 − 𝑡) 1. Lorsque 𝑡 augmente, 𝑌 et 1 − 𝑡 diminuent de sorte que
𝐶 = 𝑏 (1 − 𝑡)𝑌 diminue aussi.
7. 53𝑥 = 25𝑦+2 = 52 (𝑦+2) de sorte que 3𝑥 = 2 (𝑦 + 2). Avec 𝑥 − 2𝑦 = 8, cela donne 𝑥 = −2 et
𝑦 = −5, de sorte que 𝑥 − 𝑦 = 3.
8. (a) Soit 𝑢 = 1/𝑥 et 𝑣 = 1/𝑦. Alors le système devient 2𝑢 + 3𝑣 = 4, 3𝑢 − 2𝑣 = 19, avec
comme solution 𝑢 = 5, 𝑣 = −2 et, de là, 𝑥 = 1/𝑢 = 1/5, 𝑦 = 1/𝑣 = −1/2.
(b) Soit 𝑢 =
√
𝑥 et 𝑣 =
√
𝑦. Alors le système devient 3𝑢 + 2𝑣 = 2, 2𝑢 − 3𝑣 = 1/4, avec
comme solution 𝑢 = 1/2, 𝑣 = 1/4, et, de là, 𝑥 = 1/4, 𝑦 = 1/16.
(c) Avec 𝑢 = 𝑥2 et 𝑣 = 𝑦2, on obtient 𝑢 + 𝑣 = 13, 4𝑢 − 3𝑣 = 24, avec comme solution
𝑢 = 9, 𝑣 = 4 et, de là, 𝑥 = ±3 et 𝑦 = ±2.

23. Chapitre 4 / Les fonctions d’une variable 23
Chapitre 4 / Les fonctions d’une variable
4.2
1. (a) 𝑓 (0) = 02 + 1 = 1, 𝑓 (−1) = (−1)2 + 1 = 2, 𝑓 (1/2) = (1/2)2 + 1 = 1/4 + 1 = 5/4, et
𝑓 (
√
2) = (
√
2)2 + 1 = 2 + 1 = 3.
(b) (i) Puisque (−𝑥)2 = 𝑥2, 𝑓 (𝑥) = 𝑓 (−𝑥) pour tout 𝑥.
(ii) On a 𝑓 (𝑥+1) = (𝑥+1)2+1 = 𝑥2+2𝑥+1+1 = 𝑥2+2𝑥+2 et 𝑓 (𝑥)+ 𝑓 (1) = 𝑥2+1+2 = 𝑥2+3.
Cette égalité est vérifiée si et seulement si 𝑥2 +2𝑥 +2 = 𝑥2 +3, c’est-à-dire si et seulement
si 𝑥 = 1/2.
(iii) 𝑓 (2𝑥) = (2𝑥)2 + 1 = 4𝑥2 + 1 et 2 𝑓 (𝑥) = 2𝑥2 + 2. On a ainsi
4𝑥2
+ 1 = 2𝑥2
+ 2 ⇔ 𝑥2
= 1/2 ⇔ 𝑥 = ±
p
1/2 = ±
1
2
√
2.
2. 𝐹(0) = 𝐹(−3) = 10, 𝐹(𝑎 + ℎ) − 𝐹(𝑎) = 10 − 10 = 0.
3. (a) 𝑓 (0) = 0, 𝑓 (𝑎) = 𝑎2, 𝑓 (−𝑎) = 𝑎2 − (−𝑎 − 𝑎)2 = −3𝑎2 et 𝑓 (2𝑎) = 0.
(b) 3 𝑓 (𝑎) + 𝑓 (−2𝑎) = 3𝑎2 + [𝑎2 − (−2𝑎 − 𝑎)2] = 3𝑎2 + 𝑎2 − 9𝑎2 = −5𝑎2.
4. (a) 𝑓 (−1/10) = −10/101, 𝑓 (0) = 0, 𝑓 (1/
√
2) =
√
2/3, 𝑓 (
√
𝜋) =
√
𝜋/(1 + 𝜋),
𝑓 (2) = 2/5.
(b) 𝑓 (−𝑥) = −𝑥/(1 + (−𝑥)2) = −𝑥/(1 + 𝑥2) = − 𝑓 (𝑥) et
𝑓 (1/𝑥) = (1/𝑥)/[1 + (1/𝑥)2
] = (1/𝑥) 𝑥2
/[1 + (1/𝑥)2
] 𝑥2
= 𝑥/(1 + 𝑥2
) = 𝑓 (𝑥).
5. 𝐹(0) = 2, 𝐹(−3) =
√
19, 𝐹(𝑡 + 1) =
√
𝑡2 + 3.
6. (a) 𝐶(0) = 1 000, 𝐶(100) = 41 000 et 𝐶(101) − 𝐶(100) = 501.
(b) 𝐶(𝑥 + 1) − 𝐶(𝑥) = 2𝑥 + 301 = coût supplémentaire dû au passage de la production de
𝑥 à 𝑥 + 1.
7. (a) 𝐷(8) = 4, 𝐷(10) = 3,4 et 𝐷(10,22) = 3,334. (b) 𝑃 = 10,9.
8. (a) 𝑓 (𝑡𝑥) = 100 (𝑡𝑥)2 = 100𝑡2𝑥2 = 𝑡2 𝑓 (𝑥) (b) 𝑃(𝑡𝑥) = (𝑡𝑥)1/2 = 𝑡1/2𝑥1/2 = 𝑡1/2𝑃(𝑥)
9. (a) 𝑏 (0) = 0, 𝑏 (50) = 100/11, 𝑏 (100) = 200.
(b) 𝑏 (50+ℎ) −𝑏 (50) est le coût additionnel d’enlever ℎ % de plus que 50 % d’impuretés.
10. (a) Non : 𝑓 (2 + 1) = 𝑓 (3) = 18, alors que 𝑓 (2) + 𝑓 (1) = 8 + 2 = 10.
(b) Oui : 𝑓 (2 + 1) = 𝑓 (2) + 𝑓 (1) = −9.
(c) Non : 𝑓 (2 + 1) = 𝑓 (3) =
√
3 ≈ 1,73, alors que 𝑓 (2) + 𝑓 (1) =
√
2 + 1 ≈ 2,41.
11. (a) 𝑓 (𝑎 + 𝑏) = 𝐴(𝑎 + 𝑏) = 𝐴𝑎 + 𝐴𝑏 = 𝑓 (𝑎) + 𝑓 (𝑏)
(b) 𝑓 (𝑎 + 𝑏) = 10𝑎+𝑏 = 10𝑎 × 10𝑏 = 𝑓 (𝑎) × 𝑓 (𝑏)
12. Voir figures C4.2.12a et C4.2.12b.

24. 24 CORRIGÉS DES EXERCICES
x2
x × 1 1 ×1
1× x
x 1
x
1
Figure C4.2.12a L’aire
vaut (𝑥 +1)2 = 𝑥2 +2𝑥 +1.
x
1
x
1
Figure C4.2.12b
L’aire vaut 𝑥2 + 1.
y
1
x
1
(−3, 2)
(4, 0)
(0, 4)
(2, 3)
(−3/2, −2)
Figure C4.3.1
13. (a) Il faut 5 − 𝑥 ⩾ 0, soit 𝑥 ⩽ 5.
(b) Le dénominateur 𝑥2 − 𝑥 = 𝑥 (𝑥 − 1) doit être différent de 0, de sorte que 𝑥 ≠ 0 et
𝑥 ≠ 1.
(c) Pour commencer, le dénominateur doit être différent de 0. Ce qui exige 𝑥 ≠ 2 et
𝑥 ≠ −3. En outre, comme on ne peut prendre la racine carrée que d’un nombre positif,
la fraction (𝑥 − 1)/(𝑥 − 2) (𝑥 + 3) doit être positive. Un tableau de signes révèle que
𝐷 𝑓 =] − 3, 1] ∪ [2, +∞[. Notez en particulier que la fonction est définie en 𝑥 = 1 où elle
vaut 0.
14. (a) Définie pour 𝑥 ≠ 2 ou 𝐷 𝑓 =] − ∞, 2[∪]2, +∞[.
(b) 𝑓 (8) = 5
(c) 𝑓 (𝑥) =
3𝑥 + 6
𝑥 − 2
= 3 ⇔ 3𝑥 + 6 = 3 (𝑥 − 2) ⇔ 6 = −6, ce qui est impossible.
15. Puisque 𝑔 est manifestement définie pour 𝑥 ⩾ −2, 𝐷𝑔 = [−2, +∞[. Notez que
𝑔(−2) = 1 et 𝑔(𝑥) ⩽ 1 pour tout 𝑥 ∈ 𝐷 𝑓 . Lorsque 𝑥 va de −2 à +∞, 𝑔(𝑥) décroît
de 1 à −∞, de sorte que 𝑅𝑔 =] − ∞, 1].
4.3
1. Voir figure C4.3.1.
2. (a) 𝑓 (−5) = 0, 𝑓 (−3) = −3, 𝑓 (−2) = 0, 𝑓 (0) = 2, 𝑓 (3) = 4, 𝑓 (4) = 0.
(b) 𝐷 𝑓 = [−5, 4], 𝑅𝑓 = [−3, 4].
3. (a)
𝑥 0 1 2 3 4
𝑔(𝑥) = −2𝑥 + 5 5 3 1 −1 −3
Voir figure C4.3.3.
(b)
𝑥 −2 −1 0 1 2 3 4
ℎ(𝑥) = 𝑥2 − 2𝑥 − 3 5 0 −3 −4 −3 0 5
Voir figure C4.3.4.
(c)
𝑥 −2 −1 0 1 2
𝐹(𝑥) = 3𝑥 1
9
1
3 1 3 9
Voir figure C4.3.5.

25. Chapitre 4 / Les fonctions d’une variable 25
(d)
𝑥 −2 −1 0 1 2 3
𝐺(𝑥) = 1 − 2−𝑥 −3 −1 0 1/2 3/4 7/8
Voir figure C4.3.6.
y
− 4
− 3
− 2
− 1
1
2
3
4
5
x
1 2 3 4
Figure C4.3.3
y
− 4
− 3
1
2
3
4
5
x
− 2 1 2 3 4
Figure C4.3.4
2 1 1 2
1
2
3
2
1
y
x
Figure C4.3.5
2 1 1 2 3
1
2
3
4
2
3
1
y
x
Figure C4.3.6
4.4
1. (a) (8 − 3)/(5 − 2) = 5/3 (b) −2/3 (c) 51/5
2. Voir figures C4.4.2a, C4.4.2b et C4.4.2c.
y
1
2
3
4
x
1 2 3 4
Figure C4.4.2a
y
−5
−4
−3
−2
−1
1
x
5
1 2 3 4 6 7 8 10
Figure C4.4.2b
y
−1
1
2
3
4
x
1 2 3 4 5
Figure C4.4.2c
3. Si 𝐷 = 𝑎 + 𝑏𝑃, alors 𝑎 + 10𝑏 = 200 et 𝑎 + 15𝑏 = 150. La solution en 𝑎 et 𝑏 est 𝑎 = 300
et 𝑏 = −10, de sorte que 𝐷 = 300 − 10𝑃.
4. (a), (b) et (d) sont du premier degré ; (c) est du second degré.
5. Si 𝑃 est le prix de 𝑄 copies, alors, par la formule (4.4.2),
𝑃 − 1 400 =
3 000 − 1 400
500 − 100
(𝑄 − 100) ou 𝑃 = 1 000 + 4𝑄.
Le prix d’impression de 300 copies est donc 𝑃 = 1 000 + 4 × 300 = 2 200.
6. 𝑑1 : la pente vaut 1 et la formule (4.4.1) avec (𝑥1, 𝑦1) = (0, 2) et 𝑎 = 1 donne 𝑦 = 𝑥 + 2.
𝑑2 : la formule (4.4.2) avec (𝑥1, 𝑦1) = (0, 3) et (𝑥2, 𝑦2) = (5, 0) fournit
𝑦 − 3 =
0 − 3
5 − 0
𝑥 ou 𝑦 = −
3
5
𝑥 + 3.
𝑑3 est la droite d’équation 𝑦 = 1, de pente 0. 𝑑4 est la droite d’équation 𝑦 = 3𝑥 − 14, de
pente 3. 𝑑5 est la droite d’équation 𝑦 = 1
9 𝑥 + 2, de pente 1/9.

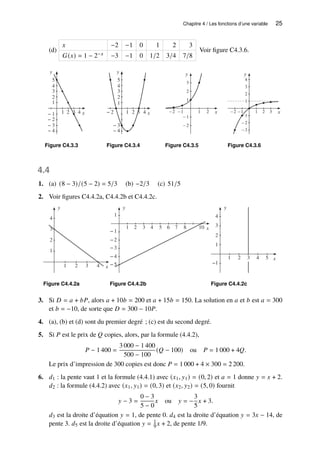
26. 26 CORRIGÉS DES EXERCICES
7. (a) 𝑑1 : 𝑦 − 3 = 2 (𝑥 − 1) ou 𝑦 = 2𝑥 + 1. (b) 𝑑2 : 𝑦 − 2 = 3−2
3−(−2) [𝑥 − (−2)] ou
𝑦 = 𝑥/5 + 12/5. (c) 𝑑3 : 𝑦 = −𝑥/2. (d) 𝑑4 : 𝑥/𝑎 + 𝑦/𝑏 = 1 ou 𝑦 = −𝑏𝑥/𝑎 + 𝑏.
8. Pour (a), la figure C4.4.8a montre que la solution est 𝑥 = 3, 𝑦 = −2. Pour (b), la
figure C4.4.8b montre que la solution est 𝑥 = 2, 𝑦 = 0. Pour (c), la figure C4.4.8c montre
qu’il n’y a pas de solution, puisque les deux droites sont parallèles.
y
x
x + y = 1
x − y = 5
(3, −2)
1
1
Figure C4.4.8a
y
x
1
1
x − y = 2
x − 2y = 2
x + y = 2
(2, 0)
Figure C4.4.8b
y
x
1
1
6x + 8y = 6
3x + 4y = 1
Figure C4.4.8c
9. Voir figures C4.4.9a, C4.4.9b et C4.4.9c.
y
x
1
1
Figure C4.4.9a
y
x
−1 1
Figure C4.4.9b
y
x
1
1
Figure C4.4.9c
10. Les points dont les coordonnées satisfont à l’inégalité 3𝑥 + 4𝑦 ⩽ 12 sont ceux qui se
trouvent sur ou sous la droite d’équation 3𝑥 + 4𝑦 = 12, comme expliqué à l’exemple 4.4.6
pour une inégalité semblable. Les points dont les coordonnées satisfont à l’inégalité
𝑥 − 𝑦 ⩽ 1, ou, de façon équivalente, 𝑦 ⩾ 𝑥 − 1, sont ceux qui se trouvent sur ou au-dessus
de la droite d’équation 𝑥 − 𝑦 = 1. Enfin, les points dont les coordonnées satisfont à
l’inégalité 3𝑥 + 𝑦 ⩾ 3, ou, de façon équivalente, 𝑦 ⩾ 3 − 3𝑥, sont ceux qui se trouvent
sur ou au-dessus de la droite d’équation 3𝑥 + 𝑦 = 3. L’ensemble de tous les points qui
satisfont aux trois inégalités est ombré dans la figure C4.4.10.
4.5
1. 0,78
2. (a) 75 − 3𝑃𝑒 = 20 + 2𝑃𝑒 et, de là, 𝑃𝑒 = 11. (b) 𝑃𝑒 = 90
3. La formule de l’équation d’une droite à l’aide de deux points donne
𝐶 − 200 =
275 − 200
150 − 100
(𝑥 − 100) ou 𝐶 =
3
2
𝑥 + 50.

27. Chapitre 4 / Les fonctions d’une variable 27
4. 𝐶 = 0,8𝑦 + 100. (Avec 𝐶 = 𝑎𝑦 + 𝑏, on sait que 900 = 1 000𝑎 + 𝑏 et 𝑎 = 80/100 = 0,8, de
sorte que 𝑏 = 100.)
5. (a) 𝑃(𝑡) = 20 000 − 2 000𝑡 (b) 𝑊(𝑡) = 500 − 50𝑡
y
x
1
2
3
2 3 4
3x + 4y = 12
3x + y = 3
x − y = 1
Figure C4.4.10
4.6
1. (a)
𝑥 −1 0 1 2 3 4 5
𝑓 (𝑥) = 𝑥2 − 4𝑥 5 0 −3 −4 −3 0 5
Voir figure C4.6.1.
(b) Minimum en 𝑥 = 2, avec 𝑓 (2) = −4. (c) 𝑥 = 0 et 𝑥 = 4.
y
− 4
− 3
− 2
− 1
1
2
3
4
5
x
− 1 1 2 3 4 5 6
f (x) = x2
− 4x
Figure C4.6.1
y
− 4
− 3
− 2
− 1
1
2
3
x
− 4− 3− 2− 1 1 2 3
f (x)=−1
2x2− x + 3
2
Figure C4.6.2
2. (a)
𝑥 −4 −3 −2 −1 0 1 2
𝑓 (𝑥) = −1
2 𝑥2 − 𝑥 + 3
2 −2, 5 0 1, 5 2 1, 5 0 −2, 5
Voir figure C4.6.2.
(b) Maximum en 𝑥 = −1 où 𝑓 (−1) = 2. (c) 𝑥 = −3 et 𝑥 = 1.
(d) 𝑓 (𝑥) 0 en (−3, 1), 𝑓 (𝑥) 0 pour 𝑥 −3 et pour 𝑥 1.
3. Minimum −4 quand 𝑥 = −2.
(a) Minimum 9 quand 𝑥 = −3.
(b)
Maximum 45 quand 𝑥 = 5.
(c) Minimum −45 quand 𝑥 = 1/3.
(d)
Maximum 40 000 quand 𝑥 = −100.
(e) Minimum −22 500 quand 𝑥 = −50.
(f)

28. 28 CORRIGÉS DES EXERCICES
4. (a) 𝑥 (𝑥 + 4). Racines 0 et −4. (b) Pas de factorisation possible. Pas de racines.
(c) −3 (𝑥 − 𝑥1) (𝑥 − 𝑥2), où les racines sont 𝑥1 = 5 +
√
15 et 𝑥2 = 5 −
√
15.
(d) 9 (𝑥 − 𝑥1) (𝑥 − 𝑥2), où les racines sont 𝑥1 = 1/3 +
√
5 et 𝑥2 = 1/3 −
√
5.
(e) −(𝑥 + 300) (𝑥 − 100). Racines −300 et 100.
(f) (𝑥 + 200) (𝑥 − 100). Racines −200 et 100.
5. (a) 𝑥 = 2𝑝 et 𝑥 = 𝑝. (b) 𝑥 = 𝑝 et 𝑥 = 𝑞. (c) 𝑥 = 1
2 𝑝 et 𝑥 = −2𝑞.
6. En développant, on obtient 𝑈(𝑥) = −(1 +𝑟2) 𝑥2 + 8 (𝑟 − 1) 𝑥. Ensuite, on applique (4.6.4)
avec 𝑎 = −(1 + 𝑟2) et 𝑏 = 8 (𝑟 − 1). 𝑈(𝑥) atteint un maximum en 𝑥 = 4 (𝑟 − 1)/(1 + 𝑟2).
7. (a) Les aires quand 𝑥 = 100, 250 et 350 sont respectivement 100 × 400 = 40 000,
250 × 250 = 62 500 et 350 × 150 = 52 500.
(b) L’aire est égale à 𝐴 = (250 + 𝑥) (250 − 𝑥) = 62 500 − 𝑥2, qui manifestement atteint un
maximum en 𝑥 = 0. Le rectangle est alors un carré.
8. (a) 𝜋(𝑄) = (𝑃𝐸 − 𝑃𝐺 − 𝛾)𝑄 = −1
2 𝑄2 + (𝛼1 − 𝛼2 − 𝛾)𝑄.
(b) Le graphique de la fonction de profit 𝜋(𝑄) = −1
2𝑄2 + (𝛼1 −𝛼2 − 𝛾)𝑄 est une parabole
dont le creux pointe vers le bas. D’après (4.6.4), le point le plus haut est atteint en
𝑄 = 𝑄 = 𝛼1 − 𝛼2 − 𝛾
et tout 𝑄 supérieur à 𝑄 donnera un point sur la partie droite descendante de la parabole.
Si 𝑄 0, c’est donc la valeur de 𝑄 qui maximise 𝜋(𝑄). Si 𝑄 ⩽ 0, pour tout 𝑄 0, on
a 𝜋(𝑄) 𝜋(0) = 0. Le profit est donc maximal en 𝑄 = 0. (On suppose, bien sûr, que
l’entreprise ne transporte pas de quantités négatives de cacao.)
(c) 𝜋(𝑄) = −1
2𝑄2 + (𝛼1 − 𝛼2 − 𝛾 − 𝑡)𝑄 et 𝑄∗ = 𝛼1 − 𝛼2 − 𝛾 − 𝑡 si 𝛼1 − 𝛼2 − 𝛾 − 𝑡 0.
(d) 𝑇 = 𝜏𝑄∗ = 𝜏 (𝛼1 −𝛼2 −𝛾 −𝜏). 𝑇 est une fonction du deuxième degré en 𝜏 ; elle vaut 0
quand 𝜏 = 0 et quand 𝜏 = 𝜏1 = 𝛼1 − 𝛼2 − 𝛾, et elle est strictement positive pour 𝜏 compris
entre 0 et 𝜏1.
(e) La taxe à l’exportation est maximale quand 𝑡 = 1
2 (𝛼1 − 𝛼2 − 𝛾).
9. (a) 361 ⩽ 377
(b) On trouve que 𝑓 (𝑥) = 𝐴𝑥2 + 𝐵𝑥 + 𝐶, où
𝐴 = 𝑎2
1 + 𝑎2
2 + · · · + 𝑎2
𝑛, 𝐵 = 2 (𝑎1𝑏1 + 𝑎2𝑏2 + · · · + 𝑎𝑛𝑏𝑛) et 𝐶 = 𝑏2
1 + 𝑏2
2 + · · · + 𝑏2
𝑛.
Maintenant, si 𝐵2 − 4𝐴𝐶 0, alors, en accord avec la formule (3.3.5), l’équation
𝑓 (𝑥) = 𝐴𝑥2 + 𝐵𝑥 + 𝐶 = 0 devrait avoir deux solutions distinctes, ce qui contredit
𝑓 (𝑥) ⩾ 0 pour tout 𝑥. Donc 𝐵2 − 4𝐴𝐶 ⩽ 0 et la conclusion en découle.
(c) L’inégalité (4.6.8) est équivalente à 1
4 𝐵2 ⩽ −𝐴𝐶.
4.7
1. (a) D’après la remarque sous l’exemple 4.7.2 et l’énoncé (4.7.6), toutes les racines entières
doivent être des facteurs de 6, à savoir ±1, ±2, ±3 et ±6. De ces 8 candidats, on trouve
que −2, −1, 1 et 3 sont toutes des racines et, comme un polynôme de degré 4 ne peut pas
avoir plus de 4 racines, on les a toutes.
L’équation peut s’écrire (𝑥 + 2) (𝑥 + 1) (𝑥 − 1) (𝑥 − 3) = 0.

29. Chapitre 4 / Les fonctions d’une variable 29
(b) Ce polynôme a les mêmes racines potentielles que (a). Mais seuls −6 et 1 sont des
solutions entières (la troisième racine est −1/2).
(c) Comme ni 1 ni −1 ne satisfont à l’équation, il n’y a pas de racines entières.
(d) On multiplie d’abord l’équation par 4 pour que les coefficients soient des entiers.
Ensuite ±1, ±2 et ±4 sont les solutions potentielles. En fait, 1, 2 et −2 sont tous les trois
solutions.
2. (a) 1 et −2. (b) 1, 5 et −5. (c) −1
3. (a) La réponse est 2𝑥2 + 2𝑥 + 4 + 3/(𝑥 − 1), car
(2𝑥3 + 2𝑥 − 1 ÷ (𝑥 − 1) = 2𝑥2 + 2𝑥 + 4
2𝑥3 − 2𝑥2
2𝑥2 + 2𝑥 − 1
2𝑥2 + 2𝑥
4𝑥 − 1
4𝑥 − 4
3 ← le reste
(b) La réponse est 𝑥2 + 1, car
(𝑥4 + 𝑥3 + 𝑥2 + 𝑥) ÷ (𝑥2 + 𝑥) = 𝑥2 + 1
𝑥4 + 𝑥3
𝑥2 + 𝑥
𝑥2 + 𝑥
0 ← pas de reste
(c) La réponse est 𝑥3 − 4𝑥2 + 3𝑥 + 1 − 4𝑥/(𝑥2 + 𝑥 + 1).
(d) La réponse est 3𝑥5 + 6𝑥3 − 3𝑥2 + 12𝑥 − 12 + (28𝑥2 − 36𝑥 + 13)/(𝑥3 − 2𝑥 + 1).
4. (a) Comme la courbe coupe l’axe 𝑂𝑥 aux points d’abscisses 𝑥 = −1 et 𝑥 = 3, on essaie
la fonction du second degré 𝑓 (𝑥) = 𝑎 (𝑥 + 1) (𝑥 − 3), pour une certaine constante 𝑎 0.
Comme la courbe passe par le point de coordonnées (1, −2), il faut 𝑓 (1) = −2. Comme
𝑓 (1) = −4𝑎, 𝑎 = 1
2 . Le polynôme proposé est 𝑦 = 1
2 (𝑥 + 1) (𝑥 − 3).
(b) Comme la fonction 𝑓 (𝑥) doit avoir trois racines 𝑥 = −3, 1, 2, on essaie la fonction du
troisième degré 𝑓 (𝑥) = 𝑏 (𝑥 + 3) (𝑥 − 1) (𝑥 − 2). Il faut 𝑓 (0) = 6𝑏 = −12. Aussi, 𝑏 = −2
et, de là, 𝑦 = −2 (𝑥 + 3) (𝑥 − 1) (𝑥 − 2).
(c) On essaie ici un polynôme du troisième degré 𝑦 = 𝑐(𝑥 + 3) (𝑥 − 2)2, où 𝑥 = 2 est
une racine double. Alors 𝑓 (0) = 12𝑐 = 6. Aussi, 𝑐 = 1
2 . Cela conduit à la formule
𝑦 = 1
2 (𝑥 + 3) (𝑥 − 2)2.
5. (a) 𝑥 + 4 (b) 𝑥2 + 𝑥 + 1 (c) −3𝑥2 − 12𝑥
6. 𝑐4 + 3𝑐2 + 5 ⩾ 5 ≠ 0 quel que soit le nombre 𝑐 choisi, de sorte que la division a toujours
un reste.

30. 30 CORRIGÉS DES EXERCICES
7. Développez le membre de droite. (Remarquez que 𝑅(𝑥) → 𝑎/𝑐 lorsque 𝑥 → +∞.)
8. La division polynomiale donne comme résultat
(𝑥2 − 𝛾𝑥 + ÷ (𝑥 + 𝛽) = 𝑥 − (𝛽 + 𝛾)
𝑥2 + 𝛽𝑥 +
− (𝛽 + 𝛾) 𝑥 +
− (𝛽 + 𝛾) 𝑥 − 𝛽(𝛽 + 𝛾)
𝛽(𝛽 + 𝛾) ← le reste
et 𝐸 = 𝛼
𝑥 − (𝛽 + 𝛾) +
𝛽 (𝛽 + 𝛾)
𝑥 + 𝛽
= 𝛼𝑥 − 𝛼 (𝛽 + 𝛾) +
𝛼𝛽 (𝛽 + 𝛾)
𝑥 + 𝛽
.
4.8
1. Voir figure C4.8.1.
y
1
2
x
1 2
y = x−1/ 3
y = x−1/ 2
y = x−1
y = x−3
Figure C4.8.1
2.
√
2
√
2
≈ 1,6325269 et 𝜋𝜋 ≈ 36,4621596.
3. (a) 23 = 8, de sorte que 𝑥 = 3/2.
(b) 1/81 = 3−4, de sorte que 3𝑥 + 1 = −4 et, de là, 𝑥 = −5/3.
(c) 𝑥2 − 2𝑥 + 2 = 2, de sorte que 𝑥2 − 2𝑥 = 0 impliquant 𝑥 = 0 ou 𝑥 = 2.
4. (a) 35𝑡 9𝑡 = 35𝑡 (32)𝑡 = 35𝑡+2𝑡 = 37𝑡 et 27 = 33, d’où 7𝑡 = 3 ou 𝑡 = 3/7.
(b) 9𝑡 = (32)𝑡 = 32𝑡 et (27)1/5/3 = (33)1/5/3 = 33/5/3 = 3−2/5, d’où 2𝑡 = −2/5 ou
𝑡 = −1/5.
4.9
1. Le montant de l’épargne après 𝑡 années est 100 (1 + 12/100)𝑡
= 100 (1,12)𝑡 . On a le
tableau suivant.
𝑡 1 2 5 10 20 30 50
100 (1, 12)𝑡 112 125, 44 176, 23 310, 58 964, 63 2 995, 99 28 900, 21

31. Chapitre 4 / Les fonctions d’une variable 31
2. Les graphiques sont tracés à la figure C4.9.2. On a le tableau suivant.
𝑥 −3 −2 −1 0 1 2 3
2𝑥 1/8 1/4 1/2 1 2 4 8
2−𝑥 8 4 2 1 1/2 1/4 1/8
y
2
4
6
8
x
−3−2 −1 1 2 3
y = 2x
y = 2−x
Figure C4.9.2
y
0.5
x
−3 −2 −1 1 2 3
y =
1
√ 2π
e− 1
2 x2
Figure C4.9.3
3. Le graphique est tracé à la figure C4.9.3. On a le tableau suivant.
𝑥 −2 −1 0 1 2
𝑦 = 1
√
2𝜋
𝑒− 1
2 𝑥2
0, 05 0, 24 0, 40 0, 24 0, 05
4. (b) et (d) ne sont pas des fonctions exponentielles. (Pour (f), noter que 𝑦 = (1/2)𝑥.)
5. (a) 16 (1,19)5 ≈ 38,18 (b) 4,40 (1,19)10 ≈ 25,06 (c) 250 000 (1,19)4 ≈ 501 335
6. On pense à une fonction de la forme 𝑦 = 𝐴𝑏𝑥, avec 𝑏 0. Alors, dans la figure 4.9.4,
puisque la courbe passe par les points de coordonnées (𝑥, 𝑦) = (0, 2) et (𝑥, 𝑦) = (2, 8),
on a 2 = 𝐴𝑏0 ou 𝐴 = 2 et 8 = 2𝑏2, de sorte que 𝑏 = 2. De là, 𝑦 = 2 × 2𝑥. Dans
la figure 4.9.5, 2
3 = 𝐴𝑏−1 et 6 = 𝐴𝑏. Il suit 𝐴 = 2 et 𝑏 = 3, de sorte que 𝑦 = 2 × 3𝑥.
Dans la figure 4.9.6, 4 = 𝐴𝑏0 et 1/4 = 𝐴𝑏4. Il suit 𝐴 = 4 et 𝑏4 = 1/16, de sorte que
𝑏 = 1/2. D’où 𝑦 = 4 (1/2)𝑥.
4.10
1. (a) ln 9 = ln 32 = 2 ln 3 (b) 1
2 ln 3 (c) ln
5
√
32 = ln 32/5 = 2
5 ln 3
(d) ln(1/81) = ln 3−4 = −4 ln 3
2. (a) ln 3𝑥 = 𝑥 ln 3 = ln 8, de sorte que 𝑥 = ln 8/ln 3.
(b) 𝑥 = 𝑒3
(c) 𝑥2 − 4𝑥 + 5 = 1 de sorte que (𝑥 − 2)2 = 0. D’où 𝑥 = 2.
(d) 𝑥 (𝑥 − 2) = 1 ou 𝑥2 − 2𝑥 − 1 = 0, de sorte que 𝑥 = 1 ±
√
2.
(e) 𝑥 = 0 ou ln(𝑥 + 3) = 0, de sorte que 𝑥 = 0 ou 𝑥 = −2.
(f)
√
𝑥 − 5 = 1 de sorte que 𝑥 = 36.

32. 32 CORRIGÉS DES EXERCICES
3. (a) 3𝑥4𝑥+2 = 8 quand 3𝑥4𝑥42 = 8 ou (12)𝑥42 = 8 de sorte que 12𝑥 = 1/2. Alors
𝑥 ln 12 = ln 1 − ln 2 = − ln 2 et, de là, 𝑥 = − ln 2/ln 12.
(b) Comme ln 𝑥2 = 2 ln 𝑥, l’équation se ramène à 7 ln 𝑥 = 6, de sorte que ln 𝑥 = 6/7 et
donc 𝑥 = 𝑒6/7.
(c) Une méthode possible est d’écrire l’équation sous la forme 4𝑥 (1 − 4−1) = 3𝑥 (3 − 1)
ou 4𝑥 × (3/4) = 3𝑥 × 2, ce qui fait (4/3)𝑥 = 8/3, impliquant 𝑥 = ln(8/3)/ln(4/3). Sinon,
on peut diviser les deux membres par 3𝑥 pour obtenir (4/3)𝑥 (1 − 1/4) = 3 − 1 = 2,
de sorte que (4/3)𝑥 = 8/3 comme précédemment. Pour les énoncés (d) à (f), utilisez la
définition 𝑎log𝑎 𝑥 = 𝑥.
(d) log2 𝑥 = 2 implique 2log2 𝑥 = 22 ou 𝑥 = 4.
(e) log𝑥 𝑒2 = 2 implique 𝑥log𝑥 𝑒2
= 𝑥2 ou 𝑒2 = 𝑥2. De là 𝑥 = 𝑒.
(f) log3 𝑥 = −3 implique 3log3 𝑥 = 3−3 ou 𝑥 = 1/27.
4. L’équation 𝐴𝑒𝑟𝑡 = 𝐵𝑒𝑠𝑡 implique directement 𝑒𝑟𝑡 /𝑒𝑠𝑡 = 𝐵/𝐴, d’où 𝑒(𝑟−𝑠) 𝑡 = 𝐵/𝐴. En
appliquant la fonction ln à chaque membre, on obtient (𝑟 − 𝑠) 𝑡 = ln(𝐵/𝐴), d’où
𝑡 =
1
𝑟 − 𝑠
ln
𝐵
𝐴
.
Autrement, on pouvait appliquer ln aux deux membres de l’équation originale,
ln 𝐴 + 𝑟𝑡 = ln 𝐵 + 𝑠𝑡, puis résoudre par rapport à 𝑡.
5. Soit 𝑡 le nombre d’années après 1990. Dans l’hypothèse d’une croissance expo-
nentielle continue, pour que le PIB des deux nations soit le même, il faut que
1,2 × 1012 × 𝑒0,09𝑡 = 5,6 × 1012 × 𝑒0,02𝑡 . Avec la réponse de l’exercice 4, on obtient
𝑡 =
1
0,09 − 0,02
ln
5,6 × 1012
1,2 × 1012
=
1
0,07
ln
14
3
≈ 22.
Les deux pays auraient donc dû avoir le même PIB environ 22 ans après 1990, soit en
2012.
6. On utilise les règles de calcul de la fonction ln 𝑥.
(a) Faux. (Posez 𝐴 = 𝑒.) (b) 2 ln
√
𝐵 = 2 ln 𝐵1/2 = 2 (1/2) ln 𝐵 = ln 𝐵
(c) ln 𝐴10 − ln 𝐴4 = 10 ln 𝐴 − 4 ln 𝐴 = 6 ln 𝐴 = 3 × 2 ln 𝐴 = 3 ln 𝐴2
(d) Faux. (Posez 𝐴 = 𝐵 = 𝐶 = 1.) (e) Correct suite à la règle (4.10.2)(b).
(f) Correct. (Utilisez (4.10.2)(b) deux fois.) (g) Faux. (Si 𝐴 = 𝑒 et 𝑝 = 2, l’égalité
devient 0 = ln 2.) (h) Correct suite à la règle (c). (i) Faux. (Prenez 𝐴=2, 𝐵=𝐶 =1.)
7. (a) exp
ln(𝑥)
− ln
exp(𝑥)
= 𝑒ln 𝑥 − ln 𝑒𝑥 = 𝑥 − 𝑥 = 0
(b) ln
𝑥4 exp(−𝑥)
= 4 ln 𝑥 − 𝑥 (c) 𝑥2/𝑦2
8. Le temps de doublement 𝑡∗ est déterminé par (1,0072)𝑡∗
= 2. À l’aide d’une calculatrice,
on trouve 𝑡∗ ≈ 96,6.
9. 𝑃(𝑡) = 1,22 × 1,034𝑡 . Le temps de doublement 𝑡∗ est donné par l’équation (1,034)𝑡∗
= 2
dont la solution est 𝑡∗ ≈ 20,7 (années).

33. Chapitre 4 / Les fonctions d’une variable 33
10. On trouve (1,035)𝑡 = 3,91 × 105/5,1 ≈ 76 666,67 et, à l’aide d’une calculatrice, 𝑡 ≈ 327.
En l’an 1969 + 327 = 2 296, chaque Zimbabwéen n’aura que 1 m2 d’espace en moyenne
pour se mouvoir.
11. Si le temps initial est 𝑡, le temps de doublement 𝑡∗ est donné par 𝐴𝑎𝑡+𝑡∗
= 2𝐴𝑎𝑡 . Cette
équation implique 𝐴𝑎𝑡 𝑎𝑡∗
= 2𝐴𝑎𝑡 , de sorte que 𝑎𝑡∗
= 2, indépendamment de 𝑡.
Exercices récapitulatifs du chapitre 4
1. (a) 𝑓 (0) = 3, 𝑓 (−1) = 30, 𝑓 (1/3) = 2, 𝑓 (
3
√
2) = 3 − 27 (21/3)3 = 3 − 27 × 2 = −51.
(b) 𝑓 (𝑥) + 𝑓 (−𝑥) = 3 − 27𝑥3 + 3 − 27 (−𝑥)3 = 3 − 27𝑥3 + 3 + 27𝑥3 = 6.
2. (a) 𝐹(0) = 1, 𝐹(−2) = 0, 𝐹(2) = 2 et 𝐹(3) = 25/13.
(b) 𝐹(𝑥) = 1 +
4
𝑥 + 4/𝑥
tend vers 1 lorsque 𝑥 devient grand positif ou négatif.
(c) Voir figure C4.R.2.
y
1
2
x
−4 −3 −2 −1 1 2 3 4
F(x) = 1 + 4x
x 2 +4
Figure C4.R.2
3. (a) 𝑓 (𝑥) ⩽ 𝑔(𝑥) quand −2 ⩽ 𝑥 ⩽ 3. (b) 𝑓 (𝑥) ⩽ 0 quand −1 ⩽ 𝑥 ⩽ 3.
(c) 𝑔(𝑥) ⩾ 0 quand 𝑥 ⩽ 3.
4. (a) 𝑥2 ⩾ 1, c’est-à-dire 𝑥 ⩾ 1 ou 𝑥 ⩽ −1.
(b) La racine carrée n’est définie que si 𝑥 ⩾ 4, mais comme 𝑥 = 4 rend le dénominateur
nul, il faut exiger 𝑥 4.
(c) Il faut que (𝑥 − 3) (5 − 𝑥) ⩾ 0, c’est-à-dire 3 ⩽ 𝑥 ⩽ 5 (faites un tableau de signes).
5. (a) 𝐶(0) = 100, 𝐶(100) = 24 100 et 𝐶(101) − 𝐶(100) = 24 542 − 24 100 = 442.
(b) 𝐶(𝑥 + 1) − 𝐶(𝑥) = 4𝑥 + 42 est le coût additionnel dû à la production d’une unité
supplémentaire.
6. (a) Pente −4. (b) Pente −3/4.
(c) La résolution en 𝑦 donne 𝑦 = 𝑏 − (𝑏/𝑎) 𝑥, de sorte que la pente vaut −𝑏/𝑎.
7. (a) La formule de l’équation d’une droite à l’aide d’un point et de sa pente donne
𝑦 − 3 = −3 (𝑥 + 2) ou 𝑦 = −3𝑥 − 3.
(b) La formule de l’équation d’une droite à l’aide de deux points donne
𝑦 − 5 =
7 − 5
2 − (−3)
(𝑥 − (−3)) ou 𝑦 = 2𝑥/5 + 31/5.

34. 34 CORRIGÉS DES EXERCICES
(c) La formule de l’équation d’une droite à l’aide de deux points donne
𝑦 − 𝑏 =
3𝑏 − 𝑏
2𝑎 − 𝑎
(𝑥 − 𝑎) ou 𝑦 = (2𝑏/𝑎) 𝑥 − 𝑏.
8. 𝑓 (2) = 3 et 𝑓 (−1) = −3 entraînent 2𝑎 + 𝑏 = 3 et −𝑎 + 𝑏 = −3, de sorte que 𝑎 = 2, 𝑏 = −1.
De là, 𝑓 (𝑥) = 2𝑥 − 1 et 𝑓 (−3) = −7. (Ou par la formule (4.4.2).)
9. Le graphique est tracé à la figure C4.R.9.
𝑥 −5 −4 −3 −2 −1 0 1
𝑦 = 𝑥2𝑒𝑥 0, 17 0, 29 0, 45 0, 54 0, 37 0 2, 7
y
1
2
3
x
−5 −4 −3 −2 −1 1 2
Figure C4.R.9
10. (1, −3) appartient au graphique si 𝑎 + 𝑏 + 𝑐 = −3, (0, −6) appartient au graphique si
𝑐 = −6 et (3, 15) appartient au graphique si 9𝑎 + 3𝑏 + 𝑐 = 15. Par conséquent, 𝑎 = 2,
𝑏 = 1 et 𝑐 = −6.
11. (a) 𝜋 = 1 000 − 1
3 𝑄
𝑄 − 800 + 1
5 𝑄
𝑄 − 100𝑄 = 100𝑄 − 8
15 𝑄2. Ici, 𝑄 = 1 500/16,
c’est-à-dire 𝑄 = 93,75, rend 𝜋 maximal.
(b) ˆ
𝜋 = 100𝑄 − 8
15 𝑄2 − 10𝑄 = 90𝑄 − 8
15 𝑄2. Donc ˆ
𝑄 = 1 350/16 = 84,375 rend ˆ
𝜋
maximal.
12. Le nouveau profit est donné par 𝜋𝜏 = 100𝑄 − 5
2 𝑄2 − 𝜏𝑄, qui atteint son maximum en
𝑄𝜏 = 1
5 (100 − 𝜏).
13. (a) La fonction de profit est 𝜋(𝑥) = 100𝑥 − 20𝑥 − 0,25𝑥2 = 80𝑥 − 0,25𝑥2, maximal en
𝑥∗ = 160.
(b) La fonction de profit est 𝜋𝜏 (𝑥) = 80𝑥 − 0,25𝑥2 − 10𝑥, maximal en 𝑥∗ = 140.
(c) La fonction de profit est 𝜋𝜏 (𝑥) = (𝑝 −𝜏−𝛼) 𝑥 − 𝛽𝑥2, maximal en 𝑥∗ = (𝑝 −𝛼−𝜏)/2𝛽.
14. (a) 𝑝(𝑥) = 𝑥 (𝑥2 + 𝑥 − 12) = 𝑥 (𝑥 − 3) (𝑥 + 4), car 𝑥2 + 𝑥 − 12 = 0 pour 𝑥 = 3 et 𝑥 = −4.
(b) ±1, ±2, ±4, ±8 sont les seules racines entières possibles. Par essai et erreur, on trouve
𝑞(2) = 𝑞(−4) = 0, de sorte que 2 (𝑥 − 2) (𝑥 + 4) = 2𝑥2 + 4𝑥 − 16 est un facteur de 𝑞(𝑥).
La division polynomiale fournit le quotient 𝑞(𝑥) ÷ (2𝑥2 +4𝑥 −16) = 𝑥 −1/2. Finalement,
𝑞(𝑥) = 2 (𝑥 − 2) (𝑥 + 4) (𝑥 − 1/2).

35. Chapitre 4 / Les fonctions d’une variable 35
15. (a) 𝑥3 − 𝑥 − 1 n’est pas nul en 𝑥 = 1, de sorte que la division laisse un reste.
(b) 2𝑥3 − 𝑥 − 1 est nul en 𝑥 = 1, de sorte que la division ne laisse pas de reste.
(c) 𝑥3 − 𝑎𝑥2 + 𝑏𝑥 − 𝑎𝑏 est nul en 𝑥 = 𝑎, de sorte que la division ne laisse pas de reste.
(d) 𝑥2𝑛 − 1 est nul en 𝑥 = −1, de sorte que la division ne laisse pas de reste.
16. On utilise (4.7.5). (a) 𝑝(2) = 8−2𝑘 = 0 pour 𝑘 = 4. (b) 𝑝(−2) = 4𝑘2 +2𝑘 −6 = 0 pour
𝑘 = −3/2 et 𝑘 = 1. (c) 𝑝(−2) = −26 + 𝑘 = 0 pour 𝑘 = 26. (d) 𝑝(1) = 𝑘2 − 3𝑘 − 4 = 0
pour 𝑘 = −1 et 𝑘 = 4.
17. Un calcul direct montre que 𝑝(2) = 1
4 23 − 22 − 11
4 2 + 15
2 = 2 − 4 − 11
2 + 15
2 = 0. En
conséquence, 𝑥 − 2 est un facteur de 𝑝(𝑥). La division de 𝑝(𝑥) par ce facteur donne
𝑝(𝑥) ÷ (𝑥 − 2) = 1
4 (𝑥2 − 2𝑥 − 15) = 1
4 (𝑥 + 3) (𝑥 − 5). Les deux autres racines sont 𝑥 = −3
et 𝑥 = 5. (Autre possibilité : 𝑞(𝑥) a les mêmes racines que 4𝑝(𝑥) = 𝑥3 − 4𝑥2 − 11𝑥 + 30.
Les racines entières de ce polynôme ne peuvent être que ±1, ±2, ±3, ±5, ±10, ±15 et
±30. Il est fastidieux de chercher les racines de cette manière.)
18. (1 + 𝑝/100)15 = 2 donne 𝑝 = 100 (21/15 − 1) ≈ 4,7 comme taux moyen annuel.
19. (a) Soit 𝐹 = 𝑎𝐶 + 𝑏. Alors 32 = 𝑎 × 0 + 𝑏 et 212 = 𝑎 × 100 + 𝑏. D’où 𝑎 = 180/100 = 9/5
et 𝑏 = 32, de sorte que 𝐹 = 9𝐶/5 + 32.
(b) Si 𝑋 = 9𝑋/5 + 32, alors 𝑋 = −40.
20. (a) ln 𝑥 = ln 𝑒𝑎𝑡+𝑏 = 𝑎𝑡 + 𝑏, de sorte que 𝑡 = (ln 𝑥 − 𝑏)/𝑎.
(b) −𝑎𝑡 = ln(1/2) = ln 1 − ln 2 = − ln 2, d’où 𝑡 = (ln 2)/𝑎.
(c) 𝑒− 1
2 𝑡2
= 21/2𝜋1/22−3, de sorte que −1
2 𝑡2 = 1
2 ln 2 + 1
2 ln 𝜋 − 3 ln 2 = −5
2 ln 2 + 1
2 ln 𝜋,
puis 𝑡2 = 5 ln 2 − ln 𝜋 = ln(32/𝜋) et finalement 𝑡 = ±
q
ln 32/𝜋
.
21. Notez que, dans le graphique de la figure 4.R.2, on a 𝑦 = 𝑓 (𝑥) =
𝑎 + 𝑏/𝑥
1 + 𝑐/𝑥
lorsque 𝑥 ≠ 0,
de sorte que 𝑦 tend vers 𝑎 quand 𝑥 prend de grandes valeurs positives ou négatives. Le
graphique montre que 𝑎 0. La fonction est discontinue en 𝑥 = −𝑐 et −𝑐 0, d’où 𝑐 0.
On a 𝑓 (0) = 𝑏/𝑐 0, donc 𝑏 0.
22. Le graphique de la fonction du second degré 𝑔 de la figure 4.R.3 est une parabole dont le
creux pointe vers le haut, donc 𝑝 0. De plus, 𝑟 = 𝑔(0) 0. Enfin, 𝑔(𝑥) a un minimum
en 𝑥 = 𝑥∗ = −𝑞/2𝑝. Comme 𝑥∗ 0 et 𝑝 0, on conclut que 𝑞 0.
23. (a) C. (b) D. (c) E. (d) B. (e) A.
(f) F. La fonction 𝑦 = 2 − ( 1
2 )𝑥 convient.
24. (a) ln(𝑥/𝑒2) = ln 𝑥 − ln 𝑒2 = ln 𝑥 − 2 pour 𝑥 0.
(b) ln(𝑥𝑧/𝑦) = ln(𝑥𝑧) − ln 𝑦 = ln 𝑥 + ln 𝑧 − ln 𝑦 pour 𝑥, 𝑦, 𝑧 0.
(c) ln(𝑒3𝑥2) = ln 𝑒3 + ln 𝑥2 = 3 + 2 ln 𝑥 pour 𝑥 0. (En général, ln 𝑥2 = 2 ln |𝑥|.)
(d) Quand 𝑥 0, notez que
1
2
ln 𝑥 −
3
2
ln(1/𝑥) − ln(𝑥 + 1) =
1
2
ln 𝑥 −
3
2
(− ln 𝑥) − ln(𝑥 + 1) = 2 ln 𝑥 − ln(𝑥 + 1)
= ln 𝑥2
− ln(𝑥 + 1) = ln[𝑥2
/(𝑥 + 1)].

36. 36 CORRIGÉS DES EXERCICES
Chapitre 5 / Les propriétés des fonctions
5.1
1. (a) 𝑦 = 𝑥2 + 1 a comme graphique celui de 𝑦 = 𝑥2 translaté vers le haut de 1 unité. Voir
figure C5.1.1a.
(b) 𝑦 = (𝑥 + 3)2 a comme graphique celui de 𝑦 = 𝑥2 déplacé de 3 unités vers la gauche.
Voir figure C5.1.1b.
(c) 𝑦 = 3 − (𝑥 + 1)2 a comme graphique celui de 𝑦 = 𝑥2 renversé vers le bas, avec le
sommet (0, 0) déplacé en (−1, 3). Voir figure C5.1.1c.
y
x
1
1
Figure C5.1.1a
y
x
− 1
1
Figure C5.1.1b
y
x
− 1
1
Figure C5.1.1c
2. (a) Le graphique de 𝑦 = 𝑓 (𝑥) est translaté de 2 unités vers la droite. Voir figure C5.1.2a.
(b) Le graphique de 𝑦 = 𝑓 (𝑥) est translaté vers le bas de 2 unités. Voir figure C5.1.2b.
(c) Le graphique de 𝑦 = 𝑓 (𝑥) a subi une réflexion par rapport à l’axe 𝑂𝑦.
Voir figure C5.1.2c.
y
x
1
1
Figure C5.1.2a
y
x
1
1
Figure C5.1.2b
y
x
1
1
Figure C5.1.2c
3. La condition d’équilibre est 106−𝑃 = 10+2𝑃 et donc 𝑃 = 32. La quantité correspondante
est 𝑄 = 106 − 32 = 74. Voir figure C5.1.3.
4. On déplace 𝑦 = |𝑥| de 2 unités vers la gauche. Ensuite, on en prend l’image par une
réflexion par rapport à l’axe 𝑂𝑥 et, enfin, on translate le graphique de 2 unités vers le
haut. Voir figure C5.1.4.
5. On trace le graphique de 𝑦 = 1/𝑥2. On le translate de 2 unités vers la gauche. Puis on en
prend l’image symétrique par rapport à l’axe 𝑂𝑥 et, enfin, on le monte de 2 unités vers le
haut. C’est la figure C5.1.5.

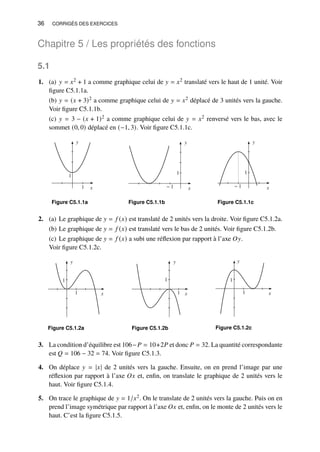
37. Chapitre 5 / Les propriétés des fonctions 37
P
Q, D, D, S
˜
32
74
P = 100 − D
P = 106 − D
P = S − 5
1
2
˜
Figure C5.1.3
y
x
1
−1
Figure C5.1.4
y
x
1
−2
Figure C5.1.5
6. 𝑓 (𝑦∗ −𝑑) = 𝑓 (𝑦∗) −𝑐 donne 𝐴(𝑦∗ −𝑑) + 𝐵(𝑦∗ −𝑑)2 = 𝐴𝑦∗ + 𝐵(𝑦∗)2 −𝑐, qui se développe
en 𝐴𝑦∗ − 𝐴𝑑 +𝐵(𝑦∗)2 −2𝐵 d𝑦∗ +𝐵𝑑2 = 𝐴𝑦∗ +𝐵(𝑦∗)2 −𝑐. D’où 𝑦∗ = [𝐵𝑑2 − 𝐴𝑑 +𝑐]/2𝐵𝑑.
5.2
1. Voir figure C5.2.1.
y
x
1
4 x2
1/x
Figure C5.2.1
2. Voir figures C5.2.2a à C5.2.2c.
y
x
Figure C5.2.2a
y
x
Figure C5.2.2b
y
x
Figure C5.2.2c
3. ( 𝑓 + 𝑔) (𝑥) = 3𝑥, ( 𝑓 − 𝑔) (𝑥) = 3𝑥 − 2𝑥3, ( 𝑓 𝑔) (𝑥) = 3𝑥4 − 𝑥6, ( 𝑓 /𝑔) (𝑥) = 3/𝑥2 − 1,
𝑓 (𝑔(1)) = 𝑓 (1) = 2 et 𝑔( 𝑓 (1)) = 𝑔(2) = 8.

38. 38 CORRIGÉS DES EXERCICES
4. Si 𝑓 (𝑥) = 3𝑥 + 7, alors 𝑓 ( 𝑓 (𝑥)) = 𝑓 (3𝑥 + 7) = 3 (3𝑥 + 7) + 7 = 9𝑥 + 28. 𝑓 ( 𝑓 (𝑥∗)) = 100
exige 9𝑥∗ + 28 = 100, de sorte que 𝑥∗ = 8.
5. ln(ln 𝑒) = ln 1 = 0, alors que (ln 𝑒)2 = 12 = 1.
5.3
1. 𝑃 = 1
3 (64 − 10𝐷)
2. 𝑃 = (157,8/𝐷)10/3
3. (a) Le domaine de définition et l’ensemble image sont R. La réciproque est 𝑥 = −𝑦/3.
(b) Le domaine de définition et l’ensemble image sont R{0}. La réciproque est 𝑥 = 1/𝑦.
(c) Le domaine de définition et l’ensemble image sont R. La réciproque est 𝑥 = 𝑦1/3.
(d) Le domaine de définition est [4, +∞[. L’ensemble image est [0, +∞[. La réciproque
est 𝑥 = (𝑦2 + 2)2.
4. (a) Comme tous les nombres de la deuxième ligne du tableau sont différents, 𝑓 admet
une fonction réciproque qui envoie chaque nombre de la deuxième ligne sur son corres-
pondant dans la première ligne. Le domaine de définition de 𝑓 −1 est {−4, −2, 0, 2, 4, 6, 8}
et 𝑓 −1(2) = −1.
(b) Comme 𝑓 (𝑥) augmente de 2 unités à chaque accroissement unitaire de 𝑥, 𝑓 (𝑥) est de
la forme 2𝑥 + 𝑎 pour une constante convenable 𝑎. Or, 𝑓 (0) = 4. Donc 𝑓 (𝑥) = 2𝑥 + 4. Si
𝑦 = 2𝑥 + 4, alors 𝑥 = (𝑦 − 4)/2 et la formule de 𝑓 −1 est 𝑓 −1(𝑥) = 1
2 𝑥 − 2.
5. 𝑓 (𝑥) = 𝑥2 n’est pas injective sur ] − ∞, +∞[ et n’a donc pas de réciproque. Sur [0, +∞[,
la fonction 𝑓 est strictement croissante et, de ce fait, admet une réciproque 𝑓 −1(𝑥) =
√
𝑥.
6. (a) 𝑓 (𝑥) = 𝑥/2 et 𝑔(𝑥) = 2𝑥 sont des fonctions réciproques.
(b) 𝑓 (𝑥) = 3𝑥 − 2 et 𝑔(𝑥) = 1
3 (𝑥 + 2) sont des fonctions réciproques.
(c) 𝐶 = 5
9 (𝐹 − 32) et 𝐹 = 9
5𝐶 + 32 sont des fonctions réciproques.
7. 𝑓 −1(𝑄) détermine le coût de 𝑄 kilos de carottes.
8. (a) Voir figure C5.3.8a.
(b) Voir figure C5.3.8b. Les triangles 𝑂𝐵𝐴 et 𝑂𝐵𝐶 sont isométriques. Le point milieu
entre 𝐴 et 𝐶 est le point 𝐵 de coordonnées ( 1
2 (𝑎 + 𝑏), 1
2 (𝑎 + 𝑏)).
9. (a) (𝑥3 − 1)1/3 = 𝑦 ⇔ 𝑥3 − 1 = 𝑦3 ⇔ 𝑥 = (𝑦3 + 1)1/3. Si 𝑥 désigne la variable
indépendante, 𝑓 −1(𝑥) = (𝑥3 + 1)1/3. R est le domaine de définition et l’ensemble image
des deux fonctions 𝑓 et 𝑓 −1.
(b) Le domaine de définition est l’ensemble des réels à l’exception de 𝑥 = 2 et, dans ce
cas,
𝑥 + 1
𝑥 − 2
= 𝑦 ⇔ 𝑥 + 1 = 𝑦 (𝑥 − 2) (1 − 𝑦) 𝑥 = −2𝑦 − 1 ⇔ 𝑥 =
−2𝑦 − 1
1 − 𝑦
=
2𝑦 + 1
𝑦 − 1
.
Avec 𝑥 comme variable indépendante, 𝑓 −1(𝑥) = (2𝑥+1)/(𝑥−1). Le domaine de définition
de la réciproque est l’ensemble des réels, à l’exception de 𝑥 = 1.

39. Chapitre 5 / Les propriétés des fonctions 39
(c) Ici, 𝑦 = (1 − 𝑥3
)1/5
+ 2 ⇔ 𝑦 − 2 = (1 − 𝑥3
)1/5
⇔ (𝑦 − 2)5
= 1 − 𝑥3
⇔ 𝑥3
= 1 − (𝑦 − 2)5
⇔ 𝑥 = [1 − (𝑦 − 2)5
]1/3
.
Avec 𝑥 comme variable indépendante,
𝑓 −1
(𝑥) = [1 − (𝑥 − 2)5
]1/3
.
R est le domaine de définition et l’ensemble image des deux fonctions 𝑓 et 𝑓 −1.
y
x
(3, 1)
(5, 3)
(1, 3)
(3, 5)
y = x
Figure C5.3.8a
y
x
C = (b, a)
A = (a, b)
B
y = x
D
E
O
Figure C5.3.8b
10. (a) Le domaine de définition est R et l’ensemble image, ]0, +∞[ de sorte que la réciproque
est définie sur ]0, +∞[. De 𝑦 = 𝑒𝑥+4, on a ln 𝑦 = 𝑥 + 4 et, de là, 𝑥 = ln 𝑦 − 4, 𝑦 0.
(b) L’ensemble image est R, qui est le domaine de définition de la réciproque.
De 𝑦 = ln 𝑥 − 4, on tire ln 𝑥 = 𝑦 + 4, et ainsi 𝑥 = 𝑒𝑦+4.
(c) Le domaine de définition est R. La fonction y est strictement croissante, avec
𝑦 → ln 2 lorsque 𝑥 → −∞ et 𝑦 → ∞ lorsque 𝑥 → +∞. L’ensemble image est donc
] ln 2, +∞[. De 𝑦 = ln 2 + 𝑒𝑥−3
, on tire 𝑒𝑦 = 2 + 𝑒𝑥−3, puis 𝑒𝑥−3 = 𝑒𝑦 − 2 et enfin
𝑥 = 3 + ln(𝑒𝑦 − 2) pour 𝑦 ln 2.
11. Il faut résoudre
𝑥 =
1
2
(𝑒𝑦
− 𝑒−𝑦
)
par rapport à 𝑦. On multiplie l’équation par 𝑒𝑦, ce qui donne
1
2
𝑒2𝑦
−
1
2
= 𝑥𝑒𝑦
ou 𝑒2𝑦 − 2𝑥𝑒𝑦 − 1 = 0. En posant 𝑒𝑦 = 𝑧, on a 𝑧2 − 2𝑥𝑧 − 1 = 0, dont la solution est
𝑧 = 𝑥 ±
√
𝑥2 + 1. Avec le signe moins, 𝑧 est négatif, ce qui n’est pas compatible avec
𝑧 = 𝑒𝑦. On retient donc
𝑧 = 𝑒𝑦
= 𝑥 +
p
𝑥2 + 1.
La fonction réciproque est donc
𝑦 = ln 𝑥 +
p
𝑥2 + 1
.

40. 40 CORRIGÉS DES EXERCICES
5.4
1. (a) La courbe coupe les axes 𝑂𝑦 et 𝑂𝑥 aux points de coordonnées (0, ±
√
3) et (±
√
6, 0)
respectivement. Elle est entièrement incluse dans le rectangle de sommets (±
√
6, ±
√
3).
En outre, elle est symétrique par rapport aux deux axes, puisque les coordonnées de ses
points sont de la forme (±
√
𝜉, ±
√
𝜂), où (𝜉, 𝜂) est un couple quelconque de nombres
positifs solution de l’équation 𝜉2 + 2𝜂2 = 6. Si on pose 𝑥 = 𝑦 , on obtient les quatre
points de coordonnées (±
√
2, ±
√
2) sur la courbe. D’autres points peuvent être obtenus
en choisissant 𝑥 quelconque compris entre −6 et 6 et en calculant la valeur de 𝑦 corres-
pondante. Voir figure C5.4.1a(5).
(b) La courbe coupe l’axe 𝑂𝑦 en (0, ±1). Elle n’a pas de points d’ordonnées telles que
𝑦2 1. Elle est symétrique par rapport aux axes. Elle se compose de deux parties :
l’une inférieure 𝑦 = −1; l’autre supérieure 𝑦 = 1. Si on pose 𝑥2 = 1, alors 𝑥2 = 9
et on a les points de coordonnées (±1, ±
√
2) et (±3, ±
√
10). Voir figure C5.4.1b(6).
x
y
−2
−1
1
2
−3 −2 −1 1 2 3
Figure C5.4.1a
y
− 2
− 1
1
2
x
− 3 − 2 − 1 1 2 3
Figure C5.4.1b
x
y
25
25
Figure C5.4.2
2. Il faut 𝑥 ⩾ 0 et 𝑦 ⩾ 0. Si le point de coordonnées (𝑎, 𝑏) appartient au graphique, celui de
coordonnées (𝑏, 𝑎) aussi. Le graphique est donc symétrique par rapport à la droite 𝑦 = 𝑥
et comprend les points (25, 0), (0, 25) et (25/4, 25/4). Pour trouver facilement les points
sur le graphique, il suffit de choisir des nombres positifs 𝑢 et 𝑣 tels que 𝑢 + 𝑣 = 5 et de
poser 𝑥 = 𝑢2 et 𝑦 = 𝑣2. Voir figure C5.4.2.
3. 𝐹(100 000) = 4 070. Le graphique est la ligne en gras tracée à la figure C5.4.3.
5.5
1. (a)
p
(2 − 1)2 + (4 − 3)2 =
√
2 (b)
√
5 (c) 1
2
√
205 (d)
√
𝑥2 + 9
(e) 2|𝑎| (f) 2
√
2
2. (5 − 2)2 + (𝑦 − 4)2 = 13 ou 𝑦2 − 8𝑦 + 12 = 0, dont les solutions sont 𝑦 = 2 et 𝑦 = 6. Une
explication géométrique est que le cercle centré en (2, 4) et de rayon
√
13 coupe la droite
𝑥 = 5 en deux points. Voir figure C5.5.2.
3. (a) 5,362 (b)
p
(2𝜋)2 + (2𝜋 − 1)2 =
√
8𝜋2 − 4𝜋 + 1 ≈ 8,209
(5) La courbe est une ellipse. Voir la section 5.5.
(6) La courbe est une hyperbole. Voir la section 5.5.

41. Chapitre 5 / Les propriétés des fonctions 41
Y
RN
4070
7500 100 000
Figure C5.4.3
y
x
5
(2, 4)
2
2
Figure C5.5.2
4. (a) (𝑥 − 2)2 + (𝑦 − 3)2 = 16
(b) Puisque le cercle est centré en (2, 5), son équation est (𝑥 −2)2 + (𝑦 −5)2 = 𝑟2. Puisque
le point de coordonnées (−1, 3) appartient au cercle, (−1−2)2 + (3−5)2 = 𝑟2 ou 𝑟2 = 13.
5. (a) Compléter les carrés mène à (𝑥 + 5)2 + (𝑦 − 3)2 = 4, de sorte que le cercle est de
rayon 2 centré en (−5, 3).
(b) (𝑥 + 3)2 + (𝑦 − 4)2 = 12, centre en (−3, 4) et rayon
√
12 = 2
√
3.
6. La condition revient à
p
(𝑥 + 2)2 + 𝑦2 = 2
p
(𝑥 − 4)2 + 𝑦2, qui se réduit à (𝑥−6)2 +𝑦2 = 42.
7. La formule peut s’écrire 𝑐𝑥𝑦 − 𝑎𝑥 + d𝑦 − 𝑏 = 0. En la comparant avec (5.5.5), 𝐴 = 𝐶 = 0
et 𝐵 = 𝑐, de sorte que 4𝐴𝐶 𝐵2 se réduit à 0 𝑐2 ou 𝑐 ≠ 0. C’est justement la condition
imposée à l’exemple 4.7.7.
8. La méthode qui consiste à compléter le carré de l’exercice 5 montre que
𝑥2
+ 𝑦2
+ 𝐴𝑥 + 𝐵𝑦 + 𝐶 = 0 ⇔ 𝑥2
+ 𝐴𝑥 + 𝑦2
+ 𝐵𝑦 + 𝐶 = 0
⇔ 𝑥2
+ 𝐴𝑥 +
1
2
𝐴
2
+ 𝑦2
+ 𝐵𝑦 +
1
2
𝐵
2
=
1
4
(𝐴2
+ 𝐵2
− 4𝐶)
⇔ 𝑥 +
1
2
𝐴
2
+ 𝑦 +
1
2
𝐵
2
=
1
4
(𝐴2
+ 𝐵2
− 4𝐶).
Sous la condition 𝐴2 + 𝐵2 4𝐶, la dernière équation est celle d’un cercle centré en
−1
2 𝐴, −1
2 𝐵
de rayon 1
2
√
𝐴2 + 𝐵2 − 4𝐶. Si 𝐴2 + 𝐵2 = 4𝐶, le graphique est réduit au point
−1
2 𝐴, −1
2 𝐵
. Pour 𝐴2 + 𝐵2 4𝐶, il n’y a pas de solution.
9. Une fois le carré complété pour 𝐷 = 𝐸 = 0, l’équation (5.5.5) est égale à
𝐴
𝑥 +
𝐵𝑦
2𝐴
2
+
1
4𝐴
(4𝐴𝐶 − 𝐵2
)𝑦2
+ 𝐹 = 0
avec 𝐴 0.
(i) Si 4𝐴𝐶 − 𝐵2 0, alors le graphique est : une ellipse si et seulement si 𝐹 0 (ou un
cercle dans le cas 4𝐴𝐶 − 𝐵2 = 4𝐴2); un seul point (−𝐵/2𝐴, 0) si et seulement si 𝐹 = 0;
l’ensemble vide si et seulement si 𝐹 0.

42. 42 CORRIGÉS DES EXERCICES
(ii) Si 4𝐴𝐶−𝐵2 = 0, alors le graphique est : deux droites parallèles 𝑥 = −𝐵𝑦/2𝐴±
p
−𝐹/𝐴
si et seulement si 𝐹 0; la droite 𝑥 = −𝐵𝑦/2𝐴 si et seulement si 𝐹 = 0; l’ensemble vide
si et seulement si 𝐹 0. (Il ne peut y avoir de parabole quand 𝐷 = 𝐸 = 0 dans (5.5.5).)
(iii) Si 4𝐴𝐶 − 𝐵2 0, alors le graphique est : une hyperbole si et seulement si 𝐹 ≠ 0; les
deux droites sécantes 𝑥 = (−𝐵 ±
√
𝐵2 − 4𝐴𝐶)𝑦/2𝐴 si et seulement si 𝐹 = 0.
5.6
1. Chaque fois, sauf pour (c), la règle définit une fonction, car elle associe à chaque élément
de l’ensemble de départ un et un seul élément de l’ensemble cible. Par exemple, en (d),
si le volume 𝑉 d’une sphère est donné, la formule 𝑉 = 4
3 𝜋𝑟3 (rappelée dans l’annexe)
implique que le rayon vaut 𝑟 = (3𝑉/4𝜋)1/3. Et la formule 𝑆 = 4𝜋𝑟2 fournit l’aire de la
surface. Par substitution de 𝑟 dans cette formule, on a
𝑆 = 4𝜋(3𝑉/4𝜋)2/3
= (36𝜋)1/3
𝑉3/2
qui exprime l’aire de la surface comme une fonction du volume. Seule (c) ne définit pas
une fonction. (Des rectangles d’aires égales peuvent avoir différents périmètres.)
2. La fonction (b) est injective et possède une réciproque : la règle qui associe sa mère à
chaque plus jeune enfant encore en vie aujourd’hui. (Même si le plus jeune enfant d’une
mère qui a plusieurs enfants n’aura pas été le même à différentes dates.) La fonction (d)
est injective et possède une réciproque : la règle qui au volume d’une sphère associe son
aire. La fonction (e) est injective et possède une réciproque : la règle qui envoie (𝑢, 𝑣) sur
(𝑢 − 3, 𝑣). La fonction (a) n’est pas injective en général et n’a donc pas de réciproque.
Exercices récapitulatifs du chapitre 5
1. Les translations à appliquer à 𝑦 = |𝑥| sont les mêmes que celles appliquées à 𝑦 = 𝑥2 à
l’exercice 5.1.1. Voir figures C5.R.1(a)-(c).
y
x
y = | x | + 1
Figure C5.R.1a
y
x
y = x + 3
Figure C5.R.1b
y
x
y = 3 – x + 1
Figure C5.R.1c
2. (a) ( 𝑓 +𝑔) (𝑥) = 𝑥2 −2 (b) ( 𝑓 −𝑔) (𝑥) = 2𝑥3 −𝑥2 −2 (c) ( 𝑓 𝑔) (𝑥) = 𝑥2 (1−𝑥) (𝑥3 −2)
(d) ( 𝑓 /𝑔) (𝑥) = (𝑥3−2)/𝑥2 (1−𝑥) (e) 𝑓 (𝑔(1)) = 𝑓 (0) = −2 (f) 𝑔( 𝑓 (1)) =𝑔(−1) =2
3. (a) La condition d’équilibre est 150 − 1
2 𝑃∗ = 20 + 2𝑃∗. On obtient donc 𝑃∗ = 52 et
𝑄∗ = 20 + 2𝑃∗ = 124.

43. Chapitre 5 / Les propriétés des fonctions 43
(b) 𝑆 = 20+2 ( b
𝑃 −2) = 16+2b
𝑃, de sorte que 𝑆 = 𝐷 quand 5b
𝑃/2 = 134. De là, b
𝑃 = 53,6,
b
𝑄 = 123,2.
(c) Avant la taxe, 𝑅∗ = 𝑃∗𝑄∗ = 6 448. Après la taxe,
b
𝑅 = ( b
𝑃 − 2) b
𝑄 = 51,6 × 123,2 = 6 357,12.
4. 𝑃 = (64 − 10𝐷)/3
5. 𝑃 = 24 − 1
5 𝐷
6. (a) 𝑥 = 50 − 1
2 𝑦 (b) 𝑥 = 5
p
𝑦/2 (c) 𝑥 = 1
3 [2 + ln(𝑦/5)], définie pour 𝑦 0
7. (a) La fonction 𝑓 est définie et strictement croissante quand 𝑒𝑥 2, c’est-à-dire
𝑥 ln 2. Son ensemble image est R, car 𝑓 (𝑥) → −∞ lorsque 𝑥 → ln 2+ et
𝑓 (𝑥) → +∞ lorsque 𝑥 → +∞. De 𝑦 = 3 + ln(𝑒𝑥 − 2), on tire ln(𝑒𝑥 − 2) = 𝑦 − 3 et donc
𝑒𝑥 −2 = 𝑒𝑦−3 ou 𝑒𝑥 = 2+𝑒𝑦−3 et finalement 𝑥 = ln(2+𝑒𝑦−3). Donc 𝑓 −1(𝑥) = ln(2+𝑒𝑥−3),
𝑥 ∈ R.
(b) Notez que 𝑓 est strictement croissante. De plus, 𝑒−𝜆𝑥 → +∞ lorsque 𝑥 → −∞ et
𝑒−𝜆𝑥 → 0 lorsque 𝑥 → +∞. Par conséquent, 𝑓 (𝑥) → 0 lorsque 𝑥 → −∞ et 𝑓 (𝑥) → 1
lorsque 𝑥 → +∞. L’ensemble image de 𝑓 , et donc le domaine de définition de 𝑓 −1, est
]0, 1[. De 𝑦 =
𝑎
𝑒−𝜆𝑥 + 𝑎
, on tire 𝑒−𝜆𝑥 + 𝑎 = 𝑎/𝑦, de sorte que 𝑒−𝜆𝑥 = 𝑎 (1/𝑦 − 1), ou
−𝜆𝑥 = ln 𝑎 + ln(1/𝑦 − 1). Ensuite, 𝑥 = −(1/𝜆) ln 𝑎 − (1/𝜆) ln(1/𝑦 − 1) et la formule de
la fonction réciproque est 𝑓 −1(𝑥) = −(1/𝜆) ln 𝑎 − (1/𝜆) ln(1/𝑥 − 1), avec 𝑥 ∈ ]0, 1[.
8. (a)
√
13 (b)
√
17 (c)
p
(2 − 3𝑎)2 = |2−3𝑎|. (Notez que 2−3𝑎 est la réponse correcte
seulement si 2 − 3𝑎 ⩾ 0, c’est-à-dire 𝑎 ⩽ 2/3. Testez en posant 𝑎 = 3.)
9. (a) (𝑥 − 2)2 + (𝑦 + 3)2 = 25 (b) (𝑥 + 2)2 + (𝑦 − 2)2 = 65
10. (𝑥−3)2+(𝑦−2)2 = (𝑥−5)2+(𝑦+4)2. Après simplification, 𝑥−3𝑦 = 7. Voir figure C5.R.10.
y
x
A = (3, 2)
B = (5, −4)
2
2
P
Figure C5.R.10
11. La fonction ne peut pas être injective, car au moins deux personnes sur les cinq auront le
même groupe sanguin.

44. 44 CORRIGÉS DES EXERCICES
Chapitre 6 / La dérivation
6.1
1. 𝑓 (3) = 2. La tangente passe par le point de coordonnées (0, 3), de sorte que sa pente est
égale à −1/3. D’où 𝑓 ′(3) = −1/3.
2. 𝑔(5) = 1, 𝑔′(5) = 1.
6.2
1. 𝑓 (5 + ℎ) − 𝑓 (5) = 4 (5 + ℎ)2 − 4 × 52 = 4 (25 + 10ℎ + ℎ2) − 100 = 40ℎ + 4ℎ2. Ainsi,
[ 𝑓 (5 + ℎ) − 𝑓 (5)]/ℎ = 40 + 4ℎ → 40 lorsque ℎ → 0. De là, 𝑓 ′(5) = 40. Cela concorde
avec (6.2.6) quand 𝑎 = 4 et 𝑏 = 𝑐 = 0.
2. (a) 𝑓 ′(𝑥) = 6𝑥 + 2
(b) 𝑓 ′(0) = 2, 𝑓 ′(−2) = −10, 𝑓 ′(3) = 20. L’équation de la tangente est 𝑦 = 2𝑥 − 1.
3. d𝐷(𝑃)/d𝑃 = −𝑏
4. 𝐶′(𝑥) = 2𝑞𝑥
5.
𝑓 (𝑥 + ℎ) − 𝑓 (𝑥)
ℎ
=
1/(𝑥 + ℎ) − 1/𝑥
ℎ
=
𝑥 − (𝑥 + ℎ)
ℎ𝑥 (𝑥 + ℎ)
=
−ℎ
ℎ𝑥 (𝑥 + ℎ)
=
−1
𝑥 (𝑥 + ℎ)
−→
ℎ→0
−
1
𝑥2
6. Pour les énoncés (a) à (c), nous appliquons la marche à suivre expliquée dans l’encadré
« Calcul de la dérivée ». Pour les énoncés (d) à (f), nous appliquons toujours cette
démarche, mais de façon plus concise.
(a) (i) 𝑓 (𝑎+ℎ) = 𝑓 (0+ℎ) = 3ℎ+2 ; (ii) 𝑓 (𝑎+ℎ)− 𝑓 (𝑎) = 𝑓 (ℎ)− 𝑓 (0) = 3ℎ+2−2 = 3ℎ ;
(iii)-(iv) [ 𝑓 (ℎ) − 𝑓 (0)]/ℎ = 3 ; (v) [ 𝑓 (ℎ) − 𝑓 (0)]/𝑖ℎ = 3 → 3 lorsque ℎ → 0, de sorte
que 𝑓 ′(0) = 3. La pente de la tangente au point de coordonnées (0, 2) est 3.
(b) (i) 𝑓 (𝑎 + ℎ) = 𝑓 (1 + ℎ) = (1 + ℎ)2 − 1 = 1 + 2ℎ + ℎ2 − 1 = 2ℎ + ℎ2 ;
(ii) 𝑓 (1 + ℎ) − 𝑓 (1) = 2ℎ + ℎ2 ; (iii)-(iv) [ 𝑓 (1 + ℎ) − 𝑓 (1)]/ℎ = 2 + ℎ ;
(v) [ 𝑓 (1 + ℎ) − 𝑓 (1)]/ℎ = 2 + ℎ → 2 lorsque ℎ → 0, de sorte que 𝑓 ′(1) = 2.
(c) (i) 𝑓 (3 + ℎ) = 2 + 3/(3 + ℎ) ; (ii) 𝑓 (3 + ℎ) − 𝑓 (3) = 2 + 3/(3 + ℎ) − 3 = −ℎ/(3 + ℎ) ;
(iii)-(iv) [ 𝑓 (3+ℎ)− 𝑓 (3)]/ℎ = −1/(3+ℎ) ; (v) [ 𝑓 (3+ℎ)− 𝑓 (3)]/ℎ = −1/(3+ℎ) → −1/3
lorsque ℎ → 0, de sorte que 𝑓 ′(3) = −1/3.
(d) [ 𝑓 (ℎ) − 𝑓 (0)]/ℎ = (ℎ3 − 2ℎ)/ℎ = ℎ2 − 2 → −2 lorsque ℎ → 0, de sorte que
𝑓 ′(0) = −2.
(e)
𝑓 (−1 + ℎ) − 𝑓 (−1)
ℎ
=
−1 + ℎ + 1/(−1 + ℎ) + 2
ℎ
, qui se simplifie en
ℎ2 − 1 + 1
ℎ(ℎ − 1)
=
ℎ
ℎ − 1
→ 0
lorsque ℎ → 0, de sorte que 𝑓 ′(0) = 0.

45. Chapitre 6 / La dérivation 45
(f) On a
𝑓 (1 + ℎ) − 𝑓 (1)
ℎ
=
(1 + ℎ)4 − 1
ℎ
=
ℎ4 + 4ℎ3 + 6ℎ2 + 4ℎ + 1 − 1
ℎ
= ℎ3
+ 4ℎ2
+ 6ℎ + 4 → 4 lorsque ℎ → 0,
de sorte que 𝑓 ′(1) = 4.
7. (a) 𝑓 (𝑥 + ℎ) − 𝑓 (𝑥) = 𝑎 (𝑥 + ℎ)2 + 𝑏 (𝑥 + ℎ) + 𝑐 − (𝑎𝑥2 + 𝑏𝑥 + 𝑐) = 2𝑎ℎ𝑥 + 𝑏ℎ + 𝑎ℎ2, donc
[ 𝑓 (𝑥 + ℎ) − 𝑓 (𝑥)]/ℎ = 2𝑎𝑥 + 𝑏 + 𝑎ℎ → 2𝑎𝑥 + 𝑏 lorsque ℎ → 0. D’où 𝑓 ′(𝑥) = 2𝑎𝑥 + 𝑏.
(b) 𝑓 ′(𝑥) = 0 pour 𝑥 = −𝑏/2𝑎. La tangente au point de maximum/minimum est parallèle
à l’axe 𝑂𝑥.
8. 𝑓 ′(𝑎) 0, 𝑓 ′(𝑏) = 0, 𝑓 ′(𝑐) 0, 𝑓 ′(𝑑) 0.
9. (a) En appliquant la formule (𝑎 − 𝑏) (𝑎 + 𝑏) = 𝑎2 − 𝑏2 avec 𝑎 =
√
𝑥 + ℎ et 𝑏 =
√
𝑥, on
obtient (
√
𝑥 + ℎ −
√
𝑥) (
√
𝑥 + ℎ +
√
𝑥) = (𝑥 + ℎ) − 𝑥 = ℎ.
(b) Par calcul direct,
𝑓 (𝑥 + ℎ) − 𝑓 (𝑥)
ℎ
=
(
p
𝑥 + ℎ −
p
𝑥) (
p
𝑥 + ℎ +
p
𝑥)
ℎ(
p
𝑥 + ℎ +
p
𝑥)
=
1
p
𝑥 + ℎ +
p
𝑥
(c) On utilise (b). Quand ℎ → 0,
𝑓 (𝑥 + ℎ) − 𝑓 (𝑥)
ℎ
=
1
√
𝑥 + ℎ +
√
𝑥
−→
ℎ→0
1
2
√
𝑥
=
1
2
𝑥−1/2
.
10. (a) 𝑓 ′(𝑥) = 3𝑎𝑥2 + 2𝑏𝑥 + 𝑐.
(b) Posez 𝑎 = 1 et 𝑏 = 𝑐 = 𝑑 = 0 pour avoir le résultat de l’exemple 6.2.2. Ensuite, posez
𝑎 = 0 pour avoir une expression du second degré comme à l’exercice 6.2.7(a).
11.
(𝑥 + ℎ)1/3 − 𝑥1/3
ℎ
=
1
(𝑥 + ℎ)2/3 + (𝑥 + ℎ)1/3𝑥1/3 + 𝑥2/3
→
1
3𝑥2/3
lorsque ℎ → 0 et
1
3𝑥2/3
=
1
3
𝑥−2/3
.
6.3
1. 𝑓 ′(𝑥) = 2𝑥 − 4, de sorte que 𝑓 (𝑥) est décroissante sur ] − ∞, 2], croissante sur [2, +∞[.
2. 𝑓 ′(𝑥) = −3𝑥2 + 8𝑥 − 1 = −3 (𝑥 − 𝑥0) (𝑥 − 𝑥1), où 𝑥0 = 1
3 (4 −
√
13) ≈ 0,13 et
𝑥1 = 1
3 (4 +
√
13) ≈ 2,54. Ensuite 𝑓 (𝑥) est décroissante sur ] − ∞, 𝑥0], croissante sur
[𝑥0, 𝑥1] et décroissante sur [𝑥1, +∞[.
3. L’expression entre crochets est la somme de deux carrés, donc n’est jamais négative, et
n’est nulle que si 𝑥1 + 1
2 𝑥2 et 𝑥2 sont tous deux nuls, ce qui n’arrive que pour 𝑥1 = 𝑥2 = 0.
L’expression entre crochets est donc toujours strictement positive si 𝑥2 ≠ 𝑥1, et 𝑥3
2 − 𝑥3
1
a donc le même signe que 𝑥2 − 𝑥1. Par conséquent, la fonction 𝑓 (𝑥) = 𝑥3 est strictement
croissante.
6.4
1. 𝐶′(100) = 203 et 𝐶′(𝑥) = 2𝑥 + 3.
2. Ici, 𝑐 est le coût marginal et aussi le coût additionnel (constant) de produire une unité de
plus, tandis que ¯
𝐶 est le coût fixe.

46. 46 CORRIGÉS DES EXERCICES
3. (a) 𝑆′(𝑌) = 𝑏 (b) 𝑆′(𝑌) = 0,1 + 0,0004𝑌
4. 𝑇′(𝑦) = 𝑡, le taux marginal d’imposition est donc constant.
5. L’interprétation de 𝑥′(0) = −3 est qu’au temps 𝑡 = 0, environ 3 barils de pétrole sont
extraits par minute.
6. (a) 𝐶′(𝑥) = 3𝑥2 − 180𝑥 + 7 500
(b) D’après (4.6.4), la fonction quadratique 𝐶′(𝑥) atteint un minimum en 𝑥 = 180/6 = 30.
7. (a) 𝜋′(𝑄) = 24 − 2𝑄 et 𝑄∗ = 12. (b) 𝑅′(𝑄) = 500 − 𝑄2
(c) 𝐶′(𝑄) = −3𝑄2 + 428,4𝑄 − 7 900
8. (a) 𝐶′(𝑥) = 2𝑎1𝑥 + 𝑏1 (b) 𝐶′(𝑥) = 3𝑎1𝑥2
6.5
1. (a) 3 (b) −1/2 (c) 133 = 2 197 (d) 40 (e) 1 (f) −3/4
2. (a) 0,6931 (b) 1,0986 (c) 0,4055 (En fait, d’après les résultats de l’exemple 7.12.2,
les valeurs précises de ces limites sont ln 2, ln 3 et ln(3/2), respectivement.)
3. (a) Voir (c).
(b) On a le tableau suivant, ou ∗ signifie « non défini ».
𝑥 0,9 0,99 0,999 1 1,001 1,01 1,1
𝑥2 + 7𝑥 − 8
𝑥 − 1
8,9 8,99 8,999 ∗ 9,001 9,01 9,1
(c) 𝑥2 + 7𝑥 − 8 = (𝑥 − 1) (𝑥 + 8), de sorte que (𝑥2 + 7𝑥 − 8)/(𝑥 − 1) = 𝑥 + 8 → 9 lorsque
𝑥 → 1.
4. (a) 5 (b) 1/5 (c) 1 (d) −2 (e) 3𝑥2 (f) ℎ2
5. (a)
1/3 − 2/3ℎ
ℎ − 2
=
3ℎ 1/3 − 2/3ℎ
3ℎ(ℎ − 2)
=
ℎ − 2
3ℎ(ℎ − 2)
=
1
3ℎ
→
1
6
lorsque ℎ → 2.
(b) Quand 𝑥 → 0, alors
(𝑥2 − 1)
𝑥2
= 1 −
1
𝑥2
→ −∞ lorsque 𝑥 → 0.
(c)
32𝑡 − 96
𝑡2 − 2𝑡 − 3
=
32 (𝑡 − 3)
(𝑡 − 3) (𝑡 + 1)
=
32
𝑡 + 1
→ 8, lorsque 𝑡 → 3 et
3
r
32𝑡 − 96
𝑡2 − 2𝑡 − 3
→
3
√
8 = 2 lorsque 𝑡 → 3.
(d)
√
ℎ + 3 −
√
3
ℎ
=
(
√
ℎ + 3 −
√
3) (
√
ℎ + 3 +
√
3)
ℎ(
√
ℎ + 3 +
√
3)
=
1
√
ℎ + 3 +
√
3
−→
ℎ→0
1
2
√
3
(e)
𝑡2 − 4
𝑡2 + 10𝑡 + 16
=
(𝑡 + 2) (𝑡 − 2)
(𝑡 + 2) (𝑡 + 8)
=
𝑡 − 2
𝑡 + 8
→ −
2
3
lorsque 𝑡 → −2.

47. Chapitre 6 / La dérivation 47
(f) On sait que 4 − 𝑥 = (2 +
√
𝑥) (2 −
√
𝑥). D’où lim
𝑥→4
2 −
√
𝑥
4 − 𝑥
= lim
𝑥→4
1
2 +
√
𝑥
=
1
4
.
6. (a)
𝑓 (𝑥) − 𝑓 (1)
𝑥 − 1
=
𝑥2 + 2𝑥 − 3
𝑥 − 1
=
(𝑥 − 1) (𝑥 + 3)
𝑥 − 1
= 𝑥 + 3 → 4 lorsque 𝑥 → 1.
(b)
𝑓 (𝑥) − 𝑓 (1)
𝑥 − 1
= 𝑥 + 3 → 5 lorsque 𝑥 → 2.
(c)
𝑓 (2 + ℎ) − 𝑓 (2)
ℎ
=
(2 + ℎ)2 + 2 (2 + ℎ) − 8
ℎ
=
ℎ2 + 6ℎ
ℎ
= ℎ + 6 → 6 lorsque ℎ → 0.
(d) On a
𝑓 (𝑥) − 𝑓 (𝑎)
𝑥 − 𝑎
=
𝑥2 + 2𝑥 − 𝑎2 − 2𝑎
𝑥 − 𝑎
=
𝑥2 − 𝑎2 + 2 (𝑥 − 𝑎)
𝑥 − 𝑎
=
(𝑥 − 𝑎) (𝑥 + 𝑎) + 2 (𝑥 − 𝑎)
𝑥 − 𝑎
= 𝑥 + 𝑎 + 2 → 2𝑎 + 2 lorsque 𝑥 → 𝑎.
(e) Même réponse qu’en (d), si on pose 𝑥 − 𝑎 = ℎ.
(f) On a
𝑓 (𝑎 + ℎ) − 𝑓 (𝑎 − ℎ)
ℎ
=
(𝑎 + ℎ)2 + 2𝑎 + 2ℎ − (𝑎 − ℎ)2 − 2𝑎 + 2ℎ
ℎ
= 4𝑎 + 4 → 4𝑎 + 4 lorsque ℎ → 0.
7. (a) 𝑥3 − 8 = (𝑥 − 2) (𝑥2 + 2𝑥 + 4), de sorte que la limite vaut 1/6.
(b) lim
ℎ→0
[
3
√
27 + ℎ − 3]/ℎ = lim
𝑢→3
(𝑢 − 3)/(𝑢3
− 27), et 𝑢3 − 27 = (𝑢 − 3) (𝑢2 + 3𝑢 + 9), de
sorte que la limite vaut lim𝑢→3 1/(𝑢2 + 3𝑢 + 9) = 1/27.
(c) 𝑥𝑛 − 1 = (𝑥 − 1) (𝑥𝑛−1 + 𝑥𝑛−2 + · · · + 𝑥 + 1), de sorte que la limite est égale à 𝑛.
6.6
1. (a) 0 (b) 4𝑥3 (c) 90𝑥9 (d) 0 (Pour rappel, 𝜋 est une constante!)
2. (a) 2𝑔′(𝑥) (b) −1
6 𝑔′(𝑥) (c) 1
3 𝑔′(𝑥)
3. (a) 6𝑥5 (b) 33𝑥10 (c) 50𝑥49 (d) 28𝑥−8 (e) 𝑥11 (f) 4𝑥−3
(g) −𝑥−4/3 (h) 3𝑥−5/2
4. (a) 8𝜋𝑟 (b) 𝐴(𝑏 + 1) 𝑦𝑏 (c) (−5/2)𝐴−7/2
5. Dans (6.2.1) (la définition de la dérivée), choisissez ℎ = 𝑥 − 𝑎. Alors 𝑎 + ℎ est remplacé
par 𝑥 et ℎ → 0 devient 𝑥 → 𝑎. Pour 𝑓 (𝑥) = 𝑥2, on a 𝑓 ′(𝑎) = 2𝑎.
6. (a) 𝐹(𝑥) = 1
3 𝑥3 + 𝐶 (b) 𝐹(𝑥) = 𝑥2 + 3𝑥 + 𝐶
(c) 𝐹(𝑥) =
𝑥𝑎+1
(𝑎 + 1)
+ 𝐶 (Dans tous les cas, 𝐶 est une constante arbitraire.)
7. (a) Avec 𝑓 (𝑥) = 𝑥2 et 𝑎 = 5, on a
lim
ℎ→0
(5 + ℎ)2 − 52
ℎ
= lim
ℎ→0
𝑓 (𝑎 + ℎ) − 𝑓 (𝑎)
ℎ
= 𝑓 ′
(𝑎) = 𝑓 ′
(5).
Par ailleurs, 𝑓 ′(𝑥) = 2𝑥 et 𝑓 ′(5) = 10. La limite est 10.

48. 48 CORRIGÉS DES EXERCICES
(b) Soit 𝑓 (𝑥) = 𝑥5. Alors 𝑓 ′(𝑥) = 5𝑥4 et la limite est égale à 𝑓 ′(1) = 5 × 14 = 5.
(c) Soit 𝑓 (𝑥) = 5𝑥2 + 10. Alors 𝑓 ′(𝑥) = 10𝑥 et c’est la valeur de la limite.
6.7
1. (a) 1 (b) 1 + 2𝑥 (c) 15𝑥4 + 8𝑥3 (d) 32𝑥3 + 𝑥−1/2 (e) 1
2 − 3𝑥 + 15𝑥2 (f) −21𝑥6
2. (a) 6
5 𝑥 − 14𝑥6 − 1
2 𝑥−1/2 (b) 4𝑥 (3𝑥4 − 𝑥2 − 1)
(c) 10𝑥9 + 5𝑥4 + 4𝑥3 − 𝑥−2 (Pour (b) et (c), commencez par développer, puis dérivez.)
3. (a) 𝑦 =
1
𝑥6
= 𝑥−6
=⇒ 𝑦′
= −6𝑥−7
, par la règle de dérivation d’une puissance (6.6.4).
(b) 𝑦 = 𝑥−1(𝑥2 + 1)
√
𝑥 = 𝑥−1𝑥2𝑥1/2 + 𝑥−1𝑥1/2 = 𝑥3/2 + 𝑥−1/2 =⇒ 𝑦′ = 3
2 𝑥1/2 − 1
2 𝑥−3/2
(c) 𝑦 = 𝑥−3/2
=⇒ 𝑦′
= −3
2 𝑥−5/2
(d) 𝑦 =
𝑥 + 1
𝑥 − 1
=⇒ 𝑦′
=
1 × (𝑥 − 1) − (𝑥 + 1) × 1
(𝑥 − 1)2
=
−2
(𝑥 − 1)2
(e) 𝑦 =
𝑥
𝑥5
+
1
𝑥5
= 𝑥−4
+ 𝑥−5
=⇒ 𝑦′
= −
4
𝑥5
−
5
𝑥6
(f) 𝑦 =
3𝑥 − 5
2𝑥 + 8
=⇒ 𝑦′
=
3 (2𝑥 + 8) − 2 (3𝑥 − 5)
(2𝑥 + 8)2
=
34
(2𝑥 + 8)2
(g) 𝑦 = 3𝑥−11 =⇒ 𝑦′ = −33𝑥−12
(h) 𝑦 =
3𝑥 − 1
𝑥2 + 𝑥 + 1
=⇒ 𝑦′
=
3 (𝑥2 + 𝑥 + 1) − (3𝑥 − 1) (2𝑥 + 1)
(𝑥2 + 𝑥 + 1)2
=
−3𝑥2 + 2𝑥 + 4
(𝑥2 + 𝑥 + 1)2
4. (a)
3
2
√
𝑥 (
√
𝑥 + 1)2
(b)
4𝑥
(𝑥2 + 1)2
(c)
−2𝑥2 + 2
(𝑥2 − 𝑥 + 1)2
5. (a) 𝑓 ′(𝐿∗) 𝑓 (𝐿∗)/𝐿∗. Voir figure C6.7.5. La pente de la tangente en 𝑃 est 𝑓 ′(𝐿∗). On
« voit » que la tangente en 𝑃 est moins raide que la droite qui joint l’origine à 𝑃, dont
la pente est 𝑓 (𝐿∗)/𝐿∗ = 𝑔(𝐿∗). (L’inégalité suit directement de la caractérisation des
fonctions dérivables concaves par l’équation (8.4.3).)
P
y
L
y = f (L)
f (L∗
)
L∗
Figure C6.7.5
(b)
d
d𝐿
𝑓 (𝐿)
𝐿
=
1
𝐿
𝑓 ′
(𝐿) −
𝑓 (𝐿)
𝐿
, comme à l’exemple 6.7.7.

49. Chapitre 6 / La dérivation 49
6. (a) 𝑦′ = 6𝑥 − 12 = 6 (𝑥 − 2) ⩾ 0 ⇔ 𝑥 ⩾ 2, d’où 𝑦 est croissante sur [2, ∞[.
(b) 𝑦′ = 𝑥3 − 3𝑥 = 𝑥 (𝑥2 − 3) = 𝑥 (𝑥 −
√
3) (𝑥 +
√
3), d’où, par un tableau de signes, on
montre que 𝑦 est croissante sur
−
√
3, 0
et sur
√
3, +∞
.
(c) 𝑦′
=
2 (2 + 𝑥2) − (2𝑥) (2𝑥)
(2 + 𝑥2)2
=
2 (2 − 𝑥2)
(𝑥2 + 2)2
=
2 (
√
2 − 𝑥) (
√
2 + 𝑥)
(𝑥2 + 2)2
.
La fonction 𝑦 est donc croissante sur [−
√
2,
√
2].
(d) 𝑦′
=
(2𝑥 − 3𝑥2) (𝑥 + 1) − (𝑥2 − 𝑥3)
2 (𝑥 + 1)2
=
−2𝑥3 − 2𝑥2 + 2𝑥
2 (𝑥 + 1)2
=
−𝑥 (𝑥 − 𝑥1) (𝑥 − 𝑥2)
(𝑥 + 1)2
,
où 𝑥1,2 = −1
2 ∓ 1
2
√
5. Alors 𝑦 est croissante sur ] − ∞, 𝑥1] et sur [0, 𝑥2].
7. (a) 𝑦′ = −1 − 2𝑥 = −3 quand 𝑥 = 1. La pente de la tangente est donc −3. Comme 𝑦 = 1
quand 𝑥 = 1, la formule (4.4.2) donne 𝑦 − 1 = −3 (𝑥 − 1) ou 𝑦 = −3𝑥 + 4.
(b) 𝑦 = 1 − 2 (𝑥2 + 1)−1, de sorte que 𝑦′ = 4𝑥/(𝑥2 + 1)2 = 1 et 𝑦 = 0 quand 𝑥 = 1.
L’équation de la tangente est 𝑦 = 𝑥 − 1.
(c) 𝑦 = 𝑥2 − 𝑥−2, d’où 𝑦′ = 2𝑥 + 2𝑥−3 = 17/4 et 𝑦 = 15/4 quand 𝑥 = 2. De là,
𝑦 = (17/4) 𝑥 − 19/4.
(d) 𝑦′
=
4𝑥3 (𝑥3 + 3𝑥2 + 𝑥 + 3) − (𝑥4 + 1) (3𝑥2 + 6𝑥 + 1)
[(𝑥2 + 1) (𝑥 + 3)]2
= −
1
9
et 𝑦 =
1
3
quand 𝑥 = 0.
D’où 𝑦 = 1
3 − 1
9 𝑥 = −(𝑥 − 3)/9.
8. 𝑅′(𝑡) = 𝑝′(𝑡) 𝑥 (𝑡)+ 𝑝(𝑡) 𝑥′(𝑡). 𝑅(𝑡) croît pour deux raisons. La première, 𝑅(𝑡) croît parce
que le prix croît. Cet accroissement est proportionnel à la quantité extraite 𝑥 (𝑡) et est
égal à 𝑝′(𝑡) 𝑥 (𝑡). Mais 𝑅(𝑡) croît aussi parce que l’extraction augmente. Sa contribution
au taux de variation de 𝑅(𝑡) doit être proportionnelle au prix et est égale à 𝑝(𝑡) 𝑥′(𝑡).
Par conséquent, 𝑅′(𝑡), le taux de variation total de 𝑅(𝑡), est la somme de ces deux
contributions.
9. (a) On utilise la règle de dérivation du quotient
𝑦 =
𝑎𝑡 + 𝑏
𝑐𝑡 + 𝑑
=⇒ 𝑦′
=
𝑎 (𝑐𝑡 + 𝑑) − (𝑎𝑡 + 𝑏)𝑐
(𝑐𝑡 + 𝑑)2
=
𝑎𝑑 − 𝑏𝑐
(𝑐𝑡 + 𝑑)2
.
(b) 𝑦 = 𝑡𝑛
𝑎
√
𝑡 + 𝑏
= 𝑎𝑡𝑛+1/2 + 𝑏𝑡𝑛 =⇒ 𝑦′ = (𝑛 + 1/2)𝑎𝑡𝑛−1/2 + 𝑛𝑏𝑡𝑛−1
(c) 𝑦 =
1
𝑎𝑡2 + 𝑏𝑡 + 𝑐
=⇒ 𝑦′
=
0 × (𝑎𝑡2 + 𝑏𝑡 + 𝑐) − 1 × (2𝑎𝑡 + 𝑏)
(𝑎𝑡2 + 𝑏𝑡 + 𝑐)2
=
−2𝑎𝑡 − 𝑏
(𝑎𝑡2 + 𝑏𝑡 + 𝑐)2
10. En raison de la règle de dérivation du produit, 𝑓 ′(𝑥) × 𝑓 (𝑥) + 𝑓 (𝑥) × 𝑓 ′(𝑥) = 1,
de sorte que 2 𝑓 ′(𝑥) × 𝑓 (𝑥) = 1. D’où 𝑓 ′(𝑥) = 1/2 𝑓 (𝑥) = 1/2
√
𝑥.
11. Si 𝑓 (𝑥) = 1/𝑥𝑛, la règle de dérivation du quotient donne
𝑓 ′
(𝑥) = (0 × 𝑥𝑛
− 1 × 𝑛𝑥𝑛−1
)/(𝑥𝑛
)2
= −𝑛𝑥−𝑛−1
,
qui est la règle de dérivation d’une puissance.

50. 50 CORRIGÉS DES EXERCICES
6.8
1. (a) d𝑦/d𝑥 = (d𝑦/d𝑢) (d𝑢/d𝑥) = 20𝑢4−1 d𝑢/d𝑥 = 20 (1 + 𝑥2)32𝑥 = 40𝑥 (1 + 𝑥2)3
(b) d𝑧/d𝑥 = (1 − 6𝑦5) (d𝑦/d𝑥) = (−1/𝑥2) 1 − 6 (1 + 1/𝑥)5
2. (a) d𝑌/d𝑡 = (d𝑌/d𝑉) (d𝑉/d𝑡) = (−3) 5 (𝑉 + 1)4𝑡2 = −15𝑡2 (𝑡3/3 + 1)4.
(b) d𝐾/d𝑡 = (d𝐾/d𝐿) (d𝐿/d𝑡) = 𝐴𝑎𝐿𝑎−1𝑏 = 𝐴𝑎𝑏 (𝑏𝑡 + 𝑐)𝑎−1
3. (a) 𝑦 =
1
(𝑥2 + 𝑥 + 1)5
= (𝑥2
+ 𝑥 + 1)−5
= 𝑢−5
, où 𝑢 = 𝑥2 + 𝑥 + 1. Par la règle de dérivation
d’une composée, 𝑦′ = (−5) 𝑢−6𝑢′ = −5 (2𝑥 + 1) (𝑥2 + 𝑥 + 1)−6.
(b) Avec 𝑢 = 𝑥 +
p
𝑥 +
√
𝑥, 𝑦 =
√
𝑢 = 𝑢1/2, de sorte que 𝑦′ = 1
2 𝑢−1/2𝑢′. Maintenant,
𝑢 = 𝑥 + 𝑣1/2, avec 𝑣 = 𝑥 + 𝑥1/2. Ensuite 𝑢′ = 1 + 1
2 𝑣−1/2𝑣′, où 𝑣′ = 1 + 1
2 𝑥−1/2. Donc,
finalement,
𝑦′
= 1
2 𝑢−1/2
𝑢′
= 1
2
𝑥 + (𝑥 + 𝑥1/2
)1/2
−1/2
1 + ( 1
2 (𝑥 + 𝑥1/2
)−1/2
(1 + 1
2 𝑥−1/2
)
.
(c) 𝑦′ = 𝑎𝑥𝑎−1(𝑝𝑥 + 𝑞)𝑏 + 𝑥𝑎𝑏𝑝(𝑝𝑥 + 𝑞)𝑏−1 = 𝑥𝑎−1(𝑝𝑥 + 𝑞)𝑏−1[(𝑎 + 𝑏)𝑝𝑥 + 𝑎𝑞]
4. (d𝑌/d𝑡)𝑡=𝑡0 = (d𝑌/d𝐾)𝑡=𝑡0 × (d𝐾/d𝑡)𝑡=𝑡0 = 𝑌′(𝐾(𝑡0))𝐾′(𝑡0)
5. d𝑌/d𝑡 = 𝐹′ ℎ(𝑡)
× ℎ′(𝑡)
6. 𝑥 = 𝑏 −
√
𝑎𝑝 − 𝑐 = 𝑏 −
√
𝑢, avec 𝑢 = 𝑎𝑝 − 𝑐. Ensuite,
d𝑥
d𝑝
= −
1
2
√
𝑢
𝑢′
= −
𝑎
2
√
𝑎𝑝 − 𝑐
.
7. (a) ℎ′(𝑥) = 𝑓 ′(𝑥2) 2𝑥 (b) ℎ′(𝑥) = 𝑔′ 𝑥𝑛 𝑓 (𝑥)
𝑛𝑥𝑛−1 𝑓 (𝑥) + 𝑥𝑛 𝑓 ′(𝑥)
8. 𝑏(𝑡) est la consommation totale de carburant après 𝑡 heures. Alors 𝑏′(𝑡) = 𝐵′ 𝑠(𝑡)
𝑠′(𝑡),
de sorte que le taux de consommation horaire est égal au taux par kilomètre multiplié par
la vitesse en km/h.
9. d𝐶/d𝑥 = 𝑞 25 − 1
2 𝑥
−1/2
10. (a) 𝑦′ = 5 (𝑥4)4 × 4𝑥3 = 20𝑥19 (b) 𝑦′ = 3 (1 − 𝑥)2 (−1) = −3 + 6𝑥 − 3𝑥2
11. (a) (i) 𝑔(5) est le montant accumulé si le taux d’intérêt annuel est 5 %, ce qui correspond
à environ 1 629 e.
(ii) 𝑔′(5) est (grosso modo) l’augmentation de cette valeur accumulée si le taux d’intérêt
est haussé de 1 %, ce qui correspond à environ 155 e.
(b) 𝑔(𝑝) = 1 000 (1 + 𝑝/100)10, donc 𝑔(5) = 1 000 × 1, 0510 = 1 628,89, arrondi au
centime d’euro le plus proche. De plus,
𝑔′
(𝑝) = 1 000 × 10 (1 + 𝑝/100)9
× 1/100 = 100 × (1 + 𝑝/100)9
,
donc 𝑔′(5) = 100 × 1,059 = 155,13, arrondi au centime d’euro le plus proche.
12. (a) 1 + 𝑓 ′(𝑥) (b) 2 𝑓 (𝑥) 𝑓 ′(𝑥) − 1 (c) 4
𝑓 (𝑥)
3
𝑓 ′(𝑥)
(d) 2𝑥 𝑓 (𝑥) + 𝑥2 𝑓 ′(𝑥) + 3
𝑓 (𝑥)
2
𝑓 ′(𝑥) (e) 𝑓 (𝑥) + 𝑥 𝑓 ′(𝑥) (f) 𝑓 ′
(𝑥)/2
p
𝑓 (𝑥)
(g) [2𝑥 𝑓 (𝑥) − 𝑥2 𝑓 ′(𝑥)]/( 𝑓 (𝑥))2 (h) [2𝑥 𝑓 (𝑥) 𝑓 ′(𝑥) − 3 ( 𝑓 (𝑥))2]/𝑥4

51. Chapitre 6 / La dérivation 51
13. (a) Si 𝑥 ≠ 0 et 0 |ℎ| |𝑥|, on a
1
ℎ
[𝜑(𝑥 + ℎ) − 𝜑(𝑥)] =
1
ℎ
1
𝑥 + ℎ
−
1
𝑥
=
−ℎ
ℎ(𝑥 + ℎ)𝑥
=
−1
(𝑥 + ℎ)𝑥
,
qui tend vers −1/𝑥2 quand ℎ → 0. En particulier, 𝜑(𝑥) = 1/𝑥 est dérivable si 𝑥 ≠ 0.
(b) Pour tout 𝑥 avec 𝑔(𝑥) ≠ 0, si 𝑓 et 𝑔 sont dérivables en 𝑥, alors : (i) en combinant
la question (a) avec la règle de dérivation d’une fonction composée, on trouve que
1/𝑔(𝑥) = 𝜑(𝑔(𝑥)) est dérivable en 𝑥 ; (ii) à l’aide de la règle de dérivation d’un produit,
on montre que 𝑓 (𝑥)/𝑔(𝑥) = 𝑓 (𝑥)[1/𝑔(𝑥)] est dérivable en 𝑥.
6.9
1. (a) 𝑦′′ = 20𝑥3 − 36𝑥2 (b) 𝑦′′ = (−1/4) 𝑥−3/2
(c) 𝑦′ = 20𝑥 (1+𝑥2)9, 𝑦′′ = 20 (1+𝑥2)9 +20𝑥 ×9×2𝑥 (1+𝑥2)8 = 20 (1+𝑥2)8 (1+19𝑥2).
2. d2𝑦/d𝑥2 = (1 + 𝑥2)−1/2 − 𝑥2 (1 + 𝑥2)−3/2 = (1 + 𝑥2)−3/2
3. (a) 𝑦′′ = 18𝑥 (b) 𝑌′′′ = 36 (c) d3𝑧/d𝑡3 = −2 (d) 𝑓 (4) (1) = 84 000
4. 𝑔′
(𝑡) =
2𝑡 (𝑡 − 1) − 𝑡2
(𝑡 − 1)2
=
𝑡2 − 2𝑡
(𝑡 − 1)2
, 𝑔′′
(𝑡) =
2
(𝑡 − 1)3
et 𝑔′′(2) = 2.
5. En notations simplifiées,
𝑦′
= 𝑓 ′
𝑔 + 𝑓 𝑔′
,
𝑦′′
= 𝑓 ′′
𝑔 + 𝑓 ′
𝑔′
+ 𝑓 ′
𝑔′
+ 𝑓 𝑔′′
= 𝑓 ′′
𝑔 + 2 𝑓 ′
𝑔′
+ 𝑓 𝑔′′
,
𝑦′′′
= 𝑓 ′′′
𝑔 + 𝑓 ′′
𝑔′
+ 2 𝑓 ′′
𝑔′
+ 2 𝑓 ′
𝑔′′
+ 𝑓 ′
𝑔′′
+ 𝑓 𝑔′′′
= 𝑓 ′′′
𝑔 + 3 𝑓 ′′
𝑔′
+ 3 𝑓 ′
𝑔′′
+ 𝑓 𝑔′′′
.
6. 𝐿 = (2𝑡 − 1)−1/2, de sorte que d𝐿/d𝑡 = −1
2 × 2 (2𝑡 − 1)−3/2 = −(2𝑡 − 1)−3/2 et
d2𝐿/d𝑡2 = 3 (2𝑡 − 1)−5/2.
7. (a) 𝑅 = 0 (b) 𝑅 = 1/2 (c) 𝑅 = 3 (d) 𝑅 = 𝜌
8. Le secrétaire à la Défense : 𝑃′ 0. L’opposition : 𝑃′ ⩾ 0 et 𝑃′′ 0.
9. d3𝐿/d𝑡3 0
6.10
1. (a) 𝑦′ = 𝑒𝑥 + 2𝑥 (b) 𝑦′ = 5𝑒𝑥 − 9𝑥2 (c) 𝑦′ = (1 × 𝑒𝑥 − 𝑥𝑒𝑥)/𝑒2𝑥 = (1 − 𝑥) 𝑒−𝑥
(d) 𝑦′ = [(1 + 2𝑥) (𝑒𝑥 + 1) − (𝑥 + 𝑥2) 𝑒𝑥]/(𝑒𝑥 + 1)2 = [1 + 2𝑥 + 𝑒𝑥 (1 + 𝑥 − 𝑥2)]/(𝑒𝑥 + 1)2
(e) 𝑦′ = −1 − 𝑒𝑥 (f) 𝑦′ = 𝑥2𝑒𝑥 (3 + 𝑥) (g) 𝑦′ = 𝑒𝑥 (𝑥 − 2)/𝑥3
(h) 𝑦′ = 2 (𝑥 + 𝑒𝑥) (1 + 𝑒𝑥)
2. (a)
d𝑥
d𝑡
= (𝑏 + 2𝑐𝑡) 𝑒𝑡
+ (𝑎 + 𝑏𝑡 + 𝑐𝑡2
) 𝑒𝑡
= (𝑎 + 𝑏 + (𝑏 + 2𝑐) 𝑡 + 𝑐𝑡2
) 𝑒𝑡
(b)
d𝑥
d𝑡
=
3𝑞𝑡2𝑡𝑒𝑡 − (𝑝 + 𝑞𝑡3) (1 + 𝑡) 𝑒𝑡
𝑡2𝑒2𝑡
=
−𝑞𝑡4 + 2𝑞𝑡3 − 𝑝𝑡 − 𝑝
𝑡2𝑒𝑡

52. 52 CORRIGÉS DES EXERCICES
(c)
d𝑥
d𝑡
= [2 (𝑎𝑡 + 𝑏𝑡2
) (𝑎 + 2𝑏𝑡) 𝑒𝑡
− (𝑎𝑡 + 𝑏𝑡2
)2
𝑒𝑡
]/(𝑒𝑡
)2
= [𝑡 (𝑎 + 𝑏𝑡) (−𝑏𝑡2
+ (4𝑏 − 𝑎) 𝑡 + 2𝑎)]𝑒−𝑡
3. (a) 𝑦′ = −3𝑒−3𝑥, 𝑦′′ = 9𝑒−3𝑥.
(b) 𝑦′ = 6𝑥2𝑒𝑥3
, 𝑦′′ = 6𝑥𝑒𝑥3
(3𝑥3 + 2).
(c) 𝑦′ = −𝑥−2𝑒1/𝑥, 𝑦′′ = 𝑥−4𝑒1/𝑥 (2𝑥 + 1).
(d) 𝑦′ = 5 (4𝑥 − 3) 𝑒2𝑥2−3𝑥+1, 𝑦′′ = 5𝑒2𝑥2−3𝑥+1(16𝑥2 − 24𝑥 + 13).
4. (a) Comme 𝑦′ = 3𝑥2 + 2𝑒2𝑥 est manifestement strictement positive partout, la fonction 𝑦
est croissante sur ] − ∞, +∞[.
(b) 𝑦′ = 10𝑥𝑒−4𝑥 + 5𝑥2 (−4) 𝑒−4𝑥 = 10𝑥 (1 − 2𝑥) 𝑒−4𝑥. Un tableau de signes donne 𝑦
croissante sur [0, 1/2].
(c) 𝑦′ = 2𝑥𝑒−𝑥2
+ 𝑥2 (−2𝑥) 𝑒−𝑥2
= 2𝑥 (1 − 𝑥) (1 + 𝑥) 𝑒−𝑥2
. Un tableau de signes donne 𝑦
croissante sur ] − ∞, −1] et sur [0, 1].
5. (a) 𝑦′ = 2𝑥𝑒−2𝑥 (1 − 𝑥). La fonction 𝑦 est donc croissante sur [0, 1].
(b) 𝑦′ = 𝑒𝑥 (1 − 3𝑒2𝑥). La fonction 𝑦 est donc croissante sur ] − ∞, −1
2 ln 3].
(c) 𝑦′ = (2𝑥 + 3) 𝑒2𝑥/(𝑥 + 2)2. La fonction 𝑦 est donc croissante sur [−3/2, +∞[.
6. (a) 𝑒𝑒𝑥
𝑒𝑥 = 𝑒𝑒𝑥+𝑥 (b) 1
2 (𝑒𝑡/2
− 𝑒−𝑡/2
) (c) −
𝑒𝑡 − 𝑒−𝑡
(𝑒𝑡 + 𝑒−𝑡 )2
(d) 𝑧2𝑒𝑧3
(𝑒𝑧3
− 1)−2/3
7. (a) 𝑦′ = 5𝑥 ln 5 (b) 𝑦′ = 2𝑥 + 𝑥2𝑥 ln 2 = 2𝑥 (1 + 𝑥 ln 2)
(c) 𝑦′ = 2𝑥2𝑥2
(1 + 𝑥2 ln 2) (d) 𝑦′ = 𝑒𝑥10𝑥 + 𝑒𝑥10𝑥 ln 10 = 𝑒𝑥10𝑥 (1 + ln 10)
6.11
1. (a) 𝑦′ = 1/𝑥 + 3, 𝑦′′ = −1/𝑥2. (b) 𝑦′ = 2𝑥 − 2/𝑥, 𝑦′′ = 2 + 2/𝑥2.
(c) 𝑦′ = 3𝑥2 ln 𝑥+𝑥2, 𝑦′′ = 𝑥 (6 ln 𝑥+5). (d) 𝑦′ = (1−ln 𝑥)/𝑥2, 𝑦′′ = (2 ln 𝑥−3)/𝑥3.
2. (a) 𝑥2 ln 𝑥 (3 ln 𝑥 + 2) (b) 𝑥 (2 ln 𝑥 − 1)/(ln 𝑥)2
(c) 10 (ln 𝑥)9/𝑥 (d) 2 ln 𝑥/𝑥 + 6 ln 𝑥 + 18𝑥 + 6
3. Pour la plupart de ces exercices, on a besoin de la règle de dérivation d’une composée.
C’est important en soi! Mais cela implique en particulier que, si 𝑢 = 𝑓 (𝑥) est une fonction
dérivable de 𝑥 telle que 𝑓 (𝑥) 0, alors
d
d𝑥
ln 𝑢 =
1
𝑢
𝑢′
=
𝑢′
𝑢
.
(a) 𝑦 = ln(ln 𝑥) = ln 𝑢 avec 𝑢 = ln 𝑥 implique 𝑦′
=
1
𝑢
𝑢′
=
1
ln 𝑥
1
𝑥
=
1
𝑥 ln 𝑥
.
(b) 𝑦 = ln
p
1 − 𝑥2 = ln 𝑢 avec 𝑢 =
√
1 − 𝑥2 implique
𝑦′
=
1
𝑢
𝑢′
=
1
√
1 − 𝑥2
−2𝑥
2
√
1 − 𝑥2
=
−𝑥
1 − 𝑥2
.
(Sinon :
√
1 − 𝑥2 = (1 − 𝑥2)1/2 ⇒ 𝑦 = 1
2 ln(1 − 𝑥2), etc.)

53. Chapitre 6 / La dérivation 53
(c) 𝑦 = 𝑒𝑥
ln 𝑥 ⇒ 𝑦′
= 𝑒𝑥
ln 𝑥 + 𝑒𝑥 1
𝑥
= 𝑒𝑥
ln 𝑥 +
1
𝑥
(d) 𝑦 = 𝑒𝑥3
ln 𝑥2
⇒ 𝑦′
= 3𝑥2
𝑒𝑥3
ln 𝑥2
+ 𝑒𝑥3 1
𝑥2
2𝑥 = 𝑒𝑥3
3𝑥2
ln 𝑥2
+
2
𝑥
(e) 𝑦 = ln(𝑒𝑥
+ 1) ⇒ 𝑦′
=
𝑒𝑥
𝑒𝑥 + 1
(f) 𝑦 = ln(𝑥2
+ 3𝑥 − 1) ⇒ 𝑦′
=
2𝑥 + 3
𝑥2 + 3𝑥 − 1
(g) 𝑦 = 2 (𝑒𝑥 − 1)−1 ⇒ 𝑦′ = −2𝑒𝑥 (𝑒𝑥 − 1)−2
(h) 𝑦 = 𝑒2𝑥2−𝑥 ⇒ 𝑦′ = (4𝑥 − 1) 𝑒2𝑥2−𝑥
4. (a) 𝑥 −1 (b) 1/3 𝑥 1 (c) 𝑥 ≠ 0
5. (a) On doit avoir 𝑥2 1, c’est-à-dire 𝑥 1 ou 𝑥 −1.
(b) ln(ln 𝑥) n’est défini que si ln 𝑥 est défini et strictement positif, c’est-à-dire pour 𝑥 1.
(c) La fraction 1/(ln(ln 𝑥) − 1) n’est définie que si ln(ln 𝑥) est défini et différent de 1.
De (b), ln(ln 𝑥) est défini lorsque 𝑥 1. De plus, ln(ln 𝑥) = 1 ⇔ ln 𝑥 = 𝑒 ⇔ 𝑥 = 𝑒𝑒.
Conclusion : 1/(ln(ln 𝑥) − 1) est défini ⇔ 𝑥 1 et 𝑥 ≠ 𝑒𝑒.
6. (a) La fonction est définie pour 4 − 𝑥2 0, soit dans ] − 2, 2[. 𝑓 ′(𝑥) = −2𝑥/(4 − 𝑥2) ⩾ 0
dans ] − 2, 0], là où 𝑦 est croissante.
(b) La fonction est définie pour 𝑥 0. 𝑓 ′(𝑥) = 𝑥2 (3 ln 𝑥 + 1) ⩾ 0 pour ln 𝑥 ⩾ −1/3, ou
𝑥 ⩾ 𝑒−1/3, de sorte que la fonction 𝑦 est croissante sur [𝑒−1/3, +∞[.
(c) La fonction est définie pour 𝑥 0 et
𝑦′
=
2 (1 − ln 𝑥) (−1/𝑥) 2𝑥 − 2 (1 − ln 𝑥)2
4𝑥2
=
(1 − ln 𝑥) (ln 𝑥 − 3)
2𝑥2
.
Un tableau de signes révèle que la fonction 𝑦 est croissante en 𝑥 tel que 1 ⩽ ln 𝑥 ⩽ 3.
Autrement dit, 𝑥 ∈ [𝑒, 𝑒3].
7. (a) (i) 𝑦 = 𝑥 − 1 (ii) 𝑦 = 2𝑥 − 1 − ln 2 (iii) 𝑦 = 𝑥/𝑒
(b) (i) 𝑦 = 𝑥 (ii) 𝑦 = 2𝑒𝑥 − 𝑒 (iii) 𝑦 = −𝑒−2𝑥 − 4𝑒−2
8. (a) 𝑓 ′(𝑥)/ 𝑓 (𝑥) = 2 ln 𝑥 + 2
(b) 𝑓 ′(𝑥)/ 𝑓 (𝑥) = 1/(2𝑥 − 4) + 2𝑥/(𝑥2 + 1) + 4𝑥3/(𝑥4 + 6)
(c) 𝑓 ′(𝑥)/ 𝑓 (𝑥) = −2/[3 (𝑥2 − 1)]
9. Pour tous ces exercices, on peut employer la dérivation logarithmique. Sinon, on peut
écrire les fonctions sous la forme 𝑓 (𝑥) = 𝑒𝑔(𝑥) et utiliser ensuite le fait que
𝑓 ′
(𝑥) = 𝑒𝑔(𝑥)
𝑔′
(𝑥) = 𝑓 (𝑥)𝑔′
(𝑥).
(a) Soit 𝑓 (𝑥) = (2𝑥)𝑥. Alors ln 𝑓 (𝑥) = 𝑥 ln(2𝑥), de sorte que
𝑓 ′(𝑥)
𝑓 (𝑥)
= 1 × ln(2𝑥) + 𝑥 ×
1
2𝑥
× 2 = ln(2𝑥) + 1.
De là,
𝑓 ′
(𝑥) = 𝑓 (𝑥) (ln(2𝑥) + 1) = (2𝑥)𝑥
(ln 𝑥 + ln 2 + 1).

54. 54 CORRIGÉS DES EXERCICES
(b) 𝑓 (𝑥) = 𝑥
√
𝑥 = 𝑒ln 𝑥
√
𝑥
= 𝑒
√
𝑥 ln 𝑥, de sorte que
𝑓 ′
(𝑥) = 𝑒
√
𝑥 ln 𝑥
×
d
d𝑥
(
√
𝑥 ln 𝑥) = 𝑥
√
𝑥
ln 𝑥
2
√
𝑥
+
√
𝑥
𝑥
= 𝑥
√
𝑥− 1
2 ( 1
2 ln 𝑥 + 1).
(c) ln 𝑓 (𝑥) = 𝑥 ln
√
𝑥 = 1
2 𝑥 ln 𝑥, de sorte que 𝑓 ′(𝑥)/ 𝑓 (𝑥) = 1
2 (ln 𝑥 + 1), ce qui donne
𝑓 ′(𝑥) = 1
2 (
√
𝑥 )𝑥 (ln 𝑥 + 1).
10. Comme ln 𝑦 = 𝑣 ln 𝑢, 𝑦′/𝑦 = 𝑣′ ln 𝑢 + 𝑣𝑢′/𝑢 et, de là, 𝑦′ = 𝑢𝑣 (𝑣′ ln 𝑢 + 𝑣𝑢′/𝑢). (Autre
méthode : noter que 𝑦 = (𝑒ln 𝑢)𝑣 = 𝑒𝑣 ln 𝑢 et utiliser ensuite la règle de dérivation de la
composée.)
11. (a) Soit 𝑓 (𝑥) = 𝑒𝑥 − (1 + 𝑥 + 1
2 𝑥2). Alors 𝑓 (0) = 0 et 𝑓 ′(𝑥) = 𝑒𝑥 − (1 + 𝑥) 0 pour tout
𝑥 0, comme montré dans l’exercice. D’où 𝑓 (𝑥) 0 pour tout 𝑥 0 et l’inégalité en
découle.
(b) Soit 𝑓 (𝑥) = ln(1 + 𝑥) − 1
2 𝑥. Alors 𝑓 (0) = 0 et de plus
𝑓 ′
(𝑥) = 1/(𝑥 + 1) −
1
2
= (1 − 𝑥)/2 (𝑥 + 1),
qui est strictement positive dans ]0, 1[. Ainsi, 𝑓 (𝑥) 0 pour 𝑥 dans ]0, 1[ et l’in-
égalité du membre de gauche est satisfaite. Pour démontrer l’autre inégalité, on pose
𝑔(𝑥) = 𝑥 − ln(1 + 𝑥). Alors 𝑔(0) = 0 et 𝑔′(𝑥) = 1 − 1/(𝑥 + 1) = 𝑥/(𝑥 + 1) 0 pour 𝑥 dans
]0, 1[. La conclusion s’ensuit.
(c) Soit 𝑓 (𝑥) = 2 (
√
𝑥 − 1) − ln 𝑥. Alors 𝑓 (1) = 0 et
𝑓 ′
(𝑥) = (1/
√
𝑥) − 1/𝑥 = (
√
𝑥 − 1)/𝑥,
qui est strictement positive pour 𝑥 tel que 𝑥 1. La conclusion s’ensuit.
Exercices récapitulatifs du chapitre 6
1. On a [ 𝑓 (𝑥 + ℎ) − 𝑓 (𝑥)]/ℎ = [(𝑥 + ℎ)2
− (𝑥 + ℎ) + 2 − 𝑥2
+ 𝑥 − 2]/ℎ
= [2𝑥ℎ + ℎ2
− ℎ]/ℎ = 2𝑥 + ℎ − 1
.
Ainsi, [ 𝑓 (𝑥 + ℎ) − 𝑓 (𝑥)]/ℎ → 2𝑥 − 1 lorsque ℎ → 0, de sorte que 𝑓 ′(𝑥) = 2𝑥 − 1.
2. [ 𝑓 (𝑥 + ℎ) − 𝑓 (𝑥)]/ℎ = −6𝑥2 + 2𝑥 − 6𝑥ℎ − 2ℎ2 + ℎ → −6𝑥2 + 2𝑥 lorsque ℎ → 0, de sorte
que 𝑓 ′(𝑥) = −6𝑥2 + 2𝑥.
3. (a) 𝑦′ = 2, 𝑦′′ = 0 (b) 𝑦′ = 3𝑥8, 𝑦′′ = 24𝑥7 (c) 𝑦′ = −𝑥9, 𝑦′′ = −9𝑥8
(d) 𝑦′ = 21𝑥6, 𝑦′′ = 126𝑥5 (e) 𝑦′ = 1/10, 𝑦′′ = 0
(f) 𝑦′ = 5𝑥4 + 5𝑥−6, 𝑦′′ = 20𝑥3 − 30𝑥−7 (g) 𝑦′ = 𝑥3 + 𝑥2, 𝑦′′ = 3𝑥2 + 2𝑥
(h) 𝑦′ = −𝑥−2 − 3𝑥−4, 𝑦′′ = 2𝑥−3 + 12𝑥−5
4. Comme 𝐶′(1 000) ≈ 𝐶(1 001) − 𝐶(1 000), si 𝐶′(1 000) = 25, le coût additionnel de
produire un peu plus de 1 000 unités est à peu près égal à 25 par unité. Si le prix par
unité est fixé à 30, le profit supplémentaire lié à l’augmentation de production légèrement
au-dessus de 1 000 unités est d’environ 30 − 25 = 5 par unité vendue.

55. Chapitre 6 / La dérivation 55
5. (a) 𝑦 = −3 et 𝑦′ = −6𝑥 = −6 en 𝑥 = 1, de sorte que 𝑦−(−3) = (−6) (𝑥−1) ou 𝑦 = −6𝑥+3.
(b) 𝑦 = −14 et 𝑦′ = 1/2
√
𝑥 − 2𝑥 = −31/4 en 𝑥 = 4, de sorte que 𝑦 = −(31/4) 𝑥 + 17.
(c) 𝑦 = 0 et 𝑦′ = (−2𝑥3 − 8𝑥2 + 6𝑥)/(𝑥 + 3)2 = −1/4 en 𝑥 = 1, de sorte que
𝑦 = (−1/4) (𝑥 − 1).
6. Cela signifie que le coût additionnel associé à l’extension de la surface d’une petite
quantité au dessus de 100 m2 est d’environ 250 e par m2.
7. (a) Comme 𝑓 (𝑥) = 𝑥3 + 𝑥, 𝑓 ′(𝑥) = 3𝑥2 + 1. (b) 𝑔′(𝑤) = −5𝑤−6
(c) Comme ℎ(𝑦) = 𝑦 (𝑦2 − 1) = 𝑦3 − 𝑦, ℎ′(𝑦) = 3𝑦2 − 1.
(d) 𝐺′(𝑡) = (−2𝑡2 − 2𝑡 + 6)/(𝑡2 + 3)2
(e) 𝜑′
(𝜉) =
(4 − 2𝜉2)
(𝜉2 + 2)2
(f) 𝐹′
(𝑠) =
−(𝑠2 + 2)
(𝑠2 + 𝑠 − 2)2
8. (a) 2𝑎𝑡 (b) 𝑎2 − 2𝑡 (c) 2𝑥𝜑 − 1/2
√
𝜑
9. (a) 𝑦′ = 20𝑢𝑢′ = 20 (5 − 𝑥2) (−2𝑥) = 40𝑥3 − 200𝑥 (b) 𝑦′
=
1
2
√
𝑢
× 𝑢′
=
−1
2𝑥2
p
1/𝑥 − 1
10. (a)
d𝑍
d𝑡
=
d𝑍
d𝑢
d𝑢
d𝑡
= 3 (𝑢2
− 1)2
2𝑢3𝑡2
= 18𝑡5
(𝑡6
− 1)2
(b)
d𝐾
d𝑡
=
d𝐾
d𝐿
d𝐿
d𝑡
=
1
2
√
𝐿
−1
𝑡2
=
−1
2𝑡2
p
1 + 1/𝑡
11. (a) 𝑥′/𝑥 = 2𝑎′/𝑎 + 𝑏′/𝑏 (b) 𝑥′/𝑥 = 𝛼𝑎′/𝑎 + 𝛽𝑏′/𝑏
(c) 𝑥′/𝑥 = (𝛼 + 𝛽) (𝛼𝑎𝛼−1𝑎′ + 𝛽𝑏𝛽−1𝑏′)/(𝑎𝛼 + 𝑏𝛽)
12. d𝑅/d𝑡 = (d𝑅/d𝑆) (d𝑆/d𝐾) (d𝐾/d𝑡) = 𝛼𝑆𝛼−1𝛽𝛾𝐾𝛾−1 𝐴𝑝𝑡𝑝−1 = 𝐴𝛼𝛽𝛾𝑝𝑡𝑝−1𝑆𝛼−1𝐾𝛾−1
13. (a) ℎ′(𝐿) = 𝑎𝑝𝐿𝑎−1(𝐿𝑎 + 𝑏)𝑝−1 (b) 𝐶′(𝑄) = 𝑎 + 2𝑏𝑄
(c) 𝑃′(𝑥) = 𝑎𝑥1/𝑞−1(𝑎𝑥1/𝑞 + 𝑏)𝑞−1
14. (a) 𝑦′ = −7𝑒𝑥 (b) 𝑦′ = −6𝑥𝑒−3𝑥2
(c) 𝑦′ = 𝑥𝑒−𝑥 (2 − 𝑥)
(d) 𝑦′ = 𝑒𝑥 [ln(𝑥2 + 2) + 2𝑥/(𝑥2 + 2)] (e) 𝑦′ = 15𝑥2𝑒5𝑥3
(f) 𝑦′ = 𝑥3𝑒−𝑥 (𝑥 − 4)
(g) 𝑦′ = 10 (𝑒𝑥 + 2𝑥) (𝑒𝑥 + 𝑥2)9 (h) 𝑦′ = 1/(2
√
𝑥 (
√
𝑥 + 1))
15. (a) 𝑦′
=
2
𝑥
ln 𝑥 ⩾ 0 si 𝑥 ⩾ 1.
(b) 𝑦′
=
𝑒𝑥 − 𝑒−𝑥
𝑒𝑥 + 𝑒−𝑥
⩾ 0 ⇔ 𝑒𝑥
⩾ 𝑒−𝑥
⇔ 𝑒2𝑥
⩾ 1 ⇔ 𝑥 ⩾ 0
(c) 𝑦′
= 1 −
3𝑥
𝑥2 + 2
=
(𝑥 − 1) (𝑥 − 2)
𝑥2 + 2
⩾ 0 ⇔ 𝑥 ⩽ 1 ou 𝑥 ⩾ 2.
(Faites un tableau de signes.)
16. (a) d𝜋/d𝑄 = 𝑃(𝑄) + 𝑄𝑃′(𝑄) − 𝑐 (b) d𝜋/d𝐿 = 𝑃𝐹′(𝐿) − 𝑤

56. 56 CORRIGÉS DES EXERCICES
Chapitre 7 / Les dérivées en action
7.1
1. En dérivant implicitement par rapport à 𝑥, on a 6𝑥 + 2𝑦′ = 0, de sorte que 𝑦′ = −3𝑥. En
explicitant l’équation donnée en 𝑦, on a 𝑦 = 5/2 − 3𝑥2/2, puis 𝑦′ = −3𝑥.
2. On dérive implicitement : 2𝑥𝑦 + 𝑥2 (d𝑦/d𝑥) = 0, d’où d𝑦/d𝑥 = −2𝑦/𝑥. On dérive à
nouveau implicitement par rapport à 𝑥, cela donne
2𝑦 + 2𝑥 (d𝑦/d𝑥) + 2𝑥 (d𝑦/d𝑥) + 𝑥2
(d2
𝑦/d𝑥2
) = 0.
On remplace d𝑦/d𝑥 par son expression et on simplifie d2𝑦/d𝑥2 = 6𝑦/𝑥2. Il est plus rapide
de dériver deux fois 𝑦 = 𝑥−2.
3. (a) Une dérivation implicite par rapport à 𝑥 donne (∗) 1 − 𝑦′ + 3𝑦 + 3𝑥𝑦′ = 0. On
explicite par rapport à 𝑦′, 𝑦′ = (1 + 3𝑦)/(1 − 3𝑥). Par définition, la fonction a comme
expression 𝑦 = (𝑥 − 2)/(1 − 3𝑥). On substitue 𝑦 dans 𝑦′, ce qui donne 𝑦′ = −5/(1 − 3𝑥)2.
En dérivant (∗) par rapport à 𝑥, on obtient −𝑦′′ + 3𝑦′ + 3𝑦′ + 3𝑥𝑦′′ = 0. On y introduit
l’expression de 𝑦′ = (1 + 3𝑦)/(1 − 3𝑥) et on résout par rapport à 𝑦′′
𝑦′′
= 6𝑦′
/(1 − 3𝑥) = −30/(1 − 3𝑥)3
.
(b) Une dérivation implicite par rapport à 𝑥 donne (∗) 5𝑦4𝑦′ = 6𝑥5, de sorte que
𝑦′ = 6𝑥5/5𝑦4 = (6/5) 𝑥1/5. En dérivant (∗) par rapport à 𝑥, on obtient
20𝑦3
(𝑦′
)2
+ 5𝑦4
𝑦′′
= 30𝑥4
.
On y introduit l’expression de 𝑦′ = 6𝑥5/5𝑦4 et on résout par rapport à 𝑦′′,
𝑦′′ = 6𝑥4𝑦−4 − 4𝑦−1(𝑦′′)2 = 6𝑥4𝑦−4 − (144/25) 𝑥10𝑦−9 = (6/25) 𝑥−4/5.
4. 2𝑢 + 𝑣 + 𝑢 (d𝑣/d𝑢) − 3𝑣2 (d𝑣/d𝑢) = 0, d’où d𝑣/d𝑢 = (2𝑢 + 𝑣)/(3𝑣2 − 𝑢). On a d𝑣/d𝑢 = 0
quand 𝑣 = −2𝑢 (à condition de supposer 3𝑣2 − 𝑢 ≠ 0). On substitue cette expression de 𝑣
dans l’équation de départ 8𝑢3 − 𝑢2 = 0. Le seul point de la courbe en lequel d𝑣/d𝑢 = 0 et
𝑢 ≠ 0 a comme coordonnées (𝑢, 𝑣) = (1/8, −1/4).
5. Dériver par rapport à 𝑥 mène à (∗) 4𝑥 + 6𝑦 + 6𝑥𝑦′ + 2𝑦𝑦′ = 0. On obtient alors
𝑦′ = −(2𝑥 + 3𝑦)/(3𝑥 + 𝑦) = −8/5 en (1, 2). Dériver (∗) par rapport à 𝑥 mène à
4 + 6𝑦′ + 6𝑦′ + 6𝑥𝑦′′ + 2 (𝑦′)2 + 2𝑦𝑦′′ = 0. On calcule en 𝑥 = 1, 𝑦 = 2 et 𝑦′ = −8/5 et on
obtient 𝑦′′ = 126/125.
6. (a) 2𝑥 + 2𝑦𝑦′ = 0, d’où, en explicitant par rapport à 𝑦′, 𝑦′ = −𝑥/𝑦.
(b) 1/2
√
𝑥 + 𝑦′/2
√
𝑦 = 0, d’où 𝑦′ = −
p
𝑦/𝑥.
(c) 4𝑥3 − 4𝑦3𝑦′ = 2𝑥𝑦3 + 𝑥23𝑦2𝑦′, d’où 𝑦′ = 2𝑥 (2𝑥2 − 𝑦3)/𝑦2 (3𝑥2 + 4𝑦).
(d) 𝑒𝑥𝑦 (𝑦 + 𝑥𝑦′) − 2𝑥𝑦 − 𝑥2𝑦′ = 0, d’où 𝑦′ = 𝑦 (2𝑥 − 𝑒𝑥𝑦)/𝑥 (𝑒𝑥𝑦 − 𝑥).
7. (a) En dérivant l’équation par rapport à 𝑥, on obtient (∗) 2𝑦 + 2𝑥𝑦′ − 6𝑦𝑦′ = 0. En posant
𝑥 = 6 et 𝑦 = 1 dans (∗), on a 2 + 12𝑦′ − 6𝑦′ = 0, de sorte que 𝑦′ = −1/3.

57. Chapitre 7 / Les dérivées en action 57
(b) On dérive (∗) implicitement par rapport à 𝑥. On obtient
2𝑦′
+ 2𝑦′
+ 2𝑥𝑦′′
− 6𝑦′
𝑦′
− 6𝑦𝑦′′
= 0. (∗∗)
En posant 𝑥 = 6, 𝑦 = 1 et 𝑦′ = −1/3 dans (∗∗), on déduit 𝑦′′ = 1/3.
8. (a) 𝑦 + 𝑥𝑦′ = 𝑔′(𝑥) + 3𝑦2𝑦′ et on isole 𝑦′.
(b) 𝑔′(𝑥 + 𝑦) (1 + 𝑦′) = 2𝑥 + 2𝑦𝑦′ et on isole 𝑦′.
(c) Pour dériver 𝑔(𝑥2𝑦) par rapport à 𝑥, on pose 𝑧 = 𝑔(𝑢), où 𝑢 = 𝑥2𝑦. Alors 𝑧′ = 𝑔′(𝑢) 𝑢′,
où 𝑢′ = 2𝑥𝑦+𝑥2𝑦′. On a donc 2 (𝑥𝑦+1) (𝑦+𝑥𝑦′) = 𝑔′(𝑥2𝑦) (2𝑥𝑦+𝑥2𝑦′). Il suffit maintenant
d’isoler 𝑦′.
9. On dérive implicitement par rapport à 𝑥 : 3𝑥2𝐹(𝑥𝑦)+𝑥3𝐹′(𝑥𝑦) (𝑦+𝑥𝑦′)+𝑒𝑥𝑦 (𝑦+𝑥𝑦′) = 1.
En posant 𝑥 = 1 et 𝑦 = 0 dans cette équation, on obtient 3𝐹(0) +𝐹′(0)𝑦′ + 𝑦′ = 1. Comme
𝐹(0) = 0, on a 𝑦′ = 1/(𝐹′(0) + 1). (Notez que 𝐹 est une fonction d’une seule variable,
dont l’argument est 𝑥𝑦.)
10. (a) On dérive par rapport à 𝑥, tout en ayant à l’esprit que 𝑦 dépend de 𝑥. Cela donne
2 (𝑥2 + 𝑦2) (2𝑥 + 2𝑦𝑦′) = 𝑎2 (2𝑥 − 2𝑦𝑦′). On résout ensuite par rapport à 𝑦′.
(b) Notez que 𝑥 = 0 impliquerait 𝑦 = 0. Mise à part cette éventualité, on voit que
𝑦′ = 0 quand 𝑥2 + 𝑦2 = 𝑎2/2 ou 𝑦2 = 1
2 𝑎2 − 𝑥2. On introduit cette expression dans
l’équation donnée 𝑥 = ±1
4 𝑎
√
6 et ainsi 𝑦 = ±1
2 𝑎
√
2. Les quatre possibilités fournissent les
coordonnées des quatre points de la courbe en lesquels la tangente est horizontale.
7.2
1. La dérivation implicite par rapport à 𝑃, en reconnaissant que 𝑄 est une fonction de 𝑃,
conduit à (d𝑄/d𝑃) × 𝑃1/2 + 𝑄 1
2 𝑃−1/2 = 0. D’où d𝑄/d𝑃 = −1
2𝑄𝑃−1
= −19/𝑃3/2
.
2. (a) 1 = 𝐶′′(𝑄∗) (d𝑄∗/d𝑃), de sorte que d𝑄∗/d𝑃 = 1/𝐶′′(𝑄∗)
(b) d𝑄∗/d𝑃 0, ce qui est admissible vu que, si le prix perçu par le producteur augmente,
la production optimale sera plus élevée.
3. (a) On prend le logarithme naturel des deux membres, ln 𝐴 − 𝛼 ln 𝑃 − 𝛽 ln𝑖 = ln 𝑆,
puis on dérive par rapport à 𝑖, ce qui donne −(𝛼/𝑃) (d𝑃/d𝑖) − 𝛽/𝑖 = 0. Il suit
d𝑃/d𝑖 = −(𝛽/𝛼) (𝑃/𝑖) 0.
(b) Une montée du taux d’intérêt déprime donc la demande et, en compensation, le prix
à l’équilibre tombe.
4. (a) On introduit (ii) et (iii) à la place de 𝐶 et 𝑀 dans l’équation (i),
𝑌 = 𝑓 (𝑌) + 𝐼 + ¯
𝑋 − 𝑔(𝑌).
(b) On dérive implicitement par rapport à 𝐼.
d𝑌/d𝐼 = 𝑓 ′
(𝑌) (d𝑌/d𝐼) + 1 − 𝑔′
(𝑌) (d𝑌/d𝐼) = ( 𝑓 ′
(𝑌) − 𝑔′
(𝑌)) (d𝑌/d𝐼) + 1 (∗)
D’où d𝑌/d𝐼 = 1/
1 − 𝑓 ′(𝑌) + 𝑔′(𝑌)
. On a 𝑓 ′(𝑌) 1. Les importations vont croître
lorsque le revenu augmente, aussi 𝑔′(𝑌) 0. Il s’ensuit que d𝑌/d𝐼 0.

58. 58 CORRIGÉS DES EXERCICES
(c) La dérivée de (∗) par rapport à 𝐼 conduit, en notation simplifiée, à
d2
𝑌/d𝐼2
= ( 𝑓 ′′
− 𝑔′′
) (d𝑌/d𝐼) + ( 𝑓 ′
− 𝑔′
) (d2
𝑌/d𝐼2
),
ainsi d2𝑌/d𝐼2 = ( 𝑓 ′′ − 𝑔′′) (d𝑌/d𝐼)/(1 − 𝑓 ′ + 𝑔′)2 = ( 𝑓 ′′ − 𝑔′′)/(1 − 𝑓 ′ + 𝑔′)3.
5. On dérive (7.2.6) par rapport à 𝜏
𝑓 ′′
(𝑃 + 𝜏) d𝑃/d𝜏 + 1
2
+ 𝑓 ′
(𝑃 + 𝜏)d2
𝑃/d𝜏2
= 𝑔′′
(𝑃) d𝑃/d𝜏
2
+ 𝑔′
(𝑃)d2
𝑃/d𝜏2
.
On simplifie la notation 𝑓 ′′(𝑃′ + 1)2 + 𝑓 ′𝑃′′ = 𝑔′′(𝑃′)2 + 𝑔′𝑃′′. On remplace 𝑃′ par
𝑃′ = 𝑓 ′/(𝑔′ − 𝑓 ′) et on résout par rapport à 𝑃′′
𝑃′′
= [ 𝑓 ′′
(𝑔′
)2
− 𝑔′′
( 𝑓 ′
)2
]/(𝑔′
− 𝑓 ′
)3
.
6. (a) On dérive (∗) par rapport à 𝜏, 𝑓 ′(𝑃) (d𝑃/d𝜏) = 𝑔′((1 − 𝜏)𝑃) [−𝑃 + (1 − 𝜏) (d𝑃/d𝜏)]
et on explicite par rapport à d𝑃/d𝜏,
d𝑃
d𝜏
=
−𝑃𝑔′((1 − 𝜏)𝑃)
𝑓 ′(𝑃) − (1 − 𝜏)𝑔′((1 − 𝜏)𝑃)
.
(b) Numérateur et dénominateur sont négatifs, de sorte que d𝑃/d𝑡 0. Une augmentation
de la taxe sur les producteurs fait monter le prix à l’équilibre.
7.3
1. 𝑓 (1) = 1 et 𝑓 ′(𝑥) = 2𝑒2𝑥−2 = 2 pour 𝑥 = 1. Selon (7.3.2), 𝑔′(1) = 1/ 𝑓 ′(1) = 1/2. La
fonction réciproque étant 𝑔(𝑥) = 1 + 1
2 ln 𝑥, 𝑔′(𝑥) = 1/2𝑥 = 1/2 pour 𝑥 = 1.
2. (a) 𝑓 ′
(𝑥) = 𝑥2
p
4 − 𝑥2 +
1
3
𝑥3 −2𝑥
2
√
4 − 𝑥2
=
4𝑥2 (3 − 𝑥2)
3
√
4 − 𝑥2
. La fonction 𝑓 est donc croissante
sur [−
√
3,
√
3 ] et décroissante sur [−2, −
√
3 ] et sur [
√
3, 2]. Voir figure C7.3.2.
y
−2
−1
1
2
x
−2 −1 1 2
Figure C7.3.2
y
x
1
2
−1 1 2
y = 1 + 1
2 x
y = √1 + x
Figure C7.4.1
(b) La fonction 𝑓 admet une réciproque sur [0,
√
3], car la fonction 𝑓 y est strictement
croissante
𝑔′
(
1
3
√
3 ) = 1/ 𝑓 ′
(1) = 3
√
3/8.

59. Chapitre 7 / Les dérivées en action 59
3. (a) 𝑓 ′(𝑥) = 𝑒𝑥−3/(𝑒𝑥−3 + 2) 0 pour tout 𝑥, de sorte que 𝑓 est strictement croissante.
De plus, 𝑓 (𝑥) → ln 2 lorsque 𝑥 → −∞ et 𝑓 (𝑥) → +∞ lorsque 𝑥 → +∞, de sorte que
l’ensemble image de 𝑓 est ] ln 2, +∞[.
(b) 𝑔(𝑥) = 3 + ln(𝑒𝑥 − 2), définie sur ] ln 2, +∞[.
(c) 𝑓 ′(3) = 1/𝑔′( 𝑓 (3)) = 1/3
4. d𝐷/d𝑃 = −0,3 × 157,8𝑃−1,3 = −47,34𝑃−1,3 de sorte que
d𝑃/d𝐷 = 1/(d𝐷/d𝑃) ≈ −0,021𝑃1,3
.
5. (a) Comme d𝑦/d𝑥 = −𝑒−𝑥−5, d𝑥/d𝑦 = 1/(d𝑦/d𝑥) = 1/−𝑒−𝑥−5 = −𝑒𝑥+5.
(b) Comme d𝑦/d𝑥 = −𝑒−𝑥/(𝑒−𝑥 + 3), d𝑥/d𝑦 = −(𝑒−𝑥 + 3)/𝑒−𝑥 = −1 − 3𝑒𝑥.
(c) La dérivation implicite par rapport à 𝑥 fournit
𝑦3
+ 𝑥 (3𝑦2
) (d𝑦/d𝑥) − 3𝑥2
𝑦 − 𝑥3
(d𝑦/d𝑥) = 2.
Il faut encore résoudre par rapport à d𝑦/d𝑥 et ensuite prendre l’inverse.
7.4
1. Si 𝑓 (𝑥) =
√
1 + 𝑥, alors 𝑓 ′(𝑥) = 1/(2
√
1 + 𝑥 ) et 𝑓 (0) = 1 et 𝑓 ′(0) = 1/2. Ainsi, (7.4.1)
donne
√
1 + 𝑥 ≈ 1 + 1
2 (𝑥 − 0) = 1 + 1
2 𝑥. Voir figure C7.4.1.
2. Ici 𝑓 (0) = 1/9 et 𝑓 ′(𝑥) = −10 (5𝑥 + 3)−3 de sorte que 𝑓 ′(0) = −10/27. Par conséquent,
(5𝑥 + 3)−2 ≈ 1/9 − 10𝑥/27.
3. (a) Comme 𝑓 (0) = 1 et 𝑓 ′(𝑥) = −(1 + 𝑥)−2, 𝑓 ′(0) = −1. Ensuite
𝑓 (𝑥) ≈ 𝑓 (0) + 𝑓 ′
(0) 𝑥 = 1 − 𝑥.
(b) Comme 𝑓 (0) = 1 et 𝑓 ′(𝑥) = 5 (1 + 𝑥)4, 𝑓 ′(0) = 5. Ensuite
𝑓 (𝑥) ≈ 𝑓 (0) + 𝑓 ′
(0) 𝑥 = 1 + 5𝑥.
(c) Comme 𝑓 (0) = 1 et 𝑓 ′(𝑥) = −1
4 (1 − 𝑥)−3/4, 𝑓 ′(0) = −1
4 . Alors
𝑓 (𝑥) ≈ 𝑓 (0) + 𝑓 ′
(0) 𝑥 = 1 −
1
4
𝑥.
4. 𝐹(1) = 𝐴 et 𝐹′(𝐾) = 𝛼𝐴𝐾𝛼−1 de sorte que 𝐹′(1) = 𝛼𝐴. Alors
𝐹(𝐾) ≈ 𝐹(1) + 𝐹′
(1) (𝐾 − 1) = 𝐴 + 𝛼𝐴(𝐾 − 1) = 𝐴(1 + 𝛼(𝐾 − 1)).
5. (a) 30𝑥2 d𝑥 (b) 15𝑥2 d𝑥 − 10𝑥 d𝑥 + 5 d𝑥 (c) −3𝑥−4 d𝑥 (d) (1/𝑥) d𝑥
(e) (𝑝𝑥𝑝−1 + 𝑞𝑥𝑞−1) d𝑥 (f) (𝑝 + 𝑞) 𝑥𝑝+𝑞−1 d𝑥 (g) 𝑟𝑝 (𝑝𝑥 + 𝑞)𝑟−1 d𝑥
(h) (𝑝𝑒𝑝𝑥 + 𝑞𝑒𝑞𝑥) d𝑥
6. (a) Si 𝑓 (𝑥) = (1+𝑥)𝑚, alors 𝑓 (0) = 1 et 𝑓 ′(0) = 𝑚, de sorte que 1+𝑚𝑥 est l’approximation
du premier degré de 𝑓 (𝑥) au voisinage de 𝑥 = 0.

60. 60 CORRIGÉS DES EXERCICES
(b) (i) 3
√
1,1 = (1 + 1/10)1/3 ≈ 1 + (1/3) (1/10) ≈ 1,033
(ii)
5
√
33 = 2 (1 + 1/32)1/5 ≈ 2 (1 + 1/160) = 2,0125
(iii)
3
√
9 = 2 (1 + 1/8)1/3 ≈ 2 (1 + 1/24) ≈ 2,083
(iv) (0,98)25 = (1 − 0,02)25 = (1 − 1/50)25 ≈ 1 − 1/2 = 1/2
7. (a) (i) Δ𝑦 = 0,61, d𝑦 = 0,6. (ii) Δ𝑦 = 0,0601, d𝑦 = 0,06.
(b) (i) Δ𝑦 = 0,011494, d𝑦 = 0,011111. (ii) Δ𝑦 = 0,001115, d𝑦 = 0,001111.
(c) (i) Δ𝑦 = 0,012461, d𝑦 = 0,0125. (ii) Δ𝑦 = 0,002498, d𝑦 = 0,0025.
8. (a) On doit dériver 3𝑥𝑒𝑥𝑦2
. On commence par utiliser la règle de dérivation du produit pour
obtenir (d/d𝑥)3𝑥 𝑒𝑥𝑦2
= 3𝑒𝑥𝑦2
+ 3𝑥 (d/d𝑥) 𝑒𝑥𝑦2
. La règle de dérivation de la composée
donne alors (d/d𝑥) 𝑒𝑥𝑦2
= 𝑒𝑥𝑦2
(𝑦2 + 𝑥2𝑦𝑦′). Par dérivation implicite sur l’ensemble, on
a 3𝑒𝑥𝑦2
+ 3𝑥𝑒𝑥𝑦2
(𝑦2 + 𝑥2𝑦𝑦′) − 2𝑦′ = 6𝑥 + 2𝑦𝑦′. En posant 𝑥 = 1, 𝑦 = 0, on obtient
3 − 2𝑦′ = 6, d’où 𝑦′ = −3/2.
(b) 𝑦 (𝑥) ≈ 𝑦 (1) + 𝑦′(1) (𝑥 − 1) = −3
2 (𝑥 − 1).
9. (a) 𝐴(𝑟 + d𝑟) − 𝐴(𝑟) est l’aire ombrée de la figure C7.4.9. Elle est à peu près égale à la
longueur du cercle intérieur, 2𝜋𝑟, multipliée par d𝑟.
(b) 𝑉(𝑟 + d𝑟) −𝑉(𝑟) est le volume de la couche située entre la sphère de rayon 𝑟 + d𝑟 et la
sphère de rayon 𝑟. Elle est à peu près égale à la surface 4𝜋𝑟2 de la sphère intérieure fois
l’épaisseur d𝑟 de la couche.
r
r + dr
Figure C7.4.9
10. En prenant le logarithme, on a ln 𝐾𝑡 = ln 𝐾 + 𝑡 ln(1 + 𝑝/100) ≈ ln 𝐾 + 𝑡𝑝/100.
Si 𝐾𝑡 = 2𝐾, alors ln 𝐾𝑡 = ln 2 + ln 𝐾 et, si 𝑡∗ désigne le temps de doublement, 𝑝 doit
être tel que ln 2 ≈ 𝑡∗ 𝑝/100, de sorte que 𝑝 ≈ 100 ln 2/𝑡∗. (Avec ln 2 ≈ 0,7, ce résultat
concorde avec la « règle du 70 » de l’exemple 7.4.3.) Le pourcentage exact 𝑝∗ vérifie
ln 2 = 𝑡∗ ln(1 + 𝑝∗/100), ou 𝑝∗ = 100 21/𝑡∗
− 1
.
11. 𝑔(0) = 𝐴 −1 et 𝑔′(𝜇) = 𝐴𝑎/(1+ 𝑏)
(1+ 𝜇)[𝑎/(1+𝑏)]−1 de sorte que 𝑔′(0) = 𝐴𝑎/(1+ 𝑏).
D’où 𝑔(𝜇) ≈ 𝑔(0) + 𝑔′(0)𝜇 = 𝐴 − 1 + 𝑎𝐴𝜇/(1 + 𝑏).
12. Comme la dérivée existe, on a limℎ→0
1
ℎ [ 𝑓 (𝑎 + ℎ) − 𝑓 (𝑎)] = 𝑓 ′(𝑎). Mais, de manière
évidente, limℎ→0
1
ℎ [ 𝑓 ′(𝑎)ℎ] = 𝑓 ′(𝑎). D’après les règles sur les limites de la section 6.5,
on a alors limℎ→0
1
ℎ [ 𝑓 (𝑎 + ℎ) − ( 𝑓 (𝑎) + 𝑓 ′(𝑎)ℎ)] = 𝑓 ′(𝑎) − 𝑓 ′(𝑎) = 0.

61. Chapitre 7 / Les dérivées en action 61
7.5
1. (a) Ici, 𝑓 ′(𝑥) = 5 (1 + 𝑥)4 et 𝑓 ′′(𝑥) = 20 (1 + 𝑥)3. Ainsi, en 𝑥 = 0, 𝑓 (0) = 1, 𝑓 ′(0) = 5 et
𝑓 ′′(0) = 20, ce qui conduit à 𝑓 (𝑥) = (1 + 𝑥)5 ≈ 1 + 5𝑥 + 1
2 20𝑥2 = 1 + 5𝑥 + 10𝑥2.
(b) 𝐴𝐾𝛼 ≈ 𝐴 + 𝛼𝐴(𝐾 − 1) + 1
2 𝛼(𝛼 − 1)𝐴(𝐾 − 1)2
(c) (1 + 3
2 𝜀 + 1
2 𝜀2)1/2 ≈ 1 + 3
4 𝜀 − 1
32 𝜀2
(d) 𝐻′(𝑥) = (−1) (1 − 𝑥)−2(−1) = (1 − 𝑥)−2 = 1 en 𝑥 = 0, et 𝐻′′(𝑥) = 2 (1 − 𝑥)−3 = 2 en
𝑥 = 0. Il s’ensuit que (1 − 𝑥)−1 ≈ 1 + 𝑥 + 𝑥2.
2. 𝑓 ′(𝑥) = (1 + 𝑥)−1, 𝑓 ′′(𝑥) = −(1 + 𝑥)−2, 𝑓 ′′′(𝑥) = 2 (1 + 𝑥)−3, 𝑓 (4) (𝑥) = −6 (1 + 𝑥)−4,
𝑓 (5) (𝑥) = 24 (1 + 𝑥)−5.
Ensuite 𝑓 (0) = 0, 𝑓 ′(0) = 1, 𝑓 ′′(0) = −1, 𝑓 ′′′(0) = 2, 𝑓 (4) (0) = −6, 𝑓 (5) (0) = 24 et
ainsi
𝑓 (𝑥) ≈ 𝑓 (0) +
1
1!
𝑓 ′
(0) 𝑥 +
1
2!
𝑓 ′′
(0) 𝑥 +
1
3!
𝑓 ′′′
(0) 𝑥3
+
1
4!
𝑓 (4)
(0) 𝑥4
+
1
5!
𝑓 (5)
(0) 𝑥5
= 𝑥 −
1
2
𝑥2
+
1
3
𝑥3
−
1
4
𝑥4
+
1
5
𝑥5
.
3. Avec 𝑓 (𝑥) = 5 (ln(1 + 𝑥) −
√
1 + 𝑥 ) = 5 ln(1 + 𝑥) − 5 (1 + 𝑥)1/2, on calcule
𝑓 ′(𝑥) = 5 (1 + 𝑥)−1 − 5
2 (1 + 𝑥)−1/2, 𝑓 ′′(𝑥) = −5 (1 + 𝑥)−2 + 5
4 (1 + 𝑥)−3/2 et,
de là, 𝑓 (0) = −5, 𝑓 ′(0) = 5
2 , 𝑓 ′′(0) = −15
4 . Le polynôme de Taylor d’ordre 2 au
voisinage de 𝑥 = 0 s’écrit 𝑓 (0) + 𝑓 ′(0) 𝑥 + 1
2 𝑓 ′′(0) 𝑥2 = −5 + 5
2 𝑥 − 15
8 𝑥2.
4. Découle de la formule (7.5.2) avec 𝑓 = 𝑈, 𝑎 = 𝑦 et 𝑥 = 𝑦 + 𝑀 − 𝑠.
5. La dérivation implicite fournit (∗) 3𝑥2𝑦 + 𝑥3𝑦′ + 1 = 1
2 𝑦−1/2𝑦′. L’introduction de 𝑥 = 0 et
𝑦 = 1 donne 1 = 1
2
1−1/2𝑦′, de sorte que 𝑦′ = 2. On dérive à nouveau (∗) par rapport à
𝑥, d’où 6𝑥𝑦 + 3𝑥2𝑦′ + 3𝑥2𝑦′ + 𝑥3𝑦′′ = −1
4 𝑦−3/2(𝑦′)2 + 1
2 𝑦−1/2𝑦′′. On introduit 𝑥 = 0, 𝑦 = 1
et 𝑦′ = 2, cela donne 𝑦′′ = 2. Finalement, 𝑦 (𝑥) ≈ 1 + 2𝑥 + 𝑥2.
6. On trouve 𝑥′(0) = 2[𝑥 (0)]2 = 2. En dérivant l’expression de 𝑥′(𝑡), on obtient
𝑥′′(𝑡) = 𝑥 (𝑡) + 𝑡𝑥′(𝑡) + 4[𝑥 (𝑡)] 𝑥′(𝑡), de sorte que
𝑥′′
(0) = 𝑥 (0) + 4[𝑥 (0)] 𝑥′
(0) = 1 + 4 × 1 × 2 = 9.
De là, 𝑥 (𝑡) ≈ 𝑥 (0) + 𝑥′(0) 𝑡 + 1
2 𝑥′′(0) 𝑡2 = 1 + 2𝑡 + 9
2 𝑡2.
7. On utilise (7.6.5) avec 𝑥 = 𝜎
p
𝑡/𝑛 , en ne retenant que trois termes du membre de droite.
8. On utilise (7.6.2) avec 𝑓 (𝑥) = (1 + 𝑥)𝑛 et 𝑥 = 𝑝/100. Alors 𝑓 ′(𝑥) = 𝑛 (1 + 𝑥)𝑛−1 et
𝑓 ′′(𝑥) = 𝑛 (𝑛 − 1) (1 + 𝑥)𝑛−2. L’approximation en découle.
9. ℎ′
(𝑥) =
(𝑝𝑥𝑝−1 − 𝑞𝑥𝑞−1) (𝑥𝑝 + 𝑥𝑞) − (𝑥𝑝 − 𝑥𝑞) (𝑝𝑥𝑝−1 + 𝑞𝑥𝑞−1)
(𝑥𝑝 + 𝑥𝑞)2
=
2 (𝑝 − 𝑞) 𝑥𝑝+𝑞−1
(𝑥𝑝 + 𝑥𝑞)2
et,
de là, ℎ′(1) = 1
2 (𝑝 − 𝑞). Comme ℎ(1) = 0, on a
ℎ(𝑥) ≈ ℎ(1) + ℎ′
(1) (𝑥 − 1) =
1
2
(𝑝 − 𝑞) (𝑥 − 1).

62. 62 CORRIGÉS DES EXERCICES
7.6
1. À la suite de l’exercice 7.5.2, 𝑓 (0) = 0, 𝑓 ′(0) = 1, 𝑓 ′′(0) = −1 et 𝑓 ′′′(𝑧) = 2 (1 + 𝑧)−3.
Alors (7.6.3) fournit
𝑓 (𝑥) = 𝑓 (0) +
1
1!
𝑓 ′
(0) 𝑥 +
1
2!
𝑓 ′′
(0) 𝑥 +
1
3!
𝑓 ′′′
(𝑧) 𝑥3
= 𝑥 −
1
2
𝑥2
+
1
3
(1 + 𝑧)−3
𝑥3
.
2. (a)
3
√
25 = 3 (1 − 2/27)1/3
≈ 3
1 −
1
3
×
2
27
−
1
9
×
4
272
≈ 2,924
(b)
5
√
33 = 2 (1 + 1/32)1/5
≈ 2
1 +
1
5 × 32
−
2
25
×
1
322
≈ 2,0125
3. (1 + 1/8)1/3 = 1 + 1/24 − 1/576 + 𝑅3 (1/8), où 0 𝑅3 (1/8) 5/(81 × 83). D’où
3
√
9 = 2 (1 + 1/8)1/3 ≈ 2,080, avec trois décimales correctes.
4. (a) On utilise la formule (7.6.3) de Taylor avec 𝑔(𝑥) = (1 + 𝑥)1/3 et 𝑛 = 2. Alors
𝑔′
(𝑥) =
1
3
(1 + 𝑥)−2/3
, 𝑔′′
(𝑥) = −
2
9
(1 + 𝑥)−5/3
et 𝑔′′′
(𝑥) =
10
27
(1 + 𝑥)−8/3
.
D’où 𝑔(0) = 1, 𝑔′(0) = 1
3 , 𝑔′′(0) = −2
9 , 𝑔′′′(𝑧) = 10
27 (1 + 𝑧)−8/3. Il s’ensuit
𝑔(𝑥) = 1 +
1
3
𝑥 −
1
9
𝑥2
+ 𝑅3 (𝑥),
où 𝑅3 (𝑥) = 1
6
10
27 (1 + 𝑧)−8/3𝑥3 = 5
81 (1 + 𝑧)−8/3𝑥3.
(b) 𝑧 ∈]0, 𝑥[ et 𝑥 ⩾ 0. D’où (1 + 𝑧)−8/3 ⩽ 1 et l’inégalité en découle.
(c) Notez que
3
√
1 003 = 10 (1 + 3 × 10−3)1/3. D’après l’approximation de la question (a),
(1 + 3 × 10−3)1/3 ≈ 1 + 1
3 × 3 × 10−3 − 1
9 (3 × 10−3)2 = 1 + 10−3 − 10−6) = 1,000999,
et ainsi
3
√
1 003 ≈ 10,00999. D’après la question (b), l’erreur 𝑅3 (𝑥) dans l’approximation
(1 + 3 × 10−3)1/3 ≈ 1,000999 satisfait à |𝑅3 (𝑥)| ⩽ 5
81 (3 × 10−3)3 = 5
3 10−9.
Par conséquent, l’erreur dans l’approximation
3
√
1 003 ≈ 10,00999 vaut
10|𝑅3 (𝑥)| ⩽
50
3
10−9
2 × 10−8
impliquant que la réponse comporte sept décimales correctes.
7.7
1. Dans chaque cas, on emploie la formule de l’élasticité (7.7.3).
(a) −3 (b) 100 (c) 1/2, car
√
𝑥 = 𝑥1/2. (d) −3/2, car 𝐴/𝑥
√
𝑥 = 𝐴𝑥−3/2.
2. El𝐾 𝑇 = 1,06. Quand les dépenses augmentent de 1 %, le volume du trafic augmente
d’environ 1,06 %.
3. (a) Une hausse de 10 % des tarifs engendre une baisse de la demande d’environ 4 %.

63. Chapitre 7 / Les dérivées en action 63
(b) Une raison pourrait être que, pour des longs trajets, les gens préfèrent l’avion si le
tarif des trains augmente. Une autre raison pourrait être que beaucoup de gens font une
navette de 60 km quotidiennement, alors que presque personne n’en fait de 300 km, et la
demande des navetteurs est susceptible d’être moins élastique.
4. (a) El𝑥𝑒𝑎𝑥 = (𝑥/𝑒𝑎𝑥)𝑎𝑒𝑎𝑥 = 𝑎𝑥
(b) El𝑥 ln 𝑥 = (𝑥/ln 𝑥) (1/𝑥) = 1/ln 𝑥
(c) El𝑥 (𝑥𝑝
𝑒𝑎𝑥
) =
𝑥
𝑥𝑝𝑒𝑎𝑥
(𝑝𝑥𝑝−1
𝑒𝑎𝑥
+ 𝑥𝑝
𝑎𝑒𝑎𝑥
) = 𝑝 + 𝑎𝑥
(d) El𝑥 (𝑥𝑝
ln 𝑥) =
𝑥
𝑥𝑝 ln 𝑥
𝑝𝑥𝑝−1
ln 𝑥 + 𝑥𝑝 1
𝑥
= 𝑝 +
1
ln 𝑥
5. El𝑥 ( 𝑓 (𝑥))𝑝 =
𝑥
( 𝑓 (𝑥))𝑝
𝑝( 𝑓 (𝑥))𝑝−1
𝑓 ′
(𝑥) = 𝑝
𝑥
𝑓 (𝑥)
𝑓 ′
(𝑥) = 𝑝 El𝑥 𝑓 (𝑥)
6. Selon (7.7.3), El𝑟 𝐷 = 1,23. Une augmentation de 1 % de revenu engendre une augmen-
tation de la demande d’environ 1,23 %.
7. ln 𝑚 = −0,02 + 0,19 ln 𝑁. Quand 𝑁 = 480 000, alors 𝑚 ≈ 11,77.
8. (a) El𝑥 𝐴 𝑓 (𝑥)
=
𝑥
𝐴 𝑓 (𝑥)
𝐴 𝑓 ′
(𝑥) =
𝑥
𝑓 (𝑥)
𝑓 ′
(𝑥) = El𝑥 𝑓 (𝑥).
(b) El𝑥 𝐴 + 𝑓 (𝑥)
=
𝑥
𝐴 + 𝑓 (𝑥)
𝑓 ′
(𝑥) =
𝑓 (𝑥) 𝑥 𝑓 ′(𝑥)/ 𝑓 (𝑥)
𝐴 + 𝑓 (𝑥)
=
𝑓 (𝑥)El𝑥 𝑓 (𝑥)
𝐴 + 𝑓 (𝑥)
.
9. (a) El𝑥 𝐴 =
𝑥
𝐴
d𝐴
d𝑥
= 0
(b) El𝑥 ( 𝑓 𝑔) =
𝑥
𝑓 𝑔
( 𝑓 𝑔)′
=
𝑥
𝑓 𝑔
( 𝑓 ′
𝑔 + 𝑓 𝑔′
) =
𝑥 𝑓 ′
𝑓
+
𝑥𝑔′
𝑔
= El𝑥 𝑓 + El𝑥𝑔
(c) El𝑥
𝑓
𝑔
=
𝑥
( 𝑓 /𝑔)
𝑓
𝑔
′
=
𝑥𝑔
𝑓
𝑔 𝑓 ′ − 𝑓 𝑔′
𝑔2
=
𝑥 𝑓 ′
𝑓
−
𝑥𝑔′
𝑔
= El𝑥 𝑓 − El𝑥𝑔
(d) El𝑥 ( 𝑓 + 𝑔) =
𝑥 ( 𝑓 ′ + 𝑔′)
𝑓 + 𝑔
=
𝑓 (𝑥 𝑓 ′/ 𝑓 ) + 𝑔(𝑥𝑔′/𝑔)
𝑓 + 𝑔
=
𝑓 El𝑥 𝑓 + 𝑔El𝑥𝑔
𝑓 + 𝑔
.
(e) Le principe est semblable à (d), mais en remplaçant +𝑔 par −𝑔 et +𝑔′ par −𝑔′.
(f) 𝑧 = 𝑓 (𝑔(𝑢)), 𝑢 = 𝑔(𝑥) ⇒ El𝑥 𝑧 =
𝑥
𝑧
d𝑧
d𝑥
=
𝑥
𝑢
𝑢
𝑧
d𝑧
d𝑢
d𝑢
d𝑥
= El𝑢 𝑓 (𝑢) El𝑥𝑢
10. (a) −5 (b)
1 + 2𝑥
1 + 𝑥
(c)
30𝑥3
𝑥3 + 1
(d) El𝑥 (5𝑥2) = 2, de sorte que El𝑥 (El𝑥 (5𝑥2)) = 0. (e)
2𝑥2
1 + 𝑥2
(f) El𝑥
𝑥 − 1
𝑥5 + 1
= El𝑥 (𝑥 − 1) − El𝑥 (𝑥5
+ 1) =
𝑥El𝑥𝑥
𝑥 − 1
−
𝑥5El𝑥𝑥5
𝑥5 + 1
=
𝑥
𝑥 − 1
−
5𝑥5
𝑥5 + 1
7.8
1. La seule fonction non continue est (a).
2. La fonction 𝑓 est discontinue en 𝑥 = 0. La fonction 𝑔 est continue en 𝑥 = 2. Les graphiques
de 𝑓 et 𝑔 sont tracés aux figures C7.8.2a et C7.8.2b.

64. 64 CORRIGÉS DES EXERCICES
y
−3
−2
1
2
3
4
x
−2 1 2 3
f
Figure C7.8.2a
y
−2
−1
1
2
3
4
x
1 2 3 4 5
g
Figure C7.8.2b
3. D’après les propriétés des fonctions continues décrites dans le livre, toutes ces fonctions
sont continues là où elles sont définies. (a) et (d) sont définies partout donc continues
partout. Dans (b), on doit exclure 𝑥 = 1. Dans (c), la fonction est définie pour 𝑥 2.
Dans (e), on doit exclure les valeurs de 𝑥 qui rendent le dénominateur nul. Ces valeurs
vérifient 𝑥2 +2𝑥 −2 = 0 ou encore (𝑥 +1)2 = 3, ce sont donc 𝑥 = ±
√
3−1. Enfin, dans (f),
la première fraction nécessite que 𝑥 0 et alors l’autre fraction est aussi définie.
4. Voir figure C7.8.4; 𝑦 est discontinue en 𝑥 = 𝑎, où l’aéroplane se trouve à la verticale du
haut de la falaise.
y
x
a
Figure C7.8.4
y
x
Figure C7.8.6
5. 𝑎 = 5. (La droite 𝑦 = 𝑎𝑥 − 1 et la parabole 𝑦 = 3𝑥2 + 1 doivent se rencontrer en 𝑥 = 1, ce
qui est vrai si et seulement si 𝑎 = 5.)
6. Voir figure C7.8.6. (Cet exemple montre que l’énoncé communément admis qui dit que
« si la fonction réciproque existe, la fonction originale et sa réciproque doivent être toutes
les deux monotones » est faux. Cela est toutefois vrai pour une fonction continue sur un
intervalle.)
7.9
1. (a) 𝐴 (b) 𝐴 (c) 𝐵 (d) 0
2. (a) lim𝑥→0+ (𝑥2 + 3𝑥 − 4) = 02 + 3 × 0 − 4 = −4
(b) |𝑥| = −𝑥 pour 𝑥 0. D’où lim
𝑥→0−
𝑥 + |𝑥|
𝑥
= lim
𝑥→0−
𝑥 − 𝑥
𝑥
= lim
𝑥→0−
0 = 0.

65. Chapitre 7 / Les dérivées en action 65
(c) |𝑥| = 𝑥 pour 𝑥 0. D’où lim
𝑥→0+
𝑥 + |𝑥|
𝑥
= lim
𝑥→0+
𝑥 + 𝑥
𝑥
= lim
𝑥→0+
2 = 2.
(d) Lorsque 𝑥 → 0+ on a
√
𝑥 → 0 et ainsi
−1
√
𝑥
→ −∞.
(e) Lorsque 𝑥 → 3+ on a 𝑥 − 3 → 0+ et ainsi
𝑥
(𝑥 − 3)
→ +∞.
(f) Lorsque 𝑥 → 3− on a 𝑥 − 3 → 0− et ainsi
𝑥
(𝑥 − 3)
→ −∞.
3. (a)
𝑥 − 3
𝑥2 + 1
=
1/𝑥 − 3/𝑥2
1 + 1/𝑥2
→ 0 lorsque 𝑥 → +∞.
(b)
r
2 + 3𝑥
𝑥 − 1
=
s
3 + 2/𝑥
1 − 1/𝑥
→
√
3 lorsque 𝑥 → +∞.
(c) 𝑎2
4. lim
𝑥→+∞
𝑓𝑖 (𝑥) = +∞ pour 𝑖 = 1, 2, 3; lim
𝑥→+∞
𝑓4 (𝑥) = 0. Alors : (a) +∞; (b) 0; (c) −∞;
(d) 1; (e) 0; (f) +∞; (g) 1; (h) +∞.
5. (a) Asymptote verticale, 𝑥 = −1. De plus, 𝑥2 ÷ (𝑥 + 1) = 𝑥 − 1 + 1/(𝑥 + 1), de sorte que
𝑦 = 𝑥 − 1 est une asymptote lorsque 𝑥 → ±∞.
(b) Pas d’asymptote verticale. De plus,
(2𝑥3
− 3𝑥2
+ 3𝑥 − 6) ÷ (𝑥2
+ 1) = 2𝑥 − 3 + (𝑥 − 3)/(𝑥2
+ 1)
de sorte que 𝑦 = 2𝑥 − 3 est une asymptote lorsque 𝑥 → ±∞.
(c) Asymptote verticale, 𝑥 = 1. De plus, (3𝑥2 + 2𝑥) ÷ (𝑥 − 1) = 3𝑥 + 5 + 5/(𝑥 − 1),
de sorte que 𝑦 = 3𝑥 + 5 est une asymptote lorsque 𝑥 → ±∞.
(d) Asymptote verticale, 𝑥 = 1. De plus
(5𝑥4
− 3𝑥2
+ 1) ÷ (𝑥3
− 1) = 5𝑥 + (−3𝑥2
+ 5𝑥 + 1)/(𝑥3
− 1)
de sorte que 𝑦 = 5𝑥 est une asymptote lorsque 𝑥 → ±∞.
6. 𝑦 = 𝐴𝑥 + 𝐴(𝑏 − 𝑐) + 𝑑 est une asymptote lorsque 𝑥 → +∞. (𝑥 = −𝑐 n’est pas une
asymptote car 𝑥 ⩾ 0.)
7. (a) Ni continue ni dérivable en 𝑥 = 1 car 𝑓 (1) = 𝐵. (b) Continue mais non dérivable
en 𝑥 = 2. (c) Ni continue ni dérivable en 𝑥 = 3. (d) Continue mais non dérivable en
𝑥 = 4.
8. 𝑓 ′(0+) = 1 et 𝑓 ′(0−) = 0. Voir figure C7.9.8.
9. C’est un peu délicat, car le dénominateur est nul en 𝑥1,2 = 2 ±
√
3. Un tableau de signes
révèle que 𝑓 (𝑥) 0 seulement sur ] − ∞, 0[ et sur ]𝑥1, 𝑥2 [. La fonction 𝑓 est croissante
sur ] − ∞, −1], sur [1, 2 +
√
3[ et sur ]2 +
√
3, +∞[. Voir aussi la figure C7.9.9.

66. 66 CORRIGÉS DES EXERCICES
y
x
1
1
f (x)
Figure C7.9.8
y
− 4
− 2
2
4
6
x
− 6 − 4 − 2 2 4 6 8
f (x) =
3x
− x2 + 4x − 1
Figure C7.9.9
7.10
1. (a) Soit 𝑓 (𝑥) = 𝑥7 − 5𝑥5 + 𝑥3 − 1. Alors 𝑓 est continue, 𝑓 (−1) = 2 et 𝑓 (1) = −4, de sorte
que, selon le théorème 7.10.1, l’équation 𝑓 (𝑥) = 0 a une solution dans ] − 1, 1[.
(b) Ici, 𝑓 (𝑥) = 𝑥3 + 3𝑥 − 8 est continue, avec 𝑓 (1) 0 𝑓 (3).
(c) Ici, 𝑓 (𝑥) =
√
𝑥2 + 1 − 3𝑥 est continue, avec 𝑓 (0) 0 𝑓 (1).
(d) Ici, 𝑓 (𝑥) = 𝑒𝑥−1 − 2𝑥 est continue, avec 𝑓 (0) 0 𝑓 (1).
2. La taille d’une personne est une fonction continue du temps (même si la croissance se
produit par poussées intermittentes, souvent durant la nuit). Le théorème 7.10.1 (et le bon
sens) donnent la conclusion.
3. Soit 𝑓 (𝑥) = 𝑥3 − 17. Alors 𝑓 (𝑥) = 0 pour 𝑥 =
3
√
17. Or, 𝑓 ′(𝑥) = 3𝑥2. On choisit
𝑥0 = 2,5. Alors 𝑓 (𝑥0) = −1,375 et 𝑓 ′(𝑥0) = 18,75. La formule (7.10.1) avec 𝑛 = 0 fournit
𝑥1 = 𝑥0 − 𝑓 (𝑥0)/ 𝑓 ′(𝑥0) = 2,5 − (−1,375)/18,75 ≈ 2,573.
4. On se souvient (voir 4.7.6) que toute racine entière de l’équation
𝑓 (𝑥) = 𝑥4
+ 3𝑥3
− 3𝑥2
− 8𝑥 + 3 = 0
doit être un facteur du terme constant 3. Une façon de voir cela directement est de
remarquer que 3 = −𝑥4 − 3𝑥3 + 3𝑥2 + 8𝑥 = 𝑥 (−𝑥3 − 3𝑥2 + 3𝑥 + 8) et, si 𝑥 est un entier,
l’expression entre crochets doit l’être aussi. Les seules solutions entières possibles sont
donc ±1 et ±3. Après essais, la seule qui convient est −3. Il y a trois autres racines
réelles qui valent approximativement 𝑥0 = −1,9, 𝑦0 = 0,4 et 𝑧0 = 1,5. En utilisant la
méthode de Newton une fois sur chacune de ces valeurs approchées, on obtient les valeurs
approximatives suivantes.
𝑥1 = −1,9 −
𝑓 (−1,9)
𝑓 ′(−1,9)
= −1,9 −
−0,1749
8,454
≈ −1,9 + 0,021 = −1,879
𝑦1 = 0,4 −
𝑓 (0,4)
𝑓 ′(0,4)
= 0,4 −
−0,4624
−8,704
≈ 0,4 − 0,053 = 0,347
𝑧1 = 1,5 −
𝑓 (1,5)
𝑓 ′(1,5)
= 1,5 −
−0,5625
16,75
≈ 1,5 + 0,034 = 1,534

67. Chapitre 7 / Les dérivées en action 67
5. Un entier proche de la solution est 𝑥 = 2. Posons 𝑓 (𝑥) = (2𝑥)𝑥 − 15. Alors
𝑓 ′(𝑥) = (2𝑥)𝑥 [ln(2𝑥) + 1]. La formule (7.10.1) avec 𝑛 = 0 donne
𝑥1 = 𝑥0 − 𝑓 (𝑥0)/ 𝑓 ′
(𝑥0) = 2 − 𝑓 (2)/ 𝑓 ′
(2) = 2 − 1/[16 (ln 4 + 1)] ≈ 1,9738.
6. Si 𝑓 (𝑥0) et 𝑓 ′(𝑥0) sont de signes opposés, comme dans la figure 7.10.1, alors la formule
(7.10.1) implique 𝑥1 𝑥0. Si elles sont de même signe, comme dans la figure 7.10.2,
alors la formule (7.10.1) implique 𝑥1 𝑥0.
7.11
1. (a) 𝛼𝑛 =
(3/𝑛) − 1
2 − (1/𝑛)
→ −
1
2
lorsque 𝑛 → +∞.
(b) 𝛽𝑛 =
1 + (2/𝑛) − (1/𝑛2)
3 − (2/𝑛2)
→
1
3
lorsque 𝑛 → +∞.
(c) 3(−1/2) + 4(1/3) = − 1/6 (d) (−1/2) × (1/3) = −1/6
(e) (−1/2) ÷ (1/3) = −3/2 (f)
p
(1/3) − (−1/2) =
p
5/6 =
√
30/6
2. (a) Quand 𝑛 → +∞, alors
2
𝑛
→ 0, de sorte que 5 −
2
𝑛
→ 5.
(b) Quand 𝑛 → +∞, alors
𝑛2 − 1
𝑛
= 𝑛 −
1
𝑛
→ +∞.
(c) Quand 𝑛 → +∞, alors
3𝑛
√
2𝑛2 − 1
=
3𝑛
𝑛
p
2 − 1/𝑛2
=
3
p
2 − 1/𝑛2
→
3
√
2
=
3
√
2
2
.
3. Pour 𝑥 fixé, on pose 𝑥/𝑛 = 1/𝑚. Alors 𝑛 = 𝑚𝑥 et, lorsque 𝑛 → +∞, 𝑚 → +∞. De là,
(1 + 𝑥/𝑛)𝑛 = (1 + 1/𝑚)𝑚𝑥 = [(1 + 1/𝑚)𝑚]𝑥 → 𝑒𝑥 lorsque 𝑚 → +∞.
7.12
1. (a) Type 0
0 . lim
𝑥→3
3𝑥2 − 27
𝑥 − 3
= lim
𝑥→3
6𝑥
1
= 18, ou en décomposant 3𝑥2 −27 = 3 (𝑥−3) (𝑥+3).
(b) Type 0
0 à répétition.
lim
𝑥→0
𝑒𝑥 − 1 − 𝑥 − 1
2 𝑥2
3𝑥3
= lim
𝑥→0
𝑒𝑥 − 1 − 𝑥
9𝑥2
= lim
𝑥→0
𝑒𝑥 − 1
18𝑥
= lim
𝑥→0
𝑒𝑥
18
=
1
18
(c) Type 0
0 à répétition.
lim
𝑥→0
𝑒−3𝑥 − 𝑒−2𝑥 + 𝑥
𝑥2
= lim
𝑥→0
−3𝑒−3𝑥 + 2𝑒−2𝑥 + 1
2𝑥
= lim
𝑥→0
9𝑒−3𝑥 − 4𝑒−2𝑥
2
=
5
2
2. (a) Type 0
0 . lim
𝑥→𝑎
𝑥2 − 𝑎2
𝑥 − 𝑎
= lim
𝑥→𝑎
2𝑥
1
= 2𝑎 (ou en décomposant 𝑥2 − 𝑎2 = (𝑥 + 𝑎) (𝑥 − 𝑎)).

68. 68 CORRIGÉS DES EXERCICES
(b) Type 0
0 à répétition.
lim
𝑥→0
2 (1 + 𝑥)1/2 − 2 − 𝑥
2(1 + 𝑥 + 𝑥2)1/2 − 2 − 𝑥
= lim
𝑥→0
(1 + 𝑥)−1/2 − 1
(1 + 2𝑥) (1 + 𝑥 + 𝑥2)−1/2 − 1
= lim
𝑥→0
−1
2 (1 + 𝑥)−3/2
2 (1 + 𝑥 + 𝑥2)−1/2 + (1 + 2𝑥)2 (−1
2 ) (1 + 𝑥 + 𝑥2)−3/2
=
−1
2
2 − 1
2
= −
1
3
.
3. (a) Type 0
0 .
lim
𝑥→1
𝑥 − 1
𝑥2 − 1
= lim
𝑥→1
1
2𝑥
=
1
2
(ou utiliser la factorisation 𝑥2 − 1 = (𝑥 + 1) (𝑥 − 1)).
(b) Type 0
0 . lim
𝑥→−2
𝑥3 + 3𝑥2 − 4
𝑥3 + 5𝑥2 + 8𝑥 + 4
= lim
𝑥→−2
3𝑥2 + 6𝑥
3𝑥2 + 10𝑥 + 8
= lim
𝑥→−2
6𝑥 + 6
6𝑥 + 10
= 3.
(c) Type 0
0 . lim
𝑥→2
𝑥4 − 4𝑥3 + 6𝑥2 − 8𝑥 + 8
𝑥3 − 3𝑥2 + 4
= lim
𝑥→2
4𝑥3 − 12𝑥2 + 12𝑥 − 8
3𝑥2 − 6𝑥
= lim
𝑥→2
12𝑥2 − 24𝑥 + 12
6𝑥 − 6
= 2.
(d) Type 0
0 . lim
𝑥→1
ln 𝑥 − 𝑥 + 1
(𝑥 − 1)2
= lim
𝑥→1
(1/𝑥) − 1
2 (𝑥 − 1)
= lim
𝑥→1
(−1/𝑥2)
2
= −
1
2
.
(e) Type 0
0 . lim
𝑥→1
1
𝑥 − 1
ln
7𝑥 + 1
4𝑥 + 4
= lim
𝑥→1
ln(7𝑥 + 1) − ln(4𝑥 + 4)
𝑥 − 1
= lim
𝑥→1
7
7𝑥 + 1
−
4
4𝑥 + 4
1
=
3
8
(f) Type 0
0 . lim
𝑥→1
𝑥𝑥 − 𝑥
1 − 𝑥 + ln 𝑥
= lim
𝑥→1
𝑥𝑥 (ln 𝑥 + 1) − 1
−1 + 1/𝑥
= lim
𝑥→1
𝑥𝑥 (ln 𝑥 + 1)2 + 𝑥𝑥 (1/𝑥)
−1/𝑥2
= −2.
(voir exemple 6.11.4 pour la dérivée de 𝑥𝑥).
4. (a) Type +∞
+∞ . lim
𝑥→+∞
ln 𝑥
𝑥1/2
= lim
𝑥→+∞
1/𝑥
(1/2) 𝑥−1/2
= lim
𝑥→+∞
2
𝑥1/2
= 0.
(b) 0. (Écrire 𝑥 ln 𝑥 =
ln 𝑥
1/𝑥
et appliquer ensuite la règle de l’Hospital.)
(c) +∞. (Écrire 𝑥𝑒1/𝑥 − 𝑥 = 𝑥 (𝑒1/𝑥 − 1) = (𝑒1/𝑥 − 1)/(1/𝑥) et appliquer ensuite la règle
de l’Hospital.)
5. La deuxième fraction n’est pas du type 0/0. La limite correcte est 5/2.
6. Type 0
0 . 𝐿 = lim
𝑣→0+
1 − (1 + 𝑣𝛽)−𝛾
𝑣
= lim
𝑣→0+
𝛾 (1 + 𝑣𝛽)−𝛾−1𝛽𝑣𝛽−1
1
. Si 𝛽 = 1, alors 𝐿 = 𝛾. Si
𝛽 1, alors 𝐿 = 0 et si 𝛽 1, alors 𝐿 = +∞.
7. Type 0
0 . Puisque
d
d𝜌
𝑐1−𝜌 = −𝑐1−𝜌 ln 𝑐, on a lim
𝜌→1
𝑐1−𝜌 − 1
1 − 𝜌
= lim
𝜌→1
−𝑐1−𝜌 ln 𝑐
−1
= ln 𝑐.
8. Type 0
0 . lim
𝑥→+∞
𝑓 (𝑥)
𝑔(𝑥)
= lim
𝑡→0+
𝑓 (1/𝑡)
𝑔(1/𝑡)
= lim
𝑡→0+
𝑓 ′(1/𝑡) (−1/𝑡2)
𝑔′(1/𝑡) (−1/𝑡2)
= lim
𝑡→0+
𝑓 ′(1/𝑡)
𝑔′(1/𝑡)
= lim
𝑥→+∞
𝑓 ′(𝑥)
𝑔′(𝑥)

69. Chapitre 7 / Les dérivées en action 69
9. Type 0
0 . 𝐿 = lim
𝑥→𝑎
𝑓 (𝑥)
𝑔(𝑥)
= lim
𝑥→𝑎
1/𝑔(𝑥)
1/ 𝑓 (𝑥)
= lim
𝑥→𝑎
−1/(𝑔(𝑥))2
−1/( 𝑓 (𝑥))2
𝑔′(𝑥)
𝑓 ′(𝑥)
= lim
𝑥→𝑎
( 𝑓 (𝑥))2
(𝑔(𝑥))2
·
𝑔′(𝑥)
𝑓 ′(𝑥)
= 𝐿2
lim
𝑥→𝑎
𝑔′(𝑥)
𝑓 ′(𝑥)
= 𝐿2
lim
𝑥→𝑎
1
𝑓 ′(𝑥)/𝑔′(𝑥)
La conclusion suit. (Ce raisonnement ne tient pas compte du problème de diviser par 0,
quand soit 𝑓 ′(𝑥), soit 𝑔′(𝑥) tend vers 0 lorsque 𝑥 tend vers 𝑎.)
Exercices récapitulatifs du chapitre 7
1. (a) 𝑦′ = −5, 𝑦′′ = 0
(b) On dérive implicitement par rapport à 𝑥, ce qui donne 𝑦3 + 3𝑥𝑦2𝑦′ = 0 et, de là,
𝑦′ = −𝑦/3𝑥. On dérive 𝑦′ = −𝑦/3𝑥 par rapport à 𝑥
𝑦′′
= −[𝑦′
3𝑥 − 3𝑦]/9𝑥2
= −[(−𝑦/3𝑥) 3𝑥 − 3𝑦]/9𝑥2
= 4𝑦/9𝑥2
.
Comme 𝑦 = 5𝑥−1/3, on obtient 𝑦′ = −(5/3) 𝑥−4/3 et 𝑦′′ = (20/9) 𝑥−7/3. Les réponses
s’obtiennent aussi en dérivant 𝑦 = 5𝑥−1/3.
(c) Comme 2𝑦′𝑒2𝑦 = 3𝑥2, 𝑦′ = (3𝑥2/2) 𝑒−2𝑦. Ensuite
𝑦′′
= 3𝑥𝑒−2𝑦
+
1
2
3𝑥2
𝑒−2𝑦
(−2𝑦′
) = 3𝑥𝑒−2𝑦
−
1
2
9𝑥4
𝑒−4𝑦
.
De l’équation 𝑒2𝑦 = 𝑥3, on tire 2𝑦 = ln 𝑥3 = 3 ln 𝑥 de sorte que 𝑦 = 3
2 ln 𝑥 et alors
𝑦′ = 3
2 𝑥−1, 𝑦′′ = −3
2 𝑥−2. En notant que 𝑒−2𝑦 = 𝑒−3 ln 𝑥 = (𝑒ln 𝑥)−3 = 𝑥−3 et
𝑒−4𝑦 = (𝑒−2𝑦)2 = 𝑥−6, on vérifie que les réponses sont les mêmes.
2. Comme 5𝑦4𝑦′ − 𝑦2 − 2𝑥𝑦𝑦′ = 0, 𝑦′
=
𝑦2
5𝑦4 − 2𝑥𝑦
=
𝑦
5𝑦3 − 2𝑥
. L’équation donnée n’étant
pas valable pour 𝑦 = 0, 𝑦′ n’est jamais nulle.
3. En dérivant implicitement par rapport à 𝑥, on a 3𝑥2+3𝑦2𝑦′ = 3𝑦+3𝑥𝑦′. Quand 𝑥 = 𝑦 = 3/2,
alors 𝑦′ = −1. Voir figure 7.R.1.
4. (a) La dérivation implicite conduit à (∗) 2𝑥𝑦 + 𝑥2𝑦′ + 9𝑦2𝑦′ = 0. En posant 𝑥 = 2 et
𝑦 = 1, on obtient 𝑦′ = −4/13.
(b) La dérivation implicite de (∗) par rapport à 𝑥 conduit à
2𝑦 + 2𝑥𝑦′
+ 2𝑥𝑦′
+ 𝑥2
𝑦′′
+ 18𝑦𝑦′
𝑦′
+ 9𝑦2
𝑦′′
= 0.
La réponse est obtenue en introduisant 𝑥 = 2, 𝑦 = 1 et 𝑦′ = −4/13, puis en résolvant
en 𝑦′′.
5. 1
3 𝐾−2/3𝐿1/3 + 1
3 𝐾1/3𝐿−2/3(d𝐿/d𝐾) = 0 et, de là, d𝐿/d𝐾 = −𝐿/𝐾.
6. Par dérivation implicite par rapport à 𝑥, 𝑦′/𝑦 + 𝑦′ = −2/𝑥 − 0,4 (ln 𝑥)/𝑥. On résout en 𝑦′,
𝑦′
=
−(2/𝑥) (1 + 1
5 ln 𝑥)
1 + 1/𝑦
qui est nul pour 1 + 1
5 ln 𝑥 = 0, c’est-à-dire ln 𝑥 = −5 ou encore 𝑥 = 𝑒−5.

70. 70 CORRIGÉS DES EXERCICES
7. (a) Utilisez (iii) pour remplacer 𝑇 dans (ii), uis servez-vous de l’expression résultante
pour remplacer 𝐶 dans (i).
(b) d𝑌/d𝐼 = 𝑓 ′
((1 − 𝛽)𝑌 − 𝛼) (1 − 𝛽) (d𝑌/d𝐼) + 1. La résolution en d𝑌/d𝐼 conduit à
d𝑌
d𝐼
=
1
1 − (1 − 𝛽) 𝑓 ′((1 − 𝛽)𝑌 − 𝛼)
.
(c) Puisque 𝑓 ′ ∈]0, 1[ et 𝛽 ∈]0, 1[, on a (1 − 𝛽) 𝑓 ′((1 − 𝛽)𝑌 − 𝛼) ∈]0, 1[, de sorte que
d𝑌/d𝐼 0.
8. (a) Par dérivation implicite par rapport à 𝑥, 2𝑥 − 𝑦 − 𝑥𝑦′ + 4𝑦𝑦′ = 0, de sorte que
𝑦′ = (𝑦 − 2𝑥)/(4𝑦 − 𝑥).
(b) Tangente horizontale en (1, 2) et (−1, −2). (𝑦′ = 0 quand 𝑦 = 2𝑥. Introduisez 𝑦 =
2𝑥 dans l’équation donnée.) Tangentes verticales en (2
√
2,
√
2/2) ≈ (2,8 ; 0,7) et en
(−2
√
2, −
√
2/2) ≈ (−2,8 ; −0,7). (Il y a une tangente verticale quand le dénominateur de
l’expression de 𝑦′ est 0, c’est-à-dire quand 𝑥 = 4𝑦.) Voir figure 7.R.2.
9. (a) 𝑦′
=
2 − 2𝑥𝑦
𝑥2 − 9𝑦2
= −
1
2
en (−1, 1).
(b) Une tangente horizontale requiert 𝑦′ = 0, c’est-à-dire 𝑥𝑦 = 1. En introduisant 𝑦 = 1/𝑥
dans l’équation donnée, on obtient 𝑥4 = −3, qui n’a pas de solution. Cela correspond à la
figure 7.R.3.
10. (a) Comme on doit avoir
1 + 𝑥
1 − 𝑥
0,
le domaine de définition de 𝑓 est l’intervalle −1 𝑥 1. Lorsque 𝑥 → 1−, on a
𝑓 (𝑥) → +∞; lorsque 𝑥 → −1−, on a 𝑓 (𝑥) → −∞. Puisque 𝑓 ′(𝑥) = 1/(1 − 𝑥2) 0
quand −1 𝑥 1, 𝑓 est strictement croissante et l’ensemble image de 𝑓 est R.
(b) De 𝑦 =
1
2
ln
1 + 𝑥
1 − 𝑥
découle ln
1 + 𝑥
1 − 𝑥
= 2𝑦 et encore
1 + 𝑥
1 − 𝑥
= 𝑒2𝑦
. La réciproque est
𝑔(𝑦) = (𝑒2𝑦 − 1)/(𝑒2𝑦 + 1). 𝑔′( 1
2 ln 3) = 3/4.
11. (a) 𝑓 (𝑒2) = 2 et 𝑓 (𝑥) = ln 𝑥 (ln 𝑥 − 1)2 = 0 quand ln 𝑥 = 0 et quand ln 𝑥 = 1, de sorte que
𝑥 = 1 ou 𝑥 = 𝑒.
(b) 𝑓 ′(𝑥) = (3/𝑥) (ln 𝑥 − 1) (ln 𝑥 − 1/3) 0 quand 𝑥 𝑒. D’où 𝑓 est strictement
croissante sur [𝑒, +∞[. Elle admet donc une fonction réciproque ℎ. Selon (7.3.2) et parce
que 𝑓 (𝑒2) = 2, on a ℎ′(2) = 1/ 𝑓 ′(𝑒2) = 𝑒2/5.
12. (a) 𝑓 ′(𝑥) = 2/(2𝑥 + 4) = (𝑥 + 2)−1 et 𝑓 ′′(𝑥) = −(𝑥 + 2)−2. D’où 𝑓 (0) = ln 4, 𝑓 ′(0) = 1/2
et 𝑓 ′′(0) = −1/4. Alors 𝑓 (𝑥) ≈ 𝑓 (0) + 𝑓 ′(0) 𝑥 + 1
2 𝑓 ′′(0) 𝑥2 = ln 4 + 𝑥/2 − 𝑥2/8.
(b) 𝑔′(𝑥) = −(1/2) (1+𝑥)−3/2 et 𝑔′′(𝑥) = (3/4) (1+𝑥)−5/2. D’où 𝑔(0) = 1, 𝑔′(0) = −1/2
et 𝑔′′(0) = 3/4. Alors 𝑔(𝑥) ≈ 1 − 𝑥/2 + 3𝑥2/8.
(c) ℎ′(𝑥) = 𝑒2𝑥 + 2𝑥𝑒2𝑥 et ℎ′′(𝑥) = 4𝑒2𝑥 + 4𝑥𝑒2𝑥. D’où ℎ(0) = 0, ℎ′(0) = 1 et ℎ′′(0) = 4.
Alors ℎ(𝑥) ≈ 𝑥 + 2𝑥2.
13. (a) 𝑥 d𝑥/
√
1 + 𝑥2 (b) 8𝜋𝑟 d𝑟 (c) 400𝐾3 d𝐾 (d) −3𝑥2 d𝑥/(1 − 𝑥3).

71. Chapitre 7 / Les dérivées en action 71
14. d 𝑓 (𝑥) = 𝑓 ′(𝑥) d𝑥 = 3𝑥2 d𝑥/2
√
1 + 𝑥3. Ensuite,
Δ 𝑓 (2) ≈ d 𝑓 (2) = 3 × 22
(0,2)/2
p
1 + 23 = 0,4.
15. Avec 𝑥 = 1
2 et 𝑛 = 5, la formule (7.6.6) fournit
𝑒
1
2 = 1 +
1
2
1!
+
( 1
2 )2
2!
+
( 1
2 )3
3!
+
( 1
2 )4
4!
+
( 1
2 )5
5!
+
( 1
2 )6
6!
𝑒𝑧
où 𝑧 est un certain nombre compris entre 0 et 1
2 . Maintenant,
𝑅6 ( 1
2 ) =
( 1
2 )6
6!
𝑒𝑧
( 1
2 )6
6!
2 =
1
23040
≈ 0,00004340
où on a employé le fait que 𝑧 1
2 implique 𝑒𝑧 𝑒
1
2 2. Il vient
𝑒
1
2 ≈ 1 +
1
2
1!
+
( 1
2 )2
2!
+
( 1
2 )3
3!
+
( 1
2 )4
4!
+
( 1
2 )5
5!
= 1 +
1
2
+
1
8
+
1
48
+
1
384
+
1
3840
≈ 1,6486979.
Comme l’erreur est inférieure à 0,000043, l’approximation 𝑒
1
2 ≈ 1,649 est correcte
jusqu’à la troisième décimale.
16. 𝑦′ + (1/𝑦) 𝑦′ = 1 ou (∗) 𝑦𝑦′ + 𝑦′ = 𝑦. Quand 𝑦 = 1, on a 𝑦′ = 1/2. On dérive (∗) par
rapport à 𝑥, (𝑦′)2 + 𝑦𝑦′′ + 𝑦′′ = 𝑦′. Avec 𝑦 = 1 et 𝑦′ = 1/2, on trouve 𝑦′′ = 1/8 de sorte
que 𝑦 (𝑥) ≈ 1 + 1
2 𝑥 + 1
16 𝑥2.
17. (a) Continue pour tout 𝑥 ≠ 0. (b) Continue pour tout 𝑥 0. (Notez que 𝑥2 + 2𝑥 + 2
n’est jamais nul.) (c) Continue pour tout 𝑥 dans ] − 2, 2[.
18. (a) Comme 1 = 𝑓 ′(𝑦2) 2𝑦𝑦′, 𝑦′
=
1
2𝑦 𝑓 ′(𝑦2)
.
(b) Comme 𝑦2 + 𝑥2𝑦𝑦′ = 𝑓 ′(𝑥) − 3𝑦2𝑦′, 𝑦′
=
𝑓 ′(𝑥) − 𝑦2
𝑦 (2𝑥 + 3𝑦)
.
(c) Comme 𝑓 ′(2𝑥 + 𝑦) (2 + 𝑦′) = 1 + 2𝑦𝑦′, 𝑦′
=
1 − 2 𝑓 ′(2𝑥 + 𝑦)
𝑓 ′(2𝑥 + 𝑦) − 2𝑦
.
19. El𝑟 (𝐷marg) = −0,165 et El𝑟 (𝐷rhm) = 2,39. Pour chaque augmentation du revenu de 1 %,
la demande en margarine diminue d’environ 0,165 %, pendant que la demande de repas
hors de la maison croît approximativement de 2,39 %.
20. (a) 5 (en utilisant la formule (7.7.3)).
(b) 1/3 (compte tenu de 3
√
𝑥 = 𝑥1/3 et (7.7.3)).
(c) El𝑥 (𝑥3
+ 𝑥5
) =
𝑥
𝑥3 + 𝑥5
(3𝑥2
+ 5𝑥4
) = (5𝑥2
+ 3)/(𝑥2
+ 1), par (7.7.2).
(Vous pouvez aussi utiliser l’exercice 7.7.9d.)
(d) 2𝑥/(𝑥2 − 1), en utilisant les parties (c) et (d) de l’exercice 7.7.9.
21. Poser 𝑓 (𝑥) = 𝑥3 − 𝑥 − 5. Alors 𝑓 ′(𝑥) = 3𝑥2 − 1. Si 𝑥0 = 2, la formule (7.10.1) avec 𝑛 = 1
donne 𝑥1 = 2 − 𝑓 (2)/ 𝑓 ′(2) = 2 − 1/11 ≈ 1,909.

72. 72 CORRIGÉS DES EXERCICES
22. La fonction 𝑓 est continue, 𝑓 (1) = 𝑒 − 3 0 et 𝑓 (4) = 𝑒2 − 3 0. D’après le
théorème 7.10.1(a), une racine de 𝑓 se trouve dans ]1, 4[. Comme 𝑓 ′(𝑥) 0, la solution
est unique. La formule (7.10.1) fournit 𝑥1 = 1 − 𝑓 (1)/ 𝑓 ′(1) = −1 + 6/𝑒 ≈ 1,21.
23. (a) lim
𝑥→3−
(𝑥2
− 3𝑥 + 2) = 9 − 9 + 2 = 2
(b) Tend vers +∞.
(c)
3 −
√
𝑥 + 17
𝑥 + 1
tend vers +∞ lorsque 𝑥 → −1−, mais vers −∞ lorsque 𝑥 → −1+.
La limite lorsque 𝑥 → −1 n’existe donc pas.
(d) lim
𝑥→0
(2 − 𝑥) 𝑒𝑥 − 𝑥 − 2
𝑥3
(type 0
0 ) = lim
𝑥→0
−𝑒𝑥 + (2 − 𝑥) 𝑒𝑥 − 1
3𝑥2
(type 0
0 )
= lim
𝑥→0
−𝑒𝑥 − 𝑒𝑥 + (2 − 𝑥) 𝑒𝑥
6𝑥
= lim
𝑥→0
−𝑥𝑒𝑥
6𝑥
= lim
𝑥→0
−𝑒𝑥
6
= −
1
6
(Simplifier par 𝑥 à l’avant-dernière étape évite d’employer la règle de l’Hospital une
troisième fois.)
(e) On a lim
𝑥→3
1
𝑥 − 3
−
5
𝑥2 − 𝑥 − 6
= lim
𝑥→3
𝑥2 − 6𝑥 + 9
𝑥3 − 4𝑥2 − 3𝑥 + 18
(type 0
0 )
= lim
𝑥→3
2𝑥 − 6
3𝑥2 − 8𝑥 − 3
(type 0
0 ) = lim
𝑥→3
2
6𝑥 − 8
=
1
5
.
(f) lim
𝑥→4
𝑥 − 4
2𝑥2 − 32
(type 0
0 ) = lim
𝑥→4
1
4𝑥
=
1
16
. Une autre façon de faire est de noter que
2𝑥2
− 32 = 2(𝑥2
− 16) = 2(𝑥 − 4)(𝑥 + 4),
puis d’éliminer 𝑥 − 4.
(g) Si 𝑥 ≠ 2, alors
𝑥2 − 3𝑥 + 2
𝑥 − 2
=
(𝑥 − 2) (𝑥 − 1)
𝑥 − 2
= 𝑥 − 1, qui tend vers 1 lorsque 𝑥 → 2.
(h) Si 𝑥 ≠ −1, alors
4 −
√
𝑥 + 17
2𝑥 + 2
=
(4 −
√
𝑥 + 17 ) (4 +
√
𝑥 + 17 )
(2𝑥 + 2) (4 +
√
𝑥 + 17 )
=
16 − 𝑥 − 17
(2𝑥 + 2) (4 +
√
𝑥 + 17 )
=
−1
2 (4 +
√
𝑥 + 17 )
qui tend vers −
1
16
lorsque 𝑥 → −1.
(i) lim
𝑥→∞
(ln 𝑥)2
3𝑥2
=
1
3
lim
𝑥→∞
ln 𝑥
𝑥
2
= 0 (voir 7.12.3).
24. Quand 𝑥 → 0, le numérateur tend vers
√
𝑏 −
√
𝑑 et le dénominateur vers 0. La limite
n’existe donc pas pour 𝑑 ≠ 𝑏. Quand 𝑑 = 𝑏, cependant,
lim
𝑥→0
√
𝑎𝑥 + 𝑏 −
√
𝑐𝑥 + 𝑏
𝑥
(type 0
0 ) = lim
𝑥→0
1
2 𝑎(𝑎𝑥 + 𝑏)−1/2 − 1
2 𝑐(𝑐𝑥 + 𝑏)−1/2
1
=
𝑎 − 𝑐
2
√
𝑏
.

73. Chapitre 8 / Fonctions concaves et convexes 73
25. Type 0
0 . lim
𝑥→0
𝑎𝑥 − 𝑏𝑥
𝑒𝑎𝑥 − 𝑒𝑏𝑥
= lim
𝑥→0
𝑎𝑥 ln 𝑎 − 𝑏𝑥 ln 𝑏
𝑎𝑒𝑎𝑥 − 𝑏𝑒𝑏𝑥
=
ln 𝑎 − ln 𝑏
𝑎 − 𝑏
.
26. 𝑥1 = 0,9 − 𝑓 (0,9)/ 𝑓 ′(0,9) ≈ 0,9247924, 𝑥2 = 𝑥1 − 𝑓 (𝑥1)/ 𝑓 ′(𝑥1) ≈ 0,9279565,
𝑥3 = 𝑥2 − 𝑓 (𝑥2)/ 𝑓 ′(𝑥2) ≈ 0,9280338 et 𝑥4 = 𝑥3 − 𝑓 (𝑥3)/ 𝑓 ′(𝑥3) ≈ 0,9280339.
Il semble que la réponse correcte à trois décimales soit 0,928.
Chapitre 8 / Fonctions concaves et convexes
8.2
1. Le graphique de 𝑓 visible en figure 8.2.9 consiste en deux segments de droites unis au
sommet. Si deux points 𝑎 et 𝑏 appartiennent au même segment, incluant le pic, alors les
deux inégalités (8.2.1) et (8.2.2) sont toutes deux remplies avec égalité. En revanche, si
ces deux points 𝑎 et 𝑏 sont sur des segments différents, alors seule (8.2.1) est vérifiée. La
fonction est concave, mais non strictement concave.
2. (a) Quand la fonction 𝑓 est strictement concave, alors l’inégalité (8.2.1) est vérifiée
strictement pour tous 𝑎 et 𝑏 distincts de 𝐼 et pour tout 0 𝜆 1; elle est donc vérifiée de
manière faible. Elle est aussi vérifiée en tant qu’égalité si 𝑎 = 𝑏 ou si 𝜆 = 0 ou 𝜆 = 1.
(b) Si le graphique de la fonction est une droite, alors les inégalités (8.2.1) et (8.2.2) sont
toutes deux vérifiées avec égalité pour tous 𝑎 et 𝑏 de 𝐼 et tout 𝜆 ∈ [0, 1]. La fonction 𝑓
est donc à la fois concave et convexe.
(c) La fonction définie par 𝑓 (𝑥) = 0 pour tout réel 𝑥 est un exemple de fonction concave
mais non strictement concave. C’est aussi le cas de toute fonction du premier degré ou de
la fonction de l’exercice 1.
(d) Quand une fonction est strictement concave, l’inégalité (8.2.1) est vérifiée strictement
pour tous 𝑎 et 𝑏 distincts de 𝐼 et tout 0 𝜆 1. Cette inégalité stricte est en contradiction
avec l’inégalité (8.2.2), la fonction ne peut donc pas être convexe.
3. La fonction associée au graphique de la figure 8.2.7 est strictement concave, tandis que
la fonction associée au graphique de la figure 8.2.8 est strictement convexe.
4. Pour un niveau de production 𝑄 0 donné, supposons que l’entreprise compare les
coûts totaux : (i) 𝑐(𝑄) de produire 𝑄 sur le site de production initial, sans ouverture d’un
nouveau site; (ii) 2𝑐( 1
2 𝑄) d’utiliser deux sites de production en répartissant la production
de manière égale. Comme 𝑐 est strictement convexe, on a 𝑐
1
2𝑄
= 𝑐
1
2 𝑄 + 1
2 × 0
1
2 𝑐(𝑄) + 1
2 𝑐(0) = 1
2 𝑐(𝑄), d’où 2𝑐( 1
2 𝑄) 𝑐(𝑄). L’option (ii) est moins chère, l’entreprise
a intérêt à répartir sa production sur deux sites.
5. Considérons les deux niveaux de revenus 𝑦 et 𝑧, avec 𝑧 𝑦. On sait grâce à l’exemple 5.2.1
et à la figure 5.4.9 représentant la fonction impôt sur le revenu qu’une hausse du revenu
imposable de 𝑦 à 𝑧 entraîne à la fois une hausse de l’impôt sur le revenu de 𝑇(𝑦) à 𝑇(𝑧)
et une hausse du taux moyen de [𝑇(𝑧) − 𝑇(𝑦)]/(𝑧 − 𝑦) sur les 𝑧 − 𝑦 dollars de revenu
supplémentaire. Or, ce taux moyen est la pente 𝑠(𝑦, 𝑧) de la fonction impôt sur le revenu 𝑇.

74. 74 CORRIGÉS DES EXERCICES
D’après le point (iii) du théorème 8.2.1, 𝑇 est donc convexe. Comme le graphique de 𝑇
est formé de segments de droite, 𝑇 ne peut cependant pas être strictement convexe.
6. Supposons que 𝑓 soit croissante mais non strictement croissante. Il existe alors 𝑎, 𝑏 de 𝐼
tels que 𝑎 𝑏 et 𝑓 (𝑎) = 𝑓 (𝑏) = 𝑓 (𝑥) pour tout 𝑥 de ]𝑎, 𝑏[. Ainsi,
𝑓 (𝑎) = 𝑓 (𝑏) = 𝑓
1
2
(𝑎 + 𝑏)
≯
1
2
[ 𝑓 (𝑎) + 𝑓 (𝑏)],
ce qui enfreint les conditions de stricte concavité. Par conséquent, si 𝑓 est croissante et
strictement concave, elle est nécessairement strictement croissante.
7. (a) Pour tout 𝑎 et tout 𝑥 de ] − ∞, +∞[ avec 𝑥 ≠ 𝑎, la pente de 𝑥2 vérifie 𝑠(𝑎, 𝑥) =
(𝑥2 − 𝑎2)/(𝑥 − 𝑎) = 𝑥 + 𝑎. Cette fonction est, de manière évidente, strictement croissante
en 𝑥. Ainsi, 𝑥2 est strictement convexe sur ] − ∞, +∞[.
(b) Pour tout 𝑎 et tout 𝑥 de [0, +∞[ avec 𝑥 ≠ 𝑎, la pente de 𝑥𝑛 vérifie
𝑠(𝑎, 𝑥) = (𝑥𝑛
− 𝑎𝑛
)/(𝑥 − 𝑎) =
𝑛
Õ
𝑘=1
𝑥𝑛−𝑘
𝑎𝑘−1
.
Lorsque 𝑥 varie sur l’intervalle [0, +∞[, chaque terme de la somme est strictement
croissant en 𝑥 à part le dernier terme constant 𝑎𝑛−1. La somme entière 𝑠(𝑎, 𝑥) est donc
strictement croissante en 𝑥. La fonction puissance 𝑥𝑛 est donc strictement convexe sur
[0, +∞[.
(c) Si 𝑛 est pair, alors la pente de la fonction 𝑦 = (−𝑥)𝑛 vérifie
𝑠(−𝑎, −𝑥) =
(−𝑥)𝑛 − (−𝑎)𝑛
(−𝑥) − (−𝑎)
=
𝑥𝑛 − 𝑎𝑛
𝑎 − 𝑥
= −𝑠(𝑎, 𝑥).
On a démontré que, lorsque 𝑎 ⩾ 0 et 𝑥 ⩾ 0, alors 𝑠(𝑎, 𝑥) est strictement croissante en
𝑥. Ainsi, 𝑠(−𝑎, −𝑥) est strictement décroissante en 𝑥, et donc strictement décroissante en
−𝑥. On en conclut que, si 𝑛 est pair, 𝑥𝑛 est strictement convexe sur ] − ∞, 0].
(d) Si 𝑛 est impair, alors
𝑠(−𝑎, −𝑥) =
(−𝑥)𝑛 − (−𝑎)𝑛
(−𝑥) − (−𝑎)
=
−𝑥𝑛 + 𝑎𝑛
𝑎 − 𝑥
= 𝑠(𝑎, 𝑥).
Dans ce cas, si 𝑎 ⩾ 0 et 𝑥 ⩾ 0, alors 𝑠(−𝑎, −𝑥) est strictement croissante en 𝑥, et donc
strictement décroissante en −𝑥. On en conclut que, si 𝑛 est impair, 𝑥𝑛 est strictement
concave sur ] − ∞, 0].
8. (i) La fonction 𝑓 (𝑥) = ln 𝑥 est croissante en 𝑥. L’inégalité de l’exercice 2.6.8 entraîne que
1
2 𝑎 + 1
2 𝑏 ⩾
√
𝑎𝑏, d’où
ln 1
2 𝑎 + 1
2 𝑏
⩾ ln
√
𝑎𝑏
= ln
√
𝑎
+ ln
√
𝑏
= 1
2 ln 𝑎 + 1
2 ln 𝑏.
On en conclut que ln 𝑥 est « milieu-concave », et donc concave. (ii) D’après l’inégalité de
l’exercice 2.6.8, les deux nombres 𝑒𝑎 et 𝑒𝑏 vérifient 1
2 𝑒𝑎 + 1
2 𝑒𝑏 ⩾
√
𝑒𝑎𝑒𝑏 = 𝑒
1
2 𝑎+ 1
2 𝑏. On
en déduit que la fonction 𝑓 (𝑥) = 𝑒𝑥 est « milieu-convexe », et donc convexe.

75. Chapitre 8 / Fonctions concaves et convexes 75
9. La définition de la concavité implique que l’inégalité est vérifiée pour 𝑛 = 2. Prenons
pour hypothèse de récurrence qu’elle est aussi vérifiée lorsque 𝑛 = 𝑘, pour 𝑘 = 2, 3, . . .
Supposons à présent que 𝑛 = 𝑘 + 1 et que les 𝑘 + 1 constantes strictement positives
𝜆𝑖 (𝑖 = 1, . . . , 𝑘 + 1) sont telles que
Í𝑘+1
𝑖=1 𝜆𝑖 = 1. Définissons maintenant, pour tout
𝑖 = 1, . . . , 𝑘, la nouvelle constante strictement positive 𝜃𝑖 = 𝜆𝑖/(1 − 𝜆𝑘+1). De manière
évidente, l’hypothèse
Í𝑘+1
𝑖=1 𝜆𝑖 = 1 entraîne
Í𝑘
𝑖=1 𝜃𝑖 = 1. Notons 𝑥𝑘 la somme
Í𝑘
𝑖=1 𝜃𝑖𝑥𝑖.
Alors
𝑘+1
Õ
𝑖=1
𝜆𝑖𝑥𝑖 = (1 − 𝜆𝑘+1)𝑥𝑘
+ 𝜆𝑘+1𝑥𝑘+1.
Comme 𝑓 est concave et 0 𝜆𝑘+1 = 1 −
Í𝑘
𝑖=1 𝜆𝑖 1, on a
𝑓
𝑘+1
Õ
𝑖=1
𝜆𝑖𝑥𝑖
!
⩾ (1 − 𝜆𝑘+1) 𝑓 (𝑥𝑘
) + 𝜆𝑘+1 𝑓 (𝑥𝑘+1)
Mais l’hypothèse de récurrence implique 𝑓 (𝑥𝑘) ⩾
Í𝑘
𝑖=1 𝜃𝑖 𝑓 (𝑥𝑖). Comme 𝜆𝑘+1 1, les
définitions ci-dessus entraînent
𝑓
𝑘+1
Õ
𝑖=1
𝜆𝑖𝑥𝑖
!
⩾ (1 − 𝜆𝑘+1)
𝑘
Õ
𝑖=1
𝜃𝑖 𝑓 (𝑥𝑖) + 𝜆𝑘+1 𝑓 (𝑥𝑘+1) =
𝑘+1
Õ
𝑖=1
𝜆𝑖 𝑓 (𝑥𝑖).
Ce qui achève la démonstration par récurrence.
8.3
1. Les définitions impliquent que, pour tous 𝑎 et 𝑏 distincts de 𝐼 et tout 0 𝜆 1, on a
𝑓 (𝜆𝑎 + (1 − 𝜆)𝑏) 𝜆 𝑓 (𝑎) + (1 − 𝜆) 𝑓 (𝑏) et 𝑔(𝜆𝑎 + (1 − 𝜆)𝑏) ⩾ 𝜆𝑔(𝑎) + (1 − 𝜆)𝑔(𝑏).
En ajoutant ces deux inégalités, on montre que la fonction ℎ(𝑥) = 𝑓 (𝑥) + 𝑔(𝑥) vérifie
ℎ(𝜆𝑎 + (1 − 𝜆)𝑏) 𝜆ℎ(𝑎) + (1 − 𝜆)ℎ(𝑏). La fonction 𝑓 + 𝑔 est donc strictement concave.
2. L’inverse de la fonction strictement concave 𝑔(𝑥) =
√
𝑥, définie pour tout 𝑥 ⩾ 0, est
la fonction croissante convexe ℎ(𝑥) = 𝑥2, définie pour tout 𝑥 ⩾ 0. Alors, si 𝑎 ⩾ 0, la
fonction 𝑓 (𝑥) = 𝑎𝑥2 + 𝑏 = 𝑎ℎ(𝑥) + 𝑏, définie pour tout 𝑥 ⩾ 0, est une fonction croissante
de la fonction convexe ℎ(𝑥). Elle est donc convexe.
3. Vous pouvez utiliser la fonction 𝑓 (𝑥) = 𝑐, où 𝑐 est une constante, comme exemple de
fonction non strictement concave. Et vous pouvez prendre la fonction 𝑔(𝑦) = 𝑐′, où 𝑐′ est
une constante, comme exemple de fonction croissante concave non strictement croissante.
Dans chacun des deux cas, la fonction composée ℎ(𝑥) = 𝑔( 𝑓 (𝑥)) est une constante : elle
n’est donc pas strictement concave.
4. Comme hypothèse de récurrence, supposons que la fonction définie sur l’intervalle 𝐼 par
𝑓 𝑘
∗ (𝑥) = min{ 𝑓𝑖 (𝑥) : 𝑖 = 1, 2, . . . , 𝑘} est concave si les 𝑘 fonctions 𝑓𝑖 (𝑥) (𝑖 = 1, 2, . . . , 𝑘)
sont toutes concaves. Nous l’avons montré en section 8.3 dans le cas 𝑘 = 2. Supposons que
c’est vrai pour un 𝑘 ⩾ 2. Alors 𝑓 𝑘+1
∗ (𝑥) = min{ 𝑓 𝑘
∗ (𝑥), 𝑓𝑘+1(𝑥)}, où 𝑓 𝑘
∗ (𝑥) est concave
d’après l’hypothèse de récurrence. Si on suppose que 𝑓𝑘+1(𝑥) est aussi concave, alors
𝑓 𝑘+1
∗ (𝑥) est le minimum de deux fonctions concaves; elle est donc concave. Cela achève
l’étape d’hérédité.

76. 76 CORRIGÉS DES EXERCICES
5. (a) En reprenant le raisonnement de l’exemple 8.3.2, la fonction
𝑓 (𝑥) = −|𝑥 − 1| = − max{𝑥 − 1, 1 − 𝑥}
est concave, tandis que la fonction 𝑔(𝑥) = |𝑥 + 1| = max{𝑥 + 1, −𝑥 − 1} est convexe.
(b) Notez que 𝑓 (𝑥) + 𝑔(𝑥) = |𝑥 + 1| − |𝑥 − 1| est égal à : −(𝑥 + 1) − (1 − 𝑥) = −2 sur
] − ∞, −1[ ; (𝑥 + 1) − (1 − 𝑥) = 2𝑥 sur ] − 1, 1[ ; (𝑥 + 1) − (𝑥 − 1) = 2 sur ]1, +∞[. Ainsi,
sur l’intervalle ]𝑎, 𝑏[, la fonction 𝑓 + 𝑔 est : (i) convexe sauf si ]𝑎, 𝑏[ inclut 𝑥 = 1, où il
y a un point anguleux; (ii) concave sauf si ]𝑎, 𝑏[ inclut −1, où il y a un deuxième point
anguleux; (iii) à la fois concave et convexe si ]𝑎, 𝑏[ n’inclut ni −1 ni 1; (iv) ni concave ni
convexe si ]𝑎, 𝑏[ inclut à la fois −1 et 1. Voir la figure C8.3.5 qui représente le graphique
de 𝑓 + 𝑔.
x
y
−3 −2 −1 1 2 3
−2
−1
1
2
1
Figure C8.3.5
6. D’après la question (a) de l’exercice 8.2.7, la fonction 𝑓 (𝑥) = 𝑥2 est strictement convexe
sur ] − ∞, +∞[, avec pour ensemble image [0, +∞[. De plus, la fonction 𝑔(𝑦) = 𝑦𝑚 est
à la fois strictement convexe et strictement croissante sur [0, +∞[. La fonction composée
𝑔( 𝑓 (𝑥)) = (𝑥2)𝑚 = 𝑥𝑛 est donc strictement convexe sur ] − ∞, +∞[.
8.5
1. Soit 𝑓 (𝑥) = ln 𝑥 définie pour tout 𝑥 0. On a 𝑓 ′′(𝑥) = −𝑥−2 0, donc ln 𝑥 est strictement
concave sur ]0, +∞[. Soit 𝑔(𝑥) = 𝑒𝑥définie pour tout réel 𝑥, on a 𝑔′′(𝑥) = 𝑒𝑥 0, donc
𝑒𝑥 est strictement convexe sur l’ensemble des nombres réels.
2. Les deux premières dérivées de ℎ(𝑥) = −𝑥2+𝑥3 sont ℎ′(𝑥) = −2𝑥+3𝑥2 et ℎ′′(𝑥) = −2+6𝑥.
Ainsi, ℎ′′(𝑥) 0 ⇔ 𝑥 1
3 et ℎ′′(𝑥) 0 ⇔ 𝑥 1
3 . Par conséquent, ℎ est : (a) concave
sur ]𝑎, 𝑏[ si et seulement si 0 ⩽ 𝑎 𝑏 ⩽ 1
3 ; (b) convexe sur ]𝑎, 𝑏[ si et seulement si
1
3 ⩽ 𝑎 𝑏 ; (c) ni concave ni convexe sur ]𝑎, 𝑏[ si et seulement si 𝑎 1
3 𝑏. Voir la
figure C8.5.2, qui représente le graphique de ℎ(𝑥).
3. En dérivant ℎ(𝑥) = 𝑔( 𝑓 (𝑥)) deux fois à l’aide de la règle de dérivation d’une fonction
composée, on obtient ℎ′(𝑥) = 𝑔′( 𝑓 (𝑥)) 𝑓 ′(𝑥) puis, en utilisant la règle de dérivation
du produit, ℎ′′(𝑥) = 𝑔′′( 𝑓 (𝑥))( 𝑓 ′(𝑥))2 + 𝑔′( 𝑓 (𝑥)) 𝑓 ′′(𝑥). Comme les hypothèses sont
𝑓 ′′ ⩽ 0, 𝑔′ ⩾ 0 et 𝑔′′ ⩽ 0, on a ℎ′′(𝑥) ⩽ 0, donc ℎ(𝑥) est concave.

77. Chapitre 8 / Fonctions concaves et convexes 77
x
y
1
1/ 3 2/ 3
− 0,1
0,1
0,2
Figure C8.5.2
4. Soit la fonction 𝑓 (𝑥) = −𝑥4, définie pour tout réel 𝑥. D’après l’exercice 8.3.6, la fonction
puissance paire 𝑥4 est strictement convexe, donc 𝑓 est strictement concave. Pourtant,
𝑓 ′′(𝑥) = −12𝑥2 ≮ 0 en 𝑥 = 0.
5. (a) Comme 𝑓 ′(𝑥) ≠ 0 pour tout 𝑥 de 𝐼, d’après le théorème 7.3.1 sur la dérivée de la
fonction réciproque, la réciproque 𝑔(𝑦) = 𝑓 −1(𝑦) est bien définie et dérivable pour tout
𝑦 de l’ensemble image 𝑓 (𝐼), avec 𝑔′( 𝑓 (𝑥)) = 1/ 𝑓 ′(𝑥). De plus, comme 𝑓 ′(𝑥) ≠ 0,
la fonction 𝑔 est deux fois dérivable, avec 𝑔′′( 𝑓 (𝑥)) = − 𝑓 ′′(𝑥)/[ 𝑓 ′(𝑥)]3, comme dans
l’équation (7.3.3).
(b) Si 𝑓 ′ 0, alors 𝑓 ′′ et 𝑔′′ sont de même signe. Si 𝑓 ′ 0, alors 𝑓 ′′ et 𝑔′′ sont de signes
opposés.
(c) Quand 𝑓 ′(𝑥) ≠ 0 et 𝑓 ′′(𝑥) ≠ 0 pour tout 𝑥 de 𝐼, on a les propriétés suivantes, qui
renforcent les résultats de la section 8.3 : (i) si 𝑓 ′ 0 sur tout 𝐼 et si 𝑓 est strictement
concave, sa réciproque 𝑔 vérifie 𝑔′ 0 et est strictement convexe; (ii) si 𝑓 ′ 0 sur tout 𝐼
et si 𝑓 est strictement convexe, sa réciproque 𝑔 vérifie 𝑔′ 0 et est strictement concave;
(iii) si 𝑓 ′ 0 sur tout 𝐼 et si 𝑓 est strictement concave, sa réciproque 𝑔 vérifie 𝑔′ 0
et est strictement concave; (iv) si 𝑓 ′ 0 sur tout 𝐼 et si 𝑓 est strictement convexe, sa
réciproque 𝑔 vérifie 𝑔′ 0 et est strictement convexe;
8.6
1. (a) Comme 𝑓 ′(𝑥) = 3𝑥2 + 3𝑥 − 6 = 3 (𝑥 − 1) (𝑥 + 2), 𝑥 = −2 et 𝑥 = 1 sont des points
critiques. Un tableau de signes montre que 𝑓 est croissante sur ] − ∞, −2] et sur [1, +∞[.
(b) 𝑓 ′′(𝑥) = 6𝑥 + 3 = 0 en 𝑥 = −1/2 en changeant de signe, c’est donc l’abscisse d’un
point d’inflexion.
2. (a) 𝑓 ′′(𝑥) = 2𝑥 (𝑥2 − 3)/(1 + 𝑥2)3. Un tableau de signes montre que 𝑓 est convexe sur
[−
√
3, 0] et sur [
√
3, +∞[. Les abscisses des points d’inflexion sont 𝑥 = −
√
3, 0,
√
3.
(b) 𝑔′′(𝑥) = 4 (1 + 𝑥)−3 0 quand 𝑥 −1, de sorte que 𝑔 est (strictement) convexe sur
] − 1, +∞[. Il n’y a pas de point d’inflexion.
(c) ℎ′′(𝑥) = (2 + 𝑥) 𝑒𝑥, de sorte que ℎ est convexe sur [−2, +∞[ et il y a un point
d’inflexion en 𝑥 = −2.

78. 78 CORRIGÉS DES EXERCICES
3. Les réponses s’obtiennent directement à partir des signes des dérivées.
(a) 𝑦′ = −𝑒−𝑥 (1 + 𝑥), 𝑦′′ = 𝑥𝑒−𝑥. Il y a un point d’inflexion en 𝑥 = 0. La fonction est
concave sur ] − ∞, 0], convexe sur [0, +∞[.
(b) 𝑦′
= (𝑥 − 1)/𝑥2
, 𝑦′′
= (2 − 𝑥)/𝑥3
. Il y a un point d’inflexion en 𝑥 = 2. La fonction est
convexe sur ]0, 2], concave sur [2, +∞[.
(c) 𝑦′ = 𝑥2𝑒−𝑥 (3 − 𝑥), 𝑦′′ = 𝑥𝑒−𝑥 (𝑥2 − 6𝑥 + 6). Il y a trois points d’inflexion en 𝑥1 = 0,
𝑥2 = 3 −
√
3 et 𝑥3 = 3 +
√
3. La fonction est concave sur ] − ∞, 𝑥1], convexe sur [𝑥1, 𝑥2],
concave sur [𝑥2, 𝑥3], convexe sur [𝑥3, +∞[.
(d) On a
𝑦′
=
1 − 2 ln 𝑥
𝑥3
et 𝑦′′
=
6 ln 𝑥 − 5
𝑥4
.
Il y a un point d’inflexion en 𝑥0 = 𝑒5/6 ≈ 2,30. La fonction est concave sur ]0, 𝑥0], convexe
sur [𝑥0, +∞[.
(e) 𝑦′ = 2𝑒𝑥 (𝑒𝑥 − 1), 𝑦′′ = 2𝑒𝑥 (2𝑒𝑥 − 1). Il y a un point d’inflexion en 𝑥0 = − ln 2. La
fonction est concave sur ] − ∞, − ln 2], convexe sur [− ln 2, +∞[.
(f) 𝑦′ = 𝑒−𝑥 (2 − 𝑥2), 𝑦′′ = 𝑒−𝑥 (𝑥2 − 2𝑥 − 2). Il y a deux points d’inflexion en 𝑥1 = 1 −
√
3
et 𝑥2 = 1 +
√
3. La fonction est convexe sur ] − ∞, 𝑥1], concave sur [𝑥1, 𝑥2], convexe sur
[𝑥2, +∞[.
4. Il y a quatre points d’inflexion en 𝑥 = 0, 𝑥 = 1, 𝑥 = 3 et 𝑥 = 5.
5. Comme 𝑓 (−1) = 1, on a −𝑎 + 𝑏 = 1. De plus, 𝑓 ′(𝑥) = 3𝑎𝑥2 + 2𝑏𝑥 et 𝑓 ′′(𝑥) = 6𝑎𝑥 + 2𝑏,
donc 𝑓 ′′(1/2) = 0 conduit à 3𝑎 + 2𝑏 = 0. En résolvant les deux équations simultanément
en 𝑎 et 𝑏, on obtient 𝑎 = −2/5 et 𝑏 = 3/5.
Exercices récapitulatifs du chapitre 8
1. La fonction 𝑓 (𝑥) =
√
𝑥 est concave tandis que 𝑔(𝑦) = 𝑦3 est convexe. La fonction com-
posée s’écrit ℎ(𝑥) = 𝑔( 𝑓 (𝑥)) =
√
𝑥
3
= 𝑥3/2, avec ℎ′(𝑥) = 3
2 𝑥1/2 et ℎ′′(𝑥) = 3
2 𝑥−1/2 0.
Cette fonction ℎ est donc strictement convexe pour 𝑥 0. Aucune contradiction n’est
possible car les résultats de la section 8.3 ne disent rien au sujet des fonctions convexes
d’une fonction concave.
2. (a) 𝑔′(𝑥) = 9𝑥2 − 𝑥4 et 𝑔′′(𝑥) = 18𝑥 − 4𝑥3.
(b) 𝑔 est croissante sur l’intervalle (−3, 3) et concave sur chacun des intervalles ]− 3
2
√
2, 0[
et ] 3
2
√
2, +∞[.
(c) La figure C8.R.2 montre le graphique de 𝑔 et les points d’inflexion correspondant à
𝑥 = 0 et 𝑥 = ±3
2
√
2 ≈ ±2,1213.
3. 𝑓 ′(𝑎) = 𝑓 ′(𝑐) = 0, 𝑓 ′(𝑏) 0, 𝑓 ′′(𝑎) 0, 𝑓 ′′(𝑏) = 0 et 𝑓 ′′(𝑐) 0. Seule la combinaison
(b) est donc correcte.
4. (a) 𝑓 ′′(𝑥) = 12𝑥 − 24. La fonction 𝑓 est donc concave sur ] − ∞, 2] et convexe sur
[2, +∞[.
(b) 𝑓 ′′(𝑥) = 8𝑥−3 pour 𝑥 ≠ 0. La fonction 𝑓 est donc concave sur ] − ∞, 0[ et convexe
sur ]0, +∞[.

79. Chapitre 9 / Optimisation 79
x
y
1
− 4 − 3 − 2 − 1 2 3 4
20
− 20
Figure C8.R.2
(c) 𝑓 ′′(𝑥) =
2𝑥3 − 96𝑥
(𝑥2 + 16)3
. La fonction 𝑓 est donc concave sur ] − ∞, −4
√
3] et [0, 4
√
3],
mais convexe sur [−4
√
3, 0] et [4
√
3, +∞[.
5. 𝑓 ′(𝑥) = −𝑥−2𝑒1/𝑥 et 𝑓 ′′(𝑥) = 2𝑥−3𝑒1/𝑥 + 𝑥−4𝑒1/𝑥 = 𝑥−4𝑒1/𝑥 (2𝑥 + 1). La fonction 𝑓 est
donc concave sur ] − ∞, −1
2 ], mais convexe sur [−1
2 , 0[ et sur ]0, +∞[. (Elle n’est pas
définie en 𝑥 = 0. De plus, 𝑒1/𝑥 → 0 quand 𝑥 → 0−, mais 𝑒1/𝑥 → ∞ quand 𝑥 → 0+. La
fonction tend vers 1 quand 𝑥 → ∞ et quand 𝑥 → −∞.) Voir figure C8.R.5.
x
y
1
2
− 2 − 1 1 2 3
− 2
Figure C8.R.5 𝑦 = 𝑒1/𝑥
y
x
y
x
f g
Figure C8.R.7
6. La dérivée seconde est 𝐶′′(𝑥) = 6𝑎𝑥 +2𝑏. 𝐶(𝑥) est donc concave sur [0, −𝑏/3𝑎], convexe
sur [−𝑏/3𝑎, +∞[. Il y a un seul point d’inflexion, situé en 𝑥 = −𝑏/3𝑎.
7. Voir figure C8.R.7. Nous avons montré à la section 8.3 que le minimum de deux fonctions
concaves quelconques est concave.
Chapitre 9 / Optimisation
9.1
1. (a) Comme le dénominateur n’est jamais inférieur à 4, on a 𝑓 (𝑥) ⩽ 2 pour tout 𝑥. Mais
𝑓 (0) = 2, de sorte que 𝑥 = 0 maximise 𝑓 (𝑥).
(b) Comme 𝑔(−2) = −3 et 𝑔(𝑥) ⩾ −3 pour tout 𝑥, 𝑥 = −2 minimise 𝑔(𝑥). Comme
𝑔(𝑥) → +∞ lorsque 𝑥 → +∞, il n’y a pas de maximum.

80. 80 CORRIGÉS DES EXERCICES
(c) Comme 1 + 𝑥4 ⩾ 1, on a ℎ(𝑥) ⩽ 1 pour tout 𝑥. Or ℎ(0) = 1, donc 𝑥 = 0 maximise ℎ.
Quand 𝑥 ∈ [−1, 1], on a 1 + 𝑥4 ⩽ 2, d’où ℎ(𝑥) ⩾ 1
2 . Il s’ensuit que ℎ est minimale aux
points 𝑥 = ±1.
(d) Pour tout 𝑥, on a 2 + 𝑥2 ⩾ 2 et donc 2/(2 + 𝑥2) ⩽ 1, ce qui implique que
−2/(2 + 𝑥2) ⩾ −1 = 𝐹(0). Ainsi, il y a un minimum −1 en 𝑥 = 0, mais pas de maximum.
(e) Maximum 2 en 𝑥 = 1. Pas de minimum.
(f) Minimum 99 en 𝑥 = 0. Pas de maximum. (Quand 𝑥 → ±∞ , 𝐻(𝑥) → 100.)
9.2
1. 𝑦′ = 1,06 − 0,08𝑥. Donc 𝑦′ ⩾ 0 pour 𝑥 ⩽ 13,25 et 𝑦′ ⩽ 0 pour 𝑥 ⩾ 13,25. Ainsi, 𝑦 atteint
un maximum en 𝑥 = 13,25.
2. On a
ℎ′
(𝑥) =
8 (3𝑥2 + 4) − (8𝑥) (6𝑥)
(3𝑥2 + 4)2
=
8 (2 −
√
3𝑥) (2 +
√
3𝑥)
(3𝑥2 + 4)2
.
Les points de coordonnées 𝑥1 = −2
√
3/3 et 𝑥2 = 2
√
3/3 sont donc critiques. Un tableau
de signes montre que ℎ′(𝑥) 0 sur ] − ∞, 𝑥1 [ et sur ]𝑥2, +∞[, tandis que ℎ′(𝑥) 0 sur
]𝑥1, 𝑥2 [.
Par conséquent, ℎ est strictement décroissante sur ] − ∞, 𝑥1], strictement croissante sur
[𝑥1, 𝑥2] et à nouveau strictement décroissante sur [𝑥2, +∞[. Puis, comme ℎ(𝑥) → 0
lorsque 𝑥 → ±∞, il s’ensuit que le maximum de ℎ se produit en 𝑥2 = 2
√
3/3 et le
minimum en 𝑥1 = −2
√
3/3.
3. ℎ′(𝑡) = 1/2
√
𝑡 − 1
2 = (1 −
√
𝑡)/2
√
𝑡. On voit que ℎ′(𝑡) ⩾ 0 sur [0, 1] et ℎ′(𝑡) ⩽ 0 sur
[1, +∞[. Conformément au point (i) du théorème 9.2.1, 𝑡 = 1 maximise ℎ(𝑡).
4. On a
𝑓 ′
(𝑥) =
4𝑥(𝑥4 + 1) − 2𝑥2 · 4𝑥3
(𝑥4 + 1)2
=
4𝑥 − 4𝑥5
(𝑥4 + 1)2
=
4𝑥(1 + 𝑥2)(1 + 𝑥)(1 − 𝑥)
(𝑥4 + 1)2
.
Pour 𝑥 restreint à l’intervalle [0, +∞[, on trouve que 𝑓 (𝑥) croît sur [0, 1] mais décroît
sur [1, +∞[. La fonction 𝑓 a donc un maximum 𝑓 (1) = 1 en 𝑥 = 1.
5. 𝑔′(𝑥) = 3𝑥2 ln 𝑥 + 𝑥3/𝑥 = 𝑥2 (3 ln 𝑥 + 1), donc 𝑔′(𝑥) = 0 quand ln 𝑥 = −1
3 , c’est-à-dire
𝑥 = 𝑒−1/3. On constate que 𝑔′(𝑥) ⩽ 0 sur ]0, 𝑒−1/3] et 𝑔′(𝑥) ⩾ 0 sur [𝑒−1/3, +∞[,
ainsi 𝑥 = 𝑒−1/3 rend 𝑔(𝑥) minimal. Comme 𝑔(𝑥) → +∞ lorsque 𝑥 → +∞, il n’y a pas de
maximum.
6. 𝑓 ′(𝑥) = 3𝑒𝑥 (𝑒2𝑥 − 2). Donc 𝑓 ′(𝑥) = 0 quand 𝑒2𝑥 = 2 ou 𝑥 = 1
2 ln 2. Si 𝑥 1
2 ln 2, alors
𝑓 ′(𝑥) 0 et, si 𝑥 1
2 ln 2, alors 𝑓 ′(𝑥) 0, ainsi en 𝑥 = 1
2 ln 2 𝑓 atteint un minimum.
Notez que 𝑓 (𝑥) tend vers +∞ lorsque 𝑥 → +∞, aussi 𝑓 n’a pas de maximum.
7. 𝑦′ = 𝑥𝑒−𝑥 (2 − 𝑥), donc 𝑦′ 0 sur ]0, 2[ et 𝑦′ 0 sur ]2, 4[. Ainsi, 𝑦 a un maximum
4𝑒−2 ≈ 0,54 en 𝑥 = 2.

81. Chapitre 9 / Optimisation 81
8. (a) 𝑦′ = 𝑒𝑥 − 2𝑒−2𝑥 et 𝑦′′ = 𝑒𝑥 + 4𝑒−2𝑥. De là 𝑦′ = 0 quand 𝑒𝑥 = 2𝑒−2𝑥 ou 𝑒3𝑥 = 2
ou encore 𝑥 = 1
3 ln 2. Comme 𝑦′′ 0 partout, la fonction est convexe et il s’agit d’un
minimum.
(b) 𝑦′ = −2 (𝑥 − 𝑎) − 4 (𝑥 − 𝑏) = 0 quand 𝑥 = 1
3 (𝑎 + 2𝑏). C’est un maximum puisque
𝑦′′ = −6.
(c) 𝑦′ = 1/𝑥 − 5 = 0 quand 𝑥 = 1
5 . C’est un maximum puisque 𝑦′′ = −1/𝑥2 0 pour tout
𝑥 strictement positif.
9. 𝑑′(𝑥) = 2 (𝑥 − 𝑎1) + 2 (𝑥 − 𝑎2) + · · · + 2 (𝑥 − 𝑎𝑛) = 2[𝑛𝑥 − (𝑎1 + 𝑎2 + · · · + 𝑎𝑛)]. Ainsi,
𝑑′(𝑥) = 0 pour 𝑥 = ¯
𝑥 tel que ¯
𝑥 = 1
𝑛 (𝑎1 + 𝑎2 + · · · + 𝑎𝑛), la moyenne arithmétique de 𝑎1,
𝑎2, . . ., 𝑎𝑛. Comme 𝑑′′(𝑥) = 2𝑛 0, ¯
𝑥 minimise 𝑑(𝑥).
10. (a) 𝑓 ′(𝑥) = 𝑘 − 𝐴𝛼𝑒−𝛼𝑥 = 0 quand 𝑥 = 𝑥0 = (1/𝛼) ln(𝐴𝛼/𝑘). Notez que 𝑥0 0 si et
seulement si 𝐴𝛼 𝑘. En outre, 𝑓 ′′(𝑥) = 𝐴𝛼2𝑒−𝛼𝑥 0 pour tout 𝑥 ⩾ 0. Ainsi, 𝑥0 est une
solution du problème de minimisation.
(b) En substituant l’expression de 𝐴 dans la réponse à la question (a), on obtient l’ex-
pression de la hauteur optimale 𝑥0. Sa valeur augmente lorsque 𝑝0 (probabilité d’être
submergées) ou 𝑉 (coût d’une inondation) augmente, mais diminue lorsque 𝛿 (taux d’in-
térêt) ou 𝑘 (coût marginal de la construction) augmente. Les signes de ces réponses sont
clairement ceux qu’un économiste attend (à vrai dire, pas seulement les économistes!).
9.3
1. (a) Comme 𝜋(𝐿) = 320
√
𝐿 − 40𝐿, on a
𝜋′
(𝐿) =
160
√
𝐿
− 40 =
40 (4 −
√
𝐿)
√
𝐿
.
On voit que 𝜋′(𝐿) ⩾ 0 pour 0 ⩽ 𝐿 ⩽ 16, tandis que 𝜋′(16) = 0 et 𝜋′(𝐿) ⩽ 0 pour
𝐿 ⩾ 16, d’où 𝐿 = 16 maximise le profit.
(b) La fonction de profit est 𝜋(𝐿) = 𝑓 (𝐿) − 𝑤𝐿. La condition du premier ordre est
𝜋′(𝐿∗) = 𝑓 ′(𝐿∗) − 𝑤 = 0.
(c) La condition du premier ordre en (b) définit 𝐿∗ comme une fonction de 𝑤. En dérivant
par rapport à 𝑤, 𝑓 ′′(𝐿∗) (d𝐿∗/d𝑤) − 1 = 0 ou (d𝐿∗/d𝑤) = 1/ 𝑓 ′′(𝐿∗) 0. (Si le coût du
travail croît, la quantité optimale de travail décroît.)
2. (a) 𝜋(𝑄) = 𝑄(𝑎 − 𝑄) − 𝑘𝑄 = (𝑎 − 𝑘)𝑄 − 𝑄2. Alors 𝜋′(𝑄) = (𝑎 − 𝑘) − 2𝑄 = 0 pour
𝑄 = 𝑄∗ = 1
2 (𝑎 − 𝑘). C’est un maximum de 𝜋, car 𝜋′′(𝑄) 0. Le profit monopolistique
est 𝜋(𝑄∗) = −( 1
2 (𝑎 − 𝑘))2 + (𝑎 − 𝑘) 1
2 (𝑎 − 𝑘) = 1
4 (𝑎 − 𝑘)2.
(b) d𝜋(𝑄∗)/d𝑘 = −1
2 (𝑎 − 𝑘) = −𝑄∗, comme dans la question (c) de l’exemple 9.3.4.
(c) La nouvelle fonction de profit est ˆ
𝜋(𝑄) = 𝜋(𝑄) + 𝑠𝑄 = (𝑎 − 𝑘)𝑄 − 𝑄2 + 𝑠𝑄. De là,
ˆ
𝜋′(𝑄) = 𝑎−𝑘 −2𝑄+𝑠 = 0 quand ˆ
𝑄 = 1
2 (𝑎−𝑘 +𝑠). Évidemment, ˆ
𝑄 = 1
2 (𝑎−𝑘 +𝑠) = 𝑎−𝑘
à condition que 𝑠 = 𝑎 − 𝑘, qui est la subvention nécessaire pour inciter le monopoliste à
produire 𝑎 − 𝑘 unités.

82. 82 CORRIGÉS DES EXERCICES
3. Voir figures C9.3.3a et C9.3.3b. Si 𝑥 = 9, tout sera coupé. On doit donc avoir 𝑥 9. En
dérivant la formule du volume 𝑉, on obtient 𝑉′(𝑥) = 12𝑥2 −144𝑥+324 = 12(𝑥−3)(𝑥−9).
Donc 𝑉′(𝑥) 0 si 𝑥 3, mais 𝑉′(𝑥) 0 si 3 𝑥 9. Le théorème 9.2.1 implique que
le volume de la boîte est maximal quand le carré découpé à chaque coin mesure 3 cm de
côté. Le volume est donc 12 × 12 × 3 = 432 cm3.
18
18 x
x
Figure C9.3.3a
x
18 − 2x
18 − 2x
Figure C9.3.3b
p
x
a + k
p(x) = a + k (1 − e−cx
)
a
Figure C9.3.4
4. 𝑝′(𝑥) = 𝑘𝑐𝑒−𝑐𝑥 0 et 𝑝′′(𝑥) = −𝑘𝑐2𝑒−𝑐𝑥 0 pour tout 𝑥. Il n’y a pas de maximum et
𝑝(𝑥) → 𝑎 + 𝑘 lorsque 𝑥 → +∞. Voir figure C9.3.4.
5. On a
𝑇
′
(𝑤) = 𝑎
𝑝𝑏 (𝑏𝑤 + 𝑐)𝑝−1𝑤 − (𝑏𝑤 + 𝑐)𝑝
𝑤2
= 𝑎 (𝑏𝑤 + 𝑐)𝑝−1 𝑏𝑤(𝑝 − 1) − 𝑐
𝑤2
,
qui est nulle pour 𝑤∗ = 𝑐/𝑏 (𝑝 − 1). C’est forcément le point de minimum, car 𝑇
′
(𝑤) est
négative pour 𝑤 𝑤∗ et positive pour 𝑤 𝑤∗.
9.4
1. 𝑓 ′(𝑥) = 8𝑥 − 40 = 0 pour 𝑥 = 5. 𝑓 (0) = 80, 𝑓 (5) = −20 et 𝑓 (8) = 16. Maximum 80 en
𝑥 = 0. Minimum −20 en 𝑥 = 5. Voir figure C9.4.1.
f (x) = 4x2
− 40x + 80
−20
20
40
60
80
x
5
3 4
1 2 6 7 8
y
Figure C9.4.1
2. Dans tous les cas, en raison du théorème des bornes atteintes, le maximum et le minimum
existent. On suit la méthode décrite avant l’exemple 9.4.1.

83. Chapitre 9 / Optimisation 83
(a) 𝑓 ′(𝑥) = −2 pour tout 𝑥 dans [0, 3]. Par conséquent, le maximum et le minimum
sont atteints aux extrémités de l’intervalle [0, 3]. Comme 𝑓 (0) = −1 et 𝑓 (3) = −7, le
maximum est en 𝑥 = 0, le minimum en 𝑥 = 3(7).
(b) 𝑓 (−1) = 𝑓 (2) = 10 et 𝑓 ′(𝑥) = 3𝑥2 − 3 = 0 en 𝑥 = ±1. Le seul point critique de
l’intervalle [−1, 2] est 𝑥 = 1, en lequel 𝑓 (1) = 6. Il y a deux maxima aux bornes et un
minimum en 𝑥 = 1.
(c) Comme 𝑓 (𝑥) = 𝑥 + 1/𝑥, 𝑓 (1/2) = 𝑓 (2) = 5/2 aux bornes. De plus,
𝑓 ′
(𝑥) = 1 − 1/𝑥2
= 0
en 𝑥 = ±1. Le seul point critique de l’intervalle [ 1
2 , 2] est 𝑥 = 1, en lequel 𝑓 (1) = 2. Il y
a deux maxima aux bornes et un minimum en 𝑥 = 1.
(d) Aux bornes, on a 𝑓 (−1) = 4 et 𝑓 (
√
5) = 0. Comme 𝑓 ′(𝑥) = 5𝑥2 (𝑥2 − 3), il y a deux
points critiques dans l’intervalle [−1,
√
5] en 𝑥 = 0 et 𝑥 =
√
3. Les valeurs prises par
la fonction en ces points sont 𝑓 (0) = 0 et 𝑓 (
√
3) = −6
√
3. Le maximum se produit en
𝑥 = −1 et le minimum en 𝑥 =
√
3.
(e) 𝑓 ′(𝑥) = 3𝑥2 − 9 000𝑥 + 6 × 106 = 3 (𝑥 − 1 000) (𝑥 − 2 000) = 0 quand 𝑥 = 1 000 et
𝑥 = 2 000. En ces points critiques, 𝑓 (1 000) = 2,5 × 109 et 𝑓 (2 000) = 2 × 109. Il y a un
minimum en la borne 𝑥 = 0 et un maximum en 𝑥 = 3 000.
3. 𝑔′(𝑥) = 2
5 𝑥𝑒𝑥2
(1 − 𝑒2−2𝑥2
). Points critiques : 𝑥 = 0 et 𝑥 = ±1. Ici 𝑥 = 2 est un point de
maximum, 𝑥 = 1 et 𝑥 = −1 sont des points de minimum.
(Notez que 𝑔(2) = 1
5 (𝑒4 + 𝑒−2) 𝑔(0) = 1
5 (1 + 𝑒2).)
4. (a) La commission est de, respectivement, 4 819 e, 4 900 e, 4 800 e et
𝐶 =
1
10
(60 + 𝑥) (800 − 10𝑥) = 4 800 + 20𝑥 − 𝑥2
, 𝑥 ∈ [0, 20].
(Quand il y a 60 + 𝑥 passagers, la compagnie charter, gagnant 800 − 10𝑥 par passager,
gagne (60 + 𝑥) (800 − 10𝑥). Le club de sport gagne 1/10 de ce montant.)
(b) La fonction du second degré 𝐶 atteint son minimum en 𝑥 = 10, de sorte que la
commission est maximale avec 70 voyageurs.
5. (a) 𝑓 (𝑥) = ln 𝑥 (ln 𝑥 − 1)2. 𝑓 (𝑒1/3) = 4/27, 𝑓 (𝑒2) = 2, 𝑓 (𝑒3) = 12. Les racines sont
𝑥 = 1 et 𝑥 = 𝑒.
(b) 𝑓 ′(𝑥) = (3/𝑥) (ln 𝑥 − 1) (ln 𝑥 − 1/3). Minimum 0 en 𝑥 = 1 et en 𝑥 = 𝑒. Maximum 12
en 𝑥 = 𝑒3.
(c) 𝑓 ′(𝑥) 0 sur [𝑒, 𝑒3], d’où 𝑓 (𝑥) admet une réciproque. 𝑔′(2) = 1/ 𝑓 ′(𝑒2) = 𝑒2/5.
6. (a) Comme ( 𝑓 (2) − 𝑓 (1))/(2 − 1) = (4 − 1)/1 = 3 et 𝑓 ′(𝑥) = 2𝑥, on a 𝑓 ′(𝑥) = 3 quand
𝑥 = 𝑥∗ = 3/2.
(b) ( 𝑓 (1) − 𝑓 (0))/1 = (0 − 1)/1 = −1 et 𝑓 ′(𝑥) = −𝑥/
√
1 − 𝑥2 = −1 quand
𝑥 =
√
1 − 𝑥2. Après avoir élevé au carré chaque membre de l’équation, on obtient
𝑥2 = 1 − 𝑥2 et ainsi 𝑥2 = 1
2 . Deux solutions, 𝑥 = ±1
2
√
2, desquelles seule la positive
vérifie 𝑥 =
√
1 − 𝑥2. Il faut donc 𝑥 = 𝑥∗ = 1
2
√
2.
(7) En réalité, rien que le signe de 𝑓 ′ (𝑥) indiquait que le maximum se produirait en la borne inférieure et le minimum
en la borne supérieure de l’intervalle.

84. 84 CORRIGÉS DES EXERCICES
(c) ( 𝑓 (6) − 𝑓 (2))/4 = −1/6 et 𝑓 ′(𝑥) = −2/𝑥2 = −1/6 quand −12/𝑥2 = −1 ou
𝑥2 = 12, et ainsi 𝑥 = ±
√
12. La solution demandée dans [2, 6] est 𝑥 = 𝑥∗ =
√
12 = 2
√
3.
(d) ( 𝑓 (4) − 𝑓 (0))/4 = 1/4 = (
√
25 −
√
9)/4 = (5 − 3)/4 = 1/2 et
𝑓 ′
(𝑥) =
1
2
2𝑥/
p
9 + 𝑥2 = 𝑥/
p
9 + 𝑥2 = 1/2 quand 2𝑥 =
p
9 + 𝑥2.
Après avoir élevé au carré chaque membre de l’équation, on obtient 4𝑥2 = 9 + 𝑥2 et
ainsi 3𝑥2 = 9. Il y a deux solutions, 𝑥 = ±
√
3, desquelles seule la positive vérifie
𝑥/
√
9 + 𝑥2 = 1/2. On a donc 𝑥 = 𝑥∗ =
√
3.
7. En un point au moins, l’embarcation a la même direction que la droite qui joint 𝐴 à 𝐵
(même si cette droite touche le rivage).
8. La fonction 𝑓 n’est pas continue en 𝑥 = −1 et 𝑥 = 1. Elle n’atteint pas de maximum, car
𝑓 (𝑥) est arbitrairement proche de 1 lorsque 𝑥 est suffisamment proche de 1, alors qu’il
n’y a pas de valeur de 𝑥 pour laquelle 𝑓 (𝑥) = 1. De même, il n’y a pas de minimum.
9. La fonction 𝑓 a un maximum en 𝑥 = 1 et un minimum pour tout 𝑥 1. (Tracez votre
propre graphique.) Malgré la discontinuité de la fonction en 𝑥 = 1 et son domaine ni
fermé, ni borné.
9.5
1. 𝜋(𝑄) = 10𝑄 − 1
1 000 𝑄2 − (5 000 + 2𝑄) = 8𝑄 − 1
1 000 𝑄2 − 5 000. Comme
𝜋′
(𝑄) = 8 −
1
500
𝑄 = 0
pour 𝑄 = 4 000 et 𝜋′′(𝑄) = − 1
500 0, une production de 𝑄 = 4 000 rend le profit
maximal.
2. (a) Voir figure C9.5.2.
1000
2000
3000
4000
Q
R(Q) = 80Q
C(Q) = Q2
+ 10Q + 900
10 Q0 30 Q∗ 40 50
Figure C9.5.2
(b) (i) L’exigence est 𝜋(𝑄) ⩾ 0 et 𝑄 ∈ [0, 50], c’est-à-dire −𝑄2 + 70𝑄 − 900 ⩾ 0 et
𝑄 ∈ [0, 50]. L’entreprise doit produire au moins 𝑄0 = 35 − 5
√
13 ≈ 17 unités.
(ii) Le profit est le plus grand en 𝑄∗ = 35.

85. Chapitre 9 / Optimisation 85
3. Le profit est donné par 𝜋(𝑥) = −0,003𝑥2 + 120𝑥 − 500 000, maximal en 𝑥 = 20 000.
4. (a) 𝜋(𝑄) = 1 840𝑄 − (2𝑄2 + 40𝑄 + 5 000) = 1 800𝑄 − 2𝑄2 − 5 000. Comme
𝜋′(𝑄) = 1 800 − 4𝑄 = 0 pour 𝑄 = 450 et 𝜋′′(𝑄) = −4 0, il s’ensuit que 𝑄 = 450 rend
le profit maximal.
(b) 𝜋(𝑄) = 2 200𝑄 − 2𝑄2 − 5 000. Comme 𝜋′(𝑄) = 2 200 − 4𝑄 = 0 pour 𝑄 = 550 et
𝜋′′(𝑄) = −4 0, il s’ensuit que 𝑄 = 550 rend le profit maximal.
(c) 𝜋(𝑄) = −2𝑄2 −100𝑄 −5 000. Ici, 𝜋′(𝑄) = −4𝑄 −100 0 pour tout 𝑄 ⩾ 0, de sorte
que la borne de l’intervalle 𝑄 = 0 rend le profit maximal.
5. (a) 𝜋(𝑄) = 𝑄𝑃(𝑄) − 𝐶(𝑄) = −0,01𝑄2 + 14𝑄 − 4 500, maximal en 𝑄 = 700.
(b) El𝑄𝑃(𝑄) = (𝑄/𝑃(𝑄))𝑃′(𝑄) = 𝑄/(𝑄 − 3 000) = −1 pour 𝑄∗ = 1 500.
(c) 𝑅(𝑄) = 𝑄𝑃(𝑄) = 18𝑄 − 0,006𝑄2, de sorte que 𝑅′(𝑄) = 18 − 0,012𝑄 = 0 quand
𝑄∗ = 1 500.
6. 𝜋′(𝑄) = 𝑃 − 𝑎𝑏𝑄𝑏−1 = 0 quand 𝑄𝑏−1 = 𝑃/𝑎𝑏, c’est-à-dire 𝑄 = (𝑃/𝑎𝑏)1/(𝑏−1). De plus,
𝜋′′(𝑄) = −𝑎𝑏 (𝑏 − 1)𝑄𝑏−2 0 pour tout 𝑄 0, c’est donc un maximum pour 𝜋.
9.6
1. 𝑓 ′(𝑥) = 3𝑥2 − 12 = 0 en 𝑥 = ±2. Un tableau de signes montre qu’en 𝑥 = 2 il y a un
minimum local et, en 𝑥 = −2, un maximum local. Comme 𝑓 ′′(𝑥) = 6𝑥, c’est confirmé
par le théorème 9.6.2.
2. (a) Strictement décroissante, donc pas de points critiques.
(b) 𝑓 ′(𝑥) = 3𝑥2 − 3 = 0 pour 𝑥 = ±1. Comme 𝑓 ′′(𝑥) = 6𝑥, on a 𝑓 ′′(−1) = −6 et
𝑓 ′′(1) = 6 et, de là, 𝑥 = −1 est un maximum local et 𝑥 = 1 est un minimum local.
(c) 𝑓 ′(𝑥) = 1 − 1/𝑥2 = 0 quand 𝑥 = ±1. Avec 𝑓 ′′(𝑥) = 2/𝑥3, on a 𝑓 ′′(−1) = −2 et
𝑓 ′′(1) = 2 et, de là, en 𝑥 = −1 il y a un maximum local et en 𝑥 = 1, un minimum local.
(d) 𝑓 ′(𝑥) = 5𝑥4 − 15𝑥2 = 5𝑥2 (𝑥2 − 3) et 𝑓 ′′(𝑥) = 20𝑥3 − 30𝑥. Trois points critiques,
𝑥 = 0 et 𝑥 = ±
√
3. Comme 𝑓 ′′(0) = 0, alors que
𝑓 ′′
(−
√
3) = −20 × 3
√
3 + 30
√
3 = −30
√
3 0 et 𝑓 ′′
(
√
3) = 30
√
3 0,
il y a un maximum local en 𝑥 = −
√
3 et un minimum local en 𝑥 =
√
3.
(e) Cette parabole admet un minimum local (et global) en 𝑥 = 3.
(f) 𝑓 ′(𝑥) = 3𝑥2 + 6𝑥 = 3𝑥 (𝑥 + 2) et 𝑓 ′′(𝑥) = 6𝑥 + 6. il y a deux points critiques, 𝑥 = 0
et 𝑥 = −2. Comme 𝑓 ′′(0) = 6 et 𝑓 ′′(−2) = −6, on a un maximum local en 𝑥 = −2 et un
minimum local en 𝑥 = 0.
3. Voir figure C9.6.3.
(a) La fonction 𝑓 (𝑥) est définie si et seulement si 𝑥 ≠ 0 et 𝑥 ⩾ −6. 𝑓 (𝑥) = 0 en 𝑥 = −6 et
en 𝑥 = −2. En tout autre point 𝑥 de son domaine de définition, 𝑓 (𝑥) a le même signe que
(𝑥 + 2)/𝑥, autrement dit 𝑓 (𝑥) 0 quand 𝑥 ∈] − 6, −2[ ou 𝑥 ∈]0, +∞[.

86. 86 CORRIGÉS DES EXERCICES
y
− 4
− 2
2
4
6
8
x
− 6 − 4 − 2 2 8 10
4 6
Figure C9.6.3
(b) On calcule la dérivée de 𝑓 .
𝑓 ′
(𝑥) = −
2
𝑥2
√
𝑥 + 6 +
𝑥 + 2
𝑥
1
2
√
𝑥 + 6
=
−4𝑥 − 24 + 𝑥2 + 2𝑥
2𝑥2
√
𝑥 + 6
=
(𝑥 + 4) (𝑥 − 6)
2𝑥2
√
𝑥 + 6
À l’aide d’un tableau de signes, on observe que 𝑓 ′(𝑥) 0 si −6 𝑥 −4, 𝑓 ′(𝑥) 0
si −4 𝑥 0, 𝑓 ′(𝑥) 0 si 0 𝑥 6, 𝑓 ′(𝑥) 0 si 6 𝑥. De là, 𝑓 est strictement
décroissante sur [−4, 0[ et sur ]0, 6], strictement croissante sur [−6, −4] et sur [6, +∞[. Il
découle du test de la dérivée première (théorème 9.6.1) que les points d’abscisses 𝑥 = −4
et 𝑥 = 6 sont respectivement un maximum local et un minimum local, dont les valeurs
sont 𝑓 (−4) = 1
2
√
2 et 𝑓 (6) = 4
3
√
8 = 8
√
2/3. De plus, en accord avec la définition (9.6.2),
au point 𝑥 = −6 se produit un autre minimum local.
(c) Comme lim𝑥→0
√
𝑥 + 6 =
√
6 0, alors que lim𝑥→0− (1 + 2/𝑥) = −∞ et
lim𝑥→0+ (1 + 2/𝑥) = +∞, on conclut que lim𝑥→0− 𝑓 (𝑥) = −∞ et lim𝑥→0+ 𝑓 (𝑥) = +∞.
Enfin,
lim
𝑥→+∞
𝑓 ′
(𝑥) = lim
𝑥→+∞
𝑥2 − 2𝑥 − 24
2𝑥2
1
√
𝑥 + 6
= lim
𝑥→∞
1
2
−
1
𝑥
−
12
𝑥2
1
√
𝑥 + 6
→
1
2
× 0 = 0.
4. Regardez le point 𝑎. Puisqu’il s’agit du graphique de 𝑓 ′(𝑥), on a 𝑓 ′(𝑥) 0 à gauche
de 𝑎, 𝑓 ′(𝑎) = 0 et 𝑓 ′(𝑥) 0 à droite de 𝑎, de sorte que 𝑎 est l’abscisse d’un minimum
local. Aux points 𝑏 et 𝑒, comme 𝑓 ′(𝑥) 0 de part et d’autre de ces points, ils ne peuvent
pas être les abscisses d’extremum. En 𝑐, 𝑓 passe par un maximum local et en 𝑑, par un
minimum local.
5. (a) 𝑓 ′(𝑥) = 3𝑥2 + 2𝑎𝑥 + 𝑏, 𝑓 ′′(𝑥) = 6𝑥 + 2𝑎. 𝑓 ′(0) = 0 exige 𝑏 = 0. 𝑓 ′′(0) ⩾ 0 exige
𝑎 ⩾ 0. Si 𝑎 = 0 et 𝑏 = 0, alors 𝑓 (𝑥) = 𝑥3 + 𝑐. Cette fonction n’a pas de minimum local
en 𝑥 = 0. Donc 𝑓 a un minimum local en 0 si et seulement si 𝑎 0 et 𝑏 = 0.
(b) 𝑓 ′(1) = 0 et 𝑓 ′(3) = 0 exigent 3 + 2𝑎 + 𝑏 = 0 et 27 + 6𝑎 + 𝑏 = 0, équivalent à 𝑎 = −6
et 𝑏 = 9.
6. (a) 𝑓 ′(𝑥) = 𝑥2𝑒𝑥 (3 + 𝑥). Utilisez un tableau de signes pour montrer qu’en 𝑥 = −3 il y
a un minimum local (et global). Pas de maximum local. (𝑥 = 0 est l’abscisse d’un point
d’inflexion.)

87. Chapitre 9 / Optimisation 87
(b) 𝑔′(𝑥) = 𝑥2𝑥 (2 + 𝑥 ln 2). En 𝑥 = 0, il y a un minimum local et en 𝑥 = −2/ln 2, un
maximum local.
7. 𝑓 (𝑥) = 𝑥3 + 𝑎𝑥 + 𝑏 → +∞ lorsque 𝑥 → +∞ et 𝑓 (𝑥) → −∞ lorsque 𝑥 → −∞.
Conformément au théorème des valeurs intermédiaires, la fonction continue 𝑓 admet au
moins une racine réelle . On calcule 𝑓 ′(𝑥) = 3𝑥2 + 𝑎. Il y a donc deux cas.
Si 𝑎 ⩾ 0, on a 𝑓 ′(𝑥) 0 pour tout 𝑥 ≠ 0 et de ce fait 𝑓 est strictement croissante. Il n’y a
donc qu’une seule racine réelle. Notez que 4𝑎3 + 27𝑏2 ⩾ 0 dans ce cas.
Si 𝑎 0, on a 𝑓 ′(𝑥) = 0 quand 𝑥 = ±
p
−𝑎/3 = ±
√
𝑝, où 𝑝 = −𝑎/3. Comme 𝑓 ′′(𝑥) = 3𝑥,
la fonction 𝑓 passe par un maximum local en 𝑥 = −
√
𝑝, où 𝑦 = 𝑏 + 2𝑝
√
𝑝 et par un
minimum local en 𝑥 =
√
𝑝, où 𝑦 = 𝑏 − 2𝑝
√
𝑝. Si l’une de ces valeurs extrêmes locales
est 0, l’équation a une racine double, ce qui est le cas si et seulement si 4𝑝3 = 𝑏2,
c’est-à-dire si et seulement si 4𝑎3 + 27𝑏2 = 0. Sinon, l’équation a trois racines réelles si
et seulement si le maximum local est strictement positif et le minimum local strictement
négatif. Cela arrive si et seulement si
𝑏 −2𝑝
√
𝑝 et 𝑏 2𝑝
√
𝑝 ⇔ |𝑏| 2𝑝
√
𝑝 ⇔ 𝑏2
4𝑝3
⇔ 4𝑎3
+ 27𝑏2
0.
Exercices récapitulatifs du chapitre 9
1. (a) 𝑓 ′(𝑥) =
4𝑥
(𝑥2 + 2)2
. D’où 𝑓 (𝑥) décroît pour 𝑥 ⩽ 0, croît pour 𝑥 ⩾ 0.
(b) 𝑓 ′′(𝑥) = 4 (2 − 3𝑥2
)/(𝑥2
+ 2)3
. Il y a des points d’inflexion en 𝑥 = ±1
3
√
6.
(c) 𝑓 (𝑥) → 1 lorsque 𝑥 → ±∞. Voir figure C9.R.1.
y
1
x
− 4 − 2 2 4
Figure C9.R.1
2. (a) 𝑄′(𝐿) = 3𝐿 (8 − 1
20 𝐿) = 0 pour 𝐿∗ = 160 et 𝑄(𝐿) est croissante sur [0, 160],
décroissante sur [160, 200], de sorte que 𝑄∗ = 160 maximise 𝑄(𝐿).
(b) La production par travailleur est 𝑄(𝐿)/𝐿 = 12𝐿 − 1
20 𝐿2 et cette fonction du second
degré a un maximum en 𝐿∗∗ = 120. On a 𝑄′(120) = 𝑄(120)/120 = 720. En général
(voir exemple 6.7.6), (d/d𝐿) (𝑄(𝐿)/𝐿) = (1/𝐿) (𝑄′(𝐿) − 𝑄(𝐿)/𝐿). Si 𝐿 0 maximise
la production par travailleur, on doit avoir 𝑄′(𝐿) = 𝑄(𝐿)/𝐿.
3. Si 𝑦 est le côté parallèle à la rive et 𝑥 l’autre côté, 2𝑥+𝑦 = 1 000, de sorte que 𝑦 = 1 000−2𝑥.
L’aire entourée mesure 𝑥𝑦 = 1 000𝑥−2𝑥2, et cette fonction du second degré a un maximum
quand 𝑥 = 250 et donc 𝑦 = 500.
4. (a) 𝜋 = −0,0016𝑄2 + 44𝑄 − 0,0004𝑄2 − 8𝑄 − 64 000 = −0,002𝑄2 + 36𝑄 − 64 000 et
𝑄 = 9 000 maximise 𝜋.

88. 88 CORRIGÉS DES EXERCICES
(b) On a
El𝑄𝐶(𝑄) =
𝑄
𝐶(𝑄)
𝐶′
(𝑄) =
0,0008𝑄2 + 8𝑄
0,0004𝑄2 + 8𝑄 + 64 000
≈ 0,12
quand 𝑄 = 1 000. Cela signifie que, quand 𝑄 augmente de 1 % à 1 000, les coûts vont
augmenter d’environ 0,12 %.
5. Le profit en fonction de 𝑄 a comme expression
𝜋(𝑄) = 𝑃𝑄 − 𝐶 = (𝑎 − 𝑏𝑄2
)𝑄 − 𝛼 + 𝛽𝑄 = −𝑏𝑄3
+ (𝑎 + 𝛽)𝑄 − 𝛼.
Alors 𝜋′(𝑄) = −3𝑏𝑄2 + 𝑎 + 𝛽 s’annule quand 𝑄2 = (𝑎 + 𝛽)/3𝑏 et donc
𝑄 =
p
(𝑎 + 𝛽)/3𝑏.
Cette valeur de 𝑄 maximise le profit, car 𝜋′′(𝑄) = −6𝑏𝑄 ⩽ 0 pour tout 𝑄 ⩾ 0.
6. (a) Pour 𝑥 0, on a 𝑅 = 𝑝
√
𝑥, 𝐶 = 𝑤𝑥 + 𝐹 et 𝜋(𝑥) = 𝑝
√
𝑥 − 𝑤𝑥 − 𝐹.
(b) 𝜋′(𝑥) = 0 quand 𝑤 = 𝑝/2
√
𝑥. (Coût marginal = prix × productivité marginale.) Alors
𝑥 = 𝑝2/4𝑤2. De plus, 𝜋′′(𝑥) = −1
4 𝑝𝑥−3/2 0 pour tout 𝑥 0, de sorte que le profit est
maximal sur ]0, +∞[. Quand 𝑥 = 𝑝2/4𝑤2, alors 𝜋 = 𝑝2/2𝑤 − 𝑝2/4𝑤 − 𝐹 = 𝑝2/4𝑤 − 𝐹.
C’est donc le profit maximal si 𝐹 ⩽ 𝑝2/4𝑤 ; sinon, l’entreprise ferait mieux de ne pas
démarrer la production et de choisir 𝑥 = 0.
7. (a) 𝑔 est définie pour 𝑥 −1.
(b) 𝑔′(𝑥) = 1 − 2/(𝑥 + 1) = (𝑥 − 1)/(𝑥 + 1), 𝑔′′(𝑥) = 2/(𝑥 + 1)2.
(c) Comme 𝑔′(𝑥) 0 sur ] − 1, 1[, 𝑔′(1) = 0 et 𝑔′(𝑥) 0 sur ]1, +∞[, 𝑥 = 1 est un point
de minimum (global). Comme 𝑔′′(𝑥) 0 pour tout 𝑥 −1, la fonction 𝑔 est convexe et
il n’y a pas de point d’inflexion. Quand 𝑥 → (−1)−, 𝑔(𝑥) → +∞ et, quand 𝑥 → +∞,
𝑔(𝑥) → +∞. Voir figure C9.R.7.
y
−1
1
2
3
4
x
−1 1 2 3
Figure C9.R.7
y
−0,2
−0,1
0,1
0,2
x
−1 1 2
y
x
Figure C9.R.8
8. (a) 𝐷 𝑓 =] − 1, +∞[.
(b) Un tableau de signes montre que 𝑓 ′(𝑥) ⩾ 0 sur ] − 1, 1] et 𝑓 ′(𝑥) ⩽ 0 sur [1, +∞[.
Par conséquent, 𝑓 a un maximum en 𝑥 = 1 et n’a pas de minimum.
𝑓 ′′
(𝑥) =
−𝑥 (𝑥2 + 𝑥 − 1)
(𝑥 + 1)2
= 0

89. Chapitre 9 / Optimisation 89
quand 𝑥 = 0 et 𝑥 = 1
2 (
√
5 − 1). (Le point 𝑥 = 1
2 (−
√
5 − 1) est en dehors du domaine de
définition.) Puisque 𝑓 ′′(𝑥) change de signe en 𝑥 = 0, il s’agit d’un point d’inflexion.
(c) 𝑓 (𝑥) → −∞ lorsque 𝑥 → (−1)+. Voir la figure C9.R.8.
9. (a) Comme
ℎ′
(𝑥) =
𝑒𝑥 (2 − 𝑒2𝑥)
(2 + 𝑒2𝑥)2
,
ℎ est croissante sur ]−∞, 1
2 ln 2 ] et décroissante sur [ 1
2 ln 2, +∞[. Donc ℎ a un maximum
en 𝑥 = 1
2 ln 2. Elle n’a pas de minimum.
(b) En fait, ℎ est strictement croissante sur ] − ∞, 1
2 ln 2], qui inclut ] − ∞, 0]. On a aussi
lim
𝑥→−∞
ℎ(𝑥) = 0 et ℎ(0) = 1/3. D’où ℎ définie sur ] − ∞, 0] admet une réciproque définie
sur ]0, 1/3] et à valeurs dans ] − ∞, 0]. Pour trouver l’expression de cette réciproque, on
remarque que
𝑒𝑥
2 + 𝑒2𝑥
= 𝑦 ⇔ 𝑦 (𝑒𝑥
)2
− 𝑒𝑥
+ 2𝑦 = 0.
Cette équation du second degré en 𝑒𝑥 a comme racines
𝑒𝑥
= [1 ±
q
1 − 8𝑦2]/2𝑦.
On exige que la solution vérifie 𝑥 ⩽ 0 et ainsi 𝑒𝑥 ⩽ 1 quand 0 𝑦 1/3. Maintenant, en
prenant la racine carrée positive, on a 𝑒𝑥 1/2𝑦 6 quand 0 𝑦 1/3. On doit donc
avoir
𝑒𝑥
= [1 −
q
1 − 8𝑦2]/2𝑦
et ainsi 𝑥 = ln(1 −
p
1 − 8𝑦2 ) − ln(2𝑦). Avec 𝑥 comme variable indépendante, ℎ−1(𝑥) =
ln(1−
√
1 − 8𝑥2 )−ln(2𝑥). La fonction et sa réciproque sont représentées à la figure C9.R.9.
y
−1,5
−1,0
−0,5
0,5
x
−1,5 −1,0 −0,5 0,5
h
h−1
Figure C9.R.9
y
x
−2
−1
1
2
−5 −4 −3 −2 −1 1 2 3 4 5
f (x) =
6x3
x4
+ x2
+ 2
Figure C9.R.12
10. (a) 𝑓 ′(𝑥) = 4𝑒4𝑥 + 8𝑒𝑥 − 32𝑒−2𝑥, 𝑓 ′′(𝑥) = 16𝑒4𝑥 + 8𝑒𝑥 + 64𝑒−2𝑥.
(b) 𝑓 ′(𝑥) = 4𝑒−2𝑥 (𝑒3𝑥 + 4) (𝑒3𝑥 − 2). D’où 𝑓 (𝑥) est croissante sur [ 1
3 ln 2, +∞[, décrois-
sante sur ] − ∞, 1
3 ln 2]. 𝑓 ′′(𝑥) 0 pour tout 𝑥 de sorte que 𝑓 est strictement convexe.
(c) Minimum (global) en 1
3 ln 2. Pas de maximum, car 𝑓 (𝑥) → +∞ lorsque 𝑥 → +∞.

90. 90 CORRIGÉS DES EXERCICES
11. (a) Comme 3
√
𝑢 est défini pour tout 𝑢, les seules valeurs de 𝑥 qui n’appartiennent pas au
domaine de définition sont celles pour lesquelles 𝑥2 − 𝑎 = 0 ou 𝑥 = ±
√
𝑎. Le domaine
de définition de 𝑓 est l’ensemble de tous les 𝑥 tels que 𝑥 ≠ ±
√
𝑎. Comme 3
√
𝑢 0 si et
seulement si 𝑢 0, le dénominateur de l’expression de 𝑓 (𝑥),
3
√
𝑥2 − 𝑎, est strictement
positif si et seulement si 𝑥2 𝑎, autrement dit, si et seulement si 𝑥 −
√
𝑎 ou 𝑥
√
𝑎.
Le numérateur de l’expression de 𝑓 (𝑥) est 𝑥 et, d’après un tableau de signes, 𝑓 (𝑥) est
strictement positive sur ] −
√
𝑎, 0[ et sur ]
√
𝑎, ∞[. Comme
𝑓 (−𝑥) =
−𝑥
3
p
(−𝑥)2 − 𝑎
= −
𝑥
3
√
𝑥2 − 𝑎
= − 𝑓 (𝑥),
le graphique de 𝑓 est symétrique par rapport à l’origine.
(b) Après avoir écrit
3
√
𝑥2 − 𝑎 sous la forme (𝑥2 − 𝑎)1/3, la dérivée est
𝑓 ′
(𝑥) =
1 × (𝑥2 − 𝑎)1/3 − 𝑥 × 1
3 (𝑥2 − 𝑎)−2/3 × 2𝑥
(𝑥2 − 𝑎)2/3
=
𝑥2 − 𝑎 − 𝑥 · 1
3 2𝑥
(𝑥2 − 𝑎)4/3
=
1
3 (𝑥2 − 3𝑎)
(𝑥2 − 𝑎)4/3
.
La deuxième égalité a été obtenue en multipliant numérateur et dénominateur par
(𝑥2 − 𝑎)2/3. Il est clair que 𝑓 ′(𝑥) n’est pas définie en ±
√
𝑎. Mis à part ces points, le déno-
minateur est toujours strictement positif (car (𝑥2 −𝑎)4/3 = ((𝑥2 −𝑎)1/3)4). Le numérateur,
1
3 (𝑥2 − 3𝑎) = 1
3 (𝑥 +
√
3𝑎) (𝑥 −
√
3𝑎), est nul en 𝑥 = ±
√
3𝑎, positif sur ] − ∞, −
√
3𝑎]
et sur [
√
3𝑎, +∞[. Comme 𝑓 et 𝑓 ′ ne sont pas définies en ±
√
𝑎, 𝑓 (𝑥) est croissante sur
] − ∞, −
√
3𝑎 [ et sur ]
√
3𝑎, +∞[, décroissante sur ] −
√
3𝑎, −
√
𝑎 [, sur ] −
√
𝑎,
√
𝑎 [ et sur
]
√
𝑎,
√
3𝑎 [. Il s’ensuit que 𝑓 passe par un maximum local en 𝑥 = −
√
3𝑎 et un minimum
local en 𝑥 =
√
3𝑎.
(c) En dérivant encore une fois, on obtient
𝑓 ′′
(𝑥) =
2
3 𝑥 (𝑥2 − 𝑎)4/3 − 1
3 (𝑥2 − 3𝑎) · 4
3 (𝑥2 − 𝑎)1/3 · 2𝑥
(𝑥2 − 𝑎)8/3
=
2
9 𝑥 (9𝑎 − 𝑥2)
(𝑥2 − 𝑎)7/3
.
La deuxième égalité a été obtenue en divisant numérateur et dénominateur par (𝑥2 −𝑎)1/3,
puis en simplifiant le numérateur. L’expression finale de 𝑓 ′′(𝑥) montre qu’il y a un point
d’inflexion en −3
√
𝑎, 0 et 3
√
𝑎(8).
12. Après avoir divisé le numérateur et le dénominateur par 𝑥3, on note que 𝑓 (𝑥) → 0 lorsque
𝑥 → ±∞. La dérivée est
𝑓 ′
(𝑥) =
18𝑥2 (𝑥4 + 𝑥2 + 2) − 6𝑥3 (4𝑥3 + 2𝑥)
(𝑥4 + 𝑥2 + 2)2
=
−6𝑥2 (𝑥4 − 𝑥2 − 6)
(𝑥4 + 𝑥2 + 2)2
=
−6𝑥2 (𝑥2 − 3) (𝑥2 + 2)
(𝑥4 + 𝑥2 + 2)2
.
Aussi, 𝑥 = 0 et 𝑥 = ±
√
3 sont des points critiques. De plus, 𝑓 ′ change de signe, du négatif au
positif lorsque 𝑥 passe par −
√
3, puis redevient négative lorsque 𝑥 passe par
√
3. Il s’ensuit
qu’en 𝑥 =
p
3 il y a un maximum local (et global) et en 𝑥 = −
p
3, un minimum local (et
global). Par contre, 𝑥 = 0 est un point d’inflexion. En outre, comme 𝑓 (−𝑥) = − 𝑓 (𝑥) quel
que soit 𝑥, le graphique est symétrique par rapport à l’origine. Voir figure C9.R.12.
(8) 𝑓 ′′ (𝑥) est nulle en ces points et change de signe en chacun d’eux.

91. Chapitre 10 / Intégration 91
Chapitre 10 / Intégration
10.1
1. (a) 1
14 𝑥14 + 𝐶 (b) 2
5 𝑥2√
𝑥 + 𝐶. (Notez que 𝑥
√
𝑥 = 𝑥 × 𝑥1/2 = 𝑥3/2.)
(c) 2
√
𝑥 + 𝐶. (Notez que 1/
√
𝑥 = 𝑥−1/2.)
(d) 8
15 𝑥
15
8 + 𝐶. (Notez que
q
𝑥
p
𝑥
√
𝑥 =
p
𝑥
√
𝑥3/2 =
√
𝑥 × 𝑥3/4 =
√
𝑥7/4 = 𝑥7/8.)
(e) −𝑒−𝑥 + 𝐶 (f) 4𝑒
1
4 𝑥 + 𝐶 (g) −3
2 𝑒−2𝑥 + 𝐶 (h) (1/ln 2) 2𝑥 + 𝐶
2. (a) 𝐶(𝑥) = 3
2 𝑥2 +4𝑥+40 (En effet, 𝐶(𝑥) =
∫
(3𝑥+4) d𝑥 =
3
2
𝑥2
+4𝑥+𝐶. Alors 𝐶(0) = 40
entraîne 𝐶 = 40.)
(b) 𝐶(𝑥) = 1
2 𝑎𝑥2 + 𝑏𝑥 + 𝐶0
3. (a)
∫
(𝑡3
+ 2𝑡 − 3) d𝑡 =
∫
𝑡3
d𝑡 +
∫
2𝑡 d𝑡 −
∫
3 d𝑡 = 1
4 𝑡4
+ 𝑡2
− 3𝑡 + 𝐶
(b)
∫
(𝑥 − 1)2
d𝑥 =
∫
(𝑥2
− 2𝑥 + 1) d𝑥 = 1
3 𝑥3
− 𝑥2
+ 𝑥 + 𝐶.
Ou bien : comme
d
d𝑥
(𝑥 − 1)3
= 3 (𝑥 − 1)2
, on a
∫
(𝑥 − 1)2
d𝑥 = 1
3 (𝑥 − 1)3
+ 𝐶1.
Cela correspond à la première réponse, avec 𝐶1 = 𝐶 + 1/3.
(c)
∫
(𝑥 − 1) (𝑥 + 2) d𝑥 =
∫
(𝑥2
+ 𝑥 − 2) d𝑥 = 1
3 𝑥3
+ 1
2 𝑥2
− 2𝑥 + 𝐶
(d) Soit développer d’abord (𝑥 + 2)3 = 𝑥3 + 6𝑥2 + 12𝑥 + 8, pour obtenir
∫
(𝑥 + 2)3
d𝑥 = 1
4 𝑥4
+ 2𝑥3
+ 6𝑥2
+ 8𝑥 + 𝐶,
soit
∫
(𝑥 + 2)3
d𝑥 = 1
4 (𝑥 + 2)4
+ 𝐶1.
(e)
∫
(𝑒3𝑥
− 𝑒2𝑥
+ 𝑒𝑥
) d𝑥 = 1
3 𝑒3𝑥
− 1
2 𝑒2𝑥
+ 𝑒𝑥
+ 𝐶
(f)
∫
𝑥3 − 3𝑥 + 4
𝑥
d𝑥 =
∫
𝑥2
− 3 +
4
𝑥
d𝑥 = 1
3 𝑥3
− 3𝑥 + 4 ln |𝑥| + 𝐶
4. (a) D’abord simplifier la fonction sous le signe intégrale :
(𝑦 − 2)2
√
𝑦
=
𝑦2 − 4𝑦 + 4
√
𝑦
= 𝑦3/2
− 4𝑦1/2
+ 4𝑦−1/2
.
Et, de là,
∫
(𝑦 − 2)2
√
𝑦
d𝑦=
∫
(𝑦3/2
− 4𝑦1/2
+ 4𝑦−1/2
) d𝑦= 2
5 𝑦5/2
− 8
3 𝑦3/2
+ 8𝑦1/2
+ 𝐶.
(b) Effectuer la division polynomiale
𝑥3
𝑥 + 1
= 𝑥2
− 𝑥 + 1 −
1
𝑥 + 1
, puis
∫
𝑥3
𝑥 + 1
d𝑥 =
𝑥3
3
−
𝑥2
2
+ 𝑥 − ln |𝑥 + 1| + 𝐶.

92. 92 CORRIGÉS DES EXERCICES
(c)
d
d𝑥
(1 + 𝑥2
)16
= 16 (1 + 𝑥2
)15
× 2𝑥 = 32𝑥 (1 + 𝑥2
)15
, d’où
∫
𝑥 (1 + 𝑥2
)15
d𝑥 = 1
32 (1 + 𝑥2)16 + 𝐶.
5. (a) et (b) : dérivez chaque membre de droite et vérifiez si c’est la fonction sous le signe
intégrale. (Pour (a) voir aussi exercice 10.5.5.)
6. (a) La figure 10.1.1 montre que l’équation du second degré 𝑓 ′(𝑥) = 0 a des racines en
𝑥 = −1 et 𝑥 = 3. On a donc 𝑓 ′(𝑥) = 𝐴(𝑥 + 1)(𝑥 − 3).
(b) La figure 10.1.1 montre aussi que 𝑓 ′(1) = −1, de sorte que 𝐴 = 1/4, d’où 𝑓 ′(𝑥) =
1
4 (𝑥 + 1)(𝑥 − 3) = 1
4 𝑥2 − 1
2 𝑥 − 3
4 . En intégrant, on obtient 𝑓 (𝑥) = 1
12 𝑥3 − 1
4 𝑥2 − 3
4 𝑥 + 𝐶.
Puisque 𝑓 (0) = 2, on a 𝐶 = 2.
(c) Voir figure C10.1.6.
y
−1
1
2
x
−3 −2 −1 1 2 3 4
f
Figure C10.1.6
y
−1
1
2
x
−4 −3 −2 −1 1 2
f
Figure C10.1.7
7. Le graphique de 𝑓 ′(𝑥) à la figure 10.1.2 a l’allure d’une fonction polynomiale de degré 3
dont les racines sont −3, −1 et 1, avec 𝑓 ′(0) = −1. Aussi
𝑓 ′
(𝑥) =
1
3
(𝑥 + 3) (𝑥 + 1) (𝑥 − 1) =
1
3
𝑥3
+ 𝑥2
−
1
3
𝑥 − 1.
Si 𝑓 (0) = 0, l’intégration donne 𝑓 (𝑥) = 1
12 𝑥4 + 1
3 𝑥3 − 1
6 𝑥2 − 𝑥. La figure C10.1.7 présente
le graphique de cette fonction 𝑓 .
8. Dérivez le membre de droite et vérifiez s’il s’agit bien de la fonction sous le signe intégrale.
9. Dérivez le membre de droite. (Après avoir appris la méthode par substitution à la section
10.6, cette intégrale deviendra facile.)
10. (a) 1
10 (2𝑥 + 1)5 + 𝐶 (b) 2
3 (𝑥 + 2)3/2 + 𝐶 (c) −2
√
4 − 𝑥 + 𝐶
11. (a) 𝐹(𝑥) =
∫
(
1
2
𝑒𝑥
− 2𝑥) d𝑥 =
1
2
𝑒𝑥
− 𝑥2
+ 𝐶. Alors 𝐹(0) = 1
2 entraîne 𝐶 = 0.
(b) 𝐹(𝑥) =
∫
(𝑥 − 𝑥3
) d𝑥 =
1
2
𝑥2
−
1
4
𝑥4
+ 𝐶. Alors 𝐹(1) = 5
12 entraîne 𝐶 = 1
6 .
12. La forme générale de 𝑓 ′ est 𝑓 ′(𝑥) = 1
3 𝑥3 + 𝐴. Aussi, 𝑓 (𝑥) = 1
12 𝑥4 + 𝐴𝑥 + 𝐵. Si on exige
𝑓 (0) = 1 et 𝑓 ′(0) = −1, alors 𝐵 = 1 et 𝐴 = −1, de sorte que 𝑓 (𝑥) = 1
12 𝑥4 − 𝑥 + 1.

93. Chapitre 10 / Intégration 93
13. 𝑓 ′(𝑥) =
∫
(𝑥−2
+ 𝑥3
+ 2) d𝑥 = −𝑥−1
+
1
4
𝑥4
+ 2𝑥 + 𝐶. Comme 𝑓 ′
(1) =
1
4
, on a
1
4
= −1 +
1
4
+ 2 + 𝐶
ou 𝐶 = −1. Une nouvelle intégration conduit à
𝑓 (𝑥) =
∫
(−𝑥−1
+
1
4
𝑥4
+ 2𝑥 − 1) d𝑥 = − ln 𝑥 +
1
20
𝑥5
+ 𝑥2
− 𝑥 + 𝐷.
Comme 𝑓 (1) = 0, on a 0 = − ln 1 +
1
20
+ 1 − 1 + 𝐷 ou 𝐷 = −
1
20
.
10.2
1. (a) 𝐴 =
∫ 1
0
𝑥3
d𝑥 =
1
4
𝑥4
1
0
=
1
4
14
−
1
4
04
=
1
4
(b) 𝐴 =
∫ 1
0
𝑥10
d𝑥 =
1
11
𝑥11
1
0
=
1
11
2. (a)
∫ 2
0
3𝑥2
d𝑥 = 𝑥3
2
0
= 8 (b) 1/7
(c) 𝑒 − 1/𝑒 (voir la région ombrée de la figure C10.2.2). (d) 9/10
y
x
−1 1
f (x) = ex
Figure C10.2.2
y
−1
x
A
y = 1/x3
−2 −1
Figure C10.2.3
3. Voir figure C10.2.3. 𝐴 = −
∫ −1
−2
𝑥−3
d𝑥 = − −
1
2
𝑥−2
−1
−2
= −
−
1
2
− −
1
8
=
3
8
.
4. 𝐴 = 1
2
∫ 1
−1
(𝑒𝑥
+ 𝑒−𝑥
) d𝑥 =
1
2
(𝑒𝑥
− 𝑒−𝑥
)
1
−1
= 𝑒 − 𝑒−1
5. (a)
∫ 1
0
𝑥 d𝑥 =
1
2
𝑥2
1
0
=
1
2
(b) 16/3
(c)
∫ 3
−2
1
2
𝑥2
−
1
3
𝑥3
d𝑥 = (
1
6
𝑥3
−
1
12
𝑥4
)
3
−2
=
1
12
𝑥3
(2 − 𝑥)
3
−2
= −
27
12
+
32
12
=
5
12
(d) −12/5 (e) 41/2
(f)
∫ 3
2
1
𝑡 − 1
+ 𝑡
d𝑡 =
ln(𝑡 − 1) +
1
2
𝑡2
3
2
= ln 2 +
9
2
−
4
2
= ln 2 +
5
2
6. (a) 𝑓 (𝑥) = 𝑥3 − 3𝑥2 + 2𝑥 et donc 𝑓 ′(𝑥) = 3𝑥2 − 6𝑥 + 2 = 0 quand 𝑥0 = 1 −
√
3/3 et
𝑥1 = 1 +
√
3/3. On a 𝑓 ′(𝑥) 0 ⇔ 𝑥 𝑥0 ou 𝑥 𝑥1. De plus,
𝑓 ′
(𝑥) 0 ⇔ 𝑥0 𝑥 𝑥1.

94. 94 CORRIGÉS DES EXERCICES
Ainsi 𝑓 est (strictement) croissante sur ] −∞, 𝑥0] et sur [𝑥1, +∞[ et (strictement) décrois-
sante sur [𝑥0, 𝑥1].
(b) Voir figure C10.2.6.
∫ 1
0
𝑓 (𝑥) d𝑥 =
∫ 1
0
(𝑥3
− 3𝑥2
+ 2𝑥) d𝑥 =
𝑥4
4
− 𝑥3
+ 𝑥2 1
0
=
1
4
− 0 =
1
4
L’aire de la région ombrée est égale à 1
4 .
y
−1
1
2
x
−1 1 2
Figure C10.2.6
y
x
−2000
−1000
1000
2000
y = 4000 − x
f
Figure C10.2.7
7. (a) 𝑓 ′
(𝑥) = −1 + 3 000 000/𝑥2
= 0 quand 𝑥 =
√
3 000 000 = 1 000
√
3. (Rappelez-vous
𝑥 0.) 𝑥 = 1 000
√
3 maximise le profit. Voir figure C10.2.7.
(b) 𝐼 =
1
2 000
4 000𝑥 −
1
2
𝑥2
− 3 000 000 ln 𝑥
3 000
1 000
= 2 000 − 1 500 ln 3 ≈ 352.
8. (a) 6/5 (b) 26/3 (c) 𝛼 (𝑒𝛽 − 1)/𝛽 (d) − ln 2
10.3
1. (a)
1
2
𝑥2
+
1
3
𝑥3
5
0
= 325/6 (b) 0 (c) ln 9 (d) 𝑒 − 1 (e) −136 (f) 687/64
(g)
∫ 4
0
1
2
𝑥1/2
d𝑥 =
1
2
×
2
3
𝑥3/2
4
0
=
8
3
(h)
∫ 2
1
1 + 𝑥3
𝑥2
d𝑥 =
∫ 2
1
1
𝑥2
+ 𝑥
d𝑥 =
−
1
𝑥
+
1
2
𝑥2
2
1
= 2
2.
∫ 𝑏
𝑐
𝑓 (𝑥) d𝑥 =
∫ 𝑏
𝑎
𝑓 (𝑥) d𝑥 −
∫ 𝑐
𝑎
𝑓 (𝑥) d𝑥 = 8 − 4 = 4
3. Soit 𝐴 =
∫ 1
0
𝑓 (𝑥) d𝑥 et 𝐵 =
∫ 1
0
𝑔(𝑥) d𝑥. Alors les deux équations donnent 𝐴 − 2𝐵 = 6 et
2𝐴 + 2𝐵 = 9, système dont la solution est 𝐴 = 5 et 𝐵 = −1/2 et, de là, 𝐼 = 𝐴 − 𝐵 = 11/2.
4.
∫ 1
0
(𝑥𝑝+𝑞
+ 𝑥𝑝+𝑟
) d𝑥 =
𝑥𝑝+𝑞+1
𝑝 + 𝑞 + 1
+
𝑥𝑝+𝑟+1
𝑝 + 𝑟 + 1
1
0
=
1
𝑝 + 𝑞 + 1
+
1
𝑝 + 𝑟 + 1
5. La valeur de 𝑓 ′(1) implique 𝑎 + 𝑏 = 6. De plus, 𝑓 ′′(𝑥) = 2𝑎𝑥 + 𝑏. La valeur de 𝑓 ′′(1)
implique 2𝑎 + 𝑏 = 18. Il s’ensuit que 𝑎 = 12 et 𝑏 = 6 et, de là, 𝑓 ′(𝑥) = 12𝑥2 − 6𝑥. Mais
alors 𝑓 (𝑥) =
∫
(12𝑥2 −6𝑥) d𝑥 = 4𝑥3 −3𝑥2 +𝐶, et, puisqu’on veut
∫ 2
0
(4𝑥3 −3𝑥2 +𝐶) = 18,
il faut que 16 − 8 + 2𝐶 = 18 ou 𝐶 = 5.

95. Chapitre 10 / Intégration 95
6. (a)
h1
9
𝑒3𝑡−2
+ ln(𝑡 + 2)
i 3
0
=
1
9
(𝑒7
− 𝑒−2
) + ln(5/2)
(b)
∫ 1
0
(𝑥2
+ 2)2
d𝑥 =
∫ 1
0
(𝑥4
+ 4𝑥2
+ 4) d𝑥 =
1
5
𝑥5
+
4
3
𝑥3
+ 4𝑥
1
0
= 83/15
(c) Notez que
𝑥2 + 𝑥 +
√
𝑥 + 1
𝑥 + 1
=
𝑥(𝑥 + 1) + (𝑥 + 1)1/2
𝑥 + 1
= 𝑥 + (𝑥 + 1)−1/2
,
On a donc
∫ 1
0
𝑥2 + 𝑥 +
√
𝑥 + 1
𝑥 + 1
d𝑥 = ( 1
2 𝑥2
+ 2(𝑥 + 1)1/2
)
1
0
= 1
2 + 2
√
2 − 2 = 2
√
2 − 3
2 .
(d) On a
𝐴
𝑥 + 𝑏
𝑥 + 𝑐
+
𝑑
𝑥
= 𝐴
𝑥 + 𝑐 + 𝑏 − 𝑐
𝑥 + 𝑐
+
𝑑
𝑥
= 𝐴 +
𝐴(𝑏 − 𝑐)
𝑥 + 𝑐
+
𝑑
𝑥
.
Il suffit alors d’intégrer,
∫ 𝑏
1
𝐴
𝑥 + 𝑏
𝑥 + 𝑐
+
𝑑
𝑥
d𝑥 = 𝐴
𝑏 − 1 + (𝑏 − 𝑐) ln[(𝑏 + 𝑐)/(1 + 𝑐)]
+ 𝑑 ln 𝑏.
7. Selon la formule (10.3.6), 𝐹′(𝑥) = 𝑥2 + 2. Pour trouver 𝐺′(𝑥), on utilise la règle de
dérivation d’une fonction composée. On obtient 𝐺′(𝑥) = 2𝑥 [(𝑥2)2 + 2] = 2𝑥5 + 4𝑥.
8. 𝐻′(𝑡) = 2𝑡𝐾(𝑡2) 𝑒−𝜌𝑡2
, d’après la formule (10.3.8) et la règle de dérivation d’une fonction
composée.
9. On utilise la formule (10.3.8) pour trouver les dérivées.
(a) 𝑡2 (b) −𝑒−𝑡2
(c) 2/
√
𝑡4 + 1
(d) ( 𝑓 (2) − 𝑔(2)) × 0 − ( 𝑓 (−𝜆) − 𝑔(−𝜆)) × (−1) = 𝑓 (−𝜆) − 𝑔(−𝜆).
10. De 𝑦2 = 3𝑥, on tire 𝑥 = 1
3 𝑦2, qui, introduit dans l’autre équation, donne 𝑦 +1 = ( 1
3 𝑦2 −1)2
ou 𝑦 (𝑦3 − 6𝑦 − 9) = 0. Or, 𝑦3 − 6𝑦 − 9 = (𝑦 − 3) (𝑦2 + 3𝑦 + 3), avec 𝑦2 + 3𝑦 + 3, qui
n’est jamais nul. D’où (0, 0) et (3, 3) sont les coordonnées des seuls points d’intersection.
L’aire de la région située entre les paraboles est
𝐴 =
∫ 3
0
(
√
3𝑥 − 𝑥2
+ 2𝑥) d𝑥 = 6.
Voir figure C10.3.10.
11. 𝑊(𝑇) =
𝐾
𝑇
(−1/𝜌) 𝑒−𝜌𝑡
𝑇
0
= 𝐾(1 − 𝑒−𝜌𝑇
)/𝜌𝑇. Ici 𝑊(𝑇) → 0 lorsque 𝑇 → +∞ et, par
la règle de l’Hospital, 𝑊(𝑇) → 𝐾 lorsque 𝑇 → 0+. Pour 𝑇 0, on trouve 𝑊′(𝑇) =
𝐾𝑒−𝜌𝑇 (1 + 𝜌𝑇 − 𝑒𝜌𝑇 )/𝜌𝑇2 0, car 𝑒𝜌𝑇 1 + 𝜌𝑇 (voir exercice 6.11.11). On conclut
que 𝑊(𝑇) est strictement décroissante et que 𝑊(𝑇) ∈]0, 𝐾[.
12. (a) On a
𝑓 ′
(𝑥) =
2
√
𝑥 + 4 (
√
𝑥 + 4 − 2)
0
pour tout 𝑥 0. Par ailleurs, 𝑓 (𝑥) → −∞ lorsque 𝑥 → 0, tandis que 𝑓 (𝑥) → +∞ lorsque
𝑥 → +∞. Par conséquent, 𝑓 est strictement croissante sur ]0, +∞[ et à valeurs dans R.

96. 96 CORRIGÉS DES EXERCICES
La fonction 𝑓 admet donc une réciproque définie sur R. Pour trouver l’expression de la
réciproque, on note que
𝑦 = 4 ln(
√
𝑥 + 4 − 2) ⇔ ln(
√
𝑥 + 4 − 2) = 𝑦/4 ⇔
√
𝑥 + 4 = 𝑒𝑦/4
+ 2
⇔ 𝑥 + 4 = (𝑒𝑦/4
+ 2)2
⇔ 𝑥 = 𝑒𝑦/2
+ 4𝑒𝑦/4
.
La réciproque est 𝑔(𝑥) = 𝑒𝑥/2 + 4𝑒𝑥/4.
(b) Voir figure C10.3.12.
y + 1 = (x − 1)2
y2
= 3x
y
−1
1
2
3
4
x
−1 1 3 4 5 6
Figure C10.3.10
y
−5
5
10
−5 5 10x
B
A a
a
f
g
y = x
Figure C10.3.12
(c) On peut observer à la figure C10.3.12 les graphiques de 𝑓 et 𝑔 symétriques par rapport
à la droite d’équation 𝑦 = 𝑥. De ce fait, aire 𝐴 = aire 𝐵. Mais aire 𝐵 est la différence
entre l’aire d’un rectangle de base 𝑎 et hauteur 10 et l’aire sous le graphique de 𝑔 sur
l’intervalle [0, 𝑎],
𝐴 = 𝐵 = 10𝑎 −
∫ 𝑎
0
(𝑒𝑥/2
+ 4𝑒𝑥/4
) d𝑥 = 10𝑎 − 2𝑒𝑎/2
− 16𝑒𝑎/4
+ 2 + 16.
Comme 𝑎 = 𝑓 (10) = 4 ln(
√
14−2), on a 𝑒𝑎/2 = (
√
14−2)2 = 14−4
√
14+4 = 18−4
√
14
et aussi 𝑒𝑎/4 =
√
14 − 2. De là,
𝐴 = 𝐵 = 10𝑎 − 2 (18 − 4
√
14) − 16 (
√
14 − 2) + 18 = 40 ln(
√
14 − 2) + 14 − 8
√
14 ≈ 6,26.
10.4
1. 𝑥 (𝑡) = 𝐾 −
∫ 𝑡
0
¯
𝑢𝑒−𝑎𝑠
𝑑𝑠 = 𝐾 − ¯
𝑢 (1 − 𝑒−𝑎𝑡
)/𝑎. Notez que 𝑥 (𝑡) → 𝐾 − ¯
𝑢/𝑎 lorsque
𝑡 → +∞. Si 𝐾 ⩾ ¯
𝑢/𝑎, le puits ne sera jamais vide.
2. (a) Soit 𝑛 le nombre total d’individus. Le nombre d’individus dont le revenu est compris
dans l’intervalle [𝑏, 2𝑏] est donné par
𝑁 = 𝑛
∫ 2𝑏
𝑏
𝐵𝑟−2
d𝑟 = 𝑛−𝐵𝑟−1
2𝑏
𝑏
=
𝑛𝐵
2𝑏
.
Leurs revenus cumulés égalent
𝑀 = 𝑛
∫ 2𝑏
𝑏
𝐵𝑟−2
𝑟 d𝑟 = 𝑛
∫ 2𝑏
𝑏
𝐵𝑟−1
d𝑟 = 𝑛𝐵 ln𝑟
2𝑏
𝑏
= 𝑛𝐵 ln 2.
Le revenu moyen est donc 𝑚 = 𝑀/𝑁 = 2𝑏 ln 2.

97. Chapitre 10 / Intégration 97
(b) La demande totale est donnée par
𝑥 (𝑝) =
∫ 2𝑏
𝑏
𝑛𝐷(𝑝, 𝑟) 𝑓 (𝑟) d𝑟 =
∫ 2𝑏
𝑏
𝑛𝐴𝑝𝛾
𝑟 𝛿
𝐵𝑟−2
d𝑟
= 𝑛𝐴𝐵𝑝𝛾
∫ 2𝑏
𝑏
𝑟 𝛿−2
d𝑟 = 𝑛𝐴𝐵𝑝𝛾 𝑟 𝛿−1
𝛿 − 1
2𝑏
𝑏
= 𝑛𝐴𝐵𝑝𝛾
𝑏𝛿−1 2𝛿−1 − 1
𝛿 − 1
.
3. On a 𝑆 = (1/𝑟) 𝑒𝑟𝑡
𝑇
0
= (𝑒𝑟𝑇
− 1)/𝑟, de sorte que 𝑒𝑟𝑇 − 1 = 𝑟𝑆. En résolvant par rapport
à 𝑇, on obtient 𝑇 = 1
𝑟 ln(1 + 𝑟𝑆).
4. (a) 𝐾(5) − 𝐾(0) =
∫ 5
0
(3𝑡2
+ 2𝑡 + 5) d𝑡 = 175
(b) 𝐾(𝑇) − 𝐾0 = (𝑇3 − 𝑡3
0) + (𝑇2 − 𝑡2
0) + 5 (𝑇 − 𝑡0)
5. (a) Voir figure C10.4.5.
50
100
150
t
2 4 6 8 10
f
g
Figure C10.4.5
y
1
2
3
4
5
6
x
1 3
2 4 5
A
y = x √1 + x
Figure C10.5.2
(b)
∫ 𝑡
0
𝑔(𝜏) − 𝑓 (𝜏)
d𝜏 =
∫ 𝑡
0
2𝜏3
− 30𝜏2
+ 100𝜏) d𝜏 =
1
2
𝑡2
(𝑡 − 10)2
⩾ 0 pour tout 𝑡.
(c) On a
∫ 10
0
𝑝(𝑡) 𝑓 (𝑡) d𝑡 =
∫ 10
0
−𝑡3
+ 9𝑡2
+ 11𝑡 − 11 + 11/(𝑡 + 1)
d𝑡
= 940 + 11 ln 11 ≈ 966,38
tandis que
∫ 10
0
𝑝(𝑡)𝑔(𝑡) d𝑡 =
∫ 10
0
𝑡3
− 19𝑡2
+ 79𝑡 + 121 − 121/(𝑡 + 1)
d𝑡
= 3 980/3 − 121 ln 11 ≈ 1 036,52.
L’option 𝑔 doit être choisie.
6. La quantité à l’équilibre est 𝑄∗ = 600, où 𝑃∗ = 80. Alors
SC =
∫ 600
0
(120 − 0,2𝑄) d𝑄 = 36 000 et SP =
∫ 600
0
(60 − 0,1𝑄) d𝑄 = 18 000.

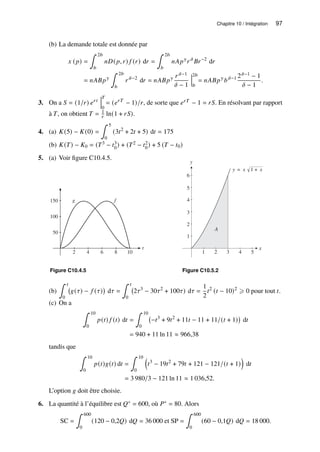
98. 98 CORRIGÉS DES EXERCICES
7. L’équilibre est atteint quand 6 000/(𝑄∗ + 50) = 𝑄∗ + 10. La seule solution positive est
𝑄∗ = 50 et 𝑃∗ = 60. Alors
𝑆𝐶 =
∫ 50
0
h 6 000
𝑄 + 50
− 60
i
d𝑄 = [6 000 ln(𝑄 + 50) − 60𝑄]
50
0
= 6 000 ln 2 − 3 000
et SP =
∫ 50
0
(50 − 𝑄) d𝑄 = 1 250.
10.5
1. (a) Formule (10.5.1) avec 𝑓 (𝑥) = 𝑥 et 𝑔′(𝑥) = 𝑒−𝑥 :
∫
𝑥𝑒−𝑥
d𝑥 = 𝑥 (−𝑒−𝑥
) −
∫
1 × (−𝑒−𝑥
) d𝑥 = −𝑥𝑒−𝑥
− 𝑒−𝑥
+ 𝐶.
(b)
∫
3𝑥𝑒4𝑥
d𝑥 = 3𝑥 ×
1
4
𝑒4𝑥
−
∫
3 ×
1
4
𝑒4𝑥
d𝑥 =
3
4
𝑥𝑒4𝑥
−
3
16
𝑒4𝑥
+ 𝐶
(c)
∫
(1+𝑥2
)𝑒−𝑥
d𝑥 = (1+𝑥2
) (−𝑒−𝑥
)−
∫
2𝑥 (−𝑒−𝑥
) d𝑥 = −(1+𝑥2
)𝑒−𝑥
+2
∫
𝑥𝑒−𝑥
d𝑥
La dernière intégrale a été calculée en (a), ce qui donne
∫
(1 + 𝑥2
)𝑒−𝑥
d𝑥 = −(1 + 𝑥2
)𝑒−𝑥
− 2𝑥𝑒−𝑥
− 2𝑒−𝑥
+ 𝐶 = −(𝑥2
+ 2𝑥 + 3)𝑒−𝑥
+ 𝐶.
(d)
∫
𝑥ln 𝑥 d𝑥 =
1
2
𝑥2
ln 𝑥 −
∫
1
2
𝑥2 1
𝑥
d𝑥 =
1
2
𝑥2
ln 𝑥 −
∫
1
2
𝑥 d𝑥 =
1
2
𝑥2
ln 𝑥 −
1
4
𝑥2
+ 𝐶
2. (a)
∫ 1
−1
𝑥 ln(𝑥 + 2) d𝑥 =
1
2
𝑥2
ln(𝑥 + 2)
1
−1
−
∫ 1
−1
1
2
𝑥2 1
𝑥 + 2
d𝑥
=
1
2
ln 3 −
1
2
∫ 1
−1
𝑥 − 2 +
4
𝑥 + 2
d𝑥 = 2 −
3
2
ln 3
(b) Pour rappel, d
d𝑥
2𝑥 = 2𝑥 ln 2 et donc 2𝑥/ln 2 est une primitive de 2𝑥. Il s’ensuit que
∫ 2
0
𝑥2𝑥
d𝑥 = 𝑥
2𝑥
ln 2
2
0
−
∫ 2
0
2𝑥
ln 2
d𝑥 =
8
ln 2
−
2𝑥
(ln 2)2
2
0
=
8
ln 2
−
4
(ln 2)2
−
1
(ln 2)2
=
8
ln 2
−
3
(ln 2)2
.
(c) On commence par intégrer par parties l’intégrale indéfinie. Par (10.5.1) avec
𝑓 (𝑥) = 𝑥2 et 𝑔(𝑥) = 𝑒𝑥,
∫
𝑥2
𝑒𝑥
d𝑥 = 𝑥2
𝑒𝑥
−
∫
2𝑥𝑒𝑥
d𝑥. (∗)
Pour calculer cette dernière intégrale, on utilise à nouveau la méthode par parties. Avec
𝑓 (𝑥) = 2𝑥 et 𝑔(𝑥) = 𝑒𝑥, on obtient
∫
2𝑥𝑒𝑥
d𝑥 = 2𝑥𝑒𝑥
−
∫
2𝑒𝑥
d𝑥 = 2𝑥𝑒𝑥
− (2𝑒𝑥
+ 𝐶).

99. Chapitre 10 / Intégration 99
On introduit cette expression dans (∗), cela donne
∫
𝑥2
𝑒𝑥
d𝑥 = 𝑥2
𝑒𝑥
− 2𝑥𝑒𝑥
+ 2𝑒𝑥
+ 𝐶,
et, de là,
∫ 1
0
𝑥2
𝑒𝑥
d𝑥 = (𝑥2
𝑒𝑥
− 2𝑥𝑒𝑥
+ 2𝑒𝑥
)
1
0
= (𝑒 − 2𝑒 + 2𝑒) − (0 − 0 + 2) = 𝑒 − 2.
Autrement, et de façon plus compacte, on utilise la formule (10.5.2).
∫ 1
0
𝑥2
𝑒𝑥
d𝑥 = 𝑥2
𝑒𝑥
1
0
−2
∫ 1
0
𝑥𝑒𝑥
d𝑥
= 𝑒 − 2
h
𝑥𝑒𝑥
1
0
−
∫ 1
0
𝑒𝑥
d𝑥
i
= 𝑒 − 2
𝑒 − 𝑒𝑥
1
0
= 𝑒 − 2
(d) On doit écrire la fonction sous le signe intégrale sous la forme d’un produit 𝑓 (𝑥)𝑔′(𝑥).
Si on pose 𝑓 (𝑥) = 𝑥 et 𝑔′(𝑥) =
√
1 + 𝑥 = (1 + 𝑥)1/2, alors, comment trouver 𝑔 ? Un peu
de réflexion mène à choisir 𝑔(𝑥) = 2
3 (1 + 𝑥)3/2. Alors (10.5.2) conduit à
∫ 3
0
𝑥
√
1 + 𝑥 d𝑥 = 𝑥 ×
2
3
(1 + 𝑥)3/2
3
0
−
∫ 3
0
1 ×
2
3
(1 + 𝑥)3/2
d𝑥
= 3 ×
2
3
× 43/2
−
2
3
2
5
(1 + 𝑥)5/2
3
0
= 16 −
4
15
(45/2
− 1)
= 16 −
4
15
× 31 = 7 +
11
15
=
116
15
.
Sinon, on aurait pu calculer d’abord la primitive 𝑥
√
1 + 𝑥 et ensuite l’intégrale définie par
la définition (10.2.3). La figure C10.5.2 montre la région sous le graphique de 𝑦 = 𝑥
√
1 + 𝑥
sur l’intervalle [0, 3]. La valeur 7 + 11
15 est-elle une estimation acceptable de l’aire 𝐴?
3. (a)
∫ 4
1
√
𝑡 ln 𝑡 d𝑡 =
∫ 4
1
𝑡1/2
ln 𝑡 d𝑡 =
2
3
𝑡3/2
ln 𝑡
4
1
−
2
3
∫ 4
1
𝑡3/2
(1/𝑡) d𝑡
=
16
3
ln 4 −
2
3
2
3
𝑡3/2
4
1
=
16
3
ln 4 −
28
9
(b)
∫ 2
0
(𝑥 − 2) 𝑒−𝑥/2
d𝑥 = (𝑥 − 2) (−2) 𝑒−𝑥/2
2
0
−
∫ 2
0
(−2) 𝑒−𝑥/2
d𝑥
= −4 − 4𝑒−𝑥/2
2
0
= −4 − 4 (𝑒−1
− 1) = −4𝑒−1
(c)
∫ 3
0
(3 − 𝑥) 3𝑥
d𝑥 = (3 − 𝑥) (3𝑥
/ln 3)
3
0
−
∫ 3
0
(−1) (3𝑥
/ln 3) d𝑥
= 26/(ln 3)2
− 3/ln 3
4. La formule générale découle de (10.5.1) et fournit, dans le cas 𝑓 (𝑥) = ln 𝑥,
∫
ln 𝑥 d𝑥 = 𝑥 ln 𝑥 − 𝑥 + 𝐶.
5. Formule (10.5.1) avec 𝑓 (𝑥) = ln 𝑥 et 𝑔′(𝑥) = 𝑥𝜌. (Sinon, dériver simplement le membre
de droite.)

100. 100 CORRIGÉS DES EXERCICES
6. (a) Par la formule (10.5.2),
∫ 𝑇
0
𝑡𝑒−𝑟𝑡
d𝑡 = 𝑡
−1
𝑟
𝑒−𝑟𝑡
𝑇
0
−
∫ 𝑇
0
−1
𝑟
𝑒−𝑟𝑡
d𝑡 =
−𝑇
𝑟
𝑒−𝑟𝑇
+
1
𝑟
∫ 𝑇
0
𝑒−𝑟𝑡
d𝑡
=
−𝑇
𝑟
𝑒−𝑟𝑇
+
1
𝑟
−1
𝑟
𝑒−𝑟𝑡
𝑇
0
=
1
𝑟2
(1 − (1 + 𝑟𝑇) 𝑒−𝑟𝑇
).
Multiplier cette expression par 𝑏.
(b)
∫ 𝑇
0
(𝑎 + 𝑏𝑡) 𝑒−𝑟𝑡
d𝑡 = 𝑎
∫ 𝑇
0
𝑒−𝑟𝑡
d𝑡 + 𝑏
∫ 𝑇
0
𝑡𝑒−𝑟𝑡
d𝑡 et utiliser (a).
(c)
∫ 𝑇
0
(𝑎 − 𝑏𝑡 + 𝑐𝑡2
) 𝑒−𝑟𝑡
d𝑡 = 𝑎
∫ 𝑇
0
𝑒−𝑟𝑡
d𝑡 − 𝑏
∫ 𝑇
0
𝑡𝑒−𝑟𝑡
d𝑡 + 𝑐
∫ 𝑇
0
𝑡2
𝑒−𝑟𝑡
d𝑡.
Utilisez ensuite les résultats précédents,
∫ 𝑇
0
𝑡2
𝑒−𝑟𝑡
d𝑡 = 𝑡2
−1
𝑟
𝑒−𝑟𝑡
𝑇
0
−
∫ 𝑇
0
2𝑡
−1
𝑟
𝑒−𝑟𝑡
d𝑡
= −
1
𝑟
𝑇2
𝑒−𝑟𝑇
+
2
𝑟
∫ 𝑇
0
𝑡𝑒−𝑟𝑡
d𝑡.
10.6
1. (a) 1
9 (𝑥2 + 1)9 + 𝐶 (poser 𝑢 = 𝑥2 + 1, d’où d𝑢 = 2𝑥 d𝑥).
(b) 1
11 (𝑥 + 2)11 + 𝐶 (poser 𝑢 = 𝑥 + 2).
(c) ln |𝑥2 − 𝑥 + 8| + 𝐶 (poser 𝑢 = 𝑥2 − 𝑥 + 8).
2. (a) 1
24 (2𝑥2 + 3)6 + 𝐶 (poser 𝑢 = 2𝑥2 + 3, de sorte que d𝑢 = 4𝑥 d𝑥).
(b) Si on pose 𝑢 = 𝑥3 + 2, on a d𝑢 = 3𝑥2 d𝑥 et
∫
𝑥2
𝑒𝑥3+2
d𝑥 =
∫
1
3
𝑒𝑢
d𝑢 =
1
3
𝑒𝑢
+ 𝐶 =
1
3
𝑒𝑥3+2
+ 𝐶.
(c) On pourrait essayer 𝑢 = 𝑥 + 2, ce qui donne d𝑢 = d𝑥 et
∫
ln(𝑥 + 2)
2𝑥 + 4
d𝑥 =
∫
ln 𝑢
2𝑢
d𝑢.
Comme ce n’est pas plus simple que l’intégrale initiale, on essaie 𝑢 = ln(𝑥 + 2).
Alors d𝑢 =
d𝑥
𝑥 + 2
et
∫
ln(𝑥 + 2)
2𝑥 + 4
d𝑥 =
∫
1
2 𝑢 d𝑢 = 1
4 (𝑢)2
+ 𝐶 = 1
4 (ln(𝑥 + 2))2
+ 𝐶.
(d) Première possibilité : 𝑢 = 1 + 𝑥. Alors d𝑢 = d𝑥 et
∫
𝑥
√
1 + 𝑥 d𝑥 =
∫
(𝑢 − 1)
√
𝑢 d𝑢 =
∫
(𝑢3/2
− 𝑢1/2
) d𝑢
=
2
5
𝑢5/2
−
2
3
𝑢3/2
+ 𝐶 =
2
5
(1 + 𝑥)5/2
−
2
3
(1 + 𝑥)3/2
+ 𝐶.
Deuxième possibilité : 𝑢 =
√
1 + 𝑥. Alors 𝑢2 = 1 + 𝑥 et 2𝑢𝑑𝑢 = d𝑥. Alors l’intégrale
devient
∫
𝑥
√
1 + 𝑥 d𝑥 =
∫
(𝑢2 − 1)𝑢2𝑢 d𝑢 =
∫
(2𝑢4 − 2𝑢3) d𝑢, etc. Vérifiez que vous
obtenez la même réponse(9).
(9) En réalité, même une intégration par parties donnerait des résultats. Voir exercice 10.5.2(d).

101. Chapitre 10 / Intégration 101
(e) Si on pose 𝑢 = 1 + 𝑥2, on a 𝑥2 = 𝑢 − 1 et d𝑢 = 2𝑥 d𝑥, de sorte que
∫
𝑥3
(1 + 𝑥2)3
d𝑥 =
∫
𝑥2 × 𝑥
(1 + 𝑥2)3
d𝑥 =
1
2
∫
𝑢 − 1
𝑢3
d𝑢
=
1
2
∫
(𝑢−2
− 𝑢−3
) d𝑢 = −
1
2
𝑢−1
+
1
4
𝑢−2
+ 𝐶
=
−1
2 (1 + 𝑥2)
+
1
4 (1 + 𝑥2)2
+ 𝐶.
(f) Si on pose 𝑢 =
√
4 − 𝑥3, 𝑢2 = 4 − 𝑥3 et 2𝑢 d𝑢 = −3𝑥2 d𝑥. Ainsi,
∫
𝑥5
p
4 − 𝑥3 d𝑥 =
∫
𝑥3
p
4 − 𝑥3 𝑥2
d𝑥 =
∫
(4 − 𝑢2
) 𝑢 (−
2
3
) 𝑢 d𝑢
=
∫
(−
8
3
𝑢2
+
2
3
𝑢4
) d𝑢 = −
8
9
𝑢3
+
2
15
𝑢5
+ 𝐶
= −
8
9
(4 − 𝑥3
)3/2
+
2
15
(4 − 𝑥3
)5/2
+ 𝐶.
3. (a) Avec 𝑢 =
√
1 + 𝑥2, 𝑢2 = 1 + 𝑥2, de sorte que 𝑢 d𝑢 = 𝑥 d𝑥. Si 𝑥 = 0, alors 𝑢 = 1;
si 𝑥 = 1, alors 𝑢 =
√
2. De là,
∫ 1
0
𝑥
p
1 + 𝑥2 d𝑥 =
∫ √
2
1
𝑢2
d𝑢 =
1
3
𝑢3
√
2
1
=
1
3
(2
√
2 − 1).
(b) 1/2. (Posez 𝑢 = ln 𝑥.)
(c) 1
2 (𝑒2 − 𝑒2/3). (Posez 𝑢 = 2/𝑥.)
(d) Méthode 1.
∫ 8
5
𝑥
𝑥 − 4
d𝑥 =
∫ 8
5
𝑥 − 4 + 4
𝑥 − 4
d𝑥 =
∫ 8
5
1 +
4
𝑥 − 4
d𝑥 = [(𝑥 + 4 ln(𝑥 − 4)]
8
5
= 3 + 4 ln 4.
Méthode 2. Introduisez la nouvelle variable 𝑢 = 𝑥 − 4. Ensuite, d𝑢 = d𝑥 et 𝑥 = 𝑢 + 4.
Quand 𝑥 = 5, 𝑢 = 1 et quand 𝑥 = 8, 𝑢 = 4, de sorte que
∫ 8
5
𝑥
𝑥 − 4
d𝑥 =
∫ 4
1
𝑢 + 4
𝑢
d𝑢 =
∫ 4
1
𝑢 + 4
𝑢
d𝑢 =
∫ 4
1
1+
4
𝑢
d𝑢 = (𝑢+4 ln 𝑢)
4
1
= 3+4 ln 4.
4.
∫ 𝑥
3
2𝑡 − 2
𝑡2 − 2𝑡
d𝑡 = ln(𝑡2
− 2𝑡)
𝑥
3
= ln(𝑥2
− 2𝑥) − ln 3 = ln 1
3 (𝑥2
− 2𝑥). L’équation à résoudre
devient ln 1
3 (𝑥2 − 2𝑥) = ln( 2
3 𝑥 − 1) = ln 1
3 (2𝑥 − 3) ou 𝑥2 − 2𝑥 = 2𝑥 − 3 ou encore,
𝑥2 − 4𝑥 + 3 = 0, dont les solutions sont 𝑥 = 1 et 𝑥 = 3. Mais seul 𝑥 = 3 appartient au
domaine spécifié 𝑥 2, c’est donc la seule solution.
5. Posez 𝑧 = 𝑥 (𝑡). Alors d𝑧 = 𝑥′(𝑡) d𝑡 et le résultat découle de (10.6.2).
6. (a) 𝐼 =
∫ 1
0
(𝑥4
− 𝑥9
) (𝑥5
− 1)12
d𝑥 =
∫ 1
0
−𝑥4
(𝑥5
− 1)13
d𝑥. Posez 𝑢 = 𝑥5 − 1. Alors
d𝑢 = 5𝑥4 d𝑥. On utilise maintenant (9.6.2) en même temps que le fait que 𝑢 = −1 quand
𝑥 = 0 et 𝑢 = 0 quand 𝑥 = 1. L’intégrale devient
𝐼 = −
∫ 0
−1
1
5
𝑢13
d𝑢 = −
1
70
𝑢14
0
−1
=
1
70
.

102. 102 CORRIGÉS DES EXERCICES
(b) Avec 𝑢 =
√
𝑥, on a 𝑢2 = 𝑥 et 2𝑢 d𝑢 = d𝑥. Ensuite(10)
∫
ln 𝑥
√
𝑥
d𝑥 = 2
∫
ln 𝑢2
d𝑢 = 4
∫
ln 𝑢 d𝑢 = 4 (𝑢 ln 𝑢 − 𝑢) + 𝐶
= 4
√
𝑥 ln
√
𝑥 − 4
√
𝑥 + 𝐶 = 2
√
𝑥 ln 𝑥 − 4
√
𝑥 + 𝐶.
(c) Avec 𝑢 = 1 +
√
𝑥, on a (𝑢 − 1)2 = 𝑥. Aussi 2 (𝑢 − 1) d𝑢 = d𝑥. On utilise à nouveau
(10.6.2) ainsi que le fait que 𝑢 = 1 quand 𝑥 = 0 et 𝑢 = 3 quand 𝑥 = 4. L’intégrale
devient(11)
∫ 3
1
2 (𝑢 − 1)
√
𝑢
d𝑢 = 2
∫ 3
1
(𝑢1/2
− 𝑢−1/2
) d𝑢 = 2 (
2
3
𝑢3/2
− 2𝑢1/2
)
3
1
=
8
3
.
7. (a) On pose 𝑢 = 1 + 𝑒
√
𝑥. Alors on a d𝑢 =
1
2
√
𝑥
𝑒
√
𝑥
d𝑥. Maintenant 𝑥 = 1 donne 𝑢 = 1 + 𝑒
et 𝑥 = 4 donne 𝑢 = 1 + 𝑒2. D’où
∫ 4
1
𝑒
√
𝑥
√
𝑥 (1 + 𝑒
√
𝑥)
d𝑥 =
∫ 1+𝑒2
1+𝑒
2 d𝑢
𝑢
= 2 ln 𝑢
1+𝑒2
1+𝑒
= 2 ln(1 + 𝑒2
) − 2 ln(1 + 𝑒).
(b) Il semble naturel de poser 𝑢 = 𝑒𝑥 + 1, puis d𝑢 = 𝑒𝑥 d𝑥 et ainsi
d𝑥 = d𝑢/𝑒𝑥
= d𝑢/(𝑢 − 1).
Quand 𝑥 = 0, 𝑢 = 2, quand 𝑥 = 1/3, 𝑢 = 𝑒1/3 + 1. D’où(12)
∫ 1/3
0
d𝑥
𝑒𝑥 + 1
=
∫ 𝑒1/3+1
2
1
𝑢 (𝑢 − 1)
d𝑢 =
∫ 𝑒1/3+1
2
1
𝑢 − 1
−
1
𝑢
d𝑢
= ln |𝑢 − 1| − ln |𝑢|
𝑒1/3+1
2
=
1
3
− ln(𝑒1/3
+ 1) + ln 2 = ln 2 − ln(𝑒−1/3
+ 1),
car
1
3
− ln(𝑒1/3
+ 1) = ln[𝑒1/3
/(𝑒1/3
+ 1)] = − ln(𝑒−1/3
+ 1).
(c) On pose 𝑧4 = 2𝑥 − 1. Alors on a 4𝑧3 d𝑧 = 2 d𝑥. Et 𝑥 = 8,5 donne 𝑧 = 2 et 𝑥 = 41
donne 𝑧 = 3. L’intégrale devient
∫ 3
2
2𝑧3 d𝑧
𝑧2 − 𝑧
= 2
∫ 3
2
𝑧2 d𝑧
𝑧 − 1
= 2
∫ 3
2
𝑧 + 1 +
1
𝑧 − 1
d𝑧
= 2
1
2 𝑧2
+ 𝑧 + ln(𝑧 − 1)
3
2
= 7 + 2 ln 2.
(10) L’intégration par parties marcherait aussi avec 𝑓 (𝑥) = ln 𝑥 et 𝑔′ (𝑥) = 1/
√
𝑥.
(11) La substitution 𝑢 =
p
1 +
√
𝑥 marche aussi.
(12) Si la fonction à intégrer était écrite
𝑒−𝑥
1 + 𝑒−𝑥
, la substitution naturelle 𝑡 = 𝑒−𝑥 (ou encore mieux 𝑢 = 1 + 𝑒−𝑥),
soit d𝑡 = −𝑒−𝑥 d𝑥, marche bien. Vérifiez que vous obtenez la même réponse.

103. Chapitre 10 / Intégration 103
8. Posez 𝑢 = 𝑥1/6. Alors 𝐼 = 6
∫
𝑢8
1 − 𝑢2
d𝑢. Puis
𝑢8
(−𝑢2 + 1)
= −𝑢6
− 𝑢4
− 𝑢2
− 1 +
1
(−𝑢2 + 1)
.
D’où 𝐼 = −
6
7
𝑥7/6
−
6
5
𝑥5/6
− 2𝑥1/2
− 6𝑥1/6
− 3 ln |1 − 𝑥1/6
| + 3 ln |1 + 𝑥1/6
| + 𝐶.
9. On trouve 𝑓 (𝑥) =
1
𝑎 − 𝑏
𝑎𝑐 + 𝑑
𝑥 − 𝑎
−
𝑏𝑐 + 𝑑
𝑥 − 𝑏
.
(a)
∫
𝑥 d𝑥
(𝑥 + 1) (𝑥 + 2)
=
∫
−1 d𝑥
𝑥 + 1
+
∫
2 d𝑥
𝑥 + 2
= − ln |𝑥 + 1| + 2 ln |𝑥 + 2| + 𝐶
(b)
∫
(1 − 2𝑥) d𝑥
(𝑥 + 3) (𝑥 − 5)
=
∫
−
7
8
1
𝑥 + 3
−
9
8
1
𝑥 − 5
d𝑥 =−
7
8
ln |𝑥 + 3| −
9
8
ln |𝑥 − 5| + 𝐶
10.7
1. (a)
∫ 𝑏
1
𝑥−3
d𝑥 = (−
1
2
𝑥−2
)
𝑏
1
=
1
2
−
1
2
𝑏−2
→
1
2
lorsque 𝑏 → +∞. Par conséquent,
∫ +∞
1
1
𝑥3
d𝑥 =
1
2
.
(b)
∫ 𝑏
1
𝑥−1/2
d𝑥 = 2𝑥1/2
𝑏
1
= 2𝑏1/2
− 2 → +∞ lorsque 𝑏 → +∞. L’intégrale diverge.
(c) 1
(d)
∫ 𝑎
0
𝑥
√
𝑎2 − 𝑥2
d𝑥 = −
p
𝑎2 − 𝑥2
𝑎
0
= 𝑎
2. (a)
∫ +∞
−∞
𝑓 (𝑥) d𝑥 =
∫ 𝑏
𝑎
1
𝑏 − 𝑎
d𝑥 =
1
𝑏 − 𝑎
𝑥
𝑏
𝑎
=
1
𝑏 − 𝑎
(𝑏 − 𝑎) = 1
(b)
∫ +∞
−∞
𝑥 𝑓 (𝑥) d𝑥 =
1
𝑏 − 𝑎
∫ 𝑏
𝑎
𝑥 d𝑥 =
1
2 (𝑏 − 𝑎)
𝑏
𝑎
𝑥2
=
1
2 (𝑏 − 𝑎)
(𝑏2
− 𝑎2
) =
1
2
(𝑎 + 𝑏)
(c)
1
3 (𝑏 − 𝑎)
𝑥3
𝑏
𝑎
=
1
3
𝑏3 − 𝑎3
𝑏 − 𝑎
=
1
3
(𝑎2
+ 𝑎𝑏 + 𝑏2
)
3. Avec des notations simplifiées et le résultat de l’exemple 10.7.1, on a les résultats suivants.
(a)
∫ +∞
0
𝑥𝜆𝑒−𝜆𝑥
d𝑥 = −𝑥𝑒−𝜆𝑥
+∞
0
+
∫ +∞
0
𝑒−𝜆𝑥
d𝑥 =
1
𝜆
(b)
∫ ∞
0
(𝑥 − 1/𝜆)2
𝜆𝑒−𝜆𝑥
d𝑥 = − (𝑥 − 1/𝜆)2
𝑒−𝜆𝑥
∞
0
+
∫ ∞
0
2 (𝑥 − 1/𝜆) 𝑒−𝜆𝑥
d𝑥
= 1/𝜆2
+ 2
∫ ∞
0
𝑥𝑒−𝜆𝑥
d𝑥 − (2/𝜆)
∫ ∞
0
𝑒−𝜆𝑥
d𝑥
= 1/𝜆2
+ 2/𝜆2
− 2/𝜆2
= 1/𝜆2
où on a exploité le résultat de l’exemple 10.7.1 et la question (a) de façon à déduire
l’avant-dernière égalité.

104. 104 CORRIGÉS DES EXERCICES
(c) On a
∫ +∞
0
(𝑥 − 1/𝜆)3
𝜆𝑒−𝜆𝑥
d𝑥 = − (𝑥 − 1/𝜆)3
𝑒−𝜆𝑥
+∞
0
+
∫ +∞
0
3 (𝑥 − 1/𝜆)2
𝑒−𝜆𝑥
d𝑥
= −1/𝜆3
+ (3/𝜆)
∫ +∞
0
(𝑥 − 1/𝜆)2
𝜆𝑒−𝜆𝑥
d𝑥
= −1/𝜆3
+ (3/𝜆) (1/𝜆2
) = 2/𝜆3
où on a utilisé le résultat de la question (b) pour justifier l’avant-dernière égalité.
4. La première intégrale diverge, car
∫ 𝑏
0
𝑥
1 + 𝑥2
d𝑥 = 1
2 ln(1 + 𝑥2)
𝑏
0
= 1
2 ln(1 + 𝑏2) → +∞ lorsque 𝑏 → +∞.
Par ailleurs, ∫ 𝑏
−𝑏
𝑥
1 + 𝑥2
d𝑥 =
1
2
ln(1 + 𝑥2
)
𝑏
−𝑏
= 0
pour tout 𝑏, de sorte que la limite lorsque 𝑏 → +∞ est 0.
5. (a) 𝑓 ′(𝑥) = (1 − 3 ln 𝑥)/𝑥4 = 0 en 𝑥 = 𝑒1/3 et passe du positif au négatif en ce point. Par
conséquent, 𝑓 a un maximum en (𝑒1/3, 1/3𝑒). Comme 𝑓 (𝑥) → −∞ lorsque 𝑥 → 0+, il
n’y a pas de minimum. En utilisant la règle de l’Hospital, on trouve aussi que 𝑓 (𝑥) → 0
lorsque 𝑥 → +∞.
(b)
∫ 𝑏
𝑎
𝑥−3
ln 𝑥 d𝑥 = −
1
2
𝑥−2
ln 𝑥
𝑏
𝑎
+
∫ 𝑏
𝑎
1
2
𝑥−3
d𝑥 =
−
1
2
𝑥−2
ln 𝑥 −
1
4
𝑥−2
𝑏
𝑎
.
Elle diverge quand 𝑏 = 1 et 𝑎 → 0. Mais
∫ ∞
1
𝑥−3 ln 𝑥 d𝑥 = 1/4.
6.
1
1 + 𝑥2
⩽
1
𝑥2
pour 𝑥 ⩾ 1 et
∫ 𝑏
1
d𝑥
𝑥2
= −
1
𝑥
𝑏
1
= 1 −
1
𝑏
−→
𝑏→+∞
1, de sorte que, d’après le
théorème de comparaison 10.7.1, l’intégrale converge.
7. À condition que les deux intégrales soient convergentes, l’intégrale est la somme de
𝐼1 = lim
𝜀→0+
∫ 3
−2+𝜀
1/
√
𝑥 + 2
d𝑥 et 𝐼2 = lim
𝜀→0+
∫ 3−𝜀
−2
1/
√
3 − 𝑥
d𝑥.
Ici, 𝐼1 = lim
𝜀→0+
2
√
𝑥 + 2
3
−2+𝜀
= lim
𝜀→0+
2
√
5 − 2
√
𝜀
= 2
√
5
et 𝐼2 = lim
𝜀→0+
−2
√
3 − 𝑥
3−𝜀
−2
= lim
𝜀→0+
−2
√
𝜀 + 2
√
5
= 2
√
5.
8. (a) 𝑧 =
∫ 𝜏
0
(1/𝜏)𝑒−𝑟𝑠
d𝑠 = (1 − 𝑒−𝑟 𝜏
)/𝑟𝜏
(b) 𝑧 =
∫ 𝜏
0
2 (𝜏 − 𝑠)𝜏−2
𝑒−𝑟𝑠
d𝑠 = (2/𝑟𝜏) [1 − (1/𝑟𝜏) (1 − 𝑒−𝑟 𝜏
)]
9.
∫
𝑥−2
d𝑥 = −𝑥−1
+𝐶. Si on calcule
∫ 1
−1
𝑥−2
d𝑥 comme −𝑥−1
1
−1
, on tombe sur la réponse
inacceptable −2. L’erreur provient de ce que 𝑥−2 diverge vers +∞ lorsque 𝑥 → 0 (en fait,
∫ 1
−1
𝑥−2
d𝑥 diverge vers +∞).

105. Chapitre 10 / Intégration 105
10. Grâce à la réponse de l’exercice 10.6.6(b), on trouve
∫ 1
ℎ
(ln 𝑥/
√
𝑥) d𝑥 = (2
√
𝑥 ln 𝑥 − 4
√
𝑥)
1
ℎ
= −4 − (2
√
ℎ ln ℎ − 4
√
ℎ) → −4.
Lorsque ℎ → 0+, la règle de l’Hospital nous permet de déduire que
√
ℎ ln ℎ = ln ℎ/ℎ−1/2
→ 0.
L’intégrale donnée converge donc vers −4.
11.
∫ 𝐴
1
𝑘
𝑥
−
𝑘2
1 + 𝑘𝑥
d𝑥 = 𝑘 ln
1
1/𝐴 + 𝑘
− 𝑘 ln
1
1 + 𝑘
→ 𝑘 ln
1
𝑘
− 𝑘 ln
1
1 + 𝑘
= ln
1 +
1
𝑘
𝑘
lorsque 𝐴 → +∞
Ainsi, 𝐼𝑘 = ln
1 + 1
𝑘
𝑘
tend vers ln 𝑒 = 1 lorsque 𝑘 → +∞.
12. La substitution 𝑢 = (𝑥 − 𝜇)/
√
2𝜎 donne d𝑢 = d𝑥/(𝜎
√
2) et ainsi d𝑥 = 𝜎
√
2 d𝑢. Elle est
utilisée pour les énoncés (a) à (c).
(a)
∫ +∞
−∞
𝑓 (𝑥) d𝑥 =
1
√
𝜋
∫ +∞
−∞
𝑒−𝑢2
d𝑢 = 1, par (10.7.9).
(b) En utilisant (a) et l’exemple 10.7.3, on obtient
∫ +∞
−∞
𝑥 𝑓 (𝑥) d𝑥 =
1
√
𝜋
∫ +∞
−∞
(𝜇 +
√
2𝜎𝑢)𝑒−𝑢2
d𝑢 = 𝜇.
(c) On a
∫ +∞
−∞
(𝑥 − 𝜇)2
𝑓 (𝑥) d𝑥 =
∫ +∞
−∞
2𝜎2
𝑢2 1
𝜎
√
2𝜋
𝑒−𝑢2
𝜎
√
2 d𝑢 = 𝜎2 2
√
𝜋
∫ +∞
−∞
𝑢2
𝑒−𝑢2
d𝑢.
Une intégration par parties mène à
∫ 𝑏
𝑎
𝑢2𝑒−𝑢2
d𝑢 = −1
2 𝑢𝑒−𝑢2
+
∫ 𝑏
𝑎
1
2 𝑒−𝑢2
d𝑢 pour
tous réels 𝑎 et 𝑏. Comme (𝑢𝑒−𝑢2
)
𝑏
𝑎
= 𝑏𝑒−𝑏2
− 𝑎𝑒−𝑎2
→ 0 quand 𝑎 → −∞ et
𝑏 → ∞, on a
∫ +∞
−∞
𝑢2𝑒−𝑢2
d𝑢 =
∫ +∞
−∞
1
2 𝑒−𝑢2
d𝑢 = 1
2
√
𝜋 d’après la question (a). D’où
∫ +∞
−∞
(𝑥 − 𝜇)2 𝑓 (𝑥) d𝑥 = 𝜎2.
Exercices récapitulatifs du chapitre 10
1. (a) −16𝑥 + 𝐶 (b) 55𝑥 + 𝐶 (c) 3𝑦 − 1
2 𝑦2 + 𝐶 (d) 1
2𝑟2 − 16
5 𝑟5/4 + 𝐶 (e) 1
9 𝑥9 + 𝐶
(f) 2
7 𝑥7/2 + 𝐶 (𝑥2√
𝑥 = 𝑥2 × 𝑥1/2 = 𝑥5/2) (g) −1
4 𝑝−4 + 𝐶 (h) 1
4 𝑥4 + 1
2 𝑥2 + 𝐶
2. (a) 𝑒2𝑥 + 𝐶 (b) 1
2 𝑥2 − 25
2 𝑒2𝑥/5 + 𝐶 (c) −1
3 𝑒−3𝑥 + 1
3 𝑒3𝑥 + 𝐶 (d) 2 ln |𝑥 + 5| + 𝐶
3. (a)
∫ 12
0
50 d𝑥 = 50𝑥
12
0
= 600 (b)
∫ 2
0
(𝑥 −
1
2
𝑥2
) d𝑥 = (
1
2
𝑥2
−
1
6
𝑥3
)
2
0
=
2
3
(c)
∫ 3
−3
(𝑢 + 1)2
d𝑢 =
1
3
(𝑢 + 1)3
3
−3
= 24 (d)
∫ 5
1
2
𝑧
d𝑧 = 2 ln 𝑧
5
1
= 2 ln 5

106. 106 CORRIGÉS DES EXERCICES
(e)
∫ 12
2
3
𝑡 + 4
d𝑡 = 3 ln(𝑡 + 4)
12
2
= 3(ln 16 − ln 6) = 3 ln(8/3)
(f) 𝐼 =
∫ 4
0
𝑣
p
𝑣2 + 9 d𝑣 = 1
3 (𝑣2 + 9)3/2
4
0
= 98/3. (Ou introduire 𝑧 =
√
𝑣2 + 9. Alors
𝑧2 = 𝑣2 + 9 et 2𝑧 d𝑧 = 2𝑣 d𝑣, ou 𝑣 d𝑣 = 𝑧 d𝑧. Quand 𝑣 = 0, 𝑧 = 3, quand 𝑣 = 4, 𝑧 = 5, de
sorte que 𝐼 =
∫ 5
3
𝑧2
d𝑧 =
1
3
𝑧3
5
3
=
98
3
.)
4. (a) 5/4 (voir exemple 10.7.2). (b)
1
20
(1 + 𝑥4
)5
1
0
=
31
20
(c) 5𝑡𝑒−𝑡
+∞
0
−
∫ +∞
0
5𝑒−𝑡
d𝑡 = 5𝑒−𝑡
+∞
0
= −5
(d)
∫ 𝑒
1
(ln 𝑥)2
d𝑥 = 𝑥 (ln 𝑥)2
𝑒
1
−2
∫ 𝑒
1
ln 𝑥 d𝑥 = 𝑒 − 2 (𝑥 ln 𝑥 − 𝑥)
𝑒
1
= 𝑒 − 2
(e)
2
9
(𝑥3
+1)3/2
2
0
=
2
9
(93/2
−1) =
52
9
(f)
1
3
ln(𝑒3𝑧
+5)
0
−∞
=
1
3
(ln 6−ln 5) =
1
3
ln(6/5)
(g)
1
4
𝑥4
ln(2𝑥)
𝑒/2
1/2
−
1
4
∫ 𝑒/2
1/2
𝑥3
d𝑥 =
1
4
(𝑒/2)4
−
1
16
[(𝑒/2)4
− (1/2)4
] =
1
256
(3𝑒4
+ 1)
(h) Introduire 𝑢 =
√
𝑥. Alors 𝑢2 = 𝑥 et 2𝑢 d𝑢 = d𝑥.
Ensuite
∫ +∞
1
𝑒−
√
𝑥
√
𝑥
d𝑥 =
∫ +∞
1
𝑒−𝑢 2𝑢 d𝑢
𝑢
= 2
∫ +∞
1
𝑒−𝑢
d𝑢 = 2𝑒−1
.
5. (a) En posant 𝑢 = 9 +
√
𝑥, on a 𝑥 = (𝑢 − 9)2 et ainsi d𝑥 = 2 (𝑢 − 9) d𝑢. Par ailleurs, 𝑢 = 9
quand 𝑥 = 0 et 𝑢 = 14 quand 𝑥 = 25. D’où
∫ 25
0
1
9 +
√
𝑥
d𝑥 =
∫ 14
9
2 (𝑢 − 9)
𝑢
d𝑢 =
∫ 14
9
2 −
18
𝑢
d𝑢 = 10 − 18 ln
14
9
.
(b) En posant 𝑢 =
√
𝑡 + 2, on a 𝑡 = 𝑢2 − 2 et ainsi d𝑡 = 2𝑢 d𝑢. De plus, 𝑢 = 2 quand 𝑡 = 2
et 𝑢 = 3 quand 𝑡 = 7. De là,
∫ 7
2
𝑡
√
𝑡 + 2 d𝑡 =
∫ 3
2
(𝑢2
− 2)𝑢 × 2𝑢 d𝑢 = 2
∫ 3
2
(𝑢4
− 2𝑢2
) d𝑢 = 2 1
5 𝑢5 − 2
3 𝑢3
3
2
= 2
243
5
−
54
3
−
32
5
−
16
3
=
422
5
−
76
3
= 886/15.
(c) En posant 𝑢 =
3
√
19𝑥3 + 8, on a 𝑢3 = 19𝑥3 +8 et ainsi 3𝑢2 d𝑢 = 57𝑥2 d𝑥. De plus, 𝑥 = 0
donne 𝑢 = 2 et 𝑥 = 1 donne 𝑢 = 3. Par conséquent,
∫ 1
0
57𝑥2 3
p
19𝑥3 + 8 d𝑥 =
∫ 3
2
3𝑢3
d𝑢 =
3
4
𝑢4
3
2
=
195
4
.
6. (a) 𝐹′(𝑥) = 4 (
√
𝑥 − 1), car
∫ 𝑥
4
(𝑢1/2
+ 𝑥𝑢−1/2
) d𝑢 = 2
3 𝑢3/2
+ 2𝑥𝑢1/2
𝑥
4
=
8
3
𝑥3/2
−
16
3
− 4𝑥.
(b) D’après (10.3.8), 𝐹′(𝑥) = ln 𝑥 − (ln
√
𝑥) (1/(2
√
𝑥)) = ln 𝑥 − ln 𝑥/(4
√
𝑥).

107. Chapitre 10 / Intégration 107
7. 𝐶(𝑌) = 0,69𝑌 + 1 000
8. En intégrant la fonction du coût marginal, on obtient
𝐶(𝑥) = 𝐶0 +
∫ 𝑥
0
(𝛼𝑒𝛽𝑢
+ 𝛾) d𝑢 = 𝐶0 +
𝛼
𝛽
𝑒𝛽𝑢
𝑥
0
=
𝛼
𝛽
(𝑒𝛽𝑥
− 1) + 𝛾𝑥 + 𝐶0.
9. Soit 𝐴 =
∫ 3
−1
( 𝑓 (𝑥) d𝑥 et 𝐵 =
∫ 3
−1
𝑔(𝑥)) d𝑥. Alors 𝐴+𝐵 = 6 et 3𝐴+4𝐵 = 9, ce qui conduit
à 𝐴 = 15 et 𝐵 = −9. Ensuite 𝐼 = 𝐴 + 2𝐵 = −3.
10. (a) Comme dans l’exemple 10.4.3, on a besoin de trouver d’abord 𝑃∗ et 𝑄∗. La condition
d’équilibre implique 𝑓 (𝑄∗) = 100 − 0,05𝑄∗ = 𝑔(𝑄∗) = 0,1𝑄∗ + 10, de sorte que
0,15𝑄∗ = 90 ou 𝑄∗ = 600. Alors 𝑃∗ = 𝑔(𝑄∗) = 0,1𝑄∗ + 10 = 70. De plus,
SC =
∫ 600
0
( 𝑓 (𝑄) − 𝑃∗
) d𝑄 =
∫ 600
0
(30 − 0,05𝑞) 𝑑𝑞 = 30𝑄 −
0,05
2
𝑄2 600
0
= 9 000
SP =
∫ 600
0
(𝑃∗
− 𝑔(𝑄)) d𝑄 =
∫ 600
0
(60 − 0,1𝑄) d𝑄 = 60𝑄 −
0,1
2
𝑄2 600
0
= 18 000
Voir figure C10.R.10a.
(b) L’équilibre a lieu quand 50/(𝑄∗ + 5) = 4,5 + 0,1𝑄∗. En éliminant les fractions et en
simplifiant, on obtient (𝑄∗)2 + 50𝑄∗ − 275 = 0. La seule solution strictement positive est
𝑄∗ = 5 et, de là, 𝑃∗ = 5.
SC =
∫ 5
0
50
𝑄 + 5
− 5
d𝑄 = [50 ln(𝑄 + 5) − 5𝑄]
5
0
= 50 ln 2 − 25
SP =
∫ 5
0
(5 − 4,5 − 0,1𝑄) d𝑄 = (0,5𝑄 − 0,05𝑄2
)
5
0
= 2,5 − 1,25 = 1,25
Voir figure C10.R.10b.
p
q
100
p*
= 70
10
q*
= 600
p = f (q)
SC
S P
p = g(q)
Figure C10.R.10a
p
q
10
SC
SP
p*
= 5
q*
= 5
p = f (q)
p = g(q)
Figure C10.R.10b
11. (a) 𝑓 ′(𝑡) = 4 ln 𝑡(2 − ln 𝑡)/𝑡2, 𝑓 ′′(𝑡) = 8[(ln 𝑡)2 − 3 ln 𝑡 + 1]/𝑡3.
(b) (𝑒2, 16/𝑒2) est un maximum local, (1, 0) est un minimum local (et global). Voir
figure C10.R.11.
(c) Aire =
32
3
. (Suggestion :
∫
𝑓 (𝑡) d𝑡 =
4
3
(ln 𝑡)3
+ 𝐶.)

108. 108 CORRIGÉS DES EXERCICES
y
1
2
3
4
5
x
5 10 15
y
x
Figure C10.R.11
12. (a)
∫ +∞
0
𝑓 (𝑟) d𝑟 =
∫ +∞
0
1
𝑚
𝑒−𝑟/𝑚
d𝑟 = 1 (comme dans l’exemple 10.7.1) et
∫ +∞
0
𝑟 𝑓 (𝑟) d𝑟 =
∫ +∞
0
𝑟
1
𝑚
𝑒−𝑟/𝑚
d𝑟 = 𝑚 (comme dans l’exercice 10.7.3(a)),
le revenu moyen est donc 𝑚.
(b) 𝑥 (𝑝) = 𝑛
∫ +∞
0
(𝑎𝑟 − 𝑏𝑝) 𝑓 (𝑟) d𝑟
= 𝑛
𝑎
∫ +∞
0
𝑟 𝑓 (𝑟) d𝑟 − 𝑏𝑝
∫ +∞
0
𝑓 (𝑟) d𝑟
= 𝑛 (𝑎𝑚 − 𝑏𝑝)
d’après les résultats de la question (a).
Chapitre 11 / Mathématiques financières
et modèles dynamiques
11.1
1. (a) (i) 8 000 (1 + 0,05/12)5×12 ≈ 10 266,87 (ii) 8 000 (1 + 0,05/365)5×365 ≈ 10 272,03
(b) 𝑡 = ln 2/ln(1 + 0,05/12) ≈ 166,7. Cela prend environ 166,7/12 ≈ 13,9 années.
2. (a) 5 000 (1 + 0,03)10 ≈ 6 719,58
(b) 37,17 années. (En effet, 5 000 (1,03)𝑡 = 3 × 5 000, ainsi 𝑡 = ln 3/ln 1,03 ≈ 37,17.)
3. On résout (1+ 𝑝/100)100 = 100 par rapport à 𝑝. Pour cela, on élève à la puissance 1/100,
1 + 𝑝/100 =
100
√
100, d’où 𝑝 = 100 (
100
√
100 − 1) ≈ 100 (1,047 − 1) = 4,7.
4. (a) (i) Après 2 ans : 2 000 (1,07)2 = 2 289,80.
(ii) Après 10 ans : 2 000 (1,07)10 ≈ 3 934,30.
(b) 2 000 (1,07)𝑡 = 6 000 donne (1,07)𝑡 = 3, de sorte que 𝑡 = ln 3/ln 1,07 ≈ 16,2 années.
5. Utilisez la formule (11.1.2).
(a) 𝐼 = (1 + 0,17/2)2 − 1 = (1 + 0,085)2 − 1 = 0,177225 ou 17,72 %.
(b) 100[(1,0425)4 − 1] ≈ 18,11 % (c) 100[(1 + 0,17/12)12 − 1] ≈ 18,39 %

109. Chapitre 11 / Mathématiques financières et modèles dynamiques 109
6. Le taux annuel effectif dans le cas (ii) est (1 + 0,2/4)4 − 1 = 1,054 − 1 ≈ 0,2155 0,215,
de sorte que la proposition (i) est (légèrement) plus avantageuse.
7. (a) 12 000 × (1,04)15 ≈ 21 611,32. (b) 50 000 × (1,05)−5 ≈ 39 176,31.
8. 100 [(1,02)12 − 1] ≈ 26,82 %.
9. Soit 𝑖 le taux annuel nominal. Selon (11.1.2), 0,28 = (1 + 𝑖/4)4 − 1, de sorte que
𝑖 = 4 ( 4
p
1,28 − 1) ≈ 0,25 ou 25 %.
11.2
1. (a) 8 000𝑒0,05×5 = 8 000𝑒0,25 ≈ 10 272,20
(b) 8 000𝑒0,05𝑡 = 16 000 ou 𝑒0,05𝑡 = 2. Dès lors, 𝑡 = ln 2/0,05 ≈ 13,86 années.
2. (a) (i) 1 000 (1 + 0,05/12)120 ≈ 1 647 (ii) 1 000𝑒0,05×10 ≈ 1 649
(b) (i) 1 000 (1 + 0,05/12)600 ≈ 12 119 (ii) 1 000𝑒0,05×50 ≈ 12 182
3. (a) 𝑒0,1 − 1 ≈ 0,105, de sorte que le taux effectif est d’environ 10,5 %.
(b) Même réponse.
4. Si elle perd 90 % de sa valeur, alors 𝑒−0,1𝑡∗
= 1/10, de sorte que −0,1𝑡∗ = − ln 10, soit
𝑡∗ = (ln 10)/0,1 ≈ 23 années.
5. 𝑒−0,06𝑡∗
= 1/2, de sorte que 𝑡∗ = ln 2/0,06 ≈ 11,55 années.
11.3
1. (i) La valeur actuelle est égale à 350 000 × 1,08−10 ≈ 162 117,72.
(ii) 350 000 × 𝑒−0,08×10 ≈ 157 265,14.
2. (i) La valeur actuelle est égale à 50 000 × 1,0575−5 ≈ 37 806,64.
(ii) 50 000 × 𝑒−0,0575×5 ≈ 37 506,83.
3. (a) On trouve 𝑓 ′(𝑡) = 0,05 (𝑡 + 5) (35 − 𝑡) 𝑒−0,05𝑡 . Manifestement, 𝑓 ′(𝑡) 0 pour 𝑡 35
et 𝑓 ′(𝑡) 0 pour 𝑡 35, de sorte que 𝑡 = 35 rend 𝑓 maximale ( 𝑓 (35) ≈ 278).
(b) 𝑓 (𝑡) → 0 lorsque 𝑡 → +∞. Voir la figure C11.3.3.
y
100
200
t
30 60 90
Figure C11.3.3

110. 110 CORRIGÉS DES EXERCICES
11.4
1. (a) 𝑠𝑛 =
3
2
1 −
1
3
𝑛
(b) 𝑠𝑛 → 3
2 lorsque 𝑛 → +∞ (c)
∞
Õ
𝑛=1
1
3𝑛−1
=
3
2
.
2. Par la formule (11.4.5), on a les résultats suivants.
(a)
1/5
1 − 1/5
= 1/4 (b)
0,1
1 − 0,1
=
0,1
0,9
=
1
9
(c)
517
1 − 1/1,1
= 5 687
(d)
𝑎
1 − 1/(1 + 𝑎)
= 1 + 𝑎 (e)
5
1 − 3/7
=
35
4
3. (a) Série géométrique de raison 1/8. Sa somme vaut 8/(1 − 1/8) = 64/7.
(b) Série géométrique de raison −3. Elle diverge.
(c) Série géométrique. Sa somme vaut 21/3/(1 − 2−1/3).
(d) Ce n’est pas une série géométrique. (On peut toutefois démontrer que sa somme est
égale à ln 2.)
4. (a) Raison 𝑘 = 1/𝑝. Converge vers 1/(𝑝 − 1) pour |𝑝| 1 mais diverge pour |𝑝| ⩽ 1.
(b) Raison 𝑘 = 1/
√
𝑥. Converge vers 𝑥
√
𝑥/(
√
𝑥 − 1) pour
√
𝑥 1, c’est-à-dire pour 𝑥 1
mais diverge pour 0 𝑥 ⩽ 1.
(c) Raison 𝑘 = 𝑥2. Converge vers 𝑥2/(1 − 𝑥2) pour |𝑥| 1 mais diverge pour 𝑥 ⩾ 1.
5. Série géométrique de raison (1 + 𝑝/100)−1. Sa somme vaut
𝑏/[1 − (1 + 𝑝/100)−1
] = 𝑏 (1 + 100/𝑝).
6. Notez 𝑥 le nombre d’années au-delà de 1971 pendant lesquelles les ressources de fer
auraient duré. L’équation à résoudre est 794+794×1,05+· · ·+794× (1,05)𝑥 = 249×103.
Selon la formule (11.4.3), cette équation est équivalente à
794[1 − (1,05)𝑥+1
]/(1 − 1,05) = 249 × 103
ou (1,05)𝑥+1 = 249 × 103 × 0,05/794 + 1 = 12 450/794 + 1 ≈ 16,68. Une calculatrice
donne 𝑥 ≈ (ln 16,68/ln 1,05) − 1 ≈ 56,68. Les ressources seront épuisées au milieu de
l’année 2028.
7. 1 824 × 1,02 + 1 824 × 1,022 + · · · + 1 824 × 1,02𝑛 = (1 824/0,02) (1,02𝑛+1 − 1,02) doit
être égal à 128 300. Aussi, 𝑛 ≈ 43,77. Les ressources vont durer jusqu’en 2037.
8. (a) Comme la raison de cette série est 𝑒−𝑖𝑡 , sa somme est égale à
𝑓 (𝑡) =
𝑃(𝑡) 𝑒−𝑖𝑡
1 − 𝑒−𝑖𝑡
=
𝑃(𝑡)
𝑒𝑖𝑡 − 1
.
(b) 𝑓 ′(𝑡) =
𝑃′(𝑡) (𝑒𝑖𝑡 − 1) − 𝑃(𝑡)𝑟𝑒𝑖𝑡
(𝑒𝑖𝑡 − 1)2
, et 𝑡∗ 0 peut rendre 𝑓 (𝑡) maximale seulement si
𝑓 ′(𝑡∗) = 0, c’est-à-dire si 𝑃′(𝑡∗) (𝑒𝑖𝑡∗
− 1) = 𝑟𝑃(𝑡∗) 𝑒𝑖𝑡∗
, ce qui implique
𝑃′(𝑡∗)
𝑃(𝑡∗)
=
𝑟
1 − 𝑒−𝑖𝑡∗ .

111. Chapitre 11 / Mathématiques financières et modèles dynamiques 111
(c) lim
𝑟→0
𝑟
1 − 𝑒−𝑖𝑡∗ (type 0
0 ) = lim
𝑟→0
1
𝑡∗𝑒−𝑖𝑡∗ =
1
𝑡∗
.
9. Comme le terme général de chacune de ces séries ne tend pas vers 0 lorsque 𝑛 → +∞,
toutes ces séries divergent.
10. (a) Série géométrique de raison 100/101 qui converge vers 100.
(b) Diverge d’après (11.4.10).
(c) Converge d’après (11.4.10).
(d) Diverge, car le terme d’ordre 𝑛 est 𝑎𝑛 = (1 + 𝑛)/(4𝑛 − 3) → 1/4 lorsque 𝑛 → +∞.
(e) Série géométrique de raison −1/2 qui converge vers −1/3.
(f) Série géométrique de raison 1/
√
3 convergente vers
√
3/(
√
3 − 1).
11. Voir la figure C11.4.11. Quand 𝑝 1,
Í∞
𝑛=1(1/𝑛𝑝) = 1 +
Í∞
𝑛=2(1/𝑛𝑝) est finie, car
la somme
Í∞
𝑛=2(1/𝑛𝑝) correspond aux rectangles ombrés dont la somme des aires est
certainement inférieure à l’aire de la région sous la courbe d’équation 𝑦 = 1/𝑥𝑝 sur
[1, +∞[, qui vaut 1/(𝑝 − 1). Quand 𝑝 ⩽ 1, la somme
Í∞
𝑛=1(1/𝑛𝑝) correspond aux plus
grands rectangles de la figure dont la somme des aires est supérieure à l’aire de la région
sous la courbe d’équation 𝑦 = 1/𝑥𝑝 sur [1, +∞[, elle-même non bornée dans le cas
𝑝 ⩽ 1. Par conséquent,
Í∞
𝑛=1(1/𝑛𝑝) diverge.
y
1
x
1 2 3 4
y = 1/x p
Figure C11.4.11
11.5
1. Utilisez (11.5.2) avec 𝑛 = 15, 𝑖 = 0,12 et 𝑎 = 3 500. Cela donne
𝑃15 =
3 500
0,12
1 −
1
(1,12)15
≈ 23 838.
2. Il y a 10 ans, le solde était de 100 000 (1,04)−10 ≈ 67 556,42.
3. 10 000 (1,063 + 1,062 + 1,06 + 1) = 10 000(1,064 − 1)/(1,06 − 1)) ≈ 43 746,16.
4. La valeur future après 10 ans dans le cas (i) est manifestement 13 000 e, alors que, selon
(11.5.3), la valeur correspondante dans le cas (ii) est
𝐹10 =
1 000
0,06
(1,0610
− 1) = 13 180,80.
La proposition (ii) est meilleure.

112. 112 CORRIGÉS DES EXERCICES
5. L’offre (i) est meilleure, car la valeur actuelle de l’offre (ii) est égale à
4 600 +
4 600
0,06
1 −
1
(1,06)4
≈ 20 539.
6. En utilisant (11.5.4), on obtient
1 500
0,08
= 18 750.
7. Si 𝑎 désigne le plus grand montant, alors, selon la formule (11.5.4), 𝑎/𝑖 = 𝐾, de sorte que
𝑎 = 𝑖𝐾.
8. C’est une série géométrique qui commence par 𝑎 = 𝐷/(1 + 𝑖) et de raison
𝑘 = (1 + 𝑔)/(1 + 𝑖).
Elle converge si et seulement si 𝑘 1, c’est-à-dire si et seulement si 𝑔 𝑖. La somme
vaut
𝑎
1 − 𝑘
=
𝐷/(1 + 𝑖)
1 − (1 + 𝑔)/(1 + 𝑖)
=
𝐷
𝑖 − 𝑔
.
9. 𝑉0 =
∫ 15
0
500𝑒−0,06𝑡
d𝑡 = 500
−1
0,06
𝑒−0,06𝑡 15
0
=
500
0,06
1 − 𝑒−0,9
≈ 4945,25
𝑉15 = 𝑒0,06×15𝑉0 = 𝑒0,9𝑉0 ≈ 2,4 596 × 4945,25 ≈ 12 163,3
11.6
1. (a) Selon la formule (11.6.2), les paiements annuels sont
𝑎 = 0,07 ×
80 000
(1 − (1,07)−10)
≈ 11 390,20.
(b) Selon (11.6.2), on trouve 𝑎 =
0,07
12
×
80 000
[1 − (1 + 0,07/12)−120]
≈ 928,87.
2. En utilisant la formule (11.5.3), on trouve
8 000
0,07
[1,076
− 1] ≈ 57 226,33.
Quatre ans après le dernier dépôt, vous avez 57 226,33 × 1,074 ≈ 75 012,05.
3. En intérêt composé annuellement, on a𝑖 = 31/20−1 ≈ 0,0565, de sorte que le taux d’intérêt
est d’environ 5,65 %. En intérêt composé instantanément, on a 𝑒20𝑖 = 3, de sorte que
𝑖 = ln 3/20 ≈ 0,0549, et le taux est d’environ 5,49 %.
4. La valeur actuelle de l’échéancier (ii) est
120 000 × 1,115
0,115
[1 − (1,115)−8
] ≈ 676 444.
La valeur actuelle de l’échéancier (iii) est
220 000 +
70 000
0,115
[1 − (1,115)−12
] ≈ 663 841.
Donc (iii) est meilleur marché. Si le taux d’intérêt passe à 12,5 %, les valeurs actuelles
des échéanciers (ii) et (iii) sont égales à 659 076 et 643 743, respectivement, de sorte que
(iii) est aussi le meilleur placement.

113. Chapitre 11 / Mathématiques financières et modèles dynamiques 113
11.7
1. 𝑖 doit satisfaire à −50 000 + 30 000/(1 + 𝑖) + 30 000/(1 + 𝑖)2 = 0. Avec 𝑠 = 1/(1 + 𝑖), cela
donne 𝑠2 + 𝑠 − 5/3 = 0, dont la solution positive 𝑠 = −1/2 +
p
23/12 ≈ 0,884, de sorte
que 𝑖 ≈ 0,13.
2. L’équation (11.7.1) est ici 𝑎/(1 + 𝑖) + 𝑎/(1 + 𝑖)2 + · · · = −𝑎0, ce qui conduit à 𝑎/𝑖 = −𝑎0
ou 𝑖 = −𝑎/𝑎0.
3. Par hypothèse, 𝑓 (0) = 𝑎0 + 𝑎1 + · · · + 𝑎𝑛 0. De plus, 𝑓 (𝑖) → 𝑎0 0 lorsque 𝑖 → +∞.
Et 𝑓 ′(𝑖) = −𝑎1 (1 + 𝑖)−2 − 2𝑎2 (1 + 𝑖)−3 − · · · − 𝑛𝑎𝑛(1 + 𝑖)−𝑛−1 0, de sorte que 𝑓 (𝑖) est
strictement décroissante. Cela garantit qu’il y a un unique taux de rendement interne avec
𝑖 0.
4. Le prix maximal est 400 000 1/1,175 + (1/1,175)2 + · · · + (1/1,175)7
≈ 1 546 522,94,
c’est-à-dire environ 1,546 million.
5. D’après (11.7.1), le taux interne de rentabilité doit vérifier
−100 000 +
10 000
1 + 𝑖
+
10 000
(1 + 𝑖)2
+ · · · +
10 000
(1 + 𝑖)20
= 0.
Après avoir divisé tous les termes par 10 000 et posé 𝑠 =
1
(1 + 𝑖)
, il est à démontrer que
l’équation
𝑓 (𝑠) = 𝑠20
+ 𝑠19
+ · · · + 𝑠2
+ 𝑠 − 10 = 0
admet une solution unique strictement positive. Comme 𝑓 (0) = −10 et 𝑓 (1) = 10,
en raison du théorème des valeurs intermédiaires (théorème 7.10.1), il existe un nombre
𝑠∗ compris entre 0 et 1 tel que 𝑓 (𝑠∗) = 0. Ce 𝑠∗ est l’unique racine strictement posi-
tive, car 𝑓 ′(𝑠) 0 pour tout 𝑠 0. En fait, suivant à (11.4.3), 𝑓 (𝑠) peut s’écrire
𝑓 (𝑠) = −10 + (𝑠 − 𝑠21)/(1 − 𝑠) et 𝑓 (𝑠∗) = 0 ⇔ (𝑠∗)21 − 11𝑠∗ + 10 = 0. L’exercice
7.R.26 demande une valeur approchée de l’unique racine de cette équation dans l’inter-
valle ]0, 1[. La réponse est 𝑠 = 𝑠∗ = 0,928 et, de là, 𝑟∗ = 1/𝑠∗ −1 ≈ 0,0775, ce qui signifie
que le taux interne de rentabilité est d’environ 7,75 %.
6. En appliquant (11.5.2) avec 𝑎 = 1 000 et 𝑛 = 5, on obtient l’équation
𝑃5 = (1 000/𝑖)
1 − 1/(1 + 𝑖)5
= 4 340
à résoudre par rapport à 𝑖. Pour 𝑖 = 0,05 ou 𝑝 = 5 %, la valeur actuelle est 4 329,48; pour
𝑖 = 0,045 ou 𝑝 = 4,5 %, la valeur actuelle est 4 389,98. Comme d𝑃5/d𝑖 0, il s’ensuit
que 𝑝 est légèrement inférieur à 5 %.
11.8
1. (a) 𝑥𝑡 = 𝑥0 (−2)𝑡 (b) 𝑥𝑡 = 𝑥0 (5/6)𝑡 (c) 𝑥𝑡 = 𝑥0 (−0,3)𝑡
2. (a) 𝑥𝑡 = −4𝑡. (b) 𝑥𝑡 = 2 (1/2)𝑡 +4 (c) 𝑥𝑡 = (13/8) (−3)𝑡 −5/8 (d) 𝑥𝑡 = −2 (−1)𝑡+4

114. 114 CORRIGÉS DES EXERCICES
3. L’équation aux différences implique 𝛼𝑃𝑡 −𝛽 = 𝛾−𝛿𝑃𝑡+1 ou 𝑃𝑡+1 = −(𝛼/𝛿)𝑃𝑡 +(𝛽+𝛾)/𝛿.
Selon (11.8.4), 𝑃𝑡 =
−
𝛼
𝛿
𝑡
𝑃0 −
𝛽 + 𝛾
𝛼 + 𝛿
+
𝛽 + 𝛾
𝛼 + 𝛿
.
11.9
1. Les fonctions (c) et (d) sont les seules qui aient un taux de croissance relatif constant.
Cela est en accord avec (11.9.3) (Notez que 2𝑡 = 𝑒(ln 2) 𝑡 ).
2. (a) 𝐾(𝑡) = (𝐾0 − 𝐼/𝛿) 𝑒−𝛿𝑡 + 𝐼/𝛿
(b) (i) 𝐾(𝑡) = 200−50𝑒−0,05𝑡 et 𝐾(𝑡) tend vers 200 par valeurs inférieures quand 𝑡 → +∞.
(ii) 𝐾(𝑡) = 200 + 50𝑒−0,05𝑡 et 𝐾(𝑡) tend vers 200 par valeurs supérieures quand 𝑡 → +∞.
3. 𝑁(𝑡) = 𝑃(1 − 𝑒−𝑘𝑡 ). Alors 𝑁(𝑡) → 𝑃 lorsque 𝑡 → +∞.
4. 𝑁′(𝑡) = 0,02𝑁(𝑡) + 4 × 104. La solution avec 𝑁(0) = 2 × 106 est
𝑁(𝑡) = 2 × 106
(2𝑒0,02𝑡
− 1).
5. 𝑃(10) = 657 donne 606𝑒10𝑘 = 657 ou 𝑒10𝑘 = 657/606. En prenant le logarithme naturel
des deux membres, on a 10𝑘 = ln(657/606), de sorte que
𝑘 = 0,1 ln(657/606) ≈ 0,00808.
𝑃(15) ≈ 684, 𝑃(40) ≈ 837 et 𝑃(55) ≈ 945 (en arrondissant au million).
6. Le pourcentage de bactéries encore en vie après 𝑡 secondes satisfait à 𝑝(𝑡) = 100𝑒−𝛿𝑡 ,
où 𝑝(7) = 70,5, de sorte que 𝛿 = − ln 0,705/7 ≈ 0,05. Donc 𝑝(30) = 100𝑒−30𝛿 ≈ 22,3%
sont encore en vie après 30 secondes. Comme 100𝑒−𝛿𝑡 = 5 quand 𝑡 ≈ ln 20/0,05 ≈ 60, il
faut environ 60 secondes pour en tuer 95 %.
7. (a) 𝑥 = 𝐴𝑒−0,5𝑡 (b) 𝐾 = 𝐴𝑒0,02𝑡 (c) 𝑥 = 𝐴𝑒−0,5𝑡 + 10 (d) 𝐾 = 𝐴𝑒0,2𝑡 − 500
(e) 𝑥 = 0,1/(3 − 𝐴𝑒0,1𝑡 ) et 𝑥 ≡ 0. (f) 𝐾 = 1/(2 − 𝐴𝑒𝑡 ) et 𝐾 ≡ 0.
8. (a) 𝑦 (𝑡) = 250 +
230
1 + 8,2𝑒−0,34𝑡
(b) 𝑦 (𝑡) → 480 lorsque 𝑡 → +∞. Voir figure C11.9.8.
100
200
300
400
500
t
5 10 15 20
Tracteurs (en milliers)
(1950) (1960) (1970)
0
0
Figure C11.9.8

115. Chapitre 11 / Mathématiques financières et modèles dynamiques 115
9. (a) En appliquant (11.9.11), on trouve 𝑁(𝑡) = 1 000/(1 + 999𝑒−0,39𝑡 ). Après 20 jours,
𝑁(20) ≈ 710 ont développé la grippe.
(b) On a
800 =
1 000
1 + 999𝑒−0,39𝑡∗ ⇔ 999𝑒−0,39𝑡∗
=
1
4
,
de sorte que 𝑒−0,39𝑡∗
=
1
3 996
et 0,39𝑡∗ = ln 3 996. 𝑡∗ ≈ 21 jours.
(c) Après environ 35 jours, 999 auront ou ont eu la grippe. 𝑁(𝑡) → 1 000 lorsque
𝑡 → +∞.
10. (a) Quand 𝑓 ≠ 𝑟, l’équation peut encore s’écrire
𝑥′
= (𝑟 − 𝑓 ) 𝑥
1 −
𝑥
(1 − 𝑓 /𝑟)𝐾
.
Il y a deux solutions constantes 𝑥 ≡ 0 et 𝑥 ≡ (1 − 𝑓 /𝑟)𝐾, bien que cette dernière soit
négative et donc sans signification dans le contexte, à moins que 𝑓 ⩽ 𝑟. Avec ¯
𝑟 = 𝑟 − 𝑓
et ¯
𝐾 = (1 − 𝑓 /𝑟)𝐾, l’équation est 𝑥 = ¯
𝑟𝑥
1 −
𝑥
¯
𝐾
. Selon la formule (11.9.11), la solution
est
𝑥 (𝑡) =
¯
𝐾
1 +
¯
𝐾 − 𝑥0
𝑥0
𝑒−¯
𝑟𝑡
=
(1 − 𝑓 /𝑟)𝐾
1 +
(1 − 𝑓 /𝑟)𝐾 − 𝑥0
𝑥0
𝑒−(𝑟− 𝑓 ) 𝑡
.
Dans le cas où 𝑓 = 𝑟, l’équation se réduit à 𝑥′ = −𝑟𝑥2/𝐾. Par séparation des variables,
on écrit − d𝑥/𝑥2 = (𝑟/𝐾) d𝑡, et l’intégration fournit 1/𝑥 = 𝑟𝑡/𝐾 + 𝐶. Si 𝑥 (0) = 𝑥0,
on a 𝐶 = 1/𝑥0 et la solution est
𝑥 =
1
𝑟𝑡/𝐾 + 1/𝑥0
→ 0 quand 𝑡 → +∞.
(b) Quand 𝑓 𝑟, la solution de l’équation différentielle donnée dans la question (a) est
encore valable même si ¯
𝐾 et ¯
𝑟 sont négatifs. À cause du fait que le taux 𝑓 dépasse le
taux de reconstitution 𝑟, le stock de poissons diminue continuellement. En effet, lorsque
𝑡 → +∞, on a 𝑒−(𝑟− 𝑓 ) 𝑡 → +∞ et la solution de l’équation satisfait en fait à 𝑥 (𝑡) → 0.
Autrement dit, le stock de poissons va vers l’extinction.
11. À environ 11 h 26. (En effet, en mesurant le temps en heures, avec 𝑡 = 0 pris à midi, on a
𝑇′ = 𝑘(20 − 𝑇) avec 𝑇(0) = 35 et 𝑇(1) = 32. La température du corps au moment 𝑡 est
donnée par 𝑇(𝑡) = 20+15𝑒−𝑘𝑡 avec 𝑘 = ln(5/4). Dans l’hypothèse où la température était
de 37 degrés au moment de la mort 𝑡∗, alors 𝑡∗ = − ln(17/15)/ln(5/4) ≈ −0,56 heures,
ou environ 34 minutes avant midi.)
11.10
1. L’équation est à variables séparées :
∫
𝑥4
d𝑥 =
∫
(1−𝑡) d𝑡, donc 1
5 𝑥5 = 𝑡 − 1
2 𝑡2 +𝐶1, qui
implique 𝑥5 = 5𝑡 − 5
2 𝑡2 + 5𝐶1, d’où 𝑥 = 5
q
5𝑡 − 5
2 𝑡2 + 5𝐶1 = 5
q
5𝑡 − 5
2 𝑡2 + 𝐶, avec 𝐶 = 5𝐶1.
Comme 𝑥 (1) = 1, on a 𝐶 = −3/2.

116. 116 CORRIGÉS DES EXERCICES
2. (a) d𝑥/d𝑡 = 𝑒2𝑡 /𝑥2. Séparer :
∫
𝑥2
d𝑥 =
∫
𝑒2𝑡
d𝑡. Intégrer : 1
3 𝑥3 = 1
2 𝑒2𝑡 + 𝐶1. Résoudre
par rapport à 𝑥,
𝑥3
=
3
2
𝑒2𝑡
+ 3𝐶1 =
3
2
𝑒2𝑡
+ 𝐶,
avec 𝐶 = 3𝐶1. De là, 𝑥 = 3
q
3
2 𝑒2𝑡 + 𝐶(13).
(b) d𝑥/d𝑡 = 𝑒−𝑡 𝑒𝑥. Séparer :
∫
𝑒−𝑥
d𝑥 =
∫
𝑒−𝑡
d𝑡. Intégrer : −𝑒−𝑥 = −𝑒−𝑡 + 𝐶1.
Résoudre par rapport à 𝑥 : 𝑒−𝑥 = 𝑒−𝑡 + 𝐶, avec 𝐶 = −𝐶1. De là, −𝑥 = ln(𝑒−𝑡 + 𝐶),
de sorte que 𝑥 = − ln(𝑒−𝑡 + 𝐶).
(c) Application directe de (11.10.3) 𝑥 = 𝐶𝑒3𝑡 − 6.
(d) Semblable à (a), 𝑥 = 7
p
(1 + 𝑡)7 + 𝐶.
(e) De (11.10.5), on obtient 𝑥 = 𝐶𝑒2𝑡
+ 𝑒2𝑡
∫
(−𝑡) 𝑒−2𝑡
d𝑡 = 𝐶𝑒2𝑡
− 𝑒2𝑡
∫
𝑡𝑒−2𝑡
d𝑡. Ici
∫
𝑡𝑒−2𝑡
d𝑡 = 𝑡(−1
2 ) 𝑒−2𝑡
+ 1
2
∫
𝑒−2𝑡
d𝑡 = (−1
2 𝑡 − 1
4 ) 𝑒−2𝑡
et donc 𝑥 = 𝐶𝑒2𝑡 − 𝑒2𝑡 (−1
2 𝑡 − 1
4 ) 𝑒−2𝑡 = 𝐶𝑒2𝑡 + 1
2 𝑡 + 1
4 .
(f) Par la formule (11.10.5),
𝑥 = 𝐶𝑒−3𝑡
+ 𝑒−3𝑡
∫
𝑒3𝑡
𝑡𝑒𝑡2−3𝑡
d𝑡 = 𝐶𝑒−3𝑡
+ 𝑒−3𝑡
∫
𝑡𝑒𝑡2
d𝑡 = 𝐶𝑒−3𝑡
+ 1
2 𝑒𝑡2−3𝑡
.
3. L’équation est à variables séparées : d𝑘/𝑘 = 𝑠𝛼𝑒𝛽𝑡 d𝑡, de sorte que ln 𝑘 =
𝑠𝛼
𝛽
𝑒𝛽𝑡
+ 𝐶1 ou
𝑘 = 𝑒
𝑠𝛼
𝛽 𝑒𝛽𝑡
𝑒𝐶1 = 𝐶𝑒
𝑠𝛼
𝛽 𝑒𝛽𝑡
. Avec 𝑘(0) = 𝑘0, on a 𝑘0 = 𝐶𝑒
𝑠𝛼
𝛽 et donc 𝑘 = 𝑘0𝑒
𝑠𝛼
𝛽 (𝑒𝛽𝑡 −1)
.
4. (a) 𝑌′ = 𝛼 (𝑎 − 1)𝑌 + 𝛼 (𝑏 + ¯
𝐼)
(b) 𝑌 =
𝑌0 −
𝑏 + ¯
𝐼
1 − 𝑎
𝑒−𝛼 (1−𝑎) 𝑡
+
𝑏 + ¯
𝐼
1 − 𝑎
→
𝑏 + ¯
𝐼
1 − 𝑎
lorsque 𝑡 → +∞.
5. De (iii), 𝐿 = 𝐿0𝑒𝛽𝑡 , de sorte que 𝐾′ = 𝛾𝐾𝛼𝐿0𝑒𝛽𝑡 , une équation à variables séparées.
∫
𝐾−𝛼 d𝐾 =
∫
𝛾𝐿0𝑒𝛽𝑡 d𝑡. Ensuite,
1
1 − 𝛼
𝐾1−𝛼
=
𝛾𝐿0
𝛽
𝑒𝛽𝑡
+ 𝐶1. De là,
𝐾1−𝛼
=
𝛾𝐿0 (1 − 𝛼)
𝛽
𝑒𝛽𝑡
+ (1 − 𝛼) 𝐶1.
En 𝑡 = 0, on a 𝐾1−𝛼
0 =
𝛾𝐿0 (1 − 𝛼)
𝛽
+ (1 − 𝛼) 𝐶1. Puis,
𝐾1−𝛼
=
(1 − 𝛼)𝛾𝐿0
𝛽
(𝑒𝛽𝑡
− 1) + 𝐾1−𝛼
0 ,
d’où on trouve
𝐾 =
(1 − 𝛼)𝛾
𝛽
𝐿0 (𝑒𝛽𝑡
− 1) + 𝐾1−𝛼
0
1/(1−𝛼)
.
(13) Il est important d’insérer la constante d’intégration à cette étape. L’ajouter plus tard conduit à une erreur :
1
3 𝑥3 = 1
2 𝑒2𝑡 , 𝑥3 = 3
2 𝑒2𝑡 , 𝑥 = 3
q
3
2 𝑒2𝑡 + 𝐶. Cela est une solution seulement si 𝐶 = 0 et n’est pas la solution générale.

117. Chapitre 11 / Mathématiques financières et modèles dynamiques 117
6.
𝑡
𝑥
d𝑥
d𝑡
= 𝑎 est à variables séparées :
d𝑥
𝑥
= 𝑎
d𝑡
𝑡
, de sorte que
∫
d𝑥
𝑥
= 𝑎
∫
d𝑡
𝑡
.
L’intégration conduit à ln 𝑥 = 𝑎 ln 𝑡 + 𝐶1, et, de là, 𝑥 = 𝑒𝑎 ln 𝑡+𝐶1 = (𝑒ln 𝑡 )𝑎𝑒𝐶1 = 𝐶𝑡𝑎, avec
𝐶 = 𝑒𝐶1 . Cela montre que les seules fonctions qui ont une élasticité constante sont de la
forme 𝑥 = 𝐶𝑡𝑎.
Exercices récapitulatifs du chapitre 11
1. (a) 5 000 × 1,0310 ≈ 6 719,58
(b) 5 000 (1,03)𝑡∗
= 10 000 de sorte que (1,03)𝑡∗
= 2 ou 𝑡∗ = ln 2/ln 1,03 ≈ 23,45.
2. (a) 8 000 × 1,053 = 9 261 (b) 8 000 × 1,0513 ≈ 15 085,19
(c) (1,05)𝑡∗
= 4 de sorte que 𝑡∗ = ln 4/1,05 ≈ 28,5.
3. Si vous empruntez 𝑎 e au taux annuel de 11 % avec paiement annuel des intérêts, la dette
à la fin de la première année s’élève à 𝑎 (1 + 11/100) = 𝑎 (1,11) ; si vous empruntez au
taux annuel de 10 % avec paiement mensuel des intérêts, la dette au bout d’un an s’élève
à 𝑎 (1 + 10/(12 × 100))12 ≈ 1,1047𝑎, de sorte que le plan (ii) est préférable.
4. 15 000𝑒0,07×12 ≈ 34 745,50
5. (a) 8 000𝑒0,06×3 ≈ 9 577,74 (b) 𝑡∗ = ln 2/0,06 ≈ 11,6
6. On utilise la formule (11.4.5).
(a) Le premier terme est 44 et la raison 0,56. La somme vaut donc
44
1 − 0,56
= 100
(b) Le premier terme est 20 et la raison 1/1,2. La somme vaut donc
20
1 − 1/1,2
= 120.
(c)
3
1 − 2/5
= 5
(d) Le premier terme est (1/20)−2 = 400 et la raison 1/20. La somme vaut donc
400
1 − 1/20
=
8 000
19
.
7. (a)
∫ 𝑇
0
𝑎𝑒−𝑖𝑡
d𝑡 = (
𝑎
𝑖
) (1 − 𝑒−𝑖𝑇
) (b)
𝑎
𝑖
, la même qu’en (11.5.4).
8. 5 000 (1,04)4 = 5 849,29
9. On utilise la formule(11.5.3) qui donne la valeur acquise d’une annuité
5 000
0,04
[(1,04)4
− 1] = 21 232,32.
10. Le dernier des huit paiements aura lieu le 1er janvier 2006, au moment où la somme
initiale 10 000 aura rapporté des intérêts pendant 10 ans. Le montant cherché 𝐾 doit
être solution de l’équation 10 000 × (1,04)10 + 𝐾[(1,04)8 − 1]/0,04 = 70 000. On trouve
𝐾 ≈ 5 990,47, arrondi à la deuxième décimale, mais la valeur exacte dépend des règles
d’arrondi appliquées par la banque lorsqu’elle calcule l’intérêt!

118. 118 CORRIGÉS DES EXERCICES
11. (a) Conformément à la formule (11.6.2), le paiement annuel est
500 000
0,07 (1,07)10
(1,0710 − 1)
≈ 71 188,80.
(b) Le montant total perçu par la banque est égal à 10 fois l’annuité de 71 188, 75, mais
chaque annuité a été perçue à une époque différente. Il n’est pas pertinent de les additionner
sans les actualiser. Si toutefois on additionnait ces montants (ce qui n’a pas de sens), on
obtiendrait 711 887, 50.
(c) Si la personne doit payer deux fois par an, le montant sera de
500 000
0,035 (1,035)20
(1,03520 − 1)
≈ 35 180,50.
Le montant total perçu par la banque est égal à 20 fois le versement semestriel de
35 180, 50, mais chaque montant a été perçu à une époque différente. Il n’est pas pertinent
de les additionner sans les actualiser. Si toutefois on additionnait ces montants (ce qui n’a
pas de sens), on obtiendrait 703 610, 80.
12. (a) La valeur actuelle vaut
3200
0,08
[1 − (1,08)−10
] = 21 472,26.
(b) La valeur actuelle vaut 7 000 +
3 000
0,08
[1 − 1,08−5
] = 18 978,13.
(c) Quatre ans auparavant, la valeur actuelle est
4 000
0,08
[1 − (1,08)−10
] = 26 840,33.
La valeur actuelle au moment où Lucie doit choisir est 26 840,33 × 1,08−4 = 19 728,44.
L’option (a)) est à conseiller à Lucie.
13. (a) 𝑓 ′
(𝑡) = 100𝑒
√
𝑡/2
𝑒−𝑖𝑡
1
4
√
𝑡
−𝑖
. On voit que 𝑓 ′(𝑡) = 0 quand 𝑡 = 𝑡∗ = 1/16𝑖2. Comme
𝑓 ′(𝑡) 0 lorsque 𝑡 𝑡∗ et 𝑓 ′(𝑡) 0 lorsque 𝑡 𝑡∗, il suit que 𝑡∗ rend 𝑓 (𝑡) maximale.
(b) 𝑓 ′
(𝑡) = 200𝑒−1/𝑡
𝑒−𝑖𝑡
1
𝑡2
− 𝑖
. On voit que 𝑓 ′(𝑡) = 0 lorsque 𝑡 = 𝑡∗ = 1/
√
𝑖. Comme
𝑓 ′(𝑡) 0 lorsque 𝑡 𝑡∗ et 𝑓 ′(𝑡) 0 lorsque 𝑡 𝑡∗, il suit que 𝑡∗ rend 𝑓 (𝑡) maximale.
14. (a) La recette totale est 𝐹(10) =
∫ 10
0
(1 + 0,4𝑡) d𝑡 = (𝑡 + 0,2𝑡2
)
10
0
= 30.
(b) Voir l’exemple 10.5.3.
15. (a) 𝑥𝑡 = (−0,1)𝑡 (b) 𝑥𝑡 = −2𝑡 + 4 (c) 𝑥𝑡 = 4
3
2
𝑡
− 2
16. (a) 𝑥 = 𝐴𝑒−3𝑡 (b) 𝑥 = 𝐴𝑒−4𝑡 + 3 (c) 𝑥 = 1/(𝐴𝑒−3𝑡 − 4) et 𝑥 ≡ 0.
(d) 𝑥 = 𝐴𝑒− 1
5 𝑡
(e) 𝑥 = 𝐴𝑒−2𝑡 + 5/3 (f) 𝑥 = 1/(𝐴𝑒− 1
2 𝑡 − 2) et 𝑥 ≡ 0.
17. (a) Séparable.
∫
𝑥−2 d𝑥 =
∫
𝑡 d𝑡 et ainsi −1/𝑥 = 1
2 𝑡2 + 𝐶1, ou 𝑥 = 1/(𝐶 − 1
2 𝑡2) avec
𝐶 = −𝐶1. Autre solution, 𝑥(𝑡) ≡ 0.
(b) Utilisation directe de (11.10.3). On obtient 𝑥 = 𝐶𝑒−3𝑡/2 − 5.
(c) Utilisation directe de (11.10.3). On obtient 𝑥 = 𝐶𝑒3𝑡 − 10.

119. Chapitre 12 / Algèbre des matrices 119
(d) Utilisation de (11.10.5), 𝑥 = 𝐶𝑒−5𝑡 + 10𝑒−5𝑡
∫
𝑡𝑒5𝑡 d𝑡.
Ici,
∫
𝑡𝑒5𝑡 d𝑡 = 𝑡 1
5 𝑒5𝑡 − 1
5
∫
𝑒5𝑡 d𝑡 = 1
5 𝑡𝑒5𝑡 − 1
25 𝑒5𝑡 .
Ainsi, 𝑥 = 𝐶𝑒−5𝑡 + 10𝑒−5𝑡 ( 1
5 𝑡𝑒5𝑡 − 1
25 𝑒5𝑡 ) = 𝐶𝑒−5𝑡 + 2𝑡 − 2
5 .
(e) 𝑥 = 𝐶𝑒−𝑡/2
+ 𝑒−𝑡/2
∫
𝑒𝑡/2
𝑒𝑡
d𝑡 = 𝐶𝑒−𝑡/2
+ 𝑒−𝑡/2
∫
𝑒3𝑡/2
d𝑡
= 𝐶𝑒−𝑡/2
+ 𝑒−𝑡/2 2
3
𝑒3𝑡/2
= 𝐶𝑒−𝑡/2
+
2
3
𝑒𝑡
.
(f) 𝑥 = 𝐶𝑒−3𝑡
+ 𝑒−3𝑡
∫
𝑡2
𝑒3𝑡
d𝑡 = 𝐶𝑒−3𝑡
+ 𝑒−3𝑡
1
3
𝑡2
𝑒3𝑡
−
2
3
∫
𝑡𝑒3𝑡
d𝑡
= 𝐶𝑒−3𝑡
+
1
3
𝑡2
−
2
3
𝑒−3𝑡
1
3
𝑡𝑒3𝑡
−
1
3
∫
𝑒3𝑡
d𝑡
= 𝐶𝑒−3𝑡
+
1
3
𝑡2
−
2
9
𝑡 +
2
27
.
18. (a) 𝑉(𝑥) = (𝑉0 + 𝑏/𝑎) 𝑒−𝑎𝑥 − 𝑏/𝑎
(b) 𝑉(𝑥∗) = 0 fournit 𝑥∗ = (1/𝑎) ln(1 + 𝑎𝑉0/𝑏).
(c) 0 = 𝑉( ˆ
𝑥) = (𝑉𝑚 + 𝑏/𝑎) 𝑒−𝑎 ˆ
𝑥 − 𝑏/𝑎 fournit 𝑉𝑚 = (𝑏/𝑎) (𝑒𝑎 ˆ
𝑥 − 1).
(d) On a 𝑥∗ = (1/0,001) ln(1 + 0,001 × 12 000/8) ≈ 916 et
𝑉𝑚 = (8/0,001) (𝑒0,001×1200
− 1) = 8 000 (𝑒1,2
− 1) ≈ 18 561.
Chapitre 12 / Algèbre des matrices
12.1
1. (a) (2, 2) (b) (2, 3) (c) (𝑚, 𝑛)
2. A =
©
­
­
«
1 0 0
0 1 0
0 0 1
ª
®
®
¬
3. 𝑢 = 3 et 𝑣 = −2. (L’égalisation des éléments de la ligne 1 et de la colonne 3 donne 𝑢 = 3.
Ensuite, l’égalisation de ceux de la ligne 2 et de la colonne 3 donne 𝑢 − 𝑣 = 5 et, de là,
𝑣 = −2. Les autres éléments doivent alors être vérifiés, mais c’est évident.)
12.2
1. Les équations (a), (c), (d) et (f) sont du premier degré en 𝑥, 𝑦, 𝑧 et 𝑤, tandis que (b) et (e)
ne sont pas du premier degré par rapport à ces variables.
2. Oui, avec 𝑥1, 𝑥2, 𝑦1 et 𝑦2 toutes constantes, le système est du premier degré en 𝑎, 𝑏, 𝑐 et 𝑑.
3. Les trois lignes sont









2𝑥1 + 4𝑥2 + 6𝑥3 + 8𝑥4 = 2
5𝑥1 + 7𝑥2 + 9𝑥3 + 11𝑥4 = 4
4𝑥1 + 6𝑥2 + 8𝑥3 + 10𝑥4 = 8

120. 120 CORRIGÉS DES EXERCICES
4. Le système s’écrit















𝑥2 + 𝑥3 + 𝑥4 = 𝑏1
𝑥1 + 𝑥3 + 𝑥4 = 𝑏2
𝑥1 + 𝑥2 + 𝑥4 = 𝑏3
𝑥1 + 𝑥2 + 𝑥3 = 𝑏4
avec comme solution















𝑥1 = −2
3 𝑏1 + 1
3 (𝑏2 + 𝑏3 + 𝑏4)
𝑥2 = −2
3 𝑏2 + 1
3 (𝑏1 + 𝑏3 + 𝑏4)
𝑥3 = −2
3 𝑏3 + 1
3 (𝑏1 + 𝑏2 + 𝑏4)
𝑥4 = −2
3 𝑏4 + 1
3 (𝑏1 + 𝑏2 + 𝑏3).
(L’addition des 4 équations, puis la division par 3, donne
𝑥1 + 𝑥2 + 𝑥3 + 𝑥4 =
1
3
(𝑏1 + 𝑏2 + 𝑏3 + 𝑏4).
La soustraction de chacune des équations initiales de cette nouvelle équation donne les
expressions de 𝑥1, 𝑥2, 𝑥3, 𝑥4. Une autre méthode serait une élimination systématique des
variables en commençant par 𝑥4 par exemple.)
5. (a) L’ensemble des biens détenus par l’individu 𝑗.
(b) 𝑎𝑖1 + 𝑎𝑖2 + · · · + 𝑎𝑖𝑛 est le stock total du bien 𝑖 possédé par tous les individus. Le
premier cas est 𝑖 = 1.
(c) 𝑝1𝑎1𝑗 + 𝑝2𝑎2𝑗 + · · · + 𝑝𝑚𝑎𝑚 𝑗
6. Le système d’équations est















0,712𝑌 − 𝐶 = −95,05
𝑋 − 𝑌 − 𝑆 + 𝐶 = 0
0,158𝑋 − 𝑆 + 0,158𝐶 = 34, 30
𝑋 = 93,53
Résoudre la première équation pour exprimer 𝑌 comme une fonction de 𝐶. Introduire
cette expression de 𝑌 et 𝑋 = 93,53 dans la troisième équation. La résoudre pour obtenir
𝑆 comme une fonction de 𝐶. Insérer ces résultats dans la deuxième équation et résoudre
par rapport à 𝐶. Puis, finalement résoudre par rapport à 𝑌 et 𝑆. La solution est 𝑋 = 93,53,
𝑌 ≈ 482,11, 𝑆 ≈ 49,73 et 𝐶 ≈ 438,31.
12.3
1. A + B =
1 0
7 5
, 3A =
0 3
6 9
.
2. A + B =
1 0 4
2 4 16
, A − B =
−1 2 −6
2 2 −2
et 5A − 3B =
−3 8 −20
10 12 8
.

121. Chapitre 12 / Algèbre des matrices 121
12.4
1. a + b =
5
3
, a − b =
−1
−5
, 2a + 3b =
13
10
et −5a + 2b =
−4
13
.
2. a + b + c = (−1, 6, −4), a − 2b + 2c = (−3, 10, 2), 3a + 2b − 3c = (9, −6, 9)
3. D’après les définitions de l’addition vectorielle et de la multiplication d’un vecteur
par un nombre réel, le membre de gauche de l’équation doit être égal au vecteur
3 (𝑥, 𝑦, 𝑧) + 5 (−1, 2, 3) = (3𝑥 − 5, 3𝑦 + 10, 3𝑧 + 15). Pour qu’il soit égal au vecteur
(4, 1, 3), les éléments correspondants doivent être égaux. L’équation est donc équivalente
au système d’équations 3𝑥 − 5 = 4, 3𝑦 + 10 = 1 et 3𝑧 + 15 = 3, dont la solution évidente
est 𝑥 = 3, 𝑦 = −3 , 𝑧 = −4.
4. Ici x = 0, donc, pour tout 𝑖, le 𝑖ème élément vérifie 𝑥𝑖 = 0.
5. Rien, car 0x = 0, quel que soit x.
6. On cherche les nombres 𝑡 et 𝑠 tels que 𝑡(2, −1) +𝑠(1, 4) = (4, −11). L’équation vectorielle
est équivalente à (2𝑡 + 𝑠, −𝑡 + 4𝑠) = (4, −11). Les deux composantes sont égales lorsque
(i) 2𝑡 + 𝑠 = 4 et (ii) −𝑡 + 4𝑠 = −11. Ce système a comme solution 𝑡 = 3, 𝑠 = −2, de sorte
que (4, −11) = 3 (2, −1) − 2 (1, 4).
7. 4x − 2x = 7a + 8b − a, de sorte que 2x = 6a + 8b et x = 3a + 4b.
8. a · a = 5, a · b = 2 et a · (a + b) = 7. On constate que a · a + a · b = a · (a + b).
9. Le produit scalaire des deux vecteurs est
𝑥2
+ (𝑥 − 1) 𝑥 + 3 × 3𝑥 = 𝑥2
+ 𝑥2
− 𝑥 + 9𝑥 = 2𝑥2
+ 8𝑥 = 2𝑥 (𝑥 + 4).
Il est nul pour 𝑥 = 0 et 𝑥 = −4.
10. (a) x = (5, 7, 12) (b) u = (20, 18, 25), (c) u · x = 526.
11. (a) Le revenu de la firme est p · z. Ses coûts sont p · x.
(b) Profit = recette - coûts = p · z − p · x = p · (z − x) = p · y. Si p · y 0, la firme fait
une perte égale à −p · y.
12. Vecteur d’intrants =
0
1
; vecteur d’extrants =
2
0
; coûts = (1, 3)
0
1
= 3;
recette = (1, 3)
2
0
= 2; valeur de l’extrant net = (1, 3)
2
−1
= 2 − 3 = −1;
perte = coûts − recette = 3 − 2 = 1, de sorte que profit = −1.
12.5
1. (a) AB =
0 −2
3 1
−1 4
1 5
=
0 × (−1) + (−2) × 1 0 × 4 + (−2) × 5
3 × (−1) + 1 × 1 3 × 4 + 1 × 5
=
−2 −10
−2 17
et BA =
12 6
15 3
.

122. 122 CORRIGÉS DES EXERCICES
(b) AB =
26 3
6 −22
et BA =
©
­
­
«
14 6 −12
35 12 4
3 3 −22
ª
®
®
¬
.
(c) AB n’est pas définie. BA =
©
­
­
«
−1 4
3 4
4 8
ª
®
®
¬
.
(d) AB =
©
­
­
«
0 0 0
0 4 −6
0 −8 12
ª
®
®
¬
et BA = (16), une matrice (1, 1).
2. 3A + 2B − 2C + D =
−1 15
−6 −13
; AB =
0 0
0 0
; C(AB) =
0 0
0 0
en utilisant le résultat
précédent.
3. A + B =
©
­
­
«
4 1 −1
9 2 7
3 −1 4
ª
®
®
¬
, A − B =
©
­
­
«
−2 3 −5
1 −2 −3
−1 −1 −2
ª
®
®
¬
, AB =
©
­
­
«
5 3 3
19 −5 16
1 −3 0
ª
®
®
¬
,
BA =
©
­
­
«
0 4 −9
19 3 −3
5 1 −3
ª
®
®
¬
, (AB)C = A(BC) =
©
­
­
«
23 8 25
92 −28 76
4 −8 −4
ª
®
®
¬
.
4. (a)
1 1
3 5
𝑥1
𝑥2
=
3
5
(b)
©
­
­
«
1 2 1
1 −1 1
2 3 −1
ª
®
®
¬
©
­
­
«
𝑥1
𝑥2
𝑥3
ª
®
®
¬
=
©
­
­
«
4
5
1
ª
®
®
¬
(c)
2 −3 1
1 1 −1
©
­
­
«
𝑥1
𝑥2
𝑥3
ª
®
®
¬
=
0
0
5. (a) et (b) A − 2I =
0 2
1 3
. La matrice C doit être d’ordre (2, 2). Avec C =
𝑐11 𝑐12
𝑐21 𝑐22
,
on doit avoir
0 2
1 3
𝑐11 𝑐12
𝑐21 𝑐22
=
1 0
0 1
ou
2𝑐21 2𝑐22
𝑐11 + 3𝑐21 𝑐12 + 3𝑐22
=
1 0
0 1
.
La dernière équation matricielle a pour unique solution 𝑐11 = −3/2, 𝑐12 = 1, 𝑐21 = 1/2
et 𝑐22 = 0.
(c) B − 2I =
0 0
3 0
, de sorte que la première ligne de toute matrice produit (B − 2I) D
doit être (0, 0). Par conséquent, aucune telle matrice D ne peut exister.
6. On sait que A est une matrice (𝑚, 𝑛). Soit B une matrice (𝑝, 𝑞). La matrice produit AB
est définie si et seulement si 𝑛 = 𝑝 et la matrice produit BA est définie si et seulement si
𝑞 = 𝑚. Pour que les produits AB et BA soient définis, il est nécessaire et suffisant que B
soit une matrice (𝑛, 𝑚).
7. On sait par l’exercice précédent que B doit être une matrice (2, 2). Soit B =
𝑥 𝑦
𝑧 𝑤
.

123. Chapitre 12 / Algèbre des matrices 123
Alors
BA =
𝑥 𝑦
𝑧 𝑤
1 2
2 3
=
𝑥 + 2𝑦 2𝑥 + 3𝑦
𝑧 + 2𝑤 2𝑧 + 3𝑤
AB =
1 2
2 3
𝑥 𝑦
𝑧 𝑤
=
𝑥 + 2𝑧 𝑦 + 2𝑤
2𝑥 + 3𝑧 2𝑦 + 3𝑤
De là, BA = AB si et seulement si (i) 𝑥 + 2𝑦 = 𝑥 + 2𝑧, (ii) 2𝑥 + 3𝑦 = 𝑦 + 2𝑤,
(iii) 𝑧 + 2𝑤 = 2𝑥 + 3𝑧 et (iv) 2𝑧 + 3𝑤 = 2𝑦 + 3𝑤. Les équations (i) et (iv) sont toutes les
deux vraies si et seulement si 𝑦 = 𝑧 ; alors, les équations (ii) et (iii) sont également toutes
les deux vraies si et seulement si, en plus, 𝑥 = 𝑤 − 𝑦. En résumé, il faut et il suffit que
𝑦 = 𝑧 et 𝑥 = 𝑤 − 𝑦. Les matrices B qui commutent avec A sont de la forme
B =
𝑤 − 𝑦 𝑦
𝑦 𝑤
= 𝑤
1 0
0 1
+ 𝑦
−1 1
1 0
où 𝑦 et 𝑤 peuvent être n’importe quels nombres réels.
8. T(Ts) =
©
­
­
«
0,85 0,10 0,10
0,05 0,55 0,05
0,10 0,35 0,85
ª
®
®
¬
©
­
­
«
0,25
0,35
0,40
ª
®
®
¬
=
©
­
­
«
0,2875
0,2250
0,4875
ª
®
®
¬
12.6
1. A(B + C) = AB + AC =
3 2 6 2
7 4 14 6
2. On commence par effectuer le produit
©
­
­
«
𝑎 𝑑 𝑒
𝑑 𝑏 𝑓
𝑒 𝑓 𝑐
ª
®
®
¬
©
­
­
«
𝑥
𝑦
𝑧
ª
®
®
¬
=
©
­
­
«
𝑎𝑥 + d𝑦 + 𝑒𝑧
d𝑥 + 𝑏𝑦 + 𝑓 𝑧
𝑒𝑥 + 𝑓 𝑦 + 𝑐𝑧
ª
®
®
¬
.
Ensuite,
(𝑥, 𝑦, 𝑧)
©
­
­
«
𝑎𝑥 + d𝑦 + 𝑒𝑧
d𝑥 + 𝑏𝑦 + 𝑓 𝑧
𝑒𝑥 + 𝑓 𝑦 + 𝑐𝑧
ª
®
®
¬
= (𝑎𝑥2
+ 𝑏𝑦2
+ 𝑐𝑧2
+ 2 d𝑥𝑦 + 2𝑒𝑥𝑧 + 2 𝑓 𝑦𝑧),
qui est une matrice (1, 1).
3. Un calcul direct montre que (AB)C et A(BC) sont des matrices égales à la matrice
D = (𝑑𝑖 𝑗) carrée d’ordre 2 dont les quatre éléments sont
𝑑𝑖 𝑗 = 𝑎𝑖1𝑏11𝑐1𝑗 + 𝑎𝑖1𝑏12𝑐2𝑗 + 𝑎𝑖2𝑏21𝑐1𝑗 + 𝑎𝑖2𝑏22𝑐2𝑗
pour 𝑖 = 1, 2 et 𝑗 = 1, 2.
4. (a)
©
­
­
«
5 3 1
2 0 9
1 3 3
ª
®
®
¬
(b) (1, 2, −3)
5. (a) On a (A + B)(A − B) = A2 − AB + BA − B2 ≠ A2 − B2 à moins que AB = BA.

124. 124 CORRIGÉS DES EXERCICES
(b) De même, (A − B)(A − B) = A2 − AB − BA + B2 ≠ A2 − 2AB + B2 à moins que
AB = BA.
Dans les deux cas, (a) et (b), il y a égalité si et seulement si AB = BA.
6. (a) Vérification directe par multiplication.
(b) AA = (AB)A = A(BA) = AB = A, de sorte que A est idempotente. Juste permuter
A et B pour montrer que B est idempotente.
(c) On suppose, par hypothèse d’induction, que A𝑘 = A pour 𝑘 = 1.
Alors A𝑘+1 = A𝑘A = AA = A, ce qui achève la démonstration par induction.
7. Si P3Q = PQ, alors P5Q = P2 (P3Q) = P2 (PQ) = P3Q = PQ.
8. (a) Une vérification directe fournit
(i) A2
= (𝑎 + 𝑑)A − (𝑎𝑑 − 𝑏𝑐)I2 =
𝑎2 + 𝑏𝑐 𝑎𝑏 + 𝑏𝑑
𝑎𝑐 + 𝑐𝑑 𝑏𝑐 + 𝑑2
.
(b) La matrice A de la question (a) est telle que A2 = 0 si 𝑎 + 𝑑 = 0 et 𝑎𝑑 = 𝑏𝑐. Un
exemple de matrice A telle que A2 = 0 ≠ A est A =
1 1
−1 −1
.
(c) Selon la question (a), A3 = (𝑎 + 𝑑)A2 − (𝑎𝑑 − 𝑏𝑐)A. Ainsi, A3 = 0 implique
(𝑎 + 𝑑)A2 = (𝑎𝑑 − 𝑏𝑐)A et, de là, en multipliant chaque membre par A encore une fois,
on a (𝑎 + 𝑑)A3 = (𝑎𝑑 − 𝑏𝑐)A2. Si A3 = 0, deux cas peuvent se présenter : (i) A2 = 0;
(ii) 𝑎𝑑 − 𝑏𝑐 = 0. Mais, dans le second cas, on a (𝑎 + 𝑑)A2 = 0, ce qui conduit à deux
sous-cas : (ii)(a) A2 = 0; (ii)(b) 𝑎𝑑 − 𝑏𝑐 = 0 et (𝑎 + 𝑑) = 0. Même dans le cas (ii)(b), le
résultat de la question (a) implique A2 = 0, ce qui est donc vrai dans tous les cas.
12.7
1. A′ =
©
­
­
­
«
3 −1
5 2
8 6
3 2
ª
®
®
®
®
¬
, B′ = (0, 1, −1, 2), C′ =
©
­
­
­
«
1
5
0
−1
ª
®
®
®
®
¬
.
2. (a) A′ =
3 −1
2 5
, B′ =
0 2
2 2
, (A + B)′ =
3 1
4 7
, (𝛼A)′ =
−6 2
−4 −10
,
AB =
4 10
10 8
, (AB)′ =
4 10
10 8
= B′A′ et A′B′ =
−2 4
10 14
.
(b) Vérifier les règles de transposition (12.7.2) à (12.7.5) est maintenant très facile.
3. On vérifie directement que, pour chacune des deux matrices, l’élément en position 𝑖𝑗 est
égal à l’élément 𝑗𝑖 pour 𝑖 = 1, 2, 3 et 𝑗 = 1, 2, 3.
4. La symétrie exige 𝑎2 − 1 = 𝑎 + 1 et 𝑎2 + 4 = 4𝑎. La deuxième équation admet l’unique
racine 𝑎 = 2, qui satisfait aussi la première équation.
5. Non! Par exemple :
0 0
0 1
1 1
1 1
=
0 0
1 1
.

125. Chapitre 12 / Algèbre des matrices 125
6. Dans le cas général, pour tout entier naturel 𝑛 3, on a
((A1A2 · · · A𝑛−1)A𝑛)′
= A′
𝑛(A1A2 · · · A𝑛−1)′
.
On pose, comme hypothèse d’induction que le résultat est vrai pour 𝑛−1. Alors la dernière
expression devient A′
𝑛A′
𝑛−1 · · · A′
2A′
1. Le résultat est donc vrai pour 𝑛.
7. (a) Vérification par multiplication directe.
(b)
𝑝 𝑞
−𝑞 𝑝
𝑝 −𝑞
𝑞 𝑝
=
𝑝2 + 𝑞2 0
0 𝑝2 + 𝑞2
=
1 0
0 1
⇔ 𝑝2 + 𝑞2 = 1.
(c) Si P′P = Q′Q = I𝑛, alors
(PQ)′
(PQ) = (Q′
P′
) (PQ) = Q′
(P′
P)Q = Q′
I𝑛Q = Q′
Q = I𝑛.
8. (a) TS =
©
­
­
«
𝑝3 + 𝑝2𝑞 2𝑝2𝑞 + 2𝑝𝑞2 𝑝𝑞2 + 𝑞3
1
2 𝑝3 + 1
2 𝑝2 + 1
2 𝑝2𝑞 𝑝2𝑞 + 𝑝𝑞 + 𝑝𝑞2 1
2 𝑝𝑞2 + 1
2 𝑞2 + 1
2 𝑞3
𝑝3 + 𝑝2𝑞 2𝑝2𝑞 + 2𝑝𝑞2 𝑝𝑞2 + 𝑞3
ª
®
®
¬
= S, car 𝑝+𝑞 = 1.
Un calcul semblable montre que T2 = 1
2 T + 1
2 S. Pour obtenir la formule de T3, il n’est
plus nécessaire de considérer les éléments séparément. Il faut multiplier chaque membre
de la dernière équation à gauche par T et utiliser TS = S pour obtenir
T3
= TT2
= T(
1
2
T +
1
2
S) =
1
2
T2
+
1
2
TS =
1
2
(
1
2
T +
1
2
S) +
1
2
S =
1
4
T +
3
4
S.
(b) On démontre par induction que la formule qui convient pour T𝑛 est
T𝑛
= 21−𝑛
T + (1 − 21−𝑛
)S. (∗)
La formule est vraie pour 𝑛 = 1(14). On suppose (∗) vraie pour 𝑛 = 𝑘. On prémultiplie
par T et on utilise les deux dernières inégalités de (a). On obtient
T𝑘+1
= TT𝑘
= T(21−𝑘
T + (1 − 21−𝑘
)S) = 21−𝑘
T2
+ (1 − 21−𝑘
)TS
= 21−𝑘
(
1
2
T +
1
2
S) + (1 − 21−𝑘
)S
= 2−𝑘
T + 2−𝑘
S + S − 2 · 2−𝑘
S = 2−𝑘
T + (1 − 2−𝑘
)S,
ce qui est la formule (∗) pour 𝑛 = 𝑘 + 1.
12.8
1. (a) La méthode d’élimination de Gauss produit
1 1 3
3 5 5
−3
∼
1 1 3
0 2 −4
1/2
∼
1 1 3
0 1 −2
−1
∼
1 0 5
0 1 −2
La solution est donc 𝑥1 = 5, 𝑥2 = −2.
(14) Et aussi pour 𝑛 = 2, 3, d’après la question (a).

126. 126 CORRIGÉS DES EXERCICES
(b) La méthode d’élimination de Gauss produit
1 2 1 4
1 −1 1 5
2 3 −1 1
©
­
«
ª
®
¬
−1 −2
∼
1 2 1 4
0 −3 0 1
0 −1 −3 −7
©
­
«
ª
®
¬
−1/3
∼
1 2 1 4
0 1 0 −1/3
0 −1 −3 −7
©
­
­
«
ª
®
®
¬
1 −2 ∼
1 0 1 14/3
0 1 0 −1/3
0 0 −3 −22/3
©
­
­
«
ª
®
®
¬−1/3
∼
1 0 1 14/3
0 1 0 −1/3
0 0 1 22/9
©
­
­
«
ª
®
®
¬ −1
∼
1 0 0 20/9
0 1 0 −1/3
0 0 1 22/9
©
­
­
«
ª
®
®
¬
La solution est donc : 𝑥1 = 20/9, 𝑥2 = −1/3, 𝑥3 = 22/9.
(c) La solution générale est : 𝑥1 = (2/5)𝑠, 𝑥2 = (3/5)𝑠, 𝑥3 = 𝑠, avec 𝑠 nombre réel
quelconque.
2. La méthode d’élimination de Gauss supprime 𝑥 des deuxième et troisième équations, et
ensuite 𝑦 de la troisième équation. On arrive ainsi à la matrice augmentée suivante :
©
­
­
«
1 1 −1 1
0 1 −3/2 −1/2
0 0 𝑎 + 5/2 𝑏 − 1/2
ª
®
®
¬
.
Quel que soit 𝑧, les deux premières équations impliquent
𝑦 = −
1
2
+
3
2
𝑧 et 𝑥 = 1 − 𝑦 + 𝑧 =
3
2
−
1
2
𝑧.
À la dernière équation, on voit que si 𝑎 ≠ −5
2 il y a une unique solution 𝑧 = (𝑏− 1
2 )
(𝑎+ 5
2 ).
Si 𝑎 = −5
2 , il n’y a pas de solutions si 𝑏 ≠ 1
2 , mais il y a un degré de liberté si 𝑏 = 1
2 (avec
𝑧 arbitraire).
3. En effectuant successivement les opérations élémentaires suivantes :
(i) soustraire la troisième équation de la première;
(ii) soustraire la nouvelle première équation des deux autres;
(iii) permuter la deuxième et la troisème équation;
(iv) multiplier la deuxième équation par −3 et l’ajouter à la troisième équation, on trouve
©
­
­
«
𝑤 𝑥 𝑦 𝑧
2 1 4 3 1
1 3 2 −1 3𝑐
1 1 2 1 𝑐2
ª
®
®
¬
∼
©
­
­
«
1 0 2 2 1 − 𝑐2
0 1 0 −1 2𝑐2 − 1
0 0 0 0 −5𝑐2 + 3𝑐 + 2
ª
®
®
¬
.
De la dernière matrice découle l’existence d’une solution si et seulement si
−5𝑐2
+ 3𝑐 + 2 = 0,

127. Chapitre 12 / Algèbre des matrices 127
autrement dit, si et seulement si 𝑐 = 1 ou 𝑐 = −2/5. Pour ces valeurs particulières de 𝑐,
les solutions sont 𝑥 = 2𝑐2 − 1 + 𝑡, 𝑦 = 𝑠, 𝑧 = 𝑡, 𝑤 = 1 − 𝑐2 − 2𝑠 − 2𝑡, quels que soient les
valeurs de 𝑠 et 𝑡. Pour les autres valeurs de 𝑐, il n’y a pas de solution(15).
4. Déplacer la première ligne en troisième position et appliquer la méthode d’élimination
de Gauss. Voici les matrices augmentées successives
©
­
­
«
1 2 1 𝑏2
3 4 7 𝑏3
𝑎 1 𝑎 + 1 𝑏1
ª
®
®
¬
∼
©
­
­
«
1 2 1 𝑏2
0 −2 4 𝑏3 − 3𝑏2
0 1 − 2𝑎 1 𝑏1 − 𝑎𝑏2
ª
®
®
¬
∼
©
­
­
«
1 2 1 𝑏2
0 1 −2 3
2 𝑏2 − 1
2 𝑏3
0 1 − 2𝑎 1 𝑏1 − 𝑎𝑏2
ª
®
®
¬
∼
©
­
­
«
1 2 1 𝑏2
0 1 −2 3
2 𝑏2 − 1
2 𝑏3
0 0 3 − 4𝑎 𝑏1 + (2𝑎 − 3
2 )𝑏2 + ( 1
2 − 𝑎)𝑏3
ª
®
®
¬
.
En regardant l’élément de la 3e ligne et de la 3e colonne de la dernière matrice, il est
évident qu’il y a une solution unique si et seulement si 3 − 4𝑎 ≠ 0 ou encore 𝑎 ≠ 3/4.
5. On pose 𝑎 = 3/4 dans la matrice de l’exercice 12.8.4. La dernière ligne de la matrice
devient
(0, 0, 0, 𝑏1 −
1
4
𝑏3).
Par conséquent, si 𝑏1 ≠ 1
4 𝑏3, il n’y a pas de solution. Si 𝑏1 = 1
4 𝑏3, il y a une infinité
de solutions. Pour un réel arbitraire 𝑡, il y a une solution unique avec 𝑧 = 𝑡. Ensuite,
la deuxième équation donne 𝑦 = 3
2 𝑏2 − 1
2 𝑏3 + 2𝑡 et enfin la première équation donne
𝑥 = −2𝑏2 + 𝑏3 − 5𝑡.
12.9
1. a + b = (3, 3) et −1
2 a = (−2,5; 0,5). Voir figure C12.9.1.
2. (a) (i) 𝜆 = 0 donne x = (−1, 2) = b; (ii) 𝜆 = 1/4 donne x = (0, 7/4) ; (iii) 𝜆 = 1/2
donne x = (1, 3/2) ; (iv) 𝜆 = 3/4 donne x = (2, 5/4) ;t (v) 𝜆 = 1 donne x = (3, 1) = a.
Voir figure C12.9.2.
(b) Quand 𝜆 parcourt [0, 1], le vecteur x parcourt le segment compris entre les extrémités
de a et b de la figure C12.9.2. En effet, conformément à la formule d’une droite déterminée
par deux points, l’équation de la droite 𝑑 qui passe par les points de coordonnées (3, 1)
et (−1, 2) est 𝑥2 = −1
4 𝑥1 + 7
4 ou 𝑥1 + 4𝑥2 = 7. Les coordonnées (𝑥1, 𝑥2) de tout point de 𝑑
satisfont à l’équation 𝑥1+4𝑥2 = 7 et sont égales à (−1+4𝜆, 2−𝜆) pour𝜆 = 1
4 (𝑥1+1) = 2−𝑥2.
Il y a donc une correspondance bijective entre les points : (i) du segment qui joint a = (3, 1)
et b = (−1, 2) ; (ii) dont les coordonnées peuvent s’écrire (−1 + 4𝜆, 2 −𝜆) pour un certain
𝜆 dans [0, 1].
(15) La réponse finale peut prendre différentes formes équivalentes selon la manière dont les opérations élémentaires
ont été effectuées.

128. 128 CORRIGÉS DES EXERCICES
(c) C’est la droite 𝑑 : si on pose 𝜆 ∈ R, le raisonnement précédent nous donne une
correspondance entre les points : (i) appartenant à la droite 𝑑 et passant par a = (3, 1)
et b = (−1, 2) ; (ii) dont les coordonnées peuvent s’écrire (−1 + 4𝜆, 2 − 𝜆) pour tout 𝜆
dans R.
y
x
1
1
(−2, 4)
b
a + b
a
(5, −1)
− 1
2 a
(−2.5, 0.5)
(3, 3)
Figure C12.9.1
y
x
1
−1 1 2 3
b
a
λ = 0
λ = 1/4
λ = 1/2
λ = 3/4
λ = 1
Figure C12.9.2
3. Voir figure C12.9.3.
P R
Q
S 5 (3,22, 4)
y
x
z
Figure C12.9.3
4. (a) Une droite passant par (0, 2, 3) parallèle à l’axe 𝑂𝑥.
(b) L’unique plan qui contient à la fois l’axe 𝑂𝑧 et la droite 𝑦 = 𝑥 dans le plan 𝑂𝑥𝑦.
5. kak = 3, kbk = 3, kck =
√
29. Et |a · b| = 6 ⩽ kakkbk = 9.
6. (a) 𝑥1 (1, 2, 1) + 𝑥2 (−3, 0, −2) = (𝑥1 − 3𝑥2, 2𝑥1, 𝑥1 − 2𝑥2) = (5, 4, 4) quand 𝑥1 = 2 et
𝑥2 = −1.
(b) 𝑥1 et 𝑥2 doivent vérifier 𝑥1 (1, 2, 1)+𝑥2 (−3, 0, −2) = (−3, 6, 1). Ensuite 𝑥1 −3𝑥2 = −3,
2𝑥1 = 6 et 𝑥1 − 2𝑥2 = 1. Les deux premières équations conduisent à 𝑥1 = 3 et 𝑥2 = 2, ce
qui est en contradiction avec la dernière équation.
7. Les vecteurs de (a) et (c) sont orthogonaux; les vecteurs de (b) ne le sont pas.
8. Les vecteurs sont orthogonaux si et seulement si leur produit scalaire est nul – autrement
dit, si et seulement si 𝑥2 − 𝑥 − 8 − 2𝑥 + 𝑥 = 𝑥2 − 2𝑥 − 8 = 0, ce qui revient à 𝑥 = −2 et
𝑥 = 4.

129. Chapitre 12 / Algèbre des matrices 129
9. Si P est orthogonale et si c𝑖 et c𝑗 sont deux colonnes distinctes de P, alors c′
𝑖c𝑗 est
l’élément de la ligne 𝑖 et de la colonne 𝑗 de la matrice P′P = I, de sorte que c′
𝑖c𝑗 = 0.
Si r𝑖 et r𝑗 sont deux lignes distinctes de P, alors r𝑖r′
𝑗 est l’élément de la ligne 𝑖 et de la
colonne 𝑗 de PP′ = I, et on a de nouveau r𝑖r′
𝑗 = 0.
10. (kak + kbk)2 = kak2 + 2kakkbk + kbk2, tandis que
ka + bk2
= (a + b) · (a + b) = kak2
+ 2a · b + kbk2
.
Il s’ensuit que (kak + kbk)2 − ka + bk2 = 2 (kakkbk − a · b) ⩾ 0 en raison de l’inégalité
de Cauchy-Schwarz (12.9.7).
12.10
1. (a) 𝑥1 = 3𝑡 +10 (1−𝑡) = 10−7𝑡, 𝑥2 = (−2) 𝑡 +2 (1−𝑡) = 2−4𝑡 et 𝑥3 = 2𝑡 + (1−𝑡) = 1+𝑡.
(b) 𝑥1 = 1, 𝑥2 = 3 − 𝑡 et 𝑥3 = 2 + 𝑡.
2. (a) Pour montrer que a appartient à 𝑑, posez 𝑡 = 0.
(b) La direction de 𝑑 est donnée par (−1, 2, 1) et l’équation du plan P est
(−1) (𝑥1 − 2) + 2 (𝑥2 − (−1)) + 1 (𝑥3 − 3) = 0 ou − 𝑥1 + 2𝑥2 + 𝑥3 = −1.
(c) Il faut que 3 (−𝑡 + 2) + 5 (2𝑡 − 1) − (𝑡 + 3) = 6, de sorte que 𝑡 = 4/3. C’est le point de
coordonnées (2/3, 5/3, 13/3).
3. On note d’abord que (5, 2, 1) − (1, 0, 2) = (4, 2, −1) et (2, −1, 4) − (1, 0, 2) = (1, −1, 2)
sont deux vecteurs de ce plan. Le vecteur normal (𝑝1, 𝑝2, 𝑝3) au plan doit être orthogonal
à ces vecteurs, c’est-à-dire tel que
(4, 2, −1) · (𝑝1, 𝑝2, 𝑝3) = 4𝑝1 + 2𝑝2 − 𝑝3 = 0,
(1, −1, 2) · (𝑝1, 𝑝2, 𝑝3) = 𝑝1 − 𝑝2 + 2𝑝3 = 0.
Une solution de ces deux équations est (𝑝1, 𝑝2, 𝑝3) = (1, −3, −2). La formule (12.10.6)
avec (𝑎1, 𝑎2, 𝑎3) = (2, −1, 4) conduit à (1, −3, −2) · (𝑥1 − 2, 𝑥2 + 1, 𝑥3 − 4) = 0 ou
𝑥1 − 3𝑥2 − 2𝑥3 = −3(16).
4. 2𝑥 + 3𝑦 + 5𝑧 ⩽ 𝑚, avec 𝑚 ⩾ 75.
5. (a) Vérification directe.
(b) (𝑥1, 𝑥2, 𝑥3) = (−2, 1, −1) + 𝑡(−1, 2, 3) = (−2 − 𝑡, 1 + 2𝑡, −1 + 3𝑡)
(16) Une autre approche serait de partir de l’équation générale 𝑎𝑥 + 𝑏𝑦 + 𝑐𝑧 = 𝑑 d’un plan et d’exiger qu’elle soit
satisfaite par les coordonnées des trois points : 𝑎 + 2𝑐 = 𝑑, 5𝑎 + 2𝑏 + 𝑐 = 𝑑, 2𝑎 − 𝑏 + 4𝑐 = 𝑑. On résout en 𝑎, 𝑏 et
𝑐 comme fonction de 𝑑, puis on introduit dans 𝑎𝑥 + 𝑏𝑦 + 𝑐𝑧 = 𝑑 et on simplifie 𝑑.

130. 130 CORRIGÉS DES EXERCICES
Exercices récapitulatifs du chapitre 12
1. (a) A =
2 3 4
3 4 5
(b) A =
1 −1 1
−1 1 −1
2. (a) A − B =
3 −2
−2 2
(b) A + B − 2C =
−3 −4
−2 −8
(c) AB =
−2 4
2 −3
(d) C(AB) =
2 −1
6 −8
(e) AD =
2 2 2
0 2 3
(f) DC n’est pas définie.
(g) 2A − 3B =
7 −6
−5 5
(h) (A − B)′ =
3 −2
−2 2
(i) et (j) : (C′A′)B′ = C′(A′B′) =
−6 5
−4 5
(k) Pas définie.
(l) D′D =
©
­
­
«
2 4 5
4 10 13
5 13 17
ª
®
®
¬
3. (a)
2 −5
5 8
𝑥1
𝑥2
=
3
5
(b)
©
­
­
­
«
1 1 1 1
1 3 2 4
1 4 8 0
2 0 1 −1
ª
®
®
®
®
¬
©
­
­
­
«
𝑥
𝑦
𝑧
𝑡
ª
®
®
®
®
¬
=
©
­
­
­
«
𝑎
𝑏
𝑐
𝑑
ª
®
®
®
®
¬
(c)
©
­
­
«
𝑎 − 1 3 −2
𝑎 2 −1
1 −2 3
ª
®
®
¬
©
­
­
«
𝑥
𝑦
𝑧
ª
®
®
¬
=
©
­
­
«
5
2
1
ª
®
®
¬
4. A + B =
©
­
­
«
0 −4 1
8 6 4
−10 9 15
ª
®
®
¬
, A − B =
©
­
­
«
0 6 −5
−2 2 6
−2 5 15
ª
®
®
¬
, AB =
©
­
­
«
13 −2 −1
0 3 5
−25 74 −25
ª
®
®
¬
,
BA =
©
­
­
«
−33 1 20
12 6 −15
6 4 18
ª
®
®
¬
, (AB)C = A(BC) =
©
­
­
«
74 −31 −48
6 25 38
−2 −75 −26
ª
®
®
¬
.
5. Les deux matrices produits du membre de gauche de l’équation sont
2𝑎 + 𝑏 𝑎 + 𝑏
2𝑥 𝑥
et
𝑎 𝑏
2𝑎 + 𝑥 2𝑏
et leur différence est
𝑎 + 𝑏 𝑎
𝑥 − 2𝑎 𝑥 − 2𝑏
.
En posant cette matrice égale à celle du membre de droite,
2 1
4 4
, on obtient 𝑎 + 𝑏 = 2,
𝑎 = 1, 𝑥 − 2𝑎 = 4 et 𝑥 − 2 = 4. D’où 𝑎 = 𝑏 = 1, 𝑥 = 6.
6. (a) A2 =
©
­
­
«
𝑎2 − 𝑏2 2𝑎𝑏 𝑏2
−2𝑎𝑏 𝑎2 − 2𝑏2 2𝑎𝑏
𝑏2 −2𝑎𝑏 𝑎2 − 𝑏2
ª
®
®
¬

131. Chapitre 12 / Algèbre des matrices 131
(b) (C′BC)′ = C′B′(C′)′ = C′(−B)C = −C′BC. A est antisymétrique si et seulement si
𝑎 = 0.
(c) A′
1 = 1
2 (A′ + A′′) = 1
2 (A′ + A) = A1, de sorte que A1 est symétrique. Il est aussi
facile de démontrer que A2 est antisymétrique, de même que toute matrice carrée A est
la somme A1 + A2 d’une matrice symétrique A1 et d’une matrice antisymétrique A2.
7. (a) 1 4 1
2 2 8
−2
∼
1 4 1
0 −6 6
−1/6
∼
1 4 1
0 1 −1
−4
∼
1 0 5
0 1 −1
La solution est 𝑥1 = 5, 𝑥2 = −1.
(b)
2 2 −1 2
1 −3 1 0
3 4 −1 1
©
­
«
ª
®
¬
∼
1 −3 1 0
2 2 −1 2
3 4 −1 1
©
­
«
ª
®
¬
−2 −3
∼
1 −3 1 0
0 8 −3 2
0 13 −4 1
©
­
«
ª
®
¬
1/8 ∼
1 −3 1 0
0 1 −3/8 1/4
0 13 −4 1
©
­
­
«
ª
®
®
¬
−13
∼
1 −3 1 0
0 1 −3/8 1/4
0 0 7/8 −9/4
©
­
­
«
ª
®
®
¬ 8/7
∼
1 −3 1 0
0 1 −3/8 1/4
0 0 1 −18/7
©
­
­
«
ª
®
®
¬
3
∼
1 0 −1/8 3/4
0 1 −3/8 1/4
0 0 1 −18/7
©
­
­
«
ª
®
®
¬ 3/8 1/8
∼
1 0 0 3/7
0 1 0 −5/7
0 0 1 −18/7
©
­
­
«
ª
®
®
¬
La solution est 𝑥1 = 3/7, 𝑥2 = −5/7, 𝑥3 = −18/7.
(c) 1 3 4 0
5 1 1 0
−5
∼
1 3 4 0
0 −14 −19 0
−1/14
∼
1 3 4 0
0 1 19/14 0
!
−3 ∼
1 0 −1/14 0
0 1 19/14 0
!
La solution est 𝑥1 = (1/14) 𝑥3, 𝑥2 = −(19/14) 𝑥3, où 𝑥3 est arbitraire (un degré de liberté).
8. Par la méthode d’élimination de Gauss,
1 𝑎 2 0
−2 −𝑎 1 4
2𝑎 3𝑎2 9 4
©
­
­
«
ª
®
®
¬
−2 −2𝑎
∼
1 𝑎 2 0
0 𝑎 5 4
0 𝑎2 9 − 4𝑎 4
©
­
­
«
ª
®
®
¬
−𝑎
∼
1 𝑎 2 0
0 𝑎 5 4
0 0 9 − 9𝑎 4 − 4𝑎
©
­
«
ª
®
¬
Pour 𝑎 = 1, la dernière équation est superflue et la solution est 𝑥 = 3𝑡 − 4, 𝑦 = −5𝑡 + 4,
𝑧 = 𝑡, avec 𝑡 arbitraire. Si 𝑎 ≠ 1, on a (9 − 9𝑎) 𝑧 = 4 − 4𝑎, de sorte que 𝑧 = 4/9. Les deux
autres équations deviennent alors 𝑥 + 𝑎𝑦 = −8/9 et 𝑎𝑦 = 16/9. Si 𝑎 = 0, il n’y a pas de
solution. Si 𝑎 ≠ 0, la solution est 𝑥 = −8/3, 𝑦 = 16/9𝑎 et 𝑧 = 4/9.
9. kak =
√
35, kbk =
√
11 et kck =
√
69. De plus, |a · b| = |(−1) × 1 + 5 × 1 + 3 × (−3)| =
| − 5| = 5. Alors kak kbk =
√
35
√
11 =
√
385 est clairement supérieur à |a · b| = 5.
L’inégalité de Cauchy-Schwarz est donc vérifiée.

132. 132 CORRIGÉS DES EXERCICES
10. (a) Si PQ − QP = P, alors PQ = QP + P et ainsi
P2
Q = P(PQ) = P(QP + P)
= (PQ)P + P2
= (QP + P)P + P2
= QP2
+ 2P2
.
D’où P2Q − QP2 = 2P2. En outre,
P3
Q = P(P2
Q) = P(QP2
+ 2P2
) = (PQ)P2
+ 2P3
= (QP + P)P2
+ 2P3
= QP3
+ 3P3
.
D’où P3Q − QP3 = 3P3.
(b) Pour démontrer le résultat dans le cas général 𝑘, on procède par induction. On
suppose que la proposition est vraie dans le cas 𝑛 = 𝑘, soit P𝑘Q − QP𝑘 = 𝑘P𝑘. Alors,
pour 𝑛 = 𝑘 + 1, on a P𝑘+1
Q = P(P𝑘
Q) = P(QP𝑘
+ 𝑘P𝑘
) = (PQ)P𝑘
+ 𝑘P𝑘+1
= (QP + P)P𝑘
+ 𝑘P𝑘+1
= QP𝑘+1
+ (𝑘 + 1)P𝑘+1
.
La proposition est vraie pour 𝑛 = 𝑘 + 1, grâce à l’hypothèse d’induction.
Chapitre 13 / Déterminants, matrices inverses
et formes quadratiques
13.1
1. (a) 3 × 6 − 2 × 0 = 18 (b) 𝑎𝑏 − 𝑏𝑎 = 0 (c) (2 − 𝑥)(−𝑥) − 1 · 8 = 𝑥2 − 2𝑥 + 8
(d) (𝑎 + 𝑏)2 − (𝑎 − 𝑏)2 = 4𝑎𝑏 (e) 3𝑡 2𝑡−1 − 3𝑡−12𝑡 = 3𝑡−12𝑡−1(3 − 2) = 6𝑡−1
2. Voir figure C13.1.2. L’aire du parallélogramme ombré est égale à 3 × 6 = 18 =
3 0
2 6
.
(3, 0)
(2, 6)
Figure C13.1.2
3. (a) La règle de Cramer donne
𝑥 =
8 −1
5 −2
3 −1
1 −2
=
−16 + 5
−6 + 1
=
11
5
, 𝑦 =
3 8
1 5
3 −1
1 −2
=
15 − 8
−6 + 1
=
7
−5
= −
7
5
.
(b) 𝑥 = 4 et 𝑦 = −1. (c) 𝑥 =
𝑎 + 2𝑏
𝑎2 + 𝑏2
, 𝑦 =
2𝑎 − 𝑏
𝑎2 + 𝑏2
, à condition que 𝑎2 + 𝑏2 ≠ 0.

133. Chapitre 13 / Déterminants, matrices inverses et formes quadratiques 133
4. Les nombres 𝑎 et 𝑏 doivent être tels que 𝑎 + 1 = 0 et 𝑎 − 3𝑏 = −10 ou 𝑎 = −1 et 𝑏 = 3.
5. L’expression du déterminant est (2 − 𝑥) (−𝑥) − 8 = 0 ou 𝑥2 − 2𝑥 − 8 = 0. La solution est
𝑥 = −2 ou 𝑥 = 4.
6. La matrice produit est AB =
𝑎11𝑏11 + 𝑎12𝑏21 𝑎11𝑏12 + 𝑎12𝑏22
𝑎21𝑏11 + 𝑎22𝑏21 𝑎21𝑏12 + 𝑎22𝑏22
, de déterminant
|AB| = (𝑎11𝑏11 + 𝑎12𝑏21) (𝑎21𝑏12 + 𝑎22𝑏22) − (𝑎11𝑏12 + 𝑎12𝑏22) (𝑎21𝑏11 + 𝑎22𝑏21).
D’autre part, |A||B| = (𝑎11𝑎22 −𝑎12𝑎21) (𝑏11𝑏22 −𝑏12𝑏21). Si on effectue courageusement
les produits de chaque membre, si, ensuite, on simplifie quatre termes dans l’expression
de |A||B|, on s’aperçoit que les deux expressions sont égales.
7. Si A = B =
1 0
0 1
, alors |A + B| = 4, alors que |A| + |B| = 2. (On a |A + B| ≠ |A| + |B|
pour la plupart des matrices A et B.)
8. Écrire le système sous la forme
(
𝑌 − 𝐶 = 𝐼0 + 𝐺0
−𝑏𝑌 + 𝐶 = 𝑎
)
.
Ensuite, la règle de Cramer fournit
𝑌 =
𝐼0 + 𝐺0 −1
𝑎 1
1 −1
−𝑏 1
=
𝑎 + 𝐼0 + 𝐺0
1 − 𝑏
, 𝐶 =
1 𝐼0 + 𝐺0
−𝑏 𝑎
1 −1
−𝑏 1
=
𝑎 + 𝑏 (𝐼0 + 𝐺0)
1 − 𝑏
.
Au lieu d’utiliser la règle de Cramer, on peut plus facilement trouver l’expression de
𝑌 : (i) en résolvant la deuxième équation pour obtenir 𝐶 = 𝑎 + 𝑏𝑌 ; (ii) en substituant
cette expression de 𝐶 dans la première équation; (iii) en résolvant l’équation obtenue par
rapport à 𝑌 ; (iv) en utilisant 𝐶 = 𝑎 + 𝑏𝑌 pour obtenir 𝐶.
9. (a) L’équation 𝑋1 = 𝑀2 indique que les exportations de la nation 1 sont égales aux
importations de la nation 2. De même, 𝑋2 = 𝑀1.
(b) Les substitutions suggérées conduisent aux deux équations
𝑌1 = 𝑐1𝑌1 + 𝐴1 + 𝑚2𝑌2 − 𝑚1𝑌1; 𝑌2 = 𝑐2𝑌2 + 𝐴2 + 𝑚1𝑌1 − 𝑚2𝑌2
ou (1 − 𝑐1 − 𝑚1)𝑌1 − 𝑚2𝑌2 = 𝐴1; −𝑚1𝑌1 + (1 − 𝑐2 − 𝑚2)𝑌2 = 𝐴2
qui sous forme matricielle s’écrivent
1 − 𝑐1 − 𝑚1 −𝑚2
−𝑚1 1 − 𝑐2 − 𝑚2
𝑌1
𝑌2
=
𝐴1
𝐴2
Pour que ce système ait une solution, il faut supposer
𝐷 = (1 − 𝑐1 − 𝑚1) (1 − 𝑐2 − 𝑚2) − 𝑚1𝑚2 ≠ 0.
La règle de Cramer fournit alors
𝑌1 = [𝐴2𝑚2 + 𝐴1 (1 − 𝑐2 + 𝑚2)]/𝐷, 𝑌2 = [𝐴1𝑚1 + 𝐴2 (1 − 𝑐1 + 𝑚1)]/𝐷.

134. 134 CORRIGÉS DES EXERCICES
(c) 𝑌2 est une fonction du premier degré de 𝐴1. Les économistes supposent généra-
lement que 𝐷, défini en question (b), est strictement positif, comme c’est le cas si
les paramètres 𝑐1, 𝑐2, 𝑚1, 𝑚2 sont tous suffisamment petits. Alors l’augmentation de
𝐴1 d’une unité change 𝑌2 d’un facteur 𝑚1/𝐷 ⩾ 0, de sorte que 𝑌2 croît lorsque 𝐴1
croît. Voici une explication économique : une augmentation de 𝐴1 fait monter le revenu
de la nation 1,𝑌1. Cela à son tour fait augmenter les importations, 𝑀1. Cependant, comme
la nation 1 importe ce que la nation 2 exporte, le revenu de la nation 2, 𝑌2, augmente, etc.
13.2
1. (a) La règle de Sarrus conduit à
1 −1 0
1 3 2
1 0 0
= 0 − 2 + 0 − 0 − 0 − 0 = −2.
(b) Par la règle de Sarrus,
1 −1 0
1 3 2
1 2 1
= 3 − 2 − 0 − 0 − 4 − (−1) = −2.
(c) Comme 𝑎21 = 𝑎31 = 𝑎32 = 0, le seul terme non nul du développement (13.2.3) est le
produit des éléments de la diagonale principale. Dès lors, le déterminant vaut 𝑎𝑑𝑓 (17).
(d) Par la règle de Sarrus,
𝑎 0 𝑏
0 𝑒 0
𝑐 0 𝑑
= 𝑎𝑒𝑑 + 0 + 0 − 𝑏𝑒𝑐 − 0 − 0 = 𝑒(𝑎𝑑 − 𝑏𝑐).
2. AB =
©
­
­
«
−1 −1 −1
7 13 13
5 9 10
ª
®
®
¬
, |A| = −2, |B| = 3, |AB| = |A||B| = −6.
3. (a) Le déterminant de la matrice des coefficients vaut |A| =
1 −1 1
1 1 −1
−1 −1 −1
= −4. Les
numérateurs de (13.2.5) sont
2 −1 1
0 1 −1
−6 −1 −1
= −4 ,
1 2 1
1 0 −1
−1 −6 −1
= −8 ,
1 −1 2
1 1 0
−1 −1 −6
= −12.
De là, (13.2.5) fournit la solution 𝑥1 = 1, 𝑥2 = 2 et 𝑥3 = 3. Le remplacement de ces
valeurs dans le système confirme que c’est bien la solution.
(b) Le déterminant de la matrice des coefficients est égal à −2 et les numérateurs
de (13.2.5) sont tous nuls. L’unique solution est donc 𝑥1 = 𝑥2 = 𝑥3 = 0.
(c) Suivez la démarche de la question (a). On trouve 𝑥 = 1, 𝑦 = 2 et 𝑧 = 3.
4. Par la règle de Sarrus, le déterminant est (1+𝑎) (1+𝑏) (1+𝑐)+1+1−(1+𝑏)−(1+𝑎)−(1+𝑐)
et, après simplification, on obtient l’expression donnée.
(17) Lla règle de Sarrus donne la même réponse.

135. Chapitre 13 / Déterminants, matrices inverses et formes quadratiques 135
5. tr(A) = 𝑎 + 𝑏 − 1 = 0 et donc 𝑏 = 1 − 𝑎. De plus, |A| = −2𝑎𝑏 = 12 de sorte que
−2𝑎 (1 − 𝑎) = 12 ou 𝑎2 − 𝑎 − 6 = 0. Les racines de cette équation sont 𝑎 = 3 et 𝑎 = −2.
Les solutions sont donc (𝑎, 𝑏) = (3, −2) ou (𝑎, 𝑏) = (−2, 3).
6. Par la règle de Sarrus, l’expression du déterminant est 𝑝(𝑥) = (1 − 𝑥)3+ 8 + 8 − 4(1 − 𝑥) −
4(1−𝑥) −4(1−𝑥) = −𝑥3 +3𝑥2 +9𝑥+5. L’équation qu’on veut résoudre est donc l’équation
du troisième degré −𝑥3 + 3𝑥2 + 9𝑥 + 5 = 0. On ne dispose pas de formule générale simple
pour résoudre ce type d’équation, mais puisque c’est une équation polynomiale avec des
coefficients entiers, d’après (4.7.7), chaque racine entière de l’équation (s’il en existe)
doit diviser le terme constant 5. Les seuls candidats pour des racines entières sont donc
±5 et ±1. On remarque facilement que 𝑝(5) = 0 et 𝑝(−1) = 0, et donc que 𝑥 − 5 et
𝑥 + 1 doivent être des facteurs de 𝑝(𝑥). Donc 𝑝(𝑥) = (𝑥 − 5)(𝑥 + 1)𝑞(𝑥), et à l’aide de la
division polynomiale on obtient 𝑞(𝑥) = 𝑥 + 1. Ainsi, 𝑥 = −1 est une racine double et le
déterminant est nul si et seulement si 𝑥 = −1 ou 𝑥 = 5.
7. (a) |A𝑡 | = 2𝑡2 − 2𝑡 + 1 = 2 (𝑡 − 1
2 )2 + 1
2 0 pour tout 𝑡. (Sinon, montrez que le polynôme
du deuxième degré n’a pas de racines réelles.)
(b) On a
A3
𝑡 =
©
­
­
«
1 2𝑡 − 2𝑡2 𝑡 − 𝑡2
4𝑡 − 4 5𝑡 − 4 −𝑡2 + 4𝑡 − 3
2 − 2𝑡 𝑡2 − 4𝑡 + 3 𝑡3 − 2𝑡 + 2
ª
®
®
¬
.
Quand 𝑡 = 1, on trouve A3
𝑡 = I3.
8. (a) La substitution de 𝑇 = 𝑑 + 𝑡𝑌 dans l’expression de 𝐶 fournit 𝐶 = 𝑎 − 𝑏𝑑 + 𝑏 (1 − 𝑡)𝑌.
La substitution de 𝐶 dans l’expression de 𝑌 fournit alors 𝑌 = 𝑎 + 𝑏 (𝑌 − 𝑑 − 𝑡𝑌) + 𝐴0. On
résout ensuite par rapport à 𝑌, 𝑇 et 𝐶 de manière à déduire les réponses données en (b)
ci-après.
(b) On écrit le système
©
­
­
«
1 −1 0
−𝑏 1 𝑏
−𝑡 0 1
ª
®
®
¬
©
­
­
«
𝑌
𝐶
𝑇
ª
®
®
¬
=
©
­
­
«
𝐴0
𝑎
𝑑
ª
®
®
¬
. Avec 𝐷 =
1 −1 0
−𝑏 1 𝑏
−𝑡 0 1
= 1+𝑏𝑡 −𝑏,
la règle de Cramer fournit(18)
𝑌 =
𝐴0 −1 0
𝑎 1 𝑏
𝑑 0 1
𝐷
=
𝑎 − 𝑏𝑑 + 𝐴0
1 − 𝑏 (1 − 𝑡)
, 𝐶 =
1 𝐴0 0
−𝑏 𝑎 𝑏
−𝑡 𝑑 1
𝐷
=
𝑎 − 𝑏𝑑 + 𝐴0𝑏 (1 − 𝑡)
1 − 𝑏 (1 − 𝑡)
,
𝑇 =
1 −1 𝐴0
−𝑏 1 𝑎
−𝑡 0 𝑑
𝐷
=
𝑡(𝑎 + 𝐴0) + (1 − 𝑏)𝑑
1 − 𝑏 (1 − 𝑡)
.
(18) Ce problème est destiné à vous entraîner à l’utilisation de la règle de Cramer, mais il est aussi là pour vous mettre
en garde contre l’excès d’utilisation de cette règle, car la résolution des équations par simple élimination est beaucoup
plus efficace.

136. 136 CORRIGÉS DES EXERCICES
13.3
1. Chacun de ces trois déterminants est une somme de 4! = 24 termes.
(a) Dans ce cas, il n’y a qu’un terme non nul. Selon (13.3.4), la valeur de ce déterminant
est 24.
(b) Deux termes seulement sont non nuls : le produit des éléments de la diagonale
principale qui est 1 × 1 × 1 × 𝑑, affecté d’un signe + et le terme
1 0 0 1
0 1 0 0
0 0 1 0
a 𝑏 𝑐 𝑑
.
Comme il y a 5 lignes qui montent, le signe de ce produit 1 × 1 × 1 × 𝑎 doit être −. La
valeur du déterminant est finalement 𝑑 − 𝑎.
(c) Il y a quatre termes non nuls : 1×1×1×11−1×1×4×4−1×(−3)×1×3−2×1×1×2 = 0
2. Avec A =
©
­
­
­
­
«
𝑎11 𝑎12 . . . 𝑎1𝑛
0 𝑎22 . . . 𝑎2𝑛
.
.
.
.
.
.
...
.
.
.
0 0 . . . 𝑎𝑛𝑛
ª
®
®
®
®
®
¬
et B =
©
­
­
­
­
«
𝑏11 𝑏12 . . . 𝑏1𝑛
0 𝑏22 . . . 𝑏2𝑛
.
.
.
.
.
.
...
.
.
.
0 0 . . . 𝑏𝑛𝑛
ª
®
®
®
®
®
¬
,
il est facile de voir que la matrice produit AB est triangulaire supérieure, avec les éléments
𝑎11𝑏11, 𝑎22𝑏22, . . . , 𝑎𝑛𝑛𝑏𝑛𝑛 sur la diagonale principale. Le déterminant |AB| est, selon (4),
le produit des 𝑛 nombres 𝑎𝑖𝑖𝑏𝑖𝑖. D’autre part, |A| = 𝑎11𝑎22 · · · 𝑎𝑛𝑛 et |B| = 𝑏11𝑏22 · · · 𝑏𝑛𝑛,
de sorte que l’égalité |AB| = |A||B| en découle immédiatement.
3. +𝑎12𝑎23𝑎35𝑎41𝑎54. (Quatre lignes entre les couples d’éléments encadrés montent de
gauche à droite.)
4. −𝑎15𝑎24𝑎32𝑎43𝑎51. (Il y a neuf lignes qui montent de gauche à droite.)
5. En examinant soigneusement comment la formule (13.3.2) s’applique à cette matrice
(4, 4), on constate que son seul terme non nul est le produit de ses éléments diagonaux.
L’équation s’écrit alors (2 − 𝑥)4 = 0, et la solution est 𝑥 = 2.
13.4
1. (a) AB =
13 16
29 36
, BA =
15 22
23 34
, A′B′ =
15 23
22 34
, B′A′ =
13 29
16 36
.
(b) |A| = |A′| = −2 et |B| = |B′| = −2. Ainsi, |AB| = 4 = |A||B|.
(c) |A′B′| = 4 et |A′||B′| = (−2) × (−2) = 4.
2. A′ =
©
­
­
«
2 1 1
1 0 2
3 1 5
ª
®
®
¬
, |A| = |A′| = −2.

137. Chapitre 13 / Déterminants, matrices inverses et formes quadratiques 137
3. (a) 0 (une colonne entièrement nulle). (b) 0 (lignes 1 et 4 proportionnelles).
(c) (𝑎1 − 𝑥) (−𝑥)3 = 𝑥4 − 𝑎1𝑥3. (Utiliser la définition d’un déterminant et observer qu’un
seul terme est non nul.)
4. |AB| = |A||B| = −12, 3|A| = 9, | − 2B| = (−2)3 (−4) = 32,
|4A| = 43|A| = 43 × 3 = 192. |A| + |B| = −1, alors que |A + B| n’est pas déterminé.
5. A2 =
©
­
­
«
𝑎2 + 6 𝑎 + 1 𝑎2 + 4𝑎 − 12
𝑎2 + 2𝑎 + 2 3 8 − 2𝑎2
𝑎 − 3 1 13
ª
®
®
¬
et |A| = 𝑎2 − 3𝑎 + 2.
6. (a) Comme les deux premières colonnes sont proportionnelles, le déterminant est nul en
raison de la propriété (v) du théorème 13.4.1.
(b) Si on additionne la colonne 2 à la colonne 3, on voit que deux colonnes sont propor-
tionnelles.
(c) La première ligne est 𝑥 − 𝑦 fois la seconde ligne, donc les deux premières lignes sont
proportionnelles.
7. X′X =
©
­
­
«
4 3 2
3 5 1
2 1 2
ª
®
®
¬
et |X′X| = 10.
8. Par la règle de Sarrus, par exemple, |A𝑎 | = 𝑎 (𝑎2 +1)+4+4−4(𝑎2 +1)−𝑎−4 = 𝑎2 (𝑎−4).
En posant 𝑎 = 1, on a |A1| = −3 et |A6
1| = |A1|6 = (−3)6 = 729. (Notez à quel point c’est
plus simple que de calculer A6
1, puis d’évaluer son déterminant.)
9. Comme P′P = I𝑛, de (13.4.1) il vient |P′||P| = |I𝑛| = 1. Or, |P′| = |P| par la règle (ii) du
théorème 13.4.1, de sorte que |P|2 = 1. D’où |P| = ±1.
10. (a) Comme A2 = I𝑛, de (13.4.1), il suit que |A|2 = |A2| = |I𝑛| = 1 ou |A| = ±1.
(b) Vérification directe par multiplication matricielle.
(c) On a (I𝑛 − A) (I𝑛 + A) = I𝑛I𝑛 − AI𝑛 + I𝑛A − AA = I𝑛 − A + A − A2 = I𝑛 − A2 et
cette expression est égale à 0 si et seulement si A2 = I𝑛.
11. (a) La première égalité est vraie, la seconde est fausse. (La seconde égalité devient vraie
si le facteur 2 externe est remplacé par 4.)
(b) Généralement fausse. (Les deux déterminants du membre de droite sont nuls, même
si 𝑎𝑑 − 𝑏𝑐 ≠ 0.)
(c) Les deux égalités sont vraies.
(d) Vrai. (Le deuxième déterminant s’obtient en soustrayant deux fois la première ligne
de la seconde.)
12. Nous avons à démontrer B(PQ) = (PQ)B. En utilisant plusieurs fois l’associativité de la
multiplication matricielle ainsi que les égalités BP = PB et BQ = QB, on obtient
B(PQ) = (BP)Q = (PB)Q = P(BQ) = P(QB) = (PQ)B.

138. 138 CORRIGÉS DES EXERCICES
13. Soit A =
©
­
­
«
0 𝑐 𝑏
𝑐 0 𝑎
𝑏 𝑎 0
ª
®
®
¬
. Calculer A2, puis utiliser (13.4.1).
14. Additionner les 𝑛 − 1 dernières lignes à la première. Chaque élément de la première ligne
devient alors 𝑛𝑎 + 𝑏. Mettre ce facteur en évidence. Additionner ensuite la première
ligne multipliée par −𝑎 aux autres 𝑛 − 1 lignes. Concrètement,
𝐷𝑛 =
𝑎 + 𝑏 𝑎 · · · 𝑎
𝑎 𝑎 + 𝑏 · · · 𝑎
.
.
.
.
.
.
...
.
.
.
𝑎 𝑎 · · · 𝑎
=
𝑛𝑎 + 𝑏 𝑛𝑎 + 𝑏 · · · 𝑛𝑎 + 𝑏
𝑎 𝑎 + 𝑏 · · · 𝑎
.
.
.
.
.
.
...
.
.
.
𝑎 𝑎 · · · 𝑎 + 𝑏
= (𝑛𝑎 + 𝑏)
1 1 · · · 1
𝑎 𝑎 + 𝑏 · · · 𝑎
.
.
.
.
.
.
...
.
.
.
𝑎 𝑎 · · · 𝑎 + 𝑏
= (𝑛𝑎 + 𝑏)
1 1 · · · 1
0 𝑏 · · · 0
.
.
.
.
.
.
...
.
.
.
0 0 · · · 𝑏
La dernière matrice est triangulaire supérieure avec comme éléments diagonaux
1, 𝑏, 𝑏, ..., 𝑏. Son déterminant est égal à 𝑏𝑛−1. D’où 𝐷𝑛 = (𝑛𝑎 + 𝑏)𝑏𝑛−1.
13.5
1. (a) 2. (Soustraire la ligne 1 des lignes 2 et 3 pour obtenir un déterminant dont les éléments
de la première colonne sont 1, 0, 0. Développer ensuite par rapport à la première colonne.)
(b) On pourrait envisager de développer par rapport à la deuxième ligne ou par rapport à
la troisième colonne, car elles ont deux éléments nuls. Mais il vaut mieux effectuer une
opération élémentaire sur une ligne ou une colonne de manière à n’avoir au plus qu’un
élément non nul. Par exemple
1 2 3 4
0 −1 0 11
2 −1 0 3
−2 0 −1 3
−2 −2
=
1 2 3 4
0 −1 0 11
0 −5 −6 −5
0 4 5 11
=
−1 0 11
−5 −6 −5
4 5 11
−5 −4
=
−1 0 11
0 −6 −60
0 5 551
= −1 −6 −60
5 55
= −(−330 + 300) = 30.
(c) 0. (Les colonnes 2 et 4 sont proportionnelles.) Pour calculer des déterminants, on peut
effectuer les opérations élémentaires sur les lignes ou sur les colonnes, mais les opérations
sur les colonnes n’ont pas de sens lors de la résolution des systèmes d’équations selon la
méthode d’élimination de Gauss.
2. Dans chacun de ces trois cas, on développe par rapport à la dernière colonne (restante).
Les réponses sont les suivantes.
(a) 𝑎 (−𝑏𝑐) − 𝑎𝑏𝑐 (b) (−𝑎)𝑏(−𝑐𝑑) (c) 1 × 5 × 3 × 4 × 6 = 360

139. Chapitre 13 / Déterminants, matrices inverses et formes quadratiques 139
13.6
1. (a) En utilisant (13.6.4), on obtient
3 0
2 −1
1/3 0
2/3 −1
=
1 0
0 1
.
(b) Utilisez (13.6.4).
2. Par un calcul direct, on obtient AB =
©
­
­
«
1 0 0
𝑎 + 𝑏 2𝑎 + 1/4 + 3𝑏 4𝑎 + 3/2 + 2𝑏
0 0 1
ª
®
®
¬
.
On a donc AB = I si et seulement si 𝑎 + 𝑏 = 4𝑎 + 3/2 + 2𝑏 = 0 et 2𝑎 + 1/4 + 3𝑏 = 1.
C’est vrai si et seulement si 𝑎 = −3/4 et 𝑏 = 3/4.
3. (a)
𝑥
𝑦
=
2 −3
3 −4
−1
3
5
=
−4 3
−3 2
3
5
=
3
1
(b)
𝑥
𝑦
=
−4 3
−3 2
8
11
=
1
−2
(c)
𝑥
𝑦
=
−4 3
−3 2
0
0
=
0
0
4. De A3 = I, on déduit A2A = I, de sorte que A−1 = A2 = 1
2
−1
√
3
−
√
3 −1
.
5. (a) |A| = 1, A2 =
©
­
­
«
0 1 1
1 1 2
1 1 1
ª
®
®
¬
, A3 =
©
­
­
«
1 1 2
2 2 3
1 2 2
ª
®
®
¬
, et donc A3 − 2A2 + A − I3 = 0.
(b) La dernière égalité dans (a) est équivalente à A(A2 − 2A + I3) = A(A − I3)2 = I3, de
sorte que A−1 = (A − I3)2.
(c) La question (b) suggère le choix P = (A − I3)−1 =
©
­
­
«
0 0 1
1 0 1
0 1 0
ª
®
®
¬
.
Alors A = [(A − I3)2]−1 = P2. La matrice −P convient aussi. On a donc
P = ±(A − I3)−1
= ±
©
­
­
«
−1 1 0
0 0 1
1 0 0
ª
®
®
¬
−1
= ±
©
­
­
«
0 0 1
1 0 1
0 1 0
ª
®
®
¬
.
6. (a) AA′ =
21 11
11 10
, |AA′| = 89 et (AA′)−1 =
1
89
10 −11
−11 21
.
(b) Non, on a vu à l’exemple 12.7.4 que la matrice AA′ doit être symétrique. Son
inverse (AA′)−1 doit donc aussi être symétrique, en raison de la remarque qui suit le
théorème 13.6.1.
7. Par calcul direct, on obtient B2 + B =
3/2 −5
−1/4 3/2
+
−1/2 5
1/4 −1/2
=
1 0
0 1
= I.
On peut soit vérifier par multiplication matricielle directe que B3 − 2B + I = 0, soit, un
peu plus facilement, utiliser la relation B2 + B = I pour arriver à B2 = I − B et ainsi
B3
− 2B + I = B(I − B) − 2B + I = B − B2
− 2B + I = −B2
− B + I = 0.

140. 140 CORRIGÉS DES EXERCICES
De plus, B2 + B = I implique B(B + I) = I. D’après (13.6.4),
B−1
= B + I =
1/2 5
1/4 1/2
.
8. Soit B = X(X′X)−1X′. Alors A2= (I𝑚 − B) (I𝑚 − B) = I𝑚 − B − B + B2. Ici
B2= (X(X′X)−1X′)(X(X′X)−1X′) = X(X′X)−1(X′X) (X′X)−1X′ = X(X′X)−1X′ = B.
D’où A2 = I𝑚 − B − B + B = I𝑚 − B = A.
9. Comme AB =
−7 0
−2 10
, on a CX = D − AB =
−2 3
−6 7
. Mais C−1 =
−2 1
3/2 −1/2
,
de sorte que X =
−2 1
0 1
.
10. (a) Si C2 + C = I, alors C(C + I) = I et C−1 = C + I = I + C.
(b) Comme C2 = I − C, il s’ensuit que
C3
= C2
C = (I − C)C = C − C2
= C − (I − C) = −I + 2C.
Et ensuite, C4 = C3C = (−I + 2C)C = −C + 2C2 = −C + 2 (I − C) = 2I − 3C.
13.7
1. (a) |A| = 10 − 12 = −2 et l’adjointe est
𝐶11 𝐶21
𝐶12 𝐶22
=
5 −3
−4 2
. La matrice inverse est
donc
A−1
= −
1
2
5 −3
−4 2
=
−5/2 3/2
2 −1
.
(b) L’adjointe de B est
adj B =
©
­
­
«
𝐶11 𝐶21 𝐶31
𝐶12 𝐶22 𝐶32
𝐶13 𝐶23 𝐶33
ª
®
®
¬
=
©
­
­
«
1 4 2
2 −1 4
4 −2 −1
ª
®
®
¬
et |B| = 𝑏11𝐶11 + 𝑏21𝐶21 + 𝑏31𝐶31 = 1 × 1 + 2 × 4 + 0 × 2 = 9 selon un développement
suivant la première colonne. De là,
B−1
=
1
9
(adj B) =
1
9
©
­
­
«
1 4 2
2 −1 4
4 −2 −1
ª
®
®
¬
.
(c) Comme la deuxième colonne de C est l’opposée du double de la troisième, le déter-
minant de C est nul et l’inverse de la matrice n’existe pas.
2. La matrice inverse est
1
|A|
©
­
­
«
𝐶11 𝐶21 𝐶31
𝐶12 𝐶22 𝐶32
𝐶13 𝐶23 𝐶33
ª
®
®
¬
=
1
72
©
­
­
«
−3 5 9
18 −6 18
6 14 −18
ª
®
®
¬
.

141. Chapitre 13 / Déterminants, matrices inverses et formes quadratiques 141
3. Le déterminant de I − A vaut |I − A| = 0,496 et la matrice adjointe est
adj(I − A) =
©
­
­
«
0,72 0,64 0,40
0,08 0,76 0,32
0,16 0,28 0,64
ª
®
®
¬
.
De là, (I − A)−1
=
1
0,496
adj(I − A) ≈
©
­
­
«
1,45161 1,29032 0,80645
0,16129 1,53226 0,64516
0,32258 0,56452 1,29032
ª
®
®
¬
, arrondi à la
cinquième décimale. Si vous voulez une réponse exacte, notez que
1 000
496
=
125
62
et
adj(I − A) =
©
­
­
«
0,72 0,64 0,40
0,08 0,76 0,32
0,16 0,28 0,64
ª
®
®
¬
=
1
25
©
­
­
«
18 16 10
2 19 8
4 7 16
ª
®
®
¬
.
Cela donne (I − A)−1
=
5
62
©
­
­
«
18 16 10
2 19 8
4 7 16
ª
®
®
¬
.
4. Soit B la matrice (𝑛, 𝑝) dont les éléments de la 𝑘-ième colonne sont 𝑏1𝑘, 𝑏2𝑘, . . . , 𝑏𝑛𝑘. Les
𝑝 systèmes de 𝑛 équations à 𝑛 inconnues peuvent s’écrire AX = B, où A est une matrice
(𝑛, 𝑛) et X, une matrice (𝑛, 𝑝). En suivant la méthode appliquée à l’exemple 13.7.2, les
mêmes opérations élémentaires sur les lignes qui transforment la matrice (A : I) d’ordre
(𝑛, 2𝑛) en (I : A−1) vont aussi transformer la matrice (A : B) d’ordre (𝑛, (𝑛 + 𝑝)) en la
matrice (I : B∗), où B∗ est la matrice des 𝑏∗
𝑖 𝑗
(19). Quand 𝑘 = 𝑟, la solution du système est
𝑥1 = 𝑏∗
1𝑟 , 𝑥2 = 𝑏∗
2𝑟 , . . . , 𝑥𝑛 = 𝑏∗
𝑛𝑟 .
5. (a) Utilisez les opérations élémentaires.
1 2
3 4
1 0
0 1
−3
∼
1 2
0 −2
1 0
−3 1
−1/2
∼
1 2
0 1
1 0
3/2 −1/2
!
−2
∼
1 0
0 1
−2 1
3/2 −1/2
!
(b)
1 2 3
2 4 5
3 5 6
©
­
«
1 0 0
0 1 0
0 0 1
ª
®
¬
−2 −3
∼
1 2 3
0 0 −1
0 −1 −3
©
­
«
1 0 0
−2 1 0
−3 0 1
ª
®
¬
∼
1 2 3
0 −1 −3
0 0 −1
©
­
«
1 0 0
−3 0 1
−2 1 0
ª
®
¬
−1
−1
∼
1 2 3
0 1 3
0 0 1
©
­
«
1 0 0
3 0 −1
2 −1 0
ª
®
¬
−2
∼
1 0 −3
0 1 3
0 0 1
©
­
«
−5 0 2
3 0 −1
2 −1 0
ª
®
¬ −3 3
∼
1 0 0
0 1 0
0 0 1
©
­
«
1 −3 2
−3 3 −1
2 −1 0
ª
®
¬
(c) On observe que la troisième ligne est la même que la première multipliée par −3.
Aussi, le déterminant étant nul, la matrice n’a pas d’inverse.
(19) En fait, comme ces opérations sur les lignes sont au total équivalentes à prémultiplier par A−1, il doit être vrai
que B∗ = A−1B.

142. 142 CORRIGÉS DES EXERCICES
13.8
1. (a) Le déterminant |A| de la matrice des coefficients vaut |A| =
1 2 −1
2 −1 1
1 −1 −3
= 19.
Les déterminants de (13.8.2) valent
−5 2 −1
6 −1 1
−3 −1 −3
= 19 ,
1 −5 −1
2 6 1
1 −3 −3
= −38 ,
1 2 −5
2 −1 6
1 −1 −3
= 38.
Conformément à (13.8.4), la solution est 𝑥 = 19/19 = 1, 𝑦 = −38/19 = −2 et
𝑧 = 38/19 = 2. On peut facilement vérifier que cette solution est correcte en introduisant
ces valeurs dans le système initial.
(b) Le déterminant |A| de la matrice des coefficients s’écrit
1 1 0 0
1 0 1 0
0 1 1 1
0 1 0 1
.
Si on soustrait la quatrième colonne de la deuxième, il ne reste qu’un élément non nul
dans la deuxième colonne. Le déterminant est réduit à
−
1 1 0
0 1 1
0 0 1
= −1.
Vérifiez que les autres déterminants de (13.8.2) valent
3 1 0 0
2 0 1 0
6 1 1 1
1 1 0 1
= 3 ,
1 3 0 0
1 2 1 0
0 6 1 1
0 1 0 1
= −6 ,
1 1 3 0
1 0 2 0
0 1 6 1
0 1 1 1
= −5 ,
1 1 0 2
1 0 1 3
0 1 1 6
0 1 0 1
= 5.
Conformément à (13.8.4), la solution est 𝑥 = −3, 𝑦 = 6, 𝑧 = 5 et 𝑢 = −5. On peut
facilement vérifier que cette solution est correcte en introduisant ces valeurs dans le
système initial(20).
2. Le déterminant du système est égal à −10, de sorte que la solution est unique. Les
déterminants (13.8.2) sont
𝐷1 =
𝑏1 1 0
𝑏2 −1 2
𝑏3 3 −1
, 𝐷2 =
3 𝑏1 0
1 𝑏2 2
2 𝑏3 −1
, 𝐷3 =
3 1 𝑏1
1 −1 𝑏2
2 3 𝑏3
.
(20) Il y a une façon bien plus rapide de résoudre ce système de quatre équations : si on soustrait la quatrième équation
de la troisième, on a immédiatement 𝑧 = 5; la deuxième équation donne alors 𝑥 = −3; la première 𝑦 = 6; et enfin la
dernière 𝑢 = −5.

143. Chapitre 13 / Déterminants, matrices inverses et formes quadratiques 143
En développant chacun de ces déterminants par rapport à la colonne (𝑏1, 𝑏2, 𝑏3), on
obtient 𝐷1 = −5𝑏1 + 𝑏2 + 2𝑏3, 𝐷2 = 5𝑏1 − 3𝑏2 − 6𝑏3, 𝐷3 = 5𝑏1 − 7𝑏2 − 4𝑏3. En
divisant par −10, on a finalement 𝑥1 = 1
2 𝑏1 − 1
10 𝑏2 − 1
5 𝑏3, 𝑥2 = −1
2 𝑏1 + 3
10 𝑏2 + 3
5 𝑏3,
𝑥3 = −1
2 𝑏1 + 7
10 𝑏2 + 2
5 𝑏3.
3. Selon le théorème 13.8.2, le système admet des solutions non triviales si et seulement
si le déterminant de la matrice des coefficients est égal à 0. Le développement selon la
première ligne fournit
𝑎 𝑏 𝑐
𝑏 𝑐 𝑎
𝑐 𝑎 𝑏
= 𝑎
𝑐 𝑎
𝑎 𝑏
− 𝑏
𝑏 𝑎
𝑐 𝑏
+ 𝑐
𝑏 𝑐
𝑐 𝑎
= 𝑎 (𝑏𝑐 − 𝑎2
) − 𝑏 (𝑏2
− 𝑎𝑐) + 𝑐(𝑎𝑏 − 𝑐2
) = 3𝑎𝑏𝑐 − 𝑎3
− 𝑏3
− 𝑐3
.
Le système admet des solutions autres que la solution triviale nulle si et seulement si
3𝑎𝑏𝑐 − 𝑎3 − 𝑏3 − 𝑐3 = 0.
13.9
1. 𝑥1 = 1
4 𝑥2 + 100, 𝑥2 = 2𝑥3 + 80, 𝑥3 = 1
2 𝑥1. La solution est 𝑥1 = 160, 𝑥2 = 240, 𝑥3 = 80,
comme l’implique (∗∗).
2. (a) Soit 𝑥 et 𝑦 les productions totales respectives des industries 𝐴 et 𝐼. Elles doivent
vérifier 𝑥 = 1
6 𝑥 + 1
4 𝑦 + 60 et 𝑦 = 1
3 𝑥 + 1
4 𝑦 + 60 ou encore 5
6 𝑥 − 1
4 𝑦 = 60 et −1
3 𝑥 + 3
4 𝑦 = 60.
(b) La solution est 𝑥 = 1440/13 et 𝑦 = 1680/13.
3. (a) Aucun secteur ne se fournit lui-même.
(b) Le montant total de l’input 𝑖 requis pour produire une unité de chaque output.
(c) Ce vecteur colonne donne le nombre d’unités de chaque input nécessaires à produire
une unité de l’output 𝑗.
(d) Aucune interprétation économique sensée. (Les biens sont habituellement exprimés
dans des unités différentes, de sorte que cela n’a pas de sens de les additionner. Comme
on dit : « on n’additionne pas des pommes et des poires! »)
4. 0,8𝑥1 − 0,3𝑥2 = 120 et −0,4𝑥1 + 0,9𝑥2 = 90, avec solution 𝑥1 = 225 et 𝑥2 = 200.
5. Le système de Leontief pour le modèle à trois secteurs est









0,9𝑥1 − 0,2𝑥2 − 0,1𝑥3 = 85
−0,3𝑥1 + 0,8𝑥2 − 0,2𝑥3 = 95
−0,2𝑥1 − 0,2𝑥2 + 0,9𝑥3 = 20
et il admet comme solution 𝑥1 = 150, 𝑥2 = 200 et 𝑥3 = 100.
6. La matrice input-output est
A =
©
­
­
«
0 𝛽 0
0 0 𝛾
𝛼 0 0
ª
®
®
¬
.

144. 144 CORRIGÉS DES EXERCICES
Les sommes des éléments de chaque colonne sont inférieures à 1 à condition que 𝛼 1,
𝛽 1 et 𝛾 1, respectivement. En particulier, le produit 𝛼𝛽𝛾 1.
7. Le vecteur quantité x0 doit satisfaire à (∗), (I𝑛 − A) x0 = b et le vecteur prix p′
0, à (∗∗),
p′
0(I𝑛 − A) = v′. En multipliant (∗∗) à droite par x0 et en utilisant (∗), on obtient
v′
x0 = (p′
0(I𝑛 − A)) x0 = p′
0((I𝑛 − A) x0) = p′
0b.
13.10
1. (a) −1, −5;
7
3
,
1
1
(b) 5, −5;
1
1
,
−2
3
(c) 2, 3, 4;
©
­
­
«
1
0
0
ª
®
®
¬
,
©
­
­
«
0
1
0
ª
®
®
¬
,
©
­
­
«
0
0
1
ª
®
®
¬
2. D’abord, Av1 = 3v1 donne 𝑎 − 𝑐 = 3, 𝑏 − 𝑒 = 0 et 𝑐 − 𝑓 = −3. Puis Av2 = v2 implique
𝑎 + 2𝑏 + 𝑐 = 1, 𝑏 + 2𝑑 + 𝑒 = 2 et 𝑐 + 2𝑒 + 𝑓 = 1. Enfin, Av3 = 4v3 fournit 𝑎 − 𝑏 + 𝑐 = 4,
𝑏 − 𝑑 + 𝑒 = −4 et 𝑐 − 𝑒 + 𝑓 = 4. En soustrayant l’équation 𝑎 − 𝑏 + 𝑐 = 4 de 𝑎 + 2𝑏 + 𝑐 = 1,
on obtient 𝑏 = −1 et 𝑎 + 𝑐 = 3. En soustrayant 𝑎 + 𝑐 = 3 de 𝑎 − 𝑐 = 3, on a 𝑐 = 0 et donc
𝑎 = 3. Une approche analogue pour les autres lignes de A conduit à la solution
A =
©
­
­
«
3 −1 0
−1 2 −1
0 −1 3
ª
®
®
¬
.
13.11
1. (a) Les valeurs propres sont 1 et 3 et les vecteurs propres associés,
1
−1
et
1
1
.
La matrice ayant pour colonnes les vecteurs normalisés s’écrit P =
1/
√
2 1/
√
2
−1/
√
2 1/
√
2
!
.
D’où P−1AP = diag(1, 3).
(b) P =
©
­
­
«
1/
√
2 1/
√
2 0
−1/
√
2 1/
√
2 0
0 0 1
ª
®
®
¬
(c) P =
©
­
­
«
0
√
2/2 −
√
2/2
−4/5 3
√
2/10 3
√
2/10
3/5 2
√
2/5 2
√
2/5
ª
®
®
¬
2. (a) L’équation caractéristique peut se simplifier en (1−𝜆)[𝜆2 +𝜆−3(1+ 𝑘)] = 0. Comme
le polynôme 𝜆2 + 𝜆 − 3(1 + 𝑘) n’est pas un multiple de (1 − 𝜆)2, au moins une racine doit
être différente de 1.
(b) Toutes les racines sont réelles si et seulement si 𝜆2 + 𝜆 − 3(1 + 𝑘) = 0 a deux racines
réelles, ce qui est vrai si et seulement si 𝑘 ⩾ −13/12. Si 𝑘 = 3, les valeurs propres sont
−4, 1 et 3.
(c) P′A3P =
©
­
­
«
1 0 0
0 −4 0
0 0 3
ª
®
®
¬
, comme promis par le théorème 13.11.2.

145. Chapitre 13 / Déterminants, matrices inverses et formes quadratiques 145
3. (a) A2 = (PDP−1)(PDP−1) = PD(P−1P)DP−1 = PDIDP−1 = PD2P−1
(b) La formule est valide pour 𝑚 = 1. Supposons qu’elle est aussi valide pour 𝑚 = 𝑘.
Alors
A𝑘+1
= AA𝑘
= PDP−1
(PD𝑘
P−1
) = PD(P−1
P)D𝑘
P−1
= PDID𝑘
P−1
= PDD𝑘
P−1
= PD𝑘+1
P−1
La formule reste donc vraie pour 𝑚 = 𝑘 + 1. Par induction, elle est donc valable pour tous
les entiers strictement positifs 𝑚.
4. D’après (13.11.1), les deux matrices AB et A−1(AB)A = BA ont les mêmes valeurs
propres.
13.12
1. (a) Ici 𝑎11 = −1, 𝑎12 = 1 (pas 2!) et 𝑎22 = −6. D’où 𝑎11 0 et 𝑎11𝑎22−𝑎2
12 = 6−1 = 5 0.
D’après (13.12.7), 𝑄(𝑥1, 𝑥2) est donc définie négative.
(b) Ici 𝑎11 = 4, 𝑎12 = 1 et 𝑎22 = 25. D’où 𝑎11 0 et 𝑎11𝑎22 − 𝑎2
12 = 100 − 1 = 99 0.
D’après (13.12.5), 𝑄(𝑥1, 𝑥2) est donc définie positive.
2. 𝑎11𝑥2
1 + 2𝑎12𝑥1𝑥2 + 2𝑎13𝑥1𝑥3 + 𝑎22𝑥2
2 + 2𝑎23𝑥2𝑥3 + 𝑎33𝑥2
3
3. (a)
1 1
1 1
(b)
𝑎 1
2 𝑏
1
2 𝑏 𝑐
(c)
©
­
­
«
3 −1 3/2
−1 1 0
3/2 0 3
ª
®
®
¬
4. A =
©
­
­
­
«
3 −1 2 4
−1 1 3/2 0
2 3/2 1 −1
4 0 −1 1
ª
®
®
®
®
¬
5. (a) Définie positive. (b) Définie positive. (c) Semi-définie négative. (d) Définie
négative.
6. Comme A est symétrique, d’après le point (a) du théorème 13.11.4, toutes les valeurs
propres sont réelles. D’après le point (b) du théorème 13.12. 1, elles sont toutes positives
si et seulement si A est semi-définie positive. Puisque |A| = 0 si et seulement si 0 est
une valeur propre, toutes les valeurs propres doivent être positives. La conclusion suit du
point (a) du théorème 13.12.1.
7. La matrice associée A est
3 −1
2 (5 + 𝑐)
−1
2 (5 + 𝑐) 2𝑐
dont le déterminant |A| = 6𝑐 − 1
4 (5 + 𝑐)2. Celui-ci peut être factorisé en
|A| = −1
4 (𝑐 − 𝑐1)(𝑐 − 𝑐2),
où 𝑐1 = 7 − 2
√
6 ≈ 2.1 et 𝑐2 = 7 + 2
√
6 ≈ 11.9. En appliquant les tests (13.12.5) à
(13.12.8), on montre que 𝑄 est définie positive pour 𝑐1 𝑐 𝑐2, semi-définie positive
pour 𝑐1 ⩽ 𝑐 ⩽ 𝑐2 et indéfinie si et seulement si 𝑐 𝑐1 or 𝑐 𝑐2.

146. 146 CORRIGÉS DES EXERCICES
8. Pour tout vecteur x de dimension 𝑛, on a x′Ax = x′(B′B)x = (Bx)′(Bx) = kBxk2 ⩾ 0,
donc A est semi-définie positive. Elle est définie positive si et seulement si Bx ≠ 0 pour
tout x ≠ 0, ce qui est vrai si et seulement si |B| ≠ 0.
9. (a) Comme 𝑄 est définie positive, on a 𝑄(0, . . . , 𝑥𝑖, . . . , 0) = 𝑎𝑖𝑖𝑥2
𝑖 0 pour tout 𝑥𝑖 ≠ 0.
Il s’ensuit que 𝑎𝑖𝑖 0.
(b) De nouveau, comme 𝑄 est définie positive, pour tous 𝑖, 𝑗 avec 𝑖 𝑗, on a
𝑅(𝑥𝑖, 𝑥𝑗) = 𝑄(0, . . . , 𝑥𝑖, . . . , 𝑥𝑗, . . . , 0) 0
à moins que 𝑥𝑖 = 𝑥𝑗 = 0. Mais 𝑅(𝑥𝑖, 𝑥𝑗) est une forme quadratique à deux variables 𝑥𝑖 et
𝑥𝑗 dont la matrice symétrique associée est
B =
𝑎𝑖𝑖 𝑎𝑖 𝑗
𝑎𝑗𝑖 𝑎𝑗 𝑗
.
Puisque 𝑄 est définie positive, 𝑅 l’est aussi. D’après le point (a) du théorème 13.2.1, on
a alors |B| 0.
10. D’après le point (a) du théorème 13.11.4, toutes les valeurs propres sont réelles. Si A est
définie négative, alors, d’après le point (c) du théorème 13.12.1, toutes les valeurs propres
𝜆1, . . . , 𝜆𝑛 sont négatives. La fonction définie par 𝜓(𝜆) = (−1)𝑛𝜑(𝜆) doit alors vérifier
𝜓(𝜆) = (𝜆 − 𝜆1)(𝜆 − 𝜆2) · · · (𝜆 − 𝜆𝑛) = (𝜆 + 𝑟1)(𝜆 + 𝑟2) · · · (𝜆 + 𝑟𝑛),
où 𝑟𝑖 = −𝜆𝑖 est positif. En développant le produit, on obtient de manière évidente un
polynôme dont les coefficients sont tous positifs. Par ailleurs, si tout coefficient 𝑎𝑖 de
𝜓(𝜆) est positif, alors 𝜓(𝜆) ⩾ 𝑎0 0 pour tout 𝜆 ⩾ 0. Seul un nombre négatif peut donc
être une valeur propre.
Exercices récapitulatifs du chapitre 13
1. (a) 5 (−2) − (−2) 3 = −4 (b) 1 − 𝑎2 (c) 6𝑎2𝑏 + 2𝑏3 (d) 𝜆2 − 5𝜆
2. (a) −4
(b) 1. (Soustraire la ligne 1 des lignes 2 et 3. Ensuite soustraire deux fois la ligne 2 de
la ligne 3. Le déterminant qui en résulte n’a qu’un élément non nul dans sa troisième
colonne.)
(c) 1. (Utiliser exactement les mêmes opérations sur les lignes que pour (a).)
3. En prenant la transposée des deux membres, on obtient A−1 − 2I2 = −2
1 1
1 0
,
de sorte que
A−1
= 2I2 − 2
1 1
1 0
=
2 0
0 2
−
2 2
2 0
=
0 −2
−2 2
.
En utilisant (13.6.3), on obtient
A =
0 −2
−2 2
−1
= −
1
4
2 2
2 0
=
−1/2 −1/2
−1/2 0
.

147. Chapitre 13 / Déterminants, matrices inverses et formes quadratiques 147
4. (a) On développe en cofacteurs par rapport à toute ligne ou colonne qui contient un zéro.
On obtient |A𝑡 | = 𝑡 + 1, de sorte que A𝑡 est inversible si et seulement si 𝑡 ≠ −1.
(b) Multiplier l’équation donnée à droite par A1 conduit à BA1 + X = I3.
De là, X = I3 − BA1 =
©
­
­
«
0 0 −1
0 0 −1
−2 −1 0
ª
®
®
¬
.
5. (a) En développant par rapport à la troisième colonne, on obtient le déterminant
|A| =
𝑞 −1 𝑞 − 2
1 −𝑝 2 − 𝑝
2 −1 0
= (𝑞 − 2)
1 −𝑝
2 −1
− (2 − 𝑝)
𝑞 −1
2 −1
= (𝑞 − 2) (−1 + 2𝑝) − (2 − 𝑝) (−𝑞 + 2) = (𝑞 − 2) (𝑝 + 1).
On a aussi
|A + E| =
𝑞 + 1 0 𝑞 − 1
2 1 − 𝑝 3 − 𝑝
3 0 1
= (1 − 𝑝)
𝑞 + 1 𝑞 − 1
3 1
= 2 (𝑝 − 1) (𝑞 − 2).
(b) A + E est inversible quand 𝑝 ≠ 1 et 𝑞 ≠ 2.
(c) Manifestement, |E| = 0. Dès lors, |BE| = |B||E| = 0, de sorte que BE n’a pas
d’inverse.
6. Le déterminant de la matrice des coefficients est
−2 4 −𝑡
−3 1 𝑡
𝑡 − 2 −7 4
= 5𝑡2
− 45𝑡 + 40 = 5 (𝑡 − 1) (𝑡 − 8).
Aussi, d’après la règle de Cramer, il y a une unique solution si et seulement si 𝑡 ≠ 1 et
𝑡 ≠ 8.
7. On voit que (I − A) (I + A + A2 + A3) = I + A + A2 + A3 − A − A2 − A3 − A4 = I − A4 = I.
Ensuite, utilisez (13.6.4).
8. (a) Cela devient facile après avoir remarqué que
U2
=
©
­
­
­
­
«
1 1 . . . 1
1 1 . . . 1
.
.
.
.
.
.
...
.
.
.
1 1 . . . 1
ª
®
®
®
®
®
¬
©
­
­
­
­
«
1 1 . . . 1
1 1 . . . 1
.
.
.
.
.
.
...
.
.
.
1 1 . . . 1
ª
®
®
®
®
®
¬
=
©
­
­
­
­
«
𝑛 𝑛 . . . 𝑛
𝑛 𝑛 . . . 𝑛
.
.
.
.
.
.
...
.
.
.
𝑛 𝑛 . . . 𝑛
ª
®
®
®
®
®
¬
= 𝑛U.
(b) Il faut d’abord remarquer que
A =
©
­
­
«
4 3 3
3 4 3
3 3 4
ª
®
®
¬
=
©
­
­
«
1 0 0
0 1 0
0 0 1
ª
®
®
¬
+
©
­
­
«
3 3 3
3 3 3
3 3 3
ª
®
®
¬
= I3 + 3U

148. 148 CORRIGÉS DES EXERCICES
grâce à la question (a), on peut écrire
(I3 + 3U) (I3 + 𝑏U) = I3 + (3 + 𝑏 + 3 × 3𝑏U) = I3 + (3 + 10𝑏)U.
Cela devient égal à I3 si on choisit 𝑏 = −3/10. Dès lors
A−1
= (I3 + 3U)−1
= I3 − (3/10)U =
©
­
­
«
1 0 0
0 1 0
0 0 1
ª
®
®
¬
−
©
­
­
«
3
10
3
10
3
10
3
10
3
10
3
10
3
10
3
10
3
10
ª
®
®
¬
=
1
10
©
­
­
«
7 −3 −3
−3 7 −3
−3 −3 7
ª
®
®
¬
.
9. De la première équation, on déduit Y = B−AX. La substitution dans la deuxième équation
conduit à X = 2A−1B − C, d’où Y = AC − B.
10. (a) La méthode d’élimination de Gauss pratiquée avec les opérations élémentaires sur les
lignes indiquées fournit
𝑎 1 4 2
2 1 𝑎2 2
1 0 −3 𝑎
©
­
­
«
ª
®
®
¬
∼
1 0 −3 𝑎
2 1 𝑎2 2
𝑎 1 4 2
©
­
­
«
ª
®
®
¬
−2 −𝑎
∼
1 0 −3 𝑎
0 1 𝑎2 + 6 −2𝑎 + 2
0 1 3𝑎 + 4 −𝑎2 + 2
©
­
­
«
ª
®
®
¬
−1 ∼
1 0 −3 𝑎
0 1 𝑎2 + 6 −2𝑎 + 2
0 0 −𝑎2 + 3𝑎 − 2 −𝑎2 + 2𝑎
©
­
­
«
ª
®
®
¬
Le système admet donc une solution unique si et seulement si −𝑎2 +3𝑎 −2 ≠ 0, autrement
dit, si et seulement si 𝑎 ≠ 1 et 𝑎 ≠ 2.
Si 𝑎 = 2, la dernière ligne ne contient plus que des 0 et il y a donc une infinité de solutions.
Si 𝑎 = 1, il n’y a pas de solution.
(b) En appliquant les mêmes opérations élémentaires sur les lignes de la matrice étendue
associée qu’en (a), la quatrième colonne est transformée de la façon suivante,
©
­
­
«
𝑏1
𝑏2
𝑏3
ª
®
®
¬
→
©
­
­
«
𝑏3
𝑏2
𝑏1
ª
®
®
¬
→
©
­
­
«
𝑏3
𝑏2 − 2𝑏3
𝑏1 − 𝑎𝑏3
ª
®
®
¬
→
©
­
­
«
𝑏3
𝑏2 − 2𝑏3
𝑏1 − 𝑏2 + (2 − 𝑎)𝑏3
ª
®
®
¬
.
La matrice étendue finale est
©
­
­
«
1 0 −3 𝑏3
0 1 𝑎2 + 6 𝑏2 − 2𝑏3
0 0 −𝑎2 + 3𝑎 − 2 𝑏1 − 𝑏2 + (2 − 𝑎)𝑏3
ª
®
®
¬
.
Il y a une infinité de solutions si et seulement si tous les éléments de la dernière ligne
sont égaux à 0, ce qui sera le cas, soit si (i) 𝑎 = 1 et 𝑏1 − 𝑏2 + 𝑏3 = 0, soit si (ii) 𝑎 = 2 et
𝑏1 = 𝑏2.

149. Chapitre 13 / Déterminants, matrices inverses et formes quadratiques 149
11. (a) |A| = −2. On a aussi A2 − 2I2 =
11 −6
18 −10
= A, de sorte que A2 + 𝑐A = 2I2 si
𝑐 = −1. Il s’ensuit que A( 1
2 A − 1
2 I2) = I2, donc A−1 = 1
2 (A − I2) =
5 −3
9 −11/2
.
(b) Si B2 = A, alors |B|2 = |A| = −2, ce qui est impossible.
12. Notez d’abord que A′A = I𝑛 implique A′ = A−1 d’après (13.6.5), de sorte que
AA′ = I𝑛. Mais alors, toujours d’après (13.6.5), on a
(A′
B−1
A) (A′
BA) = A′
B−1
(AA′
)BA = A′
B−1
I𝑛BA = A′
(B−1
B)A = A′
I𝑛A = A′
A = I𝑛.
À nouveau d’après (16.6.5), (A′BA)−1 = A′B−1A.
13. Pour une fois, nous employons l’élimination, mais non systématique. On résout la première
équation, ce qui donne 𝑦 = 3 − 𝑎𝑥. La deuxième donne alors 𝑧 = 2 − 𝑥 et la quatrième
𝑢 = 1 − 𝑦. On substitue tous ces résultats dans la troisième et on obtient
3 − 𝑎𝑥 + 𝑎 (2 − 𝑥) + 𝑏 (1 − 3 + 𝑎𝑥) = 6 ou 𝑎 (𝑏 − 2) 𝑥 = −2𝑎 + 2𝑏 + 3.
C’est l’unique solution pourvu que 𝑎 (𝑏 − 2) ≠ 0. La solution complète est
𝑥 =
2𝑏 − 2𝑎 + 3
𝑎 (𝑏 − 2)
, 𝑦 =
2𝑎 + 𝑏 − 9
𝑏 − 2
, 𝑧 =
2𝑎𝑏 − 2𝑎 − 2𝑏 − 3
𝑎 (𝑏 − 2)
, 𝑢 =
7 − 2𝑎
𝑏 − 2
.
14. Le déterminant du membre de gauche est égal à
(𝑎 + 𝑥) 𝑑 − 𝑐 (𝑏 + 𝑦) = (𝑎𝑑 − 𝑏𝑐) + (d𝑥 − 𝑐𝑦),
qui est bien la somme des déterminants de droite.
15. |B3| = |B|3. Comme B est une matrice (3, 3), on a |−B| = (−1)3|B| = −|B|. Comme
B3 = −B, il s’ensuit que |B|3 = −|B| et, de là, |B|(|B|2 + 1) = 0. La dernière équation
implique |B| = 0 et de ce fait B ne peut pas avoir d’inverse.
16. L’astuce est de constater que les développements en cofacteurs de |A|, |B| et |C| par
rapport à leur 𝑟ième ligne prennent les formes respectives
Í𝑛
𝑗=1 𝑎𝑟 𝑗𝐶𝑟 𝑗,
Í𝑛
𝑗=1 𝑏𝑟 𝑗𝐶𝑟 𝑗 et
Í𝑛
𝑗=1(𝑎𝑟 𝑗 + 𝑏𝑟 𝑗)𝐶𝑟 𝑗 pour exactement les mêmes cofacteurs 𝐶𝑟 𝑗 (𝑗 = 1, 2, . . . , 𝑛). Alors
il est évident que
|C| =
𝑛
Õ
𝑗=1
(𝑎𝑟 𝑗 + 𝑏𝑟 𝑗)𝐶𝑟 𝑗 =
𝑛
Õ
𝑗=1
𝑎𝑟 𝑗𝐶𝑟 𝑗 +
𝑛
Õ
𝑗=1
𝑏𝑟 𝑗𝐶𝑟 𝑗 = |A| + |B|.
17. Ce n’est pas une bonne idée de vouloir ici passer en force. Il vaut mieux remarquer que les
lignes 1 et 3 et les lignes 2 et 4 du déterminant ont beaucoup en commun. Aussi, on soustrait
la ligne 3 de la 1 et la ligne 4 de la 2. Conformément au théorème 13.4.1(vi), cela ne change

150. 150 CORRIGÉS DES EXERCICES
pas la valeur du déterminant. Cela donne, si on utilise ensuite le théorème 13.4.1(iii),
0 𝑎 − 𝑏 0 𝑏 − 𝑎
𝑏 − 𝑎 0 𝑎 − 𝑏 0
𝑥 𝑏 𝑥 𝑎
𝑎 𝑥 𝑏 𝑥
= (𝑎 − 𝑏)2
0 1 0 −1
−1 0 1 0
𝑥 𝑏 𝑥 𝑎
𝑎 𝑥 𝑏 𝑥
= (𝑎 − 𝑏)2
0 1 0 0
−1 0 1 0
𝑥 𝑏 𝑥 𝑎 + 𝑏
𝑎 𝑥 𝑏 2𝑥
.
La dernière égalité provient de l’addition de la colonne 2 à la colonne 4 dans le déterminant
du milieu. Si on développe le dernier déterminant par rapport à la ligne 1, on obtient
successivement
−(𝑎 − 𝑏)2
−1 1 0
𝑥 𝑥 𝑎 + 𝑏
𝑎 𝑏 2𝑥
= −(𝑎 − 𝑏)2
[−2𝑥2
+ 𝑏 (𝑎 + 𝑏) − 2𝑥2
+ 𝑎 (𝑎 + 𝑏)]
= (𝑎 − 𝑏)2
[4𝑥2
− (𝑎 + 𝑏)2
]
= (𝑎 − 𝑏)2
[2𝑥 − (𝑎 + 𝑏)][2𝑥 + (𝑎 + 𝑏)].
Si 𝑎 ≠ 𝑏, les solutions sont 𝑥1 = 1
2 (𝑎 + 𝑏) et 𝑥2 = −1
2 (𝑎 + 𝑏). Si 𝑎 = 𝑏, le déterminant est
nul, quel que soit 𝑥.
18. D’après la règle (12.7.3) et le point (ii) du théorème 13.4.1, pour tout 𝜆, on a
|A − 𝜆I| = |(A − 𝜆I)′
| = |A′
− 𝜆I|.
Il s’ensuit que |A − 𝜆I| = 0 ⇔ |A′ − 𝜆I| = 0, donc A et A′ ont bien les mêmes valeurs
propres.
19. D’après la définition d’une valeur propre, 𝜆 = 0 ⇔ A est singulière ⇔ |A| = 0. Ainsi, si
𝜆 ≠ 0, alors A a une inverse. Alors, pour ce 𝜆 ≠ 0 et tout x ≠ 0 vérifiant Ax = 𝜆x, on a
x = 𝜆A−1x ou A−1x = (1/𝜆)x. Il s’ensuit que 1/𝜆 est une valeur propre de A−1.
20. On a
|A − I| =
𝑎11 − 1 𝑎12 . . . 𝑎1𝑛
𝑎21 𝑎22 − 1 . . . 𝑎2𝑛
.
.
.
.
.
.
...
.
.
.
𝑎𝑛1 𝑎𝑛2 . . . 𝑎𝑛𝑛 − 1
.
On peut additionner les 𝑛−1 autres lignes à la première ligne sans changer le déterminant.
Pour chaque 𝑗, le 𝑗ième élément de la première ligne de ce nouveau déterminant est
Í𝑛
𝑖=1 𝑎𝑖 𝑗 − 1. Comme, par hypothèse, toutes les sommes des colonnes de A valent 1, la
première ligne doit être 0. Il s’ensuit que |A − I| = 0, donc 1 est une valeur propre de A.
21. (a) −1 avec
©
­
­
«
1
−1
2
ª
®
®
¬
; 0 avec
©
­
­
«
1
−1
1
ª
®
®
¬
; 2 avec
©
­
­
«
2
1
1
ª
®
®
¬
. (b) 0 avec
©
­
­
«
1
1
1
ª
®
®
¬
; 1 avec
©
­
­
«
−1
0
1
ª
®
®
¬
; 3 avec
©
­
­
«
1
−2
1
ª
®
®
¬
.

151. Chapitre 14 / Les fonctions de plusieurs variables 151
Chapitre 14 / Les fonctions de plusieurs variables
14.1
1. 𝑓 (0, 1) = 1 × 0 + 2 × 1 = 2, 𝑓 (2, −1) = 0, 𝑓 (𝑎, 𝑎) = 3𝑎 et 𝑓 (𝑎 + ℎ, 𝑏) − 𝑓 (𝑎, 𝑏) = ℎ.
2. 𝑓 (0, 1) = 0, 𝑓 (−1, 2) = −4, 𝑓 (104, 10−2) = 1, 𝑓 (𝑎, 𝑎) = 𝑎3.
𝑓 (𝑎 + ℎ, 𝑏) = (𝑎 + ℎ) 𝑏2 = 𝑎𝑏2 + ℎ𝑏2 et 𝑓 (𝑎, 𝑏 + 𝑘) − 𝑓 (𝑎, 𝑏) = 2𝑎𝑏𝑘 + 𝑎𝑘2.
3. 𝑓 (1, 1) = 2, 𝑓 (−2, 3) = 51, 𝑓 (1/𝑥, 1/𝑦) = 3/𝑥2 − 2/𝑥𝑦 + 1/𝑦3, 𝑝 = 6𝑥 + 3ℎ − 2𝑦,
𝑞 = −2𝑥 + 3𝑦2 + 3𝑦𝑘 + 𝑘2.
4. (a) 𝑓 (−1, 2) = 1, 𝑓 (𝑎, 𝑎) = 4𝑎2, 𝑓 (𝑎 + ℎ, 𝑏) − 𝑓 (𝑎, 𝑏) = 2 (𝑎 + 𝑏) ℎ + ℎ2.
(b) 𝑓 (𝑡𝑥, 𝑡𝑦) = (𝑡𝑥)2 + 2 (𝑡𝑥) (𝑡𝑦) + (𝑡𝑦)2 = 𝑡2 (𝑥2 + 2𝑥𝑦 + 𝑦2) = 𝑡2 𝑓 (𝑥, 𝑦) pour tout 𝑡, y
compris 𝑡 = 2.
5. 𝐹(1, 1) = 10, 𝐹(4, 27) = 60, 𝐹(9, 1/27) = 10, 𝐹(3,
√
2 ) = 10
√
3 ×
6
√
2,
𝐹(100, 1 000) = 1 000, 𝐹(2𝐾, 2𝐿) = 10 × 25/6𝐾1/2𝐿1/3 = 25/6𝐹(𝐾, 𝐿).
6. (a) Comme le dénominateur doit être différent de 0, la fonction est définie pour les (𝑥, 𝑦)
tels que 𝑦 ≠ 𝑥 − 2.
(b) Comme on ne peut prendre les racines carrées que des nombres positifs, il faut exiger
2 − (𝑥2 + 𝑦2) ⩾ 0 ou 𝑥2 + 𝑦2 ⩽ 2.
(c) On pose 𝑎 = 𝑥2 + 𝑦2. Il faut (4 − 𝑎) (𝑎 − 1) ⩾ 0, ou 1 ⩽ 𝑎 ⩽ 4. (Utilisez un
tableau de signes.) Les domaines de définition de (b) et (c) sont les régions ombrées des
figures C14.1.6b et C14.1.6c.
y
x
x2 + y2 ≤ √2
2
Figure C14.1.6b
y
x
1 2
Figure C14.1.6c
7. (a) 𝑒𝑥+𝑦 ≠ 3 ou 𝑥 + 𝑦 ≠ ln 3.
(b) Puisque (𝑥 − 𝑎)2 ⩾ 0 et (𝑦 − 𝑏)2 ⩾ 0, il suffit que 𝑥 ≠ 𝑎 et 𝑦 ≠ 𝑏, car on ne peut
prendre le logarithme que des nombres strictement positifs.
(c) 𝑥 𝑎 et 𝑦 𝑏.

152. 152 CORRIGÉS DES EXERCICES
14.2
1. (a)
𝜕𝑧
𝜕𝑥
= 2,
𝜕𝑧
𝜕𝑦
= 3. (b)
𝜕𝑧
𝜕𝑥
= 2𝑥,
𝜕𝑧
𝜕𝑦
= 3𝑦2
. (c)
𝜕𝑧
𝜕𝑥
= 3𝑥2
𝑦4
,
𝜕𝑧
𝜕𝑦
= 4𝑥3
𝑦3
.
(d)
𝜕𝑧
𝜕𝑥
=
𝜕𝑧
𝜕𝑦
= 2 (𝑥 + 𝑦)
2. (a)
𝜕𝑧
𝜕𝑥
= 2𝑥,
𝜕𝑧
𝜕𝑦
= 6𝑦. (b)
𝜕𝑧
𝜕𝑥
= 𝑦,
𝜕𝑧
𝜕𝑦
= 𝑥.
(c)
𝜕𝑧
𝜕𝑥
= 20𝑥3
𝑦2
− 2𝑦5
,
𝜕𝑧
𝜕𝑦
= 10𝑥4
𝑦 − 10𝑥𝑦4
. (d)
𝜕𝑧
𝜕𝑥
=
𝜕𝑧
𝜕𝑦
= 𝑒𝑥+𝑦
(e)
𝜕𝑧
𝜕𝑥
= 𝑦𝑒𝑥𝑦
,
𝜕𝑧
𝜕𝑦
= 𝑥𝑒𝑥𝑦
. (f)
𝜕𝑧
𝜕𝑥
= 𝑒𝑥
/𝑦,
𝜕𝑧
𝜕𝑦
= −𝑒𝑥
/𝑦2
.
(g)
𝜕𝑧
𝜕𝑥
=
𝜕𝑧
𝜕𝑦
= 1/(𝑥 + 𝑦) (h)
𝜕𝑧
𝜕𝑥
= 1/𝑥,
𝜕𝑧
𝜕𝑦
= 1/𝑦.
3. (a) 𝑓 ′
𝑥 (𝑥, 𝑦) = 7𝑥6, 𝑓 ′
𝑦 (𝑥, 𝑦) = −7𝑦6, 𝑓 ′
𝑥𝑦 (𝑥, 𝑦) = 0.
(b) 𝑓 ′
𝑥 (𝑥, 𝑦) = 5𝑥4 ln 𝑦, 𝑓 ′
𝑦 (𝑥, 𝑦) = 𝑥5/𝑦, 𝑓 ′′
𝑥𝑦 (𝑥, 𝑦) = 5𝑥4/𝑦.
(c) 𝑓 (𝑥, 𝑦) = (𝑥2 − 2𝑦2)5 = 𝑢5, où 𝑢 = 𝑥2 − 2𝑦2. Alors
𝑓 ′
𝑥 (𝑥, 𝑦) = 5𝑢4
𝑢′
1 = 5 (𝑥2
− 2𝑦2
)4
2𝑥 = 10𝑥 (𝑥2
− 2𝑦2
)4
.
De la même façon, 𝑓 ′
𝑦 (𝑥, 𝑦) = 5𝑢4𝑢′
𝑦 = 5 (𝑥2 − 2𝑦2)4 (−4𝑦) = −20𝑦 (𝑥2 − 2𝑦2)4.
Enfin,
𝑓 ′′
𝑥𝑦 (𝑥, 𝑦) = (
𝜕
𝜕𝑦
) (10𝑥 (𝑥2
− 2𝑦2
)4
) = 10𝑥 × 4 (𝑥2
− 2𝑦2
)3
(−4𝑦) = −160𝑥𝑦 (𝑥2
− 2𝑦2
)3
.
4. (a) 𝑧′
𝑥 = 3, 𝑧′
𝑦 = 4 et 𝑧′′
𝑥𝑥 = 𝑧′′
𝑥𝑦 = 𝑧′′
𝑦𝑥 = 𝑧′′
𝑦𝑦 = 0.
(b) 𝑧′
𝑥 = 3𝑥2𝑦2, 𝑧′
𝑦 = 2𝑥3𝑦, 𝑧′′
𝑥𝑥 = 6𝑥𝑦2, 𝑧′′
𝑦𝑦 = 2𝑥3 et 𝑧′′
𝑥𝑦 = 6𝑥2𝑦.
(c) 𝑧′
𝑥 = 5𝑥4 − 6𝑥𝑦, 𝑧′
𝑦 = −3𝑥2 + 6𝑦5, 𝑧′′
𝑥𝑥 = 20𝑥3 − 6𝑦, 𝑧′′
𝑦𝑦 = 30𝑦4, et 𝑧′′
𝑥𝑦 = −6𝑥.
(d) 𝑧′
𝑥 = 1/𝑦, 𝑧′
𝑦 = −𝑥/𝑦2, 𝑧′′
𝑥𝑥 = 0, 𝑧′′
𝑦𝑦 = 2𝑥/𝑦3 et 𝑧′′
𝑥𝑦 = −1/𝑦2.
(e) 𝑧′
𝑥 = 2𝑦 (𝑥 + 𝑦)−2, 𝑧′
𝑦 = −2𝑥 (𝑥 + 𝑦)−2, 𝑧′′
𝑥𝑥 = −4𝑦 (𝑥 + 𝑦)−3, 𝑧′′
𝑦𝑦 = 4𝑥 (𝑥 + 𝑦)−3 et
𝑧′′
𝑥𝑦 = 2 (𝑥 − 𝑦) (𝑥 + 𝑦)−3.
(f) 𝑧′
𝑥 = 𝑥 (𝑥2 +𝑦2)−1/2, 𝑧′
𝑦 = 𝑦 (𝑥2 +𝑦2)−1/2, 𝑧′′
𝑥𝑥 = 𝑦2 (𝑥2 +𝑦2)−3/2, 𝑧′′
𝑦𝑦 = 𝑥2 (𝑥2 +𝑦2)−3/2
et 𝑧′′
𝑥𝑦 = −𝑥𝑦 (𝑥2 + 𝑦2)−3/2.
5. (a) 𝑧′
𝑥 = 2𝑥, 𝑧′
𝑦 = 2𝑒2𝑦, 𝑧′′
𝑥𝑥 = 2, 𝑧′′
𝑦𝑦 = 4𝑒2𝑦, 𝑧′′
𝑥𝑦 = 0.
(b) 𝑧′
𝑥 = 𝑦/𝑥, 𝑧′
𝑦 = ln 𝑥, 𝑧′′
𝑥𝑥 = −𝑦/𝑥2, 𝑧′′
𝑦𝑦 = 0, 𝑧′′
𝑥𝑦 = 1/𝑥.
(c) 𝑧′
𝑥 = 𝑦2 − 𝑦𝑒𝑥𝑦, 𝑧′
𝑦 = 2𝑥𝑦 − 𝑥𝑒𝑥𝑦, 𝑧′′
𝑥𝑥 = −𝑦2𝑒𝑥𝑦, 𝑧′′
𝑦𝑦 = 2𝑥 − 𝑥2𝑒𝑥𝑦,
𝑧′′
𝑥𝑦 = 2𝑦 − 𝑒𝑥𝑦 − 𝑥𝑦𝑒𝑥𝑦.
(d) 𝑧 = 𝑥𝑦 = (𝑒ln 𝑥)𝑦 = 𝑒𝑦 ln 𝑥 = 𝑒𝑢 avec 𝑢 = 𝑦 ln 𝑥. Ensuite,
𝑧′
𝑥 = 𝑒𝑢
𝑢′
𝑥 = 𝑥𝑦
(𝑦/𝑥) = 𝑦𝑥𝑦−1
.
De même, 𝑧′
𝑦 = 𝑒𝑢𝑢′
𝑦 = 𝑥𝑦 ln 𝑥. En outre, 𝑧′′
𝑥𝑥 = (𝜕/𝜕𝑥) (𝑦𝑥𝑦−1) = 𝑦 (𝑦 − 1) 𝑥𝑦−2(21),
𝑧′′
𝑦𝑦 = (𝜕/𝜕𝑦) (𝑥𝑦 ln 𝑥) = 𝑥𝑦 (ln 𝑥)2 et 𝑧′′
𝑥𝑦 = (𝜕/𝜕𝑦) (𝑦𝑥𝑦−1) = 𝑥𝑦−1 + 𝑦𝑥𝑦−1 ln 𝑥.
(21) Quand on dérive 𝑥𝑦−1 partiellement par rapport à 𝑥, on traite 𝑦 comme une constante, de sorte que la règle
d𝑥𝑎/d𝑥 = 𝑎𝑥𝑎−1 s’applique.

153. Chapitre 14 / Les fonctions de plusieurs variables 153
6. (a) 𝐹′
𝑆 = 2,26 × 0,44𝑆−0,56𝐸0,48 = 0,9944𝑆−0,56𝐸0,48,
𝐹′
𝐸 = 2,26 × 0,48𝑆0,44𝐸−0.52 = 1,0848𝑆0,44𝐸−0,52.
(b) On a 𝑆𝐹′
𝑆 + 𝐸𝐹′
𝐸 = 𝑆 × 2,26 × 0,44𝑆−0,56
𝐸0,48
+ 𝐸 × 2,26 × 0,48𝑆0,44
𝐸−0,52
= 0,44 𝐹 + 0,48 𝐹 = 0,92 𝐹,
de sorte que 𝑘 = 0,92.
7. 𝑥𝑧′
𝑥 +𝑦𝑧′
𝑦 = 𝑥[2𝑎 (𝑎𝑥+𝑏𝑦)]+𝑦[2𝑏 (𝑎𝑥+𝑏𝑦)] = (𝑎𝑥+𝑏𝑦) 2 (𝑎𝑥+𝑏𝑦) = 2 (𝑎𝑥+𝑏𝑦)2 = 2𝑧.
8. 𝜕𝑧/𝜕𝑥 = 𝑥/(𝑥2 + 𝑦2), 𝜕𝑧/𝜕𝑦 = 𝑦/(𝑥2 + 𝑦2), 𝜕2𝑧/𝜕𝑥2 = (𝑦2 − 𝑥2)/(𝑥2 + 𝑦2)2 et
𝜕2𝑧/𝜕𝑦2 = (𝑥2 − 𝑦2)/(𝑥2 + 𝑦2)2. Donc 𝜕2𝑧/𝜕𝑥2 + 𝜕2𝑧/𝜕𝑦2 = 0.
9. (a) 𝑠′
𝑥 (𝑥, 𝑦) = 2/𝑥 et de là 𝑠′
𝑥 (20, 30) = 2/20 = 1/10.
(b) 𝑠′
𝑦 (𝑥, 𝑦) = 4/𝑦 et de là 𝑠′
𝑦 (20, 30) = 4/30 = 2/15.
14.3
1. Si 𝑥2 + 𝑦2 = 6, alors 𝑓 (𝑥, 𝑦) =
√
6 − 4. L’équation 𝑥2 + 𝑦2 = 6 est celle d’une courbe de
niveau 𝑐 =
√
6 − 4 de 𝑓 .
2. 𝑓 (𝑥, 𝑦) = 𝑒𝑥2−𝑦2
+ (𝑥2 − 𝑦2)2 = 𝑒𝑐 + 𝑐2 quand 𝑥2 − 𝑦2 = 𝑐, de sorte que la dernière
équation représente une courbe de niveau 𝑒𝑐 + 𝑐2 de 𝑓 .
3. Au point d’intersection de ces deux courbes de niveau, 𝑓 devrait prendre deux valeurs
différentes, ce qui est impossible si 𝑓 est une fonction.
4. De façon générale, le graphique de 𝑔(𝑥, 𝑦) = 𝑓 (𝑥) dans l’espace à trois dimensions est la
surface engendrée par le déplacement du graphique de 𝑧 = 𝑓 (𝑥) parallèlement à l’axe 𝑂𝑦
dans les deux sens. Le graphique de 𝑔(𝑥, 𝑦) = 𝑥 est le plan contenant l’axe 𝑂𝑦 qui fait un
angle de 45◦ avec le plan 𝑂𝑥𝑦. Le graphique de 𝑔(𝑥, 𝑦) = −𝑥3 est celui de la figure C14.3.4.
(Ce graphique non borné n’est représenté que partiellement, naturellement.)
z
y
x
Figure C14.3.4
5. Voir les figures C14.3.5a et b, qui sont toutes deux en deux parties. Seul un détail du
graphique est représenté pour la question (a).

154. 154 CORRIGÉS DES EXERCICES
x
y
z
z = 3 − x − y
(0, 0, 3)
(3, 0, 0)
(0, 3, 0)
Figure C14.3.5a1
y
x
3 − x − y = c
c = 5
c = 3
c = 1
Figure C14.3.5a2
y
x
z
√3
z = 3 − x2
− y2
Figure C14.3.5b1
y
x
c = √2
c = 1
c = 0
3 − x2
− y2
= c
Figure C14.3.5b2
6. (a) Le point de coordonnées (2, 3) appartient à la courbe de niveau 𝑧 = 8 ou 𝑓 (2, 3) = 8.
Les points de coordonnées (𝑥, 3) sont situés sur la droite 𝑦 = 3 parallèle à l’axe 𝑂𝑥. Cette
droite coupe la courbe de niveau 𝑧 = 8 quand 𝑥 = 2 et 𝑥 = 5.
(b) Lorsque 𝑦 varie avec 𝑥 = 2 fixé, le minimum de 𝑓 (2, 𝑦) est 8 quand 𝑦 = 3.
(c) En 𝐴, tout mouvement dans le sens croissant de 𝑥 mène à des courbes de niveaux
plus élevés et tout mouvement dans le sens décroissant de 𝑥 mène à des courbes de
niveaux moins élevés, de sorte que 𝑓 ′
𝑥 (𝑥, 𝑦) 0. De même, tout mouvement dans le sens
croissant de 𝑦 mène à des courbes de niveaux plus élevés et tout mouvement dans le sens
décroissant de 𝑥 mène à des courbes de niveaux moins élevés, de sorte que 𝑓 ′
𝑦 (𝑥, 𝑦) 0.
En 𝐵 : 𝑓 ′
𝑥 (𝑥, 𝑦) 0, 𝑓 ′
𝑦 (𝑥, 𝑦) 0. En 𝐶 : 𝑓 ′
𝑥 (𝑥, 𝑦) = 0, 𝑓 ′
𝑦 (𝑥, 𝑦) = 0. Enfin, pour faire
croître 𝑧 de 2 unités au départ de 𝐴, les augmentations requises de 𝑥 et 𝑦 sont d’environ
1 et 0,6 respectivement. D’où 𝑓 ′
𝑥 ≈ 2/1 = 2 et 𝑓 ′
𝑦 ≈ 2/0,6 = 10/3.
7. (a) Il est éclairant de regarder la figure comme un diagramme de courbes de niveau d’une
montagne. Les points de même altitude sont reliés entre eux. À proximité de 𝑃, le terrain
monte dans le sens positif de l’axe 𝑂𝑥 et donc 𝑓 ′
𝑥 (𝑃) 0 et descend dans le sens positif
de l’axe 𝑂𝑦, de sorte que 𝑓 ′
𝑦 (𝑃) 0. Près de 𝑄, les pentes sont en sens contraires selon
les axes. Donc 𝑓 ′
𝑥 (𝑄) 0 et 𝑓 ′
𝑦 (𝑄) 0.
(b) (i) La droite d’équation 𝑥 = 1 n’a pas de point commun avec les courbes de niveaux
données. (ii) La droite d’équation 𝑦 = 2 coupe la courbe de niveau 𝑧 = 2 en 𝑥 = 2 et
𝑥 = 6 (approximativement).
(c) En partant du point (6, 0) sur l’axe 𝑂𝑥 et en parcourant la droite d’équation
2𝑥 + 3𝑦 = 12, la première courbe de niveau rencontrée est celle de niveau 𝑧= 𝑓 (𝑥, 𝑦) =1.
Plus loin, les courbes rencontrées sont de niveaux plus élevés avec 3 comme niveau
maximal, là où la droite touche tout juste la courbe de niveau 𝑧 = 3.

155. Chapitre 14 / Les fonctions de plusieurs variables 155
8. Les inégalités annoncées à propos des dérivées partielles impliquent
𝐹(1, 0) − 𝐹(0, 0) =
∫ 1
0
𝐹′
𝑥 (𝑥, 0) d𝑥 ⩾
∫ 1
0
2 d𝑥 = 2;
𝐹(2, 0) − 𝐹(1, 0) =
∫ 2
1
𝐹′
𝑥 (𝑥, 0) d𝑥 ⩾ 2; 𝐹(0, 1) − 𝐹(0, 0) =
∫ 1
0
𝐹′
𝑦 (0, 𝑦) d𝑦 ⩽ 1;
𝐹(1, 1) − 𝐹(0, 1) =
∫ 1
0
𝐹′
𝑥 (𝑥, 1) d𝑥 ⩾ 2; 𝐹(1, 1) − 𝐹(1, 0) =
∫ 1
0
𝐹′
𝑦 (1, 𝑦) d𝑦 ⩽ 1.
14.4
1. Voir les figures C14.4.1a à c.
y
z
x
(a, 0, 0)
x = a
Figure C14.4.1a
x
y
z
(0, b, 0)
y = b
Figure C14.4.1b
y
x
z
y
x
z = c
(0, 0, c)
Figure C14.4.1c
2. (a) 𝑑 =
p
(4 − (−1))2 + (−2 − 2)2 + (0 − 3)2 =
√
25 + 16 + 9 =
√
50 = 5
√
2
(b) 𝑑=
p
(𝑎 + 1 − 𝑎)2 + (𝑏 + 1 − 𝑏)2 + (𝑐 + 1 − 𝑐)2 =
√
3
3. (𝑥 − 2)2 + (𝑦 − 1)2 + (𝑧 − 1)2 = 25
4. Il s’agit de la sphère centrée au point de coordonnées (−3, 3, 4) et dont le rayon mesure 5
unités.
5. (𝑥 − 4)2 + (𝑦 − 4)2 + (𝑧 − 1
2 )2 mesure le carré de la distance qui sépare le point de
coordonnées (4, 4, 1
2 ) d’un point quelconque de coordonnées (𝑥, 𝑦, 𝑧) du paraboloïde.
14.5
1. (a) 𝑓 (−1, 2, 3) = 1 et 𝑓 (𝑎 + 1, 𝑏 + 1, 𝑐 + 1) − 𝑓 (𝑎, 𝑏, 𝑐) = 2𝑎 + 2𝑏 + 2𝑐 + 3.
(b) 𝑓 (𝑡𝑥, 𝑡𝑦, 𝑡𝑧) = (𝑡𝑥) (𝑡𝑦) + (𝑡𝑥) (𝑡𝑧) + (𝑡𝑦) (𝑡𝑧) = 𝑡2 (𝑥𝑦 + 𝑥𝑧 + 𝑦𝑧) = 𝑡2 𝑓 (𝑥, 𝑦, 𝑧).
2. (a) Comme la somme de tous les exposants vaut 1,053, 𝑦 deviendrait 21,053 ≈ 2,07 fois
plus grand.
(b) ln 𝑦 = ln 2,9 + 0,015 ln 𝑥1 + 0,25 ln 𝑥2 + 0,35 ln 𝑥3 + 0,408 ln 𝑥4 + 0,03 ln 𝑥5

156. 156 CORRIGÉS DES EXERCICES
3. (a) La première semaine, le fonds achète 120/50 = 2,4 millions d’actions, puis suc-
cessivement 120/60 = 2 millions, 120/45 = 2,667 millions, 120/40 = 3 millions,
120/75 = 1,6 million et enfin 120/80 = 15 millions la sixième semaine. Au total,
13,167 millions d’actions.
(b) La moyenne arithmétique des prix est 350/6 = 58,33. Mais, à ce prix moyen, les
13,167 millions d’actions que le fonds a acquis lui auraient coûté
13,167 × 58,33 = 768,031 millions,
soit 48,031 millions de plus que prévu. Le prix moyen par action peut aussi être calculé
comme suit 720/13,167 = 54,68 par action. Un peu d’arithmétique montre que ce prix
est la moyenne harmonique des six prix, telle qu’elle est définie dans l’exemple 11.5.2.
4. (a) Chaque semaine 𝑤, la banque A aura acheté 100/𝑝𝑤 millions d’euros, pour un
montant total 𝑒 =
Í𝑛
𝑤=1 100/𝑝𝑤 millions d’euros.
(b) Comme la banque A aura payé 100𝑛 millions de dollars, le prix 𝑝 par euro que la
banque A aura payé, en moyenne, est 𝑝 = 100𝑛/𝑒.
D’où 1/𝑝 = 𝑒/100𝑛 = (1/𝑛)
Í𝑛
𝑤=1 1/𝑝𝑤 dollars par euro, impliquant que 𝑝 est
la moyenne harmonique de 𝑝1, . . ., 𝑝𝑛. Comme celle-ci est strictement inférieure
à la moyenne arithmétique (sauf dans le cas où 𝑝𝑤 est le même chaque semaine), c’est
un avantage escompté de l’étalement du coût en dollars.
5. (a) Comme chaque machine produit quotidiennement 60 unités, chaque unité produite
requiert 480/60 = 8 minutes.
(b) et (c) La production totale s’élève à
Í𝑛
𝑖=1(𝑇/𝑡𝑖) = 𝑇
Í𝑛
𝑖=1(1/𝑡𝑖). Si les 𝑛 machines
étaient également efficaces, le temps nécessaire pour chaque unité serait
𝑛𝑇
𝑇
𝑛
Õ
𝑖=1
(1/𝑡𝑖) = 𝑛
𝑛
Õ
𝑖=1
(1/𝑡𝑖),
la moyenne harmonique de 𝑡1, . . . , 𝑡𝑛.
14.6
1. 𝐹′
𝑥 (𝑥, 𝑦, 𝑧) = 2𝑥𝑒𝑥𝑧 + 𝑥2𝑧𝑒𝑥𝑧 + 𝑦4𝑒𝑥𝑦 et donc 𝐹′
𝑥 (1, 1, 1) = 4𝑒 ;
𝐹′
𝑦 (𝑥, 𝑦, 𝑧) = 3𝑦2𝑒𝑥𝑦 + 𝑥𝑦3𝑒𝑥𝑦 et donc 𝐹′
𝑦 (1, 1, 1) = 4𝑒 ;
𝐹′
𝑧 (𝑥, 𝑦, 𝑧) = 𝑥3𝑒𝑥𝑧 et donc 𝐹′
𝑧 (1, 1, 1) = 𝑒.
2. (a) 𝑓 ′
𝑥 = 2𝑥, 𝑓 ′
𝑦 = 3𝑦2 et 𝑓 ′
𝑧 = 4𝑧3. (b) 𝑓 ′
𝑥 = 10𝑥, 𝑓 ′
𝑦 = −9𝑦2 et 𝑓 ′
𝑧 = 12𝑧3.
(c) 𝑓 ′
𝑥 = 𝑦𝑧, 𝑓 ′
𝑦 = 𝑥𝑧 et 𝑓 ′
𝑧 = 𝑥𝑦. (d) 𝑓 ′
𝑥 = 4𝑥3/𝑦𝑧, 𝑓 ′
𝑦 = −𝑥4/𝑦2𝑧 et 𝑓 ′
𝑧 = −𝑥4/𝑦𝑧2.
(e) 𝑓 (𝑥, 𝑦, 𝑧) = (𝑥2 + 𝑦3 + 𝑧4)6 = 𝑢6, si on pose 𝑢 = 𝑥2 + 𝑦3 + 𝑧4.
Alors 𝑓 ′
𝑥 = 6𝑢5
𝑢′
1 = 6 (𝑥2
+ 𝑦3
+ 𝑧4
)5
2𝑥 = 12𝑥 (𝑥2
+ 𝑦3
+ 𝑧4
)5
,
𝑓 ′
𝑦 = 6𝑢5
𝑢′
2 = 6 (𝑥2
+ 𝑦3
+ 𝑧4
)5
3𝑦2
= 18𝑦2
(𝑥2
+ 𝑦3
+ 𝑧4
)5
,
𝑓 ′
𝑧 = 6𝑢5
𝑢′
3 = 6 (𝑥2
+ 𝑦3
+ 𝑧4
)5
4𝑧3
= 24𝑧3
(𝑥2
+ 𝑦3
+ 𝑧4
)5
.
(f) 𝑓 (𝑥, 𝑦, 𝑧) = 𝑒𝑥𝑦𝑧 = 𝑒𝑢, si on pose 𝑢 = 𝑥𝑦𝑧. On peut alors écrire 𝑓 ′
𝑥 = 𝑒𝑢𝑢′
𝑥 = 𝑒𝑥𝑦𝑧 𝑦𝑧.
De même, 𝑓 ′
𝑦 = 𝑒𝑢𝑢′
𝑦 = 𝑒𝑥𝑦𝑧𝑥𝑧 et 𝑓 ′
𝑧 = 𝑒𝑢𝑢′
𝑧 = 𝑒𝑥𝑦𝑧𝑥𝑦.

157. Chapitre 14 / Les fonctions de plusieurs variables 157
3. Comme 𝜕𝑇/𝜕𝑥 = 𝑘𝑦/𝑑𝑛 et 𝜕𝑇/𝜕𝑦 = 𝑘𝑥/𝑑𝑛 sont toutes deux strictement positives, le
nombre de voyageurs augmente si la taille de chaque ville augmente, ce qui est plausible.
Comme 𝜕𝑇/𝜕𝑑 = −𝑛𝑘𝑥𝑦/𝑑𝑛+1est strictement négative, le nombre de voyageurs diminue
si la distance entre les villes est plus grande, ce qui semble aussi plausible.
4. (a) 𝑔(2, 1, 1) = −2, 𝑔(3, −4, 2) = 352 et 𝑔(1, 1, 𝑎 + ℎ) − 𝑔(1, 1, 𝑎) = 2𝑎ℎ + ℎ2 − ℎ.
(b) 𝑔′
𝑥 = 4𝑥 − 4𝑦 − 4, 𝑔′
𝑦 = −4𝑥 + 20𝑦 − 28, 𝑔′
3 = 2𝑧 − 1. Les dérivées partielles d’ordre
deux sont : 𝑔′′
𝑥𝑥 = 4, 𝑔′′
𝑥𝑦 = −4, 𝑔′′
𝑥𝑧 = 0, 𝑔′′
𝑦𝑥 = −4, 𝑔′′
𝑦𝑦 = 20, 𝑔′′
𝑦𝑧 = 0, 𝑔′′
𝑧𝑥 = 0, 𝑔′′
𝑧𝑦 = 0
et 𝑔′′
𝑧𝑧 = 2.
5. 𝜕𝜋/𝜕𝑝 = 1
2 𝑝(1/𝑟 + 1/𝑤), 𝜕𝜋/𝜕𝑟 = −1
4 𝑝2/𝑟2, 𝜕𝜋/𝜕𝑤 = −1
4 𝑝2/𝑤2.
6. Les dérivées partielles premières sont 𝑤′
𝑥 = 3𝑦𝑧 + 2𝑥𝑦 − 𝑧3, 𝑤′
𝑦 = 3𝑥𝑧 + 𝑥2
et 𝑤′
𝑧 = 3𝑥𝑦−3𝑥𝑧2. Les dérivées partielles secondes sont 𝑤′′
𝑥𝑥 = 2𝑦, 𝑤′′
𝑥𝑦 = 𝑤′′
𝑦𝑥 = 3𝑧+2𝑥,
𝑤′′
𝑥𝑧 = 𝑤′′
𝑧𝑥 = 3𝑦 − 3𝑧2, 𝑤′′
𝑦𝑦 = 0, 𝑤′′
𝑦𝑧 = 𝑤′′
𝑧𝑦 = 3𝑥 et 𝑤′′
𝑧𝑧 = −6𝑥𝑧.
7. 𝑓 ′
𝑥 = 𝑝′(𝑥), 𝑓 ′
𝑦 = 𝑞′(𝑦), 𝑓 ′
𝑧 = 𝑟′(𝑧).
8. (a)
©
­
­
«
2𝑎 0 0
0 2𝑏 0
0 0 2𝑐
ª
®
®
¬
(b) En posant 𝑔 = 𝐴𝑥𝑦𝑏𝑧𝑐, la matrice hessienne s’écrit
©
­
­
«
𝑎 (𝑎 − 1)𝑔/𝑥2 𝑎𝑏𝑔/𝑥𝑦 𝑎𝑐𝑔/𝑥𝑧
𝑎𝑏𝑔/𝑥𝑦 𝑏 (𝑏 − 1)𝑔/𝑦2 𝑏𝑐𝑔/𝑦𝑧
𝑎𝑐𝑔/𝑥𝑧 𝑏𝑐𝑔/𝑦𝑧 𝑐(𝑐 − 1)𝑔/𝑧2
ª
®
®
¬
,
sous forme compacte.
9. On pose 𝑤 = 𝑢ℎ, où 𝑢 = (𝑥 − 𝑦 + 𝑧)/(𝑥 + 𝑦 − 𝑧). Alors
𝜕𝑤/𝜕𝑥 = ℎ𝑢ℎ−1
𝜕𝑢/𝜕𝑥, 𝜕𝑤/𝜕𝑦 = ℎ𝑢ℎ−1
𝜕𝑢/𝜕𝑦 et 𝜕𝑤/𝜕𝑧 = ℎ𝑢ℎ−1
𝜕𝑢/𝜕𝑧.
Avec 𝑣 = 𝑥 + 𝑦 − 𝑧, on a 𝜕𝑢/𝜕𝑥 = (2𝑦 − 2𝑧)/𝑣2, 𝜕𝑢/𝜕𝑦 = −2𝑥/𝑣2 et 𝜕𝑢/𝜕𝑧 = 2𝑥/𝑣2.
D’où
𝑥𝜕𝑤/𝜕𝑥 + 𝑦𝜕𝑤/𝜕𝑦 + 𝑧𝜕𝑤/𝜕𝑧 = ℎ𝑢ℎ−1
𝑣−2
[𝑥 (2𝑦 − 2𝑧) + 𝑦 (−2𝑥) + 𝑧2𝑥] = 0.
(Dans les termes de la section 15.7, la fonction 𝑤 de trois variables est homogène de
degré 0. Le théorème d’Euler 15.7.1 fournit ce résultat immédiatement.)
10. De 𝑓 = 𝑥𝑦𝑧
, on obtient ln 𝑓 = 𝑦𝑧 ln 𝑥. En dérivant par rapport à 𝑥, on a 𝑓 ′
𝑥/ 𝑓 = 𝑦𝑧/𝑥 et ainsi
𝑓 ′
𝑥 = 𝑓 𝑦𝑧/𝑥 = 𝑥𝑦𝑧
𝑦𝑧/𝑥 = 𝑦𝑧𝑥𝑦𝑧−1. En dérivant par rapport à 𝑦, on a 𝑓 ′
𝑦/ 𝑓 = 𝑧𝑦𝑧−1 ln 𝑥
et ainsi 𝑓 ′
𝑦 = 𝑧𝑦𝑧−1(ln 𝑥) 𝑥𝑦𝑧
. En dérivant par rapport à 𝑧, on a 𝑓 ′
𝑧 / 𝑓 = 𝑦𝑧 (ln 𝑦) (ln 𝑥) et
ainsi 𝑓 ′
𝑧 = 𝑦𝑧 (ln 𝑥) (ln 𝑦) 𝑥𝑦𝑧
.
11. Pour (𝑥, 𝑦) ≠ (0, 0), 𝑓 ′
𝑥 = 𝑦 (𝑥4 + 4𝑥2𝑦2 − 𝑦4) (𝑥2 + 𝑦2)−2 et
𝑓 ′
𝑦 (𝑥, 𝑦) = 𝑥 (𝑥4
− 4𝑥2
𝑦2
− 𝑦4
) (𝑥2
+ 𝑦2
)−2
.

158. 158 CORRIGÉS DES EXERCICES
D’où, quand 𝑦 ≠ 0, 𝑓 ′
𝑥 (0, 𝑦) = −𝑦. C’est aussi valable pour 𝑦 = 0, car
𝑓 ′
𝑥 (0, 0) = lim
ℎ→0
[ 𝑓 (ℎ, 0) − 𝑓 (0, 0)]/ℎ = 0.
De même, 𝑓 ′
𝑦 (𝑥, 0) = 𝑥 pour tout 𝑥. Ensuite, 𝑓 ′′
𝑥𝑦 (0, 𝑦) = (𝜕/𝜕𝑦) 𝑓 ′
𝑥 (0, 𝑦) = −1 pour tout
𝑦. En particulier, 𝑓 ′′
𝑥𝑦 (0, 0) = −1. De même, 𝑓 ′′
𝑦𝑥 (𝑥, 0) = (𝜕/𝜕𝑥) 𝑓 ′
2 (𝑥, 0) = 1 pour tout 𝑥
et ainsi 𝑓 ′′
𝑦𝑥 (0, 0) = 1. La dérivation directe pour (𝑥, 𝑦) ≠ (0, 0) conduit à
𝑓 ′′
𝑥𝑦 (𝑥, 𝑦) = 𝑓 ′′
𝑦𝑥 (𝑥, 𝑦) =
𝑥6 + 9𝑥4𝑦2 − 9𝑥2𝑦4 − 𝑦6
(𝑥2 + 𝑦2)3
. (∗)
En conclusion, à l’exclusion de l’origine, les deux dérivées croisées sont égales, confor-
mément au théorème de Young. À l’origine, toutefois, on a vu que 𝑓 ′′
𝑥𝑦 (0, 0) = −1 et
𝑓 ′′
𝑦𝑥 (0, 0) = 1. Par conséquent, au moins une des deux fonctions 𝑓 ′′
𝑥𝑦 et 𝑓 ′′
𝑦𝑥 doit y être
discontinue. En effet, de (∗), il suit que 𝑓 ′′
𝑥𝑦 (𝑥, 0) = 1 pour tout 𝑥 ≠ 0 et 𝑓 ′′
𝑥𝑦 (0, 𝑦) = −1
pour tout 𝑦 ≠ 0. On peut donc trouver des points aussi près de (0, 0) que l’on veut en les-
quels 𝑓 ′′
𝑥𝑦 est égale à 1 et aussi en lesquels 𝑓 ′′
𝑥𝑦 est égale à −1. La fonction 𝑓 ′′
𝑥𝑦 n’est
donc pas continue en (0, 0). En suivant le même raisonnement, on établit que 𝑓 ′′
𝑦𝑥
n’est pas continue en (0, 0).
14.7
1. Voir les figures C14.7.1a-à f.
−3 −2 −1 1 2 3
x
−3
−2
−1
1
2
3
y
Figure C14.7.1a
𝑥2 + 𝑦2 2
x
y
Figure C14.7.1b
𝑥 ⩾ 0, 𝑦 ⩾ 0
−4 −3 −2 −1 1 2 3
x
−4
−3
−2
−1
1
2
3
y
Figure C14.7.1c
𝑥2 + 𝑦2 8
−1 1 2 3
x
−1
1
2
3
y
Figure C14.7.1d
𝑥 ⩾ 0, 𝑦 ⩾ 0, 𝑥𝑦 ⩾ 1
−3 −2 −1
1 2
x
−1
−1
−1
1
2
y
Figure C14.7.1e
𝑥𝑦 ⩾ 1
1 2 3 4
x
1
2
3
4
y
Figure C14.7.1f
√
𝑥 +
√
𝑦 ⩽ 2

159. Chapitre 14 / Les fonctions de plusieurs variables 159
2. (a) Soit (𝑠1, 𝑡1) et (𝑠2, 𝑡2) appartenant tous deux à 𝑆 × 𝑇, avec 𝑠1, 𝑠2 ∈ 𝑆 et 𝑡1, 𝑡2 ∈ 𝑇.
Pour tout 𝜆 ∈ [0, 1] donné, soit 𝑠0 = 𝜆𝑠1 + (1 − 𝜆)𝑠2 et 𝑡0 = 𝜆𝑡1 + (1 − 𝜆)𝑡2. Alors
(𝑠0, 𝑡0) = 𝜆(𝑠1, 𝑡1) + (1 − 𝜆)(𝑠2, 𝑡2). De plus, comme 𝑆 et 𝑇 sont tous deux convexes, on
a 𝑠0 ∈ 𝑆 et 𝑡0 ∈ 𝑇. Il s’ensuit que (𝑠0, 𝑡0) appartient à 𝑆 × 𝑇, donc 𝑆 × 𝑇 est un ensemble
convexe.
(b) Oui, 𝑆 × 𝑇 est un ensemble convexe de R𝑚. Le raisonnement algébrique de la ques-
tion (a) fonctionne pour les ensembles convexes plus généraux 𝑆 ⊆ R𝑚 et 𝑇 ⊆ R𝑛 ainsi
que les points (s1, t1) et (s2, t2) de 𝑆 × 𝑇.
14.8
1. La fonction dont le graphique est tracé à gauche est strictement convexe. La fonction
correspondant à la courbe du milieu est ni convexe ni concave (elle semble convexe à
gauche, mais concave à droite). La fonction représentée à droite est concave, mais pas
strictement concave.
2. 𝑓 ′′
11 = −12 0, 𝑓 ′′
12 = 2𝑎 + 4, 𝑓 ′′
22 = −2 0. Comme 𝑓 ′′
11 0, la fonction n’est jamais
convexe. Elle est concave si et seulement si 𝑓 ′′
11 𝑓 ′′
22 − ( 𝑓 ′′
12)2 = 24− (2𝑎+4)2 ⩾ 0, ce qui est
vrai si et seulement si (𝑎+2)2 ⩽ 6, c’est-à-dire si et seulement si −2−
√
6 ⩽ 𝑎 ⩽ −2+
√
6.
Elle n’est ni concave ni convexe si et seulement si 𝑎 −2 −
√
6 or 𝑎 −2 +
√
6.
3. Pour les questions (a) et (b), on utilise les résultats du théorème 14.8.1.
(a) 𝑧 est strictement concave car c’est la somme de quatre fonctions concaves, 𝑥, 𝑦, −𝑒𝑥
et −𝑒𝑥+𝑦, dont deux sont strictement concaves.
(b) 𝑧 est strictement convexe car c’est la somme de trois fonctions convexes, 𝑒𝑥+𝑦, 𝑒𝑥−𝑦
et −1
2 𝑦, dont deux sont strictement convexes.
(c) En suivant la suggestion, on remarque que la forme quadratique 𝑤 est semi-définie
positive, donc 𝑤 est convexe, mais non strictement convexe.
4. (a) Cela se déduit directement de (14.8.7).
(b) En suivant la suggestion, notez que, puisque 𝑓 (0, 0) = 0, la définition de 𝑔 conduit à
𝑔(𝜆 ; 𝑥, 𝑦) = 𝑓 (𝜆𝑥, 𝜆𝑦)/𝜆 =
𝑓 (𝜆𝑥, 𝜆𝑦) − 𝑓 (0, 0)
𝜆 − 0
= 𝑠(0, 𝜆), (∗)
où 𝑠(0, 𝜆) est la pente de 𝑓 (𝜆𝑥, 𝜆𝑦), vue comme une fonction de 𝜆 définie pour tout 𝜆 ⩾ 0.
Si 𝑓 est concave, alors, pour tout 𝜇 ∈ [0, 1] et tout 𝜆, 𝜆′ 0, on a
𝑓 (𝜇(𝜆𝑥, 𝜆𝑦) + (1 − 𝜇)(𝜆′
𝑥, 𝜆′
𝑦)) ⩾ 𝜇 𝑓 (𝜆𝑥, 𝜆𝑦) + (1 − 𝜇) 𝑓 (𝜆′
𝑥, 𝜆′
𝑦), (∗∗)
ce qui entraîne que 𝑓 (𝜆𝑥, 𝜆𝑦) est concave en tant que fonction de 𝜆. D’après le théo-
rème 8.2.1, 𝑔(𝜆 ; 𝑥, 𝑦) = 𝑠(0, 𝜆) est décroissante en fonction de 𝜆.
(c) Supposons que 𝑓 soit strictement concave. Par une modification évidente de (∗∗),
la fonction 𝑓 (𝜆𝑥, 𝜆𝑦) de 𝜆 serait strictement concave. Alors, d’après le théorème 8.2.1,
on aurait 𝑔(𝜆 ; 𝑥, 𝑦) = 𝑠(0, 𝜆) strictement décroissante en fonction de 𝜆. Cela contredit
l’hypothèse que 𝑔(𝜆 ; 𝑥, 𝑦) est indépendante de 𝜆.

160. 160 CORRIGÉS DES EXERCICES
14.9
1. 𝜕𝑀/𝜕𝑌 = 0,14 et 𝜕𝑀/𝜕𝑟 = −0,84 × 76,03 (𝑟 − 2)−1,84 = −63,8652 (𝑟 − 2)−1,84. Ainsi,
𝜕𝑀/𝜕𝑌 est strictement positive et 𝜕𝑀/𝜕𝑟 strictement négative, ce qui s’accorde avec
l’intuition économique classique.
2. (a) Comme 𝑌′
𝐾 = 𝑎𝐴𝐾𝑎−1 et 𝑌′
𝐿 = 𝑎𝐵𝐿𝑎−1,
𝐾𝑌′
𝐾 + 𝐿𝑌′
𝐿 = 𝑎𝐴𝐾𝑎
+ 𝑎𝐵𝐿𝑎
= 𝑎 (𝐴𝐾𝑎
+ 𝐵𝐿𝑎
) = 𝑎𝑌.
(b) 𝐾𝑌′
𝐾 + 𝐿𝑌′
𝐿 = 𝐾𝑎𝐴𝐾𝑎−1
𝐿𝑏
+ 𝐿𝐴𝐾𝑎
𝑏𝐿𝑏−1
= 𝑎𝐴𝐾𝑎
𝐿𝑏
+ 𝑏𝐴𝐾𝑎
𝐿𝑎
= (𝑎 + 𝑏)𝐴𝐾𝑎
𝐿𝑏
= (𝑎 + 𝑏)𝑌
(c) Comme 𝑌′
𝐾 =
2𝑎𝐾𝐿5 − 𝑏𝐾4𝐿2
(𝑎𝐿3 + 𝑏𝐾3)2
et 𝑌′
𝐿 =
2𝑏𝐾5𝐿 − 𝑎𝐾2𝐿4
(𝑎𝐿3 + 𝑏𝐾3)2
,
𝐾𝑌′
𝐾 + 𝐿𝑌′
𝐿 =
2𝑎𝐾2𝐿5 − 𝑏𝐾5𝐿2 + 2𝑏𝐾5𝐿2 − 𝑎𝐾2𝐿5
(𝑎𝐿3 + 𝑏𝐾3)2
=
𝐾2𝐿2 (𝑎𝐿3 + 𝑏𝐾3)
(𝑎𝐿3 + 𝑏𝐾3)2
=
𝐾2𝐿2
𝑎𝐿3 + 𝑏𝐾3
= 𝑌.
Notez que, d’après la section 15.6, les fonctions de (a), (b) et (c) sont homogènes de
degré 𝑎, 𝑎 + 𝑏 et 1, respectivement. Les résultats obtenus sont donc des conséquences
immédiates du théorème d’Euler 15.6.1.
3. 𝐷′
𝑝 (𝑝, 𝑞) = −𝑏𝑞−𝛼, 𝐷′
𝑞 (𝑝, 𝑞) = 𝑏𝑝𝛼𝑞−𝛼−1. Ainsi, 𝐷′
𝑝 (𝑝, 𝑞) 0, montrant que la
demande faiblit lorsque le prix monte. Et 𝐷′
𝑞 (𝑝, 𝑞) 0, montrant que la demande
augmente à mesure que le prix d’un produit concurrent augmente.
4. 𝐹′
𝐾 = 𝑎𝐹/𝐾, 𝐹′
𝐿 = 𝑏𝐹/𝐿 et 𝐹′
𝑀 = 𝑐𝐹/𝑀, de sorte que
𝐾𝐹′
𝐾 + 𝐿𝐹′
𝐿 + 𝑀𝐹′
𝑀 = (𝑎 + 𝑏 + 𝑐)𝐹.
5. 𝜕𝐷/𝜕𝑝 et 𝜕𝐸/𝜕𝑞 sont normalement strictement négatives, car la demande d’un bien
baisse quand son prix augmente. Si les biens sont des substituts, cela signifie que la
demande augmente quand le prix de l’autre bien augmente. Les signes sont donc habi-
tuellement 𝜕𝐷/𝜕𝑞 0 et 𝜕𝐸/𝜕𝑝 0.
6. 𝜕𝑈/𝜕𝑥𝑖 = 𝑒−𝑥𝑖 , pour 𝑖 = 1, . . . , 𝑛.
7. 𝑌′
𝐾 = (−𝜇/𝜌)𝑎 (−𝜌)𝐾−𝜌−1
𝐴𝑒𝜆𝑡
𝑎𝐾−𝜌
+ 𝑏𝐿−𝜌
−(𝜇/𝜌)−1
= 𝜇𝑎𝐾−𝜌−1
𝐴𝑒𝜆𝑡
𝑎𝐾−𝜌
+ 𝑏𝐿−𝜌
−(𝜇/𝜌)−1
,
𝑌′
𝐿 = (−𝜇/𝜌)𝑏 (−𝜌)𝐿−𝜌−1
𝐴𝑒𝜆𝑡
𝑎𝐾−𝜌
+ 𝑏𝐿−𝜌
−(𝜇/𝜌)−1
= 𝜇𝑏𝐿−𝜌−1
𝐴𝑒𝜆𝑡
𝑎𝐾−𝜌
+ 𝑏𝐿−𝜌
−(𝜇/𝜌)−1
D’où 𝐾𝑌′
𝐾 + 𝐿𝑌′
𝐿 = 𝜇 (𝑎𝐾−𝜌 + 𝑏𝐿−𝜌)𝐴𝑒𝜆𝑡
𝑎𝐾−𝜌 + 𝑏𝐿−𝜌
−(𝜇/𝜌)−1
= 𝜇𝑌.
De nouveau, cette fonction est homogène de degré 𝜇. Le résultat obtenu est donc une
conséquence immédiate du théorème d’Euler 15.6.1.

161. Chapitre 14 / Les fonctions de plusieurs variables 161
14.10
1. (a) El𝑥 𝑧 = 1 et El𝑦𝑧 = 1. (b) El𝑥 𝑧 = 2 et El𝑦𝑧 = 5. (c) El𝑥 𝑧 = 𝑛 + 𝑥 et El𝑦𝑧 = 𝑛 + 𝑦.
(d) El𝑥 𝑧 = 𝑥/(𝑥 + 𝑦) et El𝑦𝑧 = 𝑦/(𝑥 + 𝑦).
2. On pose 𝑧 = 𝑢𝑔 avec 𝑢 = 𝑎𝑥𝑑
1 + 𝑏𝑥𝑑
2 + 𝑐𝑥𝑑
3 . Alors
El𝑥1 𝑧 = El𝑢𝑢𝑔
El𝑥1 𝑢 = 𝑔(𝑥1/𝑢)𝑎 d𝑥𝑑−1
1 = 𝑎𝑑𝑔𝑥𝑑
1 /𝑢.
De même, El𝑥2 𝑧 = 𝑏𝑑𝑔𝑥𝑑
2 /𝑢 et El𝑥3 𝑧 = 𝑐𝑑𝑔𝑥𝑑
3 /𝑢. Par conséquent,
El𝑥1 𝑧 + El𝑥2 𝑧 + El𝑥3 𝑧 = 𝑑𝑔(𝑎𝑥𝑑
1 + 𝑏𝑥𝑑
2 + 𝑐𝑥𝑑
3 )/𝑢 = 𝑑𝑔.
(Ce résultat découle facilement du fait que 𝑧 est homogène de degré 𝑑𝑔 et de l’équation
d’Euler en termes d’élasticités (12.7.3).)
3. El𝑥𝑖 𝑧 = 𝑝 + 𝑎𝑖𝑥𝑖 pour 𝑖 = 1, . . . , 𝑛.
4.
𝜕
𝜕𝑚
𝑝𝐷
𝑚
= 𝑝
𝑚𝐷′
𝑚 − 𝐷
𝑚2
=
𝑝
𝑚2
(𝑚𝐷′
𝑚 − 𝐷) =
𝑝𝐷
𝑚2
[El𝑚𝐷 − 1] 0 si et seulement si
El𝑚𝐷 1, de sorte que 𝑝𝐷/𝑚 augmente avec 𝑚 si El𝑚𝐷 1(22).
Exercices récapitulatifs du chapitre 14
1. 𝑓 (0, 1) = −5, 𝑓 (2, −1) = 11, 𝑓 (𝑎, 𝑎) = −2𝑎 et 𝑓 (𝑎 + ℎ, 𝑏) − 𝑓 (𝑎, 𝑏) = 3ℎ.
2. 𝑓 (−1, 2) = −10, 𝑓 (2𝑎, 2𝑎) = −4𝑎2, 𝑓 (𝑎, 𝑏 + 𝑘) − 𝑓 (𝑎, 𝑏) = −6𝑏𝑘 − 3𝑘2,
𝑓 (𝑡𝑥, 𝑡𝑦) − 𝑡2 𝑓 (𝑥, 𝑦) = 0.
3. 𝑓 (3, 4, 0) = 5, 𝑓 (−2, 1, 3) =
√
14, 𝑓 (𝑡𝑥, 𝑡𝑦, 𝑡𝑧) =
p
𝑡2𝑥2 + 𝑡2𝑦2 + 𝑡2𝑧2 = 𝑡 𝑓 (𝑥, 𝑦, 𝑧).
4. (a) 𝐹(0, 0) = 0, 𝐹(1, 1) = 15 et 𝐹(32, 243) = 15 × 2 × 9 = 270.
(b) 𝐹(𝐾 + 1, 𝐿) − 𝐹(𝐾, 𝐿) = 15 (𝐾 + 1)1/5
𝐿2/5
− 15𝐾1/5
𝐿2/5
= 15𝐿2/5
[(𝐾 + 1)1/5
− 𝐾1/5
]
est le supplément produit à la suite d’une unité de capital supplémentaire, à peu près égal
à la productivité marginale du capital.
(c) 𝐹(32 + 1, 243) − 𝐹(32, 243) ≈ 1,667. De plus, 𝐹′
𝐾 (𝐾, 𝐿) = 3𝐾−4/5𝐿2/5, ainsi
𝐹′
𝐾 (32, 243) = 3 × 32−4/5
2432/5
= 3 × 2−4
× 32
= 27/16 ≈ 1,6875.
Comme attendu, 𝐹(32 + 1, 243) − 𝐹(32, 243) est proche de 𝐹′
𝐾 (32, 243).
(d) 𝐹 est homogène de degré 3/5.
5. (a) 𝜕𝑌/𝜕𝐾 ≈ 0,083𝐾0,356𝑆0,562 et 𝜕𝑌/𝜕𝑆 ≈ 0,035𝐾1,356𝑆−0,438.
(b) La pêche est multipliée par 21,356+0,562 = 21,918 ≈ 3,779.
(22) En utilisant les formules de l’exercice 7.7.9, le résultat découle aussi du fait que El𝑚 ( 𝑝𝐷/𝑚) = El𝑚 𝑝 +El𝑚𝐷 −
El𝑚𝑚 = El𝑚𝐷 − 1.

162. 162 CORRIGÉS DES EXERCICES
6. (a) Pour tout (𝑥, 𝑦). (b) Pour (𝑥, 𝑦) tels que 𝑥𝑦 ⩽ 1.
(c) Pour (𝑥, 𝑦) tels que 𝑥2 + 𝑦2 2.
7. (a) 𝑥 + 𝑦 1 (b) 𝑥2 ⩾ 𝑦2 et 𝑥2 + 𝑦2 ⩾ 1 . Donc 𝑥2 + 𝑦2 ⩾ 1 et |𝑥| ⩾ |𝑦|.
(c) 𝑦 ⩾ 𝑥2, 𝑥 ⩾ 0 et
√
𝑥 ⩾ 𝑦. Finalement, 0 ⩽ 𝑥 ⩽ 1 et
√
𝑥 ⩾ 𝑦 ⩾ 𝑥2.
8. (a)
𝜕𝑧
𝜕𝑥
= 10𝑥𝑦4
(𝑥2
𝑦4
+ 2)4
(b)
√
𝐾(
𝜕𝐹
𝜕𝐾
) = 2
√
𝐾(
√
𝐾 +
√
𝐿) (
1
2
√
𝐾
) =
√
𝐾 +
√
𝐿
(c) 𝐾𝐹′
𝐾 + 𝐿𝐹′
𝐿 = 𝐾(
1
𝑎
) 𝑎𝐾𝑎−1
(𝐾𝑎
+ 𝐿𝑎
)1/𝑎−1
+ 𝐿 (
1
𝑎
) 𝑎𝐿𝑎−1
(𝐾𝑎
+ 𝐿𝑎
)1/𝑎−1
= (𝐾𝑎
+ 𝐿𝑎
) (𝐾𝑎
+ 𝐿𝑎
)1/𝑎−1
= 𝐹.
(d)
𝜕𝑔
𝜕𝑡
= 3/𝑤 + 2𝑤𝑡, de sorte que
𝜕2𝑔
𝜕𝑤𝜕𝑡
= −3/𝑤2
+ 2𝑡.
(e) 𝑔′
𝑡3
= 𝑡3 (𝑡2
1 + 𝑡2
2 + 𝑡2
3)−1/2 (f) 𝑓 ′
𝑥 = 4𝑥𝑦𝑧 + 2𝑥𝑧2, 𝑓 ′′
𝑥𝑧 = 4𝑥𝑦 + 4𝑥𝑧.
9. (a) 𝑓 (0, 0) = 36, 𝑓 (−2, −3) = 0, 𝑓 (𝑎 + 2, 𝑏 − 3) = 𝑎2𝑏2.
(b) 𝑓 ′
𝑥 = 2 (𝑥 − 2) (𝑦 + 3)2, 𝑓 ′
𝑦 = 2 (𝑥 − 2)2 (𝑦 + 3).
10. Vu que 𝑔(−1, 5) = 𝑔(1, 1) = 30, les deux points appartiennent à la même courbe de
niveau.
11. Si 𝑥 − 𝑦 = 𝑐 ≠ 0, alors 𝐹(𝑥, 𝑦) = ln(𝑥 − 𝑦)2 + 𝑒2 (𝑥−𝑦) = ln 𝑐2 + 𝑒2𝑐, c’est-à-dire une
constante.
12. (a) 𝑓 ′
𝑥 (𝑥, 𝑦) = 4𝑥3 − 8𝑥𝑦, 𝑓 ′
𝑦 (𝑥, 𝑦) = 4𝑦 − 4𝑥2 + 4.
(b) Il faut trouver tous les (𝑥, 𝑦) qui vérifient les deux équations (i) 4𝑥3 − 8𝑥𝑦 = 0 et
(ii) 4𝑦 − 4𝑥2 + 4 = 0. L’équation (i) implique 4𝑥 (𝑥2 − 2𝑦) = 0, autrement dit 𝑥 = 0 ou
𝑥2 = 2𝑦. Quand 𝑥 = 0, (ii) fournit 𝑦 = −1 et, de là, (𝑥, 𝑦) = (0, −1) est une solution.
Quand 𝑥2 = 2𝑦, (ii) se réduit à 4𝑦 − 8𝑦 + 4 = 0 ou 𝑦 = 1. Mais alors 𝑥2 = 2, de sorte que
𝑥 = ±
√
2. Deux nouvelles solutions sont (𝑥, 𝑦) = (±
√
2, 1).
13. (a) Le long de l’axe 𝑂𝑥, le graphique a la forme en bol d’une fonction strictement
convexe dans le plan 𝑂𝑥𝑧. Mais, le long de l’axe 𝑂𝑦, le graphique a la forme en dôme
d’une fonction strictement concave dans le plan 𝑂𝑥𝑧. Cette fonction n’est donc ni concave
ni convexe.
(b) La matrice hessienne est
f′′
=
2 0
0 −2
,
avec comme déterminant |f′′| = −4 0. Cette inégalité entraîne que les quatre conditions
des équations (14.8.7) à (14.8.10) sont toutes non satisfaites. La fonction 𝑓 n’est donc ni
concave ni convexe.
14. (a) (i) 𝑓 ′′
11 = −2 ⩽ 0, 𝑓 ′′
22 = 0 ⩽ 0, et 𝑓 ′′
11 𝑓 ′′
22 − ( 𝑓 ′′
12)2 = 0 ⩾ 0. D’après (14.8.3)
(ou (14.8.7)), 𝑓 est concave. (ii) 𝑓 (𝑥) = (𝑥 − 𝑦) + (−𝑥2) est la somme de fonctions
concaves. Elle est donc concave.

163. Chapitre 14 / Les fonctions de plusieurs variables 163
(b) Notez que −𝑒− 𝑓 (𝑥,𝑦) = 𝐹( 𝑓 (𝑥, 𝑦)), où 𝐹(𝑢) = −𝑒−𝑢. Mais 𝐹′(𝑢) = 𝑒−𝑢 0 et
𝐹′′(𝑢) = −𝑒−𝑢 0, où 𝐹 est (strictement) croissante et concave. D’après le point (iii) du
théorème 14.8.1, 𝑧 = −𝑒− 𝑓 (𝑥,𝑦) est donc concave.
15. (a) 𝑓 ′′
11 = 2𝑎, 𝑓 ′′
12 = 2𝑏, 𝑓 ′′
22 = 2𝑐, et 𝑓 ′′
11 𝑓 ′′
22 − ( 𝑓 ′′
12)2 = 2𝑎2𝑐 − (2𝑏)2 = 4(𝑎𝑐 − 𝑏2). Le
résultat se déduit ensuite de (14.8.5) et (14.8.6).
(b) D’après (14.8.3), 𝑓 est concave si et seulement si 𝑎 ⩽ 0, 𝑐 ⩽ 0 et 𝑎𝑐 − 𝑏2 ⩾ 0.
D’après (14.8.4), 𝑓 est convexe si et seulement si 𝑎 ⩾ 0, 𝑐 ⩾ 0 et 𝑎𝑐 − 𝑏2 ⩾ 0.
16. (a) El𝑥 𝑧 = 3, El𝑦𝑧 = −4.
(b) El𝑥 𝑧 = 2𝑥2/(𝑥2 + 𝑦2) ln(𝑥2 + 𝑦2), El𝑦𝑧 = 2𝑦2/(𝑥2 + 𝑦2) ln(𝑥2 + 𝑦2).
(c) El𝑥 𝑧 = El𝑥 (𝑒𝑥𝑒𝑦) = El𝑥𝑒𝑥 = 𝑥, El𝑦𝑧 = 𝑦.
(d) El𝑥 𝑧 = 𝑥2/(𝑥2 + 𝑦2), El𝑦𝑧 = 𝑦2/(𝑥2 + 𝑦2).
17. (a) 𝜕𝐹/𝜕𝑦 = 𝑒2𝑥2 (1 − 𝑦) (−1) = −2𝑒2𝑥 (1 − 𝑦).
(b) 𝐹′
𝐿 = (ln 𝐾) (ln 𝑀)/𝐿, 𝐹′′
𝐿𝑀 = (ln 𝐾)/𝐿𝑀
(c) 𝑤 = 𝑥𝑥 𝑦𝑥 𝑧𝑥 donne ln 𝑤 = 𝑥 ln 𝑥 + 𝑥 ln 𝑦 + 𝑥 ln 𝑧. En dérivant chaque membre de cette
équation par rapport à 𝑥, on obtient 𝑤′
𝑥/𝑤 = 1 × ln 𝑥 + 𝑥 (1/𝑥) + ln 𝑦 + ln 𝑧 ou
𝑤′
𝑥 = 𝑤 (ln 𝑥 + 1 + ln 𝑦 + ln 𝑧) = 𝑥𝑥
𝑦𝑥
𝑧𝑥
(ln(𝑥𝑦𝑧) + 1).
18. (a) On commence par dériver partiellement par rapport à 𝑥 et on obtient
𝜕𝑝
𝑧/𝜕𝑥𝑝
= 𝑒𝑥
ln(1 + 𝑦)
quel que soit l’entier naturel 𝑝. Si on dérive de façon répétée par rapport à 𝑦, on obtient
successivement 𝜕𝑝+1/𝜕𝑦𝜕𝑥𝑝 = 𝑒𝑥 (1 + 𝑦)−1, puis 𝜕𝑝+2/𝜕𝑦2𝜕𝑥𝑝 = 𝑒𝑥 (−1) (1 + 𝑦)−2, etc.
Par récurrence sur 𝑞, on a 𝜕𝑝+𝑞/𝜕𝑦𝑞𝜕𝑥𝑝 = 𝑒𝑥 (−1)𝑞−1(𝑞 − 1)!(1 + 𝑦)−𝑞. Cette dérivée
partielle devient (−1)𝑞−1(𝑞 − 1)! en (𝑥, 𝑦) = (0, 0).
(b) Poser 𝑧 = 𝑧1 + 𝑧2 − 𝑧3, où 𝑧1 = 𝑥𝑒𝑥 × 𝑦𝑒𝑦, 𝑧2 = 𝑒𝑥 × 𝑦𝑒𝑦 et 𝑧3 = 𝑒𝑥 × 𝑒𝑦. Pour
𝑛 = 1, 2, . . . , on peut facilement démontrer par induction que (d/d𝑢)𝑛𝑢𝑒𝑢 = 𝑒𝑢 (𝑢 + 𝑛).
Alors 𝜕𝑝+𝑞𝑧1/𝜕𝑥𝑝𝜕𝑦𝑞 = (d/d𝑥)𝑝𝑒𝑥𝑥(d/d𝑦)𝑞𝑒𝑦 𝑦 = 𝑒𝑥 (𝑥 + 𝑝)𝑒𝑦 (𝑦 + 𝑞), tandis que
𝜕𝑝+𝑞𝑧2/𝜕𝑥𝑝𝜕𝑦𝑞 = (d/d𝑥)𝑝𝑒𝑥 (d/d𝑦)𝑞𝑒𝑦 𝑦 = 𝑒𝑥𝑒𝑦 (𝑦 + 𝑞), et 𝜕𝑝+𝑞𝑧3/𝜕𝑥𝑝𝜕𝑦𝑞 = 𝑒𝑥𝑒𝑦.
En rassemblant les termes, on obtient
𝜕𝑝+𝑞
𝑧/𝜕𝑥𝑝
𝜕𝑦𝑞
= 𝑒𝑥+𝑦
[(𝑥 + 𝑝 + 1)(𝑦 + 𝑞) − 1].
En (𝑥, 𝑦) = (0, 0), cela se simplifie en (𝑝 + 1)𝑞 − 1.
19. 𝑢′
𝑥 = 𝑎𝑢/𝑥 et 𝑢′
𝑦 = 𝑏𝑢/𝑦, de sorte que 𝑢′′
𝑥𝑦 = 𝑎𝑢′
𝑦/𝑥 = 𝑎𝑏𝑢/𝑥𝑦. De là,
𝑢′′
𝑥𝑦/𝑢′
𝑥𝑢′
𝑦 = 1/𝑢 (𝑢 ≠ 0).
Ensuite,
1
𝑢′
𝑥
𝜕
𝜕𝑥
𝑢′′
𝑥𝑦
𝑢′
𝑥𝑢′
𝑦
=
1
𝑢′
𝑥
×
−𝑢′
𝑥
𝑢2
= −
1
𝑢2
=
1
𝑢′
𝑦
𝜕
𝜕𝑦
𝑢′′
𝑥𝑦
𝑢′
𝑥𝑢′
𝑦
.

164. 164 CORRIGÉS DES EXERCICES
Chapitre 15 / Les dérivées partielles en action
15.1
1. (a)
d𝑧
d𝑡
= 𝐹′
𝑥 (𝑥, 𝑦)
d𝑥
d𝑡
+ 𝐹′
𝑦 (𝑥, 𝑦)
d𝑦
d𝑡
= 1 × 2𝑡 + 2𝑦 × 3𝑡2
= 2𝑡 + 6𝑡5
Vérification : 𝑧 = 𝑡2 + (𝑡3)2 = 𝑡2 + 𝑡6, de sorte que d𝑧/d𝑡 = 2𝑡 + 6𝑡5
.
(b)
d𝑧
d𝑡
= 𝑝𝑥𝑝−1
𝑦𝑞
𝑎 + 𝑞𝑥𝑝
𝑦𝑞−1
𝑏 = 𝑥𝑝−1
𝑦𝑞−1
(𝑎𝑝𝑦 + 𝑏𝑞𝑥) = 𝑎𝑝
𝑏𝑞
(𝑝 + 𝑞) 𝑡𝑝+𝑞−1
Vérification : 𝑧 = (𝑎𝑡)𝑝 (𝑏𝑡)𝑞 = 𝑎𝑝𝑏𝑞𝑡𝑝+𝑞, de sorte que d𝑧/d𝑡 = 𝑎𝑝
𝑏𝑞
(𝑝 + 𝑞)𝑡𝑝+𝑞−1
.
2. (a)
d𝑧
d𝑡
= (ln 𝑦 + 𝑦/𝑥) × 1 + (𝑥/𝑦 + ln 𝑥) (1/𝑡)
= ln(ln 𝑡) + ln 𝑡/(𝑡 + 1) + (𝑡 + 1)/𝑡 ln 𝑡 + ln(𝑡 + 1)/𝑡
(b)
d𝑧
d𝑡
= 𝐴𝑎
𝑒𝑎𝑡
𝑥
+ 𝐵𝑏
𝑒𝑏𝑡
𝑦
= 𝑎 + 𝑏
3.
d𝑧
d𝑡
= 𝐹′
𝑥 (𝑡, 𝑦) + 𝐹′
𝑦 (𝑡, 𝑦)𝑔′
(𝑡). Si 𝐹(𝑡, 𝑦) = 𝑡2 + 𝑦𝑒𝑦 et 𝑔(𝑡) = 𝑡2, alors 𝐹′
𝑥 (𝑡, 𝑦) = 2𝑡,
𝐹′
𝑦 (𝑡, 𝑦) = 𝑒𝑦 + 𝑦𝑒𝑦 et 𝑔′(𝑡) = 2𝑡. De là, d𝑧/d𝑡 = 2𝑡(1 + 𝑒𝑡2
+ 𝑡2
𝑒𝑡2
).
4.
d𝑌
d𝐿
= 𝐹′
𝐾 (𝐾, 𝐿)𝑔′
(𝐿) + 𝐹′
𝐿 (𝐾, 𝐿)
5.
d𝑌
d𝑡
= 10𝐿 −
1
2
𝐾−1/2
0,2 + 10𝐾 −
1
2
𝐿−1/2
0,5𝑒0,1𝑡
= 35 − 7
√
5/100 quand 𝑡 = 0.
Ainsi, 𝐾 = 𝐿 = 5.
6. (a) Si 𝑧 = 𝐹(𝑥, 𝑦) = 𝑥 + 𝑦 avec 𝑥 = 𝑓 (𝑡) et 𝑦 = 𝑔(𝑡), alors 𝐹′
𝑥 = 𝐹′
𝑦 = 1. La formule de
dérivation d’une composée (15.1.1) fournit
d𝑧
d𝑡
= 1 × 𝑓 ′
(𝑡) + 1 × 𝑔′
(𝑡) = 𝑓 ′
(𝑡) + 𝑔′
(𝑡).
(b) est comme (a), sauf que 𝐹′
𝑦 = −1. Par conséquent, la formule de dérivation d’une
composée (15.1.1) fournit d𝑧/d𝑡 = 𝑓 ′
(𝑡) − 𝑔′
(𝑡).
(c) Si 𝑧 = 𝐹(𝑥, 𝑦) = 𝑥𝑦 avec 𝑥 = 𝑓 (𝑡) et 𝑦 = 𝑔(𝑡), alors 𝐹′
𝑥 (𝑥, 𝑦) = 𝑦, 𝐹′
𝑦 (𝑥, 𝑦) = 𝑥,
d𝑥/d𝑡 = 𝑓 ′
(𝑡) et d𝑦/d𝑡 = 𝑔′
(𝑡). La formule de dérivation d’une composée (15.1.1) fournit
d𝑧
d𝑡
= 𝐹′
𝑥 (𝑥, 𝑦)
d𝑥
d𝑡
+ 𝐹′
𝑦 (𝑥, 𝑦)
d𝑦
d𝑡
= 𝑦 𝑓 ′
(𝑡) + 𝑥𝑔′
(𝑡) = 𝑓 ′
(𝑡)𝑔(𝑡) + 𝑓 (𝑡)𝑔′
(𝑡).
(d) Si 𝑧 = 𝐹(𝑥, 𝑦) =
𝑥
𝑦
avec 𝑥 = 𝑓 (𝑡) et 𝑦 = 𝑔(𝑡), alors
𝐹′
𝑥 (𝑥, 𝑦) =
1
𝑦
, 𝐹′
𝑦 (𝑥, 𝑦) = −
𝑥
𝑦2
,
d𝑥
d𝑡
= 𝑓 ′
(𝑡) et
d𝑦
d𝑡
= 𝑔′
(𝑡).
La formule de dérivation d’une composée (15.1.1) fournit
d𝑧
d𝑡
= 𝐹′
𝑥 (𝑥, 𝑦)
d𝑥
d𝑡
+ 𝐹′
𝑦 (𝑥, 𝑦)
d𝑦
d𝑡
=
1
𝑦
𝑓 ′
(𝑡) −
𝑥
𝑦2
𝑔′
(𝑡)
=
𝑦 𝑓 ′(𝑡) − 𝑥𝑔′(𝑡)
𝑦2
=
𝑓 ′(𝑡)𝑔(𝑡) − 𝑓 (𝑡)𝑔′(𝑡)
(𝑔(𝑡))2
.

165. Chapitre 15 / Les dérivées partielles en action 165
(e) Si 𝑧 = 𝐹(𝑥, 𝑦) = 𝐺(𝑥), indépendant de 𝑦, avec 𝑥 = 𝑓 (𝑡), alors 𝐹′
𝑥 = 𝐺′ et 𝐹′
𝑦 = 0. La
formule de dérivation d’une composée (15.1.1) fournit
d𝑧
d𝑡
= 𝐺′
(𝑥) 𝑓 ′
(𝑡), qui est la règle
de dérivation d’une composée dans le cas des fonctions d’une seule variable.
7. Soit 𝑈(𝑥) = 𝑢(𝑥, ℎ(𝑥)). Alors
𝑈′
(𝑥) = 𝑢′
𝑥 + 𝑢′
𝑧 ℎ′
(𝑥) =
𝛼𝑥𝛼−1
𝑥𝛼 + 𝑧𝛼
+
𝛼𝑧𝛼−1
𝑥𝛼 + 𝑧𝛼
−
𝛼
𝑧
4𝑎
3
𝑥3
(𝑎𝑥4
+ 𝑏)−2/3
.
Comme le terme dans les grandes parenthèses est égal à −𝛼𝑥𝛼/𝑧 (𝑥𝛼 + 𝑧𝛼), après simpli-
fication, on a
𝑈′
(𝑥) =
𝛼𝑥𝛼−1
𝑥𝛼 + 𝑧𝛼
−
𝛼𝑥𝛼
𝑧 (𝑥𝛼 + 𝑧𝛼)
4𝑎𝑥3
3𝑧2
=
𝛼𝑥𝛼−1(3𝑧3 − 4𝑎𝑥4)
3 (𝑥𝛼 + 𝑧𝛼) 𝑧3
.
Or, 𝑧3 = 𝑎𝑥4 + 𝑏. D’où 3𝑧3 − 4𝑎𝑥4 = 3𝑏 − 𝑎𝑥4. Dès lors, 𝑈′(𝑥) = 0 quand
𝑥 = 𝑥∗ = 4
p
3𝑏/𝑎, alors que 𝑈′(𝑥) 0 pour 𝑥 𝑥∗ et 𝑈′(𝑥) 0 pour 𝑥 𝑥∗. Par
conséquent, 𝑥∗ rend bien 𝑈 maximal .
8. On dérive (15.1.1) par rapport à 𝑡, avec 𝐹 au lieu de 𝑓 ,
d2
𝑧/d𝑡2
= (d/d𝑡)[𝐹′
𝑥 (𝑥, 𝑦) d𝑥/d𝑡] + (d/d𝑡)[𝐹′
𝑦 (𝑥, 𝑦) d𝑦/d𝑡].
Or,
d
d𝑡
[𝐹′
𝑥 (𝑥, 𝑦)
d𝑥
d𝑡
] = [𝐹′′
𝑥𝑥 (𝑥, 𝑦)
d𝑥
d𝑡
+ 𝐹′′
𝑥𝑦 (𝑥, 𝑦)
d𝑦
d𝑡
]
d𝑥
d𝑡
+ 𝐹′
𝑥 (𝑥, 𝑦)
d2𝑥
d𝑡2
et
d
d𝑡
[𝐹′
𝑦 (𝑥, 𝑦)
d𝑦
d𝑡
] = [𝐹′′
𝑦𝑥 (𝑥, 𝑦)
d𝑥
d𝑡
+ 𝐹′′
𝑦𝑦 (𝑥, 𝑦)
d𝑦
d𝑡
]
d𝑦
d𝑡
+ 𝐹′
𝑦 (𝑥, 𝑦)
d2𝑦
d𝑡2
.
En additionnant et en supposant 𝐹′′
𝑥𝑦 = 𝐹′′
𝑦𝑥, on obtient la formule attendue.
9. (a) En utilisant les taux d’accroissement, on écrit
𝑓 ′
1 (0, 0) = lim
ℎ→0
1
ℎ
[ 𝑓 (ℎ, 0) − 𝑓 (0, 0)] = lim
ℎ→0
1
ℎ
× 0 = 0
et 𝑓 ′
2 (0, 0) = lim
𝑘→0
1
𝑘
[ 𝑓 (0, 𝑘) − 𝑓 (0, 0)] = lim
𝑘→0
1
𝑘
×
𝑘3
𝑘2
= 1.
(b) Pour 𝑡 ≠ 0, on a 𝑧(𝑡) =
𝑏3𝑡3
𝑎2𝑡2 + 𝑏2𝑡2
. Ainsi, 𝑧(𝑡) =
𝑏3𝑡
𝑎2 + 𝑏2
pour tout 𝑡, d’où
𝑧′
(0) =
𝑏3
𝑎2 + 𝑏2
.
(c) D’après la question (a), on a
𝑓 ′
1 (𝑥(0), 𝑦(0))
d𝑥
d𝑡
+ 𝑓 ′
2 (𝑥(0), 𝑦(0))
d𝑦
d𝑡
= 𝑏.
D’après la question (b), comme 𝑎 ≠ 0 et 𝑏 ≠ 0, cette expression n’est pas égale à 𝑧′(0).

166. 166 CORRIGÉS DES EXERCICES
(d) Il n’y a pas de contradiction, car 𝑓 n’est pas de classe 𝐶1 en (0, 0). En effet, on a
𝑓 ′
2 (𝑥, 𝑦) =
3𝑦2(𝑥2 + 𝑦2) − 𝑦3(2𝑦)
(𝑥2 + 𝑦2)2
pour tout (𝑥, 𝑦) ≠ (0, 0). Ainsi, pour tout 𝑥 ≠ 0 on a 𝑓 ′
2 (𝑥, 0) = 0, tandis que 𝑓 ′
2 (0, 0) = 1.
15.2
1. (a) 𝜕𝑧/𝜕𝑡 = 𝐹′
𝑥 (𝑥, 𝑦)𝜕𝑥/𝜕𝑡 + 𝐹′
𝑦 (𝑥, 𝑦)𝜕𝑦/𝜕𝑡 = 1 × 1 + 2𝑦𝑠 = 1 + 2𝑡𝑠2,
𝜕𝑧/𝜕𝑠 = (𝜕𝑧/𝜕𝑥) (𝜕𝑥/𝜕𝑠) + (𝜕𝑧/𝜕𝑦) (𝜕𝑦/𝜕𝑠) = 1 × (−1) + 2𝑦𝑡 = −1 + 2𝑡2𝑠.
(b) 𝜕𝑧/𝜕𝑡 = 4𝑥2𝑡 + 9𝑦2 = 8𝑡𝑥 + 9𝑦2 = 8𝑡3 − 8𝑡𝑠 + 9𝑡2 + 36𝑡𝑠3 + 36𝑠6,
𝜕𝑧/𝜕𝑠 = 4𝑥 (−1) + 9𝑦26𝑠2 = −4𝑥 + 54𝑠2𝑦2 = −4𝑡2 + 4𝑠 + 54𝑡2𝑠2 + 216𝑡𝑠5 + 216𝑠8.
2. (a) Soit 𝑧 = 𝐹(𝑥, 𝑦) = 𝑥𝑦2 avec 𝑥 = 𝑡 + 𝑠2 et 𝑦 = 𝑡2𝑠. Alors 𝐹′
𝑥 (𝑥, 𝑦) = 𝑦2,
𝐹′
𝑦 (𝑥, 𝑦) = 2𝑥𝑦, 𝜕𝑥/𝜕𝑡 = 1 et 𝜕𝑦/𝜕𝑡 = 2𝑡𝑠. Ensuite, (15.2.1) fournit
𝜕𝑧/𝜕𝑡 = 𝐹′
𝑥 (𝑥, 𝑦) (𝜕𝑥/𝜕𝑡) + 𝐹′
𝑦 (𝑥, 𝑦) (𝜕𝑦/𝜕𝑡)
= 𝑦2
+ 2𝑥𝑦2𝑡𝑠 = (𝑡2
𝑠)2
+ 2 (𝑡 + 𝑠2
) 𝑡2
𝑠2𝑡𝑠 = 𝑡3
𝑠2
(5𝑡 + 4𝑠2
).
De la même manière, on trouve 𝜕𝑧/𝜕𝑠 = 𝑦22𝑠 + 2𝑥𝑦𝑡2 = 2𝑡5𝑠 + 4𝑡4𝑠3.
(b)
𝜕𝑧
𝜕𝑡
= 𝐹′
𝑥 (𝑥, 𝑦)
𝜕𝑥
𝜕𝑡
+ 𝐹′
𝑦 (𝑥, 𝑦)
𝜕𝑦
𝜕𝑡
=
2𝑦
(𝑥 + 𝑦)2
𝑒𝑡+𝑠
+
−2𝑠𝑥
(𝑥 + 𝑦)2
𝑒𝑡𝑠
=
2 (1 − 𝑠) 𝑒𝑡𝑠+𝑡+𝑠
(𝑒𝑡+𝑠 + 𝑒𝑡𝑠)2
et,
de la même manière,
𝜕𝑧
𝜕𝑠
=
2 (1 − 𝑡) 𝑒𝑡𝑠+𝑡+𝑠
(𝑒𝑡+𝑠 + 𝑒𝑡𝑠)2
.
3.
𝜕𝑧
𝜕𝑟
= 2𝑟
𝜕𝐹
𝜕𝑢
+ (1/𝑟)
𝜕𝐹
𝜕𝑤
,
𝜕𝑧
𝜕𝑠
= −4𝑠
𝜕𝐹
𝜕𝑣
+ (1/𝑠)
𝜕𝐹
𝜕𝑤
.
4.
𝜕𝑧
𝜕𝑡1
= 𝐹′
(𝑥) 𝑓 ′
𝑥 (𝑡1, 𝑡2),
𝜕𝑧
𝜕𝑡2
= 𝐹′
(𝑥) 𝑓 ′
𝑦 (𝑡1, 𝑡2).
5.
𝜕𝑥
𝜕𝑠
= 𝐹′
𝑥 + 𝐹′
𝑦 𝑓 ′
(𝑠) + 𝐹′
𝑧𝑔′
𝑥 (𝑠, 𝑡),
𝜕𝑥
𝜕𝑡
= 𝐹′
𝑧𝑔′
𝑦 (𝑠, 𝑡).
6.
𝜕𝑧
𝜕𝑥
= 𝐹′
𝑥 𝑓 ′
𝑥 (𝑥, 𝑦) + 𝐹′
𝑦2𝑥ℎ(𝑦) et
𝜕𝑧
𝜕𝑦
= 𝐹′
𝑥 𝑓 ′
𝑦 (𝑥, 𝑦) + 𝐹′
𝑦𝑥2
ℎ′
(𝑦) + 𝐹′
𝑤 (−1/𝑦2
).
7. (a)
𝜕𝑤
𝜕𝑡
=
𝜕𝑤
𝜕𝑥
𝜕𝑥
𝜕𝑡
+
𝜕𝑤
𝜕𝑦
𝜕𝑦
𝜕𝑡
+
𝜕𝑤
𝜕𝑧
𝜕𝑧
𝜕𝑡
= 𝑦2
𝑧3
× 2𝑡 + 2𝑥𝑦𝑧3
× 0 + 3𝑥𝑦2
𝑧2
× 1 = 5𝑠2
𝑡4
(b)
𝜕𝑤
𝜕𝑡
= 2𝑥
𝜕𝑥
𝜕𝑡
+ 2𝑦
𝜕𝑦
𝜕𝑡
+ 2𝑧
𝜕𝑧
𝜕𝑡
=
𝑥
√
𝑡 + 𝑠
+ 2𝑠𝑦𝑒𝑡𝑠
= 1 + 2𝑠𝑒2𝑡𝑠
8. (a) On peut écrire 𝑧 = 𝐹(𝑢1, 𝑢2, 𝑢3), avec 𝑢1 = 𝑡, 𝑢2 = 𝑡2 et 𝑢3 = 𝑡3. Alors
d𝑧
d𝑡
= 𝐹′
𝑢1
𝑑𝑢1
d𝑡
+ 𝐹′
𝑢2
𝑑𝑢2
d𝑡
+ 𝐹′
𝑢3
𝑑𝑢3
d𝑡
= 𝐹′
𝑢1
(𝑡, 𝑡2
, 𝑡3
) + 𝐹′
𝑢2
(𝑡, 𝑡2
, 𝑡3
) 2𝑡 + 𝐹′
𝑢3
(𝑡, 𝑡2
, 𝑡3
) 3𝑡2
.
(b) On a 𝑧 = 𝐹(𝑡, 𝑓 (𝑡), 𝑔(𝑡2
))
=⇒
d𝑧
d𝑡
= 𝐹′
𝑥 (𝑡, 𝑓 (𝑡), 𝑔(𝑡2
)) + 𝐹′
𝑦 (𝑡, 𝑓 (𝑡), 𝑔(𝑡2
)) 𝑓 ′
(𝑡) + 𝐹′
𝑧 (𝑡, 𝑡2
, 𝑡3
)𝑔′
(𝑡2
) 2𝑡.

167. Chapitre 15 / Les dérivées partielles en action 167
9. d𝑍/d𝐺 = 1 + 2𝑌 d𝑌/d𝐺 + 2𝑟 d𝑟/d𝐺
10. d𝑍/d𝐺 = 1 + 𝐼′
𝑌 (𝑌, 𝑟) d𝑌/d𝐺 + 𝐼′
𝑟 (𝑌, 𝑟) d𝑟/d𝐺
11. 𝜕𝐶/𝜕𝑝1 = 𝑎𝜕𝑄1/𝜕𝑝1 + 𝑏𝜕𝑄2/𝜕𝑝1 + 2𝑐𝑄1𝜕𝑄1/𝜕𝑝1
= −𝛼1 𝐴(𝑎 + 2𝑐𝐴𝑝−𝛼1
1 𝑝
𝛽1
2 )𝑝−𝛼1−1
1 𝑝
𝛽1
2 + 𝛼2𝑏𝐵𝑝𝛼2−1
1 𝑝
−𝛽2
2
𝜕𝐶/𝜕𝑝2 = 𝑎𝜕𝑄1/𝜕𝑝2 + 𝑏𝜕𝑄2/𝜕𝑝2 + 2𝑐𝑄1𝜕𝑄1/𝜕𝑝2
= 𝛽1 𝐴(𝑎 + 2𝑐𝐴𝑝−𝛼1
1 𝑝
𝛽1
2 )𝑝−𝛼1
1 𝑝
𝛽1−1
2 − 𝛽2𝑏𝐵𝑝𝛼2
1 𝑝
−𝛽2−1
2
12. (a) On pose 𝑣 = 𝑥3 + 𝑦3 + 𝑧3 − 3𝑥𝑦𝑧, de sorte que 𝑢 = ln 𝑣. Alors
𝜕𝑢/𝜕𝑥 = (1/𝑣) (𝜕𝑣/𝜕𝑥) = (3𝑥2
− 3𝑦𝑧)/𝑣.
Pareillement, 𝜕𝑢/𝜕𝑦 = (3𝑦2 − 3𝑥𝑧)/𝑣 et 𝜕𝑢/𝜕𝑧 = (3𝑧2 − 3𝑥𝑦)/𝑣. D’où
𝑥
𝜕𝑢
𝜕𝑥
+ 𝑦
𝜕𝑢
𝜕𝑦
+ 𝑧
𝜕𝑢
𝜕𝑧
=
1
𝑣
(3𝑥3
− 3𝑥𝑦𝑧) +
1
𝑣
(3𝑦3
− 3𝑥𝑦𝑧) +
1
𝑣
(3𝑧3
− 3𝑥𝑦𝑧) =
3𝑣
𝑣
= 3.
(b) Le résultat se démontre à l’aide de (a), en appliquant quelques opérations algébriques
élémentaires.
13. On a
𝜕𝑧
𝜕𝑥
= 𝑓 ′(𝑥2𝑦)
𝜕
𝜕𝑥
(𝑥2𝑦) = 𝑓 ′(𝑥2𝑦)2𝑥𝑦 et de même
𝜕𝑧
𝜕𝑦
= 𝑓 ′(𝑥2𝑦)𝑥2.
On obtient le résultat après quelques opérations algébriques élémentaires.
14.
𝜕𝑢
𝜕𝑟
=
𝜕 𝑓
𝜕𝑥
𝜕𝑥
𝜕𝑟
+
𝜕 𝑓
𝜕𝑦
𝜕𝑦
𝜕𝑟
+
𝜕 𝑓
𝜕𝑧
𝜕𝑧
𝜕𝑟
+
𝜕 𝑓
𝜕𝑤
𝜕𝑤
𝜕𝑟
15.
𝜕𝑢
𝜕𝑟
= 𝑦𝑧𝑤 + 𝑥𝑧𝑤 + 𝑥𝑦𝑤𝑠 + 𝑥𝑦𝑧 (1/𝑠) = 28
15.3
1. La formule (15.3.2) donne 𝑦′
= −
𝐹′
𝑥
𝐹′
𝑦
= −
4𝑥 + 6𝑦
6𝑥 + 2𝑦
= −
2𝑥 + 3𝑦
3𝑥 + 𝑦
.
2. (a) On pose 𝐹(𝑥, 𝑦) = 𝑥2𝑦. Alors 𝐹′
𝑥 = 2𝑥𝑦, 𝐹′
𝑦 = 𝑥2, 𝐹′′
𝑥𝑥 = 2𝑦, 𝐹′′
𝑥𝑦 = 2𝑥, 𝐹′′
𝑦𝑦 = 0, de
sorte que 𝑦′
= −
𝐹′
𝑥
𝐹′
𝑦
= −
2𝑥𝑦
𝑥2
= −
2𝑦
𝑥
. De plus, grâce à l’équation (15.3.5),
𝑦′′
= −
1
(𝐹′
𝑦)3
𝐹′′
𝑥𝑥 (𝐹′
𝑦)2
− 2𝐹′′
𝑥𝑦 𝐹′
𝑥 𝐹′
𝑦 + 𝐹′′
𝑦𝑦 (𝐹′
𝑥)2
= −
1
𝑥6
[2𝑦𝑥4
− 2 (2𝑥) (2𝑥𝑦) 𝑥2
] =
6𝑦
𝑥2
(voir aussi exercice 7.1.2.).
(b) On pose 𝐹(𝑥, 𝑦) = 𝑥 − 𝑦 + 3𝑥𝑦. Alors 𝐹′
𝑥 = 1 + 3𝑦, 𝐹′
𝑦 = −1 + 3𝑥, 𝐹′′
𝑥𝑥 = 0, 𝐹′′
𝑥𝑦 = 3
et 𝐹′′
𝑦𝑦 = 0. Ensuite 𝑦′
= −
𝐹′
𝑥
𝐹′
𝑦
= −
(1 + 3𝑦)
(−1 + 3𝑥)
. En utilisant l’équation (15.3.5),
𝑦′′
= −
1
(𝐹′
2)3
𝐹′′
𝑥𝑥 (𝐹′
2)2
− 2𝐹′′
𝑥𝑦 𝐹′
1𝐹′
2 + 𝐹′′
𝑦𝑦 (𝐹′
𝑥)2
=
6 (1 + 3𝑦) (−1 + 3𝑥)
(−1 + 3𝑥)3
=
6 (1 + 3𝑦)
(−1 + 3𝑥)2
.

168. 168 CORRIGÉS DES EXERCICES
(c) On pose 𝐹(𝑥, 𝑦) = 𝑦5 − 𝑥6. On a 𝐹′
𝑥 = −6𝑥5, 𝐹′
𝑦 = 5𝑦4, 𝐹′′
𝑥𝑥 = −30𝑥4, 𝐹′′
𝑥𝑦 = 0,
𝐹′′
𝑦𝑦 = 20𝑦3, de sorte que 𝑦′ = −𝐹′
𝑥/𝐹′
𝑦 = −(−6𝑥5/5𝑦4) = 6𝑥5/5𝑦4. En utilisant l’équa-
tion (15.3.5),
𝑦′′
= −
1
(5𝑦4)3
(−30𝑥4
) (5𝑦4
)2
+ 20𝑦3
(−6𝑥5
)2
=
6𝑥4
𝑦4
−
144𝑥10
25𝑦9
.
3. (a) Avec 𝐹(𝑥, 𝑦) = 2𝑥2 + 𝑥𝑦 + 𝑦2, on a 𝑦′ = −𝐹′
𝑥/𝐹′
𝑦 = −(4𝑥 + 𝑦)/(𝑥 + 2𝑦) = −4 en (2, 0).
De plus, en utilisant (15.3.2), 𝑦′′ = −(28𝑥2 +14𝑦2 +14𝑥𝑦)/(𝑥 +2𝑦)3. En (2, 0), 𝑦′′ = −14.
L’équation de la tangente passant par le point de coordonnées (2, 0) et de pente −4 est
𝑦 = −4𝑥 + 8.
(b) 𝑦′ = 0 exige 𝑦 = −4𝑥. En introduisant cette expression dans l’équation originale,
on obtient l’équation du second degré 14𝑥2 − 8 = 0. Les racines de cette équation sont
𝑥 ± 2
√
7/7. On a des tangentes horizontales aux deux points (𝑎, −4𝑎) et (−𝑎, 4𝑎), où
𝑎 = 2
√
7/7.
4. Avec 𝐹(𝑥, 𝑦) = 3𝑥2 − 3𝑥𝑦2 + 𝑦3 + 3𝑦2, on a
𝐹′
𝑥 (𝑥, 𝑦) = 6𝑥 − 3𝑦2
et 𝐹′
𝑦 (𝑥, 𝑦) = −6𝑥𝑦 + 3𝑦2
+ 6𝑦,
de sorte que, selon (15.3.2), ℎ′(𝑥) = 𝑦′ = −(6𝑥 − 3𝑦2)/(−6𝑥𝑦 + 3𝑦2 + 6𝑦). Pour 𝑥 proche
de 1 et donc (𝑥, 𝑦) proche de (1, 1), on a ℎ′(1) = −(6 − 3)/(−6 + 3 + 6) = −1.
5. 𝐷′
𝑃 0 et 𝐷′
𝑖 0. En dérivant l’équation par rapport à 𝑖, on obtient
𝐷′
𝑃 (d𝑃/d𝑖) + 𝐷′
𝑖 = 0,
et ainsi d𝑃/d𝑖 = −𝐷′
𝑖/𝐷𝑃 0. Une montée du taux d’intérêt affaiblit la demande et le
prix baisse pour compenser.
6. d𝑃/d𝑅 = 𝑓 ′
𝑅 (𝑅, 𝑃)/(𝑔′(𝑃) − 𝑓 ′
𝑃 (𝑅, 𝑃)). Il est plausible que 𝑓 ′
𝑅 (𝑅, 𝑃) 0 (la
demande augmente lorsque les dépenses de publicité augmentent) et 𝑔′(𝑃) 0,
𝑓 ′
𝑃 (𝑅, 𝑃) 0, de sorte que d𝑃/d𝑅 0.
7. La dérivation de l’équation par rapport à 𝑥 et 𝑦 fournit (i) 1 − 𝑎𝑧′
𝑥 = 𝑓 ′(𝑦 − 𝑏𝑧) (−𝑏𝑧′
𝑥)
et (ii) −𝑎𝑧′
𝑦 = 𝑓 ′(𝑦 − 𝑏𝑧) (1 − 𝑏𝑧′
𝑦). Si 𝑏𝑧′
𝑥 ≠ 0, on explicite (i) par rapport à 𝑓 ′ et on
introduit dans (ii) 𝑎𝑧′
𝑥 + 𝑏𝑧′
𝑦 = 1. Si 𝑏𝑧′
𝑥 = 0, alors (i) implique 𝑎𝑧′
𝑥 = 1. Mais alors
𝑧′
𝑥 ≠ 0, de sorte que 𝑏 = 0 et à nouveau 𝑎𝑧′
𝑥 + 𝑏𝑧′
𝑦 = 1.
15.4
1. (a) Pour 𝐹(𝑥, 𝑦, 𝑧) = 3𝑥 + 𝑦 − 𝑧, l’équation donnée s’écrit 𝐹(𝑥, 𝑦, 𝑧) = 0 et
𝜕𝑧
𝜕𝑥
= −
𝐹′
𝑥
𝐹′
𝑧
= −
3
−1
= 3.
(b)
𝜕𝑧
𝜕𝑥
= −
(𝑦𝑧 + 𝑧3 − 𝑦2𝑧5)
(𝑥𝑦 + 3𝑥𝑧2 − 5𝑥𝑦2𝑧4)

169. Chapitre 15 / Les dérivées partielles en action 169
(c) Pour 𝐹(𝑥, 𝑦, 𝑧) = 𝑒𝑥𝑦𝑧 − 3𝑥𝑦𝑧, l’équation donnée s’écrit 𝐹(𝑥, 𝑦, 𝑧) = 0. Donc
𝐹′
𝑥 (𝑥, 𝑦, 𝑧) = 𝑦𝑧𝑒𝑥𝑦𝑧 − 3𝑦𝑧, 𝐹′
𝑧 (𝑥, 𝑦, 𝑧) = 𝑥𝑦𝑒𝑥𝑦𝑧 − 3𝑥𝑦, et, d’après (15.4.2),
𝑧′
𝑥 = −
𝐹′
𝑥
𝐹′
𝑧
= −
(𝑦𝑧𝑒𝑥𝑦𝑧 − 3𝑦𝑧)
(𝑥𝑦𝑒𝑥𝑦𝑧 − 3𝑥𝑦)
= −
𝑦𝑧 (𝑒𝑥𝑦𝑧 − 3)
𝑥𝑦 (𝑒𝑥𝑦𝑧 − 3)
= −
𝑧
𝑥
.
(Sinon, l’équation 𝑒𝑐 = 3𝑐 a deux solutions. De 𝑥𝑦𝑧 = 𝑐 (𝑐 constante), on trouve 𝑧′
𝑥
beaucoup plus facilement.)
2. La dérivation partielle par rapport à 𝑥 conduit à (∗) 3𝑥2 + 3𝑧2𝑧′
𝑥 − 3𝑧′
𝑥 = 0, de sorte que
𝑧′
𝑥 = 𝑥2/(1 − 𝑧2). Par symétrie, 𝑧′
𝑦 = 𝑦2/(1 − 𝑧2). Pour trouver 𝑧′′
𝑥𝑦, on dérive (∗) par
rapport à 𝑦, ce qui donne 6𝑧𝑧′
𝑦𝑧′
𝑥 + 3𝑧2𝑧′′
𝑥𝑦 − 3𝑧′′
𝑥𝑦 = 0 et, de là, 𝑧′′
𝑥𝑦 = 2𝑧𝑥2𝑦2/(1 − 𝑧2)3.
(Sinon, on peut aussi dériver 𝑧′
𝑥 = 𝑥2/(1 − 𝑧2) par rapport à 𝑦, en traitant 𝑧 comme une
fonction de 𝑦 et en utilisant l’expression de 𝑧′
𝑦.)
3. (a) Dans ce cas, l’équation (∗) est
𝑃
2
√
𝐿∗
= 𝑤, ce qui donne 𝐿∗ = 𝑃2/4𝑤2. Puis on calcule
𝜕𝐿∗/𝜕𝑃 = 𝑃/2𝑤2 0 et 𝜕𝐿∗/𝜕𝑤 = −𝑃2/2𝑤3 0.
(b) La condition du premier ordre est
𝑃 𝑓 ′
(𝐿∗
) − 𝐶′
𝐿 (𝐿∗
, 𝑤) = 0. (∗)
Pour calculer les dérivées partielles de 𝐿∗, on doit dériver partiellement (∗) par rapport à
𝑃 et 𝑤.
D’abord par rapport à 𝑃 : la dérivée partielle de 𝑃 𝑓 ′(𝐿∗) requiert la règle de
dérivation du produit. Le résultat est 𝑓 ′(𝐿∗) + 𝑃 𝑓 ′′(𝐿∗) (𝜕𝐿∗/𝜕𝑃). Puis, la dérivée
partielle de 𝐶′
𝐿 (𝐿∗, 𝑤) est 𝐶′′
𝐿𝐿 (𝐿∗, 𝑤) (𝜕𝐿∗/𝜕𝑃). De là, la dérivée de (∗) par rap-
port à 𝑃 est 𝑓 ′(𝐿∗) + 𝑃 𝑓 ′′(𝐿∗) (𝜕𝐿∗/𝜕𝑃) − 𝐶′′
𝐿𝐿 (𝐿∗, 𝑤) (𝜕𝐿∗/𝜕𝑃) = 0. La réponse
𝜕𝐿∗/𝜕𝑃 = − 𝑓 ′(𝐿∗)/(𝑃 𝑓 ′′(𝐿∗) − 𝐶′′
𝐿𝐿 (𝐿∗, 𝑤)) est obtenue en isolant 𝜕𝐿∗/𝜕𝑃. Ensuite,
en dérivant par rapport à 𝑤, la dérivation de (∗) conduit à
[𝑃 𝑓 ′′
(𝐿∗
) − 𝐶′′
𝐿𝐿 (𝐿∗
, 𝑤)](𝜕𝐿∗
/𝜕𝑤) − 𝐶′′
𝐿𝑤 (𝐿∗
, 𝑤) = 0.
La réponse 𝜕𝐿∗/𝜕𝑤 = 𝐶′′
𝐿𝑤 (𝐿∗, 𝑤)/(𝑃 𝑓 ′′(𝐿∗) − 𝐶′′
𝐿𝐿 (𝐿∗, 𝑤)) est obtenue en isolant
𝜕𝐿∗/𝜕𝑤.
4. Par la formule (15.4.2), 𝑧′
𝑥 = −
𝑦𝑥𝑦−1 + 𝑧𝑥 ln 𝑧
𝑦𝑧 ln 𝑦 + 𝑥𝑧𝑥−1
et 𝑧′
𝑦 = −
𝑥𝑦 ln 𝑥 + 𝑧𝑦𝑧−1
𝑦𝑧 ln 𝑦 + 𝑥𝑧𝑥−1
.
5. La dérivation implicite donne 𝑓 ′
𝑃 (𝑅, 𝑃)𝑃′
𝑤 = 𝑔′
𝑤 (𝑤, 𝑃) + 𝑔′
𝑃 (𝑤, 𝑃)𝑃′
𝑤 . De là,
𝑃′
𝑤 = −𝑔′
𝑤 (𝑤, 𝑃)/(𝑔′
𝑃 (𝑤, 𝑃) − 𝑓 ′
𝑃 (𝑅, 𝑃)) 0,
car 𝑔′
𝑤 0, 𝑔′
𝑃 0 et 𝑓 ′
𝑃 0.
6. 𝐹′
𝑥 (𝑥, 𝑦) = 𝑒𝑦−3 + 𝑦2 et 𝐹′
𝑦 (𝑥, 𝑦) = 𝑥𝑒𝑦−3 + 2𝑥𝑦 − 2. La pente de la tangente à la courbe
de niveau 𝐹(𝑥, 𝑦) = 4 au point de coordonnées (1, 3) est
𝑦′
= −𝐹′
𝑥 (1, 3)/𝐹′
𝑦 (1, 3) = −10/5 = −2.
L’équation de cette tangente est 𝑦 = −2𝑥 + 5.

170. 170 CORRIGÉS DES EXERCICES
7. On prend le logarithme des deux membres (1 + 𝑐 ln 𝑦) ln 𝑦 = ln 𝐴 + 𝛼 ln 𝐾 + 𝛽 ln 𝐿. On
dérive partiellement par rapport à 𝐾, ce qui donne
𝑐
𝑦
𝜕𝑦
𝜕𝐾
ln 𝑦 + (1 + 𝑐 ln 𝑦)
1
𝑦
𝜕𝑦
𝜕𝐾
=
𝛼
𝐾
.
Puis, on résout par rapport à 𝜕𝑦/𝜕𝐾, ce qui donne 𝜕𝑦/𝜕𝐾 = 𝛼𝑦/𝐾(1+2𝑐 ln 𝑦). La dérivée
partielle 𝜕𝑦/𝜕𝐿 est trouvée de la même manière : 𝜕𝑦/𝜕𝐿 = 𝛽𝑦/𝐿(1 + 2𝑐 ln 𝑦).
15.5
1. Le taux marginal de substitution est 𝑅𝑦𝑥 = 20𝑥/30𝑦, de sorte que 𝑦/𝑥 = (2/3) (𝑅𝑦𝑥)−1.
L’élasticité est 𝜎𝑦𝑥 = −1.
2. (a) 𝑅𝑦𝑥 = (𝑥/𝑦)𝑎−1 = (𝑦/𝑥)1−𝑎
(b) 𝜎𝑦𝑥 = El𝑅𝑦𝑥 (𝑦/𝑥) = El𝑅𝑦𝑥 (𝑅𝑦𝑥)1/(1−𝑎) = 1/(1 − 𝑎)
3. Si 𝐹(𝐾, 𝐿) = 𝐴𝐾𝑎 𝐿𝑏, les dérivées partielles sont 𝐹′
𝐾 = 𝑎𝐹/𝐾, 𝐹′
𝐿 = 𝑏𝐹/𝐿,
𝐹′′
𝐾 𝐿 = 𝑎𝑏𝐹/𝐾𝐿, ainsi que 𝐹′′
𝐾 𝐾 = 𝑎 (𝑎 − 1)𝐹/𝐾2 et 𝐹′′
𝐿𝐿 = 𝑏 (𝑏 − 1)𝐹/𝐿2. Mais
alors le numérateur de l’expression de 𝜎𝑦𝑥 est
−𝐹′
𝐾 𝐹′
𝐿 (𝐾𝐹′
𝐾 + 𝐿𝐹′
𝐿) = −(𝑎𝐹/𝐾) (𝑏𝐹/𝐿) (𝑎 + 𝑏)𝐹 = −𝑎𝑏 (𝑎 + 𝑏)𝐹3
/𝐾𝐿
et le dénominateur 𝐾𝐿
(𝐹′
𝐿)2
𝐹′′
𝐾 𝐾 − 2𝐹′
𝐾 𝐹′
𝐿 𝐹′′
𝐾 𝐿 + (𝐹′
𝐾 )2
𝐹′′
𝐿𝐿
= 𝐾𝐿𝐹3
[𝑏2
𝑎 (𝑎 − 1) − 2𝑎2
𝑏2
+ 𝑎2
𝑏 (𝑏 − 1)]/𝐾2
𝐿2
= − 𝑎𝑏 (𝑎 + 𝑏)𝐹3
/𝐾𝐿.
Il s’ensuit que 𝜎𝐾 𝐿 = 1.
15.6
1. Comme 𝑓 (𝑡𝑥, 𝑡𝑦) = (𝑡𝑥)4 + (𝑡𝑥)2 (𝑡𝑦)2 = 𝑡4𝑥4 + 𝑡2𝑥2𝑡2𝑦2 = 𝑡4 (𝑥4 + 𝑥2𝑦2) = 𝑡4 𝑓 (𝑥, 𝑦), 𝑓
est homogène de degré 4.
2. 𝑥 (𝑡𝑝, 𝑡𝑟) = 𝐴(𝑡𝑝)−1,5
(𝑡𝑟)2,08
= 𝐴𝑡−1,5
𝑝−1,5
𝑡2,08
𝑟2,08
= 𝑡−1,5
𝑡2,08
𝐴𝑝−1,5
𝑟2,08
= 𝑡0,58
𝑥 (𝑝, 𝑟).
La fonction est donc homogène de degré 0,58 . (Sinon, utilisez le résultat de l’exem-
ple 14.1.4.)
3. 𝑓 (𝑡𝑥, 𝑡𝑦) = (𝑡𝑥) (𝑡𝑦)2 +(𝑡𝑥)3 = 𝑡3 (𝑥𝑦2 +𝑥3) = 𝑡3 𝑓 (𝑥, 𝑦), 𝑓 est donc homogène de degré 3.
Reprenons les propriétés (15.6.2) à (15.6.5).
(15.6.2) : 𝑥 𝑓 ′
𝑥 (𝑥, 𝑦) + 𝑦 𝑓 ′
𝑦 (𝑥, 𝑦) = 𝑥 (𝑦2 + 3𝑥2) + 𝑦 (2𝑥𝑦) = 3 (𝑥3 + 𝑥𝑦2) = 3 𝑓 (𝑥, 𝑦).
(15.6.3) : Il est facile de voir que 𝑓 ′
𝑥 (𝑥, 𝑦) = 𝑦2 + 3𝑥2 et 𝑓 ′
𝑦 (𝑥, 𝑦) = 2𝑥𝑦 sont homogènes
de degré 2.
(15.6.4) : 𝑓 (𝑥, 𝑦) = 𝑥3
+ 𝑥𝑦2
= 𝑥3
[1 + (𝑦/𝑥)2
] = 𝑥3
𝑓 (1, 𝑦/𝑥)
= 𝑦3
[(𝑥/𝑦)3
+ 𝑥/𝑦] = 𝑦3
𝑓 (𝑥/𝑦, 1)
.
(15.6.5) : 𝑥2 𝑓 ′′
𝑥𝑥 +2𝑥𝑦 𝑓 ′′
𝑥𝑦 +𝑦2 𝑓 ′′
𝑦𝑦 = 𝑥2 (6𝑥)+2𝑥𝑦 (2𝑦)+𝑦2 (2𝑥) = 6𝑥3+6𝑥𝑦2 = 3×2 𝑓 (𝑥, 𝑦).

171. Chapitre 15 / Les dérivées partielles en action 171
4. 𝑓 (𝑡𝑥, 𝑡𝑦) = (𝑡𝑥) (𝑡𝑦)/[(𝑡𝑥)2 + (𝑡𝑦)2] = 𝑡2𝑥𝑦/𝑡2 [𝑥2 + 𝑦2] = 𝑓 (𝑥, 𝑦) = 𝑡0 𝑓 (𝑥, 𝑦).Donc 𝑓 est
homogène de degré 0. En utilisant les formules des dérivées partielles de cette fonction
calculées à l’exemple 11.2.1(b), on a
𝑥
𝜕 𝑓
𝜕𝑥
+ 𝑦
𝜕 𝑓
𝜕𝑦
=
𝑥𝑦3 − 𝑥3𝑦 + 𝑥3𝑦 − 𝑥𝑦3
(𝑥2 + 𝑦2)
2
= 0 = 0 × 𝑓 ,
comme l’affirme le théorème d’Euler.
5. 𝐹(𝑡𝐾, 𝑡𝐿) = 𝐴(𝑎 (𝑡𝐾)−𝜌
+ 𝑏(𝑡𝐿)−𝜌
)−1/𝜌
= 𝐴(𝑡−𝜌
𝑎𝐾−𝜌
+ 𝑡−𝜌
𝑏𝐿−𝜌
)−1/𝜌
= (𝑡−𝜌
)−1/𝜌
𝐴(𝑎𝐾−𝜌
+ 𝑏𝐿−𝜌
)−1/𝜌
qui se simplifie en 𝑡𝐹(𝐾, 𝐿). En utilisant l’exemple 15.6.3, on obtient
𝐹(𝐾, 𝐿)/𝐿 = 𝐹(𝐾/𝐿, 1) = 𝐴[𝑎 (𝐾/𝐿)−𝜌
+ 𝑏]−1/𝜌
.
6. L’équation (15.6.1) exige que, pour un certain nombre 𝑘, on ait 𝑡3𝑥3 + 𝑡2𝑥𝑦 = 𝑡𝑘 (𝑥3 + 𝑥𝑦)
pour tout 𝑡 0 et tout (𝑥, 𝑦). En particulier, pour 𝑥 = 𝑦 = 1, on doit avoir 𝑡3 + 𝑡2 = 2𝑡𝑘
pour tout 𝑡 0. Pour 𝑡 = 2, on a 12 = 2 × 2𝑘 ou 2𝑘 = 6. Pour 𝑡 = 4, on a 80 = 2 × 4𝑘 ou
4𝑘 = 40. Mais 2𝑘 = 6 implique 4𝑘 = 36. Les deux valeurs de 𝑘 devant être différentes, 𝑓
n’est homogène d’aucun degré.
7. Des équations (15.6.6) et (15.6.7), avec 𝑘 = 1, on obtient 𝑓 ′′
𝑥𝑥 = (−𝑦/𝑥) 𝑓 ′′
𝑥𝑦 et
𝑓 ′′
𝑦𝑦 = (−𝑥/𝑦) 𝑓 ′′
𝑦𝑥. Compte tenu que 𝑓 ′′
𝑥𝑦 = 𝑓 ′′
𝑦𝑥, on a
𝑓 ′′
𝑥𝑥 𝑓 ′′
𝑦𝑦 − ( 𝑓 ′′
𝑥𝑦)2
= (−𝑦/𝑥) 𝑓 ′′
𝑥𝑦 (−𝑥/𝑦) 𝑓 ′′
𝑥𝑦 − ( 𝑓 ′′
𝑥𝑦)2
= 0.
8. Comme 𝑓 ′
𝑦 (𝑥, 𝑦) est homogène de degré 1 d’après (15.6.3), on a
12 = 𝑓 ′
𝑦 (4, 6) = 𝑓 ′
𝑦 (2 × 2, 2 × 3) = 2 𝑓 ′
𝑦 (2, 3).
Mais alors 𝑓 ′
𝑦 (2, 3) = 12/2 = 6. D’après le théorème d’Euler 15.6.1,
2 𝑓 (2, 3) = 2 𝑓 ′
𝑥 (2, 3) + 3 𝑓 ′
𝑦 (2, 3) = 2 × 4 + 3 × 6 = 26.
De là, 𝑓 (2, 3) = 13. Enfin, 𝑓 (6, 9) = 𝑓 (3 × 2, 3 × 3) = 32 𝑓 (2, 3) = 9 × 13 = 117, grâce à
la définition (15.6.1).
9. Soit 𝐶 et 𝐷 le numérateur et le dénominateur de l’expression de 𝜎𝑦𝑥 dans l’exercice
15.5.3. Comme 𝐹 est homogène de degré 1, le théorème d’Euler entraîne 𝐶 = −𝐹′
𝑥 𝐹′
𝑦 𝐹 et
(15.6.6) et (15.6.7) entraînent 𝑥𝐹′′
𝑥𝑥 = −𝑦𝐹′′
𝑥𝑦 et 𝑦𝐹′′
𝑦𝑦 = −𝑥𝐹′′
𝑦𝑥 = −𝑥𝐹′′
𝑥𝑦. Par conséquent,
𝐷 = 𝑥𝑦
(𝐹′
𝑦)2
𝐹′′
𝑥𝑥 − 2𝐹′
𝑥 𝐹′
𝑦 𝐹′′
𝑥𝑦 + (𝐹′
𝑥)2
𝐹′′
𝑦𝑦
= −𝐹′′
𝑥𝑦
𝑦2
(𝐹′
𝑦)2
+ 2𝑥𝑦𝐹′
𝑥 𝐹′
2 + 𝑥2
(𝐹′
𝑥)2
= −𝐹′′
𝑥𝑦 (𝑥𝐹′
𝑥 + 𝑦𝐹′
𝑦)2
= −𝐹′′
𝑥𝑦 𝐹2
grâce à nouveau au théorème d’Euler. Il en résulte que
𝜎𝑥𝑦 = 𝐶/𝐷 = (−𝐹′
𝑥 𝐹′
𝑦 𝐹)/(−𝐹′′
𝑥𝑦 𝐹𝑦
) = 𝐹′
𝑥 𝐹′
𝑦/𝐹𝐹′′
𝑥𝑦.

172. 172 CORRIGÉS DES EXERCICES
15.7
1. (a) Homogène de degré 1.
(b) Remarquez que 𝑥𝑔′
𝑥 + 𝑦𝑔′
𝑦 +𝑧𝑔′
𝑧 = 𝑔(𝑥, 𝑦, 𝑧) +2. Comme ce n’est pas égal à 𝑘𝑔(𝑥, 𝑦, 𝑧)
quel que soit 𝑘, le théorème d’Euler implique que 𝑔 n’est pas homogène.
(c) ℎ(𝑡𝑥, 𝑡𝑦, 𝑡𝑧) =
√
𝑡𝑥 +
√
𝑡𝑦 +
√
𝑡𝑧
𝑡𝑥 + 𝑡𝑦 + 𝑡𝑧
=
√
𝑡 (
√
𝑥 +
√
𝑦 +
√
𝑧 )
𝑡(𝑥 + 𝑦 + 𝑧)
= 𝑡−1/2
ℎ(𝑥, 𝑦, 𝑧) pour tout
𝑡 0. La fonction ℎ est donc homogène de degré −1/2.
(d) 𝐺(𝑡𝑥, 𝑡𝑦) =
√
𝑡𝑥𝑡𝑦 ln
(𝑡𝑥)2 + (𝑡𝑦)2
𝑡𝑥𝑡𝑦
= 𝑡
√
𝑥𝑦 ln
𝑡2 (𝑥2 + 𝑦2)
𝑡2𝑥𝑦
= 𝑡𝐺(𝑥, 𝑦) pour tout
𝑡 0. La fonction 𝐺 est donc homogène de degré 1.
(e) 𝑥𝐻′
𝑥 + 𝑦𝐻′
𝑦 = 𝑥 (1/𝑥) + 𝑦 (1/𝑦) = 2. Puisque 2 n’est pas égal à 𝑘(ln 𝑥 + ln 𝑦) quelle
que soit la constante 𝑘, par le théorème d’Euler, 𝐻 n’est pas homogène.
(f) Homogène de degré 𝑛.
2. (a) Les calculs conduisent à
𝑓 (𝑡𝑥1, 𝑡𝑥2, 𝑡𝑥3) =
(𝑡𝑥1𝑡𝑥2𝑡𝑥3)2
(𝑡𝑥1)4 + (𝑡𝑥2)4 + (𝑡𝑥3)4
1
𝑡𝑥1
+
1
𝑡𝑥2
+
1
𝑡𝑥3
=
𝑡6 (𝑥1𝑥2𝑥3)2
𝑡4 (𝑥4
1 + 𝑥4
2 + 𝑥4
3)
1
𝑡
1
𝑥1
+
1
𝑥2
+
1
𝑥3
= 𝑡 𝑓 (𝑥1, 𝑥2, 𝑥3).
Ainsi, on voit que 𝑓 est homogène de degré 1.
(b) Les calculs mènent à
𝑥 (𝑡𝑣1, 𝑡𝑣2, . . . , 𝑡𝑣𝑛) = 𝐴 𝛿1 (𝑡𝑣1)−𝜌
+ 𝛿2 (𝑡𝑣2)−𝜌
+ · · · + 𝛿𝑛(𝑡𝑣𝑛)−𝜌−𝜇/𝜌
= 𝐴 𝑡−𝜌
(𝛿1𝑣
−𝜌
1 + 𝛿2𝑣
−𝜌
2 + · · · + 𝛿𝑛𝑣
−𝜌
𝑛 )
−𝜇/𝜌
= (𝑡−𝜌
)−𝜇/𝜌
𝐴 𝛿1𝑣
−𝜌
1 + 𝛿2𝑣
−𝜌
2 + · · · + 𝛿𝑛𝑣
−𝜌
𝑛
−𝜇/𝜌
= 𝑡𝜇
𝐴 𝛿1𝑣
−𝜌
1 + 𝛿2𝑣
−𝜌
2 + · · · + 𝛿𝑛𝑣
−𝜌
𝑛
−𝜇/𝜌
= 𝑡𝜇
𝑥 (𝑥1, 𝑥2, 𝑥3).
Ainsi, 𝑥 est homogène de degré 𝜇.
3. Toutes sont homogènes de degré 1, comme il est facile de le vérifier à partir de (15.7.1).
4. Posons 𝑠 = 𝑥1 + · · · + 𝑥𝑛. Alors 𝑣′
𝑥𝑖
= 𝑢′
𝑥𝑖
− 𝑎/𝑠, de sorte que
Í𝑛
𝑖=1 𝑥𝑖𝑣′
𝑥𝑖
=
Í𝑛
𝑖=1 𝑥𝑖𝑢′
𝑥𝑖
−
Í𝑛
𝑖=1 𝑎𝑥𝑖/𝑠 = 𝑎 − 𝑎 = 0. Selon le théorème d’Euler 15.7.1, 𝑣 est homogène de degré 0.
5. (a) On utilise la définition (15.7.6). On suppose que (𝑥1𝑦1)2 + 1 = (𝑥2𝑦2)2 + 1. Alors
(𝑥1𝑦1)2 = (𝑥2𝑦2)2. Si 𝑡 0, alors
(𝑡𝑥1𝑡𝑦1)2
+ 1 = (𝑡𝑥2𝑡𝑦2)2
+ 1 ⇔ 𝑡4
(𝑥1𝑦1)2
+ 1 = 𝑡4
(𝑥2𝑦2)2
+ 1
⇔ 𝑡4
(𝑥1𝑦1)2
= 𝑡4
(𝑥2𝑦2)2
⇔ (𝑥1𝑦1)2
= (𝑥2𝑦2)2
.
Ainsi, 𝑓 est homothétique.
(b) De
2 (𝑥1𝑦1)2
(𝑥1𝑦1)2 + 1
=
2 (𝑥2𝑦2)2
(𝑥2𝑦2)2 + 1
, on déduit
2 (𝑥1𝑦1)2
[(𝑥2𝑦2)2
+ 1] = 2 (𝑥2𝑦2)2
[(𝑥1𝑦1)2
+ 1]

173. Chapitre 15 / Les dérivées partielles en action 173
et ainsi (𝑥1𝑦1)2 = (𝑥2𝑦2)2. Pour tout 𝑡 0, on a
2(𝑡𝑥1𝑡𝑦1)2
(𝑡𝑥1𝑡𝑦1)2 + 1
=
2(𝑡𝑥2𝑡𝑦2)2
(𝑡𝑥2𝑡𝑦2)2 + 1
⇔
2𝑡4(𝑥1𝑦1)2
𝑡4(𝑥1𝑦1)2 + 1
=
2𝑡4(𝑥2𝑦2)2
𝑡4(𝑥2𝑦2)2 + 1
⇔
(𝑥1𝑦1)2
𝑡4(𝑥1𝑦1)2 + 1
=
(𝑥2𝑦2)2
𝑡4(𝑥2𝑦2)2 + 1
Notons à présent que, pour 𝑎, 𝑏 0 quelconques,
𝑎
𝑡4𝑎 + 1
=
𝑏
𝑡4𝑏 + 1
⇔ 𝑎𝑏𝑡4
+ 𝑎 = 𝑎𝑏𝑡4
+ 𝑏 ⇔ 𝑎 = 𝑏
Nous avons donc démontré que pour tout 𝑡 0, on a
2(𝑡𝑥1𝑡𝑦1)2
(𝑡𝑥1𝑡𝑦1)2 + 1
=
2(𝑡𝑥2𝑡𝑦2)2
(𝑡𝑥2𝑡𝑦2)2 + 1
⇔ (𝑥1𝑦1)2
= (𝑥2𝑦2)2
.
Ainsi, 𝑓 est homothétique.
(c) 𝑓 (1, 0) = 1 = 𝑓 (0, 1), mais 𝑓 (2, 0) = 4 ≠ 8 = 𝑓 (0, 2). Cela suffit à montrer que
𝑓 n’est pas homothétique.
(d) Comme 𝑔(𝑥, 𝑦) = 𝑥2𝑦 est homogène de degré 3 et que 𝑢 → 𝑒𝑢 est strictement
croissante, 𝑓 est homothétique conformément au théorème 15.7.2.
6. (a) ℎ(𝑡x) = 𝑓 ((𝑡𝑥1)𝑚
, . . . , (𝑡𝑥𝑛)𝑚
) = 𝑓 (𝑡𝑚
𝑥𝑚
1 , . . . , 𝑡𝑚
𝑥𝑚
𝑛 )
= (𝑡𝑚
)𝑟
𝑓 (𝑥𝑚
1 , . . . , 𝑥𝑚
𝑛 ) = 𝑡𝑚𝑟
ℎ(x),
de sorte que ℎ est homogène de degré 𝑚𝑟.
(b) Homogène de degré 𝑠𝑝. (c) Homogène de degré 𝑟 pour 𝑟 = 𝑠, pas homogène pour
𝑟 ≠ 𝑠. (d) Homogène de degré 𝑟 + 𝑠. (e) Homogène de degré 𝑟 − 𝑠.
7. Si on définit Δ = ln 𝐶(𝑡w, 𝑦) − ln 𝐶(w, 𝑦), il suffit de démontrer que Δ = ln 𝑡, car alors
𝐶(𝑡w, 𝑦)/𝐶(w, 𝑦) = 𝑒Δ = 𝑡. On calcule
Δ =
𝑛
Õ
𝑖=1
𝑎𝑖 [ln(𝑡𝑤𝑖) − ln 𝑤𝑖] +
1
2
𝑛
Õ
𝑖,𝑗=1
𝑏𝑖 𝑗 [ln(𝑡𝑤𝑖) ln(𝑡𝑤 𝑗)
− ln 𝑤𝑖 ln 𝑤 𝑗] + ln 𝑦
𝑛
Õ
𝑖=1
𝑐𝑖 [ln(𝑡𝑤𝑖) − ln 𝑤𝑖].
Comme ln(𝑡𝑤𝑖) − ln 𝑤𝑖 = ln 𝑡 + ln 𝑤𝑖 − ln 𝑤𝑖 = ln 𝑡 et
ln(𝑡𝑤𝑖) ln(𝑡𝑤 𝑗) − ln 𝑤𝑖 ln 𝑤 𝑗 = (ln 𝑡)2
+ ln 𝑡 ln 𝑤𝑖 + ln 𝑡 ln 𝑤 𝑗,
l’expression de Δ se réduit à
Δ = ln 𝑡
𝑛
Õ
𝑖=1
𝑎𝑖 +
1
2
(ln 𝑡)2
𝑛
Õ
𝑖,𝑗=1
𝑏𝑖 𝑗 +
1
2
ln 𝑡
𝑛
Õ
𝑗=1
ln 𝑤𝑖
𝑛
Õ
𝑖=1
𝑏𝑖 𝑗
+
1
2
ln 𝑡
𝑛
Õ
𝑖=1
ln 𝑤 𝑗
𝑛
Õ
𝑗=1
𝑏𝑖 𝑗 + ln 𝑦 ln 𝑡
𝑛
Õ
𝑖=1
𝑐𝑖.
D’où Δ = ln 𝑡 + 0 + 0 + 0 + 0 = ln 𝑡, à cause des conditions imposées aux paramètres 𝑎𝑖,
𝑏𝑖 𝑗 et 𝑐𝑖.

174. 174 CORRIGÉS DES EXERCICES
15.8
1. Dans chaque cas, on utilise l’approximation 𝑓 (𝑥, 𝑦) ≈ 𝑓 (0, 0) + 𝑓 ′
𝑥 (0, 0) 𝑥 + 𝑓 ′
𝑦 (0, 0) 𝑦.
(a) 𝑓 ′
𝑥 (𝑥, 𝑦) = 5 (𝑥+1)4 (𝑦+1)6 et 𝑓 ′
𝑦 (𝑥, 𝑦) = 6 (𝑥+1)5 (𝑦+1)5, de sorte que 𝑓 ′
𝑥 (0, 0) = 5
et 𝑓 ′
𝑦 (0, 0) = 6. Comme 𝑓 (0, 0) = 1, 𝑓 (𝑥, 𝑦) ≈ 1 + 5𝑥 + 6𝑦.
(b) 𝑓 ′
𝑥 (𝑥, 𝑦) = 𝑓 ′
𝑦 (𝑥, 𝑦) = 1
2 (1 + 𝑥 + 𝑦)−1/2, d’où 𝑓 ′
𝑥 (0, 0) = 𝑓 ′
𝑦 (0, 0) = 1/2. Comme
𝑓 (0, 0) = 1, on a 𝑓 (𝑥, 𝑦) ≈ 1 + 1
2 𝑥 + 1
2 𝑦.
(c) 𝑓 ′
𝑥 (𝑥, 𝑦) = 𝑒𝑥 ln(1 + 𝑦), 𝑓 ′
𝑦 (𝑥, 𝑦) = 𝑒𝑥/(1 + 𝑦). Comme 𝑓 ′
𝑥 (0, 0) = 0, 𝑓 ′
𝑦 (0, 0) = 1 et
𝑓 (0, 0) = 0, on a 𝑓 (𝑥, 𝑦) ≈ 𝑦.
2. 𝑓 (𝑥, 𝑦) ≈𝐴𝑥𝑎
0 𝑦𝑏
0 + 𝑎𝐴𝑥𝑎−1
0 𝑦𝑏
0 (𝑥 − 𝑥0) + 𝑏𝐴𝑥𝑎
0 𝑦𝑏−1
0 (𝑦 − 𝑦0)
= 𝐴𝑥𝑎
0 𝑦𝑏
0 [1 + 𝑎 (𝑥 − 𝑥0)/𝑥0 + 𝑏 (𝑦 − 𝑦0)/𝑦0]
3. On écrit la fonction sous la forme 𝑔∗(𝜇, 𝜀) = (1 + 𝜇)𝑎 (1 + 𝜀)𝛼𝑎 − 1, où 𝑎 = 1/(1 − 𝛽).
Alors
𝜕𝑔∗
(𝜇, 𝜀)/𝜕𝜇 = 𝑎 (1 + 𝜇)𝑎−1
(1 + 𝜀)𝛼𝑎
et 𝜕𝑔∗
(𝜇, 𝜀)/𝜕𝜀 = (1 + 𝜇)𝑎
𝛼𝑎 (1 + 𝜀)𝛼𝑎−1
.
De là, 𝑔∗(0, 0) = 0, 𝜕𝑔∗(0, 0)/𝜕𝜇 = 𝑎, 𝜕𝑔∗(0, 0)/𝜕𝜀 = 𝛼𝑎 et
𝑔∗
(𝜇, 𝜀) ≈𝑎𝜇 + 𝛼𝑎𝜀 = (𝜇 + 𝛼𝜀)/(1 − 𝛽).
4. 𝑓 (0,98 ; −1,01) ≈ −5 − 6 (−0,02) + 9 (−0,01) = −4,97. Comme la valeur exacte est
−4,970614, l’erreur est égale à 0,000614.
5. (a) 𝑓 (1,02 ; 1,99) = 1,1909
(b) 𝑓 (1,02 ; 1,99) ≈ 𝑓 (1, 2) + 0,02 × 8 − 0,01 × (−3) = 1,19. L’erreur est égale à 0,0009.
6. 𝑣(1,01 ; 0,02) ≈ 𝑣(1, 0) + 𝑣′
𝑥 (1, 0) × 0,01 + 𝑣′
𝑦 (1, 0) × 0,02 = −1 − 1/150.
7. On utilise la formule (15.8.4).
(a) On a
𝜕𝑧
𝜕𝑥
= 2𝑥 et
𝜕𝑧
𝜕𝑦
= 2𝑦. En (1, 2, 5), ces dérivées partielles sont égales à
𝜕𝑧
𝜕𝑦
= 2 et
𝜕𝑧
𝜕𝑥
= 4. L’équation du plan tangent est 𝑧 − 5 = 2 (𝑥 − 1) + 4 (𝑦 − 2) ⇔ 𝑧 = 2𝑥 + 4𝑦 − 5.
(b) En dérivant partiellement 𝑧 = (𝑦 − 𝑥2) (𝑦 − 2𝑥2) = 𝑦2 − 3𝑥2𝑦 + 2𝑥4, on obtient
𝜕𝑧
𝜕𝑥
= −6𝑥𝑦 + 8𝑥3
et
𝜕𝑧
𝜕𝑦
= 2𝑦 − 3𝑥2
. En (1, 3, 2), ces dérivées partielles valent
𝜕𝑧
𝜕𝑥
= −10
et
𝜕𝑧
𝜕𝑦
= 3. L’équation du plan tangent est
𝑧 − 2 = −10 (𝑥 − 1) + 3 (𝑦 − 3) ⇔ 𝑧 = −10𝑥 + 3𝑦 + 3.
8. 𝑔(0) = 𝑓 (x0), 𝑔(1) = 𝑓 (x). La formule (15.2.3) fournit
𝑔′
(𝑡) = 𝑓 ′
1 (x0
+ 𝑡(x − x0
)) (𝑥1 − 𝑥0
1) + · · · + 𝑓 ′
𝑛(x0
+ 𝑡(x − x0
)) (𝑥𝑛 − 𝑥0
𝑛).
En posant 𝑡 = 0, on obtient 𝑔′(0) = 𝑓 ′
1 (x0) (𝑥1 − 𝑥0
1) + · · · + 𝑓 ′
𝑛(x0) (𝑥𝑛 − 𝑥0
𝑛) et la formule
attendue en découle.

175. Chapitre 15 / Les dérivées partielles en action 175
9. Le plan tangent (15.8.10) passe par (𝑥, 𝑦, 𝑧) = (0, 0, 0) si et seulement si
− 𝑓 (𝑥0, 𝑦0) = 𝑓 ′
𝑥 (𝑥0, 𝑦0) (−𝑥0) + 𝑓 ′
𝑦 (𝑥0, 𝑦0) (−𝑦0).
En changeant le signe de chaque membre de l’équation et en remplaçant (𝑥0, 𝑦0) par (𝑥, 𝑦),
on obtient la caractérisation d’Euler (15.8.2) d’une fonction 𝑓 (𝑥, 𝑦) homogène de degré 1.
10. (a) Le long de la courbe 𝑥 = 𝛼𝑦2, pour tout 𝑦 ≠ 0, le point (𝛼𝑦2, 𝑦) est situé sur la courbe
de niveau 𝑓 (𝑥, 𝑦) = 𝛼/(1 + 𝛼2).
(b) Quand 𝛼 = 1, par exemple, on a 𝑓 (𝑦2, 𝑦) = 1
2 pour tout 𝑦 ≠ 0 et pourtant, quand
𝑦 = 0, on a 𝑓 (𝑦2, 𝑦) = 𝑓 (0, 0) = 0. La fonction 𝑓 n’est donc pas continue en (0, 0).
(c) Pour tout (𝑥, 𝑦) ≠ (0, 0), les dérivées partielles 𝑓 ′
1 (𝑥, 𝑦) et 𝑓 ′
2 (𝑥, 𝑦) existent, de manière
évidente, et sont continues. De plus, on a 𝑓 ′
1 (0, 0) = limℎ→0 [ 𝑓 (ℎ, 0) − 𝑓 (0, 0)]/ℎ = 0, et
de même 𝑓 ′
2 (0, 0) = 0.
(d) Comme 𝑓 est continue et dérivable en tout point (𝑥, 𝑦) ≠ (0, 0), pour toutes les
directions (ℎ, 𝑘) ≠ (0, 0), la dérivée est donnée par ∇(ℎ,𝑘) 𝑓 (𝑥, 𝑦) = 𝑓 ′
𝑥 (𝑥, 𝑦) ℎ+ 𝑓 ′
𝑦 (𝑥, 𝑦) 𝑘.
En (𝑥, 𝑦) = (0, 0), si (ℎ, 𝑘) ≠ (0, 0) est une direction telle que ℎ ≠ 0, alors
∇(ℎ,𝑘) 𝑓 (0, 0) = lim
𝜃→0
1
𝜃
[ 𝑓 (𝜃ℎ, 𝜃𝑘) − 𝑓 (0, 0)] = lim
𝜃→0
1
𝜃
𝜃3ℎ𝑘2
𝜃2ℎ2 + 𝜃4𝑘4
=
𝑘2
ℎ
.
Mais, si (0, 𝑘) est une direction telle que 𝑘 ≠ 0, alors
∇(0,𝑘) 𝑓 (0, 0) = lim
𝜃→0
1
𝜃
[ 𝑓 (0, 𝜃𝑘) − 𝑓 (0, 0)] = 0.
(e) Comme 𝑓 n’est pas continue en (0, 0), elle n’est pas dérivable en (0, 0).
15.9
1. Tant (a) que (b) donnent d𝑧 = (𝑦2 + 3𝑥2) d𝑥 + 2𝑥𝑦 d𝑦.
2. On peut soit utiliser la définition de la différentielle (15.9.1), soit les règles de calcul des
différentielles, comme nous le faisons ici.
(a) d𝑧 = d(𝑥3) + d(𝑦3) = 3𝑥2 d𝑥 + 3𝑦2 d𝑦
(b) d𝑧 = (d𝑥) 𝑒𝑦2
+ 𝑥 (d𝑒𝑦2
). Mais d(𝑒𝑦2
) = 𝑒𝑦2
d𝑦2 = 𝑒𝑦2
2𝑦 d𝑦. D’où
d𝑧 = 𝑒𝑦2
d𝑥 + 2𝑥𝑦𝑒𝑦2
d𝑦 = 𝑒𝑦2
(d𝑥 + 2𝑥𝑦 d𝑦).
(c) d𝑧 = d ln 𝑢, où 𝑢 = 𝑥2 − 𝑦2. Alors d𝑧 =
1
𝑢
d𝑢 =
2𝑥 d𝑥 − 2𝑦 d𝑦
𝑥2 − 𝑦2
.
3. (a) d𝑧 = 2𝑥𝑢 d𝑥 + 𝑥2 (𝑢′
𝑥 d𝑥 + 𝑢′
𝑦 d𝑦) (b) d𝑧 = 2𝑢 (𝑢′
𝑥 d𝑥 + 𝑢′
𝑦 d𝑦)
(c) d𝑧 =
1
𝑥𝑦 + 𝑦𝑢
(𝑦 + 𝑦𝑢′
𝑥) d𝑥 + (𝑥 + 𝑢 + 𝑦𝑢′
𝑦) d𝑦
4. 𝑇(𝑥, 𝑦, 𝑧) = [𝑥2 + 𝑦2 + 𝑧2]1/2 = 𝑢1/2, où 𝑢 = 𝑥2 + 𝑦2 + 𝑧2. Ensuite
d𝑇 =
1
2
𝑢−1/2
d𝑢 = 𝑢−1/2
(𝑥 d𝑥 + 𝑦 d𝑦 + 𝑧 d𝑧).

176. 176 CORRIGÉS DES EXERCICES
Pour 𝑥 = 2, 𝑦 = 3 et 𝑧 = 6, on calcule 𝑢 = 49, 𝑇 = 7 et
d𝑇 =
1
7
(𝑥 d𝑥 + 𝑦 d𝑦 + 𝑧 d𝑧) =
1
7
(2 d𝑥 + 3 d𝑦 + 6 d𝑧).
Par conséquent,
𝑇(2 + 0,01; 3 − 0,01; 6 + 0,02) ≈𝑇(2, 3, 6) +
1
7
[2 × 0,01 + 3 (−0,01) + 6 × 0,02]
= 7 +
1
7
× 0,11 ≈ 7,015714.
Une calculatrice donne une meilleure approximation :
√
49,2206 ≈ 7,015739.
5. Enprenant ladifférentielledechaquemembredel’équation, onobtient d(𝑈𝑒𝑈 ) = d(𝑥
√
𝑦).
D’où 𝑒𝑈 d𝑈 + 𝑈𝑒𝑈 d𝑈 =
√
𝑦 d𝑥 + (𝑥/2
√
𝑦) d𝑦. Ensuite,
d𝑈 =
p
𝑦 d𝑥/(𝑒𝑈
+ 𝑈𝑒𝑈
) + 𝑥 d𝑦/2
p
𝑦(𝑒𝑈
+ 𝑈𝑒𝑈
).
6. d𝑋 = 𝐴𝛽𝑁𝛽−1𝑒𝜌𝑡 d𝑁 + 𝐴𝑁𝛽 𝜌𝑒𝜌𝑡 d𝑡
7. d𝑋1 = 𝐵𝐸𝑋𝐸−1𝑁1−𝐸 d𝑋 + 𝐵(1 − 𝐸) 𝑋𝐸 𝑁−𝐸 d𝑁
8. (a) d𝑈 = 2𝑎1𝑢1 d𝑢1 + · · · + 2𝑎𝑛𝑢𝑛 d𝑢𝑛
(b) d𝑈 = 𝐴(𝛿1𝑢
−𝜌
1 + · · · + 𝛿𝑛𝑢
−𝜌
𝑛 )−1−1/𝜌 (𝛿1𝑢
−𝜌−1
1 d𝑢1 + · · · + 𝛿𝑛𝑢
−𝜌−1
𝑛 d𝑢𝑛)
9. d(ln 𝑧) = 𝑎1 d(ln 𝑥1) + · · · + 𝑎𝑛 d(ln 𝑥𝑛), de sorte que
d𝑧/𝑧 = 𝑎1 d𝑥1/𝑥1 + 𝑎2 d𝑥2/𝑥2 + · · · + 𝑎𝑛 d𝑥𝑛/𝑥𝑛.
10. (a) d2𝑧 = 2 d𝑥 d𝑦 + 2 (d𝑦)2
(b) d𝑧/d𝑡 = 3𝑡2 +4𝑡3 et (d2𝑧/d𝑡2) (d𝑡)2 = (6𝑡 +12𝑡2) (d𝑡)2. Mais l’expression de d2𝑧 issue
de (a) fournit (4𝑡 + 8𝑡2) (d𝑡)2.
15.10
1. (a) Les deux équations sont en (𝑢, 𝑣, 𝑥, 𝑦), il y a donc 4 − 2 = 2 degrés de liberté.
(b) 5 − 2 = 3 degrés de liberté. (c) 4 − 3 = 1 degrés de liberté.
2. Il y a 6 variables 𝑌, 𝐶, 𝐼, 𝐺, 𝑇 et 𝑖, et 3 équations. Par conséquent, il y a 6 − 3 = 3 degrés
de liberté.
3. Soit 𝑚 le nombre d’équations et 𝑛 le nombre d’inconnues.
(a) 𝑚 = 3, 𝑛 = 2; une infinité de solutions. (b) 𝑚 = 𝑛 = 2; pas de solution.
(c) 𝑚 = 𝑛 = 2; une infinité de solutions.
4. (a) 𝑚 = 1, 𝑛 = 100; une infinité de solutions.
(b) 𝑚 = 1, 𝑛 = 100; pas de solution. On constate que la règle de comptage échoue
lamentablement.

177. Chapitre 15 / Les dérivées partielles en action 177
15.11
1. La différentiation conduit aux deux équations 𝑎 d𝑢 + 𝑏 d𝑣 = 𝑐 d𝑥 + 𝑑 d𝑦 et
𝑒 d𝑢 + 𝑓 d𝑣 = 𝑔 d𝑥 + ℎ d𝑦. Puis leur résolution par rapport à d𝑢 et d𝑣 donne
d𝑢 = [(𝑐 𝑓 − 𝑏𝑔) d𝑥 + (𝑑𝑓 − 𝑏ℎ) d𝑦]/𝐷 et d𝑣 = [(𝑎𝑔 − 𝑐𝑒) d𝑥 + (𝑎ℎ − 𝑑𝑒) d𝑦]/𝐷, où
𝐷 = 𝑎 𝑓 − 𝑏𝑒. Les dérivées partielles demandées se lisent aisément.
2. (a) La différentiation conduit à 𝑢3 d𝑥 + 𝑥3𝑢2 d𝑢 + d𝑣 = 2𝑦 d𝑦 et 3𝑣 d𝑢 + 3𝑢 d𝑣 − d𝑥 = 0.
La résolution par rapport à d𝑢 et d𝑣 avec 𝐷 = 9𝑥𝑢3 − 3𝑣 donne
d𝑢 = (−3𝑢4
− 1) d𝑥/𝐷 + 6𝑦𝑢 d𝑦/𝐷 et d𝑣 = (3𝑥𝑢2
+ 3𝑢3
𝑣) d𝑥/𝐷 − 6𝑦𝑣 d𝑦/𝐷.
(b) 𝑢′
𝑥 = (−3𝑢4 − 1)/𝐷, 𝑣′
𝑥 = (3𝑥𝑢2 + 3𝑢3𝑣)/𝐷
(c) 𝑢′
𝑥 = 283/81 et 𝑣′
𝑥 = −64/27
3. Puisqu’on ne demande que les dérivées partielles de 𝑦1 et 𝑦2 par rapport à 𝑥1, on calcule
la différentielle du système par rapport à 𝑥1.
3 −
𝜕𝑦1
𝜕𝑥1
− 9𝑦2
2
𝜕𝑦2
𝜕𝑥1
= 0 et 3𝑥2
1 + 6𝑦2
1
𝜕𝑦1
𝜕𝑥1
−
𝜕𝑦2
𝜕𝑥1
= 0.
La résolution de ce système fournit 𝜕𝑦1/𝜕𝑥1 = (3 − 27𝑥2
1 𝑦2
2)/𝐽 et
𝜕𝑦2/𝜕𝑥1 = (3𝑥2
1 + 18𝑦2
1)/𝐽 avec 𝐽 = 1 + 54𝑦2
1𝑦2
2.
Une autre méthode serait, surtout si on a besoin de toutes les dérivées partielles, de
différentier totalement le système suivant,
(i) 3 d𝑥1 +2𝑥2 d𝑥2 −d𝑦1 −9𝑦2
2 d𝑦2 = 0, (ii) 3𝑥2
1 d𝑥1 −2 d𝑥2 +6𝑦2
1 d𝑦1 −d𝑦2 = 0.
En posant d𝑥2 = 0 et en résolvant par rapport à d𝑦1 et d𝑦2, on obtient d𝑦1 = 𝐴 d𝑥1 et
d𝑦2 = 𝐵 d𝑥1, où 𝐴 = 𝜕𝑦1/𝜕𝑥1 et 𝐵 = 𝜕𝑦2/𝜕𝑥1.
4. On dérive partiellement par rapport à 𝑀, en se rappelant que 𝑌 et 𝑖 sont des fonctions des
variables indépendantes 𝑎 et 𝑀, 𝐼′(𝑖) 𝑖′
𝑀 = 𝑆′(𝑌) 𝑌′
𝑀 et 𝑎𝑌′
𝑀 + 𝐿′(𝑖) 𝑖′
𝑀 = 1. On écrit ces
deux équations sous la forme classique d’un système de deux équations à deux inconnues
(
− 𝑆′
(𝑌) 𝑌′
𝑀 + 𝐼′
(𝑖) 𝑖′
𝑀 = 0
𝑎𝑌′
𝑀 + 𝐿′
(𝑖) 𝑖′
𝑀 = 1.
La solution en est, que ce soit par élimination ou par la formule (3.6.4),
𝑌′
𝑀 =
𝐼′(𝑖)
𝑆′(𝑌) 𝐿′(𝑖) + 𝑎𝐼′(𝑖)
et 𝑖′
𝑀 =
𝑆′(𝑌)
𝑆′(𝑌) 𝐿′(𝑖) + 𝑎𝐼′(𝑖)
.
5. La dérivation partielle par rapport à 𝑥 conduit à 𝑦 + 𝑢′
𝑥𝑣 + 𝑢𝑣′
𝑥 = 0 et 𝑢 + 𝑥𝑢′
𝑥 + 𝑦𝑣′
𝑥 = 0.
La résolution en 𝑢′
𝑥 et 𝑣′
𝑥 fournit
𝑢′
𝑥 =
𝑢2 − 𝑦2
𝑦𝑣 − 𝑥𝑢
=
𝑢2 − 𝑦2
2𝑦𝑣
, 𝑣′
𝑥 =
𝑥𝑦 − 𝑢𝑣
𝑦𝑣 − 𝑥𝑢
=
2𝑥𝑦 − 1
2𝑦𝑣
où on a introduit 𝑥𝑢 = −𝑦𝑣 et 𝑢𝑣 = 1 − 𝑥𝑦. La dérivation partielle de 𝑢′
𝑥 par rapport à 𝑥
donne enfin
𝑢′′
𝑥𝑥 =
𝜕2𝑢
𝜕𝑥2
=
𝜕
𝜕𝑥
𝑢′
𝑥 =
2𝑢𝑢′
𝑥2𝑦𝑣 − (𝑢2 − 𝑦2) 2𝑦𝑣′
𝑥
4𝑦2𝑣2
=
(𝑢2 − 𝑦2) (4𝑢𝑣 − 1)
4𝑦2𝑣3
.
(La réponse peut prendre différentes formes.)

178. 178 CORRIGÉS DES EXERCICES
6. (a) La différentiation conduit aux équations :
d𝑌 = d𝐶 + d𝐼 + d𝐺, d𝐶 = 𝐹′
𝑌 d𝑌 + 𝐹′
𝑇 d𝑇 + 𝐹′
𝑖 d𝑖 et d𝐼 = 𝑓 ′
𝑌 d𝑌 + 𝑓 ′
𝑖 d𝑖.
De là, d𝑌 = 𝐹′
𝑇 d𝑇 + d𝐺 + (𝐹′
𝑖 + 𝑓 ′
𝑖 ) d𝑖
/(1 − 𝐹′
𝑌 − 𝑓 ′
𝑌 ).
(b) 𝜕𝑌/𝜕𝑇 = 𝐹′
𝑇 /(1 − 𝐹′
𝑌 − 𝑓 ′
𝑌 ) 0, de sorte que 𝑌 décroît lorsque 𝑇 croît. Mais si
d𝑇 = d𝐺 avec d𝑖 = 0, alors d𝑌 = 1 + 𝐹′
𝑇
d𝑇/(1 − 𝐹′
𝑌 − 𝑓 ′
𝑌 ) ; elle est strictement positive
sous la condition 𝐹′
𝑇 −1.
7. (a) 6 − 3 = 3
(b) La différentiation suivie d’un regroupement des termes en d𝑌, d𝑖 et d𝐼 du membre
de gauche donne (i) (𝐶′
𝑌 − 1) d𝑌 + 𝐶′
𝑖 d𝑖 + d𝐼 = − d𝛼 (ii) 𝐹′
𝑌 d𝑌 + 𝐹′
𝑖 d𝑖 − d𝐼 = − d𝛽
(iii) 𝐿′
𝑌 d𝑌 + 𝐿′
𝑖 d𝑖 = d𝑀. Avec d𝛽 = d𝑀 = 0, on a
d𝑌 = −(𝐿′
𝑖/𝐷) d𝛼, d𝑖 = (𝐿′
𝑌 /𝐷) d𝛼 et d𝐼 = [(𝐹′
𝑖 𝐿′
𝑌 − 𝐹′
𝑌 𝐿′
𝑖)/𝐷] d𝛼,
où 𝐷 = 𝐿′
𝑖 (𝐶′
𝑌 + 𝐹′
𝑌 − 1) − 𝐿′
𝑌 (𝐶′
𝑖 + 𝐹′
𝑖 ).
8. (a) Il y a 3 variables et 2 équations, de sorte qu’il y a (en général) un degré de liberté.
(b) On prend la différentielle de chaque équation :
0 = 𝛼𝑃 d𝑦 + 𝐿′
(𝑖) d𝑖 et 𝑆′
𝑦 d𝑦 + 𝑆′
𝑖 d𝑖 + 𝑆′
𝑔 d𝑔 = 𝐼′
𝑦 d𝑦 + 𝐼′
𝑖 d𝑖.
On trouve d𝑦/d𝑔 = −𝐿′(𝑖)𝑆′
𝑔/𝐷 et d𝑖/d𝑔 = 𝛼𝑃𝑆′
𝑔/𝐷, où 𝐷 = 𝐿′(𝑖) (𝑆′
𝑦−𝐼′
𝑦)−𝛼𝑃(𝑆′
𝑖−𝐼′
𝑖 ).
9. (a) Par différentiation,
2𝑢𝑣 d𝑢 + 𝑢2
d𝑣 − d𝑢 = 3𝑥2
d𝑥 + 6𝑦2
d𝑦 et 𝑒𝑢𝑥
(𝑢 d𝑥 + 𝑥 d𝑢) = 𝑣 d𝑦 + 𝑦 d𝑣.
Au point 𝑃, ces équations deviennent 3 d𝑢 + 4 d𝑣 = 6 d𝑦 et d𝑣 = 2 d𝑥 − d𝑦. De là,
d𝑢 = 2 d𝑦 − (4/3) d𝑣 = −(8/3) d𝑥 + (10/3) d𝑦. On a aussi 𝜕𝑢/𝜕𝑦 = 10/3 et 𝜕𝑣/𝜕𝑥 = 2.
(b) Δ𝑢 ≈ d𝑢 = −(8/3) 0,1 + (10/3) (−0,2) = −14/15 ≈ −0,93,
Δ𝑣 ≈ d𝑣 = 2 (0,1) + (−1) (−0,2) = 0,4.
10. On prend les différentielles et on pose d𝑝2 = d𝑚 = 0 :
(i) 𝑈′′
𝑥1 𝑥1
d𝑥1 + 𝑈′′
𝑥1 𝑥2
d𝑥2 = 𝑝1 d𝜆 + 𝜆 d𝑝1 ; (ii) 𝑈′′
𝑥2 𝑥1
d𝑥1 + 𝑈′′
𝑥2 𝑥2
d𝑥2 = 𝑝2 d𝜆;
(iii) 𝑝1 d𝑥1 + d𝑝1 𝑥1 + 𝑝2 d𝑥2 = 0. La résolution en d𝑥1 conduit en particulier à
𝜕𝑥1
𝜕𝑝1
=
𝜆𝑝2
2 + 𝑥1 (𝑝2𝑈′′
𝑥1 𝑥2
− 𝑝1𝑈′′
𝑥2 𝑥2
)
𝑝2
1𝑈′′
𝑥2 𝑥2
− 2𝑝1 𝑝2𝑈′′
𝑥1 𝑥2
+ 𝑝2
2𝑈′′
𝑥1 𝑥1
.
Exercices récapitulatifs du chapitre 15
1. (a) d𝑧/d𝑡 = 6 × 4𝑡 + 3𝑦29𝑡2 = 24𝑡 + 27𝑡2𝑦2 = 24𝑡 + 243𝑡8
(b) d𝑧/d𝑡 = 𝑝𝑥𝑝−1𝑎 + 𝑝𝑦𝑝−1𝑏 = 𝑝𝑡𝑝−1(𝑎𝑝 + 𝑏𝑝)
Dans (a) 𝑧 = 6 (2𝑡2) + (3𝑡3)3 = 12𝑡2 + 27𝑡9, de sorte que d𝑧/d𝑡 = 24𝑡 + 243𝑡8.
Dans (b), 𝑧 = (𝑎𝑡)𝑝 + (𝑏𝑡)𝑝 = 𝑎𝑝𝑡𝑝 + 𝑏𝑝𝑡𝑝, de sorte que d𝑧/d𝑡 = (𝑎𝑝 + 𝑏𝑝)𝑝𝑡𝑝−1.

179. Chapitre 15 / Les dérivées partielles en action 179
2. 𝜕𝑧/𝜕𝑡 = 𝐺′
𝑢 (𝑢, 𝑣) 𝜙′
𝑡 (𝑡, 𝑠) et 𝜕𝑧/𝜕𝑠 = 𝐺′
𝑢 (𝑢, 𝑣) 𝜙′
𝑠 (𝑡, 𝑠) + 𝐺′
𝑣 (𝑢, 𝑣) 𝜓′(𝑠).
3. 𝜕𝑤/𝜕𝑡 = 2𝑥 × 1 + 3𝑦2 × 1 + 4𝑧3𝑠 = 2𝑥 + 3𝑦2 + 4𝑠𝑧3 = 4𝑠4𝑡3 + 3𝑠2 + 3𝑡2 − 6𝑡𝑠 + 2𝑠 + 2𝑡,
𝜕𝑤/𝜕𝑠 = 2𝑥 − 3𝑦2 + 4𝑡𝑧3 = 4𝑠3𝑡4 − 3𝑠2 − 3𝑡2 + 6𝑡𝑠 + 2𝑠 + 2𝑡.
4. 𝑋 = 𝑁𝑔(𝑢), où 𝑢 = 𝜑(𝑁)/𝑁. Alors d𝑢/d𝑁 = [𝜑′(𝑁)𝑁−𝜑(𝑁)]/𝑁2 = (1/𝑁) (𝜑′(𝑁)−𝑢)
et, par la règle de dérivation du produit et de la composée,
d𝑋
d𝑁
= 𝑔(𝑢) + 𝑁𝑔′
(𝑢)
d𝑢
d𝑁
= 𝑔(𝑢) + 𝑔′
(𝑢) (𝜑′
(𝑁) − 𝑢).
On dérive le membre de droite par rapport à 𝑁,
d2𝑋
d𝑁2
= 𝑔′
(𝑢)
d𝑢
d𝑁
+ 𝑔′′
(𝑢)
d𝑢
d𝑁
𝜑′
(𝑁) − 𝑢
+ 𝑔′
(𝑢)
𝜑′′
(𝑁) −
d𝑢
d𝑁
=
1
𝑁
𝑔′′
𝜑(𝑁)/𝑁
𝜑′
(𝑁) − 𝜑(𝑁)/𝑁
2
+ 𝑔′
𝜑(𝑁)/𝑁
𝜑′′
(𝑁).
5. (a) On prend le logarithme naturel de la fonction : ln 𝐸 = ln 𝐴 − 𝑎 ln 𝑝 + 𝑏 ln 𝑚, puis on
calcule la dérivée : 𝐸′/𝐸 = −𝑎 (𝑝′/𝑝) + 𝑏 (𝑚′/𝑚).
(b) ln 𝑝 = ln 𝑝0 + 𝑡 ln(1,06), de sorte que 𝑝′/𝑝 = ln 1,06. De même, 𝑚′/𝑚 = ln 1,08.
Ensuite, 𝐸′/𝐸 = −𝑎 ln 1,06 + 𝑏 ln 1,08 = ln(1,08𝑏/1,06𝑎) = ln 𝑄.
6. En dérivant chaque membre par rapport à 𝑥 en tenant 𝑦 constant, on obtient
3𝑥2
ln 𝑥 + 𝑥2
= (6𝑧2
ln 𝑧 + 2𝑧2
) 𝑧′
𝑥.
Quand 𝑥 = 𝑦 = 𝑧 = 𝑒, 𝑧′
𝑥 = 1/2. On dérive une seconde fois
6𝑥 ln 𝑥 + 5𝑥 = (12𝑧 ln 𝑧 + 10𝑧) (𝑧′
𝑥)2
+ (6𝑧2
ln 𝑧 + 2𝑧2
) 𝑧′′
𝑥𝑥.
Quand 𝑥 = 𝑦 = 𝑧 = 𝑒 et 𝑧′
𝑥 = 1/2, 𝑧′′
𝑥𝑥 = 11/16𝑒.
7. 𝑅𝑦𝑥 = 𝐹′
𝑥/𝐹′
𝑦 = −𝑥/10𝑦. D’où 𝑦/𝑥 = −(1/10)𝑅−1
𝑦𝑥, de sorte que
𝜎𝑦𝑥 = El𝑅𝑦𝑥 (𝑦/𝑥) = −1.
8. (a) TMS = 𝑅𝑦𝑥 = 𝑈′
𝑥/𝑈′
𝑦 = 2𝑦/3𝑥 (b) TMS = 𝑅𝑦𝑥 = 𝑦/(𝑥 + 1)
(c) TMS = 𝑅𝑦𝑥 = (𝑦/𝑥)3
9. (a) −1 (b) 2𝑎𝑐 (c) 4
(d) Non homogène. (À supposer 𝐹 homogène, alors, selon le théorème d’Euler, pour une
certaine constante 𝑘, on aurait eu 𝑥1𝑒𝑥1+𝑥2+𝑥3 + 𝑥2𝑒𝑥1+𝑥2+𝑥3 + 𝑥3𝑒𝑥1+𝑥2+𝑥3 = 𝑘𝑒𝑥1+𝑥2+𝑥3 ,
pour tout 𝑥1, 𝑥2, 𝑥3 positifs, et 𝑥1 + 𝑥2 + 𝑥3 = 𝑘. Ce qui est évidemment impossible pour
(𝑥1, 𝑥2, 𝑥3) quelconque.)
10. Comme 𝑦/𝑥 = (𝑅𝑦𝑥)1/3, 𝜎𝑦𝑥 = El𝑅𝑦𝑥 (𝑦/𝑥) = 1/3.

180. 180 CORRIGÉS DES EXERCICES
11. On prend l’élasticité par rapport à 𝑥 des deux membres de l’équation,
El𝑥 (𝑦2
𝑒𝑥
𝑒1/𝑦
) = El𝑥 𝑦2
+ El𝑥𝑒𝑥
+ El𝑥𝑒1/𝑦
= 0.
On a El𝑥 𝑦2 = 2El𝑥 𝑦 et El𝑥𝑒𝑥 = 𝑥. De plus, El𝑥𝑒1/𝑦 = El𝑥𝑒𝑢, où 𝑢 = 1/𝑦, de
sorte que El𝑥𝑒𝑢 = 𝑢El𝑥 (1/𝑦) = (1/𝑦) (El𝑥1 − El𝑥 𝑦) = −(1/𝑦)El𝑥 𝑦. Finalement,
2El𝑥 𝑦 + 𝑥 − (1/𝑦)El𝑥 𝑦 = 0 ou El𝑥 𝑦 = 𝑥𝑦/(1 − 2𝑦)(23).
12. (a) Pour tout 𝑡 0, on a 𝑓 (𝑡𝑥, 𝑡𝑦) = (𝑡𝑥)𝑔(𝑡𝑥/𝑡𝑦) = 𝑡𝑥𝑔(𝑥/𝑦) = 𝑡 𝑓 (𝑥, 𝑦), donc 𝑓 est
homogène de degré 1.
(b) En utilisant un raisonnement analogue à celui de la question (a), on montre que t 𝐹
est homogène de degré 𝑘.
(c) À l’aide de la réponse à l’exemple 15.7.3 dans le cas de la fonction générique de Cobb-
Douglas, on montre que 𝐺 est homogène de degré (𝑎 −𝑏) + (𝑏 −𝑐) + (𝑐 −𝑑) + (𝑑 −𝑎) = 0.
13. Comme 𝐹 est homogène de degré 1, selon (15.6.6) ou (15.6.7), on a 𝐾𝐹′′
𝐾 𝐾 + 𝐿𝐹′′
𝐾 𝐿 = 0,
de sorte que 𝐹′′
𝐾 𝐿 = −(𝐾/𝐿)𝐹′′
𝐾 𝐾 0 puisque 𝐹′′
𝐾 𝐾 0 et 𝐾 0, 𝐿 0.
14. Dériver 𝑓 (𝑡𝑥1, . . . , 𝑡𝑥𝑛) = 𝑔(𝑡) 𝑓 (𝑥1, . . . , 𝑥𝑛) par rapport à 𝑡 et poser 𝑡 = 1, comme dans
la démonstration du théorème d’Euler 15.7.1. Cela conduit à
𝑛
Õ
𝑖=1
𝑥𝑖 𝑓 ′
𝑥𝑖
(𝑥1, . . . , 𝑥𝑛) = 𝑔′
(1) 𝑓 (𝑥1, . . . , 𝑥𝑛).
D’où par le théorème d’Euler, 𝑓 doit être homogène de degré 𝑔′(1). En réalité, 𝑔(𝑡) = 𝑡𝑘
où 𝑘 = 𝑔′(1).
15. d𝑢 + 𝑒𝑦 d𝑥 +𝑥𝑒𝑦 d𝑦 +d𝑣 = 0 et d𝑥 + 𝑒𝑢+𝑣2
d𝑢 + 𝑒𝑢+𝑣2
2𝑣 d𝑣 −d𝑦 = 0. Au point donné, ces
équations se réduisent à d𝑢 + d𝑣 = −𝑒 d𝑥 − 𝑒 d𝑦 et d𝑢 = −𝑒 d𝑥 + 𝑒 d𝑦, ce qui implique
𝑢′
𝑥 = −𝑒, 𝑢′
𝑦 = 𝑒, 𝑣′
𝑥 = 0 et 𝑣′
𝑦 = −2𝑒.
16. (a) Après différentiation, on rassemble dans le membre de gauche tous les termes en d𝑝
et d𝐿,
(i) 𝐹′
(𝐿) d𝑝 + 𝑝𝐹′′
(𝐿) d𝐿 = d𝑤, (ii) 𝐹(𝐿) d𝑝 + (𝑝𝐹′
(𝐿) − 𝑤) d𝐿 = 𝐿 d𝑤 + d𝐵.
Comme 𝑝𝐹′(𝐿) = 𝑤, (ii) se simplifie en d𝑝 = (𝐿 d𝑤 + d𝐵)/𝐹(𝐿). On introduit cette
expression dans (i) et on résout par rapport à d𝐿, ce qui donne
d𝐿 = [(𝐹(𝐿) − 𝐿𝐹′
(𝐿)) d𝑤 − 𝐹′
(𝐿) d𝐵]/𝑝𝐹(𝐿)𝐹′′
(𝐿).
Il s’ensuit que
𝜕𝑝
𝜕𝑤
=
𝐿
𝐹(𝐿)
,
𝜕𝑝
𝜕𝐵
=
1
𝐹(𝐿)
,
𝜕𝐿
𝜕𝑤
=
𝐹(𝐿) − 𝐿𝐹′(𝐿)
𝑝𝐹(𝐿)𝐹′′(𝐿)
,
𝜕𝐿
𝜕𝐵
= −
𝐹′(𝐿)
𝑝𝐹(𝐿)𝐹′′(𝐿)
.
(23) On a utilisé les règles sur l’élasticité de l’exercice 7.7.9. Si vous n’êtes pas à l’aise avec ces formules, vous pouvez
calculer 𝑦′ par dérivation implicite et utiliser ensuite El𝑥 𝑦 = (𝑥/𝑦) 𝑦′.

181. Chapitre 15 / Les dérivées partielles en action 181
(b) Comme toutes les variables qui contiennent 𝑝 sont strictement positives, et que
𝐹′(𝐿) 0 et 𝐹′′(𝐿) 0, il est clair que 𝜕𝑝/𝜕𝑤, 𝜕𝑝/𝜕𝐵, et 𝜕𝐿/𝜕𝐵 sont toutes strictement
positives.
Le signe de 𝜕𝐿/𝜕𝑤 est l’opposé du signe de 𝐹(𝐿) − 𝐿𝐹′(𝐿). Par les équations du
modèle, on a 𝐹′(𝐿) = 𝑤/𝑝 et 𝐹(𝐿) = (𝑤𝐿 + 𝐵)/𝑝. D’où 𝐹(𝐿) − 𝐿𝐹′(𝐿) = 𝐵/𝑝 0.
Par conséquent, 𝜕𝐿/𝜕𝑤 0.
17. (a) 𝛼𝑢𝛼−1 d𝑢 + 𝛽𝑣𝛽−1 d𝑣 = 2𝛽 d𝑥 + 3𝑦2 d𝑦 et
𝛼𝑢𝛼−1
𝑣𝛽
d𝑢 + 𝑢𝛼
𝛽𝑣𝛽−1
d𝑣 − 𝛽𝑣𝛽−1
d𝑣 = d𝑥 − d𝑦.
En 𝑃, on trouve 𝜕𝑢/𝜕𝑥 = 2−𝛽/𝛼 , 𝜕𝑢/𝜕𝑦 = −2−𝛽/𝛼 , 𝜕𝑣/𝜕𝑥 = (2𝛽 − 2−𝛽)/𝛽2𝛽−1,
𝜕𝑣/𝜕𝑦 = (2−𝛽 + 3)/𝛽2𝛽−1.
(b) 𝑢(0,99; 1,01) ≈𝑢(1, 1) + 𝜕𝑢(1, 1)/𝜕𝑥 × (−0,01) + 𝜕𝑢(1, 1)/𝜕𝑦 × 0,01
= 1 − 2−𝛽
/100𝛼 − 2−𝛽
/100𝛼 = 1 − 2−𝛽
/50𝛼.
18. (a) 𝑆 =
∫ 𝑇
0
𝑒−𝑟 𝑥
(𝑒𝑔𝑇 −𝑔𝑥
− 1) d𝑥 = 𝑒𝑔𝑇
∫ 𝑇
0
𝑒−(𝑟+𝑔) 𝑥
d𝑥 −
∫ 𝑇
0
𝑒−𝑟 𝑥
d𝑥
=
𝑒𝑔𝑇 − 𝑒−𝑟𝑇
𝑟 + 𝑔
+
𝑒−𝑟𝑇 − 1
𝑟
.
Par conséquent, 𝑟(𝑟 + 𝑔)𝑆 = 𝑟𝑒𝑔𝑇 + 𝑔𝑒−𝑟𝑇 − (𝑟 + 𝑔).
(b) Une dérivation implicite par rapport à 𝑔 donne
𝑟𝑆 = 𝑟𝑒𝑔𝑇
(𝑇 + 𝑔𝜕𝑇/𝜕𝑔) + 𝑒−𝑟𝑇
+ 𝑔𝑒−𝑟𝑇
(−𝑟𝜕𝑇/𝜕𝑔) − 1
de sorte que 𝜕𝑇/𝜕𝑔 = [𝑟𝑆 + 1 − 𝑟𝑇𝑒𝑔𝑇 − 𝑒−𝑟𝑇 ]/𝑟𝑔(𝑒𝑔𝑇 − 𝑒−𝑟𝑇 ).
19. (a) La condition nécessaire du premier ordre pour un maximum est
𝑃′
(𝑡) = 𝑉′
(𝑡) 𝑒−𝑖𝑡
− 𝑖𝑉(𝑡) 𝑒−𝑖𝑡
− 𝑚𝑒−𝑖𝑡
= 0.
Après simplification par 𝑒−𝑖𝑡 , on voit que 𝑡∗ ne peut rendre la valeur actuelle maximale
que si l’équation donnée est satisfaite. L’équation dit que l’accroissement marginal 𝑉′(𝑡∗)
en valeur de marché par unité de temps en gardant la voiture un peu plus longtemps doit
être égal à la somme du coût annuel de maintenance plus les intérêts non gagnés 𝑖𝑉(𝑡∗)
par unité de temps passé à attendre.
(b) On dérive à nouveau 𝑃(𝑡) :
𝑃′′
(𝑡) = 𝑉′′
(𝑡) 𝑒−𝑖𝑡
− 𝑖𝑉′
(𝑡) 𝑒−𝑖𝑡
− 𝑖𝑉′
(𝑡) 𝑒−𝑖𝑡
+ 𝑖2
𝑉(𝑡) 𝑒−𝑖𝑡
+ 𝑖𝑚𝑒−𝑖𝑡
.
On regroupe les termes
𝑃′′
(𝑡) = [𝑉′′
(𝑡) − 𝑖𝑉′
(𝑡)]𝑒−𝑖𝑡
+ [𝑉′
(𝑡) − 𝑖𝑉(𝑡) − 𝑚](−𝑖𝑒−𝑖𝑡
).
Au point critique 𝑡∗, le dernier crochet vaut 0. La condition 𝑃′′(𝑡∗) 0 revient à 𝐷 =
𝑉′′(𝑡∗) − 𝑖𝑉′(𝑡∗) 0.

182. 182 CORRIGÉS DES EXERCICES
(c) On prend la différentielle de (∗) : 𝑉′′(𝑡∗) d𝑡∗ = d𝑖 𝑉(𝑡∗) + 𝑖 𝑉′(𝑡∗) d𝑡∗ = d𝑚. De là
𝜕𝑡∗
𝜕𝑖
=
𝑉(𝑡∗)
𝑉′′(𝑡∗) − 𝑖𝑉′(𝑡∗)
=
𝑉(𝑡∗)
𝐷
et
𝜕𝑡∗
𝜕𝑚
=
1
𝑉′′(𝑡∗) − 𝑖𝑉′(𝑡∗)
=
1
𝐷
.
En supposant 𝑉(𝑡∗) 0 (sinon, il serait préférable de supprimer la voiture tout de suite),
les deux dérivées partielles sont strictement négatives. Une légère augmentation du taux
d’intérêt ou du coût d’entretien va pousser le propriétaire à vendre la voiture un peu
plus tôt.
Chapitre 16 / Les intégrales multiples
16.1
1. (a)
∫ 2
0
∫ 1
0
(2𝑥 + 3𝑦 + 4) d𝑥
d𝑦 =
∫ 2
0
(𝑥2
+ 3𝑥𝑦 + 4𝑥)
𝑥=1
𝑥=0
d𝑦 =
∫ 2
0
(5 + 3𝑦) d𝑦
=
5𝑦 +
3
2
𝑦2
2
0
= 16
(b)
∫ 𝑎
0
∫ 𝑏
0
(𝑥 − 𝑎)(𝑥 − 𝑏) d𝑥
d𝑦 =
∫ 𝑎
0
1
3
𝑥3
−
1
2
(𝑎 + 𝑏)𝑥2
+ 𝑎𝑏𝑥
𝑥=𝑏
𝑥=0
d𝑦
=
∫ 𝑎
0
1
3
𝑏3
−
1
2
(𝑎 + 𝑏)𝑏2
+ 𝑎𝑏2
d𝑦
= 𝑎
1
3
𝑏3
+
1
2
𝑎𝑏2
−
1
2
𝑏3
=
1
6
𝑎𝑏2
(3𝑎 − 𝑏)
(c) 16 ln 2 − 3 ln 3 − 5 ln 5.
2.
1
𝑏
(𝑒𝑏 − 𝑒𝑏/𝑎) +
1
𝑎
− 1.
3. 𝑘𝑎 = 2 + 4/(𝑎2 + 3𝑎) 2 pour tout 𝑎 0.
4. L’intégrale intérieure est égale à
∫ 1
−2
[𝑥2
𝑦3
− (𝑦 +1)2
] d𝑦 =
1
4
𝑥2
𝑦4
−
1
3
(𝑦 + 1)3
𝑦=1
𝑦=−2
=
1
4
𝑥2
−
8
3
−4𝑥2
−
1
3
= −
15
4
𝑥2
−3.
La double intégrale est donc égale à
𝐼 = −
∫ 2
0
15
4
𝑥2
+ 3
d𝑥 = −
5
4
𝑥3
+ 3𝑥
𝑥=2
𝑥=0
= −(10 + 6) = −16.
16.3
1. L’aire de la région ombrée est la différence entre les aires : (i) du carré unité; (ii) du
triangle dont les coins ont pour coordonnées (𝑧 − 1, 1), (1, 𝑧 − 1) et (1, 1). La différence
entre ces aires est égale à 1 − 1
2 (2 − 𝑧)2.

183. Chapitre 17 / Optimisation sans contraintes 183
16.4
1. Pour 𝑖 = 1, 2, 3, on a
∭
𝐶
𝑥2
𝑖 d𝑥1 d𝑥2 d𝑥3 =
∫ 1
0
𝑥2
d𝑥 =
1
3
, d’où
∭
𝐶
(𝑥2
1 + 𝑥2
2 + 𝑥2
3) d𝑥1 d𝑥2 d𝑥3 = 3
∫ 1
0
𝑥2
d𝑥 = 1.
Chapitre 17 / Optimisation sans contraintes
17.1
1. Les conditions du premier ordre 𝑓 ′
𝑥 (𝑥, 𝑦) = −4𝑥 + 4 = 0 et 𝑓 ′
𝑦 (𝑥, 𝑦) = −2𝑦 + 4 = 0 sont
toutes les deux satisfaites quand 𝑥 = 1 et 𝑦 = 2.
2. (a) 𝑓 ′
𝑥 (𝑥, 𝑦) = 2𝑥 −6 et 𝑓 ′
𝑦 (𝑥, 𝑦) = 2𝑦 +8. Ces dérivées partielles s’annulent au seul point
de coordonnées (𝑥, 𝑦) = (3, −4).
(b) 𝑓 (𝑥, 𝑦) = 𝑥2 − 6𝑥 + 32 + 𝑦2 + 8𝑦 + 42 + 35 − 32 − 42 = (𝑥 − 3)2 + (𝑦 + 4)2 + 10 ⩾ 10
pour tout (𝑥, 𝑦). Or, 𝑓 (3, −4) = 10. Donc (3, −4) minimise 𝑓 .
3. 𝐹′
𝐾 = −2 (𝐾 − 3) − (𝐿 − 6) et 𝐹′
𝐿 = −4 (𝐿 − 6) − (𝐾 − 3), de sorte que les conditions du
premier ordre sont −2 (𝐾 − 3) − (𝐿 − 6) = 0,65, −4 (𝐿 − 6) − (𝐾 − 3) = 1,2. La seule
solution de ce système de deux équations est (𝐾, 𝐿) = (2,8; 5,75).
4. (a) 𝑃(10, 8) = 𝑃(12, 10) = 98
(b) Conditions du premier ordre : 𝑃′
𝑥 = −2𝑥 + 22 = 0, 𝑃′
𝑦 = −2𝑦 + 18 = 0. Solution :
𝑥 = 11 et 𝑦 = 9, où le profit est égal à 𝑃(11, 9) = 100.
17.2
1. Nous vérifions que les conditions du point (a) du théorème 17.2.2 sont satisfaites dans les
trois cas.
(a) Pour tout (𝑥, 𝑦), 𝜕2𝜋/𝜕𝑥2 = −0,08 ⩽ 0, 𝜕2𝜋/𝜕𝑦2 = −0,02 ⩽ 0;
(𝜕2𝜋/𝜕𝑥2) (𝜕2𝜋/𝜕𝑦2) − (𝜕2𝜋/𝜕𝑥𝜕𝑦)2 = 0,0015 ⩾ 0.
(b) Pour tout (𝑥, 𝑦), 𝑓 ′′
𝑥𝑥 = −4, 𝑓 ′′
𝑥𝑦 = 0 et 𝑓 ′′
𝑦𝑦 = −2, d’où 𝑓 ′′
𝑥𝑥 𝑓 ′′
𝑦𝑦 − ( 𝑓 ′′
𝑥𝑦)2 = 0.
(c) Avec 𝜋 = 𝐹(𝐾, 𝐿) − 0,65𝐾 − 1,2𝐿, on a 𝜋′′
𝐾 𝐾 = −2, 𝜋′′
𝐾 𝐿 = −1 et 𝜋′′
𝐿𝐿 = −4, donc
𝜋′′
𝐾 𝐾 𝜋′′
𝐿𝐿 − (𝜋′′
𝐾 𝐿)2 = 7.
2. (a) Profit : 𝜋(𝑥, 𝑦) = 24𝑥 + 12𝑦 − 𝐶(𝑥, 𝑦) = −2𝑥2 − 4𝑦2 + 4𝑥𝑦 + 64𝑥 + 32𝑦 − 514. Point
critique en 𝑥 = 40, 𝑦 = 24, où 𝜋(40, 24) = 1 150. Puisque 𝜋′′
𝑥𝑥 = −4 ⩽ 0, 𝜋′′
𝑦𝑦 = −8 ⩽ 0
et 𝜋′′
𝑥𝑥 𝜋′′
𝑦𝑦 − (𝜋′′
𝑥𝑦)2 = 16 ⩾ 0, c’est un maximum.
(b) Avec 𝑦 = 54 − 𝑥, l’expression du profit est
ˆ
𝜋 = −2𝑥2
− 4 (54 − 𝑥)2
+ 4𝑥 (54 − 𝑥) + 64𝑥 + 32 (54 − 𝑥) − 514
= −10𝑥2
+ 680𝑥 − 10 450.

184. 184 CORRIGÉS DES EXERCICES
Il y a un maximum quand ˆ
𝜋′(𝑥) = 0, ce qui se produit en 𝑥 = 34. Alors 𝑦 = 54 − 34 = 20.
Le maximum est atteint en 𝑥 = 34, 𝑦 = 20, où la valeur maximale est 1 110.
3. On résout l’équation de budget par rapport à 𝑥, ce qui donne 𝑥 = 108 − 3𝑦 − 4𝑧. En se
servant de cette expression, la fonction d’utilité en fonction de 𝑦 et 𝑧 est donnée par
𝑈 = (108 − 3𝑦 − 4𝑧) 𝑦𝑧.
Les conditions nécessaires du premier ordre sont 𝑈′
𝑦 = 108𝑧 − 6𝑦𝑧 − 4𝑧2 = 0 et
𝑈′
𝑧 = 108𝑦 − 3𝑦2 − 8𝑦𝑧 = 0. Comme il est supposé que 𝑦 et 𝑧 sont strictement posi-
tives, ces deux équations se réduisent à 6𝑦 + 4𝑧 = 108 et 3𝑦 + 8𝑧 = 108 et ont comme
solution 𝑦 = 12 et 𝑧 = 9(24). Le maximum 3 888 est atteint en 𝑥 = 36, 𝑦 = 12, 𝑧 = 9.
4. (a) 𝜋(𝑥, 𝑦) = 𝑝𝑥 + 𝑞𝑦 − 𝐶(𝑥, 𝑦) = (25 − 𝑥) 𝑥 + (24 − 2𝑦) 𝑦 − (3𝑥2
+ 3𝑥𝑦 + 𝑦2
)
= −4𝑥2
− 3𝑥𝑦 − 3𝑦2
+ 25𝑥 + 24𝑦
(b) 𝜋′
𝑥 = −8𝑥 − 3𝑦 + 25 = 0 et 𝜋′
𝑦 = −3𝑥 − 6𝑦 + 24 = 0 quand (𝑥, 𝑦) = (2, 3). Ensuite,
𝜋′′
𝑥𝑥 = −8 ⩽ 0, 𝜋′′
𝑦𝑦 = −6 ⩽ 0 et 𝜋′′
𝑥𝑥 𝜋′′
𝑦𝑦 − (𝜋′′
𝑥𝑦)2 = (−8) (−6) − (−3)2 = 39 ⩾ 0. Aussi
(𝑥, 𝑦) = (2, 3) maximise le profit.
5. Le profit est donné par 𝜋(𝑥, 𝑦) = 𝑝𝑥 +𝑞𝑦 −𝑥2 −𝑥𝑦 − 𝑦2 −𝑥 − 𝑦 −14. Il y a un point critique
(𝑥∗, 𝑦∗) en 𝑥∗ = 1
3 (2𝑝 − 𝑞 − 1) et 𝑦∗ = 1
3 (−𝑝 + 2𝑞 − 1). Sous les hypothèses 𝑞 2𝑝 − 1
et 𝑞 1
2 (𝑝 + 1), le point intérieur (𝑥∗, 𝑦∗), avec 𝑥∗ 0 et 𝑦∗ 0, remplit les conditions
suffisantes du théorème 17.2.2 pour que ce soit un maximum.
6. (a) 𝑥∗ = 𝑝/2𝛼, 𝑦∗ = 𝑞/2𝛽 et les conditions du second ordre sont satisfaites.
(b) 𝜋∗(𝑝, 𝑞) = 𝑝𝑥∗ + 𝑞𝑦∗ − 𝛼 (𝑥∗)2 − 𝛽(𝑦∗)2 = 𝑝2/4𝛼 + 𝑞2/2𝛽. De là,
𝜕𝜋∗
(𝑝, 𝑞)/𝜕𝑝 = 𝑝/2𝛼 = 𝑥∗
.
Augmenter le prix 𝑝 d’une unité fait augmenter le profit optimal d’environ 𝑥∗, la quantité
produite du premier bien. 𝜕𝜋∗(𝑝, 𝑞)/𝜕𝑞 = 𝑦∗ a la même interprétation.
7. La contrainte consiste en 𝑧 = 4𝑥 + 2𝑦 − 5. Après avoir remplacé 𝑧 par son expression, on
cherche (𝑥, 𝑦) qui rend minimal 𝑃(𝑥, 𝑦) = 𝑥2 + 𝑦2 + (4𝑥 +2𝑦 −5)2 par rapport à 𝑥 et 𝑦. Les
conditions du premier ordre sont 𝑃′
𝑥 = 34𝑥 + 16𝑦 − 40 = 0, 𝑃′
𝑦 = 16𝑥 + 10𝑦 − 20 = 0 et la
solution 𝑥 = 20/21, 𝑦 = 10/21. Comme 𝑃′′
𝑥𝑥 = 34, 𝑃′′
𝑥𝑦 = 16 et 𝑃′′
𝑦𝑦 = 10, les conditions
du second ordre indiquent qu’il s’agit d’un minimum. Cette valeur minimale est 525/441.
8. Pour vérifier que les conditions suffisantes du point (i) du théorème 17.2.2 sont remplies,
on calcule 𝑓 ′′
𝑥𝑥 = 𝑎 (𝑎−1)𝐴𝑥𝑎−2𝑦𝑏, 𝑓 ′′
𝑥𝑦 = 𝑓 ′′
𝑦𝑥 = 𝑎𝑏𝐴𝑥𝑎−1𝑦𝑏−1 et 𝑓 ′′
𝑦𝑦 = 𝑏 (𝑏−1)𝐴𝑥𝑎𝑦𝑏−2.
Ensuite, 𝑓 ′′
𝑥𝑥 𝑓 ′′
𝑦𝑦 − ( 𝑓 ′′
𝑥𝑦)2 = 𝑎𝑏𝐴2𝑥2𝑎−2𝑦2𝑏−2
1 − (𝑎 + 𝑏)
. On suppose 𝑎 + 𝑏 ⩽ 1. Alors
𝑎 ⩽ 1 et 𝑏 ⩽ 1 aussi. Si 𝑥 0 et 𝑦 0, alors 𝑓 ′′
𝑥𝑥 ⩽ 0 et 𝑓 ′′
𝑦𝑦 ⩽ 0 et 𝑓 ′′
𝑥𝑥 𝑓 ′′
𝑦𝑦 − ( 𝑓 ′′
𝑥𝑦)2 ⩾ 0,
ce qui permet de conclure que 𝑓 est concave pour 𝑥 0, 𝑦 0.
(24) Le théorème 17.2.1 ne peut pas être utilisé pour démontrer directement le caractère optimal. Néanmoins, il peut
être appliqué au problème équivalent de maximiser ln𝑈. Voir théorème 17.6.6.

185. Chapitre 17 / Optimisation sans contraintes 185
17.3
1. (a) 𝑓 ′
𝑥 = −2𝑥 + 6, 𝑓 ′
𝑦 = −4𝑦 + 8, 𝑓 ′′
𝑥𝑥 = −2, 𝑓 ′′
𝑥𝑦 = 0 et 𝑓 ′′
𝑦𝑦 = −4.
(b) En (3, 2) se produit un maximum local, car 𝐴 = −2 0 et 𝐴𝐶 − 𝐵2 = 8 0. Le
théorème 13.2.1 implique que (3, 2) est un maximum (global).
2. (a) 𝑓 ′
𝑥 = 2𝑥 + 2𝑦2, 𝑓 ′
𝑦 = 4𝑥𝑦 + 4𝑦, 𝑓 ′′
𝑥𝑥 = 2, 𝑓 ′′
𝑥𝑦 = 4𝑦, 𝑓 ′′
𝑦𝑦 = 4𝑥 + 4.
(b) 𝑓 ′
𝑦 = 0 ⇔ 4𝑦 (𝑥 + 1) = 0 ⇔ 𝑥 = −1 ou 𝑦 = 0. Si 𝑥 = −1, alors 𝑓 ′
𝑥 = 0 pour 𝑦 = ±1.
Si 𝑦 = 0, alors 𝑓 ′
𝑥 = 0 pour 𝑥 = 0. La nature de ces trois points critiques est donnée dans
le tableau.
(𝑥, 𝑦) 𝐴 𝐵 𝐶 𝐴𝐶 − 𝐵2 Type de point critique
(0, 0) 2 0 4 8 Minimum local
(−1, 1) 2 4 0 −16 Point-selle
(−1, −1) 2 −4 0 −16 Point-selle
3. (a) Les dérivées partielles premières et secondes de 𝑓 sont 𝑓 ′
𝑥 (𝑥, 𝑦) = (2𝑥 − 𝑎𝑦) 𝑒𝑦,
𝑓 ′
𝑦 (𝑥, 𝑦) = 𝑥 (𝑥 − 𝑎𝑦 − 𝑎) 𝑒𝑦, 𝑓 ′′
𝑥𝑥 (𝑥, 𝑦) = 2𝑒𝑦, 𝑓 ′′
𝑥𝑦 (𝑥, 𝑦) = (2𝑥 − 𝑎𝑦 − 𝑎) 𝑒𝑦 et
𝑓 ′′
𝑦𝑦 (𝑥, 𝑦) = 𝑥 (𝑥 −𝑎𝑦 −2𝑎) 𝑒𝑦. Les points critiques sont les solutions du système des deux
équations (i) 2𝑥 − 𝑎𝑦 = 0; (ii) 𝑥 (𝑥 − 𝑎𝑦 − 𝑎) = 0.Si 𝑥 = 0, alors (i) donne 𝑦 = 0 (car
𝑎 ≠ 0). Si 𝑥 ≠ 0, alors (ii) donne 𝑥 = 𝑎𝑦 + 𝑎, tandis que (i) donne 𝑥 = 1
2 𝑎𝑦. De là, 𝑥 = −𝑎
et 𝑦 = −2.
Conclusion : Il y a deux points critiques, (0, 0) et (−𝑎, −2).
Pour déterminer la nature de chaque point critique (𝑥0, 𝑦0), on utilise le test de la dérivée
seconde avec 𝐴 = 𝑓 ′′
𝑥𝑥 (𝑥0, 𝑦0), 𝐵 = 𝑓 ′′
𝑥𝑦 (𝑥0, 𝑦0), et 𝐶 = 𝑓 ′′
𝑦𝑦 (𝑥0, 𝑦0). Le test donne le
résultat suivant.
Point 𝐴 𝐵 𝐶 𝐴𝐶 − 𝐵2 Résultat
(0, 0) 2 −𝑎 0 −𝑎2 Point-selle
(−𝑎, −2) 2𝑒−2 −𝑎𝑒−2 𝑎2𝑒−2 −𝑎2𝑒−4 Minimum local
(b) Le point critique tel que 𝑥∗ ≠ 0 est (𝑥∗, 𝑦∗) = (−𝑎, −2). En ce point, on a
𝑓 ∗
(𝑎) = 𝑓 (−𝑎, −2) = −𝑎2
𝑒−2
et d 𝑓 ∗
(𝑎)/𝑑𝑎 = −2𝑎𝑒−2
.
Par ailleurs, pour la fonction ˆ
𝑓 (𝑥, 𝑦, 𝑎) = (𝑥2 − 𝑎𝑥𝑦)𝑒𝑦, on a
ˆ
𝑓 ′
𝑎 (𝑥, 𝑦, 𝑎) = −𝑥𝑦𝑒𝑦
et ˆ
𝑓 ′
𝑎 (𝑥∗
, 𝑦∗
, 𝑎) = −𝑥∗
𝑦∗
𝑒𝑦∗
= −2𝑎𝑒−2
.
L’équation ˆ
𝑓 ′
𝑎 (𝑥∗, 𝑦∗, 𝑎) = d 𝑓 ∗(𝑎)/d𝑎 est donc correcte. C’est aussi ce que dit le théorème
de l’enveloppe, voir formule (17.7.3).
4. (a) Dans les trois cas, (0, 0) est un point critique en lequel 𝑧 = 0 et 𝐴 = 𝐵 = 𝐶 = 0, de
sorte que 𝐴𝐶 − 𝐵2 = 0.

186. 186 CORRIGÉS DES EXERCICES
(b) Dans le cas (i), 𝑧 ⩽ 0 pour tout (𝑥, 𝑦), de sorte qu’il y a un maximum à l’origine.
Dans le cas (ii), 𝑧 ⩾ 0 pour tout (𝑥, 𝑦), de sorte qu’il y a un minimum à l’origine. Dans le
cas (iii), 𝑧 prend des valeurs strictement positives et strictement négatives en des points
arbitrairement proches de l’origine, de sorte qu’il y a un point-selle.
5. (a) Il faut 1 + 𝑥2𝑦 0. Quand 𝑥 = 0, 𝑓 (0, 𝑦) = 0. Quand 𝑥 ≠ 0,
1 + 𝑥2
𝑦 0 ⇔ 𝑦 −1/𝑥2
.
La figure montre un morceau de la surface représentative de 𝑓 . Notez que 𝑓 = 0 sur l’axe
𝑂𝑥 et sur l’axe 𝑂𝑦.
(b) 𝑓 ′
𝑥 (𝑥, 𝑦) = 2𝑥𝑦/(1 + 𝑥2
𝑦) et 𝑓 ′
𝑦 (𝑥, 𝑦) = 𝑥2
/(1 + 𝑥2
𝑦). Ici, 𝑓 ′
𝑥 = 𝑓 ′
𝑦 = 0 en tous points
(0, 𝑏) avec 𝑏 ∈ R.
(c) 𝑓 ′′
𝑥𝑥 (𝑥, 𝑦) =
2𝑦 − 2𝑥2𝑦2
(1 + 𝑥2𝑦)2
, 𝑓 ′′
𝑥𝑦 (𝑥, 𝑦) =
2𝑥
(1 + 𝑥2𝑦)2
et 𝑓 ′′
𝑦𝑦 (𝑥, 𝑦) =
−𝑥4
(1 + 𝑥2𝑦)2
.
Les dérivées partielles secondes en tous les points de coordonnées (0, 𝑏) sont
𝑓 ′′
𝑥𝑥 (0, 𝑏) = 2𝑏, 𝑓 ′′
𝑥𝑦 (0, 𝑏) = 0 et 𝑓 ′′
𝑦𝑦 (0, 𝑏) = 0. De là, 𝐴𝐶 − 𝐵2 = 0 en tous les points
critiques. Le test de la dérivée seconde n’est pas concluant.
(d) Notez que 𝑓 (0, 𝑏) = 0 en tout point critique (0, 𝑏). En examinant le signe de
𝑓 (𝑥, 𝑦) = ln(1 + 𝑥2𝑦) au voisinage de chaque point critique, on s’aperçoit que 𝑓 admet
un maximum local quand 𝑏 0; un point-selle quand 𝑏 = 0; et un minimum local quand
𝑏 0. Voir figure C17.3.5.
x
y
z
z = ln(1 + x2
y)
Figure C17.3.5
y
1
2
x
−1 1
y = 2x2
y = x2
y = (k/h)x
Figure C17.3.6
6. (a) 𝑓 (𝑥, 𝑦) = 0 le long de chacune des deux paraboles 𝑦 = 𝑥2 et 𝑦 = 2𝑥2.
(b) Voir figure C17.3.6. Le domaine {(𝑥, 𝑦) ∈ R2 : 𝑥2 𝑦 2𝑥2} sur lequel 𝑓 (𝑥, 𝑦) est
strictement négative est ombré.
(c) 𝑓 ′
1 (𝑥, 𝑦) = 8𝑥3 − 6𝑥𝑦 et 𝑓 ′
2 (𝑥, 𝑦) = 2𝑦 − 3𝑥2. L’origine est le seul point critique, avec
𝑓 (0, 0) = 0. Comme le montre la figure, 𝑓 (𝑥, 𝑦) prend des valeurs strictement positives et
strictement négatives en des points arbitrairement proches de (0, 0), de sorte que l’origine
est un point-selle.
(d) 𝑔(𝑡) = 𝑓 (𝑡ℎ, 𝑡𝑘) = (𝑡𝑘 − 𝑡2ℎ2) (𝑡𝑘 − 2𝑡2ℎ2) = 2ℎ4𝑡4 − 3ℎ2𝑘𝑡3 + 𝑘2𝑡2, de sorte que
𝑔′(𝑡) = 8ℎ4𝑡3 − 9ℎ2𝑘𝑡2 + 2𝑘2𝑡 et 𝑔′′(𝑡) = 24ℎ4𝑡2 − 18ℎ2𝑘𝑡 + 2𝑘2. De là, 𝑔′(0) = 0 et
𝑔′′(0) = 2𝑘2. Pour 𝑘 ≠ 0, il y a donc un minimum local strict en 𝑡 = 0. Pour 𝑘 = 0,
𝑔(𝑡) = 2𝑡4ℎ4 admet aussi un minimum local strict en 𝑡 = 0.

187. Chapitre 17 / Optimisation sans contraintes 187
17.4
1. (a) 𝜋 = 𝑃1𝑄1 +𝑃2𝑄2 −𝐶(𝑄1, 𝑄2) = −2𝑄2
1 −4𝑄2
2 +180𝑄1 +160𝑄2. Cette fonction atteint
un maximum en 𝑄∗
1 = 45, 𝑄∗
2 = 20, avec 𝑃∗
1 = 110, 𝑃∗
2 = 100 et 𝜋∗ = 5 650.
(b) Soit 𝑃 = 𝑃1 = 𝑃2. Alors 𝑄1 = 100 − 1
2 𝑃, 𝑄2 = 45 − 1
4 𝑃, de sorte que le profit
s’exprime en fonction de 𝑃 par
b
𝜋 = (𝑃 − 20) (𝑄1 + 𝑄2) = (𝑃 − 20)
145 −
3
4
𝑃
= −
3
4
𝑃2
+ 160𝑃 − 2 900.
Il est maximal quand 𝑃 = 320/3. Le profit correspondant s’élève à 16 900/3. La diminu-
tion du profit est donc : 5 650 − 16 900/3 = 50/3.
(c) Le nouveau profit est e
𝜋 = −2𝑄2
1−4𝑄2
2+175𝑄1+160𝑄2, avec maximum en 𝑄1 = 43,75,
𝑄2 = 20 et prix 𝑃1 = 112,50 et 𝑃2 = 100. Le profit maximisé est 5 428,125. Le nombre
d’unités vendues sur le marché 1 baisse, le prix monte et les profits sont moindres. Sur le
marché 2, le nombre d’unités vendues et le prix ne varient pas.
2. (a) 𝜋 = −𝛽1𝑃2
1 −𝛽2𝑃2
2 +(𝛼1+𝛿𝛽1)𝑃1+(𝛼2+𝛿𝛽2)𝑃2−𝛾−𝛿 (𝛼1+𝛼2), 𝑃∗
1 = (𝛼1+𝛿𝛽1)/2𝛽1,
𝑃∗
2 = (𝛼2 + 𝛿𝛽2)/2𝛽2. Les conditions du second ordre sont manifestement satisfaites, car
𝜋′′
𝑃1 𝑃1
= −2𝛽1, 𝜋′′
𝑃1 𝑃2
= 0 et 𝜋′′
𝑃2 𝑃2
= −2𝛽2.
(b) La nouvelle fonction de profit est
ˆ
𝜋 = −𝛽1𝑃2
− 𝛽2𝑃2
+ (𝛼1 + 𝛿𝛽1)𝑃 + (𝛼2 + 𝛿𝛽2)𝑃 − 𝛾 − 𝛿 (𝛼1 + 𝛼2)
et il est facile de voir que le prix qui rend le profit maximal est
ˆ
𝑃 =
𝛼1 + 𝛼2 + 𝛿(𝛽1 + 𝛽2)
2 (𝛽1 + 𝛽2)
.
(c) Dans le cas 𝛿 = 0, les réponses à la question (a) se simplifient en
𝑃∗
1 =
𝛼1
2𝛽1
et 𝑃∗
2 =
𝛼2
2𝛽2
et le profit maximal en
𝜋(𝑃∗
1, 𝑃∗
2) =
𝛼2
1
4𝛽1
+
𝛼2
2
4𝛽2
− 𝛼.
Mais, si la discrimination par le prix est interdite, la réponse à la question (b) devient
ˆ
𝑃 =
𝛼2 + 𝛼1
2 (𝛽1 + 𝛽2)
,
avec profit maximal
ˆ
𝜋( ˆ
𝑃1) =
(𝛼1 + 𝛼2)2
4 (𝛽1 + 𝛽2)
− 𝛾.
La perte de profit est donc
𝜋(𝑃∗
1, 𝑃∗
2) − ˆ
𝜋( ˆ
𝑃) =
(𝛼1𝛽2 − 𝛽1𝛼2)2
4𝛽1𝛽2(𝛽1 + 𝛽2)
⩾ 0.
Notez que cette perte est nulle si et seulement si 𝛼1𝛽2 = 𝛽1𝛼2, auquel cas 𝑃∗
1 = 𝑃∗
2 et
l’entreprise va faire payer le même prix sur chaque marché de toute manière.

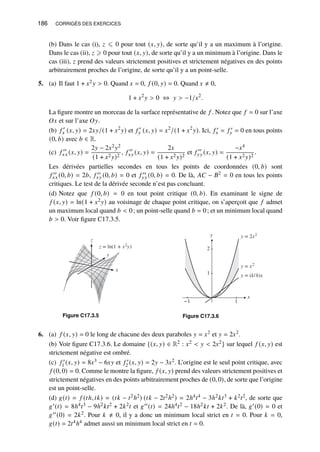
188. 188 CORRIGÉS DES EXERCICES
3. Comme au point (c) de l’exemple 17.4.2, imposer une taxe 𝜏 par unité vendue sur le
marché 1 signifie que la nouvelle fonction de profit est b
𝜋(𝑄1, 𝑄2) = 𝜋(𝑄1, 𝑄2) − 𝜏𝑄1. Le
choix optimal de production sur le marché 1 est alors b
𝑄1 = (𝑎1 −𝛼−𝜏)/2𝑏1 (voir le texte)
et la recette de la taxe est 𝑇(𝜏) = 𝜏(𝑎1 −𝛼−𝜏)/2𝑏1 = [𝜏(𝑎1 −𝛼)−𝜏2]/2𝑏1. Cette fonction
du second degré atteint un maximum quand 𝑇′(𝜏) = 0, de sorte que 𝜏 = 1
2 (𝑎1 − 𝛼).
4. (a) Les quatre points donnés sont (𝑥0, 𝑦0) = (0 ; 11,29), (𝑥1, 𝑦1) = (1 ; 11,40),
(𝑥2, 𝑦2) = (2 ; 11,49) et (𝑥3, 𝑦3) = (3 ; 11,61), où 𝑥0 correspond à 1970, etc.(25). En
mettant en application la méthode des moindres carrés expliquée à l’exemple 17.4.4, on
trouve
𝜇𝑥 = 1
4 (0 + 1 + 2 + 3) = 1,5, 𝜇𝑦 = 1
4 (11,29 + 11,40 + 11,49 + 11,61) = 11,45,
𝜎𝑥𝑥 = 1
4 [(0 − 1,5)2 + (1 − 1,5)2 + (2 − 1,5)2 + (3 − 1,5)2] = 1,25.
De plus, 𝜎𝑥𝑦 =1
4 [(−1,5) (11,29 − 11,45) + (−0,5) (11,40 − 11,45)
+ (0,5) (11,49 − 11,45) + (1,5) (11,61 − 11,45)]
qui est égal à 0,13125. La formule (∗∗) mène à
ˆ
𝑎 = 𝜎𝑥𝑦/𝜎𝑥𝑥 = 0,105 et ˆ
𝑏 = 𝜇𝑦 − ˆ
𝑎𝜇𝑥 ≈ 11,45 − 0,105 × 1,5 = 11,29.
(b) Avec 𝑧0 = ln 274, 𝑧1 = ln 307, 𝑧2 = ln 436 et 𝑧3 = ln 524, les quatre points donnés
sont (𝑥0, 𝑧0) = (0 ; 5,61), (𝑥1, 𝑧1) = (1 ; 5,73), (𝑥2, 𝑧2) = (2 ; 6,08) et (𝑥3, 𝑧3) = (3 ; 6,26).
Comme précédemment, 𝜇𝑥 = 1,5 et 𝜎𝑥𝑥 = 1,25. De plus,
𝜇𝑧 = 1
4 (5,61 + 5,73 + 6,08 + 6,26) = 5,92
et 𝜎𝑥𝑧 ≈1
4 [(−1,5) (5,61 − 5,92) + (−0,5) (5,73 − 5,92) + (0,5) (6,08 − 5,92)
+ (1,5) (6,26 − 5,92)] = 0,2875.
De là, ˆ
𝑐 = 𝜎𝑥𝑧/𝜎𝑥𝑥 = 0,23, ˆ
𝑑 = 𝜇𝑧 − ˆ
𝑐𝜇𝑥 = 5,92 − 0,23 × 1,5 = 5,575.
(c) Si les tendances ln(PIB) = 𝑎𝑥 + 𝑏 et ln(FA) = 𝑐𝑥 + 𝑑 se sont poursuivies, alors AE
atteint 1 % du PNB en un temps 𝑥 solution de ln(AE/PNB) = ln 0,01 ou
(𝑐 − 𝑎) 𝑥 + 𝑑 − 𝑏 = ln 0,01.
D’où 𝑥 = (𝑏 − 𝑑 + ln 0,01)/(𝑐 − 𝑎). En introduisant ces estimations dans les résultats des
parties (a) et (b), on obtient
𝑥 ≈ (11,29 − 5,575 − 4,605)/(0,23 − 0,105) = 1,11/0,125 = 8,88.
Le but aurait été atteint à la fin de 1978.
5. (a) Le profit cumulé des deux firmes est 𝑝𝑥 + 𝑞𝑦 − (5 + 𝑥) − (3 + 2𝑦), ou, en remplaçant
𝑥 et 𝑦 par leurs expressions, (𝑝 − 1) (29 − 5𝑝 + 4𝑞) + (𝑞 − 2) (16 + 4𝑝 − 6𝑞) − 8. Après
simplification, 26𝑝 + 24𝑞 − 5𝑝2 − 6𝑞2 + 8𝑝𝑞 − 69. C’est une fonction concave de 𝑝
et 𝑞. Les conditions du premier ordre sont les deux équations 26 − 10𝑝 + 8𝑞 = 0 et
(25) Les 𝑦𝑡 sont des valeurs approchées comme d’ailleurs tous les autres résultats.

189. Chapitre 17 / Optimisation sans contraintes 189
24 − 12𝑞 + 8𝑝 = 0. Leur unique solution est 𝑝 = 9, 𝑞 = 8, qui fournit un maximum. Les
niveaux de production correspondants sont 𝑥 = 16 et 𝑦 = 4. Le profit de la firme 𝐴 est
123 et celui de la firme 𝐵 est 21.
(b) Le profit de la firme 𝐴 est maintenant donné par
𝜋𝐴(𝑝) = (𝑝 − 1) (29 − 5𝑝 + 4𝑞) − 5 = 34𝑝 − 5𝑝2
+ 4𝑝𝑞 − 4𝑞 − 34,
avec 𝑞 fixé. Ce polynôme du second degré atteint sa plus grande valeur en
𝑝 = 𝑝𝐴(𝑞) =
1
5
(2𝑞 + 17).
De même, le profit de la firme 𝐵 est 𝜋𝐵 (𝑞) = 𝑞𝑦 − 3 − 2𝑦 = 28𝑞 − 6𝑞2 + 4𝑝𝑞 − 8𝑝 − 35,
avec 𝑝 fixé. Ce polynôme du second degré atteint sa plus grande valeur en
𝑞 = 𝑞𝐵 (𝑝) =
1
3
(𝑝 + 7).
(c) L’équilibre a lieu lorsque (𝑝, 𝑞) satisfait simultanément aux deux équations
𝑝 = 𝑝𝐴(𝑞) = 1
5 (2𝑞 + 17) et 𝑞 = 𝑞𝐵 (𝑝) = 1
3 (𝑝 + 7). Après substitution de la deuxième
équation dans la première 𝑝 = 1
5
21
3 (𝑝 + 7) + 17
ou, après élimination des fractions,
15𝑝 = 2𝑝 + 14 + 51. Les prix sont donc respectivement 𝑝 = 5 et 𝑞 = 4, les niveaux de
production 𝑥 = 20, 𝑦 = 12, et les profits 75 pour 𝐴 et 21 pour 𝐵.
(d) Au départ du point de coordonnées (9, 8), la firme 𝐴 se déplace d’abord vers
𝑝𝐴(8) = 33/5 = 6,6, alors la firme 𝐵 répond en se déplaçant en
𝑞𝐵 (6,6) = 13,6/3 ≈ 4,53,
ensuite la firme 𝐴 répond en se déplaçant près de 𝑝𝐴(4,53) = 26,06/5 = 5,212, etc. Après
le premier mouvement horizontal au départ de (9, 8), le processus se poursuit par des
mouvements alternés verticaux vers le bas depuis la courbe 𝑝 = 𝑝𝐴(𝑞), et horizontaux
depuis la courbe 𝑞 = 𝑞𝐵 (𝑝), comme le montre la figure C17.4.5. Ces mouvements ne
traversent jamais les courbes et à la limite, le processus converge vers le point d’équilibre
(5, 4) déterminé dans la question (c).
q
2
4
6
8
10
p
2 6
4 8 10 12 14
(5, 4)
q = qB (p)
p = pA(q)
(9, 8)
Figure C17.4.5

190. 190 CORRIGÉS DES EXERCICES
17.5
1. (a) 𝑓 ′
𝑥 (𝑥, 𝑦) = 4−4𝑥 et 𝑓 ′
𝑦 (𝑥, 𝑦) = −4𝑦. Le seul point critique est (1, 0), avec 𝑓 (1, 0) = 2.
(b) 𝑓 (𝑥, 𝑦) atteint le maximum 2 en (1, 0) et le minimum −70 en (−5, 0). (L’existence
d’un maximum et d’un minimum est assurée par le théorème des bornes atteintes. Le
long de la frontière, la fonction vaut 4𝑥 − 50, avec 𝑥 ∈ [−5, 5]. Son maximum est −30 en
𝑥 = 5 et son minimum, −70 en 𝑥 = −5.)
2. (a) Comme la fonction continue 𝑓 est définie sur l’ensemble borné et fermé 𝑆 (voir la
figure C17.5.2), le théorème des bornes atteintes assure l’existence d’un maximum et
d’un minimum pour 𝑓 sur 𝑆.
y
x
4
4
(3, 3)
(III)
(II)
(IV)
(I)
Figure C17.5.2
y
3
x
5
S
0
IV
(4,3) III (5,3)
II
I
V
Figure C17.5.3
Les points critiques sont les solutions de
(𝑖) 𝑓 ′
𝑥 (𝑥, 𝑦) = 3𝑥2
− 9𝑦 = 0 et (𝑖𝑖) 𝑓 ′
𝑦 (𝑥, 𝑦) = 3𝑦2
− 9𝑥 = 0.
De (i), 𝑦 = 1
3 𝑥2, expression que l’on introduit dans (ii) 1
3 𝑥 (𝑥3 − 27) = 0. Les
seules solutions sont 𝑥 = 0 et 𝑥 = 3. Le seul point critique intérieur à 𝑆 est donc
(𝑥, 𝑦) = (3, 3). On continue en examinant le comportement de 𝑓 (𝑥, 𝑦) sur la frontière
de 𝑆, plus précisément le long des quatre côtés de 𝑆.
(I) 𝑦 = 0, 𝑥 ∈ [0, 4]. Alors 𝑓 (𝑥, 0) = 𝑥3 + 27, qui a un minimum en 𝑥 = 0 et un maximum
en 𝑥 = 4.
(II) 𝑥 = 4, 𝑦 ∈ [0, 4]. Alors 𝑓 (4, 𝑦) = 𝑦3 − 36𝑦 + 91. La fonction 𝑔(𝑦) = 𝑦3 − 36𝑦 + 91,
𝑦 ∈ [0, 4] est telle que 𝑔′(𝑦) = 3𝑦2 −36 = 0 en 𝑦 =
√
12. Les éventuelles valeurs extrêmes
dans le cas (II) sont en (4, 0), (4,
√
12) et (4, 4).
(III) 𝑦 = 4, 𝑥 ∈ [0, 4]. Alors 𝑓 (𝑥, 4) = 𝑥3 − 36𝑥 + 91 et, comme en (II), les éventuelles
valeurs extrêmes sont en (0, 4), (
√
12, 4) et (4, 4).
(IV) 𝑥 = 0, 𝑦 ∈ [0, 4]. Comme dans le cas (I), les éventuelles valeurs extrêmes sont en
(0, 0) et (0, 4).
Finalement, six candidats en lesquels la fonction vaut 𝑓 (3, 3) = 0, 𝑓 (0, 0) = 27,
𝑓 (4, 0) = 𝑓 (0, 4) = 91, 𝑓 (4,
√
12) = 𝑓 (
√
12, 4) = 91 − 24
√
12 ≈ 7,86. La conclusion est
aisée : maximum 91 en (0, 4) et en (4, 0), minimum 0 en (3, 3).
(b) L’ensemble 𝑆 =
(𝑥, 𝑦) : 𝑥2 + 𝑦2 ⩽ 1 considéré se compose de tous les points
situés à l’intérieur ou sur la frontière du cercle centré sur l’origine et de rayon 1. C’est un

191. Chapitre 17 / Optimisation sans contraintes 191
ensemble borné et fermé et 𝑓 (𝑥, 𝑦) = 𝑥2 + 2𝑦2 − 𝑥 est une fonction continue. Le théorème
des bornes atteintes assure l’existence d’un maximum et d’un minimum pour 𝑓 sur 𝑆.
Les points critiques pour 𝑓 se produisent là où 𝑓 ′
𝑥 (𝑥, 𝑦) = 2𝑥−1 = 0 et 𝑓 ′
𝑦 (𝑥, 𝑦) = 4𝑦 = 0.
La seule solution est (𝑥1, 𝑦1) = (1/2, 0), point intérieur de 𝑆.
Une valeur extrême qui ne se produit pas en un point intérieur doit se produire sur la
frontière de 𝑆, à savoir 𝑥2 + 𝑦2 = 1. Sur ce cercle, 𝑦2 = 1 − 𝑥2 et donc les valeurs prises
par la fonction sont
𝑓 (𝑥, 𝑦) = 𝑥2
+ 2𝑦2
− 𝑥 = 𝑥2
+ 2 (1 − 𝑥2
) − 𝑥 = 2 − 𝑥 − 𝑥2
où 𝑥 parcourt l’intervalle [−1, 1](26). La fonction 𝑔(𝑥) = 2 − 𝑥 − 𝑥2 admet un point
critique intérieur à [−1, 1], à savoir 𝑥 = −1/2. Les valeurs extrêmes de 𝑔(𝑥) se produisent
forcément soit en cette valeur de 𝑥, soit en l’une ou l’autre des extrémités ±1 de l’intervalle
[−1, 1]. Les valeurs extrêmes de 𝑓 (𝑥, 𝑦) sur la frontière de 𝑆 se produisent parmi les points
(𝑥2, 𝑦2) = (−1
2 , 1
2
√
3), (𝑥3, 𝑦3) = (−1
2 , −1
2
√
3), (𝑥4, 𝑦4) = (1, 0), (𝑥5, 𝑦5) = (−1, 0).
Or, 𝑓 ( 1
2 , 0) = −1
4 , 𝑓 (−1
2 , ±1
2
√
3) = 9
4 , 𝑓 (1, 0) = 0 et 𝑓 (−1, 0) = 2. Conclusion : maximum
9/4 en (−1/2,
√
3/2) et en (−1/2, −
√
3/2), minimum −1/4 en (1/2, 0).
3. L’ensemble 𝑆 apparaît à la figure C17.5.3. Comme il est borné et fermé et comme la
fonction 𝑓 est continue, il y a un maximum sur 𝑆. Les points critiques ont comme
coordonnées les solutions du système d’équations 𝜕 𝑓 /𝜕𝑥 = 9 − 12 (𝑥 + 𝑦) = 0 et
𝜕 𝑓 /𝜕𝑦 = 8 − 12 (𝑥 + 𝑦) = 0. Mais les équations 12 (𝑥 + 𝑦) = 9 et 12 (𝑥 + 𝑦) = 8
sont contradictoires. Ce système n’a pas de solution. La valeur maximale de 𝑓 se produit
sur la frontière de 𝑆, composée de 5 côtés. De deux choses l’une, le maximum se produit
ou en l’un des 5 sommets ou en un point intérieur des 5 arêtes. Aux sommets, la fonc-
tion prend les valeurs 𝑓 (0, 0) = 0, 𝑓 (5, 0) = −105, 𝑓 (5, 3) = −315, 𝑓 (4, 3) = −234 et
𝑓 (0, 1) = 2.
On examine maintenant le comportement de 𝑓 le long des 5 arêtes.
(I) 𝑦 = 0, 𝑥 ∈]0, 5[. Le comportement de 𝑓 est celui de la fonction
𝑔1 (𝑥) = 𝑓 (𝑥, 0) = 9𝑥 − 6𝑥2
pour 𝑥 ∈]0, 5[. Si cette fonction admet un maximum sur ]0, 5[, il doit se produire en un
point critique dont l’abscisse est la solution de 𝑔′
1(𝑥) = 9 − 12𝑥 = 0 ou 𝑥 = 3/4. On
calcule 𝑔1 (3/4) = 𝑓 (3/4, 0) = 27/8.
(II) 𝑥 = 5, 𝑦 ∈]0, 3[. On définit 𝑔2 (𝑦) = 𝑓 (5, 𝑦) = 45 + 8𝑦 − 6 (5 + 𝑦)2 pour 𝑦 ∈]0, 3[.
Ici, 𝑔′
2(𝑦) = −52 − 12𝑦, toujours strictement négatif sur ]0, 3[. Il n’y a donc pas de points
critiques sur cette arête.
(III) 𝑦 = 3, 𝑥 ∈]4, 5[. On définit 𝑔3 (𝑥) = 𝑓 (𝑥, 3) = 9𝑥 + 24 − 6 (𝑥 + 3)2 pour 𝑥 ∈]4, 5[.
Ici, 𝑔′
3(𝑥) = −27 − 12𝑥, toujours strictement négatif sur ]4, 5[. Il n’y a donc pas de points
critiques sur cette arête.
(26) Il est fréquent d’oublier cette restriction.

192. 192 CORRIGÉS DES EXERCICES
(IV) −𝑥 + 2𝑦 = 2 ou 𝑦 = 𝑥/2 + 1, avec 𝑥 ∈]0, 4[. On définit
𝑔4 (𝑥) = 𝑓 (𝑥, 𝑥/2 + 1) = −27𝑥2
/2 − 5𝑥 + 2
pour 𝑥 ∈]0, 4[. Ici, 𝑔′
4 (𝑥) = −27𝑥 −5, toujours strictement négatif sur ]0, 4[. Il n’y a donc
pas de points critiques sur cette arête.
(V) 𝑥 = 0, 𝑦 ∈]0, 1[. On définit 𝑔5 (𝑦) = 𝑓 (0, 𝑦) = 8𝑦 − 6𝑦2. Alors 𝑔′
5 (𝑦) = 8 − 12𝑦 = 0
en 𝑦 = 2/3 et 𝑔5 (2/3) = 𝑓 (0, 2/3) = 8/3.
Après avoir comparé les valeurs prises par 𝑓 aux 5 sommets de la frontière et aux 2 points
des arêtes notées (I) et (V) respectivement, on conclut que le maximum de 𝑓 se produit
en (3/4, 0) et vaut 27/8.
4. (a) Les conditions du premier ordre 2𝑎𝑥𝑦+𝑏𝑦+2𝑦2 = 0 et 𝑎𝑥2 +𝑏𝑥+4𝑥𝑦 = 0 doivent avoir
(𝑥, 𝑦) = (2/3, 1/3) comme solution. Aussi, 𝑎 = 1 et 𝑏 = −2. De plus, 𝑐 = 1/27, de sorte
que 𝑓 (2/3, 1/3) = −1/9. Comme 𝐴 = 𝑓 ′′
𝑥𝑥 (2/3, 1/3) = 2/3, 𝐵 = 𝑓 ′′
𝑥𝑦 (2/3, 1/3) = 2/3 et
𝐶 = 𝑓 ′′
𝑦𝑦 (2/3, 1/3) = 8/3, le théorème 13.3.1 montre qu’il s’agit d’un minimum.
(b) Maximum 193/27 en (2/3, 8/3). Minimum −1/9 en (2/3, 1/3).
5. (a) D’abord, 𝑓 ′
𝑥 (𝑥, 𝑦) = 𝑒−𝑥 (1 − 𝑥) (𝑦 − 4) 𝑦 = 0 quand 𝑥 = 1 ou 𝑦 = 0 ou 𝑦 = 4. Ensuite,
𝑓 ′
𝑦 (𝑥, 𝑦) = 2𝑥𝑒−𝑥 (𝑦 − 2) = 0 quand 𝑥 = 0 ou 𝑦 = 2. Les points critiques sont (1, 2), (0, 0)
et (0, 4).
De plus,
𝑓 ′′
𝑥𝑥 (𝑥, 𝑦) = 𝑒−𝑥
(𝑥 − 2) (𝑦2
− 4𝑦), 𝑓 ′′
𝑥𝑦 (𝑥, 𝑦) = 𝑒−𝑥
(1 − 𝑥) (2𝑦 − 4) et 𝑓 ′′
𝑦𝑦 = 2𝑥𝑒−𝑥
.
Voici la nature des points critiques.
(𝑥, 𝑦) 𝐴 𝐵 𝐶 𝐴𝐶 − 𝐵2 Type de point
(1, 2) 4𝑒−2 0 𝑎2𝑒−1 8𝑒−2 Minimum local
(0, 0) −4 0 −16 Point-selle
(0, 4) 0 4 0 −16 Point-selle
(b) L’ensemble image de 𝑓 n’est borné ni supérieurement, ni inférieurement. Il n’y a
pas de maximum global, car 𝑓 (1, 𝑦) = 𝑒−1(𝑦2 − 4𝑦) → +∞ lorsque 𝑦 → +∞. Il n’y
a pas de minimum global, car 𝑓 (−1, 𝑦) = −𝑒(𝑦2 − 4𝑦) tend vers −∞ lorsque 𝑦 → +∞.
(c) L’ensemble 𝑆 est manifestement borné. La frontière de 𝑆 se compose des quatre côtés
d’un rectangle et les points de ces côtés appartiennent à 𝑆. Donc 𝑆 est fermé. Comme
𝑓 est continue, le théorème des bornes atteintes garantit l’existence d’un maximum et
d’un minimum global de 𝑓 sur 𝑆. Le seul point critique de 𝑓 intérieur à 𝑆 est celui de
coordonnées (1, 2). La fonction y prend la valeur 𝑓 (1, 2) = −4𝑒−1 ≈ −1,4715. Les quatre
côtés sont examinés séparément (voir figure 17.5.5).
(i) Le long de (I), 𝑦 = 0 et 𝑓 (𝑥, 𝑦) = 𝑓 (𝑥, 0) est identiquement nulle.
(ii) Le long de (II), 𝑥 = 5 et 𝑓 (𝑥, 𝑦) = 5𝑒−5(𝑦2 − 4𝑦) pour 𝑦 ∈ [0, 4]. Sa plus petite
valeur est atteinte en 𝑦 = 2 et sa plus grande valeur en 𝑦 = 0 et en 𝑦 = 4. Les valeurs de
la fonction sont 𝑓 (5, 2) = −20𝑒−5 ≈ −0,1348 et 𝑓 (5, 0) = 𝑓 (5, 4) = 0.

193. Chapitre 17 / Optimisation sans contraintes 193
(iii) Le long de (III), 𝑦 = 4 et 𝑓 (𝑥, 𝑦) = 𝑓 (𝑥, 4) = 0.
(iv) Enfin, le long de (IV), 𝑥 = 0 et 𝑓 (𝑥, 𝑦) = 𝑓 (0, 𝑦) = 0. En résumé, 𝑓 atteint sa plus
petite valeur −4𝑒−1 sur 𝑆 au point de coordonnées (1, 2) et sa plus grande valeur 0 en
tous les points des segments (I), (III) et (IV).
(d) 𝑦′
= −
𝑓 ′
𝑥 (𝑥, 𝑦)
𝑓 ′
𝑦 (𝑥, 𝑦)
= −
𝑒−𝑥 (1 − 𝑥) (𝑦 − 4) 𝑦
2𝑥𝑒−𝑥 (𝑦 − 2)
=
(𝑥 − 1) (𝑦 − 4) 𝑦
2𝑥 (𝑦 − 2)
= 0 quand 𝑥 = 1 et
𝑦 = 4 − 𝑒.
x
y
5
4
(1, 2)
(I)
(II)
(III)
(IV)
Figure C17.5.5
6. (a) Fermé et borné, donc compact. (b) Ouvert et non borné. (c) Fermé et borné,
donc compact. (d) Fermé et non borné. (e) Fermé et non borné. (f) Ouvert et non
borné.
7. Soit 𝑔(𝑥) = 1 sur [0, 1[, 𝑔(𝑥) = 2 sur [1, 2]. Alors 𝑔 présente une discontinuité en 𝑥 = 1
et l’ensemble {𝑥 : 𝑔(𝑥) ⩽ 1} = [0, 1[ n’est pas fermé. (Tracez vous-même le graphique
de 𝑔.)
17.6
1. (a) Les conditions du premier ordre 𝑓 ′
𝑥 (𝑥, 𝑦, 𝑧) = 2 − 2𝑥 = 0, 𝑓 ′
𝑦 (𝑥, 𝑦, 𝑧) = 10 − 2𝑦 = 0 et
𝑓 ′
𝑧 (𝑥, 𝑦, 𝑧) = −2𝑧 = 0 ont une solution unique (𝑥, 𝑦, 𝑧) = (1, 5, 0), en laquelle la fonction
doit admettre un maximum.
(b) Les conditions du premier ordre sont 𝑓 ′
𝑥 (𝑥, 𝑦, 𝑧) = −2𝑥 − 2𝑦 − 2𝑧 = 0,
𝑓 ′
𝑦 (𝑥, 𝑦, 𝑧) = −4𝑦 − 2𝑥 = 0, 𝑓 ′
𝑧 (𝑥, 𝑦, 𝑧) = −6𝑧 − 2𝑥 = 0. Des deux dernières équa-
tions, on tire 𝑦 = −1
2 𝑥 et 𝑧 = −1
3 𝑥. En substituant dans la première équation, on obtient
−2𝑥 + 𝑥 + 2
3 𝑥 = 0, et donc 𝑥 = 0, impliquant 𝑦 = 𝑧 = 0. Ainsi (𝑥, 𝑦, 𝑧) = (0, 0, 0) est le
point en lequel se produit le maximum.
2. (a) 𝑓 (𝑥) = 𝑒−𝑥2
et 𝑔(𝑥) = 𝐹( 𝑓 (𝑥)) = ln(𝑒−𝑥2
) = −𝑥2 ont un unique maximum en 𝑥 = 0.
(b) Seul 𝑥 = 0 maximise 𝑓 (𝑥). Mais 𝑔(𝑥) = 5 est maximale en tout point 𝑥 puisqu’elle
est constante.
3. Selon la règle de dérivation des fonctions composées, 𝑔′
𝑥𝑖
(x) = 𝐹′( 𝑓 (x)) 𝑓 ′
𝑥𝑖
(x) pour
𝑖 = 1, 2, . . . , 𝑛. Comme 𝐹′ ≠ 0 partout, la proposition est démontrée.

194. 194 CORRIGÉS DES EXERCICES
4. Calculer 𝑓 ′
𝑥 n’a rien de compliqué. La dérivée de
∫ 𝑧
𝑦
𝑒𝑡2
d𝑡 par rapport à 𝑦, en tenant 𝑧
constant, s’obtient en utilisant (10.3.7) : elle est égale à −𝑒𝑦2
. La dérivée de
∫ 𝑧
𝑦
𝑒𝑡2
d𝑡 par
rapport à 𝑧, en tenant 𝑦 constant, s’obtient en utilisant (10.3.6) : elle est égale à 𝑒𝑧2
.
D’où 𝑓 ′
𝑦 = 2 − 𝑒𝑦2
et 𝑓 ′
𝑧 = −3 + 𝑒𝑧2
. Puisque chacune des trois dérivées partielles ne
dépend que d’une variable et s’annule pour des valeurs différentes de cette variable, il y
a 8 points critiques qui sont
(𝑥, 𝑦, 𝑧) = (3, ±
√
ln 2, ±
√
ln 3 ) et (𝑥, 𝑦, 𝑧) = (2, ±
√
ln 2, ±
√
ln 3 ),
où toutes les combinaisons de signes sont permises.
5. (a) Comme 𝐹(𝑢) = 1
2 (𝑒𝑢 − 𝑒−𝑢) est strictement croissante, le problème est équivalent à
max 𝑥2 + 𝑦2 − 2𝑥 sous la condition (𝑥, 𝑦) ∈ 𝑆.
(b) ln 𝑢 est strictement croissant pour 𝑢 0. Le problème est donc équivalent à
max ln 𝐴 + 𝑎1 ln 𝑥1 + · · · + 𝑎𝑛 ln 𝑥𝑛
sous la condition 𝑥1 + · · · + 𝑥𝑛 = 1.
17.7
1. (a) Le profit 𝜋 = 𝑝𝑥 − 𝑎𝑥 − 𝑏𝑥2 − 𝑡𝑥 admet un maximum en 𝑥∗ = (𝑝 − 𝑎 − 𝑡)/2𝑏, avec
𝜋∗ = (𝑝 − 𝑎 − 𝑡)2/4𝑏.
(b) 𝜕𝜋∗/𝜕𝑝 = 2 (𝑝 −𝑎 −𝑡)/4𝑏 = 𝑥∗. Si on augmente 𝑝 de d𝑝 dollar, avec d𝑝 petit, alors le
profit optimal augmente approximativement de 𝑥∗ d𝑝 dollars. (Pour chacune des 𝑥∗ unités
vendues, la recette s’accroît de d𝑝 dollar.)
2. (a) La fonction de profit est 𝜋 = 𝜋(𝐿, 𝑃, 𝑤) = 𝑃
√
𝐿 −𝑤𝐿. La valeur de 𝐿 qui maximise le
profit doit satisfaire à 𝜋′
𝐿 (𝐿, 𝑃, 𝑤) = 𝑃/2
√
𝐿−𝑤 = 0, ce qui donne 𝐿 = (𝑃/2𝑤)2. Comme
𝜋′′
𝐿𝐿 = −𝑃/4𝐿3/2 0 pour tout 𝐿, le profit est maximal en 𝐿 = 𝐿∗(𝑃, 𝑤) = (𝑃/2𝑤)2.
(b) La fonction de valeur est
𝜋∗
(𝑃, 𝑤) = 𝜋(𝐿∗
, 𝑃, 𝑤) = 𝑃
√
𝐿∗ − 𝑤𝐿∗
= 𝑃(𝑃/2𝑤) − 𝑤(𝑃/2𝑤)2
= 𝑃2
/4𝑤.
Alors 𝜕𝜋∗/𝜕𝑃 = 𝑃/2𝑤 =
√
𝐿∗ = 𝜋′
𝑃 (𝐿∗, 𝑃, 𝑤). Enfin,
𝜕𝜋∗
/𝜕𝑤 = −𝑃2
/4𝑤2
= −𝐿∗
= 𝜋′
𝑤 (𝐿∗
, 𝑃, 𝑤).
Le théorème de l’enveloppe est donc confirmé dans cet exemple.
3. (a) 𝜋 = 𝑝(𝐾2/3 + 𝐿1/2 +𝑇1/3) −𝑟𝐾 − 𝑤𝐿 − 𝑞 et 𝐾∗ = 8
27 𝑝3𝑟−3. Les conditions du premier
ordre pour un maximum sont
𝜋′
𝐾 =
2
3
𝑝𝐾−1/3
− 𝑟 = 0, 𝜋′
𝐿 =
1
2
𝑝𝐿−1/2
− 𝑤 = 0, 𝜋′
𝑇 =
1
3
𝑝𝑇−2/3
− 𝑞 = 0.
D’où 𝐾−1/3 = 3𝑟/2𝑝, 𝐿−1/2 = 2𝑤/𝑝 et 𝑇−2/3 = 3𝑞/𝑝. En élevant chaque membre de
𝐾−1/3 = 3𝑟/2𝑝 à la puissance −3, on obtient
𝐾∗
= (3𝑟/2𝑝)−3
= (2𝑝/3𝑟)3
= (8/27)𝑝3
𝑟−3
.
De même, on trouve 𝐿∗ = 1
4 𝑝2𝑤−2, 𝑇∗ = 1
3
√
3
𝑝3/2𝑞−3/2.

195. Chapitre 17 / Optimisation sans contraintes 195
(b) 𝑄∗ = 4
9 𝑝2𝑟−2 + 1
2 𝑝𝑤−1 + 1
√
3
𝑝1/2𝑞−1/2, de sorte que
𝜕𝑄∗
/𝜕𝑟 = −
8
9
𝑝2
𝑟−3
= −𝜕𝐾∗
/𝜕𝑝.
4. 𝜕𝑄∗/𝜕𝑟 = (𝜕/𝜕𝑟) (𝜕 ˆ
𝜋∗/𝜕𝑝) = (𝜕/𝜕𝑝) (𝜕 ˆ
𝜋∗/𝜕𝑟) = (𝜕/𝜕𝑝) (−𝐾∗) = −𝜕𝐾∗/𝜕𝑝. Les
autres égalités se démontrent de la même manière.
5. (a) On prend la différentielle de 𝑝𝐹′
𝐾 (𝐾∗, 𝐿∗) = 𝑟 sans oublier la règle de dérivation du
produit
𝐹′
𝐾 (𝐾∗
, 𝐿∗
) d𝑝 + 𝑝 d(𝐹′
𝐾 (𝐾∗
, 𝐿∗
)) = d𝑟
où 𝑟 est le coût unitaire du capital. Ensuite, d(𝐹′
𝐾 (𝐾∗, 𝐿∗)) = 𝐹′′
𝐾 𝐾 (𝐾∗, 𝐿∗) d𝐾∗ +
𝐹′′
𝐾 𝐿 (𝐾∗, 𝐿∗) d𝐿∗(27). Cela explique la première des deux équations (en remplaçant d𝐾
par d𝐾∗ et d𝐿 par d𝐿∗). La deuxième s’obtient de la même manière.
(b) On arrange le système d’équations en plaçant les différentielles des variables exogènes
𝑝, 𝑟 et 𝑤 dans le membre de droite et en omettant d’indiquer que les dérivées partielles
sont calculées en (𝐾∗, 𝐿∗).
𝑝𝐹′′
𝐾 𝐾 d𝐾∗
+ 𝑝𝐹′′
𝐾 𝐿 d𝐿∗
= d𝑟 − 𝐹′
𝐾 d𝑝
𝑝𝐹′′
𝐿𝐾 d𝐾∗
+ 𝑝𝐹′′
𝐿𝐿 d𝐿∗
= d𝑤 − 𝐹′
𝐿 d𝑝
Poser Δ = 𝐹′′
𝐾 𝐾 𝐹′′
𝐿𝐿 − 𝐹′′
𝐾 𝐿 𝐹′′
𝐿𝐾 = 𝐹′′
𝐾 𝐾 𝐹′′
𝐿𝐿 − (𝐹′′
𝐾 𝐿)2. Ensuite, grâce à (3.6.4) et après
simplification par 𝑝, on obtient
d𝐾∗
=
−𝐹′
𝐾 𝐹′′
𝐿𝐿 + 𝐹′
𝐿 𝐹′′
𝐾 𝐿
𝑝Δ
d𝑝 +
𝐹′′
𝐿𝐿
𝑝Δ
d𝑟 +
−𝐹′′
𝐾 𝐿
𝑝Δ
d𝑤.
De la même manière,
d𝐿∗
=
−𝐹′
𝐿 𝐹′′
𝐾 𝐾 + 𝐹′
𝐾 𝐹′′
𝐿𝐾
𝑝Δ
d𝑝 +
−𝐹′′
𝐿𝐾
𝑝Δ
d𝑟 +
𝐹′′
𝐾 𝐾
𝑝Δ
d𝑤.
On peut maintenant lire les dérivées partielles demandées.
𝜕𝐾∗
𝜕𝑝
=
−𝐹′
𝐾 𝐹′′
𝐿𝐿 + 𝐹′
𝐿 𝐹′′
𝐾 𝐿
𝑝(𝐹′′
𝐾 𝐾 𝐹′′
𝐿𝐿 − (𝐹′′
𝐾 𝐿)2)
,
𝜕𝐿∗
𝜕𝑝
=
−𝐹′
𝐿 𝐹′′
𝐾 𝐾 + 𝐹′
𝐾 𝐹′′
𝐿𝐾
𝑝(𝐹′′
𝐾 𝐾 𝐹′′
𝐿𝐿 − (𝐹′′
𝐾 𝐿)2)
,
𝜕𝐾∗
𝜕𝑟
=
𝐹′′
𝐿𝐿
𝑝(𝐹′′
𝐾 𝐾 𝐹′′
𝐿𝐿 − (𝐹′′
𝐾 𝐿)2)
,
𝜕𝐿∗
𝜕𝑟
=
−𝐹′′
𝐿𝐾
𝑝(𝐹′′
𝐾 𝐾 𝐹′′
𝐿𝐿 − (𝐹′′
𝐾 𝐿)2)
,
𝜕𝐾∗
𝜕𝑤
=
−𝐹′′
𝐾 𝐿
𝑝(𝐹′′
𝐾 𝐾 𝐹′′
𝐿𝐿 − (𝐹′′
𝐾 𝐿)2)
,
𝜕𝐿∗
𝜕𝑤
=
𝐹′′
𝐾 𝐾
𝑝(𝐹′′
𝐾 𝐾 𝐹′′
𝐿𝐿 − (𝐹′′
𝐾 𝐿)2)
.
(c) Les conditions du second ordre suffisantes pour qu’il y ait un maximum local strict
entraînent que 𝐹′′
𝐾 𝐾 0, 𝐹′′
𝐿𝐿 0 et 𝐹′′
𝐾 𝐾 𝐹′′
𝐿𝐿 (𝐹′′
𝐾 𝐿)2) 0. Il s’ensuit que 𝜕𝐾∗/𝜕𝑟 et
𝜕𝐿∗/𝜕𝑤 sont tous deux strictement négatifs. Comme nous n’avons pas d’information sur
le signe de 𝐹′′
𝐾 𝐿, les signes des autres dérivées partielles restent indéterminés. Comme
𝐹′′
𝐾 𝐿 = 𝐹′′
𝐿𝐾 , on observe que 𝜕𝐾∗/𝜕𝑤 = 𝜕𝐿∗/𝜕𝑟.
(27) Pour voir pourquoi, notez que d𝑔(𝐾∗, 𝐿∗) = 𝑔′
𝐾 (𝐾∗, 𝐿∗) d𝐾∗ + 𝑔′
𝐿 (𝐾∗, 𝐿∗) d𝐿∗. Ensuite, posez 𝑔 = 𝐹′
𝐾 .

196. 196 CORRIGÉS DES EXERCICES
6. (a) (i) 𝑅′
𝑥1
(𝑥∗
1, 𝑥∗
2) + 𝑠 = 𝐶′
𝑥1
(𝑥∗
1, 𝑥∗
2) (revenu marginal + subvention = coût marginal).
(ii) 𝑅′
𝑥2
(𝑥∗
1, 𝑥∗
2) = 𝐶′
𝑥2
(𝑥∗
1, 𝑥∗
2) + 𝑡 = 0 (revenu marginal = coût marginal + taxe).
(b) 𝜋′′
𝑥1 𝑥1
= 𝑅′′
𝑥1 𝑥1
− 𝐶′′
𝑥1 𝑥1
0 et
𝐷 = 𝜋′′
𝑥1 𝑥1
𝜋′′
𝑥2 𝑥2
− (𝜋′′
𝑥1 𝑥2
)2 = (𝑅′′
𝑥1 𝑥1
− 𝐶′′
𝑥1 𝑥1
) (𝑅′′
𝑥2 𝑥2
− 𝐶′′
𝑥2 𝑥2
) − (𝑅′′
𝑥1 𝑥2
− 𝐶′′
𝑥1 𝑥2
)2 0.
(c) On prend les différentielles totales de (i) et (ii), cela donne
(𝑅′′
𝑥1 𝑥1
− 𝐶′′
𝑥1 𝑥1
) d𝑥∗
1 + (𝑅′′
𝑥1 𝑥2
− 𝐶′′
𝑥1 𝑥2
) d𝑥∗
2 = −𝑑𝜎,
(𝑅′′
𝑥2 𝑥1
− 𝐶′′
𝑥2 𝑥1
) d𝑥∗
1 + (𝑅′′
𝑥2 𝑥2
− 𝐶′′
𝑥2 𝑥2
) d𝑥∗
2 = d𝜏.
On résout par rapport à d𝑥∗
1 et d𝑥∗
2 et on remet en ordre
d𝑥∗
1 =
−(𝑅′′
𝑥2 𝑥2
− 𝐶′′
𝑥2 𝑥2
)𝑑𝜎 − (𝑅′′
𝑥1 𝑥2
− 𝐶′′
𝑥1 𝑥2
) d𝜏
𝐷
,
d𝑥∗
2 =
(𝑅′′
𝑥2 𝑥1
− 𝐶′′
𝑥2 𝑥1
)𝑑𝜎 + (𝑅′′
𝑥1 𝑥1
− 𝐶′′
𝑥1 𝑥1
) d𝜏
𝐷
.
On voit maintenant que les dérivées partielles sont
𝜕𝑥∗
1
𝜕𝜎
=
−𝑅′′
𝑥2 𝑥2
+ 𝐶′′
𝑥2 𝑥2
𝐷
0,
𝜕𝑥∗
1
𝜕𝜏
=
−𝑅′′
𝑥1 𝑥2
+ 𝐶′′
𝑥1 𝑥2
𝐷
0,
𝜕𝑥∗
2
𝜕𝜎
=
𝑅′′
𝑥2 𝑥1
− 𝐶′′
𝑥2 𝑥1
𝐷
0,
𝜕𝑥∗
2
𝜕𝜏
=
𝑅′′
𝑥1 𝑥1
− 𝐶′′
𝑥1 𝑥1
𝐷
0,
les signes provenant des hypothèses de l’exercice et du fait que 𝐷 0 par (b). Notez que
ces signes sont en accord avec les intuitions économiques. Par exemple, si la taxe sur le
bien 2 augmente, la production du bien 1 augmente, tandis que celle du bien 2 diminue.
(d) C’est une conséquence des expressions de (c), car 𝑅′′
𝑥1 𝑥2
= 𝑅′′
𝑥2 𝑥1
et 𝐶′′
𝑥1 𝑥2
= 𝐶′′
𝑥2 𝑥1
.
Exercices récapitulatifs du chapitre 17
1. Les conditions du premier ordre
𝑓 ′
𝑥 (𝑥, 𝑦) = −4𝑥 + 2𝑦 + 18 = 0 et 𝑓 ′
𝑦 (𝑥, 𝑦) = 2𝑥 − 2𝑦 − 14 = 0
sont satisfaites en (𝑥, 𝑦) = (2, −5). De plus, 𝑓 ′′
𝑥𝑥 = −4, 𝑓 ′′
𝑥𝑦 = 2 et 𝑓 ′′
𝑦𝑦 = −2, de sorte que
𝑓 ′′
𝑥𝑥 𝑓 ′′
𝑦𝑦 − ( 𝑓 ′′
𝑥𝑦)2 = 4. Les conditions du point (a) du théorème 17.2.2 sont satisfaites.
2. (a) La fonction de profit est 𝜋(𝑄1, 𝑄2) = 120𝑄1 +90𝑄2 −0,1𝑄2
1 −0,1𝑄1𝑄2 −0,1𝑄2
2. Les
conditions du premier ordre pour que le profit soit maximal sont
𝜋′
𝑄1
(𝑄1, 𝑄2) = 120 − 0,2𝑄1 − 0,1𝑄2 = 0
𝜋′
𝑄2
(𝑄1, 𝑄2) = 90 − 0,1𝑄1 − 0,2𝑄2 = 0.
On trouve (𝑄1, 𝑄2) = (500, 200). En outre,
𝜋′′
𝑄1𝑄1
(𝑄1, 𝑄2) = −0,2 ⩽ 0, 𝜋′′
𝑄1𝑄2
(𝑄1, 𝑄2) = −0,1 et 𝜋′′
𝑄2𝑄2
(𝑄1, 𝑄2) = −0,2 ⩽ 0.
Comme 𝜋′′
𝑄1𝑄1
𝜋′′
𝑄2𝑄2
− (𝜋′′
𝑄1𝑄2
)2 = 0,03 ⩾ 0, (500, 200) maximise le profit.

197. Chapitre 17 / Optimisation sans contraintes 197
(b) La fonction de profit est maintenant
ˆ
𝜋(𝑄1, 𝑄2) = 𝑃1𝑄1 + 90𝑄2 − 0,1𝑄2
1 − 0,1𝑄1𝑄2 − 0,1𝑄2
2.
Les conditions du premier ordre pour que le profit soit maximal deviennent
ˆ
𝜋′
𝑄1
= 𝑃1 − 0,2𝑄1 − 0,1𝑄2 = 0 et ˆ
𝜋′
𝑄2
= 90 − 0,1𝑄1 − 0,2𝑄2 = 0.
De manière à imposer le choix 𝑄1 = 400, les conditions du premier ordre impliquent
𝑃1 − 80 − 0,1𝑄2 = 0 et 90 − 40 − 0,2𝑄2 = 0. Il s’ensuit que 𝑄2 = 250 et 𝑃1 = 105.
3. (a) Les coordonnées des points critiques sont telles que
𝑃′
𝑥 (𝑥, 𝑦) = −0,2𝑥 − 0,2𝑦 + 47 = 0 et 𝑃′
𝑦 (𝑥, 𝑦) = −0,2𝑥 − 0,4𝑦 + 48 = 0.
La solution est 𝑥 = 230 et 𝑦 = 5. De plus, 𝑃′′
𝑥𝑥 = −0,2 ⩽ 0, 𝑃′′
𝑥𝑦 = −0,2 et 𝑃′′
𝑦𝑦 = −0,4 ⩽ 0.
Comme 𝑃′′
𝑥𝑥 𝑃′′
𝑦𝑦 − (𝑃′′
𝑥𝑦)2 = 0,04 ⩾ 0, (230, 5) rend le profit maximal.
(b) Avec la production totale 𝑥 + 𝑦 = 200, ou 𝑦 = 200 − 𝑥, la nouvelle fonction de profit
est ˆ
𝜋(𝑥) = 𝑓 (𝑥, 200 − 𝑥) = −0,1𝑥2 + 39𝑥 + 1 000. Il est facile de voir que cette fonction
admet un maximum en 𝑥 = 195. Alors 𝑦 = 200 − 195 = 5.
4. (a) Les points critiques sont
(i) 𝑓 ′
𝑥 (𝑥, 𝑦) = 3𝑥2
− 2𝑥𝑦 = 𝑥 (3𝑥 − 2𝑦) = 0
(ii) 𝑓 ′
𝑦 (𝑥, 𝑦) = −𝑥2
+ 2𝑦 = 0.
De (i), 𝑥 = 0 ou 3𝑥 = 2𝑦. Si 𝑥 = 0, alors (ii) fournit 𝑦 = 0. Si 3𝑥 = 2𝑦, alors (ii) fournit
3𝑥 = 𝑥2 et ainsi 𝑥 = 0 ou 𝑥 = 3. Si 𝑥 = 3, alors (ii) fournit 𝑦 = 𝑥2/2 = 9/2. Les points
critiques sont (0, 0) et (3, 9/2).
(b) Les points critiques sont données par :
(i) 𝑓 ′
𝑥 (𝑥, 𝑦) = 𝑦𝑒4𝑥2−5𝑥𝑦+𝑦2
(8𝑥2 − 5𝑥𝑦 + 1) = 0;
(ii) 𝑓 ′
𝑦 (𝑥, 𝑦) = 𝑥𝑒4𝑥2−5𝑥𝑦+𝑦2
(2𝑦2 − 5𝑥𝑦 + 1) = 0 .
Si 𝑦 = 0, alors (i) est satisfait et (ii) n’est vrai que si 𝑥 = 0. Si 𝑥 = 0, alors (ii) est
satisfait et (i) n’est vrai que si 𝑦 = 0. D’où en plus de (0, 0), tout autre point critique doit
être tel que 8𝑥2 − 5𝑥𝑦 + 1 = 0 et 2𝑦2 − 5𝑥𝑦 + 1 = 0. On soustrait la deuxième équation
de la première 8𝑥2 = 2𝑦2 ou 𝑦 = ±2𝑥. On introduit 𝑦 = −2𝑥 dans 8𝑥2 − 5𝑥𝑦 + 1 = 0,
cela donne 18𝑥2 + 1 = 0. Cette équation n’a pas de solution. On introduit 𝑦 = 2𝑥 dans
8𝑥2 − 5𝑥𝑦 + 1 = 0, cela donne −2𝑥2 + 1 = 0 ou 𝑥 = ±1
2
√
2. Les points critiques sont
(−1
2
√
2, −
√
2), (0, 0) et ( 1
2
√
2,
√
2).
(c) Les coordonnées des points critiques sont telles que
(i) 𝑓 ′
𝑥 (𝑥, 𝑦) = 24𝑥𝑦 − 48𝑥 = 24𝑥 (𝑦 − 2) = 0 ;
(ii) 𝑓 ′
𝑦 (𝑥, 𝑦) = 12𝑦2
+ 12𝑥2
− 48𝑦 = 12 (𝑥2
+ 𝑦2
− 4𝑦) = 0.
En raison de (i), 𝑥 = 0 ou 𝑦 = 2. Si 𝑥 = 0, alors (ii) fournit 𝑦 (𝑦 − 4) = 0, soit 𝑦 = 0 ou
𝑦 = 4. Ainsi (0, 0) et (0, 4) sont des points critiques. Si 𝑦 = 2, alors (ii) fournit 𝑥2 −4 = 0,
soit 𝑥 = ±2. De là, (2, 2) et (−2, 2) sont aussi des points critiques.

198. 198 CORRIGÉS DES EXERCICES
5. Les coordonnées des points critiques sont telles que 𝑓 ′
𝑥 (𝑥, 𝑦, 𝑎) = 2𝑎𝑥 − 2 = 0 et
𝑓 ′
𝑦 (𝑥, 𝑦, 𝑎) = 2𝑦 − 4𝑎 = 0, soit 𝑥 = 𝑥∗(𝑎) = 1/𝑎 et 𝑦 = 𝑦∗(𝑎) = 2𝑎. La fonction de
valeur optimale est 𝑓 ∗(𝑎) = 𝑎 (1/𝑎)2 − 2 (1/𝑎) + (2𝑎)2 − 4𝑎(2𝑎) = −(1/𝑎) − 4𝑎2. D’où
(d/d𝑎) 𝑓 ∗(𝑎) = (1/𝑎2) − 8𝑎. Par ailleurs, (𝜕/𝜕𝑎) 𝑓 (𝑥, 𝑦, 𝑎) = 𝑥2 − 4𝑦 = (1/𝑎2) − 8𝑎 en
(𝑥∗(𝑎), 𝑦∗(𝑎)). Cela est en accord avec le théorème de l’enveloppe.
6. (a) Avec 𝜋 = 𝑝(𝐾𝑎 + 𝐿𝑏 + 𝑇𝑐) − 𝑟𝐾 − 𝑤𝐿 − 𝑞𝑇, les conditions du premier ordre pour
que (𝐾∗, 𝐿∗,𝑇∗) soit un maximum de 𝜋 sont
𝜋′
𝐾 = 𝑝𝑎 (𝐾∗
)𝑎−1
− 𝑟 = 0, 𝜋′
𝐿 = 𝑝𝑏(𝐿∗
)𝑎−1
− 𝑤 = 0, 𝜋′
𝑇 = 𝑝𝑐(𝑇∗
)𝑎−1
− 𝑞 = 0.
Solution : 𝐾∗ = (𝑎𝑝/𝑟)1/(1−𝑎), 𝐿∗ = (𝑏𝑝/𝑤)1/(1−𝑎), 𝑇∗ = (𝑐𝑝/𝑞)1/(1−𝑎).
(b) 𝜋∗ = Γ + des termes qui ne dépendent pas de 𝑟, avec
Γ = 𝑝(𝑎𝑝/𝑟)𝑎/(1−𝑎)
− 𝑟(𝑎𝑝/𝑟)1/(1−𝑎)
.
Des calculs algébriques mènent à
Γ = (𝑎/𝑟)𝑎/(1−𝑎)
𝑝1/(1−𝑎)
− (𝑎𝑝)1/(1−𝑎)
𝑟−𝑎/(1−𝑎)
= (𝑎𝑎/(1−𝑎)
− 𝑎1/(1−𝑎)
)𝑝1/(1−𝑎)
𝑟−𝑎/(1−𝑎)
= (1 − 𝑎)𝑎𝑎/(1−𝑎)
𝑝1/(1−𝑎)
𝑟−𝑎/(1−𝑎).
Ensuite
𝜕𝜋∗
𝜕𝑟
=
𝜕Γ
𝜕𝑟
= −𝑎𝑎𝑎/(1−𝑎)
𝑝1/(1−𝑎)
𝑟−𝑎/(1−𝑎)−1
= −𝑎1/(1−𝑎)
𝑝1/(1−𝑎)
𝑟−1/(1−𝑎)
= −(𝑎𝑝/𝑟)1/(1−𝑎)
.
(c) On applique (17.7.3) à ce cas-ci, où 𝜋(𝐾, 𝐿,𝑇, 𝑝, 𝑟, 𝑤, 𝑞) = 𝑝𝑄 − 𝑟𝐾 − 𝑤𝐿 − 𝑞𝑇 avec
𝑄 = 𝐾𝑎 + 𝐿𝑏 + 𝑇𝑐 et 𝜋∗(𝑝, 𝑟, 𝑤, 𝑞) = 𝑝𝑄∗ − 𝑟𝐾∗ − 𝑤𝐿∗ − 𝑞𝑇∗. Les dérivées partielles
de 𝜋 calculées en (𝐾∗, 𝐿∗,𝑇∗, 𝑝, 𝑟, 𝑤, 𝑞) avec la quantité produite 𝑄∗, devraient conduire à
𝜕𝜋∗/𝜕𝑝 = 𝜋′
𝑝 = 𝑄∗, 𝜕𝜋∗/𝜕𝑟 = 𝜋′
𝑟 = −𝐾∗, 𝜕𝜋∗/𝜕𝑤 = 𝜋′
𝑤 = −𝐿∗ et 𝜕𝜋∗/𝜕𝑤 = 𝜋′
𝑤 = −𝑇∗.
Grâce à la question (b), on a la deuxième égalité. Les trois autres équations peuvent être
vérifiées de la même manière à la faveur de calculs algébriques assez laborieux.
7. (a) 𝑓 ′
𝑥 = 𝑒𝑥+𝑦 + 𝑒𝑥−𝑦 − 3
2 , 𝑓 ′
𝑦 = 𝑒𝑥+𝑦 − 𝑒𝑥−𝑦 − 1
2 , 𝑓 ′′
𝑥𝑥 = 𝑒𝑥+𝑦 + 𝑒𝑥−𝑦, 𝑓 ′′
𝑥𝑦 = 𝑒𝑥+𝑦 − 𝑒𝑥−𝑦,
𝑓 ′′
𝑦𝑦 = 𝑒𝑥+𝑦 + 𝑒𝑥−𝑦. Ensuite, 𝑓 ′′
𝑥𝑥 ⩾ 0, 𝑓 ′′
𝑦𝑦 ⩾ 0 et
𝑓 ′′
𝑥𝑥 𝑓 ′′
𝑦𝑦 − ( 𝑓 ′′
𝑥𝑦)2
= (𝑒𝑥+𝑦
+ 𝑒𝑥−𝑦
)2
− (𝑒𝑥+𝑦
− 𝑒𝑥−𝑦
)2
= 4𝑒𝑥+𝑦
𝑒𝑥−𝑦
= 4𝑒2𝑥
⩾ 0,
de sorte que 𝑓 est convexe.
(b) En tout point critique, on a 𝑒𝑥+𝑦 = 1 et 𝑒𝑥−𝑦 = 1
2 , de sorte que 𝑥+𝑦 = 0 et 𝑥−𝑦 = − ln 2.
Le seul point critique est dès lors (𝑥, 𝑦) = (−1
2 ln 2, 1
2 ln 2), en lequel
𝑓 (𝑥, 𝑦) =
1
2
(3 + ln 2).
Comme 𝑓 est convexe, c’est un minimum.
8. (a) 𝑓 ′
𝑥 (𝑥, 𝑦) = 2𝑥 − 𝑦 − 3𝑥2, 𝑓 ′
𝑦 (𝑥, 𝑦) = −2𝑦 − 𝑥, 𝑓 ′′
𝑥𝑥 (𝑥, 𝑦) = 2 − 6𝑥, 𝑓 ′′
𝑥𝑦 (𝑥, 𝑦) = −1,
𝑓 ′′
𝑦𝑦 (𝑥, 𝑦) = −2. Les coordonnées des points critiques sont déterminées par les équations

199. Chapitre 17 / Optimisation sans contraintes 199
2𝑥 − 𝑦 − 3𝑥2 = 0 et −2𝑦 − 𝑥 = 0. Selon la dernière équation 𝑦 = −𝑥/2 et, dans ce cas, la
première équation devient 5
2 𝑥−3𝑥2 = 0. Il y a donc deux points critiques, (𝑥1, 𝑦1) = (0, 0)
et (𝑥2, 𝑦2) = (5/6, −5/12). La nature de ces points est déterminée dans le tableau suivant.
(𝑥, 𝑦) 𝐴 𝐵 𝐶 𝐴𝐶 − 𝐵2 Type de point
(0, 0) 2 −1 −2 −5 Point-selle
( 5
6 , − 5
12 ) −3 −1 −2 5 Maximum local
(b) 𝑓 est concave sur l’ensemble des points tels que 𝑓 ′′
𝑥𝑥 ⩽ 0, 𝑓 ′′
𝑦𝑦 ⩽ 0, 𝑓 ′′
𝑥𝑥 𝑓 ′′
𝑦𝑦 −( 𝑓 ′′
𝑥𝑦)2 ⩾0,
c’est-à-dire là où 2 − 6𝑥 ⩽ 0, −2 ⩽ 0 et (2 − 6𝑥) (−2) − (−1)2 ⩾ 0. Ces conditions sont
équivalentes à 𝑥 ⩾ 1/3 et 𝑥 ⩾ 5/12. Comme 5/12 1/3, 𝑓 est concave sur l’ensemble 𝑆
composé de tous les (𝑥, 𝑦) tels que 𝑥 ⩾ 5/12. Le point critique (𝑥2, 𝑦2) = (5/6, −5/12)
trouvé dans la question (a) appartient à 𝑆. Comme 𝑓 est concave sur 𝑆, c’est un point en
lequel 𝑓 atteint un maximum (global) sur 𝑆 et 𝑓max = 25
36 − 25
144 + 25
72 − 125
216 = 125
432 .
9. (a) Pour qu’un point soit critique, il faut que ses coordonnées satisfassent à 𝑥 − 1 = −𝑎𝑦
et 𝑎 (𝑥 − 1) = 𝑦2 − 2𝑎2𝑦. Ces deux équations impliquent −𝑎2𝑦 = 𝑎 (𝑥 − 1) = 𝑦2 − 2𝑎2𝑦.
De là, 𝑎2𝑦 = 𝑦2, dont les solutions sont 𝑦 = 0 ou 𝑦 = 𝑎2. Comme 𝑥 = 1 − 𝑎𝑦, les points
critiques sont (1, 0) et (1 − 𝑎3, 𝑎2)(28).
(b) La fonction de valeur optimale au point critique de la question (a) est
1
2
(1 − 𝑎3
)2
− (1 − 𝑎3
) + 𝑎3
(−𝑎3
) −
1
3
𝑎6
+ 𝑎2
𝑎4
= −
1
2
+
1
6
𝑎6
,
dont la dérivée partielle par rapport à 𝑎 est 𝑎5. Par ailleurs, la dérivée partielle de 𝑓
par rapport à 𝑎, en tenant 𝑥 et 𝑦 constantes, est 𝜕 𝑓 /𝜕𝑎 = 𝑦 (𝑥 − 1) + 2𝑎𝑦2. Calculée en
𝑥 = 1− 𝑎3, 𝑦 = 𝑎2, cette dérivée partielle est aussi égale à 𝑎5, ce qui confirme le théorème
de l’enveloppe.
(c) 𝑓 ′′
𝑥𝑥 = 1, 𝑓 ′′
𝑦𝑦 = −2𝑦 + 2𝑎2, 𝑓 ′′
𝑥𝑦 = 𝑎 et 𝑓 ′′
𝑥𝑥 𝑓 ′′
𝑦𝑦 − ( 𝑓 ′′
𝑥𝑦)2 = 𝑎2 − 2𝑦. Donc 𝑓 est convexe
si et seulement si −2𝑦 + 2𝑎2 ⩾ 0 et −2𝑦 + 𝑎2 ⩾ 0, ce qui est équivalent à 𝑎2 ⩾ 𝑦 et
𝑎2 ⩾ 2𝑦. Par conséquent, 𝑓 (𝑥, 𝑦) est convexe sur la partie du plan 𝑂𝑥𝑦 pour laquelle
𝑦 ⩽ 1
2 𝑎2.
10. (a) 𝑝 = 𝐶′
𝑥 (𝑥∗, 𝑦∗) et 𝑞 = 𝐶′
𝑦 (𝑥∗, 𝑦∗) sont les conditions bien connues qui traduisent le
fait qu’à l’optimum le prix de chaque bien doit être égal au coût marginal.
(b) Dans une notation simplifiée, à l’optimum (𝑥∗, 𝑦∗), ˆ
𝜋′
𝑥 = 𝐹 + 𝑥𝐹′
𝑥 + 𝑦𝐺′
𝑥 − 𝐶′
𝑥 = 0 et
ˆ
𝜋′
𝑦 = 𝑥𝐹′
𝑦 + 𝐺 + 𝑦𝐺′
𝑦 − 𝐶′
𝑦 = 0.
L’interprétation en est la suivante : le revenu marginal = le coût marginal, comme d’ha-
bitude, avec le fait qu’un changement de quantité produite de l’un des deux biens affecte
en même temps le revenu de l’autre marché.
(c) La fonction de profit est
𝜋 = 𝑥 (𝑎 − 𝑏𝑥 − 𝑐𝑦) + 𝑦 (𝛼 − 𝛽𝑥 − 𝛾𝑦) − 𝑃𝑥 − 𝑄𝑦 − 𝑅,
(28) Comme il avait été demandé de vérifier que (1 − 𝑎3, 𝑎2) était un point critique, il suffisait de vérifier si ces
valeurs de 𝑥 et 𝑦 rendaient bien les dérivées partielles nulles.

200. 200 CORRIGÉS DES EXERCICES
donc les conditions du premier ordre sont 𝜕𝜋/𝜕𝑥 = 𝑎 − 2𝑏𝑥 − 𝑐𝑦 − 𝛽𝑦 − 𝑃 = 0,
𝜕𝜋/𝜕𝑦 = −𝑐𝑥 + 𝛼 − 𝛽𝑥 − 2𝛾𝑦 − 𝑄 = 0.
(d) 𝜕2𝜋/𝜕𝑥2 = −2𝑏, 𝜕2𝜋/𝜕𝑦2 = −2𝛾, 𝜕2𝜋/𝜕𝑥𝜕𝑦 = −(𝛽 + 𝑐). Les dérivées partielles
d’ordre 2 sont strictement négatives et
Δ = (𝜕2
𝜋/𝜕𝑥2
) (𝜕2
𝜋/𝜕𝑦2
) − (𝜕2
𝜋/𝜕𝑥𝜕𝑦)2
= 4𝛾𝑏 − (𝛽 + 𝑐)2
,
de sorte que la conclusion annoncée en découle.
Chapitre 18 / Optimisation sous contraintes d’égalité
18.1
1. (a) L(𝑥, 𝑦) = 𝑥𝑦 − 𝜆(𝑥 + 3𝑦 − 24). Les conditions du premier ordre L′
𝑥 = 𝑦 − 𝜆 = 0,
L′
𝑦 = 𝑥 − 3𝜆 = 0 impliquent 𝑥 = 3𝑦. La contrainte devient alors 3𝑦 + 3𝑦 = 24, de sorte
que 𝑦 = 4 et ensuite 𝑥 = 12.
(b) En utilisant (∗∗) de l’exemple 18.1.3 avec 𝑎 = 𝑏 = 𝑝 = 1, 𝑞 = 3 et 𝑚 = 24, on a
𝑥 = 1
2 (24/1) = 12, 𝑦 = 1
2 (24/3) = 4.
2. Avec L = −40𝑄1 + 𝑄2
1 − 2𝑄1𝑄2 − 20𝑄2 + 𝑄2
2 − 𝜆 (𝑄1 + 𝑄2 − 15), les conditions du
premier ordre sont L′
𝑥 = −40 + 2𝑄1 − 2𝑄2 −𝜆 = 0, L′
𝑦 = −2𝑄1 − 20 + 2𝑄2 −𝜆 = 0. Elles
entraînent −40 + 2𝑄1 − 2𝑄2 = −2𝑄1 − 20 + 2𝑄2, de sorte que 𝑄1 − 𝑄2 = 5.
Ensemble, cette équation et la contrainte mènent à la solution 𝑄1 = 10, 𝑄2 = 5, avec
𝜆 = −30.
3. (a) Conformément à (∗∗) dans l’exemple 18.1.3, 𝑥 = 3
10 𝑚 et 𝑦 = 1
10 𝑚.
(b) 𝑥 = 10, 𝑦 = 6 250 000. (c) 𝑥 = 8/3, 𝑦 = 1.
4. (a) Avec L(𝑥, 𝑦) = 𝑥2 + 𝑦2 − 𝜆 (𝑥 + 2𝑦 − 4), les conditions du premier ordre sont
L′
𝑥 = 2𝑥 − 𝜆 = 0 et L′
𝑦 = 2𝑦 − 2𝜆 = 0. De ces équations, on tire 2𝑥 = 𝑦 et on
introduit ce résultat dans la contrainte, cela donne 𝑥 + 4𝑥 = 4 ou 𝑥 = 4/5 et, de là,
𝑦 = 2𝑥 = 8/5, avec 𝜆 = 2𝑥 = 8/5.
(b) La même méthode qu’en (a) conduit à 2𝑥 − 𝜆 = 0 et 4𝑦 − 𝜆 = 0, de sorte que 𝑥 = 2𝑦.
De la contrainte, on obtient 𝑥 = 8 et 𝑦 = 4, avec 𝜆 = 16.
(c) Les conditions du premier ordre impliquent 2𝑥 + 3𝑦 = 𝜆 = 3𝑥 + 2𝑦, ce qui donne
𝑥 = 𝑦. La solution est donc (𝑥, 𝑦) = (50, 50) avec 𝜆 = 250.
5. La contrainte de budget s’écrit 2𝑥 + 4𝑦 = 1 000, de sorte qu’avec
L(𝑥, 𝑦) = 100𝑥𝑦 + 𝑥 + 2𝑦 − 𝜆 (2𝑥 + 4𝑦 − 1 000),
les conditions du premier ordre sont L′
𝑥 = 100𝑦 + 1 − 2𝜆 = 0 et L′
𝑦 = 100𝑥 + 2 − 4𝜆 = 0.
En éliminant 𝜆 de ces équations, on obtient 𝑥 = 2𝑦. On introduit ce résultat dans la
contrainte, cela donne 2𝑥 + 2𝑥 = 1 000. Ainsi, 𝑥 = 250 et 𝑦 = 125.
6. La formule (∗∗) de l’exemple 18.1.3 avec 𝑥, 𝑦, 𝑝, 𝑞 et 𝑚 remplacées respectivement par
𝑚, ℓ, 1/𝑤, 1 et 𝑇0 conduit à 𝑚 = 𝑎𝑤𝑇0/(𝑎 + 𝑏) et ℓ = 𝑏𝑇0/(𝑎 + 𝑏).

201. Chapitre 18 / Optimisation sous contraintes d’égalité 201
7. Le problème est : max −0,1𝑥2 − 0,2𝑥𝑦 − 0,2𝑦2 + 47𝑥 + 48𝑦 − 600 sous la contrainte
𝑥 + 𝑦 = 200. Avec L(𝑥, 𝑦) = −0,1𝑥2 − 0,2𝑥𝑦 − 0,2𝑦2 + 47𝑥 + 48𝑦 − 600 − 𝜆 (𝑥 + 𝑦 − 200),
les conditions du premier ordre sont
L′
𝑥 = −0,2𝑥 − 0,2𝑦 + 47 − 𝜆 = 0 et L′
𝑦 = −0,2𝑥 − 0,4𝑦 + 48 − 𝜆 = 0.
Après élimination de 𝑥 et 𝜆, on a 𝑦 = 5 et la contrainte de budget donne 𝑥 = 195, avec
𝜆 = 7.
8. (a) 𝑃(𝑥, 𝑦) = (96 − 4𝑥) 𝑥 + (84 − 2𝑦) 𝑦 − 2𝑥2 − 2𝑥𝑦 − 𝑦2 = −6𝑥2 − 3𝑦2 − 2𝑥𝑦 + 96𝑥 + 84𝑦
(b) 𝑃′
𝑥 (𝑥, 𝑦) = −12𝑥 − 2𝑦 + 96, 𝑃′
𝑦 (𝑥, 𝑦) = −6𝑦 − 2𝑥 + 84. Le seul point critique est
(𝑥, 𝑦) = (6, 12).
(c) Le lagrangien s’écrit L(𝑥, 𝑦) = −6𝑥2 − 3𝑦2 − 2𝑥𝑦 + 96𝑥 + 84𝑦 − 𝜆 (𝑥 + 𝑦 − 11) et les
conditions du premier ordre,
L′
𝑥 = −12𝑥 − 2𝑦 + 96 − 𝜆 = 0 et L′
𝑦 = −6𝑦 − 2𝑥 + 84 − 𝜆 = 0.
L’élimination de 𝜆 conduit à 10𝑥 − 4𝑦 = 12. La contrainte est 𝑥 + 𝑦 = 11. La solution de
ce système de deux équations est 𝑥 = 4, 𝑦 = 7. Comme 𝑃(4, 7) = 673 𝑃(6, 12) = 792,
la restriction de production fait diminuer le profit de 119.
9. (a) Avec L = 𝑥𝑎 +𝑦−𝜆 (𝑝𝑥+𝑦−𝑚), les conditions du premier ordre pour que (𝑥∗, 𝑦∗) soit
solution du problème sont (i) L′
𝑥 = 𝑎 (𝑥∗)𝑎−1 −𝜆𝑝 = 0; (ii) L′
𝑦 = 1−𝜆 = 0. D’où 𝜆 = 1 et
𝑥∗ = 𝑥∗(𝑝, 𝑚) = 𝑘 𝑝−1/(1−𝑎) avec 𝑘 = 𝑎1/(1−𝑎). Ensuite, 𝑦∗ = 𝑦∗(𝑝, 𝑚) = 𝑚 − 𝑘 𝑝−𝑎/(1−𝑎).
(b) 𝜕𝑥∗
/𝜕𝑝 = −𝑥∗
/𝑝(1−𝑎) 0, 𝜕𝑥∗
/𝜕𝑚 = 0, 𝜕𝑦∗
/𝜕𝑝 = 𝑎𝑥∗
/(1−𝑎) 0 et 𝜕𝑦∗
/𝜕𝑚 = 1.
(c) La dépense optimale sur le bien 𝑥 est 𝑝𝑥∗(𝑝, 𝑚) = 𝑘 𝑝−𝑎/(1−𝑎), de sorte que
El𝑝 𝑝𝑥∗(𝑝, 𝑚) = −𝑎/(1 − 𝑎) 0. En particulier, la dépense sur le bien 𝑥 va diminuer
lorsque son prix augmente.
(d) On voit que 𝑥∗ = (1/2𝑝)2, 𝑦∗ = 𝑚 − 1/4𝑝, de sorte que
𝑈∗
(𝑝, 𝑚) =
√
𝑥∗ + 𝑦∗
= (1/2𝑝) + 𝑚 − 1/4𝑝 = 𝑚 + 1/4𝑝
et l’égalité proposée devient évidente.
10. (a) Avec L(𝑥, 𝑦) = 100 − 𝑒−𝑥 − 𝑒−𝑦 − 𝜆(𝑝𝑥 + 𝑞𝑦 − 𝑚), les conditions du premier ordre
L′
𝑥 = L′
𝑦 = 0 impliquent 𝑒−𝑥 = 𝜆𝑝 et 𝑒−𝑦 = 𝜆𝑞. De là, 𝑥 = − ln(𝜆𝑝) = − ln 𝜆 − ln 𝑝,
𝑦 = − ln 𝜆 − ln 𝑞. On introduit ces expressions de 𝑥 et 𝑦 dans la contrainte, cela donne
−𝑝(ln 𝜆 + ln 𝑝) − 𝑞 (ln 𝜆 + ln 𝑞) = 𝑚 et ainsi ln 𝜆 = −(𝑚 + 𝑝 ln 𝑝 + 𝑞 ln 𝑞)/(𝑝 + 𝑞). Par
conséquent, 𝑥 (𝑝, 𝑞, 𝑚) = [𝑚+𝑞 ln(𝑞/𝑝)]/(𝑝+𝑞), 𝑦 (𝑝, 𝑞, 𝑚) = [𝑚+ 𝑝 ln(𝑝/𝑞)]/(𝑝+𝑞).
(b) 𝑥 (𝑡𝑝, 𝑡𝑞, 𝑡𝑚) = [𝑡𝑚 + 𝑡𝑞 ln(𝑡𝑞/𝑡𝑝)]/(𝑡𝑝 + 𝑡𝑞) = 𝑥 (𝑝, 𝑞, 𝑚), ce qui montre que 𝑥 est
homogène de degré 0. De même, on peut voir que 𝑦 (𝑝, 𝑞, 𝑚) est homogène de degré 0.
(c) Vérification directe.
18.2
1. Selon (∗∗) de l’exemple 18.1.3, la solution est 𝑥∗ = 3𝑚/8, 𝑦∗ = 𝑚/12, avec 𝜆 = 9𝑚3/512.
La fonction de valeur optimale est 𝑓 ∗(𝑚) = (𝑥∗)3𝑦∗ = 9𝑚4/2 048, de sorte que
d 𝑓 ∗(𝑚)/d𝑚 = 9𝑚3/512 = 𝜆.

202. 202 CORRIGÉS DES EXERCICES
2. (a) Avec L = 𝑟𝐾 + 𝑤𝐿 − 𝜆 (
√
𝐾 + 𝐿 − 𝑄), les conditions du premier ordre sont
L′
𝐾 = 𝑟 − 𝜆/2
√
𝐾∗ = 0, L′
𝐿 = 𝑤 − 𝜆 = 0. On introduit 𝜆 de la dernière équation
dans la première, cela donne
√
𝐾∗ = 𝑤/2𝑟. Ensuite 𝐾∗ = 𝑤2/4𝑟2 et, de la contrainte, il
suit 𝐿∗ = 𝑄 − 𝑤/2𝑟.
(b) La fonction de valeur optimale est 𝐶∗(𝑄) = 𝑟𝐾∗ + 𝑤𝐿∗ = 𝑤𝑄 − 𝑤2/4𝑟, de sorte que
d𝐶∗(𝑄)/d𝑄 = 𝑤 = 𝜆.
3. (a) 𝑥 + 2𝑦 = 𝑎 entraîne 𝑦 = 1
2 𝑎 − 1
2 𝑥, d’où 𝑥2 + 𝑦2 = 𝑥2 + ( 1
2 𝑎 − 1
2 𝑥)2 = 5
4 𝑥2 − 1
2 𝑎𝑥 + 1
4 𝑎2.
Cette fonction du second degré atteint un minimum en 𝑥 = 𝑎/5, d’où 𝑦 = 2𝑎/5.
(b) L(𝑥, 𝑦) = 𝑥2 + 𝑦2 − 𝜆 (𝑥 + 2𝑦 − 𝑎). Les conditions nécessaires sont L′
𝑥 = 2𝑥 − 𝜆 = 0,
L′
𝑦 = 2𝑦 − 2𝜆 = 0, impliquant 2𝑥 = 𝑦. La contrainte donne alors 𝑥 = 𝑎/5 et ensuite
𝑦 = 2𝑎/5, 𝜆 = 2𝑎/5.
(c) Voir figure C18.2.3. Il s’agit de trouver le point sur la droite 𝑥 + 2𝑦 = 𝑎 le plus
proche de l’origine. Comme aucun point de la droite n’est plus loin que tous les autres de
l’origine, le problème de maximisation correspondant n’a pas de solution.
y
x
(a/5, 2a/5)
a
a/2
Figure C18.2.3
4. (a) Avec L(𝑥, 𝑦) =
√
𝑥 + 𝑦 − 𝜆 (𝑥 + 4𝑦 − 100), les conditions du premier ordre
pour que (𝑥∗, 𝑦∗) soit solution du problème sont (i) 𝜕L/𝜕𝑥 = 1/2
√
𝑥∗ − 𝜆 = 0 et
(ii) 𝜕L/𝜕𝑦 = 1 − 4𝜆 = 0. De (ii), 𝜆 = 1/4. On introduit cette valeur de 𝜆 dans (i), ce
qui donne
√
𝑥∗ = 2 ou 𝑥∗ = 4. Alors 𝑦∗ = 25 − 1
4 × 4 = 24 et l’utilité maximale vaut
𝑈∗ =
√
𝑥∗ + 𝑦∗ = 26.
(b) On désigne les nouvelles valeurs optimales de 𝑥 et 𝑦 par ˆ
𝑥 et ˆ
𝑦. Si 𝑥 passe de 100 à
101, on a encore 𝜆 = 1/4 et ˆ
𝑥 = 4. La contrainte donne maintenant 4 + 4ˆ
𝑦 = 101, ce qui
entraîne ˆ
𝑦 = 97/4 = 24,25, avec ˆ
𝑈 =
√
ˆ
𝑥 + ˆ
𝑦 = 26,25. L’accroissement de la fonction
d’utilité optimale est ˆ
𝑈 − 𝑈∗ = 0,25 = 𝜆(29).
(c) Les conditions nécessaires d’optimalité s’écrivent maintenant
𝜕L/𝜕𝑥 = 1/2
√
𝑥∗ − 𝜆𝑝 = 0, 𝜕L/𝜕𝑦 = 1 − 𝜆𝑞 = 0.
En poursuivant de la même façon que dans (a), on trouve 𝜆 = 1/𝑞,
√
𝑥∗ = 𝑞/2𝑝 et ainsi
𝑥∗ = 𝑞2/4𝑝2, avec 𝑦∗ = 𝑚/𝑞 − 𝑞/4𝑝(30).
(29) En règle générale, l’augmentation de l’utilité est approximativement égale à la valeur du multiplicateur de
Lagrange.
(30) Notez que 𝑦∗ 0 ⇔ 𝑚 𝑞2/4𝑝. Notez aussi que, si on explicite la contrainte par rapport à 𝑦, la fonction
d’utilité devient 𝑢(𝑥) =
√
𝑥 + (𝑚 − 𝑝𝑥)/𝑞. On voit que 𝑢′ (𝑥) = 1/2
√
𝑥 − 𝑝/𝑞 = 0 pour 𝑥∗ = 𝑞2/4𝑝2 et
𝑢′′ (𝑥) = −(1/4) 𝑥−3/2 0 quand 𝑥 0. On a bien trouvé le maximum.

203. Chapitre 18 / Optimisation sous contraintes d’égalité 203
5. (a) Conditions du premier ordre : (i) 𝛼/(𝑥∗ − 𝑎) = 𝜆𝑝 ; (ii) 𝛽/(𝑦∗ − 𝑏) = 𝜆𝑞. De là,
𝑝𝑥∗ = 𝑝𝑎 + 𝛼/𝜆 et 𝑞𝑦∗ = 𝑞𝑏 + 𝛽/𝜆. Substituer ces expressions dans la contrainte mène à
𝑚 = 𝑝𝑥∗ + 𝑞𝑦∗ = 𝑝𝑎 + 𝑞𝑏 + (𝛼 + 𝛽)/𝜆 = 𝑝𝑎 + 𝑞𝑏 + 1/𝜆, d’où 1/𝜆 = 𝑚 − (𝑝𝑎 + 𝑞𝑏). Les
expressions (∗∗) sont maintenant facilement établies(31).
(b) On dérive partiellement
𝑈∗
= 𝛼[ln 𝛼 + ln(𝑚 − (𝑎𝑝 + 𝑏𝑞)) − ln 𝑝] + 𝛽[ln 𝛽 + ln(𝑚 − (𝑎𝑝 + 𝑏𝑞)) − ln 𝑞],
en se rappelant que 𝛼 + 𝛽 = 1,
𝜕𝑈∗
𝜕𝑚
=
𝛼
𝑚 − (𝑝𝑎 + 𝑞𝑏)
+
𝛽
𝑚 − (𝑝𝑎 + 𝑞𝑏)
=
1
𝑚 − (𝑝𝑎 + 𝑞𝑏)
= 𝜆 0.
Et aussi,
𝜕𝑈∗
𝜕𝑝
=
−𝛼𝑎
𝑚 − (𝑝𝑎 + 𝑞𝑏)
−
𝛼
𝑝
+
−𝛽𝑎
𝑚 − (𝑝𝑎 + 𝑞𝑏)
=
−𝑎
𝑚 − (𝑝𝑎 + 𝑞𝑏)
−
𝛼
𝑝
= −𝑎𝜆 −
𝛼
𝑝
,
tandis que
−
𝜕𝑈∗
𝜕𝑚
𝑥∗
= −𝜆
𝑎 +
𝛼
𝜆𝑝
= −𝑎𝜆 −
𝛼
𝑝
,
de sorte que
𝜕𝑈∗
𝜕𝑝
= −
𝜕𝑈∗
𝜕𝑚
𝑥∗
. La dernière égalité s’obtient de la même manière.
6. 𝑓 (𝑥,𝑇) = 𝑥
∫ 𝑇
0
[−𝑡3
+ (𝛼𝑇2
+ 𝑇 − 1) 𝑡2
+ (𝑇 − 𝛼𝑇3
) 𝑡] d𝑡
= 𝑥
𝑇
0
[−1
4 𝑡4 + (𝛼𝑇2 + 𝑇 − 1) 1
3 𝑡3 + (𝑇 − 𝛼𝑇3) 1
2 𝑡2]
= −
1
6
𝛼𝑥𝑇5
+
1
12
𝑥𝑇4
+
1
6
𝑥𝑇3
=
1
12
𝑥𝑇3
(2 + 𝑇 − 2𝛼𝑇2
)
Un calcul semblable, mais plus facile montre que 𝑔(𝑥,𝑇) =
∫ 𝑇
0
(𝑥𝑡𝑇 − 𝑥𝑡2
) d𝑡 = 1
6 𝑥𝑇3.
Le lagrangien pour le problème du producteur est
L =
1
12
𝑥𝑇3
(2 + 𝑇 − 2𝛼𝑇2
) − 𝜆(
1
6
𝑥𝑇3
− 𝑀).
Les deux conditions du premier ordre sont
1
12
𝑇3
(2 + 𝑇 − 2𝛼𝑇2
) −
1
6
𝜆𝑇3
= 0 et
1
12
𝑥𝑇2
(6 + 4𝑇 − 10𝛼𝑇2
) −
1
2
𝜆𝑥𝑇2
= 0.
Ces équations impliquent 𝜆 = 1
2 (2 + 𝑇 − 2𝛼𝑇2) = 1
6 (6 + 4𝑇 − 10𝛼𝑇2). Il s’ensuit que
4𝛼𝑇2 = 𝑇. Une solution est 𝑇 = 0, mais elle n’est pas compatible avec la contrainte
1
6 𝑥𝑇3 = 𝑀. La solution intéressante est 𝑇 = 1/4𝛼, qui entraîne 𝜆 = 1 + 1/16𝛼. En
l’introduisant dans la contrainte 𝑔(𝑥,𝑇) = 𝑀, on détermine 𝑥 = 6𝑀𝑇−3 = 384𝑀𝛼3.
(31) On peut interpréter 𝑎 et 𝑏 comme les quantités minimales de subsistance des deux biens, auquel cas l’hypothèse
𝑝𝑎 + 𝑞𝑏 𝑚 signifie que le consommateur peut se permettre d’acheter (𝑎, 𝑏).

204. 204 CORRIGÉS DES EXERCICES
Comme 𝑥𝑇3 = 6𝑀, le profit maximal est
𝑓 ∗
(𝑀) = 𝑀 + 𝑀/8𝛼 − 𝛼𝑀/16𝛼2
= 𝑀 + 𝑀/16𝛼,
dont la dérivée par rapport à 𝑀 est en effet 𝜆(32).
18.3
1. (a) Avec L(𝑥, 𝑦) = 3𝑥𝑦 − 𝜆 (𝑥2 + 𝑦2 − 8), les conditions du premier ordre sont
L′
𝑥 = 3𝑦 − 2𝜆𝑥 = 0 et L′
𝑦 = 3𝑥 − 2𝜆𝑦 = 0.
Elles peuvent aussi s’écrire (i) 3𝑦 = 2𝜆𝑥 et (ii) 3𝑥 = 2𝜆𝑦. Si 𝑥 = 0, alors (i) donne
𝑦 = 0; par contre, si 𝑦 = 0, alors (ii) donne 𝑥 = 0. Mais (𝑥, 𝑦) = (0, 0) ne réalise pas la
contrainte. Par conséquent, 𝑥 ≠ 0 et 𝑦 ≠ 0. En égalant le rapport des membres de gauche
de (i) et (ii) au rapport des membres de droite, on a 𝑦/𝑥 = 𝑥/𝑦 ou 𝑥2 = 𝑦2. Enfin, en
exploitant la contrainte, 𝑥2 = 𝑦2 = 4. Les quatre candidats à la solution sont donc (2, 2) et
(−2, −2) avec 𝜆 = 3/2, et (2, −2) et (−2, 2) avec 𝜆 = −3/2. Les valeurs correspondantes
de la fonction sont 𝑓 (2, 2) = 𝑓 (−2, −2) = 12 et 𝑓 (2, −2) = 𝑓 (−2, 2) = −12.
Comme 𝑓 est continue sur l’ensemble borné fermé qu’est un cercle, le maximum et le
minimum existent. D’après les valeurs prises par la fonction, (2, 2) et (−2, −2) sont les
seules solutions possibles du problème de maximisation et (−2, 2) et (2, −2) les seules
possibles du problème de minimisation.
(b) Avec L = 𝑥 + 𝑦 − 𝜆 (𝑥2 + 3𝑥𝑦 + 3𝑦2 − 3), les conditions du premier ordre sont
1 − 2𝜆𝑥 − 3𝜆𝑦 = 0 et 1 − 3𝜆𝑥 − 6𝜆𝑦 = 0. Ces équations donnent
1 = 2𝜆𝑥 + 3𝜆𝑦 = 3𝜆𝑥 + 6𝜆𝑦.
En particulier, 𝜆 (3𝑦 + 𝑥) = 0. Comme 𝜆 = 0 est impossible, 𝑥 = −3𝑦. En introduisant
cette expression de 𝑥, la contrainte devient 3𝑦2 = 3, d’où 𝑦 = ±1.
Il y a donc deux candidats : (𝑥, 𝑦, 𝜆) = (3, −1, 1
3 ) et (𝑥, 𝑦, 𝜆) = (−3, 1, −1
3 ). Comme la
fonction objectif est continue et la courbe de contrainte est bornée fermée (en fait une
ellipse – voir (5.5.5)), le théorème des bornes atteintes garantit l’existence d’extrema. Les
valeurs de la fonction sont 𝑓 (3, −1) = 2 et 𝑓 (−3, 1) = −2. Le maximum se produit en
(3, −1), le minimum en (−3, 1).
2. (a) Avec L = 𝑥2 + 𝑦2 − 2𝑥 + 1 − 𝜆 (𝑥2 + 4𝑦2 − 16), les conditions du premier ordre
sont (i) 2𝑥 − 2 − 2𝜆𝑥 = 0 et (ii) 2𝑦 − 8𝜆𝑦 = 0. L’équation (i) implique 𝑥 ≠ 0 et, de
là, 𝜆 = 1 − 1/𝑥, tandis que l’équation (ii) entraîne 𝑦 = 0 ou 𝜆 = 1/4. Si 𝑦 = 0, alors
𝑥2 = 16 − 4𝑦2 = 16, de sorte que 𝑥 = ±4, qui donne alors 𝜆 = 1 ∓ 1/4. Si 𝑦 ≠ 0, alors
(32) On note que le maximum en lui-même est beaucoup plus facile à déterminer si on introduit la contrainte
𝑀 = 1
6 𝑥𝑇 3 dans la fonction objectif 𝑓 (𝑥,𝑇 ), qui devient alors la fonction −𝛼𝑀𝑇 2 + 1
2 𝑀𝑇 + 𝑀 de 𝑇 seulement,
avec 𝛼 et 𝑀 comme paramètres. La condition du premier ordre pour que 𝑇 rende cette expression maximale est
−2𝛼𝑀𝑇 +
1
2
𝑀 = 0,
impliquant 𝑇 = 1/4𝛼. Cette méthode ne permet cependant pas de trouver 𝜆.

205. Chapitre 18 / Optimisation sous contraintes d’égalité 205
𝜆 = 1/4 et (i) donne 2𝑥 − 2 − 𝑥/2 = 0, d’où 𝑥 = 4/3. La contrainte 𝑥2 + 4𝑦2 = 16 fournit
4𝑦2 = 16 − 16/9 = 128/9, de sorte que 𝑦 = ±
p
32/9 = ±4
√
2/3.
Il y a donc quatre candidats : (𝑥, 𝑦, 𝜆) = (4, 0, 3/4) ; (𝑥, 𝑦, 𝜆) = (−4, 0, 5/4) ; (𝑥, 𝑦, 𝜆) =
(4/3, 4
√
2/3, 1/4) et (𝑥, 𝑦, 𝜆) = (4/3, −4
√
2/3, 1/4).
L’examen des valeurs prises par la fonction conduit au résultat suivant : le maximum
est 25, atteint en (𝑥, 𝑦, 𝜆) = (−4, 0, 5/4), le minimum est 11/3, atteint en (𝑥, 𝑦, 𝜆) =
(4/3, ±4
√
2/3, 1/4).
(b) Le lagrangien s’écrit L = ln (2 + 𝑥2) + 𝑦2 −𝜆 (𝑥2 +2𝑦 −2). Les conditions du premier
ordre pour que (𝑥, 𝑦) amène au minimum sont (i) 𝜕L/𝜕𝑥 = 2𝑥/(2 + 𝑥2) − 2𝜆𝑥 = 0,
(ii) 𝜕L/𝜕𝑦 = 2𝑦 − 2𝜆 = 0, (iii) 𝑥2 + 2𝑦 = 2.
De (i) découle 𝑥 1/(2 + 𝑥2
) − 𝜆
= 0, soit 𝑥 = 0 ou 𝜆 = 1/(2 + 𝑥2
).
Si 𝑥 = 0, alors (iii) donne 𝑦 = 1, de sorte que (𝑥1, 𝑦1) = (0, 1) est un premier candidat
à la solution. Si 𝑥 ≠ 0, alors 𝑦 = 𝜆 = 1/(2 + 𝑥2
) , par (ii). On introduit l’expression
𝑦 = 1/(2 + 𝑥2
) dans (iii) et on obtient
𝑥2
+ 2/(2 + 𝑥2
) = 2 ⇔ 2𝑥2
+ 𝑥4
+ 2 = 4 + 2𝑥2
⇔ 𝑥4
= 2 ⇔ 𝑥 = ±
4
√
2.
De (iii), 𝑦 = 1 − 1
2 𝑥2 = 1 − 1
2
√
2. D’où
(𝑥2, 𝑦2) = (
4
√
2, 1 − 1
2
√
2) et (𝑥3, 𝑦3) = (−
4
√
2, 1 − 1
2
√
2)
sont deux nouveaux candidats. On compare les valeurs prises par la fonction
𝑓 (𝑥1, 𝑦1) = 𝑓 (0, 1) = ln 2 + 1 ≈ 1,69,
𝑓 (𝑥2, 𝑦2) = 𝑓 (𝑥3, 𝑦3) = ln (2 +
√
2 ) + (1 − 1
2
√
2 )2
= ln (2 +
√
2 ) + 3
2 −
√
2 ≈ 1,31.
On conclut que le minimum de 𝑓 (𝑥, 𝑦) soumise à la contrainte se produit en (𝑥2, 𝑦2) et
(𝑥3, 𝑦3).
3. (a) L = 𝑥 + 𝑦 − 𝜆(𝑥2 + 𝑦 − 1). Les équations L′
𝑥 = 1 − 2𝜆𝑥 = 0, L′
𝑦 = 1 − 𝜆 = 0 et
𝑥2 + 𝑦 = 1 ont comme solution 𝑥 = 1/2, 𝑦 = 3/4 et 𝜆 = 1.
(b) Voir la figure C18.3.3, qui montre le maximum en (𝑥, 𝑦) =
1
2 , 3
4
. Le problème de
minimisation n’a pas de solution, car 𝑓 (𝑥, 1 − 𝑥2) = 𝑥 + 1 − 𝑥2 → −∞ lorsque 𝑥 → +∞.
y
x
−1 1
y = 1 − x2
( 1
2 , 3
4 )
1
2
x + y =
x + y = 5
4
Figure C18.3.3

206. 206 CORRIGÉS DES EXERCICES
(c) La solution du nouveau problème est 𝑥 = 0,5 et 𝑦 = 0,85. La variation de la fonction
de valeur optimale est 𝑓 ∗(1,1) − 𝑓 ∗(1) = (0,5+0,85) − (0,5+0,75) = 0,1. Comme 𝜆 = 1,
on a 𝜆 × 𝑑𝑐 = 1 × 0,1 = 0,1. Dans ce cas, (18.2.3) est vérifiée avec égalité. (C’est dû à la
forme particulière des fonctions 𝑓 et 𝑔.)
4. (a) Avec L = 24𝑥 − 𝑥2 + 16𝑦 − 2𝑦2 − 𝜆(𝑥2 + 2𝑦2 − 44), les conditions du premier ordre
sont (i) L′
𝑥 = 24 − 2𝑥 − 2𝜆𝑥 = 0 et (ii) L′
𝑦 = 16 − 4𝑦 − 4𝜆𝑦 = 0. De (i), 𝑥 (1 + 𝜆) = 12 et
de (ii) 𝑦 (1 + 𝜆) = 4. Après élimination de 𝜆 de (i) et (ii), on obtient 𝑥 = 3𝑦 = 12/(1 + 𝜆),
avec 𝜆 ≠ −1. On introduit ce résultat dans la contrainte, 11𝑦2 = 44, soit 𝑦 = ±2 et, de
là, 𝑥 = ±6. Il y a deux candidats, (𝑥, 𝑦) = (6, 2) avec 𝜆 = 1 et (𝑥, 𝑦) = (−6, −2) avec
𝜆 = −3. Le calcul de la fonction objectif en ces deux points mène à conclure que le seul
maximum possible est en (𝑥, 𝑦) = (6, 2). Comme la fonction objectif est continue et la
courbe de la contrainte, bornée fermée, le théorème des bornes atteintes garantit qu’il y a
bien un maximum en ce point.
(b) Selon la formule (18.2.3), la variation est à peu près égale à 𝜆 × 1 = 1.
5. (a) 𝑄 = x′Ax, où x′ est le vecteur ligne (𝑥1, 𝑥2) et A est la matrice
2 7
7 2
.
(b) On a L = 2𝑥2
1 + 14𝑥1𝑥2 + 2𝑥2
2 − 𝜆(𝑥2
1 + 𝑥2
2 − 1). Les conditions du premier ordre sont
L′
1 = 4𝑥1 + 14𝑥2 − 2𝜆𝑥1 = 0 et L′
2 = 14𝑥1 + 4𝑥2 − 2𝜆𝑥2 = 0. En divisant chaque équation
par 2, on observe que ces deux équations peuvent être réécrites Ax = 𝜆x. Tout vecteur
non nul remplissant les conditions du premier ordre est donc un vecteur propre de A, et
le multiplicateur de Lagrange est la valeur propre associée.
(c) Comme 𝑄(x) = x′Ax est une fonction continue, elle atteint à la fois un maximum et
un minimum sur le cercle unité x′x = 𝑥2
1 + 𝑥2
2 = 1, qui est un ensemble fermé et borné. Il
existe donc un maximum en x+ et un minimum en x− qui vérifient x′x = 1 ainsi que les
conditions du premier ordre Ax = 𝜆x, ou encore x′Ax = 𝜆. La plus grande valeur propre
est donc le maximum et la plus petite, le minimum.
(d) L’équation caractéristique s’écrit
0 =
2 − 𝜆 7
7 2 − 𝜆
= (2 − 𝜆)2
− 49 = 𝜆2
− 4𝜆 − 45 = (𝜆 − 2)2
− 49.
Ses racines sont les deux valeurs propres 𝜆+ = 9 et 𝜆− = −5. Leur sont respectivement
associés les deux vecteurs propres x+ et x− qui vérifient
−7 7
7 −7
x+
= 0 et
7 7
7 7
x−
= 0.
En les normalisant de sorte que x′x = 1, on obtient respectivement les vecteurs orthogo-
naux x+ = ±1
2
√
2 (1, 1)′ et x− = ±1
2
√
2 (1, −1)′. Les vecteurs ±1
2
√
2 (1, 1)′ sont les deux
points de maximum sous contrainte de 𝑄, tandis que ±1
2
√
2 (1, −1)′ sont les deux points
de minimum sous contrainte.

207. Chapitre 18 / Optimisation sous contraintes d’égalité 207
18.4
1. Poser 𝑦 = 2 − 𝑥 réduit le problème à la maximisation de 𝑥(2 − 𝑥) = 2𝑥 − 𝑥2, qui a pour
solution 𝑥 = 1. La valeur optimale de 𝑦 devient donc 2−𝑥 = 1. En utilisant la méthode du
multiplicateur de Lagrange avec le lagrangien L(𝑥, 𝑦) = 𝑥𝑦 − 𝜆(𝑥 + 𝑦 − 2), les conditions
du premier ordre sont 𝑦 − 𝜆 = 0, 𝑥 − 𝜆 = 0, avec l’unique solution 𝑥 = 𝑦 = 𝜆 = 1 vérifiant
la contrainte 𝑥 + 𝑦 = 2. Alors, quand 𝜆 = 1, on a L(2, 2) = 2 L(1, 1) = 1, de sorte
que (1, 1) ne produit pas de maximum pour L. (En fait, L(𝑥, 𝑦) admet un point-selle en
(1, 1).)
2. Le problème des systèmes de trois équations à deux inconnues n’est pas qu’ils soient
plus difficiles à résoudre, c’est qu’ils sont souvent incompatibles – c’est-à-dire qu’il est
impossible de les résoudre. Les équations 𝑓 ′
𝑥 (𝑥, 𝑦) = 𝑓 ′
𝑦 (𝑥, 𝑦) = 0 ne sont pas valides au
point optimal.
3. (a) Avec L = 2𝑥 + 3𝑦 − 𝜆 (
√
𝑥 +
√
𝑦 − 5), les conditions du premier ordre sont
L′
𝑥 (𝑥, 𝑦) = 2 − 𝜆/2
√
𝑥 = 0, L′
𝑦 (𝑥, 𝑦) = 3 − 𝜆/2
√
𝑦 = 0. On a donc 𝜆 = 4
√
𝑥 = 6
√
𝑦, d’où
𝑦 = 4𝑥/9. Ainsi, 𝑥 = 9 et 𝑦 = 4, avec 𝜆 = 12.
(b) Voir figure C18.4.3. Déplacez la droite d’équation 2𝑥 + 3𝑦 = 𝑐 le plus loin possible
dans la direction nord-est. La solution est en (𝑥, 𝑦) = (0, 25).
(c) Comme 𝑔(𝑥, 𝑦) est continûment différentiable seulement sur l’ensemble 𝐴 des (𝑥, 𝑦)
tels que 𝑥 0 et 𝑦 0, le théorème ne s’applique pas au point (𝑥, 𝑦) = (0, 25).
y
x
x + y = 5
2x + 3y = 75
2x + 3y = 50
P
(25, 0)
2x + 3y = 30
(0, 25)
Figure C18.4.3
4. Avant d’essayer de trouver le minimum demandé, on observe le graphique de la courbe
d’équation 𝑔(𝑥, 𝑦) = 0, que montre la figure C18.4.4. Elle se compose de trois parties :
(i) la courbe continue d’équation 𝑦 =
√
𝑥 (𝑥 + 1) dans le quadrant positif;
(ii) la courbe continue d’équation 𝑦 = −
√
𝑥 (𝑥 + 1), image de (i) par une réflexion par
rapport à l’axe 𝑂𝑥 ;
(iii) le point isolé (−1, 0). Le problème consiste à trouver le point de la courbe le
plus proche du point de coordonnées (−2, 0). Géométriquement, il est évident que
ce minimum se produit au point isolé (−1, 0), où 𝑓 (−1, 0) = 1. Avec le lagrangien
L = (𝑥 + 2)2 + 𝑦2 − 𝜆(𝑦2 − 𝑥 (𝑥 + 1)2), on a L′
𝑥 = 2 (𝑥 + 2) + 𝜆((𝑥 + 1)2 + 2𝑥 (𝑥 + 1))

208. 208 CORRIGÉS DES EXERCICES
et L′
𝑦 = 2𝑦 (1 − 𝜆). Notez que L′
𝑦 = 2𝑦 (1 − 𝜆) = 0 seulement si 𝜆 = 1 ou 𝑦 = 0. Pour
𝜆 = 1, on a L′
𝑥 = 3 (𝑥 + 1)2 + 2 0 quel que soit 𝑥. Pour 𝑦 = 0, la contrainte donne 𝑥 = 0
ou 𝑥 = −1. En 𝑥 = 0, L′
𝑥 = 4 + 𝜆 = 0 et en 𝑥 = −1, L′
𝑥 = 2.
La méthode des multiplicateurs de Lagrange ne fournit que la solution éventuelle
(𝑥, 𝑦) = (0, 0) avec 𝜆 = −4, qui ne correspond pas à un minimum local. Le mini-
mum global en (−1, 0) ne satisfait pas aux conditions du premier ordre L′
𝑥 = L′
𝑦 = 0
pour quelque valeur de 𝜆 que ce soit, car L′
𝑥 = 2 en ce point. La méthode des multiplica-
teurs de Lagrange ne peut donc pas identifier ce minimum. Notez qu’en (−1, 0) à la fois
𝑔′
𝑥 (−1, 0) et 𝑔′
𝑦 (−1, 0) sont nuls.
x
y
− 3 − 2 − 1 1 2 3
− 6
− 5
− 4
− 3
− 2
− 1
1
2
3
4
5
6
d
(x,y)
y2 = x(1+ x)2
Figure C18.4.4
18.5
1. Le lagrangien L = 10𝑥1/2𝑦1/3 − 𝜆(2𝑥 + 4𝑦 − 𝑚) est concave en (𝑥, 𝑦). D’après le théo-
rème 18.5.1, la solution du point (a) de l’exercice 13.2.8 est donc un maximum.
2. Avec L = ln 𝑥 + ln 𝑦 − 𝜆(𝑝𝑥 + 𝑞𝑦 − 𝑚), L′
𝑥 = 1/𝑥 − 𝑝𝜆, L′
𝑦 = 1/𝑦 − 𝑞𝜆, L′′
𝑥𝑥 = −1/𝑥2,
L′′
𝑥𝑦 = 0 et L′′
𝑦𝑦 = −1/𝑦2. De plus, 𝑔′
𝑥 = 𝑝 et 𝑔′
𝑦 = 𝑞. De là,
𝐷(𝑥, 𝑦, 𝜆) = −𝑞2
/𝑥2
− 𝑝2
/𝑦2
0.
La condition (i) du théorème 18.5.2 est vérifiée.
3. Comme 𝐷(𝑥, 𝑦, 𝜆) = 10, le théorème 18.5.2 dit que (𝑎/5, 2𝑎/5) est un minimum local.
4. Avec L = 𝑥𝑎 + 𝑦𝑎 − 𝜆(𝑝𝑥 + 𝑞𝑦 − 𝑚), les conditions du premier ordre sont
L′
𝑥 = 𝑎𝑥𝑎−1
− 𝜆𝑝 = 0 et L′
𝑦 = 𝑎𝑦𝑎−1
− 𝜆𝑞 = 0.

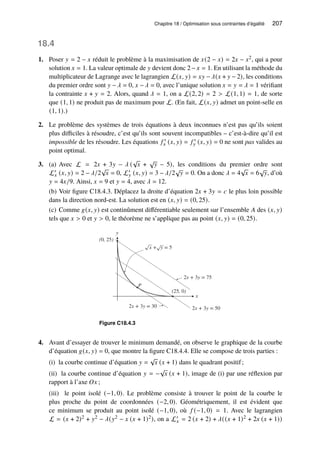
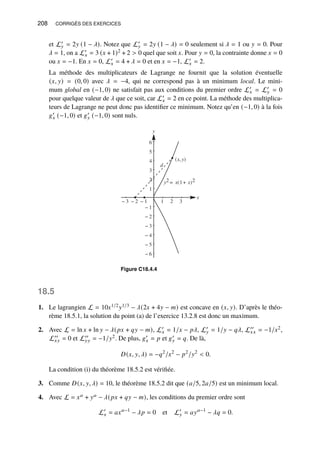
209. Chapitre 18 / Optimisation sous contraintes d’égalité 209
Si 𝜆 = 0, alors (𝑥, 𝑦) = (0, 0), et la contrainte n’est pas satisfaite. Il en découle que 𝜆 ≠ 0
et aussi 𝑥 = (𝜆𝑝/𝑎)1/(𝑎−1), 𝑦 = (𝜆𝑞/𝑎)1/(𝑎−1). L’introduction de ces valeurs de 𝑥 et 𝑦
dans la contrainte de budget mène à
(𝜆/𝑎)1/(𝑎−1)
(𝑝𝑎/(𝑎−1)
+ 𝑞𝑎/(𝑎−1)
) = 𝑚.
Afin de simplifier les notations, on pose 𝑅 = 𝑝𝑎/(𝑎−1) + 𝑞𝑎/(𝑎−1). On a alors
(𝜆/𝑎)1/(1−𝑎)
= 𝑚/𝑅.
Par conséquent, 𝑥 = 𝑚𝑝1/(𝑎−1)/𝑅 et 𝑦 = 𝑚𝑞1/(𝑎−1)/𝑅.
18.6
1. (a) L(𝑥, 𝑦, 𝑧) = 𝑥2+𝑦2+𝑧2−𝜆(𝑥+𝑦+𝑧−1), de sorte que L′
𝑥 = 2𝑥−𝜆 = 0, L′
𝑦 = 2𝑦−𝜆 = 0,
L′
𝑧 = 2𝑧 − 𝜆 = 0. Il s’ensuit que 𝑥 = 𝑦 = 𝑧. La seule solution des conditions nécessaires
est (1/3, 1/3, 1/3) avec 𝜆 = 2/3.
(b) Le problème consiste à déterminer la plus courte distance entre l’origine et le plan
d’équation 𝑥 + 𝑦 + 𝑧 = 1. Le problème de maximisation correspondant n’a pas de solution.
2. 𝑥 =
1/2
1/2 + 1/3 + 1/4
390
4
= 45, 𝑦 =
1/3
1/2 + 1/3 + 1/4
390
3
= 40,
𝑧 =
1/4
1/2 + 1/3 + 1/4
390
6
= 15.
3. (a) Avec le lagrangien L(𝑥, 𝑦, 𝑧) = 𝑥 +
√
𝑦 − 1/𝑧 − 𝜆(𝑝𝑥 + 𝑞𝑦 + 𝑟𝑧 − 𝑚), les conditions
du premier ordre sont, en plus de la contrainte
(i) L′
𝑥 = 1 − 𝜆𝑝 = 0; (ii) L′
𝑦 = 1
2 𝑦−1/2 − 𝜆𝑞 = 0; (iii) L′
𝑧 = 𝑧−2 − 𝜆𝑟 = 0.
(b) Des équations de (a), on tire 𝜆 = 1/𝑝 et, de là, 1
2 𝑦−1/2 = 𝑞/𝑝, de sorte que 𝑦 = 𝑝2/4𝑞2
et finalement 𝑧 =
p
𝑝/𝑟. On introduit ces expressions de 𝑦 et 𝑧 dans la contrainte de budget
et on résout par rapport à 𝑥, cela donne 𝑥 = 𝑚/𝑝 − 𝑝/4𝑞 −
p
𝑟/𝑝.
(c) Substitution directe.
(d) 𝜕𝑈∗/𝜕𝑚 = 1/𝑝 = 𝜆, comme on s’y attend depuis la section 14.2.
4. Le lagrangien est L(𝑥, 𝑦, ℓ) = 𝛼 ln 𝑥 + 𝛽 ln 𝑦 + (1 − 𝛼 − 𝛽) ln(𝐿 − ℓ) − 𝜆 (𝑝𝑥 + 𝑞𝑦 − 𝑤ℓ).
Il admet un point critique en la solution (𝑥∗, 𝑦∗, ℓ∗) des équations suivantes :
(i) L′
𝑥 = 𝛼/𝑥∗−𝜆𝑝 = 0; (ii) L′
𝑦 = 𝛽/𝑦∗−𝜆𝑞 = 0; (iii) L′
ℓ = −(1−𝛼−𝛽)/(𝐿−ℓ∗)+𝜆𝑤 = 0.
De (i) et (ii), 𝑞𝑦∗ = (𝛽/𝛼)𝑝𝑥∗, tandis que de (i) et (iii) ℓ∗ = 𝐿 − [(1 − 𝛼 − 𝛽)/𝑤𝛼]𝑝𝑥∗.
On introduit dans la contrainte de budget et on résout par rapport à 𝑥∗. Cela donne
𝑥∗ = 𝛼𝑤𝐿/𝑝, 𝑦∗ = 𝛽𝑤𝐿/𝑞 et ℓ∗ = (𝛼 + 𝛽)𝐿.
5. Comme les contraintes se réduisent à ℎ + 2𝑘 + ℓ = 0 et 2ℎ − 𝑘 − 3ℓ = 0, 𝑘 = −ℎ et ℓ = ℎ.
Mais alors 𝑥2 + 𝑦2 + 𝑧2 = 200 + 3ℎ2 ⩾ 200 pour tout ℎ, de sorte que 𝑓 est maximale pour
ℎ = 0. Ensuite 𝑘 = ℓ = 0 aussi et on conclut que (𝑥, 𝑦, 𝑧) = (10, 10, 0) est solution du
problème de minimisation.

210. 210 CORRIGÉS DES EXERCICES
6. Ici, L = 𝑎2
1𝑥2
1 + · · · + 𝑎2
𝑛𝑥2
𝑛 − 𝜆 (𝑥1 + · · · + 𝑥𝑛 − 1). Les conditions nécessaires sont
L′
𝑥𝑗
= 2𝑎2
𝑗𝑥𝑗 − 𝜆 = 0, pour 𝑗 = 1, . . . , 𝑛,
ce qui conduit à 𝑥𝑗 = 𝜆/2𝑎2
𝑗. En les introduisant dans la contrainte, on trouve la relation
1 = 1
2𝜆 (1/𝑎2
1 + · · · + 1/𝑎2
𝑛). Donc, pour 𝑗 = 1, . . . , 𝑛, on a
𝑥𝑗 =
1/𝑎2
𝑗
1/𝑎2
1 + · · · + 1/𝑎2
𝑛
=
1/𝑎2
𝑗
Í𝑛
𝑖=1(1/𝑎2
𝑖 )
.
Si au moins un 𝑎𝑖 est nul, la valeur minimale est 0; elle est atteinte en posant le 𝑥𝑖
correspondant égal à 1, les autres 𝑥𝑗 étant tous nuls.
7. Le lagrangien s’écrit L = 𝑥 + 𝑦 −𝜆 (𝑥2 +2𝑦2 + 𝑧2 −1) − 𝜇 (𝑥 + 𝑦 + 𝑧 −1). Les coordonnées
de ses points critiques sont telles que (i) L′
𝑥 = 1−2𝜆𝑥−𝜇 = 0; (ii) L′
𝑦 = 1−4𝜆𝑦−𝜇 = 0;
(iii) L′
𝑧 = −2𝜆𝑧 − 𝜇 = 0. De (ii) et (iii), on a 1 = 𝜆(4𝑦 − 2𝑧), et en particulier 𝜆 ≠ 0.
De (i) et (ii), 𝜆(𝑥 − 2𝑦) = 0 et aussi 𝑥 = 2𝑦. En substituant cette expression de 𝑥 dans
les contraintes, on obtient 6𝑦2 + 𝑧2 = 1 et 3𝑦 + 𝑧 = 1. Alors 𝑧 = 1 − 3𝑦 implique
1 = 6𝑦2 + (1−3𝑦)2 = 15𝑦2 −6𝑦 +1. De là, 𝑦 = 0 ou 𝑦 = 2/5, impliquant 𝑥 = 0 ou 𝑥 = 4/5
et 𝑧 = 1 ou 𝑧 = −1/5. Les seuls candidats sont (𝑥, 𝑦, 𝑧) = (0, 0, 1) avec 𝜆 = −1/2, 𝜇 = 1
et (𝑥, 𝑦, 𝑧) = (4/5, 2/5, −1/5) avec 𝜆 = 1/2, 𝜇 = 1/5. Comme 𝑥 + 𝑦 est nul en (0, 0, 1) et
vaut 6/5 en (4/5, 2/5, −1/5), ce sont respectivement le minimum et le maximum(33).
8. (a) Pour la fonction d’utilité de Cobb-Douglas donnée, on a 𝑈′
𝑥𝑗
(x) = 𝛼𝑗𝑈(x)/𝑥𝑗. Alors
(18.6.6) dans le cas 𝑘 = 1 implique 𝑝𝑗/𝑝1 = 𝑈′
𝑥𝑗
(x)/𝑈′
𝑥1
(x) = 𝛼𝑗𝑥1/𝛼1𝑥𝑗. D’où
𝑝𝑗𝑥𝑗 = (𝑎𝑗/𝑎1)𝑝1𝑥1. On introduit cette expression dans la contrainte de budget pour
𝑗 = 2, . . . , 𝑛, ce qui donne 𝑝1𝑥1 + (𝑎2/𝑎1)𝑝1𝑥1 + · · · + (𝑎𝑛/𝑎1)𝑝1𝑥1 = 𝑚, impliquant
𝑝1𝑥1 = 𝑎1𝑚/(𝑎1 + · · · + 𝑎𝑛). De même, 𝑝𝑗𝑥𝑗 = 𝑎𝑗 𝑚/(𝑎1 + · · · + 𝑎𝑛) pour 𝑘 = 1, . . ., 𝑛.
(b) De (18.6.6) dans le cas 𝑘 = 1, on a 𝑥𝑎−1
𝑗 /𝑥𝑎−1
1 = 𝑝𝑗/𝑝1 et ainsi
𝑥𝑗/𝑥1 = (𝑝𝑗/𝑝1)−1/(1−𝑎)
ou 𝑝𝑗𝑥𝑗/𝑝1𝑥1 = (𝑝𝑗/𝑝1)1−1/(1−𝑎)
= (𝑝𝑗/𝑝1)−𝑎/(1−𝑎)
.
On introduit cette expression dans la contrainte de budget pour 𝑗 = 2, . . . , 𝑛, ce qui donne
𝑝1𝑥1
h
1 + (𝑝2/𝑝1)−𝑎/(1−𝑎)
+ · · · + (𝑝𝑛/𝑝1)−𝑎/(1−𝑎)
i
= 𝑚
de sorte que
𝑝1𝑥1 = 𝑚𝑝−𝑎/(1−𝑎)
1
. 𝑛
Õ
𝑖=1
𝑝−𝑎/(1−𝑎)
𝑖 .
Le même raisonnement pour chaque 𝑗 conduit à
𝑝𝑗𝑥𝑗 = 𝑚𝑝−𝑎/(1−𝑎)
𝑗
. 𝑛
Õ
𝑖=1
𝑝−𝑎/(1−𝑎)
𝑖
pour 𝑗 = 1, . . ., 𝑛.
(33) Les deux contraintes déterminent la courbe d’intersection entre un ellipsoïde (voir figure 14.4.1 du livre) et un
plan. Comme un ellipsoïde est un ensemble borné fermé de l’espace de dimension trois, la courbe en question l’est
aussi et la fonction objectif 𝑥 + 𝑦, continue, atteint obligatoirement un maximum et un minimum sur cet ensemble
borné fermé.

211. Chapitre 18 / Optimisation sous contraintes d’égalité 211
18.7
1. (a) Comme L = 𝑥 + 𝑎 ln 𝑦 −𝜆(𝑝𝑥 + 𝑞𝑦 − 𝑚), on a L′
𝑥 = 1 −𝜆𝑝 = 0, L′
𝑦 = 𝑎/𝑦∗ −𝜆𝑞 = 0.
D’où 𝜆 = 1/𝑝 et, de là, après introduction dans la deuxième équation, 𝑦∗ = 𝑎𝑝/𝑞. La
contrainte de budget fournit alors 𝑥∗ = 𝑚/𝑝 − 𝑎. Comme le lagrangien est concave, c’est
bien la solution.
(b) 𝑈∗ = 𝑥∗ + 𝑎 ln 𝑦∗ = 𝑚/𝑝 − 𝑎 + 𝑎 ln 𝑎 + 𝑎 ln 𝑝 − 𝑎 ln 𝑞. Ensuite,
𝜕𝑈∗
/𝜕𝑝 = −𝑚/𝑝2
+ 𝑎/𝑝, 𝜕𝑈∗
/𝜕𝑞 = −𝑎/𝑞, 𝜕𝑈∗
/𝜕𝑚 = 1/𝑝
et 𝜕𝑈∗/𝜕𝑎 = ln 𝑎 + ln 𝑝 − ln 𝑞.
(c) 𝜕L/𝜕𝑝 = −𝜆𝑥, 𝜕L/𝜕𝑞 = −𝜆𝑦, 𝜕L/𝜕𝑚 = 𝜆 et 𝜕L/𝜕𝑎 = ln 𝑦. Le calcul de ces quatre
dérivées partielles en (𝑥∗, 𝑦∗) montre que le théorème de l’enveloppe est confirmé.
2. Ici, L = 𝑥 + 4𝑦 + 3𝑧 − 𝜆 (𝑥2 + 2𝑦2 + 1
3 𝑧2 − 𝑏). Les conditions du premier ordre sont
(i) L′
𝑥 = 1 − 2𝜆𝑥 = 0; (ii) L′
𝑦 = 4 − 4𝜆𝑦 = 0; (iii) L′
𝑧 = 3 − 2
3𝜆𝑧 = 0. Par
conséquent, 𝜆 ≠ 0 et ainsi 𝑥 = 1/2𝜆, 𝑦 = 1/𝜆, 𝑧 = 9/2𝜆. On introduit ces expres-
sions dans la contrainte, cela donne [(1/4) + 2 + (27/4)]𝜆−2 = 𝑏 et ainsi 𝜆2 = 9/𝑏,
impliquant 𝜆 = ±3/
√
𝑏. La valeur de la fonction objectif est 𝑥 + 4𝑦 + 3𝑧 = 18/𝜆.
Dès lors, 𝜆 = −3/
√
𝑏 détermine le minimum. C’est (𝑥, 𝑦, 𝑧) = (𝑎, 2𝑎, 9𝑎), où
𝑎 = −
√
𝑏/6. Enfin, d 𝑓 ∗(𝑏)/d𝑏 = −3/
√
𝑏 = 𝜆.
3. (a) 𝑥 = 𝑎𝑀/𝛼, 𝑦 = 𝑏𝑀/𝛽, 𝑧 = 𝑐𝑀/𝛾, 𝜆 = 1/2𝑀, où
𝑀 =
√
𝐿/
q
𝑎2/𝛼 + 𝑏2/𝛽 + 𝑐2/𝛾 .
(Les conditions du premier ordre donnent 𝑥 = 𝑎/2𝜆𝛼, 𝑦 = 𝑏/2𝜆𝛽, 𝑧 = 𝑐/2𝜆𝛾. La solution
est obtenue en substituant ces expressions dans la contrainte et en résolvant par rapport
à 𝜆.)
(b) On trouve 𝑀 =
√
𝐿/5 et les valeurs de 𝑥, 𝑦 et 𝑧 en découlent.
(c) Lorsque 𝐿 = 100, 𝑀 = 2 et 𝜆 = 1/4. L’augmentation de la valeur maximale,
lorsque 𝐿 passe de 100 à 101, est d’environ 𝜆 × 1 = 0,25. L’augmentation effective est
5 (
√
101 −
√
100 ) ≈ 0,249378.
4. (a) Avec L = 𝑥2 + 𝑦2 + 𝑧 − 𝜆 (𝑥2 + 2𝑦2 + 4𝑧2 − 1), les conditions nécessaires sont
(i) 𝜕L/𝜕𝑥 = 2𝑥 − 2𝜆𝑥 = 0; (ii) 𝜕L/𝜕𝑦 = 2𝑦 − 4𝜆𝑦 = 0; (iii) 𝜕L/𝜕𝑧 = 1 − 8𝜆𝑧 = 0.
De (i), 2𝑥 (1 − 𝜆) = 0, de sorte qu’il y a deux possibilités : 𝑥 = 0 ou 𝜆 = 1.
(A) Soit 𝑥 = 0. De (ii), 2𝑦 (1 − 2𝜆) = 0, soit 𝑦 = 0 ou 𝜆 = 1/2.
(A.1) Si 𝑦 = 0, la contrainte donne 4𝑧2 = 1 ou 𝑧2 = 1/4 ou encore 𝑧 = ±1/2. L’équation
(iii) donne 𝜆 = 1/8𝑧 et il y a deux candidats, 𝑃1 de coordonnées (0, 0, 1/2) avec 𝜆 = 1/4
et, 𝑃2 de coordonnées (0, 0, −1/2) avec 𝜆 = −1/4.
(A.2) Si 𝜆 = 1/2, alors (iii) donne 𝑧 = 1/8𝜆 = 1/4. De la contrainte, il suit que 2𝑦2 = 3/4
(on a supposé 𝑥 = 0) et, de là, 𝑦 = ±
p
3/8 = ±
√
6/4. Les nouveaux candidats sont 𝑃3
de coordonnées (0,
√
6/4, 1/4) avec 𝜆 = 1/2 et 𝑃4 de coordonnées (0, −
√
6/4, 1/4) avec
𝜆 = 1/2.

212. 212 CORRIGÉS DES EXERCICES
(B) Soit 𝜆 = 1. L’équation (iii) donne 𝑧 = 1/8 et (ii) donne 𝑦 = 0. De la contrainte, il vient
𝑥2 = 15/16, de sorte que 𝑥 = ±
√
15/4. Candidats : 𝑃5 de coordonnées (
√
15/4, 0, 1/8)
avec 𝜆 = 1 et 𝑃6 de coordonnées (−
√
15/4, 0, 1/8) avec 𝜆 = 1.
On désigne par 𝑓𝑘 la valeur de la fonction objectif pour 𝑘 = 1, 2, . . . , 6 où 𝑃𝑘 désigne
chacun des 6 candidats. Les calculs fournissent 𝑓1 = 1/2, 𝑓2 = −1/2, 𝑓3 = 𝑓4 = 5/8 et
𝑓5 = 𝑓6 = 17/16. Après comparaison, 1
4
√
15, 0, 1
8
et −1
4
√
15, 0, 1
8
(avec 𝜆 = 1) sont
les solutions du problème de maximisation et 0, 0, −1
2
est la solution du problème de
minimisation.
(b) Δ 𝑓 ∗ ≈ 𝜆Δ𝑐 = 1 × 0,02 = 0,02
5. Le lagrangien est L = 𝑟𝐾 + 𝑤𝐿 − 𝜆 (𝐾1/2𝐿1/4 − 𝑄). Les conditions nécessaires pour
que (𝐾∗, 𝐿∗) soit une solution du problème sont (i) L′
𝐾 = 𝑟 − 1
2𝜆(𝐾∗)−1/2(𝐿∗)1/4 = 0;
(ii) L′
𝐿 = 𝑤 − 1
4𝜆(𝐾∗)1/2(𝐿∗)−3/4 = 0; (iii) (𝐾∗)1/2(𝐿∗)1/4 = 𝑄. Ensemble (i) et
(ii) impliquent 𝑟/𝑤 = 2𝐿∗/𝐾∗ et ainsi 𝐿∗ = 𝑟𝐾∗/2𝑤. On introduit cela dans (iii) :
𝑄 = (𝐾∗)1/2(𝑟𝐾∗/2𝑤)1/4 = (𝐾∗)3/42−1/4𝑟1/4𝑤−1/4. La résolution par rapport à 𝐾∗ donne
la réponse 𝐾∗ = 21/3𝑟−1/3𝑤1/3𝑄4/3. Ensuite,
𝐿∗
= 2−2/3
𝑟2/3
𝑤−2/3
𝑄4/3
, 𝐶∗
= 3 × 2−2/3
𝑟2/3
𝑤1/3
𝑄4/3
, 𝜆 = 24/3
𝑟2/3
𝑤1/3
𝑄1/3
.
Les égalités (∗) de l’exemple 18.7.3 se vérifient facilement.
6. On obtient
𝜕𝐾∗
𝜕𝑤
=
𝜕
𝜕𝑤
𝜕𝐶∗
𝜕𝑟
=
𝜕
𝜕𝑟
𝜕𝐶∗
𝜕𝑤
=
𝜕𝐿∗
𝜕𝑟
,
grâce aux deux premières égalités (∗) de l’exemple 18.7.3.
7. (a) Avec L =
√
𝑥 + 𝑎𝑦 − 𝜆 (𝑝𝑥 + 𝑞𝑦 − 𝑚), les conditions du premier ordre pour que
(𝑥∗, 𝑦∗) soit solution du problème sont 𝑝𝑥∗ + 𝑞𝑦∗ = 𝑚 et (i) L′
𝑥 = 1/2
√
𝑥∗ − 𝜆𝑝 = 0,
(ii) L′
𝑦 = 𝑎 − 𝜆𝑞 = 0. D’où 𝜆 = 𝑎/𝑞 et 𝑥∗(𝑝, 𝑞, 𝑎, 𝑚) = 𝑞2/4𝑎2 𝑝2, 𝑦∗(𝑝, 𝑞, 𝑎, 𝑚) =
𝑚/𝑞 − 𝑞/4𝑎2 𝑝. Le lagrangien est concave en (𝑥, 𝑦), de sorte que c’est bien la solution.
La fonction d’utilité indirecte est 𝑈∗(𝑝, 𝑞, 𝑎, 𝑚) =
√
𝑥∗ + 𝑎𝑦∗ = 𝑞/4𝑎𝑝 + 𝑎𝑚/𝑞.
(b) Les dérivées partielles de 𝑈∗ par rapport aux quatre paramètres 𝑝, 𝑞, 𝑚 et 𝑎 sont
𝜕𝑈∗
/𝜕𝑝 = −𝑞/4𝑎𝑝2
, 𝜕𝑈∗
/𝜕𝑞 = 1/4𝑎𝑝 − 𝑎𝑚/𝑞2
, 𝜕𝑈∗
/𝜕𝑚 = 𝑎/𝑞
et 𝜕𝑈∗/𝜕𝑎 = −𝑞/4𝑎2 𝑝 + 𝑚/𝑞.
Par ailleurs, avec L(𝑥, 𝑦, 𝑝, 𝑞, 𝑎, 𝑚) =
√
𝑥 + 𝑎𝑦 − 𝜆 (𝑝𝑥 + 𝑞𝑦 − 𝑚), les dérivées partielles
premières de L calculées en (𝑥∗, 𝑦∗) sont 𝜕L∗/𝜕𝑝 = −𝜆𝑥∗ = −(𝑎/𝑞) (𝑞2/4𝑎2 𝑝2) =
−𝑞/4𝑎𝑝2, 𝜕L∗/𝜕𝑞 = −𝜆𝑦∗ = −(𝑎/𝑞) (𝑚/𝑞 − 𝑞/4𝑎2 𝑝) = 1/4𝑎𝑝 − 𝑎𝑚/𝑞2, 𝜕L∗/𝜕𝑚 = 𝜆
et 𝜕L∗/𝜕𝑎 = 𝑦∗ = 𝑚/𝑞 − 𝑞/4𝑎2 𝑝.
Le théorème de l’enveloppe est confirmé dans tous les cas.
Exercices récapitulatifs du chapitre 18
1. (a) Le lagrangien est L(𝑥, 𝑦) = 3𝑥+4𝑦−𝜆(𝑥2+𝑦2−225) et les conditions du premier ordre
impliquent 3−2𝜆𝑥 = 0 et 4−2𝜆𝑦 = 0, d’où 3𝑦 = 4𝑥 = 6𝜆. En introduisant ces valeurs dans

213. Chapitre 18 / Optimisation sous contraintes d’égalité 213
les contraintes, on obtient 𝑥2 = 81, d’où 𝑥 = ±9. Les deux solutions à toutes les conditions
du premier ordre sont (𝑥, 𝑦, 𝜆) = ±(9, 12, 1/6). Or, le lagrangien L(𝑥, 𝑦) est concave ou
concave selon que 𝜆 ⩾ 0 ou 𝜆 ⩽ 0. D’après le théorème 18.5.1, (𝑥, 𝑦) = (9, 12) est donc
un point de maximum et (𝑥, 𝑦) = (−9, −12) un point de minimum.
(b) Selon (18.2.3), 𝑓 ∗(225 − 1) − 𝑓 ∗(225) ≈ 𝜆(−1) = −1/6.
2. (a) 𝑥 = 2𝑚/5𝑝, 𝑦 = 3𝑚/5𝑞. (b) 𝑥 = 𝑚/3𝑝, 𝑦 = 2𝑚/3𝑞. (c) 𝑥 = 3𝑚/5𝑝, 𝑦 = 2𝑚/5𝑞.
3. (a) Si les ventes 𝑥 du premier bien s’accroissent, l’augmentation nette du profit par
unité d’augmentation de 𝑥 est la somme des trois termes : (i) 𝑝(𝑥∗), gain en recette
issu du surcroît de production; (ii) −𝑝′(𝑥∗) 𝑥∗, perte de revenu lors de la vente de
𝑥∗ unités à un prix réduit; (iii) −𝐶′
𝑥 (𝑥∗, 𝑦∗), opposé du coût marginal de la produc-
tion supplémentaire. En fait, 𝑝(𝑥∗) + 𝑝′(𝑥∗) 𝑥∗ est la dérivée de la fonction de recette
𝑅(𝑥) = 𝑝(𝑥) 𝑥 en 𝑥 = 𝑥∗, habituellement appelée la recette marginale. La première condi-
tion du premier ordre 𝑝(𝑥∗) = 𝐶′
𝑥 (𝑥∗, 𝑦∗) − 𝑥∗ 𝑝′(𝑥∗) dit que la recette marginale doit
être égale au coût marginal (partiel). Idem pour la deuxième condition du premier ordre
𝑞(𝑦∗) = 𝐶′
𝑦 (𝑥∗, 𝑦∗) − 𝑦∗𝑞′(𝑦∗), en cas d’augmentation des ventes 𝑦 du second bien.
(b) Compte tenu de la restriction 𝑥 + 𝑦 ⩽ 𝑚, on doit ajouter la condition 𝜆 ⩾ 0, avec
𝜆 = 0 si ˆ
𝑥 + ˆ
𝑦 𝑚.
4. (a) Le lagrangien est L(𝑥, 𝑦) = 𝑈(𝑥, 𝑦) − 𝜆[𝑝𝑦 − 𝑤(24 − 𝑥)]. Les conditions du premier
ordre impliquent 𝑝𝑈′
𝑥 = 𝑤𝑈′
𝑦 = 𝜆𝑤𝑝, ce qui immédiatement conduit à (∗∗).
(b) En dérivant (∗) et (∗∗) par rapport à 𝑤, on obtient 𝑝𝑦′
𝑤 = 24 − 𝑥 − 𝑤𝑥′
𝑤 et
𝑝(𝑈′′
11𝑥′
𝑤 + 𝑈′′
12𝑦′
𝑤 ) = 𝑈′
𝑦 + 𝑤(𝑈′′
21𝑥′
𝑤 + 𝑈′′
22𝑦′
𝑤 ). La solution de ces deux équations
du premier degré est la formule proposée de 𝑥′
𝑤 = 𝜕𝑥/𝜕𝑤.
5. (a) Avec L = 𝑥2 + 𝑦2 − 2𝑥 + 1 − 𝜆 ( 1
4 𝑥2 + 𝑦2 − 𝑏), les conditions du premier ordre
sont (i) L′
𝑥 = 2𝑥 − 2 − 1
2𝜆𝑥 = 0; (ii) L′
𝑦 = 2𝑦 − 2𝜆𝑦 = 0; (iii) 1
4 𝑥2 + 𝑦2 = 𝑏. De (ii), il
vient (1 − 𝜆) 𝑦 = 0 et donc 𝜆 = 1 ou 𝑦 = 0.
(I) Cas 𝜆 = 1. Alors (i) donne 𝑥 = 4
3 et, de (iii), on tire 𝑦2 = 𝑏 − 1
4 𝑥2 = 𝑏 − 4
9 , ce qui
donne 𝑦 = ±
q
𝑏 − 4
9 . Il y a deux candidats,
(𝑥1, 𝑦1) = 4/3,
r
𝑏 −
4
9
!
et (𝑥2, 𝑦2) = 4/3, −
r
𝑏 −
4
9
!
.
(II) Cas 𝑦 = 0. De (iii), 𝑥2 = 4𝑏, c’est-à-dire 𝑥 = ±2
√
𝑏. Deux candidats supplémentaires :
(𝑥3, 𝑦3) = (2
√
𝑏, 0) et (𝑥4, 𝑦4) = (−2
√
𝑏, 0). La fonction objectif prend les valeurs
suivantes : 𝑓 (𝑥1, 𝑦1) = 𝑓 (𝑥2, 𝑦2) = 𝑏 − 1/3, 𝑓 (𝑥3, 𝑦3) = (2
√
𝑏 − 1)2 = 4𝑏 − 4
√
𝑏 + 1,
𝑓 (𝑥4, 𝑦4) = (−2
√
𝑏 − 1)2 = 4𝑏 + 4
√
𝑏 + 1. Clairement, le maximum se produit en
(𝑥4, 𝑦4). Pour savoir lequel des trois autres couples (𝑥3, 𝑦3), (𝑥1, 𝑦1) ou (𝑥2, 𝑦2) conduit
au minimum, on doit décider lequel des deux nombres 4𝑏 − 4
√
𝑏 + 1 ou 𝑏 − 1
3 est le plus
petit. Leur différence est
4𝑏 − 4
√
𝑏 + 1 − 𝑏 −
1
3
= 3 𝑏 −
4
3
√
𝑏 +
4
9
= 3
√
𝑏 −
2
3
2
0

214. 214 CORRIGÉS DES EXERCICES
puisque 𝑏 4
9 . Le minimum se produit en (𝑥1, 𝑦1) et (𝑥2, 𝑦2). La contrainte 𝑥2/4+ 𝑦2 = 𝑏
décrit l’ellipse de la figure C18.R.5. La fonction objectif 𝑓 (𝑥, 𝑦) = (𝑥 − 1)2 + 𝑦2 fournit le
carré de la distance entre les points de coordonnées (𝑥, 𝑦) et (1, 0). Les courbes de niveau
de 𝑓 sont dès lors des cercles centrés en (1, 0) et la figure montre les deux qui passent
par les points de minimum et de maximum.
y
x
−4
−2
2
4
−4 −2 2 4 6
(x1,y 1)
(x3,y 3)
(x 2,y2)
(x 4 ,y4)
Figure C18.R.5
(b) Pour 𝑥 = −2
√
𝑏, 𝑦 = 0, 𝑓 ∗(𝑏) = 4𝑏 + 4
√
𝑏 + 1. Puisque 𝜆 = 4 + 2/
√
𝑏, l’égalité
suggérée est facilement vérifiée.
6. (a) Avec L(𝑥, 𝑦) = 𝑣(𝑥) + 𝑤(𝑦) − 𝜆 (𝑝𝑥 + 𝑞𝑦 − 𝑚), les conditions du premier ordre
fournissent 𝑣′(𝑥) = 𝜆𝑝 et 𝑤′(𝑦) = 𝜆𝑞. D’où 𝑣′(𝑥)/𝑤′(𝑦) = 𝑝/𝑞.
(b) Comme L′′
𝑥𝑥 = 𝑣′′(𝑥), L′′
𝑦𝑦 = 𝑤′′(𝑦) et L′′
𝑥𝑦 = 0, on constate que le lagrangien est
concave.
7. (a) Avec L = 𝑥2 − 2𝑥 + 1 + 𝑦2 − 2𝑦 − 𝜆[(𝑥 + 𝑦)
p
𝑥 + 𝑦 + 𝑏 − 2
√
𝑎], les conditions du
premier ordre sont (i) L′
𝑥 = 2𝑥 − 2 − 𝜆[
p
𝑥 + 𝑦 + 𝑏 + (𝑥 + 𝑦)/2
p
𝑥 + 𝑦 + 𝑏 ] = 0 et
(ii) L′
𝑦 = 2𝑦 − 2 − 𝜆[
p
𝑥 + 𝑦 + 𝑏 + (𝑥 + 𝑦)/2
p
𝑥 + 𝑦 + 𝑏 ] = 0.
Les conditions du premier ordre impliquent 2𝑥 − 2 = 2𝑦 − 2, de sorte que 𝑥 = 𝑦. La
contrainte donne 2𝑥
√
2𝑥 + 𝑏 = 2
√
𝑎. Après substitution dans la contrainte, élévation au
carré et simplification, on obtient la deuxième équation de (∗).
(b) On prend les différentielles (i) d𝑥 = d𝑦 ; (ii) 6𝑥2 d𝑥 + 𝑥2 𝑑𝑏 + 2𝑏𝑥 d𝑥 = 𝑑𝑎. On
identifie facilement dans ces équations les dérivées partielles de 𝑥 et 𝑦 par rapport à 𝑎
et 𝑏, 𝜕𝑥/𝜕𝑎 = 1/2𝑥 (3𝑥 + 𝑏) et 𝜕𝑥/𝜕𝑏 = −𝑥/2 (3𝑥 + 𝑏). Et, de là,
𝜕2𝑥
𝜕𝑎2
=
𝜕
𝜕𝑎
𝜕𝑥
𝜕𝑎
=
𝜕
𝜕𝑎
1
6𝑥2 + 2𝑏𝑥
= −
12𝑥 + 2𝑏
(6𝑥2 + 2𝑏𝑥)2
𝜕𝑥
𝜕𝑎
= −
12𝑥 + 2𝑏
(6𝑥2 + 2𝑏𝑥)3
= −
6𝑥 + 𝑏
4𝑥3 (3𝑥 + 𝑏)3
.

215. Chapitre 19 / Programmation linéaire 215
Chapitre 19 / Programmation linéaire
19.1
1. (a) Sur la figure C19.1.1a, on voit que la solution est à l’intersection des deux droites
d’équations 3𝑥1 +2𝑥2 = 6 et 𝑥1 +4𝑥2 = 4. Solution : max = 36/5 pour (𝑥1, 𝑥2) = (8/5, 3/5).
(b) Sur la figure C19.1.1b, on voit que la solution est à l’intersection des deux droites
d’équations 𝑢1 + 3𝑢2 = 11 et 2𝑢1 + 5𝑢2 = 20. Solution : min = 104 pour (𝑢1, 𝑢2) = (5, 2).
x2
x1
1
2
3
1 2 3 4
P
3x1
+ 4x2
= c
Figure C19.1.1a
u2
u1
5
5 10
10u1 + 27u2 = c
P
Figure C19.1.1b
2. (a) Un graphique montre que la solution est à l’intersection des droites d’équations
−2𝑥1 + 3𝑥2 = 6 et 𝑥1 + 𝑥2 = 5. D’où max = 98/5 pour (𝑥1, 𝑥2) = (9/5, 16/5).
(b) La solution est celle du système des deux équations 2𝑥1 + 3𝑥2 = 13 et 𝑥1 + 𝑥2 = 6.
D’où max = 49 pour (𝑥1, 𝑥2) = (5, 1)
(c) La solution est celle du système 𝑥1 − 3𝑥2 = 0 et 𝑥1 = 2. D’où max = −10/3 pour
(𝑥1, 𝑥2) = (2, 2/3).
3. L’ensemble 𝐴 correspond au polygone ombré de la figure C19.1.3.
(a) La solution est manifestement le point le plus haut 𝑃, car c’est celui dont l’ordon-
née 𝑥2 est la plus élevée. Ce point 𝑃 est situé à l’intersection des droites d’équations
−2𝑥1 + 𝑥2 = 2 et 𝑥1 + 2𝑥2 = 8 et ses coordonnées sont (𝑥1, 𝑥2) = (4/5, 18/5).
(b) Le point de 𝐴 qui a l’abscisse la plus grande est manifestement le point 𝑄 de coor-
données (8, 0).
(c) La droite d’équation 3𝑥1 +2𝑥2 = 𝑐 pour une certaine valeur de 𝑐 est tracée en pointillés
à la figure C19.1.3. Plus 𝑐 augmente, plus la droite s’éloigne vers le nord-est. Celle qui a
encore un point commun avec 𝐴 est celle qui passe par le point 𝑄 de coordonnées (8, 0),
en lequel la fonction objectif a la valeur 24.
(d) La droite d’équation 2𝑥1 − 2𝑥2 = 𝑐 (ou 𝑥2 = 𝑥1 − 𝑐/2) fait un angle de 45◦ avec
l’axe 𝑂𝑥1 et le coupe en 𝑐/2. Plus 𝑐 diminue, plus la droite monte vers la gauche. La
droite de cette famille qui a la valeur de 𝑐 la plus petite et encore un point en commun
avec 𝐴 est celle qui passe par le point 𝑃 de coordonnées (4/5, 18/5) en lequel la fonction
objectif prend la valeur minimale −28/5.

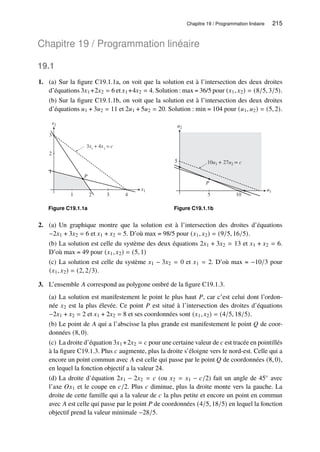
216. 216 CORRIGÉS DES EXERCICES
(e) La droite d’équation 2𝑥1 + 4𝑥2 = 𝑐 est parallèle à celle d’équation 𝑥1 + 2𝑥2 = 8 de la
figure. Lorsque 𝑐 augmente, elle s’éloigne de plus en plus vers le nord-est. Celle qui a des
points communs avec 𝐴 et qui a la plus grande valeur de 𝑐 manifestement coïncide avec
la droite d’équation 𝑥1 + 2𝑥2 = 8. Dès lors, tous les points du segment compris entre 𝑃 et
𝑄 sont solutions.
(f) La droite d’équation −3𝑥1 − 2𝑥2 = 𝑐 est parallèle à la droite en pointillés de la figure
et coupe l’axe 𝑂𝑥1 en −𝑐/3. Lorsque 𝑐 augmente, la droite se déplace vers le nord-est,
de sorte que la solution est en 𝑄 de coordonnées (8, 0) où la fonction objectif vaut −24.
(On pourrait aussi raisonner comme ceci : rendre minimum −3𝑥1 − 2𝑥2 sous la contrainte
(𝑥1, 𝑥2) dans 𝐴 est équivalent à rendre maximum 3𝑥1 + 2𝑥2 sous la contrainte (𝑥1, 𝑥2)
dans 𝐴. La solution est donc la même que celle de la question (c).)
x2
x1
P
A
Q
8
4
− 2x1 + x2 = 2
3x1 + 2x2 = c
x1 + 2x2 = 8
Figure C19.1.3
4. (a) Il n’y a pas de maximum. Regardez la figure C19.1.4. À valeurs croissantes de 𝑐, la
droite en pointillés d’équation 𝑥1 + 𝑥2 = 𝑐 se déplace vers le nord-est et possède toujours
un point (𝑐, 0) commun avec la région ombrée représentant l’ensemble réalisable.
(b) Maximum en 𝑃(1, 0). Les courbes de niveau sont les mêmes qu’en (a), mais la
direction de croissance est inversée.
5. La pente de la droite d’équation 20𝑥1 + 𝑡𝑥2 = 𝑐 doit se trouver entre −1/2 (la pente de la
frontière farine) et −1 (la pente de la frontière beurre). Pour 𝑡 = 0, la droite est verticale
et la solution est le point 𝐷 dans la figure 19.1.2 du livre. Pour 𝑡 ≠ 0, la pente de la droite
est −20/𝑡. D’où −1 ⩽ −20/𝑡 ⩽ −1/2, ce qui implique 𝑡 ∈ [20, 40].
6. Le problème PL est : max 700𝑥 + 1 000𝑦 s. c.









3𝑥 + 5𝑦 ⩽ 3 900
𝑥 + 3𝑦 ⩽ 2 100
2𝑥 + 2𝑦 ⩽ 2 200
, 𝑥 ⩾ 0 , 𝑦 ⩾ 0.
Une figure qui montrerait l’ensemble admissible et une courbe de niveau de la fonction
objectif ferait apparaître que la solution se trouve au point d’intersection des droites

217. Chapitre 19 / Programmation linéaire 217
d’équations 3𝑥 + 5𝑦 = 3 900 et 2𝑥 + 2𝑦 = 2 200. La résolution de ces équations fournit
𝑥 = 800 et 𝑦 = 300. La firme doit produire 800 appareils de type 𝐴 et 300 de type 𝐵.
x2
−1
1
2
3
4
−1 1 2 3 4 5 6
−x1 + x2 = −1
−x1 + 3x2 = 3
x1 + x2 = c
x1
Figure C19.1.4
19.2
1. (a) Voir figure C19.1.1a ci-dessus. Quand 3𝑥1 + 2𝑥2 ⩽ 6 est remplacé par 3𝑥1 + 2𝑥2 ⩽ 7
dans l’exercice 19.1.1, l’ensemble réalisable s’agrandit, car la droite qui passe par 𝑃 est
déplacée vers la droite. Le nouveau point optimal est l’intersection des droites d’équations
3𝑥1 + 2𝑥2 = 7 et 𝑥1 + 4𝑥2 = 4 et ses coordonnées sont (𝑥1, 𝑥2) = (2, 1/2). L’ancienne
valeur optimale de la fonction objectif était 36/5. La nouvelle est
3 × 2 + 4 ×
1
2
= 8 =
40
5
,
soit une augmentation de 𝑢∗
1 = 4/5.
(b) Quand 𝑥1 + 4𝑥2 ⩽ 4 est remplacé par 𝑥1 + 4𝑥2 ⩽ 5, l’ensemble réalisable s’agrandit,
car la droite d’équation 𝑥1 + 4𝑥2 = 4 est déplacée vers le haut. Le nouveau point optimal
se trouve à l’intersection des droites d’équations 3𝑥1 + 2𝑥2 = 6 et 𝑥1 + 4𝑥2 = 5 et
ses coordonnées sont (𝑥1, 𝑥2) = (7/5, 9/10). L’ancienne valeur optimale de la fonction
objectif était 36/5. La nouvelle est 39/5, soit une augmentation de 𝑢∗
2 = 3/5.
(c) En multipliant les deux contraintes ⩽ par 4/5 et 3/5, respectivement, et en addition-
nant, on obtient
(4/5) (3𝑥1 + 2𝑥2) + (3/5) (𝑥1 + 4𝑥2) ⩽ 6 × (4/5) + 4 × (3/5),
qui se réduit à 3𝑥1 + 4𝑥2 ⩽ 36/5.
2. min 8𝑢1 + 13𝑢2 + 6𝑢3 sous la contrainte
(
𝑢1 + 2𝑢2 + 𝑢3 ⩾ 8
2𝑢1 + 3𝑢2 + 𝑢3 ⩾ 9
, 𝑢1 ⩾ 0, 𝑢2 ⩾ 0, 𝑢3 ⩾ 0.
3. (a) min 6𝑢1 + 4𝑢2 sous la contrainte
(
3𝑢1 + 𝑢2 ⩾ 3
2𝑢1 + 4𝑢2 ⩾ 4
, 𝑢1 ⩾ 0, 𝑢2 ⩾ 0.

218. 218 CORRIGÉS DES EXERCICES
(b) max 11𝑥1 + 20𝑥2 sous la contrainte
(
𝑥1 + 2𝑥2 ⩽ 10
3𝑥1 + 5𝑥2 ⩽ 27
, 𝑥1 ⩾ 0, 𝑥2 ⩾ 0.
4. (a) Un graphique montre que la solution est au croisement des droites d’équations
𝑥1 + 2𝑥2 = 14 et 2𝑥1 + 𝑥2 = 13. D’où max = 9 pour (𝑥∗
1, 𝑥∗
2) = (4, 5).
(b) Le dual s’énonce min 14𝑢1 + 13𝑢2 sous la contrainte
(
𝑢1 + 2𝑢2 ⩾ 1
2𝑢1 + 𝑢2 ⩾ 1
, 𝑢1 ⩾ 0, 𝑢2 ⩾ 0.
Un graphique montre que la solution est au croisement des droites d’équations
𝑢1 + 2𝑢2 = 1 et 2𝑢1 + 𝑢2 = 1. D’où min = 9 pour (𝑢∗
1, 𝑢∗
2) = (1/3, 1/3).
19.3
1. (a) Au vu de la figure C19.3.1a, il est clair que, lorsque 𝑐 augmente, la droite en pointillés
se déplace de plus en plus vers le nord-est de sorte qu’elle a à la fois sa plus grande valeur
de 𝑐 et encore un point en commun avec l’espace réalisable lorsqu’elle passe par le point 𝑃,
dont les coordonnées sont (𝑥, 𝑦) = (0, 3). Le maximum associé est 2 × 0 + 3 × 7 = 21.
(b) À la figure C19.3.1b, lorsque 𝑐 diminue, la droite en pointillés se déplace vers le
sud-ouest. La plus petite valeur de 𝑐 pour laquelle elle a encore un point commun avec
l’espace réalisable est celle pour laquelle elle passe par le point 𝑃, dont les coordonnées
sont (𝑢1, 𝑢2) = (0, 1). Le minimum associé est 20𝑢1 + 21𝑢2 = 21.
(c) Oui, car le maximum du primal (a) et le minimum du dual (b) sont égaux à 21.
y
x
P
2x + 7y = c
1
1
Figure C19.3.1a
u2
u1
1
P 20u1 + 21u2 = c
Figure C19.3.1b
2. max 300𝑥1 + 500𝑥2 sous la contrainte
(
10𝑥1 + 25𝑥2 ⩽ 10 000
20𝑥1 + 25𝑥2 ⩽ 8 000
, 𝑥1 ⩾ 0 , 𝑥2 ⩾ 0. La
solution peut être déterminée graphiquement. Elle est 𝑥∗
1 = 0, 𝑥∗
2 = 320 et la valeur de la
fonction objectif 160 000, la même valeur que celle obtenue à l’exemple 19.1.2 pour la
valeur optimale du problème primal.
3. (a) Le profit réalisé par la vente de 𝑥1 petits téléviseurs et 𝑥2 téléviseurs moyens est donné
par 400𝑥1 + 500𝑥2. La première contrainte, 2𝑥1 + 𝑥2 ⩽ 16, dit que le temps utilisé de

219. Chapitre 19 / Programmation linéaire 219
la ligne 1 ne peut pas dépasser le nombre d’heures disponibles. Idem pour les autres
contraintes.
(b) L’illustration graphique du problème à la figure C19.3.3 rend évidente la solution
max = 3 800 pour 𝑥1 = 7 et 𝑥2 = 2.
(c) Si on relâche la première contrainte en 2𝑥1 + 𝑥2 ⩽ 17, la solution se déplace vers
l’intersection des deux droites d’équations 2𝑥1 + 𝑥2 = 17 et 𝑥1 + 2𝑥2 = 11. La nouvelle
solution est 𝑥1 = 23/3, 𝑥2 = 5/3, en laquelle le profit vaut 3 900. Relâcher la deuxième
contrainte en 𝑥1 + 4𝑥2 ⩽ 17 ne fait pas de différence, car une part de la capacité de la
ligne 2 reste de toute façon inutilisée en (7, 2).
Si on relâchait la troisième contrainte 𝑥1 + 2𝑥2 ⩽ 12, la solution ne serait plus à
l’intersection des droites d’équations 2𝑥1 + 𝑥2 = 16 et 𝑥1 + 2𝑥2 = 12, à savoir en
(𝑥1, 𝑥2) = (20/3, 8/3), car cela violerait la deuxième contrainte 𝑥1 + 4𝑥2 ⩽ 16. En
revanche, ainsi qu’un graphique précis le laisse supposer, la solution se produit là
où les deux premières contraintes sont liantes, à l’intersection des droites d’équations
2𝑥1 + 𝑥2 = 16 et 𝑥1 + 4𝑥2 = 16, soit en (𝑥1, 𝑥2) = (48/7, 16/7). Le profit qui en résulte
est 27 200/7 = 3 885 + 5
7 3 900. C’est donc la capacité de la ligne 1 qu’il convient
d’accroître. Si la capacité de la ligne 3 était augmentée d’une heure par jour, une partie
de cette augmentation serait gaspillée à cause des limites de capacité des lignes 1 et 2.
x2
5
x1
5 10
2x1 + x2 = 16
400x1 + 500x2 = constante
x1 + 2x2 = 11
(x*
1 ,x *
2 ) = (7, 2)
x1 + 4x2 = 16
Figure C19.3.3
19.4
1. Selon la formule (19.4.1), △𝑧∗ = 𝑢∗
1 △𝑏1 + 𝑢∗
2 △𝑏2 = 0 × 0,1 + 1 × (−0,2) = −0,2.
2. (a) Le problème est analogue à l’exercice 19.3.3. max 300𝑥1 + 200𝑥2 sous la
contrainte







6𝑥1 + 3𝑥2 ⩽ 54
4𝑥1 + 6𝑥2 ⩽ 48 ,
5𝑥1 + 5𝑥2 ⩽ 50
𝑥1 ⩾ 0, 𝑥2 ⩾ 0

220. 220 CORRIGÉS DES EXERCICES
où 𝑥1 et 𝑥2 sont les nombres d’unités produites de A et B, respectivement. Un graphique
précis le montrerait, la solution se trouve à l’intersection des droites d’équations
6𝑥1 + 3𝑥2 = 54 et 5𝑥1 + 5𝑥2 = 50,
soit en (𝑥1, 𝑥2) = (8, 2). Le profit maximal est 300 × 8 + 200 × 2 = 2 800.
(b) Le problème dual s’énonce
min (54𝑢1 + 48𝑢2 + 50𝑢3) s. c.









6𝑢1 + 4𝑢2 + 5𝑢3 ⩾ 300
3𝑢1 + 6𝑢2 + 5𝑢3 ⩾ 200
𝑢1, 𝑢2, 𝑢3 ⩾ 0
.
Comme la solution optimale du primal est 𝑥∗
1 = 8, 𝑥∗
2 = 2, deux valeurs strictement posi-
tives, les deux premières contraintes du dual sont satisfaites avec égalité en (𝑢∗
1, 𝑢∗
2, 𝑢∗
3).
Mais la deuxième contrainte du primal est satisfaite avec inégalité, car 4𝑥∗
1+6𝑥∗
2 = 44 48.
D’où 𝑢∗
2 = 0, avec 6𝑢∗
1 + 5𝑢∗
3 = 300 et 3𝑢∗
1 + 5𝑢∗
3 = 200. Par conséquent, 𝑢∗
1 = 100/3,
𝑢∗
2 = 0 et 𝑢∗
3 = 20. En outre, la valeur optimale 54𝑢∗
1 + 48𝑢∗
2 + 50𝑢∗
3 = 2 800 du dual est
égale à la valeur optimale du primal.
(c) Augmentation du profit optimal : Δ𝜋∗ = 𝑢∗
1 × 2 + 𝑢∗
3 × 1 = 260/3.
19.5
1. 4𝑢∗
1 + 3𝑢∗
2 = 3 2 et 𝑥∗ = 0; 5𝑢∗
1 + 7𝑢∗
2 = 7 et 𝑦∗ = 3 0. Aussi, 4𝑥∗ + 5𝑦∗ = 15 20 et
𝑢∗
1 = 0; 3𝑥∗ + 7𝑦∗ = 21 et 𝑢∗
2 = 1 0. On voit que (19.5.1) et (19.5.2) sont satisfaites.
2. (a) Voir figure C19.5.2. Le minimum est atteint en (𝑦∗
1, 𝑦∗
2) = (3, 2).
y2
5
10
y1
5 10 15
(3)
y1 + 2y2 = Z0
(1)
(3, 2)
(2)
(4)
Figure C19.5.2
(b) Le dual est :
max 15𝑥1 + 5𝑥2 − 5𝑥3 − 20𝑥4 s. c.
(
𝑥1 + 𝑥2 − 𝑥3 + 𝑥4 ⩽ 1
6𝑥1 + 𝑥2 + 𝑥3 − 2𝑥4 ⩽ 2
, 𝑥𝑗 ⩾ 0, 𝑗 = 1, . . . , 4.
Le maximum est en (𝑥∗
1, 𝑥∗
2, 𝑥∗
3, 𝑥∗
4) = (1/5, 4/5, 0, 0).

221. Chapitre 19 / Programmation linéaire 221
(c) Si la première contrainte est changée en 𝑦1 + 6𝑦2 ⩾ 15,1, la solution du primal est
encore à l’intersection des droites (1) et (2) à la figure C19.5.2, mais avec (1) légèrement
translatée vers le haut. La solution du dual est totalement inchangée. Dans les deux
problèmes, la solution optimale s’accroît de (15,1 − 15) × 𝑥∗
1 = 0,02.
3. (a) min 10 000𝑦1 + 8 000𝑦2 + 11 000𝑦3 sous la contrainte
(
10𝑦1 + 20𝑦2 + 20𝑦3 ⩾ 300
20𝑦1 + 10𝑦2 + 20𝑦3 ⩾ 500
, 𝑦1 ⩾ 0, 𝑦2 ⩾ 0, 𝑦3 ⩾ 0.
(b) Le dual est : max 300𝑥1 + 500𝑥2 sous la contrainte









10𝑥1 + 20𝑥2 ⩽ 10 000
20𝑥1 + 10𝑥2 ⩽ 8 000
20𝑥1 + 20𝑥2 ⩽ 11 000
, 𝑥1 ⩾ 0, 𝑥2 ⩾ 0.
Il est illustré graphiquement dans la figure C19.5.3, où (1) désigne la première contrainte,
(2) la deuxième et (3) la troisième. Les droites parallèles en pointillés sont des courbes
de niveau de la fonction objectif 300𝑥1 + 500𝑥2. On voit sur la figure que l’optimum
se produit au point où les droites (1) et (3) se coupent, c’est-à-dire en un point où les
première et troisième contraintes sont satisfaites avec égalités. Là, 10𝑥∗
1 + 20𝑥∗
2 = 10 000
et 20𝑥∗
1 +20𝑥∗
2 = 11 000. La solution est 𝑥∗
1 = 100 et 𝑥∗
2 = 450. Le maximum de la fonction
objectif est 300 × 100 + 500 × 450 = 255 000.
100
200
300
400
500
600
700
800
900
1 000
x 2
x 1
100 200 300 400 500 600 700 800 900 1 000
(2)
(1)
(3)
100
200
300
400
500
600
700
800
900
1 000
100 200 300 400 500 600 700 800 900 1 000
Figure C19.5.3
Comme les variables du problème dual sont toutes deux positives à l’optimum, les condi-
tions de complémentarité impliquent que les deux contraintes du problème primal doivent

222. 222 CORRIGÉS DES EXERCICES
être satisfaites avec égalité à l’optimum : 10𝑦∗
1 + 20𝑦∗
3 = 300 et 20𝑦∗
1 + 20𝑦∗
3 = 500. Par
conséquent, la solution du primal est 𝑦∗
1 = 20, 𝑦∗
2 = 0, 𝑦∗
3 = 5 et la valeur de la fonction
objectif à l’optimum est 10 000 × 20 + 8 000 × 0 + 11 000 × 5 = 255 000. De plus, la
deuxième contrainte du problème dual est satisfaite avec inégalité stricte à l’optimum,
puisque 20 × 𝑥∗
1 + 10 × 𝑥∗
2 = 6 000 8 000. Par conséquent, la variable correspondante
du problème dual doit être nulle à l’optimum, donc 𝑦∗
2 = 0. Avec les deux équations
précédentes, on en déduit que 𝑦∗
1 = 20 et 𝑦∗
3 = 5. La valeur de la fonction objectif au
maximum est 10 000 × 20 + 8 000 × 0 + 11 000 × 5 = 255 000.
(c) Si le coût de l’utilisation horaire de l’usine 1 augmente de 100, cela n’a pas d’effet
sur les contraintes du primal, mais cela accroît de 100 le membre de droite de la pre-
mière contrainte du problème dual. En première approximation, on pourrait annoncer
une augmentation de coût de 100 × 20 = 2 000 en choisissant le même point admissible
(𝑦∗
1, 𝑦∗
2, 𝑦∗
3) = (20, 0, 5) pour le primal. Cela pourrait toutefois surestimer l’augmentation
du coût minimum, car il pourrait être préférable de transférer une partie de la production
de l’usine 1, devenue désormais plus chère, ailleurs. Pour obtenir la réponse exacte, on
vérifie si la production est transférée en se tournant vers le dual. Il est inchangé à part la
contrainte (1) devenue 10𝑥1 + 20𝑥2 ⩽ 10 100. En regardant à nouveau la figure C19.5.3,
la solution du dual se trouve encore à l’intersection des droites (1) et (3), même après
que (1) a été déplacée. En particulier, la solution du primal modifié satisfait exactement
les mêmes contraintes (y compris les contraintes de positivité) avec égalités et se trouve
donc au même point. L’estimation précédente de 2 000 comme accroissement du coût
était précise.
4. (a) Quand 𝑥3 = 0, la solution est 𝑥1 = 𝑥2 = 1/3. Quand 𝑥3 = 3, la solution est 𝑥1 = 1 et
𝑥2 = 2.
(b) Soit 𝑧max la valeur maximale de la fonction objectif. Si 0 ⩽ 𝑥3 ⩽ 7/3, alors
𝑧max(𝑥3) = 2𝑥3 + 5/3 pour 𝑥1 = 1/3 et 𝑥2 = 𝑥3 + 1/3. Si 7/3 𝑥3 ⩽ 5, alors
𝑧max(𝑥3) = 𝑥3 + 4 pour 𝑥1 = 𝑥3 − 2 et 𝑥2 = 5 − 𝑥3. Si 𝑥3 5, alors 𝑧max(𝑥3) = 9
pour 𝑥1 = 3 et 𝑥2 = 0. Comme 𝑧max(𝑥3) est croissante, le maximum est 9 pour 𝑥3 ⩾ 5.
(c) La solution du problème initial est 𝑥1 = 3 et 𝑥2 = 0, avec 𝑥3 nombre arbitraire
supérieur à 5.
Exercices récapitulatifs du chapitre 19
1. (a) 𝑥∗ = 3/2, 𝑦∗ = 5/2. (Un graphique montrerait que la solution est à l’intersection des
droites d’équations 𝑥 + 𝑦 = 4 et −𝑥 + 𝑦 = 1.)
(b) Le dual s’écrit min 4𝑢1 + 𝑢2 + 3𝑢3 sous la contrainte
(
𝑢1 − 𝑢2 + 2𝑢3 ⩾ 1
𝑢1 + 𝑢2 − 𝑢3 ⩾ 2
, 𝑢1 ⩾ 0, 𝑢2 ⩾ 0, 𝑢3 ⩾ 0.
Compte tenu des conditions de complémentarité, la solution du dual est 𝑢∗
1 = 3/2,
𝑢∗
2 = 1/2 et 𝑢∗
3 = 0.

223. Chapitre 19 / Programmation linéaire 223
2. (a) Considérez le programme linéaire donné comme le primal et notez-le (P). Son dual
est max −𝑥1 + 𝑥2 sous la contrainte













−𝑥1 + 2𝑥2 ⩽ 16
𝑥1 − 2𝑥2 ⩽ 6
−2𝑥1 − 𝑥2 ⩽ −8
− 4𝑥1 − 5𝑥2 ⩽ −15
, 𝑥1 ⩾ 0, 𝑥2 ⩾ 0.
Il est désigné par (D). Si vous tracez l’ensemble admissible de (D) et une droite d’équation
−𝑥1 + 𝑥2 = 𝑐, vous observez que lorsque 𝑐 augmente, la droite se déplace vers le nord-
ouest. La droite dont l’équation a la plus grande valeur de 𝑐 et qui a une intersection
non vide avec l’ensemble admissible coupe ce dernier au point de coordonnées (0, 8),
à l’intersection des trois droites d’équations −𝑥1 + 2𝑥2 = 16, −2𝑥1 − 𝑥2 = −8, et 𝑥1 = 0.
Celles-ci définissent trois des contraintes, mais la contrainte 𝑥1 ⩾ 0 est redondante.
(b) On voit que, quand 𝑥1 = 0 et 𝑥2 = 8, les deuxième et quatrième contraintes de (D) ne
sont pas liantes de sorte que 𝑦2 = 𝑦4 = 0 à l’optimum de (P). De plus, comme 𝑥2 = 8 0,
la deuxième contrainte de (P) doit être liante à l’optimum – autrement dit, 2𝑦1 − 𝑦3 = 1.
Mais alors la fonction objectif de (P) peut être réduite de 16𝑦1 + 6𝑦2 − 8𝑦3 − 15𝑦4 à
16𝑦1 − 8𝑦3 = 8 (2𝑦1 − 𝑦3) = 8. On en conclut que tout (𝑦1, 𝑦2, 𝑦3, 𝑦4) de la forme
(𝑦1, 𝑦2, 𝑦3, 𝑦4) = ( 1
2 (1 + 𝑏), 0, 𝑏, 0) doit résoudre (P), à condition que ses composantes
soient positives et que la première contrainte de (P) soit satisfaite(34). La première
contrainte se réduit à −1
2 (1 + 𝑏) − 2𝑏 ⩾ −1 ou 𝑏 ⩽ 1
5 . En conclusion, ( 1
2 (1 + 𝑏), 0, 𝑏, 0)
est optimal à condition que 0 ⩽ 𝑏 ⩽ 1
5 .
(c) La fonction objectif (D) est changée en 𝑘𝑥1 + 𝑥2, mais les contraintes restent les
mêmes. La solution (0, 8) trouvée dans la question (a) reste aussi inchangée à condition
que la pente −𝑘 de la courbe de niveau 𝑥2 = 8 − 𝑘𝑥1 passant par le point (0, 8) reste
positive et pas inférieure à la pente 1/2 de la droite −𝑥1 + 2𝑥2 = 16. Donc 𝑘 ⩽ −1
2 .
3. (a) 𝑥∗ = 0, 𝑦∗ = 4. (Un graphique montrerait que la solution est à l’intersection des droites
d’équations 𝑥 = 0 et 4𝑥 + 𝑦 = 4.)
(b) Le problème dual s’écrit max 4𝑢1 + 3𝑢2 + 2𝑢3 − 2𝑢4 sous la contrainte
(
4𝑢1 + 2𝑢2 + 3𝑢3 − 𝑢4 ⩽ 5
𝑢1 + 𝑢2 + 2𝑢3 + 2𝑢4 ⩽ 1
𝑢1, 𝑢2, 𝑢3, 𝑢4 ⩾ 0 .
Compte tenu des conditions de complémentarité, sa solution est
𝑢∗
1 = 1, 𝑢∗
2 = 𝑢∗
3 = 𝑢∗
4 = 0.
4. (a) Pour trouver a = (5, 5, 7), on pose 𝜆 = 1/2. Pour avoir b = (7, 5, 5) il faut que
6𝜆 + 2 = 7, −2𝜆 + 6 = 5 et −6𝜆 + 10 = 5, mais ces équations n’ont pas de solution.
Notez que les vecteurs d’output admissibles sont les points du segment allant de (8, 4, 4)
à (2, 6, 10). Le point a est situé sur ce segment, mais ce n’est pas le cas de b.
(34) Nous savons déjà que la deuxième contrainte est satisfaite avec égalité.

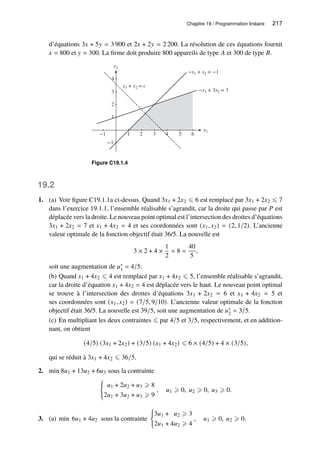
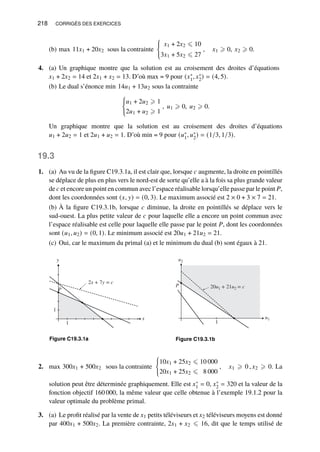
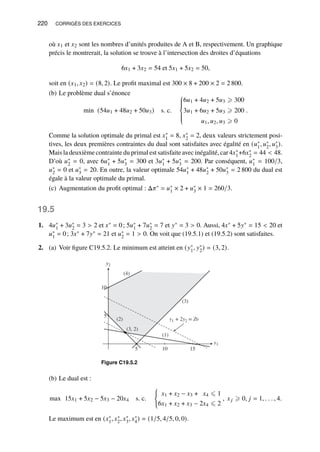
224. 224 CORRIGÉS DES EXERCICES
(b) On envisage le cas où on peut jeter de l’output. En question (a), nous avons vu que a
peut être produit même si on ne jette pas d’output. b n’est possible que si l’entreprise a
l’autorisation de jeter de l’output et qu’il existe un scalaire 𝜆 de [0, 1] tel que 6𝜆 + 2 ⩾ 7,
−2𝜆+6 ⩾ 5 et −6𝜆+10 ⩾ 5. Ces inégalités se simplifient en 𝜆 ⩾ 5/6, 𝜆 ⩽ 1/2, 𝜆 ⩽ 5/6,
qui sont incompatibles.
(c) La recette est 𝑅(𝜆) = 𝑝1𝑥1 + 𝑝2𝑥2 + 𝑝3𝑥3 = (6𝑝1 − 2𝑝2 − 6𝑝3)𝜆 + 2𝑝1 + 6𝑝2 + 10𝑝3,
avec 𝑅′(𝜆) égale à la constante 𝑠 = 6𝑝1 − 2𝑝2 − 6𝑝3. Si 𝑠 0, alors la recette 𝑅(𝜆) est
maximisée en 𝜆 = 1; si 𝑠 0, alors elle est maximisée en 𝜆 = 0. Les deux usines peuvent
rester toutes deux en activité uniquement dans le cas particulier où 𝑠 = 0.
5. (a) Si les nombres d’unités produites des trois biens sont 𝑥1, 𝑥2 et 𝑥3, le profit est donné par
6𝑥1 + 3𝑥2 + 4𝑥3 et le temps utilisé des deux machines est 3𝑥1 + 𝑥2 + 4𝑥3 et 2𝑥1 + 2𝑥2 + 𝑥3,
respectivement. Le problème posé est dès lors
max 6𝑥1 + 3𝑥2 + 4𝑥3 sous la contrainte
(
3𝑥1 + 𝑥2 + 4𝑥3 ⩽ 𝑏1
2𝑥1 + 2𝑥2 + 𝑥3 ⩽ 𝑏2
, 𝑥1, 𝑥2, 𝑥3 ⩾ 0 .
(b) L’ensemble admissible est le polygone ombré de la figure C19.R.5. Les droites
notées I, II, et III montrent où les différentes contraintes sont satisfaites avec éga-
lités. Les droites en pointillés sont des courbes de niveau de la fonction objectif
100𝑦1 + 100𝑦2. On voit que la fonction objectif passe par sa plus petite valeur en 𝑃,
intersection des droites I et II. Les coordonnées (𝑦∗
1, 𝑦∗
2) de 𝑃 sont données par les deux
équations 3𝑦∗
1 + 2𝑦∗
2 = 6 et 𝑦∗
1 + 2𝑦∗
2 = 3, d’où (𝑦∗
1, 𝑦∗
2) = (3/2, 3/4). La valeur optimale
de la fonction objectif est 100 (𝑦∗
1 + 𝑦∗
2) = 225.
y2
1
2
3
4
5
y1
1 2 3 4 5 6 7
II
I
III
100y1 + 100y2 = constante
P
Figure C19.R.5
(c) Puisque le dual a une solution, en raison du théorème de la dualité, le problème (a)
a aussi une solution optimale, notée (𝑥∗
1, 𝑥∗
2, 𝑥∗
3). Comme la troisième contrainte du dual
est satisfaite avec inégalité, on doit avoir 𝑥∗
3 = 0. En outre, les deux contraintes du
primal doivent à l’optimum être satisfaites avec égalités (liantes), car les deux variables

225. Chapitre 20 / Programmation non linéaire 225
sont positives à l’optimum. De là, 3𝑥∗
1 + 𝑥∗
2 = 100 et 2𝑥∗
1 + 2𝑥∗
2 = 100, ce qui donne
𝑥∗
1 = 𝑥∗
2 = 25. Le profit maximal est 6𝑥∗
1 + 3𝑥∗
2 + 4𝑥∗
3 = 225, égal à la valeur du primal,
comme attendu.
(d) Comme première approximation, le profit augmente de 𝑦∗
1 Δ𝑏1 = 1,5. Le nouveau
profit maximal serait 226,5. Pour que cette approximation soit exacte, le point optimal du
dual doit être inchangé quand 𝑏1 passe de 100 à 101. C’est manifestement vrai, comme
on le voit sur la figure C19.R.5.
(e) La valeur maximale du primal est égale à la valeur minimale du dual. Compte tenu de
la même approximation qu’à la question (d), c’est égal à 𝑏1𝑦∗
1 + 𝑏2𝑦∗
2, qui est clairement
homogène de degré 1 en 𝑏1 et 𝑏2. Plus généralement, soit 𝐹(𝑏1, 𝑏2) la valeur minimale du
dual obtenue dans la question (b). Pour un 𝛼 0 quelconque, minimiser 𝛼𝑏1𝑦1+𝛼𝑏2𝑦2 sur
l’ensemble admissible du dual fournit la même solution (𝑦∗
1, 𝑦∗
2) que minimiser 𝑏1𝑦1+𝑏2𝑦2
sur le même ensemble admissible. Par conséquent,
𝐹(𝛼𝑏1, 𝛼𝑏2) = 𝛼𝐹(𝑏1, 𝑏2)
quel que soit 𝛼 0, et 𝐹 est homogène de degré 1.
Chapitre 20 / Programmation non linéaire
20.1
1. (a) Avec L = −𝑥2 − 𝑦2 − 𝜆 (𝑥 − 3𝑦 + 10), en raison de (20.1.2) et (20.1.3),
(i) L′
𝑥 = −2𝑥 − 𝜆 = 0; (ii) L′
𝑦 = −2𝑦 + 3𝜆 = 0; (iii) 𝜆 ⩾ 0 avec 𝜆 = 0 si 𝑥 − 3𝑦 −10.
Dans le cas 𝜆 = 0, (i) et (ii) impliquent 𝑥 = 𝑦 = 0, en contradiction avec 𝑥 − 3𝑦 ⩽ −10.
Donc 𝜆 0, et de (iii), 𝑥 − 3𝑦 = −10. En outre, (i) et (ii) impliquent 𝜆 = −2𝑥 = 2
3 𝑦, de
sorte que 𝑦 = −3𝑥. Compte tenu de 𝑥 − 3𝑦 = −10, 𝑥 = −1 et alors 𝑦 = 3. Comme il est
facile de voir que le lagrangien est concave, la solution est (𝑥, 𝑦) = (−1, 3).
(b) Voir la figure C20.1.1. La solution est le point de la droite d’équation 𝑥 − 3𝑦 = −10
le plus proche de l’origine.
y
x
–10 –5 –1
3
2
1
x –3y = –10
Figure C20.1.1
2. (a) Les conditions KKT sont (i) 1
2
√
𝑥
− 𝜆𝑝 = 0; (ii) 1
2
√
𝑦 − 𝜆𝑞 = 0;
(iii) 𝜆 ⩾ 0, et 𝜆 = 0 si 𝑝𝑥 + 𝑞𝑦 𝑚. En se débarrassant des fractions dans (i) et
(ii), on a 1 = 2𝜆𝑝
√
𝑥 = 2𝜆𝑞
√
𝑦, d’où il découle que 𝑥, 𝑦, 𝜆 sont toutes strictement
positives et aussi que 𝑦 = 𝑝2𝑥/𝑞2. Comme 𝜆 0, l’équation de budget 𝑝𝑥 + 𝑞𝑦 = 𝑚

226. 226 CORRIGÉS DES EXERCICES
est satisfaite, impliquant 𝑥 = 𝑚𝑞/(𝑝𝑞 + 𝑝2). La valeur correspondante de 𝑦 se trouve
facilement et les fonctions de demande sont
𝑥 = 𝑥 (𝑝, 𝑞, 𝑚) =
𝑚𝑞
𝑝 (𝑝 + 𝑞)
, 𝑦 = 𝑦 (𝑝, 𝑞, 𝑚) =
𝑚𝑝
𝑞 (𝑝 + 𝑞)
.
Ces fonctions de demande résolvent le problème, car il est facile de voir que L(𝑥, 𝑦) est
concave.
(b) Il est aisé de vérifier que les fonctions de demande sont homogènes de degré 0, comme
attendu.
3. (a) Avec L = 4 − 1
2 𝑥2 − 4𝑦 − 𝜆(6𝑥 − 4𝑦 − 𝑎), les conditions KKT s’écrivent
(i) 𝜕L/𝜕𝑥 = −𝑥 − 6𝜆 = 0; (ii) 𝜕L/𝜕𝑦 = −4 + 4𝜆 = 0; (iii) 𝜆 ⩾ 0 (avec 𝜆 = 0
si 6𝑥 − 4𝑦 𝑎).
(b) De (ii), 𝜆 = 1, de sorte que (i) donne 𝑥 = −6. De (iii) et de la contrainte donnée,
𝑦 = −9 − 1
4 𝑎. Comme le lagrangien est concave, on a trouvé la solution.
(c) 𝑉(𝑎) = 𝑎 + 22, de sorte que 𝑉′(𝑎) = 1 = 𝜆.
4. (a) L(𝑥, 𝑦) = 𝑥2 + 2𝑦2 − 𝑥 − 𝜆(𝑥2 + 𝑦2 − 1). Les conditions KKT s’écrivent
(i) 2𝑥 − 1 − 2𝜆𝑥 = 0; (ii) 4𝑦 − 2𝜆𝑦 = 0; (iii) 𝜆 ⩾ 0 avec 𝜆 = 0 si 𝑥2 + 𝑦2 1.
(b) Par (ii), 𝑦 (2 − 𝜆) = 0, de sorte que soit (I) 𝑦 = 0, soit (II) 𝜆 = 2.
(I) 𝑦 = 0. Si 𝜆 = 0, alors par (i), 𝑥 = 1/2 et (𝑥, 𝑦) = (1/2, 0) est un candidat à l’optimum
(car il vérifie toutes les conditions KKT). Si 𝑦 = 0 et 𝜆 0, alors par (iii) et 𝑥2 + 𝑦2 ⩽ 1,
𝑥2 + 𝑦2 = 1. Mais alors 𝑥 = ±1, de sorte que (𝑥, 𝑦) = (±1, 0) sont candidats, avec 𝜆 = 1/2
et 3/2, respectivement.
(II) 𝜆 = 2. Dans ce cas, de (i), 𝑥 = −1/2 et (iii) donne 𝑦2 = 3/4, de sorte que 𝑦 = ±
√
3/2.
Ainsi, (−1/2, ±
√
3/2) sont encore deux candidats avec 𝜆 = 2.
(c) Puisque 𝑓 est continue et que l’ensemble des points admissibles est fermé et borné, le
théorème des bornes atteintes assure qu’il existe un maximum. Le ou les points maximum
se trouvent parmi les cinq points qui remplissent les conditions nécessaires. En évaluant
𝑥2 + 2𝑦2 − 𝑥 en chacun de ces points, on trouve que la valeur maximale est 9/4, atteinte
en (−1/2,
√
3/2) et en (−1/2, −
√
3/2).
5. (a) Avec le lagrangien L(𝑥, 𝑦) = 2 − (𝑥 − 1)2 − 𝑒𝑦2
− 𝜆(𝑥2 + 𝑦2 − 𝑎), les conditions
KKT sont (i) −2 (𝑥 − 1) − 2𝜆𝑥 = 0; (ii) −2𝑦𝑒𝑦2
− 2𝜆𝑦 = 0; (iii) 𝜆 ⩾ 0, avec 𝜆 = 0 si
𝑥2 + 𝑦2 𝑎. De (i), 𝑥 = (1 + 𝜆)−1. En outre, (ii) se réduit à 𝑦 (𝑒𝑦2
+ 𝜆) = 0 et ainsi 𝑦 = 0
(car 𝑒𝑦2
+ 𝜆 est toujours strictement positif).
(I) : On suppose que 𝜆 = 0. Alors l’équation (i) donne 𝑥 = 1. On doit avoir dans ce cas
𝑎 ⩾ 𝑥2 + 𝑦2 = 1.
(II) : On suppose que 𝜆 0. Alors (iii) donne 𝑥2 + 𝑦2 = 𝑎 et ainsi 𝑥 = ±
√
𝑎 (pour rappel,
𝑦 = 0). Comme 𝑥 = 1/(1 + 𝜆) et 𝜆 0, on doit avoir 0 𝑥 1, de sorte que 𝑥 =
√
𝑎 et
𝑎 = 𝑥2 1. Reste à trouver la valeur de 𝜆 et à vérifier qu’elle est strictement positive. De
l’équation (i), il vient 𝜆 = 1/𝑥 − 1 = 1/
√
𝑎 − 1 0.
Le seul point dont les coordonnées remplissent les conditions KKT est
(𝑥, 𝑦) = (1, 0) si 𝑎 ⩾ 1 et (
√
𝑎, 0) si 0 𝑎 1. La valeur correspondante de 𝜆
est 0 ou 1/
√
𝑎 − 1, respectivement.

227. Chapitre 20 / Programmation non linéaire 227
(b) Comme L′
𝑥𝑥 = −2−2𝜆 0, L′
𝑦𝑦 = −𝑒𝑦2
(2+4𝑦2) −2𝜆 0 et L′
𝑥𝑦 = 0, le lagrangien
L(𝑥, 𝑦) est concave, et la solution est donnée dans les deux cas (I) et (II) de la question (a).
(c) Si 𝑎 ∈]0, 1[, on a 𝑓 ∗(𝑎) = 𝑓 (
√
𝑎, 0) = 2 − (
√
𝑎 − 1)2 − 1 = 2
√
𝑎 − 𝑎, et pour 𝑎 ⩾ 1
on a 𝑓 ∗(𝑎) = 𝑓 (1, 0) = 1. d 𝑓 ∗(𝑎)/d𝑎 = 0 = 𝜆.
Notez que pour obtenir d 𝑓 ∗(𝑎)/d𝑎 quand 𝑎 = 1, il faut vérifier séparément si les dérivées
à droite et à gauche de 1 (voir 7.9.3), à savoir
( 𝑓 ∗
)′
(1+
) = lim
ℎ→0+
𝑓 ∗(1 + ℎ) − 𝑓 ∗(1)
ℎ
et ( 𝑓 ∗
)′
(1−
) = lim
ℎ→0−
𝑓 ∗(1 + ℎ) − 𝑓 ∗(1)
ℎ
existent et sont égales. Or, les dérivées à gauche et à droite sont respectivement égales
aux dérivées des fonctions dérivables 𝑔−(𝑎) = 2
√
𝑎 − 𝑎 et 𝑔+(𝑎) = 1 en 𝑎 = 1, qui sont
toutes deux nulles. En conclusion, ( 𝑓 ∗)′(1) existe et est égale à 0.
6. Avec L = 𝑎𝑄 − 𝑏𝑄2 − 𝛼𝑄 − 𝛽𝑄2 + 𝜆𝑄, les conditions KKT pour que 𝑄∗ résolve le
problème sont (i) dL/d𝑄 = 𝑎 −𝛼 −2 (𝑏 + 𝛽)𝑄∗ +𝜆 = 0; (ii) 𝜆 ⩾ 0, avec 𝜆 = 0 si 𝑄∗ 0.
D’après le théorème 20.1.1, ces conditions sont aussi suffisantes, car le lagrangien est
concave. On trouve 𝑄∗ = (𝑎 − 𝛼)/2 (𝑏 + 𝛽) et 𝜆 = 0 si 𝑎 𝛼, tandis que 𝑄∗ = 0 et
𝜆 = 𝛼 − 𝑎 si 𝑎 ⩽ 𝛼. (Voir aussi l’exemple 4.6.3.)
20.2
1. (a) En écrivant les contraintes sous la forme
𝑔1 (𝑥, 𝑦) = 𝑥 + 𝑒−𝑥
− 𝑦 ⩽ 0 et 𝑔2 (𝑥, 𝑦) = −𝑥 ⩽ 0,
le lagrangien est L = 1
2 𝑥 − 𝑦 − 𝜆1 (𝑥 + 𝑒−𝑥 − 𝑦) − 𝜆2 (−𝑥). Les conditions KKT sont alors
(i) 1
2 − 𝜆1 (1 − 𝑒−𝑥) + 𝜆2 = 0; (ii) −1 + 𝜆1 = 0; (iii) 𝜆1 ⩾ 0, avec 𝜆 = 0 si 𝑥 + 𝑒−𝑥 𝑦 ;
(iv) 𝜆2 ⩾ 0, avec 𝜆 = 0 si 𝑥 0.
(b) De (ii), 𝜆1 = 1, de sorte que de (iii), 𝑥 + 𝑒−𝑥 = 𝑦. Soit 𝑥 = 0, soit 𝑥 0. Dans ce
dernier cas, (iv) implique 𝜆2 = 0. Alors (i) implique 1
2 − (1 − 𝑒−𝑥) = 0 ou 𝑒−𝑥 = 1
2 . Par
conséquent, 𝑥 = ln 2 et 𝑦 = 𝑥 + 𝑒−𝑥 = ln 2 + 1
2 . Si 𝑥 = 0, alors (i) implique 𝜆2 = −1
2 , ce
qui contredit 𝜆2 ⩾ 0. On conclut que (𝑥, 𝑦) = (ln 2, ln 2 + 1
2 ) est le seul point qui vérifie
les conditions KKT, avec (𝜆1, 𝜆2) = (1, 0). (En faisant un graphique des contraintes et en
étudiant les courbes de niveau 1
2 𝑥 − 𝑦 = 𝑐, il est facile de voir que le point trouvé résout
bien le problème de maximisation.)
2. Le lagrangien est L = 𝛼 ln 𝑥 + (1 − 𝛼) ln 𝑦 −𝜆 (𝑝𝑥 + 𝑞𝑦 − 𝑚) − 𝜇 (𝑥 − ¯
𝑥), et les conditions
KKT pour que (𝑥∗, 𝑦∗) soit une solution du problème sont :
(i) L′
𝑥 =
𝛼
𝑥∗
− 𝜆𝑝 − 𝜇 = 0; (ii) L′
𝑦 =
1 − 𝛼
𝑦∗
− 𝜆𝑞 = 0;
(iii) 𝜆 ⩾ 0, et 𝜆 = 0 si 𝑝𝑥∗ + 𝑞𝑦∗ 𝑚 ; (iv) 𝜇 ⩾ 0, et 𝜇 = 0 si 𝑥∗ ¯
𝑥.
On suppose que 𝛼 ∈]0, 1[, auquel cas (ii) implique 𝜆 0 et ainsi (iii) assure
𝑝𝑥∗
+ 𝑞𝑦∗
= 𝑚.
On suppose 𝜇 = 0. Alors, de (i) et (ii) on déduit
𝛼/𝑝𝑥∗
= (1 − 𝛼)/𝑞𝑦∗
ou 𝑞𝑦∗
= (1 − 𝛼)𝑝𝑥∗
/𝛼.

228. 228 CORRIGÉS DES EXERCICES
Alors la contrainte de budget entraîne 𝑝𝑥∗ +(1−𝛼)𝑝𝑥∗/𝛼 = 𝑚, d’où il suit que 𝑥∗ = 𝑚𝛼/𝑝
et 𝑦∗ = (1 − 𝛼)𝑚/𝑞, avec 𝜆 = 1/𝑚. Cela vaut tant que 𝑥∗ ⩽ ¯
𝑥, c’est-à-dire 𝑚 ⩽ 𝑝 ¯
𝑥/𝛼.
On suppose 𝜇 0. Alors 𝑥∗ = ¯
𝑥 et 𝑦∗ = 𝑚/𝑞 − 𝑝 ¯
𝑥/𝑞 = (𝑚 − 𝑝 ¯
𝑥)/𝑞, avec
𝜆 = (1− 𝛼)/(𝑚 − 𝑝 ¯
𝑥) et 𝜇 = 𝛼/¯
𝑥 −𝜆𝑝 = (𝛼𝑚 − 𝑝 ¯
𝑥)/¯
𝑥 (𝑚 − 𝑝 ¯
𝑥). Notez que si 𝑚 𝑝 ¯
𝑥/𝛼,
alors 𝑚 𝑝 ¯
𝑥 puisque 𝛼 1. On conclut que, si 𝑚 𝑝 ¯
𝑥/𝛼, alors 𝜆 et 𝜇 sont tous les
deux strictement positifs et les conditions (i)-(iv) sont vérifiées.
Comme L′
𝑥𝑥 = −𝛼/𝑥2 0, L′
𝑦𝑦 = −𝛼/𝑦2 0 et L′
𝑥𝑦 = 0, le lagrangien L(𝑥, 𝑦) est
concave et on a trouvé la solution dans les deux cas.
3. (a) L’ensemble réalisable est la partie ombrée de la figure C20.2.3.
y
1
2
3
4
5
6
7
x
−2 −1 1 2 3 4 5 6 7
II
(−1, 5)
I
III
(3, 1)
Figure C20.2.3
y
x
x + ay = c
1
x + y = 0
1
x2
+ y2
= 1
Figure C20.2.4
(b) Avec les contraintes
𝑔1 (𝑥, 𝑦) = −𝑥 − 𝑦 ⩽ −4, 𝑔2 (𝑥, 𝑦) = −𝑥 ⩽ 1, 𝑔3 (𝑥, 𝑦) = −𝑦 ⩽ −1,
le lagrangien s’écrit L = 𝑥 + 𝑦 − 𝑒𝑥 − 𝑒𝑥+𝑦 − 𝜆1 (−𝑥 − 𝑦 + 4) − 𝜆2 (−𝑥 − 1) − 𝜆3 (−𝑦 + 1).
En formulant les conditions de complémentarité comme en (20.1.5), les conditions KKT
se résument à l’existence de nombres positifs 𝜆1, 𝜆2 et 𝜆3 tels que :
(i) L′
𝑥 = 1 − 𝑒𝑥 − 𝑒𝑥+𝑦 + 𝜆1 + 𝜆2 = 0; (ii) L′
𝑦 = 1 − 𝑒𝑥+𝑦 + 𝜆1 + 𝜆3 = 0;
(iii) 𝜆1 (−𝑥 − 𝑦 + 4) = 0; (iv) 𝜆2 (−𝑥 − 1) = 0; (v) 𝜆3 (−𝑦 + 1) = 0.
De (ii), 𝑒𝑥+𝑦 = 1+𝜆1 +𝜆3. La substitution dans (i) fournit 𝜆2 = 𝑒𝑥 +𝜆3 ⩾ 𝑒𝑥 0. Comme
𝜆2 0, (iv) implique 𝑥 = −1. Une solution doit forcément appartenir à la droite (II) de
la figure C.20.2.3, ce qui montre que la troisième contrainte 𝑦 ⩾ 1 doit être relâchée(35).
De (v) découle 𝜆3 = 0, et alors (ii) donne
𝜆1 = 𝑒𝑥+𝑦
− 1 ⩾ 𝑒4
− 1 0.
D’où de (iii), la première contrainte est active, c’est-à-dire 𝑦 = 4−𝑥 = 5. La seule solution
possible est (𝑥∗, 𝑦∗) = (−1, 5).
(c) Comme L(𝑥, 𝑦) est concave, on a trouvé le point optimal, (𝑥∗, 𝑦∗) = (−1, 5).
(35) Cela s’explique algébriquement en remarquant que, à cause de 𝑥 + 𝑦 ⩾ 4 et 𝑥 = −1, on a
𝑦 ⩾ 4 − 𝑥 = 5 1.

229. Chapitre 20 / Programmation non linéaire 229
4. (a) L’ensemble réalisable est ombré dans la figure C20.2.4. (La fonction à maximiser est
𝑓 (𝑥, 𝑦) = 𝑥 + 𝑎𝑦. Les courbes de niveau de cette fonction sont des droites de pente −1/𝑎
lorsque 𝑎 ≠ 0 et des droites verticales lorsque 𝑎 = 0. La droite en pointillés de la figure
est une de ces courbes de niveau (pour 𝑎 ≈ −0,25). Le maximum de 𝑓 se produit au point
de l’ensemble réalisable qui va être déterminé par un déplacement parallèle de la droite
aussi loin que possible vers la droite(36) tout en restant en contact avec la région ombrée.
Pour appliquer la méthode de la section 20.2, on écrit la seconde contrainte −𝑥 − 𝑦 ⩽ 0 et
on considère le lagrangien L(𝑥, 𝑦) = 𝑥 + 𝑎𝑦 −𝜆1 (𝑥2 + 𝑦2 − 1) +𝜆2 (𝑥 + 𝑦). Les conditions
KKT sont (i) L′
𝑥 (𝑥, 𝑦) = 1 − 2𝜆1𝑥 + 𝜆2 = 0; (ii) L′
𝑦 (𝑥, 𝑦) = 𝑎 − 2𝜆1𝑦 + 𝜆2 = 0;
(iii) 𝜆1 ⩾ 0, avec 𝜆1 = 0 si 𝑥2 + 𝑦2 1; (iv) 𝜆2 ⩾ 0, avec 𝜆2 = 0 si 𝑥 + 𝑦 0.
(b) De (i) découle 2𝜆1𝑥 = 1 + 𝜆2 ⩾ 1. Mais (iii) implique 𝜆1 ⩾ 0, de sorte que, en fait,
𝜆1 0 et 𝑥 0. Comme 𝜆1 0, il suit de (iii) que 𝑥2 + 𝑦2 = 1 et ainsi tout éventuel
maximum aura lieu en un point de ce demi-cercle où 𝑥 0.
(I) Cas 𝑥+𝑦 = 0. Comme 𝑥2 +𝑦2 = 1 et 𝑥 0, la seule solution est 𝑥 = 1
2
√
2 et 𝑦 = −1
2
√
2.
En additionnant les équations (i) et (ii), on obtient 0 = 1+𝑎−2𝜆1(𝑥+𝑦)+2𝜆2 = 1+𝑎+2𝜆2
puisque 𝑥 + 𝑦 = 0. Mais 𝜆2 ⩾ 0, donc 𝑎 = 1 − 2𝜆2 ⩽ −1 dans ce cas. L’équation (i) avec
𝜆2 = 1
2 (1 − 𝑎) et 𝑥 = 1
2
√
2 conduit alors à 𝜆1 = (1 + 𝜆2)/2𝑥 = (1 − 𝑎)/4𝑥 =
√
2(1 − 𝑎)/4.
(II) Cas 𝑥 + 𝑦 0. Alors (iv) implique 𝜆2 = 0, de sorte que (i) et (ii) se réduisent à
1 − 2𝜆1𝑥 = 0 et 𝑎 − 2𝜆1𝑦 = 0 et ainsi 𝑥 = 1/(2𝜆1) et 𝑦 = 𝑎/(2𝜆1). La substitution dans
𝑥2 + 𝑦2 = 1 fournit (1/4𝜆1)2 (1 + 𝑎2) = 1 et donc 𝜆1 = 1
2
√
1 + 𝑎2 . Cela donne
𝑥 =
1
√
1 + 𝑎2
et 𝑦 =
𝑎
√
1 + 𝑎2
.
Comme 𝑥 + 𝑦 = (1 + 𝑎)(1 + 𝑎2)−1/2 0 dans ce cas, cela se produit quand 𝑎 −1.
Conclusion : les seuls couples qui satisfont aux conditions KKT sont les suivants
(𝑥∗
, 𝑦∗
) =
(
1
2
√
2, −1
2
√
2
si𝑎 ⩽ −1
1/
√
1 + 𝑎2, 𝑎/
√
1 + 𝑎2
si𝑎 −1
.
Comme l’ensemble réalisable est borné et fermé et comme 𝑓 est continue, ces valeurs
extrêmes sont forcément atteintes.
5. Le lagrangien est L = 𝑦 − 𝑥2 + 𝜆𝑦 + 𝜇 (𝑦 − 𝑥 + 2) − 𝜈 (𝑦2 − 𝑥), dont les points critiques
sont tels que (i) −2𝑥 − 𝜇 + 𝜈 = 0; (ii) 1 + 𝜆 + 𝜇 − 2𝜈𝑦 = 0. De plus, les conditions de
complémentarité exigent (iii) 𝜆 ⩾ 0, avec 𝜆 = 0 si 𝑦 0; (iv) 𝜇 ⩾ 0, avec 𝜇 = 0 si
𝑦 − 𝑥 −2; (v) 𝜈 ⩾ 0, avec 𝜈 = 0 si 𝑦2 𝑥.
De (ii), on a 2𝜈𝑦 = 1 +𝜆 + 𝜇 0, d’où 𝑦 0 et 𝜈 0, ce qui entraîne, d’après (v), 𝑦2 = 𝑥.
L’équation (iii) implique aussi 𝜆 = 0 et 2𝜈𝑦 = 1 + 𝜇. L’équation (i) donne 𝑥 = 1
2 (𝜈 − 𝜇).
On suppose 𝜇 0. Alors 𝑦 − 𝑥 + 2 = 𝑦 − 𝑦2 + 2 = 0 avec comme racines 𝑦 = −1 et 𝑦 = 2.
Seule 𝑦 = 2 est admissible. Ensuite 𝑥 = 𝑦2 = 4. Comme 𝜆 = 0, les conditions (i) et (ii)
deviennent −𝜇 + 𝜈 = 8 et 𝜇 − 4𝜈 = −1, de sorte que 𝜈 = −7/3, ce qui contredit 𝜈 ⩾ 0.
Aussi, (𝑥, 𝑦) = (4, 2) n’est pas un candidat. Par conséquent, 𝜇 = 0. D’où 𝑥 = 1
2 𝜈 = 𝑦2
et, par (ii), 1 = 2𝜈𝑦 = 4𝑦3. De là, 𝑦 = 4−1/3, 𝑥 = 4−2/3, qui est le seul candidat. C’est la
solution avec 𝜆 = 0, 𝜇 = 0 et 𝜈 = 1/2𝑦 = 4−1/6.
(36) Pourquoi vers la droite?

230. 230 CORRIGÉS DES EXERCICES
6. (a) Voir la figure C20.2.6. Pour que (𝑥, 𝑦) soit admissible, il faut que 𝑒−𝑥 ⩽ 𝑦 ⩽ 2/3 et
ainsi 𝑒𝑥 ⩾ 3/2, ce qui en particulier implique 𝑥 0.
y
1
2
x
1 2
y = 2/3
y = e−x
(x∗
, y∗
)
Figure C20.2.6
(b) Le lagrangien est L = −(𝑥 + 1
2 )2 − 1
2 𝑦2 − 𝜆1 (𝑒−𝑥 − 𝑦) − 𝜆2 (𝑦 − 2
3 ). Les conditions
du premier ordre sont :
(i) L′
𝑥 (𝑥, 𝑦) = −(2𝑥 + 1) + 𝜆1𝑒−𝑥 = 0; (ii) L′
𝑦 (𝑥, 𝑦) = −𝑦 + 𝜆1 − 𝜆2 = 0;
(iii) 𝜆1 ⩾ 0, avec 𝜆1 = 0 si 𝑒−𝑥 𝑦 ; (iv) 𝜆2 ⩾ 0, avec 𝜆2 = 0 si 𝑦 2/3.
De (i), 𝜆1 = (2𝑥 + 1)𝑒𝑥 ⩾ 3/2, à cause de (a), impliquant 𝑦 = 𝑒−𝑥. De (ii),
𝜆2 = 𝜆1 − 𝑦 ⩾ 3/2 − 2/3 0, d’où 𝑦 = 2/3 à cause de (iv). Voici donc le candidat à la
solution (𝑥∗, 𝑦∗) = (ln(3/2), 2/3), avec 𝜆1 = 3[ln(3/2) + 1/2] et 𝜆2 = 3 ln(3/2) + 5/6.
Il est facile de voir que le lagrangien est concave comme une fonction de (𝑥, 𝑦) quand
𝜆1 ⩾ 0. C’est donc bien la solution. Autre raisonnement possible : on suppose 𝜆1 = 0.
Alors, de (ii), 𝑦 = −𝜆2 ⩽ 0, contredisant 𝑦 ⩾ 𝑒−𝑥. Aussi 𝜆1 0 et (iii) donne 𝑦 = 𝑒−𝑥.
On suppose 𝜆2 = 0. Alors, de (ii), 𝜆1 = 𝑦 = 𝑒−𝑥 et (i) donne 𝑒−2𝑥 = 2𝑥 + 1. On définit
𝑔(𝑥) = 2𝑥 + 1 − 𝑒−2𝑥. Alors 𝑔(0) = 0 et 𝑔′(𝑥) = 2 + 2𝑒−2𝑥 0. L’équation 𝑒−2𝑥 = 2𝑥 + 1
n’a pas de solution en dehors de 𝑥 = 0. D’où 𝜆2 0, etc.
7. (a) Avec L = 𝑥𝑧 + 𝑦𝑧 − 𝜆(𝑥2 + 𝑦2 + 𝑧2 − 1), les conditions KKT sont (i) 𝑧 − 2𝜆𝑥 = 0;
(ii) 𝑧 − 2𝜆𝑦 = 0; (iii) 𝑥 + 𝑦 − 2𝜆𝑧 = 0; (iv) 𝜆 ⩾ 0, avec 𝜆 = 0 si 𝑥2 + 𝑦2 + 𝑧2 1.
(b) Si 𝜆 = 0, chaque point (𝑥, 𝑦, 0) avec 𝑥 + 𝑦 = 0 et 𝑥2 + 𝑦2 ⩽ 1 satisfait aux conditions
KKT. Mais la valeur de 𝑥𝑧 + 𝑦𝑧 en ces points est 0 : ce n’est donc évidemment pas la
valeur maximale. Dans le cas 𝜆 0 et donc 𝑥2 + 𝑦2 + 𝑧2 = 1, alors (i) et (ii) impliquent
𝑥 = 𝑦 = 𝑧/2𝜆. Il s’ensuit que (𝑧2/4𝜆2) + (𝑧2/4𝜆2) + 𝑧2 = 1, donc 𝑧2 = 4𝜆2/(4𝜆2 + 2).
Mais alors (iii) implique que 𝑧/𝜆 = 2𝜆𝑧 et, puisque 𝑧 ≠ 0, 2𝜆2 = 1. Ainsi, 𝑧2 = 1
2 . Les
points vérifiant les conditions KKT sont ( 1
2 , 1
2 , 1
2
√
2) et (−1
2 , −1
2 , −1
2
√
2), avec 𝜆 = 1
2
√
2.
Le théorème des bornes atteintes garantit l’existence d’un maximum, qui correspond à
l’un de ces deux points.
20.3
1. (a) Avec L(𝑥, 𝑦) = 𝑥 +ln(1+ 𝑦) −𝜆(16𝑥 + 𝑦 −495), les conditions KKT pour que (𝑥∗, 𝑦∗)
soit une solution sont : (i) L′
𝑥 (𝑥∗, 𝑦∗) = 1 − 16𝜆 ⩽ 0 ( = 0 si 𝑥∗ 0) ;
(ii) L′
𝑦 (𝑥∗
, 𝑦∗
) =
1
1 + 𝑦∗
− 𝜆 ⩽ 0 ( = 0 si 𝑦∗
0) ; (iii) 𝜆 ⩾ 0 avec 𝜆 = 0
si 16𝑥∗ + 𝑦∗ 495; (iv) 𝑥∗ ⩾ 0, 𝑦∗ ⩾ 0; (v) 16𝑥∗ + 𝑦∗ ⩽ 495.

231. Chapitre 20 / Programmation non linéaire 231
(b) Notez que le lagrangien est concave. Un point dont les coordonnées satisfont aux
conditions KKT sera donc un maximum. De la condition (i), 𝜆 ⩾ 1/16 0, et (iii) et
(v) impliquent (vi) 16𝑥∗ + 𝑦∗ = 495. Dans le cas 𝑥∗ = 0, (v) donne 𝑦∗ = 495 et, de (ii),
𝜆 = 1/496, en contradiction avec 𝜆 ⩾ 1/16. D’où 𝑥∗ 0 et, par (i), 𝜆 = 1/16. Dans le
cas 𝑦∗ = 0, (ii) implique 𝜆 ⩾ 1, en contradiction avec 𝜆 = 1/16. D’où 𝑦∗ 0 et, de (ii),
𝑦∗ = 15 et, selon (v), 𝑥∗ = 30. La seule solution qui satisfait aux conditions KKT est
(𝑥∗, 𝑦∗) = (30, 15), avec 𝜆 = 1/16.
(c) L’utilité va augmenter d’environ 𝜆 × 5 = 5/16. (En réalité, la nouvelle solution est
(30 + 5
16 , 15) et l’augmentation de la fonction d’utilité est 5/16. C’est dû au fait que la
fonction d’utilité est quasiment du premier degré.)
2. Le lagrangien sans multiplicateurs de Lagrange pour les contraintes de positivité s’écrit
L = 𝑥𝑒𝑦−𝑥 − 2𝑒𝑦 − 𝜆 (𝑦 − 1 − 𝑥/2), de sorte que les conditions du premier ordre (20.3.3)
et (20.3.4) sont :
(i) L′
𝑥 = 𝑒𝑦−𝑥−𝑥𝑒𝑦−𝑥+1
2𝜆 ⩽ 0 (= 0 si 𝑥 0) ; (ii) L′
𝑦 = 𝑥𝑒𝑦−𝑥−2𝑒−𝜆 ⩽ 0 (= 0 si 𝑦 0) ;
(iii) 𝜆 ⩾ 0 avec 𝜆 = 0 si 𝑦 1 + 1
2 𝑥. Si 𝑥 = 0, alors (i) implique 𝑒𝑦 + 1
2𝜆 ⩽ 0, ce qui est
impossible. Donc 𝑥 0 et, de (i), il vient (iv) 𝑥𝑒𝑦−𝑥 = 𝑒𝑦−𝑥 + 1
2𝜆. On suppose d’abord
que 𝜆 0. Alors (iii) et 𝑦 ⩽ 1 + 𝑥/2 impliquent (v) 𝑦 = 1 + 1
2 𝑥. D’où 𝑦 0 et de (ii), on
a 𝑥𝑒𝑦−𝑥 = 2𝑒 + 𝜆. D’après (iv) et (v),
𝜆 = 2𝑒𝑦−𝑥
− 4𝑒 = 2𝑒(𝑒− 1
2 𝑥
− 2).
Mais alors, 𝜆 0 implique 𝑒− 1
2 𝑥 2, ce qui contredit 𝑥 ⩾ 0. La seule possibilité est
donc 𝜆 = 0. Ensuite, (iv) donne 𝑥 = 1. Si 𝑦 0, alors (ii) fournit 𝑒𝑦−1 = 2𝑒, et ainsi
𝑦 − 1 = ln(2𝑒) = ln 2 + 1. Avec 𝑥 = 1, cela contredit la contrainte 𝑦 ⩽ 1 + 1
2 𝑥. De là,
𝑦 = 0, et le seul couple qui convient est (𝑥, 𝑦) = (1, 0) avec 𝜆 = 0(37).
3. Le lagrangien est L = 𝑥1 +3𝑥2 −𝑥2
1 −𝑥2
2 −𝑘2 −𝜆(𝑥1 −𝑘) − 𝜇 (𝑥2 −𝑘). Un triplet admissible
(𝑥∗
1, 𝑥∗
2, 𝑘∗) résout le problème si et seulement si il existe des nombres 𝜆 et 𝜇 tels que
(i)
𝜕L
𝜕𝑥1
= 1 − 2𝑥∗
1 − 𝜆 ⩽ 0 (= 0 si 𝑥∗
1 0) ; (ii)
𝜕L
𝜕𝑥2
= 3 − 2𝑥∗
2 − 𝜇 ⩽ 0 (= 0 si 𝑥∗
2 0);
(iii)
𝜕L
𝜕𝑘
= −2𝑘∗ + 𝜆 + 𝜇 ⩽ 0 (= 0 si 𝑘∗ 0) ; (iv) 𝜆 ⩾ 0 avec 𝜆 = 0 si 𝑥∗
1 𝑘∗ ;
(v) 𝜇 ⩾ 0 avec 𝜇 = 0 si 𝑥∗
2 𝑘∗.
Si 𝑘∗ = 0, alors les contraintes exigent 𝑥∗
1 = 0 et 𝑥∗
2 = 0, et ainsi (i) et (ii) impliquent
𝜆 ⩾ 1 et 𝜇 ⩾ 3, ce qui contredit (iii). D’où 𝑘∗ 0. Ensuite, si 𝜇 = 0, alors (ii) et (iii)
impliquent 𝑥∗
2 ⩾ 3/2 et 𝜆 = 2𝑘∗ 0. Ainsi, 𝑥∗
1 = 𝑘∗ = 1/4, en contradiction avec 𝑥∗
2 ⩽ 𝑘∗.
Ainsi, 𝜇 0, ce qui implique 𝑥∗
2 = 𝑘∗. Maintenant, si 𝑥∗
1 = 0 𝑘∗, alors 𝜆 = 0, ce qui
contredit (i). Ainsi, 0 𝑥∗
1 = 1
2 (1 − 𝜆). Ensuite, si 𝜆 0, alors
𝑥∗
1 = 𝑘∗
= 𝑥∗
2 =
1
2
(1 − 𝜆) =
1
2
(3 − 𝜇) =
1
2
(𝜆 + 𝜇)
(37) Le théorème des bornes atteintes ne peut pas s’appliquer ici, car l’ensemble réalisable n’est pas borné. En effet, il
inclut les points de coordonnées (𝑥, 0) pour des valeurs de 𝑥 arbitrairement grandes. Néanmoins, il avait été supposé
que le problème avait une solution.

232. 232 CORRIGÉS DES EXERCICES
en raison de (i), (ii) et (iii) respectivement. Mais les deux dernières égalités ne sont
satisfaites que si 𝜆 = −1/3 et 𝜇 = 5/3, ce qui contredit 𝜆 ⩾ 0. Ainsi, 𝜆 = 0 en fin de
compte, avec 𝑥∗
2 = 𝑘∗ 0, 𝜇 0, 𝑥∗
1 = 1
2 (1 − 𝜆) = 1
2 . Maintenant, de (iii) découle
𝜇 = 2𝑘∗ et ainsi, de (ii), 3 = 2𝑥∗
2 + 𝜇 = 4𝑘∗. La seule solution possible est, dès lors,
(𝑥∗
1, 𝑥∗
2, 𝑘∗) = (1/2, 3/4, 3/4), avec 𝜆 = 0 et 𝜇 = 3/2. Finalement, avec 𝜆 = 0 et 𝜇 = 3
2 ,
le lagrangien 𝑥1 + 3𝑥2 − 𝑥2
1 − 𝑥2
2 − 𝑘2 − 3
2 (𝑥2 − 𝑘) est une fonction du second degré de
(𝑥1, 𝑥2, 𝑘), qui atteint un maximum au point critique (𝑥∗
1, 𝑥∗
2, 𝑘∗). Ainsi qu’il a été établi
à la fin de la méthode de la section 20.3, c’est aussi suffisant pour que (𝑥∗
1, 𝑥∗
2, 𝑘∗) soit la
solution du problème.
Exercices récapitulatifs du chapitre 20
1. Avec L = 10 − (𝑥 − 2)2 − (𝑦 − 1)2 − 𝜆(𝑥2 + 𝑦2 − 𝑎), les conditions KKT sont
(i) L′
𝑥 = −2 (𝑥 − 2) − 2𝜆𝑥 = 0; (ii) L′
𝑦 = −2 (𝑦 − 1) − 2𝜆𝑦 = 0; (iii) 𝜆 ⩾ 0,
avec 𝜆 = 0 si 𝑥2 + 𝑦2 𝑎. Puisque le lagrangien est concave quand 𝜆 ⩾ 0, ces conditions
sont suffisantes pour un maximum. Premier cas, 𝜆 = 0. Alors (𝑥, 𝑦) = (2, 1). C’est valable
quand 𝑎 ⩾ 𝑥2 + 𝑦2 = 5. Deuxième cas, 𝜆 0. Alors (i) implique 𝑥 = 2/(1 + 𝜆) et (ii)
implique 𝑦 = 1/(1 + 𝜆). Comme (iii) implique 𝑥2 + 𝑦2 = 𝑎, on a 5/(1 + 𝜆)2 = 𝑎 et ainsi
𝜆 =
p
5/𝑎 − 1, qui est strictement positif lorsque 𝑎 5.
La solution est (𝑥, 𝑦) = (2
p
𝑎/5,
p
𝑎/5).
2. (a) Avec L = 𝑥𝑦 − 𝜆1 (𝑥2 + 𝑟𝑦2 − 𝑚) − 𝜆2 (−𝑥 + 1), les conditions KKT pour
que (𝑥∗, 𝑦∗) soit solution du problème sont (i) L′
𝑥 = 𝑦∗ − 2𝜆1𝑥∗ + 𝜆2 = 0;
(ii) L′
𝑦 = 𝑥∗ − 2𝑟𝜆1𝑦∗ = 0; (iii) 𝜆1 ⩾ 0, avec 𝜆1 = 0 si (𝑥∗)2 + 𝑟(𝑦∗)2 𝑚 ;
(iv) 𝜆2 ⩾ 0, avec 𝜆2 = 0 si 𝑥∗ 1; (v) (𝑥∗)2 + 𝑟(𝑦∗)2 ⩽ 𝑚 ; (vi) 𝑥∗ ⩾ 1.
(b) À (ii) et (vi) de la question (a), on voit que 𝜆1 = 0 est impossible. Donc 𝜆1 0 et, à
(iii) et (v), on voit que (vii) (𝑥∗)2 + 𝑟(𝑦∗)2 = 𝑚.
(I) : On suppose 𝜆2 = 0. Alors de (i) et (ii), 𝑦∗ = 2𝜆1𝑥∗ et 𝑥∗ = 2𝜆1𝑟𝑦∗, de sorte que
𝑥∗ = 4𝜆2
1𝑟𝑥∗. Mais (vi) implique 𝑥∗ ≠ 0. De là, 𝜆2
1 = 1/4𝑟 et donc 𝜆1 = 1/2
√
𝑟. Ensuite,
𝑦∗ = 𝑥∗/
√
𝑟. On introduit dans (vii) et on résout par rapport à 𝑥∗. Cela donne 𝑥∗ =
p
𝑚/2
et 𝑦∗ =
p
𝑚/2𝑟. Notez que
𝑥∗
⩾ 1 ⇔
p
𝑚/2 ⩾ 1 ⇔ 𝑚 ⩾ 2.
D’où pour 𝑚 ⩾ 2, un candidat à la solution 𝑥∗ =
p
𝑚/2 et 𝑦∗ =
p
𝑚/2𝑟, avec 𝜆1 = 1/2
√
𝑟
et 𝜆2 = 0.
(II) : On suppose 𝜆2 0. Alors 𝑥∗ = 1 et de (vii), on tire 𝑟(𝑦∗)2 = 𝑚 − 1. Par (ii), on a
𝑦∗ ⩾ 0, de sorte que
𝑦∗
=
p
(𝑚 − 1)/𝑟.
On introduit ces valeurs dans (i) et (ii), puis on résout par rapport à 𝜆1 et 𝜆2. On obtient
𝜆1 = 1/2
p
𝑟(𝑚 − 1) et ensuite 𝜆2 = (2 − 𝑚)/
p
𝑟(𝑚 − 1). Notez que
𝜆2 0 ⇔ 1 𝑚 2.
D’où pour 1 𝑚 2, le seul candidat est 𝑥∗ = 1, 𝑦∗ =
p
(𝑚 − 1)/𝑟, avec
𝜆1 = 1/2
p
𝑟(𝑚 − 1) et 𝜆2 = (2 − 𝑚)/
p
𝑟(𝑚 − 1).

233. Chapitre 20 / Programmation non linéaire 233
La fonction objectif est continue et l’ensemble réalisable est manifestement borné fermé.
Par conséquent, en vertu du théorème des bornes atteintes, il y a un maximum. Les
candidats trouvés sont bien les solutions du programme(38).
(c) Pour 𝑚 ⩾ 2, 𝑉(𝑟, 𝑚) = 𝑚/2
√
𝑟, de sorte que 𝑉′
𝑚 = 1/2
√
𝑟 = 𝜆1 et 𝑉′
𝑟 = −𝑚/4
√
𝑟3.
Pour 1 𝑚 2, 𝑉(𝑟, 𝑚) =
p
(𝑚 − 1)/𝑟, de sorte que 𝑉′
𝑚 = 1/2
p
𝑟(𝑚 − 1) = 𝜆1 et
𝑉′
𝑟 = −(1/2)
p
(𝑚 − 1)/𝑟3.
(d) Pour 𝑚 ⩾ 2, L′
𝑟 = −𝜆1 (𝑦∗)2 = −(1/2
√
𝑟)𝑚/2𝑟 = −𝑚/4
√
𝑟3. Pour 1 𝑚 2,
L′
𝑟 = −𝜆1 (𝑦∗
)2
= −[1/2
p
𝑟(𝑚 − 1)](𝑚 − 1)/𝑟 = −(1/2)
p
(𝑚 − 1)/𝑟3.
On retrouve bien que 𝜕𝑉(𝑟, 𝑚)/𝜕𝑟 = 𝜕L/𝜕𝑟.
3. (a) Voir figure C.20.R.3. Si 𝑎 = 0, c’est un programme linéaire dont la solution est 𝑃, de
coordonnées (𝑥1, 𝑥2) = (2 000, 2 000/3).
x2
1000
2000
3000
4000
x1
1000 2000 3000 4000
500x1 + 250x2 = c
P
Figure C20.R.3
(b) Si 𝑎 ⩾ 0, on suit les techniques de la section 20.10 et on écrit le lagrangien
L = (500 − ⊣§1) §1 + 250§2 − 𝜆1 (0,04𝑥1 + 0,03𝑥2 − 100)
− 𝜆2 (0,025𝑥1 + 0,05𝑥2 − 100)
− 𝜆3 (0,05𝑥1 − 100) − 𝜆4 (0,08𝑥2 − 100).
Alors les conditions KKT (avec les contraintes de positivité) sont : il existe des nombres
𝜆1, 𝜆2, 𝜆3 et 𝜆4, tels que
(i) 𝜕L/𝜕𝑥1 = 500 − 2𝑎𝑥1 − 0,04𝜆1 − 0,025𝜆2 − 0,05𝜆3 ⩽ 0 (= 0 si 𝑥1 0) ;
(ii) 𝜕L/𝜕𝑥2 = 250 − 0,03𝜆1 − 0,05𝜆2 − 0,08𝜆4 ⩽ 0 (= 0 si 𝑥2 0) ;
(iii) 𝜆1 ⩾ 0, et 𝜆1 = 0 si 0,04𝑥1 + 0,03𝑥2 100;
(38) Sinon, L′′
𝑥𝑥 = −2𝜆1 ⩽ 0, L′′
𝑦𝑦 = −2𝑟𝜆1 ⩽ 0 et Δ = L′′
𝑥𝑥 L′′
𝑦𝑦 − (L′′
𝑥𝑦)2 = 4𝑟𝜆2
1 − 1. Dans ce cas, 𝑚 ⩾ 2,
Δ = 0 et si 1 𝑚 2, Δ = 1/(𝑚 − 1) 0. Dans les deux cas, L(𝑥, 𝑦) est concave. Les conditions KKT sont donc
suffisantes pour qu’il y ait un maximum.

234. 234 CORRIGÉS DES EXERCICES
(iv) 𝜆2 ⩾ 0, et 𝜆2 = 0 si 0,025𝑥1 + 0,05𝑥2 100;
(v) 𝜆3 ⩾ 0, et 𝜆3 = 0 si 0,05𝑥1 100;
(vi) 𝜆4 ⩾ 0, et 𝜆4 = 0 si 0,08𝑥2 100.
(c) Les conditions KKT sont suffisantes à l’optimalité puisqu’il est facile de véri-
fier que le lagrangien est concave en (𝑥1, 𝑥2) pour 𝑎 ⩾ 0. Pour savoir quand
(𝑥1, 𝑥2) = (2 000, 2 000/3) reste optimal, on doit trouver des multiplicateurs de Lagrange
tels que toutes les conditions KKT sont encore satisfaites. Notez que (i) et (ii) doivent
encore être satisfaites avec égalité. En outre, les inégalités (iv) et (vi) sont strictes, de
sorte que 𝜆2 = 𝜆4 = 0. Ensuite, (ii) donne 𝜆1 = 25 000/3. Il reste à vérifier pour quelles
valeurs de 𝑎, il est possible de satisfaire à (i) pour un 𝜆3 qui satisfait aussi à (v). De (i),
0,05𝜆3 = 500 − 4 000𝑎 − 0,04 (25 000/3) = 500/3 − 4 000𝑎 ⩾ 0 si et seulement si
𝑎 ⩽ 1/24.
4. Avec le lagrangien L = 𝑅(𝑄) − 𝐶(𝑄) − 𝜆 (−𝑄), les conditions KKT pour que 𝑄∗ soit
solution sont (i) 𝑅′(𝑄∗) − 𝐶′(𝑄∗) + 𝜆 = 0; (ii) 𝜆 ⩾ 0, avec 𝜆 = 0 si 𝑄∗ 0.
Ces conditions sont aussi suffisantes, car le lagrangien est concave en 𝑄. Une condition
suffisante (et nécessaire) pour que 𝑄∗ = 0 soit optimal est que 𝜋′(0) ⩽ 0, ou de façon
équivalente, 𝑅′(0) ⩽ 𝐶′(0). (Faites une figure.)
5. (a) Le problème de maximisation posé s’écrit : max (−𝑟𝐾 −𝑤𝐿) s.c. −
√
𝐾𝐿 ⩽ −𝑄. Avec
le lagrangien L = −𝑟𝐾 − 𝑤𝐿 − 𝜆 (−
√
𝐾𝐿 + 𝑄), les conditions KKT pour que (𝐾∗, 𝐿∗)
soit solution sont
(i) L′
𝐾 = −𝑟 + 𝜆 (
√
𝐿∗/2
√
𝐾∗) = 0; (ii) L′
𝐿 = −𝑤 + 𝜆 (
√
𝐾∗/2
√
𝐿∗) = 0;
(iii) 𝜆 ⩾ 0 (𝜆 = 0 si
√
𝐾∗𝐿∗ 𝑄).
Manifestement 𝜆 = 0 contredirait (i) et (ii), de sorte que 𝜆 0 et (iv)
√
𝐾∗𝐿∗ = 𝑄. En
éliminant 𝜆 de (i) et (ii), on trouve 𝐿∗ = 𝑟𝐾∗/𝑤. Ensuite, (iv) fournit 𝐾∗ = 𝑄
p
𝑤/𝑟 et
𝐿∗ = 𝑄
p
𝑟/𝑤.
(b) 𝑐∗(𝑟, 𝑤, 𝑄) = 𝑟𝐾∗ +𝑤𝐿∗ = 2𝑄
√
𝑟𝑤, de sorte que 𝜕𝑐∗/𝜕𝑟 = 𝑄
p
𝑤/𝑟 = 𝐾∗. Si le prix 𝑟
du capital augmente de d𝑟, alors le coût minimum augmentera d’environ 𝐾∗ d𝑟 et le choix
optimal du capital injecté, de 𝑟. L’équation 𝜕𝑐∗/𝜕𝑤 = 𝑄
p
𝑟/𝑤 = 𝐿∗ s’interprète de la
même façon.