Le document présente une série d'exercices en géométrie et en mathématiques pour une révision. Il aborde divers sujets, tels que les cercles, les triangles, les calculs d'angles et d'aire, ainsi que des problèmes d'algèbre et d'inéquations. Chaque section comprend des questions pratiques et des démonstrations à réaliser.
![Page 1 de 7
Révision 1 (Géométrie)
I. NOTE BIEN: ( Très important)
Soit ( C) un cercle de centre O et de diamètre [AB] tel que AB = 6 cm. Sur le cercle ( C) et du
même côté par rapport à (AB) on place deux points M et N tel que l’arc 𝑚𝑒𝑠𝐴𝑀̂ = 80° et l’arc
𝑚𝑒𝑠 𝐵𝑁̂ = 60°.
1) Tracer la figure.
2) Calculer A𝑀̂ 𝐵 et 𝑚𝑒𝑠𝑀𝑁̂ .
3) Quelle est la nature du triangle ANB ?
4) Calculer les angles A𝐵̂ 𝑀 et N𝐵̂A.
5) Quelle est la nature du triangle OBN.
6) Calculer la longueur de l’arc 𝐵𝑁̂ .
7) Calculer l’aire du secteur circulaire AOM.
8) Les droites (AM) et (BN) se coupent en R et les droites (AN) et (BM) se coupent en I.
Montrer que (RI) est perpendiculaire à (AB).
9) Calculer la mesure de l’angle A𝑅̂B et celle de A𝐼̂B.
II. Tracer un cercle ( O) de diamètre [AB], de centre O et de rayon 5 cm. Placer un point C sur (O)
tel que A𝐵̂C= 60° et soit H le projeté orthogonal de C sur (AB).
1) Déterminer la nature du triangle CHB.
2) Calculer CH et HA et en déduire AC.
3) Soit K le pied de la perpendiculaire menée de O sur (AC). Calculer OK.
4) La tangente en A à (O) coupe la droite (OK) en E. Calculer OE puis AE.
III.
1) Calculer le plus grand commun diviseur (PGCD) de 154 et 112.
2) Simplifier la fraction
112
154
pour la rendre irréductible.
3) On pose m =
112
154
+
1
8
.
a. Ecrire le nombre m sous forme d’une fraction irréductible.
b. Le nombre m est-il décimal ? Justifier
Nom:…………………
Classe de EB9
Sujet: Mathématiques
LaCitéCulturelle
Scientifique
(Mraige)
Révision: Fiche 1
Date: Aout, 2016
Durée:………..](https://image.slidesharecdn.com/fiche1derevisioneb9-160901173156/85/Fiche-1-de-revision-eb9-1-320.jpg)
![Page 2 de 7
IV. On donne 2 cercles C( O ; R) et C’(O’ ;R’) tangents extérieurement en un point A. Une tangente
extérieure touche le cercle ( C) en M et le cercle (C’) en N. La tangente commune intérieure en A
coupe MN en B.
1) Faire une figure.
2) Montrer que B est le milieu de [MN].
3) En déduire que le triangle AMN est rectangle en A.
4) Trouver la nature du quadrilatère OMNO’. Justifier.
V. On donne deux cercles C( O ;R) et C’(O’ ;R’) sécants en A et B. Soit [AM] le diamètre du cercle
(C ) et [AN] le diamètre du cercle ( C’).
1) Tracer la figure.
2) Montrer que les points M, B et N sont alignés.
3) Comparer OO’ et MN et déduire la nature du quadrilatère OO’NM.
VI. ( Pythagore)
1) XYZ est un triangle tel que XY= 4,8 ; XZ= 3,6 et YZ= 6 cm. Le triangle XYZ est-il
rectangle ?
2) Un triangle ABC rectangle en A est tel que AB= 8 cm et AC= 15 cm. La hauteur issue de A
dans le triangle ABC coupe [BC] en H. La médiane issue de H dans la triangle AHC coupe
[AC] en I.
a. Construire la figure.
b. Calculer HI.
VII. (Théorème de milieux)
Sur la figure ci-contre on a :
B, C et A sont alignés.
N , O et P sont alignés.
B est le milieu de [MP].
C est le milieu de [MO].
AN= 5 cm ; NO= 4 cm et OP = 3 cm.
1) Démontrer que (CB) // (OP) et
calculer CB.
2) Démontrer que A est le milieu de
[MN].
BON TRAVAIL](https://image.slidesharecdn.com/fiche1derevisioneb9-160901173156/85/Fiche-1-de-revision-eb9-2-320.jpg)
![Page 4 de 7
Révision 3
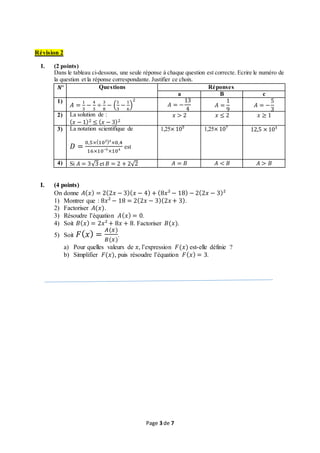
I. (3 points)
On considère le tableau suivant :
1) Montrer que c’est un tableau de
proportionnalité.
2) Calculer le coefficient de proportionnalité
et déduire l’équation de sa fonction
linéaire.
I. (4 points)
On donne les polynômes : 𝑃( 𝑥) = (2𝑥 − 3)( 𝑥 + 4) − 𝑥² + 16 et 𝑄( 𝑥) = ( 𝑥 + 5)2 − 1
1) Factoriser 𝑃(𝑥) et 𝑄(𝑥).
2) Résoudre les équations suivantes :
a) 𝑃( 𝑥) = 0.
b) 𝑃( 𝑥) = 𝑄( 𝑥).
c) 𝑄( 𝑥) = 24.
3) Soit : 𝐹( 𝑥) =
𝑃(𝑥)
𝑄(𝑥)
a) Pour quelles valeurs de x, 𝐹(𝑥) est-elle définie ?
b) Simplifier 𝐹(𝑥) puis résoudre 𝐹( 𝑥) =
1
2
.
II. (2 points)
1) Prouver que pour tout nombre différent de zéro, l’inéquation 𝑥² + 𝑦² ≥ 2𝑥𝑦 est toujours
vraie.
2) Déduire que si 𝑥 𝑒𝑡 𝑦 sont non nulles avec la même signe alors
𝑥
𝑦
+
𝑦
𝑥
≥ 2.
III. (6 points)
1) Dans un repère orthonormé d’axes x’Ox, y’Oy, placer les points A(1 ;3), B( 5 ;8) et C(5 ;3).
2) Calculer les mesures de [AB],[AC] et [BC], puis déduire la nature du triangle ABC.
3) Déterminer les coordonnées du point D, tel que 𝐶𝐴⃗⃗⃗⃗⃗ = 𝐵𝐷⃗⃗⃗⃗⃗⃗
4) Quelle est la nature du quadrilatère ACBD ? Justifier.
5) Déterminer les coordonnées du point I le milieu de [AC] et du point J celui de [AB].
6) Déduire la longueur du segment IJ.
7) Prouver que le quadrilatère OACB est un
parallélogramme.
IV. (5 points)
Dans la figure suivante, on donne un cercle (C ) de centre
O et de rayon 3 cm, BP= AB et 𝐵𝐴̂ 𝑁 = 30°.
1) Calculer AP,BN et AN.
2) Calculer AQ et BQ.
3) Vérifier que M est le milieu de [AP].
4) Vérifier que (OM) est perpendiculaire à (AB).
5) Trouver le lieu géométrique du point P lorsque M
varie sur ( C).
BON TRAVAIL
0,16 × 10² 1,3̅
3 3
4
×
25
100
÷
3
4
M](https://image.slidesharecdn.com/fiche1derevisioneb9-160901173156/85/Fiche-1-de-revision-eb9-4-320.jpg)


