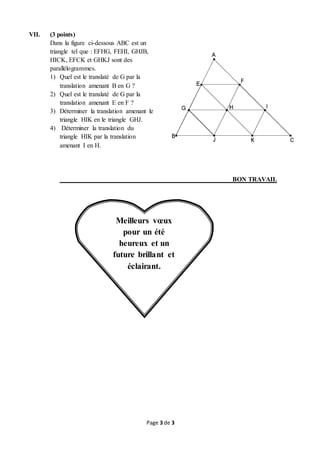
Le document présente un examen de mathématiques pour une classe de 3ème semestre, comprenant des questions sur des sujets variés tels que l'arithmétique, la géométrie, et les pourcentages. Les élèves doivent justifier leurs réponses, factoriser des expressions, résoudre des équations et effectuer des constructions géométriques. L'examen est structuré en plusieurs sections avec des points attribués à chaque question.

1. Page 1 de 3
CCS Mathématiques Juin 2015
Classe de EB7 Examen du 𝟑é𝒎𝒆 semestre Durée : 120 min
Nom :…………………………………..
I. (2 points)
Dans le tableau suivant, une seule réponse est correcte. Trouver la bonne réponse avec
justification.
Nb Questions Réponses
A B C
1 5² × 25² × (5²)⁴ 5¹² × 5² 5¹⁶ 5¹²
2 Le PGCD de 16 et 48 3 48 16
3 La notation scientifique de
37,05 × 10⁵ est
0,3705 × 10⁷ 3,705 × 10⁶ 3,705 × 10⁴
4
𝐴 = (
2
3
−
5
2
) ×
9
4
+
1
2
= 𝐴 = −
29
8
𝐴 =
29
8
𝐴 =
29
7
II. (4 points)
On donne 𝐴( 𝑥) = (2𝑥 − 3)( 𝑥 − 1) − (2𝑥 − 3)(4 − 𝑥)
1) Factoriser 𝐴(𝑥).
2) Développer et réduire 𝐴(𝑥).
3) Calculer 𝐴(0), 𝐴(−1).
4) Résoudre l’équation 𝐴( 𝑥) = 4𝑥² + 8𝑥 + 4
III. (4 points)
1) Trois voitures sur 75 sont accidentées. Quel pourcentage cela représente-t-il ?
2) Avec 3,5 𝑙 de peinture, on peut peindre 14 m².
a) Quelle est l’aire qu’on peut peindre avec 12 𝑙 de peinture ?
b) Quelle est la quantité de peinture nécessaire pour peindre 23 m² ?
3) Un marchand achète trois pièces d’un tissu de mesures respectives 30 m, 25 m et 40 m.
La première pièce coûte 600000 LL.
Trouver le prix de chacune des deux autres.
IV. (2 points)
B et C sont deux points fixes tels que BC= 3 cm.
1) Trouver le lieu géométrique de point variable M tel que BM= 7 cm.
2) Trouver le lieu géométrique de point variable N tel que (CN) et (BC) sont
perpendiculaires.

2. Page 2 de 3
V. (4 points)
Voir la figure ci-dessous, puis répondre aux questions suivantes :
1
1) Trouver la mesure de l’angle 𝐴𝐻̂ 𝐵.
2) Prouver que (EI) est parallèle à (KL).
3) Les droites (JE) est (BH) sont-elles parallèles ? Justifier.
4) Trouver x et y.
VI. (6 points)
1) Construire l’ angle 𝑋𝑂̂ 𝑌 = 120°, puis construire la bissectrice de cet angle, [OZ).
2) Placer un point A sur [Oz) sachant que OA= 6cm.
3) A et B sont les projetés orthogonaux de A respectivement sur [Ox) et [Oy).
4) Placer les points S et T les symétriques de A par rapport à B et C respectivement.
5) Montrer que les triangles OAC et OAB sont superposables.
6) Prouver que OS= OT.
7) Montrer que BOS et COT sont superposables.
8) Calculer les mesures de 𝑂𝐴̂ 𝐵, 𝑂𝐴̂ 𝐶, 𝐴𝑆̂ 𝑂 𝑒𝑡 𝐴𝑇̂ 𝑂.

3. Page 3 de 3
VII. (3 points)
Dans la figure ci-dessous ABC est un
triangle tel que : EFHG, FEHI, GHJB,
HICK, EFCK et GHKJ sont des
parallélogrammes.
1) Quel est le translaté de G par la
translation amenant B en G ?
2) Quel est le translaté de G par la
translation amenant E en F ?
3) Déterminer la translation amenant le
triangle HIK en le triangle GHJ.
4) Déterminer la translation du
triangle HIK par la translation
amenant I en H.
BON TRAVAIL
Meilleurs vœux
pour un été
heureux et un
future brillant et
éclairant.