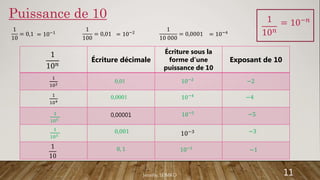
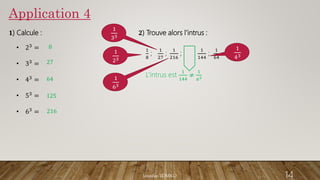
Le document aborde les puissances et les propriétés associées aux exposants en mathématiques. Il inclut des exemples de calculs avec des puissances, des applications de règles pour manipuler ces puissances, ainsi qu'une introduction à la notation scientifique. Jennifer Tomko présente des propriétés des puissances, des exemples de notation et des exercices pratiques.

1. Puissances
Classe : EB7
Matière : Mathématiques
Préparé par : Jennifer TOMKO
1

2. Puissance d’un nombre
𝑎 × 𝑎 × 𝑎 × … × 𝑎
𝑛 fois
= 𝑎𝑛
5 × 5 × 5 × 5
4 fois
= 54
7 × 7 × 7 × 7 × 7
5 fois
= 75
base
exposant
ou
puissance
• 𝑎𝑛
s’appelle la puissance 𝑛ème de
𝑎.
2
Jennifer TOMKO

3. 2
1
Propriétés
3
Jennifer TOMKO
(−5)4× (−5)3
73 × 93
= (−5)4+3
= (−5)7
= (7 × 9)3
= 633
𝑎𝑛 × 𝑎𝑚 = 𝑎𝑛+𝑚
𝑎𝑛
× 𝑏𝑛
= (𝑎 × 𝑏)𝑛
−5 × −5 × −5 × −5
−5 × −5 × −5
7 × 7 × 7
9 × 9 × 9

4. 4
3
Propriétés
4
Jennifer TOMKO
𝑎𝑛
𝑎𝑚
= 𝑎𝑛−𝑚
𝑎𝑛
𝑏𝑛
= (𝑎
𝑏)𝑛
3×3×3×3×3×3×3×3
3×3×3×3×3
38
35
= (3)8−5
= (3)3
65
25 =
6
2
5
= (3)5

5. 5
Propriétés
5
Jennifer TOMKO
(𝑎𝑛)𝑚 = 𝑎𝑛×𝑚
(−23
)2
= (−2)3×2
= (−2)6
−2 × −2 × (−2) × −2 × −2 × (−2)

6. Remarque
6
Jennifer TOMKO
• Si 𝑎 > 0, alors 𝑎𝑛 > 0
• Si 𝑎 < 0, alors 𝑎𝑛
> 0 si 𝑛 est pair
𝑎𝑛
< 0 si 𝑛 est impair
32
= 9
23 = 8
(−2)4
= −2 × −2 × −2 × (−2)
(−2)3= −2 × −2 × (−2)
= 16
= − 8
Signe de 𝑎𝑛

7. Application 1
7
Jennifer TOMKO
45 × 42 =
105
× 103
=
12,3 4 × 12,3 5 =
30 × 313 =
42 × 45 × 43 =
𝑎 × 𝑎2
=
45+2 = 47
105+3 = 108
(12,3)4+5
= (12,3)9
30+13 =313
42+5+3 = 410
𝑎1+2 = 𝑎3

8. Application 2
8
Jennifer TOMKO
84 5
= 8……
… … 3 … = 1315
(7…)6 = 742
20
13 5
7
5
3
2 5
=
510
53 … = 518
𝑎2 3 = 𝑎…
310
……
6
6

9. Puissance de 10
9
Jennifer TOMKO
102 = 10 × 10 = 100
103 = 10 × 10 × 10 = 1 000
10𝑛 = 1 0 . . . . . . . . 0
𝑛 zéro
106 = 1 000 000
6 zéros
108 = 100 000 000
8 zéros
Puissance d’exposant positif Puissance d’exposant négatif
10−2 =
1
102 = 0,01
1
100
=
10−5
=
1
105 = 0,00001
1
100 000
=
10−𝑛 =
1
10𝑛 =
𝑛 chiffres après la virgule
0,0 . . . 1
10−1 =
1
10
= 0,1
à la 5ème place
après la virgule

10. Puissance de 10
10
Jennifer TOMKO
Nombre Nombre de zéros
Écriture sous la
forme d’une
puissance de 10
Exposant de 10
10
1 000
1
100
100 000 000
1
3
0
2
101
103
100
102
1
3
0
2
8 108
8

11. Puissance de 10
11
Jennifer TOMKO
1
10𝑛
Écriture décimale
Écriture sous la
forme d’une
puissance de 10
Exposant de 10
1
102
1
104
0,00001
10−3
1
10
1
10
= 0,1
1
100
= 0,01
= 10−1 = 10−2
1
10 000
= 0,0001 = 10−4
1
10𝑛
= 10−𝑛
0,01 10−2
−2
0,0001 10−4 −4
1
105
10−5 −5
1
103
0,001 −3
0, 1 10−1
−1

12. Puissance de 10
12
Jennifer TOMKO
 Tous les puissances de 10 sont des nombres positifs.
107 > 0 ; 10−15 > 0
 (−10)𝑛 est un nombre positif si 𝑛 est pair.
(−10)4
= 104
= 10 000
 (−10)𝑛
est un nombre négatif si 𝑛 est impair.
(−10)3= −103= −1 000
Remarque

13. Application 3
Écris sous forme de puissances.
1) Le carré de 4.
2) Le cube de
5
7
.
3) La puissance cinquième de 7.
4) 8,9 exposant 9.
5) 10 exposant 3.
6) La puissance d’exposant 7 de
1
3
.
7) L’opposé du carré de 13,2.
8) L’opposé de la puissance quatrième de 19.
9) Le carré de 𝑥.
1) 42
2)
5
7
3
3) 75
4) (8,9)9
5) 103
6)
1
3
7
7) −(13,2)2
8) −194
9) 𝑥2
13
Jennifer TOMKO

14. Application 4
𝟏) Calcule :
• 23 =
• 33 =
• 43
=
• 53 =
• 63 =
8
27
64
125
216
𝟐) Trouve alors l’intrus :
1
8
;
1
27
;
1
216
;
1
144
;
1
64
.
L’intrus est
1
144
≠
1
𝑎3
1
23
1
33
1
63
1
43
14
Jennifer TOMKO

15. Notation scientifique
15
Jennifer TOMKO
264 0 ,9 = 2 ,64 09 × 10 …
0 ,07 = 7 × 10 …
3
− 2
Un nombre positif en notation scientifique est de la forme : 𝒂 × 𝟏 𝟎 𝒑
𝑎 est un nombre
décimal avec
1 ≤ 𝑎 < 10
𝑝 un entier
0 ,9 × 102
= 9 × 10 …
1
15 × 10 −2
= 1, 5 × 10 …
− 1

16. Application 5
85 milliards : 85 × 109
Écris en notation scientifique.
71 milliers :
240 millions :
13,7 milliards :
3 504,62 × 108 =
0,086 × 105 =
71 × 103
240 × 106
13,7 × 109
3,50462 × 1011
8,6 × 103
= 8,5 × 1010
= 7,1 × 104
= 2,4 × 108
= 1,37 × 1010
16
Jennifer TOMKO