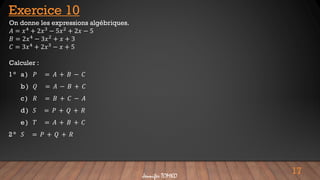
Le document traite des expressions algébriques, comprenant des définitions, des exemples de monômes, et des explications de calculs tels que l'addition et la soustraction d'expressions algébriques. Il fournit également des exercices pratiques pour réduire des termes semblables et évaluer des expressions pour des valeurs spécifiques de variables. Enfin, le document montre comment multiplier des monômes et donne des exercices pour calculer le périmètre et l'aire d'une figure en utilisant des expressions algébriques.