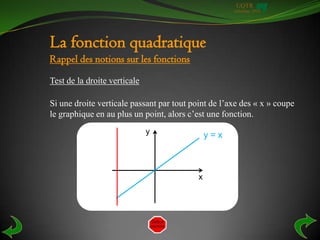
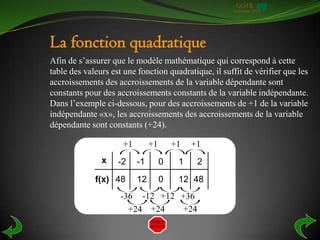
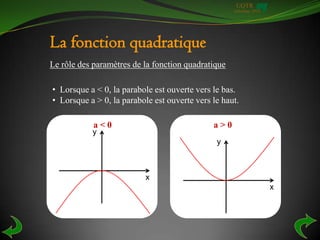
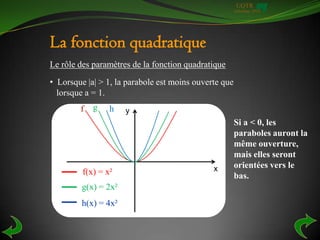
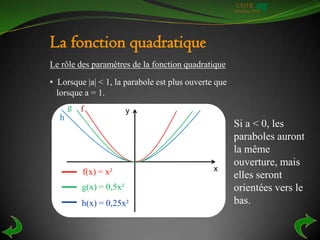
Le document traite des fonctions quadratiques, en présentant leurs concepts fondamentaux, leur représentation graphique et leur équation sous forme de polynôme de degré 2. Il décrit comment vérifier qu'une relation est une fonction à l'aide du test de la droite verticale, et explique comment trouver la règle d'une fonction quadratique à partir d'une table de valeurs. De plus, divers exercices sont fournis pour appliquer ces notions.

1. UQTR
Automne 2010
La fonction quadratique
Cette section contient les notions essentielles pour
comprendre les fonctions quadratiques. En
cliquant sur le bouton «théorie», il vous sera
possible de choisir le sujet de votre choix.
Théorie
Veuillez noter qu’en tout temps, vous pourrez
retourner au début de la section en cliquant sur le
bouton .
Exercices

2. UQTR
Automne 2010
La fonction quadratique
Rappel des notions sur les fonctions.
Secondaire 4 : technico-sciences.
Références
y
x

3. UQTR
Automne 2010
La fonction quadratique
Rappel des notions sur les fonctions
Qu’est-ce qu’une fonction?
Une fonction est une relation entre deux ensembles qui associe à
tout élément du premier ensemble un élément unique bien
déterminé du deuxième ensemble.
Pour vérifier si c’est véritablement une fonction dans le plan, on
peut faire le test de la droite verticale, expliqué à la prochaine page.

4. UQTR
Automne 2010
La fonction quadratique
Rappel des notions sur les fonctions
Test de la droite verticale
Si une droite verticale passant par tout point de l’axe des « x » coupe
le graphique en au plus un point, alors c’est une fonction.
y y=x
x

5. UQTR
Automne 2010
La fonction quadratique
Rappel des notions sur les fonctions
Pour tracer une fonction à partir de son équation, on peut créer
une table de valeurs afin de repérer facilement les coordonnées
dans le plan.
f(x) = -3x + 6
y
Pour x = 0 Pour x = 3
y = -3(0) + 6 y = -3(3) + 6 (0,6)
y=6 y = -3
x
x 0 1 2 3
f(x) 6 3 0 -3 (3,-3)

6. UQTR
Automne 2010
La fonction quadratique
Rappel des notions sur les fonctions
Dans une fonction de la forme : y = ax + b, «b» est l’endroit où la
droite croise l’axe des y et «a» représente l’inclinaison de la droite.
Si «a» est un nombre négatif, l’inclinaison de la droite sera vers le
bas (de gauche à droite).
y y = 2x
y = 0,5x
(0,-3) x
y = -x - 3

7. UQTR
Automne 2010
La fonction quadratique
La fonction quadratique, aussi appelée « fonction pôlinomiale de
degré 2 », est une fonction dont la règle est un polynôme de degré 2 à
une variable. La représentation graphique d’une fonction quadratique
dont la règle est de f(x) = a(bx)², où a et b n’égalent pas 0, est une
parabole dont le sommet se situe à l’origine du plan cartésien.
f(x) = 3(2x)² y
x -2 -1 0 1 2
f(x) 48 12 0 12 48 x
(-2,48) (2,48)

8. UQTR
Automne 2010
La fonction quadratique
Afin de s’assurer que le modèle mathématique qui correspond à cette
table des valeurs est une fonction quadratique, il suffit de vérifier que les
accroissements des accroissements de la variable dépendante sont
constants pour des accroissements constants de la variable indépendante.
Dans l’exemple ci-dessous, pour des accroissements de +1 de la variable
indépendante «x», les accroissements des accroissements de la variable
dépendante sont constants (+24).
+1 +1 +1 +1
x -2 -1 0 1 2
f(x) 48 12 0 12 48
-36 -12 +12 +36
+24 +24 +24

9. UQTR
Automne 2010
La fonction quadratique
Il existe une autre forme de la règle de la fonction quadratique de la
forme f(x) = a(bx)². Il suffit d’appliquer la loi des exposants pour en
arriver à une équation équivalente de la forme f(x) = ax².
f(x) = 5(3x)²
f(x) = 5(3²)(x²)
f(x) = 5(9)(x²)
f(x) = 45x²

10. UQTR
Automne 2010
La fonction quadratique
Le rôle des paramètres de la fonction quadratique
• Lorsque a < 0, la parabole est ouverte vers le bas.
• Lorsque a > 0, la parabole est ouverte vers le haut.
a<0 a>0
y
y
x
x

11. UQTR
Automne 2010
La fonction quadratique
Le rôle des paramètres de la fonction quadratique
• Lorsque |a| > 1, la parabole est moins ouverte que
lorsque a = 1.
f g h y
Si a < 0, les
paraboles auront la
même ouverture,
mais elles seront
x orientées vers le
f(x) = x² bas.
g(x) = 2x²
h(x) = 4x²

12. UQTR
Automne 2010
La fonction quadratique
Le rôle des paramètres de la fonction quadratique
• Lorsque |a| < 1, la parabole est plus ouverte que
lorsque a = 1.
g f y
h
Si a < 0, les
paraboles auront
la même
ouverture, mais
f(x) = x² x
elles seront
g(x) = 0,5x² orientées vers le
h(x) = 0,25x² bas.

13. UQTR
Automne 2010
La fonction quadratique
Comment trouver la règle d’une fonction quadratique?
Il est possible de déterminer la règle d’une fonction quadratique de
la forme f(x) = ax² à partir de sa table de valeurs. Voici les étapes :
1) Substituer les coordonnées d’un point de la table de valeurs à x et
à f(x) dans la règle f(x) = ax².
2) Résoudre l’équation obtenue à l’étape 1 afin de déterminer la
valeur de a.
3) Écrire la règle sous la forme f(x) = ax² avec la valeur de a
déterminée à l’étape 2.

14. UQTR
Automne 2010
La fonction quadratique
Comment trouver la règle d’une fonction quadratique?
x -2 -1 0 1 2 * Il est possible de
faire les mêmes étapes
f(x) 48 12 0 12 48
à partir d’un
f(x) = ax²
graphique
étape 1: 48 = a(-2)² dont on connaît un
étape 2: 48 = 4a point autre que le
a = 12 sommet.*
étape 3: f(x) = 12x²
Exercices

15. UQTR
Automne 2010
Exercices
#1 Voici la règle d’une fonction quadratique : f(x) = 4(2x)².
Complète la table de valeurs suivante.
x -2 -1 0 1 2
f(x)

16. UQTR
Automne 2010
Exercices
#2 Écris les règles des fonctions quadratiques suivantes sous la forme
f(x) = ax².
a) f(x) = 4(5x)²
b) f(x) = -6(2x)²
c) f(x) = 0,5(-4x)²

17. UQTR
Automne 2010
Exercices
#3 Détermine la règle des fonctions quadratiques suivantes.
a) x 0 1 2 3 4
f(x) 0 4 16 36 64
b) x -2 -1 0 1 2
f(x) -10 -2,5 0 -2,5 -10

18. UQTR
Automne 2010
Exercices
#4 Voici une table de valeurs dans laquelle sont indiqués deux couples
d’une fonction.
x -5 2 6 10
f(x) 0 6 54
Reproduis et complète la table de valeurs en
considérant que f est une fonction:
a) affine (une droite de la forme f(x) = ax+b);
b) quadratique de la forme f(x) = ax².

19. UQTR
Automne 2010
Corrigé des exercices
#1 Voici la règle d’une fonction quadratique : f(x) = 4(2x)².
Complète la table de valeurs suivante.
x -2 -1 0 1 2
f(x) 64 16 0 16 64

20. UQTR
Automne 2010
Corrigé des exercices
#2 Écris les règles des fonctions quadratiques suivantes sous la forme
f(x) = ax².
a) f(x) = 4(5x)² f(x) =100x²
b) f(x) = -6(2x)² f(x) = -24x²
c) f(x) = 0,5(-4x)² f(x) = 8x²

21. UQTR
Automne 2010
Corrigé des exercices
#3 Détermine la règle des fonctions quadratiques suivantes.
a) x 0 1 2 3 4
f(x) = 4x²
f(x) 0 4 16 36 64
b) x -2 -1 0 1 2
f(x) = -2,5x²
f(x) -10 -2,5 0 -2,5 -10

22. UQTR
Automne 2010
Corrigé des exercices
#4 Voici une table de valeurs dans laquelle sont indiqués deux couples
d’une fonction.
a) Il faut trouver la règle de la fonction affine de la
forme f(x) = ax + b. Ensuite, on peut déterminer
les valeurs manquantes algébriquement.
La règle de la fonction affine est f(x) = 12x – 18.
x -5 1,5 2 6 10
f(x) -78 0 6 54 102

23. UQTR
Automne 2010
Corrigé des exercices
#4 Voici une table de valeurs dans laquelle sont indiqués deux couples
d’une fonction.
b) Il faut trouver la règle de la fonction quadratique
de forme f(x) = ax². Ensuite, on peut déterminer
les valeurs manquantes algébriquement.
La règle de la fonction quadratique est f(x) = 1,5x².
x -5 0 2 6 10
f(x) -37,5 0 6 54 150

24. UQTR
Automne 2010
Références
• Bernier, J-F., Boucher, C., Jacques, M., Marotte, L. &
Rodrigue, V. (2010). Intersection, 2ème cycle du
secondaire, 2ème année, manuel de l’élève B. Technico-
sciences. Montréal: Chenelière Éducation inc.
• Desraps, R., Bernier, J-F., Boucher, C., Jacques, M.,
Marotte, L. & Rodrigue, V. (2010). Intersection, 2ème cycle
du secondaire, 2ème année, guide d’accompagnement
pédagogique. Technico-sciences. Montréal: Chenelière
Éducation inc.