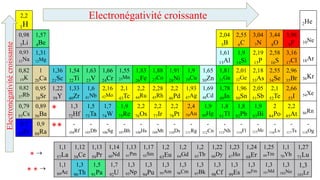
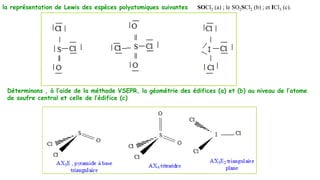
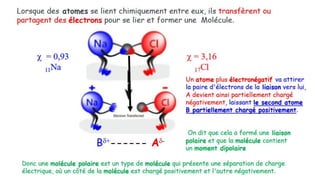
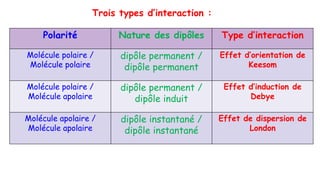
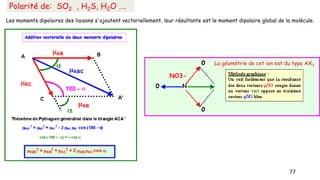
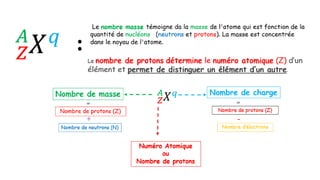
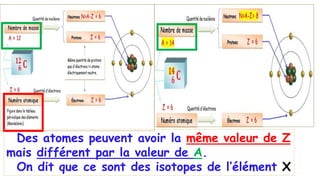
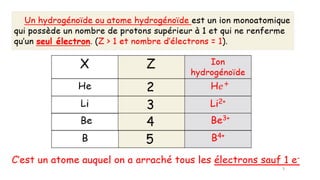
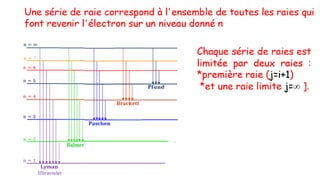
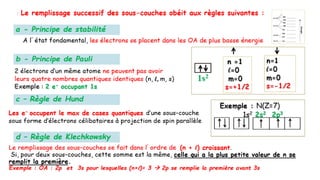
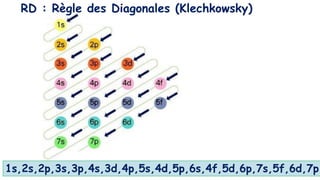
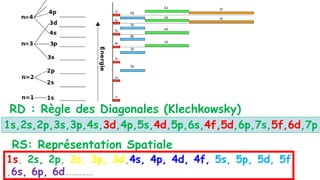
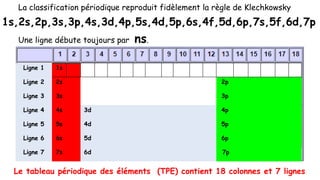
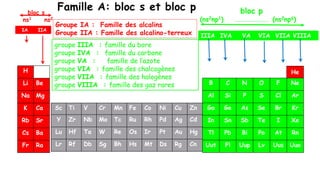
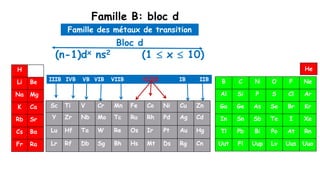
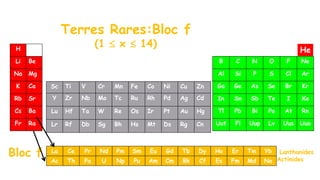
Le document traite de l'atomistique et de la liaison chimique, détaillant les calculs des niveaux d'énergie de l'atome d'hydrogène et des transitions électroniques. Il aborde également la structure électronique, la configuration des atomes selon la règle de Klechkowski, ainsi que les différences entre les propriétés paramagnétiques et diamagnétiques des éléments. Des exemples sont fournis pour illustrer comment les éléments chimiques sont classés dans le tableau périodique selon leur structure et leurs caractéristiques électroniques.

1. Structure de la matière
Professeur Asmaa HAKAM
a.hakam@um5r.ac.ma
AT MISTIQUE
AT MISTIQUE
Module : Atomistique / Liaison Chimique
Résumé d’Atomistique
et Liaison Chimique

4. Des atomes peuvent avoir la même valeur de Z
mais différent par la valeur de A.
On dit que ce sont des isotopes de l’élément X

10. 1.Calculer les valeurs des différents niveaux d'énergie de l'atome d'hydrogène. Les schématiser
2.Quelle est la longueur d'onde du photon provoquant la transition d'un électron du niveau
fondamental au niveau n=3.
1)
2)
𝜟𝑬 = 𝒉𝝂 =
𝒉𝒄
𝝀
(𝐸𝑛=
𝑍2
𝑛2
𝐸1𝐻)

11. 1) Calculer en A° la longueur d’onde de la raie correspondante à la transition entre les niveaux n2=3 et n1=2
dans le cas de l’atome d’hydrogène. (1 point)
2) A quelle série appartient cette raie ? (1 point)
3) Donner la raie limite de cette série. (1 point)
4) Calculer en A° la longueur d’onde de la raie correspondante à la même transition dans le cas de l’ion
hydrogènoïde du béryllium (Be). (1 point)
Ritz :
1
𝜆𝑗→𝑖
= 𝑍2𝑅𝐻
1
𝑛𝑖
2 −
1
𝑛𝑗
2

12. J
E
eV
E
E
E
E
19
19
1
2
10
12
,
261
10
6
,
1
2
,
163
2
,
163
)
6
,
217
(
4
,
54

















L’énergie que doit absorber
un ion Be3+ pour que l’électron
passe du niveau fondamental
au premier niveau excité est
donnée par la relation:
ΔE = E2 – E1.
E
hc


 
0
1 2 76,1A
  

13. C’est-à-dire déterminer pour chaque électron les
valeurs de ses quatre nombres quantiques: (n ,l , m , s )
Configuration électronique des éléments
Etablir la configuration électronique d’un élément ,
consiste à décrire le cortège électronique de celui-ci:
C’est-à-dire attribuer à chaque électron de l’atome une place:
(couche/ sous-couche/ case quantique/ spin)
Structure électroniques
La combinaison ,de ces quatre nombres ,
est unique pour un électron donné.

17. RD : Règle des Diagonales (Klechkowsky)
1s,2s,2p,3s,3p,4s,3d,4p,5s,4d,5p,6s,4f,5d,6p,7s,5f,6d,7p

18. RD : Règle des Diagonales (Klechkowsky)
1s,2s,2p,3s,3p,4s,3d,4p,5s,4d,5p,6s,4f,5d,6p,7s,5f,6d,7p
RS: Représentation Spatiale
1s, 2s, 2p, 3s, 3p, 3d,4s, 4p, 4d, 4f, 5s, 5p, 5d, 5f
,6s, 6p, 6d…………

19. La classification périodique reproduit fidèlement la règle de Klechkowsky
Une ligne débute toujours par ns.
1s,2s,2p,3s,3p,4s,3d,4p,5s,4d,5p,6s,4f,5d,6p,7s,5f,6d,7p
Ligne 1 1s
Ligne 2 2s 2p
Ligne 3 3s 3p
Ligne 4 4s 3d 4p
Ligne 5 5s 4d 5p
Ligne 6 6s 5d 6p
Ligne 7 7s 6d 7p
Le tableau périodique des éléments (TPE) contient 18 colonnes et 7 lignes

20. Ligne 1
n=1
Ligne 2
n=2
Ligne 3
n=3
Ligne 4
n=4
Ligne 5
n=5
Le tableau périodique des éléments (TPE) contient 18 colonnes et 7 lignes
Ici je n’ai représenté que les 5 premières périodes

23. bloc p
(ns2np1) .…………….…… (ns2np6)
IIIA IVA VA VIA VIIA VIIIA
groupe IIIA : famille du bore
groupe IVA : famille du carbone
groupe VA : famille de l’azote
groupe VIA : famille des chalcogènes
groupe VIIA : famille des halogènes
groupe VIIIA : famille des gaz rares
IA IIA
bloc s
ns1 ns2
Groupe IA : Famille des alcalins
Groupe IIA : Famille des alcalino-terreux
H
Li Be
Na Mg
K Ca
Rb Sr
Cs Ba
Fr Ra
B C N O F Ne
Al Si P S Cl Ar
Ga Ge As Se Br Kr
In Sn Sb Te I Xe
Tl Pb Bi Po At Rn
Uut Fl Uup Lv Uus Uuo
He
Sc Ti V Cr Mn Fe Co Ni Cu Zn
Y Zr Nb Mo Tc Ru Rh Pd Ag Cd
Lu Hf Ta W Re Os Ir Pt Au Hg
Lr Rf Db Sg Bh Hs Mt Ds Rg Cn
Famille A: bloc s et bloc p

24. Bloc d
(n-1)dx ns2 (1  x  10)
IIIB IVB VB VIB VIIB VIIIB IB IIB
Famille des métaux de transition
Famille B: bloc d
Sc Ti V Cr Mn Fe Co Ni Cu Zn
Y Zr Nb Mo Tc Ru Rh Pd Ag Cd
Lu Hf Ta W Re Os Ir Pt Au Hg
Lr Rf Db Sg Bh Hs Mt Ds Rg Cn
H
Li Be
Na Mg
K Ca
Rb Sr
Cs Ba
Fr Ra
B C N O F Ne
Al Si P S Cl Ar
Ga Ge As Se Br Kr
In Sn Sb Te I Xe
Tl Pb Bi Po At Rn
Uut Fl Uup Lv Uus Uuo
He

25. Bloc f
Terres Rares:Bloc f
(1  x  14)
H
Li Be
Na Mg
K Ca
Rb Sr
Cs Ba
Fr Ra
Sc Ti V Cr Mn Fe Co Ni Cu Zn
Y Zr Nb Mo Tc Ru Rh Pd Ag Cd
Lu Hf Ta W Re Os Ir Pt Au Hg
Lr Rf Db Sg Bh Hs Mt Ds Rg Cn
B C N O F Ne
Al Si P S Cl Ar
Ga Ge As Se Br Kr
In Sn Sb Te I Xe
Tl Pb Bi Po At Rn
Uut Fl Uup Lv Uus Uuo
He
La Ce Pr Nd Pm Sm Eu Gd Tb Dy
Ac Th Pa U Np Pu Am Cm Bk Cf
Ho Er Tm Yb
Es Fm Md No
Lanthanides
Actinides

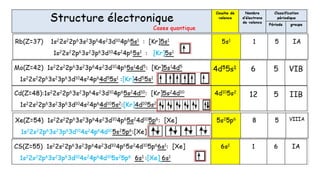
26. Rb(Z=37) 1s22s22p63s23p64s23d104p65s1 : [Kr]5s1
1s22s22p63s23p63d104s24p65s1 : [Kr]5s1
5s1 1 5 IA
Structure électronique
Cases quantique
Couche de
valence
Nombre
d’électrons
de valence
Classification
périodique
Période groupe
Cd(Z=48):1s22s22p63s23p64s23d104p65s24d10: [Kr]5s24d10
1s22s22p63s23p63d104s24p64d105s2:[Kr]4d105s2
4d105s2
12 5 IIB
Xe(Z=54) 1s22s22p63s23p64s23d104p65s24d105p6: [Xe]
1s22s22p63s23p63d104s24p64d105s25p6:[Xe]
5s25p6 8 5 VIIIA
CS(Z=55) 1s22s22p63s23p64s23d104p65s24d105p66s1: [Xe]
1s22s22p63s23p63d104s24p64d105s25p6 6s1 :[Xe] 6s1
6s1 1 6 IA

27. La règle de Klechkowsky ne permet pas d’obtenir toujours la bonne configuration électronique réelle des
atomes. A partir de n = 3 de nombreuses exceptions à cette règle apparaissent.
Nous ne chercherons pas à justifier toutes ces exceptions mais on peut expliquer certaines d’entre elles en
admettant qu’une sous-couche totalement remplie ou à demi remplie apporte une stabilité supplémentaire.
Ainsi la configuration (d5 s1 ) est plus stable que la configuration (d4 s2 ) : ( Cr et Mo)
De même la configuration (d10 s1) est plus stable que la configuration (d9 s2) :(Cu,Ag etAu)
(n-1)d5ns1
(n-1)d10ns1

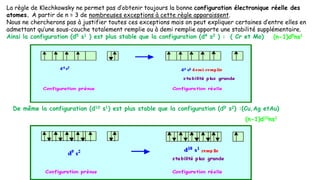
28. Cr(Z=24) : 1s22s22p63s23p64s13d5 :[Ar]4s13d5
1s22s22p63s23p63d54s1: [Ar]3d54s1
3d54s1 6 4 VIB
Structure électronique
Cases quantique
Couche
de
valence
Nombre
d’électrons
de valence
Classification
périodique
Période groupe
Mo(Z=42) : 1s22s22p63s23p64s23d104p65s14d5: [Kr]5s14d5
1s22s22p63s23p63d104s24p64d55s1 :[Kr]4d55s1
4d55s1
6 5 VIB
Cu(Z=29) : 1s22s22p63s23p64s13d10 : [Ar]4s13d10
1s22f.s22p63s23p63d104s1 : [Ar]3d104s1
3d104s1 11 4 IB
Ag(Z=47) : 1s22s22p63s23p64s23d104p65s14d10 :[Kr] 5s14d10
1s22s22p63s23p63d104s24p64d105s1: [Kr] 4d105s1
4d105s1 11 5 IB
Au(Z=79): 1s22s22p63s23p64s23d104p65s24d105p66s14f145d10
[Xe] 6s1 4f14 5d10
[Xe] 4f14 5d10 6s1
5d106s1 11 6 IB
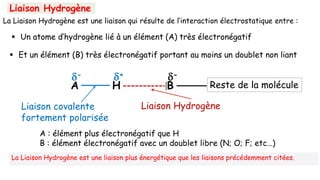
Les éléments qui font exception à la règle de Klechköwsky :

33. H
Sc Zn Br
Rb Mo Ag Cd I Xe
Placer ces mêmes éléments chimiques dans le tableau périodique ci-dessous
n=1
n=2
n=3
n=4
n=5
n=6
n=7
30Zn , 54Xe , 35Br, 21Sc , 48Cd , 37Rb ,47Ag, 42Mo, 53I ,27Co
27Co

34. Elément Couche de valence Case quantique Paramagnétique Diamagnétique
F 2s22p5 OUI -
Cr 3d54s1 OUI -
Fe 3d64s2 OUI -
Cu 3d104s1 OUI -
Zn 3d104s2 NON Diamagnétique
Ga 4s24p1 OUI -
Mo 4d55s1 OUI -
I 5s25p5 OUI -
La présence d’électrons célibataires dans un atome, molécule ou un cristal
confère à ce système des propriétés paramagnétiques.
En l’absence d’électrons célibataires la matière est dite diamagnétique

35. Rayon atomique
𝒓𝐜𝐨𝐯(𝑨) =
𝒅𝑨−𝑨
𝟐
𝒅𝑨−𝑨

36. Dans un même groupe , quand Z augmente, du haut vers le bas, le nombre de
couches augmente et par conséquent le rayon augmente.
Z(X1)  Z(X2)  r(X1)  r(X2)
Des éléments qui ont la même structure électronique, on dit qu’ils sont
isoélectroniques: lorsque Z augmente, le rayon diminue.
L’augmentation de Z entraîne l’augmentation de la charge au niveau du noyau
et par conséquent une contraction.
Z(X)  Z(Y)  r(X)  r(Y)
Dans une même période, quand Z augmente, de gauche vers la droite, le
nombre de couches est constant, mais Z (ou Z*) augmente donc Fa augmente
et par conséquent le rayon diminue.
Z(X1)  Z(X3)  r(X1)  r(X3)

37. Ca; Cr ; Fe ; Cu ;Zn et Br appartiennent tous à la même période n=4
r(Br)  r(Zn)  r(Cu)  r(Fe)  r(Cr)  r(Ca)
r
𝒓𝒏 =
𝒏∗𝟐
𝒁∗
𝒓𝟏𝑯
Si Z* augmente, FA augmente et le rayon diminue
r

38. IA VIIIA
n=1 IIA IIIA IVA VA VIA VIIA
n=2 F
n=3 IIIB IVB VB VIB VIIB VIIIB IB IIB
n=4
n=5 I
n=6
n=7
L’électronégativité 𝛘 caractérise la tendance qu’a un atome à attirer les
électrons à lui: capacité d’un atome à attirer des électrons d’atomes voisins.

39. On attribue l’effet d’écran au type d’électron considéré suivant la règle.
Ces règles empiriques sont applicables pour les premières périodes mais
deviennent très aléatoires lorsque n  4.
n* : nombre quantique apparent
L’énergie d’un électron situé sur un niveau n est donnée par la relation :
Type d’électron Même groupe Groupes (n-1) Groupes ˂ (n-1)
1s 0,30 - -
(ns),(np) 0,35 0,85 1
(nd),(nf) 0,35 1 1
𝐸𝑛 =
𝑍
∗2
𝑛∗2
𝐸1𝐻
n 1 2 3 4 5 6
n* 1 2 3 3,7 4 4,2
𝒁𝒊
∗
= 𝒁 − 𝝈𝒋→𝒊

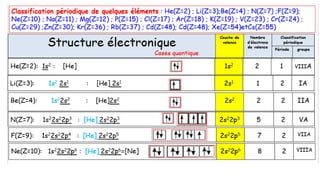
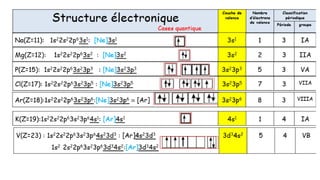
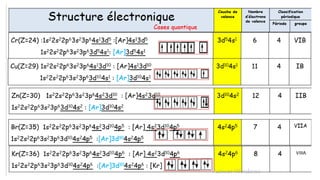
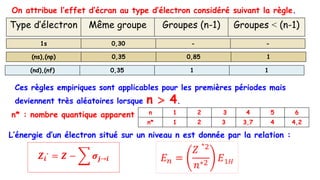
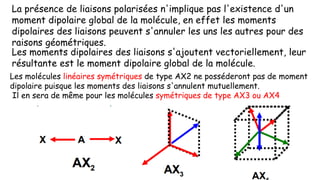
40. Potassium K(Z=19) : 1s22s22p63s23p64s1
Électron de cœur : 1s22s22p63s23p6
Électron de valence : 4s1
Groupes de Slater : (1s2) (2s22p6) (3s23p6) (4s1)
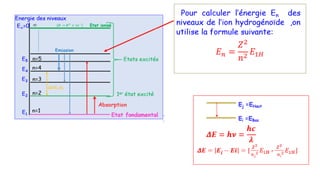
𝑬𝒏 =
𝒁
∗𝟐
𝒏∗𝟐
𝑬𝟏𝑯
𝒁𝒊
∗
= 𝒁 − 𝝈𝒋→𝒊
Des électrons d’un même groupe « ressentent » la même charge effective.
Ils ont donc une même énergie et sont à la même distance du noyau.
[1s] [2s ,2p] [3s ,3p] [4s,4p]
Z=19 2e- 8e- 8e- 1e-

41.  Calcul des charges nucléaires effectives Z*
1s(K), Z*
2s2p(K), Z*
3s3p(K) et Z*
4s4p(K)
)
𝑍1𝑠
∗
(𝐊) = 𝑍(K) − (1𝜎1𝑠→1𝑠
= 19 – (1x 0,30) = 18,7
𝑍2𝑠2𝑝
∗
(𝐊) = 𝑍(K) − (7𝜎2𝑠2𝑝→2𝑠2𝑝 + 2𝜎1𝑠→2𝑠2𝑝
= 19 – ((7x 0,35) + (2x0,85))= 14,85
𝑍3𝑠3𝑝
∗
(𝐊) = 𝑍(K) − (7𝜎3𝑠3𝑝→3𝑠3𝑝 + 8𝜎2𝑠2𝑝→3𝑠3𝑝 + 2𝜎1𝑠→3𝑠3𝑝
= 19 – ((7x 0,35) + (8x0,85)+(2x1))= 7,75
𝑍4𝑠4𝑝
∗
(𝐊) = 𝑍(K) − (8𝜎3𝑠3𝑝→4𝑠4𝑝 + 8𝜎2𝑠2𝑝→4𝑠4𝑝 + 2𝜎1𝑠→4𝑠4𝑝
= 19 – ((8x 0,85) + (8x1)+(2x1))= 2,2

42.  Calcul des énergies E1s(K), E2s2p(K), E3s3p(K) et E4s4p(K)
𝐸1𝑠 𝐾 =
𝑍1𝑠
∗2
𝑛∗2 𝐸1H =
(18,7)2
12 −13,6 =-4755,784 eV
𝐸2𝑠2𝑝 𝐾 =
𝑍2𝑠2𝑝
∗2
𝑛∗2 𝐸1H =
(14,85)2
22 −13,6 =-749,776 eV
𝐸3𝑠3𝑝 𝐾 =
𝑍3𝑠3𝑝
∗2
𝑛∗2 𝐸1H =
(7,75)2
32 −13,6 =-90,76 eV
𝐸4𝑠4𝑝 𝐾 =
𝑍4𝑠4𝑝
∗2
𝑛∗2 𝐸1H =
(2,2)2
3,72 −13,6 =-4,808 eV

43.  Calcul de l’énergie totale du potassium K:
K(Z=19): 1s22s22p63s23p6 4s1
L’énergie totale d’un atome =
Somme des énergies de chaque électron
E(K)=2E1s(K)+8E2s2p(K)+8E3s3p(K)+1E4s4p(K)
E(K)=2(-4755,78)+8(-749,77)+8(-90,76)+1(-4,808)
E(K)=-16240,608 eV

44. Ordre de départ des électrons en cas d’ionisation
 Pour les éléments du bloc s , les électrons s partent en premier.
Exemple : Mg(Z=12 ; 12 e-)
Mg+(Z=12 ; 11e- )
Mg2+(Z=12 ; 10e- )
1s2 2s2 2p6 3s2
1s2 2s2 2p6 3s1
1s2 2s2 2p6
 Pour les éléments du bloc p, les électrons p partent en premier.
Exemple : P (Z=15 ; 15 e-)
P+ (Z=15 ; 14 e-)
P2+ (Z=15 ; 13 e-)
1s2 2s2 2p6 3s2 3p3
1s2 2s2 2p6 3s2 3p2
1s2 2s2 2p6 3s2 3p1

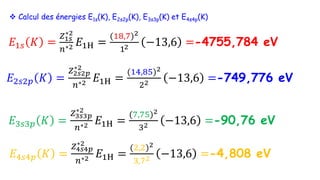
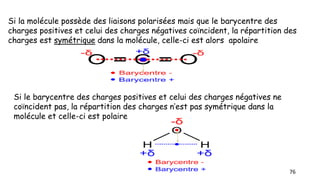
45. Fe(Z=26 ; 26 e-)1s2 2s2 2p6 3s2 3p6 3d6 4s2
En cas d’ionisation ce sont les e- (4s) qui partent avant les e- (3d)
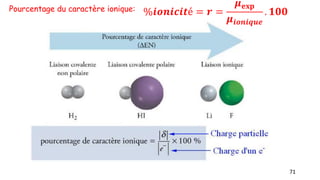
En cas d’ionisation des éléments du bloc d , ils perdront d’abord deux
électrons s avant de perdre ,éventuellement , un ou plusieurs de leurs
électrons d.
Fe+ (Z=26 ; 25 e-)
Fe2+ (Z=26 ; 24 e-)
Fe3+ (Z=26 ; 23 e-)
1s2 2s2 2p6 3s2 3p6 3d6 4s1
1s2 2s2 2p6 3s2 3p6 3d6
1s2 2s2 2p6 3s2 3p6 3d5
Zn(Z=30) 1s22s22p63s23p64s23d10 : [Ar] 4s23d10 :(RD)
1s22s22p63s23p63d104s2 : [Ar] 3d104s2 :(DS)
Formation de l’ion Zn2+
:1s22s22p63s23p63d10 : [Ar] 3d10

46. Le molybdène (Mo) appartient à la famille du chrome Cr (Z=24) et à la 5ème période.
1. Donner sa structure électronique selon la règle de Klechkowsky et selon la disposition
spatiale ainsi que son numéro atomique.
2. Le molybdène appartient-il aux métaux de transition ? Justifier votre réponse.
3. Quels sont les propriétés magnétiques du molybdène quand il est isolé ?
2) Mo présente les orbitales s et d comme orbitales de valence, ils appartiennent donc au bloc d :
Mo est un métal de transition
3) Mo est paramagnétique car il présente des électrons célibataires
1) Cr(Z=24) :1s22s22p63s23p64s13d5 :[Ar]4s13d5
Mo appartient donc à la période n=5 et à la famille VIB (ns1(n-1)d5), sa configuration
électronique de valence sera alors 5s14d5
1s22s22p63s23p63d104s24p64d55s1
Mo : 1s22s22p63s23p64s23d104p65s14d5

47. Déterminer la configuration électronique et donner le numéro atomique de l’élément situé dans la même
période que le fer, Fe(Z=26), et appartenant à la même famille que le carbone, C(Z=6). Est-ce que cet
élément fait partie des métaux de transition ? Pourquoi ?
 La configuration électronique du C (Z=6) est : 1s2 2s22p2
C appartient au groupe IVA
 La configuration électronique du Fe (Z=26) est:
RD :1s22s22p63s23p64s23d6
RS :1s22s22p63s23p63d64s2
Il faut déterminer la configuration électronique du Fe et du C pour connaitre la période
et le groupe de X ( l’élément recherché)
même période
même famille
X

48.  La configuration électronique du C (Z=6) est : 1s2 2s22p2
C appartient au groupe IVA
 La configuration électronique du Fe (Z=26) est:
RD :1s22s22p63s23p64s23d6
RS :1s22s22p63s23p63d64s2
Sa couche de valence : 3d64s2 donc Fe appartient à la période n=4
L’élément recherché appartenant au groupe IVA et de
période n=4 est X(Z=32):1s22s22p63s23p64s23d104p2
Déterminer la configuration électronique et donner le numéro atomique de l’élément situé dans la même
période que le fer, Fe(Z=26), et appartenant à la même famille que le carbone, C(Z=6). Est-ce que cet
élément fait partie des métaux de transition ? Pourquoi ?
L’élément X, à chercher ,appartient donc à la période n=4 et à la famille IVA (ns2np2), sa
configuration électronique de valence sera alors 4s24p2 .
X ne fait pas partie des métaux de transition car l’orbitale d est totalement remplie et
l’orbitale p commence à se remplir ( OA p contient 2 électrons)

49. La colonne de l’azote, N(Z=7), comporte dans l’ordre les éléments suivants : N, P, As, Sb, Bi.
a. Donner la structure électronique de l’azote à l’état fondamental.
b. Donner la structure électronique à l’état fondamental et le numéro atomique de Sb.
c. Les éléments de la famille d’azote perdent-ils ou gagnent-ils les électrons pour acquérir la structure
la plus stable.
a) N(Z=7): 1s22s22p3 N appartient à la période n=2
b) P(Z=15): 1s22s22p63s23p3 P appartient à la période n=3
As appartient à la période n=4
Sb appartient à la période n=5
État fondamental Sb : 1s22s22p63s23p64s23d104p65s24d105p3
Sb(Z) =51
c) Les éléments de la famille d’azote gagnent des électrons pour
acquérir la structure la plus stable du gaz rare de la même période

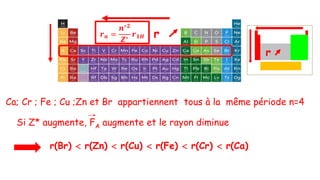
50. Calcul de la charge nucléaire effective Z* perçue par chaque électron de
l’atome de chlore Cl (Z=17, 17 électrons)
Cl
[1s2] [ 3s2 ; 3p5]
+17
Cl (Z=17, 17électrons) : 1s22s22p63s 23p5 configuration électronique à l’état fondamental
Électron de cœur : 1s22s22p6
Électron de valence :3s23p5
Groupes de Slater : (1s2) (2s22p6) (3s23p5)
[2s2 ; 2p6 ]
𝒁𝒊
∗
= 𝒁 − 𝝈𝒋→𝒊

51. Calcul des charges nucléaires effectives Z*
1s(Cl), Z*
2s2p(Cl) et Z*
3s3p(Cl)
  7
,
16
30
,
0
17
1
1
)
(
1 






s
s
Z
Cl
s
Z 
85
,
12
15
,
4
17
)]
85
,
0
(
2
)
35
,
0
(
7
[
17
2
2
1
2
2
2
2
2
7
)
(
2
2 

















p
s
s
p
s
p
s
Z
Cl
p
s
Z 

1
,
6
9
,
10
17
)
(
3
3
)]
1
(
2
)
85
,
0
(
8
)
35
.
0
(
6
[
17
)
(
3
3
3
3
1
2
3
3
2
2
8
3
3
3
3
6
)
(
3
3























Cl
p
s
Z
Cl
p
s
Z
p
s
s
p
s
p
s
p
s
p
s
Z
Cl
p
s
Z 


𝒁𝒊
∗
= 𝒁 − 𝝈𝒋→𝒊

52.  Calcul des énergies E1s(Na), E2s2p(Na) et E3s3p(Na)
eV
H
E
n
p
s
Z
Cl
p
s
E 4165
,
561
)
6
,
13
(
2
)
2
(
2
)
85
,
12
(
1
)
2
2
*
2
2
(
)
(
2
2 





eV
H
E
n
p
s
Z
Cl
p
s
E 228
,
56
)
6
,
13
(
2
)
3
(
2
)
1
,
6
(
1
)
2
2
*
3
3
(
)
(
3
3 





eV
H
E
n
s
Z
Cl
s
E 904
,
3792
)
6
,
13
(
2
)
1
(
2
)
7
,
16
(
1
)
2
2
*
1
(
)
(
1 





𝑬𝒏 =
𝒁
∗𝟐
𝒏∗𝟐
𝑬𝟏𝑯

53.  Calcul de l’énergie totale du sodium Cl:
1 2 2 3 3
( ) 2 ( ) 8 ( ) 7 ( )
2( 3792,904) 8( 561,4165) 7( 56,228)
7585,808 4491,332 393,596
12470,736
s s p s p
E Cl E Cl E Cl E Cl
eV
  
     
   
 
Cl (Z=17): 1s22s22p63s2
L’énergie totale d’un atome = Somme des énergies de chaque électron
E(Cl)
E(Cl)
3p5

54. calculons l’ énergies de première ionisation du Chlore Cl (Z=17)
EI1 correspond à la réaction : Cl  Cl+ + 1e- : énergie de 1ère ionisation de Cl
EI1 = E(Cl+) - E(Cl)
Structure de
Cl : (1s2
) (2s2
2p6
) (3s2
3p5
)
Cl+
: (1s2
) (2s2
2p6
) (3s2
3p4
).
E(Cl) = 2E1s(Cl) + 8E2s2p(Cl) +7E3s3p(Cl)
E(Cl+
) = 2E1s(Cl+
) + 8E2s2p(Cl+
) + 6E3s3p(Cl+
)
Avec E1s(Cl) = E1s(Cl+
) et E2s2p(Cl) = E2s2p(Cl+
)

55. EI1 = E(Cl+) - E(Cl)
EI1 = [2E1s(Cl+) + 8E2s2p(Cl+) + 6E3s3p(Cl+)] - [2E1s(Cl) + 8E2s2p(Cl) + 7E3s3p(Cl+)]
Calculons
 
3 3 3 3 3 3 2 2 3 3 1 3 3
( ) 5 8 2
17 5(0,35) 8 . 0,85 +2(1)
6,45
s p s p s p s p s p s s p
Z Cl Z   

  
 
    
 
  

*2 2
( ) (6,45)
3 3
( ) ( ) ( 13,6) 62,866
3 3 1
2 2
(3)
Z Cl
s p
E Cl E eV
s p H
n

     

EI1 = 6E3s3p(Cl+
) - 7E3s3p(Cl)
E3s3p(Cl) = - 56,23 eV
EI1(Cl) = 6E3s3p(Cl+
) - 7E3s3p(Cl) = 6 (-62,866) – 7 (-56,23)
= - 377,196 + 393,61 = 16,414 eV

56. Donner la structure électronique à l’ état fondamental et le numéro atomique:
A- du deuxième élément X1 de la première série des métaux de transition .
A quel groupe chimique appartient cet élément?
B- du deuxième élément X2 du groupe VIIA.
A quelle famille appartient cet élément?
C- de l’élément X3 appartenant au groupe IA et à la 4ème période .
A quelle famille appartient cet élément?
D- de l’élément Rb appartenant à la même famille que X3 et qui se situe à la cinquième
période.
1s
2s 2p
3s 3p
4s 3d 4p
5s 4d 5p
6s 4f 5d 6p
7s 5f 6d 7p
première série des métaux de transition
deuxième série des métaux de transition

57. A) Deuxième élément X1 de la première série des métaux de transition :
Première série métaux de transitions couche de valence de type 4s23d
X1 : 1s22s22p63s23p64s23d2 X1(Z=22) Groupe IVB famille des métaux de transition
B) Deuxième élément X2 du groupe VIIA
couche de valence VIIA de type ns2p5 avec n=3
X2 : 1s22s22p63s23p5 X2(Z=17) Groupe VIIA famille des Halogènes
C) Elément X3 appartenant au groupe IA et à la 4ème période n=4 :
couche de valence de type ns1
X3 : 1s22s22p63s23p64s1 X3(Z=19) Groupe IA famille des Alcalins
D) L’élément Rb appartenant à la même famille que X3 et qui se situe à la cinquième période n=5.
couche de valence de type ns1 avec n=5
Rb : 1s22s22p63s23p64s23d10 4p65s1 Rb(Z=37) Groupe IA famille des Alcalins

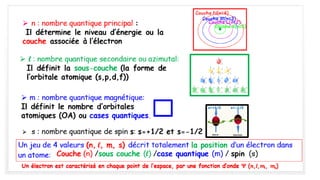
58. Be [1s2] [2s2]
E1 E2 EBe = 2 E1 + 2 E2
Be+ [1s2] [2s1]
E1 E'2 EBe
+ = 2 E1 + E'2
E.I1 = EBe
+ - EBe = E'2 - 2 E2
Be2+ [1s2]
E1 EBe
2+ = 2 E1
E.I2 = EBe
2+ - EBe
+ = -E'2
Be3+ [1s1]
E'1 EBe
3+ = E'1
E.I3 = EBe
3+ - EBe
2+ = E'1 - 2 E1
Be4+ EBe
4+ = 0
E.I4 = EBe
4+ - EBe
3+ = -E'1
Structure électronique Energie de l’élément X Energie d’ionisation

59. Calcul des diverses énergies :
Z*E2 = 4 - 0,35 - (2 * 0,85 ) = 1,95
E2 = -13,6 * 1,952/22 = -12,92 eV
Z*E'2 = 4 - (2 * 0,85 ) = 1,95 + 0,35 = 2,3
E'2 = -13,6 * 2,32/22 = -17,99 eV
Z*E1 = 4 - 0,3 = 3,7
E1 = -13,6 * 3,72/12 = -186,18 eV
Z*E'1 = 4
E'1 = -13,6 * 42/12 = -217,6 eV
Calcul des énergies d'ionisation successives :
E.I1 = EBe
+ - EBe = E'2 - 2 E2 = -17,99 - 2 (12,92 ) = 7,85 eV
E.I2 = EBe
2+ - EBe
+ = -E'2 = 17,99 eV
E.I3 = EBe
3+ - EBe
2+ = E'1 - 2 E1 = -217,6 - 2(-186,18 ) = 154,76 eV
E.I4 = EBe
4+ - EBe
3+ = -E'1 = 217,6 eV

60. Révisions Liaisons Chimiques

62. La molécule est symbolisée par :
 A : atome central
C’est la somme (m + n) qui définit la géométrie de base de la molécule
m + n Géométrie de base
2
3
4
5
6
Linéaire
Triangulaire plane
Tétraédrique
Bipyramide trigonale
Octaédrique
 X : atome lié à A
 m : nombre
d’atomes X liés à A
 E : doublets libres autour de A
 n : nombre de doublets libres
autour de A
AXmEn

66. 2,2
1H 2He
0,98
3Li
1,57
4Be
2,04
5B
2,55
6C
3,04
7N
3,44
8O
3,98
9F 10Ne
0,93
11Na
1,31
12Mg
1,61
13Al
1,9
14Si
2,19
15P
2,58
16S
3,16
17Cl 18Ar
0,82
19K
1
20Ca
1,36
21Sc
1,54
22Ti
1,63
23V
1,66
24Cr
1,55
25Mn
1,83
26Fe
1,88
27Co
1,91
28Ni
1,9
29Cu
1,65
30Zn
1,81
31Ga
2,01
32Ge
2,18
33As
2,55
34Se
2,96
35Br 36Kr
0,82
37Rb
0,95
38Sr
1,22
39Y
1,33
40Zr
1,6
41Nb
2,16
42Mo
2,1
43Tc
2,2
44Ru
2,28
45Rh
2,2
46Pd
1,93
47Ag
1,69
48Cd
1,78
49In
1,96
50Sn
2,05
51Sb
2,1
52Te
2,66
53I 54Xe
0,79
55Cs
0,89
56Ba
* 1,3
72Hf
1,5
73Ta
1,7
74W
1,9
75Re
2,2
76Os
2,2
77Ir
2,2
78Pt
2,4
79Au
1,9
80Hg
1,8
81Tl
1,8
82Pb
1,9
83Bi
2
84Po
2,2
85At 86Rn
0,7
87Fr
0,9
88Ra
** -
104Rf
-
105Db
-
106Sg
-
107Bh
-
108Hs
-
109Mt
-
110Ds
-
111Rg
-
112Cn
-
113Nh
-
114Fl
-
115Mc
-
116Lv
-
117Ts
-
118Og
1,1
57La
1,12
58Ce
1,13
59Pr
1,14
60Nd
1,13
61Pm
1,17
62Sm
1,2
63Eu
1,2
64Gd
1,2
65Tb
1,22
66Dy
1,23
67Ho
1,24
68Er
1,25
69Tm
1,1
70Yb
1,27
71Lu
1,1
89Ac
1,3
90Th
1,5
91Pa
1,7
92U
1,3
93Np
1,3
94Pu
1,3
95Am
1,3
96Cm
1,3
97Bk
1,3
98Cf
1,3
99Es
1,3
100Fm
1,3
101Md
1,3
102No
1,3
103Lr
Electronégativité
croissante
Electronégativité croissante
* 
* * 

68. la représentation de Lewis des espèces polyatomiques suivantes SOCl2 (a) ; le SO2SCl2 (b) ; et ICl3 (c).
Déterminons , à l’aide de la méthode VSEPR, la géométrie des édifices (a) et (b) au niveau de l’atome
de soufre central et celle de l’édifice (c)

70. 70
Différence d'électronégativité détermine la nature de la liaison
covalente entre 2 éléments :
• liaison apolaire lorsque la différence est nulle ;
• liaison polaire quand la différence n'est pas nulle ;
• liaison ionique quand la différence est tellement forte qu'un
des éléments a attiré complètement les électrons : les atomes
sont devenus des ions et portent des charges électriques entières.
Électronégativité 
Capacité d'un atome à attirer le nuage électronique d'une liaison
covalente dans laquelle il est engagé

71. 71
Pourcentage du caractère ionique:

72. Trois types d’interaction :
Polarité Nature des dipôles Type d’interaction
Molécule polaire /
Molécule polaire
dipôle permanent /
dipôle permanent
Effet d’orientation de
Keesom
Molécule polaire /
Molécule apolaire
dipôle permanent /
dipôle induit
Effet d’induction de
Debye
Molécule apolaire /
Molécule apolaire
dipôle instantané /
dipôle instantané
Effet de dispersion de
London

73. Liaison Hydrogène
La Liaison Hydrogène est une liaison qui résulte de l’interaction électrostatique entre :
Reste de la molécule
A
-
H
+ -
B
Liaison covalente
fortement polarisée
Liaison Hydrogène
A : élément plus électronégatif que H
B : élément électronégatif avec un doublet libre (N; O; F; etc…)
 Un atome d’hydrogène lié à un élément (A) très électronégatif
 Et un élément (B) très électronégatif portant au moins un doublet non liant
La Liaison Hydrogène est une liaison plus énergétique que les liaisons précédemment citées.

74. Les facteurs qui contribuent à déterminer la Polarité des molécules sont les
formes géométriques des molécules et le type de liaison entre leurs atomes.
Les dipôles sont donc un ensemble de charges séparées dans un atome ou
une molécule. Ils sont causés par une distribution inégale des électrons.
Le moment dipolaire d’une molécule est la somme vectorielle des moments
dipolaires permanents des liaisons composant cette molécule
Une molécule est dite polaire quand elle possède un moment
dipolaire permanent , sinon elle est appelée apolaire.
Connaissant sa géométrie par la méthode VSEPR, on peut
rapidement estimer la présence d’un moment dipolaire
permanent

75. 75
La présence de liaisons polarisées n'implique pas l'existence d'un
moment dipolaire global de la molécule, en effet les moments
dipolaires des liaisons peuvent s'annuler les uns les autres pour des
raisons géométriques.
Les moments dipolaires des liaisons s'ajoutent vectoriellement, leur
résultante est le moment dipolaire global de la molécule.
Les molécules linéaires symétriques de type AX2 ne posséderont pas de moment
dipolaire puisque les moments des liaisons s'annulent mutuellement.
Il en sera de même pour les molécules symétriques de type AX3 ou AX4

76. 76
Si le barycentre des charges positives et celui des charges négatives ne
coïncident pas, la répartition des charges n’est pas symétrique dans la
molécule et celle-ci est polaire
Si la molécule possède des liaisons polarisées mais que le barycentre des
charges positives et celui des charges négatives coïncident, la répartition des
charges est symétrique dans la molécule, celle-ci est alors apolaire

77. 77
Polarité de: SO2 , H2S, H2O ….
La géométrie de cet ion est du type AX3
NO3-
Les moments dipolaires des liaisons s'ajoutent vectoriellement, leur résultante est le moment dipolaire global de la molécule.

78. Couple / Polarité Nature des
dipôles
Types d’interactions de Van
der Waals
(CO2, SO3)
Molécule apolaire / Molécule apolaire
Dipôle instantané /
Dipôle instantané
Effet de dispersion de London
(CH4, H2S)
Molécule apolaire / Molécule polaire
Dipôle induit /
Dipôle permanent
Effet d’induction de Debye
(SO2, ICl)
Molécule polaire / Molécule polaire
Dipôle permanent /
Dipôle permanent
Effet d’orientation de Keesom
(H2O, CH3OH)
Molécule polaire / Molécule polaire
Dipôle permanent /
Dipôle permanent
Effet d’orientation de Keesom
+ Liaison Hydrogène
Les différents types d’interactions qui s’exercent entre les molécules des couples :
(CO2, SO3); (CH4, H2S); (SO2, ICl) et (H2O, CH3OH) sont :

79. 79
Les forces intramoléculaires attirent les atomes dans une molécule et sont
responsables de la stabilité des molécules (Fintermoléculaire < Fintramoléculaire).
Les forces intermoléculaires sont responsables des propriétés de la matière
dans sa masse: points de fusion, d'ébullition.
Pour passer de l’état liquide à l’état gazeux, il faut casser les interactions
intermoléculaires. Plus ces interactions sont fortes et nombreuses, plus la
température d’ébullition est élevée.
Solubilisation et miscibilité: Plus les molécules d’un soluté peuvent donner des
interactions avec celles d’un solvant et plus grande sera la solubilité dans ce
solvant
il en est de même pour la miscibilité entre deux liquides.