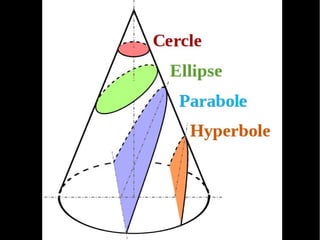
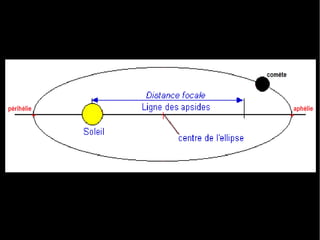
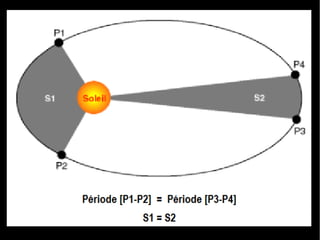
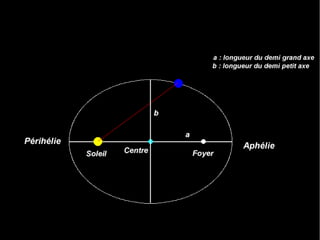
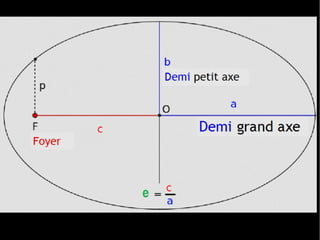
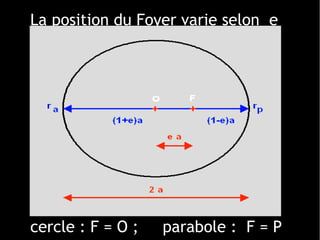
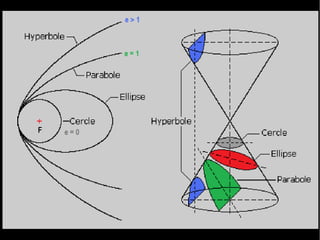
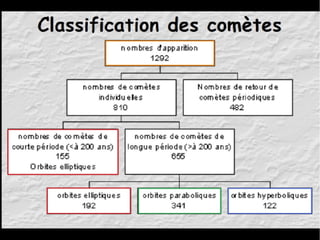
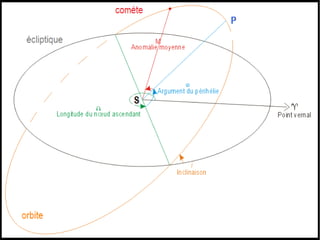
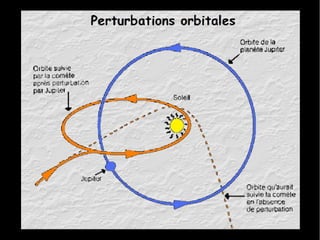
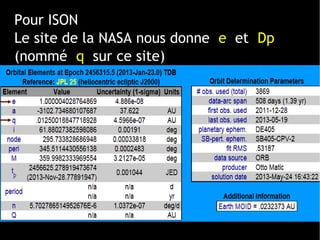
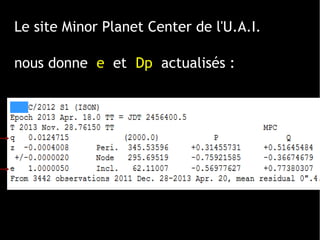
Le document traite du calcul de la vitesse d'une comète, en se basant sur les lois de Kepler et des méthodes astronomiques complexes pour déterminer les paramètres orbitaux. Il explique comment la trajectoire des comètes, notamment celle de la comète ISON, peut être calculée et comprend des formules précises pour évaluer la vitesse au périhélie. En conclusion, la vitesse estimée de la comète ISON lors de son passage au périhélie est d'environ 377 km/s.

1. Comment calculer sa vitesse
lors du passage près du Soleil ?
Comète C/2012 ISON

2. m^3 / kg / s^2

3. 1 ligne 2 ligne 3 ligne 4 ligne
0
2
4
6
8
10
12
1 colonne
2 colonne
3 colonne
Pour calculer les éphémérides d'une comète,
il est nécessaire de connaître
6 paramètres orbitaux.
Ils se calculent à partir des observations par
des méthodes assez complexes
(Laplace, Gauss, Olbers).

4. Le mouvement d'une comète
est régi par les mêmes lois
que celles des planètes
ou de tout corps céleste :
la gravitation
et
la conservation de l'énergie.

5. Mathématiquement, la trajectoire
se traduit par 3 lois énoncées
en 1618 par Képler :

6. 1 ligne 2 ligne 3 ligne 4 ligne
0
2
4
6
8
10
12
1 colonne
2 colonne
3 colonne
1.
L'orbite est une conique
(cercle, ellipse, parabole ou hyperbole)
dont le Soleil est un foyer.
La trajectoire est plane.

8. La trajectoire de ISON est hyperbolique.

9. 1 ligne 2 ligne 3 ligne 4 ligne
0
2
4
6
8
10
12
1 colonne
2 colonne
3 colonne
Le périhélie est le point de la
trajectoire le plus proche du Soleil.
L'aphélie est le point de la
trajectoire le plus loin du Soleil.
La ligne aphélie - périhélie forme
le grand axe.

11. 1 ligne 2 ligne 3 ligne 4 ligne
0
2
4
6
8
10
12
1 colonne
2 colonne
3 colonne
2. loi des aires :
La ligne joignant
le Soleil et le corps céleste
parcourt
des aires identiques
en des temps égaux

13. 1 ligne 2 ligne 3 ligne 4 ligne
0
2
4
6
8
10
12
1 colonne
2 colonne
3 colonne
La 2e loi de Képler
implique que la vitesse
sur l'orbite est variable et
plus rapide au périhélie.

14. 1 ligne 2 ligne 3 ligne 4 ligne
0
2
4
6
8
10
12
1 colonne
2 colonne
3 colonne
3.
Le rapport
(période de révolution)²
_____________________
(grand axe de l'ellipse)³
est constant.

15. 1 ligne 2 ligne 3 ligne 4 ligne
0
2
4
6
8
10
12
1 colonne
2 colonne
3 colonne
On l'écrit aussi
T² = a³
T est la période en années.
a est le demi-grand axe en U.A.

16. 1 ligne 2 ligne 3 ligne 4 ligne
0
2
4
6
8
10
12
1 colonne
2 colonne
3 colonne
Nicolas COPERNIC émit l'idée d'héliocentrisme,
Tycho BRAHE fit les observations des positions
des trajectoires,
Johannes KEPLER trouva les lois géométriques,
Isaac NEWTON les démontra,
EINSTEIN les ajusta.

17. 1 ligne 2 ligne 3 ligne 4 ligne
0
2
4
6
8
10
12
1 colonne
2 colonne
3 colonne
Eléments décrivant une ellipse :

20. cercle : F = O ; parabole : F = P
La position du Foyer varie selon e

21. 1 ligne 2 ligne 3 ligne 4 ligne
0
2
4
6
8
10
12
1 colonne
2 colonne
3 colonne
L'excentricité e mesure le
degré d'aplatissement de la trajectoire :
e = distance entre les foyers / grand axe
e>1 pour une hyperbole
e=1 pour une parabole
e<1 pour une ellipse
e=0 pour un cercle

24. 1 ligne 2 ligne 3 ligne 4 ligne
0
2
4
6
8
10
12
1 colonne
2 colonne
3 colonne
Les paramètres orbitaux
permettant le calcul de position sont :
a : le demi grand axe
e : excentricité
tp : date du périhélie
ω ou Peri : argument (angle) du périhélie
Ω ou Node : longitude du noeud ascendant
i : inclinaison de l'orbite sur l'écliptique

26. Une trajectoire hyperbolique
est un cas très rare,
ou lié à une perturbation de trajectoire
elliptique.
L'excentricité demeure faible
et e est proche de 1.

28. La loi des aires
La conservation de l'énergie
L'énergie liée à la vitesse :
Ec = ½ m V²
L'énergie liée à la gravitation :
Ep = - G Ms m / r
Le calcul de la vitesse d'une comète
fait intervenir :

29. et :
G = constante de Gravitation
Ms = masse du Soleil
r = distance au foyer
Dp = distance au périhélie
V² = G Ms ( 2/r - 1/a )
V, la vitesse d'une comète
se calcule par la formule :
et : Dp = a (1 - e)

30. Il nous reste à estimer e et Dp
grâce aux observations.
Vp² = G Ms ( 1 + e )/Dp
En remplaçant a par la valeur précédente,
On obtient :

31. Pour ISON
Le site de la NASA nous donne e et Dp
(nommé q sur ce site)

32. Le site Minor Planet Center de l'U.A.I.
nous donne e et Dp actualisés :

33. on obtient :
Calcul avec la comète ISON C/2012 S1 :
Vp = 377 km/s
( <5 fois la distance Terre-
Lune)
( 300 000 fois la Terre)
( 150 millions de km)
( faible hyperbole)

34. on obtient Vp = 30 km/s
Vp² = G Ms ( 1 + e )/Dp
Pour le cas de la Terre (ellipse), avec :

35. on obtient Vp = 42 km/s
Vp² = G Ms ( 1 + e )/Dp
Pour le cas Terre, la vitesse limite
parabolique d'échappement au Soleil est:

36. Donc la vitesse de la comète ISON C/2012 S1
à son passage au périhélie le 28 nov. 2013
sera d'environ :
Vp = 377 km/s
= 1,36 million km/h

37. Références :
Eléments orbitaux ISON C/2012 S1 :
http://www.minorplanetcenter.net/mpec/K13/K13H38.html
http://ssd.jpl.nasa.gov/sbdb.cgi?sstr=ison&orb=1

38. Sites Web intéressants :
Informations détaillées sur les comètes (en français) :
http://www.astrosurf.com/cometes/description/Com_des.html
Mathématiques des coniques (en anglais) :
http://www.braeunig.us/space/orbmech.htm#hyperbolic
http://en.wikipedia.org/wiki/Hyperbolic_trajectory
Ephémérides des petits objets :
http://www.minorplanetcenter.net/iau/MPEph/MPEph.html

39. © Bruno CARTIGNY
Mai 2013
Club d'Astronomie : Astro Club 85
http://astroclub85.free.fr/