Ce mémoire présente un modèle de planification d'un réseau de quatrième génération (4G) basé sur un réseau de troisième génération (3G) existant, traitant spécifiquement du problème d'affectation des cellules aux commutateurs. Le modèle proposé cherche à minimiser les coûts d'investissement tout en maximisant l'utilisation des équipements 3G, et il est évalué par une approche heuristique utilisant la recherche taboue. Les résultats montrent que la méthode taboue peut approcher la solution optimale avec un écart moyen ne dépassant pas 30%.


















![1
CHAPITRE 1
INTRODUCTION
La planification d’un r´eseau mobile consiste `a d´eterminer l’ensemble des compo-
santes mat´erielles et logicielles de ces syst`emes, les positionner, les interconnecter et les utiliser
de fa¸con optimale, en respectant, entre autres, une s´erie de contraintes de qualit´e de service
[50]. Ce processus qui peut ˆetre `a la fois long et coˆuteux a lieu avant la mise en op´eration
du r´eseau. Pour les r´eseaux de premi`ere g´en´eration (1G), de deuxi`eme g´en´eration (2G) et de
troisi`eme g´en´eration (3G), une s´erie de recherches ont ´et´e men´ees et visent `a minimiser les
coˆuts des ´equipements, tout en maintenant une communication de qualit´e et une capacit´e
´elev´ee [34], [23]. Toutefois, ces derni`eres ann´ees, les recherches portent surtout sur l’analyse
des r´eseaux de quatri`eme g´en´eration (4G), dont l’objectif est d’offrir toute une gamme de
services (l’acc`es rapide `a l’Internet, le commerce ´electronique, la vid´eoconf´erence, la t´el´e-
m´edecine, l’apprentissage `a distance, etc.) ayant chacun ses caract´eristiques et contraintes
particuli`eres [22], [33]. Quelques tentatives ont ´et´e faites pour proposer des mod`eles qui per-
mettent de faire la planification de tels r´eseaux [18]. Ces mod`eles, dans l’ensemble, apportent
des solutions au probl`eme de planification pour les zones d´epourvues de toute infrastructure
[42], [48]. Mais, qu’en est-il si la planification de ces r´eseaux se r´ealise `a partir d’un r´eseau
existant ? Ainsi, ce m´emoire traite du probl`eme de planification des r´eseaux 4G `a partir d’un
r´eseau 3G existant. Dans ce contexte, la planification consiste `a maximiser l’utilisation des
´equipements du r´eseau 3G d´ej`a en place, tout en minimisant les coˆuts induits par l’ajout de
ceux consituant le r´eseau 4G. Ce chapitre d’introduction d´efinit d’abord les concepts de base
des r´eseaux mobiles. Ensuite, les ´el´ements de la probl´ematique y seront pr´esent´es, suivi des
objectifs de la recherche. Ce chapitre se termine par l’organisation de la suite du document.
1.1 D´efinitions et concepts de base
Un r´eseau mobile est un r´eseau de communication compos´e de cellules, g´en´erale-
ment consid´er´ees de forme hexagonale. Ces cellules sont toutes juxtapos´ees l’une `a l’autre afin
d’assurer une meilleure couverture de la zone g´eographique consid´er´ee. Ces cellules peuvent
ˆetre de tailles variables allant des picocellules aux cellules parapluie, comme d´ecrit dans [50].
En se basant sur cette r´epartition cellulaire, les r´eseaux mobiles op`erent en mode infrastruc-
ture, o`u tous les ´echanges transitent par un point d’acc`es, la station de base, desservant
chacune une cellule sur une couverture sans fil donn´ee. Plusieurs g´en´erations de r´eseaux](https://image.slidesharecdn.com/2011germineseide-140603143923-phpapp02/85/2011-germine-seide-19-320.jpg)
![2
mobiles se sont d´efil´ees `a travers le temps. Ce sont la 1G avec un mode de transmission
analogique, la 2G qui marqua le passage `a l’`ere num´erique, la 3G qui permet d’int´egrer des
services de voix et de donn´ees, et de nos jours, les r´eseaux de prochaine g´en´eration.
Un R´eseau Mobile de Prochaine G´en´eration (RMPG) est un r´eseau permettant l’in-
t´egration flexible et efficace des diff´erentes technologies d’acc`es mobiles existantes, et facilitant
leur ´evolution ainsi que leur int´egration avec de nouvelles et futures technologies d’acc`es [17].
Dans ces r´eseaux, les stations de base sont de type multi-mode parce qu’elles int`egrent de
multiples interfaces radio leur permettant de communiquer avec les diff´erents r´eseaux mobiles
h´et´erog`enes int´egrant le RMPG. Les RMPG co¨ıncident de pr`es avec la 4`eme g´en´eration de
r´eseaux mobiles. Cette g´en´eration comporte des ´equipements pouvant permettre aux op´era-
teurs de rationaliser leurs coˆuts. Dans la suite de ce document, le terme 4G sera utilis´e pour
d´esigner les RMPG.
Lorsqu’un utilisateur se d´eplace `a l’int´erieur du r´eseau, l’UE (User Equipment) se
raccorde `a une station de base en fonction de la puissance de son signal. Quand cette puis-
sance atteint un seuil minimal, des op´erations sont effectu´ees pour relayer la communication
par une nouvelle cellule. Un tel m´ecanisme est connu sous le nom de rel`eve [20]. La rel`eve per-
met ainsi `a un utilisateur en cours d’appel de maintenir sa connexion active et une qualit´e de
communication suffisante durant ses d´eplacements `a travers les diff´erentes cellules du r´eseau.
Les r´eseaux 4G comportent deux types de rel`eves : une rel`eve horizontale ou intra-r´eseau, et
une rel`eve verticale ou inter-r´eseaux.
La rel`eve horizontale s’effectue entre cellules de mˆeme type de technologie d’acc`es
d’un r´eseau mobile homog`ene. Suivant que ces cellules sont desservies ou non par un mˆeme
commutateur, la rel`eve horizontale est dite simple ou complexe. Sur la figure 1.1, l’UE dans
son parcours passe de la cellule C9 `a la cellule C10, toutes deux reli´ees au commutateur
Com3. Dans ce cas, la rel`eve est dite simple et n’entraˆıne que la mise `a jour des param`etres
de localisation du UE aux stations de base B9 `a B10. Quand l’UE communique avec les
stations de base B5 de la cellule C5 et B8 de la cellule C8 desservies respectivement par
les commutateurs Com2 et Com4, la rel`eve s’effectue avec changements de commutateurs et
est dite complexe. Suite `a cette rel`eve, Com2 transmet le profil de l’utilisateur ainsi que les
informations concernant son nouvel emplacement au commutateur Com4. Ces informations
seront ensuite enregistr´ees dans les bases de donn´ees pr´evues `a cet effet.](https://image.slidesharecdn.com/2011germineseide-140603143923-phpapp02/85/2011-germine-seide-20-320.jpg)
![3
Figure 1.1 Types de rel`eves
Une rel`eve verticale fait intervenir des cellules appartenant `a des r´eseaux d’acc`es de
technologies diff´erentes tels que l’UMTS (Universal Mobile Telecommunications System), le
WiMAX (Worldwide Interoperability for Microwave Access), la LTE (Long Term Evolution),
le GSM (Global System for Mobile Communication) et le Wi-Fi (Wireless Fidelity) [36]. Ainsi,
quand l’UE, dans son parcours, arrive `a la fronti`ere de sa cellule, le m´ecanisme de rel`eve est
d´eclench´e par la BS (Base Station) qui contrˆole cette cellule. Si la cellule cible partage le mˆeme
commutateur d’interconnexion que la cellule courante, la rel`eve verticale est dite simple et
entraˆıne une mise `a jour de la position du UE, un ´equilibrage du trafic, et l’allocation ou non
de nouveaux canaux. Dans le cas contraire, la rel`eve verticale est consid´er´ee comme complexe
et les op´erations pr´e-cit´ees s’ex´ecutent par l’interm´ediaire de plusieurs commutateurs, ce qui
rend cette rel`eve encore plus coˆuteuse.
La planification d’un r´eseau mobile 4G `a partir d’un r´eseau mobile 3G consiste `a r´e-
organiser le r´eseau 3G initialement ´etabli et fonctionnel de mani`ere `a desservir un plus grand
nombre d’usagers, et par cons´equent, `a g´erer un trafic plus volumineux. Cette r´eorganisation
peut entraˆıner, soit l’ajout de nouveaux ´equipements 4G et le retrait de certains ´equipements
3G existants, soit la substitution de tous les ´equipements 3G existants. La planification de
ce r´eseau ´etendu comprend plusieurs phases, dont le choix des architectures, l’´evaluation de
la demande de trafic, la conception topologique r´ealis´ee `a partir des affectations des ´equipe-
ments des diff´erents r´eseaux et l’analyse de performance. L’approche qui sera retenue dans
ce m´emoire tiendra compte de toutes ces phases, `a l’exception de la phase d’´evaluation de la](https://image.slidesharecdn.com/2011germineseide-140603143923-phpapp02/85/2011-germine-seide-21-320.jpg)
![4
demande de trafic dont le r´esultat proviendra d’un travail d´ej`a r´ealis´e, comme le montrent
[24] et [59] pour son approche s´equentielle `a la r´esolution du probl`eme de planification. Mais
avant, une pr´esentation des architectures qui participent dans le r´eseau ´etendu sera faite afin
de justifier le choix de celles retenues.
Chaque g´en´eration de r´eseaux mobiles vient avec plusieurs propositions d’architec-
tures ; les plus ´etudi´ees sont pr´esent´ees dans la suite de cette section. Ainsi, deux grandes
technologies ont-elles domin´e la troisi`eme g´en´eration des r´eseaux mobiles. Ce sont : l’UMTS,
repr´esent´e par la figure 1.2, et le CDMA2000, illustr´e `a la figure 1.3 [61]. Ces deux r´eseaux
poss`edent plusieurs niveaux d’´equipements. Les deux premiers niveaux constituent le sous-
syst`eme radio et le troisi`eme niveau correspond au sous-syst`eme r´eseau.
Figure 1.2 Architecture du r´eseau 3G/UMTS
Dans les r´eseaux 3G, l’interconnexion entre les sous-r´eseaux se fait au moyen du
RNC (Radio Network Controller) dans l’UMTS et du BSC (Base Station Controller) dans
le CDMA2000. Les nœuds RNC et BSC sont reli´es chacun `a deux routeurs du sous-syst`eme
r´eseau. Les routeurs de l’UMTS sont le MSC (Mobile Switching Center) pour le domaine
`a commutation de circuits et le SGSN (Serving GPRS Support Node) pour le domaine `a
commutation de paquets. Le CDMA2000 comporte ´egalement pour son domaine `a commu-
tation de circuit le routeur MSC et un deuxi`eme routeur pour la prise en charge du domaine
`a commutation de paquets, comme l’indique la figure 1.2. De ces architectures, l’UMTS est
celle qui sera retenue dans la planification du r´eseau 4G.](https://image.slidesharecdn.com/2011germineseide-140603143923-phpapp02/85/2011-germine-seide-22-320.jpg)
![5
Figure 1.3 Architecture du r´eseau 3G/CDMA2000
Deux grandes technologies sont en phase de devenir leader en ce qui concerne l’offre
de l’Internet mobile `a haut d´ebit prˆon´e pour la quatri`eme g´en´eration [54]. Ce sont : le WiMAX
mobile de la figure 1.4 qui fait r´ef´erence `a la norme IEEE 802.16, et la LTE de la figure 1.5
d´evelopp´ee par le groupe 3GPP (3G Partnership Project). Ces deux technologies pr´esentent,
entre autres, une diff´erence significative au niveau de leur architecture. En effet, le r´eseau
LTE comporte deux niveaux d’´equipements. Le premier est constitu´e uniquement d’eNode
B (E-UTRAN Node B) et le deuxi`eme comporte les nœuds MME (Mobility Management
Entity) et le SGW (Serving Gateway). Le r´eseau WiMAX comprend trois niveaux dont celui
des BS, des nœuds ASN-GW (Access Service Network Gateway) et d’un routeur desservant
les autres nœuds du r´eseau cœur, comme pr´esent´e `a la figure 1.5.
Figure 1.4 Architecture du r´eseau 4G/WiMAX](https://image.slidesharecdn.com/2011germineseide-140603143923-phpapp02/85/2011-germine-seide-23-320.jpg)
![6
Figure 1.5 Architecture du r´eseau 4G/LTE
Dans le cadre de ce m´emoire, la technologie LTE, r´ef´erenc´ee `a la figure 1.5, sera
consid´er´ee pour faire une extension du r´eseau UMTS. Ce choix est justifi´e par le fait que
plusieurs entreprises en t´el´ecommunications, comme Cisco, Ericsson et Alcatel-Lucent se
tournent de plus en plus vers cette technologie qui offre une vari´et´e d’options pour am´eliorer
les capacit´es de leur r´eseau [58], [28].
1.2 ´El´ements de la probl´ematique
La planification des r´eseaux mobiles est un processus it´eratif compos´e de plusieurs
phases, pr´esentant chacune un degr´e de complexit´e diff´erent [52]. Dans le cadre de ce m´e-
moire, la phase de la planification qui traite de l’affectation des nœuds du r´eseau est celle
qui sera trait´ee. Elle consiste `a d´eterminer, `a partir des sch´emas d’affectation, la topologie
d’interconnexion qui permet de r´eduire les coˆuts du r´eseau et le nombre d’op´erations de
mises `a jour engendr´ees par les rel`eves. `A cet effet, le probl`eme d’affectation est divis´e en
deux sous-probl`emes : l’affectation des nœuds du r´eseau 4G et l’affectation des nœuds du
r´eseau 3G au r´eseau 4G. Chaque sous-probl`eme s’apparente au probl`eme d’affectation trait´e
respectivement dans les r´eseaux de 2`eme et de 3`eme g´en´erations. Dans chacun des cas, les
solutions propos´ees consistent `a rapprocher le probl`eme d’affectation, de certains probl`emes
tr`es connus, comme le partitionnement des graphes et la localisation d’entrepˆots [50]. Ainsi,
pour le premier sous-probl`eme, les cellules des r´eseaux 2G et 3G sont consid´er´ees comme les
nœuds du graphe `a partitionner et les arcs repr´esentent les diff´erents coˆuts de rel`eve entre les
cellules. Pour le deuxi`eme sous-probl`eme, les cellules repr´esentent les usines, le coˆut de liaison
leurs productions, et les commutateurs les entrepˆots o`u la production des usines est stock´ee.](https://image.slidesharecdn.com/2011germineseide-140603143923-phpapp02/85/2011-germine-seide-24-320.jpg)
![7
Le probl`eme de partitionnement des graphes et celui de la localisation d’entrepˆots ont ´et´e
d´emontr´es NP-difficiles [38], [27], [57]. Puisque le probl`eme d’affectation peut se ramener soit
au probl`eme de partitionnement des graphes, soit au probl`eme de la localisation d’entrepˆots,
il est donc consid´er´e ´egalement comme un probl`eme NP-difficile. Par cons´equent, le probl`eme
ne peut pas ˆetre r´esolu avec les m´ethodes standards, comme les algorithmes `a ´enum´eration
exhaustive. En effet, pour n cellules et m commutateurs, il a ´et´e montr´e que ces algorithmes
permettent d’explorer un nombre de mn
sch´emas d’affectations possibles [26], [56], [34]. De
toutes ces combinaisons, choisir la meilleure qui permet de minimiser le coˆut du r´eseau serait
trop long en termes de temps de calcul.
Figure 1.6 Architecture typique d’un r´eseau 3G/UMTS ´etendu vers 4G/LTE
De ces diff´erents travaux, il en d´ecoule que le probl`eme d’affectation est directement
li´e aux nombres d’´equipements et aux niveaux d’emplacements de ses ´equipements dans
le r´eseau. Ainsi, sur l’architecture de la figure 1.6, le r´eseau pr´esente principalement deux
niveaux d’´equipements. Le premier niveau comporte les nœuds eNode B, Node B et RNC. Le
deuxi`eme niveau d’´equipements comporte les MME et les S-GW du r´eseau cœur 4G/LTE, les
SGSN et les MSC du r´eseau cœur 3G/UMTS. En se basant sur ce sch´ema, le probl`eme dans
le r´eseau ´etendu consiste `a trouver une topologie d’interconnexion bas´ee sur une m´ethode
d’affectation optimale des eNode B et des SGSN aux MME et SGW. Ce r´eseau, avec ses
deux niveaux d’´equipements, se rapproche de l’architecture 2G. Mais, une grande diff´erence
se situe au niveau du nombre de nœuds constituant le 2`eme niveau. En effet, le r´eseau
2G prend en compte l’affectation des Node B n vers un seul commutateur MSC m, ce qui
repr´esente mn
affectations. Le r´eseau ´etendu pr´esent´e `a la figure 1.6 est compos´e de m MME](https://image.slidesharecdn.com/2011germineseide-140603143923-phpapp02/85/2011-germine-seide-25-320.jpg)


![10
CHAPITRE 2
ANALYSE DU PROBL`EME DE PLANIFICATION
La planification des r´eseaux mobiles pr´esente beaucoup de d´efis, tant au niveau
architecture, qu’au niveau d’´evolutivit´e. En effet, une bonne connaissance des architectures
permet aux planificateurs de mieux g´erer les ressources en place, de faciliter l’´evolution du r´e-
seau en int´egrant des technologies plus performantes, qui leur permettent de fournir en mˆeme
temps des services de bonne qualit´e. Ce chapitre passe alors en revue les travaux majeurs
traitant des diff´erents aspects du probl`eme de planification des r´eseaux mobiles, tels qu’abor-
d´es dans la litt´erature. En premier lieu, une description des ´equipements des architectures
participant `a la planification du r´eseau sera faite. Cette description permettra de d´eceler les
d´efis de recherche que les nouvelles technologies apportent au probl`eme de planification. De
ces d´efis, l’affectation des cellules aux commutateurs est celui qui sera pr´esent´e et ´etudi´e, telle
qu’abord´ee dans les g´en´erations pr´ec´edentes de r´eseaux mobiles. Pour chaque g´en´eration, les
m´ethodes de r´esolution utilis´ees seront d´ecrites. Enfin, une analyse comparative des diff´erents
travaux sera r´ealis´ee, en mettant en exergue les ´el´ements de solution qu’ils apportent dans la
r´esolution du probl`eme de planification d’un r´eseau mobile 4G.
2.1 Caract´eristiques des r´eseaux 3G/UMTS
L’UMTS, depuis sa premi`ere version sortie en 1999, a ´et´e sujet `a de nombreuses
am´eliorations. En 2001, une interface r´eseau de type TD-SCDMA (Time Division Synchro-
nous Code Division Multiple Access) a ´et´e ajout´e, offrant un meilleur d´ebit par rapport au
TD-CDMA (Time Division-CDMA) de la premi`ere version. En cons´equence, dans le r´eseau
cœur, la signalisation a ´et´e d´epartag´ee de la transmission de donn´ees. En 2002, le support
de l’IP (Internet Protocol) au niveau du r´eseau cœur, de mˆeme que le HSDPA (High-Speed
Downlink Packet Access), ont ´et´e ajout´es [4]. En 2005, le d´ebit en amont (Uplink) sera accru
au moyen du m´ecanisme HSUPA (High-Speed Uplink Packet Access) [8]. Ces am´eliorations se
rattachent plus pr´ecis´ement au niveau des ´equipements, de leur performance et des interfaces
d’interconnexion, telles qu’illustr´ees dans les tableaux B.1 `a B.5. Mais, dans l’ensemble, l’ar-
chitecture des r´eseaux UMTS garde une structure inh´erente aux r´eseaux mobiles, compos´ee
d’un r´eseau d’acc`es et d’un r´eseau cœur [61].](https://image.slidesharecdn.com/2011germineseide-140603143923-phpapp02/85/2011-germine-seide-28-320.jpg)
![11
2.1.1 R´eseau d’acc`es 3G/UMTS
L’UTRAN est le nom attribu´e au r´eseau d’acc`es de l’UMTS. Il r´ealise les transferts
de trafic de donn´ees et de signalisation entre l’appareil mobile (UE) et le r´eseau cœur [2]. Il
comprend principalement deux entit´es : le Node B et le RNC, repr´esent´ees `a la figure 2.1. Le
Node B ´etablit la connexion de l’utilisateur en transmettant des signaux radio et les flux de
donn´ees entre l’interface radio et le RNC. Cette op´eration se r´ealise au moyen de l’interface
Iub reliant ces deux nœuds. Les RNC, quant `a eux, font la gestion des ressources radio et
des ph´enom`enes de rel`eves. Ils communiquent entre eux via l’interface Iur et sont reli´es aux
Node B par l’interface Iub [5], [6], [7]. Ils servent d’interm´ediaire entre l’appareil mobile (UE)
et le r´eseau cœur en transitant les informations de voix et de donn´ees, respectivement, au
moyen des interfaces Iu-cs et Iu-ps de la figure 2.2.
Figure 2.1 Architecture du r´eseau d’acc`es de l’UMTS : UTRAN
2.1.2 R´eseau cœur 3G/UMTS
Le r´eseau cœur, repr´esent´e `a la figure 2.2, assure suivant le service utilis´e, la connexion
des terminaux mobiles (UE) au PDN (Packet Data Network) ou au RTPC (R´eseau T´el´epho-
nique Public Commut´e). Dans [62], l’auteur pr´esente une subdivision du r´eseau en deux](https://image.slidesharecdn.com/2011germineseide-140603143923-phpapp02/85/2011-germine-seide-29-320.jpg)
![12
domaines : un domaine `a commutation de paquets, le PS-CN (Packet Switch-Core Network)
et un domaine `a commutation de circuit, le CS-CN (Circuit Switch-Core Network). Le do-
maine `a commutation de paquets comprend un SGSN (Serving GPRS Support Node) qui se
charge du routage des paquets, de l’authentification et du cryptage des informations de l’uti-
lisateur au moyen des donn´ees du HLR (Home Location Register). Il comprend ´egalement
le GGSN (Gateway GPRS Support Node) utilis´e comme passerelle pour la commutation de
paquets avec les r´eseaux externes, tels que l’Internet, les LANs, les WANs, les r´eseaux GPRS,
les r´eseaux ATM. C’est `a ce niveau que les proc´edures de tarification sont ´etablies. Le do-
maine `a commutation de circuit consiste en un MSC (Mobile Service Switching Center) et un
GMSC (Gateway Mobile Switching Center) [3]. Le MSC est responsable de la signalisation
requise pour l’´etablissement, la fermeture et le maintien des connexions. Il est aussi charg´e
des fonctions radio telles que, le reroutage d’appels ainsi que l’allocation des canaux radio des
appareils mobiles. Le GMSC met en forme, convertit les protocoles employ´es par le r´eseau
mobile et interagit avec le HLR pour obtenir des informations de routage. Le HLR et le VLR
(Visitor Location Register) sont des bases de donn´ees situ´ees dans le syst`eme domiciliataire
de l’utilisateur. Ces bases de donn´ees contiennent toutes les informations relatives `a l’utili-
sateur [10]. Ces informations d´efinissent le profil de ce dernier et consistent, entre autres, en
un num´ero de t´el´ephone, une cl´e authentification, les services autoris´es, les zones de roaming
associ´ees aux MSC et les param`etres de localisation du UE tout au long de son parcours.
Figure 2.2 Architecture du r´eseau cœur de l’UMTS](https://image.slidesharecdn.com/2011germineseide-140603143923-phpapp02/85/2011-germine-seide-30-320.jpg)
![13
2.2 Caract´eristiques des r´eseaux 4G/LTE
L’´evolution `a long terme est l’´equivalent fran¸cais du terme anglais LTE. Elle d´esigne
un projet r´ealis´e par l’organisme de standardisation 3GPP œuvrant `a r´ediger des techniques
qui permettront d’am´eliorer la norme UMTS des r´eseaux cellulaires 3G, vers la quatri`eme
g´en´eration, pour faire face aux futures ´evolutions technologiques. Les buts poursuivis pour
la LTE consistent en une am´elioration de l’efficacit´e spectrale qui permettra le transfert des
donn´ees `a tr`es haut d´ebit, de l’ordre de 50 Mbps, avec une port´ee plus importante, un nombre
d’appels par cellule plus ´elev´e que dans l’UMTS et une latence plus faible, telles qu’illustr´ees
dans les tableaux B.1 `a B.5. La quatri`eme g´en´eration pr´esente, pour l’am´elioration des ser-
vices, des plateformes multi-technologiques capables de supporter de nouvelles applications
innovatrices. De mˆeme que ces pr´ec´edentes, la 4G pr´esente une architecture qui comporte un
r´eseau d’acc`es : l’E-UTRAN et un r´eseau cœur v´ehiculant que des paquets de donn´ees [46].
Elle est dite pour cela tout-IP.
2.2.1 R´eseau d’acc`es 4G/LTE
Le r´eseau d’acc`es LTE est constitu´e d’un nœud unique l’Evolved Node B ou eNode
B, repr´esent´e `a la figure 2.3. Il regroupe en une entit´e unique les fonctionnalit´es des nœuds
Node B et RNC de l’UMTS. La principale fonction de l’eNode B est d’acheminer les flux de
donn´ees de l’UE vers l’EPC (Evolved Packet Core Network) au moyen des fonctions comme le
RRM (Radio Ressource Management) et le CAC (Call Admission Control). Cette op´eration
est r´ealis´ee en utilisant l’interface S1 qui relie l’E-UTRAN aux composantes de l’EPC. L’E-
UTRAN dispose d’une nouvelle interface X2 unique au r´eseau LTE. Cette interface a pour
principal rˆole de r´ealiser des ´echanges de donn´ees et de signaux de connexion entre diff´erents
eUTRAN. Pr´esent´e ainsi, la planification des r´eseaux d’acc`es devient tr`es simple avec un
nombre r´eduit de nœuds et d’interfaces. Cette simplicit´e entraˆıne une r´eduction des pertes de
paquets qui peuvent subvenir en cas de rel`eve, celle des coˆuts d’op´eration et une diminution
du temps de latence dans le syst`eme.](https://image.slidesharecdn.com/2011germineseide-140603143923-phpapp02/85/2011-germine-seide-31-320.jpg)

![15
Le MME comporte les fonctionnalit´es de base de la signalisation dans la connexion
du terminal mobile au r´eseau. Il fournit les informations n´ecessaires `a l’identification de
l’usager au moment de son authentification dans le syst`eme, en se servant des informations
provenant du HSS. En se servant des fonctions du plan de contrˆole, il fait la gestion des
sessions des utilisateurs authentifi´es. Il est responsable des fonctions de gestion de la mobilit´e
telles que la coordination de la signalisation pour les rel`eves inter-SGW, et n´egocie la qualit´e
de service `a offrir. Le MME est responsable de la diffusion des messages de paging quand
l’UE est dans l’incapacit´e de recevoir les paquets qui lui sont destin´es. Il fait la mise `a jour
des param`etres de localisation de l’UE se retrouvant dans une zone qui n’est pas prise en
charge par le MME [11]. Il joue un rˆole cl´e dans la rel`eve entre les diff´erentes technologies,
en s´electionnant le nœud qui va mettre en place la porteuse, le default bearer, afin d’´etablir
la communication entre les deux architectures.
Le SGW est d´efini pour g´erer les ”donn´ees utilisateur”et est impliqu´e dans le routage
et la transmission de paquets de donn´ees entre les eUTRAN et le r´eseau cœur. L’´echange des
paquets est achemin´e par le SGW au PDN-GW par l’interface S5. Le SGW est connect´e `a l’
eUTRAN via l’interface S1-U qui sert de relai entre l’utilisateur et le EPC. Il op`ere comme
une ancre locale qui sert pour la mobilit´e inter-eNode B et permet de faire la rel`eve entre les
syst`emes mobiles de diff´erentes g´en´erations, comme LTE et UMTS.
Le P-GW est le nœud qui relie l’utilisateur mobile aux autres r´eseaux PDN, tels que
les r´eseaux IP, PSTN et non-3GPP. L’acc`es aux r´eseaux IP et PSTN se fait par l’interm´ediaire
de l’IMS. Le PDN Gateway agit comme un routeur par d´efaut par lequel transitent les
requˆetes de l’utilisateur. Il effectue l’allocation d’adresses IP pour chaque Terminal Mobile,
le filtrage des paquets pour chaque usager, et comptabilise les octets ´echang´es dans la session
de ce dernier `a des fins de facturation.
Le HSS se pr´esente comme une version ´evolu´ee du HLR. Il permet de stocker des
informations d’abonnement pouvant servir au contrˆole des appels et `a la gestion de session
des utilisateurs r´ealis´e par le MME. Il entrepose, pour l’identification des utilisateurs, la
num´erotation et le profil des services auxquels ils sont abonn´es. En plus des donn´ees d’au-
thentification des utilisateurs, il contient les informations de souscription pour les autres
r´eseaux, comme le GSM, le GPRS, 3G, LTE et IMS.
Le PCRF est une entit´e qui ex´ecute principalement deux grandes tˆaches. La pre-
mi`ere est de g´erer la qualit´e de service que requiert le r´eseau, et alloue en cons´equence les
porteuses bearer appropri´ees. La deuxi`eme tˆache se rapporte principalement `a la tarification.](https://image.slidesharecdn.com/2011germineseide-140603143923-phpapp02/85/2011-germine-seide-33-320.jpg)
![16
En effet, le PCRF g`ere les politiques de facturation qui doivent ˆetre prises en compte par le
PDN-GW et applicables en fonction des actions de l’utilisateur.
L’IMS est une architecture r´ecemment appliqu´ee dans les r´eseaux mobiles qui per-
mettent aux op´erateurs de t´el´ecommunications d’offrir des services sur IP `a valeur ajout´ee.
Cette nouvelle architecture permet d’´etablir des sessions multim´edia ind´ependamment du
type d’acc`es `a Internet utilis´e. Cette architecture est aussi capable de supporter, sur un r´e-
seau tout IP dans une mˆeme session, des applications en temps r´eel telles que la voix et la
vid´eo ; et des applications non temps r´eel telles que le Push to Talk et la messagerie instanta-
n´ee. L’IMS est utilis´e aussi bien par les terminaux mobiles des r´eseaux GPRS et UMTS, que
par les usagers fixes `a large bande, comme xDSL, cˆable, etc. L’IMS pr´esente une interface
aux r´eseaux en mode circuit, comme le RTCP et le GSM, et fournit une interface normalis´ee
bas´ee sur le protocole SIP pour l’acc`es aux services.
En r´esum´e, les r´eseaux 4G/LTE se distinguent des r´eseaux 3G/UMTS par trois
grands aspects. Une nouvelle interface radio avec les technologies OFDM (Orthogonal Fre-
quency Division Multiplexing) en amont, le SC-FDMA (Single Carrier - Frequency Division
Multiple Access) en uplink et MIMO (Multiple Input Multiple Output), lui permettant de
supporter des largeurs de bande allant de 1.4 `a 20 MHz [14], [9]. Les r´eseaux UMTS utilisent,
pour leur interface radio, le W-CDMA (Wideband Code Division Multiple Access) d’une lar-
geur de bande allant jusqu’`a 5 MHz [1], [13]. Au niveau de l’architecture, le r´eseau d’acc`es
LTE est r´eduit `a une entit´e unique, l’eNode B, tel que d´ecrit dans [12]. Il remplit `a la fois le
rˆole des Node B et des RNC de l’UMTS, ce qui apporte une grande r´eduction du d´elai d’acc`es
et du nombre d’op´erations dans le r´eseau. Les r´eseaux bas´es sur la technologie LTE offrent,
pour les nouveaux services, une architecture tout-IP au moyen de l’IMS. Celle-ci remplace
ainsi dans l’UMTS le domaine `a commutation de circuits h´erit´e du GSM et le domaine `a
commutation de paquets du GPRS.
2.3 Probl`eme d’affectation
L’un des probl`emes de la planification les plus ´etudi´es dans la litt´erature est le
probl`eme d’affectation [25], [34], [53]. Ce dernier consiste `a d´eterminer un patron d’affectation
des cellules `a des commutateurs dans le but de minimiser une fonction de coˆut, tout en
respectant un certain nombre de contraintes. Dans les sections suivantes seront pr´esent´es les
travaux r´ealis´es pour traiter le probl`eme dans le cas des r´eseaux 2G, 3G et 4G.](https://image.slidesharecdn.com/2011germineseide-140603143923-phpapp02/85/2011-germine-seide-34-320.jpg)
![17
2.3.1 Cas des r´eseaux 2G
Deux niveaux d’´equipements sont consid´er´es dans les r´eseaux 2G. Le niveau 1
comporte les BTS (Base Transceiver Station) occupant chacune une cellule, alors que le
niveau 2 est compos´e des commutateurs MSC, comme illustr´e `a la figure 2.5. Dans ce contexte,
r´esoudre le probl`eme d’affectation revient `a trouver un patron d’affectation des cellules aux
commutateurs MSC. Plus particuli`erement, en consid´erant un ensemble de n cellules et de
m commutateurs, il faut d´eterminer parmi les couples d’affectation (n, m) avec n ∈ N et
m ∈ M, laquelle permettra de minimiser une fonction de coˆut, compos´ee du coˆut de liaison
entre les BTS des cellules et les MSC, et du coˆut de rel`eve entre deux cellules n et n desservies
par une mˆeme BTS.
Figure 2.5 Exemple d’architecture 2G
Le mod`ele r´esultant du travail de Houeto [34] est une fonction quadratique qui tra-
duit le coˆut des liaisons et le coˆut des rel`eves simples et complexes. La minimisation de la
fonction est soumise `a des contraintes, comme l’unicit´e et la capacit´e des nœuds. Dans ce
mod`ele, une cellule sera affect´ee `a un seul commutateur et le trafic provenant de la cellule ne
doit pas d´epasser la capacit´e du commutateur. Pour ´evaluer la performance de cette m´ethode,
un algorithme de recherche taboue est utilis´e, puisque le probl`eme a ´et´e initialement prouv´e
NP-difficile [44].](https://image.slidesharecdn.com/2011germineseide-140603143923-phpapp02/85/2011-germine-seide-35-320.jpg)

![19
avec :
– hij le coˆut r´eduit par unit´e de temps d’une rel`eve complexe entre les cellules i et j ;
– yij variable d´ecisionnelle qui vaut 1 si les cellules i, j avec (i = j) sont reli´ees au mˆeme
commutateur k, et 0 sinon.
Les auteurs Pierre et Houeto [51] font une adaptation de la m´ethode de r´esolution
utilis´ee par [34] au probl`eme d’affectation pour les r´eseaux mobiles en g´en´eral. Leur objectif
est de d´eterminer un profil d’affectation qui minimisera `a la fois les ressources affect´ees, les
coˆuts des rel`eves et les coˆuts de cˆablage dans le r´eseau. Pour y parvenir, ils proposent un
mod`ele math´ematique d´eriv´e de 2.1 et une m´ethode bas´ee sur la m´etaheuristique de recherche
taboue, pour obtenir des solutions acceptables en des temps de calcul raisonnables.
2.3.2 Cas des r´eseaux 3G
Les r´eseaux 3G pr´esentent une architecture tout `a fait diff´erente des r´eseaux pr´e-
c´edents, avec l’ajout de deux nouveaux ´equipements : le SGSN et le RNC, comme le montre
la figure 1.2. Ces r´eseaux 3G v´ehiculent deux types de trafic : un trafic de voix et un trafic
de donn´ees. Dans cette nouvelle architecture, le Node B acheminera les deux types de trafic.
Les RNC ajout´es serviront de nœuds de liaison pour diriger le trafic de voix vers les MSC et
le trafic de donn´ees vers les SGSN. Ces changements seront `a la base d’une nouvelle formula-
tion du probl`eme d’affectation des cellules aux commutateurs. Cette section consid`ere alors
certains travaux qui ont ´et´e r´ealis´es pour r´esoudre le probl`eme d’affectation des r´eseaux 3G,
compos´e de Node B i, de RNC j, de MSC l, et de SGSN k [24], [59].
Pour solutionner ce probl`eme, Diallo [24] le divise en deux sous-affectations : une
affectation des Node B i aux RNC j et l’affectation des RNC j aux MSC k et aux SGSN l.
En consid´erant le cas de la domiciliation simple, l’auteur propose un mod`ele math´ematique
prenant en compte les coˆuts de liaisons entre les ´equipements du r´eseau et les coˆuts de rel`eves
entre les cellules, puis une m´ethode de recherche taboue pour le r´esoudre. Cette fonction est
soumise aux contraintes d’unicit´e des affectations, et aux contraintes de capacit´e en com-
mutation de paquets et en commutation de circuit des RNC, des SGSN et des MSC. Ainsi,
pour affecter i Node B `a j RNC et j RNC `a k MSC et l SGSN, le probl`eme d’optimisation
math´ematique pour la domiciliation simple revient `a minimiser une fonction regroupant le](https://image.slidesharecdn.com/2011germineseide-140603143923-phpapp02/85/2011-germine-seide-37-320.jpg)
![20
coˆut des affectations de l’´equation 2.3 et le coˆut des rel`eves de l’´equation 2.4.
Minimiser(f1 + f2)
f1 =
i∈I j∈J
cijxij +
j∈J k∈K
cjkxjk +
j∈J l∈L
cjlxjl (2.3)
f2 =
i∈I i ∈I j∈J j ∈J
hmsc
ii (1 − yii )(1 − Y msc
jj ) +
i∈I i ∈I j∈J j ∈J
hsgsn
ii (1 − yii )(1 − Y sgsn
jj ) (2.4)
o`u
– cijxij, cjkxjk et cjlxjl d´esignent le coˆut de cˆablage, respectivement, des Node B au RNC,
des RNC au MSC et des RNC au SGSN ;
– hsgsn
ii (1 − yii ) et hmsc
ii (1 − yii )(1 − Y msc
jj ) d´esignent le coˆut total des rel`eves impliquant
respectivement un changement de SGSN et de MSC ;
avec
– hsgsn
ii et hmsc
ii , les coˆuts r´eduits par unit´e de temps des rel`eves complexes entre les Node
B i et i , impliquant respectivement un changement de SGSN et un changement de
MSC ;
– yii , une variable d´ecisionnelle qui vaut 1 si les Node B i, i avec i = i sont reli´es au
mˆeme RNC et 0 sinon ;
– Y msc
jj et Y sgsn
jj , des variables d´ecisionnelles qui valent 1 si les RNC j, j avec j = j sont
reli´ees respectivement au mˆeme MSC et au mˆeme SGSN, et 0 sinon ;
– cij, le coˆut d’amortissement de la liaison entre les Node B i et le RNC j ;
– cjk et cjl, les coˆuts d’amortissement des liaisons entre les RNC j et respectivement les
MSC k, les SGSN l ;
– xij une variable d´ecisionnelle qui vaut 1 si le Node B i est reli´e au RNC j et 0 sinon ;
– xjk et xjl, les variables d´ecisionnelles qui valent 1 si le RNC j est reli´e respectivement
au MSC k, et au SGSN l, et 0 sinon.
L’approche propos´ee par St-Hilaire [59] est une approche globale qui subdivise le
probl`eme en trois sous-probl`emes. Pour cette approche, l’auteur formule un mod`ele math´e-
matique qui regroupe la formulation faite de chacun des sous-probl`emes pris s´epar´ement.
Ensuite, une ´evaluation du mod`ele est r´ealis´ee au moyen de la recherche taboue. L’objectif
principal de l’auteur consiste `a s´electionner le nombre, l’emplacement, le type de nœuds du](https://image.slidesharecdn.com/2011germineseide-140603143923-phpapp02/85/2011-germine-seide-38-320.jpg)

![22
– xkt
3 une variable d´ecisionnelle qui vaut 1 si un MSC de type t ∈ T3 est install´e `a un site
k ∈ S3, et 0 sinon ;
– xlt
4 une variable d´ecisionnelle qui vaut 1 si un SGSN de type t ∈ T4 est install´e `a un site
k ∈ S4, et 0 sinon.
2.3.3 Cas des r´eseaux 4G
Les r´eseaux de prochaine g´en´eration orientent la planification des r´eseaux cellulaires
vers de nouvelles avenues de recherche. En effet, les tendances portent de plus en plus vers
une int´egration transparente des technologies sans fil existantes, comme les syst`emes GSM,
LAN, AdHoc en un environnement totalement h´et´erog`ene [37], [41]. Cette nouvelle vague de
pens´ee distingue la 4`eme g´en´eration des g´en´erations pr´ec´edentes, o`u seul primait le besoin
de d´eveloppement de nouvelles normes et de nouveaux standards. Les syst`emes 4G sont
compl`etement orient´es vers l’utilisateur final, en fournissant des services vari´es `a haut d´ebit
et sans coupure `a travers les r´eseaux. Toutefois, la migration des syst`emes actuels vers la
4`eme g´en´eration constitue un ´enorme d´efi. Dans la litt´erature, plusieurs travaux abordent ce
probl`eme en consid´erant plusieurs aspects [22], [41].
Les chercheurs Beaubrun et al. [22] ´elaborent les principaux facteurs qui doivent ˆetre
pris en compte par les concepteurs des futurs r´eseaux mobiles. Ce sont : la couverture radio,
l’architecture, l’allocation des ressources, l’itin´erance globale et l’ing´enierie de trafic. Chacun
de ces facteurs traite d’un aspect particulier du probl`eme de planification. Les chercheurs
proposent dans ce cas une approche modulaire qui subdivise le probl`eme de planification
des r´eseaux de prochaine g´en´eration en des sous-probl`emes plus faciles `a r´esoudre. Les sous-
probl`emes li´es `a l’allocation des ressources et l’itin´erance globale seront retenus pour analyse,
parce qu’ils sont li´es aux probl`emes d’affectation des cellules. Une bonne allocation des res-
sources doit permettre au r´eseau d’assurer la continuit´e de la connexion de l’utilisateur en
d´eplacement. Dans les r´eseaux de prochaine g´en´eration, cette mobilit´e implique un d´eplace-
ment `a travers des r´eseaux utilisant des technologies diff´erentes, ce qui n´ecessite la gestion
de diff´erents types de trafic, avec des d´ebits et des d´elais diff´erents.
Beaubrun et al. proposent, `a cet effet, une m´ethode d’optimisation des ressources
du r´eseau bas´ee sur l’utilisation faite de ses ressources. Ils consid`erent les param`etres des
diff´erents types de trafic et le mod`ele de mobilit´e pour ´evaluer la quantit´e de ressources `a
allouer `a chaque utilisateur suivant ses besoins. Ainsi, le syst`eme pourra r´eguler l’utilisation
faite de la bande passante lors du passage d’un service gourmand en ressources (jeux vid´eo,](https://image.slidesharecdn.com/2011germineseide-140603143923-phpapp02/85/2011-germine-seide-40-320.jpg)
![23
streaming etc..) vers un autre service moins exigeant (SMS, courriel). Ce qui permet en outre
de garantir une bonne qualit´e de service en termes de probabilit´e de blocage de nouveaux
appels, et de temps de latence dˆu aux rel`eves. L’itin´erance globale permet de g´erer efficace-
ment la mobilit´e globale de l’utilisateur dans ces syst`emes multi-technologiques, tout en lui
permettant d’acc´eder `a ses services quelque soit sa position g´eographique. Une solution au
probl`eme d’itin´erance globale des r´eseaux de prochaine g´en´eration a ´et´e propos´ee dans [21].
Les auteurs pr´esentent une nouvelle passerelle intelligente appel´ee WING (Wireless Networ-
king Gateway) qui facilite les ´echanges inter-syst`emes et permet de convertir les formats de
signaux et de messages d’un r´eseau `a un autre. WING contrˆole les appels de rel`eve, assure une
interop´erabilit´e entre les sous-syst`emes lors de l’itin´erance globale, et effectue une r´eduction
du trafic de signalisation au niveau des bases de donn´ees lors des mises `a jour des param`etres
de localisation du UE.
2.3.4 Cas des r´eseaux d’extension
Il existe tr`es peu de travaux qui traitent de l’extension des r´eseaux mobiles. L’auteur
Chamberland propose dans [23], une approche globale qui regroupe les trois sous-probl`emes
de la planification, pour aborder le probl`eme d’extension. La m´ethode de r´esolution propos´ee
comprend un mod`ele math´ematique et une m´ethode d’´enum´eration implicite. Le mod`ele com-
mence par repr´esenter le r´eseau existant. L’objectif de l’auteur est de d´eterminer le nombre,
l’emplacement des nouveaux nœuds `a ajouter, de s´electionner les nœuds existants `a enlever
de mani`ere `a minimiser une fonction de coˆut (CL(v) + CN (x)) exprim´ee en fonction :
– du coˆut d’ajout des liens et interfaces des nouveaux nœuds, et du coˆut de retrait des
liens et interfaces de certains nœuds existants.
CL(v) =
i∈S1 j∈S2 m∈M12
(aijm
12 (vijm
12 − ¯vijm
12 ) + Aijm
12 (vijm
12 − ¯vijm
12 )+
)
+
j∈S2 k∈S3 m∈M23
(ajkm
23 (vjkm
23 − ¯vjkm
23 ) + Ajkm
23 (vjkm
23 − ¯v23jkm
)+
)
+
j∈S2 l∈S4 m∈M24
(ajlm
24 (vjlm
24 − ¯vjlm
24 ) + Ajlm
24 (vjlm
24 − ¯vjlm
24 )+
) (2.7)
– du coˆut d’installation et de connexion des nouveaux nœuds, et du coˆut de retrait de](https://image.slidesharecdn.com/2011germineseide-140603143923-phpapp02/85/2011-germine-seide-41-320.jpg)
![24
certains nœuds existants.
CN (x) =
t∈T1
(bt
1(
i∈S1
(xit
1 − ¯xit
1 )) + Bt
1(
i∈S1
(¯xit
1 − xit
1 )+
)
+
t∈T2
(bt
2(
j∈S2
(xjt
2 − ¯xit
2 )) + Bt
2(
i∈S2
(¯xit
2 − xit
2 )+
)
+
t∈T3
(bt
3(
k∈S3
(xkt
3 − ¯xit
3 )) + Bt
3(
i∈S3
(¯xit
3 − xit
3 )+
)
+
t∈T4
(bt
4(
l∈S4
(xlt
4 − ¯xit
4 )) + Bt
4(
i∈S4
(¯xit
4 − xit
4 )+
) (2.8)
avec
– ¯xit
1 une variable d´ecisionnelle qui vaut 1 si le Node B de type t ∈ T1 est install´e `a un
site i ∈ S1 dans le r´eseau en place, et 0 sinon ;
– ¯vijm
12 repr´esentant le nombre de liens de type m ∈ M12 pour connecter un Node B install´e
`a un site i ∈ S1, `a un RNC install´e `a un site j ∈ S2, dans le r´eseau en place ;
– Aijm
12 (Ajkm
23 , Ajlm
24 ) les coˆuts de retraits des liens et des interfaces de type m ∈ M12
(m ∈ M23, m ∈ M24) install´es entre les sites i ∈ S1 et j ∈ S2 (i ∈ S2 et j ∈ S3, i ∈ S2
et j ∈ S4) ;
– Bt
1, Bt
2, Bt
3, et Bt
4 repr´esentant respectivement, le coˆut de retrait d’un Node B (RNC,MSC,
SGSN) de type t ∈ T1 (t ∈ T2, t ∈ T3, t ∈ T4).
Ce mod`ele est sujet aux contraintes d’unicit´e des affectations des nœuds, de capacit´e
des liens et des ´equipements. De mˆeme, les contraintes d’int´egralit´e et de non n´egativit´e
doivent ˆetre respect´ees. Pour ´evaluer la performance du mod`ele, l’auteur utilise l’algorithme
Branch-and-bound qui prend en param`etres, le nombre de Node B, de RNC, de MSC et de
SGSN, et les diff´erents types de liens et interfaces.
L’´evaluation `a grande ´echelle du travail a ´et´e faite par St-Hilaire [60]. L’auteur se
base sur un algorithme de recherche taboue semblable `a [23], qui ex´ecute des mouvements
vari´es en fonction des types de nœuds, de liens et interfaces disponibles. Il calcule le meilleur
coˆut de l’extension `a l’ajout et/ou au retrait de certains nœuds.](https://image.slidesharecdn.com/2011germineseide-140603143923-phpapp02/85/2011-germine-seide-42-320.jpg)
![25
2.4 M´ethodes de r´esolution bas´ees sur des heuristiques
Dans cette section, trois des principales heuristiques adapt´ees au probl`eme d’af-
fectation seront d´ecrites. Ce sont : le recuit simul´e, la recherche taboue et les agorithmes
m´em´etiques [43], [51], [53].
2.4.1 Recuit simul´e
Le recuit simul´e est un algorithme de recherche locale bas´ee sur la notion de voisi-
nage entre les configurations. Chaque configuration S est obtenue en appliquant un ensemble
de mouvements M(S) d´efinis de fa¸con al´eatoire suivant le crit`ere de M´etropolis. De mani`ere
g´en´erale, un mouvement est automatiquement accept´e s’il am´eliore le coˆut de la solution
actuelle. Sinon, il sera appliqu´e selon une probabilit´e qui d´epend d’une certaine temp´erature.
Selon le crit`ere de M´etropolis, plus la temp´erature est ´elev´ee, plus il est possible d’accepter de
mauvaises solutions [39]. Ainsi, en adaptant le recuit simul´e au probl`eme d’affectation, une
am´elioration de la solution sera toujours accept´ee alors qu’une augmentation de la fonction
de coˆut sera accept´ee avec une certaine probabilit´e qui d´epend de la temp´erature [43].
2.4.2 Recherche taboue
L’algorithme de recherche taboue consiste `a am´eliorer it´erativement une solution
initiale afin d’aboutir `a une solution finale respectant les contraintes de capacit´e et d’unicit´e
des affectations aux commutateurs. Cette am´elioration se r´ealise au moyen de mouvements
qui permettent de passer d’une solution `a une autre dans un espace de recherche pr´ed´efini. Cet
algorithme est bas´e sur un m´ecanisme de m´emoire (liste taboue) qui exclut les mouvements
d´ej`a effectu´es et ´evite d’y revenir pendant un certain nombre d’it´erations.
Pour r´esoudre le probl`eme d’affectation des cellules aux commutateurs dans les
r´eseaux mobiles, les auteurs dans [25], [34], [51] et [59] proposent une solution initiale qui
affecte chaque Node B i au RNC j le plus proche. De mˆeme, chaque RNC j sera affect´e
simultan´ement aux MSC k et SGSN l les plus proches. L’algorithne tabou, dans le but
d’am´eliorer la solution initiale, effectue des mouvements sur l’ensemble des nœuds. Quand
il s’agit d’un mouvement de r´eaffectation, le Node B i sera r´eaffect´e au RNC j , ensuite, le
RNC j sera r´eaffect´e `a un MSC k et SGSN l qui g´en`erent le plus faible gain. D’autres types
de mouvements, comme le retrait et le changement du type d’un Node B i, d’un RNC j, d’un
MSC k et d’un SGSN l d´ej`a install´es sont ´egalement consid´er´es. L’algorithme sauvegarde
chaque mouvement effectu´e dans une liste taboue pendant un nombre kmax it´erations, ce qui
repr´esente le crit`ere d’arrˆet de l’algorithme. `A chaque it´eration, une ´evaluation de la solution](https://image.slidesharecdn.com/2011germineseide-140603143923-phpapp02/85/2011-germine-seide-43-320.jpg)
![26
permet de v´erifier le respect des contraintes de capacit´e. En cas de non-respect, une p´enalit´e
est ajout´ee au coˆut de la solution.
2.4.3 Algorithmes m´em´etiques
L’algorithme m´em´etique, contrairement aux diff´erentes m´ethodes d´ej`a ´etudi´ees,
tend `a faire ´evoluer, non pas une seule, mais plusieurs configurations (chromosomes) dont
l’ensemble constitue une population. Les candidats qui participent `a la reproduction sont
choisis de fa¸con al´eatoire et les chromosomes sont mut´es suivant une certaine probabilit´e.
Ainsi, l’adaptation au probl`eme d’affectation vise `a trouver `a partir d’une population initiale
de chromosomes, la meilleure affectation qui permet de minimiser le coˆut du r´eseau, tout en
respectant les contraintes de capacit´es des commutateurs et celles li´ees `a l’unicit´e des affec-
tations des cellules aux commutateurs. Les solutions obtenues du probl`eme sont des chaˆınes
de chromosomes. Chaque chaˆıne repr´esente le sch´ema d’affectation recherch´e, o`u chaque case
de la chaˆıne re¸coit le num´ero du commutateur auquel la cellule est affect´ee. La longueur de la
chaˆıne est ´egale au nombre de cellules et restera inchang´ee, car toutes les cellules doivent ˆetre
affect´ees. La valeur maximale d’un g`ene de ces chromosomes est ´egale au nombre maximal
de commutateurs du r´eseau. Cet algorithme comporte des op´erateurs g´en´etiques de s´election,
de croisement et de mutation œuvrant `a faire varier les populations.
Les auteurs Hedible et al. [32], et Suresh et al. [55] proposent un mod`ele math´e-
matique coupl´e de l’algorithme g´en´etique pour r´esoudre le probl`eme d’affectation des cellules
aux commutateurs. Ce mod`ele math´ematique inclut une fonction objective `a minimiser qui
comptabilise les coˆuts de liaisons et de rel`eves entre les nœuds. Cette fonction est soumise `a
des contraintes de capacit´e et d’unicit´e des affectations. Les auteurs d´efinissent une popula-
tion initiale, puis alt`ere cette solution au moyen de deux types d’op´erateurs g´en´etiques : un
op´erateur de croisement et un op´erateur de mutation. La solution obtenue est ensuite ´evalu´ee
pour la v´erification du respect des contraintes.
Les auteurs Quintero et al. [53] s’inspirent de l’approche utilis´ee par [32] `a laquelle ils
appliquent un algorithme de recherche locale. L’algorithme obtenu porte le nom d’algorithme
m´em´etique. En effectuant des tests de comparaison avec d’autres heuristiques, comme la
recherche taboue, les r´esultats montrent que la m´ethode propos´ee apporte une am´elioration
sur la fonction de coˆut obtenue par la recherche taboue.](https://image.slidesharecdn.com/2011germineseide-140603143923-phpapp02/85/2011-germine-seide-44-320.jpg)
![27
2.5 Analyse des travaux
Ce chapitre pr´esente principalement les deux approches utilis´ees pour traiter le pro-
bl`eme d’affectation et d’extension dans la planification des r´eseaux mobiles. La premi`ere
approche est dite globale parce qu’elle int`egre tous les aspects du probl`eme. C’est une ap-
proche qui est tr`es fastidieuse et requiert beaucoup de temps d’impl´ementation. Toutefois,
elle s’av`ere ˆetre tr`es efficace dans la prise de d´ecision du planificateur dans le cas d’une nou-
velle implantation, pour pr´evoir une extension du syst`eme en place ou tout simplement dans
la maintenance du r´eseau. Ces d´ecisions se basent alors sur la coh´erence et la pr´eservation
des interactions qui existent entre chaque sous-probl`eme. L’auteur St-Hilaire pr´esente dans
[59] un cadre global de planification des r´eseaux mobiles. L’auteur a pu montrer l’efficacit´e
de cette m´ethode, mais certaines limitations sont `a signaler. En effet, l’auteur ne consid`ere
pas la notion de mobilit´e qui rel`eve d’une grande importance dans les r´eseaux mobiles. Cette
mobilit´e consiste mˆeme un champ d’expertise dans le domaine des t´el´ecommunications. De
plus, avec l’av`enement des r´eseaux de prochaine g´en´eration qui se proposent de regrouper di-
vers environnements mobiles et incompatibles en une infrastructure unique [21], une approche
globale doit n´ecessairement tenir compte de l’itin´erance globale.
La seconde approche est dite s´equentielle et permet de cibler un probl`eme sp´ecifique
de la planification. Dans cette approche, chaque probl`eme est trait´e s´epar´ement, facilitant
ainsi la tˆache du planificateur en l’aidant `a d´etecter une panne pr´ecise, sans avoir `a passer `a
travers les autres ´etapes de la planification. C’est dans ce contexte que se situe le travail r´ealis´e
par Diallo dans [25]. Dans ce travail, l’auteur traite directement du probl`eme d’affectation
des cellules, et d´efinit les concepts de rel`eve simple et de rel`eve complexe li´es `a la mobilit´e. Ce
travail ne fait pas une gestion de la mobilit´e `a proprement parler. Il tient compte de la notion
d’itin´erance, en permettant aux op´erateurs d’estimer dans la planification, le coˆut de la mise
`a jour des informations `a la suite d’une rel`eve. Ce travail pr´esente ´egalement des r´esultats
assez concluants, mais l’auteur ne pr´esente aucune garantie dans la migration de ces r´eseaux,
vers un r´eseau de prochaine g´en´eration.
Le probl`eme li´e `a l’´evolutivit´e des r´eseaux mobiles vers des r´eseaux de nouvelle
g´en´eration est souvent pos´e quand l’op´erateur d´esire augmenter le nombre de ses abonn´es.
L’´evolution du r´eseau existant peut se r´ealiser, soit en ´etendue territoriale (milieux urbains,
p´eriurbains et ruraux), soit simplement en diversifiant les services offerts, soit les deux `a la
fois. Ce dernier cas est celui qui est consid´er´e dans ce m´emoire, et consiste essentiellement
en une mise `a jour du r´eseau, soit par l’ajout de nouveaux ´equipements, soit par le retrait de
certains ´equipements d´ej`a en place. Dans son approche de r´esolution, Chamberland [23] uti-](https://image.slidesharecdn.com/2011germineseide-140603143923-phpapp02/85/2011-germine-seide-45-320.jpg)
![28
lise une approche gloable de planification. Cependant, le travail ne refl`ete pas une migration
vers un r´eseau de nouvelle g´en´eration. Les auteurs dans [37] ont tent´e d’apporter une solution
au probl`eme de planification, dans l’´evolutivit´e d’un r´eseau existant vers un r´eseau de pro-
chaine g´en´eration. Ce travail ne pr´esente qu’une architecture d’interconnexion de diff´erentes
technologies, et ne traite que de la performance de l’architecture.
Bien que plusieurs travaux aient ´et´e effectu´es sur la planification des r´eseaux mobiles
[22]-[59], l’aspect du probl`eme li´e `a l’´evolutivit´e d’un r´eseau mobile existant dans un cadre
multi-technologique laisse certaines avenues de recherche non encore explor´ees. Ainsi, ce tra-
vail consistera `a planifier un r´eseau 4G/LTE `a partir d’un r´eseau 3G/UMTS, d´ej`a en place et
fonctionnel. Cet aspect diff´erencie ce m´emoire des travaux qui ont fait l’objet d’analyse dans
ce chapitre. Plus sp´ecifiquement, l’aspect de la planification qui sera abord´e dans ce travail est
l’affectation des cellules aux commutateurs. Il consistera alors `a affecter les nouveaux eNode
B aux SGW et MME, et `a affecter les nœuds existants SGSN de l’UMTS aux mˆemes SGW
et MME. Puisque les travaux des r´eseaux pr´ec´edents ne peuvent pas s’adapter au probl`eme
de planification d’un r´eseau 4G `a partir d’un r´eseau 3G existant, alors une nouvelle approche
sera utilis´ee pour traiter ce probl`eme dans le cadre de ce m´emoire.](https://image.slidesharecdn.com/2011germineseide-140603143923-phpapp02/85/2011-germine-seide-46-320.jpg)
![29
CHAPITRE 3
MOD´ELISATION DU PROBL`EME D’AFFECTATION DANS LA
PLANIFICATION D’UN R´ESEAU 4G
Faire ´evoluer un r´eseau existant vers un r´eseau 4G requiert une allocation des
ressources les plus efficaces [21]. De ce fait, le probl`eme d’affectation pr´esente un grand d´efi
et doit avoir une consid´eration particuli`ere dans la planification des r´eseaux mobiles. Ce
probl`eme a fait l’objet de nombreuses ´etudes dans la litt´erature, plus pr´ecis´ement pour les
r´eseaux de deuxi`eme (2G) et de troisi`eme (3G) g´en´eration [35], [51]. Pour aborder le probl`eme
dans le cas des r´eseaux 4G, dans la suite de ce chapitre, seront d´efinis certains concepts de
base, utiles `a la formulation du probl`eme. Ensuite, l’architecture du r´eseau sera pr´esent´ee, et
permettra au moyen des ensembles d´ecrivant les ´equipements, et des variables, d’´elaborer le
mod`ele math´ematique propos´e. Ce chapitre se termine par une analyse de la compl´exit´e du
probl`eme, dans le but de trouver une m´ethode de r´esolution ad´equate.
3.1 Concepts de base
Le probl`eme d’affectation des cellules aux commutateurs consiste, de fa¸con g´e-
n´erale, `a d´eterminer un patron d’affectation des cellules aux commutateurs dans le but de
minimiser une fonction de coˆut quadratique, tout en respectant les contraintes de capacit´es
de ces commutateurs. Dans la planification d’un r´eseau 4G r´ealis´ee `a partir d’un r´eseau 3G
existant, le probl`eme d’affectation consiste `a trouver un patron d’affectation entre les nœuds
eNode B, SGSN, MME et SGW qui permet de minimiser cette fonction de coˆut, tout en res-
pectant certaines contraintes. Il convient alors de consid´erer les affectations entre les nœuds
du r´eseau 4G et les affectations entre les nœuds des r´eseaux 3G et 4G. De ce fait, deux types
de rel`eves sont `a consid´erer : une rel`eve horizontale et une rel`eve verticale qui peuvent ˆetre
simples ou complexes. Ce m´emoire tient compte uniquement de la rel`eve horizontale inter-4G
et de la rel`eve verticale entre les r´eseaux 3G et 4G.
3.1.1 Rel`eve horizontale simple
Au niveau du r´eseau 4G, la rel`eve horizontale simple est d´eclench´ee au niveau des
nœuds eNode B, reli´es `a un mˆeme MME et un mˆeme SGW. Le terminal mobile qui se trouve
`a la fronti`ere de sa cellule courante envoie une requˆete de rel`eve `a l’eNode B e desservant cette
cellule. Cette requˆete peut ˆetre intercept´ee directement par la cellule destination desservie par](https://image.slidesharecdn.com/2011germineseide-140603143923-phpapp02/85/2011-germine-seide-47-320.jpg)
![30
un eNode B e au moyen de l’interface X2, ou en passant par le MME et le SGW communs
`a e et e au moyen de l’interface S1 repr´esent´ee `a la figure 3.1 [15].
Figure 3.1 Rel`eve simple via interface X2 du r´eseau LTE
3.1.2 Rel`eve horizontale complexe
Dans cette rel`eve, le transfert des informations d’un usager passant d’une cellule `a
une autre fait intervenir des eNode B diff´erents, soient e, e , eux mˆemes reli´es `a des MME et
des SGW diff´erents, telle qu’illustr´ee `a la figure 3.2. Ainsi, l’eNode B source e d´eclenche le
m´ecanisme de rel`eve en envoyant, au moyen de l’interface S1, une requˆete au MME qui lui
est affect´e. Le MME `a son tour v´erifie les informations re¸cues de la rˆequette et les achemine
`a l’eNode B cible e auquel elles sont destin´ees. Les op´erations li´ees `a la rel`eve s’ach`event
quand l’eNode B e re¸coit la confirmation sur la reception des informations de l’eNode B e
[47].
Figure 3.2 Rel`eve horizontale complexe dans le r´eseau LTE](https://image.slidesharecdn.com/2011germineseide-140603143923-phpapp02/85/2011-germine-seide-48-320.jpg)
![31
3.1.3 Rel`eve verticale simple
La rel`eve verticale fait intervenir les cellules appartenant `a des technologies d’acc`es
radio diff´erentes [19]. Cette rel`eve permet ainsi d’assurer la continuit´e des services quand le
type d’acc`es utilis´e n’est plus offert sur la couverture courante de l’utilisateur [16]. ´Etant
donn´e que ce m´emoire traite de la planification d’un r´eseau 4G `a partir d’un r´eseau 3G,
la rel`eve verticale fera usage des interfaces Iub et Iu pour le r´eseau 3G bas´e UMTS, et des
interfaces S1 et S4 pour le r´eseau 4G bas´e LTE, comme le montre la figure 3.3. Les principaux
nœuds qui interviennent dans la connexion des deux r´eseaux sont : le SGSN du r´eseau UMTS,
le MME et le SGW du r´eseau LTE. Ainsi, pour effectuer le transfert d’informations `a travers
le r´eseau, une requˆete est envoy´ee par l’eNode B source via l’interface S1 au MME. Ce
dernier, informe alors le SGW et le SGSN destination au moyen des interfaces S11, S3 et S4
desservant la cellule o`u l’UE se dirige [20]. Ainsi, les ´echanges effectu´es lors de cette rel`eve
permettent de maintenir la session de l’utilisateur sans interruption pendant que ce dernier
se d´eplace `a travers les r´eseaux d’acc`es diff´erents.
Figure 3.3 Rel`eve verticale entre les r´eseaux LTE et UMTS
3.1.4 Rel`eve verticale complexe
La rel`eve verticale est dite complexe quand l’eNode B et le SGSN sont chacun li´es `a
des MME et SGW diff´erents, comme illustr´ee `a la figure 3.4. Par cons´equent, tout transfert](https://image.slidesharecdn.com/2011germineseide-140603143923-phpapp02/85/2011-germine-seide-49-320.jpg)


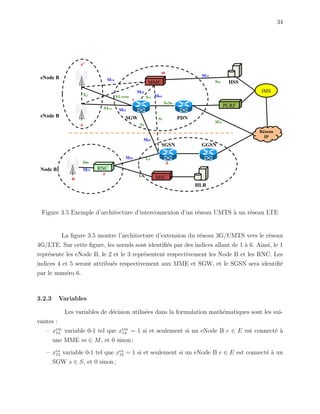












![47
3.5 Analyse de la complexit´e du mod`ele math´ematique
L’analyse de la complexit´e du probl`eme d’affectation dans la planification d’un
r´eseau 4G `a partir d’un r´eseau 3G existant est influenc´ee par le nombre et les niveaux des
´equipements dans l’architecture. En effet, plus il existe des niveaux d’´equipements et plus il
existe des combinaisons d’affectations. Plus il existe des combinaisons et plus nombreuses sont
les op´erations de mises `a jour en cas de rel`eve, plus sp´ecifiquement en cas de rel`eve complexe.
En effet, l’architecture r´esultante de l’affectation fait intervenir des ´equipements appartenant
`a des niveaux diff´erents, de technologies diff´erentes et par cons´equent regroupe un ensemble
de caract´eristiques, plus diversifi´es les uns les autres. Ainsi, l’analyse de la compl´exit´e du
probl`eme sera bas´ee sur l’analyse faite de la complexit´e des deux r´eseaux impliqu´es dans
l’architecture.
Les deux niveaux que pr´esente le r´eseau 4G/LTE le rapprochent de l’architecture
des r´eseaux 2G. Dans les travaux r´ealis´es pour r´esoudre le probl`eme d’affectation des r´eseaux
2G, les auteurs montrent l’´equivalent de ce probl`eme `a celui du partitionnment des graphes
[51], [53]. Par analogie, chaque cellule desservie par un eNode B dans le r´eseau 4G/LTE et
par un Node B du r´eseau 3G/UMTS sera consid´er´ee comme un sommet du graphe. Les coˆuts
des rel`eves horizontale et verticale entre chaque paire de nœuds repr´esentent, en l’occurrence
un arc reliant deux sommets du graphe. Le probl`eme d’affectation dans le pr´esent contexte
devient donc un probl`eme NP-difficile. Il faut donc exclure l’usage d’une m´ethode exacte.
Les m´ethodes exactes, comme l’algorithme `a ´enum´eration exhaustive, sont de com-
plexit´e exponentielle. Elles offrent une solution exacte, mais peuvent exploser avec la taille
du probl`eme. En effet, avec e eNode B, g SGSN, s SGW et m MME ou q SGM, le principe
de r´esolution consisterait `a effectuer un nombre de (m + s)e
et (m + s)g
ou de q(e+g)
com-
binaisons [40]. Trouver dans ce cas les sch´emas d’affectations qui permettront de r´eduire le
coˆut tout en estimant la capacit´e de chacun des nœuds MME, SGW ou SGM, n´ecessiterait
un temps de traitement important. Tel que d´efini, le probl`eme d’affectation se pr´esente alors
comme un probl`eme d’optimisation dont le but est de trouver une solution minimisant le
coˆut des affectations et celui des rel`eves de mani`ere `a r´eduire le coˆut d’extension, assurer une
meilleure couverture de la zone consid´er´ee, tout en respectant les contraintes de capacit´es des
nœuds du r´eseau cœur. Cette caract´eristique oriente vers le choix d’une heuristique qui offre
en un temps raisonnable des r´esultats qui convergent vers l’optimum. De ces algorithmes, la
recherche taboue sera utilis´ee.](https://image.slidesharecdn.com/2011germineseide-140603143923-phpapp02/85/2011-germine-seide-65-320.jpg)
![48
CHAPITRE 4
ADAPTATION DE LA RECHERCHE TABOUE AU PROBL`EME DE
PLANIFICATION DES R´ESEAUX 4G/LTE
Ce chapitre porte essentiellement sur l’adaptation de la recherche taboue au pro-
bl`eme de planification dans les r´eseaux 4G. Ainsi, la prochaine section fera une description
sommaire de l’heuristique, suivie des ´etapes d’adaption aux r´eseaux mobiles 4G. Ensuite,
dans les sections subs´equentes, seront d´ecrites les ´etapes menant `a la g´en´eration de la solu-
tion initiale, pour finir par la description et l’adaptation des m´ecanismes de m´emoire `a court,
`a moyen et `a long terme, utilis´es pour am´eliorer les coˆuts des solutions initiales obtenues.
4.1 Adaptation de la recherche taboue aux r´eseaux 4G
La recherche taboue est une recherche locale, dont le principe de fonctionnement
repose essentiellement sur l’exploration de l’ensemble des voisins de la solution courante.
Deux principaux param`etres sont `a consid´erer dans cet algorithme : la liste taboue et la te-
nure de la solution. La liste taboue est une m´emoire propre `a l’algorithme, qui garde la trace
des solutions d`ej`a explor´ees afin de ne pas les reproduire. Cette m´emoire permet d’exclure
certains choix de mouvements, et par cons´equent restreindre les voisinages de la solution du
probl`eme. La notion de tenure est la dur´ee du statut tabou d’une solution. Elle est utilis´ee
pour indiquer pendant combien d’it´erations, le mouvement g´en´erant cette solution reste ta-
bou [29].
L’adaptation de la recherche taboue au probl`eme d’affectation dans la planification
des r´eseaux 4G commence par la cr´eation d’une solution initiale. Cette solution est g´en´er´ee
`a partir des donn´ees d´ecrivant les caract´eristiques du r´eseau et fournies en param`etre au
probl`eme. Le r´esultat obtenu est une topologie pr´esentant le mode d’affectation des eNode B
et des SGSN aux composantes MME, SGW ou SGM. Puisque le r´eseau UMTS est pr´ealable-
ment ´etabli, alors les premiers ´el´ements qui seront affect´es sont les nouveaux nœuds `a ajouter
au r´eseau UMTS. Pour ce faire, la solution initiale effectue l’affectation en partant du niveau
d’´equipements le plus bas de la hi´erarchie, les eNode B, vers le niveau le plus haut compos´e
des MME, des SGW ou des SGM. La deuxi`eme affectation r´ealise l’interconnexion des deux
r´eseaux. Alors, en se basant sur le principe d’affectation ascendante, les SGSN seront `a leur
tour affect´es aux composantes MME, SGW ou SGM. Le r´esultat issu de la solution initiale](https://image.slidesharecdn.com/2011germineseide-140603143923-phpapp02/85/2011-germine-seide-66-320.jpg)


![51
C(n) telle que :
C(n) ≤ (Cmin + α(Cmax − Cmin)) (4.1)
Les nœuds candidats, Cmax, repr´esentent l’ensemble des SGW et des MME du
r´eseau. Alors, Cmax sera ´egale `a |M| ou `a |S|. Le premier nœud du r´eseau, Cmin, sera ´egal `a 0, et
α repr´esente la graine al´eatoire comprise dans les intervalles [0, |M|] et [0, |S|], comme indiqu´e
dans l’algorithme 1. Pour chaque affectation, l’algorithme renvoie un coˆut total compos´e de
la sommation des coˆuts de liaison entre les eNode B et les SGW et MME, et celle des coˆuts de
liaisons entre les SGSN et les SGW et MME auxquels ils sont affect´es. L’algorithme s’arrˆete
quand tous les eNode B et tous les SGSN sont affect´es.
Tableau 4.5 Affectation des eNode B aux MME et SGW
eNode B MME SGW
0 2 0
1 0 1
2 1 2
3 0 1
4 1 2
5 0 1
6 1 0
7 2 2
8 1 0
9 2 1
Tableau 4.6 Affectation des SGSN aux MME et SGW
SGSN MME SGW
0 1 2
1 0 1
2 2 0
3 0 1
4 1 2
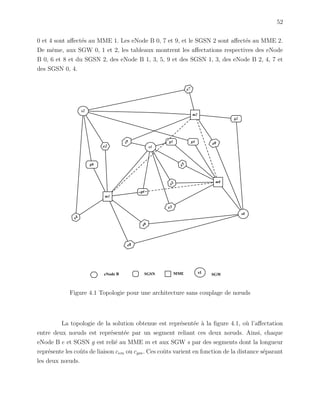
Pour illustrer les r´esultats issus de l’ex´ecution de l’algorithme 1, un r´eseau com-
portant 10 eNode B, 5 SGSN, 3 MME et 3 SGW sera consid´er´e. Cette ex´ecution est r´ealis´ee
avec comme unique contrainte, celle d’affecter chaque eNode B e et chaque SGSN g `a un
seul MME m et un seul SGW s. Les tableaux 4.5 et 4.6 montrent les r´esultats de la solution
initiale. Chaque case de ces tableaux comporte l’indice du MME m et du SGW s auxquels
l’eNode B e et le SGSN g sont affect´es. Ainsi, les tableaux 4.5 et 4.6 indiquent, que les eNode
B 1, 3 et 5 et les SGSN 1 et 3 sont affect´es au MME 0. Les eNode B 2, 4, 6 et 8 et les SGSN](https://image.slidesharecdn.com/2011germineseide-140603143923-phpapp02/85/2011-germine-seide-69-320.jpg)
![53
Algorithme 1 Pseudo code de la solution initiale stochastique pour l’architecture sans couplage
de nœuds
Lecture :
- du nombre d’eNode B e, de MME m, de SGW s, de SGSN g,
- des coˆuts de liaison TabCLeNB MME, TabCLeNB SGW, TabCL SGSN MME et
TabCL SGSN SGW
Cmin = 0
CmaxMME = m, CmaxSGW = s
idMME = 0, idSGW = 0
affectationeNB MME = 0, affectationeNB SGW = 0
affectationSGSN MME = 0, affectationSGSN SGW = 0
CAffectation = 0
Pour tout E[i] faire
idMME = Cmin + r.nextInt(CmaxMME − Cmin)
affectationeNB MME[i][idMME] = 1
CAffectation = +TabCLeNB MME[i][idMME]
idSGW = Cmin + r.nextInt(CmaxSGW − Cmin)
affectationeNB SGW[i][idSGW] = 1
CAffectation = +TabCLeNB SGW[i][idSGW]
Fin Pour
Affecter l’eNode B i au MME idMME et au SGW idSGW
Pour tout G[j] faire
idMME = Cmin + r.nextInt(CmaxMME − Cmin)
affectationSGSN MME[j][idMME] = 1
CAffectation = +TabCL SGSN MME[j][idMME]
idSGW = Cmin + r.nextInt(CmaxSGW − Cmin)
affectationSGSN SGW[j][idSGW] = 1
CAffectation = +TabCL SGSN SGW[j][idSGW]
Fin Pour
Affecter le SGSN j au MME idMME et au SGW idSGW](https://image.slidesharecdn.com/2011germineseide-140603143923-phpapp02/85/2011-germine-seide-71-320.jpg)



![57
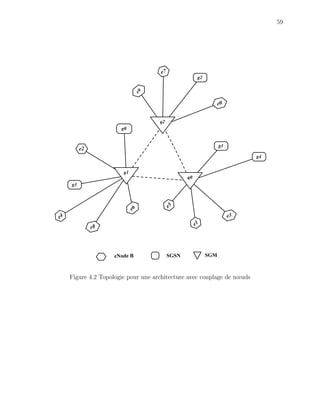
4.2.2 Solutions initales pour l’architecture avec couplage de nœuds
Les algorithmes al´eatoire et de coˆut minimum seront repr´esent´es respectivement
par les algorithmes 3 et 4. Ils re¸coivent en entr´ee le nombre d’eNode B, de SGSN et de
SGM ; les coˆuts de liaisons entre les eNode B et les SGM du tableau 4.11, de mˆeme que
les coˆuts de liaisons entre les SGSN et les SGM du tableau 4.12. Les coˆuts de liaisons ont
´et´e g´en´er´es par une application Matlab, dont les explications se trouvent au chapitre 5. Un
exemple de r´esultats de ces algorithmes sera pr´esent´e dans les sections suivantes pour un
r´eseau comportant 10 eNode B, 5 SGSN et 3 SGM.
Tableau 4.11 Coˆuts de liaisons des eNode B aux SGM
eNode B SGM
0 1 2
0 12 8 8
1 10 0 6
2 6 10 3
3 12 6 6
4 7 12 6
5 0 6 3
6 10 12 6
7 12 10 6
8 6 6 3
9 6 12 6
Tableau 4.12 Coˆuts de liaisons des SGSN aux SGM
SGSN SGM
0 1 2
0 8 8 8
1 16 10 6
2 6 8 3
3 13 12 6
4 6 10 6
L’ex´ecution de l’algorithme 3 affecte chaque eNode B e et chaque SGSN g `a un SGM
q choisi de fa¸con al´eatoire dans la liste des nœuds candidats C(n), telle que d´ecrite dans la
relation 4.1. Les candidats repr´esentent l’ensemble des nœuds SGM du r´eseau. Dans ce cas,
Cmax sera ´egale `a |Q|. La valeur de Cmin sera ´egale `a 0 et α sera compris dans l’intervalle [0 ,
|Q|]. L’algorithme prend fin quand tous les eNode B et tous les SGSN sont affect´es. Le coˆut](https://image.slidesharecdn.com/2011germineseide-140603143923-phpapp02/85/2011-germine-seide-75-320.jpg)

![60
Algorithme 3 Pseudo code de la solution initiale stochastique pour l’architecture sans couplage
de nœuds
Lecture : du nombre d’eNode B e, de MME m, de SGW s, de SGSN g, des coˆuts de liaison
TabCLeNB SGM et TabCL SGSN SGM
Cmin = 0
CmaxSGM = q
idSGM = 0
affectationeNB SGM = 0, affectationSGSN SGM = 0
CAffectation = 0
Pour tout E[i] faire
idSGM = Cmin + r.nextInt(CmaxSGM − Cmin)
affectationeNB SGM[i][idSGM] = 1
CAffectation = +TabCLeNB SGM[i][idSGM]
Fin Pour
Affecter le l’eNode B i au SGM idSGM
Pour tout G[j] faire
idSGM = Cmin + r.nextInt(CmaxSGM − Cmin)
affectationSGSN SGM[j][idSGM] = 1
CAffectation = +TabCLeNB SGM[j][idSGM]
Fin Pour
Affecter le SGSN j au SGM idSGM](https://image.slidesharecdn.com/2011germineseide-140603143923-phpapp02/85/2011-germine-seide-78-320.jpg)


![63
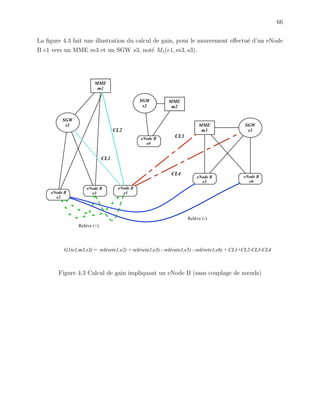
4.3 M´emoire `a court terme
La m´emoire `a court terme ou tabou de base est le premier m´ecanisme d´eclench´e
`a l’ex´ecution de l’algorithme de recherche taboue d´ecrit dans la figure 4.7. `A partir de la
solution initiale g´en´er´ee, la m´emoire `a court terme ex´ecute un ensemble de mouvements. Ces
mouvements permettent de g´en´erer de nouvelles solutions devant am´eliorer la solution de
d´epart. Un certain nombre de ces solutions sont gard´ees en m´emoire (Liste Taboue), `a des
fins d’utilisation lors de l’application des m´ecanismes `a moyen et `a long terme. Dans la suite
de cette section seront d´ecrites les diff´erentes caract´eristiques de la m´emoire `a court terme.
Ce sont : les types de mouvements, les gains g´en´er´es `a l’application de ces mouvements, la
liste taboue, le crit`ere d’aspiration qui permet d’annuler le caract`ere tabou d’un mouvement
et en dernier lieu, la fonction qui permet d’´evaluer la solution trouv´ee.
4.3.1 Mouvements
Soit s ∈ S, une solution courante. Soit N(s) l’ensemble des solutions voisines de
s, obtenues en faisant varier s au moyen de mouvements. Pour la m´emoire `a court terme, les
mouvements consistent `a faire la r´eaffectation des nœuds eNode B e, et SGSN g aux ´equipe-
ments du r´eseau cœur. Ces mouvements de r´eaffectation diff`erent, suivant que l’architecture
consid`ere, ou non un couplage de nœuds.
Dans l’architecture sans couplage de nœuds, plusieurs types de mouvements de
r´eaffectation peuvent ˆetre ´elabor´es. Ainsi, pour passer de la solution initiale fournie par les
algorithmes 1 et 2 `a une nouvelle solution, quatre types de mouvements sont utilis´es. Ils
consistent en une :
– r´eaffectation d’un eNode B e `a un MME m, not´e M1(e, m) ;
– r´eaffectation d’un eNode B e `a un SGW s, not´e M2(e, s) ;
– r´eaffectation d’un SGSN g `a un MME m, not´e M3(g, m) ;
– r´eaffectation d’un SGSN g `a un SGW s, annot´ee M4(g, s).
Une telle vari´et´e de mouvements fait accroˆıtre l’ensemble des solutions possibles de
l’algorithme. Pour limiter le choix des solutions et respecter les sch´emas des rel`eves complexes
des figures 3.2 et 3.4, les mouvements seront regroup´es comme dans [25]. Ainsi M1(e, m) et
M2(e, s) constitueront un seul mouvement M1(e, s, m). De mˆeme, M3(e, m) et M4(e, s) se
regroupent en un mouvement M2(g, s, m). Dans chacun des cas, un changement d’eNode B](https://image.slidesharecdn.com/2011germineseide-140603143923-phpapp02/85/2011-germine-seide-81-320.jpg)




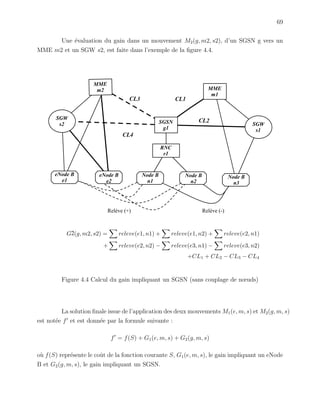



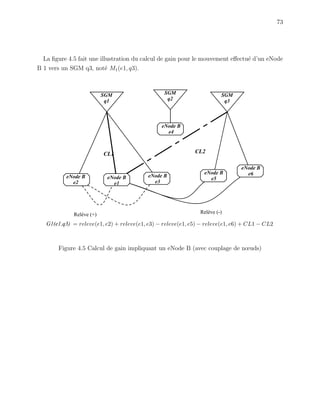
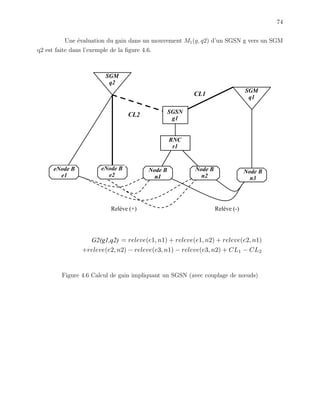






![81
Entity
Mouvement tabou?
Générer la solution initiale
Évaluation de la solution initiale
Générer les tableaux de gains
Initialisation des
variables Nbiter =0,
bestiter =0; bestsol=0
Choisir les mouvements de types M1 et M2 de gain minimal
Appliquer le Mouvement choisi; Mettre à jour la
liste taboue; Mettre à jour les tableaux de gain;
Obtenir la solution s' ;
Ajouter la soution s' dans les tableau statistique
Nbiter = Nbiter+1
S:=s'
Si évaluation évaluation(bestsol)
Alors bestiter:=Nbiter
S remplace la plus ancienne meilleure solution dans tabest[]
Autres mouvements ?
Nbiter-bestiter > kmax?
Choix d'une solution s de tabest[]
nonrespect=0 nonrespect++solution s faisable ?
Nonrespect=0 > = Drespect?
Nbiter = Nbiter+1; S:=s'
Si évaluation(s) < évaluation(bestsol) alors bestiter:=Nbiter
i=i+1 i<count?
Appliquer mouvement M3
Mise à jour de la liste taboue
Mise à jour des tables de gain
Appliquer mouvement M1
Mise à jour de la liste taboue
Mise à jour des tables de gain
Nbiter-bestiter > kmax?
OuiNon Non
Non
Non
Non
Non
Intensification
Non
Diversification
Oui
Oui
Oui
Oui
Oui
Oui
Tabou de base
Figure 4.7 Algorithme Tabou](https://image.slidesharecdn.com/2011germineseide-140603143923-phpapp02/85/2011-germine-seide-99-320.jpg)
![82
CHAPITRE 5
IMPL´EMENTATION ET ANALYSE DES R´ESULTATS
En regard aux objectifs du mod`ele propos´e, ce chapitre pr´esente les ´etapes d’im-
pl´ementation d’une application pouvant servir `a la planification d’un r´eseau 4G/LTE `a partir
d’un r´eseau 3G/UMTS existant. Cette application est un programme informatique ex´ecutant
les diff´erentes ´etapes de l’algorithme de recherche taboue (RT). Elle repose sur des classes et
des m´ethodes, d´ecrivant les fonctionnalit´es des trois m´ecanismes de m´emoire propres `a l’algo-
rithme. Cette application est constitu´ee d’un ensemble de codes ex´ecutables qui, en utilisant
les param`etres cl´es `a la RT, permettent d’´evaluer la performance de la m´ethode de r´esolution
propos´ee. Ainsi, dans la suite de ce chapitre seront pr´esent´es : la m´ethode utilis´ee pour mo-
d´eliser le trafic g´en´er´e par les diff´erents ´equipements du r´eseau, les formats de fichiers utilis´es
en entr´ee et en sortie du programme. De mˆeme, les classes et les m´ethodes ayant servi dans
l’impl´ementation seront d´ecrites pour ensuite discuter des diff´erents r´esultats qui permettront
de montrer l’efficacit´e de la m´ethode propos´ee.
5.1 Pr´esentation des donn´ees utilis´ees
Dans cette section sont d´ecrits : la m´ethode de mod´elisation du trafic du r´eseau,
les formats des fichiers d’entr´ee et du fichier de sortie de l’application, de mˆeme que l’envi-
ronnement mat´eriel et logiciel utilis´e pour l’application.
5.1.1 Mod´elisation du trafic
Le programme de simulation utilis´e pour la mod´elisation du trafic est une appli-
cation Matlab qui s’inspire de [24] et [34], respectivement pour les r´eseaux 3G et 2G. En
cons´equence, plusieurs fonctions doivent ˆetre modifi´ees pour introduire le trafic du r´eseau
4G/LTE. Ainsi, en consid´erant l’architecture avec couplage des nœuds MME et SGW en une
entit´e unique, le SGM, les trafics qui seront consid´er´es sont : un trafic entre les eNode B et
les SGM, au niveau du r´eseau 4G, ensuite, un trafic entre les SGSN et les SGM entre les
r´eseaux 3G et 4G.
Pour mod´eliser ce trafic, les coˆuts de liaisons entre les ´equipements seront consid´er´es.
Pour le r´eseau 4G/LTE, le coˆut de liaison entre les cellules et les SGM sera proportionnel `a la](https://image.slidesharecdn.com/2011germineseide-140603143923-phpapp02/85/2011-germine-seide-100-320.jpg)
![83
distance les s´eparant. Pour r´ealiser l’interconnexion du r´eseau 3G/UMTS avec le r´eseau LTE
tout-IP, et par souci de compatibilit´e, seul le trafic de donn´ees provenant du r´eseau 3G/UMTS
sera consid´er´e. Ainsi, entre un SGSN et un SGM, le coˆut de liaison sera proportionnel `a la
distance les s´eparant.
Pour mod´eliser le trafic en commutation de paquets dans le r´eseau ´etendu, ce travail
consid`ere que le taux d’appels en trafic de donn´ees, fi, provenant des nœuds eNode B et
Node B 1
, suit une loi gamma de moyenne et de variance ´egales `a l’unit´e. De plus, pour tenir
compte des temps de s´ejour des paquets `a l’int´erieur des cellules ou temps de service, ce
travail consid`ere, comme dans [24], que ces temps de service sont distribu´es selon une loi
exponentielle de param`etre 1. En cons´equence, pour un nœud (eNode B ou Node B) i situ´e
dans une cellule j ayant x voisins, l’intervalle [0, 1] est divis´e en x + 1 sous intervalles en
choisissant x nombres al´eatoires uniform´ement distribu´es entre 0 et 1. `A la fin de la p´eriode
de service dans la cellule j, l’appel peut ˆetre, soit transf´er´e au i`eme
voisin, pour i = 1, ..., x,
avec une probabilit´e de rel`eve rij ´egale `a la longueur du i`eme
intervalle, soit termin´e avec une
probabilit´e ´egale `a la longueur du x + 1`eme
intervalle. Pour trouver alors les volumes d’appels
et les taux de rel`eves coh´erents, les cellules sont consid´er´ees comme des files d’attente de type
M/M/1 formant un r´eseau de Jackson [30], [45]. Les taux d’arriv´ees de paquets αi dans les
cellules `a l’´equilibre sont obtenus en r´esolvant le syst`eme suivant :
fi = αi −
k
j=1
αirij avec i = 1, 2, 3, ..., k
o`u
– k repr´esente le nombre total de cellules du r´eseau ;
– rij repr´esente la probabilit´e de rel`eve entre i et j ;
– fi les taux d’appels en trafic de paquets provenant des cellules i.
L’interconnexion des r´eseaux 3G et 4G pr´esente de nouvelles consid´erations au ni-
veau du trafic ´echang´e entre les eNode B et les Node B. En effet, puisque les eNode B sont de
plus grande capacit´e que les Node B, alors ce travail consid`ere que ces derniers re¸coivent un
volume de trafic pouvant seoir `a leur capacit´e. Sera donc choisi comme volume d’appel d’un
eNode B i et d’un Node B n, la longueur moyenne de la file d’attente de chaque nœud, cor-
respondant au type de trafic. Par cons´equent, les taux de rel`eves horizontale hij et verticale
hvin seront d´efinis par :
1. Node B g´en´erant des trafics vers les SGSN](https://image.slidesharecdn.com/2011germineseide-140603143923-phpapp02/85/2011-germine-seide-101-320.jpg)




![88
syst`eme d’exploitation est la version 10.5.8 de Mac OS X, avec un processeur d’une vitesse
de 2.8 GHz et d’une taille m´emoire de 4 GB, pour une fr´equence de 1067 Mhz DDR3. La
g´en´eration des fichiers de trafic et de capacit´e des ´equipements pour le r´eseau sera r´ealis´ee
au moyen d’un programme Matlab, qui utilise une fonction al´eatoire servant `a mod´eliser la
demande en trafic des ´equipements du r´eseau.
5.2 Conception de l’application
La phase de conception de l’outil de planification est r´ealis´ee au moyen du langage
de mod´elisation unifi´e (UML) [31], [49]. Elle se compose principalement d’un diagramme de
classes et d’un diagramme d’´etats transitions.
5.2.1 Diagramme de classes
Le diagramme de classes est utilis´e pour capturer la structure statique de l’outil
de planification propos´e. Il identifie la structure des classes et les associations qui existent
entre elles, comme le montre la figure 5.1. Chacune des classes comporte, les attributs et
les op´erations de l’objet qu’elle repr´esente. Entre les classes sont d´efinis soit une relation
d’h´eritage, soit une association non sym´etrique, l’agr´egation. Par exemple, les classes SolGain
et Mouvement h´eritent respectivement des classes Solution et ListeTaboue (sp´ecification),
alors qu’il existe une agr´egation entre les classes Donn´ees, Intensification, Diversification et
la classe principale qui est Probl`eme. Cette relation traduit l’id´ee que toute action sur une
de ces classes entraˆıne n´ecessairement une action sur la classe Probl`eme.
La notion de package 3G/UMTS utilis´ee est un ensemble de classes qui permettent
de g´erer les affectations au niveau du r´eseau 3G. Ce package g´en`ere d’abord les affectations
entre les Node B et les RNC, ensuite, celles des RNC aux SGSN et MSC. La principale
fonctionnalit´e de ce package est de pouvoir g´en´erer en sortie, un fichier o`u sont d´efinis les
sch´emas d’affectation des Node B aux SGSN.
”Diversification.java” impl´emente le m´ecanisme de la m´emoire `a long terme de l’ap-
plication. Cette classe comprend une m´ethode principale compte() qui permet de sauvegarder
les statistiques des solutions obtenues, tout au long de l’application des m´emoires `a court et `a
moyen terme. Ces statistiques serviront de solutions initiales au red´emarrage de l’application,
dont le nombre est fix´e au moyen d’un attribut de relance nbstart.
”Donn´ees.java”comporte les informations relatives aux r´eseaux de simulation. Cette
classe renseigne sur la taille du r´eseau au moyen d’attributs, comme nbeNB, nbSGSN, nbSGM](https://image.slidesharecdn.com/2011germineseide-140603143923-phpapp02/85/2011-germine-seide-106-320.jpg)



![92
choix_mvt();
cmTaboue();
RechercheTaboue();
Donnees mydata;
Solution lasol;
Solution sol_init;
Gain legain;
ListeTabou plaLT;
Intensification intense;
Diversification diverse;
double bestfaisable;
Noeud[] noeud;
Problème
compte()
int nbstart;
int [][] stat_sol;
Diversification
LectureFic()
LectureFicCapacite()
LectureFicAffectation()
int nbeNB;
int nbSGM;
int nbNB;
int nbSGSN;
int totalNoeud;
double[] TabCapENB;
double[] TabCapSGM;
double[] TabCapSGSN ;
double[][] TabCoutLENB_SGM;
double[][] TabCoutLSGSN_SGM;
double[][] TabAffecNB_SGSN;
double[][] TabCoutReleveENB_ENB;
double[][] TabCoutReleveENB_NB;
double[][] TabCoutReleveNB_ENB;
double[] capaciteResiduelleSGM;
double[][] coutReleve;
double[][] TabCoutLSGSN;
double[][] TabCoutLNoeud_SGM;
double[] capaciteNoeud;
Noeud[] noeud;
Données
générerGain()
getCoutRelève()
tabGainMAJ()
double [][] tabGainNoeud_SGM;
int nbeNodeB, nbSGM, nbNB,
nbSGSN, totalNoeud;
Noeud[] noeud;
Gain
mvtEgal()
int SGM;
int noeudId;
Mouvement
String type;
int noeudId;
Noeud
set();
Solution sol;
Gain gain;
double eval;
double[]
capaciteResiduelleSGM;
double obj;
SolGain
intensifie()
ListeTabou liste1,
liste2;
SolGain[] bestSol
Gain gain
Solution sol
int[] Noeud_SGM;
int compteur;
int solnum;
Intensification
appartient()
noeud tete,
queue;
int taille,
compte;
ListeTaboue
initialise()
initialiseDiv()
vérifierContraintes()
FonctionObjectif()
int nbrEnodeB,
nbrSGM, nbrNB,
nbrSGSN;
int[][]
affectationNoeudSGM;
Solution
Extension3G-4G
3G/UMTS
Affectation
Node B-SGSN
SolutionDiversification Intensification
Probleme
Figure 5.1 Diagramme de classes de l’application
5.2.2 Diagramme d’´etats-transitions
Le diagramme d’´etats-transitions, illustr´e `a la figure 5.2, est utilis´e pour expri-
mer le comportement dynamique des objets. Il permet de d´ecrire les changements d’´etats du
programme au travers des trois m´ecanismes de m´emoire. Un ´etat est caract´eris´e par un des
m´ecanismes de m´emoire : court, moyen et long terme. Une transition repr´esente le passage
instantan´e d’un ´etat vers un autre et est d´eclench´ee suivant la valeur des param`etres MMT](https://image.slidesharecdn.com/2011germineseide-140603143923-phpapp02/85/2011-germine-seide-110-320.jpg)
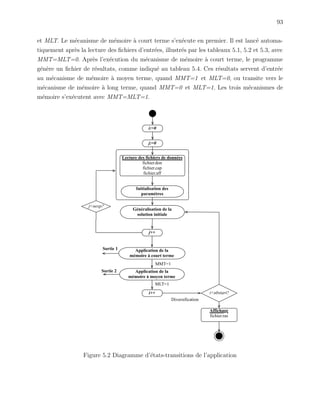


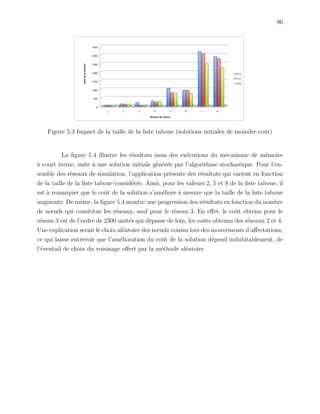


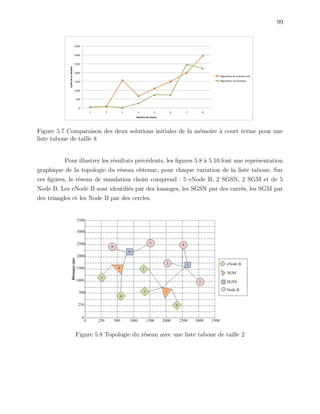
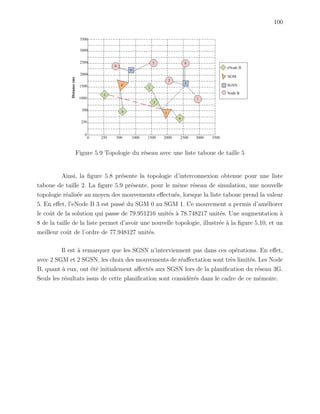

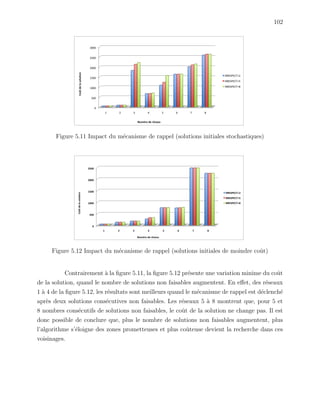

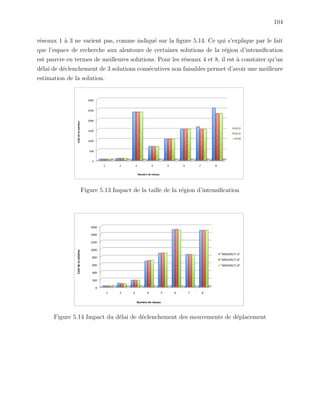
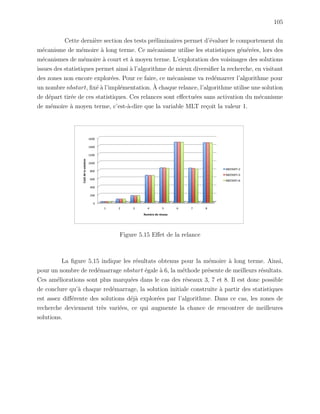
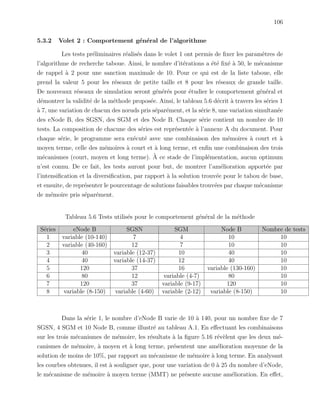
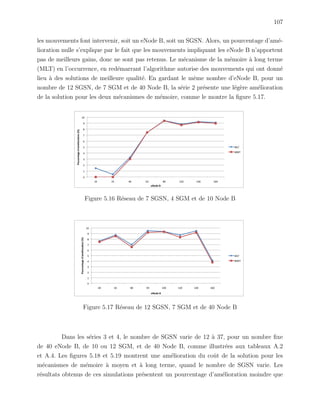
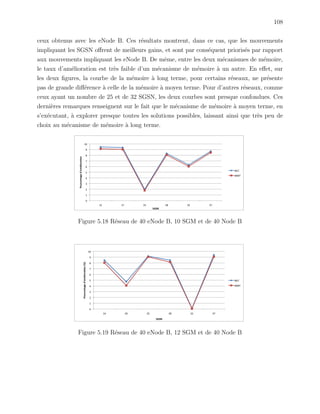
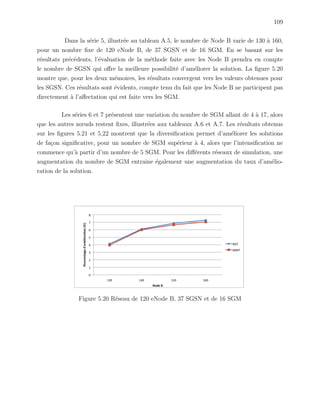
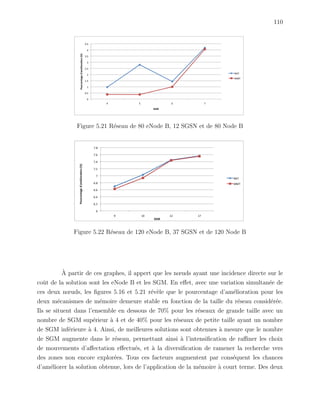
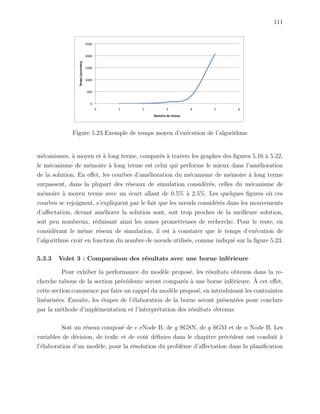



![115
o`u Nh
− d´esigne l’ensemble des (n-1) valeurs minimales de la matrice triangulaire hh
T et IN− ,
la fonction indicatrice des ensembles N−
LB =
e∈E
min(ceq
17) +
e∈E
min(cgq
67) +
k−1
p=1
k
q=p+1
IK− hT (p, q).hT (p, q)+
+
e∈E
min(Hvgq
67) +
e∈E
min(Hv
gq
67) (5.22)
L’impl´ementation de la borne inf´erieure est faite au moyen d’un programme r´ealis´e
en Matlab, tir´e de [24]. Le programme re¸coit en entr´ee le mod`ele, tel que d´ecrit dans 5.19,
mais libre des contraintes de capacit´es ´elabor´ees dans 5.10, 5.12 et 5.12. Ainsi pour chaque
r´eseau de simulation du tableau 5.6, le programme fait la lecture des fichiers de donn´ees
d´ecrivant les matrices les coˆuts de liaisons des eNode B au SGM, celles des coˆuts de liaisons
des SGSN au SGM, ainsi que les coˆuts des rel`eves horizontale et verticale. La valeur obtenue
de la borne sera ensuite compar´ee aux r´esultats obtenus de la recherche taboue du volet 2,
pour d´eterminer l’´ecart moyen existant entre ces deux valeurs.
Ainsi, les tableaux 5.7 `a 5.14 montrent que les solutions obtenues par la recherche
taboue sont assez proches de la borne inf´erieure. Dans le cas de la variation des eNode B, les
tableaux 5.7 et 5.8 pr´esentent un rapprochement de la borne `a mesure que le nombre d’eNode
B augmente. Dans ces deux tableaux, la borne pr´esente un ´ecart ne d´epassant pas 25% des
solutions obtenues de la recherche taboue. De mˆeme, les tableaux 5.9 et 5.10 montrent le mˆeme
comportement pour les SGSN. Pour certains r´eseaux comme indiqu´es dans les tableaux 5.9 `a
5.12, l’´ecart est compris entre 17% et 26% sur l’ensemble des r´eseaux de simulation consid´er´es.
Toutefois, dans le cas des tableaux 5.8 et 5.13 les ´ecarts tombent mˆeme en dessous de 1%.
Tableau 5.7 ´Ecart par rapport `a la borne inf´erieure pour la s´erie 1
eNode B 10 25 40 63 80 120 140 160
´Ecart (%) 24.6256 23.8733 20.0696 18.4292 10.3127 14.7053 7.751 9.7606
Tableau 5.8 ´Ecart par rapport `a la borne inf´erieure pour la s´erie 2
eNode B 40 65 80 93 100 120 140 160
´Ecart (%) 21.8378 23.1038 12.6167 8.0445 15.9576 0.12311 19.644 8.6314](https://image.slidesharecdn.com/2011germineseide-140603143923-phpapp02/85/2011-germine-seide-133-320.jpg)

![117
CHAPITRE 6
CONCLUSION
Ce chapitre de conclusion fait une synth`ese de la d´emarche utilis´ee dans ce m´e-
moire, pour tenter d’apporter une solution aux probl`emes li´es `a la planification d’un r´eseau
de quatri`eme g´en´eration. Pour ce faire, les diff´erentes ´etapes de la solution propos´ee ayant
conduit `a l’impl´ementation seront d´ecrites, suivies des limitations du travail. Ce chapitre se
termine par l’´enum´eration de quelques propositions pour des recherches futures.
6.1 Synth`ese des travaux
Le but principal de ce m´emoire a ´et´e de r´esoudre le probl`eme d’affectation des
cellules, dans le cadre de la planification d’un r´eseau mobile 4G `a partir d’un r´eseau mobile 3G
existant. Pour ce faire, diff´erents travaux ayant approch´e le mˆeme probl`eme dans les r´eseaux
pr´ec´edents ont ´et´e consid´er´es [17]-[59]. Ces travaux sont divis´es suivant qu’ils utilisent une
approche de r´esolution globale ou s´equentielle. Ainsi, l’analyse des travaux pour les r´eseaux 2G
d´emontre que le probl`eme d’affectation consiste `a trouver des sch´emas d’affectation entre, un
nombre de n cellules et de m commutateurs, en tenant compte des contraintes de capacit´es de
ces derniers, et de l’unicit´e des affectations des cellules `a ces commutateurs. Avec les r´eseaux
3G, deux types de trafic : la voix et les donn´ees, sont consid´er´es. Pour ces r´eseaux, les travaux
distinguent deux niveaux d’affectation : le niveau 1 qui traite du probl`eme d’affectation des
Node B (cellules) aux contrˆoleurs RNC, et le niveau 2 o`u les RNC sont affect´es en mˆeme temps
aux MSC et aux SGSN. Dans ce m´emoire, le r´eseau utilis´e prend en compte deux technologies
diff´erentes : celle de la 3G et celle de la 4G. Le mod`ele utilis´e permet alors d’affecter les eNode
B (cellules) et les SGSN en mˆeme temps, aux MME et aux SGW. Telles que pr´esent´ees, ces
affectations pr´esentent une grande similitude avec le niveau 2 des r´eseaux 3G. Mais, elles se
d´emarquent par l’ajout de nouveaux ´equipements et le type de trafic consid´er´e.
Pour r´esoudre le probl`eme, une mod´elisation faite `a partir des formules math´ema-
tiques a ´et´e propos´ee. Ce mod`ele prend en compte, les affectations des eNode B du r´eseau
4G et celles des SGSN du r´eseau 3G, aux ´equipements du r´eseau cœur 4G, les MME et les
SG-W. Ce mod`ele, tout en minimisant le coˆut total de l’architecture obtenue des affectations,
devrait respecter plusieurs contraintes telles que : les contraintes de capacit´es des MME et
des SG-W et les contraintes d’unicit´e des affectations des eNode B et des SGSN `a ces MME et](https://image.slidesharecdn.com/2011germineseide-140603143923-phpapp02/85/2011-germine-seide-135-320.jpg)


![120
R´EF´ERENCES
[1] 23.101 (2009). General Universal Mobile Telecommunications System (UMTS) architec-
ture, 9.0.0 ´edition.
[2] 23.110 (2009). Universal Mobile Telecommunications System (UMTS) access stratum ;
Services and functions, 9.0.0 ´edition.
[3] 23.205 (2010). Bearer-independent circuit-switched core network ; Stage 2, 9.1.0 ´edition.
[4] 25.308 (2010). High Speed Downlink Packet Access (HSDPA) ; Overall description ; Stage
2, 9.4.0 ´edition.
[5] 25.410 (2009). UTRAN Iu interface : General aspects and principles, 9.0.0 ´edition.
[6] 25.420 (2010). UTRAN Iur interface general aspects and principles, 9.1.0 ´edition.
[7] 25.426 (2009). UTRAN Iur and Iub interface data transport & transport signalling for
DCH data streams, 9.0.0 ´edition.
[8] 25.950 (2005). UTRA High Speed Downlink Packet Access (HSDPA), 4.0.1 ´edition.
[9] 25.996 (2009). Spacial channel model for Multiple Input Multiple Output (MIMO) simu-
lations, 9.0.0 ´edition.
[10] 29.016 (2009). General Packet Radio Service (GPRS) ; Serving GPRS Support Node
(SGSN) - Visitors Location Register (VLR) ; Gs interface network service specification,
9.0.0 ´edition.
[11] 29.118 (2010). Mobility Management Entity (MME) and Visitor Location Register (VLR)
SGs interface specification, 9.4.0 ´edition.
[12] 36.323 (2010). Evolved Universal Terrestrial Radio Access (E-UTRA) ; Packet Data
Convergence Protocol (PDCP) specification, 9.0.0 ´edition.
[13] 36.800 (2009). Universal Terrestrial Radio Access (UTRA) and Evolved Universal Ter-
restrial Radio Access (E-UTRA) ; Extended UMTS / LTE 800 Work Item Technical
Report, 9.0.0 ´edition.
[14] 37.976 (2010). Measurements of radiated performance for MIMO and multi-antenna
reception for HSPA and LTE terminals, 1.1.0 ´edition.
[15] 3GPP TS 23.401 (2010). General Packet Radio Service (GPRS) enhancements for Evol-
ved Universal Terrestrial Radio Access Network (E-UTRAN) access, 9.7.0 ´edition.
[16] ABONDO, C. (2005). Gestion de la Qualit´e de Service dans les syst`emes mobiles de
prochaine g´en´eration. Th`ese de doctorat, ´Ecole Polytechnique de Montr´eal.](https://image.slidesharecdn.com/2011germineseide-140603143923-phpapp02/85/2011-germine-seide-138-320.jpg)
![121
[17] ALI, B. ET AL. (2008). Gestion des ressources et de la qualit´e de service dans un r´eseau
mobile h´et´erog`ene de prochaine g´en´eration. M´emoire de maˆıtrise, ´Ecole Polytechnique
de Montr´eal.
[18] AMZALLAG, D. LIVSCHITZ, M. et NAOR, J.RAZ, D. (2005). Cell planning of 4g cellu-
lar networks : algorithmic techniques and results. 2005 6th IEE International Conference
on 3G and Beyond. 1–5.
[19] ANDREI, V., POPOVICI, E., FRATU, O. et HALUNGA, S. (2009). The architecture
of a software module, supporting vertical handover in heterogenous networks. Proc. of
International Conference on Science ETAI Conference. 26–29.
[20] BAJZIK, L., HORVATH, P., KOROSSY, L. et VULKAN, C. (2007). Impact of intra-lte
handover with forwarding on the user connections. Mobile and Wireless Communications
Summit, 2007. 16th IST. IEEE, 1–5.
[21] BEAUBRUN, R., PIERRE, S. et CONAN, J. (2005). An approach for managing global
mobility and roaming in the next-generation wireless systems. vol. 28, 571–581.
[22] BEAUBRUN, R., PIERRE, S. et CONAN, J. (2005). Methodologie de planification des
futurs reseaux mobiles. Canadian Conference on Electrical and Computer Engineering,
2005. 1161–1164.
[23] CHAMBERLAND, S. (2004). An efficient heuristic for the expansion problem of cellular
wireless networks. Computers and Operations Research, 31, 1769–1791.
[24] DIALLO, M. (2004). Affectation des cellules aux commutateurs dans les r´eseaux mobiles
de troisi`eme g´en´eration. M´emoire de maˆıtrise, ´Ecole Polytechnique de Montr´eal.
[25] DIALLO, M., PIERRE, S. et BEAUBRUN, R. (2010). A tabu search approach for
assigning node bs to switches in umts networks. Wireless Communications, IEEE Tran-
sactions on, 9, 1350 –1359.
[26] FIDUCCIA, C. et MATTHEYSES, R. (1988). A linear-time heuristic for improving
network partitions. Papers on Twenty-five years of electronic design automation. ACM,
241–247.
[27] GAREY, M. et JOHNSON, D. (1979). Computers and Intractability : A Guide to the
Theory of NP-completeness. WH Freeman & Co. New York, NY, USA.
[28] GHOSH, A., RATASUK, R., MONDAL, B., MANGALVEDHE, N. et THOMAS, T.
(2010). LTE-advanced : next-generation wireless broadband technology [Invited Paper].
Wireless Communications, IEEE, 17, 10–22.
[29] GLOVER, F. (1989). Tabu search 1.](https://image.slidesharecdn.com/2011germineseide-140603143923-phpapp02/85/2011-germine-seide-139-320.jpg)
![122
[30] HARRISON, P. et PATEL, N. (1992). Performance Modelling of Communication Net-
works and Computer Architectures (International Computer S. Addison-Wesley Long-
man Publishing Co., Inc.
[31] HASSAN, G. (2006). Designing concurrent, distributed, and real-time applications with
UML. Addison-Wesley Professional.
[32] HEDIBLE, C. et PIERRE, S. (2000). Genetic algorithm for the assignment of cells to
switches in personal communication networks. Electrical and Computer Engineering,
2000 Canadian Conference on. IEEE, vol. 2, 1077–1081.
[33] HOSSAIN, E. (2008). Heterogeneous Wireless Access Networks : Architectures and Pro-
tocols. Springer Verlag.
[34] HOUETO, O. E. F. (1999). Affectation de cellules a des commutateurs dans les reseaux
de communications personnelles. M´emoire de maˆıtrise, Ecole Polytechnique, Montreal,
Canada.
[35] HURLEY, S. (2002). Planning effective cellular mobile radio networks. IEEE transac-
tions on vehicular technology, 51, 243–253.
[36] HWANG, Y. et PARK, A. (2008). Vertical handover platform over applying the open
API for WLAN and 3G LTE systems. Vehicular Technology Conference, 2008. VTC
2008-Fall. IEEE 68th. IEEE, 1–5.
[37] JAMALIPOUR, A., MIRCHANDANI, V. et KIBRIA, M. (2005). Dimensioning of an
enhanced 4g/b3g infrastructure for voice traffic. Personal, Indoor and Mobile Radio
Communications, 2005. PIMRC 2005. IEEE 16th International Symposium on. IEEE,
vol. 3, 2003–2007.
[38] KERNIGHAN, B. et LIN, S. (1970). An efficient heuristic procedure for partitioning
graphs. Bell System Technical Journal, 49, 291–307.
[39] KIRKPATRICK, S. (1984). Optimization by simulated annealing : Quantitative studies.
Journal of Statistical Physics, 34, 975–986.
[40] LEFEBVRE, M. (2003). Cours et exercices de probabilit´es appliqu´ees : incluant les
notions de base de statistique. Presses inter Polytechnique.
[41] MAKAYA, C. et PIERRE, S. (2008). An analytical framework for performance eva-
luation of ipv6-based mobility management protocols. Wireless Communications, IEEE
Transactions on, 7, 972 –983.
[42] MANOLAKIS, K., IBING, A. et JUNGNICKEL, V. (2008). Performance evaluation of
a 3gpp lte terminal receiver. Wireless Conference, 2008. EW 2008. 14th European. 1–5.](https://image.slidesharecdn.com/2011germineseide-140603143923-phpapp02/85/2011-germine-seide-140-320.jpg)
![123
[43] MENON, S. et GUPTA, R. (2004). Assigning cells to switches in cellular networks
by incorporating a pricing mechanism into simulated annealing. Systems, Man, and
Cybernetics, Part B : Cybernetics, IEEE Transactions on, 34, 558–565.
[44] MERCHANT, A. et SENGUPTA, B. (1994). Multiway graph partitioning with appli-
cations to PCS networks. INFOCOM’94. Networking for Global Communications., 13th
Proceedings IEEE. IEEE, 593–600.
[45] MOLLOY, M. (1989). Fundamentals of performance modeling. Macmillan Pub. Co.
[46] MONTILLA BRAVO, A., MORENO, J. et SOTO, I. (2004). Advanced positioning and
location based services in 4g mobile-ip radio access networks. Personal, Indoor and Mo-
bile Radio Communications, 2004. PIMRC 2004. 15th IEEE International Symposium
on. vol. 2, 1085 – 1089 Vol.2.
[47] MYUNG, H. (2008). Technical Overview of 3GPP LTE. Polytechnic University of New
York.
[48] OLSSON, M., SULTANA, S., ROMMER, S., FRID, L. et MULLIGAN, C. (2009). Sys-
tem architecture evolution (SAE) and the evolved packet core. Driving the mobile broad-
band revolution. Elsevier Ltd.
[49] PENDER, T., MCSHEFFREY, E., VARVERIS, L. et BOOKS24X7, I. (2003). UML
bible. Wiley.
[50] PIERRE, S. (2003). R´eseaux et syst`emes informatiques mobiles : Fondements, architec-
tures et applications. Presses inter Polytechnique.
[51] PIERRE, S. et HOUETO, F. (2002). A tabu search approach for assigning cells to
switches in cellular mobile networks. Computer Communications, 25, 464–477.
[52] PILIOURAS, T. C. M. (2004). Network design : management and technical perspectives.
CRC Press, seconde ´edition.
[53] QUINTERO, A. et PIERRE, S. (2002). A memetic algorithm for assigning cells to
switches in cellular mobile networks. IEEE communications letters, 6, 484–486.
[54] RAO, G. et RADHAMANI, G. (2008). WiMAX : a wireless technology revolution. CRC
Press.
[55] SAKTHIVEL, S. et SURESH, R. (2006). A Genetic Algorithm Approach for Assigning
Mobile Base Stations to Switches in Cellular Mobile Networks. International Journal of
Soft Computing, 1, 166–169.
[56] SANCHIS, L. (1989). Multiple-way network partitioning. Computers, IEEE Transac-
tions on, 38, 62–81.](https://image.slidesharecdn.com/2011germineseide-140603143923-phpapp02/85/2011-germine-seide-141-320.jpg)
![124
[57] SKORIN-KAPOV, J. (1990). Tabu search applied to the quadratic assignment problem.
ORSA Journal on computing, 2, 33–45.
[58] SPIEGEL, C., BERKMANN, J., BAI, Z., SCHOLAND, T., DREWES, C., BRUCK,
G., GUNZELMANN, B. et JUNG, P. (2008). Mimo schemes in utra lte, a comparison.
Proceedings of the IEEE Vehicular Technology Conference.
[59] ST-HILAIRE, M. (2006). Planification globale des r´eseaux mobiles de troisi`eme g´en´era-
tion. Th`ese de doctorat, ´Ecole Polytechnique de Montr´eal.
[60] ST-HILAIRE, M., CHAMBERLAND, S. et PIERRE, S. (2006). Global expansion model
for mobile networks. Communications Letters, IEEE, 10.
[61] TABBANE, S. (2000). Handbook of mobile radio networks. Artech House.
[62] TANENBAUM, A. (2002). Computer Networks. Prentice-Hall International, Inc., qua-
tri`eme ´edition.](https://image.slidesharecdn.com/2011germineseide-140603143923-phpapp02/85/2011-germine-seide-142-320.jpg)
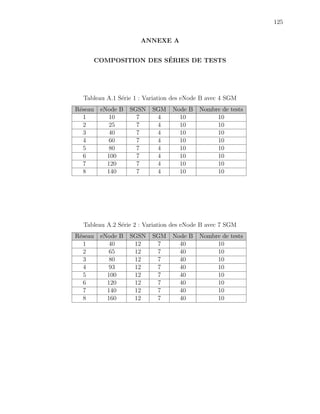
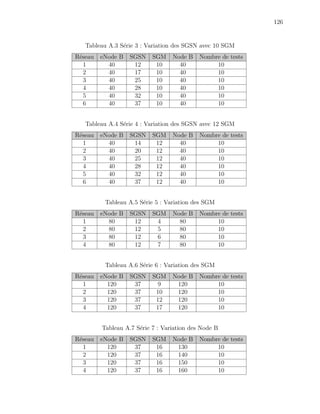
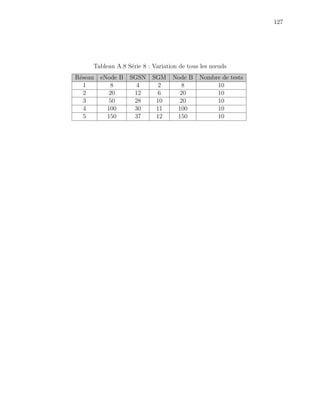

![129
Tableau B.2 Comparaison des terminologies des sous-syst`emes radio des r´eseaux 4G et 3G
(suite)
Termes du LTE
D´efinition ´Equivalence dans l’UMTS
PDCCH Physical Downlink Control
Channel
High Speed – Shared Control Channel (HS-
SCCH) [for HSPA+] or Dedicated Physical
Control Channel (DPCCH) [for a R99 chan-
nel]
PCFICH Physical Control Format In-
dicator Channel
NA
PHICH Physical Hybrid ARQ Indi-
cation Channel
E-DCH HARQ Indication Channel (E-
HICH) [for HSPA+] or NA [for a R99 chan-
nel]
PRACH Physical Random Access
Channel
Physical Random Access Channel (PRACH)
PUSCH Physical Uplink Shared
Channel
E-DCH Dedicated Physical Data Channel
(E-DPDCH) [for HSPA+] or Dedicated Phy-
sical Data Channel (DPCCH) [for a R99
channel]
PUCCH Physi-
cal
Uplink Control Channel E-DCH Dedicated Physical Control Channel
(E-DPCCH) [for HSPA+] or Dedicated Phy-
sical Control Channel (DPCCH) [for a R99
channel]](https://image.slidesharecdn.com/2011germineseide-140603143923-phpapp02/85/2011-germine-seide-147-320.jpg)

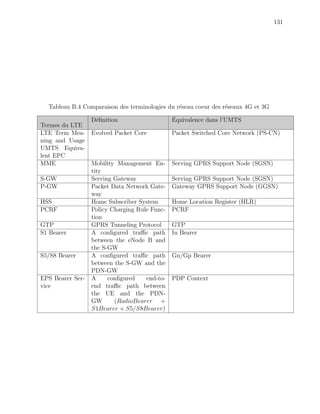
![132
Tableau B.5 Autres terminologies des r´eseaux 4G et 3G
Termes du LTE
D´efinition ´Equivalence dans l’UMTS
UE User Equipment (the mobile device) UE
IMSI International Mobile Subscriber Iden-
tity [Mobile Country Code (MCC), Mo-
bile Network Code (MNC) and Mobile
Identification Number (MIN)]
IMSI
IMEI International Mobile Equipment Iden-
tity
IMEI
Downlink (DL) Transmissions from the network to the
mobile
Downlink (DL)
Uplink (UL) Transmissions from the mobile to the
network
Uplink (UL)
Ciphering Over-the-air privacy Ciphering
Attach Initial registration process Attach
MIB, SIB Master Information Block and System
Information Block
MIB, SIB
DCI Downlink Control Information High Speed – Shared Control
Channel (HS- SCCH)
UCI Uplink Control Information E-DCH – Absolute Grant Chan-
nel (E- AGCH) and E-DCH – Re-
lative Grant Channel (E-RGCH)
C-RNTI Cell Radio Network Temporary Identi-
fier
High Speed – RNTI (H-RNTI)
CQI Channel Quality Indicator CQI
HARQ Hybrid ARQ HARQ
Handover Redirection of traffic from one base sta-
tion to another
Handover
Measurement
Control events
A1, A2, A3, A4,
A5, B1, B2
Thresholds for cell selection and han-
dover
Measurement Control e1a, e1b,
e1c, e1d, e1j](https://image.slidesharecdn.com/2011germineseide-140603143923-phpapp02/85/2011-germine-seide-150-320.jpg)