Le document traite de la commande électrique à réglage vectoriel pour des moteurs asynchrones, mettant en avant les avantages de leur utilisation par rapport aux moteurs à courant continu. Il aborde l'analyse mathématique, la synthèse de systèmes, ainsi que des études expérimentales concernant le levage mécanique avec convertisseurs fréquentiels. L'objectif principal est d'étudier et d'optimiser ces commandes pour améliorer leur performance dans des applications réelles.
![-{
rT1a"Tr-'i n-r-I
i rtfl -]IIl .
tûf*E[iïtrE 11
I NL.JLII I LL Ft
I 'l IFuNItrFFFæ|TF i-**F æi lF1&.
L +.J! ËI Il kl tH! I ** Hh eéill#r.a=
ruËîff #T *fr ilifË*eFil#tJË
,nw
PtlJR t'tBTËt'{Tlff'l
$U TITHE TT
R H Ë1 TETTEFFfr
ElfX [I trlH ! F H
lEll-t gtrg I kl I
rftl Êrnlltr liirFÂfiilnl lr
LIT TJLIIIL IYILLFTIEILTUL
nf,n
I ntt
ilfr fll I Â lf l fifr n!"1 ô trljh,lFR
Itt L, k rIt çt Itt rJ I tr-lt?Ittu-tJ
' I -{ na rt - ' *-DE
ELE l:TF,I#liE ,{ HEGL{GE 1''E[IT*F,IEL
' 'L:U-fr{L-$A"t-l
rES ,{FFÂRETT,S trE LEl,'ÂGE''
*ÛUTEII{IJE LË 311t1/gt DEVAI'Jï tA [$h4l*i$$l*$i û'ËXAil4Ei'l :
"Mr,$Et{Ë*ijztil Ê, FÊ#FE$$rilH , |'Jf{lllËH$lTE ds BtlilA 'FÊE$iÛEriT
"Mr KA$$lnl{ v, MÂlTHf nE f,ftiiFEHEfi*f , UFll:rfR$lTt iie nLlLrA =E}iilMllJiiTfijx
-itlir $TËFAP{Ûtl tl, I'dAiTftE ûË f*ItlFEËËlrj*E , EFJ$ET LAËliûLjAT -iHiÂït4ii'iAiEiiÊ
-ir,lr ZILËFI$HI il, MA|TËE AE CûiïFËËËf,jr;F, Ul',JlVEÊËiTE ds ËtlDÊ -8,-;*idii{nTËUn
-ir,lrFÊYLûY L fdÂITAE ûE ççirltËtËllr.iE, LJfiit/ERFiTf; d* BL!ûê -RÂPF*fiTEljfi
-i,ir $ALli! H. ïdÂiiË[ A$$lËiAlÉi, ilHiYEt$lTE ric $tlûÂ -iliiriii](https://image.slidesharecdn.com/32-530-58-1-2-231026172714-2ae41f31/85/32-530-58-1-2-pdf-1-320.jpg)
!['U?r -Yto- {$ ''t r8-1- ]
THE$E
^^uvu
FHE$ÊI'ITEE A
I
L'l"fNlvHn$nË FE H-laA
. NSTITUT nffi ffffisÂh$Qt"H
PûIJR L'OBTEfrTISI'I
$u TiTRr ffi
ryAfiffiTgN
lllnullry r ]r r
Ëf{ ûËl{lE MEtA}llolJE
PAfi
MÛUAICI MÛ}IAMMED
''CTMMÀNIJE EI$CTRISUE À EEËLAGE YECTTRIET
T}ES A,PFÂRËILS SA LEYAËK"
$0uTrHuË LE 3 1/$ 1/$S $Erf,f{T Lâ çS}$M[$$r*Fl B rffsfdru :
-Hr Ëfff*û{tn$ û. FR$.FE$$.gli& , tl$lY$fr$lïË de Btlll$ 'pgËslFffiT
-Mr KA$$tSil l, $#$TnË $fr tfrHFËSEHfÊ ,'llffiïfi&$lïH d+ BtlR,* "gï{A}*l*lATEtlÏ
.il{r $TfFAî{*f l, MSIT*Ë tfi *S$ffgg$,$f , Ël{gfT ;gfiHÛl}AT 'EHShdlfiATElJfi
.Hr ITLEH$KI y. MAITRI '$E
tûf{ffrnËff*[ ,ltiltrllEË$TïË Se ELI$& "E]t*ffiffATËt]R
-MrFAyLSt i. tu{Alïfrfi *Ë {.û$lFfrft[ffiûË - UftiVËfr$lïË $,s $LISA "pAFFtllÏ Ëilfl
.Mr $Allllll. f'dA$Rn A$$l$TfiHT , uNtYËft$lTE dç Bt|[A -ll'llilTE
32-530-58-1](https://image.slidesharecdn.com/32-530-58-1-2-231026172714-2ae41f31/85/32-530-58-1-2-pdf-2-320.jpg)














![22.
Ces dernières formules représentent les parties néelles du v6rc-
teur "espace" résultant exprimê dans une forme complexe et notê dans
le systÈme triphasÉ fixer ou erx - OpÉrateur tounnant faisant les
transformations du système tournant à celui {ixÉ triphasÉ:
Puisque :
eJ-=CO5'X+jSinX
â.eJ- = gjx.gJt:zo-= eJ(t20-+xl=
g2.gJx = eJ(x-12o.t = C,'S(X-lZOo)
cos{12Oo+x) + jsin(l?Oo+x}
+ jsi n (x-l20o )
En substituant ces relations dang le systÈme d,équations (ç) on
obtient 3
irr = Re(i6,gq3s1g + jia.cosx - is,,sinx + jîa.sinx)
= ia,CoSX -i'SinX
ie = Re{lcog(x + 1?oo] + jsin(x + laoo) rtiA. + jis.l]
= ia,cgrs(x + 12Oo) + jia.sin(x + llQol +
+ jin.cox (x + 12Oo ) i e:,gin (x + l20o )
= ia, cos(x + 12Oo) - is. sin(x + lZOo)
ig = Re{lcos(x 1200] + jsin(x 120û]rtia, + jiE'r]
= ia, cos( x 1200) ig, sin( x t?Oo)
Touteg les nelations obtenues gont valables pout* le systèrne lié
àux axÊ5 biphasé du rotor d'une machine synchFone c.à.d. dans le sys-
tàme des coordonnÉes d - q . Pour cela il faut substituer les indices
d - q avec les indices A, et 8,.
Pour le cas du courant, rorsque le systÈne des coordonnéeg
tourne à une vitesge de rotation di+férente de la vitesge synchrone,
la position de ce systÈme est dÉterminÉe paF l,angle X* entre leg
axes tour'nants et les axes du système immobire tfig. l-4).
tre systÈme tourne à une vitegse hfr< = dx*/dt et la position du
vecteur esp;rccl régultant du courant est définie par l,angle
tr*=o(-Xr.](https://image.slidesharecdn.com/32-530-58-1-2-231026172714-2ae41f31/85/32-530-58-1-2-pdf-17-320.jpg)


![I
I
I
I
T
t
I
I
I
I
I
t
I
I
I
I
I
I
t
Iii
I
25,
machine et enbrassent tous les enroulements. D3ns le cas gÉnÉral,
quand les axes des mÊmes phases du stator et du rotor ne coincident
Fêsr alors les inductances mutuelles du rotor et du stator sont éga-
les :
= Le= cosÊ)a- = Le= cog(wt + go )
= Lez cos€}ao = Lrz cos (wt + êo + Zn./S)
= Ll= cosêa= = Lr:a cos{wt ç Ë}o + 4n./S} etc.._
utilisant Le système d'Équations (11), nous Ërupons:
V- = iJ-. + {is, + ie}Lrr * i-La- + irrLao + icl.â=
V- = irrl-r + (i.o + ir=)Lrr * i-L;- * irr|-s-.ts i=L-=
9- = id-r + (i6 + irlLrr * i-Lc- * ir,Lea.r i=Lc=
En utiligant r'Équation gD Fa.^ FopÉnateur â, r,équation(pe par
l'opérateur s2 et en additionnant Ur^, lp asv) c,r on obtient:
va + av- + azve = (i.q + aip + aaiclLr + fi;, + ic + (i,a + ic,)a +
+ (ia + ir')allLrr + i-(Lrztrog$ar * al-r=cos€ls- * alLr,:zcosêc-) +
+ iu (Lr=cosêao * a'-r=c.'scL'' * aÊ Lr=cosgbu ) + io (L.=c.,s.rar +
* rl r=ggsC}rl= + al Lr=tros€lee l
Suivant la dÊfinition:
(zfs, {lt^ + agl- + azV., =V- - vecteur espec.. d,un f lux
magnÉtique embrassé de 1'enroulement du stator
En tenant compte des formuleg suivanteg:
i- = (2/3, (i.q + si. + atic)
et
(2/3, (ig + ie + ia.a + ic,a + i*r.â * ia.as + ir,.az) =
= l2f3l (i= + aic + aaia) + (2./J) (i= + ai- + aeis) =
= i-â-= + ire-t = -i-
Alons:
Q.13, (ia + ein + aeiclLr + (Z/]irl(ie, + ie +
+ (i.q + iela + (ia + i'lat lLer=, i-(La _ Lrr)
La relation du flux magnÉtique embnassé du stator dÉterminée par
les courants Ou rotor V-- peut-€tre écrite ainsi !
La-
l-âb
tq=
En
( 12)](https://image.slidesharecdn.com/32-530-58-1-2-231026172714-2ae41f31/85/32-530-58-1-2-pdf-20-320.jpg)
![tg
tg
=
æ
€
æ
*
G
Ë
€
ë
E
E
Ë
æ
G
G
æl
E
G
26-
W-^ = (i- + air, + a2i=)Le=cos(wt + êo) +
+ (ai- + aaia + i=)Lr=cos(wt + e|o + 4rr/3] +
+ (ae i- + ia + àie ) Lr:accls (wt + gç, + Ar./3)
Puisque ê^- = fu.' = {Jb= = €}o + wt et utirisant ces reration=:
i- = (Z/5, (i-+51ir+a2i-)
ir. â-a = (Z/3, (ai -+sa i r,+i =)
i-s--a - (Z/J, (aa i -+i rrai =)
trn peut Écrire :
V'- = i^Lez f aocos(wt + ç61 * a-rcos{wt + €b + Zn./3} +
+ a-zcos (wt + Clo + 4tt/S) I -
= (2/31 i-Lea. gJ (wù' + ittot
Par conséquent re vecteur résultant du flux du staton peut Ëtne
représenté de t.elle maniàre :
V- = i-(Lr - Lrr) + (zlsri-Lr=.er <w*+€o>
r orr obtient !
( 14t
( 13)
Puisquel Lr.r = -t -^/Z et Ll = L:l * l--
donc' Lr - Lrr = Lrr + L- = L- - inductance totale équivalent
de la phase dÉterrninÉe par le fl.ux du counant de sa phase et les flux
des phases voisines du stator.
L- = (3/2r l-- = (3/2rLr= = (S./Zr1--
- inductance du champ
magnétique principal calculée pour une phase de ra machine triphasÉe
.,u l'inductance mutuelle du stator et du rotor.
En supFoEiant que wt+€lo = or
9)-= i.L-* i-l--.grs
D'une manière analoguer on obtient !
Vl* = i-L-,,e-r- + i-l*
t- = L=-L=z = Lrr + (S/Zll-,' = L-r + L-
où : t* - inductantre totare équivalente de ra phase du
rotor déterminée par les flux de ses courants et des csurants des
phases voisine!s.
l*e - inductence de fuite
l- -inductance mutuelre du stator et du rotor du frux](https://image.slidesharecdn.com/32-530-58-1-2-231026172714-2ae41f31/85/32-530-58-1-2-pdf-21-320.jpg)



![I
I
I
t
3ù
'l
t
I
I
I
rl
I
t
I
I
rlt
I
Pour le circuit du stator :
r
lt-=u--*jl.tro
I
li-=i*+jirt]
I
I g- = Vo + ill)-c
L
D
t
I
I
û
I
I
I
Pour le rotor, il faut transfsrmer les vecteups rÉsultants du
systÈme A'-E' lié avec le rotor et tournant à la vitesse du eoton w
au systÈme biphasÉ tournant X -Y possÉdant une vitesse de rotation
Wrc .
Bn sait que :
(27'
Notation' des vecteurs "espace"
nésultants dans le systÈme
biphasÉ A'J' liÉ au rotor
dÉrivée d{-ldt sur les axes tournants X-Y
seront !
dQ-.
=
-.Êcrswrct
+
-.sinwxt
llF = l.11-a, + Llh^9..j
i- = i-a, + iFB.. j
Vn=V-^. +P--..i
Les projections de la
(guivant la formule (7') )
dv- d9--
dt (xl
d?-
dt (y)
0ù;
rJV-n
dt
dp-*
dt
aV-'
=-.sinr*rt+-.troswrt
dt
dV-. dv-
et - projections de la dÉrivée
-
dans
dt dt dt
, le sYstène {ixe cr-.s.
Pour transformer ccls dernières équations, il faut considÉrer 1e
dÉrivÉes guivantes :
d dlp--
--tp-gg;clshlrtl
=
-
CoEiw].t - 9-.*t*=inwr.t
dt dt
d dV--
-|:|{.!rsin$rkt)
=
-
sinwr.t + V-grn1",Êcrstdrt
dt dt](https://image.slidesharecdn.com/32-530-58-1-2-231026172714-2ae41f31/85/32-530-58-1-2-pdf-25-320.jpg)





![lr
ll
I
It
Ir
It
,l
I
I
t
t
I
I
I
I
I
I
t
I
t
ji
36-
Dsrc :
L: *-
ll^ = lJra
+ jura = i-*-
+ jt-t-g = I-R..
i-,- * i-,*
dV-
dt
aV-
- :w9-
dt
ty-
ry- E I-l* + I-l*
Eonclusion !
En utilisant les Équations de Pank-fiorev dans les di{fÉrentg
systèmes de coordonnÉes r GrFl peut sirnpli{ier ,== O"orGlssus dynami-
gues.
Il est trés commode d'utiliser les axes cr - B pout^ analyser les
procédés dynamiqueg dans les machines ou le stator est symÉtrique et
le rotor asymÉtriquÊ.
D - trBUPLE ELECTRtrHAËNETIEUE D'UNE l"IAtrHINE ASYNCHRBNE.
On peut trouvern d'abond, la nelation de la puissancE] Électro-
magnÉtique des machines à courant alternatif. Pour un système
syrnÉtrique et tenant compte des relations suivantes ,6il
u-* uo +U= - O et i-* iu + i* = O
où u- r llc r tl€ r i- r is et i= - valeuns instantanÉeg
La relation de puissance instantanée de toutes 1es phases peut
Etre écrite de telle manière !
p=u-i-+rrsi5+uoi=
Si les courants et les tensions ne conFtrrtent pas de composante:
nulles (iorttolr orr obtient la valeur de la puie'sance instantanÉe en
utilisant l'équation suivante :
. p = (3/2, Re E u^i I - produit scalaire des vecteups corl^es-
pondants p.oup le système triphasé.
t](https://image.slidesharecdn.com/32-530-58-1-2-231026172714-2ae41f31/85/32-530-58-1-2-pdf-31-320.jpg)







![r lrt
I La fonction principale d'un tel système de rÉglage consiste à
I
varier la vitesge de rotation d'une machine asynchrone et former
f les processus transitoires et statiques selon les lois nÉcessaires
I Par ailleurs r cÊ système doit exÉcuter les fonctions guivantes:
I
10' Transformen leg valeurs de sortie de cette commande électni.
I guer à savoir Ao, i-r [r- rnesurÉs dans le systÈme de coordonnÉes
- tournant liÉ avec le vecteur {lux magnÉtique embrassê du rotor;
I ?o) Optimiser le proceseius transitoire du système tournant ana-
I logiquement aux commandes Électriques à ceurant continu ]
I
3o) Eompenser les composantes non-linéaires des Équations d'une
I rnachine asynchrone;
40) Exercer 1'opération invense du passage du système tqurnan:
I au système fixe;
50) Fittrer le flux magnétique et le courant du stator des har.
I
moni guels supéri eul^ets;;
I âo) Obtenir les impulsions de =srtie de ce système, commoder
r
poup le rÉglage de l'onduleur d'un convertisseur frÉquentiel.
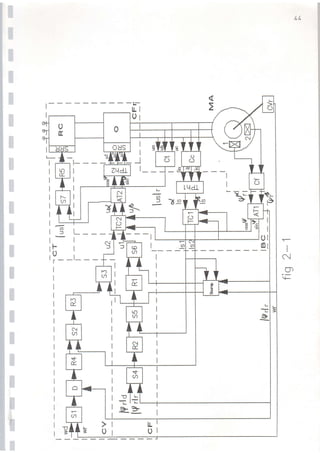
f Le schÉma fonctionnel d'une telle commande Électrique
I frÉquentielle evec le réglage vectoriel est reprÉsentÉ sur la
I
f i gure 2-r..
I A- LE trIRCUIT PRINCIPAL (DE PUISSANCE }
!
C'est un convertisseur de fréquentresi aveltr un redreEiEieup trom-
I mandÉ tCF-1. IL se cclmpose d'un redresseur commandé à thyristsrs
tRCl et à'un onduleur à thyristors Efd.fB|
t
I
I
I
lii
I
Le convertisseur permet de varier l'amplitude et la
fréquence de 1a tension aux bornes d'une machine asynchrone. Le
redresgeur commandé rÉg1e I'amplitude et I'ondul.eur fait varier
la frÉquentre de la tension de sortie.](https://image.slidesharecdn.com/32-530-58-1-2-231026172714-2ae41f31/85/32-530-58-1-2-pdf-40-320.jpg)









![56-
I
I
I
I
t
I
t
I
t
I
t
Tr )) Tr.
temps T1
g1
de
On pose 3
Kr.
Tr.=-ett
ld=
peut compensEl|^ Ia composantEl
fonctisn der transfert sera l
on
La
wr (s) -
K:e(TrlL''l
s (T},s + 1)
Hai selon 1e critÊne d'optimisation appelÉ optimum techriqr.rk7
|
L'- |
I
l(2 = zr, T,
I
Al.rs t'-":::-::=:
=transfert
du contour ouvert optimisÉ se.a '
I
zTpS(TrS + 1)
Donc
"
:-::::"=o'
*"'"=*:*' o' ""*"" {ermÉ optimisé sera
I
ZT-age + 2T;'S + t
I
Donc, grâce à I'optimisation, la variation de la valeur de sor- |
tie du contour optimisé dépend seulement de la petite constante de
I
temps Tr.
Pour'= ="Tn:";.oo'"]oo'"":":'=:," ==-'":'
='=r,, I
' z.!o
y=
L=+ =o,ror I
La fonction de passage est caractérisÉe.pan Ia valeur I
;rïï:ïî
nésrase $ = 4rs r er par rernps du premier mâx'
I
I
I
t
T
I
t
I
{:}
I.l
T
,f](https://image.slidesharecdn.com/32-530-58-1-2-231026172714-2ae41f31/85/32-530-58-1-2-pdf-50-320.jpg)
![I
I
I
t
I
I
I
I
I
I
I
I
I
I
I
I
I
I
:l
$t
t
56r
Le temps de réglage t- = Br4 t.'-.trette optimisation est obtenue
dans des conditions pratiques. Parfois trn appelle ce critère
d'optimisation, l'optimum de
^craùr.f€J
2Û l Pour le contour du rÉglage du {lux raagnÉtique embrassÉ du
rotor lP-l r cln utilise le rÉgulateur suivant 3
K:r€i + 14-
hlnz (s) =
s
La fonction de transfert du contour ouvent
total du rotor sera :
a=T=K+[ (Ks/K.e]S + 1l
l^f ' :e (s) =
si(T=S + 1' (2T'.l5l + 2Tr.,S + l)
En passant à la forme de notation suivante, (forne de Vichne-
gradskii ), on obtient !
hf' :e(p) = otr r
Ps+APl+Bp+1
azT=K*
(&o= - racine gÉométrique moyslnnet
(appelée fréquenctr gÉnénalisÉe)
2T rz
ff=
2T,
a=T=l(*
{fo
B=
D'où
aaT:rlL
B = !z,trTF-!/sAe
du rÉglage de {lux
AoF
En tragant cette courbe sur le diegrâmme de Vichnegradski et en
(
cherchant le rapport d'attÉnuation F r on peut dÉterniner les
t
coe'fficients A et B et Fap ËonsÉquent le coefficient K+ .](https://image.slidesharecdn.com/32-530-58-1-2-231026172714-2ae41f31/85/32-530-58-1-2-pdf-51-320.jpg)

![58
Avec un contour de deuxiÈme ordre
on peut récr.ir.e cette éqr-ration ainsi :
hJi, tsl =
4Tt,SSs(ZTr, + l) +l
I
2ïrr 5z + 4Tl.,Ei +t
4TrS(?Tgege + 2Tr., +l) + I
BTr:sgs BTrzga + 4T,,S +l
(s
Sr
l,t
lt
Il
I
ll
I
rI
,l
I
I
t
t
t
I
I
I
I
I
I
I
t
ljl
I
DE RtrTATIT]N
1l Le contour du courant (I-a ):
La fonction de transfert de ce contour srt^a :
(L'-1 -r
hlr (sl =
où
B_-=çALzuL _EEX REËULATEURS DU DE REELAEE DE LA VITESSE
qui est supÉrieur
- intégral de f-:
4 Eir) (T}'S + l)
= 1/Tr
Four trornpelnser la grande constante de temps T1
à ï, , i1 faut r-rtiriser' Lrn r.égr-rlateur' propor.tionnel
1fu5 + 14.
lrlH:r =
s
En prenant l,optimum
l(=
Tr=
IL
Alors la {onction de
fermÉ optimisÉ sera :
technique on choisit
Lt-
Kc, =
ZT l.Tp
trangfert du contour de rÉglage de courant
ùlr-:r (s) =
ZT.,agr+ZT},S+l](https://image.slidesharecdn.com/32-530-58-1-2-231026172714-2ae41f31/85/32-530-58-1-2-pdf-53-320.jpg)
![I
I
I
I
I
I
I
I
I
I
I
I
I
t
I
I
I
I
I
I
ilr
2l Le contour de rÉglage de la vitesse de
Le couple ÉlectromagnÉtique d'une machine
minÉ par:
l{ = (3./2)nn=;ù-|I-=
sù p - nombre de paires de pâles
en posant a
59
rotation.
asynchrone est dÉter-
l'l = l{rrltll_1t-=
Par analogie des contoups des courants, ici on utilisé un régul,
teur proportionnel - intÉgral :
Ith+=Kir+tG/S
La fonction de trangfent du contouF ouveFt du
vitegse de r.otaticrn ser.â !
réglage de la
Jrf '- (gl =
KcKlnl9- | t (K?./KËts +t I
.ldcztraga + zr,s +ll
A treuse du bloc de division (voir fig ll qui gÉnère la normali-
sation de l'erreur de ta vitesse de rotation par le module du flux
rnagnÉtique total du rotor, la fonction de transfert peut Être Écrite
ainsi !
KeK;r r K-
" LË=*']
Jrf'-(g) =
52 (2Tr,2Sz + 2Tr. + 1'
La fonction de transfert du contour fenmÉ de la vitesse g'epe !
Kz
5+1
l(É
hL (s) =
2Tre3 ZT,.,J J
Sa+ g1S+
l("rltr Krfia Kml(c
Les valeups apFroximatives des coefficients
vent Être déterrninées si trn change le polynôrne :
Kz
s2 +_s+1
Ka
des rÉgulateurs Feu-](https://image.slidesharecdn.com/32-530-58-1-2-231026172714-2ae41f31/85/32-530-58-1-2-pdf-54-320.jpg)





![I
I
I
I
o
I
.l
T
I
it
Ir
lr
l:
l:
65-
L'erreur de poursuite :
K
Ç-(fl = h|o-conna- - hf =
-
,r.
F
e- <r2t2t "
f
.1 2
ZorcoS- a +
7.
J2 {2
+ srz.sin r + csin+ "J
Le processusi transitoire est montrÉ sur la {ig 3 - 3
Le couple ÉlectrornagnÉtique est dÉterminÉ par le thÉorème de
composition de Laplace et par la {ormule suivante :
SZT'rJ-1S (2Trr ge + 2T,S + 1l
tt[.r ts] = -
c.à.d l
4(2Tl.)4Ei4 + El(ZTr,lsS:s + El(zTrrlsSt + gTl,Ei + 1
l'l(c) = Jl<
L'
.t2 .t2 {2 J?
fcos-a-Zsin-c+-rsin-
22?2
{2 .r7
2
or+](https://image.slidesharecdn.com/32-530-58-1-2-231026172714-2ae41f31/85/32-530-58-1-2-pdf-60-320.jpg)
![,E
i=
t:
t=
l_
l_=
l_..
I'=
l;
E=
E=
E=
E=
F;
E.-
E- 1:
E :
É:
EF :
66-
IV ETUDES EXPERIHENTALES
DE LA CT]HHANDE ELECTRIEUE A REELAGE VEtrTNRIEL
Les expÉriences se sont dÉroulÉes au laboretoire deg ', Eomrnandes
et machines ÉlectriqLles " de I'Institut des Hines de Leningrad Fen-
dant le mois de septembre 1gg"
On a utiligé pouP cela l'installation expérimentale conpor^tant:
- un moteur asynchrone
- un convertissËtut^ fréquentiel à thyristors
- un système de réglage vectoriel
Le schérna fonctionnel de cette installation est montré sur^ le
desgin 2, - t
Le système de rÉglage est conçu paF des bltrcs construits par la
chaire des machines Électriques de t'Institut des Hines de Leningrad.
Le circuit principal de puissance de la commande Électrique est
un moteur asynchrone du type AE lâtf3fâ/+, avec trornme charge une
machine à courant continu de type rH.El5 et un convertiss€luF fréquen-
tiel à thyristors standard de type Tn4-15. Les enroulements secondai-
res de cei tronvelrtisseurg sont hnanchÉs (couplés) en étoile (y) gtu
couplage triangle (A).
Par conséquent la valeur de la tengion de sortie du nednegseur
augmente. Le contrôle de ces valeursi et de la position du vecteur du
{lux magnétique s'exerce par des captçlurs de Hsll de type ffxr-z
installés le long des axes or - I de la machinei asynchrone.
En qualitÉ de capteurs de courant on utilise des capteurs du
typer$TrK-40 à la gortie du convertisseur dans chaque phase.
On dispose à 1'entrÉe du moteur asynchrone d'un capteur de ten-
sion poup le contour du rÉglage de tension.
. Dn a effectuÉ les essais sur cette installation.](https://image.slidesharecdn.com/32-530-58-1-2-231026172714-2ae41f31/85/32-530-58-1-2-pdf-61-320.jpg)









![I
I
I
I
I
I
I
I
I
I
I
t
I
I
I
I
I
I
76
V-BLOtrS DES SYSTEHESi DE REGLAËE VECTT]RIEL SUR
BAgiE DE trTRCUITS INTEERES
A-BASE D'ELEI'IENT DES SYSTEPIES VEtrTORIELS [4 a,gJ
1 ) Flul.tiplicateurs opÉrationnels-intÉgrales
Leg Élérnents des systèmes de rÉglage vectoriel fabriqués; pal^
I'Ingtitut des Flineg de Leningrad sont cnêes sur la base circuits
intÉgrés (CI) de large utilisation : les amplificateurs opérationnel
de type K 153 et K 14O et des paires de transistors (soondonnÉs) K5C
et K 15ç . L'utilisation des circuits intÉgrÉs diminuent la dimengic
et le poids . Efl outre ces trI Augmentent la rapidité de fonctisnne-
ment et la suretÉ des systèmes . Le choix du multiplicateur opéra-
tionnel est déterminÉ par !
- la rapidité de {onctionnement
- et 1'exactitude
L'amplificateur K 153 Y Dl est optimisé suivant ces principaux
paramètresrc'est pourqtroi on peut rÉaliser tout le système vectoriel
à l'aide de cet amplificateur . Pour certains blocs r of, utilige des
amplificateurs de type K 14O . I'amplificateun K 14O Y Dl a des cir-
cuits de correctisn compliquÉs , mais passèdent de grandes valeurg c
ldo et Ko . en cette vertu il peut Être utilisÉ en qualitÉ
d'intégrateur et de rÉgulateur intégrable . La prÉcision des opêna-
tions exÉcutées dÉpend des É1érnents qui rÉalisent leg circuits opÉr:
tionnels . On r{:co,nfiande d'utiliser des condensateuns précis de typt
K 7O-7 et des rÉsistances Ê?-ZqT . Ees résistanc€rs pGr trettent
d'obtenir unei précision statique égale à Or5 *
I
J
I](https://image.slidesharecdn.com/32-530-58-1-2-231026172714-2ae41f31/85/32-530-58-1-2-pdf-71-320.jpg)




![=
=
=
l*
t_
t:
t*-
I
t:
l=_=
l=
t=
t-
l=
E
Æ=
E-
E=
E=
E :
E=
-
E
E=
E=I
E::
81
mission cts't ptrsitif ; âvec les couplages 1-4 , 2-3 et 7-9 ce coeffi-
cient est négatif . La borne 9 ,aveic 1O-1 dÉbranchÉ, peut Ëtre uti-
lisÉe Four accorder à la gortie du multiplicateun 1'amplificateur de
puissance . L'accord du rnultiplicateur est fait de Ia manière sui-
vante !
10) on Établit une tension Êtalon Égale
la rÉsistance R12t
2l' ) on fixe la tengion de gortie zéro
I'entrée 2t
à (6 + 9) V à f 'aide de
avec la tension zÉro de
30 ) r]n Ëgale la tension de ssrtie de Yl qui egt Égale à
(O + 10û) mV à la tension de l'*nt"É= l elle mËme égale à tC
V par l'intermédiaire de la rÉsistance variable R3t
40) à l'aide de Ia rÉsistance Rê trn donne la tension sur la ba=
de T? assunant l'atténuation maximum du signal d'entrée 2
Le csefficient de tnansmission du multiplicateur varie à 1'aide
de la rÉsistance R12 . Dans le tableau 2 on montre les caractéristi-
ques du multiplicateur construif. à l'aide du circuit intÉgré
K SO4 HT 4 . Ees canactÉristiquels sont obtenues expÉrimentalement
Les essais d'échauffement du multiplicateur sont fait dans gamme= de
tempÉrat.r"== A= (5 +.4Olotr . Le rnuLtiplicateuF e unei bonne prÉci=io.n
dans tous les quadrantg (pas moing de OtS X) . La prÉcision du multi
plicateur dépend de la stabilité des tensiong d'alimentation
g;i 1a stabilité des tengion= n'est pas suffisante r alor.s iI
faut fournir des tensisng à la régistance R12 et aux diviseuPs R3-R4
et R5-R7 des stabilisateurs sêparés . Les essais montrent que
I'utilisation des paires de transigtorg (accordÉs) à effet de champ
permet pratiquement de ge dÉbarrasser de l'in{luence des caractéris-
tiques tension-courant non-LinÉaires sur la prÉcision du rnultiptica-
teur et permet d'atténuer entièrement la dépendance de la rÉsistancs
du collecteur-emetteur des transistors à effet de champ de la
tempÉrature](https://image.slidesharecdn.com/32-530-58-1-2-231026172714-2ae41f31/85/32-530-58-1-2-pdf-76-320.jpg)



















![I
I
I
I
I
]
I
,l
I
I
t
I
I
I
'l
I
I
I
I
10?
2- Ghoix du rnoteur
7.-t> Calcul d,aprÈs la charge
max imal e;
Fl't = 15 f - rÉgime faible
La puissance du moteuF Eln rÉgime stahle
Buand P = Glu
Avec P - Résistance du dÉplacement de translation
Glu, Vl 125OOO. 14r5
N. = 37 khl
er?oo.2o 6l?00.0rgo
h
Lo = 0rg0 - Rendement du mécanisme
Le msteur le plus proche ËrvElc FFI = 15 f e'st le moteur t"lTH
type 511--a avclc Nd = 45 kw et HTF 4lz-a avec Nd = J4 khf .
Donc nous prenons Ie moteur de 45 khf.
2-2, Calcul d,après la charge équivalente !
Nous pFenons un coe{ficient d'utilisation avrc la charge du
pont roulant K- = 0r5 et quand la charge est max Kr = OrZ
Nombre de dérnanrerges en I heure Zo = IZO
Goe{ oolz s 1155 - troe{ de la surchaFg=r de dÉnar*ages
La durée d'un dÉmarrage Ta-- = I s.
Le rapport du temps de fonctionnement du moteun pendant le
dérnarrage et du temps en régime stable est :
Zo.X 120. I
lÇr-=
="*
=-;;;-=0ro3
Coe{ficient de charge Équivalente:
r0
Y- = { ( Or4.K, + OrÉ } K- * Kgrc,
t-
trharge équivalente
.^
Pr= = FrYt = lzs.0r6s = Blroo
Puigsance nécessaire du moteur si p -
,-
- ooy
= .[ tor4.Ot? + 016 ]OrS + O'OJ lrSSz = O165
KN
Ps
I
Ir
I
P=. Vl Blooo. 14r5
N-
ê1200.0r8 61200. OrE
?[14 khf](https://image.slidesharecdn.com/32-530-58-1-2-231026172714-2ae41f31/85/32-530-58-1-2-pdf-96-320.jpg)






![I
I
I
I
I
I
t
I
I
I
I
I
T
I
I
I
I
I
.l
I
Jr
I
Le nombre de dents Équivalentes sera :
Four le pignon : Z-r - Zt./[ (cosF]sl = ?,2/Qr96Ë:r = 24
pour la roue i Zuz, = Zzlf (cosFlsJ = 139./Or966rt =153
Les csefficients de configuratians de dent= respectivement
Z,,r et Z-z ( Tab. SCI -t131):
Yr = Or414 ? Yz = Or515
Les contraintes de flexion 3
. Pour Le pignon:
nrr = (13.l"lprl/(ma.Zr.b.yrl = (13.âo5) f (a13?.2?.7r5,or414)
= 128 HPa
Pour la roue:
trçc = (r-t.y1l /yz, = (128.0r414) /Ot515 = 1O2rS l{Pa
troefficient de transformation aux chatrges de calculs :
,ô
Y'-- = Kr.. Kr'. Hr. = Or5. Or2. I = Or I (Tab. 15 -E 131l
avec Kx = 1 (coefticient de correction qui dépend de
'0 r0
x
I rr; Pour^ Yr orz Kr. = Iro)
Les charges de calculs du pignon !
rfl
7o = Zol-.Y--' = 619. 1O7.Or 1 = êr?. 10ê
Hombre de cycles de base et taux de fatigue3
Limite
t-t' =
7s= 3. 10ê I m=É (Tab.6-t131)
à la fatigue pour le pignon :
o-r.orl(Za/7e] = 432 ê.t(3. 1Oê]./(6r9. 10é) =
376 l"lPa ( Rq-.- = 7BS HPa
Pour la roue:
H
fr-r' = tr-r..-{(Zà/Zp} = 432.
avec:
et
ê.f t3. ltts)/(1r1,10ê) =
= 510 l'lPa { Re-r-
tÀ
7. = z",=.Y-' = 1t1.lo'r'.ot1 = Irl'lod'{ l. -
m=6 (Tab.â-t131'
1o* i](https://image.slidesharecdn.com/32-530-58-1-2-231026172714-2ae41f31/85/32-530-58-1-2-pdf-103-320.jpg)
![I
I
I
4-3) SÉcuritÉ à la fatigue:
Pour le pignon :
2. R--*. û-r 2. ?8O.432
n=
Û--*. {r-1 +Ko'.R--*} 12,'(43?+1r7.gBO)
tnl à l14 (Tab..tt ttsl )
Les contraintes en tt'tpal:
âvec K'o = 1r7 ( HË > ZSO rTab. 1A - tl3l)
Pour la roue:
2.98O.432
Il= =3t?4
I
I
1O2r3(432 +1rZ.9EO)
Vérif ication à la gol.iditÉ statique
H"t = l'lre.ldcr = éO5- lr} = ??6 Nm
avec l{a = LrZ (troefficient dynamique
Les contraintes de flexion :
= 3115
;tnJ è lr7
(Tab. 11 -E lSl )
;Tab. 2E)
{
I
I
)
I
]
I
I
I
I
I
I
I
I
I
i
I
H'or ZZh
T'+:f+-=12El-:
tLr éo5
153rÉ l"tPa
Analogiquenent trn obtient pour la roue i t, + = IZS HFa
La sêcurité d'élasticitÉ sera pour :
- Le pignon: n = Rr-r-/tr'+ = ?BS./lSSré = Srll
tnl à ? (Tah. tt )
- La t^truet ! n = ZSS.11ZS = 6.5El
tnl Z 2r4 (Tab.. lt )
4-4' DÉterrnination des dimensions du 2ro- étage
E'est un eingr^€lnagel à dentures droites:
i= = 5r? - Taux de rapport i
lTz = Z6FO Nm { Sur l,arbre du pignon }
lTs = 1SSOO Nm (Sur I'arbre de la roue l
Leg matériaux sont identiques à ceux du !-- Étage.
D'après le Tab. â, nous aup{f,n5 les paramétres suivants:
Pour le pignon : Zu = S.lOa ; m=6](https://image.slidesharecdn.com/32-530-58-1-2-231026172714-2ae41f31/85/32-530-58-1-2-pdf-104-320.jpg)
![m
I
I
I
U
I
I
-l
I
:-t
I
I
]
I
t
,l
I
,l
I
I
I
I
I
Jl
I
240. HRC
Erf= =
K*-
= 1?40 I'lFa
K*. = lr0 (Tab-
240,45
=-
1
Four la roue 2 26 =
Alors Z.a = lrl.lOé
Pour la roue ! Z-s =
Donc pouF le pignon :
3. 10é' I m = ?
Z-,=/iz = 1r1.1Oé./5r2 = = ?r1,lOs
6t-
111 -
5. lo7
1r1,10ê
= 174OOO N./crns
3?8O.10-r
1CIr35.5n?. 11102
0135.364 = l2B mm.
mr-
lzo
t-
lZ,'=
24 1
Pour la roue
27.H8
Erlo =
-
K*-'
Âr-
27.2=5 - ; l.10-
l- E 111OOO N/cmr
.lt'. lz, t. loE
H3'r,10-1
= 1O5(5r2+l)
-.i2'frl2=
zb
= 1 llO HPa.
Cette contrainte egt utilisÉe pout le calcul suivant.
Hsment de calcul pouF Ie pignon l
Her = Fla.K- = 2650. lr$ = 39f|0 Nm avË1tr K- = lr5
Alors I'entr'axe â." sçlra !
3
a€ = tOS (ite+l)
= 3614 cm.
Largeur de la coul^ctnne: ! = -.âw =
En fin de compte nous eupons :
Ew = 4OO mm ; b=14Omm
Le diamétre primitif du pignon sera :
dr = Za-/(iz + I ) = 2.4OO/(5r2 + I ) = 129 rnrn
F-s = 432 l'lPa donc !
frl+ = 114.r-1./(tnl.K'c,) = l14.?,60/Ir4.l14 = lBE Flpa
tn] = 114 iK'o = 1n4 d'après Tab. 11-12.](https://image.slidesharecdn.com/32-530-58-1-2-231026172714-2ae41f31/85/32-530-58-1-2-pdf-105-320.jpg)

![I
I
I
I
I
t
I
t
I
I
t
t
I
I
I
I
I
I
I
Jl
t
113
Za = 5. 10?
Roue = Z.s = Zo:r. '-- = 2rl.1Oê.Orl. = 2t1.1O!:'
7a = 3. lF
Er r'-r = f-r.'{(Z,5fZo,=} = 432,â.13. 1æ/1r1.10é'=
= 51O HPa { FL = 785 l'lPa-
Pour la roue ! f '-r = 432 â"[3. Iæ/2r12. lts =
= o72 FlPa { R-
La gÉcurité à la {atigue !
-Pignon:n=
-Roue n=3rÊ5
4-l:,, Vérification à la solidité -statique
H'-= = Hp:a.Ka = 2650. Irl = 2915 Nrn
Les contraintes de {lexion :
t'+ = {r+.H'p=/ltlp= = 121 r2. lrl = 13313 l'lPa
Pour la roue z c'+ = 112175 lIPa
SÉcuritÉ d'ÉlastitritÉ :
2.R--*.t-t/ f{r--*(r-t + K'o.R---}l =
2.?8O.432/t1?112(342 + 117.9BO)l = 3r33
n = R--rn/tr'+ = ]:fjf,/13313 = S'BB
n=7El5/112r?5=&rT
- Pignon !
- Roue :
donc n à ?rt
5- Ealcul des arbres
5-l) Premier
Les charges:
Leg efforts:
- tangentiel
- axial
- radial
arbre
l"lr = 432 Nm
-
- F- = Fc.tgB = f2650.tg(14059')
- F- = Fe.tgg{/cosp =
= l?650.tg (2Oo | lcos (14o59')
1?650 N
= 33?O
=47ô7Nt](https://image.slidesharecdn.com/32-530-58-1-2-231026172714-2ae41f31/85/32-530-58-1-2-pdf-107-320.jpg)

![I
t
I
I
I
I
T
It
It
ll
l:
l:
r15
Or Aa = (4767.0,O95/O,325,
= 1750 N
81 = 1767 1750 = 3017 N
lloaent de flexLon rnaxinal :
lf.---- = Àr.â = 175O-O.23 =
lfo-<rr-rr) = Ar (a - bl2l =
= 337 Nn
b) Plan horizontal :
Àz - F+..c|{a + c} =
= 1255O.OrO95/O 1325 =
= 3570 N
Bz = 1265O
= B9BO N
3570 =
!f.---- = l..a = 3670.0123
lfsnrrr-rr) = Àz(a-bl2) =
llonent de flexlon total 3
l.fa - )â.li11.1- + i.J Ma'et + !l-t
= 9A2 Nn (Votr fig
Dl.anétre du prenler arbre
Section I-I
+ (339O.O,0683/ (2.O,325) ) =
402,5 Nn
L75O(O,23 -O,O75/21 =
ftg C
= 844 Nn
3670 (O,23 O,A75l2l = 7L6 Nn
ll1.r =f M1'*---t -F !1.----t I !!42 r5' + 844' = 935 Nn
lllcrrï-rtr1 = f 337r + 7L6'
l,lonent de torslon : l{a =
l,iouent Idéal de flexLon :
= 791 Nn
= 432 Nn
!lr
(93512)+ l1f935' + â32,
)
sf
219
4321(O,2.86)
ctrl = 29 mm
aI
dr_- > Et uù./(o,2.[ ]]](https://image.slidesharecdn.com/32-530-58-1-2-231026172714-2ae41f31/85/32-530-58-1-2-pdf-109-320.jpg)

![I
I
I
I
I
I
I
I
I
I
t
I
t
I
I
I
I
I
I
,f
I
r17
t Les contraintes de torsion dans la section II-II
d
ç= l4+.1{O12.dt---rr) = !t321(O12.O2O53) = 17r3 }lPa
t Le coeffLclent de sécurLté dens la seetLon II-ff
nc' = €r|.Gtn = or85 -324/L7.3 = 1519 > [n] * 2
'L
* Contraintes de flexl.on denË Ia sectLon II-II
6c = l{rrrt-t-f(O'1.dtrr-tt) = 79Ll(O'1.O7O53) = 63r28 }!Pa
evec !ltr---r = 791 Nm
Le nonbre de cycles de base de I'arbre sera:
nb = 5'10tt
n=g
Z=, = 619:l0tt
Pulgue Zct ) Zu , La linite de résistance à Ia fatigue est
êgale à d-r = !!32 ltlPa-
Le coefficlent de concentration des contralntes de flexion
Pour Ia section II-II ( changement de diamétre et raccordenent)
hfe
T = 2,9 ; d-= fr:0,04
'E-II
vv
ftgr 5
Pour les rapports ( h/r ) et ( rld )
VI rI ( Appendl.ce t 13I )
et d'après le tableau.
Ko = 2 t}O.
Le csefficl-ent Ko = (K. * K,'ll €r. âvec Ko - 2r3O et
l{- = Or25 (1ab-9} ( état de surface }
et €re = OITO (Tab-B) ( dlnenslon de I'arbre )
Ko = (2r3 + Or25 l/Or7 = 316l!-
4l](https://image.slidesharecdn.com/32-530-58-1-2-231026172714-2ae41f31/85/32-530-58-1-2-pdf-111-320.jpg)


![I
I
I
I
t
I
t
I
I
I
I
t
T
I
I
I
I
I
I
:
.r:
I
I
1.20
D' aprèe la figure I
f,!|19 = O
Ar(a+b+c) - F=g(b+c) +
alors :
= - E-â = -3390 N
Fs3.C E-z.dzl2 = Q
âr = [F=r(b+c) - Frz.c * F-a.dz/Zll( a+b+c] =
= [ 15,07 .O1225 â,.767.O,O95 + 3r39.O' â,32/2llA,t25
- 3165 kN
Br = -Àr ' E-z * F-g = 3'65 11767 + L5rQ7 = 61553 kN
r Réactions dens le plan horizontal:
ll -+
At=
= 3,8fxN
fig 9
f,Èl^ = O
Fùgi.â Fo=. (a+b) + 82. (a+b+c) = O
Bz = [F-2.(a+b) - Fgs.â ]/(a+b+c] -
= [12,65.O r23. - 4LrA.O'1llO1325
âa = F+.a - Fot + Bz = ItttA L2265
r Les nonents de flerlon :
- ptan vertlcâl
A
a b
#
ct
6 5Nm
Brx c
= -J'79 kN
3179 = 2â 196 KN
Bt= Ç65 xn/
B
At x a=3
632 Nm 1tg. t0](https://image.slidesharecdn.com/32-530-58-1-2-231026172714-2ae41f31/85/32-530-58-1-2-pdf-114-320.jpg)

![â
*
ll
t
I
I
I
I
I
I
t
I
I
I
t
I
o
I
I
o
I
o
;
T
ji
I
Ce eoeffLclent est largenent sufflsant; c'est
fait pas de vérification des sectLons à gauche et
pignon-
pourguoi on
à droite du
5-31 Calcul du troislène
l'l= = 135OS hlm i d-r^ I
F.- = 4114 kN
Fr* = 15rÛ? kN
F-r=O
arbre
sJ135O{r./ (ûr3.Et&} = ??r? rnrn
* Réactions!:
+Br = Frr.a/(a+b) =
= â16â kN
+Àr = 15 rA7-4164
= 10r1t3 kN
Ez = Ftr.a/(a+b)
= L2r74 kN
z = 28'66 kN
ùlonents de flexion:
v - 1Or43.O'1 =
= I rAâ3 kNn
l'fh = 28;66.O11 = 2,866 kNn
-F l'loment idÉa1 de flexion:
Ua = lâl4r. + )tt (Èlr)t + (!l.t.)2 =
= 8'445 kNn
)t(3 ,O5 + {3, Ost + 13,5r ) =
!f-. = fl.O/432 + 21866, = 3rO5 kNn
!lÈ = lfa = 1315 kNm
* Dlaaétre de la sectlon Eoils la r{rrre:
d 2 t{}ltl (o,1-[o].] = rJB,aaïLoBl (o;1.123] =99,2 nn
avec [o]. = 123 MPa
Prenone .d = 95 nrn l d-1- = 92 rZ mn
,043 KNx rn
Mtors lon
:
= {3500 ilxrn](https://image.slidesharecdn.com/32-530-58-1-2-231026172714-2ae41f31/85/32-530-58-1-2-pdf-116-320.jpg)

![I
I
I
I
I
I
I
I
I
I
I
I
t
I
I
I
I
I
I
l'l
I
X - Facteur radial
v - Facteur de rgtation ; v =1 pour^ tous les paliers puisque
les bagues intÉrieures tournent.
Y - Facteur axial
Pour les rsulements à une rangÉe de billes à contact oblique
( angle de contact = 4Oo ), nous âvons :
e = Irl4 {Tah. 31}
Les charges axiales aux points 'A' et ,8, sont :
Ra- = e.FLâ = 1114.4rO&6 = 4t365 kN
Rn- - t.Rs = l0rEl kN
= Re'- Ra'= l0rg - 4.-365 = é1175 l F-
Pour cette raison la {orce axiale F- est dirigÉe vers le
point 'â'.
Donc Fn- = Ra- = 16rg kN
Fa- = Rs'- F- = l0rg - 3139 = 7r4t kN
Fa-/R* =7t41/4t066 ) e = 1114 donc:
X =Or57 Y=ûrg3
Fs-lftg = lÛrE/9-r473 < Ë! = Irl4 donc:
[=1 Y=Or55t14]
Alors
poun le point 'A'i
P = Or57.4rOêê a 0193.41 = ?rZL
donc E = 9121 (7O5. IOOO. 6O/IQ-, i./.:t =
On choisit donc le roulement 40 BT
et Ëo = ?5OO daN
pour le point 'Ê' P = 1.1.?1473
donc E = 15r41.4(7O5. 1OOO.âQ/lOp.rt,/s
On choisit donc le roulement à deux
tact oblique 4O BE 33 avec tr = 54OO
32rO9 kN = 32O? daN
OS avec tr = 345O daN
.t Or55. 10rB
= 53170 kN
rangÉes de
daN et Eo =
= 15r413
=537O daN
billes à cûn-
45OO daN](https://image.slidesharecdn.com/32-530-58-1-2-231026172714-2ae41f31/85/32-530-58-1-2-pdf-118-320.jpg)

![ff
I
I
I
I
I
I
I
I
I
I
t
I
t
I
I
I
I
t
lr
I
Cg = Pr-r.LrO92 = 1555 daN
0n prendre pour les 2 palLêrs les
55 BC {)2 avec une chârge dynanlgue
r26
nènes roulenents
Sd = 335O daN et une
charge statlgue S = 255O daN
7- Calcul du tarnbour
llatérlau
Fonte FT 15
RÊ-r- = 15 daN
doo-p= = 75 daN/nm2
[ct]oo-- = 6=o^--ltrrl = 7515 = 15 daN
avec [n] = 5 coefflcl-ent de sêcurlté
La force naxlnale de tenslon du câble !E--* = 3116 kN
donc I'épaisseur de Ia parol du tanbour !
t' = El(t.Iafoo---) = 3L16.LOal(OrO2. 15.lOt) = 1O'5 nn
avec t = OrO2 D .- pas entre 2 spires
Prenonsg=19nn.
L'axe du tanbour: La résultante de tenslon des 2 câbles:
R = 2E = 6312 kN
La charge sur le polnt d'appul 'À':
Rr = R-Lzll11+L2) = = 5312-575/ (735+575)= = 27'7 kN
Rg=P-Rr=35'5kN
Ro = R.le/lg = = 6312.(575-115)/995= = 29'2 kN = 292O daN
Rc = R - Rp = 63,'2 2912 = = 34 kN
735 s
fig 1](https://image.slidesharecdn.com/32-530-58-1-2-231026172714-2ae41f31/85/32-530-58-1-2-pdf-120-320.jpg)
![I
I
I
I
I
I
t
I
I
I
I
I
I
t
I
I
I0
t
I
lr
I
fLg 2
ftg 3
Les nonents fléchissants:
Àu polnt 'D' :
iltlc = Rr.lr = 27 17 -Or2-LOz = 554O Nm
Àu polnt 'C':
lilr:. - RB.(1= - l=) = 355OO(0,1c76 O7C6O) = 4O9O Nn
donc Mo--* = Mso = 554O Nn = l{rar:r
Puisque sur I'axe aucune charge n'est exercée Hr--- = ltrac-r
donc le dLamètre de l'arbre sera:
d ) 3{Mrar-tl (O'1.IO]r) = 3{5540/ (O,1.93.1OG) - O,O85 n
evec Ia]o = 6-t-l (K'or. [n] ) = 260l (L,â.21 = 93 ]tPa
Ici d-r = 26O MPa limite à la fatigue de flexion pour
L27
I
I
I
t
I
I
ls = 460
DI (n=73s (c=175](https://image.slidesharecdn.com/32-530-58-1-2-231026172714-2ae41f31/85/32-530-58-1-2-pdf-121-320.jpg)






![û =f
rt<tt
J'
I
I
I
It
lr
lr
lr
lr
lr
l:
(= er/f = Lzsooolo,oob4
ContraLnte totale:
(or)t + d.
1E ( R-ar- =
' = J8r35r + 4-213, = 9125 daN/mnt
25 daN/nnr
= 23.1O6 Pa = 23 ltPa
134
( 2,3daN/mn'
Q,= 62,5 5rN
KN
9-2) Calcul de 1.écrou du crochet
Contrainte de clsaillement adnissible:
[-L]-.- - O'5.[oJc=-oa = Ot6-iO = 42 l1Pa ( d2OO N/cni )
Hauteur de 1'écrou:
H = Q/(n-dr-k.-L--fC]) avec d1 = 5o nm; k, = o,g7 tpour
filetage de profil nêtrtque); ktr = O,E6 - coefficient dépendant du
rapport du diamètre du filetage et du pâs.
H l 125OOOl (n-5.O,97 -O,86-r!2OO) = 39 nn
DÀanêtre extérieur de l'écrou:
Do = lr$ d = Lr8.64 = 115 rnn
9-3) Cholx du palLer du crochet
On le falt d'après la chargre statlgue-
Charge de calcul:
F- = Q.Ka = L25 OOO - Lr25 = 156 OOO N
K.r = Lr25 - coefflcient dynanique.
= 125 xN
fts 3](https://image.slidesharecdn.com/32-530-58-1-2-231026172714-2ae41f31/85/32-530-58-1-2-pdf-128-320.jpg)

![I
I
,l
i36
Hr------- = Jâ.W++l (F - do) = J6'A5,r9/ (L2 - 7t5) =
I = 1CIr7 cm. Prenons H = llO mm
l'loment f 1Échissant dang la section IV-IV:
I H+ = 1.P=/? = OrO?5- t5ft}Oç/? = 5B5O Nm = 5B5OOO Ncm
Eontraintes de f lexion:
I
{r+ = M+/(Or1.ds} = 585OOO/lArl.OrOOg:t} = 91r5. lOê Pa = ?lr5 l'lPa
I Coefficient de sécurité:
n = €r,,r.R--r-/tr+ = OrB.35r3/9I 15 = 3t1
I Enl = / avec Êr =orB ( tab B )
9-5) Palier des Poulies
I
I1 y a 4 roulements à billes.
I La charge sul^ un roulement Eer^a: Glr = Et4 = 1?5OOO./4 = 31?5O N
Le nombre de tour-s du roulement pÉup Dpourrr = 4OO mm et la
r vitesse du câble V = 2? m/min.
trharge dynarnique de base pour. le roulement:
I
E = F- (n.1r- f Lâââârstto
I . avË!tr F- = Gl = 3125O N = 3125 daN
- n =V/tn(Dr, +çl-r51-)l =29/{1r.t0r4çO'O1E}} 3?3t./min
I lr' = 10 OOO h alors:
c = 3125(23, 10000/166êê)tt?to = ?495 daN
I
On choisit le roulement BO Btr O3 avec C = 95OO daN et
-
I Eo = TEOO daN.
do = d+lr-r-ir--enoenrt * (5 + 10) filtn = (â4 + l0]mm =
= 74 mm. Prenons do =75 mm
9-él Chsix du frein
On le choisit d'après le moment de freinage;
f'lç^ = t'L.0o.Blio aveic:
(.
l'L = lrlr = 135OO Nm
io = 32rS - Taux de transmission du rÉducteun'
I
I
I
tia
I
I](https://image.slidesharecdn.com/32-530-58-1-2-231026172714-2ae41f31/85/32-530-58-1-2-pdf-130-320.jpg)






![r
I
I
I
I
I
I
I
I
I
T
I
I
t
I
I
I
I
I
I ,:i
I
144
l{.r =
4aaT:zT*,
l{=
-=T==Or35&
K4
= 35. 1O2
4.2.1O-2.ûr356. 1O-2
l{= = l.?r25. 1O-2
ss + E.1o-4 E2 + 4.10-2 S + I
transfert dr-r circuit de vitesse en prenant en
I'optimum symÉtnique srFa:
2t3 2t3
F Or 1û?. 1O2
4.3163. 1O-2 22r52.1O-2
1r5.4.CIr93El = 5ré3
Hg{S} =
E}.10-ê
La 'fenctign de
congi dÉrati on
J
l1'
4. Hf,r. Tr.'
F.+r = t].f})pl{- =
P={
2r3 213
=
-
= OrOl?7
180,16
lde =
32, l{r{. Ta ,, 3?.5r63. tO-=
B. lO-2 S
lrlw (5) =
64. 1O-s54 + â4. 1O_.,5=I + 32. 10_45:2 + B. 1O_r25 + I
I
fl6 = = 35rE
?"f2. Tl,
La fonctign de transfert par ra perturbation s;era!
1 ,39. 1O-r. (2. 1O-4fi2 + 2.10-=S +l ) S
tr['r (Si) =
br4.1ûr-7Ei4 ç Ér4. 1O-5S:s .. 3r?. l6-rt5:a + g. lO-zS + 1](https://image.slidesharecdn.com/32-530-58-1-2-231026172714-2ae41f31/85/32-530-58-1-2-pdf-138-320.jpg)
![I
I
I
I
I
I
I
I
I
I
I
I
I
I
I
t
I
I
I
l
I
{âË
L..tJ
ËÏËLÏÛGËâFI{IE
1) ËË===1,:er=1.:à TJ.*. .Fr:tr=v =.F.
"ThÉr=ri= ds= =y=tènes âg=Er-vis" l{sscsu "Flë.ËLil..:â", 1??3,
=i *s.r'ta,st-i V.A" ,Favl=v V"Ë. ,Ê*ruda.ki:v V,?.
"Sy=tème de :*éç1.*.9= des cr=r*rnand== ÉS.ectriql-isË âvÊr des int:teur=
a=ynchrcns=" " Lsni r:gr'ad , LËhlTP, 1ç??.
3] Ëculçakav Ê.â,
"Réç1age frÉq*e,ntie'1
4l Vagint:v *, ï"
d*= i*atslrrg âËynchr-sne=".t'ls==t:ri "fnÊr-giË"
"T*lachins= É1scÈ-i'iql-r€=", Le::i.ngrad "Ênergie', 1çÉ8.
El lJ-. --
-L
lr' r. r.-
-l-
1
-il FliJvd,l-ll Fl .I- r rs-adl-È:- I'
"FrûEEË=us tran=iti:ireg dsn= leg lnarhines à =eurant alterr':st!f "
t4n=rnr r t 4FlE
&3 Ëiegannv=*i *.U. =t autr'e=,
"Sy=t**:== de rÊglaçe =ubar-dsnnÉ de= =g*:E*andes Élect-riqlisË av=c
csnvgr'tisËgu-!''E de= =*upapE=" I l'la=colrr "FnËrgiF" r ïçF3.
?i Lebedev E" oN=iraarl,: Ç. u Pi=àr'ac FI", 5!.=ç*nt:r.=ki *.
"*Égiag= des cærnr*ands= É1=rtri*Li== à rr=ui''*+r:t cc:n-i.inu â thyris-
È .-.e- =
rl r l.T*e r r,r i ll Fn <i_. .a i
--
li
Lul = 5 l:s=LL:+- I Li a-! Hl -
Ë] âis:<eev V.1.'. rS*,rlt*cu U, n *sudahsv V. rPavlrv V.
"fj.=n:ent= dr-:-
=y=t=*e dç =,=iniir*,*d= É1=ct--iqu= **Éque*tiel âvÊr
r*g1age v=cti=r'iel =ubr:rdsnnÉ"i lTc=csur "EnÊrgiEn'.
?l Ela=rhh:e F.
"Ëâ= pr'irip der *eldsri=ntiÉr'Ll-g , dir-gr-r-:dlage fiir- dir- trans-
vscàcr- -r'egelung vr=n dr'eh$=lsç+=hinerl.; Sierneng Teits=hr-i*t;
1F?1 - t'J 4= - ft 1*.
1i--î] FlËter- S., *ippper-g=r- H.
"ti= tr-si':=v==tai-- r'egeli-ing fiii- den *eld*ri=*ti"=tgn betrieb ein=r.
A=ynchr-' r:r:-r*a==h i r:* "
Eien=n= ?=it==hri+t"" 1?Tl - iii 45 - H 3.J.](https://image.slidesharecdn.com/32-530-58-1-2-231026172714-2ae41f31/85/32-530-58-1-2-pdf-139-320.jpg)
![I
I
I
I
I
I
I
I
I
I
I
I
I
I
I
I
I
I
!
J
t
11) Lagæeiler- F. , *ichter i"i.
"FluE=rfÉung in Ê=ynchrannaschinsn"
Sie*iens Eeit=chrift ", 1ç"S - lri 4= - H 1+.
l=i Lesnhar-d H. , Gahr.iel Ë. , Nardiy tr.
"Field-ilr'i=nted ssntrç3 *f a, standerd AC rnstsr u=i*g micr::pr*-
ceËsfrrÉrr ; IEEË tr'an=g=tis*s on i*du=try âptrlicatifrnË",
1çA$ - çDL I*-1& - l{û? , i*a,rch/apr-i1.
1=: Pav!.ev lr!.8.
"[:rer*ples ds cal=ul des eppareil= de lÊvage"
i-er:ingr*,d "Pla.chinnstrûËr.:iÊ,, r l??&.
14! trhevslier A.
"Le çiiide du des=ine,teur ind*=tr.ie1 ,,
Hschette t==hnique ; Éditian 1?Eil-1"E}?.
15! ËÊAË J.F.
"vites=e vsria-bis, petit * peiit, 1= nsteur a=ynchrr:ne,,.
ïndu=trie= =t techr:ique ?r] jui* 1?gô
i.5} LËAruHARD W.
"ËE*tr'irl s* *x nachine= r*ith the help sf nicrselectrcriicE,,
IF*C Systp' Esntral in Psr*=r El.ectrr:nic= a*d Electr-ical Erive= ,
Lauganne 1ç43
1?l LEnruHÊRS tÀf.
"C=ntr-el t:f eigctrical Sr-ive="
Ëditign 5FËIh|GER-VEFL*Ë l?gs
:.*} E{JHLËE H.
"Ë1 ectrsni qu=
Editian SUlqtS
:.?i EÛ58 E. H,
de p*ig=srice"
{ ôfr{
t rTtl
"FE$rÊr- ELectri:ni=s s.*d AE Dr-ivE=,'
Editic* :Pc*=ntice-Hal! rErigi=g|c*d Ëriff=rNer* Jer=ey, 1çE'&](https://image.slidesharecdn.com/32-530-58-1-2-231026172714-2ae41f31/85/32-530-58-1-2-pdf-140-320.jpg)


