4SI-Algo-2025 manuel et resumé de programmation

Algorithmique et Programmation*** 4ième
SI Prof. Mme
FATMA Knani
REVISION et RAPPEL
Les fonctions prédéfinies sur les types numériques et les chaines
Nom Description
x  abs(a)
x = abs(a)
Retourne la valeur absolue de a
x  arrondi(a)
x = round(a)
Retourne l'entier arrondi le plus proche de a
 L’entier pair le plus proche, si la partie décimale = 0.5
x  ent(a)
x = int(a)
Retourne la partie entière de a
Partie entière 20.25 partie décimale
x  racinecarré(a)
x = sqrt(a)
Retourne la racine carrée de a positif
Il faut ajouter la bibliothèque : from math import sqrt
x  aléa(a,b)
x = randint(a,b)
Retourne aléatoirement un entier entre [a,b]
 Ajouter la bibliothèque : from random import randint
x  ord(c)
x = ord(c)
Retourne le code ASCII (entier positif) du caractère c
c  chr(x)
c = chr(x)
Retourne le caractère dont le code ASCII est x
Ch1 sous_chaine(ch, d, f)
Ch1 = ch[d : f]
Retourne une partie de la chaine ch à partir de la position d jusqu’à la
position
f-1 (f exclue). Le 1er
caractère est de l’ordre 0
L long(ch)
L = len(ch )
Retourne la longueur d’une chaine (le nombre de caractères)
Ch  convch(nb)
Ch = str(nb)
Convertie une valeur numérique nb en une chaîne de caractères
n  valeur (ch)
n = int(ch)
ou
n = float(ch)
Convertir une chaine de caractère en une valeur numérique (entier ou réel ;
sinon erreur)
Ch1 effacer (ch, d, f)
CH1 = CH[:d] + CH[f:]
Retourne une chaîne Ch1 après avoir effacé des caractères de la chaîne ch
à partir de la position d jusqu’à la position f (f exclue).
chm  majus(ch)
chm = ch.upper( )
Convertit une chaine en majuscule
p  pos(ch2,ch1)
p = ch1.find (ch2)
Retourne la position de la 1ère
occurrence de ch2 dans la chaine ch1.
si ch2 existe dans ch1 elle renvoie sa position. Sinon, elle renvoie -1
x  estnum(ch)
x = ch.isdecimal()
Retourne Vrai si la chaine est numérique
(en python : contient seulement des caractères chiffres : ni virgule, ni signe-)
Ordre de priorité entre les opérateurs arithmétiques , logiques et relationnels
1 | P a g e
(1) Les parenthèses
(2) non
(3) * , / , // (div), % (mod) , et
(4) + , - , ou
(5) < , > , <= , >= , != , == , in (), not in

SI Prof. Mme
FATMA Knani
Le type tableau
Le type Enregistrement
Déclaration en algorithmique
TDNT TDO
Nouveaux Types Objet Type / Nature
Nom_Type_Enregistrement=Enregistrement
Champ1 : Type1
Champ2, Champ3 : Type2
………
ChampN : TypeM
Fin
Nom_Enregistremen
t
Nom_Type_Enregistrement
Déclaration en Python
Nom_Enregistrement = { } « signifie Enregistrement
vide »
Nom_Enregistrement = dict (Champ1 = Type1 , Champ2 = Type2 , … ,
ChampN = TypeN)
E = dict(Nom_Enregistrement)
Accès à un champ d’enregistrement
Notation en algorithmique Notation en Python
Nom_Enregistrement . Nom_Champ Nom_ Enregistrement [ " Nom_Champ" ]
2 | P a g e
En
Algorithme
TDNT TDO
Nouveaux Types Objet Type / Nature
Tableau à une
dimension
Nom_type_tab = Tableau de N Type_élément Nom_tableau Nom_type_tab
Tableau à deux
dimensions
Nom_type_mat = Tableau de N lignes * M
colonnes de Type _élément
Nom_matric
e
Nom_type_mat
En Python
Tableau à une
dimension
from numpy import array
T = array ( [Type-element()] * N )
Tableau à deux
dimensions
from numpy import array
T = array ( [[Type-element()] * colonnes ]* lignes)

SI Prof. Mme
FATMA Knani
Les structures de
contrôle
conditionnelles
Syntaxe Algorithmique Syntaxe Python
Forme simple
réduite
Initialisation
Si Condition alors
Traitement
Finsi
if condition:
Traitement ;
Forme alternative
ou complète
Initialisation
Si Condition Alors
Traitement1
Sinon
Traitement2
FinSi
if condition1:
Traitement1
else:
Traitement2
Forme généralisée
Initialisation
Si Condition1 Alors
Traitement1
Sinon Si Condition2 Alors
Traitement2
Sinon Si ………………
Sinon
TraitementN
FinSi
if condition1:
Traitement1
elif condition2:
Traitement2
elif …………
else:
TraitementN
Structure à choix
multiples
Initialisation
Selon sélecteur
valeur1 : trait1
valeur2, valeur4, valeur6 : trait2
valeur7 .. valeur10 : trait3
………
valeur_n-1 : trait_n-1
Sinon trait_n
Fin selon
NB. La variable sélecteur doit être de type scalaire
match selecteur :
case valeur1 :
trait1
case valeur1,valeur2:
trait2
……
3 | P a g e

SI Prof. Mme
FATMA Knani
Les boucles
Structure de contrôle itérative complète (Pour)
En algorithme En Python
Pour compteur de début à fin [Pas = valeur_pas] faire
Traitement à répéter
Finpour
for compteur in range(debut, fin + 1, pas) :
Structure de contrôle itérative à condition d'arrêt
Deux Formulations
La boucle REPETER La boucle TANTQUE
Répéter
Jusqu'a (Condition_Arrêt)
Tant que NON (Condition d'arrêt) faire
Fin TantQue
En
algorithme
En Python
Pas de correspondance. Toutefois, on peut utiliser :
valide = False
while valide == False :
Traitement
valide = ( Condition(s) de sortie )
while Condition :
4 | P a g e

SI Prof. Mme
FATMA Knani
En algorithmique Implémentation en python
Fonction Nom_fonction (pf1: type1 ; pf2: type2 ; … ;
pfn : typen) : Type de résultat
DEBUT
Traitement
Retourner VRésultat
FIN
def Nom_fonction (pf1, pf2 , … , pfn ) :
Traitement
[return VRésultat]
Procédure Nom_procédure (pf1: type1 ; pf2: type2 ; …
@ pfn : typen)
DEBUT
Traitement
FIN
Appel
Mode de passage
En algorithme En Python
Si le mode de passage est par référence (par adresse), on
ajoutera le symbole @ avant le nom du paramètre.
(N.B. la valeur du paramètre effectif sera modifiée
après exécution de sous-programme)
Procédure Nom_procédure (@pf1 : type1 , @pf2 :
type2 , … , pfn : typen)
Début
Traitement
Fin
Nom_module (pf1 , pf2 , … , pfn) :
Traitement
N.B. : En python, les paramètres de type
dictionnaire, tableau et fichier sont, par
défaut passés par référence.
5 | P a g e
Les modules
Module En algorithmique Implémentation en python
Fonction Objet  Nom_fonction (liste des paramètres
effectifs)
Objet  Nom_module (liste des paramètres
effectifs)
Procédure Nom_procédure (liste des paramètres effectifs) Nom_module (liste des paramètres effectifs)

SI Prof. Mme
FATMA Knani
Exercice 1 (SP 2023)
Exercice 2
6 | P a g e

SI Prof. Mme
FATMA Knani
Soit T est un tableau d’éléments de type chaîne (n est un entier impair compris entre 5 et
99). Chaque chaîne (chaîne alphanumérique) doit être composée obligatoirement par des
lettres et des chiffres et contenir au maximum 20 caractères.
À partir du tableau T, on veut extraire deux tableaux T1 et T2. Le tableau T1 contiendra
les entiers extraits des chaines de T. Le tableau T2 contiendra les chaines alphabétiques
extraites de T.
Puis on affichera :
 Tous les entiers premiers de trois chiffres.
 Toutes les chaines palindromes alphabétiques
 La chaîne alphabétique la plus longue.
Exemple : n=7
Le programme affichera :
Tous les entiers premiers de trois chiffres sont : 101 , 419 , 103
Toutes les chaînes palindromes sont : bonnob , elle, enne
La chaine alphabétique la plus longue est : bonnechannce
Exercice 3
Écrire un programme qui permet de remplir un tableau T de n chiffres (6<n<30) puis
cherche et affiche la plus longue séquence de valeurs en ordre croissant des chiffres.
Exemple :
Pour le tableau suivant, le plus longue séquence croissante est : 2 4 6 9
7 | P a g e
4
1
8
9
0
6
7
2
4
6
9
1
3
5
0
8
8
7
4

SI Prof. Mme
FATMA Knani
Exercice 4
Un nombre est dit repdigit (ou uniforme) est un entier naturel strictement positif formé d’un
seul chiffre ou par la répétition d’un même chiffre.
Exemples :
x = 3 est un nombre repdigit
x = 1111211 n’est pas un nombre repdigit
Travail demandé : Écrire l'algorithme d'un module permettant de stocker dans un tableau T
d'enregistrements tous les éléments repdigit paires qui se trouvent dans une matrice carrée M.
Chaque enregistrement du tableau est composé de :
- NumL : l’indice de la ligne
- NumC : l’indice de la colonne
- Contenu : nombre repdigit paire
Exemple : Pour N = 4 et M :
Exercice 5
Les données de n (7 < n < 30) élèves sont regroupées dans un tableau enregistrements T.
La structure d'un enregistrement est comme suit :
 Identifiant : Entier
 Date :
o Jour : Entier
o Mois : Entier
o An : Entier
 Moyenne : Réel
 Rang : Entier
On se propose de saisir les données de n élèves puis de calculer et d’afficher le
nombre des admis, des redoublants ainsi que la moyenne générale de la classe.
Travail à faire :
1. Faire l’algorithme du programme principal.
2. Faire les algorithmes des modules envisagés.
8 | P a g e
0 1 2 3
0 4 555 292 1
1 134 22 80 987
2 765 44444 330 67
3 211 120 9 666
T sera : 0
0
4
1
1
22
2
1
44444
3
3
666
0 1 2 3

SI Prof. Mme
FATMA Knani
Chap 1 : Les fichiers textes et binaires
a- Définition : Un fichier est un ensemble structuré de données de même type nommé et
enregistré sur un support de stockage..
b- Types de fichiers :
 Fichier texte : appelé aussi imprimable ou ASCII, c'est un fichier contenant des lignes
composées de caractères. Ce fichier est directement lisible par un logiciel tel que le bloc note.
 Fichier de données (binaire typé) : fichier basé sur une structure de donnée (fichier de réels,
de caractères, d'enregistrements, ...). Il contient du code binaire (non lisible directement)
c- Déclaration en algorithmique (1ère méthode)
Tableau de Déclaration des Objets (T.D.O)
Objet Type/Nature
Fichier texte Nom_Fichier Fichier texte
Fichier de données Nom_Fichier Fichier de Type _élément
d- Déclaration en algorithmique (2ème
méthode)
Tableau de Déclaration des Nouveaux Types (T.D.N.T)
Fichier texte Nom_Type = Fichier texte
Fichier de données Nom_Type = Fichier de Type _élément
Tableau de Déclaration des Objets (T.D.O)
Objet Type/Nature
Fichier texte Nom_Fichier Nom_Type
Fichier de données Nom_Fichier Nom_Type
 La position initiale du pointeur dans un fichier texte ou de données est Zéro.
 Type_Element peut être : Entier, Réel, chaîne, Booléen, Tableau, Enregistrement.
 Un fichier possède deux noms : un nom logique (interne) : c’est le nom du fichier
déclaré et utilisé par le programme (exp : Eleve) et un nom physique (externe) :
c’est le nom du fichier utilisé par le système d’exploitation (exp : fichier_eleve.dat )
9 | P a g e

SI Prof. Mme
FATMA Knani
Les fonctions et les procédures prédéfinies sur les fichiers textes
Ouverture
Ouvrir ( "CheminNom_Physique" ,
Nom_Logique ,"Mode" )
Avec mode d’ouverture égal à :
 r" : Ouverture d'un fichier existant en Lecture seule.
"w" : Ouverture en Écriture seule. Si le fichier existe,
son contenu sera effacé, sinon il sera créé.
 "a" : Ouverture en mode Ajout à la fin (append). Si le
fichier n'existe pas, il sera créé.
Nom_Logique = open ("Chemin
Nom_Physique","Mode")
f=open("D:4SIeleve.txt","r")
Lecture
Lire ( Nom_Logique , Ch )
Lecture de la totalité d’un fichier.
Lire(f, lg)
Nom_Logique = open ("cheminNom_Physique" , "r" )
Ch = Nom_Logique.read ( ) ou bien
T = Nom_Logique.readlines ( )
Lire_Ligne ( Nom_Logique , Ch )
Lecture d’une ligne depuis un fichier texte.
Lire_Ligne (f, lg)
Nom_Logique = open ("chemin
Nom_fichier.extension", "r" )
Ch = Nom_Logique.readline ( )
Écriture
Ecrire ( Nom_Logique , Ch )
Écriture de la chaîne Ch dans un fichier texte sans
retour à la ligne.
Ecrire (f, lg)
Nom_Logique = open ("cheminNom_fichier.txt" , "w
ou a" )
Nom_Logique.write ( Ch )
f.write (lg)
Ecrire_nl ( Nom_Logique , Ch)
Écriture de la chaîne Ch dans un fichier texte et retour
à une nouvelle ligne
Ecrire_nl (f, lg)
Nom_Logique = open ("cheminNom_fichier.txt" , "w
ou a" )
Nom_Logique.write ( Ch + " n" )
f.write (lg + " n")
Tester fin fichier
Fin_Fichier ( Nom_Logique )
Retourner VRAI si le pointeur est à la fin du fichier
Sinon elle retourne FAUX.
Fin_Fichier (f)
ch= Nom_logique.readline()
While ch != "" :
Traitement
ch = Nom_logique.readline()
N.B. : La fin d’un fichier texte est la chaine vide
Fermeture
Fermer ( Nom_Logique ) Fin_Fichier (f) Nom_Logique.close ( ) f.close ( )
Application 1 :
On veut créer un fichier texte , nommé physiquement « mots.txt » et logiquement F .
Remplir ce fichier par des chaînes de caractères non vides puis calculer et afficher le nombre de
mots dans ce fichier.
Le remplissage du fichier s’arrête lorsque l’utilisateur répond par « N » à la question « Voulez-
vous continuer la saisie O / N ? ».
Travail demandé :
1- Faire l’algorithme du programme principal.
2- Faire les algorithmes des modules envisagés.
3- Donner le programme Python correspondant.
10 | P a g e

SI Prof. Mme
FATMA Knani
Correction
En algorithmique En Python
# Correction de Mme FATMA Knani
# Procédure Remplissage_Fichier pour remplir un fichier par
des chaînes non vides
Procédure Remplissage_Fichier (@ f : Fichier Texte)
Début
Ouvrir (nomphy, f , "w") #création du fichier mots.txt
Répéter
Répéter
Ecrire ("Saisir une chaîne : "), Lire (ch)
Jusqu’à ch ≠ ""
Ecrire_nl (f, ch)
Répéter
Ecrire ("Voulez-vous continuer la saisie
O / N ? ") , Lire (rep)
Jusqu’à (majus (rep) dans [ "N".."O"] {"O" , "N"}
Jusqu’à (majus (rep)= N")
Fermer (f)
Fin
# Fonction Nettoyage pour supprimer les espaces
supplémentaires et les espaces au début et à la fin d’une chaîne
Fonction Nettoyage (ch : chaîne) : chaîne
Début
Tantque (pos("⊔⊔", ch) ≠ -1 ) Faire # Le symbole ⊔ signifie espace
p  pos("⊔⊔", ch)
ch  effacer (ch, p, p+1)
FinTantque
Si ch[0] = "⊔" Alors
ch  effacer (ch, 0, 1)
FinSi
Si ch [long(ch) -1 ] = "⊔" Alors
ch  effacer (ch, long( ch )-1 , long( ch ))
FinSi
Retourner ch
Fin
# Fonction Nombre_mot pour calculer le nombre de mots dans
une chaîne. Sachant que nombre de mots = nombre d’espaces
+1
Fonction Nombre_mot (ch : chaîne) : entier
Début
nbm  1
Pour i de 0 à long(ch) -1 Faire
Si ch [ i ] = "⊔" Alors
nbm  nbm +1
FinSi
FinPour
Retourner nbm
Fin
def Remplissage_Fichier() : # On ne peut pas
mettre f comme paramètre non encore défini
#global f Mettre global f ou bien return f
f = open(nomphy, "w")
stop=False
while (stop == False) :
valid=False
while not valid:
ch = input("Saisir une phrase : ")
valid= ch != ""
f.write (ch+"n")
rep = input("Voulez-vous continuer la
saisie O/N ? ")
while not "N"<=rep.upper()<="O":
rep = input("Voulez-vous continuer la
saisie O/N ? ")
stop = rep.upper() == "N"
f.close()
return f
def Nettoyage(ch) :
while ch.find(" ") != -1 :
p = ch.find(" ")
ch = ch[:p] + ch[p+1:]
if ch[0] == " " :
ch=ch[1:]
if ch[len(ch)-1] == " " :
ch = ch[:len(ch)-1]
return ch
def Nombre_mot (ch) :
nbm = 1
for i in range (0, len (ch)) :
if ch[i] ==" " :
nbm = nbm + 1
return nbm
def Comptage (f) :
f = open(nomphy , "r")
nbmot = 0
ch = f.readline()
while ch != "" :
ch = Nettoyage(ch)
nbmot= nbmot + Nombre_mot (ch)
ch=f.readline()
f.close()
return nbmot
11 | P a g e
T.D.O
Objet Type
Ch,
nomphy
chaîne
rep caractère
T.D.O
Objet Type
p entier
T.D.O
Objet Type
i , nbm Entier

SI Prof. Mme
FATMA Knani
# Fonction Comptage pour calculer le nombre de mots dans le
fichier
Fonction Comptage (f : Fichier Texte) : entier
Début
Ouvrir (nomphy, f , "r")
nbmot  0
Tantque Non Fin_Fichier (f) Faire
Lire_Ligne (f, ch)
ch1  Nettoyage (ch)
nbmot  nbmot + Nombre_mot (ch1)
FinTantque
Fermer (f)
Retourner nbmot
Fin
#Algorithme du programme principal
ALGORITHME Mot
DÉBUT
nomphy  "C:4SImots.txt"
Remplissage_Fichier (f)
Ecrire ("Le nombre de mots dans le fichier = ",
comptage (f))
FIN
T.D.O.G
Objet Type/Nature
nomphy chaîne
Remplissage_Fichier Procédure
Comptage Fonction
f Fichier Texte
# Programme principal
nomphy="C:/4SI/mots.txt"
f=Remplissage_Fichier()
print ("Le nombre de mots dans le fichier = ",
Comptage (f))
12 | P a g e
T.D.O
Objet Type/Nature
Ch , ch1 Chaîne
nbmot Entier
Nettoyage Fonction
Nombre_Mo
t
Fonction

SI Prof. Mme
FATMA Knani
Les fonctions et les procédures prédéfinies sur les fichiers de données
Ouverture
Ouvrir ( "CheminNom_Physique" , Nom_Logique ,"Mode" )
Avec mode d’ouverture égal à :
 rb" : Ouverture d'un fichier en Lecture seule.
"wb" : Ouverture en Écriture. Si le fichier existe,
son contenu sera effacé, sinon il sera créé.
 "ab" : Ouverture en mode Ajout à la fin (append).
Si le fichier n'existe pas, il sera créé.
Nom_Logique = open ("CheminNom_Physique",
"Mode")
Lecture
Lire ( Nom_Logique , Objet )
Lecture d’un enregistrement d’un fichier.
import pickle as pic
Objet = pic.load ( Nom_Logique )
ou
from pickle import *
objet=load(nom_logique)
Écriture
Ecrire ( Nom_Logique , Objet )
from pickle import dump
dump (objet, nom_logique)
Tester fin fichier
Fin_Fichier ( Nom_Logique ) Nom_Logique = open(chemin, "rb")
FinFichier = False
while FinFichier == False :
try :
E = load(nom_logique)
Traitement…
except :
FinFichier = True
Fermeture
Fermer ( Nom_Logique ) Nom_Logique.close ( )
Application 2 :
On veut créer un fichier typé , nommé physiquement « Eleves.dat » et logiquement Fe.
Remplir ce fichier par les noms et les moyennes de N élèves avec (10≤N≤35) puis afficher la
moyenne de la classe et la liste des noms des élèves admis.
Travail demandé :
1- Faire l’algorithme du programme principal.
2- Faire les algorithmes des modules envisagés.
3- Donner le programme Python correspondant.
Correction
En algorithmique En Python
13 | P a g e

SI Prof. Mme
FATMA Knani
# Correction de Mme FATMA Knani
Procédure Saisir (@ n : entier)
Début
Répéter
Ecrire ("Saisir le nombre d’élèves : ")
Lire (n)
Jusqu’à n  [2..20]
Fin
Procédure Remplissage_Fichier (n : entier ; @ f :fichelv)
Début
Ouvrir (nomphy, f , "wb")
Pour i de 0 à n-1 Faire
Ecrire ("Saisir le nom de l’élève N° ", i), Lire (e.nom)
Ecrire ("Saisir la moyenne de l’élève N° ", i), Lire (e.moy)
Ecrire (f, e)
FinPour
Fermer (f)
Fin
Fonction Moyenne (n : entier ; f :fichelv) : réel
Début
Ouvrir (nomphy, f , "rb")
s  0
Lire (f, e)
s  s + e.moy
FinPour
Fermer (f)
Retourner (s/n)
Fin
Procédure Affichage (n : entier ; f :fichelv)
Début
Ouvrir (nomphy, f , "rb")
Ecrire_nl ("La liste des admis : ")
Tantque Non Fin_Fichier (f) Faire # ou boucle Pour
Lire (f, e)
Si e.moy ≥ 10 Alors
Ecrire_nl (e.nom)
FinSi
FinTantque
Fermer (f)
Fin
#Algorithme du programme principal
def Remplissage_Fichier () :
global f
valide = False
while valide == False :
n = int (input("Donner le nombre
d’élèves : "))
valide = (2<=n<=20)
f = open (nomphy, "wb")
for i in range (n) :
e = dict(nom=str(),moy=float())
e["nom"]= input ("Saisir le nom de
l’élève N°"+ str(i+1) +":")
while e["nom"]=='':
e["nom"]= input ("Saisir le nom de
l’élève N°"+ str(i+1) +":")
ok=False
while not ok:
e["moy"]= float (input( "Saisir la
moyenne de l’élève N°"+ str(i+1)+":"))
ok= 0<=e["moy"]<=20
dump (e , f)
f.close()
return n
def Moyenne (n,f) :
f = open (nomphy, "rb")
s = 0
for i in range (n) :
e= load (f)
s= s + e ["moy"]
f.close()
return s/n
def Affichage (f) :
f = open (nomphy, "rb")
14 | P a g e
T.D.O
Obje
t
Type/Nature
e Eleve
T.D.O
Objet Type/Nature
i Entier
e Eleve
s Réel
T.D.O
Objet Type/Nature
i Entier
e Eleve

SI Prof. Mme
FATMA Knani
ALGORITHME Admis
DÉBUT
nomphy  "c:3SIeleves.dat"
Saisir (n)
Remplissage_Fichier (n,f)
Ecrire_nl ("La moyenne de la classe est : ", Moyenne (n, f))
Affichage (n,f)
FIN
print ("La liste des admis : ")
'''for i in range (n) :
e= load (f)
if (e["moy"] >= 10) :
print (e ["nom"])'''
# ou bien sans utiliser le paramètre n
dans l'en-tête :
fin_fichier = False
while fin_fichier == False :
try :
e= load (f)
if (e["moy"] >= 10) :
print (e ["nom"])
except :
fin_fichier = True
f.close ( )
# Programme principal
from pickle import *
nomphy = "eleves.dat"
n=Remplissage_Fichier()
print ("La moyenne de la classe est : ",
Moyenne (n,f))
Affichage (f)
15 | P a g e
T.D.O
Objet Type/Nature
nomphy Chaîne
n Entier
f Fichelv
Saisir Procédure
Remplissage _Fichier Procédure
Moyenne Fonction
Affichage Procédure
T.D.N.T
Type
Eleve = Enregistrement
nom : chaîne
moy : Réel
Fin
Fichelv= Fichier d'Eleve

SI Prof. Mme
FATMA Knani
Chap 2 : Les algorithmes de tri
Le mot TRI en informatique désigne l’action d’ordonner des objets selon un critère
(croissant/décroissant).
Il existe plusieurs algorithmes de tri :
 Tri par sélection
 Tri à bulles
 Tri par insertion
 Tri Shell
 Tri rapide
 Tri fusion
 Tri comptage, …..
1- Tri par Sélection :
Principe :
1- Comparer tous les éléments du tableau pour sélectionner le plus petit/grand
2- Permuter le plus petit/grand élément trouvé avec le premier élément du tableau.
3- Refaire les étapes 1 et 2 : chercher le plus petit/grand élément du tableau sauf le premier puis
l’échanger avec le second élément et ainsi de suite.
Ce processus est répété (N-1) fois sachant que N = nombre d’élément du tableau qu’on veut trier.
Procédure Tri_Selection ( n : entier ; @ t :tab)
Début
Pour i de 0 à n-2 faire
posmin  i
Pour j de i+1 à n-1 faire
Si t[posmin] > t[j] alors
posmin  j
FinSi
FinPour
Si posmin ≠ i alors
aux  t[i]
t[i]  t[posmin]
t[posmin]  aux
FinSi
FinPour
Fin
16 | P a g e
# permut (t[i] ,
t[posmin] )
def Tri_Selection(n,t):
for i in range(n-1):
pmin=i
for j in range(i+1,n):
if t[j]<t[pmin]:
pmin=j
if pmin != i:
aux = t[pmin]
t[pmin] = t[i]
t[i] = aux

SI Prof. Mme
FATMA Knani
2- Tri à bulles :
Principe :
C’est une méthode de tri qui consiste à comparer les éléments du tableau par paires adjacentes
(consécutifs).
On peut la traduire par l’algorithme formel suivant (si tri croissant) :
1- Comparer la première paire d’éléments T[0] et T[1],
2- Si T[0]>T[1] alors permuter T[0] et T[1],
3- Aller à la paire suivante et répéter les étapes 1 et 2 jusqu’à comparer la dernière paire T[N-2]
et T[N-1]
4- On recommence les étapes 1 et 2 ( parcours de 0 à N-2, Puis de 0 à N-3) jusqu’à aucune
permutation n’a été effectuée et tous les éléments du tableau sont triés.
Procédure TriBulle ( n : entier, @t :tab)
Début
Répéter
Echange  Faux
Pour i de 0 à n-2 faire
Si t[i] > t[i+1] alors
aux  t[i]
t[i]  t[i+1]
t[i+1]  aux
Echange  Vrai
FinSi
FinPour
n n-1
Jusqu’à non Echange # ou Echange =Faux
Fin
def tri_bull(n,t):
echange=True
while echange :
echange=False
for i in range (n-1) :
if (t[i]>t[i+1]):
aux=t[i]
t[i]=t[i+1]
t[i+1]=aux
echange=True
n=n-1
3- Tri par Insertion :
Principe :
C’est une méthode de tri qui consiste à prendre les éléments de la liste un par un puis insérer chacun
dans sa bonne place de façon que les éléments traités forment une sous liste triée (comme le jeu de
cartes).
Cette méthode peut se traduire par les étapes suivantes :
1- On commence par T[1], le deuxième élément .
2- Comparer l’élément choisi avec tous ses précédents dans la liste et l’insérer dans sa bonne
place (après avoir décalé à droite, les éléments qui lui sont supérieurs (si tri croissant) ).
3- Répéter l’étape 2 pour l’élément suivant jusqu'à arriver au dernier l’élément T[N-1].
17 | P a g e
# permut (t[i] ,
t[i+1] )

SI Prof. Mme
FATMA Knani
Procédure tri Insertion( n : entier, @t :tab)
Début
V ß T[i] ; j ß i
TantQue (j>=1) Et (V<T[j-1]) Faire
T[j] ß T[j-1]
j ß j-1
Fin TantQue
T[j] ß V
Fin Pour
Fin
def Tri_Insertion(n,TC,TV):
for i in range(1,n):
X = TC[i]
Y = TV[i]
j = i
while (j>=1) and (X<TC[j-1]) :
TC[j] = TC[j-1]
TV[j] = TV[j-1]
j = j-1
TC[j] = X
TV[j] = Y
4- Tri Shell (Donald L. Shell, en 1959) :
Ce tri est une amélioration du tri par insertion. Dans le tri par insertion, un élément passe à
sa place en progressant lentement, case par case. L'accélération consiste à faire des grands
pas, puis des pas de plus en plus petits, jusqu'à, évidemment, des pas de 1 pour que le
tableau soit trié.
 Le calcul du pas est basé sur cette formule (suite) :
p  3*p+1
Procédure Tri_shell(@ T: Tab ; N : entier)
Début
P  1
Tant que (p<N) faire
p  3*p+1
Fin tant que
Tant que (p > 1) faire
p  p div 3
Pour i de p à N-1 faire
temp  T[i]
j  i
18 | P a g e

SI Prof. Mme
FATMA Knani
Tant que (j>p-1) et (T[j-p] > temp) faire # OU j>=p
T[j]  T[j-p]
j  j-p
Fin tant que
T[j]  temp
Fin pour
Fin tant que
Fin
Fin tant q
Application :
Tri Par Fusion
19 | P a g e

SI Prof. Mme
FATMA Knani
Chap 3 : La Récursivité
La récursivité est une méthode algorithmique qui consiste à appeler un sous-programme dans son
propre corps (module qui s'appelle lui-même).
Principe :
 Le sous-programme récursif fait appel à lui-même jusqu’à ce qu’il atteigne une
condition d’arrêt (convergence vers un point d’arrêt).
 À chaque appel, il y a mémorisation d’une nouvelle valeur d'un même paramètre
formel.
 La récursivité utilise toujours la pile du programme en cours (pour stocker les données
intermédiaires : problème : déborde lorsque le nombre des appels devient important).
Activité :
Calculer la factorielle d’un entier positif N , notée N! = 1*2*…*N et0! = 1
 On peut utiliser une méthode itérative ou récursive :
Algorithme itératif Algorithme récursif
Fonction Factorielle (n : Entier) : Entier
Début
F ← 1
Pour i de 2 à n Faire
F← F * i
Fin Pour
Retourner F
Fin
Fonction Factorielle (n : Entier) : Entier
Début
Si (n = 0) Alors Retourner 1
# Si n < 2 ou Si (n=0) ou (n= 1) Alors Retourner 1
Sinon Retourner n * Factorielle(n-1)
FinSi
Fin
20 | P a g e

SI Prof. Mme
FATMA Knani
I)
II) On veut écrire un algorithme récursif intitulé verif qui permet de vérifier si un tableau T rempli
par N entiers est trié dans l’ordre croissant ou non.
Pour cela on vous demande de compléter le tableau ci-dessous en mettant Valide ou Invalide
dans la colonne correspondante pour chaque définition de la fonction verif.
Justifier votre réponse dans le cas où la définition est invalide.
21 | P a g e
Applications

SI Prof. Mme
FATMA Knani
III)
Pour chaque exercice suivant, écrire un module récursif solution.
1. Calculer la somme de n premiers entiers.
Exemple : Pour N=7 , la somme des 7 premiers entiers est : 1+2+3+4+5+6+7 = 28
2. Saisir un entier N paire.
3. Calculer et renvoyer le nombre de caractères voyelles majuscules dans une chaine ch.
4. Inverser une chaine de caractère
5. Calculer la somme de chiffres d’une chaine de caractères ch.
Exemple : Pour ch = ’’4SI 2024’’, la fonction retourne 12.
6. Calculer la somme des éléments d’un Tableau.
7. Tester si une chaine est palindrome ou non.
 Nous appelons "palindrome" un mot ou une phrase qui se lit de la même façon dans les deux
sens (de gauche à droite et de droite à gauche ).
Exemple : radar, rotor, été, AZZA, 123454321.
8. Calculer et afficher la valeur de Xn
avec X un réel donné.
Exemple : Pour X = 2 et n = 8, la fonction retourne 28
= 256
9. Vérifier la primalité d'un nombre n.
10. Afficher les entiers compris entre 2 bornes a et b.
11. Tester l’existence d’un entier E dans un Tableau.
12. Vérifier l’existence d’un entier m dans un tableau T contenant n entiers, en utilisant la
technique de la recherche dichotomique.
NB : Nous supposons que le tableau est déjà trié dans l’ordre croissant.
13. Trier un tableau T de n entiers dans l’ordre décroissant
(utiliser la méthode de tri par sélection).
22 | P a g e

SI Prof. Mme
FATMA Knani
Chap 4 : Les algorithmes récurrents
Un algorithme ou un traitement est dit récurrent s’il utilise un procédé itératif ou récursif pour donner
un résultat qui peut dépendre de P résultats précédents, on parle alors d’un algorithme ou d’un
traitement récurrent d’ordre P.
Exemple : Un algorithme récurrent d’ordre 2 est un algorithme donnant un résultat dépendant de
deux résultats précédents.
1- Les algorithmes récurrents d’ordre 1 :
Activité 1 : Somme matrice
Écrire l’algorithme d’un module qui permet de calculer la somme des éléments d’une matrice
carrée d'entiers d'ordre n (4  n  20).
Activité 2 : Suite de Thue-Morse ( Suites de chaînes de caractères)
La suite de Thue-Morse consiste à remplacer toute occurrence du caractère "0" par la chaine "01"
et toute occurrence du caractère "1" par la chaine "10", etc.
Exemple : Si on part de la chaine "0" , on aura les transformations suivantes :
Suite récurrente d'ordre ??? ………..
Écrire un programme qui calculer et affiche le Nème
terme de la suite de Thue-Morse à partir d'un
caractère A ("0" ou "1" ) donné.
2- Les algorithmes récurrents d’ordre 2 :
Activité 3 : Suite de Fibonacci
Leonard de Pise, plus connu sous le nom de Fibonacci, étudia du point de vue numérique la
reproduction des lapins. Il considère qu'un couple de jeunes lapins met une saison pour devenir
adulte, attend une deuxième saison de gestation, puis met au monde un couple de jeunes lapins à
chaque saison suivante.
En supposant que les lapins ne meurent jamais, nous obtenons donc le schéma ci-dessous :
 Cette suite est définie par la relation récurrente suivante :
U1 = 0
U2 = 1
Un = Un-1 + Un-2 pour tout n >=2
 Écrire un module (itératif, puis récursif) qui permet de calculer les nième
termes de la
suite de fibonacci pour un terme n donné.
23 | P a g e

SI Prof. Mme
FATMA Knani
Activité 4 : Triangle de Pascal
Le triangle de Pascal est une présentation des coefficients
binomiaux dans un tableau triangulaire (Matrice). Pour calculer les
coefficients du binôme : on remplit la matrice en mettant des 1 à la
première colonne, des 1 sur la diagonale principale et en remplissant
le reste du matrice suivant la règle suivante : chaque coefficient
s'obtient comme la somme du coefficient qui est juste au-dessus de lui, et du
coefficient qui est à la gauche de ce dernier :
M [ligne, colonne] = M [ligne-1, colonne] + M [ligne-1, colonne-1]
On se propose de remplir et d’afficher les n premières lignes du Triangle de Pascal (3  n 
100). Ecrire une solution itératif, puis récursif.
a) Proposez un algorithme modulaire du problème,
b) Déduisez les algorithmes correspondants,
c) Traduisez et testez la solution obtenue.
Activité 5 : Nombre d’OR
appelé nombre d'or, dont une valeur approchée est 1,618033988……. (appelé phi ou Φ)
 Soient deux suites U et V définies à partir de :
La suite Vn tend vers une limite appelée nombre d'or.
On suppose que le nième
terme de la suite V soit Vn , donc un nombre approché du nombre
d'or avec une précision e dès que |Vn - Vn-1 e.
 Ecrire un module qui permet de calculer et d’afficher Vn et son rang à 10-4
près.
24 | P a g e

SI Prof. Mme
FATMA Knani
Exercice n°1 :
Soit k, n deux entiers naturels et U une suite définie par :
1. Quel est l’ordre de récurrence de la suite U ? justifier
2. Calculer les termes U1, U2 et U3 pour k=4.
3. Parmi les trois propositions suivantes, laquelle qui correspond au rôle de la suite U.
- la suite U permet de calculer la factorielle de k : k !
- la suite U permet de calculer k à la puissance n : kn
- la suite U permet de calculer le produit de n et k : n * k
 Ecrire une version itérative puis une version récursive d’un algorithme d’une fonction qui permet
de calculer Un pour tout entier n supérieur ou égale à 0.
Exercice n°2 :
Soit la suite U définit comme suit :
U0=1
U1=2
Un=Un-1+Un-2 pour tout n>=2 et n pair
Un=Un-1+Un-2+Un-3 pour tout n>=3 et n impair
4
1. Quel est l'ordre de récurrence de cette suite ?
2. Ecrire un programme qui permet de calculer et d’afficher les Nième
termes de cette suite (2<n<=20).
Exercice n°3 :
Soit la suite ROBINSON définie comme suit :
U0=X (X étant un entier positif donnée)
Un+1= nombre d’apparition de chaque chiffre dans Un
Exemple : Si U0=1 alors
U1 = 11 (1 Se répète 1 fois dans U0)
U2=21 (1 Se répète 2 fois dans U1)
U3=1211 (2 Se répète 1 fois et 1 se répète 1 fois dans U2)
U4=3112 (1 Se répète 3 fois et 2 se répète 1 fois dans U3)
U5=132112 (Etc…)
1. Quel est l'ordre de récurrence de cette suite ?
2. Ecrire un algorithme puis la traduction en python d’un programme qui permet de saisir un
entier positif X représentant la valeur de U0 puis calculer et afficher les n premières termes de
cette suite (2<n<=20).
25 | P a g e
U0=1
Un+1= k * Un
Applications

SI Prof. Mme
FATMA Knani
Chap 5 : Les algorithmes arithmétiques
L'arithmétique est une branche des mathématiques qui étudie les relations entre les nombres
Exemples : calcul de la factorielle, calcul de puissance, calcul de PGCD, de PPCM, test de primalité ,
étude de nombres parfaits, conversion entre les bases de numération, nombres de
combinaison, étude de règles de divisibilité, …
I) Primalité d’un nombre :
Un nombre est dit premier : s'il admet exactement 2 diviseurs distincts : 1 et lui-même.
Exemples : 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, …
 Ecrire une fonction itérative puis récursive qui vérifie si un entier est premier ou
non.
Fonction premier(x :entier) : booléen
Debut
i  2
Tant que (n mod i ≠ 0 ) et (i<=n div 2) Faire
i  i + 1
Fin Tantque
Retourner i > n div 2
Fin
def premier1(n):
i=2
x=True
while x and i<=n // 2 :
if n%i==0 :
x=False
else :
i=i+1
return x and n>1
II) Calcul du PGCD :
Le plus grand commun diviseur de deux entiers a et b est le plus grand entier permettant de
diviser a et b. On le note PGCD (a,b).
Ecrire une fonction itérative puis récursive qui détermine le PGCD de 2 entiers a et b
par la méthode de soustractions successives.
Traitement
 Si a>b : a a - b et b ne change pas.
 Si a<b : b b - a et a ne change pas
 Le traitement s'arrête lorsque a=b
26 | P a g e
Fonction premier(n,d :entier) :
booléen
Début
Si d > n div 2 alors
Retourner Vrai
Sinon Si n mod d = 0 alors
Retourner Faux
Sinon
Retourner premier(n,d+1)
FinSi
Fin

SI Prof. Mme
FATMA Knani
Version itérative Version récursive
Fonction pgcd_Difference(a, b : entier) : entier
Début
Tant que (a ≠ b) Faire
Si a >b Alors
a  a - b
Sinon
b  b - a
Fin Si
Fin Tant que
Retourner a
Fin
Fonction pgcd_Difference(a,b : entier) : entier
Début
Si (a = b) Alors
retourner a
Sinon Si (a > b) Alors
retourner pgcd_Difference (a-b,b)
Sinon
retourner pgcd_Difference (a,b-a)
Fin Si
Fin
Ecrire un programme qui permet de saisir 2 entiers positive a et b et déterminer leur PGCD par la
méthode de divisions euclidiennes.
Fonction pgcd_Euclide (a,b : entier) : entier
Début
Répéter
R A Mod B
A B
B R
Jusqu'à B = 0
Retourner a
Fin
Fi
III) Calcul du PPCM :
Le plus petit commun multiple de deux entiers a et b est le plus petit entier multiple à la fois de a et
b. On le note PPCM (a,b).
Traitement
 Si a=b, le PPCM est a (ou b)
Sinon, chercher les multiples de a en ordre croissant et s’arrêter s’il est multiple aussi de b.
Ecrire une fonction itérative puis récursive qui détermine le PPCM de 2 entiers a et b.
27 | P a g e
Fonction pgcd_Euclide (a,b : entier) : entier
Début
Si (b = 0) Alors
Retourner a
Sinon
Retourner pgcd_Euclide(b, a mod b)
Fin Si

SI Prof. Mme
FATMA Knani
IV) Décomposition d’un entier en produit de facteurs premiers :
La décomposition d’un entier en produit de facteurs premiers consiste à écrire cet entier sous la
forme d’un produit de ses diviseurs premiers.
Pour décomposer un entier n en produit de facteurs premiers :
 Vérifier si n est divisible par 2, si oui continuer à le diviser par 2 et le remplacer par n div 2
jusqu’à ce qu’il ne soit plus multiple de 2
 Refaire l’étape précédente pour 3, 4, ...
 Refaire les deux étapes précédentes jusqu’à n = 1
Ecrire une module itératif puis récursif qui décompose un entier en produit de facteurs
premiers.
V) Calcul de :
 Ecrire l’algorithme d’une fonction qui permet de chercher le nombre d’arrangement de
deux entiers donnés n et p, avec (1 ≤ p ≤ n).
 Ecrire l’algorithme d’une fonction qui permet de chercher le nombre de combinaison de p
éléments parmi n, avec (0 ≤ p ≤ n).
VI) Règles de divisibilité :
Un entier N est divisible par un entier M, si le reste de la division euclidienne de N par M est nul
Divisibilité par 3 :
Un entier est divisible par 3 si la somme de ses chiffres est divisible par 3.
Exemple : Soient les entiers suivants : 6, 42, 191, 39, 41, 30, 20, 13 et 8.
 dans cette liste d'entiers, encerclez ceux qui sont divisibles par 3.
Fonction Div_3 (ch : Chaine) : Chaine
Début
Somme  0
Pour i de 0 à Long (ch) -1 Faire
Somme  Somme + Valeur (ch[i])
FinPour
Retourner Somme Mod 3 = 0
Fin
28 | P a g e

SI Prof. Mme
FATMA Knani
Un entier est divisible par 4 si le nombre formé par ses deux derniers chiffres est divisible par 4.
Exemples : 6287 n'est pas divisible par 4 (car 87 n'est pas divisible par 4),
4120 l'est (car 20 = 5 x 4, donc divisible par 4).
Fonction Div_4 (m : Entier) : Chaine
Début
Retourner (m Mod 100) Mod 4 = 0
Fin
Un entier est divisible par 5 si son chiffre d’unités est égal à 0 ou 5.
Exemples : 6287 n'est pas divisible par 5, car 7 {0, 5}
4120 est divisible par 5, car 0 {0, 5}
3635 est divisible par 5, car 5 {0, 5}
Fonction Div_5 (m : Entier) : Chaine
Début
Retourner (2*m) Mod 10 = 0
Fin
VII) Conversions entre les bases de numération :
Un système de numération est une méthode de comptage fondée sur une base de numération
qui est un entier supérieur ou égal à 2. Soit N une base de numération, le système sera doté de N
chiffres allant de 0 à N-1.
Exemples de bases de numération :
1- Conversion d’un nombre décimal vers une autre base :
 On se propose de convertir les nombres décimaux du fichier FD en leurs équivalents
en base b1 (b1[2,9]). Ces derniers sont à stockés dans un fichier texte FB.
2-Conversion d’un nombre d’une base vers la base décimale :
3-Conversion d'un nombre hexadécimal en binaire :
29 | P a g e
Base Système Symboles
2 binaire 0 et 1
8 octal 0, 1, 2, 3, 4, 5, 6 et 7
10 décimal 0, 1, 2, 3, 4, 5, 6, 7, 8 et 9
16 hexadécimale 0, 1, 2, 3, 4, 5, 6, 7, 8, 9
A, B, C, D, E et F

SI Prof. Mme
FATMA Knani
4-Conversion d'un nombre binaire en octal :
5- Conversion d'un nombre d'une base B1 en une base B2 :
On se propose de convertir un nombre d'une base B1 en base B2, avec 2  b1  16 et 2 
b2  16.
30 | P a g e

SI Prof. Mme
FATMA Knani
Chap 6 : Les algorithmes d'approximation
I) Recherche du point fixe d’une fonction :
En mathématiques, pour une application f d'un ensemble E, un élément x de E est un point
fixe de f si f(x) = x.
 Graphiquement, les points fixes d'une fonction f s'obtient
en traçant la droite d'équation y = x : Tous les points
d'intersection de la courbe représentative de f avec cette
droite sont alors les points fixes de f.
Activité :
En utilisant le logiciel graph, chercher les points fixes de ces
fonctions :
 f(x) = 1 - sin(x)
 f(x) = cos(x)
Écrire un programme qui calcule et affiche une valeur approchée du point fixe de la fonction f
avec une précision epsilon (à 10-4
près).
Algorithme Python
Fonction f (x : réel) : Réel
Début
Retourner 1-sin(x)
Fin
Fonction Point() :
Début
x  0.5 {choix arbitraire}
Tant que abs(f(x)-x)>0.00001 Faire
x  f(x)
Fin Tant que
Retourner x
Fin
OU
xprec  0.5
xact  f(xprec )
Tant que abs(xact-xprec)>0.00001 Faire
xprec  xact
xact  f(xact )
Fin Tant que
def f(x):
return 1-sin(x)
def point():
x=0.5
while abs(f(x)-x)>0.00001:
x=f(x)
return x
print(point())
31 | P a g e

SI Prof. Mme
FATMA Knani
II) Calcul de valeurs approchées de constantes connues :
1) Valeur approchée de :
π
En utilisant la formule d’Euler :
Π
6
2
=1+
1
2
2 +
1
3
2 +
1
4
2 +
1
5
2 +.....+
1
n
2
Ecrire un programme Python qui calcule et affiche une valeur approchée de π avec une erreur
maximale ε. La valeur de ε est un réel donné. Le calcul s’arrête quand la différence entre deux
termes consécutifs devient inférieure ou égale à ε = 10-5
.
Algorithme Python
Fonction Pi_Euler (Ep : réel) : Réel
Début
S2 ←1, i ←2 # S2 ← 0 i ←1
Répéter
S1 ← S2
S2 ← S1 + 1 / (i*i)
i  i + 1
Jusqu'à abs(RacineCarrée (6*S2) -
RacineCarrée (6*S1)) < Ep
Retourner RacineCarrée (6*S2)
Fin
from math import sqrt
def pi_eul (ep):
s1=1
s2=1+(1/4)
i=3
while abs(sqrt(6*s2)-sqrt(6*s1))>= ep :
s1=s2
s2=s2+1/(i*i)
i=i+1
return sqrt(6*s2)
En utilisant la formule de Wallis :
Π
2
=
2
1
∗
2
3
∗
4
3
∗
4
5
∗
6
5
∗
6
7
∗
8
7
∗
8
9
∗.......∗
2i
2(i−1)+1
∗
2i
2i+1
Fonction Pi_ Wallis(Ep : réel) : Réel
Début
P2 ←1
i ← 1
Répéter
P1 ← P2
P2 ← P2 * ((2*i)/(2*(i-1)+1))* ((2*i)/(2*i+1))
i  i + 1
Jusqu'à abs(2*P2 - 2*P1) < Ep
Retourner 2*P2
Fin
def pi(epsilon):
Pp=2
Pa= 2*2/3
i=2
while abs(2*Pa – 2*Pp)>epsilon:
Pp=Pa
Pa=Pa*(2*i/(2*i-1))*(2*i/(2*i+1))
i=i+1
return 2*Pa
2) Valeur approchée de e (Euler) :
E ou nombre exponentiel ou nombre de Neper est une constante représentant la base de l’algorithme
népérien. Elle est égale à 2.7182818284 5904523536 …
e = 1 + (1/1!) + (1/2!) + (1/3!) + (1/4!) + (1/5!) + (1/6!) + ... + (1/n!)
32 | P a g e

SI Prof. Mme
FATMA Knani
Algorithme Python
Fonction e(Ep : réel) : Réel
Début
S2 ←1
i ← 1
F ← 1
Répéter
S1 ← S2
S2 ← S2 + 1 / (F*i)
F  F*i
i  i + 1
Jusqu'à abs(S2 - S1) < Ep
Retourner S2
Fin
def fact(x):
f=1
for i in range(1,x+1):
f=f*i
return f
def neper():
s1=1 ; s2=2 ; i=2
while abs(s2-s1)> 0.0001:
s1=s2
s2=s2+1/fact(i)
i=i+1
return s2
def neper1(ep):
s1=1 ; s2=2 ; i=2
F=1
while abs(s2-s1)> ep:
s1=s2
s2=s2+1/(F*i)
F=F*i
i=i+1
return s2
Applications
Exercice -1-
Soit la formule de Leibniz
π
4
=1−
1
3
+
1
5
−
1
7
+
1
9
−...
1. Donner le terme de cette formule dans le cas général
2. Donner un algorithme qui permet de calculer une valeur approché de π avec une erreur
maximale ε. La valeur de ε est une donnée.
Exercice -2-
La racine carrée approchée d’un nombre réel R par la méthode de Newton, définit de la façon
suivante :
U0 = R
Un+1 = (Un+ R / Un) / 2
Cette suite converge vers √Rle calcul est arrêté lorsque  R - Un
2
 < e, où e est un réel positif
saisi au clavier.
Donner un algorithme qui permet de calculer une valeur approché de √R
33 | P a g e

SI Prof. Mme
FATMA Knani
34 | P a g e

SI Prof. Mme
FATMA Knani
Exercice -3-
Ecrire un programme Python qui calcule et affiche la valeur de π en utilisant cette formule.
Π
4
=1−
1
3
+
1
5
−
1
7
+
1
9
.......
(−1)
i
(2i+1)
..
Exercice -4-
Pour x très proche de zéro on a :
cos( x )=1−
x
2
2 !
+
x
4
4 !
−
x
6
6 !
+.. ... ... .
(−1)
n
x
2 n
2n !
et
sin s(x)=
x1
1!
−
x3
3!
+
x5
5!
−
x7
7!
+
x9
9!
.........+
(−1)i
x(2i+1)
(2i+1)!
Calculer cos (x) puis sin(x) en utilisant les formules ci-dessus :
 Le calcul s’arrête quand la différence entre deux termes consécutifs devient inférieure ou
égale à e, où e est un réel positif saisi au clavier.
La dernière somme calculée est une valeur approchée de cos (x) / sin(x).
Exercice -5-
35 | P a g e

SI Prof. Mme
FATMA Knani
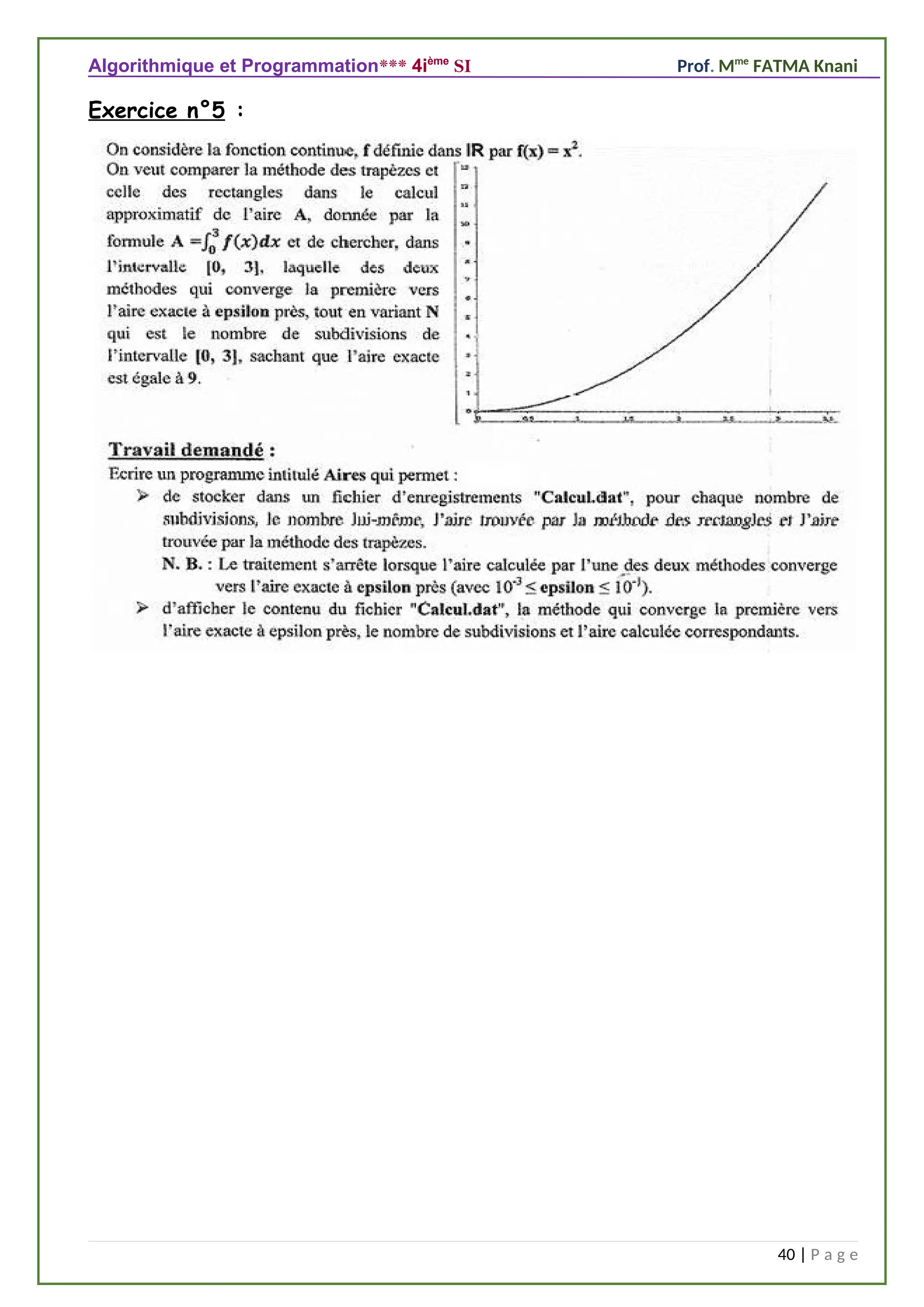
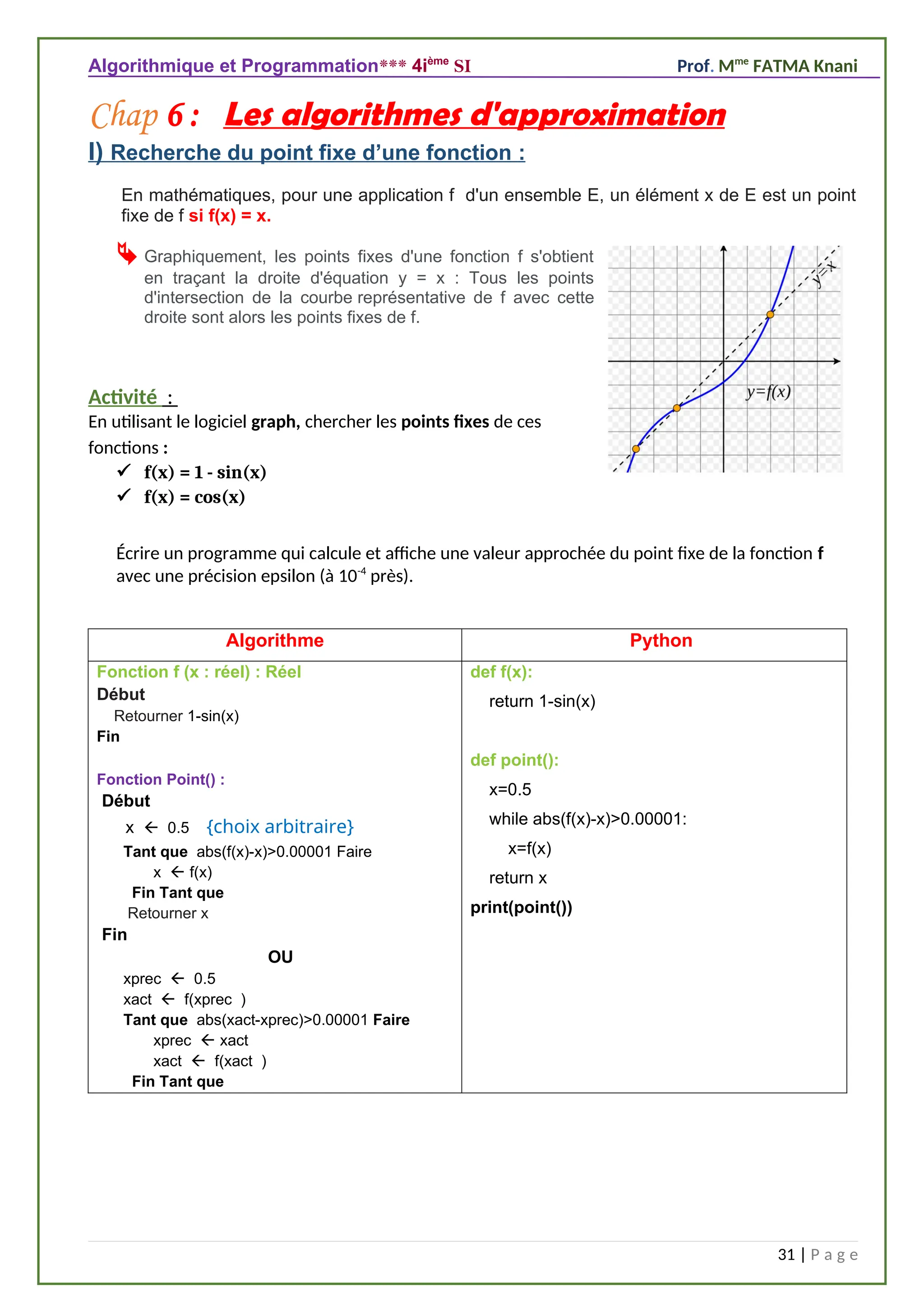
III) Calcul d’aires :
Soit une fonction f continue et croissante dans l'intervalle [a,b].
Si nous ne connaissons pas de primitive de la fonction f, nous ne pouvons pas calculer ∫a
b
f (x)dx
Nous chercherons alors, à en déterminer une valeur approchée.
En mathématiques, l’intégrale ∫a
b
f (x)dx
d’une fonction réelle positive dans
l’intervalle [a,b] est la valeur de l’aire du domaine délimité par l’axe des
abscisses et la courbe représentative de la fonction.
 Donc on va décomposer l’intervalle [a,b] en sous-
intervalle de même largeur (b-a)/n, avec : a=borne
inferieure de l’intégrale ; b=borne supérieure de
l’intégrale ; n=nombre de sous-intervalles (de
subdivisions)
1- Méthode de rectangle :
Sur chaque intervalle [ai, ai+1] est représenté un rectangle de largeur ai+1 – ai et de hauteur : h= (b-a)/n
Nous proposons de calculer, en utilisant la méthode des rectangles, l'aire résultante de la
courbe de la fonction f : x  1/ (1+x2
) sur un intervalle [a, b] donné.
2- Méthode de trapèzes :
Dans cette méthode, pour calculer
l’aire de toute la surface, il suffit de
calculer la somme de toutes les
surfaces des trapèzes, et non des
rectangles, entre a et b.
36 | P a g e

SI Prof. Mme
FATMA Knani
En utilisant la méthode des trapèzes, écrire un module qui calcule l'aire résultante de la
courbe de la fonction
f : x  1/ (1+x2
) sur un intervalle [a, b] donné.
Applications
Exercice n°1 : (Bac 2017)
37 | P a g e

SI Prof. Mme
FATMA Knani
38 | P a g e

SI Prof. Mme
FATMA Knani
39 | P a g e

SI Prof. Mme
FATMA Knani
Exercice n°5 :
40 | P a g e

SI Prof. Mme
FATMA Knani
Chap 7 : Programmation d'une interface
graphique
TP n° 1 : (Bac Pratique 2023)
41 | P a g e

SI Prof. Mme
FATMA Knani
42 | P a g e

SI Prof. Mme
FATMA Knani
43 | P a g e

SI Prof. Mme
FATMA Knani
TP n°2 : (Bac Pratique Prototype 2023)
44 | P a g e

SI Prof. Mme
FATMA Knani
45 | P a g e

SI Prof. Mme
FATMA Knani
46 | P a g e

SI Prof. Mme
FATMA Knani
TP n° 3 : (Inspiré du Bac Pratique 2011)
47 | P a g e

4SI-Algo-2025 manuel et resumé de programmation

Contenu connexe

Tendances

Similaire à 4SI-Algo-2025 manuel et resumé de programmation

Dernier

4SI-Algo-2025 manuel et resumé de programmation