Le document traite des concepts fondamentaux en analyse mathématique, y compris les limites, la continuité, les dérivées, et les intégrales. Chacun de ces sujets est détaillé avec des définitions, des exemples, et des théorèmes essentiels. Il aborde aussi des applications pratiques comme les dérivées et les intégrales dans divers contextes mathématiques.

1. Analyse
Didier Müller, janvier 2012
www.nymphomath.ch

3. Table des matières
1. Limites
1.1. Les limites dans la vie courante.....................................................................................................................................1
1.2. Exemple introductif.......................................................................................................................................................2
1.3. Définition et notations...................................................................................................................................................3
1.4. Opérations sur les limites..............................................................................................................................................4
1.5. Calcul de limites quand x → a, a fini............................................................................................................................4
1.6. Calcul de limites quand x → ∞......................................................................................................................................5
1.7. Une limite célèbre..........................................................................................................................................................7
1.8. Ce qu'il faut absolument savoir.....................................................................................................................................7
2. Continuité
2.1. Continuité en un point...................................................................................................................................................9
2.2. Continuité sur un intervalle...........................................................................................................................................9
2.3. Opérations sur les fonctions continues........................................................................................................................10
2.4. Deux théorèmes fondamentaux sur les fonctions continues........................................................................................11
2.5. Ce qu'il faut absolument savoir...................................................................................................................................12
3. Dérivées
3.1. Un peu d'histoire..........................................................................................................................................................13
3.2. Définition de la dérivée...............................................................................................................................................13
3.3. La dérivée seconde......................................................................................................................................................17
3.4. Dérivées de fonctions usuelles....................................................................................................................................19
3.5. Règles de dérivation....................................................................................................................................................19
3.6. Théorèmes relatifs aux fonctions dérivables...............................................................................................................21
3.7. Ce qu'il faut absolument savoir...................................................................................................................................24
4. Applications des dérivées
4.1. Calculs de tangentes à des courbes..............................................................................................................................25
4.2. Problèmes de taux d'accroissement.............................................................................................................................28
4.3. Problèmes d'optimisation.............................................................................................................................................29
4.4. Méthode de Newton-Raphson.....................................................................................................................................32
4.5. Ce qu'il faut absolument savoir...................................................................................................................................32
5. Étude de fonctions
5.1. Asymptotes..................................................................................................................................................................33
5.2. Points fixes..................................................................................................................................................................33
5.3. Croissance et concavité (rappels)................................................................................................................................34
5.4. Méthode.......................................................................................................................................................................35
5.5. Un exemple complet....................................................................................................................................................35
5.6. Ce qu'il faut absolument savoir...................................................................................................................................38
6. Étude de courbes paramétrées
6.1. Définitions...................................................................................................................................................................39
6.2. Exemple de courbes paramétrées : figures de Lissajous.............................................................................................39
6.3. Asymptotes..................................................................................................................................................................40
6.4. Dérivées et points particuliers.....................................................................................................................................41
6.5. Méthode.......................................................................................................................................................................41
6.6. Deux exemples complets.............................................................................................................................................42
6.7. Ce qu'il faut absolument savoir...................................................................................................................................45

4. 7. Intégrales
7.1. Un peu d'histoire..........................................................................................................................................................47
7.2. Calcul d'aire.................................................................................................................................................................47
7.3. Définition de l'intégrale définie...................................................................................................................................48
7.4. Le théorème fondamental du calcul intégral...............................................................................................................49
7.5. Recherche de primitives..............................................................................................................................................50
7.6. Retour au problème du calcul d'aire............................................................................................................................53
7.7. Calcul de l'intégrale définie.........................................................................................................................................54
7.8. Intégrales impropres....................................................................................................................................................55
7.9. Ce qu'il faut absolument savoir...................................................................................................................................56
8. Applications des intégrales
8.1. Aire entre deux courbes...............................................................................................................................................57
8.2. Volume d'un solide de révolution................................................................................................................................58
8.3. Longueur d'une courbe plane.......................................................................................................................................59
8.4. Aire d'une surface de révolution..................................................................................................................................60
8.5. Mouvement rectiligne..................................................................................................................................................61
8.6. Ce qu'il faut absolument savoir...................................................................................................................................62
9. Équations différentielles
9.1. Introduction.................................................................................................................................................................63
9.2. L'équation y' = f(x).......................................................................................................................................................63
9.3. L'équation à variables séparables y'⋅ g(y) = h(x)........................................................................................................64
9.4. L'équation homogène y' =g
y
x ..............................................................................................................................64
9.5. L'équation linéaire y' + p(x)⋅ y = q(x)..........................................................................................................................65
9.6. Applications des équations différentielles d'ordre 1....................................................................................................65
9.7. Ce qu'il faut absolument savoir...................................................................................................................................67

5. LIMITES 1
1. Limites
1.1. Les limites dans la vie courante
La notion de vitesse, et en particulier la vitesse d'un objet à un instant précis, est,
Vitesse instantanée étonnamment, subtile et difficile à définir précisément. Considérez cette affirmation :
« À l'instant où le cheval a franchi la ligne d'arrivée, il galopait à 64 km/h ». Comment
peut-on étayer une telle affirmation ? Une photographie ne serait d'aucune aide, puisque
sur le cliché, le cheval est immobile ! Il y a une sorte de paradoxe à essayer de quantifier
le mouvement à un moment précis puisqu'en se focalisant sur un seul instant on stoppe
le mouvement !
Rappelons que la vitesse est la distance parcourue ∆x divisée par le temps ∆t qu'il a fallu
pour la parcourir. Pour avoir la vitesse instantanée, on choisira  t 0 . On ne peut pas
prendre ∆t = 0, puisqu'on aurait une division par 0. La vitesse instantanée est donc une
limite.
Zénon d'Elée Les problèmes de mouvement étaient un des thèmes centraux de Zénon et d'autres
(Elée, env. −490 − philosophes dès le 5ème siècle avant Jésus Christ. L'approche moderne, rendue célèbre
Elée, env. −425) par Newton, ne considère plus la vitesse à un instant donné, mais sur un petit intervalle
de temps contenant cet instant.
On a vu dans le chapitre consacré aux droites comment calculer la pente d'une droite.
Pente d'une courbe
Qu'en est-il pour une courbe ? Contrairement aux droites, la pente d'une courbe n'est pas
en un point constante. Par exemple, quand les coureurs du Tour de France gravissent un col, la
pente n'est pas toujours la même ; certains tronçons sont plus raides que d'autres.
Comme la pente d'une droite est le déplacement vertical ∆y divisé par le déplacement
horizontal ∆x, la pente en un point précis d'une courbe sera obtenu en choisissant
 x 0 , autrement dit en prenant deux points « proches » sur la courbe. La pente d'une
courbe en un point est donc elle aussi une limite.
La notion de limite est particulièrement utile pour étudier le comportement d'une
fonction au voisinage d'un trou ou d'un bord de son domaine de définition.
Voisinage d'un trou Voisinage d'un bord du domaine
Didier Müller - LCP - 2012 Cahier Analyse

6. 2 CHAPITRE 1
1.2. Exemple introductif
sin  x
Soit la fonction f  x= dont nous allons étudier le comportement au voisinage
x
0
de a = 0, car elle est indéfinie en ce point, puisqu'on aurait .
0
Méthode numérique La méthode numérique consiste à construire un petit tableau de valeurs.
Dans notre cas, on se rapprochera de 0 en venant depuis la gauche (i.e. en prenant des
nombres plus petits que 0) et depuis la droite (i.e. en prenant des nombres plus grands
que 0). D'après le tableau ci-dessous, il semblerait que la limite de f(x) quand x tend
vers 0 est 1.
Attention ! Dans les méthodes numériques, les angles sont toujours exprimés en
radians !
gauche  a  droite
x –0.1 –0.01 –0.001 –0.0001 0 0.0001 0.001 0.01 0.1
f(x) 0.99833 0.99998 0.99999 0.99999 indéfini 0.99999 0.99999 0.99998 0.99833
Méthode géométrique Nous allons prouver que le résultat de l'analyse numérique est exact par
une méthode géométrique ad hoc.
D
Regardons le dessin ci-contre.
B
Aire du triangle OCB ≤ Aire du secteur OCB ≤ Aire du triangle OCD,
ta n x
d'où :
1 2 x 1
⋅1⋅sin  x⋅1 ⋅  ⋅1⋅tan  x
s in x
2 2 2
x Après simplifications :
0 A C sin  x x tan x
1
Après division par sin(x) (d'après le dessin sin(x) > 0) :
L'arc de cercle BC est une portion du
x 1
cercle trigonométrique (de rayon 1). 1 
sin  x cos  x
Puis en inversant tout :
sin  x
1 cos  x
x
Comme on fait tendre x vers 0, cos(x) tend vers 1 et il résulte que :
sin  x
1 1
x
On vient de démontrer que, en venant depuis la droite (puisque l'angle x
est positif), la limite de la fonction f(x) tend vers 1.
On remarque rapidement que le résultat est le même en venant depuis la
sin − x sin  x
gauche (i.e. x < 0), puisque = et cos(–x) = cos(x).
−x x
Comme la limite à gauche est égale à la limite à droite, on dit que la limite existe et
qu'elle est égale à 1.
sin  x
On l'écrit : lim =1
x 0 x
Remarque importante
Si la limite à gauche est différente de la limite à droite, on dit que la limite n'existe pas.
Cahier Analyse Didier Müller - LCP - 2012

7. LIMITES 3
sin  x
Graphe de , avec un trou en x = 0
x
1.3. Définition et notations
Définition Soit f une fonction définie sur un intervalle ouvert contenant a. Elle peut ne pas être
définie en a.
La limite de f en a est le nombre vers lequel se rapproche la valeur de f(x) quand x se
rapproche aussi près qu'on veut de a, mais avec x ≠a.
Notations Il existe de nombreuses notations pour indiquer les limites à gauche et à droite. Voici
celle que nous utiliserons :
Limite à gauche Limite à droite
lim f x = L lim f  x= L
x a x a
xa xa
Rappelons encore une fois que lim f x = L ⇔ lim f  x= L et lim f  x=L .
x a xa x a
xa xa
{
Exercice 1.1 – 1 si x  1
Soit la fonction f(x) = 2 si x = 1
3 si x  1
Donnez : a. lim f x  b. lim f x  c. lim f x  d. f(1)
x 1 x 1 x 1
x1 x1
Didier Müller - LCP - 2012 Cahier Analyse

8. 4 CHAPITRE 1
1.4. Opérations sur les limites
Si f et g admettent des limites finies quand x  a , avec a fini ou infini, alors :
lim  k⋅f  x=k⋅lim f  x , où k est un nombre réel
x a xa
lim  f  x g  x=lim f  xlim g x (idem pour « – »)
x a xa x a
lim  f  x⋅g  x=lim f  x⋅lim g  x
x a xa xa
lim f  x
f  x x  a
lim = si lim g x≠0
x a g x lim g  x x a
xa
n
x a

lim  f  x= n lim f  x
x a
On va maintenant classer les limites en différentes catégories, puis on développera des
techniques de résolution pour chacune de ces catégories. On cherchera d'abord des
limites quand x tend vers un nombre fini, puis quand x tend vers l'infini.
1.5. Calcul de limites quand x → a, a fini
Limites de fonctions Introduisons d'abord une définition intuitive de la continuité :
continues en a « Une fonction est continue dans un intervalle si on peut la dessiner d'un bout à l'autre
de l'intervalle sans lever le crayon. »
Si f est continue en a, la limite en a est égale à l'image de a.
2 2
Exemples lim 3 x x =3⋅ 5=80
5
x 5
lim sin  x=sin
x

3
 3
3
=
2
N  x
Limite du quotient Soit la fonction f  x=
D x
de deux fonctions
1er cas : c1
Si lim N  x=c1 et lim D  x=c 2≠0 , alors lim f  x= .
dénominateur non nul x a x a x a c2
2ème cas : Seule une des trois réponses suivantes est possible :
numérateur non nul et 1. lim f  x=∞
dénominateur nul x a
2. lim f  x=−∞
x a
3. lim f  x n'existe pas car lim f  x≠lim f  x
x a x a x a
xa xa
Pour déterminer la bonne réponse, il faut donc comparer la limite à gauche et la limite à
droite. Si elles sont égales, la bonne réponse sera la 1. ou la 2. Si elles sont différentes,
la bonne réponse sera la 3.
Si le numérateur et le dénominateur tendent tous les deux vers 0, on a une forme
indéterminée.
Cahier Analyse Didier Müller - LCP - 2012

9. LIMITES 5
3ème cas : a. N(x) et D(x) sont des polynômes
numérateur et Si N(a) = 0, N(x) est divisible par (x–a) et si D(a) = 0, D(x) est aussi divisible par
dénominateur nuls (x–a). On peut donc simplifier la fraction par (x–a).
2
x – 5 x6  x−2 x−3 x−3 1
Exemple : lim =lim =lim =−
x – x – 2 x  2  x−2 x1 x  2 x1
2
x2 3
b. N(x) et D(x) ne sont pas des polynômes
Dans certains cas on peut simplifier.
Exemple : lim
 x – 2 =lim x–2 =lim
1
=
1
x4 x –4 x4   x−2  x 2 x  4  x 2 4
Dans d'autres cas, il faut une autre méthode, par exemple numérique ou géométrique
(voir l'exemple introductif).
Nous verrons dans le chapitre 3, consacré aux dérivées, le théorème de l'Hôpital, qui
pourra être utilisé dans un pareil cas.
Calculez, si elles existent, les limites suivantes :
Exercice 1.2
2 2 2
x –2 x 2 x x – 1 3 x – 2 x 2
1. lim 2. lim 3 3. lim
x 0 x x – 1 x 1 x 0 x1
2 2 2
x 2 x – 15 x 2 x – 15 x 2 x – 15
4. lim 2 5. lim 2 6. lim 2
x – 5 x 8 x15 x3 x 8 x15 x−3 x 8 x15
2 2 2
x – 2 x1 x 1 x – 3 x2
7. lim 8. lim 9. lim
x  2 ∣x – 4∣
2 2
Aide pour les ex. 13-16 : x 1 x –1 x2 x – 4 x 4
x2
  a  b  a –  b=a – b
2 2 2
x – 3 x2 x – 5 x6 x x – 2
10. lim 2
11. lim 2 12. lim 2
Remarque utile pour les x2 x – 4 x 4 x3 2x –6x x 1  x – 1
x2
calculs
Quand x≈0, alors sin(x) ≈x 13. lim
x –1 14. lim
 x 2 x –  2 15. lim
x–5
et tan(x) ≈x. x 1 x –1 x 1 x –1 x 5  2 x –1 – 3
2
Attention, cela ne marche que x sin 2 x sin 2 x
16. lim 17. lim 18. lim
quand x est proche de 0 ! x 0  x 1 – 1
2
x 0 x x 0 sin 3 x 
sin  x –1 sin  x x
Aide pour les ex. 23-24 : 19. lim 20. lim 2
21. lim 2
x 1 x–1 x 0 2 x x x 1  x – 1
comparer les limites à gauche
et à droite tan3 x ∣x∣ ∣x−2∣
22. lim 23. lim 24. lim 2
x 0 3x x 0 x x2 x −3 x2
1.6. Calcul de limites quand x → ∞
Quand on divise un nombre fini par un nombre tendant vers l'infini, le résultat tend vers
Principe du gâteau zéro.
d'anniversaire
Plus le nombre d'invités
est grand, plus la part de
gâteau est petite.
Didier Müller - LCP - 2012 Cahier Analyse

10. 6 CHAPITRE 1
Théorème 1
Limite d'une
fonction polynôme En +∞ (respectivement –∞), toute fonction polynôme a la même limite que son terme de
degré le plus élevé.
quand x → ∞
Démonstration
n n– 1 n –2
lim  an x an – 1 x an – 2 x a 1 xa0  =
x ∞
n a n – 1 1 an – 2 1 a1 1 a0 1 n
lim an x 1    =lim a x
x ∞ an x  a n x2 a n x n−1  x  ∞ n
 a n xn
0 0 0 0
Théorème 2
Limite d'une
fonction rationnelle En +∞ (respectivement –∞), toute fonction rationnelle a la même limite que le rapport
des termes de plus haut degré du numérateur et du dénominateur.
quand x → ∞
En effet, d'après le théorème 1 :
{
0 si n  m
n n–1 n
a n x a n – 1 x a1 xa0  an x an
lim m m– 1 =lim m = si n = m
x ∞ bm x bm – 1 x b1 xb0  x ∞ bm x bn
∞ ou – ∞ si n  m
0
Formes Des expressions du type « », « 0⋅∞ », « ∞ », « ∞−∞ » sont dites indéterminées.
∞
0
indéterminées
Lorsqu'un calcul de limites conduit à une forme indéterminée, on ne peut pas conclure
 x =∣x∣
2 immédiatement ; il faut généralement faire quelques transformations en utilisant par
exemple les formules que vous trouverez dans la marge.
Exemples
∣x∣ = { x si x0
– x si x  0
a. lim   x 24 x 4 – x  = lim    x2 – x = lim ∣x2∣ – x =
2
x∞ x∞ x∞
lim  x2 – x = 2
lim  x 2b xc = x∞
x ∞
lim x
x ∞
∣ b∣
2
b. lim   x 2−2 x 42 x = lim    x−1232 x =
x−∞ x−∞
Refaites les deux exemples
ci-contre en utilisant la
troisième formule !
x−∞ 
lim   x−1  1
2
 3
 x−1 
2 2 x = lim ∣x−1∣ 1
x−∞ 
3
 x−1 2

2 x =
0
lim ∣x−1∣ 2 x = lim − x12 x = lim  x1 = –∞.
x−∞ x−∞ x−∞
Calculez, si elles existent, les limites suivantes :
Exercice 1.3
2 2 2
2x –3x 3 x – x1 2x – x
1. lim 2 2. lim 3 3. lim
x∞ 3 x – 5 x1 x−∞ x x x−∞ x2
3 2 2 2
x 3 x  x−1 x −4 x3
4. lim 2 5. lim 2 6. lim 2
x∞ x –1 x∞ x 3 x x∞ 2 x 5
7. lim
2
x −5 x6
8. lim
 x 2−3− x 9. lim
 x 2−4x3
2
x−∞ 2 x −6 x x−∞ x x∞ x1
10. lim  x –  x2 1 11. lim 2 x x 21
x∞ x−∞
Cahier Analyse Didier Müller - LCP - 2012

11. LIMITES 7
1.7. Une limite célèbre
Dans le chapitre consacré aux logarithmes, nous avions déjà vu cette limite célèbre, qui
est la définition du nombre e (dont la valeur est 2.718281828459...) :
x x
lim 1
x∞  1
x
=e . De plus, on a aussi lim 1
x−∞   1
x
=e .
C'est ici l'occasion de remarquer que l'on peut facilement se tromper en faisant des
Où est la faute de raisonnements qui semblent justes. On pourrait en effet se dire que quand x tend vers
raisonnement ? l'infini, 1/x tend vers 0, et qu'il reste alors 1 puissance infini, donc 1. Or, ce n'est pas la
réponse exacte. Aussi est-il toujours prudent de vérifier sa réponse par une petite
analyse numérique.
1
Remarquez bien que
On a aussi : lim 1 y y =e .
quand x → ±∞, y → 0, y0
1 1
puisque y= . En effet, en substituant y par , on retrouve la première limite.
x x
Calculez, si elles existent, les limites suivantes :
Exercice 1.4
x5 3x x
Il faut utiliser les opérations
1. lim 1
x∞  1
x
2. lim 1
x∞  
1
x
3. lim 1
x∞  2
x
du § 1.4 et parfois travailler x x
 
1
par substitution pour se
ramener à la définition de e.
4. lim 1−
x∞  1
x
5. lim 1 – 4 x x
x 0
6. lim
x∞
x
1 x
x1
7. lim
x∞  
x3
x−1
8. lim 13 tan 2  xcot
x 0
2
x 
1.8. Ce qu'il faut absolument savoir
Connaître les définitions de limite, limite à gauche, limite à droite t ok
sin  x
Savoir prouver que lim =1 t ok
x 0 x
Savoir résoudre les types de limites vus dans ce chapitre t ok
Didier Müller - LCP - 2012 Cahier Analyse

12. 8 CHAPITRE 1
Cahier Analyse Didier Müller - LCP - 2012

13. CONTINUITÉ 9
2. Continuité des fonctions
2.1. Continuité en un point
Définition On dit qu'une fonction f est continue en x = a si les trois conditions suivantes sont
satisfaites :
- f(a) existe dans ℝ ,
- les limites à gauche et à droite existent dans ℝ et sont égales,
- les limites à gauche et à droite sont égales à f(a).
Version courte, mais équivalente :
f est continue en a si lim f x = f  a .
x a
Où les fonctions ci-dessous sont-elles discontinues ?
2
x – x– 2
a. f  x=
x –2
On remarque que f(2) n'est pas défini, ce qui entraîne que f est discontinue en 2.
{
2
x – x– 2
si x≠2
b. f(x) = x– 2
1 si x=2
2
x – x–2  x – 2 x1
Comme f(2) = 1, f est définie en 2, et lim =lim =3 existe,
x2 x–2 x 2 x–2
mais lim f x ≠ f 2  .
x 2
Donc, f est discontinue en 2.
{
1
si x≠0
c. f(x) = x 2
1 si x=0
1
Comme f(0) = 1, f est définie en 0, mais lim f x =lim 2 =∞
.
x 0 x 0 x
Aussi, f est discontinue en 0.
d. f(x) = [x]
La fonction partie entière f(x) = [x] présente une discontinuité en chaque valeur
entière de x parce que lim [ x ] n'existe pas si n est un entier.
x n
2.2. Continuité sur un intervalle
Définition graphique Donnons tout d'abord une définition graphique intuitive :
« Une fonction f est continue si on peut dessiner son graphe sans lever le crayon. »
Didier Müller - LCP - 2010 Cahier Analyse

14. 10 CHAPITRE 2
Continuité à gauche et Une fonction est continue à droite en un nombre a si lim f x = f  a et continue à
x a
continuité à droite xa
gauche en un nombre a si lim f x = f  a .
x a
xa
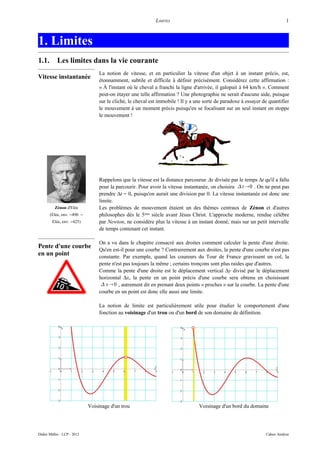
Esquissez le graphe d'une fonction qui est continue partout sauf en x = 3, et qui est
Exercice 2.1
continue à gauche en 3.
Un parking fait payer 2 francs pour la première heure (ou fraction d'heure) et 1 franc
Exercice 2.2
pour chaque heure suivante jusqu'à un maximum journalier de 10 francs.
a. Représentez graphiquement ce tarif de parking en fonction du temps.
b. Remarquez les discontinuités de cette fonction et expliquez leur signification à
quelqu'un qui met sa voiture dans ce garage.
Continuité sur un On dit qu'une fonction est continue sur un intervalle si elle est continue en tout point
intervalle de l'intervalle. Aux extrémités de l'intervalle, il faut comprendre continue par continue à
droite ou continue à gauche.
Rappel Toutes les fonctions suivantes sont continues sur leur domaine de définition :
Une fonction est une règle qui - polynomiales (elles sont continues dans ℝ )
assigne à chaque élément x - rationnelles
d'un ensemble A exactement - racines
un élément, noté f(x), d'un - trigonométriques
ensemble B. L'ensemble A est - trigonométriques réciproques (arcsin, arccos, arctan, arccot)
appelé le domaine de - exponentielles
définition de la fonction. - logarithmes
Attention ! Une fonction continue sur son domaine de définition n'est pas forcément
continue dans ℝ . Par exemple, tan(x) est continue sur son domaine de définition, mais
pas dans ℝ .
2.3. Opérations sur les fonctions continues
Soient f et g deux fonctions définies sur un intervalle I ; soit un réel a ∈ I. Si les
fonctions f et g sont continues en a, alors
1. λ·f est continue en a ( ∈ℝ ),
2. f + g est continue en a (idem pour « – »),
Chacun de ces résultats
découle de la loi des limites 3. f·g est continue en a,
correspondante f
4. est continue en a si g(a) ≠ 0 et discontinue si g(a) = 0.
(voir chapitre 1, § 1.4) g
5. Si une fonction g est continue au point a et une fonction f est continue au point g(a),
alors f °g est continue en a.
ln  xarctan  x
Où la fonction f  x= 2 est-elle continue ?
x –1
La fonction y = ln(x) est continue pour x > 0 et y = arctan(x) est continue sur ℝ . Il
s'ensuit que la fonction ln(x) + arctan(x) est continue sur ]0 ; +∞[, d'après la règle 2.
La fonction du dénominateur est polynomiale et donc partout continue. D'autre part,
x2 − 1 est nul quand x = 1 et x = −1.
Finalement, f est continue sur les intervalles ]0 ; 1[ et ]1 ; +∞[.
Cahier Analyse Didier Müller - LCP - 2010

15. CONTINUITÉ 11
Expliquez pourquoi les fonctions ci-dessous sont discontinues pour la valeur de a
Exercice 2.3
donnée. Dessinez le graphe de ces fonctions.
2
x –1
a. f(x) = a = −1
x1
{
2
x −1
si x≠−1
b. f(x) = x1 a = −1
6 si x=−1
{
2
x −2 x−8
c. f(x) = si x≠4 a=4
x−4
3 si x=4
d. f(x) =
{1−x si
2
x −2 x si
x≤2
x2
a=2
Expliquez pourquoi les fonctions ci-dessous sont continues en chaque point de leur
Exercice 2.4
domaine de définition. Précisez ce domaine de définition.
4
x 17
a. f  x= 2 b. f t =2 t  25 – t 2
6 x x – 1
x 2
c. f  x=e sin 5 x d. f  x=arcsin  x – 1
f  x=cos e x 
4
e. f t=ln t –1 f.
2.4. Deux théorèmes fondamentaux sur les fonctions continues
Théorème de Bolzano
Si f est une fonction continue sur [a, b] telle que f(a) et f(b) ont des signes opposés, alors
il existe au moins un réel c dans l'intervalle ouvert ]a, b[ tel que f(c) = 0.
Moins formel :
« Une fonction continue ne peut changer de signe qu'après s'être annulée. »
Théorème de la valeur intermédiaire
Bernhard Bolzano Si f est une fonction continue sur [a, b] et f(a) ≠ f(b), alors, pour tout réel u strictement
(Prague, 5/10/1781 - compris entre f(a) et f(b), il existe au moins un réel c de l'intervalle ouvert ]a, b[ tel que
Prague, 18/12/1848) f(c) = u.
Le théorème de la valeur
intermédiaire certifie qu'une
fonction continue passe par
toutes les valeurs intermédiaires
entre les valeurs f(a) et f(b).
Attention ! L'inverse n'est
pas vrai ! En effet, pour un
réel c strictement compris
entre a et b, il n'existe pas
forcément un réel u = f(c) dans
l'intervalle ]f(a), f(b)[.
Didier Müller - LCP - 2010 Cahier Analyse

16. 12 CHAPITRE 2
Y a-t-il équivalence entre la propriété de la valeur intermédiaire et la continuité ?
Exercice 2.5 Autrement dit, est-ce que si une fonction satisfait la propriété de la valeur intermédiaire,
cela signifie-t-il qu'elle est continue ? La réponse est non.
{  1
sin si x≠0
Montrez que la fonction f(x) = x est un contre-exemple.
0 si x=0
Le théorème de la valeur intermédiaire est mis à contribution dans la localisation des
racines des équations, ainsi que le montre l'exemple suivant :
Quand u = 0, on peut aussi
utiliser le théorème de « Montrez qu'une racine de l'équation 4x3 − 6x2 + 3x − 2 = 0 est située entre 1 et 2. »
Bolzano, qui est un cas
particulier du théorème de la Posons f(x) = 4x3 − 6x2 + 3x − 2. Nous sommes à la recherche d'une solution de
valeur intermédiaire. l'équation donnée, c'est-à-dire d'un nombre c situé entre 1 et 2 tel que f(c) = 0. Voilà
pourquoi nous prenons a = 1, b = 2 et u = 0, en vue d'exploiter ce théorème. On a :
f(1) = 4 − 6 + 3 − 2 = −1 < 0 et f(2) = 32 − 24 + 6 − 2 = 12 > 0
Donc f(1) < 0 < f(2) et u = 0 est bien un nombre situé entre f(1) et f(2). De plus, f, étant
une fonction polynomiale, est continue. Dans ces conditions, le théorème de la valeur
intermédiaire affirme l'existence d'un nombre c entre 1 et 2 tel que f(c) = 0. Autrement
dit, l'équation 4x3 − 6x2 + 3x − 2 = 0 a au moins une racine dans l'intervalle ]1 ; 2[.
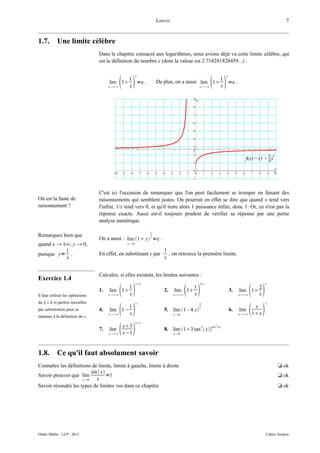
Algorithme de L'algorithme le plus simple permettant de
recherche de zéros trouver un zéro d'une fonction est la
d'une fonction méthode de dichotomie. On commence
avec deux abscisses a et b qui encadrent
un zéro de la fonction. À chaque itération,
on coupe l'intervalle en deux sous-
Les algorithmes de recherche intervalles [a, c] et [c, b], c = (a + b)/2
des zéros d'une fonction sont étant le milieu de a et b. On garde le sous-
étudiés en analyse numérique. intervalle qui contient un zéro, puis on
recoupe en deux ce sous-intervalle, et ainsi
de suite. L'intervalle encadrant le zéro
devient ainsi de plus en plus petit.
La méthode de dichotomie garantit la
convergence vers un zéro lorsque la Étapes successives de la méthode de dichotomie
fonction est continue. avec comme intervalle initial [a1; b1].
1
Exercice 2.6 Montrez que la fonction sin(4x4+3x+2) a une racine comprise entre 0 et
2
, puis
calculez-la à 0.01 près.
2.5. Ce qu'il faut absolument savoir
Connaître la définition de la continuité en un point t ok
Connaître la définition de la continuité à gauche, à droite, sur un intervalle t ok
Reconnaître une fonction continue t ok
Dire où une fonction est discontinue t ok
Connaître le théorème de Bolzano t ok
Connaître le théorème de la valeur intermédiaire t ok
Connaître la méthode de dichotomie t ok
Cahier Analyse Didier Müller - LCP - 2010

17. DÉRIVÉES 13
3. Dérivées
3.1. Un peu d'histoire
Isaac Newton est né le jour de Noël 1642, l'année de la mort de Galilée, à Woolsthorpe,
petit bourg de la région de Lincoln, sur la côte est de l'Angleterre. Admis au Trinity
College de Cambridge en 1661, il se familiarise avec les œuvres de Descartes, Galilée,
Wallis et Isaac Barrow. Entre 1665 et 1666, il est contraint de quitter l'Université de
Cambridge qui ferme ses portes à cause de la peste qui sévit dans la région. De retour à
Woolsthorpe, c'est au cours de cette parenthèse qu'il pose les fondements du calcul
infinitésimal, de la nature de la lumière blanche et de sa théorie de l'attraction
universelle. De retour à Cambridge en 1669, il succède à Isaac Barrow à la chaire de
mathématiques de l'Université, qu'il conservera jusqu'en 1695. En 1671, il conçoit lui-
même un télescope à miroir, exceptionnel pour l'époque, qui grossit 40 fois. Le 11
Isaac Newton
janvier 1672, il est élu à la Royal Society de Londres. En 1687, Newton publie son
(Woolsthorpe, 25/12/1643 -
œuvre maîtresse, Principes mathématiques de philosophie naturelle, exposant sa théorie
Londres, 31/3/1727)
de l'attraction universelle. En 1693, il plonge dans une profonde dépression qui
marquera la fin de sa période créatrice. Les Méthodes des fluxions, qu'il avait écrites en
1671, ne seront publiées qu'en 1736, après sa mort. Newton y faisait alors naître le
calcul infinitésimal, en même temps que Leibniz dont le Calcul différentiel fut, lui,
édité en 1686. À l'époque, les deux hommes s'étaient vivement opposés, chacun
revendiquant la paternité de la découverte. À la mort de Newton, le débat continua.
Leibniz est né à Leipzig le 1er juillet 1646. Il est donc parfaitement contemporain à
Newton. À quinze ans, maîtrisant les langues anciennes, il entre à l'université de Leipzig
pour étudier le droit mais il y découvre Kepler, Galilée et Descartes, ce qui l'incite à
s'initier aux mathématiques. En 1663 il soutient une thèse sur le principe
d'individuation, part étudier les mathématiques à Iena, puis le droit à Altorf où il obtient
Gottfried Wilhelm von Leibniz un doctorat en 1667. En 1672, Leibniz rejoint une mission diplomatique à la cour de
(Leipzig, 1/7/1645 - Louis XIV – pour convaincre le roi de conquérir l'Égypte. Là, il se lie avec les grands
Hannover, 14/11/1716) esprits de l'époque, dont le mathématicien hollandais Christiaan Huygens (1629-1695),
se plonge dans la lecture de Pascal et invente une machine à calculer. Leibniz est ébloui
par les méthodes que lui dévoile Huygens ; au cours d'un voyage à Londres en 1673, il
rencontre des mathématiciens anglais à qui il montre ses premiers travaux et assiste à
des séances de la Royal Society dont il est élu membre étranger. De retour à Paris, il
retrouve Huygens qui l'encourage vivement à poursuivre ses recherches. À l'issue de
son séjour parisien, il élabore le calcul différentiel. En 1684, il publie son Calcul
différentiel. Il fonde en 1700 l'académie de Berlin dont il est le premier président.
Leibniz est aussi célèbre en tant que théologien et philosophe.
D'autres grands noms sont liés à l'intégration. Citons entre autres Jacques Bernoulli
(1654-1705), Jean Bernoulli (1667-1748) le frère de Jacques, Daniel Bernoulli (1700-
Christiaan Huygens 1782) le fils de Jean, le marquis de l'Hôpital (1661-1704), Leonhard Euler (1707-
(La Haye, 14/4/1629 - 1783), Joseph Louis Lagrange (1736-1813), Pierre Simon de Laplace (1749-1827) et
La Haye, 8/7/1695) Augustin Cauchy (1789-1857).
3.2. Définition de la dérivée
f  x 0 x – f  x 0 
Définition 1 Si la limite f '  x 0= lim existe, elle est appelée fonction dérivée
 x 0 x
de la fonction f. f est alors dite dérivable.
Remarque : ∆x peut être positif ou négatif. Si ∆x > 0 on parle de dérivée à droite ; si
∆x < 0, on parle de dérivée à gauche. La fonction est dérivable si la
dérivée à droite et la dérivée à gauche existent et si elles sont égales.
Didier Müller - LCP - 2011 Cahier Analyse

18. 14 CHAPITRE 3
∆x est un accroissement
(une variation) de la
variable x.
f(x0+∆x) – f(x) est
l'accroissement de f .
f  x 0 x – f  x 0
est
x
le taux d'accroissement
moyen.
Quand ∆x → 0, on parle
de taux de variation
instantané.
Attention ! ∆x ne signifie pas ∆·x. Cela signifie « un petit accroissement de x ». On ne
peut pas séparer le ∆ du x.
Interprétation La valeur f '(x0) est la pente de la tangente à la courbe f(x) en x = x0.
géométrique
De cette interprétation géométrique, on peut déduire que :
Si f ' > 0 sur un intervalle, alors f est croissante sur cet intervalle.
Si f ' < 0 sur un intervalle, alors f est décroissante sur cet intervalle.
Si f ' = 0 en un point, alors ce point est un extremum de la fonction ou un point
d'inflexion à tangente horizontale.
minimum maximum points d'inflexion à tangente
(extrema) horizontale (chaise)
Définition 2 Si une fonction f(x) est dérivable en tout point de l'intervalle I = ]a ; b[, elle est dite
dérivable sur l'intervalle I.
Notations Il existe plusieurs notations pour désigner la dérivée d'une fonction y = f(x) :
dy
f '(x), f ', y', ˙ ,
y
dx
La dernière notation a été introduite par Leibniz.
Elle remplace parfois avantageusement les autres notations. En effet, dans de nombreux
calculs, on est en droit de travailler comme s'il s'agissait d'un rapport banal, ce qui
donne un aspect immédiat à certains résultats.
Une fonction dérivable en un point est continue en ce point.
Dérivabilité et
continuité Attention ! La réciproque est fausse : une fonction continue n'est pas forcément
dérivable. Par exemple la fonction y = |x| est continue mais pas dérivable en x = 0 (les
dérivées à gauche et à droite ne sont pas égales). Il en est ainsi pour toutes les fonctions
possédant des « pointes ».
Cahier Analyse Didier Müller - LCP - 2011

19. DÉRIVÉES 15
Sur le graphe de la fonction f(x) ci-dessous, indiquez les valeurs approximatives de x
Exercice 3.1 pour lesquelles :
1
a. f(x) = 0 b. f ' (x) = 0 c. f ' (x) = 1 d. f ' (x) = –4 e. f ' (x) = –
2
Indication
Utilisez l'interprétation
géométrique de la dérivée.
Esquissez le graphe de sin(x) et utilisez ce graphe pour décider si la dérivée de sin(x) en
Exercice 3.2
x = 3π est positive ou négative.
En utilisant la définition 1 de la dérivée, trouvez algébriquement la dérivée f ' de
Exercice 3.3
1
Pour trouver f(x+∆x), il suffit
a. f(x) = x3 + 5 b. f(x) =
x
de remplacer le symbole « x » c. f(x) =  x d. f(t) = 3t2 + 5t
par « x+∆x ».
Trouvez la pente des tangentes à la parabole y = x2 aux points A(1; 1) et D(−2; 4).
Exercice 3.4
Utilisez la définition 1 pour estimer numériquement la dérivée de
Exercice 3.5
a. f(x) = xx en x = 2

b. f(x) = ln(cos(x)) en x = Travaillez toujours en radians !
4
c. f(x) = sin(ex) en x = 3
1
Exercice 3.6 La position d'un mobile est donnée par l'équation du mouvement s = f(t) =
1t
, où t
est mesuré en secondes et s en mètres. Calculez la vitesse du mobile après 2 secondes.
Didier Müller - LCP - 2011 Cahier Analyse

20. 16 CHAPITRE 3
Esquissez le graphe de la fonction dérivée de chacune des fonctions ci-dessous :
Exercice 3.7
a. b. c.
d. e. f.
En mettant en correspondance les courbes de f(x) et f ' (x) de l'exercice 3.7, remplissez
Exercice 3.8 les cases vides du tableau ci-dessous avec les réponses suivantes (il y a un intrus) :
= 0, = 0, = 0, < 0, > 0, ∞, min ou max
point pt. d'infl. à
f(a) décroît croît minimum maximum
d'inflexion tg. horiz.
f ' (a)
Dans une expérience de laboratoire, le nombre de bactéries après t heures est donné par
Exercice 3.9 n = f(t).
a. Quelle est la signification de f ' (5) ? En quelles unités s'exprime f ' (5) ?
b. Si la quantité de nourriture et d'espace n'est pas limitée, lequel des deux nombres
f ' (5) et f ' (10) sera le plus grand ?
a. Dessinez une courbe dont la pente partout positive croît continûment.
Exercice 3.10 b. Dessinez une courbe dont la pente partout positive décroît continûment.
c. Dessinez une courbe dont la pente partout négative croît continûment.
d. Dessinez une courbe dont la pente partout négative décroît continûment.
Dessinez un graphe possible de y = f(x) connaissant les informations suivantes sur la
Exercice 3.11 dérivée :
• f ' (x) > 0 pour 1 < x < 3
• f ' (x) < 0 pour x < 1 ou x > 3
• f ' (x) = 0 en x = 1 et x = 3
a. Sur un même système d'axes, dessinez les graphes de f(x) = sin(x) et g(x) = sin(2x),
Exercice 3.12 pour x compris entre 0 et 2π.
b. Sur un deuxième système d'axes identique au premier, esquissez les graphes de f ' (x)
et g' (x) et comparez-les.
Par des expériences, on peut constater que le chemin parcouru ( l) par un corps en chute
Exercice 3.13 libre est proportionnel au carré du temps écoulé :
g
l(t) = t2 où g est la gravité terrestre (9.81 m/s2).
2
a. Quelle est la vitesse moyenne entre le moment t et le moment t + ∆t ?
Quand ∆t → 0, la vitesse moyenne tend, par définition, vers la vitesse instantanée au
moment t.
b. Quelle est la vitesse instantanée au moment t ?
Cahier Analyse Didier Müller - LCP - 2011

21. DÉRIVÉES 17
3.3. La dérivée seconde
Comme la dérivée est elle-même une fonction (cf. ex. 3.7), on peut souvent calculer sa
dérivée. Pour une fonction f, la dérivée de sa dérivée est appelée dérivée seconde et
notée f ''.
Que nous dit la dérivée seconde ?
Rappelons que la dérivée d'une fonction nous dit si une fonction croît ou décroît.
Si f ' > 0 sur un intervalle, alors f est croissante sur cet intervalle.
Remarque Si f ' < 0 sur un intervalle, alors f est décroissante sur cet intervalle.
On peut aussi calculer la
dérivée troisième, quatrième, Puisque f '' est la dérivée de f ' :
etc. Cependant, elles ont Si f '' > 0 sur un intervalle, alors f ' est croissante sur cet intervalle.
moins d'intérêt que les Si f '' < 0 sur un intervalle, alors f ' est décroissante sur cet intervalle.
dérivées première et seconde.
Ainsi la question devient : qu'indique le fait que f ' soit croissante ou décroissante ?
Lorsque f ' est croissante, la courbe f se redresse : elle est convexe.
Lorsque f ' est décroissante, la courbe f s'infléchit vers le bas : elle est concave.
Deux trucs mnémotechniques
Pour se rappeler la différence
entre convexe et concave,
penser qu'une courbe concave a
la forme d'une caverne.
Si la dérivée seconde est
positive, on peut imaginer que
« la courbe sourit ».
Inversement, quand elle est
négative, « elle tire la tronche ».
Pour trouver les points d'inflexion (point noir sur la figure ci-dessus) de f(x), il faut
poser f '' (x) = 0 et résoudre. Mais attention ! Il faudra vérifier que c'est bien un point
d'inflexion : f '' (x−ε) et f '' (x+ε) devront être de signe opposé.
Pour la fonction f donnée ci-dessous, décidez où la dérivée seconde est positive et où
Exercice 3.14
elle est négative.
Didier Müller - LCP - 2011 Cahier Analyse

22. 18 CHAPITRE 3
Donnez trois moyens de faire la différence entre un minimum local d'une fonction f, un
Exercice 3.15
maximum local et un point d'inflexion à tangente horizontale .
Chacun des graphes ci-dessous montre la position de quatre wagonnets se déplaçant sur
Exercice 3.16
une ligne droite en fonction du temps. Les échelles de tous les graphes sont les mêmes.
Quel(s) wagonnet(s) a (ont) :
Rappels de physique a. une vitesse constante ?
La fonction vitesse est la b. la plus grande vitesse initiale ?
dérivée de la fonction horaire c. une vitesse nulle ?
(position). La fonction d. une accélération nulle ?
accélération est la dérivée de e. une accélération toujours positive ?
la fonction vitesse. f. une accélération toujours négative ?
(I) (II) (III) (IV)
x x x x
t t t t
Trouvez algébriquement la dérivée seconde de
Exercice 3.17 1
a. f(x) = x3 + 5 en x = 1 b. f(x) = en x = 2
(suite de l'ex. 3.3) x
c. f(x) =  x en x = 1 d. f(t) = 3t2 + 5t en t = –1
Dessinez sur le graphe de la fonction f ci-dessous les « bouts de la fonction f » où f ≥ 0
Exercice 3.18 (en vert), f ' ≥ 0 (en rouge) et f '' ≥ 0 (en bleu).
On se donne les abscisses suivantes : –2.25, –1.6, –1.2, –0.5, 0, 0.7, 1.55, 2.
Dites pour lesquelles de ces abscisses…
a. f et f '' sont non nulles et de même signe.
b. au moins deux des valeurs de f, f ' et f '' sont nulles.
a. Dessinez une courbe dont la première et la seconde dérivée sont partout positives.
Exercice 3.19 b. Dessinez une courbe dont la seconde dérivée est partout négative, mais dont la
première dérivée est partout positive.
c. Dessinez une courbe dont la seconde dérivée est partout positive, mais dont la
première dérivée est partout négative.
d. Dessinez une courbe dont la première et la seconde dérivée sont partout négatives.
Cahier Analyse Didier Müller - LCP - 2011

23. DÉRIVÉES 19
3.4. Dérivées de fonctions usuelles
Pour éviter de toujours recalculer les mêmes dérivées à partir de la définition 1, on peut
construire une table des dérivées.
Les tables ci-dessous regroupent les fonctions usuelles. a et n sont des constantes.
f (x) f ' (x) f (x) f ' (x)
a 0 sin(x) cos(x)
n n– 1
x n⋅x cos(x) –sin(x)
1
1 1 2
 x= x 2 tan(x) 2 =1tan  x
2 x cos  x
1 1 2
ln(x) cot(x) − 2 =−1−cot  x
x sin  x
loga(x) 1 1
arcsin(x)
x ln a  1 – x2
x x 1
e e arccos(x) −
 1 – x2
x x 1
a a ln a arctan(x) 2
1 x
1
|x| sgn(x) (x ≠ 0) arccot(x) − 2
1x
3.5. Règles de dérivation
Soient f et g deux fonctions dérivables et λ un nombre réel. Les propriétés suivantes
servent au calcul des dérivées :
Les démonstrations de ces 1. (f + g) ' = f ' + g' 2. (f – g) ' = f ' – g'
propriétés, longues et '
fastidieuses, découlent de la
définition 1.
3. (λ·f) ' = λ·f ' 4. 
f
g
=
f ' g – f g'
g
2
5. (f·g) ' = f ' ·g + f·g' 6.  g° f '=g ' ° f ⋅f '
La règle la plus difficile est la sixième. Elle concerne la dérivation de fonctions
composées. Nous la traiterons en détails un peu plus loin.
3 exemples de calculs 1. Dérivons h(x) = ex + x3
de dérivées
On a f(x) = ex , g(x) = x3 et h(x) = f(x) + g(x).
 
D'après la règle 1 : h'  x=e x  3 x2
f ' g'
sin  x
2. Dérivons h x= x
e
f  x
On a f(x) = sin(x) , g(x) = ex et h x=
g  x
f' g f g'
D'après la règle 4 : h'  x=
  sin x  =
cos  x⋅e – ⋅e cos  x−sin  x
x x
x 2 x

e  e
g2
Didier Müller - LCP - 2011 Cahier Analyse

24. 20 CHAPITRE 3
2 x
3. Dérivons h x= x ⋅3
On a f(x) = x2 , g(x) = 3x et h(x) = f(x)·g(x).
D'après la règle 5 : h'  x=2 x⋅3  ⋅3 ln3= x⋅3 2 x ln 3
 x 
x 2 x x
f' g f g'
a, b, c, d sont des nombres réels. On donne f(x). Calculez f ' (x) pour les cas suivants :
Exercice 3.20
1. x+1 2. 2x 3. –3x+5 4. ax+b
La règle 6 n'intervient dans
aucun des ces calculs, car il 5. x2 6. 4x2–5x–4 7. 2x3+2x+6 8. ax2+bx+c
n'y a pas de fonctions
9. 0 10. ax3+bx2+cx+d 11. (x+5)(x–3) 12. (3x2+5)(x2–1)
composées. 2
a x5 x – x5
13. (ax+b)(cx+d) 14. 15. 16. 2
x x –1 x – 2 x1
3 1
17. x 18. 3
x 19.  x2 20.
x
Rappel sur la Envisageons les fonctions f(x) = 6x − 4 et g x = x . On peut les appliquer à la queue
composition de fonctions leu leu, par exemple : la fonction « f suivie de g ».
Prenons un exemple : 5 → f → 26 → g →  26
Pour x, on aura :
Les flèches représentent les
machines (les fonctions). Pour
x → f → 6x − 4 → g → 6 x – 4
obtenir le résultat, on remplace
le carré représente par ce qui est On écrira g  f  x=  6 x – 4 ou g ° f  x=  6 x – 4 .
au début de la flèche.
De même avec la « fonction g suivie de f » :
Remarquez bien que l'ordre x→ g→  x → f → 6 x – 4
des opérations est l'inverse de
On écrira f  g x=6  x – 4 ou f ° g  x=6  x – 4 .
l'ordre d'écriture!
3 exemples d'utilisation 1. Dérivons h x=sin  x . Le schéma est x → f →  x → g→ sin  x .
de la règle 6 1

D'après la règle 6 : h'  x=cos  x⋅
En anglais, la règle 6 s'appelle
g '° f 
2 x
f '
the chain rule.
x2 2 2
2. Dérivons h x=e . Le schéma est x → f → x → g→ e .
x
2
 
D'après la règle 6 : h '  x= e x ⋅2 x
g '° f f'
3. Dérivons h x=ln ∣cos3 x ∣ .
2
Le schéma est x → f → 3 x → g→ cos 3 x  → k→ ln ∣cos 3 x ∣ .
2 2 2
1
 2 2
D'après la règle 6 : h'  x= 2 ⋅−sin 3 x ⋅6 x =−6 x tan 3 x 
On peut aussi voir une  g '° f
cos 3 x  f'
k ' °g ° f
composition de fonctions
comme l'emboîtement de Remarquez que l'on dérive les fonctions successivement de droite à gauche tout en
poupées russes. On « dérive gardant intact « l'intérieur » des fonctions. On parle souvent de dérivée de l'intérieur.
toutes les poupées » de Pour se rappeler l'ordre de dérivation, il est utile quand on débute de faire le petit
l'extérieur vers l'intérieur. schéma fléché.
Cahier Analyse Didier Müller - LCP - 2011

25. DÉRIVÉES 21
a et b sont des nombres réels. On donne f(x). Calculez f ' (x) pour les cas suivants :
Exercice 3.21
1.  x 25 x – 1 2.   x – 1 2
3
3. x
2
 2 x1
Rappelez-vous que l'erreur la
1
plus courante dans le calcul 4.  2 x – 1  2 x – 1 5.  x2 –16   4 – x 6. (x2+5x–1)5
3
des dérivées est l'oubli de la
dérivée intérieure ! 7. (3x2–x–1)(2x–3)3 8. (2x2–x–1)3 9. (x+2)3x2
10. sin(x) + cos(x) 11. tan(x) – x 12. sin(2x–1)
13. sin5(4x) 14.  sin  x 15. cos3   x
1
16. 17. e2x 18. eax+b
tan 2 x
19. esin(x) 20. exsin(x) 21. cos(2x) e4x
22. ln(3x) 23. ln(sin(4x)) 24. ln(ln(x))
3
25. ln(ex) 26. 3 x 2
–2 x–1 27.  xtan  x

32 x 2
x 9
28.  cos 3 x 29. 30.
 1 x x3
x –x
e –e
31. arctan(2–x) 32. sin2x + cos2x 33. x –x
e e
3
34.  x  1 x
2
35.  cos2  x 3sin 2 x  36. arcsin(2x)
37. x2e 38. xx
3.6. Théorèmes relatifs aux fonctions dérivables
Soit f : [a ; b] → ℝ telle que :
Théorème de Rolle
1. f est continue sur [a ; b]
2. f est dérivable sur ]a ; b[
Michel Rolle (1652-1719) 3. f(a) = f(b).
est un mathématicien Alors il existe une valeur c dans l'intervalle ]a ; b[ telle que f ' (c) = 0.
français.
Démonstration
Puisque la fonction f est continue sur [a ; b], elle admet une valeur maximale M et une
valeur minimale m sur [a ; b]. Deux cas sont alors possibles :
a. M = m. Dans ce cas, f est constante et on a f ' (x) = 0 pour tout x dans ]a ; b[.
b. M > m. Dans ce cas, il existe un x tel que f(x) = M ou f(x) = m, avec x dans ]a ; b[.
Pour fixer les idées, supposons que ce soit M : il existe donc une valeur c dans
l'intervalle ]a ; b[ telle que f(c) = M. Comme M est un maximum, alors f '(c) = 0.
t
Didier Müller - LCP - 2011 Cahier Analyse

26. 22 CHAPITRE 3
Soit f : [a ; b] → ℝ telle que :
Théorème des
accroissements finis 1. f est continue sur [a ; b]
(aussi appelé théorème de 2. f est dérivable sur ]a ; b[.
la moyenne) f b  – f a 
Alors il existe au moins une valeur c dans l'intervalle ]a ; b[ où : = f ' c
b –a
A gauche :
Illustration du théorème des
accroissements finis
A droite :
La fonction auxiliaire F(x)
Voici une conséquence pratique
du théorème des accroissements
finis :
Démonstration
si une voiture relie Zurich à
Bâle à une vitesse moyenne de On va utiliser le théorème de Rolle.
112 km/h, alors il y a un f b – f  a
Définissons une fonction auxiliaire F  x= f  x−  x−a  .
moment où la vitesse b–a
instantanée de la voiture (la f b – f  a
La dérivée de cette fonction F est F '  x= f '  x− .
vitesse lue au compteur) est b–a
exactement de 112 km/h. F vérifie les trois hypothèses du théorème de Rolle. Donc il existe une valeur c dans
f b – f  a
l'intervalle ]a ; b[ telle que F'(c) = 0. Donc f ' c=
b–a
t
Ce théorème est aussi appelé « Théorème des accroissements finis généralisé ».
Théorème de
Cauchy Soient f et g deux fonctions continues sur [a ; b], dérivables sur ]a ; b[. Supposons que
g(a) ≠ g(b) et que g' ne s'annule pas sur ]a ; b[.
f b – f a  f ' c
Alors il existe une valeur c dans l'intervalle ]a ; b[ telle que : =
g b – g a g '  c
Démonstration
La démonstration est analogue à celle du théorème des accroissements finis, en posant
comme fonction auxiliaire : F(x) = [g(b) – g(a)]f(x) – [f(b) – f(a)]g(x).
La dérivée de cette fonction F est F'(x) = [g(b) – g(a)]f '(x) – [f(b) – f(a)]g'(x).
Augustin Louis Cauchy
F vérifie les trois hypothèses du théorème de Rolle. Donc, il existe une valeur c dans
(Paris, 21/8/1789 -
Sceaux, 23/5/1857) l'intervalle ]a ; b[ telle que F'(c) = 0. Donc [g(b) – g(a)]f '(x) = [f(b) – f(a)]g'(x), ce qui
f b – f a f ' c
implique bien que = .
g b – g a g '  c
t
Cahier Analyse Didier Müller - LCP - 2011

27. DÉRIVÉES 23
Soient f et g deux fonctions telles que :
Règle de l'Hôpital
1. lim f x =lim g  x=0
x a xa
2. il existe un voisinage V de a tel que f et g sont dérivables dans V{a}.
3. g' ne s'annule pas dans V{a}
f '  x
4. lim existe.
x a g '  x
Alors :
f  x f '  x
lim =lim
x a g x x  a g '  x
Démonstration
Guillaume François Antoine Choisissons x ≠ a arbitraire dans V. En appliquant le théorème de Cauchy, nous avons :
Marquis de l'Hôpital f  x− f a f ' 
= , où ξ est un nombre compris entre a et x.
(Paris, ?/?/1661 - g  x− g a  g ' 
Paris, 2/2/1704) f  x f ' 
Mais par la condition 1, on sait que f(a) = g(a) = 0. Par conséquent : =
g  x  g ' 
Si x → a, alors ξ tend aussi vers a, puisque ξ est compris entre x et a.
f '  x f ' 
En outre, si lim = A , lim existe et est égale à A.
x a g '  x  a g ' 
f  x f '  f '  x
Par conséquent, il est évident que : lim =lim =lim =A ,
x a g x  a g '  x  a g '  x
f  x f '  x
et en définitive : lim =lim .
x a g x x  a g '  x t
Remarque importante
La règle de l'Hôpital est aussi valable si a = ±∞, ou si lim f = ±∞ et lim g = ±∞.
Utilisation de la règle de La règle de l'Hôpital permet de remplacer une limite par une autre qui peut être plus
l'Hôpital simple. Cette règle s'utilise en trois étapes :
f  x 0
1. Vérifier que est une forme indéterminée ( , 0·∞ ou ∞ ). ∞
g x  0
On peut au besoin réitérer ce Si ce n'est pas le cas, on ne peut pas utiliser la règle de l'Hôpital.
processus plusieurs fois. 2. Dériver f(x) et g(x) séparément.
f '  x
3. Calculer lim
x a g '  x
Exemples Solutions
sin 2 x
Calculons lim Puisque lim sin 2 x=0 et lim x=0 , on a bien une forme indéterminée.
x 0 x x 0 x 0
sin 2 x 2cos  2 x
La règle de l'Hôpital peut s'appliquer : lim =lim =2 .
x 0 x x 0 1
x x 2
e Ici, nous avons lim e =1 et lim x =0 .
Calculons lim 2 x 0 x 0
x 0 x x
e
lim 2 n'est donc pas une forme indéterminée. La solution est +∞.
x 0 x
Si on avait appliqué (à tort) la règle de l'Hôpital, on aurait obtenu :
x x x
e e e 1
lim 2 =lim =lim = .
x 0 x x0 2 x x 0 2 2
Didier Müller - LCP - 2011 Cahier Analyse

28. 24 CHAPITRE 3
La règle de l'Hôpital ne s'applique pas au calcul des limites ci-dessous, bien que celles-
Exercice 3.22
ci existent. Expliquez pourquoi et calculez ces limites par une autre méthode.
a. lim
xsin x
b. lim 2
3x
c. lim
sin
 1
x
x ∞ x x 0 x 1 x 0 1
x
Calculez les limites suivantes, si elles existent, en utilisant la règle de l'Hôpital.
Exercice 3.23 N'oubliez pas de d'abord contrôler si vous avez le droit d'utiliser cette règle !
2 5 4 3 2
x 2 x−3 x −2 x  x 2 x −4 x2
a. lim b. lim 3
x 1 x−1 x 1 x −3 x 2
c. lim
x 0
x
xsin x  x 1 
d. lim 1 – xtan  
x
2
m m
ln  x−1 x −a
e. lim f. lim n n (m ≠ n)
xe x−e x a x −a
1−sin  x sin a x−sin b x
g. lim 2 h. lim (a ≠ −b)
x  cot  x x 0 sin a xsin b x
2
sin   x x−1
i. lim j. lim 3 2
x 0 x x 1 x −2 x  x
3.7. Ce qu'il faut absolument savoir
Connaître la définition de la dérivée en tant que limite t ok
Comprendre l'interprétation géométrique de la dérivée t ok
Connaître les dérivées des fonctions usuelles t ok
Connaître les six règles de dérivation par cœur t ok
Pouvoir dériver n'importe quelle fonction t ok
Connaître le théorème de l'Hôpital et savoir l'appliquer t ok
Cahier Analyse Didier Müller - LCP - 2011

29. APPLICATIONS DES DÉRIVÉES 25
4. Applications des dérivées
4.1. Calculs de tangentes à des courbes
On cherche parfois à connaître l'équation d'une droite tangente à une fonction.
Rappels sur les droites Rappelons qu'une droite a pour équation y = mx + h, où m est la pente de la droite.
Il est aussi utile de savoir qu'une droite de pente m passant par le point A(x0; y0) a pour
équation y – y0 = m(x – x0).
Rappelons enfin que f ' (a) donne la pente de la tangente à la courbe f(x) en x = a.
Si le point de tangence T(xT ; yT) est donné, le problème est simple à résoudre.
Cas où le point de
tangence est connu 1. Calculer m = f ' (xT). C'est la pente de la tangente.
2. Introduire les coordonnées du point de tangence (xT ; yT) dans l'équation
y – yT = m(x – xT).
3. Simplifier cette équation pour en obtenir une de la forme y = mx + h.
Exemple Soit la fonction f  x=  3 x et le point T(3; 3). Donnez l'équation de la tangente à la
courbe passant par le point T.
Le point T appartient à la courbe ( f  x=  3⋅3=3 ). C'est donc le point de tangence.
1. f '  x=
 3 ⇒ f ' 3= 1 =m
La numérotation correspond à 2 x 2
celle du plan de résolution. 1
2. y – 3=  x – 3 
2
x 3
3. y= 
2 2
Pour les fonctions f suivantes, donnez l'équation de la tangente au graphe de f en xT :
Exercice 4.1
a. 2
f  x=5 x – 6 x 2 xT = 1 b. f  x=  x xT = 4
3x–2
c. f  x= xT = 0
5 x1
Didier Müller - LCP - 2012 Cahier Analyse

30. 26 CHAPITRE 4
Si le point A(x0 ; y0) n'est pas le point de tangence, le problème est un peu plus
Cas où le point de
compliqué. Il faut d'abord trouver xT, l'abscisse du point de tangence.
tangence n'est pas
connu 1. Calculer f ' (x).
2. Poser y0 – f (xT) = f ' (xT )(x0 – xT) et résoudre pour trouver xT .
3. yT = f (x T ).
4. m = f ' (xT).
5. Introduire les coordonnées du point de tangence (xT ; yT) dans l'équation
y – yT = m(x – xT).
6. Simplifier cette équation pour en obtenir une de la forme y = mx + h.
L'équation du point 2 provient de y – yT = m(x – xT). En effet, m = f '(xT ) et comme le
point A appartient à la droite, ses coordonnées doivent satisfaire l'équation de celle-ci.
3
Exemple Soit la fonction f  x= x et le point A(1; -3).
9
Donnez l'équation de la tangente à la courbe passant par le point A.
2
x
La numérotation correspond à 1. f '  x= .
3
celle du plan de résolution. 3 2
xT xT 3 2
2. – 3– = 1 – xT  . En développant, on trouve 2 xT − 3 xT − 27 = 0 .
9 3
Par tâtonnement, on trouve xT = 3.
3. yT = f (3) = 3
4. m = f ' (3 ) = 9/3 = 3
5. y − 3 = 3(x − 3)
6. y = 3x − 6
Pour les fonctions f suivantes, donnez l'équation de la tangente passant par le point A :
Exercice 4.2 2
x
a. f  x= A(–1 ; –3)
5
b. f(x) = 2·ln(x) A(0 ; –4)
c. f(x) = ex A(0 ; 0)
Cahier Analyse Didier Müller - LCP - 2012

31. APPLICATIONS DES DÉRIVÉES 27
Sur l'écran du jeu vidéo que montre la figure ci-dessous, on peut voir des avions qui
Exercice 4.3
descendent de gauche à droite en suivant la trajectoire indiquée et qui tirent au rayon
laser selon la tangente à leur trajectoire en direction des cibles placées sur l'axe Ox aux
abscisses 1, 2 , 3 et 4.
2 x1
On sait que la trajectoire de l'avion a pour équation y= .
x
a. La cible no 4 sera-t-elle touchée si le joueur tire au moment où l'avion est en (1 ; 3) ?
b. Déterminez l'abscisse de l'avion permettant d'atteindre la cible no 2.
Exercice 4.4
On veut prolonger un segment de parabole
par deux droites, de sorte que la fonction f
obtenue soit partout dérivable (voir dessin
ci-contre).
Complétez la formule ci-dessous avec les
équations des droites :
{
..................... si x– 1
2
x
f(x) = –2 x si – 1x3
2
..................... si x3
L'angle sous lequel se coupent les graphes de deux fonctions f et g en leur point
Exercice 4.5 d'intersection I est l'angle que forment leurs tangentes au point I.
Rappel Trouvez l'angle d'intersection des graphes des fonctions f et g suivantes :
Angle entre deux droites a. f(x) = x2 g(x) = x3
de pentes m1 et m2 : x
2
b. f(x) = x2 g  x= 3
∣ ∣
m2 – m1 4
tan = π
1m1 m2 c. f(x) = sin(x) g(x) = cos(x) 0≤ x≤
2
Didier Müller - LCP - 2012 Cahier Analyse

32. 28 CHAPITRE 4
1
Exercice 4.6 Soit f  x=
x
a. Esquissez le graphe de f(x) pour x > 0.
b. Soit un point A sur le graphe de f (d'abscisse supérieure à 0). Calculez l'aire du
triangle OAB, où O est l'origine et B est le point d'intersection de la tangente au
graphe de f en A avec l'axe horizontal.
ax − 2
Exercice 4.7 On donne la fonction f ( x) = .
8 − bx
Calculez a et b de telle manière que le graphe de f passe par le point   1;
1
3
et que la
7
tangente au graphe de f au point (2 ; f(2)) ait une pente égale à .
2
4.2. Problèmes de taux d'accroissement
Exercice résolu Une brèche s'est ouverte dans les flancs d'un pétrolier. Supposons que le pétrole
s'écoulant du tanker s'étend autour de la brèche selon un disque dont le rayon augmente
de 2 m/s. À quelle vitesse augmente la surface de la marée noire quand le rayon de la
nappe de pétrole est de 60 m ?
Solution Soit A l'aire du disque (en m2), r le rayon du disque (en m) et t le temps écoulé depuis
l'accident (en secondes) .
Dans ce genre de problème, la
dA dA dr
notation de Leibniz est très = ⋅
pratique.
On va utiliser la relation suivante :   
dt dr dt
cherché à calculer donné
Cela peut paraître étrange, mais
dr
on peut faire comme si ces Le taux d'accroissement du rayon est =2 m/s (voir la donnée).
dt
dérivées étaient des fractions !
dA
Il faut maintenant exprimer A par rapport à r pour pouvoir calculer .
dr
L'aire du disque A est donnée par la formule : A = πr2.
Le modèle de résolution
ci-contre est applicable à tous dA dA
En dérivant A par rapport à r, on obtient : =2 r . Comme r = 60, =120 .
les exercices qui suivent. dr dr
dA
On veut le taux d'accroissement de l'aire polluée par rapport au temps, c'est-à-dire .
dt
dA dA dr dA
D'après la relation de départ = ⋅ , on trouve que =120⋅2=754 m2/s.
dt dr dt dr
a. Si les arêtes d'un cube de 2 cm de côtés croissent de 1 cm/min, comment le volume
Exercice 4.8 croît-il ?
b. Si l'aire d'une sphère de 10 cm de rayon croît de 5 cm2/min, comment le rayon croît-
il ?
c. Soit un cône dont le rayon de la base et égal à la hauteur. Si le volume de ce cône
haut de 10 cm croît de 15 cm3/min, comment la hauteur croît-elle ?
À l'altitude de 4000 pieds, une fusée s'élève verticalement à une vitesse de 880 pieds par
Exercice 4.9 seconde. Une caméra au sol, située à 3000 pieds de la rampe de lancement, la filme.
À quelle vitesse doit augmenter l'angle d'élévation de cette caméra pour qu'elle ne perde
pas de vue la fusée ?
Une échelle longue de 5 mètres est appuyée contre un mur. Quand l'extrémité posée sur
Exercice 4.10 le sol est à une distance de 4 mètres du mur, l'échelle glisse à une vitesse de 2 m/s. À
quelle vitesse l'extrémité appuyée contre le mur glisse-t-elle alors vers le bas ?
Cahier Analyse Didier Müller - LCP - 2012

33. APPLICATIONS DES DÉRIVÉES 29
4.3. Problèmes d'optimisation
Beaucoup de problèmes pratiques conduisent à la détermination des valeurs maximales
et minimales prises par une quantité variable. Ces valeurs, qui sont les plus favorables
dans un contexte donné, sont appelées valeurs optimales. Déterminer ces valeurs
constitue un problème d'optimisation.
Voici la marche à suivre pour résoudre un problème d'optimisation :
Plan de résolution
1. Exprimer la quantité variable Q à rendre optimale (maximale ou minimale) comme
fonction d'une ou de plusieurs variables.
2. Si Q dépend de plus d'une variable, disons n variables, trouver (n–1) équations liant
ces variables.
3. Utiliser ces équations pour exprimer Q comme fonction d'une seule variable et
déterminer l'ensemble D des valeurs admissibles de cette variable.
4. Calculer les extrema de Q (sans oublier de contrôler ce qui se passe aux bords de D).
Il faut donc dériver Q par rapport à la variable utilisée et poser Q' = 0.
5. Vérifier le résultat : a-t-on bien trouvé l'optimum cherché ?
On dispose d'une corde d'une longueur L pour construire un enclos rectangulaire le long
Premier exemple de d'un mur rectiligne.
problème
a a
b
Quelles dimensions faut-il donner à cet enclos pour que le pré qu'il délimite ait une aire
maximale ?
Résolution 1. Soit A l'aire délimitée par l'enclos. On a évidemment : A = a·b
La numérotation correspond à 2. L = 2·a + b ⇒ b = L – 2·a
celle du plan de résolution.
3. A = a·(L – 2·a) = a·L – 2·a2
L
L'aire A doit être positive, donc D(a) = [0 ; ].
2
Sur le bord gauche de D, a vaut 0 ce qui correspond à une aire nulle.
L
Sur le bord droit de D, a vaut ce qui correspond à une aire nulle.
2
dA L L
4. = L – 4a =0 ⇒ a= et b=
da 4 2
5. Pour a = 0.25·L, on trouve une aire de 0.125 L2.
Comparons ce résultat avec l'aire obtenue pour a = 0.24·L et a = 0.26·L. Dans les
deux cas, on obtient une aire de 0.1248·L2. On a donc bien trouvé l'aire maximale.
On aurait aussi pu calculer la dérivée seconde de A en a = 0.25·L, et étudier son
2
d A
signe. On a : 2 =– 4 .
da
La fonction A est partout concave (c'est une parabole), donc aussi en a = 0.25·L. Le
résultat est donc bien un maximum.
Didier Müller - LCP - 2012 Cahier Analyse

34. 30 CHAPITRE 4
Soit la figure ci-dessous :
Deuxième exemple
Le polygone PQRS est un carré. Pour quelle valeur de α l'aire A est-elle maximum ?
Trouvez la longueur du segment PS quand l'aire A est maximum.
Résolution 1. A = carré PQRS – (secteur OTP – triangle OPS)
2
= sin  –  
2
2 1
2
2

 1
⋅⋅1 – cos ⋅sin  =sin  –  cos ⋅sin 
2 2
2. rien à faire
3. A=sin 2  –
 1
 cos ⋅  . D = 0; 
2 2
sin
2 [ ]
dA 1 1
=2 sin  cos  –   =sin 2 cos – sin 
2 2
4. – sin cos 
d 2 2
1−2sin 2  cf. formulaire 
dA °
=0⇔ 2cos =sin ⇔ tan = 2⇔=1.107 radians =63.345
d
Sur le bord gauche de D (α = 0), l'aire vaut 0.
 
Sur le bord droit de D ( = ), l'aire vaut 1 – ≅ 0.2146.
2 4
dA dA
5. Si α < 1.107, 0 . Si α > 1.107, 0 .
d d
On a donc bien un maximum.
La réponse est donc : PS=sin =0.894
Parmi tous les rectangles de périmètre 2p, quel est celui dont l'aire est maximale ?
Exercice 4.11 Quelle est son aire ?
Vous disposez d'une plaque de carton carrée, de côté a. On vous demande de fabriquer
Exercice 4.12 une boîte à chaussures sans couvercle de volume maximum. Pour cela, vous découperez
quatre carrés dans les coins de la plaque pour obtenir une croix, puis vous relèverez les
bords.
Dimensionnez une boîte de conserve cylindrique d'un décimètre cube, l'objectif étant
Exercice 4.13 d'utiliser le moins de fer-blanc possible.
Un fil de longueur L doit être coupé en deux parties de manière à pouvoir former un
Exercice 4.14 triangle équilatéral avec l'une et un carré avec l'autre. Comment faut-il couper ce fil pour
que l'aire totale des deux figures construites soit
a. maximale
b. minimale ?
Cahier Analyse Didier Müller - LCP - 2012

35. APPLICATIONS DES DÉRIVÉES 31
Le gardien d'un phare (point A) doit rejoindre le plus rapidement possible sa maison
Exercice 4.15 côtière (point B). Il se déplace en canot à la vitesse de 4 km/h et à pied à la vitesse de 5
km/h. Où doit-il accoster (point P) pour que le temps de parcours soit minimal ? La côte
est supposée rectiligne.
Une fenêtre romane est formée d'un rectangle surmonté d'un demi-disque. Supposons
Exercice 4.16 que le périmètre p de la fenêtre soit donné.
Calculez les dimensions de la fenêtre romane laissant passer le maximum de lumière.
Dessinez cette fenêtre en prenant p = 7.14 mètres.
On considère une famille de droites de pente négative passant par le point de
Exercice 4.17
coordonnées (3; 2).
Pour quelle droite de la famille le triangle délimité par la droite et les axes de
coordonnées a-t-il la plus petite aire ?
À midi, un navire B est repéré à 40 km à l'est d'un navire A. A se déplace à la vitesse de
Exercice 4.18 20 km/h dans la direction 30oE, tandis que B se dirige à la vitesse de 10 km/h dans la
Pour simplifier, on admettra direction 30oW (les angles sont mesurés avec la direction N).
que la surface de la mer est À quelle heure les navires seront-ils le plus proche l'un de l'autre ?
plate... Quelle sera alors la position du navire B par rapport à A ?
On fabrique un cornet de forme conique en
Exercice 4.19 rejoignant les bords rectilignes d'un secteur
circulaire d'angle φ et de rayon r (voir ci-
contre).
Quel est le volume du cornet de capacité
maximale ?
Formules pour le cône s est l'apothème du cône, θ l'angle au
sommet, r le rayon de la base, h la hauteur
et φ l'angle de développement.
Alat = r s Atot = r r s
1 2
V = r h
3
sin 
 r
2
=
s
=2 sin 
2
Didier Müller - LCP - 2012 Cahier Analyse

36. 32 CHAPITRE 4
4.4. Méthode de Newton-Raphson
En analyse numérique, la méthode de Newton-Raphson, est un algorithme efficace
pour approcher un zéro d'une fonction. De manière informelle, le nombre de décimales
correctes double à chaque étape.
Partant d'une valeur f  xn
approximative raisonnable d'un Par récurrence, on définit la suite xn par : x n1 = xn – . En principe, cette suite va
f '  x n
zéro x0 d'une fonction f, on
approche la fonction par sa converger vers a.
tangente au point (x0; f(x0)).
Cette tangente est une fonction
affine dont on sait trouver
l'unique zéro (que l'on appellera
x1). Ce zéro de la tangente sera
généralement plus proche du
« vrai » zéro de la fonction (a).
On recommence les mêmes
calculs en partant cette fois de
x1, ce qui va nous donner
l'abscisse x2, etc.
Exercice
Retrouvez la valeur de xn+1 en
partant de l'équation de la droite
y−y0 = m(x−x0)
Si la fonction présente un extremum local, il y a un risque que la méthode ne converge
pas, car la valeur de la dérivée est nulle en un extremum et le nouveau point à l'infini.
3
Exemple Cherchons un zéro de la fonction f  x=cos  x – x .
2
La dérivée est f '  x=– sin  x – 3 x .
Nous savons que le zéro se situe entre 0 et 1. Prenons comme valeur de départ x0 = 0.5.
f  x 0 cos 0.5– 0.5
3
x1 = x0 – =0.5 – 2 =1.11214
f '  x0  – sin 0.5 – 3⋅0.5
f  x 1 cos 1.11214 – 1.11214
3
x 2= x1 – =1.11214 – 2 =0.90967
f '  x1  – sin 1.11214 – 3⋅1.11214
f  x2 cos 0.90967 – 0.90967
3
x 3= x2 – =0.90967 – 2 =0.86626
f '  x 2 – sin 0.90967  – 3⋅0.90967
f  x3 cos 0.86626  – 0.86626
3
x 4= x3 – =0.86626 – 2 =0.86547
3 f '  x 3 – sin 0.86626  – 3⋅0.86626
f  x=cos  x – x
f  x4 cos 0.86547  – 0.86547
3
x 5 = x4 – =0.86547 – 2 =0.86547
f '  x 4 –sin 0.86547  – 3⋅0.86547
Après cinq itérations, les cinq premiers chiffres après la virgule sont déjà exacts.
Cherchez le zéro de la fonction ex + sin(x) − 3.
Exercice 4.20
4.5. Ce qu'il faut absolument savoir
Calculer une tangente à une courbe t ok
Connaître la notation de Leibniz pour les dérivées t ok
Résoudre un problème de taux d'accroissement t ok
Connaître la démarche pour résoudre un problème d'optimisation t ok
Connaître la méthode de Newton-Raphson t ok
Cahier Analyse Didier Müller - LCP - 2012

37. ÉTUDE DE FONCTIONS 33
5. Étude de fonctions
5.1. Asymptotes
Asymptote verticale La droite x = a est dite asymptote verticale (A. V.) de la fonction f si l'une au moins
des conditions suivantes est vérifiée :
lim f  x=∞ (ou –∞ ) lim f  x=∞ (ou –∞ )
x a x a
xa xa
Une A. V. ne peut exister que si la fonction est discontinue en x = a.
Asymptote affine La droite d'équation y = mx + h est une asymptote affine de la courbe représentative de
la fonction f si
Remarque lim [ f x – mx h]=0 (propriété analogue en – ∞ )
x∞
Si m = 0, l'asymptote est
horizontale. Les valeurs m et h sont calculés avec les formules suivantes :
Il faut donc commencer par f  x
m= lim h= lim [ f  x−m x] (idem en –∞ )
calculer m. Si m tend vers x∞ x x∞
l'infini, il n'y a pas
d'asymptote affine. Attention ! L'asymptote affine n'est pas forcément la même en +∞ et en –∞. Il faut
donc étudier les deux cas.
3
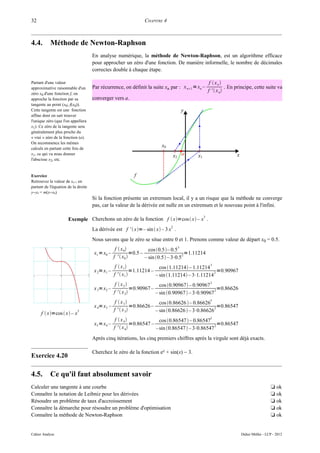
x
Ci-dessous, le graphe de la fonction , qui possède deux asymptotes verticales
2
x –4
(en bleu) et une asymptote affine (en vert).
Remarquez que la fonction est discontinue en x = –2 et x = 2.
5.2. Points fixes
Soit E un ensemble et f : E  E une fonction. On dit que x∈ E est un point fixe de f
si f(x) = x.
Didier Müller - LCP - 2011 Cahier Analyse

38. 34 CHAPITRE 5
5.3. Croissance et concavité (rappels)
Le signe de la dérivée d'une fonction f renseigne sur sa croissance et sa décroissance.
Si f ' > 0 sur un intervalle, alors f est croissante sur cet intervalle.
Si f ' < 0 sur un intervalle, alors f est décroissante sur cet intervalle.
La dérivée seconde f '' renseigne sur la concavité de la fonction.
Si f '' > 0 sur un intervalle, alors f est convexe sur cet intervalle.
Si f '' < 0 sur un intervalle, alors f est concave sur cet intervalle.
Lorsque f ''(c) = 0, alors il y a un point d'inflexion en c.
Dérivée nulle On sait, d'après le chapitre sur les dérivées, que lorsque f '(c) = 0, on a, en c, soit un
minimum, soit un maximum, soit un point d'inflexion à tangente horizontale.
Pour déterminer dans lequel des trois cas on se trouve, trois méthodes sont possibles :
1. Étudier la valeur de la fonction f(x) dans le voisinage de c.
2. Étudier le signe de la dérivée f '(x) dans le voisinage de c.
3. Calculer f ''(c).
Les quatre tableaux suivants montrent tous les cas possibles.
x c–ε c c+ε x c–ε c c+ε
f(x) f(c–ε)>f(c) f(c) f(c+ε)>f(c) f(x) f(c–ε)<f(c) f(c) f(c+ε)<f(c)
f '(x) f '(c–ε)<0 0 f '(c+ε)>0 f '(x) f '(c–ε)>0 0 f '(c+ε)<0
f ''(x) f ''(c)>0 f ''(x) f ''(c)<0
f(c) est un minimum f(c) est un maximum
x c–ε c c+ε x c–ε c c+ε
f(x) f(c–ε)>f(c) f(c) f(c+ε)<f(c) f(x) f(c–ε)<f(c) f(c) f(c+ε)>f(c)
f '(x) f '(c–ε)<0 0 f '(c+ε)<0 f '(x) f '(c–ε)>0 0 f '(c+ε)>0
f ''(x) f ''(c)=0 f ''(x) f ''(c)=0
f(c) est un point d'inflexion à tangente horizontale (2 cas)
Exemple Soit la fonction f(x) = –x2 + 4x – 3.
f '(x) = –2x + 4 et f ''(x) = –2.
En posant f '(x) = 0, on trouve un point critique en x = 2 (voir définition à l'étape 6 de
la méthode présentée au § 5.4).
D'où le tableau :
x 2–ε 2 2+ε
f(x) <1 1 <1
f '(x) + 0 –
f ''(x) –2
f(2) est un maximum
Exercice-test Esquissez la courbe d'une fonction f où l'on trouve les quatre cas décrits dans les
tableaux ci-dessus. Mettez en évidence les points où f '(x) = 0.
Cahier Analyse Didier Müller - LCP - 2011

39. ÉTUDE DE FONCTIONS 35
5.4. Méthode
L'étude d'une fonction f comprend huit étapes. Vous trouverez au § 5.5 un exemple qui vous servira d'aide-mémoire.
1. Ensemble de définition Déterminer le domaine D où la fonction f(x) est définie.
2. Parité Voir si la fonction est paire, impaire, périodique ou rien du tout. Cela
permet, si la fonction est « agréable », de gagner du temps par la suite.
La fonction f est paire si f(x) = f(–x), et impaire si f(x) = –f(–x), ∀ x.
3. Signe de la fonction Chercher les zéros, puis faire un tableau pour voir où la fonction est
négative, positive ou nulle.
4. Asymptotes verticales, trous Calculer la ou les asymptotes verticales et trouver les éventuels trous.
5. Asymptotes affines Calculer la ou les asymptotes affines et, si demandé, trouver le position-
nement de la courbe par rapport à ces asymptotes.
6. Croissance et points critiques Un point c de l'ensemble de définition est un point critique si f '(c) = 0 ou
si f '(c) n'existe pas.
Calculer la dérivée et chercher ses zéros. Faire un tableau pour voir
comment la fonction croît. Identifier les minima, les maxima et les points
d'inflexion à tangente horizontale (en utilisant une des trois méthodes du
§ 5.3).
7. Concavité et points d'inflexion Chercher la concavité de la fonction et les points d'inflexion. Pour cela,
calculer la dérivée seconde si elle n'est pas trop compliquée (cette
méthode est la seule qui garantit de trouver tous les points d'inflexion).
Faire un tableau. Calculer les pentes des tangentes aux points d'inflexion.
Dessiner la courbe en utilisant les renseignements glanés aux étapes 1 à 7.
8. Représentation graphique Faire un grand dessin où l'on représente le graphe de la fonction, les
asymptotes et les points particuliers.
5.5. Un exemple complet
3
x
Étudions la fonction f  x= 2 .
 x – 1
1. Ensemble de définition L'ensemble de définition de f est D = ℝ {1}.
2. Parité f est paire si f(x) = f(–x). Est-ce le cas ?
3 3
 – x –x
Si la fonction est paire ou impaire, on f – x= 2= 2 ≠ f  x . f n'est donc pas paire.
 – x – 1   x1
peut alors n'étudier que le côté positif.
Le côté négatif se déduira du côté f est impaire si f(x) = – f(–x). Est-ce le cas ?
positif. 3 3
 – x x
− f  – x=− 2= 2 ≠ f x  . f n'est donc pas impaire.
 x1  x1
En fait, puisque le domaine de définition D n'est pas symétrique, il est
évident que la fonction ne peut être ni paire, ni impaire.
Didier Müller - LCP - 2011 Cahier Analyse

40. 36 CHAPITRE 5
3. Signe de la fonction Cherchons d'abord le(s) zéro(s) de f :
3
x 3
f  x=0 ⇒ 2 =0 ⇒ x =0 ⇒ x=0 .
 x –1
Le signe de la fonction est donné par le tableau suivant (dans la première
ligne, on met les valeurs de x trouvées aux étapes 1 et 3) :
x <0 0 ]0;1[ 1 >1
x3 – 0 + +
(x – 1)2 + + + +
f(x) – 0 + +
4. Asymptotes verticales (A.V.), Les asymptotes verticales, s'il y en a, se trouvent aux abscisses trouvées à
trous l'étape 1. Il s'agit de vérifier que ce sont bien des asymptotes verticales et
non pas des trous.
On peut s'aider du tableau de signes de lim f  x=∞ et lim f  x=∞
l'étape 3 pour déterminer le signe de x 1 x 1
x1 x1
l'infini.
Si on avait un trou, on trouverait que la limite à gauche est égale à la
limite à droite et que ces limites seraient égales à un nombre.
5. Asymptotes affines (A.A.) Une asymptote affine est de la forme y = m·x + h. On va analyser ce qui
se passe en –∞ et en +∞.
2 2 2
f  x x x x
Du côté de +∞ m= lim = lim 2 = lim 2 = lim 2 =1
x∞ x x∞  x−1 x ∞ x −2 x1 x ∞ x
 
3 2
x 2 x −x
h= lim [ f  x−m x]= lim 2 − x = lim 2
x∞ x ∞  x−1 x∞ x −2 x1
2
2x
= lim 2 =2
x∞ x
Du côté de +∞, l' A.A. est donc y = x + 2.
Du côté de –∞ Idem que pour +∞ (le signe ne change rien).
2
6. Croissance et points critiques x  x – 3
f '  x= 3 s'annule en 0 et 3.
 x – 1
Les points du graphe dont les abscisses sont des points critiques de f sont
27
donc (0 ; 0) et (3 ; ).
4
La croissance de f est donnée par le tableau suivant (dans la première
ligne, on met les valeurs de x trouvées aux étapes 1 et 6) :
x 0 1 3
f '(x) + 0 + – 0 +
27
f(x)  0   
4
pt. d'infl. minimum
à tg. hor.
Cahier Analyse Didier Müller - LCP - 2011

41. ÉTUDE DE FONCTIONS 37
7. Concavité et points d'inflexion 6x
f ' '  x= 4 s'annule en 0.
 x – 1
La concavité de f est donnée par le tableau suivant (dans la première
ligne, on met les valeurs de x trouvées aux étapes 1 et 7) :
x 0 1
f ''(x) – 0 + +
f(x) ∩ 0 ∪ ∪
pt. d'infl.
Calcul de la pente de la tangente Il y a un seul point d'inflexion en (0 ; 0).
au point d'inflexion 2
0 0 – 3 0
m= f '  x= 2 = =0
 0– 1 1
(on savait déjà d'après l'étape 6 que c'était un point d'inflexion à tangente
horizontale).
8. Représentation
graphique
On trace d'abord les
asymptotes trouvées aux
étapes 4 et 5.
On place ensuite tous les
points que l'on a trouvés
aux étapes 3, 6 et 7.
On trace enfin la courbe
d'après les indices
récoltés aux étapes 2, 3, 6
et 7. Les tableaux en
particulier sont d'une aide
très précieuse.
Il est conseillé de calculer
d'autres points de la
fonction et de les reporter
sur le dessin.
Didier Müller - LCP - 2011 Cahier Analyse

42. 38 CHAPITRE 5
Exercice 5.1
Étudiez les fonctions suivantes selon l'exemple du § 5.5. Vous trouverez des corrigés sur le site de ce cours.
– 3 x4
Fonctions 1. f  x=
2 x3
rationnelles 2 2
x –4x –5 – 83 x – 12 x13
2. f  x= 2 aide : f ' '  x= 2 3
2 x – 4 x3  x – 4 x3
2
x  x – 3 64 – x
3. f  x= 2 aide : f ' '  x= 4
 x – 2  x – 2
3 3 2
x 2 2  – x 6 x 3 x – 2 
4. f  x= 2 aide : f ' '  x= 2 3
x 1  x 1 
f ' ' s'annule en −0.8056, 0.38677, 6.41883
Autres types de 5. f  x= 1 – x2
fonctions –
x2
6. f  x=e 2
2 –2 x
7. f  x= 2 x 2 x – 1⋅e
2
ln  x 1
8. f  x=
2x
x x
9. f  x=e – 5e 1 http://ow.ly/5Hpp8
4 3
Exercice 5.2 Voici le graphe de la fonction f  x=– x  4 x  x5 . Malheureusement, les axes ont
disparu. Remettez les axes et graduez-les (la graduation n'est pas la même sur l'abscisse
et l'ordonnée).
5.6. Ce qu'il faut absolument savoir
Trouver les asymptotes d'une fonction t ok
Connaître les huit étapes de la méthode par cœur t ok
Maîtriser parfaitement chaque étape de la méthode t ok
Cahier Analyse Didier Müller - LCP - 2011

43. ÉTUDE DE COURBES PARAMÉTRÉES 39
6. Étude de courbes paramétrées
6.1. Définitions
Soit deux fonctions f et g définies sur le même sous-ensemble D⊂ℝ . Le point M(t) de
coordonnées (f(t) ; g(t)) décrit un sous-ensemble (C) du plan lorsque t varie dans un
intervalle I.
Remarques
Une représentation paramétrique d’une courbe (C) est un système d’équations où les
La courbe (C) n’est pas coordonnées des points de la courbe sont exprimées en fonction d’un paramètre
nécessairement le graphe (souvent noté t, k, θ, …).
d’une fonction ; c’est
pourquoi on parle de courbe
paramétrée et non pas de
(C) : {
x = f t 
y = g t 
fonction paramétrée.
Ces équations sont appelées équations paramétriques de (C).
On peut parfois, en éliminant
le paramètre t entre les deux
équations, obtenir y comme
On note parfois également { x = xt
y = yt 
fonction de x, et ramener
l’étude de la courbe à celle Si l’on veut que cette définition ait un sens, il faut que x(t) et y(t) existent
d’une courbe définie par une simultanément.
relation y = h(x).
C’est pourquoi le domaine de définition D de la courbe (C) est l’intersection des
domaines de définition Dx et Dy des fonctions x(t) et y(t). On a donc D= D x ∩ D y .
Soit a et b deux nombres réels. Trouvez le domaine de définition de la courbe
Exercice 6.1
paramétrée : {
x =  t −a
y =  b −t
6.2. Exemple de courbes paramétrées : figures de Lissajous
Les figures de Lissajous (ou courbes
de Bowditch) sont de la forme :
{x = a sin t 
y = b sin n t

avec 0≤≤ et n≥1
2
En électronique, on peut faire
apparaître des figures de Lissajous
sur un oscilloscope.
Jules Antoine Lissajous
(Versailles, 4/3/1822 -
Plombières, 24/6/1880)
{x = sin 5t 
y = cos3t 
, t∈[0; 2[
Didier Müller - LCP - 2010 Cahier Analyse

44. 40 CHAPITRE 6
6.3. Asymptotes
Asymptote verticale On obtient une telle asymptote lorsque x tend vers une valeur finie a et y
tend vers une valeur infinie.
lim xt =a , avec a∈ℝ
t t0
lim y t=±∞
t t 0
L’asymptote verticale est une droite qui a pour équation x = a.
Si x(t) – a est positif, la courbe est à droite de l’asymptote, sinon elle est à
gauche.
La courbe coupe l’asymptote lorsque x(t) = a.
Asymptote verticale x = 1
Asymptote horizontale
Cette fois, x tend vers l’infini et y tend vers une valeur finie b lorsque t
tend vers t0.
lim xt =±∞
t t 0
lim y t=b , avec b∈ℝ
t t0
L’asymptote horizontale est une droite qui a pour équation y = b.
Si y(t) – b est positif, la courbe est en dessus de l’asymptote, sinon elle est
en dessous.
Asymptote horizontale y = 1.5 La courbe coupe l’asymptote lorsque y(t) = b.
Une asymptote oblique ne peut exister que si x et y tendent tous deux vers
Asymptote oblique
l’infini lorsque t tend vers t0. Cette condition est nécessaire mais pas
suffisante.
lim xt =±∞
t t0
lim y t=±∞
t t0
La droite y = mx + h est une asymptote oblique si :
yt 
m=lim ∈ ℝ
t t0 xt
Asymptote oblique y = −x − 1 h=lim  y t −m⋅x t  ∈ ℝ
t t 0
Ces formules sont analogues à celles rencontrées au chapitre 5, page 33.
Si m = ∞, il n'y a pas d'asymptote
oblique.
La position de la courbe est donnée par le signe de y(t) – mx(t) – h.
Si cette expression est positive, la courbe est en dessus de l’asymptote,
sinon, elle est en dessous.
Cahier Analyse Didier Müller - LCP - 2010

45. ÉTUDE DE COURBES PARAMÉTRÉES 41
6.4. Dérivées et points particuliers
Les valeurs de t décrivant le domaine d’étude, on étudie, lorsque c’est possible, le signe
Dérivées dx dy
des dérivées et .
dt dt
Comme pour les fonctions d’une seule variable (voir chapitre 5), on présentera les
résultats sous forme d’un tableau, qui est constitué de deux tableaux accolés, donnant
les variations de x et y (voir § 6.6).
Regardons deux points voisins de la courbe : M(t0) et M(t0 + ε). La droite passant par
dy
Calcul de ces deux points tend vers la tangente à la courbe au point M(t0) lorsque ε tend vers zéro.
dx
La pente de la droite passant par M(t0) et M(t0 + ε) est :
On peut écrire : yt 0 – yt 0 
y 't yt 0 – yt 0 yt 0 – y t 0  
m= y ' x = mt 0 ;= = ⋅ =
x 't xt 0 – xt 0   x t0  – x t0  x t 0  – x t 0 

dy dy
donne la pente de la t 
dx dt 0 dy
tangente à la courbe. Lorsque ε tend vers 0, la pente tend vers = t 0  .
dx dx
t 0 
dt
Si x’(t0) ≠ 0 et y’(t0) = 0, la courbe admet une tangente horizontale en M(t0).
Points particuliers
Si x’(t0) = 0 et y’(t0) ≠ 0, la courbe admet une tangente verticale en M(t0).
Si x’(t0) = 0 et y’(t0) = 0, la courbe admet un point singulier en M(t0).
y 't
On pourra compléter le tableau des dérivées par une ligne donnant les valeurs de
x' t
pour les valeurs de t figurant déjà dans ce tableau.
6.5. Méthode
L’étude d’une courbe paramétrée comprend six étapes.
1. Domaine de définition Déterminer le domaine D où la courbe est définie.
2. Asymptotes Déterminer, s’il y en a, les A.V, les A.H et les A.O.
dx dy dy
3. Dérivées et tableau de variation Calculer , et . Faire le tableau de variation.
dt dt dx
4. Points particuliers Déterminer, s’il y en a, les points à tangente verticale, les points à
tangente horizontale et les points singuliers.
Calculer la limite de la pente de la tangente aux points singuliers, i.e.
dy
m=lim t
t  a dx
5. Intersection avec les axes Trouver les t qui satisfont x(t) = 0 et y(t) = 0.
6. Représentation graphique Dessiner la courbe en utilisant les renseignements glanés aux étapes 1 à 5.
Il n’est pas interdit de calculer certains points de la courbe, afin de faire
un dessin plus précis.
Didier Müller - LCP - 2010 Cahier Analyse

46. 42 CHAPITRE 6
6.6. Deux exemples complets
Premier exemple
{
2
t
x =
t –1
Étudions la courbe
t
y = 2
t –1
1. Domaine de L’ensemble de définition de la courbe est D = ℝ {−1 ; 1}.
définition
2.1. Asymptote Il y a une A. V. quand t = −1, puisque
verticale (A. V.)
{
1
lim x t=−
t−1 2
{
lim yt =−∞
lim y t n ' existe pas , car t −1
t−1
t−1
lim yt =∞
t −1
t−1
{
lim xt =∞
2.2. Asymptotes t ∞
Quand t ∞ , il y a une A. H., car
horizontales (A. H.) lim y t =0
t ∞
{
lim xt =−∞
t −∞
Quand t −∞ , il y a une A. H., car
lim y t =0
t −∞
2.3. Asymptotes Il y a une A. O. quand t = 1, puisque
obliques (A. O.)
{ {
lim x t=−∞
t 1
lim x t n ' existe pas , car t1
t 1
lim x t=∞
t 1
t1
{
lim yt=−∞
t 1
lim y t  n ' existe pas, car t 1
t 1
lim yt=∞
t 1
t 1
t 1
2
t –1 t 1 t 1
Calcul de m m=lim 2 =lim =lim =
t 1 t t 1 t t 1 t1 2
t–1 1
2 2 3 2
t 1 t 2t−t t1 −t −t 2 t
Calcul de h h=lim 2 – ⋅ =lim 2 =lim 2 =
t 1 t – 1 2 t – 1 t 1 2t −1  t 1 2t −1
2 2
1 −t − 2t t−1 1 −t −2 t  1 −3 3
lim = lim = ⋅ =−
2 t  1 t −1t1 2 t  1 t 1  2 2 4
1 3
L’A. O. a donc pour équation y= x – .
2 4
Cahier Analyse Didier Müller - LCP - 2010

47. ÉTUDE DE COURBES PARAMÉTRÉES 43
2 2
3. Dérivées et tableau dx 2 t t – 1 – t t – 2 t t t – 2
= 2 = 2= 2 s’annule en t = 0 et t = 2.
de variations dt t – 1 t – 1 t – 1 
2 2 2 2
dy t – 1 – 2 t – t –1 t 1
= 2 2 = 2 2 =– 2 2 ne s’annule pas.
dt t – 1 t – 1 t – 1
2 2 2 2 2
dy t 1 t – 1 t 1 t−1 t 1
=– 2 2⋅ =– 2 2⋅ =− 2 ne s’annule pas.
dx t – 1  t t – 2  t−1 t1 t t −2 tt−2 t 1
Les valeurs de t intéressantes sont t = –1, 0, 1 et 2 (valeurs trouvées aux étapes 1 et 3). Il
faut aussi voir ce qui se passe quand t → ±∞.
t –∞ –1 0 1 2 +∞
1
x –∞  –  0   4  +∞
2
dx 0 − − 0 +
+ +
dt
2
y 0−   0    0+
3
dy
− – –1 – − –5 −
dt
A. H. A. V. tangente A. O tangente A. H.
verticale verticale
4. Points particuliers En inspectant le tableau ci-dessus, on s'aperçoit qu'il n’y a pas de points singuliers, mais
deux points à tangente verticale.
5. Intersection avec Il y a une seule intersection en t = 0. Le point d'intersection est (0 ; 0).
les axes
6. Représentation En bleu, les trois asymptotes.
graphique
Didier Müller - LCP - 2010 Cahier Analyse

48. 44 CHAPITRE 6
Second exemple
{
1
x = 2t − 2
Étudions la courbe t
2
y = 2tt
1. Domaine de L’ensemble de définition de la courbe est D = ℝ *
définition
{
lim xt=−∞
t 0
2. Asymptotes Il y a une asymptote horizontale quand t = 0, puisque
lim y t=0
t 0
Il n'y a pas d'asymptotes quand t ±∞ .
3. Dérivées et tableau dx 2
=2 3 s’annule en t = −1.
de variations dt t
dy
=2 2t s’annule en t = −1.
dt
3 3 3
dy 1t 1t t t 1 t t1 t
= = = 3 = = 2 ne s'annule jamais.
dx 1 t3 1 t 1
2
t 1t −t1 t −t1
1 3 3
t t
Les valeurs de t intéressantes sont t = –1 et 0 (valeurs trouvées aux étapes 1 et 3). Il faut
aussi voir ce qui se passe quand t → ±∞.
t –∞ –1 0 +∞
x –∞  –3   +∞
dx + 0 +
−
dt
y +∞  –1  0  +∞
dy
− 0 + 2 +
dt
dy 1
−
dx 3
Point Asymptote
singulier horizontale
4. Points particuliers En inspectant le tableau, on s'aperçoit qu'il y a un point singulier en t = −1. Il est utile
dy
dans ce cas de calculer −1 pour connaître la pente de la tangente en ce point.
dx
1
5. Intersections avec xt =0⇒ t = 3 qui correspond au point (0 ; 2.22)
les axes 2
yt =0 ⇒ t =−2 qui correspond au point (−4.25 ; 0)
6. Représentation En esquissant le dessin de cette courbe, on s'apercevra que cette courbe contient un
graphique
point double. Pour le calculer, il faut résoudre {
x t = x s
y t = y s
avec t≠s .
Ce n'est en général pas facile ! En résolvant le système avec Mathematica, on a trouvé
t=– 1 –  2 et s= – 1 2 . Ces deux valeurs correspondent au point (−5 ; 1).
Cahier Analyse Didier Müller - LCP - 2010

49. ÉTUDE DE COURBES PARAMÉTRÉES 45
Exercice 6.2 Étudiez et dessinez les courbes suivantes selon les exemples du § 6.6 (a > 0).
{
2
t
x t =
{
2 2
x t = t 1t
a. b. 3
y t = t3 t
y t = 2
1t
{ {
3t 3t
x t = 3 x t = 3
1t 1t
c. 2 d. 2
3t 3t
y t = 3 y t = 2
1t 1t
{ {
e−t e−t
x t  = x t  =
t t
e. f.
1 1
y t = y t =
t t−1 t t2
{
ln t
g.
x t =
y t =
t
t ln t 
h. { x t =
y t =
a t −sin t 
a1−cost 
{ {
3 3
x t = a cos t  x t = a cos t 
i. j.
y t = a sin 3 t y t = a sin t
6.7. Ce qu’il faut absolument savoir
Trouver les asymptotes d’une courbe paramétrée t ok
Trouver les points particuliers d’une courbe paramétrée t ok
Connaître les six étapes de la méthode par cœur t ok
Maîtriser parfaitement chaque étape de la méthode t ok
Didier Müller - LCP - 2010 Cahier Analyse

50. 46 CHAPITRE 6
{
3a t
x=
Folium de Descartes 1t
3
y =t x
{
x = cost 2cos 2t
Trèfle gauche y = sin t −2 sin 2 t
z = −2sin 3t 
Cahier Analyse Didier Müller - LCP - 2010

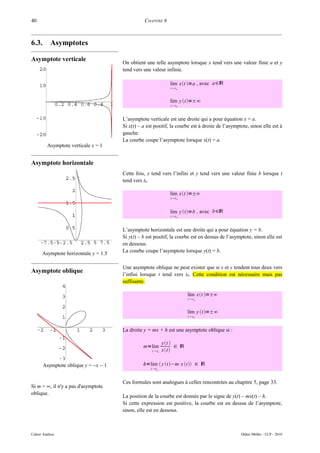
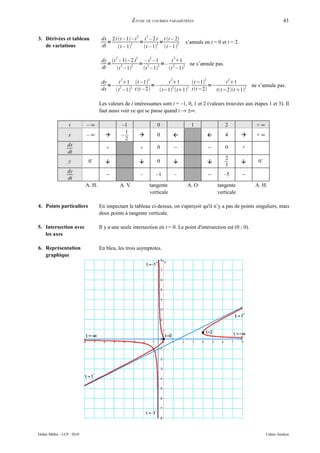
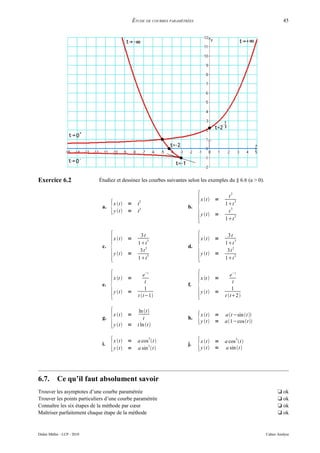
51. INTÉGRALES 47
7. Intégrales
7.1. Un peu d'histoire
Les calculs d'aire de figures géométriques simples comme les rectangles, les polygones
et les cercles sont décrits dans les plus anciens documents mathématiques connus. La
première réelle avancée au-delà de ce niveau élémentaire a été faite par Archimède, le
génial savant grec. Grâce à la technique d'Archimède, on pouvait calculer des aires
bornées par des paraboles et des spirales. Au début du 18 ème siècle, plusieurs
mathématiciens ont cherché à calculer de telles aires de manière plus simple à l'aide de
limites. Cependant, ces méthodes manquaient de généralité. La découverte majeure de la
résolution générale du problème d'aire fut faite indépendamment par Newton et Leibniz
(voir le chapitre 3) lorsqu'ils s'aperçurent que l'aire sous une courbe pouvait être obtenue
en inversant le processus de différentiation. Cette découverte, qui marqua le vrai début
Archimède de Syracuse de l'analyse, fut répandue par Newton en 1669 et ensuite publiée en 1711 dans un
(Syracuse, -287 - article intitulé De Analysis per Aequationes Numero Terminorum Infinitas.
Syracuse, -212) Indépendamment, Leibniz découvrit le même résultat aux environs de 1673 et le
formula dans un manuscrit non publié daté du 11 novembre 1675.
7.2. Calcul d'aire
Dans ce paragraphe, nous allons étudier le deuxième problème majeur de l'analyse (le
premier problème était de trouver la tangente à une courbe qui nous a conduit à la
découverte des dérivées) :
Le problème du calcul d'aire
Soit une fonction f continue et non négative sur un intervalle [a, b].
Trouver l'aire entre le graphe de f et l'abscisse dans l'intervalle [a, b].
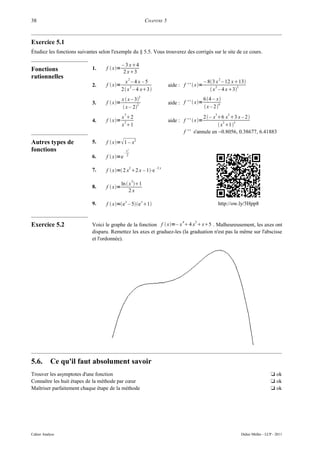
5
Que vaut l'aire sous la courbe 4
4 + sin(x) entre 1 et 6 (voir 3
dessin ci-contre) ? 2
1
1 2 3 4 5 6
L'idée est de subdiviser l'intervalle [a, b] en plusieurs sous-intervalles de même largeur
[x0, x1], [x1, x2], ... , [xn–1, xn], avec x0=a et xn=b.
La largeur de chaque sous-intervalle est égale à la largeur de l'intervalle [a, b] divisé par
b–a
le nombre de sous-intervalles, c'est-à-dire : de  x= .
n
Pour chaque i = 0, 1, ... , n–1, on dessine un rectangle ayant comme base le segment
Georg Friedrich Bernhard xixi+1 et comme hauteur f(xi) (voir dessins page suivante).
Riemann
(Breselenz, 17/9/1826 - Ainsi, l'aire du ième rectangle (hauteur x largeur) est :
Selasca, 20/7/1866) f  xi  ×  x
L'aire totale des n rectangles est :
n –1
Note : cette somme est appelée A n= ∑ f  x i ⋅ x
somme de Riemann. i=0
Didier Müller - LCP - 2010 Cahier Analyse

52. 48 CHAPITRE 7
Lorsque le nombre n de sous-intervalles augmente, la largeur de chaque sous-intervalle
diminue et l'approximation de l'aire sous la courbe devient plus précise. À la limite,
nous obtenons l'expression exacte pour l'aire A :
Rappel
3 n– 1
b–a
∑ xi = x0  x1 x 2 x 3 A= lim
n ∞
∑ f  x i ⋅ x avec  x=
n
i=0 i=0
5 5
4 4
3 3
2 2
1 1
1 2 3 4 5 6 1 2 3 4 5 6
Approximation avec 10 rectangles : aire = 19.8691 Approximation avec 30 rectangles : aire = 19.6745
Voici trois manières d'approcher l'aire sous la courbe 4+sin(x). Les deux premières
Exercice 7.1 utilisent cinq rectangles, la troisième cinq trapèzes.
5 5
L'aire exacte est 19.5801. 4 4
3 3
a. 2 b. 2
1 1
1 2 3 4 5 6 1 2 3 4 5 6
5
4
3
c.
2 Calculez ces trois approximations.
1
1 2 3 4 5 6
7.3. Définition de l'intégrale définie
D'une manière générale, et indépendamment du calcul d'aire, la quantité
n– 1
A= lim ∑ f  x i ⋅ x
n ∞ i=0
(si la limite existe) est appelée intégrale définie de la fonction f(x) de a à b. Elle est
Note importante notée
b b
∫ f  x dx est un nombre. ∫ f  x dx
a a
Les nombres a et b sont appelés bornes d'intégration et x variable d'intégration.
« dx » est un symbole insécable (on ne peut pas séparer le d du x). Il indique que l'on
intègre sur x. Il se place toujours en dernière position et marque la fin de l'intégrale.
Cahier Analyse Didier Müller - LCP - 2010

53. INTÉGRALES 49
7.4. Le théorème fondamental du calcul intégral
L'usage de la définition de l'intégrale
b n–1
∫ f  x dx=nlim ∑ b−a⋅f  xi 
∞ n
a i=0
se révèle être très peu pratique car demandant des calculs longs et parfois difficiles.
Cependant, pour certaines fonctions (pas toutes), il existe une alternative plus simple. Il
se trouve qu'il y a une relation entre intégration et différenciation. Cette relation
s'appelle le théorème fondamental du calcul intégral.
Théorème fondamental Soit une fonction f continue définie sur l'intervalle [a, b]. Alors
b
du calcul intégral
∫ f  x dx= F b− F a
a
où F(x) est une fonction telle que F'(x) = f(x).
Note
∫ f  x dx est une fonction
On dit que F(x) est la primitive de f(x) et on écrit F  x=∫ f  xdx .
Preuve du théorème Pour simplifier, nous allons prouver le théorème pour une fonction f positive sur
l'intervalle [a, b]. Le cas général est similaire.
Pour tout nombre réel x compris entre a et b, notons A(x) l'aire bornée par la courbe,
l'abscisse, la droite verticale passant par a et celle passant par x. Ceci définit une
fonction A(x).
Considérons le changement de la valeur A(x) quand x augmente d'une petite quantité h.
Si h est suffisamment petit, la différence entre A(x) et A(x+h) est approximativement
égale à l'aire du rectangle de largeur h et de hauteur f(x), donc d'aire h·f(x). Ainsi :
A xh− A x≈h⋅f  x
En divisant par h, on obtient :
A xh − A x
≈ f  x
h
Plus h sera petit, plus petite sera l'erreur de l'approximation ci-dessus. À la limite, nous
aurons :
A xh – A x
lim = f  x
h 0 h
Didier Müller - LCP - 2010 Cahier Analyse

54. 50 CHAPITRE 7
Cette limite n'est rien d'autre que la dérivée A'(x) de la fonction A(x). Nous avons donc
montré que :
En d'autres termes, A(x) est la A'(x) = f(x)
primitive de f(x) (les Anglo- Supposons maintenant que F(x) est une primitive de f(x). Ainsi :
Saxons disent volontiers
antidérivée ou encore intégrale F'(x) = f(x) = A'(x)
indéfinie). Donc
F'(x) – A'(x) = [F–A]'(x) = 0
Cela signifie que la fonction F–A est constante sur l'intervalle [a, b] (car sa dérivée est
nulle). Supposons que [F–A](x) = C.
Ainsi :
F(x) = A(x) + C
Comme A(a) = 0, nous pouvons déterminer C en posant x = a :
F(a) = 0 + C
Ainsi :
F(x) = A(x) + F(a) ou A(x) = F(x) – F(a)
Il s'ensuit que
b
∫ f  x dx= A b= F b− F a
a
Q.E.D.
Exemple Reprenons notre exemple de départ, à savoir calculer l'aire sous la courbe de la fonction
f(x) = 4 + sin(x), dans l'intervalle [1, 6].
Une primitive possible de f(x) est F(x) = 4x – cos(x). On peut le vérifier aisément en
dérivant F(x).
Attention ! Donc, d'après le théorème fondamental du calcul intégral :
Il faut toujours travailler en
6
radians !
∫ 4sin xdx =24−cos 6 −  =19.580132
 4−cos 1
1 F 6 F 1
7.5. Recherche de primitives
Soit donnée la fonction F(x) = x2. Sa dérivée est F'(x) = f(x) = 2x. Supposons maintenant
que l'on ait « oublié » la fonction F(x) et qu'on n'ait retenu que sa dérivée f(x). Est-il
possible de retrouver la fonction originale F(x) ?
Cette recherche de la fonction originale est appelée recherche d'une primitive.
Dériver
F  x=x 2 f  x=2 x
Chercher une primitive
Remarquons au passage qu'il existe une infinité de primitives pour une fonction f(x). En
effet, rappelons-nous que la dérivée d'une constante est nulle.
Donc F(x) = x2 + 2, F(x) = x2 – 5 sont aussi des primitives de f(x) = 2x.
Cependant, toutes les primitives de f(x) = 2x sont de la forme F(x) = x2 + C .
Cahier Analyse Didier Müller - LCP - 2010

55. INTÉGRALES 51
En vous appuyant sur vos souvenirs des dérivées, trouvez les primitives ci-dessous :
Exercice 7.2
∫ 4 dx = ∫ 6 x dx = ∫ x2 dx =
dx
∫ −cos  x dx = ∫ e x dx = ∫x =
dx d
∫ sin d  = ∫ 2x = ∫ cos2  =
Vous trouverez une liste des primitives les plus courantes dans votre formulaire de
mathématiques.
Propriétés des
(1) ∫ k⋅f  x dx= k ∫ f  x dx
primitives (2) ∫  f  x g x  dx=∫ f  x dx∫ g  x dx (idem pour « – »)
En utilisant votre formulaire et les deux propriétés ci-dessus, trouvez les primitives
Exercice 7.3
suivantes :
4
5x
a. ∫ cot  xdx b. ∫ 12 dx c. ∫ 7sin 3x dx
d. ∫ 5 cos 2 x−e5x 9 dx e. ∫ 2tan  x dx f. ∫ 3x dx
3
x 1
g. ∫ x dx (aide : transformez cette fonction en somme de puissances de x).
Cette importante méthode est couramment utilisée pour transformer un problème
Intégration par d'intégration compliqué en un problème plus simple. Elle peut se résumer ainsi :
substitution
Pas 1. Poser u = g(x). Tout le problème est de bien choisir g(x) !
du
Pas 2. Calculer = g '  x .
dx
Pas 3. Faire la substitution u = g(x), du = g'(x) dx.
À partir d'ici, plus aucun x ne doit subsister dans l'intégrale. Si tel était le cas, cela
voudrait dire que la substitution du pas 1 n'était pas judicieuse.
Pas 4. Trouver la primitive.
Pas 5. Remplacer u par g(x), pour obtenir le résultat en fonction de x.
Premier exemple Évaluer ∫ sin 2  xcos  x dx .
du
Si on pose u = sin(x), on aura = cos(x), donc du = cos(x)dx.
dx
3 3
u sin  x
Ainsi, ∫ sin 2  xcos  x dx=∫ u2 du= 3 C = 3
C
 cos x
Deuxième exemple Évaluer ∫ x dx .
du 1 1 1
Si on pose u=  x , on aura = , donc du= dx et 2 du= dx .
dx 2  x 2 x x
 cos x
Ainsi, ∫ x dx=∫ 2 cos u  du=2 ∫ cos u du=2 sin u C=2 sin  xC
Didier Müller - LCP - 2010 Cahier Analyse

56. 52 CHAPITRE 7
Trouvez les primitives ci-dessous en faisant la substitution indiquée :
Exercice 7.4
a. ∫ 2 x x 21 23 dx u = x2 + 1
b. ∫ cos3  xsin  xdx u = cos(x)
∫ 
sin x
c. dx u=  x
x
3 x dx
d. ∫ u = 4x2 + 5
 4 x2 5
Trouvez les primitives ci-dessous. Vous vérifierez chaque résultat en le dérivant.
Exercice 7.5
a. ∫ x2− x 23 dx b. ∫ cos 8 xdx
2
x
c. ∫ t  7t 212 dt d. ∫ dx
 x 31
5
x dx sin  
e. ∫ f. x
2
4 x 1
3
∫ x 2 dx
2
x dx
g. ∫ cos2  x 3 h. ∫ sin 5 3 cos 3d 
sin 3d 
∫ cos2 cos 3
2
i. j. ∫ x e x dx
ln  x
k. ∫ x
dx l. ∫ x2  x3 2dx
2
8x
m. ∫ 3 x  1−2 x 2 dx n. ∫ x 32 dx
tan 4 x x2
Les questions o, p et q
o. ∫ cos 4 x dx p. ∫ x1 dx
nécessitent une opération
préalable. q. ∫ cos3  d  2
(indication : rappelez-vous que cos sin =1 )
2
Si nous voulons poursuivre notre projet de ramener des problèmes compliqués à des
Intégration par problèmes simples, nous pouvons examiner la possibilité d'exprimer l'intégrale d'un
parties produit de deux fonctions f et g en termes des intégrales de f et g. Essayons d'inverser la
règle pour la dérivée d'un produit :
(f·g)' = f ' ·g + f·g'
En intégrant, on obtient :
f  x⋅g x =∫ f '  x⋅g  x dx∫ f  x⋅g '  xdx
D'où la règle d'intégration par parties :
∫ f  x⋅g '  xdx = f  x⋅g  x−∫ f '  x⋅g  xdx
Utilité de la formule La formule de l'intégration par parties ne résout que très partiellement le problème que
d'intégration par nous nous sommes posé. Analysons-la : elle s'applique à un produit de fonctions dont
parties nous devons pouvoir dériver l'une (f→f ' ) et intégrer l'autre (g'→g). Mais son point
faible réside dans le fait qu'elle ramène l'intégrale d'un produit (f·g') à l'intégrale d'un
autre produit (f ' ·g).
Son utilisation n'a donc de sens que si le calcul de la deuxième intégrale est plus simple
que celui de la première.
Cahier Analyse Didier Müller - LCP - 2010

57. INTÉGRALES 53
Exemple ∫ x e x dx =?
Les deux facteurs peuvent très facilement être dérivés et intégrés. Comme la dérivée de
x est 1, on va poser :
f (x) = x g'(x) = ex
d'où : f ' (x) = 1 g(x) = ex (+C)
Remarque
et nous trouvons : ∫ x e x dx =x e x −∫ e x dx .
Lors d'une résolution en
utilisant cette technique, il
La nouvelle intégrale (celle à droite du « = ») est facile à résoudre : ∫ e x dx =e x
arrive que l'on doive intégrer Donc : ∫ x e x dx =x e x −e x C= x−1e x C
par parties plusieurs fois.
Vérifions le résultat en dérivant : ((x–1)·ex)' = (x–1)·ex + ex = x·ex
Trouvez les primitives suivantes, en intégrant par parties :
Exercice 7.6
x
a. ∫ x cos x dx b. ∫ e x dx
x
c. ∫ x3 ln∣4 x∣ dx d. ∫  x1 dx
ln ∣x∣
e. ∫ 2 x sin 3 xdx f. ∫ x
dx
g. ∫ t2 et dt h. ∫ x2 sin x dx
i. ∫ e x  x2 x1 dx j. ∫ e−x sin  xdx
7.6. Retour au problème du calcul d'aire
Nous avons introduit la notion d'intégrale à partir du problème du calcul d'aire sous une
Exercice 7.7 courbe (voir § 7.2). Ce problème avait une restriction : la fonction f devait être positive
dans l'intervalle [a, b]. Que se passe-t-il si ce n'est pas le cas ? Pour le découvrir,
calculez successivement les intégrales définies ci-dessous (voir § 7.3) :
 
0 4 2
∫ sin x dx = ∫ sin x dx = ∫ sin x dx =
0 0 0
3
 2 2
∫ sin x dx = ∫ sin  xdx = ∫ sin  x dx =
0 0 0
3 0 0
∫ sin  x dx = ∫ sin  x dx = ∫ sin x dx =
0 − 
Voici le graphe de sin(x) dans l'intervalle [−π ; 3π]. Que constatez-vous d'étrange et
comment l'expliquez-vous ?
À votre avis, qu'entend-on par le terme aire signée ?
Didier Müller - LCP - 2010 Cahier Analyse

58. 54 CHAPITRE 7
7.7. Calcul de l'intégrale définie
b b
Propriétés de (1) ∫ k⋅f  x dx=k⋅∫ f  x dx
l'intégrale définie a a
b b b
Comme vous avez pu le (2) ∫  f  x g  x  dx=∫ f  x dx∫ g x dx (idem pour « – »)
constater au § 7.6, l'intégrale a a a
définie représente l'aire a
signée comprise entre la (3) ∫ f  x dx=0
a
courbe et l'axe Ox dans un
b a
intervalle donné. Cela signifie
que l'aire est comptée
(4) ∫ f  x dx=−∫ f  x dx
a b
négativement quand la b c b
fonction est négative. (5) ∫ f  x dx=∫ f x dx∫ f  xdx (avec a ≤ c ≤ b)
Cette constatation aide à a a c
comprendre les propriétés ci- b b
contre. (6) ∫ f  x dx≤∫ g  x dx si f(x) ≤ g(x) pour tout x dans [a, b]
a a
S'il est impossible de trouver Chaque fois que c'est possible, le calcul de l'intégrale définie entre les bornes a et b se
une primitive, on peut toujours fait en deux temps. Premièrement, trouver une primitive F(x) de la fonction f(x) à
approcher numériquement le intégrer ; deuxièmement calculer F(b) – F(a).
résultat par la somme des 3
rectangles définis au § 7.2. Comme exemple, calculons ∫ x 2 x2 dx .
–1
4
x
Étape 1 : ∫ x2 x 2 dx=∫  2 xx 3 dx =x 2 4 C
3 4 4
Étape 2 : ∫ x 2 x2 dx =32 3 −−12 −1  =9 81 −1 1 = 28
4 4 4 4
–1
Calculez les intégrales définies ci-dessous :
Exercice 7.8
3 2 2
a. ∫x 3
dx b. ∫ x 1x  dx 3
c. ∫ t 2−2t 8dt
2 −1 1
3 2 9
d. ∫ 12 dx e. ∫  13 − 22 x−4  dx f. ∫  x dx
1 x 1 x x 1

9 4 3 4
−
3
g. ∫ 2 y  y dy h. ∫  −5  x− x  dx
2
i. ∫ cos  x dx
4 1 x −
4

2 2 
2 x
j. ∫  x sin 2  x  dx k. ∫ dx l. ∫ x2 cos  xdx
 0  13 x 2 0
6
a. Calculez l'aire sous la courbe y = x2 + 1 dans l'intervalle [0, 3].
Exercice 7.9
b. Calculez l'aire au-dessus de l'axe Ox mais en dessous de la courbe y = (1–x)(x–2).
Pour toutes les questions ci-
c. Calculez l'aire du domaine borné par la courbe y = 3sinx et l'abscisse dans
4
contre, il est vivement l'intervalle [0, ].
3
recommandé de faire une
esquisse. d. Calculez l'aire du domaine borné par la courbe y = x3 – 5x2 + 6x et l'abscisse dans
l'intervalle [0, 3].
2 3π / 4
Exercice 7.10 a. Calculez ∫ 2x − 3 dx b. Calculez ∫ cos x dx
0 0
Cahier Analyse Didier Müller - LCP - 2010

59. INTÉGRALES 55
7.8. Intégrales impropres
Une intégrale définie est dite impropre (ou généralisée) dans deux cas :
1. une ou les deux bornes sont à l'infini
ou 2. la fonction n'est pas continue dans l'intervalle d'intégration.
Si la fonction f est continue dans l'intervalle d'intégration, on définit :
Premier cas
∞ b b b
∫ f  xdx =b∞ ∫ f  x dx
lim et ∫ f  xdx =alim ∫ f  x dx
−∞
a a −∞ a
Dans les deux cas, si la limite existe et n'est pas infinie, on dit que l'intégrale converge.
Autrement, elle diverge.
∞ 0 ∞
De plus, ∫ f  xdx =∫ f  xdx ∫ f  x dx .
−∞ −∞ 0
∞
Exemple 1 ∫ dx2 =?
1 x
dx 1
On a : ∫ x2 =− x C=F  x
∞ b
dx dx 1
D'où : ∫ x 2 =blim ∫ x 2 =blim F b− F 1=blim − b −−1=1
1 ∞ 1 ∞  ∞
0
Cette intégrale converge vers 1.
∞
Exemple 2 ∫ dx
x
=?
1
dx
On a : ∫ x
=ln∣x∣C=F  x
∞ b
∫ dx =blim ∫ dx =blim F b− F 1=blim lnb −ln 1 =∞
 
D'où :
1 x ∞ 1 x ∞ ∞
0
∞
Cette intégrale diverge.
Si la fonction f est discontinue en c dans l'intervalle [a, b] (c peut être une des bornes
Second cas d'intégration), alors
b  b
∫ f  x dx=limc ∫ f  x dxlimc ∫ f  x dx
 
a a 
c c
2  2
dx dx dx
Exemple 3 ∫  x−12 =lim ∫  x−12 lim ∫  x−12
 1  1
=?
0 0 
1 1
dx 1
On a : ∫ 2 =− C =F  x
 x−1  x−1

dx 1
Calcul de la première limite : lim ∫ =lim − −1=∞
 1 0
2
 x−1  1 −1
1 1
2
dx 1
Calcul de la seconde limite : lim ∫ 2 =lim −1 =∞
 1   x−1  1 −1
1 1
Cette intégrale diverge. Si on avait appliqué naïvement la formule sans prendre de
précaution, on aurait trouvé F(2) – F(0) = −1−1 = −2. Résultat aberrant puisque f n'est
jamais négative : l'intégrale définie ne peut pas être négative non plus !
Didier Müller - LCP - 2010 Cahier Analyse

60. 56 CHAPITRE 7
Calculez les intégrales impropres ci-dessous :
Exercice 7.11
∞ ∞ ∞
a. ∫ e−x dx b. ∫ dx c. ∫ 2
dx
0 1 x  4
2
x −1
∞ 0 0
dx dx
d. ∫ 3
e. ∫ 3
f. ∫ e 3 x dx
e x ln  x −∞ 2 x−1 −∞
∞ ∞ 4
g. ∫ x dx3
h. ∫ 2 x 2 dx i. ∫ dx
2
−∞ −∞  x 3 3  x−3
 
2 3 2
cos x
j. ∫ tan  xdx k. ∫ dx l. ∫  1−sin  x dx
0 0 x−2 0
7.9. Ce qu'il faut absolument savoir
Comprendre comment calculer une aire avec une somme de rectangle t ok
Connaître le théorème fondamental de l'analyse et savoir le démontrer t ok
Savoir ce qu'est une primitive t ok
Trouver une primitive par la méthode de substitution t ok
Intégrer par partie t ok
Calculer une intégrale définie t ok
Calculer l'aire comprise entre une courbe de l'axe des x t ok
Cahier Analyse Didier Müller - LCP - 2010

61. APPLICATIONS DES INTÉGRALES DÉFINIES 57
8. Applications des intégrales définies
8.1. Aire entre deux courbes
Problème Soient f et g deux fonctions continues dans l'intervalle [a, b] telles que f(x) ≥ g(x), pour
a ≤ x ≤ b. Calculer l'aire A du domaine délimité par ces deux courbes.
Solution Si g est positive (g ≥ 0) dans l'intervalle [a, b], alors
A = « aire sous f » – « aire sous g »
donc
b b b
A=∫ f  xdx−∫ g  xdx =∫ [ f  x – g  x] dx
a a a
Cette formule est aussi valable quand les fonctions ne sont pas partout positives.
En effet, si g prend des valeurs négatives dans l'intervalle [a, b], on translate les deux
courbes verticalement vers le haut de sorte que la fonction g soit partout positive ou
nulle. Il s'agit donc de trouver le minimum m de g sur [a, b], puis de soustraire m (car
m<0) à f(x) et à g(x). Puisque les deux courbes sont translatées de la même façon, il est
clair que l'aire entre les deux courbes ne va pas changer. On a alors :
b b
Les m se sont simplifiés
A=∫ [ f x  – m – g  x – m ] dx=∫ [ f  x – g  x]dx
a a
On donne les fonctions f et g. Calculez l'aire du domaine borné délimité par les deux
Exercice 8.1 fonctions.
2 2
a. f  x= x g  x=8− x
2 2
b. f  x= x −3 x2 g  x=−x −x6
3 2 3 2
c. f  x= x −5 x 6 x g  x= x −7 x 12 x
1 3
d. f  x= x g  x= 2 x
4
Calculez l'aire du domaine compris entre les courbes des fonctions f et g et les droites
verticales x = a et x = b.
e. f(x) = x2 + 1 g(x) = x a = –1 b=2
f. f(x) = x3 g(x) = x a=0 b=2
1
g. Calculez l'aire du domaine compris entre les courbes y = x, y= , et les droites
x
horizontales y = 1 et y = 2.
Didier Müller - LCP - 2010 Cahier Analyse

62. 58 CHAPITRE 8
8.2. Volume d'un solide de révolution
Problème Soit f une fonction continue et non négative sur l'intervalle [a, b].
Trouver le volume V du solide généré par la révolution autour de l'axe Ox de la portion
de courbe y = f(x) comprise entre x = a et x = b.
2 3 4
0 1
3
2
2.5
2
1.5 0
1
0.5
-2
1 2 3 4
2
0
-2
Volume de révolution obtenu en faisant tourner la courbe de gauche autour de l'axe Ox
Solution L'idée est la même que lorsque l'on cherchait l'aire sous une courbe. On va découper
(méthode des disques) l'intervalle [a, b] en n sous-intervalles de même largeur [x0, x1], [x1, x2], ... , [xn–1, xn],
avec x0 = a et xn = b.
La largeur de chaque sous-intervalle est égale à la largeur de l'intervalle [a, b] divisé par
b–a
le nombre de sous-intervalles, c'est-à-dire :  x= . Pour chaque i = 0, 1, ... , n–1,
n
on dessine un rectangle ayant comme base le segment xixi+1 et comme hauteur f(xi).
Lorsqu'ils tourneront autour de l'axe Ox, chacun de ces rectangles va définir un cylindre
très fin (presque un disque) de volume π·[f(xi)]2∆x.
Le volume du corps de révolution sera la somme de tous ces cylindres :
n
V = lim
n ∞
∑ ⋅[ f  x]2  x
i=1
qui n'est rien d'autre que l'intégrale définie :
b
V =∫ [ f  x] dx
2
a
2 3 4
0 1
2
0
-2
2
0
-2
Volume de révolution approché par une série de cylindres.
Cahier Analyse Didier Müller - LCP - 2010

63. APPLICATIONS DES INTÉGRALES DÉFINIES 59
Calculez le volume des solides générés par la révolution autour de l'axe Ox des courbes
Exercice 8.2
suivantes et donnez le nom (quand ils en ont un) de ces solides :
a. y = 4, –1 ≤ x ≤ 3
b. y = 3x, 0≤x≤2
c. y = x + 1, 0≤x≤3
d. y=  R − x ,
2 2
–R ≤ x ≤ R
e. y=  3− x , x ≥ –1
f. y = x2, 0≤x≤2
g. Donnez la formule permettant de trouver le volume engendré par une révolution
autour de l'axe Oy, puis calculez le volume du solide généré par la révolution
autour de l'axe Oy de la courbe : y = x3, 0 ≤ y ≤ 1.
h. Trouvez le volume du corps engendré par la révolution autour de l'axe Oy de la
courbe x=  1 y , y ≤ 3.
8.3. Longueur d'une courbe plane
Définition préalable Une fonction est lisse sur un intervalle si sa dérivée est continue sur cet intervalle.
Problème Soit f une fonction lisse dans l'intervalle [a, b].
Trouver la longueur L de la courbe y = f(x) de a à b.
Solution L'idée consiste à découper l'intervalle [a, b] en n sous-intervalles [x0, x1], [x1, x2], ...,
[xn–1, xn] de largeur ∆x.
On pose évidemment x0 = a et xn = b.
On relie ensuite par une ligne polygonale les points P0, P1, ..., Pn.
On obtiendra une bonne approximation de la longueur de la courbe en additionnant les
longueurs Lk des n différents segments, pour k = 1, ..., n.
Regardons un segment. Le théorème de Pythagore nous donne facilement sa longueur
s :
 s= x2 y2
Que l'on peut aussi écrire :
   
2 2 2
 x  y y
 s=  ⋅ x= 1 ⋅ x
2
 x  x2
x
Si l'on regarde de segment [xk–1, xk], on peut écrire :

2
L k = 1
 xk – xk – 1 
f  xk  – f  x k – 1 
⋅ xk – xk – 1 
D'après le théorème des accroissements finis,
Voir La dérivée § 3.6
f  x k  – f  x k – 1
= f ' k  où xk–1 < ξk < xk
x k – xk – 1
Par conséquent,
L k = 1[ f '  k ]2⋅ x
Donc, la longueur de la ligne polygonale est
n
L=∑  1[ f ' k ] ⋅ x
2
k=1
Didier Müller - LCP - 2010 Cahier Analyse

64. 60 CHAPITRE 8
Si nous augmentons maintenant le nombre de sous-intervalles de sorte que ∆x→0, alors
la longueur de la courbe polygonale va approcher la longueur de la courbe y = f(x). Par
définition, ce n'est rien d'autre que l'intégrale définie suivante :
b
L=∫  1[ f '  x] dx
2
a
a. Calculez la longueur de la courbe y = 2x entre les points (1, 2) et (2, 4) en utilisant
Exercice 8.3 la formule ci-dessus, puis vérifiez votre réponse à l'aide du théorème de Pythagore.
3
b. Calculez la longueur de la courbe y= x 2 – 1 de x = 0 à x = 1.
2
c. 1. Calculez la longueur de la courbe y= x 3 de x = 1 à x = 8.
2. Pourquoi ne peut-on pas utiliser telle quelle la formule pour calculer la
longueur de cette courbe entre –1 et 8 ? Donnez un moyen de s'en sortir.
d. Calculez la longueur de la courbe y=  1 – x 2 de x = 0 à x = 1.
8.4. Aire d'une surface de révolution
Problème Soit f une fonction lisse et non négative sur l'intervalle [a, b].
Trouver l'aire de la surface générée par la révolution autour de l'axe Ox de la portion de
courbe y = f(x) comprise entre x = a et x = b.
Solution L'idée est un peu la même que pour calculer la longueur d'une courbe : on va approcher
la courbe par une ligne polygonale. En faisant tourner cette ligne polygonale autour de
l'axe Ox, la surface obtenue sera composée de troncs de cônes circulaires droits mis bout
à bout.
Si r1 est le rayon du grand cercle de base, r2 le rayon du petit et g la longueur d'une
génératrice du tronc de cône, son aire latérale vaut :
Acône = π(r1 + r2)·g
Reprenons notre surface de révolution dont on veut connaître l'aire. Coupons-la en
tranches de largeur ∆x, comme le ferait un boucher avec un jambon. Ces tranches sont
« à peu près » des cônes tronqués. L'aire latérale du tronc de cône no k est :
Le théorème de la valeur
A k =2⋅f mk ⋅L k
intermédiaire nous assure que
mk existe.
f  x k – 1  f  xk 
avec mk compris entre xk–1 et xk et tel que f mk = .
2
Lors des calculs de la longueur d'une courbe du § 8.3, nous avons calculé que
L k = 1[ f '  k ]2⋅ x , donc
A k =2⋅f mk ⋅ 1[ f '  k ]2⋅ x
L'aire de la surface totale est la somme :
n
A=∑ 2 ⋅f  mk ⋅ 1[ f ' k ] ⋅ x
2
k=1
Quand on augmente le nombre de segments, leur longueur diminue, et forcément ξ se
Le calcul intégral avancé nous rapproche de m. Si on suppose qu'à la limite ces points sont confondus, on trouve
apprend que cette supposition l'intégrale suivante :
est en fait inutile car f et f ' sont b
A=2∫ f  x  1 f '  x dx
2
toutes deux continues.
a
Cahier Analyse Didier Müller - LCP - 2010

65. APPLICATIONS DES INTÉGRALES DÉFINIES 61
2 3 4
0 1
3
2
2.5
2
1.5 0
1
0.5
-2
1 2 3 4
2
0
-2
Surface de révolution obtenue en faisant tourner autour de l'axe Ox la ligne polygonale approchant la courbe
Problème semblable Pour une fonction exprimée sous la forme x = g(y), avec g'(y) continue sur l'intervalle
[c, d] et g(y) ≥ 0 pour c ≤ y ≤ d, l'aire de la surface générée par la révolution de g(y)
autour de l'axe Oy est donnée par la formule :
d
A=2 ∫ g  y  1g '  y dy
2
c
Trouvez l'aire de la surface engendrée par la révolution autour de l'axe Ox des courbes
Exercice 8.4 suivantes :
1
a. y=  1 – x 2 , 0 x b. y = 7x, 0 x1
2
c. y=  4 – x2 −1 x1
Trouvez l'aire de la surface engendrée par la révolution autour de l'axe Oy des courbes
suivantes :
d. x=9 y1 0 y 2 e. x=  9 – y 2 −2 y2
3
f. y=  3 x 0 y 2
8.5. Mouvement rectiligne
Remarque Pour introduire les dérivées, nous avions parlé du problème de calculer la vitesse
Dans ce paragraphe, nous instantanée d'un mobile connaissant son horaire s(t). Nous avions vu que la vitesse v(t)
supposerons que tous les est la dérivée de l'horaire et l'accélération a(t) la dérivée de la vitesse :
mouvements se font sur une
2
ligne droite. ds dv d s
v t = s' t = et at =v ' t= =
dt dt dt 2
Inversement, on déduit que l'horaire est l'antidérivée de la vitesse et que la vitesse est
l'antidérivée de l'accélération :
st =∫ v t dt et v t=∫ at  dt
Ainsi, si la fonction vitesse d'un mobile est connue, on peut trouver sa position à
condition d'avoir suffisamment d'informations pour déterminer la constante
d'intégration.
Didier Müller - LCP - 2010 Cahier Analyse

66. 62 CHAPITRE 8
Exemple Trouvez la fonction horaire d'une particule se déplaçant avec une vitesse v(t) = cos(π·t)
le long d'une ligne droite, en sachant qu'en t = 0, s = 4.
1
La fonction horaire est st =∫ v t dt =∫ cos  t dt= sin tC .

1
Comme s = 4 quand t = 0, il suit que 4= s0 = sin 0 C=C .


0
1
Ainsi, st= sin  t 4 .

Déplacement et distance Le changement de position, ou déplacement, du mobile dans un laps de temps [t1, t2]
parcourue est donné par la formule :
t2
∫ vt dt =s t2 − st 1
t1
La distance parcourue par le mobile dans ce même laps de temps peut être différente
du déplacement. Elle est donnée par la formule :
t2
∫∣vt ∣dt
t1
Donnez la fonction horaire s(t) d'un mobile sachant que
Exercice 8.5
a. v(t) = t3 – 2t2 + 1 ; s(0) = 1
b. a(t) = 4 ; v(0) = 1 ; s(0) = 0
c. a(t) = 4cos(2t) ; v(0) = –1 ; s(0) = –3
d. Trouvez la position, la vitesse et l'accélération en t = 1, si v t=sin  

2
t et
sachant que s = 0 quand t = 0.
Donnez le déplacement et la distance parcourue par une particule le long d'une droite
sachant que
e. v(t) = t2 + t – 2 ; 0≤t≤2
f. a(t) = t – 2 ; v(0) = 0 ; 1≤t≤5
1
g. at = ; v(0) = 2 ; 0≤t≤3
 5t 1
h. Sachant qu'un mobile en chute libre dans le vide subit une accélération a(t) = –g,
trouvez les formules de la vitesse v(t) et de l'horaire s(t).
8.6. Ce qu'il faut absolument savoir
Calculer l'aire entre deux courbes t ok
Calculer le volume d'un solide de révolution autour d'un des axes t ok
Trouver les valeurs de la constante C d'après les données initiales t ok
Cahier Analyse Didier Müller - LCP - 2010

67. ÉQUATIONS DIFFÉRENTIELLES 63
9. Équations différentielles
9.1. Introduction
Une équation différentielle est une relation entre une ou plusieurs fonctions inconnues
et leurs dérivées. L'ordre d'une équation différentielle correspond au degré maximal de
différenciation auquel une des fonctions inconnues a été soumise.
Ainsi, une équation différentielle d'ordre n est une équation de la forme
R(x ; y ; y'; y''; ... ; y(n)) = 0.
Toute fonction qui vérifie, pour tout x, l'équation R(x ; y ; y'; y''; ... ; y(n)) = 0 est une
solution de cette équation.
Résoudre une équation différentielle consiste à déterminer l'ensemble des fonctions qui
en sont solutions.
Les équations différentielles sont utilisées pour construire des modèles mathématiques
de phénomènes physiques et biologiques, par exemple pour l'étude de la radioactivité ou
la mécanique céleste. Par conséquent, les équations différentielles représentent un vaste
champ d'étude, aussi bien en mathématiques pures qu'en mathématiques appliquées.
1. xy' – y = 0 est une équation différentielle du premier ordre.
Exemples L'une des solutions est donnée par y = x. L'ensemble des solutions est donné par
l'ensemble des fonctions de la forme y = λx, avec ∈ℝ .
2. y'' + 4y = 0 est une équation différentielle d'ordre 2.
L'une des solutions est donnée par y = sin(2x), une autre par cos(2x). Les solutions
de cette équation sont de la forme y = λcos(2x) + µsin(2x),  , ∈ℝ .
3. y''' + y' – 2 ex = 0 est une équation différentielle d'ordre 3.
La fonction y = ex est solution de cette équation.
Trouvez les équations différentielles qui ont pour solution générale les fonctions y = f(x)
Exercice 9.1 données ci-dessous, α, β et γ étant des constantes.
a. y=αx b. y = αex
1
y = sin(x + α)
2
c. d. y=  x 
2
e. y = α x2 + β x + γ
9.2. L'équation y' = f(x)
Une équation différentielle d'ordre 1
R(x ; y ; y') = 0
admet, sous certaines conditions, une solution qui dépend d'une constante réelle
arbitraire (constante d'intégration). Pour caractériser l'une des fonctions f, solution de
R(x ; y ; y') = 0, il faut se donner une condition initiale.
Méthode de résolution Soit l'équation y' = f(x).
Si F est une primitive de f, alors la solution générale de l'équation proposée est donnée
par y = F(x) + α, ∈ℝ .
1
Exemple y' = cos(2x) admet comme solution générale y= sin 2 x , ∈ℝ .
2
Didier Müller - LCP - 2011 Cahier Analyse

68. 64 CHAPITRE 9
Résolvez les équations suivantes :
Exercice 9.2
a. y' = 0 b. y' + 2x = 0
1
c. y' = sin(x)cos(x) d. y' = 2
1 x
x x –1
e. y' = f. y' =
 1 x 2 x1
9.3. L'équation à variables séparables y'⋅ g(y) = h(x)
Méthode de résolution Une équation différentielle du type y'⋅ g(y) = h(x) est dite « à variables séparables ».
Si G et H sont des primitives respectives de g et h, la solution d'une telle équation est
donnée par :
G(y) = H(x) + α, ∈ℝ
Exemple L'équation (x – 1)y' – 2y = 0 peut se ramener à
1 2 dy 1 2 dy 2
y' = ou = ⇒ = dx
y x –1 dx y x – 1 y x–1
à condition d'écarter provisoirement la solution y = 0. En intégrant, on obtient :
– ln∣∣
ln ∣y∣ =2ln ∣x – 1∣ , ∈ℝ *
c
c'est-à-dire ln ∣∣=ln  x – 1 , d'où la solution y= x – 1 , ∈ℝ .
y 2 2
Résolvez les équations suivantes :
Exercice 9.3
a. y' sin(x) = y cos(x) b. y2 + (x+1)y' = 0
c. xy' – ky = 0, k ∈ℝ * d. y' =2 x  1− y2
e. x2y' + y = 3 f. yy' = x
g. y' – xe-y = 0 h. y = ln(y')
9.4. L'équation homogène y ' = g 
y
x
Méthode de résolution Pour résoudre l'équation y' = g
y
x  y
, on pose =z (y = xz et y' = z + xz') : on obtient
x
ainsi une équation différentielle à variables séparables.
y
Exemple xy' = x + y est une équation homogène, car elle peut s'écrire : y' =1 .
x
1
En posant y = xz, on obtient l'équation z + xz' = 1 + z, d'où z '= .
x
Sa solution générale est z = ln|x| + α, ∈ℝ .
D'où la solution générale de l'équation proposée : y= x ln∣x∣
Résolvez les équations suivantes :
Exercice 9.4
a. xy' = x – y b. xy2y' = x3 + y3
c. x – y + xy' = 0 d. (x2– y2)y' = xy
Cahier Analyse Didier Müller - LCP - 2011

69. ÉQUATIONS DIFFÉRENTIELLES 65
9.5. L'équation linéaire y' + p(x)⋅ y = q(x)
Méthode de résolution Soit l'équation à résoudre y' + p(x)⋅ y = q(x).
∫ p x dx
1. Calculer =e . µ est appelé facteur d'intégration.
d
2. Poser  y= q x .
dx
3. Intégrer les deux côtés de l'équation obtenue en 2 et résoudre pour y.
Exemple Résoudre y' – 4xy = x.
∫ −4 x dx −2 x 2
Comme p(x) = –4x, le facteur d'intégration vaut =e =e .
d –2 x 2
–2 x 2
Remarque On pose e y= x e .
dx
Cette équation aurait aussi pu 1 – 2x
– 2 x2 – 2 x2 2
se résoudre par séparation des On intègre : e y=∫ x e dx=− e C
4
variables. 1 2x
2
D'où l'on tire : y=− C e
4
Résolvez les équations suivantes :
Exercice 9.5
a. y' + y tan(x) = sin(2x) b. x2y' + y = 1
c. y' − x3 = xy d. y' sin(x) − y cos(x) = cot(x)
e. (x+1)y' − 2y = (x+1)3 f. xy' − y = ln(x)
Résolvez les équations suivantes avec les conditions initiales indiquées :
Exercice 9.6
a. xy' − 2y = 2 – x , y(0.5) = 0 b. 2xy' + y = 1 , y(1) = 2
c. xy' + y = xcos(x) , y 

2
=1 d. y' + y = e−x , y(0) = 0
2
e. y' = y + 3x + 2 , y(0) = −3 f. xy' + 3y = – , y(−1) = −3
x
9.6. Applications des équations différentielles d'ordre 1
Trouver une courbe du plan passant par le point (0; 3) et dont la pente de la tangente au
Géométrie 2x
point (x; y) est de 2 .
y
dy 2 x
On a y' = = et la condition initiale y(0) = 3.
dx y 2
On doit résoudre l'équation différentielle à variables séparables : y2dy = 2xdx.
1 3 2
D'où : ∫ y 2 dy=∫ 2 x dx ⇒
3
y = x C .
3
De la condition initiale, on déduit que C = 9. La courbe est donc y=  3 x 27 .
2
Trouvez une courbe du plan passant par le point indiqué et dont la pente de la tangente
Exercice 9.7 au point (x; y) est également donnée.
2
y
a. (1; −1) ; pente =
3x
b. (2; 0) ; pente = x e y
Didier Müller - LCP - 2011 Cahier Analyse

70. 66 CHAPITRE 9
Au temps t = 0, un réservoir contient 4 lb de sel dissous dans 100 gal d'eau. Supposons
Mélanges
qu'une saumure contenant 2 lb de sel par gallon d'eau s'écoule dans le réservoir à un
débit de 5 gal/min et que la solution obtenue s'échappe du réservoir aussi avec un débit
de 5 gal/min. La solution est conservée uniforme par un mélangeur. Quelle est la
quantité de sel dans le réservoir après 10 min (t = 10) ?
Soit y(t) la quantité de sel (en livres) au temps t. Commençons par trouver une
dy
expression de , la vitesse de variation de la quantité de sel au temps t.
dt
5
10 lb de sel pénètrent chaque minute dans le réservoir, et yt  en sortent.
100
dy yt
On a donc =10 – .
dt 20
1 lb = 1 livre = 453,6 grammes dy y t
 =10 est une équation différentielle linéaire d'ordre 1.
dt 20
1 gal = 1 gallon = On a aussi la condition initiale y(0) = 4. Résolvons.
3.8 litres (USA) ou
∫1 / 20dt t / 20
4.5 litres (GB) =e =e
d t /20 t /20
e y=10 e
dt
y=∫ 10 e
t / 20 t /20 t / 20
e dt =200 e C
−t / 20
yt =200C e
D'après la condition initiale, 4 = 200 + C ⇒ C = −196.
−t/ 20
Donc, yt =200−196 e .
−0.5
Après 10 minutes, la quantité de sel sera y10=200−196e =81.1 lb.
Au temps t = 0, un réservoir contient 25 lb de sel dissous dans 50 gal d'eau. Supposons
Exercice 9.8 qu'une saumure contenant 4 lb de sel par gallon d'eau s'écoule dans le réservoir à un
débit de 2 gal/min et que la solution obtenue s'échappe du réservoir aussi avec un débit
de 2 gal/min. La solution est conservée uniforme par un mélangeur.
a. Quelle est la quantité de sel dans le réservoir au temps t ?
b. Quelle est la quantité de sel dans le réservoir après 25 min ?
Un réservoir d'une capacité de 1000 gallons contient initialement 500 gal d'une saumure
Exercice 9.9 contenant 50 lb de sel. Au temps t = 0, de l'eau pure est ajoutée à un débit de 20 gal/min
et la solution obtenue est évacuée avec un débit de 10 gal/min.
Combien de sel y aura-t-il dans le réservoir quand il commencera à déborder ?
La loi de Torricelli donne une relation entre la vitesse d'écoulement d'un liquide par
Exercice 9.10 l'orifice d'un récipient et la hauteur de liquide au-dessus de l'orifice.
Soit h(t) la hauteur de liquide contenu dans le récipient au-dessus de l'orifice au temps t
et A(h) l'aire de la surface du liquide quand la hauteur du liquide est h. On a la relation :
dh
A h = – k h
dt
où k est une constante positive dépendant de certains facteurs, comme la viscosité du
liquide et l'aire de la section du trou d'écoulement.
Au temps t = 0, un réservoir cylindrique d'un mètre de rayon contient 4 mètres d'eau au-
dessus de l'orifice. La constante k vaut 0.025.
a. Trouvez h(t).
b. Après combien de minutes le réservoir arrêtera-t-il de se vider ?
Cahier Analyse Didier Müller - LCP - 2011

71. ÉQUATIONS DIFFÉRENTIELLES 67
En mathématiques, en économie et en biologie, on parle d'un phénomène à croissance
Croissance
exponentielle (ou géométrique) lorsque la croissance en valeur absolue de la
exponentielle population est proportionnelle à la population existante, c'est-à-dire lorsque le taux de
croissance est constant.
Une croissance exponentielle s'exprime en mathématiques :
• pour un phénomène discret (on prend des mesures à intervalle régulier) sous
forme d'une progression géométrique,
• pour un phénomène continu (on essaie de calculer ce qui se passe entre deux
mesures consécutives) sous forme d'une fonction exponentielle.
Soit y(t) la population en question. Comme la croissance en valeur absolue de la
dy
population est proportionnelle à la population existante, cela se traduit par = ky où
dt
k est le facteur de proportionnalité, avec y(0) = y0.
Cette équation est à variables séparables et peut donc être résolue comme vu plus haut.
∫ dy =∫ k dt
y
ln|y| = kt + C
kt C C kt
∣y∣=e =e ⋅e
De la condition initiale y(0) = y0, il suit que eC = y0 . Par conséquent, la solution de
dy kt
l'équation différentielle = ky est y= y0 e .
dt
Selon les données de l'ONU, la population mondiale au début de l'année 1990 était
Exercice 9.11
d'environ 5.3 milliards d'habitants, avec un taux de croissance de 2% par an. En utilisant
le modèle de la croissance exponentielle, estimez la population mondiale au début de
l'année 2015.
Le nombre de bactéries dans une culture croît de manière exponentielle au taux de 1%
Exercice 9.12
par heure. En supposant qu'il y ait actuellement 10'000 bactéries, trouvez...
a. le nombre de bactéries au temps t ;
b. le nombre de bactéries après 5 heures ;
c. le temps nécessaire pour obtenir 45'000 bactéries.
9.7. Ce qu'il faut absolument savoir
Résoudre une équation à variables séparables t ok
Résoudre une équation homogène t ok
Résoudre une équation linéaire t ok
Didier Müller - LCP - 2011 Cahier Analyse

72. 68 ANALYSE
Solutions des exercices
Chapitre 1 Chapitre 3
1.1. a. −1 b. 3 c. n'existe pas d. 2 3.1. a. x = –1, 1, 2, 3 b. x ≅ –0.3, 1.45, 2.6
c. x ≅ –0.1, 1, 2.8 d. x ≅ –0.8
1.2. 1. –2 2. –1 3. 2 e. x ≅ –0.4, 1.75, 2.4
4. 4 5. 0 6. n'existe pas 3.2. La dérivée est négative, car la pente de la
tangente en 3π est négative.
7. 0 8. +∞ 9. +∞
y
10. –∞ 11. 1/6 12. n'existe pas 1
1 3
13. 14. 15. 3 0 1 2 3 4 5 6 7 8 9 10 11 x
2 2 2
-1
2
16. 2 17. 2 18.
3
1 1
3.3. a. 3x2 b. – c. d. 6t + 5
19. 1 20. 1 21. +∞ x
2
2 x
22. 1 23. n'existe pas 24. n'existe pas
3.4. Calculons d'abord la pente de la sécante AB :
2
CB 1 x –1
pente = tan = = =
AC x
1.3. 1. 2/3 2. 0 3. –∞ 2 x x
2
=2 x
4. +∞ 5. 1 6. 1/2 x
7. 1/2 8. –2 9. 1 Si B tend vers A, ∆x tend vers 0 et la pente de la
sécante tend vers 2. La pente de la tangente au
10. 0 11. –∞ point A est donc :
lim (pente de la sécante AB) = lim (2+∆x) = 2
B A x  0
1.4. 1. e 2. e3 3. e2
La pente en A' est de −4.
4. 1/e 5. e−4 6. 1/e
7. e4 8. e3
3.5. a. 6.77259 b. –1 c. 6.5981
1
3.6. – m/s
Chapitre 2 9
3.7.
2.3. a. f(−1) n'est pas défini b. x – 1 f  x≠ f – 1
lim
a. b.
c. lim f x ≠ f  4 d. lim f x ≠ f 2
x 4 x2
x2
2.4. voir § 2.3.
c. d.
1 1
a. D = {x∣x≠– , } b. D = [−5; 5]
2 3
c. D = ℝ d. D = [ –  2 ;  2 ]
e. D = ] –∞ ;– 1[∪]1;∞[ f. D = {x∣x≥0}
e. f.
2.5. f satisfait la propriété de la valeur intermédiaire,
mais est en discontinue en 0.
2.6. environ 0.36
Cahier Analyse Didier Müller - LCP - 2012

73. 69 ANALYSE
3.9. a. Le taux instantané de variation du nombre de 3.20. 1. 1 2. 2 3. –3
bactéries après 5 heures, exprimé en nombre 4. a 5. 2x 6. 8x–5
de bactéries par heure. 7. 6x2+2 8. 2ax+b 9. 0
b. f ' (10) > f ' (5) car f(t) est une fonction 10. 3ax2+2bx+c 11. 2x+2 12. 12x3+4x
exponentielle. a −6
13. 2acx+ad+bc 14. – 2 15. 2
x  x – 1
3.12. a. x9 1 1
16. – 17. 18. 3 2
2 x 3x
2 3
x – 1
1.5 2 –1
19. 3 20.
1 3x 2  x3
0.5
1 2 3 4 5 6
3.21.
-0.5
2 x5 2
-1 1. 2.
2  x 25 x – 1
3
3x–1
-1.5
2
5 x 2 x
-2 3. 4. 2 x – 1
b.  2 x1
g'HxL
1
2 5. 5 x 4  4 – x 6. 5(2x+5)(x2+5x–1)4
2
1 7. (30x2–26x–3)(2x–3)2 8. 3(2x2–x–1)2(4x–1)
9. x(5x+4)(x+2)2 10. cos(x) – sin(x)
1 2 3 4 5 6
11. tan2(x) 12. 2cos(2x–1)
-1
cos x 
13. 20sin4(4x)cos(4x) 14.
2  sin  x
-2
–3 2 2
15. sin   xcos   x 16. –
∆ l l(t + ∆ t ) − l(t ) 2 x 2
sin 2 x
3.13. a. vmoyenne = = =
∆t ∆t 17. 2e2x 18. aeax+b
g 2 g 2 19. cos(x) esin(x) 20. (sinx+cosx) ex
t t – t 2 2 2
2 2 g t 2t  t  t – t
= 1
t 2 t 21. 2(2cos(2x)–sin(2x))e4x 22.
x
g g
= 2 t t = g t   t 1
2 2 23. 4ctg(4x) 24.
x ln  x
x g 2 3 x – 1
b. v t= lim = lim  g t  t = g t 25. 1 26.
t  0 t t 0 2 3 3 x – 2 x – 1
3 2 2
2
2tan  x 3 sin 3 x
3.14. La dérivée seconde est négative si x < −1 et 27. 28. –
2  xtan  x 2  cos 3 x
positive si x > −1. Elle est nulle quand x = 1, ce
qui signale un point d'inflexion.
29.
2 x1
30.
 x3 x2 6 x – 9
21 x  1x 2 x32  x 29
3.15. Voir http://www.nymphomath.ch/
–1
MADIMU2/ANALY/COR3-15.PDF 31. 2 32. 0
x – 4 x5
3.16. a. III et IV b. II c. IV 4 4 x 1 x1
33. 34.
4  1 x  x 2 1 x
x
–x 2
d. III et IV e. I f. II e e 
2
3.17. a. 6 b. 1/4 c. –1/4 d. 6 35. 0 36.
 1 – 4 x2
3.18. a. –2.25, –0.5, 2 b. 0, 1.55 37. 2ex2e−1 38. (1+ln(x)) xx
Cahier Analyse Didier Müller - LCP - 2012

74. SOLUTIONS DES EXERCICES 70
3.22. a. 1 b. 0 c. 0
Chapitre 5
1 5.2. Repérer les points critiques et d'inflexion
3.23. a. 4 b. 1 c.
2
2 1 m m–n
d. e. f. a
 e n
1 a–b
g. h. i. ∞
2 ab
j. n'existe pas
Chapitre 4
1
4.1. a. y = 4x – 3 b. y = 4 x + 1 c. y = 13x – 2
6 9
4.2. a. y = –2x – 5 et y= x –
5 5
Chapitre 6
b. y = 2ex – 4 c. y = ex
– 1  5 6.1. D = [a ; b]
4.3. a. oui b.
2
{
1
– 3x – si x  – 1 Chapitre 7
2
x2 7.1. a. 20.1762 b. 19.0553 c. 19.6157
4.4. f(x) = – 2x si – 1 x3
2 5
x
9 7.3. a. lnsinx + C b.
+C
x– si x  3 12
2 5x
7 5 e
c. – cos 3 xC d. sin 2 x – 9 xC
4.5. a. 0 ; 8.13° b. 30.94° c. 70.53° 3 2 5
x
3
4.6. b. 1 e. -2 lncosx + C f. C
ln 3 
34 8
4.7. a = 3 ; b = 5 ou a= 9 ; b= 3 g.
2
 x  x37C
7
1 3
4.8. a. 12 cm3/min b. 16  cm/min c. 20 cm/min
1 2 24 1 4
4.9. environ 6.05 ˚/s 7.4. a. 24 x 1 C b. –
4
cos  xC
3
4.10. – 8/3 m/s c. – 2cos   xC
2
d.
4
 4 x 25C
p p
4.11. Le carré de côté 2 et d'aire
4
2a a 1 2 4 1
4.12. Base carrée de côté 3 , hauteur 6 7.5. a. – 8 2 – x  C b.
8
sin 8 xC
3

1 2 3
4.13. hauteur = diamètre = 3 4
dm c.
21
7 t2 12  2 C d.
3
 x 1C

4.14. a. ne faire que le carré
b. l=
9L
pour le triangle
e. –
1
16
2 –2
4 x 1 C f.
1
5
cos
5
x 
C
94  3 1 3 1 6
g. tan  x C h. sin 3 C
3 18
4.15. PB = 3 km
1 1 x 2
2p p i. – tan cos 3C j. e C
4.16. rectangle : largeur : 4 hauteur : 4 3 2
3
1 2 2 3
ln ∣x∣C  x  2 2 C
4.17. La droite de pente – 2 k.
2
l.
9
3
3
1 8
ln∣x 2∣C
3
4.18. À 14h. Le navire B sera alors à 20 km de A dans la m. – 1 – 2 x 2  2 C n.
2 3
direction 150oE.
3 1
2 r o. C p. x + ln|x+1| + C
4.19. cm3 4cos 4 x
9 3 3
sin 
q. sin – C
4.20. 0.81944 3
Didier Müller - LCP - 2012 Cahier Analyse

75. 71 ANALYSE
7.6. a. x·sinx + cosx + C b. e–x(–1–x) + C 8.4. a. π b. 35  2  c. 8π
d. 40  82  e. 24π f. 24.1179
 
4
x 1
c. ln∣4 x∣ – C
4 4
4
t 2
d.
2
 x – 2   x1C 8.5. a. st = – t3 t1 b. s(t) = 2t2 + t
4 3
3
e. 
2 1
3 3 
sin 3 x – x cos 3 x C
c. s(t) = –cos(2t)–t–2
e. 2/3; 3
d. s = 2/π; v=1; a=0
f. –10/3; 17/3
1 2 g. 204/25; 204/25
f. ln  xC g. et(t2–2t+2) + C
2
h. −x2cosx + 2xsinx + 2cosx + C
i. e x  x2 – x2C Chapitre 9
1 –x
j. – e cos  xsin  xC
2
9.1. a. xy' = y b. y' = y
c. y'' + y = 0 d. xy'' – y' = 0
7.8. a. 65/4 b. 81/10 c. 22/3 e. y''' = 0
d. 2/3 e. –1/3 f. 52/3
9.2. a. y = α, ∈ℝ b. y = α x2
g. 844/5 h. –55/3 i. 2 1 2
2 c. y= sin  x d. y = arctan(x) + α
 2
j. 2  3 k. 0.868 l. −2π
9 e. y=  1 x 2 f. y = x – ln(x+1)2 + α
1
7.9. a. 12 b. 1/6 c. 15/2 9.3. a. y = α sin(x) b. y=
ln ∣  x1∣
d. 37/12 c. y = α xk d. y = sin(x2 + α)
1
1 e. y=3 e x
f. y=± x 2
7.10. a. 5/2 b. 2 –
2
7.11. a. 1 b. diverge c. ln(5/3) ∣1 2
g. y=ln  x
2 ∣ h. y=ln ∣ ∣1
− x
d. 1/2 e. –1/4 f. 1/3 2
x  3
9.4. a. y= b. y= x  ln ∣ x3∣
g. 0 h. 0 i. diverge 2x
j. diverge k. ln(1/2) l. 2 c. y= x⋅ln

x d. x=± y  – 2ln  y
9.5. a. y = −2cos2(x) + α cos(x)
Chapitre 8 1
b. y=1 e x
2
c. y= – x 2 – 2 ex / 2
8.1. a. 64/3 b. 9
1
c. 9 d. 5/3 d. y= sin  x –
e. 9/2 f. 5/2 2sin  x
g. 1 e. y = (x + α)(x + 1)2
f. y = αx – ln(x) – 1
8.2. a. cylindre : 64π b. cône : 24π
1
c. cône tronqué : 21π d. sphère :
4
R
3 9.6. a. 2x2 + x – 1 b. y=1
3 x
xsin  xcos x
32 c. y= d. y = xe−x
e. paraboloïde : 8π f.  x
5 2
4– x
3 e. y = 2ex – 3x – 5 f. y= 3
g.  h. 8π x
5
 
2
–3 x
8.3. a.  5 b. 1.4397 c. 1. 7.6337 9.7. a. y= 2  x1 b. y= – ln 3 –
2
d. π/2
Cahier Analyse Didier Müller - LCP - 2012

76. SOLUTIONS DES EXERCICES 72
9.8. a. y= 200 – 175e – t /25
b. 136 lb
9.9. 25 lb
9.10. a. h(t) = (2 – 0.003979t)2
b. environ 8.4 min
9.11. 8.7 milliards
9.12. a. y=10000 e 0.01 t
b. 10'513
c. environ 150 heures
Didier Müller - LCP - 2012 Cahier Analyse