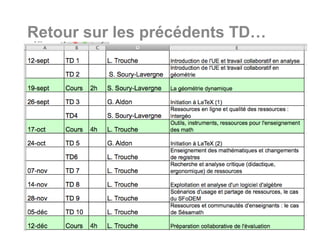
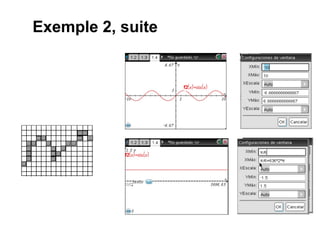
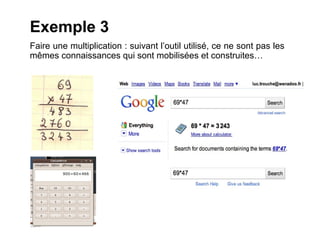
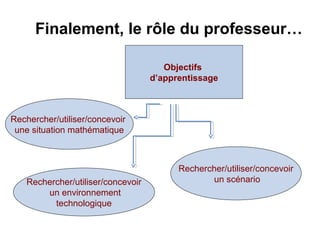
Le document présente un travail collaboratif d'étudiants en mathématiques utilisant des environnements numériques pour concevoir des ressources pédagogiques. Il s'interroge sur l'impact des outils numériques dans l'enseignement des mathématiques et évoque les mutations des pratiques éducatives à l'ère digitale. Les étudiants sont encouragés à analyser et réfléchir sur l'utilisation des outils technologiques et la nature de l'apprentissage en mathématiques.

1. Des outils de calcul aux instruments
du travail mathématique
UE e-culture
Master EADM
2012-2013
Une approche de la pratique,
de l’apprentissage et de
l’enseignement des
mathématiques dans des
environnements numériques
Luc Trouche, EducTice-S2HEP, Ecole Normale Supérieure de Lyon
luc.trouche@ens-lyon.fr - http://ens-lyon.academia.edu/LucTrouche

2. Evaluation UE, dernière version !
Un travail collaboratif exploitant la plateforme Spiral et ses outils,
réalisé en binôme, avec une part personnelle :
- les étudiants travailleront par deux ;
- ils choisiront un thème mathématique, un objectif didactique et
un niveau scolaire (par exemple : la dérivation des fonctions,
introduction, classe de première scientifique) ;
- ils organiseront une recherche raisonnée de ressources pour
l’enseignement de ce thème dans ce contexte ;
- ils retiendront 3 ressources, en justifiant ce choix, et les
composeront pour réaliser une situation d’enseignement
soigneusement décrite ;
- ce travail commun au binôme sera mis en ligne (avant la fin du
mois de décembre), accompagné d’une analyse individuelle de
chacun des deux participants, situant sa contribution personnelle
et proposant une analyse critique du résultat.

3. L’UE eCulture, rappels
Les questions suivantes seront traitées :
• quels sont les outils utiles, nécessaires pour
faire/apprendre/enseigner les mathématiques ? Comment
comprendre les rapports des élèves, des professeurs, avec ces
outils ?
• quelles sont les ressources nécessaires pour concevoir un
enseignement de mathématiques ? Quel est le travail sur les
ressources que fait un enseignant ? Comment analyser la
participation des élèves à ce travail ? Quelle est la contribution
des technologies, anciennes ou nouvelles, à ce travail ?
• comment comprendre le bouleversement qu’Internet introduit,
dans les systèmes d’information et de communication en général,
dans la documentation des enseignants de mathématiques en
particulier ?

4. Réflexions sur l’eCulture, rappels
L’UE questionnera les nouvelles manières de faire, d’apprendre et
d’enseigner les mathématiques à l’ère du numérique
L’avènement du numérique constitue un bouleversement des
façons de s’informer et de communiquer, aussi important que
l’avènement de l’écriture (Pédauque 2006) et de l’imprimerie
Il y a une logique de l’écriture (Goody 1985) : listes, tableaux,
formules, schéma ; il y a une logique du numérique : programme,
hypertexte, lecture-écriture, pensée en réseau
Cela touche nécessairement la pratique des mathématiques à
tous les niveaux (relation forte entre le développement de l’écriture
et le développement des mathématiques)
Ressources numériques pour les mathématiques, une
métamorphose du travail des enseignants (Gueudet & Trouche
2010)

5. Réflexions sur l’eCulture
Commentaires des étudiants après le premier cours
L'utilisation de Framapad est un bon moyen (gratuit et libre) de se
répartir les différentes tâches de travail et de décomposer un problème
en plusieurs sous problèmes- il nous permet d'échanger des
informations rapidement, et aussi la correction instantané par nos
collègues, qui apportent toujours des améliorations. C'est enrichissant.
Il était intéressant de jongler entre de l'analyse et de l'algèbre en
groupe. Beaucoup d'aide et d'idées pour tenter de résoudre les
problèmes même si la géométrie a posé des problèmes de constructions
Nous avons rencontré certaines difficultés pour savoir quels outils
utiliser et comment les utiliser. Un peu de pratique du logiciel serait
utile afin de mieux se concentrer sur la résolution du problème.
Il faut retenir qu'internet peut être une bonne source d'information
mais pas que... il faut faire attention et bien réfléchir par soi-même sur
la question posée en utilisant plusieurs outils mathématiques

6. Retour sur les précédents TD…

7. Le programme de la journée
Cours
• quelle organisation de l’espace du cours ?
• les outils pour les mathématiques, leur enseignement
• les effets des outils
• exemples…
• des concepts pour situer la place des outils dans cet
enseignement
TD
• traitement de problèmes dans des environnements numériques,
… et réflexion

8. Quelle organisation de l’espace du
cours ?
Inventaire des outils et projet didactique… Etude d’une vidéo qui
met en évidence la très grande variété des dispositifs qui sont mis
en œuvre par un professeur dans le cadre de son cours…
Organisation du cours du jour en fonction des outils disponibles…

9. Les outils pour les mathématiques
Des outils toujours présents :
outils de comptes pour la
société, outils de calcul pour les
savants, ou pour
l’enseignement, issus de
l’expérience et assistant l’activité
des hommes.
Ci-contre, le timith, outil de
‘calcul automatique’ du blé
« Le calcul, on le voit, se fait tout
seul » (Bourdieu 2003)

10. Les outils pour les mathématiques
Ci-dessus, une tablette de problèmes (deuxième millénaire avant
notre ère, 10cm x 10 cm, plusieurs centaines de problèmes).
Des outils hautement structurés, concentrant des connaissances,
articulés avec un ensemble d’artefacts (Neugebauer & Sachs 1945)

11. Les outils pour les mathématiques
Des évolutions notables avec les outils informatiques :
 le regroupement des outils dans une même enveloppe ;
 des outils ‘de poche’, polyvalents
 la multiplication des images ;
 le changement de paradigme (de la flèche au filet).

12. Les outils pour les mathématiques
Une superposition
permanente entre anciens et
nouveaux outils, des phases
de transition qui peuvent être
longue
Illustration ci-contre :
plusieurs siècles en France
pour passer du calcul à
jetons au calcul à plume

13. Les outils pour les mathématiques
Ou des superpositions courtes (une dizaine d’années de
cohabitation entre règles à calcul et calculatrices…)

14. Sujet de controverses dans
l’enseignement…
Un sujet ancien…
« Le boulier corrompt l’enseignement
de l’arithmétique. La principale utilité
de cet enseignement est d’exercer de
bonne heure, chez l’enfant, les
capacités d’abstraction, de lui
apprendre à voir de tête, par les yeux
de l’esprit. Lui mettre les choses sous
les yeux de la chair, c’est d’aller
Extrait de la rubrique le
directement contre l’esprit de cet
boulier-compteur, le
enseignement.
boulier numérateur, etc.
dans le dictionnaire La nature a donné aux enfants leurs
pédagogique de F. dix doigts pour boulier ; au lieu de leur
Buisson (1911) en donner un second, il faut leur
apprendre à se passer du premier ».

15. Sujet de controverses dans
l’enseignement…
Mathema, connaissance et pensée
pure…
« Puisqu’une machine à compter est
possible, une machine à raisonner est
possible. Et l’algèbre est déjà une
sorte de machine à raisonner : vous
tournez la manivelle, et vous obtenez
sans fatigue un résultat auquel la
pensée n’arriverait qu’avec des
peines infinies.
L’algèbre ressemble à un tunnel :
vous passez sous la montagne, sans
vous occuper des villages et des
Alain, 1932, Propos sur chemins tournants, vous êtes de
l’éducation. l’autre côté et vous n’avez rien vu »

16. Sujet de controverses dans
l’enseignement…
Aristo, Bulletin
d’information
pour le corps
enseignant
(1971)
« Pour le professeur formé aux rigueurs de la discipline
mathématique, l’introduction de la règle à calcul dès les
classes moyennes peut poser un vrai cas de conscience ».

17. Les effets des outils
Effets sur la production des mathématiques, exemples :
•le théorème de Mohr (1672) - Mascheroni (1797) : toute
construction à la règle et au compas peut être réalisée au
compas seul http://en.wikipedia.org/wiki/Mohr–Mascheroni_theorem
•les aspects expérimentaux (Zagier 2005).
Effets sur les programmes d’étude, exemples :
•le passage de la plume d’oie à la plume de fer et l’arithmétique
•l’introduction des calculatrices graphiques et l’analyse
Effets sur le travail enseignant :
•foisonnement de ressources et accélération technologique ;
•nouvelles opportunités de collaboration

18. Les effets des outils
Effets sur l’enseignement lui-même :
De nouveaux moyens :
• de représentation des connaissances
• de manipulation des objets
• d’exploration des problèmes
• de validation des solutions
• de collaboration (élèves, professeurs)
Effets sur les modes de travail des élèves et la
conceptualisation des mathématiques :
• le paradigme du filet ;
• les effets des images, la confusion entre les objets et leur
représentation (« c’est tout vu… »)

19. Exemple 1
« Magie et image ont mêmes lettres… », une nécessaire
analyse des images, un écart irréductible entre le territoire et
ses cartes, les objets mathématiques et leurs représentations…

20. Exemple 2
Mise en évidence (sur une calculatrice type TI-spire) des
problèmes posés par la coexistence du calcul exact et du calcul
approché, et par la gestion discrète de phénomènes continus
(typiquement : les pixels des écrans)
x x x x x x x x x x x x x x x
x : P i x e l s s o l l i c i t é s p a r l 'a l g o r i t h m e

21. Exemple 2, suite

22. Exemple 3
Faire une multiplication : suivant l’outil utilisé, ce ne sont pas les
mêmes connaissances qui sont mobilisées et construites…

23. Exemple 4
Trouver une parabole tangente à trois droites données,
différentes résolutions dans des environnements différents
(papier-crayon, calculatrice dynamique, Geogebra) :
- des questions initiales nécessaires si l’on veut engager des
méthodes de résolution efficientes : qu’est-ce qu’une parabole ?
Y a-t-il toujours une (des) solution (s) ? Qu’est-ce qu’une
tangente à une parabole a de spécifique (par rapport à une
tangente à une autre courbe ?
- avec un grapheur, possibilité de s’engager dans une démarche
de résolution approchée, où l’activité débouche sur une
découverte du rôle des coefficients de l’équation de la parabole.
y = -7,3x - 24,075
y = -1,3x - 9,075
y = 7,7x - 9,075

24. Exemple 4, suite…
L’activité, dans un environnement spécifique (écran fait de pixels)
développe des connaissances spécifiques, par exemple une
« définition d’une tangente » qui émerge : « une droite est
d’autant plus tangente à une courbe qu’elle a plus de points
communs avec elle », liée à la mobilisation de zooms de plus en
plus rapprochés (définition liée aux modes de validation de la
solution graphique)
Une définition dynamique du coefficient c, liée aux modes d’action
sur la figure (« c augmente quand la courbe monte », et
réciproquement, d’où l’idée que ce coefficient est négatif dans les
deux cas ci-dessous)

25. Quelques concepts théoriques…
Pour penser l’intégration des outils dans l’apprentissage des
mathématiques…
Un artefact Un sujet Relations dialectiques entre les
sujets et les artefacts qu’ils
Genèse instrumentale
utilisent
Les artefacts : des propositions
Les instruments : des
Instrumentation constructions individuelles
Deux processus en étroite
relation, instrumentation et
Instrumentalisation
instrumentalisation
Un instrument = une Un instrument, entité mixte
partie de l’artefact + des (matérielle et psychologique),
schèmes d’utilisation résultat d’une genèse

26. Quelques concepts théoriques…
Un schème = organisation invariante de l’activité pour réaliser un
type de tâche (Piaget, Vergnaud)
Le développement humain repose sur le développement d’un
répertoire de schèmes :
• schème du saut à la perche ;
• schème de descente d’un escalier ;
• schème de résolution d’une équation algébrique…
Schème = des gestes structurés par des connaissances
Dans le cas des mathématiques, ces connaissances sont des
« théorèmes-en-actes » et des « concepts-en-actes », bien
souvent implicites (Vergnaud 1999)
Petit exercice d’illustration : recherche des triangles rectangles
ABC tels que AB est le carré de AC (qui font apparaître que,
“naturellement”, on pense que le carré d’un nombre est plus
grand que le nombre…)

27. Quelques concepts théoriques…
Instrumentation
L’instrumentation est un processus
par lequel les contraintes et
potentialités de l’artefact
conforment l’activité du sujet. Il se
développe à travers l’émergence
“Si la fonction augmente rapidement, et l’évolution de schèmes pour la
c’est bon. Par contre, si la fonction
réalisation de tâches
oscille fortement, alors pas de limite
infinie”. On peut émettre l’hypothèse Exemple, étudier, avec une
que le schème de l’étudiant intègre une calculatrice graphique, la limite en
connaissance du type “si la limite de f
+ ∞ de la fonction qui, à x, associe
est infinie, alors f est nécessairement
croissante”.
f(x) = ln(x) + 100 sin(x)

28. Quelques concepts théoriques…
Instrumentalisation
Faire sien un objet, c’est « y mettre
du sien »
Ni une diversion, ni un braconnage…
mais une contribution essentielle au
développement des artefacts
Comme conséquence, l’idée d’une
conception continuée et distribuée
des artefacts (logiciels, ressources
pour les exploiter) : tout utilisateur est
un concepteur…
Les ressorts des communautés
d’utilisateurs, de développeurs…

29. Finalement, le rôle du professeur…
Objectifs
d’apprentissage
Rechercher/utiliser/concevoir
une situation mathématique
Rechercher/utiliser/concevoir
Rechercher/utiliser/concevoir un scénario
un environnement
technologique

30. Exercice 1, à achever
collaborativement…
La question est : par combien de zéros se termine n !
Mieux, peut-on définir (c’est-à-dire programmer sur une machine)
une suite f, qui, pour tout n, calcule f(n) égal au nombre de zéros
qui sont à la fin de l’écriture de (n !) ?
Le problème a été bien avancé en cours : il s’agit d’en faire un
énoncé, assorti d’une description de la mise en œuvre
(l’organisation de l’espace de la classe et de l’espace du problème),
pour un niveau scolaire donné, et un objectif d’enseignement précis.

31. Exercice 2, à préparer pour le TD
suivant…
Problème de géométrie : peut-on construire
un polygone connaissant le milieu de ses
côtés ? (environnement technologique :
GeoGebra)
• étude mathématique du problème ;
• construction d’un scénario pour des élèves
de tel ou tel niveau scolaire…

32. Références
Bourdieu, P. (2003). Images d' Algérie: une affinité élective. Arles : Actes sud
Brousseau, G. (2005). Recherches en éducation mathématique, APMEP 457, 213-224,
http://www.apmep.asso.fr/IMG/pdf/Brousseau.pdf
Buisson, F. (dir.) (1911). Le nouveau dictionnaire de pédagogie et d’instruction primaire, INRP
http://www.inrp.fr/edition-electronique/lodel/dictionnaire-ferdinand-buisson/
Neugebauer, 0., & Sachs, A. (1945). Mathematical Cuneiform Texts. New Haven: American
oriental society.
Trouche, L. (1995). E pur, si muove. Repères-IREM, 20, 16-28.
Trouche, L. (2000), La parabole du gaucher et de la casserole à bec verseur, éléments de
méthode pour une étude des processus d’apprentissage dans un environnement de
calculatrices complexes, Educational Studies in Mathematics, 41(3), 239-264,
http://www.springerlink.com/index/N1HP281710152520.pdf
Trouche, L. (2005). Des outils de calcul aux instruments du travail mathématique, conférence
à l’université d’été Le calcul sous toutes ses formes http://www3.ac-
clermont.fr/pedago/maths/pages/site_math_universite/CD-UE/Menu_pour_Internet.htm
Vergnaud, G. (1999). A quoi sert la didactique, Sciences humaines 24,
http://www.scienceshumaines.com/a-quoi-sert-la-didactique-_fr_11865.html
Zagier, D. (2005). Les aspects expérimentaux en théorie des nombres, conférence à
l’université d’été Le calcul sous toutes ses formes http://www3.ac-
clermont.fr/pedago/maths/pages/site_math_universite/CD-UE/Menu_pour_Internet.htm