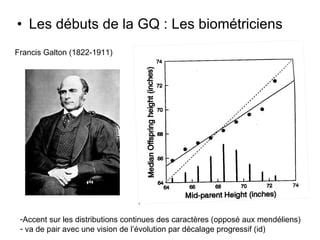
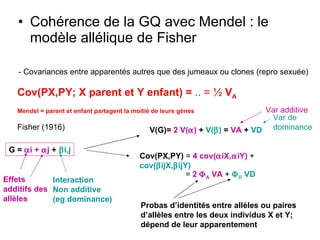
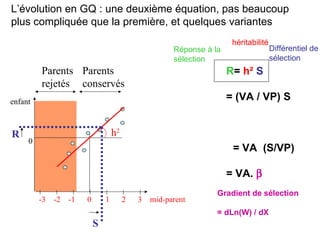
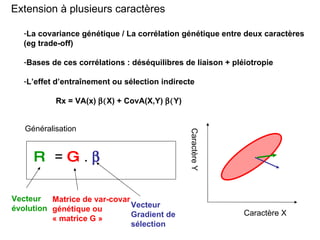
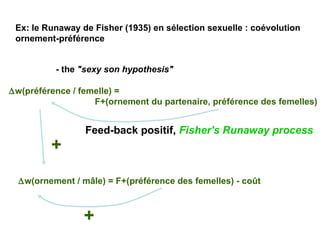
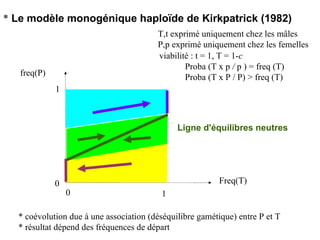
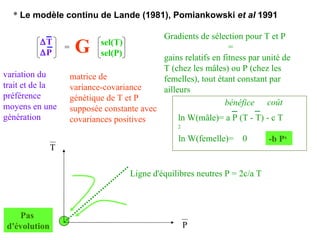
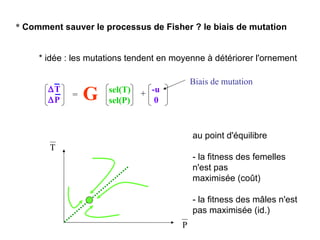
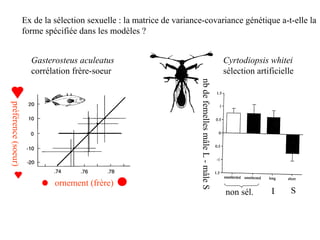
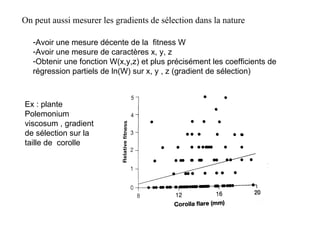
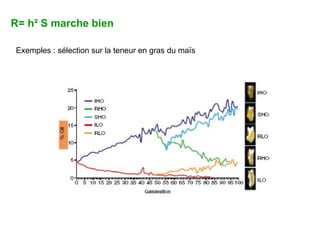
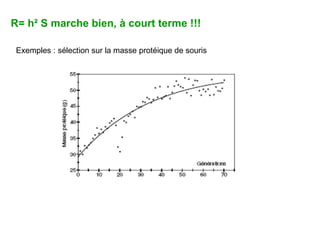
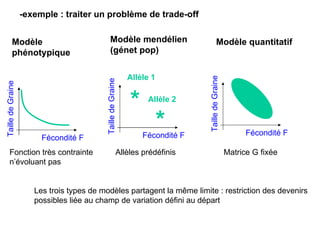
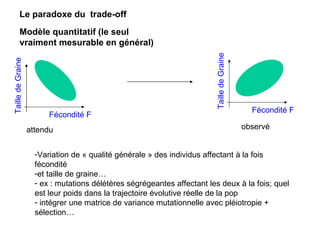
Le document présente la modélisation de l'évolution et de la génétique quantitative, en abordant trois méthodes principales : l'optimisation phénotypique, la théorie des jeux et la dynamique adaptative. Il décrit également les modèles d'hérédité, la transmission des caractères phénotypiques, et les limites de la génétique quantitative à long terme, tout en soulignant l'importance des covariances génétiques et de la mesure des variances. Enfin, il illustre ces concepts à travers des exemples, comme la sélection sexuelle et les modèles de Fisher, tout en mettant en avant les défis de la mesure en biologie évolutive.

1. Modélisation en évolution et génétique quantitative Patrice DAVID

2. Le problème : modéliser l’évolution d’un ou plusieurs caractères sous diverses conditions 3 méthodes Phénotypique Optimisation Théorie des jeux Dynamique adaptative Génétique des pops locus Modifieurs Fréquences, déséquilibres de liaison Génétique quanti Variance génétique Héritabilité Gradient de sélection

3. 3 façons de représenter la transmission des caractères Phénotypique Hérédité uniparentale clonale Génétique des pops Lois de Mendel Génétique quanti Hérédité quantitative

4. 1) La GQ comme modèle de transmission des phénotypes 2) Un exemple de modèle d’évolution formalisé en GQ 3) Le gros avantage de la GQ : le lien avec des paramètres mesurables 4) Les limites; évolution à long terme 5) Résumé PLAN

5. 1) La GQ comme modèle de transmission des phénotypes 2) Un exemple de modèle d’évolution formalisé en GQ 3) Le gros avantage de la GQ : le lien avec des paramètres mesurables 4) Les limites; évolution à long terme 5) Résumé

6. Les débuts de la GQ : Les biométriciens Francis Galton (1822-1911) Accent sur les distributions continues des caractères (opposé aux mendéliens) va de pair avec une vision de l’évolution par décalage progressif (id) portrait

7. La GQ en une équation, et en plus elle est pas compliquée P = G + E La déviation Phénotypique (1 individu par rapport à sa pop) La déviation Génotypique (1 individu par rapport à sa pop) La déviation Environnementale (1 individu par rapport à sa pop) Jusqu’ici, un exercice purement formel; ça ne sert à rien si G et E restent indéterminés V P = V G + V E (Cov(G,E)=0)

8. P = G + E Cov(PX,PY; X et Y jumeaux) = Cov(Gx+Ex,Gy+Ey) = Cov(Gx,Gy)+Cov(Gx,Ey)+Cov(Ex,Gy)+Cov(Ex,Ey) = Cov(Gx,Gy) = (sachant que Gx=Gy…) Cov(Gx,Gx) = V(Gx) = V G G est la moyenne d’un même génotype répliqué (cloné) et distribué au hasard dans les environnements Déterminer G Autre écriture de la même chose : ressemblance entre clones Généralisation = L’hérédité en GQ se représente comme une ressemblance (=covariance) entre apparentés dans une population

9. Cohérence de la GQ avec Mendel : le modèle allélique de Fisher - Covariances entre apparentés autres que des jumeaux ou clones (repro sexuée) Cov(PX,PY; X parent et Y enfant) = .. = ½ V A Mendel = parent et enfant partagent la moitié de leurs gènes Fisher (1916) G =  i +  j +   i,j V(G)= 2 V(  ) + V(  ) = VA + VD Cov(PX,PY) = 4 cov(  iX,  iY) + cov(  ijX,  ijY) = 2  A VA +  D VD Effets additifs des allèles Interaction Non additive (eg dominance) Var additive Var de dominance Probas d’identités entre allèles ou paires d’allèles entre les deux individus X et Y; dépend de leur apparentement

10. Quelques aspects du modèle de Fisher Le modèles peut intégrer autant de locus qu’on veut et rester valide, pour peu que les effets des locus s’additionnent entre eux… Une famille n’est pas un génotype : plus de la moitié de la VA ségrège à l’intérieur d’une famille de plein frères On ressemble plus à son plein-frère qu’à ses parents…

11. L’évolution en GQ : une deuxième équation, pas beaucoup plus compliquée que la première, et quelques variantes R = h² S = (VA / VP) S = VA (S/VP) = VA.  -3 -2 -1 0 1 2 3 mid-parent enfant 0 Parents rejetés Parents conservés S R Réponse à la sélection héritabilité Différentiel de sélection Gradient de sélection = dLn(W) / dX h 2

12. Extension à plusieurs caractères La covariance génétique / La corrélation génétique entre deux caractères (eg trade-off) Bases de ces corrélations : déséquilibres de liaison + pléiotropie L’effet d’entraînement ou sélection indirecte Rx = VA(x)  X) + CovA(X,Y)  Y) Généralisation R = G .  Vecteur évolution Matrice de var-covar génétique ou « matrice G » Vecteur Gradient de sélection Caractère X Caractère Y

13. 1) La GQ comme modèle de transmission des phénotypes 2) Un exemple de modèle d’évolution formalisé en GQ 3) Le gros avantage de la GQ : le lien avec des paramètres mesurables 4) Les limites; évolution à long terme 5) Résumé

14. Ex: le Runaway de Fisher (1935) en sélection sexuelle : coévolution ornement-préférence  w(préférence / femelle) = F+(ornement du partenaire, préférence des femelles) - the "sexy son hypothesis" Feed-back positif, Fisher's Runaway process  w(ornement / mâle) = F+(préférence des femelles) - coût + +

15. * Le modèle monogénique haploïde de Kirkpatrick (1982) T,t exprimé uniquement chez les mâles P,p exprimé uniquement chez les femelles viabilité : t = 1, T = 1- c Proba (T x p / p ) = freq (T) Proba (T x P / P) > freq (T) * coévolution due à une association (déséquilibre gamétique) entre P et T * résultat dépend des fréquences de départ Freq(T) freq(P) 0 1 0 1 Ligne d'équilibres neutres

16. -b P x Pas d'évolution * Le modèle continu de Lande (1981), Pomiankowski et al 1991  T  P G sel(T) sel(P) = variation du trait et de la préférence moyens en une génération matrice de variance-covariance génétique de T et P supposée constante avec covariances positives Gradients de sélection pour T et P = gains relatifs en fitness par unité de T (chez les mâles) ou P (chez les femelles), tout étant constant par ailleurs ln W(mâle)= a P (T - T) - c T 2 bénéfice coût ln W(femelle)= 0 Ligne d'équilibres neutres P = 2c/a T P T

17. -u 0 * Comment sauver le processus de Fisher ? le biais de mutation * idée : les mutations tendent en moyenne à détériorer l'ornement  T  P G sel(T) sel(P) = + Biais de mutation P T au point d'équilibre - la fitness des femelles n'est pas maximisée (coût) - la fitness des mâles n'est pas maximisée (id.)

18. 1) La GQ comme modèle de transmission des phénotypes 2) Un exemple de modèle d’évolution formalisé en GQ 3) Le gros avantage de la GQ : le lien avec des paramètres mesurables 4) Les limites; évolution à long terme 5) Résumé

19. Les variances et covariances génétiques peuvent se mesurer !!! (c’est pénible mais ça se fait) Le principe = mesurer des covariances entre individus dont les relations d’apparentement sont connues ( pédigrées in natura ) ou fabriquées (pédigrées contrôlées au labo, croisements) Méthodes statistiques basées sur les modèles aléatoires Ex familles de demi-frères : Variance inter-familles = covariance intra-famille = ¼ VA Autre façon : mesurer l’héritabilité réalisée grâce à la réponse à une sélection artificielle H² = S / R

20. Ex de la sélection sexuelle : la matrice de variance-covariance génétique a-t-elle la forme spécifiée dans les modèles ? Gasterosteus aculeatus Cyrtodiopsis whitei corrélation frère-soeur sélection artificielle ornement (frère) préférence (soeur) nb de femelles mâle L - mâle S L S non sél.

21. On peut aussi mesurer les gradients de sélection dans la nature Avoir une mesure décente de la fitness W Avoir une mesure de caractères x, y, z Obtenir une fonction W(x,y,z) et plus précisément les coefficients de régression partiels de ln(W) sur x, y , z (gradient de sélection) Ex : plante Polemonium viscosum , gradient de sélection sur la taille de corolle

22. R= h² S marche bien Exemples : sélection sur la teneur en gras du maïs

23. R= h² S marche bien, à court terme !!! Exemples : sélection sur la masse protéique de souris

24. 1) La GQ comme modèle de transmission des phénotypes 2) Un exemple de modèle d’évolution formalisé en GQ 3) Le gros avantage de la GQ : le lien avec des paramètres mesurables 4) Les limites; évolution à long terme 5) Résumé

25. -démarche typique d’un modèle de GQ 1) exprimer en termes simples les gradients de sélection 2) supposer la matrice G constante, éventuellement d’une forme contrainte 3) annuler le gradient de sélection pour trouver des équilibres s’il y en a; sinon rechercher des cycles-limites Pb : la matrice G (ou la variance génétique) n’est pas une constante fixée dans la nature Elle résulte d’un processus de mutation + sélection + recombinaison + dérive … dont le résultat dépend de l’architecture génétique du trait (nombre, position, effets des allèles)

26. -exemple d’architecture : modèle infinitésimal (Kimura, Bulmer) Une infinité de locus à effets très petits, additifs Distribution gaussienne des valeurs de G (Loi normale) VG ne diminue pas avec la sélection directionnelle -exemple d’architecture : modèle gaussien (Lande) Un nombre fini de locus, additifs; effets des allèles sur le phénotype = valeurs aléatoires gaussiennes Distribution gaussienne des valeurs de G VG dépend de la variance de mutation, de la sélection, et de la recombinaison et peut atteindre une valeur stationnaire

27. -exemple : traiter un problème de trade-off Modèle phénotypique Modèle mendélien (génet pop) Modèle quantitatif Fécondité F Taille de Graine Fonction très contrainte n’évoluant pas Fécondité F Taille de Graine * * Allèle 1 Allèle 2 Fécondité F Taille de Graine Allèles prédéfinis Matrice G fixée Les trois types de modèles partagent la même limite : restriction des devenirs possibles liée au champ de variation défini au départ

28. Le paradoxe du trade-off Modèle quantitatif (le seul vraiment mesurable en général) Fécondité F Taille de Graine Fécondité F Taille de Graine attendu observé Variation de « qualité générale » des individus affectant à la fois fécondité et taille de graine… ex : mutations délétères ségrégeantes affectant les deux à la fois; quel est leur poids dans la trajectoire évolutive réelle de la pop intégrer une matrice de variance mutationnelle avec pléiotropie + sélection…

29. 1) La GQ comme modèle de transmission des phénotypes 2) Un exemple de modèle d’évolution formalisé en GQ 3) Le gros avantage de la GQ : le lien avec des paramètres mesurables 4) Les limites; évolution à long terme 5) Résumé

30. La GQ c’est Assez facile mais il faut aimer les variances et les covariances Un mode de représentation des l’hérédité adapté aux caractères continus à déterminisme multilocus plus ou moins « boîte noire » dans des espèces sexuées Avantageux pour pouvoir comparer les modèles avec de vraies mesures : il est possible (mais coûteux en temps et en énergie) de mesurer des variances génétiques en labo et dans la nature, et l’évolution de traits / la sélection sur des traits… mais essayez donc de mesurer des fréquences d’allèles modifieurs… Limité par des hypothèses passe-partout (constance de la variance génétique fixée de l’extérieur) qui sont super pratiques pour les calculs mais insatisfaisantes (c’est un peu vrai de tous les modèles d’évolution) L’évolution de la matrice G peut être considérée comme un problème ouvert en biologie de l’évolution

31. 3 façons de mater la matrice G dans un modèle A l’anglaise A l’américaine A la bourrin -on suppose G constante, d’un trait de plume, et on y croit (méthode culottée mais élégante et facile, produit des formules compactes et simples) -on bricole un modèle multilocus (eg infinitésimal, gaussien) et on se lance dans les calculs (méthode compliquée, mais on obtient des formules qui épatent la galerie avec plein de  et de  ) -on simule un million d’allèles et de locus avec des simuls individu-centrées (bourrin et efficace, la grosse Bertha, on n’a pas besoin d’avoir sucé les maths au biberon, mais attention à ne pas s’égarer dans la jungle des paramètres)