Télécharger pour lire hors ligne
Téléchargé parIES Reyes Católicos EPV
"Les triangles"
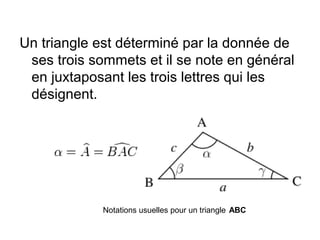
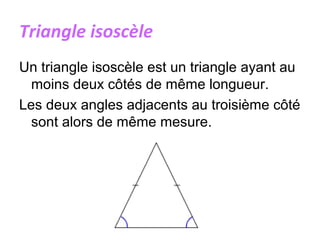
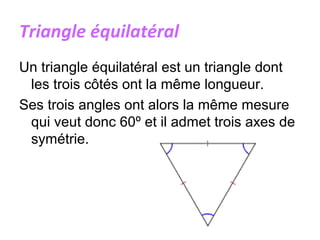
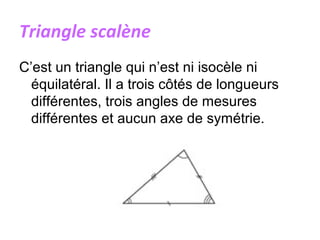
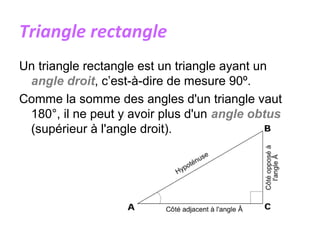
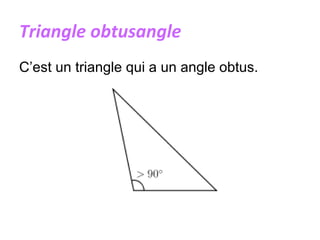
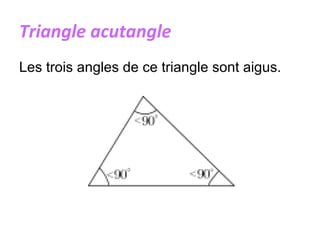
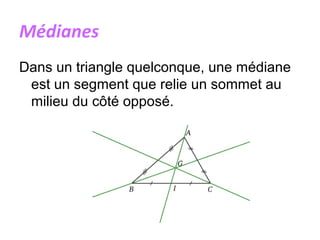
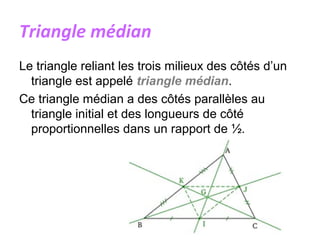
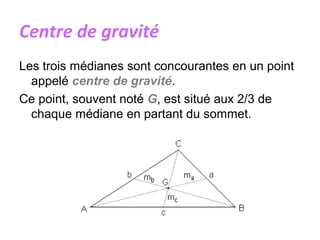
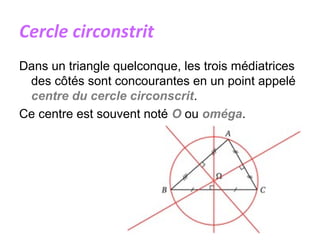
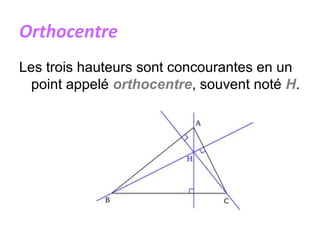
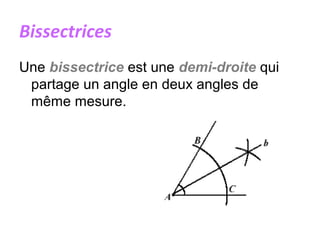
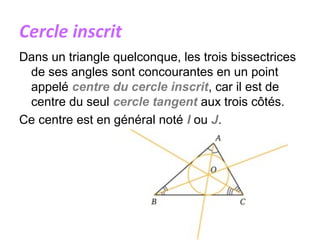
Un triangle est une figure plane délimitée par trois côtés et trois sommets. Il peut être classé en plusieurs types, tels que isocèle, équilatéral, scalène, rectangle, obtusangle et acutangle, en fonction des longueurs de ses côtés et de la mesure de ses angles. Des constructions géométriques associées, telles que les médianes, les hauteurs et les bissectrices, ainsi que les concepts de centre de gravité, d'orthocentre et de cercle inscrit, sont également discutés.
Contenu connexe
"Les triangles"
- 1.
- 2. Définition Un triangle esune figure plane, formée par trois points appelés sommets; par les trois segments qui les relient, appelés côtés, délimitant un domaine du plan appelé intérieur. Le triangle est aussi le polygone le plus simple qui délimite une portion du plan.
- 3. Un triangle estdéterminé par la donnée de ses trois sommets et il se note en général en juxtaposant les trois lettres qui les désignent. Notations usuelles pour un triangle ABC
- 4.
- 5. Triangle isoscèle Un triangleisoscèle est un triangle ayant au moins deux côtés de même longueur. Les deux angles adjacents au troisième côté sont alors de même mesure.
- 6. Triangle équilatéral Un triangleéquilatéral est un triangle dont les trois côtés ont la même longueur. Ses trois angles ont alors la même mesure qui veut donc 60º et il admet trois axes de symétrie.
- 7. Triangle scalène C’est untriangle qui n’est ni isocèle ni équilatéral. Il a trois côtés de longueurs différentes, trois angles de mesures différentes et aucun axe de symétrie.
- 8. Triangle rectangle Un trianglerectangle est un triangle ayant un angle droit, c’est-à-dire de mesure 90º. Comme la somme des angles d'un triangle vaut 180°, il ne peut y avoir plus d'un angle obtus (supérieur à l'angle droit).
- 9. Triangle obtusangle C’est untriangle qui a un angle obtus.
- 10. Triangle acutangle Les troisangles de ce triangle sont aigus.
- 11.
- 12. Médianes Dans un trianglequelconque, une médiane est un segment que relie un sommet au milieu du côté opposé.
- 13. Triangle médian Le trianglereliant les trois milieux des côtés d’un triangle est appelé triangle médian. Ce triangle médian a des côtés parallèles au triangle initial et des longueurs de côté proportionnelles dans un rapport de ½.
- 14. Centre de gravité Lestrois médianes sont concourantes en un point appelé centre de gravité. Ce point, souvent noté G, est situé aux 2/3 de chaque médiane en partant du sommet.
- 15. Cercle circonstrit Dans untriangle quelconque, les trois médiatrices des côtés sont concourantes en un point appelé centre du cercle circonscrit. Ce centre est souvent noté O ou oméga.
- 16. Hauteurs Si les troissommets sont distincs, une hauteur est une droite passant par un sommet et perpendiculaire au côté opposé.
- 17. Orthocentre Les trois hauteurssont concourantes en un point appelé orthocentre, souvent noté H.
- 18. Bissectrices Une bissectrice estune demi-droite qui partage un angle en deux angles de même mesure.
- 19. Cercle inscrit Dans untriangle quelconque, les trois bissectrices de ses angles sont concourantes en un point appelé centre du cercle inscrit, car il est de centre du seul cercle tangent aux trois côtés. Ce centre est en général noté I ou J.