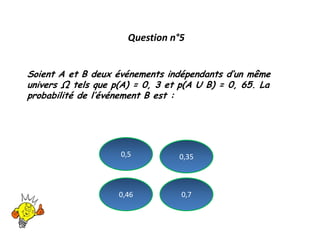
Le document présente un questionnaire à choix multiples comportant huit questions sur différentes notions de probabilités et de mathématiques. Les questions incluent des scénarios tels que le tir à la cible, la durée de fonctionnement d'un moteur, et des problèmes liés aux lancers de dés. Chaque question nécessite l'application de concepts mathématiques pour calculer des probabilités ou démontrer des propriétés.