Le document présente un projet d'analyse numérique réalisé à l'École Nationale d'Ingénieurs de Tunis, portant sur des méthodes de décomposition simple en 1D, notamment les méthodes de différences finies pour résoudre des équations aux dérivées ordinaires. Il traite des conditions aux limites de Dirichlet et Neumann, de la méthode de Schwarz alternée et parallèle, ainsi que de l'optimisation de la solution à l'aide de MATLAB. Le projet souligne l'importance des conditions aux limites et présente des résultats d'erreurs et d'ordres de convergence.

1. Université Tunis El Manar
Ecole Nationale d’ingénieurs de Tunis
Département de Génie Civil
Projet d’Analyse Numérique
Méthode de décomposition simple en 1D par
recouvrement
Réalisé par
Yassine Elaroui
Bilel Gabsi
Encadré par
Monsieur Rjaibi Badereddine
Année Universitaire : 2018-2019
1

2. Remerciements
On tient à remercier Monsieur Badereddine Rjaibi pour
les efforts fournis dans la réussite de ce projet. Nous avons
grandement apprécié votre soutien, votre implication et votre
expérience tout au long de cette période.
On désire aussi remercier les professeurs de l’École Nationale
d’Ingénieurs de Tunis, qui nous ont fourni les outils nécessaires
à la réalisation du projet.
2

3. Table des matières
1 Introduction Et Généralités 7
2 Méthodes de différences finies 9
2.1 Conditions aux limites de Dirichlet . . . . . . . . . 9
2.1.1 Algorithme numérique . . . . . . . . . . . . 9
2.1.2 Programmation sur Matlab . . . . . . . . . 10
2.2 Conditions aux limites de Neumann . . . . . . . . 14
2.2.1 Algorithme numérique . . . . . . . . . . . . 14
2.2.2 Programmation sur Matlab . . . . . . . . . 14
2.2.3 Coclusion . . . . . . . . . . . . . . . . . . 16
3 Méthode de Schwarz alternée 17
3.1 Introduction . . . . . . . . . . . . . . . . . . . . . 17
3.2 Programmation sur Matlab . . . . . . . . . . . . . 18
3.2.1 Code script . . . . . . . . . . . . . . . . . . 18
3.2.2 Erreur . . . . . . . . . . . . . . . . . . . . 18
3.3 Optimisation . . . . . . . . . . . . . . . . . . . . . 18
4 Méthode de Schwarz parallèle 22
4.1 Programmation sur Matlab . . . . . . . . . . . . . 22
4.1.1 Code script . . . . . . . . . . . . . . . . . . 22
4.1.2 Erreur . . . . . . . . . . . . . . . . . . . . 23
3

4. 5 Conclusion 25
4

5. Table des figures
2.1 Script de la solution approchée U . . . . . . . . . . 11
2.2 Courbe représentative de la solution exacte et de la
solution approchée . . . . . . . . . . . . . . . . . . 11
2.3 Erreur E pour f(x0) = 0 , f(xN ) = sin(3) et N = 10 12
2.4 Erreur E pour f(x0) = 0 , f(xN ) = sin(3) et N = 16 12
2.5 Erreur E pour f(x0) = 1 , f(xN ) = 3 et N = 10 . 12
2.6 Code script de l’ordre de convergence en imposant
les conditions de Dirichlet . . . . . . . . . . . . . . 13
2.7 Ordre de convergence (Log(E) en fonction de Log(h)) 13
2.8 Ordre de convergence pour les conditions de Dirichlet 14
2.9 Script de la solution approchée U par les conditions
de Neumann . . . . . . . . . . . . . . . . . . . . . 15
2.10 Erreur pour un nombre de points d’interpolations
N = 5 . . . . . . . . . . . . . . . . . . . . . . . . 15
2.11 Erreur pour un nombre de points d’interpolations
N = 10 . . . . . . . . . . . . . . . . . . . . . . . . 16
2.12 Code script de l’ordre de convergence en imposant
les conditions de Neumann . . . . . . . . . . . . . 16
2.13 Ordre de convergence pour les conditions de Neumann 16
3.1 Représentation graphique du domaine Ω . . . . . . 17
3.2 Représentation graphique de la méthode de Schwarz
alternée . . . . . . . . . . . . . . . . . . . . . . . 19
5

6. 3.3 Algorithme et représentation de l’erreur de la mé-
thode de Schwarz . . . . . . . . . . . . . . . . . . 20
3.4 Algorithme optimisé de l’erreur de la méthode de
Schwarz . . . . . . . . . . . . . . . . . . . . . . . 21
3.5 Erreur sur ]0,Xm1[ (à gauche) sur ]Xm,1[ (à droite) 21
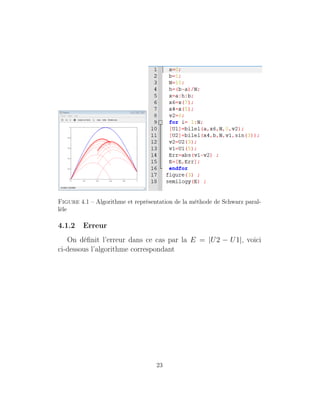
4.1 Algorithme et représentation de la méthode de Schwarz
parallèle . . . . . . . . . . . . . . . . . . . . . . . 23
4.2 Algorithme et représentation de l’erreur de la mé-
thode de Schwarz parallèle . . . . . . . . . . . . . 24
6

7. Chapitre 1
Introduction Et Généralités
Au 19ème siècle, les physiciens Claude Navier et George Stokes
ont étudier les comportements très variés et complexes d’un fluide
en écoulement. Pendant longtemps ces équations n’ont pas pu être
analysé qu’à partir d’approximations, car dans la plupart des cas
ces équations ne possèdent pas de solutions analytiques.
Ces astreintes nous ont menées a recourir aux algorithmes de
simulation numérique tel que la méthode de différences finies
qui nous permet de discrétiser le domaine de calcul afin d’obtenir
une solution a ces équations.
Dans notre cas on se projette sur l’étude de l’ équation aux
dérivés ordinaires (1.1) tout en connaissant le résultat antérieu-
rement.
−f (x) + f(x) = 10sin(3x) ∀x ∈]0, 1[ (1.1)
La solution exacte de (1.1) est



fexacte(x) = fhomogene(x) + fparticuliere(x)
fhomogene(x) = c1 exp x + c2 exp −x
fparticuliere(x) = c3sin(3x)
Pour pouvoir déterminer la solution exacte de (1.1) il faudra
7

8. imposer des conditions aux limites, on introduit dans ce contexte :
les conditions aux limites de dirichlet



−f (x) + f(x) = 10sin(3x) ∀x ∈]0, 1[
f(0) = 0
f(1) = sin(3)
les conditions aux limites de Neumann



−f (x) + f(x) = 10sin(3x) ∀x ∈]0, 1[
f (0) = 3
f (1) = 3cos(3)
D’où un calcul analytique donne
fexacte(x) = sin(3x) (1.2)
Enfin dans le but d’approcher (1.2) on a employer deux méthodes :
Méthode de Schwarz parallèle
Méthode de Schwarz alternée
Dans la continuité du travail réalisé, on s’est penché sur l’opti-
misation de la solution obtenu, c’est là qu’on réalise l’importance
des conditions aux limites choisi.
C’est le temps d’exécution sous machine qui tranchera entre le
choix des C.L de Dirichlet ou celle de Neumann.
Pour se faire on a utilisé sous Matlab la fonction Polyfit afin
de déterminer l’ordre de convergence puisqu’on sait que l’erreur E
vérifie l’inégalité (1.3)
E < c × hp
(1.3)
log E = log c + p × log h (1.4)
Avec p l’ordre de convergence de la méthode.
8

9. Chapitre 2
Méthodes de différences finies
2.1 Conditions aux limites de Dirichlet
2.1.1 Algorithme numérique
On suppose que le domaine d’étude Ω =]0, 1[ et le pas h = 1
N+1
avec N ∈ N∗



−f (x) + f(x) = 10sin(3x) ∀x ∈]0, 1[
f(0) = 0
f(1) = sin(3)
En appliquant la formule de Taylor au 2éme ordre
f(xi + h) = f(xi) + h × f (xi) +
h2
2
× f (xi) + o(h2
) (2.1)
f(xi − h) = f(xi) − h × f (xi) +
h2
2
× f (xi) + o(h2
) (2.2)
D’où on obtient la solution du système précédant
f (xi) =
−2f(xi) + f(xi + h) + f(xi − h)
h2
9

10. Pour i = 1
g(x1) +
f(x0)
h2
=
(−2 + h2
)f(x1) − f(x2)
h2
Pour i = N
g(xN ) +
f(xN−1)
h2
=
(−2 + h2
)f(xN ) − f(xN+1)
h2
Avec
g(xi) =
(−2 + h2
)f(xi) − f(xi+1) − f(xi−1)
h2
∀i ∈ N∗
Donc finalement on aura le système matriciel
AU =B
1
h2











2 + h2
−1 0 . . . . . . 0
−1 2 + h2
−1 . . . . . . 0
0 −1 ... ... . . . 0
... ... ... ... ...
... ... ... ... ...
2 + h2
−1
0 . . . . . . 0 −1 2 + h2






















f(x1)
f(x2)
...
...
f(xN−2)
f(xN−1)
f(xN )











=












g(x1) + f(x0)
h2
g(x2)
...
...
g(xN−2)
g(xN−1)
g(xN ) + f(xN−1)
h2












2.1.2 Programmation sur Matlab
Code script
L’algorithme suivant nous permet d’obtenir la solution appro-
chée et d’évaluer l’erreur de la simulation numérique.
10

11. Figure 2.1 – Script de la solution approchée U
Figure 2.2 – Courbe représentative de la solution exacte et de la solution
approchée
Erreur
Afin d’optimiser la solution approchée et s’assurer qu’elle tend
vers la solution exacte il faut que l’erreur E → 0.
11

12. Or, On a remarqué que l’erreur dépend de deux facteurs : les
nombres de points d’interpolation et les conditions aux limites
fixées.
Nombres de points d’interpolation
Pour f(x0) = 0 et f(xN ) = sin(3) pour N = 10, on obtient
une erreur E=
Figure 2.3 – Erreur E pour f(x0) = 0 , f(xN ) = sin(3) et N = 10
Pour N = 16 on obtient une erreur E=
Figure 2.4 – Erreur E pour f(x0) = 0 , f(xN ) = sin(3) et N = 16
Conditions aux limites
Pour un nombre de points d’interpolation fixé N = 10 et en chan-
geant les conditions aux limites.
Figure 2.5 – Erreur E pour f(x0) = 1 , f(xN ) = 3 et N = 10
D’où on conclut que l’erreur est assez bien dépendante de les
conditions aux limites que par le nombre de points d’interpolation
N.
12

13. Ordre de convergence
En utilisant l’algorithme suivant
Figure 2.6 – Code script de l’ordre de convergence en imposant les condi-
tions de Dirichlet
On obtient comme résultat
Figure 2.7 – Ordre de convergence (Log(E) en fonction de Log(h))
13

14. Figure 2.8 – Ordre de convergence pour les conditions de Dirichlet
2.2 Conditions aux limites de Neumann
2.2.1 Algorithme numérique
Soit le système suivant



−f (x) + f(x) = 10sin(3x) ∀x ∈]0, 1[
f (0) = 3
f (1) = 3cos(3)
Afin de résoudre E.D.O Neumann propose la méthode dans lequel
on impose aux extrémités des valeurs de dérivé bien décrite au
dessus.
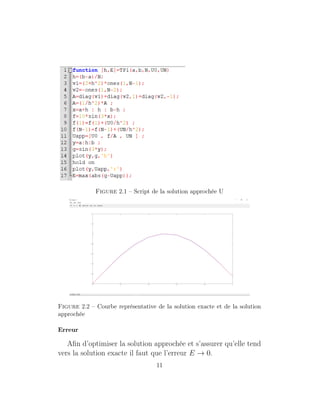
2.2.2 Programmation sur Matlab
Code script
L’algorithme suivant nous permet d’obtenir la solution appro-
chée et d’évaluer l’erreur de la simulation numérique.
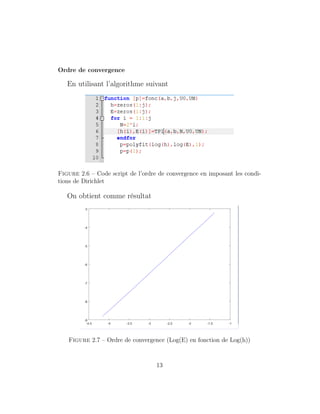
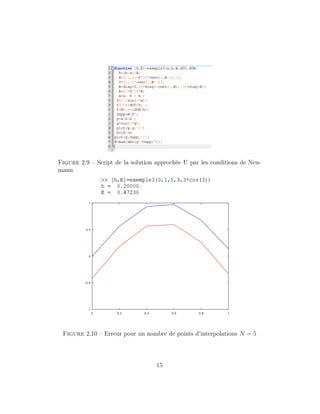
Erreur
Nombres de points d’interpolation
Pour N = 5 on obtient l’erreur suivante
Or si on augmente le nombre de points d’interpolations N la
valeur de l’erreur tend à diminuer.
14

15. Figure 2.9 – Script de la solution approchée U par les conditions de Neu-
mann
Figure 2.10 – Erreur pour un nombre de points d’interpolations N = 5
15

16. Figure 2.11 – Erreur pour un nombre de points d’interpolations N = 10
Ordre de convergence
Afin de déterminer l’ordre de convergence, on propose la mé-
thode décrite ci dessous
Figure 2.12 – Code script de l’ordre de convergence en imposant les condi-
tions de Neumann
Figure 2.13 – Ordre de convergence pour les conditions de Neumann
2.2.3 Coclusion
Comme conclusion on peut juger que la méthode est plus per-
formante dans notre cas puisqu’elle admet un ordre de convergence
supérieur.
16

17. Chapitre 3
Méthode de Schwarz alternée
3.1 Introduction
La méthode de schwarz est une technique classique de décom-
position de domaines afin de résoudre les équations aisément.
Dans notre cas notre domaine est Ω =]0, 1[ soit la représenta-
tion suivante : Comme on l’a indiquer auparavant en utilisera les
Figure 3.1 – Représentation graphique du domaine Ω
conditions de Dirichlet pour la résolution de l’E.D.O (1.1) dans
tout ce qui suit.
On introduit dans un premier les deux systèmes décrivant la dé-
composition de Ω avec U1 la solution correspondante à l’intervalle
]0,Xm1[ et U2 la solution correspondante à l’intervalle ]Xm2,1[.
17

18. 


−U1 (x) + U1(x) = 10sin(3x) ∀x ∈]0, 1[
U1(0) = 0
U1(Xm1) = U2(Xm2)



−U2 (x) + U2(x) = 10sin(3x) ∀x ∈]0, 1[
U2(1)) = sin(3)
U2(Xm1) = U2(Xm2)
3.2 Programmation sur Matlab
3.2.1 Code script
Dans un premier temps on introduit l’algorithme de la méthode
de Schwarz alternée figure 3.2
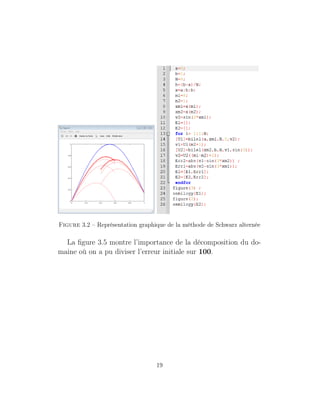
Par ailleurs cette algorithme nous a permis d’obtenir la figure
3.2 on remarque aussi d’après 3.2 la dépendance de chaque courbe
par rapport à l’autre.
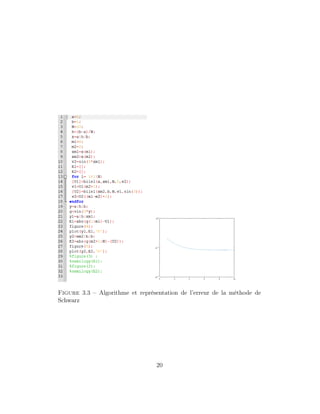
3.2.2 Erreur
Afin d’estimer l’erreur on a eut recours à l’algorithme 3.3, on re-
marque une erreur d’interpolation flagrante E=0.1, on doit donc
penser a optimiser notre algorithme afin de garantir de meilleur
résultat.
3.3 Optimisation
Dans cette partie, on propose l’étude de l’erreur sur chacun des
intervalles, tout en étudiant l’effet de la variation des intervalles
sur l’erreur, c’est-à-dire en changeant les valeurs de Xm1 et Xm2.
18

19. Figure 3.2 – Représentation graphique de la méthode de Schwarz alternée
La figure 3.5 montre l’importance de la décomposition du do-
maine où on a pu diviser l’erreur initiale sur 100.
19

20. Figure 3.3 – Algorithme et représentation de l’erreur de la méthode de
Schwarz
20

21. Figure 3.4 – Algorithme optimisé de l’erreur de la méthode de Schwarz
Figure 3.5 – Erreur sur ]0,Xm1[ (à gauche) sur ]Xm,1[ (à droite)
21

22. Chapitre 4
Méthode de Schwarz parallèle
Ce qui différencie la méthode de Schwarz parallèle à la
méthode de Schwarz alternée est la dépendance de la solution
U1 a n+1 de la solution U2 a l’itération n ce qui nous donne les
systèmes suivants :



−U1 (x) + U1(x) = 10sin(3x) ∀x ∈]0, Xm1[
Un+1
1 (0) = 0
Un+1
1 (Xm1) = Un
2 (Xm1)



−U2 (x) + U2(x) = 10sin(3x) ∀x ∈]Xm2, 1[
Un+1
2 (1)) = sin(3)
Un+1
2 (Xm1) = Un
1 (Xm2)
4.1 Programmation sur Matlab
4.1.1 Code script
On introduit l’algorithme correspondant à la méthode de Schwarz
parallèle
22

23. Figure 4.1 – Algorithme et représentation de la méthode de Schwarz paral-
lèle
4.1.2 Erreur
On définit l’erreur dans ce cas par la E = |U2 − U1|, voici
ci-dessous l’algorithme correspondant
23

24. Figure 4.2 – Algorithme et représentation de l’erreur de la méthode de
Schwarz parallèle
24

25. Chapitre 5
Conclusion
Ce projet nous avons pu estimer l’importance des méthodes
numériques dans la résolution des problèmes mathématiques à
travers leurs complexités de résolution, l’erreur d’interpolation et
enfin l’optimisation de ces algorithmes
25