Le projet porte sur la manipulation de nuages de points lidar, visant à intégrer diverses capacités de traitement, telles que l'agrégation, la déformation rigide et non rigide, et la détection d'irrégularités. L'opération d'agrégation s'appuie sur l'algorithme ICP (Iterative Closest Point) et ses variantes, en mettant l'accent sur les déformations non rigides adaptées aux mesures. Ce travail est réalisé dans le cadre d'un projet de fin d'études à l'École Nationale d'Ingénieurs de Tunis, en collaboration avec l'Université de Perpignan Via Domitia.

1. Université de Perpignan Via Domitia
Calcul Haute Performance, Simulation
École Nationale d’Ingénieurs de Tunis
Département Technologies de l’Information et de la Communication
Projet Fin d’Etudes
Agrégation, Déformation et irrégularités
Manipulation de nuages de points LIDAR
Réalisé par :
SMIDA Mahdi
Encadré par :
M. BARIOU Marcel
Classe : M2 CHiPS | 3 A informatique
Entreprise d’accueil :
Année universitaire : 2017/2018

2. Signatures
Responsable UPVD
M.BARBOTEU Michaël
Encadrant Entreprise
M.BARIOU Marcel

3. Résumé
Le présent projet [1], lié à la manipulation de nuages de points LIDAR, a pour objectif
d’aboutir à l’intégration de plusieurs capacités de traitement soit sous forme d’une amélio-
ration éventuelle de l’existant, soit par la réalisation de nouveaux greffons (plug-in) de trai-
tement, destinés, a priori, à être intégrés dans l’outil CloudCompare [4] ou déposés sur des
serveurs comme service en ligne :
• agrégation de nuage de points dénommé par l’anglicisme «registration»,
• déformation de nuage de points de manière rigide ou non rigide,
• irrégularités, détection d’anomalie dans des structures régulières.
L’opération d’agrégation ou de recalage de nuages de points, s’appuie communément sur l’al-
gorithme de recalage des nuages de point ICP(Iterative Closest Point) et ses variantes que nous
allons particulièrement étudier. La déformation rigide, assez simple à mettre en oeuvre n’est
pas nécessairement adaptée à notre problématique, nous nous intéresserons davantage à des
déformations non rigides qui sont des transformations non linéaires entre points de référence
(amer) parfaitement identifiés sur le parcours de mesures.
Mots-clés : Iterative Closet Point, SVD, Transformation, Recalage 3D, Alignement, LI-
DAR, Nuage de points.
i

4. Abstract
The present project [1], about LIDAR point cloud manipulation, aims to achieve the inte-
gration of several processing capacities either in the form of an improvement of the existing
one, either by making new plugins, to be integrated into CloudCompare or to set up on online
services[4] :
• 3D Pointcloud registration,
• Rigid and non-rigid 3D Pointcloud deformation,
• irregularities, anomaly detection in regular structures.
The operation of aggregation or registration of point clouds is commonly based on the Itera-
tive Closest Point and its variants, which we will study in particular. The rigid deformation,
quite simple to implement is not necessarly adapted to our problematic, we will be interes-
ted more in non-rigid deformations which are nonlinear transformations between reference
points perfectly identified on the course of measurements.
Keywords : Iterative Closest Point, SVD, Transformation, 3D Registration, Alignment;
LIDAR, Point Cloud.
ii

5. Table des matières
INTRODUCTION GÉNÉRALE 1
I INTRODUCTION GÉNÉRALE 1
II Contexte de travail 4
II.1 Présentation de l’entreprise EXAMETRICS . . . . . . . . . . . . . . . . . . . . 4
II.1.1 EXAMETRICS . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4
II.1.2 Domaine d’expertise de l’entreprise . . . . . . . . . . . . . . . . . . . 4
II.1.3 Exemple de Produit photogrammétrique EXAMETRICS . . . . . . . . 6
II.1.4 Les solutions EXAMETRICS et leurs marchés . . . . . . . . . . . . . . 6
II.1.5 La R&D chez EXAMETRICS, stratégie de développement . . . . . . . . 9
II.1.6 Compétences et ressources humaines . . . . . . . . . . . . . . . . . . . 9
II.1.7 Ré-orientation de compétences . . . . . . . . . . . . . . . . . . . . . . 10
II.2 La conduite du projet d’agrégation de nuage de points . . . . . . . . . . . . . . 11
II.2.1 La première partie . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11
II.2.2 La deuxième partie . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12
II.2.3 La troisième partie . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12
II.3 Technologies impliquées . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13
II.3.1 Matériel . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13
II.3.2 Logiciels et librairies utilisés . . . . . . . . . . . . . . . . . . . . . . . . 14
III Greffon (Plugin) CloudCompare 16
III.1 Mise en place des prérequis . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 16
III.2 Développement du greffon CloudCompare . . . . . . . . . . . . . . . . . . . . 18
III.2.1 Problématique posée . . . . . . . . . . . . . . . . . . . . . . . . . . . . 18
III.2.2 Présentation de l’IHM . . . . . . . . . . . . . . . . . . . . . . . . . . . 19
III.2.3 Notions géométriques liées à l’affichage . . . . . . . . . . . . . . . . . 20
III.3 Optimisation du traitement . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 21
III.4 Conclusions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 25
IV Etudes bibliographiques sur le recalage I.C.P. 27
IV.1 Problème de recalage . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 28
IV.1.1 Les outils mathématiques nécessaires . . . . . . . . . . . . . . . . . . . 29
iii

6. TABLE DES MATIÈRES
IV.1.2 Mesures de distance Euclidiennes . . . . . . . . . . . . . . . . . . . . . 30
IV.1.3 Estimation de la transformation . . . . . . . . . . . . . . . . . . . . . . 30
IV.2 L’algorithme ICP et ses variantes . . . . . . . . . . . . . . . . . . . . . . . . . . 32
V Réalisation et test 37
V.1 L’algorithme ICP dans la librairie Open3D . . . . . . . . . . . . . . . . . . . . 37
V.1.1 Open3d : Point-to-point ICP . . . . . . . . . . . . . . . . . . . . . . . . 37
V.1.2 Open3d : Point-to-plane ICP . . . . . . . . . . . . . . . . . . . . . . . . 39
V.2 L’algorithme ICP dans la librairie VTK . . . . . . . . . . . . . . . . . . . . . . 41
V.2.1 Adaptation de l’outil à l’algorithme ICP de VTK . . . . . . . . . . . . . 41
V.2.2 ICP VTK test de performance et de convergence . . . . . . . . . . . . . 43
V.3 Maquettes ICP Basique et ICP parallèle . . . . . . . . . . . . . . . . . . . . . . 45
V.3.1 ICP : Implémentation séquentielle . . . . . . . . . . . . . . . . . . . . 45
V.3.2 ICP : Implémentation paralléle . . . . . . . . . . . . . . . . . . . . . . 46
VI Le recalage par caractéristiques étendues 47
VI.1 Parcours bibliographique sommaire . . . . . . . . . . . . . . . . . . . . . . . . 49
VI.1.1 Notes de lecture : EFFICIENT VARIANT OF ICP . . . . . . . . . . . . . 49
VI.1.2 Notes de lecture : A ROBUST LINEAR FEATURES-BASED REGISTRA-
TION . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 50
VI.1.3 Notes de lecture : FEATURE-BASED REGISTRATION . . . . . . . . . 51
VI.1.4 Note lecture : ALTERNATIVE METHODOLOGIES FOR LIDAR CALI-
BRATION . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 52
VI.1.5 Fiche lecture de : MULTI-FEARURED REGISTRATION . . . . . . . . . 53
VI.1.6 lecture de : Georeferenced Point Clouds : A Survey of Features and
Point Cloud Management . . . . . . . . . . . . . . . . . . . . . . . . . 55
VI.1.7 Note de lecture : STRIP ADJUSTMENT USING CONJUGATE PLANAR
AND LINEAR FEATURES . . . . . . . . . . . . . . . . . . . . . . . . . 55
VI.1.8 Extensions et travaux à venir . . . . . . . . . . . . . . . . . . . . . . . 57
VIIConclusions 59
Bibliographie 62
iv

7. Table des figures
II.1 Reconstruction photogrammétrique par Exametrics . . . . . . . . . . . . . . . 6
II.2 Principe de l’écholocation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 14
III.1 Lidar employé . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 17
III.2 IHM plugin CloudCompare . . . . . . . . . . . . . . . . . . . . . . . . . . . . 20
III.3 Méthode 1 : état initial . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 21
III.4 Méthode 1 : état intermédiaire . . . . . . . . . . . . . . . . . . . . . . . . . . . 22
III.5 Méthode 1 : Résultat de l’intersection . . . . . . . . . . . . . . . . . . . . . . . 23
III.6 Méthode 2 : État initial . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 24
III.7 Méthode 2 : Enregistrement du fichier LAS . . . . . . . . . . . . . . . . . . . . 25
IV.1 Exemple simplifié SVD . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 31
IV.2 (a) Le point le plus proche - (b) Tir normal . . . . . . . . . . . . . . . . . . . . 35
IV.3 Paires sur les limites du nuage . . . . . . . . . . . . . . . . . . . . . . . . . . . 36
V.1 État initial avant le recalage Point-to-point ICP . . . . . . . . . . . . . . . . . . 38
V.2 Résultat du recalage Point-to-point ICP . . . . . . . . . . . . . . . . . . . . . . 39
V.3 État initial avant le recalage Point-to-plane ICP . . . . . . . . . . . . . . . . . 40
V.4 Résultat du recalage Point-to-plane ICP . . . . . . . . . . . . . . . . . . . . . . 41
V.5 Etat intial d’utilitaire ICP basé sur VTK . . . . . . . . . . . . . . . . . . . . . . 42
V.6 Résultat de l’utilitaire ICP basé sur VTK . . . . . . . . . . . . . . . . . . . . . . 43
V.7 Courbe des temps d’exécutions en fonction du nombre d’itérations . . . . . . 44
V.8 Courbe de convergence . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 44
V.9 Appariement après 50 itérations . . . . . . . . . . . . . . . . . . . . . . . . . . 45
v

8. Glossaire
BIM Building information modeling. 2
ICL Iterative Closest Line. 50
ICP Iterative Closest Point. i, 27
IMU Inertial module unit Centrale inertielle. 5, 17
LIDAR light detection and ranging. i, ii, 16
NDVI normalized difference vegetation index. 6
SVD Singular value decomposition. 29, 31
VTK The Visualization Toolkit. 41
vi

9. Chapitre I
INTRODUCTION GÉNÉRALE
A
u cours de ces dernières années, l’évolution technique de scan 3-D et d’arpen-
tage et de topographie est devenu de plus en plus remarquable et accessible
par l’apport de la mesure par LIDAR. Les premiers pas ont été effectués par les
LIDARs satellitaires, aéroportés, les LIDARs fixes au sols et enfin les LIDARs
mobiles terrestres. Ces déclinaisons sont également associées à un accroissement considérable
de la résolution comme de la cadence d’acquisition des points. Derrière cette importante évo-
lution,vient le besoin d’avoir une vision par ordinateur des données tridimensionnelles de
qualité et proche de la réalité en terme de mesures et de précision. Aussi, si l’acquisition a
fait de grands progrès, le traitement du nuage de points connaît une grande effervescence au
niveau mondial
Les applications de la télédétection par laser sont très nombreuses et offrent des avantages
incontestables. Il suffit d’un seul balayage d’une durée de quelques minutes pour produire
une représentation de l’objet ou de la zone analysée dans un référentiel 3D, sous la forme
d’un nuage de points. Les cadences d’acquisitions atteignent plusieurs millions de points par
seconde sur les LIDARs professionnels haut de gamme. Mais on peut aussi se satisfaire de
quelques milliers de points par seconde comme c’est le cas sur les LIDARs mobile terrestres
d’entrée de gamme. L’exploitation de ce nuage peut cibler plusieurs applications :
1. restitution volumique avec drapage dans une image, de la zone ou de l’objet analysés, afin
d’obtenir de meilleures performances de restitution 3D que la stricte photogrammétrie,
2. identification d’objet ou d’obstacle avec une connaissance dimensionnelle précise dans
un référentiel 3D,
3. réingénierie dimensionnelle sur des objets ou des constructions c’est à dire mesures au
sens strict,
4. aide à la navigation autonome pour véhicules terrestres, tels que la voiture.
1

10. CHAPITRE I. INTRODUCTION GÉNÉRALE
Cependant, l’approche quantitative, en terme de mesures précises, n’est pas assez présente
dans le traitement des données issues d’un LIDAR. Dans ce contexte, la précision de mesure
représente un enjeu scientifique et économique majeur du fait de la sensibilité des ces données
et de leurs applications. Les villes intelligentes ou les Smart Cities représentent l’un de ces
domaines d’applications à travers le BIM, ainsi que la foresterie.
Les travaux de la présente étude s’attachent à explorer les processus de calage de nuages dis-
tincts de points, "REGISTRATION", ayant une zone commune (chevauchement géométrique).
Ce processus est couramment sollicité dans la phase d’agrégation de nuages distincts :
1. lors de relevé de données LIDAR sur un grand ensemble géographique, il est procédé à
des séquences de relevés indépendants sur des zones connexes en s’assurant qu’il y ait
des chevauchements géographiques entre ces deux zones connexes, lors de l’acquisition
des données. C’est cette communalité de points qui permettra d’agréger les deux zones
pour en faire une seule, sous forme d’un nuage, de points, unique.
2. en d’autres circonstances on cherche à accroître la densité de points sur une zone afin
d’améliorer la facilité de traitement, ceci nous conduit également à agréger deux nuages
distincts en ayant le meilleur calage possible entre ces deux nuages, dans ce cas la zone
analysée est commune aux deux nuages.
Aussi la connexion entre ces zones est assurée en recherchant des points communs (plus
exactement des zones communes identifiées par des propriétés de voisinage de points appar-
tenant à ces zones) entre deux zones (l’une dans le nuage de référence et l’autre dans le nuage
à recaler avec le nuage de référence) et en les fusionnant. Historiquement l’algorithme I.C.P.
(Iterative Closest Point), par son antériorité et au prix de nombreuses variantes a largement
occupé la scène dans ce domaine en mobilisant l’énergie de nombreux travaux de recherche.
Il peut donner des résultats satisfaisants dans des cas très spécifiques (ce qui explique les va-
riantes) mais en limitant également son utilisation pour l’agrégation de deux nuages de points
(versus une agrégation chaînée de nuages de points consécutivement connexes). Mais rien ne
nous empêche de chaîner une suite d’agrégation, deux premiers nuages donneront un résultat
satisfaisant et nous pouvons ensuite tenter l’agrégation à un troisième et ainsi de suite. La
présente étude sera phasée en deux étapes :
1. après une première recherche bibliographique, vu le rôle fondateur et la popularité de
l’algorithme I.C.P. et des investigations qui se poursuivent sur celui-ci, afin de surmon-
ter ses insuffisances, il est procédé à une identification des variantes de cet algorithme et
2

11. CHAPITRE I. INTRODUCTION GÉNÉRALE
aux tests de ceux-ci afin de s’approprier de la connaissance et de la méthodologie d’agré-
gation en examinant son adéquation possible aux problématiques rencontrées, par les
mesures effectuées par EXAMETRICS, ces points seront analysés,
2. ayant connaissance, a priori, des limites de l’algorithme, tout en l’ayant testé, une se-
conde recherche bibliographique poursuit la première en examinant particulièrement les
nouveaux axes de recherches qui, sans exclure nécessairement l’I.C.P., le complète dans
certains cas par l’addition de nouvelles approches, s’attachant à rechercher des zones
géométriques homologues entre deux nuages (points, lignes, plans, surfaces convexes).
Cependant en préambule à la présente étude il a été procédé à un premier travail de dé-
couverte [3] de la structure d’un nuage de points, organisé dans un format largement utilisé
dans la profession (*.las), et d’un outil également très connu dans le métier CloudCompare
permettant la manipulation, la visualisation et certains traitements sur des nuages de points
LIDAR. A cette fin, afin de se familiariser avec les approches géométriques et statistiques de
la manipulation de nuages de points et découvrir la bibliothèque de traitement associée (fon-
dation C++ de CloudCompare) mettant en œuvre une grande variété d’algorithmes, il a été
procédé à la construction d’un greffon (plugin) permettant d’assurer l’intersection d’un nuage
de points avec un plan. Compte tenu des tolérances de calcul nécessaires, ce plan s’avère être
un parallélépipède borné dont la hauteur est assimilée à la tolérance de mesure.
3

12. Chapitre II
Contexte de travail
II.1 Présentation de l’entreprise EXAMETRICS
II.1.1 EXAMETRICS
Créée en 2012, suite à l’autorisation par décrets en 2012, pour une entreprise, de travailler
avec des drones aériens, EXAMETRICS est une TPE située à Saint-Estève près de Perpignan.
Son chiffre d’affaires est en croissance permanente et elle est constituée de 4 personnes (2
ingénieurs plus deux techniciens de bureau d’études), auxquelles il faut joindre un intervenant
externe, expérimenté, encadrant les travaux de recherche et développement . Elle cible pour
2018 un chiffre d’affaires de 300 Ke. EXAMETRICS est une société d’ingénierie spécialisée
dans l’acquisition par drone, entre autres, de données numériques de topographie et de leur
traitement. Elle a été fondée par Henri Borreill, ingénieur en traitement du signal et de l’image
et Christophe Puerto, ingénieur topographe.
II.1.2 Domaine d’expertise de l’entreprise
EXAMETRICS déploie une activité de services topographiques reposant sur trois piliers :
1. acquisition de données,
2. traitement et analyse des données,
3. présentation des résultats,
le tout reposant sur une activité de recherche et de développement qui s’est peu à peu installée
au cours des trois dernières années afin de soutenir sa croissance. L’acquisition des données
peut être faite par des drones aériens, terrestres ou aquatiques. Ses marchés :
1. Agriculture de précision : topographie, détection de carence minérale ou sanitaire et de
stress hydrique.
4

13. CHAPITRE II. CONTEXTE DE TRAVAIL
2. Inspection, contrôle qualité, surveillance de grands ouvrages d’art : barrages, canaux,
transport d’électricité ( inspection de pylône), dépôts sédimentaires, recueil d’échan-
tillons,
3. Topographie aérienne : plans 2D, 3D , orthophotographies, cubatures, évaluation impact
visuel.
4. Modélisation 3D : photogrammétrie, communication, intégration paysagère.
En matière d’outillage d’acquisition de données, nous citerons les plateformes instrumentées,
aériennes, terrestres ou aquatiques. Par exemple un drone de précision comme le Novadem
U130, plateforme instrumentée en appareil photographique, caméra dans le visible, l’infra-
rouge ou le proche infrarouge, ou un drone nautique de bathymétrie. En revanche, les instru-
ments LIDAR (dotés d’IMU.), éventuellement accompagnés de balises GPS posées au sol, sont
uniquement à mobilité terrestre à ce jour. Les capteurs, toujours de plus en plus précis, citons :
1. appareils photographiques numériques haute définition (42 millions de pixels pour le
SONY A7R II),
2. caméras thermiques et proche Infra-Rouge,
3. LIDAR (50 000 points/seconde),
apportent une masse importante de données qu’il faut savoir traiter et souvent de manière très
distincte et le plus rapidement possible.
Le traitement et l’analyse des données conduits en bureau d’études, s’appuient sur une
diversité d’outils sophistiqués du marché, permettant de conduire des travaux de traitement
d’images, de maillage et de photogrammétrie, comme de dépouillement et de traitements sta-
tistiques des données. Cette étape importante en bureau d’étude, exigeant en amont un temps
important de nettoyage et de préparation des données et en aval une présentation synthétique
des résultats obtenus, est le cœur de la création de valeur pour la société EXAMETRICS. C’est
cette activité qui doit connaître un développement important, avec un accroissement de la
productivité et la mise en place de verrous technologiques logiciels et algorithmiques afin de
faire la différence avec la concurrence et apporter un meilleur service à la clientèle de l’en-
treprise. C’est ceci qui conduit à une stratégie de développement fondée sur la R&D source
d’innovation.
5

14. CHAPITRE II. CONTEXTE DE TRAVAIL
La présentation des résultats se fait sous forme de rapports circonstanciés, de mise à dispo-
sition de représentation 3D, de bases de données, voire de fichiers s’implantant sur un Système
d’Informations Géographiques (S.I.G.) ou de C.A.O.
II.1.3 Exemple de Produit photogrammétrique EXAMETRICS
La figure suivante présente le résultat d’un traitement photogrammétrique , de reconstruc-
tion 3D, effectué sur une collection de photographies prise avec drone sur un fort en Méditer-
ranée .
Figure II.1 – Reconstruction photogrammétrique par Exametrics
II.1.4 Les solutions EXAMETRICS et leurs marchés
La suite des solutions EXAMETRICS répond aux attentes des marchés suivants :
• Agriculture :
Les méthodes proposées permettent un diagnostic précis pour faire un état des lieux
précis des parcelles et d’optimiser les intrants et les récoltes. Avec l’utilisation du drone
l’agriculture rentre dans une nouvelle dimension :
– Comptage des sujets manquants ou chétifs.
– Zonage des adventices.
– Détection de stress hydrique et NDVI.
6

15. CHAPITRE II. CONTEXTE DE TRAVAIL
– Mesure de surfaces complexes.
– Zonage des carences et maladies.
– Mesure des pentes d’écoulement des eaux.
Parmi les avantages, nous citerons une précision inégalée, une vision globale, un mode
opératoire simple et rapide permettant d’anticiper l’évolution des croissances et d’es-
timer les volumes de récoltes. Ainsi des diagnostics précis, au service du végétal opti-
misent les intrants et les coûts et, par la même, accroissent la productivité de l’exploita-
tion agricole.
• Inspection
Les drones multirotor d’Exametrics permettent un contrôle de tout type d’installation.
Rapide, bon marché, facile à mettre en œuvre, le drone peut inspecter les endroits les
plus inaccessibles, avec une grande précision et en minimisant les risques.
– Réduction des risques humains.
– Rapidité et économie.
– Production en continue.
– Tout contrôle géolocalisé en génie civil.
– Survol aisé, ou vol stationnaire, pour prise de vue géolocalisée dans les grandes
fermes solaires et/ou éoliennes.
– Inspection précise des grands réseaux de transport en aérien de l’eau, du gaz et de
l’électricité.
• Topographie aérienne
Après acquisition des données (photos aériennes), les images sont traitées par un logi-
ciel de photogrammétrie pour générer un modèle 3D. Ce modèle 3D utilise des points
de calage au sol pour une précision optimale dans le référentiel de mesure. Ainsi nous
conduisons des opérations de :
– réalisation de plans topographiques 2D et 3D,
– modélisations numériques de terrains,
– production d’orthophotographies,
– relevé de surfaces verticales ou orthophotographies complexes.
7

16. CHAPITRE II. CONTEXTE DE TRAVAIL
– calculs de cubatures pour les carriers ou tout stockage en grand volume de maté-
riaux,
– simulation d’intégration paysagère, notamment les appréciations des impacts de
construction,
Précis, économique, simple et rapide à mettre en œuvre, en bref une solution de qualité
supérieure.
• Modélisation 3D
La modélisation 3D offre une précision inégalée. Notre modélisation 3D par photogram-
métrie, issue de photos aériennes de drones EXAMETRICS, est effectuée au moyen des
meilleurs logiciels du marché. Examétrics réussit à combiner le nuage de points, généré
au scan 3D Leica C10, à celui issu de la photogrammétrie aérienne pour reconstruire un
modèle 3D extrêmement précis ou chaque cote sera respectée avec une grande précision.
Ceci permet d’effectuer :
– des relevés d’architecture (plan, coupe)
– des analyses de déformation dans le domaine du génie civil,
– des simulations propres à l’urbanisme, impact visuel, occultation de la lumière,
éclairage, exposition aux vents,
– des campagnes de communication interactive,
– de la modélisation urbaine 3D,
– des simulations de catastrophes naturelles (inondation : contribution au GEMAPI).
Nous pouvons ainsi établir des modèles 3D complexes, avec une grande précision suffi-
sante en nous inscrivant également, à terme, dans de grands standards de mise à dispo-
sition de données (CityGML) dans le cadre d’initiatives telles que SmartCity.
• Relevé LIDAR
Avec un LIDAR mobile offrant une capacité d’acquisition de 45 000 points par seconde,
EXAMETRICS aspire à mesurer tout type de surfaces et de volumes pour :
– le BIM
– la foresterie
– la reconnaissance de formes au sein de nuage de points permet de construire des
nomenclatures géolocalisées des plus diverses.
8

17. CHAPITRE II. CONTEXTE DE TRAVAIL
Ces derniers résultats sont ciblés, en s’appuyant peu à peu sur des travaux en appren-
tissage profond (I.A) afin de maîtriser progressivement, les objectifs avancés.
II.1.5 La R&D chez EXAMETRICS, stratégie de développement
EXAMETRICS a fait le choix d’opérer sur des marchés où la plus-value réelle se construit à
travers la maîtrise de verrous technologiques exigeant des connaissances profondes de ceux-ci
(Algorithmique et codage) : - la maîtrise du traitement et de l’analyse des informations extraites
des données collectées (Images, nuages de points LIDAR, données de bathymétrie, etc...).
Concernant le LIDAR, depuis deux ans EXAMETRICS a conduit des travaux dans sa mise en
oeuvre, avec des offres de services sur le marché de la foresterie, de l’agriculture et du B.I.M., et
des investigations de R&D. Face aux attentes des marchés concernés il y a nécessité d’accroître
la productivité en ayant une offre de services et d’outils plus performants et mieux maîtrisés,
ce qui implique une implication forte en algorithmique et en ingénierie logicielle.
Aussi, c’est tout naturellement qu’EXAMETRICS cherche à s’inscrire dans un écosystème ca-
pable de l’accompagner dans sa courbe d’apprentissage de ces nouvelles connaissances. Ainsi,
l’adhésion à l’accueil de stagiaires issu.e.s d’un enseignement de haut niveau, comme la mise
en œuvre de démarche de thèse de recherche sont des processus appropriés à cette nouvelle
approche du développement de l’entreprise.
La maîtrise future, par l’entreprise, des connaissances acquises, suite à ces travaux, sera d’au-
tant plus forte que les personnes porteuses de mémoires ou de thèses seront susceptibles de
rejoindre EXAMETRICS, et que les travaux se poursuivront en matière de R&D tout en conti-
nuant à collaborer avec les organismes de formation et de recherche dont ils ou elles sont
issu.e.s. Le débouché industriel de ces travaux cible l’atteinte de nouveaux marchés avec de
nouvelles pratiques, ce qui est une mutation forte pour l’entreprise, tant au niveau des res-
sources humaines que des technologies.
II.1.6 Compétences et ressources humaines
Les compétences se répartissent entre l’acquisition des données proprement dites, le traite-
ment des données acquises en bureau d’études, et la relation client ce qui nécessite des savoir-
9

18. CHAPITRE II. CONTEXTE DE TRAVAIL
faire spécifiques, concernant :
• l’acquisition :
– préparation de l’instrumentation sur les plateformes (drones) d’acquisition,
– pilotage de drones,
– établissement administratif des plans de vol.
• le traitement des données :
– nettoyage et préparation des données collectées,
– analyse et traitement des données, en s’appuyant sur des logiciels divers, 3DRe-
shaper, Garmin, Autocad, Covadis, afin de générer des rapports de cubatures, des
plants topographiques, d’analyser des photos aériennes, et de conduire des travaux
de photogrammétrie.
• la relation client :
– prospection et participation à des salons,
– préparation des devis,
– suivi des projets et des clients.
Les technologies d’acquisition évoluant en permanence, EXAMETRICS s’assure que les em-
ployés, formés en conséquence, soient en capacité permanente d’évoluer vers les nouvelles
technologies.
II.1.7 Ré-orientation de compétences
Aujourd’hui, l’entreprise oriente son expertise vers le traitement de nuages de points issus
de balayage Laser LIDAR (Light detection and ranging) et l’automatisation des opérations de
traitement associées. Ceci est une rupture importante par rapport aux méthodes de travail
antérieures, la relation technologique la plus forte reste la manipulation de nuages à l’instar
de ce qui se fait en photogrammétrie. Cependant le nuage de points LIDAR, bien plus riche
en densité d’informations (quoique bruitée) apporte également une plus grande précision des
données acquises. Les approches technologiques (algorithmique) sont totalement différentes
du traitement d’images. Ceci ouvre de nouvelles perspectives et porte d’avantage l’accent sur
10

19. CHAPITRE II. CONTEXTE DE TRAVAIL
le registre de la mesure et de la géométrie algorithmique.
Cela a conduit EXAMETRICS à faire ses premiers travaux dans les domaines :
• du B.I.M (Builder Informations Models), à savoir la cotation dimensionnelle du patri-
moine construit dans le domaine architectural, après des relevés LIDAR,
• de la foresterie, où le relevé par LIDAR permet d’offrir une solution de substitution aux
mesures dendrométriques, telles que pratiquées dans l’exploitation forestière.
Le présent rapport de stage traite une problématique transversale à tous les marchés d’ac-
quisition de données par LIDAR, le recalage de deux nuages de points, avec une zone géogra-
phique commune.
II.2 La conduite du projet d’agrégation de nuage de points
L’introduction générale faisait apparaître deux étapes dans la méthodologie de travail, concer-
nant le traitement de l’agrégation, le calage des nuages de points. Cependant compte tenu de
la spécificité du traitement de nuages de points LIDAR, ces deux étapes ont été précédées
d’un phase d’apprentissage et de découverte d’un outil de manipulation de nuages de points
CLOUD_COMPARE et de familiarisation avec les structures de nuages de points LIDAR. En
effet cet outil, un logiciel libre (créé au sein du C.E.A. et de l’E.D.F.), toujours en développement
très actif, est en fait un cadriciel de développement en langage C++ [30]. Outre ces fonction-
nalités opérationnelles, il était nécessaire de connaître l’architecture de son logiciel, car l’outil
est une cible pour certains greffons spécifiques que le projet serait amené à développer, mais il
peut être également envisageable d’utiliser sa bibliothèque C++, pour l’intégrer dans d’autres
applications.
II.2.1 La première partie
Cette première partie de stage s’est déroulée en collaboration avec trois étudiants de l’IME-
RIR lors d’un projet industriel d’une durée de deux mois.
Il s’agissait d’une phase d’initiation et de découverte pour bien s’adapter avec la manipula-
tion des nuages de point. Plus précisément, elle avait comme objectif :
• La découverte de l’outil CloudCompare, outil privilégié de manipulation de nuage de
points LIDAR.
• L’analyse des codes sources(QT/C++) de l’outil.
11

20. CHAPITRE II. CONTEXTE DE TRAVAIL
• La découverte des éléments structurants des fichiers de données (*.las).
• La création d’un greffon permettant l’intersection avec tolérance de nuages de points
avec des objets géométriques, et la collecte de points contenus dans le volume de tolé-
rance.
Le premier objet géométrique, retenu pour intersecter un nuage de points, était le plan. En
fait, des tolérances de mesures sont nécessaires et le plan s’avère être un parallélépipède borné
dans l’espace.
II.2.2 La deuxième partie
Cette partie était principalement destinée à l’étude de l’algorithme ICP (Iterative Closet
Point) en le testant sur des jeux de données afin d’étudier la convergence et la performance de
chaque implémentation. Pour la conduire, il a été procédé :
• à une phase de recherche bibliographique afin d’effectuer un état de l’art dans le domaine
et compte tenu de l’antériorité importante des travaux :
– d’évaluer les problèmes de convergence rencontrées,
– d’examiner les différentes variantes qui ont été développées,
– de tenter de classer les cas d’utilisation spécifiques des différentes variantes,
• d’assurer le prototypage de quelques variantes pour évaluer leur performance et mieux
comprendre les problématiques rencontrées.
En entamant cette étude nous avions connaissance par les recherches bibliographiques des
limites de l’algorithme, comme d’autres approches qui se mettent en place. Cependant, il faut
avoir présent à l’esprit que l’I.C.P. peut s’avérer performant quand certaines conditions ini-
tiales sont rassemblées et n’est absolument pas abandonné. Donc la maîtrise de cet algorithme
reste un passage recommandé pour qui œuvre dans son amélioration algorithmique.
II.2.3 La troisième partie
En respect de ce qui est indiqué, une troisième partie de l’étude s’est intéressée aux nou-
velles approches, basées sur les caractéristiques géométriques saillantes des nuages de
points (zones de points caractéristiques, identification d’au moins deux lignes non parallèles,
identification de plan borné) en ayant la possibilité de trouver pour chaque caractéristique
12

21. CHAPITRE II. CONTEXTE DE TRAVAIL
identifiée dans un nuage (le nuage de référence) son élément homologue dans le second nuage,
en conséquence il a été procédé :
• à une seconde phase de recherche bibliographique afin d’effectuer un état de l’art dans
le domaine de la caractérisation géométrique des nuages de points en s’appuyant sur ces
caractéristiques identifiées afin d’évaluer les paramètres de transformation (translation,
rotation, mise à l’échelle) dénommée transformation de Helmert [13], pour assurer le
calage du second nuage de point sur le nuage de référence.
• en nous appuyant sur les références bibliographiques identifiées, à un cahier des charges
de prototypage mettant cette méthodologie en œuvre : une approche mixant la zone de
points, le couple de droites et un plan borné.
II.3 Technologies impliquées
II.3.1 Matériel
Un LIDAR est un laser doté d’une capacité :
• de balayage mécanique planaire et volumétrique, du fait de deux mouvements, un ba-
layage planaire (éventail) associé à la rotation de ce plan,
• de mesure de temps de vol de l’écho suite à une émission laser, associée à des données
accélérométriques, gyrométriques et magnétométriques, permettant de calculer les co-
ordonnées x, y, z (longitude, latitude, altitude) dans le référentiel initial de l’instrument
de mesure.
Ces dernières données sont issues d’une centrale inertielle intégrée au LIDAR.
D’une manière courante, après traitement, les données obtenues sont mises à disposition
au format *.las qui est un standard de présentation des données LIDAR (ce n’est pas le seul).Il
s’avère être le plus répandu, donc un standard de fait adopté par le LIDAR GEOSLAM d’EXA-
METRICS.
13

22. CHAPITRE II. CONTEXTE DE TRAVAIL
Figure II.2 – Principe de l’écholocation
A partir de la différence entre ces deux temps (Emission signal et réception de l’écho c.a.d
“temps de vol”), il est possible d’en déduire la distance entre l’émetteur et le point de réflexion,
les autres acquisitions une fois fusionnées avec cette données permettent un géoréférence-
ment de l’écho dans le référentiel de l’instrument de mesure.
En effectuant ce type de mesure dans plusieurs orientations, il est alors possible de “scan-
ner” une pièce. Cette méthode a donc comme résultat de produire un nuage de points au format
*.las au prix de traitements complémentaires et représentatif de la zone analysée.
C’est sur ce type de fichier de données que notre projet s’appuie. Le traitement de ce nuage
permet l’extraction de formes géométriques plus ou moins complexes selon le domaine d’ap-
plication.
II.3.2 Logiciels et librairies utilisés
L’ensemble des travaux s’appuie sur des logiciels libres. En effet au vu de leur complexité, il
est pertinent d’y associer une large population de développeurs et de testeurs afin d’aboutir le
plus rapidement possible à des versions stables et robustes. Il n’en demeure pas moins que le
développement s’avère chronophage et peuplé d’embûches. Parmi ces logiciels nous citerons :
• CLOUDCOMPARE (Licence GNU/GPL) : Logiciel libre de visualisation et traitement de
14

23. CHAPITRE II. CONTEXTE DE TRAVAIL
nuages de points LIDAR en 3D, construit sur une bibliothèque pouvant être intégrée dans
des développements C++, mais non pourvue d’une API d’interface au langage PYTHON.
.
• PCL (Licence BSD) : Point Cloud Library [26] une bibliothèque d’ algorithmes Libres de
droits pour des tâches de traitement de nuage 3D de points LIDAR et dotée d’une API
PYTHON.
• PDAL (Licence GNU/GPL) : Point Data Abstraction Library [29] : est une librairie de
traitement de nuage de points LIDAR, mettant en œuvre de nombreux algorithmes, dont
certains empruntés à PCL et dotée d’une API PYTHON.
• QT SDK , QT Creator (Licence Qt [31]) : librairie graphique développée en en C++. .
• VTK (Licence BSD) : Visualization Toolkit[28] (VTK) est un logiciel libre pour du trai-
tement graphique 3D et traite nuage de points et images. C’est une bibliothèque C++
doté d’API Tcl/Tk, Java, et Python. Le plus ancien dans ce type de logiciel VTK inclut un
large spectre d’algorithmes, scalaire, vectoriel, tensoriel, texture et maillage.
• OPEN3D[27] (Licence MIT) : Bibliothèque libre de droits, de traitement de données 3D,
écrite en C++ et dotée d’une API Python, elle tente de substituer à PDAL en offrant un
haut niveau de parallélisation.
15

24. Chapitre III
Greffon (Plugin) CloudCompare
Introduction
Dans ce chapitre, après avoir introduit les prérequis du traitement de nuages de points nous
abordons le développement d’un greffon CloudCompare dédié à l’extraction d’un sous nuage
de points à partir d’un fichier *.las. Ce travail a été effectué dans le cadre d’une collaboration
avec une équipe de 3 étudiants de 3ème année de L’IMERIR, lors d’un projet de deux mois,
piloté par EXAMETRICS [3] [2].
III.1 Mise en place des prérequis
Cette section est destinée pour définir les prérequis.
Définition 1 (LIDAR). La télédétection par laser ou LIDAR, acronyme de l’expression en langue
anglaise light detection and ranging ou « laser detection and ranging » (soit en français « détec-
tion et estimation de la distance par la lumière » ou « par laser »), est une technique de mesure
à distance fondée sur l’analyse du temps de vol d’une impulsion LIDAR se réfléchissant sur un
objet. Le LIDAR employé par EXAMETRICS est un instrument GEOSLAM, type Z-REVO. Il s’agit
d’un laser (longueur d’onde de 905nm) terrestre (poids 1 Kg) , porté à mains par un opérateur qui
se déplace en marchant (3 à 4 km/h) dans la zone à analyser. Le laser actif à une zone de balayage
dans un éventail plan ouvert à 270°. Le mouvement de rotation circulaire de la tête portant le laser
permet d’avoir une exploration volumique, (270° x 360°) l’éventail plan effectuant une rotation
permanente. La fréquence de rotation de la tête est de 2 Hz.
La résolution angulaire dans l’éventail plan est de 0.625 °, soit 432 angles de tir dans le plan de
l’éventail. Le balayage de l’éventail se fait en 10ms (100 Hz), ce qui permet une cadence d’acqui-
sition de 43 200 points par seconde sachant qu’un seul point est acquis sur chaque tir laser. Ceci
correspond à un volume de stockage de données de l’ordre de 170 Kbytes/s, soit 10 MB/min. La
précision relative point à point est de 2 à 3 cm, la précision absolu pour une boucle de mesure de
10 mn (100 MB de données) est de 30 cm.
16

25. CHAPITRE III. GREFFON (PLUGIN) CLOUDCOMPARE
Doté d’un IMU, cet outil offre l’avantage de pouvoir effectuer des relevés dans des zones où le
signal GPS est masqué, cependant l’inconvénient de cette technologie est lié à la dérive des accé-
léromètres avec le temps. Ceci nécessite de recommander des campagnes de mesures de quelques
dizaines de minutes pour limiter cette dérive, ou d’user d’artifice de rebouclage de parcours si l’al-
gorithme de fusion de données est en capacité de les détecter et de procéder à des recalages de la
centrale inertielle au cours de la fusion des données.
Figure III.1 – Lidar employé
Définition 2 (Nuage de points). Ensemble de points donnés dans un système de coordonnées (gé-
néralement X,Y,Z [Longitude, latitude, altitude]) dans le référentiel de l’instrument de mesure : le
LIDAR) et issu du processus de mesure par LIDAR. A l’issue d’une campagne de balayage ce denier
fournit un fichier compressé *.rosbag qui rassemble des données d’accélérométrie, de gyrométrie et
de magnétométrie pour ce qui nous concerne. La fusion de ces données, effectuée hors acquisition
par un logiciel spécialisé, fournit le nuage de points (un point est un écho élémentaire) au format
*.las l’unité de mesure étant le mètre, le tout étant fourni dans le référentiel de l’instrument de
mesure.
Définition 3 (Format *.las/*.Laz). C’est le format standard pour les données LIDAR qui regroupe
différentes informations.
Le *.laz est un format compressé du “*.las”.
Les spécifications détaillées des formats *.Las sont disponibles sur les liens suivants :
17

26. CHAPITRE III. GREFFON (PLUGIN) CLOUDCOMPARE
• http ://www.asprs.org/a/society/committees/standards/asprs_las_format_v10.pdf
• http ://www.asprs.org/a/society/committees/standards/asprs_las_format_v11.pdf
• http ://www.asprs.org/a/society/committees/standards/asprs_las_format_v12.pdf
• http ://www.asprs.org/a/society/committees/standards/LAS_1_3_r11.pdf
• http ://www.asprs.org/a/society/committees/standards/LAS_1_4_r11.pdf
la dernière version est la version 1.4 à sa révision candidate 13 de Juillet 2015. lL’ASPRS (
American Society for Photogrammetry & Remote Sensing) est la propriétaire de la spécification
*.las. Ce standard est maintenu par un groupe de travail animé par le comité de direction de
l’ASPRS. Les fichiers GEOSLAM issus du post-traitement de conversion au format *.las, utilise
la version 1.0 en fournissant uniquement la position géométrique de chaque écho élémentaire.
Pour le GEOSLAM, l’écho élémentaire, est le premier écho en retour pour une émission donnée. la
période d’émission est de l’ordre de 22µ secondes. En outre le post-traitement fournit le fichier de
trajectographie (x, y, z) de l’origine du référentiel de l’instrument, échantillonné à une période de
10 secondes associé à cet échantillonnage est donné le quaternion donnant le vecteur directeur de
l’émission laser du LIDAR.
Définition 4 (Matrice de transformation). Dans le plan cartésien, une matrice de transformation
est une matrice qui appliquée aux coordonnées d’un point initial représentées par une matrice
colonne permet de trouver celle de son image transformée par une opération géométrique donnée
(translation, rotation, mise à l’échelle). Les coordonnées de la nouvelle image sont alors obtenues
en effectuant la multiplication de chaque pont de l’image initiale sous forme de matrice colonne
(les coordonnées d’un point) par la matrice correspondant à la transformation géométrique que
l’on désire opérer. Il s’agit de la transformation de Helmert [13].
III.2 Développement du greffon CloudCompare
III.2.1 Problématique posée
Le but est de créer un outil, sous forme de greffon (plugin) permettant de sélectionner et
d’extraire les points d’un nuage, sachant que le critère de sélection est l’intersection de ce
nuage de points avec un objet géométrique. Il était proposé de rechercher les points intersec-
tant un plan de l’espace, dans une zone bornée de l’espace. Par ailleurs, l’introduction d’une
tolérance de mesure ramenait le problème à la recherche des points contenus dans un paral-
lélépipède rectangle. Les données initiales sont extrêmement simples :
18

27. CHAPITRE III. GREFFON (PLUGIN) CLOUDCOMPARE
• le plan est défini par deux vecteurs orthogonaux dans un plan et issu du même point,
ils donnent implicitement la normale au plan et les bornes de recherche de point en
association avec la tolérance définie ci-après,
• une tolérance de mesure définit ce qui peut être assimilé à la hauteur du parallélépipède
d’intersection
Fort de ces trois données géométriques il était demandé, en s’aidant de la bibliothèque de
développement de CloudCompare d’extraire du nuage sous forme d’un fichier *.las ou d’un
tableau Numpy, les points présents au sein du parallélépipède de tolérance.
Ce développement avait trois objectifs :
• découvrir la manipulation de nuage de points,
• se familiariser avec l’architecture de CloudCompare et notamment sa bibliothèque de
développement en C++, afin de conduire le développement demandé,
• s’initier aux manipulations et transformations géométriques en s’appuyant sur les outils
élémentaires en 3D qu’ils s’agissent de matrices ou de quaternions.
III.2.2 Présentation de l’IHM
La définition de deux points A et B détermine le vecteur normal au plan désiré. Le bouton
glissant juste dessous permet de déplacer un point (point du plan) du vecteur entre A et B pour
complètement définir notre plan, en donnant un point du plan appartenant au segment AB.
Un bornage (longueur, largeur) définissent l’aire d’intersection, enfin la tolérance est utilisée
pour préciser la hauteur de la “boîte de tolérance” permettant le calcul d’intersection et la
collecte des points du nuage appartenant à cette zone (volume) de tolérance.
19

28. CHAPITRE III. GREFFON (PLUGIN) CLOUDCOMPARE
Figure III.2 – IHM plugin CloudCompare
L’I.H.M permet de sélectionner 2 algorithmes, le premier est linéaire/itératif et est exécuté
en langage Python pour les premiers tests. Le deuxième utilise les octree/récursif (bibliothèque
CloudCompare) et permet une optimisation en temps du calcul. Au clic sur le bouton “Com-
pute/Calculer” l’algorithme sélectionné est exécuté dans un fil d’exécution parallèle (thread)
séparé afin de ne pas bloquer l’IHM.
III.2.3 Notions géométriques liées à l’affichage
Calcul des coordonnées du point appartenant au vecteur
Soit i un point du vecteur normal
−−−−→
AB permettant de définir notre plan. Comme décrit dans
l’IHM, on déplace le point i entre A et B avec un “Slider”. Afin de connaître les coordonnées
de ce point, qui appartient au plan, nous réalisons les calculs suivants :
• Données :
– k : coefficient entre 0 et 1 définissant la position de i (k = 0 alors i = A, k = 1 alors i
= B)
– les coordonnées du point A
– les coordonnées du point B
• Calcul de i :
ix = k × (Bx − Ax) + Ax (III.1)
De même pour iy iz
20

29. CHAPITRE III. GREFFON (PLUGIN) CLOUDCOMPARE
Création du plan borné
Dans l’outil CloudCompare, la génération du plan borné se fait à partir de 4 points. Dans
notre interface, nous définissons le plan avec un vecteur normal
−−−−→
AB et un point i appartenant
à ce vecteur. Partant du point i deux vecteurs normés du plan (donc orthogonaux à la normale,
non colinéaires et orthogonaux entre eux) sont définis afin de permettre d’élaborer 4 points
qui sont transmis à une méthode spécifique de CloudCompare pour la construction complète
du parallélépipède rectangle de tolérance.
III.3 Optimisation du traitement
Le traitement de fichier de nuage de points (extension *.las) volumineux peut être chrono-
phage. Pour minimiser le temps de traitement dans ce cas là, il est nécessaire de trouver de
nouvelles méthodes afin d’optimiser son traitement, deux méthodes sont proposées.
Méthode 1 : Filtre par distances
La première méthode consiste à utiliser des outils déjà présent dans CloudCompare :
• Calcul de distances entre le nuage de points et les faces du parallélépipède.
• Filtre par valeurs négatives, ce qui nécessite de respecter l’orientation des vecteurs lors
des calculs dans le trièdre de référence.
Figure III.3 – Méthode 1 : état initial
21

30. CHAPITRE III. GREFFON (PLUGIN) CLOUDCOMPARE
En interne, CloudCompare va d’abord calculer l’arbre d’octrees de notre nuage afin d’opti-
miser le temps de ses calculs. Toujours dans cette optique, il propose également de paralléliser
les calculs sur les cœurs disponibles de la machine.
L’outil de calcul de distances va donc générer en mémoire (dans un tableau spécifique de
scalaire) une valeur de distance entre les points du nuage et les faces de notre parallélépipède.
On obtient le nuage suivant Figure III.3 (en bleu on distingue le parallélépipède et les points
du nuage qui lui sont internes).
Figure III.4 – Méthode 1 : état intermédiaire
22

31. CHAPITRE III. GREFFON (PLUGIN) CLOUDCOMPARE
Sur le tableau spécifique de scalaire on applique maintenant le filtre par valeur (paramétré
pour ne prendre que les valeurs négatives) ce qui permet de ne retenir que les valeurs internes
à notre parallélépipède rectangle de tolérance.
Figure III.5 – Méthode 1 : Résultat de l’intersection
La sélection des points est correctement réalisée. Cette méthode n’est pas complètement
implémentée dans le greffons mais le code source est disponible sur GitHub. On peut notam-
ment y trouver comment utiliser une fenêtre interne à CloudCompare dans notre greffons.
Cela peut permettre d’appeler la fenêtre de calcul des distances depuis notre greffon.
Méthode 2 : Coupure transversale
La deuxième méthode consiste à faire des coupures transversales du nuage de points en se
basant sur l’outil ‘Crop’ de CloudCompare et en modifiant principalement deux paramètres du
parallélépipède :
• Dimension : Longueur, largeur et hauteur (tolérance).
• Position du centre de la boite : cela revient à appliquer une translation de la boîte de sa
position initiale aux valeurs du vecteur de la nouvelle position souhaitée.
23

32. CHAPITRE III. GREFFON (PLUGIN) CLOUDCOMPARE
Figure III.6 – Méthode 2 : État initial
Ce greffon fait appel à la fonction "Crop" qui prend comme paramètres les dimensions du
parallélépipède et le nom du nouveau nuage qui va contenir le résultat. Le bouton "Compute"
permet d’appliquer la fonctionnalité d’extraction après la modification de la position ainsi que
des dimensions du parallélépipède de sélection.
24

33. CHAPITRE III. GREFFON (PLUGIN) CLOUDCOMPARE
Figure III.7 – Méthode 2 : Enregistrement du fichier LAS
De plus, le bouton "Compute" fait apparaître une fenêtre modale qui s’affiche pour choi-
sir des options de résolution pour l’enregistrement du fichier LAS qui contiendra les points
extraits du nuage principal, par le parallélépipède de sélection.
Inconvénient
Cependant, cette méthode ne prend pas en compte les rotations du parallélépipède rec-
tangle, elle est limitée aux coupures transversales d’un nuage du points. Le développement de
la mise en œuvre de la matrice de rotation, appliqué aux points délimitant le parallélépipède
de sélection, n’a pas été effectué.
III.4 Conclusions
En conclusion, cette première partie de stage est le fruit d’un travail d’équipe pour découvrir
la bibliothèque CloudCompare qui est l’environnement de traitement du nuages de points et
d’accueil des différents algorithmes implémentés dans le logiciel libre CloudCompare. Cette
initiation, a servi de prétexte à la création d’un greffon d’extraction de points d’un nuage, par
25

34. CHAPITRE III. GREFFON (PLUGIN) CLOUDCOMPARE
un parallélépipède rectangle intersectant ce nuage de points. Ce développement a été conduit
dans le langage compilé C++ et le langage interprété Python.
26

35. Chapitre IV
Etudes bibliographiques sur le recalage
I.C.P.
Introduction
La technique de recalage s’avère nécessaire pour l’agrégation d’images ou de nuages de
points de zones géographiques/géométriques voisines, ayant en commun, pour le moins, une
zone partielle de chevauchement, sur laquelle on s’appuiera pour mettre en œuvre le proces-
sus d’agrégation. Dans nos travaux, nous nous intéressons uniquement aux nuages de points
LIDAR, limités à deux nuages :
• un premier nuage de référence,
• un second nuage ayant partie ou quasi totalité de commune, géographiquement et/ou
géométriquement, avec le premier,
Les acquisitions de points ont été faites selon des points de vue distincts (donc des référen-
tiels distincts) liés à l’orientation, la translation, et la distance. Le recalage consiste à trouver
la transformation (sous forme de matrice ou de quaternions intégrant : rotation, translation,
mise à l’échelle) afin de faire coïncider les points homologues, si ils sont identifiables, ou des
zones similaire par critères de voisinage.
L’algorithme ICP est l’un des algorithmes les plus populaires pour résoudre ce problème
d’agrégation ("REGISTRATION"). Fondamentalement c’est un algorithme itératif de minimi-
sation qui ne converge pas toujours, ou offre un temps de convergence rédhibitoire.
Dans ce chapitre, on s’intéresse à l’algorithme ICP 3-D et à ces variantes, des prototypages
d’implémentation sont effectués et qualifiés. Dans un chapitre suivant, on abordera l’état de
l’art dans la fusion de nuages tentant :
• d’identifier des primitives géométriques dans le premier nuage,
27

36. CHAPITRE IV. ETUDES BIBLIOGRAPHIQUES SUR LE RECALAGE I.C.P.
• de trouver leurs homologues dans le second nuage,
et sur la base de cette identification les modalités d’évaluation de l’opérateur de transformation.
IV.1 Problème de recalage
La formulation mathématique du problème de recalage étudié est un problème de minimi-
sation, sachant que la transformation optimale revient à minimiser la fonction d’erreur basée
sur la distance euclidienne entre le nuage de référence N1 et le nuage NT issu de la transfor-
mation appliquée au second nuage N2 à aligner :
• N1 = {P1, ..., Pnp}
• N2 = {Q1, ..., Qnq}
L’erreur quadratique à minimiser est donnée par :
(R, S, T) =
1
np
np
i=1
pi − RSqi −
−→
T 2
(IV.1)
où :
• pi et qi sont des points homologues entre N1 et N2,
• R représente la matrice de rotation,
• S représente le facteur de mise à l’échelle,
−→
T
• est le vecteur de translation.
Ceci est la représentation la plus générale de la transformée de Helmert. Concernant la zone
de chevauchement, si on est capable de l’isoler, afin de normaliser, la représentation de cette
zone, dans deux nuages, que l’on considère comme identique, on évalue le centre de masse
de cette zone, ce sera notre donnée de translation. Ceci revient en fait à caler le barycentre la
zone commune sur l’origine du référentiel de l’instrument de mesure. Ensuite l’essentiel de la
transformation relève de rotations, dont il faut évaluer les paramètres.
Les centres de masse d’un nuage de point N1 = {P1, ..., Pnp} est donné par l’expression
qui suit :
1
np
np
i=1
pi (IV.2)
28

37. CHAPITRE IV. ETUDES BIBLIOGRAPHIQUES SUR LE RECALAGE I.C.P.
Le centre de masse est évalué pour les zones communes homologues des nuages de réfé-
rence et à recaler. Ensuite avant de calculer la transformation, pour caler le second nuage sur
le nuage de référence, les centres de masse respectifs de chaque nuage sont soustrait de chaque
point à traiter. Cette opération assure une sorte de normalisation géométrique par rapport au
référentiel. Ceci sera d’autant plus vrai entre les deux nuages que les bornes des zones géo-
graphiques et/ou géométriques retenues seront identiques ou proches. Comme il faut assurer
assurer un appariement entre un nuage de référence et un nouveau nuage mesuré, idéalement
pour un point du nouveau nuage il faut trouver son homologue dans le nuage de référence.
On se contentera du point le plus proche (le plus similaire) dans le nuage de référence. Cou-
ramment ceci est réalisé par l’algorithme kd-tree. Ces points étant identifiés, il faut trouver la
transformation (rotation, translation et mise à l’échelle) qui permet de faire coïncider au mieux
les deux nuages. Cet algorithme s’appuie sur un arbre binaire, du même nom, qui est construit
par le découpage récursif de l’espace en deux et le classement des points en conséquence, en
fonction de l’espace d’appartenance et la granularité du découpage.
Les étapes de la transformation sont les suivantes :
• pour chaque point dans un nuage de référence il faut trouver le point le plus proche
(similaire) son homologue dans le nuage à recaler, ceci met couramment en œuvre l’al-
gorithme de recherche kd-tree, ce qui réduit la complexité à O(n lg n) contre O(n2
)
• ensuite on calcule la transformation (rotation, translation, mise à l’échelle) en s’appuyant
sur des outils d’algèbre linéaire matrice et quaternions,
• on applique cette transformation au nuage à recaler,
• on évalue la fonction d’erreur et si le seuil n’est pas atteint on reprend au premier point.
IV.1.1 Les outils mathématiques nécessaires
Au vu des publications il est retenu couramment :
• pour la recherche des points ou zones homologues indiquons l’algorithme kd-tree cité
précédemment, auquel il faut ajouter la méthode des Octree avec la méthode optimisée
de Morton pour parcourir les cubes de voxels,
• les opérateurs de transformation sont construits à partir des outils d’algèbre linéaire
(matrices, quaternion, décomposition SVD d’autres approches plus rares s’appuient sur
des méthodes statistiques et notamment la méthode de Monte-Carlo,
29

38. CHAPITRE IV. ETUDES BIBLIOGRAPHIQUES SUR LE RECALAGE I.C.P.
• le problème de mise à l’échelle est important, diverses approches :
– matrices orthonormales,
– recherche de valeurs propres,
– dérivées partielles avec un facteur unique de mise à l’échelle,
– dérivées partielles avec un facteur de mise à l’échelle pour chaque axe du référentiel
3D,
• la prise compte des erreurs de mesures, des points aberrants ou des zones occultées(exemple
courant nécessitant une seconde mesure sur la même zone selon un autre point de vue)
est fondamentale
IV.1.2 Mesures de distance Euclidiennes
Nous examinons les mesures de distance Euclidienne qui est la mesure de distance “natu-
relle”. Elles sont utilisées entre entités géométriques (points, droites, plans, etc.). Ces distances
sont utilisées dans les algorithmes d’estimation de transformation géométrique.[33]
Distance point-point : La distance entre deux points x et y de l’espace Euclidien de di-
mension p (p = 3 dans notre cas), ces points sont représentés respectivement par des vecteurs
de coordonnées homogènes de taille ((p + 1) × 1) notés x ∼ (¯x x) et y ∼ (¯y y) avec x = 0
et y = 0, est donnée par :
d2
PP(x, y) =
¯x
x
−
¯y
y
2
(IV.3)
Distance point-hyperplan : La distance entre un point x et un hyperplan Π ( droite en
2 dimensions et un plan en 3 dimensions), représentés respectivement par des vecteurs de
coordonnées homogènes de taille ((p+1)×1) notés x et Π avec x = 0 et ¯Π = 0, est donnée
par :
d2
PH(x, Π) =
(x Π)2
x2 ¯Π
2 (IV.4)
IV.1.3 Estimation de la transformation
Le problème de la recherche de la rotation et de la translation entre deux ensembles de
points correspondants est connu sous le nom de problème d’estimation de la transformation
30

39. CHAPITRE IV. ETUDES BIBLIOGRAPHIQUES SUR LE RECALAGE I.C.P.
rigide. Il joue un rôle crucial dans de nombreuses applications robotiques telles que la loca-
lisation et le mappage simultanés (SLAM), la reconstruction de surface et l’étalonnage des
capteurs inertiels. Ce problème est bien étudié dans la littérature .
Parmi les solutions proposés on peut citer la méthode SVD[32] qui se base sur la décom-
position en valeurs singulières d’une matrice calculée en utilisant la représentation standard
des transformations.
+
Figure IV.1 – Exemple simplifié SVD
La recherche de la matrice de transformation rigide optimale peut être décomposée en plu-
sieurs étapes :
1. Trouvez les centroïdes (centre de masse) des deux jeux de données A et B :
centroïdA =
1
N
×
N
i=1
Pi
A, avecP = (x, y, z) (IV.5)
de même pour centroïdB de l’ensemble de points B
2. En utilisant les vecteurs de centre de masse, caler les centroïdes des deux ensembles de
points à l’origine, puis trouver la rotation optimale (matrice R) :
La méthode la plus simple est d’utiliser la décomposition de valeur singulière (SVD), car
cette fonction est largement disponible dans de nombreux langages de programmation
(Matlab, Octave, C avec LAPACK, C ++ avec OpenCV...). SVD est une puissante baguette
magique en algèbre linéaire pour résoudre toutes sortes de problèmes numériques. Il
suffit de savoir que le SVD va décomposer une matrice E en 3 autres matrices, telles
31

40. CHAPITRE IV. ETUDES BIBLIOGRAPHIQUES SUR LE RECALAGE I.C.P.
que :
SV D(E) = [U, S, V ]
tel que
E = USV T
(IV.6)
Sachant que E pourrait être la matrice de représentation des deux ensembles de points
suivants, chaque point ∈ R3
• N1 = {P1, ..., Pnp}
• N2 = {Q1, ..., Qnq}
A étant la matrice représentative de N1 et B étant la matrice représentative de N2 ,
E = ABT
∈ R3x3
, la construction se faisant avec le même nombre de points dans
chaque nuage c.a.d que np = nq.
L’étape suivante consiste à accumuler une matrice, appelée H, et à utiliser SVD pour
trouver la rotation comme suit :
H =
N
i=1
(Pi
A − centroïdA)(Pi
B − centroïdB)T
(IV.7)
SV D(H) = [U, S, V ]
R = V UT
3. Trouver la translation t
t = −R × centroidA + centroidB (IV.8)
IV.2 L’algorithme ICP et ses variantes
Le premier algorithme ICP a été proposé par Paul Besl et Neil McKay dans un livre, désor-
mais célèbre, paru en 1992 dans IEEE Transactions on PAMI.
Depuis cette publication, différentes versions de l’algorithme ont été publiées soit, pour
accélérer les performances de l’algorithme, soit pour améliorer l’exactitude des informations.
Théoriquement, le principe de l’algorithme ICP présenté est le suivant :
• Élection de l’ensemble des points
32

41. CHAPITRE IV. ETUDES BIBLIOGRAPHIQUES SUR LE RECALAGE I.C.P.
• Effectuer un échantillonnage en associant, deux à deux, les points homologues d’un
nuage à l’autre,
• Pondération éventuelle des paires correspondantes
• Rejeter des paires pour éliminer les valeurs aberrantes,
• Affectation d’un seuil d’erreur, critère de convergence,
• La réduction de l’erreur de manière itérative.
Chaque étape de l’algorithme peut être réalisée d’une façon différente, d’où la richesse de
l’algorithme ICP et, également, l’une des explications de l’existence de plusieurs variantes de
ce dernier.
L’étape de la sélection des points du nuage
Cette étape d’initialisation diffère d’une variante à un autre. En effet, la sélection se fait en
prenant en considération soit :
• Tout le nuage de points
• Un échantillonnage linéaire 1 point sur n (n à définir dans [1,10] par exemple)
• Un échantillonnage aléatoire selon une loi uniforme
• une sélection des points avec une distribution de la normale à ces points soit la plus
élevés, ce qui évite une sélection de points appartenant à une même surface plane,
Pour l’échantillonnage normal la structure changeante de relief (même modeste)peuvent
jouer un rôle critique. Par ailleurs, la distribution selon la normale est simple, consommation
basse mais sa robustesse est faible ( Converge parfaitement que dans des nuages sans cour-
bures).
Ainsi, l’échantillonnage d’un seul des deux nuages de points n’a pas un effet considérable,
même si on permute les rôles des nuages, sur la convergence de l’algorithme car cette stratégie
d’échantillonnage de l’algorithme ICP préserve sa commutativité (Secret-key algorithm ).
Bruit + Distorsion + échantillons réduits = Mauvais résultats
En conclusion, un échantillon très dense et non bruité est le meilleur choix pour cette étape.
En effet, nous préservons toujours la densité d’un nuage dans cette opération commutative.
33

42. CHAPITRE IV. ETUDES BIBLIOGRAPHIQUES SUR LE RECALAGE I.C.P.
L’étape de l’appariement des points homologues
Les différentes façons, de conduire cette étape, étudiées dans la littérature sont :
• Faire correspondre à chaque point de nuage échantillonné le point le plus proche dans
l’autre nuage.
• Exécuter un tir normal à la surface induite par le point et ses voisins.
• Assurer un étalonnage inverse.
• Trouver des compatibilités complémentaires avec le point source ( il faut une caracté-
ristique autre que les coordonnées géométriques telle que la couleur ou l’intensité de
l’écho), dans le cas de nos travaux nous ne disposons, pour un point, que de ses seules
coordonnées dans R3
.
La solution la plus répandue pour cette étape de recherche et classification de cette étape c’est
un recours à l’algorithme Kd-tree afin de parcourir rapidement les nuages dont les points
sont classés dans des arbres binaires selon des critères spatiaux, ceci permet de minimiser la
complexité des opérations en O(n lg n) contre O(n2
).
Définition 5 (kd-tree). L’algorithme Kd-Tree s’appuie sur une structuration
des données par une partition binaire récursive de l’espace permettant ainsi
de stocker des points en les rattachant à un arbre binaire. Ceci permet de faire
des recherches (recherche par plage, plus proche voisin, etc.) plus rapidement
qu’en parcourant linéairement le tableau de points. Les arbres k-d sont des
cas particuliers d’arbres BSP (binary space partition trees).
Cette structure a été proposée par Jon Louis Bentley de l’Université Stanford
en 1975.
L’algorithme kd-tree, peut être utilisé avec chaque variante de l’étape. Cependant, le kd-
tree avec la technique de recherche du plus proche n’est efficace qu’avec des nuages de points
présentant un minimum de courbures comme c’est illustré dans la figure suivante.
34

43. CHAPITRE IV. ETUDES BIBLIOGRAPHIQUES SUR LE RECALAGE I.C.P.
Figure IV.2 – (a) Le point le plus proche - (b) Tir normal
Pondération
Il existe plusieurs possibilités, citons :
• Pondération constante
• Pondération inférieure pour les points ayant une distance point à point plus élevée
Poids = 1 −
distance(P1P2)
distance_maximale
(IV.9)
• Poids basé sur la compatibilité de la normale
Rejet de points
Il s’agit des points identifiés comme aberrants, à savoir :
• Distance (paire de points) > distance donnée
• Les n % pires paires basées sur une métrique( par exemple n=10)
• Paire où l’un des deux points n’est pas compatible avec son voisin ( couleur , intensité
,etc..)
• Paires sur les limites du nuage. C’est à dire passer d’un état (a) à un état (b) comme le
montre la figure ci-dessous.
35

44. CHAPITRE IV. ETUDES BIBLIOGRAPHIQUES SUR LE RECALAGE I.C.P.
Figure IV.3 – Paires sur les limites du nuage
Minimisation de l’erreur
Cette étape est très intéressantes et il y a plusieurs stratégies pour la passer :
• Pour l’estimation de la transformation on peut utiliser :
– la décomposition matricielle en valeur singulière,
– les quaternions,
– les matrices orthogonales.
• Pour la minimisation de l’erreur il y a les méthodes :
– Point à point
– Point à plan
36

45. Chapitre V
Réalisation et test
Introduction
Ce chapitre est consacré à l’étape de réalisation et test. Il a pour objectif de présenter et tester
les limites des algorithmes déjà implémentés dans certaines librairies et de les comparer avec
nos propositions de code. Nous présentons l’environnement de développement et les librairies
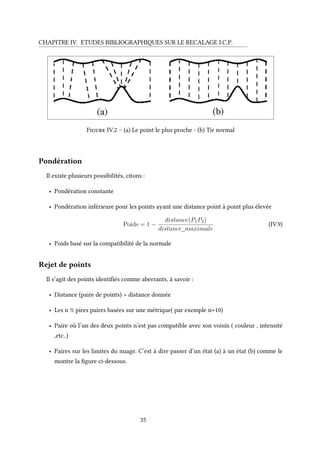
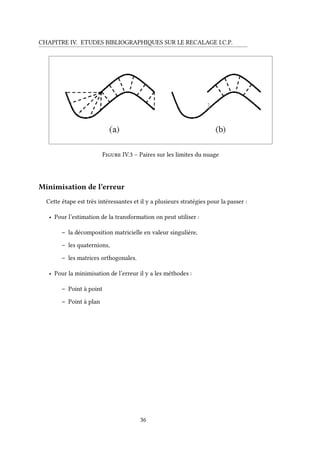
adoptées. Nous allons ensuite montrer quelques courbes illustrant la performance d’exécution
et notamment la vitesse de convergence des algorithmes.
V.1 L’algorithme ICP dans la librairie Open3D
Open3D est une bibliothèque libre de droits qui prend en charge le développement rapide
de logiciels traitant des données 3D. Sa mise en oeuvre s’appuie sur le "notebook" JUPYTER.
Ce cadriciel est hautement optimisé et configuré pour la parallélisation.
Cette libraire propose deux variantes de l’algorithme ICP, la première se base sur "point-
to-point ICP" et la deuxième sur the point-to-plane ICP [Rusinkiewicz2001].
V.1.1 Open3d : Point-to-point ICP
En général, l’algorithme ICP itère sur deux étapes comme nous l’avons précisé dans le cha-
pitre précédent, à savoir :
• Trouver un ensemble de correspondance K = {(p, q)} à partir du nuage de points cibles
P et du nuage de points source Q transformé avec la matrice de transformation initiale
T.
• Mettre à jour la transformation T en minimisant une fonction E(T) définie sur l’en-
semble de correspondance K.
37

46. CHAPITRE V. RÉALISATION ET TEST
Dans ce cas "Point-to-point ICP" proposé par Besl et McKay en 1992 [réf article] la fontion
E(T) est comme suit :
E(T) =
(p,q)∈k
p − T × q 2
(V.1)
La transformation T est composée d’une matrice de rotation 3∗3 et d’un vecteur de transla-
tion. Donc, la classe développée TransformationEstimationPointToPoint, avec Open3D, fournit
des fonctions permettant de calculer les matrices résiduelles et jacobiennes de l’objectif. Par
défaut, registration_icp s’exécute jusqu’à la convergence ou atteint un nombre maximal d’ité-
rations (30 par défaut). Ce paramètre peut être modifié pour offrir plus de temps de calcul et
améliorer ainsi les résultats.
Figure V.1 – État initial avant le recalage Point-to-point ICP
Nous observons dans la figure ci-dessus, notre greffon implémenté avec le langage Python
et qui utilise l’état initial d’Open3D avant l’exécution de l’algorithme de recalage point-to-
point ICP. Les fichiers de nuages de points source et destination ont comme extension *.pcd.
Pour les paramètres d’entrée de notre algorithme, nous avons fixé le seuil de convergence
à 0.02 et le nombre maximale d’itérations à 30, sans application d’une transformation initiale.
Le nuage en rouge est la source (celui à recaler) et celui en bleu c’est le nuage de destination
(le nuage de référence).
38

47. CHAPITRE V. RÉALISATION ET TEST
Dans la figure ci-dessous, nous montrons le résultat de l’algorithme sur deux petits nuages
synthétiques de test.
Figure V.2 – Résultat du recalage Point-to-point ICP
Le nuage de points recalé est en vert.La couleur bleue est propre au nuage de référence.
V.1.2 Open3d : Point-to-plane ICP
L’algorithme Point-to-plane ICP [ChenAndMedioni1992] utilise une fonction E(T) sui-
vante (formule V.2), différente de l’algorithme Point-to-point ICP (formule V.1).
E(T) =
(p,q)∈k
((p − T × q) −
−−→
np )2
(V.2)
Avec l’utilisation
−−→
np la normale du point p, dans l’expression E(T) à minimiser, l’article
[Rusinkiewicz2001] a montré que l’algorithme ICP point à plan a une vitesse de convergence
plus rapide que l’algorithme ICP point à point.
Dans Open3D, l’appel de cet algorithme se fait aussi avec registration_icp mais en appelant
la classe d’estimation TransformationEstimationPointToPlane.
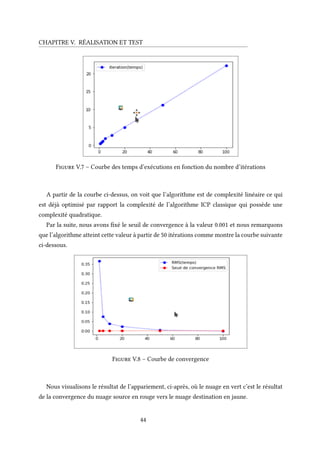
Ainsi, nous avons appliqué les deux différents algorithmes sur des jeux de données de 198835
points pour le nuage source et 137833 pour le nuage destination, trouvés dans les données de
39

48. CHAPITRE V. RÉALISATION ET TEST
test de la librairie.
Ci-dessous la figure de l’état initial des deux nuages de points source et destination avant
l’application du deuxième algorithme Point-to-plane.
Figure V.3 – État initial avant le recalage Point-to-plane ICP
Après avoir appliqué l’algorithme Point-to-plane avec notre outil, 30 itérations était suf-
fisantes pour que notre nuage source de point converge avec un ensemble de points corres-
pondants égal à 123471 points. Cependant, il avait besoin de 144 itérations avec l’algorithme
Point-to-point pour qu’il converge et pour qu’on obtient la matrice de transformation adéquate
pour reproduire presque le même nombre de points correspondants.
La figure ci-dessous montre ces résultats de convergence.
40

49. CHAPITRE V. RÉALISATION ET TEST
Figure V.4 – Résultat du recalage Point-to-plane ICP
V.2 L’algorithme ICP dans la librairie VTK
VTK est un logiciel libre destiné à l’infographie 3D, le traitement d’image et la visuali-
sation. Il se compose d’une bibliothèque de classes C ++ et de plusieurs couches d’interface
interprétées, y compris en Java et Python. VTK supporte une grande variété d’algorithmes
de visualisation, y compris les méthodes scalaires, vectorielles, tensorielles, volumétriques et
volumétriques, ainsi que des techniques de modélisation avancées telles que la modélisation
implicite, la réduction polygonale, le lissage, la découpe et la triangulation Delaunay. En addi-
tion, il propose dans sa bibliothèque un algorithme ICP.
V.2.1 Adaptation de l’outil à l’algorithme ICP de VTK
L’implémentation d’ICP dans VTK se base sur la minimisation d’erreur au sens des moindres
carrés pour obtenir un meilleur appariement après un certain nombre d’itérations.
La figure ci-dessous montre l’état initial de l’utilitaire basé sur VTK. Les entrées de trai-
tement sont des fichiers de *.LAS. Le nombre maximum d’itérations doit être fixé avant de
procéder à l’application de l’algorithme.
41

50. CHAPITRE V. RÉALISATION ET TEST
Figure V.5 – Etat intial d’utilitaire ICP basé sur VTK
Nous avons utilisé l’environnement conda pcp-env "point cloud processing" préparé initia-
lement par Open3D. C’est un environnement dédié au traitement de nuage de points et qui
regroupe un ensemble de librairies très utiles citons PDAL et JSON que nous avons exploités
pour la lecture et l’écriture rapide des données géométriques dans les fichiers *.LAS. Par rap-
port à l’utilitaire basé sur Open3D, nous avons ajouté l’exportation du fichier résultat sous
l’extension *.LAS.
42

51. CHAPITRE V. RÉALISATION ET TEST
Figure V.6 – Résultat de l’utilitaire ICP basé sur VTK
La figure ci-dessus montre le résultat de l’appariement des nuages de points de test. La
section en bas est un affichage de trace pour chaque étape effectuée par l’utilisateur. Ainsi,
nous visualisons la distance moyenne et le temps d’exécution d’ICP à l’issue de la procédure
de traitement.
V.2.2 ICP VTK test de performance et de convergence
Cette partie est consacrée à tester la robustesse de l’algorithme ICP implémenté dans la
librairie VTK. Donc, pour commencer nous avons effectué une acquisition avec LIDAR au
BusinessLab à l’IMERIR pour avoir des nuages de points de test. Puis, nous avons utilisé notre
plugin CloudCompare (cf. chapitre III) pour l’extraction de deux nuages source et destination
de tailles 30 780 points et 38 955 points respectivement.
43

52. CHAPITRE V. RÉALISATION ET TEST
Figure V.7 – Courbe des temps d’exécutions en fonction du nombre d’itérations
A partir de la courbe ci-dessus, on voit que l’algorithme est de complexité linéaire ce qui
est déjà optimisé par rapport la complexité de l’algorithme ICP classique qui possède une
complexité quadratique.
Par la suite, nous avons fixé le seuil de convergence à la valeur 0.001 et nous remarquons
que l’algorithme atteint cette valeur à partir de 50 itérations comme montre la courbe suivante
ci-dessous.
Figure V.8 – Courbe de convergence
Nous visualisons le résultat de l’appariement, ci-après, où le nuage en vert c’est le résultat
de la convergence du nuage source en rouge vers le nuage destination en jaune.
44

53. CHAPITRE V. RÉALISATION ET TEST
Figure V.9 – Appariement après 50 itérations
V.3 Maquettes ICP Basique et ICP parallèle
V.3.1 ICP : Implémentation séquentielle
L’implémentation de la maquette en Annexe est développée sur Jupyter Notebook via le
langage de programmation Python et en utilisant la librairie Numpy. En outre, cette implé-
mentation est basée sur la programmation orientée objet. Essentiellement une classe mère qui
regroupe les méthodes et les attributs communs entre les classes filles prévues basiques et
parallèles.
Algorithm 1 Algorithme ICP basique
Donnée : source, destination nuages de points
Résultat : res nuage résultat
Début ICP
initialiser res = source
Tant que le nuage res est proche de la destination
Pour chaque point pi dans res, on cherche le point le plus proche qi dans destination.
Empiler les qi dans un nouveau nuage de points cible.
Calculer la transformation R, T entre res et le nuage cible.
Appliquer la transformation calculée sur le nuage res afin de le mettre à jour.
fin Tant que
fin ICP
Nous constatons que la limites de cet algorithme décrit au dessus c’est le nombre de com-
45

54. CHAPITRE V. RÉALISATION ET TEST
paraisons qui augmente exponentiellement en fonction du nombre de points dans les nuages.
La méthode de la comparaison de distance pour chercher le point le plus proche est très gour-
mande en temps de calcul.
En conséquence, l’exploitation de la parallélisation sur GPU, pour optimiser le temps de calcul
de la recherche des points les plus proche, est indispensable.
V.3.2 ICP : Implémentation paralléle
Cette sous section détaille la méthode parallèle de l’algorithme ICP en utilisant PyCUDA
qui est une API Python pour accéder au calcul parallèle sur la carte GPU CUDA fournie par
Nvidia.
Par observation, chaque point du nuage de points source l’algorithme calcule sa distance
euclidienne avec tous les points de la destination et cela pour chaque itération. Puis, on sé-
lectionne les points avec la distance minimale. Par conséquent, la partie CUDA est conçue en
trois parties :
1. Initialisation : Charger le nuage de points destination dans la mémoire globale de l’en-
vironnement CUDA, de sorte que chaque thread puisse y accéder sans copie inutile.
2. Trouver la correspondance : La fonction réelle pour trouver le point de correspondance
(point homologue) dans destination pour un seul point dans source, enregistrer le cor-
respondant dans le nouveau nuage res, et afficher la distance minimale.
3. Réduction : ressembler les distances totales calculées par chaque thread. Cette valeur est
utilisée pour déterminer si le seuil est atteint et si la boucle doit être terminée ou non.
46

55. Chapitre VI
Le recalage par caractéristiques
étendues
Introduction
Comme nous venons de le voir dans les chapitres précédents, l’I.C.P. rencontre des dif-
ficultés de convergence , en effet il lui est donné insuffisamment d’indices pour faciliter la
construction, réponse que tente d’apporter les variantes. Une autre tendance apparaît, la vo-
lonté de caractériser le nuage de points. Ainsi des axes de recherche travaillent sur des défini-
tions d’attributs de caractérisation, le triptyque de base reste :
• le point,
• la ligne,
• le plan.
Cependant, partant du point élémentaire ou l’homologue n’est pas toujours identifiable
dans le nuage à associer au nuage de référence on travaillera sur des amas locaux assimilables
à des amers, dont on trouve les homologues d’un nuage de points à l’autre. Concernant la
ligne, il s’agit, pour calculer nos paramètres de transformation, d’identifier deux lignes non
colinéaires dans le nuage de référence et de retrouver leurs homologues dans le nuage à trans-
former, en respect de contraintes que l’on présentera plus tard. Un plan identifié dans le nuage
de référence avec son homologue dans le nuage à transformer c’est une grande richesse d’infor-
mation, de nombreux vecteurs, des normales. Les recherches en cours s’intéressent également
à des formes plus complexes, la sphère, le cylindre.
Aussi le recalage d’un nuage de points LIDAR est d’autant plus précis qu’il pourra prendre
en compte plusieurs caractéristiques, de ce nuage de points à recaler, également identifiable
dans le nuage de référence.
Le recalage («registration») de nuage de point est une opération couramment nécessaire
dans les chaînes de traitement. En effet une campagne de mesures sur un site nécessite plu-
sieurs relevés indépendants. Une autre situation courante est la volonté d’accroître la densité
47

56. CHAPITRE VI. LE RECALAGE PAR CARACTÉRISTIQUES ÉTENDUES
des points sur une zone donnée. Ces divers relevés, tout en ayant des zones communes, peuvent
être effectués selon :
• des points de vue (référentiel instrument) distincts,
• des échelles (distance de la prise de vue) différentes,
ce qui complexifie d’autant les recalages de deux nuages de points. Les points ou échos en
retour sont positionnés dans le référentiel de l’instrument de mesure, suite à sa calibration
et le positionnement des référentiels initiaux n’est pas nécessairement le même si toutes les
précautions ne sont pas prise dans ce sens.
Ainsi des points ou objets homologues d’un nuage à un autre peuvent être positionnés
dans deux référentiels, ayant subi translation et rotation l’un par rapport à l’autre. Le recalage
nécessite d’être en capacité d’évaluer cette translation et cette rotation. Cette évaluation sera
d’autant plus aisée que nous trouverons des homologies entre le nuage de référence et le nuage
à recaler.
Mais divers travaux ont mis en évidence l’obtention de recalages d’autant meilleurs que
plusieurs caractéristiques du nuage de points, sont sollicités pour la conduite de cette opé-
ration. Nous les passons rapidement en revue en nous appuyant sur [7] afin de dégager des
priorités dans la maîtrise de leur mise en œuvre.
Des propositions sont faites pour utiliser toutes géométries (lignes, points, plans) de zones
homologues, d’un nuage de point à l’autre, faisant office d’amers en quelque sorte. Cepen-
dant cette maîtrise nécessite une gradation de compétences, sachant que toutes extractions de
caractéristique requièrent des démarches spécifiques.
Afin d’éliminer les inconsistances d’un nuage de point à l’autre toute une méthodologie doit
être mise à l’œuvre et ceci est crucial si on cherche de la qualité (précision) dimensionnelle. Le
processus de recalage doit pouvoir répondre à quatre problématiques [15] :
• l’extraction de primitives géométriques, points remarquables, des lignes, des plans,
les structures géométriques basique (cylindres, sphères, polygône)
• l’estimation de la meilleure transformation géométrique, associant rotation, trans-
lation, mise à l’échelle, afin d’établir la meilleure correspondance possible entre homo-
logues dans deux nuages de points,
• la mesure et la qualification de la mise en correspondance des homologues de
deux nuages,
• l’adoption de la bonne stratégie de mise en correspondance.
48

57. CHAPITRE VI. LE RECALAGE PAR CARACTÉRISTIQUES ÉTENDUES
VI.1 Parcours bibliographique sommaire
Même si nos avions quelque peu connaissance des limites (convergence ou non, temps de
calcul) de l’ICP classique EXAMETRICS y est confronté tous les jours en production à son
bureau d’études, les lectures le confirmaient, il était nécessaire d’acquérir les fondamentaux
afin d’aller plus loin. L’objectif de l’entreprise est de s’approprier les technologies et les algo-
rithmes de traitement, le passage par les fondamentaux est nécessaire.
Afin d’identifier les axes de travaux à venir des compléments bibliographiques nous aident
à éclairer le paysage afin de cerner l’état d’avancement des nouvelles approches du recalage
ou des extensions apparaissant dans la famille des algorithmes ICP déjà très peuplée. Nous en
donnons ci-après un résumé très sommaire et un approfondissement sera nécessaire.
VI.1.1 Notes de lecture : EFFICIENT VARIANT OF ICP
Szymon Rusinskiewicz Marc Levoy Standford university [8]
L’algorithme I.C.P. est connu pour une large utilisation dans le recalage de nuage de points
par rapport à une référence, quand la position initiale du nuage à recaler est connue et qu’il
possède une zone commune avec le nuage de référence.
Les variantes de l’ICP peuvent intervenir dans différentes phases de l’algorithme. Dans le
cas présent nous nous calons uniquement sur la géométrie. Le principe repose sur la mini-
misation de la distance entre deux groupes de points a priori homologues entre le nuage de
référence et le nuage à recaler. Les transformations à appliquer concernent, ses rotations, des
translations et des mises à l’échelle, voire des redressements dans le cas de dérive de certaines
mesures géométriques. mais on s’intéresse à des surfaces homologues que l’on tente d’appai-
rer.
Disposer d’une transformation initiale qui diminue la distance initiale est un facteur positif
d’amélioration de la convergence. En absence de celle-ci, la convergence est fortement liée à
la qualité de l’estimateur initial. Cet estimateur peut être apprécié selon diverses méthodes :
• utilisation de la trajectoire du scanner,
• recherche de caractéristiques de surface,
• signatures de surface par spin de nuage par analogie avec le spin d’image.
49

58. CHAPITRE VI. LE RECALAGE PAR CARACTÉRISTIQUES ÉTENDUES
VI.1.2 Notes de lecture : A ROBUST LINEAR FEATURES-BASED RE-
GISTRATION
Les balayage multiple de zone enrichit la densité des nuages de point et évite l’occultation
de certaines parties. La difficulté étant d’assurer le calage correct des zones se chevauchant
dans un système commun de coordonnées. [10]
Il est adopté un enregistrement fin et un enregistrement grossier tous deux basés sur la
reconnaissance de caractéristiques géométriques. Un algorithme Ransac identifie un triplet de
lignes, dans un nuage de points. Les lignes homologues sont recherchées dans le second nuage.
Il existe des méthodes de recalage rigides et non rigides :
• mise en correspondance de caractéristiques géométriques (points, lignes, plans, sphère,
cylindre), sous réserve de trouver les éléments adaptés dans la scène dont le filtrage est
coûteux et de disposer de règles de description de formes particulièrement pertinentes,
• passage par un maillage et détection de surfaces homologues locales,
• passage par la gestion des points mettant généralement en œuvre l’algorithme ICP, qui
malgré sa popularité et la diversité de ses variantes, se heurte au nombre d’itérations
nécessaires et la non assurance de sa convergence, vu que le calcul de ses paramètres de
transformation se fait pas à pas. Les recherches actuelles s’orientent vers une première
étape grossière permettant d’initialiser au mieux la phase de démarrage de l’algorithme
ICP sollicité.
Donc 4 problèmes à traiter :
• extraction des primitives géométriques, en disposant de descripteurs de forme perti-
nents,
• trouver les paramètres de transformation,
• trouver des critères de similarité pour associer les éléments homologues d’un nuage de
points à l’autre, afin de les faire coïncider,
• définir une stratégie de convergence.
En zone urbaines, les lignes sont plus faciles à trouver, intersection de plans. Il faut noter le
développement du cadriciel du «Robust Line Matching & Registration, RLMR» qui est décrit.
Survol ICL (Iterative Closest Line), par analogie avec ICP seule la matrice de rotation est
prise en compte. Autre approche pour le calcul de la translation. ici pour la recherche de la
50

59. CHAPITRE VI. LE RECALAGE PAR CARACTÉRISTIQUES ÉTENDUES
transformation d’Helmert, la contrainte est qu’il faut que les extrémités de segment soient
des points homologues du nuage de référence au nuage à recaler, l’échelle est identique (on
s’installe dans le même volume d’observation [cube ou parallélépipède].
VI.1.3 Notes de lecture : FEATURE-BASED REGISTRATION
Note : en faire un document de référence même si il date, c’est une piste de solution.
[7] Avant tout recalage de nuage de points, ces derniers doivent être repositionnés, si ce
n’est le cas, dans un référentiel commun. Les paramètres de transformation (rotation, trans-
lation et mise à l’échelle) doivent être définis. A cette fin les propriétés des caractéristiques
géométriques homologues sont analysées statistiquement afin d’évaluer les transformations
nécessaires à opérer. C’est ce qui est conduit dans la présente proposition
Connu comme premier outil de recalage, bénéficiant de certaines améliorations, l’algo-
rithme ICP a largement occupé la scène du recalage avec une promotion excessive. Trouver
des points homologues d’un nuage à un autre, sauf amers bien spécifiques, reste difficile. Des
tentatives sont conduites entre courbes/lignes identifiées entre deux nuages et la minimisation
de leur distance à leur plan d’appartenance. D’autres tentatives en création d’image raster (z
en paramètre) sont conduites. La qualité du recalage reste faible.
En scènes urbaines, le point, la droite et le plan ont la priorité des recherches en cours.
Néanmoins l’hypothèse d’homologie point à point est à rejeter, tout au plus peut-on envisager
de rechercher des zones locales sous-jacentes de surface (minimisant la distance points/surface
au sens des moindres carrés) et pouvant coïncider d’un nuage à l’autre.
Cependant en travaillant les caractéristiques suivantes :
• points,
• lignes,
• surfaces,
il est possible d’aboutir à une paramétrisation de la transformée d’Helmert. En trouvant, au
minimum 3 points homologues de manière manuelle il est possible de définir :
• les termes de la matrice de transformation,
• le facteur d’échelle,
• le vecteur de translation.
51

60. CHAPITRE VI. LE RECALAGE PAR CARACTÉRISTIQUES ÉTENDUES
Concernant les lignes, il est nécessaire d’avoir une colinéarité entre les deux lignes homo-
logues.
VI.1.4 Note lecture : ALTERNATIVE METHODOLOGIES FOR LIDAR
CALIBRATION
[14] Deux approches sont toujours privilégiées pour le recalage de deux nuages de points
de mesures sur des zones communes :
• une approche calée sur l’instrumentation, prenant en compte ses dérives (corrigées par
une transformation géométrique), et respectant une mise en œuvre stricte de la procé-
dure de mesure,
• une approche calée donnée, essayant de reconstituer la géométrie commune aux deux
nuages de points en s’affranchissant du bruit de mesure ou de la redondance des données.
Fondamentalement cet article revient sur les écarts géométriques, entre deux campagnes
de mesures, induit par la calibration des instruments et notamment la position des référentiels
de mesures au moment de l’acquisition à des moments différents. Ceci engendre déjà les écarts
systématiques qu’il nous faut retirer, sans oublier l’échelle ou la distance de la prise de mesure.
Deux procédures de recalage sont abordées :
• la méthode simplifiée n’utilise que les données géométriques, parfaitement représen-
tatives des données mises à disposition par le LIDAR, il faut estimer les écarts géomé-
triques entre les deux zones communément chevauchées, sous réserve qu’il n’y ait pas de
dérive intrinsèque de l’instrument de mesure, en prenant la précaution de la correction
minimale suite à des passages multiples sur une même zone.
• la méthode rigoureuse exige en outre la connaissance de la trajectographie de l’instru-
ment de mesures, et elle met en évidence le poids des erreurs du écarts entre les réfé-
rentiels de navigation. Considérant que l’identification de points homologues est im-
possible, cette méthode s’appuie sur un maillage à base de réseau de triangles irrégulier
(T.I.N.) dont la normale à la surface est estimée et il est procédé à la recherche du triangle
(le plus homologue) en utilisant la matrice de variance-covariance dans le second nuage,
sur les triangles d’une zone locale et l’évaluation de l’écart angulaire entre les normales
du triangle initial du premier nuage et le triangle sélecté dans le second.
52

61. CHAPITRE VI. LE RECALAGE PAR CARACTÉRISTIQUES ÉTENDUES
Les deux approches nécessitent une construction du paramétrage de correction en tra-
vaillant sur des zones locales pour leur estimation.
VI.1.5 Fiche lecture de : MULTI-FEARURED REGISTRATION
[15] Par l’apport immédiat des trois dimensions, la mesure par LIDAR supplante peu à peu
les apports de la photogrammétrie. Cela est vrai tant pour les lidar satellitaires, aéroportés
ou terrestres mobiles. Cependant l’extraction de l’information dimensionnelle d’un nuage de
points LIDAR est d’autant plus précise qu’elle peut prendre en compte plusieurs caractéris-
tiques de ce nuage de points.
Le recalage («registration») de nuage de point est une opération couramment nécessaire
dans les chaînes de traitement. En effet, une campagne de mesures sur un site nécessite plu-
sieurs relevés indépendants. Ces derniers tout en ayant des zones communes peuvent être
effectués selon :
• des points de vue (référentiel instrument),
• des échelles (distance de la prise de vue),
distincts, ce qui complexifie d’autant les recalages de deux nuages de points. Les points ou
écho en retour sont positionnés dans le référentiel de l’instrument de mesure.
Ainsi des points ou objets homologues d’un nuage à un autre peuvent être positionnés
dans deux référentiels, ayant subi translation et rotation l’un par rapport à l’autre. Le recalage
nécessite d’être en capacité d’évaluer cette translation et cette rotation.
Mais divers travaux ont mis en évidence l’obtention de recalages d’autant meilleurs que
plusieurs caractéristiques du nuage de points, sont sollicités pour la conduite de cette opéra-
tion. Nous les passons rapidement en revue en nous appuyant sur [[7] afin de dégager des
priorités dans la maîtrise de leur mise en œuvre.
Des propositions sont faites pour utiliser toutes géométries (lignes, points, plans) de zones
homologues, d’un nuage de point à l’autre, faisant office d’amers en quelque sorte. Cepen-
dant cette maîtrise nécessite une gradation de compétences, sachant que toutes extractions de
caractéristique requièrent des démarches spécifiques.
Afin d’éliminer les inconsistances d’un nuage de point à l’autre toute une méthodologie doit
être mise à l’œuvre et ceci est crucial si on cherche de la qualité (précision) dimensionnelle.
Il existe une véritable panoplie de solutions en matière de recalage et d’agrégation de nuage
de points :
53

62. CHAPITRE VI. LE RECALAGE PAR CARACTÉRISTIQUES ÉTENDUES
• L’algorithme I.C.P. est le plus communément utilisé avec de nombreuses variantes, compte
tenu des résultats souvent insatisfaisants :
– ICP avec calibration,
– ICP en projection point/point,
– ICP en recherche d’appariement de surfaces,
• d’autres méthodes calées sur l’identification de caractéristiques précises, groupe de points,
lignes, surfaces, formes géométriques, dont on recherche la superposition stricte,
• d’autres méthodes relevant de l’imagerie (géométrie 2D) après projection sur des plans
dans le triède de référence ont été également abordées, ainsi que l’utilisation de la trans-
formation de caractéristiques 2D à invariance d’échelle (SIFT),
• les axes de recherche actuelle s’orientent peu à peu vers la reconnaissance de forme,
la reconnaissance d’objet 3D, l’analyse de forme d’histogramme et la construction de
descripteur locaux de surface en s’appuyant sur divers outils de classification fournis
par l’apprentissage profond.
Bien que les travaux de la présente note porte sur l’I.C.P qui reste malgré ses imperfections
capable d’agréger une paire de nuages de points, nous effectuons néanmoins un survol des
autres approches, notamment celles basées sur les recherches de caractéristiques géométriques
homologues d’un nuage à l’autre. Le processus de recalage doit pouvoir répondre à quatre
problématiques :
• l’extraction de primitives géométriques, points remarquables, des lignes, des plans, les
structures géométriques basique (cylindres, sphères, polygône)
• estimer le meilleure transformation géométrique, associant rotation, translation, mise
à l’échelle, afin d’établir la meilleure correspondance possible entre homologues dans
deux nuages de points,
• trouver une mesure de la qualité de la mise en correspondance des homologues de deux
images,
• adopter la bonne stratégie de mise en correspondance.
Ces approches sont rassemblées dans le concept RSTG (Rotation, Scale (mise à l’échelle),
Translation, et compatibilité géométrique). Les auteurs étudient un schéma de transformation
de lignes, an ayant au moins deux lignes homologues d’un nuage de points à un autre.
54

63. CHAPITRE VI. LE RECALAGE PAR CARACTÉRISTIQUES ÉTENDUES
A l’issue de la transformation, l’objectif est de minimiser l’écart entre les primitives du
nuage de référence et celles du nuage transformé. l’opération est conduite sur droite et sur
plan.
VI.1.6 lecture de : Georeferenced Point Clouds : A Survey of Features
and Point Cloud Management
[6] Ce document parcourt les caractérisation possibles de nuages de points, ainsi que les
choix de traitement adoptés, selon les caractéristiques de ce même nuage de points. Un nuage
de points se caractérise par une organisation non structuré de points géolocalisés dans un
repère 3D et avec des frontières relativement peu définies. En général, chaque point peut avoir
d’autres attributs : intensité, normale, couleur, heure d’acquisition (nx; ny; nz; z; r; g; b;
nIR; T). Ceci n’est pas le cas dans les nuages traités chez EXAMETRICS. La notion d’échelle
n’existe pas a priori, mais la recherche d’éléments homologues doit se faire dans une même
zone géométrique et selon les modalités d’acquisition des nuages, la densité de points peut
varier fortement d’un nuage à l’autre, pour une même zone géométrique.
Dans le cas présent l’acquisition d’un écho unique (le premier) fournit ses coordonnées et
l’heure d’acquisition. Nous disposons uniquement de la position géométrique du point et de
son heure d’acquisition, en temps normé (pour les fichiers *.las).
Toutes autres caractéristiques (primitives géométriques) , ne peuvent être construite que
par calcul issus des données précédentes :
• lignes et droites,
• normales à des surfaces locales,
• plans,
• formes géométriques élémentaires.
VI.1.7 Note de lecture : STRIP ADJUSTMENT USING CONJUGATE PLA-
NAR AND LINEAR FEATURES
[5] Partant du principe qu‘il n’est pas possible de trouver de manière native, des points
homologues dans des zones de chevauchement de de deux nuages de points distincts, la pré-
sente méthode développe l’identification locale de plans et de droites dont l’homologie (au
sens morphologique du terme) est identifiable d’un nuage de points à l’autre, ceci permettant
un recalage du second nuage par rapport au premier pris comme référence.
55

64. CHAPITRE VI. LE RECALAGE PAR CARACTÉRISTIQUES ÉTENDUES
Des règles de calibration et des procédures de mesures sont fortement recommandées afin
d’avoir la meilleure reproductibilité possible. L’image complémentaire peut dans certains cas
résoudre des ambiguïtés d’identification de caractéristiques homologues d’un nuage à l’autre.
Les sources d’erreurs intrinsèques à un LIDAR sont analysées ou extrait de bibliographies.
Le vecteur de direction de mobilité (roulis, tangage, lacet) peut influer sur l’écart de mesures.
Le principe de recalage s’appuie essentiellement sur les corrections des erreurs intrinsèques à
un LIDAR.
Ce qui s’approche de notre problématique est l’extraction de primitives géométriques. En
premier lieu il est nécessaire de corriger les écarts de positionnement du référentiel de l’ins-
trument de mesure, à moins que la procédure de mesure ait pris les précautions nécessaires
pour limiter ou éviter cet écart. Sur des zones supposées homologues, on extrait les normales
sur une surface locale (calculées selon un critère RMS/LSA) , dans le référentiel de l’instrument
de mesures et on identifie l’écart angulaire éventuel entre les deux zones homologues.
Par ailleurs sans rechercher strictement des zones homologues très précises, on peut faire
l’hypothèse d’une similarité de densité d’écho dans certaines zones, notamment celles à l’in-
tersection de plan. Ainsi une analyse en composante principale peut nous donner les axes
de faibles variances et de forte variance. L’axe de forte variance donnerait l’orientation de la
droite si elle existe, les deux autres axes étant les deux autres axes orthogonaux.
56

65. CHAPITRE VI. LE RECALAGE PAR CARACTÉRISTIQUES ÉTENDUES
VI.1.8 Extensions et travaux à venir
La problématique de recalage de nuage de points est transversale à toutes les activités de
manipulation de nuage de points quelles que soient les domaines d’application et notamment
dans tout ce qui relève du domaine de la mesure dans lequel EXAMETRICS souhaite prendre
ses parts de marché. Cette maîtrise est fondamentale.
Ces travaux ont permis à la société EXAMETRICS de prendre pied, même modestement,
dans les algorithmes de recalage et d’identifier les problématiques statistiques et géométriques
auxquels il faut trouver une réponse afin d’obtenir un recalage de nuage de points satisfaisant.
Quelques algorithmes ont été mis en œuvre sur des exemples de nuages de points dont cer-
tains issus des mesures EXAMETRICS. Le point d’entrée est donné maintenant il faut pouvoir
poursuivre tout en maintenant une veille technologique opiniâtre sur le sujet. En outre, au fur
et à mesure de la production de prototype donnant quelques résultats le processus d’indus-
trialisation doit être envisagé (ré-écriture en langage C++).
Dans l’immédiat il apparaît nécessaire de s’atteler à l’identification des primitives géomé-
triques de base : - le segment (horizontal et vertical), - le plan, - les surfaces convexes, - les
coins. La maîtrise de l’ordonnancement des points s’avérera particulièrement pertinent, no-
tamment, si on souhaite mettre en œuvre de manière efficace l’algorithme S.V.D. Il s’agit de
mettre en œuvre un ou des dérivés de l’algorithme I.C.P. par l’utilisation des possibilités d’iden-
tification d’objets ou de zones homologues entre le nuage de référence et le nuage à agréger,
en s’appuyant sur une plus grande diversité de caractéristiques de ces nuages. La poursuite
des travaux chez EXAMETRICS et notamment un sujet de thèse à venir, proposé par EXA-
METRICS, y contribueront.
Concernant le processus industriel qui vient derrière pour le déploiement, sachant que l’ob-
jectif, à terme, est de mettre à disposition des clients, des processus de traitement sur des ser-
veurs distants à base de machines virtuelles multi-coeurs extensibles les précautions suivantes
sont à prendre en compte dès la maquette algorithmique :
• s’assurer de la parallélisation ("thread") possible de tous les processus itératifs lourds,
• déléguer vers des processeurs spécialisés de type CUDA ce qui est possible et pertinent,
• enfin, compte tenu de la complexité des traitements et des conflits de versions de librai-
57

66. CHAPITRE VI. LE RECALAGE PAR CARACTÉRISTIQUES ÉTENDUES
ries qui peuvent se présenter entre deux traitements distincts faisant appel aux mêmes
librairies mais à des versions distinctes, il faut dans la phase d’industrialisation envisa-
ger d’isoler certains traitements dans des conteneurs spécialisés (Type Docker/Swarm
qui est un choix) tout en gérant leur orchestration.
Ceci assurera la stabilité de fonctionnement et la performance des processus industriali-
sés, y compris sur des versions anciennes de certaines librairies, en permettant de les faire
cohabiter, au prix de la maîtrise de l’orchestration des échanges entre conteneurs , avec de
nouveaux processus fondés sur les mêmes librairies mais à des versions plus récentes. C’est
une contrainte fondamentale pour assurer, dans l’avenir, la disponibilité du service aux futurs
clients d’EXAMETRICS, sans avoir à reprendre la ré-écriture des processus industrialisés dès
que les bibliothèques de logiciel, dont ils dépendent, évoluent.
58

67. Chapitre VII
Conclusions
S
ur le plan professionnel et d’une façon générale, un stage représente sans doute
une expérience enrichissante pour chaque stagiaire indépendamment du fait
qu’il en sorte avec des satisfactions ou des déceptions, l’essentiel c’est la décou-
verte.
Sur le plan personnel, ce stage a été très enrichissant dans la mesure où il m’a permis de
bien comprendre les aspects techniques de l’acquisition et surtout les enjeux du traitement de
nuages de points LIDAR. Mais plus encore, il m’a permis d’acquérir des compétences rares et
de me familiariser avec un environnement complexe en mettant en pratique la manipulation
des nuages de points qui constitue une nouvelle thématique de recherche et de développement
très active. En effet, même si l’acquisition et les équipements associés connaissent des amé-
liorations constantes, les outils de traitement et notamment les bibliothèques de logiciel font
l’objet d’une activité très foisonnante en matière de recherche algorithmique vu la complexité
du problème, qu’il s’agisse du nettoyage des nuages de points de leur agrégation ou de l’ex-
traction de l’information qu’ils portent.
À titre d’apprentissage, il semble intéressent de mettre en évidence les questions qui se
posent autour de la manipulation des nuages de points issues d’un laser LIDAR. Ainsi, savoir
comment exploiter cette technologie moderne pour répondre, par exemple, aux attentes de
l’industrie de la construction (BIM), de l’exploitation durable de la la nature (foresterie) est
une enjeu passionnant. Au centre de ces questions, se trouvent naturellement les problèmes
de traitement de ces données massives, géolocalisées, donc en 3 dimensions. En effet, mon
stage adressait ces problématiques, plus précisément, le problème de recalage des nuages de
points. Ainsi, la particularité de ce projet réside également dans la cohabitation du domaine
mathématique et du développement informatique, qui sont liés par l’algorithmique.
En premier lieu, il est primordial de prendre connaissance, de manière permanente, de l’état
de l’art des technologies impliquées, de la physique qui les soutient, des fondations mathéma-
tiques du traitement 3D et de la construction progressive des algorithmes avec leur forces et
59

68. CHAPITRE VII. CONCLUSIONS
leur insuffisances. C’est une attitude à cultiver, que ce soit pendant la phase de mise en place de
l’environnement de développement ou durant le développement, lui même, qui peut remettre
en cause les premiers choix. Ceci nécessite de s’adapter à ses situations changeantes. +
Ainsi, Nous avons mis en exécution un greffon en C + + d’extraction d’un sous nuage dans le
logiciel libre CloudCompare. Ce fut un contact d’apprentissage très efficace de la manipulation
et de la navigation dans un nuage de point, d’un strict point de vue géométrique.
Par la suite, nous avons focalisé nos travaux sur un problème complexe de vision par ordi-
nateur qui est le problème d’agrégation de nuages distincts en cherchant les zones communes.
Nous avons dû effectuer une étude bibliographique préalable très approfondie, en déchiffrant
de nombreux articles qui existent, sur le sujet, dans la littérature spécialisée afin de découvrir
les solutions proposées, leurs forces et leur faiblesses. Les comprendre était une première dif-
ficulté à franchir, suggérer des améliorations et les implanter un véritable défi.
La phase d’implémentation, également, nécessitait la découverte de bibliothèques logicielles
très élaborées, ayant déjà une longue histoire. Découvrir, VTK, PDAL, OPEN3D et PCL était
intéressant pour comparer certains critères de performance et de convergence de ICP, l’algo-
rithme de nos préoccupations, afin de mettre en place des greffons qui utilisent ces biblio-
thèque pour améliorer ou, ambition suprême, remplacer cet algorithme. Cela nous a permis,
aussi, de faire des maquettes de l’algorithme ICP et ICP parallèle sur des technologies CUDA.
Par ailleurs et en outre le souci de parallélisation est constant, car l’objectif dans la phase in-
dustrielle est de pouvoir déployer les applicatifs, sur des serveurs distants multi-coeurs. Ceci
est d’ailleurs en cours sur d’autres travaux de développement plus avancés au sein d’EXAME-
TRICS.
Pour terminer, je souligne que c’est grâce à la société EXAMETRICS qu’il m’a été donné
l’occasion d’être le premier étudiant de notre Master 2 CHIPS, depuis sa création, à effectuer
son projet de fin d’étude dans une entreprise industrielle et commerciale de la région de Per-
pignan.
Pour cela, comme pour l’accompagnement et l’encadrement qui a été mis en place par
EXAMETRICS, je voudrais exprimer ma sincère et profonde reconnaissance à ses di-
rigeants fondateurs et à tous ceux qui travaillent pour cette entreprise, même si nous
nous sommes peu vus, à l’exception de mon encadrant direct qui assurait le relais. Nous étions
dans des locaux distincts et éloignés et leur charge de travail de production prenait l’essentiel
60

69. CHAPITRE VII. CONCLUSIONS
de leur temps. Cependant mes travaux étaient très suivis et les encouragements permanents.
61

70. Bibliographie
[1] R&D Exametrics.
Agrégation Déformation Irrégularité manipulation de nuages de points LIDAR
Cahier des charges fonctionnelles Exametrics-R&d 10 mars 2018 St Estève France
[2] Clément Matysiak Jules Malard Noé Pichot Mahdi Smida.
Rapport Projet Industriel IMERIR - Projet LIDAR - Exametrics Années 2017-2018
Promotion Dessertine Rapport final projet LIDAR Mars 2018
[3] R&D Exametrics.
Découverte Cloud-Compare Manipulation de nuages de points Cahier des charges
projet IMERIR découverte Lidar Exametrics-R&D Février 2018 St Estève France
[4] Daniel Girardeau-Montaut.
“Détection de changement sur des données géométriques tridimensionnelles”.
Thèse de doctorat de l’École Nationale Supérieure des Télécommunications, 15 Mai 2006,
Paris, France.
[5] A. F. Habib a, *, A. P. Kersting a, Z. Ruifanga, M. Al-Durgham a, C. Kim a, D. C. Lee.
Lidar strip adjustemnt using conjugate linear features in overlapping strip
• Dept. of Geomatics Engineering, University of Calgary, 2500 University Dr.
NW,Calgary, Alberta, T2N 1N4, Canada, , habib@geomatics.ucalgary.ca.
• Department of Geo-Informatics, Sejong University, Seoul, South Korea,
dclee@sejong.ac.kr
[6] Johannes Otepka , Sajid Ghuffar, Christoph Waldhauser, Ronald Hochreiter and Norbert
Pfeifer.
Georeferenced Point Clouds : A Survey of Features and Point Cloud Management
[7] J.J. Jaw*, T.Y. Chuang.
Feature-based registration of terrestrial lidar points clouds Department of Civil
Engineering, National Taiwan University, 1, Roosevelt Rd., Sec. 4, Taipei 10617, Taiwan,
China – (jejaw,d95521008)@ntu.edu.tw
62

71. BIBLIOGRAPHIE
[8] Szymon Rusinkiewicz, Marc Levoy, .
Efficient variants of ICP algorithm
Stanford University
[9] Martyna Poreba, François Goulette.
A robust linear feature-based procedure for automated registration of point
clouds.
(MINES ParisTech)
[10] JA. Al-Rawabdeh a*, H. Al-Gurrani a, K. Al-Durgham a, I. Detchev a, F. He b, N. El-Sheimy
a, and A. Habib b.
A robust registration algorithm for point cloud from UAV images for change de-
tection
Dep’t of Geomatics Engineering, University of Calgary, 2500 University Dr. NW, Calgary,
AB, Canada T2N 1N4 - (amalrawa, htattya, kmaldurg, i.detchev, elsheimy)@ucalgary.ca
Lyles School of Civil Engineering, Purdue University, 47907 West Lafayette, IN, USA -
ahabib@purdue.edu
[11] von Kurt Leimer.
External Sorting Of Point Clouds
BACHELORARBEIT zur Erlangung des akademischen Grades Bachelor Of Science im Rah-
men des Studiums Medieninformatik und Visual Computing eingereicht
[12] Islem JEBARI.
Recalage de données 3D aériennes et terrestres pour cartographie numérique
Université ISTIA 2009 Angers
[13] Sasa Milenkovic1.
Quaternion Based Helmert Transformation
Research · June 2015 DOI : 10.13140/RG.2.1.2915.6004 Republic Geodetic Authority — Ser-
bia AGROS Control Centre
[14] Ayman Habib *, Ki In Bang, Ana Paula Kersting and Jacky Chow.
Alternative Methodologies for LiDAR System Calibration
Department of Geomatics Engineering, The University of Calgary, 2500 University
Drive NW, T2N 1N4, Calgary, AB, Canada; E-Mails : kibang@ucalgary.ca (K.B.);
ana.kersting@ucalgary.ca (A.K.); jckchow@ucalgary.ca (J.C.)
63

72. BIBLIOGRAPHIE
[15] Tzu-Yi Chuang and Jen-Jer Jaw .
Multi-Feature Registration of Point Clouds
Department of Civil Engineering, National Taiwan University, Taipei City, Taiwan 10617;
jtychuang@ntu.edu.tw * Correspondence : jejaw@ntu.edu.tw; Tel. : +886-2-3366-4276
Academic Editors : Jie Shan, Juha Hyyppä, Richard Gloaguen and Prasad S. Thenkabail
Received : 23 October 2016; Accepted : 12 March 2017; Published : 16 March 2017
[16] Ana Paula Kersting, Ruifang Zhai, Ayman Habib,.
Strip adjustement using conjugate planar and linear features in overlapping
strips
Dept. of Geomatics Engineering, University of Calgary, 2500 University Dr. NW, Calgary,
Alberta, T2N 1N4, Canada. ana.kersting@ucalgary.ca, rzhai@geomatics.ucalgary.ca, ha-
bib@geomatics.ucalgary.ca
[17] Adrien Gressin, C. Mallet, J. Demantké, Nicolas David
Towards 3D lidar point cloud registration improvement using optimal neighbo-
rhood knowledge.
Université Paris-Est – IGN/SR, MATIS, 73 avenue de Paris, 94160 Saint-Mandé, France
[18] F. Pommerleau, F. Colas, R. Siegward.
A Review of Point Cloud Registration Algorithms for Mobile Robotics
Space Robotics Laboratory – University of Toronto Toronto, Canada,
f.pomerleau@gmail.com Inria, Villers-lès-Nancy, F-54600, France CNRS, Loria, UMR
7503, Vandoeuvre-lès-Nancy, F-54500, France Université de Lorraine, Vandoeuvre-
lès-Nancy, F-54500, Francefrancis.colas@inria.fr Autonomous Systems Lab – ETH
ZurichZurich, Switzerlandrsiegwart@ethz.ch
[19] Georgios D. Evangelidis and Radu Horaud.
Joint Alignment of Multiple Point Sets with Batch and Incremental Expectation-
Maximization
[20] Francois Pomerleau Francis Colas RolandSiegwart Stephane Magnenat
Comparing ICP Variants on Real-World Data Sets Open-source library and
experimental protocol.
Space Robotics Laboratory – University of Toronto Toronto, Canada,
f.pomerleau@gmail.com Inria, Villers-lès-Nancy, F-54600, France CNRS, Loria, UMR
7503, Vandoeuvre-lès-Nancy, F-54500, France Université de Lorraine, Vandoeuvre-
64

73. BIBLIOGRAPHIE
lès-Nancy, F-54500, Francefrancis.colas@inria.fr Autonomous Systems Lab – ETH
ZurichZurich, Switzerlandrsiegwart@ethz.ch
[21] Ying He ,Bin Liang , Jun Yang, Shunzhi Li, Jin He
An Iterative Closest Points Algorithm for Registration of 3D Laser Scanner Point
Clouds with Geometric Features
Shenzhen Graduate School, Harbin Institute of Technology, Shenzhen 518055,
China Department of Automation, Tsinghua University, Beijing 100084, China; he-
j15@mails.tsinghua.edu.cn Shenzhen Graduate School, Tsinghua University, Shenzhen
518055, China; yangjun603@mail.tsinghua.edu.cn (J.Y.); lisz15@mails.tsinghua.edu.cn
(S.L.) Correspondence : heying@hitsz.edu.cn (Y.H.); bliang@tsinghua.edu.cn (B.L.); Tel. :
+86-010-6279-7036 (Y.H.)
Webographie
[22] Python : https://www.python.org
[23] cProfile : https://docs.python.org/2/library/profile
[24] PyCuda : https://mathema.tician.de/software/pycuda
[25] Numpy : https://www.numpy.org
[26] Pcl : http://www.pointclouds.org/documentation/
[27] Open3d : http://www.open3d.org/docs/index.html
[28] Vtk : https://www.vtk.org/doc/nightly/html/annotated.html
[29] Pdal : https://pdal.io/project/docs.html
[30] C++ : http://devdocs.io/cpp/
[31] Qt : http://doc.qt.io/
[32] Svd : http://web.mit.edu/be.400/www/SVD/Singular_Value_
Decomposition.htm
[33] Mesures de distance : https://tel.archives-ouvertes.fr/
tel-00004360/document
65

74. Annexes
Utilitaire ICP Basé sur VTK
1 #NEEDS VTK v t k _ v i s u a l i z e r TKINTER PDAL JSON NUMPY PANDAS LASPY
2 #BY Mahdi SMUIDA
3 # 2018
4
5 #VTK
6 import vtk
7 from v t k _ v i s u a l i z e r import ∗
8 #TKINTER
9 import t k i n t e r as tk
10 from t k i n t e r . messagebox import ∗
11 from t k i n t e r . f i l e d i a l o g import ∗
12 #PDAL
13 import pdal
14 #JSON
15 import json
16 #NUMPY
17 import numpy as np
18 #PANDAS
19 import pandas as pd
20 #LASPY
21 import laspy
22
23 import time
24 from datetime import datetime
25 from datetime import t i m e d e l t a
26
27
28 c l a s s App ( tk . Tk ) :
29
30 def _ _ i n i t _ _ ( s e l f ) :
31 tk . Tk . _ _ i n i t _ _ ( s e l f ) # c r e a t e window
32 s e l f . filenameSource = " " # v a r i a b l e to s t o r e filename
33 s e l f . filenameTarget = " " # v a r i a b l e to s t o r e filename
34 # v a r i a b l e to s t o r e filename
35 s e l f . s o u r c e P i p e l i n e = " "
36 s e l f . t a r g e t P i p e l i n e = " "
66

75. ANNEXES
37 s e l f . o u t P i p e l i n e = " "
38 s e l f . filenameOutput = " "
39
40 l a b e l = Label ( s e l f , t e x t = "EXAMETRICS : I . C . P TOOLS" , fg = " red " , font
=( " H e l v e t i c a " , 20) ) . pack ( )
41 l a b e l = Label ( s e l f , t e x t = "VTK BASED" , fg = " green " , font =( " H e l v e t i c a " ,
15) ) . pack ( )
42 photo = PhotoImage ( f i l e = " exametrics_icon . png " )
43 canvas = Canvas ( s e l f , width =350 , height =200)
44 canvas . create_image ( 3 5 0 / 2 , 200/2 , anchor=CENTER , image=photo )
45 canvas . pack ( )
46 " " " SECTION " " "
47 l = LabelFrame ( s e l f , t e x t = " STEP 1 : INPUT SECTION " , padx =30 , pady
=0)
48 l . pack ( f i l l = " both " , expand= " yes " )
49
50 " " " Source Button " " "
51 tk . Button ( l , t e x t = " INPUT ∗ ∗ SOURCE ∗ ∗ LAS FILE " , command= s e l f .
recupereSource ) . pack ( )
52 " " " Target Button " " "
53 tk . Button ( l , t e x t = " INPUT ∗ ∗ TARGET ∗ ∗ LAS FILE " , command= s e l f .
recupereTarget ) . pack ( )
54
55
56 " " " SECTION " " "
57 l 1 = LabelFrame ( s e l f , t e x t = " STEP 2 : COMPUTE SECTION " , padx =30 ,
pady =30)
58 l 1 . pack ( f i l l = " both " , expand= " yes " )
59
60 " " " SECTION " " "
61
62 v i s = LabelFrame ( s e l f , t e x t = " STEP 3 : V i s u a l i z a t i o n " , padx =30 , pady
=30)
63 v i s . pack ( f i l l = " both " , expand= " yes " )
64 " " " V i s u a l i z e Button " " "
65 tk . Button ( vis , t e x t = " V i s u a l i z e " , command= s e l f . V i s u a l i z e ) . pack ( )
66
67
68 " " "MAX i t e r a t i o n input " " "
69 s e l f . spinbox = tk . Spinbox ( l1 , from_ =2 , to =200)
70 s e l f . spinbox . pack ( pady =3)
71 tk . Button ( l1 , t e x t = ’ Send max i t e r a t i o n value >> ’ , command= s e l f .

76. ANNEXES
maxIteration ) . pack ( )
72
73 s e l f . v = StringVar ( l1 , value = ’ output ’+ s t r ( datetime . now ( ) ) + ’ . l a s ’ )
74 s e l f . e = Entry ( l1 , t e x t v a r i a b l e = s e l f . v )
75 s e l f . e . pack ( )
76
77 " " " Compute Button " " "
78 tk . Button ( l1 , t e x t = " Compute " , command= s e l f . Compute ) . pack ( )
79
80
81 " " " SECTION " " "
82 s e l f . l 2 = LabelFrame ( s e l f , t e x t = "TRACE SECTION " , padx =30 , pady =30)
83 s e l f . l 2 . pack ( f i l l = " both " , expand= " yes " )
84
85 s e l f . mainloop ( )
86
87
88 def o p e n f i l e ( s e l f ) :
89 s e l f . filename = askopenfilename ( t i t l e = " Open f i l e " )
90
91 def maxIteration ( s e l f ) :
92 x= s e l f . spinbox . get ( )
93 type ( x ) == i n t
94 i f i n t ( x ) >200 or i n t ( x ) <2:
95 messagebox . showerror ( "ERROR" , "MAX ITERATION VALUE MUST BE AN
INTEGER BETWEEN 1 AND 200 " )
96 e l s e :
97 return i n t ( x )
98
99
100
101 def r e a d L a s F i l e ( s e l f , f i l e p a t h ) :
102 pip= {
103 " p i p e l i n e " : [
104 {
105 " type " : " r e a d e r s . l a s " ,
106 " filename " : f i l e p a t h
107 } ,
108
109 ]
110 }
111 p i p e l i n e = pdal . P i p e l i n e ( json . dumps ( pip ) )

77. ANNEXES
112 p i p e l i n e . v a l i d a t e ( )
113 p i p e l i n e . execute ( )
114 return p i p e l i n e
115
116
117 def recupereSource ( s e l f ) :
118 s e l f . filenameSource = askopenfilename ( t i t l e = " Open Source LAS F i l e " ,
f i l e t y p e s =[( ’ l a s f i l e s ’ , ’ . l a s ’ ) , ( ’ l a s f i l e s ’ , ’ . l a s ’ ) ] )
119 i f s e l f . filenameSource != " " :
120 l a b e l = Label ( s e l f . l2 , t e x t = " Source point Cloud i s s u c c e s s f u l l y
loaded . . . " , bg= " yellow " )
121 l a b e l . pack ( )
122 e l s e :
123 Label ( s e l f . l2 , t e x t = " Choose your Source point Cloud Pl e as e " , bg
= " red " ) . pack ( )
124
125
126
127 def recupereTarget ( s e l f ) :
128 s e l f . filenameTarget = askopenfilename ( t i t l e = " Open Source LAS F i l e " ,
f i l e t y p e s =[( ’ l a s f i l e s ’ , ’ . l a s ’ ) , ( ’ l a s f i l e s ’ , ’ . l a s ’ ) ] )
129 i f s e l f . filenameTarget != " " :
130 l a b e l = Label ( s e l f . l2 , t e x t = " Target point Cloud i s s u c c e s s f u l l y
loaded . . . " , bg= " yellow " )
131 l a b e l . pack ( )
132 e l s e :
133 Label ( s e l f . l2 , t e x t = " Choose your Target point Cloud Pl e as e " , bg
= " red " ) . pack ( )
134
135
136
137 def pipelineToxyz ( s e l f , p i p e l i n e ) :
138 " " " transform l a s f i l e information j u s t to XYZ information to our
point Cloud c l a s s " " "
139 arr = p i p e l i n e . arrays [ 0 ]
140 d e s c r i p t i o n = arr . dtype . descr
141 c o l s = [ c o l f o r col , __ in d e s c r i p t i o n ]
142 df = pd . DataFrame ( { c o l : arr [ c o l ] f o r c o l in c o l s } )
143 arr = p i p e l i n e . arrays [ 0 ]
144 xyz=np . array ( [ np . array ( df [ ’X ’ ] ) , np . array ( df [ ’Y ’ ] ) , np . array ( df [ ’Z ’
] ) ] ) . T
145 return xyz

78. ANNEXES
146
147 def V i s u a l i z e ( s e l f ) :
148 i f ( s e l f . filenameSource == " " ) or ( s e l f . filenameTarget == " " ) :
149 Label ( s e l f . l2 , t e x t = " Verify your input " , bg= " red " ) . pack ( )
150 e l i f s e l f . filenameOutput == " " :
151 Label ( s e l f . l2 , t e x t = " Wait . . . " , bg= " red " ) . pack ( )
152 s e l f . s o u r c e P i p e l i n e = s e l f . r e a d L a s F i l e ( s e l f . filenameSource )
153 s e l f . t a r g e t P i p e l i n e = s e l f . r e a d L a s F i l e ( s e l f . filenameTarget )
154 xyzSource= s e l f . pipelineToxyz ( s e l f . s o u r c e P i p e l i n e )
155 xyzTarget = s e l f . pipelineToxyz ( s e l f . t a r g e t P i p e l i n e )
156 xyzoutput = s e l f . pipelineToxyz ( s e l f . o u t P i p e l i n e )
157 # Renderer
158
159 #TARGET POINTCLOUD
160 pointCloud = PointCloud ( )
161 f o r k in range ( len ( xyzSource ) ) :
162 pointCloud . addPoint ( xyzSource [ k ] )
163 sourceActor = pointCloud . vtkActor
164
165 sourceActor . GetMapper ( ) . S c a l a r V i s i b i l i t y O f f ( )
166 sourceActor . GetProperty ( ) . SetColor ( 1 , 0 , 0) # ( R , G, B )
167 sourceActor . GetProperty ( ) . S e t P o i n t S i z e ( 4 )
168
169
170 #TARGET POINTCLOUD
171 pointCloud2 = PointCloud ( )
172 f o r k in range ( len ( xyzTarget ) ) :
173 pointCloud2 . addPoint ( xyzTarget [ k ] )
174 t a r g e t A c t o r = pointCloud2 . vtkActor
175
176 t a r g e t A c t o r . GetMapper ( ) . S c a l a r V i s i b i l i t y O f f ( )
177 t a r g e t A c t o r . GetProperty ( ) . SetColor ( 0 , 0 , 1 ) # ( R , G, B )
178 t a r g e t A c t o r . GetProperty ( ) . S e t P o i n t S i z e ( 4 )
179
180
181
182
183 #OUTPUT POINTCLOUD
184
185 outputPointCloud = PointCloud ( )
186 f o r k in range ( len ( xyzoutput ) ) :
187 outputPointCloud . addPoint ( xyzoutput [ k ] )

79. ANNEXES
188 outputActor = outputPointCloud . vtkActor
189
190 outputActor . GetMapper ( ) . S c a l a r V i s i b i l i t y O f f ( )
191 outputActor . GetProperty ( ) . SetColor ( 0 , 1 , 0) # ( R , G, B )
192 outputActor . GetProperty ( ) . S e t P o i n t S i z e ( 4 )
193
194 renderer = vtk . vtkRenderer ( )
195 renderWindow = vtk . vtkRenderWindow ( )
196 # i n t e r a c t o r
197 renderWindowInteractor = vtk . vtkRenderWindowInteractor ( )
198
199 renderer . AddActor ( sourceActor )
200 renderer . AddActor ( t a r g e t A c t o r )
201 renderer . AddActor ( outputActor )
202
203 renderer . SetBackground ( 0 , 0 , 0)
204 renderer . ResetCamera ( )
205
206 # Render Window
207
208 renderWindow . AddRenderer ( renderer )
209 # I n t e r a c t o r
210
211 renderWindowInteractor . SetRenderWindow ( renderWindow )
212 # Begin I n t e r a c t i o n
213 renderWindow . Render ( )
214 renderWindowInteractor . S t a r t ( )
215
216 " " " f i g = p l t . f i g u r e ( )
217 ax = f i g . add_subplot ( 1 1 1 , p r o j e c t i o n = ’3d ’ )
218 ax . p l o t ( xyzSource [ : , 0 ] , xyzSource [ : , 1 ] , xyzSource [ : , 2 ] )
219 p l t . show ( )
220
221
222 l a b e l = Label ( s e l f , t e x t =" ICP i s Running . . . " , bg =" yellow " )
223 l a b e l . pack ( ) " " "
224
225 def Compute ( s e l f ) :
226 # Verify input t e s t
227 i f s e l f . filenameSource == " " or s e l f . filenameTarget == " " :
228 Label ( s e l f . l2 , t e x t = " Verify your input " , bg= " red " ) . pack ( )
229 #TRACE MAX ITERATION

80. ANNEXES
230 x= s e l f . spinbox . get ( )
231 l a b e l = Label ( s e l f . l2 , t e x t = " ICP s t a r t running with " + x + "
i t e r a t i o n " , fg = " red " )
232 l a b e l . pack ( )
233
234 s e l f . s o u r c e P i p e l i n e = s e l f . r e a d L a s F i l e ( s e l f . filenameSource )
235 s e l f . t a r g e t P i p e l i n e = s e l f . r e a d L a s F i l e ( s e l f . filenameTarget )
236
237 xyzSource= s e l f . pipelineToxyz ( s e l f . s o u r c e P i p e l i n e )
238 xyzTarget = s e l f . pipelineToxyz ( s e l f . t a r g e t P i p e l i n e )
239
240 s t a r t = time . process_time ( )
241
242 t a r g e t P o i n t s = vtk . v t k P o i n t s ( )
243 s o u r c e P o i n t s = vtk . v t k P o i n t s ( )
244 t a r g e t V e r c t i c e s = vtk . vtkCellArray ( )
245 s o u r c e V e r c t i c e s = vtk . vtkCellArray ( )
246
247 t a r g e t = vtk . vtkPolyData ( )
248 source = vtk . vtkPolyData ( )
249
250 f o r i in range ( len ( xyzSource ) ) :
251 id = s o u r c e P o i n t s . I n s e r t N e x t P o i n t ( xyzSource [ i ] [ 0 ] , xyzSource [ i
] [ 1 ] , xyzSource [ i ] [ 2 ] )
252 s o u r c e V e r c t i c e s . I n s e r t N e x t C e l l ( 1 )
253 s o u r c e V e r c t i c e s . I n s e r t C e l l P o i n t ( id )
254
255 f o r i in range ( len ( xyzTarget ) ) :
256 id = t a r g e t P o i n t s . I n s e r t N e x t P o i n t ( xyzTarget [ i ] [ 0 ] , xyzTarget [ i
] [ 1 ] , xyzTarget [ i ] [ 2 ] )
257 t a r g e t V e r c t i c e s . I n s e r t N e x t C e l l ( 1 )
258 t a r g e t V e r c t i c e s . I n s e r t C e l l P o i n t ( id )
259
260
261 t a r g e t . S e t P o i n t s ( t a r g e t P o i n t s )
262 source . S e t P o i n t s ( s o u r c e P o i n t s )
263 t a r g e t . S e t V e r t s ( t a r g e t V e r c t i c e s )
264 source . S e t V e r t s ( s o u r c e V e r c t i c e s )
265 i f vtk . VTK_MAJOR_VERSION <= 5 :
266 t a r g e t . Update ( )
267 source . Update ( )
268

81. ANNEXES
269 # ============ run ICP ==============
270 icp = vtk . v t k I t e r a t i v e C l o s e s t P o i n t T r a n s f o r m ( )
271 #RMS
272 icp . SetMaximumMeanDistance ( 0 . 0 0 0 0 1 )
273 icp . CheckMeanDistanceOn ( )
274 icp . SetSource ( source )
275 icp . SetTarget ( t a r g e t )
276 icp . GetLandmarkTransform ( ) . SetModeToRigidBody ( )
277 # icp . DebugOn ( )
278 icp . SetMaximumNumberOfIterations ( s e l f . maxIteration ( ) )
279 #SAMPLING WITH ALL THE POINT CLOUD
280 icp . SetMaximumNumberOfLandmarks ( source . GetNumberOfPoints ( ) ) ;
281 icp . StartByMatchingCentroidsOn ( )
282 icp . Modified ( )
283 icp . Update ( )
284
285 i c p T r a n s f o r m F i l t e r = vtk . vtkTransformPolyDataFilter ( )
286 i f vtk . VTK_MAJOR_VERSION <= 5 :
287 i c p T r a n s f o r m F i l t e r . SetInput ( source )
288 e l s e :
289 i c p T r a n s f o r m F i l t e r . SetInputData ( source )
290 i c p T r a n s f o r m F i l t e r . SetTransform ( icp )
291 i c p T r a n s f o r m F i l t e r . Update ( )
292 transformedSource = i c p T r a n s f o r m F i l t e r . GetOutput ( )
293
294 p r i n t ( icp . GetMeanDistance ( ) )
295 #TRACE Distance
296 d i s t = Label ( s e l f . l2 , t e x t = " Mean d i s t a n c e i s " + s t r ( icp .
GetMeanDistance ( ) ) , fg = " black " , font =( " A r i a l " , 11) ) . pack ( )
297
298 e l a p s e d _ t i m e _ s e c s = time . process_time ( ) −s t a r t
299
300 msg = " ICP Execution took : " + s t r ( e l a p s e d _ t i m e _ s e c s ) + " secs "
301
302
303 Label ( s e l f . l2 , t e x t =msg , fg = " green " , font =( " A r i a l " , 10) ) . pack ( )
304 output =[]
305 f o r index in range ( len ( xyzSource ) ) :
306 point = [ 0 , 0 , 0 ]
307 transformedSource . GetPoint ( index , point )
308 # output p o i n t s in a l i s t
309 output = output +[ point ]

82. ANNEXES
310 # p r i n t ( output )
311 a l l x =[]
312 a l l y =[]
313 a l l z =[]
314 f o r index in range ( len ( xyzSource ) ) :
315 a l l x . append ( output [ index ] [ 0 ] )
316 a l l y . append ( output [ index ] [ 1 ] )
317 a l l z . append ( output [ index ] [ 2 ] )
318
319 header = laspy . header . Header ( )
320 s e l f . filenameOutput = s e l f . e . get ( )
321 o u t f i l e = laspy . f i l e . F i l e ( s e l f . filenameOutput , mode= "w" , header=
header )
322
323 xmin = np . f l o o r ( np . min ( a l l x ) )
324 ymin = np . f l o o r ( np . min ( a l l y ) )
325 zmin = np . f l o o r ( np . min ( a l l z ) )
326 o u t f i l e . header . o f f s e t = [ xmin , ymin , zmin ]
327 o u t f i l e . header . s c a l e = [ 0 . 0 0 0 0 0 0 0 1 , 0 . 0 0 0 0 0 0 0 1 , 0 . 0 0 0 0 0 0 0 1 ]
328
329 o u t f i l e . x =np . array ( a l l x )
330 o u t f i l e . y =np . array ( a l l y )
331 o u t f i l e . z=np . array ( a l l z )
332 o u t f i l e . c l o s e ( )
333
334 s e l f . o u t P i p e l i n e = s e l f . r e a d L a s F i l e ( s e l f . filenameOutput )
335 v= Label ( s e l f . l2 , t e x t = " You can V i s u a l i z e r e s u l t s now" , fg = " white "
, bg= " red " ) . pack ( )
336
337
338 c l a s s PointCloud :
339
340 def _ _ i n i t _ _ ( s e l f , zMin = −10.0 , zMax = 1 0 . 0 , maxNumPoints=1 e6 ) :
341 s e l f . maxNumPoints = maxNumPoints
342 s e l f . vtkPolyData = vtk . vtkPolyData ( )
343 s e l f . c l e a r P o i n t s ( )
344 mapper = vtk . vtkPolyDataMapper ( )
345 mapper . SetInputData ( s e l f . vtkPolyData )
346 #mapper . SetColorModeToDefault ( )
347 mapper . SetScalarRange ( zMin , zMax )
348 mapper . S e t S c a l a r V i s i b i l i t y ( 1 )
349 s e l f . vtkActor = vtk . vtkActor ( )

83. ANNEXES
350 s e l f . vtkActor . SetMapper ( mapper )
351
352
353 def addPoint ( s e l f , point ) :
354 i f s e l f . v t k P o i n t s . GetNumberOfPoints ( ) < s e l f . maxNumPoints :
355 p o i n t I d = s e l f . v t k P o i n t s . I n s e r t N e x t P o i n t ( point [ : ] )
356 s e l f . vtkDepth . InsertNextValue ( point [ 2 ] )
357 s e l f . v t k C e l l s . I n s e r t N e x t C e l l ( 1 )
358 s e l f . v t k C e l l s . I n s e r t C e l l P o i n t ( p o i n t I d )
359 e l s e :
360 r = random . randint ( 0 , s e l f . maxNumPoints )
361 s e l f . v t k P o i n t s . S e t P o i n t ( r , point [ : ] )
362 s e l f . v t k C e l l s . Modified ( )
363 s e l f . v t k P o i n t s . Modified ( )
364 s e l f . vtkDepth . Modified ( )
365
366 def c l e a r P o i n t s ( s e l f ) :
367 s e l f . v t k P o i n t s = vtk . v t k P o i n t s ( )
368 s e l f . v t k C e l l s = vtk . vtkCellArray ( )
369 s e l f . vtkDepth = vtk . vtkDoubleArray ( )
370 s e l f . vtkDepth . SetName ( ’ DepthArray ’ )
371 s e l f . vtkPolyData . S e t P o i n t s ( s e l f . v t k P o i n t s )
372 s e l f . vtkPolyData . S e t V e r t s ( s e l f . v t k C e l l s )
373 s e l f . vtkPolyData . GetPointData ( ) . S e t S c a l a r s ( s e l f . vtkDepth )
374 s e l f . vtkPolyData . GetPointData ( ) . S e t A c t i v e S c a l a r s ( ’ DepthArray ’ )
375
376
377 i f __name__ == " __main__ " :
378
379 import warnings
380 warnings . s i m p l e f i l t e r ( a c t i o n = ’ ignore ’ , category =FutureWarning )
381 App ( )
Utilitaire ICP Basé sur OPEN3D
1
2 #NEEDS TKINTER and OPEN3D
3 #BY Mahdi SMUIDA
4 # 2018
5 #TKINTER
6 import t k i n t e r as tk
7 from t k i n t e r . messagebox import ∗

84. ANNEXES
8 from t k i n t e r . f i l e d i a l o g import ∗
9 import os , sys
10 #NUMPY
11 import numpy as np
12
13 #OPEN 3D
14 from py3d import ∗
15 import copy
16 import time
17 from datetime import datetime
18 from datetime import t i m e d e l t a
19
20
21 c l a s s App ( tk . Tk ) :
22
23 def _ _ i n i t _ _ ( s e l f ) :
24 tk . Tk . _ _ i n i t _ _ ( s e l f )
25 s e l f . filenameSource = " "
26 s e l f . filenameTarget = " "
27 s e l f . source = None
28 s e l f . t a r g e t = None
29 s e l f . tr an sf orm at io n = None
30
31 l a b e l = Label ( s e l f , t e x t = "EXAMETRICS : I . C . P TOOLS" , fg = " red " , font
=( " H e l v e t i c a " , 20) ) . pack ( )
32 l a b e l = Label ( s e l f , t e x t = "OPEN 3D BASED" , fg = " green " , font =( "
H e l v e t i c a " , 15) ) . pack ( )
33 photo = PhotoImage ( f i l e = " exametrics_icon . png " )
34 canvas = Canvas ( s e l f , width =350 , height =200)
35 canvas . create_image ( 3 5 0 / 2 , 200/2 , anchor=CENTER , image=photo )
36 canvas . pack ( )
37
38
39 " " " SECTION " " "
40 l = LabelFrame ( s e l f , t e x t = " STEP 1 : INPUT SECTION " , padx =30 , pady
=0)
41 l . pack ( f i l l = " both " , expand= " yes " )
42
43 " " " Source Button " " "
44 tk . Button ( l , t e x t = " INPUT ∗ ∗ SOURCE ∗ ∗ PCD FILE " , command= s e l f .
recupereSource ) . pack ( )
45 " " " Target Button " " "

85. ANNEXES
46 tk . Button ( l , t e x t = " INPUT ∗ ∗ TARGET ∗ ∗ PCD FILE " , command= s e l f .
recupereTarget ) . pack ( )
47
48
49
50
51
52 " " " SECTION " " "
53
54 l 1 = LabelFrame ( s e l f , t e x t = " STEP 2 : COMPUTE SECTION " , padx =30 ,
pady =30)
55 l 1 . pack ( f i l l = " both " , expand= " yes " )
56
57 " " " SECTION " " "
58
59 v i s = LabelFrame ( s e l f , t e x t = " STEP 3 : V i s u a l i z a t i o n " , padx =30 , pady
=30)
60 v i s . pack ( f i l l = " both " , expand= " yes " )
61 " " " V i s u a l i z e Button " " "
62 tk . Button ( vis , t e x t = " V i s u a l i z e Before ICP " , command= s e l f . V i s u a l i z e
) . pack ( )
63 tk . Button ( vis , t e x t = " V i s u a l i z e R e s u l t " , command= s e l f .
v i s u a l i z e R e s u l t ) . pack ( )
64
65 " " "MAX i t e r a t i o n input " " "
66 s e l f . spinbox = tk . Spinbox ( l1 , from_ =2 , to =200)
67 s e l f . spinbox . pack ( pady =3)
68 tk . Button ( l1 , t e x t = ’ Send max i t e r a t i o n value >> ’ , command= s e l f .
maxIteration ) . pack ( )
69
70
71 " " " Compute Button " " "
72 tk . Button ( l1 , t e x t = " Compute ICP : point to point " , command= s e l f .
Compute ) . pack ( )
73 tk . Button ( l1 , t e x t = " Compute ICP : point to plane " , command= s e l f .
ComputePlane ) . pack ( )
74 " " " SECTION " " "
75 s e l f . l 2 = LabelFrame ( s e l f , t e x t = "TRACE SECTION " , padx =30 , pady =30)
76 s e l f . l 2 . pack ( f i l l = " both " , expand= " yes " )
77
78 s e l f . mainloop ( )
79

86. ANNEXES
80
81
82 def maxIteration ( s e l f ) :
83 x= s e l f . spinbox . get ( )
84 type ( x ) == i n t
85 i f i n t ( x ) <2:
86 messagebox . showerror ( "ERROR" , "MAX ITERATION VALUE MUST BE AN
INTEGER > 2 " )
87 e l s e :
88 return i n t ( x )
89
90
91 def recupereSource ( s e l f ) :
92 s e l f . filenameSource = askopenfilename ( t i t l e = " Open Source PCD F i l e " ,
f i l e t y p e s =[( ’ pcd f i l e s ’ , ’ . pcd ’ ) ] )
93 i f s e l f . filenameSource != " " :
94 l a b e l = Label ( s e l f . l2 , t e x t = " Source point Cloud i s s u c c e s s f u l l y
loaded . . . " , bg= " yellow " )
95 l a b e l . pack ( )
96 s e l f . source = read_point_cloud ( s e l f . filenameSource )
97 e l s e :
98 Label ( s e l f . l2 , t e x t = " Choose your Source point Cloud Pl e as e " , bg
= " red " ) . pack ( )
99
100
101
102 def recupereTarget ( s e l f ) :
103 s e l f . filenameTarget = askopenfilename ( t i t l e = " Open Source PCD F i l e " ,
f i l e t y p e s =[( ’ pcd f i l e s ’ , ’ . pcd ’ ) , ( ’ pcd f i l e s ’ , ’ . pcd ’ ) ] )
104 i f s e l f . filenameTarget != " " :
105 l a b e l = Label ( s e l f . l2 , t e x t = " Target point Cloud i s s u c c e s s f u l l y
loaded . . . " , bg= " yellow " )
106 l a b e l . pack ( )
107
108 s e l f . t a r g e t = read_point_cloud ( s e l f . filenameTarget )
109 e l s e :
110 Label ( s e l f . l2 , t e x t = " Choose your Target point Cloud Pl e as e " , bg
= " red " ) . pack ( )
111
112
113 def V i s u a l i z e ( s e l f ) :
114 s e l f . source . paint_uniform_color ( [ 1 , 0 , 0 ] )

87. ANNEXES
115 s e l f . t a r g e t . paint_uniform_color ( [ 0 , 0 , 1 ] )
116 draw_geometries ( [ s e l f . source , s e l f . t a r g e t ] )
117
118 def ComputePlane ( s e l f ) :
119 sourceToArray= np . asarray ( s e l f . source . p o i n t s )
120 targetToArray = np . asarray ( s e l f . t a r g e t . p o i n t s )
121 p r i n t ( len ( sourceToArray ) )
122 p r i n t ( len ( targetToArray ) )
123 # s e u i l
124 t h r e s h o l d = 0 . 0 2
125 # I n i t i a l T r a n s l a t i o n
126 t r a n s _ i n i t = np . asarray (
127 [ [ 0 . 8 6 2 , 0 . 0 1 1 , −0.507 , 0 . 5 ] ,
128 [ −0.139 , 0 . 9 6 7 , −0.215 , 0 . 7 ] ,
129 [ 0 . 4 8 7 , 0 . 2 5 5 , 0 . 8 3 5 , −1.4] ,
130 [ 0 . 0 , 0 . 0 , 0 . 0 , 1 . 0 ] ] )
131 # I n i t i a l alignment
132 e v a l u a t i o n = e v a l u a t e _ r e g i s t r a t i o n ( s e l f . source , s e l f . target ,
threshold , t r a n s _ i n i t )
133 Label ( s e l f . l2 , t e x t = " Before ICP " + s t r ( e v a l u a t i o n ) , fg = " red " ) . pack ( )
134 #COMPUTE r e g i s t r a t i o n with point to point e s t i m a t i o n
135 reg_p2l = r e g i s t r a t i o n _ i c p ( s e l f . source , s e l f . target , threshold ,
t r a n s _ i n i t , TransformationEstimationPointToPlane ( ) , ICPConvergenceCriteria
( max_iteration = s e l f . maxIteration ( ) ) )
136 # apply tr an sf or ma ti on
137 reg_p2l . t ra nsf or ma ti on
138
139 Label ( s e l f . l2 , t e x t = " After ICP " + s t r ( reg_p2l ) , fg = " green " ) . pack ( )
140 Label ( s e l f . l2 , t e x t = " Transformation matrix i s : n " + s t r ( reg_p2l .
t ran sf or ma ti on ) , fg = " green " ) . pack ( )
141 s e l f . tr an sf orm at io n = reg_p2l . tr an sf or ma ti on
142
143 def Compute ( s e l f ) :
144 sourceToArray= np . asarray ( s e l f . source . p o i n t s )
145 targetToArray = np . asarray ( s e l f . t a r g e t . p o i n t s )
146 # s e u i l
147 t h r e s h o l d = 0 . 0 2
148 # I n i t i a l T r a n s l a t i o n
149 t r a n s _ i n i t = np . asarray (
150 [ [ 0 . 8 6 2 , 0 . 0 1 1 , −0.507 , 0 . 5 ] ,
151 [ −0.139 , 0 . 9 6 7 , −0.215 , 0 . 7 ] ,
152 [ 0 . 4 8 7 , 0 . 2 5 5 , 0 . 8 3 5 , −1.4] ,

88. ANNEXES
153 [ 0 . 0 , 0 . 0 , 0 . 0 , 1 . 0 ] ] )
154 # I n i t i a l alignment
155 e v a l u a t i o n = e v a l u a t e _ r e g i s t r a t i o n ( s e l f . source , s e l f . target ,
threshold , t r a n s _ i n i t )
156 Label ( s e l f . l2 , t e x t = " Before ICP " + s t r ( e v a l u a t i o n ) , fg = " red " ) . pack ( )
157 #COMPUTE r e g i s t r a t i o n with point to point e s t i m a t i o n
158 reg_p2p = r e g i s t r a t i o n _ i c p ( s e l f . source , s e l f . target , threshold ,
t r a n s _ i n i t , TransformationEstimationPointToPoint ( ) , ICPConvergenceCriteria
( max_iteration = s e l f . maxIteration ( ) ) )
159 reg_p2p . t ran sf or ma ti on
160
161 Label ( s e l f . l2 , t e x t = " After ICP " + s t r ( reg_p2p ) , fg = " green " ) . pack ( )
162 Label ( s e l f . l2 , t e x t = " Transformation matrix i s : n " + s t r ( reg_p2p .
t ran sf or ma ti on ) , fg = " green " ) . pack ( )
163 s e l f . tr an sf orm at io n =reg_p2p . tr an sf or ma ti on
164
165 def d r a w _ r e g i s t r a t i o n _ r e s u l t ( s e l f , source , target , tr ans fo rm at io n ) :
166 source_temp = copy . deepcopy ( source )
167 target_temp = copy . deepcopy ( t a r g e t )
168 source_temp . paint_uniform_color ( [ 0 , 1 , 0 ] )
169 target_temp . paint_uniform_color ( [ 0 , 0 , 0 . 9 2 9 ] )
170 source_temp . transform ( t ra ns fo rm at io n )
171 draw_geometries ( [ source_temp , target_temp ] )
172
173
174
175 def v i s u a l i z e R e s u l t ( s e l f ) :
176 s e l f . d r a w _ r e g i s t r a t i o n _ r e s u l t ( s e l f . source , s e l f . target , s e l f .
t ran sf or ma ti on )
177
178
179
180 i f __name__ == " __main__ " :
181
182 import warnings
183 warnings . s i m p l e f i l t e r ( a c t i o n = ’ ignore ’ , category =FutureWarning )
184 App ( )
Maquette ICP sur Jupyter Notebook
1 # coding : utf −8
2

89. ANNEXES
3 # In [ 1 ] :
4
5 " " " " t h i s notebook i s written by− Mahdi SMIDA { email : eng . smida@gmail . com
} " " "
6 " " " ∗ . Las f o r pointCloud " " "
7 # L i b r a r i e s
8 import numpy as np
9 from m p l _ t o o l k i t s . mplot3d import Axes3D
10 import m a t p l o t l i b . pyplot as p l t
11 import time
12 import pdal
13 import json
14 import ipyvolume . pylab as p3
15 import pandas as pd
16 import math
17
18
19 # In [ 2 ] :
20
21 # PointCloud Class
22 c l a s s PC ( o b j e c t ) :
23 def _ _ i n i t ( s e l f , other ) :
24 i f i s i n s t a n c e ( other , PC ) :
25 s e l f . initFromPC ( other )
26 s e l f . pts = None
27 s e l f . normPts=None
28 s e l f .Num= 0
29 s e l f . center = None
30
31 def getPointCloudInformation ( s e l f ) :
32 return " < Point cloud Points :% s normPts :% s Num:% s center :% s > " % (
s e l f . pts , s e l f . normPts , s e l f .Num , s e l f . center )
33
34 def initFromNdArray ( s e l f , other ) :
35 s e l f . pts = np . copy ( other )
36 s e l f .Num = other . shape [ 0 ]
37 s e l f . normalize ( )
38
39 def Sampling ( s e l f ) :
40 x= s e l f . pts [ 0 : : 1 6 ]
41 return x
42

90. ANNEXES
43 def initFromArray ( s e l f , other ) :
44 s e l f . pts =np . copy ( other )
45 s e l f .Num= len ( other )
46 s e l f . normalize ( )
47
48 def initFromPC ( s e l f , other ) :
49 a s s e r t i s i n s t a n c e ( other , PC )
50 s e l f . pts = np . copy ( other . pts )
51 s e l f .Num = other .Num
52 s e l f . normalize ( )
53
54 def normalize ( s e l f ) :
55 a s s e r t s e l f .Num !=0
56 s e l f . center = np . mean ( s e l f . pts , a x i s =0)
57 s e l f . normPts = s e l f . pts − s e l f . center
58
59 def applyTransformation ( s e l f , R=None , T=None ) :
60 s e l f . pts = s e l f . pts . dot ( R . T ) +T . T
61 s e l f . normalize ( )
62
63 def DisplayPcWithMatplotlib ( pointCloud ) :
64 # MatplotLib v i s u a l i s a t i o n
65 f i g u r e = p l t . f i g u r e ( )
66 ax = f i g u r e . add_subplot ( 1 1 1 , p r o j e c t i o n = ’ 3d ’ )
67 ax . s c a t t e r ( pointCloud . pts [ : , 0 ] , pointCloud . pts [ : , 1 ] , pointCloud . pts
[ : , 2 ] , c= ’ r ’ , marker= ’ . ’ )
68 ax . s e t _ x l a b e l ( ’X ’ )
69 ax . s e t _ y l a b e l ( ’Y ’ )
70 ax . s e t _ z l a b e l ( ’Z ’ )
71 p l t . show ( )
72
73 def DisplayPcWithIpyvolume ( pointCloud , c l r ) :
74 p3 . f i g u r e ( )
75 s = p3 . s c a t t e r ( pointCloud . pts [ : , 0 ] , pointCloud . pts [ : , 1 ] , pointCloud .
pts [ : , 2 ] , c o l o r = clr , s i z e =2)
76 p3 . squarelim ( )
77 p3 . show ( )
78
79
80
81 # In [ 3 ] :
82

91. ANNEXES
83
84 # Basic i t e r a t i v e C l o s e s t point algorithm
85 c l a s s BasicICP ( o b j e c t ) :
86 # i n i t
87 def _ _ i n i t _ _ ( s e l f , source , target , r e i n i t = F a l s e ) :
88 s e l f . source = source
89 s e l f . t a r g e t = t a r g e t
90 a s s e r t s e l f . source .Num == s e l f . t a r g e t .Num
91 s e l f . r e s u l t = PC ( )
92 s e l f . r e s u l t . initFromPC ( source )
93 PC . initFromPC ( s e l f . r e s u l t , source )
94 s e l f . r e i n i t = r e i n i t
95 # Point Cloud R e g i s t r a t i o n return Rotation and t r a n s l a t i o n
96 def getPCRegistation ( s e l f , t r g t ) :
97 a s s e r t s e l f . r e s u l t and t r g t
98 a s s e r t s e l f . r e s u l t .Num == t r g t .Num
99
100 H = np . dot ( s e l f . r e s u l t . normPts . T , t r g t . normPts )
101 U, S , Vt = np . l i n a l g . svd (H)
102 R=np . dot ( Vt . T , U . T )
103 # i f Refkection
104 i f np . l i n a l g . det ( R ) < 0 :
105 Vt [ 2 , : ] ∗= −1
106 R = np . dot ( Vt . T , U . T )
107 #Warn i f SVD i s not c o r r e c t l y performed
108 Epsilon =0.0001
109 i f abs ( np . l i n a l g . det ( R ) −1.0)> Epsilon :
110 Warning ( ’ Point Cloud R e g i s t r a t i o n u n s t a b l e ! ’ )
111 T= t r g t . center −s e l f . r e s u l t . center . dot ( R . T )
112 p r i n t ( R )
113 p r i n t ( T )
114 return R , T
115 #Compute correspondence
116 def computeCorrespondence ( s e l f ) :
117 a s s e r t s e l f . r e s u l t and s e l f . t a r g e t
118 a s s e r t s e l f . r e s u l t .Num == s e l f . t a r g e t .Num
119 #Main icp algorithm
120 def solveMe ( s e l f ) :
121 p r i n t ( ’ Solve Me ICP Algorithm ’ , s e l f . _ _ c l a s s _ _ . __name__ )
122 d i s t a n c e t h r e s h o l d =0.001
123 maxIteration =10
124 i t e r a t i o n =0

92. ANNEXES
125 currentDist , t r g t = s e l f . computeCorrespondence ( )
126 p r i n t ( " Current Distance before S t a r t i n g %f " , c u r r e n t D i s t )
127 # BasicICP ( loop )
128 while c u r r e n t D i s t > d i s t a n c e t h r e s h o l d and i t e r a t i o n < maxIteration :
129 #Compute Transformation
130 R , T = s e l f . getPCRegistation ( t r g t )
131 #Apply t ran sf or ma ti on
132 s e l f . r e s u l t . applyTransformation ( R , T )
133 # Compute correspondence
134 currentDist , t r g t = s e l f . computeCorrespondence ( )
135 # Next i t e r a t i o n
136 i t e r a t i o n +=1
137 p r i n t ( " I t e r a t i o n : %5d , with t o t a l d i s t a n c e : %f " % ( i t e r a t i o n ,
c u r r e n t D i s t ) )
138 return s e l f . r e s u l t . pts , s e l f . r e s u l t . DisplayPcWithIpyvolume ( " red " )
139
140
141
142 # In [ 4 ] :
143
144 c l a s s ICP ( BasicICP ) :
145 def _ _ i n i t _ _ ( s e l f , source , target , r e i n i t = F a l s e ) :
146 super ( ICP , s e l f ) . _ _ i n i t _ _ ( source , target , r e i n i t )
147
148 def g e t P C R e g i s t r a t i o n ( s e l f , t r g t ) :
149 return super ( ICP , s e l f ) . g e t P C R e g i s t r a t i o n ( t r g t )
150
151 def computeCorrespondence ( s e l f ) :
152 super ( ICP , s e l f ) . computeCorrespondence ( )
153 # i n i t index Array & t o t a l d i s t a n c e to zeros
154 indexArray = np . zeros ( s e l f . r e s u l t .Num, dtype=np . i n t )
155 t o t a l D i s t a n c e = 0 . 0
156
157 f o r r e s u l t I n d e x , r e s u l t V a l u e in enumerate ( s e l f . r e s u l t . pts ) :
158 minIndex , minDistance = −1, math . i n f
159 f o r targetIndex , t a r g e t V a l u e in enumerate ( s e l f . t a r g e t . Sampling
( ) ) :
160 d i s t a n c e = np . l i n a l g . norm ( r e s u l t V a l u e − t a r g e t V a l u e )
161 i f d i s t a n c e < minDistance :
162 minDistance , minIndex = distance , t a r g e t I n d e x
163 indexArray [ r e s u l t I n d e x ] = minIndex
164 t o t a l D i s t a n c e += minDistance

93. ANNEXES
165
166 t r g t = PC ( )
167 xyz= s e l f . t a r g e t . pts [ indexArray , 0 : 3 ]
168 t r g t . initFromNdArray ( xyz )
169 PC . initFromNdArray ( trgt , xyz )
170 return t o t a l D i s t a n c e , t r g t
171
172
173 # In [ 5 ] :
174
175 #Read Las F i l e
176 filename = ’ . / bun045 . l a s ’
177 pip= {
178 " p i p e l i n e " : [
179 {
180 " type " : " r e a d e r s . l a s " ,
181 " filename " : filename
182 } ,
183
184 ]
185 }
186 p i p e l i n e = pdal . P i p e l i n e ( json . dumps ( pip ) )
187 p i p e l i n e . v a l i d a t e ( )
188 get_ipython ( ) . run_line_magic ( ’ time ’ , ’ n_points = p i p e l i n e . execute ( ) ’ )
189 p r i n t ( ’ P i p e l i n e s e l e c t e d { } p o i n t s ( { : . 1 f } pts ) ’ . format ( n_points , n_points )
)
190
191 " " " transform l a s f i l e information j u s t to XYZ information to our point
Cloud c l a s s " " "
192 arr = p i p e l i n e . arrays [ 0 ]
193 d e s c r i p t i o n = arr . dtype . descr
194 c o l s = [ c o l f o r col , __ in d e s c r i p t i o n ]
195 df = pd . DataFrame ( { c o l : arr [ c o l ] f o r c o l in c o l s } )
196 arr = p i p e l i n e . arrays [ 0 ]
197 xyz=np . array ( [ np . array ( df [ ’X ’ ] ) , np . array ( df [ ’Y ’ ] ) , np . array ( df [ ’Z ’ ] ) ] ) . T
198 pointCloud = PC ( )
199 pointCloud . initFromArray ( xyz )
200 PC . initFromArray ( pointCloud , xyz )
201 pointCloud . DisplayPcWithIpyvolume ( ’ red ’ )
202
203
204 # In [ 6 ] :

94. ANNEXES
205
206 #Read Las F i l e
207 filename = ’ . / bun090 . l a s ’
208 pip= {
209 " p i p e l i n e " : [
210 {
211 " type " : " r e a d e r s . l a s " ,
212 " filename " : filename
213 } ,
214 ]
215 }
216 p i p e l i n e = pdal . P i p e l i n e ( json . dumps ( pip ) )
217 p i p e l i n e . v a l i d a t e ( )
218 get_ipython ( ) . run_line_magic ( ’ time ’ , ’ n_points = p i p e l i n e . execute ( ) ’ )
219 p r i n t ( ’ P i p e l i n e s e l e c t e d { } p o i n t s ( { : . 1 f } pts ) ’ . format ( n_points , n_points )
)
220
221 " " " transform l a s f i l e information j u s t to XYZ information to our point
Cloud c l a s s " " "
222 arr = p i p e l i n e . arrays [ 0 ]
223 d e s c r i p t i o n = arr . dtype . descr
224 c o l s = [ c o l f o r col , __ in d e s c r i p t i o n ]
225 df = pd . DataFrame ( { c o l : arr [ c o l ] f o r c o l in c o l s } )
226 arr = p i p e l i n e . arrays [ 0 ]
227 xyz=np . array ( [ np . array ( df [ ’X ’ ] ) , np . array ( df [ ’Y ’ ] ) , np . array ( df [ ’Z ’ ] ) ] ) . T
228 # p r i n t ( ( output ) )
229 pointCloud2 = PC ( )
230 pointCloud2 . initFromArray ( xyz )
231 PC . initFromArray ( pointCloud2 , xyz )
232 pointCloud2 . DisplayPcWithIpyvolume ( " yellow " )
233 # p r i n t ( output )
234
235
236 # In [ 7 ] :
237
238 i c p S o l v e r =ICP ( pointCloud , pointCloud2 , F a l s e )
239 # p r i n t ( pointCloud . Sampling ( ) )
240 get_ipython ( ) . run_line_magic ( ’ time ’ , ’ i c p S o l v e r . solveMe ( ) ’ )
241
242
243 # In [ 8 ] :
244

95. ANNEXES
245 p r i n t ( len ( pointCloud . Sampling ( ) ) )
246
247
248 # In [ 9 ] :
249
250 p3 . f i g u r e ( )
251 # Source
252 s = p3 . s c a t t e r ( pointCloud . pts [ : , 0 ] , pointCloud . pts [ : , 1 ] , pointCloud . pts
[ : , 2 ] , c o l o r = " black " , s i z e =2)
253 # D e s t i n a t i o n
254 s = p3 . s c a t t e r ( pointCloud2 . pts [ : , 0 ] , pointCloud2 . pts [ : , 1 ] , pointCloud2 . pts
[ : , 2 ] , c o l o r = " yellow " , s i z e =2)
255 s= p3 . s c a t t e r ( i c p S o l v e r . r e s u l t . pts [ : , 0 ] , i c p S o l v e r . r e s u l t . pts [ : , 1 ] , i c p S o l v e r
. r e s u l t . pts [ : , 2 ] , c o l o r = " blue " , s i z e =2)
256 #p3 . xyzlim ( − 0 . 2 , 0 . 2 )
257 #p3 . animation_control ( s ) # shows c o n t r o l s f o r animation c o n t r o l s
258 p3 . show ( )
Classe ICP parallèle
1 c l a s s IcpPara ( BasicICP ) :
2
3
4 # ________________________________________________________________
5 def _ _ i n i t _ _ ( s e l f , source , target , NumCore=0 , r e i n i t = F a l s e ) :
6 super ( IcpPara , s e l f ) . _ _ i n i t _ _ ( source , target , r e i n i t )
7 #Cuda u t i l i t i e s
8 s e l f . computeCorrespondenceWithCuda=None
9 s e l f . distances_gpu =None
10 s e l f . NumCore= s e l f . source .Num i f NumCore<=0 e l s e NumCore
11 p r i n t ( " Cuda cores f o r P a r a l l e l ICP s e t to " , s e l f . NumCore )
12 s e l f . initCuda ( )
13 # ________________________________________________________________
14
15 def initCuda ( s e l f ) :
16 " " "
17 I n i t i a l i z e CUDA environment
18 − Create CUDA C program , and compile i t
19 − Copy d e s t i n a t i o n PointCloud to CUDA g l o b a l and constant value
20 − Create handler of f i n d _ c l o s e s t f u nc t io n in CUDA
21 " " "
22 mod = SourceModule ( " " "

96. ANNEXES
23 # d e f i n e ROW ( " " " + s t r ( s e l f . source .Num) + " " " )
24 # d e f i n e OFFSET ( " " " + s t r ( s e l f . NumCore ) + " " " )
25 __constant__ f l o a t t a r g e t [ROW] [ 3 ] ;
26
27
28 __global__ void getTarget ( f l o a t ∗ r e t ) {
29 i n t idx = threadIdx . x ;
30 r e t [ idx ∗3]= t a r g e t [ idx ] [ 0 ] ;
31 r e t [ idx ∗3+1] = t a r g e t [ idx ] [ 1 ] ;
32 r e t [ idx ∗3+2] = t a r g e t [ idx ] [ 2 ] ;
33 }
34
35
36 __global__ void c l o s e s t P o i n t ( f l o a t ∗ res , f l o a t ∗ ret , f l o a t ∗
d i s t a n c e s )
37 {
38 f o r ( i n t idx = threadIdx . x ; idx < ROW; idx += OFFSET ) {
39 f l o a t x_source = res [ idx ∗ 3 ] ;
40 f l o a t y_source = res [ idx ∗ 3 + 1 ] ;
41 f l o a t z_source = res [ idx ∗ 3 + 2 ] ;
42 f l o a t x_distance , y_distance , z_distance , min_distance ,
d i s t a n c e ;
43 i n t min_index= −1;
44
45 f o r ( i n t i =0 ; i <ROW; i ++) {
46 x _ d i s t a n c e = t a r g e t [ i ] [ 0 ] ;
47 y_distance = t a r g e t [ i ] [ 1 ] ;
48 z _ d i s t a n c e = t a r g e t [ i ] [ 2 ] ;
49
50 d i s t a n c e =( x_source−x _ d i s t a n c e ) ∗ ( x_source−x _ d i s t a n c e ) +
( y_source−y_distance ) ∗ ( y_source−y_distance ) +( z_source −z _ d i s t a n c e ) ∗ (
z_source −z _ d i s t a n c e ) ;
51 i f ( distance < min_distance | | min_index <0) {
52 min_distance = d i s t a n c e ;
53 min_index= i ;
54 }
55 }
56 r e t [ idx ∗ 3 ] = t a r g e t [ min_index ] [ 0 ] ;
57 r e t [ idx ∗3+1] = t a r g e t [ min_index ] [ 1 ] ;
58 r e t [ idx ∗3+2] = t a r g e t [ min_index ] [ 2 ] ;
59 d i s t a n c e s [ idx ] = s q r t ( min_distance ) ;
60 }

97. ANNEXES
61 }
62 " " " )
63 targetCuda , _ = mod . g e t _ g l o b a l ( ’ t a r g e t ’ )
64 s e l f . t a r g e t . pts . dtype= np . f l o a t 3 2
65 a s s e r t s e l f . t a r g e t . pts . dtype==np . f l o a t 3 2
66 pycuda . d r i v e r . mem_get_info ( )
67 cuda . memcpy_htod ( targetCuda , s e l f . t a r g e t . pts )
68 d i s t a n c e s = np . zeros ( s e l f . source .Num, dtype=np . f l o a t 3 2 )
69 s e l f . distances_gpu = gpuarray . to_gpu ( d i s t a n c e s )
70 s e l f . computeCorrespondenceWithCuda ( ’ c l o s e s t P o i n t ’ )
71 getDistCuda = mod . g e t _ f u n c t i o n ( ’ getDistance ’ )
72 # ________________________________________________________________
73 def g e t P C R e g i s t r a t i o n ( s e l f , t r g t ) :
74 return super ( IcpPara , s e l f ) . g e t P C R e g i s t r a t i o n ( t r g t )
75 # ________________________________________________________________
76 def computeCorrespondence ( s e l f ) :
77 super ( IcpPara , s e l f ) . computeCorrespondence ( )
78 t r g t = np . zeros ( [ s e l f . s r c .Num, 3 ] , dtype=np . f l o a t 3 2 )
79 s e l f . computeCorrespondenceCuda ( cuda . In ( s e l f . r e s u l t . pts ) , cuda . Out (
t r g t ) , s e l f . distances_gpu , block =( s e l f . NumCore , 1 , 1) )
80 return gpuarray . sum ( s e l f . distances_gpu ) . get ( ) , PC ( t r g t )
81
82 # ________________________________________________________________

98. ANNEXES