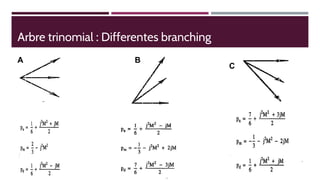
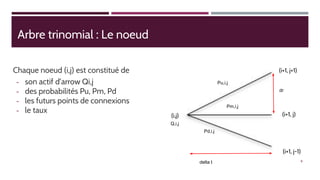
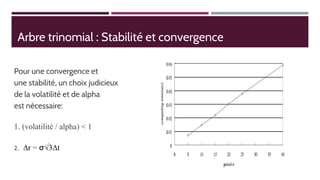
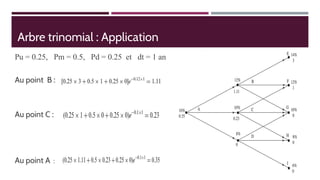
Ce document présente l'implémentation du modèle Hull-White à un facteur en utilisant Python, en expliquant les concepts liés à l'arbre trinomial et aux méthodes de valorisation des actifs financiers. Les perspectives et les limites de ce modèle, ainsi que des exemples pratiques, sont également discutés. Des liens vers des ressources supplémentaires, y compris du code sur GitHub, sont fournis.

1. IMPLÉMENTATION DU MODÈLE DE HULL ET WHITE
AVEC PYTHON
1
Master 2 Finance de Marché et Gestion des Risques
Présenté par :
● Fabricio VIEIRA DA SILVA ALMEIDA
● Ali B. SIDIBE
● Ayten YAGBASAN

2. Plan
◼ Le modèle de Hull et White
◼ Arbre trinomial
◼ Implémentation avec Python
◼ Perspectives et limites
2

3. Modèle Hull-White one-factor
◼ Modèle no-arbitrage avec un seule source de perturbations
◼ Si ⇒ Ho et Lee
◼ Si est constant ⇒ Modèle de Vasicek
◼ Hypothèse économique et mathématique solide et traçable.
3

4. Modèle Hull-White one-factor
◼ Calibrable sur la structure du taux observée à t = 0 :
avec on obtient le taux forward instantané à l’instant actuel de
maturité t. 4

5. Arbre trinomial
◼ Développé pour la première fois par Phelim Boyle en 1986.
◼ Nécessaire pour l'évaluation de certains types d’actif financiers de
type américains.
◼ Un concept proche des méthodes des différences finies.
5

6. Arbre trinomial : Differentes branching
66
A B
C

7. Arbre trinomial : Choix d’orientation
La décision de passer d’une orientation à l’autre est dictée par jmax et jmin.
Empiriquement pour assurer la stabilité de l’arbre, on choisit
sous la contraint que jmin = -jmax
❏ Si j = jmax : branching C
❏ Si j = jmin : branching B
❏ Si jmin < j < jmax : branching A
77

8. Arbre trinomial : Le noeud
Chaque noeud (i,j) est constitué de
- son actif d’arrow Qi,j
- des probabilités Pu, Pm, Pd
- les futurs points de connexions
- le taux
888
(i,j)
(i+1, j+1)
(i+1, j)
(i+1, j-1)
Pd,i,j
Pm,i,j
Pu,i,j
Q,i,j
delta t
dr

9. Arbre trinomial : Généralisation
L’arbre trinomial de (Hull-White) peut-être généralisé à tout modèle de la forme :
Pour Hull- White : Pour Black–Karasinski :
Si g est la fonction inverse de f alors l’actualisation se fait par :
au lieu de
99

10. Arbre trinomial : Stabilité et convergence
Pour une convergence et
une stabilité, un choix judicieux
de la volatilité et de alpha
est nécessaire:
1. (volatilité / alpha) < 1
2. ∆r = 𝞂√3∆t
1010

11. Arbre trinomial : Application
Pu = 0.25, Pm = 0.5, Pd = 0.25 et dt = 1 an
Au point B :
Au point C :
Au point A : 1111

12. Environnement technique
◼ Code disponible sur Github:
https://github.com/fmgrlab/hull_white_model
◼ Site Web de démonstration:
http://fmgrlab..com/
◼ Environnement : Python, Jupiter, Numpy, Github.
12

13. Limites
◼ Forte corrélation entre les produits de taux de maturité différentes.
◼ Non calibrable sur la volatilité.
◼ Disparition des phénomènes extrêmes due à la normalité.
13

14. Perspectives
◼ Estimation des paramètres: volatilité et vitesse de retour à la
moyenne.
◼ Implémenter un modèle dans lequel le pas de temps 𝝙t n’est pas
constant.
◼ Récupérer directement les taux à travers Bloomberg. 14