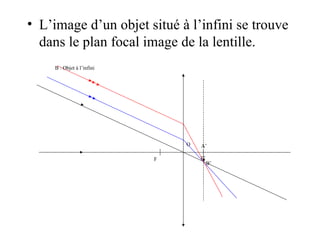
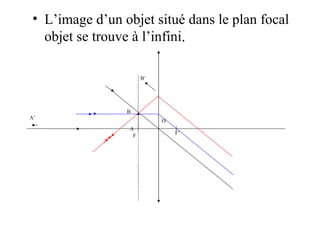
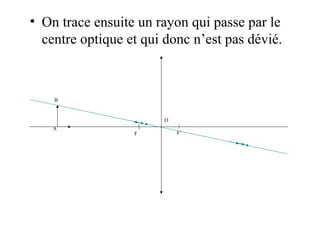
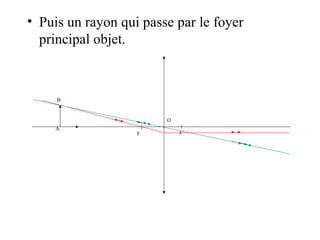
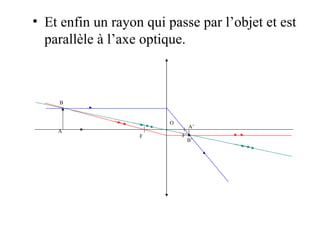
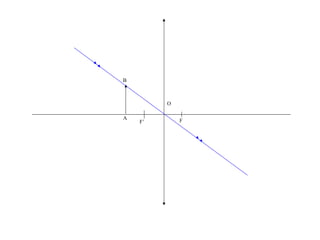
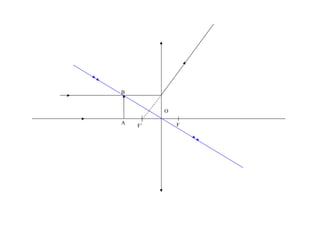
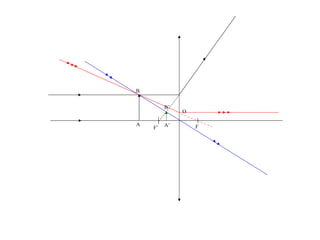
Le document traite des lentilles minces convergentes, en expliquant leurs caractéristiques, propriétés et relations optiques. Il décrit les concepts de foyer principal image, foyer principal objet, distance focale et vergence, ainsi que la construction d'une image à travers une lentille. Enfin, le texte précise les relations de conjugaison et de grandissement liées aux lentilles.

1. Lentilles minces convergentes

2. On symbolise une lentille convergente par: Symbole

3. 2. Caractéristiques Une lentille mince convergente est plus étroite sur les bords qu’en son centre. Le centre de symétrie de la lentille est son centre optique noté en général O. La droite passant par O et perpendiculaire au plan de la lentille est l’axe optique de la lentille. Cet axe est orienté dans le sens de propagation de la lumière.

4. 3. Propriétés

5. Les rayons lumineux passant par O ne sont pas déviés par la lentille. Rayon lumineux Lentille convergente O : centre optique

6. Les rayons lumineux incidents parallèles à l’axe optique se coupent après la lentille en un point de l’axe, noté F’, appelé foyer principal image . F’ : foyer principal image O

7. A l’inverse, les rayons lumineux émergents de la lentille parallèlement à l’axe optique proviennent d’un point de l’axe noté F appelé foyer principal objet. O F : foyer principal objet

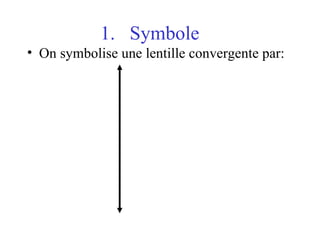
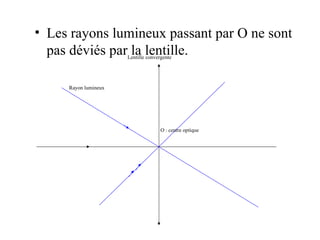
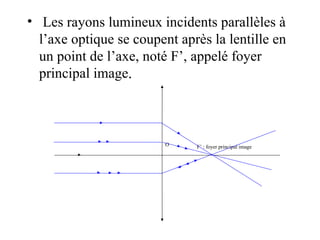
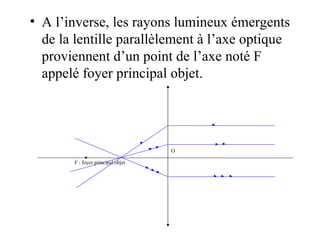
8. La mesure algébrique du segment [OF’], notée OF’ ou f’ est caractéristique de la lentille et est appelé la distance focale de la lentille. On a : OF’ = - OF = f’ . f’ s’exprime en mètre. La vergence C d’une lentille est : C=1/f’. Elle s’exprime en dioptrie de symbole  . (1  = 1m -1 )‏

9. Le plan passant par un foyer et perpendiculaire à l’axe optique est appelé plan focal (image ou objet). Les rayons issus d’un objet à l’infini sont parallèles entre eux. 4. Objets et images à l’infini

10. L’image d’un objet situé à l’infini se trouve dans le plan focal image de la lentille. O F F’ B : Objet à l’infini A’ B’

11. L’image d’un objet situé dans le plan focal objet se trouve à l’infini . O F F’ A’ A B B’

12. 5. Construction d’une image On veut construire l’image d’un objet à travers une lentille dont on connaît la distance focale. On commence par placer sur l’axe optique la lentille, l’objet puis les foyers principaux images et objets (on connaît f’, donc OF et OF’ car f’ = OF’ = - OF). O A B F F’

13. On trace ensuite un rayon qui passe par le centre optique et qui donc n’est pas dévié. O A B F F’

14. Puis un rayon qui passe par le foyer principal objet. O A B F F’

15. Et enfin un rayon qui passe par l’objet et est parallèle à l’axe optique. O A B F F’ A’ B’

16. Remarque: Parfois le foyer principal image F’ est situé avant la lentille et le foyer principal objet est situé après la lentille. O A B F’ F

17. O A B F’ F

18. O A B F’ F

19. O A B F’ F A’ B’

20. 6. Relation de de conjugaison 1 1 1 C OA’ OA f’ Relation de conjugaison de Descartes. (le prime est en premier). Exercice: OA= - 5,0 cm et f’ = 3,0 cm, calculer OA’ (réponse: 7,5 cm)

21. 7. Relation de grandissement Le grandissement (latéral) est:  A’B’ A B La relation de grandissement est:  A’B’ OA’ A B OA