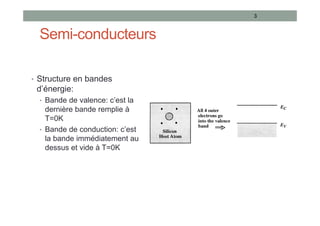
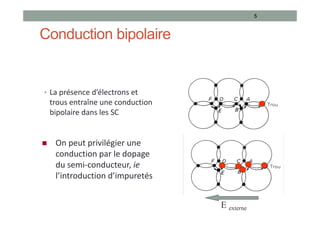
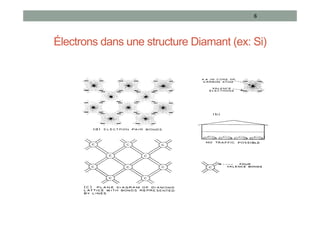
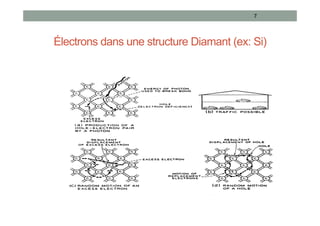
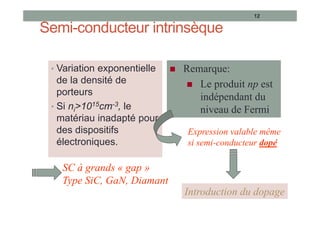
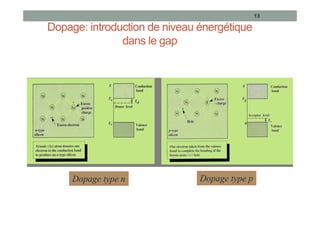
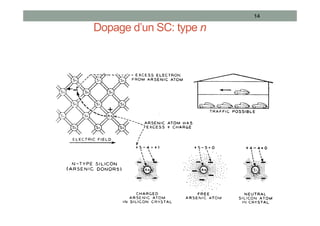
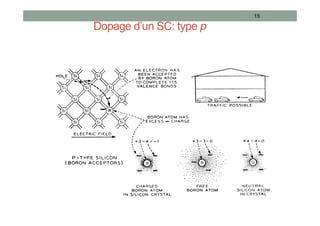
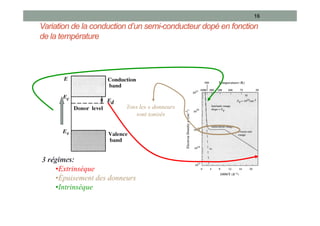
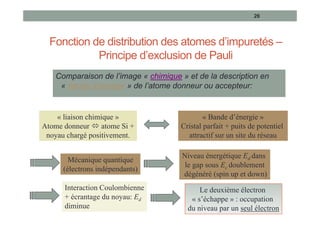
Le document traite des semi-conducteurs à l'équilibre, leur dopage, la structure en bandes d'énergie, et la densité de porteurs, en expliquant les concepts clés tels que la conduction bipolaire et la position du niveau de Fermi. Il aborde également les semi-conducteurs hors équilibre, les processus de génération et recombinaison, et les courants dans ces matériaux. Des équations mathématiques et des modèles sont présentés pour décrire le comportement des semi-conducteurs en fonction de différentes conditions de température et de dopage.

1. CHAPITRE 1A
Rappels:
Semi-conducteur à l’équilibre
1

2. Semi-conducteurs à l’équilibre
• Dopage des semi-conducteurs
• Semi-conducteur intrinsèque
• Le dopage n et p
• Calcul de la densité de porteurs extrinsèques
2

3. Semi-conducteurs
• Structure en bandes
d’énergie:
• Bande de valence: c’est la
dernière bande remplie à
T=0K
• Bande de conduction: c’est
la bande immédiatement au
dessus et vide à T=0K
3

4. Notion de trous (+e !)
• La notion de bandes
permet d’introduire le
porteur de charge positif
: un trou
4
 Aux températures
différentes de 0 K,
électrons « montent » dans
BC, laissent des « trous »
dans la BV

5. Conduction bipolaire
• La présence d’électrons et
trous entraîne une conduction
bipolaire dans les SC
5
 On peut privilégier une
conduction par le dopage
du semi‐conducteur, ie
l’introduction d’impuretés
E externe

6. Électrons dans une structure Diamant (ex: Si)
6

7. Électrons dans une structure Diamant (ex: Si)
7

8. Densité de porteurs dans les bandes
• Fonction de Fermi:
• Densité d’états:
• Densité de porteurs:
8
Eg
kT
F
E
E
e
E
f /
)
(
1
1
)
( 


2
/
1
2
/
3
2
*
2
)
(
2
2
1
)
( C
c
C E
E
m
E
N 











2
/
1
2
/
3
2
*
2
)
(
2
2
1
)
( E
E
m
E
N V
v
v 














C
E
n
C dE
E
f
E
N
n ).
(
).
(



V
E
p
v dE
E
f
E
N
p ).
(
).
(

9. Densité de porteurs dans les bandes
• Approximation de Boltzmann:
• Si le niveau de Fermi est à plus de « 3kT » du minimum de la
bande de conduction ou du maximum de la bande de valence, on
peut simplifier la fonction de distribution:
9
kT
E
E
e
E
n
f F
/
)
(
)
( 

 kT
E
E
e
E
n
f F
/
)
(
)
( 


kT
E
E
e
E
p
f F
/
)
(
)
(



kT
E
E
e
E
p
f F
/
)
(
)
(




10. Densité de porteurs dans les bandes
• Dans ces conditions (Boltzmann), la densité de
porteurs libres s’écrit:
• Dans la bande de conduction (électrons):
• Dans la bande de valence (trous):
10
)
exp(
kT
E
E
N
n F
C
C


 )
exp(
kT
E
E
N
n F
C
C



)
exp(
kT
E
E
N
p v
F
v


 )
exp(
kT
E
E
N
p v
F
v



avec
2
/
3
2
*
2
2 








h
kT
m
N C
C
2
/
3
2
*
2
2 








h
kT
m
N C
C
2
/
3
2
*
2
2 








h
kT
m
N v
v
2
/
3
2
*
2
2 








h
kT
m
N v
v
avec

11. Loi d’action de masse np=ni
2
• Dans un semi-conducteur intrinsèque, la densité de
trous est égale à la densité d’électrons:
• En faisant n=p, on obtient le niveau de Fermi
intrinsèque:
11
2
2
/
3
*
*
3
2
)
exp(
)
(
2
4 i
g
h
e n
kT
E
m
m
kT
np 










)
ln(
2
2 V
C
V
C
Fi
i
N
N
kT
E
E
E
E 




12. Semi-conducteur intrinsèque
• Variation exponentielle
de la densité de
porteurs
• Si ni>1015cm-3, le
matériau inadapté pour
des dispositifs
électroniques.
12
SC à grands « gap »
Type SiC, GaN, Diamant
 Remarque:
 Le produit np est
indépendant du
niveau de Fermi
Expression valable même
si semi-conducteur dopé
Introduction du dopage

13. Dopage: introduction de niveau énergétique
dans le gap
13
Dopage type n Dopage type p

14. Dopage d’un SC: type n
14

15. Dopage d’un SC: type p
15

16. Variation de la conduction d’un semi-conducteur dopé en fonction
de la température
16
3 régimes:
•Extrinsèque
•Épuisement des donneurs
•Intrinsèque
Tous les « donneurs
sont ionisés

17. Calcul de la position du niveau énergétique
Ed ou Ea
• Le problème « ressemble »
au modèle de l’atome
d’hydrogène
• Introduction du Rydberg
« modifié » :
17
2
0
0
*
6
.
13 

















m
m
E
E C
d
Exemple de dopants et leurs énergies
eV
n
e
m
En 2
2
2
0
4
0
6
.
13
)
4
(
2





18. Densité de porteurs extrinsèques:
• nb d’électrons différents du nb de trous
• Mais loi d’action de masse toujours valable, avec n.p=cte
(sauf si dopage trop élevé).
• Pour déterminer ces concentrations (n et p), on écrit la
neutralité électrique du système.
18
0



 n
p
n
cste
n
p
n i 
 2
.
0
)
( 2
2



 i
A
D n
n
N
N
n
D
A N
p
N
n 



19. Densité de porteurs extrinsèques:
• Semi-conducteurs type n (ND>NA):
• Dans la pratique (ND, NA, et ND – NA >> )ni si bien que:
19
 
  




 










 




2
1
2
2
2
1
2
2
4
)
(
2
1
4
)
(
2
1
i
A
D
A
D
i
A
D
A
D
n
N
N
N
N
p
n
N
N
N
N
n
)
/(
2
A
D
i
A
D
N
N
n
p
N
N
n





20. Niveau de Fermi dans un SC dopé
• Si le SC n’est pas dégénéré, l’approximation de
Boltzmann reste valable:
• Type n et p respectivement
• Soit un niveau de Fermi type n et type p donné par:
20
)
exp(
)
exp(
kT
E
E
N
N
N
p
kT
E
E
N
N
N
n
V
F
V
D
A
F
C
C
A
D
p
n










))
/(
ln(
))
/(
ln(
D
A
V
V
F
A
D
C
C
F
N
N
N
kT
E
E
N
N
N
kT
E
E
p
n







21. Différence Ef - Efi
• Au lieu d’exprimer Ef en fonction de Nc et Nv, on peut
écrire:
type n
type p
21










i
d
i
f
n
N
kT
E
E ln










i
a
f
i
n
N
kT
E
E ln
Fi
e

22. • On peut alors exprimer les densité d’électrons et de trous
à l’équilibre par:
22
kT
e
i
kT
E
E
i
kT
e
i
kT
E
E
i
Fi
Fi
F
Fi
Fi
F
e
n
e
n
p
e
n
e
n
n
/
/
)
(
/
/
)
(










avec:
0
0






Fi
F
Fi
Fi
F
Fi
E
E
e
E
E
e

 type n
type p
Équations de
Boltzmann
Différence Ef - Efi

23. Semi-conducteurs dégénérés:
approximation de Joyce –Dixon
• Dans ce cas , l’approximation de Boltzmann n’est
plus valable pour le calcul:
• soit de n et p
• soit de la position du niveau de Fermi:
on utilise alors l’approximation de Joyce-Dixon:
23


















V
V
V
C
C
C
F
N
p
N
p
kT
E
N
n
N
n
kT
E
E
8
1
ln
8
1
ln

24. Peuplement des niveaux d’impuretés : gel des porteurs
• En fonction de la température, le niveau d’impureté
est plus ou moins peuplé. Supposons un SC « avec »
ND donneurs et NA accepteurs (ND>NA)
• À T=0K
•BV =>pleine
•EA => NA électrons
•ED => ND-NA électrons
•BC => vide
24

25. Peuplement des niveaux d’impuretés : gel des porteurs
• À température non nulle: les électrons sont redistribués
mais leur nombre reste constant !!!. L’équation de
neutralité électrique permet de connaître leur répartition:
25
A
a
i
D
d
i
N
p
n
p
N
n
n
n






)
(
)
(
a
A
D
d p
p
N
N
n
n 




n, p : électrons (trous) libres dans BC (BV)
nd (pa) : électrons (trous) liés aux donneurs (accepteurs)

26. Fonction de distribution des atomes d’impuretés –
Principe d’exclusion de Pauli
Comparaison de l’image « chimique » et de la description en
« bande d’énergie » de l’atome donneur ou accepteur:
26
« liaison chimique »
Atome donneur  atome Si +
noyau chargé positivement.
« Bande d’énergie »
Cristal parfait + puits de potentiel
attractif sur un site du réseau
Mécanique quantique
(électrons indépendants)
Niveau énergétique Ed dans
le gap sous Ec doublement
dégénéré (spin up et down)
Interaction Coulombienne
+ écrantage du noyau: Ed
diminue
Le deuxième électron
« s’échappe » : occupation
du niveau par un seul électron

27. Probabilité d’occupation du niveau
d’impureté
• Proba d’occupation et nb d’électrons sur Ed:
• Proba de non occupation et nb de trous sur Ea:
27
)
exp
2
1
1
(
kT
E
E
f
f
d
n



kT
E
E
N
n
f
d
d
d



exp
2
1
1
)
exp
4
1
1
(
kT
E
E
f
a
f
p



kT
E
E
N
p
a
f
a
a



exp
4
1
1

28. Niveau « donneur »:le facteur 1/2
• Atome de Phosphore (col V):
• États électroniques 3s² 3p3 : 2e s et 2e p participent aux
liaisons  1e sur le niveau ED (le 5° !)
• il (le 5° !) possède un spin particulier up ou down
• Une fois l’e parti (f(E)) la « case » vide peut
capturer un spin up ou down => le mécanisme (la
proba.) de capture est augmenté / à l’émission.
28
)
(
)
( E
f
E
fD 

29. Semi-conducteur fortement dopé
• Si dopage trop important, les impuretés se « voient »
(rayon de Bohr 100 angströms)
le niveau d’énergie associé s’élargit
• Un effet important est la diminution du « Gap » du SC et
donc ni augmente!!:
29
meV
K
T
N
E d
g
2
/
1
18
)
(
300
10
5
.
22 










pour le Silicium

30. CHAPITRE 1B
Semi-conducteurs hors équilibre
30

31. Plan:
• Recombinaison et génération
• Courants dans les SC
• Équation de densité de courants
• Équations de continuité
• Longueur de Debye
• Équation de Poisson
• Temps de relaxation diélectrique
31

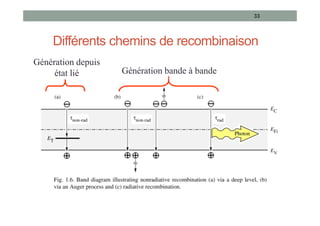
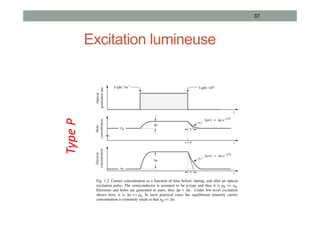
32. Phénomènes de Génération - Recombinaison
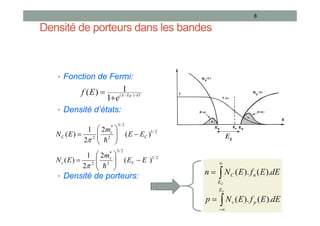
• Loi d’action de masse:
• À l’équilibre thermodynamique:
• Hors équilibre: apparition de phénomènes de Génération -
Recombinaison
• création ou recombinaison de porteurs :
Unité [g]=[r]=s-1cm-3
• Taux net de recombinaison:
32
r
g
r
g
g
r
g th





 '
'
' avec
th
g
r
r 
 '
externe interne
2
i
n
np 

33. Différents chemins de recombinaison
33
Génération bande à bande
Génération depuis
état lié

34. Recombinaison: 2 « chemins » possibles
• Recombinaison directe électron-trou
• Processus fonction du nombre d’électron et de trous
• Exemple: type n +excitation lumineuse en faible injection (
ie )
• En régime de faible injection le nombre de porteurs
majoritaires n’est pas affecté.
34
p
p
p
r



n
n
n
r



p
p
p 

 0 0
0 n
n
n
n 



0
n
p
n 




35. Recombinaison: 2 « chemins » possibles
• Recombinaison par centres de recombinaison:
• En général ces centres se trouvent en milieu de bande interdite
• Le taux de recombinaison s’écrit:
• Où est caractéristique du centre recombinant
• Si les 2 processus s’appliquent:
35
m

)
(
1
1
1
p
n
m





n
p
n
n
np
r
i
i
m 



2
1 2

Équation de
Shockley-Read

36. Recombinaison: 2 « chemins » possibles
• Si semi-conducteur peu dopé: on applique SR
• Si semi-conducteur dopé n:
• Si région « vide » de porteurs (ex: ZCE)
36
p
p
p
r



0
2



m
i
n
r

Taux net de génération.
Création de porteurs

37. Excitation lumineuse
37
Type P

38. Recombinaison radiative ou non
38

39. Recombinaisons de surface
39

40. Courants dans les SC
• Courant de conduction: présence de champ électrique
• Si E=0, vitesse des électron=vitesse thermique (107 cm/s) mais =>
vitesse moyenne nulle car chocs (« scattering ») avec le réseau +
impuretés.
• Libre parcours moyen (« mean free path »):
40
o
A
100
. 
 
vth
l ps
1
.
0



41. Courants dans les SC
• Courant de conduction: présence de champ électrique
• Entre deux chocs, les électrons sont accélérés uniformément
suivant
• Accélération:
• Vitesse:
• Mobilité:
41
*
/m
qE



E

µE
m
qE
v 


 *
/

*
/m
q
µ 

Si : 1500 cm2/Vs
GaAs: 8500 cm2/Vs
In0.53Ga0.47As:11000 cm2/Vs

42. Courants dans les SC
• La densité de courant de conduction s’écrit:
• Pour les électrons:
• Pour les trous:
• Pour l’ensemble:
42
E
neµ
v
ne
J n
n
n
c 

 E
neµ
v
ne
J n
n
n
c 


E
peµ
v
pe
J p
p
p
c 

 E
peµ
v
pe
J p
p
p
c 


E
peµ
neµ
J
J
J p
n
p
n
total
c )
( 


 E
peµ
neµ
J
J
J p
n
p
n
total
c )
( 




43. Courants dans les SC
• Importance de la mobilité sur les composants
• Mobilité la plus élevée possible
• => vitesse plus grande pour un même E
• Facteurs limitants:
• Dopage
• Défauts (cristallins, structuraux, …)
• Température
• Champ électrique de saturation + géométrie
43

44. Courants dans les SC
• Vitesse de saturation des électrons
• La relation linéaire vitesse – champ valide uniquement
pour:
• Champ électrique pas trop élevé
• Porteurs en équilibre thermique avec le réseau
• Sinon:
• Au-delà d’un champ critique, saturation de la vitesse
• Apparition d’un autre phénomène: « velocity overshoot »
pour des semiconducteurs multivallée.
• Régime balistique:pour des dispositifs de dimensions
inférieures au libre parcours moyen (0.1µm)
44

45. Vitesse de saturation
• Différents
comportement en
fonction du SC
45
Survitesse
(« overshoot »)

46. 46
Survitesse dans le cas de SC
multi vallées

47. Courants dans les SC
• Courant de diffusion:
• Origine: gradient de concentration
• Diffusion depuis la région de forte concentration vers la région de
moindre [].
• 1° loi de Fick:
47
dx
dp
D
p
dx
dn
D
n
p
x
D
n
x
D




nb d’e- qui diffusent par unité de
temps et de volume (flux)
nb de h+ qui diffusent par unité de
temps et de volume (flux)

48. Courants dans les SC
• Courant de diffusion: somme des deux contributions
(électrons et trous):
• Constante ou coefficient de diffusion
[ ]=cm2/s.
48
dx
dp
eD
dx
dn
eD
p
n
e
J p
n
x
D
x
D
diff




 )
(
p
n
D ,

49. Courants dans les SC
• Courant total: somme des deux contributions (si elles existent)
de conduction et diffusion:
• D et µ expriment la faculté des porteurs à se déplacer. Il existe
une relation entre eux: relation d’Einstein:
49
)
(
)
(
dx
dp
D
dx
dn
D
e
E
peµ
neµ
J
J
J
J
J
J
p
n
p
n
T
p
n
diff
cond
T








e
kT
µ
D

e
kT
µ
D


50. Équations de continuité – longueur de diffusion
• G et R altèrent la distribution des
porteurs donc du courant
50
G
R
e
x
dx
x
dJ
A
dt
t
x
dn
x
A
G
R
e
x
J
e
x
x
J
A
dt
t
x
dn
x
A
n
n
n


















)
(
)
,
(
)
(
)
(
)
,
(
 On obtient alors les équations de
continuité pour les électrons et les trous:
n
n
n
g
r
dx
dJ
e
dt
t
x
dn



1
)
,
(
n
n
n
g
r
dx
dJ
e
dt
t
x
dn



1
)
,
(
p
p
p
g
r
dx
dJ
e
dt
t
x
dp




1
)
,
(
p
p
p
g
r
dx
dJ
e
dt
t
x
dp




1
)
,
(

51. Équations de continuité – longueur de diffusion
• Exemple: cas où le courant est exclusivement du à
de la diffusion:
51
dx
dp
eD
diff
J
dx
dn
eD
diff
J
p
p
n
n



)
(
)
(
dx
dp
eD
diff
J
dx
dn
eD
diff
J
p
p
n
n



)
(
)
( n
n
n
n
dx
n
d
D
dt
dn

0
2
2



n
n
n
n
dx
n
d
D
dt
dn

0
2
2



p
p
p
p
dx
p
d
D
dt
dp

0
2
2



p
p
p
p
dx
p
d
D
dt
dp

0
2
2




52. Équations de continuité – longueur de
diffusion
• En régime stationnaire, les
dérivées par rapport au temps
s’annulent:
• Solutions:
52
2
0
0
2
0
2
)
(
n
n
n L
n
n
D
n
n
dx
n
n
d 




 2
0
0
2
0
2
)
(
n
n
n L
n
n
D
n
n
dx
n
n
d 





2
0
0
2
0
2
)
(
p
p
p L
p
p
D
p
p
dx
p
p
d 




 2
0
0
2
0
2
)
(
p
p
p L
p
p
D
p
p
dx
p
p
d 





n
L
x
e
n
n
x
n
x
n /
0 )
0
(
)
)
(
(
)
( 




 n
L
x
e
n
n
x
n
x
n /
0 )
0
(
)
)
(
(
)
( 





 Longueur de diffusion: représente la
distance moyenne parcourue avant
que l’électron ne se recombine avec
un trou (qq microns voire qq mm)
 Ln ou Lp >> aux dispos VLSI
 R et G jouent un petit rôle sauf
dans qq cas précis (Taur et al)
n
n
n D
L 
 n
n
n D
L 
 p
p
p D
L 
 p
p
p D
L 


53. Équation de Poisson
• Elle est dérivée de la première équation de Maxwell. Elle relie le
potentiel électrique et la densité de charge:
• Dans les SC, deux types de charges (fixes et mobiles):
53
sc
x
dx
dE
dx
V
d

 )
(
2
2




 
)
(
)
(
)
(
)
(
2
2
x
N
x
N
x
n
x
p
e
dx
V
d
A
D
sc








Charge mobiles
(électrons et trous)
Charges fixes
(dopants ionisés)

54. Longueur de Debye
• Si on écrit l’équation de Poisson dans un type n en exprimant n en
fonction de :
• Si Nd(x) => Nd+Nd(x) , alors Fi est modifié de Fi
54
Fi

 
kT
e
i
d
sc
Fi Fi
e
n
x
N
e
dx
d /
2
2
)
( 





en remarquant que: V(x)=Fi cte
)
(
2
2
2
x
N
e
kT
N
e
dx
d
d
sc
Fi
sc
d
Fi











55. Longueur de Debye
• Signification physique?
• Solution de l’équation différentielle du 2° degré:
• La « réponse » des bandes n’est pas abrupte mais « prend »
quelques LD ( si Nd=1016 cm-3, LD=0.04µm). Dans cette
région, présence d’un champ électrique (neutralité électrique
non réalisée)
55
D
Fi
L
x
A 

 exp

D
sc
D
N
e
kT
L 2


avec

56. Temps de relaxation diélectrique
• Comment évolue dans le temps la densité de
porteurs majoritaires ?
• Équation de continuité (R et G négligés):
56
x
J
e
t
n n




 1
n
n E
E
J 
 /

 sc
en
x
E

/




or et
d’où
sc
n
n
t
n






Solution: )
/
exp(
)
( sc
n
t
t
n 



sc
n


  Temps de relaxation diélectrique ( 10-12 s)