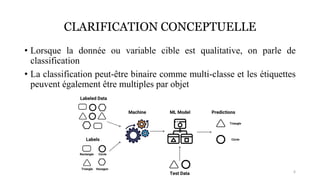
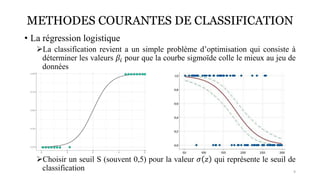
La classification est une méthode en Intelligence Artificielle qui consiste a ranger des élements dans différentes catégories prédéfinies sans intervention de l'humain, de maniere autonome. Ici, vous en saurez plus par rapport a ce type d'apprentissage supervisé (car nécéssite un entrainement de modele) et découvirez comment elle peut etre mis en place.

1. L’apprentissage supervisé : classification
Intelligence Artificielle et Applications
UNIVERSITE D’ABOMEY-CALAVI
*_*_*_*_*_*
ECOLE POLYTECHNIQUE D’ABOMEY-CALAVI
*_*_*_*_*_*
DÉPARTEMENT DE GENIE INFORMATIQUE ET Télécoms
*_*_*_*_*_*
Année académique : 2024-2025

2. GROUPE N°1:
MEMBRES DU GROUPE :
BAKPE Espéro
ESSOU Fructueux
NOM DE L’ENSEIGNANT :
Dr. Ratheil HOUNDJI

3. PLAN
Introduction
Clarifications conceptuelles
Méthodes courantes de classification
Processus de classification
Conclusion
3
Métriques de mesure de performance

4. INTRODUCTION
4

5. CLARIFICATION CONCEPTUELLE
• L’apprentissage supervisé est une méthode d’apprentissage
automatique consistant a apprendre une fonction de prédiction
d’étiquettes (données quantitatives et qualitatives) à base d’exemples
clairement étiquetées (données d’entraînement)
5

6. CLARIFICATION CONCEPTUELLE
• Lorsque la donnée ou variable cible est qualitative, on parle de
classification
• La classification peut-être binaire comme multi-classe et les étiquettes
peuvent également être multiples par objet
6

7. METHODES COURANTES DE CLASSIFICATION
• Plusieurs méthodes existent et sont utilisées selon le cas présenté :
➢La régression logistique
➢Les Support Vector Machines (SVM)
➢Le K-Nearest Neighbor (K-NN)
➢Les arbres de décisions
➢etc.
• Nous vous présenterons ici deux méthodes : la régression logistique et
les SVM 7

8. METHODES COURANTES DE CLASSIFICATION
• La régression logistique
➢Utilisée pour des tâches de classification binaire linéaire
➢Prédit une probabilité d’appartenance d’une observation à une classe sur la
base d’un modèle linéaire, souvent la fonction sigmoïde définit comme suit :
8
𝜎 𝑧 =
1
1 + 𝑒−𝑧
Ici, on aura
𝑧 = ෍
𝑖
𝛽𝑖𝑥𝑖

9. METHODES COURANTES DE CLASSIFICATION
• La régression logistique
➢La classification revient a un simple problème d’optimisation qui consiste à
déterminer les valeurs 𝛽𝑖 pour que la courbe sigmoïde colle le mieux au jeu de
données
➢Choisir un seuil S (souvent 0,5) pour la valeur 𝜎 𝑧 qui représente le seuil de
classification 9

10. METHODES COURANTES DE CLASSIFICATION
• Support Vector Machines (SVM) ou Machines à Vecteurs Supports
➢Principe : séparer un ensemble de données en deux classes à l’aide d’une frontière en
maximisant la marge
➢Les vecteurs supports sont les points qui définissent les droites extrêmes
➢La marge est l’espace entre les droites extrêmes ou la distance entre la frontière et les
vecteurs supports
➢Ici, on parle de SVM linéaire car les classes sont linéairement séparables 10

11. METHODES COURANTES DE CLASSIFICATION
• Support Vector Machines (SVM) ou Machines à Vecteurs Supports
➢Pour rendre l’algorithme plus flexible, on peut tolérer un nombre
d’observation biaisantes, mais cela augmente son biais.
11
3 enregistrements
dans la marge

12. METHODES COURANTES DE CLASSIFICATION
• Support Vector Machines (SVM) ou Machines à Vecteurs Supports
➢Dans le cas ci-dessus, le SVM linéaire sera fortement biaisé, il ne fonctionnera
peu, voire pas. On utilise alors une autre méthode.
12

13. METHODES COURANTES DE CLASSIFICATION
• Support Vector Machines (SVM) ou Machines à Vecteurs Supports
➢Principe : on définit une fonction appelée noyau définit dans la dimension des
observations qui amènera ces dernières dans la dimension supérieure, et ceci
dans le but de pouvoir les y séparer avec un hyperplan
➢Le dataset ci-dessus est non linéairement séparable. Prenons pour noyau la
fonction suivante
13
𝑓 𝑥 = 𝑥3

14. METHODES COURANTES DE CLASSIFICATION
• Support Vector Machines (SVM) ou Machines à Vecteurs Supports
➢On obtient la nouvelle représentation suivante et une séparation est possible
➢La classe de la nouvelle variable sera déterminée par sa position par rapport à
cette nouvelle droite dans le même espace 14

15. AUTRES METHODES
• Les arbres de décisions
oLe dataset est injecté par la racine
o Les feuilles représentent les classes objectifs
o Chacun des autres noeuds représente une
interrogation sur une variable dont la réponse oriente
dans la progression dans l’arbre.
15

16. AUTRES METHODES
• Les forts aléatoires
oUn ensemble d’arbres de décision ou chacun d’eux a été entrainé sur des
ensembles légèrement diffèrents.
oLa classe majoritaire est sélectionnée
16

17. METRIQUES DE MESURE DE PERFORMANCE
• Matrice de confusion :
• Exactitude ou Accuracy : 𝑎𝑐𝑐𝑢𝑟𝑎𝑐𝑦 =
𝑇𝑃+𝑇𝑁
𝑇𝑃+𝑇𝑁+𝐹𝑃+𝐹𝑁
• Précision : 𝑝𝑟𝑒𝑐𝑖𝑠𝑖𝑜𝑛 =
𝑇𝑃
𝑇𝑃+𝐹𝑃
• Rappel ou Recall : 𝑟𝑒𝑐𝑎𝑙𝑙 =
𝑇𝑃
𝑇𝑃+𝐹𝑁
• Score F1 :
2
𝐹1
=
1
𝑝𝑟𝑒𝑐𝑖𝑠𝑖𝑜𝑛
+
1
𝑟𝑒𝑐𝑎𝑙𝑙
17

18. METRIQUES DE MESURE DE PERFORMANCE
• Exemple :
18
Id Y_attendus Y_prédits
1 0 0
2 1 1
3 0 0
4 1 0
5 1 1
6 0 1
7 1 1
8 0 0
9 0 1
10 1 1
Matrice de confusion :
𝑨𝒄𝒄𝒖𝒓𝒂𝒄𝒚 =
3 + 4
10
= 0.70
𝑷𝒓𝒆𝒄𝒊𝒔𝒊𝒐𝒏 =
4
4 + 2
= 0.67
𝑹𝒆𝒄𝒂𝒍𝒍 =
4
4 + 1
= 0.80
𝑭𝟏 = 2 ∗
0.67 ∗ 0.8
0.67 + 0.8
= 0.73
3
2
1
4

19. PROCESSUS DE CLASSIFICATION
• Prétraitement de la donnée
➢Gérer les données manquantes
➢Gérer les variables qualitatives en les encodant
➢Mise à l’échelle des variables
• Séparation du dataset en données d’entraînement et de test
• Entraînement
• Mesure des performances
19

20. CONCLUSION
20

21. MERCI DE VOTRE
ATTENTION
21