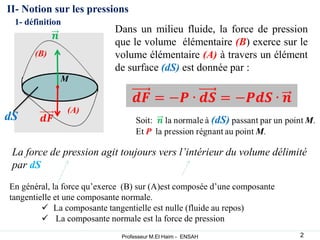
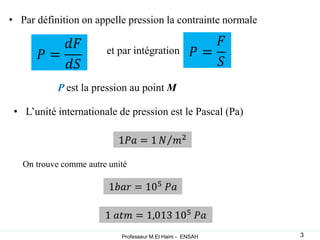
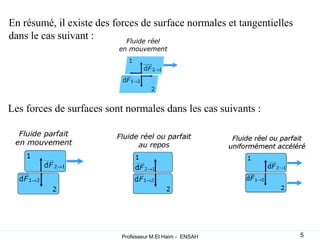
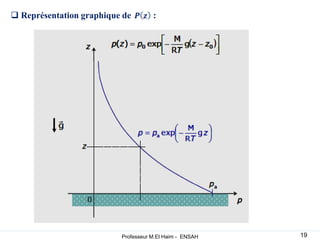
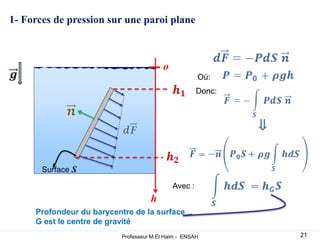
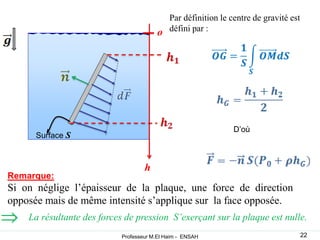
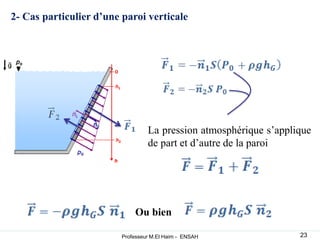
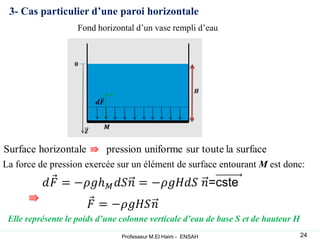
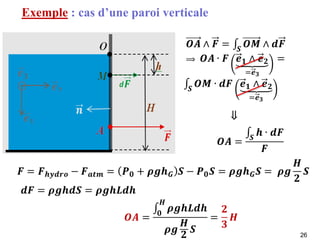
La statique des fluides étudie l'équilibre des fluides au repos, en se concentrant sur les forces de volume dues au poids et les forces de surface dues à la pression. Les concepts de pression atmosphérique, pression absolue et forces hydrostatiques sont fondamentaux, permettant de comprendre comment ces forces interagissent dans des fluides incompressibles et compressibles. L'application du principe d'Archimède explique la poussée que subit un objet immergé, ainsi que les conditions de flottaison.

1. Statique des Fluides
Chapitre II

2. La statique des fluides est la science qui étudie les conditions d’équilibre des fluides
au repos.
Plus précisément, elle concerne toutes les situations dans lesquelles il n’y a pas de
mouvement relatif entre les particules fluides :
 fluides au repos
 fluides uniformément accélérés
Donc il n’y a pas de contraintes tangentielles dues aux frottements entre particules.
Les forces misent en jeu sont uniquement :
Forces de volume dues au poids
Forces de surface dues à la pression.
Rq:
Quand le fluide est un liquide (eau par exemple), la théorie est appelée l’hydrostatique.
En hydrostatique, le fluide étant au repos, les lois établies pour un fluide parfait s’appliqueront
à un fluide réel.
I- Introduction
Professeur M.El Haim - ENSAH 1

3. II- Notion sur les pressions
La force de pression agit toujours vers l’intérieur du volume délimité
par dS
Dans un milieu fluide, la force de pression
que le volume élémentaire (B) exerce sur le
volume élémentaire (A) à travers un élément
de surface (dS) est donnée par :
dS
(A)
(B)
M
En général, la force qu’exerce (B) sur (A)est composée d’une composante
tangentielle et une composante normale.
 La composante tangentielle est nulle (fluide au repos)
 La composante normale est la force de pression
1- définition
2
Professeur M.El Haim - ENSAH

4. • Par définition on appelle pression la contrainte normale
et par intégration
• L’unité internationale de pression est le Pascal (Pa)
On trouve comme autre unité
P est la pression au point M
3
Professeur M.El Haim - ENSAH

5. mais
La pression au point M ne dépend pas de l’orientation de la
surface dS
4
Professeur M.El Haim - ENSAH

6. En résumé, il existe des forces de surface normales et tangentielles
dans le cas suivant :
Les forces de surfaces sont normales dans les cas suivants :
5
Professeur M.El Haim - ENSAH

7. 2- Pression atmosphérique et pression absolue-pression effective :
 Pression atmosphérique : est la pression de l’air en un lieu donné.
Au niveau de la mer : Patm = 1 atm ≈1,013 bar = 760 mmHg
 Pression absolue- Pression effective
Lorsque la pression d’un fluide est supérieure à la pression atmosphérique on dit que ce fluide
est sous pression.
Lorsque la pression du fluide est inférieure à la pression atmosphérique, on dit que le fluide
est sous vide.
Une pression nulle (P=0 Pa) correspond à un vide parfait qui correspond en fait à une absence
totale de particules (atomes ou molécules).
oLa pression absolue est la pression mesurée par rapport au
vide absolu. Elle est toujours positive.
oLa pression relative se définit par rapport à la pression
atmosphérique :cette pression peut donc prendre une valeur
positive (sous pression) ou une valeur négative (sous vide)
La relation suivante permet de passer de l'une à l'autre:
6
Professeur M.El Haim - ENSAH

8. II- Équation fondamentale de la statique des fluides
Les forces de volume : le poids du fluide donné par:
Les forces de surface : dues à la pression ; on peut décomposer la
résultante en trois composantes :
Considérons un élément de volume de forme parallélépipédique à
l’intérieur d’un fluide en équilibre, de volume dV = dxdydz,
dans un repère cartésien:
7
Professeur M.El Haim - ENSAH

9. Puisque les forces de surface sont nécessairement normales, la composante suivant z
correspond aux forces de pression s’exerçant sur les surfaces perpendiculaires à
l’axe z . Donc :
Car par un développement au premier ordre, on a :
8
Professeur M.El Haim - ENSAH

10. o Par analogie sur les deux autres axes :
o La force de surface se résume alors à :
Au total, on a:
et
9
Professeur M.El Haim - ENSAH

11.  En vertu du principe fondamental de la dynamique, l’ensemble
des forces agissant sur la particule fluide équivaut au produit de sa
masse par son accélération :
Par conséquent, on a:
D’où
Si le fluide est au repos , dans ce cas:
(Équation locale)
10
Professeur M.El Haim - ENSAH

12. Dans le cas d’un fluide au repos, en supposant , on a:
D’où
C’est l’équation différentielle à résoudre pour connaître
la pression en tout point du fluide au repos
11
Professeur M.El Haim - ENSAH

13. III- l’équation hydrostatique pour un fluide
incompressible & un fluides compressibles
Un fluide est dit incompressible si l’on peut considérer que sa masse
volumique est en tout point la même
Par ailleurs, on peut considérer que l’accélération de la pesanteur est une constante
Par conséquent :
Et par intégration :
Soit:
1- Fluide incompressible
12
Professeur M.El Haim - ENSAH

14. On considère au sein de ce fluide homogène et au repos, deux points distincts A et B,
d’altitudes respectives et , alors on peut écrire la relation suivante entre les pressions
et :
Ou bien:
La plupart du temps, on prendra le niveau de référence correspondant à la surface libre
du fluide où :
h : hauteur de fluide sous le niveau de référence
13
Professeur M.El Haim - ENSAH

15. Cette relation permet de calculer la pression en tout point du liquide, connaissant la
pression atmosphérique et la profondeur de ce point par rapport à la surface libre.
 Représentation graphique de la pression dans les liquides :
14
Professeur M.El Haim - ENSAH

16. Remarque :
La pression dans un fluide homogène ne dépend que de la différence de
l’hauteur et de la masse volumique. Cela a des conséquences importantes:
– Pour une altitude donnée la pression est la même ;
– La surface libre d’un fluide est plane.
Pression indépendante de la forme du
récipient
15
Professeur M.El Haim - ENSAH

17. APPLICATION
Mesure de la pression atmosphérique (Baromètre de Torricelli, ~ 1643)
Soit un récipient contenant du mercure de masse volumique 13600Kg/m3. On
plonge dans le récipient un tube vertical, le niveau de la surface du mercure à
l’intérieur du tube se stabilise à une hauteur h = 0.76 m. Sachant que le vide règne
dans la partie supérieure du tube, déterminer la pression à la surface du mercure
contenu dans le récipient?
16
Professeur M.El Haim - ENSAH

18. 2- Fluide compressible
Masse molaire
du gaz
D’où compressibilité
Pour connaître la pression en tout point du gaz, on part de l’équation
fondamentale de la statique des fluides:
17
Professeur M.El Haim - ENSAH

19. constant si la température est homogène
Où la constante se définit par rapport à la pression pour un niveau de référence
Donc :
on l’intègre:
18
Professeur M.El Haim - ENSAH

20.  Représentation graphique de :
19
Professeur M.El Haim - ENSAH

21. IV- Force de pression :Forces s’exerçant sur une surface immergée
(forces hydrostatiques)
On peut désormais s’intéresser à la détermination des forces s’exerçant
sur les surfaces solides immergées.
On sait que:
est la force de pression élémentaire s’exerçant sur
la surface élémentaire dS
Pour connaître la force totale s’exerçant sur une surface S, il suffit d’intégrer :
20
Professeur M.El Haim - ENSAH

22. 1- Forces de pression sur une paroi plane
h
o
Surface S
Où:
Donc:
Avec :
Profondeur du barycentre de la surface
G est le centre de gravité
21
Professeur M.El Haim - ENSAH

23. o
Surface S
h
D’où
Remarque:
Si on néglige l’épaisseur de la plaque, une force de direction
opposée mais de même intensité s’applique sur la face opposée.
La résultante des forces de pression S’exerçant sur la plaque est nulle.
Par définition le centre de gravité est
défini par :
22
Professeur M.El Haim - ENSAH

24. 2- Cas particulier d’une paroi verticale
La pression atmosphérique s’applique
de part et d’autre de la paroi
Ou bien
23
Professeur M.El Haim - ENSAH

25. 3- Cas particulier d’une paroi horizontale
Fond horizontal d’un vase rempli d’eau
La force de pression exercée sur un élément de surface entourant M est donc:
Elle représente le poids d’une colonne verticale d’eau de base S et de hauteur H
24
Professeur M.El Haim - ENSAH

26. V- Point d’application d’une force hydrostatique (centre
de poussée) :
Il faut alors calculer le moment de la force
par rapport à un point O quelconque, puis
identifier ce moment à la résultante des
moments élémentaires par rapport à ce
même point O
25
Professeur M.El Haim - ENSAH

27. Exemple : cas d’une paroi verticale
26

28. V- Effort exercé sur un objet totalement immergé : Poussée d’Archimède
On cherche l’effort exercé sur un objet immergé, c’est-à-dire la force totale exercée
par le fluide sur l’obstacle qui occupe le volume V totalement entouré par le fluide.
On sait que la force exercée par le fluide sur le solide
immergé s’exprime come :
La formule du gradient permet de passer d’une intégrale de
surface à une intégrale de volume :
Dans le cas présent, si l’on identifie le scalaire f à la pression, on obtient :
27

29. Or, l’équation fondamentale da la statique des fluides permet d’écrire :
Remarques1 :
•Pour un corps partiellement immergé, le volume déplacé est
égal au volume immergé
•on admettra que le point d’application de la poussée
d’Archimède est le centre de masse de la partie immergée du
solide.
Tout corps plongé dans un fluide au repos subit une force
verticale, dirigée de bas en haut et opposée au poids du
volume de fluide déplacé
28
Professeur M.El Haim - ENSAH

30. Remarques 2 :
1- Si : le solide flotte.
2- Si : le solide est immergé et il reste en suspension dans le
liquide.
3-Si : le solide est immergé et il touche le fond du contenant
du liquide.
Variation de la position du solide dans un liquide en fonction la masse volumique
29
Professeur M.El Haim - ENSAH