Téléchargé 160 fois
Téléchargé parchagra bassem
Problème De Sac à Dos
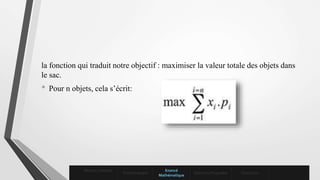
Le document aborde le problème de sac à dos, une question centrale en optimisation combinatoire, en discutant de sa formulation mathématique et des solutions proposées par différentes méthodes de résolution, incluant tant des techniques exactes que des heuristiques. Il présente également des algorithmes tels que le best fit decreasing et la méthode de branch and bound, soulignant leur pertinence dans le contexte contemporain de la recherche informatique. Enfin, il mentionne que ce problème et ses variantes continuent d'être un sujet d'étude actif dans le domaine.
Contenu connexe
Problème De Sac à Dos
- 1. Projet R-O Complexité: ProblèmeDe Sac à Dos
- 2. Plan • Mise Encontexte • Problématique • Enoncé mathématique • Solutions Proposées • Conclusion 2
- 3. Plan • Mise Encontexte • Problématique • Enoncé mathématique • Solutions Proposées • Conclusion 3
- 4. Mise en contexte Miseen contexte Problématique Enoncé Mathématique Solutions Proposées Conclusion • Article Reducibility Among Combinatorial Problems de Richard Karp en 1972 . • Les 21 problèmes NP-complets de Karp ont marqué une étape importante de l'histoire de la théorie de la complexité des algorithmes. 4
- 5. Plan • Mise Encontexte • Problématique • Enoncé mathématique • Solutions Proposées • Conclusion 5
- 6. Problématique 6 1|2 Histoire du problème Miseen contexte Domaines concernés Enoncé mathématique Variantes Conclusion et perspective Sac du cambrioleur Capacité est limitée Chaque objet possède un poids et une valeur Le voleur doit optimiser la valeur Totale des objets Mise en contexte Problématique Enoncé Mathématique Solutions Proposées Conclusion
- 7. Question qui sepose? Quels sont les objets que l’on doit prendre pour maximiser le coût transporté tout en respectant la contrainte de poids du sac? Mise en contexte Problématique Enoncé Mathématique Solutions Proposées Conclusion
- 8. Plan • Mise Encontexte • Problématique • Enoncé mathématique • Solutions Proposées • Conclusion 8
- 9. Formulation mathématique • Touteformulation commence par un énoncé des données: Problème: choisir un sous ensemble d’objet d’utilité maximale à placer dans un sac tel la capacité du sac soit respectée. Données: • W : capacité maximale du sac • I : ensemble de n objets • Pi: pour chaque objet i € I , pi représente son utilité • wi : chaque objet i a un poids w Mise en contexte Problématique Enoncé Mathématique Solutions Proposées Conclusion
- 10. Pour quatre objets(n = 4) et un sac à dos d'un poids maximal de 30 kg (W = 30), nous avons par exemple les données suivantes: • Ensuite, il nous faut définir les variables qui représentent en quelque sorte les actions ou les décisions qui amèneront à trouver une solution: • xi: une variable associée à un objet i de la façon suivante : xi = 1 si l’objet i est mis dans le sac xi = 0 si l’objet i n’est pas mis dans le sac Objets 1 2 3 4 pi 7 4 3 3 wi 13 12 8 10 Mise en contexte Problématique Enoncé Mathématique Solutions Proposées Conclusion
- 11. • Une solutionpossible au problème ? x1 = 0, x2 = 1, x3 = 1, et x4 = 1 • La contrainte est elle respectée? x1.w1 + x2.w2 + x3.w3 + x4.w4 ≤ W il suffit de calculer cette somme : 0 × 13 + 1 × 12 + 1 × 8 + 1 ×10 = 30, ce qui est bien inférieur ou égal à 30. Nous parlons alors de solution réalisable. Mais ce n’est pas nécessairement la meilleure solution. Mise en contexte Problématique Enoncé Mathématique Solutions Proposées Conclusion
- 12. la fonction quitraduit notre objectif : maximiser la valeur totale des objets dans le sac. • Pour n objets, cela s’écrit: Mise en contexte Problématique Enoncé Mathématique Solutions Proposées Conclusion
- 13. Plan • Mise Encontexte • Problématique • Enoncé mathématique • Solutions Proposées • Conclusion 13
- 14. • Il existedeux grandes catégories de méthodes de résolution de problèmes d’optimisation combinatoire : les méthodes exactes: permettent d’obtenir la solution optimale à chaque fois, mais le temps de calcul peut être long si le problème est compliqué à résoudre les méthodes approchées: - encore appelées heuristiques, permettent d’obtenir rapidement une solution approchée, donc pas nécessairement optimale. - a pour but de trouver une solution avec un bon compromis entre la qualité de la solution et le temps de calcul Méthode d Résolution Mise en contexte Problématique Enoncé Mathématique Solutions Proposées Conclusion
- 15. Le Best FitDecreasing (BFD) (meilleur remplissage par ordre décroissant): •Triant tous les objets par ordre décroissant de poids • Sélectionnant les objets un à un dans l’ordre du tri et en ajoutant l’objet sélectionné dans le sac le plus lourd tel que la contrainte de poids maximal reste respectée. Déroulons cet algorithme sur notre exemple : Best Fit Decreasing Algorithme Mise en contexte Problématique Enoncé Mathématique Solutions Proposées Conclusion
- 16. Best Fit DecreasingAlgorithme Mise en contexte Problématique Enoncé Mathématique Solutions Proposées Conclusion Première étape: Objets 2 3 1 4 5 6 7 Pi 4 4 3 3 3 2 1 Objets 2 3 1 4 5 6 7 Pi 4 4 3 3 3 2 1 Xi 1 1 2 2 2 1 2 Deuxième étape:
- 17. Best Fit DecreasingAlgorithme Mise en contexte Problématique Enoncé Mathématique Solutions Proposées Conclusion Objets 2 3 1 4 5 6 Pi 4 4 3 3 3 3 Xi 1 1 2 2 2 3 Cette solution est optimale, mais cet algorithme est imparfait comme le montre le cas suivant : =>La qualité de cet algorithme est de rester rapide même si le nombre d’objets augmente considérablement tout en approchant de moins d’un facteur 2 la solution optimale
- 18. Best Fit DecreasingAlgorithme Mise en contexte Problématique Enoncé Mathématique Solutions Proposées Conclusion • First Fit - FF : on place au fur et à mesure les objets dans le premier sac possible . • Worst Fit - WF : on place au fur et à mesure les objets dans le sac le plus léger possible . • Best Fit – BF : on place, au fur et à mesure, les objets dans le sac le plus lourd possible . • First Fit Decreasing et Worst Fit Decreasing – FFD etWFD : on trie les objets dans l’ordre des poids décroissant puis on applique FF / WF.
- 19. La méthode deBranch and Bound
- 20. 1. Recherche desolution initiale: On va utiliser une approche glouton. En commençant par le premier objet, on met des objets dans le sac à dos tant que la capacité le permet. 2. Principe d’évaluation: Le principe d’évaluation a pour objectif de connaître la qualité des nœuds à traiter La méthode de Branch and Bound utilise deux types de bornes: - une borne inférieure de la fonction d’utilité du problème initial, - une borne supérieure de la fonction d’utilité.
- 21. - si pourun sous-problème la borne supérieure est plus petite que la borne inférieure du problème, l’exploration du sous-ensemble correspondant est inutile 3. Le principe de séparation : - Le principe de séparation consiste à diviser le problème en un certain nombre de sous problèmes qui ont chacun leur ensemble de solutions réalisables. En résolvant tous les sous problèmes et en prenant la meilleure solution trouvée, on est assuré d'avoir résolu le problème initial. Ce principe de séparation est appliqué de manière récursive à chacun des sous ensembles tant que celui-ci contient plusieurs solutions
- 22. . Condition d’arret: Laprocédure de séparation d’un ensemble s’arrête lorsqu’une des conditions suivantes est vérifiée : - on connaît la meilleure solution de l’ensemble ; - on connaît une solution meilleure que toutes celles de l’ensemble ; - on sait que l’ensemble ne contient aucune solution admissible 4. Stratégie de parcours : - La stratégie de parcours est la règle qui permet de choisir le prochain sommet à séparer parmi l’ensemble des sommets de l’arborescence
- 23. Plan • Mise Encontexte • Problématique • Enoncé mathématique • Solutions Proposées • Conclusion 23
- 24. Le Problème desac à dos est un problème qui est toujours d’actualité. En effet, dans la recherche en informatique, le problème du sac à dos et ses dérivés sont encore beaucoup étudiés. Il en existe de nombreuses variantes : sac à dos multi- dimensions (plusieurs poids par objet), plusieurs fonctions objectif, etc. De nombreux algorithmes exacts et approchés sont proposés pour ce type de problèmes. Les chercheurs ne sont pas près de partir en vacances… Conclusion Mise en contexte Problématique Enoncé Mathématique Solutions Proposées Conclusion
- 25.
Notes de l'éditeur
- #3 Nous allons commencer cette présentation par une introduction durant laquelle nous allons introduire la problématique, l’organisme d’accueil ainsi que la méthodologie Nous expliciterons ensuite le contexte du projet. Puis Nous enchainerons par les parties étude des besoins, etude conceptuelle et réalisation pour finir avec la conclusion et les perspectives envisagées.
- #4 Nous allons commencer cette présentation par une introduction durant laquelle nous allons introduire la problématique, l’organisme d’accueil ainsi que la méthodologie Nous expliciterons ensuite le contexte du projet. Puis Nous enchainerons par les parties étude des besoins, etude conceptuelle et réalisation pour finir avec la conclusion et les perspectives envisagées.
- #5 Au cours de ces dernières années, le secteur de télécommunication a vécu un progrès spectaculaire et une mutation structurelle suite à la vague de privatisation et l'ouverture du marché aux opérateurs privé. En effet, suite à l'existence de plusieurs opérateurs dans le même pays, le client a la possibilité de choisir l’opérateur auquel il va confier son contrat . Pour cette raison il vise sans doute à celui qui propose une vue d'ensemble complète sur l'évolution technologique, des offres exceptionnelles et innovantes ainsi que des promotions régulières. D’où l’apparition d’une cooccurrence exponentielle entre les opérateurs Télécom
- #6 Nous allons commencer cette présentation par une introduction durant laquelle nous allons introduire la problématique, l’organisme d’accueil ainsi que la méthodologie Nous expliciterons ensuite le contexte du projet. Puis Nous enchainerons par les parties étude des besoins, etude conceptuelle et réalisation pour finir avec la conclusion et les perspectives envisagées.
- #7 Étant donné que dans un tel marché, le client est l'unique décideur du succès et suite à cet environnement mouvementé et incertain, les opérateurs télécom se trouvent dans l'obligation d'améliorer leurs compétences, de répondre au besoin du client dans le bref délais et d’assurer l’exclusivité . D'où la nécessité de personnaliser leurs systèmes de facturation afin de garantir l’expansion et maintenir la confrontation à la concurrence. Parmi ces systèmes de facturation qui existent sur le marché on trouve le progiciel majeur BSCS .
- #9 Nous allons commencer cette présentation par une introduction durant laquelle nous allons introduire la problématique, l’organisme d’accueil ainsi que la méthodologie Nous expliciterons ensuite le contexte du projet. Puis Nous enchainerons par les parties étude des besoins, etude conceptuelle et réalisation pour finir avec la conclusion et les perspectives envisagées.
- #14 Nous allons commencer cette présentation par une introduction durant laquelle nous allons introduire la problématique, l’organisme d’accueil ainsi que la méthodologie Nous expliciterons ensuite le contexte du projet. Puis Nous enchainerons par les parties étude des besoins, etude conceptuelle et réalisation pour finir avec la conclusion et les perspectives envisagées.
- #24 Nous allons commencer cette présentation par une introduction durant laquelle nous allons introduire la problématique, l’organisme d’accueil ainsi que la méthodologie Nous expliciterons ensuite le contexte du projet. Puis Nous enchainerons par les parties étude des besoins, etude conceptuelle et réalisation pour finir avec la conclusion et les perspectives envisagées.