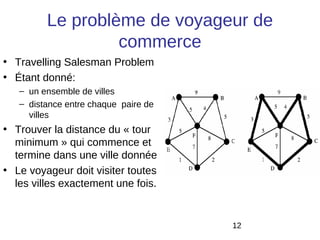
Le document traite des problèmes de décision et d'optimisation en informatique décisionnelle, en présentant des exemples tels que le problème SAT et le problème du voyageur de commerce. Il explore la complexité de ces problèmes, ainsi que les concepts de convexité et de programmation linéaire. Des applications pratiques dans divers domaines tels que l'allocation de fréquences et la gestion du trafic sont également mentionnées.

1. Chapitre 1
Notions préliminaires
Master Informatique Décisionnelle et Intelligence appliquée à la gestion
Hend Bouziri
Maître Assistant, ESSEC de Tunis
LARODEC ISG
Laboratoire de Recherche Opérationnelle, de DEcision et de
Contrôle de processus
1

2. Typologie de problèmes
• Problème de décision,
• Problème d’optimisation
2

3. Problème de décision
• Un problème de décision est défini par:
– un nom,
– des paramètres génériques,
– une question.
• Exemples
– Problème de CLIQUE
– Graphe G=(S,A), 1<k<n=Card(S)
– Existe t ’il une clique d’ordre k dans G?
– SAT
– N var. logiques xj
– k clauses Ck sur les xj
– Existe t’il une fonction de vérité telle que toutes les clauses
soient vraies?
3

4. Problème SAT
• Boolean Satisfiability Problem
– Le premier problème classé NP-complet
• Applications possibles
– Diagnostic de systèmes
– Cryptographie
• L’expression booléenne doit être une
conjonction de clauses ;
– les clauses sont représentées par des disjonctions de
k variables (k-SAT)
• Exemple:
– Pour N=3, k=2,
– soit la fonction (expression) logique:
• (v1∨v2)∧(¬v1∨v3)∧(¬v2∨v1)
• Fonction satisfiable si v1=vrai,v2=faux et v3=vrai
4

5. Complexité du SAT
• Pour N=100,
– taille espace de recherche = 2100≈1030!
• Evaluation de 1000 chaînes / sec ; 15
milliards d’années pour évaluer moins de
1% de l’espace.
• Attention!
– k>2, problème NP-complet ;
– k=2, Algorithme polynomial
5

6. Problème d’optimisation
• Un problème d’optimisation
– Encore appelé problème de programmation
mathématique
– consiste à trouver, parmi un ensemble donné,
un élément :
• Qui peut être un vecteur de IRn un vecteur
d’entiers, une fonction...
• minimisant ou maximisant une fonction
donnée de cet ensemble sur IR.
6

7. Pourquoi Optimiser?
7

8. Problème d’optimisation
• Dans tout problème d’optimisation on se
doit de définir :
– les variables
– le ou les objectifs
– les contraintes
8

9. Problème d’optimisation
• Problème d’optimisation continu: à
variable continue
– Chercher un optimum d’une fonction continue
• Sans ou avec contraintes
• Applications: physique,…
• Problème d’optimisation combinatoire:
– ou problèmes discrets
– les variables sont dénombrables
9

10. Exemple d’applications industrielles
• Allocation de fréquences
• Optimisation de réseaux téléinformatiques
• Localisation d'entrepôts
• Optimisation de tournées de
distribution/ramassage
• Optimisation de chaînes de production
• Optimisation de planning/emplois du temps
• Gestion du trafic aérien/ferroviaire
10

11. Problème d’optimisation
combinatoire
• Tous les modèles sont des simplifications
de la réalité.
• Problème ==> Modèle ==> Solution
• Exemple de problèmes d’OC
– TSP
– Sac à dos
– ordonnancement
– coloration de graphes
11

12. Le problème de voyageur de
commerce
• Travelling Salesman Problem
• Étant donné:
– un ensemble de villes
– distance entre chaque paire de
villes
• Trouver la distance du « tour
minimum » qui commence et
termine dans une ville donnée
• Le voyageur doit visiter toutes
les villes exactement une fois.
12

13. Remarque
• Version décisionnelle de TSP :
– Étant donné un ensemble de villes, distance
entre chaque paire de villes, et une borne B,
– Existe-t-il un tour qui
• commence et se termine dans une ville donnée,
• Visite chaque ville exactement une seule fois
• Admet une distance totale au plus égale à B?
13

14. Complexité des problèmes
combinatoire
• TSP  n villes ville=élément d’une permutation
• Taille de l’espace de recherche = n!
• Problème TSP symétrique :
– dist(x,y)=dist(y,x)
• TSP symétrique : n! / 2,
• |S| = n!/2n = (n-1)! / 2 ; n>6 (TSP > SAT)
• 10 villes = 181 000 solutions
• 20 villes = 10 000 000 000 000 000 solutions
• 50 villes = 100 000 000 000 000 000 000 000
000 000 000 000 000 000 000 000 000 000 000
000 000 solutions !!!
14

15. Attention concernant la complexité
• Voir cours complexité
• On peut avoir un problème classé
– NP-complet
– qui admet des instances (ou des cas)
« faciles ».
15

16. Convexité
• Définition 1.1
– Étant donné deux points de IRn, x et y. une
combinaison de x et y est un point z donné par:
– z=λx +(1-λ)y.
∀ λ est un réel entre 0 et 1.
– Si λ différent de 0 et 1 alors z est dit une combinaison
stricte de x et de y.
• Définition 1.2
– Un ensemble S ⊆ IRn est convexe s’il contient toutes
les combinaisons convexe des points x et y.
• Remarques: IRn est convexe, tout singleton est
convexe, ∅ est convexe.
16

17. Exemples d’ensembles convexes
• Dans IR1, tout intervalle est un ensemble
convexe et tout ensemble convexe est un
intervalle.
• Dans IR2
17

18. Fonction convexe
• Soit S ⊆IRn un ensemble convexe,
• la fonction f:S →IR1 est dite convexe dans S si
pour toute paire de points x et y de S, on a:
• f(λx +(1-λ)y) ≤ λf(x) +(1-λ)f(y)
λ ∈ IR1 et 0≤λ≤1.
• Si S=IRn, on dit simplement que f est convexe.
• Exemple:
– Toute fonction linéaire est convexe dans tout
ensemble convexe S.
• Remarque:
– Une fonction qui n’est pas convexe est concave.
18

19. Représentation graphique
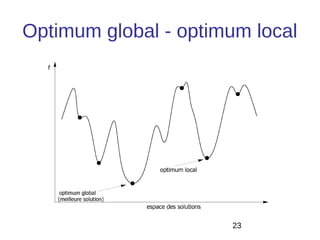
• Intuitivement, une
fonction convexe
admet l’allure
suivante:
• Ici c:[0,1]⊆IR→IR
• La condition de
convexité implique
que graphiquement
tjs la « corde» se
situe au dessus de la
fonction.
19

20. • Exemple:
• Une classe importante
des problèmes • La fonction c(x) définit
d’optimisations concerne sur [0,1] est convexe
la minimisation de et admet plusieurs
fonctions convexes sur optimima locaux mais
des ensembles convexes tous globaux
• Dans de tels problèmes :
optimum local
=
optimum global.
20

21. Instance d’un problème
d’optimisation
• Un problème d’optimisation est un
ensemble d’instances du problème.
• Informellement:
– une instance est donnée par un ensemble de
donnée (en input) et suffisamment de
données pour formuler une solution
– Un problème est une collection d’instances
générées de la même manière.
21

22. • Résoudre un problème (plus précisément
une instance du problème)
• consiste à trouver une (ou plusieurs)
solution s* ∈ X optimisant la valeur de la
fonction de coût f.
• Une telle solution s* s'appelle une solution
optimale ou un optimum global.
22

23. Optimum global - optimum local
23

24. Instance de problème
d’optimisation combinatoire
• Un problème d’optimisation est défini par un
ensemble d’instances
• A chaque instance d’un problème d’optimisation
combinatoire est associé :
– un ensemble discret de solutions S (espace de
recherche),
– un sous-ensemble X de S représentant les solutions
admissibles (réalisables)
– et une fonction de coût f (ou fonction objectif) qui
assigne à chaque solution s∈ X le nombre réel (ou
entier) f(s).
24

25. Plus formellement
• Une instance I d'un problème de
minimisation est un couple (X, f) où:
– X⊆ S est un ensemble fini de solutions
admissibles, et f une fonction de coût à
minimiser.
– f : X → R. Le problème est de trouver s* ∈ X
tel que f(s*) ≤ f(s) pour tout élément s ∈ X.
• N.b: d’une manière similaire on peut
définir un problème de maximisation en
remplaçant ≤ par ≥.
25

26. Définition encore plus formelle
• Un problème d’optimisation (minimisation)
P=(S,f) est donné par:
Minimiser f(s) (fonction à minimiser)
Avec gi(s) ≤ 0, i=1..m (contraintes d’inégalités)
hj(s)=0, j=1…p (contraintes d’égalité)
– Avec f, g et h fonctions dans IRn.
26

27. • Si f est concave, g est convexe et h est
linéaire alors on parle d’un problème de
programmation convexe.
• Pour un problème de programmation
convexe optimum local=optimum global
27

28. Problème de programmation
linéaire
• Si f, g, h sont fonctions linéaires, on parle
de problème de programmation linéaire.
• Chaque problème dans cette classe est
réduit à la sélection d’une solution parmi
un ensemble fini de solutions possibles.
• Ce problème est alors de type
combinatoire
28

29. Programmation linéaire en 0-1
• Exemple: Problème de sac à dos
• Définissant pour chaque objet une variable de
décision binaire
– xi= 1 si l’objet i est retenu
– xi= 0 sinon
• Déterminer une sélection optimale:
– Max Σcixi
– Sous Σvixi≤ b (volume ou poids du sac)
• Plusieurs applications réelles
• Pb: Comment modéliser?
29

30. Modélisation: Contraintes
• La plupart des problèmes réels possèdent des
contraintes.
• Exemple : Problème d’emploi du temps :
• Liste des cours, classes, étudiants / classe, professeur /
classe, salles disponibles, taille des salles, logistique des
salles (vidéo, …).
• Exemple de contraintes :
– Toute classe doit être affectée à une salle disponible avec un
nombre de places suffisant et des facilités requises,
– Les étudiants affectés à plusieurs classes ne doivent pas être
affectés au même temps.
– Les professeurs ne doivent pas être affecté à des cours en
parallèle.
30

31. Exemple: Le problème de voyageur
de commerce
• Dans une instance du problème TSP
– Données (input):
• n>0 (entier) nombre de villes,
• Les distances entre toutes paires de villes (matrice
de dimension n×n.
– Un tour est un cycle (chemin fermé) qui passe
une et une seule fois par chaque ville (et donc
revient à la ville de départ) →contraintes
31

32. Modélisation: Objectif
• Enjeux économique,
performance,..
• Dans un problème
d’affectation de fréquences,
plusieurs objectifs:
– Min Nombre de sites (coût)
– Min Interférences
– Max Trafic écoulé
32

33. Classification des méthodes de
résolution
• Algorithmes évaluant des solutions
complètes
• Algorithmes évaluant des solutions
partielles (incomplète, problème réduit)
• Algorithmes exacts
• Algorithmes approximatifs.
33