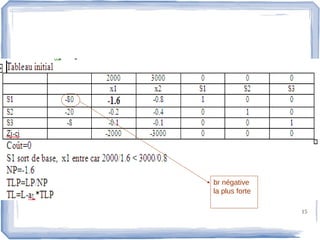
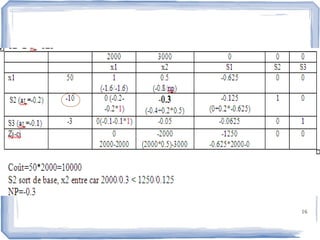
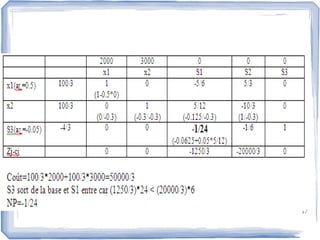
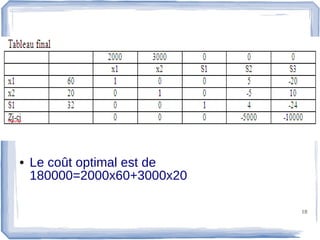
La dualité en programmation linéaire établit une relation entre un problème primal et son problème dual, avec des solutions optimales équivalentes. Le document explique les interprétations économiques et les propriétés de la dualité, ainsi que des algorithmes pour résoudre ces problèmes. Un exemple est fourni pour illustrer la minimisation des coûts dans le cadre du problème dual.