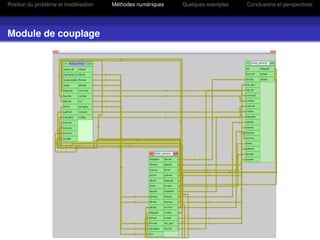
Le document présente des méthodes numériques pour résoudre des systèmes couplés fluide-structure, avec un accent sur le code_saturne et le code_aster. Il aborde la modélisation des équations de conservation ainsi que des exemples de simulations de mouvements vibratoires sous écoulement. Les conclusions mettent en évidence les défis et perspectives pour le développement de modèles plus performants et adaptés aux applications réelles.

1. Position du problème et modélisation Méthodes numériques Quelques exemples Conclusions et perspectives
Solveur itératif pour la résolution de
systèmes couplés fluide structure
Couplage Code_Saturne Code_Aster Salomé YACS
Elisabeth Longatte
EDF R&D
Collaboration MFEE / SINETICS / AMA / LaMSID
Novembre 2010

2. Position du problème et modélisation Méthodes numériques Quelques exemples Conclusions et perspectives
Objectifs
1 Position du problème et modélisation
2 Méthodes numériques
3 Quelques exemples
4 Conclusions et perspectives

3. Position du problème et modélisation Méthodes numériques Quelques exemples Conclusions et perspectives
Equations de conservation
Fluide homogène newtonien en écoulement incompressible, de
viscosité constante et uniforme
˜
divU = 0 Ωf
˜
1 dU 1 1 ˜
˜
= − 2 eZ − grad p + ∆U Ωf
UR dt FR RE
Solide en petites transformations, de matériau élastique linéaire
isotrope
∂2ξ UR 2
D =− e + divσ Ωs
∂t
2 FR Z
2
1 t
D ( ξ+ ξ) = (1 + ν)σ − νTr(σ)1 Ωs
2

4. Position du problème et modélisation Méthodes numériques Quelques exemples Conclusions et perspectives
Equations d’interface
Condition cinématique
∂ξ
˜ ˜
UR U(x ) = D ˜
(X , t) Γfs = Ωf ∩ Ωs
∂t
Condition dynamique
2 ˜
˜ ˜
CY [−p(x )1 + ˜ ˜ ˜ ˜
d(x )].n(x ) = σ(x ).n(x ) Γfs = Ωf ∩ Ωs
RE
avec CY = MUR 2
Couplage interfacial
˜
x = x = X + Dξ

5. Position du problème et modélisation Méthodes numériques Quelques exemples Conclusions et perspectives
Problème modèle
Petites vibrations d’une paroi solide rigide indéformable au
voisinage d’un fluide parfait en écoulement à potentiel
dU
divU = 0 = −gradp
dt
˜
avec U = UR U
Développement à l’ordre 1 en λ
U = V + λv p = P + λp
avec λ = D << 1
et V = Ψ

6. Position du problème et modélisation Méthodes numériques Quelques exemples Conclusions et perspectives
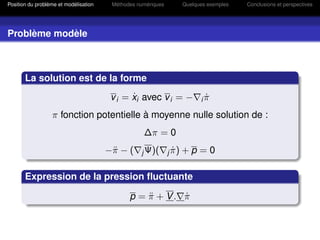
Problème modèle
Equations linéarisées
ivi =0
∂v i
+ j (V i v j + Vjvi) + ip =0
∂t
Après développement
ivi =0
∂v i
+ i [v j ( j Ψ)] +( j Ψ)[ jvi − vj] + ip =0
∂t

7. Position du problème et modélisation Méthodes numériques Quelques exemples Conclusions et perspectives
Problème modèle
La solution est de la forme
˙
v i = xi avec v i = − iπ
˙
π fonction potentielle à moyenne nulle solution de :
∆π = 0
−¨ − (
π j Ψ)( j π)
˙ +p =0
Expression de la pression fluctuante
p = π + V. π
¨ ˙

8. Position du problème et modélisation Méthodes numériques Quelques exemples Conclusions et perspectives
Evolution spatio temporelle de l’interface
Condition à la paroi vibrante
˙
(V + v ).n = x s .n sur Σ

9. Position du problème et modélisation Méthodes numériques Quelques exemples Conclusions et perspectives
Condition à la paroi vibrante
Ordre 0
V .n = 0 sur Σ
Ordre 1
[(V + v ).n ]|Σ =
V (M).n + V (M).(n − n) + [V (M ) − V (M)].n + (v .n)|Σ
D’où
˙
v .n|Σ = x s .n + V (M). Σ (x s .n) + (divΣ V )(x s .n)
∂π
˙
˙
= −x s .n − (divΣ V )x s .n − V . Σ (x s .n)
∂n |Σ

10. Position du problème et modélisation Méthodes numériques Quelques exemples Conclusions et perspectives
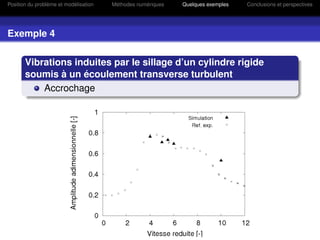
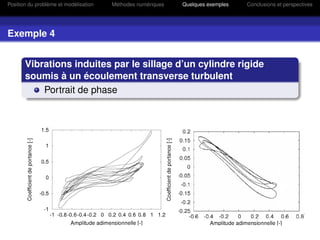
Effet du fluide en écoulement sur les mouvements de la structure
Soit une base de modes propres (sans fluide) Xi (r )
x s = Σai (t)X i (r )
Expression de la pression fluctuante
xfi = − iπ p = π + V. π
¨ ˙
∂π
˙
= x s˙.n − (div V )x s .n − V . (x s .n)
∂n
implique p(r , t) = Σ[aj Φ1 (r ) + aj Φ2 (r ) + aj φ3 (r )]
¨ j ˙ j j
Matrice de couplage
¨ ˙ 2
F = −[mij ]A + [mij ]V A + ([mij ]Vo + [mij ]P)A

11. Position du problème et modélisation Méthodes numériques Quelques exemples Conclusions et perspectives
Résolution du système couplé
Problème modèle
¨ ˙ 2
F = −[mij ]A + [mij ]V A + ([mij ]V + [mij ]P)A
˙
Termes de composition de vitesse V A engendrant un
amortissement (positif ou négatif)
2
Termes quasi-statiques V A et PA
Classe 1 : développement en petites perturbations
Relation linéaire entre cinématique et distribution de
contrainte à l’interface
Cas linéaire : résolution d’un problème aux valeurs propres
Combinaison avec une méthode de superposition
Cas non linéaire : introduction de corrélations empiriques

12. Position du problème et modélisation Méthodes numériques Quelques exemples Conclusions et perspectives
Résolution du système couplé
Classe 2 : méthode itérative
Non linéarité de l’interface
Conditions aux limites non connues explicitement, non
résolues implicitement à l’interface
Résolution par une méthode itérative (point fixe)
Conditions aux limites imposées explicitement
Recherche d’une solution satisfaisant les conditions de
compatibilité à l’interface

13. Position du problème et modélisation Méthodes numériques Quelques exemples Conclusions et perspectives
Opérateur de Dirichlet Neumann
Méthode itérative
Formulation non linéaire
Relaxation, stabilité conditionnelle
Fonction du module de couplage
Avancée en temps (convergence, point fixe)
Transferts de champs entre modèles fluide et solide
(cinématique et contraintes à l’interface)
F f = F(u ifs )
u
u ifs = U(F f )
F
u ifs = U ◦ F(u ifs )
u

14. Position du problème et modélisation Méthodes numériques Quelques exemples Conclusions et perspectives
Avancée en temps
Méthode de point fixe
Prédiction du déplacement de l’interface
n+1,k
u fsi = u fsi u n+1,k −1 , u n+1,k −1
s ˙s
Résolution du système fluide
pn+1,k = p pn , v n , u n+1,k
f fsi
n+1,k
vf = v pn , v n , u n+1,k
f fsi
Calcul des contraintes exercées par le fluide sur la paroi
solide
F n+1,k = F pn+1,k , v n+1,k )
f f

15. Position du problème et modélisation Méthodes numériques Quelques exemples Conclusions et perspectives
Avancée en temps
Méthode de point fixe
Résolution du système solide
u n+1,k = u u n , u n , u n , F n+1,k
s s ˙ s ¨s f
Convergence sur le déplacement
u n+1,k − u n+1,k −1
s s
≤ε
u n+1,0
s
Passage à l’itération suivante ou sous itération

16. Position du problème et modélisation Méthodes numériques Quelques exemples Conclusions et perspectives
Algorithme de résolution

17. Position du problème et modélisation Méthodes numériques Quelques exemples Conclusions et perspectives
Exemples of prédicteurs
Prédicteurs explicites (déplacement)
u P,n+1 = u n
s s
u P,n+1 = u n + ∆t u n
s s ˙s
3∆t n ∆t n−1
u P,n+1 = u n +
s s ˙
u − ˙
u
2 s 2 s
P,n+1 ∆t 2 n
us = u n + ∆t u n +
s ˙s ¨
u
2 s
P,n+ 1 ∆t n
us 2
= un +
s u˙
2 s
1
P,n+ 2 ∆t n ∆t 2 n
us = un +
s ˙
u + u¨
2 s 8 s
P,n+ 1 5∆t n ∆t n−1
us 2
= un +
s ˙
u − ˙
u
8 s 8 s

18. Position du problème et modélisation Méthodes numériques Quelques exemples Conclusions et perspectives
Exemples of prédicteurs
Prédicteurs explicites (contrainte)
f P,n+1 = f n
f f
f P,n+1 = f n+1
f f
P,n+1 1 n 1 n+1
ff = f + ff
2 f 2
P,n+1
ff = 2f f − f P,n
f n
f
P,n+1
ff = 2f n+1 − f P,n
ff f

19. Position du problème et modélisation Méthodes numériques Quelques exemples Conclusions et perspectives
Exemples of prédicteurs
Prédiction correction (déplacement initial)
3∆t n ∆t n−1
u P,n+1 = u n +
s s ˙
u − u˙
2 s 2 s
Prédiction correction (boucle itérative)
P,n+1,k
us = u n+1,k −1
s

20. Position du problème et modélisation Méthodes numériques Quelques exemples Conclusions et perspectives
Propriétés de convergence
Conservation du bilan d’énergie
Méthode de prédiction correction (explicite)

21. Position du problème et modélisation Méthodes numériques Quelques exemples Conclusions et perspectives
Propriétés de convergence
Méthode itérative
Stabilité conditionnelle

22. Position du problème et modélisation Méthodes numériques Quelques exemples Conclusions et perspectives
Transfert de champs
Méthode de projection
Poids résiduels, interpolations
Interfaces non conformes
ns nf
u [f ,j] = Πij u [s,i] Ξs,i = Ξf ,j Πij
i=1 j=1

23. Position du problème et modélisation Méthodes numériques Quelques exemples Conclusions et perspectives
Transfert de champs
Condensation
Compatibilité des modélisations de l’interface (formulation,
discrétisation, maillage, dimension)
Condensation 2D ou 3D vers 1D (éléments poutres)
Calcul de moyennes spatiales des champs pariétaux

24. Position du problème et modélisation Méthodes numériques Quelques exemples Conclusions et perspectives
Module de couplage

25. Position du problème et modélisation Méthodes numériques Quelques exemples Conclusions et perspectives
Exemples
Décomposition en problèmes élémentaires
Effets du fluide (sans écoulement permanent)
Accrochage fréquentiel
Effets induits par la turbulence (effets de Reynolds)
Bifurcation instationnaire (couplage non conservatif)

26. Position du problème et modélisation Méthodes numériques Quelques exemples Conclusions et perspectives
Exemple 1
Petits mouvements vibratoires d’un cylindre dans un
réseau de cylindres fixes soumis à un écoulement
transversal en régime laminaire
Modélisation

27. Position du problème et modélisation Méthodes numériques Quelques exemples Conclusions et perspectives
Exemple 1
Petits mouvements vibratoires d’un cylindre dans un
réseau de cylindres fixes soumis à un écoulement
transversal en régime laminaire
Vitesse réduite critique d’instabilité dynamique

28. Position du problème et modélisation Méthodes numériques Quelques exemples Conclusions et perspectives
Exemple 1
Petits mouvements vibratoires d’un cylindre dans un
réseau de cylindres fixes soumis à un écoulement
transversal en régime laminaire
Evolution de la fréquence et de l’amortissement en
fonction de la vitesse réduite

29. Position du problème et modélisation Méthodes numériques Quelques exemples Conclusions et perspectives
Exemple 1
Petits mouvements vibratoires d’un cylindre dans un
réseau de cylindres fixes soumis à un écoulement
transversal en régime laminaire
Comparaison au modèle théorique de Connors
1/2
URC m2πξ
= KConnors
fn D ρf D 2

30. Position du problème et modélisation Méthodes numériques Quelques exemples Conclusions et perspectives
Exemple 1
Petits mouvements vibratoires d’un cylindre dans un
réseau de cylindres fixes soumis à un écoulement
transversal en régime laminaire
Post instabilité

31. Position du problème et modélisation Méthodes numériques Quelques exemples Conclusions et perspectives
Exemple 2
Petits mouvements vibratoires d’un réseau de cylindres
soumis à un écoulement transversal en régime laminaire
Modélisation

32. Position du problème et modélisation Méthodes numériques Quelques exemples Conclusions et perspectives
Exemple 2
Petits mouvements vibratoires d’un réseau de cylindres
soumis à un écoulement transversal en régime laminaire
Critère de stabilité (phase)
Fo sinΦ
CFS = −
ωxo

33. Position du problème et modélisation Méthodes numériques Quelques exemples Conclusions et perspectives
Exemple 3
Petits mouvements vibratoires d’un conduit flexible
parcouru par un écoulement axial interne en régime
laminaire
Modélisation

34. Position du problème et modélisation Méthodes numériques Quelques exemples Conclusions et perspectives
Exemple 3
Petits mouvements vibratoires d’un conduit flexible
parcouru par un écoulement axial interne en régime
laminaire
Couplage non conservatif

35. Position du problème et modélisation Méthodes numériques Quelques exemples Conclusions et perspectives
Exemple 3
Petits mouvements vibratoires d’un conduit flexible
parcouru par un écoulement axial interne en régime
laminaire
Couplage non conservatif

36. Position du problème et modélisation Méthodes numériques Quelques exemples Conclusions et perspectives
Exemple 4
Vibrations induites par le sillage d’un cylindre rigide
soumis à un écoulement transverse turbulent
Modélisation LES (Re = 3900)

37. Position du problème et modélisation Méthodes numériques Quelques exemples Conclusions et perspectives
Exemple 4
Vibrations induites par le sillage d’un cylindre rigide
soumis à un écoulement transverse turbulent
Accrochage

38. Position du problème et modélisation Méthodes numériques Quelques exemples Conclusions et perspectives
Exemple 4
Vibrations induites par le sillage d’un cylindre rigide
soumis à un écoulement transverse turbulent
Accrochage

39. Position du problème et modélisation Méthodes numériques Quelques exemples Conclusions et perspectives
Exemple 4
Vibrations induites par le sillage d’un cylindre rigide
soumis à un écoulement transverse turbulent
Portrait de phase

40. Position du problème et modélisation Méthodes numériques Quelques exemples Conclusions et perspectives
Exemple 5
Petits mouvements vibratoires d’un réseau de cylindres
soumis à un écoulement transverse turbulent
Modélisation

41. Position du problème et modélisation Méthodes numériques Quelques exemples Conclusions et perspectives
Conclusions et perspectives
Synthèse
Module de couplage
Démonstrateur prototype
Adhérence aux versions de développement de
Code_Saturne, Code_Aster et Salomé
Performance, CPU, parallélisme
Verrous à lever
Passage à l’échelle réelle
Réduction de modèle
Homogénéisation
Couplage de modèles (micro macro, hybride RANS LES)