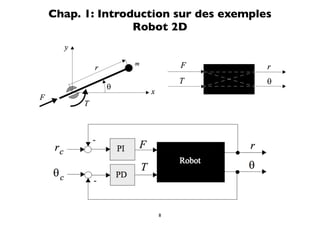
Le document traite de la coordination de systèmes multivariables et des dispositifs dynamiques distribués, abordant des sujets tels que la représentation d'état, la linéarisation, la discrétisation et la commande d'état. Il présente un syllabus détaillé des cours avec des études de cas et des méthodes d'analyse, y compris des exemples pratiques comme l'entraînement électrique et le pendule inversé. Les concepts clés incluent la modélisation, l'observation d'état et l'optimisation de la commande.

1. Systèmes Multivariables
Coordination de systèmes et de
dispositifs dynamiques distribués
Dr. Denis Gillet (IEL)
http://graaasp.epfl.ch/#item=space_851

2. Support:
Polycopié Systèmes multivariables (2011) de D. Gillet
qui est disponible en ligne
http://graaasp.epfl.ch/attachment/385
2

3. Syllabus
• Représentation d'état (21 septembre): Introduction. Exemples qualitatifs. Représentation
d'état analogique.
• Représentation d'état (28 septembre): Simulation. Représentation d'état discrète.
• Etude de cas (5 octobre): Introduction ex catherdra à l'étude de cas et exercices.
• Linéarisation (12 octobre): Trajectoires et points de fonctionnement. Commande a priori.
Linéarisation locale. Linéarisation globale.
• Discrétisation (19 octobre): Discrétisation de modèles linéaires (prise en compte de
convertisseurs AD & DA). Méthodes de calcul de l'exponentielle de matrice.
• Analyse dynamique des systèmes MIMO discrets et Principe de la commande d'état (26
octobre): Solution de l'équation d'état discrète. Matrice de transfert. Stabilité, Formes canoniques.
Synthèse constructive du régulateur.
• Commande d'état SISO (2 novembre): Formule d'Ackermann pour le régulateur. Commande à
réponse pile.
• Observation d'état (9 novembre): Méthode constructive. Formule d'Ackermann pour
l'observateur. Observabilité.
• Etude de cas (16 novembre): Etude de cas au laboratoire - ME A0 392.
• Commande d'état optimale (23 novembre): Introduction à la commande d'état MIMO.
Solution du problème optimal par Lagrange.
• Commande d'état optimale (30 novembre): Commande optimale linéaire quadratique (LQR)
stationnaire.
• Etude de cas (7 décembre): Etude de cas au laboratoire - ME A0 392 (assistant: Alain Bock). 0.5
pts de bonus (sur la base d'un rapport à rendre pour le 7 janvier par email à Alain Bock)!
• Estimation d'état optimale (14 décembre).
• Fonctions de navigation et révision (21 décembre).
3

4. Chap. 1: Introduction sur des exemples
Entraînement électrique
Rétroaction classique
Commande en cascade
4

5. Chap. 1: Introduction sur des exemples
Entraînement électrique
Commande d’état
5

6. Chap. 1: Introduction sur des exemples
Pendule inversé
Applications
Interactions dynamiques
6

7. Chap. 1: Introduction sur des exemples
Pendule inversé
Commande d’état
7

8. Chap. 1: Introduction sur des exemples
Robot 2D
8

9. Chap. 1: Linéarité
Additivité f (x + y) = f (x) + f (y)
+ Homogénéité f (αx) = αf (x)
Principe de
superposition
f (αx + βy) = αf (x) + βf (y)
Comportement proportionnel
˙
y(t) ˙
y(t)
u(t) u(t)
y(t) = f [u(t), t] = au(t)
˙ y(t) = f [u(t), t] = au(t) + b
˙
9

10. Chap. 1: Linéarité
u1 → y1 = au1
˙
u2 → y2 = au2
˙
u = αu1 + βu2 → y = a(αu1 + βu2 ) = α(au1 ) + β(au2 ) = αy1 + β y2
˙ ˙ ˙
Le principe de superposition s’applique
u1 → y1 = au1 + b
˙
u2 → y2 = au2 + b
˙
u = αu1 + βu2 → y = a(αu1 + βu2 ) + b = α(au1 ) + β(au2 ) + b = αy1 + β y2
˙ ˙ ˙
Le principe de superposition ne s’applique pas
10

11. Chap. 1: Signaux discrets
w(tk )
t1 t5
t2 t3 t4
t
t−3 t−2 t−1 t0
h est la période d’échantillonnage tk = kh
w(tk ) = w(kh) → w(k)
Les techniques avancées de commande n’ont de sens
qu’implantées sur ordinateurs, donc numériques
11

12. Chap. 1: Etat d’un système
x1 , x2 , . . . , xn
u1 , u2 , . . . , ur y1 , y2 , . . . , yp
État
• Actions • Réactions
• Causes Entrées
ce qui est susceptible Sorties • Effets
d’évoluer
• Données • Résultats
• Moyens disponibles Conditions initiales • Comportements qui
pour influencer le doivent être
système observés ou modifiés
• Excitation • Réponse du système
• Grandeurs pouvant • Observations
Perturbations
être manipulées • Mesures
• Influence de l’environnement sur le système
• Grandeurs ne pouvant pas être manipulées
Le modèle est une représentation mathématique qui décrit les
interactions entre les entrées et l’état, et entre l’état et les sorties
12

13. Chapitre 2
Représentation d’état
13

14. Entraînement électrique
Electrical Drive
i
θ J
R
u ui
f
Partie électrique Partie mécanique
u(t) = Ri(t) + ui (t) J ω(t) = M (t) − f ω(t)
˙
ui (t) = kω(t) ˙
θ(t) = ω(t)
M (t) = ki(t)
14

15. Entraînement électrique
Electrical Drive
i
θ J
R
u ui
f
Modèle physique Choix des variables d’état
2 x1 (t) = θ(t)
ω(t) = − J
˙ 1 k
+ f ω(t) + k
JR u(t)
R x2 (t) = ω(t)
˙
ω(t) = θ(t) y(t) = θ(t)
Modèle d’état: équation d’état Modèle d’état: équation de sortie
x1 (t) = x2 (t)
˙ y(t) = x1 (t)
2
x2 (t) = − J k + f x2 (t) +
˙ 1
R
k
JR u(t)
15

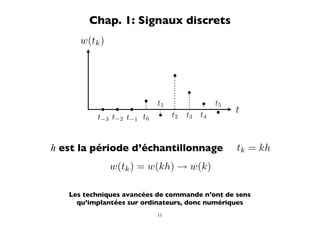
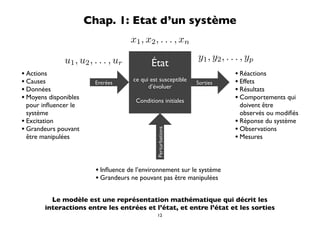
16. Systèmes analogiques non linéaires
Nonlinear continuous time systems
 
x1 (t) = f1 [x1 (t) , . . . , xn (t) , u1 (t) , . . . ur (t) , t]
˙ x1 (t)
˙
x2 (t) = f2 [x1 (t) , . . . , xn (t) , u1 (t) , . . . ur (t) , t]
˙
 x2 (t)
˙ 
 
.
. x (t) = 
˙ . 
.  .
. 
xn (t) = fn [x1 (t) , . . . , xn (t) , u1 (t) , . . . ur (t) , t]
˙ xn (t)
˙
 
y1 (t) = g1 [x1 (t) , . . . , xn (t) , u1 (t) , . . . ur (t) , t] y1 (t)
y2 (t) = g2 [x1 (t) , . . . , xn (t) , u1 (t) , . . . ur (t) , t]  y2 (t) 
 
.
. y (t) =  . 
.  .
. 
yp (t) = gp [x1 (t) , . . . , xn (t) , u1 (t) , . . . ur (t) , t] yp (t)
     
x1 (t) u1 (t) f1 [x (t) , u (t) , t]
 x2 (t)   u2 (t)   f2 [x (t) , u (t) , t] 
     
x (t) =  .  u (t) =  .  f [x (t) , u (t) , t] =  . 
 .
.   .
.   .
. 
xn (t) ur (t) fn [x (t) , u (t) , t]
16

17. Systèmes analogiques non linéaires
Nonlinear continuous time systems
x1 (t) = f1 [x1 (t) , . . . , xn (t) , u1 (t) , . . . ur (t) , t]
˙
x2 (t) = f2 [x1 (t) , . . . , xn (t) , u1 (t) , . . . ur (t) , t]
˙
.
.
.
xn (t) = fn [x1 (t) , . . . , xn (t) , u1 (t) , . . . ur (t) , t]
˙
y1 (t) = g1 [x1 (t) , . . . , xn (t) , u1 (t) , . . . ur (t) , t]
y2 (t) = g2 [x1 (t) , . . . , xn (t) , u1 (t) , . . . ur (t) , t]
.
.
.
yp (t) = gp [x1 (t) , . . . , xn (t) , u1 (t) , . . . ur (t) , t]
x(t) = f [x(t), u(t), t]
˙
y(t) = g [x(t), u(t), t]
17

18. 2.1.3: Sélection des variables d’état
Selection of the state variables
a¨ (t) + sin z(t)
ω ˙ = u1 (t)
2
v(t) + cos z(t)
˙ ˙ = u2 (t)
˙
z(t) = αt
Ne pas prendre en considération les dérivées des entrées
18

19. Systèmes analogiques linéaires
Linear continuous time systems
x(t) = f [x(t), u(t), t]
˙
Non linéaire
y(t) = g [x(t), u(t), t]
x(t) = A(t)x(t) + B(t)u(t)
˙
Linéaire
y(t) = C(t)x(t) + D(t)u(t)
x(t) = Ax(t) + Bu(t)
˙ Linéaire et
y(t) = Cx(t) + Du(t) stationnaire
19

20. Entraînement électrique
Electrical Drive
i
θ J
R
u ui
f
Modèle d’état: équation d’état Modèle d’état: équation de sortie
x1 (t) = x2 (t)
˙ y(t) = x1 (t)
1 k2 k
x2 (t) = −
˙ + f x2 (t) + u(t)
J R JR
a b
Modèle d’état: équation d’état Modèle d’état: équation de sortie
x1 (t)
˙ 0 1 x1 (t) 0 x1 (t)
= + u(t) y(t) = 1 0
x2 (t)
˙ 0 a x2 (t) b x2 (t)
20

21. 2.3: Méthode de Runge-Kutta
1
x (kh + h) ≈ x (kh) + [a(kh) + 2b (kh) + 2c (kh) + d (kh)]
6
y (kh) = g [x (kh) , u (kh) , kh]
a (kh) = hf [x (kh) , u (kh) , kh]
a(kh)
b (kh) = hf x (kh) + 2 , u kh + h , kh + h
2 2
b(kh)
c (kh) = hf x (kh) + 2 , u kh + 2 , kh + h
h
2
d (kh) = hf [x (kh) + c (kh) , u (kh + h) , kh + h]
21

22. Systèmes discrets non linéaires
Nonlinear discrete time systems
x1 (k + 1) = f1 [x1 (k), . . . , xn (k), u1 (k), . . . , ur (k), k]  
x (k + 1) = f [x (k), . . . , x (k), u (k), . . . , u (k), k] x1 (k + 1)
2 2 1 n 1 r  x2 (k + 1) 
.  
. x(k + 1) =  . 
.  .
. 
x (k + 1) = f [x (k), . . . , x (k), u (k), . . . , u (k), k]
n n 1 n 1 r xn (k + 1)
 
y1 (k) = g1 [x1 (k), . . . , xn (k), u1 (k), . . . , ur (k), k] y1 (k)
y (k) = g [x (k), . . . , x (k), u (k), . . . , u (k), k]  y (k) 
2 2 1 n 1 r  2 
. y(k) =  . 
.
.  .
. 
y (k) = g [x (k), . . . , x (k), u (k), . . . , u (k), k] yp (k)
p p 1 n 1 r
     
x1 (k) u1 (k) f1 [x(k), u(k), k]
 x (k)   u (k)   f [x(k), u(k), k] 
 2   2   2 
x(k) =  .  u(k) =  .  f [x(k), u(k), k] =  . 
 .
.   .
.   .
. 
xn (k) ur (k) fn [x(k), u(k), k]
22

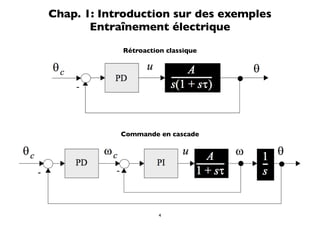
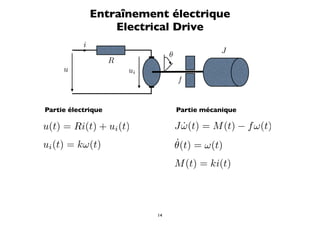
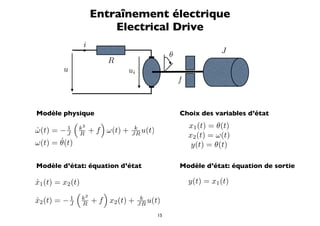
23. Entraînement électrique
Electrical Drive
i
θ J
R
u ui
f
Modèle analogique
θ(s) A 1 b
G(s) = = τ =− A=−
U (s) s (1 + sτ ) a a
Modèle discret vu au travers de convertisseurs AD DA
α = −e−h/τ
G(s)
H(z) = 1 − z −1 Z L−1 b1 = A [h − τ (1 + α)]
s
b2 = A [τ (1 + α) + hα]
θ(z) b1 z −1 + b2 z −2 b1 z −1 + b2 z −2
H(z) = = =
U (z) (1 − z −1 ) (1 + αz −1 ) 1 + (α − 1) z −1 − αz −2
23

24. 2.5: FT → Modèle d’état
Y (z) b0 + b1 z −1 + b2 z −2 + . . . + bn z −n
H (z) = =
U (z) 1 + a1 z −1 + a2 z −2 + . . . + an z −n
(b1 − a1 b0 ) z −1 + (b2 − a2 b0 ) z −2 + . . . + (bn − an b0 ) z −n
Y (z) = b0 U (z) + U (z)
1 + a1 z −1 + a z −2 + . . . + a z −n
2 n
˜
Y (z)
˜
Y (z) (b1 − a1 b0 ) z −1 + (b2 − a2 b0 ) z −2 + . . . + (bn − an b0 ) z −n
=
U (z) 1 + a1 z −1 + a2 z −2 + . . . + an z −n
˜
Y (z) U (z)
= ≡ Q (z)
(b1 − a1 b0 ) z −1 + (b2 − a2 b0 ) z −2 + . . . + (bn − an b0 ) z −n 1 + a1 z −1 + a2 z −2 + . . . + an z −n
24

25. FT → Modèle d’état
Y (z) b0 + b1 z −1 + b2 z −2 + . . . + bn z −n
H (z) = =
U (z) 1 + a1 z −1 + a2 z −2 + . . . + an z −n
(b1 − a1 b0 ) z −1 + (b2 − a2 b0 ) z −2 + . . . + (bn − an b0 ) z −n
Y (z) = b0 U (z) + U (z)
1 + a1 z −1 + a z −2 + . . . + a z −n
2 n
˜
Y (z)
˜
Y (z) (b1 − a1 b0 ) z −1 + (b2 − a2 b0 ) z −2 + . . . + (bn − an b0 ) z −n
=
U (z) 1 + a1 z −1 + a2 z −2 + . . . + an z −n
˜
Y (z) U (z)
= ≡ Q (z)
(b1 − a1 b0 ) z −1 + (b2 − a2 b0 ) z −2 + . . . + (bn − an b0 ) z −n 1 + a1 z −1 + a2 z −2 + . . . + an z −n
U (z) = Q (z) + a1 z −1 Q (z) + a2 z −2 Q (z) + . . . + an z −n Q (z)
25

26. FT → Modèle d’état
Y (z) b0 + b1 z −1 + b2 z −2 + . . . + bn z −n
H (z) = =
U (z) 1 + a1 z −1 + a2 z −2 + . . . + an z −n
(b1 − a1 b0 ) z −1 + (b2 − a2 b0 ) z −2 + . . . + (bn − an b0 ) z −n
Y (z) = b0 U (z) + U (z)
1 + a1 z −1 + a z −2 + . . . + a z −n
2 n
˜
Y (z)
˜
Y (z) (b1 − a1 b0 ) z −1 + (b2 − a2 b0 ) z −2 + . . . + (bn − an b0 ) z −n
=
U (z) 1 + a1 z −1 + a2 z −2 + . . . + an z −n
˜
Y (z) U (z)
= ≡ Q (z)
(b1 − a1 b0 ) z −1 + (b2 − a2 b0 ) z −2 + . . . + (bn − an b0 ) z −n 1 + a1 z −1 + a2 z −2 + . . . + an z −n
˜
Y (z) = (b1 − a1 b0 ) z −1 Q (z) + (b2 − a2 b0 ) z −2 Q (z) + . . . + (bn − an b0 ) z −n Q (z)
26

27. FT → Modèle d’état
Q (z) = −a1 z −1 Q (z) − a2 z −2 Q (z) − . . . − an z −n Q (z) + U (z)
˜
Y (z) = (b1 − a1 b0 ) z −1 Q (z) + (b2 − a2 b0 ) z −2 Q (z) + . . . + (bn − an b0 ) z −n Q (z)
W1 (z) = z −1 Q (z)
W (z) = z −2 Q (z)
2
.
.
.
W (z) = z −n Q (z)
n
zW1 (z) = Q (z) = −a1 W1 (z) − a2 W2 (z) − . . . − an Wn (z) + U (z)
zW (z) = z −1 Q (z) = W1 (z)
2
.
.
.
zW (z) = z −n+1 Q (z) = Wn−1 (z)
n
˜
Y (z) = (b1 − a1 b0 )W1 (z) + (b2 − a2 b0 )W2 (z) + . . . + (bn − an b0 )Wn (z)
˜
Y (z) = b0 U (z) + Y (z)
27

28. FT → Modèle d’état
   
−a1 −a2 . . . −an−1 −an 1
 1 0 ... 0 0   
   0
 .
. .
. 
w (k + 1) =  0 1 . .  w (k) + 
 .
.

 u (k)

 .

  .
 . .. 
. . 0 0  0 
0 ... 0 1 0 0
Φw gw
y (k) = b1 − a1 b0 b2 − a2 b0 . . . bn − an b0 w (k) + b0 u (k)
cT
w
Y (z) b0 + b1 z −1 + b2 z −2 + . . . + bn z −n
H (z) = =
U (z) 1 + a1 z −1 + a2 z −2 + . . . + an z −n
28

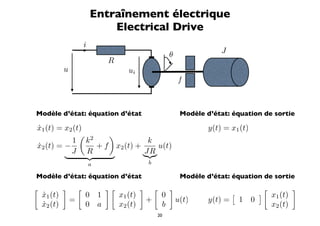
29. Entraînement électrique
Electrical Drive
i
θ J
R
u ui
f
Modèle discret vu au travers de convertisseurs AD DA
θ(z) b1 z −1 + b2 z −2 b1 z −1 + b2 z −2
H(z) = = =
U (z) (1 − z −1 ) (1 + αz −1 ) 1 + (α − 1) z −1 − αz −2
α = −e−h/τ b1 = A [h − τ (1 + α)] b2 = A [τ (1 + α) + hα]
Modèle d’état discret artificiel correspondant
w1 (k + 1) − (α − 1) α w1 (k) 1
= + u(k)
w2 (k + 1) 1 0 w2 (k) 0
w1 (k)
y(k) = θ(k) = b1 b2 + [0] u(k)
w2 (k)
29

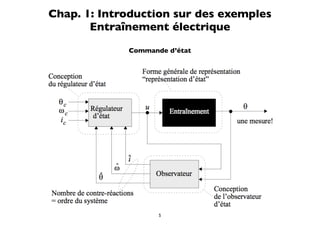
30. Modèle d’état/State-space model
Analogique/Continuous Discret/Discrete
Non linéaire
Nonlinear
x (t) = f [x (t) , u (t) , t]
˙ x (k + 1) = f [x (k) , u (k) , k]
y (t) = g [x (t) , u (t) , t] y (k) = g [x (k) , u (k) , k]
Linéaire
x (t) = A (t) x (t) + B (t) u (t)
˙ x (k + 1) = Φ(k)x (k) + Γ(k)u (k)
Linear
y (t) = C (t) x (t) + D (t) u (t) y (k) = C(k)x (k) + D(k)u (k)
time-invariant
stationnaire
Linéaire et
Linear and
x (t)
˙ = Ax (t) + Bu (t) x (k + 1) = Φx (k) + Γu (k)
y (t) = Cx (t) + Du (t) y (k) = Cx (k) + Du (k)
30