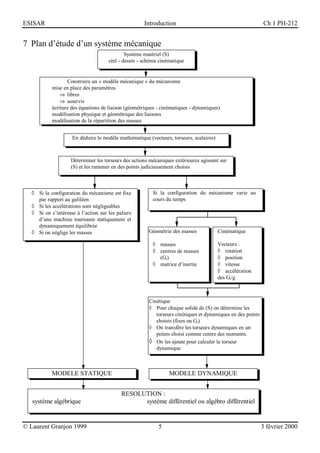
Le document présente une introduction à la mécanique des solides, mettant en avant la notion de système et de modèle pour étudier les interactions matérielles. Il aborde les hypothèses en mécanique classique, les limitations de cette approche et les applications contemporaines dans des domaines comme la robotique. La méthodologie pour modéliser les systèmes mécaniques est également exposée, soulignant l'importance des actions mécaniques et des référentiels dans l'analyse des mouvements.