Ce document présente une étude sur les prédicteurs conformes sparses, mettant l'accent sur l'utilisation du lasso comme outil de sélection des variables dans un cadre de régression linéaire. Il décrit des méthodes expérimentales pour la validation de ces prédicteurs, ainsi que des résultats de performance sur des données simulées et réelles. Les conclusions soulignent l'efficacité des prédicteurs conformes sparses, notamment lorsque le nombre de variables dépasse le nombre d'observations.

1. Pr´dicteurs Conformes Sparses
e
Universit´ Paris-Est – Marne-la-Vall´e
e e
Groupe de travail pr´vision
e
Crest, 8 Avril 2011
M. Hebiri (UMLV) SCP 8 Avril 2011 1 / 21

2. Outline
1 Cadre de travail
2 Pr´-requis
e
3 Pr´dicteurs Conformes Sparses
e
Lasso Conformal Predictor
Famille de pr´dicteurs conformes
e
4 Exp´riences num´riques
e e
M´thodes et comparaison
e
Performances
M. Hebiri (UMLV) SCP 8 Avril 2011 2 / 21

3. Cadre Transductif
R´f´rences:
ee
Vapnik ’98
Joachims ’99
M. Hebiri (UMLV) SCP 8 Avril 2011 3 / 21

4. Mod`le de r´gression lin´aire
e e e
Observations: En = {(x1 , y1 ), . . . , (xn , yn ), xnew }
yi = xi β ∗ + ξi
Vecteur des variables : xi = (xi,1 , . . . , xi,p ) ∈ Rp , i≥1
Nouvelle observation : xnew ∈ Rp
R´sponse : yi ∈ R,
e i≥1
Param`tre inconnu : β ∗ = (β1 , . . . , βp ) ∈ Rp
e ∗ ∗
Bruit : ξi ∼ N (0, σ 2 ), σ 2 connu.
M. Hebiri (UMLV) SCP 8 Avril 2011 4 / 21

5. Objectifs
Objectif I : Etant donn´ En et ε > 0, construire un pr´dicteur conforme
e e
(intervalle de confiance) Γε de niveau 1 − ε pour ynew
Outil : Mesure de conformit´ entre xnew et les xi d´j` observ´s
e ea e
distance (g´om´trique, voisinage, etc.)
e e
distance de similarit´ : ` d´finir par la suite
e a e
Objectif II : Exploiter la sparsit´ du mod`le (beaucoup de composantes
e e
dans β ∗ sont ´gale ` zero) si n´cessaire
e a e
Outil : Recourrir ` une proc´dure de s´lection de variables (LASSO, etc.)
a e e
Remarque : ce deuxi`me objectif est particuli`rement int´ressant lorsque
e e e
→ le nombre de variables est tr`s grand (comparativement au nombre
e
d’observations)
→ le nombre de variables vraiment pertinentes est petit
M. Hebiri (UMLV) SCP 8 Avril 2011 5 / 21

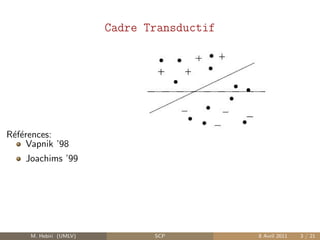
6. Pr´diction Conforme :
e Vovk et al. ’05
Notations :
y ∈ R : valeur possible de ynew
|A| : cardinal de l’ensemble A
Score de Non-conformit´ α(y) = (α1 (y), . . . , αn (y), αnew (y))
e
αi (y) : similarit´ entre (xnew , y) et (xi , yi )
e
information relative : p-value
1
p(y) = | {i ∈ {1, . . . , n, new} : αnew (y) ≤ αi (y)} |
n+1
1
p(y) ∈ [ n+1 ; 1]
plus p(y) est petite, moins la paire test´e (xnew , y) est vraisemblable
e
(ce choix fait de y une valeur aberrante lorsqu’elle est combin´e avec
e
xnew )
Pr´dicteur Conforme Γε : valeurs y ∈ R telle que p(y) > ε.
e
M. Hebiri (UMLV) SCP 8 Avril 2011 6 / 21

7. Estimateur LASSO : Tibshirani ’96
LASSO
n p
ˆ 1 2
β = Argmin (yi − xi β) + λ |βj |
β∈Rp n i=1 j=1
Param`tre de r´gularisation : λ
e e
Motivation :
ˆ
Solution sparse β (i.e., beaucoup de coefficients r´duits ` 0)
e a
R´sultats interpr´tables quand le mod`le est sparse
e e e
M. Hebiri (UMLV) SCP 8 Avril 2011 7 / 21

8. Algorithmique
Solution approch´e : LARS algorithme (Efron et al. ’04)
e
Algorithme LARS : données de diabètes
600
400
200
Coefficients βj
0
−200
−400
−600
0 0.2 0.4 0.6 0.8 1
mc
( Σ | βj | ) / ( Σ | βj |)
ˆ ˆ
→ βλ1 , . . . , βλK : approximations de la solution LASSO aux points de
transition λ = λ1 , . . . , λK
M. Hebiri (UMLV) SCP 8 Avril 2011 8 / 21

9. Suite...
ˆ
Etape k : µk = xk βλk = xk (xk xk )−1 (xk y −
ˆ λk
sk )
2
vecteur des r´ponses : y = (y1 , . . . , yn )
e
matrice des donn´es : x = (x1 , . . . , xn )
e
vecteur signe : sk
xk est la restriction de x aux colonnes correspondant aux variables
s´lectionn´es
e e
ˆ
Ne prend pas en compte xnew dans la construction de β !
M. Hebiri (UMLV) SCP 8 Avril 2011 9 / 21

10. Pr´dicteurs Conformes Sparses
e
On consid`re les donn´es augment´es : x = (x1 , . . . , xn , xnew ) et
e e e
y = (y1 , . . . , yn , y)
Pour tout point de transition λk , on d´finit l’estimateur LASSO µk
e ˆ
sur la base de xk et y
On d´finit le score de Non-conformit´
e e
αk (y) := |y − µk | = |Ak + Ck + Bk y|
ˆ
o` | · | s’interpr`te composante par composante et
u e
 Ak = (ak , . . . , ak , ak ) := (I − Hk ) (y1 , . . . , yn , 0)

1 n new
Bk = (bk , . . . , bk , bk ) := (I − Hk ) (0, . . . , 0, 1)
1 n new
Ck = (ck , . . . , ck , ck ) := λk xk (xk xk )−1 sk

1 n new 2
Les αk (y) sont lin´aires par morceaux
e
M. Hebiri (UMLV) SCP 8 Avril 2011 10 / 21

11. Pr´dicteurs Conformes Sparses
e
1
p-value: pk (y) = n+1 | i : αi (y) ≤ αnew (y) |
k k
Pr´dicteur ` l’´tape k : Γε = {y ∈ R : pk (y) > ε}
e a e k
Proposition
k k
Les points y tels que αi (y) = αnew (y) existent
k = bk
i) si bi new : quand y est ´gal `
e a
ak − ak + ck − ck
i new i new ak + ak + ck + ck
i new i new
− et − .
bk − bk
i new bk + bk
i new
ii) si bk = bk = 0 : lorsque y est ´gal `
i new e a
ak + ak + ck + ck
i new i new
−
2bk
i
Conformal Lasso Predictor Γε : le plus petit Γε
opt k
M. Hebiri (UMLV) SCP 8 Avril 2011 11 / 21

12. Exemple de pr´dicteurs conformes
e
Conformal predictors when n=300
80
60
40
20
k
Γε
0
−20
y
new
−40
CoLP
−60
−80
0 10 20 30 40 50
iteration
→ Le Conformal Lasso Predictor est le plus petit intervalle
→ Dans cet exemple, il contient la vraie valeur de ynew
→ En g´n´ral : ∀λ fix´ P(ynew ∈ Γλ ) ≥ 1 − ε
e e e
M. Hebiri (UMLV) SCP 8 Avril 2011 12 / 21

13. Extension
Estimateur de la forme :
µ = u(x, s)y + v(x, s)
ˆ
o` u(·) et v(·) sont des fonctions constantes par morceaux par rapport ` y
u a
On s’int´resse `
e a
CoLP: u(x, s) = xk (xk xk )−1 xk
v(x, s) = −λk xk (xk xk )−1 sk
CoRP: u(x, s) = x(x x + µIp )−1 x et v = 0
CENeP: u(x, s) = xk (xk xk + µk Ik )−1 xk
v(x, s) = −λk xk (xk xk )−1 sk
M. Hebiri (UMLV) SCP 8 Avril 2011 13 / 21

14. Cadre exp´rimental
e
Tous les intervalles de confiance construits sont de niveau
1 − ε = 90%
Toutes les exp´riences de simulations sont r´p´t´es M = 1000 fois
e e ee
Mesures de performance :
Pr´cision : taille de l’intervalle
e
M
Validit´ : VALε = M −1
e I(ynew ∈ (Γε )m )
opt
m=1
S´lection de variable : reconstitution du support de β ∗
e
M´thodes de r´f´rence :
e ee
S´lection de variables : LASSO original (Tibshirani ’96) et
e
l’Elastic-Net original (Zou & Hastie ’05) (bas´ sur le crit`re BIC)
e e
Pr´cision et validit´ : CoRP (Vovk et al. ’05)
e e
M. Hebiri (UMLV) SCP 8 Avril 2011 14 / 21

15. Donn´es simul´es avec p = 50
e e
A∗ = {j : βj = 0} : ensemble des variables pertinentes
∗
Exemple(a): A∗ = {1}; d´croissance exponentielle des corr´lations
e e
entre les variables successives {15, . . . , 35}
Exemple(b): A∗ = {1, . . . , 5} ∪ {10, . . . , 25} ; les corr´lations sont
e
comme dans l’Exemple(a)
Exemple(c): A∗ = {1, . . . , 15}; trois groupes de variables tr`se
corr´l´es : G1 = {1, . . . , 5}, G2 = {6, . . . , 10} and G1 = {11, . . . , 15}
ee
Exemple(d): A∗ = {1, . . . , p}; d´croissance exponentielle des
e
corr´lations entre les variables successives {1, . . . , p}
e
M. Hebiri (UMLV) SCP 8 Avril 2011 15 / 21

16. Validit´
e
Table: Contrˆle de VALε
o
Exemple[n/σ] CoRP CoLP CoLaRP CENeP
Ex (a)[300/1] 0.90± 0.02 0.88± 0.02 0.85± 0.02 0.88± 0.02
Ex (a)[300/7] 0.89± 0.02 0.91± 0.02 0.89± 0.02 0.90± 0.02
Ex (a)[300/15] 0.89± 0.02 0.89 ± 0.02 0.88± 0.02 0.89± 0.02
Ex (b)[300/1] 0.90± 0.02 0.88± 0.02 0.87± 0.02 0.87± 0.02
Ex (c)[300/1] 0.90± 0.02 0.90± 0.02 0.89± 0.02 0.90± 0.02
Ex (d)[300/1] 0.89± 0.02 0.90± 0.02 0.90± 0.02 0.90± 0.02
Ex (a)[50/3] 0.89± 0.02 0.67± 0.03 0.41± 0.03 0.79± 0.02
Ex (a)[20/3] 0.86± 0.02 0.60± 0.03 0.30± 0.03 0.69± 0.03
Exemple[n/σ] CoRP CoLP Stopped-CoLP 2-PN-CoLP
Ex (a)[50/7] 0.85± 0.02 0.62± 0.03 0.82± 0.02 0.88± 0.02
Ex (b)[50/1] 0.88± 0.02 0.56± 0.03 0.82± 0.02 0.91 ± 0.02
Ex (c)[20/15] 0.88± 0.02 0.61± 0.03 0.77± 0.03 0.90± 0.02
Ex (d)[20/1] 0.90± 0.02 0.60± 0.03 0.79± 0.02 0.89± 0.02
M. Hebiri (UMLV) SCP 8 Avril 2011 16 / 21

17. S´lection de variables :
e Exemple(b)[300/5]
50 50
45 45
40 40
35 35
30 30
Iteration
Iteration
25 25
20 20
CoLP
15 CoRLaP 15 CENeP
Lasso Elastic−Net
10 10
5 5
0 0
0 5 10 15 20 25 30 35 40 45 50 0 5 10 15 20 25 30 35 40 45 50
Variable index Variable index
M. Hebiri (UMLV) SCP 8 Avril 2011 17 / 21

18. Pr´cision :
e Exemple(b)[n/5]
4
90 x 10
2.5
Selected predictor
80
Selected predictor
Failed predictor
70 2
60
Intervals sizes
Intervals sizes
1.5
50
40
1
30
20
0.5
10
0 0
0 5 10 15 20 25 30 35 40 45 50 0 50 100 150 200 250 300 350 400
Iteration Iteration
M. Hebiri (UMLV) SCP 8 Avril 2011 18 / 21

19. Donn´es R´elles
e e
On utilise les donn´es “House Boston” (506 observations et 13 variables)
e
On ajoute artificiellement 483 variables bruits → p = 500
On effectue 150 permutations des lignes de la matrice des donn´es et
e
du vecteur r´ponse
e
→ on s´lectionne n = 50 couples (xi , yi )
e
→ on choisit une lignes au hasard comme ´tant (xnew , ynew )
e
Table: contrˆle de VALε et du numbre de variables bruits s´lectionn´es (variables
o e e
X14 ` X500 ) (p = 500 et n = 50).
a
CoRP CoLP CENeP Stopped-CoLP 2-PN-CoLP
VALε 0.93± 0.01 0.43± 0.04 0.85± 0.02 0.85± 0.02 0.93± 0.01
Noise 100 % 20.3 % 4.0 % 5.9 % 5.9 %
M. Hebiri (UMLV) SCP 8 Avril 2011 19 / 21

20. Conclusion
Pr´dicteurs Conformes Sparses
e
→ crit`re naturelle de s´lection de l’intervalle optimal
e e
→ bonne performance dans le cas p ≤ n
→ correction dans le cas p > n : permet d’´galer (ou d’am´lorer)
e e
les performances du CoRP (avec une pr´cisioin toujours meilleure)
e
Validit´ th´orique (Vovk et al. ’05)
e e
Perspective : consistance en s´lection de variables (th´orique) lorsque
e e
la s´lection est bas´e sur le crit`re de pr´cision !
e e e e
M. Hebiri (UMLV) SCP 8 Avril 2011 20 / 21

21. Merci de votre attention
M. Hebiri (UMLV) SCP 8 Avril 2011 21 / 21