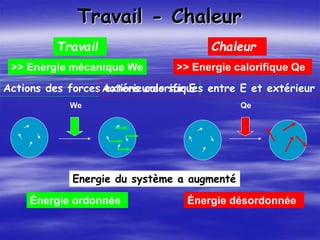
Le document aborde les concepts fondamentaux de la thermodynamique, en détaillant les systèmes thermodynamiques, les transformations et les propriétés des substances. Il explore également les principes de travail et de chaleur, ainsi que les relations entre les différentes fonctions d'état. Enfin, des équations d'état et des diagrammes thermodynamiques sont présentés pour aider à la compréhension des comportements de la matière sous diverses conditions.

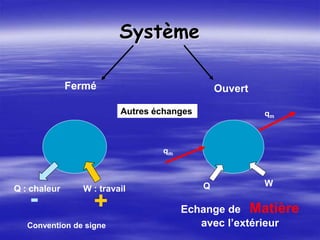

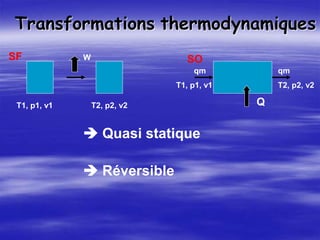




![Equations d’état
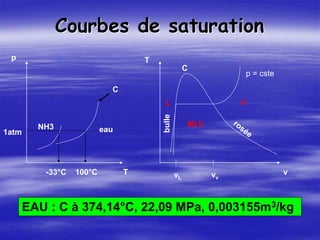
LIQUIDE v = cste p
COURBE DE VAPORISATION L V
Antoine ln psat = A - [ B / (Tsat – C)]
Eau A = 11,68 B = 3816 C = 46,13 T °K, p bars
Imcompressible
pour un liquide v = vL h = hL
u = uL s = sL
à la Température du pb](https://image.slidesharecdn.com/1193770-230715171135-5dbefb0b/85/1193770-ppt-14-320.jpg)



![Energie interne d’une substance
LIQUIDE u = f(T) u = uL à la température du Pb ou
du = C(T).dT et Du = C.DT à C cst
GAZ PARFAIT u = f(T) et du = Cv(T).dT
Si Cv cst [gaz idéal] => Du = Cv.DT
C chaleur spécifique du liquide (J/kg°K)
Cv chaleur spécifique à volume constant du gaz (J/kg°K)](https://image.slidesharecdn.com/1193770-230715171135-5dbefb0b/85/1193770-ppt-22-320.jpg)


![Enthalpie d’une substance
LIQUIDE A- cas général p.v<<u => h = u = f(T)
=> h = hL à la température du Pb ou
dh = C(T).dT et Dh = Du = C.DT à C cst
GAZ PARFAIT h = f(T) et dh = Cp(T).dT
Si Cp cst [gaz idéal] => Dh = Cp.DT
Cp chaleur spécifique à pression constante du gaz (J/kg°K)
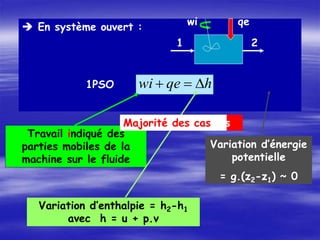
h = u + p.v
B- cas des pompes Dh = Du + D(pv) et
Du << D(pv) => Dh = D(pv)](https://image.slidesharecdn.com/1193770-230715171135-5dbefb0b/85/1193770-ppt-26-320.jpg)