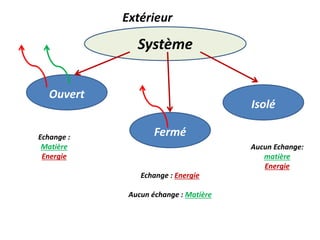
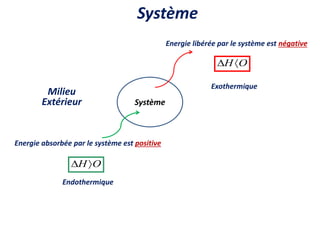
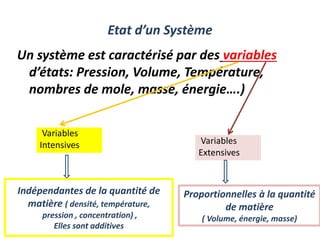
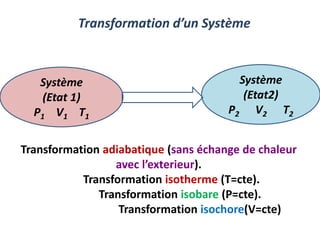
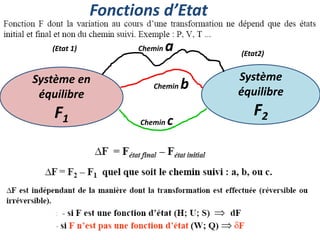
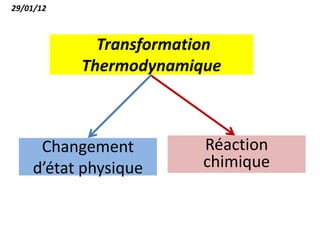
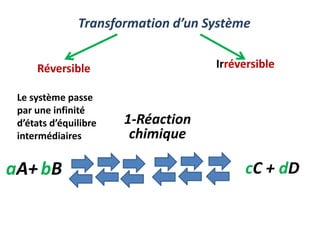
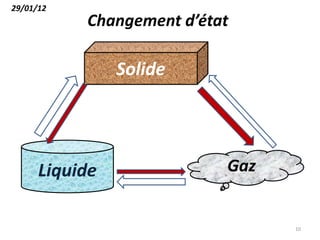
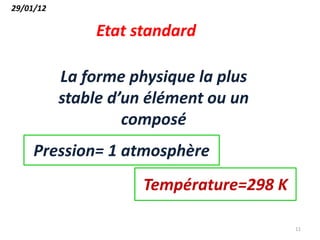
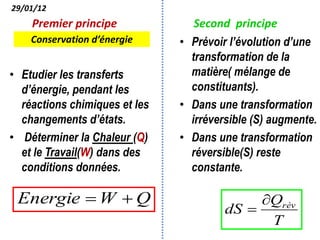
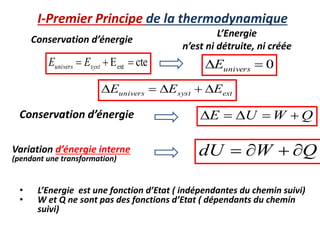
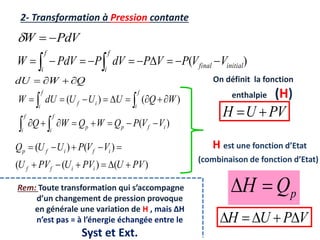
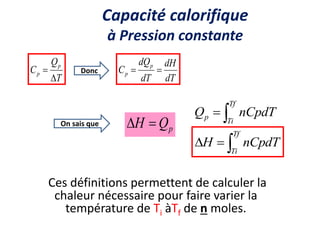
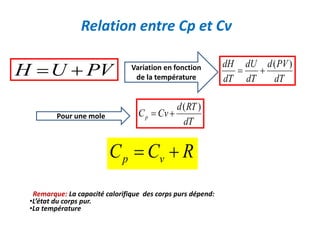
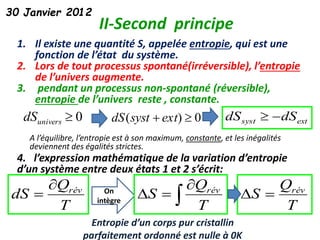
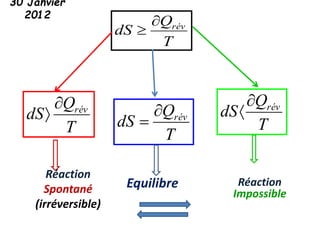
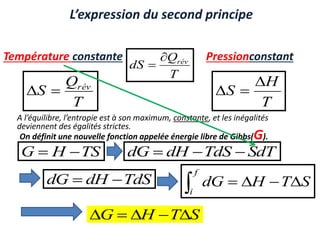
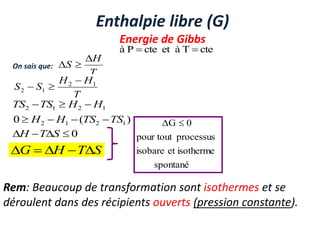
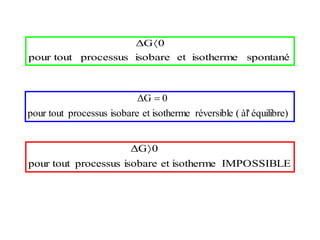
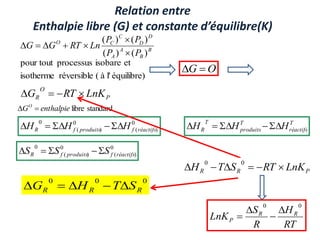
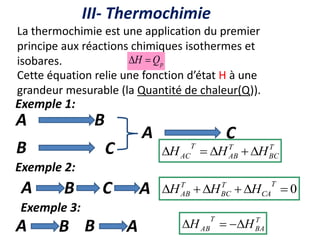
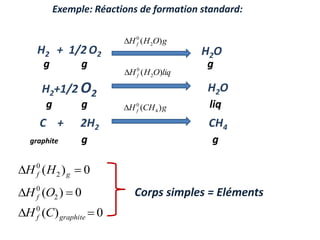
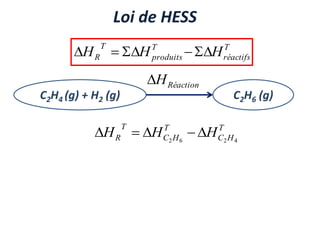
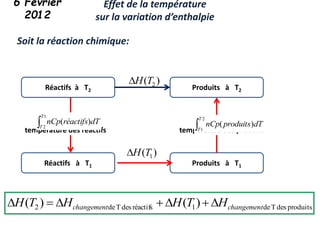
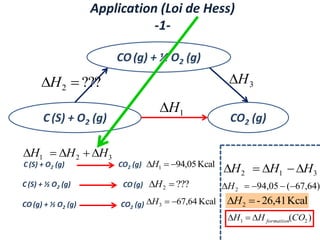
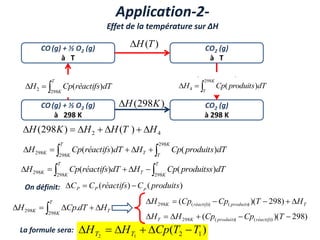
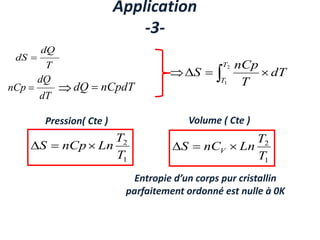
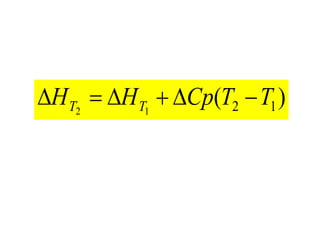Le document présente une introduction à la thermodynamique, abordant les concepts clés tels que l'énergie interne, l'entropie, et les transformations thermodynamiques. Il explique les premiers et seconds principes de la thermodynamique, ainsi que les notions d'enthalpie et de chaleur spécifique. En outre, il discute des transformations réversibles et irréversibles, ainsi que des applications pratiques comme la thermochimie.

1. Introduction à la
Thermodynamique
22/01/2012
U= énergie interne
H= enthalpie
S= entropie
W= travail
Q= chaleur
G= Enthalpie libre

2. • Le langage et l’esprit thermodynamique est de
prévoir la transformation de la matière dans des
conditions données.
• La thermodynamique ne s’intéresse qu’aux états
en équilibres .
• Est-ce que la transformation peut être spontanée
( irréversible), non spontanée(réversible)?
• Jusqu'où la transformation peut elle se faire?
La thermodynamique
repose sur deux notions:
Energie Entropie
chaleur,
travail mécanique,
(électrique ), rayonnement .
• Mesure le Désordre
• L’entropie de l’Univers augmente
• L’entropie d’un équilibre reste
constante

3. Système
Ouvert
Fermé
Isolé
Echange :
Matière
Energie
Echange : Energie
Aucun échange : Matière
Aucun Echange:
matière
Energie
Extérieur

4. Système
Energie absorbée par le système est positive
Système
Milieu
Extérieur
O
H 

O
H

Energie libérée par le système est négative
Exothermique
Endothermique

5. Un système est caractérisé par des variables
d’états: Pression, Volume, Température,
nombres de mole, masse, énergie….)
Etat d’un Système
Variables
Intensives Variables
Extensives
Indépendantes de la quantité de
matière ( densité, température,
pression , concentration) ,
Elles sont additives
Proportionnelles à la quantité
de matière
( Volume, énergie, masse)

6. Transformation adiabatique (sans échange de chaleur
avec l’exterieur).
Transformation isotherme (T=cte).
Transformation isobare (P=cte).
Transformation isochore(V=cte)
Système
(Etat 1)
P1 V1 T1
Système
(Etat2)
P2 V2 T2
Transformation d’un Système

7. Fonctions d’Etat
Système en
équilibre
F1
Système
équilibre
F2
(Etat 1)
(Etat2)
Chemin a
Chemin b
Chemin c

8. Changement
d’état physique
Transformation
Thermodynamique
Réaction
chimique
29/01/12

9. Transformation d’un Système
Réversible Irréversible
Le système passe
par une infinité
d’états d’équilibre
intermédiaires
aA+bB cC + dD
1-Réaction
chimique

10. Solide
Liquide Gaz
Changement d’état
10
29/01/12

11. Etat standard
11
29/01/12
Pression= 1 atmosphère
Température=298 K
La forme physique la plus
stable d’un élément ou un
composé

12. Premier principe
• Etudier les transferts
d’énergie, pendant les
réactions chimiques et les
changements d’états.
• Déterminer la Chaleur (Q)
et le Travail(W) dans des
conditions données.
Second principe
• Prévoir l’évolution d’une
transformation de la
matière( mélange de
constituants).
• Dans une transformation
irréversible (S) augmente.
• Dans une transformation
réversible(S) reste
constante.
Q
W
Energie 

T
Q
dS rév


Conservation d’énergie
29/01/12

13. I-Premier Principe de la thermodynamique
Q
W
U
E 




Q
W
dU 



Conservation d’énergie
Variation d’énergie interne
(pendant une transformation)
0

 univers
E
ext
syst
univers E
E
E 




cte
Eext 

 syst
univers E
E
L’Energie
n’est ni détruite, ni créée
Conservation d’énergie
• L’Energie est une fonction d’Etat ( indépendantes du chemin suivi)
• W et Q ne sont pas des fonctions d’Etat ( dépendants du chemin
suivi)

14. Enthalpie (H)
Pour étudier un système simplement , on doit garder un
maximum de paramètres constants(isobares, isochorse,
…..)
0


 PdV
W

Q
W
Q
U 






1- Transformation à Volume constant

 





 v
initial
final Q
Q
U
U
U
dU
Ceci relie ∆U à Qv , donc Qv est
une fonction d’Etat
distance
Force
W
Travail 


distance
surface
Volume 

surface
Volume
distance 
Volume
W surface
Force


v
Q
U 


15. v
Q
U 

Variation d’Energie Interne

16. 2- Transformation à Pression contante
PdV
W 


)
( initial
final
f
i
f
i
V
V
P
V
P
dV
P
PdV
W 








 

Q
W
dU 



)
(
)
(
)
(
i
f
p
p
f
i
f
i
f
i
i
f
f
i
V
V
P
Q
W
Q
W
Q
W
Q
U
U
U
dU
W





















)
(
)
(
(
)
(
)
(
PV
U
PV
U
PV
U
V
V
P
U
U
Q
i
i
f
f
i
f
i
f
p











On définit la fonction
enthalpie (H)
PV
U
H 

H est une fonction d’Etat
(combinaison de fonction d’Etat)
p
Q
H 

Rem: Toute transformation qui s’accompagne
d’un changement de pression provoque
en générale une variation de H , mais ∆H
n’est pas = à l’énergie échangée entre le
Syst et Ext.
V
P
U
H 





17. p
Q
H 

Variation d’Enthalpie
n
RT
U
H 




)
(PV
U
H 





18. Capacité calorifique
• La chaleur spécifique d’une substance , la
quantité de chaleur , qu’il faut fournir à 1
gramme de cette substance pour élever sa
température d’1 degré centigrade.
T
Q
C


T
Q
nC v
v


T
nC
Q p
p 


molaire
spécifique
Chaleur
e
Calorifiqu
Capacité Masse


-1
1
-1
1
-1
.mol
Cal.K
g.mol
.K
Cal.g
e
Calorifiqu
Capacité 




T
C
Q 


T
nC
Q v
v 


T
Q
nC
p
p



19. dT
dH
dT
dQ
C
p
p 

T
Q
C
p
p


Ces définitions permettent de calculer la
chaleur nécessaire pour faire varier la
température de Ti àTf de n moles.
p
Q
H 
 

Tf
Ti
p nCpdT
Q



Tf
Ti
nCpdT
H
Capacité calorifique
à Pression constante
On sais que
Donc

20. Ces définitions permettent de calculer la
chaleur nécessaire pour faire varier la
température de Ti àTf de n moles.
Capacité calorifique
à volume constant
On sais que
Donc
dT
dU
dT
dQ
C v
v 

T
Q
C v
v


v
Q
U 



Tf
Ti
v nCvdT
Q



Tf
Ti
nCvdT
U

21. Relation entre Cp et Cv
PV
U
H 
 dT
PV
d
dT
dU
dT
dH )
(


dT
RT
d
Cv
Cp
)
(


Variation en fonction
de la température
Pour une mole
R
C
C v
p 

Remarque: La capacité calorifique des corps purs dépend:
•L’état du corps pur.
•La température

22. 30 Janvier 2012
II-Second principe
ext
syst dS
dS 

0

univers
dS 0
)
( 
 ext
syst
dS
A l’équilibre, l’entropie est à son maximum, constante, et les inégalités
deviennent des égalités strictes.
4. l’expression mathématique de la variation d’entropie
d’un système entre deux états 1 et 2 s’écrit:
1. Il existe une quantité S, appelée entropie, qui est une
fonction de l’état du système.
2. Lors de tout processus spontané(irréversible), l’entropie
de l’univers augmente.
3. pendant un processus non-spontané (réversible),
entropie de l’univers reste , constante.
T
Q
dS rév

 On
intègre 



T
Q
S rév
T
Q
S rév


Entropie d’un corps pur cristallin
parfaitement ordonné est nulle à 0K

23. T
Q
dS rév


T
Q
dS rév


T
Q
dS rév


T
Q
dS rév


Réaction
Spontané
(irréversible)
Equilibre Réaction
Impossible
30 Janvier
2012

24. L’expression du second principe
Pressionconstant
Température constante
T
Q
dS rév


T
Q
S rév


T
H
S



A l’équilibre, l’entropie est à son maximum, constante, et les inégalités
deviennent des égalités strictes.
On définit une nouvelle fonction appelée énergie libre de Gibbs(G).
TS
H
G 
 SdT
TdS
dH
dG 


TdS
dH
dG 

S
T
H
G 




S
T
H
dG
f
i






25. Enthalpie libre (G)
Energie de Gibbs
Rem: Beaucoup de transformation sont isothermes et se
déroulent dans des récipients ouverts (pression constante).
T
H
S



On sais que:
cte
T
à
et
cte
P
à 

T
H
H
S
S 1
2
1
2



1
2
1
2 H
H
TS
TS 


)
(
0 1
2
1
2 TS
TS
H
H 



0



 S
T
H
spontané
isotherme
et
isobare
processus
pour tout
0
ΔG 
S
T
H
G 





26. spontané
isotherme
et
isobare
processus
pour tout
0
ΔG
équilibre)
àl'
(
réversible
isotherme
et
isobare
processus
pour tout
0
ΔG 
IMPOSSIBLE
isotherme
et
isobare
processus
pour tout
0
ΔG

27. Relation entre
Enthalpie libre (G) et constante d’équilibre(K)
B
B
A
A
D
D
C
C
O
P
P
P
P
Ln
RT
G
G
)
(
)
(
)
(
)
(







P
O
R LnK
RT
G 



équilibre)
l'
à
(
réversible
isotherme
et
isobare
processus
pour tout
O
G 

standard
libre
enthalpie
GO


T
réactifs
T
produits
T
R H
H
H 




0
)
(
0
)
(
0
réactifs
f
produits
f
R H
H
H 




0
)
(
0
)
(
0
réactifs
f
produits
f
R S
S
S 




0
0
0
R
R
R S
T
H
G 




P
R
R LnK
RT
S
T
H 





0
0
RT
H
R
S
LnK R
R
P
0
0





28. III- Thermochimie
T
BC
T
AB
T
AC H
H
H 




La thermochimie est une application du premier
principe aux réactions chimiques isothermes et
isobares. p
Q
H 

Cette équation relie une fonction d’état H à une
grandeur mesurable (la Quantité de chaleur(Q)).
Exemple 1:
A C
A B
B C
A
A B C 0






T
CA
T
BC
T
AB H
H
H
Exemple 2:
Exemple 3:
A B B A
T
BA
T
AB H
H 




29. Enthalpie de Formation d’un composé = la chaleur Dégagée ou
Absorbée ,∆H f lorsqu'une mole du composé est formée à partir des
éléments à pression constante.
Définitions
Enthalpie de Formation standard d’un composé=s’est la chaleur
Dégagée ou Absorbée ,∆H 0
f lorsqu'une mole du composé est
formée à partir des éléments à P=1 atm à T.
Éléments dans leur état
stable sous 1 atm à T
Composé dans leur état
stable sous 1 atm à T
0
f
H

Rem: l’enthalpie standard de formation des
éléments par définition=0 0
)
(
0

 éléments
H f

30. Exemple: Réactions de formation standard:
H2 + 1/2 O2 H2O
H2+1/2 O2 H2O
g g liq
g
g
g
C + 2H2 CH4
graphite g g
0
)
( 2
0

 g
f H
H
0
)
(
0

 graphite
f C
H
0
)
( 2
0

 O
H f
g
O
H
H f )
( 2
0

liq
O
H
H f )
( 2
0

g
CH
H f )
( 4
0

Corps simples = Eléments

31. T
réactifs
T
produits
T
R H
H
H 




Loi de HESS
C2H4 (g) + H2 (g) C2H6 (g)
Réaction
H

T
H
C
T
H
C
T
R H
H
H 4
2
6
2






32. Effet de la température
sur la variation d’enthalpie
Soit la réaction chimique:
Réactifs à T2 Produits à T2
)
( 2
T
H

Réactifs à T1 Produits à T1
)
( 1
T
H

Changement de
température des réactifs
Changement de
température des produits
produits
des
T
de
1
réactifs
des
T
de
2 )
(
)
( changement
changement H
T
H
H
T
H 






6 Février
2012

1
2
)
(
T
T
dT
réactifs
nCp

2
1
)
(
T
T
dT
produits
nCp

33. Application (Loi de Hess)
-1-
C (S) + O2 (g) CO2 (g)
1
H

3
2
1 H
H
H 




CO (g) + ½ O2 (g)
3
H

???
2 
H
3
1
2 H
H
H 




C (S) + O2 (g) CO2 (g)
C (S) + ½ O2 (g)
CO2 (g)
CO (g)
CO (g) + ½ O2 (g)
Kcal
05
,
94
1 

H
Kcal
64
,
67
3 

H
???
2 
H
Kcal
26,41
-
2 
H
)
64
,
67
(
94,05
2 



H
)
( 2
1 CO
H
H formation




34. CO (g) + ½ O2 (g)
à T
CO2 (g)
à T
)
(T
H

CO (g) + ½ O2 (g)
à 298 K
CO2 (g)
à 298 K
)
298
( K
H

Changement de
température des réactifs
Changement de
température des produits
Application-2-
Effet de la température sur ∆H



T
K
dT
réactifs
Cp
H
298
2 )
( 


K
T
dT
produits
Cp
H
298
4 )
(
4
2 )
(
)
298
( H
T
H
H
K
H 







 




K
T
T
T
K
K dT
produits
Cp
H
dT
réactifs
Cp
H
298
298
298 )
(
)
(

 




T
K
T
T
K
K dT
produitss
Cp
H
dT
réactifs
Cp
H
298
298
298 )
(
)
(
On définit: )
(
)
( produits
C
réactifs
C
C p
P
P 


T
T
K
K H
dT
Cp
H 



 298
298 . T
produits
réactifs
K H
T
Cp
Cp
H 




 )
298
)(
( )
(
)
(
298
)
( 1
2
1
2
T
T
Cp
H
H T
T 





)
298
)(
( )
(
)
(
298 




 T
Cp
Cp
H
H réactifs
produits
K
T
La formule sera:

35. Application
-2-
)
)(
(
)
( 1
2
1
2 1
1
2
T
T
Cp
Cp
H
T
T
Cp
H
H réactifs
produits
T
T
T 










Capacités calorifiques
molaires à pression
constante
Cp(cal/mol.K)
Calculons maintenant :
Avec
????
393
2



 K
T H
H
)
298
393
(
298
393 





 Cp
H
H K
K
  )
298
393
(
)
(
1/2
)
(
)
( 2
2
298
393 






 O
Cp
CO
Cp
CO
Cp
H
H K
K
  )
298
393
(
)
2
/
05
,
7
(
97
,
6
96
,
8
67640
393 






 K
H
mol
Kcal
H K /
79
,
67
393 


mol
Kcal
H K /
64
,
67
298 


)
298
393
(
( )
(
)
(
298
393 





 réactifs
produits
K
K Cp
Cp
H
H

36. )
( 1
2
1
2
T
T
Cp
H
H T
T 






37. Application
-3-
T
dQ
dS 
 


2
1
T
T
dT
T
nCp
S
dT
dQ
nCp  nCpdT
dQ 


1
2
T
T
Ln
nCp
S 


1
2
T
T
Ln
nC
S V 


Pression( Cte ) Volume ( Cte )
Entropie d’un corps pur cristallin
parfaitement ordonné est nulle à 0K

38. 5 Février
2012(Férié)

39. La réaction de combustion de 104g d’acide
malonique cristallisé
s’accompagne d’une variation d’énergie interne égale
à -865,7 KJ lorsqu’elle est réalisée à volume constant
et à la température de 25°C. Calculer la chaleur de
combustion à pression constante de l’acide
malonique à cette température.
• C=12, H= 1 et R = 8,32 J.K-1.mol-1
Application-4-
6 Février
2012

40. • La combustion biologique des aliments réalisée par les cellules est à
la base du mécanisme de la respiration.
• Le glucose par exemple est oxydé et donne des produits stables et
simples CO2 et H2O.
• Les données thermodynamiques de la réaction à 25°C sont
et
Application-5-
1
0
.
7
,
2825 


 mol
KJ
H 1
0
.
5
,
2867 


 mol
KJ
G
1- Calculer la variation d’entropie standard de cette réaction
d’oxydation du glucose.
2-La dénaturation (coupure des liaisons peptidiques par chauffage) de la
myoglobine s’accompagne à 25 °C des variations d’enthalpie et
d’enthalpie libre suivantes:
et
Calculer et comparer les résultats obtenus à la première et
à lseconde question.
1
0
.
6
,
175 

 mol
KJ
H
1
0
.
8
,
56 

 mol
KJ
G
??
0

S

41. Solubilité des Solides
• La concentration (S)du soluté solide pur est
constante, donc ,K= S
• On sais que , que l’influence de la température sur
la constante est:
Soluté
Pur solide
Soluté en solution
concentration X2
2
)
(ln
RT
H
dT
K
d 

2
)
(ln
)
(ln
RT
H
dT
S
d
dT
K
d fusion




0

 
fusion
H
On intègre constante
1






T
R
H
LnS
fusion
Solubilité augmente avec la température
b

 ax
y