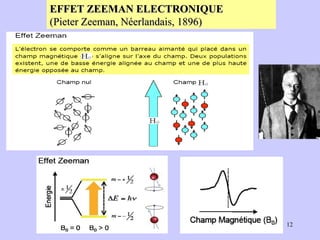
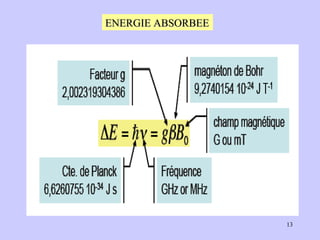
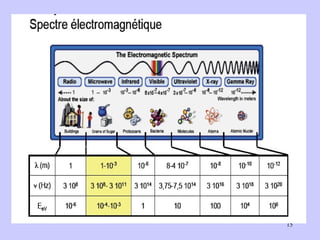
Le document traite de la spectrométrie de résonance paramagnétique électronique (RPE), une technique développée pour étudier les systèmes paramagnétiques, en particulier les ions de transition. Il aborde les concepts fondamentaux du paramagnétisme, l'effet Zeeman, et les applications de la RPE dans les domaines agroalimentaires, pharmaceutiques et biomédicaux. La RPE est présentée comme une méthode non destructive et quantitative, capable de fournir des informations sur les radicaux libres et les moments magnétiques des spins électroniques.

1. SPECTROMETRIE DE RESONANCE PARAMAGNETIQUE ELECTRONIQUE - RPE - Par Pr. J. BENNAZHA

2. * RPE DES IONS DE TRANSITION * INTRODUCTION * LE PARAMAGNETISME * EFFET ZEEMAN ELECTRONIQUE * EQUATION D’ONDE DE SCHRODINGER * STRUCTURE DES RAIES SPECTRALES * SPECTROMETRE RPE * PHENOMENES LIES A LA RPE * EXEMPLES DE SPECTRES RPE * RPE ET ALIMENTS IRRADIES * PRODUITS PHARMACEUTIQUES IRRADIES PLAN DU COURS

3. INTRODUCTION RPE ELECTRON CELIBATIARE Champ magnétique H Moyen puissant pour étudier les systèmes paramagnétiques

4. DEVELOPPEMENT DE LA RPE * 1945  la première observation d’un signal RPE * 1952  Le physicien (OXFORD) jette les bases théoriques et expérimentales, de cette nouvelle spectroscopie * 1952  1 er spectre d’un radical libre * 1960  développement par des chimistes: Bloembergen, Purcell, Pound, …en // à leurs travaux sur la RMN.

5. Principaux domaines d’application de la RPE  Domaine Agroalimentaire: Contrôle de la qualité des aliments irradiés (Gamma, RX,…): viandes, épices, sucres, fruits et légumes, …  Domaine Pharmaceutique: Contrôle des médicaments ,… (Irradiés pour conservation) Domaine Biomédical: * Contrôle d’implants, matériel médical,.. ( Irradiés pour stérilisation ) * Radiations absorbées par patients sous radiothérapie, ex: Spectre email des dents/Radical CO 2 -  Meilleur dosimètre biologique * Personnes accidentés dans l’industrie nucléaire (Chernobyl) * Survivants des bombes atomiques (Nagasaki et Hiroshima) * Imagerie à faibles fréquences DOSIMETRIE

6. CHIMIE : Détection des centres paramagnétiques : * Matrices inorganiques (Mn 2+, Cu 2+,… ) * Matrices organiques (Radicaux libres, …) Catalyse Réactions polymériques, Cinétique des réactions, Photosynthèse, PHYSIQUE :  Semi-conducteurs, métaux,…, matériaux magnétiques ,… GEOLOGIE :  Datations, Géochronologie Succès de la RPE  * Non Destructive * Qualitative * Quantitative Biologie:  Radicaux dans les tissus vivants  Réactions enzymatiques

7. LE PARAMAGNETISME * L’influence d’un aimant  (Hext),????? * Alignement des dipôles magnétiques (O 2 ) // à H avec même sens * Substance paramagnétique  Substance Attirée par un aimant

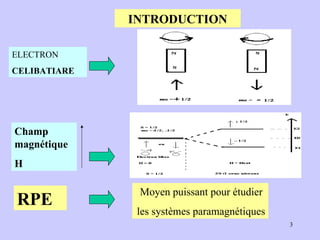
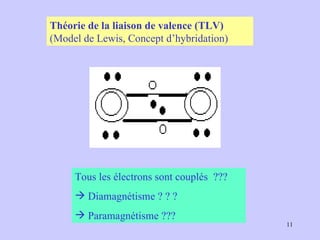
8. Comparaison des complexes [Fe(CN) 6 ] 4- et [Mn(H 2 O) 6 ] 2+ Le complexe hexacyanoferrat(II) est diamagnétique, car il contient le cation Fe 2+ ( système d 6 ) et six ligands anioniques CN - ( ligands à 2 électrons ) avec tous les électrons appariés en doublets (hybridation d 2 sp 3 ). Le complexe hexaaquamanganèse(II) est paramagnétique, le cation Mn 2+ ( système d 5 ) et six ligands neutres H 2 O ( ligands à 2 électrons ) avec 5 électrons non appariés (hybridation sp 3 d 2 ). Un cristal de sel K 4 [Fe(CN) 6 ] est alors repoussé par un champs magnétique non uniforme, mais l'effet diamagnétique est très faible et ne peut être démontré qu'avec un appareillage très fin. Un cristal du sel [Mn(H 2 O) 6 ]SO 4 est alors attiré par un champs magnétique non uniforme, l'effet paramagnétique est fort et peut être démontré avec un système expérimental simple. Magétisme moléculaire

9. * Comportement d’un  paramagnétique sous l’effet de Hext * Notion de SPIN

10. Explication de l’origine du paramagnétisme de O 2 Théorie des orbitales moléculaires (TOM), (config. électronique) 2 électrons célibataires (non appariés)  Paramagnétisme de O 2 Rq. Les entités O 2 + et O 2 - sont aussi paramagnétiques (1 e célibataire) (σ1sl) 2 (σ1s*) 2 (σ2sl) 2 (σ2s*) 2 (σ2pxl) 2 (π2pyl) 2 (π2pzl) 2 (π2py*) 1 (π2pz*) 1

11. Théorie de la liaison de valence (TLV) (Model de Lewis, Concept d’hybridation) Tous les électrons sont couplés ??? Diamagnétisme ? ? ? Paramagnétisme ???

12. EFFET ZEEMAN ELECTRONIQUE (Pieter Zeeman, Néerlandais, 1896)

13. ENERGIE ABSORBEE

14. CLASIFICACION GENERAL DE LAS ESPECTROSCOPIAS

16. La RPE est une absorption

17. Forme de la raie RPE Model Lorentzien : La particule qui absorbe de l'énergie  un oscillateur harmonique Interactions entre particules  collision entre ces particules Une collision = modification brusque de la phase de l'oscillateur Forme Lorentzienne Model Gaussien : Défauts d'uniformité de Hext, Hétérogénéité de l'échantillon étudié Défauts d'uniformités à distribution aléatoire  Courbe en cloche de Gauss Forme Gaussienne

18. LA RPE EST AUSSI QUANTITATIVE

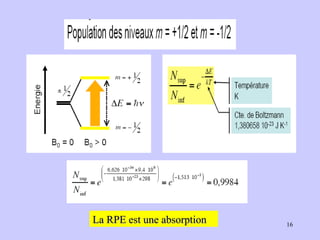
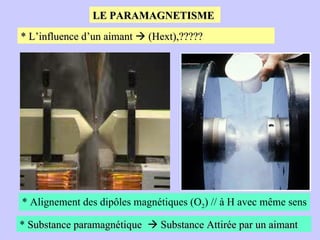
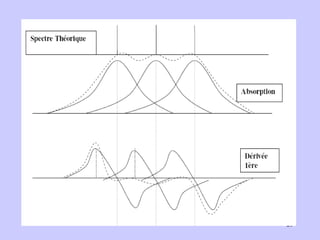
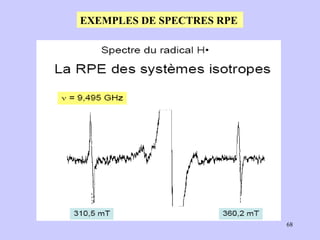
19. Un spectre RPE est caractérisé par : 1-Sa forme (L ou G) 2- Sa position (g, H0) 3- Sa largeur ΔHpp 4- Son amplitude App Schéma de spectre RPE/ amplitude App et largeur du spectre ΔHpp [Poole, 1983]

21. Conditions pour avoir un signal RPE: 1- Un ou plusieurs électrons non appariés  substance paramagnétique 2- Centres paramagnétiques sous forme de traces (matrices inorg.) ou dilués (soluté/solution) ( une Concentration élevée  disparition du signal)

23. SPECTROMETRE RPE (SCHEMA DE PRINCIPE)

24. SPECTROMETRE RPE

25. Spectromètre FSTM

26. H : Hamiltonien du système: Opérateur tenant compte de toutes les interactions Ψ : Fonction d’onde : décrivant le mouvement ondulatoire de la particule E : Énergie du système : valeurs propres de H Équation d’onde de Schrödinger (Mécanique quantique) Particule en mouvement  Énergie ?  Équation de Schrödinger HΨ = EΨ HΨ = EΨ  Équation différentielle très compliquée  Solutions exactes pour cas simples

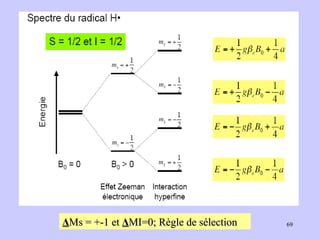
27. Cas de l’atome d’Hydrogène (ou Hydrogenoîde : Ze+, 1e ) HΨ = EΨ H = -ħ 2 /2m . Δ + V – Ze 2 /r = V , Δ = opérateur Laplatien = d 2 /dx 2 + d 2 /dy 2 +d 2 /dz 2 ) Ψ = Ψ n, l, ml = Rn, l (r) . Yl, ml (θ, φ) -ħ 2 /2m . Δ Ψ –Ze 2 /r Ψ – EΨ = 0 (Ei ? pour les quelles det = 0) En = -[( Z 2 . e 4 . m 2 )/ 2 ħ ]. [1/n 2 ]

28. On a pu mettre en évidence les séries spectrales suivantes (déjà trouvées par BOHR) : Dans l’UV  Série de Lyman  ν = R (1/1 2 – 1/n 2 ), n= 2, 3, 4, … Dans le visible  Série de Balmer  ν = R (1/2 2 – 1/n 2 ), n= 3, 4, 5,… Dans l’ IR  Série de Pashen  ν = R (1/3 2 – 1/n 2 ), n= 4, 5, 6,… Dans l’ IR  Série de Brackett  ν = R (1/4 2 – 1/n 2 ), n= 5, 6, 7,…. Valeurs propres : En = -[( Z 2 . e 4 . m 2 )/ 2 ħ ]. [1/n 2 ]  En dépend uniquement de n. ΔE = Em-En = hν ; ν = R (1/m 2 – 1/n 2 ) : Formule de Balmer * Niveaux d’énergie dans l’atome d’hydrogène avec des séries d’émissions * Chaque niveau d ‘énergie est associée à un mouvement de l’électron sur son orbite

29. Spectre de l’atome d’hydrogène

30. Structures des raies spectrales  Structure fine  Structure Hyperfine  Structure Superhyperfine

31. Structure fine Si ion ou molécule possède plusieurs électrons non appariés  S > 1/2 ( Cas Haut spin par exemple, champ cristallin faible ) Interaction entre spins voisins Terme (Energie) supplémentaire (S.D.S)  HΨ = EΨ 2S+1 sous niveaux, 2S raies

32. Structure hyperfine Si Moment magnétique de spin du noyau  I ≠ 0 Moment magnétique de spin de l’électron  S Pour un même ion Terme supplémentaire (I.A.S) (à introduire dans l’hamiltonien et résoudre HΨ = EΨ de nouveau) 2I +1 sous niveaux et 2I+1 raies

33. Si Moment magnétique de spin du noyau  I ≠ 0 Moment magnétique de spin de l’électron  S L’électron d’un ion en interaction avec des noyaux voisins ( I ≠ 0 et les I’ ≠ 0)) Structure Superhyperfine Terme supplémentaire (I.A.S) (à introduire dans l’hamiltonien et résoudre HΨ = EΨ de nouveau) (2I+1) x (2nI’+1) raies

35. HAMILTONIEN DE SPIN ET SES PARAMETRES H = g β H S + S A I Terme « S A I »: Interaction électron (S) – noyau (I non nul)  Interaction hyperfine I : Opérateur de spin nucléaire g : facteur de Landé (de décomposition spectrale) A : Constante de couplage hyperfin (e - noyau). Terme « g β H S » : Interaction électron (S, opérateur de spin) - Hext  Effet Zeeman électronique

36. * g permet d’identifier les centres responsables du paramagnétisme (ex : Mn 2+ , Cu 2+ ,…etc) * g dépend de la symétrie du site cristallographique du centre paramagnétique gx 0 0 g = 0 gy 0 0 0 gz soit Hext ║ Z * g permet d’apprécier le degré de localisation des électrons des substances paramagnétiques (Chimie organique) Facteur de Landé g *g comme tenseur donne des informations sur la symétrie des champs locaux qui agissent sur l’e à spin non couplé. g  Position de la raie , indépendant de l’instrument ,  /RMN ) g (électron libre) = 2,00232 * Si g ≈ g (électron libre)  ∩ spin- orbite faible (‘’pas d’orbite ‘’)  e délocalisé * Si g ≠ g (électron libre)  ∩ spin- orbite forte (e pris dans l’orbite)  e localisé

37. Facteur g de quelques espèces à S = 1/2 Cu (acac) 2 2,13 Mo O (SCN) 5 2- 1.935 VO (acac) 2 1.968 Cp 2 TiCl 2 AlCl 2 1.975 e - 2.0023 ° CH 3 2.0026 C 14 H 10 anión 2.0029 (antraceno) SO 2 - 2.0056 {(CH 3 ) 3 C} 2 NO 2.0063

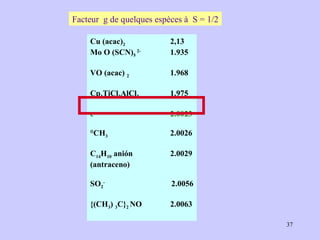
38. g J = 1 + [J(J+1) + S(S+1) – L(L+1)]/2J(J+1) L : moment orbital S : moment de spin J : moment orbital total : J = L+ S (couplage Russell-Saunders) Cas de l’électron libre E libre  pas d’orbite  L = 0 et J = S D’où : g (e) = 2 (valeur plus précise : 2,00232)

40. * A : et aussi un tenseur dans le cas général Facteur A (Constante du couplage hyperfin) * Informations sur les noyaux voisins immédiats de l’e étudié (leur I = 0 ou non…valeur de I à partir du spectre,…) * Traduit l’ ∩ entre moment magnétique de spin – moment magnétique de l’e. * Valeur de A permet d’identifier les centres paramagnétiques A  Distance entre deux raies consécutives / Interaction hyperfine

41. X ≡ Y ≡ Z gx = gy = gz  gx = gy = gz = g X ≡ Y ≠ Z  (gx = gy ) ≠ gz  gx = gy = g┴ ; gz = g║ X ≠Y ≠ Z gx ≠ gy ≠ gz  g 1 , g 2 , g 3 ISOTROPIE/ANISOTROPIE (SYMETRIES EN RPE)

42. Exemple de calcul des énergies Cas: Effet Zeeman (e et Hext) Hamiltonien de spin : H = g β H S sans ( « S A I ») Cas d'un électron en présence de Hext (║Oz)  H1 = g β Hz Sz Sz : Opérateur de spin Hz : Champ orienté selon Oz S = 1/2 et deux orientations possibles: Ms = +1/2, Ms = -1/2 Avec deux états (│S, Ms>): │+1/2, +1/2> et │+1/2, -1/2> L'action de l'opérateur Sz s'écrit: Sz│S, Ms> = Ms│S, Ms>, Sz│1/2, +1/2> = +1/2│1/2, +1/2> Sz│1/2, -1/2> = -1/2│1/2, -1/2> Calculons Hz│S, Ms> Hz│1/2, +1/2> = g β Hext Sz│1/2, +1/2> = (g β Hext)/2. │1/2, +1/2> Hz│1/2, -1/2> = g β Hext Sz│1/2, -1/2> = -(g β Hext)/2. │1/2, -1/2> Les deux états possibles: E 1 = (g β Hext)/2 et E 2 = - (g β Hext)/2

43. Hext : oblige les spins à s’orienter  décomposition des niveaux énergétiques H0 : fournit un quantum d’énergie hν 0  transitions par absorption d’énergie (ν 0 Є zone micro-onde) Il y’ a absorption  il y’a résonance  Condition de résonance Δ E= E+ - E- = g β H 0 = h ν 0 Règles de sélection RPE  Δm s = +-1 et Δm I = 0

44. Cas idéal ? 1- Radicaux libres en solution Radicaux libres ?  on a au moins 1e célibataire en général 2- Elément para. Sous forme de traces dans une matrice diamagnétique (ex: Mn 2+ / MgO) Hamiltonien = Hamiltonien de spin : H = g β H S + S A I Couplage hyperfin Effet ?  Dégénérescence des niveaux Zeeman en 2I+1 sous niveaux ( -I < -I+1 < …..< m I < …I-1 < I)  μ N aura 2I+1 orientations possibles et à probabilités égales

47. Phénomènes liés à la RPE Phénomène de relaxation  Relaxation spin-réseau  Relaxation spin-spin  T 1 : Temps de relaxation spin - réseau  T 2 : Temps de relaxation spin - spin

48. T1: Temps au bout duquel l'E absorbée par les spins baisse n fois, par suite d'échange d'E du spins  réseau. (le système de spin perd de l'E) T2: Temps au bout duquel se fait le rétablissement de l'équilibre dans le système de spins après transfert d'E spins  spins voisins. (le système de spins ne perd pas d'E) Phénomène relaxation spin-spin >> Phénomène relaxation spin-réseau T2 < < T1

49. Phénomène de saturation (si n 1 = n 2 ) Conseil : Éviter de travailler avec des puissances élevées.

50. RPE des ions de transition μ eff (S) ≡ μ exp  Le paramagnétisme des ions du groupe de Fer est dû au spin seul Couche 3d découverte  Action directe des Ligands/ion central Étouffement du moment orbitalaire L

51. μ eff (J = L+S) ≡ μ exp  Le paramagnétisme des ions des terres rares est dû à la contribution du moment orbital et de spin Couche 4f non découverte (protégée par 5s 2 5p 6 )  Pas d’action du C.Cr. sur le mouvement des électrons f.  Magnétisme du à L et S (Couplage Russell- Saunders)

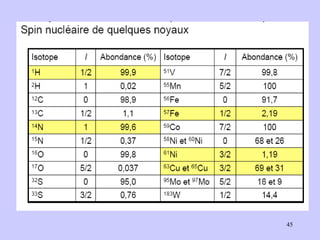
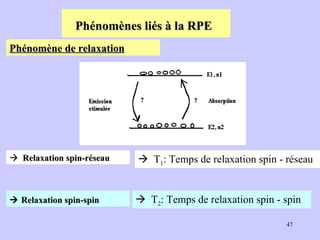
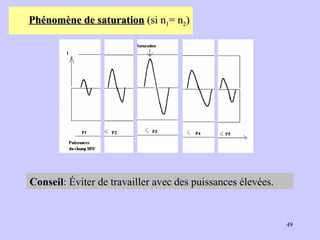
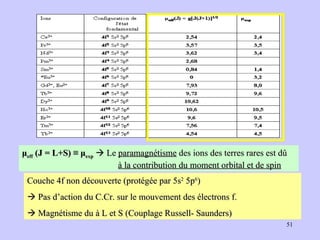
52. Exemple : [Fe(CN) 6 ] 3- et [Fe(H 2 O) 6 ] 3+ Fe 3+ : 3d 5 Fe 3+ : ion libre (pas de ligands) 3dz 2 , 3dx 2 -y 2 , 3dxy, 3dxz, 3dyz 4s 4px, 4py, 4pz 4dz 2 , 4dx 2 -y 2 , 4dxy, 4dxz, 4dyz μ exp = 1.75 μ B  μ th = [q(q+2)] 1/2 μB , q = 1 (1 e. cél.). [Fe(CN) 6 ] 3- avec 1 électron cél.  Complexe paramagnétique  Signal RPE Cas du complexe [ Fe(CN) 6 ] 3+ Complexes de symétrie octaédrique

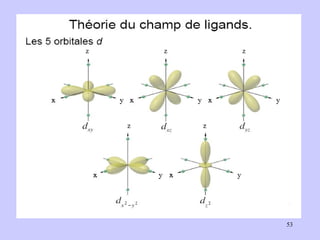
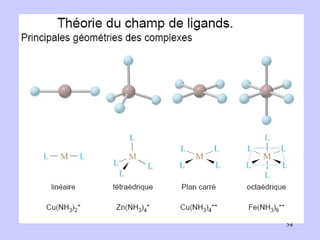
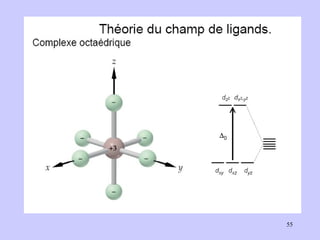
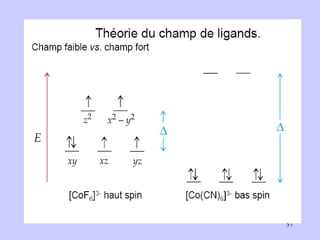
58. I - < Br - < Cl - < F - < OH - < C 2 O 4 2- ≈ H 2 O < EDTA 4- < NH 3 < NO - 2 < < CN - < CO CN -  Champ cristallin fort  Fe 3+ à OA bas spin (BS) Cas du complexe [ Fe(CN) 6 ] 3+

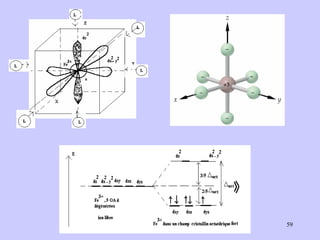
60. μ exp = 5,80 μ B  μ th = [5(5+2)] 1/2 μ B = 5,91 μ B [Fe(H 2 O) 6 ] 3+  avec 5 électrons célibataires Complexe paramagnétique  signal RPE possible Cas du complexe [Fe(H 2 O) 6 ] 3+ H 2 O  Champ cristallin ≈ faible  Fe 3+ à OA haut spin (HS)

61. Cas du complexe [Fe(H 2 O) 6 ] 3+

62. Complexes de symétrie tétraédrique et plan carrée Exemple : [Ni(CN 4 )] 2- et [NiCl 4 ] 2- [NiCl 4 ] 2- , Cl - : ligand faible et Complexe paramagnétique  H.S Hybridation sp 3  Complexe tétraédrique

63. [Ni(CN 4 )] 2- , CN - : ligand fort et Complexe diamagnétique  B.S Hybridation dsp 2  Complexe plan carré

64. Dans le cadre du champ cristallin Symétrie tétraédrique : [NiCl 4 ] 2- , H. S Complexe paramagnétique Les ligands ne pointent vers aucune O.A d Mais sont plus près des O.A d dirigées vers le milieu des arêtes (a/2) que vers celles dirigées vers le centre des faces (a(2) 1/2 )  O.A d déstabilisées  ( dxy, dxz et dyz )  t2g  E augmentée  O.A d stabilisées  dz 2 , dx 2 -y 2  eg  E abaissée

65. Symétrie plan carrée : [Ni(CN 4 )] 2- , B. S Complexe diamagnétique

66. Théorie du champ cristallin: Explication de la couleur Transition d-d , complexe octaédrique d'élément de transition (t 2g  e g ) Absorption de photon de la lumière visible [400 nm - 800 nm] Exemple : [Ti(H 2 O) 6 ] 3+  Ti 3+ : 3d 1

67. Détermination de  oct  oct = h  = hc/  = (6,62 10 -34 J.s).(3.00 10 8 m.s -1 )/ (510. 10 -9 m) = 3,88 10 -19 J pour 1 mole d'ions [Ti(H 2 O) 6 ] 3+  oct = (3,88 10-19 J). (6,02 10 23 ions/mol) = 234.10 3 J.mol-1 = 234 KJ.mol -1 En nombre d'onde:  oct = 1/  = 1/ 510 10 -7 cm = 19 607 cm -1 Pour 1 ligand H 2 O   oct = (19 607)/6 = 3268 cm -1  On peut comparer la force des ligands: I - < Br - < Cl - < F - < OH - < C 2 O 4 2- ≈ H 2 O < EDTA 4- < NH 3 < CN - < CO

68. EXEMPLES DE SPECTRES RPE

69. Δ Ms = +-1 et Δ MI=0; Règle de sélection

72. Cu 2+: 3d 9 S = ½ I = 3/2  2I + 1 orientations possibles de μ N m I = -3/2, -1/2, +1/2, +3/2 Δm s = +-1 et Δm I = 0 CAS DU CUIVRE

73. SPECTRE RPE DE CU 2+ ANISOTROPE 4 raies hyperfines non résolues

77. Mn 2+: 3d 5 Cas: Champ cristallin fort (B.S) S= ½ I = 5/2  2I + 1 orientations possibles de μ N m I = -5/2, -3/2, -1/2, +1/2, +3/2, +5/2 Δm s = +-1 Et Δm I = 0 CAS DU MANGANESE

78. Spectre RPE : Mn 2+ /MgO Facteur g ? h  = g  H centr . Constante de couplage hyperfin: A?

79. Structure fine :55 Mn (S = 5/2)  Interaction Spin e – Spin e  Niveaux d’énergie de spin  2S+1 = 6  2S raies = 5 (5 paquets) , Δ S = +-1  Intensités des paquets : 5,8,9,8,5 Structure fine et hyperfine Mn 2+ : (3d 5 ) Cas: Champ cristallin faible (H.S) Dégénérescence à H = 0 (En absence de champ) Raie 1 2 3 4 5

80. Structure hyperfine : 55 Mn (I= 5/2)  Inter. Spin e – Spin N  2I+1 raies (6 raies) Δ M I = 0, Δ M S =-+1  Intensités: égales Spectre RPE de Mn 2+ / amphibole (structure fine/Structure hyperfine ).

81. Spectres RPE : Plusieurs noyaux à spins identiques (Protons , I = 1/2) 1H 2H 3H 1:1 1:2:1 1:3:3:1

82. Radical: H OC° H COOH ? ? Radical : ° C H 2 OH

83. 1 er H de CH ( A 1 > ) 2 eme H de OH ( A 2 <) 4 raies possibles de même intensités Radical: H OC° H COOH

85. 4 H  (A  = 4,90G)  5 raies (1:4:6:4:1) 4 H  (A  = 1,83G )  5(x5) raies = 25 raies  Rapports d’intensités ???  Diagramme

86. Radicales sólo con núcleos I = 1/2 1 H(99.985%) I = 1/2 12 C(98.892%) I = 0 No interacciona 1 H (1, 4, 5, 8) n+1 = 5 1 H (2, 3, 6, 7) n+1 = 5 nº de líneas = 5 x 5 = 25 a 1 (exp) = 4.90 G (Quinteto) a 2 (exp) = 1.83 G (Quinteto) C 10 H 8 1 2 3 4 5 6 7 8

88. Effet des 4 H  Effet des 4 H 

90. H=  I L A L S

92. Número de líneas:  (2nI i + 1) = n + 1 Intensidad: Coeficientes del desarrollo de (1 + x) n 1 1 1 2 1 1 3 3 1 1 4 6 4 1 1 5 10 10 5 1 Spin I = 1/2 1 H, Sistemas con n núcleos equivalentes (I = 1/2) . 1 2 3 4 5 6 H(1, 2, 5, 6) n + 1 = 5 líneas (1:4:6:4:1) H(3,4) n + 1 = 3 líneas (1:2:1) Nº total de líneas = 5 x 3 = 15

94. TEST anti-oxydant d’un produit X %d’inhibition X = ((ref – test)/(ref- bdf) )x 100 Ref : signal ref du DPPH/solvant Test : signal du DPPH +produit X à tester bdf : signal du bruit de fond

95. Techniques de marquage et de piégeage de spin Marquage de spin (spin labeling) Piégeage de spin (spin trapping)

96. SPIN TRAPPING Spin Traps ( Nitrosocompuestos, nitronas) Del análisis del espectro de del aducto se puede deducir la estructura del radical R. R . + ST AS . Radical inestable Spin trap (diamagnético) Aducto de spin: persistente

100. Spectre RPE Nitroxyles (NO) en solution 5.10 -4 M /albumine 4% PCA: Composé hydrophile qui se lie peu à l’albumine Mouvement libre  Spectre isotrope NFA: Substance lipophile qui se lie majoritairement à l’albumine Fraction liée  Spectre anisotrope Marquage de spin (Spin labeling) Si entités instables  Piégeage de spin par autres molécules (Spin trapping)  Groupements reporters de leur environnement  Microviscosité, Micropolarité, pH (intracellulaire, implants, tube digestif, …), ...

102. INTERACCIONES HIPERFINAS Diagrama de niveles para dos núcleos equivalentes I= 1 Radical nitronil-nitróxido en benceno Intensidad: 1:2:3:2:1 Núcleos con I>1/2 2 nitrógenos equivalentes I= 1 (300K)

103. Intérêt d’étudier les sucres par RPE ? 1- Spectre RPE +- stable (dosimétrie) 2- Leur présence dans nos aliments et médicaments

104. Spectres RPE de sucres irradiés avec une dose de 50Gy de source 60 Co

105. Courbe d’étalonnage des sucres irradiés au 60 Co

106. Application de la dosimétrie : Spectres RPE de fragments d’os de travailleurs auprès d’une source de cobalt 60, à San Salvador

107. Ref. : Revista Brasileira de Fisica Médica, Vomume 1, Nùmero1 , 2005

108. Skript zur Vorlesung von A. Schweiger

109. 107 Ag  I = ½ ; 109 Ag  I = ½ 2nI+1 lines = 7; Pascal triangal 

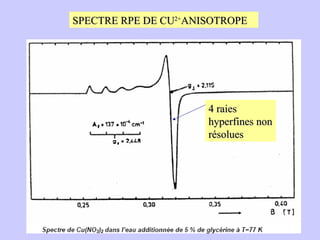
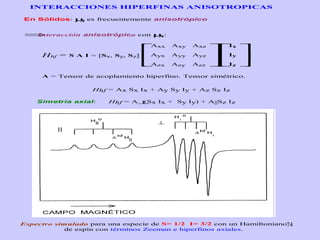
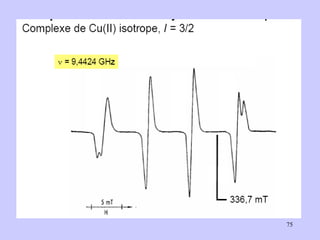
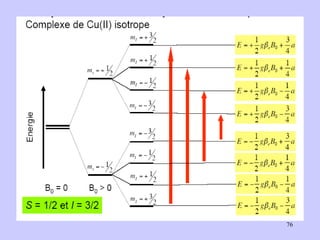
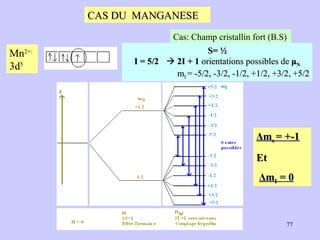
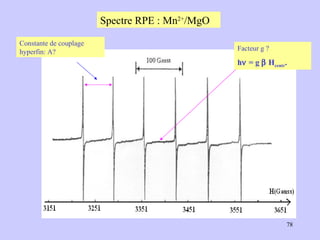
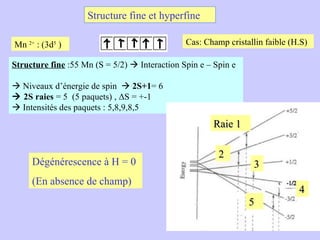
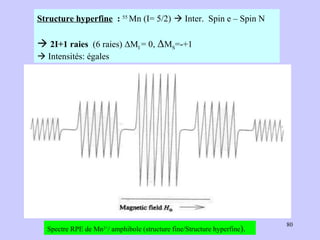
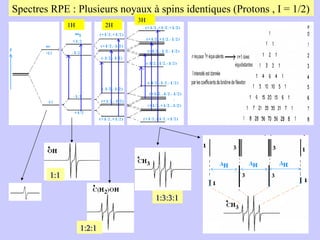
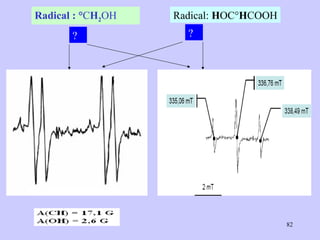
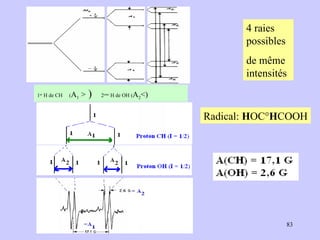
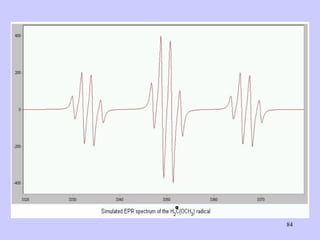
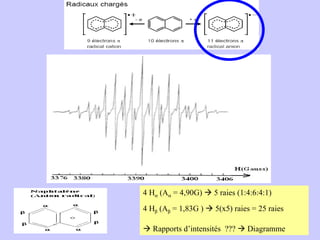
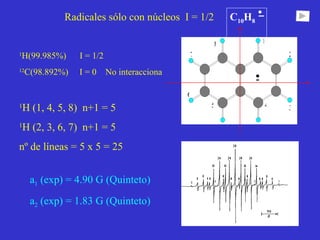
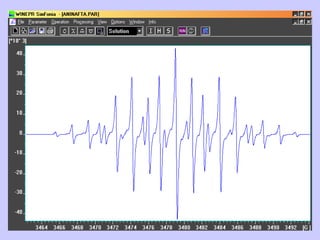
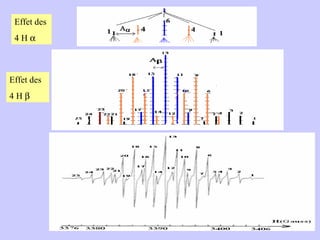
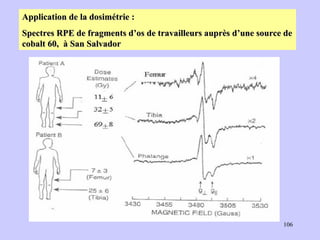
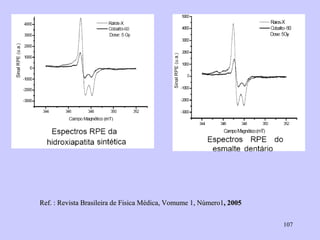
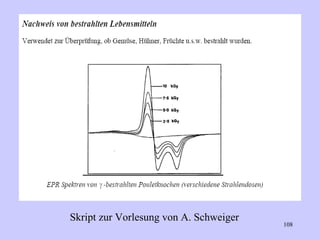
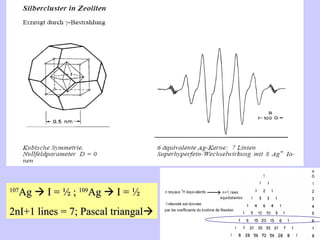
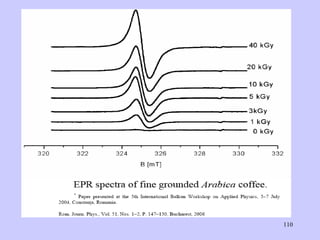
111. Aspect quantitative de la RPE  appareil à 2 cavités (Echantillon + Etalon)  Enregistrement dans les mêmes conditions Échantillon [spins]? I(échantillon) connue Étalon [spins] connue I(etalon) connue I (signal )  [centres paramagnétiques]

112. APLICACIONES Efectos de las irradiaciones Defectos en cristales ej.: Centros de color en haluros alcalinos Detección óptica de Resonancia Magnética Influencia de impurezas en semiconductores Campos cristalinos en monocristales Microcristales con iones magnéticos etc FÍSICA GEOLOGÍA Datación Procesos de oxidación-reducción Birradicales y moléculas en su estado triplete Investigaciones cinéticas Comportamiento de radicales libres en corrosión Comportamiento de pinturas bajo irradiación UV Investigación de Polímeros Estudio de mecanismos de reacción etc QUÍMICA Sonoquímica in situ

113. Efecto de los Rayos X sobre compuestos biológicos Detección de drogas Control de alimentos irradiados Reacciones enzimáticas Fotosíntesis Observación de iones y elementos de transición Propiedades magnéticas anormales de ácidos nucleicos etc BIOLOGÍA Investigación de reacciones carcinogenésicas Estudio de la sangre y de microorganismos Estudio de radicales libres en tejidos vivos Fotosíntesis Técnicas de “spin label” Técnicas de”spin probe” “ Técnicas de imaging” etc MEDICINA

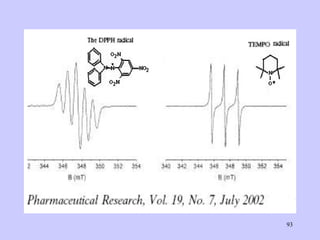
114. BIBLIOGRAPHIE * Electron spin resonance by Dr. Phil Rieger, Brown University, 2005 * La résonance paramagnétique électronique, A. KASTLER (Lauréat du Prix Nobel), Dunod, Paris, 1968. * La résonance paramagnétique électronique, M.CHE, D.OLIVIER, L. BONNEVOIT, P. MERIAUNDEAU, 1980 * Chimie générale, M.Garric, Dunod University, 1976 * © 1999 International Consultative Group on Food Irradiation Report. * Journal officiel de l'union européenne (11-3-2003) * Electron spin resonance studies of some irradiated pharmaceuticals M. Gibella et al.; Radiation Physics and Chemistry ; 58(2000)69-76.[1] M. Le Bars, A. Bouroche, L'ionisation dans l'industrie agroalimentaire , Editions INRA, 1998. * L. Saint-Lèbe, J. Raffi, Le traitement ionisant des aliments , Cah. Nutr. Diét., 30, 1995, 117-123. * Comité Mixte d'Experts OMS (Organisation mondiale pour la Santé), FAO (Food and Agricultural * * * * * Organization), AIEA (Agence Internationale pour l'Energie Atomique), Salubrité des aliments irradiés, Ser. Rap. Techn. N°659, OMS, Genève, 1981. * J. Raffi, J-J. Belliardo, Potential new methods in identification of irradiated food , CCE, EUR 13331 EN, 1991. * Rapport scientifique, E. Marchioni (Faculty of pharmacy, strasbourg), H. Delincée (Institute of Nutrutional Physiology, Karlsrushe), 2002. * Doctorat, A. MARFAK, Radiolyse gamma des flavonoides Etude de leur réactivité avec les radicaux issus des alcools : formation des depsides.Université de Limoge, France, 2003. * Spectrométrie RPE, IMACSEN, PHILIPE TUREK , DESS. p:// * Pharmaceutical Research, Vol. 19, N° 7, July 2002. * Etude toxicologique transfrantalière destinée à évaluer le risque encouru lors de la consommation d’aliments gras ionisés; Rapport final/Schlussbericht INTERREG II/ Projet N° 3.171; 2002. * RPE, principe et applications biomédicales, R. DEBUYST et al. LOUVAIN MED. 118: 205-213, 1999. * Facts on Food Irradiation,International Consultative Group on Food Irradiation (ICGFI), 1999