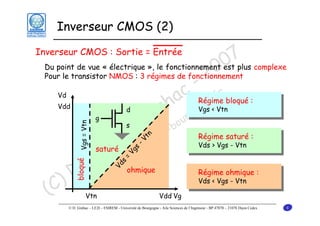
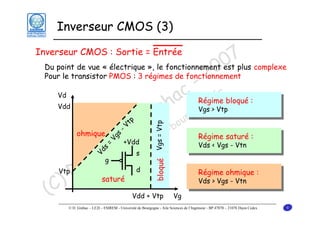
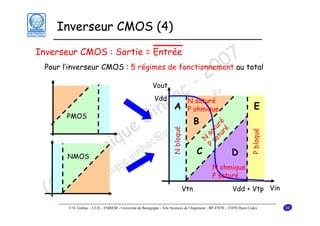
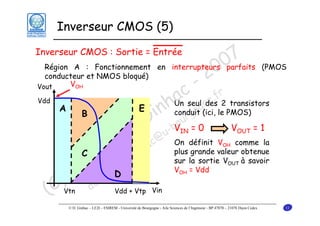
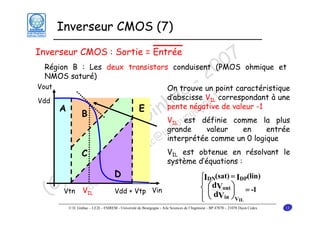
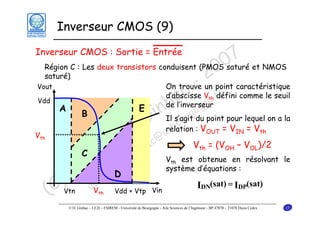
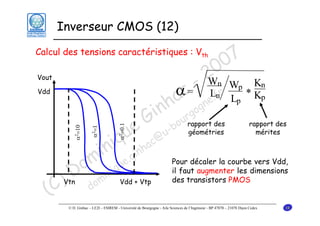
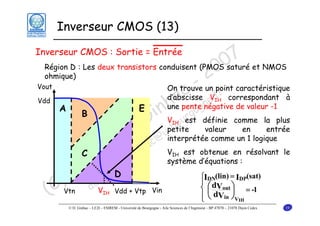
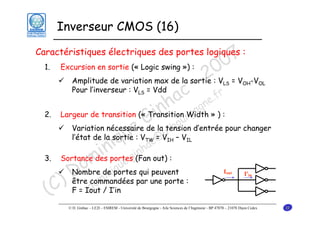
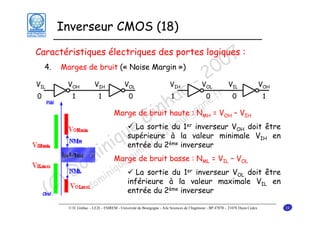
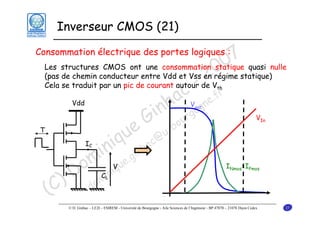
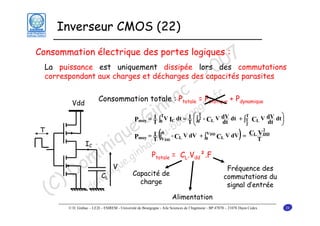
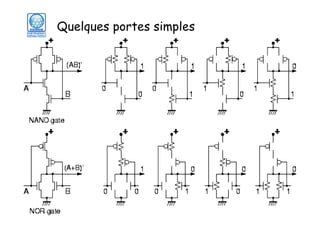
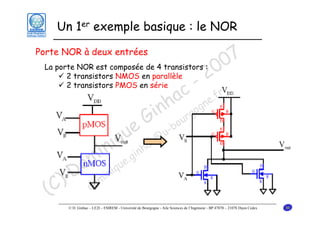
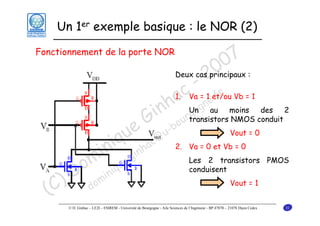
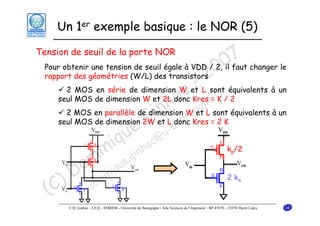
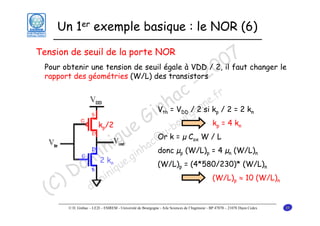
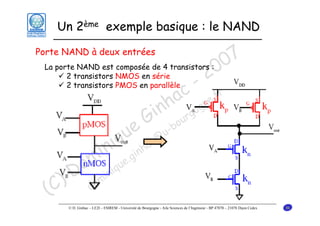
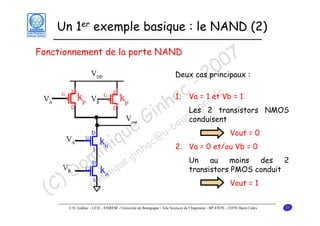
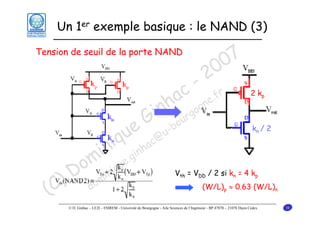
Le document traite des principes fondamentaux de la microélectronique numérique, notamment de la technologie CMOS, qui combine des transistors NMOS et PMOS pour réaliser des opérations logiques. Il présente des détails sur le fonctionnement et le design des inverseurs CMOS, y compris les régimes de fonctionnement des transistors et les calculs associés aux tensions caractéristiques. L'objectif du cours est de fournir une compréhension approfondie de la structure et du fonctionnement des circuits logiques en utilisant la technologie CMOS.

1. Micro
7
Électronique 00
2
- r
Chapitre 3
c e.f
a gn
nh rgo
i Principes de la
G -bou
e @u technologie
u c
i q nha
CMOS
in .gi
om inique
D m
) do
(C
Dominique GINHAC
dginhac@u-bourgogne.fr

2. Plan du cours
7
0
0
2
1- Introduction sur la microélectronique numérique
- r
c e.f
a gn
3- Bases de la technologie CMOS o
nh rg
i u
Généralités
G -bo
Inverseur CMOS e
u c@u
Portes NOR et NAND
i q nha
in élémentaires
.gi
4- Design de m
oportesique
D min
) d des
5-Technologie o composants
(C
2- Physique des semi conducteurs
© D. Ginhac – LE2I – ESIREM - Université de Bourgogne - Aile Sciences de l’Ingénieur - BP 47870 – 21078 Dijon Cedex
2

3. CMOS : Principes généraux
7
0
0
2
u
iq
- r
c e.f
a gn
nh rgo
i u
G -bo
e
in .gin
om inique
D m
) do
(C
c@
ha
u
© D. Ginhac – LE2I – ESIREM - Université de Bourgogne - Aile Sciences de l’Ingénieur - BP 47870 – 21078 Dijon Cedex
3

4. Définition
7 NMOS et
0
La structure CMOS est un assemblage de transistors
0
PMOS dans l’objectif d’effectuer une opération logique plus ou
2
moins complexe
- r
c e.f
a gn
h o
nlogiquergCMOS est constituée :
i u
Une porte
G réseau de transistors PMOS
d’un bo
e d’un uréseau de transistors NMOS
u c@
iq Cesnha sont connectés :
in .gi réseaux
entrées
m que aux sortie
o i ni
à la
D m
aux alimentations (masse et vdd)
) do
(C
CMOS = Complementary MOS = NMOS + PMOS
© D. Ginhac – LE2I – ESIREM - Université de Bourgogne - Aile Sciences de l’Ingénieur - BP 47870 – 21078 Dijon Cedex
4

5. Définition (2)
7 NMOS et
0
La structure CMOS est un assemblage de transistors
0
PMOS dans l’objectif d’effectuer une opération logique plus ou
2
moins complexe
- r
c Pourquoi Complementary ?
a gne.f
nh parce que chaque réseau de
i urgo
Tout simplement,
G est-bchargé d’effectuer soit la mise
o
transistors
e la @u à 1 de la fonction logique :
u c
à 0, soit mise
i q nha
in .gi Le réseau P effectue la mise à 1 en
au potentiel
om inique mettant la sortieeffectue la Vdd à 0 en
Le réseau N
mise
D m mettant la sortie au potentiel 0V
) do
(C
CMOS = Complementary MOS = NMOS + PMOS
© D. Ginhac – LE2I – ESIREM - Université de Bourgogne - Aile Sciences de l’Ingénieur - BP 47870 – 21078 Dijon Cedex
5

6. Structures Complementary MOS
7 base de la
0
La structure CMOS permet de construire l’élément de
0
logique à effet de champ : l’inverseur composé d’un seul transistor
2
NMOS et d’un seul transistor PMOS
- r
c e.f
a gn
nh rgdes transistors :
i u o
Interconnexions
G -bo
e Source du PMOS reliée à Vdd
u c@u
iq nha Source du NMOS reliée à la masse
in .gi
om inique Grilles attaquées par l'entrée
D m
Drains connectés à la sortie
) do
(C
CMOS = Complementary MOS = NMOS + PMOS
+Vdd
s
Entrée
d
Sortie
d
s
© D. Ginhac – LE2I – ESIREM - Université de Bourgogne - Aile Sciences de l’Ingénieur - BP 47870 – 21078 Dijon Cedex
6

7. Inverseur CMOS
7 comme
0
Du point de vue « logique », un inverseur CMOS est vu
0
double interrupteur en série
2
- r
c e.f
a gn
nh rgo
i u
G -bo
e @u
u c
i q nha
in .gi
om inique
D m
) do
(C
Inverseur CMOS : Sortie = Entrée
+Vdd
s
Entrée
I
QU
ZZ
un
ENTREE = 0
PMOS : Conducteur / Bloqué
NMOS : Conducteur / Bloqué
SORTIE = 1
d
Sortie
d
s
ENTREE = 1
PMOS : Conducteur / Bloqué
NMOS : Conducteur / Bloqué
SORTIE = 0
© D. Ginhac – LE2I – ESIREM - Université de Bourgogne - Aile Sciences de l’Ingénieur - BP 47870 – 21078 Dijon Cedex
7

8. Inverseur CMOS (2)
7 complexe
0
Du point de vue « électrique », le fonctionnement est plus
0
Pour le transistor NMOS : 3 régimes de fonctionnement
2
- r
c Régime bloqué :
a gne.f
nh rgo
i u
G -bo
e @u
u c
Régime saturé :
i q nha
saturé
in .gi
om iniqueohmique
Régime ohmique :
D m
) do
(C
Inverseur CMOS : Sortie = Entrée
Vd
Vtn
Vgs < Vtn
d
g
-V
tn
s
s
=
Vg
s
Vds > Vgs - Vtn
Vd
bloqué
Vgs = Vtn
Vdd
Vds < Vgs - Vtn
Vdd Vg
© D. Ginhac – LE2I – ESIREM - Université de Bourgogne - Aile Sciences de l’Ingénieur - BP 47870 – 21078 Dijon Cedex
8

9. Inverseur CMOS (3)
7 complexe
0
Du point de vue « électrique », le fonctionnement est plus
0
Pour le transistor PMOS : 3 régimes de fonctionnement
2
- r
c Régime bloqué :
a gne.f
nh rgo
i u
G -bo
e @u
ohmique
u c
Régime saturé :
i q nha
in .gi
om inique
Régime ohmique :
D m
) do saturé
(C
Inverseur CMOS : Sortie = Entrée
Vd
Vdd
g
Vtp
s
d
Vgs = Vtp
+Vdd
Vds < Vgs - Vtn
bloqué
Vd
s
=
Vg
s
-V
tp
Vgs > Vtp
Vdd + Vtp
Vds > Vgs - Vtn
Vg
© D. Ginhac – LE2I – ESIREM - Université de Bourgogne - Aile Sciences de l’Ingénieur - BP 47870 – 21078 Dijon Cedex
9

10. Inverseur CMOS (4)
7 total
0
Pour l’inverseur CMOS : 5 régimes de fonctionnement au
0
2
- r
c e.f
a gn
E
nhA rgo
i uB
G -bo
e @u
u c
i q nha
C
D
in .gi
om inique
D m
) do
(C
Inverseur CMOS : Sortie = Entrée
Vout
Vdd
N ohmique
P saturé
Vtn
P Vgs
bloqué bloqué= Vt
NMOS
N bloqué
PMOS
N
P sa
sa tu
tu ré
ré
N saturé
P ohmique
Vdd + Vtp Vin
© D. Ginhac – LE2I – ESIREM - Université de Bourgogne - Aile Sciences de l’Ingénieur - BP 47870 – 21078 Dijon Cedex
10

11. Inverseur CMOS (5)
7 (PMOS
Région A : Fonctionnement en interrupteurs 0
0 parfaits
conducteur et NMOS bloqué)
2
V
- r
c e.f
a g des 2 transistors
Un seul n
A
E
nhconduit (ici, le PMOS)
B
i urgo
G -bVo = 0 V = 1
e @u
u c On définit V comme la
iq nha plus grande valeur obtenue
in .gi
C
sur la sortie V
à savoir
m que
o iniD
V = Vdd
D m
) do
(C
Inverseur CMOS : Sortie = Entrée
Vout
OH
bloqué
Vgs = Vt
Vdd
Vtn
IN
OUT
OH
OUT
OH
Vdd + Vtp Vin
© D. Ginhac – LE2I – ESIREM - Université de Bourgogne - Aile Sciences de l’Ingénieur - BP 47870 – 21078 Dijon Cedex
11

12. Inverseur CMOS (6)
7 bloqué
0
Région E : Fonctionnement en interrupteurs parfaits (PMOS
0
et NMOS conducteur)
2
- r
c e.f
a g des 2 transistors
Un seul n
A
E
nhconduit (ici, le NMOS)
B
i urgo
G -bVo = 1 V = 0
e @u
u c On définit V comme la
iq nha plus petite valeur obtenue
in .gi
C
sur la sortie V
à savoir
m que V
o iniD
V =0
D m
) do
(C
Inverseur CMOS : Sortie = Entrée
Vout
bloqué
Vgs = Vt
Vdd
OL
Vtn
IN
OUT
OL
OUT
OL
Vdd + Vtp Vin
© D. Ginhac – LE2I – ESIREM - Université de Bourgogne - Aile Sciences de l’Ingénieur - BP 47870 – 21078 Dijon Cedex
12

13. Inverseur CMOS (7)
7 ohmique et
0
Région B : Les deux transistors conduisent (PMOS
0
NMOS saturé)
2
- r
On trouve un point caractéristique
c e correspondant à une
d’abscisse V .f
a négative de valeur -1
h gogn
pente
A
E
B
inV uest définie comme la plus
r
G grande valeur en entrée
bo
e @uinterprétée comme un 0 logique
u c
iq nha V est obtenue en résolvant le
in .gi
C
système d’équations :
m que
o iniD
D m
⎧I (sat) = I (lin)
⎪ d
) V do
⎨ ⎛ V ⎞ = -1
C
⎜
⎟
(
⎪ ⎝ dV ⎠
Inverseur CMOS : Sortie = Entrée
Vout
Vdd
Vgs = Vt
IL
bloqué
IL
IL
DN
Vtn
IL
Vdd + Vtp Vin
DP
out
⎩
in VIL
© D. Ginhac – LE2I – ESIREM - Université de Bourgogne - Aile Sciences de l’Ingénieur - BP 47870 – 21078 Dijon Cedex
13

14. Inverseur CMOS (8)
7
0
0
2
Calcul des tensions caractéristiques : VIL
VIL
⎧IDN(sat) = IDP(lin)
⎪
est obtenue à partir du système d’équations : ⎨ ⎛ dVout ⎞ = -1
⎜
⎟
⎪ ⎝ dVin ⎠V
⎩
IL
u
iq
- r
c e.f
a gn
nh rgo
i u
G -bo
e
in .gin
om inique
D m
) do
(C
c@
ha
u
Avec
© D. Ginhac – LE2I – ESIREM - Université de Bourgogne - Aile Sciences de l’Ingénieur - BP 47870 – 21078 Dijon Cedex
14

15. Inverseur CMOS (9)
7 et NMOS
Région C : Les deux transistors conduisent (PMOS0
0 saturé
saturé)
2point caractéristique
- r
On trouve un
c e défini comme le seuil
d’abscisse V .f
a gn
de l’inverseur
h
A
E
nIl s’agitgo point pour lequel on a la
B
i ur du
G relation : V = V = V
bo
e @uV
u c
i q nha
V = (V – V )/2
n .gi
i
C
V est obtenue en résolvant le
m que
o iniD
système d’équations :
D m
) dVo
I (sat) = I (sat)
C
(
Inverseur CMOS : Sortie = Entrée
Vout
th
Vgs = Vt
Vdd
bloqué
th
Vtn
th
Vdd + Vtp Vin
OUT
th
IN
OH
th
OL
th
DN
DP
© D. Ginhac – LE2I – ESIREM - Université de Bourgogne - Aile Sciences de l’Ingénieur - BP 47870 – 21078 Dijon Cedex
15

16. Inverseur CMOS (10)
7la tension de
0
V est défini comme le seuil de l’inverseur pour lequel
0
sortie est égale à la tension d’entrée
2
- r
c e.f
a gn
nh rgo
i u
G -bo
e @u
u c
i q nha
in .gi
om inique
D m
Avec
) do
(C
Calcul des tensions caractéristiques : Vth
IDN(sat) = IDP(sat)
th
© D. Ginhac – LE2I – ESIREM - Université de Bourgogne - Aile Sciences de l’Ingénieur - BP 47870 – 21078 Dijon Cedex
16

17. Inverseur CMOS (11)
7½ V
0
Pour obtenir un inverseur symétrique, il faut avoir V =
0
2
- r
c avec V = - V
= a
1
On a donc
e.f
h gogn
i n ur
G -bo
e @u
= 1
u c
i q nha
in .gi
om inique
D m
) do
(C
Calcul des tensions caractéristiques : Vth
IDN(sat) = IDP(sat)
th
tn
DD
tp
© D. Ginhac – LE2I – ESIREM - Université de Bourgogne - Aile Sciences de l’Ingénieur - BP 47870 – 21078 Dijon Cedex
17

18. Inverseur CMOS (12)
7
0
0
2
Calcul des tensions caractéristiques : Vth
Vout
u
iq
α2=0.1
α2=1
α2=10
Vdd
- Wnr Wp * Κn
=
αc L.n L Κp
a gne f p
nh rgo
i u
G -bo
e
in .gin
om inique
D m
) do
(C
Vtn
c@
ha
Vdd + Vtp
u
rapport des
géométries
rapport des
mérites
Pour décaler la courbe vers Vdd,
il faut augmenter les dimensions
des transistors PMOS
© D. Ginhac – LE2I – ESIREM - Université de Bourgogne - Aile Sciences de l’Ingénieur - BP 47870 – 21078 Dijon Cedex
18

19. Inverseur CMOS (13)
7 et NMOS
Région D : Les deux transistors conduisent (PMOS0
0 saturé
ohmique)
2
- r
On trouve un point caractéristique
c e
d’abscisse V.f correspondant à
apentegnégative de valeur -1
h go n
une
A
E
B
inV uest définie comme la plus
G petiter valeur en entrée
bo
e @uinterprétée comme un 1 logique
u c
iq nha V est obtenue en résolvant le
in .gi
C
système d’équations :
m que
o iniD
D m
⎧I (lin) = I (sat)
⎪ d
) doV
⎨ ⎛ V ⎞ = -1
C
⎜
⎟
(
⎪ ⎝ dV ⎠
⎩
Inverseur CMOS : Sortie = Entrée
Vout
Vdd
Vgs = Vt
IH
bloqué
IH
IH
DN
Vtn
IH
Vdd + Vtp Vin
DP
out
in VIH
© D. Ginhac – LE2I – ESIREM - Université de Bourgogne - Aile Sciences de l’Ingénieur - BP 47870 – 21078 Dijon Cedex
19

20. Inverseur CMOS (14)
7
0
0
2
Calcul des tensions caractéristiques : VIH
VIH
⎧IDN(lin) = IDP(sat)
⎪
est obtenue à partir du système d’équations : ⎨ ⎛ dVout ⎞ = -1
⎜
⎟
⎪ ⎝ dVin ⎠V
⎩
IH
u
iq
- r
c e.f
a gn
nh rgo
i u
G -bo
e
in .gin
om inique
D m
) do
(C
c@
ha
u
Avec
© D. Ginhac – LE2I – ESIREM - Université de Bourgogne - Aile Sciences de l’Ingénieur - BP 47870 – 21078 Dijon Cedex
20

21. Inverseur CMOS (15)
Premier bilan sur l’inverseur CMOS
Vout
Vout
7
0
0
2
- r
c e.f
a gn
nh rgo
i u
G -bo
e
u
iq
VOH + VOL
2
VOL
VIL
Vth
VIH
Sortie
NMOS
PMOS
< Vtn
VOH
Bloqué
Ohmique
B
in .gin
om inique
D m
) do
(C
Entrée
A
Vin
VOH
Région
VIL
VOH
Saturé
Ohmique
Vth
Vth
Saturé
Saturé
D
VIH
VOL
Ohmique
Saturé
E
> (Vdd + Vtp)
VOL
Ohmique
Bloqué
c@
ha
C
u
Vin
© D. Ginhac – LE2I – ESIREM - Université de Bourgogne - Aile Sciences de l’Ingénieur - BP 47870 – 21078 Dijon Cedex
21

22. Inverseur CMOS (16)
7
0
0
2
Caractéristiques électriques des portes logiques :
1.
Excursion en sortie (« Logic swing ») :
c e.f
a gn
nh Width » ) :
i u
2. Largeur de transition (« Transition rgo
G la tension d’entrée pour changer
bo
Variation nécessaire de
eV =@Vu- – V
u c
l’état de la sortie :
i q nha
inportesg(Fan out) :
3. Sortance des
. i
ue
om deniportes qui peuvent
q
Nombre
D commandées par une porte :
i
être om
) F = Iout / I’in
d
(C
Amplitude de variation max de la sortie : VLS = VOH-VOL
Pour l’inverseur : VLS = Vdd
r
TW
IH
IL
Iout
I'in
© D. Ginhac – LE2I – ESIREM - Université de Bourgogne - Aile Sciences de l’Ingénieur - BP 47870 – 21078 Dijon Cedex
22

23. Inverseur CMOS (17)
7
0
0
2
Caractéristiques électriques des portes logiques :
4.
Marges de bruit (« Noise Margin »)
- r
c e.f
a gn
nh rgo
i u
G -bo
e
Capacité d’une porte à éliminer le bruit sur les entrées
(bruit par couplage capacitif, résistif, bruit thermique, …)
u
iq
in .gin
om inique
D m
) do
(C
VTW
Rappels :
c@
ha
u
VOHmin : tension minimale de
sortie représentant un état haut
VOLmax : tension maximale de
sortie représentant un état bas
VIHmin
:
tension
minimale
d'entrée pour laquelle on est à
l'état bas en sortie
VILmax
:
tension
maximale
d'entrée pour laquelle on est à
l'état haut en sortie
© D. Ginhac – LE2I – ESIREM - Université de Bourgogne - Aile Sciences de l’Ingénieur - BP 47870 – 21078 Dijon Cedex
23

24. Inverseur CMOS (18)
7
0
0
2
Caractéristiques électriques des portes logiques :
4.
VIL
0
Marges de bruit (« Noise Margin »)
- r
c e.f
a gn
nh rgoN = V – V
Marge de bruit haute :
i u
G -bo
La sortie du 1 inverseur V doit être
e @
supérieureu à la valeur minimale V
en
u cdu 2 inverseur
iq entréea
inMargeinh bruit basse : N = V – V
m que.g de
o ini La sortie du 1 inverseur V doit être
D m inférieure à la valeur maximale V en
) do
entrée du 2
inverseur
(C
VOH
VIH
VOL
1
1
0
VIH
VOL
VOH
0
1
VIL
0
1
MH
OH
er
IH
OH
IH
ème
ML
er
IL
OL
OL
ème
© D. Ginhac – LE2I – ESIREM - Université de Bourgogne - Aile Sciences de l’Ingénieur - BP 47870 – 21078 Dijon Cedex
IL
24

25. Inverseur CMOS (19)
7
0
0
2
Caractéristiques électriques des portes logiques :
4. Marges de bruit idéales
- V r = Vdd
c e.f
a gnV = 0
nh rgo V = Vdd / 2
i u
G -bo V = VDD / 2
e
OHmin
OLmax
u
iq
in .gin
om inique
D m
) do
(C
IHmin
c@
ha
u
ILmax
Donc :
NMH = Vdd / 2
NML = Vdd / 2
© D. Ginhac – LE2I – ESIREM - Université de Bourgogne - Aile Sciences de l’Ingénieur - BP 47870 – 21078 Dijon Cedex
25

26. Inverseur CMOS (20)
7
0
4. Marges de bruit idéales et caractéristique de l’inverseur
0
2
- r
c e.f
a gn
nh rgo
i u
G -bo
e @u
u c
i q nha
in .gi
om inique
D m
) do
(C
Caractéristiques électriques des portes logiques :
Vout
Vout
Vin
VOH
Vout
VOH
VOH + VOL
2
VOL
VOL
VIL
Vth
VIH
Vin
Vth
VIH
Vin
VIL
© D. Ginhac – LE2I – ESIREM - Université de Bourgogne - Aile Sciences de l’Ingénieur - BP 47870 – 21078 Dijon Cedex
26

27. Inverseur CMOS (21)
7 quasi nulle
0
Les structures CMOS ont une consommation statique
0
(pas de chemin conducteur entre Vdd et Vss en régime statique)
2V
Cela se traduit par un pic de courant autour de
- r
c e.f
a gn
nh rgo
i u
G -bo
e @u
u c
i q nha
in .gi
om inique
D m
) do
(C
Consommation électrique des portes logiques :
th
Vdd
Vout
VIn
T
IC
CL
V
INmos=IPmos
© D. Ginhac – LE2I – ESIREM - Université de Bourgogne - Aile Sciences de l’Ingénieur - BP 47870 – 21078 Dijon Cedex
27

28. Inverseur CMOS (22)
7
0
La puissance est uniquement dissipée lors des commutations
0
correspondant aux charges et décharges des capacités parasites
2
- r
c = Pe.f + P
Consommation totale :a
P
h gogn
i n ur
G -bo
e @u
)
u c(
i q nha
in .gi P = C .V ².F
om inique
D m
) do
(C
Consommation électrique des portes logiques :
totale
Vdd
statique
dynamique
T
⎞
1 T
1⎛
Pmoy = T ∫0 V IC dt = T ⎜ ∫02 - CL V dV dt + ∫T CL V dV dt ⎟
dt
dt
T
⎝
T
⎠
2
2
V
C V
1 0
Pmoy = T ∫VDD - CL V dV + ∫0 DD CL V dV = L T DD
IC
totale
CL
V
L
dd
Fréquence des
commutations du
signal d’entrée
Capacité de
charge
Alimentation
© D. Ginhac – LE2I – ESIREM - Université de Bourgogne - Aile Sciences de l’Ingénieur - BP 47870 – 21078 Dijon Cedex
28

29. Quelques portes simples
7
0
0
2
u
iq
- r
c e.f
a gn
nh rgo
i u
G -bo
e
in .gin
om inique
D m
) do
(C
c@
ha
u
© D. Ginhac – LE2I – ESIREM - Université de Bourgogne - Aile Sciences de l’Ingénieur - BP 47870 – 21078 Dijon Cedex
29

30. Un 1er exemple basique : le NOR
7
0
La porte NOR est composée de 4 transistors :
0
2 transistors NMOS en parallèle
2
2 transistors PMOS en série
- r
c e.f
a gn
nh rgo
i u
G -bo
e @u
u c
i q nha
in .gi
om inique
D m
) do
(C
Porte NOR à deux entrées
© D. Ginhac – LE2I – ESIREM - Université de Bourgogne - Aile Sciences de l’Ingénieur - BP 47870 – 21078 Dijon Cedex
30

31. Un 1er exemple basique : le NOR (2)
7
0
Deux cas20
principaux :
- r
1. c = 1 et/ou Vb = 1
a Va gne.f
nh rUno au moins conduit 2
i u transistors NMOS des
g
G -bo
e
Fonctionnement de la porte NOR
u
iq
in .gin
om inique
D m
) do
(C
c@
ha
u
Vout = 0
2. Va = 0 et Vb = 0
Les 2 transistors PMOS
conduisent
Vout = 1
© D. Ginhac – LE2I – ESIREM - Université de Bourgogne - Aile Sciences de l’Ingénieur - BP 47870 – 21078 Dijon Cedex
31

32. Un 1er exemple basique : le NOR (3)
Tension de seuil de la porte NOR
7
0
0
2
Définition : Vth = Va = Vb = Vout
Conditions supposées :
1. Commutations simultanées de Va et Vb
2. (W/L)nA = (W/L)nB
.fr
3. (W/L)pA = (W/L)pB
ne
u
iq
c
a g
nh rgo
i u
G -bo
e
in .gin
om inique
D m
) do
(C
c@
ha
u
En comparaison
© D. Ginhac – LE2I – ESIREM - Université de Bourgogne - Aile Sciences de l’Ingénieur - BP 47870 – 21078 Dijon Cedex
32

33. Un 1er exemple basique : le NOR (4)
7
0
0
2
Tension de seuil de la porte NOR
Définition : Vth = Va = Vb = Vout
Conditions supposées :
1. Commutations simultanées de Va et Vb
2. (W/L)nA = (W/L)nB
.fr
3. (W/L)pA = (W/L)pB
ne
u
iq
c
a g
nhk etgV = - V , on obtient :
i k = ur o
Si
G -bo
e
in .gin
om inique
D m
) do
(C
n
c@
ha
u
p
tn
tp
Vth (Nor) = (VDD + Vtn ) / 3
Vth(Inv) = VDD / 2
A.N. : VDD = 5 V et Vtn = 1V
VTH(Inv) = 2.5 V
Vth(Nor) = 2 V
© D. Ginhac – LE2I – ESIREM - Université de Bourgogne - Aile Sciences de l’Ingénieur - BP 47870 – 21078 Dijon Cedex
33

34. Un 1er exemple basique : le NOR (5)
7 changer le
Pour obtenir une tension de seuil égale à VDD / 2, 0faut
0 il
rapport des géométries (W/L) des transistors
2
- r
2 MOS en série de dimension W et L sont équivalents à un
c =K
seul MOS de dimension W et 2L donc Kres e.f / 2
a gn
nh Wgo L sont équivalents à un
2 MOS en parallèle de dimension
et
iet L doncr Kres = 2 K
G -bou
seul MOS de dimension 2W
e @u
u c
i q nha
k /2
in .gi
om inique
D m
2k
) do
(C
Tension de seuil de la porte NOR
p
n
© D. Ginhac – LE2I – ESIREM - Université de Bourgogne - Aile Sciences de l’Ingénieur - BP 47870 – 21078 Dijon Cedex
34

35. Un 1er exemple basique : le NOR (6)
7 changer le
Pour obtenir une tension de seuil égale à VDD / 2, 0faut
0 il
rapport des géométries (W/L) des transistors
2
- r
c e.f
a gn
V h V / o si k / 2 = 2 k
in = urg 2 k = 4 k
G -bo
k /2
e @u k = µ C W / L
u c Or
iq nha donc µ (W/L) = 4 µ (W/L)
in .gi
m2 k que
(W/L) = (4*580/230)* (W/L)
o i ni
D m
(W/L) ≈ 10 (W/L)
) do
(C
Tension de seuil de la porte NOR
th
DD
p
n
p
p
n
ox
p
n
p
n
n
p
n
p
© D. Ginhac – LE2I – ESIREM - Université de Bourgogne - Aile Sciences de l’Ingénieur - BP 47870 – 21078 Dijon Cedex
n
35

36. Un 2ème exemple basique : le NAND
7
La porte NAND est composée de 4 transistors : 0
0
2 transistors NMOS en série
2
2 transistors PMOS en parallèle
- r
c e.f
a gn
nh rgo
i u
G -bo
e @u
u c
i q nha
in .gi
om inique
D m
) do
(C
Porte NAND à deux entrées
© D. Ginhac – LE2I – ESIREM - Université de Bourgogne - Aile Sciences de l’Ingénieur - BP 47870 – 21078 Dijon Cedex
36

37. Un 1er exemple basique : le NAND (2)
7
0
Deux cas20
principaux :
- r
1. c = 1 et Vb = 1
a Va gne.f
nh rLes 2 transistors
i u conduisent
go
G -bo
e
Fonctionnement de la porte NAND
u
iq
in .gin
om inique
D m
) do
(C
c@
ha
u
NMOS
Vout = 0
2. Va = 0 et/ou Vb = 0
Un
au
moins
des
2
transistors PMOS conduit
Vout = 1
© D. Ginhac – LE2I – ESIREM - Université de Bourgogne - Aile Sciences de l’Ingénieur - BP 47870 – 21078 Dijon Cedex
37

38. Un 1er exemple basique : le NAND (3)
Tension de seuil de la porte NAND
u
iq
7
0
0
2
- r
c e.f
a gn
nh rgo
i u
G -bo
e
in .gin
om inique
D m
) do
(C
c@
ha
u
2 kp
kn / 2
Vth = VDD / 2 si kn = 4 kp
(W/L)p ≈ 0.63 (W/L)n
© D. Ginhac – LE2I – ESIREM - Université de Bourgogne - Aile Sciences de l’Ingénieur - BP 47870 – 21078 Dijon Cedex
38

39. 7
0
0
2
- r
c e.f
a
A suivre… gn
nh rgo
i u
G -bo
e @u
u c
iq
n .ginha
i
om inique
D m
) do
(C