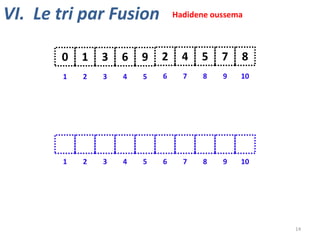
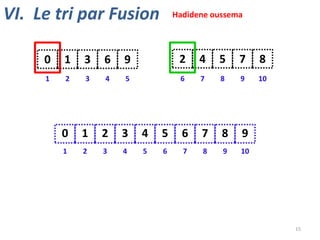
Le document présente plusieurs algorithmes de tri, y compris le tri à bulles, le tri par sélection, le tri par insertion et le tri par shell. Chaque méthode est décrite avec des détails sur son fonctionnement et son efficacité. Le tri par fusion est également mentionné à la fin du document.
![II. Le tri à bulles
Hadidene Oussema
Def Proc Tri_a_bulles (var T : tab ; n : entier )
répéter 23 13 23 23
23 13 23 13
2
5
8
2
8
5
5
8
5
tr vrai
Pour i de 1 à n-1 faire
Si (t[i]>t[i+1]) alors trié
Tableau
proc permut(t[i],t[i+1])
tr faux
Fin si
Fin pour
jusqu’à (tr)
Fin Tri_a_bulles
1](https://image.slidesharecdn.com/animationstris-131202130652-phpapp01/75/Animations-tris-1-2048.jpg)
![III. Le tri par sélection
Hadidene Oussema
Def Proc Tri_selection (var T : tab ; n : entier )
5
Pour 23 1 à n-1 13
i de 2
faire 8
P Fn pos_min(t,i,n)
Si (P≠i) alors
Tableau trié
proc permut(t[i],t[P])
Fin si
Fin pour
Fin Tri_selection
2](https://image.slidesharecdn.com/animationstris-131202130652-phpapp01/85/Animations-tris-2-320.jpg)
![IV. Le tri par insertion
Hadidene Oussema
Def Proc Tri_insertion (var T : tab ; n : entier )
Pour i de 2 à n faire
Si (T[i-1] > T[i]) alors 8
23
2
13
5
E T[i]
Pi
Tableau trié
tant que (T[P-1] > e) et (P > 1) faire
T[P] t[p-1]
P P-1
Fin tant que
T[P] E
Fin si
Fin pour
Fin Tri_insertion
3](https://image.slidesharecdn.com/animationstris-131202130652-phpapp01/85/Animations-tris-3-320.jpg)
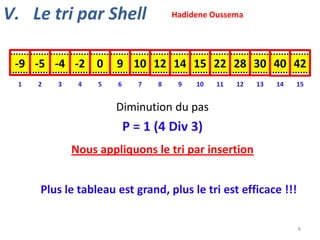
![Def Proc Tri_Shell (var T : tab ; n : entier )
Hadidene Oussema
p0
Tant que (p<n) faire
Clause 0
p (3 * p) + 1
Fin tant que
Tant que (p ≠ 1) faire
p p div 3
Pour i de p+1 à n faire
e T[i]
ji
Tant que (j>p) et (T[j-p]>e) faire
Clause 1
Clause 2
T[j] T[j-p]
Clause 3
j j-P
Fin tant que
T[j] e
Fin pour
Fin tant que
Fin Tri_Shell
9
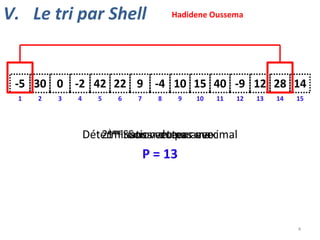
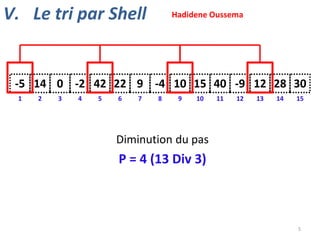
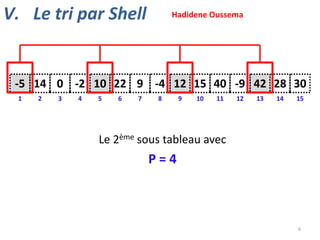
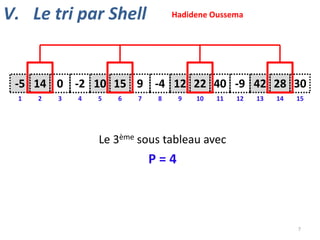
V. Le tri par Shell](https://image.slidesharecdn.com/animationstris-131202130652-phpapp01/85/Animations-tris-9-320.jpg)
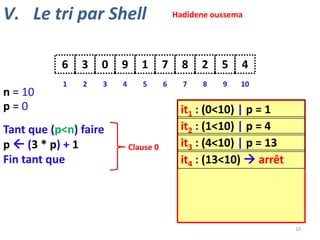
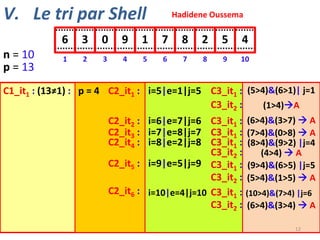
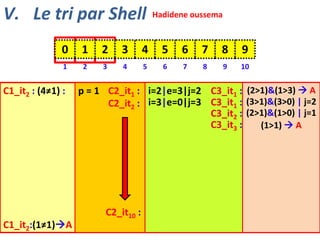
![V. Le tri par Shell
Hadidene Oussema
6
n = 10
p = 13
3
0
9
1
7
8
2
5
4
1
2
3
4
5
6
7
8
9
10
Tant que (p ≠ 1) faire
p p div 3
Pour i de p+1 à n faire
e T[i]
ji
Tant que (j>p) et (T[j-p]>e)
faire
Clause 2
Clause 3
T[j] T[j-p]
j j-P
Fin tant que
T[j] e
Fin pour
Fin tant que
Clause 1
11](https://image.slidesharecdn.com/animationstris-131202130652-phpapp01/85/Animations-tris-11-320.jpg)