Le document présente une introduction aux processus stochastiques, en se concentrant sur les chaînes de Markov et les processus de Poisson. Il inclut des définitions, des classifications des états, des théorèmes limites, ainsi que des applications comme les files d'attente. Des exercices et des exemples illustrent l'utilisation de ces concepts statistiques dans divers contextes pratiques.


![Introduction
On peut d´ finir un processus stochastique comme etant une famille {Xt }t∈T de variables al´ atoires
e ´ e
ind´ x´ es par le temps t. Les mots processus et stochastique signifient respectivement fonction et al´ atoire.
e e e
Alors qu’une variable al´ atoire X associe a chaque ω ∈ Ω une r´ alisation X(ω), un processus stochastique
e ` e
{Xt }t∈T associe a chaque ω une fonction (ou trajectoire) {Xt (ω)}t∈T :
`
T → E
,
t → Xt (ω)
o` E est l’espace d’arriv´ e des variables al´ atoires Xt . Passer des variables al´ atoires aux processus sto-
u e e e
chastiques revient a passer en analyse des points aux fonctions. A
` ` titre d’exemple, la trajectoire d’une
mouche en fonction du temps peut etre mod´ lis´ e par un processus stochastique a valeurs dans E = R3 .
ˆ e e `
Lorsque l’ensemble des temps T est au plus d´ nombrable (par exemple T = N), on parle de processus
e
stochastiques a temps discret. Lorsqu’il est continu (i.e. T = [0; t0 ] ou T = R+ ), on parle de processus
`
stochastiques a temps continu.
`
Dans tout ce cours, on abr` ge les expressions “variable al´ atoire” en v.a. et “ind´ pendantes et identique-
e e e
ment distribu´ es” en i.i.d.
e
Les situations r´ elles pouvant etre mod´ lis´ es par des processus stochastiques sont nombreuses. En voici
e ˆ e e
quelques exemples :
E XEMPLES :
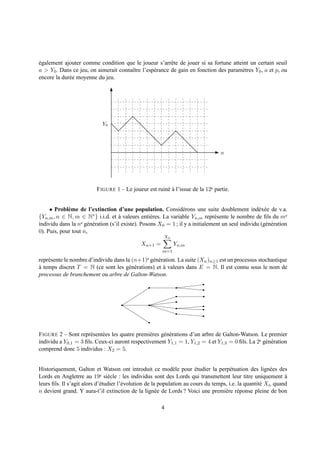
• Probl` me de la ruine du joueur. Consid´ rons une suite de v.a. (Yn )n≥1 i.i.d. dont la loi commune
e e
est d´ finie par
e
IP(Y1 = 1) = p et IP(Y1 = −1) = 1 − p
et une quantit´ initiale (d´ terministe ou al´ atoire) Y0 ∈ Z ind´ pendante des v.a. Yn . On d´ finit la marche
e e e e e
al´ atoire simple par
e
Xn+1 = Xn + Yn+1
= Y0 + Y1 + . . . + Yn + Yn+1 ,
pour tout n ∈ N. La suite (Xn )n≥1 est un processus stochastique a temps discret T = N (ce sont les
`
instants n = 0, 1, 2 . . .) et a valeurs dans E = Z. La suite (Xn )n≥1 repr´ sente l’´ volution de la fortune
` e e
d’un joueur (jouant a pile ou face, a la roulette...) gagnant un montant fixe (ici 1 euro) avec probabilit´ p et
` ` e
perdant le mˆ me montant avec probabilit´ 1 − p. Les parties, dont les r´ sultats sont les Yn , sont suppos´ es
e e e e
ind´ pendantes. La fortune du joueur a l’issue de la n
e ` e partie est X . La quantit´ Y repr´ sente la fortune
n e 0 e
initiale du joueur.
Le joueur est ruin´ (et donc arrˆ te de jouer) d` s que la suite (Xn )n≥1 touche l’axe des abscisses. On peut
e e e
3](https://image.slidesharecdn.com/coursprostoc-121002170116-phpapp02/85/Cours-stochastic-processes-3-320.jpg)
![sens : si le nombre moyen IE[Y0,1 ] de fils de chaque individu est elev´ , la population devrait rapidement
´ e
ı ` l’inverse, si IE[Y0,1 ] est proche de 0, la population devrait s’´ teindre.
croˆtre. A e
• S´ ries temporelles ou chronologiques. Les s´ ries temporelles peuvent etre mod´ lis´ es par des
e e ˆ e e
processus stochastiques. Elles peuvent illustrer le nombre de morts suite a des accidents de la route dans
`
un pays donn´ durant un intervalle de temps, le nombre de passagers dans les transports a´ riens ou encore
e e
les valeurs de clˆ tures journali` res du CAC40.
o e
4000
3500
EuStockMarkets[, 3]
3000
2500
2000
1500
1992 1993 1994 1995 1996 1997 1998
Time
F IGURE 3 – Valeurs de clˆ tures journali` res du CAC40 de 1991 a 1998.
o e `
Un des objectifs principaux de l’´ tude d’une s´ rie temporelle est la pr´ vision des r´ alisations futures, tr` s
e e e e e
souvent pour des raisons economiques (pr´ voir l’´ volution de la demande d’un produit pour ajuster au
´ e e
mieux les moyens de production, pr´ voir l’´ volution d’un march´ financier...).
e e e
Les s´ ries temporelles feront l’objet de tout un cours en GIS5.
e
• Files d’attente. La salle de r´ servation d’une grande gare SNCF donne une bonne repr´ sentation
e e
d’une file d’attente (queue en anglais). Elle comprend un certain nombre de guichets et des clients qui sont
soit en train d’ˆ tre servis, soit en attente qu’un guichet se lib` re. Le nombre total de ces clients pr´ sents
e e e
dans la salle de r´ servation au temps t est not´ Nt . Le hasard intervient dans les arriv´ es des clients ainsi
e e e
que dans la dur´ e des services. La suite (Nt )t≥0 est un processus stochastique a temps continu et a valeurs
e ` `
dans E = N. L’objectif est d’´ tudier l’´ volution de Nt au cours du temps afin d’optimiser le nombre de
e e
guichets n´ cessaires pour satisfaire en un temps raisonnable les clients.
e
On peut egalement mod´ liser par une file d’attente un syst` me informatique dans lequel les nouvelles
´ e e
tˆ ches se mettent en attente avant d’ˆ tre trait´ es, ou encore un poste de travail dans une usine.
a e e
Les files d’attentes seront etudi´ es en d´ tails dans ce cours.
´ e e
En GIS3 ou en GIS4, vous avez d´ j` vu des processus stochastiques : n’importe quelle suite de v.a. i.i.d.
ea
en est un exemple ! L’ind´ pendance entre les variables facilite les calculs et permet d’obtenir sans trop
e
d’efforts des th´ or` mes limites int´ ressants (Loi des Grands Nombres, Th´ or` me Central Limite...). Mal-
e e e e e
heureusement, l’ind´ pendance n’est pas un ph´ nom` ne courant dans la nature. Int´ grer de la d´ pendance
e e e e e
entre les variables permet de mod´ liser plus fid` lement la r´ alit´ . Il y a n´ anmoins un coˆ t a payer ; les
e e e e e u `
calculs sont plus durs et les th´ or` mes plus chers.
e e
Les processus stochastiques que nous etudierons dans ce cours prendront en compte une certaine d´ pen-
´ e
dance entre les variables ; une d´ pendance de type markovienne (ou de Markov). Cela signifie que l’´ volu-
e e
tion future du processus ne d´ pend de son pass´ que par l’interm´ diaire du pr´ sent. Par exemple pour
e e e e
d´ cider au mieux du 21e coup a jouer dans une partie d’´ checs, il suffit de connaˆtre la configuration du jeu
e ` e ı
a l’issue du 20e coup, le d´ tail des 19 premiers coups n’ayant alors aucune importance.
` e
5](https://image.slidesharecdn.com/coursprostoc-121002170116-phpapp02/85/Cours-stochastic-processes-5-320.jpg)










![Lemme 1.2.5 Pour tout entier n et tous etats i et j,
´
IP(Ni ≥ n + 1 | X0 = j) = IP(Ti < +∞ | X0 = j) IP(Ni ≥ n | X0 = i) .
Les etats transients sont ceux dans lesquels on ne passe qu’un nombre fini de fois. Par opposition, on
´
revient une infinit´ de fois dans un etat r´ current.
e ´ e
Proposition 1.2.6 Les conditions suivantes sont equivalentes :
´
(1) l’´ tat i est r´ current : IP(Ti < +∞|X0 = i) = 1 ;
e e
(2) conditionnellement a X0 = i, la chaˆne de markov (Xn )n∈N revient presque sˆ rement une infinit´
` ı u e
de fois en i :
IP(Ni = +∞ | X0 = i) = 1 ;
(n)
(3) la s´ rie
e pi,i diverge.
Proposition 1.2.7 Les conditions suivantes sont equivalentes :
´
(4) l’´ tat i est transient : IP(Ti < +∞|X0 = i) < 1 ;
e
(5) conditionnellement a X0 = i, la v.a. Ni est presque sˆ rement finie et suit la loi g´ om´ trique de
` u e e
param` tre αi = IP(Ti < +∞|X0 = i) :
e
∀n ∈ N, IP(Ni = n | X0 = i) = αn (1 − αi ) ;
i
(n)
(6) conditionnellement a X0 = i, la v.a. Ni est int´ grable : IE[Ni |X0 = i] =
` e pi,i < +∞.
(n)
Remarquons que l’identit´ entre l’esp´ rance conditionnelle IE[Ni |X0 = i] et la s´ rie
e e e pi,i est valable
quelle que soit la nature de cette derni` re, en la consid´ rant comme un el´ ment de [0; +∞]. Elle repose sur
e e ´e
le th´ or` me de Fubini.
e e
IE[Ni | X0 = i] = IE 1 Xn =i
1 X0 = i
n≥1
= IE[1 Xn =i | X0 = i]
1
n≥1
= IP(Xn = i | X0 = i)
n≥1
(n)
= pi,i .
n≥1
Les deux propositions ci-dessus se d´ montrent simultan´ ment.
e e
D´ monstration Prouvons (1) ⇒ (2). En combinant, IP(Ti < +∞|X0 = i) = 1 et le Lemme 1.2.5, il
e
vient :
IP(Ni ≥ n + 1 | X0 = i) = IP(Ni ≥ n | X0 = i) = . . . = IP(Ni ≥ 1 | X0 = i),
16](https://image.slidesharecdn.com/coursprostoc-121002170116-phpapp02/85/Cours-stochastic-processes-16-320.jpg)
![en it´ rant. Par ailleurs, {Ni ≥ 1} = {Ti < +∞}. On en d´ duit que pour tout n, IP(Ni ≥ n|X0 = i) = 1.
e e
Il ne reste plus qu’` faire tendre n vers l’infini pour obtenir (2) :
a
IP(Ni = +∞ | X0 = i) = IP {Ni ≥ n} X0 = i
n≥1
= lim IP(Ni ≥ n | X0 = i)
n→+∞
= 1.
L’implication (2) ⇒ (3) repose sur :
(n)
pi,i = IE[Ni | X0 = i] ≥ (+∞) IP(Ni = +∞ | X0 = i) = +∞ .
n≥1
Supposons (4) : αi = IP(Ti < +∞|X0 = i) < 1. Le Lemme 1.2.5 donne :
IP(Ni ≥ n + 1 | X0 = i) = αi IP(Ni ≥ n | X0 = i) = . . . = αn IP(Ni ≥ 1 | X0 = i) .
i
Ainsi,
IP(Ni ≥ n + 1 | X0 = i) = αn IP(Ti < +∞ | X0 = i) = αn+1 .
i i
On en d´ duit d’une part que Ni est presque sˆ rement finie
e u
IP(Ni = +∞ | X0 = i) = lim IP(Ni ≥ n | X0 = i) = 0
n→+∞
(car αi < 1) et d’autre part que sa loi est g´ om´ trique de param` tre αi . Ce qui prouve (5).
e e e
IP(Ni = n | X0 = i) = IP(Ni ≥ n | X0 = i) − IP(Ni ≥ n + 1 | X0 = i) = αn (1 − αi ) .
i
L’implication (5) ⇒ (6) est imm´ diate :
e
αi
IE[Ni | X0 = i] = IP(Ni ≥ n | X0 = i) = < +∞ .
1 − αi
n≥1
Enfin, (3) ⇒ (1) et (6) ⇒ (4) sont respectivement les contrapos´ es de (4) ⇒ (6) et (1) ⇒ (3). Les
e
boucles sont boucl´ es !
e
La r´ currence et la transience sont des propri´ t´ s de classe irr´ ductible :
e ee e
Proposition 1.2.8 Si les etats i et j communiquent alors ils sont tous deux r´ currents ou tous deux tran-
´ e
sients.
Ainsi, tous les etats appartenant a la mˆ me classe irr´ ductible qu’un etat transient (resp. r´ current), le seront
´ ` e e ´ e
egalement. La classe sera alors qualifi´ e de transiente (resp. r´ currente).
´ e e
(k) (l)
D´ monstration Si les etats i et j communiquent, il existe deux instants k et l tels que pi,j > 0 et pj,i > 0.
e ´
Soit m ≥ k + l. Partant de i, une facon d’y revenir en m pas consiste a d’abord aller en j en l pas, puis d’y
¸ `
revenir en m − k − l pas pour enfin aller en i en k pas :
(m) (l) (m−k−l) (k)
pi,i ≥ pi,j pj,j pj,i .
17](https://image.slidesharecdn.com/coursprostoc-121002170116-phpapp02/85/Cours-stochastic-processes-17-320.jpg)
![De la mˆ me mani` re,
e e
(m) (k) (m−k−l) (l)
pj,j ≥ pj,i pi,i pi,j .
(m) (m)
Les deux s´ ries m pi,i et
e m pj,j sont donc de mˆ me nature. Les Propositions 1.2.6 et 1.2.7 permettent
e
alors de conclure.
Proposition 1.2.9 La probabilit´ de sortir d’une classe irr´ ductible r´ currente est nulle. Plus pr´ cis´ ment,
e e e e e
si i est un etat r´ current et C(i) sa classe alors
´ e
(n)
∀j ∈ C(i), ∀n ∈ N, IP(Xn = j | X0 = i) = pi,j = 0 .
/
(n)
D´ monstration Soit j ∈ C(i) et supposons par l’absurde qu’il existe un entier n tel que pi,j > 0. Il
e /
(m) (m)
existe alors un entier m tel que pj,i > 0. Dans le cas contraire, i.e. ∀m pj,i = 0, l’´ tat i ne pourrait etre
e ˆ
r´ current puisqu’il existerait une probabilit´ non nulle de quitter i et de ne jamais y revenir. D` s lors, les
e e e
etats i et j communiquent, ce qui contredit j ∈ C(i).
´ /
Proposition 1.2.10 Toute chaˆne de Markov homog` ne sur un espace d’´ tats fini a au moins un etat
ı e e ´
r´ current. En particulier, toute chaˆne irr´ ductible sur un espace d’´ tats fini est r´ currente.
e ı e e e
D´ monstration Montrons que, etant donn´ un etat i transient, le nombre moyen de passage par l’´ tat i en
e ´ e ´ e
partant d’un etat j, i.e. IE[Ni |X0 = j], est finie. Cette affirmation repose sur le Lemme 1.2.5, la Proposition
´
1.2.7, le fait que IE[Z] = n≥1 IP(Z ≥ n) pour une v.a. positive Z et le calcul suivant :
IE[Ni | X0 = j] = IP(Ni ≥ n + 1 | X0 = j)
n∈N
= IP(Ti < +∞ | X0 = j) IP(Ni ≥ n | X0 = i)
n∈N
= IP(Ti < +∞ | X0 = j) IP(Ni ≥ n | X0 = i)
n∈N
= IP(Ti < +∞ | X0 = j)(1 + IE[Ni | X0 = i])
< +∞ .
Donc, presque sˆ rement, chaque etat de E est visit´ un nombre fini de fois. C’est impossible : E etant fini,
u ´ e ´
notre chaˆne fr´ quente au moins l’un des etats de E une infinit´ de fois.
ı e ´ e
1.2.3 P´ riodicit´
e e
D´ finition 1.2.11 La p´ riode d’un etat i est l’entier d(i) d´ fini par
e e ´ e
(n)
d(i) = PGCD{n ≥ 1, pi,i > 0} .
Lorsque d(i) = 1, l’´ tat i est qualifi´ de ap´ riodique.
e e e
18](https://image.slidesharecdn.com/coursprostoc-121002170116-phpapp02/85/Cours-stochastic-processes-18-320.jpg)


![Consid´ rons enfin une chaˆne de Markov (Xn )n∈N a espace d’´ tats E fini et de matrice de transition P .
e ı ` e
Supposons de plus que la suite (Xn )n∈N converge en loi vers une mesure de probabilit´ sur E, not´ e ν :
e e
pour tout j ∈ E, lim µn (j) = ν(j) .
n→+∞
Puisque E est fini, l’application lin´ aire t P est continue donc t P t µn converge (coordonn´ e par coor-
e e
donn´ e) vers
e t P t ν, lorsque n tend vers l’infini. D’autre part, t P t µ = t µ
n n+1 converge egalement (coor-
´
donn´ e par coordonn´ e) vers la loi t ν. Celle-ci v´ rifie donc t P t ν = t ν, ou encore ν = νP . En conclusion,
e e e
si la suite (Xn )n∈N converge en loi vers une mesure de probabilit´ alors cette loi limite est n´ cessairement
e e
une mesure stationnaire pour la chaˆne de Markov correspondante.
ı
1.3.2 Lorsque l’espace d’´ tats E est fini
e
Consid´ rons une chaˆne de Markov homog` ne (Xn )n∈N a espace d’´ tats fini E et de matrice de transition
e ı e ` e
P . Comme la somme des coefficients sur chaque ligne de P vaut 1, tout vecteur a coordonn´ es constantes
` e
est vecteur propre de P associ´ a la valeur propre 1. Une matrice carr´ e et sa transpos´ e ayant les mˆ mes
e` e e e
valeurs propres, 1 est donc egalement valeur propre de t P . Notons E1 l’espace propre associ´ a la valeur
´ e`
propre 1 pour t P :
E1 = {v ∈ RCard(E) , tP v = v} .
On vient de montrer que dim E1 ≥ 1. D` s lors, tout vecteur (colonne) t π appartenant a E1 et dont la
e `
somme des coordonn´ es vaut 1, produit un vecteur ligne π, loi de probabilit´ sur E et v´ rifiant π = πP .
e e e
C’est donc une mesure stationnaire pour la chaˆne de Markov de matrice de transition P . En conclusion,
ı
l’existence d’au moins une mesure stationnaire est automatique lorsque l’espace d’´ tats E est fini.
e
Lorsque la chaˆne est irr´ ductible (dans ce cas, tous les etats sont r´ currents), l’espace propre E1 est de
ı e ´ e
dimension 1, ce qui implique l’unicit´ de la mesure stationnaire.
e
Proposition 1.3.2 Consid´ rons une chaˆne de Markov homog` ne a espace d’´ tats fini E et de matrice de
e ı e ` e
transition P . Elle admet au moins une mesure stationnaire. Si la chaˆne est irr´ ductible alors il y a unicit´
ı e e
de la mesure stationnaire (notons-la π). Dans ce cas, elle charge tous les etats
´
π(i) > 0, pour tout i ∈ E
et le temps moyen de retour en i est egal a l’inverse de π(i) :
´ `
1
IE[T (i) | X0 = i] = , pour tout i ∈ E.
π(i)
Cependant, l’existence et l’unicit´ de la mesure stationnaire π n’assure pas la convergence en loi de la suite
e
(Xn )n∈N vers π. Cette convergence repose en fait sur l’ap´ riodicit´ de la chaˆne.
e e ı
Le r´ sultat suivant est non trivial. Il ne sera pas d´ montr´ .
e e e
Th´ or` me 1.3.3 Consid´ rons une chaˆne de Markov homog` ne (Xn )n∈N a espace d’´ tats fini E et de
e e e ı e ` e
matrice de transition P . Supposons de plus que la chaˆne est irr´ ductible et ap´ riodique. Notons π sa
ı e e
mesure stationnaire.
(1) La matrice P n converge quand n tend vers l’infini vers une matrice dont toutes les lignes sont
egales a π.
´ `
21](https://image.slidesharecdn.com/coursprostoc-121002170116-phpapp02/85/Cours-stochastic-processes-21-320.jpg)
![(2) Quelle que soit la loi de X0 , la suite (Xn )n∈N convergence en loi quand n tend vers l’infini vers
π : pour tout etat i, IP(Xn = i) → π(i).
´
Les points (1) et (2) s’interpr` tent par de l’ind´ pendance asymptotique : en deux instants eloign´ s l’un de
e e ´ e
l’autre, la chaˆne se comporte de mani` re presque ind´ pendante. En effet, les quantit´ s IP(Xn = j|X0 = i)
ı e e e
et IP(Xn = j) tendent toutes les deux vers la mˆ me limite π(j). Elles sont donc proches asymptotiquement,
e
ce qui donne
IP(Xn = j , X0 = i) ≃ IP(Xn = j) IP(X0 = i) .
En utilisant l’invariance par translation dans le temps, la relation ci-dessus se g´ n´ ralise en
e e
IP(Xn+m = j , Xm = i) ≃ IP(Xn+m = j) IP(Xm = i) .
Consid´ rons une nouvelle fois l’exemple du bit informatique dont la matrice de transition est donn´ e par
e e
p 1−p
P = .
1−p p
La chaˆne de Markov correspondante est irr´ ductible si et seulement si p < 1. Dans ce cas, l’unique
ı e
mesure stationnaire est le vecteur ligne π = (1/2, 1/2). Si de plus p > 0, alors la chaˆne est ap´ riodique.
ı e
Le th´ or` me limite s’applique :
e e
1
∀i ∈ {0, 1}, lim IP(Xn = i) = .
n→+∞ 2
Autrement dit, quelque soit le bit initial X0 et quelle que soit la valeur de 0 < p < 1, au bout d’un certain
temps, le bit sortant suit une loi uniforme sur {0, 1}.
Lorque p = 0, la matrice de transition devient
0 1
P = .
1 0
La chaˆne est alors 2−p´ riodique. Puisque P 2 est egale a la matrice identit´ , il en va de mˆ me pour toutes
ı e ´ ` e e
les puissances paires de P , tandis que les puissances impaires sont egales a P . Par cons´ quent, le coefficient
´ ` e
(n) (n)
p0,0 prend alternativement les valeurs 0 et 1 : la suite (p0,0 )n∈N ne peut converger.
(n)
Terminons par une comparaison. La Th´ or` me 1.3.3 stipule que, sous les bonnes hypoth` ses, pi,j tend
e e e
vers une limite strictement positive (Proposition 1.3.2). Ceci concerne le cas o` j est r´ current. Lorsque
u e
(n)
j est transient, pi,j tend vers 0. En effet, l’esp´ rance conditionnelle IE[Nj |X0 = i] est finie (voir la
e
d´ monstration de la Proposition 1.2.10). Par cons´ quent, la s´ rie
e e e
(n)
pi,j = IP(Xn = j | X0 = i)
n≥1 n≥1
= IE[1 Xn =j | X0 = i]
1
n≥1
= IE[Nj | X0 = i]
(n)
est convergente. Son terme g´ n´ ral, i.e. pi,j , tend donc vers 0 quand n tend vers l’infini.
e e
22](https://image.slidesharecdn.com/coursprostoc-121002170116-phpapp02/85/Cours-stochastic-processes-22-320.jpg)
![1.3.3 Lorsque l’espace d’´ tats E est infini
e
L’´ tude th´ orique de la convergence en loi d’une chaˆne de Markov devient plus d´ licate lorsque l’espace
e e ı e
e `
d’´ tats E est infini. A plus forte raison que dans la partie pr´ c´ dente, les r´ sultats qui suivent ne seront pas
e e e
d´ montr´ s.
e e
Consid´ rons une chaˆne de Markov homog` ne (Xn )n∈N irr´ ductible et r´ currente, a espace d’´ tats infini E
e ı e e e ` e
E , a coordonn´ es
et de matrice de transition P . On peut alors montrer qu’il existe un vecteur colonne v ∈ R ` e
strictement positives, v´ rifiant t P v = v. Si la somme des coordonn´ es de v est finie
e e
M := v(j) < +∞ , (1.2)
j∈E
alors il suffit de renormaliser le vecteur v par sa masse totale M pour obtenir une mesure stationnaire (qui
sera unique). Cependant la condition (1.2) n’est pas toujours v´ rifi´ e. Une hypoth` se suppl´ mentaire sur
e e e e
la chaˆne doit etre faite pour assurer l’existence (et l’unicit´ ) d’une mesure stationnaire.
ı ˆ e
D´ finition 1.3.4 Consid´ rons une chaˆne de Markov homog` ne irr´ ductible et r´ currente a espace d’´ tats
e e ı e e e ` e
infini E. Soit i ∈ E. Le temps de retour T (i) a i est fini presque sˆ rement (car i est r´ current). Si, de plus,
` u e
IE[T (i)|X0 = i] < +∞ ,
l’´ tat i est qualifi´ de r´ current positif. Dans le cas contraire, i est qualifi´ de r´ current nul.
e e e e e
ˆ
Etre r´ current nul signifie que l’on revient presque sˆ rement en temps fini en cet etat mais que le temps de
e u ´
retour est plutˆ t long. Si long que son esp´ rance est infinie.
o e
La marche al´ atoire simple et sym´ trique (i.e. avec p = 1/2) sur Z est un exemple de chaˆne de Markov
e e ı
pour laquelle tous les etats sont r´ currents nuls.
´ e
Le th´ or` me suivant etablit que la r´ currence positive est une propri´ t´ de classe (mˆ me chose pour la
e e ´ e ee e
r´ currence nulle) : c’est une condition n´ cessaire et suffisante pour l’existence d’une mesure stationnaire.
e e
Si c’est le cas, il y a unicit´ de la mesure stationnaire.
e
Th´ or` me 1.3.5 Soit (Xn )n∈N une chaˆne de Markov homog` ne irr´ ductible, a espace d’´ tats infini E.
e e ı e e ` e
Sont equivalentes :
´
(i) tous les etats sont r´ currents positifs ;
´ e
(ii) il existe au moins un etat r´ current positif ;
´ e
(iii) la chaˆne (Xn )n∈N admet (au moins) une mesure stationnaire.
ı
Lorsque ces conditions sont v´ rifi´ es, il y a unicit´ de la mesure statonnaire. Notons-la π. Elle est d´ finie
e e e e
par :
1
∀i ∈ E, = IE[T (i) | X0 = i] .
π(i)
Si de plus, la chaˆne (Xn )n∈N est ap´ riodique alors :
ı e
(1) la matrice P n converge quand n tend vers l’infini vers une matrice dont toutes les lignes sont egales
´
aπ;
`
(2) quelle que soit la loi de X0 , la suite (Xn )n∈N convergence en loi quand n tend vers l’infini vers π :
pour tout etat i, IP(Xn = i) → π(i).
´
23](https://image.slidesharecdn.com/coursprostoc-121002170116-phpapp02/85/Cours-stochastic-processes-23-320.jpg)




![Proposition 2.1.3 La somme de n v.a. ind´ pendantes de loi exponentielle de param` tre λ suit une loi,
e e
appal´ e loi Gamma de param` tres n et λ et not´ e Γ(n, λ), dont la densit´ est donn´ e par :
e e e e e
λn xn−1 −λx
f (x) = e 1 x≥0 .
1
(n − 1)!
2.1.2 Pr´ sentation du processus de Poisson
e
D´ finition 2.1.4 Soit (Xn )n≥1 une suite de v.a. ind´ pendantes et de mˆ me loi, exponentielle de param` tre
e e e e
λ. Posons S0 = 0 et pour tout entier n ≥ 1, Sn = X1 + . . . + Xn . Pour tout r´ el t ≥ 0, d´ finissons la v.a.
e e
Nt , a valeurs enti` res, par :
` e
Nt = n ⇔ Sn ≤ t < Sn+1 .
Le processus stochastique {Nt }t≥0 est appel´ processus de Poisson d’intensit´ λ.
e e
Le processus de Poisson est un mod` le de comptage d’´ v´ nements al´ atoires isol´ s dans le temps, comme
e e e e e
des “tops” d’horloge s´ par´ s par des dur´ es al´ atoires. Dans ce mod` le :
e e e e e
• Xn est la dur´ e s´ parant le (n − 1)e top du ne ;
e e
• Sn est la date a laquelle survient le ne top. D’apr` s la Proposition 2.1.3, la v.a. Sn suit la loi Gamma
` e
de param` tres n et λ ;
e
• Nt est le nombre de tops compt´ s entre l’instant 0 et l’instant t :
e
Nt = 1 Sn ≤t .
1
n≥1
Nt
5
4
3
2
1
0 t
S1 S2 S3 S4 S5
X1 X2 X4 X5 X6
F IGURE 2.1 – Ci-dessus est repr´ sent´ e la trajectoire simul´ e d’un processus de Poisson d’intensit´
e e e e
λ = 1/2 sur l’intervalle [0; 10]. On constate que d’assez longues p´ riodes sans aucun top alternent
e
avec des rafales de tops rapproch´ s : il n’y a pas d’autre explication a la fameuse “loi des s´ ries” ch` re
e ` e e
aux journalistes. Si des ev´ nements (comme par exemple des accidents d’avion) arrivent rarement, de
´ e
mani` re impr´ visible et ind´ pendante, on ne peut pas imaginer qu’ils surviennent a des intervalles de
e e e `
temps r´ guliers. Il faut plutˆ t s’attendre a les voir survenir parfois de mani` re rapproch´ e, par “s´ ries”.
e o ` e e e
Soit 0 ≤ s ≤ t des r´ els. La diff´ rence Nt − Ns est appel´ e accroissement. Elle est egale au nombre de
e e e ´
tops entre les instants s et t.
28](https://image.slidesharecdn.com/coursprostoc-121002170116-phpapp02/85/Cours-stochastic-processes-28-320.jpg)
![Th´ or` me 2.1.5 Consid´ rons un processus de Poisson {Nt }t≥0 d’intensit´ λ. Il v´ rifie les propri´ t´ s sui-
e e e e e ee
vantes :
(P1) {Nt }t≥0 est un processus de comptage ; il est a valeurs enti` res, v´ rifie N0 = 0 p.s. et pour tous
` e e
r´ els 0 ≤ s ≤ t, Ns ≤ Nt .
e
(P2) {Nt }t≥0 est un processus a accroissements ind´ pendants ; pour tout entier k et pour toute suite
` e
d’instants 0 < t1 < t2 < . . . < tk , les accroissements Nt2 − Nt1 , . . . , Ntk − Ntk−1 sont des v.a.
ind´ pendantes.
e
(P3) Les accroissements du processus {Nt }t≥0 sont poissonniens ; pour tous r´ els 0 ≤ s < t, la v.a.
e
Nt − Ns suit la loi de Poisson de param` tre λ(t − s) ;
e
(P4) {Nt }t≥0 est un processus homog` ne ou a accroissements stationnaires ; pour tous instants 0 ≤
e `
t1 < t2 et s ≥ 0, la v.a. Nt2 +s − Nt1 +s suit la mˆ me loi que Nt2 − Nt1 . ;
e
(P5) {Nt }t≥0 est un processus d’´ v´ nements rares ; IP(Nt+h − Nt ≥ 2) = o(h).
e e
Nous ne d´ montrerons pas ces r´ sultats et nous nous contenterons de quelques commentaires.
e e
Par d´ finition, un processus de Poisson est une fonction du hasard et du temps, a valeurs enti` res, qui est
e ` e
croissante dans le temps. De plus,
IP(N0 = 0) = 1 − IP(N0 = 0) ≥ 1 − IP(X1 = 0) = 1 .
C’est donc un processus de comptage.
La d´ monstration de la propri´ t´ (P2) est li´ e a l’absence de m´ moire de la loi exponentielle (Proposi-
e ee e ` e
tion 2.1.1). Elle signifie que les nombres de tops compt´ s dans des intervalles de temps disjoints sont
e
ind´ pendants. En particulier, les nombres de tops dans les intervalles [0; t] et ]t; t + s] sont ind´ pendants.
e e
C’est la propri´ t´ (P3) qui est a l’origine du nom du processus de Poisson. La probabilit´ pour qu’il y ait
ee ` e
n tops entre les instants s et t (avec s < t) est donn´ e par :
e
(λ(t − s))n −λ(t−s)
IP(Nt − Ns = n) = e .
n!
En particulier,
IE[Nt − Ns ] = λ(t − s) .
Le nombre moyen de tops compt´ s dans un intervalle de temps est donc proportionnel a la longueur de cet
e `
intervalle et le coefficient de proportionnalit´ n’est autre que λ. Par cons´ quent, le nombre moyen de tops
e e
par unit´ de temps est egal a λ, fort justement appel´ intensit´ du processus. La dur´ e moyenne entre deux
e ´ ` e e e
tops etant de 1/λ (ce sont des exponentielles de param` tre λ), il est normal de compter λ tops par unit´ de
´ e e
temps en moyenne.
Avec la condition N0 = 0 p.s., le nombre de tops jusqu’` l’instant t est distribu´ selon la loi de Poisson de
a e
param` tre λt :
e
Nt ∼ P(λt) .
La propri´ t´ (P4) est une cons´ quence imm´ diate de (P3) : les v.a. Nt2 +s − Nt1 +s et Nt2 − Nt1 suivent
ee e e
toutes les deux la loi de Poisson de param` tre λ((t2 + s) − (t1 + s)) = λ(t2 − t1 ).
e
La propri´ t´ (P5) signifie que la probabilit´ de compter plus d’un top dans un petit intervalle de temps est
ee e
n´ gligeable. Elle d´ coule egalement de la propri´ t´ (P3). Rappelons tout d’abord que f (h) = o(h) signifie
e e ´ ee
que le rapport f (h)/h tend vers 0 quand h tend vers 0. La notation o(h) a un caract` re infinit´ simal (et en
e e
aucun cas global). Puisque
IP(Nt+h − Nt = 0) = e−λh = 1 − λh + o(h)
29](https://image.slidesharecdn.com/coursprostoc-121002170116-phpapp02/85/Cours-stochastic-processes-29-320.jpg)
![et
IP(Nt+h − Nt = 1) = (λh)e−λh = λh + o(h) ,
on en d´ duit que
e
IP(Nt+h − Nt ≥ 2) = 1 − IP(Nt+h − Nt = 0) − IP(Nt+h − Nt = 1) = o(h) .
R´ ciproquement, un processus stochastique v´ rifiant les propri´ t´ s (P1), (P2), (P4) et (P5) est un processus
e e ee
de Poisson. Il v´ rifie donc egalement la propri´ t´ (P3).
e ´ ee
Les instants de saut d’un processus de Poisson v´ rifient la propri´ t´ int´ ressante suivante : lorsqu’on sait
e ee e
qu’exactement n sauts ont eu lieu dans l’intervalle [0; t], la distribution de ces sauts dans [0; t] est celle de
n points tir´ s uniform´ ment au hasard dans cet intervalle.
e e
Proposition 2.1.6 Conditionnellement en {Nt = n}, la loi du vecteur (S1 , . . . , Sn ) des n premiers instants
de saut d’un processus de Poisson est la mˆ me que celle du r´ ordonnement par ordre croissant d’une suite
e e
de n v.a. ind´ pendantes et de mˆ me loi uniforme sur [0; t]. Autrement dit, si on tire des v.a. U1 , . . . , Un
e e
ind´ pendantes de loi uniforme sur [0; t] et si on les r´ ordonne en posant
e e
U(1) = min Ui < U(2) < . . . < U(n) = max Ui ,
1≤i≤n 1≤i≤n
alors la loi conditionnelle de (S1 , . . . , Sn ) sachant Nt = n est la mˆ me que celle de (U(1) , . . . , U(n) ).
e
e ´
D´ monstration Nous d´ montrons uniquement le cas n = 1. Etant donn´ s des r´ els 0 ≤ u ≤ t, on peut
e e e
ecrire :
´
IP(S1 ≤ u, Nt = 1) = IP(Nu = 1, Nt = 1)
= IP(Nu = 1, Nt − Nu = 0)
= IP(Nu = 1) IP(Nt − Nu = 0) ,
du fait de l’ind´ pendance des accroissements (P2). Par la propri´ t´ (P3), les v.a. Nu et Nt − Nu suivent
e ee
des lois de Poisson de param` tres respectifs λu et λ(t − u) (o` λ est l’intensit´ du processus). Ainsi,
e u e
IP(S1 ≤ u, Nt = 1) = IP(Nu = 1) IP(Nt − Nu = 0)
= λue−λu × e−λ(t−u)
= λue−λt .
Finalement,
u
IP(S1 ≤ u | Nt = 1) = .
t
Autrement dit, la fonction de r´ partition de la v.a. S1 conditionnellement a {Nt = 1} est celle d’une loi
e `
uniforme sur l’intervalle [0; t].
Terminons en donnant deux r´ sultats sur la superposition de processus de Poisson ind´ pendants et sur
e e
l’op´ ration inverse de d´ composition.
e e
Proposition 2.1.7
30](https://image.slidesharecdn.com/coursprostoc-121002170116-phpapp02/85/Cours-stochastic-processes-30-320.jpg)
![1. Soient {Nt1 }t≥0 et {Nt2 }t≥0 deux processus de Poisson ind´ pendants (i.e. tout ev´ nement li´ a
e ´ e e `
l’un est ind´ pendant de tout ev´ nement li´ a l’autre), d’intensit´ s respectives λ1 et λ2 . On appelle
e ´ e e` e
superposition de ces deux processus le processus somme :
∀t ≥ 0, Nt = Nt1 + Nt2 .
Alors {Nt }t≥0 est encore un processus de Poisson d’intensit´ λ1 + λ2 .
e
2. Inversement, si {Nt }t≥0 est un processus de Poisson d’intensit´ λ, on associe aux instants de saut
e
(Sn )n∈N de ce processus une suite de v.a. (Yn )n∈N ind´ pendantes, ind´ pendantes du processus
e e
{Nt }t≥0 , et de mˆ me loi de Bernoulli :
e
∀n ∈ N, IP(Yn = 1) = p et IP(Yn = 0) = 1 − p .
Soit {Nt′ }t≥0 le processus dont les instants de saut sont les (Sn )n∈N tels que Yn = 1. Alors, {Nt′ }t≥0
est encore un processus de Poisson d’intensit´ λ′ = pλ.
e
Voici deux exemples d’application :
– Sur une voie a double sens, si les flux de v´ hicules venant de droite et de gauche sont deux processus
` e
de Poisson d’intensit´ respectives λ1 et λ2 , pouvant etre consid´ r´ s comme ind´ pendants, alors le
e ˆ ee e
flux global de v´ hicules est encore un processus de Poisson d’intensit´ λ1 + λ2 .
e e
– Si le flux global de v´ hicules est un processus de Poisson d’intensit´ λ et que 5% des v´ hicules sont
e e e
rouges alors le flux des v´ hicules rouges est encore un processus de Poisson d’intensit´ λ′ = 0, 05λ.
e e
2.1.3 Simulation et mod´ lisation
e
De nombreuses situations sont mod´ lis´ es par les processus de Poisson : arriv´ es de clients dans une file
e e e
d’attente, appels a un central t´ l´ phonique, d´ sint´ gration de particules radioactives, pannes de composants
` ee e e
electroniques, passages de voitures sur une route a grande circulation non embouteill´ e. . . Pour se faire une
´ ` e
id´ e concr` te de ce qu’est un processus de Poisson, rien ne vaut la simulation. On peut bien sˆ r programmer
e e u
en suivant la d´ finition, ce qui implique des tirages successifs de variables exponentielles. On peut aussi
e
appliquer la propri´ t´ (P3) et la Proposition 2.1.6 : pour simuler des ev´ nements poissoniens sur l’intervalle
ee ´ e
de temps [0; t], on commence par choisir la valeur n prise par Nt suivant la loi P(λt), puis on simule les
dates d’arriv´ es de ces n ev´ nements en les tirant au hasard suivant la loi uniforme sur [0; t]. En R, cela
e ´ e
donne :
n = rpois(1,λt)
v = runif(n,0,t)
w = sort(v)
Le vecteur w contient les instants de sauts S1 , . . . , Sn du processus de Poisson d’intensit´ λt sur l’intervalle
e
[0; t].
Il est important de comprendre quelles hypoth` ses de mod´ lisation l’utilisation d’un processus de Poisson
e e
sous-entend. Dire que des ev´ nements surviennent selon un processus de Poisson, c’est supposer qu’`
´ e a
chaque instant, l’arriv´ e du prochain ev´ nement est parfaitement impr´ visible, i.e. ind´ pendante de ce qui
e ´ e e e
a pr´ c´ d´ . On suppose de plus que l’intensit´ (nombre moyen d’´ v´ nements par unit´ de temps) reste
e e e e e e e
constante. Supposons que l’on souhaite mod´ liser des arriv´ es de clients dans un magasin. Les questions
e e
sont les suivantes.
– Les clients arrivent-ils un par un (´ v´ nements rares) ?
e e
31](https://image.slidesharecdn.com/coursprostoc-121002170116-phpapp02/85/Cours-stochastic-processes-31-320.jpg)
![– Le temps qui s’est ecoul´ depuis l’arriv´ e du dernier client est-il sans incidence sur les chances d’en
´ e e
voir arriver un bientˆ t (accroissements ind´ pendants) ?
o e
– Dans une seconde fix´ e, les chances de voir arriver un client sont-elles constantes (homog´ n´ it´ en
e e e e
temps) ?
Mˆ me si les r´ ponses a ces questions sont g´ n´ ralement plutˆ t n´ gatives, il est raisonnable de commencer
e e ` e e o e
par mod´ liser cette situation par un processus de Poisson. Lorsque cette premi` re mod´ lisation conduit
e e e
a des r´ sultats aberrants, on a recours a des mod` les plus sophistiqu´ s qui sont des g´ n´ ralisations du
` e ` e e e e
processus de Poisson. Par exemple, les processus de renouvellement sont des processus de comptage
d’´ v´ nements rares s´ par´ s par des dur´ es ind´ pendantes, mais de loi autre qu’exponentielle. Les processus
e e e e e e
de Poisson non homog` nes sont des processus de comptage, a accroissements ind´ pendants, d’´ v´ nements
e ` e e e
rares, mais la loi de Nt+h − Nt d´ pend de t. L’int´ rˆ t des processus de Poisson compos´ s r´ side dans la
e ee e e
possibilit´ d’ajouter, a chaque top, une v.a. enti` re plutˆ t que d’augmenter syst´ matiquement de 1. Ceci
e ` e o e
permet en particulier de tenir compte des arriv´ es group´ es dans les mod` les d’attente.
e e e
Signalons enfin que le processus de Poisson peut etre etendu a des dimensions sup´ rieures a 1. Les tops
ˆ ´ ` e `
sont alors interpr´ t´ s comme des points de l’espace, pouvant par exemple mod´ lis´ s les individus d’une
ee e e
esp` ce prot´ g´ e dans un parc naturel. Dans la fenˆ tre [0; 20]2 , le nombre de points d’un processus de Pois-
e e e e
son (bi-dimensionnel) d’intensit´ λ suit la loi de Poisson de param` tre λ × 202 . Puis, en ces points, nous
e e
centrons des disques dont les rayons sont des v.a. i.i.d. L’union de ces disques forme un sous-ensemble
al´ atoire Γ, appel´ Mod` le Bool´ en ; voir la Figure 2.2. Le Mod` le Bool´ en permet de mod´ liser de nom-
e e e e e e e
breux ph´ nom` nes physiques ou biologiques : la porosit´ d’un milieu ou d’un mat´ riau, la propagation
e e e e
d’une maladie sur un territoire, etc.
F IGURE 2.2 – Trois simulations du Mod` le Bool´ en. Dans les trois cas, les rayons sont distribu´ s selon la
e e e
loi exponentielle de param` tre 1. L’intensit´ du processus de Poisson sous-jacent vaut, de gauche a droite,
e e `
λ = 1, 4, 7. Il n’est donc pas etonnant que l’ensemble Γ (en noir) remplisse de plus en plus la fenˆ tre
´ e
[0; 20]2 . Dans la derni` re simulation, est-il possible de traverser la fenˆ tre [0; 20]2 , disons de gauche a
e e `
droite, tout en restant dans Γ ?
Voici le code en R produisant ces simulations :
n = rpois(1,λL2 )
X = runif(n,0,L)
Y = runif(n,0,L)
R = rexp(n,1)
plot(0 :L, 0 :L, type=”n”, xlab=””, ylab=””)
32](https://image.slidesharecdn.com/coursprostoc-121002170116-phpapp02/85/Cours-stochastic-processes-32-320.jpg)
![for (i in 1 :n) points(X[i],Y[i],cex=R[i],pch=16)
2.2 Processus markoviens de sauts
Les Processus markoviens de sauts sont la g´ n´ ralisation des chaˆnes de Markov au temps continu.
e e ı
Le passage du temps discret au temps continu se fait en remplacant le pas de temps fixe d’une chaˆne de
ı
Markov par des intervalles de temps al´ atoires ind´ pendants de loi exponentielle. Le processus de Poisson
e e
sera notre premier exemple de processus markoviens de sauts. Un second sera li´ aux files d’attente et sera
e
abord´ dans la derni` re partie de ce cours.
e e
2.2.1 D´ finition et exemples
e
Consid´ rons un ensemble E fini ou d´ nombrable et une suite croissante de v.a. (Sn )n∈N a valeurs dans
e e `
R+ . Un processus de sauts {Xt }t≥0 a espace d’´ tats E et d’instants de sauts (Sn )n∈N est un processus
` e
stochastique dont la valeur ne peut changer qu’en ses instants de sauts :
∀n ∈ N, ∃!x ∈ E tel que ∀t ∈ [Sn ; Sn+1 [, Xt = x .
Nous nous int´ ressons exclusivement a une classe particuli` re de processus de sauts, appel´ s processus
e ` e e
markoviens de sauts. Ces processus evoluent de la mani` re suivante. Supposons que le processus se trouve
´ e
a l’´ tat x a l’issu du saut intervenant a l’instant Sn .
` e ` `
1. Le temps de s´ jour dans l’´ tat x, a savoir la v.a. Sn+1 − Sn , suit la loi exponentielle de param` tre
e e ` e
λ(x). Le param` tre de cette loi peut donc d´ pendre de l’´ tat x o` le processus se trouve. Mais a part
e e e u `
cette d´ pendance en l’´ tat x, la v.a. Sn+1 − Sn est ind´ pendante du pass´ du processus.
e e e e
` l’instant Sn+1 , le processus saute de l’´ tat x vers l’´ tat y (avec y = x) avec une probabilit´ qx,y ,
2. A e e e
quantit´ ind´ pendante de Sn+1 − Sn et du pass´ .
e e e
L’´ volution du processus est donc d´ termin´ e par la suite (λ(x))x∈E et par la matrice Q := (qx,y )x,y∈E .
e e e
Voici une d´ finition plus formelle :
e
D´ finition 2.2.1 Un processus de sauts {Xt }t≥0 a espace d’´ tats E et d’instants de sauts (Sn )n∈N est
e ` e
markovien s’il existe :
• une suite born´ e (λ(x))x∈E de r´ els strictement positifs,
e e
• une matrice Q = (qx,y )x,y∈E de r´ els positifs v´ rifiant
e e
∀x ∈ E, qx,x = 0 et qx,y = 1 ,
y∈E
telles que, pour tout entier n, pour tous etats x0 , x1 , . . . , xn , xn+1 et pour tous r´ els positifs t1 , . . . , tn ,
´ e
tn+1 :
XSn+1 = xn+1 , XSn = xn , Sn − Sn−1 > tn , . . . ,
IP
Sn+1 − Sn > tn+1 XS1 = x1 , S1 − S0 > t1 , XS0 = x0
XSn+1 = xn+1 ,
= IP XSn = xn (2.3)
Sn+1 − Sn > tn+1
= e−λ(xn )tn+1 qxn ,xn+1 . (2.4)
33](https://image.slidesharecdn.com/coursprostoc-121002170116-phpapp02/85/Cours-stochastic-processes-33-320.jpg)

![markov = function(x0 ,T,λ,Q)
{ X = x0
T = T - rexp(1,λ[x0 ])
while (T > 0)
{ U = runif(1,0,1)
R = qX,x1
i=1
while (R < U)
{i=i+1
R = R + qX,xi
}
X = xi
T = T - rexp(1,λ[xi ])
}
X
}
Le cœur de cette routine consiste a choisir le prochain etat visit´ par le processus selon le vecteur de
` ´ e
probabilit´ (qX,xi )i≥1 , l’´ tat occup´ etant X. Cette simulation peut se simplifier consid´ rablement suivant
e e e´ e
le contexte (processus de Poisson, automate binaire).
2.2.2 Probabilit´ s de transition et g´ n´ rateur de Markov
e e e
Le r´ sultat suivant est l’analogue de la propri´ t´ de Markov et de l’homog´ n´ it´ en temps qui d´ finissent
e ee e e e e
habituellement les chaˆnes de Markov. Comme dans le cas discret, cela conduit a une caract´ risation simple
ı ` e
de la loi du processus.
Proposition 2.2.2 Un processus markovien de sauts {Xt }t≥0 a espace d’´ tats E satisfait les deux egalit´ s
` e ´ e
suivantes : pour tout entier n, pour tous etats x0 , x1 , . . . , xn , xn+1 et pour toute suite croissante de r´ els
´ e
positifs 0 < t1 < . . . < tn < tn+1 ,
IP(Xtn+1 = xn+1 | Xtn = xn , . . . , Xt1 = x1 , X0 = x0 ) = IP(Xtn+1 = xn+1 | Xtn = xn )
= IP(Xtn+1 −tn = xn+1 | X0 = xn ) .
D` s lors, la probabilit´ conditionnelle IP(Xt = y|Xs = x) ne d´ pend que des etats x, y et de l’accroisse-
e e e ´
ment t − s, ce qui justifie la notation suivante. Pour tout r´ el positif t et pour tous etats x, y, la probabilit´
e ´ e
de transition de x vers y sur un intervalle (de temps) de longueur t est d´ finie par :
e
p(t) := IP(Xt = y | X0 = x) .
x,y
(t)
Attention, la notation px,y ne pr´ cise pas le nombre de sauts pour aller de l’´ tat x a l’instant 0 a l’´ tat y a
e e ` ` e `
l’instant t.
(t)
La matrice P (t) := (px,y )x,y∈E est appel´ e matrice de transition sur un intervalle (de temps) de longueur
e
t. Comme dans le cas discret, la taille de la matrice P (t) d´ pend du cardinal de E (´ ventuellement infini),
e e
ses coefficients sont des r´ els positifs et la somme de ces coefficients sur toute une ligne vaut 1.
e
Comme dans le cas discret, la loi µt de la v.a. Xt est obtenue par produit matriciel entre la loi initiale µ0
(i.e. celle de X0 ) et la matrice de transition P (t) :
µt = µ0 P (t) .
35](https://image.slidesharecdn.com/coursprostoc-121002170116-phpapp02/85/Cours-stochastic-processes-35-320.jpg)










![2.4 Exercices
Exercice 1 : Bit informatique poissonnien
Consid´ rons un processus de Poisson {Nt }t≥0 d’intensit´ λ et une v.a. X0 , ind´ pendante du processus
e e e
{Nt }t≥0 , valant −1 ou 1 avec probabilit´ 1/2. Soit {Xt }t≥0 le processus a valeurs dans {−1, 1}, changeant
e `
de signe a chaque saut du processus {Nt }t≥0 et issu de X0 .
`
1. Apr` s avoir donn´ une expression de Xt en fonction de Nt et de X0 , d´ terminer son esp´ rance et
e e e e
sa variance.
2. Calculer la probabilit´ pour que la valeur du bit au temps t0 soit la mˆ me qu’initialement. Puis la
e e
limite de cette probabilit´ quand t0 → +∞. Comparer avec le bit informatique a temps discret. On pourra
e `
utiliser la formule
∞
z 2k 1 z
= e + e−z .
(2k)! 2
k=0
Exercice 2 : Temps d’attente de voyageurs
Supposons que des voyageurs en partance pour Londres arrivent a la gare Lille Europe selon un processus
`
de Poisson d’intensit´ λ. Le d´ part de leur train est pr´ vu au temps t0 (nous conviendrons que la gare ouvre
e e e
ses portes au temps t = 0).
1. Calculer le nombre moyen de voyageurs prenant ce train.
2. Calculer la moyenne de la somme des temps d’attente de ces voyageurs.
Exercice 3 : Loi binomiale et processus de Poisson
Comme il fait beau ce matin, je prends mon petit-d´ jeuner dans le jardin. Des merles et des moineaux
e
viennent chiper des miettes de pain que j’´ parpille volontairement sur la table. Les passages des merles et
e
des moineaux peuvent etre mod´ lis´ s par deux processus de Poisson ind´ pendants d’intensit´ s respectives
ˆ e e e e
λ et λ′ .
1. Calculer la probabilit´ pour que le premier oiseau venant sur la table soit un merle.
e
2. Calculer la probabilit´ pour que les deux premiers oiseaux venant sur la table soient des merles.
e
3. Quelle est la loi du nombre d’oiseaux venant sur la table jusqu’au temps t ? Sachant que ce nombre
vaut n, quelle est la loi du nombre de merles venant sur la table jusqu’au temps t ?
Exercice 4 : Radioactivit´
e
Une source radioactive emet des particules selon un processus de Poisson d’intensit´ λ. Chaque particule
´ e
est emise suivant une direction al´ atoire, de loi uniforme sur [0; 2π], et ind´ pendante des autres particules.
´ e e
Un compteur Geiger, plac´ pr` s de la source, enregistre les particules emises de direction comprise entre
e e ´
−π/4 et π/4. Quelle est la loi du nombre de particules enregistr´ es jusqu’au temps t ?
e
Exercice 5 (Examen 2009) :
Une fois la nuit tomb´ e, Pierre et Paul se retrouvent a l’observatoire afin de contempler des etoiles filantes.
e ` ´
Le passage des etoiles filantes dans le ciel est mod´ lis´ par un processus de Poisson d’intensit´ 0.1 (l’unit´
´ e e e e
de temps etant la minute), not´ {Nt }t≥0 . Soit Xn le temps al´ atoire s´ parant le passage de la (n − 1) ´
´ e e e e etoile
filante du passage de la ne.
46](https://image.slidesharecdn.com/coursprostoc-121002170116-phpapp02/85/Cours-stochastic-processes-46-320.jpg)
![1. Quelle est la probabilit´ pour Pierre et Paul de ne voir aucune etoile filante durant la premi` re heure
e ´ e
d’observation ? Quel est le nombre moyen d’´ toiles filantes qu’ils devraient voir durant cette premi` re
e e
heure d’observation ? Et pendant la seconde heure d’observation ?
2. Paul est de nature impatiente (seulement pour cette question) : s’il ne voit aucune etoile filante
´
durant 20 minutes (cons´ cutives) alors il s’en va ! Quelle est la probabilit´ qu’il en voit exactement 3 ?
e e
Plus g´ n´ ralement, quelle est la loi du nombre d’´ toiles filantes que Paul verra ? En d´ duire le nombre
e e e e
moyen d’´ toiles filantes que l’impatient Paul verra.
e
3. On suppose enfin que Paul est arriv´ en retard au rendez-vous (disons au temps t0 > 0 alors que
e
Pierre est arriv´ au temps t = 0).
e
(a) Sachant qu’aucune etoile filante n’est pass´ e avant l’arriv´ e de Paul, quelle est la loi du temps
´ e e
qu’il devra patienter pour en observer une ?
(b) Supposons dans cette question que t0 = 20. Sachant qu’une seule etoile filante est pass´ e avant
´ e
l’arriv´ e de Paul, quelle aurait et´ la probabilit´ pour Paul de la voir s’il etait arriv´ 5 minutes plus tˆ t ?
e ´e e ´ e o
Exercice 6 : Loi g´ om´ trique et processus de Poisson
e e
Je souhaite traverser une route a grande circulation dont le flux de v´ hicules peut etre mod´ lis´ par un
` e ˆ e e
processus de Poisson d’intensit´ λ = 1 (l’unit´ etant la minute). Depuis l’ablation de mes deux jambes, il
e e´
me faut tout de mˆ me 3 minutes pour traverser une telle route. Avant de me lancer, je pr´ f` re r´ fl´ chir un
e ee e e
peu. . .
1. Quelle est la loi du nombre de v´ hicules que je dois laisser passer avant de pouvoir traverser ?
e
2. Quel est le temps moyen d’attente avant de traverser ?
Exercice 7 (Examen 2010) : Probl` mes de simulations
e
Pr´ cisons que les g´ n´ rateurs mentionnn´ s ci-dessous g´ n` rent des v.a. ind´ pendantes entre elles, mais
e e e e e e e
aussi de tout le reste !
1. Comment simuler une loi exponentielle de param` tre 2 lorsqu’on dispose uniquement d’un g´ n´ rateur
e e e
de loi exponentielle de param` tre 1 ?
e
2. Comment simuler un processus de Poisson d’intensit´ 1 sur l’intervalle [0; 100] sans utiliser de lois
e
exponentielles (quel que soit le param` tre) ?
e
` e 1
3. A partir de la simulation pr´ c´ dente et d’un g´ n´ rateur de loi de Bernoulli de parm` tre 2 , comment
e e e e
e 1
simuler un processus de Poisson d’intensit´ 2 sur l’intervalle [0; 100] ?
Exercice 8 : Deux automates binaires d´ pendants
e
Consid´ rons un syst` me a deux composants identiques tel que, en cas de panne de l’un des deux compo-
e e `
sants, l’autre puisse aussi tomber en panne. Les hypoth` ses de mod´ lisation sont les suivantes.
e e
• Le temps de fonctionnement de chaque composant suit la loi E(λ).
• Le temps de r´ paration d’un composant seul (pendant le fonctionnement de l’autre) suit la loi E(µ).
e
• Le temps de r´ paration des deux composants simultan´ ment suit la loi E(ν).
e e
• En cas de panne d’un des composants, l’autre continue a fonctionner avec probabilit´ c.
` e
• Toutes les v.a. du mod` le sont ind´ pendantes.
e e
Soit Zt l’´ tat du syst` me au temps t : Zt ∈ E = {00, 10, 01, 11} o` , par exemple, l’´ tat 01 signifie que le
e e u e
premier composant est en panne tandis que le second est en fonctionnement.
1. Nous admettons que {Zt }t≥0 est un processus markovien de sauts sur E. Pr´ ciser cependant la
e
47](https://image.slidesharecdn.com/coursprostoc-121002170116-phpapp02/85/Cours-stochastic-processes-47-320.jpg)

![Annexe : quelques formules
Voici quelques formules ultra classique du calcul des probabilit´ s dont vous ne pourrez pas vous passer
e
durant ce cours.
On se donne un tripl´ (Ω, F, IP) o` :
e u
– Ω est un ensemble ;
– F est une tribu sur Ω, i.e. une tr` s grande famille de sous-ensembles de Ω ;
e
– IP est une mesure de probabilit´ sur Ω : les seuls sous-ensembles de Ω pouvant etre mesur´ s par IP
e ˆ e
sont ceux de la tribu F.
Dans la suite, A, B et (An )n∈N sont dans la tribu F.
[A1] On a toujours
IP An ≤ IP(An )
n∈N n∈N
avec egalit´ si et seulement si les ev´ nements An , n ∈ N, sont deux a deux disjoints.
´ e ´ e `
[A2] Supposons que la famille (An )n∈N forme une partition de Ω, i.e. les An , n ∈ N, sont deux a deux
`
disjoints et leur union remplit tout Ω. Alors ;
IP(B) = IP(B ∩ An ) = IP(B | An ) IP(An ) .
n∈N n∈N
[A3] Les ev´ nements A et B sont ind´ pendants si et seulement si IP(A ∩ B) = IP(A) IP(B), ce qui s’´ crit
´ e e e
encore
IP(A | B) = IP(A) d` s que IP(B) > 0.
e
[A4] Si la suite (An )n∈N est croissante, i.e. An ⊂ An+1 , alors
IP An = lim IP(An ) .
n→∞
n∈N
[A5] Si la suite (An )n∈N est d´ croissante, i.e. An ⊃ An+1 , alors
e
IP An = lim IP(An ) .
n→∞
n∈N
[A6] La probabilit´ d’un ev´ nement est egale a l’esp´ rance de son indicatrice :
e ´ e ´ ` e
IP(A) = IE [1 A ] .
1
49](https://image.slidesharecdn.com/coursprostoc-121002170116-phpapp02/85/Cours-stochastic-processes-49-320.jpg)