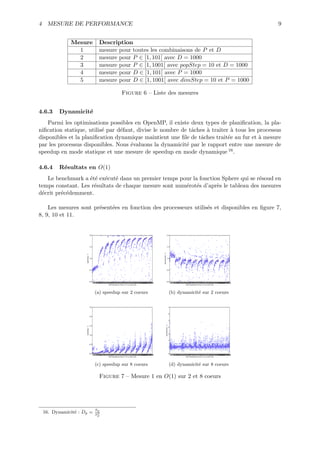
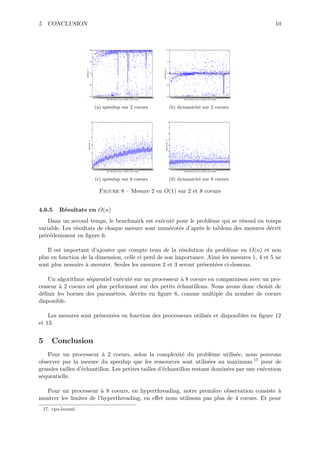
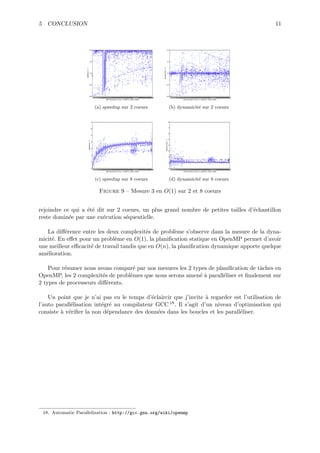
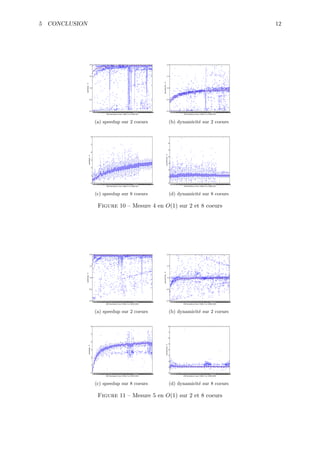
Le document aborde la parallélisation et les modèles de programmation, en se concentrant sur des algorithmes pour le produit matriciel et le tri d'un tableau binaire. Il propose des solutions détaillées avec des pseudo-codes, des implémentations en C++, et des considérations sur la performance. Le tout est structuré autour d'exemples concrets et de diagrammes illustrant le design des classes et l'utilisation d'OpenMP.

1. Parall´lisation & mod`les
e e
de programmation
Caner Candan
M2 MIHP
6 mars 2011
Table des mati`res
e
1 Produit matriciel 2
´
1.1 Enonc´ . . . . . . . . . .
e . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2
1.2 Solution . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2
1.2.1 La diffusion . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2
1.2.2 Le produit . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3
1.2.3 L’impl´mentation
e . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3
2 D´coupage d’un tableau binaire
e 3
´
2.1 Enonc´ . . . . . . . . . . . . . .
e . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3
2.2 Solution . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4
2.2.1 D´terminer l’index . . .
e . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4
2.2.2 Cr´er le tableau binaire
e . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4
2.2.3 Impl´mentation . . . . .
e . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4
3 Design 5
3.1 Diagramme de classes . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5
3.2 Surcharge d’op´rateur . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
e 5
4 Mesure de performance 6
4.1 Pr´ambule . . . . . . . . . . . . . . . . .
e . . . . . . . . . . . . . . . . . . . . . . . 6
4.2 Identifier les ressources les plus utilis´es
e . . . . . . . . . . . . . . . . . . . . . . . 6
4.3 Pseudo-code de la fonction apply . . . . . . . . . . . . . . . . . . . . . . . . . . . 6
4.4 La fonction en parall`le . . . . . . . . .
e . . . . . . . . . . . . . . . . . . . . . . . 6
4.5 Speed-up . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7
4.6 Mesures . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7
4.6.1 Fonctions objectifs . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8
4.6.2 Benchmark . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8
4.6.3 Dynamicit´ . . . . . . . . . . . .
e . . . . . . . . . . . . . . . . . . . . . . . 9
4.6.4 R´sultats en O(1) . . . . . . . .
e . . . . . . . . . . . . . . . . . . . . . . . 9
4.6.5 R´sultats en O(n) . . . . . . . .
e . . . . . . . . . . . . . . . . . . . . . . . 10
5 Conclusion 10
1

2. 1 PRODUIT MATRICIEL 2
1 Produit matriciel
1.1 ´
Enonc´
e
Matrice : D´crire un algorithme PRAM pour le mod`le EREW qui utilise O(n3 ) processeurs
e e
pour multiplier deux matrices de taille n ∗ n. 1
1.2 Solution
Une solution consisterait ` diffuser dans un premier temps toutes les donn´es des matrices `
a e a
multiplier ` chaque processus puis de faire le produit des matrices en prenant le soin que chaque
a
processus utilise les donn´es qui leur est propre.
e
1.2.1 La diffusion
En respectant le mod`le EREW, les matrices A et B ∈ Kn∗n sont copi´es, dans un premier
e e
temps, n fois dans les cubes A et B ∈ Kn∗n∗n . Ceci permet de r´server une dimension du cube
e
a
` un processus et ´viter toute lecture concurrente.
e
L’algorithme 1 pr´sente le pseudo-code de la fonction de diffusion qui prend comme donn´e
e e
en entr´e une matrice M ∈ Kn∗n et retourne un cube M ∈ Kn∗n∗n . Elle est exprim´e en
e e
2 ´tapes. La premi`re consiste ` affecter, en utilisant O(n2 ) processeurs, chaque point de la
e e a
matrice dans la premi`re dimension du cube. La deuxi`me ´tape effectue la copie en diffusion 2
e e e
de chaque point de la matrice situ´ ` la premi`re dimension du cube vers les autres dimensions
ea e
du cube en utilisant O(log n) processeurs et pour une matrice enti`re en O(n2 ∗ log n).
e
Donn´es : M ∈ Kn∗n , n ∈ N
e
R´sultat : M ∈ Kn∗n∗n
e
1 d´but
e
2 parall`le
e
3 pour i ← 0 ` n faire
a
4 parall`le
e
5 pour j ← 0 ` n faire
a
6 m (0, i, j) ← m(i, j)
7 parall`le
e
8 pour s ← 0 ` log2 n faire
a
9 parall`le
e
10 pour h ← 0 ` s2 faire
a
11 parall`le
e
12 pour i ← 0 ` n faire
a
13 parall`le
e
14 pour j ← 0 ` n faire
a
15 m (2s + h, i, j) ← m (h, i, j)
16 fin
Algorithme 1 : Copie de matrice en diffusion
n
1. cij = k=0 aik bkj : http://fr.wikipedia.org/wiki/Produit_matriciel
2. Hot potato routing : http://en.wikipedia.org/wiki/Hot_potato_routing

3. ´
2 DECOUPAGE D’UN TABLEAU BINAIRE 3
1.2.2 Le produit
En appliquant le mod`le EREW, le produit matriciel prend en param`tre les cubes A et
e e
B ∈ Kn∗n∗n tel que chaque processus utilise sa dimension de cube respective pour lire les
donn´es de aij et bij .
e
L’algorithme 2 pr´sente le pseudo-code de la fonction de produit matriciel qui prend comme
e
donn´e en entr´e les cubes A et B ∈ Kn∗n∗n et retourne une matrice C ∈ Kn∗n . L’affectation
e e
des valeurs dans la matrice C se fait en O(n2 ) et le produit de cij se fait en O(n).
Donn´es : A, B ∈ Kn∗n∗n , n ∈ N
e
R´sultat : C ∈ Kn∗n
e
1 d´but
e
2 parall`le
e
3 pour i ← 0 ` n faire
a
4 parall`le
e
5 pour j ← 0 ` n faire
a
6 c(i, j) ← n a(p, i, k) ∗ b(p, k, j)
k=0
7 fin
Algorithme 2 : Produit matriciel
1.2.3 L’impl´mentation
e
Apr`s avoir d´crit la fonction de diffusion et le produit matriciel respectant tous deux le
e e
mod`le EREW, nous allons voir l’implementation d’un produit de deux matrices A et B ∈ Kn∗n
e
produisant une troisi`me matrice C ∈ Kn∗n .
e
L’algorithme 3 d´crit l’impl´mentation.
e e
Donn´es : A, B ∈ Kn∗n , n ∈ N
e
R´sultat : C ∈ Kn∗n
e
1 d´but
e
2 A ← dif f usion(A, n)
3 B ← dif f usion(B, n)
4 C ← produit(A , B )
5 fin
Algorithme 3 : Impl´mentation du produit matriciel
e
2 D´coupage d’un tableau binaire
e
2.1 ´
Enonc´
e
D´coupage d’un tableau : Soit A un tableau de longueur n dont les ´l´ments sont soit des
e ee
0 soit des 1. Concevez un algorithme EREW de complexit´ O(log n) utilisant O(n) processeurs
e
pour ranger tous les ´l´ments 1 ` la droite du tableau tout en maintenant leur ordre relatif
ee a
(propri´t´ de stabilit´ des ´l´ments).
ee e ee
Hint : effectuer un calcul de pr´fixe pour d´terminer quel devrait ˆtre la position de chaque
e e e
´l´ment.
ee

4. ´
2 DECOUPAGE D’UN TABLEAU BINAIRE 4
2.2 Solution
Notre tableau ´tant binaire, contenant que des 0 et 1, il devient facile de compter le nombre
e
de 1 en sommant toutes les valeurs du tableau pour ensuite d´terminer ` quel index placer les
e a
0 et 1.
Toute fois pour respecter l’´nonc´ et avoir une complexit´ en O(log n), nous allons devoir
e e e
utiliser la fonction calculant la somme des pr´fixes.
e
2.2.1 D´terminer l’index
e
L’algorithme 4 permet de d´terminer l’index qui constituera la fronti`re entre les 0 et 1 dans
e e
le tableau. Pour cela il prend en param`tre le tableau binaire B ∈ Kn ainsi que la taille du
e
tableau n ∈ N .
Donn´es : B ∈ Kn , n ∈ N
e
R´sultat : i ∈ N
e
1 d´but
e
2 i ← n − calcul somme pref ixe(B)
3 fin
Algorithme 4 : Trouver l’index
2.2.2 Cr´er le tableau binaire
e
L’algorithme 5 prend en param`tre l’index et la taille et cr´e un tableau binaire tri´ en
e e e
fonction de l’index, 0 ` gauche et 1 ` droite.
a a
Donn´es : i, n ∈ N
e
R´sultat : B ∈ Kn
e
1 d´but
e
2 parall`le
e
3 pour j ← 0 ` i faire
a
4 B (i) ← 0
5 parall`le
e
6 pour j ← i ` n faire
a
7 B (i) ← 1
8 fin
Algorithme 5 : Cr´ation du tableau binaire tri´
e e
2.2.3 Impl´mentation
e
L’algorithme 6 illustre la solution.
Donn´es : B ∈ Kn
e
R´sultat : B ∈ Kn
e
1 d´but
e
2 i ← trouver index(B)
3 B ← creer tableau binaire(i)
4 fin
Algorithme 6 : D´coupage d’un tableau binaire
e

5. 3 DESIGN 5
3 Design
Tous les exercices ont ´t´ d´velopp´s en C++ en utilisant le paradigme de programmation
ee e e
objet et le design qui suit a ´t´ ´labor´ pour regrouper les diff´rents composants de calculs.
ee e e e
N´anmoins une recherche a ´t´ effectu´ pour d´terminer les limites de OpenMP et C++. Il
e ee e e
semblerait que les conteneurs fournit par la STL 3 ne soient pas threadsafe 4 . Une ´tude 5 donne
e
une liste non-exhaustive des pr´cautions ` prendre lors de l’utilisation de OpenMP en C++.
e a
Cependant la version OpenMP 3.0 apporte des concepts nouveaux permettant l’utilisation no-
tamment des iterateurs. On peut ainsi, par exemple, s’affranchir de simple indexeur de tableau
et ´tendre la parall´lisation sur des listes chaˆ ees.
e e ın´
3.1 Diagramme de classes
Figure 1 – Diagramme de classes
Deux grandes familles d’op´ration coexistent. Elles sont pr´sent´es en figure 1. Les op´rations
e e e e
de calcul ` param`tre unique “OMPComputeUnary” et celles ` deux param`tres “OMPCompu-
a e a e
teBinary”. Tous deux renvoient un r´sultat. Elles sont pr´fix´es de “OMP” pour OpenMP 6 . Le
e e e
calcul de somme des pr´fixes prenant un seul param`tre en entr´e “OMPVector” et renvoyant
e e e
un “Atom”, cette classe se situe dans la famille “OMPComputeUnary”. Le produit matriciel se
situe, quant ` lui, dans la famille “OMPComputeBinary”, cette classe prend deux param`tres
a e
“OMPMatrix” et retourne le mˆme type. On peut imaginer d’autres op´rations comme, par
e e
exemple, un produit vectoriel.
3.2 Surcharge d’op´rateur
e
Compte tenu des possibilit´s offertes par le langage C++, comme la surcharge des op´rateurs,
e e
l’op´rateur ∗ se voit ainsi surcharg´ dans la classe “OMPMatrix” afin d’appeler implicitement
e e
la classe “OMPMatrixProduct” pour le calcul du produit matriciel. Ainsi en ´crivant le code
e
C = A ∗ B ceci revient ` ´crire C = OM P M atrixP roduct()(A, B).
ae
3. Standard Template Library : http://www.sgi.com/tech/stl/
4. On dit qu’un programme ou qu’une portion de code est thread-safe s’il fonctionne correctement durant une
ex´cution simultan´e par plusieurs threads (processus l´gers). http://fr.wikipedia.org/wiki/Threadsafe
e e e
5. C++ and OpenMP : http://www.compunity.org/events/pastevents/parco07/parco_cpp_openmp.pdf
6. Open Multi-Processing : http ://openmp.org/

6. 4 MESURE DE PERFORMANCE 6
4 Mesure de performance
Je profite de ce rapport pour parler d’un travail qui m’a ´t´ demand´ en entreprise. Nous uti-
ee e
lisons le framework EO 7 pour d´velopper nos algorithmes ´volutionnaires 8 . Le sujet consistait
e e
a
` impl´menter, au framework EO, un parall´lisme ` m´moire partag´e en utilisant OpenMP.
e e a e e
4.1 Pr´ambule
e
Avant de commencer il est important de pr´ciser que les EA 9 travaillent sur une population
e
d’individu aussi appel´ ´chantillon. Un individu ´tant repr´sent´ par un point dans l’´chantillon,
ee e e e e
la complexit´ d’un probl`me est d´finit par le nombre de dimensions pour chaque individu.
e e e
Le probl`me est repr´sent´ par la fonction objectif qui prend en param`tre un individu (un
e e e e
point dans l’´chantillon) et ´value toutes ses dimensions pour en d´duire la qualit´ 10 . La qualit´
e e e e e
est le crit`re de comparaison d’un point dans son ´chantillon.
e e
4.2 Identifier les ressources les plus utilis´es
e
Un test de profiling a ´t´ ex´cut´ afin d’identifier les ressources les plus utilis´es dans le
ee e e e
framework EO. Le test nous a permit d’identifier une fonction qui est utilis´e par une grande
e
majorit´ des op´rateurs 11 EO. Il s’agit de la fonction “apply”. Elle prend en param`tres une
e e e
population d’individu et un op´rateur. Cette fonction va it´rer sur tous les individus de la
e e
population et appliquer l’op´rateur. Il peut ˆtre int´ressant d’optimiser cette fonction. Nous
e e e
allons nous limiter ` transformer le code s´quentiel en parall`le.
a e e
4.3 Pseudo-code de la fonction apply
L’algorithme 7 prend en param`tre une population ainsi qu’un op´rateur ` appliquer `
e e a a
chaque individu.
Donn´es : P ∈ Kn , F ∈ Operateur
e
R´sultat : B ∈ Kn
e
1 d´but
e
2 pour i ← 0 ` n faire
a
3 F (P (i))
4 fin
Algorithme 7 : La fonction apply
4.4 La fonction en parall`le
e
L’algorithme 8 transforme la fonction “apply” en parall`le en utilisant le mod`le PRAM
e e
CREW 12 et O(n) processeurs pour parcourir tous les individus de la population.
7. Evolving Object, http://eodev.sf.net
8. Algorithme ´volutionnaire : http://fr.wikipedia.org/wiki/Algorithme_evolutionnaire
e
9. Algorithmes ´volutionnaires
e
10. Fitness en anglais
11. Op´rateurs de s´lection et variation
e e
12. Concurantial Read Exclusive Write

7. 4 MESURE DE PERFORMANCE 7
Donn´es : P ∈ Kn , F ∈ Operateur
e
R´sultat : B ∈ Kn
e
1 d´but
e
2 parall`le
e
3 pour i ← 0 ` n faire
a
4 F (P (i))
5 fin
Algorithme 8 : La fonction omp apply
4.5 Speed-up
Apr`s avoir cr´e la fonction alternative employant le parall´lisme ` m´moire partag´e, appel´
e e e a e e e
“omp apply”, nous allons ´tudier une solution de mesure du speed-up 13 .
e
L’´quation, en figure 2, pr´sente une m´thode de mesure du speed-up et est impl´ment´e
e e e e e
dans l’algorithme 9.
P,D
M esure du Speedup = r Spkl
k=0,l=0
Figure 2 – Mesure du Speedup
Une description des param`tres est disponible dans la figure 3.
e
Param`tres
e Description
p la taille minimum de la population
popStep le pas d’iteration de la population
P la taille maximum de la population
d la taille minimum de la dimension
dimStep le pas d’iteration de la dimension
D la taille maximum de la dimension
r le nombre d’ex´cution pour chaque com-
e
binaison de p et d
Figure 3 – Description des param`tres utilis´s
e e
4.6 Mesures
En prenant en compte les param`tres d´crits pr´c´demment, nous allons lancer les tests sur
e e e e
deux architectures mat´rielles diff´rentes pr´sent´ en figure 4.
e e e e
Pour visualiser l’´volution du speed-up, nous utilisons un outil de g´n´ration de graphiques 15 ,
e e e
avec les donn´es produits par les tests.
e
T∗
13. Sp = T1 : http://en.wikipedia.org/wiki/Speedup
p
15. Utilisation de matplotlib en python pour g´n´rer des boites a moustache
e e `

8. 4 MESURE DE PERFORMANCE 8
Donn´es : p, P, popStep, d, D, dimStep, r ∈ N
e
1 d´but
e
2 pour k ← p ` P faire
a
3 pour l ← d ` D faire
a
4 pour m ← 0 ` r faire
a
5 Ts ← 0
6 Tp ← 0
7 d´but
e
8 t1 ← omp get wtime()
9 ... code sequentiel avec k et l ex´cut´ m fois ...
e e
10 apply( ... )
11 t2 ← omp get wtime()
12 Ts ← t2 − t1
13 fin
14 d´but
e
15 t1 ← omp get wtime()
16 ... code parall`le avec k et l ex´cut´ m fois ...
e e e
17 omp apply( ... )
18 t2 ← omp get wtime()
19 Tp ← t2 − t1
20 fin
Ts
21 ... on conserve le speed-up Tp pour k et l ...
22 fin
Algorithme 9 : La fonction de mesure du speedup
Processeur Nombre de coeurs Fr´quence
e Cache L1
Intel Centrino vPro 2 2.40GHz 3072KB
Intel Core i7 8 (hyperthreading 14 ) 2.67GHz 8192KB
Figure 4 – Architectures mat´rielles
e
4.6.1 Fonctions objectifs
Il est important de simuler toutes les compl´xit´s de probl`mes que l’on peut ˆtre amen´
e e e e e
a e
` r´soudre. Pour nos tests, le choix a ´t´ orient´ vers deux fonctions objectifs de complexit´
ee e e
diff´rente pr´sent´ en figure 5.
e e e
Fonction objectifs Complexit´ en temps
e Algorithme
La fonction Sphere O(1) Sphere = n individuk
k=0
Probl`me ` temps variable quelconque
e a O(n) usleep(U (0, 1) ∗ 10)
Figure 5 – Fonctions objectifs
4.6.2 Benchmark
Pour faciliter et automatiser les tests, une liste de mesures a ´t´ ´labor´ avec les param`tres
e ee e e
d´crits pr´c´demment et un script contenant l’ensemble des tests ` ex´cuter a ´t´ cr´e. La liste
e e e a e ee e
des mesures est pr´sent´e en figure 6.
e e

9. 4 MESURE DE PERFORMANCE 9
Mesure Description
1 mesure pour toutes les combinaisons de P et D
2 mesure pour P ∈ [1, 101[ avec D = 1000
3 mesure pour P ∈ [1, 1001[ avec popStep = 10 et D = 1000
4 mesure pour D ∈ [1, 101[ avec P = 1000
5 mesure pour D ∈ [1, 1001[ avec dimStep = 10 et P = 1000
Figure 6 – Liste des mesures
4.6.3 Dynamicit´
e
Parmi les optimisations possibles en OpenMP, il existe deux types de planification, la pla-
nification statique, utilis´ par d´faut, divise le nombre de tˆches ` traiter ` tous les processus
e e a a a
disponibles et la planification dynamique maintient une file de tˆches trait´e au fur et ` mesure
a e a
par les processus disponibles. Nous ´valuons la dynamicit´ par le rapport entre une mesure de
e e
speedup en mode statique et une mesure de speedup en mode dynamique 16 .
4.6.4 R´sultats en O(1)
e
Le benchmark a ´t´ ex´cut´ dans un premier temps pour la fonction Sphere qui se r´soud en
ee e e e
temps constant. Les r´sultats de chaque mesure sont num´rot´s d’apr`s le tableau des mesures
e e e e
d´crit pr´c´demment.
e e e
Les mesures sont pr´sent´es en fonction des processeurs utilis´s et disponibles en figure 7,
e e e
8, 9, 10 et 11.
2.0 2.0
1.5 1.5
dynamicity - 1
speedup - 1
1.0 1.0
0.5 0.5
0.0 13 6791115192327313539434751555963677175798387919599104110116
245 8112162024283236404448525660646872768084889296101107113119
014182226303438424650545862667074788286909498102108114120
13172125293337414549535761656973778185899397 103109115121
105111117
100106112118 0.0 13 6791115192327313539434751555963677175798387919599104110116
245 8112162024283236404448525660646872768084889296101107113119
014182226303438424650545862667074788286909498102108114120
13172125293337414549535761656973778185899397 103109115121
105111117
100106112118
100 iterations from 1,1 to 101,101 100 iterations from 1,1 to 101,101
(a) speedup sur 2 coeurs (b) dynamicit´ sur 2 coeurs
e
2.5 7
6
2.0
5
1.5
dynamicity - 1
4
speedup - 1
3
1.0
2
0.5
1
0.0 13 6791115192327313539434751555963677175798387919599104110116
245 8112162024283236404448525660646872768084889296101107113119
014182226303438424650545862667074788286909498102108114120
13172125293337414549535761656973778185899397 103109115121
105111117
100106112118 0 13 6791115192327313539434751555963677175798387919599104110116
245 8112162024283236404448525660646872768084889296101107113119
014182226303438424650545862667074788286909498102108114120
13172125293337414549535761656973778185899397 103109115121
105111117
100106112118
100 iterations from 1,1 to 101,101 100 iterations from 1,1 to 101,101
(c) speedup sur 8 coeurs (d) dynamicit´ sur 8 coeurs
e
Figure 7 – Mesure 1 en O(1) sur 2 et 8 coeurs
Sp
16. Dynamicit´ : Dp =
e d
Sp

10. 5 CONCLUSION 10
2.0 2.0
1.5 1.5
dynamicity - 2
speedup - 2
1.0 1.0
0.5 0.5
0.0 123456789111417202326293235384144475053565962656871747780838689929598
101316192225283134374043464952555861646770737679828588919497101
121518212427303336394245485154576063666972757881848790939699
100 0.0 123456789111417202326293235384144475053565962656871747780838689929598
101316192225283134374043464952555861646770737679828588919497101
121518212427303336394245485154576063666972757881848790939699
100
100 iterations from 1,1000 to 101,1000 100 iterations from 1,1000 to 101,1000
(a) speedup sur 2 coeurs (b) dynamicit´ sur 2 coeurs
e
6 8
7
5
6
4
5
dynamicity - 2
speedup - 2
3 4
3
2
2
1
1
0 123456789111417202326293235384144475053565962656871747780838689929598
101316192225283134374043464952555861646770737679828588919497101
121518212427303336394245485154576063666972757881848790939699
100 0 123456789111417202326293235384144475053565962656871747780838689929598
101316192225283134374043464952555861646770737679828588919497101
121518212427303336394245485154576063666972757881848790939699
100
100 iterations from 1,1000 to 101,1000 100 iterations from 1,1000 to 101,1000
(c) speedup sur 8 coeurs (d) dynamicit´ sur 8 coeurs
e
Figure 8 – Mesure 2 en O(1) sur 2 et 8 coeurs
4.6.5 R´sultats en O(n)
e
Dans un second temps, le benchmark est ex´cut´ pour le probl`me qui se r´soud en temps
e e e e
variable. Les r´sultats de chaque mesure sont num´rot´s d’apr`s le tableau des mesures d´crit
e e e e e
pr´c´demment en figure 6.
e e
Il est important d’ajouter que compte tenu de la r´solution du probl`me en O(n) et non
e e
plus en fonction de la dimension, celle ci perd de son importance. Ainsi les mesures 1, 4 et 5 ne
sont plus nessaire ` mesurer. Seules les mesures 2 et 3 seront pr´sent´es ci-dessous.
a e e
Un algorithme s´quentiel ex´cut´ sur un processeur ` 8 coeurs en comparaison avec un pro-
e e e a
cesseur ` 2 coeurs est plus performant sur des petits ´chantillons. Nous avons donc choisit de
a e
d´finir les bornes des param`tres, d´crits en figure 6, comme multiple du nombre de coeurs
e e e
disponible.
Les mesures sont pr´sent´es en fonction des processeurs utilis´s et disponibles en figure 12
e e e
et 13.
5 Conclusion
Pour un processeur ` 2 coeurs, selon la complexit´ du probl`me utilis´e, nous pouvons
a e e e
observer par la mesure du speedup que les ressources sont utilis´es au maximum 17 pour de
e
grandes tailles d’´chantillon. Les petites tailles d’´chantillon restant domin´es par une ex´cution
e e e e
s´quentielle.
e
Pour un processeur ` 8 coeurs, en hyperthreading, notre premi`re observation consiste `
a e a
montrer les limites de l’hyperthreading, en effet nous utilisons pas plus de 4 coeurs. Et pour
17. cpu-bound

11. 5 CONCLUSION 11
2.0 2.0
1.5 1.5
dynamicity - 3
speedup - 3
1.0 1.0
0.5 0.5
0.0 123456789111417202326293235384144475053565962656871747780838689929598
101316192225283134374043464952555861646770737679828588919497101
121518212427303336394245485154576063666972757881848790939699
100 0.0 123456789111417202326293235384144475053565962656871747780838689929598
101316192225283134374043464952555861646770737679828588919497101
121518212427303336394245485154576063666972757881848790939699
100
100 iterations from 1,1000 to 1001,1000 100 iterations from 1,1000 to 1001,1000
(a) speedup sur 2 coeurs (b) dynamicit´ sur 2 coeurs
e
7 8
6 7
6
5
5
dynamicity - 3
4
speedup - 3
4
3
3
2
2
1 1
0 123456789111417202326293235384144475053565962656871747780838689929598
101316192225283134374043464952555861646770737679828588919497101
121518212427303336394245485154576063666972757881848790939699
100 0 123456789111417202326293235384144475053565962656871747780838689929598
101316192225283134374043464952555861646770737679828588919497101
121518212427303336394245485154576063666972757881848790939699
100
100 iterations from 1,1000 to 1001,1000 100 iterations from 1,1000 to 1001,1000
(c) speedup sur 8 coeurs (d) dynamicit´ sur 8 coeurs
e
Figure 9 – Mesure 3 en O(1) sur 2 et 8 coeurs
rejoindre ce qui a ´t´ dit sur 2 coeurs, un plus grand nombre de petites tailles d’´chantillon
ee e
reste domin´e par une ex´cution s´quentielle.
e e e
La diff´rence entre les deux complexit´s de probl`me s’observe dans la mesure de la dyna-
e e e
micit´. En effet pour un probl`me en O(1), la planification statique en OpenMP permet d’avoir
e e
une meilleur efficacit´ de travail tandis que en O(n), la planification dynamique apporte quelque
e
am´lioration.
e
Pour r´sumer nous avons compar´ par nos mesures les 2 types de planification de tˆches en
e e a
OpenMP, les 2 complexit´s de probl`mes que nous serons amen´ ` parall´liser et finalement sur
e e ea e
2 types de processeurs diff´rents.
e
Un point que je n’ai pas eu le temps d’´claircir que j’invite ` regarder est l’utilisation de
e a
l’auto parall´lisation int´gr´ au compilateur GCC
e e e 18 . Il s’agit d’un niveau d’optimisation qui
consiste ` v´rifier la non d´pendance des donn´es dans les boucles et les parall´liser.
a e e e e
18. Automatic Parallelization : http://gcc.gnu.org/wiki/openmp

12. 5 CONCLUSION 12
2.0 2.0
1.5 1.5
dynamicity - 4
speedup - 4 1.0 1.0
0.5 0.5
0.0 123456789111417202326293235384144475053565962656871747780838689929598
101316192225283134374043464952555861646770737679828588919497101
121518212427303336394245485154576063666972757881848790939699
100 0.0 123456789111417202326293235384144475053565962656871747780838689929598
101316192225283134374043464952555861646770737679828588919497101
121518212427303336394245485154576063666972757881848790939699
100
100 iterations from 1000,1 to 1000,101 100 iterations from 1000,1 to 1000,101
(a) speedup sur 2 coeurs (b) dynamicit´ sur 2 coeurs
e
6 7
5 6
5
4
dynamicity - 4
4
speedup - 4
3
3
2
2
1 1
0 123456789111417202326293235384144475053565962656871747780838689929598
101316192225283134374043464952555861646770737679828588919497101
121518212427303336394245485154576063666972757881848790939699
100 0 123456789111417202326293235384144475053565962656871747780838689929598
101316192225283134374043464952555861646770737679828588919497101
121518212427303336394245485154576063666972757881848790939699
100
100 iterations from 1000,1 to 1000,101 100 iterations from 1000,1 to 1000,101
(c) speedup sur 8 coeurs (d) dynamicit´ sur 8 coeurs
e
Figure 10 – Mesure 4 en O(1) sur 2 et 8 coeurs
2.0 2.0
1.5 1.5
dynamicity - 5
speedup - 5
1.0 1.0
0.5 0.5
0.0 123456789111417202326293235384144475053565962656871747780838689929598
101316192225283134374043464952555861646770737679828588919497101
121518212427303336394245485154576063666972757881848790939699
100 0.0 123456789111417202326293235384144475053565962656871747780838689929598
101316192225283134374043464952555861646770737679828588919497101
121518212427303336394245485154576063666972757881848790939699
100
100 iterations from 1000,1 to 1000,1001 100 iterations from 1000,1 to 1000,1001
(a) speedup sur 2 coeurs (b) dynamicit´ sur 2 coeurs
e
6 8
7
5
6
4
5
dynamicity - 5
speedup - 5
3 4
3
2
2
1
1
0 123456789111417202326293235384144475053565962656871747780838689929598
101316192225283134374043464952555861646770737679828588919497101
121518212427303336394245485154576063666972757881848790939699
100 0 123456789111417202326293235384144475053565962656871747780838689929598
101316192225283134374043464952555861646770737679828588919497101
121518212427303336394245485154576063666972757881848790939699
100
100 iterations from 1000,1 to 1000,1001 100 iterations from 1000,1 to 1000,1001
(c) speedup sur 8 coeurs (d) dynamicit´ sur 8 coeurs
e
Figure 11 – Mesure 5 en O(1) sur 2 et 8 coeurs

13. 5 CONCLUSION 13
2.0 2.0
1.5 1.5
variable_dynamicity - 2
variable_speedup - 2 1.0 1.0
0.5 0.5
0.0 123456789111417202326293235384144475053565962656871747780838689929598
101316192225283134374043464952555861646770737679828588919497101
121518212427303336394245485154576063666972757881848790939699
100 0.0 123456789111417202326293235384144475053565962656871747780838689929598
101316192225283134374043464952555861646770737679828588919497101
121518212427303336394245485154576063666972757881848790939699
100
100 iterations from 2,1000 to 202,1000 100 iterations from 2,1000 to 202,1000
(a) speedup sur 2 coeurs (b) dynamicit´ sur 2 coeurs
e
7 3.5
6 3.0
5 2.5
variable_dynamicity - 2
variable_speedup - 2
4 2.0
3 1.5
2 1.0
1 0.5
0 123456789111417202326293235384144475053565962656871747780838689929598
101316192225283134374043464952555861646770737679828588919497101
121518212427303336394245485154576063666972757881848790939699
100 0.0 123456789111417202326293235384144475053565962656871747780838689929598
101316192225283134374043464952555861646770737679828588919497101
121518212427303336394245485154576063666972757881848790939699
100
100 iterations from 8,1000 to 808,1000 100 iterations from 8,1000 to 808,1000
(c) speedup sur 8 coeurs (d) dynamicit´ sur 8 coeurs
e
Figure 12 – Mesure 2 en O(n) sur 2 et 8 coeurs
2.0 2.0
1.5 1.5
dynamicity - 3
speedup - 3
1.0 1.0
0.5 0.5
0.0 123456789111417202326293235384144475053565962656871747780838689929598
101316192225283134374043464952555861646770737679828588919497101
121518212427303336394245485154576063666972757881848790939699
100 0.0 123456789111417202326293235384144475053565962656871747780838689929598
101316192225283134374043464952555861646770737679828588919497101
121518212427303336394245485154576063666972757881848790939699
100
100 iterations from 2,1000 to 2002,1000 100 iterations from 2,1000 to 2002,1000
(a) speedup sur 2 coeurs (b) dynamicit´ sur 2 coeurs
e
8 3.0
7
2.5
6
2.0
variable_dynamicity - 3
variable_speedup - 3
5
4 1.5
3
1.0
2
0.5
1
0 123456789111417202326293235384144475053565962656871747780838689929598
101316192225283134374043464952555861646770737679828588919497101
121518212427303336394245485154576063666972757881848790939699
100 0.0 123456789111417202326293235384144475053565962656871747780838689929598
101316192225283134374043464952555861646770737679828588919497101
121518212427303336394245485154576063666972757881848790939699
100
100 iterations from 8,1000 to 8008,1000 100 iterations from 8,1000 to 8008,1000
(c) speedup sur 8 coeurs (d) dynamicit´ sur 8 coeurs
e
Figure 13 – Mesure 3 en O(n) sur 2 et 8 coeurs