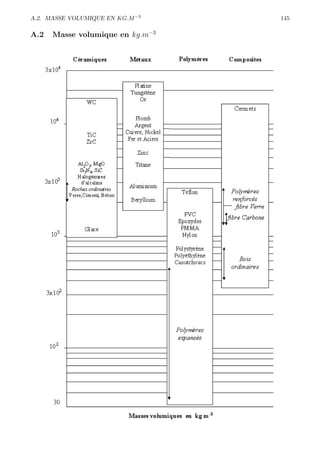
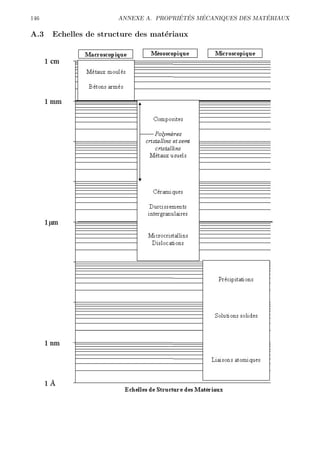
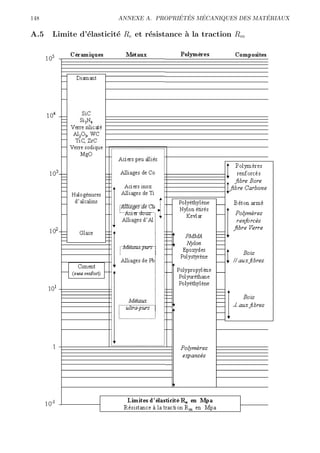
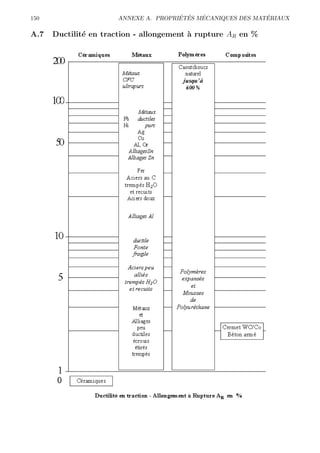
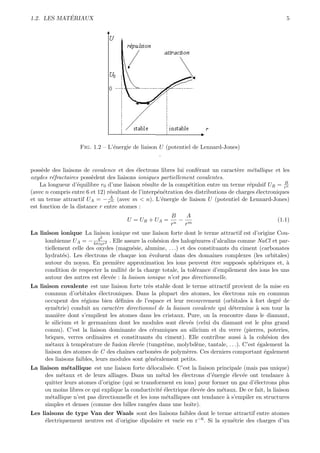
Le document traite des principes de la mécanique des solides et des matériaux, en se concentrant sur des concepts tels que l'élasticité, la plasticité et la rupture. Il présente divers aspects des matériaux, les lois mécaniques fondamentales, les comportements sous déformation et les théories associées. Ce contenu est destiné à l'enseignement et inclut des références aux essais mécaniques et à la dynamique des milieux déformables.

1. M´canique du solide et des mat´riaux
e e
´
Elasticit´-Plasticit´-Rupture
e e
Jean-Claude Charmet
Documents concernant l’enseignement (Cours, TD, Pr´ceptorats, TP) sur
e
http ://www.pmmh.espci.fr/fr/Enseignement
Rubrique : Supports de l’enseignement de m´canique des solides
e
ESPCI - Laboratoire d’Hydrodynamique et M´canique Physique
e

2. ii

3. Table des mati`res
e
1 MATERIAUX 1
1.1 La Science des mat´riaux . . . . . . . . . . . . . . . . .
e . . . . . . . . . . . . . . . . . 1
1.2 Les mat´riaux . . . . . . . . . . . . . . . . . . . . . . . .
e . . . . . . . . . . . . . . . . . 2
1.2.1 Les classes de mat´riaux et leurs propri´t´s . . .
e ee . . . . . . . . . . . . . . . . . 3
1.2.2 La liaison chimique et les propri´t´s m´caniques
ee e . . . . . . . . . . . . . . . . . 4
1.2.3 Raideur et r´sistance ultime . . . . . . . . . . . .
e . . . . . . . . . . . . . . . . . 6
1.2.4 Entre raideur et rupture . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10
1.3 La m´canique des solides continus . . . . . . . . . . . .
e . . . . . . . . . . . . . . . . . 11
1.3.1 Les essais en m´canique . . . . . . . . . . . . . .
e . . . . . . . . . . . . . . . . . 11
1.3.2 L’essai de traction simple . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12
1.3.3 Les modes de ruine . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13
1.3.4 H´t´rog´n´it´ et anisotropie . . . . . . . . . . . .
ee e e e . . . . . . . . . . . . . . . . . 13
1.3.5 Le Comportement m´canique des mat´riaux . . .
e e . . . . . . . . . . . . . . . . . 14
´ ´
2 ETAT MECANIQUE 15
2.1 Milieux d´formables . . . . . . . . . . . . . . . . . . . . . . . . . .
e . . . . . . . . . . . 15
2.1.1 Forces externes et ´quilibre m´canique . . . . . . . . . . . .
e e . . . . . . . . . . . 15
2.1.2 Forces internes, forces de surface et transmission des efforts . . . . . . . . . . . 15
2.1.3 Raideur, rigidit´, ´tat m´canique local . . . . . . . . . . . .
e e e . . . . . . . . . . . 16
2.2 Les contraintes . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 16
´
2.2.1 Etat m´canique local . . . . . . . . . . . . . . . . . . . . . .
e . . . . . . . . . . . 16
2.2.2 Le tenseur des contraintes . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 18
2.2.3 Propri´t´s du tenseur des contraintes . . . . . . . . . . . . .
ee . . . . . . . . . . . 20
2.2.4 Repr´sentation des contraintes . . . . . . . . . . . . . . . .
e . . . . . . . . . . . 22
2.3 La loi fondamentale de la dynamique . . . . . . . . . . . . . . . . . . . . . . . . . . . . 26
2.3.1 Equation de l’´quilibre dynamique . . . . . . . . . . . . . .
e . . . . . . . . . . . 26
2.3.2 Conditions aux limites . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 28
2.4 Les d´formations . . . . . . . . . . . . . . . . . . . . . . . . . . . .
e . . . . . . . . . . . 28
´
2.4.1 Etat local de d´formation . . . . . . . . . . . . . . . . . . .
e . . . . . . . . . . . 29
2.4.2 Les grandes d´formations . . . . . . . . . . . . . . . . . . .
e . . . . . . . . . . . 30
2.4.3 Les petites d´formations . . . . . . . . . . . . . . . . . . . .
e . . . . . . . . . . . 31
2.4.4 Le tenseur des d´formations . . . . . . . . . . . . . . . . . .
e . . . . . . . . . . . 34
2.4.5 Propri´t´s du tenseur des d´formations . . . . . . . . . . .
ee e . . . . . . . . . . . 35
2.4.6 Repr´sentation des d´formations . . . . . . . . . . . . . . .
e e . . . . . . . . . . . 36
2.5 Continuit´ et compatibilit´ des d´formations . . . . . . . . . . . .
e e e . . . . . . . . . . . 36
2.6 Lois de comportement : relations contraintes - d´formations . . . .
e . . . . . . . . . . . 37
2.7 R´sum´ Contraintes - D´formations . . . . . . . . . . . . . . . . .
e e e . . . . . . . . . . . 38
´
3 ELASTICITE ´ 39
3.1 Le travail de d´formation . . . . . . . . .
e . . . . . . . . . . . . . . . . . . . . . . . . . 39
3.1.1 Le travail virtuel de d´formation .
e . . . . . . . . . . . . . . . . . . . . . . . . . 39
3.1.2 Les potentiels ´lastiques . . . . . .
e . . . . . . . . . . . . . . . . . . . . . . . . . 40
3.1.3 Relation avec la thermodynamique . . . . . . . . . . . . . . . . . . . . . . . . . 41
iii

4. iv `
TABLE DES MATIERES
3.2 L’´lasticit´ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
e e . . . . . . . . . . 42
3.2.1 Les deux ´lasticit´s . . . . . . . . . . . . . . . . . . . . . . . .
e e . . . . . . . . . . 42
3.2.2 L’´lasticit´ lin´aire . . . . . . . . . . . . . . . . . . . . . . . .
e e e . . . . . . . . . . 42
3.2.3 L’´lasticit´ lin´aire isotrope . . . . . . . . . . . . . . . . . . .
e e e . . . . . . . . . . 43
3.3 Les modules ´lastiques . . . . . . . . . . . . . . . . . . . . . . . . . .
e . . . . . . . . . . 43
3.3.1 Module d’Young et coefficient de Poisson . . . . . . . . . . . . . . . . . . . . . 43
3.3.2 Module de Coulomb . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 44
3.3.3 Modules de Lam´ . . . . . . . . . . . . . . . . . . . . . . . . .
e . . . . . . . . . . 44
3.3.4 Modules de compressibilit´ et de cisaillement . . . . . . . . .
e . . . . . . . . . . 44
3.4 Les ´quations de l’´lasticit´ . . . . . . . . . . . . . . . . . . . . . . .
e e e . . . . . . . . . . 45
3.4.1 La loi de Hooke . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 45
3.4.2 Les modules effectifs . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 46
3.4.3 L’´quation de Lam´ . . . . . . . . . . . . . . . . . . . . . . .
e e . . . . . . . . . . 47
3.5 Les probl`mes plans . . . . . . . . . . . . . . . . . . . . . . . . . . .
e . . . . . . . . . . 48
3.5.1 La d´formation plane . . . . . . . . . . . . . . . . . . . . . .
e . . . . . . . . . . 48
3.5.2 La contrainte plane . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 49
3.5.3 Lieux caract´ristiques des probl`mes plans . . . . . . . . . . .
e e . . . . . . . . . . 50
3.6 Ondes et vibrations . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 52
3.6.1 Les ondes de volume . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 52
3.6.2 Barres, plaques et blocs . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 54
3.6.3 Les ondes de flexion . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 55
3.7 Th´or`mes ´nerg´tiques en ´lasticit´ lin´aire . . . . . . . . . . . . . .
e e e e e e e . . . . . . . . . . 57
3.7.1 R´ciprocit´ des chargements . . . . . . . . . . . . . . . . . . .
e e . . . . . . . . . . 57
3.7.2 Th´or`mes ´nerg´tiques . . . . . . . . . . . . . . . . . . . . .
e e e e . . . . . . . . . . 58
3.8 Flexion et flambement . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 59
3.8.1 Flexion des poutres . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 59
3.8.2 Flambement des poutres . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 62
3.9 Le contact . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 64
3.9.1 Le contact : ph´nom`ne m´canique local . . . . . . . . . . . .
e e e . . . . . . . . . . 64
3.9.2 Le contact en dimension d = 3 . . . . . . . . . . . . . . . . . . . . . . . . . . . 65
3.9.3 Poin¸on plan rigide ` base circulaire sous chargement normal
c a . . . . . . . . . . 66
3.9.4 Le contact de Hertz . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 67
e ´
3.10 R´sum´ Elasticit´ . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
e e . . . . . . . . . . 69
4 PLASTICITE ´ 71
4.1 Le comportement plastique . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 71
4.1.1 Le seuil de plasticit´ . . . . . . . . . . . . . . . . . . . . . . . . . .
e . . . . . . . 71
4.1.2 Influence des d´formations plastiques sur les propri´t´s m´caniques
e ee e . . . . . . . 72
4.1.3 Le comportement plastique pur . . . . . . . . . . . . . . . . . . . . . . . . . . . 73
4.1.4 Instabilit´ plastique et ´coulement libre . . . . . . . . . . . . . . .
e e . . . . . . . 75
4.1.5 La striction stable . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 77
4.2 Fronti`re ´lastique et fronti`re d’´coulement . . . . . . . . . . . . . . . . .
e e e e . . . . . . . 77
4.2.1 La fronti`re ´lastique . . . . . . . . . . . . . . . . . . . . . . . . . .
e e . . . . . . . 77
4.2.2 La fronti`re d’´coulement . . . . . . . . . . . . . . . . . . . . . . .
e e . . . . . . . 79
4.3 Crit`res de plasticit´ et d’´coulement . . . . . . . . . . . . . . . . . . . . .
e e e . . . . . . . 80
4.3.1 Effet d’une pression isotrope . . . . . . . . . . . . . . . . . . . . . . . . . . . . 81
4.3.2 Sym´tries du domaine de r´sistance . . . . . . . . . . . . . . . . .
e e . . . . . . . 81
4.3.3 Crit`re de Tresca et Courbe intrins`que de Caquot . . . . . . . . .
e e . . . . . . . 82
4.3.4 Crit`res de Von Mis`s et Coulomb . . . . . . . . . . . . . . . . . .
e e . . . . . . . 83
4.4 Les ´quations de la plasticit´ . . . . . . . . . . . . . . . . . . . . . . . . .
e e . . . . . . . 84
4.4.1 Les mat´riaux ductiles . . . . . . . . . . . . . . . . . . . . . . . . .
e . . . . . . . 85
4.4.2 Chargement radial et d´formation simple . . . . . . . . . . . . . .
e . . . . . . . 87
4.4.3 Loi de Hooke g´n´ralis´e . . . . . . . . . . . . . . . . . . . . . . . .
e e e . . . . . . . 88
4.4.4 Travail plastique . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 89

5. `
TABLE DES MATIERES v
4.5 La plasticit´ ` l’´chelle microscopique . . . . . . . . . . . . . . . . .
ea e . . . . . . . . . . 91
4.5.1 Le glissement dans un monocristal . . . . . . . . . . . . . . . . . . . . . . . . . 91
4.5.2 Les dislocations . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 93
4.5.3 Action d’un champ de contrainte externe sur une dislocations . . . . . . . . . . 98
4.5.4 Obstacles intrins`ques au mouvement des dislocations . . . .
e . . . . . . . . . . 102
4.5.5 Obstacles externes au mouvement des dislocations . . . . . . . . . . . . . . . . 106
4.5.6 Vers la plasticit´ macroscopique . . . . . . . . . . . . . . . . .
e . . . . . . . . . . 107
4.6 R´sum´ Plasticit´ . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
e e e . . . . . . . . . . 109
5 RUPTURE 111
5.1 R´sistance th´orique ` la rupture . . . . . . . . . . . . . . . . . . . . .
e e a . . . . . . . . . 112
5.1.1 La contrainte th´orique de clivage . . . . . . . . . . . . . . . .
e . . . . . . . . . 112
5.1.2 L’´nergie superficielle des solides . . . . . . . . . . . . . . . . .
e . . . . . . . . . 113
5.1.3 L’effet d’´chelle . . . . . . . . . . . . . . . . . . . . . . . . . . .
e . . . . . . . . . 113
5.2 Approche en force et en contrainte . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 114
5.2.1 Le coefficient de concentration des contraintes . . . . . . . . . . . . . . . . . . . 115
5.2.2 La contrainte de rupture effective . . . . . . . . . . . . . . . . . . . . . . . . . . 116
5.3 La rupture fragile . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 116
5.3.1 Fissure et modes de rupture . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 116
5.3.2 Les phases de chargement . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 117
5.3.3 Les hypoth`ses du mod`le de rupture fragile . . . . . . . . . . .
e e . . . . . . . . . 117
5.3.4 Le mod`le de rupture fragile . . . . . . . . . . . . . . . . . . .
e . . . . . . . . . 118
5.3.5 Coefficient de concentration k et facteur d’intensit´ K . . . . .
e . . . . . . . . . 118
5.4 La correction d’´lasto-plasticit´ . . . . . . . . . . . . . . . . . . . . . .
e e . . . . . . . . . 119
5.4.1 Autonomie de la zone critique . . . . . . . . . . . . . . . . . . . . . . . . . . . . 119
5.4.2 Mod`le d’Irwin en plasticit´ confin´e . . . . . . . . . . . . . . .
e e e . . . . . . . . . 119
5.4.3 Mod`le de Barenblatt . . . . . . . . . . . . . . . . . . . . . . .
e . . . . . . . . . 120
5.5 La t´nacit´ des mat´riaux . . . . . . . . . . . . . . . . . . . . . . . . .
e e e . . . . . . . . . 121
5.5.1 Condition d’amor¸age . . . . . . . . . . . . . . . . . . . . . . .
c . . . . . . . . . 121
5.5.2 La t´nacit´ th´orique . . . . . . . . . . . . . . . . . . . . . . . .
e e e . . . . . . . . . 122
5.5.3 Le paradoxe de la t´nacit´ . . . . . . . . . . . . . . . . . . . . .
e e . . . . . . . . . 122
5.5.4 La t´nacit´ effective . . . . . . . . . . . . . . . . . . . . . . . .
e e . . . . . . . . . 122
5.6 Approche ´nerg´tique . . . . . . . . . . . . . . . . . . . . . . . . . . .
e e . . . . . . . . . 123
5.6.1 Crit`re ´nerg´tique pour la rupture brutale . . . . . . . . . . .
e e e . . . . . . . . . 124
5.6.2 Le bilan d’´nergie . . . . . . . . . . . . . . . . . . . . . . . . .
e . . . . . . . . . 124
5.6.3 Condition d’amor¸age et taux de restitution de l’´nergie . . . .
c e . . . . . . . . . 125
5.6.4 Stabilit´ et propagation . . . . . . . . . . . . . . . . . . . . . .
e . . . . . . . . . 125
5.6.5 Courbe d’´quilibre d’une fissure . . . . . . . . . . . . . . . . .
e . . . . . . . . . 126
5.6.6 Influence du type de chargement . . . . . . . . . . . . . . . . . . . . . . . . . . 126
5.7 La longueur de Griffith . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 127
5.7.1 Taux de restitutiton d’´nergie . . . . . . . . . . . . . . . . . . .
e . . . . . . . . . 128
´
5.7.2 Energie de fissuration et longueur absolue . . . . . . . . . . . . . . . . . . . . . 129
´
5.7.3 Energie de fissuration et t´nacit´ : La relation entre GC et KC
e e . . . . . . . . . 130
5.8 La propagation des fissures . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 131
5.8.1 La courbe d’´quilibre et la propagation contrˆl´e . . . . . . . .
e oe . . . . . . . . . 132
5.8.2 La stabilit´ de la propagation . . . . . . . . . . . . . . . . . . .
e . . . . . . . . . 132
5.8.3 Influence du type de chargement . . . . . . . . . . . . . . . . . . . . . . . . . . 133
5.9 Les m´canismes de la rupture brutale . . . . . . . . . . . . . . . . . .
e . . . . . . . . . 134
5.9.1 Le d´chirement ductile des m´taux . . . . . . . . . . . . . . . .
e e . . . . . . . . . 134
5.9.2 Le clivage fragile des c´ramiques . . . . . . . . . . . . . . . . .
e . . . . . . . . . 135
5.10 La r´sistance ` la rupture des mat´riaux fragiles . . . . . . . . . . . .
e a e . . . . . . . . . 136
5.10.1 R´sistance ` la rupture . . . . . . . . . . . . . . . . . . . . . .
e a . . . . . . . . . 136
5.10.2 La statistique de la rupture fragile . . . . . . . . . . . . . . . . . . . . . . . . . 138
5.11 R´sum´ Rupture . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
e e . . . . . . . . . 141

6. vi `
TABLE DES MATIERES
A Propri´t´s m´caniques des mat´riaux
e e e e 143
A.1 Temp´ratures de fusion et de ramollissement(*) en °K .
e . . . . . . . . . . . . . . . . . 144
A.2 Masse volumique en kg.m−3 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 145
A.3 Echelles de structure des mat´riaux . . . . . . . . . . . .
e . . . . . . . . . . . . . . . . . 146
A.4 Module d’Young en Gpa . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 147
A.5 Limite d’´lasticit´ Re et r´sistance ` la traction Rm
e e e a . . . . . . . . . . . . . . . . . 148
Re
A.6 Limite d’´lasticit´ normalis´e : E . . . . . . . . . . . .
e e e . . . . . . . . . . . . . . . . . 149
A.7 Ductilit´ en traction - allongement ` rupture AR en %
e a . . . . . . . . . . . . . . . . . 150
A.8 T´nacit´ KC en M P a.m
e e 1/2 ` l’ambiante . . . . . . . . .
a . . . . . . . . . . . . . . . . . 151
A.9 Energie de rupture GC en kJ.m−2 ` l’ambiante . . . . .
a . . . . . . . . . . . . . . . . . 152
B Op´rateurs diff´rentiels - Formulaire
e e 153
B.1 Coordonn´es cart´siennes . . . . . . .
e e . . . . . . . . . . . . . . . . . . . . . . . . . . . 154
B.1.1 Scalaire φ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 154
B.1.2 Vecteur u . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 154
B.1.3 Contrainte σ et D´formation ε
e . . . . . . . . . . . . . . . . . . . . . . . . . . . 154
B.2 Coordonn´es polaires . . . . . . . . . .
e . . . . . . . . . . . . . . . . . . . . . . . . . . . 155
B.2.1 Scalaire φ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 155
B.2.2 Vecteur u . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 155
B.2.3 Contrainte σ et D´formation ε
e . . . . . . . . . . . . . . . . . . . . . . . . . . . 155
B.3 Coordonn´es sph´riques . . . . . . . .
e e . . . . . . . . . . . . . . . . . . . . . . . . . . . 156
B.3.1 Scalaire φ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 156
B.3.2 Vecteur u . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 156
B.3.3 Contrainte σ et D´formation ε
e . . . . . . . . . . . . . . . . . . . . . . . . . . . 156
C Bibliographie 157

7. Chapitre 1
MATERIAUX
1.1 La Science des mat´riaux
e
Alors que la r´sistance des structures et des mat´riaux est un domaine qui nous concerne tous dans
e e
notre vie quotidienne, elle est rest´e pendant des si`cles le parent pauvre des “Sciences”. Essayer de
e e
comprendre pourquoi se produisent des catastrophes telles que l’effondrement d’un pont ou la rupture
d’un barrage ´tait le lot des hommes de l’art dont les connaissances ´taient surtout affaire d’empirisme
e e
et de tradition.
C’est en 1638, sur la fin de sa vie, que Galil´e (1564-1642) publia son “Dialoghi delle due nuove
e
scienze”, premier ouvrage publi´ qui traitait s´rieusement de r´sistance m´canique. Il ´tudia l’influence
e e e e e
de la section sur la r´sistance statique des tiges, montrant que la charge de rupture ´tait bien propor-
e e
tionnelle ` l’aire de la section droite, et s’int´ressa aussi, avec plus ou moins de bonheur (il ne pouvait
a e
b´n´ficier des travaux de Isaac Newton (1642-1727) sur le principe de l’action et de la r´action), ` la
e e e a
r´sistance en flexion de divers types de poutres.
e
Alors qu’il partageait avec les Grecs leur m´pris pour les Sciences appliqu´es, Isaac Newton y
e e
apporta deux outils d’importance primordiale : le calcul diff´rentiel et sa troisi`me loi, plus connue
e e
sous le nom de “Principe de l’action et de la r´action”. Cette loi stipule que si un corps pesant exerce sur
e
un corps support une force due ` l’action de la pesanteur (contact statique) ou ` celle de l’acc´l´ration
a a ee
(contact dynamique), ce support exerce en sens inverse une force de r´action ´gale et oppos´e sur le
e e e
corps pesant. Si les lois de Newton nous donnent les forces auxquelles une structure peut ˆtre soumise,
e
elle ne nous donne aucune information sur les forces de r´action au sein des mat´riaux qui la compose.
e e
Comment et pourquoi la structure r´siste-t-elle ? La r´ponse fut donn´e par Robert Hooke (1635-
e e e
´
1703). Etudiant l’allongement produit par l’action de charges croissantes appliqu´es sur divers mat´riaux,
e e
il ´tablit une relation de proportionnalit´, dans la limite de pr´cision des mesures de l’´poque, et il
e e e e
formula la loi de l’´lasticit´ qui porte son nom en 1679 dans son trait´ “ De potentia restituva” sous la
e e e
forme “Ut tensio, sic vis”. Telle tension, telle force, car en latin tensio signifie g´n´ralement ´tirement
e e e
et non tension - au sens de force - bien que les romains aient souvent confondu les deux acceptions.
Nous savons aujourd’hui que cette loi s’applique bien ` presque tous les solides usuels (cristallins ou
a
amorphes) aux faibles contraintes mais que les mat´riaux constitutifs des structures biologiques la
e
suivent rarement. Cependant, pour les structures et les mat´riaux usuels, elle joue un rˆle essentiel.
e o
Malgr´ leur richesse, les id´es de Hooke ne d´bouch`rent que cent ans plus tard sous la forme
e e e e
des concepts de Contrainte et de D´formation introduits par Augustin Cauchy (1789-1857). Bien
e
que recouvrant des notions tr`s simples ces deux termes restent souvent myst´rieux et rebutants.
e e
Jusqu’alors les ´tudes avaient port´ sur des structures plus ou moins ´labor´es pour lesquelles les
e e e e
analyses en terme d’allongement et de force ne distinguaient pas ce qui ´tait la contribution de la
e
g´om´trie de la structure de celle intrins`que au mat´riau. La d´finition de l’´tat m´canique local en
e e e e e e e
terme de contrainte et de d´formation a v´ritablement sorti la Science des Mat´riaux de l’impasse.
e e e
L’id´e qu’un mat´riau puisse ˆtre caract´ris´ par une rigidit´ intrins`que est due ` Thomas Young
e e e e e e e a
(1773-1829) qui d´montrait ainsi que la d´formation globale d’une structure r´sulte en fait de la com-
e e e
binaison de la raideur du mat´riau et de la taille et de la forme de cette structure. Cependant on
e
doit ` Henri Navier (1785-1836) d’avoir formul´ math´matiquement le concept d´velopp´ par Thomas
a e e e e
1

8. 2 CHAPITRE 1. MATERIAUX
Young, en s’appuyant sur les notions de d´formation et de contrainte formul´es par Augustin Cau-
e e
chy. Les bases ´taient pos´es pour entreprendre la r´solution analytique des probl`mes de calcul des
e e e e
structures.
Fort de ces progr`s, le d´but du XIXe si`cle fut la p´riode privil´gi´e des tentatives de pr´diction
e e e e e e e
des r´sistances pratiques des mat´riaux ` partir des connaissances acquises sur les forces des liaisons
e e a
interatomiques et des catastrophes, les r´sultats obtenus s’´cartant de plusieurs ordres de grandeur
e e
des valeurs exp´rimentales. Il fallut attendre plus d’un si`cle pour voir se dessiner une approche
e e
satisfaisante des m´canismes comportementaux au del` de la zone ´lastique : ductilit´ et plasticit´,
e a e e e
fragilit´ et rupture. En effet, ce n’est qu’en 1920 que A. Griffith publia son article r´volutionnaire sur
e e
la r´sistance ` la rupture des solides. et ce n’est qu’en 1934 que Geoffrey Taylor sugg´ra l’existence de
e a e
dislocations dans les cristaux pour interpr´ter les propri´t´s de ductilit´ des m´taux purs.
e ee e e
La Science des Mat´riaux disposait enfin des outils conceptuels n´cessaires ` son d´veloppement.
e e a e
Les travaux de Griffith et de Taylor sont ` la base des m´thodes d’´laboration de nos mat´riaux
a e e e
modernes. Le d´veloppement conjoint des nouveaux mat´riaux et des moyens de calcul par ´l´ments
e e ee
finis permet aujourd’hui aux ing´nieurs de concevoir des structures m´caniquement fiables de plus en
e e
plus complexes comme en t´moignent les r´alisations de haute technologie du pont de Normandie ou
e e
du viaduc de Millau pour ne citer que le domaine des ouvrages d’art.
1.2 Les mat´riaux
e
Le physico-chimiste ´tudie les propri´t´s de la mati`re, m´taux, alliages, verres, polym`res, tissus
e ee e e e
biologiques,. . .mais ne s’occupe que rarement des mat´riaux correspondants. Les mat´riaux sont de
e e
la mati`re travaill´es par l’homme pour fabriquer des objets. Le process d’´laboration procure au
e e e
mat´riau une certaine microstructure qui ` son tour d´termine ses propri´t´s chimiques, physiques,
e a e ee
m´caniques, ´lectriques, thermiques. Il s’agit l` des propri´t´s intrins`ques du mat´riau. La synth`se
e e a ee e e e
des mat´riaux en laboratoire s’appuie sur la trilogie mise en oeuvre- structure - propri´t´s :.
e ee
Proc´d´s de fabrication
e e Coul´e, frittage, d´pˆts (´lectrolytique,. . .)
e e o e
Mise en forme par d´formation
e Laminage, extrusion, ´tirage, forgeage, emboutissage,
e
martelage, . . .
Mise en forme par enl`vement de
e Usinage, rectification, d´coupe (chalumeau, laser, jet
e
mati`re
e d’eau), ´lectro´rosion, . . .
e e
Traitements thermiques Recuit, trempe, vieillissement, revenu, . . .
Assemblage Soudage, collage, rivetage, boulonnage, vissage, fret-
tage, . . .
Traitement de surface Grenaillage, rodage, trempe superficielle, revˆtement
e
par d´pˆt (´lectrolytique, phase vapeur, projection,
e o e
. . .)
...
Tab. 1.1 – Proc´d´s de mise en oeuvre
e e
Type de Liaison, Mol´cules
e Type et taille
Syst`me cristallin, Ordre
e a
` longue et courte distance
Polym`res
e Taux de r´ticulation et de cristallinit´
e e
H´t´rog´n´it´s chimiques
ee e e e S´gr´gation aux joints de grains
e e
Pr´cipit´s coh´rents, incoh´rents
e e e e Dimension, forme, fraction volumique
Composites Plis, fibres (courtes longues trichytes)
Texture, Porosit´e
...
Tab. 1.2 – Microstructure

9. ´
1.2. LES MATERIAUX 3
M´caniques
e Modules et limites ´lastiques, ´crouissage (contrainte
e e
d’´coulement), charge ` la rupture, vitesse de fluage,
e a
ductilit´, allongement r´parti, ` rupture, taux de
e e a
striction, viscosit´, capacit´ d’amortissement, duret´,
e e e
r´sistance (fatigue, usure, abrasion, . . .) . . .
e
Tab. 1.3 – Propri´t´s m´caniques
ee e
1.2.1 Les classes de mat´riaux et leurs propri´t´s
e e e
L’ing´nieur groupe les mat´riaux en trois classes correspondant approximativement ` trois types
e e a
de comportement.
Mat´riaux
e Comportement Propri´t´s
ee
Verres et c´ramiques
e Duret´ et fragilit´
e e Isolants et r´fractaires
e
M´taux et Alliages
e Ductilit´
e Conducteurs et R´flecteurs
e
Polym`res
e D´formabilit´
e e
Tab. 1.4 – Les trois classes de mat´riaux
e
Cette classification recoupe celle des mat´riaux en fonction de leur type de liaison chimique. Ce
e
r´sultat n’est pas fortuit dans la mesure o` une grande partie des propri´t´s physiques et en particulier
e u ee
des propri´t´s m´caniques sont conditionn´es par les propri´t´s des liaisons chimiques.
ee e e ee
Liaison covalente
Bore Fibres
Carbone diamant Poudres abrasives - fibres
Silicium - germanium Composants ´lectroniques
e
Carbures - nitrures Meules, paliers, fibres r´fractaires
e
Polym`res
e Thermodurcissables
Liaison ionique
Alumine, silice, zircone Abrasifs, r´fractaires
e
Verres Vitres, emballages, fibres
Oxydes et carbures d’uranium Industrie nucl´aire
e
Liaison m´tallique
e
Aluminium Alliages l´gers
e
Zinc Bˆtiment, fonderie
a
Titane A´ronautique
e
Zirconium Industrie chimique, gaines combustible nucl´aire
e
Cuivre Laitons, bronzes
Or, Argent Monnaies, brasures, photographie, contacts
Etain, Plomb Plomberie, soudure
Tantale R´fractaire, ´lectronique
e e
Fer, Cobalt, Nickel Aciers, fontes, superalliages
Chaˆınes covalentes avec liaisons Van der Waals ou Hydrog`ne e
Polym`res
e Thermoplastiques
Elastom`res
e
Bois, Papiers, Cartons
Ciments, B´tons
e
Tab. 1.5 – Mat´riaux et type de liaisons chimiques
e
A ces trois classes s’ajoute la classe des composites qui permet une grande souplesse de combinai-
sons de propri´t´s.
ee

10. 4 CHAPITRE 1. MATERIAUX
Fig. 1.1 – La classe des mat´riaux composites
e
.
1.2.2 La liaison chimique et les propri´t´s m´caniques
e e e
Pour r´sister aux efforts qui lui sont appliqu´s un mat´riau n’a d’autre ressource que de se d´former
e e e e
de mani`re ` stocker ou ` dissiper l’´nergie qui lui est fournie. Dans les mat´riaux cristallins la
e a a e e
d´formation est associ´e ` de l´g`res variations des distances interatomiques, mais elles entraˆ
e e a e e ınent
des variations consid´rables de l’´nergie de coh´sion (´nergie interne). Ainsi, pour comprendre les
e e e e
caract´ristiques m´caniques des mat´riaux comme leur module il faut descendre ` l’´chelle atomique.
e e e a e
Deux facteurs ont un effet pr´pond´rant sur ces propri´t´s :
e e ee
Les forces qui retiennent les atomes les uns aux autres (les liaisons atomiques). Elles agissent comme
de petits ressorts qui lient un atome ` ses proches voisins dans l’´tat solide.
a e
La mani`re dont les atomes sont empil´s (l’empilement atomique) qui va d´terminer le nombre de
e e e
ressorts par unit´ de surface et l’angle sous lequel ils sont ´tir´s.
e e e
Les liaisons atomiques
Les propri´t´s des mat´riaux sont fortement corr´l´es au type de liaison entre atomes car il
ee e ee
d´termine l’´nergie de coh´sion de la mati`re, la force n´cessaire pour ´carter les atomes les uns
e e e e e e
des autres jusqu’` rupture, le coefficient de dilatation, la conductibilit´ ´lectrique ou thermique, la
a e e
stabilit´ des phases, la r´activit´, . . .. Le chimiste distingue deux types de liaisons : les liaisons fortes
e e e
(ionique, covalente et m´tallique) toutes assez r´sistantes qui se d´sagr`gent entre 1000 et 5000 °K et
e e e e
les liaisons faibles ou secondaires (Van der Waals et hydrog`ne) relativement faibles qui fondent
e
entre 100 et 500 °K.
La temp´rature de fusion du corps est un bon indicateur de la r´sistance de ses liaisons
e e
Liaisons Ionique ou Covalente M´tallique
e Van der Waals
Energie 10 5 0,1
Tab. 1.6 – Energie de liaison typique en eV/atome
La coh´sion des m´taux et des c´ramiques est enti`rement due ` des liaisons fortes, covalentes et
e e e e a
ioniques pour les c´ramiques, m´talliques et covalentes pour les m´taux. Ces liaisons fortes et rigides
e e e
se caract´risent par des modules m´caniques ´lev´s.
e e e e
Bien que beaucoup plus faibles, les liaisons secondaires n’en sont pas moins importantes. Elles sont
responsables de liens entre les mol´cules de polym`res, leur permettant d’exister ` l’´tat solide. Sans
e e a e
elles, l’eau bouillirait ` -80°C et la vie sur terre n’existerait pas.
a
Il faut cependant garder ` l’esprit que de nombreux atomes sont retenus les uns aux autres par
a
des liaisons mixtes qui combinent plusieurs sortes de liaisons ´l´mentaires. Ainsi le carbone graphite
ee

11. ´
1.2. LES MATERIAUX 5
Fig. 1.2 – L’´nergie de liaison U (potentiel de Lennard-Jones)
e
.
poss`de des liaisons de covalence et des ´lectrons libres lui conf´rant un caract`re m´tallique et les
e e e e e
oxydes r´fractaires poss`dent des liaisons ioniques partiellement covalentes.
e e
B
La longueur d’´quilibre r0 d’une liaison r´sulte de la comp´tition entre un terme r´pulsif UR = rn
e e e e
(avec n compris entre 6 et 12) r´sultant de l’interp´n´tration des distributions de charges ´lectroniques
e e e e
A
et un terme attractif UA = − rm (avec m < n). L’´nergie de liaison U (potentiel de Lennard-Jones)
e
est fonction de la distance r entre atomes :
B A
U = UR + UA = − (1.1)
rn rm
La liaison ionique La liaison ionique est une liaison forte dont le terme attractif est d’origine Cou-
q2
lombienne UA = − 4πε0 r2 . Elle assure la coh´sion des halog´nures d’alcalins comme NaCl et par-
e e
tiellement celle des oxydes (magn´sie, alumine, . . .) et des constituants du ciment (carbonates
e
hydrat´s). Les ´lectrons de chaque ion ´voluent dans des domaines complexes (les orbitales)
e e e
autour du noyau. En premi`re approximation les ions peuvent ˆtre suppos´s sph´riques et, `
e e e e a
condition de respecter la nullit´ de la charge totale, la tol´rance d’empilement des ions les uns
e e
autour des autres est ´lev´e : la liaison ionique n’est pas directionnelle.
e e
La liaison covalente est une liaison forte tr`s stable dont le terme attractif provient de la mise en
e
commun d’orbitales ´lectroniques. Dans la plupart des atomes, les ´lectrons mis en commun
e e
occupent des r´gions bien d´finies de l’espace et leur recouvrement (orbitales ` fort degr´ de
e e a e
sym´trie) conduit au caract`re directionnel de la liaison covalente qui d´termine ` son tour la
e e e a
mani`re dont s’empilent les atomes dans les cristaux. Pure, on la rencontre dans le diamant,
e
le silicium et le germanium dont les modules sont ´lev´s (celui du diamant est le plus grand
e e
connu). C’est la liaison dominante des c´ramiques au silicium et du verre (pierres, poteries,
e
briques, verres ordinaires et constituants du ciment). Elle contribue aussi ` la coh´sion des
a e
m´taux ` temp´rature de fusion ´lev´e (tungst`ne, molybd`ne, tantale, . . .). C’est ´galement la
e a e e e e e e
liaison des atomes de C des chaˆ ınes carbon´es de polym`res. Ces derniers comportant ´galement
e e e
des liaisons faibles, leurs modules sont g´n´ralement petits.
e e
La liaison m´tallique est une liaison forte d´localis´e. C’est la liaison principale (mais pas unique)
e e e
des m´taux et de leurs alliages. Dans un m´tal les ´lectrons d’´nergie ´lev´e ont tendance `
e e e e e e a
quitter leurs atomes d’origine (qui se transforment en ions) pour former un gaz d’´lectrons plus
e
ou moins libres ce qui explique la conductivit´ ´lectrique ´lev´e des m´taux. De ce fait, la liaison
ee e e e
m´tallique n’est pas directionnelle et les ions m´talliques ont tendance ` s’empiler en structures
e e a
simples et denses (comme des billes rang´es dans une boˆ
e ıte).
Les liaisons de type Van der Waals sont des liaisons faibles dont le terme attractif entre atomes
´lectriquement neutres est d’origine dipolaire et varie en r−6 . Si la sym´trie des charges d’un
e e

12. 6 CHAPITRE 1. MATERIAUX
atome existe en moyenne dans le temps (neutralit´ ´lectrique), la distribution instantan´e autour
ee e
du noyau ne l’est pas, cr´ant un moment dipolaire al´atoire. Ce moment induit un moment
e e
similaire sur un atome voisin et les deux dipˆles ainsi form´s s’attirent. Ce sont ces liaisons qui
o e
sont responsables de l’´tat liquide des gaz ` basse temp´rature, lorsque l’agitation thermique est
e a e
trop faible pour les rompre, et la glace n’existe que grˆce aux liaisons hydrog`ne.
a e
C’est par la formation de liaisons fortes et faibles que la mati`re se condense pour passer de l’´tat
e e
gazeux ` l’´tat liquide ou solide. Les liaisons faibles des liquides ordinaires ont fondu ; pour cette raison
a e
ils opposent une forte r´sistance ` la compression mais faible ` la traction ou au cisaillement. Leur
e a a
module de compressibilit´ K est grand devant celui des gaz, mais leur module de cisaillement G et
e
leur module d’Young E sont nuls. De mani`re g´n´rale les modules d´pendent de l’´tat des liaisons
e e e e e
(solides ou fondues) et de la structure de la mati`re.
e
´
Etat Liaisons Modules
Faibles Fortes K G et E
Liquides rompues — grand nuls (E = G = 0)
Cristaux liquides rompues — grand quasi nuls (E G 0)
Caoutchoucs ´tablies
e ´tablies
e grand petits (E G K)
Verres — ´tablies
e grand grands (E G K)
Cristaux — ´tablies
e grand grands (E G K)
Tab. 1.7 – Liaisons chimiques et ´tats de la mati`re
e e
L’empilement des atomes
La fa¸on dont les atomes sont empil´s est ´galement une donn´e importante pour d´terminer les
c e e e e
propri´t´s m´caniques des mat´riaux. De nombreux mat´riaux (presque tous les m´taux et c´ramiques)
ee e e e e e
sont constitu´s d’un assemblage de petits cristaux dans lesquels les atomes sont empil´s en une struc-
e e
ture r´guli`re r´p´t´e dans les trois dimensions. Les cristaux les plus simples peuvent ˆtre mod´lis´s
e e e ee e e e
en assimilant les atomes ` des sph`res dures. Il s’agit l` cependant d’une simplification consid´rable
a e a e
quoique commode. En simplifiant encore plus un corps pur avec une seule taille de sph`res dures e
aux liaisons non directives aura tendance ` s’organiser en une structure compacte o` les sph`res sont
a u e
rang´es sans contrainte autre que g´om´trique. Le Cuivre est un bon exemple de mat´riau r´pondant `
e e e e e a
ces conditions. Les caract´ristiques principales de l’empilement atomique s’expriment au travers de la
e
masse volumique du mat´riau qui est l’expression de la masse et du diam`tre des atomes constituants,
e e
mais aussi de la densit´ de l’empilement dans le cristal. La plupart des m´taux ont de fortes densit´s
e e e
parce que leurs atomes sont lourds et empil´s de fa¸on compacte.
e c
Les verres min´raux sont constitu´s d’oxydes (comme SiO2 ) amorphes dans lesquels l’empilement
e e
n’est pas cristallin. Ainsi, la silice vitreuse, du fait des liaisons covalentes Si − O reste solide bien au
dessus de 1000°C. L’ajout de N a2 O diminue la rigidit´ de la structure et abaisse la temp´rature de
e e
ramollissement (` laquelle on peut travailler le verre sodique usuel des bouteilles et des vitres) aux
a
alentours de 700°C en brisant une partie des liaisons covalentes.
La masse volumique des polym`res et de nombreuses c´ramique est plus faible que celle des m´taux
e e e
parce que les atomes constituants (C, H, O) sont plus l´gers et qu’ils adoptent des structures d’empi-
e
lement non compact (cf. annexe A.2).
1.2.3 Raideur et r´sistance ultime
e
La connaissance du potentiel de Lennard-Jones (1.1) permet de calculer la force interatomique
F = dU et la longueur au repos r0 (F = 0) de la liaison qui correspond au minimum de l’´nergie U de
dr e
la liaison. Lorsque l’on ´tire la liaison la force croˆ progressivement jusqu’` la valeur maximale FM
e ıt a
pour une longueur rM correspondant ` la dissociation de la liaison qui se produit au point d’inflexion
a
dF
de la courbe U (r). La pente S = dr de la courbe F (r) d´finit la raideur de la liaison. Au repos, F = 0
e
d2 U
et r = r0 , elle a pour valeur S0 = dr2 |r0 .

13. ´
1.2. LES MATERIAUX 7
´
Fig. 1.3 – Energie et r´sistance d’une liaison
e
.
Elle augmente depuis cette valeur lorsque la liaison est de plus en plus comprim´e, traduisant la
e
r´sistance de plus en plus grande du mat´riau ` la compression hydrostatique. Au contraire, lorsque la
e e a
liaison est ´tir´e, sa raideur diminue jusqu’` s’annuler au point de dissociation r = rM o` la liaison ne
e e a u
pr´sente plus de r´sistance ` la traction. Pour de faibles variations r − r0 de la longueur de la liaison
e e a
autour de sa valeur d’´quilibre r = r0 , la force de r´sistance F = S0 (r − r0 ) varie donc lin´airement
e e e
avec r − r0 pour tous les mat´riaux. On peut donc calculer la valeur S0 de la raideur de la liaison en
e
fonction de sa nature ` partir de courbes th´oriques U (r). C’est le domaine de la physique du solide
a e
et de la chimie quantique.
S0
Type de liaison S0 (N.m−1 ) E= r0 (Gpa)
Covalentes, liaison C − C 180 1000
Ionique pure (i.e Na-Cl) 9 - 21 30 - 70
M´tallique pure (i.e Cu-Cu)
e 15 - 40 30 - 150
Hydrog`ne (i.e H2 O − H2 O)
e 2 8
Van der Waals (cires, polym`res)
e 1 2
Tab. 1.8 – Raideurs de liaisons : valeur typiques
La coh´sion d’un mat´riau cristallin ´tant assur´e par les liaisons interatomiques, leur raideur
e e e e
permet th´oriquement de calculer les modules ´lastiques du mat´riau ` condition de prendre en compte
e e e a
la structure cristalline qui va d´finir les directions des liaisons par rapport ` l’effort appliqu´ d’o` un
e a e u
comportement g´n´ralement anisotrope.
e e
Pour passer de la raideur microscopique (liaison) ` la raideur macroscopique (module d’Young E )
a
associ´ ` chaque type de liaison, donc ` chaque classe de mat´riau, consid´rons le mod`le simple dans
ea a e e e
A
lequel tous les atomes sont situ´s sur un r´seau cubique (cf. Fig. 1.3). N = r2 ´tant le nombre de liaisons
e e e
0
qui traversent une section droite d’aire A normale ` la force macroscopique appliqu´e f , la r´sistance
a e e
` la traction microscopique de chaque liaison faiblement ´tir´e de r0 ` r ´tant F = S0 (r − r0 ), la
a e e a e
force macroscopique appliqu´e est donc f = N F = A S0 r−r0 . R´´crite en terme de contrainte, densit´
e r
0
r0 ee e
f r−r0
surfacique de force σ = A et de d´formation, variation relative d’allongement ε = r0 , cette relation
e
devient σ = S0 ε. Soit l’expression du module d’Young E = σ caract´risant la raideur macroscopique
r
0
ε e
S0
en fonction de la raideur microscopique E = r0 .
En comparant les ordres de grandeur ainsi calcul´s (Tab. 1.8) avec les valeurs mesur´es (cf. annexe A.4),
e e

14. 8 CHAPITRE 1. MATERIAUX
on constate un bon accord pour les mat´riaux cristallins : c´ramiques et m´taux. On peut ´galement
e e e e
noter la tr`s bonne corr´lation entre les valeurs des modules ´lastiques et les temp´ratures de fusion
e e e e
des mat´riaux (cf. annexe A.1) qui traduisent bien la r´sistance des liaisons. Ainsi le diamant qui
e e
pr´sente le plus fort module d’Young connu est aussi le mat´riau dont la temp´rature de fusion est la
e e e
plus ´lev´e.
e e
Le mod`le pr´c´dent permet ´galement d’estimer la limite th´orique de r´sistance ultime ` la
e e e e e e a
traction σM d’un mat´riau en fonction de son type de liaison. C’est la contrainte associ´e ` la force
e e a
FM qui conduit ` la dissociation de la liaison au maximum de la courbe F (r), donc au point d’inflexion
a
de la courbe U (r) ou encore ` la valeur S = 0 de la raideur. Il lui correspond une d´formation maximale
a e
εM associ´e ` la longueur maximale rM d’extension de la liaison.
e a
m+1 1
σM 1 m + 1 n−m n + 1 n−m
= εM = −1 (1.2)
E n+1 n+1 m+1
E
Pour un cristal ionique, m=1 et n=9, la limite ultime ` la traction est σM
a 15 et la d´formation
e
σM 1 1
εM 20% . En faisant varier m de 1 ` 6 et n de 6 ` 12, le rapport E varie assez peu, entre 10 et 25
a a
et εM varie entre 10 et 30%.
Le cas particulier des polym`res
e
D’apr`s (Tab. 1.8) tous les mat´riaux v´ritablement ` l’´tat solide devraient avoir des modules
e e e a e
´lastiques sup´rieurs ` la valeur minimale calcul´e de 2 GPa. Or, pour la classe des mat´riaux po-
e e a e e
lym`res, les estimations bas´es sur la raideur des liaisons pr´sentent une divergence de plusieurs ordres
e e e
de grandeur par rapport aux valeurs mesur´es. Ceci provient de leur structure particuli`re. Les po-
e e
lym`res sont constitu´s de tr`s longues mol´cules. Bien que les atomes qui en constituent le squelette
e e e e
(g´n´ralement compos´ d’atomes de carbone) soient li´s par des liaisons covalentes rigides, la longueur
e e e e
de ces chaˆınes les rend flexibles et, selon les conditions, ces chaˆ
ınes s’arrangent
– au hasard et non en structures p´riodiques tridimensionnelles (polym`res amorphes)
e e
– se replient les unes sur les autres de mani`re sym´trique et r´guli`re ` la mani`re d’une rame de
e e e e a e
papier informatique (polym`res cristallins)
e
– ou pr´sentent une structure mixte contenant ` la fois des zones amorphes et des zones cristallis´es.
e a e
Fig. 1.4 – Structure des polym`res
e
– ` gauche : amorphe partiellement cristallis´
a e
– ` droite : fortement r´ticul´ par de nombreux ponts covalents interchaˆ
a e e ınes
Leurs propri´t´s m´caniques sont conditionn´e par l’indice de cristallinit´, le degr´ de pontage entre
ee e e e e
les chaˆ
ınes et la densit´ des liaisons faibles interchaˆ
e ınes de type Van der Waals. Les liaisons le long
du squelette des macromol´cules et les pontages occasionnels entre chaˆ
e ınes (liaisons covalentes tr`s
e

15. ´
1.2. LES MATERIAUX 9
raides) ne participent que tr`s peu ` la raideur globale, sauf ` tr`s forte d´formation lorsque toutes les
e a a e e
chaˆınes sont compl`tement ´tir´es. Ce sont les liaisons secondaires faibles (inter-chaˆ
e e e ınes de type Van
der Waals) qui contrˆlent les propri´t´s m´caniques des polym`res.
o ee e e
Or la densit´ des liaisons faibles inter-chaˆ
e ınes ´tant une fonction de la temp´rature, la temp´rature
e e e
de fusion du mat´riau doit ˆtre remplac´e par la temp´rature de transition vitreuse Tg qui caract´rise
e e e e e
la transition entre un ´tat normal basse temp´rature (T < Tg ) dans lequel les liaisons faibles sont
e e
´tablies et un ´tat fondu haute temp´rature (T > Tg ) dans lequel les liaisons secondaires ont fondu.
e e e
La plupart des polym`res tr`s flexibles ont partiellement fondu ` l’ambiante. Au del` de Tg les po-
e e a a
Fig. 1.5 – Influence de Tg sur la structure des ´lastom`res
e e
– ` gauche : amorphe ` T > Tg pontage inter-chaˆ
a a ınes covalents occasionnels
– ` droite : ` T < Tg liaisons Van des Waals secondaires inter-chaˆ
a a ınes ´tablies au niveau des groupes
e
lym`res non pont´s fondent compl`tement et deviennent des liquides visqueux, les polym`res r´ticul´s
e e e e e e
deviennent visco´lastiques (PVC) ou caoutchouteux (Polystyr`ne butadi`ne). Cette fusion des liaisons
e e e
secondaires est la cause de leurs propri´t´s m´caniques particuli`res comme par exemple la formabi-
ee e e
lit´ du poly´thyl`ne ou la grande d´formabilit´ ´lastique du caoutchouc. Sous contrainte les chaˆ
e e e e ee ınes
peuvent alors facilement glisser les unes sur les autres partout o` il n’y a pas de pont, ce qui explique
u
la grande d´formabilit´ et la faible valeur des modules ´lastiques des polym`res ` l’ambiante.
e e e e a
Par contre, en dessous de Tg les polym`res sont de v´ritables solides de module ´lastique ≥ 2 GPa.
e e e
Leur module est ´lev´ par suite de la formation de ponts Van der Waals dont la densit´ avoisine 1.
e e e
La simple exp´rience qui consiste ` refroidir un morceau de caoutchouc ` la temp´rature de l’azote
e a a e
liquide permet de rendre compte de la qualit´ de la pr´diction th´orique. En effet ce dernier devient
e e e
alors rigide (et cassant) et son module passe rapidement d’une valeur 1 MPa ` une valeur normale
a
d’environ 4 GPa.
L’autre param`tre qui caract´rise le comportement m´canique des polym`res est leur degr´ de
e e e e e
r´ticulation qui mesure la densit´ de ponts covalents inter-chaˆ
e e ınes. La rigidit´ des polym`res augmente
e e
corr´lativement ` l’augmentation de leur taux de r´ticulation pour tendre vers la limite du diamant
e a e
que l’on peut consid´rer comme un polym`re dont toutes les liaisons sont pont´es. les polym`res les
e e e e
plus rigides ont aujourd’hui des modules comparables ` celui de l’aluminium. Le module d’Young est
a
donc une fonction croissante de la densit´ de ponts covalents, mˆme pour les caoutchoucs au dessus
e e
de la temp´rature de transition vitreuse, en dessous de Tg leur module ´tant ´lev´ par suite de la
e e e e
formation de ponts Van der Waals dont la densit´ avoisine 1 (cf. Fig. 1.6).
e
La haute ´lasticit´ caoutchoutique
e e
Pour les mat´riaux tels que les ´lastom`res et les tissus biologiques, les conformations des chaˆ
e e e ınes
macromol´culaires peuvent ˆtre consid´rablement modifi´es par les d´formations quasiment sans varia-
e e e e e
tion des distances interatomiques et le comportement du mat´riau r´sulte de la variation de r´sistance
e e e
au changement de conformation des macromol´cules, d´senchevˆtrement, ´tirement, alignement, res-
e e e e
ponsables de la haute ´lasticit´ caoutchoutique, ´lasticit´ d’origine entropique. La d´formation se pro-
e e e e e
duit quasiment ` contrainte constante et les pelotes s’´tirent progressivement, la faible r´sistance
a e e

16. 10 CHAPITRE 1. MATERIAUX
Fig. 1.6 – Influence de la Tg et du taux de r´ticulation
e
Fig. 1.7 – L’´lasticit´ d’origine entropique
e e
a
` cet ´tirement provenant de l’agitation thermique qui tend ` r´emmˆler les chaˆ
e a e e ınes. A tr`s haute
e
d´formation, le module tangent croˆ brutalement car ce sont les liaisons covalentes du squelette car-
e ıt
bon´ de la plupart des chaˆ
e ınes qui sont maintenant ´tir´es et la rupture (fragile) intervient sans
e e
accroissement notable de d´formation.
e
1.2.4 Entre raideur et rupture
Si un mat´riau suivait ` l’´chelle macroscopique les lois microscopiques jusqu’` rupture il stockerait
e a e a
une quantit´ d’´nergie m´canique ´gale ` la somme des ´nergies de toutes ses liaisons chimiques, c’est
e e e e a e
a
` dire du mˆme ordre que celle contenue dans une masse ´quivalente d’explosif. A la rupture cette
e e
´nergie serait brutalement lib´r´e en une v´ritable explosion. Manger s’apparenterait ` allumer dans
e ee e a
sa bouche un bˆton de dynamite.
a
Heureusement, il n’en est rien car les r´sistances RM ultimes mesur´es (cf. annexe A.5 et A.6)
e e
E
sont de plusieurs ordres de grandeur inf´rieures ` la limite th´orique σM
e a e 10 . Au del` d’un seuil
a

17. ´
1.3. LA MECANIQUE DES SOLIDES CONTINUS 11
de contrainte, les mat´riaux cristallins dissipent l’exc´dent d’´nergie m´canique en se d´formant de
e e e e e
mani`re irr´versible supportant des allongements sup´rieurs ` la valeur th´orique εM
e e e a e 10% sans
cons´quence dangereuse (cf. annexe A.7). Mais il faut alors les comprimer fortement pour leur redonner
e
leur forme initiale et au bout de quelques cycles, le processus de d´gradation par fatigue provoque
e
leur rupture. Le comportement particulier des ´lastom`res provient du changement de conformation
e e
Mat´riau
e D´formation (%)
e Contrainte (MPa) ´
Energie stockable(J.kg −1 )
Bronze 0,3 400 70
Bois d’If (arc) 0,9 120 900
Corne 4,0 90 1500
Cheveux humains 30 160 13000
Caoutchouc 300 7 8000
Acier ` ressort
a 0,3 700 130
Tendon 8,0 70 2500
Tab. 1.9 – Capacit´s de stockage d’´nergie
e e
des macromol´cules et non de l’extension des liaisons fortes du squelette et conduit ` une r´ponse
e a e
r´versible jusqu’` rupture mais non lin´aire de sorte que leurs grandes d´formations s’obtiennent `
e a e e a
faible niveau de contrainte limitant leur capacit´ de stockage.
e
1.3 La m´canique des solides continus
e
C’est le domaine de la Science qui ´tudie et mod´lise le comportement de la mati`re en prenant
e e e
en compte, contrairement ` la M´canique Rationnelle, sa d´formabilit´. Comme les d´formations
a e e e e
d´pendent non seulement des forces, mais aussi de la temp´rature, il faut ´galement prendre en compte
e e e
les lois d’´change de chaleur et les principes de la Thermodynamique. Contrairement ` ces principes
e a
bien ´tablis, les lois de d´formation sont loin d’ˆtre simples et connues avec autant de certitude. Si
e e e
th´orie et calculs sont n´cessaires pour mod´liser et pr´dire, la th´orie doit ˆtre pr´c´d´e d’observations
e e e e e e e e e
et les calculs v´rifi´s par l’exp´rience.
e e e
Avec l’av`nement des mat´riaux composites modernes, la Science des Mat´riaux ne peut plus faire
e e e
l’impasse sur la texture de la mati`re pour pr´ciser les lois de comportement. En passant directement
e e
de l’´chelle microscopique, l’angstr¨m des liaisons atomiques, aux dimensions macroscopiques on oublie
e o
que les mat´riaux comportent des textures aux ´chelles m´soscopiques interm´diaires (cf. annexe A.3),
e e e e
textures qui vont influer consid´rablement sur certaines de leurs propri´t´s, tout particuli`rement sur
e ee e
leurs caract´ristiques de r´sistance m´canique.
e e e
Cependant, il faut garder pr´sent ` l’esprit le fait que tous les d´veloppements th´oriques sont bas´s
e a e e e
sur la conception fondamentale d’un milieu continu dont les transformations sont continues. Or nous
savons que la mati`re est discontinue ` l’´chelle mol´culaire, souvent mˆme ` une ´chelle beaucoup
e a e e e a e
plus grande : cristaux d’un m´tal, grains d’une roche, granulats d’un b´ton. Mais la M´canique se
e e e
place ` une ´chelle macroscopique, c’est ` dire ` une ´chelle suffisamment grande pour que la mati`re
a e a a e e
apparaisse comme continue, sauf ´ventuellement le long de certaines surfaces de discontinuit´ comme
e e
les fractures.
1.3.1 Les essais en m´canique
e
Dimensionner des structures pour qu’elles puissent supporter le chargement n´cessite la r´solution
e e
compl`te du probl`me m´canique associ´. Aux ´quations de conservation (masse, impulsion, ´nergie) il
e e e e e e
faut adjoindre les lois de comportement des mat´riaux constitutifs, ´quations d’´tat reliant contrainte
e e e
et d´formation.
e
L’´tablissement de la loi de comportement d’un mat´riau est g´n´ralement ph´nom´nologique,
e e e e e e
bas´e sur l’exp´rimentation macroscopique et l’identification des param`tres dans le cadre de la for-
e e e
mulation thermodynamique. Cependant l’identification exp´rimentale du comportement m´canique
e e

18. 12 CHAPITRE 1. MATERIAUX
d’un mat´riau est par nature une op´ration d´licate car elle ne peut s’effectuer qu’` partir d’essais
e e e a
m´canique sur des ´prouvettes qui, par leur taille, doivent ˆtre consid´r´es comme des structures. Or,
e e e ee
on ne peut d´duire le champ de contraintes ` partir des efforts globaux dans une structure, condition
e a
n´cessaire ` l’identification du comportement, que si l’on connaˆ d´j` le comportement. Pour vaincre
e a ıt e a
cette difficult´, force nous est de recourir ` des g´om´tries et des sollicitations sp´cifiques permettant de
e a e e e
d´duire les variables m´caniques locales ` partir des grandeurs globales quel que soit le comportement.
e e a
Les essais m´caniques classiques s’effectuent donc sur des ´prouvettes normalis´es et des sollicitations
e e e
particuli`res telles que la traction uniaxiale d’un barreau long, la torsion ou la mise en pression interne
e
d’un tube mince,. . .
1.3.2 L’essai de traction simple
L’essai de traction met habituellement en ´vidence trois stades principaux dans l’´volution du
e e
comportement du mat´riau (cf. Fig. 1.8)
e
Fig. 1.8 – Essai de traction : r´ponse typique
e
Un comportement ´lastique lin´aire ou non (domaine 1) pour lequel aucune d´formation r´siduelle
e e e e
ne se maintient apr`s d´charge.
e e
Un stade de d´formation plastique parfait (domaine 2) et avec ´crouissage (domaine 3) caract´ris´
e e e e
par une d´formation r´siduelle irr´versible apr`s d´charge, l’ensemble du comportement ´tant
e e e e e e
compl`tement ind´pendant du temps, notamment de la vitesse de chargement.
e e
Une ´tape d’endommagement (domaine 4) conduisant ` la rupture. L’endommagement se ma-
e a
nifeste par l’alt´ration progressive des propri´t´s m´caniques qui accompagne, habituellement
e ee e
pour d’assez grandes d´formations ou sous sollicitations cycliques, la formation et la croissance
e
de microfissures et microcavit´s, alt´ration pouvant aller jusqu’` la rupture. Naturellement li´es
e e a e
a
` la d´formation elle mˆme les lois d’endommagement doivent ˆtre coupl´es aux lois de com-
e e e e
portement et l’ensemble d´termine le comportement r´el du mat´riau. Selon les mat´riaux, la
e e e e
rupture peut se produire plus ou moins tˆt, notamment en stade ´lastique ou plastique avant
o e
endommagement.
Cependant, dans bien des cas le temps intervient et la courbe d’essai obtenue est une fonc-
tion de la vitesse de sollicitation (domaine 5). Ainsi un arrˆt ` contrainte constante s’accompagne
e a
d’une d´formation de fluage, un arrˆt ` d´formation constante s’accompagne d’une relaxation de la
e e a e
contrainte, une sollicitation cyclique d’hyst´resis. C’est la manifestation de la viscosit´ du mat´riau
e e e
visco-´lasticit´ ou visco-´lasto-plasticit´.
e e e e

19. ´
1.3. LA MECANIQUE DES SOLIDES CONTINUS 13
1.3.3 Les modes de ruine
Les modes de ruine d’une structure d´pendent des sollicitations m´caniques, thermiques, chimiques
e e
qu’elle subit, des d´fauts qu’elle contient et des propri´t´s du mat´riau. Ils comprennent :
e ee e
Le flambage instabilit´ r´sultant d’une diminution d’´nergie sous faible perturbation des conditions
e e e
aux limites. Au del` d’un seuil de compression, une structure allong´e fl´chit brutalement, cette
a e e
configuration devenant ´nerg´tiquement plus favorable.
e e
Les agressions chimiques oxydation et corrosion sous contrainte.
Les ruptures par endommagement cr´ation de nouvelles surfaces au sein du mat´riau. A l’´chelle
e e e
des atomes les m´canismes d’endommagement se classent en trois types g´n´riques :
e e e
– Les clivages, rupture de liaisons en traction avec cr´ation d’une fissure, concernent les mat´riaux
e e
cristallis´s. Un m´canisme analogue intervient dans les craquelures des polym`res, dans le
e e e
b´ton plus ou moins cristallis´, dans les verres, dans les ruptures intergranulaires.
e e
– Les glissements, d´calage sous cisaillement des liaisons entre les atomes de deux plans ato-
e
miques adjacents sont ` l’origine de la d´formation plastique ; Ils peuvent conduire ` une
a e a
instabilit´ de la structure, striction ou d´chirure ductile (plastic collapse) lorsque la diminu-
e e
tion de section qu’ils induisent ne peut plus ˆtre compens´e par l’´crouissage (durcissement)
e e e
du mat´riau. La d´formation plastique provoque aussi l’apparition de petites cavit´s internes ;
e e e
Leur croissance et leur coalescence conduisent ` la rupture. Sous sollicitation cycliques, les
a
glissements n’´tant pas parfaitement r´versibles, il finissent par d´t´riorer la surface des pi`ces
e e ee e
aboutissant aux ruptures de fatigue.
– Les cavitations par diffusion de lacunes : m´canisme tr`s important en fluage n´cessitant des
e e e
temp´ratures ´lev´es de fonctionnement ou de fortes irradiations.
e e e
Ces m´canismes
e de ruine interagissent avec les m´canismes chimiques (migration de gaz dans les
e
cavit´s, blocage des
e glissements par des atomes de solut´ ou des pr´cipit´s, modification de l’´nergie
e e e e
des joints de grains ou des surfaces par migration d’impuret´s, r´actions chimiques sur les surfaces
e e
nouvellement cr´´es
ee et conduisent ` l’apparition de fissures ` l’´chelle macroscopique.
a a e
1.3.4 H´t´rog´n´it´ et anisotropie
e e e e e
Entre l’´chelle de la macro m´canique ou m´canique des milieux continus (la mati`re est consid´r´e
e e e e ee
comme une boite noire) et l’´chelle atomique de la micro m´canique (ou l’on ´tudie les ph´nom`nes
e e e e e
´l´mentaires : d´fauts d’empilement, mouvement des dislocations, interactions avec les d´fauts ponc-
ee e e
tuels lacunes, interstitiels,. . .), existent dans les mat´riaux r´els des ´chelles interm´diaires d’inho-
e e e e
mog´n´it´ structurale (grains de polycristaux ; phases de m´taux ou d’alliages de polym`res ; charges,
e e e e e
particules ou fibres de renforcement des composites m´talliques, c´ramiques ou ` matrice polym`re ;
e e a e
granulats des b´tons ; pores ;. . .) qui constituent la texture des mat´riaux (cf. annexe A.3). Cette
e e
texture va influer consid´rablement sur certaines de leurs propri´t´s, tout particuli`rement sur leurs
e ee e
caract´ristiques de r´sistance m´canique. Elle est ` l’origine des diff´rences consid´rables constat´es
e e e a e e e
entre les valeurs th´oriques d´duites des propri´t´s des liaisons et les valeurs mesur´es. Il aura fallu
e e ee e
attendre la d´couverte (` partir des ann´es 1930) des d´fauts (Griffith) et des dislocations (Taylor) et
e a e e
la prise en compte de leurs effets pour expliciter ces diff´rences. Les mat´riaux r´els ne sont pas ho-
e e e
mog`nes. Comportement m´canique et endommagement d´pendent non seulement de la composition
e e e
chimique globale, mais aussi de l’arrangement des diverses phases. C’est bien sˆr le cas des mat´riaux
u e
composites artificiels dans lesquels on introduit volontairement ` l’´laboration diverses phases (ma-
a e
trice et ´l´ments de renforcement, fibres, charges, . . .), mais les mat´riaux naturels utilis´s depuis
ee e e
longtemps sont pour la plupart des composites naturels comme le bois. Les moyens actuels d’observa-
tion et d’analyse chimique locale ont largement contribu´ au d´veloppement d’une nouvelle approche
e e
plus d´ductive de la m´canique des solides, la m´so m´canique qui tente de r´aliser un passage du
e e e e e
microscopique au macroscopique en d´finissant le comportement macroscopique ` partir de la des-
e a
cription de la texture, des m´canismes ´l´mentaires de d´formation et d’endommagement et de leur
e ee e
int´gration dans le processus de changement d’´chelle conduisant ` la d´finition de la loi de compor-
e e a e
tement macroscopique. Cette derni`re approche est plus complexe, moins ´tablie, mais plus riche et
e e
mieux fond´e physiquement.
e

20. 14 CHAPITRE 1. MATERIAUX
• Anisotropie
De part la constitution anisotrope du mat´riau, ´troitement reli´e ` l’h´t´rog´n´it´ de sa microstruc-
e e e a ee e e e
ture, son comportement m´canique est anisotrope (d´pendance de la r´ponse vis-`-vis de la direction
e e e a
de sollicitation) et cette anisotopie ´voluera avec la d´formation qui modifie l’organisaion de la mi-
e e
crostructure. Cependant, lorsque la microstructure pr´sente certains ´l´ments de sym´trie il en est de
e ee e
mˆme de l’anisotropie et la loi de comportement correspondante doit respecter ces ´l´ments de sym´trie.
e ee e
L’origine physique de l’anisotropie est l’h´t´rog´n´it´ de la microstructure. Si l’on d´compose celle-ci
ee e e e e
en ´l´ments homog`nes, l’anisotropie macroscopique r´sulte d’une anisotropie ´l´mentaire, celle des
ee e e ee
´l´ments homog`nes de la microstructure, et d’une anisotropie d’organisation, attach´e ` l’agencement
ee e e a
spatial de ces ´l´ments homog`nes.
ee e
L’anisotropie ´l´mentaire est d´termin´e par l’anisotropie des m´canismes de d´formation, elle
ee e e e e
mˆme li´e ` l’anisotropie de la structure interne de l’´l´ment (liaisons atomiques, directions de
e e a ee
glissement cristallographique, d´faut d’emplilement, directions de diffusion, . . .).
e
L’anisotropie d’organisation r´sulte de l’h´t´rog´n´it´ de la microstructure : forme, orientation et
e ee e e e
r´partition spatiale de grains, inclusions, cavit´s, textures, . . ..
e e
Si cette complexit´ des textures et de leur ´volution rend difficile le passage micro-macro, elle offre
e e
en contrepartie des possibilit´s quasi infinies de modulation des propri´t´s m´caniques des mat´riaux.
e ee e e
1.3.5 Le Comportement m´canique des mat´riaux
e e
Un corps ne pouvant r´sister ` la sollicitation appliqu´e qu’en se d´formant, l’analyse de la rigidit´
e a e e e
des structures en terme de force et d’allongement ne permet pas de distinguer la contribution de la
g´om´trie de celle, intrins`que, du mat´riau. Pour ce faire, il faut d´finir en tout point de la structure
e e e e e
un ´tat m´canique local ind´pendant de sa g´om´trie. La caract´risation de cet ´tat local en terme
e e e e e e e
de contrainte σ et de d´formation ε - la relation entre ces grandeurs et leurs d´riv´es temporelles
e e e
d´finissant la loi de comportement macroscopique - fait l’objet du second chapitre.
e
La plupart des structures ´tant con¸ues pour supporter un chargement ` temp´rature ambiante
e c a e
en n’accusant que de faibles d´formations, le troisi`me chapitre de ce volume est consacr´ ` la loi de
e e ea
comportement ´lastique des mat´riaux.
e e
Au del` d’un chargement critique les mat´riaux ductiles (particuli`rement les m´taux) pr´sentent
a e e e e
un comportement fluide et s’´coulent sous contrainte.
e
Cet ´coulement s’arrˆte lorsque le chargement est r´duit en dessous du seuil critique mais le mat´riau
e e e e
s’est d´form´ de mani`re permanente. Ce comportement plastique est exploit´ dans les proc´d´s de
e e e e e e
mise en forme (laminage, emboutissage,...) imposant au mat´riau une d´formation importante mais
e e
permanente.
Le quatri`me chapitre est d´di´ aux lois de comportement plastique. Les m´canismes g´n´riques `
e e e e e e a
petite ´chelles (micro ou m´soscopique) ` l’origine de ce comportement sont mis en relation avec les
e e a
propri´t´s m´caniques macroscopiques mesurables.
ee e
Tout mat´riau fortement sollicit´ s’endommage progressivement jusqu’` pr´senter des d´fauts ma-
e e a e e
croscopiques. La m´canique de la rupture a pour objet l’´tude de ces d´fauts et l’´tablissement des
e e e e
donn´es exp´rimentales permettant de d´terminer leur cin´tique de propagation et la taille critique
e e e e
au-del` de laquelle, pour une sollicitation donn´e, la rupture brutale se produit. Cette rupture peut
a e
ˆtre provoqu´e par une surcharge occasionnelle ou, plus insidieusement, par un m´canisme de fatigue
e e e
au cours duquel les fissures se forment et croisent lentement sous chargement plus faible lorsque ce
dernier est appliqu´ de mani`re cyclique.
e e
Le cinqui`me chapitre est d´di´ aux lois de comportement ` rupture et aux m´canismes d’endomma-
e e e a e
gement associ´s.
e

21. Chapitre 2
´ ´
ETAT MECANIQUE
2.1 Milieux d´formables
e
2.1.1 Forces externes et ´quilibre m´canique
e e
→
−
La loi fondamentale de la dynamique m→ = −γ F appliqu´e ` un corps en ´quilibre m´canique
e a e e
statique implique la nullit´ de la r´sultante et du moment r´sultant des efforts externes appliqu´s.
e e e e
→
− −
→
F =0 M =0 (2.1)
– Si le nombre d’efforts externes est ´gal au nombre d’´quations, le corps est en ´tat d’´quilibre
e e e e
isostatique et les efforts sont enti`rement d´termin´s.
e e e
– Si ce nombre est sup´rieur au nombre d’´quations, le corps est en ´tat d’´quilibre hyperstatique
e e e e
et la d´termination des efforts implique la prise en compte de la d´formation du milieu pour
e e
obtenir les ´quations compl´mentaires.
e e
2.1.2 Forces internes, forces de surface et transmission des efforts
Sous l’action d’efforts externes tout corps se d´forme. Cette d´formation fait apparaˆ des forces
e e ıtre
internes dont l’origine se situe ` l’´chelle atomique. Ce sont les liaisons atomiques distendues (ou com-
a e
prim´es) qui exercent des forces de rappel qui tendent ` ramener les atomes ` leur position d’´quilibre
e a a e
et le corps dans son ´tat initial. Ces forces se caract´risent par un rayon d’action de l’ordre de quelques
e e
distances interatomiques. Or la M´canique des Milieux Continus, th´orie macroscopique, ne consid`re
e e e
que des distances grandes par rapport aux dimensions atomiques et leur rayon d’action doit ˆtre e
consid´r´ comme nul ` cette ´chelle. Les forces de rappel ` l’origine de l’existence des forces internes
ee a e a
sont des forces ` courte port´e qui ne se transmettent qu’` leur environnement imm´diat.
a e a e
Il en r´sulte que les forces exerc´es sur une partie du corps par les parties environnantes agissent
e e
directement par sa surface. Les forces internes sont sont des forces surfaciques, des actions de contact.
Fig. 2.1 – Principe de l’action et de la r´action : l’action de la partie A sur la partie B est ´gale et
e e
oppos´e ` l’action de la partie B sur la partie A
e a
→
− →
−
Consid´rons un corps soumis ` l’action des forces externes F G et F D . L’´quilibre m´canique
e a e e
→
− →
−
statique impose F G + F D = 0. S´parons par la pens´e ce corps en deux parties A et B.
e e
→
− →
−
L’´quilibre de la partie A prise isol´ment impose l’existence d’une force f (B/A) telle que F G +
e e
→
−
f (B/A) = 0, force interne repr´sentant l’action de la partie B sur la partie A.
e
→
−
R´ciproquement,l’´quilibre de la partie B prise isol´ment impose l’existence d’une force f (A/B) telle
e e e
→
− →
−
que F D + f (A/B) = 0, force interne repr´sentant l’action de la partie A sur la partie B.
e
15

22. 16 ´ ´
CHAPITRE 2. ETAT MECANIQUE
Il r´sulte de l’´quilibre du corps pris dans son ensemble que la r´sultante des forces internes est
e e e
toujours nulle :
→
− →
−
f (B/A) + f (A/B) = 0 (2.2)
2.1.3 Raideur, rigidit´, ´tat m´canique local
e e e
Un corps ne pouvant r´sister ` la sollicitation appliqu´e qu’en se d´formant, l’essai de traction
e a e e
donne acc`s ` la raideur K de l’´prouvette d´finie comme le rapport de la force F de traction `
e a e e a
l’allongement ∆l r´sultant. La raideur K prend en compte ` la fois la g´om´trie de l’´prouvette et la
e a e e e
rigidit´ intrins`que du mat´riau.
e e e
L’exp´rience ` montr´ que pour ´tirer de la mˆme quantit´ ∆l deux ´prouvettes du mˆme mat´riau
e a e e e e e e e
Fig. 2.2 – Raideur de l’´prouvette et rigidit´ du mat´riau
e e e
de mˆme longueur initiale l mais d’aire de section droite S diff´rentes, la force F ` appliquer varie
e e a
proportionnellement ` S.
a
Elle a ´galement montr´ qu’` aire de section S et ` force F fix´es, l’allongement r´sultant ∆l varie
e e a a e e
proportionnellement ` la longueur initiale l.
a
Il en r´sulte que la raideur K varie proportionnellement ` S et inversement proportionnellement ` l
e a a
de sorte que la relation F = K∆l se met sous la forme
F ∆l
=E (2.3)
S l
la quantit´ E ind´pendante de la g´om´trie de l’´prouvette ´tant une caract´ristique intrins`que du
e e e e e e e e
mat´riau : sa rigidit´.
e e
Les variables d´crivant l’´tat m´canique local, ind´pendamment de la g´om´trie de la structure,
e e e e e e
seront donc :
– la contrainte σ = F : densit´ surfacique de force
S e
∆l
– la d´formation ε = l : variation relative de longueur
e
2.2 Les contraintes
Elles caract´risent l’´tat de sollicitation m´canique (efforts internes) en tout point du mat´riau,
e e e e
ind´pendamment de sa nature et de ses caract´ristiques de r´sistance.
e e e
2.2.1 ´
Etat m´canique local
e
Pour caract´riser l’´tat de sollicitation m´canique (efforts internes) en tout point du mat´riau
e e e e
ind´pendamment de la g´om´trie du corps, la description en terme de force est insuffisante, il faut
e e e
introduire la notion de densit´ surfacique de force.
e

23. 2.2. LES CONTRAINTES 17
Le vecteur contrainte
→
−
Si la force de contact r´sultante f repr´sentant l’action exerc´e par la partie A sur la section de
e e e
→
− → →
− −
coupe de la partie B doit bien ´quilibrer la force externe F soit f + F = 0, elle n’a pas de raison,
e
sauf cas particulier, d’ˆtre uniform´ment r´partie (en module et/ou en direction) sur cette section.
e e e
→
− →
− →
− →
−
Chaque ´l´ment d’aire dS supportera une force ´l´mentaire d f = T ds telle que S T dS = f . La
ee ee
→
−
densit´ surfacique de force T , appel´e vecteur contrainte, est une fonction du point courant M de la
e e
section de coupe. Plutˆt que d’employer le terme section de coupe, nous utiliserons d´sormais le terme
o e
de facette plus adapt´ au fait que les coupes sont virtuelles.
e
Fig. 2.3 – Le vecteur contrainte T d´pend du point M et de l’orientation n de la facette
e
En un point M0 donn´ consid´rons deux sections de coupe S et S caract´ris´e respectivement par
e e e e
→ et →. Pour chacune d’elles le vecteur contrainte → v´rifie :
−
leurs orientations n
−
n
−
T e
→
− →
− →
− →
−
sur S T dS = f sur S T dS = f (2.4)
S S
→
− →
− →
−
En M0 : T (M0 , →) = T (M0 , n ).
−
n
→
−
Le vecteur contrainte T est ´galement une fonction de l’orientation → de la facette.
e −
n
Le volume repr´sentatif ´l´mentaire
e ee
→
−
Le vecteur contraintes T repr´sentant au point M la densit´ surfacique de force sur la facette
e e
→ peut ´galement s’exprimer sous la forme :
−
d’orientation n e
→
− →
−
→
− f f
T (M, →) =
−
n = lim (2.5)
S S→0 S
Lorsque l’on fait tendre l’aire S vers z´ro en partant de l’´chelle de la dimension du corps, le rapport
e e
f
S qui ´volue d’abord de mani`re continue pr´sente de fortes fluctuations lorsque l’on s’approche de
e e e
l’´chelle des dimensions atomiques pour laquelle la notion de milieu continu perd son sens.
e
Dans les mat´riaux r´els ces fluctuations apparaissent plus tˆt ` l’´chelle caract´ristique des h´t´rog´n´it´s
e e o a e e ee e e e
de sa texture, typiquement de l’´chelle du grain (100 µm) dans les mat´riaux cristallins ` celle des gra-
e e a
nulats (1 cm) dans les b´tons. Cette ´chelle d´finit la dimension du volume repr´sentatif ´l´mentaire
e e e e ee
de la th´orie des milieux continus, la taille de la “particule”, offrant l’avantage d’´viter toute hypoth`se
e e e
sur la constitution de la mati`re.
e
Rep`re local, contraintes normales et de cisaillement
e
n e e e − − →
n r
−
Au point M , pour une facette de direction →, on d´finit le rep`re local - tri`dre direct - M, →, →, t
−
→ → →
− − −
de telle mani`re que les vecteurs T , n , r soient coplanaires.
e
→
−
Dans ce rep`re les composantes du vecteur contrainte T (M, →) sont σnn , σrn , σtn , le premier in-
e −n
dice faisant r´f´rence ` l’axe de projection, le second ` l’orientation → du plan de la facette. Par
ee a a −n
→
−
construction on a toujours σtn = 0 et les composantes non nulles de T sont sa composante normale
σnn selon → appel´e contrainte normale not´e σ et sa composante tangentielle σrn situ´e dans le plan
−n e e e
de la facette perpendiculaire ` → appel´e contrainte de cisaillement not´e τ .
a−n e e

24. 18 ´ ´
CHAPITRE 2. ETAT MECANIQUE
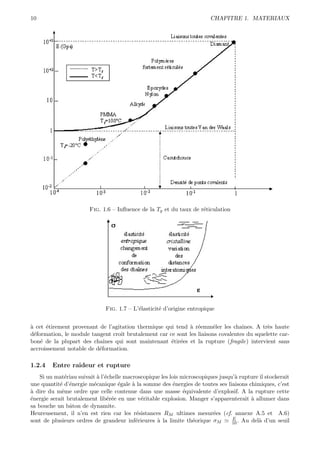
Fig. 2.4 – Le rep`re local de la facette : M, n, r, t
e
→
−
contrainte normale σ C’est la composante de T qui tire lorsqu’elle est parall`le ` → ou qui pousse
e a− n
si elle est antiparall`le ` n
e a →. Le signe de σ est donc intrins`que : σ > 0 pour la traction et σ < 0
− e
pour la compression.
→
−
contrainte de cisaillement τ C’est la composante de T qui agit ` la mani`re d’une “cisaille”, d’o`
a e u
son nom.
La dimension des composantes de contrainte est [ML−1 T−2 ] : rapport de la force [MLT−2 ] ` l’aire
a
[L 2 ] de la section sur laquelle elle s’exerce. Son unit´ est le Pascal P a (ou N.m−2 ). En pratique cette
e
unit´ est trop petite et l’unit´ courante du m´canicien est le M´gapascal M P a (ou M N.m−2 ), voire
e e e e
le Gigapascal GP a (ou GN.m−2 ).
L’´tat m´canique local au point M sera donc d´termin´ si l’on connaˆ en ce point les composantes
e e e e ıt
→
−
σ et τ de tous les vecteurs contraintes T (M, →) associ´s ` toutes les facettes d’orientation → possibles
−
n e a −
n
passant par ce point.
En chaque point M , parmi toutes les directions de facettes possibles, certaines supporteront un
cisaillement maximal tandis que d’autres supporteront une traction maximale. Il est important de faire
une distinction entre les deux types de composantes normale et tangentielle car l’exp´rience montre
e
que tout mat´riau pr´sente, selon sa nature, un seuil caract´ristique de contrainte σC ou τC selon son
e e e
mode de ruine, seuil au del` duquel il c`de.
a e
– Les mat´riaux dits ductiles - tels les m´taux - c`dent par d´formation plastique lorsque le ci-
e e e e
saillement maximal τM atteint le seuil τC .
– Les mat´riaux dits fragiles - tels le verre - c`dent lorsque la traction maximale σM atteint le
e e
seuil σC .
2.2.2 Le tenseur des contraintes
En un point M donn´, il existe n´cessairement des relations entre les divers vecteurs contrainte
e e
T associ´s aux diverses facettes de normales n passant par ce point. Pour s’en convaincre, il suffit de
e
consid´rer l’´quilibre d’une “particule” de centre M . Pour une telle particule, de surface externe S,
e e
les vecteurs contrainte doivent v´rifier :
e
→
− → ∧ →dS = 0
− −
T dS = 0 r T (2.6)
S S
traduisant respectivement la nullit´ de la r´sultante des efforts exerc´s par son environnement et de son
e e e
moment. D’un point de vue math´matique, cela implique l’existence d’un op´rateur liant en chaque
e e
→
− → de la facette sur laquelle il s’applique.
−
point M le vecteur contrainte T ` l’orientation n
a
Isolons au sein de la mati`re un t´tra`dre ´l´mentaire M ABC dont les trois faces M BC, M AC et
e e e ee
M AB sont les trois faces du tri`dre M, x1 , x2 , x3 .
e
La quatri`me ABC caract´ris´e par sa normale → de composantes (cosinus directeurs) :
e e e −n
SM BC SM AC SM AB
n1 = n2 = n3 = (2.7)
SABC SABC SABC

25. 2.2. LES CONTRAINTES 19
→
−
supporte un vecteur contrainte T (M, →) de composantes (T1 ,T2 ,T3 ) repr´sentant l’action du reste du
−
n e
corps sur ABC.
−
→ −
→ −
→
De la mˆme mani`re T1 (M, −→), T2 (M, −→) et T3 (M, −→) repr´senteront respectivement l’action
e e −
−x1 −
−x2 −
−x3 e
du reste du corps sur M BC, M AC et M AB.
´
Fig. 2.5 – Equilibre : T´tra`dre, Parall´l´pip`de
e e ee e
´
Equilibre des forces L’´quilibre du t´tra`dre qui doit s’´crire en terme de force et non en terme de
e e e e
contrainte (densit´ surfacique de force) implique la relation :
e
→
− −
→ −
→ −
→
T (M, →)SABC + T1 (M, −→)SM BC + T2 (M, −→)SM AC + T3 (M, −→)SM AB = 0
−
n −
−x1 −
−x2 −
−x3 (2.8)
→
− →
−
Comme, en vertu du principe de l’action et de la r´action, T (M, −→) = − T (M, →), cette
e −
x −
x
relation s’´crit en tenant compte des relations (2.7) :
e
→
− −
→ −
→ −
→
T (M, →) = T1 (M, − )n1 + T2 (M, − )n2 + T3 (M, − )n3
−
n →
x1 →
x2 →
x3 (2.9)
→
−
En introduisant les composantes σ1i , σ2i , σ3i des vecteurs contraintes Ti (M, →) i ∈ {1, 2, 3}
−i
x
repr´sentant les actions des faces M BC, M AC et M AB sur le reste du corps :
e
−
→
T1 (M, − ) = σ11 − + σ21 − + σ31 −
→
x1 →
x1 →
x2 →
x3
−
→
T2 (M, − ) = σ12 − + σ22 − + σ32 −
→
x2 →
x1 →
x2 →
x3 (2.10)
−
→
T3 (M, − ) = σ13 − + σ23 − + σ33 −
→
x3 →
x1 →
x2 →
x3
→
−
Finalement la relation (2.10) entre T (M, →) et → s’´crit de mani`re g´n´rale :
−
n − e
n e e e
→
−
T (M, →) = σ →
−
n −
n (2.11)
a
` l’aide du tenseur σ(M ) dont les composantes dans le rep`re M, x1 , x2 , x3 sont :
e
σ11 σ12 σ13
σ(M ) = σ21 σ22 σ23 (2.12)
σ31 σ32 σ33
La connaissance des vecteurs contraintes agissant sur trois facettes orthogonales de normales
x1 , x2 , x3 suffit ` d´terminer au point M l’´tat de contrainte caract´ris´ par le tenseur des
a e e e e
→
− →) sur toute facette contenant M .
−
contraintes σ, donc le vecteur contrainte T (M, n

26. 20 ´ ´
CHAPITRE 2. ETAT MECANIQUE
´
Equilibre des moments De mˆme que pour la r´sultante des forces, l’´quilibre impose que le mo-
e e e
ment r´sultant soit nul. En raisonnant cette fois sur une particule parall´l´pip`diques ´l´mentaire
e ee e ee
de volume dx1 dx2 dx3 et en calculant la composante selon l’axe x3 du moment r´sultant :
e
σ21 dx2 dx3 dx1 = σ12 dx1 dx3 dx2 σ21 = σ12 (2.13)
aire aire
De mani`re analogue on obtient avec les deux autres composantes du moment : σ23 = σ32 et
e
σ31 = σ13 . La sym´trie du tenseur des contraintes :
e
σ =t σ σij = σji (2.14)
est une cons´quence directe de la nullit´ du moment r´sultant
e e e
Les composantes de σ forment deux groupes ditincts :
– Les composantes de la diagonale principale σij avec i = j composantes normales (traction > 0
ou compression < 0) dirig´es selon les normales aux facettes.
e
– Les composantes hors diagonale σij avec i = j composantes tangentielles (cisaillement) contenues
dans le plan des facettes.
2.2.3 Propri´t´s du tenseur des contraintes
e e
Rep`re principal et invariants
e
Le tenseur σ(M ) d´finissant l’´tat de contrainte en un point M est un op´rateur intrins`que qui lie
e e e e
la normale n→ ` une facette passant par ce point au vecteur contrainte qui s’applique ` cette facette :
− a a
→
−
T (M, →)
−
n (2.15)
Cette d´finition est ind´pendante du rep`re choisi, seule sa repr´sentation, les valeurs de ses compo-
e e e e
santes, d´pend du rep`re.
e e
Comme pour tout tenseur sym´trique de rang 2, il existe toujours un rep`re particulier, le rep`re prin-
e e e
cipal dans lequel le tenseur des contraintes σ(M ) a pour repr´sentation une matrice diagonale dont
e
les composantes sont appel´es contraintes principales σ1 , σ2 et σ3 . Ce sont les valeurs propres toujours
e
r´elles de l’op´rateur . Notons que le tenseur σ est toujours d´fini par six quantit´s ind´pendantes,
e e e e e
ses six composantes dans un rep`re quelconque ou ses trois contraintes principales auxquelles il faut
e
associer les trois angles d’Euler d´finissant la position du rep`re principal par rapport ` celui du
e e a
laboratoire.
Les contraintes principales σ1 , σ2 et σ3 - ainsi que le tenseur σ lui-mˆme - v´rifient l’´quation
e e e
caract´ristique :
e
3 2
Det(σ − λδ) = 0 λ3 − I1 λ2 + I2 λ − I3 = 0 σ − I1 σ + I2 σ − I3 δ = 0 (2.16)
et sont ind´pendantes du rep`re choisi de sorte que les trois coefficients I1 ,I2 et I3 sont des combi-
e e
naisons de composantes de σ invariantes par changement de rep`re. Ces coefficients repr´sentent le
e e
jeu d’invariants du tenseur : sa trace Tr, la somme des d´terminants mineurs des composantes de sa
e
diagonale principale et son d´terminant Det.
e
I1 = δ · σ = Tr(σ) = σ11 + σ22 + σ33 = σ1 + σ2 + σ3
1 (4) 2 2 2
I2 = 2δ · σ · σ = σ11 σ22 − σ12 + σ22 σ33 − σ32 + σ33 σ11 − σ31 = σ1 σ2 + σ2 σ3 + σ3 σ1
(6)
I3 = 1 δ
6 · σ · σ · σ = Det(σ) = 1 δijk δpqr σip σjq σkr = σ1 σ2 σ3
6
Il existe une infinit´ de jeux d’invariants combinaisons du jeu pr´c´dent. La combinaison la plus usit´e
e e e e
est le jeu d’invariants d´fini par :
e
∗ ∗
I1 = Tr(σ) I1 = I1 ∗
I1 = I1 = Tr(σ)
∗ 2 ∗ 2 ∗2 ∗
I2 = Tr(σ ) I2 = I1 − 2I2 2I2 = (I1 − I2 )
∗ 3 ∗ ∗ ∗ ∗ 3 2
I3 = Tr(σ ) I3 = I1 − 3I1 I2 + 3I3 6I3 = 2I3 − 3I1 I2 + I3 = 2Tr(σ ) − 3Tr(σ)Tr(σ ) + Tr3 (σ)
3 3

27. 2.2. LES CONTRAINTES 21
Sph´rique et d´viateur
e e
Tout ´tat de contrainte est d´composable en la somme de deux ´tats :
e e e
Le sph´rique ´tat isotrope caract´ris´ par la contrainte normale moyenne (traction ou compression)
e e e e
σm = Tr(σ) auquel est associ´e la partie sph´rique S = σm δ du tenseur σ. Il est enti`rement
e e e
caract´ris´ par la contrainte normale moyenne σm et, du fait de son isotropie, il est diagonal
e e
dans tout rep`re : Tr(S) = Tr(σ) = 3σm . C’est la g´n´ralisation de la notion de pression.
e e e
Le tenseur des contraintes en hydrostatique a donc pour expression σ = σm δ = −pδ , la pression
p, contrainte normale de compression n´gative pour le m´canicien ´tant d´finie positive par
e e e e
l’hydrodynamicien.
Le d´viateur ´tat anisotrope traduisant les d´viations par rapport ` l’isotropie moyenne et ca-
e e e a
Tr(σ−S)2
ract´ris´ par la contrainte d´viatorique moyenne (cisaillement) σd =
e e e 3 auquel est
associ´e la partie d´viateur D = σd π du tenseur σ.
e e
σ = S + D = σm δ + σd π (2.17)
Sa trace Tr(D) = 0 est nulle par d´finition. Il est caract´ris´ par les cinq autres param`tres
e e e e
ind´pendants de σ, la contrainte d´viatorique (cisaillement) moyenne σd et les quatre param`tres
e e e
ind´pendants du tenseur des directions π qui caract´rise les directions principales de σ d’o` son
e e u
nom. Ce dernier est toujours d´fini par quatre quantit´s ind´pendantes :
e e e
– Ses six composantes dans un rep`re quelconque li´es par les deux relations Tr(π) = 0 et
e e
2
Tr(π ) = 3.
– Ses trois valeurs propres π1 , π2 et π3 - li´es par les relations pr´c´dentes de sorte que π1 , π2 et
e e e
π3 sont des fonctions d’un seul param`tre µ - auxquelles il faut associer les trois angles d’Euler
e
d´finissant la position du rep`re principal par rapport ` celui du laboratoire.
e e a
En d’autres termes, π ne poss`de qu’un seul invariant ind´pendant.
e e
Contraintes octa´driques
e
Fig. 2.6 – Contraintes octa`driques
e
Les huit facettes (cf. Fig : 2.6) de normales →(± √3 , ± √3 , ± √3 ) constituant un octa`dre rep´r´
−
n 1 1 1
e ee
dans le syst`me d’axes principal de σ admettent la mˆme composante normale σnn = σm et la mˆme
e e e
→
− →) de
−
composante de cisaillement σrn = σd . Le vecteur contrainte de chacune de ces facettes T (M, n
→
−
composantes (± √3 σ1 , ± √3 σ1 , ± √3 σ1 ) a pour module | T |2 = 1 (σ1 + σ2 + σ3 ). Ses composantes locales
1 1 1
3
2 2 2
sont :
→ −
−
σnn = T · → = 3 Tr(σ1 + σ2 + σ3 ) = σm
n 1
→
− Tr(D)2 1
σrn = | T |2 − σnn =
2
3 = 3 (σ1 − σ2 )2 + (σ2 − σ3 )2 + (σ3 − σ1 )2 = σd

28. 22 ´ ´
CHAPITRE 2. ETAT MECANIQUE
2.2.4 Repr´sentation des contraintes
e
Espace des contraintes
Le tenseur σ au point M ´tant exprim´ dans son rep`re principal, l’´tat m´canique au point M est
e e e e e
alors d´crit par la somme de trois sollicitations simples de traction (ou de compression pour les com-
e
posantes de contraintes principales n´gatives) appliqu´es selon chacune des directions de contraintes
e e
principales. Dans l’espace des contraintes, rep`re orthonorm´ d’axes O, σ1 , σ2 , σ3 , l’´tat m´canique au
e e e e
−→−
point M caract´risant le tenseur σ(M ) est repr´sent´ par le vecteur OM (σ1 , σ2 , σ3 ). C’est la somme de
e e e
−→
−
l’´tat m´canique correspondant au sph´rique S(M ) = σm δ caract´ris´ par le vecteur OH(σm , σm , σm )
e e e e e
1 1 1
port´ par la droite ∆ de cosinus directeurs (± √3 , ± √3 , ± √3 ) et de l’´tat m´canique correspondant au
e e e
−→
−
d´viateur D(M ) = σd π caract´ris´ par le vecteur OH(σ1 − σm , σ2 − σm , σ3 − σm ) contenu dans le plan
e e e
perpendiculaire ` ∆ d’origine H. Cette repr´sentation, applicable ` tout tenseur sym´trique de rang
a e a e
Fig. 2.7 – Espace des contraintes - Surfaces de charge et de rupture
2, prendra tout son sens en m´canique pour repr´senter la loi de comportement plastique dans laquelle
e e
n’intervient que le d´viateur des contraintes caract´ristique du cisaillement. En particulier, les crit`res
e e e
de plasticit´ des diverses classes de mat´riaux ductiles - qui c`dent en cisaillement - seront repr´sent´s
e e e e e
dans cet espace par une surface de r´volution d’axe ∆ appel´e surface de charge( ). Tant que l’´tat
e e e
−→
−
de contrainte au point M sera tel que le vecteur OM sera int´rieur du cylindre bord´ par cette surface,
e e
le mat´riau se comportera de mani`re ´lastique et ne pr´sentera pas de d´formation permanente. D`s
e e e e e e
−→
−
que ce vecteur OM viendra au contact de cette surface, l’´coulement plastique irr´versible se produira
e e
en ce point et le mat´riau pr´sentera apr`s d´charge des d´formations permanentes.
e e e e e
De la mˆme mani`re, les crit`res de rupture des mat´riaux fragiles - qui c`dent en traction - seront
e e e e e
repr´sent´s par une seconde surface - de forme plus complexe, localement perpendiculaire ` chacun
e e a
des trois axes - appel´e surface de rupture( ).
e
Cercles de Mohr
La repr´sentation de Otto Mohr de l’´tat m´canique pr´sente l’avantage d’un diagramme plan
e e e e
ne comportant que des cercles et des droites et s’appuie sur la repr´sentation du vecteur contrainte
e
→
−
T (M, →) = σ(M )→ associ´ ` la facette de normale → dans le rep`re local de la facette (cf. sec-
−
n −
n e a −n e
tion 2.2.1) de sorte qu’il n’y admet que deux composantes σnn et σrn . Elle d´finit l’´tat m´canique au
e e e
point M du corps dans l’espace local des contraintes caract´ris´ par le plan O, σnn , σrn comme l’en-
e e
→
−
semble des points P extr´mit´s du vecteur T (M, →) pour toutes les valeurs possibles de l’orientation
e e −n
→. Ce lieu est d´fini par le syst`me des trois ´quations :
−n e e e
→ · → = 1 σnn = → · → = (σ(M ) · →) · →
− −
n n
− −
T n − −
n n 2 2 → →
− −
σnn + σrn = T · T = (σ(M ) · →) · (σ(M ) · →)
−
n −
n

29. 2.2. LES CONTRAINTES 23
Fig. 2.8 – Espace de Mohr des contraintes locales
En supposant, sans perte de g´n´ralit´, σ1 < σ2 < σ3 les points repr´sentatifs se situent dans le plan
e e e e
σnn , σnt ` l’int´rieur d’un domaine compris entre les trois cercles principaux centr´s sur l’axe Oσnn ,
a e e
σ +σ |σ −σ |
de centre i 2 j et de rayon i 2 j .
Les cercles principaux correspondent ` l’annulation d’un des cosinus directeurs ni de →, c’est-`-
a −n a
dire que la direction consid´r´e appartient ` un plan principal. Cette situation est fort heureusement
ee a
courante, qu’il s’agisse de probl`mes plans o` lorsqu’une direction principale est ´vidente, soit parce
e u e
que la facette est libre de charge, soit par raison de sym´trie.
e
→
−
Dans ce cas le vecteur T (M, →) = σ(M )→ appartient lui aussi au plan principal consid´r´. C’est
−n −
n ee
cette propri´t´ qui rend la construction de Mohr aussi efficace.
ee
Dans ce qui suit, nous nous limiterons ` l’´tude des cercles principaux et nous consid´rerons,
a e e
sans perte de g´n´ralit´, que la direction → appartient au plan principal σ1 , σ2 c’est-`-dire que la
e e e −
n a
composante n3 de la normale ` la facette est nulle. L’´tat de contrainte au point M ´tant repr´sent´
a e e e e
Fig. 2.9 – Espace mat´riel - Espace de Mohr des contraintes locales
e
par le tenseur σ diagonal dans son rep`re principal O, X1 , X2 , X3 , la direction de la normale → ` la
e − a
n
facette consid´r´e sera donc caract´ris´e dans le plan principal O, X1 , X2 par l’angle θ - rep´r´ dans
ee e e ee
le sens trigonom´trique - avec l’axe principal OX1 et les vecteurs unitaires de son rep`re local →, →
e e − −
n r
→
− →(cos θ, sin θ, 0) et →(− sin θ, cos θ, 0). Les
− −
-( t ´tant confondu avec X3 )- ont pour composantes : n
e r
→
−
composantes locales de son vecteur contrainte T sont :
→ −
−
σnn = T · → = → · σ → = σ1 cos2 θ + σ2 sin2 θ σnn = σ1 +σ2 − σ2 −σ1 cos 2θ
n −
n −
n 2 2
→ → → →
− − − · σ − = (σ2 − σ1 ) sin θ cos θ σrn = σ2 −σ1 sin 2θ
σrn = T · r = r n 2

30. 24 ´ ´
CHAPITRE 2. ETAT MECANIQUE
d´finissant les ´quations param`triques du cercle principal σ1 , σ2 dans le plan de Mohr σnn , σrn :
e e e
(σnn − σ1 +σ2 2
2 ) + σnn − ( σ2 −σ1 )2 = 0 Centre
2
2 OI = σ1 +σ2
2 Rayon R= σ2 −σ1
2
→
−
Le point P du plan σnn , σrn extr´mit´ du vecteur T (M, →) est assujetti ` parcourir ce cercle lorsque
e e −
n a
la facette tourne dans le rep`re mat´riel OX1 X2 .
e e
Notons imm´diatement que, par suite de la pr´sence du signe ”-” dans l’´quation de σnn , le cercle est
e e e
d´crit dans le sens des aiguilles d’une montre lorsque l’angle θ de la facette tourne dans le sens
e
trigonom´trique.
e
G´om´triquement :
e e
→
− −
−→ − → − →
T (M, →) = OP = OI + IP
−
n σnn = OI − R cos 2θ σrn = R sin 2θ
Le cercle ´tant toujours repr´sent´ dans le rep`re local →, → , la figure repr´sente exactement, en
e e e e − −
n r e
→
−
module et en direction, la configuration du vecteur T (M, →) dans le rep`re local. Mais, dans le cas
−
n e
→
− − − − → − →
−
particulier des cercles principaux, grˆce ` la propri´t´ de coplanarit´ de T (M, →), →, →, X 1 et X 2 il
a a ee e n n r
est possible de repr´senter ´galement sur la mˆme figure la position du rep`re local par rapport aux
e e e e
axes principaux. Si l’angle X1 M n est ´gal ` θ, l’angle au centre σ1 IP est ´gal ` −2θ et l’angle σ1 σ2 P
e a e a
est ´gal ` θ. Les segments σ2 P et σ1 P sont respectivement parall`les aux directions principales X1 et
e a e
X2 .
→
−
Lorsque θ varie de 0 ` π le point P repr´sentatif de T (M, →) d´crit le demi cercle depuis le point σ1
a 2 e − e
n
→
−
pour θ = 0 - premi`re direction principale pour laquelle T (M, →) align´ sur O→ ` pour composantes
e −n e − a
n
π
locales σnn = σ1 et σrn = 0 jusqu’au point σ2 pour θ = 2 - seconde direction principale pour laquelle
→
−
T (M, →) align´ sur O→ ` pour composantes locales σnn = σ2 et σnr = 0.
−n e − a
n
La composante de cisaillement σrn passe par un maximum M σnr = R = σ2 −σ1 lorsque θ = π c’est-`-
2 4 a
dire pour une direction bissectrice du rep`re principal.
e
Lorsqu’une direction principale est connue, ce qui est fr´quent, il est plus rare de connaˆ
e ıtre
´galement les deux autres. Dans le rep`re de mesure O, x1 , x2 , X3 -(OX3 ´tant la direction principale
e e e
connue)- le tenseur σ(M ) d´crivant l’´tat de contrainte au point M aura donc pour composantes :
e e
σ11 σ12 0
σ(M ) = σ21 σ22 0
0 0 σ3
Comme on ne s’int´resse qu’au plan principal perpendiculaire ` OX3 , on pourra se limiter au sous
e a
tenseur plan dont les composantes dans les rep`res O, x1 , x2 et O, X1 , X2 principal seront respective-
e
ment :
σ11 σ12 σ1 0
σ= σ=
σ21 σ22 0 σ2
Connaissant σ dans le rep`re O, x1 , x2 , il est ais´ de trouver les contraintes principales σ1 et σ2 et la
e e
position du rep`re principal O, X1 , X2 par la simple construction du cercle de Mohr (Fig. 2.10) :
e
−
→
– Le vecteur contrainte T1 de la facette de normale →1 a pour composantes (σ11 , σ21 ) dans le
−
x
rep`re →1 , →2 . Son rep`re local →, → ´tant confondu avec le rep`re →1 , →2 , ses composantes
e − − x x e − − e
n r e − −x x
locales seront σnn = σ11 et σrn = σ21 . Dans le plan de Mohr O, σnn , σrn l’extr´mit´ de son
e e
−
→
vecteur T1 se situera au point P1 .
−
→
– Le vecteur contrainte T2 de la facette de normale →2 a pour composantes (σ12 , σ22 ) dans le rep`re
−x e
→1 , →2 . Son rep`re local →, → se d´duisant du rep`re →1 , →2 par rotation de π , → = →2 et
− −
x x e − −
n r e e − −x x −
n −x
2
→ = −→1 et ses composantes locales seront σnn = σ22 et σrn = −σ12 . Dans le plan de Mohr
−r −
x
−
→
O, σnn , σrn l’extr´mit´ de son vecteur T2 se situera au point P2 .
e e

31. 2.2. LES CONTRAINTES 25
Fig. 2.10 – Construction du cercle de Mohr
Comme deux facettes perpendiculaires ont les extr´mit´s de leur vecteur contrainte diam´tralement
e e e
oppos´es, le cercle de Mohr sera le cercle de diam`tre P1 , P2 centr´ sur Oσnn - puisque par sym´trie
e e e e
σ11 +σ22 1 2 + 4σ 2 . Les
de σ : σ12 = σ21 - au point I tel que OI = 2 et de rayon R = 2 (σ22 − σ11 ) 12
contraintes principales σ1 = OI + R et σ1 = OI − R s’en d´duisent imm´diatement. L’angle orient´ α
e e e
2σ12
entre le rep`re principal O, X1 , X2 et le rep`re O, x1 , x2 est d´termin´ par la relation tg2α = σ22 −σ11 .
e e e e
σ11 +σ22
– La position du centre du cercle conduit ` l’´galit´ OI =
a e e 2 = σ1 +σ2
2
1 2
– Le cisaillement maximal, en valeur absolue ´gal ` R, conduit ` l’´galit´ R =
e a a e e 2 (σ22 − σ11 )2 + 4σ12 =
σ2 −σ1
2
Ces deux ´galit´s ne font que traduire les invariants tensoriels du sous tenseur σ ; En effet, par
e e
d´composition de σ en sph´rique S et en d´viateur D :
e e e
1 0 − cos 2α sin 2α 1 0 1 0
σ = OI +R σ = OI +R
0 1 sin 2α cos 2α 0 1 0 −1
dans le rep`re O, x1 , x2 et dans le rep`re principal O, X1 , X2 , on v´rifie bien :
e e e
Tr(S) = 2OI Det(D) = −R
Notons enfin que la repr´sentation de Mohr, d´velopp´e dans le cadre de la m´canique, est ap-
e e e e
plicable dans tous les domaines de la physique o` l’on manipule des tenseurs sym´triques de rang 2
u e
comme par exemple le tenseur des susceptibilit´s di´lectriques.
e e
Cisaillement pur
Le cas particulier du cisaillement pur correspond ` σ1 = −σ2 . La contrainte moyenne σm est nulle :
a
OI=0. Les facettes orient´es ` π des facettes principales sont soumises au seul cisaillement. Le tenseur
e a 4
des contraintes se r´duit ` son d´viateur qui a pour expressions respectivement dans le rep`re principal
e a e e
π
M, X1 , X2 et dans le rep`re ` 4 : M, x1 , x2 :
e a
−σ 0 0 σ
σ= σ=
0 σ σ 0

32. 26 ´ ´
CHAPITRE 2. ETAT MECANIQUE
π
Fig. 2.11 – Cisaillement pur, rep`re principal : M, X1 , X2 rep`re `
e e a 4 : M, x1 , x2
2.3 La loi fondamentale de la dynamique
2.3.1 Equation de l’´quilibre dynamique
e
Nous ne nous sommes pr´occup´s, jusqu’ici, que de l’´quilibre m´canique statique d’une particule
e e e e
de mati`re centr´e au point M soumise de la part du milieu environnant ` des forces de contact
e e a
→
− →).
−
caract´ris´es par leur densit´ surfacique T (M, n
e e e
Il faut maintenant prendre en compte les forces de volume et d’acc´l´ration support´es par cette
ee e
particule pour ´tablir l’´quation de l’´quilibre dynamique. A l’´chelle du milieu continu, ces forces
e e e e
seront caract´ris´es par leurs densit´s massiques :
e e e
– acc´l´ration : ρ→(M )
ee −
γ
→
−
– force externe : ρ X (M )
→
−
ρ(M ) ´tant la masse volumique du milieu mat´riel, →(M ) l’acc´l´ration et X (M ) la densit´ massique
e e −γ ee e
de force externe auxquelles il est soumis.
En m´canique, la densit´ massique de force la plus fr´quemment rencontr´e est la gravit´ → qui permet
e e e e e−g
de prendre en compte l’effet de poids propre de la structure.
´
Equilibre m´canique global Isolons au sein d’un milieu mat´riel un volume V limit´ par une sur-
e e e
face S. Ce volume est soumis aux densit´s massiques de forces externes γ
e → et →(M ) et ` la
− −
X a
→
−
densit´ surfacique de forces T (M, →) exerc´e par la mati`re environnante. La loi fondamentale
e −
n e e
→
−
de la dynamique m→ = −γ F s’´crit sous la forme d’un bilan int´gral ´tendu au volume V :
e e e
→
− →
−
ρ→dV =
−
γ ρ X dV + T dS
V V S
→
−
Comme les actions de contact sont li´es par la relation T = σ →, le th´or`me de la divergence
e −
n e e
permet de transformer l’int´grale sur S en int´grale sur V
e e
→
−
T dS = σ · →dS =
−
n Div(σ)dV
S S V
et le bilan s’´crit :
e
→
−
ρ→dV =
−
γ ρ X dV + Div(σ)dV
V V V
Ce bilan ´tant ind´pendant du volume V choisi, il en r´sulte l’´quation de l’´quilibre dynamique :
e e e e e
→
−
Divσ + ρ X − ρ→ = 0
−γ (2.18)
´
Equilibre m´canique local Cette ´quation s’´tablit ´galement en consid´rant l’´quilibre d’une par-
e e e e e e
ticule parall´l´pip`de de masse volumique ρ et de volume ´l´mentaire dV = dx1 dx2 dx3 centr´e
ee e ee e
au point M o` l’´tat de contrainte est caract´ris´ par le tenseur σ, la densit´ massique de force
u e e e e
→
−
externe par X et l’acc´l´ration par → :
ee −
γ

33. 2.3. LA LOI FONDAMENTALE DE LA DYNAMIQUE 27
´
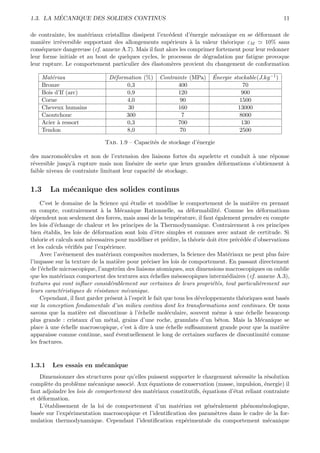
Fig. 2.12 – Equilibre dynamique d’une particule de mati`re
e
→
− →
−
ρ→dV = ρ X dV +
−
γ T dS
f aces
En projection sur l’axe x1 , l’´quilibre des forces :
e
→
−
f aces T dS = {[σ11 + 1 ∂σ11 ] − [σ11 − 2 ∂σ11 ]}dx2 dx3
2 ∂x1
1
∂x1
+{[σ12 + 1 ∂σ12 ] − [σ12 − 1 ∂σ12 ]}dx1 dx3
2 ∂x2 2 ∂x2
+{[σ13 + 1 ∂σ13 ] − [σ13 − 1 ∂σ13 ]}dx1 dx2
2 ∂x3 2 ∂x3
→
− ∂σ1j
T dS = dV = [Divσ]composante1 dV
f aces
∂xj
En regroupant les 3 projections on retrouve l’´quation (2.18) de l’´quilibre dynamique sous la
e e
forme de 3 ´quations diff´rentielles scalaires qui s’´crivent en coordonn´es cart´siennes :
e e e e e
∂σij
+ ρXi − ργi = 0 (2.19)
∂xj
avec sommation sur l’indice j r´p´t´ selon la convention d’Einstein dite des indices muets.
e ee
Notons que cette ´quation ne fait pas appel ` la nature du milieu consid´r´, celle-ci ´tant prise en
e a ee e
compte dans l’´quation d’´tat ou loi de comportement du mat´riau. Ainsi, en hydrostatique, la loi de
e e e
→
−
comportement s’´crit [σ = −pδ, → = 0, X = ρ→] et l’´quation de l’´quilibre conduit ` l’´quation de
e −γ −
g e e a e
→
−
→ = − p + ρ→ = 0 qui ne s’applique qu’aux fluides au repos.
− −
l’hydrostatique Div(−pδ) + ρ g g

34. 28 ´ ´
CHAPITRE 2. ETAT MECANIQUE
2.3.2 Conditions aux limites
L’´quation de l’´quilibre dynamique est l’´quation diff´rentielle qui r´git l’´volution spatiale de
e e e e e e
l’´tat de contrainte caract´ris´ par le tenseur σ au sein de la mati`re. Pour d´terminer l’´tat de
e e e e e e
contrainte r´gnant en tout point d’une structure, il faut ´tablir la solution de cette ´quation qui v´rifie
e e e e
les conditions impos´es - g´n´ralement en terme de forces externes et de d´placement - ` sa p´riph´rie.
e e e e a e e
Fig. 2.13 – Conditions aux limites
Prenons l’exemple d’un ballon de football. Lorsque le joueur frappe le ballon, la pointe de sa
→
−
chaussure exerce une densit´ surfacique de force f sur la zone d’impact. → ´tant la normale ext´rieure
e − e
n e
au point M de la surface impact´e du ballon, l’´quilibre m´canique impose que le vecteur contrainte
e e e
→
− →
−
associ´ T (M, →) soit ´gal ` f .
e −
n e a
→
− →
−
T (M, →) = σ(M ) · → = f
−n −n (2.20)
Au point M en orientant la normale ext´rieur au ballon → selon Ox3 , la condition aux limites impose
e −
n
les valeurs de σ13 , σ23 et σ33
σ11 σ12 σ13 0 f1 σ11 σ12 f1
→
−
T (M, →) =
−
n σ21 σ22 σ23 · 0 = f2 =⇒ σ(M ) = σ21 σ22 f2
σ31 σ32 σ33 1 f3 f1 f2 f3
→
−
Mais apr`s l’impact,d`s que le ballon est en vol, f ≡ 0 et la normale ext´rieure → ` la surface du
e e e − a
n
ballon est direction principale ` valeur propre nulle. Il en est de mˆme pour toute surface libre de
a e
charge.
Notons que les conditions aux limites n’impliquent aucune condition sur les valeurs des composantes
de contrainte σ11 , σ22 et σ12 du sous tenseur associ´es aux facettes de normale perpendiculaire ` →.
e a−n
Ainsi, dans le cas du ballon, la pression de gonflage induit des contraintes de traction dans l’enveloppe
qui confine l’air sous pression.
2.4 Les d´formations
e
Sous l’action d’un chargement, tous les corps subissent un changement de forme, de position et
d’orientation entre un ´tat initial avant application de la charge et un ´tat final cons´cutif ` son
e e e a
application. Les d´formations caract´risent le changement de forme local en tout point du mat´riau,
e e e
ind´pendamment de sa nature et de ses caract´ristiques de r´sistance.
e e e

35. ´
2.4. LES DEFORMATIONS 29
2.4.1 ´
Etat local de d´formation
e
La transformation g´om´trique qui d´crit le passage d’un petit ´l´ment de mati`re de l’´tat initial
e e e ee e e
a e
` l’´tat final se d´compose en Translation, Rotation et D´formation, cette derni`re ´tant seule respon-
e e e e
sable du changement de forme du petit ´l´ment. Translation et Rotation sont des mouvements de corps
ee
rigides qui traduisent les changements de position et d’orientation. Du point de vue de l’´tat final,
e
Rotation et D´formation ne sont pas commutatives. Si l’on ne s’int´resse qu’au changement de forme
e e
du petit ´l´ment et non plus ` sa position absolue les deux configurations finales sont ´quivalentes
ee a e
pour un chargement donn´. e
Fig. 2.14 – Transformation g´om´trique de passage entre l’´tat initial et l’´tat final
e e e e
Seule la D´formation responsable des variations de longueur et des distorsions angulaires ca-
e
ract´rise le changement de forme. Elle seule sera li´e ` la contrainte appliqu´e au travers de la loi de
e e a e
comportement du mat´riau. C’est la variable pertinente du m´canicien.
e e
Petites et grandes d´formations
e
Cependant, lors de l’application de deux chargements successifs, il faut tenir compte de l’ordre
des chargements puisque le second agit sur un ´tat interm´diaire - position, orientation et forme -
e e
induit par le premier, ´tat qui devient le nouvel ´tat de r´f´rence pour le calcul de la r´partition des
e e ee e
contraintes induit par le second chargement. Le calcul de la r´partition des contraintes induit par le
e
second chargement doit s’effectuer ` partir de la forme modifi´e par le premier. L’´tat de contrainte
a e e
est donc diff´rent de celui qui serait obtenu si le second chargement ´tait appliqu´ ` l’´tat initial sans
e e ea e
tenir compte de la D´formation induite par le premier.
e
Ce n’est que dans le cas o` les variations de position, orientation et forme seront suffisamment
u
faibles que l’on pourra les n´gliger et consid´rer qu’en premi`re approximation le second chargement
e e e
agit ´galement sur la g´om´trie initiale, n´gligeant les variations de g´om´trie induites par le premier
e e e e e e
chargement. Il faudra donc distinguer le cas des petites d´formations comme celles des mat´riaux
e e
cristallins travaillant en r´gime ´lastique de celui des grandes d´formations comme celles qui inter-
e e e
viennent dans les op´rations de formage et d’emboutissage des m´taux en r´gime plastique ou celles
e e e
des ´lastom`res supportant de grandes d´formations en r´gime ´lastique.
e e e e e
Principe de superposition
Une approche classique de r´solution d’un probl`me m´canique - connue sous le nom de Principe de
e e e
superposition - consiste ` d´composer la sollicitation appliqu´e ` une structure en une somme de solli-
a e e a
citations ´l´mentaires pour lesquelles il est ais´ de d´terminer, ` partir de la g´om´trie initiale, l’´tat
ee e e a e e e
de contrainte et la d´formation induite correspondante, puis de d´terminer l’´tat de d´formation global
e e e e
par addition de ces ´tats ´l´mentaires de d´formation. De part son principe mˆme, cette approche se
e ee e e
r´f`re toujours ` la g´om´trie initiale et n’est donc applicable qu’en petites d´formations.
ee a e e e

36. 30 ´ ´
CHAPITRE 2. ETAT MECANIQUE
Extension et glissement
Fig. 2.15 – Extension et glissement
A l’´chelle microscopique, le changement de forme se caract´rise par un changement de longueur et
e e
un changement d’orientation des liaisons atomiques. A l’´chelle macroscopique, lorsqu’une structure
e
se d´forme, un segment de longueur l voit varier sa longueur, mais aussi sa direction.
e
– La variation de longueur se caract´rise par l’extension e = l+∆l ou l’allongement relatif ε = ∆l .
e l l
– La variation de direction est pour sa part le r´sultat de la composition des deux op´rations de
e e
Rotation et de D´formation. Afin de s’affranchir de la rotation et de ne retenir que la distorsion
e
de forme, il suffit de suivre l’´volution au cours de la d´formation de l’angle ϕ form´ par deux
e e e
directions initialement orthogonales. Le glissement γ est d´fini comme l’angle compl´mentaire
e e
π
ϕ − 2.
L’allongement relatif ε ´tant d´fini par le rapport de deux longueurs et le glissement γ ´tant d´fini
e e e e
par un angle, la d´formation est une grandeur sans dimension, donc sans unit´ de mesure.
e e
2.4.2 Les grandes d´formations
e
Nous nous limiterons ` la pr´sentation simplifi´e dans un essai classique de traction. On enregistre
a e e
l’allongement ∆l d’une ´prouvette de section initiale S0 et de longueur initiale l0 en fonction de la
e
force appliqu´e F . Pour caract´riser le comportement du mat´riau on s’affranchit de la g´om´trie
e e e e e
F
de l’´prouvette en introduisant la contrainte nominale de traction σn = S0 et l’extension (stretch)
e
e = l+∆l = 1 + ∆l = 1 + εn , εn = ∆l ´tant la d´formation nominale d’extension. La courbe d’essai
l l l e e
F, ∆l trac´e dans le plan σn ,εn est alors repr´sentative du comportement en traction du seul mat´riau.
e e e
Fig. 2.16 – D´formations nominale et vraie
e
Tant que l’allongement ∆l reste petit devant la longueur initiale l0 , typiquement tant εn < 1%,
on peut n´gliger les variations de forme de l’´prouvette et les grandeurs nominales σn et εn sont
e e

37. ´
2.4. LES DEFORMATIONS 31
repr´sentatives de l’´tat de contrainte et de d´formation vraies du mat´riau. C’est le r´gime des pe-
e e e e e
tites d´formations.
e
Cependant, lorsque l’´prouvette s’allonge de mani`re importante, comme c’est le cas pour les
e e
m´taux en r´gime plastique pour lesquels la d´formation nominale ` rupture atteint quelques dizaines
e e e a
de % ou les ´lastom`res en r´gime ´lastique pour lesquels elle peut atteindre quelques centaines de %,
e e e e
on constate exp´rimentalement que l’aire de section droite S d´croˆ au fur et ` mesure de l’allongement
e e ıt a
de l’´prouvette. Il est donc naturel, pour s’affranchir de la g´om´trie de l’´prouvette, de prendre `
e e e e a
tout instant du chargement les dimensions vraies S < S0 et l > l0 pour d´finir les vraies contrainte
e
et d´formation. La d´finition de la d´formation vraie devient incr´mentale au sens o`, sous l’action
e e e e u
de la contrainte vraie σ = F ` un instant donn´ du chargement, le mat´riau subit un accroissement
S a e e
d’extension de = l+dl auquel correspond l’accroissement de d´formation vraie dε = dl . La d´formation
l e l e
vraie ε lorsque l’´prouvette s’est allong´e de ∆l s’obtient par int´gration :
e e e
l0 +∆l dl ∆l
ε= = Ln(1 + ) = Ln(1 + εn ) (2.21)
l0 l l
C’est le r´gime des grandes d´formations.
e e
2.4.3 Les petites d´formations
e
La plupart des structures ´tant constitu´es de mat´riaux cristallins peu d´formables travaillant
e e e e
en r´gime ´lastique, l’approximation des petites d´formations est largement suffisante. Elle offre de
e e e
plus l’avantage du principe de superposition. Nous nous limiterons ` la pr´sentation de la th´orie des
a e e
petites d´formations.
e
La trajectoire d’une particule
Fig. 2.17 – Trajectoire d’une particule et affinit´ tangente
e
→
−
Au cours de l’application du chargement une particule de mati`re de coordonn´es initiales X se
e e
d´place pour occuper une nouvelle position de coordonn´es finales → . La transformation g´om´trique
e e −x e e
qui d´finit le passage de l’´tat initial de r´f´rence ` l’´tat final d´form´ est donc caract´ris´e dans
e e ee a e e e e e
→→
− −
un mˆme rep`re fixe par la fonctionnelle vectorielle → = F ( X ). Si l’on se limite ` une petite r´gion,
e e −
x a e
boule de volume dV0 autour d’un point mat´riel P0 , le centre P0 se translate en P et les points voisins
e
Q0 se d´placent en Q. Leur ensemble forme la boule d´form´e de volume dV . Un d´veloppement limit´
e e e e e
→ = γ(→)d→ en appelant γ(→) = Grad→(→) le tenseur gradient de la transformation
−
conduit ` d x
a
− −
X X
−
X
− −
F X
au point P0 . La relation :
→ →
− − ∂xi dV
d→ = γ( X )d X
−
x dxi = dXj Det(γ) = (2.22)
∂Xj dV0
d´finit l’affinit´ tangente ` la transformation au point P0 . Le Jacobien Det(γ) de la transformation
e e a
´tant par d´finition le rapport du volume dV de la boule d´form´e au volume dV0 de la boule initiale.
e e e e
Notons que γ contient les informations locales de changement de forme (d´formation) et d’orientation
e
(rotation) de la boule initiale.

38. 32 ´ ´
CHAPITRE 2. ETAT MECANIQUE
Le vecteur d´placement
e
Fig. 2.18 – Vecteur d´placement et affinit´ tangente
e e
Plutˆt que de caract´riser la transformation affine tangente par les positions finales → des points
o e −
x
→
−
mat´riels de position X dans l’´tat initial, il est plus commode d’´tudier le champ de d´placement
e e e e
→ induit par la transformation et d´fini par →(→) = → − →. En appelant G = Grad→ le tenseur
−u e − −
u X − −
x X −
u
→ →
− −
gradient du champ de d´placement au point P0 , la transformation affine tangente d→ = γ( X )d X
e −
x
s’´crit alors en terme de d´placement :
e e
→ →
− − ∂ui
d→ = G( X )d X
−
u dui = dXj G=γ−δ (2.23)
∂Xj
Notons que G, comme γ, contient lui aussi les informations locales de changement de forme (d´formation)
e
et d’orientation (rotation) de la boule initiale.
→
−
La d´formation ´tant seule responsable des changements de longueur, le segment d X de longueur
e e
→ →
− −
initiale L telle que L2 =t d X · d X prend par d´formation pure la longueur finale l telle que l2 =t
e
→
− →
− → −
− →
−
d→ · d→. Avec d→ = d X + d→, l2 = L2 +t d→ · d X +t d X · d→ +t d→ · d→. Comme d→ = Gd X ,
−
x − x −x −
u −
u u −u − u −
u
→t
− →
− 2 −L2 →
−
l2 = L2 +t d X ( G + G +t GG)d X . Le rapport l L2 associ´ ` la variation de longueur du segment d X
ea
est fonction du tenseur sym´trique t G + G +t GG qui caract´rise la d´formation pure.
e e e
Gradient de d´placement et petites d´formations
e e
La description math´matique des d´formations se simplifie consid´rablement lorsque la forme ini-
e e e
tiale de la structure est peu modifi´e sous l’action du chargement. Dans ce cas, la variation de forme
e
→
− →
−
de la boule initiale de centre P0 est telle que d→ = d X + d→ d X soit γ = δ + G δ. Les variations
−
x −u
2 −L2
relatives de longueur sont tr`s petites l L2
e 2 l−L et les composantes Gij de G sont petites devant
L
l’unit´. On peut donc n´gliger le terme t GG par rapport au terme G +t G et la d´formation pure
e e e
est repr´sent´e par la partie sym´trique du gradient de d´placement G. Sa partie compl´mentaire
e e e e e
antisym´trique repr´sentera la rotation locale.
e e
L’approximation des petites d´formations s’applique ` la plupart des structures travaillant en
e a
domaine ´lastique pour lesquelles Gij d´passe rarement 10−3 .
e e
Translation, rotation et d´formation
e
En d´composant G en sa partie sym´trique ε et sa partie antisym´trique Ω :
e e e
G11 G12 G13
G= G21 G22 G23 =
G31 G32 G33

39. ´
2.4. LES DEFORMATIONS 33
2G11 G12 + G21 G13 + G31 0 G12 − G21 G13 − G31
1 1
G12 + G21 2G22 G23 + G32 + −(G12 − G21 ) 0 G23 − G32
2 2
G13 + G31 G23 + G32 2G33 −(G13 − G31 ) −(G23 − G32 ) 0
ε Ω
ε et Ω sont li´s ` G par :
e a
1 1 ∂ui ∂uj 1 1 ∂ui ∂uj
ε = (G +t G) εij = ( + ) Ω = (G −t G) Ωij = ( − ) (2.24)
2 2 ∂Xj ∂Xi 2 2 ∂Xj ∂Xi
avec, par construction :
ε =t ε εij = εji Ω = −t Ω Ωij = −Ωji
– La partie antisym´trique Ω qui ne comporte que trois composantes ind´pendantes induit dans
e e
→
−
la boule de centre P0 un champ de d´placement d→ = Ωd X correspondant ` la rotation locale
e −
u a
de la boule de vecteur ω→ tel que d→ = Ωd→ = → ∧ →. Le vecteur rotation locale → d´finissant
− −u
−
X − −
ω X − e
ω
l’axe, le sens et l’amplitude de la rotation locale a pour composantes ω1 = −Ω23 ,ω2 = −Ω31
et ω3 = −Ω12 soit ωi = −Ωjk avec {i, j, k} permutation circulaire du groupe {1, 2, 3}. C’est
l’analogue du vecteur tourbillon des hydrodynamiciens.
– La partie sym´trique ε qui ne comporte que six composantes ind´pendantes induit dans la boule
e e
→
−
de centre P0 un champ de d´placement d→ = εd X correspondant ` la d´formation locale. Cette
e −
u a e
partie du champ de d´placement - associ´e ` la d´formation pure - est la seule responsable du
e e a e
changement de forme de la boule.
Le d´placement → d’un point Q0 de la boule est la somme :
e −u
→(Q0 ) = →(P0 ) + →(P0 ) ∧ d→ + ε(P0 )d→
−
u −
u −
ω
−
X
−
X
T ranslation Rotation D´f ormation
e
Fig. 2.19 – D´placements de translation Q0 Q , rotation Q Q et d´formation Q Q
e e
– d’un d´placement de corps rigide compos´ de la translation →0 du centre P0 de la boule et de
e e −u
→
−
→ ∧ X de la boule autour du vecteur →(P0 ) associ´ ` la partie antisym´trique
− −
la rotation locale ω ω ea e
Ω.
→
−
– d’un d´placement εd X responsable du changement de forme par d´formation associ´ ` la partie
e e ea
sym´trique ε(P0 )
e

40. 34 ´ ´
CHAPITRE 2. ETAT MECANIQUE
2.4.4 Le tenseur des d´formations
e
D´finition
e
Dans le cadre de la th´orie des petites d´formations, l’´tat de d´formation en un point M est
e e e e
donc caract´ris´ par le tenseur sym´trique ε(M ) et la relation donnant le d´placement d’extr´mit´
e e e e e e
→(M, →) d’un segment unitaire d’origine M et de direction → est donn´e par :
−
u
−
l
−
l e
→(M, →) = ε(M )→
−
u
−
l
−
l (2.25)
ε(M ) caract´rise au point M la relation entre les vecteurs d´placement → de segments unitaires de
e e −u
→
−
diff´rentes orientations l . Comme dans le cas du tenseur des contraintes, la connaissance des vecteurs
e
d´placement d’extr´mit´ u1 , u2 et u3 de trois segments orthogonaux de longueur unitaire d’origine M
e e e
respectivement orient´s selon les axes M x1 , M x2 et M x3 suffit ` d´terminer en ce point M l’´tat de
e a e e
e →(M, →) et → s’´crit de mani`re g´n´rale ` l’aide du tenseur
−
d´formation. la relation (2.25) entre u
−
l
−
l e e e e a
ε(M ) dont les composantes dans le rep`re M, x1 , x2 , x3 sont :
e
ε11 ε12 ε13
ε(M ) = ε21 ε22 ε23
ε31 ε32 ε33
Rep`re local, extension, distorsion et glissement
e
Au point M o` l’´tat local de d´formation est caract´ris´ par le tenseur ε(M ), le d´placement
u e e e e e
→
− →
−
d’extr´mit´ →(M, l ) d’un segment unitaire d’origine M orient´ dans la direction l induit d’une part
e e− u e
une variation de la longueur du segment et d’autre part un changement d’orientation. Pour caract´risere
→ − →
− − →
− →
−
ces deux effets, introduisons le rep`re local tri`dre direct M, l , →, t associ´ ` la direction l tel l ,
e e r ea
→ et → soient coplanaires.
−r −u
→
−
Dans ce rep`re les composantes du vecteur d´placement →(M, l ) sont εll , εrl , εtl , le premier indice
e e −
u
→
−
faisant r´f´rence ` l’axe de projection, le second ` l’orientation l du segment. Par construction on a
ee a a
→ →
− −
toujours εtl = 0 et les composantes non nulles de → sont sa composante normale εll = →(M, l ) · l
−
u −
u
→
− → −
−
selon l appel´e extension et sa composante perpendiculaire εrl = →(M, l ) · → situ´e dans le plan
e −
u r e
→ →
− −
de glissement l , r appel´e distorsion.
e
→
−
d´formation normale εll C’est la composante de → qui ´tire lorsqu’elle est parall`le ` l ou qui
e −u e e a
→
−
contracte si elle est antiparall`le ` l . Le signe de εll est donc intrins`que : εll > 0 pour l’extension
e a e
et εll < 0 pour la contraction.
En petites d´formations, elle caract´rise le changement de longueur du segment car :
e e
→
− → −
− →
− →
− →
−
l = l + →(M, l ) = l + εll l + εrl →
u −
r |l |= (1 + εll )2 + ε2
rl 1 + εll
d´formation de distorsion εrl C’est la composante de → qui change l’orientation de l en la faisant
e −
u
→ →
− −
tourner dans le plan de glissement l , r . En petites d´formations, elle caract´rise la variation
e e
d’orientation du segment car :
εrl
tgα = α εrl
1 + εll
ce qui revient ` confondre le pied C de l’arc BC et celui H de la perpendiculaire BH et `
a a
assimiler la distorsion εrl ` l’angle α
a
Rappelons que nous ne nous int´ressons ici qu’` l’effet de la d´formation pure. A ce changement
e a e
de direction il faut ajouter celui induit par la rotation locale pour d´finir de mani`re absolue la
e e
→
−
nouvelle direction de l .
Pour un segment unitaire orient´ selon la direction perpendiculaire → on obtiendrait de la mˆme
e −r e
mani`re dans son rep`re local r
e e →, −→ les composantes locales εrr et ε . La sym´trie de la d´formation
− − l e e
lr
pure t ε = ε impliquant la relation εlr = −εrl

41. ´
2.4. LES DEFORMATIONS 35
Fig. 2.20 – Petites d´formations, distorsion et glissement
e
Les directions l et r ´tant initialement perpendiculaires, leurs d´form´es l et r font un angle ϕ
e e e
π → →
− − → →
− −
reli´ au glissement γlr par γlr = ϕ − 2 . Soit l · r = −| l || r | sin γlr . Au premier ordre sin γlr γlr ,
e
→
− →
− →
− → −
− → − →
− −
| l | = | l |(1+εll ) | l | et de la mˆme mani`re |→ | |→|. Comme par ailleurs l ·→ = ( l +→( l ))·
e e − r −r r u
→ → →→→ →→ →→
− − − − − − − − − → → →→→
− − − − −
(→ + →(→)) = →( l )· r + l · u ( r )+ u ( l )· u ( r ) →( l )· r + l · u ( r ) = εrl −εlr = −2εlr = 2εlr
− − −
r u r −
u −
u
→ →
− −
puisque l · r = 0, le glissement est ´gal au double de la distorsion.
e
2.4.5 Propri´t´s du tenseur des d´formations
e e e
Le tenseur ε(M ) d´finissant l’´tat de d´formation en un point M est un op´rateur intrins`que,
e e e e e
→
−
sym´trique par construction, qui lie le vecteur d´placement d’extr´mit´ →(M, l ) du segment uni-
e e e e −u
→
−
taire l d’origine M ` son orientation. Cette d´finition est ind´pendante du rep`re choisi, seule sa
a e e e
repr´sentation, les valeurs de ses composantes, d´pend du rep`re.
e e e
Comme le tenseur des contraintes, il poss`de les propri´t´s communes aux tenseur sym´triques de
e ee e
rang 2. Toutes les propri´t´s du tenseur des contraintes σ - en particulier : valeurs principales, di-
ee
rections principales, invariants, sph´rique et d´viateur - (cf. section 2.2.3) s’appliquent au tenseur
e e
→
−
des d´formations ε. Il suffit de remplacer la normale → ` la facette par le segment l et le vecteur
e − a
n
→
− →
−
contrainte T (M, →) par le vecteur d´placement d’extr´mit´ →(M, l ).
−n e e e− u
La d´composition en sph´rique et d´viateur ε = S + D = εm δ + εd π admet une interpr´tation
e e e e
simple, mais physiquement fondamentale. La variation relative de volume θ = dV d’une particule au
V
cours d’une petite d´formation est l’invariant θ = 3εm = Tr(ε). En effet la longueur d´form´e d’un
e e e
→
−
segment unitaire d’orientation l i = →i ´tant li = 1 + εii , la variation de volume dV d’un cube d’arˆte
− e
x e
unit´ sera (1 + ε11 )(1 + ε22 )(1 + ε33 ) − 1 = Tr(ε). La d´formation sera donc la somme :
e e
Fig. 2.21 – Changement de volume et changement de forme
– d’une d´formation sph´rique isotrope (S) (gonflement ou d´gonflement) caract´ris´ par l’exten-
e e e e e
sion moyenne εm prenant en compte la variation totale de volume θ = 3εm = Tr(ε) ` forme
a
constante.
– d’une d´formation d´viatrice anisotrope (D) prenant en compte le changement de forme ` volume
e e a
constant (Tr(D) = 0).
Du point de vue des mat´riaux, si la d´formation ´lastique induit toujours, sauf cas particuliers,
e e e
un changement de volume, la d´formation plastique s’effectue au contraire ` volume constant et ne
e a
fait intervenir que le d´viateur des d´formations.
e e

42. 36 ´ ´
CHAPITRE 2. ETAT MECANIQUE
2.4.6 Repr´sentation des d´formations
e e
Les repr´sentations du tenseur des contraintes (σ) sont ´videmment transposables au tenseur des
e e
d´formations (ε) (cf. section 2.2.4).
e
La repr´sentation de Mohr dans un plan principal de d´formation permet de dessiner directement la
e e
Fig. 2.22 – Affinit´ : la transformation d’un cercle en une ellipse
e
section d´form´e d’une particule dans le plan principal. Le cercle de rayon unit´ est d´form´ en une
e e e e e
ellipse de demi axes principaux 1 + ε1 , 1 + ε2
2.5 Continuit´ et compatibilit´ des d´formations
e e e
Revenons un instant au cas g´n´ral de la transformation affine tangente (´quation : 2.22) qui
e e e
d´crit l’´volution d’une particule de mati`re de volume dV au cours de l’application d’un chargement.
e e e
Pour que cette transformation existe, il faut qu’il y ait correspondance biunivoque entre chaque point
dV
mat´riel du domaine dans l’´tat initial et dans l’´tat final, ce qui implique que dV0 = Detγ soit
e e e
strictement positif. Detγ > 0 n’est autre que l’expression de la condition de continuit´ sur laquelle
e
est bas´e la m´canique des milieux continus. En d´coulent les cons´quences suivantes :
e e e e
1. Tous points mat´riels formant un ensemble connexe (volume, surface, courbe) forment toujours
e
un ensemble connexe de mˆme nature au cours de la distorsion.
e
2. Tout point mat´riel situ´ ` l’int´rieur d’une surface ferm´e reste ` l’int´rieur de cette surface
e e a e e a e
transform´e par la distorsion.
e
3. Les points mat´riels qui forment dans la configuration de r´f´rence la fronti`re d’un milieu
e ee e
continu en forment encore la fronti`re quelque soit l’´volution de la distorsion.
e e
4. La masse contenue ` l’int´rieur d’une surface mat´rielle ferm´e reste constante au cours de la
a e e e
distorsion. Par surface mat´rielle on entend une surface constitu´e toujours par les mˆmes points
e e e
mat´riels, surface qui se d´place et se d´forme par rapport au r´f´rentiel (aspect Lagrangien). Ce
e e e ee
terme s’oppose au terme de surface g´om´trique qui d´signe une surface invariable par rapport
e e e
au r´f´rentiel. Au cours de la distorsion les points mat´riels traversent la surface g´om´trique
ee e e e
(aspect Eul´rien).
e
La conservation de la masse (dans le r´f´rentiel fixe) : dm = ρdV = ρ0 dV0 permet d’´crire la
ee e
condition de continuit´ sous la forme :
e
ρDetγ = ρ0 ρ − ρ0 + ρ(Detγ − 1) = 0

43. ´
2.6. LOIS DE COMPORTEMENT : RELATIONS CONTRAINTES - DEFORMATIONS 37
– En m´canique des fluides γ − δ = Grad→dt. Pour dt → 0, Detγ − 1 = Det(δ + Grad→dt) − 1
e −
v −v
se r´duit, en ne gardant que les termes du premier ordre du d´veloppement, ` Tr(Grad→dt) =
e e a −v
Div v→dt. La variation de masse volumique Dρ = ρ − ρ0 , en suivant les particules de mati`re,
− e
conduit ` l’expression de l’´quation lagrangienne de conservation de la masse :
a e
Dρ
+ ρDiv→ = 0
−
v
Dt
– En M´canique des solides, o` les atomes sont astreints ` rester sur le r´seau cristallin, on ne
e u a e
peut pas d´coupler Rotation locale et D´formation et la continuit´ de la mati`re implique des
e e e e
restrictions sur la mani`re dont ´volue l’´tat de d´formation d’un point ` un autre.
e e e e a
→
− →
−
En petites d´formations, si l’on applique une transformation d→ = Gd X = (Ω + ε)d X va-
e −
u
Fig. 2.23 – Continuit´ : compatibilit´ des d´formations
e e e
riant al´atoirement d’une particule mat´rielle ` une autre, la d´form´e ne sera pas continue.
e e a e e
Pour assurer cette continuit´, il faut que d→ soit une diff´rentielle exacte, c’est ` dire que G
e −
u e a
s’identifie ` Grad u
a → , ce qui implique que RotD G = 0, soit RotD (ε + Ω) = 0. L’int´grabilit´
− e e
portera ` la fois sur ε et Ω, mais comme les deux grandeurs ne sont pas ind´pendantes, la
a e
condition d’int´grabilit´ peut s’´crire uniquement en terme de ε, la grandeur de r´f´rence du
e e e ee
m´canicien. Cette condition s’´crit sous la forme de six ´quations diff´rentielles aux d´riv´es
e e e e e e
partielles secondes des composantes de ε :
∂ 2 εpr
Inc(ε) = RotD (RotG (ε)) = RotG (RotD (ε)) = 0 Incij (ε) = δipq δjrs (2.26)
∂xq ∂xs
δijk ´tant la composante du tenseur δ compl`tement antisym´trique de rang 3 telle que :
e e e
δijk = +1 si {ijk} est une permutation paire du groupe {123}
δijk = −1 si {ijk} est une permutation impaire du groupe {123}
δijk = 0 dans tous les autres cas (δijk comporte au moins deux indices ´gaux).
e
2.6 Lois de comportement : relations contraintes - d´formations
e
En aucun cas nous n’avons fait appel jusqu’ici ` la nature et aux propri´t´s m´caniques du mat´riau.
a ee e e
Pour ´tablir la relation entre le changement de forme d’une structure et les efforts qui lui sont appliqu´s,
e e
i.e. la relation Contraintes - D´formations, et l’usage que fera le mat´riau du travail qui lui est fourni,
e e
il faut faire appel ` la loi de comportement du mat´riau, son ´quation d’´tat en termes de σ et ε vraies
a e e e
qui s’´crit de mani`re g´n´rale comme une fonctionnelle tensorielle des tenseurs de contrainte et de
e e e e
d´formation et de leurs d´riv´es temporelles :
e e e
dσ dε
F{σ, , . . . , ε, , . . .} = 0
dt dt

44. 38 ´ ´
CHAPITRE 2. ETAT MECANIQUE
Fig. 2.24 – Comportement caract´ristique d’un mat´riau en traction
e e
2.7 R´sum´ Contraintes - D´formations
e e e
´
Description de l’Etat M´canique Local
e
Contrainte D´formation
e
→
−
T (M, n→) = σ → D´finition →(M, →) = ε→
− −
n e −
u
−
l
−
l
σij = σji Sym´trie
e εij = εji
Principe Fondamental de la Dynamique Relation D´formation - D´placement
e e
→
−
Divσ + ρ X = ρ→−γ 2ε = Grad→ +t Grad→
−
u −u
∂σij dV →
−
∂xj + ρXi = ργi V = Trε = div u
Conditions aux Limites Conservation de la Masse
→=→
−
σ(M ) n
−
f
∂ 2 εpr
Incij (ε) = δipq δjrs ∂xq ∂xs
Description Ind´pendante du Comportement du Mat´riau
e e
´
Equation d’Etat du Mat´riau
e
dσ dε
F{σ, , . . . , ε, , . . .} = 0
dt dt
Description du Comportement du Mat´riau en σ et ε vraies.
e

45. Chapitre 3
´ ´
ELASTICITE
L’exp´rience montre que si la d´formation du mat´riau est suffisamment faible, il reprend son ´tat
e e e e
primitif non d´form´ lors de la suppression des efforts ext´rieurs ayant provoqu´ sa d´formation.
e e e e e
Le comportement ´lastique parfait correspond ` une r´versibilit´ m´canique parfaite. Le tenseur des
e a e e e
d´formations ε est alors une variable d’´tat et sa donn´e d´termine, de mani`re biunivoque, le ten-
e e e e e
seur des contraintes σ. Le travail de d´formation d´velopp´ entre deux ´tats d’´quilibre est alors
e e e e e
ind´pendant du chemin suivi entre ces deux ´tats.
e e
3.1 Le travail de d´formation
e
3.1.1 Le travail virtuel de d´formation
e
Le travail de d´formation est d´fini comme celui des forces externes et d’inertie. Si le champ de
e e
d´placement se r´duit ` un mouvement de corps rigide, translation et rotation qui n’induisent pas
e e a
de variation des forces internes, le travail de d´formation est nul. Au sein d’un mat´riau isolons un
e e
Fig. 3.1 – Travail de d´formation
e
volume V de mati`re limit´ par une surface S soumis aux efforts virtuels :
e e
→∗
−
– volumiques : inertie −ρ→∗ et externe ρ X regroup´s sous la forme de la densit´ volumique de
−
γ e e
→∗
−
force f
→∗
−
– surfaciques : action T des parties environnantes
Le travail virtuel de d´formation W dans le champ de d´placement virtuel → s’´crit :
e e − e
u
→∗ →
− − →∗ →
− −
W = f u dV + T u dS
V S
→∗ →∗
− − ∗
Au syst`me de forces f , T est associ´ au sein de la mati`re un tenseur des contraintes σ
e e e
statiquement admissible, c’est ` dire v´rifiant en volume l’´quation fondamentale de la dynamique
a e e
→∗
− →∗
−
Divσ + f = 0 et en surface les conditions aux limites T = σ →.
∗ ∗−
n
39

46. 40 ´ ´
CHAPITRE 3. ELASTICITE
Au d´placement → cin´matiquement admissible continu et d´rivable est associ´ le tenseur des
e −
u e e e
d´formations ε .
e
Le travail de d´formation W peut alors s’´crire :
e e
→∗ →
− − → σ ∗ →dS
− −
W = V f u dV + S u n W = V fi∗ ui dV + S
∗
σij ui nj dS
→∗ →
− − ∗ →
− ∗
∗
d(σij ui )
= V[f u + Div(σ ) u ]dV = V [fi ui + dxj ]dV
→∗
− ∗
∂σij
= V ( f + Div(σ ))→ dV +
∗ −
Tr(σ Grad→ )dV
− ∗ ∂ui
∗t ∗
u V u = V (fi + ∂xj )ui dV + V σij ∂xj dV
∗ ∗ ∗ ∗
= V Tr(σ ε )dV − V Tr(σ Ω )dV = V σij εij dV − V σij Ωij dV
∗ ∗ ε dV
W = V Tr(σ ε )dV W = V σij ij
Le travail virtuel de d´formation W peut donc s’´crire soit en terme de forces externes, soit en
e e
terme de forces internes :
∗ →∗ →
− − →∗ →
− −
W = Tr(σ ε )dV = f u dV + T u dS (3.1)
V V S
dW
et sa densit´ volumique
e dV s’´crit sous la forme :
e
dW ∗
= Tr(σ ε ) (3.2)
dV
3.1.2 Les potentiels ´lastiques
e
Fig. 3.2 – Potentiels d’´lasticit´ parfaite
e e
Pour une ´volution r´elle d’un ´tat d’´quilibre (σ ,ε ) ` un ´tat d’´quilibre voisin (σ + dσ ,ε + dε),
e e e e a e e
selon la variable d’´tat choisie, on pourra d´finir deux densit´s volumiques de potentiel :
e e e
∗
– Avec σ = σ et ε = dε, la densit´ volumique de potentiel d’´lasticit´ π(ε) se d´finit par :
e e e e
∂π ∂π
dπ = Tr(σdε) σ= σij = (3.3)
∂ε ∂εij
Le tenseur des d´formations ε est alors une variable d’´tat et sa donn´e d´termine de mani`re
e e e e e
biunivoque le tenseur des contraintes. σ
∗
– Avec ε = ε et σ = dσ, la densit´ volumique de potentiel compl´mentaire ω(σ) se d´finit par :
e e e
∂ω ∂ω
dω = Tr(εdσ) ε= εij = (3.4)
∂σ ∂σij
Le tenseur des contraintes σ est ´galement une variable d’´tat et sa donn´e d´termine de mani`re
e e e e e
biunivoque le tenseur des d´formations ε.
e

47. ´
3.1. LE TRAVAIL DE DEFORMATION 41
Ces potentiels sont li´s par les relations d(π + ω) = dTr(σε).
e
Par int´gration ` partir d’un ´tat de r´f´rence sans contrainte ni d´formation initiales :
e a e ee e
ε σ dW
π(ε) = Tr(σdε) ω(σ) = Tr(εdσ) = π(ε) + ω(σ) = Tr(σε) (3.5)
0 0 dV
Cf. Figure 3.2. Le potentiel d’´lasticit´ ou potentiel des d´formations π(ε) repr´sente la densit´ vo-
e e e e e
lumique d’´nergie ´lastique stock´e dans le milieu sous l’action des forces externes.
e e e
3.1.3 Relation avec la thermodynamique
La d´finition du travail de d´formation est purement m´canique et ne peut avoir de relation
e e e
avec les fonctions thermodynamiques que pour des situations thermiques particuli`res, en pratique
e
essentiellement dans des conditions isothermes ou adiabatiques.
Premier principe
En appelant E, F et S les densit´s volumiques d’´nergie interne, d’´nergie libre et d’entropie
e e e
et T la temp´rature absolue le premier principe de la thermodynamique appliqu´ ` une particule de
e ea
volume V limit´ par une surface S indique que la variation infinit´simale d’´nergie interne est ´gale `
e e e e a
la diff´rence entre la quantit´ de chaleur re¸ue et le travail des forces internes. Il s’´crit :
e e c e
δEdV = δQdV − δ → • →dS +
− −
q n δW dV
V V S V
δQ ´tant la densit´ volumique de quantit´ de chaleur re¸ue et → le flux de chaleur sortant. Compte
e e e c −
q
→ • →dS =
− −
tenu de la relation (3.3) et de S q n →dV , lors d’une variation de d´formation δε le
−
V Div q e
premier principe implique la relation :
δE = Tr(σ • δε) + δQ − δDiv→
−
q (3.6)
Second principe
Pour la particule le second principe s’´crit :
e
δQ →
−q →
δSdV − dV + δ • − dS ≥ 0
n
V V T S T
→ −
−q →
−q →
−q − → −
Avec S T • →dS = V Div T dV , F = E − T S et Div T = T Div→ − T12 → • T , compte tenu du
n 1 −
q q
premier principe il s’´crit finalement sous la forme de l’in´galit´ de Clausius-Duhem traduisant le fait
e e e
que l’incr´ment de dissipation volumique dΨ est non n´gatif :
e e
1 → → −
δΨ = δΨ1 + δΨ2 = Tr(σ • δε) − (δF + SδT ) − δ− • T ≥ 0
q (3.7)
T
– δΨ1 = Tr(σ • δε) − (δF + SδT ) est l’incr´ment de dissipation volumique intrins`que.
e e
→
−
– δΨ2 = T δ → • T est l’incr´ment de dissipation volumique thermique.
1 −
q e
La r´versibilit´ thermodynamique implique dΨ1 + dΨ2 = 0.
e e
– La r´versibilit´ thermique dΨ2 = 0 est assur´e en particulier en conditions adiabatiques (→ = 0)
e e e −q
→
−
et isothermes ( T = 0) g´n´ralement rencontr´es en m´canique.
e e e e
– La r´versibilit´ m´canique dΨ1 = 0 d´finit l’´lasticit´ parfaite, comportement d’un milieu capable
e e e e e e
de stocker sans pertes l’´nergie fournie par les forces ext´rieures en se d´formant et de la restituer
e e e
en totalit´ de lors du d´chargement.
e e
La r´versibilit´ m´canique dψ1 = 0 ´lasticit´ parfaite implique dF = −SdT + T r(σdε) conduisant
e e e e e
aux relations :
dE = T dS + Tr(σdε) dF = −SdT + Tr(σdε) dΦ = −SdT + Tr(εdσ) (3.8)
∂E ∂π ∂Φ ∂ω
σ= = σ = ∂F = ∂π
∂ε T ∂ε
ε=− = (3.9)
∂ε S ∂ε ∂σ T ∂σ

48. 42 ´ ´
CHAPITRE 3. ELASTICITE
Φ = F − T r(σε) ´tant le potentiel thermodynamique. Ces formules sont la g´n´ralisation des formules
e e e
de la thermodynamique des gaz o` Tr(σε) = −pV .
u
En m´canique, dans la grande majorit´ des cas, les vitesses de d´formations sont suffisamment
e e e
lentes pour assurer l’´quilibre thermique en conditions isothermes de sorte que dT = 0. En prenant
e
comme ´tat de r´f´rence thermodynamique F = Φ = 0 le corps non d´form´ ε = 0 ` temp´rature
e ee e e a e
T = Cte pour s’affranchir des d´formations de dilatation thermique le potentiel ´lastique π s’identifie
e e
alors ` l’´nergie libre F et le potentiel ´lastique compl´mentaire ω s’identifie ` l’oppos´ du potentiel
a e e e a e
thermodynamique Φ.
3.2 L’´lasticit´
e e
3.2.1 Les deux ´lasticit´s
e e
Les mat´riaux pr´sentent en de¸` d’un certain seuil de chargement qui leur est propre un compor-
e e ca
tement ´lastique quasi r´versible caract´ris´ par une densit´ volumique de potentiel ´lastique π(ε) qui
e e e e e e
s’identifie en r´gime isotherme T = T0 ` leur densit´ volumique d’´nergie libre F(ε). A l’incr´ment de
e a e e e
d´formation dε correspond l’´tat de contrainte tel que :
e e
∂π ∂F ∂E ∂S
σ= = = − T0
∂ε ∂ε T ∂ε T ∂ε T
Cette expression montre que l’origine de l’´lasticit´ est double : une contribution provient de la varia-
e e
tion d’´nergie interne associ´e ` la d´formation, l’autre provient de celle de l’entropie. Selon les classes
e e a e
de mat´riaux ces deux contributions peuvent ˆtre d’ordres de grandeur tr`s diff´rents.
e e e e
– Pour les mat´riaux tr`s d´formables comme les ´lastom`res, les conformations des chaˆ
e e e e e ınes ma-
cromol´culaires peuvent ˆtre consid´rablement modifi´es par les d´formations quasiment sans
e e e e e
variation des distances interatomiques et le terme entropique, responsable de la haute ´lasticit´
e e
caoutchoutique, devient pr´pond´rant. Les d´formations r´sultantes sont importantes et le com-
e e e e
portement ´lastique est non lin´aire du fait de l’´volution de r´sistance au changement de confor-
e e e e
mation des macromol´cules, d´senchevˆtrement, ´tirement, alignement. La contrainte augmente
e e e e
bien avec la d´formation puisque l’entropie diminue, la structure interne du mat´riau pelotes
e e
initialement d´sordonn´e s’ordonnant par ´tirement des chaˆ
e e e ınes macromol´culaires.
e
– La variation d’´nergie interne est pr´pond´rante pour les mat´riaux cristallins pour lesquels
e e e e
de l´g`res variations des distances interatomiques associ´es ` la d´formation entraˆ
e e e a e ınent des
variations consid´rables de l’´nergie de coh´sion alors que l’entropie n’est quasiment pas mo-
e e e
difi´e. Ce type de comportement ´lastique lin´aire commun ` la plupart des structures s’´tudie
e e e a e
g´n´ralement dans le cadre des petites d´formations en ´lasticit´ lin´aire objet des d´veloppements
e e e e e e e
de ce chapitre.
3.2.2 L’´lasticit´ lin´aire
e e e
En de¸` de leur seuil d’´coulement plastique (mat´riaux ductiles) ou de rupture (mat´riaux fragiles)
ca e e e
les mat´riaux cristallins pr´sentent une r´ponse ´lastique lin´aire. Elle se traduit donc par une relation
e e e e e
de proportionnalit´ entre les tenseurs σ et ε. Dans ce cas les potentiels π(ε) = F(ε) et ω(σ) = −Φ(σ)
e
sont ´gaux (Cf. Fig. 3.3) et la densit´ volumique d’´nergie ´lastique stock´e s’exprime sous la forme :
e e e e e
1 dW 1
π(ε) = F = = Tr(σε) (3.10)
2 dV 2
F se r´duit ` une fonction homog`ne de degr´ 2 des composantes de ε mais aussi de σ. C’est
e a e e
une forme quadratique d´finie positive ; Le th´or`me d’Euler sur les fonctions homog`nes conduit ` la
e e e e a
relation :
1 1 ∂F 1 ∂F
F = Tr(σε) = Tr(ε ) = Tr(σ ) (3.11)
2 2 ∂ε T 2 ∂σ T
∂F
L’´nergie libre F permet, en ´lasticit´ lin´aire seulement, de d´duire les d´formations par ε =
e e e e e e ∂σ T
.

49. ´
3.3. LES MODULES ELASTIQUES 43
Fig. 3.3 – Potentiels d’´lasticit´ lin´aire
e e e
3.2.3 L’´lasticit´ lin´aire isotrope
e e e
La plupart des mat´riaux sont ´labor´s sous forme polycristalline. Comme en m´canique des
e e e e
milieux continus on ne s’int´resse qu’` des particules de mati`re dont les dimensions sont grandes
e a e
devant celles des microcristaux, l’isotropie macroscopique du mat´riau r´sulte g´n´ralement d’une
e e e e
moyenne des propri´t´s anisotropes des nombreux microcristaux constituant la particule et les pro-
ee
pri´t´s m´caniques ´lastiques ne d´pendent pas de l’orientation au sein de la mati`re, contrairement
ee e e e e
au cas des monocristaux ou des composites.
Soumis ` un champ de contrainte suffisamment faible pour que ces mat´riaux restent en de¸`
a e ca
de leur seuil de plasticit´, les coefficients de la relation contrainte - d´formation en r´gime ´lastique
e e e e
lin´aire, les modules ´lastiques de ces mat´riaux, sont des constantes ind´pendantes de l’amplitude de
e e e e
la contrainte appliqu´e.
e
L’´nergie libre F d’un mat´riau isotrope, ´tant une fonction homog`ne de degr´ 2 des composantes
e e e e e
de ε ou de σ, est un scalaire invariant par changement de rep`re. F ne peut donc d´pendre que des
e e
2 2
invariants quadratiques {Tr2 (ε), Tr(ε) } ou {Tr2 (σ), Tr(σ) } :
2 2
mε Tr2 (ε) + mε Tr(ε ) = F = mσ Tr2 (σ) + mσ Tr(σ )
1 2 1 2 (3.12)
{mε , mε } et {mσ , mσ } constituants des couples de deux modules ind´pendants caract´risant le com-
1 2 1 2 e e
portement ´lastique lin´aire isotrope. Ces couples ne sont pas ind´pendants et il est possible d’exprimer
e e e
les modules d’un couple en fonction de ceux de l’autre. De mˆme, par combinaison, il est possible de
e
d´finir d’autres couples de modules.
e
Les mat´riaux isotropes sont caract´ris´s par 2 modules ´lastiques ind´pendants.
e e e e e
3.3 Les modules ´lastiques
e
3.3.1 Module d’Young et coefficient de Poisson
Vers 1800 Young, m´decin de formation, s’int´resse ` l’´lasticit´ de la corn´e. En proc´dant `
e e a e e e e a
des essais de traction uniaxiale, il constate que la d´formation ε mesur´e selon l’axe de traction est
e e
σ
proportionnelle ` la contrainte σ appliqu´e. Il d´finit le coefficient de proportionnalit´ E = ε .
a e e e
Poisson compl`te l’analyse en constatant que l’allongement dans la direction de l’axe de traction
e
s’accompagne d’un raccourcissement plus faible proportionnel dans les directions perpendiculaires. Il
d´finit positif le coefficient de proportionnalit´ η = − ε⊥ .
e e ε
– Le Module d’Young E a la dimension d’une contrainte et se mesure g´n´ralement en GPa (cf. an-
e e
nexe A.4). Il repr´sente la contrainte qu’il faudrait appliquer pour obtenir une d´formation unit´
e e e
soit doubler la longueur initiale. Aucun mat´riau ne r´pond lin´airement ` une telle contrainte,
e e e a
la plupart ont c´d´ bien avant.
e e
– Le Coefficient de Poisson η est un nombre sans dimension compris dans l’intervalle {0, 1 }. A 2
l’exception des ´lastom`res comme le caoutchouc dont le coefficient de Poisson η 1 , la plupart
e e 2
des mat´riaux isotropes continus ont un coefficient de Poisson compris dans l’intervalle {0, 25 −
e
0, 35} .

50. 44 ´ ´
CHAPITRE 3. ELASTICITE
Fig. 3.4 – Modules : Young, Poisson, Coulomb
– Les mat´riaux structurellement complexes peuvent avoir des coefficient de Poisson sup´rieurs
e e
a
` 0,5. C’est le cas des granulaires, des poreux, des textiles et de nombreux tissus biologiques
comme les muscles qui gonflent fortement lorsqu’on les contracte avec un coefficient de Poisson
η 1. A l’oppos´ le coefficient de Poisson du li`ge η 0. Un bouchon ne s’allonge pas quand
e e
on l’´treint dans un bouche bouteille.
e
3.3.2 Module de Coulomb
Coulomb proc`de ` des essais de torsion (cisaillement pur) et constate que le glissement γ est
e a
τ
proportionnel au cisaillement τ appliqu´. Il d´finit le coefficient de proportionnalit´ G = γ . Le module
e e e
de Coulomb G a la dimension d’une contrainte et se mesure g´n´ralement en GPa. Il repr´sente le
e e e
cisaillement qu’il faudrait appliquer pour obtenir un glissement d’un radian.
3.3.3 Modules de Lam´
e
Lam´, qui s’int´ressait ` la propagation des ondes, introduit le couple de modules {λ, µ} tels que
e e a
l’´nergie libre (cf. Eq. 3.12), exprim´e en termes d’invariants du tenseur des d´formation s’´crive
e e e e
2
F = λ Tr2 (ε) + µTr(ε ). Les modules de lam´ λ et µ ayant tous deux la dimension d’une contrainte.
2 e
3.3.4 Modules de compressibilit´ et de cisaillement
e
La d´formation se d´composant en un changement de volume ` forme constante et un changement
e e a
de forme ` volume constant (cf. 2.4.5) ces deux op´rations seront caract´ris´es respectivement par
a e e e
les modules K et µ.
– Le changement de volume ` forme constante est une d´formation isotrope. Le module K ´tablit
a e e
la relation σm = Kθ = 3Kεm entre la contrainte moyenne σm et la variation relative de volume
r´sultante θ = dV = 3εm .
e V
Dans le cas d’une compression hydrostatique dp ` laquelle est associ´e la valeur moyenne σm =
a e
dp
−dp, la relation σm = Kθ s’´crit K = −V dV . Le module de compressibilit´ K, dont la dimension
e e

51. ´ ´ ´
3.4. LES EQUATIONS DE L’ELASTICITE 45
est celle d’une contrainte, n’est autre que l’inverse du coefficient de compressibilit´ thermody-
e
1 dV
namique χ = − V dp .
– Le changement de forme ` volume constant est une d´formation qui ne fait intervenir que les
a e
d´viateurs des contraintes et des d´formations caract´ris´s par les contrainte σd et d´formation
e e e e e
εd d´viatoriques moyennes. Le module de cisaillement µ, dont la dimension est celle d’une
e
contrainte, ´tablit la relation σd = 2µεd entre ces deux grandeurs.
e
3.4 Les ´quations de l’´lasticit´
e e e
3.4.1 La loi de Hooke
Relation de Young
A partir de la d´finition de E et de η la relation contrainte d´formation s’´crit :
e e e
σ1 0 0 ε1 0 0 1 0 0
σ1
σ= 0 0 0 =⇒ ε= 0 ε2 0 = 0 −η 0
E
0 0 0 0 0 ε3 0 0 −η
Tout ´tat de contrainte se r´duisant ` un ´tat triaxial dans ses axes principaux, le principe de superpo-
e e a e
sition permet de le d´composer σ en trois ´tats de contraintes uniaxiaux orthogonaux, de calculer pour
e e
chacun la d´formation r´sultante puis de sommer ces trois d´formations pour obtenir le tenseur des
e e e
d´formations ε associ´ ` σ. Cette relation tensorielle, ´tablie dans le rep`re principal, est intrins`que.
e ea e e e
Elle s’´crit dans un rep`re quelconque sous la forme de l’´quation de Young :
e e e
Eε = −ηTr(σ)δ + (1 + η)σ Eεij = −ησkk δij + (1 + η)σij (3.13)
Relation de Lam´
e
2
La relation contrainte - d´formation r´sultant de la relation σ =
e e ∂F
∂ε T
, avec F = λ Tr2 (ε)+µTr(ε ),
2
s’´crit alors :
e
σ = λTr(ε)δ + 2µε σij = λεkk δij + 2µεij (3.14)
Relation de Hooke
En d´composant σ = S σ + Dσ = σm δ + σd π σ et ε = S ε + Dε = εm δ + εd π ε en parties sph´riques
e e
et d´viatoriques, le comportement ´lastique d’un milieu isotrope est enti`rement caract´ris´ par la loi
e e e e e
de Hooke :
S σ = 3KS ε Dσ = 2µDε π σ = π ε (3.15)
Le tenseur des contraintes σ et celui des d´formations ε admettent les mˆmes directions principales
e e
en tout point. Ils ont mˆme tenseur des directions π.
e
Relations entre les modules
Ayant d´fini 3 couples de modules {E, η}, {λ, µ} et {K, µ} ainsi que le module G, ´tablissons les
e e
relations qui lient ces modules entre-eux.
1. Module de cisaillement.
En ne consid´rant dans l’´quation (3.13) que les composantes de cisaillement σij avec i = j on
e e
obtient la relation γij = 2εij = 2(1+η) qui s’identifie ` la d´finition σij = Gγij du module de
E a e
E
Coulomb G conduisant ` la relation G = 2(1+η) .
a
En ne consid´rant dans l’´quation (3.14) que les composantes de cisaillement σij avec i = j on
e e
obtient la relation σij = 2µεij = µγij qui, compar´e ` σij = Gγij , conduit ` la relation G ≡ µ.
e a a
Le module de Coulomb G s’identifie au module de cisaillement µ.
Le module de cisaillement µ, qui lie ´galement les d´viateurs de σ et de ε (cf. Eq. 3.15), quantifie
e e
la r´sistance au changement de forme (` volume constant) des mat´riaux.
e a e

52. 46 ´ ´
CHAPITRE 3. ELASTICITE
2. Relations entre {E, η}, {λ, µ} et {K, µ}
Pour ´tablir ces relations, il faut r´soudre le syst`me lin´aire de six ´quations alg´briques consti-
e e e e e e
tuant les ´galit´s tensorielles (3.13) ou (3.14). Pour ce faire, prenons la trace de la relation
e e
d’Young (3.13) et celle de la relation de Lam´ (3.14). Compte tenu de Tr(δ) = 3, elle conduisent
e
aux relations :
ETr(ε) = (1 − 2η)Tr(σ) Tr(σ) = (3λ + 2µ)Tr(ε) (3.16)
entre les traces de σ et de ε. De la relation de Hooke (3.15) on tire les relations :
E 2
K= =λ+ µ (3.17)
3(1 − 2η) 3
En rempla¸ant dans la relation d’Young (3.13) Tr(σ) par son expression en fonction de Tr(ε)
c
tir´e de la relation (3.16) puis en r´solvant en terme de σ, cette ´quation s’´crit :
e e e e
ηE E
σ= Tr(ε)δ + ε
(1 + η)(1 − 2η) 1+η
Par identification avec la relation de Lam´ (3.14) on obtient les relations cherch´es :
e e
ηE E
λ= µ= (3.18)
(1 + η)(1 − 2η) 2(1 + η)
En rempla¸ant dans la relation de Lam´ (3.14) Tr(ε) par son expression en fonction de Tr(σ)
c e
tir´e de la relation (3.16) puis en r´solvant en terme de ε, cette ´quation s’´crit :
e e e e
λ 1
ε=− Tr(σ)δ + σ
2µ(3λ + 2µ) 2µ
Par identification avec la relation d’Young (3.13) on obtient les relations cherch´es :
e
µ(3λ + 2µ) λ
E= η= (3.19)
λ+µ 2(λ + µ)
3.4.2 Les modules effectifs
Les ´tats de contrainte σ et de d´formation ε ´tant d´crits dans le rep`re principal :
e e e e e
σ1 0 0 ε1 0 0
σ= 0 σ2 0 ⇔ ε= 0 ε2 0
0 0 σ3 0 0 ε3
σ1
d´finissons les modules effectifs {E ∗ , η ∗ } par les relations : E ∗ =
e ε1 et η∗ = − ε2 .
ε1
1. D´formation libre
e
La relation de Young (3.13) est directement applicable et la d´finition des modules effectifs
e
{E ∗ , η ∗ } coincide avec celle des modules {E, η}
2. D´formation interdite selon l’axe x3
e
Dans ce cas ε3 = 0 et la composante de contrainte σ3 est li´e aux contraintes σ1 et σ2 par la
e
relation : σ3 = η(σ1 + σ2 ). La relation d’Young est applicable aux sous ´tats plans :
e
σ1 0 ε1 0
σ= ⇔ ε=
0 σ2 0 ε2
a
` condition de remplacer les modules vrais du mat´riaux par les modules effectifs :
e
E η
E∗ = η∗ = (3.20)
1 − η2 1−η

53. ´ ´ ´
3.4. LES EQUATIONS DE L’ELASTICITE 47
3. D´formation interdite selon les axes x2 et x3
e
η
Dans ce cas ε2 = ε3 = 0, σ2 = σ3 = 1−η σ1 , le coefficient de Poisson effectif η ∗ = 0. Le probl`me
e
devient unidimensionnel en d´formation et le module d’Young effectif vaut :
e
E(1 − η)
E∗ = = λ + 2µ (3.21)
(1 − 2η)(1 + η)
Lorsque la d´formation est interdite lat´ralement, E ∗ > E, le mat´riau paraˆ plus rigide du fait de la
e e e ıt
frustration de l’effet Poisson.
Fig. 3.5 – Modules effectifs : Compression uniaxiale
3.4.3 L’´quation de Lam´
e e
En combinant l’´quation de l’´quilibre dynamique (cf. Eq. 2.18) v´rifi´e par le tenseur des contraintes
e e e e
σ, la d´finition du tenseur de d´formation ε en terme de d´placement → (cf. Eq. 2.24), la d´finition de
e e e −
u e
2→
d u−
l’acc´l´ration γ = dt2 et l’´quation d’´tat du mat´riau (cf. Eq. 3.14), on obtient, par ´limination de
ee e e e e
σ et de ε entre ces 3 ´quations, l’´quation de Lam´ de l’´lasticit´ lin´aire isotrope en terme de champ
e e e e e e
de d´placement :
e
→
− d2 →
−
u
(λ + µ)Grad(Div→) + µ∆→ + ρ X = ρ 2
−u −u
dt
→
− d2 →
−
u
(λ + µ)Rot(Rot→) + (λ + 2µ)∆→ + ρ X = ρ 2
−
u −u (3.22)
dt
1 ρ→− ρ d2 →
−
u
Grad(Div→) + ∆→ + X =
−u −
u
1 − 2η µ µ dt2
Elle diff`re de l’´quation de Laplace par le terme Grad(Div→) qui en fait toute sa richesse, mais
e e −
u
aussi toute sa complexit´. Elle est aux mat´riaux ´lastiques lin´aires isotropes ce qu’est l’´quation de
e e e e e
Navier-Stokes aux fluides newtoniens.
Forces de volume constantes ou nulles
Dans la plupart des cas la d´formation d’une structure r´sulte de l’action des efforts appliqu´s ` sa
e e e a
surface (chargement externe n’intervenant dans la solution ´lastique que par l’interm´diaire des condi-
e e
tions aux limites) et de celle du poids propre de la structure (efforts dus ` la pesanteur correspondant
a
a
` une densit´ volumique de force constante).
e
→
−
Lorsque les forces de volume f sont constantes l’´quation de Lam´ se r´duit ` :
e e e a
1 ρ→ →
− −
Grad(Div→) + ∆→ + f = 0
−
u −
u
1 − 2η µ

54. 48 ´ ´
CHAPITRE 3. ELASTICITE
Sa divergence - qui d´termine la variation de volume au cours de la d´formation - est une fonction
e e
harmonique. De la relation lin´aire entre σ et ε il r´sulte que la trace du tenseur des contraintes est
e e
´galement une fonction harmonique :
e
∆(Div→) = ∆(Tr(ε)) = 0
−
u ∆(Tr(σ)) = 0 (3.23)
3.5 Les probl`mes plans
e
Dans le cas des structures en feuillets minces ou des structures de grande longueur charg´es unique-
e
ment dans le plan de section droite, il est possible de r´duire l’´tude ` celle d’un probl`me m´canique
e e a e e
bidimensionnel plan.
Au sens math´matique, un probl`me est bidimensionnel lorsque toutes les grandeurs ne sont fonc-
e e
tion que de deux des trois coordonn´es d’espace. Cette seule restriction ne simplifie pas les probl`mes
e e
d’´lasticit´ car si le champ de d´placement → ne d´pend que de x1 , x2 la d´formation ε33 = ∂u3 et les
e e e −u e e ∂x
3
gradients ∂u3 , ∂u3 sont nuls mais ∂u1 et ∂u2 donc ε31 et ε32 ne le sont en g´n´ral pas. Le tenseur des
1
∂x ∂x
2
∂x
3
∂x
3
e e
d´formations ε poss`de encore 5 composantes non nulles au lieu de 6 et le tenseur des contraintes σ 6
e e
composantes non nulles.
Afin de simplifier le probl`me ´lastique, on impose comme condition suppl´mentaire que l’axe x3
e e e
soit direction principale en tout point ce qui implique que le chargement de la structure, invariant par
translation selon x3 , s’effectue dans le plan de section droite {x1 , x2 }. Il faut alors distinguer le cas
des d´formations planes de celui des contraintes planes.
e
3.5.1 La d´formation plane
e
En d´formation plane l’axe x3 est en tout point direction principale ` valeur propre nulle du tenseur
e a
des d´formations ε impliquant ε33 = 0, ε13 = 1 ∂u1 = 0 et ε23 = 1 ∂u2 = 0 d’o` u3 = 0
e 2 ∂x
3
2 ∂x
3
u
L’axe x3 est ´galement direction principale du tenseur des contraintes σ impliquant σ13 = σ23 = 0,
e
mais, la d´formation ε33 ´tant nulle, en d´formation plane les sections adjacentes ne sont pas libres de
e e e
se d´former par effet Poisson selon x3 , elles se gˆnent mutuellement et cette frustration est ` l’origine
e e a
d’une contrainte σ33 = 0. Sa valeur σ33 = η(σ11 +σ22 ) se d´duit directement de la loi de comportement
e
1
´lastique ε33 = E (σ33 − η(σ11 + σ22 )) (cf. relation d’Young Eq. 3.13).
e
La d´formation plane concerne donc des structures de grande longueur invariantes en forme et en
e
chargement par translation selon l’axe x3 telles que des tunnels ou des feuillets minces ins´r´s entre
ee
deux blocs suffisamment rigides pour ˆtre consid´r´s comme ind´formables.
e ee e
Les tenseurs σ , ε et le champ de d´placement → satisfont alors aux relations d’un probl`me
e −
u e
bidimensionnel :
ε11 ε12 u1 (x1 , x2 ) σ11 σ12 u3 = 0
ε= ⇒ u= ⇒ σ= avec
ε12 ε22 u2 (x1 , x2 ) σ12 σ22 σ33 = η(σ11 + σ22 )
(3.24)
a
` condition de remplacer dans la relation de Young E ∗ ε = (1 + η ∗ )σ − η ∗ Tr(σ)δ les modules vrais du
mat´riaux par les modules effectifs (cf. Eq. 3.20) :
e
E η
E∗ = η∗ =
1 − η2 1−η
→ →
− −
L’´quation de l’´quilibre ´lastique statique DivD σ + ρ X = 0 se r´duit ` :
e e e e a
∂σ11 ∂σ12 ∂σ21 ∂σ22
+ + ρX1 = 0 + + ρX2 = 0 ρX3 = 0
∂x1 ∂x2 ∂x1 ∂x2
→
−
la derni`re ´quation impliquant que la force de volume ρ X ait une composante X3 = 0 sur l’axe x3 .
e e
→ −
−
Lorsque les forces de volume se r´duisent au poids propre de la structure X = → implique que l’axe
e g
x3 soit horizontal.
Compte tenu de la relation σ33 = η(σ11 + σ22 ) et de l’´quation g´n´rale (3.23) la solution d’un
e e e
probl`me de d´formation plane passe par la r´solution de :
e e e
∆(σ11 + σ22 ) = 0 (3.25)

55. `
3.5. LES PROBLEMES PLANS 49
Fonction de contrainte
Lorsque l’on n´glige les forces de volumes l’´quation de l’´quilibre ´lastique statique se r´duit ` :
e e e e e a
∂σ11 ∂σ12 ∂σ21 ∂σ22
+ =0 + =0
∂x1 ∂x2 ∂x1 ∂x2
Les composantes σ11 ,σ22 et σ12 se d´duisent alors d’une fonction de contrainte arbitraire χ(x1 , x2 ) par
e
les relations :
∂2χ ∂2χ ∂2χ
σ11 = σ22 = σ12 = − (3.26)
∂x22 ∂x2
1 ∂x1 ∂x2
Mais les 3 composantes σ11 ,σ22 et σ12 ne sont pas ind´pendantes puisqu’elles s’expriment au moyen
e
des deux seules composantes u1 , u2 du champ de d´placement. La relation de Young conduit alors ` la
e a
∗ (ε + ε ) = (1 − η ∗ )(σ + σ ) = (1 − η ∗ )∆χ. Comme ε
relation E 11 22 11 22 33 = 0 entraˆıne ε11 + ε22 = Div→−
u
et comme Div u → v´rifie l’´quation(3.23) la fonction de contrainte est une fonction biharmonique :
− e e
∆(∆χ) = 0 σ33 = η∆χ (3.27)
3.5.2 La contrainte plane
Le probl`me de la contrainte plane
e
En contrainte plane l’axe x3 est en tout point direction principale ` valeur propre nulle du tenseur
a
des contraintes σ impliquant σ13 = σ23 = σ33 = 0.
Le tenseur des d´formations ε d´duit de la loi de comportement ´lastique lin´aire (cf. relation
e e e e
η
d’Young Eq. 3.13) comporte une composante ε33 = ∂u3 = − E (σ11 + σ22 ) fonction de x1 , x2 . La com-
∂x
3
posante u3 du champ de d´placement est donc une fonction de x1 , x2 , x3 lin´aire en x3 . En cons´quence
e e e
∂u3 ∂u3
∂x1 = 0 et ∂x2 = 0 impliquant ε13 = 0, ε23 = 0 et σ13 = 0, σ23 = 0.
Le seul probl`me r´ellement bidimensionnel de contrainte plane vraie doit donc satisfaire ` ε33 = 0,
e e a
c’est ´galement un probl`me de d´formation plane. Il correspond ` σ11 + σ22 = 0. C’est le cisaillement
e e e a
pur.
La contrainte quasi plane
Fig. 3.6 – Feuillet mince en contrainte quasi plane
Pour un feuillet mince et vertical, sans force de volume autre que la gravit´, sollicit´ dans son
e e
plan de section droite par un chargement sym´trique sur l’´paisseur, condition n´cessaire pour que le
e e e
feuillet ne fl´chisse pas hors de son plan, on pourra d´finir rigoureusement un probl`me de contrainte
e e e
moyenne plane en d´finissant les composantes du tenseur des contraintes moyen par :
e
e/2
< σij >= σij (x1 , x2 , x3 )dx3 (3.28)
−e/2

56. 50 ´ ´
CHAPITRE 3. ELASTICITE
En effet, σi1 et σi2 ´tant des fonctions paires de x3 par sym´trie du chargement, il en est de mˆme
e e e
∂σi1 ∂σi2 ∂σi3 −→
−
de ∂x1 et ∂x2 donc de ∂x3 puisque DivD σ = Cte. En cons´quence la primitive σi3 est une fonction
e
impaire de x3 dont la valeur moyenne prise selon l’´paisseur e est rigoureusement nulle. Avec < ε33 >=
e
η
− E (< σ11 > + < σ22 >) et ` condition de raisonner sur les valeurs moyennes selon l’´paisseur du
a e
feuillet, le probl`me de contraintes quasi-planes s’´crit comme un vrai probl`me bidimensionnel :
e e e
< σ11 > < σ12 > < ε11 > < ε12 > < ε13 >=< ε23 >= 0
σ= ⇒ ε= avec η
< σ12 > < σ22 > < ε12 > < ε22 > < ε33 >= − E (< σ11 > + < σ22 >)
(3.29)
la relation de Young conservant sa forme habituelle : E < ε >= (1 + η) < σ > −ηTr(< σ >)δ. La
d´formation ε33 ´tant libre en contrainte plane les sections adjacentes sont libres de se d´former par
e e e
effet Poisson selon x3 , il n’y a pas de frustration donc E et η sont les vrais modules du mat´riau.
e
Compte tenu de la relation < σ33 >= 0 et de l’´quation g´n´rale (3.23) la solution d’un probl`me
e e e e
de contrainte plane passe par la r´solution de :
e
∆(< σ11 > + < σ22 >) = 0 (3.30)
3.5.3 Lieux caract´ristiques des probl`mes plans
e e
Loi de similitude
Le fait que l’´quation r´gissant les probl`mes plans ∆(< σ11 > + < σ22 >) = 0 en contraintes
e e e
planes et ∆(σ11 + σ22 ) = 0 en d´formation plane ne contienne aucun module ´lastique implique
e e
que, ` g´om´trie et ` chargement donn´, la r´partition des contraintes au sein d’une section droite du
a e e a e e
mat´riau est ind´pendante du mat´riau ´tudi´. Cette propri´t´ remarquable est ` la base des m´thodes
e e e e e ee a e
d’analyse exp´rimentale des contraintes telles que la photo´lasticim´trie qui utilise des mod`les en
e e e e
mat´riau photo´lastique transparent comme le verre, le PMMA (Polym´tacrylate de m´thyle) connu
e e e e
sous le nom commercial de Plexiglas ou diverses r´sines comme les araldites et polyur´thanes pour
e e
d´terminer l’´tat plan de contraintes car il n’y a pas n´cessit´ d’une mise ` l’´chelle des modules
e e e e a e
´lastiques du mat´riau mod`le et du mat´riau r´el.
e e e e e
Le tenseur σ repr´sentant l’´tat plan de contrainte ´tant caract´ris´ dans le syst`me d’axe x1 , x2
e e e e e e
par ces trois composantes σ11 , σ12 , σ22 , en chaque point du mod`le il admet un syst`me d’axes propres
e e
dans lequel il se d´compose en sph´rique S et d´viateur D sous la forme :
e e e
σI 0 1 1 0 1 1 0
σ= = S + D = (σI + σII ) + (σI − σII )
0 σII 2 0 1 2 0 −1
σI +σII est repr´sentatif du sph´rique tandis que σI −σII est repr´sentatif du d´viateur des contraintes.
e e e e
Lieux caract´ristiques
e
Fig. 3.7 – Isoclines - Isochromes - Isopaches - Isostatiques

57. `
3.5. LES PROBLEMES PLANS 51
Isoclines Une isocline - mˆme inclinaison - est le lieu des points du mod`le charg´ ou les directions
e e e
des contraintes principales σI et σII font un angle α constant par rapport ` la direction de
a
r´f´rence x1 . L’´quation implicite du r´seau des isoclines dans le rep`re x1 , x2 est :
ee e e e
2σ12 (x1 , x2 )
tg2α =
σ11 (x1 , x2 ) − σ22 (x1 , x2 )
Le r´seau des isoclines est un r´seau obtenu exp´rimentalement en photo´lasticit´.
e e e e e
Isochromes Une isochrome - mˆme couleur - est le lieu des points du mod`le charg´ o` la diff´rence
e e e u e
σI − σII des contraintes principales est constante. Le r´seau des isochromes mat´rialise les iso-
e e
valeurs du cisaillement maximal
1 σ11 (x1 , x2 ) − σ22 (x1 , x2 ) 2 2
τmax = (σI − σII ) = ( ) + σ12 (x1 , x2 ) = Cte
2 2
en tout point du mod`le. Il est repr´sentatif de l’´tat d´viatorique et s’obtient exp´rimentalement
e e e e e
en photo´lasticit´.
e e
Isopaches Une isopache - mˆme ´paisseur - est le lieu des points du mod`le charg´ o` la varia-
e e e e u
tion d’´paisseur δe(x1 , x2 ) = e0 ε33 (x1 , x2 ) est constante. Comme en contraintes planes ε33 =
e
η
− E (σ11 + σ22 ), c’est aussi le lieu des points du mod`le o` la somme σI + σII des contraintes
e u
principales est constante. Le r´seau des isopaches mat´rialise les isovaleurs de l’´paisseur en
e e e
tout point du mod`le. Il est repr´sentatif de l’´tat sph´rique et s’obtient exp´rimentalement par
e e e e e
interf´rom´trie.
e e
Fig. 3.8 – Isostatiques des neuds du bois et d’une tˆte de f´mur
e e
Isostatiques Les isostatiques sont les trajectoires des contraintes principales. Comme les lignes de
courant en m´canique des fluides, elles repr´sentent la mani`re dont les efforts s’´coulent ` travers
e e e e a
le mod`le. Elle sont tangentes aux contraintes principales en tout point, formant un double r´seau
e e
de lignes orthogonales. En particulier, un bord de mod`le non charg´ est une isostatique pour une
e e
des contraintes principales, les isostatiques de l’autre contrainte d´bouchant perpendiculairement
e
sur ce bord libre de charge. L’´quation diff´rentielle implicite du r´seau des isostatiques est donc :
e e e
dx2 2σ12 (x1 , x2 ) dx2 dx2 2 σ12 (x1 , x2 )
tgθ = tg2θ = = (1 − ( ) )
dx1 σ11 (x1 , x2 ) − σ22 (x1 , x2 ) dx1 dx1 σ11 (x1 , x2 ) − σ22 (x1 , x2 )

58. 52 ´ ´
CHAPITRE 3. ELASTICITE
Ce r´seau tr`s important car les isostatiques sont les trajectoires potentielles des fissures. Il ne
e e
s’obtient pas directement exp´rimentalement. Son trac´ s’effectue ` partir du relev´ des isoclines,
e e a e
en tra¸ant au sommet d’un quadrillage les croix correspondant ` l’orientation des contraintes
c a
principales dont la direction est fournie par l’angle de l’isocline passant par ce point, puis en
tra¸ant les courbes enveloppes.
c
Dans les structures qui soutiennent la mati`re vivante la nature aligne les fibres r´sistantes le
e e
long de lignes de ferraillage qui mat´rialisent les isostatiques. La figure 3.8 pr´sente les lignes
e e
isostatiques ` l’encastrement des branches sur un tronc d’arbre et dans une tˆte de f´mur, lignes
a e e
que l’on retrouve tr`s nettement dans la direction des fibres du bois ` l’emplacement des noeuds
e a
et dans les fibres osseuses.
Tous ces r´seaux respectent les sym´tries du mod`le et de son chargement.
e e e
3.6 Ondes et vibrations
La propagation des ondes ´lastiques r´sulte de la comp´tition entre les forces d’inertie et les forces
e e e
de rappel ´lastique correspondant ` un ´change oscillant entre l’´nergie cin´tique et l’´nergie ´lastique.
e a e e e e e
Un milieu isotrope poss`de deux modules ´lastiques caract´risant la compressibilit´ (changement de
e e e e
volume ` forme constante) et la r´sistance au cisaillement (changement de volume ` forme constante).
a e a
Il peut propager en volume simultan´ment mais de mani`re d´coupl´e des ondes de dilatation com-
e e e e
pression, ondes longitudinales dont la polarisation →L (champ de d´placement de la mati`re induit
−
u e e
par le passage de l’onde) est parall`le ` la direction de propagation de l’onde et des ondes de cisaille-
e a
ment sans dilatation, ondes transversales dont la polarisation →T est perpendiculaire ` la direction
−
u a
de propagation.
3.6.1 Les ondes de volume
Afin d’´tablir la forme g´n´rale de la c´l´rit´ des ondes de volume dans les solides, consid´rons le
e e e ee e e
→
−
mod`le scalaire simple d’une onde de pulsation ω et de vecteur d’onde k se propageant ` la vitesse
e a
V dans la direction x au sein d’un milieu mat´riel de module E ∗ et de masse volumique ρ induisant
e
x
sur son passage un d´placement local de la mati`re u = u0 sin ω(t − V ) (cf. fig. 3.9).
e e
Fig. 3.9 – Propagation d’une onde
La densit´ volumique d’´nergie cin´tique 1 ρ( ∂u )2 prend la valeur maximale 1 ρω 2 u2 tandis que la
e e e 2 ∂t 2 0
1
densit´ volumique d’´nergie ´lastique 2 σε prend, compte tenu du comportement ´lastique du milieu
e e e e
σ = E ∗ ε = E ∗ ∂u , la valeur maximale 1 E ∗ ω 2 ( u0 )2 . L’´galit´ des valeurs maximales de ces deux formes
∂x 2 V e e
d’´nergie conduit ` la forme g´n´rale de la vitesse du son :
e a e e
E∗
V = (3.31)
ρ
Les vitesses typiques de propagation du son dans les solides sont de l’ordre de quelques milliers de
m.s−1 .
Dans un milieu ´lastique isotrope de dimensions caract´ristiques D grandes devant la longueur
e e
→
−
d’onde λ, (λ D), et en l’absence de forces de volumes X = 0 l’´quation de Lam´ du mouvement
e e

59. 3.6. ONDES ET VIBRATIONS 53
s’´crit (cf. eq. 3.22) :
e
d2 →
−
u d2 →
−
u
(λ + µ)Grad(Div→) + µ∆→ = ρ 2
−u −
u (λ + µ)Rot(Rot→) + (λ + 2µ)∆→ = ρ 2
−
u −
u (3.32)
dt dt
Tout champ de vecteur → est d´composable en la somme de 2 champs →L et →T tels que :
−
u e −
u −
u
→ = →L + →T
− − − Div→L = 0 Rot→L = 0
−
u −
u
u u u avec (3.33)
Div→T = 0 Rot→T = 0
−
u −
u
Les ondes longitudinales
Fig. 3.10 – Propagation d’une onde longitudinale
Ce sont des ondes de compression-traction induisant un d´placement de la mati`re →L dans la
e e − u
→
−
direction de propagation d´finie par le vecteur d’onde k (cf. fig. 3.10). La divergence du champ de
e
d´placement →L n’est pas nulle, traduisant des variations locales de volume (extension-contraction)
e −u
au passage de l’onde. Par contre le rotationnel du champ de d´placement →L est nul.
e −
u
L’´quation (3.32) se r´duit alors ` l’´quation de propagation des ondes longitudinales :
e e a e
d2 →
−
u
(λ + 2µ)∆→ = ρ 2
−
u (3.34)
dt
dont la vitesse de propagation est :
λ + 2µ E∗ 1−η
VL = = avec E∗ = E (3.35)
ρ ρ (1 + η)(1 − 2η)
Les ondes transversales
Fig. 3.11 – Propagation d’une onde transverse
Ce sont des ondes de cisaillement induisant un d´placement de la mati`re →T perpendiculaire `
e e − u a
→
−
la direction de propagation d´finie par le vecteur d’onde k (cf. fig. 3.11). La divergence du champ de
e
d´placement →T est nulle, traduisant une absence de variation locale de volume au passage de l’onde.
e −
u
Par contre le rotationnel du champ de d´placement →L est non nul. L’´quation (3.32) se r´duit alors
e −
u e e
a e
` l’´quation de propagation des ondes longitudinales :
d2 →
−
u
µ∆→ = ρ 2
−
u (3.36)
dt

60. 54 ´ ´
CHAPITRE 3. ELASTICITE
dont la vitesse de propagation est :
µ E∗ E
VT = = avec E∗ = (3.37)
ρ ρ 2(1 + η)
Le rapport des vitesses longitudinale et transverse ne d´pend que du coefficient de Poisson η :
e
VT 1 − 2η 1 VT 1 1
= <√ = pour η = (3.38)
VL 2(1 − η) 2 VL 2 3
3.6.2 Barres, plaques et blocs
Les expressions des vitesses de propagation des ondes longitudinales (eq. 3.35) et transverse (eq.
3.37) ont ´t´ obtenues dans l’hypoth`se ou les dimensions D du milieu sont grandes devant la longueur
ee e
d’onde λ. Elles doivent ˆtre modifi´es si les dimensions du milieu perpendiculaires ` la direction de
e e a
propagation deviennent comparables ou inf´rieures ` la longueur d’onde λ.
e a
Ondes longitudinales
Pour un milieu de dimensions caract´ristiques L
e λ dans la direction de propagation et l, h dans
les directions perpendiculaires, on distinguera (cf. fig. 3.12) les trois cas :
– Barres : l, h λ
– Plaques : h λ et l λ
– Blocs : l, h λ
Fig. 3.12 – Barres, plaques et blocs
1. Barres
Comme l, h λ, les d´formations εll et εhh induites par effet Poisson sont libres et le module
e
´quivalent ` retenir dans l’expression de la vitesse de propagation est le module vrai E ∗ = E du
e a
mat´riau (cf. section 3.4.2).
e
2. Plaques
En d´composant la plaque en une s´rie de poutre de hauteur h
e e λ et de largeur λ la d´formation
e
et εhh induite par effet Poisson reste libre mais la d´formation εll est nulle, les effets Poisson
e
des poutres adjacentes dans la direction l se contrariant mutuellement. Le module ´quivalent
e
` retenir dans l’expression de la vitesse de propagation est le module apparent E ∗ = 1−η2 du
a E
mat´riau.
e
3. Blocs

61. 3.6. ONDES ET VIBRATIONS 55
En d´composant le bloc en une s´rie de poutre de hauteur et de largeur λ les d´formations εhh
e e e
et εll sont nulles, les effets Poisson des poutres adjacentes dans les directions h et l se contrariant
mutuellement. Le module ´quivalent ` retenir dans l’expression de la vitesse de propagation est
e a
∗ =E 1−η
le module apparent E (1+η)(1−2η) du mat´riau.
e
Les vitesses longitudinales de propagation correspondantes sont :
E 1−η
VL = ρ VL = E 1−η2
ρ
1
VL = E
ρ (1+η)(1−2η) (3.39)
Barres Plaques Blocs
Ondes transverses
La d´formation induite par le cisaillement s’effectuant ` volume constant, (Div→T = 0), l’effet
e a −u
Poisson n’intervient pas et la vitesse de l’onde transverse VT ne d´pend pas des dimensions transversales
e
a
` la direction de propagation.
3.6.3 Les ondes de flexion
Les ondes de flexion des plaques et des coques
Les structures minces, comme les plaques et les coques, propagent ´galement des ondes transver-
e
sales dispersives de flexion. Pour des longueurs d’onde λ grandes devant l’´paisseur h mais petites
e
devant la largeur l et la longueur L de la plaque, la propagation est r´gie par l’´quation d’onde :
e e
∂2ξ h3 E
D∆2 ξ + ρh = 0 avec D = E∗ et E∗ = (3.40)
∂t2 12 1 − η2
→−
−
ξ(x1 , x2 ) ´tant la d´form´e de la surface neutre de la plaque. Les solutions du type ξ(→, t) = ξ0 cos( k →−
e e e −
x x
ωt) conduisent ` l’´quation de dispersion et ` la vitesse de groupe :
a e a
D 2 dω E 1 E∗
ω= k VG = = kh = kh (3.41)
ρh dk 1 − η 2 3ρ 3ρ
Dans le cas d’une plaque mince dont deux bords parall`les de longueur L sont libres et les deux autres
e
de largeur l soumis ` conditions d’appui simple ξ ne d´pend plus de y et l’´quation d’onde s’´crit par
a e e e
int´gration sur l dans la direction y :
e
∂4ξ ∂2ξ ∂4ξ ∂2ξ
Dl + ρhl 2 = 0 E∗I + ρS 2 = 0 (3.42)
∂x4 ∂t ∂x4 ∂t
avec I moment quadratique de flexion et S aire de la section droite, ` :
a
E∗I 2 dω E∗
ω= k VG = = kh (3.43)
ρS dk 3ρ
1. Pour une plaque large (l ≈ L > λ h) la d´formation εll est interdite (d´formation plane
e e
(εll = 0, σll = 0) et le module ´quivalent E
e ∗ doit ˆtre pris ´gal au module de d´formation plane
e e e
E ∗ = 1−η2 .
E
2. Pour une poutre ´troite (L > λ
e l ≈ h) la d´formation εll est libre (contrainte plane σll =
e
0, εll = 0) et le module ´quivalent E ∗ doit ˆtre pris ´gal au module d’Young E.
e e e
Pour une structure de masse surfacique w, l’´quation d’onde s’´crit plus g´n´ralement D∆2 ξ +
e e e e
d2 ξ
w dt2 = 0 avec ξ( x→) d´form´e de sa surface neutre. Mais w peut varier d’un point ` un autre
− e e a
w = w(→), traduisant soit des variations locales d’´paisseur h(→), soit des variations locales de
−x e −
x
masse volumique ρ(→). Les solutions de la forme ξi = ξi (→)cos(ωi t + ϕi ) conduisent ` l’´quation
−x −x a e
∆ 2 ξ(→) − w 2 ξ(→) = 0, les conditions aux limites fournissant la suite des fr´quences propres w ad-
−
x −
x e
i i
missibles. L’amplitude de la d´form´e associ´e ξi (→) est appel´e mode propre d’ordre i de la structure.
e e e −
x e

62. 56 ´ ´
CHAPITRE 3. ELASTICITE
Ainsi, dans le cas simple d’une plaque rectangulaire (´paisseur h et masse volumique ρ constantes,
e
longueur L et largeur l) en appui simple sur son pourtour : d´placement ξ(± L , x2 ) = ξ(x1 , ± 2 ) = 0
e 2
l
∂ 2ξ ∂ 2ξ
et moment fl´chissant ∼ ∂x2 (± L , x2 ) = ∂x2 (x1 , ± 2 x2 ) = 0 l’´quation aux modes propres admet une
e 2
l
e
1 2
solution analytique :
mπx1 nπx2 Eh m n
ξm,n (→) = A sin
−
x sin ωm,n = π 2 h [( )2 + ( )2 ]
2) L
(3.44)
L l 12w(1 − η l
Les modes propres de vibration d’une structure
Le d´placement u(→, t) d’un point d’une structure mince en vibration normalement ` sa surface
e −x a
peut s’´crire ` tout instant comme combinaison lin´aire d’un ensemble de N modes propres :
e a e
N
u(→, t) =
−
x ηi (t)ξ(→)
−
x (3.45)
i=1
ηi repr´sentant le coefficient d’influence (de pond´ration) du mode i. Pour une structure continue N
e e
est infini, mais on obtient en g´n´ral une bonne ´valuation de u(→, t) en se limitant ` un nombre
e e e −x a
fini de modes. Chaque mode propre ξi est orthogonal relativement ` la distribution de masse de la
a
structure d’o` le nom de mode normal.
u
w(→)ξi (→)ξj (→)dS = Mi δij
−
x −
x −
x (3.46)
S
Mi ´tant la masse g´n´ralis´e du mode propre i.
e e e e
→−
−
Pour une structure soumise ` une densit´ surfacique de force ext´rieure F (→, t), en rempla¸ant
a e e x c
u(→, t) par son d´veloppement, les ´quations de Lagrange du mouvement (inertie mγ = forces
−x e e
ext´rieures F -amortissement visqueux f -rappel ´lastique K) :
e e
∂2u ∂u
m 2
=F −f − Ku (3.47)
∂t ∂t
se s´parent en N ´quations diff´rentielles ind´pendantes :
e e e e
∂ 2 ηi ∂ηi Fi
2
+ 2βi 2
+ ωi η i = avec Fi = F (→, t)ξi (→)dS
−
x −
x (3.48)
∂t ∂t Mi S
d´finissant les coefficients d’influence des diff´rents modes, Fi ´tant la force g´n´ralis´e et βi le coef-
e e e e e e
ficient d’amortissement associ´s au mode i. Ainsi la connaissance des modes propres d’une structure
e
(r´partition spatiale, fr´quence, amortissement) permet de calculer la r´ponse d’une structure com-
e e e
plexe ` une sollicitation ext´rieure connue.
a e
Un cas particulier important en pratique est celui d’une densit´ surfacique de force dont la
e
r´partition spatiale n’est pas fonction du temps : F (→, t) = F (→)H(t) ; la d´pendance temporelle
e −
x −x e
H(t) ´tant la mˆme en tout point. F (→) peut alors se d´composer en int´grale de Fourier sous la
e e −
x e e
→ − →
− −
forme : F (→) = S F ( X )δ(→ − X )dS et la lin´arit´ des ´quations permet d’obtenir la r´ponse de la
−x x e e e e
a →,t) comme superposition des r´ponses ´l´mentaires aux forces F (→)H(t)
−
structure ` la sollicitation F( x e ee
−
X
→
− →
−
o` F ( X ) est l’amplitude de la force ponctuelle appliqu´e en X . La force g´n´ralis´e du mode ξi est
u e e e e
→
− →
−
Fi = S F (→, t)ξ(→)dS = F ( X )ξi ( X )H(t) et l’´quation (3.48) du coefficient d’influence du mode i
−
x −x e
devient : →
− →
−
∂ 2 ηi ∂ηi 2 F ( X )ξi ( X )
+ 2βi + ωi η i = H(t) (3.49)
∂t2 ∂t Mi
Pour une excitation sinuso¨
ıdale H(t) = exp(Iωt) ` la pulsation ω, la solution de cette ´quation
a e
→ →
− −
conduit ` η = α (ω) avec α (ω) = 1 F ( X )ξi ( X ) (I nombre imaginaire tel que I 2 =-1).
a i i i 2
Mi (ωi −ω 2 )+2Iβi ω
→
−
La r´ponse impulsionnelle de la structure ` la force ponctuelle F ( X )H(t) est alors donn´e par
e a e
u(→, t) = Re( exp(Iωt) N αi (ω)ξi (→)). La r´ponse de la structure ` la sollicitation F (→, t) s’ob-
−
x i=1
−x e a −
x
tient alors par superposition des r´ponses ´l´mentaires ci-dessus.
e ee

63. ´ ` ´ ´ ´ ´ ´
3.7. THEOREMES ENERGETIQUES EN ELASTICITE LINEAIRE 57
→
− →
−
La r´ponse du mode ξi (→) d´pend de la valeur ξi ( X ) de ce mode au point X d’application
e −x e
de l’excitation. Elle est maximale lorsque ω ≈ ωi . Il sera donc possible, en choisissant la fr´quence
e
→
−
d’excitation ω et le point d’application X de l’excitation de mani`re ad´quate, de s´lectionner un
e e e
mode donn´. Si ui d´signe l’amplitude du d´placement pour ω = ωi :
e e e
N →
− →
−
1 F ( X )ξi ( X ) →
ui (→) ≈
−
x ξi (− )
x (3.50)
Mi i=1
2βi ωi
L’expression de la r´ponse impulsionnelle s’applique ´galement au cas d’une sollicitation ` fr´quence
e e a e
nulle, c’est ` dire au cas d’une d´form´e statique. En faisant ω = 0, la d´form´e statique d’une structure
a e e e e
→
− →
−
sous la sollicitation ponctuelle F( X ) au point X s’´crit :
e
→
−
→
−
N
1 ξi (→)ξi ( X )
−
x
uS (→) = F ( X )
−
x 2 (3.51)
i=1
Mi Mi ωi
3.7 Th´or`mes ´nerg´tiques en ´lasticit´ lin´aire
e e e e e e e
Ces th´or`mes ne s’appliquent que lorsque le mat´riau pr´sente un comportement parfaitement
e e e e
´lastique lin´aire caract´ris´ par sa capacit´ ` stocker et ` restituer sans pertes la totalit´ du travail
e e e e ea a e
fourni par les efforts externes lors de la d´formation.
e
3.7.1 R´ciprocit´ des chargements
e e
Fig. 3.13 – R´ciprocit´ des chargements
e e
(1) (2) (1) (2)
Pour un chargement de l’´tat initial σ = 0, ε = 0 ` l’´tat final σ = σ +σ , ε = ε +ε l’´nergie
e a e e
(1) (2)
´lastique accumul´e F = F11 + F22 + F12 selon le trajet de chargement σ → σ est la somme de
e e
(i)
trois termes, Fij d´signant l’´nergie ´lastique stock´e sous l’action de la contrainte σ au cours de
e e e e
(j) (1)
la d´formation ε . L’application lente et r´versible du premier chargement σ de 0 ` σ entraˆ
e e a ıne
une d´formation proportionnelle progressive ε conduisant ` une d´formation interm´diaire ε(1) et `
e a e e a
1 (1) (1)
une ´nergie ´lastique stock´e F11 = 2 Tr(σ ε ). A partir de cet ´tat interm´diaire, l’application
e e e e e
(2)
lente et r´versible du second chargement σ de 0 ` σ
e a entraˆ une d´formation proportionnelle
ıne e
(2) (1)
progressive ε conduisant ` une d´formation finale ε qui s’ajoute ` ε et ` une ´nergie ´lastique
a e a a e e
1 (2) (2) (1)
stock´e F22 = 2 Tr(σ ε ). Mais durant cette ´tape la contrainte ´tablie constante σ travaille dans
e e e
(1) (2)
le champ de d´formation ε stockant l’´nergie ´lastique F12 = Tr(σ ε ). Dans l’´tat final l’´nergie
e e e e e
´lastique totale stock´e est :
e e
1 (1) (1) 1 (2) (2) (1) (2)
F = F11 + F22 + F12 = Tr(σ ε ) + Tr(σ ε ) + Tr(σ ε )
2 2
(2) (1)
Pour le trajet de chargement σ →σ on obtient de mˆme :
e
1 (2) (2) 1 (1) (1) (2) (1)
F = F22 + F11 + F21 = Tr(σ ε ) + Tr(σ ε ) + Tr(σ ε )
2 2

64. 58 ´ ´
CHAPITRE 3. ELASTICITE
(2)
F21 repr´sentant cette fois l’´nergie ´lastique stock´e par le travail de la contrainte ´tablie σ dans
e e e e e
(1) (1)
le champ de d´formation ε cr´e par σ .
e e
L’ind´pendance vis ` vis du trajet suivi implique l’´galit´ des termes F12 et F21 (r´ciprocit´).
e a e e e e
L’´nergie totale F ne se r´duit pas ` la somme F11 +F22 des ´nergies associ´es ` chaque chargement
e e a e e a
suppos´ appliqu´ seul. Il existe un terme crois´ F12 + F21 = 2F12 = 2F21 qui traduit la d´pendance
e e e e
(1) (2)
quadratique de l’´nergie. Dans l’application lente et r´versible du chargement de 0 ` σ = σ + σ ,
e e a
(1) (2)
la d´formation croˆ proportionnellement de 0 ` ε = ε + ε et l’´nergie ´lastique totale stock´e est
e ıt a e e e
bien :
1 (1) (2) (1) (2) 1 1 1
F = Tr (σ + σ )(ε + ε ) = F11 + (F12 + F21 ) + F22
2 2 2 2
Le travail de la contrainte du premier chargement dans le champ de d´formation cr´e par le second
e e
est ´gal au travail de la contrainte du second chargement dans le champ de d´formation cr´e par le
e e e
premier.
3.7.2 Th´or`mes ´nerg´tiques
e e e e
En ´lasticit´ lin´aire, dans le cas habituel o` les efforts ext´rieurs appliqu´s aux structures sont
e e e u e e
pr´pond´rants (force de volume et poids propre n´gligeables), le travail de d´formation d’une structure
e e e e
→
−
de volume V se r´duit au travail des forces ext´rieures appliqu´es (densit´ surfacique de force T ou
e e e e
→
−
chargement ponctuel T ) sur sa surface S dans le champ de d´placement ´lastique → qu’elles induisent
e e −
u
et l’´nergie ´lastique stock´e s’´crit d’apr`s (3.1) et (3.10) :
e e e e e
1 1 1 →→
−− 1 →→
− −
UE = W = Tr(σε)dV = T u dS = Tiui (3.52)
2 2 V 2 S 2 i
de sorte que :
→ ∂U E
− → = ∂U
−
E
T = → u →
− (3.53)
∂−
u ∂T
→
−
dans lesquelles T et → forment un couple de variables conjugu´es dont le produit ` la dimension
−
u e a
d’une ´nergie. Il faut donc prendre ce produit au sens des charges et des d´placements g´n´ralis´s,
e e e e e
ainsi si une force correspond ` un d´placement, un moment correspondra ` un d´placement angulaire.
a e a e
S’en d´duisent trois th´or`mes d’application pratique permettant de d´terminer soit les efforts,
e e e e
soit les d´placements en calculant l’´nergie ´lastique stock´e dans la structure.
e e e e
Formule de Maxwell-Betti
→−
−
Avec V Tr(σε)dV = S f →dS la r´ciprocit´ des chargements Tr(σ 1 ε2 ) = Tr(σ 2 ε1 ) s’´crit direc-
u e e e
tement sous la forme :
→ →
− − → −
−
T 1 x 2 = T 2 →1
x
Pour deux ´tats d’´quilibre d’une mˆme structure ´lastique, le travail des sollicitations ext´rieures du
e e e e e
1er ´tat dans le champ de d´placement du 2nd est ´gal au travail des sollicitations ext´rieures du 2nd
e e e e
´tat dans le champ de d´placement du 1er.
e e
Th´or`me de Castigliano
e e
→
− →
−
L’´nergie ´lastique U E d’une structure supportant des charges Q appliqu´es aux points X est une
e e e
→→
− − →
−
fonction quadratique des Q ( X ) et la relation →( X ) = → → d´termine le d´placement ´lastique →
− −
∂U E
u − − e e e u
∂ Q (X )
→
− →
−
au point X ` l’aplomb de la charge Q .
a
→
−
Pour d´terminer la d´form´e de la structure en tout point, appliquons au point → la charge P .
e e e −
x
→→
− − →−
−
L’´nergie U E devient une fonction quadratique des Q ( X ) et de P (→). Le d´placement → au point →),
e x e −u −
x
→
− →
− →→
− −
E( Q , P )
fonction de P et des charges Q , est donn´ par →(→) = ∂U →
e − −
u x − . Dans la limite o` le chargement
u
∂P

65. 3.8. FLEXION ET FLAMBEMENT 59
→→
− − →
−
P ( x ) → 0, le d´placement →(→) est une fonction des seules charges Q donn´e par :
e − −
u x e
E → → → →
− − − −
→(→) = ∂U ( Q ( X ), P ( x ) →
− −
u x − →
→−
− P (− )=0
∂ P (→)
x x
Le th´or`me de Castigliano permet de calculer en tout point le champ de d´placement induit par un
e e e
→
−
chargement Q par application de la m´thode dite de la charge fictive.
e
Formule de M´nabr´a
e e
→
−
Pour un probl`me hyperstatique o` le nombre des r´actions d’appuis inconnues R j , est sup´rieur
e u e e
au nombre d’´quations de la statique et ne permet pas d’exprimer toutes les r´actions en fonction
e e
→
−
de la g´om´trie de la structure et des charges ext´rieures Q i l’´nergie de la structure est de la forme
e e e e
→ →
− −
U E = f ( Q i , R j ). L’´quilibre correspondant au minimum de cette ´nergie, les r´actions d’appuis seront
e e e
d´termin´es par les relations :
e e
E
→j = ∂U = 0
−u →
−
∂ Rj
traduisant le fait que les appuis sont des points fixes.
Principe des travaux virtuels
−
→
Pour le champ de d´placement virtuel δu calculons :
e
– δWext (→) le travail des forces ext´rieures (fourni au syst`me)
−u e e
→) le travail des forces int´rieures (absorb´ par le syst`me) correspondant ` une augmen-
−
– δWint ( u e e e a
tation de l’´nergie interne
e
−
→ −
→ −
→
Si la diff´rence ∆(δu) = Wint (δu) − Wext (δu) est :
e
−
→ −
→ −
→
– ∆(δu) < 0 δWext (δu) > δWint (δu) le d´placement est physiquement possible (hors ´quilibre)
e e
−
→ −
→ −
→
– ∆(δu) = 0 δWext (δu) = δWint (δu) le d´placement est le champ d’´quilibre (solution d’´quilibre
e e e
m´canique)
e
−
→ −
→ −
→
– ∆(δu) > 0 δWext (δu) < δWint (δu) le d´placement est physiquement impossible.
e
3.8 Flexion et flambement
3.8.1 Flexion des poutres
Flexion circulaire
Consid´rons un ´l´ment de poutre de section droite rectangulaire (b, h), de longueur dx soumis `
e ee a
un moment de flexion M .
Fig. 3.14 – Flexion circulaire

66. 60 ´ ´
CHAPITRE 3. ELASTICITE
Dans l’hypoth`se de la flexion faible, les sections droites restent planes et tournent les unes par
e
rapport aux autres. Ainsi, les deux sections extrˆmes de l’´l´ment de poutre de longueur dx, initia-
e ee
lement parall`les, forment un angle dϕ. La d´form´e de flexion de l’´l´ment est un arc de cercle de
e e e ee
rayon R tel que :
dx = Rdϕ (3.54)
La surface neutre (y = 0), l’origine ´tant prise au barycentre de la section droite, conservant sa
e
longueur dx les fibres sup´rieures (y > 0) subiront un allongement et les fibres sup´rieures (y < 0) un
e e
raccourcissement δdx(y) tel que :
δdx(y) = ydϕ (3.55)
La surface de cote y, (y > 0), subit donc une d´formation d’extension ` laquelle est associ´e une
e a e
contrainte de traction :
δdx y y
ε(y) = = σ(y) = Eε = E (3.56)
dx R R
La r´partition des contraintes dans la section droite est donc invariante sur la largeur b et varie
e
lin´airement dans l’´paisseur h de l’´l´ment de poutre, Traction au dessus de la surface neutre, Com-
e e ee
pression en dessous.
Le torseur des efforts (R, M ) sur la section terminale vaut :
b h/2 y
R´sultante R =
e S 0 dz −h/2 E R dy =
σdS = 0
b h/2 2
Moment M = S yσdS = 0 dz −h/2 E y dy R = E
RI
b h/2 3
avec I = 0 dz −h/2 y 2 dy = bh
12
I ´tant le moment quadratique de flexion de la section droite.
e
Le torseur des efforts appliqu´s (0, M ) se r´duisant au moment M , les conditions aux limites seront
e e
assur´es pour :
e
EI My My
= M ⇒ ε(y) = σ(y) = (3.57)
R EI I
L’´nergie ´lastique stock´e vaut :
e e e
1 1 y2 E EI 1M
UE = σεdV = E 2
dV = dx y 2 dydz = dx = dx
2 V 2 V R 2R2 S 2R 2 2R
1
U E = M dϕ (3.58)
2
Poutre console
Consid´rons une poutre de section droite rectangulaire (b, h), de longueur L encastr´e en x = L et
e e
soumise ` son extr´mit´ libre (x = 0) ` une force transversale F .
a e e a
Fig. 3.15 – Poutre console
R´partition des Contraintes
e
• Equilibre statique

67. 3.8. FLEXION ET FLAMBEMENT 61
La force F qui tend ` faire fl´chir la poutre induit ` l’encastrement un moment M = F L qui tend
a e a
a
` le faire pivoter dans le sens horaire. Le torseur RE , ME des r´actions d’encastrement se compose
e
→
− →
− −
→ −
→
donc d’une r´action R E oppos´e ` F et d’un moment M E oppos´ ` M tels que :
e e a ea
→
− →
−
R´sultante R E + F = 0 RE = F
e
−
→ −
→
Moment M E + M = 0 ME = F L
• Moment de flexion M (x)
Dans une section droite d’abscisse x, l’action de la partie droite de la poutre se traduit par un
torseur d’efforts R(x), M (x) donn´ par :
e
→
− →
−
Effort tranchant Rx = F
−→
Moment fl´chissant M x de module F (L − x)
e
• D´form´e y(x)
e e
L’´quation diff´rentielle de la d´form´e s’´crit :
e e e e e
EI d2 y
= M (x) EI 2 = −M (x) = −F (L − x)
R dx
Par int´gration la pente de la d´form´e s’´crit :
e e e e
dy x dy F L2
EI = −F x(L − ) tg(ϕ) ≈ ϕ = (L) =
dx 2 dx 2EI
dy
compte tenu de la condition d’encastrement dx (0) = 0. ϕ repr´sentant l’angle de pente d’extr´mit´ en
e e e
x = L.
Par int´gration la d´form´e s’´crit :
e e e e
1 x F L3
EIy = − F x2 (L − ) δ = y(L) =
2 3 3EI
compte tenu de la condition d’encastrement y(0) = 0. δ repr´sentant la fl`che d’extr´mit´ en x = L.
e e e e
• Contraintes σ(x, y)
On d´montre que les contraintes induites par l’effort tranchant R(x) sont n´gligeables devant celles
e e
induites par le moment fl´chissant M (x) lorsque la poutre est longue : L
e h, b.
En vertu de (3.57) la r´partition des contraintes et celle des d´formations d´pendent maintenant
e e e
de l’abscisse x :
M (x)y F σ M (x)y F
σ(x, y) = = y(L − x) ε= ε(x, y) = = y(L − x) (3.59)
I I E EI EI
Les contraintes sont maximales sur les faces externes y = ± h , lin´airement d´croissantes de la section
2 e e
d’encastrement ` la section terminale libre, soit :
a
Fh
σM (x) = (L − x) (3.60)
2I
´
Energie ´lastique
e
Par calcul ` l’aide des forces internes :
a
1 F2 L 2 2 3
U E = U int = 2 V σεdV = 2EI 2
y 2 (L − x)2 dV = 2EI 0 (L − x)2 dx = F L
V
F
6EI
ou
1 L dϕ 1 L M 1 L F2 L F 2 L3
U E = U int = 2 0 M dx dx = 2 0
2 2
R dx = 2EI 0 M dx = 2EI 0 (L − x) dx = 6EI
Par calcul ` l’aide des forces externes :
a
1 F 2 L3
U E = U ext = F δ =
2 6EI

68. 62 ´ ´
CHAPITRE 3. ELASTICITE
3.8.2 Flambement des poutres
Les mat´riaux ne c`dent pas de la mˆme fa¸on suivant qu’ils travaillent en tension ou en compres-
e e e c
sion. Lorsqu’un ´l´ment travaille en tension, qu’il s’agisse d’une corde, d’une tige d’acier ou du tendon
ee
d’un muscle, il s’´tire tout en restant rectiligne et la rupture survient g´n´ralement ` l’endroit le plus
e e e a
faible de l’´l´ment. En revanche le comportement des mat´riaux vis-`-vis d’une compression d´pend
ee e a e
de leur longueur. Une courte tige de m´tal, un petit mur de brique ou un os court conservera sa forme
e
sous compression jusqu’au moment o` se produira un ph´nom`ne de destruction par ´crasement local.
u e e e
Pour une mˆme force de compression, une tige plus longue mais de mˆme section, un mur plus haut
e e
ou un mˆt de bateau se courbera avant de rompre. La flexion d’un solide rectiligne et allong´ sous
a e
l’effet de forces qui le compriment suivant sa longueur est une instabilit´ m´canique appel´e flambage,
e e e
ou encore flambement.
Charge critique de flambage
Le flambage est une transition vers une configuration de plus basse ´nergie. Lors de la compression
e
d’une tige par une force F , la structure commence par se comprimer jusqu’` une force critique FC
a
au del` de laquelle la configuration flamb´e est ´nerg´tiquement plus favorable. L’analyse lin´aire
a e e e e
permet de d´terminer la force critique FC seuil de l’instabilit´ mais ne fournit aucune indication sur
e e
l’´volution du syst`me pour des efforts appliqu´s F > FC . Le flambage est analogue ` la flexion dont
e e e a
il se distingue par l’existence de la force seuil FC .
Fig. 3.16 – Flexion et Flambement
Consid´rons, comme ´tat de r´f´rence, une tige de longueur L, de moment d’inertie I et de module
e e ee
d’Young E comprim´e par la force FC au seuil de la transition entre la compression et le flambement.
e
Juste au del` du seuil de flambement F FC la d´form´e caract´ris´e par sa fl`che petite δ est r´gie
a e e e e e e
EI 1 d2 y δ
par l’´quation de flexion faible R = −M (x). En estimant la courbure R ≈ dx2 ∼ L2 et le moment
e
fl´chissant M ∼ FC δ, la charge critique de flambage est donn´e par :
e e
EI
FC ∼ (3.61)
L2
Charge critique d’Euler
La force de compression axiale FC susceptible de produire le flambage d’une tige ou d’une colonne
calcul´e exactement par le math´maticien suisse L´onard Euler (1707-1783) est :
e e e
EI π 2 EI
FC = k = 2 (3.62)
L2 Lef f
k ´tant une constante sans dimension qui d´pend des degr´s de libert´ des extr´mit´s de la tige et
e e e e e e
Lef f la longueur de la poutre en appuis simples admettant la mˆme charge critique FC .
e
La force qui provoque le flambage d´pend :
e
– de l’inverse du carr´ de la longueur libre de la tige
e
Plus la tige est courte, mieux elle r´siste. Ce r´sultat a une ´norme influence pratique sur la
e e e
forme et le poids des structures, tant artificielles que naturelles.
– de la rigidit´ de la tige
e
Pour r´sister au flambage, un module de Young ´lev´ est essentiel d’o` l’´laboration fibres
e e e u e
sp´ciales ` haute rigidit´ - en bore ou en graphite - pour produire des mat´riaux composites tr`s
e a e e e
performants.

69. 3.8. FLEXION ET FLAMBEMENT 63
Appui Charge d’Euler FC Longueur effective Lef f
Simple-simple 1 L
1
Encastr´-encastr´
e e 4 2L
Encastr´-simple
e 2,04 0, 7L
1
Encastr´-libre
e 4 2L
Tab. 3.1 – Valeurs de k et de Lef f pour quelques types d’appui
– du moment d’inertie de la section droite
La gamme des mat´riaux ` module d’Young ´lev´ ´tant restreinte, un moyen simple et ´conomique
e a e ee e
pour rigidifier une tige consiste ` changer la g´om´trie de sa section pour augmenter sa rai-
a e e
deur ` masse constante. Le moment d’inertie de flexion ´tant I = S y 2 dS et la masse lin´ique
a e e
m = ρ S dS la structure la plus rigide en flexion ` masse donn´e sera celle qui repoussera la
a e
mati`re le plus loin possible de l’axe de flexion.
e
La charge de flambage d’une tige n’est pas n´cessairement sa charge de rupture. Pour une tige
e
longue le flambage peut survenir pour des chargements tr`s faibles. De ce fait, si la force de compression
e
disparaˆ la tige peut se redresser sans dommage. C’est le m´canisme de d´fense des poils de tapis ou
ıt, e e
de paillasson, des herbes et des jeunes pousses que l’on pi´tine.
e
Coefficient de charge et crit`re de qualit´ du mat´riau
e e e
La comparaison de l’efficacit´ d’´l´ments structuraux travaillant en tension ou en compression
e ee
passe par l’estimation du poids minimal de l’´l´ment capable de supporter une charge F donn´e sur
ee e
une port´e L donn´e : son coˆt pond´ral. Comme la r´sistance d’un ´l´ment travaillant en traction
e e u e e ee
est quasi ind´pendante de L alors que celle d’un ´l´ment comprim´, limit´e par le flambage d’Euler,
e ee e e
diminue comme L−2 , le coˆt pond´ral peut varier ´norm´ment.
u e e e
Un rapport simple permet de quantifier l’efficacit´ d’un ´l´ment : son coefficient de charge C d´fini
e ee e
comme le rapport de la charge F ` la port´e L :
a e
F
C= (3.63)
L
Plus C est ´lev´, plus l’´l´ment est efficace en compression. L’efficacit´ croˆ si la conception d’ensemble
e e ee e ıt
de la structure permet d’augmenter la charge ou de r´duire la port´e.
e e
Ainsi une bicyclette poss`de des roues de grand diam`tre peu charg´es. C est petit le gain en poids
e e e
est substantiel en utilisant des rayons travaillant en traction.
La charge d’une automobile est plus importante et le diam`tre des roues plus petit. C est grand et les
e
jantes travaillent en compression.
L’augmentation du coefficient de charge est un moyen commode d’´viter le flambage. Ce n’est
e
pas toujours possible, la port´e et la charge roulante d’un pont sont des donn´es incontournables.
e e
Dans les structures ` faible coefficient de charge, il est plus difficile de traiter efficacement les charges
a
compressives que les charges en tension. C’est pourtant une situation tr`s courante, aussi bien dans
e
les structures biologiques que dans celles fabriqu´es par l’homme. Il faut donc trouver des moyens de
e
r´soudre ce probl`me sans inconv´nient r´dhibitoire.
e e e e
Trois moyens sont utilis´s pour ´viter le flambage sans entraˆ
e e ıner pour autant des poids ou des
coˆts suppl´mentaires quand le coefficient de charge de la structure C est faible :
u e
– La pr´contrainte du mat´riau en appliquant une tension pr´alable aux ´l´ments qui risqueraient
e e e ee
de plier. Le gonflage des pneus ´vitant le flambement des flancs ou la pression hydrostatique de
e
la s`ve empˆchant le flambage des parois des cellules animales ou v´g´tales en sont des exemples.
e e e e
– Le choix de la forme de la section afin d’augmenter le moment d’inertie. Les structures pleines
sont remplac´es par des tubes creux (bambou, la plupart des os) ou des profil´s. Les mat´riaux
e e e
en plaques ou en feuilles peuvent ˆtre dot´s de renforts pliss´s, coll´s ou soud´s (tˆle ondul´e)
e e e e e o e
ou constitu´s de structures sandwich pliss´es (carton) ou nid d’abeille (cloisons placoplˆtre).
e e a

70. 64 ´ ´
CHAPITRE 3. ELASTICITE
– Par le choix du mat´riau le plus favorable. A faible coefficient de charge certains mat´riaux
e e
r´sistent beaucoup mieux que d’autres ` la compression. Pour une charge de flambement F et
e a
une port´e L fix´es le module ´lastique E et le moment d’inertie I v´rifient la relation d’Euler
e e e e
EI
F ∼ L2 . La masse de la structure portante est m = ρLS (S aire de section droite et ρ masse
volumique du mat´riau). La structure la plus efficace tant du point de vue pond´ral que du point
e e
de vue ´conomique sera la structure la plus l´g`re. La g´om´trie de la section droite va fixer la
e e e e e
L2 L2
relation S = f (I) ∼ f ( FE ), soit m ∼ ρLf ( FE ).
– La dimension caract´ristique de section droite d’une tige est (S)
√ 4 e
√ √ L son moment d’inertie
ρ
√ L2 F .
I ∼ ( S) soit S ∼ I et une masse m ∼ E
– Les dimensions caract´ristiques de section droite des panneaux sont l’´paisseur h << L et
e e
la largeur l de l’ordre de L. S ∼ Lh et I ∼ Lh 3 , soit S ∼ (IL2 )1/3 et une masse m =
ρE −1/3 L7/3 F 1/3 .
ρ ρ
La quantit´ critique est le rapport √E (tiges) ou E 1/3 (panneaux). On utilise pour les comparaisons
e
les rapports inverses appel´s crit`res de qualit´ du mat´riau. Plus ces rapports sont grands, plus le
e e e e
mat´riau r´siste ` la compression.
e e a
√
E 1/3
Mat´riau
e E (Mpa) ρ (kg.dm−3 ) ρ
E
ρ
Acier 210000 7,8 59 7,7
Aluminium 73000 2,8 99 15,0
B´ton
e 15000 2,5 49 10,0
Composites fibre de carbone 200 2,0 223 29,0
Bois tendre 10000 0,35 290 61,4
Bois dur 12000 0,65 170 35,5
Tab. 3.2 – Crit`res de qualit´ typiques de quelques mat´riaux
e e e
On peut se servir de ces deux crit`res de qualit´ pour classer divers mat´riaux naturels ou
e e e
synth´tiques en fonction de leur r´sistance au flambage. Le tableau illustre la raison des choix faits `
e e a
la fois dans l’industrie et par la nature. Ainsi, pour fabriquer des panneaux, l’aluminium est environ
deux fois plus efficace que l’acier, ce qui explique son emploi pour le fuselage et les ailes des avions.
L’acier reste tr`s utilis´ parce qu’il est facile d’augmenter le moment d’inertie I de la section (profil´s,
e e e
raidisseurs soud´s ou rivet´s). Le bois est un mat´riau ` crit`re de qualit´ ´lev´ tr`s utilis´ depuis la
e e e a e ee e e e
mise au point de colles efficaces et de traitement anti-pourrissement.
3.9 Le contact
Lorsque deux corps en contact ponctuel sont press´s l’un contre l’autre, ils se d´forment localement
e e
pour cr´er une aire de contact de dimension caract´ristique a petite devant les rayons de courbure R
e e
des deux corps au point de contact, aire sur laquelle se r´partit l’effort de contact. Les contraintes
e
σ induites sont ainsi concentr´es dans une petite r´gion autour du point de contact et leur intensit´
e e e
d´croˆ rapidement lorsque l’on s’en ´loigne.
e ıt e
3.9.1 Le contact : ph´nom`ne m´canique local
e e e
Sous l’action d’une charge normale concentr´e F agissant sur un milieu ´lastique semi infini la
e e
contrainte radiale σrr d´pend, par sym´trie, de la distance r au point d’application de la charge.
e e
L’´quilibre d’une demi sph`re d = 3 (ou d’un demi cylindre de longueur unit´ en dimension d = 2)
e e e
dont la surface est d’ordre S ∼ r d−1 s’´crit F ∼ σ S et conduit ` la loi variation de la contrainte :
e a
rr
1
σ∼ (3.64)
rd−1
En ´lasticit´ lin´aire il en va de mˆme pour les d´formations et la variation du d´placement s’obtient
e e e e e e
par int´gration :
e
d=2 σ∼1 r ε∼ 1 r u ∼ ln r
1 (3.65)
d=3 σ ∼ r2 ε ∼ r12 u∼ 1 r

71. 3.9. LE CONTACT 65
Les contraintes d´croissent rapidement lorsque l’on s’´loigne du point de contact. Le contact est un
e e
ph´nom`ne m´canique local. Pour autant que les dimensions L (et pas seulement les rayons de courbure
e e e
R) des corps en contact soient grandes devant celle a de l’aire de contact, la distribution des contraintes
de contact ne d´pend pas de mani`re critique ni de la forme exacte des corps loin de cette zone, ni
e e
du d´tail du mode de transmission vers la r´gion de contact des efforts ext´rieurs appliqu´s. Quelque
e e e e
soit la mani`re dont la pression p se r´partit sur l’aire de contact, la distribution des contraintes et
e e
des d´placements tend lorsque r
e a vers celle cr´e par la force concentr´e F ´gale ` l’int´grale de p
e e e a e
sur l’aire de contact. La distribution des contraintes peut ˆtre calcul´e avec une bonne approximation
e e
en consid´rant, qu’` l’´chelle de l’aire de contact, chacun des deux corps est un solide semi infini
e a e
limit´ par un plan, le plan de contact et les contraintes se concentrent dans un petit volume de
e
dimension caract´ristique ad autour du point de contact. Pour des d´formations suffisamment faibles
e e
pour rester dans le domaine de validit´ de l’´lasticit´ lin´aire, la solution d’un probl`me de contact
e e e e e
s’obtient par application du principe de superposition une fois connue la r´ponse en d´placement et
e e
en contrainte ` une charge ponctuelle concentr´e au point de contact. Cette approximation est mise
a e
en d´faut en ce qui concerne les d´placements r´sultant d’un contact en dimension d = 2 par suite de
e e e
la divergence logarithmique u ∼ lnr. Il faut alors tenir compte de la forme r´elle des corps pour lever
e
l’ind´termination r´sultant de cette approximation.
e e
3.9.2 Le contact en dimension d = 3
Le probl`me du contact en dimension d = 3 se ram`ne ` celui du demi espace ´lastique limit´ par un
e e a e e
→−
−
plan infini charg´ par une distribution de forces F (→ ) qui ne doit satisfaire qu’` l’unique condition
e x a
de s’annuler ` l’infini afin de pouvoir d´finir une zone de contact loin de laquelle les d´formations
a e e
s’annulent.
Le tenseur de Green du contact
Fig. 3.17 – Contact ponctuel en dimension 3
Dans le demi espace, le contact doit satisfaire l’´quation de l’´quilibre ´lastique : Grad(Div→) +
e e e −
u
→ = 0 et les conditions aux limites σiz = −Fi sur le plan z = 0, le vecteur unitaire de la
−
(1 − 2η)∆ u
normale au milieu ´tant dirig´ dans le sens des z n´gatifs. Par convention → d´signe un vecteur appar-
e e e − e
x
tenant au plan de contact z = 0 et x→ un vecteur quelconque du demi espace, pouvant ´ventuellement
− e
appartenir au plan de contact. Le champ de d´placement →, cr´´ au point → par une charge ponctuelle
e −u ee −x
→
−
F plac´e ` l’origine est :
e a
1 2(1−η)r+z [2r(ηr+z)+z 2 ]x
ux = 4πG { r(r+z) Fx + r3 (r+z)2
(xFx + yFy ) + [ xzr3
x
− (1 − 2η) r(r+z) ]Fz }
2(1−η)r+z [2r(ηr+z)+z 2 ]y
1 yz y
uy = 4πG { r(r+z) Fy + r3 (r+z)2
(xFx + yFy ) + [ r3 − (1 − 2η) r(r+z) ]Fz } (3.66)
1 1−2η z 2(1−η) 2
uz = 4πG {[ r(r+z) + r3 ](xFx + yFy ) + [ r + z3 ]Fz }
r
E
avec G = 2(1+η) et r = x2 + y 2 + z 2 . Ces relations conduisent ` la d´finition du tenseur de Green G
a e
(r´ponse en d´placement ` une force concentr´e ` l’origine) du contact :
e e a e a
→(→) = G(→)→
− −
u x − −
x F (3.67)

72. 66 ´ ´
CHAPITRE 3. ELASTICITE
La solution g´n´rale du contact ´lastique
e e e
Par application du principe de superposition la solution du probl`me de contact ´lastique de densit´
e e e
→−
−
surfacique de force F (→ ) quelconque se met sous la forme :
x
→(→) =
− −
u x x − →− −
x
−
G(→ − →) F (→ )d→
− x x (3.68)
S
Le tenseur des d´formations s’en d´duit facilement par la relation 2ε = Grad→ + t Grad→ et
e e −
u −
u
celui tenseur des contraintes par la loi de Hooke Eε = (1 + η)σ − ηTr(σ)δ.
Fig. 3.18 – Les diff´rents types de contact : poin¸onnement - pression impos´e - Hertz
e c e
Bien que ces ´quations fournissent la solution formelle des probl`mes de contact, champs de
e e
d´placement, d´formation et contraintes, lorsque la distribution surfacique des charges est connue,
e e
les solutions analytiques n’existent que pour des g´om´tries et des chargements particuliers. Il en va
e e
de mˆme pour la solution du probl`me inverse dans le cas o` le champ de d´placement est impos´
e e u e e
dans la zone de contact (poin¸onnement) ou dans celui du contact de Hertz dans lequel les corps en
c
contact soumis ` un chargement ext´rieur s’adaptent l’un ` l’autre en se d´formant mutuellement de
a e a e
sorte que ni la r´partition des contraintes dans l’aire de contact, ni les d´formations ne sont connues
e e
a
` priori. Il faudra alors recourir ` d’autres approches.
a
3.9.3 Poin¸on plan rigide ` base circulaire sous chargement normal
c a
La r´partition de pression p(ρ) compatible avec la condition uz = Cte = δ sous le poin¸on est
e c
p(ρ) = p0 2 . La charge totale est P = S p(ρ)dS = 2πa2 p0 et la pression moyenne pm = πa2 = 2p0 .
P
1− ρ2
a
Fig. 3.19 – R´partition de pression et isostatiques du poin¸onnement
e c
Le calcul des int´grales de superposition (Sneddon 1946) conduit au champ de d´placement dont
e e
on d´duit les champs de d´formation et de contrainte.
e e
Plastification et rupture
Du fait de la discontinuit´ des contraintes sur le pourtour de l’aire de contact, le cisaillement
e
y est maximal et la plastification s’amorce sur le pourtour de l’aire de contact comme le montre

73. 3.9. LE CONTACT 67
Fig. 3.20 – Plastification : Isovaleurs de Van Mises - Coupe d’un laiton α poin¸onn´
c e
exp´rimentalement la coupe d’un poin¸onnement dans du laiton α et th´oriquement les isovaleurs de
e c e
Van Mis`s . La rupture se produira dans un mat´riau fragile ` partir du pourtour de l’aire de contact
e e a
comme le montre les isostatiques de la figure 3.19.
3.9.4 Le contact de Hertz
Lorsque deux corps ´lastiques entrent en contact ponctuel, ils s’´crasent localement (se d´forment)
e e e
de mani`re ` former une aire de contact non nulle. Il s’agit d’un probl`me complexe puisque ni l’aire
e a e
de contact ni la r´partition de charge qui en r´sulte ne sont connues ` priori.
e e a
Approche dimensionnelle
Dans le contact ´lastique de Hertz il est int´ressant d’estimer comment les d´formations et les
e e e
contraintes croissent avec la charge P appliqu´e ` l’aide d’un raisonnement dimensionnel. De ce fait
e a
on peut se limiter au cas simple de deux sph`res en contact selon une aire circulaire plane de rayon
e
a sous l’action d’une force pressante P normale ` l’aire de contact. Chaque sph`re de rayon Ri est
a e
un solide ´lastique lin´aire caract´ris´ par son module d’Young Ei et son coefficient de Poisson ηi .
e e e e
L’´crasement δi des surfaces s’effectuant parall`lement ` l’axe des centres, il n’y a pas de d´placement
e e a e
dans le plan de contact. Il s’agit d’un probl`me de d´formation plane et le module ´lastique ` prendre
e e e a
en compte est Ei ∗ = Ei .
1−η 2
i
Tant que δi a ou a Ri l’´tat de d´formation dans chaque corps au voisinage de la zone de
e e
contact est d´fini par une d´formation εi ∼ δi correspondant au rapport d’un d´placement δi sur une
e e a e
δ
base initiale de longueur a. On aurait pu na¨ıvement proc´der ` une estimation du type εi ∼ Rii mais
e a
cela aurait ´t´ en contradiction avec l’aspect localis´e de la d´formation de contact. La pression de
ee e e
contact σ ∼ a2 induit dans la r´gion de contact les d´formations εi ∼ E ∗ ∼ a2P ∗ et l’´crasement total
P
e e σ
E
e
i i
δ = δ1 + δ2 ∼ a(ε1 + ε2 ) ∼ P
a2 E ∗
, E ∗ module ´lastique ´quivalent du contact tel que
e e 1
E∗ = 1
E1∗ + 1
E2 .
∗
1 d2 z δi
Mais l’´crasement δi est reli´ ` la courbure de la sph`re par la relation
e ea e Ri ≈ dρ1 ∼ a2 de sorte que
a2
l’´crasement total δ ∼ , R∗ rayon ´quivalent du contact d´fini par
e R∗ e e 1 1 1
R∗ = R1 + R2 .
Il r´sulte de l’´galit´ des deux expressions de δ la loi du contact de Hertz :
e e e
E ∗ a3 √ P R∗ a2
P ∼ P ∼ E ∗ R∗ δ 1/2 a3 ∼ δ∼ (3.69)
R∗ E∗ R∗
Le contact de Hertz est un exemple de comportement macrosopique force d´placement non lin´aire
e e
bien que le comportement microscopique contrainte d´formation du mat´riau soit lin´aire. L’´nergie
e e e e
´lastique accumul´e dans le contact est donn´e par :
e e e
δ 2 P P 2/3 2 P 5/3 2
UE = P dδ ∼ ∗2/3 R∗1/3
dP = ∗2/3 R∗1/3
= Pδ (3.70)
0 3 0 E 5E 5

74. 68 ´ ´
CHAPITRE 3. ELASTICITE
Du fait de la non lin´arit´ de la loi du contact, P ∼ E ∗ R1/2 δ 3/2 l’expression U E = 1 P δ n’est pas
e e 2
applicable. La p´n´tration δ ne peut pas ˆtre calcul´e par d´rivation de l’´nergie ´lastique U E par
e e e e e e e
rapport ` la charge appliqu´e P . Il faut ´galement d´terminer le potentiel compl´mentaire Ω :
a e e e e
δ P 5/3 2 ∗ ∗1/2 5/2 a5 E √
UE = 2
0 P dδ = 5 E ∗2/3 R∗1/3 = 5 E R δ = 2 P δ = 2 E ∗ R∗2
5 5 P = dU = E ∗ R∗ δ 1/2
dδ
P 3 3 ∗ ∗1/2 5/2 P 5/3 P 2/3
(3.71)
Ω= E
0 δdP = P δ − U = 5 P δ = 5 E R δ = 2 E ∗2/3 R∗1/3
5
dΩ
δ = dP = E ∗2/3 R∗1/3
Mais U E s’´crit aussi U E = 2 V σεdV puisque la relation microscopique σ = E ∗ ε est lin´aire. En
e 1
e
estimant comme pr´c´demment ε ∼ a , U
e e δ E ∼ E ∗ ( δ )2 V = E ∗ a2 V , V ´tant le volume des corps dans
e
a R∗2
lesquels agissent les d´formations d’´crasement, la comparaison des deux expressions de U E conduit
e e
` V ∼ a3 traduisant l’aspect local des d´formations de contact.
a e
Contact bille rigide - plan d´formable
e
Ce probl`me particulier est associ´ aux essais de duret´ Rockwell et Brinell qui donnent acc`s `
e e e e a
la r´sistance plastique d’un mat´riau par la mesure de la taille de l’empreinte plastique produite par
e e
une bille rigide press´e contre l’´chantillon plan.
e e
Fig. 3.21 – Contact de Hertz : bille rigide sur plan d´formable
e
Dans l’aire de contact circulaire de rayon a petit devant le rayon R du p´n´trateur sph´rique
e e e
1 ρ2
rigide, l’enfoncement uz de la surface plane, assimil´ ` la parabole ausculatrice, est uz = δ(1 − 2 a2 ).
ea
La r´partition de pression de Hertz p(ρ) compatible avec cette condition, la charge totale P et la
e
pression moyenne pm sont donn´es par :
e
ρ2 2 P 2
p(ρ) = p0 1 − P = p(ρ)dS = πa2 p0 pm = = p0 . (3.72)
a2 S 3 πa2 3
Le calcul des int´grales de superposition (Huber 1904) conduit au champ de d´placement dont on
e e
d´duit les champs de d´formation et de contrainte.
e e
Fig. 3.22 – R´partition des contraintes en surface
e
La contrainte radiale σρρ prend sa valeur maximale p0 1+2η sur le pourtour de l’aire de contact.
3
Le poin¸onnement d’un mat´riau fragile, comme un bloc de verre, par un indenteur sph´rique rigide
c e e

75. ´ ´ ´ ´
3.10. RESUME ELASTICITE 69
Fig. 3.23 – La plastification commence sur l’axe, sous l’aire de contact, au point de Hertz
de rayon R ne produit pas de plastification sous l’aire de contact mais une rupture qui s’initie sous
la forme d’un anneau circulaire de rayon a tel que σρρ = σR , o` σR est la contrainte de rupture du
u
mat´riau.
e
Fig. 3.24 – Isostatiques et cˆne de rupture de Hertz
o
La rupture se produit le long de l’isostatique σ3 et conduit ` la formation d’un tronc de cˆne de
a o
rupture, le cˆne de Hertz.
o
3.10 e ´
R´sum´ Elasticit´
e e
Loi de Hooke
Eε = −ηTr(σ)δ + (1 + η)σ Young Eεij = −ησkk δij + (1 + η)σij
σ = λTr(ε)δ + 2µε Lame σij = λεkk δij + 2µεij
S σ = 3KS ε Hooke Dσ = 2µDε π σ = π ε
´
Equation de Lam´ en d´placement
e e
→
− 2→
−
(λ + µ)Grad(Div→) + µ∆→ + ρ X = ρ ddtu
−u −
u 2
→
− 2→
−
(λ + µ)Rot(Rot→) + (λ + 2µ)∆→ + ρ X = ρ ddtu
−u −
u 2
1 →) + ∆→ + ρ → = ρ d2 →
− − − −
u
1−2η Grad(Div u u µX µ dt2
Relations entre les modules ´lastiques
e
ηE E
λ= (1+η)(1−2η) G=µ= 2(1+η)
E = µ(3λ+2µ)
λ+µ η= λ
2(λ+µ)
E
K = 3(1−2η) K= λ + 2µ
3

76. 70 ´ ´
CHAPITRE 3. ELASTICITE
Potentiel d’´lasticit´ et ´nergie ´lastique
e e e e
Le travail de d´formation W s’´crit soit en terme de forces externes, soit en terme de forces internes :
e e
→→
−− →→
−−
W = Tr(σε)dV = f u dV + T u dS
V V S
En l’absence de forces de volume, l’´nergie ´lastique stock´e s’´crit :
e e e e
⇒ ´lasticit´ lin´aire
e e e
dU E ε dU E 1
dV = 0 Tr(σdε) dV = 2 Tr(σε)
→ →
− − →−
−
U E = 2 S T →dS
dU E 1
UE = V dV dV = S T d u dS u

77. Chapitre 4
´
PLASTICITE
Lorsqu’un mat´riau est sollicit´ jusqu’` rupture, les essais montrent que la contrainte de rupture
e e a
σR est une grandeur pr´sentant de fortes fluctuations pouvant mˆme d´passer la d´cade pour certains
e e e e
mat´riaux et que le mode de ruine d´pend de la nature du mat´riau. Ainsi la rupture peut interve-
e e e
nir brutalement quasi sans d´formation pr´alable pour les mat´riaux qualifi´s aujourd’hui de fragiles,
e e e e
tandis qu’elle n’intervient qu’apr`s une ´tape de grande d´formation permanente pour les mat´riaux
e e e e
qualifi´s aujourd’hui de ductiles. Nous savons maintenant que les mat´riaux fragiles rompent brutale-
e e
ment au del` d’une certaine tension, tandis que les mat´riaux ductiles s’´coulent plastiquement avant
a e e
de rompre sous cisaillement. Si la rupture est toujours l’´tape ultime de la ruine des structures, elle
e
est pr´c´d´e d’une ´tape de plastification pour les mat´riaux ductiles.
e e e e e
4.1 Le comportement plastique
Le comportement plastique est celui d’un corps solide qui prend des d´formations permanentes
e
sans se fissurer. On admet g´n´ralement que ces d´formations permanentes se produisent au del` d’un
e e e a
seuil de contrainte appel´ seuil de plasticit´ ou limite d’´lasticit´.
e e e e
4.1.1 Le seuil de plasticit´
e
En dessous du seuil de plasticit´ les d´formations ne restent pas toujours parfaitement ´lastiques
e e e
(frottements internes), mais apr`s d´charge, le corps doit reprendre progressivement mais int´gralement
e e e
sa forme initiale. Le seuil de plasticit´ doit ˆtre vu comme une sch´matisation commode : au del`
e e e a
du seuil les d´formations permanentes deviennent beaucoup plus importantes que les d´formations
e e
´lastiques. La d´finition du seuil est conventionnelle (cf. Fig. 4.1) et d´pend de la pr´cision des moyens
e e e e
de mesure utilis´s. La limite d’´lasticit´ vraie (point A) d´finie par la valeur de la contrainte σV
e e e e
qui produit une d´formation permanente dans le premier grain de la microstructure du mat´riau est
e e
inaccessible ` la mesure exp´rimentale. Lorsque le nombre de grains plastifi´s augmente la d´formation
a e e e
permanente devient accessible ` la mesure. Elle est d´finie comme la d´formation εp mesur´e apr`s
a e e e e
une d´charge ´lastique (trajet BC) qui r´cup`re la partie de d´formation ´lastique εe , les propri´t´s
e e e e e e ee
´lastiques (modules ´lastiques) ´tant suppos´es raisonnablement non modifi´es par le tr`s faible taux
e e e e e e
de plastification subit par le mat´riau (identit´ des pentes des trajets OA et BC). A cette d´formation
e e e
d´finie conventionnellement par εp = 2.10
e −2 (ou 10−5 selon la pr´cision des moyens de mesure utilis´s)
e e
correspond le seuil d’´lasticit´ conventionnelle σC (εp ) appel´ seuil de plasticit´. En pratique, le seuil
e e e e
de plasticit´ est appel´ limite d’´lasticit´ σe du mat´riau, terminologie prˆtant ` confusion puisqu’il
e e e e e e a
s’agit en r´alit´ d’une limite d’´lasticit´ conventionnelle.
e e e e
En g´n´ral la r´sistance ` la d´formation plastique d´pend plus ou moins, selon les mat´riaux
e e e a e e e
et la temp´rature, de la vitesse de d´formation (visco-plasticit´ ) et de l’histoire des d´formations
e e e e
permanentes d´j` subies par le mat´riau soit au cours du processus d’´laboration, soit au cours de
ea e e
sollicitations ant´rieures (´crouissage). On constate exp´rimentalement que lorsqu’un solide a ´t´
e e e ee
soumis ` une contrainte non isotrope, il poss`de vis-`-vis d’un nouveau chargement un seuil ´gal ` la
a e a e a
71

78. 72 ´
CHAPITRE 4. PLASTICITE
Fig. 4.1 – Seuil de plasticit´
e
plus grande valeur de la charge ant´rieure. Ainsi, sur la figure 4.1 repr´sentant la courbe de charge
e e
(force Q, d´placement q), le seuil de plasticit´ ` la premi`re charge OB correspond au point A. A la
e ea e
seconde charge CB , le seuil de plasticit´ correspond au point B . L’absence de co¨
e ıncidence rigoureuse
entre B et B et la boucle d´charge-recharge BCB sont la cons´quence d’un effet de frottement
e e
interne. Pour des chargement infiniment lents, les frottements internes n’interviennent pas, les points
B et B et les trajets BC et CB sont confondus, la plasticit´ est alors ind´pendante du temps, absence
e e
d’effet visqueux. Dans ce cas, le nouveau seuil de plasticit´ au point B confondu avec B est bien ´gal
e e
a
` la valeur de la plus grande charge atteinte lors de la charge pr´c´dente, point B. C’est cette ´vidence
e e e
exp´rimentale qui justifie la notion de seuil d’´coulement.
e e
Grˆce ` leur ductilit´, les mati`res plastifiables peuvent ˆtre moul´es sous l’action de contraintes
a a e e e e
suffisantes et gardent ensuite leur forme sous des contraintes plus faibles. Tous les m´taux non alli´s
e e
et certains alliages pr´sentent une phase de comportement plastique. La d´formation plastique est
e e
utilis´e dans les op´rations de corroyage : forgeage, estampage, emboutissage, laminage, filage, pliage,
e e
...
Les terres, l’argile et la plupart des pˆtes sont plastifiables. Enfin, les corps r´put´s fragiles, b´tons,
a e e e
roches, verres, ... soumis ` pression hydrostatique suffisamment ´lev´e cessent d’ˆtre fragiles et ac-
a e e e
qui`rent un comportement plastique vis-`-vis des contraintes additionnelles.
e a
4.1.2 Influence des d´formations plastiques sur les propri´t´s m´caniques
e e e e
D´formations plastiques mod´r´es
e e e
Des d´formations plastiques mod´r´es n’entraˆ
e ee ınent pas de changement des modules d’´lasticit´
e e
dans les corps compacts. Leurs trois effets essentiels sont :
Fig. 4.2 – Durcissement, ductilit´ et effet Bauschinger
e
– Le durcissement
´e
El´vation du seuil de plasticit´ pour des contraintes de mˆme nature et de mˆme signe que
e e e
celles qui ont produit l’´coulement plastique. La courbe de charge (sans d´charge) σ = f (ε)
e e

79. 4.1. LE COMPORTEMENT PLASTIQUE 73
est une fonction non d´croissante de ε traduisant le durcissement du mat´riau ´crouissage ou
e e e
dσ
work-hardening : dε > 0.
– La r´duction de la ductilit´
e e
C’est la diminution de l’allongement possible avant rupture. La position du point de rupture R
n’est quasiment pas modifi´e par les d´charges AO2 , BO3 , ... Ces d´charges ont pour effet de
e e e
d´placer l’origine des d´formations de O en O2 puis O3 , ... r´duisant progressivement l’allonge-
e e e
ment restant ` parcourir jusqu’` la rupture. On observe g´n´ralement une diminution progressive
a a e e
du durcissement au fur et ` mesure que l’on se rapproche du point de rupture R. La courbe de
a
2
charge σ = f (ε) est une fonction croissante de ε : dσ > 0, mais cette d´riv´e d´croˆ : d σ < 0.
dε e e e ıt dε2
– L’effet Bauschinger
On observe g´n´ralement une diminution (en valeur absolue) du seuil de plasticit´ pour des
e e e
contraintes de mˆme nature mais de signes oppos´s ` celles qui ont produit la d´formation
e e a e
plastique, soit |σ2 | < |σ1 |. Dans tous les cas on observe une r´duction de l’amplitude du domaine
e
´lastique : |σ2 | − |σ1 | < σ2 − σ1 . Dans le cas des m´taux pour lesquels σ 1 = −σ1 on a σ2 > −σ2 .
e e
D´formations plastiques importantes
e
Des d´formations plastiques importantes ont pour effet d’´tirer et d’orienter les grains cristallins
e e
ou les chaˆınes de polym`res. Sous l’effet du laminage intense, le mat´riau initialement isotrope de-
e e
vient anisotrope entraˆ ınant le changement de ses modules d’´lasticit´. Les m´taux fortement plastifi´s
e e e e
prennent une texture, les roches une schistosit´.
e
Les modifications produites par les d´formations plastiques peuvent dans tous les cas ˆtre rat-
e e
tach´es ` un changement de structure ` une certaine ´chelle. Dans certains cas ces changements sont
e a a e
d´finitifs, mais il arrive assez souvent que le corps ait tendance ` reprendre tr`s lentement sa struc-
e a e
ture initiale. Dans le cas des m´taux ce ph´nom`ne est appel´ restauration : apr`s d´charge d’une
e e e e e e
´prouvette, plus on attend pour la recharger plus l’´crouissage s’estompe car le durcissement disparaˆ
e e ıt
par annihilation lente des dislocations.
4.1.3 Le comportement plastique pur
Dans la pratique la vitesse de d´formation est suffisamment lente pour que l’on puisse n´gliger les
e e
effets de frottement interne : absence de d´formation diff´r´e ou de recouvrance retard´e. La plasticit´
e ee e e
pure est ind´pendante du temps.
e
L’´lasto-plasticit´ parfaite
e e
Elle correspond au cas id´al o` le seuil d’´coulement est une constante mat´rielle ind´pendante de
e u e e e
la valeur de la d´formation plastique atteinte. L’´crouissage ou durcissement est nul. Le comportement
e e
plastique parfait est sch´matis´ par le mod`le d’un patin id´al ` frottement sec (cf. Fig 4.3) dont le
e e e e a
seuil de glissement correspond au seuil d’´coulement σe ind´pendant de εp . Au del` du seuil, quand
e e a
σ ≥ σe le patin n’oppose aucune r´sistance additionnelle au glissement. Ce mod`le ne permet pas
e e
de d´finir la d´formation plastique εp au del` du seuil puisqu’il ne comporte aucun m´canisme de
e e a e
contention de la d´formation plastique, il est par contre tr`s utile pour repr´senter la notion de seuil
e e e
d’´coulement plastique libre (non contenu) le Yield point. L’´lasticit´ est repr´sent´e par le ressort de
e e e e e
raideur E mont´ en s´rie. Tant que la contrainte σ < σe , le patin est bloqu´, seul le ressort travaille
e e e
et la relation σ = f (ε) s’´crit σ = Eε = Eεe . La d´formation totale est d’origine purement ´lastique
e e e
jusqu’au point A. Lorsque l’on cherche ` augmenter la contrainte σ appliqu´e au del` de σe , le patin
a e a
se met ` glisser sans opposer de r´sistance, le mat´riau se plastifie, la contrainte reste plafonn´e ` la
a e e e a
valeur σe et le mat´riau s’´coule plastiquement. Sa d´formation totale ε = εe +εp est alors la somme de
e e e
la d´formation ´lastique constante εe = Eσe et de la d´formation plastique εp dont la loi d’´volution
e e e e
est ind´termin´e dans ce mod`le ´l´mentaire. Si l’on proc`de ` une d´charge ` partir de l’´tat de
e e e ee e a e a e
d´formation atteint au point B le patin se bloque instantan´ment arrˆtant l’´coulement plastique de
e e e e
sorte que εp = εp (B) tandis que le ressort se d´tend progressivement et la d´formation ´lastique suit la
e e e
loi εe = Eσ (σ < σe ) de sorte qu’apr`s d´charge compl`te la d´formation permanente est εp = εp (B).
e e e e
Un nouveau chargement retendra le ressort jusqu’` revenir au point B au del` duquel l’´coulement
a a e

80. 74 ´
CHAPITRE 4. PLASTICITE
Fig. 4.3 – Plasticit´ parfaite : le mod`le du patin ` frottement sec
e e a
plastique reprendra ` σ = σe fix´. Le fait que le seuil d’´coulement soit ind´pendant de l’amplitude
a e e e
de la d´formation plastique εp traduit bien l’absence d’´crouissage du mat´riau. En ´lasto-plasticit´
e e e e e
parfaite il n’existe pas de relation biunivoque entre σ et εp .
L’´lasto-plasticit´ ´crouissante
e ee
Le mod`le le plus simple consiste ` mettre en parall`le sur le patin un ressort de raideur K appel´e
e a e e
module d’´crouissage qui correspond au m´canisme de cr´ation des contraintes internes n´cessaires
e e e e
pour contenir l’´coulement plastique. Tant que la contrainte σ < σe , le patin est bloqu´, seul le ressort
e e
Fig. 4.4 – Plasticit´ ´crouissante : le mod`le du patin ` frottement sec
ee e a
E travaille et la relation σ = f (ε) s’´crit σ = Eε = Eεe . La d´formation totale est d’origine purement
e e
´lastique jusqu’au point A.
e
Lorsque l’on cherche ` augmenter la contrainte σ appliqu´e au del` de σe , le patin se met `
a e a a
glisser opposant toujours la r´sistance σe , le mat´riau se plastifie mais le ressort K vient limiter
e e
l’´coulement possible de sorte que σ = σe + Kεp est la somme de la contrainte seuil du patin et de
e
la contrainte σI = Kεp = σ − σe du ressort K. Le ressort ´lastique se d´forme ´galement selon la loi
e e e
d’´lasticit´ σ = Eεe . La d´formation totale ε = εe +εp au point B est alors la somme de la d´formation
e e e e
σ σ−σe
´lastique εe = E et de la d´formation plastique εp = K de sorte que la r´ponse σ = f (ε) s’´crit :
e e e e
1 1 1 1 1 1 1
ε = ( E + K )σ − K σe soit ε(B) − ε(A) = E (σ(B) − σ(A)) avec E = E + K . E pente du segment AB
est appel´ module tangent. Comme E
e K, E K. Ce mod`le simple met en ´vidence le caract`re
e e e
incr´mental des lois de la plasticit´.
e e
De mani`re plus g´n´rale, il y aura une relation biunivoque σ = f (ε) dont la lin´arisation locale au
e e e e
voisinage d’un point B de la zone plastique conduit imm´diatement ` la d´finition du module tangent
e a e
E (σ) = dσ d’o` son appellation et ` l’´criture incr´mentale dσ = Kdεp de la loi de plasticit´, le
dε u a e e e
module tangent E (σ) et le module d’´crouissage K(σ) ´tant tout deux des fonctions d´croissantes de
e e e
la contrainte σ rendant compte de la diminution progressive du durcissement lorsque la plastification.
Si l’on proc`de ` une d´charge ` partir de l’´tat de d´formation atteint au point B le patin se
e a e a e e
bloque instantan´ment arrˆtant l’´coulement plastique de sorte que εp = εp (B) tandis que le ressort
e e e
se d´tend progressivement et la d´formation ´lastique suit la loi εe = Eσ (σ < σ(B)). Apr`s d´charge
e e e e e
compl`te la d´formation permanente est εp = εp (B). Mais le ressort K qui supportait la contrainte
e e
σI = Kεp (B) reste tendu par suite du blocage du patin. Il exerce donc sur le patin une contrainte

81. 4.1. LE COMPORTEMENT PLASTIQUE 75
−σI .C’est grˆce ` l’existence de cette contrainte interne induite par la plastification que l’´coulement
a a e
plastique peut rester confin´. La plastification ´crouissante s’accompagne toujours de la cr´ation de
e e e
contraintes internes de confinement. A l’´chelle microscopique tous les grains ne se plastifient pas en
e
mˆme temps et l’´coulement des grains qui se plastifient est contenu par les d´formations ´lastiques des
e e e e
grains non plastifi´s, ces d´formations ´tant ` l’origine des contraintes internes. Cependant, au cours de
e e e a
l’´crouissage, le nombre de grains en r´gime ´lastique diminue tandis que le nombre de grains passant
e e e
en ´coulement plastique augmente. Il existe donc un point au del` duquel l’´coulement plastique ne
e a e
peut plus ˆtre contenu, et la ruine intervient alors inexorablement.
e
Ce simple mod`le met ´galement en ´vidence une deuxi`me caract´ristique fondamentale des lois
e e e e e
de plasticit´, son caract`re non univoque :
e e
– Si au point B on augmente la contrainte appliqu´e σ, la plastification se poursuit selon la loi
e
dσ
σ = f (ε) d´finie de mani`re incr´mentale par K(σ) = dεp .
e e e
– Si au contraire on la diminue, on rentre ` nouveau en r´gime ´lastique et la d´charge σ = f (ε)
a e e e
s’identifie simplement ` la loi de l’´lasticit´.
a e e
Chaque point de la courbe de charge σ = f (ε) doit ˆtre consid´r´ comme un point de bifurcation
e ee
possible ce qui revient ` dire que la courbe σ = f (ε) est la limite du domaine de comportement
a
´lastique du mat´riau pour la sollicitation consid´r´e.
e e ee
L’effet Bauschinger
Ce mod`le simple permet ´galement de rendre compte sch´matiquement de l’effet Bauschinger.
e e e
Fig. 4.5 – Effet Bauschinger : le mod`le du patin ` frottement sec
e a
Partant de l’´tat de repos, la contrainte σ appliqu´e peut varier entre −σe et σe avant que le
e e
patin ne se mette en mouvement. Le domaine ´lastique AA initial (d´formation purement ´lastique
e e e
du ressort E sans glissement du patin plastique εp = 0) est d´fini par −σe < σ < σe . Appliquons
e
maintenant une charge σ > σe de sorte que le patin glisse puis se bloque ` la nouvelle position
a
d’´quilibre B. Le ressort K est alors tendu par la contrainte interne σI = Kεp et le patin supporte la
e
charge σ −σI qui doit en valeur absolue rester inf´rieure ` σe afin que le patin reste bloqu´. Le domaine
e a e
´lastique BB apr`s plastification εp (d´formation purement ´lastique du ressort E sans glissement
e e e e
du patin plastique εp = Cte) est donc d´fini par σI − σe < σ < σI + σe . Il s’est bien agrandi du cot´
e e
de la contrainte de plastification initiale et r´duit pour la contrainte de signe oppos´. Dans ce mod`le
e e e
simple, le domaine ´lastique garde une amplitude constante 2σe , mais il se translate de σI , ´crouissage,
e e
r´duisant la ductilit´ en se rapprochant du point de rupture.
e e
4.1.4 Instabilit´ plastique et ´coulement libre
e e
La figure 4.6 repr´sente la courbe de charge typique F = f (u) d’un mat´riau ductile sollicit´ en
e e e
traction uniaxiale, essai classique dans lequel F est la force appliqu´e ` l’´prouvette (longueur initiale
e a e
l0 , aire de section droite initiale S0 ) et u l’allongement r´sultant mesur´ par le d´placement de la
e e e

82. 76 ´
CHAPITRE 4. PLASTICITE
traverse mobile de la machine d’essai). Moyennant une affinit´ de coefficient S0 selon l’axe des forces
e
et l0 selon celui des d´placements, cette courbe repr´sente ´galement la relation σn = f (εn ) entre
e e e
d´formation et contrainte nominales. Sch´matiquement elle se d´compose en trois domaines :
e e e
Fig. 4.6 – Instabilit´ plastique : courbes de charge nominale et vraie
e
– Un domaine ´lastique
e
OB caract´ris´ par une tr`s forte pente (module d’Young E) correspondant ` une d´formation
e e e a e
´lastique maximale ε ∼ 10−3 . La fin du domaine ´lastique est caract´ris´e par la limite ´lastique
e e e e e
conventionnelle Re (point B) correspondant ` un allongement plastique permanent r´siduel εP
a e
de 0, 2%. La limite ´lastique vraie σe pour laquelle le premier cristal se plastifie (point A), non
e
mesurable, est port´e ici pour m´moire.
e e
– Un domaine d’´coulement plastique contenu
e
BM caract´ris´ par l’allongement plastique uniform´ment r´parti Au et la r´sistance ultime `
e e e e e a
la traction Rm . La d´formation plastique reste homog`ne sur le corps de l’´prouvette. Tous les
e e e
tron¸ons de l’´prouvette se d´forment de la mˆme mani`re et la r´duction d’aire de section droite
c e e e e e
qui en r´sulte est la mˆme quelque soit la section droite consid´r´e. C’est le domaine de plasticit´
e e ee e
utilisable pour les op´rations de formage et d’emboutissage. Les d´formations atteignent quelques
e e
dizaines de % et il faut utiliser la contrainte vraie telle que F = σn S0 = σS et la d´formation
e
vraie ε = Ln(1 + εn ) pour repr´senter la loi de comportement ε = g(σ) qui ne se confond plus
e
avec la courbe de charge σn = f (εn ).
– Un domaine d’instabilit´ plastique
e
Au del`, domaine M R, la courbe de charge pr´sente une pente n´gative, traduisant une instabilit´
a e e e
m´canique plastique conduisant rapidement ` la rupture (point R) caract´ris´e par l’allongement
e a e e
a
` rupture Ar encore appel´ ductilit´ en traction. Plus Ar est grand et plus le mat´riau est ductile
e e e
et apte ` l’utilisation pour les op´rations de formage.
a e
L’´coulement plastique libre
e
Au point M une section particuli`re de l’´prouvette travers´e par un d´faut toujours pr´sent dans
e e e e e
les mat´riaux r´els se d´forme plus rapidement que les autres. Son aire devient plus petite, la contrainte
e e e
y augmente et la d´formation plastique se localise au voisinage de cette section : c’est la striction.
e
Le mat´riau a atteint sa limite de r´sistance. La plastification n’´volue plus de mani`re homog`ne le
e e e e e
long de l’´prouvette, l’´coulement plastique n’est plus contenu dans la zone de striction tandis que la
e e
d´formation s’arrˆte dans le reste de l’´prouvette. L’instabilit´ plastique se produit lorsque dσn = 0 et
e e e e dε
n
correspond au maximum dF = 0 de la courbe de charge. L’´coulement plastique devenu libre dans la
e
zone de striction entraˆ un allongement rapide de l’´prouvette et une diminution de la force impos´e
ıne e e
par la machine d’essai dont la vitesse d’allongement est limit´e.
e

83. ` ´ ` ´
4.2. FRONTIERE ELASTIQUE ET FRONTIERE D’ECOULEMENT 77
Le seuil d’instabilit´ plastique
e
En terme de loi de comportement le seuil d’instabilit´ dF = 0 est tel que dσ = − dS . L’exp´rience
e σ S e
montre que, si la d´formation plastique est suffisamment grande, la plastification des mat´riaux s’ef-
e e
fectue ` volume constant ce qui permet de relier les variations de S ` celle de l par la relation
a a
dS
S = − dl = −dε. L’instabilit´ plastique correspond donc au point de la loi de comportement tel que
l e
σ = dσ au del` duquel le durcissement du mat´riau n’est plus suffisant pour accommoder l’augmen-
dε a e
tation de contrainte appliqu´e. La condition de d´formation ` volume constant permet ´galement de
e e a e
pr´ciser la mani`re dont la loi de comportement ε = g(σ) se d´duit de la courbe de charge σn = f (εn )
e e e
au travers des transformations : ε = Ln(1 + εn ) et σ = σn (1 + εn ).
4.1.5 La striction stable
Dans certains polym`res la courbe de charge Q = f (q) pr´sente un maximum au del` duquel, il
e e a
n’y a plus durcissement mais palier plastique.
Fig. 4.7 – Striction stable des polym`res
e
Les polym`res, comme le poly´thyl`ne pr´sentent une striction stable qui ne conduit pas ` la
e e e e a
rupture. dσn s’annule ` assez faible contrainte et la striction commence. Toutefois le col ne devient
dε
n
a
jamais instable, il s’allonge de mani`re importante car pour ce mat´riaux l’´crouissage ` forte contrainte
e e e a
est consid´rable accommodant l’augmentation de contrainte dˆ ` la r´duction de section de la zone
e ua e
de striction. Ce comportement ´trange r´sulte de l’alignement des chaˆ
e e ınes polym´riques dans le col le
e
long de la direction d’´tirement. Les polym`res ´tir´s (compl`tement strictionn´s) sont beaucoup plus
e e e e e e
r´sistants que les polym`res non ´tir´s.
e e e e
4.2 Fronti`re ´lastique et fronti`re d’´coulement
e e e e
La sollicitation de traction utilis´e jusqu’ici pour la caract´risation du comportement plastique est
e e
fonction d’un seul param`tre de charge, la force de traction Q ` laquelle est associ´ le d´placement q.
e a e e
G´n´ralisons les notions de limite ´lastique et de limite d’´coulement plastique au cas des sollicitations
e e e e
complexes caract´ris´es par l’´tat de contrainte σ.
e e e
4.2.1 La fronti`re ´lastique
e e
Partant de l’´tat de repos σ = 0 on cherche ` d´terminer l’ensemble de tous les ´tats de contraintes
e a e e
σ = 0 faisant apparaˆ ıtre une d´formation permanente. Dans l’espace des contraintes cet ensemble
e
d´finit une surface d’´quation f (σ) = 0 que l’on nomme fronti`re ´lastique. Cette surface ´galement
e e e e e
appel´e surface de charge est ind´pendante du trajet de chargement et de l’horaire suivis pour l’at-
e e
teindre puisque σ = f (ε) est biunivoque en r´gime ´lastique. En g´n´ral, l’´crouissage du mat´riau
e e e e e e
modifie la fronti`re ´lastique. Lorsqu’elle n’est pas modifi´e par l’apparition des d´formations plas-
e e e e
tiques, le mat´riau est dit plastique parfait.
e

84. 78 ´
CHAPITRE 4. PLASTICITE
Lorsque le point de charge atteint la surface de charge avec une vitesse dirig´e vers l’ext´rieur, il ne
e e
peut la franchir mais l’entraˆ avec lui. Cette translation s’accompagne ´galement d’une d´formation
ıne e e
de la surface de charge.
Par contre, d`s que la vitesse de charge est dirig´e vers l’int´rieur le point de charge quitte
e e e
la surface de charge pour rentrer dans le domaine ´lastique, la d´formation plastique s’arrˆte et la
e e e
surface de charge se fige.
Fig. 4.8 – Domaine ´lastique, surface de charge et ´crouissage
e e
Pour illustrer ce comportement reprenons le mod`le simple du patin ` frottement sec (Cf. Fig 4.9)
e a
soumis cette fois ` deux chargements X et Y , les deux ressorts de raideurs kX et kY symbolisant
a
le comportement plastique ´crouissant et les deux ressorts de raideurs EX et EY symbolisant le
e
comportement ´lastique. Le seuil de r´sistance au glissement S du patin ´tant suppos´ ind´pendant
e e e e e
de la direction de glissement le patin glissera dans la direction de la r´sultante des efforts qui lui sont
e
appliqu´s lorsque l’amplitude de cette r´sultante atteindra le seuil S et ce, quelle que soit la direction
e e
de cette r´sultante. Partant de l’´tat initial o` les ressorts de contention sont au repos (X0 = Y0 = 0)
e e u
l’action des efforts X et Y se traduit simplement par des d´formations ´lastiques dans les ressorts
√ e e
EX et EY tant que le module X 2 + Y 2 de la r´sultante reste inf´rieur au seuil de glissement S.
e e
√
La limite ´lastique sera atteinte lorsque X 2 + Y 2 = S. La fronti`re ´lastique initiale, cercle de
e e e
rayon S centr´ sur l’origine O, a pour ´quation : f (X, Y ) = X 2 + Y 2 − S 2 = 0 Pour un trajet de
e e
Fig. 4.9 – Mod`le du patin ` frottement sec
e a
→
−
charge radial aboutissant au point I de la fronti`re ´lastique initiale la force appliqu´e F (X, Y ) = OI
e e e
→
−
fait l’angle θ avec l’axe OX. Un incr´ment d F de la force induit un glissement du patin plastique
e
→
− →
−
dxP dans la direction F , une force interne d F 0 (dX0 , dY0 ) avec dX0 = kx dx0 et dY0 = ky dy0 dans
les ressorts de contention et le centre O du domaine ´lastique se d´place dans la direction β telle
e e
dY0 ky dy0 ky
dX0 = tgβ = kx dx0 = kx tgθ. Si l’´crouissage est isotrope kx = ky , β = θ et le centre du domaine
e

85. ` ´ ` ´
4.2. FRONTIERE ELASTIQUE ET FRONTIERE D’ECOULEMENT 79
→
−
´lastique se d´place dans la direction OI de l’effort appliqu´. Une d´charge, diminution de F , provoque
e e e e
→
−
l’arrˆt du glissement mais les ressorts de contention plastique restent soumis ` l’effort interne d F 0 .
e a
Partant d’un ´tat ´croui (C centre du domaine ´lastique) sans effort externe appliqu´ mais o` les
e e e e u
ressorts de contention sont tendu (X0 = Y0 = 0), l’action d’un effort se traduit simplement par des
d´formations ´lastiques dans les ressorts EX et EY tant que le module (X − X0 )2 + (Y − Y0 )2 de
e e
la r´sultante appliqu´e au patin reste inf´rieur au seuil de glissement S . La nouvelle limite ´lastique
e e e e
sera atteinte lorsque (X − X0 ) 2 + (Y − Y )2 = S. La fronti`re ´lastique ´crouie, cercle de rayon S
e e e
0
centr´ sur l’origine C(X0 , Y0 ), a pour ´quation : f (X, Y ) = (X − X0 )2 + (Y − Y0 )2 − S 2 = 0. A seuil
e e
de glissement S constant la fronti`re ´lastique ne se d´forme pas, sa translation traduit l’´crouissage
e e e e
et l’effet Bauschinger.
Effectuons maintenant le trajet de charge CP qui am`ne le point de charge sur la fronti`re ´lastique
e e e
→
−
´crouie au point P o` la r´sultante des efforts appliqu´s au patin est F (X − X0 , Y − Y0 ). Au point
e u e e
→
−
P appliquons alors un incr´ment de charge δ F (dX , dY ) = P P dans une direction P P diff´rente de
e e
CP . En vertu de la propri´t´ de la loi de glissement, l’accroissement de d´formation plastique δxP
ee e
s’effectuera dans la direction de la r´sultante actuelle, c’est ` dire CP et non dans celle de l’incr´ment
e a e
P P . Par contre son amplitude d´pendra ` la fois de l’amplitude et de la direction de l’incr´ment de
e a e
charge. Pour un mat´riau isotrope la d´formation ´lastique instantan´e cr´e par l’incr´ment de charge
e e e e e e
s’effectue elle dans la direction P P de cet incr´ment.
e
Cette propri´t´ se v´rifie facilement avec un fil ´crouissable ´tir´ au del` du seuil de plasticit´.
ee e e e e a e
La force de traction F ayant conduit ` l’allongement plastique actuel ´tant maintenue constante, ap-
a e
pliquons un petit couple de torsion dC. La r´ponse ´lastique instantan´e est une l´g`re torsion qui
e e e e e
s’annule avec le retrait du couple dC. Par contre dC g´n´re ´galement un incr´ment de d´formation
e e e e e
plastique sous la forme d’un petit ´tirement suppl´mentaire du fil et non d’une petite torsion.
e e
Ce mod`le met en ´vidence la diff´rence fondamentale entre les d´formations ´lastique et plastique :
e e e e e
l’incr´ment de d´formation ´lastique suit la direction de l’incr´ment de charge, tandis que l’incr´ment
e e e e e
de d´formation plastique suit la direction de la charge appliqu´e.
e e
4.2.2 La fronti`re d’´coulement
e e
Comme le montre l’essai de traction tout mat´riau admet une limite de r´sistance au del` de
e e a
laquelle la d´formation plastique ne peut plus ˆtre contenue. Au del` de cette limite la structure
e e a
´volue rapidement vers la rupture. D’une mani`re g´n´rale la fronti`re d’´coulement sera la surface
e e e e e e
enveloppe F (σ) = 0 de toutes les fronti`res ´lastiques ayant atteint le seuil d’´coulement plastique
e e e
libre, elle d´finira la limite de r´sistance du mat´riau comme fonction de la sollicitation impos´e, c’est
e e e e
le crit`re d’´coulement.
e e
Dans une structure l’´tat de contrainte cr´e par les efforts ext´rieurs appliqu´s n’est en g´n´ral pas
e e e e e e
homog`ne et varie d’un point ` un autre. La limite ´lastique n’est pas atteinte simultan´ment en tous
e a e e
points et les ´l´ments macroscopiques de structure n’ayant pas encore atteint leur limite d’´coulement
ee e
plastique libre contiennent les ´l´ments l’ayant atteint jusqu’au moment o` toute la structure s’´coule
ee u e
plastiquement librement. Ainsi, mˆme si le mat´riau constitutif de la structure est un mat´riau `
e e e a
comportement plastique parfait, ce qui revient ` dire que pour un volume ´l´mentaire en ´tat de
a ee e
contrainte homog`ne la fronti`re ´lastique initiale se confond avec la fronti`re d’´coulement, la r´ponse
e e e e e e
globale de la structure en terme de chargement pr´sente habituellement un ´crouissage et, en terme
e e
de param`tres de chargement Q1 , Q2 , · · · la surface de charge se distingue de la surface d’´coulement.
e e
Partant de l’origine imposons au point de charge P un trajet de charge qui s’en ´loigne. La fronti`re
e e
´lastique initiale est atteinte en P0 . A partir de cet instant la plastification commence et le point P ,
e
bloqu´ sur la fronti`re, suit le trajet P0 P1 entraˆ
e e ınant avec lui la fronti`re ´lastique : c’est l’´crouissage
e e e
a e
` l’´chelle de la structure. Si on proc`de ` une d´charge la d´formation plastique cesse instantan´ment
e a e e e
et la fronti`re ´lastique ´crouie se fige tandis que P rebrousse chemin et rentre ` l’int´rieur de la
e e e a e
fronti`re ´lastique ´crouie : c’est la d´charge ´lastique. Au point limite de chargement P1 la limite de
e e e e e
r´sistance est atteinte et l’´coulement plastique ne peut plus ˆtre contenu. En modifiant le trajet de
e e e
charge le point limite de chargement P1 d´crit dans l’espace des param`tres de chargement Q1 , Q2 , · · ·
e e
une surface lieu des points de chargement limite. Cette surface est appel´ surface de chargement limite.
e

86. 80 ´
CHAPITRE 4. PLASTICITE
Fig. 4.10 – Fronti`res ´lastiques et surface de chargement limite
e e
4.3 Crit`res de plasticit´ et d’´coulement
e e e
Pour un ´l´ment de mati`re en ´tat de contrainte homog`ne la fronti`re ´lastique, initiale ou ´crouie,
ee e e e e e e
f (σ) = 0 repr´sente le crit`re de plasticit´. La fronti`re d’´coulement, surface enveloppe F (σ) = 0 de
e e e e e
toutes les fronti`res ´lastiques ayant atteint le seuil d’´coulement plastique libre apr`s ´crouissage,
e e e e e
d´finit la limite de r´sistance du mat´riau comme fonction de la sollicitation homog`ne impos´e :
e e e e e
c’est le crit`re d’´coulement ou limite de r´sistance. Ces deux crit`res sont confondus pour les corps
e e e e
a
` comportement plastique parfait.
Pour un corps a comportement plastique anisotrope les fonctions f et F d´pendent ´videmment
e e
des axes utilis´s, elle d´pendront donc dans le cas g´n´ral des trois invariants du tenseur σ d´finissant
e e e e e
la sollicitation impos´e et des trois angles d’Euler rep´rant les axes principaux de σ par rapport aux
e e
axes mat´riels d’anisotropie.
e
Pour un corps ` comportement plastique isotrope tel que les conditions n´cessaires au d´clenchement
a e e
ou ` la poursuite de l’´coulement plastique soient ind´pendantes de la direction de sollicitation par
a e e
rapport ` la mati`re on peut toujours confondre les axes propres de σ et les axes mat´riels de sorte
a e e
que les crit`res f et F sont obligatoirement des invariants de σ. Les crit`res s’´criront donc soit en
e e e
terme d’invariants F (I1 , I2 , I3 ) = 0 soit en terme de contraintes principales F (σ1 , σ2 , σ3 ) = 0. Dans
l’espace σ1 , σ2 , σ3 des contraintes principales le domaine F < 0 est appel´ domaine de r´sistance. Ce
e e
n’est pas le domaine ´lastique mais celui des d´formations plastiques contenues.
e e
Comme toute d´formation plastique conduit inexorablement ` la rupture finale du mat´riau par
e a e
traction ce domaine est limit´ par deux nappes distinctes (Cf. Fig 4.11) : l’une ΣP correspondant `
e a
l’´coulement plastique et l’autre ΣR ` la rupture. La nappe ΣR est tangente aux trois plans σ1 =
e a
σR , σ2 = σR , σ3 = σR au point S o` elle rencontre l’axe des contraintes isotropes σ1 = σ2 = σ3 ,
u
traction hydrostatique, ce qui nous ram`ne ` la notion de contrainte de rupture σR d’un mat´riau en
e a e
traction.
Fig. 4.11 – Allure probable des deux nappes en projection sur le plan σ1 , σ2
Mˆme dans le cas de grandes d´formations plastiques la s´paration se termine par une rup-
e e e

87. ` ´ ´
4.3. CRITERES DE PLASTICITE ET D’ECOULEMENT 81
ture fragile, clivage sur la nappe ΣR . Les causes de cet effet sont diverses : l’endommagement par
d´veloppement de fissures microscopiques, l’´crouissage augmentant la r´sistance au glissement mais
e e e
diminuant souvent la r´sistance au clivage, la viscosit´ agissant dans le mˆme sens que l’´crouissage
e e e e
quand la d´formation plastique s’acc´l`re et la modification de l’´tat de contrainte induite par la
e ee e
modification de la forme ext´rieure du corps sous l’action des d´formations plastiques.
e e
Nous limiterons l’´tude aux principaux crit`res d’´coulement plastique, surface ΣP , mais il faudra
e e e
garder en m´moire le fait que ces crit`res ne pr´jugent pas du mode de rupture final.
e e e
4.3.1 Effet d’une pression isotrope
Pour un corps r´put´ homog`ne et sans vides le domaine des d´formations plastiques contenues
e e e e
s’´tend ind´finiment du cot´ des pressions (contrainte n´gative) sur l’axe ∆(σ1 = σ2 = σ3 ). La plas-
e e e e
tification s’effectuant ` volume constant (d´formation isotrope nulle) une compression hydrostatique,
a e
quelle que soit son amplitude, ne produit ni rupture ni ´coulement plastique comme l’ont d´montr´es
e e e
les exp´riences de Bridgmann et Cook.
e
Cependant ce r´sultat est mis en d´faut pour les corps pr´sentant des vides ou de graves d´faut
e e e e
d’homog´n´it´. Une pression hydrostatique peut alors induire des d´formations plastiques importantes
e e e e
voire mˆme la rupture. Ainsi :
e
– Les m´taux fritt´s et le b´ton sec r´pondent ` un crit`re ferm´ du cot´ des pressions avec une
e e e e a e e e
r´sistance ` la traction faible (li´e ` la faible coh´sion du mat´riau).
e a e a e e
– Les textiles tiss´s pr´sentent au contraire une tr`s faible r´sistance ` la compression (li´e au
e e e e a e
flambement des fils) compar´e ` leur r´sistance en traction.
e a e
Fig. 4.12 – Crit`res ferm´s : mat´riaux h´t´rog`nes et textiles
e e e ee e
4.3.2 Sym´tries du domaine de r´sistance
e e
Le crit`re F doit ˆtre sym´trique en σ1 = σ2 = σ3 . L’axe ∆(σ1 = σ2 = σ3 ) des contraintes isotropes
e e e
est l’axe de sym´trie ternaire de la fronti`re d’´coulement ΣP (F = 0) et les plans σ1 = σ2 , σ2 = σ3 et
e e e
σ1 = σ3 plans de sym´trie. La section de ΣP par un plan perpendiculaire ` ∆ poss`de une sym´trie
e a e e
ternaire. Pour d´terminer compl`tement ΣP il suffit de la d´terminer dans un angle di`dre ´gal ` π .
e e e e e a 3
−→
−
Dans l’espace Oσ1 , Oσ2 , Oσ3 des contraintes principales, le vecteur OM de composantes σ1 , σ2 , σ3 qui
d´crit l’´tat de contrainte en un point du corps est assujetti ` rester dans le domaine d´limit´ par ΣP .
e e a e e
−→
−
Il se d´compose en un vecteur OH(σm , σm , σm ) port´ par ∆ axe des contraintes normales moyennes
e e
−→
−
σm et d’un vecteur perpendiculaire HM (σ1 − σm , σ2 − σm , σ3 − σm ) dans le plan perpendiculaire ` ∆ a
d’origine H.
−→− √ √
Le vecteur OH de module 3σm = 33 Tr(σ) caract´rise le sph´rique des contraintes.
e e
−→−
Le vecteur HM caract´rise le d´viateur de contraintes. σd ´tant la contrainte d´viatorique moyenne
e e e e
et J2 = |(σ1 − σm )(σ2 − σm ) + σ1 − σm )(σ3 − σm ) + σ2 − σm )(σ3 − σm )| la valmeur absolue du second
2 √ √
invariant du d´viateur, son module |HM | = Tr(σ D ) = 2J2 = 3σd = 2 σI , σI = √2 σd ´tant
e 3
3
e
l’intensit´ des contraintes. Dans le r´f´rentiel Hσ1 , Hσ2 , Hσ3 perspectives des axes Oσ1 , Oσ2 , Oσ3
e ee
−→
−
dans le plan perpendiculaire ` ∆ en H caract´risant le d´viateur, le vecteur HM a pour composantes
a e e
3
2 (σi − σm ).
• En traction simple d’amplitude σ selon Oσ1 :
−→
− 2
3σm = σ |HM |2 = σ 2 soit σ = σI (4.1)
3

88. 82 ´
CHAPITRE 4. PLASTICITE
Fig. 4.13 – Sym´tries du domaine de r´sistance, plan du d´viateur et espace des contraintes
e e e
−→−
Le vecteur HM a pour composantes 2 3 σ, − 3 3 σ, − 3 3 σ sur les perspectives Hσ1 , Hσ2 , Hσ3 des
3 2
1
2
1
2
trois axes Oσ1 , Oσ2 , Oσ3 . Dans le plan du d´viateur, il est port´ par la perspective Hσ1 de la partie
e e
positive de l’axe Oσ1 .
L’´tat de compression simple d’amplitude −σ sera donc le point sym´trique par rapport ` l’origine
e e a
H sur le mˆme axe.
e
• En cisaillement pur dans le plan σ1 , σ2 caract´ris´ par σ1 = τ , σ2 = −τ et σ3 = 0 :
e e
−→
− √
σ = σ D σm = 0 |HM |2 = 2τ 2 soit σI = 3τ (4.2)
−→
−
Le vecteur HM a pour composantes 3 τ, − 3 τ, 0 sur les trois axes Hσ1 , Hσ2 , Hσ3 . Dans le plan du
2 2
d´viateur, il est port´ par la perpendiculaire ` l’axe Hσ3 .
e e a
4.3.3 Crit`re de Tresca et Courbe intrins`que de Caquot
e e
En 1870 Tresca, effectuant des exp´riences sur le plomb, admet que la d´formation plastique se
e e
produit en un point lorsque sur une facette passant par ce point la cission (module du cisaillement)
atteint une valeur caract´ristique du mat´riau c’est ` dire lorsque la cission maximale τM = 1 (σ1 −σ3 )
e e a 2
lorsque σ1 ≥ σ2 ≥ σ3 atteint une valeur d´termin´e k, r´sistance au cisaillement du mat´riau. Ce
e e e e
crit`re est bien adapt´ au comportement des m´taux purs et ` certains alliages, un changement de
e e e a
signe des contraintes ne change pas la limite d’´coulement : F (−σ1 , −σ2 , −σ3 ) = F (σ1 , σ2 , σ3 ).
e
Fig. 4.14 – Crit`re de Tresca et courbe intrins`que de Caquot
e e
Pour les autres corps Mohr (1900), se basant sur l’id´e que la d´formation plastique s’op`re par
e e e
glissement, propose une g´n´ralisation du crit`re de Tresca sous la forme : τ = f (σ), τ cission et σ
e e e
contrainte normale support´es par la facette de glissement. f est une fonction d´croissante de σ (les
e e
σ > 0 sont des tractions) et la courbe limite τ = f (σ) du plan σ, τ dite courbe de r´sistance intrins`que
e e
ou courbe intrins`que de Caquot d´limite le domaine de r´sistance du mat´riau.
e e e e
Dans le plan σ, τ de la repr´sentation de Mohr la condition τ = f (σ) sera r´alis´e pour deux
e e e
facettes lorsque le plus grand des cercles de Mohr, ici de diam`tre σ3 , σ1 avec σ3 < σ2 < σ1 , deviendra
e

89. ` ´ ´
4.3. CRITERES DE PLASTICITE ET D’ECOULEMENT 83
bitangent ` la courbe intrins`que. Les facettes de glissement qui contiennent la direction σ2 , font
a e
π ϕ
alors un angle 4 − 2 avec la direction de la facette soumise ` la traction maximale. La condition
a
de bitangence se r´duit ` une expression du type g(σ1 , σ3 ) = 0 dans laquelle la contrainte principale
e a
σ2 n’intervient pas. Afin que le cercle limite reste bitangent ` la courbe intrins`que σ1 et σ3 doivent
a e
∂g ∂g
varier dans le mˆme sens et g v´rifie : ∂σ1 ∂σ3 < 0. La d´termination exp´rimentale de la courbe
e e e e
intrins`que s’obtient comme enveloppe des cercles limites de l’exp´rience d’´treinte avec compression
e e e
(σ1 = σ2 = −q, σ3 = −p, p > q). On constate :
– Aux tr`s grandes pressions q, pour tous les mat´riaux, la valeur de |τ | = p−q tend vers une limite
e e 2
finie, le crit`re tend vers celui de Tresca : deux droites parall`les ` Oσ. Le mat´riau aux grandes
e e a e
pressions q est capable de supporter de tr`s grandes d´formations plastiques sans rupture, mˆme
e e e
les roches les plus dures. L’application d’une pression hydrostatique pr´alable ` un corps fragile
e a
d´place le centre du cercle limite vers la gauche sur l’axe Oσ expliquant les plissements sans
e
fracture des terrains s´dimentaires ou le filage du verre ` froid.
e a
– Au sommet S de la courbe intrins`que il y a rupture avant d´formation plastique avec une forte
e e
dispersion des valeurs de la contrainte de rupture : on est pass´ sur la surface ΣR
e
Fig. 4.15 – Ductilit´ et fragilit´
e e
– Les mat´riaux diff`rent seulement par la position S du sommet de la courbe intrins`que par
e e e
a a 1
rapport ` l’origine O des contraintes, c’est ` dire par la valeur du rapport 2 OS . Ce rapport est
k
grand pour les corps ductiles, le cercle limite tangente d’abord la surface ΣP . Il est tr`s petit
e
pour les corps fragiles (b´ton, roches, c´ramiques, verres) et le cercle limite tangente d’abord ΣR
e e
au voisinage de S. La ductilit´ se caract´rise ´galement par le rapport des limites σT ` la traction
e e e a
simple et σC ` la compression simple. Pour les corps tr`s ductiles, ce rapport est ´gal ` 1 car
a e e a
σC = σT = 2k. Pour les corps fragiles, il est tr`s petit (de 1/10 ` 1/100) car σT = σR
e a σT = 2k.
4.3.4 Crit`res de Von Mis`s et Coulomb
e e
Dans le cas des terres denses o` l’on observe des glissements la loi τ = f (σ) n’est que grossi`rement
u e
respect´e. Le crit`re de la courbe intrins`que n’est donc pas rigoureux. De nombreux essais ont montr´
e e e e
que pour tous les mat´riaux (m´taux, terres, roches, b´tons) la contrainte principale interm´diaire σ2
e e e e
joue un rˆle. Si son influence reste limit´e dans le cas des m´taux o` lorsque l’on fait varier σ2 de σ1
o e e u
a
` σ3 , ` σ3 = Cte la valeur critique de σ1 varie de 10%, elle est au contraire tr`s importante dans le
a e
cas des roches pour lesquelles la r´sistance ` l’´treinte (σ1 = σ2 = −q, σ3 = −p, p > q) est double de
e a e
la r´sistance ` la compression simple (σ2 = 0, σ1 = −q, σ3 = −p, p > q).
e a
Pour prendre en compte la contrainte principale interm´diaire, il faut revenir ` la d´finition du
e a e
crit`re en terme d’invariants des contraintes F (I1 , I2 , I3 ) = 0. Pour les corps tr`s ductiles l’exp´rience
e e e
montre que seul intervient le d´viateur des contraintes σ D = σ − σm δ avec σm contrainte normale
e
moyenne telle que 3σm = I1 . On peut donc substituer aux invariants I2 et I3 de σ les invariants J2
2 2 2
et J3 correspondant de son d´viateur σ D puisque J1 = Tr(σ D ) = 0, 2J2 = Tr(σ D ) = Tr(σ ) − 3σm
e
et J3 = Det(σ D ). Le crit`re s’´crit alors : F (J2 , J3 ) = g(σm ). La section droite de cette surface dans
e e
tout plan perpendiculaire ` l’axe de sym´trie ternaire ∆(σ1 = σ2 = σ3 ) de la surface ΣP est limit´e
a e e
par la courbe d’´quation φ(J2 , J3 ) = g(σm ) = Cte. Aux fortes pressions la surface ΣP se rapproche
e
d’un cylindre de g´n´ratrices parall`les ` ∆ et la constante g(σm ) devient ind´pendante de σm (Cf.
e e e a e
Fig. 4.13).

90. 84 ´
CHAPITRE 4. PLASTICITE
Crit`res de Von Mis`s et de Tresca
e e
• Le crit`re de Von Mis`s J2 = k 2 en est la forme la plus simple obtenue lorsque φ ne d´pend ni
e e e √
−→−
de J3 ni de σm . Comme |HM |2 = 2J2 = 2k 2 c’est un cylindre circulaire d’axe ∆ et de rayon r = 2k.
D’apr`s (4.2) la r´sistance au cisaillement τ est σC = k et d’apr`s (4.1) la r´sistance ` la traction σ
e √ e e e a
est σT = k 3.
• Le crit`re de Tresca qui s’´crit σ1 − σ3 = 2k lorsque σ1 ≥ σ2 ≥ σ3 , correspondant ` un plan
e e a
parall`le ` ∆ et ` Oσ2 coupant l’axe Oσ1 ` l’abscisse 2k et dont la trace sur le plan perpendiculaire `
e a a a a
∆ est une droite parall`le ` Hσ2 . En faisant jouer les sym´tries le crit`re de Tresca Sup|σi − σj | = 2k
e a e e
est un cylindre d’axe ∆ ayant pour base, dans le plan perpendiculaire ` ∆, un hexagone r´gulier.
a e
D’apr`s σ1 − σ3 = 2k la r´sistance au cisaillement σ1 = τ , σ3 = −τ est σC = k et la r´sistance `
e e e a
la traction σ1 = σ, σ3 = 0 est σT = 2k.
Fig. 4.16 – Crit`res de Von Mis`s et Tresca
e e
• Ces deux crit`res sont voisins. En prenant comme r´f´rence la r´sistance en cission pure k,
e ee e
l’hexagone de Tresca est circonscrit au cercle de Von Mis`s car les deux figures sont tangentes aux
e
points repr´sentatifs du cisaillement pur. Par sym´trie les r´sistances en traction et compression sont
e e e
´gales dans chacun des crit`res, mais, ` r´sistances au cisaillement k ´gales, la r´sistance ` la traction
e √ e a e e e a
est σT = k 3 pour Von Mis`s et σT = 2k pour le crit`re de Tresca. L’´cart relatif maximal entre les
√ e e e
deux crit`res donn´ par k 2k = 13% intervient pour une sollicitation de traction pure. L’exp´rience
e e 3−2k
e
donne pour les m´taux des r´sultats compris entre les deux, en g´n´ral plus proches de Von Mis`s.
e e e e e
De ce fait il est fr´quemment utilis´ d’autant qu’il pr´sente une r´gularit´ math´matique commode
e e e e e e
compar´e ` celui de Tresca.
e a
Crit`res de Schleicher et de Coulomb
e
Pour faire intervenir la contrainte moyenne σm la g´n´ralisation la plus simple des crit`res pr´c´dents
e e e e e
consiste ` remplacer la constante k pr´c´dente par une fonction de σm : J2 = f (σm ) g´n´ralisation du
a e e e e
crit`re de Von Mis`s connue sous le nom de crit`re de Schleicher. Ce crit`re donne de bons r´sultats
e e e e e
pour les roches en prenant f (σm ) = A|σm |α avec α un peu < 1. La valeur α = 1 correspond au crit`re e
de Coulomb d´finissant le frottement sec. La r´sistance au glissement τ augmente proportionnelle-
e e
ment ` la charge de compression moyenne σm , leur rapport constant µ = tgϕ ´tant le coefficient de
a e
frottement. La coh´sion σC est la r´sistance ultime ` la traction g´n´ralement faible.
e e a e e
4.4 Les ´quations de la plasticit´
e e
Rappelons la diff´rence fondamentale entre les d´formations ´lastique et plastique : l’incr´ment de
e e e e
E
d´formation ´lastique dε suit la direction de l’incr´ment de contrainte dσ qui le provoque, tandis que
e e e
P
l’incr´ment de d´formation plastique dε d´pend plus de l’´tat de contrainte σ qui le rend possible
e e e e

91. ´ ´
4.4. LES EQUATIONS DE LA PLASTICITE 85
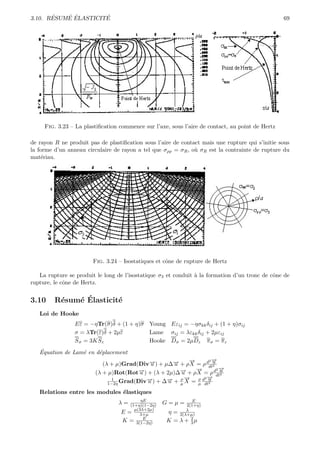
Fig. 4.17 – Crit`re de Coulomb
e
que de l’incr´ment de contrainte dσ qui le provoque.
e
E P
En effectuant la partition de la d´formation totale ε = ε + ε en d´formation ´lastique et plas-
e e e
P
tique, la d´formation plastique ε dans un ´tat donn´ est une fonctionnelle d´pendant ` la fois des
e e e e a
contraintes σ de l’´tat consid´r´ et de leur ´volution au cours de tous les ´tats pr´c´dents. En intro-
e ee e e e e
P
duisant un temps conventionnel τ pour d´crire cette histoire, t d´signant l’´tat actuel, la relation ε ,
e e e
P
σ s’´crit : ε (t) = F[σ(τ ), σ(t)] avec −∞ < τ < t. Il est clair qu’` une mˆme valeur de d´formation
e a e e
P
ε peut correspondre une infinit´ d’´tats de contrainte σ. On ne peut ´crire la loi de comportement
e e e
plastique sous forme finie comme en ´lasticit´ car elle est de nature incr´mentale.
e e e
Devant la difficult´ de raisonner sur des fonctionnelles non lin´aires on utilise l’hypoth`se dite des
e e e
variables cach´es : la donn´e de l’histoire σ(τ ) peut ˆtre remplac´e par celles des valeurs actuelles αk (t)
e e e e
d’un certain nombre de variables cach´es dites param`tres d’´crouissage repr´sent´es (pour des raisons
e e e e e
de simplicit´) par le vecteur →(t) fonctionnelle de σ(τ ) et dont la connaissance, jointe ` celle de σ(t),
e −
α a
d´termine l’´tat du corps. En plasticit´ classique, ind´pendante du temps, les ´quations incr´mentales
e e e e e e
s’´crivent :
e
dε = Y(σ, →)dσ−
P P
α dε = 0
dα→ = K(σ, →)dσ
− −α →=0
−
dα (4.3)
en r´gime plastique en r´gime ´lastique
e e e
Pour r´soudre un probl`me de plasticit´, il faut donc connaˆ :
e e e ıtre
– La fonction de charge f (σ, →) = 0 qui ´volue au cours du chargement
−
α e
– La fonction d’´coulement Y(σ, →) qui lie l’incr´ment de d´formation plastique dε ` l’accrois-
− P
e α e e a
sement de chargement dσ
– La loi d’´crouissage K(σ, →) qui lie l’´volution d→ du param`tre d’´crouissage ` l’accroissement
e −α e −α e e a
de chargement dσ
La description de l’´coulement plastique est un probl`me distinct de celle de l’´crouissage. Il faut
e e e
´tablir les lois d’´volution des param`tres d’´crouissage permettant de d´terminer la d´formation de
e e e e e e
la surface de charge et la loi d’´coulement plastique afin d’´tablir ` chaque incr´ment de contrainte
e e a e
l’´tat de d´formation plastique induit.
e e
4.4.1 Les mat´riaux ductiles
e
Loi d’´coulement
e
Nous nous limiterons au cas des mat´riaux cristallins ductiles pour lesquels, au moins de mani`re
e e
P
approch´e, l’exp´rience montre que l’´coulement plastique dε s’effectue dans la direction du gradient
e e e
∂f
∂σ
de la surface de charge ´crouie f (σ, →) = 0, Le mat´riau suit une loi d’´coulement associ´e ` la
e −
α e e e a
surface de charge et la fonction d’´coulement Y(σ, →) est enti`rement d´termin´e par la connaissance
e −α e e e
de la surface de charge f (σ, →) = 0. Au voisinage de la fronti`re ´lastique initiale la contention
−α e e
des grains plastifi´s par leurs voisins non plastifi´s limite leur d´formation plastique ` un ordre de
e e e a
grandeur ´gal ` celui des d´formations ´lastiques des grains non plastifi´s. La d´formation plastique
e a e e e e
s’accompagne n´cessairement d’une variation de volume. Mais l’exp´rience montre que lorsque la
e e

92. 86 ´
CHAPITRE 4. PLASTICITE
Fig. 4.18 – Loi d’´coulement plastique des mat´riaux ductiles
e e
d´formation plastique croˆ la variation permanente de volume (variation plastique) devient n´gligeable
e ıt e
a e
` l’´chelle des d´formations plastiques, la plastification s’effectue ` volume constant et la fonction de
e a
charge ne d´pend plus que du d´viateur des contraintes σ D . La surface d’´coulement confondue avec
e e e
→) est donc un cylindre de g´n´ratrices parall`les ` la droite ∆ d’´quation
−
la surface de charge f (σ D , α e e e a e
σ = σm δ repr´sentant les ´tats de contrainte isotrope justifiant les crit`res de Von Mis`s et de Tresca
e e e e
(Cf. section 4.3). En r´gime ´lastique la variation relative de volume Tr(ε) est associ´e au coefficient
e e e
de Poisson η par ETr(ε) = (1 − 2η)Tr(σ). Au del` de la limite ´lastique la plastification ` volume
a e a
1
constant (d´formation ´lastique n´gligeable) Tr(ε) ≈ Tr(εD ) = 0 implique η = 2 , le coefficient de
e e e
poisson passe progressivement de η < 1 ` η = 1 lorsque la d´formation plastique progresse.
2 a 2 e
Loi d’´crouissage isotrope
e
L’´volution de la surface de charge au cours de l’´coulement peut ˆtre complexe et, en plus du
e e e
d´placement qui accompagne le point de charge, elle subit un changement de forme modifiant ainsi les
e
seuils de plasticit´ pour tous les autres chargements. A partir d’une forme initiale f (σ) = 0 le sch´ma
e e
d’´volution le plus simple est celui de l’´crouissage isotrope. Il se traduit par une simple dilatation
e e
homoth´tique de la surface de charge par rapport ` l’origine. Un seul param`tre scalaire d’´crouissage
e a e e
α suffit ` d´crire cette ´volution .
a e e
Sous ces restrictions, la seule donn´e de la fonction de charge f (σ, α) = 0 permet de caract´riser
e e
a
` la fois la fonction d’´coulement et la fonction d’´crouissage, conduisant ` une forte simplification du
e e a
probl`me.
e
Relation de Von Mis`s
e
Le crit`re de Von Mis`s, bien adapt´ aux m´taux ductiles, s’´crit en pr´sence d’´crouissage isotrope
e e e e e e e
caract´ris´ par la fonction ψ(α) :
e e
1 2 ∂f ∂J2
f ≡ J2 − ψ(α) = Tr(σ D ) − ψ(α) ⇒ = = σD
2 ∂σ ∂σ
P
et la loi d’´coulement se r´duit ` une proportionnalit´ entre l’incr´ment de d´formation plastique dε
e e a e e e
et le d´viateur des contrainte σ D qui le g´n`re. Dans l’espace tridimensionnel des contraintes princi-
e e e
pales, la fronti`re d’´coulement est un cylindre circulaire dont l’axe est la droite ∆(σ1 = σ2 = σ3 ) et
e e
la vitesse de d´formation plastique est repr´sent´e par un vecteur dirig´ selon la normale ext´rieure
e e e e e
au cylindre.
La fonction de charge initiale de Von Mis`s, en l’absence d’´crouissage ψ(α) = 0, s’´crit plus
e e e
commod´ment sous la forme :
e
σI − σe ⇒ fe (σ) = σI − σe = 0

93. ´ ´
4.4. LES EQUATIONS DE LA PLASTICITE 87
avec σe limite d’´lasticit´ initiale en traction simple et σI intensit´ des contraintes ou contrainte
e e e
´quivalente au sens de Von Mis`s :
e e
2
3 3 2 3 Tr(σ D ) 3
σI = 3J2 = σD σD = Tr(σ D ) = √ = √ σd
2 2 2 3 2
qui s’assimile ` la contrainte axiale dans le cas de la traction simple puisque :
a
     
1 0 0 2 0 0 4 0 0
1  2 1
σ = σ  0 0 0  ⇒ σ D = 3 σ  0 −1 0  ⇒ σ D = 9 σ 2  0 1 0 
    
0 0 0 0 0 √−1 0 0 1
2 = 1 Tr(σ 2 ) = 2 σ 2
σd 2
⇒ σd = 3 σ et σI = 23
√ σd = σ
3 D 9
Un ´tat de contrainte complexe σ peut ˆtre assimil´ ` celui d’une traction pure ´quivalente d’amplitude
e e ea e
σI .
4.4.2 Chargement radial et d´formation simple
e
Lorsque les charges externes varient de mani`re monotone proportionnellement ` un seul param`tre
e a e
cin´matique t appel´ temps conventionnel en tout point de la structure le tenseur σ varie proportion-
e e
nellement ` lui mˆme en gardant une orientation fixe correspondant ` un trajet de chargement radial
a e a
dans l’espace des contraintes. Son tenseur des directions π σ ne d´pend pas de t. Dans ce cas, le char-
e
gement est soit un chargement simple ` un param`tre (traction uniaxiale, flexion d’une poutre dont la
a e
section droite pr´sente un axe de sym´trie, le moment fl´chissant ´tant parall`le ` cet axe, ...) soit `
e e e e e a a
un chargement composite (torsion+traction,...) tel que les efforts appliqu´s dans les diff´rents modes
e e
de sollicitation restent toujours proportionnels au cours du temps.
P
Si de plus le mat´riau est isotrope ` ´crouissage isotrope, les directions principales de dε co¨
e ae ıncident
avec celles de σD , qui sont aussi celles de σ. Comme σ garde une direction constante au cours du char-
P
gement, il en va de mˆme pour dε . Il est alors possible d’int´grer les ´quations incr´mentales et
e e e e
P
d’obtenir des relations finies entre les variables σ et ε comme dans le cas ´lastique. C’est la simplifi-
e
cation dite de la d´formation simple.
e
A l’intensit´ des contraintes ou contrainte ´quivalente de Von Mis`s σI = 3 σ D σ D qui s’assimile
e e e 2
a
` la contrainte axiale dans le cas d’une traction simple est associ´e la d´formation plastique cumul´e :
e e e
√ 2
2 T r(εD ) √
εI = ε D εD = 2 = 2εd
3 3
1
En traction simple, la plastification s’effectuant ` volume constant (η = 2 ) :
a
   
1 0 0 2 0 0
P ε
σ = σ 0 0 0  ⇒ ε = εD =  0 −1 0 
  
2
0 0 0 0 0 −1
et εI = ε de la mˆme mani`re que σI = σ. Hencky et Mis`s ont ´tabli la relation :
e e e e
2σI 2σI
σD = εD = (ε − εS ) (4.4)
3εI 3εI
qui lie les d´viateurs de σ et de ε.
e
Cette relation traduit simplement l’´galit´ π σ = π ε des tenseurs des directions de σ et de ε sous
e e
la forme :
σD εD √ √
πσ = = = π ε puisque εI = 2εd et 2σI = 3σd
σd εd
L’´quation de plasticit´ se ram`ne donc ` la d´termination de la fonction ϕ telle que εI = ϕ(σI ).
e e e a e
En d´formation simple cette fonction est universelle, valable pour tous les chargements radiaux
e
monotones.

94. 88 ´
CHAPITRE 4. PLASTICITE
Loi de Hollomon
La courbe σI = φ(εI ) obtenue exp´rimentalement par un essai de traction d´finit la fonction φ
e e
inverse de ϕ. Diverses formes analytiques ont ´t´ retenues pour son ajustement en r´gime plastique.
ee e
La plus usit´e, car bien adapt´e ` l’´crouissage des m´taux, est la loi d’Hollomon :
e e a e e
σI = Aεχ
I 0≤χ<1 (4.5)
Selon la valeur de l’exposant d’´crouissage χ, cette loi permet de repr´senter une ´volution continue
e e e
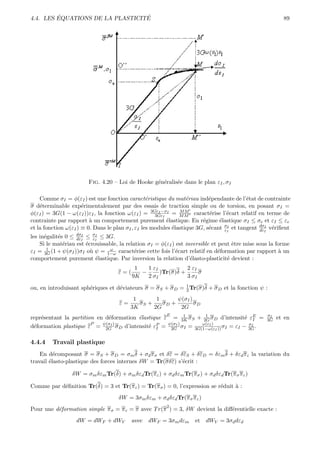
Fig. 4.19 – Loi d’Hollomon
de la fonction d’´crouissage entre la plasticit´ parfaite pour χ = 0 et la plasticit´ ´crouissante pour
e e e e
χ < 1. En pratique, comme le montre le tableau ci-dessous, χ < 1 traduisant la diminution progressive
du durcissement lorsque la plastification progresse. Les probl`mes d’´lasto-plasticit´ en d´formation
e e e e
M´taux et Alliages
e RP (Mpa) A (MPa) χ
Acier doux recuit 210 500 0,28
Acier 0,6% C tremp´ revenu
e 520 1270 0,15
Acier alli´ lamin´
e e 630 100 0,14
Acier inoxydable recuit 590 1280 0,45
Cuivre recuit 60 320 0,54
Laiton α (70-30) recuit 80 900 0,49
Aluminium recuit 40 180 0,20
Al Cu Mg (2024) 310 700 0,16
Tab. 4.1 – Exposant d’´crouissage. RP limite de r´sistance en traction
e e
simple se ram`nent ` celui de la traction plastique simple d’une ´prouvette ´quivalente soumise `
e a e e a
3 2
la contrainte σI = 2 Tr(σ D ) d´duite de
e l’´tat de contrainte actuel et pr´sentant une d´formation
e e e
2
plastique cumul´e
e εI = 2 Tr(εD ) d´duite
3 e de l’´tat de d´formation plastique cumul´e actuelle ce qui
e e e
permet de donner un sens plus large ` l’exposant d’´crouissage de la loi d’Hollomon d´fini en traction.
a e e
4.4.3 Loi de Hooke g´n´ralis´e
e e e
L’´coulement plastique s’effectuant ` volume constant, le tenseur des d´formations plastiques cu-
e a e
P
mul´es ε s’identifie au d´viateur du tenseur des d´formations ε. La relation de Hencky-Mis`s s’´crit
e e e e e
σ D = 2σI εD = 2σI (ε−εS ) et lie les d´viateurs de σ et de ε. En adjoignant la relation de compressibilit´
3ε
I
3ε
I
e e
σm = 3Kεm ou σ S = KTr(ε)δ liant les sph´riques de σ et de ε et prenant en compte les variations de
e
volume induites par la partie ´lastique des d´formations la loi de Hooke se g´n´ralise facilement :
e e e e
2 σI 2 σI
σ = σ S + σ D = (K − )Tr(ε)δ + ε (4.6)
9 εI 3 εI
σd σI
En r´gime ´lastique pur la relation σ D = 2GεD conduit `
e e a εd = 2G et εI = 3G soit :
2 2 2
σ = (K − G)Tr(ε) + 2Gε ou σ = (K − [3G])Tr(ε) + [3G]ε
3 9 3
afin de conserver la mˆme forme de loi en r´gime plastique et ´lasto-plastique.
e e e

95. ´ ´
4.4. LES EQUATIONS DE LA PLASTICITE 89
Fig. 4.20 – Loi de Hooke g´n´ralis´e dans le plan εI , σI
e e e
Comme σI = φ(εI ) est une fonction caract´ristique du mat´riau ind´pendante de l’´tat de contrainte
e e e e
σ d´terminable exp´rimentalement par des essais de traction simple ou de torsion, en posant σI =
e e
φ(εI ) = 3G(1 − ω(εI ))εI , la fonction ω(εI ) = 3GεI −σI = M M ” caract´rise l’´cart relatif en terme de
3GεI
MM
e e
contrainte par rapport ` un comportement purement ´lastique. En r´gime ´lastique σI ≤ σe et εI ≤ εe
a e e e
et la fonction ω(εI ) ≡ 0. Dans le plan σI , εI les modules ´lastique 3G, s´cant σI et tangent dσI v´rifient
e e ε
I
dε
I
e
dσI σI
les in´galit´s 0 ≤ dεI ≤ εI ≤ 3G.
e e
Si le mat´riau est ´crouissable, la relation σI = φ(εI ) est inversible et peut ˆtre mise sous la forme
e e e
1 ω
εI = 3G (1 + ψ(σI ))σI o` ψ = 1−ω caract´rise cette fois l’´cart relatif en d´formation par rapport ` un
u e e e a
comportement purement ´lastique. Par inversion la relation d’´lasto-plasticit´ devient :
e e e
1 1 εI 2 εI
ε=( − )Tr(σ)δ + σ
9K 2 σI 3 σI
1
ou, en introduisant sph´riques et d´viateurs σ = σ S + σ D = 3 Tr(σ)δ + σ D et la fonction ψ :
e e
1 1 ψ(σI )
ε= σS + σD + σD
3K 2G 2G
E 1 1 σI
repr´sentant la partition en d´formation ´lastique ε = 3K σ S + 2G σ D d’intensit´ εE =
e e e e I 3G et en
P ψ(σI ) P = ψ(σI ) σ = ω(εI ) σI
d´formation plastique ε = 2G σ D d’intensit´ εI
e e 2G I 3G(1−ω(εI )) σI = εI − 3G .
4.4.4 Travail plastique
En d´composant σ = σ S + σ D = σm δ + σd π σ et δε = δεS + δεD = δεm δ + δεd π ε la variation du
e
travail ´lasto-plastique des forces internes δW = Tr(σδε) s’´crit :
e e
δW = σm δεm Tr(δ) + σm δεd Tr(π ε ) + σd δεm Tr(π σ ) + σd δεd Tr(π σ π ε )
Comme par d´finition Tr(δ) = 3 et Tr(π ε ) = Tr(π σ ) = 0, l’expression se r´duit ` :
e e a
δW = 3σm δεm + σd δεd Tr(π σ π ε )
2
Pour une d´formation simple π σ = π ε = π avec T r(π ) = 3, δW devient la diff´rentielle exacte :
e e
dW = dWF + dWV avec dWF = 3σm dεm et dWV = 3σd dεd

96. 90 ´
CHAPITRE 4. PLASTICITE
Le travail ´lasto-plastique des forces internes ne d´pend plus du chemin suivi :
e e
εm θ εd εI
W = WF =Cte +WV =Cte WF =Cte = 3 σm dεm = σm dθ WV =Cte = 3 σd dεd = σI dεI
0 0 0 0
θ = 3εm ´tant la dilatation cubique (variation relative de volume) et σI , εI les intensit´s de contrainte
e e
et de d´formation v´rifiant σI εI = 3σd εd
e e
W (θ, σI )n’est autre que le potentiel des contraintes
σI = ∂W
∂εI σm = ∂W∂θ σ = ∂W
∂ε
σ D = ∂W∂ε=Cte
V
D
WF =Cte correspond au changement de volume ` forme constante sous l’action de la contrainte
a
normale isotrope moyenne σm . Il est de nature purement ´lastique la plastification s’effectuant `
e a
1
volume constant. Comme σm = 3Kεm = Kθ : WF =Cte = 2 Kθ2 .
WV =Cte correspond au changement de forme ` volume constant sous l’action de la contrainte
a
d´viatorique σd . Il reste de nature ´lasto-plastique et se d´compose en un terme ´lastique r´cup´rable
e e e e e e
et un terme plastique : WV =Cte = W E + W P .
Tant que la contrainte σd n’a pas atteint le seuil de r´sistance au cisaillement ce travail est de
e
nature purement ´lastique r´cup´rable WV =Cte = W E et le changement de forme r´sultant r´versible.
e e e e e
Comme σd = 2Gεd et σI = 3GεI le module de cisaillement G caract´risant la r´sistance au changement
e e
de forme : W E = 3Gε2 = 3 σd εd = 1 σI εI = 6G σI .
d 2 2
1 2
Au del`, la plastification avec changement de forme irr´versible intervient.
a e
• Pour un mat´riau plastique parfait ce seuil est la constante σI = σe et la capacit´ de stockage
e e
d’´nergie ´lastique r´cup´rable sous forme d’un changement de forme ` volume constant du corps
e e e e a
1 2
sature ` W E = 6G σe .
a
• En pr´sence d’´crouissage le seuil progresse avec la plastification augmentant la capacit´ de stockage
e e e
d’´nergie ´lastique r´cup´rable de sorte que, par ´crouissage, le travail ´lastique W E continue ` croˆ
e e e e e e a ıtre.
Cependant, la raideur d´croissant rapidement lorsque que la d´formation irr´versible progresse, le
e e e
travail d´pens´ pour d´former le corps plastiquement devient tr`s rapidement sup´rieur au travail
e e e e e
´lastique. Le travail plastique d´pens´ sous forme de chaleur et d’´nergie ´lastique de contention,
e e e e e
´nergie bloqu´e non r´cup´rable, s’´crit dans tous las cas :
e e e e e
εI 1 2
WP = σI dεI − σ
0 6G I
On ne s’int´resse qu’au travail WV =Cte de changement de forme ` volume constant, le seul qui inter-
e a
vienne au niveau de la courbe d’´crouissage σI = φ(εI ). Ce travail ´tant ind´pendant du chemin suivi
e e e
(Cf. Fig. 4.20) :
ε 1 2 ε 1 2
WV =Cte = W E + W P = 0 I σI dεI W E = 6G σI W P = 0 I σI dεI − 6G σI
SurfaceOSM M ” SurfaceO M M ”O SurfaceOSM O O
Le travail compl´mentaire WV =Cte = σI εI − WV =Cte soit la surface OSM O”O :
e
εI σI ∂ WV =Cte ∂ WV =Cte
WV =Cte = σI εI − σI dεI = εI dσI εI = εD =
0 0 ∂σI ∂σ D
n’est autre que le potentiel des d´formations plastiques (hors variation de volume).
e
Th´or`me de la d´charge
e e e
La d´charge partielle de M ` N (Cf. Fig. 4.20) suit la loi de l’´lasticit´ σ = (K − 2 G)Tr(ε)δ + 2Gε
e a e e 3
2
soit en posant λ = K − 3 G et θ = Tr(ε) :
N M N M
σ −σ = Λ(θN − θM )δ + 2G(ε − ε )

97. ´ ` ´
4.5. LA PLASTICITE A L’ECHELLE MICROSCOPIQUE 91
O
• La d´charge totale (point O avec σ = 0 et θO = 0) fournit la valeur de la d´formation plastique
e e
P
ε obtenue par chargement jusqu’au point M :
P M M
2Gε = ΛθM δ + 2Gε −σ
Si le mat´riau ´tait rest´ ´lastique lin´aire il aurait fallu lui appliquer, pour obtenir la mˆme d´formation
e e ee e e e
M fM M
ε , une contrainte : σ = ΛθM δ + 2Gε . La d´formation plastique r´sultant du chargement r´el
e e e
fM
(point M ) s’obtient donc ` partir de la diff´rence entre la contrainte fictive σ
a e solution du probl`me
e
M
´lastique lin´aire (point M ) et la contrainte vraie σ solution du probl`me ´lasto-plastique r´el. D’o`
e e e e e u
le th´or`me de la d´charge :
e e e
P 1 f
ε = (σ − σ)
2G
P
• Pour r´tablir la forme initiale et annuler ε il faut poursuivre la d´charge et appliquer un ´tat
e e e
rM rM P fM M
de contrainte σ (point I) tel que σ = −2Gε = −(σ − σ ). Cet ´tat de contrainte r´siduelle
e e
P
(induite par la plasticit´ qui a cr´´ la d´formation ε obtenue apr`s d´charge totale au point O )
e ee e e e
correspond ` la contrainte de contention et ` l’´nergie ´lastique bloqu´e. Il s’obtient aussi directement
a a e e e
fM M
a
` partir de la diff´rence entre la solution ´lastique fictive σ
e e et la solution ´lasto-plastique r´elle σ .
e e
rM
Il est auto ´quilibr´ dans le mat´riau : Div(σ ) = 0.
e e e
4.5 La plasticit´ ` l’´chelle microscopique
ea e
4.5.1 Le glissement dans un monocristal
L’exp´rience montre que les solides monocristallins se d´forment plastiquement ` basse temp´rature
e e a e
par glissements le long de directions particuli`res dans les plans cristallographiques les plus denses.
e
Contrainte th´orique de glissement
e
L’´nergie du cristal est une fonction p´riodique de la distance de glissement puisqu’un d´calage
e e e
d’une distance atomique d’un plan dense par rapport ` son voisin dans la direction du glissement
a
ram`ne l’ensemble des atomes dans des positions ´nerg´tiquement ´quivalentes. En l’absence de
e e e e
contrainte les atomes occupent des positions telles que cette ´nergie est minimale.
e
Tant que l’amplitude τ du cisaillement dans la direction du glissement γ reste faible sa suppression
entraˆ le retour en position d’´nergie minimale, le comportement est ´lastique.
ıne e e
Au del` d’un certain seuil de cission τth on franchit la barri`re ´nerg´tique et le plan glisse d’une
a e e e
distance interatomique pour se retrouver en position d’´nergie minimale. Apr`s suppression de la
e e
contrainte il reste un glissement r´siduel, le comportement est devenu plastique.
e
Fig. 4.21 – R´sistance th´orique au cisaillement
e e
La cission τ ´tant la d´riv´e de l’´nergie par rapport au glissement γ, elle est aussi p´riodique de
e e e e e
p´riode ´gale ` la distance interatomique a le long de la ligne de glissement. Au premier terme du
e e a
d´veloppement en s´rie de Fourier :
e e
2π 2π 2π
τ = τth sin x τ = τth sin bγ ≈ bγτth lorsque γ → 0
a a a

98. 92 ´
CHAPITRE 4. PLASTICITE
x ´tant le d´placement d’une moiti´ du cristal par rapport ` l’autre et b d´signant la distance entre
e e e a e
plans atomiques denses, aux faibles valeurs, o` comportement est ´lastique, le glissement γ = x est
u e b
reli´ ` la cission par τ = µγ, µ ´tant le module de cisaillement du cristal dans la direction de glissement.
ea e
D’o` l’expression de la contrainte de cission th´orique :
u e
µa µ
τth = Pour b ≈ a τth ≈ (4.7)
2πb 10
En pratique la cission critique τC mesur´e sur des monocristaux est inf´rieure de plusieurs ordres
e e
de grandeur ` la cission th´orique τth .
a e
´ e
El´ment Structure Cission critique τC (Mpa) Cission th´orique τth (Mpa)
e
Cu,Ag,Au CFC 1,0 - 0,60 - 0,92 700 - 1200
M g,Zn,Cd Hexagonal 0,83 - 0,94 - 0,58 2300
Tab. 4.2 – Cission critique et th´orique des monocristaux
e
Origine de la plasticit´ dans les m´taux
e e
Les d´formations permanentes ont toujours pour origine des m´canismes de glissement.
e e
A haute temp´rature ce sont les changements de structure voire de phase qui provoquent les glissements
e
relatifs des grains les uns par rapport aux autres.
Fig. 4.22 – Glissement intragranulaire
A temp´rature moins ´lev´e la d´formation se fait uniquement par glissement intra-grain. Le
e e e e
m´canisme le plus fr´quent est un m´canisme de translation : glissement d’une maille ou d’un nombre
e e e
entier de mailles de part et d’autre d’un plan interatomique. Apr`s glissement le r´seau atomique
e e
retrouve sa disposition initiale mais le cristal s’est d´form´ de mani`re permanente.
e e e
Il existe une diff´rence de plusieurs ordres de grandeur entre la limite ´lastique th´orique et celle
e e e
mesur´e exp´rimentalement (Cf. Tab. 4.3), ce que confirme ´galement le tableau des limites ´lastiques
e e e e
normalis´es σe (Cf. Annexe A.6). En 1934, pour lever cette contradiction entre th´orie et exp´rience,
e E e e
Module de cisaillement Limite d’´lasticit´
e e
µ
µ (Gpa) σe (Mpa) σe
Monocristaux
Al monocristal 25 0,4 60000
Ag monocristal 28 0,6 45000
Polycristaux
Al polycristal 25 30 830
Al polycristal ´croui
e 25 100 250
Alliages
Dural (AU4G) 25 360 70
Acier 80 650 120
Acier Cr − N i 80 1200 67
Tab. 4.3 – Limite ´lastique th´orique et exp´rimentale
e e e
Taylor a ´mis l’hypoth`se que le glissement des plans atomiques ne s’effectue pas d’un bloc mais
e e
progressivement par propagation d’un d´faut appel´ dislocation dans l’arrangement des atomes. Son
e e
d´placement est plus ais´ que le glissement en bloc car il n’int´resse qu’un tout petit nombre d’atomes
e e e

99. ´ ` ´
4.5. LA PLASTICITE A L’ECHELLE MICROSCOPIQUE 93
a
` la fois. Du point de vue de la d´formation macroscopique, il aboutit au mˆme r´sultat lorsque
e e e
la ligne de dislocation a balay´ tout le plan atomique, mais l’´nergie n´cessaire pour d´placer ce
e e e e
d´faut de proche en proche correspond ` celle du basculement d’une seule rang´e atomique au lieu du
e a e
basculement simultan´ de toutes les liaisons du plan de glissement. De ce fait, elle est nettement plus
e
faible que l’´nergie de basculement simultan´. Il en est de mˆme de la contrainte ` appliquer pour
e e e a
obtenir le glissement.
Fig. 4.23 – Trichite de carbure de Si dans un composite ` matrice Al (photo D. Chambolle)
a
Les trichites (whiskers en anglais), monocristaux aiguille ou filamentaires de tr`s petit diam`tre
e e
(quelques microns de diam`tre) trop petit pour contenir des dislocations, pr´sentent bien une limite
e e
µ
´lastique de l’ordre de τth = 10 d´montrant le bien fond´ de l’hypoth`se de Taylor.
e e e e
Trichite Graphite Al2 O3 Fe SiC
σe (Gpa) 19,6 15,4 12,6 20
µ (Gpa) 257 200 74 263
µ
σe 13 13 6 13
Tab. 4.4 – Trichites et limite ´lastique th´orique
e e
4.5.2 Les dislocations
Limitons l’´tude au cas o` la d´formation plastique r´sulte du d´placement des d´fauts du r´seau :
e u e e e e e
les dislocations. Les divers obstacles qu’elles doivent franchir vont conditionner l’amplitude de la
contrainte ` appliquer pour obtenir une d´formation plastique explicitant les diff´rences de duret´ entre
a e e e
covalents et m´taux, la nature de l’´crouissage, l’influence de la taille des grains, des atomes ´trangers
e e e
en solution solide, des pr´cipit´s et des inclusions. La duret´ (Cf. Tab. 4.3) croˆ du monocristal `
e e e ıt a
l’alliage traduisant l’augmentation de r´sistance au d´placement des dislocations. Ces effets ont des
e e
cons´quences pratiques importantes pour le d´veloppement de mat´riaux ` haute limite d’´lasticit´
e e e a e e
et pour la description du comportement au cours des op´rations de corroyage (mise en forme par
e
d´formation plastique) et pour la compr´hension du fluage.
e e
G´om´trie
e e
Dans un solide continu on r´alise une coupure selon une surface S s’appuyant sur une ligne l. On
e
→
−
translate ensuite les l`vres ainsi form´es l’une par rapport ` l’autre selon un vecteur b appel´ vecteur
e e a e
de B¨rgers de la dislocation. Cette op´ration n´cessite l’application d’efforts sur le solide. On supprime
u e e
la discontinuit´ ainsi cr´e au sein du mat´riau en comblant les vides cr´es par de la mati`re ou en
e e e e e
collant les l`vres s’il a fallu retirer de la mati`re pour r´aliser la translation. Apr`s collage on retire les
e e e e
efforts ext´rieurs. Il subsiste alors au sein du mat´riau un champ de contraintes internes auto´quilibr´
e e e e
ind´pendant de la surface S choisie. Il est enti`rement caract´ris´ par la donn´e de la ligne l et du
e e e e e
→
− →
−
vecteur de B¨rgers b . Cette ligne l est la dislocation caract´ris´e par son vecteur de B¨rgers b et
u e e u
→
−
son vecteur tangent t d´finissant le sens de parcours sur la ligne.
e
→ →
− −
Toute dislocation se d´compose sur la base form´e par la dislocation Coin b ⊥ t et la dislocation
e e
→ →
− −
Vis b // t correspondant ` la d´composition d’une dislocation mixte sur sa base propre. Il suffit donc
a e
d’´tudier ces deux types de dislocations. La dislocation Coin correspond ` l’insertion d’un demi plan
e a
d’atomes suppl´mentaire, comme une demi page ins´r´e entre les pages d’un livre.
e ee

100. 94 ´
CHAPITRE 4. PLASTICITE
Fig. 4.24 – Description virtuelle de la cr´ation d’une ligne de dislocation
e
Fig. 4.25 – Dislocations Coin et Vis : Aspects macroscopique et microscopique
Propri´t´s
e e
En d´signant par d→ le d´placement de chaque atome par rapport ` sa position dans le r´seau
e −
u e a e
id´al sans dislocation, le vecteur C d→ sur un contour arbitraire ferm´ (C) passant par les nœuds du
e −
u e
r´seau atomique entourant la ligne de dislocation l n’est pas nul. En orientant ce contour (C) dans
e
le sens direct (r`gle du tire bouchon) ` partir du sens d´fini par l’orientation choisie pour le vecteur
e a e
→
−
tangent t pour parcourir l le vecteur de B¨rgers de la dislocation est donn´ par :
u e
→
−
d→ =
−
u d→Grad→d→ = − b
−
u − −
u x
C C
La ligne de dislocation est le lieu des points singuliers du champ de d´formation. Elle est analogue
e
a
` la ligne tourbillon de la m´canique des fluides (circulation de la vitesse autour d’un vortex) o` ` un
e ua
conducteur parcouru par un courant ´lectrique (circulation du champ magn´tique) d’o` son nom de
e e u
vortex solide. Le champ gradient du d´placement ´tant ici un tenseur de rang 2, sa circulation est un
e e

101. ´ ` ´
4.5. LA PLASTICITE A L’ECHELLE MICROSCOPIQUE 95
Fig. 4.26 – Dislocations : Circulation de Gradu et loi des noeuds
vecteur, le vecteur de B¨rgers, au lieu d’ˆtre un scalaire comme en ´lectricit´ ou en m´canique des
u e e e e
fluides. Il en r´sulte que la ligne de dislocation l est :
e
• Soit une boucle ferm´e.
e
• Soit une ligne d´bouchant ` la surface du corps.
e a
• Soit une ligne rencontrant une autre dislocation et formant un nœud qui v´rifie l’´quation d’´quilibre
e e e
→
− →
− →
−
(loi des noeuds) b 1 + b 2 + b 2 = 0, les tangentes aux diff´rentes lignes concourant au nœud ´tant
e e
toutes orient´es dans un mˆme sens convergent ou divergent par rapport au nœud.
e e
La p´riodicit´ du r´seau impose des restrictions sur les valeurs possibles du vecteur de B¨rgers
e e e u
→
−
b des dislocations. Il doit ˆtre tel que le d´placement r´sultant r´tablisse la p´riodicit´ du r´seau.
e e e e e e e
Les vecteurs de B¨rgers sont donc des multiples des vecteurs du r´seau, (donc des distances interato-
u e
miques).
D´formation et contrainte induites
e
La condition de circulation signifie qu’en pr´sence d’une dislocation le vecteur d´placement →
e e −
u
est une fonction multivalu´e des coordonn´es subissant un accroissement donn´ lorsqu’on d´crit un
e e e e
contour ferm´ (C) autour de la ligne de dislocation l. Physiquement il n’en est rien car l’accroissement
e
repr´sente une translation suppl´mentaire des points du r´seau ´gale ` une des p´riodes ce qui n’affecte
e e e e a e
en rien son ´tat. Cela signifie simplement qu’en pr´sence de dislocations le r´seau n’est pas au repos
e e e
mais soumis ` un syst`me de contraintes responsables de la distorsion par rapport au r´seau id´al.
a e e e
Ces contraintes internes li´es au fait que les atomes ne sont pas au fond des puits de potentiel du
e
r´seau cristallin id´al forment un champ auto´quilibr´. Les dislocations sont des d´fauts thermody-
e e e e e
namiquement instables qui sont responsables de l’´nergie ´lastique bloqu´e au sein du mat´riau. On
e e e e
devrait s’attendre ` ce qu’ils disparaissent en vertu du principe du minimum d’´nergie. En pratique
a e
ces d´fauts sont pi´g´s au sein du mat´riau et n´cessitent un processus d’activation pour pouvoir
e e e e e
se d´placer et s’annihiler entre eux ou s’´vacuer hors de la mati`re. De ce fait ce sont des d´fauts
e e e e
thermodynamiquement m´tastables.
e
Par invariance par translation le gradient de d´placement Grad→ le long d’une ligne de dislocation
e −u
→
−
ne d´pend que des coordonn´es du plan perpendiculaire ` la ligne. La circulation C Grad→d→ = − b
e e a − −
u x
le long d’un circuit entourant la dislocation ne doit pas varier dans une homoth´tie de contour dans ce
e
plan. Ceci n’est possible que si Grad→, ε et σ varient comme 1 . Le champ σ d’une ligne de dislocation
−
u r
est un champ ` longue port´e.
a e
Champs de contrainte et de d´formation d’une dislocation
e
Dislocation vis Par invariance par translation et par raison de sym´trie le champ de d´placement
e e
n’admet qu’une composante uz fonction de r et ϕ mais ind´pendante de z. En d´pliant le
e e
cylindre macroscopique de hauteur unit´ d´crivant la dislocation, la d´formation correspond `
e e e a
b
un glissement simple, sans variation de volume, d’amplitude γ = 2εzφ = 2πr , soit :
0 0 0 0 0 0 0
→=
−
u 0 ε= b
0 0 1 σ= µb
0 0 1 (4.8)
4πr 2πr
b
2π ϕ 0 1 0 0 1 0
Dislocation coin Par invariance par translation le long de la ligne z de la dislocation Coin dont le
→
−
vecteur de B¨rgers b (b, 0, 0) est orient´ selon Ox, le champ de d´placement → appartient au
u e e −
u

102. 96 ´
CHAPITRE 4. PLASTICITE
Fig. 4.27 – Champ de contrainte dislocation Vis et dislocation Coin
plan x, y et ses composantes ne sont pas fonction de z. Il lui correspond un ´tat de d´formation
e e
plane et un ´tat de contrainte :
e
b 1−2η
εrr = εϕϕ = − 2π 2(1−η) 1 sin ϕ 2εrϕ = 2π 1−η 1 cos ϕ εzz = 0
r
b 1
r
µ µ (4.9)
σrr = σϕϕ = −b 2π(1−η) 1 sin ϕ σrϕ = b 2π(1−η) 1 cos ϕ σzz = η(σrr + σϕϕ )
r r
´
Energie et tension de ligne
1
L’´nergie par unit´ de longueur de dislocation E = 2 V Tr(σε)dV est aussi ´gale au travail
e e e
1 → →
− − → →
− −
2 S b σ n dS n´cessaire pour d´placer les l`vres de la coupure d’aire S de la quantit´ b , n d´signant
e e e e e
la normale ` la surface de coupure (Cf. Fig. 4.25). La seule composante de contrainte intervenant
a
→
−
dans l’expression ´tant σzϕ pour la dislocation Vis ( b // Oz et →//Oϕ) et σrϕ (ϕ = 0) pour la
e −n
→
− →//Oϕ), en posant D =
− µ µ
dislocation Coin ( b //Or et n 2π pour la dislocation Vis et D = 2π(1−η) pour
la dislocation Coin, l’´nergie par unit´ de longueur de dislocation se r´duit ` :
e e e a
1 dr 1 rSup
E = Db2 = Db2 Ln
2 r 2 rInf
et pr´sente une divergence logarithmique aux deux limites.
e
La limite inf´rieure rInf est de l’ordre de grandeur de la distance interatomique rInf ≈ b ≈ 0, 25
e
nm. Elle d´finit le cœur de la dislocation o` les positions des atomes sont telles qu’il est impossible de
e u
les d´crire par la th´orie de l’´lasticit´. La limite sup´rieure rSup correspond physiquement ` la distance
e e e e e a
moyenne lD entre deux dislocations. Dans les m´taux recuits la distance moyenne entre dislocation est
e
lD ≈ 10−4 cm. Leurs champs de contrainte s’annihilent mutuellement ` des distances de cet ordre car,
a
le champ de contraintes internes ´tant auto´quilibr´, il y a statistiquement autant de dislocations d’un
e e e
signe que de dislocations de signe contraire. L’´nergie d’une dislocation isol´e serait donc consid´rable
e e e
dans un solide de grandes dimensions. En pratique il est tr`s difficile de produire des cristaux contenant
e
de faibles densit´s de dislocation.
e
L’´nergie par unit´ de longueur de dislocation, ´nergie ´lastique pi´g´e dans le solide vaut :
e e e e e e
µb2 lD
EE ≈ Ln
4π b
Avec ces valeurs, l’ordre de grandeur de E E est de 0,6 ` 0,7µb2 .
a
A cette ´nergie il faut adjoindre l’´nergie pi´g´e dans le cœur o` les lois de l’´lasticit´ ne sont plus
e e e e u e e
µ
valables. On peut estimer la d´formation ` ε ≈ 0, 2 et la contrainte σ ≈ 10 et l’´nergie singuli`re de
e a e e
cœur vaut :
E C ≈ 0, 02µb2
Dans les m´taux, cette ´nergie singuli`re de coeur E C ne repr´sente que quelques % de l’´nergie
e e e e e
´lastique E
e E.

103. ´ ` ´
4.5. LA PLASTICITE A L’ECHELLE MICROSCOPIQUE 97
Il ne s’agit l` que d’ordres de grandeur et l’on s’accorde g´n´ralement pour prendre comme ´nergie
a e e e
par unit´ de longueur de dislocation :
e
1
E = µb2 (4.10)
2
Il n’en reste pas moins vrai que l’´nergie de dislocation reste tr`s grande par rapport ` son entropie.
e e a
1
• L’´nergie E L d’une dislocation de longueur L vaut E L = 2 µb2 L. Comme sur L il y a N b atomes,
e
L
l’´nergie par atome vaut E A = E = 1 µb3 .
e N 2
• Le nombre de positions que peut occuper une dislocation de longueur L (volume Lb2 ) dans un cube
d’arˆte L est ( L )2 . L’entropie de configuration S L correspondante est S L = kLn( L )2 , k d´signant la
e b b e
constante de Boltzman. L’entropie par atome vaut S A = S L = b kLn( L )2 .
N L b
En prenant pout L la distance moyenne entre disloctions lD l’´nergie libre par atome vaut :
e
1 b lD
F A = E A − T S A = µb3 − Ln( )2 kT (4.11)
2 lD b
Pour le cuivre µ = 4.1010 N m−2 et b ∼ 2, 5.10−10 m, l’´nergie par unit´ de longueur de dislocation vaut
= e e
E = 1, 25.10 9 Jm−1 soit E A ≈ 2eV par atome le long de la ligne de dislocation. Avec l = 10−4 cm
D
l’entropie par atome vaut S A ≈ 4.10−3 k. A l’ambiante kT ≈ 40 eV de sorte que S A
1
E A et l’´nergie
e
A ∼ E A > 0. Une dislocation augmente fortement l’´nergie libre. Bien que thermodynamique-
libre F = e
ment instables prises isol´ment, les dislocations forment des r´seaux r´seaux autostabilis´s et sont
e e e e
toujours pr´sentes dans un cristal.
e
Courber un segment de dislocation en maintenant ses deux extr´mit´s fixes augmente sa longueur
e e
l donc son ´nergie E. Cela revient ` dire qu’il existe tension de ligne de dislocation T = dE , force de
e a dl
tension r´gnant le long de la ligne de dislocation et qui tend ` la rendre rectiligne.
e a
dE 1
T = = µb2 (4.12)
dl 2
Densit´ de dislocation
e
La densit´ de dislocation ρD est d´finie comme la longueur totale de dislocation par unit´ de volume.
e e e
Dimensionnellement c’est l’inverse d’une surface, ρD se mesure en cm −2 . Les dislocations perturbent les
distances d entre plans cristallographiques et leurs orientations θ, elles sont donc visibles en microscopie
´lectronique. Localement la pr´sence d’une dislocation d´truit la condition de r´flexion de Bragg
e e e e
v´rifi´e par le plan cristallographique choisi, elle apparaˆ comme une ligne sombre sur le champ
e e ıt
d’observation comme sur ce clich´ de microscopie ´lectronique d’un acier inoxydable aust´nitique.
e e e
Nous avons un moyen exp´rimental de voir les dislocations. Il faut cependant relier la densit´ de
e e
dislocation ρD ` une quantit´ mesurable en surface. Estimons la densit´ ρD de dislocation dans un
a e e
cube ´l´mentaire de mati`re d’arˆte L petite devant la longueur des dislocations en admettant qu’il
ee e e
→
−
contient N morceaux de dislocations de longueur L de mˆme vecteur de B¨rgers b . La longueur totale
e u
de dislocation est N L dans le volume V = L3 et la densit´ de dislocation : ρD = N L = L2 = N , soit
e V
N
S
le nombre de dislocations traversant l’unit´ d’aire.
e
Fig. 4.28 – Clich´ de microscopie ´lectronique d’un acier inoxydable.
e e
Cette m´thode de comptage permet de d´terminer exp´rimentalement une densit´ approximative
e e e e
de dislocation ρD . Le tableau suivant donne les valeurs approximatives des densit´s de dislocation en
e
fonction de l’´tat du mat´riau.
e e

104. 98 ´
CHAPITRE 4. PLASTICITE
Etat ρD (cm−2 ) ∆V
V (b = 3, 1.10−10 m)
Monocristaux solidifi´s avec pr´caution
e e 102 - 103 10−13 - 10−12
Monocristaux recuits 105 - 106 10−10 - 10−9
Polycristaux recuits 106 - 107 10−9 - 10−8
Polycristaux fortement ´crouis
e 109 - 1012 10−6 - 10−3
Tab. 4.5 – Densit´ de dislocation et variation relative de volume associ´e
e e
Variation de volume induite
Le champ de glissement simple induit par une dislocation Vis n’induit pas de variation de volume.
Ce r´sultat reste vrai pour une dislocation Coin, la variation < 0 dans la r´gion en compression
e e
compensant exactement la variation > 0 dans la r´gion en traction. D’une mani`re plus g´n´rale, le
e e e e
champ de contraintes internes cr´e par la pr´sence de dislocations ´tant auto´quilibr´, < σ >= 0, la
e e e e e
variation de volume r´sultante est nulle. Cependant, le cœur des dislocations est trop d´form´ pour
e e e
ob´ir aux lois de l’´lasticit´ lin´aire. La coeur de la dislocation forme un tube de rayon r ∼ b, soit
e e e e
une section S ∼ b2 ` peu pr`s ´quivalente ` celle d’un tube de lacune. La pr´sence des dislocations se
a e e a e
traduit donc par un accroissement relatif de volume ∆V ∼ SL avec L longueur totale des dislocations
V V
contenues dans le volume V , soit ∆V ∼ ρD b2 . Cons´quence essentielle : la d´formation plastique
V e e
macroscopique li´e ` l’augmentation de la densit´ de dislocations s’accompagne d’une variation de
e a e
volume tout ` fait n´gligeable, justifiant l’hypoth`se de d´formation plastique a volume constant de la
a e e e `
m´canique des solides coh´rents.
e e
4.5.3 Action d’un champ de contrainte externe sur une dislocations
Les dislocations interagissent avec la contrainte appliqu´e au cristal, que celle-ci provienne d’une
e
action ext´rieure ou de la pr´sence de contraintes induites par des d´fauts voisins.
e e e
Force de Peach-Ko¨hler
e
Fig. 4.29 – Action d’un champ de contrainte sur une dislocation
Au sein d’un volume de mati`re V de surface ext´rieure ∂V l’existence d’une dislocation se tra-
e e
duit au par un champ de contraintes internes σ D , un champ de d´placement →D responsable de la
e −
u
→
−
distorsion du r´seau atomique et une ´nergie ´lastique pi´g´e ED . L’application d’efforts T cr´e un
e e e e e e
champ de contrainte externe σ , un champ de d´placement → et une ´nergie ´lastique stock´e ET
−
e
e u e e e
ind´pendante de ED . L’´nergie ´lastique emmagasin´e est E = ED + ET .
e e e e
• Dislocation pr´existante
e
→ −
−
Si les forces T varient, leur travail ´l´mentaire δW = ∂V T δ →dV est ´gal ` la variation de l’´nergie
ee u e a e
´lastique emmagasin´e δE = δET + δED . La variation d’´nergie ´lastique pi´g´e δED est ´gale au
e e e e e e e
travail des forces fD = σ D →, → normale ext´rieure ` ∂V , dans le champ de d´placement δ → cr´e par
− −
n n e a e − e
u

105. ´ ` ´
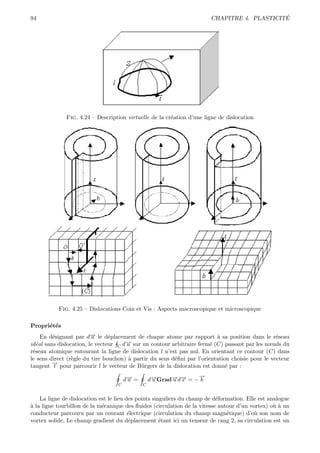
4.5. LA PLASTICITE A L’ECHELLE MICROSCOPIQUE 99
→
−
T . Or, ces forces fD sont nulles, la surface ´tant libre de charge en l’absence de chargement externe,
e
et leur travail donc la variation δED le sont ´galement.
e
La variation d’´nergie se r´duit ` la seule variation d’´nergie ´lastique δET ´gale au travail des
e e a e e e
forces externes δW . Elle ne d´pend pas de la pr´sence de la dislocation. En d’autres termes une
e e
mesure des constantes ´lastiques ne permet pas de d´tecter les dislocations. Il faut que les dislocations
e e
se d´placent pour qu’elles soient m´caniquement d´tectables sous la forme d’une d´formation plastique
e e e e
irr´versible.
e
• Cr´ation d’une Dislocation
e
→
−
A l’inverse cr´ons au sein de la mati`re soumise aux actions externes T ayant stock´ une ´nergie
e e e e
→
−
´lastique ET une dislocation de vecteur de B¨rgers b en appliquant les efforts TD sur la surface
e u
→
−
de coupure SD s’appuyant sur la ligne l orient´e de vecteur tangent t . Le travail W d´pens´ par
e e e
→
−
les forces TD pour d´placer de b les l`vres de la coupure est ´gal ` l’´nergie ED de la dislocation
e e e a e
→−
− →
−
auquel il faut ajouter le travail ∂V T →D dS des forces ext´rieures ´tablies T dans le champ →D cr´e
u e e −u e
→
−
→) b dS des contraintes σ sur la face origine du circuit de B¨rgers
−
par la dislocation et celui − SD (σ n u
de la surface de coupure SD de normale ext´rieure →. Le signe n´gatif provient de la convention
e −
n e
e
d’orientation du circuit de B¨rgers et σ est la somme des contraintes appliqu´es σ et d’´ventuelles
u e e
contraintes internes provenant de sources comme par exemples d’autres dislocations.
e e e
→−
−
u − →
n
−
Au total l’´nergie ´lastique emmagasin´e E = ED + ET + ∂V T →D dS − SD (σ →) b dS doit rester
´gale ` ED + ET . Il en r´sulte l’´galit´ :
e a e e e
→→
−−
T u D dS = − →
−
(σ →) b dS
n
∂V SD
• D´placement d’une Dislocation
e
Lorsqu’une dislocation existante se d´place de δ →(s), s ´tant l’abscisse curviligne de la ligne de
e −
x e
dislocation l, le travail des efforts externes correspondant est :
δW =
→ →
− −
T δ u D dS = δ − →
n
−
(σ →) b dS =
→ −
−
[(σ →) ∧ t ]δ →ds
−
n x
∂V SD l
→ −
−
En ´crivant ce travail sous la forme δW = l F δ →ds, l’action du champ de contrainte σ sur une
e x
→
−
dislocation de vecteur de B¨rgers b se r´duit ` une force par unit´ de longueur de dislocation appel´e
u e a e e
force de Peach-K¨hler :
o
→
− →
−
F = (σ →) ∧ t
− n (4.13)
→
− →
−
Cette force est toujours normale au plan d´fini par les vecteurs t et (σ b ). En particulier elle est
e
toujours perpendiculaire ` la ligne de dislocation l.
a
Plan de glissement et force de mont´e
e
→
− →
−
Le plan de glissement π d’un segment de dislocation est le plan d´fini par les vecteurs t et b .
e
→ →
− − → →
− −
Une dislocation Vis admet une infinit´ ( b // t ) de plans de glissement alors qu’il est unique ( b ⊥ t )
e
pour une dislocation Coin. La particularit´ physique du plan de glissement, r´sultant de la structure
e e
microscopique de la dislocation, fait qu’elle ne peut se d´placer plus ou moins facilement que dans
e
ce plan. Mais le seul d´placement possible de la dislocation ` basse temp´rature s’effectue dans la
e a e
→
−
direction de b car il suffit de d´placements relativement petits des atomes entourant le cœur pour
e
→
−
d´caler le demi plan suppl´mentaire d’une distance b en conservant l’organisation du r´seau cristallin
e e e
(glissement conservatif ).
→
−
Dans le rep`re local d´fini par la tangente t ` la ligne de dislocation l, sa normale → (appartenant
e e a −
n
→
− → →
− −
→ = t ∧ n la facette du plan de glissement
−
au plan de glissement π contenant t ) et sa binormale ν
→
−
de normale → est soumise ` un vecteur contrainte T = σ → produit par le champ externe σ.
−
ν a −ν
→
− →
−
La cission r´solue τ , contrainte de cisaillement dans la direction de glissement b vaut τ = →σ b =
e −
ν b
→
−
b σ → (par sym´trie de σ) avec b module de →.
−ν e
−
b
b
→
− →
− →
− →− −
−
La force de Peach-K¨hler F ´tant ⊥ ` t c’est sa composante F ⊥ = ( F →)→ dans le plan π qui
o e a n n
d´termine les possibilit´s de glissement, de multiplication et de franchissements d’obstacles ` basse
e e a

106. 100 ´
CHAPITRE 4. PLASTICITE
Fig. 4.30 – Glissement d’une dislocation Coin
→ →−
− − → → −
− − → −
−
temp´rature. Comme [(σ b )∧ t ]→ = b σ( t ∧ →) = b σ → elle est directement li´e ` la cission r´solue
e n n ν e a e
τ par F⊥ = τ b→.
−n
La seule direction de glissement autoris´ d’une dislocation Coin ` basse temp´rature ´tant parall`le
e a e e e
→
− →
−
a
` b , cette force se r´duit ` F⊥ = τ b .
e a
→ →
− − →
−
On appelle F − F ⊥ force de mont´e. C’est la partie de F qui tend ` faire quitter le plan de
e a
glissement. Un tel mouvement (non conservatif ), appel´ mont´e de la dislocation quelque soit son
e e
sens le long de la direction ⊥ ` π, n’est possible que si les atomes du demi plan exc´dentaire s’en
a e
´chappe par diffusion d’atome ou de lacune ce qui n´cessite une activation thermique importante donc
e e
une temp´rature ´lev´e.
e e e
M´canisme de glissement d’une dislocation Coin
e
Le champ de contrainte externe exerce une force f = τ b par unit´ de longueur de ligne de dis-
e
location. Si cette force est suffisante pour vaincre la r´sistance au mouvement la ligne de dislocation
e
se d´place au sein du cristal provoquant une marche plastique d’amplitude b. Le mouvement de la
e
dislocation correspond ` la rupture des liaisons des atomes de cœur puis ` leur restauration avec leurs
a a
plus proches voisins dans le sens du mouvement. Ce processus est beaucoup plus ais´ que le glissement
e
d’un bloc d’un demi cristal par rapport ` l’autre qui n´cessiterait la rupture simultan´e de toutes
a e e
les liaisons, donc des ´nergies et des contraintes appliqu´es beaucoup plus intenses. Le m´canisme
e e e
Fig. 4.31 – Glissement macroscopique induit par le mouvement d’une dislocation
de d´calage des deux demi cristaux obtenus lorsque la dislocation a balay´ la totalit´ de l’aire du
e e e
plan de glissement s’apparente ` celui employ´ pour d´placer un tapis. Le d´placement d’un bloc du
a e e e
tapis en tirant sur un bord met en jeu une force importante pour vaincre l’effort de frottement qui se
d´veloppe sur la totalit´ de la surface du tapis (´quivalent d’un mouvement en bloc de l’ensemble du
e e e
plan de glissement). Il est beaucoup plus ais´ de d´placer le tapis en lan¸ant un pli (´quivalent de la
e e c e
dislocation) qui, se propageant de proche en proche, conduira au mˆme d´placement final mais avec
e e
un effort beaucoup plus faible.

107. ´ ` ´
4.5. LA PLASTICITE A L’ECHELLE MICROSCOPIQUE 101
Fig. 4.32 – Analogie de Mott
D´formation macroscopique induite
e
Pour un bloc initialement cubique d’arˆte L, lorsque la dislocation ` parcouru la distance L, elle
e a
a balay´ une aire A = L
e 2 provoquant un glissement macroscopique moyen γ = b que l’on peut ´crire
e
L
2 →
−
γ = bL3 = bA . Une dislocation de vecteur de burgers b balayant une aire δA au sein d’un volume de
L V
mati`re V produira un accroissement de glissement macroscopique :
e
bδA
δγ = (4.14)
V
Par ailleurs, la densit´ de dislocation dans ce mˆme volume est ρD = N L , N ´tant le nombre de
e e V e
dislocations de vecteur de B¨rgers b et de longueur L. Si chacune des dislocations se d´place d’une
u e
distance moyenne lD elle balaye une surface δA = LlD et produit un glissement δγ = bLlD . Le V
glissement macroscopique total γ = N δγ = N L blD = ρD blD . En pratique seule une fraction ρm des
V
dislocations est mobile. v ´tant leur vitesse moyenne la vitesse de glissement macroscopique est
e
γ = ρm bv
˙ (4.15)
.
La densit´ initiale de dislocations n’autorise pas une d´formation plastique de grande amplitude.
e e
Mˆme en supposant que toutes les dislocations soient mobiles la d´formation plastique maximale d’un
e e
grain de polycristal recuit de taille typique φ=100 µm contenant une densit´ ρD = 108 cm−2 de dislo-
e
cations de vecteur de B¨rgers b = 2, 5.10
u −8 cm est limit´e ` γ = ρ bφ = 2, 5%.
e a D
• Dislocations d’accommodation g´om´trique
e e
Pour former un solide par d´formation plastique il faut une densit´ de dislocation ρG dite densit´
e e e
de dislocation d’accommodation g´om´trique.
e e
Fig. 4.33 – Flexion plastique et densit´ d’accomodation g´om´trique
e e e
Estimons la densit´ ρG n´cessaire dans le cas simple d’une poutre en flexion en tra¸ant un circuit
e e c
de B¨rgers ABCD dans le cristal non d´form´. Il devient AB CD dans le cristal fl´chi. Le d´faut
u e e e e
de fermeture du circuit BB est ´gal au vecteur de B¨rgers total N b, N ´tant le nombre de disloca-
e u e
tions d’accommodation g´om´trique n´cessaire. La densit´ ρG ,nombre de dislocations par unit´ d’aire,
e e e e e
n´cessaire est ρG = N = ABxAD = Rb car N = AB −AB et ABAD = AB . Avec b = 2, 5.10−10 m et
e S
N 1
b
−AB
R
ρD = 105 cm−2 La densit´ de dislocation ρD initialement pr´sente est insuffisante pour atteindre une
e e
d´formation plastique importante. Il faut donc admettre l’existence de m´canismes de multiplication
e e
des dislocations, ce que confirme l’exp´rience.
e

108. 102 ´
CHAPITRE 4. PLASTICITE
R (m) 0,01 0,1 1
ρG (cm−2 ) 4.107 4.106 4.105
ρG
ρD 400 40 4
Tab. 4.6 – Densit´ d’accomodation g´om´trique en flexion
e e e
• Moulin de Frank-Read
Le moulin de Frank-Read est un des m´canismes efficaces de multiplication des dislocations.
e
Fig. 4.34 – Multiplication des dislocations : m´canisme de Frank-Read
e
Sous l’effet de la cission τ qui s’exerce sur le plan de glissement la dislocation, ancr´e en deux
e
points A et B distants de L, se courbe de telle mani`re qu’un ´l´ment d’arc ds soit en ´quilibre sous
e ee e
l’action combin´e de la force F⊥ = τ b et de la tension de ligne T = 1 µb2 . θ ´tant l’angle sous lequel
e 2 e
on voit le segment ds depuis le centre de courbure, l’´quilibre des forces F⊥ ds = 2T sin 2 ≈ T θ = TR
e θ ds
d´finit le rayon de courbure R = 2 µb . Lorsque τ augmente R diminue jusqu’` atteindre L pour
e 1
τ a 2
µb
τF R = (4.16)
L
contrainte critique d’activation du moulin, l’arc devient instable, tourne autour des points A et B
distants de L et la recombinaison des portions de signes oppos´s en regard ´jecte une boucle qui se
e e
propage par glissement et recr´e un nouveau segment AB qui d´marre un nouveau cycle. Un moulin
e e
de Frank-Read peut ainsi produire jusqu’` 500 boucles (Cf. Fig. 4.35).
a
Fig. 4.35 – Marches superficielles sur une surface d’Aluminium polie ´lectrolytiquement r´sultant de
e e
l’´mergence de deux dislocations Vis. (J.M. Marchin, G. Wyon, Acta. Met. 10 (1962) 915)
e
4.5.4 Obstacles intrins`ques au mouvement des dislocations
e
La d´formation plastique commence quand la cission sur le plan de glissement atteint une valeur
e
critique capable de mettre les dislocations en mouvement. Cette force critique qui caract´rise le seuil
e
de plasticit´ et son ´volution au cours de la d´formation va d´pendre de la r´sistance oppos´e au
e e e e e e
mouvement des dislocations. Cette r´sistance provient de la r´sistance des liaisons du r´seau, de
e e e
l’´crouissage et des joints de grain.
e

109. ´ ` ´
4.5. LA PLASTICITE A L’ECHELLE MICROSCOPIQUE 103
R´sistance du r´seau atomique Force de Peierls-Nabarro
e e
L’´nergie de cœur le long d’une dislocation est minimale lorsque celle-ci suit une rang´e atomique
e e
dense, vall´e de Peierls. Pour passer d’une vall´e ` la suivante et faire basculer les liaisons atomiques, il
e e a
faut franchir une barri`re de potentiel ∆EP N ` laquelle correspond une cission critique τP N traduisant
e a
la r´sistance du r´seau au glissement des dislocations. Lorsque les vall´es ne sont pas trop profondes
e e e
le passage d’une vall´e ` l’autre ne s’effectue pas d’un bloc, mais par propagation d’une d´viation o`
e a e u
d’un d´crochement. Le cristal, de part sa structure atomique et son type de liaison, va exercer une
e
r´sistance comme s’il existait un frottement au mouvement des dislocations, r´sistance conduisant `
e e a
un seuil d’´coulement τP N beaucoup plus ´lev´ dans les covalents et les ioniques que dans les m´taux.
e e e e
Fig. 4.36 – Friction de r´seau, d´viation et d´crochement
e e e
• Liaisons ionique et covalentes
Dans les cristaux ioniques les glissements am`nent face ` face des ions de mˆme signe provoquant
e a e
une grande d´pense d’´nergie Coulombienne, dans les covalents les liaisons sont tr`s orient´es et tr`s
e e e e e
rigides. Dans ces mat´riaux la profondeur de vall´es est particuli`rement grande, les dislocations ont
e e e
tendance ` ˆtre rectilignes et ` prendre des orientations cristallographiques particuli`res. La plupart
ae a e
des c´ramiques sont intrins`quement fragiles, les liaisons ioniques ou covalentes opposent une ´norme
e e e
force de friction de r´seau au d´placement des dislocations, quasi impossible ` l’ambiante. Quand
e e a
une dislocation se d´place dans une telle structure elle doit briser puis reconstituer les liaisons cours
e
de son mouvement, ce qui s’apparente ` la travers´e d’une forˆt en arrachant et en replantant tous
a e e
les arbres rencontr´s sur le passage. La rupture brutale intervient toujours avant la plastification car
e
E
la contrainte τP N est une fraction importante du module d’Young E, typiquement 30 . Leur duret´, e
si ´lev´es que le seul moyen de la mesurer consiste ` indenter la c´ramique avec un p´n´trateur en
e e a e e e
diamant, est ` l’origine de leur utilisation comme abrasif ou outil de coupe (diamant, carbures, oxydes,
a
nitrures. . .).
Fig. 4.37 – R´sistance au mouvement des liaisons ionique, covalente et m´tallique
e e
• Liaison m´tallique
e
Les m´taux purs sont intrins`quement ductiles car la liaison m´tallique est d´localis´e et les vall´es
e e e e e e
de Peierls beaucoup moins profondes. Le passage d’une dislocation d´place les atomes situ´s au-dessus
e e
de son plan de glissement par rapport ` ceux qui sont en dessous, mais elle n’a qu’un faible effet sur
a
les liaisons ´lectrons-ions, son mouvement s’apparente ` une promenade ` travers des herbes hautes.
e a a
Le r´seau n’exerce qu’une l´g`re force de traˆ
e e e ınage sur la dislocation mobile. La contrainte τP N est
E
typiquement de l’ordre 1000 ou moins pour des m´taux mous comme le cuivre ou le plomb. A la
e

110. 104 ´
CHAPITRE 4. PLASTICITE
temp´rature ambiante ou au-dessus presque tous les m´taux purs courants sont r´sistants ` la rupture
e e e a
qui n’intervient qu’apr`s une forte plastification.
e
R´sistance du r´seau de dislocations r´seau de Frank
e e e
Les dislocations dans un cristal non ´croui forment un r´seau tridimensionnel de densit´ ρD appel´
e e e e
−1/2
r´seau de Frank dans lequel la distance moyenne entre dislocations lD = ρD . Ces dislocations
e
interagissent entre elles et se placent en position d’´nergie minimale dans les vall´es de potentiel. Pour
e e
d´placer une dislocation dans son plan de glissement il faut lui faire franchir des collines qui r´sultent
e e
des interactions avec les autres dislocations. Parmi les dislocations environnantes, certaines sont dans
des plans de glissement parall`les ` celui de la dislocation ` d´placer, les autres traversent, percent,
e a a e
son plan de glissement, ce sont les arbres de la forˆt.
e
Deux dislocations qui s’intersectent peuvent se combiner pour former une dislocation de vecteur
→
− →
− →
− →
−
de B¨rgers b 1 + b 2 et d’´nergie 1 | b 1 + b 2 |2 . Lorsque b1 b2 > 0 la jonction est r´pulsive et le
u e 2 e
franchissement de l’arbre produit un cran mais lorsque b1 b2 < 0 cette jonction diminue l’´nergie, elle
e
est attractive et stable. Ces jonctions attractives peuvent servir de point d’ancrage pour les sources de
−1/2
Frank-Read. Leur distance moyenne ´tant de l’ordre de L = 2l = 2ρD , puisqu’il y a en moyenne un
e
arbre attractif sur deux, la contrainte d’activation du moulin de Frank-Read τF R = µb est de l’ordre
L
√
de τC = µb ρD .
2
Fig. 4.38 – Interactions avec la forˆt
e
Pour faire glisser les dislocations au milieu du r´seau de Frank-Read la contrainte appliqu´e doit
e e
ˆtre sup´rieure au seuil :
e e
√
τC ≈ µb ρD (4.17)
Lorsque ρD augmente τC augmente traduisant l’´crouissage du mat´riau ` l’´chelle macroscopique.
e e a e
• Microd´formation du cristal
e
Tant que la contrainte appliqu´e τ ne d´passe pas la force de Peierls-Nabarro τP N , les dislocations
e e
sont immobiles et le mat´riau se comporte de fa¸on parfaitement ´lastique.
e c e
D`s qu’elles commencent ` bouger, elles forment des arcs entres les points d’ancrage et balayent
e a
des aires A conduisant ` une d´formation macroscopique suppl´mentaire produisant une diminution
a e e
apparente du module d’´lasticit´. Cependant, tant que τ reste inf´rieur au seuil d’instabilit´ des arcs
e e e e
τF R elles reviennent ` leur position initiale ` la d´charge. Le cristal reste ´lastique mais la courbe
a a e e
contrainte d´formation pr´sente de petites boucles d’hyst´r´sis. Ce ph´nom`ne dissipatif an´lastique
e e ee e e e
correspond ` l’accroissement du frottement interne avec l’augmentation de la d´formation.
a e
Le moment o` τ atteint la limite d’instabilit´ τF R des arcs co¨
u e ıncide avec la micro limite ´lastique
e
difficile ` mesurer car correspondant ` de tr`s faibles d´formations.
a a e e
Puis, au fur et ` mesure que τ croit, la densit´ ρD des dislocations augmente et la forˆt devient de
a e e
plus en plus dense provoquant un fort durcissement. Les lignes de glissement se raccourcissent mais
leur distance diminue ´galement. Comme les distances entre points d’ancrage sont distribu´es statisti-
e e
quement il existe des zones dures aux endroits o` la forˆt est plus touffue. Lorsqu’une dislocation glisse
u e
dans une telle forˆt elle abandonne des boucles de dislocation autour des zones dures. Le passage des
e
dislocations successives provoque donc la cr´ation d’´cheveaux de dislocations fortement stabilis´s. La
e e e

111. ´ ` ´
4.5. LA PLASTICITE A L’ECHELLE MICROSCOPIQUE 105
Fig. 4.39 – Dislocations dans un alliage hastalloy : Recuit, Ecroui, Ecroui ` 15% avec formation d’amas
a
(photos CEA.SRMA)
r´sistance au mouvement des dislocations correspond ` la contrainte n´cessaire pour franchir les es-
e a e
paces plus clairsem´s. Les passages entre zones dures se bouchent progressivement par l’accumulation
e
des boucles conduisant au durcissement d’´crouissage. L’´crouissage est un mode de durcissement tr`s
e e e
utilis´ (tubes de Cu, fil ´tir´, acier de pr´contrainte,...).
e e e e
• Restauration
Si l’´crouissage est trop important il empˆche la poursuite des op´rations de corroyage et peut mˆme
e e e e
provoquer des ruptures, le r´seau de Frank ´tant quasi compl`tement fig´. Pour r´tablir la ductilit´ il
e e e e e e
faut d´bloquer les dislocations en for¸ant des mouvements en dehors des plans de glissements. Pour
e c
ce faire il faut permettre aux atomes et aux lacunes de diffuser au sein du mat´riau ce qui implique
e
une activation thermique forte, c’est l’op´ration de recuit au cours de laquelle les dislocations voisines
e
de signes oppos´s, comme celles formant des dipˆles, vont s’annihiler tandis que les dislocations de
e o
mˆme signe vont se placer les unes pr`s des autres afin de minimiser leur ´nergie d’interaction. La
e e e
mont´e, rendue possible par la migration de lacunes jusqu’au cœur des dislocations les am`nent ` ´gale
e e ae
distance les unes des autres, formant des parois de dislocations qui introduisent une d´sorientation et
e
qui partagent les grains en sous grains, c’est la polygonisation. Puis certains sous grains vont croˆ ıtre
au d´pens des autres, formant les germes de grains nouveaux, c’est la recristallisation. On aboutit
e
finalement ` une structure nouvelle de grains qui ont retrouv´s une faible densit´ de dislocation et
a e e
donc, par abaissement de la duret´, une nouvelle capacit´ ` subir un corroyage par ´crouissage. La
e ea e
taille des grains recristallis´s est fonction croissante de la temp´rature de recuit et d´croissante de
e e e
l’´crouissage pr´alable. Pour que la recristallisation ait lieu, il faut que l’´crouissage pr´alable ait
e e e e
d´pass´ un seuil critique. C’est tout l’art du forgeron qui alterne ´crouissage m´canique et recuit de
e e e e
restauration.
R´sistance des joints de grain
e
Les mat´riaux polycristallins sont form´s de grains poss´dant des orientations cristallographiques
e e e
diff´rentes s´par´es par des joints de grains. Quand la contrainte appliqu´e τ d´passe la r´sistance
e e e e e e
interne τP N de frottement du r´seau le glissement des dislocations s’amorce dans les grains poss´dant
e e
les plans de glissement d’orientation la plus favorable par rapport au cisaillement impos´. Puis, lorsque
e
τ − τP N atteint la valeur critique d’activation τF R , les sources de dislocations ´mettent des boucles
e
qui viennent se bloquer sur les joints de grains formant des empilements jusqu’` ce que la force en
a
retour exerc´e sur la source l’empˆche de fonctionner. Une fois bloqu´es les premi`res sources actives
e e e e
l’augmentation de τ d´clenche des glissements dans des grains moins favorablement orient´s. Comme
e e
les empilements de dislocations cr´ent des concentrations de contrainte aux joints de grain, celles-ci
e
peuvent ` leur tour activer les sources proches des joints dans les grains voisins. Les dislocations ´mises
a e
par les sources proches des joints traversent alors les grains et viennent buter sur les joints des grains
suivants. La distance entre empilements est alors de l’ordre de la taille d du grain. De proche en proche
la propagation des glissements passe ainsi de grain en grain.
1
La loi d’´volution τY = τP N + kY √d de la r´sistance au cisaillement τY d’un grain ´tablie par
e e e

112. 106 ´
CHAPITRE 4. PLASTICITE
√
Hall et Petch est bien confirm´e exp´rimentalement. La contrainte τY = τP N + µb ρD ` appliquer
e e a
pour obtenir une d´formation γ ´tant la somme de la contrainte seuil initial τP N de r´sistance du
e e e
√
r´seau atomique et de la contrainte de durcissement d’´crouissage µb ρD , comme γ est li´ ` ρD par
e e ea
γ = blD ρD et la distance moyenne lD parcourue par les dislocations est proportionnelle ` la taille d
a
√
du grain, le facteur de Petch kY varie comme γ. A mˆme niveau d’´crouissage γ, la r´sistance au
e e e
cisaillement sera d’autant plus ´lev´e que le grain est petit.
e e
La relation de Hall-Petch ´tablie au niveau du grain se g´n´ralise et s’applique ` la limite d’´lasticit´
e e e a e e
RP du polycristal :
1
RP = σI + kY √ (4.18)
d
σI ´tant li´ ` la contrainte seuil de glissement des dislocations (limite ´lastique initiale) et le facteur
e ea e
de Petch kY ` la contrainte d’activation des sources (´crouissage). Si la contrainte interne σI d´pend
a e e
fortement de la temp´rature, le facteur de Petch kY n’en d´pend pas.
e e
4.5.5 Obstacles externes au mouvement des dislocations
Les m´canismes intrins`ques de durcissement permettent d’agir sur la duret´ des corps purs. Mais
e e e
pour agir sur les propri´t´s m´caniques il faut plus de souplesse. Pour ce faire il suffit de combiner
ee e
traitements thermiques, irradiation,... et introduction d’atomes ´trangers sous forme de solution solide,
e
de pr´cipit´s ou d’inclusions, c’est ` dire employer des alliages.
e e a
Durcissement de solution solide
Les impuret´s peuvent se mettre en solution dans un m´tal solide. Par exemple dans le laiton,
e e
alliage de Cu et de Zn, les atomes de Zn de rayon a0 + ∆a0 remplacent des atomes de Cu de rayon
a0 pour former une solution solide de substitution d´sordonn´e. A l’ambiante le Cu peut dissoudre
e e
jusqu’` 30% de Zn. Les atomes de Zn ´tant plus gros que ceux du Cu leur substitution dans le r´seau
a e e
du Cu cr´e des dilatations locales du r´seau cristallin.
e e
Une dislocation Coin aura donc tendance ` se positionner au voisinage des atomes de Zn qui
a
dilatent le r´seau pour diminuer sont ´nergie. Ce faisant, elle s’allonge ce qui a pur effet d’augmenter
e e
son ´nergie. De ce fait, la dislocation adopte une position d’´quilibre forme des zigzags aplatis entre
e e
les atomes de solut´ qui se trouvent dans son plan de glissement, tout en restant proche d’une ligne
e
droite moyenne.
Ces pi´geages au voisinage des atomes de solut´ rendent rugueux le plan de glissement augmentant
e e
la r´sistance au mouvement des dislocations, franchissement d’une barri`re ´nerg´tique pour d´crocher
e e e e e
d’un atome de solut´ afin de s’accrocher a un autre. Le durcissement par les solutions solides conduit
e `
a
` une augmentation de la r´sistance au mouvement des dislocations dont la contrainte critique varie
e
approximativement en racine carr´e de la concentration en solut´.
e e
Cependant ce mode de durcissement, efficace ` l’ambiante pour de nombreux alliages m´talliques
a e
comme le laiton monophas´, les bronzes, les aciers inoxydables,... perd rapidement de son efficacit´ avec
e e
l’augmentation de la temp´rature qui autorise la diffusion des atomes de solut´ lib´rant le mouvement
e e e
des dislocations et provoquant le fluage.
Durcissement par les pr´cipit´s
e e
Une mani`re tr`s efficace de durcir une matrice m´tal ou c´ramique est d’y introduire des pr´cipit´s
e e e e e e
d’une seconde phase. La plupart des aciers sont durcis par des pr´cipit´s de carbures ainsi obtenus.
e e
C’est aussi le cas typique des alliages d’aluminium Al − Cu comme AU 4G connu sous le nom de
duralumin pour rappeler son fort durcissement par rapport ` Al.
a
De petites particules peuvent ´galement ˆtre introduites dans des m´taux ou c´ramiques par
e e e e
d’autres moyens. Le plus simple est de mˆler un disperso¨ (un oxyde par exemple) dans un m´tal
e ıde e
en poudre (c’est le cas pour le plomb ou l’aluminium) puis de compacter et de fritter le m´lange des
e
poudres.
Les deux moyens conduisent ` des particules petites et dures sur la trajectoire des dislocations.
a
Les pr´cipit´s coh´rents avec le r´seau de la matrice seront franchis par cisaillement. Par contre,
e e e e

113. ´ ` ´
4.5. LA PLASTICITE A L’ECHELLE MICROSCOPIQUE 107
les dislocations ne peuvent pas p´n´trer dans les pr´cipit´s incoh´rents, elles doivent les contourner,
e e e e e
abandonnant des boucles qui entourent les pr´cipit´s.
e e
Fig. 4.40 – De gauche a droite : Cisaillement d’un pr´cipit´ dans super alliage ` base de N i - Boucles
` e e a
de dislocations laiss´es autour des pr´cipit´s par leur contournement dans un alliage ` base de N i
e e e a
sollicit´ de mani`re cyclique. photos M. Clavel
e e
• Contournement d’un pr´cipit´
e e
Fig. 4.41 – Contournement d’un pr´cipit´ par une dislocation et abandon d’une boucle
e e
Le contournement s’effectue selon le m´canisme d’Orowan, analogue ` celui de la source de Frank-
e a
Read, en laissant une boucle de dislocation autour de chaque pr´cipit´. La contrainte critique :
e e
µb
τOR = (4.19)
L − 2R
est donn´e par la formule de Frank-Read (Cf. Eq. 4.16) ` condition de remplacer L par L − 2R, R
e a
´tant le rayon du pr´cipit´ dans le plan de glissement de la dislocation.
e e e
La contrainte τC n´cessaire faire avancer la dislocation par contournement des obstacles est ´lev´e.
e e e
Pour s’en convaincre, utilisons l’analogie du gonflage d’un ballon de baudruche dans une cage ` oiseaux,
a
les barreaux repr´sentent les obstacles. Il faut exercer une forte pression pour que le ballon d´borde
e e
des barreaux, mais quand cela s’est produit il n’y a plus de difficult´ ` poursuivre son gonflage.
ea
Dans tous les cas la contrainte critique augmente lorsque diminue la distance entre pr´cipit´s. Le
e e
durcissement maximal est produit par des pr´cipit´s durs et rapproch´s.
e e e
4.5.6 Vers la plasticit´ macroscopique
e
La courbe de consolidation du monocristal
√
La limite d’´coulement τY = M ax{τP N , τSS , τP P } + µb ρ r´sulte des diverses contributions ` la
e e a
r´sistance ` l’avancement des dislocations :
e a
• La force de Peierls-Nabarro σP N traduisant la r´sistance des liaisons du r´seau.
e e
• Le durcissement de solution solide σSS .
• Le durcissement des pr´cipit´s ou des particules σP P .
e e
√
• Le durcissement d’´crouissage αµb ρ
e
Le monocristal
Crit`re de plasticit´ L’´coulement plastique se produit ` partir de la multiplication et du d´placement
e e e a e
collectif irr´versible d’un nombre suffisant de dislocations. Quel que soit le m´canisme consid´r´
e e ee

114. 108 ´
CHAPITRE 4. PLASTICITE
(multiplication, franchissement d’obstacles. . .), une force suffisante, la composante F⊥ = τ b de
la force de Peach-Koehler, doit s’exercer sur les dislocations. Avec → normale au plan de glisse-
−
ν
ment, n→ direction de glissement dans ce plan, σ contrainte appliqu´e et τC la cission critique le
− e
→σ →| − τC pour chaque famille de dislocations
− −
crit`re de plasticit´ se met sous la forme f (σ) = | n ν
e e
consid´r´e. A basse temp´rature seul un petit nombre de syst`mes de glissement (plans et direc-
ee e e
tions de glissement dans ces plans), dits syst`mes de glissement facile, cristallographiquement
e
d´termin´s, sont susceptibles d’ˆtre activ´s plastiquement. A chaque syst`me de glissement facile
e e e e e
est associ´ son propre crit`re f (σ) et donc sa propre cission r´duite critique τC , le cristal ne
e e e
pouvant se d´former plastiquement que lorsque l’´tat de contrainte σ permet d’annuler l’une des
e e
fonctions de charge (ou plusieurs simultan´ment), les autres restant n´gatives. Dans l’espace des
e e
contraintes la surface de charge ou crit`re du monocristal a la forme d’un hyperpoly`dre.
e e
Loi d’´crouissage Les cissions r´duites critiques τC jouent le rˆle de param`tres d’´crouissage dont
e e o e e
il faut pr´ciser l’´volution au cours de l’´coulement plastique. Ceci conduit ` d´finir d’autres
e e e a e
param`tres physiques d’´crouissage dont d´pendent les cissions. Compte tenu du rˆle majeur
e e e o
des interactions entre dislocations dans l’´crouissage des m´taux purs, il est logique de chercher
e e
a
` relier les cissions r´duites critiques aux densit´s de dislocations pr´sentes dans l’´l´ment de
e e e ee
volume consid´r´. Le mod`le d’interactions du r´seau de Franck conduit ` une loi d’´crouissage
ee e e a e
√
isotrope τC = µb ρD . D’autres relations peuvent ˆtre ´tudi´es pour traduire des cin´matiques
e e e e
d’´crouissage plus complexes. Il reste alors ` exprimer les lois d’´volution des densit´s ρD , mais
e a e e
il est tr`s difficile d’aboutir ` des expresssions suffisamment de g´n´rales.
e a e e
Loi d’´coulement plastique Les relations entre taux de d´formation plastique et taux de contrainte
e e
pr´sentent le mˆme genre de dificult´s.
e e e
D’un point de vue purement cin´matique, il faut remplacer la relation scalaire d’Orowan γ =
e ˙
ρm bv, (ρm ´tant la densit´ de dislocations mobiles et v leur vitesse moyenne), par une relation
e e
vectorielle donnant la vitesse de d´placement relatif de deux plans cristallographiques de la mˆme
e e
famille, puis g´n´raliser ` l’ensemble des syst`mes de glissement.
e e a e
Mais, au-del`, il faut ´galement pr´ciser quelle est la fraction ρm de la densit´ totale de disloca-
a e e e
tions ρ qui est mobile sous le chargement actuel et quelle est son ´volution en fonction de σ et
e
pr´ciser l’´volution de la vitesse moyenne de d´placement des dislocations.
e e e
Autant de probl`mes qui, bien qu’ayant ´t´ trait´s dans de nombreux cas particuliers, n’ont
e ee e
pas aujourd’hui de r´ponse suffisamment g´n´rale pour garantir un passage explicite sur un
e e e
large domaine de validit´ de l’´chelle des d´fauts cristallins ` celle du comportement global du
e e e a
monocristal.
Le polycristal
En plus des difficult´s d´j` ´voqu´es pour le monocristal, la plasticit´ du polycristal pr´sente de
e eae e e e
nouveaux degr´s de complexit´ majoritairement li´s ` la pr´sence des joints de grain qui constituent
e e e a e
des structures complexes de d´fauts, rarement r´ductibles ` de simples arrangements plans de dislo-
e e a
cations. Leur influence sur le comportement plastique du polycristal s’exerce ` plusieurs niveaux :
a
• Au niveau microscopique, cette influence est d´termin´e par la nature des interactions entre
e e
dislocations de r´seau et d´fauts constituant le joint. Aux effets de force-image s’ajoutent des ef-
e e
fets d’obstacle ` la propagation des dislocations responsables de la formation d’empilements et de
a
concentrations de contraintes susceptibles d’activer dans les grains voisins des sources de dislocations
assurant la transmission de l’´coulement plastique de grain ` grain. Le joint de grain (site privil´gi´
e a e e
de s´gr´gation d’impuret´s, de pr´cipitation, ...) agit ´galement de mani`re plus complexe, aussi bien
e e e e e e
comme source que comme puits de dislocations.
• A un niveau interm´diaire, le joint est responsable de la formation, dans son voisinage, d’une
e
zone cristalline riche en d´fauts en moyenne plus ´crouie que l’int´rieur des grains. En d´coule une
e e e e
h´t´rog´n´it´ de comportement du grain partag´ en domaines plus ou moins ´crouis qui font du grain
ee e e e e e
lui-mˆme une structure complexe dont le comportement moyen est, du fait de la non-lin´arit´ de la
e e e
plasticit´, fort ´loign´ de celui du monocristal isol´.
e e e e

115. ´ ´ ´
4.6. RESUME PLASTICITE 109
• Enfin, ` un niveau macroscopique, le joint de grains intervient comme fronti`re entre deux cristaux
a e
d’orientations diff´rentes. Mˆme si chaque grain est d´form´ plastiquement de mani`re uniforme la
e e e e e
d´formation plastique n’est plus globalement compatible. Il en r´sulte un champ de contraintes internes
e e
qui conduit ` des fluctuations importantes de la contrainte locale d’un grain ` l’autre, ne redonnant
a a
qu’en moyenne les contraintes appliqu´es ` l’´l´ment polycristallin.
e a ee
Au-del` de l’effet individuel des joints de grains, le comportement global du polycristal est d´termin´
a e e
par la distribution d’ensemble des joints (position, orientation, dimensions), r´gissant les formes et les
e
tailles des grains mais aussi par les orientations cristallines propres ` chaque grain et leur ´volution
a e
au cours de l’´coulement. Pour analyser pr´cis´ment ces diff´rents param`tres et leur influence il ne
e e e e e
suffit pas d’avoir connaissance de leurs probabilit´s, il faut encore connaˆ
e ıtre leur distribution spa-
tiale, la r´ponse d’un grain donn´ d´pendant aussi des d´tails de son voisinage, orientation, forme et
e e e e
dimensions de ses proches voisins, voire de grains plus ´loign´s qui interagissent ` distance avec lui.
e e a
Le passage micro-macro
Compar´e ` l’approche macrocopique purement ph´nom´nologique dans laquelle les param`tres
e a e e e
d’´crouissage sont des variables cach´es sans signification physique ´tablie, la compr´hension des
e e e e
m´canismes aux ´chelles micro et m´soscopiques qui d´crit les param`tres les plus importants de
e e e e e
l’agr´gat polycristallin (texture cristallographique ou morphologique) et traite le polycristal comme
e
un mat´riau composite incompl`tement d´crit de mani`re statistique, permet de pr´ciser la nature
e e e e e
physique de l’´crouissage et de la r´sistance plastique.
e e
Bien que l’´tude des m´canismes physiques ` l’origine de la plasticit´ macroscopique ne permette
e e a e
pas, en l’´tat actuel des connaissances, d’assurer le passage complet du comportement microscopique
e
au comportement macroscopique, elle n’en reste pas moins un guide pr´cieux pour l’´laboration des
e e
mat´riaux destin´s ` r´sister aux d´formations plastiques.
e e a e e
4.6 R´sum´ Plasticit´
e e e
Seuil de Plasticit´
e
Elasticite ε = εE si σ ≤ σe
Plasticite ε = εE + εP si σ > σe
Au del` de la limite ´lastique, chaque point de la courbe de charge est un point de bifurcation. La
a e
plastification s’effectue par changement de forme ` volume constant et ne d´pend que du d´viateur
a e e
des contraintes σ D . Cela correspond ` une r´sistance limite du mat´riau au cisaillement.
a e e
M´taux ductiles
e
Dans l’espace des contraintes, le crit`re de plasticit´ ou surface de charge f (σ) = 0 d´finit la limite
e e e
´lastique ´crouie pour un ´tat de chargement donn´. Dans le cas des m´taux, la surface de charge est
e e e e e

116. 110 ´
CHAPITRE 4. PLASTICITE
bien repr´sent´e par le cylindre de Von Mis`s.
e e e
Pour un ´crouissage isotrope (dilatation du cylindre au cours de la plastification), l’´coulement
e e
P
plastique s’effectue normalement ` cette surface et l’incr´ment de d´formation plastique dε a mˆmes
a e e e
directions propres que le d´viateur σ D des contraintes appliqu´es.
e e
Pour une d´formation simple (trajet radial dans l’espace des contraintes conservant les directions
e
P
propres de σ D ), il existe une relation biunivoque entre σ D et la d´formation plastique cumul´e ε qui
e e
admettent mˆmes directions principales.
e
2
Tr(σ D ) 3 2 3
σD σd = 3 σI = 2 Tr(σ D ) = √ σd
2
P
2
Tr(εD ) 2 2 √
ε = εD εd = 3 εI = 3 Tr(εD ) = 2εd
P 3 εI
πσ = πε ε = 2 σI σ D εI = ϕ(σI )
P
Toute sollicitation complexe σ D , ε se ram`ne ` une sollicitation de traction ´quivalente caract´ris´e
e a e e e
par la contrainte vraie σI intensit´ des contrainte ou contrainte ´quivalente au sens de Von Mis`s et
e e e
l’intensit´ εI de la d´formation plastique cumul´e.
e e e
Au del` de la limite ´lastique, la loi de Hollomon
a e
σI = Aεχ
I 0≤χ<1
d´crit l’´crouissage des m´taux ductiles.
e e e
Travail ´lasto-plastique
e
Pour effectuer un changement de forme irr´versible ` volume constant, il faut d´penser un travail
e a e
plastique :
εI 1 2
WP = σI dεI − σ
0 6G I
Ce travail est d´pens´ sous forme de chaleur (pertes plastiques) et d’´nergie ´lastique de contention
e e e e
(bloqu´e non r´cup´rable).
e e e

117. Chapitre 5
RUPTURE
Lorsqu’un mat´riau est sollicit´ jusqu’` rupture, les essais montrent que la contrainte de rupture
e e a
σR est une grandeur pr´sentant de fortes fluctuations pouvant mˆme d´passer la d´cade pour certains
e e e e
mat´riaux et que le mode de ruine d´pend de la nature du mat´riau. Ainsi la rupture peut interve-
e e e
nir brutalement quasi sans d´formation pr´alable pour les mat´riaux qualifi´s aujourd’hui de fragiles,
e e e e
tandis qu’elle n’intervient qu’apr`s une ´tape de grande d´formation permanente pour les mat´riaux
e e e e
qualifi´s aujourd’hui de ductiles. Nous savons maintenant que les mat´riaux fragiles rompent brutale-
e e
ment au del` d’une certaine tension, tandis que les mat´riaux ductiles s’´coulent plastiquement sous
a e e
cisaillement avant de rompre. Si la rupture est toujours l’´tape ultime de la ruine des structures, elle
e
est pr´c´d´e d’une ´tape de plastification pour les mat´riaux ductiles. Ce document traitera principa-
e e e e e
lement de la rupture fragile au sens macroscopique d’un mat´riau, c’est ` dire une rupture intervenant
e a
sans plastification macroscopique notable, ce qui n’exclut pas une plastification microscopique en tˆte
e
de fissure.
La m´canique de la rupture a pour objet l’´tude des fissures macroscopiques, la d´termination des
e e e
champ des contraintes et de d´formations correspondants et l’´tablissement des donn´es exp´rimentales
e e e e
permettant de d´terminer la cin´tique de propagation des d´fauts et leur taille critique au-del` de la-
e e e a
quelle, pour une sollicitation donn´e, la rupture instable se produit. Le d´veloppement th´orique de
e e e
la m´canique de la rupture, important depuis les ann´es 1960, doit beaucoup aux progr`s r´alis´s
e e e e e
conjointement dans la mise au point des m´thodes de contrˆle non destructif.
e o
Contrainte critique et taille critique de d´faut
e
Rupture brutale La sollicitation croissante d’une pi`ce comportant une fissure de longueur aC se
e
traduit dans une premi`re ´tape (´tape d’ouverture) par un ´cartement progressif des l`vres du
e e e e e
d´faut. Lorsque la contrainte appliqu´e σ atteint une valeur critique σC (aC ) d’autant plus faible
e e
que la taille aC du d´faut est grande, la fissure s’allonge rapidement (´tape de propagation) ce
e e
qui conduit brutalement ` la rupture de la pi`ce.
a e
Rupture de fatigue Lorsque la sollicitation est une fonction du temps t (corrosion sous contrainte,
fluage en temp´rature) ou du nombre de cycles N (fatigue cyclique), la taille aC de la fissure aug-
e
mente progressivement et, lorsque la contrainte critique σC (aC ) atteint la valeur de la contrainte
appliqu´e σ, la pi`ce rompt brutalement. Ce m´canisme de fatigue par croissance de la taille du
e e e
d´faut produit une rupture brutale diff´r´e au bout d’un temps tR (σ) (ou d’un nombre de cycle
e ee
NR (σ)).
La figure 5.1 d´crit le sch´ma de principe illustrant la variation de la dimension a d’une fissure
e e
avec le nombre de cycles N , en fatigue, ou le temps t, en corrosion sous contrainte ou en fluage,
et la taille de d´faut critique aC ` rupture, pour une sollicitation donn´e. La taille a du d´faut
e a e e
croˆ avec N ou t tandis que la contrainte de rupture σR d´croˆ Pour un d´faut de taille
ıt e ıt. e
a = aC donn´e, il existe donc une contrainte critique σC = σ(aC ) provoquant la rupture.
e
R´ciproquement, pour une contrainte σ = σC donn´e, il existe une taille maximale de d´faut
e e e
admissible aC = a(σC ) pour que la structure ne casse pas.
111

118. 112 CHAPITRE 5. RUPTURE
Fig. 5.1 – Principe de la rupture diff´r´e
ee
5.1 R´sistance th´orique ` la rupture
e e a
5.1.1 La contrainte th´orique de clivage
e
L’´nergie interne d’un monocristal est une fonction p´riodique de la distance atomique a. Au
e e
repos les atomes occupent les positions d’´nergie minimale. Tant que la contrainte de traction σ
e
appliqu´e perpendiculairement au plan atomique reste faible sa suppression entraˆ le retour en
e ıne
position d’´nergie minimale, le comportement est ´lastique. Au del` d’un certain seuil de traction σth
e e a
correspondant au franchissement du col ´nerg´tique la s´paration intervient par clivage, rupture de
e e e
l’ensemble des liaisons chimiques entre les atomes de deux plans adjacents.
Fig. 5.2 – Contrainte th´orique de clivage
e
La contrainte σ ´tant la d´riv´e de l’´nergie par rapport ` l’extension, elle oscille avec la mˆme
e e e e a e
p´riode a distance interatomique. Au premier ordre du d´veloppement en s´rie de Fourier la contrainte
e e e
σ s’´crit :
e
2π
σ = σth sin x = σth sin 2πε σ 2πσth ε lorsque ε → 0
a
x ´tant le d´placement d’une moiti´ du cristal par rapport ` l’autre. Aux faibles d´formations l’iden-
e e e a e
tification avec la loi de Hooke σ = Eε permet de relier raideur et r´sistance par :
e
E E
σth = σth ≈
2π 10
ordre de grandeur confirm´ par la th´orie des ´nergies de liaison (Cf. Eq. 1.2 et Fig. 1.3).
e e e
Les liaisons chimiques ´tant responsable de la coh´sion du mat´riau ` l’´chelle atomique il est
e e e a e
normal de trouver une relation entre la raideur E (Module d’Young) et la r´sistance en traction σth
e
(contrainte de rupture).

119. ´ ´ `
5.1. RESISTANCE THEORIQUE A LA RUPTURE 113
5.1.2 L’´nergie superficielle des solides
e
Le clivage cr´e deux nouvelles surfaces dont les atomes voient leur environnement modifi´, ils n’ont
e e
plus autant de proches voisins que les atomes en volume. Il en r´sulte, comme pour les liquides, une
e
tension de surface donc une ´nergie superficielle γ. L’´nergie de s´paration W S ` fournir pour cr´er
e e e a e
par clivage les deux nouvelles surfaces d’aire S est W S = 2γS.
´
Fig. 5.3 – Energie superficielle et contrainte th´orique de clivage
e
Supposant, avec Griffith, que l’´nergie ´lastique mobilisable pour assurer le clivage est celle stock´e
e e e
au voisinage du plan de s´paration dans un volume V = Sa, S ´tant l’aire de clivage et a la distance
e e
1 1
interatomique. 2 σε = 2E σ 2 ´tant la densit´ volumique d’´nergie ´lastique stock´e, l’´nergie mobilisable
e e e e e e
1
est W El = 2E σ 2 Sa. Le clivage intervient donc pour une contrainte σth telle que W El = W S , soit
2
aσth = 4γE. Dans l’´tablissement de cette relation on suppose que les liaisons atomiques continuent
e
d’ob´ir ` la loi de Hooke jusqu’` rupture. Ce n’est pas le cas, la courbe force de rappel - ´cart ` la
e a a e a
position d’´quilibre d´duite du potentiel de Lennard-Jones s’´carte de la loi lin´aire d’une mani`re
e e e e e
approximativement parabolique, la force croissant moins vite que l’´cart. Compte tenu de la propri´t´
e ee
g´om´trique des paraboles, la contrainte maximale calcul´e par la loi lin´aire est surestim´e d’un
e e e e e
facteur 2, ainsi la relation :
γE
σth =
a
est une bonne approximation de la r´sistance th´orique ` la rupture en traction de la plupart des
e e a
solides.
En rapprochant les deux expressions de σth = 2π et σth = γE , γ, E et a sont li´s par :
E
a e
4π 2 γ = Ea (5.1)
.
5.1.3 L’effet d’´chelle
e
Dans les solides cristallins la structure mol´culaire se r´arrange compl`tement au moment de la
e e e
solidification et les tensions superficielles mesur´es en phase liquide ne permettent pas n´cessairement
e e
d’en d´duire l’´nergie de surface de l’´tat solide. En revanche, le verre n’est g´n´ralement pas cristallis´
e e e e e e
lorsqu’il se solidifie ` partir d’un ´tat liquide ou pˆteux ; sa structure mol´culaire n’est pas sensiblement
a e a e
modifi´e. L’extrapolation ` 15°C des mesures de la tension superficielle du verre ` des temp´ratures
e a a e
comprises entre 745°C et 1110°C donne pour le verre solide une ´nergie de surface γ=0,56 N.m−1 =0,56
e
J.m−2 . Le module d’Young E du verre ordinaire est d’environ 62000 MPa. La r´sistance th´orique `
e e a
E 4 MPa ou σ = γE 4 MPa
la traction du verre est, selon le mode de calcul, σth = 2π = 10 th a = 1, 3.10
avec a de l’ordre de 2A ˚ (2.10−10 m).
La contrainte de rupture en traction de baguettes de verre d’environ 1 mm de diam`tre est de l’ordre
e
de 170 MPa, valeur pr`s de 100 fois plus faible que la valeur calcul´e. Cependant, une diminution du
e e
diam`tre augmente la contrainte de rupture et les fibres les plus fines, les whiskers, ont une contrainte de
e

120. 114 CHAPITRE 5. RUPTURE
rupture d´passant 13600 MPa, correspondant parfaitement ` la pr´vision th´orique. Cet effet d’´chelle
e a e e e
n’est pas l’apanage du verre et la contrainte de rupture th´orique n’est pas une abstraction scientifique
e
on sait l’atteindre ou s’en approcher en laboratoire pour la quasi-totalit´ des mat´riaux.
e e
Mat´riaux
e γ (J.m−2 ) E (Gpa) σth (Gpa)
Fer 2,0 210 46
Cuivre 1,65 120 31
Zinc 0,75 90 18
Aluminium 0,90 73 18
Tungst`ne
e 3,0 360 73
Diamant 5,4 1200 180
Chlorure de sodium 0,115 43 6,2
Oxyde d’aluminium 4,6 420 67
Verre ordinaire 0,54 70 14
´
Tab. 5.1 – Energie superficielle, Module d’Young et R´sistance th´orique
e e
La r´sistance effective ` la rupture σR des mat´riaux massifs de nos structures est 10 ` 100 fois
e a e a
plus faible que la contrainte de coh´sion σth de la mati`re (somme des forces de liaison de la section
e e
la plus faible).
Bien que sa valeur moyenne soit fonction d´croissante de la taille de l’´chantillon, σR pr´sente
e e e
toujours une grande dispersion quel que soit le soin pris pour op´rer sur des ´chantillons identiques
e e
dans des conditions identiques. Une chaˆ de mol´cules devrait pr´senter une r´sistance effective ´gale
ıne e e e e
a
` la r´sistance th´orique, ce sont les in´vitables d´fauts qui sont responsables des effets d’´chelle et
e e e e e
de dispersion. Du fait de leur r´partition statistique plus un ´chantillon est volumineux et plus les
e e
d´fauts qu’il contient peuvent ˆtre de taille importante diminuant sa r´sistance ` la rupture.
e e e a
Fig. 5.4 – dispersion de la contrainte de rupture et effet d’´chelle
e
Deux th´ories, l’une fond´e sur des consid´rations de forces et de contraintes, l’autre due ` Griffith
e e e a
fond´e sur des bilans ´nerg´tiques, ont permis de jeter les bases de la m´canique de la rupture et sont
e e e e
a
` l’origine de son d´veloppement. Les arguments fond´s sur l’´nergie sont les plus importants, les plus
e e e
fondamentaux et les plus universels, mais commen¸ons par exposer les arguments fond´s sur les forces
c e
et les contraintes.
5.2 Approche en force et en contrainte
Les variations locales de g´om´trie d’une structure sous sollicitation peuvent conduire ` une ampli-
e e a
fication locale du champ de contrainte par rapport ` sa valeur moyenne, c’est la notion de concentration
a
des contraintes. Toute variation brutale de section amplifie localement les contraintes entraˆ ınant un
affaiblissement corr´latif de la structure, mais l’introduction de trous, d’encoches ou de fissures est
e
particuli`rement n´faste.
e e
Il est instructif d’´tudier le r´seau des isostatiques, trajectoires le long desquelles se transmet la
e e
contrainte dans la masse d’un corps solide supportant une charge. Analogues des lignes de courant en
hydrodynamique elles mettent en ´vidence les difficult´s d’´coulement des contraintes.
e e e

121. 5.2. APPROCHE EN FORCE ET EN CONTRAINTE 115
Fig. 5.5 – Variations locales de g´om´trie et concentration des contraintes
e e
Dans une plaque uniforme soumise ` traction uniaxiale, les isostatiques sont parall`les, l’´coulement
a e e
est laminaire.
Si la pi`ce comporte un ´tranglement sym´trique et progressif, les isostatiques se resserrent dans la
e e e
partie ´troite et le niveau de contrainte augmente ` cet endroit, c’est l’analogue de l’augmentation de
e a
vitesse par conservation du d´bit.
e
Les isostatiques se concentrent ` la pointe d’une rayure ou d’une fissure accroissant tr`s fortement
a e
l’intensit´ de la contrainte locale de mani`re analogue au contournement d’une plaque perpendiculaire
e e
a e
` l’´coulement. La rupture qui intervient le long de la rayure est exploit´e par le vitrier pour couper
e
le verre.
5.2.1 Le coefficient de concentration des contraintes
La pr´sence d’un trou de petite taille dans une plaque en traction uniforme produit une concen-
e
tration de la contrainte localis´e au bord du trou caract´ris´e par le coefficient de concentration de
e e e
contrainte k rapport de la contrainte locale σm ` la contrainte σ0 appliqu´e au loin. Les r´sultats
a e e
principaux du calcul du champ de contraintes (Inglis 1913) au voisinage d’un trou elliptique perc´ e
dans une plaque de taille grande devant ses dimensions, 2b et 2c ´tant le petit et le grand axe de
e
l’ellipse, mise en traction perpendiculairement au grand axe sont regroup´s sur la figure 5.6.
e
Fig. 5.6 – Concentration de contrainte autour d’un trou elliptique
Au voisinage des sommets du grand axe apparaˆ une forte concentration de la contrainte de
ıt
traction. Sa valeur maximale σm en bord d’ellipse est ` cet endroit σm = k = 1 + 2 c = 1 + 2 ρ ,
a σ0 b
c
avec ρ rayon de courbure en extr´mit´ du grand axe (cρ = b2 ). k = 3 dans le cas du trou circulaire
e e
(b = c = ρ). La contrainte de traction diminue pour tendre vers σ0 lorsque l’on s’´loigne de l’ellipse le
e
long du grand axe.
Aux sommets du petit axe 2b de l’ellipse, r`gne au contraire une contrainte de compression, d’am-
e
plitude σ0 tendant ` s’annuler lorsque l’on s’´loigne de l’ellipse le long du petit axe.
a e

122. 116 CHAPITRE 5. RUPTURE
Si les trous elliptiques sont rarement rencontr´s en pratique, la solution reste valable pour des
e
ouvertures dont la forme en est peu ´loign´e telles que les fissures (ellipse aplatie) ou les ouvertures
e e
a
` angles assez vifs comme les hublots et les ´coutilles. Le coefficient de concentration de contrainte
e
k et, par voie de cons´quence, la contrainte σm augmentent tr`s rapidement avec l’aplatissement de
e e
l’ellipse de sorte que rapidement :
c c
k≈2 =2 (5.2)
b ρ
5.2.2 La contrainte de rupture effective
Les mat´riaux fragiles renferment une multitude de fissures internes dont le rayon d’extr´mit´ ρ, la
e e e
fissure ´tant vue comme une ellipse tr`s aplatie, est de l’ordre d’une dimension atomique a et la rupture
e e
intervient lorsqu’en tˆte de fissure la contrainte maximale locale σm atteint la valeur de la contrainte de
e
rupture th´orique en traction σth . Comme σm varie proportionnellement ` la contrainte appliqu´e σ0 ,
e a e
c
le facteur de proportionnalit´ ´tant justement le coefficient de concentration de contrainte k ≈ 2 ρ ,
ee
la contrainte de rupture effective σR : σR = σk est tr`s inf´rieure ` la valeur th´orique. a ´tant de
th
e e a e e
l’ordre de 1˚, un d´faut non visible de taille caract´ristique c 1 µm conduit ` un facteur k de l’ordre
A e e a
de 102 correspondant bien ` l’ordre de grandeur du rapport constat´ exp´rimentalement.
a e e
γE
Avec σth = a , on obtient la relation de Griffith reliant la contrainte de rupture σR ` la taille c
a
du d´faut :
e
2
σR c ≈ γE (5.3)
relation qui montre que la r´sistance effective ` la rupture σR est li´e ` la taille du plus grand d´faut
e a e a e
existant justifiant ` la fois la dispersion sur σR li´e ` la distribution des d´fauts et l’effet d’´chelle
a e a e e
puisque statistiquement plus le volume est grand et plus il contient de grands d´fauts.
e
5.3 La rupture fragile
A l’´chelle macroscopique une fissure peut ˆtre consid´r´e comme une ellipse de grand axe 2c dont
e e ee
le petit axe 2b, donc le rayon ρ, tend vers 0. Dans ce cas, le coefficient de concentration de contrainte
k diverge induisant une discontinuit´ et une divergence des contraintes en tˆte de fissure. La fissure
e e
doit alors ˆtre vue comme une discontinuit´ au sein d’un milieu continu.
e e
5.3.1 Fissure et modes de rupture
La rupture est caract´ris´e (au moins localement) par la s´paration irr´versible (g´n´ralement les
e e e e e e
liaisons chimiques rompues ne se r´tablissent pas par suite de la pr´sence in´vitable de polluant) d’un
e e e
milieu continu de part et d’autre d’une surface g´n´ratrice S. La coupure ainsi cr´e est appel´e fissure.
e e e e
Fig. 5.7 – fissure et modes de rupture
C’est une surface de discontinuit´ pour le champ de d´placement. Le saut [→] = →+ − →− est le
e e −
u −
u −
u
d´placement d’ouverture de la fissure.
e
Sa composante un normale ` S est l’ouverture, ´cartement des l`vres de la fissure. Elle ne peut, `
a e e a

123. 5.3. LA RUPTURE FRAGILE 117
l’´vidence, ˆtre n´gative.
e e e
Sa composante tangentielle ut est le glissement relatif des l`vres de la fissure.
e
Lorsque la s´paration est effective, les l`vres sont libres de charge et les vecteurs contrainte des
e e
facettes de chaque l`vre s’annulent.
e
→
−
T = σ→ = 0
−
n
Cette condition n’est ´videmment pas applicable aux fissures ferm´es qui imposent une condition de
e e
frottement entre les l`vres, comme cela se produit dans les roches sous pression.
e
On distingue trois modes de rupture :
– Le mode I appel´ de mani`re ´vidente mode d’ouverture.
e e e
– Le mode II appel´ mode de glissement plan.
e
– Le mode III appel´ mode de glissement antiplan ou mode de d´chirure, celui mobilis´ lorsque
e e e
l’on d´chire une feuille de papier.
e
5.3.2 Les phases de chargement
Lors du chargement d’une pi`ce fissur´e, on distingue deux phases :
e e
La phase d’ouverture pendant laquelle, la fissure immobile s’ouvre, les l`vres s’´cartant sans chan-
e e
gement g´om´triquee de la surface S. Cette phase se poursuit jusqu’` un chargement critique
e e a
autorisant la fissure ` se propager en s’agrandissant. A ce chargement critique correspond la
a
condition d’amor¸age.
c
La phase de propagation Au del` du chargement critique d’amor¸age, la fissure s’agrandit (avance)
a c
soit dans le plan tangent ` S soit dans d’autres directions (branchement), c’est la phase de
a
propagation qui pourra ˆtre contrˆl´e (propagation dite stable) ou non (propagation dite instable
e oe
conduisant ` la rupture brutale ou catastrophique).
a
Fig. 5.8 – Ouverture et propagation d’une fissure
5.3.3 Les hypoth`ses du mod`le de rupture fragile
e e
– Le mat´riau est suppos´ homog`ne, isotrope ` comportement ´lastique lin´aire jusqu’` rupture.
e e e a e e a
La courbe de traction de la structure macroscopique pr´sente un comportement lin´aire jusqu’`
e e a
rupture ; On parle alors de rupture fragile ` l’´chelle macroscopique ce qui n’exclut pas l’existence
a e
d’une ductilit´ ` plus petite ´chelle au voisinage de la fissure pour autant que la plastification
e a e
reste strictement confin´e au voisinage de la fissure.
e
– On n´glige les forces de volume et les acc´l´rations, la rupture dynamique ´tant exclue.
e ee e
– On se restreint aux probl`mes bidimensionnels (d’´paisseur e) en contrainte plane (cas des
e e
plaques minces) et en d´formation plane (cas des plaques ´paisses). L’origine O ´tant prise en
e e e
tˆte de fissure, l’axe Ox1 sera pris dans le prolongement de la fissure.
e
Fig. 5.9 – Ouverture et propagation d’une fissure

124. 118 CHAPITRE 5. RUPTURE
On s’attend donc ` ce que le mod`le pr´sente une divergence des contraintes physiquement sans
a e e
signification au voisinage de la tˆte de fissure, mais la solution repr´sentera bien l’´volution spatiale
e e e
du champ de contrainte induit par la fissure au del` d’un petit rayon r0 .
a
5.3.4 Le mod`le de rupture fragile
e
Le r´sultat essentiel en ´lasticit´ lin´aire a ´t´ ´tabli par Irwin. Le premier terme du d´veloppement
e e e e e ee e
limit´ du champ de contrainte au voisinage d’une fissure est le mˆme pour tous les probl`mes (char-
e e e
gement et g´om´trie de fissure) correspondant ` un mode d’ouverture donn´. Pour chaque mode, ce
e e a e
premier terme est connu ` un facteur multiplicatif pr`s not´ K facteur d’intensit´ de contrainte. La
a e e e
solution d’un probl`me de fissure se ram`ne donc en ´lasticit´ lin´aire ` la d´termination du facteur
e e e e e a e
K qui ne d´pend que de la g´om´trie de la fissure et du type de chargement. Dans un probl`me r´el, la
e e e e e
solution sera souvent une combinaison lin´aire des trois modes, combinaison rendue possible en raison
e
du principe de superposition des solutions en ´lasticit´ lin´aire. Le mode I est cependant physiquement
e e e
le mode le plus important puisque l’ouverture de la fissure conduit assez facilement ` la rupture. Les
a
autres modes ne sont pas toujours faciles ` contrˆler, en particulier en pr´sence de frottement des
a o e
l`vres. En mode I la fissure se propage dans son propre plan par raison de sym´trie. On s’int´ressera
e e e
donc essentiellement au mode I.
Champ de d´placement Champ de contrainte
e
→= K
− r →
− (5.4)
u 2µ 2π f (κ, θ) σ = √K f (θ)
2πr
η ´tant le coefficient de Poisson et µ le module de cisaillement, κ = 3 − 4η en d´formation plane et
e e
3−η
κ = 1+η en contrainte plane. σ33 = η(σ11 + σ22 ) en d´formation plane et σ33 = 0 en contrainte plane.
e
Fig. 5.10 – Traction en tˆte de fissure
e
Les facteurs d’intensit´ de contraintes sont aussi des facteurs de discontinuit´ des d´placements.
e e e
Cette interpr´tation appliqu´e ` KI d´gage une condition de compatibilit´ importante, n’apparaissant
e e a e e
pas de fa¸on ´vidente en terme de contrainte, ` savoir KI ≥ 0. En cons´quence la contrainte σ22 (r, θ =
c e a e
0) juste en avant de la fissure est toujours ≥ 0. En mode I la tˆte de fissure travaille toujours en traction
e
(travail ` l’ouverture). Il ne faut cependant pas oublier que ces champs correspondent seulement au
a
premier terme du d´veloppement limit´. D`s que l’on s’´loigne de la fissure, d’autres termes r´guliers
e e e e e
1
√ lorsque r → 0.
interviennent. On peut seulement affirmer qu’ils seront n´gligeables devant r
e
5.3.5 Coefficient de concentration k et facteur d’intensit´ K
e
Il est important de ne pas confondre le coefficient de concentration de contrainte k qui ne donne
qu’une information locale ` la pointe mˆme de la fissure et le facteur d’intensit´ de contrainte K qui
a e e
d´crit l’ensemble de la singularit´ spatiale du champ de contrainte. Si k est sans dimension, K est le
e e
√
produit d’une contrainte par la racine carr´e d’une longueur [K] = [σ][L]1/2 et se mesure en MPa. m.
e
Le passage ` la limite permettant de d´finir une fissure comme la limite d’un trou elliptique
a e
compl`tement aplati conduit naturellement ` une relation entre les deux grandeurs, la longueur inter-
e a
venant dans K ´tant reli´e ` la taille c du d´faut par la relation d’Irwin :
e e a e
Lim π √
K= σm ρ
ρ→0 2
σm ´tant la contrainte en tˆte de la fissure elliptique et ρ son rayon de courbure.
e e
Pour une fissure elliptique aplatie de longueur 2c dans une plaque infinie (en pratique de dimensions
c
grandes devant c) soumise ` une traction σ, σm = kσ avec k = 2 ρ , le passage ` la limite conduit `
a a a
√
KI = σ πc .

125. ´ ´
5.4. LA CORRECTION D’ELASTO-PLASTICITE 119
Fig. 5.11 – Facteur d’intensit´ de contrainte
e
Citons comme autre exemple le cas classique d’une fissure lat´rale de longueur c d´bouchant sur
e e
le cot´ d’une plaque semi infinie soumise ` une traction homog`ne σ perpendiculaire ` la fissure pour
e a e a
√ √
laquelle KI = 1, 122σ πc ≈ 2σ c.
On retrouve bien le fait annonc´ que K est une fonction du chargement et de la g´om´trie du
e e e
probl`me. Les expressions de K pour diverses g´om´tries et divers chargements sont tabul´es dans les
e e e e
ouvrages sp´cialis´s.
e e
5.4 La correction d’´lasto-plasticit´
e e
La solution ´lastique n’est pas physiquement r´aliste. Les contraintes en tˆte de fissure sont ´crˆt´es
e e e e ee
par la plasticit´, particuli`rement dans les m´taux.
e e e
Fig. 5.12 – Correction d’´lasto-plasticit´
e e
5.4.1 Autonomie de la zone critique
La divergence des contraintes en tˆte de fissure est physiquement sans signification. Au voisi-
e
nage imm´diat de la tˆte de fissure les contraintes seront au minimum ´crˆt´es par l’apparition de
e e e ee
d´formations plastiques. Il existe en tˆte de fissure un domaine, de rayon r0 caract´ristique du mat´riau,
e e e e
dans lequel la d´gradation est telle que toute description par une loi de comportement type milieu
e
continu est illusoire. L’hypoth`se de l’autonomie de la zone critique, sous-jacente ` toutes les th´ories
e a e
de la rupture fragile revient ` admettre que la forme de la zone critique et les valeurs critiques des
a
champs qui y r`gnent sont les mˆmes pour chaque classe de mat´riaux quelle que soit la g´om´trie
e e e e e
de la pi`ce et son chargement. A l’ext´rieur de cette zone les champs de contrainte correspondent
e e
pratiquement ` ceux donn´s par la th´orie ´lastique.
a e e e
L’´tat critique de la fissure (condition d’amor¸age) sera r´put´ atteint lorsque les contraintes σ sur
e c e e
le cercle de rayon r0 v´rifieront certaines relations caract´ristiques du mat´riau, le rayon r0 ´tant lui
e e e e
mˆme une de ces caract´ristiques. A l’appui de cette hypoth`se, plusieurs solutions plastiques, dont
e e e
celle de Rice dans laquelle le champ ´lastique ` l’ext´rieur d’une zone plastique circulaire correspond
e a e
bien ` celui pr´vu par la th´orie ´lastique ` un l´ger d´calage d’origine pr`s.
a e e e a e e e
5.4.2 Mod`le d’Irwin en plasticit´ confin´e
e e e
Le mod`le d’Irwin s’applique aux conditions de contrainte plane. Le mat´riau est suppos´ ˆtre
e e e e
parfaitement plastique, sans consolidation et ob´ir au crit`re de Tresca 2k = R
e e P , RP ´tant la limite
e

126. 120 CHAPITRE 5. RUPTURE
´lastique du mat´riau. La contrainte σyy qui s’applique sur le plan prolongeant la fissure est principale,
e e
constante dans la zone plastifi´e et vaut RP . En zone ´lastique la contrainte σyy = √K dans le plan
e e 2πr
1 K 2
θ = 0 atteint la limite RP ` une distance ry telle que ry =
a 2π ( RP ) . En r´alit´, la zone d´form´e
e e e e
Fig. 5.13 – zone plastique d’Irwin et crack tip opening displacement
plastiquement est plus ´tendue de fa¸on ` respecter l’´quilibre des contraintes. Il faut compenser la
e c a e
troncature de la distribution ´lastique pour x ≤ ry . En faisant l’hypoth`se simple selon laquelle la
e e
distribution ´lastique de la contrainte σyy est translat´e d’une quantit´ X l’´galit´ des aires hachur´es
e e e e e e
1 K 2
conduit ` X = ry , soit R = 2ry . La dimension de la zone plastique est donc : R = π ( RP ) .
a
Ce calcul est ´videmment approximatif l’´quilibre des contraintes n’´tant assur´ que dans le plan
e e e e
prolongeant la fissure. Il n’est valable que si la dimension de la zone plastique reste assez petite
(hypoth`se de zone plastique confin´e). La fissure accompagn´e de sa zone plastique se comporte
e e e
comme une fissure ´lastique fictive de longueur (c + R). R appel´e correction de zone plastique d’Irwin
e e
est utilis´e pour mieux repr´senter la fissure dans le cas o` la plasticit´ commence ` devenir importante.
e e u e a
Ce mod`le ne peut pr´tendre repr´senter correctement la forme de la zone plastique dans tout le plan.
e e e
Des calculs analytiques et num´riques plus ´volu´s montrent que l’estimation fournie conduit, dans
e e e
tous les cas, ` un tr`s bon ordre de grandeur peu affect´ par l’´crouissage. Par contre, les formes de
a e e e
la zone plastique sont fortement d´pendantes du probl`me trait´.
e e e
Le profil de la fissure est ´mouss´ par la plasticit´. Les l`vres s’´cartent ` leur extr´mit´ d’une
e e e e e a e e
K2
quantit´ δ appel´e ´cartement de fissure ou Crack Tip Opening Displacement, CTOD. δ ≈ ERP (E
e e e
est le module de Young) est un bon ordre de grandeur.
5.4.3 Mod`le de Barenblatt
e
Pour lever la divergence des contraintes et des d´formations en pointe de fissure, Barenblatt `
e a
´mis l’hypoth`se des forces de coh´sion confin´es dans le plan de fissure au voisinage de sa pointe.
e e e e
Physiquement, bien que les liaisons soient rompues, les atomes des deux l`vres continuent de s’attirer
e
tant que l’´cartement δ des l`vres de la fissure n’est pas trop grand. Aux faibles ´cartements la r´ponse
e e e e
est quasi ´lastique, mais l’attraction s’annule pour les ´cartements importants d´passant une certaine
e e e
valeur δm correspondant ` une longueur de bec R petite devant la taille c de la fissure. La force
a
d’attraction F est une fonction non lin´aire de l’´cartement δ. Ces forces r´gularisent le champ de
e e e
contrainte lorsque le facteur d’intensit´ de contrainte K qui leur est associ´ compense exactement
e e
celui K de la th´orie lin´aire. Dans l’hypoth`se d’autonomie de la zone critique la forme du bec de
e e e
longueur R est ind´pendante de la g´om´trie de la structure et du chargement et la force F devient
e e e
fonction non lin´aire de la distance ` la tˆte de fissure. La solution du probl`me de la fissure charg´e
e a e e e
par des contraintes de coh´sion qui tendent ` la fermer conduit aux deux r´sultats important :
e a e √
– Le facteur d’intensit´ de contrainte est li´ aux forces de coh´sion par K = π2 0 σ(x) dx
e e e π √
x
– Le profil d’ouverture du bec δ(x) varie comme x3/2 au lieu de x1/2 dans le mod`le ´lastique. Le
e e
bec est pointu, ce qui est physiquement satisfaisant.
Physiquement, le mod`le de Barenblatt est satisfaisant puisque les champs m´caniques sont d’am-
e e
plitude finie dans tout le solide. Du point de vue pratique, le calcul, qui doit prendre en compte la

127. ´ ´ ´
5.5. LA TENACITE DES MATERIAUX 121
Fig. 5.14 – forces de coh´sion mod`le de Barenblatt
e e
fonction non lin´aire F (x) est moins simple que celui des facteurs d’intensit´ de contrainte, d’o` l’usage
e e u
r´pandu du mod`le ´lastique qui se trouve ainsi justifi´.
e e e e
Fig. 5.15 – Craquelure dans un polym`re photo Schirrer
e
Les ´tudes sur polym`re ont montr´ que cette forme de bec est assez bien v´rifi´e. Dans de nombreux
e e e e e
cas, la rupture des polym`res amorphes r´sulte du d´veloppement de craquelures (ou craze) fissures
e e e
dont les faces sont pont´es par des fibrilles. Ce sont des faisceaux de chaˆ
e ınes polym´riques extraites
e
de la matrice. Elles sont relativement align´es, comme dans un polym`re fortement ´tir´. Lorsque
e e e e
l’ouverture de la craquelure augmente, la longueur des fibrilles augmente, non par fluage, mais par
poursuite de l’extraction des chaˆ
ınes qui finissent par c´der cr´ant une v´ritable fissure.
e e e
5.5 La t´nacit´ des mat´riaux
e e e
La correction d’´lasto-plasticit´ levant la divergence non physique des contraintes en tˆte de fissure,
e e e
le mod`le de fissure en ´lasticit´ lin´aire est ` la base de la plupart des th´ories de la rupture fragile au
e e e e a e
sens macroscopique du terme. En mode d’ouverture sym´trique, mode I le plus important en pratique,
e
il conduit ` la notion de seuil critique, non pas pour la contrainte qui diverge toujours en tˆte de fissure,
a e
mais pour le facteur d’intensit´ de contrainte K.
e
5.5.1 Condition d’amor¸age
c
Le crit`re de rupture, condition d’amor¸age de la propagation de la fissure en mode d’ouverture
e c
s’´crit alors sous la forme simple :
e
K = KC (5.5)
– Le facteur d’intensit´ de contrainte K uniquement fonction du chargement σ et de la g´om´trie,
e e e
en particulier de la taille c de fissure est solution d’un probl`me d’´lasticit´ lin´aire.
e e e e
– KC est une caract´ristique physique du mat´riau appel´e t´nacit´. La t´nacit´, dont l’unit´ de
e e e e e e e e
√ √
mesure est le MPa m , s’obtient via la relation KC = K(σR , c) ≈ σR c par la d´termination
e
exp´rimentale du chargement critique σR provoquant la rupture d’´prouvettes normalis´es pr´entaill´es
e e e e e
pour dont la forme analytique de la fonction K(σ, c) est connue.

128. 122 CHAPITRE 5. RUPTURE
5.5.2 La t´nacit´ th´orique
e e e
La t´nacit´ d’un mat´riau, caract´ristique intrins`que donc ind´pendante de la taille c de ses
e e e e e e
d´fauts, mesure sa r´sistance au clivage. Elle est donc fonction de l’´nergie superficielle γ. La rupture
e e e
2
intervenant sous l’action de la concentration de contrainte pour une contrainte effective telle σR c ≈ γE,
√ √
la t´nacit´ th´orique vaut KC ≈ σR c = γE.
e e e
Ainsi pour le verre et l’acier doux :
γ (Jm−2 ) E (GPa) σth (GPa) KCth (MPa.m1/2 ) KC (MPa.m1/2 )
Verre 0,54 70 14 0,19 0,7
Acier doux 2 210 46 0,65 140
´
Tab. 5.2 – Energie superficielle, Module d’Young et R´sistance th´orique
e e
Compte tenu du faible intervalle de valeurs de l’´nergie superficielle, (γ 0,5-5 J.m−2 ) la t´nacit´
e e e
d’un mat´riau, qui varie comme la racine carr´e de sa raideur, reste du mˆme ordre de grandeur
e e e
(KC 0,1-1 MPa.m1/2 ) pour la quasi totalit´ des c´ramiques et des m´taux.
e e e
5.5.3 Le paradoxe de la t´nacit´
e e
La concentration des contraintes a longtemps ´t´ consid´r´e comme expliquant de fa¸on satis-
ee ee c
faisante la diff´rence entre les r´sistances exp´rimentale et th´orique des solides. Cependant, si l’on
e e e e
accepte totalement cette explication, la plupart des mat´riaux solides devraient ˆtre fragiles et se
e e
rompre ` la mani`re du verre. En admettant, avec Griffith, que le diam`tre effectif d’extr´mit´ d’une
a e e e e
fissure est de l’ordre de grandeur de la distance interatomique, environ 1˚, une fissure superficielle de
A
c
taille c amplifie localement les contraintes d’un facteur k ≈ 2 ρ
Taille de d´faut c
e 1 µm 1 cm 1m
Coefficient de concentration de contrainte k 200 20000 200000
Une fissure de 1cm devrait r´duire la r´sistance th´orique d’un facteur 20000, auquel cas les vitrages,
e e e
qui ont souvent des fissures de cette taille, pourraient difficilement survivre. Sur des structures de tr`se
grande taille comme des bateaux, on rencontre parfois des fissures de plus d’un m`tre de long, qui
e
produiraient une concentration de contraintes d’un facteur 200000, impliquant que la structure en
question ne supporterait mˆme pas son propre poids ! De plus, apr`s des ann´es d’usage, il apparaˆ
e e e ıt
souvent, dans une grande structure (un navire, un pont ou une automobile), des fissures, des rayures,
des points de rouille, . . .Le calcul du facteur de concentration des contraintes, ` la mani`re d’Inglis,
a e
pour le plus important de ces d´fauts, conduit ` des r´sultats effarants. Or ces structures continueront `
e a e a
assurer leur fonction avec une fiabilit´ satisfaisante pendant des dizaines, voire des centaines d’ann´es.
e e
5.5.4 La t´nacit´ effective
e e
La t´nacit´ r´elle (d´termin´e exp´rimentalement) de la plupart des mat´riaux est sup´rieure ` la
e e e e e e e e a
t´nacit´ th´orique (voir tableau ci-dessous et Annexe A.8).
e e e
Mat´riau
e γ (J.m−2 ) W S (J.m−2 ) σR (MPa)
Acier doux 2,0 500000 400
Acier haute r´sistance
e 2,0 10000 1000
Alliages d’aluminium 0,9 10000 400
Bois 0,1 15000 100
Os 0,2 1700 120
Verre et c´ramique
e 0,5 1-10 170
√
Comme KC = γE , cela revient ` admettre que l’´nergie superficielle γ dans cette expression doit
a e
ˆtre remplac´e par une ´nergie de s´paration GC > γ. Mˆme dans le cas de mat´riaux r´put´s fragiles
e e e e e e e e

129. ´ ´
5.6. APPROCHE ENERGETIQUE 123
comme le verre, l’´nergie de s´paration GC est sup´rieure ` l’´nergie superficielle γ. L’origine physique
e e e a e
de cet ´cart tient au fait que, non seulement il faut s´parer les atomes et les mol´cules au niveau
e e e
de la fracture (´nergie γ), mais de plus toute la structure fine du mat´riau se trouve d´sorganis´e au
e e e e
voisinage de cette fracture jusqu’` des distances ´loign´es parfois de plusieurs centim`tres. Des liaisons
a e e e
atomiques peuvent ˆtre bris´es ` des distances allant jusqu’` 500000 fois la maille atomique et l’´nergie
e e a a e
totale n´cessaire ` la rupture de ces liaisons plus ou moins ´loign´es est tr`s sup´rieure ` γ dans les
e a e e e e a
mat´riaux ductiles. Mˆme pour des mat´riaux cassants comme le verre, l’´nergie de s´paration est
e e e e e
environ dix fois plus ´lev´e que la valeur de l’´nergie de cr´ation des surfaces. Lorsqu’un mat´riau est
e e e e e
caract´ris´ par une ´nergie de s´paration ´lev´e (i.e. acier ou bois) la valeur de l’´nergie W
e e e e e e e S n´cessaire
e
a
` la formation d’une fissure est souvent bien sup´rieure ` 100000 fois l’´nergie de cr´ation γ des
e a e e
surfaces traduisant un m´canisme de fracturation d’une grande efficacit´ pour absorber des quantit´s
e e e
importantes d’´nergie dans des r´gions ´loign´es de la fracture.
e e e e
S’il faut bien fournir une ´nergie 2γdS pour accroˆ de dS la surface de fissure, la cr´ation d’une
e ıtre e
zone ` fort endommagement en tˆte de fissure n´cessite une quantit´ d’´nergie suppl´mentaire justifiant
a e e e e e
le fait que la t´nacit´ r´elle soit sup´rieure ` la t´nacit´ th´orique. Le rayon de cette zone ´tant de
e e e e a e e e e
l’ordre de R = π ( KP )2 et la contrainte de l’ordre de RP , pour faire progresser la fissure de dS, il faut
1
R
C
aussi fournir de l’´nergie pour obtenir cet endommagement. L’´nergie suppl´mentaire ` fournir pour
e e e a
2
(RP )2 KC
cr´er cet endommagement dans le volume balay´ RdS est de l’ordre de W E RdS = E dS = GC dS
e e
a
` comparer ` 2γdS.
a
– Pour les mat´riaux fragiles comme le verre, γ ∼0,5 J.m−2 , E ∼70 GPa, RP ∼170 MPa et
e
KC ∼0,5 MPa.m1/2 soit W S ∼3 J.m−2 et R ∼3 µm.
– Pour les mat´riaux tenaces comme l’acier doux, γ ∼2 J.m−2 , E ∼210 GPa, RP ∼400 MPa et
e
KC ∼100 MPa.m1/2 soit W S ∼5.105 J.m−2 et R ∼20 cm.
Les mat´riaux peu tenaces (fragiles) ont une ´nergie de s´paration GC qui reste de l’ordre de
e e e
l’´nergie superficielle γ et la th´orie du clivage donne bien le bon ordre de grandeur KC
e e KCth , la
zone d’endommagement en pointe de fissure restant tr`s limit´e.
e e
Les mat´riaux tenaces (ductiles ou rendus tenace par d’autres m´canismes comme les fibrilles des
e e
polym`res) ont une ´nergie de s´paration GC tr`s sup´rieure ` l’´nergie superficielle γ. KC >> KCth
e e e e e a e
et la th´orie du clivage n’est pas adapt´e. L’´nergie n´cessaire ` la rupture est quasi enti`rement
e e e e a e
consomm´e dans la zone d’endommagement de grande taille dont la croissance accompagne celle de
e
la fissure.
Fig. 5.16 – Sillage plastique bordant une fissure de fatigue dans un acier inoxydable. Photo ETCA-
CREA
5.6 Approche ´nerg´tique
e e
La th´orie des concentrations de contrainte suppose implicitement que, si en un point quelconque
e
du solide, la contrainte locale est suffisante pour briser une liaison atomique alors la fissure se propage
a
` travers l’ensemble du solide provoquant la rupture. Or, dans la plupart des mat´riaux existent des
e
d´fauts locaux et certains atomes sont trop ´loign´es de leurs voisins pour assurer une bonne coh´sion
e e e e
des liaisons et, malgr´ cela, ces mat´riaux ne se brisent pas spontan´ment, beaucoup sont mˆme tr`s
e e e e e
solides. La concentration de contrainte ne suffit pas, ` elle seule, ` rendre compte du m´canisme
a a e

130. 124 CHAPITRE 5. RUPTURE
de rupture, c’est une condition n´cessaire mais non suffisante pour s´parer atomes et mol´cules et
e e e
permettre la rupture. Comme tout m´canisme (horloge, moteur...), il a besoin d’ˆtre aliment´ avec la
e e e
bonne forme d’´nergie. Un mat´riau ou une structure qui supporte une charge se comporte comme un
e e
ressort : il stocke de l’´nergie ´lastique. Cette ´nergie se r´partit dans un volume consid´rable de la
e e e e e
structure. Pour qu’une rupture se produise, une part suffisante de cette ´nergie doit ˆtre transmise `
e e a
l’endroit de la fissure pour actionner effectivement le m´canisme de rupture.
e
5.6.1 Crit`re ´nerg´tique pour la rupture brutale
e e e
Le point commun ` la rupture brutale des structures est la pr´sence de fissures, r´sultant souvent
a e e
d’un soudage d´ficient. La rupture brutale est caus´e par la croissance, ` la vitesse du son dans le
e e a
mat´riau, de fissures pr´existantes qui soudainement deviennent instables. Illustrons ce comportement
e e
a
` l’aide d’un ballon de baudruche. Un ballon gonfl´ est un r´servoir d’´nergie ´lastique, celle du gaz
e e e e
comprim´ et celle de la membrane tendue, l’´nergie totale augmentant avec la pression de gonflage. La
e e
cr´ation d’un d´faut par enfoncement d’une aiguille provoque l’explosion du ballon dont la membrane
e e
se brise par rupture brutale bien avant d’avoir atteint sa limite ´lastique. Mais si le ballon n’est que
e
partiellement gonfl´, le trou cr´e par l’aiguille est un d´faut stable provoquant simplement une fuite
e e e
d’air. Enfin si le ballon perc´ est gonfl´ rapidement, il finit par atteindre une pression qui le fait
e e
brutalement ´clater. En d’autres termes le ballon a atteint une pression critique ` laquelle le d´faut
e a e
cr´´ par l’´pingle devient instable.
ee e
5.6.2 Le bilan d’´nergie
e
Pour agrandir la surface d’un d´faut il faut d´chirer la mati`re ce qui consomme une ´nergie de
e e e e
s´paration dU S = GC dS produit de l’´nergie de s´paration du mat´riau par l’aire d´chir´e.
e e e e e e
Tant que l’´nergie m´canique dU M EC restitu´e au cours de cette d´chirure est plus faible que
e e e e
l’´nergie dU S n´cessaire ` la s´paration, la d´chirure ne se produit pas, sinon elle enfreindrait les lois
e e a e e
de la thermodynamique, et le d´faut reste stable, autrement dit il s’ouvre sans s’agrandir.
e
Lorsque l’´nergie m´canique emmagasin´e U M EC est suffisante pour que la fraction dU M EC res-
e e e
titu´e au cours de la d´chirure dS soit sup´rieure ` l’´nergie consomm´e dU S , le syst`me lib`re plus
e e e a e e e e
d’´nergie qu’il n’en consomme et le d´faut, devenu instable, s’agrandit brusquement. A chaque d´faut
e e e
est associ´ un chargement limite fonction de la taille initiale du d´faut et de la g´om´trie de la pi`ce
e e e e e
qui le qu’elle contient, chargement au-del` duquel l’´nergie disponible dans la pi`ce devient suffisante
a e e
pour fournir l’´nergie n´cessaire ` la propagation du d´faut.
e e a e
Consid´rons le syst`me thermodynamiquement isol´ constitu´ d’une plaque contenant une fissure
e e e e
de longueur c dans un mat´riau d’´paisseur e et du syst`me de mise en charge σ. L’´nergie totale U
e e e e
de ce syst`me doit rester constante.
e
U = U EXT + U EL + U S = U M EC + U S = Cte
Cette ´nergie se d´compose en :
e e
´
– U S Energie de s´paration utilis´e pour cr´er la fissure de longueur 2c.
e e e
´
– U EL Energie ´lastique stock´e au sein de la plaque, potentiel des efforts internes.
e e
´
– U EXT Energie potentielle des efforts impos´s.
e
Avec U M EC = U EXT + U EL ´nergie m´canique totale du syst`me.
e e e
Ces diff´rentes ´nergies d´pendent bien ´videmment, ` ´paisseur e = Cte, de la longueur de fissure
e e e e ae
c. La longueur d’´quilibre de la fissure est donc fix´e par la condition :
e e
dU dU M EC dU S
= + =0
dc dc dc
S M EC
Si la fissure s’allonge de dc > 0, sa surface croˆ de dS = edc ⇒ dU > 0 et dU dc < 0. Accroˆ
ıt dc ıtre
la longueur de fissure consomme de l’´nergie et l’accroissement d’´nergie de s´paration est pr´lev´ sur
e e e e e
l’´nergie m´canique disponible U M EC .
e e
Physiquement la fissure ne peut croˆ que par lib´ration des tensions qui la tiennent ferm´e. Pour
ıtre e e
allonger r´ellement la fissure encore faut-il que l’´nergie m´canique U M EC du syst`me soit suffisante
e e e e
M EC S
pour que sa variation − dU dc puisse compenser l’accroissement dU n´cessaire ` la s´paration.
dc e a e

131. ´ ´
5.6. APPROCHE ENERGETIQUE 125
Fig. 5.17 – Allongement d’une fissure par lib´ration des tensions.
e
5.6.3 Condition d’amor¸age et taux de restitution de l’´nergie
c e
S 1 dU S
La quantit´ dU =
e dS e dc n’est autre que l’´nergie de s´paration GC caract´ristique propre au
e e e
mat´riau. La quantit´ :
e e
dU M EC 1 dU M EC
G=− =− (5.6)
dS e dc
est appel´e logiquement taux de restitution d’´nergie. Le crit`re de rupture ou condition d’amor¸age
e e e c
´quivalent au crit`re K = KC s’´crit donc :
e e e
GC − G = 0 soit G = GC (5.7)
Comme K, G est une fonction du chargement σ, de la g´om´trie de la pi`ce et du d´faut, en particulier
e e e e
de sa longueur c, solution d’un probl`me m´canique ´lastique en th´orie de la rupture fragile.
e e e e
L’´quilibre G = GC est :
e
2
– instable si d U < 0, soit dG > 0
dS 2 dS
2
– stable si d U > 0, soit dG < 0
dS 2 dS
5.6.4 Stabilit´ et propagation
e
L’apport de l’approche ´nerg´tique est la mise en ´vidence de la stabilit´ de l’´quilibre de la fissure
e e e e e
et les conditions de contrˆle de sa propagation que l’on peut r´sumer dans le tableau ci-dessous, v
o e
´tant la vitesse de propagation de la fissure.
e
G < GC G = GC G > GC
Fermeture ´
Equilibre (v = 0) Propagation (v > 0)
dG dG
dS ≤ 0 Stable dv ≤ 0 Contrˆl´e
oe
dG dG
dS > 0 Instable dv > 0 Catastrophique
´
G < GC Energie m´canique mobilisable insuffisante pour accroˆ la longueur de fissure, celle-ci se
e ıtre
referme (ou se cicatrice dans le cas de certains mat´riaux comme les adh´sifs).
e e
G = GC La fissure en ´quilibre (v=0 mais fissure ouverte) sous l’action du chargement.
e
– Si dG ≤ 0 ´quilibre stable : toute fluctuation entraˆ
dS e ınant un accroissement de la longueur de
fissure provoque une diminution du taux de restitution d’´nergie et la fissure tend ` reprendre
e a
sa longueur d’´quilibre en r´gressant.
e e
– Si dG > 0 ´quilibre instable : toute fluctuation entraˆ
dS e ınant un accroissement de la longueur
de fissure provoque une augmentation du taux de restitution d’´nergie et la fissure se met `
e a
croˆ (v = 0 fissure se propageant plus ou moins rapidement).
ıtre
´
G > GC Energie mobilisable exc´dentaire pour accroˆ la longueur de la fissure, celle ci est donc en
e ıtre
r´gime de propagation. Il faut alors s’int´resser ` la cin´tique de propagation qui sera contrˆl´e
e e a e oe
par l’´volution du taux de restitution d’´nergie en fonction de la vitesse de fissure.
e e
– Si dG < 0 la propagation est dite contrˆl´e, la fissure progresse ` vitesse d´croissante vers un
dv oe a e
nouvel ´tat d’´quilibre (fissure plus grande)
e e
– Si dG = 0 la fissure progresse ` vitesse constante.
dv a
dG
– Si dv > 0 la propagation est dite catastrophique, la fissure progresse ` vitesse croissante et
a
provoque la rupture de la pi`ce.
e
Si l’´nergie en exc`s n’est pas dissip´e par d’autres m´canismes, cas des mat´riaux fragiles,
e e e e e

132. 126 CHAPITRE 5. RUPTURE
la vitesse de clivage augmente rapidement jusqu’` atteindre une vitesse proche de la vitesse
a
des ondes de surface de Rayleigh. L’´nergie exc´dentaire est dissip´e dans la propagation des
e e e
ondes associ´es, d’o` le bruit caract´ristique accompagnant ce type de rupture.
e u e
5.6.5 Courbe d’´quilibre d’une fissure
e
Le taux de restitution d’´nergie G(σ, c) ´tant fonction du chargement σ et de la longueur c de la
e e
fissure, la longueur d’´quilibre ceq donn´e par G(σ, ceq ) = GC est fonction du chargement impos´ σ.
e e e
A l’´chelle de la structure au chargement Q correspond un allongement q dont le taux de croissance
e
dq
dQ est d’autant plus grand que la fissure pr´existante est longue. Autrement dit la fissure s’ouvrant
e
dq
sans progresser sous l’action du chargement Q la souplesse (inverse de la raideur) apparente λ = dQ
de la structure est une fonction croissante de la longueur de fissure c. Ce r´gime d’ouverture perdure
e
jusqu’au chargement v´rifiant la condition d’amor¸age G(Q, c) = GC pour la fissure de longueur c.
e c
Fig. 5.18 – Courbe d’´quilibre ou d’amor¸age de propagation
e c
Dans le plan de chargement Q, q la condition d’amor¸age devient la courbe d’amor¸age Q = f (q)
c c
param`tr´e en longueur de fissure. Elle s´pare le plan de chargement en deux r´gions :
e e e e
– La r´gion inf´rieure correspond au domaine d’ouverture (la fissure s’ouvre sous l’action du char-
e e
gement sans variation de sa longueur)
– La r´gion sup´rieure correspond au domaine de propagation (la fissure s’agrandit sous l’action
e e
du chargement).
5.6.6 Influence du type de chargement
La th´orie de la rupture fragile suppose un comportement lin´aire q = λ(c)Q jusqu’au point
e e
d’amor¸age. A longueur de fissure c donn´e :
c e
– Les efforts impos´s d´rivent d’un potentiel U EXT dont la variation dU EXT = −Qdq est l’oppos´e
e e e
du travail dW = Qdq des efforts impos´s consid´r´s comme externes au syst`me.
e ee e
– Les efforts internes d´rivent d’un potentiel U EL ´nergie ´lastique stock´e dans le mat´riau dont
e e e e e
la variation dU EL = 1 Qdq = 1 qdQ (´lasticit´ lin´aire).
e e e
2 2
L’´nergie m´canique U M EC = U EXT + U EL est ´galement un potentiel ind´pendant du trajet de
e e e e
chargement suivi que celui-ci s’effectue ` d´placement impos´, ` charge impos´ ou comme combinaison
a e e a e
des deux. Sous chargement croissant un d´faut nucl´ant de petite taille va croˆ jusqu’` atteindre la
e e ıtre a
dimension d’´quilibre 2ceq appel´e longueur de Griffith ind´pendante elle aussi du type de chargement
e e e
utilis´ pour atteindre l’´quilibre.
e e
Par contre, au del` de l’amor¸age, le type de chargement influe sur le comportement en propagation.
a c
Il est donc int´ressant de d´finir l’origine de l’´nergie m´canique motrice de la fissuration pour les deux
e e e e
types de chargement extrˆmes : chargement ` force ou ` d´placement impos´.
e a a e e
´
Equilibre ` d´placement impos´ Le d´placement q0 ´tant impos´ brutalement ` l’instant initial,
a e e e e e a
le d´faut va croˆ jusqu’` la longueur d’´quilibre c. La force r´sultante Q est d´termin´e ` tout
e ıtre a e e e e a
instant par la r´ponse du mat´riau q = λ(c)Q, la souplesse λ ´tant fonction croissante de la taille
e e e

133. 5.7. LA LONGUEUR DE GRIFFITH 127
Fig. 5.19 – Energie m´canique en ´lasticit´ lin´aire
e e e e
Fig. 5.20 – Fissure ` d´placement impos´ et ` charge impos´e
a e e a e
c du d´faut.
e
A dq = 0 entraˆ ınant dQ = − dλ Q < 0 la force Q ne travaille pas et la variation du potentiel des
λ
efforts externes dU EXT = Qdq = 0. La variation d’´nergie ´lastique dU EL = 1 qdQ en ´lasticit´
e e 2 e e
lin´aire vaut alors dU
e EL = 1 q dQ = − 1 Q2 dλ < 0. Il en va de mˆme de la variation d’´nergie
e e
2 0 2
1
m´canique dU M EC = dU EXT + dU EL = − 2 Q2 dλ < 0.
e
Finalement : dU M EC < 0 avec dU EXT = 0 et dU EL < 0. L’´nergie motrice de fissuration est
e
pr´lev´e sur la r´serve d’´nergie ´lastique stock´e. La propagation ult´rieure sera contrˆlable.
e e e e e e e o
´
Equilibre ` force impos´e La charge Q0 ´tant impos´e brutalement ` l’instant initial, le d´faut va
a e e e a e
croˆ jusqu’` la longueur d’´quilibre c.
ıtre a e
A dQ = 0, entraˆ ınant dq = Q0 dλ, le d´placement r´sultant q ´tant d´termin´ ` tout instant par
e e e e ea
la r´ponse du mat´riau q = λ(c)Q. La force Q0 travaille dans le d´placement q et la variation
e e e
du potentiel des efforts externes vaut cette fois dU EXT = −dW EXT = −Q0 dq < 0, celle de
1 1
l’´nergie ´lastique stock´e dU EL = 2 Qdq vaut 2 Q2 dλ > 0 et la variation d’´nergie m´canique
e e e 0 e e
dU M EC = dU EXT + dU EL = −dU EL = − 1 Q2 dλ < 0.
2 0
Finalement : dU M EC < 0 avec dW EXT = −dU EXT > 0 et dU EL > 0. L’´nergie motrice
e
de fissuration est pr´lev´e sur le travail des forces externes dont une moiti´ sert ` augmenter
e e e a
l’´nergie ´lastique stock´e. La propagation ult´rieure sera catastrophique.
e e e e
5.7 La longueur de Griffith
La longueur de Griffith d’´quilibre d’une fissure ´tant ind´pendante du trajet de chargement,
e e e
imposons ` une plaque fissur´e de grande dimension devant la longueur de fissure 2c et d’´paisseur e
a e e
un chargement uniforme σ normal ` la fissure. L’´nergie qu’il a fallu fournir pour cr´er cette fissure est
a e e
U S = GC S = 2GC ec. Le calcul exact en coordonn´es elliptiques (Inglis) de l’´nergie ´lastique stock´e
e e e e
dans la plaque est fastidieux, mais son estimation est ais´e. A la contrainte appliqu´e σ correspond une
e e
σ
d´formation de l’ordre de E , E ´tant le module d’Young du mat´riau, et la densit´ volumique d’´nergie
e e e e e
1 σ2 1 σ2
´lastique est de l’ordre de 2 E . L’´nergie ´lastique est de l’ordre de 2 E V , V volume caract´ristique
e e e e
associ´ ` la taille de la fissure, seule dimension associ´e ` ce probl`me plan, et non pas le volume
e a e a e
total de la plaque de taille infinie car, physiquement, une fissure ne perturbe le champ de contrainte de

134. 128 CHAPITRE 5. RUPTURE
fa¸on significative que dans une petite zone en son voisinage et seule l’´nergie m´canique disponible
c e e
dans cette zone sera mobilisable pour la faire progresser.
V = 4πc2 e ´tant le volume du cylindre, rayon 2c ´paisseur e, entourant la fissure, l’´nergie ´lastique
e e e e
stock´e vaut U
e EL = 2πc2 eσ 2 , la variation d’´nergie m´canique, moteur de la fissuration, vaut, ` force
e e a
E
impos´e, dU
e M EC = −dU EL et le taux de restitution d’´nergie G = − dU M EC = 4πcσ 2 . dG > 0,
e dS E dS
l’´quilibre G = GC est instable (´quilibre a chargement impos´) et la longueur d’´quilibre de Griffith :
e e ` e e
1 E
LC = π GC σ2 telle que πσ 2 LC = GC E.
Fig. 5.21 – Longueur d’´quilibre de Griffith et ´nergie motrice
e e
L’´nergie U S absorb´e par le syst`me pour cr´er une fissure varie comme c. A chargement impos´
e e e e e
σ, l’´nergie m´canique |U
e e M EC | lib´r´e par le syst`me pendant la cr´ation de la fissure varie elle comme
e e e e
2 eσ 2
c2 . Il dispose donc de l’´nergie motrice U m = |U M EC | − U S = πc E − 2GC ec pour faire progresser la
e
m
fissure. La variation d’´nergie dU fournie par le syst`me pour agrandir (dc > 0) les fissures de taille
e dc e
c:
– est n´gative si 2c < LC inf´rieure ` la longueur de Griffith, le syst`me consomme de l’´nergie.
e e a e e
Il n’y a donc aucune raison ´nerg´tique pour que ces fissures se propagent. Si de telles fissures
e e
pr´existent, elles sont stables et g´n´ralement sans danger.
e e e
– est positive si 2c > LC sup´rieure ` la longueur de Griffith ces fissures, le syst`me fournit
e a e
de l’´nergie pour agrandir ces fissures. Elles sont donc instables et se propagent rapidement
e
conduisant ` la rupture.
a
5.7.1 Taux de restitutiton d’´nergie
e
G, solution du probl`me ´lastique lin´aire, se d´termine ` partir de la g´om´trie et du chargement
e e e e a e e
de la pi`ce et son expression analytique se calcule ais´ment pour fissure bidimensionnelle, le raisonne-
e e
ment portant sur une ´paisseur e unit´.
e e
La structure bidimensionnelle d’aire S et d’´paisseur e unit´ contenant la fissure de longueur c est
e e
limit´e par le contour C. Lors de l’accroissement dc de la longueur de fissure le contour C se d´forme
e e
dans le champ de d´placement → qu’il induit et :
e −u
– La variation de l’´nergie ´lastique U EL = 1 S σεdS s’´crit par application du principe des
e e 2 e
→ −
−
travaux virtuels δU EL = 2 C+F δ T · →dl, l’int´gration portant sur le contour total : contour
1
u e
→ → − →
− − −
ext´rieur C et contour de fissure F . Soit ∂c U EL = 1 C+F { T ∂∂c + → ∂∂c }dl. La fissure ´tant
e ∂
2
u u T e
→
− →
−
T
libre de charge T = 0 et ∂∂c = 0 sur F , le contour d’int´gration se r´duit au contour ext´rieur
e e e
→ u
− → → ∂→
− −
C et ∂c U EL = 1 C { T ∂∂c + − ∂c }dl.
∂
2 u T
→ →
− − u → →
− − u
– La variation du travail des forces ext´rieures ∂c W EXT = C T T ∂∂c = C T ∂∂c car l’effort
e ∂
externe ne travaille pas sur la partie de C o` les d´placements sont impos´s.
u e e

135. 5.7. LA LONGUEUR DE GRIFFITH 129
Finalement, le taux de restitution d’´nergie :
e
→
−
∂ ∂ 1 → ∂→ → ∂ T
− −u
G=− (U EXT + U EL ) = (W EXT − U EL ) = {T −−
u }dl (5.8)
∂c ∂c 2 C ∂c ∂c
Cette expression permet de calculer G connaissant les valeurs des champs sur le contour ext´rieur C
e
de la structure ou de le mesurer. Elles permettent ´galement de d´terminer G exp´rimentalement les
e e e
champs m´caniques consid´r´s forces impos´es et d´placements r´sultants ´tant exp´rimentalement
e ee e e e e e
accessibles.
5.7.2 ´
Energie de fissuration et longueur absolue
La longueur de Griffith est une longueur absolue, rapport de la densit´ surfacique d’´nergie de
e e
2
fissuration GC du mat´riau ` la densit´ volumique d’´nergie ´lastique σ dans la structure. La longueur
e a e e e E
critique de stabilit´ LC d’une fissure est, a niveau donn´ de contrainte de traction σ, proportionnelle
e ` e
a e
` l’´nergie de s´paration GC . Cette grandeur et la nature des m´canismes dont elle d´pend sont des
e e e
caract´ristiques tr`s importantes, tant en biologie que dans les divers domaines techniques.
e e
On constate que la valeur habituellement admise pour la r´sistance ` la traction - celle que l’on
e a
mesure en tirant sur une ´prouvette de forme r´guli`re - n’est que m´diocrement corr´l´e avec l’´nergie
e e e e ee e
de s´paration. Pour les m´taux, la corr´lation est mˆme invers´e : les aciers mous de faible r´sistance
e e e e e e
a
` la traction sont peu fragiles, tandis que les durs qui ont une grande r´sistance ` la traction sont
e a
cassants.
L’´chelle des dimensions de la structure joue un rˆle important. En effet, la longueur de Griffith
e o
´tant une grandeur absolue pour un mat´riau et un niveau de contrainte donn´s, cette longueur est
e e e
la mˆme qu’il s’agisse d’une mouche ou d’un p´trolier. C’est l` que la th´orie de Griffith prend toute
e e a e
son importance :
Dans les petits objets Une fissure risque d’ˆtre critique d`s lors qu’elle fait plus de quelques mil-
e e
lim`tres, il est alors plus sˆr d’utiliser un mat´riau dur ` haute r´sistance dont le travail de
e u e a e
fracture est assez faible.
Dans les grandes structures Les dimensions des ouvertures intentionnelles (i.e. portes ou hublots)
ou accidentelles (i.e. fissures) doivent ˆtre proportionn´es ` la longueur critique. Un alliage tr`s
e e a e
ductile de travail de fracture ´lev´ est alors pr´f´rable. Ces mat´riaux solides, mais ne r´sistant
e e ee e e
pas aux fortes contraintes de traction, devront ˆtre utilis´s avec des contraintes faibles, afin que
e e
la taille des fissures critiques reste acceptable. Pour l’acier doux ordinaire utilis´ en construction
e
m´tallique la longueur critique est de l’ordre de 2m pour une contrainte de 80 MPa.
e
Une structure charg´e doit ˆtre vue comme un syst`me ´nerg´tique potentiellement instable, un
e e e e e
r´servoir accumulant de l’´nergie qui cherche ` s’´chapper ` l’instar d’un explosif chimique. Celui-ci
e e a e a
ne doit pas exploser sous l’effet d’un ´chauffement localis´, provoqu´ par exemple par un petit impact.
e e e
Si l’´chauffement ne concerne qu’un tr`s petit volume, la perte de chaleur dans l’environnement sera
e e
sup´rieure ` la production de chaleur issue de la d´gradation chimique et la r´action explosive ne
e a e e
divergera pas. Pour lib´rer la totalit´ de l’´nergie explosive, il faut activer un certain volume critique.
e e e
Le travail des sp´cialistes est de faire en sorte que l’explosif stocke une ´nergie chimique suffisante,
e e
mais que cette ´nergie ne se lib`re que dans des conditions parfaitement d´termin´es. La lib´ration
e e e e e
d’une grande quantit´ d’´nergie stock´e se trouve bloqu´e par une barri`re ´nerg´tique coupl´e avec
e e e e e e e e
un effet dimensionnel (ou effet d’´chelle).
e
Dans le cas d’un mat´riau sous contrainte, cette dimension critique est la longueur de Griffith. Pour les
e
niveaux de contrainte que l’on rencontre dans les structures ordinaires, la quantit´ d’´nergie stock´e
e e e
par unit´ de masse est tr`s inf´rieure ` l’´nergie chimique des explosifs. C’est pourquoi, lors des essais
e e e a e
de traction, la rupture d’une ´prouvette ne s’accompagne que d’un bruit mod´r´. Maintenant que l’on
e ee
parvient, en laboratoire, ` approcher la r´sistance th´orique de nombreux solides, on constate qu’au
a e e
voisinage de la limite de rupture la quantit´ d’´nergie de d´formation stock´e par le mat´riau s’ap-
e e e e e
proche de l’´nergie totale des liaisons chimiques. La rupture de ces ´chantillons hyperr´sistants lib`re
e e e e
une ´nergie par unit´ de masse de mati`re peu diff´rente de celle d’un explosif comme la dynamite.
e e e e
Lors de la rupture des trichites on observe une v´ritable explosion et l’´mission d’un petit nuage de
e e

136. 130 CHAPITRE 5. RUPTURE
poussi`re ou de fum´e. En outre, il ne reste pratiquement rien de l’´chantillon qui est totalement
e e e
d´sint´gr´.
e e e
5.7.3 ´
Energie de fissuration et t´nacit´ : La relation entre GC et KC
e e
Pour un niveau de contrainte σ donn´ on trouve une longueur critique de d´faut LC telle que
e e
σ 2 LC ≈ KC dans l’approche en terme de force K = KC et σ 2 LC ≈ GC E dans l’approche en terme
2
e a 2
d’´nergie G = GC conduisant ` la relation : KC ≈ GC E.
GC est une caract´ristique du mat´riau qu’il faut d´terminer exp´rimentalement.
e e e e
Mouton pendule de Charpy. La diff´rence d’´nergie potentielle du pendule, caract´ris´e par la
e e e e
diff´rence des angles de lˆcher et de remont´e, est ´gale ` l’´nergie consomm´e pour provoquer
e a e e a e e
la rupture au choc de l’´prouvette pr´entaill´e. Cette ´nergie, appel´e r´silience, comprend trois
e e e e e e
termes : l’´nergie de s´paration proprement dite 2γS, l’´nergie ´lastique U EL proportionnelle
e e e e
au carr´ de la limite ´lastique σe et l’´nergie plastique (GC − 2γ)S. L’´nergie ´lastique ´tant
e e e e e e
calcul´e ` partir de la connaissance de σe et de la g´om´trie de l’´prouvette la r´silience est une
e a e e e e
mesure de GC .
Transition fragile ductile. Pour les mat´riaux fragiles la r´silience se r´duit pratiquement ` U EL +
e e e a
2γS autorisant la d´termination de l’´nergie superficielle γ du mat´riau.
e e e
Les mat´riaux ductiles, comme les m´taux, pr´sentent une variation brutale de r´silience autour
e e e e
d’une temp´rature caract´ristique appel´e temp´rature de transition fragile-ductile. En dessous
e e e e
de cette temp´rature, l’´nergie de rupture se r´duit ` l’´nergie de s´paration γ, le mat´riau
e e e a e e e
se comporte comme un mat´riau fragile. L’activation thermique est trop faible pour mobiliser
e
les dislocations et la rupture de clivage ne s’accompagne pas de dissipation plastique. Au del` a
de cette temp´rature, l’endommagement et la dissipation plastique thermiquement activ´e aug-
e e
mentent fortement l’´nergie dissip´e, donc la r´silience. La fragilisation peut ˆtre obtenue par
e e e e
vieillissement, corrosion chimique (le Ga abaisse tr`s fortement l’´nergie de rupture de l’alumi-
e e
nium, l’eau celle du verre d’o` la d´coupe sous arrosage), traitement thermique et irradiation
u e
aux neutrons.
Fig. 5.22 – Mouton de Charpy, Transition fragile ductile, Pelage des adh´sifs
e
Pelage des adh´sifs. La mˆme grandeur GC mesure la force des adh´sifs. En suspendant un poids
e e e
mg ` un petit morceau d´roul´ de ruban adh´sif d’´paisseur e et de largeur b, le ruban ne se
a e e e e
d´roule pas sur le bord du rouleau, comme dans le cas d’une pelote de ficelle, mais le long du
e
plan de sym´trie vertical. Le pelage du ruban ` π est assimilable ` la propagation d’une fissure
e a 2 a
entre la partie d´roulante et la partie coll´e sur le rouleau. La charge critique produisant le
e e
d´roulement rapide du ruban (rupture brutale) est li´e ` l’´nergie de rupture GC de l’adh´sif de
e e a e e
mani`re particuli`rement simple. Lors du d´collement d’une longueur dx de ruban qui consomme
e e e
l’´nergie de s´paration dW S = GC bdx la charge externe mg effectue un travail dW = mgdx.
e e
L’´nergie ´lastique associ´e ` l’allongement de la partie d´coll´e dx ´tant n´gligeable du fait de la
e e e a e e e e
raideur ´lev´e du ruban, l’´galit´ dW = dW S conduit ` la relation GC = mg . Typiquement, b=2
e e e e a b
cm, m=1 kg, et g=l0 m.s−2 , ce qui donne GC =500 J.m−2 valeur raisonnable pour les adh´sifs. e

137. 5.8. LA PROPAGATION DES FISSURES 131
Fig. 5.23 – M´thode de la souplesse
e
M´thode de la souplesse. Elle d´coule directement des relations G = 1 q 2 ∂λ ` charge Q impos´
e e 2 ∂c a e
1 2 ∂λ
et G = − 2 Q ∂c ` d´placement q impos´. On r´alise deux mesures de pente des courbes force
a e e e
d´placement correspondants ` deux longueurs de fissure l´g`rement diff´rentes. Il s’agit donc
e a e e e
d’une m´thode diff´rentielle qui porte sur la variation de pente ´lastique ∆λ due ` la variation
e e e ∆c a
de g´om´trie de la fissure. La difficult´ exp´rimentale r´side dans la r´alisation de deux mod`les
e e e e e e e
identiques sauf en ce qui concerne la fissure. Il ne faut pas que la diff´rence de longueur de
e
fissure soit importante, mais il faut qu’elle soit suffisante pour entraˆ
ıner une variation de pente
d´celable exp´rimentalement.
e e
5.8 La propagation des fissures
L’ouverture d’une fissure jusqu’au point d’amor¸age est un ph´nom`ne quasi statique mais au del`,
c e e a
dans la phase de propagation, la fissuration devient un ph´nom`ne dynamique et il faut ajouter au
e e
bilan d’´nergie l’´nergie cin´tique correspondant ` la mise en mouvement de la mati`re lib´r´e par
e e e a e ee
l’agrandissement de la fissure. Dans le changement de g´om´trie correspondant ` un processus r´el de
e e a e
fissuration (augmentation dS d’aire de fissure) la conservation de l’´nergie totale du syst`me s’´crit
e e e
maintenant :
dW EXT = dU EL + dU S + dU CIN (5.9)
dU CIN ´tant la variation d’´nergie cin´tique lors de l’accroissement de surface de la fissure. La condi-
e e e
tion d’amor¸age G = GC s’´crit aussi dU CIN = 0 et la condition de propagation G > GC est
c e
´quivalente ` dU CIN > 0. L’initiation de la propagation ` partir de la configuration d’´quilibre d’ou-
e a a e
verture d’une fissure est possible d`s que G = GC . Plusieurs cas sont ` distinguer :
e a
1. Si, ` tout instant, les sollicitations externes ´voluent de mani`re ` maintenir l’´galit´ G = GC
a e e a e e
donc sans accroissement d’´nergie cin´tique, la rupture est contrˆl´e et la croissance de la fissure
e e oe
stable.
2. Mais si, ` tout instant, les sollicitations externes provoquent un accroissement d’´nergie cin´tique,
a e e
G > GC , seule la fraction dU S de l’´nergie motrice dU M EC = dW EXT − dU EL est utilis´e `
e e a
la rupture des liaisons donc ` l’accroissement de la surface de fissure, la partie compl´mentaire
a e
dU CIN = dU M EC − dU S ´tant transform´e en ´nergie cin´tique. La mani`re dont le mat´riau
e e e e e e
utilisera cette ´nergie cin´tique va conditionner le caract`re contrˆlable (stable) ou catastrophique
e e e o
(instable) de la propagation.
– Si le mat´riau ne pr´sente pas de frottement interne, mat´riau ´lastique fragile parfait, l’ac-
e e e e
croissement d’´nergie cin´tique est dissip´ dans la cr´ation de nouvelle surface et la vitesse
e e e e
de propagation de la fissure va croˆ ıtre tr`s rapidement pour atteindre une vitesse proche
e
de la vitesse du son dans le mat´riau (quelques milliers de m.s−1 ) conduisant ` la rupture
e a
catastrophique.
– Si celui-ci est dou´ de frottement interne, comme c’est le cas des polym`res et des ´lastom`res,
e e e e
le surplus d’´nergie sera dissip´e sous forme de chaleur limitant d’autant plus la vitesse de
e e
propagation que le frottement interne sera ´lev´. e e

138. 132 CHAPITRE 5. RUPTURE
3. Enfin, si l’´volution du chargement ext´rieur est telle que dans une premi`re phase il y a surplus
e e e
d’´nergie motrice (G > GC ) donc accroissement d’´nergie cin´tique puis dans une seconde phase
e e e
d´ficit d’´nergie motrice (G < GC ), le surplus d’´nergie cin´tique accumul´ dans la premi`re
e e e e e e
phase pourra ˆtre partiellement utilis´ pour compenser le d´ficit d’´nergie motrice pendant une
e e e e
partie de la seconde phase et conduire ` un ´ventuel ´quilibre (arrˆt de la propagation) de la
a e e e
fissure.
5.8.1 La courbe d’´quilibre et la propagation contrˆl´e
e oe
Ces m´canismes s’illustrent graphiquement dans le plan de chargement Q, q dont les r´gions stable
e e
(r´gime d’ouverture) et instable (r´gime de propagation) sont s´par´es par la courbe d’amor¸age. Le
e e e e c
mat´riau sera consid´r´, pour des raisons de simplicit´, fragile ` faible frottement interne.
e ee e a
La courbe d’´quilibre correspondant a la condition d’amor¸age G = GC admet deux asymptotes,
e ` c
l’une correspondant ` la raideur du mat´riau en l’absence de fissure et l’autre l’axe des q correspondant
a e
au cas o` le solide est travers´ compl`tement par une fissure coupant la ligne des forces. Elle repr´sente
u e e e
la limite du domaine de s´curit´ de la pi`ce, domaine ` l’int´rieur duquel, quelque soit le trajet de
e e e a e
charge, donc quelle que soit la longueur de fissure, on a l’assurance qu’elle ne se propage pas.
Consid´rons le trajet de charge OAD (abscisse curviligne s) au cours duquel la rupture contrˆl´e
e oe
produit un accroissement de la fissure de la longueur initiale c(A) ` la longueur finale c(D) > c(A).
a
Sur le trajet OA les l`vres de la fissure de longueur c(A) s’ouvrent progressivement sans variation de
e
sa longueur. Au del` du point A l’´volution du chargement ext´rieur est contrˆl´ de sorte qu’il d´crive
a e e oe e
la portion AD de la courbe d’´quilibre. La longueur de la fissure croˆ progressivement de c(A) ` c(D),
e ıt a
la condition G = GC ´tant v´rifi´e en tout point du trajet AD.
e e e
Le taux de restitution d’´nergie G v´rifie la relation dU M EC = −Gdc, soit d’apr`s (5.8), ∆U M EC =
e e e
1 D
− 2 A (Qdq − qdQ)ds, Q les efforts externes appliqu´s et q les d´placement correspondants, relation
e e
qui n’est autre (au signe pr`s) que la surface sous la courbe de charge, dans ce cas particulier OADO.
e
M EC S
La rupture ´tant parfaitement contrˆl´e, G = GC ou ∂U ∂c + ∂U = 0 en tout point de A ` D, cette
e oe ∂c a
surface repr´sente ´galement l’´nergie ∆U
e e e S qu’il a fallu pour agrandir la fissure. L’aire du triangle
curviligne OADO repr´sente donc l’´nergie de fissuration ` fournir pour faire progresser la fissure de
e e a
sa longueur initiale c(A) ` sa longueur finale c(D).
a
Fig. 5.24 – Courbe d’´quilibre et stabilit´ de propagation
e e
5.8.2 La stabilit´ de la propagation
e
Consid´rons maintenant le probl`me de la stabilit´ de la propagation de la fissure lorsque le trajet
e e e
de charge traverse la courbe d’´quilibre : courbe P ACEBF qui se termine en F au moment pr´cis o`
e e u
la fissure s’arrˆte.
e
1. Au point A de la courbe d’´quilibre la fissure commence ` se propager.
e a
2. Au point E une d´charge virtuelle ´lastique s’effectuant suivant le trajet rectiligne EDO dont
e e
la pente ,raideur de la pi`ce fissur´e, est une fonction univoque de la longueur de fissure, la
e e

139. 5.8. LA PROPAGATION DES FISSURES 133
Aire ´
Energie associ´e
e
Aire OACEEO ∆W EXT travail des efforts externe
Aire OEE O ∆U EL ´nergie ´lastique stock´e
e e e
Aire OADO S ´nergie de rupture dissip´e
∆U e e
Aire ACED ∆U CIN ´nergie cin´tique disponible > 0
e e
Aire OACEDO ∆U M EC = ∆U S +∆U CIN = ∆W EXT −∆U EL ´nergie motrice disponible > 0
e
fissure en propagation ` la mˆme longueur que la fissure en ´tat d’´quilibre au point D. Ces
a e e e
aires v´rifient bien le bilan ´nerg´tique ∆W
e e e EXT = ∆U EL + ∆U S + ∆U CIN
3. Au point B l’´nergie cin´tique ∆U CIN repr´sent´e par l’aire ACEBDA est maximale. Si cette
e e e e
´nergie n’´tait pas transform´e en ´nergie de rupture, la fissure arrˆterait de se propager et sa
e e e e e
nouvelle longueur d’´quilibre serait c(B).
e
Aire ´
Energie associ´e
e
Aire OOBII O ∆W EXT travail des efforts externe
Aire OII O ∆U EL ´nergie ´lastique stock´e
e e e
Aire OBGO ∆U eS ´nergie de rupture dissip´e
e
Aire OBIO ∆U M EC = ∆W EXT − ∆U EL ´nergie motrice
e
disponible > 0
4. Lorsque la fissure croˆ de B en G, la d´charge ´lastique virtuelle GO d´finit le point I sur le
ıt e e e
trajet de charge qui rentre dans le domaine de stabilit´. Il n’y a donc plus d’´nergie cin´tique
e e e
cr´´e. La diff´rence ∆U M EC − ∆U S aire BGIB est n´gative conform´ment au fait que le trajet
ee e e e
de charge est rentr´ dans le domaine de stabilit´ G < GC . La fissure ne peut croˆ
e e ıtre au del`
a
de B que si une partie au moins de l’´nergie cin´tique accumul´e entre A et B, aire ACEBDA
e e e
vient compenser le d´ficit d’´nergie motrice entre B et G.
e e
5. Si la quasi totalit´ de cette ´nergie cin´tique est utilis´e pour faire progresser la fissure, celle-ci
e e e e
se stabilisera au point H correspondant au point F du trajet de charge sur la d´charge ´lastique
e e
HF O tel que les aires ACEBDA et BHF soient ´gales. Toute l’´nergie cin´tique en exc`s a ´t´
e e e e ee
utilis´e pour compenser le d´ficit d’´nergie motrice aire BHF .
e e e
6. De B ` H Le d´ficit de force motrice ∆U S − ∆U M EC est bien ´gal ` l’aire BF H. Le point H
a e e a
Aire ´
Energie associ´e
e
Aire OOBF F O ∆W EXT travail des efforts externe
Aire OF F O ∆U EL ´nergie ´lastique stock´e
e e e
Aire OBHO ∆U eS ´nergie de rupture dissip´e
e
Aire OBF O ∆U M EC = ∆W EXT − ∆U EL ´nergie motrice
e
disponible > 0
est bien le point d’´quilibre ultime de la fissure. La rupture interviendra si la dimension de la
e
pi`ce est inf´rieure ` la longueur c(H). La rupture ne sera contrˆlable que si le trajet de charge
e e a o
revient assez tˆt dans la zone de stabilit´.
o e
L’interpr´tation g´om´trique de Berry permet cependant de comprendre au moins qualitativement le
e e e
comportement de propagation car elle suppose un calcul de l’´nergie de rupture en quasi statique.
e
Or pour de nombreux mat´riaux, l’´nergie de rupture est une fonction de la cin´tique de rupture au
e e e
travers de la d´pendance de GC avec la vitesse de propagation.
e
5.8.3 Influence du type de chargement
En rupture ` force impos´e. Lorsque le point d’amor¸age A est atteint la force Q = QA est main-
a e c
tenue constante. Une fois dans le domaine instable, U CIN augmente rapidement et toujours plus

140. 134 CHAPITRE 5. RUPTURE
Fig. 5.25 – Stabilit´ de propagation et type de chargement ` force et d´placement impos´
e a e e
vite que U S . Les courbes de chargement et d’´quilibre ne peuvent se recouper conduisant ` la
e a
rupture brutale catastrophique.
En rupture ` d´placement impos´. Lorsque le point d’amor¸age A ou B est atteint le d´placement
a e e c e
constant q = qA ou q = qB est maintenu constant.
– Si la taille initiale de la fissure est petite, amor¸age sur la partie sup´rieure de la courbe
c e
d’´quilibre au point A, il y aura d´but de propagation instable, l’arrˆt de la fissure d´pendra
e e e e
de l’importance de l’´nergie cin´tique acquise au moment ou la courbe de charge recoupe `
e e a
d´placement fix´ la courbe d’´quilibre. Le dessin correspond ` un arrˆt de fissure au point
e e e a e
A lorsque tout l’´nergie cin´tique en exc`s a ´t´ consomm´e pour agrandir la fissure. Plus
e e e ee e
la fissure initiale est petite (plus haut sur la courbe se trouve le point d’amor¸age) et plus le
c
risque de rupture catastrophique est important.
– Si la taille initiale de la fissure est grande, amor¸age sur la partie inf´rieure de la courbe
c e
d’´quilibre au point B, il n’y aura pas de propagation, la fissure va s’ouvrir diminuant la partie
e
´lastique du d´placement de la structure donc la force appliqu´e et l’on rentre imm´diatement
e e e e
dans le domaine de stabilit´.e
A d´placement impos´, une grande fissure est moins dangereuse qu’une petite. La stabilit´ de la
e e e
propagation d´pend essentiellement du mode de chargement. Le mode ` force impos´e est toujours
e a e
instable, le mode ` d´placement impos´ est habituellement stable (en pratique on se trouve presque
a e e
toujours sur la partie inf´rieure de la courbe d’amor¸age) mais il peut devenir instable dans certains
e c
cas particuliers.
5.9 Les m´canismes de la rupture brutale
e
Les deux m´canismes principaux de propagation d’une fissure sont le d´chirement ductile et le
e e
clivage fragile.
5.9.1 Le d´chirement ductile des m´taux
e e
Lorsqu’une charge suffisante est appliqu´e ` un mat´riau ductile pouvant soutenir une d´formation
e a e e
plastique importante, la rupture se d´veloppe ` partir d’une fissure, souvent une fissure de fatigue,
e a
et la surface de rupture est extrˆmement rugueuse, constitu´e de cupules traduisant l’arrachement
e e
de mati`re et la forte dissipation d’´nergie de d´formation plastique en tˆte de fissure dans la zone
e e e e
de rayon R = π ( KP )2 . Ce rayon augmentant rapidement quand RP diminue. Les fissures dans les
1
R
C
mat´riaux mous sont associ´es ` des zones plastifi´es importantes. La rupture par d´chirement ductile
e e a e e
consomme beaucoup d’´nergie par d´formation plastique et plus la zone plastique est ´tendue, plus
e e e
l’´nergie absorb´e est importante, donc plus GC et KC sont ´lev´s. C’est pourquoi les m´taux ductiles
e e e e e
ont une telle t´nacit´. D’autres mat´riaux doivent aussi leur t´nacit´ ` ce comportement, par exemple
e e e e ea
la pˆte ` modeler, et certains polym`res la doivent ` un mode de rupture similaire au d´chirement
a a e a e
ductile (formation des crazes avec arrachement des macromol´cules entre les l`vres de la fissure).
e e

141. ´
5.9. LES MECANISMES DE LA RUPTURE BRUTALE 135
Du fait de la faible force de traˆınage du r´seau atomique les m´taux sont intrins`quement ductiles.
e e e
Mˆme quand ils sont qualifi´s de purs, la plupart des m´taux contiennent de petites inclusions (ou
e e e
particules) de compos´s chimiques form´s par r´action du m´tal avec des atomes d’impuret´. Dans la
e e e e e
zone plastifi´e, la d´formation se produit autour de ces inclusions, conduisant ` la formation de cavit´s
e e a e
allong´es. Au fur et ` mesure que la d´formation plastique se poursuit, ces cavit´s se relient les unes
e a e e
aux autres et la fissure progresse par d´chirement ductile. La d´formation plastique en tˆte de fissure
e e e
transforme naturellement la fissure ´troite en une fissure plus large et cet ´largissement diminue la
e e
contrainte locale de telle fa¸on qu’` l’extr´mit´ de la fissure elle soit juste suffisante pour entretenir
c a e e
la d´formation plastique du mat´riau ´croui ` cet endroit. A temp´rature ambiante ou au-dessus,
e e e a e
presque tous les m´taux purs sont r´sistants ` la rupture mais l’ajout d’´l´ments d’alliages diminue la
e e a ee
mobilit´ des dislocations augmentant la limite ´lastique et r´duisant du mˆme coup la zone plastifi´e.
e e e e e
La formation de pr´cipit´s ou de structures cristallines de duret´ ´lev´e donc fragiles permet la propa-
e e ee e
gation de fissures qui ne peuvent plus s’´mousser et diminue la r´sistance ` la rupture entraˆ
e e a ınant une
rupture fragile. Un traitement thermique appropri´ est essentiel pour obtenir les propri´t´s m´caniques
e ee e
souhait´es, c’est tout l’art du m´tallurgiste.
e e
Fig. 5.26 – M´canismes de rupture : d´chirement ductile et clivage fragile
e e
5.9.2 Le clivage fragile des c´ramiques
e
La surface de rupture des mat´riaux tr`s durs (c´ramique, verre,. . .) pr´sente un faci`s tr`s diff´rent.
e e e e e e e
Au lieu d’ˆtre tr`s rugueuse, la surface de rupture est plane et sans asp´rit´s sugg´rant une absence
e e e e e
quasi totale de zone de d´formation plastique en tˆte de fissure (RP grand, KC faible). La contrainte
e e
locale atteint au voisinage de la tˆte de fissure des valeurs consid´rables, proches de la contrainte de
e e
rupture th´orique en traction ` condition que la fissure reste ´troite. Mˆme si on admet un certain
e a e e
´moussement de la tˆte de fissure, la contrainte locale y est n´anmoins tr`s sup´rieure ` la limite
e e e e e a
´lastique et les liaisons interatomiques sont litt´ralement rompues, la fissure se propage par clivage,
e e
s´paration des plans atomiques, et conduit ` des surfaces de rupture plates ` l’´chelle atomique.
e a a e
L’´nergie n´cessaire ` la rupture des liaisons dans un mat´riau dur est plus faible que celle que
e e a e
n´cessaire au d´chirement ductile d’o` leur fragilit´.
e e u e
A basse temp´rature, les m´taux de structure hexagonale ou cubique centr´e deviennent fragiles et
e e e
rompent par clivage comme le verre. L’abaissement de la temp´rature diminuant l’agitation thermique
e
des atomes r´duit la mobilit´ des dislocations par augmentation de la r´sistance intrins`que du r´seau
e e e e e
induisant une augmentation de la limite ´lastique et une diminution de la taille de la zone plastifi´e en
e e
tˆte de fissure jusqu’` ce qu’elle soit devenue si petite que le mode de rupture de d´chirement ductile
e a e
devienne un clivage. Pour certaines compositions d’aciers cette transition ductile-fragile survient ` des
a
temp´ratures proches de 0°C et les constructions en acier sont plus fragiles en hiver qu’en ´t´.
e ee
Des ph´nom`nes semblables apparaissent dans les polym`res ` la transition vitreuse. En dessous de
e e e a
la Tg les polym`res sont beaucoup plus fragiles. De nombreux polym`res comme les r´sines ´poxydiques
e e e e
sont toujours fragiles (faible GC ) simplement parce qu’` toute temp´rature les chaˆ
a e ınes sont fortement
r´ticul´es par des liaisons covalentes et les fissures ne sont pas ´mouss´es par plastification en tˆte de
e e e e e

142. 136 CHAPITRE 5. RUPTURE
fissure.
5.10 La r´sistance ` la rupture des mat´riaux fragiles
e a e
5.10.1 R´sistance ` la rupture
e a
Diff´rents essais m´caniques permettent de d´terminer la r´sistance ` la rupture des mat´riaux
e e e e a e
fragiles.
Essai de traction
Fig. 5.27 – Mat´riau fragile : Rupture en traction
e
M e
L’essai le plus simple est l’essai de traction. Il mesure la contrainte Rt n´cessaire pour provoquer
la propagation instable de la plus longue fissure que contient l’´chantillon. Dans un ´chantillon donn´,
e e e
si la plus longue microfissure la mieux orient´e a une longueur 2cM ax alors c’est cette fissure qui
e
d´terminera la r´sistance ` la traction. En effet, cette fissure repr´sente le maillon le plus faible,
e e a e
elle deviendra instable lorsque la contrainte moyenne de traction v´rifiera la condition d’amor¸age
e c
σ 2 πc 2 et provoquera la rupture catastrophique de l’´chantillon. La r´sistance ` la traction
M ax = KC e e a
M
Rt de l’´chantillon est donc ´gale ` la contrainte d’amor¸age du maillon le plus faible, soit :
e e a c
M KC
Rt ∼ √
πcM ax
Il y a donc deux mani`res d’am´liorer la r´sistance m´canique des c´ramiques : diminuer cM ax en
e e e e e
contrˆlant soigneusement la fabrication ou augmenter KC par alliage ou par constitution d’un com-
o
posite ` partir de cette c´ramique.
a e
Essai de flexion
Fig. 5.28 – Mat´riau fragile : Rupture en flexion
e
Les essais de traction sur les c´ramiques sont d´licats car elles tendent ` se rompre dans les
e e a
mors de la machine d’essai. Il est beaucoup plus facile de mesurer la force n´cessaire pour casser un
e
barreau dans un essai de flexion. La contrainte de traction maximale σr en surface du barreau au
moment de sa rupture est appel´e module de rupture. On pourrait penser que σr doit ˆtre ´gal `
e e e a
a M
la r´sistance ` la traction Rt . En fait, il est l´g`rement plus ´lev´ (typiquement 1,7 fois plus) car
e e e e e
la r´partition des contraintes dans l’´prouvette n’est pas homog`ne. La demi ´prouvette sup´rieure
e e e e e
travaille en compression tandis que la demi ´prouvette inf´rieure travaille en traction, cette traction
e e
´tant d’autant plus forte que l’on se rapproche de la face inf´rieure et du centre de l’´prouvette, ce
e e e
qui explique que la rupture se produise ` partir de cette face ` l’aplomb de l’appui exer¸ant la force
a a c

143. ´ ` ´
5.10. LA RESISTANCE A LA RUPTURE DES MATERIAUX FRAGILES 137
F . Statistiquement le plus grand d´faut ` plus de chance de se situer au centre de l’´prouvette, donc
e a e
dans une zone sous faible contrainte, de sorte que la rupture se d´clenchera sur un d´faut de taille
e e
inf´rieure dans la zone de forte traction, conduisant donc ` une contrainte de rupture σr sup´rieure `
e a e a
RtM.
Essai de compression
Le troisi`me type d’essai est l’essai de compression. Pour les m´taux (ou n’importe quel autre solide
e e
e M e e M
plastique) la r´sistance Rc mesur´e en compression a la mˆme signification que celle Rt mesur´e en e
traction. Mais il n’en est pas de mˆme pour les solides fragiles dont la r´sistance ` la compression est
e e a
M M
environ 15 fois plus ´lev´e, soit : Rc ≈ 15Rt . En compression, les fissures se propagent de mani`re
e e e
stable et d´vient de leur orientation initiale pour se propager parall`lement ` l’axe de compression.
e e a
La rupture n’est pas provoqu´e par la progression rapide et instable d’une fissure unique comme en
e
traction, mais par la lente progression de nombreuses fissures qui forment une zone d’´crasement.
e
Ce n’est donc pas la longueur cM ax de la plus grande fissure qui intervient, mais plutˆt la longueur
o
moyenne cM oy . La r´sistance ` la compression est, comme en traction, du type :
e a
M KC
Rt ∼ √
πcM oy
Fig. 5.29 – Mat´riau fragile : Rupture en compression
e
Pour expliquer ce ph´nom`ne, il faut revenir au mod`le de la fissure elliptique aplatie d’Inglis.
e e e
En traction, lorsque la fissure est orient´e perpendiculairement ` la contrainte, les pointes de l’ellipse
e a
sont soumises ` une forte traction provoquant la propagation instable de la fissure. En compression,
a
au contraire, les pointes sont soumises ` une forte compression et la fissure stable tend ` se fermer.
a a
Mais elle est soumise ` une contrainte de traction aux extr´mit´s du petit axe et, si on impose `
a e e a
l’infini une contrainte suffisamment grande (beaucoup plus grande qu’en traction traduisant la grande
r´sistance ` la compression), deux branchement vont apparaˆ dans la direction de la compression.
e a ıtre
Lorsque la fissure s’incline, ces points de branchement se d´placent rapidement vers les pointes avec
e
l’augmentation de l’angle d’inclinaison. Les branchements se produisent perpendiculairement ` la a
direction de la contrainte de traction, donc dans la direction de la compression.
Essai de choc thermique
Quand en versant de l’eau bouillante dans un verre le fond se d´tache avec un bruit sec, on r´invente
e e
l’essai standard de r´sistance au choc thermique. La rupture provoqu´e par de brutales variations de
e e
temp´rature est un probl`me typique des c´ramiques. Mais tandis que certaines (comme le verre
e e e
ordinaire), ne pourront encaisser qu’un choc thermique de 80°C avant de casser, d’autres (comme le
nitrure de silicium), pourront supporter une variation brutale de 500°C.
Une mani`re de mesurer la r´sistance aux chocs thermiques consiste ` laisser tomber dans de
e e a
l’eau froide un ´chantillon de c´ramique chauff´ ` des temp´ratures de plus en plus ´lev´es. L’´cart
e e ea e e e e
maximum de temp´rature ∆T (en °K) auquel il survit sans se casser donne la mesure de sa r´sistance
e e
au choc thermique. Si son coefficient de dilatation thermique est α, la couche superficielle brutalement

144. 138 CHAPITRE 5. RUPTURE
refroidie subit une contraction α∆T . Mais elle fait partie d’un solide beaucoup plus volumineux qui
est encore chaud, et ceci l’astreint ` conserver sa dimension initiale : elle doit donc supporter une
a
e e a M
contrainte de traction ´lastique Eα∆T . Si cette contrainte exc`de la r´sistance ` la traction Rt la
e
surface de la pi`ce se fissure et finalement s’´caille. Donc la temp´rature maximale supportable ∆TM ax
e e e
est donn´e par la relation : Eα∆TM ax = Rt .
e M
Pour le verre ordinaire, α est grand et ∆TM ax est faible, mais pour la plupart des c´ramiques
e
techniques, α est faible et Rt M est ´lev´e, de sorte qu’elles peuvent ˆtre refroidies brutalement de
e e e
plusieurs centaines de degr´s sans se briser.
e
5.10.2 La statistique de la rupture fragile
Il n’est jamais possible d’affirmer qu’un solide fragile ne cassera pas sous une contrainte de traction
donn´e car la rupture d´pend de la taille inconnue du plus grand d´faut maillon le plus faible. Or celle-
e e e
ci peut varier de mani`re consid´rable d’une ´prouvette ` l’autre. Seule la probabilit´ de survie d’une
e e e a e
pi`ce en fonction de la contrainte σ externe appliqu´e peut ˆtre d´termin´e pour un mat´riau fragile.
e e e e e e
La craie ` tableau est un solide fragile. Certains bˆtons de craie sont plus fragiles que d’autres.
a a
En ´crivant au tableau, on constate qu’en moyenne 3 bˆtons sur 10 cassent tandis que les 7 autres
e a
survivent. La probabilit´ de rupture PR pour cette craie, sollicit´e en flexion sous la force normalis´e
e e e
d’´criture vaudra PR = 0, 3. Si la pi`ce est un outil de coupe en c´ramique, une probabilit´ de rupture
e e e e
de 1 sur 100 peut ˆtre acceptable, car un outil se remplace facilement. Mais s’il s’agit d’un hublot
e
d’installation sous vide, dont la rupture peut causer des blessures, on souhaitera limiter fortement
le risque d’accident en choisissant une probabilit´ de rupture PR de l’ordre de l0−6 . Pour une tuile
e
du bouclier de navette spatiale, quand la rupture d’une sur 10000 peut ˆtre fatale, on visera une
e
probabilit´ de rupture PR de l’ordre de l0
e −8 .
Si un risque acceptable (la probabilit´ de rupture) peut ˆtre affect´ ` la fonction remplie par la
e e ea
pi`ce, il est alors effectivement possible de la concevoir de sorte que le risque n’exc`de pas ce maximum
e e
acceptable.
Distribution statistique de d´fauts
e
Fig. 5.30 – Distribution statistique de d´fauts
e
La craie est une c´ramique poreuse de faible t´nacit´ KC =0,9 MPa.m1/2 mal consolid´e, pleine de
e e e e
e a M
fissures et de pores. Sa r´sistance moyenne ` la traction Rt est de l’ordre de 15 MPa correspondant ` a
une taille de d´faut de l’ordre du mm. Mais la craie contient une distribution de d´fauts de diff´rentes
e e e
longueurs. Deux morceaux de craie A et B g´om´triquement identiques peuvent avoir des r´sistances
e e e
notablement diff´rentes, d’un facteur 3 ou plus. Ceci provient du fait que l’un (morceau B) a ´t´
e ee
d´coup´ de telle sorte que, par hasard, il ne contienne que des fissures courtes, tandis que l’autre
e e
(morceau A) a ´t´ taill´ de sorte qu’il contienne l’une des plus longues fissures de la distribution.
ee e
Si de petits ´chantillons g´om´triquement identiques sont d´coup´s dans un gros bloc de c´ramique
e e e e e e
fragile, ils pr´senteront une dispersion de r´sistance m´canique due ` la dispersion de la taille des
e e e a

145. ´ ` ´
5.10. LA RESISTANCE A LA RUPTURE DES MATERIAUX FRAGILES 139
d´fauts. En moyenne un gros ´chantillon ayant plus de chances de contenir l’un des plus longs d´fauts
e e e
cassera pour une contrainte plus faible qu’un ´chantillon plus petit. Il y a d´pendance de la r´sistance
e e e
par rapport au volume.
Hypoth`se du maillon le plus faible
e
Les ruptures par clivage prennent naissance ` partir d’´l´ments microstructuraux, grains, inden-
a ee
tations, qui pr´sentent une distribution statistique et c’est en g´n´ral le grain le plus gros et le plus
e e e
favorablement orient´ pour cliver, ´l´ment le moins r´sistant, qui d´clenche la rupture. La th´orie sta-
e ee e e e
tistique du maillon le plus faible s’applique ` ces ruptures fragiles. Elle repose sur quelques hypoth`ses
a e
fondamentales ` v´rifier soigneusement en pratique :
a e
– Le solide est consid´r´ comme la juxtaposition de N ´l´ments parfaitement ind´pendants et la
ee ee e
rupture de l’´l´ment le plus faible entraˆ la rupture du solide entier.
ee ıne
– A chaque ´l´ment correspond une probabilit´ de rupture P0 (σ) sous une contrainte σ donn´e.
ee e e
La probabilit´ de survie de l’´l´ment ´tant 1-P0 (σ), celle des N ´l´ments vaut selon l’hypoth`se
e ee e ee e
d’ind´pendance [1 − P0 (σ)]
e N et la probabilit´ de rupture P (σ) = 1 − [1 − P (σ)]N s’´crit aussi sous
e e
R 0
la forme
1 1
PR (σ) = 1 − exp(−N ln[ ]) = 1 − exp(−N f (σ)) avec f (σ) = ln[ ]
1 − P0 (σ) 1 − P0 (σ)
o` la fonction P0 (σ) est inconnue.
u
Effet de volume
Le volume total V ayant ´t´ subdivis´ en N ´l´ments de volume V0 , la probabilit´ de rupture du solide
ee e ee e
V
de volume V s’´crit : PR (σ, V ) = 1 − exp− V0 f (σ) fonction croissante de V .
e
Effet de contrainte inhomog`ne e
Lorsque la pi`ce est soumise ` une contrainte h´t´rog`ne, on la divise en un grand nombre de volumes
e a ee e
´l´mentaires ∆V , chacun soumis ` une contrainte σ suppos´e homog`ne sur ∆V mais fonction de la
ee a e e
position du volume ∆V consid´r´ dans la structure. Pour chacun de ces volumes ∆V la probabilit´
ee e
de rupture PR (σ, ∆V ) est donn´e par l’expression pr´c´dente avec V = ∆V . La probabilit´ de survie
e e e e
de la pi`ce est le produit des probabilit´s de survie de chacun de ses ´l´ments (tous doivent survivre
e e ee
pour que la pi`ce survive) et vaut :
e
∆V dV
1 − PR (σ, V ) = [1 − PR (σ, ∆V )] = exp( − f (σ)) PR (σ, V ) = 1 − exp(− f (σ) )
V0 V V0
en passant ` la limite continue sachant que le volume V0 reste petit devant le volume dV sur lequel on
a
admet que la contrainte σ est constante. La probabilit´ de rupture est fonction de la r´partition des
e e
contraintes dans la pi`ce. Mais quelle valeur faut-il attribuer ` σ ? En g´n´ral on utilise la plus grande
e a e e
des contraintes principales lorsqu’elle est positive. Ainsi une ´prouvette en flexion a une probabilit´ de
e e
rupture plus faible que celle de la mˆme ´prouvette en traction sous une contrainte ´gale ` celle qui
e e e a
agit sur la fibre la plus tendue en flexion. En traction, tout le volume est soumis ` la contrainte alors
a
qu’en flexion seule une mince couche proche de la surface tendue supporte la contrainte de traction
maximale. Le contrainte de rupture en flexion est plus grande que la r´sistance ` la traction.
e a
Si la d´pendance en volume est une cons´quence directe de l’hypoth`se de la th´orie du maillon le
e e e e
plus faible, reste ` pr´ciser la fonction f (σ).
a e
Th´orie de Weibull
e
Weibull a propos´ la forme empirique suivante :
e
σ − σs m σ
f (σ) = ( ) f (σ) = ( )m (5.10)
σu σu
qui rend bien compte de la dispersion exp´rimentale des contraintes de rupture des mat´riaux fragiles
e e
en traction. Dans cette expression, σs repr´sente un seuil de contrainte en dessous duquel la probabilit´
e e
de rupture est nulle. Dans la plupart des cas on suppose que σs = 0, ce que nous ferons par la suite.
Le module de Weibull m est un indicateur de la dispersion. Plus il est faible, plus cette dispersion est
importante :

146. 140 CHAPITRE 5. RUPTURE
– Pour les faibles module de Weibull, (m < 20), la distribution des d´fauts est tr`s variable d’un
e e
´chantillon ` l’autre, d’o` la dispersion des contraintes de rupture.
e a u
– Pour les forts module de Weibull, la distribution des d´fauts est tr´s peu variable d’un ´chantillon
e e e
a
` l’autre, d’o` faible dispersion des contraintes de rupture , la contrainte de rupture σR est une
u
grandeur quasi d´terministe.
e
Fig. 5.31 – Loi de Weibull de la rupture fragile
En mesurant la probabilit´ de survie PS (σ, V0 ) = 1 − PR (σ, V 0) comme le nombre d’´chantillons
e e
de mˆme volume V0 n’ayant pas cass´ sous la contrainte σ, la loi de Weibull
e e
σ m
PS (σ, V0 ) = 1 − PR (σ, V 0) = exp[−( ) ]
σu
1
est v´rifi´e si les points s’alignent dans le plan ln(ln[ 1−PR ]), ln σ sur une droite dont la pente est ´gale
e e e
au module de Weibull m. A contrainte nulle, PS = 1, tous les ´chantillons survivent. Lorsque σ aug-
e
mente PS diminue tendant vers 0 pour les fortes contraintes et tous les ´chantillons cassent. σu est la
e
contrainte telle que PS (σu , V0 ) = 1 ≈ 0,37 laissant survivre 37% des ´chantillons.
e e
Le volume effectif et la contrainte de Weibull .
V m
Dans la loi de Weibull compl`te PS (σ, V ) = exp( − V0σ m ) int´grant les effets de volume, les param`tres
e σu e e
e m
V0 et σu ne sont pas ind´pendants, seul leur produit V0 σu intervient. σM ax ´tant dans une pi`ce de
e e
volume V la valeur maximale de la contrainte majeure positive solution du probl`me ´lastique en
e e
contrainte inhomog`ne la probabilit´ de survie de la pi`ce s’´crit :
e e e e
σ m dV σM ax m Vef f σ
PS (σ, V ) = exp( − ( ) ) = exp( − ( ) ) avec V ef f = ( )m dV
V σu V0 σu V0 V σM ax
La probabilit´ de survie d’une pi`ce soumise ` contrainte inhomog`ne de maximum σM ax est ´gale `
e e a e e a
celle d’une pi`ce ´quivalente de volume Vef f en ´tat de contrainte homog`ne σM ax . L’application ` la
e e e e a
1
flexion trois points conduit ` la relation σr = Rt [2(m + 1)2 ] m entre la r´sistance en traction RM t
a M e
et le module de rupture en flexion σr , soit σr ≈ 1,7 Rt M annonc´ pour la valeur typique m = 10 des
e
c´ramiques.
e
On peut ´galement d´finir la contrainte de Weibull σw (li´e au volume effectif Vef f ) telle que :
e e e
σ m dV σw 1 1 σw Vef f m1
PS (σ, V ) = exp( − ( ) ) = exp{−( )m } avec σw = [ σ m dV ] m et =( )
V σu V0 σu V0 V σM ax V0
L’essai d’´preuve ou comment tricher avec la statistique.
e
Dans un lot de pi`ces avec une certaine distribution de r´sistances, on ´limine les plus faibles en les
e e e
chargeant toutes sous une contrainte d’´preuve donn´e. Celles qui contiennent des fissures de grande
e e
longueur cassent et il ne reste que la fraction r´sistante ` la contrainte d’´preuve. Statistiquement
e a e
parlant, les essais d’´preuve constituent une s´lection qui rejette la queue de la distribution du cˆt´
e e oe

147. ´ ´
5.11. RESUME RUPTURE 141
des faibles r´sistances. C’est une m´thode largement utilis´e pour r´duire la probabilit´ de rupture des
e e e e e
pi`ces critiques dont l’efficacit´ est remise en cause par la transformation lente au cours du temps des
e e
petits d´fauts inoffensifs en fissures dangereuses de grande dimension. Il faut donc ´prouver la pi`ce `
e e e a
intervalles r´guliers tout au long de son utilisation. Ce type de proc´dure est ´galement impos´ par la
e e e e
r´glementation pour les pi`ces critiques en mat´riau ductile comme les r´servoirs d’acier sous pression
e e e e
(chaudi`res, bouteille de gaz,. . .) pour d´tecter la croissance des fissures de fatigue.
e e
Les limites de l’approche statistique
Cette approche n’est plus valide lorsqu’une des hypoth`ses de d´part, notamment celle concernant
e e
l’ind´pendance des ´l´ments de volume est mise en d´faut.
e ee e
– Si la contrainte normale est n´gative, une propagation de la microfissure est possible, mais elle
e
se fait en g´n´ral avec une bifurcation telle que le facteur d’intensit´ de contrainte diminue. Une
e e e
telle fissure cesse d’ˆtre activ´e. Elle participe n´anmoins ` un endommagement progressif du
e e e a
mat´riau, mais l’hypoth`se du maillon le plus faible n’est pas utilisable.
e e
– Il en est de mˆme si les microfissures se propagent mais s’arrˆtent sur des obstacles qui les
e e
stabilisent (b´ton et c´ramiques).
e e
5.11 R´sum´ Rupture
e e
La rupture correspond ` une r´sistance limite du mat´riau en traction.
a e e
La contrainte de rupture effective
2
σR c = G C E KC = GC E
est li´e ` la taille c du d´faut. Elle pr´sente une dispersion li´e ` la distribution de taille des d´fauts.
e a e e e a e
√ −2 ).
Le mat´riau est caract´ris´ par sa t´nacit´ KC (Mpa m) ou son ´nergie de rupture GC (J.m
e e e e e e
Rupture fragile et rupture ductile
Rupture fragile Rupture ductile
Surface de rupture lisse Surface de rupture rugueuse
GC , KC faibles GC , KC forts
Clivage des liaisons Endommagement plastique
GC ≈ γ
La dimension caract´ristique R de la zone plastique en tˆte de fissure :
e e
KC 2
R≈( ) avec RP seuil plastique
RP
est petite pour les corps fragiles, grande pour les corps ductiles (tenaces).
Mod`le ´lastique
e e
Au voisinage de la tˆte de fissure le champ de contrainte ne d´pend que de la g´om´trie de la fissure
e e e e

148. 142 CHAPITRE 5. RUPTURE
et du type de chargement. Il est caract´ris´ par le facteur d’intensit´ de contrainte K :
e e e
K
σ=√ f (θ)
2πr
Ouverture et propagation
La propagation d’une fissure n’est possible que si l’´nergie m´canique mobilisable au voisinage de la
e e
fissure est suffisante pour contrebalancer l’´nergie de rupture n´cessaire ` son allongement.
e e a
Pour agrandir la surface d’un d´faut il faut d´chirer la mati`re ce qui consomme une ´nergie de
e e e e
s´paration dU
e S = G dS produit de l’´nergie de s´paration du mat´riau par l’aire d´chir´e.
e e e e e
C
• Ouverture du d´faut. Tant que l’´nergie m´canique dU M EC restitu´e au cours de cette d´chirure est
e e e e e
plus faible que l’´nergie dU S n´cessaire a la s´paration, la d´chirure ne se produit pas et le d´faut
e e ` e e e
reste stable, autrement dit il s’ouvre sans s’agrandir.
• Propagation du d´faut. Lorsque l’´nergie m´canique emmagasin´e U M EC est suffisante pour que la
e e e e
fraction dU M EC restitu´e au cours de la d´chirure dS soit sup´rieure ` l’´nergie consomm´e dU S , le
e e e a e e
syst`me lib`re plus d’´nergie qu’il n’en consomme et le d´faut, devenu instable, s’agrandit brusquement.
e e e e
Condition d’amor¸age et taux de restitution de l’´nergie
c e
L’´nergie totale U de l’ensemble constitu´ d’un mat´riau contenant une fissure et du syst`me de mise
e e e e
en charge doit rester constante.
U = U EXT + U EL + U S = U M EC + U S = Cte
Cette ´nergie se d´compose en :
e e
´
– U S Energie de s´paration utilis´e pour cr´er la fissure.
e e e
´
– U EL Energie ´lastique stock´e au sein de la plaque, potentiel des efforts internes.
e e
´
– U EXT Energie potentielle des efforts impos´s.
e
Avec U M EC = U EXT + U EL ´nergie m´canique totale du syst`me. Ces diff´rentes ´nergies d´pendent
e e e e e e
bien ´videmment de la taille de fissure. La longueur d’´quilibre de la fissure est donc fix´e par la
e e e
condition :
dU dU M EC dU S
= + =0
dS dS dS
S M EC
Si l’aire de fissure s’acroˆ de dS > 0, dU > 0 et dU dc < 0. Accroˆ la longueur de fissure consomme
ıt dc ıtre
de l’´nergie et l’accroissement d’´nergie de s´paration est pr´lev´ sur l’´nergie m´canique disponible
e e e e e e e
U M EC . La quantit´ G = − dU M EC est appel´e taux de restitution d’´nergie. Le crit`re de rupture ou
e e e e
dS
condition d’amor¸age s’´crit :
c e
dU
= GC − G = 0 ou G = GC K = KC
dS
d2 U dG d2 U dG
L’´quilibre G = GC est instable si
e dS 2
< 0, soit dS > 0 et stable si dS 2
> 0, soit dS < 0.
Stabilit´ et propagation
e
Les conditions de contrˆle de la propagation d’une fissure sont :
o
v ´tant la vitesse de propagation de la fissure.
e
G < GC G = GC G > GC
Fermeture ´
Equilibre (v = 0) Propagation (v > 0)
dG dG
dS ≤ 0 Stable dv ≤ 0 Contrˆl´e
oe
dG dG
dS > 0 Instable dv > 0 Catastrophique

149. Annexe A
Propri´t´s m´caniques des mat´riaux
e e e e
1. Temp´ratures de fusion et de ramollissement
e
2. Masse volumique
3. Echelles de structure des mat´riaux
e
4. Module d’Young E
5. Limite d’´lasticit´ et r´sistance ` la traction
e e e a
6. Limite d’´lasticit´ normalis´e
e e e
7. Ductilit´ en traction - allongement ` rupture
e a
8. T´nacit´
e e
9. Energie de rupture
143

150. 144 ´ ´ ´ ´
ANNEXE A. PROPRIETES MECANIQUES DES MATERIAUX
A.1 Temp´ratures de fusion et de ramollissement(*) en °K
e

151. A.2. MASSE VOLUMIQUE EN KG.M −3 145
A.2 Masse volumique en kg.m−3

152. 146 ´ ´ ´ ´
ANNEXE A. PROPRIETES MECANIQUES DES MATERIAUX
A.3 Echelles de structure des mat´riaux
e

153. A.4. MODULE D’YOUNG EN GPA 147
A.4 Module d’Young en Gpa

154. 148 ´ ´ ´ ´
ANNEXE A. PROPRIETES MECANIQUES DES MATERIAUX
A.5 Limite d’´lasticit´ Re et r´sistance ` la traction Rm
e e e a

155. ´ ´ ´
A.6. LIMITE D’ELASTICITE NORMALISEE : RE
149
E
Re
A.6 Limite d’´lasticit´ normalis´e :
e e e E

156. 150 ´ ´ ´ ´
ANNEXE A. PROPRIETES MECANIQUES DES MATERIAUX
A.7 Ductilit´ en traction - allongement ` rupture AR en %
e a

157. ´ ´ `
A.8. TENACITE KC EN M P A.M 1/2 A L’AMBIANTE 151
A.8 T´nacit´ KC en M P a.m1/2 ` l’ambiante
e e a

158. 152 ´ ´ ´ ´
ANNEXE A. PROPRIETES MECANIQUES DES MATERIAUX
A.9 Energie de rupture GC en kJ.m−2 ` l’ambiante
a

159. Annexe B
Op´rateurs diff´rentiels - Formulaire
e e
1. Coordonn´es cart´siennes
e e
2. Coordonn´es polaires
e
3. Coordonn´es sph´riques
e e
153

160. 154 ´ ´
ANNEXE B. OPERATEURS DIFFERENTIELS - FORMULAIRE
B.1 Coordonn´es cart´siennes
e e
Coordonn´es : x, y, z, Accroissements : dx, dy, dz, Longueur : ds2 = dx2 + dy 2 + dz 2
e
B.1.1 Scalaire φ
∂φ
∂x
→
− ∂φ ∂2φ ∂2φ ∂2φ
F = Gradφ = ∂y ∆φ = ∂x2
+ ∂y 2
+ ∂z 2
∂φ
∂z
B.1.2 Vecteur u
∂ux ∂ux ∂ux
∂x ∂y ∂z
G = Grad→ =
− Div→ = Trε =
−
∂uy ∂uy ∂uy ∂ux ∂uy ∂uz
u ∂x ∂y ∂z u ∂x + ∂y + ∂z
∂uz ∂uz ∂uz
∂x ∂y ∂z
∂uz ∂uy ∂ 2 ux ∂ 2 ux ∂ 2 ux
− ∂x2
+ ∂y 2
+ ∂z 2
∂y ∂z
Rot→ =
−
u ∂ux
∂z − ∂uz
∂x ∆→ =
−
u ∂ 2 uy
∂x2
+
∂ 2 uy
∂y 2
+
∂ 2 uy
∂z 2
∂uy ∂ux ∂ 2 uz ∂ 2 uz ∂ 2 uz
∂x − ∂y + +
∂x2 ∂y 2 ∂z 2
B.1.3 Contrainte σ et D´formation ε
e
∂σxx ∂σ
∂x + ∂y + ∂σxz
xy
∂z
∂σyx ∂σyy ∂σyz
DivD σ = ∂x + ∂y + ∂z
∂σzx ∂σzy
∂x + ∂y + ∂σzz
∂z
∂ux 1 ∂ux ∂uy 1 ∂ux ∂uz
∂x 2 ∂y + ∂x 2 ∂z + ∂x
1 ∂uy ∂ux ∂uy 1 ∂uy ∂uz
ε= 2 ∂x + ∂y ∂y 2 ∂z + ∂y
1 ∂uz ∂ux 1 ∂uz ∂uy ∂uz
2 ∂x + ∂z 2 ∂y + ∂z ∂z

161. ´
B.2. COORDONNEES POLAIRES 155
B.2 Coordonn´es polaires
e
Coordonn´es : r, θ, z, Accroissements : dr, rdθ, dz, Longueur : ds2 = dr2 + r2 dθ2 + dz 2
e
B.2.1 Scalaire φ
∂φ
→
− ∂r
∂2φ ∂2φ
F = Gradφ = ∂φ
r∂θ
∆φ = 1 ∂
r ∂r r ∂φ +
∂r r2 ∂θ2
+ ∂z 2
∂φ
∂z
B.2.2 Vecteur u
∂ur 1 ∂ur ∂ur
∂r r ∂θ − uθ ∂z
G = Grad→ =
−
u ∂uθ 1 ∂uθ
+ ur ∂uθ Div→ = Trε =
−
u 1 ∂rur
r ∂r + ∂uθ
r∂θ + ∂uz
∂z
∂r r ∂θ ∂z
∂uz 1 ∂uz ∂uz
∂r r ∂θ ∂z
∂ 2 ur ∂ 2 ur 2∂uθ
∂uz
− ∂uθ 1
r
∂
∂r r ∂ur +
∂r r2 ∂θ2
+ ∂z 2
− r2 ∂θ
− ur
r2
r∂θ ∂z
Rot→ =
−
u ∂ur
∂z − ∂uz
∂r ∆→ =
−
u 1
r
∂
∂r r ∂uθ +
∂r
∂ 2 uθ
r2 ∂θ2
+ ∂ 2 uθ
∂z 2
+ 2∂ur
r2 ∂θ
− uθ
r2
∂uθ ∂ur uθ
∂r − r∂θ + r
1 ∂
r ∂uz + ∂ 2 uz
+ ∂ 2 uz
r ∂r ∂r r2 ∂θ2 ∂z 2
B.2.3 Contrainte σ et D´formation ε
e
∂σrr
∂r + 1 ∂σrθ
r ∂θ + ∂σrz
∂z + σrr −σθθ
r
∂σrθ 1 ∂σθθ ∂σθz
DivD σ = ∂r + r ∂θ + ∂z + 2σrθ
r
∂σrz 1 ∂σθz ∂σzz
∂r + r ∂θ + ∂z + σr
rz
∂ur 1 1 ∂ur ∂uθ 1 ∂ur ∂uz
∂r 2 r ∂θ − uθ + ∂r 2 ( ∂z + ∂r )
ε= 1 1 ∂ur ∂uθ 1 ∂uθ 1 ∂uθ 1 ∂uz
2 r ∂θ − uθ + ∂r r ∂θ + ur 2 ( ∂z + r ∂θ )
1 ∂ur ∂uz 1 ∂uθ 1 ∂uz ∂uz
2 ( ∂z + ∂r ) 2 ( ∂z + r ∂θ ) ∂z

162. 156 ´ ´
ANNEXE B. OPERATEURS DIFFERENTIELS - FORMULAIRE
B.3 Coordonn´es sph´riques
e e
Coordonn´es : r, θ, ϕ, Accroissements : dr, rdθ, r sin θdϕ, Longueur : ds2 = dr2 ++r2 dθ2 +r2 sin 2θdϕ2
e
B.3.1 Scalaire φ
∂φ
∂r
→
− ∂φ ∂2φ
F = Gradφ = r∂θ ∆φ = 1 ∂
r2 ∂r
r2 ∂φ +
∂r
1 ∂
r2 sin θ ∂θ
sin θ ∂φ +
∂θ
1
r2 sin2 θ ∂ϕ2
∂φ
r sin θ∂ϕ
B.3.2 Vecteur u
∂ur 1 ∂ur 1 ∂ur uϕ
∂r r ∂θ − uθ r sin θ ∂ϕ − r
G = Grad→ =
−
u ∂uθ
∂r
1 ∂uθ
r ∂θ + ur 1
r sin θ
∂uθ
∂ϕ −
uϕ
r cotgθ
∂uϕ 1 ∂uϕ 1 ∂uϕ ur uθ
∂r r ∂θ r sin θ ∂ϕ + r + r cotgθ
1 ∂(r2 ur ) 1 ∂(uθ sin θ) 1 ∂uϕ
Div→ = Trε =
−
u 2
+ +
r ∂r r sin θ ∂θ r sin θ ∂ϕ
∂(uϕ sin θ) 2 1 ∂(uθ sin θ) 1 ∂uϕ
1
r sin θ ∂θ − ∂uθ
∂ϕ
∆ur − r2
ur + sin θ ∂θ + sin θ ∂ϕ
Rot→ =
−
u 1 ∂ur
r sin θ ∂ϕ
∂(ru )
− 1 ∂rϕ
r
∆→ =
−
u ∆uθ + 2
r2
∂ur uθ cos θ ∂uϕ
∂θ − 2 sin2 θ − sin2 θ ∂ϕ
1 ∂(ruθ ) ∂ur 2 ∂ur ∂uθ uϕ
r ∂r − ∂θ ∆uϕ + r2 sin2 θ ∂ϕ + cotgθ ∂ϕ − 2 sin θ
B.3.3 Contrainte σ et D´formation ε
e
∂σrr 1 ∂σrθ 1 ∂σrϕ 1
∂r + r ∂θ + r sin θ ∂ϕ + r (2σrr − σθθ − σϕϕ + σrθ cotgθ)
∂σrθ 1 ∂σθθ 1 ∂σθϕ 1
DivD σ = ∂r + r ∂θ + r sin θ ∂ϕ + r (3σrθ + (σθθ − σϕϕ )cotgθ)
∂σrϕ 1 ∂σθϕ 1 ∂σϕϕ 1
∂r + r ∂θ + r sin θ ∂ϕ + r (3σrϕ + 2σθϕ cotgθ)
∂ur 1 1 ∂ur ∂uθ 1 1 ∂ur uϕ ∂uϕ
∂r 2 r ∂θ − uθ ∂r 2 r sin θ ∂ϕ − r + ∂r
1 1 ∂ur ∂uθ 1 ∂uθ 1 1 ∂uθ uϕ 1 ∂uϕ
ε= 2 r ∂θ − uθ ∂r r ∂θ + ur 2 r sin θ ∂ϕ − r cotgθ + r ∂θ
1 1 ∂ur uϕ ∂uϕ 1 1 ∂uθ uϕ 1 ∂uϕ 1 ∂uϕ ur uθ
2 r sin θ ∂ϕ − r + ∂r 2 r sin θ ∂ϕ − r cotgθ + r ∂θ r sin θ ∂ϕ + r + r cotgθ

163. Annexe C
Bibliographie
M´canique du solide et des mat´riaux
e e
Les ouvrages de base introduisent de mani`re simple avec un formalisme tr`s l´ger les concepts
e e e
fondamentaux de la M´canique du solide et de la Science des mat´riaux.
e e
S’il ne faut lire qu’un ouvrage, c’est celui de Gordon, Structures et Mat´riaux. En seconde position
e
viennent les deux tomes Mat´riaux de Ashby et Jones, Propri´t´s et applications et Mat´riaux, mi-
e ee e
crostructure et mise en œuvre. En troisi`me position du tierc´ les deux tomes Elasticit´ et Plasticit´
e e e e
et Comportement m´canique des mat´riaux de Fran¸ois, Zaoui et Pineau, certes plus approfondis et
e e c
plus calculatoires mais toujours tr`s physiques.
e
Ouvrages de base
• Means, Stress and Strain (basic concepts for geologists), Springer Verlag (1976).
• J.E. Gordon, Structures et Mat´riaux, Pour la Science Belin (1994).
e
• M.F. Ashby, D.R.H. Jones, Mat´riaux : Propri´t´s et applications, Dunod (1996).
e ee
Pour en savoir plus
• S.Timoshenko, Th´orie de l’´lasticit´, B´ranger (1948).
e e e e
• S.Timoshenko, R´sistance des mat´riaux (tomes I et II) B´ranger (1947).
e e e
• L.Landau, E.Lifchitz, Th´orie de l’´lasticit´, Editions MIR (1990).
e e e
• E. Dieulesaint, D. Royer, Ondes ´lastiques dans les solides, Masson (1974).
e
´
• D.Fran¸ois,A. Pineau, A. Zaoui, Elasticit´ et Plasticit´, Herm`s (1992).
c e e e
• J. Mandel, Propri´t´s m´caniques des mat´riaux Eyrolles (1978).
ee e e
• M.F. Ashby, D.R.H. Jones, Mat´riaux : Microstructure et mise en forme, Dunod (1996).
e
• D.Fran¸ois,A. Pineau, A. Zaoui, Comportement m´canique des mat´riaux, Herm`s (1992).
c e e e
• C.Bathias, J.P. Ba¨
ılon, La fatigue des mat´riaux et des structures, Herm`s (1997).
e e
157