Le document traite des milieux granulaires, qui présentent des caractéristiques à la fois solides et liquides, et explore leur comportement à travers des expériences et modélisations. Il décrit comment les contraintes sont transmises dans ces milieux, en mettant en avant le modèle de Janssen pour comprendre la pression dans un silo. Les observations réalisées montrent la complexité des écoulements denses de matériaux granulaires et leur dualité dans des états variés.

1. Les milieux granulaires : entre fluide et solide
dossier personnel
Benoit Halinger, Steren Giannini
20 juin 2006
Table des mati`res
e
Introduction 2
Notions pr´liminaires
e 2
0.1 D´finition d’un milieu granulaire . . . . . . . . . . . . . . . . . . . . . . .
e 2
0.2 Tenseurs de contraintes . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2
1 L’effet de voˆ te
u 3
1.1 La propagation des contraintes . . . . . . . . . . . . . . . . . . . . . . . . 3
1.2 L’exp´rience du silo . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
e 4
1.3 Mod´lisation physique : Approche de Janssen . . . . . . . . . . . . . . .
e 8
2 Les Ecoulements denses 9
2.1 Observations . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10
2.1.1 Exp´rience du plan inclin´
e e . . . . . . . . . . . . . . . . . . . . . . 10
2.1.2 Exp´rience du tambour . .
e . . . . . . . . . . . . . . . . . . . . . . 12
2.2 Mod´lisation des ´coulements . .
e e . . . . . . . . . . . . . . . . . . . . . . 12
2.2.1 le tas de sable . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12
2.2.2 Equations moyenn´es dans
e l’´paisseur
e . . . . . . . . . . . . . . . . 15
Conclusion 18
Bibliographie 19
Contacts 19
Annexe 20
1

2. 0.1 D´finition d’un milieu granulaire
e `
TABLE DES MATIERES
Introduction
Au repos ou en ´coulement, la mati`re en grains ne manque pas de surprendre par ses
e e
propri´t´s particuli`res entre solides et liquides...
ee e
Les enjeux
Les mat´riaux granulaires sont pr´sents dans de nombreux secteurs industriels, cepen-
e e
dant leur ´tude reste tr`s r´cente. La description de leur comportement et la compr´hen-
e e e e
sion des ph´nom`nes observ´s est donc primordiale.
e e e
Une dualit´ Liquide/Solide
e
Le grand nombre de particules constituantes et la complexit´ des interactions de
e
contact conduisent ` une multitude de comportements diff´rents. Ainsi les milieux gra-
a e
nulaires existent sous plusieurs ´tats.
e
On observe donc un comportement solide sous certaines solicitations, liquide sous
d’autres, mais ´galement des comportements ayant simultan´ment les propri´t´s de ces
e e ee
deux ´tats.
e
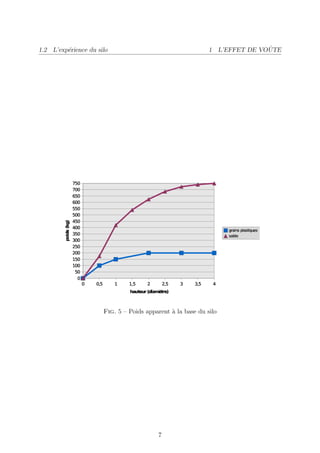
Le sablier
L’observation anodine d’un sablier soul`ve ` elle seule de multiples interrogations :
e a
Contrairement ` la clepsydre, pourquoi le sablier conserve-t-il un d´bit constant ? Pour-
a e
quoi le tas inf´rieur garde-t-il le mˆme angle de talus au cours du remplissage ?
e e
Notions pr´liminaires
e
0.1 D´finition d’un milieu granulaire
e
On appelle ici un milieu granulaire un milieu form´ d’une collection de particules
e
macroscopiques de taille sup´rieure ` 100µm. En minorant la taille de ces grains, on peut
e a
n´gliger les forces de Van der Walls, les ponts capillaires, les mouvements browniens et
e
les forces ´lectrostatiques entre les particules.
e
0.2 Tenseurs de contraintes
On souhaite d´crire le milieu granulaire comme un mat´riau continu. On introduit
e e
alors le tenseur des contraintes, qui repr´sente les forces surfaciques s’exer¸ant sur lui.
e c
On le d´finit pour un ´l´ment rectangulaire ´l´mentaire de mat´riau.[cf sch´ma 1]
e ee ee e e
En deux dimensions, les composantes du tenseur des contraintes sont les suivantes :
– σxx la composante normale, selon − , des forces surfaciques s’exer¸ant sur les faces
→
ex c
verticales
– σzz la composante normale, selon − , des forces s’exer¸ant sur les faces horizontales
→ez c
– σxz la composante tangentielle (force de cisaillement), selon − , des forces s’exer¸ant
→
ez c
sur les faces verticales
2

3. ˆ
1 L’EFFET DE VOUTE
Fig. 1 – Le tenseur des contraintes en 2 dimensions
– σzx la composante tangentielle (force de cisaillement), selon − , des forces s’exer¸ant
→
ex c
sur les faces horizontales.
D’un point de vue m´canique, c’est le mode de transmission des contraintes qui d´-
e e
termine l’´tat physique du milieu. Dans le cas d’un liquide, les contraintes tangentes sont
e
nulles, et les contraintes normales sont ´galement transmises dans toutes les directions et
e
dans tout le milieu. Dans le cas d’un solide, au contraire, les contraintes tangentes sont
souvent non-nulles et σxx peut ˆtre diff´rent de σzz (une telle diff´rence, la contrainte
e e e
d´viatorique, met syst´matiquement un liquide en mouvement : les liquides ne peuvent
e e
pas transmettre de contrainte d´viatorique).
e
Les contraintes dans un milieu granulaire
Le caract`re bivalent des milieux granulaires, entre solides et liquides, se manifeste au
e
niveau des contraintes, puisque la contrainte d´viatorique y est g´n´ralement non-nulle,
e e e
mais il existe une valeur limite au-del` de laquelle le milieu s’´coule. (cette valeur est
a e
proportionnelle ` la pression moyenne σxx +σzz qui s’exerce sur le milieu, ce qui explique
a 2
que lorsque l’on appuie sur un tas de sable, on s’enfonce, mais au fur et ` mesure la
a
pression est de plus en plus importante, le milieu s’´coule de moins en moins, le sable
e
devient solide sous la pression du doigt !)
1 L’effet de voˆ te
u
1.1 La propagation des contraintes
Lorsqu’un ensemble de grains est mis sous contrainte, la transmission des forces est
tr`s inhomog`ne. Certains grains ne sont pratiquement pas sous contrainte, alors que
e e
toute la charge repose sur d’autres. Ces derniers font parties de ”chaines de forces” bien
marqu´es.
e
Une exp´rience consiste ` exercer une pression sur un empilement de cylindres consti-
e a
tu´ d’un mat´riau bir´fringeant. (voir photo 2. On peut observer les chaˆ de forces entre
e e e ınes
3

4. 1.2 L’exp´rience du silo
e ˆ
1 L’EFFET DE VOUTE
Fig. 2 – Exp´rience de photo´lasticit´
e e e
deux polariseurs crois´s : les cylindres sont d’autant plus lumineux qu’ils sont soumis `
e a
une contrainte importante. La r´partition des forces est manifestement tr`s h´t´rog`ne.
e e ee e
exp´rience en direct : effet de voˆte dans le tube d’efferalgan
e u
1.2 L’exp´rience du silo
e
Nous allons ici observer une cons´quence de cette propagation particuli`re des forces
e e
dans un mat´riau granulaire. L’exp´rience consiste ` mesurer le poids ` la base d’un
e e a a
silo contenant un volume d´termin´ de mati`re en grains. Les mat´riaux sont ´galement
e e e e e
un param`tre d’´tude : Nous avons utilis´ du sable sec dont les grains sont d’un dia-
e e e
m`tre moyen autour du millim`tre pour notre premi`re manipulation (photo 3a). Pour
e e e
la seconde, nous avons utilis´ des granul´s de plastique de forme cylindrique dont les
e e
dimensions sont de quelques millim`tres.(photo 3b)
e
Apr`s de multiples remaniments, le dispositif final de la manipulation est le suivant
e
(voir sch´ma de la figure 4) :
e
– un silo transparent gradu´ en ”diam`tres” reli´ solidement et d’une mani`re tr`s
e e e e e
rigide au sol.
– une balance pr´sice capable de soutenir un poids maximal d’environ 4kg.
e
– un syst`me de piston qui transmet les forces de pression ` la base du silo vers la
e a
balance. Celui-ci doit coulisser sans frotter dans le silo. Il est pr´sent pour ´viter les
e e
fuites de grains.
4

5. 1.2 L’exp´rience du silo
e ˆ
1 L’EFFET DE VOUTE
Fig. 3 – Pr´sentation des dispositifs
e
Fig. 4 – Sch´ma du dispositif
e
5

6. 1.2 L’exp´rience du silo
e ˆ
1 L’EFFET DE VOUTE
Mesure Hauteur Photo Sch´ma
e Poids apparent mesur´
e
sable grains plastiques
n1
˚ D 420g 150g
n3
˚ 2D 624 200g
n5
˚ 3D 700g 200g
Tab. 1 – R´capitulatif des observations
e
On observe alors plusieurs phases lors du remplissage progressif du silo (voir tableau
1 et courbes de la figure 5) : Pour de faibles hauteurs de grains, le poids mesur´ augmente
e
lin´airement avec le volume de grains vers´. Ce qui est tr`s naturel car c’est le cas des
e e e
fluides. Cependant au del` d’une hauteur de l’ordre de deux fois le diam`tre du silo, le
a e
poids mesur´ reste casiment toujours le mˆme. Il tend vers une valeur constante, ce qui
e e
diff`re des fluides ordinaires.
e
Ces ph´nom`nes observ´s d´coulent de la dualit´ liquide/solide qui r´git un mat´riau
e e e e e e e
granulaire : Une telle mati`re ne peut ˆtre d´crite comme un fluide classique dont le poids
e e e
est directement mesurable ` la base du r´cipient qui le contient, le mat´riau pr´sente donc
a e e e
simultan´ment des caract´ristiques d’un liquide et d’un solide.
e e
Sur le principe de la voˆte architecturale, le poids des grains est en partie support´ par
u e
les paroies du silo.
6

7. 1.2 L’exp´rience du silo
e ˆ
1 L’EFFET DE VOUTE
Fig. 5 – Poids apparent ` la base du silo
a
7

8. 1.3 Mod´lisation physique : Approche de Janssen
e ˆ
1 L’EFFET DE VOUTE
1.3 Mod´lisation physique : Approche de Janssen
e
On consid`re un silo cylindrique de diam`tre D remplit d’un mat´riau granulaire. Le
e e e
mod`le choisit a ´t´ propos´ par Janssen en 1895, il reste d’une grande simplicit´.
e ee e e
il est bas´ sur 3 hypoth`ses :
e e
1. les contraintes verticales σzz ne d´pendent que de la variable d’espace z
e
2. le milieu frotte sur les parois lat´rales et se trouve sur le point de glisser : T = µs N
e
(avec µs le coefficient de frottement statique)
3. la contrainte verticale σzz appliqu´e sur le mat´riaux engendre une contrainte hori-
e e
zontale σxx qui lui est directement proportionnelle : σxx = Kσzz . (K ´tant constante,
e
pour un fluide la pression est isotrope on aurait K = 1)
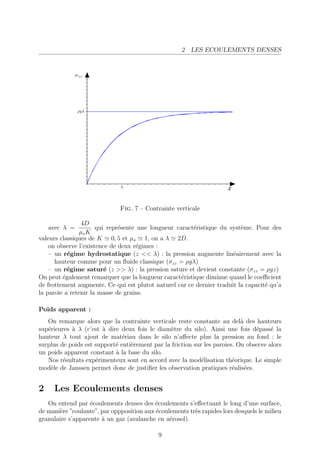
Equilibre d’une tranche ´l´mentaire de mat´riau [z, z + dz] :
ee e
Fig. 6 – Syst`me ´tudi´ : tranche cylindrique de diam`tre D
e e e e
bilan des efforts : poids, forces de pression en z et en z + dz, forces de frottement avec
la paroie.
En projetant le th´or`me fondamental de la statique sur l’axe vertical :
e e
πD2 πD2
ρgdz + (σzz |z − σzz |z+dz ) − πDdzT = 0 (1)
4 4
ce qui devient en utilisant les hypoth`ses :
e
dσzz 4Kµs
= ρg − σzz (2)
dz D
Sachant que σzz est nulle ` la surface z = 0, on en d´duit que la contrainte verticale
a e
σzz est donn´ par :
e
σzz (z) = ρgλ(1 − ez/λ ) (3)
8

9. 2 LES ECOULEMENTS DENSES
Fig. 7 – Contrainte verticale
4D
avec λ = qui repr´sente une longueur caract´ristique du syst`me. Pour des
e e e
µs K
valeurs classiques de K 0, 5 et µs 1, on a λ 2D.
on observe l’existence de deux r´gimes :
e
– un r´gime hydrostatique (z << λ) : la pression augmente lin´airement avec la
e e
hauteur comme pour un fluide classique (σzz = ρgλ)
– un r´gime satur´ (z >> λ) : la pression sature et devient constante (σzz = ρgz)
e e
On peut ´galement remarquer que la longueur caract´ristique diminue quand le coefficient
e e
de frottement augmente. Ce qui est plutot naturel car ce dernier traduit la capacit´ qu’a
e
la paroie a retenir la masse de grains.
Poids apparent :
On remarque alors que la contrainte verticale reste constante au del` des hauteurs
a
sup´rieures ` λ (c’est ` dire deux fois le diam`tre du silo). Ainsi une fois d´pass´ la
e a a e e e
hauteur λ tout ajout de mat´riau dans le silo n’affecte plus la pression au fond : le
e
surplus de poids est support´ enti`rement par la friction sur les paroies. On observe alors
e e
un poids apparent constant ` la base du silo.
a
Nos r´sultats exp´rimenteux sont en accord avec la mod´lisation th´orique. Le simple
e e e e
mod`le de Janssen permet donc de justifier les observation pratiques r´alis´es.
e e e
2 Les Ecoulements denses
On entend par ´coulements denses des ´coulements s’effectuant le long d’une surface,
e e
de mani`re ”coulante”, par oppposition aux ´coulements tr`s rapides lors desquels le milieu
e e e
granulaire s’apparente ` un gaz (avalanche en a´rosol).
a e
9

10. 2.1 Observations 2 LES ECOULEMENTS DENSES
2.1 Observations
Duplicit´ des angles
e
On constate exp´rimentalement que pour chaque type de grains, tous les tas form´s
e e
de ces grains ont un mˆme angle, appel´ angle de talus. Mais, au-del` de ce point de
e e a
vue statique, on remarque aussi que lors d’un ´coulement, sur un plan inclin´ ou dans un
e e
tambour par exemple, il existe deux angles : un angle de d´part ou d’avalanche, et un
e
angle d’arrˆt, plus petit.
e
Fig. 8 – L’angle de talus reste constant quelle qeue soit l’´chelle
e
2.1.1 Exp´rience du plan inclin´
e e
Pour mettre en ´vidence ces deux angles, nous avons r´alis´ un dispositif de plan in-
e e e
clin´.
e
On d´pose une couche de sable sur une plaque de bois recouverte de toile Emeri (pour la
e
rugosit´), dont on modifie l’inclinaison, jusqu’` ce que le milieu s’´coule. L’angle mesur´
e a e e
a
` la fin de l’avalanche est plus petit que l’angle de d´part.
e
Fig. 9 – L’exp´rience du plan inclin´ - Principe
e e
Ainsi on mesure un angle de stabilit´ maximum de 38 , et un angle de repos (ou
e ˚
d’arrˆt) de 34 .
e ˚
10

11. 2.1 Observations 2 LES ECOULEMENTS DENSES
Fig. 10 – Dispositif utilis´
e
Fig. 11 – R´sultats - angle de d´part et angle d’arret
e e
11

12. 2.2 Mod´lisation des ´coulements
e e 2 LES ECOULEMENTS DENSES
Fig. 12 – Exp´rience du tambour, dispositif de l’ENSIC
e
2.1.2 Exp´rience du tambour
e
particularit´s.. 2 zones apparaissent : une zone importante o` les grains tournent de
e u
concert avec le tambour, et une zone en forme de croissant o` les grains s’´coulent ` la
u e a
mani`re d’un fluide. / 2 angles diff´rents directmt visibles par exp´rience ` effectuer dvt
e e e a
jury.
2.2 Mod´lisation des ´coulements
e e
2.2.1 le tas de sable
Nous allons tenter dans ce paragraphe de simuler sommairement le comportement
d’un tas de sable.
Le syst`me ´tudi´ est un demi tas en 2 dimensions. Celui-ci est discr´tis´, il est
e e e e e
en r´alit´ repr´sent´ par une liste de valeurs, ces valeurs ´tant les hauteurs de chaque
e e e e e
”collonne de grains”.
Il est r´git par quelques r`gles simples qui vont d´terminer son ´volution :
e e e e
Une boucle dans le programme d´termine s’il doit y avoir effondrement ou non. Se-
e
lon la figure 13, la colonne de grains est jug´e instable si elle d´passe au moins de trois
e e
grains sa voisine. Dans ce cas l’effondrement entraine avec lui deux grains (voir plus si
la diff´rence ´tait sup´rieure ` 3). Ceci traduit l’existence de friction entre les grais : un
e e e a
grain qui s’effondre entraine avec lui d’autres grains.
On g´n`re ensuite un tas initialement stable avec un algorithme bas´ sur des choix
e e e
al´atoirs. Ce tas va maintenant ˆtre utils´ pour diverses simulations.
e e e
12

13. 2.2 Mod´lisation des ´coulements
e e 2 LES ECOULEMENTS DENSES
Fig. 13 – R`gles simples r´gissant le syst`me
e e e
´crans
e observations
Tas initial g´n´r´, au repos.
e ee
Tas apr`s le d´clanchement d’une avalanche, au repos.
e e
Superposition des deux r´sultats pr´c´dents :
e e e
on constate que l’angle du tas apr`s l’avalanche
e
est inf´rieur ` l’angle initial.
e a
Tab. 2 – Angles du tas avant et apr`s une avalanche
e
La premi`re simulation est la suivante : nous cr´ons une perturbation en ajoutant un
e e
ou deux grains ` une hauteur donn´e. Ainsi cette perturbation va, ` l’it´ration suivante,
a e a e
d´clancher une avalanche suivant les r`gles initiales. Le syst`me ´volue alors jusqu’` une
e e e e a
situation de repos apr`s un certain nombre d’it´rations.
e e
L’objectif est ici de comparer l’angle avant l’avalanche et l’angle apr`s l’avalanche. Les
e
r´sultats de la simulation sont pr´sent´s dans la tableau 2.
e e e
Cette simple simulation num´rique aboutit ainsi au mˆme r´sultat que nos observations
e e e
initiles du plan inclin´.
e
La seconde simulation consiste ` ”d´verser” en continue une certaine quantit´ de grains
a e e
au sommet du tas. Nos observations se limitent ` l’observation de la g´om´trie du tas.
a e e
13

14. 2.2 Mod´lisation des ´coulements
e e 2 LES ECOULEMENTS DENSES
´crans
e observations
Tas initial g´n´r´, au repos.
e ee
Tas apr`s l’ajout d’une grande
e
quantit´ de grains a son sommet.
e
Tab. 3 – Angle de talus ` diff´rente ´chelles
a e e
Comme pour la simulation pr´cd´dente, des avalanches ont lieu. On constate cepen-
e e
dant (voir tableau 3) que les tas ainsi cr´´s poss`dent r´guli`rement le mˆme angle que
ee e e e e
le tas initial. Il sagit de l’angle maximal observable.
Ceci n’est autre que l’observation de l’existence d’un angle de talus : peu importe la taille
du tas consid´r´, l’angle maximal qu’on peu esp´rer atteindre reste le mˆme.
ee e e
14

15. 2.2 Mod´lisation des ´coulements
e e 2 LES ECOULEMENTS DENSES
2.2.2 Equations moyenn´es dans l’´paisseur
e e
Les ´quations moyenn´es de l’´paisseur, ´tablies en 1989, permettent de rendre compte
e e e e
de l’´volution de l’´coulement d’un milieu granulaire sur un plan inclin´ d’un angle θ.
e e e
Fig. 14 – description du syst`me ´tudi´
e e e
Conservation de la masse
On consid`re un volume virtuel τ , fixe dans l’espace, limit´ par une surface ferm´e Σ,
e e e
et plong´ dans un fluide en d´placement dont la densit´ est ρ et la vitesse − . Pendant
e e e →v
un temps dt, la masse m pr´sente dans ce volume varie donc d’une quantit´
e e
dm d ∂ρ
= ρdV = dV (4)
dt dt τ τ ∂t
puisque le volume est fixe dans l’espace.
∂ρ
de plus l’hypoth`se d’incompressibilit´ assure que
e e = 0. Donc imm´diatement
e
∂t
dm
=0 (5)
dt
−−
→ − →
−
→
or l’´l´ment de surface d2 S de Σ est travers´ par un flux de masse ρ d2 S − dt. On peut
ee e v
donc ´crire
e
dm
= − →− −
→
ρ − d2 S
v (6)
dt Σ
15

16. 2.2 Mod´lisation des ´coulements
e e 2 LES ECOULEMENTS DENSES
D’o` en utilisant le th´or`me d’Ostrogradsky
u e e
div(ρ − )dV = 0
→
v (7)
τ
ceci ´tant valable pour tout volume τ , on en d´duit
e e
div − = 0
→
v (8)
ce qui s’´crit encore dans le cas de notre probl`me plan, avec − = u(x, z, t, ) − +v(x, z, t) − ,
e e →
v →
ex →
ez
∂u ∂v
+ =0 (9)
∂x ∂z
Conservation de la quantit´ de mouvement
e
∂ρ −
→
v →→ − −
→ −−
→ →
−
dV = − ρ − (− . d2 S)
v v + [σ] d2 S + F dV
τ ∂t Σ Σ τ
quantite de mouvement f lux de la quantite de mouvement f orces de surf ace f orces de volume (poids ρ − )
→
g
(10)
Nous allons ramener chaque int´grale surfacique en int´grale volumique en utilisant
e e
le th´or`me d’Ostrogradsky
e e
Concernant les forces de surface :
−−
→ −→
[σ] d2 S = div[σ]dV (11)
Σ τ
−→ ∂σxx ∂σxy ∂σxz
o` (div[σ])x =
u + +
∂x ∂y ∂z
Concernant le flux de la quantit´ de mouvement :
e
→→ −
v v
−
→
ρ − (− . d2 S) =
→
−→
div(ρvx v) − +div(ρvy − ) − +div(ρvz − ) − dV )(12)
ex → →
v ey → →
v ez
Σ τ
= → −→ →
v
−
ρ(− . grad)(− ) + − div(ρ − ) dV
v →
v →
v (13)
τ
= → −→ →
v
−
ρ(− . grad)(− )dV
v (14)
τ
Ainsi on tire de (10) :
∂ρ −→
v → −→ →
− −→ →
−
= −ρ(− . grad)(− ) + div[σ] + F
v v (15)
∂t
on reconnait ici la d´riv´e particuli`re
e e e
Dρ −
→
v −→ →
−
= div[σ] + F (16)
Dt
16

17. 2.2 Mod´lisation des ´coulements
e e 2 LES ECOULEMENTS DENSES
Equations des ´coulements
e
la conservation de la masse et de la quantit´ de mouvement donnent donc les trois
e
´quations suivantes dans le cas de notre probl`me plan
e e
∂u ∂v
+ =0 (17)
∂x ∂z
∂u ∂u ∂u ∂σxx ∂σxz
ρ +u +v = ρg sin θ − − (18)
∂t ∂x ∂z ∂x ∂z
∂v ∂v ∂v ∂σxz ∂σzz
ρ +u +v = −ρg cos θ − − (19)
∂t ∂x ∂z ∂x ∂z
L’obtention des ´quations moyenn´es s’effectue en deux ´tapes. La premi`re ´tape
e e e e e
consiste ` utiliser l’hypoth`se de couche mice pour n´gliger des termes dans les ´quations
a e e e
pr´c´dentes. La seconde ´tape consiste ` int´grer les ´quations le long de z.
e e e a e e
Afin de pouvoir comparer les ordres de grandeur des diff´rents termes des ´quations
e e
pr´c´dentes, des variables adimensionn´es not´es avec une tilde sont introduite. L’´chelle
e e e e e
de grandeur selon x est not´e L et l’´chelle de l’´paisseur de la couche est H. l’hypoth`se
e e e e
de couche mince signifie que le param`tre = H/L est petit. l’adimensionnement est
e
choisi comme suit :
x = xL
˜ z = zH
˜ ˜
t = t g/L
u = u g/L
˜ v = v g/L
˜
σxx = σ˜ ρgH cos θ σzz = σ˜ ρgH cos θ σxz = σ˜ ρgH sin θ
xx zz xz
l’addimentionnement permet donc de transformer les ´quations de conservation de la
e
forme :
∂ u ∂˜
˜ v
+ =0 (20)
∂x ∂z
˜ ˜
∂u
˜ ∂u
˜ ∂u
˜ ∂ σ˜
xx ∂ σ˜
xz
+u˜ +v˜ = sin θ − cos θ − sin θ (21)
˜
∂t ∂x
˜ ∂z
˜ ∂x˜ ∂z˜
∂˜
v ∂˜
v ∂˜
v ∂ σ˜
xz ∂ σ˜
zz
+u ˜ +v = − cos θ − sin θ − cos θ (22)
˜
∂t ∂x
˜ ∂z
˜ ∂x˜ ∂z˜
Si on n´glige
e la derni`re ´quation (22) devient
e e
∂ σ˜
zz
= −1 (23)
∂z˜
par int´gration de cette ´quation, en consid´rant que la pression est nulle ` l’interface,
e e e a
on obtient l’expression de la pression verticale dimensionn´e :
e
σzz = ρg cos θ(h − z) (24)
17

18. 2.2 Mod´lisation des ´coulements
e e 2 LES ECOULEMENTS DENSES
Obtention des ´quations finales
e
Dans le but d’obtenir les ´quations finale, il faut maintenant int´grer les ´quations
e e e
suivant z.
En ce qui concerne l’´quation (20) qui traduit la conservation de la masse, on utilise
e
∂h
le fait que v = , ainsi en int´grant suivant z :
e
∂t
∂h ∂(hu)
+ =0 (25)
∂t ∂x
Pour les ´quations de la conservation de la quantt´ de mati`re,nous supposons de plus
e e e
que la contrainte normale horizontale est proportionnelle ` la contrainte normale verti-
a
cale : σxx = kσzz . Pour une pression isotrope : k = 1, ce qui est le cas pour les fluides.
Concernant les milieux granulaires cette hypoth`se n’a rien d’´vident.
e e
Donc en utilisant σzz = ρg cos θ(h − z) et σxx = kσzz , l’´quation (18) devient donc :
e
∂u ∂u ∂u ∂h ∂τ 1
ρ +u +v = ρg cos θ tan θ − k − (26)
∂t ∂x ∂z ∂x ∂z ρg cos θ
en notant τ = σxz
On utilise enfin le fait que dans l’hypoth`se de la couche mince, la vitesse selon ex est
e
ind´pendante de z. Ainsi par int´gration suivant z :
e e
∂u ∂u ∂h τ
ρh +u = ρgh cos θ tan θ − k − (27)
∂t ∂x ∂x ρgh cos θ
La contrainte interfaciale τ qui traduit la rh´ologie du mat´riau peut, ` l’aide d’une
e e a
loi de friction, ˆtre remplac´e par µρgh cos θ, ie une contrainte tangentielle proporionnelle
e e
a
` la contrainte normale. µ repr´sente ici le coefficient de friction.
e
Finalement les ´quations moyenn´es dans l’´paisseur sont :
e e e
∂h ∂(hu)
+ =0 (28)
∂t ∂x
∂u ∂u ∂h
ρh +u = ρgh cos θ tan θ − k −µ (29)
∂t ∂x ∂x
On interpr`te ais´ment la derni`re ´quation (29) : l’acc´l´ration est compens´e par
e e e e ee e
une force de gravit´, une force de friction au fond et une force d’´talement.
e e
Conclusion
Finalement, les milieux granulaires, de par leur mode particulier de transmission des
contraintes, par les voˆtes qui les soudent mais qui sont boulervers´es ` la moindre per-
u e a
turbation, font preuve d’une dualit´ liquide/solide. Tas solide ou grains qui s’´coule dans
e e
18

19. 2.2 Mod´lisation des ´coulements
e e 2 LES ECOULEMENTS DENSES
un sablier, les comportements ´tranges des milieux granulaires se rencontrent aussi au
e
niveau de leurs ´coulements, que ce soit sur un plan ou dans un tambour.
e
D’autres domaines d’´tude concernant les milieux granulaires existent. Parmis eux
e
figurent l’´tude des interactions entre particules, les ph´nom`nes de s´gr´gation, de com-
e e e e e
paction, de dilatance, de r´sistance au cisaillement...
e
On parvient ` mod´liser des avalanches, et ` approcher les ´quations qui r´gissent
a e a e e
ces ´coulements, n´anmoins, leur port´e est tr`s limit´e. Les conditions d’applications,
e e e e e
les approximations utilis´es empˆchent toute g´n´ralisation. Par exemple, on s’est rendu
e e e e
compte que des mod´lisations effectu´es pour des ´coulements en tambour pour une cer-
e e e
rayon du tambour
taine tranche de rapports dimension des grains n’avaient plus de valeur pour des rapports
diff´rents. De nombreuses difficult´s restent ` surmonter, et aucune th´orie g´n´rale n’a
e e a e e e
encore ´t´ ´tablie dans cette science tr`s jeune mais tr`s dynamique.
eee e e
Et pour cause, ses applications dans l’industrie sont consid´rables : on estime que
e
70 % des produits fabriqu´s passent ` un moment au moins de leur ´laboration par un
e a e
stade granulaire. De l’activit´ mini`re ` la fabrication du b´ton, de l’industrie chimique ou
e e a e
pharmaceutique ` l’agroalimentaire, en passant par la mod´lisation des ´coulements py-
a e e
roclastiques et mˆme le broyage [(dont le cout global est sup´rieur ` celui du transport !)],
e e a
tous les domaines sont concern´s.e
Bibliographie
– La physique des tas de sable - Ph. Claudin - EDPscience - 1999
– Les milieux granulaires - O.Pouliquen - Cours de l’ENSTA - 2001
– Du sac de billes au tas de sable - Etienne Guyon, Jean-Paul Troadec - Odile
Jacob - 1994
– M´canique g´n´rale : Elastostatique - Ecole nationale sup´rieure de l’a´ronau-
e e e e e
tique et de l’espace - 1973
– sujets de concours : ´cole polytechnique - 1999 - ´cole normale sup´rieure de
e e e
Cachan - 2002
Contacts
V´ronique Falk, Enseignant-chercheur ` l’ENSIC Nancy
e a
19

20. 2.2 Mod´lisation des ´coulements
e e 2 LES ECOULEMENTS DENSES
Annexe
Code source du programme ”avalanche” ti-89
:Prgm
:
:EffDess
:0->ymin :hauteur->ymax
:0->xmin :hauteur->xmax
:
:{hauteur}->l
:Lign 1,0,1,hauteur
:
:hauteur->h
:While h <> 1: h-nbrAl´at(2)->h: augmente(l,{h})->l: dim(l)->di: Lign di,0,di,l[di]
e
:EndWhile
:Pause
:
:Prompt perturb :Lbl c
:l[perturb]+2->l[perturb] :Lign perturb,0,perturb,l[perturb]
:
:For i,2,dim(l),1
:If l[i-1]-l[i]=3 Then
:l[i-1]-2->l[i-1] :Lign i-1,l[i-1],i-1,l[i-1]+2,0 :l[i]+2->l[i]
:Lign i,l[i]-2,i,l[i],1
:
:ElseIf l[i-1]-l[i]=4 Then
:l[i-1]-3->l[i-1] :Lign i-1,l[i-1],i-1,l[i-1]+3,0 :l[i]+3->l[i]
:Lign i,l[i]-3,i,l[i],1
:
:ElseIf l[i-1]-l[i]>4 Then
:l[i-1]-4->l[i-1] :Lign i-1,l[i-1],i-1,l[i-1]+4,0 :l[i]+4->l[i]
:Lign i,l[i]-4,i,l[i],1
:EndIf
:EndFor
:
:Goto c
:
:EndPrgm
20