Le document est un livret de cours de mathématiques pour la classe de 6e, contenant 12 séquences qui couvrent divers concepts mathématiques tels que les nombres décimaux, les angles, et la proportionnalité. Chaque séquence est structurée en séances d'une heure et inclut des conseils de travail et des exercices de différents niveaux de difficulté. Le contenu est protégé par des droits d'auteur, et son utilisation est réservée à un usage personnel uniquement.














![— © Cned, Mathématiques 6e16
Enfin, pour terminer cette séance, voici un peu de calcul mental :
Ajouter 24, c’est ajouter 20 puis 4. Ajouter 36 c’est ajouter 30 puis 6.
Utilise cette méthode pour trouver mentalement les réponses ci-dessous :
123 + 24 = ............. 53 + 36 = ............. 432 + 63 = ............. 215 + 81 = ..............
Réponse:
123+24=14753+36=89432+63=495215+81=296
Séance 4
Je découvre le segment.
Je différencie droite, demi-droite et segment.
Pour commencer cette séance, tu vas continuer la recherche du trésor.
Exercice 17 La Carte au Trésor – suite –
Indication du pirate : « Tu as été trop loin : il faut revenir sur tes pas. Pour poursuivre ta
recherche, tu dois rejoindre le Ravin qui se trouve à la croisée de deux pistes » :
• celle sur laquelle tu te trouves
• la piste rectiligne limitée par l’Ours pétrifié et l’Arbre à thé.
• Note O le point représentant l’Ours Pétrifié et A celui de l’Arbre à Thé.
• Représente la piste rectiligne partant de O et allant jusqu’au point A. Tu viens de tracer
un segment.
On le note [OA] ou [AO] car un segment n’a pas « de sens ».
• Le segment [OA] et la demi-droite [DS) se coupent en R, le point recherché qui
représente le Ravin. Marque le point R.
Nous nous rendons alors au point R pour poursuivre notre recherche.
Tu viens de re-découvrir la notion de segment. Recopie sa définition sur ton cahier de cours à la
suite de ce qui était écrit précédemment :
Segment :
La partie de la droite (AB) comprise entre les points A
B
A et B est appelé le segment d’extrémités A et B. A ∈ [AB] B ∈ [AB]
On le note [AB] ou [BA].
On mesure la longueur d’un segment avec une règle graduée.
On note AB ou BA la longueur du segment [AB].
Les phrases suivantes ont la même signification :
« Le segment [AB] mesure 4 cm. »
ou « La longueur du segment [AB] est égale à 4 cm. »
ou « AB = 4 cm. »
Attention : il ne faut pas confondre [AB] qui désigne un segment et AB qui désigne un nombre
(puisque c’est une longueur).
Remarque : On utilise deux crochets lorsqu’on nomme un segment afin de rappeler qu’un segment
est limité à ses deux extrémités et que les deux extrémités appartiennent au segment.
je retiens
Séquence 1 — séance 4
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-16-320.jpg)
![© Cned, Mathématiques 6e — 17
Effectue directement ci-dessous l’exercice d’application suivant :
Exercice 18
1-
A B
On a représenté le segment d’extrémités
.............. et ............... .
On le note .............. ou ...............
AB = .............. cm.
2- C
D
On a représenté le segment d’extrémités ....
et ............... .
On le note .............. ou ..............
.............. = .............. cm.
3-
E
F On a représenté le segment d’extrémités ....
.............. et ............... .
On le note .............. ou ..............
.............. = .............. cm.
4-
G H I Trace en bleu le segment [GH].
GH = .......... cm.
5-
J
K L
Trace en bleu le segment [KL].
KL = .......... cm.
Effectue l’exercice 19 ci-dessous directement sur le livret.
Exercice 19
Sur cette figure sont représentés :
CD
E
• la droite .................................
• la demi-droite ........................
• le segment ..............................
Prends maintenant ton cahier d’exercices, note « exercice 20 », et effectue-le.
Exercice 20
Place deux points R et S. Trace en bleu la demi-droite [RS). Trace en vert la demi-droite
[SR).
a) Que représente la partie coloriée en bleu ou en vert ?
b) Que représente la partie coloriée à la fois en bleu et en vert ?
Effectue l’exercice 21 suivant directement sur le livret.
Séquence 1séance 4 —
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-17-320.jpg)
![— © Cned, Mathématiques 6e18
Exercice 21
On a représenté quatre points P, Q, R et S.
P
Q
R
S
Trace et nomme tous les segments ayant
pour extrémités deux de ces points.
Effectue l’exercice suivant directement sur le livret.
Exercice 22
Observe la figure ci-contre puis complète en remplaçant
B
A
C
D
F
E
les pointillés par ∈ ou ∉.
E ..............[AB] E ............. [AB) E ............. (AB)
F ..............[BC] F ............. [BC) F ............. (BC)
D .............[AC] D ........... [AC) D............. (AC)
A .............[CA]
Prends ton cahier d’exercices, note « exercice 23 » et effectue l’exercice ci-dessous :
Exercice 23
Place trois points A, B et C.
1- Trace un point M tel que : M ∉ [AB] et M ∈ [AB).
2- Trace un point N tel que : N ∈ [BC].
3- Trace un point P tel que P appartienne à [NB) et P n’appartienne pas à [BN].
4- Trace (MN), [NA] et [PM).
Nous allons maintenant apprendre ensemble à tracer un segment dont on connaît la longueur.
Lis attentivement la méthode commentée ci-dessous.
je comprends la méthode
Tracer un segment [AB] tel que AB = 5 cm
1ère
étape : On prend une règle graduée et on trace un trait allant de la graduation 0 à la graduation 5.
0 1 2 3 4 5 6 7 8 9 10
2ème
étape : On trace deux petits « traits » aux extrémités et on note le nom des points : A et B. On
peut enfin noter la longueur « au-dessus du segment », soit ici 5 cm ou bien seulement 5 (si l’unité est
le centimètre). Tu n’es pas obligé de représenter un segment horizontal : tu peux le tracer où tu veux, et
dans n’importe quelle direction.
A B5 cm
Séquence 1 — séance 4
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-18-320.jpg)
![© Cned, Mathématiques 6e — 19
Maintenant que tu sais représenter un segment dont on connaît la longueur, entraîne-toi en
effectuant l’exercice 24 sur ton cahier d’exercices. N’oublie pas avant de commencer par écrire
« Exercice 24 ».
Exercice 24
a) Trace un segment [EF] tel que EF = 7 cm.
b) Trace un segment [EG] tel que EG = 3 cm.
c) Trace un segment [FH] tel que FH = 4,5 cm
Enfin, pour terminer cette séance, voici un peu de calcul mental :
Ajouter 19, c’est ajouter 20 puis retrancher 1. Ajouter 29, c’est ajouter 30 puis retrancher 1.
Utilise cette méthode pour trouver mentalement les réponses ci-dessous.
64 + 19 =................... 67 + 29 =................... 137 + 49 =................. 248 + 39 =.................
Réponse:
64+19=8367+29=96137+49=186248+39=287
Séance 5
Je découvre le milieu d’un segment
Exercice 25
a) Trace un segment [CD] tel que CD = 8 cm.
b) Place sur ce segment le point I tel que CI = 4 cm.
c) Détermine la longueur DI (déterminer veut dire calculer).
d) Que peux-tu dire des longueurs CI et DI ?
Recopie sur ton cahier de cours, à la suite de ce que tu as déjà écrit :
Définition du milieu d’un segment :
Le milieu I du segment [AB] est le seul point du segment [AB] tel que IA = IB.
A
B
I
Les deux petits traits bleus sur le segment [AI] et sur le segment [IB]
signifient que les segments [AI] et [IB] ont la même longueur. On les
appelle « un codage ». Ils permettent de visualiser l’égalité de longueur
sur la figure. On peut utiliser de nombreux codages différents (deux
traits, trois traits, une croix, un petit cercle...) pour signifier que des
segments sont de même longueur.
Remarque : cette définition signifie que le milieu d’un segment est l’unique point
(c’est-à-dire qu’il n’y en a pas d’autre) qui vérifie à la fois les deux conditions suivantes :
• I est un point du segment [AB] (c’est-à-dire « I ∈ [AB] »)
• I est à la même distance de A que de B (c’est-à-dire « IA = IB »).
je retiens
Séquence 1séance 5 —
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-19-320.jpg)
![Effectue maintenant les exercices d’application ci-dessous sur ton livret.
Exercice 26
1- Place les milieux I, J et K respectifs
F
C
A
D
B
Edes segments [AB], [CD] et [EF] et
code les segments de même longueur.
2- Que peux-tu dire des points I, J et K ?
.....................................................................
.....................................................................
Exercice 27
1- Place les milieux I, J et K respectifs
L
M
Ndes segments [NL], [MN] et [ML] et
code les segments de même longueur.
2- Trace les droites (IM), puis (JL) et
enfin (KN).
3- Que remarques-tu ? ..............................
................................................................
................................................................
Exercice 28 La Carte au trésor – suite –
Rappel : Tu te trouves au Ravin représenté par le point R.
Indication du pirate : « Marche maintenant tout droit jusqu’au milieu de la piste rectiligne
limitée par le Ravin et la Pyramide de Mathie. »
• Nomme P le point représentant la Pyramide de Mathie.
• Trace le segment [RP].
• Place le milieu U du segment [RP]. Pour cela, mesure la longueur de ce segment.
Rejoignons maintenant le point U pour poursuivre notre recherche.
Exercice 29
Dans la figure ci-contre :
A
B
C
D
F
E
• AB = BC = CD = DA
• CE = CF
• C ∉ [AF]
Séquence 1 — séance 5
— © Cned, Mathématiques 6e20
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-20-320.jpg)
![© Cned, Mathématiques 6e — 21
1- Code les segments de même longueur.
2- On suppose de plus que C est le milieu de [AE].
Explique pourquoi : CA = CF.
..................................................................................................................................................
..................................................................................................................................................
3- Pourquoi C n’est-il pas le milieu du segment [AF] ?
..................................................................................................................................................
..................................................................................................................................................
Exercice 30
Dans la figure ci-contre, on a :
B
A
D
E
F
C
B ∈ [AC] et F ∈ [AE]. On sait également que CD
n’est pas égal à BC.
a) B est-il le milieu de [AC] ?
Explique ta réponse.
............................................................................................
............................................................................................
b) F est- il le milieu de [AE] ?
Explique ta réponse.
............................................................................................
............................................................................................
Prends ton cahier d’exercices, note « Exercice 31 » et effectue l’exercice ci-dessous.
Exercice 31
1- Trace :
a) un segment [AB] de 5 cm b) le point D tel que B soit le milieu de [AD].
c) le point E de [DB) tel que : DE = 8 cm d) le point F de [BD] tel que : BF = 3 cm
2- Calcule AD, AE, EB.
3- Que représente B pour le segment [EF] ? Justifie ta réponse
Finissons cette séance par un peu de calcul mental :
Complète les cases ci-dessous :
16 77
+5 +14 +29 +13 +39
Réponse:
1621356477
+5+14+29+13+39
116
Séquence 1séance 5 —
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-21-320.jpg)



![© Cned, Mathématiques 6e — 25
Exercice 37
Dans les différents cas suivants, construis la droite (Δ) passant par M et perpendiculaire à (d).
M
(d)
M
(d)
M
(d) M
(d)
Prends ton cahier d’exercices et effectue l’exercice suivant :
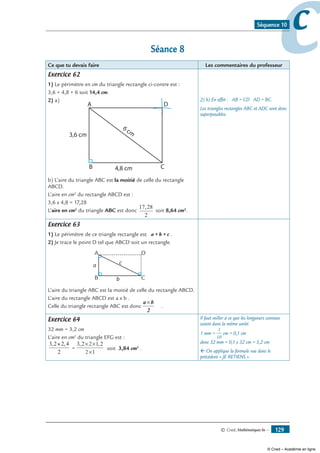
Exercice 38
1- Trace : E
F G
• la droite (d1
) passant par E et
perpendiculaire à (FG)
• la droite (d2
) passant par F et
perpendiculaire à (EG)
• la droite (d3
) passant par G et
perpendiculaire à (EF).
2- Que peux-tu dire des droites (d1
),(d2
) et (d3
) ?
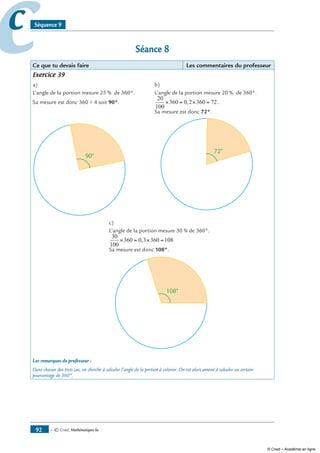
Exercice 39 La Carte au trésor – suite –
Rappel : Tu es sur la piste reliant le Ravin au point U. Tu te trouves au point P.
Indication du pirate : « Repère la piste perpendiculaire à la tienne et suis-la sur 10 km
(tu n’auras pas à nager !). »
• Trace la perpendiculaire au segment [RP] passant par le point U. Nomme-la (d).
• Place le point X tel que :
X est sur la droite (d)
X est à 10 km de U
X se trouve sur l’île.
Nous marchons jusqu’au point X. Nous nous rapprochons du trésor ...
Séquence 1séance 6 —
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-25-320.jpg)

![— © Cned, Mathématiques 6e28
Séance 7
J’étudie les positions de droites - suite -
Recopie sur ton cahier de cours et à la suite :
Définition de la médiatrice :
La médiatrice d’un segment est la droite perpendiculaire
A
B
(d)
I
à ce segment en son milieu.
Remarque : cette définition signifie que la médiatrice
d’un segment est la seule droite qui
• est perpendiculaire au segment
• le coupe en son milieu. (d) est la médiatrice de [AB] :
(d) ⊥ (AB)
et I est le milieu de [AB]
je retiens
Prends ton cahier d’exercices et effectue l’exercice suivant :
Exercice 42
Précise, en justifiant ta réponse, si la droite (d) est la médiatrice du segment [MN] dans les
différents cas suivants :
a)
M
N
(d)
b)
M
N
(d)
c)
M
N
(d)
Effectue les exercices suivants directement sur ton livret.
Exercice 43
Trace la médiatrice (d) du segment [GH] et la médiatrice (Δ) du segment [CB].
G
H
C
B
Séquence 1 — séance 7
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-28-320.jpg)
![© Cned, Mathématiques 6e — 29
Séquence 1séance 7 —
Exercice 44
O
P
Q
1- Trace les médiatrices (d1
), (d2
) et (d3
)
respectives des segments [OP], [PQ]
et [QO].
2- Que peux-tu dire des droites (d1
), (d2
)
et (d3
) ?
........................................................
........................................................
........................................................
Remarque : (d1
), (d2
) et (d3
) se lisent « dé un », « dé deux » et « dé trois ».
Exercice 45
(d1
)
Trace une droite (d2
) perpendiculaire à la droite (d1
)
puis une droite (d3
) perpendiculaire à (d1
).
Que peut-on dire des droites (d2
) et (d3
) ?
........................................................
........................................................
........................................................
Tu viens de voir que deux droites perpendiculaires toutes les deux à une même troisième droite
semblent parallèles. En fait, ce résultat est toujours vrai. À partir de maintenant, on considèrera
que ce résultat est toujours vrai : ce résultat s’appelle une propriété.
Recopie sur ton cahier de cours et à la suite la propriété suivante :
Propriété 1 :
Si deux droites sont perpendiculaires à une même troisième droite,
(d2 )
(d3
)
(d1
)
alors elles sont parallèles.
Ceci s’écrit également :
Si (d2
) ⊥ (d1
) et (d3
) ⊥ (d1
) alors (d2
) // (d3
)
je retiens
En mathématiques, on ne peut affirmer un résultat que si on l’a prouvé (on dit démontré).
Cette année, tu vas apprendre à démontrer des résultats (c’est-à-dire faire des démonstrations).
Pour cela, on ne peut utiliser que ce que l’on sait d’après l’énoncé et le cours.
Ce que l’on sait d’après l’énoncé (et éventuellement une question précédente) s’appelle les
données.
Une propriété, comme celle que nous venons de voir précédemment, est un outil important pour
faire des démonstrations.
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-29-320.jpg)
![© Cned, Mathématiques 6e — 31
Effectue les trois exercices suivants :
Exercice 47
Complète les deux plans de démonstration ci-dessous :
1-
On sait que :
(d) ⊥ (Δ) et (Δ’) ⊥ (Δ)
On applique la propriété : « Si deux droites sont perpendiculaires
à une même troisième droite, alors elles sont parallèles.»
On déduit que :
...................................
2-
On sait que :
............ et (d) ⊥ (d’)
On applique la propriété : « Si deux droites sont perpendiculaires
à une même troisième droite, alors elles sont parallèles.»
On déduit que :
(d) // (Δ)
Exercice 48
1- Démontre que (d1
) et (d3
) sont parallèles.
J
K
L
(d1)
(d2)
(d3
)
(d4
)
Tu feras un plan de démonstration.
2- Que peux-tu dire des droites (d2
) et (d4
) ?
Tu feras un plan de démonstration.
Figure à main levée
Exercice 49
On considère trois points A, B et C alignés dans cet ordre tels que AB = 4 cm et AC = 7 cm.
1- Trace la droite (d) passant par C et perpendiculaire à la droite (AB).
2- Trace la médiatrice (∆) du segment [AB].
3- Démontre que les droites (∆) et (AB) sont perpendiculaires.
Tu feras un plan de démonstration.
4- Que peux-tu dire des droites (∆) et (d) ?
Tu feras un plan de démonstration.
Séquence 1séance 7 —
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-31-320.jpg)







![© Cned, Mathématiques 6e — 39
Vocabulaire :
Soit un cercle C de centre O et
de rayon 2,5 cm.
O
C
K
L
A B
AB
C
• Un rayon est un segment
dont les extrémités sont
un point du cercle et
le centre O du cercle.
Exemples : [OC], [OL], [OK]
Le rayon est la longueur
de chaque rayon soit ici 2,5 cm.
• Une corde est un segment
dont les extrémités
sont deux points du cercle.
Exemple : [AB]
• Un diamètre est une corde qui passe
par le centre O du cercle.
Exemple : [KL]
Le diamètre est la longueur de chaque diamètre soit ici 2 x 2,5 soit 5 cm.
• L’arc AB est la plus petite portion de cercle comprise entre les points A et B.
je retiens
Les cercles sont des formes que l’on retrouve souvent dans la
nature. En voici un exemple : des cercles obtenus en lançant
une pierre à la surface d’un lac. Ces cercles ont tous le même
centre : on dit alors qu’ils sont concentriques.
© Cned
Exerce-toi maintenant à tracer des cercles en faisant l’exercice ci-dessous sur ton cahier d’exercices.
Exercice 61
1- Trace un cercle de centre Y et
de rayon 3 cm.
C
B
A
2- Trace un cercle de centre Z et
de diamètre 4 cm.
(Effectue la suite de l’exercice sur ton livret)
3- a) Trace le cercle C 1
de centre A
et passant par C.
b) Trace le cercle C 2
de centre B
et passant par C.
c) Trace le cercle C 3
de centre C
et passant par B.
Tu as vu comment tracer un cercle de diamètre 4 cm. Lis attentivement l’encadré ci-après,
il t’apprendra à tracer un cercle dont on connaît un diamètre (et non le diamètre : ce n’est pas
la même chose ! ).
Séquence 1séance 9 —
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-39-320.jpg)
![— © Cned, Mathématiques 6e40
je comprends la méthode
Tracer le cercle de diamètre [EF]
1- On veut tracer le cercle
de diamètre [EF].
2- On mesure [EF].
On trouve 6 cm.
On place alors le milieu de
[EF] à 3 cm de E sur [EF].
3- On pointe le compas sur
le milieu du segment, on
prend pour écartement
la distance entre ce point
et F (3 cm) et on trace le
cercle.
E
F E
F
0 1 2 3 4 5 6 7
E
F
Effectue maintenant les trois exercices suivants sur ton cahier d’exercices.
Exercice 62
1- Trace un segment [CD] de 7 cm.
2- On considère le cercle C de diamètre [CD]. Place O le centre du cercle C .
3- Trace le cercle C de diamètre [CD].
4- Trace une corde [CE] telle que CE = 4 cm.
5- Représente en vert l’arc DE.
Exercice 63
Trace un segment [EF] de 3 cm. Quels sont les points situés à la fois à 4 cm de E et à 5 cm
de F ?
Exercice 64
1- Trace deux points K et L tels que : KL = 6 cm.
2- Trace le cercle C de centre K et de rayon 4 cm puis le cercle C ‘ de centre L et de rayon
3 cm.
3- Hachure en vert la zone où les points sont situés à moins de 4 cm de K.
4- Hachure en bleu la zone où les points sont situés à moins de 3 cm de L.
5- Quelle est la zone où sont situés les points à moins de 4 cm de K et à moins de 3 cm de L ?
Séquence 1 — séance 9
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-40-320.jpg)
![© Cned, Mathématiques 6e — 41
Exercice 65 La Carte au trésor – suite –
Rappel : Tu te trouves au point X.
Indication du pirate : « Le point Y où tu dois aller se trouve sur la piste représentée
par la droite (d’). Il se trouve à 6 km du Gué du diable et il doit te rapprocher de l’arbre
Millénaire ».
• Note G le Gué du diable.
• Trace l’ensemble des points situés à 6 km du point G.
• Le point Y se trouve à 6 km du point G sur (d’) et il doit être en sorte que l’on se
« rapproche de M ». Place le point Y sur la carte.
Nous marchons jusqu’au point Y. Il ne reste plus qu’une étape à franchir avant de trouver le trésor !
Effectue maintenant l’exercice suivant directement sur ton cours.
Exercice 66
Construis le point A tel que A appartienne au cercle
M
O
N
de diamètre [MN] et (AN) // ( MO).
Exercice 67
Construis un point B tel que
• d’une part, B appartienne au cercle
L K
P R
de centre K passant par L.
• d’autre part : (BP) ⊥ (KR).
Finissons cette séance par un peu de calcul mental :
Complète les pointillés :
4 x ............... = 24 6 x .............. = 36 5 x .................= 45 6 x ................ = 54
Réponse:
4x6=246x6=365x9=456x9=54
Séquence 1séance 9 —
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-41-320.jpg)
![— © Cned, Mathématiques 6e42
séance 10
J’apprends à reporter des longueurs
Nous allons commencer cette séance par des exercices de reproduction de figures mathématiques.
Prends ton cahier d’exercices et effectue les exercices suivants :
Exercice 68
La figure ci-contre est représentée à
A I B
C
D
5,5 cm
4 cm
main levée. Reproduis-la à l’aide
d’une règle graduée
et d’une équerre.
I ∈ [AB]
Exercice 69
Reproduis la figure ci-contre.
3 cm 3 cm
Nous allons maintenant apprendre, à partir d’une figure, à écrire une consigne (un petit texte)
permettant à quelqu’un qui ne verrait pas la figure de pouvoir la tracer. Lis attentivement le
paragraphe ci-après :
Séquence 1 — séance 10
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-42-320.jpg)
![© Cned, Mathématiques 6e — 43
je comprends la méthode
Écrire un texte permettant de reproduire la figure ci-dessous
A B
C
D
C (d) Il s’agit de repérer les caractéristiques de
la figure pour permettre à quelqu’un qui
n’aurait pas vu la figure de pouvoir la
reproduire.
• On trace un triangle ABC.
• On trace le cercle C dont [AC] est
un diamètre .
• D est le centre du cercle C .
• On trace le segment [BD].
• La droite (d) est la droite perpendiculaire
à (AB) passant par le point B.
Attention : Quand on dit « reproduire une figure », on ne veut pas dire
A
D
C
C
B
(d)
« reproduire à l’identique », comme on pourrait le faire avec un papier calque,
mais reproduire une figure qui possède les mêmes propriétés mathématiques,
comme par exemple ici la figure ci-contre.
Entraîne-toi en effectuant sur ton cahier d’exercices, l’exercice suivant :
Exercice 70
Écris un texte permettant de reproduire cette figure.
B
C
A
I
C
D
5 cm
Séquence 1séance 10 —
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-43-320.jpg)
![— © Cned, Mathématiques 6e44
Nous allons maintenant découvrir l’utilisation du compas pour reporter des longueurs, qui est une
méthode que l’on utilise constamment en géométrie :
je comprends la méthode
Étant donné un segment [AB] et un point C, tracer un point D tel que : CD = AB
1- Je trace une demi-droite d’origine C.
2- Je prends comme écartement de compas
la longueur du segment [AB].
A B
C
x
A B
C
x
3- Je trace le cercle de centre C avec
l’écartement précédent du compas.
4- Le cercle coupe la demi-droite au point D.
x
C
C
D
x
Entraîne-toi en effectuant les quatre exercices suivants :
Exercice 71
a) Trace le point Z sur la demi-droite [Dw)
tel que : DZ = AB
b) Trace deux points X et Y sur la droite
(d) tels que : AX = AY = JK
A
B
D
w
J
A
(d)
K
Séquence 1 — séance 10
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-44-320.jpg)
![© Cned, Mathématiques 6e — 45
Séquence 1séance 10 —
Exercice 72
Construis un point Y sur la demi-droite [Fx)
x
A
B
C
D
Ftel que :
FY = AB + CD.
Exercice 73
Sans utiliser une règle, compare AY et
I
M
A
Y
N
J
K
L
KL + MN + IJ.
..................................................................
..................................................................
..................................................................
..................................................................
Exercice 74
1- Trace sans utiliser de règle graduée le cercle C
L
K
I
J
Hde centre L et de rayon HI.
2- Trace un diamètre [AB] de ce cercle.
3- Trace une corde [BC] telle que : BC = KJ.
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-45-320.jpg)

![© Cned, Mathématiques 6e — 47
je m’évalue
1- Combien y a t il de droites passant par
deux points distincts ?
® aucune droite
® une droite
® deux droites
® une infinité
2- Les points suivants :
A
C
B
® sont alignés
® semblent alignés
® ne semblent pas alignés
® semblent confondus
3- La demi-droite d’origine D et passant par
E se note :
® (DE)
® (DE]
® [DE)
® [DE]
4- Dans cette figure :
F G
H
I
® H est le milieu de [FG]
® I est le milieu de [FG]
® FH = GH
® FI + IG = FG
5- Dans la figure ci-contre, les droites :
® sont parallèles
® sont sécantes
® sont perpendiculaires
® sont confondues
6- Dans la figure ci-contre, les droites :
® sont parallèles
® sont sécantes
® sont perpendiculaires
® sont confondues
7- Dans la figure ci-contre, les droites
(d1
) et (d2
) :
(d1)
(d2)
® sont parallèles
® sont sécantes
® sont perpendiculaires
® sont confondues
8- Dans la figure ci-contre, les droites
(d1
) et (d2
) :
(d1)
(d3)
(d2)
(d2)//(d3)
® sont parallèles
® sont sécantes
® sont perpendiculaires
® sont confondues
9- Un cercle a pour diamètre 10 cm.
La longueur de n’importe quelle corde
de ce cercle :
® est égale à 10 cm
® est supérieure à 10 cm
® est inférieure ou égale à 10 cm
® est égale à 5 cm
10- Dans la figure suivante qui représente un
cercle de centre I :
I
A
B
C
® [AB] est un diamètre
® [AB] est une corde
® [BC] est un rayon
® [BC] est une corde
Séquence 1séance 10 —
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-47-320.jpg)
















































![Prends une feuille de papier calque. Écris en haut « Exercice 13 » et trace les figures demandées.
Tu pourras ensuite vérifier tes figures en superposant le calque avec la figure corrigée.
Tu feras de même pour les exercices 13, 14, 15, 16 et 17. Une fois le travail fini, tu colleras la
feuille de papier calque dans ton cahier d’exercices. N’oublie pas d’écrire les numéros des exercices.
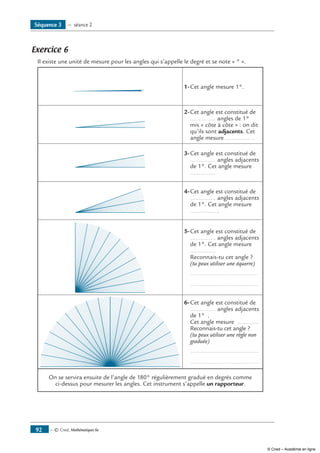
Exercice 13
Trace un angle xAy∑ de 25°, un angle zBt∂ de 75°, un angle uOv∑ de 120° et un angle eDf∑ de
164°.
Tu commenceras par décalquer les débuts de figures proposés ci-dessous.
Exercice 14
a) Construis un point D tel que FED∑ = 45º . b) Construis un point M tel que KLM∑ =135º
E F
K
L
Effectue ensuite les trois exercices ci-dessous.
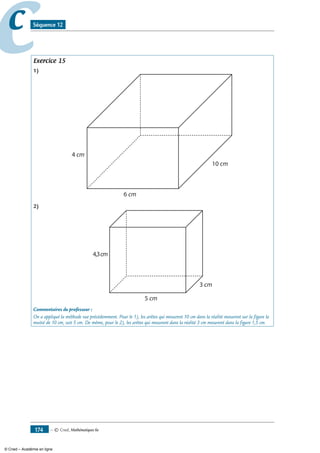
Exercice 15
a) Trace un angle CKL∑ de 92°.
b) Trace un angle GRM∑ de 68°.
Exercice 16
Construis la figure à main levée ci-contre à l’aide
A B
40°
10 cm
8
cm
C
d’une règle graduée et de ton rapporteur.
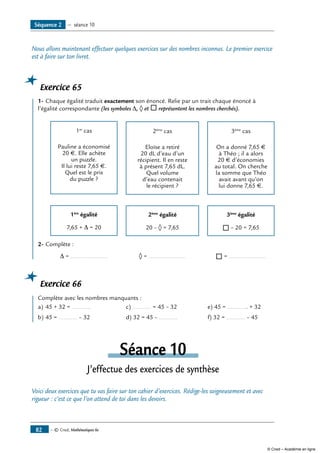
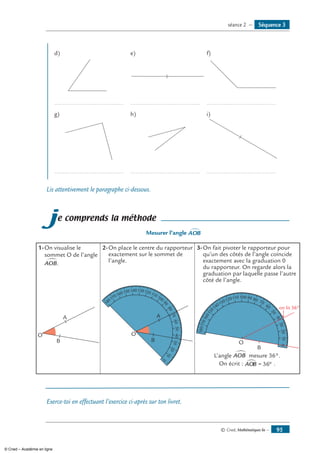
Exercice 17
1- Trace un segment [OA] tel que OA = 5 cm.
2- Place un point B tel que AOB∑ = 20° et OB = 7 cm.
3- Place un point C tel que OBC∑ =120° et BC = 6 cm.
4- Place un point D tel que BCD∑ = 70° et CD = 10 cm.
Indication :
A
O
C
D
B
tu dois obtenir une figure de ce type :
Séquence 3 — séance 3
— © Cned, Mathématiques 6e, 2008100
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-100-320.jpg)






![© Cned, Mathématiques 6e — 107
Séance 5
Je raisonne avec les angles
Nous allons dans cette séance effectuer des démonstrations utilisant les angles. Prends ton cahier
d’exercices et effectue l’exercice ci-dessous.
Exercice 26
Les points A, B et C sont-ils alignés ? Tu démontreras
ta réponse.
B A
x
y
C
84°
66°
31°
Prends ton cahier de cours et recopie le paragraphe ci-dessous.
POINTS ALIGNÉS
Dire que le point A est un point du segment [BC], ou que « B, A et C sont alignés dans
cet ordre » revient à dire que l’angle BAC∑ est plat.
B A C
Si l’angle BAC∑ est plat, alors A est un point du segment [BC].
Ceci s’écrit également : Si BAC∑ = °180 alors A ∈ [BC].
Si A est un point du segment [BC], alors l’angle BAC∑ est plat.
Ceci s’écrit également : Si A ∈ [BC] alors BAC∑ = °180 .
je retiens
Entraîne-toi à utiliser la propriété ci-dessus en effectuant les trois exercices suivants sur ton cahier
d’exercices.
Exercice 27
Démontre que le point C est sur le segment [EF].
E F
x
C
45°
y
Séquence 3séance 5 —
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-107-320.jpg)

![© Cned, Mathématiques 6e — 109
Séquence 3séance 6 —
Séance 6
Je redécouvre les triangles
Nous allons commencer par revoir ce qu’est un triangle et préciser le vocabulaire.
Recopie sur ton cahier de cours le paragraphe ci-dessous.
TriangleS
Le cas général :
Un triangle est une figure fermée à 3 côtés et 3 angles.
Le triangle représenté ci-contre se note ABC
A
B C
(ou ACB, BAC, BCA, CAB, CBA).
Les points A, B et C sont les trois sommets du triangle.
Les segments [AB], [AC] et [BC] sont ses trois côtés.
BAC∑ , ABC∑ et BCA∑ sont ses trois angles.
je retiens
Effectue sur ton livret l’exercice ci-dessous.
Exercice 30
Sur cette figure, 4 triangles sont tracés. Lesquels ?
A
B D
E
C
.................................................................................
.................................................................................
B, C et D sont alignés
Prends une feuille de papier calque et effectue l’exercice ci-dessous. Tu vérifieras ta construction
par transparence en plaçant cette feuille sur le corrigé. Tu découperas ensuite la figure tracée et la
colleras dans ton cahier d’exercices.
Exercice 31
Construis un triangle ABC tel que BC = 8 cm, CBA∑ = °50 et BCA∑ = °60 .
Tu commenceras par représenter une figure à main levée sur laquelle tu noteras les données de l’énoncé.
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-109-320.jpg)

![© Cned, Mathématiques 6e — 111
3- un triangle KLM tel que KL = 6 cm, KM = 4 cm et KLM∑ = °40 .
Figure à main levée papier calque :
Effectue l’exercice ci-dessous sur ton livret.
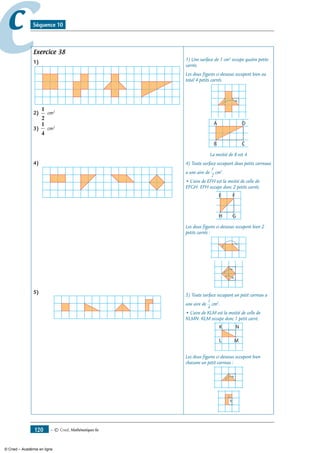
Exercice 33
Le but de cet exercice est de tracer un triangle ABC tel que AB = 5 cm, AC = 7 cm et BC = 9 cm.
1- Trace un segment [BC] de 9 cm.
2- On cherche à placer le point A.
Le point A se trouve à ............ cm du point B. Le point A se trouve donc sur le .................
de centre ........ et de rayon ................. Trace ce cercle et nomme le C 1
.
Le point A se trouve à ............ cm du point C. Le point A se trouve donc sur le .................
de centre ........ et de rayon ................. Trace ce cercle et nomme le C 2
.
3- Où se trouve le point A ? ................................................................................................
4- Place le point A et trace le triangle ABC.
Tu viens de découvrir une méthode permettant de construire un triangle dont on connaît
les longueurs des côtés. Cette méthode est détaillée ci-dessous : lis attentivement le paragraphe
qui suit.
Séquence 3séance 6 —
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-111-320.jpg)
![— © Cned, Mathématiques 6e112
je comprends la méthode
Tracer un triangle EGH tel que EG = 4 cm , HG = 3,5 cm et EH = 6 cm
1- On commence par faire une figure à main levée.
E
G
4 cm 3,5cm
H6cm
2- On trace un côté, par exemple [EH].
Il mesure 6 cm.
3- Comme EG = 4 cm, on trace un arc de cercle de centre E
et de rayon 4 cm.
HE 6 cm HE 6 cm
4- Comme HG = 3,5 cm, on trace un arc de cercle de centre
H et de rayon 3,5 cm (assez grand pour couper
le premier).
5- Les deux arcs se coupent en G.
On trace les segments [EG] et [HG].
On n’écrit pas les longueurs sur la
figure.
HE 6 cm
E
G
H
Séquence 3 — séance 6
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-112-320.jpg)




![© Cned, Mathématiques 6e — 117
TRIANGLES PARTICULIERS
Il existe plusieurs triangles particuliers. Voici leurs définitions :
Définition du triangle rectangle :
Un triangle est rectangle lorsqu’il a un angle droit.
Ci-contre, le triangle ABC est rectangle en A
A
B C(ceci signifie que l’angle qui a pour sommet le point A est un angle droit).
Définition du triangle isocèle :
Un triangle est isocèle lorsqu’il a au moins deux côtés
de la même longueur.
Ci-contre, le triangle ABC est isocèle en A
A
B
C
(ceci signifie que les côtés [AB] et [AC] ont la même longueur, soit AB = AC).
• Le point A s’appelle le sommet principal du triangle isocèle ABC.
• Le côté [BC] s’appelle la base du triangle isocèle ABC.
Définition du triangle équilatéral :
Un triangle est équilatéral lorsque ses trois côtés
ont la même longueur.
Ci-contre, le triangle ABC est équilatéral. On a AB = AC = BC.
Remarques :
A
B C
• Un triangle équilatéral ABC est isocèle en A, en B et en C.
C’est donc un triangle isocèle particulier.
• Un triangle qui n’est pas particulier est dit « quelconque ».
• Un triangle à la fois rectangle et isocèle (cela est possible)
est un « triangle rectangle isocèle ».
je retiens
Voici un exercice de recherche de triangles particuliers. Effectue-le sur ton cahier d’exercices.
N’oublie pas de justifier chaque ligne.
Exercice 38
Complète la liste ci-dessous :
A
B
C
D
E
F G
H
I
J
K
Sur la figure ci-contre :
• le triangle DKB est rectangle en B car DBK∑ = °90 .
• ...
les points K, I et H sont alignés
les points D, F, G et I sont alignés
Séquence 3séance 7 —
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-117-320.jpg)



![© Cned, Mathématiques 6e — 121
je comprends la méthode
Construire un triangle EFG isocèle en E tel que EF = 4 cm et FG = 3 cm
1- On commence par faire une figure codée
à main levée.
2- On trace un segment [FG] de 3 cm.
On prend comme écartement de
compas 4 cm. On trace un arc
de cercle de centre F
E
F
G
4 cm 4 cm
3 cm F G
3- On garde le même écartement de 4 cm et
on trace un arc de cercle de centre G qui
coupe l’autre arc.
Les deux arcs se coupent en E.
4- On trace les segments [EF] et [EG] et
on code la figure.
F G
E
F G
E
Effectue l’exercice suivant. Tu effectueras les constructions à main levée directement sur ton livret,
et les « vraies constructions » directement sur du papier calque que tu colleras sur ton livret après la
correction.
Exercice 42
Construis les figures suivantes :
1- un triangle RST isocèle en R tel que RS = 6 cm et ST = 4 cm.
Figure à main levée
Séquence 3séance 8 —
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-121-320.jpg)





![© Cned, Mathématiques 6e — 127
je m’évalue
1- L’angle DFE∑ a pour sommet :
® D
® F
® E
® [DF)
2- L’angle KLM∑ a pour côté(s) :
® [LM)
® [LM]
® [LK)
® [KM)
3- La mesure d’une angle droit, en degrés,
est :
® 45°
® 100°
® 180°
® 90°
4- L’angle ci-contre est :
N
P
Q
® aigu
® droit
® obtus
® plat
5- La bissectrice d’un angle de 106°
le coupe en deux angles adjacents de :
® 106°
® 58°
® 53°
® 212°
6- L’angle JDL∑ est plat. Les points J, L et D :
® sont alignés
® sont confondus
® sur une même droite
® ne sont pas toujours alignés
7-Le triangle DEF est isocèle en D.
On a donc :
® DE = EF
® DF = EF
® DE = DF
® DE = EF = DF
8- Le triangle KLM est rectangle en M.
® les droites (KM) et (ML) sont
perpendiculaires
® l’angle KL M∑ est droit
® l’angle KML∑ est droit
® l’angle MKL∑ est droit
9-Le triangle CVR est rectangle isocèle en V.
On a :
® CVR∑ = °90
® CR = RV
® RV = CV
® CRV∑ = °90
10- Un cercle de centre O passe par les
points H et K.
® [HK] est une corde de ce cercle
® [HK] est un diamètre de ce cercle
® le triangle OHK est équilatéral
® le triangle OHK est isocèle en O
Séquence 3séance 9 —
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-127-320.jpg)



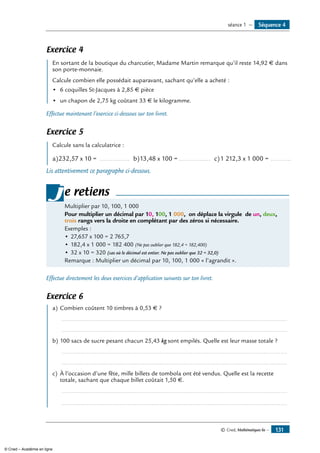
























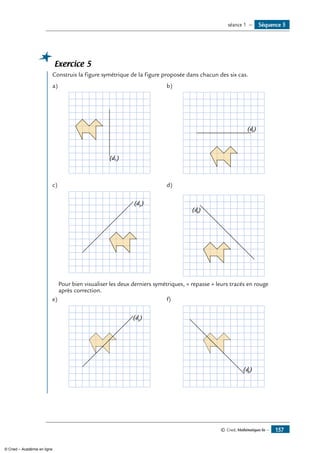

![Exercice 10
1- Construis les points A’, B’, C’, D’, E’, F’ et G’
A
B
C
D
E
G
F
(d)
symétriques des points A, B, C, D, E, F et G
par rapport à la droite (d).
2- Que peux-tu dire des points D et G ?
...............................................................
...............................................................
...............................................................
Nous allons maintenant travailler sans quadrillage. Effectue l’exercice ci-dessous sur ton livret.
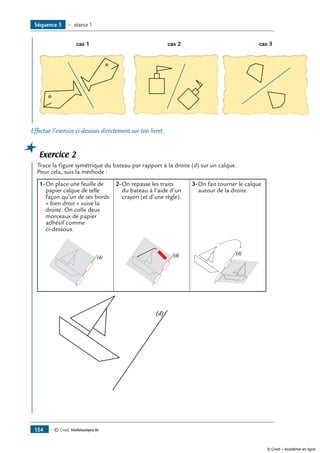
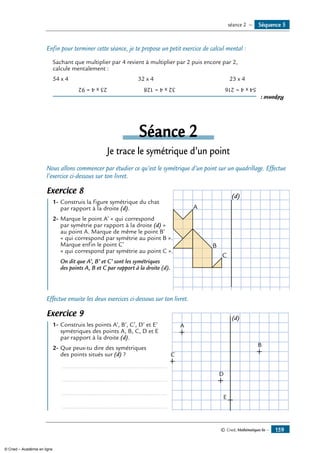
Exercice 11
On cherche à trouver une méthode géométrique
A
E
F
B
B'
A'
(d)
permettant de construire le symétrique d’un point.
1- Prends une équerre et utilise-la...
Comment sont le segment [AA’]
et la droite (d) ? le segment [BB’]
et la droite (d) ?
.........................................................
.........................................................
.........................................................
2- Prends un compas (ou une règle graduée)
et utilise-la...
Que remarques-tu à propos de AE et EA’ ?
de BF et FB’ ?
.........................................................
.........................................................
.........................................................
3- Que semble représenter la droite (d)
pour les segment [AA’] et [BB’] ?
.........................................................
.........................................................
Lis attentivement le paragraphe ci-dessous et recopie-le sur ton cahier de cours.
Séquence 5 — séance 2
— © Cned, Mathématiques 6e160
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-160-320.jpg)
![Séquence 5séance 2 —
© Cned, Mathématiques 6e — 161
SYMÉTRIQUES DE FIGURES
Symétrique d’un point
Dire que A’ est le symétrique de A par rapport à (d) signifie que :
la droite (AA’) est perpendiculaire à (d)
A
(d)
B
et la droite (d) coupe [AA’] en son milieu.
Ceci revient à dire que la droite (d) est la médiatrice du segment [AA’].
je retiens
Lis attentivemment ce qui suit et retiens bien cette méthode :
je comprends la méthode
Tracer à l’aide d’une équerre le point A’, symétrique du point A par rapport à la droite (d)
A
(d)
1- On trace (d’) la
perpendiculaire à (d)
passant par A. Les droites
(d) et (d’) se coupent en I.
2- On prend la longueur AI
comme écartement de
compas et on trace un arc
de cercle coupant (d’) de
l’autre côté de I.
3- On code la figure.
(d)
(d')I
A
I
A
(d)
(d')
A
A'
(d)
Remarque : le point A est lui aussi le symétrique du point A’ par rapport à la droite (d).
Effectue les trois exercices ci-après sur ton cahier. Tu utiliseras du papier calque pour reproduire par
transparence les figures et effectueras ensuite l’exercice sur ton papier calque (sans le plier).
Tu colleras après avoir corrigé par transparence, le papier calque dans ton cahier.
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-161-320.jpg)


![© Cned, Mathématiques 6e — 165
Tu sais maintenant ce qu’est le symétrique d’une droite et comment le construire.
Nous allons maintenant étudier le symétrique d’un segment.
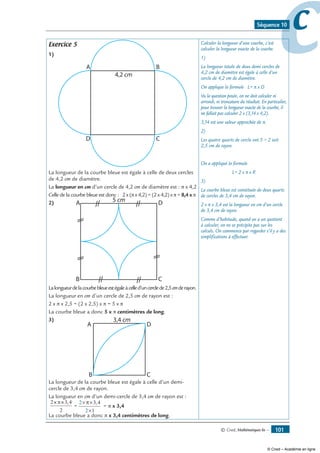
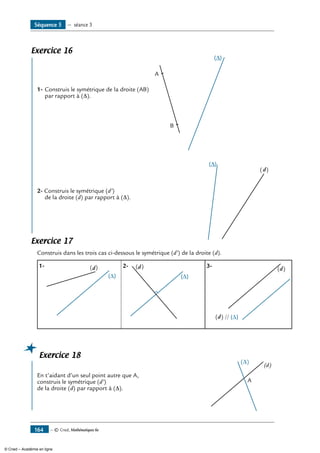
Exercice 19
1- Construis A’, B’, C’, D’, E’, F’ et G’
les symétriques de A, B, C, D, E et F
par rapport à (D).
Trace la droite (AB) et la droite (A’B’).
A
C
D E
F
G
B
(∆)
2- Complète par ∈ ou ∉ :
C ............... [AB] C’ .............. [A’B’]
D ............... [AB] D’ ............. [A’B’]
E ................ [AB] E’ .............. [A’B’]
F ................ [AB] F’ .............. [A’B’]
G ............... [AB] G’.............. [A’B’]
3- Si un point M est sur le segment [AB], alors son symétrique M’ .......................................
......................................................................................................................................
4- Marque un point K sur le segment [A’B’] puis construis son symétrique N par rapport à
(D). Que remarques-tu ?
......................................................................................................................................
Prends ton cahier de cours et recopie le paragraphe ci-dessous.
Symétrique d’un segment A
A'
B'
B
∆( )
Le symétrique d’un segment est un segment.
Ici, le symétrique du segment [AB] par rapport à la droite (Δ)
est le segment [A’B’].
Remarque : Le symétrique de tout point du segment [AB]
est donc sur le segment [A’B’].
je retiens
Effectue l’exercice ci-dessous sur ton livret.
Exercice 20
A
B
C
D
E
F
1- Trace les symétriques respectifs
des segments [AB], [CD] et [EF]
par rapport à la droite (D).
2- Mesure et compare les
longueurs AB et A’B’,
CD et C’D’, EF et E’F’.
Que remarques-tu ?
.......................................
.......................................
......................................
......................................
......................................
Séquence 5séance 3 —
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-165-320.jpg)
![Prends ton cahier de cours et recopie le paragraphe ci-après.
Propriété
Si deux segments sont symétriques l’un de l’autre,
A
A'
B'
B
(∆)
alors ils ont la même longueur.
Ici :
A’ et B’ sont les symétriques
respectifs de A et B par rapport à la droite (D)
donc : AB = A’B’
je retiens
Prends ton cahier d’exercices et effectue l’exercice ci-dessous.
Exercice 21 : Méline, Jade et Jules
Ernest affirme que deux segments de même longueur sont nécessairement symétriques.
- Jade dit : « C’est vrai. »
- Méline dit : « C’est faux. »
- Jules dit : « C’est parfois vrai et parfois faux. »
Qui a raison ? Ne justifie pas ta réponse.
Effectue l’exercice ci-dessous sur ton livret.
Exercice 22
Le point I est le milieu du segment [AB].
A
B
I
1- Trace le symétrique [A’B’] du segment [AB]
par rapport à la droite (D).
2- Construis I’ le symétrique du point I
par rapport à la droite (D).
3- Nous allons démontrer que I’ est le milieu de [A’B’].
a) On sait que : .................................................
D’après la propriété : .....................................
......................................................................
......................................................................
On conclut : I’ ∈ [A’B’].
b) Le symétrique du segment [AI] est ..........., donc : .............. = ..............
Le symétrique du segment [IB] est ..........., donc : .............. = ..............
Or I est ....................................... donc : AI =.........................................
On a :............. =............... , .................................... et ..............................................
donc A’ I’ =.........................................
Comme ............................. et que :.........................., le point I’ est le milieu de [A’B’].
Séquence 5 — séance 3
— © Cned, Mathématiques 6e166
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-166-320.jpg)
![© Cned, Mathématiques 6e — 167
Lis attentivement le paragraphe ci-dessous.
Si deux segments sont symétriques l’un de l’autre,
S
S
(∆)
A
A'
I'
B'
B
I
alors leurs milieux respectifs sont également symétriques.
Ici :
Les segments [AB] et [A’B’] sont symétriques
par rapport à la droite (D) donc leurs milieux
respectifs I et I’ sont symétriques par rapport à la droite (D) .
je retiens
Effectue l’exercice ci-dessous sur ton livret.
Exercice 23
Sur le bout de papier ci-contre, A’ est le symétrique A'
B
(d)
de A par rapport à la droite (d). Sans faire de tracé
en dehors de ta feuille, trouve une valeur approchée
de la longueur AB.
............................................................................
............................................................................
............................................................................
............................................................................
Enfin pour terminer cette séance, je te propose un petit exercice de calcul mental :
Sachant que multiplier par 20 revient à multiplier par 10 puis encore par 2,
calcule mentalement :
3,8 x 20 24,7 x 20 12,3 x 20
Réponse:
3,8x20=76 24,7x20=494 12,3x20=246
Séance 4
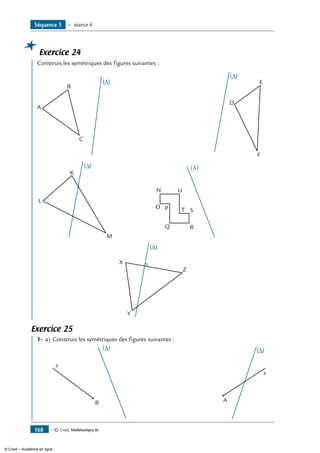
Je construis la figure symétrique d’une figure plus complexe
Nous avons vu dans les séances précédentes comment construire le symétrique d’un point, puis
d’un segment, sans quadrillage. Nous allons maintenant construire les symétriques de figures
plus complexes sans quadrillage : des triangles, ... . La méthode est la même que celle utilisée
précédemment, pense que les figures suivantes ne sont que des « ensembles de segments ».
Effectue les deux exercices ci-après sur ton livret.
Séquence 5séance 4 —
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-167-320.jpg)



![— © Cned, Mathématiques 6e172
Exercice 29
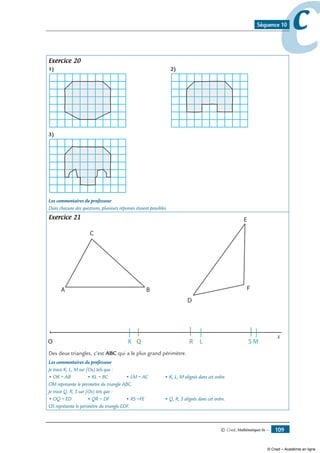
Les figures suivantes admettent des axes de symétrie. Trace-les tous !
Nous allons étudier la médiatrice d’un segment du point de vue de la symétrie axiale.
Commence par faire l’exercice ci-dessous sur ton livret.
Exercice 30
1- Trace A’ le symétrique du point A par rapport à la droite (d).
A(d)
2- Justifie pourquoi (d) est la médiatrice de [AA’].
..........................................................................................
..........................................................................................
..........................................................................................
3- Quels sont les deux axes de symétrie du segment [AA’] ?
..........................................................................................
4- Trace ces axes de couleurs différentes.
Prends ton cahier de cours et recopie soigneusement le paragraphe ci-après.
Séquence 5 — séance 5
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-172-320.jpg)
![© Cned, Mathématiques 6e — 173
MÉDIATRICE
A
(d)
B
Axes de symétrie d’un segment
Un segment [AB] possède deux axes de symétrie :
• la droite (AB) elle-même
et
• la médiatrice du segment [AB].
je retiens
Nous allons maintenant aborder une propriété très importante de la médiatrice.
Effectue l’exercice ci-dessous sur ton livret.
Exercice 31
La droite (d) désignant la médiatrice d’un segment [AB], nous cherchons à répondre à la
question suivante : « Si l’on place un point n’importe où sur (d), sa distance à A est-elle toujours
égale à sa distance à B ? ».
1- Place sur la droite (d) un point I qui n’appartient pas à [AB].
A
B
(d)
2- Quel est le symétrique du point I par rapport à (d) ? Pourquoi ?
..........................................................................................
3- Quel est le symétrique du segment [AI] ?
..........................................................................................
..........................................................................................
..........................................................................................
..........................................................................................
4- Compare AI et BI. Justifie ta réponse.
..........................................................................................
..........................................................................................
5- Place un point J sur (d) qui n’appartient pas à [AB].
Compare AJ et BJ. Justifie ta réponse.
..........................................................................................
..........................................................................................
6- Tu viens de montrer que si M ∈ (d) alors : ............... = ............... .
Séquence 5séance 5 —
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-173-320.jpg)
![— © Cned, Mathématiques 6e174
Effectue l’exercice ci-dessous sur ton livret.
Exercice 32
Nous cherchons à répondre à la question suivante :
A
B
M
N
si l’on place un point à égale distance de A et de B,
se trouve-t-il sur la médiatrice de [AB] ?
On a pris un écartement de compas au hasard
et on a tracé un arc de cercle de centre A,
puis sans changer d’écartement, un arc de cercle
de centre B (tracé bleu).
Les deux arcs se coupent en un point M.
On a ensuite changé d’écartement de compas.
On a enfin tracé avec ce nouvel écartement un arc de cercle
de centre A puis un arc de cercle de centre B (tracé vert).
Les deux arcs se coupent en un point N.
1- Trace la droite (MN). Que remarques-tu concernant (MN) ?
2- Place sur la figure à l’aide d’un compas un point O à égale distance de A et de B.
Que remarques-tu ?
3- Conjecture : Si un point K est tel que KA = KB, alors K est ..............................................
........................................................ du segment ......................................................... .
Prends ton cahier de cours et recopie soigneusement le paragraphe ci-dessous.
Propriété caractéristique de la médiatrice
A
B
M
N
• Si un point M est sur la médiatrice du segment [AB],
alors on a : MA = MB.
ou encore :
Si un point M est sur la médiatrice du segment [AB],
alors M est équidistant de A et de B.
• Si un point M vérifie : MA = MB, alors M est sur la médiatrice du segment [AB].
ou encore :
Si un point M est équidistant de A et de B, alors M est sur la médiatrice d’un segment
[AB].
Remarque : « équidistant » veut dire « à la même distance »
je retiens
Prends ton cahier d’exercices et effectue l’exercice ci-dessous.
Exercice 33 : Méline, Jade et Jules
Voici un énoncé d’exercice : « Trois points K , A et R sont tels que KA = KR. Que peux-tu
en conclure ? »
- Jade dit : « C’est facile ! Cela signifie que le point K est le milieu du segment [AR]. »
- Méline dit : « Mais non ! Cela signifie que le triangle KAR est isocèle en K. »
- Jules dit : « Cela signifie tout simplement que le point K est sur la médiatrice du segment
[AR]. »
Qui a raison ? Justifie ta réponse.
Séquence 5 — séance 5
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-174-320.jpg)
![© Cned, Mathématiques 6e — 175
Séquence 5séance 5 —
Voici la méthode géométrique permettant de tracer la médiatrice d’un segment au compas.
Cette méthode découle de la propriété précédente. Cette construction est plus précise que celle
utilisant l’équerre : dorénavant tu devras l’utiliser. Lis attentivement le paragraphe ci-dessous
et retiens-le.
je comprends la méthode
Construire avec un compas la médiatrice (d) du segment [AB]
A
B
1-On choisit un écartement
de compas quelconque
et on trace deux arcs de
cercle de même rayon,
l’un de centre A et l’autre
de centre B.
2- On fait à nouveau ce
que l’on a déja fait dans
l’étape précédente. Tu
peux garder le même
écartement de compas.
3- On trace la droite passant
par les deux points, on la
nomme (d) , et on code la
figure.
A
B
A
B
A
B
(d)
Effectue cet exercice sur ton cahier d’exercices. Prends une feuille de papier calque et recopie les
figures par transparence. Une fois la figure corrigée, tu colleras la vignette de papier calque dans
ton cahier.
Exercice 34
Trace les médiatrices des trois segments ci-dessous.
A B
C
D
E
F
Effectue l’exercice suivant sur ton cahier d’exercices. Prends une feuille de papier calque et recopie
la figure par transparence. Tu colleras cette vignette de papier calque à côté de tes réponses une fois
que tu auras corrigé.
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-175-320.jpg)
![— © Cned, Mathématiques 6e176
Exercice 35
1- Trace (d) la médiatrice du segment [AB].
A
B
C
2- Trace (d’) la médiatrice du segment [BC].
3- On nomme I le point d’intersection de (d)
et de (d’).
a) Démontre que IA = IB en recopiant le texte
ci-dessous et en complétant les pointillés :
On sait que : la droite (d)
est la .........................................................
du segment .............................................. .
Comme le point I est sur (d), on a :.................... .
b) Démontre que IB = IC en rédigeant comme précédemment.
c) Trace le cercle de centre I passant par A. Que remarques-tu ? Prouve-le.
Enfin pour terminer cette séance, je te propose un petit exercice de calcul mental :
Sachant que multiplier par 5 revient à multiplier par 10 puis diviser par 2,
calcule mentalement :
16 x 5 22 x 5 8,6 x 5
Réponse:
16x5=80 22x5=110 8,6x5=43
Séance 6
J’utilise les propriétés de la médiatrice
Nous allons durant cette séance apprendre à utiliser les propriétés de la médiatrice.
Commence par effectuer l’exercice ci-dessous sur ton livret.
Exercice 36
On cherche à placer un point X tel que :
E
F
B
• X est équidistant de E et de F
• X est à 2,5 cm de B.
1- X est équidistant de E et de F donc X se trouve
sur ................................................................
Trace-la.
2- X est à 2,5 cm de B donc X se trouve
sur ................................................................
3- Combien y-a-t-il de solution(s) au problème ? Place-les sur la figure.
Séquence 5 — séance 6
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-176-320.jpg)
![© Cned, Mathématiques 6e — 177
Prends ton cahier d’exercices et effectue l’exercice ci-dessous.
Exercice 37
Trace un cercle C de centre I et de rayon 3 cm. Place deux points K et L sur le cercle et trace
la corde [KL]. Trace le triangle KLM isocèle en M et tel que ML = 7 cm.
Nous cherchons à démontrer que la droite (IM) est la médiatrice du segment [KL].
1- Compare IK et IL.
2- Compare MK et ML.
3- Recopie le texte ci-dessous et complète les pointillés :
Comme les longueurs IK et IL sont ............................ , le point I est donc sur .....................
...........................................................................................................................................
Comme les longueurs MK et ML sont ............................ , le point M est donc sur ...............
......................................................................................................................................... .
La droite ............................ est donc la médiatrice de............................ .
Tu vas découvrir dans cet exercice une méthode géométrique permettant de placer le milieu de
n’importe quel segment. Il faudra retenir cette méthode et l’appliquer dorénavant lorsqu’on te
demandera de placer le milieu d’un segment.
Exercice 38
1- Trace la médiatrice du segment [AB].
A
C
D
B
2- Place le milieu I du segment [AB].
Tu viens de découvrir une méthode permettant
de placer le milieu d’un segment sans avoir à le mesurer.
3- Applique cette méthode pour placer le milieu J
du segment [CD] ci-contre.
Rédige le programme de ta construction.
Prends ton cahier d’exercices. Prends une feuille de papier calque et reproduis la figure proposée.
Effectue tes constructions sur le papier et calque. Corrige ensuite ta figure en la superposant au
corrigé puis colle-la dans ton cahier d’exercices.
Exercice 39
1- Construis au compas le milieu I du segment [EF].
E
F
G
2- Construis au compas le milieu J du segment [EG].
3- Que remarques-tu à propos de la droite (IJ) ?
Séquence 5séance 6 —
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-177-320.jpg)
![— © Cned, Mathématiques 6e178
Tu vas maintenant découvrir une autre méthode, basée sur la médiatrice, qui permet de construire
le symétrique d’un point uniquement à l’aide d’un compas. Effectue l’exercice ci-dessous sur
ton livret.
Exercice 40
dans cet exercice nous allons apprendre une méthode permettant de construire
le symétrique A’ d’un point A uniquement au compas.
1- Place deux points E et F sur la droite (d).
(Indication : E et F doivent être suffisamment éloignés l’un de l’autre pour la précision de
ta construction).
2- A et A’ doivent être symétriques par rapport
à la droite (d). (d) est donc
la ………….........…...… du …………....…........ [AA’].
3- E est sur la médiatrice du segment [AA’].
A
(d)
On a donc : …………......... = ………….........…...… .
Trace le cercle C de centre E et de rayon EA.
On a : A’…………..C .
4- F est sur la médiatrice du segment [AA’].
On a donc : …………......... = ………….........…...… .
Trace le cercle C ’de centre F et de rayon FA.
On a : A’…………..C ’.
5- Comme : A’…………..C et A’…………..C ’, A’ est le deuxième point d’intersection
de ........................ et ............................
je comprends la méthode
Construire le symétrique A’ d’un point A uniquement au compas
A
(d)
1- On choisit un écartement de
compas quelconque et on trace
un arc de cercle qui coupe la
droite (d) en deux points.
2- On pointe le compas
sur un des deux points
d’intersection de l’arc et
de la droite. On trace un
nouvel arc de cercle
(il faut conserver le
même écartement)
3- On pointe le compas sur
l’autre point d’intersection de
l’arc et de la droite. On trace
un nouvel arc de cercle
(on garde le même écartement)
A
(d)
A
(d)
A
(d)
Séquence 5 — séance 6
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-178-320.jpg)


![© Cned, Mathématiques 6e — 181
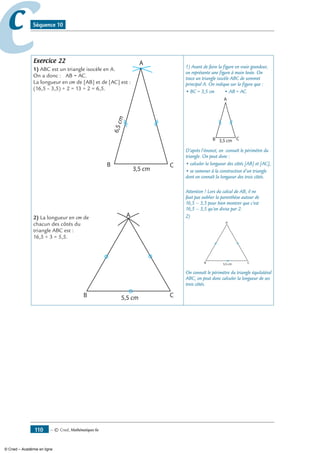
Exercice 44
Le triangle ABC est isocèle en A. Code la figure.
B C
A
1- Trace (d) la médiatrice de [BC]. Que remarques-tu ?
..........................................................................................
2- AB = ........... car le triangle ABC est ...................... en ...........
3- Comme ............... = ................, le point A est sur ..................
...................................................................
Note I le milieu de [BC].
4- • le symétrique de B par rapport à la droite (d) est ................. .
• le symétrique de A par rapport à la droite (d) est ................. .
• le symétrique de I par rapport à la droite (d) est .................. .
Le symétrique de l’angle BAI∑ est donc l’angle.............................. .
Comme un angle et son symétrique ont ........................................................................ ,
on a : .......................................... . Code la figure.
Par suite, (d) est .............................................................de BAC∑.
5- De même, le symétrique de l’angle ABC∑ est l’angle ................... .
Comme un angle et son symétrique ont ........................................................................ ,
on a : ................................ . Code la figure.
Prends ton cahier de cours et recopie le paragraphe ci-dessous.
TRIANGLE ISOCÈLE
Propriété 1
Si un triangle ABC est isocèle en A, alors :
B
C
A
• on a : ABC ACB∑ ∑=
• la médiatrice du côté [BC] est un axe de symétrie du triangle.
C’est également la bissectrice de l’angle BAC∑.
Vocabulaire :
Dans le triangle ABC isocèle en A :
• le point A est appelé sommet principal
• le côté [BC] s’appelle la base
• les angles ABC∑ etABC ACB∑ ∑= s’appellent les angles à la base : ils sont égaux.
je retiens
Prends ton cahier d’exercices et effectue les deux exercices ci-après.
Séquence 5séance 7 —
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-181-320.jpg)
![— © Cned, Mathématiques 6e182
Séquence 5 — séance 7
Exercice 45
Trace un cercle C de centre O et de rayon 4 cm. Place deux points A et B sur ce cercle
tels que OAB∑ = 40° et trace la corde [AB].
1- Quelle est la nature du triangle OAB ? Justifie ta réponse.
2- Détermine OBA∑ . Justifie ta réponse. Vérifie ensuite ta réponse en mesurant sur ta figure.
Exercice 46 : Méline, Jade et Jules
Il faut tracer un triangle ABC isocèle en A tel que ABC∑ = °52 et BC = 5,2 cm.
1- Trace uniquement une figure à main levée et code-la.
- Jade dit : « C’est impossible parce nous n’avons pas les mesures des côtés [AB] et
[AC]. »
- Méline dit : « Mais si, c’est possible ! »
- Jules dit : « Ce n’est pas à cause des mesures des côtés que c’est impossible,
c’est à cause des mesures des angles. »
Qui a raison ? Ne justifie pas ta réponse.
2- Construis un triangle ABC répondant à l’énoncé avec tes instruments de géométrie.
Effectue l’exercice ci-dessous sur ton livret.
Exercice 47
On a représenté ci-contre un triangle ABC
B
C
isocèle en A sur un petit papier qui
malheureusement s’est déchiré.
Trace la bissectrice de l’angle BAC∑
(sans compléter le tracé du triangle).
Justifie ta construction.
Effectue l’exercice suivant sur ton cahier.
Exercice 48 : Méline, Jade et Jules
1- Trace avec tes instruments le triangle EDF tel que :
FED FD E∑ ∑= = °54 et DE = 4,6 cm.
2-
- Jade dit : « Le triangle EDF est isocèle en E. »
- Méline dit : « Non ! Il est isocèle en D. »
- Jules dit : « Mais non ! Il est isocèle en F. »
Qui te semble avoir raison ? Ne justifie pas ta réponse.
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-182-320.jpg)

![— © Cned, Mathématiques 6e184
2- Déplie le papier calque, trace le « trait de pliage ».
3- Que représente ce trait pour xOy∑ ?
Prends ton cahier de cours et recopie le paragraphe ci-dessous.
BISSECTRICE
Axe de symétrie d’un angle
L’axe de symétrie d’un angle est sa bissectrice.
O
x
y
(d)
Remarque : Jusqu’à maintenant, la bissectrice avait désigné
une demi-droite. En fait, le terme de bissectrice peut désigner
également une droite : c’est le cas ici.
Ici :
L’axe de symétrie de l’angle xOy∑ est la droite (d), sa bissectrice.
je retiens
Effectue l’exercice ci-dessous sur ton livret.
Exercice 51
1- Place un point A sur la demi-droite [Ox)
O
x
y
et un point B sur la demi-droite [Oy)
tels que : OA = OB.
2- Trace le segment [AB]. Que peux-tu dire du triangle OAB ?
.............................................................................
.............................................................................
.............................................................................
3- Trace la médiatrice du segment [AB].
Que sais-tu également de cette médiatrice ? Justifie.
.............................................................................
.............................................................................
.............................................................................
Lis attentivement le paragraphe ci-dessous.
Séquence 5 — séance 8
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-184-320.jpg)
![© Cned, Mathématiques 6e — 185
je comprends la méthode
Trace la bissectrice de l’angle xOy∑ à l’aide d’un compas
O
x
y
1- On prend un écartement de compas
quelconque et on trace un arc de cercle
de centre O qui coupe les deux demi-
droites [Ox) et [Oy) en deux points
2- On prend un nouvel écartement de
compas (mais on peut aussi garder
le même) et on trace un arc de cercle
de centre A.
O
x
y
A
B
O
x
y
A
B
3- On garde le même écartement que
précédemment et on trace un arc
de cercle de centre B qui coupe le
précédent.
4- On trace la droite passant par O et
le point d’intersection des deux arcs :
c’est la bissectrice de l’angle xOy∑ .
On code la figure.
Justifications : dans le triangle AOB
isocèle en O, la droite (d) est la
médiatrice du segment [AB]. C’est aussi
la bissectrice de l’angle AOB∑ .
O
x
yB
A
O
x
y
(d)
B
A
Remarque : pour construire (d), il est inutile de nommer A et B sur la figure
(ici, ils sont nommés uniquement pour que tu comprennes mieux les explications).
Dorénavant, tu utiliseras toujours cette méthode pour construire une bissectrice. Prends une feuille
de papier calque, reproduis par transparence les angles ci-dessous et effectue l’exercice.
Séquence 5séance 8 —
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-185-320.jpg)


![— © Cned, Mathématiques 6e188
TRIANGLE ÉQUILATÉRAL
Propriété
Si un triangle ABC est équilatéral, alors :
B C
A
B C
A
• Ses trois angles sont égaux. • Les médiatrices des trois côtés
sont les trois axes de symétrie du
triangle. Ce sont également les
bissectrices des trois angles.
je retiens
Effectue l’exercice ci-dessous sur ton cahier d’exercices.
Exercice 55
1- Trace un cercle de centre O et de diamètre [EF] tel que EF = 6 cm.
2- Trace la médiatrice (d) du segment [EF].
3- Construis un point M sur (d) tel que EM = EF.
4- Démontre que : EMF MEF MFE∑ ∑ ∑
= =
Enfin pour terminer cette séance, je te propose un petit exercice de calcul mental :
Sachant que multiplier par 11 revient à multiplier par 10 et à ajouter le nombre que l’on
multiplie, calcule mentalement :
12 x 11 2,8 x 11 26 x 11
Réponse:
12x11=132 2,8x11=30,8 26x11=286
Enfin, nous allons terminer cette séquence par un test. Lis attentivement les questions et coche
directement la ou les réponses justes sur ton livret. Une fois le test effectué, reporte-toi aux corrigés,
lis-les attentivement puis entoure en rouge les bonnes réponses.
Attention ! Pour certaines questions, plusieurs réponses proposées sont justes.
Séquence 5 — séance 9
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-188-320.jpg)
![© Cned, Mathématiques 6e — 189
je m’évalue
1- Les deux figures
ci-dessous (d)
semblent-elles
symétriques
par rapport
à la droite (d) ?
® OUI
® NON
2- Les deux figures ci-dessous sont-elles
symétriques par rapport à la droite (d) ?
(d)
® OUI
® NON
3- Dire que B’ est le symétrique de B par
rapport à la droite (d) revient à dire que :
® B et B’ sont symétriques par rapport
à la droite (d)
® (d) est la médiatrice du segment
[BB’]
® B et B’ sont sur la droite (d)
® B est le symétrique de B’ par rapport
à la droite (d)
4- Le symétrique d’un angle est :
® un angle
® un triangle
® un angle de mesure différente
® un angle de même mesure
5- Combien la figure ci-dessous a-t-elle
d’axes de symétrie ?
® 6
® 12
® 4
® aucun
6- Le point M est sur la médiatrice du
segment [KL], on a donc :
® KM = KL
® KM = ML
® MK = ML
® LM = KL
7- On a LH = LR. Le point L est donc :
® sur le segment [HR]
® sur le cercle de centre H passant par R
® sur le cercle de centre R passant par H
® sur la médiatrice du segment [HR]
8- L’axe de symétrie d’un triangle FJI
isocèle en F est :
® la bissectrice de l’angle FI J∑
® la bissectrice de l’angle FJI∑
® la médiatrice du segment [IJ]
® la bissectrice de l’angle IF J∑
9-Le triangle HER possède deux angles
égaux. Ce triangle est donc :
® rectangle en H
® rectangle isocèle
® équilatéral
® isocèle
10- Un angle admet un axe de symétrie qui
est :
® parallèle à un de ses côtés
® perpendiculaire à un de ses côtés
® sa bissectrice
® confondu avec un de ses côtés
Séquence 5séance 9 —
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-189-320.jpg)





















![Séquence 7séance 1 —
© Cned, Mathématiques 6e —
Exercice 2
Complète les phrases suivantes :
K
M
R
A
1- Les sommets du quadrilatère sont les points
....... , ....... , ....... et ....... .
2- Ses côtés sont les segments .............. ,
.............. , .............. et .............. .
3- Ses angles sont .............. , .............. ,
.............. et ..............
Lis attentivement le paragraphe ci-dessous.
e retiens
Définition : un quadrilatère est une figure fermée à
quatre côtés, quatre sommets, et quatre angles.
Ici : A
B
C
D
Les quatre sommets sont les points A, B, C et D.
les quatre côtés sont les segments [AB], [BC], [CD] et [DA].
Les côtés [AB] et [CD] sont opposés.
Les côtés [BC] et [DA] sont opposés.
Les angles sont ABC
∑
, BCD
∑
, CDA
∑
et DAB
∑
.
Les angles ABC
∑
et CDA
∑
sont opposés.
Les angles BCD
∑
et DAB
∑
sont opposés.
j
Effectue les deux exercices suivants directement sur ton livret.
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-213-320.jpg)
![Exercice 3
K
R E
G T
O
U
V
1- Colorie les côtés [KG] et [TO] en bleu.
Le côté opposé à [KG] est ................ . Le côté opposé à [TO] est ................
Colorie-les en vert.
2- Colorie les angles KRE
∑
et OUV
∑
en orange.
L’angle opposé à KRE
∑
est ................ . L’angle opposé à OUV
∑
est ................ .
Colorie-les en rouge.
Exercice 4
P
V
R
KVoici un jardin dont les bordures constituent un quadrilatère.
Une coccinelle souhaite faire le tour de ce jardin.
1- Elle part du point K. Elle parcourt le segment [KV].
Arrivée au point V, elle continue son parcours
exactement sur les segments [VR] puis [RP], puis [PK].
On peut résumer son chemin de la façon suivante :
K Ë ..... Ë ..... Ë ..... Ë K
Si elle avait fait le tour toujours en partant de K
mais dans l’autre sens, son chemin aurait été :
K Ë ..... Ë ..... Ë ..... Ë K
2- Quelles sont les six autres façons possibles de faire le tour de ce jardin ?
..... Ë ..... Ë ..... Ë ..... Ë ..... ...... Ë ..... Ë ..... Ë ..... Ë .....
..... Ë ..... Ë ..... Ë ..... Ë ..... ...... Ë ..... Ë ..... Ë ..... Ë .....
..... Ë ..... Ë ..... Ë ..... Ë ..... ...... Ë ..... Ë ..... Ë ..... Ë .....
3- Les trajets suivants permettent-ils de faire le tour du jardin ? (OUI ou NON)
K Ë R Ë V Ë P Ë K .....................
K Ë P Ë V Ë R Ë K .....................
4- Pour conclure, combien y a-t-il au total de façons différentes permettant de faire le tour
de ce jardin ? ................................ .
Lis attentivement le paragraphe ci-après.
Séquence 7 — séance 1
— © Cned, Mathématiques 6e
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-214-320.jpg)
![e retiens
A
B
C
DUn quadrilatère peut se nommer de plusieurs façons :
Ici, le quadrilatère se nomme ABCD ou encore BCDA
ou CDAB ou DABC ou ADCB ou DCBA ou CBAD
ou BADC.
Les sommets A et B, par exemple, qui sont les extrémités
d’un même côté, sont consécutifs.
Les sommets A et C, par exemple, ne sont pas consécutifs.
Lorsque des sommets ne sont pas consécutifs,
on dit qu’ils sont opposés.
A et C sont donc opposés.
j
Effectue les deux exercices ci-dessous sur ton livret.
Exercice 5
K M
R
A
Écris tous les noms possibles du quadrilatère ci-dessous :
.........................................
.........................................
.........................................
.........................................
.........................................
.........................................
Avant d’effectuer l’exercice ci-dessous, rappelons que les diagonales d’un quadrilatère sont les
segments qui joignent deux sommets opposés.
[KM] et [RA] sont donc les diagonales du quadrilatère AKRM précédent. (Trace-les.)
Séquence 7séance 1 —
© Cned, Mathématiques 6e —
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-215-320.jpg)
![Exercice 6
Tracer les diagonales des deux quadrilatères ci-dessous.
K M
R
T
S
Q
L
A
Lis attentivement le paragraphe ci-dessous.
e retiens
A
C
D
B
Définition : les diagonales d’un quadrilatère sont les
deux segments dont les extrémités sont deux sommets
non consécutifs.
Ici, les deux diagonales du quadrilatère ABCD sont
les segments [AC] et [BD].
Remarque : Parfois, on appelle aussi diagonales du quadrilatère
ABCD les droites (AC) et (BD).
j
Séance 2
Je découvre le cerf-volant
Nous allons maintenant découvrir un type de quadrilatère un peu particulier. Effectue l’exercice
ci-dessous directement sur ton livret.
— © Cned, Mathématiques 6e10
Séquence 7 — séance 2
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-216-320.jpg)
![Exercice 7
Construis un quadrilatère A’B’C’D’ de mêmes
A’
x
mesures que ABCD, mais tel que :
B'A'D'
∑
= 30°. A
B
C
D
2,1
cm
4,4cm
Lis attentivement le paragraphe ci-dessous.
e retiens
Définition d’un cerf-volant : un cerf-volant est un quadrilatère dont deux côtés
consécutifs ont la même longueur ainsi que les deux autres côtés.
E
DF
G
Ici, le quadrilatère EDFG est un cerf-volant : les côtés
consécutifs [ED] et [EG] ont la même longueur ainsi
que les côtés [FG] et [FD].
Le quadrilatère E’D’F’G’ est
E'
D'
F'
G'
aussi un cerf-volant : les côtés
consécutifs [E’D’] et [F’D’]
ont la même longueur ainsi
que les côtés [F’G’] et [G’E’].
j
Effectue l’exercice ci-après.
Séquence 7séance 2 —
© Cned, Mathématiques 6e — 11
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-217-320.jpg)
![Exercice 8 Ma boîte à outils
Rends-toi à la fin de ton livret aux pages intitulées « Ma Boîte à Outils ». Retrouve la carte
qui correspond à la définition du cerf-volant et complète-la. Tu coderas également la figure
de la carte.
Effectue l’exercice ci-dessous directement sur ton livret.
Exercice 9
Voici ci-contre un cerf-volant KLMN tel que :
KL = KN et ML = MN.
1- Place les sommets K, L, M et N sur la figure.
Code l’égalité de longueur KL = KN en vert sur la figure.
Code l’égalité de longueur ML = MN en bleu sur la figure.
2- Complète :
Comme ........ = ........ , le point K est sur ............................................... du segment [LN].
Comme ........ = ........ , le point M est sur ............................................... du segment [LN].
La droite (KM) est donc la médiatrice du segment ..................
Trace le segment [LN] et la droite (KM).
3- Soit I le point d’intersection des diagonales (KM) et (LN) du cerf-volant.
Comme la droite (KM) est la médiatrice du segment .................. ,
la diagonale (KM) coupe la diagonale [LN] en son ....................... , et les diagonales
sont ....................... .
Code sur la figure ce que tu viens de démontrer.
4- Par la symétrie axiale par rapport à la droite (KM) :
• K a pour symétrique .........
• M a pour symétrique .........
• L a pour symétrique .........
• N a pour symétrique .........
La droite (KM) est donc un ........................................ du cerf-volant KLMN.
5- Par la symétrie axiale par rapport à la droite (KM) :
L’angle KLM
∑
a pour symétrique ................... .
Les angles ................ et ................ sont donc égaux.
Code-le sur la figure.
Lis attentivement le paragraphe ci-après.
Séquence 7 — séance 2
— © Cned, Mathématiques 6e12
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-218-320.jpg)

![— © Cned, Mathématiques 6e14
Exercice 12
1- Trace un segment [AB] de 4 cm. Trace la droite (d), médiatrice du segment [AB].
La droite (d) coupe le segment [AB] au point K. Marque un point E sur la droite (d).
a) Marque un point F de la droite (d) qui n’appartient pas à la demi-droite [KE).
b) Marque un autre point de la demi-droite [KE) et nomme-le G.
2- Démontre que EA = EB.
3- Démontre que FA = FB.
4- Démontre que GA = GB.
5- Quelle est la nature du quadrilatère AFBE ? Justifie ta réponse.
Quelle est la nature du quadrilatère AGBE ? Justifie ta réponse.
Lis attentivement le paragraphe ci-dessous.
e retiens
Je reconnais un cerf-volant
A
D
C
BPropriété : si un quadrilatère a une diagonale
qui est la médiatrice de l’autre diagonale,
alors ce quadrilatère est un cerf-volant.
Ici, la diagonale (AC) est la médiatrice de
la diagonale [BD] donc on peut en déduire que
ABCD est un cerf-volant.
j
Effectue l’exercice ci-dessous.
Exercice 13 Ma Boîte à Outils – suite –
Retrouve la carte qui correspond à la façon de reconnaître un cerf-volant, complète-la et
code la figure.
Effectue l’exercice ci-dessous sur ton cahier d’exercices.
Exercice 14
K
J
L
M
On se propose dans cet exercice de déterminer la nature
du quadrilatère JKLM de la figure codée ci-contre.
Tu justifieras soigneusement toutes tes réponses.
1- Que représente la droite (KM) pour le segment [JL] ?
2- Quelle est la nature du quadrilatère JKLM ?
Séquence 7 — séance 2
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-220-320.jpg)
![© Cned, Mathématiques 6e — 15
Séance 3
J’étudie le losange
Prends ton cahier d’exercices et effectue l’exercice ci-dessous.
Exercice 15
1- Trace sur du papier calque un segment [AB] de 6,5 cm de longueur. Trace le cercle Ω de
centre A et de rayon 4 cm. Trace le cercle Ω’ de centre B et de rayon 4 cm.
La lettre grecque Ω se lit « oméga ».
2- Les deux cercles se coupent aux points M et N. Trace le quadrilatère AMBN.
Démontre que ce quadrilatère est un cerf-volant.
3- a) Quelle est la particularité de ce cerf-volant ?
b) Te souviens-tu de son nom ?
Lis attentivement le paragraphe ci-après.
e retiens
Définition d’un losange : un losange est un quadrilatère dont les quatre côtés ont
la même longueur.
Ici, ABCD et A’B’C’D’ sont deux losanges : leurs quatre côtés mesurent tous 3 cm.
On a : AB = BC = CD = DA = 3 cm A’B’ = B’C’ = C’D’ = D’A’ = 3 cm
A
B
C
D
B'
A'
C'
D'
On remarque ci-dessus que des losanges peuvent avoir des côtés de même longueur et ne pas être
superposables.
j
Effectue l’exercice ci-dessous.
Séquence 7séance 3 —
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-221-320.jpg)

![© Cned, Mathématiques 6e — 17
2- Complète les phrases suivantes :
Comme EG = ED et que FG = FD
on déduit que EDFG est un ......................
Comme GE = GF et que DE = DF on en
déduit que EDFG est un ......................
donc
donc
• (EF) est un axe de ................... • (GD) est un ...... de ...............
• Les angles ..................... EDF
∑
et EGF
∑
sont ..................
Code-le sur la figure.
• Les angles opposés .........
∑ et .........
∑
sont égaux.
Code-le sur la figure.
• La diagonale (EF) est la ........................
de la diagonale [GD],
c’est-à-dire : la diagonale (EF) coupe
la ............... [GD] en son ............ et
perpendiculairement.
Code l’angle droit et les distances égales.
• La .................. (GD) est la ..................
de la ..................EF],
c’est-à-dire : la .................. (GD) coupe la
diagonale [.......] en son ...........................
et ...............................
Code les distances égales.
• Si un quadrilatère est un .......................
....................... alors ses diagonales sont
......................
• Si un quadrilatère est un losange alors ses
..................... ont le même ....................
Lis attentivement le paragraphe ci-dessous.
e retiens
Propriétés :
Si un quadrilatère est un losange alors :
D
A
B
C
• il admet deux axes de symétrie : ses diagonales
• ses diagonales sont perpendiculaires
• ses diagonales ont le même milieu
• chaque diagonale est la médiatrice de l’autre
• ses angles opposés sont égaux.
j
Séquence 7séance 3 —
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-223-320.jpg)

![© Cned, Mathématiques 6e — 19
1- Romain affirme : « Si les diagonales d’un quadrilatère sont perpendiculaires alors ce quadrilatère est
un losange ».
Es-tu d’accord ? ................... (oui / non). En effet, la figure n° ............. permet de dire
que Romain a ................... (tort / raison).
2- Damien affirme : « Si les diagonales d’un quadrilatère ont le même milieu alors ce quadrilatère est
un losange ».
Es-tu d’accord ? ................... (oui / non). En effet, la figure n° ............. permet de dire
que Damien a ................... (tort / raison).
3- Maxime pense que Romain et Damien devraient s’associer et réfléchir ensemble pour
trouver dans quel cas on est sûr d’obtenir un losange.
Es-tu d’accord avec Maxime ? ................... (oui / non). En effet, d’après les figures
n°.......... et n° .......... on constate que : « dès que les diagonales sont ............................
et ont le même ......................, le quadrilatère est un ........................... . »
On admettra cette propriété (elle est vraie mais on ne le démontrera pas ici).
Lis attentivement le paragraphe ci-dessous.
e retiens
Je reconnais un losange
D
A
B
C
Propriété :
Si un quadrilatère a ses diagonales qui :
• ont le même milieu
et
• sont perpendiculaires,
alors ce quadrilatère est un losange.
Ici, d’après le codage, les diagonales [AC] et [BD]
sont perpendiculaires et leur point commun est
le milieu de chacune d’elles, donc on peut en déduire
que ABCD est un losange.
j
Effectue l’exercice ci-dessous.
Exercice 23 Ma Boîte à Outils – suite –
Retrouve la carte qui correspond à la façon de reconnaître un losange, complète-la
et code-la.
Prends ton cahier d’exercices et effectue l’exercice ci-après.
Séquence 7séance 3 —
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-225-320.jpg)
![— © Cned, Mathématiques 6e20
Exercice 24
Les segments [AB] et [CD] sont les diagonales d’un losange.
On a : AB = 5 cm et BAC
∑
= 48 °.
1- Trace une figure à main levée.
2- Le programme de construction ci dessous est dans le désordre. Dans quel ordre faut-il
écrire les étiquettes pour pouvoir construire le losange ?
Étiquette 1 Je trace (d) la droite perpendiculaire à (AB) qui passe par M.
Étiquette 2 Je place le milieu M du segment [AB] à 2,5 cm de A sur le segment [AB].
Étiquette 3 Je construis l’angle BAx∑ de mesure 48°.
Étiquette 4 Je justifie que j’obtiens un losange : comme les diagonales [AB]
et [CD] sont perpendiculaire et ont le même milieu, je peux affirmer
que le quadrilatère ACBD est un losange.
Étiquette 5 Le point C est le point d’intersection de [Ax) et de (d).
Étiquette 6 Je trace un segment [AB] de 5 cm de longueur.
Étiquette 7 Je reporte à l’aide d’un compas un arc de cercle de centre M et de rayon
MC. Cet arc coupe la droite (d) en D.
3- Construis ce losange sur une feuille de papier calque que tu colleras dans ton cahier
d’exercices après avoir corrigé par superposition sur le corrigé.
Séance 4
J’étudie le rectangle
Prends ton cahier d’exercices et effectue l’exercice ci-dessous. Tu construiras la figure sur du papier
calque et tu la colleras sur ton cahier d’exercice une fois que tu l’auras vérifiée.
Exercice 25
Reproduis le quadrilatère CVBN représenté ci-contre à main levée. C N
V B
5 cm
3 cm
Séquence 7 — séance 4
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-226-320.jpg)
![© Cned, Mathématiques 6e — 21
Lis attentivement le paragraphe ci-dessous.
e retiens
A
D
B
C
Définition d’un rectangle : un rectangle est
un quadrilatère qui a quatre angles droits.
Ici, ABCD est un rectangle :
∑
= 90°.ABC = BCD = CDA = DAB
∑ ∑∑
j
Effectue l’exercice ci-dessous.
Exercice 26 Ma Boîte à Outils – suite –
Retrouve la carte qui correspond à la définition du rectangle, complète-la puis code-la.
Effectue l’exercice ci-dessous directement sur ton livret.
Exercice 27
D H
F G
Voici un quadrilatère DFGH qui possède trois angles droits.
Complète les phrases suivantes :
1- Trace en bleu ci-contre les droites (DH) et (FG). Trace en rouge la droite (DF).
D H
F G
Les droites (DH) et (FG) sont toutes les deux ............................
à la droite (DF). Les droites (DH) et (FG) sont donc
................................ .
2- Trace en bleu ci-contre les droites (DH) et (FG). Trace en rouge la droite (HG).
On vient de démontrer que les droites (DH) et (FG) D H
F G
sont ................................ .
La droite (GH) est ......................... à la droite (DH),
elle est donc ......................... à la droite (FG). Code la figure.
3- Le quadrilatère DFGH possède donc en fait ........ angles droits.
Par définition, c’est donc un ................................................. .
4- On a démontré dans le 2- que ses côtés opposés [DH] et [FG] sont .............................. .
De même, les côtés opposés [DF] et [HG] sont ...................................... parce qu’ils sont
tous les deux ...................................... au côté [DH].
Séquence 7séance 4 —
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-227-320.jpg)
![© Cned, Mathématiques 6e — 23
Effectue l’exercice ci-dessous.
Exercice 30 Ma Boîte à Outils – suite –
Retrouve la carte qui correspond aux axes de symétrie du rectangle, complète-la
puis code-la.
Effectue l’exercice ci-dessous directement sur ton livret.
Exercice 31
A
I
B C
D
(d)
(d')
La figure ci-contre représente un rectangle ABCD
avec ses deux axes de symétrie (d) et (d’).
I est le point d’intersection de (d) et (d’).
Complète les phrases suivantes :
1- a) Quel est le symétrique du segment [AD] par rapport à la droite (d) ? .....................
Que peux-tu en déduire concernant les longueurs des segments [AD] et [BC] ?
...............................................................
b) Quel est le symétrique du segment [AB] par rapport à la droite (d’) ? .....................
Que peux-tu en déduire concernant les longueurs des segments [AB] et [DC] ?
...............................................................
c) Quelle propriété viens-tu de démontrer ?
..................................................................................................................................
..................................................................................................................................
2- Trace les diagonales du rectangle ABCD.
a) Quel est le point d’intersection de ces diagonales ? (On ne demande pas de le justifier, on
l’admettra) .....................
b) Quel est le symétrique du segment [AC] par rapport à la droite (d’) ? .....................
Que peux-tu en déduire concernant les longueurs des segments [AC] et [BD] ?
...........................................
c) Quelle propriété viens-tu de démontrer ?
..................................................................................................................................
..................................................................................................................................
3- a) En utilisant la symétrie par rapport à la droite (d’), compare les distances IA et ID :
...........................................
En utilisant la symétrie par rapport à la droite (d), compare les distances ID et IC :
...........................................
En utilisant la symétrie par rapport à la droite (d’), compare les distances IC et IB :
...........................................
En utilisant la symétrie par rapport à la droite (d), compare les distances IB et IA :
...........................................
Séquence 7séance 4 —
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-229-320.jpg)
![— © Cned, Mathématiques 6e24
b) Compare IA et IC : ................................ puis IB et ID : .............................................
Le point I est le ................................ des diagonales [AC] et [BD]
c) Quelle propriété viens-tu de démontrer ?
..................................................................................................................................
..................................................................................................................................
Lis attentivement le paragraphe ci-dessous.
e retiens
Propriétés d’un rectangle
A
B
C
D
Si un quadrilatère est un rectangle, alors :
• ses diagonales ont la même longueur
• ses diagonales ont le même milieu
• ses côtés opposés sont parallèles
• ses côtés opposés ont la même longueur.
j
Effectue l’exercice ci-dessous.
Exercice 32 Ma Boîte à Outils – suite –
1- Retrouve la carte qui correspond aux propriétés des diagonales d’un rectangle, complète-
la et code-la.
2- Retrouve les cartes qui correspondent aux propriétés des côtés opposés d’un rectangle,
complète-les. Code la figure de la carte concernant les longueurs. Colorie les côtés
parallèles de l’autre carte.
Prends ton cahier d’exercices et effectue les deux exercices ci-dessous.
Exercice 33
Trace un rectangle ABCD dont les diagonales se coupent en O puis le cercle Ω de diamètre
[AC]. Pourquoi le cercle Ω passe-t-il par les points B et D ?
Exercice 34
1- Trace un quadrilatère dont les diagonales se coupent en leur milieu, et qui n’est pas
un rectangle.
2- Trace un quadrilatère dont les diagonales ont la même longueur, et qui n’est pas
un rectangle.
3- Essaie de tracer un quadrilatère qui n’est pas un rectangle dont les diagonales sont de
même longueur et se coupent en leur milieu. Y arrives-tu ?
Séquence 7 — séance 4
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-230-320.jpg)
![© Cned, Mathématiques 6e — 25
Lis attentivement le paragraphe ci-après.
e retiens
Je reconnais un rectangle
A
B
C
D
Propriété : Si un quadrilatère a ses diagonales
• le même milieu
et
• la même longueur,
alors ce quadrilatère est un rectangle.
Ci-contre, les diagonales [AC] et [BD] du
quadrilatère ABCD ont le même milieu et
la même longueur. On peut donc déduire que ABCD est un rectangle.
j
Effectue l’exercice ci-dessous.
Exercice 35 Ma Boîte à Outils – suite –
Retrouve la carte qui correspond à la façon de reconnaître un rectangle, complète-la et
code-la.
Prends ton cahier d’exercices et effectue l’exercice ci-dessous.
Exercice 36
Les segments [RT] et [US] sont les diagonales d’un rectangle RSTU.
Ces diagonales se coupent en V et l’on a : RT = 6 cm et TVU∑ = °53 .
1- Construis ce rectangle sur une feuille de papier calque tu colleras dans ton cahier après
avoir vérifié la construction sur le corrigé.
(commence par réfléchir sur une figure à main levée au brouillon).
2- Rédige le programme de ta construction.
(aide : essaie de t’inspirer des étiquettes de l’exercice 24)
3- Justifie pourquoi ce programme de construction donne un rectangle.
Séance 5
Je redécouvre le carré
Nous allons découvrir ensemble une définition du carré. Effectue l’exercice suivant directement sur
ton livret.
Séquence 7séance 5 —
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-231-320.jpg)


![— © Cned, Mathématiques 6e28
Nous allons découvrir ensemble des propriétés qui permettent de reconnaître un carré.
Effectue les exercices suivants directement sur ton livret.
Exercice 41
1- Construis un losange ABCD de 4,5 cm de coté tel que ABC
∑
= 90°
2- Reconnais-tu la nature de ce losange ? ..........................................................
(On ne demande pas de démontrer.)
Lis attentivement le paragraphe ci-après.
e retiens
Première façon de reconnaître un carré
A
B
C
D
Propriété : si un losange possède un angle droit
alors c’est un carré.
Ici, d’après le codage, ABCD est un losange et l’angle
∑
BAD
mesure 90° donc on peut en déduire que ABCD est un carré.
j
Effectue les exercices suivants directement sur ton livret.
Exercice 42 Ma Boîte à Outils – suite –
Retrouve la carte qui correspond à cette première façon de reconnaître un carré, complète-
la et code-la.
Exercice 43
1- Construis un rectangle EFGH tel que EF = 6,2 cm et EH = 6,2 cm.
2- Reconnais-tu la nature de ce rectangle ? .......................................................
Démontre ce que tu affirmes.
Lis attentivement le paragraphe ci-dessous.
e retiens
Deuxième façon de reconnaître un carré
A
D
C
B
Propriété : si un rectangle possède deux côtés consécutifs
de la même longueur alors c’est un carré.
Ici, d’après le codage, ABCD est un rectangle et les côtés
consécutifs [AB] et [AD] ont la même longueur donc
on peut en déduire que ABCD est un carré.
j
Séquence 7 — séance 5
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-234-320.jpg)
![© Cned, Mathématiques 6e — 29
Effectue les exercices suivants directement sur ton livret.
Exercice 44 Ma Boîte à Outils – suite –
Retrouve la carte qui correspond à la deuxième façon de reconnaître un carré, complète-la
et code-la.
Exercice 45
E
F
G
H
Complète :
Les diagonales de ce quadrilatère sont perpendiculaires et
ont le même milieu. D’après la propriété : « si les diagonales
d’un quadrilatère sont perpendiculaires et ont le même milieu,
alors ce quadrilatère est un ........................ », on déduit que
EFGH est un ................................ .
Les diagonales de ce quadrilatère ont, de plus la même longueur.
D’après la propriété : « si les diagonales d’un quadrilatère ont
la même longueur et ont le même milieu, alors ce quadrilatère
est un ........................ », on déduit que EFGH est un ................................ .
Ce quadrilatère est donc un ..................... et un ..........................
D’après la définition : « un quadrilatère qui est à la fois un rectangle et un losange est
un ....................... », on peut affirmer que EFGH est un ................................... .
Lis attentivement le paragraphe ci-dessous.
e retiens
Troisième façon de reconnaître un carré
A
D
C
B
Si un quadrilatère a ses diagonales qui :
• sont perpendiculaires
• ont le même milieu
• et ont la même longueur
alors ce quadrilatère est un carré.
Ici, les diagonales [AC] et [BD] sont telles que :
• (AC) ⊥ (BD) ,
• AC = BD
• les segments [AC] et [BD] ont le même milieu,
donc on peut en déduire que ABCD est un carré.
j
Effectue l’exercice suivant directement sur ton livret.
Exercice 46 Ma Boîte à Outils – suite –
Retrouve la carte qui correspond à la troisième façon de reconnaître un carré, complète-la
et code-la.
Effectue l’exercice suivant sur ton cahier d’exercices.
Séquence 7séance 5 —
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-235-320.jpg)

![© Cned, Mathématiques 6e — 31
Exercice 49
A
B
C
D
Voici un quadrilatère ABCD :
1- Quelle la nature précise du triangle ABD ? Justifie.
2- Quelle est la nature du quadrilatère ABCD ? Justifie.
Exercice 50
A
O
B
C
D
E
C
Dans la figure ci-contre le point O est le centre du
cercle C et A, C et E sont des points du cercle C .
1- Détermine la nature du quadrilatère OCDE .
2- Détermine la nature du quadrilatère ABCO .
Tu justifieras chacune de tes réponses.
Exercice 51
On considère un rectangle BEAU dont le côté [BE] est plus long que le côté [BU].
Le cercle Ω de centre B et de rayon BU coupe le segment [BE] au point M.
La droite passant par M et perpendiculaire à (BE) coupe [UA] au point N.
1- Trace la figure en vraie grandeur avec tes instruments.
2- Détermine la nature du quadrilatère BMNU. Justifie ta réponse.
Séquence 7séance 6 —
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-237-320.jpg)


![— © Cned, Mathématiques 6e34
Séquence 7 — séance 8
Exercice 59
E
(d)
(d')
Reproduis la figure ci-contre et termine
la construction du rectangle dont l’un
des sommets est le point E et dont les axes
de symétrie sont les droites (d) et (d’).
Séance 8
Je rédige des démonstrations
Dans cette séance, tu vas t’entraîner à rédiger des démonstrations avec des quadrilatères
(à l’aide des définitions et des propriétés que tu as apprises).
Effectue l’exercice suivant directement sur ton livret.
Exercice 60
A
B
1- Dans le cadre ci-dessous, trace au compas la médiatrice
(Δ) du segment [AB]. Elle coupe le segment [AB] au point
M. Trace ensuite le cercle Ω de diamètre [AB]. La droite
(Δ) et le cercle Ω se coupent aux points E et F.
2- Trace en vert le quadrilatère AEBF et
trace en rouge ses diagonales.
3- a) Henri a conclu : « AEBF est un losange. ».
Victor a conclu : « AEBF est un rectangle. ».
Lou-Ann affirme qu’ils ont raison tous les deux mais
Astrid dit que ce n’est pas possible.
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-240-320.jpg)
![© Cned, Mathématiques 6e — 35
D’après toi, qui a raison :
Henri ? Victor ? Lou-Ann ? Astrid ?
C’est ...................... (complète).
b) Complète les cases suivantes avec les mots :
– médiatrice – diamètre(s) – centre – diagonale(s) – longueur – alignés – cercle –
perpendiculaires – milieu – ou avec les lettres A – B – E – F – Ω – de l’énoncé
puis code la figure au fur et à mesure :
Maillon 1
Comme la droite (Δ) est la
..................... du segment ........,
d’après la définition de la .....................
....... , (Δ) coupe [AB] en son ..............
Le point ...... est donc le milieu de [AB]
et c’est le ................... du cercle Ω
Maillon 2
Les points E, M et F sont alignés et les
points E et F sont sur le ....................
de centre ......... donc :
• le segment [EF] est un ...................
du cercle Ω.
• le point M est le ..................
du segment [EF].
Maillon 3
Comme les segments [EF] et [AB] sont
deux ........................ du cercle Ω , ils
ont la même ........................... .
Maillon 4
Comme (Δ) est la ..................... du
segment ........ , d’après la définition de
la ............., on a (EF) ........ (AB).
Maillon 5
Comme les diagonales du quadrilatère
............... sont ..............................
et ont le même ................. M, je peux
conclure que AEBF est un losange.
Maillon 6
Comme les diagonales du quadrilatère
AEBF ont le même ................. M et ont
la même ................, je peux conclure
que AEBF est un rectangle.
c) Reconstitue la démonstration de Henri en écrivant simplement les numéros des
maillons dans l’ordre où ils se succèdent dans sa démonstration :
1 - ................................................................................
d) De la même manière, reconstitue la démonstration de Victor :
1 - ................................................................................
e) En conclusion, AEBF est un .................... et un ......................... donc c’est un
.................
Effectue les exercices suivants sur ton cahier d’exercices. Tu traceras les constructions sur
du papier calque puis tu les colleras dans les exercices de ton cahier au fur et à mesure que tu
les auras vérifiées sur les corrigés.
Exercice 61
1- Trace un cercle Ω de centre I et de rayon 3 cm. Trace en rouge un diamètre [EF]
de ce cercle.
2- Trace ensuite le cercle Ω’ de même centre I et de rayon 4,5 cm. Trace en bleu un diamètre
[AB] de ce cercle tel que : (AB) ⊥ (EF).
3- Quelle est la nature du quadrilatère AEBF ?
Séquence 7séance 8 —
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-241-320.jpg)

![© Cned, Mathématiques 6e — 37
3- a) Trace en vert le quadrilatère SEAU.
b) Démontre que l’angle SEA
∑
est droit.
c) Démontre que l’angle ESU
∑
est également droit.
d) Démontre que le quadrilatère SEAU est un rectangle.
e) Compare EA et ES.
f) Quelle est la nature précise du quadrilatère SEAU ?
Séance 9
J’effectue des exercices de synthèse
Effectue les trois exercices suivants sur ton cahier d’exercices.
Exercice 66
Trace un quadrilatère ABCD dont les diagonales sont perpendiculaires. Quelle est la nature
de ce quadrilatère ? Ne justifie pas ta réponse.
Exercice 67
Construis le losange RSTU dont les côtés [RS] et [TU] mesurent respectivement 3 cm et
4 cm.
Séquence 7séance 9 —
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-243-320.jpg)















![© Cned, Mathématiques 6e — 53
Exercice 22
Écris chaque fraction suivante en toutes lettres :
2
3
..........................................................................................................
7
4
..........................................................................................................
33
7
..........................................................................................................
17
11
..........................................................................................................
Exercice 23
À l’aide d’un calcul de tête, complète les égalités suivantes :
35
7
= ..................................
9
9
= .................................. 13
1
= ..................................
48
6
= .................................. 56
7
= .................................. 4
4
= ..................................
72
1
= .................................. 77
11
= .................................. 37
37
= ..................................
Prends ton cahier de cours et recopie le paragraphe ci-dessous.
e retiens
Propriétés :
• Si a est un nombre quelconque : a
a
1
=
Exemples : 103
1
103= 5 8
1
5 8
,
,=
• Si a est un nombre quelconque différent de 0 : a
a
=1
Exemples :
2 087
2 087
1=
j
Effectue les deux exercices ci-dessous sur ton livret.
Exercice 24
1- On a partagé un segment [OI] d’une unité en quatre segments superposables.
Écris dans les cases du dessous les écritures décimales, et complète les quatre fractions.
0
O I
1
.........
.........
.........
.........
.........
.........
.........
.........
Séquence 8séance 4 —
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-259-320.jpg)
![— © Cned, Mathématiques 6e54
2- On a partagé un segment [OI] d’une unité en cinq segments superposables.
Complète comme tu l’as fait dans la question précédente.
0
O I
1
.........
.........
.........
.........
0,2
.........
.........
.........
.........
.........
.........
.........
.........
.........
.........
Exercice 25
On considère les nombres :
9
7
;
5
7
;
14
13
;
8
8
;
13
14
;
2
3
;
47
47
;
3
2
1- Complète le tableau
nombres plus petits que 1 nombres égaux à 1 nombres plus grands que 1
........................................ ........................................ ........................................
2- Comment, sans calcul, reconnais-tu une fraction supérieure à 1 ? inférieure à 1 ?
.....................................................................................................................................
.....................................................................................................................................
.....................................................................................................................................
Lis attentivement le paragraphe ci-dessous.
e retiens
COMPARER UNE FRACTION À 1.
Si a et b sont des entiers quelconques, et que b est différent de 0 :
• la fraction
a
b
est inférieure à 1 si a b
• la fraction
a
b
est supérieure à 1 si a b
j
Prends ton cahier d’exercices et effectue l’exercice ci-dessous.
Exercice 26
Parmi les six fractions ci-dessous, quelles sont celles qui représentent un nombre décimal ?
Pour les autres, tu donneras la troncature au centième du nombre représenté.
a)
7
4
b)
2
3
c)
3
2
d)
11
12
e)
7
2
Séquence 8 — séance 4
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-260-320.jpg)
























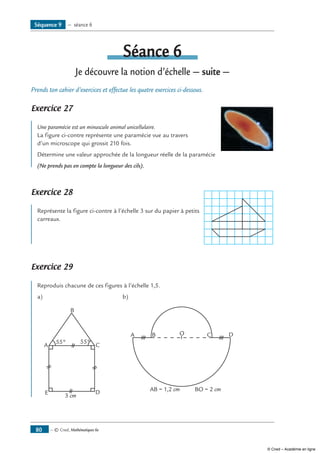




























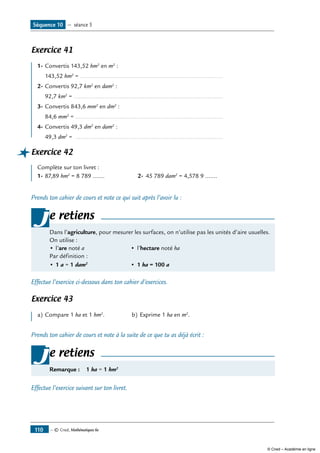






![© Cned, Mathématiques 6e — 117
Effectue les cinq exercices suivants dans ton cahier d’exercices.
Exercice 64
Calcule l’aire du triangle EFG.
G
E F
2,4 cm
32 mm
Exercice 65
1- Construis un losange ABCD tel que : AC = 5 cm et BD = 3,4 cm.
2- Calcule l’aire de ABCD.
Exercice 66 G A
F
B
E
D
C
36 cm²
49 cm²
On considère la figure ci-contre où ABFG et BCDE
sont des carrés.
Calcule l’aire du triangle ABC.
Exercice 67
Un triangle ABC rectangle en A est tel que : AB = 5 cm. Son aire est égale à 12,5 cm2
.
1- Calcule AC.
2- Qu’en déduis-tu concernant la nature du triangle ABC ?
Exercice 68
B
D C
A
A,B,Esontalignés
E
On considère la figure à main levée ci-contre
où ABCD est un rectangle.
1- a) Que représente B pour le segment [AE] ?
b) Compare AE et AB.
2- Pour AB = 3 cm et AD = 5 cm,
calcule l’aire du rectangle ABCD ainsi que
celle du triangle ADE.
3- Que remarques-tu ?
4- Penses-tu qu’on ferait la même remarque avec n’importe
quelles autres valeurs de AB et AD ? Justifie.
Séquence 10séance 8 —
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-323-320.jpg)

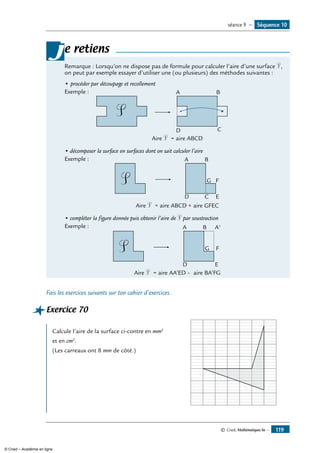
![— © Cned, Mathématiques 6e120
Exercice 71
A
E
F G
H
B
I
K
CL
MN
OD
8 mm
1,2 cm
3,2 cm
5,4 cm
J
Calcule l’aire de la surface représentée
à main levée ci-contre :
Exercice 72
Calcule l’aire de la surface ci-contre en mm2
et en cm2
(Les carreaux ont 8 mm de côté.)
Exercice 73
G
F
H D
E
C
A B
3,6 dm
5,1 dm
10,2 dm
6 dm
Calcule l’aire de la surface ci-contre sachant que :
• A ∈ [GB] • D ∈ [HC] • F ∈ [GH]
Séquence 10 — séance 9
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-326-320.jpg)
![© Cned, Mathématiques 6e — 121
Exercice 74 Un beau parc pour les enfants de la ville — suite —
1- Calcule en m2
et en ares l’aire du bassin 1.
Bassin 1
7,5 m
2- La ville a décidé de choisir le bassin qui offrira le plus de place aux enfants pour jouer.
Elle attend encore des projets. Actuellement, parmi ceux qui sont connus, y en-a-t-il qui
n’ont plus aucune chance d’être choisis ?
Exercice 75 A E
G
B
H
CID
F
On considère la figure ci-contre :
Compare l’aire des rectangles EBHG et FGID.
E ∈ [AB] F ∈ [AD] I ∈ [DC] H ∈ [BC]
Séance 10
J’effectue des exercices de révision
Prends ton cahier d’exercices et cherche les exercices suivants :
Exercice 76 A B
D C
8,3 m
Calcule l’aire de la figure
représentée en gris bleu
ci-contre en m2
et en ares.
Séquence 10séance 10 —
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-327-320.jpg)
![— © Cned, Mathématiques 6e122
Exercice 77
E F B
G
H
CJD
A
K
L
I
La ligne bleue ci-contre représente un chemin de ronde
autour d’un château-fort, vu d’en haut.
AB = 135 m, BC = 105 m et FB = 30 m
1- Montre que la longueur exacte en m de cette ligne est
(180 x �) + 240.
2- Détermine l’arrondi au dixième de cette longueur.
Exercice 78
Terre
La figure ci-contre représente un satellite se déplaçant à altitude
constante autour de la Terre. Sa trajectoire est un cercle ayant
le même centre que la Terre.
Sachant que ce cercle a 42 410 km de long, détermine une valeur
approchée de l’altitude à laquelle se déplace le satellite.
On considèrera que la Terre a 12 800 km de diamètre.
Exercice 79
A
B C
D
E
F
35 m
7,8 m
2,46 dam
D ∈[EC] F ∈[AD]
13 mSachant que l’aire de la surface gris bleu ci-contre
est 677,56 m2
calcule :
1- l’aire en m2
du rectangle ABCD
2- le périmètre de la surface grisée.
Exercice 80 C
A B
F 1
F '2
F '1
F '3
F2
F 3
On considère la figure ci-contre.
F '1
est le symétrique de F 1
par rapport à (AB),
F '2
est le symétrique de F 2
par rapport à (AC),
F '3
est le symétrique de F 3
par rapport à (BC).
Sachant que AB = 2,7 m et AC = 3,4 m, calcule l’aire
de la surface verte.
Aide : Tu utiliseras le résultat suivant que tu admettras et retiendras :
Une figure et son symétrique ont la même aire.
Enfin, nous allons terminer cette séquence par un test. Lis attentivement les questions et coche
directement la ou les réponses justes sur ton livret. Une fois le test effectué, reporte-toi aux corrigés,
lis-les attentivement puis entoure en rouge les bonnes réponses.
Séquence 10 — séance 10
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-328-320.jpg)


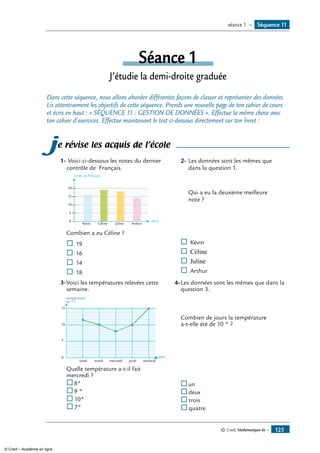









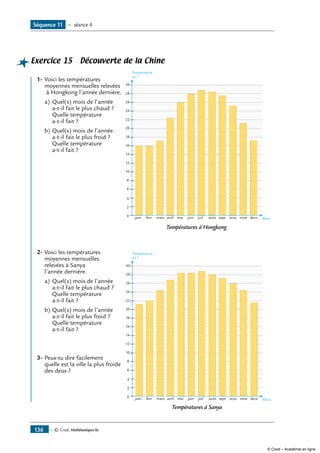







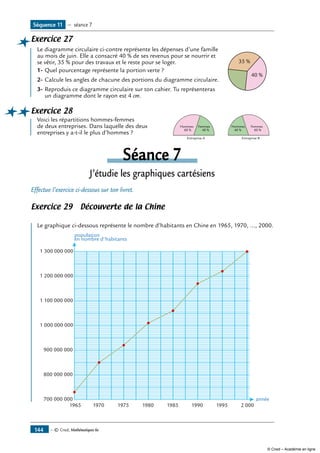










![© Cned, Mathématiques 6e — 155
Séquence 12séance 1 —
4- En utilisant le tableau précédent, écris ci-dessous ce que tu peux en conclure sur les
sommets, les faces et les arêtes des emballages n’ayant que des faces rectangulaires :
.....................................................................................................................................
.....................................................................................................................................
5- Comment appelle-t-on un solide dont toutes les faces sont des rectangles ?
.....................................................................................................................................
6- Comment appelle-t-on un solide dont toutes les faces sont des carrés ?
.....................................................................................................................................
Prends une nouvelle page de ton cahier de cours, et écris en rouge :
« SÉQUENCE 12 : PARALLÉLÉPIPÈDES RECTANGLES. VOLUMES ».
Fais de même avec ton cahier d’exercices. Recopie ensuite le paragraphe suivant dans ton cahier
d’exercices.
e retiens
Le parallélépipède rectangle
Définition :
A B
CD
E F
GH
Un parallélépipède rectangle est un solide dont toutes les faces
sont des rectangles.
Ici :
• Les sommets sont les points A , B, C , D , E , F, G et H.
• Les faces du parallélépipède rectangle sont les rectangles ABCD, EFGH,
ABFE, BCGF, DCGH et ADHE.
• Une arête est un segment dont les extrémités sont deux sommets consécutifs d’une face.
Les segments [AB], [BC] ou [BF] sont par exemple des arêtes. [BG] n’est pas une arête.
Définition :
Un parallélépipède rectangle dont toutes les faces sont
L K
JI
P O
NM
des carrés est appelé un cube.
Ici :
• Les sommets sont les points I, J, K, L, M, N, O et P.
• Les faces du cube sont les carrés IJKL, MNOP, IJNM, JKON, LKOP
et ILPM.
Propriété
Un parallélépipède rectangle a huit sommets, six faces et douze arêtes.
j
Lis attentivement ce qui suit et retiens la méthode.
je comprends la méthode
Nommer le parallélépipède rectangle représenté ci-contre
A B
C
D
E F
GH
• On commence par nommer une face : par exemple ABCD.
• Avant de continuer à nommer le parallélépipède,
* on repère :
- la face parralèle à la première (ici, c’est EFGH).
A B
C
D
E
GH
F
- les arêtes qui « relient » les deux faces considérées
(ici : [AE], [BF], [CG], [DH])
* on pense : « à A correspond E,
à B correspond F… »
A B C D E F G H• On continue de nommer le parallélépipède considéré :
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-361-320.jpg)
![— © Cned, Mathématiques 6e156
Séquence 12 — séance 2
Effectue l‘exercice suivant directement sur ton livret.
Exercice 2
A
B C
D
E
F G
H
Complète les notations du parallélépipède rectangle représenté ci-contre :
a) ABCD ................
b) ADHE ................
c) AEHD ................
d) HDCG ................
e) CGF ................
Exercice 3 « Julie et les volumes » — suite —
Julie veut représenter sur une feuille de papier blanc une petite boîte
d’allumettes en forme de parallélépipède rectangle.
Parmi les quatre figures ci-dessous, laquelle te paraît la plus adaptée ?
coche la case correspondante.
® ®
® ®
Séance 2
Je découvre la perspective cavalière
Lis attentivement et recopie le paragraphe suivant sur ton cahier de cours.
e retiens
Représentation en perspective cavalière d’un parallélépipède rectangle
• Les arêtes [AE], [BF], [CG] et [DH] qui sont parallèles et
A B
CD
E F
GH
de même longueur dans la réalité, sont représentées ici
par des segments parallèles et de même longueur.
• Les arêtes [AD], [DH] et [DC] qui ne sont pas visibles
dans la réalité sont représentées en pointillés.
• La face ABFE en avant et la face DCGH en arrière sont
représentées en vraie grandeur.
• Les arêtes [EH], [FG], [BC] et [AD] qui « relient la face avant et la face arrrière »
sont dessinées plus petites que dans la réalité.
j
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-362-320.jpg)
![© Cned, Mathématiques 6e — 157
Effectue les quatre exercices ci-dessous sur ton cahier d’exercices.
Exercice 4
A B
CD
E F
GH
1- a) Nomme toutes les faces « non visibles » de la représentation
en perspective cavalière du parallélépipède rectangle ABCDEFGH
dessinée ci-contre.
b) Nomme la face avant et la face arrière.
2- a) Nomme toutes les faces « non visibles » de la représentation
A B
CD
E F
GH
en perspective cavalière du parallélépipède rectangle ABCDEFGH
dessinée ci-contre.
b) Nomme la face avant et la face arrière.
Exercice 5
A B
CD
E
F
GH
ABCDEFGH est un parallélépipède rectangle. Précise si, dans la réalité,
les phrases suivantes sont justes ou fausses en justifiant tes réponses.
1- ADHE est un rectangle.
2- EABF n’est pas un carré.
3- EFGH est un carré.
4- BCG n’est pas un triangle rectangle.
5- AB = BC
Exercice 6
I J
KL
M N
OPOn considère le parallélépipède rectangle IJKLMNOP représenté ci-contre:
1- Nomme toutes les arêtes ayant pour extrémité le point P.
2- Nomme toutes les faces ayant le sommet L en commun
3- Nomme toutes les faces ayant pour côté l’arête [JK].
4- Quelles sont les faces parallèles à la face MNOP ?
5- Nomme toutes les arêtes parallèles à l’arête [NO].
6- Nomme toutes les arêtes perpendiculaires à l’arête [NO].
7- Nomme toutes les arêtes perpendiculaires à la face MPLI.
Exercice 7
A B
CD
E F
GH
6 cm
4 cm
5 cm
On a représenté ci-contre le parallélépipède rectangle ABCDEFGH.
Construis en vraie grandeur les faces DCGH, HGFE et CGFB.
Séquence 12séance 2 —
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-363-320.jpg)




![— © Cned, Mathématiques 6e162
Séquence 12 — séance 5
Exercice 17 « Julie et les volumes » — suite —
Les deux figures ci-dessous sont également représentées dans la dernière « page découpage »,
à la fin de ton livret. Reporte-toi à cette page et découpe soigneusement les deux figures
représentées.
Plie ensuite chacune des deux figures afin d’obtenir deux boîtes, (utilise du papier adhésif).
Quels solides obtiens-tu ?
Figure 1 : .........................................................................................
Figure 2 : .........................................................................................
Exercice 18 « Julie et les volumes » — suite —
A
E F
GH
B
CD
Julie voudrait fabriquer en carton cette petite boite de jus de fruit
ayant la forme d’un parallélépipède rectangle et représentée ci-contre.
Pour cela, elle découpe successivement avec une paire de ciseaux l’arête
[GH], l’arête [HE], l’arête [EF], l’arête [GC], l’arête [HD], l’arête [EA]
puis l’arête [FB].
Elle met à plat son découpage et elle obtient un patron de sa boite
de jus de fruit représenté ci-dessous :
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-368-320.jpg)



![— © Cned, Mathématiques 6e166
Exercice 23 « Julie et les volumes » — suite —
A
E F
GH
B
CD
12 cm
6 cm
10 cm
Julie possède un petit aquarium
qui a la forme d’un parallélépipède
de dimensions : 12 cm, 10 cm
et 6 cm qui est représenté
ci-contre. Elle a à sa disposition
des cubes de 1 cm d’arête.
1- Combien de cubes de 1 cm
d’arête peut-elle disposer
le long de l’arête [AB]
puis le long de l’arête [BF] ?
2- Combien de cubes de 1 cm
d’arête peut-elle empiler
le long de l’arête [BC] ?
3- Combien de cubes de 1 cm
d’arête peut-elle disposer
au fond de son aquarium ?
4- Combien lui faut-il de cube de 1 cm d’arête pour remplir complètement son aquarium ?
Ce nombre est appelé le volume en cm3
de l’aquarium.
5- En utilisant la méthode des questions précédentes, quel est le volume d’un cube
d’arête 7 cm ?
Lis attentivement et recopie le paragraphe suivant sur ton cahier de cours.
e retiens
Volume d’un parallélépipède rectangle
Définition : le volume V d’un parallélépipède rectangle est le produit de ses
trois dimensions.
Attention ! Les dimensions doivent toutes être exprimées dans la même unité.
Au besoin, on les convertit dans la même unité.
a
b
c
a
V = a x b x c V = a x a x a
j
Effectue les deux exercices suivants sur ton cahier d’exercices.
Exercice 24
Calcule le volume des solides suivants :
1- Un parallélépipède rectangle dont les dimensions sont : 1,2 dm ; 2,5 dm et 3 dm.
2- Un cube d’arête 6 cm.
3- Un parallélépipède rectangle dont les dimensions sont : 4 cm ; 1,6 dm et 2,5 cm.
4- Un parallélépipède rectangle dont les dimensions sont : 0,34 cm ; 5 mm et 3,6 mm.
Séquence 12 — séance 6
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-372-320.jpg)






![— © Cned, Mathématiques 6e174
Séquence 12 — séance 9
je m’évalue
1- Les faces d’un parallélépipède rectangle
sont des :
® carrés
® losanges
® rectangles
® triangles
2- Le nombre d’arêtes d’un parallélépipède
rectangle est :
® 4
® 6
® 8
® 12
3- Dans la figure
A
E F
GH
B
CD
représentée en
perspective cavalière
ci-contre, les faces
ABCD et EFGH sont :
® parallèles.
® perpendiculaires.
® sécantes.
4- Dans la figure
A
E F
GH
B
CD
représentée en
perspective cavalière
ci-contre, les arêtes
[BC] et [CG] sont :
® parallèles.
® perpendiculaires.
® sécantes.
5- Parmi les figures suivantes, quelles sont
celles qui ne représentent pas le patron
d’un cube ?
® ®
® ®
6- Les dimensions d’un parallélépipède
rectangle sont 2 cm, 5 cm et 6 cm alors
son volume est :
® 42 cm
® 104 cm2
® 60 cm3
® 13 cm3
7- 1 540 cm3
sont égaux à :
® 1 540 dm3
® 1,54 dm3
® 1 540 000 dm3
® 0, 001 54 dm3
8- 25 L sont égaux à :
® 25 000 dL
® 250 dL
® 2 500 cL
® 2,5 daL
9- 25 L sont égaux à :
® 25 dm3
® 250 dm3
® 2,5 dm3
® 25 000 cm3
10- L’aire totale des faces d’un cube de
3 cm d’arête est :
® 36 cm2
® 36 cm3
® 54 cm2
® 54 cm3
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-380-320.jpg)







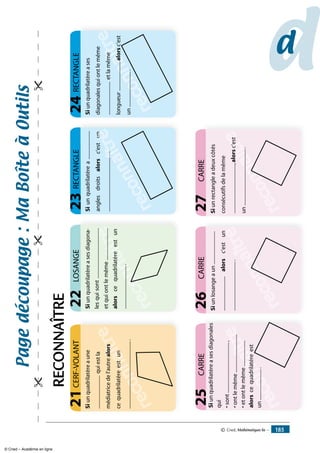



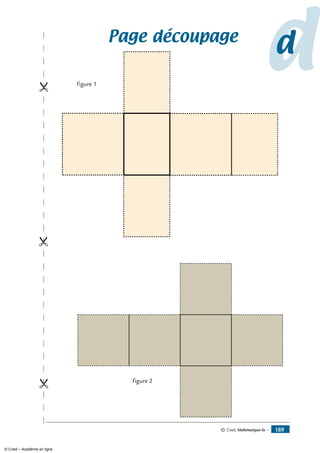






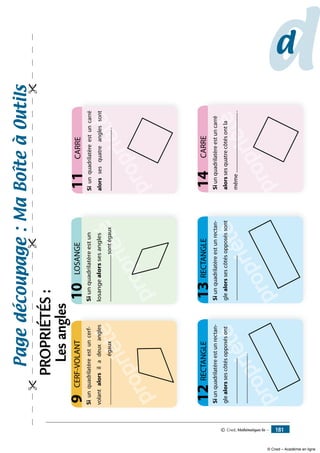
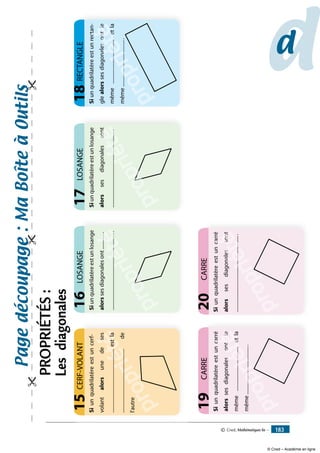













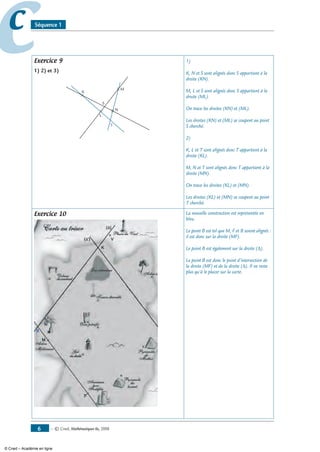
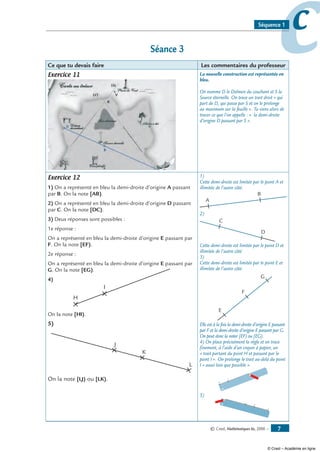

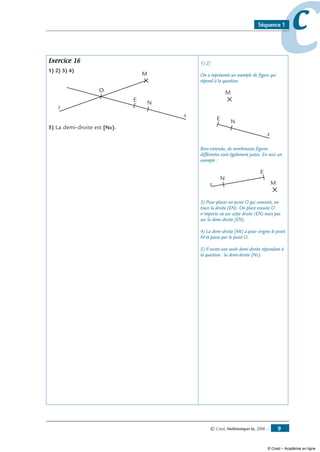
![— © Cned, mathématiques 6e, 200810
cc Séquence 1
Séance 4
Ce que tu devais faire Les commentaires du professeur
Exercice 17 Toutes les nouvelles constructions sont
représentées en bleu.
On note O le point représentant l’Ours
pétrifié.
On trace un trait droit « qui part de O et qui
s’arrête à A ». Tu viens de tracer ce que l’on
appelle le segment d’extrémités O et A, et que
l’on note [OA] ou [AO].
Ce segment coupe la demi-droite [DS) en
un point que l’on nomme R et qui représente
un ravin. C’est de là qu’il faudra partir pour
poursuivre notre recherche...
Exercice 18
1) On a représenté le segment d’extrémités A et B.
On le note [AB] ou [BA].
AB = 4 cm.
2) On a représenté le segment d’extrémités C et D.
On le note [CD] ou [DC].
DC = 6 cm.
3) On a représenté le segment d’extrémités E et F.
On le note [EF] ou [FE].
EF = 2 cm.
4) GH = 3,5 cm.
G H I
5) KL = 1,5 cm.
J
K L
1)
A B
0 1 2 3 4 5
On pouvait également écrire « le segment
d’extrémités B et A ».
2)
C
D
0
1
2
3
4
5
6
7
On pouvait également écrire « le segment
d’extrémités D et C ». Sa longueur peut
également s’écrire CD.
CD = DC = 6 cm.
Attention de ne pas écrire une égalité fausse
comme par exemple : [CD] = 6 cm
3)
E
F
0
1
2
3
On pouvait également écrire « le segment
d’extrémités F et E ». Sa longueur peut
également s’écrire FE.
FE = EF = 2 cm
Attention à ne pas confondre EF et [EF].
4)
G
H I
0 1 2 3 3,5
5)
J
K
L
0 1 21,5
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-423-320.jpg)
![© Cned, Mathématiques 6e, 2008 — 11
ccSéquence 1
Exercice 19
Sur cette figure sont représentés :
• la droite (CE).
• la demi-droite [CD).
• le segment [DE].
CD
E
Exercice 20
S
R
a) La partie en bleu ou en vert est la droite (RS)
b)La partie à la fois en bleu et en vert est le segment [RS].
On a tracé côte à côte les traits bleu et
vert entre R et S, mais normalement, ils se
superposent exactement. C’est juste pour bien
remarquer que la partie entre les point R et S
est la seule à être coloriée à la fois en bleu et
en vert : le segment [RS] est donc la réponse
de la question b).
Comme toute la droite a été coloriée, la partie
coloriée en bleu ou en vert (ou en bleu et en
vert) est donc la droite (RS).
Exercice 21
P
Q
R
S
On a tracé les 6 segments :
[PQ], [PR], [PS], [QR], [QS] et [RS].
On trace dans un premier temps tous les
segments qui ont pour extrémité le point P :
on trace les segments [PQ], [PR] et [PS].
On trace ensuite les segments d’extrémité le
point Q que l’on n’ a pas déjà tracés : on trace
[QR] et [QS].
Enfin, on trace le seul segment non déjà tracé
d’extrémité R qui est [RS].
Remarque : on pouvait bien sûr les nommer
[QP], [RP], [SP], [RQ], [SQ] et [SR].
Exercice 22
E ∈ [AB] E ∈ [AB) E ∈ (AB)
F ∉ [BC] F ∈ [BC) F ∈ (BC)
D ∉ [AC] D ∉ [AC) D ∈ (AC)
A ∈ [CA]
Pour s’aider, on a tracé en orange la demi-
droite [AC), en bleu [AB) et en vert [BC).
B
A
C
D
F
E
On a A ∈ [CA] car chaque extrémité d’un
segment lui appartient.
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-424-320.jpg)
![— © Cned, mathématiques 6e, 200812
cc Séquence 1
Exercice 23
A
B
C
M
N
P
Ecrivons en toutes lettres ce que nous avons
tracé dans la partie gauche :
1) M n’appartient pas au segment
d’extrémités A et B et M appartient à la demi-
droite d’origine A passant par B.
2) N appartient au segment d’extrémités B
et C.
3) P appartient à la demi- droite [NB) et P
n’appartient pas au segment [BN].
4) On trace la droite qui passe par M et N.
On trace le segment d’extrémités N et A.
On trace la demi-droite d’origine P passant
par M.
Exercice 24
E F
G
H
7cm
4,5cm
3cm
On a représenté dans la partie gauche une
solution juste, mais il y en a bien d’autres :
on pouvait placer les segments dans n’importe
quelle position.
Voici comment on pouvait procéder :
• On trace un segment [EF] de 7 cm de
longueur.
E F7 cm
0
1
2
3
G
3 cm
On trace un segment [EG] de 3 cm de
longueur. Une de ses extrémités est E : « on
repart donc du point E ». On peut choisir
« n’importe quelle direction » pour ce segment .
• On trace un segment [FH] de 4,5 cm de
longueur. Une de ses extrémités est F : « on
repart donc du point F ». On peut choisir
également « n’importe quelle direction » pour
ce segment.
E F
G
H
7 cm
4,5
3 cm
0
1
2
3
4
5
4,5
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-425-320.jpg)
![© Cned, Mathématiques 6e, 2008 — 13
ccSéquence 1
Séance 5
Ce que tu devais faire Les commentaires du professeur
Exercice 25
a) b)
C
D
I4 cm
c) Comme I est sur le segment [CD], on a : DI = 8 – 4 = 4.
DI = 4 cm
d) CI = 4 cm DI = 4 cm.
Les longueurs CI et DI sont égales.
a) On dit « trace un segment [CD] » dans
l’énoncé car on peut le placer n’importe où.
Une fois tracé, on dira « le segment [CD] » car
alors il n’y en aura plus qu’un.
c) On pouvait écrire de façon plus abstraite que :
DI= DC—CI =8—4=4
lalongueurDCmoinslalongueurCI
Remarque importante :
On peut faire ce calcul car I est sur le segment
[CD]. Si le point n’est pas sur le segment,
comme le point J de la figure ci-dessous, on ne
peut pas calculer DJ en faisant CD - CJ :
C D
4
J
8
6
(la figure n’est pas à l’échelle)
d) On pouvait également écrire : CI = DI.
(ce qui veut dire que les longueurs CI et DI
sont égales).
Le point I du segment [CD] tel que
CI = DI est appelé « le milieu de [CD] ».
Exercice 26
1)
F
C
A
D
B
E
J
I
K
2) Les points I, J et K semblent alignés.
1)
• Tracé du milieu I de [AB] : on mesure le
segment [AB] avec la règle graduée, on obtient
4 cm. On trace le point I de [AB] tel que :
AI = 2 cm.
• Tracé du milieu J de [CD] :
DC = 3 cm donc on trace le point J de [CD] tel
que : DJ = 1,5 cm.
• Tracé du milieu K de [EF] :
EF = 5 cm donc on trace le point K de [EF] tel
que : EK = 2,5 cm.
2) Pour pouvoir affirmer que les points I, J et
K semblent alignés, on place une règle de telle
façon que I et J soient sur le bord. On se rend
alors compte que le point K semble également
être sur le bord de la règle.
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-426-320.jpg)
![— © Cned, mathématiques 6e, 200814
cc Séquence 1
Exercice 27
1) 2)
L
M
N
I
K
J
3) On remarque que les trois droites tracées semblent passer
par le même point.
• Tracé du milieu I de [NL] :
On mesure le segment [NL] : NL= 4 cm.
On place le point I de [NL] tel que : LI = 2 cm.
• Tracé du milieu J de [MN] : MN = 5 cm.
OnplacelepointJde[MN]telque: NJ=2,5cm.
• Tracé du milieu K de [ML] : ML = 7 cm.
OnplacelepointKde[ML]telque: LK=3,5cm.
3) remarque :
Trois droites qui se coupent en un même point
sont dites « concourantes ».
Exercice 28 On note P le point représentant la Pyramide
de Mathie.
On trace le segment [RP].
On veut placer le milieu U de ce segment.
Pour cela, on commence par le mesurer.
• Le segment [RP] mesure 5 cm.
• La moitié de 5 cm est 2,5 cm.
• Le point U se trouve donc entre R et P et à
2,5 cm du point R.
• On prend alors une règle graduée, on
mesure 2,5 cm et on place le point U. On
n’oublie pas de coder la figure pour indiquer
que les deux longueurs RU et PU sont égales.
Exercice 29
1)
A B
CD
F E
2) D’après l’énoncé :
• C est le milieu de [AE] donc : CA = CE.
• CE = CF
CA = CE et CE = CF d’où CA = CF.
3) Le point C n’est pas le milieu du segment [AF] car il n’est
pas sur le segment [AF].
On pouvait bien sûr coder les segments par
d’autres signes : trois traits, quatre traits, ...
Le codage met en évidence l’égalité des
longueurs CA et CF.
Attention ! Si on a CA = CF, le point C
n’est pas nécessairement le milieu du
segment [AF].
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-427-320.jpg)
![© Cned, Mathématiques 6e, 2008 — 15
ccSéquence 1
Exercice 30
a) Le point B appartient à [AC] et d’après le codage de la
figure AB = BC donc B est le milieu de [AC].
Il faut se méfier des impressions données
par une figure. Dans la figure il semble que
les segments [AF] et [FE] aient la même
longueur. En réalité la longueur FE est
légèrement plus petite que AF.
Remarque : il existe un symbole pour signifier
« n’est pas égal à » : le symbole « ≠ ».
On aurait pu écrire :
« AF ≠ FE donc F n’est pas le mileu de [AE] ».
Exercice 31
1) a) b) c) d)
A B DE F
5 cm 3 cm
8 cm
B est le milieu de [AD]
2)
Calcul de AD
B est le milieu de [AD] donc AD = 2 x AB soit AD = 10 cm.
Calcul de AE
AE = AD – DE. AE = 10 – 8 = 2 soit AE = 2 cm.
Calcul de EB
EB = AB – AE. EB = 5 – 2 = 3 soit EB = 3 cm.
3)
B est sur [EF] et l’on a : EB = BF = 3 cm.
Le point B est donc le milieu du segment [EF].
1) a) On trace un segment [AB] de 5 cm.
A B5 cm
b) Pour obtenir le point D, on trace la demi-droite
[AB), puis le point D de la demi-droite [AB)
différent du point A tel que BD = AB = 5 cm.
A B5 cm D
c) On place E sur [DB) tel que DE = 8 cm :
A B
ED = 8 cm
DE
d) On place F sur [BD] tel que BF = 3 cm :
A B
BF = 3 cm
DE F
Remarque :
Il est conseillé d’indiquer sur ta figure tout ce
que tu sais : cela t’aidera par la suite.
2)
On pouvait aussi écrire que AD = AB + BD.
Puis AD = 5 + 5 = 10 soit AD = 10 cm.
On a AE = AD – DE car E est sur le segment
[AD].
On a EB = AB – AE car E est sur le segment
[AB].
3) Il est très important de justifier sa réponse.
Il est évident, vu la construction, que B est sur
le segment [EF], mais il faut tout de même le
rappeler.
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-428-320.jpg)


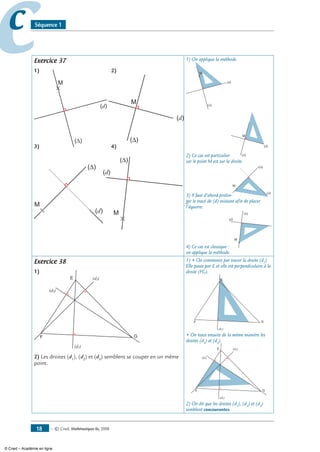
![© Cned, Mathématiques 6e, 2008 — 19
ccSéquence 1
Exercice 39 On trace la perpendiculaire (d) au segment
[RP] passant par le point U. On note « (d) »
cette droite sur la carte.
On code ensuite l’angle droit.
Plaçons maintenant le point X :
Il se trouve à 10 km du point U sur la droite (d).
1 cm sur la carte représente 2 km en réalité.
10 km = 5 x 2 km.
10 km sont donc représentés par 5 x 1 cm sur
la carte, c’est-à-dire 5 cm.
Il y a donc deux possibilités. Voici la première :
La deuxième possibilité (dans l’autre sens),
fait que le point X est dans l’eau. Ce n’est
donc pas celle-là qu’il faut retenir.
Exercice 40
A
B
F
G
M
K
Les points F, G et K doivent être alignés. On
trace donc la droite (FG).
A
B
F
G
M
On doit avoir (MK) ⊥ (AB). On trace donc
la droite perpendiculaire à (AB) passant par
le point M.
A
B
F
G
M
K est le point d’intersection de cette
perpendiculaire et de la droite (FG).
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-432-320.jpg)

![© Cned, Mathématiques 6e, 2008 — 21
ccSéquence 1
Séance 7
Ce que tu devais faire Les commentaires du professeur
Exercice 42
a) (d) n’est pas la médiatrice du segment [MN] car elle n’est
pas perpendiculaire au segment [MN].
b) (d) n’est pas la médiatrice du segment [MN] car elle ne
passe pas par le milieu du segment [MN].
c) (d) est la médiatrice du segment [MN] car elle passe par le
milieu de [MN] et elle est perpendiculaire au segment [MN].
a) Une droite passant par le milieu d’un
segment n’est pas forcément la médiatrice
du segment : il faut aussi qu’elle lui soit
perpendiculaire.
b) Une droite perpendiculaire à un segment
n’est pas forcément sa médiatrice : il faut aussi
qu’elle passe par le milieu du segment.
Exercice 43
G
H
(d)
C
B
(∆)
Voici une méthode te permettant de tracer la
médiatrice du segment [GH] :
On mesure le segment [GH]. On trouve 6 cm.
Le milieu de ce segment se trouve donc à trois
centimètres de G.
G
H0
1
2
3
4
5
6
7
On marque ensuite le milieu du segment et
on trace la perpendiculaire à la droite (GH)
passant par le milieu du segment. On utilise
pour cela l’équerre.
G
H
On prolonge enfin le trait tracé et on écrit les
codages : le « petit carré » pour indiquer l’angle
droit et, par exemple, des petits traits pour
signifier que la médiatrice coupe le segment
[GH] en deux segments de même longueur.
On fait de même pour la médiatrice du
segment [CB].
Remarque importante : une autre méthode
beaucoup plus précise te permettant de tracer
une médiatrice sera étudiée par la suite.
Exercice 44
O
P
Q(d2)
(d3)(d1)
Les droites (d1
), (d2
) et (d3
) semblent concourantes.
Pour tracer (d1
) médiatrice de [OP], on place
le milieu de [OP] et on trace la droite (d1
)
perpendiculaire à (OP) passant par ce milieu.
On pratique de même pour tracer (d2
) et (d3
).
Les droites (d1
), (d2
) et (d3
) semblent passer
par un même point.
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-434-320.jpg)

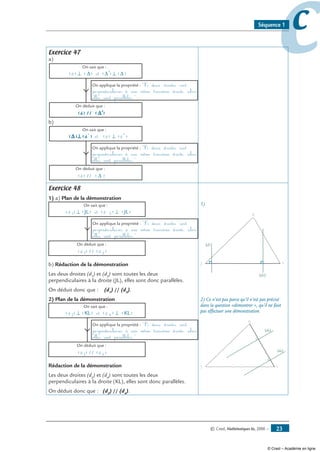
![— © Cned, mathématiques 6e, 200824
cc Séquence 1
Exercice 49
1) et 2)
A
(d)
B
C
(∆)
3) Plan de la démonstration
(∆) est la médiatrice du segment [AB]
On sait que :
On applique la définition :La médiatrice d'un segment
est la droite perpendiculaire à ce segment qui passe
On déduit que :
(∆)⊥(AB)
par son milieu
Rédaction de la démonstration
(Δ) est la médiatrice du segment [AB], elle est donc
perpendiculaire à la droite (AB). On déduit donc que :
(Δ) ⊥ (AB).
4) Plan de la démonstration
(∆) ⊥ (AB) et (d) ⊥ (AB)
On sait que :
On déduit que :
(∆) // (d)
On applique la propriété : Si deux droites sont
perpendiculaires à une même troisième droite, alors
elles sont parallèles.
Rédaction de la démonstration
Comme les deux droites (Δ) et (d) sont toutes les deux
perpendiculaires à la droite (AB), elles sont parallèles.
On déduit donc que : (Δ) // (d).
1) Les points A, B et C sont alignés dans cet
ordre tels que AB = 4 cm et AC = 7 cm, d’où :
A
B
C
3 cm
4 cm
On trace ensuite la droite (d) perpendiculaire
à la droite (AB) en C :
A
(d)
B
C
2) On trace ensuite la droite (Δ). C’est la
perpendiculaire à (AB) passant par le milieu
de [AB] :
A
(d)
B
C
(∆)
2 cm
2 cm
4) On peut remarquer que le résultat :
« (∆) est perpendiculaire à (AB) » obtenu
à la question 3) devient une donnée pour la
démonstration de la question 4).
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-437-320.jpg)

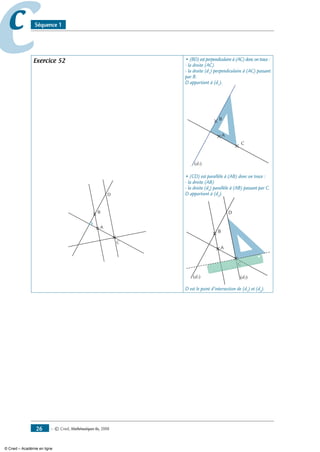


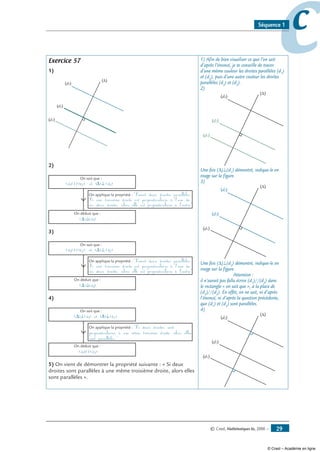
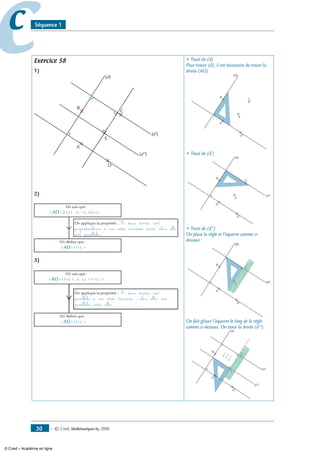

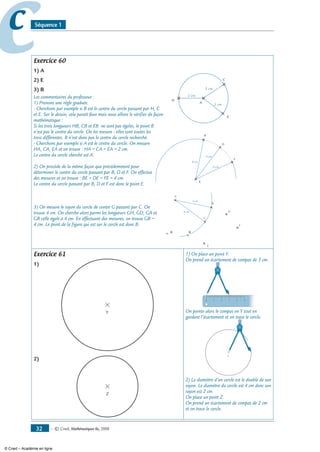
![© Cned, Mathématiques 6e, 2008 — 33
ccSéquence 1
3) a) b) c) Comment tracer le cercle de centre A passant
par C ?
C’est simple : « on pointe le compas en A et
on prend pour écartement AC ». On trace
alors le cercle.
On applique la même méthode pour les deux
autres cercles.
Exercice 62
1) 2) 3) 4) et 5)
C D
C
O
E
4 cm
DE
2) Le centre O du cercle dont [CD] est un
diamètre est le milieu de [CD] (en effet, O est
sur le segment [CD] car [CD] est un diamètre
et OC = OD = 3,5 cm)
3) On trace le cercle en utilisant la méthode
vue précédemment.
4) Comme CE = 4 cm, le point E appartient
au cercle de centre C et de rayon 4 cm. On
trace donc ce second cercle, qui coupe le cercle
C en deux points.
Le point E est un de ces points (on choisit où
l’on place la lettre E).
C
B
A
C 1
C 2
C 3
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-446-320.jpg)
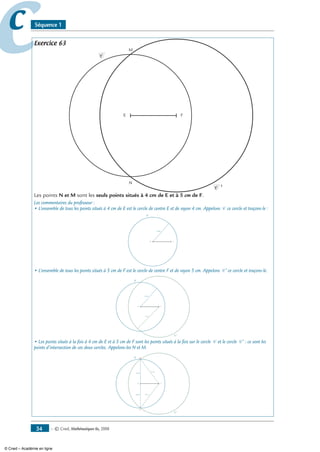
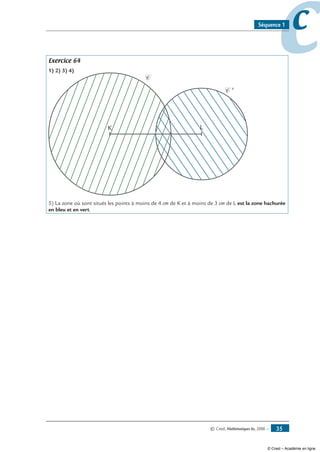
![— © Cned, mathématiques 6e, 200836
cc Séquence 1
Exercice 65
On note G le point représentant le Gué du
diable.
L’ensemble de tous les points situés à 6 km du
point G est le cercle de centre G et de rayon
6 km.
1 cm sur la carte représente 2 km en réalité.
6 km = 3 x 2 km.
6 km sont donc représentés par
3 x 1 cm soit 3 cm.
On trace le cercle de centre G et de rayon
3 cm. Il coupe la droite (d’) en deux points.
Un seul de ces deux points nous rapproche de
l’arbre Millénaire : le point Y. On note Y sur
la carte.
Le trésor n’est plus très loin ...
Exercice 66
M
O
N
A
1) Le point A est sur le cercle de diamètre
[MN]. Traçons ce cercle :
M
O
N
On doit aussi avoir (AN) // (MO).
On trace la droite (MO). Le point A est sur
la parallèle à la droite (MO) passant par N.
Traçons cette droite :
M
O
N
A
Le point A est un point d’intersection du cercle
et de cette droite. Ce n’est pas le point N, c’est
donc l’autre point d’intersection.
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-449-320.jpg)
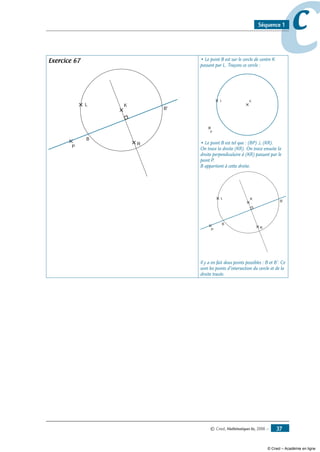
![— © Cned, mathématiques 6e, 200838
cc Séquence 1
Séance 10
Ce que tu devais faire Les commentaires du professeur
Exercice 68
A I B
C
D
5,5 cm
4 cm
On peut commencer par tracer le segment [AB].
D’après l’énoncé, on a : I ∈ [AB].
D’après les codages on a : IA = IB.
I est donc le milieu de [AB].
Comme AI = 4 cm, on a : AB = 8 cm.
On trace donc un segment [AB] et on place
son milieu I.
A I B
On trace ensuite deux segments perpendiculaires
à [AB] :
• [AD] de longueur 5,5 cm
• [BC] de longueur 4 cm
A I B
C
D
5,5 cm
4 cm
Il ne reste plus alors qu’à tracer le segment [DC].
Exercice 69
3 cm3 cm
On commence par remarquer que cette figure
est composée de 3 demi-cercles : deux de
diamètre 3 cm et un de diamètre 6 cm.
3 cm 3 cm
On trace un segment [AB] de 6 cm et son
milieu I.
3 cm 3 cmA I B
AI = IB = 3 cm. On trace ensuite un demi-
cercle de diamètre [AI], puis, du même côté,
un demi-cercle de diamètre [IB].
3 cm 3 cmA I B
On trace enfin « de l’autre côté » de (AB) un
demi-cercle de diamètre [AB].
3 cm 3 cmA I B
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-451-320.jpg)
![© Cned, Mathématiques 6e, 2008 — 39
ccSéquence 1
Exercice 70
On trace un segment [AB] de longueur 5 cm et le cercle C de
diamètre [AB].
On trace la droite perpendiculaire à (AB) passant par A puis
un point C sur cette droite tel que : AC = AB = 5 cm.
On place le point D de la demi droite [AC) tel que :
• A, C, D soient alignés dans cet ordre
• CD = AB = 5 cm.
On trace le segment [CB], la demi-droite [DB) et on place I
le point d’intersection de C et [DB), distinct de B.
BA
C
5 cm
BA
C
5 cm
C
BA
C
5 cm
C
D
BA
C
5 cm
C
D
I
Exercice 71
a) A
B
D
w
Z
b)
J
A
(d)
K
X
Y
On applique la méthode vue précédemment : on
prend pour écartement de compas la longueur AB.
On pointe le compas en D et on trace un arc de
cercle qui coupe la demi-droite [Dw) au point Z.
On prend pour écartement de compas la longueur
JK, on pointe le compas en A et on trace deux arcs
de cercles qui coupent la droite (d) aux points X et
Y.
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-452-320.jpg)
![— © Cned, mathématiques 6e, 200840
cc Séquence 1
Exercice 72
x
A
B
C
D
F
Y
On prend comme écartement de compas
la longueur du segment [AB], on pointe le
compas en F et on trace un arc de cercle qui
coupe la demi-droite [Fx).
x
A
B
C
D
F
On prend pour écartement de compas la
longueur de [CD], on pointe le compas au point
obtenu précédemment et on trace un autre arc
de cercle qui coupe la demi-droite [Fx).
x
A
B
C
D
F
Y
Exercice 73
On construit un point Z tel que AZ = KL + MN + IJ.
I
M
A
Y
N
J
K
L
Z
F
E
EF = MN
FZ = IJ
AZ est supérieur à AY donc KL + MN + IJ est supérieur à AY.
En procédant comme dans l’exercice
précédent, on cherche à placer le point Z de
[AY) tel que :
AZ = KL + MN + IJ.
Pour cela, on reporte sur la demi-droite [AY)
la longueur KL à partir de A, puis la longueur
MN « à la suite », puis la longueur IJ « à la
suite ». On obtient ainsi le point Z.
Comparer AY et KL+MN+IJ, c’est comparer
les longueurs AY et AZ, soit dire laquelle des
deux est la plus grande. D’après la figure, la
longueur AZ est plus grande que la longueur
AY.
En conclusion, KL + MN + IJ est supérieur à
AY.
On écrit : KL + MN + IJ AY
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-453-320.jpg)
![© Cned, Mathématiques 6e, 2008 — 41
ccSéquence 1
Exercice 74
L
K
I
J
H
A
B
C
C
L
K
I
J
H
1) On trace le cercle de centre L avec comme
écartement de compas la longueur HI.
2) On trace un diamètre [AB] de ce cercle (on
le choisit comme on veut).
3) Pour tracer une corde [BC] telle que
BC = KJ, il suffit de placer un point C sur le
cercle de diamètre [AB] tel que BC = KJ.
On trace pour cela un cercle de centre B et de
rayon KJ. Ce cercle coupe le cercle de diamètre
[AB] en deux points. N’importe lequel des
deux points répond à la question.
L
K
I
J
H
A
B
C
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-454-320.jpg)
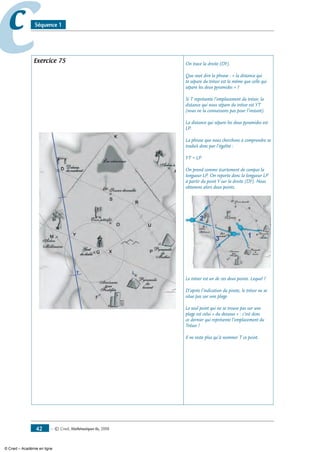
![© Cned, Mathématiques 6e, 2008 — 43
ccSéquence 1
Exercice Je m’évalue
1) Combien y a t il de droites passant par deux points distincts ?
® aucune droite
˝ une droite
® deux droites
® une infinité
2) Les points suivants :
® sont alignés
˝ semblent alignés
® ne semblent pas alignés
® semblent confondus
3) La demi-droite d’origine D et passant par E se note :
® (DE)
® (DE]
˝ [DE)
® [DE]
4) Dans cette figure :
® H est le milieu de [FG]
® I est le milieu de [FG]
˝ FH = GH
˝ FI + IG = FG
5) Dans la figure ci-contre, les droites :
® sont parallèles
˝ sont sécantes
® sont perpendiculaires
® sont confondues
6) Dans la figure ci-contre, les droites :
® sont parallèles
˝ sont sécantes
˝ sont perpendiculaires
® sont confondues
7) Dans la figure ci-contre, les droites (d1
) et (d2
) :
˝ sont parallèles
® sont sécantes
® sont perpendiculaires
® sont confondues
8) Dans la figure ci-contre, les droites (d1
) et (d2
) :
® sont parallèles
˝ sont sécantes
˝ sont perpendiculaires
® sont confondues
9) Un cercle a pour diamètre 10 cm. La longueur de n’importe
quelle corde de ce cercle :
® est égale à 10 cm
® est supérieure à 10 cm
˝ est inférieure ou égale à 10 cm
® est égale à 5 cm
10) Dans la figure suivante qui représente un cercle de centre I
˝ [AB] est un diamètre
˝ [AB] est une corde
® [BC] est un rayon
˝ [BC] est une corde
2) On ne peut pas démontrer la réponse, c’est
pourquoi on utilise le mot « « semblent ».
4) H n’ est pas le milieu de [FG] car H n’est
pas un point de [FG].
Les distances IG et IF ne sont pas égales donc I
n’est pas le milieu de [FG].
I est un point de [FG] donc FI + IG = FG.
5) Si on prolonge les tracés des droites, alors
ils se coupent.
6) Les droites se coupent en formant un angle
droit.
7) Les droites (d1
) et (d2
) sont
perpendiculaires à une même droite donc elles
sont parallèles (on peut l’affirmer car on sait
le démontrer).
8) (d2
) et (d3
) sont parallèles et (d1
)
est perpendiculaire à (d3
) donc (d1
) est
perpendiculaire à (d2
).
9) Une corde est la plus longue lorsqu’elle
est un diamètre. Tous les diamètres du cercle
mesurent 10 cm.
10) A ,B et C sont des points du cercle donc
[AB]et [BC] sont des cordes. De plus, [AB]
contient le centre I du cercle, d’où [AB] est
aussi un diamètre.
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-456-320.jpg)









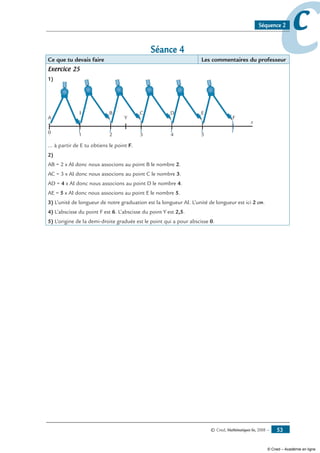























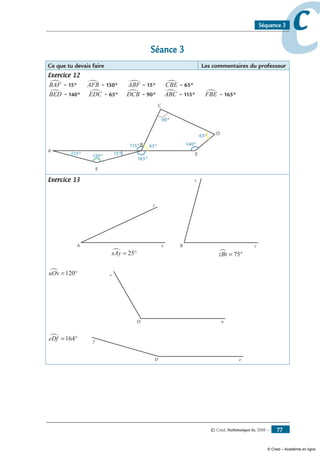
![— © Cned, mathématiques 6e, 200878
cc Séquence 3
Exercice 14
a)
E F
D
b)
K
L
M
a)
E F
[EF] étant tracé, on place correctement le
rapporteur et on fait une marque en face de la
graduation 45°.
010
20
30
40
50
60
70
90 80100
110
120
130
140
150
160
170180
E F
On trace la demi-droite d’origine E passant
par « la marque ». On place ensuite un point
D n’importe où sur cette demi-droite.
010
20
30
40
50
60
70
90 80100
110
120
130
140
150
160
170180
E F
D
Remarque : on aurait pu aussi construire le
point D « au-dessous » de [EF).
b) On effectue de même que dans le a).
Remarque : là aussi, le point M pouvait être
construit « au-dessous » de (KL).
Exercice 15
a)
CK
L
b)
GR
M
a) On commence par tracer une demi-droite
[KC) quelconque :
On place correctement le rapporteur et on fait
une marque en face de la graduation 92°.
CK
010
20
30
40
50
60
70
90 80100
110
120
130
140
150
160
170180
On trace la demi-droite d’origine K passant
par « la marque ». On place ensuite un point
L n’importe où sur cette demi-droite.
b) On effectue de même que dans le a).
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-491-320.jpg)
![© Cned, Mathématiques 6e, 2008 — 79
ccSéquence 3
Exercice 16
A B
40°
10 cm
8
cm
C
Les commentaires du professeur :
On commence par tracer un segment [AB] de 10 cm de longueur. On trace ensuite un angle BAx∑ de 40°. On place ensuite C
sur la demi-droite [Ax) tel que : AC = 8 cm. Il ne reste plus alors qu’à tracer le segment [BC].
Exercice 17
AO
C
D
20°
120°
70°
5 cm
7 cm
6cm
10 cm
B
x
y
z
Les commentaires du professeur :
• On commence par tracer un segment [OA] de 5 cm de longueur. On trace ensuite un angle AOx∑ de 20°.
On marque le point B sur [Ox) à 7 cm de O.
• On trace un angle OBy∑ de 120°. On marque le point C sur [By) à 6 cm de B.
• On trace un angle BCz∑de 70°. On marque le point D sur [Cz) à 10 cm de C.
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-492-320.jpg)

![© Cned, Mathématiques 6e, 2008 — 81
ccSéquence 3
Séance 4
Ce que tu devais faire Les commentaires du professeur
Exercice 19
1) CBA∑ = 60= 60°
2) 3) CBA∑ = 60: 2 = 60° : 2 = 30°
B A
C
D
30°
30°
1) Pour pouvoir mesurer l’angle CBA∑ , on
prolonge les tracés des côtés de cet angle.
2) On commence par calculer combien
mesurent les 2 angles adjacents égaux.
Remarque : la moitié de l’angle CBA∑ peut se
noter
CBA
2
∑
.
On place le centre du rapporteur en B et on fait
coïncider le côté [BA] avec la graduation 0°.
On fait en suite une marque en face de la
graduation 30°, et on trace la demi-droite
d’origine B passant par cette marque.
010
20
30
40
50
60
70
90 80100
110
120
130
140
150
160
170180
B A
C
4- On place ensuite un point D n’importe où
sur la demi-droite que l’on vient de tracer.
Exercice 20
a) La demi-droite [OC) est-elle la bissectrice de l’angle AOB∑ ? non
b) La demi-droite [LN) est-elle la bissectrice de l’angle KLM∑ ? oui
K
L
M
N
60°
60°
c) La demi-droite [TR) est-elle la bissectrice de l’angle UTS∑ ? non
d) La demi-droite [XV) est-elle la bissectrice de l’angle YXW∑ ? oui
Y
V W
X
45°
45°
a) Les angles AOC∑ et COB∑ sont adjacents
mais ne sont pas égaux. La demi-droite [OC)
n’est donc pas la bissectrice de l’angle AOB∑ .
A
O B
C
25°
65°
c) Les angles UTR∑ et RTS∑ sont adjacents
mais ne sont pas égaux. La demi-droite [TR)
n’est donc pas la bissectrice de l’angle UTS∑ .
U
R
S
T30°
24°
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-494-320.jpg)


![— © Cned, mathématiques 6e, 200884
cc Séquence 3
Séance 5
Ce que tu devais faire Les commentaires du professeur
Exercice 26
Je calcule ABC∑ :
ABC ABx xBy yBC∑ ∑ ∑ ∑= + +
ABC∑ = °+ °+ ° = °31 66 84 181
La mesure de l’angle ABC∑ n’est pas égale à 180° donc cet
angle n’est pas l’angle plat.
L’angle ABC∑ n’est pas plat donc les points A, B et C ne sont
pas alignés.
Pour pouvoir affirmer un résultat, on ne
peut pas se fier à une mesure, qui sera
toujours imprécise. Il faut donc utiliser une
démonstration : nous allons donc raisonner à
partir des données.
Nous connaissons les mesures des trois angles
adjacents : ABx∑ , xBy∑ et yBC∑ , dont la somme
est égale à ABC∑ .
Connaître l’angle ABC∑ nous donne des
informations d’alignement : si cet angle est
plat, les trois points A, B et C sont alignés
(sinon, ils ne le sont pas).
Nous calculons la somme des trois angles :
elle n’est pas égale à 180°. Nous savons donc
comment prouver le résultat. Il nous reste à
rédiger la démonstration : il faut faire des
phrases courtes.
Exercice 27
Je calcule ECF∑ :
ECF ECy yCx xCF∑ ∑ ∑ ∑= + +
• yCx ECy∑ ∑= = °45 (d’après le codage)
• L’angle xCF∑ est droit donc xCF∑ = °90
ECF∑ = °+ °+ ° = °45 45 90 180
ECF∑ = 180° donc C ∈ [EF].
Le point C est donc sur le segment [EF].
Nous voulons démontrer que le point C est sur
[EF], et nous ne connaissons que des mesures
d’angles. Nous pensons donc à la propriété vue
précédemment.
Pour pouvoir l’appliquer, nous devons calculer
ECF∑ .
L’angle ECF∑ est la somme de trois angles
adjacents dont on peut connaître les mesures.
Nous calculons la somme, nous trouvons 180°.
Il ne nous reste plus qu’à appliquer la propriété
pour démontrer que le point C est sur le
segment [EF].
Exercice 28
Je calcule yLM∑ :
KLM KLx xLy yLM∑ ∑ ∑ ∑= + +
• Les points K, L et M sont alignés dans cet ordre donc
KLM∑ = °180 .
58 32 180°+ °+ = °yLM∑
90 180°+ = °yLM∑
yLM∑ = °− ° = °180 90 90
L’angle yLM∑ a pour mesure 90°, c’est donc un angle
droit.
Nous connaissons des mesures d’angles.
Nous devons prouver que yLM∑ est droit.
Nous allons donc essayer de prouver que yLM∑
mesure 90°.
On pense à utiliser la propriété vue
précédemment :
« Si L ∈ [KM] alors KLM∑ = °180 ».
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-497-320.jpg)


![© Cned, Mathématiques 6e, 2008 — 87
ccSéquence 3
Exercice 31
B C
A
50° 60°
8 cm
B C
A
50° 60°
8 cm
Pour pouvoir tracer une figure répondant
à l’énoncé, nous commençons d’abord par
représenter une figure à main levée, et on
la code. Cette figure va nous permettre de
réfléchir à la manière de faire la construction :
quel point place-t-on en premier ? quel segment
ou quel angle trace-t-on en premier ?
On commence par tracer le côté [BC] qui
mesure 8 cm :
B C
On trace un angle de 50° de sommet B :
B C
010
20
30
40
50
60
70
90 80100
110
120
130
140
150
160
170180
90 100
110
120
130
150
140
160170180
80
60
70
40
50
30
20
10
0
On trace un angle de 60° de sommet C :
B C
010
20
30
40
50
60
70
90 80100
110
120
130
140
150
160
170180
90 100
110
120
130
150
140
160170180
80
60
70
40
50
30
20
10
0
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-500-320.jpg)
![— © Cned, mathématiques 6e, 200888
cc Séquence 3
Exercice 32
1)
Figure à main levée
A
B C4 cm
80° 60°
B
C
A
80° 60°
4 cm
2)
Figure à main levée
S
R T
4,5 cm
50°
4 cm
4 cm
S
R T
4,5 cm
50°
3)
Figure à main levée
M
K L
4 cm
40°
6 cm
M
K L
4 cm
40°
6 cm
M'
1) On utilise la méthode étudiée dans
l’exercice précédent. On rappelle qu’il est
toujours utile de faire une figure à main levée,
même quand cela n’est pas demandé.
2) Voici une construction possible :
• On commence par tracer un segment [RT]
de 4 cm.
• On trace ensuite un angle TRx∑ de 50°.
4 cm
x
R T
50°
• On place le point S sur [Rx) tel que RS = 4,5 cm.
• On trace enfin le segment [ST].
3) Voici une construction possible :
• On commence par tracer un segment [KL]
de 6 cm.
• On trace ensuite un angle KLx∑ de 40°.
x
K L
40°
6 cm
• Comme KM = 4 cm, on trace au compas le
cercle de centre K et de rayon 4 cm.
x
K L
40°
6 cm
• Le point M est l’un des 2 points
d’intersection de [Lx)et du cercle.
• On trace enfin le segment [KM].
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-501-320.jpg)

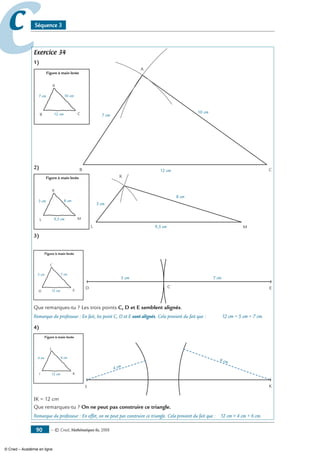
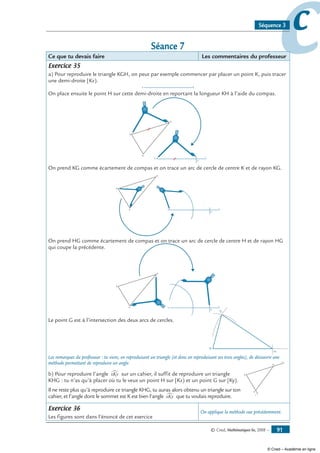
![© Cned, Mathématiques 6e, 2008 — 93
ccSéquence 3
Exercice 38
• le triangle DKB est rectangle en B car DBK∑ = °90 .
• le triangle DIK est rectangle en I car DIK∑ = °90 .
• le triangle CDB est isocèle en C car CD = CB.
• le triangle ABK est équilatéral car AB = AK = KB.
• le triangle KIJ est rectangle en J car IJK∂ = °90 .
• le triangle EDF est rectangle isocèle en D car DE = DF et
EDF∑ = °90 .
• le triangle GIH est rectangle isocèle en I car IG = IH et
GIH∑ = °90 .
A
B
C
D
E
F G
H
I
J
K
Exercice 39
1)
Figure à main levée
C
A B
4 cm
5 cm
2)
Figure à main levée
G
F E
4,5 cm
2 cm
G
F E
4,5 cm
2 cm
(d)
3)
Figure à main levée
M
K L
45°
4 cm
M
K L
45°
4 cm
x
y
1) Cette construction est la plus simple :
• On peut commencer par tracer un segment
[AB] de 5 cm de longueur.
• On trace à l’aide d’une équerre un segment
[AC] perpendiculaire à (AB) de longueur 4 cm.
• On obtient ainsi le point C. Il ne reste plus
qu’à tracer le segement [BC] et à coder le
triangle.
2)
• On peut commencer par tracer un segment
[FE] de 2 cm de longueur.
• On trace à l’aide d’une équerre la droite
(d) perpendiculaire à (FE) et passant par F.
• Le point G est à 4,5 cm du point E : on
trace donc un arc de cercle de centre E et de
rayon 4,5 cm.
• Cet arc de cercle coupe la droite (d) au
point G.
• Il ne reste plus qu’à tracer le segment [GE]
et à coder le triangle.
3)
• On peut commencer par tracer un segment
[KL] de 4 cm.
• On trace à l’aide d’une équerre une demi-
droite [Kx) perpendiculaire à (KL).
• On trace un angle KLy∑ de 45° à l’aide
d’un rapporteur.
• les demi-droites [Kx) et [Ly) se coupent en
M.
• Il ne reste plus qu’à coder le triangle.
C
A B
4 cm
5 cm
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-506-320.jpg)

![© Cned, Mathématiques 6e, 2008 — 95
ccSéquence 3
Séance 8
Ce que tu devais faire Les commentaires du professeur
Exercice 41
Figure à main levée
C
A
B
5 cm
7 cm
B C
A
7 cm
5 cm
On applique la méthode vue dans la séance 6
permettant de tracer un triangle connaissant
les longueurs de ses 3 côtés.
Le cas du triangle isocèle est particulier : une
fois le segment [BC] tracé, les deux arcs de
cercle de centres B et C ont tous les deux 5 cm
de rayon.
La méthode de construction est détaillée dans
la suite du cours.
Exercice 42
1)
Figure à main levée
T
R
S
6 cm
4 cm
S T
R
4 cm
6 cm
2)
Figure à main levée
M
K
L
4 cm
45°
M
K
L
4 cm
45°
x
3)
Figure à main levée
C
B
A
3 cm
70°
C
B
A
3 cm
70°
x
1)
On applique la méthode décrite
précédemment.
2)
• On peut commencer par tracer un segment
[KL] de 4 cm.
• On trace un angle LKx∑ de 45°.
• On sait que KM = 4 cm car le triangle KLM
est isocèle en K. On trace un arc de cercle de
centre K et de rayon 4 cm qui coupe la demi-
droite [Kx) en M.
• On trace le segment [LM] et on code le
triangle.
3)
• On peut commencer par tracer un segment
[BA] de 3 cm.
• On trace un angle BAx∑ de 70°.
• On sait que BC = 3 cm car le triangle ABC
est isocèle en B. On trace un arc de cercle de
centre B et de rayon 3 cm qui coupe la demi-
droite [Ax) en A et en C.
• On trace le segment [BC] et on code le
triangle.
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-508-320.jpg)
![— © Cned, mathématiques 6e, 200896
cc Séquence 3
Exercice 43
K
4 cmL M
Ce cas est un cas particulier de triangle
isocèle : on applique donc la méthode de
construction d’un triangle isocèle, qui va ici se
simplifier.
• On trace un segment [LM] de 4 cm.
• On prend pour écartement de compas la
longueur LM et on trace deux arcs de cercle de
centres respectifs L et M qui se coupent en K.
• On trace le triangle KLM et on le code.
Exercice 44
1)
E
2,5
cm
3 cm
I
G
J
F
H
4 cm
5cm
2cm
2) On trace :
• un triangle FGJ rectangle en G tel que :
GF = 3 cm ; GJ = 5 cm.
• un triangle EGF tel que :
GE = 2,5 cm ; EF = 2 cm.
• un triangle GIE équilatéral.
• un triangle EFH isocèle en H tel que HE = 4 cm.
1) La figure est constituée :
• d’un triangle FGJ rectangle en G tel que
GF = 3 cm et GJ = 5 cm (on le trace en
utilisant une équerre).
• d’un triangle EGF tel que :
GF = 3 cm ; GE = 2,5 cm ; EF = 2 cm.
On le trace en utilisant la méthode de
construction d’un triangle dont on connaît les
longueurs de chacun des trois côtés.
• un triangle GIE équilatéral.
On le trace en appliquant la méthode de
construction d’un triangle équilatéral (sachant
que [GE] est déjà tracé).
• un triangle EFH isocèle en H tel que
HE = 4 cm.
On le trace en appliquant la méthode de
construction d’un triangle isocèle (utilisant le
compas).
2) Ceci est une bonne réponse, mais il y en
avait d’autres.
Quand on rédige ce genre de consignes, il faut
essayer de n’écrire que ce qu’il y a d’essentiel.
Par exemple, dans la solution proposée, il
n’était pas nécessaire d’écrire :
« un triangle GIE équilatéral de côté 2,5 cm »,
car on sait déjà que [GE] est un de ses côtés et
qu’il mesure 2,5 cm.
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-509-320.jpg)

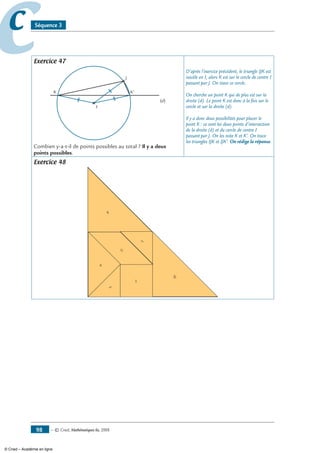


![© Cned, Mathématiques 6e, 2008 — 101
ccSéquence 3
Exercice Je m’évalue
1) L’angle DFE∑ a pour sommet :
® D
˝ F
® E
® [DF)
2) L’angle KLM∑ a pour côté(s) :
˝ [LM)
® [LM]
˝ [LK)
® [KM)
3) La mesure d’une angle droit, en degrés, est :
® 45°
® 100°
® 180°
˝ 90°
4) L’angle ci-contre est :
® aigu
® droit
˝ obtus
® plat
5) La bissectrice d’un angle de 106° le coupe en deux angles de :
® 106°
® 58°
˝ 53°
® 212°
6) L’angle JDL∑ est plat. Les points J, L et D :
˝ sont alignés
® sont confondus
˝ sur une même droite
® ne sont pas toujours alignés
7) Le triangle DEF est isocèle en D. On a donc :
® DE = EF
® DF = EF
˝ DE = DF
® DE = EF = DF
8) Le triangle KLM est rectangle en M.
˝ les droites (KM) et (ML) sont perpendiculaires
® l’angle KLM∑ est droit
˝ l’angle KML∑ est droit
® l’angle MKL∑ est droit
9) Le triangle CVR est rectangle isocèle en V. On a :
˝ CVR∑ = 90= 90°
® CR = RV
˝ RV = CV
® CRV∑ = °90
10) Un cercle de centre O passe par les points H et K.
˝ [HK] est une corde de ce cercle
® [HK] est un diamètre de ce cercle
® le triangle OHK est équilatéral
˝ le triangle OHK est isocèle en O
1) Le sommet est la « lettre du milieu » dans
la notation d’un angle.
2) Pour t’aider à répondre, tu peux tracer
rapidement sur un brouillon une figure à main
levée.
5) La moitié de 106 est 53.
Pense à tracer rapidement sur un brouillon une
figure à main levée !
6) Pense à tracer rapidement sur un brouillon
une figure à main levée !
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-514-320.jpg)
![— © Cned, mathématiques 6e, 2008102
cc Séquence 4
SÉQUENCE 4
Séance 1
Ce que tu devais faire Les commentaires du professeur
Je revise les acquis de l’école
1) c)
2) a)
3) d)
4) c)
1) Pour calculer combien Paul dépense, on
effectue 7 x 8.
2) Coline possède au total 3 fois 54 cartes plus
15 cartes. On calcule donc 3 x 54. On trouve
162. On y ajoute 15 : on trouve alors 177.
Remarque : ce calcul peut s’écrire (3 x 54) + 15
Les parenthèses signifient que l’on commence
par calculer 3 x 54.
3) Cette question était un piège : il ne fallait
pas faire de multiplication. Sébastien a gagné
7 + 9 + 13 billes soit 29 billes.
4) Pour obtenir rapidement le résultat, il
suffisait d’appliquer la règle de multiplication par
100 : il fallait décaler la virgule de 1,5 de deux
rangs vers la droite et compléter par un zéro.
Exercice 1
La vente des 29 consoles a rapporté au vendeur 317
(en euros) : x 29
317 x 29 = 9 193 2853
Le chiffre des centaines du résultat est 1. 634 .
La lettre associée à 1 est A. 9193
J’écris donc A dans la 1ère case :
[A] [__] [__] [__] [__] [__] [__] [__] [__]
— 317 x 9 (unités)
— 317 x 2 (dizaines)
(Ne pas oublier de décaler d’un rang vers la
gauche le résultat de 317 x 2 par rapport à
celui de 317 x 9)
Ce qu’on dit quand on effectue 317 x 29
• lorsqu’on effectue 317 x 9
. 9 x 7 ? 63. Je pose 3 et je retiens 6.
. 9 x 1 ? 9 ; 9 + 6 = 15 ; je pose 5 et je retiens 1.
. 9 x 3 ? 27 ; 27 + 1 = 28
• lorsqu’on effectue 317 x 2
. 2 x 7 ? 14. Je pose 4 et je retiens 1.
. 2 x 1 ? 2 ; 2 + 1 = 3
. 2 x 3 ? 6
Exercice 2
La longueur en cm de la courbe rouge est : 6,2
6,2 x 16 = 99,2 x 1,6
37,2
62, .
99,2
La longueur en mm de la courbe verte est : 73,5
73,5 x 13 = 955,5 x 1,3
955,5 mm = 95,55 cm 220,5
99,2 95,55 735, .
955,5
La courbe rouge est donc plus longue que la courbe verte.
La courbe rouge est constituée de 16 segments
de 6,2 cm.
Pour multiplier un décimal par un entier,
• on effectue la multiplication sans tenir
compte de la virgule
• on place la virgule dans le résultat
(Comme 6,2 s’écrit avec un chiffre après la
virgule, on place la virgule dans le résultat de
façon à avoir un chiffre après la virgule)
La courbe verte est constituée de 13 segments
de 73,5 mm.
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-515-320.jpg)




![© Cned, Mathématiques 6e, 2008 — 107
ccSéquence 4
Exercice 11
1) a) 5 x 1,8 x 2 = (2 x 5) x 1,8 = 10 x 1,8 = 18
b) 2 x 2 x 2 x 0,003 x 5 x 5 x 5 = (2 x 5) x (2 x 5) x (2 x 5) x 0,003 = 10 x 10 x 10 x 0,003 = 1 000 x 0,003 = 3
Commentaires du professeur :
Dans les deux produits donnés, on remarque les facteurs 2 et 5.
• 2 x 5 = 10
• Multiplier par 10 est facile.
On peut utiliser l’égalité précédente, puisque dans un produit on peut changer l’ordre des facteurs et les grouper comme on veut.
2) a) La lettre associée à 18 est la 18ème de l’alphabet, soit R. J’écris donc R dans la deuxième case du
«nom secret».
[A] [R] [__] [__][__][__][__][__][__]
b) La lettre associée à 3 est C. J’écris donc C dans la troisième case du «nom secret».
[A] [R] [C] [__][__][__][__][__][__]
Exercice 12
1) 4 x 25 = 100 8 x 125 = 1 000
2) a) 4 x 0,25 = 1 b) 0,8 x 125 = 100
Retiens ces deux égalités. Cela t’aidera à
voir comment calculer rapidement certaines
expressions.
Exercice 13
1) K = 9 x 25 x 8,1 x 4
K = (25 x 4) x (9 x 8,1)
K = 100 x 72,9
K = 7 290
2) L = 3 x 1,25 x 96 x 8
L = (1,25 x 8) x (96 x 3)
L = 10 x 288
L = 2 880
3) M = 10 x 9 x 0,4 x 9 x 25
M = 10 x (0,4 x 25) x (9 x 9)
M = 10 x 10 x 81
M = 8 100
On remarque les facteurs 25 et 4. On pense
à l’égalité : 25 x 4 = 100. Multiplier par 100
est facile.
On pense à utiliser : 125 x 8 = 1 000
On pense à utiliser : 4 x 25 = 100
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-520-320.jpg)






![— © Cned, mathématiques 6e, 2008114
cc Séquence 4
c)
4,7,3
x 9,6
2,8,3,8
42,5,7,0
45,4,0,8
2) Recherche du nom secret :
Le résultat de la multiplication à trous du 1- b) est 43,884.
Le chiffre des dixièmes de ce résultat est 8.
La 8ème lettre de l’alphabet est H. J’écris donc H dans la
quatrième case du «nom secret».
[A] [R] [C] [H][__][__][__][__][__]
c) n x 3 se termine par un 8.
En récitant la table de 3,
on constate que le seul
résultat qui se termine
par un 8 s’obtient en
effectuant 3 x 6.
Par suite, n représente
un 6.
Grâce au résultat que nous venons de trouver,
nous pouvons compléter partiellement la
multiplication à trous donnée :
obtenu en effec-
tuant 6 x n et
en ajoutant 4 de
de retenue
(6 x n) + 4 = 28
Or le nombre qui ajouté à 4 donne 28 est
28 – 4 soit 24.
Par suite : 6 x n = 24
On en déduit que n représente le chiffre 4.
Ainsi :
1
n x 3 se termine par un 7.
Lorsqu’on récite la table
de 3, on constate que seul
le résultat de 3 x 9 se
termine par un 7.
Par suite,n représente
un 9.
La suite est alors facile.
Exercice 24
On peut obtenir un nombre entier en multipliant deux
décimaux non entiers : 0,4 x 2,5 = 1 fl égalité obtenue à partir de : 4 x 25 = 100
7
x
®®®
®®
n
8
®,
3
82
7
,®
®
®
®®
7
x
®®®
®®
8
®,
3
82
7
,n
®
®®
6
3
7
x
®®®
®®
8
®,
3
82
7
,n
®
®®
6
3
7
x
®®®
®®
8
®,
3
82
7
,
®
®®
6
3
4
7
x
®®®
®®
8
®,
3
82
7
,
n
®®
6
3
4
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-527-320.jpg)



![— © Cned, mathématiques 6e, 2008118
cc Séquence 4
Séance 5
Exercice 33
1) a) 39,4 x 0,1 = 3,94
b) 115,86 x 0,01 = 1,158 6
c) 564,3 x 0,001 = 0,564 3
2) • Multiplier un décimal par 0,1 revient à déplacer sa virgule
vers la gauche de 1 rang.
• Multiplier un décimal par 0,01 revient à déplacer sa virgule
vers la gauche de 2 rangs.
• Multiplier un décimal par 0,001 revient à déplacer sa
virgule vers la gauche de 3 rangs.
564,3 = 0564,3
Remarque : Multiplier un décimal par 0,1 ;
0,01 ; 0,001 c’est le multiplier par
1
10
,
1
100
,
1
1 000
.
Exercice 34
101 9,1 930,1 9,3
10,1 910 9,301 0,093
x 0,1 -1 x 100 +20,1 x 0,01 -0,001 x 0,01
• Calcul de 101 x 0,1
Penser que : 101 = 101,0
• Calcul de 9,1 x 100
Penser que : 9,1 = 9,10
• Calcul de 9,3 x 0,01
Penser que : 9,3 = 009,3
Exercice 35
Le produit de 57 par 0,01 est 57 x 0,01 soit 0,57.
0,57 + 8,43 = 9,00 = 9
La lettre de l’alphabet associée à 9 est I. J’écris donc I dans la 5ème case du « nom secret » :
[A] [R] [C] [H][I][__][__][__][__]
Exercice 36
1) A = 0,1 x 0,1 = 0,01
2) B = 0,1 x 0,01 = 0,001
3) C = 0,01 x 0,01 = 0,000 1
1) Pour multiplier un décimal par 0,1 on
déplace sa virgule de 1 rang vers la gauche.
00,1
2) Pour multiplier un décimal par 0,01 on
déplace sa virgule de 2 rangs vers la gauche.
000,1
3) Même règle que précédemment.
000,01
Exercice 37
1) D = 10 x 0,1 = 1
2) E = 100 x 0,1 = 10
3) F = 1 000 x 0,001 = 1
10,0
100,0
1 000,0
Remarque : Pour calculer les nombres D et F
on aurait pu aussi raisonner ainsi :
D = 10 x 0,1 = 10 x
1
10
=
10
10
= 1
F=1000x0,001=1000x
1
1 000
=
1 000
1 000
=1
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-531-320.jpg)

![— © Cned, mathématiques 6e, 2008120
cc Séquence 4
Exercice 40
1)
0,01 x 134 x 100 x 0,1 = (0,01 x 100) x 134 x 0,1 = 13,4
1
La partie entière de 13,4 est 13.
La lettre de l’alphabet associée à 13 est M.
J’écris donc M dans la 6ème case du «nom secret».
[A] [R] [C] [H][I][M][__][__][__]
2)
1000x50x0,1x0,1x0,01=1000x(0,1x0,01)x50x0,1=1x50x0,1=5
0,001
La lettre de l’alphabet associée à 5 est E.
J’écris donc E dans la 7ème case du «nom secret».
[A] [R] [C] [H][I][M][E][__][__]
1) On remarque les facteurs 0,01 et 100.
0,01 x 100 = 1
On peut utiliser cette égalité vu que dans un
produit on peut changer l’ordre des facteurs et
les grouper comme on veut.
2) On remarque les facteurs 0,1 et 0,01.
0,1 x 0,01 = 0,001
Cette dernière égalité est «intéressante» vu
que : 1 000 x 0,001 = 1
On pouvait également utiliser une autre
méthode :
On remplace 1 000 par 10 x 100. Ainsi,
on peut utiliser les égalités : 10 x 0,1 = 1 et
100 x 0,01 = 1
1 000 x 50 x 0,1 x 0,1 x 0,01
= 10 x 100 x 50 x 0,1 x 0,1 x 0,01
= (10 x 0,1) x (100 x 0,01) x 50 x 0,1 = 5
1 1
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-533-320.jpg)
![© Cned, Mathématiques 6e, 2008 — 121
ccSéquence 4
Séance 6
Exercice 41
La distance en km qu’Ydriss parcourt les jours de classe, pour
suivre ses cours, est :
2,4 x 2 = 4,8
Il va 5 fois par semaine au collège.
La distance en km qu’il parcourt chaque semaine pour suivre sa
scolarité est donc :
4,8 x 5 = 24
La distance en km qu’il parcourra cette année scolaire en allant
au collège est :
24 x 36 = 864
Le chiffre des unités de 864 est 4.
La lettre de l’alphabet associée à 4 est D.
J’écris donc D dans la 8ème case du « nom secret ».
[A] [R] [C] [H][I][M][E][D][__]
L’année scolaire compte 36 semaines de classe.
Pour répondre à la question posée, il sufffit
de commencer par calculer la distance en km
qu’Ydriss parcourt chaque semaine pour suivre
ses cours.
Exercice 42
Chaque minute, l’aiguille des secondes d’une pendule fait un
tour de cadran.
1 h = 60 min
En 1 h, elle fait donc 60 tours de cadran.
1 journée = 24 h
En 1 journée, le nombre de tours de cadran que fait l’aiguille
des secondes est donc : 60 x 24 = 1 440
En 1 année de 365 jours, le nombre de tours de cadran que fait
cette aiguille est donc : 1 440 x 365 = 525 600
Si nécessaire, commence par regarder tourner
l’aiguille des secondes d’une pendule.
Combien de temps met-elle pour effectuer un
tour de cadran ?
Commençons par calculer combien de tours
elle effectue en une journée.
Exercice 43
1) Le nombre total de places du cinéma est : 36 x 18 = 648
Le nombre de places libres à la séance de 15 h était :
648 – 459 = 189
2) Le nombre de personnes ayant payé le prix normal est :
459 – 271 = 188
La recette en euros de la séance de 15 h a été
(6,40 x 188) + (5,60 x 271) soit 1 203,2 + 1 517,6
c’est-à-dire 2 720,8.
3) Le nombre de tickets vendus dans la journée a été :
(973 – 187) + 1 = 786 + 1 = 787
2) On sait combien de personnes ont payé
au tarif réduit. Pour calculer la recette de
la séance de 15 h, il faut savoir combien de
personnes ont payé au tarif normal.
3) Attention ! Le nombre de tickets vendus ne
s’obtient pas en calculant 973 – 187.
Pour t’en convaincre, imagine que le dernier
billet vendu ait porté le numéro 188.
Seulement deux billets auraient été vendus
dans la journée. Des deux calculs 188 – 187
et (188 – 187) + 1, c’est bien le deuxième qui
permet d’obtenir 2.
Lorsqu’on te demande de répondre à une
question du type de celle qui t’a été posée,
ramène-toi toujours au brouillon à un cas plus
simple, afin de vérifier que le calcul que tu
proposes a des chances d’être correct.
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-534-320.jpg)

![© Cned, Mathématiques 6e, 2008 — 123
ccSéquence 4
Séance 7
Exercice 46
Comme il y a un arbre à chaque extrémité de l’avenue, le
nombre d’intervalles entre deux arbres consécutifs est égal au
nombre d’arbres moins 1. Le nombre d’intervalles est donc :
105 – 1 = 104
La longueur en m de l’avenue est : 5,10 x 104 = 530,4
Le chiffre des centaines du résultat obtenu est 5.
La lettre de l’alphabet associée à 5 est E.
J’écris donc E dans la 9ème case du «nom secret».
[A] [R] [C] [H][I][M][E][D][E]
Il apparaît alors le nom d’un très grand savant grec (peut-être
le plus grand de l’Antiquité).
Archimède était à la fois un mathématicien, un physicien, un
ingénieur et un philosophe. Il vécut de 287 à 212 avant Jésus
Christ.
Il est l’inventeur de la roue dentée, de la poulie, du levier, de la
vis sans fin… Grâce à des machines qu’il avait fait construire
pour lancer au loin des pierres, il tint en échec pendant trois
ans les Romains qui assiégeaient sa ville (Syracuse).
Il a, par ailleurs, pris conscience en prenant son bain, de la
poussée de l’eau sur tout corps plongé dedans. Il était si joyeux,
paraît-il, d’avoir fait cette découverte, qu’il serait sorti de
son bain et aurait traversé sa ville en criant : « Euréka ! » (J’ai
trouvé)
La longueur en m de l’avenue s’obtient en
multipliant 5,10 (la distance en m séparant
deux arbres consécutifs) par le nombre
d’intervalles.
Combien y a-t-il d’intervalles ?
Il fallait se souvenir que si l’on place des
points sur une ligne (non fermée), en
plaçant un point à chaque extrémité, le
nombre d’intervalles est égal au nombre de
points moins 1.
5 points
4 intervalles
Exercice 47
Le prix du tapis en euros est : 357,10 x 0,630 07 = 224,997 99
L’arrondi au centième de ce prix est 225.
On fait une multiplication. C’est l’opération
que tu aurais faite si le tapis avait coûté 2 ou
3 dinars.
Le chiffre des millièmes du prix est 7. Par suite
l’arrondi au centième du prix est 224,99 + 0,01
soit 225.
Il était inutile, pour traiter l’exercice, de savoir
que Pierre-Yves était allé en Tunisie pour ses
30 ans. Connaître la longueur du tapis ne
servait pas non plus.
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-536-320.jpg)
![— © Cned, mathématiques 6e, 2008124
cc Séquence 4
Exercice 48
Énoncé
Florine achète 2,100 kg de pommes à 1,6 € le kilo. Elle paie avec
un billet de 5 euros.
Combien lui rend-on ?
Solution
La somme en euros qu’on rend à Florine est :
5 – (1,6 x 2,100) = 5 – 3,36 = 1,64
Ce n’est pas, bien sûr, le seul énoncé qui
convienne.
Attention ! Lorsqu’on te demande d’écrire
un énoncé, il ne faut pas oublier d’écrire la
question.
Le prix des pommes s’obtient en multipliant le
prix d’un kilo par le nombre de kilos achetés.
Exercice 49
1) Le montant total en euros des achats de Léopoldine est :
20 – 5,18 = 14,82
350 g = 0,350 kg
Le prix en euros de la limande est : 9,8 x 0,35 = 3,43
290 g = 0,290 kg
Le prix en euros des crevettes roses est : 21 x 0,29 = 6,09
Le prix total en euros des deux soupes de poisson est :
2,34 x 2 = 4,68
Le prix en euros de la mayonnaise est :
14,82 – (3,43 + 6,09 + 4,68) = 14,82 – 14,2 = 0,62
2) On ne peut calculer le prix des deux tranches de saumon vu
qu’on ne connaît pas leur « poids ».
Le prix de la limande s’obtient en multipliant
le prix d’un kilo par le nombre de kilos
achetés.
(9,8 x 0,35) + (21 x 0,29) + (2,34 x 2)
représente le prix total en euros de la limande,
des crevettes roses et des deux soupes de
poisson.
On pouvait donc calculer directement le prix
en euros de la mayonnaise en retranchant
(9,8 x 0,35) + (21 x 0,29) + (2,34 x 2) à
14,82
c’est-à-dire en effectuant :
14,82–((9,8x0,35)+(21x0,29)+(2,34x2))
ce qu’on note généralement :
14,82–[(9,8x0,35)+(21x0,29)+(2,34x2)]
(On utilise un crochet, car à l’intérieur de la
grande parenthèse, il y a des parenthèses)
Pour effectuer une expression contenant
un crochet, on commence par effectuer les
parenthèses à l’intérieur du crochet.
Ainsi, le prix en euros de la mayonnaise est :
14,82–[(9,8x0,35)+(21x0,29)+(2,34x2)]
soit14,82–(3,43+6,09+4,68)…
Le prix du saumon s’obtient en multipliant le
prix d’un kilo par le nombre de kilos achetés.
Cette question était un piège !
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-537-320.jpg)






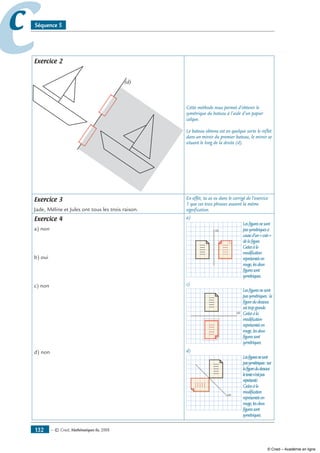
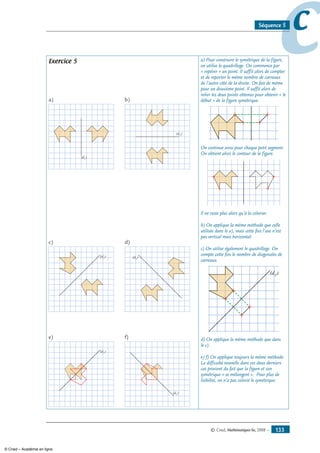

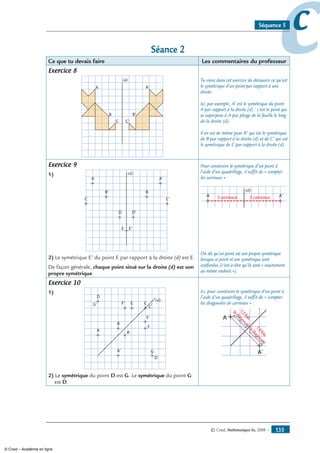
![— © Cned, mathématiques 6e, 2008136
cc Séquence 5
Exercice 11
1) Le segment [AA’] et la droite (d) semblent perpendiculaires.
Le segment [BB’] et la droite (d) semblent également
perpendiculaires.
2) D’après la figure, il semble que : AE = EA’ et que BF = FB’.
3) La droite (d) semble être la médiatrice des segments [AA’] et
[BB’].
a)
A
B
B'
A'
(d)
A'
(d)
A
B
B'
A'
(d)
On place
l’équerre de la
façon suivante
pour tester si les
droites (AA’)
et (d) semblent
perpendiculaires.
On fait de même
pour (BB’) et (d).
On vérifie avec le
compas que AE
et EA’ semblent
égales de la façon
suivante.
On fait de même
pour BF et FB’.
Exercice 12
(d)
B‘
A‘
C‘
C
A
B
On applique la méthode vue précédemment.
On utilise l’équerre et le compas.
Pour construire le point A’ :
• On trace la droite perpendiculaire à la
droite (d) passant par A.
• On prend le compas et on reporte la
distance AI à partir du point I comme ci-
dessous.
(d)
A‘
A
I
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-549-320.jpg)
![© Cned, Mathématiques 6e, 2008 — 137
ccSéquence 5
Exercice 13
(d1
)
(d2
)
A'
B
B'
A
On utilise à nouveau la méthode vue
précédemment.
Il fallait faire attention à bien lire la consigne :
A’ est le symétrique de A par rapport à la droite
(d1
). Il faut donc tracer la perpendiculaire à
la droite (d1
) passant par A puis prendre son
compas.
Il fallait ensuite construire B’, le symétrique du
point B par rapport à la droite (d2
).
Exercice 14
A
A'
B
C
C'
B'
K I
J
AJ = JA’
BI = IB’
CK = KC’
On applique à nouveau la même méthode
pour obtenir les points A’, B’ et C’.
Pourquoi n’a-t-on pas
codé sur la figure les
égalités de longueurs ?
la réponse est simple,
étudions un exemple
ci-contre. On a voulu
coder l’égalité des
deux longueurs AJ
et JA’.
Quelqu’un qui
regarde la figure va
certainement dire :
d’après la figure on
a HJ = JA’. Ce qui ici
est faux.
A
A'
B
I
C
C' B'
J
H
En fait, comme le segment [AJ] est coupé par
au moins un autre segment, on ne peut pas
coder l’égalité de longueur AJ = JA’.
De fait, on ne peut coder aucune des trois
égalités de longueur sur la figure.
Par contre, on peut toujours écrire sous la
figure les trois égalités.
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-550-320.jpg)
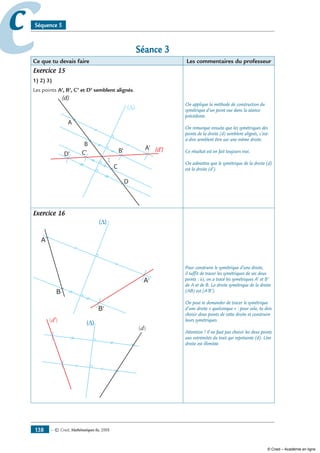

![— © Cned, mathématiques 6e, 2008140
cc Séquence 5
Exercice 19
1)
A
A'
C
C'
D
D'
E
E'
F
F'
G
G'
B
B'
K
N
2)
C ∉ [AB] C’ ∉ [A’B’]
D ∈ [AB] D’ ∈ [A’B’]
E ∈ [AB] E’ ∈ [A’B’]
F ∈ [AB] F’ ∈ [A’B’]
G ∉ [AB] G’ ∉ [A’B’]
3) Si un point M est sur le segment [AB], alors son symétrique
M’ semble être sur le segment [A’B’].
4) Le point N semble être sur le segment [AB].
1)
On construit à l’aide de l’équerre et du
compas les points A’, B’, C’, D’, E’, F’ et G’.
On trace ensuite la droite (A’B’). Cette droite
passe par les points B’, C’, D’, E’, F’ et G’.
On le savait car les point B, C, D, E, F et G
sont sur la droite (d) et le symétrique d’une
droite est une droite.
2) On remarque que parmi C, D, E, F et G,
tous les point qui sont sur le segment [AB] ont
pour symétrique un point du segment [A’B’].
De plus, les points qui ne sont pas sur [AB]
ont pour symétrique un point qui n’est pas sur
[A’B’].
3) Il fallait écrire que ce que nous avons
constaté ci-dessus pour les points A, D, E,
F semblait vrai pour tout point du segment
[AB].
4) Nous remarquons qu’inversement, le
symétrique de tout point du segment [A’B’]
semble être sur le segment [AB].
Exercice 20
2) Il semble que : AB = A’B’ CD = C’D’ EF = E’F’.
1)
Nous venons de voir que le symétrique d’un
segment est un segment. Pour construire le
symétrique de chacun des trois segments,
il suffit de commencer par construire le
symétrique de chacune de ses extrémités.
2)
On remarque que les longueurs d’un segment
et de son symétrique semblent être égales.
Par la suite, nous admettrons que ceci est
toujours vrai : un segment et son symétrique
ont toujours la même longueur.
1)
(∆)A
B
C
D
E
F
A'
B'
C'
D' E'
F'
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-553-320.jpg)
![© Cned, Mathématiques 6e, 2008 — 141
ccSéquence 5
Exercice 21
Méline et Jules ont raison ; Jade a tort.
En mathématiques, si une propriété est dite vraie (par exemple :« deux segments de même longueur sont symétriques »), cela veut
dire qu’elle est toujours vraie. Ici, lorsqu’on dit que cette propriété est fausse, on veut dire qu’elle n’est pas toujours vraie. Pour le
démontrer, il suffit alors de trouver un exemple pour lequel la propriété n’est pas vérifiée (on appelle cela un contre-exemple).
Voici un contre-exemple :
A
B
C
D [AB] et [CD] sont deux segments de même longueur. Supposons qu’ils soient symétriques par
rapport à une droite (D). Nous cherchons où peut se trouver cette droite.
Le symétrique du point B est nécessairement une extrémité du segment [CD]. Il y a donc deux possibilités : D ou C.
• Si le symétrique du point B était le point D :
(∆)
A
B
C
D
La droite (D) est nécessairement la médiatrice du segment [BD]. On voit bien alors que le
point C n’est pas le symétrique du point A. Le symétrique du point B n’est donc pas le point
D.
• Si le symétrique du point B était le point C :
(∆)
A
B
C
D La droite (D) est nécessairement la médiatrice du segment [BC]. On voit bien alors que
le point D n’est pas le symétrique du point A. Le symétrique du point B n’est donc pas le
point D.
Conclusion : les deux cas envisagés mènent à quelque chose d’impossible. Les segments [AB] et [CD] ne peuvent donc pas être
symétriques par rapport à une droite.
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-554-320.jpg)
![— © Cned, mathématiques 6e, 2008142
cc Séquence 5
Exercice 22
1) 2)
(∆)
A
B
I
B'
A'
I'
3)
a)
On sait que : I ∈ [AB]
D’après la propriété : Le symétrique du segment [AB] est le
segment [A’B’].
On conclut : I’ ∈ [A’B’]
b)
Le symétrique du segment [AI] est [A’I’], donc : AI = A’I’.
Le symétrique du segment [IB] est [I’B’], donc : IB = I’B’.
Or I est le milieu de [AB] donc : AI = IB.
On a : AI = IB, AI = A’I’ et IB = I’B’ donc A’I’ = I’B’.
Comme I’ ∈ [A’B’] et que A’I’ = I’B’, le point I’ est le milieu de
[A’B’].
1) On applique la méthode vue dans l’exercice
20 pour tracer le symétrique du segment
[AB].
2) On construit le point I’ , symétrique du
point I à l’aide de l’équerre et du compas.
3)
a)
On sait que le symétrique de tout point du
segment [AB] est sur le segment [A’B’].
Comme I est sur [AB], le point I’ est donc sur
le segment [A’B’].
b)
Nous utilisons dans cette question la propriété
suivante : « un segment et son symétrique ont
la même longueur ».
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-555-320.jpg)
![© Cned, Mathématiques 6e, 2008 — 143
ccSéquence 5
Séance 4
Ce que tu devais faire Les commentaires du professeur
Exercice 23
A'
B
B'
(d)
On construit B’ le symétrique de B par rapport à (d).
Le segment [AB] a pour symétrique par rapport à (d) le
segment [A’B’]. Ce deux segments ont donc même longueur.
On mesure le segment [A’B’].
[A’B’] mesure environ 4 cm donc [AB] mesure environ 4 cm.
On ne peut pas construire le point A car il
« sort du petit bout de papier ».
On voit que l’on peut construire le symétrique
du point B. On peut donc construire le segment
[A’B’], qui est en fait le symétrique du segment
[AB] que l’on ne peut pas construire. Comme
ces deux segments ont la même longueur, il
suffit donc de mesurer le segment [A’B’] pour
trouver la mesure de [AB].
Exercice 24
(∆)
A
B
B'
A'
C'
C
(∆)
D
E
F
E'
D'
F'
(∆)
K K'
L'M'
L
M
E'
N
O P
Q R
ST
U
N'
U' O'
P'
Q'
R'
S'
T'
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-556-320.jpg)
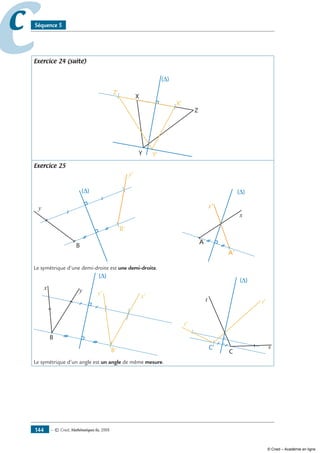
![© Cned, Mathématiques 6e, 2008 — 145
ccSéquence 5
Exercice 26
1) 4)
A'
B'
C'D'
E'
F'
O'
A
B
O
C
D
E
F
C
C
2) Les points A’, B’, C’, D’, E’ et F’ semblent appartenir à un
même cercle.
3) O’A’ = OA car les segments [OA] et [O’A’] sont
symétriques.
5) Conjecture : le symétrique du cercle C est le cercle C ’ de
centre O’ et de même rayon.
1)
On construit successivement les six points
A’, B’, C’, D’, E’ et F’. On n’a pas mis tous
les codages la figure pour ne pas nuire à la
lisiblité.
2)
Les six points construits semblent tous être sur
un même cercle.
3)
On utilise la propriété selon laquelle un
segment et son symétrique ont la même
longueur.
4) On trace le cercle de centre O’ qui passe
par A’ : il semble passer par B’, C’, D’, E’ et
F’.
5)
Il semble donc que le symétrique d’un cercle
soit un cercle de même rayon.
Nous allons admettre par la suite que ce
résultat est toujours vrai, c’est-à-dire que
le symétrique d’un cercle par rapport à une
droite est toujours un cercle de même rayon.
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-558-320.jpg)
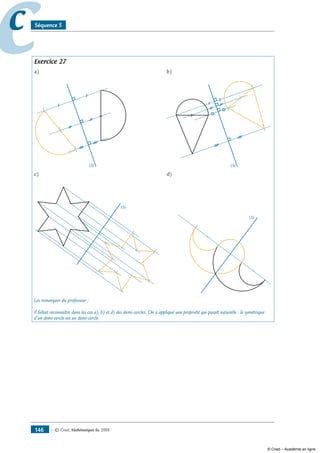

![— © Cned, mathématiques 6e, 2008148
cc Séquence 5
Exercice 30
1) 4)
A
A'
(d)
2) (d) est la médiatrice de [AA’] car A’ est le symétrique du
point A par rapport à la droite (d).
3) Les axes de symétrie du segment [AA’] sont la droite (d) et
la droite (AA’).
1)
2)
Dans la séance 2, nous avons vu que dire que
A et A’ étaient symétriques par rapport à
la droite (d) revenait à dire que (d) était la
médiatrice du segment [AA’].
3)
Chaque point de l’axe de syméytrie est son
propre symétrique. Par conséquent, par la
symétrie axiale par rapport à la droite (AA’),
tout point du segment [AA’] est son propre
symétrique : le symétrique du segment [AA’]
par rapport à la droite (AA’) est le segment
[AA’] lui-même. La droite (AA’) est donc un
axe de symétrie pour le segment [AA’].
Exercice 31
1)
A
B
(d)
I
J
2) C’est lui-même car il est sur la droite (d).
3) C’est le segment [BI] car B est le symétrique de A et I est son
propre symétrique.
4) AI = BI car le symétrique d’un segment est un segment de
même longueur.
5) AJ = BJ car J est son propre symétrique, d’où [AJ] est le
symétrique de [BJ].
6) Tu viens de montrer que si M ∈ (d) alors : MA = MB.
2) Il fallait se rappeler que tout point de
la droite (d) est son propre symétrique par
rapport à la droite (d).
3)
B est le symétrique de A
I est le symétrique de lui-même
Le segment [BI] est donc le symétrique du
segment [AI].
4) On utilise la propriété selon laquelle un
segment et son symétrique ont la même
longueur.
5) On effectue le même raisonnement que
dans le 3) avec le point J :
B est le symétrique de A
J est le symétrique de lui-même
Le segment [BJ] est donc le symétrique du
segment [AJ].
Comme ces segments sont symétriques, ils ont
donc même longueur.
6) On pourrait effectuer le même
raisonnement que celui utilisé pour I et J avec
tout point M de la médiatrice du segment
[AB]. On a donc toujours : MA = MB.
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-561-320.jpg)
![© Cned, Mathématiques 6e, 2008 — 149
ccSéquence 5
Exercice 32
A
B
M
N
O
1) La droite (MN) semble être la médiatrice du segment [AB].
2) Le point O semble être sur la droite (MN).
3) Conjecture : Si un point K est tel que KA = KB, alors K est
sur la médiatrice du segment [AB].
1) À vue d’oeil, il semble que la droite (MN)
soit la médiatrice du segment [AB]. On
utilise l’équerre, et cette observation semble
se confirmer. Toutefois, en l’absence de
démonstration, on ne peut pas en être certain.
2) Pour construire le point O, on utilise le
compas : on trace un arc de cercle de centre A,
puis avec le même écartement de compas un
autre arc de cercle de centre B. Ces deux arcs
de cercles se coupent en O. Ce point semble
être sur la droite (MN).
3) Ce qui semble être vrai pour le point O
semble être vrai pour n’importe quel point M
situé à la même distance de A et de B (on dit
aussi équidistant de A et de B).
En fait, on va admettre que ce résultat est
toujours vrai, c’est-à-dire que tout point M
équidistant de A et de B est sur la médiatrice
du segment [AB].
Exercice 33
Jules et Méline ont raison. Jade a tort.
Si trois points K, A et R sont tels que KA = KR, on sait d’après
la propriété précédente que le point K peut être n’importe
quel point de la médiatrice de [AR]. Jade a donc tort et Jules a
raison.
Méline a raison car cela veut aussi dire que le triangle KAR est
isocèle en K (par définition).
Voici une figure afin de visualiser l’énoncé de
l’exercice « trois points K, A et R sont tels que
KA = KR ».
K
A R
Exercice 34
A B
C
D
(d)
(d')
(d'')
E
F
Les remarques du professeur :
Il suffit d’appliquer la méthode expliquée précédemment. N’oublie pas, une fois chaque construction réalisée, de nommer la
médiatrice et de coder la figure.
N’oublie pas également que tu devras à partir de maintenant ne plus utiliser que cette méthode pour construire la médiatrice d’un
segment : c’est la plus fiable et la plus précise.
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-562-320.jpg)
![— © Cned, mathématiques 6e, 2008150
cc Séquence 5
Exercice 35
1) 2)
A
B
C
I
(d)
(d')
3) a)
On sait que : la droite (d) est la médiatrice du segment [AB].
Comme le point I est sur (d), on a : IA = IB.
b)
On sait que : la droite (d’) est la médiatrice du segment [BC].
Comme le point I est sur (d’), on a : IB = IC.
c) Le cercle de centre I passant par A semble passer également
par B et C.
Comme IA = IB = IC (d’après les questions a) et b)), les points
A, B et C sont sur le cercle de centre I et de rayon IA, c’est-à-
dire le cercle de centre I passant par A.
1) 2)
On utilise la construction de la médiatrice au
compas vue précédemment.
3) a)
Tout point de la médiatrice du segment [AB]
est équidistant de A et de B. I est sur cette
médiatrice donc :
IA = IB.
b)
I est également sur la médiatrice du segment
[BC], d’où par un même raisonnement :
IB = IC.
c)
Comme IA = IB et IB = IC, on a :
IA = IB = IC.
Les trois points A, B et C sont donc à la même
distance du point I, c’est-à-dire sur un même
cercle de centre I, qui passe donc par A, B et
C.
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-563-320.jpg)
![© Cned, Mathématiques 6e, 2008 — 151
ccSéquence 5
Séance 6
Ce que tu devais faire Les commentaires du professeur
Exercice 36
E
F
BX1
X2
1) X est équidistant de E et de F donc X se trouve sur la
médiatrice du segment [EF].
2) X est à 2,5 cm de B donc X se trouve sur le cercle de centre
B et de rayon 2,5 cm.
3) Il y a deux solutions au problème : X1
et X2
. Ce sont les
deux points d’intersection de la médiatrice du segment [EF] et
du cercle de centre B et de rayon 2,5 cm.
1)
L’ensemble des points équidistants de E et de F
est la médiatrice du segment [EF].
2)
L’ensemble des points situés à 2,5 cm du point
B est le cercle de centre B et de rayon 2,5 cm.
3) Les points qui sont à la fois équidistants de
E et de F et situés à 2,5 cm de B sont donc les
points d’intersection de la droite et du cercle
tracés précédemment.
Exercice 37
K
M
I
L
C
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-564-320.jpg)
![— © Cned, mathématiques 6e, 2008152
cc Séquence 5
1)
K et L sont situés sur le même cercle de centre I donc on a :
IK = IL.
2)
Le triangle KLM est isocèle en M donc MK = ML.
3)
Comme les longueurs IK et IL sont égales, le point I est donc
sur la médiatrice du segment [KL].
Comme les longueurs MK et ML sont égales, le point M est
donc sur la médiatrice du segment [KL].
La droite (IM) est donc la médiatrice du segment [KL].
1) On utilise dans cette première question
la définition du cercle de centre I. C’est
l’ensemble de tous les points situés à une
même distance de I. Comme K et L sont deux
points de ce cercle, on a donc IK = IL.
2) On utilise ici la définition d’un triangle
isocèle en M.
3) On applique la propriété caractéristique de
la médiatrice vue dans la séance précédente.
Comme les points I et M sont sur la
médiatrice du segment [KL], la droite (IM)
est donc nécessairement cette médiatrice.
Code-le sur la figure du corrigé ci-contre.
Remarque : Pour prouver qu’une droite (IM)
est la médiatrice d’un segment [KL], il suffit
de prouver que I et M sont deux points de
cette médiatrice, c’est-à-dire que I et M sont
équidistants de K et de L.
Exercice 38
1) 2)
A I
J
C
D
B
3) Pour construire le milieu J du segment [CD] à l’aide du
compas :
• On trace la médiatrice du segment [CD] à l’aide du compas.
• Cette médiatrice coupe le segment [CD] en J.
1) 2) 3)
Par définition, la médiatrice d’un segment est
la droite qui le coupe perpendiculairement en
son milieu.
Si l’on construit la médiatrice d’un segment,
on construit alors automatiquement le milieu
de ce segment : c’est le point d’intersection de
ce segment et de sa médiatrice.
Ceci constitue donc une méthode géométrique
permettant de construire le milieu de
n’importe quel segment.
Dorénavant, tu devras toujours utiliser
cette méthode lorsqu’on te demandera de
construire le milieu d’un segment.
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-565-320.jpg)
![© Cned, Mathématiques 6e, 2008 — 153
ccSéquence 5
Exercice 39
1) 2)
E
J
F
G
I
3) La droite (IJ) semble parallèle à la droite (FG).
1) 2)
On applique la méthode vue précédemment
pour construire le milieu du segment [EF],
puis le milieu du segment [EG].
3)
En fait, la droite (IJ) est parallèle à la droite
(FG), et cela est vrai pour n’importe quel
triangle ! (tu apprendras cela en 4e).
Exercice 40
1)
A
A'
E
F
(d)
C
C ’
2) A et A’ doivent être symétriques par rapport à la droite (d).
(d) est donc la médiatrice du segment [AA’].
3) E est donc sur la médiatrice du segment [AA’].
On a donc EA = EA’ .
Trace le cercle C de centre E et de rayon EA.
On a : A’ ∈ C .
4) F est sur la médiatrice du segment [AA’].
On a donc FA = FA’.
Trace le cercle C ’ de centre F et de rayon FA.
On a : A’ ∈ C ’.
5) Comme A ∈ C et A’ ∈ C ’, A’ est le deuxième point
d’intersection de C et C ’.
1) Nous avons placé « au hasard » les points
E et F sur la droite (d).
2) Nous avons déjà vu plusieurs fois (c’est un
résultat que tu dois connaître) que :
« A et A’ symétriques par rapport à la droite
(d) » revient à dire que « la droite (d) est la
médiatrice du segment [AA’] ».
3) 4) Nous savons également que tout
point de la médiatrice du segment [AA’] est
équidistant de A et de A’. Comme E et F sont
sur cette médiatrice, on doit avoir :
EA = EA’ et FA = FA’.
Comme EA = EA’, le point A’ est donc sur le
cercle de centre E et de rayon EA. On trace
donc ce cercle.
Comme FA = FA’, le point A’ est donc sur le
cercle de centre F et de rayon FA. On trace
donc ce deuxième cercle.
Le point A’ est donc le deuxième point
d’intersection des deux cercles tracés.
Ceci constitue donc une méthode pour tracer
le symétrique d’un point uniquement au
compas, car pour construire le point A’, nous
n’avons utilisé que le compas (et même pas la
règle non graduée !).
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-566-320.jpg)
![— © Cned, mathématiques 6e, 2008154
cc Séquence 5
Exercice 41
1)
A
E B
CD
(d2
)
(d1
)
2)
Jade semble avoir raison. Méline semble avoir tort.
Jules a tort. Il ignore qu’on peut toujours tracer le symétrique
d’un point par rapport à une droite.
1) On utilise la méthode précédente pour
construire dans un premier temps le point B.
A
B
(d2
)
(d1
)
On construit ensuite de la même façon les
points C, D et E.
2)
Les points A et E semblent effectivement
confondus.
En fait, c’est difficile à démontrer, mais
on pourrait démontrer qu’ils le sont
effectivement.
Exercice 42
1) a) D’après les codages de la figure, la droite (d) est
perpendiculaire au segment [AC] et passe par son milieu, c’est
donc sa médiatrice. Comme I est sur cette médiatrice, on a
donc :
IA = IC.
b) D’après les codages de la figure, la droite (d’) est
perpendiculaire au segment [BC] et passe par son milieu,
c’est donc sa médiatrice. Comme I est également sur cette
médiatrice, on a donc : IB = IC.
c) D’après le 1- a) et le 1- b) on a : IA = IC et IB = IC. On a
donc : IA = IB.
2)
J est sur la médiatrice du segment [AD] donc JA = JD.
J est également sur la médiatrice du segment [BD] donc
JB = JD.
Comme JA = JD et JB = JD, on a : JA = JB.
3)
Comme IA = IB, I est sur la médiatrice du segment [AB].
Comme JA = JB, J est sur la médiatrice du segment [AB].
Les points I et J sont donc tous les deux sur la médiatrice du
segment [AB], la droite (IJ) est donc la médiatrice du segment
[AB]. La droite (IJ) est perpendiculaire à [AB].
A
D
B
C
I
J
(d)
(d')
Dans ce type d’exercice, pense à écrire des
phrases courtes et précises.
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-567-320.jpg)
![© Cned, Mathématiques 6e, 2008 — 155
ccSéquence 5
Séance 7
Ce que tu devais faire Les commentaires du professeur
Exercice 43
A
B
C
D
E
F G
H
IJ
K
L
M
N O
0 axe
1 axe
1 axe
3 axes
0 axe
Exercice 44
B
(d)
C
A
I
1) Elle semble passer par le point A.
2) AB = AC car le triangle ABC est isocèle en A.
3) Comme AB = AC, le point A est sur la médiatrice du
segment [BC] donc sur la droite (d).
4)
• Le symétrique de B par rapport à la droite (d) est C.
• Le symétrique de A par rapport à la droite (d) est lui-même .
• Le symétrique de I par rapport à la droite (d) est lui-même .
Le symétrique de l’angle BAI∑ est donc l’angle CAI∑.
Comme un angle et son symétrique ont la même mesure,
on a : BAI CAI∑ ∑= . Par suite, (d) est la bissectrice de BAC∑.
5) De même, le symétrique de l’angle ABC∑ est l’angle ACB∑ .
Comme un angle et son symétrique ont la même mesure,
on a : ABC ACB∑ ∑= .
Le triangle ABC est isoclèle en A, on code donc
sur la figure l’égalité de longueurs AB = AC.
1) La droite (d) semble passer exactement
par le point A. Pour en être sûr, nous allons le
démontrer dans la réponse suivante.
2)
3) On utilise la propriété suivante : si un point
A est équidistant de deux points B et C, alors il
est sur la médiatrice du segment [BC].
4) Comme (d) est la médiatrice du segment
[BC], le point B a pour symétrique le point C.
On sait que tout point de (d) est son propre
symétrique par rapport à la droite (d). C’est
donc le cas pour le point A et le point I.
Connaissant les symétriques respectifs des
points B, A et I, nous connaissons donc l’angle
symétrique de l’angle BAI∑ .
5) On effectue le même raisonnement que
dans la question précédente.
Nous venons donc de démontrer dans cet
exercice que dans un triangle isocèle, la
médiatrice d’un des côtés est axe de symétrie
du triangle.
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-568-320.jpg)
![— © Cned, mathématiques 6e, 2008156
cc Séquence 5
Exercice 45
B A
O
40˚
4 cm C
1) A et B sont deux points du cercle C de centre O, donc OA = OB.
Comme OA = OB, le triangle OAB est isocèle en O.
2) Comme le triangle OAB est isocèle en O, on a :
OAB OBA∑ ∑= . Comme OAB∑ = °40 , on a : OBA∑ = °40 .
Pour tracer la figure, on commence par tracer
un cercle C de centre O et de rayon 4 cm
puis on place un point A « au hasard » sur ce
cercle.
On utilise ensuite le rapporteur pour placer un
point B tel que AOB∑ = °40 .
A
B A
O
40°
4 cm C
O
40°
A
90
90
1) On applique ici la définition du triangle
isocèle.
2) On applique la propriété vue précédemment :
si un triangle est isocèle, alors ses angles à la base
sont égaux. Comme on connaît la mesure d’un
angle à la base, on va ainsi connaître la mesure
de l’autre.
Exercice 46
1)
B
52°
5,2 cm C
A
Méline a raison, Jade et Jules ont tort.
2)
B
52°
(d)
C
A
1)
2)
Laconstructionn’est
pasimmédiate:dans
unpremiertemps,on
peutcommencerpar
tracerlecôté[BC]de
5,2cm.
Onsaitensuite
quelepointAest
nécessairement
surlamédiatrice
dusegment[BC].
Traçonsdonc(d)
lamédiatricedu
segment[BC].
B
(d)
C
Noussavonsquele
pointAesttelque:
ABC∑ = °52 .
Onprenddoncun
rapporteureton
traceunedemi-droite
[Bx)telleque:
CBx∑ = °52 .
LepointAestle
pointd’intersection
deladroite(d)etde
lademi-droite[Bx).
B
52°
(d)
C
A
x
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-569-320.jpg)
![© Cned, Mathématiques 6e, 2008 — 157
ccSéquence 5
Exercice 47
B
C
(d)
On n’avait « pas le droit » de tracer le
sommet A puis de tracer la bissectrice. Il
fallait donc réfléchir et penser à la propriété
suivante : dans un triangle ABC isocèle en
A, la bissectrice de l’angle BAC∑ est aussi la
médiatrice du côté [BC].
On trace donc à l’aide d’un compas la
médiatrice du côté [BC], on obtient alors la
droite recherchée.
Exercice 48
1)
54˚
4,6 cm
54˚
F
D E
y x
2) Jules semble avoir raison. Méline et Jade ont tort.
1) Nous avons déja vu dans la séquence 3
comment construire cette figure.
Il suffit de tracer un segment [DE] de 4,6 cm,
puis, à l’aide du rapporteur et de la règle, de
tracer deux demi-droites [Dx) et [Ey) telles
que les angles xDE∑ et yED∑ mesurent 54°.
2) Il semble, en regardant la figure, que le
triangle FDE est isocèle en F.
En fait, nous allons par la suite admettre que
lorsqu’un triangle possède deux angles de
même mesure, alors ce triangle est isocèle.
Exercice 49
Le point B est sur le segment [AC], on a donc :
ABC∑ = °− ° = °180 140 40
Je calcule EBC∑ :
ABC ABE EBC∑ ∑ ∑= +
180 140° = °+ EBC∑
EBC∑ = °− ° = °180 140 40
Les deux angles EBCet BCE∑ ∑ ont la même mesure : 40°.
Le triangle EBC possède donc deux angles égaux, il est donc
isocèle en E.
Nous devons démontrer que le triangle EBC
est isocèle.
Nous connaissons deux méthodes pour
démontrer qu’un triangle est isocèle :
• soit on démontre que deux de ses côtés ont
même longueur.
• soit on démontre que deux de ses angles ont
même mesure (d’après la propriété que nous
avons vue précédemment).
Ici, nous n’avons aucune information
concernant les longueurs, nous allons donc
utiliser la deuxième méthode.
Pour cela, on peut utiliser la donnée : « B est
sur le segment [AC]» pour déterminer l’angle
ABC∑ puis en déduire l’angle EBC∑ = °40.
Ontrouvealors: EBC∑ = °40 soit EBC ECB∑ ∑=
Le triangle EBC est donc isocèle en E.
B CA
E
40°40°
140°
N’oublie pas que pour rédiger ce type de
démonstration, il faut faire des phrases claires
et courtes !
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-570-320.jpg)
![— © Cned, mathématiques 6e, 2008158
cc Séquence 5
Séance 8
Ce que tu devais faire Les commentaires du professeur
Exercice 50
O
x
y
O
x
y
1) 2)
3) Le « trait de pliage » passe par le point O et partage l’angle
xOy∑ en deux angles de même mesure. Ce «trait de pliage»
représente donc la bissectrice de l’angle xOy∑ .
1) 2) On applique bien la consigne : on
reproduit l’angle par transparence puis on
plie le papier calque de telle sorte que les
deux demi-droites [Ox) et [Oy) coïncident
exactement. On déplie le calque et on trace le «
trait de pliage ».
3) Ce trait de pliage, qui est en fait l’axe
de symétrie de cet angle, semble être sa
bissectrice.
Par la suite, nous admettrons le résultat que
nous avons remarqué par l’expérience, à savoir
qu’un angle a un seul axe de symétrie : sa
bissectrice.
Notons bien que nous appelons bissectrice une
droite et non une demi-droite comme on l’a vu
dans la séquence 3.
Exercice 51
1)
O
A
B
x
y
2) On a OA = OB, le triangle OAB est donc isocèle en O.
3) La médiatrice du côté [AB] du triangle OAB isocèle en O est
également la bissectrice de l’angle AOB∑
1) On place un point « au hasard » sur la
demi-droite [Ox).
On prend ensuite la longueur OA comme
écartement de compas et on trace un arc de
cercle de centre O qui coupe la demi-droite
[Oy) en B. On a ainsi OA = OB.
O
A
B
x
y
2)
3) On applique la propriété vue dans la
séance précédente : « dans un triangle isocèle,
la médiatrice de la base est la bissectrice de
l’angle au sommet ».
Nous venons de découvrir une méthode
permettant de tracer la bissectrice d’un
angle sans utiliser de rapporteur !
Exercice 52
A
x
t
sy
B
C
D
E
Les remarques du professeur : On applique la méthode vue précédemment.
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-571-320.jpg)
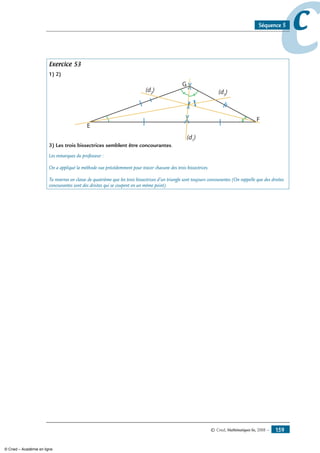

![© Cned, Mathématiques 6e, 2008 — 161
ccSéquence 5
Exercice 55
1) 2) 3)
OE
M
F
(d)
EM = EF
4)
Le point M est sur la médiatrice du segment [EF] donc on a :
ME = MF.
Le point M est tel que EM = EF.
On a donc : ME = EF = MF.
Le triangle EMF est donc équilatéral.
Les trois angles d’un triangle équilatéral ont même mesure.
On a donc :
MEF MFE EMF∑ ∑ ∑= =
2) On trace à l’aide d’un compas et d’une
règle la médiatrice du segment [EF].
3) Le point M doit être à la fois sur la droite
(d) et vérifier l’égalité EM = EF.
• Vérifier l’égalité EM = EF signifie être à une
distance EF du point E, c’est-à-dire être sur le
cercle de centre E et de rayon EF. On trace ce
cercle.
• Le point M doit être à la fois sur la droite
(d) et sur ce cercle, c’est donc un des deux
points d’intersection (on a le choix !) du cercle
et de la droite (d).
4) On veut démontrer que les trois angles
d’un triangle ont la même mesure. On pense
alors à utiliser la propriété : « si un triangle
est équilatéral, alors ses trois angles ont la
même mesure ».
Nous essayons donc de démontrer que le
triangle EFM est équilatéral. Nous pourrons
ensuite en déduire que ses trois angles ont la
même mesure.
Pour cela, étudions les longueurs de ses côtés :
On a : ME = MF car le point M est sur la
médiatrice du segment [EF].
On sait que EM = EF.
On a donc ME = MF = EF.
Le triangle EMF est donc équilatéral et ses
trois angles ont donc la même mesure.
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-574-320.jpg)
![— © Cned, mathématiques 6e, 2008162
cc Séquence 5
Exercice Je m’évalue
1) Les deux figures ci-dessous
semblent-elles symétriques par
rapport à la droite (d) ?
(d)
˝ oui
® non
2) Les deux figures ci-dessous sont-elles
symétriques par rapport à la droite (d) ?
(d)
® oui
˝ non
3) Dire que B’ est le symétrique de B par rapport à la droite (d)
revient à dire que :
˝ B et B’ sont symétriques par rapport à la droite (d)
˝ (d) est la médiatrice du segment [BB’]
® B et B’ sont sur la droite (d)
˝ B est le symétrique de B’ par rapport à la droite (d)
4) Le symétrique d’un angle est :
˝ un angle
® un triangle
® un angle de mesure différente
˝ un angle de même mesure
5) Combien la figure ci-dessous a-t-elle
d’axes de symétrie ?
˝ 6
® 12
® 4
® aucun
6) Le point M est sur la médiatrice du segment [KL], on a donc :
® KM = KL
˝ KM = ML
˝ MK = ML
® LM = KL
1) Effectivement, les deux symboles euros
semblent symétriques par rapport à la droite
(d). Si tu n’as pas bien répondu, reporte-toi à
l’exercice 1 de la séance 1 et à son corrigé pour
reprendre la notion que tu n’as pas comprise.
2) On voit bien que si on devait plier cette
feuille le long de la droite (d), les deux
symboles ne coïncideraient pas. Si tu n’as pas
bien répondu, reporte-toi à l’exercice 1 de la
séance 1 et à son corrigé.
3) Seule la troisième réponse est fausse. Nous
avons le symétrique d’un point dans la séance
2 (en particulier dans le « Je retiens »). Si tu
n’as pas bien répondu, révise cette séance.
4) Le symétrique d’un angle est un angle. On sait
de plus que c’est un angle de même mesure. Ce
n’est pas un triangle car les deux côtés d’un angle
sont des demi-droites (et non des segments). Si tu
n’as pas bien répondu, reporte-toi à la deuxième
question de l’exercice 25 de la séance 4 et au « Je
retiens » qui suit.
5) La figure possède 6 axes de symétrie. Il
fallait faire attention à ne pas en oublier et à
ne pas compter plusieurs fois le même. Si tu ne
comprends pas bien cette réponse, reporte-toi
au début de la séance 5, en particulier aux
exercices 28 et 29 ainsi qu’à leurs corrigés.
1
2
3
4
5
6
6) Les deux égalités KM = ML et MK = ML
sont en fait les mêmes puisque la longueur
KM est la longueur MK. Les deux autres
propositions sont fausses : KM et LM peuvent
être beaucoup plus grandes que KL si l’on
choisit un point M sur la médiatrice du
segment [KL] très très loin de K et de L.
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-575-320.jpg)
![© Cned, Mathématiques 6e, 2008 — 163
ccSéquence 5
7) On a LH = LR. Le point L est donc :
® sur le segment [HR]
® sur le cercle de centre H passant par R
® sur le cercle de centre R passant par H
˝ sur la médiatrice du segment [HR]
8) L’axe de symétrie d’un triangle FJI isocèle en F est :
® la bissectrice de l’angle FIJ∑
® la bissectrice de l’angle FJI∑
˝ la médiatrice du segment [IJ]
˝ la bissectrice de l’angle IFJ∑
9) Le triangle HER possède deux angles égaux. Ce triangle est
donc :
® rectangle en H
® rectangle isocèle
® équilatéral
˝ isocèle
10) Un angle admet un axe de symétrie qui est :
® parallèle à un de ses côtés
® perpendiculaire à un de ses côtés
˝ sa bissectrice
® confondu avec un de ses côtés
7) Si tu n’as pas bien compris cette question,
reporte-toi à l’exercice 32 de la séance 5 ainsi
qu’au « Je retiens » qui suit.
Une seule des quatre propositions est juste. Si
tu n’as pas bien répondu, révise le «Je retiens»
qui suit l’exercice 31.
8) Il ne fallait pas oublier la troisième
proposition car dans un triangle isocèle, la
bissectrice de l’angle du sommet principal est
également la médiatrice de la base.
Si tu n’as pas bien compris cette question,
reporte-toi à l’exercice 44 de la séance 7 ainsi
qu’à son corrigé et au « Je retiens » qui le suit.
9) C’est une propriété que l’on a admise
et qu’il faut connaître. Si tu rencontres des
difficultés sur cette question, reporte-toi aux
exercices 48 et 49, à leurs corrigés, et au « Je
retiens » qui se trouve entre ces deux exercices.
10) Cette notion a été abordée dans l’exercice
50 de la séance 8 et dans le « Je retiens » qui
suit.
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-576-320.jpg)























![© Cned, mathématiques 6e — 3
ccSéquence 7
Exercice 2
1) Les sommets du quadrilatère sont les points K, A, M et R.
2) Ses côtés sont les segments [KA], [AM], [MR] et [RK].
3) Ses angles sont KAM , AMR , HGE et RKA .
2) On fait attention à bien écrire les côtés avec
des crochets : ce sont des segments.
3) On pouvait également écrire chaque angle
d’une autre façon (par exemple l’angle KAM∑
se note également MAK∑).
Exercice 3
1) Le côté opposé à [KG] est [RE]. Le côté opposé à [TO] est
[VU].
) L’angle opposé à KRE est KGE . L’angle opposé à OUV
est OTV .
On regarde le quadrilatère de gauche. Il a par
définition quatre côtés : [KG], son côté opposé
[RE] (ils n’ont aucun sommet en commun),
puis [KR] et [GE].
On dit que [KR] et [KG] sont des côtés
consécutifs car ils ont en commun une
extrémité : K. De même, les côtés [GE]
et [KG] sont consécutifs : leur extrémité
commune est G.
Exercice 4
1)
K à V à R à P à K
Si elle avait fait le tour toujours en partant de K mais dans
l’autre sens, son chemin aurait été : K à P à R à V à K
)
V à R à P à K à V V à K à P à R à V
R à P à K à V à R R à V à K à P à R
P à K à V à R à P P à R à V à K à P
3)
K à R à V à P NON
K à P à V à R NON
4) Pour conclure, combien y a-t-il au total de façons différentes
permettant de faire le tour de ce jardin ? huit façons.
2) On a pour l’instant énuméré huit façons
de faire le tour du jardin sans « traverser le
gazon ».
3)
On voit bien sur la figure ci-dessous que le
chemin :
K à R à V à P à K
ne permet pas de faire le tour du jardin.
Les huit façons possibles de noter le tour
du jardin correspondent aux huit façons de
noter un quadrilatère. Toutefois, on n’écrit
ni les flèches, ni le sommet d’arrivée. Ainsi,
le quadrilatère qui représente le jardin peut
se nommer :
KVRP, KPRV, VRPK, VKPR, RPKV,
RVKP, PKVR, PRVK.
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-602-320.jpg)
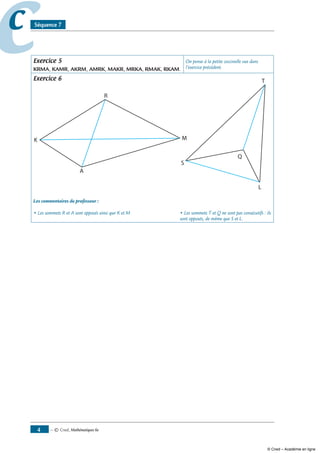
![© Cned, mathématiques 6e —
ccSéquence 7
Séance
Ce que tu devais faire Les commentaires du professeur
Exercice 7
Les commentaires du professeur :
• On observe le quadrilatère ABCD : les côtés [AB] et [AD] ont la même longueur (2,1 cm), ainsi que les côtés [CB] et [CD]
(qui mesurent tous les deux 4,4 cm).
• On commence par construire le triangle A’B’D’ : on utilise la méthode apprise à l’exercice 32 séquence 3 séance 6, 2ème
question (la revoir éventuellement).
90
90
• Ensuite, on trace un arc de cercle de centre B’ et de rayon 4,4 cm puis un arc de cercle de centre D’ et de même rayon 4,4 cm.
• Les deux arcs de cercle se coupent au point C’.
• On trace les deux derniers côtés [C’B’] et [C’D’] du quadrilatère.
Le quadrilatère que l’on vient de tracer s’appelle un cerf-volant.
Remarque : les deux cerfs-volants ABCD et A’B’C’D’ ont des côtés de même longueur,
mais ils ne sont pas superposables parce que leurs angles sont différents.
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-604-320.jpg)

![© Cned, Mathématiques 6e —
ccSéquence 7
Exercice 9
1), 2), 3) et 5)
I
2) Complète :
Comme KL = KN, le point K est sur la médiatrice du segment
[LN].
Comme ML = MN, le point M est sur la médiatrice du segment
[LN].
La droite (KM) est donc la médiatrice du segment [NL].
3) Soit I le point d’intersection des diagonales (KM) et (LN)
du cerf-volant. Comme la droite (KM) est la médiatrice du
segment [LN], la diagonale (KM) coupe la diagonale [LN] en
son milieu, et les diagonales sont perpendiculaires.
4) Par la symétrie axiale par rapport à la droite (KM) :
• K a pour symétrique K
• M a pour symétrique M
• L a pour symétrique N
• N a pour symétrique L
La droite (KM) est donc un axe de symétrie du cerf-volant
KLMN.
5) Par la symétrie axiale par rapport à la droite (KM) :
L’angle KLM a pour symétrique KNM .
Les angles KLM et KNM sont donc égaux.
1)
• On peut placer comme on veut K en « haut »
et M en « bas », ou le contraire. Par contre, K
est le sommet commun à deux côtés consécutifs
de même longueur, il en est de même pour
le point M. On ne peut donc pas les placer à
« gauche » ni à « droite ».
• On place par exemple K « en haut » et M
« en bas ». Ensuite, on place « à gauche » L et
« à droite » N. (On peut faire aussi l’inverse).
2)
• On utilise ici la seconde partie de la
propriété caractéristique de la médiatrice :
second paragraphe « JE RETIENS » de la
séquence 5 séance 5.
• Le point K est équidistant de N et de L donc
il appartient à la médiatrice du segment [LN].
Il en est de même pour le point M.
• K et M sont deux points de la médiatrice
donc cette médiatrice est la droite (KM) elle-
même.
3) On utilise la définition de la médiatrice
d’un segment (revoir éventuellement le
premier paragraphe « JE RETIENS » de la
séquence 1 séance 7). I est le milieu de [LN]
et KIN∑ = 90°
4)
• On utilise le fait que la médiatrice d’un
segment est un axe de symétrie de ce segment
(revoir éventuellement le premier paragraphe
« JE RETIENS » de la séquence 5 séance 5)
• K est son propre symétrique parce qu’il est
sur l’axe lui-même. Il en est de même pour M.
• Non seulement (KM) est un axe de symétrie
pour le segment [NL] mais encore, (KM)
est un axe de symétrie pour le cerf-volant
« entier ». On admettra que le cerf-volant
a exactement un axe de symétrie, sans le
démontrer.
5)
• Les symétriques des côtés [LK) et [LM) de
l’angle KLM∑ sont respectivement les côtés
[NK) et [NM) de l’angle KNM∑.
• Revoir au besoin le premier paragraphe
« JE RETIENS » de la séquence 5 séance 4 sur
les mesures de deux angles symétriques l’un
de l’autre.
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-606-320.jpg)

![© Cned, mathématiques 6e —
ccSéquence 7
Exercice 11
• Le quadrilatère ABCD est un cerf-volant donc d’après sa
définition, ABCD a deux côtés consécutifs de la même longueur
ainsi que les deux autres côtés.
• D’après le codage, BC = CD, donc on a : AB = AD.
• D’après le codage, on a également : AE = ED = AB, mais
on sait aussi que : AB = AD. Je peux donc affirmer que :
AE = ED = AD.
• Les trois côtés du triangle ADE ont la même longueur donc,
d’après la définition du triangle équilatéral, je peux affirmer
que le triangle ADE est équilatéral.
• On utilise la définition du cerf-volant
apprise au début de la séance 2 : Boîte à
Outils carte n°1.
• On lit les informations données par le
codage.
• On utilise : AB = AD pour remplacer AB
par AD dans l’égalité : AE = ED = AB ce qui
nous donne : AE = ED = AD.
Exercice 12
1)
) Comme le point E appartient à la médiatrice de [AB] ,
d’après la propriété caractéristique de la médiatrice, E est
équidistant de A et de B, c’est-à-dire : EA = EB.
3) F est un point de la médiatrice de [AB] donc il est aussi
équidistant de A et de B, c’est-à-dire : FA =FB.
4) G est aussi sur la médiatrice de [AB] donc on a aussi :
GA = GB.
) Comme le quadrilatère AFBE possède deux côtés consécutifs
[EA] et [EB] de la même longueur ainsi que les deux autres,
[FA] et [FB], je peux affirmer, d’après la définition du cerf-
volant, que AFBE est un cerf-volant.
6) De même, comme le quadrilatère AGBE possède deux côtés
consécutifs [EA] et [EB] de la même longueur ainsi que les deux
autres [GA] et [GB], je peux affirmer, d’après la définition du
cerf-volant, que AGBE est un cerf-volant.
1)
• On trace un segment [AB] de 4 cm.
• On trace sa médiatrice (d) au compas :
revoir au besoin le paragraphe « Je comprends
la méthode » de la séquence 5 séance 5.
• Une fois qu’on a placé le point E, on place le
point F sur la droite (d) mais « de l’autre côté
de la droite (d) par rapport au point K ».
2) , 3) et 4)
On utilise la propriété caractéristique de
la médiatrice que l’on a vue à la séquence
5 séance 5 au deuxième paragraphe « JE
RETIENS ».
5) et 6)
On utilise la définition du cerf-volant apprise
au début de cette séance.
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-608-320.jpg)
![— © Cned, mathématiques 6e10
cc Séquence 7
Exercice 13
reconnaître
diago‐
nale
cerf‐volant
reconnaître On recopie simplement les mots qui manquent
dans la carte en prenant modèle sur le
paragraphe « JE RETIENS » précédent. On
code ensuite la figure.
Exercice 14
1) D’après le codage, la droite (MK) est perpendiculaire
au segment [JL] en son milieu. D’après la définition de
la médiatrice, je peux affirmer que la droite (MK) est la
médiatrice du segment [JL].
) La diagonale (MK) du quadrilatère JKLM est la médiatrice
de l’autre diagonale [JL] donc, d’après la propriété : « si un
quadrilatère a une diagonale qui est la médiatrice de l’autre
diagonale alors ce quadrilatère est un cerf-volant », je peux
affirmer que JKLM est un cerf-volant.
1)
On utilise donc la définition de la médiatrice
vue à la séquence 1 séance 7 premier
paragraphe « JE RETIENS ».
2) On utilise la Boîte à Outils : carte n°21.
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-609-320.jpg)
![© Cned, mathématiques 6e — 11
ccSéquence 7
Séance 3
Ce que tu devais faire Les commentaires du professeur
Exercice 15
1) et )
• Comme M et N appartiennent à Ω , d’après la définition du cercle, on a AM = 4 cm et AN = 4 cm.
De même, comme M ∈ Ω’ et N ∈ Ω on a : BM = BN = 4 cm.
• Les deux côtés consécutifs [AM] et [AN] du quadrilatère AMBN ont la même longueur ainsi que les
deux autres côtés consécutifs [BM] et [BN]. D’après la définition du cerf-volant, je peux affirmer
que AMBN est un cerf-volant.
3) a) AM = AN = BN = BM = 4 cm
La particularité de ce cerf-volant est que ses quatre côtés ont la même longueur.
b) AMBN est un losange.
Les commentaires du professeur :
2) Pour prouver que AMBN est un cerf-volant, il suffit de prouver que : AM = AN et BM = BN. (ou que : • NA = NB
• et MA = MB)
La définition du cercle a été vue à la séquence 1 séance 9 premier paragraphe « Je retiens ».
3) En effet, un cerf-volant dont les quatre côtés ont la même longueur est appelé : « losange ».
Exercice 16
quadrilatère
longueur
définition
définition
définition
définition
définition
définition
définitionlongueur
définitionlongueur
définitionlongueurlongueur
définitionlongueurlongueur
définition
définition
définition
définition
définition
définition
définitionlongueur
définitionlongueur
définitionlongueur
définitionlongueur
définition
définition
définition
définition
définition
définition
définitionlongueurlongueurlongueurlongueur
On recopie simplement les mots qui manquent
dans la carte en prenant modèle sur le
paragraphe « JE RETIENS » précédent. On
code ensuite la figure.
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-610-320.jpg)
![— © Cned, mathématiques 6e12
cc Séquence 7
Exercice 17
1) Clément a raison. En effet, puisque tous les côtés d’un
losange ont la même longueur, on a bien deux côtés consécutifs
de même longueur ainsi que les deux autres côtés.
2) Non, Samia a tort. figure :
1) On a vu dans l’exercice 15 qu’un losange
est un cerf-volant qui a une particularité.
2) Un cerf-volant est un quadrilatère dont
deux côtés consécutifs ont la même longueur
ainsi que les deux autres côtés.
La longueur des quatre côtés n’ est donc pas
nécessairement la même.
Exercice 18
Les commentaires du professeur :
• On commence par représenter une figure codée à main levée.
• Comme RSTU est un losange, d’après la définition d’un losange (carte n°2 de la Boîte à Outils), on sait que :
RS = ST = TU = UR = 5 cm.
• On commence par tracer un segment [RT] de 6 cm.
• On trace un arc de cercle de centre R et de rayon 5 cm puis un arc de cercle de centre T et de même rayon : les deux arcs se
coupent au point S.
• On trace « de l’autre côté du segment [RT] » un nouvel arc de cercle de centre R et de rayon 5 cm puis un arc de cercle de
centre T et de même rayon : les deux arcs se coupent au point U.
• On termine la construction du losange en traçant ses côtés [RS], [ST], [RU] et [UT].
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-611-320.jpg)
![© Cned, Mathématiques 6e — 13
ccSéquence 7
Exercice 19
1) et 2)
3)
• Comme le triangle DEF est équilatéral, d’après la définition
d’un triangle équilatéral : DE = EF = FD = 4 cm.
• Comme le triangle FEG est aussi équilatéral on a :
FE = EG = GF = 4 cm.
• On en déduit : DE = EG = GF = FD = 4 cm.
• Les quatre côtés du quadrilatère DEGF ont la même longueur
donc, d’après la définition d’un losange, je peux affirmer que
DEGF est un losange.
1)
On revoit si nécessaire le paragraphe « Je
retiens » de la séquence 3 séance 7 sur la
définition du triangle équilatéral ainsi que la
méthode de construction vue à l’exercice 43 de
la séquence 3 séance 8.
2)
• Le triangle FEG est équilatéral et :
EF = 4 cm donc :
EG = FG = 4 cm.
• Pour construire le point G on procède
comme à la question précédente : on reporte
au compas la longueur 4 cm à partir de E puis
à partir de F. Le point G est l’intersection des
deux arcs de cercle. On termine la construction
du triangle FEG en traçant ses deux derniers
côtés [EG] et [FG].
3) Comme :
DE = EF = FD = 4 cm
et aussi :
FE = EG = GF = 4 cm,
on déduit les égalités de longueur des quatre
côtés du quadrilatère DEGF.
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-612-320.jpg)



![© Cned, mathématiques 6e — 17
ccSéquence 7
Exercice 24
1)
)
Etiquette 6 - Etiquette 3 - Etiquette - Etiquette 1 - Etiquette
– Etiquette 7 - Etiquette 4
3)
– Etiquette 7 - Etiquette 4
x
2)
• On commence par tracer un segment [AB]
de 5 cm : ce sera une première diagonale du
losange.
• On utilise le rapporteur pour tracer ce qui
sera l’angle BAC∑ , qui mesure 48° : on a déjà
tracé le côté [AB) de cet angle et le second
côté sera noté [Ax).
• Ensuite on trace la droite (d),
perpendiculaire à (AB) et passant par le
milieu M de [AB]. Cette droite sera la
seconde diagonale.
• Cette droite coupe la demi-droite [Ax) en
C.
• Puisque M doit être le milieu de [CD], le
point D doit être le symétrique du point C par
rapport à la droite (AB) : on reporte donc la
longueur MC au compas à partir de M sur la
droite (CM) mais « de l’autre côté par rapport
à la droite (AB) ». On trace alors un arc de
cercle qui coupe (CM) au point D.
• On finit de tracer les côtés du losange.
• On est sûr que c’est un losange car les
diagonales ont été construites de telle sorte
qu’elles soient perpendiculaires et se coupent
en leur milieu.
Il y avait une autre bonne réponse :
Etiquette 6 - Etiquette 2 - Etiquette 1
- Etiquette 3 - Etiquette 5 - Etiquette 7
- Etiquette 4
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-616-320.jpg)
![— © Cned, mathématiques 6e18
cc Séquence 7
Séance 4
Ce que tu devais faire Les commentaires du professeur
Exercice 25
Les commentaires du professeur :
• On commence par construire avec l’équerre et la règle graduée les deux côtés perpendiculaires [CN]
et [NB] tels que : NC = 5 cm et NB = 3 cm.
• On trace la demi-droite [Cx) perpendiculaire en C à la droite (CN) puis la demi-droite [By) C N
B
5
3
x
y
V
perpendiculaire en B à la droite (BN). Le point V est le point commun à ces deux demi-droites.
• À l’aide de l’équerre, on peut vérifier que l’angle CVB∑ semble droit. On verra par la suite à l’aide d’une démonstration que cet
angle est un angle droit.
Tu as déjà rencontré un tel quadrilatère : on l’appelle un rectangle.
Exercice 26
définition
définition
définition
définitionquadrilatère
droits On recopie simplement les mots qui manquent
dans la carte en prenant modèle sur le
paragraphe « JE RETIENS » précédent.
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-617-320.jpg)
![© Cned, mathématiques 6e — 1
ccSéquence 7
Exercice 27
1)
Les droites (DH) et (FG) sont toutes les
deux perpendiculaires à la droite (DF).
Les droites (DH) et (FG) sont donc
parallèles.
)
On vient de démontrer que les droites
(DH) et (FG) sont parallèles.
La droite (GH) est perpendiculaire à la
droite (DH), elle est donc perpendiculaire
à la droite (FG).
3) Le quadrilatère DFGH possède donc en fait 4 angles droits.
Par définition, c’est donc un rectangle.
4) On a démontré dans le 2) que ses côtés opposés [DH] et
[FG] sont parallèles. De même, les côtés opposés [DF] et [HG]
sont parallèles parce qu’ils sont tous les deux perpendiculaires
au côté [DH].
1) On utilise la propriété 1 du paragraphe
« JE RETIENS » de la séquence 1 séance 7.
2) On utilise la propriété 2 du paragraphe
« JE RETIENS » de la séquence 1 séance 8.
3) En conclusion, dès qu’un quadrilatère
possède trois angles droits, son quatrième
angle est droit également : ce quadrilatère est
donc un rectangle.
Exercice 28
reconnaître
trois
rectangle
On recopie simplement les mots qui manquent
dans la carte en prenant modèle sur le
paragraphe « JE RETIENS » précédent.
Exercice 29
Les axes de symétrie du rectangle sont les droites (d) et (d’).
On plie soigneusement de façon à faire une
bonne observation.
Seuls les pliages suivant les droites (d) et
(d’) permettent d’obtenir que les sommets,
les côtés et les angles du rectangle KLMN se
superposent exactement. Ce sont les deux
seuls axes de symétrie du rectangle.
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-618-320.jpg)
![— © Cned, mathématiques 6e0
cc Séquence 7
Exercice 30
propriété
propriété
propriété
propriété
propriétédeux
médiatrices
On recopie simplement les mots qui manquent
dans la carte en prenant modèle sur le
paragraphe « JE RETIENS » précédent.
Exercice 31
1)
a) Quel est le symétrique du segment [AD] par rapport à la
droite (d) ? [BC].
Que peux-tu en déduire concernant les longueurs des segments
[AD] et [BC] ? Elles sont égales.
b) Quel est le symétrique du segment [AB] par rapport à la
droite (d’) ? [DC].
Que peux-tu en déduire concernant les longueurs des segments
[AB] et [DC] ? Elles sont égales.
c) Quelle propriété viens-tu de démontrer ?
Si un quadrilatère est un rectangle, alors ses côtés opposés
sont de même longueur.
)
I
a) Quel est le point d’intersection de ces diagonales ? le point I
b) Quel est le symétrique du segment [AC] par rapport à la
droite (d’) ? [DB]
Que peux-tu en déduire concernant les longueurs des segments
[AC] et [BD] ? Elles sont égales.
c) Quelle propriété viens-tu de démontrer ?
Si un quadrilatère est un rectangle, alors ses diagonales sont
de même longueur.
3)
a)
En utilisant la symétrie par rapport à la droite (d’), compare les
distances IA et ID : IA =ID
En utilisant la symétrie par rapport à la droite (d), compare les
distances ID et IC : ID =IC
En utilisant la symétrie par rapport à la droite (d’), compare les
distances IC et IB : IC = IB
En utilisant la symétrie par rapport à la droite (d), compare les
distances IB et IA : IB = IA
b) Compare IA et IC : IA = IC puis IB et ID : IB = ID
Le point I est le milieu des diagonales [AC] et [BD].
c) Si un quadrilatère est un rectangle, alors ses diagonales ont
le même milieu.
1) a) par la symétrie par rapport à la droite
(d) :
A a pour symétrique B
D a pour symétrique C.
[AD] a donc pour symétrique [BC].
On utilise la propriété de la symétrie suivante
« un segment et son symétrique ont la même
longueur ».
b) Par la symétrie par rapport à la droite (d’) :
A a pour symétrique D
B a pour symétrique C.
[AB] a donc pour symétrique [DC].
c) C’est une propriété importante que l’on
devra retenir.
2) b) par rapport à la droite (d’) :
Le symétrique de A est D.
Le symétrique de C est B
Donc :
Le symétrique de [AC] est [DB].
c) N’oublie pas que les segments [AC] et
[BD] sont les diagonales.
3) a)
• En effet, [IA] et [ID] sont symétriques
par rapport à la droite (d’) (le point I est son
propre symétrique).
• [ID] et [IC] sont symétriques par rapport à
la droite (d).
• [IC] et [IB] le sont par rapport à la droite
(d’).
• [IB] et [IA] le sont par rapport à (d).
b) • IA = ID et ID = IC donc IA = IC
IB = IC et IC = ID donc IB = ID
• Comme les points A, I et C sont alignés
ainsi que les points B, I et D, on déduit que I
est le milieu des diagonales.
c) Cette propriété est importante : on devra la
retenir.
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-619-320.jpg)
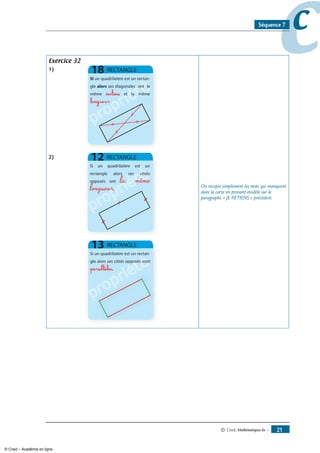
![— © Cned, mathématiques 6e22
cc Séquence 7
Exercice 33
O
• Les diagonales du rectangle ABCD se coupent en O.
• D’après la propriété : « si un quadrilatère est un rectangle
alors ses diagonales ont la même longueur et se coupent en
leur milieu », je peux affirmer que O est le milieu de [AC] et de
[BD], et que AC = BD.
• J’en déduis que : OA = OB = OC = OD
• Le cercle Ω de diamètre [AC] a pour centre le milieu O de
[AC] et son rayon est OA.
Comme OB = OD = OA, B et D appartiennent à Ω.
• Le centre d’un cercle est le milieu de son
diamètre.
• On utilise ici la carte 18 de la Boîte à
Outils.
• Comme O est le milieu de [AC] :
OA = OC = AC ÷ 2
De même, comme O est le milieu de [BD] :
OB = OD = BD ÷ 2
• On utilise la définition du cercle : séquence 1
séance 9 premier paragraphe « Je retiens ».
Les distances de B à O et de D à O sont égales
au rayon OA.
Exercice 34
1) 2)
3) Je n’y arrive pas.
Les commentaires du professeur :
3) On a beau essayer tous les cas de figures, on a toujours l’impression d’avoir un rectangle ...
Par la suite, on va admettre et retenir que ce résultat est toujours vrai, à savoir :
« Si un quadrilatère a ses diagonales qui ont le même milieu et qui ont la même longueur, alors ce quadrilatère est un
rectangle ».
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-621-320.jpg)
![© Cned, mathématiques 6e — 3
ccSéquence 7
Exercice 35
reconnaître
reconnaître
reconnaître
milieu
longueur
rectangle On recopie simplement les mots qui manquent
dans la carte en prenant modèle sur le
paragraphe « JE RETIENS » précédent.
Exercice 36
1)
)
• Je trace un segment [RT] de 6 cm.
• Je place le milieu V du segment [RT].
• Je construis l’angle TVx de mesure 53°.
• Je trace un arc de cercle de centre V et de rayon RV
(égal à 3 cm).
Il coupe la demi-droite [Vx) en U.
• Je prolonge le tracé de la droite (UV).
Je trace un autre arc de cercle de centre V et de rayon 3 cm.
Il coupe la droite (UV) en un deuxième point : le point S.
• Je trace les côtés du quadrilatère RSTU.
x
3) Les diagonales du quadrilatère RSTU ainsi construit ont la même longueur 6 cm et le même milieu
V. D’après la propriété : « Si un quadrilatère a des diagonales qui ont la même longueur et le même
milieu, alors ce quadrilatère est un rectangle », je peux affirmer que RSTU est un rectangle.
Les commentaires du professeur :
2)
On commence par tracer le segment [RT], son milieu V puis l’angle TVx∑ dont la mesure est 53°. On pense ensuite à la propriété :
« Si un quadrilatère a des diagonales qui ont la même longueur et le même milieu, alors ce quadrilatère est un rectangle », car on
veut construire un rectangle. On connaît déjà les longueurs VR et VT. On sait que l’on doit avoir VR = VT = VU = VS = 3 cm.
On pense alors à tracer le cercle de centre V et de rayon 3 cm. Il coupe la droite (Vx) en U et S. Il ne reste plus alors qu’à tracer
les côtés du quadrilatère.
3) On utilise la carte 24 de la Boîte à Outils : elle permet de reconnaître un rectangle à l’aide de ses diagonales.
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-622-320.jpg)





![© Cned, mathématiques 6e —
ccSéquence 7
Exercice 45
1) Les diagonales de ce quadrilatère sont perpendiculaires et
ont le même milieu. D’après la propriété : « si les diagonales
d’un quadrilatère sont perpendiculaires et ont le même milieu,
alors ce quadrilatère est un losange », on déduit que EFGH est
un losange.
) Les diagonales de ce quadrilatère ont, de plus, la même
longueur. D’après la propriété : « si les diagonales d’un
quadrilatère ont la même longueur et ont le même milieu, alors
ce quadrilatère est un rectangle », on déduit que ce EFGH est
un rectangle.
3) Ce quadrilatère est donc un losange et un rectangle.
D’après la définition « un quadrilatère qui est à la fois un
rectangle et un losange est un carré », on peut affirmer que
EFGH est un carré.
1)
• Le codage montre que les diagonales sont
perpendiculaires et ont le même milieu.
3) On utilise la carte 4 de la Boîte à Outils.
Exercice 46
reconnaître
reconnaître
reconnaître
reconnaître
reconnaître
perpendiculaires
milieu
longueur
carré
reconnaître
reconnaître
reconnaître
reconnaître
reconnaître
reconnaître
reconnaître
reconnaître
reconnaître
reconnaître
reconnaître
reconnaître
reconnaître
reconnaître
reconnaître
reconnaître
reconnaître
reconnaître
reconnaître
reconnaître
reconnaître
reconnaître
reconnaître
reconnaître
reconnaître
reconnaître Aide-toi du paragraphe précédent et n’oublie
pas le codage.
Exercice 47
1)
)
• Je trace un segment [EG] de 5 cm.
• Je place le milieu de ce segment.
• Je trace la perpendiculaire à ce segment en son milieu.
• Je place les points F et H de cette perpendiculaire de telle
sorte que le milieu de [EG] soit aussi le milieu de [FH] et de
telle sorte que FH = 5 cm.
Je trace le quadrilatère EFGH. J’affirme que c’est un carré.
Je justifie :
Les diagonales [EG] et [FH] ont le même milieu, elles ont la
même longueur et elles sont perpendiculaires donc d’après
la propriété : « si les diagonales d’un quadrilatère sont
perpendiculaires, ont le même milieu et ont la même longueur
alors ce quadrilatère est un carré », je peux affirmer que EFGH
est un carré.
1) On représente une figure à main levée
codée :
2)
• On trace la première diagonale [EG] de 5
cm de longueur.
• On place son milieu, appelons-le O par
exemple. On a :
OE =OG = 2,5 cm.
• On trace la droite (d), perpendiculaire en O
à la droite (EG).
• On place les deux points F et H de cette
médiatrice qui sont situés à
2,5 cm de O à l’aide d’un compas. On trace
pour cela deux arcs de cercle de centre O et de
rayon OE. Ces deux arcs coupent la droite (d)
en F et H.
• On termine la construction du carré en
traçant ses côtés.
• On utilise la carte 25.
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-628-320.jpg)


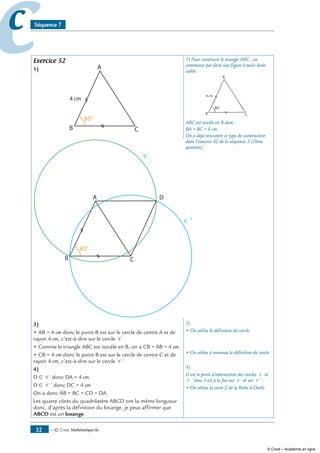
![© Cned, mathématiques 6e — 33
ccSéquence 7
Séance 7
Ce que tu devais faire Les commentaires du professeur
Exercice 53
1)
)
Les commentaires du professeur :
1) EFGH est un cerf-volant donc le côté [EF] a un côté consécutif qui a la même longueur que lui. Comme :
[EH] n’a pas la même longueur que [EF], [FG] a donc la même longueur que [EF].
Par un même raisonnement, on déduit que : EH = GH.
2)
étape 1 On trace le côté [FG] de 3 cm. On trace un angle étape 2 On trace un arc de cercle de centre G, de rayon 4 cm,
de sommet G, de côté [GF) et de mesure 130°. qui coupe le deuxième côté de l’angle en H.
F
G3 cm
90
90
étape 3 On trace un arc de cercle de centre H étape 4 On trace un autre arc de cercle, de centre F et de rayon
et de rayon HG = 4 cm. FG qui coupe le premier arc en E. On trace alors les côtés du
cerf-volant.
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-632-320.jpg)
![— © Cned, mathématiques 6e34
cc Séquence 7
Exercice 54
1)
I
2)
• Je trace un segment [JL] de 5 cm.
• Je trace un cercle de centre J et de rayon 2,5 cm.
• Je trace un cercle de centre L et de rayon 3,5 cm.
• Je place les deux points d’intersection des deux cercles I et K.
• Je trace les côtés du quadrilatère IJKL.
1) On réfléchit sur une figure à main levée codée.
I
On constate que les côtés de même longueur
sont d’une part [IJ] et [JK] et d’autre part
[IL] et [LK].
On peut commencer par tracer le triangle IJL
dont on connaît les longueurs des trois côtés.
Au besoin, revoir la rubrique « je comprends
la méthode » de la séance 6 de la séquence 3.
Comme IJKL est un cerf-volant, on a :
JK = JI = 2,5 cm
KL = LI = 3,5 cm.
On peut donc tracer le triangle JKL connaissant
les trois longueurs de ses côtés. Les cercles que
l’on trace sont en fait les mêmes que ceux qui
nous ont permis de construire le point I.
Il nous suffisait donc de tracer deux cercles : l’un
de centre J et de rayon 2,5 cm, l’autre de centre L
et de rayon 3,5 cm pour obtenir les points I et K.
Exercice 55
1)
2)
a) Voici une figure à main levée :
b) ABCD est un losange donc sa diagonale (BD) est un axe de
symétrie de ce quadrilatère. (BD) est donc la bissectrice de
l’angle ADC∑. On a donc : ADC∑ = 2 x ADB∑ = 80°.
c)
A
B C
D3 cm
80°
x
1) On pense à la carte 22 de la Boîte à
Outils. On se dit : « Si j’arrivais à construire
des diagonales perpendiculaires qui ont le
même milieu, j’obtiendrais alors un losange ».
On trace un segment de 7 cm.
On trace ensuite sa médiatrice au compas qui
le coupe en son milieu M. 5,4 ÷ 2 = 2,7
On trace deux arcs de cercle de centre M et de
rayon 2,7 cm qui coupent cette médiatrice en
deux points.
2)
b) On a utilisé la carte 6 de la boîte à outils.
c) On construit le losange de la façon suivante :
• On trace le côté [DA],
• On construit un angle ADx∑ de mesure 80°.
• On reporte au compas la longueur AD à
partir de D sur [Dx) ; on obtient le point C.
• On trace deux arcs de cercle de rayon AD, l’un
de centre A, l’autre de centre C. Ils se coupent en B.
• On trace les deux côtés qu’il reste à tracer.
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-633-320.jpg)
![© Cned, Mathématiques 6e — 35
ccSéquence 7
Exercice 56
1)
Q
R S
T
6 cm
35°
Les commentaires du professeur :
étape 1 On trace le côté [QR] de 6 cm puis un angle étape 2 On trace les perpendiculaires à la droite (QR) passant
de sommet Q, de côté [QR), de mesure 35°. par Q et R. On obtient S.
Q
6 cm
35°
Q
R S
6 cm
35°
étape 3 On trace la perpendiculaire à la droite (RS)
passant par le point S. On obtient T.
Q
R S
T
6 cm
35°
D’après la carte 23 de la boîte à outils, QRST est un rectangle.
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-634-320.jpg)
![— © Cned, mathématiques 6e36
cc Séquence 7
2)
E
F
H
5 cm
4 cm
G
Les commentaires du professeur :
étape 1 On trace le segment[EG] de 5 cm. Soit M étape 2 Comme EF = 4 cm, le point F se trouve sur le cercle de
le milieu de [EG]. Comme les diagonales d’un rectangle centre E et de rayon 4 cm. EFGH est un rectangle donc ses côtés
ont la même longueur et le même milieu, on a : opposés ont la même longueur, d’où : GH = EF = 4 cm. Le point
ME = MG = MH = MF = 2,5 cm. Les points F et H H se trouve donc sur le cercle de centre G et de rayon 4 cm
sont donc sur le cercle de centre M et de rayon 2,5 cm
soit sur le cercle de diamètre [EG].
E
2,5 cm
G
M
E GE
F
H
G
M
étape 3 On trace les quatre côtés du quadrilatère EFGH.
E GE
F
H
G
M
On a bien respecté la consigne de ne pas utiliser l’équerre.
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-635-320.jpg)
![© Cned, Mathématiques 6e — 37
ccSéquence 7
Exercice 57
J K
L
4 cm
Les commentaires du professeur :
étape 1 On trace un côté [IJ] de 4 cm, puis on trace une demi-droite d’origine J, perpendiculaire à (IJ) à l’aide d’une équerre.
On reporte ensuite la longueur IJ à partir de J sur cette demi-droite à l’aide d’un compas.
J K
4 cm
étape 2 On trace deux arcs de cercle de rayon 4 cm de centres respectifs I et K. Ces deux arcs se coupent en L.
J K
4 cm
L
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-636-320.jpg)
![— © Cned, mathématiques 6e38
cc Séquence 7
Exercice 58
1)
J
K
L
M
E
F
G
H
Les deux rectangles sont-ils toujours superposables ? NON
2)
A
B
C
D
S
T
U
R
Les deux carrés sont-ils toujours superposables ? OUI
1)
• On trace la diagonale [JL] qui mesure
6 cm, puis on cherche à tracer une deuxième
diagonale.
• On utilise la carte 24 :
JKLM est un rectangle donc cette deuxième
diagonale a la même longueur que l’autre, soit
6 cm, et les deux diagonales se coupent en leur
milieu que l’on nomme O.
On trace le cercle de centre O et de rayon 3 cm.
• On trace un diamètre [MK], mais on a un
nombre infini de possibilités. En voici trois :
J
K
K' K''
L
M
M'
M''
Si on choisit un autre diamètre pour deuxième
diagonale, on peut par exemple obtenir le
quadrilatère EFGH.
On voit facilement que ces deux rectangles ne
sont pas superposables.
2)
• On utilise la carte 25 :
Ce n’est pas la même chose pour le carré
puisque les diagonales d’un carré sont
perpendiculaires : dès qu’on trace la première
diagonale, la seconde est unique.
A
D
B
C
Il n’y a donc qu’un seul carré qui a une
diagonale de 6 cm. C’est pour cette raison que
les carrés ABCD et RSTU sont superposables.
Exercice 59 On utilise la carte 7.
A et B sont les symétriques respectifs de E par
rapport à (d) et (d’).
(Revoir au besoin la construction du
symétrique d’un point par rapport à une droite
dans la séquence 5, séance 2 ou 6)
Pour construire E’ :
• E’ est le symétrique de A par rapport à (d’),
• ou encore celui de B par rapport à (d)
• ou encore lorsqu’on reporte EB à partir de
A et EA à partir de B : E’ est le point commun
aux deux arcs de cercle.
E
(d)
(d')
A
E'
B
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-637-320.jpg)
![© Cned, Mathématiques 6e — 39
ccSéquence 7
Séance 8
Ce que tu devais faire Les commentaires du professeur
Exercice 60
1) et 2)
3)
a) C’est Lou-Ann.
b)
Maillon 1
Comme la droite (Δ) est la médiatrice du
segment [AB], d’après la définition de la
médiatrice, (Δ) coupe [AB] en son milieu. Le
point M est donc le milieu de [AB] et c’est le
centre du cercle Ω.
Maillon 2
Les points E, M et F sont alignés et les points E et
F sont sur le cercle de centre M donc :
• le segment [EF] est un diamètre du cercle Ω.
• le point M est le milieu du segment [EF].
Maillon 3
Comme les segments [EF] et [AB] sont deux
diamètres du cercle Ω, ils ont la même longueur.
Maillon 4
Comme (Δ) est la médiatrice du segment [AB],
d’après la définition de la médiatrice, on a :
(EF) ⊥ (AB).
Maillon 5
Comme les diagonales du quadrilatère AEBF
sont perpendiculaires et ont le même milieu M,
je peux conclure que AEBF est un losange.
Maillon 6
Comme les diagonales du quadrilatère AEBF ont
le même milieu M et ont la même longueur, je
peux conclure que AEBF est un rectangle.
c) démonstration de Henri : 1 – 2 – 4 – 5
d) démonstration de Victor : 1 – 2 – 3 – 6
e) En conclusion, AEBF est un losange et un rectangle donc c’est un carré.
Les commentaires du professeur :
1)
• On trace la médiatrice au compas : on revoit au besoin le paragraphe « Je comprends la méthode » de la séquence 5, séance 5.
• Pour tracer le cercle Ω, on revoit éventuellement le paragraphe « Je comprends la méthode », séquence 1, séance 9.
Ici, on a déjà le milieu de [AB] : c’est le point M commun aux droites (AB) et (Δ).
2) Les diagonales sont les segments [AB] et [EF].
3)
a) C’est Lou-Ann qui a raison. Cependant, on peut déjà le « tester » sur la figure : les quatre angles semblent être droits et les
quatre côtés semblent avoir la même longueur.
c) On utilise la carte 22.
d) On utilise la carte 24.
e) On utilise la carte 4.
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-638-320.jpg)
![— © Cned, mathématiques 6e40
cc Séquence 7
Exercice 61
1) et 2)
E
F
A
B
3 cm
3)
• Comme [EF] est un diamètre du cercle Ω, le centre I de Ω est
le milieu de [EF].
• Comme [AB] est un diamètre du cercle Ω’, le centre I de ce
cercle Ω’ est aussi le milieu de [AB].
• Les diagonales [EF] et [AB] ont donc le même milieu I.
• On sait que : (AB) ⊥ (EF). Les diagonales de AEBF sont
donc perpendiculaires.
• D’après la propriété « si un quadrilatère a ses diagonales
qui sont perpendiculaires et qui ont le même milieu alors ce
quadrilatère est un losange », je peux affirmer que AEBF est un
losange.
1) On n’oublie pas qu’un diamètre est une
corde qui passe par le centre du cercle.
2) Une fois qu’on a tracé [EF], on trace
une droite perpendiculaire à (EF) passant
par I : elle coupe Ω’ en deux points A et B
diamétralement opposés.
3)
• Comme le point I est le centre du cercle Ω,
il est le milieu du diamètre [EF].
• Comme I est aussi le centre de Ω’, c’est
également le milieu du diamètre [AB].
On utilise la carte 22 de la Boîte à Outils.
Prends le temps de recopier soigneusement
la démonstration si la tienne est incomplète :
cela t’entraînera à rédiger.
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-639-320.jpg)
![© Cned, Mathématiques 6e — 41
ccSéquence 7
Exercice 62
a) « Un carré est un losange. » OUI
« Un losange est un carré. » NON
b) « Un carré est un rectangle. » OUI
« Un rectangle est un carré. » NON
c) « Un carré est un cerf-volant. » OUI
« Un cerf-volant est un carré. » NON
d) « Les côtés opposés d’un losange ont la même longueur. »
OUI
« Les côtés opposés d’un cerf-volant ont la même longueur. »
NON
a) Un carré est un losange par définition
(carte 4 de la Boîte à Outils).
Par contre, on a rencontré beaucoup de losanges
dans cette séquence qui ne sont pas des carrés : il
suffit qu’aucun de leurs angles ne soit droit.
b) Un carré est un rectangle par définition
(carte 4 de la Boîte à Outils).
Par contre, on a rencontré beaucoup de
rectangles dans cette séquence qui ne sont pas
des carrés : il suffit que leurs côtés consécutifs
n’aient pas la même longueur.
c) Un carré est un losange donc c’est un cerf-
volant puisqu’un losange est un cerf-volant
avec la particularité d’avoir tous ses côtés de la
même longueur. Par contre, un cerf-volant n’est
pas forcément un losange comme on l’a déjà vu
dans l’exercice 17 donc encore moins un carré !
d)
Comme tous les côtés d’un losange ont la
même longueur, les côtés opposés aussi ont la
même longueur.
Par contre, les côtés opposés d’un cerf-volant
n’ont pas généralement la même longueur :
il n’y a qu’à observer, par exemple, celui du
premier paragraphe « Je retiens » de la séance
2 de cette séquence.
Exercice 63
1)
• HKJI est un losange. D’après la propriété : « si un quadrilatère
est un losange alors ses angles opposés sont égaux », je peux
affirmer que les angles KHI et KJI sont égaux.
2)
• D’après le codage, les angles HKL et KJI sont égaux mais
KJI = KHL d’après la question 1, donc on a : HKL = KHL .
• D’après la propriété « si un triangle a deux angles égaux alors
il est isocèle », je peux affirmer que le triangle HKL est isocèle.
• Comme les sommets de ses angles égaux sont H et K, le
triangle HKL est isocèle en L.
1)
• On utilise la carte 10 de la Boîte à Outils.
2)
• On utilise ici une donnée fournie par le
codage. De plus, KHI∑ = KHL∑.
• On utilise ici le second paragraphe « Je
retiens » de la séquence 5 séance 7.
• On donne une réponse complète c’est-à-
dire que l’on précise bien en quel sommet
le triangle est isocèle : on donne le nom du
sommet principal.
Exercice 64
1), 2) et 3)
A
B
B'
C
• Les segments [AB] et [AB’] sont symétriques par rapport à la
droite (AC) donc ils ont la même longueur : AB = AB’.
• De même, les segments [BC] et [B’C] sont symétriques par
rapport à la droite (AC) donc : BC = B’C.
• On a : AB = AB’ et : BC = B’C. Le quadrilatère AB’CB est
donc par définition un cerf-volant.
1) et 2)
• On revoit au besoin le paragraphe « Je
comprends la méthode » de la séquence 5
séance 6 pour construire B’.
3)
• On utilise la propriété du troisième
paragraphe « Je retiens » de la séquence 5
séance 3.
• On utilise ici la carte 1 de la Boîte à Outils.
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-640-320.jpg)
![— © Cned, mathématiques 6e42
cc Séquence 7
Exercice 65
1) , 2) et 3) a)
A
S
45°
E
U
b)
• Les angles AEU et SEU sont symétriques par rapport à la
droite (EU) donc ils ont la même mesure. AEU = SEU = 45°.
• On a :
SEA = SEU + UEA
SEA = SEU + UEA= 45° + 45° = 90°.
L’angle SEA = SEU + UEAest droit.
c)
Le triangle EAU est rectangle en A donc : EAU = 90° .
Les angles ESU et EAU = 90°sont symétriques par rapport
à la droite (EU) donc ils sont égaux. On a donc :
ESU∑ ∑= =EAU 90°
d)
Les trois angles ESU , EAU = 90°et SEA = SEU + UEAsont droits.
D’après la propriété : « Si un quadrilatère a trois angles droits,
alors c’est un rectangle », je peux affirmer que SEAU est un
rectangle.
e)
Les segments [EA] et [ES] sont symétriques par rapport à
la droite (EU) donc ils ont la même longueur c’est-à-dire :
EA = ES.
f)
[EA] et [ES] ont la même longueur. D’après la propriété : « Si
un rectangle a deux côtés consécutifs de la même longueur alors
c’est un carré », je peux affirmer que SEAU est un carré.
3)
b) Dans la symétrie axiale par rapport à la
droite (EU) :
• le symétrique de E est lui-même
• le symétrique de U est lui-même
• A et S sont symétriques
• les demi-droites [EA) et [ES) sont
symétriques
• la demi-droite [EU) est sa propre
symétrique
c)
Revoir au besoin le premier paragraphe « Je
retiens » de la séquence 5 séance 4.
d)
On utilise ici la carte 23 de la Boîte à Outils.
e) On utilise ici le troisième paragraphe « Je
retiens » de la séquence 5 séance 3.
f) On utilise ici la carte 27 de la Boîte à
Outils.
Recopie bien ces démonstrations si les
tiennes sont différentes de celles du corrigé
ou bien si elles sont incomplètes.
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-641-320.jpg)

![— © Cned, mathématiques 6e44
cc Séquence 7
Exercice 68
1)
a) Le quadrilatère ABGH a trois angles droits. D’après la
propriété : « Si un quadrilatère a trois angles droits, alors c’est
un rectangle », je peux affirmer que ABGH est un rectangle
donc HGB = 90°.
b)
• D’après les codages : GB = GD = BC = DC. Par définition, le
quadrilatère BCDG est un losange.
• D’après la propriété : « Si un quadrilatère est un losange
alors ses angles opposés sont égaux », je peux affirmer que :
BGD∑ ∑= =BCD 40°.
c)
• D’après le codage du quadrilatère DEFG, les côtés
consécutifs [DG] et [GF] ont la même longueur ainsi que les
côtés consécutifs [DE] et [EF]. Ce quadrilatère est donc par
définition un cerf-volant.
• D’après la propriété : « Si un quadrilatère est un cerf-volant
alors il admet un axe de symétrie : la diagonale qui est la
médiatrice de l’autre » et grâce aux codages, je peux déduire
que la diagonale (GE) est un axe de symétrie de DGFE.
• Les anglesHGE = HGB + BGD + DGE et EGF sont symétriques donc
DGE = =EGF 50°
d)
On a :
donc HGE = HGB + BGD + DGE= 90° + 40° + 50° = 180°.
L’angle HGE est plat donc les points H , G et E sont alignés
dans cet ordre.
2)
1)
a)
On utilise la carte 23 de la Boîte à Outils
b)
• On utilise la carte 2 de la Boîte à Outils
• On utilise la carte 10 de la Boîte à Outils
Code ce résultat sur la figure.
c)
• On utilise la carte 1 de la Boîte à Outils
• On utilise la carte 5 de la Boîte à Outils
Code ce résultat sur la figure.
d)
• Voir le premier paragraphe « Je retiens »
séquence 3 séance 5 puis l’exercice 27 séquence
3.
2)
• On commence par construire un rectangle
AHGB ayant les dimensions données. La
meilleure méthode consiste à tracer un triangle
rectangle HAB puis à utiliser le compas pour
obtenir le sommet G.
• On construit ensuite le losange BGDC. On
commence par construire l’angle BGD∑ de 40°
à l’aide d’un rapporteur. On obtient ensuite le
sommet C à l’aide du compas.
• On construit enfin le cerf-volant GFED.
Pour cela, on commence par construire le
point E qui est sur la droite (HG) d’après
le 1) d), et qui est tel que : GE = HG. On
prolonge donc le tracé du segment [HG] puis
on utilise le compas pour obtenir le point E.
À l’aide d’un compas, on trace des arcs
de cercle de rayons GD et DE de centres
respectifs G et E. Ces arcs se coupent en F.
HGE = HGB + BGD + DGE
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-643-320.jpg)


![© Cned, mathématiques 6e — 47
ccSéquence 7
) ABCD est un losange tel que les triangles ABD et BDC sont
équilatéraux. Coche les égalités vraies :
˝ AB = BC
˝ AB = DC
˝ AB = BD
¨ AC = BD
10) Dans quel cas les triangles ABC et BCD sont-ils isocèles et
superposables ?
˝ quand ABDC est un losange
¨ quand ABCD est un losange
˝ quand ABCD est un carré
¨ quand ABCD est un rectangle
9) La longueur de la diagonale [AC] est
différente de la longueur des côtés, mais
AB = BD car le triangle ABD est équilatéral.
10) Voici les deux cas où les triangles ABC et
BCD sont superposables et isocèles :
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-646-320.jpg)
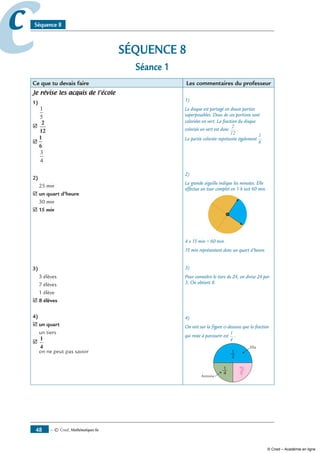
















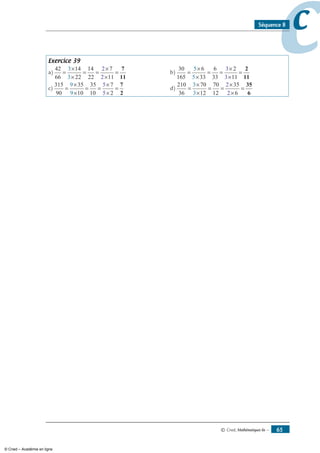



















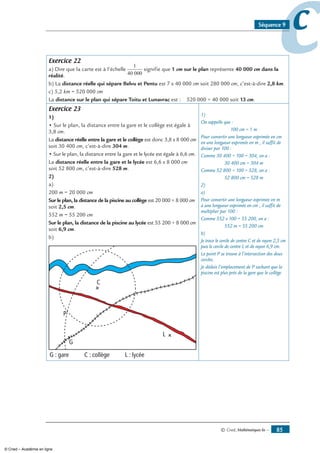


![— © Cned, mathématiques 6e88
cc Séquence 9
Exercice 29
a) b)
A‘
B‘
C‘
D‘E‘
4,5 cm
55° 55°
xy
A‘ D‘B‘ C‘1,8 cm 1,8 cm3 cm 3 cmO‘
Les remarques du professeur :
• Figure a)
On commence par tracer un carré A’C’D’E’ de côté 3 x 1,5 soit 4,5 cm. On utilise ensuite le rapporteur :
on trace deux demi-droites [A’x) et [C’y) telles que : xA C' '∑ = °55 et yC A' '∑ = °55 . Ces deux demi-droites se coupent en B’.
• Figure b)
On trace un demi-cercle de centre O’ qui a pour diamètre 2 x 1,5 soit 3 cm. On trace ensuite deux segments [A’B’] et [C’D’]
qui mesurent 1,2 x 1,5 cm (soit 1,8 cm) tels que A’, B’, O’, C’, D’ soient alignés dans cet ordre. On trace ensuite le demi-cercle
de centre O’ , qui a pour rayon O’A’, et qui se trouve « du bon côté ».
© Cned – Académie en ligne](https://image.slidesharecdn.com/214275799-cours-cned-6-eme-maths-141220090101-conversion-gate02/85/214275799-cours-cned-6-eme-maths-687-320.jpg)