Ce document présente un cours sur la gestion des risques, abordant des concepts théoriques, l'historique des crises financières, et l'évolution de la réglementation. Il explore diverses typologies et mesures des risques, ainsi que des approches pratiques pour l'optimisation et la gestion des capitaux. En outre, il couvre le risque de crédit, les normes prudentielles et les méthodes de stress-testing.




![9 L’approche standard 89
9.1 La r´glementation prudentielle . . . . . . . .
e . . . . . . . . . . . . . . . . . . . . . . . . . 89
9.2 Les pond´rations . . . . . . . . . . . . . . . .
e . . . . . . . . . . . . . . . . . . . . . . . . . 90
9.3 Les notations externes . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 91
9.4 Les proc´dures de r´duction des risques . . .
e e . . . . . . . . . . . . . . . . . . . . . . . . . 94
9.4.1 Les sˆret´s ou collat´raux . . . . . . .
u e e . . . . . . . . . . . . . . . . . . . . . . . . . 94
9.4.1.1 L’approche compl`te . . . . .
e . . . . . . . . . . . . . . . . . . . . . . . . . 94
9.4.1.2 L’approche simple . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 97
9.4.2 Les garanties et les d´riv´s de cr´dit .
e e e . . . . . . . . . . . . . . . . . . . . . . . . . 97
9.4.3 Autres consid´rations . . . . . . . . .
e . . . . . . . . . . . . . . . . . . . . . . . . . 98
9.4.3.1 Compensation de bilan . . . . . . . . . . . . . . . . . . . . . . . . . . . . 98
9.4.3.2 Le d´calage des maturit´s . .
e e . . . . . . . . . . . . . . . . . . . . . . . . . 98
9.4.3.3 L’asym´trie des devises . . .
e . . . . . . . . . . . . . . . . . . . . . . . . . 99
9.4.4 Quelques exemples . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 99
9.4.4.1 Collateralised transactions . . . . . . . . . . . . . . . . . . . . . . . . . . 99
9.4.4.2 On-balance sheet netting . . . . . . . . . . . . . . . . . . . . . . . . . . . 102
9.4.4.3 Guarantees/credit derivatives . . . . . . . . . . . . . . . . . . . . . . . . . 103
10 La m´thode IRB
e 105
10.1 Les principes g´n´raux . . . . . . . . . . . . . . . . . . . . . .
e e . . . . . . . . . . . . . . . . 105
10.1.1 Le sch´ma simplifi´e de l’approche IRB . . . . . . . . .
e e . . . . . . . . . . . . . . . . 105
10.1.2 D´finition de la d´faillance . . . . . . . . . . . . . . .
e e . . . . . . . . . . . . . . . . 106
10.1.3 La notation interne . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 106
10.2 L’exemple de la m´thode IRB pour les entreprises . . . . . . .
e . . . . . . . . . . . . . . . . 106
10.2.1 Formulation des pond´rations de risque . . . . . . . .
e . . . . . . . . . . . . . . . . 107
10.2.1.1 Dans l’approche IRB simple . . . . . . . . . . . . . . . . . . . . . . . . . . 107
10.2.1.2 Dans l’approche IRB avanc´e . . . . . . . . .
e . . . . . . . . . . . . . . . . 108
10.2.2 Justification de la m´thode IRB . . . . . . . . . . . . .
e . . . . . . . . . . . . . . . . 112
10.2.3 Param`tres de la fonction de pond´ration . . . . . . .
e e . . . . . . . . . . . . . . . . 121
10.2.3.1 La probabilit´ de d´faillance . . . . . . . . .
e e . . . . . . . . . . . . . . . . 121
10.2.3.2 La perte en cas de d´faillance . . . . . . . . .
e . . . . . . . . . . . . . . . . 121
10.2.3.3 La maturit´ . . . . . . . . . . . . . . . . . .
e . . . . . . . . . . . . . . . . 121
10.2.3.4 L’exposition en cas de d´faillance . . . . . .
e . . . . . . . . . . . . . . . . 121
10.2.4 Les exigences minimales d’´ligibilit´ . . . . . . . . . .
e e . . . . . . . . . . . . . . . . 121
10.3 Prolongements . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 122
10.3.1 Risque retail . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 122
10.3.2 Risque souverain . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 122
10.3.3 Risque banque . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 122
10.3.4 Risque financement de projet . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 122
10.3.5 Risque equity . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 122
10.4 Granularit´ du portefeuille . . . . . . . . . . . . . . . . . . . .
e . . . . . . . . . . . . . . . . 122
10.4.1 La m´thodologie . . . . . . . . . . . . . . . . . . . . .
e . . . . . . . . . . . . . . . . 122
10.4.2 Exemples . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 124
10.4.3 D´rivation du coefficient d’ajustement de granularit´ .
e e . . . . . . . . . . . . . . . . 125
10.4.3.1 La d´termination du coefficient β . . . . . .
e . . . . . . . . . . . . . . . . 125
10.4.3.2 Du coefficient β ` l’ajustement de granularit´
a e du Comit´ de Bˆle
e a . . . . . 129
10.5 Les modifications du 5 novembre 2001 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 133
IV Les mod`les de risque de cr´dit
e e 137
11 Introduction 139
12 Le mod`le de la firme
e 141
12.1 Le mod`le de Merton [1974] . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 142
e
12.2 Extensions du mod`le de Merton . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 144
e
12.2.1 G´n´ralisation de la notion de d´faut . . . . . . . . . . . . . . . . . . . . . . . . . . 144
e e e](https://image.slidesharecdn.com/gestionrisques-130221132633-phpapp01/85/Gestion-risques-5-320.jpg)
![12.2.2 Introduction de sauts dans le processus de valorisation des actifs . . . . . . . . . . 145
12.3 M´thodologie mise en place par K.M.V. Corporation . . . . . . . . . . .
e . . . . . . . . . . 146
12.3.1 Une mesure du risque de d´faut : la distance au d´faut . . . . . .
e e . . . . . . . . . . 146
12.3.2 Estimation de la distance au d´faut . . . . . . . . . . . . . . . .
e . . . . . . . . . . 147
12.3.3 Calcul de l’EDF . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 148
12.4 Une application : le mod`le CreditMetrics . . . . . . . . . . . . . . . . . .
e . . . . . . . . . . 151
13 L’approche actuarielle de CreditRisk+ 153
13.1 La d´marche . . . . . . . . . . . . . . . . . . . . .
e . . . . . . . . . . . . . . . . . . . . . . 153
13.2 Mod´lisation ` taux de d´faut fixes . . . . . . . . .
e a e . . . . . . . . . . . . . . . . . . . . . . 155
13.2.1 Occurrence de d´fauts . . . . . . . . . . . .
e . . . . . . . . . . . . . . . . . . . . . . 155
13.2.2 Pertes de d´faut . . . . . . . . . . . . . . .
e . . . . . . . . . . . . . . . . . . . . . . 156
13.2.2.1 Proc´dure de calcul et distribution
e des pertes . . . . . . . . . . . . . . . . 156
13.2.2.2 Application au cas multi-annuel . . . . . . . . . . . . . . . . . . . . . . . 157
13.3 Passage ` des taux de d´faut al´atoires . . . . . . .
a e e . . . . . . . . . . . . . . . . . . . . . . 158
13.3.1 Incertitude des taux de d´faut . . . . . . .
e . . . . . . . . . . . . . . . . . . . . . . 158
13.3.2 Analyse par secteur . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 158
13.3.3 Occurrence de d´fauts . . . . . . . . . . . .
e . . . . . . . . . . . . . . . . . . . . . . 159
13.3.4 Distribution des pertes de d´faut . . . . . .
e . . . . . . . . . . . . . . . . . . . . . . 160
13.3.4.1 Pertes de d´faut . . . . . . . . . .
e . . . . . . . . . . . . . . . . . . . . . . 160
13.3.4.2 Relation de r´currence . . . . . . .
e . . . . . . . . . . . . . . . . . . . . . . 160
13.4 Conclusion . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 161
14 L’approche Intensit´ : une approche sous forme r´duite
e e 163
14.1 Cadre de l’analyse . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 163
14.1.1 D´finition de l’intensit´ de survie . . . . . . . . . . . . . . . . .
e e . . . . . . . . . . . 164
14.1.2 Une autre approche de l’intensit´ de d´faut . . . . . . . . . . .
e e . . . . . . . . . . . 165
14.2 Les diff´rentes repr´sentations du prix de la dette risqu´e . . . . . . .
e e e . . . . . . . . . . . 165
14.2.1 Premi`res repr´sentations . . . . . . . . . . . . . . . . . . . . .
e e . . . . . . . . . . . 165
14.2.2 Th´or`me de repr´sentation du prix de la dette risqu´e . . . . .
e e e e . . . . . . . . . . . 166
14.3 Un exemple d’application : le mod`le de Jarrow et Turnbull [1995]
e . . . . . . . . . . . 166
V Le risque op´rationnel
e 169
15 La r´glementation prudentielle
e 171
15.1 La d´finition du risque op´rationnel . . . . . . . . .
e e . . . . . . . . . . . . . . . . . . . . . 171
15.2 Les approches forfaitaires . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 173
15.2.1 Basic Indicator Approach (BIA) . . . . . . . . . . . . . . . . . . . . . . . . . . 173
15.2.2 Standardised Approach (SA) . . . . . . . . . . . . . . . . . . . . . . . . . . . . 174
15.3 Annexe : composition du Risk Management Group (RMG) of the Basel Committee on
Banking Supervision . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 174
16 Les m´thodes AMA
e 177
16.1 L’approche IMA . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 177
16.2 L’approche LDA . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 179
16.2.1 Pr´sentation de la m´thode statistique
e e . . . . . . . . . . . . . . . . . . . . . . . . . 179
16.2.2 Robustesse de l’approche LDA . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 180
16.3 Le mapping IMA/LDA . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 181
16.4 L’approche Scorecard . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 182
Conclusion g´n´rale
e e 185](https://image.slidesharecdn.com/gestionrisques-130221132633-phpapp01/85/Gestion-risques-6-320.jpg)

![9.1 Evolution de la pond´ration ajust´e r en fonction de la sˆret´ ajust´e CA (E = 100) . . .
e e u e e 95
9.2 Evolution de la pond´ration ajust´e r en fonction de l’exposition E (CA = 50) . . . . . .
e e 96
10.1 Fonction de r´f´rence BRW . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
ee 108
10.2 D´riv´e premi`re de la fonction de r´f´rence BRW . . . . . . . . . . . . . . . . . . . . . .
e e e ee 109
1−PD
10.3 Ajustement de la maturit´ 1 + 0.470 × PD0.44 . . . . . . . . . . . . . . . . . . . . . . . .
e 109
10.4 Repr´sentation graphique de la fonction b (PD) . . . . . . . . . . . . . . . . . . . . . . . .
e 114
10.5 Influence du seuil α sur la probabilit´ de d´faillance conditionnelle Pi (ρ = 20%) . . . . .
e e 117
10.6 Influence du seuil α sur la probabilit´ de d´faillance conditionnelle Pi pour des valeurs
e e
donn´es de pi (ρ = 20%) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
e 117
10.7 Influence de la corr´lation ρ sur la probabilit´ de d´faillance conditionnelle Pi (α = 99.5%)
e e e 118
10.8 Influence de la corr´lation ρ sur la probabilit´ de d´faillance conditionnelle Pi pour des
e e e
valeurs donn´es de pi (α = 99.5%) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
e 118
10.9 Fonction de r´f´rence BRW (ajustement de maturit´/formule exacte) . . . . . . . . . . . .
ee e 120
10.10Impact des param`tres sur le coefficient β (valeurs par d´faut : LGD = 50%, α = 99.5%,
e e
ρ = 20% et σ [X] = 2) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 129
10.11Impact des propositions du 5 Novembre 2001 sur les pond´rations en risque (I) . . . . . .
e 135
10.12Impact des propositions du 5 Novembre 2001 sur les pond´rations en risque (II) . . . . . .
e 135
10.13Impact des propositions du 5 Novembre 2001 sur les corr´lations ρ (PD) . . . . . . . . . .
e 136
12.1 Effet de levier (d > 1) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 144
12.2 Effet de levier (d < 1) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 145
12.3 Volatilit´ des actifs, secteur d’activit´ et taille
e e de l’entreprise . . . . . . . . . . . . . . . . 147
12.4 Expected default frequency . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 148
12.5 EDF de Bangkok Metropolitan Bank . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 149
12.6 EDF de Burns Philip . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 150
12.7 Valeur de march´ de Burns Philip . . . . . . .
e . . . . . . . . . . . . . . . . . . . . . . . . . 150
13.1 Organigramme de la d´marche suivie par CreditRisk+
e . . . . . . . . . . . . . . . . . . . . 154
16.1 Distribution agr´g´e avec ζ (i, j) ∼ LN (8, 2.2) et N (i, j) ∼ P (50) . . . . . . . . . . . . . 180
e e](https://image.slidesharecdn.com/gestionrisques-130221132633-phpapp01/85/Gestion-risques-8-320.jpg)
![Liste des documents distribu´s en cours
e
1. Comit´ de Bˆle sur le Contrˆle Bancaire, Vue d’ensemble du Nouvel Accord de Bˆle sur les fonds
e a o a
propres, Document soumis ` consultation, Janvier 2001
a
2. Punjabi, S. [1998], Many happy returns, Risk Magazine, June, 71-76
3. Modalit´s de Calcul du Ratio de Solvabilit´ — Actualisation au 31 d´cembre 2000, Commission
e e e
Bancaire, Secr´tariat G´n´ral, Service des Affaires Internationales, 31 Janvier 2001
e e e
4. Derman, E. [2001], Markets and model, Risk Magazine, 14, July, 48-50
5. Rebonato, R. [2001], Model risk : new challenges, new solutions, Risk Magazine, 14, March, 87-90
6. Turc, J. [1999], Pr´sentation du march´ du risque de cr´dit, CDC March´s, S´minaire INRIA du
e e e e e
8 juin 1999
7. Basel Committee on Banking Supervision, Credit Ratings and Complementary Sources of Credit
Quality Information, Working Paper, 3, August 2000
8. Koyluoglu, H.U. et A. Hickman [1998], Reconcilable differences, Risk Magazine, 11, October,
56-62
9. Finger, C.C. [1999], Conditional approaches for CreditMetrics portfolio distributions, CreditMe-
trics Monitor, April, 14-33
10. Wilson, T. [2001], IRB approach explained, Risk Magazine, 14, May, 87-90
11. Wilson, T. [2001], Probing granularity, Risk Magazine, 14, August, 103-106
12. Basel Committee on Banking Supervision, Working Paper on the Regulatory Treatment of Opera-
tional Risk, Working Paper, 8, September 2001
13. Frachot, A., P. Georges et T. Roncalli [2001], Loss Distribution Approach for operational
risk, Groupe de Recherche Op´rationnelle, Cr´dit Lyonnais, Working Paper
e e
14. Pennequin, M. [2001], Risques op´rationnels : comment se pr´parer ` la r´forme de Bˆle, Club
e e a e a
Banque, F´d´ration des Banques Fran¸aises, 27 septembre 2001
e e c](https://image.slidesharecdn.com/gestionrisques-130221132633-phpapp01/85/Gestion-risques-9-320.jpg)

![Avant-Propos
Ceci est le support ´crit qui accompagne le cours “Introduction ` la Gestion des Risques”.
e a
L’expos´ oral du cours sera sensiblement diff´rent de ces notes. Celui-ci portera plus sur
e e
la culture financi`re du risque que sur les m´thodes.
e e
Les m´thodes seront abord´es de fa¸on plus approfondie dans deux autres cours : “La
e e c
Th´orie des Extrˆmes et la Gestion des Risques de March´” et ”La Gestion des Risques
e e e
Multiples”. C’est dans ces deux cours que nous verrons la mise en œuvre pratique des
m´thodes avec le logiciel GAUSS. A titre indicatif, le premier cours portera sur la VaR et le
e
stress-testing. Et nous aborderons les copulas, le risque de cr´dit et le risque op´rationnel
e e
dans le second cours.
Les propositions de Bˆle pour le nouvel Accord ´voluent rapidement. Par
a e
exemple, la publication le 28 septembre 2001 d’un nouveau document
consultatif sur le risque op´rationnel modifie sensiblement les proposi-
e
tions du 16 janvier 2001. Dans l’expos´ oral, je pr´senterai les derniers
e e
travaux. Certains paragraphes du pr´sent document peuvent donc ˆtre
e e
(partiellement) obsol`tes.
e
La r´daction de ce document a ´t´ faite ` partir de diff´rents travaux et articles qui ont ´t´ r´alis´s au
e ee a e ee e e
Groupe de Recherche Op´rationnelle du Cr´dit Lyonnais.
e e
1. Les chapitres de la partie “Le risque de march´” reprennent la note [HRR] que j’ai r´dig´e en
e e e
collaboration avec Sakda Hoeung et Ga¨l Riboulet.
e
2. Les chapitres sur le mod`le de Merton et l’approche Intensit´ sont extraits du rapport de stage long
e e
de Nicolas Baud.
3. Le chapitre sur CreditRisk+ est extrait du document [R] ´crit par Ga¨l Riboulet.
e e
4. La partie sur le risque op´rationnel s’inspire tr`s largement des diff´rents travaux que j’ai men´s
e e e e
avec Antoine Frachot et Pierre Georges.
Vous pouvez t´l´charger les documents originaux ` l’adresse internet du GRO : http ://gro.creditlyonnais.fr.
ee a
[B ] Baud, N. [2000], La mesure du risque de cr´dit, Groupe de Recherche Op´rationnelle, Cr´dit
e e e
Lyonnais, Rapport de Stage
[BFIMR] Baud, N., A. Frachot, P. Igigabel, P. Martineu et T. Roncalli [1999], An analysis framework
for bank capital allocation, Groupe de Recherche Op´rationnelle, Cr´dit Lyonnais, Working Paper
e e
(document disponible sur le site web du GRO)
[BN] Bezat, A. et A. Nikeghbali [2000], La th´orie des extrˆmes et la gestion des risques de march´,
e e e
GT ENSAE (document disponible sur le site web du GRO)
´
[BDNRR] Bouye, E., V. Durrleman, A. Nikeghbali, G. Riboulet et T. Roncalli [2000], Copulas for
finance : a reading guide and some applications, Groupe de Recherche Op´rationnelle, Cr´dit Lyon-
e e
nais, Working Paper (document disponible sur le site web du GRO)
[C] Costinot, A. [2000], La construction d’un programme de simulation de crise, Groupe de Recherche
Op´rationnelle, Cr´dit Lyonnais, Rapport de Stage
e e
[CRR] Costinot, A., G. Riboulet et T. Roncalli [2000], Stress-testing et th´orie des valeurs extrˆmes :
e e
une vision quantifi´e du risque extrˆme, Groupe de Recherche Op´rationnelle, Cr´dit Lyonnais,
e e e e
Working Paper (document disponible sur le site web du GRO)
[FGR] Frachot, A., P. Georges et T. Roncalli [2001], Loss Distribution Approach for operational
risk, Groupe de Recherche Op´rationnelle, Cr´dit Lyonnais, Working Paper (document disponible
e e
sur le site web du GRO)
[HRR ] Hoeung, S., G. Riboulet et T. Roncalli [1999], Les risques de march´ — R´glementations,
e e
mesures et pratiques, Groupe de Recherche Op´rationnelle, Cr´dit Lyonnais, document interne
e e
[R ] Riboulet, G. [2000], Mesure du risque de cr´dit d’un portefeuille, Groupe de Recherche Op´rationnelle,
e e
Cr´dit Lyonnais, document interne
e](https://image.slidesharecdn.com/gestionrisques-130221132633-phpapp01/85/Gestion-risques-11-320.jpg)




![CHAPITRE 1. INTRODUCTION HISTORIQUE
que les probl`mes de tarification. L’Accord de Bˆle de 1988 impose aussi une nouvelle vision du risque,
e a
beaucoup plus r´glementaire. La publication en 1994 de la m´thodologie RiskMetrics par JP Morgan
e e
permet une diffusion tr`s large des m´thodes Value-at-Risk (VaR ou valeur en risque) aussi bien aupr`s
e e e
des professionnels que des acad´miques.
e
1.2 Le d´veloppement des produits financiers
e
Il existe plusieurs types de risque (voir le chapitre suivant). Les deux principaux sont le risque de cr´dit
e
(credit risk) et le risque de march´ (market risk) — en fait, le risque op´rationnel (operational risk)
e e
est consid´r´ comme plus important que le risque de march´. Pour une premi`re d´finition, nous pouvons
ee e e e
assimiler le risque de march´ ` un risque de volatilit´ des prix des actifs et le risque de cr´dit au risque
ea e e
de d´faillance. L’Accord de Bˆle de 1988 traite de ces deux risques — pour ˆtre pr´cis, seul le risque de
e a e e
cr´dit ´tait concern´, le risque de march´ a ´t´ pris en compte plus tard. N´anmoins, il est vite apparu
e e e e ee e
que le traitement r´glementaire (capital forfaitaire) du risque de march´ ´tait mal adapt´. Les autorit´s
e ee e e
r´glementaires ont donc autoris´ les banques ` utiliser des mod`les internes pour mesurer ce risque. Cela
e e a e
n’est pas le cas du risque de cr´dit, car le march´ du cr´dit n’avait pas (et n’a toujours pas) la maturit´
e e e e
suffisante pour mesurer le risque de fa¸on rationnelle et coh´rente. Cela explique la part particuli`re
c e e
de ce cours consacr´e au risque de march´. Cependant, afin de bien cerner le risque de march´, il est
e e e
indispensable de connaˆ les diff´rents produits.
ıtre e
L’historique suivant est extrait de Jorion [2001] (voir la section 1.2.2) et de Crouhy, Galai et Mark
[2001] (section 2 du chapitre 1).
– Foreign currency futures (1972)
– Equity options (1973)
– Over-the-counter currency options (1979)
– Currency swaps (1980)
– Interest rate swaps (1981)
– Equity index options (1983)
– Interest rate caps/floors (1983)
– Swaptions (1985)
– Path-dependent options (Asian, lookback, etc.) (1987)
– CAT options (1992)
– Captions/Floortions (1993)
– Credit default options (1994)
– Weather derivatives (1997)
L’innovation financi`re a surtout concern´ dans un premier temps le march´ des changes (FX market).
e e e
Cela s’explique par la crise p´troli`re de 1973. Cette innovation s’est rapidement transmise aux march´s
e e e
d’actions (Equity market) et de taux d’int´rˆt (Bond market ou Interest Rate market), et dans
ee
une moindre mesure au march´ des mati`res premi`res (Commodity market). Il faut noter que celle-ci
e e e
s’est faite en dehors des march´s organis´s (centralized exchanges). Ce sont donc g´n´ralement des
e e e e
produits trait´s sur des march´s de gr´ ` gr´ (over-the-counter markets ou OTC markets).
e e ea e
Voyons quelques d´finitions (tr`s simplifi´es) des principaux produits.
e e e
– Un contrat ` terme (futures) fixe les caract´ristiques d’une transaction future : la maturit´ du
a e e
contrat, le cours ` terme (forward), etc.
a
– Une option est un contrat entre deux parties par lequel l’une accorde ` l’autre le droit, mais non
a
l’obligation, de lui acheter (option d’achat) ou de lui vendre (option de vente) l’actif support selon
certaines conditions. L’option est un exemple d’actif conditionnel ou d’actif contingent. Voici
quelques caract´ristiques qui permettent de d´finir le contrat :
e e
INTRODUCTION A LA GESTION DES RISQUES 6](https://image.slidesharecdn.com/gestionrisques-130221132633-phpapp01/85/Gestion-risques-16-320.jpg)
![CHAPITRE 1. INTRODUCTION HISTORIQUE
1. Le support du contrat est appel´ le sous-jacent de l’option.
e
2. Le prix convenu ` l’avance auquel peut avoir lieu la transaction est le prix d’exercice (strike).
a
3. Si la maturit´ de l’option n’est pas pr´cis´e, l’option est dite perp´tuelle.
e e e e
4. L’acheteur de l’option paye une prime (premium) au vendeur de l’option pour le droit d’exer-
cer l’option.
5. Une option d’achat est un call et une option de vente est un put.
6. Si la date d’exercice correspond ` l’´ch´ance de l’option, l’option est dite Europ´enne. Si
a e e e
l’acheteur peut exercer ` tout moment avant la maturit´ de l’option, nous avons une option
a e
Am´ricaine. Ces deux types d’option d´finissent les options Vanilles (Vanilla options).
e e
Lorsqu’il existe plusieurs dates discr`tes d’exercice, on les appelle des options Bermuda
e
La caract´risation math´matique de l’option correspond ` la d´finition de la fonction payoff :
e e a e
+
European Call (S (T ) − K)
+
European Put (K − S (T ))
Asian (Floating Strike) ¯ +
S (T ) − S
+
Asian (Fixed Strike) K −S ¯
+
Lookback (S (T ) − mint0 ≤t≤T S (t))
+
Barrier (DOC) 1[mint ≤t≤T S(t)≥L] · (S (T ) − K)
0
+
Spread (S1 (T ) − S2 (T ) − K)
+
Basket (S1 (T ) + S2 (T ) − K)
– Un swap est un ´change de deux ´ch´anciers de flux futurs. Par exemple, un swap de taux fixe/variable
e e e
(fixed/floating) est l’´change d’un taux fixe contre un taux variable (Euribor, etc.).
e
– Un cap est un contrat qui permet ` l’acheteur de se garantir contre une hausse des taux en fixant
a
un taux plafond.
1.3 L’histoire r´cente des crises financi`res
e e
La r´glementation prudentielle en mati`re de contrˆle des risques financiers est une cons´quence des
e e o e
diff´rentes crises financi`res et de leur impact sur la solvabilit´ des ´tablissements financiers. Le chapitre
e e e e
2 de Jorion [2001] pr´sente un historique assez complet des “d´sastres” financiers r´cents. Voici quelques
e e e
points de rep`re :
e
1974 Herstatt Bank — FX trading — $4.8 Mds.
1994 Orange County — Reverse repos — $1.81 Mds.
1994 Metallgesellschaft — Oil futures — $1.34 Mds.
1994 Procter & Gamble — Swaps — $0.16 Mds.
1995 Barings — Index Nikkei 225 futures — $1.33 Mds.
1997 Natwest — Swaptions — $0.13 Mds.
1998 LTCM — Liquidity crisis — $2 Mds.
Pourquoi mettre en place des m´canismes de surveillance des ´tablissements financiers par des autorit´s
e e e
de tutelle ? Lors de crises financi`res importantes (crise mexicaine, crise russe, crise asiatique, etc.), la
e
mise en place d’un prˆteur en dernier ressort s’av`re tr`s couteuse pour ´viter une crise syst´mique.
e e e e e
De mˆme, la d´faillance d’un seul ´tablissement financier peut conduire ` une contagion aux autres
e e e a
´tablissements financiers ` cause de la panique financi`re (Diamond et Dybvig [1983]). La mise en
e a e
place d’une r´glementation en mati`re des risques vise donc dans un premier temps ` limiter le risque
e e a
syst´mique, et dans un deuxi`me temps ` ´viter les d´faillances individuelles des ´tablissements financiers.
e e ae e e
´ `
1.3. L’HISTOIRE RECENTE DES CRISES FINANCIERES 7](https://image.slidesharecdn.com/gestionrisques-130221132633-phpapp01/85/Gestion-risques-17-320.jpg)

![1.4 L’´volution de la r´glementation
e e
La r´glementation prudentielle a consid´rablement ´volu´ ces vingt derni`res ann´es sous l’impulsion
e e e e e e
des travaux du Comit´ de Bˆle. Mˆme si celui-ci n’a aucun pouvoir d´cisionnel, ses recommandations
e a e e
sont reprises par les diff´rentes autorit´s de tutelle des diff´rents pays industrialis´s. Bien sˆr, il existe de
e e e e u
petites diff´rences entre les textes de Bˆle et les textes officiels.
e a
En Europe, c’est la Commission Europ´enne qui est charg´e de d´finir la CAD (Capital Adequacy
e e e
Directive). Mais la mise en œuvre revient aux diff´rentes autorit´s de tutuelle nationales. En France,
e e
c’est la Commission Bancaire (qui est rattach´e ` la Banque de France) qui contrˆle l’application de la
e a o
CAD (en fait, une version fran¸aise adapt´e ` la l´gislation fran¸aise par le Comit´ de la R´glementation
c e a e c e e
Bancaire et Financi`re — CRBF).
e
Les principales dates de l’´volution de la r´glementation sont les suivantes :
e e
1988 The Basle Capital Accord
1993 Capital Adequacy Directive
1996 Amendment to the Capital Accord to incorporate market risks
1999 A new capital adequacy framework
2001 The New Basel Capital Accord
2004 (2005 ?) Basle II
Bibliographie
[1] Amendment to the capital accord to incorporate market risks, Basle Committee on Banking Supervi-
sion, January 1996, N◦ 24
[2] Bernstein, P.L. [1995], Des Id´es Capitales, Presses Universitaires de France, Paris
e
[3] Crouhy, M., D. Galai et R. Mark [2001], Risk Management, McGraw-Hill
[4] Diamond, D.W. et P.H. Dybvig [1983] Bank runs, deposit insurance and liquidity, Journal of Political
Economy, 91(3), 401-419
[5] Jorion, P. [2001], Value at Risk : The new Benchmark for Controlling Market Risks, deuxi`me
e
´dition, McGraw-Hill
e](https://image.slidesharecdn.com/gestionrisques-130221132633-phpapp01/85/Gestion-risques-19-320.jpg)


![´
CHAPITRE 2. DEFINITION DU RISQUE
GRAPHIQUE 2.1. Les diff´rents types de risque
e
le mod`le de s´lection de portefeuille de Markowitz, l’agent maximise son esp´rance de gain pour un
e e e
niveau de risque donn´, qui est mesur´ par l’´cart-type.
e e e
Cette vision du risque n’est coh´rente que dans un monde gaussien. Cependant, nous savons depuis
e
fort longtemps que l’hypoth`se de normalit´ des rendements des actifs financiers n’est pas v´rifi´e. Ac-
e e e e
tuellement, la mesure de risque qui est la plus r´pandue est la valeur en risque (Value-at-Risk ou VaR).
e
Statistiquement, ce n’est rien d’autre que le quantile α de la perte potentielle pour un horizon donn´. e
Soit ϑ la variable al´atoire repr´sentant la perte potentielle. Notons F la distribution de probabilit´ de
e e e
ϑ. Nous avons
VaR = F−1 (α) (2.1)
Deux ´l´ments sont donc d´terminants pour calculer la valeur en risque : la distribution de probabilit´
ee e e
et le seuil de confiance.
Rating R´glementaire (march´)
e e BBB A AA AAA
α 99% 99.75% 99.9% 99.95% 99.97%
Temps de retour 100 jours 400 jours 4 ann´es
e 8 ann´es
e 13 ann´es
e
Φ−1 (α) 2.33 2.81 3.09 3.29 3.43
t−1 (α)
4 3.75 5.60 7.17 8.61 9.83
La perte moyenne E [ϑ] est d´sign´e par le terme expected loss. Dans le risque de march´, le capital
e e e
en risque (Capital-at-Risk ou CaR) correspond ` la valeur en risque. Dans le risque de cr´dit, il est ´gal
a e e
a
` la diff´rence entre le quantile et la perte moyenne — cette diff´rence est appel´e la perte exceptionelle
e e e
(unexpected loss). Dans ce dernier cas, on suppose que les marges (et les provisions) couvrent la perte
moyenne. Enfin, il nous faut d´finir aussi la charge en capital (capital charge) qui est fonction du
e
capital en risque. Cette charge en capital correspond au montant effectif de fonds propres immobilis´s e
pour assurer l’op´ration.
e
INTRODUCTION A LA GESTION DES RISQUES 12](https://image.slidesharecdn.com/gestionrisques-130221132633-phpapp01/85/Gestion-risques-22-320.jpg)
![´
CHAPITRE 2. DEFINITION DU RISQUE
GRAPHIQUE 2.2. Repr´sentation graphique de la valeur en risque
e
2.3 L’optimisation du couple rentabilit´/risque
e
Il est difficile de finir ce chapitre consacr´ au risque sans ´voquer la rentabilit´. Car le but d’une banque,
e e e
ce n’est pas de prendre le moins de risque possible, mais d’atteindre une rentabilit´ maximale pour un
e
risque donn´.e
La mesure des risques va permettre de calculer les fonds propres n´cessaires pour assurer chaque
e
op´ration financi`re. C’est donc un outil qui a plusieurs vocations. Il permet bien sˆr de dimensionner les
e e u
risques encourus en fonction du montant de ces fonds propres. Mais c’est aussi un outil indispensable pour
calculer des mesures de performances. Au niveau global, la mesure de performance la plus utilis´e est le
e
rendement des fonds propres (Return on Equity ou ROE). A des niveaux beaucoup plus fins (jusqu’au
niveau transactionel), les banques utilisent des mesures de performance ajust´e du risque (risk-adjusted
e
performance measure ou RAPM). Par exemple, le rapport du rendement esp´r´ sur le capital en risque
ee
est une mesure RAPM.
Il est donc important de consid´rer la mesure des risques non pas uniquement comme un outil r´glementaire,
e e
mais comme un outil strat´gique de d´cision pour la banque, car
e e
[...] la gestion d’une banque consiste en une gestion globale et coordonn´e, sous
e
contraintes internes et externes, de la rentabilit´ et des risques li´s aux activit´s de
e e e
´
l’´tablissement (Augros et Queruel [2000]).
e
Bibliographie
[1] Artzner, A., F. Delbaen, J-M. Eber et D. Heath [1997], Thinking coherently, Risk magazine, 10,
November, 68-71
[2] Artzner, A., F. Delbaen, J-M. Eber et D. Heath [1999], Coherent measures of risk, Mathematical
Finance, 9, 203-228
´
[3] Augros, J-C. et M. Queruel [2000], Risque de Taux d’Int´rˆt et Gestion Bancaire, Economica,
ee
Paris
´
2.3. L’OPTIMISATION DU COUPLE RENTABILITE/RISQUE 13](https://image.slidesharecdn.com/gestionrisques-130221132633-phpapp01/85/Gestion-risques-23-320.jpg)
![[4] Guldimann, Til. [1994], RiskMetricsT M Technical Document, 2nd edition, J.P. Morgan, New York
[5] Markowitz, H.M. [1987], Mean-Variance Analyses in Portfolio Choice and Capital Markets, Basil
Blackwell, Oxford](https://image.slidesharecdn.com/gestionrisques-130221132633-phpapp01/85/Gestion-risques-24-320.jpg)
![3
Le nouvel Accord de Bˆle et le ratio McDonough
a
3.1 Les fonds propres
Voici le bilan simplifi´ d’une banque
e
ACTIF PASSIF
Actifs immobilis´s
e Fonds propres
Cr´dits et prˆts
e e Dette
titres (portfeuilles de n´gociation, de placement et d’investissement)
e D´pˆts
e o
Tr´sorerie
e
Les fonds propres (ou le capital) sont un ´l´ments du passif d’une banque. Ils regroupent :
ee
– Les actions ordinaires et les certificats d’investissement,
– les r´serves,
e
– le r´sultat non distribu´,
e e
– etc.
Les autres ´l´ments du passif d’une banque sont les d´pˆts, l’´pargne des m´nages, ainsi que les dettes.
ee e o e e
A l’actif, nous trouvons les cr´dits et les prˆts aux m´nages et aux entreprises, les services, le portefeuille
e e e
de titres, etc.
Le rˆle des fonds propres est triple (Dubernet [1997]) :
o
1. Les fonds propres sont n´cessaires ` la croissance.
e a
Les fonds propres sont le moteur de l’activit´ de la banque. A cause des contraintes externes
e
(par exemple, la r´glementation) et internes (impos´es par exemple par les actionnaires), ces fonds
e e
propres dimensionnent le risque de la banque, et donc l’activit´ de la banque. La croissance de
e
l’´tablissement financier d´pend donc de l’´volution de son capital.
e e e
2. Les fonds propres sont une garantie vis-`-vis des cr´anciers.
a e
Ils servent ` garantir l’activit´ de la banque. En particulier, ils doivent permettre d’absorber les
a e
fortes pertes dues ` des ´l´ments ´xog`nes et/ou inattendus :
a ee e e
– Crise russe (risque pays — d´faut de paiement),
e
– Crise asiatique (implosion des syst`mes bancaires),
e
– Crise immobili`re (krach sp´culatif),
e e
– etc.](https://image.slidesharecdn.com/gestionrisques-130221132633-phpapp01/85/Gestion-risques-25-320.jpg)
![ˆ
CHAPITRE 3. LE NOUVEL ACCORD DE BALE ET LE RATIO MCDONOUGH
Ainsi plus leur niveau est ´lev´, plus la banque pr´sente des gages de solidit´ (` activit´ bancaire
e e e e a e
constante). Ces fonds propres sont un des ´l´ments de notation de la banque (rating), note qui
ee
conditionne le coˆt des ressources (de tr´sorerie et de long terme).
u e
3. Les fonds propres sont les ressources les plus ch`res (exigence de rentabilit´).
e e
Puisque les fonds propres permettent de couvrir les risques, ils sont r´mun´r´s. Le taux de r´mun´ration
e ee e e
est appel´ Return on Equity ou ROE. L’objectif de la banque est donc d’offrir le ROE le plus
e
´lev´ ` ses actionnaires (prendre le moins de risque et d´gager la plus de r´sultat net). Actuellement,
e ea e e
celui-ci varie fortement d’un ´tablissement financier ` un autre avec une moyenne autour de 15%.
e a
Notons que celui-ci a une influence tr`s importante sur la valeur de march´ de la banque (Market
e e
Value Added ou MVA) et conditionne (partiellement) la croissance externe (OPA, OPE, fusion,
etc.) de l’´tablissement financier.
e
3.2 Le ratio Cooke
En 1988, le Comit´ de Bˆle propose un ratio international de solvabilit´ qui doit permettre
e a e
– une meilleure ad´quation des fonds propres par rapport aux risques
e
– de renforcer la solidit´ et la stabilit´ du syst`me bancaire,
e e e
– et d’att´nuer les in´galit´s concurrentielles entre les banques.
e e e
C’est le fameux ratio Cooke (du nom du pr´sident du Comit´ de Bˆle de l’´poque) qui correspond au
e e a e
rapport entre le montant des fonds propres et celui des encours (pond´r´s) EPC de cr´dit. Plusieurs
ee e
niveaux de fonds propres sont d´finis :
e
1. Les fonds propres de base FP1 ou “noyau dur” (TIER 1).
2. Les fonds propres compl´mentaires FP2 (TIER 2).
e
3. Les fonds propres surcompl´mentaires FP3 (TIER 3).
e
Les fonds propres de base correspondent au capital et aux r´serves. Les fonds propres compl´mentaires
e e
sont plus difficiles ` d´finir, mais sont principalement constitu´s par des emprunts subordonn´s. Selon
a e e e
l’Accord de Bˆle (Basle Accord), les ´tablissements financiers doivent respecter les contraintes sui-
a e
vantes :
FP2 ≤ FP1
FP1 / EPC ≥ 4%
(FP1 + FP2 ) / EPC ≥ 8% (ratio Cooke)
Les encours pond´r´s de cr´dit concerne le bilan et le hors bilan et les pond´rations sont les suivantes
ee e e
(Bessis [1995]) :
– 0% pour les cr´ances sur des Etats de l’OCDE,
e
– 20% pour les cr´ances sur les banques et les collectivit´s locales d’Etats de l’OCDE ;
e e
– 50% pour les cr´ances garanties par une hypoth`que ou cr´dit bail immobilier ;
e e e
– 100% pour tous les autres ´l´ments d’actifs, dont les cr´dits ` la client`le.
ee e a e
L’Accord de Bˆle a ´t´ adopt´ par le Parlement Europ´en en 1993. La r´glementation a ´volu´e progressi-
a ee e e e e e
vement pour prendre en compte les risques de march´. Contrairement au risque de cr´dit, deux approches
e e
existent pour calculer les risques de march´. La premi`re approche est une m´thode forfaitaire, alors
e e e
que la seconde approche autorise les banques ` utiliser un mod`le interne. L’id´e principale est d’inciter
a e e
les banques ` construire des mod`les robustes pour calculer les risques de march´ et donc d’obtenir des
a e e
exigences en fonds propres beaucoup plus r´alistes.
e
Remarque 1 Le site internet de la Reserve Bank of New Zeland contient un exemple complet de calcul
des ratios TIER 1 et TIER 2. Le lien direct est
http ://www.rbnz.govt.nz/banking/regulation/0091769.html
INTRODUCTION A LA GESTION DES RISQUES 16](https://image.slidesharecdn.com/gestionrisques-130221132633-phpapp01/85/Gestion-risques-26-320.jpg)
![ˆ
CHAPITRE 3. LE NOUVEL ACCORD DE BALE ET LE RATIO MCDONOUGH
3.3 Bˆle II et le nouveau ratio de solvabilit´
a e
Le Comit´ de Bˆle a publi´ le 16 janvier 2001 le second document consultatif pour une r´forme (en
e a e e
profondeur) de la r´glementation prudentielle. Celui-ci fait suite ` la publication en juin 1999 d’un premier
e a
document consultatif et aux diverses r´actions de la profession. Dans le calendrier original de la r´forme,
e e
une seconde p´riode consultative devait avoir lieu jusqu’au 31 mai 2001 pour permettre la r´daction finale
e e
du nouvel Accord pour fin 2001. L’impl´mentation de celui-ci ´tait pr´vu pour janvier 2004.
e e e
Le calendrier original est actuellement retard´, et l’impl´mentation n’est d´sormais pr´vue qu’en 2005
e e e e
pour plusieurs raisons :
– Le Comit´ de Bˆle n’est pas satisfait des r´ponses fournies par les banques aux questionnaires QIS
e a e
(Quantitative Impact Study).
– La calibration aux donn´es s’av`re difficile.
e e
– Il existe des d´saccords importants entre le Comit´ de Bˆle et les associations de banques (par
e e a
exemple, sur la part du risque op´rationnel).
e
– Enfin, plusieurs questions m´thodologiques ne sont pas r´solues.
e e
Les motivations du nouvel Accord sont multiples. La premi`re d’entre elle est la modification de l’as-
e
siette des risques :
FP1 + FP2
≥ 8%
risque de cr´dit + risque op´rationnel + risque de march´
e e e
L’assiette des risques int´gre d´sormais le risque op´rationnel. Dans la version de janvier 2001,
e e e
le Comit´ de Bˆle proposait la r´partition suivante de la charge en fonds propres
e a e
Type de risque Exigence en FP R´partition
e
Cr´dit
e 6% 75%
March´ e 0.4% 5%
Op´rationnel
e 1.6% 20%
Total 8% 100%
La seconde motivation de l’Accord est de rapprocher la r´glementation des pratiques en vigueur dans
e
l’industrie pour le pilotage des risques, afin que l’exigence en fonds propres sont plus sensible au risque r´el
e
(more risk sensitive) de la banque. A terme, l’id´e est d’autoriser les banques, sous certaines conditions,
e
d’utiliser les mod`les internes pour mesurer le risque de cr´dit et le risque op´rationnel, comme cela se
e e e
fait d´j` pour le risque de march´.
ea e
[...] Le renforcement de l’´galit´ des conditions de concurrence et le meilleur alignement des
e e
exigences de fonds propres sur les risques sous-jacents sont [...] deux finalit´s importantes du
e
futur dispositif. [...] Le nouveau ratio permettra non seulement de faire converger le capital
r´glementaire — souci des autorit´s de contrˆle — et le capital ´conomique — souci des
e e o e
´tablissements — mais aussi, au-del` des exigences de fonds propres, de poser un v´ritable
e a e
cadre prudentiel pour le contrˆle bancaire des prochaines ann´es (Pujal [2001]).
o e
Le nouveau dispositif se d´compose en trois piliers :
e
1. First Pillar : Minimum Capital Requirement
2. Second Pillar : Supervisory Review Process
3. Third Pillar : Market Discipline
Le premier pilier concerne l’exigence minimale en fonds propres. Le traitement du risque de march´ e
reste inchang´. Le traitement du risque de cr´dit est revu en profondeur. Trois m´thodes sont d´sormais
e e e e
possibles pour mesurer le risque de cr´dit :
e
– L’approche standardis´e est une version actualis´e de l’approche r´glementaire actuelle. En parti-
e e e
culier, la classification est beaucoup plus fine et la notation externe (rating) est prise en compte.
ˆ ´
3.3. BALE II ET LE NOUVEAU RATIO DE SOLVABILITE 17](https://image.slidesharecdn.com/gestionrisques-130221132633-phpapp01/85/Gestion-risques-27-320.jpg)

![Depuis la publication du second document consultatif, la position du Comit´ de Bˆle a ´volu´ :
e a e e
– Les risques op´rationnels pourraient repr´senter moins de 20% de l’exigence en fonds propres.
e e
– L’approche IMA est remplac´e par l’approche AMA (Advanced Measurement Approach)
e
qui pourrait ˆtre compos´e de plusieurs m´thodes (IMA, ScoreCard, LDA, etc.). Il n’est donc
e e e
pas exclu que le Comit´ de Bˆle autorise l’utilisation des mod`les internes LDA.
e a e
Le second pilier concerne le processus de surveillance. Les autorit´s de contrˆle (la Commission Bancaire
e o
en France) disposeront d’un pouvoir beaucoup plus important. Enfin, le troisi`me pilier vise ` promouvoir
e a
une discipline de march´ plus efficace (communication publique de la structure du capital, de l’allocation
e
de fonds propres, de l’exposition aux risques et des pertes).
Bibliographie
[1] International convergence of capital measurement and capital standards, Basle Committee on Banking
Supervision, July 1988, N◦ 4
[2] Capital Adequacy Directive (CAD), directive 93/6/CEE du CONSEIL du 15 mars 1993 sur
l’ad´quation des fonds propres des entreprises d’investissement et des ´tablissements de cr´dit, Journal
e e e
Officiel des Communaut´s Europ´ennes, N◦ L 141/1-26
e e
[3] Amendment to the capital accord to incorporate market risks, Basle Committee on Banking Supervi-
sion, January 1996, N◦ 24
[4] A new capital adequacy framework, Basle Committee on Banking Supervision, June 1999, N◦ 50
[5] The New Basel Capital Accord — Consultative Document, Basle Committee on Banking Supervision,
January 2001
[6] Overview of The New Basel Capital Accord — Consultative Document, Basle Committee on Banking
Supervision, January 2001
[7] The New Basel Capital Accord : an explanatory note — Consultative Document, Basle Committee
on Banking Supervision, January 2001
[8] Basel part one : the new Accord, Risk Magazine, 14, February, 24-29
[9] The new Accord delayed, Risk Magazine, 14, July, 29-31
[10] Bessis, J. [1995], Gestion des Risques et Gestion Actif-Passif des Banques, Dalloz, Paris
[11] Dubernet, M. [1997], Gestion Actif-Passif et Tarification des Services Bancaires, Economica, Paris
[12] Pujal, A. [2001], Un nouveau ratio de solvabilit´ en 2004, Banque Magazine, 622, F´vrier, 36-39
e e](https://image.slidesharecdn.com/gestionrisques-130221132633-phpapp01/85/Gestion-risques-29-320.jpg)


![CHAPITRE 4. LA NOTION DE CAPITAL ECONOMIQUE ET L’ALLOCATION DE FONDS PROPRES
Plusieurs questions se posent alors :
– Comment d´cider la r´alisation ou non d’une op´ration ?
e e e
– Comment choisir entre deux op´rations ?
e
– Que faire lorsque l’enveloppe allou´e est enti`rement consomm´e ?
e e e
Nous voyons bien que dans ce contexte le principe de “premier arriv´, premier servi” ne
e
tient plus.
Une premi`re approche consid`re le principe d’Euler. Soit un portefeuille avec un vecteur de strat´gie
e e e
u. Notons R la mesure de risque et K le vecteur de capital ´conomique. Nous pouvons alors d´finir une
e e
mesure de performance raisonnable par (Tasche [1999], th´or`me 4.4) :
e e
a (u) = ∂u R (u) (4.1)
Le capital ´conomique est alors d´fini par K = (Ki (u)) avec
e e
ui
Ki (u) ≡ ai (u)
R (u)
ui
= ∂u R (u) (4.2)
R (u)
Dans le cas d’une mesure de risque de type Value-at-Risk gaussienne, nous retrouvons le principe de
covariance. Une deuxi`me approche consid`re l’´galisation des mesures de performance ajust´e du risque
e e e e
(RAPM) :
1. Roc (return on regulatory capital)
2. Rorac (return on risk-adjusted capital)
3. Raroc (risk-adjusted return on regulatory capital)
4. Rarorac (risk-adjusted return on risk-adjusted capital)
Par exemple, la mesure RORAC est d´finie par
e
Revenu net
RORAC = (4.3)
Capital ´conomique
e
L’id´e sous-jacente est alors de comparer cette mesure ` une cible, et seuls les projets qui pr´sentent des
e a e
performances sup´rieures ` cette cible seront retenus.
e a
Consid´rons M activit´s relativement ind´pendantes. Notons Km le capital ´conomique allou´ ` la m-
e e e e ea
i`me activit´. Soit ϕ (K) la fonction qui relie le capital ´conomique et le RORAC. C repr´sente le capital
e e e e
de la banque. Nous pouvons alors formaliser le probl`me d’allocation de la fa¸on suivante :
e c
K1 + . . . + KM ≤ C
(4.4)
ϕm (Km ) = ϕm (Km )
A moins de consid´rer l’ind´pendance entre les diff´rentes activit´s (ou de faire des hypoth`ses simplifi-
e e e e e
catrices), l’approche bottom-up est difficile ` utiliser pour faire un v´ritable exercice d’allocation de fonds
a e
propres. En fait, cette approche est beaucoup plus appropri´e pour suivre la consommation de fonds
e
propres, et ` posteriori pour mesurer la v´ritable rentabilit´ de chaque activit´.
a e e e
4.3.2 L’approche top-down
Contrairement ` l’approche bottom-up qui consiste ` consolider le risque du portefeuille bancaire depuis
a a
le niveau ´l´mentaire (la transaction) jusqu’` l’unit´ d’allocation (la ligne de m´tier), l’approche top-
ee a e e
down consiste ` d´sagr´ger une information mesur´e sur l’ensemble du portefeuille bancaire, celle-ci ´tant
a e e e e
utilis´e comme un proxy pour la mesure de risque.
e
Concr`tement, selon la m´thodologie EaR (Earnings-at-Risk) usuellement mise en œuvre dans ce
e e
contexte, le risque d’une activit´ est directement reli´ ` la volatilit´ de son r´sultat. De ce point de vue,
e ea e e
INTRODUCTION A LA GESTION DES RISQUES 22](https://image.slidesharecdn.com/gestionrisques-130221132633-phpapp01/85/Gestion-risques-32-320.jpg)
![la volatilit´ est per¸ue comme un int´grateur de l’ensemble des risques associ´s ` cette activit´.
e c e e a e
Cette d´marche est une ´tape pr´liminaire naturelle de l’allocation puisqu’elle adopte le point de vue
e e e
de l’actionnaire qui investit son capital dans diff´rentes activit´s bancaires assimil´es ` autant d’actifs
e e e a
financiers. C’est donc une m´thode proche de la th´orie du portefeuille, mais avec des particularit´s li´es
e e e e
a
` l’activit´ bancaire.
e
Remarque 2 Vous trouverez un exemple de m´thode top-down dans l’article de Baud, Frachot, Igi-
e
gabel, Martineu et Roncalli [1999].
Bibliographie
[1] Baud, N., A. Frachot, P. Igigabel, P. Martineu et T. Roncalli [1999], An Analysis Framework
for Bank Capital Allocation, Groupe de Recherche Op´rationnelle, Cr´dit Lyonnais, Working Paper
e e
[2] Denault, M. [1999], Coherent allocation of risk capital, Swiss Federal Institute of Technology, Wor-
king Paper
[3] Froot, K.A. et J.C. Stein [1998], Risk management, capital budgeting, and capital structure policy
for financial institutions : an integrated approach, Journal of Financial Economics, 47, 55-82
[4] Punjabi, S. [1998], Many happy returns, Risk, June, 71-76
[5] Tasche, D. [1999], Risk contributions and performance measurement, Zentrum Mathematik, TU
M¨nchen, Working Paper
u](https://image.slidesharecdn.com/gestionrisques-130221132633-phpapp01/85/Gestion-risques-33-320.jpg)



![5
La r´glementation prudentielle
e
Le d´veloppement des march´s financiers dans les ann´es 80 et surtout dans les ann´es 90, a conduit
e e e e
les autorit´s de contrˆle bancaire et les autorit´s de march´ ` prendre un certain nombre de d´cisions
e o e e a e
pour r´guler ces march´s. En particulier, ces d´cisions ont concern´ fortement les risques de march´.
e e e e e
Actuellement, ils existent plusieurs textes r´glementaires relatifs ` ce sujet. Nous pouvons citer par
e a
exemple celui de la Commission Bancaire dat´ du 3 Novembre 1997 et celui de la CAD [1]. Ces textes
e
r´glementaires ont eu pour effet de pousser les ´tablissements financiers ` d´velopper des mod`les internes
e e a e e
de mesure de risque.
Avant de situer les enjeux pour une banque, nous devons pr´ciser dans un premier temps la notion de
e
risque de march´. Celui-ci est pr´sent´ de la mani`re suivante dans le texte de la Commission Bancaire
e e e e
(r´f´rence [3], section 1) :
ee
Le risque de march´, d´fini comme le risque de pertes sur les positions du bilan et du hors-
e e
bilan ` la suite de variations des prix de march´, recouvre :
a e
– Les risques relatifs aux instruments li´s aux taux d’int´rˆt et titres de propri´t´ du porte-
e ee ee
feuille de n´gociation ;
e
– Le risque de change et le risque sur produits de base encourus pour l’ensemble de l’activit´
e
de bilan et hors-bilan.
Nous remarquons tout de suite le caract`re potentiel de la perte induit par cette d´finition. Et nous
e e
voyons aussi que le p´rim`tre consid´r´ est relativement large. Nous devons noter tout de mˆme que cette
e e ee e
perte doit ˆtre li´e ` des possibles variations de prix de march´.
e e a e
De la mˆme mani`re que pour le risque de cr´dit, les exigences de fonds propres relatives aux risques
e e e
de march´ s’appliquent sur une base consolid´e. Pour les mesurer, les ´tablissements ont le choix entre
e e e
deux types d’approches :](https://image.slidesharecdn.com/gestionrisques-130221132633-phpapp01/85/Gestion-risques-37-320.jpg)
![´
CHAPITRE 5. LA REGLEMENTATION PRUDENTIELLE
1. l’approche standard pr´sent´e dans les diff´rentes annexes du document [3]. Celles-ci concernent les
e e e
cat´gories suivantes de risques et sont additionn´es de mani`re arithm´tique ;
e e e e
Cat´gorie de risque
e P´rim`tre de calcul
e e
Risque de Taux Portefeuille de n´gociation
e
(risque g´n´ral et risque sp´cifique)
e e e
Risque sur Titres de Propri´t´
ee Portefeuille de n´gociation
e
(risque g´n´ral et risque sp´cifique)
e e e
Risque de Change Ensemble des op´rations qu’elles appartiennent
e
au portefeuille de n´gociation ou non
e
Risque sur mati`res premi`res
e e Ensemble des op´rations qu’elles appartiennent
e
au portefeuille de n´gociation ou non
e
Risques optionnels Options associ´es ` chacune des cat´gories de
e a e
risques pr´c´dentes
e e
2. ou l’approche mod`les internes. L’utilisation de cette m´thode, subordonn´e ` la r´alisation de
e e e a e
certaines conditions, est soumise ` l’approbation explicite du Secr´tariat G´n´ral de la
a e e e
Commission Bancaire .
Le probl`me de l’utilisation conjointe des mod`les internes et de la m´thodologie standardis´e fait l’objet
e e e e
d’un paragraphe dans l’annexe 7 du document [3]. La position de la Commission Bancaire sur ce point
est donc la suivante :
Ainsi, un ´tablissement commen¸ant ` utiliser des mod`les pour une ou plusieurs cat´gories
e c a e e
de facteurs de risque doit en principe ´tendre progressivement ce syst`me ` tous ses risques
e e a
de march´ et ne peut plus, pour les risques ´valu´s, revenir ` la m´thodologie standardis´e (`
e e e a e e a
moins que la Commission Bancaire ne lui ait retir´ son agr´ment pour ses mod`les).
e e e
La Commission Bancaire tol`re donc l’utilisation combin´e des mod`les internes et de la m´thode standar-
e e e e
dis´e. Mais elle prˆte une attention particuli`re ` la permanence des m´thodes, ainsi qu’` leur ´volution
e e e a e a e
afin de s’orienter vers un mod`le global qui tient compte de l’ensemble des risques de march´.
e e
Pour la banque, en plus de fournir une mesure plus juste des risques de march´, la construction d’un
e
mod`le interne est un projet qui permet aussi d’assainir son syst`me d’information, notamment sur le
e e
stockage et la qualit´ des donn´es. Mais le v´ritable enjeu concerne l’exigence en fonds propres. Nous
e e e
pouvons penser qu’une mesure plus r´fl´chie permet de mieux mesurer la consommation en fonds propres
e e
des activit´s de march´. Un mod`le interne est donc un ´l´ment de r´ponse dans le cadre d’un mod`le
e e e ee e e
d’allocation de fonds propres, comme peuvent l’ˆtre les outils RAROC.
e
La lecture des textes r´glementaires est int´ressante ` plusieurs titres. Elle permet de d´gager les
e e a e
crit`res d´finissant un bon mod`le selon les autorit´s r´glementaires, c’est-`-dire de d´finir les normes
e e e e e a e
de validation. Elle permet aussi de s’interroger sur les aspects m´thodologiques et le choix d’un mod`le.
e e
Elle permet enfin de repositionner les pratiques actuelles en mati`re de gestion du risque de march´ par
e e
rapport aux exigences r´glementaires.
e
5.1 Les textes officiels
Il existe plusieurs textes officiels relatifs ` la r´glementation des risques de march´. En ce qui nous
a e e
concerne, nous nous int´ressons principalement ` celui de la Commission Bancaire et celui de la CAD.
e a
Ce sont les deux textes (l’un provenant d’une autorit´ de r´glementation fran¸aise, l’autre d’une autorit´
e e c e
europ´enne) qui s’appliquent aux ´tablissements financiers fran¸ais.
e e c
La r´glementation de la Commission Bancaire a fait l’objet de plusieurs r´visions importantes qui
e e
sont pr´sent´es dans l’article [2] de la Revue d’Economie Financi`re. Dans les ann´es 80, suite ` la
e e e e a
d´r´glementation et la lib´ralisation des mouvements de capitaux, les op´rations de march´ ont connu
ee e e e
un essor consid´rable. Jusque l`, les risques de march´ ´taient relativement peu contrˆl´s. Une des
e a e e oe
cons´quences de la crise d’octobre 1987 a ´t´ la signature d’un premier accord international (l’Accord de
e ee
INTRODUCTION A LA GESTION DES RISQUES 28](https://image.slidesharecdn.com/gestionrisques-130221132633-phpapp01/85/Gestion-risques-38-320.jpg)
![´
CHAPITRE 5. LA REGLEMENTATION PRUDENTIELLE
Bˆle) sur le risque bancaire, mais celui-ci concernait plus sp´cifiquement le risque de cr´dit, c’est-`-dire
a e e a
le risque de d´faillance de la contrepartie . Ce n’est qu’en 1993 que des m´thodes standardis´es pour
e e e
mesurer les risques de march´ ont commenc´ ` ˆtre propos´es dans le cadre du Comit´ de Bˆle, sans
e e a e e e a
encore faire l’objet d’application en termes de contrˆle . Sous la pression de certains ´v`nements mar-
o e e
quants du d´but des ann´es 1990 (en particulier, la faillite de la banque Barings), de nouveaux travaux
e e
ont vu le jour, notamment l’amendement ` l’Accord sur les fonds propres de 1988 concernant les risques
a
de march´ du comit´ de Bˆle en janvier 1996. C’est sur ce texte, ainsi que sur la directive 93/6/CEE
e e a
du Conseil de l’Union Europ´enne du 15 mars 1993, que s’appuie tr`s fortement la r´glementation de la
e e e
Commission Bancaire.
Les institutions financi`res ont la possibilit´ d’utiliser leurs propres mod`les internes de mesure de
e e e
risques de march´ ` la place des m´thodes standardis´es. Ces mod`les internes doivent cependant ˆtre
ea e e e e
valid´s par l’autorit´ de tutelle, c’est-`-dire qu’ils doivent respecter des normes qualitatives et des crit`res
e e a e
qualitatifs et quantitatifs. Nous d´veloppons ceux-ci dans les paragraphes qui suivent.
e
5.2 Les normes g´n´rales
e e
Les mod`les internes doivent remplir les conditions minimales suivantes (section 1 de l’annexe 7 du
e
document [3]) :
– le syst`me de gestion des risques de l’´tablissement repose sur des principes sains et mis en œuvre
e e
de mani`re int`gre ;
e e
– l’´tablissement poss`de en nombre suffisant de personnel qualifi´ pour l’utilisation de mod`les
e e e e
´labor´s non seulement dans le domaine de la n´gociation, mais aussi dans ceux du contrˆle des
e e e o
risques, de l’audit interne et, du postmarch´ ;
e
– les mod`les de l’´tablissement ont fait la preuve sur une dur´e significative qu’ils mesurent les risques
e e e
avec une pr´cision raisonnable ;
e
– l’´tablissement effectue r´guli`rement des simulations de crise selon les modalit´s pr´cis´es ` la
e e e e e e a
section 5.5.3.
Dans la mˆme section, la Commission Bancaire pr´cise la proc´dure de soumission du mod`le et les
e e e e
modalit´s d’utilisation :
e
L’utilisation des mod`les internes pour le calcul de l’exigence prudentielle en fonds propres
e
est soumise ` l’approbation pr´alable de la Commission Bancaire, apr`s une p´riode
a e e e
de suivi et de test en situation r´elle.
e
5.3 Les crit`res qualitatifs
e
Les syst`mes de gestion des risques de march´ doivent respecter certains crit`res qualitatifs. Les
e e e
cons´quences sont relativement importantes, puisque le degr´ de conformit´ ` ces crit`res peut condi-
e e ea e
tionner le niveau du multiplicateur. Seuls les ´tablissements les respectant int´gralement pourront
e e
pr´tendre au multiplicateur minimal. Ce multiplicateur (qui correspond au (3 + ξ) de la formule 5.1
e
page 31) intervient dans le calcul de l’exigence de fonds propres et doit ˆtre consid´r´ comme un pa-
e ee
ram`tre de p´nalisation.
e e
L’ensemble des crit`res qualitatifs est pr´sent´ dans le paragraphe 2 de l’annexe 7 du document [3].
e e e
Nous pr´sentons ici un r´sum´ de ces diff´rents crit`res :
e e e e e
a. L’´tablissement financier doit disposer d’une unit´ de contrˆle des risques, responsable de la
e e o
configuration et de l’exploitation du syst`me de gestion des risques, ind´pendante des unit´s de
e e e
n´gociation. Elle doit ´tablir et analyser des rapports quotidiens sur les r´sultats produits
e e e
par les mod`les ainsi qu’une ´valuation de l’utilisation des limites de n´gociation et rend compte
e e e
directement ` l’organe ex´cutif de l’´tablissement.
a e e
b. Cette unit´ doit effectuer r´guli`rement ( au moins trimestriellement ) des contrˆles ex-post.
e e e o
´ ´
5.2. LES NORMES GENERALES 29](https://image.slidesharecdn.com/gestionrisques-130221132633-phpapp01/85/Gestion-risques-39-320.jpg)
![´
CHAPITRE 5. LA REGLEMENTATION PRUDENTIELLE
c. L’organe d´lib´rant et l’organe ex´cutif doivent ˆtre activement associ´s au processus de contrˆles
e e e e e o
des risques et le consid´rer comme un aspect essentiel de l’activit´ de l’´tablissement.
e e e
d. Les rapports quotidiens doivent ˆtre revus par des responsables disposant de l’expertise et de
e
l’autorit´ suffisantes pour exiger au besoin une r´duction des positions prises par un op´rateur
e e e
voire une diminution du degr´ d’exposition global de la banque.
e
e. Les mod`les internes doivent ˆtre ´troitement int´gr´s ` la gestion journali`re des risques.
e e e e e a e
f. Le syst`me de mesure des risques doit ˆtre utilis´ conjointement avec les limites op´rationnelles.
e e e e
g. Un programme rigoureux de simulations de crise doit r´guli`rement compl´ter l’analyse des
e e e
risques fond´e sur les r´sultats quotidiens des mod`les internes. Lorsque ses conclusions font ap-
e e e
paraˆıtre une vuln´rabilit´ particuli`re ` un ensemble donn´ de circonstances, des mesures appro-
e e e a e
pri´es doivent ˆtre prises rapidement pour r´duire ces risques.
e e e
h. Les ´tablissements doivent disposer d’un programme de v´rification du respect des r`gles
e e e
et proc´dures internes relatives au fonctionnement du syst`me de mesure des risques. Ce syst`me
e e e
fait l’objet d’une documentation d´crivant les principes de base et le d´tail des techniques de
e e
mesure utilis´es.
e
i. Une analyse ind´pendante du syst`me de mesure des risques doit ˆtre effectu´e r´guli`rement
e e e e e e
dans le cadre du processus d’un audit interne de l’´tablissement. Elle doit porter ` la fois sur les
e a
activit´s des unit´s de n´gociation et sur celles de l’unit´ ind´pendante de contrˆle des
e e e e e o
risques. R´alis´e ` intervalles r´guliers, si possible annuellement, elle doit couvrir au minimum :
e e a e
– le caract`re ad´quat de la documentation concernant le syst`me et les processus de mesure des
e e e
risques ;
– l’organisation de l’unit´ de contrˆle des risques ;
e o
– l’int´gration des mesures des risques de march´ dans la gestion journali`re des risques ;
e e e
– les proc´dures d’agr´ment des mod`les et syst`mes de valorisation ;
e e e e
– la validation de toute modification significative du processus de mesure des risques ;
– la couverture par le mod`le des diff´rents risques de march´ ;
e e e
– la fiabilit´ et l’int´grit´ du syst`me d’information et des tableaux de bord destin´s aux respon-
e e e e e
sables ;
– la pr´cision et l’exhaustivit´ des donn´es relatives aux positions ;
e e e
– le contrˆle de la coh´rence, de la mise ` jour et de la fiabilit´ des donn´es utilis´es dans les
o e a e e e
mod`les internes ainsi que de l’ind´pendance des sources ;
e e
– l’exactitude et la pertinence des hypoth`ses en mati`re de volatilit´ et corr´lations ;
e e e e
– la v´rification de la pr´cision des mod`les par le biais d’analyses ex-post fr´quentes.
e e e e
Plusieurs commentaires peuvent ˆtre faits sur ces crit`res qualitatifs. Tout d’abord, la Commission
e e
Bancaire insiste fortement sur l’organisation du syst`me des risques et notamment sur l’unit´ de contrˆle.
e e o
Sans fournir la structure d´sir´e du syst`me, elle indique des signaux forts pour l’unit´ de contrˆle
e e e e o
concernant son ind´pendance, son pouvoir et sa comp´tence. La Commission Bancaire insiste aussi
e e
sur la transparence des mod`les. Ils doivent notamment faire l’objet d’une description ´crite d´taill´e et
e e e e
doivent ˆtre aliment´s par des bases de donn´es fiables.
e e e
5.4 Les crit`res quantitatifs
e
Le choix des mod`les est laiss´ aux ´tablissements financiers. Mais ils doivent respecter un certain
e e e
nombre de r`gles, qui sont d´crites dans le paragraphe 5 de l’annexe 7 du document [3] :
e e
1. La perte potentielle est calcul´e quotidiennement.
e
2. Le niveau de confiance unilat´ral requis est de 99%.
e
3. Il est appliqu´ un choc instantan´ sur les prix ´quivalent ` une variation sur dix jours correspondant
e e e a
a
` une p´riode de d´tention de dix jours ouvr´s.
e e e
INTRODUCTION A LA GESTION DES RISQUES 30](https://image.slidesharecdn.com/gestionrisques-130221132633-phpapp01/85/Gestion-risques-40-320.jpg)

![´
CHAPITRE 5. LA REGLEMENTATION PRUDENTIELLE
la Commission Bancaire est assez impr´cise concernant le cinqui`me point. Elle ne pr´cise pas ce qui est
e e e
consid´r´ comme un accroissement notable de la volatilit´. L’appr´ciation est laiss´e ` la discr´tion de
ee e e e a e
l’unit´ de contrˆle.
e o
5.5 Autres consid´rations
e
Dans ce paragraphe, nous pr´sentons des points particuliers relatifs aux facteurs de march´, au risque
e e
sp´cifique et aux simulations de crise.
e
5.5.1 D´finition des facteurs de risque de march´
e e
D’une mani`re g´n´rale, les grandes cat´gories de facteurs concernent :
e e e e
Les taux d’int´rˆt ;
ee
Les cours de change ;
Les prix des titres de propri´t´ et de produits de base1 ;
ee
La volatilit´ des options correspondantes.
e
Plus pr´cis´ment, la commission Bancaire propose de d´finir les facteurs de risque comme les param`tres
e e e e
de march´ qui affectent la valeur des positions de n´gociation de l’´tablissement et propose un certain
e e e
nombre de recommandations :
1. Pour les taux d’int´rˆt, un ensemble de facteurs de risque doit exister pour chaque monnaie.
ee
– La mod´lisation de la courbe des taux doit faire intervenir plusieurs bandes de maturit´,
e e
afin d’appr´hender la variation de la volatilit´ des taux tout au long de l’´ch´ancier ; ` chaque
e e e e a
bande correspond au moins un facteur de risque.
– Le syst`me de mesure doit inclure des facteurs distincts destin´s ` saisir le risque li´ aux
e e a e
´carts de taux entre types d’instruments et/ou cat´gories d’´metteurs.
e e e
2. Pour les cours de change, on doit pr´voir
e des facteurs correspondant au cours contre monnaie
nationale de chaque devise.
3. Les facteurs de risque doivent exister pour chacun des march´s de titres de propri´t´. Au minimum,
e ee
un facteur de risque doit appr´hender les fluctuations des prix d’un march´ donn´ (indice de march´).
e e e e
Une m´thode plus d´taill´e consiste ` d´finir des facteurs de risque correspondant aux diff´rents
e e e a e e
secteurs du march´. L’approche la plus compl`te consiste ` retenir comme facteurs de risque les
e e a
titres sp´cifiques.
e
4. Pour les produits de base, un facteur de risque unique peut ˆtre admis lorsque les positions sont
e
faibles. En cas d’activit´ plus importante, les mod`les doivent tenir compte des diff´rences entre
e e e
qualit´s du mˆme produit et maturit´s.
e e e
5. Pour les options, on doit tenir compte de facteurs de risque appr´hendant la volatilit´ des taux/prix/-
e e
cours sous-jacents. Lorsque les positions sont importantes ou lorsque l’actif conditionnel est com-
plexe, on doit utiliser des volatilit´s diff´renci´es en fonction des ´ch´ances et le cas ´ch´ant des
e e e e e e e
prix d’exercice.
Ce dernier point est important, puisque la Commission Bancaire pr´cise comment doit ˆtre pris en
e e
compte le risque de volatilit´. D’une mani`re g´n´rale, l’aspect volatility skew 2 doit ˆtre int´gr´ dans
e e e e e e e
1 Les risques de march´ concernent aussi les produits sur mati`res premi`res. Cela apparaˆ clairement dans l’actualisation
e e e ıt
du 31 d´cembre 1998 (r´f´rence [4]) :
e ee
Enfin, par instruments sur produits de base, il faut comprendre tous contrats ` terme ou d’´change,
a e
toutes options achet´es ou tous produits d´riv´s similaires ayant pour sous-jacents des contrats sur produits
e e e
´nerg´tiques, productions agricoles ou m´taux non ferreux (par exemple aluminium, cuivre et zinc), ainsi que
e e e
les autres m´taux non pr´cieux.
e e
2 La notion de volatility skew (ou volatility smile) correspond au fait que la volatilit´ implicite des options de mˆme
e e
maturit´ n’est pas constante et qu’elle d´pend des prix d’exercice. Si nous repr´sentons sur un graphe la volatilit´ en
e e e e
fonction du prix d’exercice, nous obtenons une courbe qui ressemble souvent ` un sourire.
a
INTRODUCTION A LA GESTION DES RISQUES 32](https://image.slidesharecdn.com/gestionrisques-130221132633-phpapp01/85/Gestion-risques-42-320.jpg)
![´
CHAPITRE 5. LA REGLEMENTATION PRUDENTIELLE
le mod`le. Il est aussi int´ressant de remarquer la construction du troisi`me point. A sa lecture, la
e e e
meilleure m´thode consisterait ` prendre en compte la totalit´ des prix de titres pour d´finir les facteurs
e a e e
de risque. Cependant, ce type d’approche pose des probl`mes statistiques importants li´s ` la th´orie de
e e a e
convergence des estimateurs, de telle sorte que, concr`tement, une application ` la lettre du point 3 peut
e a
ˆtre dangereuse.
e
5.5.2 Traitement du risque sp´cifique
e
Nous rappelons que le risque sp´cifique vise ` tenir compte du risque de contrepartie li´ ` l’´metteur
e a ea e
de l’instrument (document [2], page 9). Les mod`les internes, qui prennent en compte ce risque sp´cifique,
e e
doivent satisfaire les crit`res suivants :
e
– Le mod`le est apte ` expliquer ex ante les variations historiques des valeurs du portefeuille,
e a
– il fournit la preuve de sa sensibilit´ au risque de concentration dans la composition du portefeuille,
e
– sa fiabilit´ de fonctionnement demeure bonne dans un environnement adverse,
e
– la qualit´ de ses performances est justifi´e par un contrˆle ex-post (backtesting),
e e o
– la m´thodologie sous-jacente doit ˆtre en mesure de prendre en compte le risque d’´v´nements
e e e e
impr´visibles (OPA, OPE, etc.) ainsi que le risque de d´faillance de l’´metteur.
e e e
La cons´quence imm´diate de la non prise en compte du risque sp´cifique dans le mod`le est que
e e e e
... les exigences de fonds propres pour la couverture du risque sp´cifique feront l’objet
e
d’une surcharge en capital.
Le mode de calcul de l’exigence de fonds propres est relativement peu clair dans ce cas (voir page 53 du
document [3]). N´anmoins, la Commission bancaire fournit la formule suivante :
e
– soit 3×(VaR globale) + (VaR risque sp´cifique du portefeuille global),
e
– soit 3×(VaR globale) + (VaR des sous-portefeuilles contenant du risque sp´cifique).
e
Il est difficile de faire le lien entre cette formule et la formule (5.1). Dans l’actualisation du 31 d´cembre
e
1998 (r´f´rence [4]), la Commission Bancaire est encore moins pr´cise sur le risque sp´cifique puisque le
ee e e
paragraphe traitant de ce sujet se r´duit ` “une peau de chagrin”. N´anmoins, nous pouvons penser que
e a e
le coefficient 3 est en fait le coefficient multiplicatif 3 + ξ. En notant VaR sp la VaR du risque sp´cifique
e
(c’est-`-dire la VaR risque sp´cifique du portefeuille global ou la VaR des sous-portefeuilles contenant du
a e
risque sp´cifique), il est possible que la vraie formulation soit
e
60 60
1 1
FP (t) = max P (t − 1) + VaR sp (t − 1) , (3 + ξ) × P (t − i) + VaR sp (t − i) (5.2)
60 i=1
60 i=1
Il est int´ressant de noter que la Commission Bancaire fait explicitement r´f´rence ` la VaR (Value-at-
e ee a
Risk) que nous pouvons traduire sous le terme de “valeur en risque”. Mˆme si cela n’est pas affirm´
e e
parfaitement, la m´thode interne de r´f´rence est clairement la VaR.
e ee
5.5.3 Simulations de crise
Nous rappelons que les simulations de crise font partie des normes g´n´rales d’acceptation de la m´thode
e e e
interne. C’est donc un point important dans la mise en place d’un mod`le interne. Celles-ci font d’ailleurs
e
l’objet d’un paragraphe dans le texte de la Commission Bancaire. 7 points sont alors ´voqu´s :
e e
1. Les ´tablissements... doivent se doter d’un programme de simulations de crise ` la fois ri-
e a
goureux et complet. Ces simulations, qui permettent d’identifier les ´v`nements susceptibles d’avoir
e e
une forte incidence, constituent un ´l´ment-cl´ de l’´valuation du niveau des risques.
ee e e
2. Elles doivent couvrir toute la gamme des facteurs, y compris les ´v´nements ` probabilit´ r´duite.
e e a e e
Elles doivent aussi rendre compte de l’impact de ces ´v´nements sur les produits lin´aires et non
e e e
lin´aires.
e
3. Les simulations de crise doivent revˆtir un caract`re quantitatif et qualitatif. En outre, l’´tablissement
e e e
doit dresser l’inventaire des mesures ` prendre pour r´duire ses risques et pr´server son capital. Leurs
a e e
conclusions doivent ˆtre communiqu´es syst´matiquement ` la direction g´n´rale, et p´riodiquement,
e e e a e e e
au conseil d’administration.
´
5.5. AUTRES CONSIDERATIONS 33](https://image.slidesharecdn.com/gestionrisques-130221132633-phpapp01/85/Gestion-risques-43-320.jpg)
![´
CHAPITRE 5. LA REGLEMENTATION PRUDENTIELLE
4. L’exercice prudentiel consiste ` tester sur le portefeuille courant des situations pass´es de pertuba-
a e
tions majeures, en tenant compte des fortes variations de prix et de la vive r´duction de la liquidit´
e e
associ´es ` ces ´v´nements et/ou ` ´valuer la sensibilit´ des positions de march´ aux modifications
e a e e ae e e
des hypoth`ses de volatilit´ et corr´lations, ce qui n´cessite une mesure des marges de fluctuations
e e e e
de ces valeurs dans le pass´ et un calcul sur la base des chiffres extrˆmes.
e e
5. Ces sc´narios doivent notamment comprendre les situations que l’´tablissement identifie comme
e e
´tant les plus d´favorables, sur la base des caract´ristiques de son portefeuille.
e e e
6. La Commission Bancaire peut demander ` l’´tablissement d’´valuer l’impact de sc´narios qu’elle a
a e e e
d´finis et de lui communiquer l’ensemble des conclusions.
e
7. Les r´sultats doivent ˆtre revus ` intervalles r´gulier par la Direction G´n´rale et ˆtre pris en
e e a e e e e
compte dans la d´finition des limites et strat´gies fix´es. En outre, si la simulation fait apparaˆ
e e e ıtre
une vuln´rabilit´ particuli`re ` un ensemble donn´ de circonstances, l’´tablissement doit prendre
e e e a e e
rapidement les mesures n´cessaires ` une gestion ad´quate de ces risques.
e a e
Nous voyons ici l’importance de la direction g´n´rale dans le syst`me de gestion des risques. Celle-ci
e e e
doit ˆtre continuellement inform´e. Il est int´ressant de noter que le cœur du mod`le interne doit ˆtre
e e e e e
bas´ sur les ´v´nements extrˆmes. Le mod`le doit donc bien mesurer une perte potentielle, un risque
e e e e e
extrˆme. Enfin, nous devons aussi remarquer l’importance de la Commission Bancaire qui, si elle le
e
d´sire, peut intervenir et demander ` l’´tablissement de chiffrer des sc´narios.
e a e e
5.6 Dispositif prudentiel de contrˆle ex post li´ ` l’utilisation des
o ea
mod`les internes
e
Les contrˆles ex post visent ` s’assurer que le degr´ de couverture observ´ correspond
o a e e
bien au niveau de confiance de 99%. Voici quelques ´l´ments pour mener ` bien ces contrˆles :
ee a o
1. Ils sont r´alis´s ` partir des r´sultats r´els et/ou hypoth´tiques.
e e a e e e
2. Ils sont r´alis´s au moins trimestriellement et les donn´es des douze derniers mois glissants doivent
e e e
ˆtre utilis´es.
e e
Ces contrˆles permettent notamment de calculer les exceptions. Une exception correspond ` une date o`
o a u
la perte d´passe le risque calcul´ par le mod`le. La Commission Bancaire utilise le nombre d’exceptions
e e e
pour valider le mod`le et pour d´terminer le coefficient multiplicateur (3 + ξ). Elle d´finie le concept de
e e e
probabilit´ cumul´e des exceptions comme la probabilit´ d’obtenir au maximum le nombre d’exceptions
e e e
indiqu´ avec un taux de couverture effectif de 99%. Voyons de fa¸on concr`te comment le calcul est
e c e
effectu´. Si κ d´signe la variable qui prend la valeur 1 dans le cas d’une exception, alors κ est une variable
e e
1
al´atoire de Bernoulli de param`tre p = 100 (nous avons une chance sur 100 pour que κ corresponde ` une
e e a
exception lorsque le taux effectif de couverture est de 99%). Si on consid´re une p´riode [t1 , t2 ] comprenant
e e
N jours ouvr´s. Pendant cette p´riode, et sous l’hypoth`se que les ´v´nements sont ind´pendants, la
e e e e e e
probabilit´ d’avoir n exceptions est ´gale `
e e a
N −n
Pr (X = n) = CN pn (1 − p)
n
avec X la variable al´atoire correspondant au nombre d’exceptions pour la p´riode [t1 , t2 ]. X correspond
e e
N
bien sˆr ` une variable al´atoire Binomiale Bp . La probabilit´ cumul´e d’avoir n exceptions a donc pour
u a e e e
expression
n
N −i
Pr (X ≤ n) = CN pi (1 − p)
i
i=1
La Commission Bancaire d´finit alors trois zones pour ´valuer les r´sultats des contrˆles ex post et pour
e e e o
appliquer le compl´ment ´ventuel au coefficient multiplicateur 3 :
e e
Zone D´finition de la zone
e Valeur de ξ
Verte Pr (X ≤ n) < 95% 0
Orange Pr (X ≤ n) < 99.99% 0–1
Rouge Pr (X ≤ n) ≥ 99.99% 1
INTRODUCTION A LA GESTION DES RISQUES 34](https://image.slidesharecdn.com/gestionrisques-130221132633-phpapp01/85/Gestion-risques-44-320.jpg)

![crit`res peut conditionner le niveau de multiplicateur. Ici, nous avons l’impression que ce niveau est
e
presque enti`rement d´termin´ par la proc´dure de backtesting.
e e e e
L’actualisation du 31 d´cembre 1998 permet de pr´ciser et de modifier certains points. En premier
e e
lieu, le backtesting porte sur la Valeur en Risque sur un jour, et non sur la Valeur en Risque pour
une p´riode de d´tention de 10 jours. Ensuite, les contrˆles doivent porter sur les 250 derniers jours
e e o
ouvrables. Cela est important, car si nous supposons que les “douze derniers mois” correspondent ` 260
a
jours, les zones sont d´finies diff´rement ` cause du caract`re escalier de la loi Binomiale :
e e a e
Zone N = 250 N = 260
Verte moins de 5 exceptions moins de 6 exceptions
Orange entre 5 et 9 exceptions entre 6 et 10 exceptions
Rouge plus de 10 exceptions plus de 11 exceptions
Enfin, les exceptions doivent ˆtre communiqu´es ` la Commission Bancaire :
e e a
Afin de permettre ` la Commission Bancaire de v´rifier en permanence l’ad´quation du facteur
a e e
compl´mentaire, l’´tablissement informe sans d´lai et, en tout ´tat de cause, dans les cinq
e e e e
jours ouvrables, le Secr´tariat G´n´ral de la Commission Bancaire, des d´passements r´v´l´s
e e e e e ee
par leur programme de contrˆle ex-post qui, en fonction du tableau ci-dessus, impliqueraient
o
un rel`vement du facteur compl´mentaire.
e e
Bibliographie
[1] Capital Adequacy Directive (CAD), directive 93/6/CEE du CONSEIL du 15 mars 1993 sur
l’ad´quation des fonds propres des entreprises d’investissement et des ´tablissements de cr´dit, Journal
e e e
Officiel des Communaut´s Europ´ennes, N◦ L 141/1-26
e e
[2] La surveillance prudentielle des risques de march´ support´s par les ´tablissements de cr´dit, Com-
e e e e
mission Bancaire, Service des ´tudes bancaires, article pour la Revue d’Economie Financi`re, 26 juin
e e
1996
[3] Modalit´s de Calcul du Ratio de Solvabilit´ — Actualisation au 31 d´cembre 1997, Commission
e e e
Bancaire, Cellule de contrˆle des Risques de march´, 3 novembre 1997
o e
[4] Modalit´s de Calcul du Ratio de Solvabilit´ — Actualisation au 31 d´cembre 1998, Commission
e e e
Bancaire, Secr´tariat G´n´ral, Service des Affaires Internationales, 30 d´cembre 1998
e e e e](https://image.slidesharecdn.com/gestionrisques-130221132633-phpapp01/85/Gestion-risques-46-320.jpg)



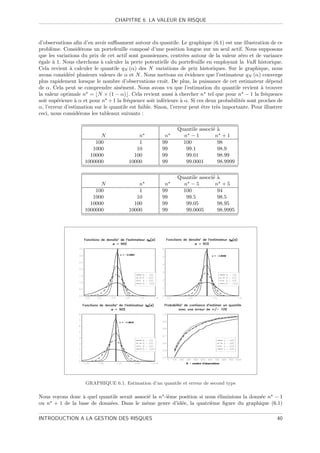
![CHAPITRE 6. LA VALEUR EN RISQUE
montre comment ´volue la probabilit´ d’estimer un quantile avec une erreur de plus ou moins 10%. Le
e e
probl`me est le mˆme que celui consid´r´ pr´c´demment. Nous voyons bien que cette probabilit´ “de
e e ee e e e
confiance” croˆ avec le nombre d’observations. Et il est int´ressant de remarquer la diff´rence entre le
ıt e e
seuil de confiance de 99% et les autres seuils de confiance.
Remarque 5 Si les autorit´s de r´gulation d´cident d’augmenter le seuil de confiance, cela aura un im-
e e e
pact tr`s important sur la gestion des bases de donn´es, qui devront ˆtre plus longues. A titre d’illustration,
e e e
il n’est pas possible d’estimer une VaR historique ` 99.9% avec moins de 1000 observations.
a
6.1.3 La VaR Monte-Carlo
La VaR Monte-Carlo est bas´e sur la simulation des facteurs de march´ F (t) dont on se donne une
e e
loi de distribution a priori, de pr´f´rence admissible avec l’historique. Nous pouvons alors valoriser le
ee
portefeuille avec les facteurs simul´s. Si nous utilisons N simulations, nous pouvons alors d´terminer N
e e
variations simul´es du portefeuille, que nous assimilons ` N pertes potentielles. Il suffit ensuite de calculer
e a
le quantile correspondant tout comme pour la m´thode de la VaR historique. Les deux m´thodes sont
e e
donc tr`s semblables. La seule diff´rence est que l’une des m´thodes utilise les facteurs pass´s, alors que
e e e e
l’autre utilise des facteurs simul´s. Une autre diff´rence concerne la taille N de l’´chantillon pour la calcul
e e e
du quantile, qui n’est pas contraint dans le cas de la VaR Monte-Carlo.
A titre d’illustration, le sch´ma 6.2 montre les diff´rentes ´tapes de l’algorithme lorsque les facteurs
e e e
de march´ correspondent aux variations des prix des actifs. Cette m´thode est tr`s int´ressante, puisque
e e e e
nous pouvons calculer directement la VaR pour une p´riode de d´tention de T jours mˆme si les facteurs
e e e
de march´ correspondent ` une p´riode de 1 jour.
e a e
Il faut cependant noter que cette m´thode n´cessite un ordinateur tr`s performant car elle est coˆteuse
e e e u
en temps de calcul (elle convient difficilement au calcul journalier d’une VaR pour un nombre trop
grand d’actifs). De plus, elle demande un effort important de mod´lisation puisque celle-ci d´terminera
e e
enti`rement les trajectoires des facteurs de march´ que l’on utilise pour le calcul de la VaR.
e e
6.1.4 Pertinence des mesures VaRs
Nous avons vu que la VaR param´trique ne convenait pas pour les portefeuilles d’options. Toutes les
e
mesures ne sont donc pas pertinentes pour n’importe quel type de portefeuille. Le tableau suivant montre
le p´rim`tre d’utilisation des VaRs en fonction de la normalit´ des facteurs de march´ et de la lin´arit´
e e e e e e
du portefeuille :
Normalit´ des facteurs
e
Instruments lin´aires
e Oui Non
Param´trique
e
Oui Monte-Carlo Historique
Historique
Monte-Carlo
Non Historique
Historique
source : Boulier, Brabant, Dalaud et Dieu [1997]
A noter que nous pouvons aussi utiliser la m´thode de Monte Carlo lorsque les facteurs ne sont pas
e
normaux, mais dans ce cas, elle peut ˆtre extrˆmement difficile ` mettre en place si elle pr´sente des
e e a e
sp´cificit´s importantes.
e e
´
6.1. DEFINITION 41](https://image.slidesharecdn.com/gestionrisques-130221132633-phpapp01/85/Gestion-risques-51-320.jpg)


![CHAPITRE 6. LA VALEUR EN RISQUE
pouvons par exemple consid´rer que les niveaux de confiance 98.5% et 99.5% sont tr`s proches du fait de
e e
leur faible ´cart absolu, ou au contraire les consid´rer tr`s diff´rents, car la VaR ` 99.5% a 3 fois moins
e e e e a
de chance d’ˆtre d´pass´e que la VaR ` 98.5%.
e e e a
6.2.2 Une explication du facteur multiplicatif (3 + ξ)
Les mod`les internes de risques de march´ sont majoritairement bas´s sur les m´thodes VaR. Or, ces
e e e e
m´thodes ne donnent qu’une approximation de la vraie distribution pour mod´liser la variation des prix.
e e
C’est pourquoi il est n´cessaire de corriger l’estimation du quantile par un facteur de prudence. Celui-
e
ci correspond implicitement au facteur multiplicatif. Comme Stahl [1997] le montre, ce facteur, souvent
pr´sent´ comme arbitraire, a des fondements th´oriques rigoureux (dans le cadre d’une VaR gaussienne).
e e e
Le probl`me est le suivant : ´tant donn´ une variable al´atoire X de loi quelconque dont nous connais-
e e e e
sons les deux premiers moments µ et σ 2 , ` quelle distance relative par rapport ` l’´cart-type se situe le
a a e
quantile α ? Pour cela, nous utilisons l’in´galit´ de Bienaym´-Tchebyshev :
e e e
1
Pr (|X − µ| > kσ) ≤ (6.9)
k2
Si la loi est sym´trique, nous avons
e
1
Pr (X ≤ µ + kσ) ≥ 1 − (6.10)
2k 2
Or cette probabilit´ n’est rien d’autre que la fonction de r´partition F :
e e
1
F (µ + kσ) ≥ 1 − (6.11)
2k 2
Au seuil de confiance de α et si nous d´signons par F −1 la fonction inverse de r´partition (qui n’est rien
e e
d’autre que la fonction de quantile), nous en d´duisons que
e
1
X ≤ µ + kσ ⇐⇒ F −1 1 − =α (6.12)
2k 2
et donc
1
k≤
2 − 2α
En n´gligeant la tendance µ et en assimilant X ` la perte potentielle, celle-ci se situe donc ` k ´carts-types.
e a a e
Or la VaR telle qu’elle est calcul´e se situe ` c = Φ−1 (α) ´carts-types. Le ratio k est le coefficient de
e a e c
multiplication qui permet d’ˆtre sˆr que la VaR correspond bien ` un quantile au moins ´gal ` α lorsque
e u a e a
nous utilisons une approximation gaussienne et ceci quelle que soit la vraie fonction de distribution.
Remarque 6 Il est facile de montrer que lorsque la fonction de distribution est asym´trique, une borne
e
−1
sup´rieure de k est (1 − α) .
e
Le tableau suivant contient les valeurs du ratio pour diff´rentes valeurs de α.
e
sym´trique
e asym´trique
e
α c k k/ c k k/ c
90.00 1.28 2.24 1.74 3.16 2.47
95.00 1.64 3.16 1.92 4.47 2.72
99.00 2.33 7.07 3.04 10.00 4.30
99.25 2.43 8.16 3.36 11.55 4.75
99.50 2.58 10.00 3.88 14.14 5.49
99.75 2.81 14.14 5.04 20.00 7.12
99.99 3.72 70.71 19.01 100.00 26.89
INTRODUCTION A LA GESTION DES RISQUES 44](https://image.slidesharecdn.com/gestionrisques-130221132633-phpapp01/85/Gestion-risques-54-320.jpg)
![CHAPITRE 6. LA VALEUR EN RISQUE
Nous remarquons qu’effectivement lorsque le seuil de confiance est ´gal ` 99%, ce ratio est proche de 3
e a
(lorsque la fonction de densit´ est sym´trique). Supposons que les autorit´s r´glementaires fixent le seuil
e e e e
de confiance ` 99.5%, dans ce cas le ratio est proche de 4. Si les autorit´s r´glementaires prenaient alors
a e e
cette valeur pour fixer le coefficient multiplicateur, cette mesure aurait pour incidence d’augmenter les
fonds propres de 41.4% par rapport ` la situation actuelle.
a
Il y a une remarque int´ressante ` faire concernant l’analyse pr´c´dente. Dans cette pr´sentation, la
e a e e e
VaR correspond ` c · σ, mais nous consid´rons que la borne sup´rieure de la vraie VaR est en fait k · σ.
a e e
L’exigence en fonds propres correspond donc ` cette valeur k · σ. Or les exceptions sont d´termin´es en
a e e
fonction de la VaR c · σ, et non en fonction de la VaR k · σ. Si nous poussons l’analyse jusqu’au bout, il
aurait ´t´ plus logique de d´terminer les exceptions en fonction de k ·σ. Donc, ce coefficient multiplicateur
ee e
trouve bien une justification, mais les autorit´s r´glementaires ont fait preuve de beaucoup de prudence,
e e
puisque la probabilit´ que la perte potentielle d´passe le montant des fonds propres est bien inf´rieure `
e e e a
1%.
6.2.3 Le choix de la distribution de probabilit´
e
Ce choix est primordial dans le calcul des VaRs param´trique et de Monte-Carlo. G´n´ralement, nous
e e e
utiliserons une loi normale ou log-normale pour mod´liser les facteurs F (t). Cela implique que la distri-
e
bution de F (t) est enti`rement d´termin´e par les deux premiers moments µ et Σ. L’utilisation en finance
e e e
de la normalit´ repose sur des arguments de facilit´ d’utilisation. Mais nous savons depuis fort longtemps
e e
que les s´ries financi`res ne sont ni normales ni log-normales. En revanche, il est facile de calculer la
e e
variance d’une combinaison des composantes d’un vecteur gaussien. De mˆme, la simulation de nombres
e
al´atoires normaux est tr`s ais´e ` partir d’un g´n´rateur de nombres al´atoires uniformes pour le cas
e e e a e e e
a
` une dimension, ou d’une d´composition de Cholesky ou en valeurs singuli`res pour le cas ` plusieurs
e e a
dimensions.
Certains auteurs ont tent´ de justifier le recours ` la loi normale par le th´or`me central-limite qui
e a e e
´tablit la convergence vers la loi normale sous des hypoth`ses peu contraignantes. Soit (Xn ) une suite de
e e
variables al´atoires ind´pendantes et identiquement distribu´es, alors
e e e
n
Xi − E (Xi ) L
√ −→ N (0, 1) (6.13)
i=1
σ (Xi ) n
Cependant, la convergence en loi n’est rien d’autre qu’une convergence des fonctions de r´partition. Cette
e
convergence est beaucoup plus rapide dans les r´gions proches de la moyenne. Feller [1968] a d’ailleurs
e
3
montrer que l’approximation n’est valable qu’autour de n 4 ´carts-types de la moyenne. Nous pouvons
e
alors facilement construire des exemples qui illustrent le probl`me du th´or`me central-limite dans la
e e e
m´thodologie VaR param´trique. L’exemple suivant est propos´ par Boulier, Brabant, Dalaud et
e e e
Dieu [1997]. Les auteurs consid`rent un mod`le macro-´conomique de type APT o` les rentabilit´s sont
e e e u e
d´crites par l’´volution al´atoire d’une trentaine de facteurs ´conomiques, qu’ils supposent ind´pendants et
e e e e e
3
de mˆme loi. L’approximation n’est alors valable qu’autour de 30 4
e √ 12.819 ´carts-types de la moyenne.
e
Or l’´cart-type de la loi normale r´sultante est 30
e e 5.477 fois plus grande que l’´cart-type initial.
e
Cela implique que l’approximation n’est plus valable au del` de la probabilit´ de 99.04%. Pour cet
a e
exemple, les VaRs au-del` de 99% ne font plus partie du domaine de validit´ de l’approximation par
a e
la loi normale. Dans le cas des portefeuilles de taux d’int´rˆt, il est recommand´ d’utiliser au moins 13
ee e
facteurs. En utilisant le mˆme raisonnement, cela voudrait dire que les VaRs au-del` de 97.12% sont en
e a
dehors du domaine de validit´ d´fini par Feller5 . Cette analyse peut ˆtre une nouvelle explication
e e e
de l’utilisation d’un facteur multiplicatif.
Comme nous l’avons d´j` signal´, la variable al´atoire X de loi normale N (µ, σ) est enti`rement
ea e e e
2
caract´ris´e par ces deux premiers moments µ = E (X) et σ 2 = E (X − µ) . Nous rappelons que
e e
cette fonction de distribution est utilis´ en finance car elle est facilement manipulable, mais il existe de
e
nombreux travaux qui pr´sentent des arguments contredisant l’id´e que les variations des prix des actifs
e e
sont normaux. Cela vient notamment du fait que les moments d’ordre 3 et 4 d’une s´rie financi`re sont
e e
1
5 La valeur de la probabilit´ qui d´finit le domaine de validit´ est Φ n 4 .
e e e
´
6.2. QUELQUES REFLEXIONS SUR LA VAR 45](https://image.slidesharecdn.com/gestionrisques-130221132633-phpapp01/85/Gestion-risques-55-320.jpg)
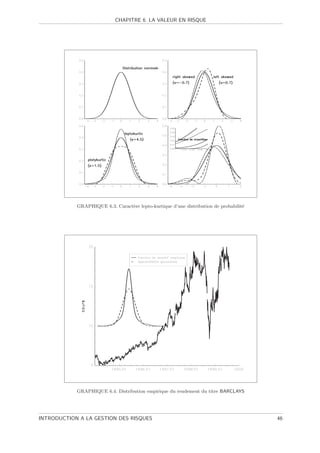
![CHAPITRE 6. LA VALEUR EN RISQUE
tr`s diff´rents de ceux de la loi normale. La skewness υ (ou moment centr´ d’ordre 3) est un coefficient
e e e
d’asym´trie de la fonction de densit´, alors que la kurtosis κ (ou moment centr´ d’ordre 4) est une mesure
e e e
d’aplatissement. Nous avons
3
E (X − µ)
υ =
σ3
4
E (X − µ)
κ =
σ4
Pour la loi normale, υ et κ valent respectivement 0 et 3. Si υ 0 (resp. υ 0), on dit que la distribution
est asym´trique ` droite (resp. ` gauche). Lorsque κ est sup´rieur ` 3, la distribution pr´sente des queues
e a a e a e
´paisses (elle est lepto-kurtique). Le graphique (6.3) pr´sente diff´rentes fonctions de densit´6 . Lorsque
e e e e
les distributions pr´sentent des queues de distribution ´paisses, le quantile α est alors bien au del` (en
e e a
valeur absolue) du quantile gaussien correspondant. Prenons par exemple la figure en bas ` gauche. Celle-
a
ci contient le graphe des fonctions de r´partition pour le segment x ∈ [−3, −2]. Pour la loi gaussienne,
e
nous v´rifions bien que le quantile ` 1% est −2.33. Or pour cette valeur, la quatri`me distribution
e a e
pr´sente une valeur de 5% pour la fonction de r´partition. Le quantile ` 1% est en fait bien au-del` de
e e a a
−2.33. Le graphique (6.4) correspond ` l’´volution du cours du titre Barclays depuis 1994. Nous avons
a e
estim´ la fonction de densit´ des variations du cours en utilisant la m´thode non param´trique du noyau
e e e e
d’Epanechnikov et compar´ celle-ci avec la fonction de densit´ gaussienne estim´e par la m´thode des
e e e e
moments. L’estimation classique bas´e sur les deux premiers moments ne permet donc pas de prendre en
e
compte les queues ´paisses.
e
L’´volution du titre Barclays nous interpelle sur le probl`me de la stationnarit´ du processus. Nous
e e e
pouvons penser qu’une approximation gaussienne ne peut ˆtre valide que localement. Cela pose alors le
e
probl`me de la longueur de l’historique utilis´ pour la VaR param´trique. Les instance r´glementaires
e e e e
exigent un historique d’au moins 1 an. Contrairement ` l’id´e fort r´pandue que plus l’historique
a e e
est long, meilleure sera la mesure des risques, l’utilisation d’un historique trop long peut
avoir des cons´quences n´fastes sur la VaR param´trique. Car, dans ce cas l`, il est parfaitement
e e e a
clair que les propri´t´s d’ergodicit´ et de stationnarit´ ne sont pas respect´es. L’utilisation d’un historique
ee e e e
long doit ˆtre plutˆt r´serv´ ` la VaR historique.
e o e ea
L’utilisation de la loi normale pour la VaR param´trique n’en demeure pas moins incontournable. Il
e
convient donc d’apporter une attention particuli`re ` l’estimation de la matrice de covariance.
e a
6.2.4 L’estimation de la matrice de covariance
Nous notons F (t0 ; N ) la matrice des facteurs observ´s pour t = t0 − 1, . . . , t0 − N avec
e
F (t0 − 1)
.
.
.
F (t0 ; N ) = F (t0 − n) (6.14)
.
.
.
F (t0 − N )
Consid´rons une matrice diagonale Λ de dimension N × N avec 1 diag (Λ) = 1. Λ est appel´e la matrice
e e
e ˆ ˆ
des poids des observations. Nous d´finissons µ et Σ par
µ = F (t0 ; N ) Λ 1
ˆ (6.15)
6 Nous avons g´n´r´ celles-ci en utilisant la fonction de densit´ d’Edgeworth (Rubinstein [1998]) :
e e e e
υ 3 κ−3 4 υ2 5
f (x) = b (x) 1 + x − 3x + x − 6x2 + 3 + x − 10x3 + 15x
6 24 72
avec b la fonction de densit´ Binomiale.
e
´
6.2. QUELQUES REFLEXIONS SUR LA VAR 47](https://image.slidesharecdn.com/gestionrisques-130221132633-phpapp01/85/Gestion-risques-57-320.jpg)

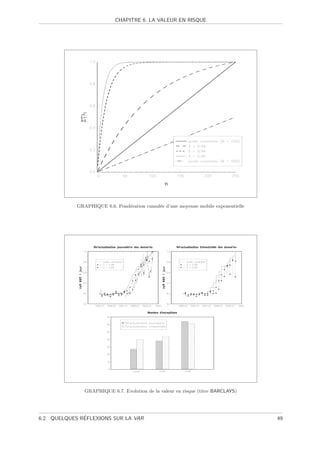
![CHAPITRE 6. LA VALEUR EN RISQUE
Voyons un exemple montrant la diff´rence entre les deux exemples. Nous consid´rons une position
e e
longue sur le titre BARCLAYS. Le graphique (6.7) pr´sente l’´volution de la VaR avec deux types de
e e
r´actualisation. La taille de l’´chantillon est fix´ ` 250 jours de trading. En p´riode de crise, la VaR
e e e a e
RiskMetrics est plus grande que la VaR avec les poids constants. Ce ph´nom`ne s’inverse lors des p´riodes
e e e
calmes (ou apr`s les p´riodes de crises). Cela se comprend ais´ment ` cause de la forme des poids. Si nous
e e e a
consid´rons le nombre d’exceptions (pour information, le nombre de jours de trading est ´gal ` 1136),
e e a
la VaR avec poids constants est la plus performante pour cet exemple. Cela tient au fait que la VaR
RiskMetrics sous-estime le risque pour les p´riodes calmes, ce qui implique que d`s qu’il y a une variation
e e
plus importante, nous obtenons une exception. Cela se voit tr`s bien si nous consid´rons la localisation
e e
des exceptions. Celles-ci ont des positions diff´rentes selon la m´thodologie. Enfin, nous remarquons que
e e
la fr´quence de r´actualisation a une influence non n´gligeable sur la qualit´ de la VaR.
e e e e
Si nous calculons le temps de retour moyen empirique pour l’exemple pr´c´dent, nous constatons qu’il
e e
est l´g`rement inf´rieur au temps de retour moyen th´orique. Cela veut dire que nos mesures VaR ont
e e e e
sous-estim´ la perte potentielle. Hendricks [1996] remarque ce mˆme ph´nom`ne. Il compare douze
e e e e
m´thodologies diff´rentes et constate que
e e
Virtually all of the approaches produce accurate 95th percentile risk measures. The 99th
percentile risk measures, however, are somewhat less reliable and generally cover only between
98.2 percent and 98.5 percent of the outcomes. On the one hand, these deficiencies are small
when considered on the basis of the percentage of outcomes missclassified. On the other hand,
the risk measures would generally need to be increased across the board by 10 percent or
more to cover precisely 99 percent of outcomes.
6.2.4.1 Un exercice de backtesting
Ce paragraphe s’attache ` d´terminer la mani`re optimale de calculer la matrice de covariance. Notre
a e e
approche se base sur le calcul du nombre d’exceptions observ´es sur un historique des cours d’´tablissements
e e
financiers depuis 1994.
Nous nous pla¸ons dans le cadre d’une VaR analytique sous l’hypoth`se de rendements gaussiens. Nous
c e
sommes donc en mesure de d´terminer un intervalle de confiance ` une certaine probabilit´ ` partir
e a e a
des deux premiers moments. Nous comparons ici de mani`re qualitative la validit´ de ces intervalles de
e e
confiance selon la m´thode choisie pour l’estimation des deux premiers moments. Les r´sultats qui suivent
e e
permettent de visualiser de mani`re dynamique les caract´ristiques sur la VaR associ´es ` ces m´thodes.
e e e a e
Les estimateurs retenus pour le calcul des rendements moyens et des volatilit´s sont les m´thodes de
e e
poids constants et de poids exponentiels (λ = 0.94). L’enjeu inh´rent au choix de la m´thode d’estimation
e e
de ces param`tres est capital ; il s’agit d’obtenir une r´activit´ optimale aux variations du march´, tout
e e e e
en conservant une inertie suffisante pour ne pas trop sur ou sous-estimer les variations possibles. A priori,
une m´thode reposant sur des poids constants accusera un petit peu de retard pour r´hausser son niveau
e e
dans une p´riode ` forte volatilit´. De mˆme, la m´thode reposant sur des poids exponentiels risque de
e a e e e
largement sur-estimer la VaR apr`s une courte p´riode d’agitation.
e e
Afin d’illustrer ce ph´nom`ne, nous proposons par la suite d’´tudier le nombre d’exceptions observ´es
e e e e
sur le cours de certains ´tablissements financiers par p´riode. Une exception est d´finie comme une valeur
e e e
du titre en dehors de l’intervalle de confiance pr´vu. Nous consid´rons les cas de positions longues et
e e
courtes sur un titre, ce qui nous am`ne ` d´finir des bornes sup´rieures et inf´rieures de notre intervalle.
e a e e e
Nous nous sommes attach´s ` respecter les crit`res quantitatifs de la Commission Bancaire pour le calcul
e a e
de la VaR. Ainsi avons nous retenu un niveau de confiance de 1% sur une p´riode de d´tention de 1 jour.
e e
De mˆme, l’estimation des moments des distributions des rendements quotidiens ont ´t´ calcul´s sur un
e ee e
historique d’un an renouvel´ tous les trois mois. Tout ceci nous a permis de d´terminer les s´ries des deux
e e e
bornes Lu et Ld de notre intervalle pour les rendements journaliers :
Lu
t = µt − Φ−1 (0.5%) × σ t
Ld
t = µt + Φ−1 (0.5%) × σ t
o` Φ−1 (0.5%) est le quantile ` 0.5% de la loi normale centr´e r´duite (Φ−1 (0.5%)
u a e e 2.575). µt et σ t sont
respectivement la moyenne et l’´cart-type estim´s du rendement ` l’instant t.
e e a
INTRODUCTION A LA GESTION DES RISQUES 50](https://image.slidesharecdn.com/gestionrisques-130221132633-phpapp01/85/Gestion-risques-60-320.jpg)
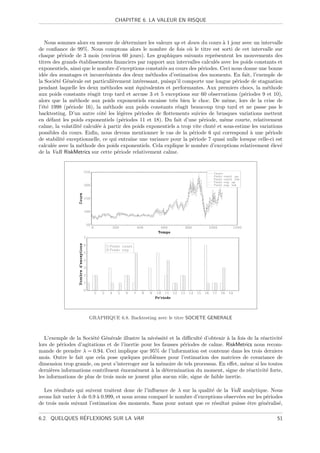
![CHAPITRE 6. LA VALEUR EN RISQUE
l’´tude des s´ries des cours sur les ´tablissements financiers pousse ` choisir un coefficient λ favorisant
e e e a
une m´moire plus longue, c’est–`-dire une inertie plus importante. Il semble, de mani`re qualitative,
e a e
que la valeur optimale de ce coefficient dans ce cas l` soit de l’ordre de 0.96.
a
Nous notons, toutefois, que la valeur optimale de λ est susceptible de varier selon les
march´s8 . Aussi, le coefficient obtenu ne peut ˆtre adapt´ pour l’ensemble des s´ries fi-
e e e e
nanci`res. Nous conseillons plutˆt une ´tude du march´ ` consid´rer au pr´alable, qui
e o e e a e e
permettrait de d´terminer le λ optimal.
e
GRAPHIQUE 6.9. D´termination de la valeur optimale pour λ
e
6.2.4.2 Les approches conditionnelles de l’estimation de la matrice de covariance
Les approches pr´c´dentes de l’estimation la matrice de covariance reposent sur l’hypoth`se que Σ est
e e e
une matrice constante au cours du temps. Cette hypoth`se a ´t´ vivement critiqu´e par de nombreux
e ee e
´conom`tres (voir les survey [1], [6] et [29]). Afin de prendre en compte les effets h´t´rosc´dastiques,
e e ee e
Engle [1982] introduit une nouvelle classe de processus connus sous le nom de mod`les ARCH. A la suite
e
de cet article, de nombreux travaux dans le domaine de la mod´lisation de la variance conditionnelle ont
e
vu le jour et plusieurs formes de g´n´ralisation ont ´t´ introduites. Dans un premier temps, Bollerslev
e e ee
[1986] propose d’introduire un effet “autor´gressif” dans l’´quation de variance conditionnelle (mod`les
e e e
GARCH). Ensuite, plusieurs formes d’extension au cas multidimensionnel sont apparues.
Le cas unidimensionnel
Soit le processus unidimensionnel {yt } en temps discret d´fini par
e
yt = µ + εt (6.17)
8 Cette ´tude a d´j` ´t´ men´e par RiskMetrics, et met en ´vidence des diff´rences notables de λ selon les march´s (places
e eae e e e e e
financi`res et produits) et la p´riode de d´tention. λ = 0.94 est une valeur moyenne bas´e sur un crit`re de moindres carr´s
e e e e e e
de la variance quotidienne des rendements. Dans le cadre de la VaR, nous pensons que ce crit`re n’est pas le plus appropri´
e e
et qu’il est pr´f´rable de consid´rer un crit`re de minimisation du nombre d’exceptions.
ee e e
INTRODUCTION A LA GESTION DES RISQUES 52](https://image.slidesharecdn.com/gestionrisques-130221132633-phpapp01/85/Gestion-risques-62-320.jpg)
![CHAPITRE 6. LA VALEUR EN RISQUE
GRAPHIQUE 6.10. Valeur optimale de λ pour diff´rents titres
e
avec εt un processus stochastique. Sous l’hypoth`se de normalit´ et de constance de la variance, nous
e e
avons
εt | It−1 ∼ N 0, σ 2 (6.18)
o` It−1 repr´sente l’information pass´e. Lorsque nous estimons la variance avec la m´thode pr´sent´e
u e e e e e
pr´c´demment, nous faisons l’hypoth`se implicite que le processus est celui ci-dessus. Comme nous savons
e e e
que ce n’est pas la bonne repr´sentation, les estimations sont refaites r´guli`rement pour tenir compte
e e e
que la variance change au cours du temps. En revanche, les mod`les de type ARCH supposent que
e
εt | It−1 ∼ N 0, h2
t (6.19)
Conditionnellement ` l’information pass´, εt n’est plus un bruit blanc. Selon la sp´cification de h2 , nous
a e e t
d´finissons plusieurs types de mod`les. Par exemple, yt est un processus ARCH(p) si
e e
p
h2 = α 0 +
t α i ε2
t−i (6.20)
i=1
Dans le cas d’un processus GARCH(p,q), nous avons
p q
h2 = α 0 +
t α i h2 +
t−i β i ε2
t−i (6.21)
i=1 i=1
A titre illustratif, nous avons repr´sent´ sur le graphique (6.11) la variance conditionnelle du rendement
e e
du titre BARCLAYS estim´e ` partir d’un mod`le GARCH(1,1). A partir des estimations, il est alors
e a e
possible de construire des pr´visions de la variance conditionnelle Et h2 . Dans le cas des m´thodes
e t+h e
pr´sent´es au paragraphe pr´c´dent, la seule pr´vision possible de la variance en t+h est en fait la variance
e e e e e
e e a e ´
observ´e en t, ce qui n’est pas le cas des mod`les ` variances conditionnelles. L’´tude de Dave et Stahl
[1998] montre bien que d’un point de vue dynamique, les approches traditionnelles d’estimation de la
matrice de covariance pr´sentent un biais lorsque les s´ries ne sont pas stationnaires. Les auteurs ont fait
e e
une ´tude exhaustive sur le march´ des changes en consid´rant 5 m´thodes : la m´thode historique, la VaR
e e e e e
analytique avec des poids constants, la VaR RiskMetrics et les mod`le GARCH(1,1) et Tail GARCH(1,1).
e
´
6.2. QUELQUES REFLEXIONS SUR LA VAR 53](https://image.slidesharecdn.com/gestionrisques-130221132633-phpapp01/85/Gestion-risques-63-320.jpg)
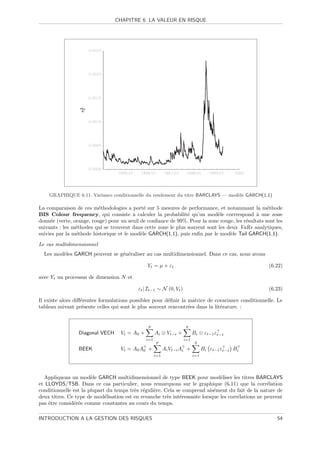

![CHAPITRE 6. LA VALEUR EN RISQUE
1
des innovations. Ce coefficient ´tant d´termin´, nous appliquons la T α rule, qui consiste ` passer
e e e a
1
de la VaR 1 jour ` la VaR T jours en multipliant par T α .
a
– La derni`re m´thode consiste tout simplement ` d´terminer la matrice de variance-covariance des
e e a e
rendements ` T jours. Cette approche n´cessite un historique assez long des donn´es et ne peut
a e e
pas ˆtre appliqu´e ` tous les horizons. Toutefois, elle permet d’obtenir la v´ritable matrice de
e e a e
variance-covariance historique. Reste alors le probl`me de l’ad´quation du mod`le ` cette maturit´.
e e e a e
Les articles rencontr´s dans la litt´rature s’attachent plus particuli`rement ` tester la validit´ de la
e e e a e
premi`re approche et ` d´velopper la deuxi`me m´thodologie au travers de mod`les semi-param´triques.
e a e e e e e
il n’y a pas de consensus arrˆt´ sur la question. Diebold et al. [15], [10] testent la proc´dure de scaling
ee e
sur des actifs soumis ` une dynamique de type GARCH. Leur argumentation repose sur la formule de
a
Drost-Nijman qui permet de corriger la volatilit´ ` T jours ` partir de celle obtenue ` 1 jour, sous certaines
ea a a
conditions de r´gularit´ et pour des horizons suffisamment longs. Leurs deux principales conclusions sont
e e
les suivantes :
– pour un horizon sup´rieur ` 10-15 jours, la volatilit´ n’est pas pr´visible. Autrement dit, les mod`les
e a e e e
a
` volatilit´ conditionnelle ne sont plus valables pour T 10 ;
e
– dans tous les cas, le scaling amplifie les fluctuations de la volatilit´. Mˆme si en moyenne le coefficient
√ e e
T peut sembler conservateur, le v´ritable rapport entre les deux volatilit´s est souvent bien au-
√ e e
dessous ou bien au-dessus de T .
Danielsson et De Vries [11], [12] proposent une autre approche fond´e sur des r´sultats de la
e e
th´orie des valeurs extrˆmes. Ils ´mettent quelques r´serves sur l’application de la m´thode propos´e
e e e e e e
par RiskMetrics pour un horizon de 10 jours, mˆme si les conclusions ne s’appliquent pas uniquement
e
au passage de la VaR 1 jour ` la VaR 10 jours. C’est plus la m´thode fond´e sur l’unique estimation
a e e
de la matrice de variance-covariance qui est remise en cause. Les tests et simulations qu’ils ont effectu´s
e
aboutissent aux conclusions suivantes :
– RiskMetrics sous-estime la VaR ` 1 jour par rapport ` une m´thode fond´e sur la th´orie des
a a e e e
extrˆmes surtout pour la mesure des risques rares (i.e. 0.05% et 0.005%). Nous notons ici que les
e
r´sultats obtenus pour une VaR ` 1% sont comparables pour les deux m´thodes.
e a e
– Pour des pr´visions ` 10 jours, la m´thode de RiskMetrics bas´e sur le scaling sur-estime la VaR
e a e e
1
obtenue par la T α rule (en moyenne, le coefficient α obtenu vaut 4.6).
√
Ces diff´rents r´sultats ne font ressortir aucun consensus quant ` l’application du coefficient T . Les
e e a
seules conclusions tir´es soulignent que dans une approche purement RiskMetrics, le scaling n’est pas
e
forc´ment conservateur (amplification des fluctuations) et qu’en le comparant ` des m´thodes plus fines,
e a e
il peut s’av´rer trop conservateur.
e
6.2.5.2 Un exercice de simulation
Pour illustrer les id´es ´nonc´es ci-dessus, nous avons effectuer quelques simulations de rendements de
e e e
diff´rents actifs. Nous avons consid´r´ successivement une dynamique de type GARCH, puis un mod`le `
e ee e a
volatilit´ stochastique (Hull-White). Dans ces deux cas, nous simulons des trajectoires du cours, dont nous
e
calculons les vraies √
volatilit´s ` 1 jour et ` 10 jours, puis nous comparons le rapport de ces deux volatilit´s
e a a e
avec le coefficient 10. Cette approche a seulement le m´rite de tester la validit´ de l’approximation
√ e e
effectu´e par la T rule, mais ne nous apporte aucune information quant ` la pertinence d’une VaR
e a
analytique de type RiskMetrics qui ne d´pend que de la matrice de variance-covariance.
e
Mod`le GARCH
e
Nous supposons ici que le rendement 1 jour d’un actif peut ˆtre mod´lis´ par un GARCH(1,1). Cette
e e e
hypoth`se n’est pas tr`s restrictive et semble cadrer avec la dynamique observ´e sur les march´s de
e e e e
certains titres. Nous simulons donc un processus yt tel que :
yt = σ t εt
σ2
t = w + αyt−1 + βσ 2
2
t−1
εt ∼ N ID(0, 1)
INTRODUCTION A LA GESTION DES RISQUES 56](https://image.slidesharecdn.com/gestionrisques-130221132633-phpapp01/85/Gestion-risques-66-320.jpg)

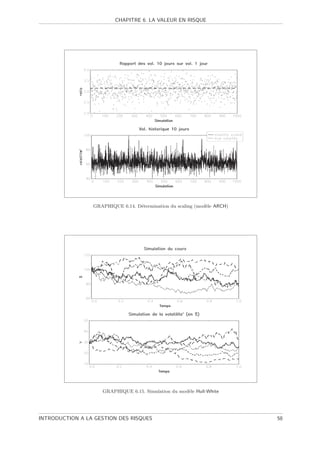
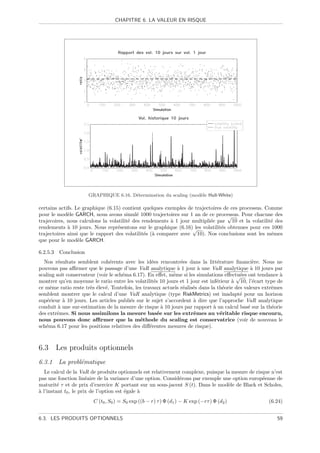
![CHAPITRE 6. LA VALEUR EN RISQUE
VaR 1 jour VaR 1 jour
(RiskMetrics) (th. des extrˆmes)
e
-
√
VaR 10 jours VaR 1 jour × 10 VaR 10 jours
(th. des extrˆmes)
e (RiskMetrics) (RiskMetrics)
-
ou
√
VaR 10 jours VaR 10 jours VaR 1 jour × 10
(th. des extrˆmes)
e (RiskMetrics) (RiskMetrics)
-
GRAPHIQUE 6.17. Positions relatives des VaRs
avec b le cost-of-carry et Φ la fonction de r´partition de la loi normale centr´e et r´duite,
e e e
1 S 1 √ √
d1 = √ ln 0 + bτ + σ τ et d2 = d1 − σ τ (6.25)
σ τ K 2
Consid´rons un portefeuille avec une position longue sur cette option, la variation du portefeuille entre t0
e
et t0 +h est ´gale ` C (t + h, S (t + h))−C (t0 , S0 ). Nous ne pouvons pas assimiler le risque du portefeuille
e a
a
` une distribution normale ou log-normale, car le prix de l’option BS est une fonction non-lin´aire du prix
e
du sous-jacent S (t) qui correspond ` une distribution log-normale dans le mod`le de Black et Scholes.
a e
Notons fS la fonction de densit´ de S (t) et C (S) la fonction de la prime d’achat. Comme la fonction C
e
est bijective, nous avons alors
fS C −1 (C)
fC (C) = (6.26)
∂S C (C −1 (C))
Puisque ∂S C (S) n’est pas une fonction affine de S, le distribution du prix de l’option n’est pas log-
normale. Il n’est donc pas possible d’utiliser une m´thode de type matrice de covariance pour calculer la
e
VaR d’une option.
6.3.2 Les solutions
Plusieurs auteurs ont alors propos´ des m´thodes de types analytique ou Monte Carlo pour calculer
e e
la mesure de risque des produits non lin´aires. Les m´thodes analytiques sont g´n´ralement bas´e sur
e e e e e
des approximations de Taylor. Par exemple, Britten-Jones et Schaefer [1997] proposent d’utiliser
´
une expansion partielle ` l’ordre 2 afin de tenir compte du Gamma de l’option. Cardenas, Fruchard,
a
Koehler, Michel et Thomazeau [1997] int`grent dans leur analyse le risque de volatilit´ en consid´rant
e e e
le Vega de l’option. G´n´ralement, ces m´thodes sont assez lourdes ` mettre en place d’un point de vue
e e e a
technique, surtout dans le cas multidimensionnel. D’un autre cˆt´, les m´thodes de Monte Carlo sont
oe e
beaucoup moins complexes, mais pr´sentent parfois des temps de calcul prohibitifs.
e
Finalement, la m´thode historique (parfois coupl´e avec une m´thode Monte Carlo) semble ˆtre une
e e e e
m´thode de compromis int´ressante. Cependant, elle n´cessite une gestion tr`s efficace des bases de
e e e e
INTRODUCTION A LA GESTION DES RISQUES 60](https://image.slidesharecdn.com/gestionrisques-130221132633-phpapp01/85/Gestion-risques-70-320.jpg)
![CHAPITRE 6. LA VALEUR EN RISQUE
donn´es. En effet, celles-ci doivent contenir beaucoup plus d’information (par exemple, les surfaces de
e
volatilit´) que celles des actifs lin´aires. Nous devons aussi mentionner le fait que dans l’esprit des textes
e e
r´glementaires, la m´thode doit prendre en compte les risques de volatilit´. Implicitement, cela suppose
e e e
donc que les pricers utilis´s pour le calcul de la VaR soient des pricers int´grant le smile. Cela pose
e e
quelques difficult´s, car il n’existe pas de “paradigme dominant” de type Black et Scholes comme dans
e
le cas du pricing sans smile. Plusieurs mod`les existent, mais tous ne sont pas de mˆme robustesse. De
e e
plus, la qualit´ d’un pricer avec smile d´pend de l’impl´mentation. Il existe ainsi plusieurs logiciels de
e e e
valorisation d’options de change bas´e sur la m´thode de Dupire, mais tous donnent un prix diff´rent,
e e e
car les m´thodes d’interpolation du smile sont diff´rentes, les donn´es utilis´es sont diff´rentes, certains
e e e e e
utilisent des artifices num´riques pour assurer la convergence, etc. Il convient donc d’ˆtre tr`s prudent
e e e
lors du choix de la m´thodologie d’une VaR sur des produits non lin´aires.
e e
Remarque 7 La m´thode historique est largement utilis´e par les banques pour calculer les VaRs op-
e e
tionnelles. Cependant, il semble que la Commission Bancaire demande de plus en plus d’´viter cette
e
m´thodologie au profit de m´thodes plus robustes.
e e
6.3.3 La gestion du risque des produits optionnels
Les produits optionnels sont parmi les actifs les plus risqu´s dans l’activit´ d’une salle de march´. Ils
e e e
font donc l’objet d’une surveillance quotidienne importante. La Commission Bancaire insiste fortement
sur le contrˆle des risques des activit´s de d´riv´s :
o e e e
– d´riv´s actions ;
e e
– produits structur´s (options sur plusieurs sous-jacents) ;
e
– exotiques de taux ;
– options de change (FX) ;
– d´riv´s de cr´dit ;
e e e
– etc.
En particulier, la Commission Bancaire demande que les pricers soient valid´s par une unit´ quantitative
e e
ind´pendante du Front Office. Derni`rement, elle a aussi propos´ de calculer des r´factions pour “risque
e e e e
de mod`le” et “risque de param`tres”.
e e
Voici une liste (non-exhaustive) des diff´rents risques li´s aux actifs contingents :
e e
1. Le risque de mod`le ou risque de mispricing
e
2. Le risque d’impl´mentation
e
3. Le risque de param`tres
e
4. Le risque de volatilit´ ou risque de smile
e
5. Le risque de convexit´
e
6. Le risque de corr´lation
e
Afin de ne pas alourdir le cours, nous verrons des exemples tr`s simples sans entrer dans les d´tails
e e
math´matiques. Pour cela, nous utiliserons les r´flexions men´es par Rebonato [2001] et Derman [2001].
e e e
6.4 Conclusion
Comme nous avons pu le voir, les mod`les de mesure des risques de march´ demandent beaucoup de
e e
savoir-faire. Celui-ci ne doit pas seulement concerner les instruments de march´ ou les aspects financiers,
e
mais aussi les outils statistiques et la gestion des bases de donn´es. Cependant, pour reprendre l’expression
e
de Boulier et al. [1997], mesurer n’est pas g´rer. La gestion des risques de march´ ne consiste pas
e e
seulement ` mesurer son risque. Elle cherche surtout ` l’analyser, ` le comprendre. En d´finitive, elle
a a a e
passe par la compr´hension de la micro-structure de son risque de march´.
e e
Toutefois, il est difficile de finir cette section sans ´voquer les pol´miques autour la VaR. Cette mesure
e e
ea e ´
– nous l’avons d´j` vu – pose de nombreux probl`mes statistiques. Aux Etats-Unis, cela a conduit ` des
a
6.4. CONCLUSION 61](https://image.slidesharecdn.com/gestionrisques-130221132633-phpapp01/85/Gestion-risques-71-320.jpg)
![CHAPITRE 6. LA VALEUR EN RISQUE
attaques assez violentes de la part des ´conom`tres et des statisticiens. D’autres critiques plus th´oriques
e e e
ont ´t´ faites. En premier lieu, elles concernent l’impossibilit´ de mod´lisation du futur par le pass´ (voir
ee e e e
la controverse entre Nassim Taleb et Phillipe Jorion — r´f´rences [21], [27] et [28]). En second lieu, elles
ee
portent sur la coh´rence de la VaR en tant que mesure des risques. D’apr`s l’axiomatique d´velopp´e
e e e e
par Artzner, Delbaen, Eber et Heath [1998], la VaR ne v´rifie pas la propri´t´ fondamentale de
e ee
sous-additivit´9 . Deux types de mesures coh´rentes du risque ont alors ´t´ propos´s. Soit X la variable
e e ee e
e e ¨
al´atoire d´crivant la position nette du portefeuille, Embrechts, Kluppelberg et Milkosh [1997]
d´finissent de la fa¸on suivante :
e c
= E −X| X ≤ x− (6.27)
Dans ce cas, n’est plus un quantile (comme pour la VaR), mais l’esp´rance de perte au del` d’un certain
e a
quantile (qui pourrait ˆtre ´ventuellement le niveau de la VaR). Artzner, Delbaen, Eber et Heath
e e
[1997] ont sugg´r´e une deuxi`me mesure de risque proche de la pr´c´dente :
ee e e e
= sup E −X| X ≤ x− , P = p p ∈ ℘ (6.28)
avec ℘ l’ensemble des distributions de probabilit´s des ´tats de la nature. ℘ est aussi appel´ l’ensemble
e e e
des “sc´narios g´n´ralis´s”. Dans ce cas, pour chaque sc´nario appartenant ` ℘, on calcule l’esp´rance
e e e e e a e
de perte (x− = 0) ou l’esp´rance de perte au del` d’un certain quantile (x− 0), puis on d´termine la
e a e
plus grande valeur parmi tous les sc´narios de ℘. Comme le font remarquer les auteurs, cela exige une
e
r´flexion approfondie pour d´finir ℘ :
e e
The generalized scenarios method is the universal coherent risk measurement method : it
requires thinking before calculating, which can only improve risk management.
Bibliographie
[1] Andersen, T.G. [1994], Stochastic autoregressive volatility : a framework for volatility modeling,
Mathematical Finance, 4, 75-102
[2] Artzner, A., F. Delbaen, J-M. Eber et D. Heath [1997], Thinking coherently, Risk magazine, 10,
November, 68-71
[3] Artzner, A., F. Delbaen, J-M. Eber et D. Heath [1998], Coherent measures of risk, Eidgen¨ssische
o
Technische Hochschule, Z¨rick, Working Paper
u
[4] Baker, M., J. Tattersall et R. Wilson [1996], Cad and beyond, Risk Magazine, 9-2, February
[5] Bollerslev, T. [1986], Generalized autoregressive conditional heteroskedasticity, Journal of Econo-
metrics, 50, 987-1008
[6] Bollerslev, T., R.F. Engle et D.B. Nelson [1993], ARCH models, in The Handbook of Econo-
metrics, Volume 4, chapter 11
[7] Boulier, J-F., A. Brabant, R. Dalaud et A-L. Dieu [1997]. Risques de march´ : Vue de Profil,
e
Direction de la Recherche et de l’Innovation, Cr´dit Commercial de France, Quants, 28
e
[8] Britten-Jones, M. et S.M. Schaefer [1997], Non-linear Value at Risk, London Business School,
Working Paper
´
[9] Cardenas, J., E. Fruchard, E. Koehler, C. Michel et I. Thomazeau [1997], VaR : One step
beyond, Risk magazine, 10, October, 72-75
[10] Christoffersen, P.F., F.X. Diebold et T. Schuermann [1998], Horizon Problems and Extreme
Events in Financial Risk Management, FRBNY Economic Policy Review
[11] Danielsson, J. et C.G. de Vries [1997a], Value-at-Risk and Extreme Returns, Tinbergen Institute
Rotterdam, Mimeo
[12] Danielsson, J. et C.G. de Vries [1997b], Beyond the Sample : Extreme Quantile and Probability
Estimation, Tinbergen Institute Rotterdam, Mimeo
9 Cela veut dire que la VaR globale de deux portefeuilles peut ˆtre sup´rieure ` la somme des VaRs individuelles des
e e a
deux portefeuilles !
INTRODUCTION A LA GESTION DES RISQUES 62](https://image.slidesharecdn.com/gestionrisques-130221132633-phpapp01/85/Gestion-risques-72-320.jpg)
![´
[13] Dave, R.D. et G Stahl [1999], On the accuracy of VaR estimates based on the variance-covariance
approach, Olsen Associates, Z¨rich, Working Paper
u
[14] Derman, E. [2001], Markets and model, Risk Magazine, 14, July, 48-50
[15] Diebold, F.X., A. Hickman, A. Inoue et T. Schuermann [1997], Converting 1-Day Volatility to h-
√
Day volatility : Scaling by h is worse than you think, The Wharton School, University of Pennsylvania,
97-34
[16] Engle, R.F. [1982], Autoregressive conditional Heteroskedasticity with estimates of the variance of
the U.K. inflation, Econometrica, 50, 987-1008
¨
[17] Embrechts, P., Kluppelberg, C. et T. Mikosch [1997], Modelling Extremal Events for Insurance
and Finance, Springer-Verlag, Berlin
[18] Feller, W. [1968], An introduction to probability theory and its applications, volume 1, trois`me
e
´dition, John Wiley Sons, New York
e
[19] Guldimann, Til. [1994], RiskMetricsT M Technical Document, 2nd edition, J.P. Morgan, New York
[20] Hendricks, D. [1996], Evaluation of Value-at-Risk models using historical data, Federal Reserve
Board of New York, FRBNY Economic Policy Review, April, 39-69
[21] Jorion, P. [1997], In defense of VaR, Derivatives Strategy
[22] Lopez, J. [1998], Methods for evaluating Value-at-Risk estimates, Federal Reserve Bank of New
York
[23] Rebonato, R. [2001], Model risk : new challenges, new solutions, Risk Magazine, 14, March, 87-90
[24] Rouvinez, C. [1997], Going greek with VaR, Risk Magazine, 10, February
[25] Rubinstein, M. [1998], Edgeworth binomial trees, Journal of Derivatives, spring, 20-27
[26] Stahl, G. [1997], Three cheers, Risk Magazine, 10, May
[27] Taleb, N. [1997a], The world according to Nassim Taleb, interview by editor Joe Kolman, Derivatives
Strategy, December/January
[28] Taleb, N. [1997b], Against Value-at-Risk : Nassim Taleb replies to Phillipe Jorion, document non
publi´
e
[29] Taylor, S.J. [1994], Modeling stochastic volatility : a review and comparative study, Mathematical
Finance, 4, 183-204](https://image.slidesharecdn.com/gestionrisques-130221132633-phpapp01/85/Gestion-risques-73-320.jpg)

![7
Les programmes de stress-testing
Comme le pr´conisent les autorit´s r´glementaires, les ´tablissements financiers doivent effectuer
e e e e
r´guli`rement des simulations de crise afin de connaˆ
e e ıtre le montant des pertes potentielles en cas de
fluctuations dangereuses et importantes du march´. Il faut tout de suite pr´ciser que malgr´ le caract`re
e e e e
obligatoire, ces simulations de crises ne sont en aucun cas utilis´s pour calculer l’exigence en fonds propres.
e
Cependant, l’utilisation de simulations de crises est l’un des quatre principes de base d´finis e
par la Commission Bancaire pour qu’un mod`le interne soit valid´. Le but de ces simulations
e e
est alors de compl´ter le dispositif de mesure des risques, et notamment les mesures de VaR 1 .
e
Ces simulations de crises, parfois appel´es sc´narios de stress, et plus connu sous le terme anaglais stress
e e
testing, doivent ˆtre des outils pour appr´hender l’exposition de la banque ` une crise grave. Contrairement
e e a
a
` la VaR, elles doivent permettre de r´pondre ` la question suivante :
e a
Quel est le montant de perte auquel la banque doit faire
face lors de la prochaine crise si le portefeuille de
n´gociation ne change pas ?
e
La notion de probabilit´ disparaˆ Statistiquement, les stress testing font donc r´f´rence ` un maximum,
e ıt. ee a
et non ` un quantile. C’est une vision du risque extrˆme. Le point de vue est donc assez diff´rent de celui
a e e
de la VaR, puisque le r´gulateur est beaucoup moins concern´ par cette mesure (mˆme si la m´thodologie
e e e e
doit lui ˆtre communiqu´e). Les mesures fournies par les stress testing sont avant tout destin´es au risk
e e e
management et ` la direction g´n´rale. Celles-ci doivent faire l’objet d’une analyse d´taill´e afin de
a e e e e
bien comprendre l’exposition de la banque et afin de bien v´rifier que ce risque extrˆme est ` un
e e a
niveau supportable :
The art of stress testing should give the institution a deeper understanding of the specific
portfolios that could be put in jeopardy given a certain situation. The question then would be :
“Would this be enough to bring down the firm ?” That way, each institution can know exactly
what scenario it is they do not want to engage in (Michael Ong, ABN Amro, in Dunbar et
Irving [1998]).
Deux grandes familles de stress testing existent : les m´thodes objectives et les m´thodes dites subjec-
e e
tives. Le premier type utilise les faits historiques (des faits qui se sont r´ellement pass´s) pour construire
e e
les sc´narios, alors que la seconde famille est bas´e sur des hypoth`ses de travail. Pour ˆtre plus pr´cis,
e e e e e
nous pouvons classer les stress testing selon trois approches (Dunbar et Irving [1998]) :
1 Une´tude men´e par Tucker et Lawrence [1998] sur le risk management aupr`s de 679 institutions de 25 pays montre
e e e
que 93% des risk managers consid`rent qu’une mesure VaR est insuffisante comme mesure de risque.
e](https://image.slidesharecdn.com/gestionrisques-130221132633-phpapp01/85/Gestion-risques-75-320.jpg)
![CHAPITRE 7. LES PROGRAMMES DE STRESS-TESTING
1. La premi`re est la plus simple : elle consiste ` utiliser les donn´es des crises pass´es et ` employer la
e a e e a
m´thode de simulation historique sur ces p´riodes troubl´es pour calculer une perte potentielle
e e e
maximale (et non une VaR). L’´tablissement financier a alors une estimation de ce que causerait
e
la survenance de ces mˆmes crises avec le portefeuille de n´gociation actuel.
e e
2. La deuxi`me approche est une analyse structur´e des sc´narios. Les ´v`nements historiques sont
e e e e e
utilis´s en les appliquant aux conditions actuelles de march´. Par exemple, nous pouvons analyser
e e
l’incidence de la hausse des taux de 1994 par la Federal Reserve Bank si elle survenait aujourd’hui.
Contrairement ` la premi`re m´thode qui utilisent les donn´es historiques, cette m´thode va donc
a e e e e
utiliser des donn´es simul´es ` partir des donn´es actuelles et des ´v`nements pass´s.
e e a e e e e
3. La troisi`me approche est une analyse de sc´narios sp´cifiques. Pour cela, il convient d’identifier une
e e e
situation qui risque de menacer l’´tablissement financier. Cette m´thode ne fait donc pas r´f´rence
e e ee
aux ´v`nements pass´s, mais utilisent des hypoth`ses sur les crises potentielles futures.
e e e e
Les stress testing sont donc des suites de questions que doit se poser l’´tablissement financier sur son
e
risque :
In essence, a comprehensive stress-testing programme asks a series of “what if” questions
that force risks managers to try to predict what risk banks could face next time disaster strikes
(Dunbar et Irving [1998]).
Par exemple, voici le genre de questions que peut se poser la banque :
– Quel est l’impact d’une hausse des taux directeurs de 100 points de base ?
– Que se passe-t-il si la courbe des taux s’inverse ?
– Quelles sont les r´percussions d’une d´valuation ?
e e
– Que se passe-t-il en l’absence de liquidit´ ?
e
– Quel est l’impact d’une hausse des prix de l’immobilier ?
– etc.
Il est tout d’abord important de noter qu’il n’existe pas aujourd’hui de standard plus pr´cis pour
e
l’´laboration des sc´narios de crise. On se contentera donc dans un premier temps d’avoir ` l’esprit la
e e a
probl´matique suivante : un programme de simulation de crise doit ˆtre en mesure de r´pondre ` ces trois
e e e a
questions :
– Quelles seront les pertes si le sc´nario X se produit ?
e
– Quels sont les pires sc´narios pour l’institution ?
e
– Que pouvons-nous faire pour limiter les pertes dans ce cas ?
Sachant par ailleurs que l’int´rˆt de la Commission Bancaire est que ces simulations puissent influencer
ee
directement les choix de la direction en mati`re de gestion du risque, il faut avoir en tˆte deux autres
e e
exigences :
– la cr´dibilit´ du sc´nario aux yeux de la direction g´n´rale ;
e e e e e
– la bonne lisibilit´ pour cette derni`re de l’exposition du portefeuille aux diff´rents facteurs de risque
e e e
pr´alablement d´finis.
e e
7.1 Directions m´thodologiques choisies par les institutions bancaires
e
Nous fournissons ici les r´sultats d’une enquˆte men´e par Deloitte Touche en 1999 aupr`s de 200
e e e e
banques dans le monde sur le Risk Management et publi´e en mai 2000 dans la revue Banque Magazine :
e
L’utilisation du stress testing (en % des ´tablissements interrog´s)
e e
Actuels Envisag´se
1 Sc´narios reposant sur la politique et l’´conomie
e e 40% 45%
2 Sc´narios chocs march´s
e e 70% 55%
3 Chocs historiques 65% 58%
4 Stress testing global 30% 50%
5 Micro-stress testing 44% 29%
6 Th´orie des valeurs extrˆmes
e e 5% 24%
INTRODUCTION A LA GESTION DES RISQUES 66](https://image.slidesharecdn.com/gestionrisques-130221132633-phpapp01/85/Gestion-risques-76-320.jpg)

![CHAPITRE 7. LES PROGRAMMES DE STRESS-TESTING
– d’impliquer dans sa construction un grand nombre de personnes aux comp´tences vari´es et jusqu’`
e e a
des niveaux de responsabilit´ tr`s ´lev´s ;
e e e e
– de cr´er r´guli`rement de nouveaux sc´narios adapt´s aux changements politiques et ´conomiques.
e e e e e e
Exemple 1 Herv´ Goulletquer, Senoir Economist au Cr´dit Lyonnais, nous a fourni un exemple de
e e
sc´nario de crise concernant une baisse de Wall Street difficilement g´rable (voir Costinot, Riboulet and
e e
Roncalli [2000]). Aux Etats-Unis, sous le double effet d’une activit´ qui ralentit et d’une inflation qui
e
devient moins sage, le march´ des actions se retourne assez brutalement (−8% sur un mois pour l’indice
e
Dow Jones). La R´serve f´d´rale est incapable de r´pondre de suite ` cette baisse brutale des cours. Les
e e e e a
taux courts restent en l’´tat tout au long du mois concern´. Le dollar subit la pression baissi`re li´e
e e e e
aux rapatriements de capitaux vers l’Europe et le Japon. L’Euro s’appr´cierait de 3 cents par rapport
e
au Dollar (toujours en un mois). La hausse de la Livre serait un peu plus forte (6 cents). Dans ce
contexte de sortie de capitaux du pays, et aussi dans un environnement qui dans un premier temps reste
marqu´ par la crainte de plus d’inflation, le march´ obligataire est mal orient´. Le rendement ` 10 ans
e e e a
d’une obligation du Tr´sor am´ricain se tend assez nettement (+55 bp). En Europe, la hausse de l’Euro
e e
freine la remont´e des taux longs (+20 bp en un mois). Dans ces conditions, la baisse du CAC40 peut
e
difficilement se comparer ` celle de Wall Street. Elle n’atteint que 5%. Et la BCE ne juge pas utile de
a
revoir son r´glage mon´taire.
e e
7.4 La m´thode WCS
e
Boudoukh, Richardson et Whitelaw [1995] d´finisse l’analyse “worst-case scenario” (ou WCS) de
e
la fa¸on suivante :
c
WCS asks the following question : what is the worst that can happen to the value of the
firm’s trading portfolio over a given period (eg, 20 trading days) ?
Comme l’explique Bahar, Gold, Kitto et Polizu [1997], l’utilisation de l’analyse WCS est motiv´e
e
par les pr´occupations r´elles des risk managers :
e e
...VaR has been criticised at a more fundamental level — that it asks the wrong question...
VaR requires a probability that loss shocks, over a short horizon, will not exceed a certain
figure. This is often interpreted as expressing the number of times a loss shock in excess of the
subjective threshold would occur over a long time horizon. But managers are more likely be
concerned with the probability of realising a specific loss shock, rather than the probability
of landing in a region of large loss shocks.
L’analyse WCS consiste ` diviser une p´riode de r´f´rence T en N sous-intervalles de mˆme longueur. Soit
a e ee e
Xn la variable al´atoire d´crivant la position nette du portefeuille pour le n-i`me sous-intervalle. Dans ce
e e e
contexte, nous pouvons d´finir la mesure de VaR ` partir du nombre de sous-intervalles qui pr´sentent
e a e
une perte sup´rieure ` une valeur donn´e x− :
e a e
N
1[Xn ≤x− ]
n=1
=1−α (7.1)
N
avec α le seuil de confiance. Pr´sent´ de cette fa¸on, x− n’est rien d’autre que la mesure VaR. En
e e c
revanche, l’analyse WCS consid`re la distribution de la perte maximale (ou la fonction de distribution
e
du pire) parmi les sous-intervalles. On cherche donc ` caract´riser la fonction de distribution GN de
a e
χ− = min (X1 , . . . , Xn , . . . , XN ). Si nous supposons que les variables al´atoires Xn sont ind´pendantes
N e e
et de mˆme loi de distribution F, nous avons
e
GN (x) = Pr χ− ≤ x
N
= 1 − Pr (X1 x, . . . , Xn x, . . . , XN x)
N
= 1 − [1 − F (x)] (7.2)
Notons gN et f les fonctions de densit´ correspondantes, nous pouvons montrer facilement que
e
N −1
gN (x) = N × [1 − F (x)] f (x) (7.3)
INTRODUCTION A LA GESTION DES RISQUES 68](https://image.slidesharecdn.com/gestionrisques-130221132633-phpapp01/85/Gestion-risques-78-320.jpg)
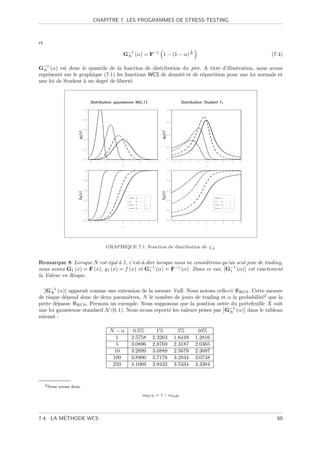
![CHAPITRE 7. LES PROGRAMMES DE STRESS-TESTING
Lorsque l’horizon consid´r´ est un jour de trading et pour α ´gal ` 1%, la mesure de risque est bien ´gale
ee e a e
a
` 2.33, la Valeur en Risque. Lorsque nous prenons 5 jours de trading, la mesure de risque passe ` 2.88.
a
Nous voyons bien que le risque d´pend alors du nombre de jours de trading consid´r´. La coubure de la
e ee
fonction G−1 (α) en fonction de N nous donne une certaine vision “dynamique” du risque3 . A partir
N
de la fonction de distribution du pire, nous pouvons construire d’autres mesures de risque. Par exemple,
nous pouvons consid´r´ l’esp´rance du pire η (N ) d´finie par
ee e e
η (N ) = −E [χN ]
N −1
≡ −N × [1 − F (x)] f (x) x dx (7.5)
Comme le montre le graphique (7.2), cette esp´rance du pire d´pend fortement de la fonction de densit´
e e e
et notamment de la queue gauche de celle-ci. Nous voyons clairement que dans le cas o` la fonction de
u
distribution des pertes potentielles est leptokurtique (cas de la Student T1 ), la diff´rence de risque entre
e
cette distribution et la distribution gaussienne estim´e peut croˆ tr`s fortement avec N .
e ıtre e
GRAPHIQUE 7.2. L’influence de la queue de distribution sur η (N )
On associe g´n´ralement l’analyse WCS aux simulations de crises, car elles sont toutes les deux li´es `
e e e a
la notion de temps de retour. En g´n´ral, une m´thodologie VaR a du mal ` appr´hender les crises. En
e e e a e
effet, les temps de retour bas´s sur les VaRs manquent g´n´ralement de r´alisme. L’analyse WCS ou la
e e e e
th´orie des extrˆmes, qui fait l’objet de la prochaine section, sont des outils plus adapt´s dans ces cas-l`
e e e a
(Boulier, Brabant, Dalaud et Dieu [1997]) :
On remarque d’abord le r´alisme des r´sultats obtenus par la m´thode statistique des
e e e
extrˆmes. Ainsi, lors du krach d’octobre 1987, la variation quotidienne la plus forte de l’indice
e
MSCI France fut de 8.4%. Cette chute correspond ` une dur´e de retour estim´e ` treize ans
a e e a
par la m´thode des extrˆmes, alors que l’approche par la loi normale fournit une dur´e de
e e e
retour de l’ordre de dix milliards d’ann´es. Ici la m´thode param´trique est mise en d´faut
e e e e
parce que le quantile consid´r´ (99.97%) a trait ` un ´v´nement tr`s rare.
ee a e e e
3 Cependant, comme les variables al´atoires Xn sont ind´pendantes, cette dynamique ne tient pas compte des effets de
e e
contagion.
INTRODUCTION A LA GESTION DES RISQUES 70](https://image.slidesharecdn.com/gestionrisques-130221132633-phpapp01/85/Gestion-risques-80-320.jpg)
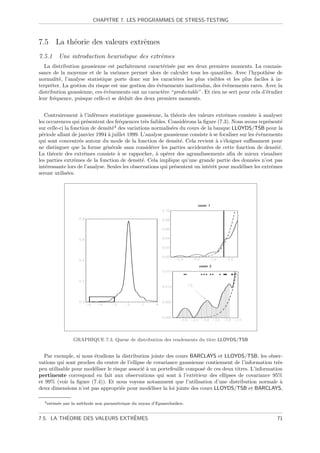
![CHAPITRE 7. LES PROGRAMMES DE STRESS-TESTING
puisque de nombreuses r´alisations sont dans des domaines qui pr´sentent des occurences tr`s faibles (qui
e e e
sont ´gales num´riquement ` z´ro).
e e a e
GRAPHIQUE 7.4. Distribution jointe des rendements des titres BARCLAYS et LLOYDS/TSB
Il faut bien comprendre que la th´orie des valeurs extrˆmes, mˆme si elle est li´e aux recherches dans
e e e e
le domaine des queues ´paisses, n’est pas un outil de mod´lisation du caract`re leptokurtique
e e e
d’une distribution. En fait, elle permet de caract´riser la loi des extrema. Dans la section pr´c´dente,
e e e
nous d´terminions la distribution des minima ` partir de la fonction de densit´ qui les engendrent. La
e a e
th´orie des valeurs extrˆmes va nous permettre, en particulier, d’estimer directement la distribution `
e e a
partir des donn´es. L’id´e est donc la suivante :
e e
Que pouvons nous dire de la distribution limite lim GN (x)
N −→∞
sans faire d’hypoth`ses sur la distribution F ?
e
Comme l’explique McNeil [1998a], nous ne pouvons affirmer que la th´orie des valeurs extrˆmes permet
e e
de pr´dire le futur avec certitude. Mais le pass´ contient assez d’information (qui n’est pas forc´ment
e e e
observable) sur les extrema pour pouvoir mod´liser G∞ (x), sans pour autant vouloir connaˆ la fonction
e ıtre
F. Et cela est possible, car sous certaines conditions, G∞ (x) ne peut ˆtre d´cliner qu’en un nombre
e e
tr`s limit´ de lois de distribution (voir l’annexe 7.5.6.1 pour une d´monstration intuitive).
e e e
7.5.2 La th´orie classique
e
7.5.2.1 Pr´sentation des 3 lois d’extrˆmes
e e
Nous reprenons les notations introduites pour d´finir la distribution du pire. Nous consid´rons N varia-
e e
bles al´atoires X1 , . . . , Xn , . . . , XN ind´pendantes et de mˆme loi de distribution F dont nous cherchons `
e e e a
´tudier le comportement des extrˆmes χ− = min (X1 , . . . , Xn , . . . , XN ) et χ+ = max (X1 , . . . , Xn , . . . , XN ).
e e N N
Pour cela, nous pouvons utiliser la statistique d’ordre Y sur X, c’est-`-dire que nous avons
a
χ− = Y1 ≤ · · · ≤ Yn ≤ · · · ≤ YN = χ+
N N (7.6)
k(N )
Consid´rons alors la variable al´atoire Λ =
e e (Yn ). Embrechts, Resnick et Samorodnitsky
n=1
[1997] donnent diff´rents exemples d’utilisation de Λ en finance :
e
INTRODUCTION A LA GESTION DES RISQUES 72](https://image.slidesharecdn.com/gestionrisques-130221132633-phpapp01/85/Gestion-risques-82-320.jpg)
![CHAPITRE 7. LES PROGRAMMES DE STRESS-TESTING
1
– Si (y) = k(N ) × y, Λ correspond ` la moyenne des k (N )-i`mes pertes les plus importantes ;
a e
– Si (y) = (y − − y)+ et k (N ) = N , Λ repr´sente la somme des pertes plus grandes qu’un seuil ;
e
– Si (y) = y et k (N ) = αN , Λ est le quantile α de X.
Avec la th´orie des extrˆmes, nous nous int´ressons directement ` Λ = Y1 et Λ = YN . Pour cela, nous
e e e a
avons besoin du th´or`me de Fisher-Tippet qui permet de caract´riser la loi de distribution des extrˆmes :
e e e e
Th´or`me 1 (Th. 3.2.3 de Embrechts, Kl¨ ppelberg et Mikosch (1997)) Supposons N variables
e e u
al´atoires X1 , . . . , Xn , . . . , XN ind´pendantes et de mˆme loi de distribution F. S’il existe des constantes
e e e
aN et bN et une distribution limite non d´g´n´r´e G telles que
e e e e
χ+ − bN
N
lim Pr ≤x = G (x) ∀x ∈ R (7.7)
N −→∞ aN
alors G appartient ` l’un des trois types suivants de distribution :
a
0 x≤0 0
Type I (Frechet) G (x) = g (x) =
exp (−x−α ) x0 αx−(1+α) exp (−x−α )
α α−1 α
exp (− (−x) ) x≤0 α (−x) exp (− (−x) )
Type II (Weibull) G (x) = g (x) =
1 x0 0
Type III (Gumbel) G (x) = exp (−e−x ) x∈R g (x) = exp (−x − e−x )
C’est l’un des r´sultats les plus importants de la th´orie des extrˆmes : sous certaines conditions, la loi
e e e
de distribution des extrˆmes est l’une des trois lois param´triques pr´c´dentes. En fait, nous pouvons
e e e e
caract´riser ces trois types de distribution par une distribution unique (Coles et Tawn [1999]) :
e
1
−ξ
x−µ
G (x) = exp − 1 + ξ (7.8)
σ
d´fini sur le support ∆ = x : 1 + ξ x−µ 0 et que nous notons G (µ, σ, ξ). Cette fonction de distribu-
e σ
tion correspond ` la loi de probabilit´ de Von Mises, mais elle est plus connue sous le nom de “Generalized
a e
Extreme Value distribution” (GEV). Nous avons alors les correspondances suivantes :
Frechet ξ = α−1 0
Weibul ξ = −α−1 0
Gumbel ξ −→ 0
Remarquons que les param`tres µ et σ sont en fait les limites de bN et aN . A titre d’illustration, voyons
e
quelques exemples de distribution GEV. Pour cela, nous pouvons facilement montrer que la fonction de
densit´ correspondante est
e
−( 1+ξ ) 1
−ξ
1 x−µ ξ
x−µ
g (x) = 1+ξ exp − 1 + ξ (7.9)
σ σ σ
Les graphiques (7.5) et (7.6) pr´sentent des fonctions de densit´ et de r´partition pour diff´rentes valeurs
e e e e
de param`tre. Lorsque µ varie, nous remarquons une translation des fonctions. µ est donc un param`tre
e e
de localisation. σ joue le rˆle d’une variance, c’est pourquoi nous le consid´rons comme un param`tre
o e e
de dispersion. Enfin, le param`tre ξ est li´ au caract`re leptokurtique de la fonction de distribution F.
e e e
C’est pourquoi on lui donne g´n´ralement le nom d’indice de queue ou d’indice de valeur extrˆme (Drees
e e e
[1997]).
´ ˆ
7.5. LA THEORIE DES VALEURS EXTREMES 73](https://image.slidesharecdn.com/gestionrisques-130221132633-phpapp01/85/Gestion-risques-83-320.jpg)
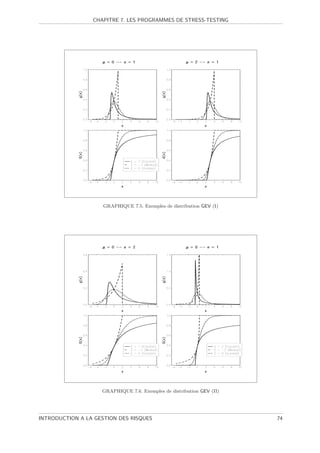
![CHAPITRE 7. LES PROGRAMMES DE STRESS-TESTING
7.5.2.2 Quelques remarques sur les lois d’extrˆmes
e
L’´tude des lois d’extrˆme est tr`s int´ressante. C’est un domaine de recherche prolifique. Dans ce
e e e e
paragraphe, nous pr´sentons quelques r´sultats remarquables.
e e
Remarque 9 Reprenons l’analyse WCS et appliquons celle-ci au maximum χ+ . Nous avons alors
N
N
GN (x) = F (x)
N −1
gN (x) = N × F (x) f (x) (7.10)
et
lim GN (x) = G (x) (7.11)
N →∞
Il est alors int´ressant d’´tudier la vitesse de convergence qui permet d’avoir une id´e de la p´riode de
e e e e
r´f´rence de l’analyse WCS pour que celle-ci soit “´quivalente” ` la th´orie des extrˆmes.
ee e a e e
Voyons un exemple. Nous consid´rons la distribution gaussienne standard. Nous savons que la loi des
e
extrˆmes correspondante est une Gumbel. Sur le graphique (7.7), nous remarquons que l’approximation
e
de G1 (x) par une loi de Gumbel est moins bonne que celle de G10000 (x). Nous consid´rons mainte-
e
GRAPHIQUE 7.7. Convergence de GN vers la distribution de Gumbel lorsque F est gaussienne
nant plusieurs distributions : la loi gaussienne, la loi exponentielle, la loi de Student T4 et la loi α-stable
sym´trique5 S0.7 (1, 0, 0). Pour mesurer la convergence, Coles et Tawn [1999] proposent d’´tudier gra-
e e
x−bN
phiquement le comportement de − ln − ln GN aN en fonction de N et de le comparer celui-ci
de la loi limite. Pour les lois gaussienne et exponentielle, la loi limite est la distribution de Gumbel.
Pour les deux autres, c’est la distribution de Fr´chet. Le probl`me est de construire les suites (aN ) et
e e
χ+ −b
(bN ). Pour la loi exponentielle, nous pouvons montrer que si aN = 1 et bN = − ln (N ), NaN N converge
bien en loi vers la famille de type III. Pour les autres lois, la connaissance des suites (aN ) et (bN ) n’est
5 voir Nolan [1999].
´ ˆ
7.5. LA THEORIE DES VALEURS EXTREMES 75](https://image.slidesharecdn.com/gestionrisques-130221132633-phpapp01/85/Gestion-risques-85-320.jpg)
![CHAPITRE 7. LES PROGRAMMES DE STRESS-TESTING
GRAPHIQUE 7.8. Convergence de certaines distributions vers la distribution de Fr´chet
e
pas toujours v´rifi´e6 . Dans ce cas, nous pouvons construire les suites num´riquement en adoptant un
e e e
crit`re de bonne ad´quation7 entre GN x−bN et la loi limite G (x). Les r´sultats sont pr´sent´s sur le
e e aN e e e
graphique (7.8). Nous voyons ainsi que la convergence de la loi exponentielle est bien plus rapide que celle
de la loi gaussienne. Et les distributions qui ont des queues leptokurtiques (c’est le cas des distributions
T4 et S0.7 (1, 0, 0)) pr´sentent des vitesses de convergence plus faibles.
e
Remarque 10 Le quantile G−1 (α) d’ordre α pour la distribution GEV est donn´ par la formule suivante :
e
σ −ξ
G−1 (α) = µ − 1 − (− ln α) (7.12)
ξ
Ce quantile est donc fortement influenc´8 par les deux param`tres σ et ξ. A titre d’illustration, le graphique
e e
(7.9) pr´sente diff´rentes courbes de quantiles en fonction de ξ. Intuitivement, nous comprenons que plus
e e
la distribution F poss`de de la variance et plus elle est leptokurtique, plus ce quantile sera ´l´v´.
e ee e
Remarque 11 Nous pouvons montrer que le mode de la distribution GEV est atteint pour la valeur
ξ
µ+σ (1 − ξ) . Quant ` la moyenne E χ+ , nous pouvons la calculer facilement en utilisant une proc´dure
a N e
d’int´gration num´rique de type Gauss-Legendre ou Gauss-Hermite.
e e
Nous avons maintenant presque tous les ´l´ments pour appliquer la th´orie des valeurs extrˆmes ` la
ee e e a
gestion du risque. Soit P la perte potentielle d’un portefeuille. Mesurer le risque revient alors ` analyser
a
6 Coles et Tawn [1999] fournissent deux expressions pour (a ) et (b ) pour la loi gaussienne, mais celles-ci s’av`rent
e
N N
num´riquement non ad´quates, notamment pour des faibles valeurs de N . C’est pourquoi nous avons aussi pr´f´r´ utiliser
e e ee e
la m´thode num´rique de construction des suites pour la loi gaussienne.
e e
7 Nous avons utilis´ une norme
e 2 pour le crit`re d’ad´quation.
e e
8 En effet, nous avons
σ
∂α G−1 (α) = (7.13)
α (− ln α)1+ξ
INTRODUCTION A LA GESTION DES RISQUES 76](https://image.slidesharecdn.com/gestionrisques-130221132633-phpapp01/85/Gestion-risques-86-320.jpg)
![CHAPITRE 7. LES PROGRAMMES DE STRESS-TESTING
GRAPHIQUE 7.9. Quantile de la distribution GEV
la loi du maximum de −P, c’est-`-dire la distribution du pire. A partir de celle-ci, nous pouvons calculer
a
les quantiles du pire, l’esp´rance ou le mode du pire, les temps de retour, etc. Avant de voir quelques
e
applications, il reste cependant ` d´velopper l’inf´rence statistique et les m´thodes d’estimation d’une
a e e e
distribution GEV.
7.5.2.3 Estimation des param`tres de la distribution GEV
e
Il existe plusieurs m´thodes pour estimer les param`tres de la distribution GEV. Nous pouvons par
e e
exemple citer les m´thodes d’estimation de l’indice de queue (de type Hill ou Pickands — voir Drees,
e
De Haan et Resnick [1998]), la m´thode des moments ou encore les m´thodes de seuil (bas´e par
e e e
exemple sur la distribution de Pareto g´n´ralis´e). Mais celle qui reste la plus populaire et qui sous
e e e
certaines conditions est la plus efficace est la m´thode du Maximum de Vraisemblance9 .
e
Soit θ le vecteur des param`tres. Nous avons
e
µ
θ= σ
ξ
Nous consid´rons un ´chantillon de donn´es {Xt } de dimension T = ϕN avec ϕ ∈ R. Nous divisons cet
e e e
´chantillon en N blocs et nous d´finissons χ+ de la fa¸on suivante
e e n c
χ+ = max
n X1+n(t−1) , t = 1, . . . , ϕ (7.14)
L’expression de la vraisemblance de l’observation n est donc
−( 1+ξ ) 1
−ξ
1 χ+ − µ
n
ξ
χ+ − µ
n
L χ+ ; θ
n = 1+ξ exp − 1 + ξ (7.15)
σ σ σ
9 Nous utilisons ici les notations et la terminologie de Davidson et MacKinnon [1993], ouvrage de r´f´rence sur la
ee
question du maximum de vraisemblance.
´ ˆ
7.5. LA THEORIE DES VALEURS EXTREMES 77](https://image.slidesharecdn.com/gestionrisques-130221132633-phpapp01/85/Gestion-risques-87-320.jpg)
![CHAPITRE 7. LES PROGRAMMES DE STRESS-TESTING
Nous en d´duisons l’expression suivante pour la log-vraisemblance :
e
1
−ξ
1+ξ χ+ − µ
n χ+ − µ
n
χ+ ; θ = − ln σ −
n ln 1 + ξ − 1+ξ (7.16)
ξ σ σ
L’estimateur du maximum de vraisemblance correspond alors `
a
N
ˆML = arg max
θ χ+ ; θ (7.17)
n
θ∈Θ n=1
avec Θ l’espace des param`tres. L’estimation de l’expression (7.17) est relativement ais´e ` condition de
e e a
prendre quelques pr´cautions, notamment pour la sp´cification de Θ (` cause de la singularit´ au point
e e a e
ξ = 0). Pour les applications, nous avons utilis´ l’algorithme de Bryoden-Flectcher-Goldfarb-Shanno en
e
utilisant un jacobien analytique (voir l’annexe 7.5.6.2).
7.5.3 Le concept de temps de retour
Pour appliquer la th´orie des extrˆmes ` la finance, il est n´cessaire d’introduire la notion de temps de
e e a e
retour. Consid´rons un ´v´nement E ayant une probabilit´ d’occurence ´gale ` α. La loi d’apparition de
e e e e e a
cet ´v´nement est alors une variable al´atoire g´om´trique de probabilit´ α. Son esp´rance math´matique
e e e e e e e e
est
1
τ= (7.18)
α
τ est le temps de retour de E.
Exemple 2 Consid´rons une VaR 99%. Le temps de retour associ´ ` l’´v´nement “d´passement de la
e e a e e e
VaR” est
1
τ= = 100 (7.19)
1 − 0.99
Si la p´riode de d´tention est de 1 jour, le temps de retour de la VaR 99% est 100 jours. Cela veut dire
e e
qu’on d´passe la VaR journali`re en moyenne tous les 100 jours.
e e
−1
D´finition 1 Soit α = Pr {χ+ ≤ x}. Le temps de retour de l’´v´nement Pr {χ+ x} est ´gal ` (1 − α)
e n e e n e a
p´riodes de r´f´rence. Le temps de retour en jours est donc
e ee
1
τ =ϕ (7.20)
1−α
Remarque 12 Nous pouvons comparer les r´sultats entre une V aR traditionnelle et une V aR GEV `
e a
partir de la relation suivante :
αGEV = 1 − ϕ (1 − αVAR ) (7.21)
7.5.4 Applications
´
Nous reportons les r´sultats obtenus par Bezat et Nikeghbali [2000] et Bouye, Durrleman, Ni-
e
keghbali, Riboulet et Roncalli [2000] avec la base de donn´es LME (les cours consid´r´s sont celui
e ee
de l’aluminium AL, du forward 15 mois de l’aluminium AL-15 et du cuivre CU).
Nous ´laborons des sc´narios de crise de la mani`re suivante. On se donne des temps de retour ´lev´s
e e e e e
de l’ordre de 5 ans, 10 ans, 25 ans, 50 ans, 75 ans et 100 ans et on utilise la formule (7.20) pour calculer
la variation maximale n´gative des cours sur une journ´e. Les r´sultats obtenus sont10 :
e e e
10 Pour information, la valeurs des param`tres estim´s sont
e e
Param`tres
e AL AL-15 CU
µ 0.022 0.018 0.028
σ 0.007 0.006 0.013
ξ 0.344 0.275 0.095
INTRODUCTION A LA GESTION DES RISQUES 78](https://image.slidesharecdn.com/gestionrisques-130221132633-phpapp01/85/Gestion-risques-88-320.jpg)
![CHAPITRE 7. LES PROGRAMMES DE STRESS-TESTING
Echelles de Risque (en variation journali`re)
e
pour des positions longues (en %)
Temps de Retour AL AL-15 CU
5 -6.74 -4.82 -8.03
10 -8.57 -5.90 -9.35
25 -11.75 -7.68 -11.23
50 -14.91 -9.36 -12.76
75 -17.14 -10.49 -13.70
100 -18.92 -11.38 -14.39
Echelles de Risque (en variation journali`re)
e
pour des positions courtes (en %)
Temps de Retour AL AL-15 CU
5 6.96 5.79 7.53
10 8.35 7.10 8.82
25 10.46 9.20 10.73
50 12.32 11.12 12.34
75 13.52 12.39 13.36
100 14.43 13.38 14.12
Nous avons report´ en outre sur les figures (7.10) et (7.11) la densit´ des lois d’extrˆmes estim´es ainsi
e e e e
que la relation entre l’´chelle de risque et le temps de retour dans le cas des positions longues.
e
Notons qu’il existe d’autres alternatives ` l’utilisation de la GEV. Costinot, Riboulet et Roncalli
a
[2000] utilisent une approche dite semi-param´trique en s’appuyant sur le fait que les s´ries financi`res
e e e
appartiennent au domaine d’attraction de la distribution de Fr´chet. Les quantiles extrˆmes se d´duisent
e e e
des quantiles empiriques ` partir d’une simple homoth´tie param´tr´e par l’indice de queue (voir aussi
a e e e
les travaux de Straetmans [1999,2000]). Dans cette approche, l’indice de queue est alors donn´ pare
l’estimateur de Hill.
GRAPHIQUE 7.10. Estimation des densit´ des lois des extrˆmes
e e
´ ˆ
7.5. LA THEORIE DES VALEURS EXTREMES 79](https://image.slidesharecdn.com/gestionrisques-130221132633-phpapp01/85/Gestion-risques-89-320.jpg)
![CHAPITRE 7. LES PROGRAMMES DE STRESS-TESTING
GRAPHIQUE 7.11. Relation entre l’´chelle de risque et le temps de retour
e
7.5.5 Le cas multidimensionnel
Cette partie fera l’objet d’un d´veloppement dans le cours “Gestion des risques multiples”. Pour une
e
´
premi`re approche, vous pouvez consulter Bezat et Nikeghbali [2000] et Bouye, Durrleman, Ni-
e
keghbali, Riboulet et Roncalli [2000].
7.5.6 Annexes
7.5.6.1 Forme g´n´rale d’une loi d’extrˆmes
e e e
Nous pouvons montrer que la forme g´n´rale d’une loi d’extrˆmes est exp (h (x)). Nous avons GN (x) =
e e e
N
F (x) et
N N −1
dGN (x) = F (x) ln F (x) dN + N F (x) f (x) dx (7.22)
Nous en d´duisons que
e
f (x)
d ln GN (x) = ln F (x) dN + N dx := hN (x) (7.23)
F (x)
Il est alors facile de montrer que sous certaines conditions de r´gularit´, hN (x) = h (x) lorsque N −→ ∞
e e
et F (x) −→ 1− . En introduisant une contrainte de stabilit´ (la distribution des extrema d’un sous-
e
´chantillon doit ˆtre la mˆme que celle de l’´chantillon original), Boulier, Brabant, Dalaud et Dieu
e e e e
[1997] montrent que h est la solution d’une ´quation fonctionnelle qui ne poss`de que trois solutions.
e e
7.5.6.2 Jacobien analytique de la fonction de log-vraisemblance
Nous avons
1
1 + ξ − ω− ξ
∂µ χ+ ; θ
n =
σω
1
(1 + ξ) − ω − ξ (χ+ − µ) − σω
n
∂σ χ+ ; θ
n =
σ2 ω
1 1 (χ+ − µ) (χ+ − µ)
∂ξ χ+ ; θ
n = 1 − ω− ξ 2 ln ω −
n
− n
(7.24)
ξ ξσω σω
INTRODUCTION A LA GESTION DES RISQUES 80](https://image.slidesharecdn.com/gestionrisques-130221132633-phpapp01/85/Gestion-risques-90-320.jpg)
![avec
χ+ − µ
n
ω =1+ξ (7.25)
σ
Bibliographie
[1] Bahar, R., M. Gold, T. Kitto et C. Polizu [1997], Making the best of the worst, Risk Magazine,
10, August
[2] Bezat, A. et A. Nikeghbali [2000], La th´orie des extrˆmes et la gestion des risques de march´, GT
e e e
ENSAE
[3] Boudoukh, J., M. Richardson et R. Whitelaw [1995], Expect the worst, Risk Magazine, 8,
September
[4] Boulier, J-F., A. Brabant, R. Dalaud et A-L. Dieu [1997]. Risques de march´ : Vue de Profil,
e
Direction de la Recherche et de l’Innovation, Cr´dit Commercial de France, Quants, 28
e
´
[5] Bouye, E., V. Durrleman, A. Nikeghbali, G. Riboulet et T. Roncalli [2000], Copulas for
finance : a reading guide and some applications, Groupe de Recherche Op´rationnelle, Cr´dit Lyonnais,
e e
Working Paper
[6] Coles, S. [1998], Extreme value theory and applications, A course presented at the 44th Reuni˜o
a
Annual de RBRAS, S˜o Paulo, 26-30 July
a
[7] Coles, S. et J. Tawn [1999], Statistical methods for extreme values, A course presented at the 1988
RSS conference, Strathclyde, September 1998
[8] Costinot, A., G. Riboulet et T. Roncalli [2000], Stress-testing et th´orie des valeurs extrˆmes :
e e
une vision quantifi´e du risque extrˆme, Groupe de Recherche Op´rationnelle, Cr´dit Lyonnais, Working
e e e e
Paper
[9] Davidson, R. et J. MacKinnon [1993], Estimation and Inference in Econometrics, Oxford University
Press, Oxford
[10] Drees, H. [1997], Optimal rates of convergence for estimates of the extreme value index, University
of Cologne, Technical report
[11] Drees, H., L. De Haan et S. Resnick [1998], How to make a Hill plot, University of Cologne,
Technical report
[12] Dunbar, N. et R. Irving [1998], This is the way the world ends, Risk Magazine, 11, December
¨
[13] Embrechts, P., Kluppelberg, C. et T. Mikosch [1997], Modelling Extremal Events for Insurance
and Finance, Springer-Verlag, Berlin
[14] Embrechts, P., Resnick, S.I. et G. Samorodnitsky [1997], Extreme value theory as a risk ma-
nagement tool, Departement Mathematik, ETHZ, Z¨rich, Preprint
u
[15] Embrechts, P., Resnick, S.I. et G. Samorodnitsky [1998], Living on the edge, Risk Magazine,
11, January
[16] McNeil, A.J. [1997a], On extremes and crashes, Departement Mathematik, ETHZ, Z¨rich, Preprint
u
[17] McNeil, A.J. [1997b], Estimating the tails of loss severity distributions using extreme value theory,
ASTIN Bulletin, 27, 117-137
[18] McNeil, A.J. [1998a], History repeating, Risk Magazine, 11, January
[19] McNeil, A.J. [1998b], Calculating quantile risk measures for financial return series using extreme
value theory, Departement Mathematik, ETHZ, Z¨rich, Preprint
u
[20] McNeil, A.J. [1999], Extreme value theory for risk managers, Departement Mathematik, ETHZ,
Z¨rich, Preprint
u
[21] Tucker, T et A. Lawrence [1998], Chain reaction, FOW, November, 25-28](https://image.slidesharecdn.com/gestionrisques-130221132633-phpapp01/85/Gestion-risques-91-320.jpg)




![´ ´ ´ ´
CHAPITRE 8. PRESENTATION GENERALE DU RISQUE DE CREDIT
– La d´gradation de la qualit´ du cr´dit constitue la troisi`me source de risque portant sur une dette.
e e e e
Si la perception de la qualit´ de l’emprunteur se d´t´riore, la prime de risque accord´e par les
e ee e
march´s financiers s’accroˆ en cons´quence. De plus, si l’emprunteur b´n´ficie d’une note de la part
e ıt e e e
d’une agence de notation, celle-ci est susceptible de se d´grader suite ` la perception n´gative des
e a e
march´s.
e
Notons que les risques de d´faut et de d´gradation sont fortement corr´l´s dans la mesure o` la d´gradation
e e ee u e
de la qualit´ de la contrepartie peut ˆtre pr´curseur d’un d´faut. Ce sont n´anmoins deux risques bien
e e e e e
distincts. Le risque de d´gradation se traduit par une possible d´valorisation de la dette au cours sa
e e
p´riode de vie. Les pertes li´es ` la d´gradation de la qualit´ de la contrepartie se r´alisent donc en cas
e e a e e e
de vente anticip´e de la dette sans qu’un d´faut se soit pour autant produit.
e e
8.2 Le march´ du risque de cr´dit
e e
C’est un march´ tr`s h´t´rog`ne puisque le risque de cr´dit prend diff´rentes formes. On distingue
e e ee e e e
n´anmoins deux grandes cat´gories. La premi`re correspond aux prˆts bancaires (et plus g´n´ralement
e e e e e e
aux diff´rentes facilit´s de cr´dit telles que les lignes de cr´dit confirm´es ou non confirm´es). Dans ce
e e e e e e
cas l`, l’´v´nement de cr´dit (credit event) est un risque de d´faillance (ou de contrepartie). La seconde
a e e e e
cat´gorie correspond aux obligations risqu´es. Cela explique en partie que les banques utilisent des outils
e e
diff´rents pour mesurer et g´rer le risque de cr´dit selon le portfeuille consid´r´. La principale diff´rence
e e e ee e
tient au choix de l’horizon temporel (default mode (DM) paradigm et Mark-to-market (MTM)
paradigm).
8.2.1 Le march´ des prˆts bancaires
e e
Ce n’est pas un march´ au sens ´conomique du terme. Le risque de cr´dit provient d’une asym´trie
e e e e
d’information entre la banque et son client.
– Prˆts court terme et long terme ;
e
– Lignes de cr´dit confirm´es et non confirm´es ;
e e e
– Financement structur´s ;
e
– etc.
8.2.2 Le march´ des obligations risqu´es
e e
En ce qui concerne le march´ des obligations risqu´es (risky bond), Turc [1999] consid´re que la
e e e
probl´matique du risque de cr´dit est triple :
e e
D’une part, l’´mission des obligations implique une probl´matique de la demande de cr´dit : pourquoi
e e e
se financer par obligation ? D’autre part elle est achet´e, ´chang´e, agr´ment´e de d´riv´s en tout genre,
e e e e e e e
sujette ` sp´culation d’o` une probl´matique de trading, ou d’interm´diation financi`re : comment prendre
a e u e e e
en compte le risque de d´faut dans le prix d’un produit d´riv´ ? Enfin, l’obligation est partie int´grante du
e e e e
portefeuille d’un investisseur, ce qui engendre un probl´matique de gestion : comment g´rer un portfeuille
e e
avec risque de cr´dit, comment estimer le risque globalement encouru par le d´tenteur de ce portefeuille ?
e e
L’investisseur en obligations risqu´es cherche un placement plus rentable que celui des obligations d’´tat
e e
(sovereign debt). La diff´rence entre la rentabilit´ d’une obligation risqu´e et d’une obligation sˆre est
e e e u
appel´e le spread de taux. Deux composantes expliquent ce spread de taux : le spread de cr´dit (risque
e e
de d´pr´ciation de la qualit´ de signature de l’emprunteur) et la liquidit´ (profondeur du carnet d’ordre).
e e e e
8.2.3 Les d´riv´s de cr´dit
e e e
Contrairement aux prˆts bancaires et aux obligations risqu´es qui sont une source de risque de cr´dit,
e e e
les d´riv´s du cr´dit sont des instruments financiers hors bilan qui permettent de transf´rer le risque de
e e e e
l’actif ` une contrepartie sans c´der cet actif.
a e
1. Premi`re g´n´ration de d´riv´s de cr´dit
e e e e e e
INTRODUCTION A LA GESTION DES RISQUES 86](https://image.slidesharecdn.com/gestionrisques-130221132633-phpapp01/85/Gestion-risques-96-320.jpg)
![– Credit Guarantees
– Revolving Credit
– Repo Market
– Asset Swaps
– Structured Notes
2. Deuxi`me g´n´ration de d´riv´s de cr´dit
e e e e e e
– Credit default swaps (CDS)
– Default digital put
– Total return swaps
– Credit linked notes
– Spread Options
3. Troisi`me g´n´ration de d´riv´s de cr´dit
e e e e e e
– First-to-defaults (F2D)
– First losses
– Collateralized bond obligations (CBO)
– Collateralized loan obligations (CLO)
– Collateralized debt obligations (CDO)
– Basket credit derivatives
Bibliographie
[1] Credit risk modelling : current practices and applications, Basle Committee on Banking Supervision,
April 1999, N◦ 49
[2] Legras, J. et L. Bonnat [2001], Le Cooke est mort, vive le Cooke, Cr´dit Commercial de France,
e
Quants, 38
[3] Turc, J. [1999], Pr´sentation du march´ du risque de cr´dit, CDC March´s, S´minaire INRIA du 8
e e e e e
juin 1999](https://image.slidesharecdn.com/gestionrisques-130221132633-phpapp01/85/Gestion-risques-97-320.jpg)


![CHAPITRE 9. L’APPROCHE STANDARD
5. The Inter-American Development Bank (IADB)
6. The European Investment Bank (EIB)
7. The Nordic Investment Bank (NIB)
8. The Caribbean Development Bank (CDB)
9. The Council of Europe Development Bank (CEDB)
Pour les banques, les autorit´s r´glementaires ont le choix entre deux options. Dans la premi`re
e e e
option, la pond´ration d´pend de la notation du pays et non de la banque. Par exemple, la
e e
pond´ration 20% est applicable aux banques dont le si`ge social est dans un ´tat not´ AAA ` AA-. Dans
e e e e a
la seconde option, la pond´ration d´pend de la notation de la banque et de la maturit´ de
e e e
la cr´ance. Ainsi, une pond´ration plus favorable est appliqu´e aux cr´ances d’une dur´e inf´rieure ou
e e e e e e
´gale ` 3 mois. Afin de bien comprendre les deux options, voici quelques exemples :
e a
Caract´ristiques de la cr´ance
e e Pond´ration
e
Rating du pays Rating de la banque Maturit´ e Option 1 Option 2
1 AAA BBB 1 mois 20% 20%
2 AAA BBB 10 ans 20% 50%
3 BB+ AA 3 mois 100% 20%
4 BB+ AA 1 an 100% 20%
5 non not´e A 4 mois 100% 50%
6 A non not´e 4 mois 50% 50%
Pour les entreprises d’investissement (securities firms), les pond´rations sont les mˆmes que celles
e e
des banques.
Les pond´rations pour les entreprises (corporates) s’appliquent aussi aux compagnies d’assurance
e
(insurance companies). Contrairement aux banques, il n’y a qu’une seule option et seule la notation
de l’entreprise est prise en compte. N´anmoins, le d´coupage des classes de rating est diff´rent de celui
e e e
des emprunteurs souverains. Concernant les entreprises non not´es, le Comit´ de Bˆle consid`re que leurs
e e a e
cr´ances ne sont pas g´n´ralement de qualit´ faible (signal low credit quality) et qu’une pond´ration
e e e e e
de 150% serait trop p´nalisante.
e
Enfin, les cr´ances garanties par des biens immobiliers r´sidentiels (claims secured by residential
e e
property) et par des biens immobiliers commerciaux (claims secured on commercial real estate) sont
pond´r´es respectivement ` 50% et 100%. Concernant les actifs de la banque de r´seau (retail assets),
ee a e
aucune m´thodologie n’a encore ´t´ propos´e.
e ee e
9.3 Les notations externes
Le cœur de l’approche standard (Standardized Approach ou SA) est bien sˆr les notations externes.
u
Celles-ci sont faites par des organismes externes d’´valuation de cr´dit (External Credit Assessment
e e
Institution ou ECAI). Nous pouvons citer par exemple les agences de rating les plus c´l`bres Standard
ee
Poor’s, Moody’s, Fitch IBCA et DCR. La Banque de France fournit aussi une notation appel´e “code BdF”.
e
Nous pouvons aussi mentionner que la COFACE produit des notes pays. Les autorit´s r´glementaires
e e
auront donc ` valider les ECAI que pourront utiliser les banques. Pour cela, une ECAI devra v´rifier
a e
diff´rents crit`res d’´ligibilit´ (voir les paragraphes 53 ` 62 du document [1]) :
e e e e a
– Objectivit´ (m´thodologie rigoureuse et valid´e par un backtesting)
e e e
– Ind´pendance (pas de pressions politiques ou ´conomiques susceptibles d’influencer la notation)
e e
– Acc`s international et transparence
e
– Information (publication des m´thodologies d’´valuation)
e e
– Ressources
9.3. LES NOTATIONS EXTERNES 91](https://image.slidesharecdn.com/gestionrisques-130221132633-phpapp01/85/Gestion-risques-101-320.jpg)
![CHAPITRE 9. L’APPROCHE STANDARD
– Cr´dibilit´
e e
La principale difficult´ va ˆtre le mapping des diff´rentes notations. Le 30 avril 2001, le Comit´ de Bˆle
e e e e a
proposait la correspondance suivante entre les deux grandes agences internationales de notation :
Prime High Grade Upper Lower
Maximum Safety High Quality Medium Grade Medium Grade
SP AAA AA+ AA AA- A+ A A- BBB+ BBB BBB-
Moody’s Aaa Aa1 Aa2 Aa3 A1 A2 A3 Baa1 Baa2 Baa3
Non Investment Speculative Highly Substantial In Poor
Grade Speculative Risk Standing
SP BB+ BB BB- B+ B B- CCC+ CCC CCC-
Moody’s Ba1 Ba2 Ba3 B1 B2 B3 Caa1 Caa2 Caa3
Extremely May be Default
Speculative in Default
SP CC C D
Moody’s Ca C
Des travaux sont en cours pour obtenir un mapping plus exhaustif. A titre d’exemple, Bardos [2001]
propose le rapprochement suivant entre les cotations Banque de France et les ratings SP pour les risques
pond´r´s Corporate :
ee
Notation AAA ` AA-
a A+ ` A-
a BBB+ ` BB-
a BB- ` C
a non not´
e
Cote BdF A37 Autres A37 47 57, 67, 58, 59, 68 et 69
Pond´ration
e 20% 50% 100% 150% 100%
A titre d’exemples, voici quelques notations que nous pouvons trouver sur le site de SP :
http ://www.standardandpoors.com/RatingsActions/index.html
– Extrait de Sovereign Ratings List (October 11, 2001) :
Local Currency Foreign Currency
Long- Short- Long- Short-
Sovereign term Outlook term term Outlook term
rating rating rating rating
Argentina CCC+ Negative C CCC+ Negative C
Belgium AA+ Stable A-1+ AA+ Stable A-1+
Canada AAA Stable A-1+ AA+ Stable A-1+
Colombia BBB Negative A-3 BB Negative B
Denmark AAA Stable A-1+ AAA Stable A-1+
France AAA Stable A-1+ AAA Stable A-1+
Suriname B Watch Neg B- Watch Neg
INTRODUCTION A LA GESTION DES RISQUES 92](https://image.slidesharecdn.com/gestionrisques-130221132633-phpapp01/85/Gestion-risques-102-320.jpg)



![CHAPITRE 9. L’APPROCHE STANDARD
GRAPHIQUE 9.2. Evolution de la pond´ration ajust´e r en fonction de l’exposition E (CA = 50)
e e
avec HE la d´cote li´e ` la volatilit´ de l’exposition, HC la d´cote li´e ` la volatilit´ de la sˆret´ et HF X
e e a e e e a e u e
la d´cote li´e au risque de change. Pour calculer ces d´cotes, nous avons deux possibilit´s :
e e e e
– utiliser des d´cotes prudentielles standard donn´es par le Comit´ de Bˆle,
e e e a
– ou les estimer statistiquement.
L’annexe 3 du document [1] pr´sente les estimations des d´cotes prudentielles standard (en %) lorsque
e e
la p´riode de d´tention est 10 jours et la valorisation et la reconstitution des marges sont journali`res
e e e
(10-business day haircuts assuming daily mark-to-market and daily remargining) :
Notation Maturit´ r´siduelle
e e Emprunteurs souverains Banques/Entreprises
0 ` 1 an
a 0.5 1
AAA ` AA
a 1` 5 ans
a 2 4
+5 ans 4 8
0 ` 1 an
a 1 2
A ` BBB
a 1` 5 ans
a 3 6
+5 ans 6 12
BB 20
Esp`ces
e 0
Or 15
Actions d’un indice principal 20
Actions d’une bourse “internationale” 30
Risque FX 8
Consid´rons une sˆret´ de de $100 sur une obligation du tr´sor AAA. Si la maturit´ r´siduelle de l’obli-
e u e e e e
gation est 10 ans et si la sˆret´ est en esp`ces dans la devise de l’obligation, alors nous avons
u e e
100
CA = = $96.153
1 + 0.04 + 0 + 0
INTRODUCTION A LA GESTION DES RISQUES 96](https://image.slidesharecdn.com/gestionrisques-130221132633-phpapp01/85/Gestion-risques-106-320.jpg)
![CHAPITRE 9. L’APPROCHE STANDARD
Si la devise de l’obligation et la devise des esp`ces sont diff´rentes, il y a un risque de change et nous
e e
obtenons
100
CA = = $89.285
1 + 0.04 + 0 + 0.08
Supposons maintenant que la sˆret´ correspond ` de l’or, nous avons
u e a
100
CA = = $84.033
1 + 0.04 + 0.15 + 0
Consid´rons maintenant une obligation d’´tat BB, une sˆret´ constitu´e par des actions d’une bourse
e e u e e
“internationale” (mais qui ne sont pas dans un indice principal) libell´es dans une devise ´trang`re. La
e e e
valeur ajust´e de la sˆret´ devient
e u e
100
CA = = $63.291
1 + 0.20 + 0.30 + 0.08
Si nous appliquons le risque r´siduel, nous obtenons (1 − 15%) × $63, 291 = $53, 797. Dans ce dernier cas,
e
la valeur ajust´e du colat´ral apr`s prise en compte du risque r´siduel ne repr´sente que la moiti´ de la
e e e e e e
valeur nominale de la protection.
Dans le cadre d’une estimation interne des d´cotes, celle-ci doit v´rifier les mˆmes crit`res quantitatifs
e e e e
que ceux pour le risque de march´. En particulier, la p´riode de d´tention est fix´e ` 10 jours et le seuil
e e e e a
de confiance est 99%.
Quelque soit l’approche retenue pour calculer les d´cotes (standard ou mod`le interne), les valeurs de
e e
celles-ci doivent ˆtre modifi´es
e e
– si la p´riode N de reconstitution des marges pour les op´rations de march´ est sup´rieure ` la
e e e e a
journ´e
e
N +9
H = H10 (9.8)
10
– ou si la p´riode N de revalorisation pour les op´rations de prˆts garantis est sup´rieure ` la journ´e2
e e e e a e
N + 19
H = H10 (9.9)
10
H10 repr´sente ici la d´cote ` 10 jours.
e e a
9.4.1.2 L’approche simple
Dans cette approche, la pond´ration applicable ` la partie non couverte (E − C) est celle de la contre-
e a
partie ou de l’emprunteur et la pond´ration applicable ` la sˆret´ C est celle de l’instrument de couverture
e a u e
(avec un plancher de 20%).
9.4.2 Les garanties et les d´riv´s de cr´dit
e e e
Pour tenir compte de garanties (et des d´riv´s de cr´dit), certaines conditions doivent ˆtre remplies
e e e e
(voir les articles 183 ` 199 du document [1]) :
a
– la garantie est directe, explicite, irr´vocable et inconditionnelle ;
e
– information publique ;
– etc.
2 Dans ce cas, la p´riode de d´tention standard est 20 jours ouvr´s et non 10 jours ouvr´s.
e e e e
´ ´
9.4. LES PROCEDURES DE REDUCTION DES RISQUES 97](https://image.slidesharecdn.com/gestionrisques-130221132633-phpapp01/85/Gestion-risques-107-320.jpg)
![CHAPITRE 9. L’APPROCHE STANDARD
Dans le cas d’une couverture proportionnelle, on calcule les risques pond´r´s de la fa¸on suivante
ee c
r × E = r × (E − GA ) + [(r × w) + g (1 − w)] GA (9.10)
avec GA le montant de la garantie ajust´ du risque de change et g la pond´ration du risque de la garantie.
e e
Nous remarquons que dans le cas d’une protection totale (E = GA ), cette expression devient
r = (r × w) + g (1 − w) (9.11)
et r = g si w est ´gal ` z´ro. La m´thode de calcul est proche de celle issue de l’approche simple pour
e a e e
les sˆret´s. En effet, si nous posons w ´gal ` z´ro, nous avons
u e e a e
r × E = r × (E − GA ) + g × GA (9.12)
Dans le cas d’une couverture par tranches (senior et junior), nous distinguons deux cas :
1. Le risque de cr´dit sur la tranche junior GJ est transf´r´ et le risque de cr´dit sur la tranche senior
e ee e
GS est conserv´ :
e
r × E = r × GS + [(r × w) + g (1 − w)] GJ (9.13)
Cela revient donc ` une couverture proportionelle avec GA = GJ = E − GS .
a
2. Le risque de cr´dit sur la tranche junior GJ est conserv´ et le risque de cr´dit sur la tranche senior
e e e
GS est transf´r´ :
ee
r × E = [(r × w) + g (1 − w)] GS
On consid`re dans ce cas que le risque sur la tranche junior (qui est un risque de premi`re perte)
e e
doit ˆtre d´duit du montant des fonds propres.
e e
Concernant les risques r´siduels, voici les valeurs de w calcul´e par le Comit´ de Bˆle :
e e e a
w Garantie
0 Garantie souveraine
0.15 Autres garanties
0.15 D´riv´s de cr´dit
e e e
9.4.3 Autres consid´rations
e
9.4.3.1 Compensation de bilan
Le Comit´ de Bˆle reconnait les accords de compensation de bilan dans le portefeuille bancaire des
e a
prˆts et d´pˆts. N´anmoins, la contrepartie doit satisfaire certains crit`res. Dans ce cas, le facteur de
e e o e e
pond´ration du risque r´siduel w est ´gal ` 0.
e e e a
9.4.3.2 Le d´calage des maturit´s
e e
Un d´calage de maturit´ intervient losque la maturit´ r´siduelle de la couverture est plus faible que
e e e e
celle de l’exposition sous-jacente. Dans ce cas, la pond´ration corrig´e r est
e e
r si TCRM ≤ 1 an
r = TCRM TCRM
1− TE r+ TE r si 1 an ≤ TCRM ≤ TE
avec r la pond´ration de l’exposition, r la pond´ration ajust´e de l’exposition, TE la maturit´ de l’ex-
e e e e
position et TCRM la maturit´ de la couverture CRM.
e
INTRODUCTION A LA GESTION DES RISQUES 98](https://image.slidesharecdn.com/gestionrisques-130221132633-phpapp01/85/Gestion-risques-108-320.jpg)
![CHAPITRE 9. L’APPROCHE STANDARD
9.4.3.3 L’asym´trie des devises
e
Nous rappelons que la valeur ajust´e du collat´ral CA est
e e
C
CA = (9.14)
1 + HE + HC + HF X
Dans le cadre d’une compensation de bilan, la valeur ajust´e du d´pˆt re¸u D est
e e o c
D
DA = (9.15)
1 + HF X
Concernant les garanties et les d´riv´s de cr´dit, une formule analogue existe
e e e
G
GA =
1 + HF X
9.4.4 Quelques exemples
Nous reproduisons ici les exemples donnn´s par le Comit´ de Bˆle (annexe 4 du document [1]).
e e a
9.4.4.1 Collateralised transactions
Flat repo with a bank counterparty, not satisfying the conditions for zero w
Bank A repos out $1,000-worth of 10-year AAA-rated sovereign securities to Bank B (risk weighted
at 20%) and receives $1,000 in cash collateral. Revaluation and remargining are conducted daily. There
is no currency mismatch or maturity mismatch. In this case a haircut of 4% is applied to the sovereign
securities lent out while there is no haircut for the collateral received, since it is cash. Then the adjusted
value of the collateral, CA , is
C
CA =
1 + HE + HC + HF X
$1000
=
1 + 0.04 + 0 + 0
= $962
In order to calculate the risk weighted assets, the exposure E, CA , the weight for remaining risks (w =
0.15), and the risk weight of counterparty (r = 0.2) are inserted into the equation below. Note that the
exposure ($1,000) exceeds the adjusted value of collateral ($962).
r ×E = r × max ((E − (1 − w) CA ) , w × E)
= 0.2 × (1000 − 0.85 × 962)
= $36.50
So, the risk weighted assets will be $36.50 (r = 20% and r = 3.65%).
Flat reverse repo with a bank counterparty
This is the opposite side of the transaction in Example above. Bank B takes in $1,000 worth of 10-year
AAA-rated sovereign securities (from this banks perspective these securities are the collateral received)
and provides $1,000 in cash to Bank A (counterparty risk weight 50%). Revaluation and remargining are
conducted daily. There is no currency mismatch or maturity mismatch. In this case a haircut of 4% is
applied to the sovereign securities reverse repoed in (i.e. taken as collateral) while there is no haircut for
the cash posted. Then the adjusted value of the collateral, CA , is
$1000
CA =
1 + 0 + 0.04 + 0
= $962
´ ´
9.4. LES PROCEDURES DE REDUCTION DES RISQUES 99](https://image.slidesharecdn.com/gestionrisques-130221132633-phpapp01/85/Gestion-risques-109-320.jpg)



![9.4.4.3 Guarantees/credit derivatives
Loan to an unrated corporate fully guaranteed by a third-party corporate eligible for a 20% risk weight
A bank has lent $1000 to an unrated corporate and has obtained a guarantee for the full amount from
a third-party corporate (20% counterparty risk weight). The formula is
r × E = r × (E − GA ) + [(r × w) + g (1 − w)] GA
Here E = GA = $1000, r = 100%, g = 20%, w = 0.15 and so the risk-weighted assets are
r ×E = [(100% × 15%) + 20% (1 − 15%)] × $1000
= $320
Loan to an unrated corporate fully protected by a guarantee with a third-party bank eligible for a 20%
risk weight
A bank has lent $1000 to an unrated corporate and has obtained a guarantee for the full amount from
a third-party bank (20% counterparty risk weight). Since the guarantor is a bank, a zero w applies. So,
the risk weighted assets will be
r ×E = [(100% × 0%) + 20% (1 − 0%)] × $1000
= $200
Note that this result is equivalent to the present substitution approach.
Pro rata guarantee from bank
Bank A has an exposure of $1000 with a three-year residual maturity, and has obtained a pro rata
guarantee of $500 of this exposure, also with a three-year residual maturity. The formula for r is
r ×E = r × (E − GA ) + [(r × w) + g (1 − w)] GA
= 100% × ($1000 − $500) + [(100% × 0%) + 20% × (1 − 0%)] × $500
= $600
Bibliographie
[1] Basel Committee on Banking Supervision, The Standardized Approach to Credit Risk — Consultative
Document, Supporting document to the New Basel Capital Accord, January 2001
[2] Bardos [2001], Statistiques de d´faillance selon les cotations, Banque de France, Secretariat G´n´ral,
e e e
Direction des Entreprises, Observatoire des Entreprises](https://image.slidesharecdn.com/gestionrisques-130221132633-phpapp01/85/Gestion-risques-113-320.jpg)


![´
CHAPITRE 10. LA METHODE IRB
1. Le risque porte sur une ou des personnes individuelles.
2. Le risque porte sur certains produits (cartes de cr´dits, prˆts aux particuliers, cr´dit bail, d´couverts,
e e e e
cr´dits aux logements, etc.).
e
3. L’exposition est d’un montant relativement faible.
4. L’exposition est “comprise” parmi un grand nombre d’expositions comparables (notion de granu-
larit´ du portefeuille).
e
Comme nous l’avons vu, les composantes de risque sont la probabilit´ de d´faillance, la perte en cas
e e
de d´faillance et l’exposition en cas de d´faillance. Une quatri`me composante concerne la maturit´
e e e e
M. Quelle que soit la m´thode (simple ou avanc´e), les probabilit´s de d´faillance sont estim´es par la
e e e e e
banque et doivent correspondre ` une moyenne conservatrice des probabilit´s de d´faillance sur le long
a e e
terme (conservative view of a long-run average PD). Bien sˆr, ces probabilit´s de d´faillance sont li´es
u e e e
a
` la construction des notations internes. Dans l’approche simple, les valeurs de LGD sont fournies par
les autorit´s de r´gulation. Le document consultatif de Janvier 2001 propose une valeur de 50% pour la
e e
plupart des transactions (dettes seniors) et 75% pour les dettes subordonn´es. Dans la m´thode avanc´e,
e e e
c’est la banque elle-mˆme qui fournit la valeur. En r`gle g´n´rale, l’exposition en cas de d´faillance sera
e e e e e
´gale au montant nominal du cr´dit. Le calcul des risques pond´r´s RWA correspond alors
e e ee
RWA = r × EAD (10.1)
avec r la pond´ration “interne” calcul´e ` partir de PD, LGD, M et la fonction de risques pond´r´s.
e e a ee
La banque peut alors calculer la valeur totale des risques pond´r´s par portefeuille (c’est-`-dire pour
ee a
chaque classe d’exposition) en faisant une simple somme. Finalement, un facteur d’ajustement qui refl`te
e
la granularit´ du portefeuille est appliqu´ pour obtenir la valeur finale des risques pond´r´s.
e e ee
10.1.2 D´finition de la d´faillance
e e
On remarque que la notion cl´ dans cette approche est donc la d´faillance. Dans les paragraphes 139
e e
a
` 151 du document [3], celle-ci est d´finie de la fa¸on suivante :
e c
La d´faillance d’une contrepartie donn´e est suppos´e ˆtre survenue si l’un des quatres ´v´nements
e e e e e e
a eu lieu
1. L’emprunteur ne peut plus honorer ses obligations de remboursement (principal, int´rˆts ou com-
ee
mission) en totalit´.
e
2. Il est survenu un ´v´nement de cr´dit (par exemple, une provision sp´cifique).
e e e e
3. L’emprunteur est en d´faut de paiement depuis 90 jours sur l’un de ses cr´dits.
e e
4. L’emprunteur est en faillite juridique.
On voit donc que cette d´finition recouvre deux types de cr´ances : les cr´ances contentieuses (le risque
e e e
de perte est constat´) et les cr´ances douteuses (le risque de perte est potentiel). Le Comit´ de Bˆle
e e e a
est conscient que cela peut poser des probl`mes de p´rim`tre. C’est pourquoi des travaux sont en cours
e e e
concernant le mapping d’estimations bas´es sur d’autres d´finitions.
e e
10.1.3 La notation interne
Celle-ci est au cœur de la m´thode IRB. La table 10.1 est un exemple de syst`me de notation interne. En
e e
g´n´ral, c’est un syst`me avec diff´rents niveaux (grade) et ` chaque niveau est associ´e une probabilit´
e e e e a e e
de d´faillance. Ce syst`me de notation fera l’objet d’une validation par les autorit´s de r´glementation et
e e e e
la banque devra d´montrer qu’il est conforme aux exigences minimum depuis au moins trois ans.
e
10.2 L’exemple de la m´thode IRB pour les entreprises
e
Nous reprenons ici les grandes lignes du chapitre 2 du document [3]. Le Comit´ de Bˆle remarque que
e a
les banques utilisent un syst`me de notation interne bas´ sur 10 notes en moyenne.
e e
INTRODUCTION A LA GESTION DES RISQUES 106](https://image.slidesharecdn.com/gestionrisques-130221132633-phpapp01/85/Gestion-risques-116-320.jpg)
![´
CHAPITRE 10. LA METHODE IRB
Rating Degree of risk Definition Borrower category
by self-assessment
1 No essential risk Extremely high degree of certainty of repayment
2 Negligible risk High degree of certainty of repayment
3 Some risk Sufficient certainty of repayment
A Better There is certainty of repayment, but substential changes in
4 B than the environment in the future may have some impact on
C average this incertainty Normal
A There are no problems foreseeable in the future, but a strong
5 B Average likelihood of impact from changes in the environment
C
A There are no problems foreseeable in the future, but the future
6 B Tolerable cannot be considered entirely safe.
C
7 Lower than There are no problems at the current time but the financial position
average of the borrower is relatively weak
A Needs There are problems with lending terms or fulfilment, or the borrower’s Needs
8 preventive business conditions are poor or unstable, or there are other factors attention
B management requiring careful management
9 Needs There is a high likelihood of bankruptcy in the future In danger of bankruptcy
10 I serious The borrower is in serious financial straits and “effectively bankrupt” Effectively bankrupt
II management The borrower is bankrupt Bankrupt
TABLE 10.1. Exemple de syst`me de notation interne (Ieda, Marumo et Yoshiba [2000])
e
10.2.1 Formulation des pond´rations de risque
e
Les pond´rations de risque (risk weights) sont obtenues ` partir d’une fonction sp´cifique continue (risk
e a e
weight function). Nous avons
r = RW (PD, LGD, M) (10.2)
et
RWA = r × EAD
= RW (PD, LGD, M) × EAD (10.3)
Les valeurs de PD, LGD, M et EAD sont exprim´es en chiffres r´els (par exemple, 100% correspond `
e e a
une valeur de 100).
Dans l’approche IRB simple, la maturit´ n’est pas prise en compte. Dans ce cas, la maturit´ moyenne
e e
des expositions est suppos´e ´gale ` 3 ans. Nous avons
e e a
LGD
r = RW = min × BRW (PD) , 12.5 × LGD (10.4)
50
RW repr´sente la pond´ration associ´e ` des valeurs donn´es des composantes de risques et BRW est la
e e e a e
fonction dite benchmark calibr´e pour une perte en cas de d´faillance ´gale ` 50%. Dans la m´thode IRB
e e e a e
avanc´e, la maturit´ est prise en compte. Nous avons alors
e e
LGD
RW = min × BRW (PD) × [1 + (M − 3) b (P D)] , 12.5 × LGD
50
Si la maturit´ M est ´gale ` 3 ans, nous retrouvons la formule de l’approche IRB simple. Le terme
e e a
1 + (M − 3) b (P D) est un facteur d’´chelle multiplicatif lin´aire en M . b (P D) est ici une fonction de la
e e
probabilit´ de d´faillance.
e e
10.2.1.1 Dans l’approche IRB simple
Le Comit´ de Bˆle d´finit la fonction BRW de la fa¸on suivante :
e a e c
1 − PD
BRW (PD) = 976.5 × Φ 1.118 × Φ−1 (PD) + 1.288 × 1 + 0.470 × (10.5)
PD0.44
Dans cette formule, PD est exprim´e en valeur d´cimale (par exemple, 1% correspond ` 0.01). Le Comit´
e e a e
de Bˆle indique que cette fonction de r´f´rence (Benchmark Risk Weight function) est la r´sultante du
a ee e
produit de trois facteurs s´par´s :
e e
´
10.2. L’EXEMPLE DE LA METHODE IRB POUR LES ENTREPRISES 107](https://image.slidesharecdn.com/gestionrisques-130221132633-phpapp01/85/Gestion-risques-117-320.jpg)
![´
CHAPITRE 10. LA METHODE IRB
– Le terme Φ 1.118 × Φ−1 (PD) + 1.288 repr´sente la somme des pertes esp´r´es et non esp´r´es
e ee ee
associ´e ` un portefeuille infiniment granulaire de prˆts de maturit´ 1 an et de perte en cas de
e a e e
d´faillance ´gale ` 100%. La calibration a ´t´ faite ` partir d’un mod`le de risque de cr´dit ` la
e e a ee a e e a
Merton avec un seul facteur de risque syst´matique. Le seuil de confiance et la corr´lation moyenne
e e
des actifs ont ´t´ fix´s respectivement ` 99.5% et 20%.
ee e a
1−PD
– Le terme 1 + 0.470 × PD0.44 est un coefficient d’ajustement qui refl`te une maturit´ moyenne ´gale
e e e
a
` 3 ans.
– Le facteur d’´chelle 976.50 a ´t´ calibr´ pour des valeurs PD et LGD par d´faut ´gales ` 0.7% et
e ee e e e a
50%. Dans ce cas, la fonction BRW (PD) prend la valeur 100%.
Sur le graphique 10.1, nous avons repr´sent´ la fonction de r´f´rence BRW (PD) en fonction de la proba-
e e ee
bilit´ de d´faillance. Nous remarquons que celle-ci croˆ tr`s vite — voir le graphique 10.2 repr´sentant
e e ıt e e
la d´riv´e premi`re ∂ BRW (PD) /∂ PD. Afin de bien mesurer l’impact de l’ajustement de maturit´
e e e e
1−PD
1 + 0.470 × PD0.44 — c’est-`-dire la passage d’une maturit´ un an ` une maturit´ trois ans, le gra-
a e a e
phique 10.3 montre le coefficient d’ajustement dans la formule BRW (PD). Enfin, nous avons report´ e
les valeurs des pond´rations (en %) des actifs risqu´s dans les tables 10.2 ` 10.4. Nous v´rifions que la
e e a e
fonction de r´f´rence a bien ´t´ calibr´e afin que la pond´ration soit approximativement 100% pour une
ee ee e e
probabilit´ de d´faillance ´gale ` 0.7% et une perte en cas de d´faillance ´gale ` 50%.
e e e a e e a
GRAPHIQUE 10.1. Fonction de r´f´rence BRW
ee
Nous pouvons comparer la m´thode SA avec la m´thode IRB simple. La table 10.5 pr´sente les valeurs
e e e
implicites de PD et LGD pour une valeur RW donn´e. La relation est bien sˆr lin´aire par rapport ` la
e u e a
variable LGD.
10.2.1.2 Dans l’approche IRB avanc´e
e
Cette approche diff`re sensiblement de la m´thode simple. En effet, les valeurs de perte en cas de
e e
d´faillance ne sont plus fix´es par le r´gulateur (50% et 75%), mais sont estim´es par la banque. Ensuite,
e e e e
la maturit´ est explicitement prise en compte (elle peut l’ˆtre aussi dans la m´thode simple). Dans ce
e e e
cas, la valeur de la pond´ration devient
e
LGD
RW = min × BRW (PD) × [1 + (M − 3) b (PD)] , 12.5 × LGD (10.6)
50
INTRODUCTION A LA GESTION DES RISQUES 108](https://image.slidesharecdn.com/gestionrisques-130221132633-phpapp01/85/Gestion-risques-118-320.jpg)
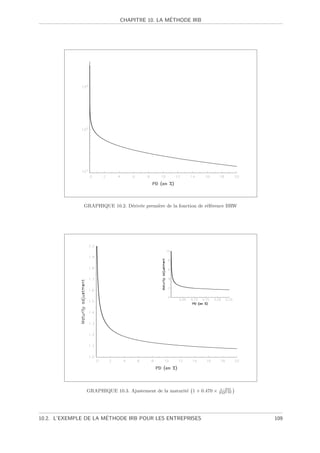
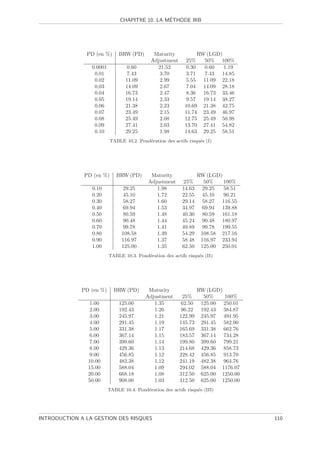
![´
CHAPITRE 10. LA METHODE IRB
RW
PD (en %) 20% 50% 100% 150%
0.025 79.08
0.05 52.25
0.075 40.82
0.10 34.19 85.46
0.25 19.26 48.15 96.30
0.50 12.41 31.02 62.04 93.06
0.75 9.59 23.98 47.97 71.95
1.00 8.00 20.00 40.00 60.00
2.50 4.54 11.34 22.68 34.02
5.00 3.02 7.54 15.09 22.63
7.50 2.41 6.03 12.05 18.08
10.00 2.07 5.18 10.37 15.55
25.00 1.60 4.00 8.00 12.00
50.00 1.60 4.00 8.00 12.00
TABLE 10.5. Relation implicite entre la probabilit´ de d´faillance et la perte en cas de d´faut pour une valeur
e e e
RW donn´e
e
La fonction de r´f´rence ne change pas. Le terme 1 + (M − 3) b (PD) intervient ici comme un facteur de
ee
diminution (M 3) ou d’augmentation (M 3) de la pond´ration.
e
La fonction b (PD) repr´sente la sensibilit´ de la pond´ration par rapport ` la maturit´. Par exemple, si
e e e a e
b (PD) est ´gal ` z´ro, la maturit´ M n’a pas d’influence sur la pond´ration. Notons que pour des raisons
e a e e e
´videntes, nous devons v´rifier que
e e
1 + (M − 3) b (PD) 0 (10.7)
ou encore pour M 3
1
b (PD) (10.8)
3−M
Pour l’instant, le Comit´ de Bˆle n’a pas fix´ d´finitivement la fonction b (PD). Les premiers travaux
e a e e
montrent que cette fonction d´pend de l’approche consid´r´e pour traiter le risque de cr´dit : approche
e ee e
Mark-to-Market ou approche Default Mode. Dans la premi`re approche (MtM), la calibration du
e
Comit´ de Bˆle sugg`re cette fonction
e a e
0.0235 × (1 − PD)
b (PD) = 0.44 (10.9)
PD +0.470 × (1 − PD)
Dans ce cas, la valeur de la pond´ration devient
e
LGD
RW = × BRW (PD) × [1 + (M − 3) b (PD)]
50
LGD 1 − PD
= × 976.5 × Φ 1.118 × Φ−1 (PD) + 1.288 × 1 + 0.470 × ×
50 PD0.44
0.0235 × (1 − PD)
1 + (M − 3) 0.44
PD +0.470 × (1 − PD)
LGD
= × 976.5 × Φ 1.118 × Φ−1 (PD) + 1.288 ×
50
1 − PD 1 − PD
1 + 0.470 × + 0.0235 × (M − 3) × (10.10)
PD0.44 PD0.44
Cela revient ` d´finir une nouvelle fonction de r´f´rence :
a e ee
1 − PD 1 − PD
BRW (PD) = 976.5 × Φ 1.118 × Φ−1 (PD) + 1.288 × 1 + 0.470 × + 0.0235 × (M − 3) ×
PD0.44 PD0.44
(10.11)
Nous remarquons que le coefficient d’ajustement de la maturit´ est maintenant plus complexe puisqu’il
e
comprend deux termes :
´
10.2. L’EXEMPLE DE LA METHODE IRB POUR LES ENTREPRISES 111](https://image.slidesharecdn.com/gestionrisques-130221132633-phpapp01/85/Gestion-risques-121-320.jpg)
![´
CHAPITRE 10. LA METHODE IRB
β (PD, M )
PD (en %) β (PD) M = 0.5 M =1 M =3 M =5 M =7
0.025 2.81 0.55 1.00 2.81 4.61 6.42
0.05 2.33 0.67 1.00 2.33 3.66 4.99
0.075 2.11 0.72 1.00 2.11 3.23 4.34
0.10 1.98 0.75 1.00 1.98 2.96 3.94
0.25 1.65 0.84 1.00 1.65 2.31 2.96
0.50 1.48 0.88 1.00 1.48 1.96 2.44
0.75 1.40 0.90 1.00 1.40 1.80 2.20
1.00 1.35 0.91 1.00 1.35 1.71 2.06
2.50 1.23 0.94 1.00 1.23 1.46 1.70
5.00 1.17 0.96 1.00 1.17 1.33 1.50
7.50 1.14 0.97 1.00 1.14 1.27 1.41
10.00 1.12 0.97 1.00 1.12 1.23 1.35
25.00 1.06 0.98 1.00 1.06 1.13 1.19
50.00 1.03 0.99 1.00 1.03 1.06 1.10
TABLE 10.6. Facteur d’ajustement de la maturit´
e
1−PD
1. Le premier terme 1 + 0.470 × PD0.44 est le terme de correction pour passer d’une maturit´ 1 an
e
a
` une maturit´ moyenne 3 ans. Il est strictement sup´rieur ` 1 si la probabilit´ de d´faillance est
e e a e e
inf´rieure ` 100%.
e a
1−PD
2. Le second terme 0.0235 × (M − 3) × PD0.44 est le terme de correction qui prend en compte de fa¸on
c
explicite la maturit´. Il peut ˆtre positif ou n´gatif.
e e e
Nous remarquons que si la maturit´ est ´gale ` un an (M = 1), nous avons
e e a
BRW (PD) = 976.5 × Φ 1.118 × Φ−1 (PD) + 1.288 (10.12)
Nous retrouvons bien la fonction de r´f´rence qui a ´t´ calibr´e pour une maturit´ ´gale ` un an. Si la
ee ee e ee a
maturit´ vaut trois ans, alors nous obtenons l’´galit´ BRW (PD) = BRW (PD). La table 10.6 pr´sente
e e e e
les valeurs des facteurs d’ajustement de maturit´e
1 − PD
β (PD) = 1 + 0.470 × (10.13)
PD0.44
et
1 − PD 1 − PD
β (PD, M ) = 1 + 0.470 × 0.44 + 0.0235 × (M − 3) × (10.14)
PD PD0.44
L’incidence sur la valeur de la pond´ration est pr´sent´e dans la table 10.7.
e e e
Dans l’approche DM, la calibration du Comit´ de Bˆle sugg`re une fonction polynomiale
e a e
+
b (PD) = 7.6752 × PD2 −1.9211 × PD +0.0774 (10.15)
Dans ce cas, b (PD) prend syst´matiquement la valeur z´ro si la probabilit´ de d´faillance est sup´rieure
e e e e e
a
` 5%. A titre de comparaison, l’incidence sur la pond´ration est pr´sent´e dans la table 10.8. Nous
e e e
remarquons que la sensibilit´ de la pond´ration ` la maturit´ est beaucoup moins forte dans l’approche
e e a e
DM que dans l’approche MtM (voir le graphique 10.4).
10.2.2 Justification de la m´thode IRB
e
Dans ce paragraphe, nous suivons l’expos´ de Wilson [2001a]. Consid´rons un portefeuille Π de I
e e
cr´dits. Notons LGDi la perte nominale en cas de d´faillance. LGDi est une variable al´atoire de moyenne
e e e
Ei et d’´cart-type Ei · σ i . Nous supposons que la probabilit´ de d´faillance du i-i`me cr´dit d´pend d’un
e e e e e e
mod`le factoriel :
e
Pi = Pi (X1 , . . . , Xn ) (10.16)
INTRODUCTION A LA GESTION DES RISQUES 112](https://image.slidesharecdn.com/gestionrisques-130221132633-phpapp01/85/Gestion-risques-122-320.jpg)
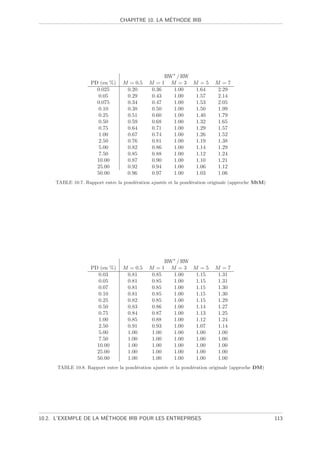
![´
CHAPITRE 10. LA METHODE IRB
GRAPHIQUE 10.4. Repr´sentation graphique de la fonction b (PD)
e
Le d´faut Di est alors une variable al´atoire dont la distribution est une loi de Bernoulli de param`tre
e e e
Pi . Nous avons donc E [Di ] = Pi et σ 2 [Di ] = Pi (1 − Pi ). La perte du portefeuille L est al´atoire
e
I
L= Di · LGDi (10.17)
i=1
Nous pouvons calculer les deux premiers moments sous l’hypoth`se que les d´fauts et les pertes nominales
e e
sont ind´pendantes. Nous avons
e
I
E [L] = E Di · LGDi
i=1
I
= E [Di · LGDi ]
i=1
I
= E [Di ] E [LGDi ]
i=1
I
= Ei · Pi (10.18)
i=1
INTRODUCTION A LA GESTION DES RISQUES 114](https://image.slidesharecdn.com/gestionrisques-130221132633-phpapp01/85/Gestion-risques-124-320.jpg)
![´
CHAPITRE 10. LA METHODE IRB
et
I
σ 2 [L] = σ2 Di · LGDi
i=1
I
= σ 2 [Di · LGDi ]
i=1
I
2
= E (Di · LGDi −E [Di · LGDi ])
i=1
I
= E Di E LGD2 − E2 [Di ] E2 [LGDi ]
2
i
i=1
I
= σ 2 [Di ] + E2 [Di ] σ 2 [LGDi ] + E2 [LGDi ] − E2 [Di ] E2 [LGDi ]
i=1
I
= Pi (1 − Pi ) + Pi2 Ei σ 2 + Ei − Pi2 Ei
2
i
2 2
i=1
I
= Ei Pi (1 − Pi ) + σ 2 Pi
2
i (10.19)
i=1
Notons que cette moyenne et cet ´cart-type sont des variables conditionnelles aux r´alisations des facteurs
e e
X1 , . . . , Xn . Dans ce cadre d’analyse, Wilson [2001a] consid´r`re un portefeuille ΠM “´quivalent” au
ee e
portfeuille original Π. Ce nouveau portefeuille est construit en rempla¸ant chaque cr´dit par M cr´dits
c e e
ind´pendants d’exposition Ei /M et de mˆme probabilit´ de d´faillance Pi (X1 , . . . , Xn ). Lorsque M tend
e e e e
vers l’infini, nous obtenons un portefeuille not´ Π∞ . C’est le portefeuille infiniment granulaire du Comit´
e e
de Bˆle (infinitely fine-grained portfolio). Notons L∞ la perte de ce portefeuille. Nous avons
a
I M
1
E [LM ] = Ei · Pi
i=1 m=1
M
I
= Ei · Pi
i=1
= E [L] (10.20)
et
I M
1 2
σ 2 [LM ] = E Pi (1 − Pi ) + σ 2 Pi
i=1 m=1
M2 i i
I
1
= Ei Pi (1 − Pi ) + σ 2 Pi
2
i
M i=1
1 2
= σ [L] (10.21)
M
Nous en d´duisons que E [L∞ ] = E [L] et σ 2 [L∞ ] = 0. Conditionnellement aux r´alisations des facteurs,
e e
la distribution de perte L∞ est une variable al´atoire sˆre qui prend la valeur E [L] :
e u
Pr {L∞ = E [L]} = 1 (10.22)
L’al´a du portefeuille infiniment granulaire ne porte donc plus que sur les facteurs X1 , . . . , Xn . Si nous
e
supposons un seul facteur X de distribution H et si Pi est une fonction croissante du facteur, l’inverse
de la distribution de la perte est donc
I
F−1 (α) :=
∞ Ei · Pi H−1 (α) (10.23)
i=1
´
10.2. L’EXEMPLE DE LA METHODE IRB POUR LES ENTREPRISES 115](https://image.slidesharecdn.com/gestionrisques-130221132633-phpapp01/85/Gestion-risques-125-320.jpg)
![´
CHAPITRE 10. LA METHODE IRB
La contribution du cr´dit i est donc SRCi = Ei · Pi H−1 (α) .
e
Dans le paragraphe 172 du document [3], le Comit´ de Bˆle explique que la formule de la fonction de
e a
r´f´rence BRW a ´t´ calibr´e en utilisant un mod`le ` la Merton avec un seul facteur. Pour retrouver son
ee ee e e a
expression, nous utilisons les r´sultats de Finger [1999]. Soit Zi la valeur de l’actif normalis´e. Dans
e e
le mod`le de Merton, la d´faillance intervient si Zi passe en dessous d’une barri`re Bi :
e e e
Di = 1 ⇔ Zi Bi (10.24)
ou encore
Φ (Zi ) Pi (10.25)
La valeur normalis´e de l’actif est mod´lis´e de la fa¸on suivante
e e e c
√
Zi = ρX + 1 − ρεi (10.26)
avec X le facteur de risque syst´matique et εi le facteur de risque individuel. Les variables al´atoires Zi ,
e e
Z et εi sont ind´pendantes de distribution N (0, 1). Pour interpr´ter le param`tre ρ, nous calculons
e e e
E [Zi Zj ] = E ρX 2 + (1 − ρ) εi εj + X ρ (1 − ρ) (εi+ εj )
= ρ (10.27)
ρ est donc la corr´lation (constante) des valeurs des actifs. Nous pouvons maintenant caract´riser la
e e
probabilit´ de d´faillance conditionnelle
e e
Pi = Pr {Di = 1 | X}
= Pr {Zi Bi | X}
√
= Pr ρX + 1 − ρεi Bi
√
Bi − ρX
= Pr εi √
1−ρ
√
Bi − ρX
= Φ √ (10.28)
1−ρ
Notons pi la probabilit´ de d´faillance non conditionnelle. Nous remarquons que
e e
pi = Pr {Zi Bi } = Φ (Bi ) (10.29)
Nous en d´duisons que
e
√
Φ−1 (pi ) − ρX
Pi = Φ √ (10.30)
1−ρ
Une couverture au seuil de confiance α implique donc une contribution individuelle ´gale `1
e a
√
Φ−1 (pi ) − ρΦ−1 (1 − α)
SRCi = Ei · Pi = Ei · Φ √ (10.31)
1−ρ
Pour α = 99.5% et ρ = 20% (valeurs pr´sent´es dans le paragraphe 172 du document [3]), nous obtenons
e e
SRCi = Ei · Φ 1.118Φ−1 (pi ) + 1.288 (10.32)
Nous pouvons noter que la probabilit´ conditionnelle Pi est extrˆmement sensible au seuil de confiance
e e
α et ` la corr´lation ρ (voir les graphiques 10.5 ` 10.8).
a e a
1 car la relation entre la probabilit´ de d´faillance conditionnelle et le facteur X est d´croissante.
e e e
INTRODUCTION A LA GESTION DES RISQUES 116](https://image.slidesharecdn.com/gestionrisques-130221132633-phpapp01/85/Gestion-risques-126-320.jpg)
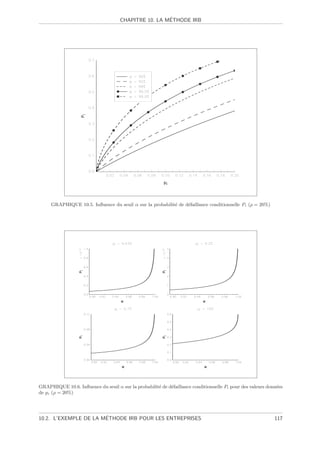
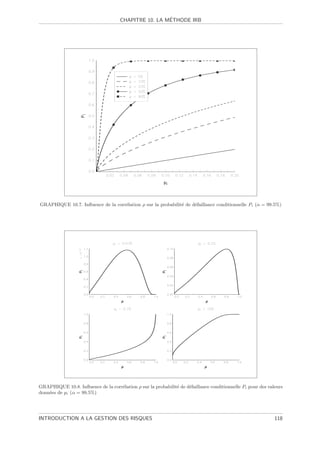

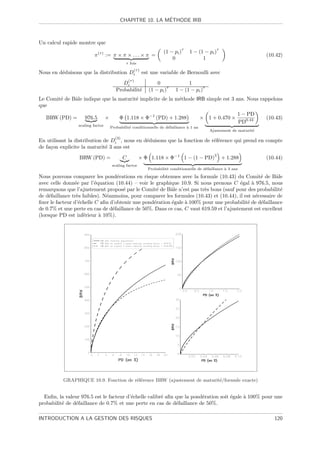
![´
CHAPITRE 10. LA METHODE IRB
10.2.3 Param`tres de la fonction de pond´ration
e e
10.2.3.1 La probabilit´ de d´faillance
e e
Si le cr´dit n’est pas prot´g´ par une technique CRM, la probabilit´ de d´faillance est celle associ´e `
e e e e e e a
la note interne ` laquelle l’emprunteur est affect´ pour un horizon d’un an. Dans le cas d’une protection,
a e
nous devons distingu´ l’approche IRB simple de l’approche IRB avanc´e :
e e
– Dans la premi`re approche, la probabilit´ de d´faillance ajust´e PD (qui est applicable uniquement
e e e e
a
` la partie couverte de l’exposition) est
PD = w × PD + (1 − w) × PDG (10.45)
o` PDG est la probabilit´ de d´faillance de la garantie et w est le facteur de risque r´siduel (0 ou
u e e e
15%).
– Dans la deuxi`me approche, la probabilit´ de d´faillance ajust´e PD est celle de la garantie.
e e e e
10.2.3.2 La perte en cas de d´faillance
e
Nous rappelons que les pertes en cas de d´faillance sont r´glementaires (50% ou 75%) dans l’approche
e e
simple. Dans le cas d’existence de suret´s, la perte en cas de d´faillance ajust´e LGD est
e e e
CA
LGD = max 1 − (1 − w) × × LGD, w × LGD (10.46)
E
o` E est l’exposition et CA la valeur ajust´e des suret´s. Si le colat´ral est physique (une r´sidence par
u e e e e
exemple), alors la perte en cas de d´faillance ajust´e LGD est donn´e par le tableau suivant
e e e
Condition LGD
C
E ≤ 30% 50%
C
E 140% 40%
C
30% E ≤ 140% 1− 1 ×
7
C
E × 50%
Dans l’approche avanc´e, les banques pourraient utiliser leurs propres estimations.
e
10.2.3.3 La maturit´
e
Celle-ci n’intervient explicitement que dans le cas de l’approche avanc´e. La maturit´ correspond ` la
e e a
dur´e r´siduelle maximum avec un plancher ´gal ` un an.
e e e a
10.2.3.4 L’exposition en cas de d´faillance
e
C’est l’encours nominal du cr´dit.
e
10.2.4 Les exigences minimales d’´ligibilit´
e e
Celles-ci sont nombreuses (voir les paragraphes 189 ` 261 du document [3]). Elles concernent
a
– la notation,
– l’audit interne et externe,
– la surveillance du risque de cr´dit,
e
– la qualification du personnel,
– l’estimation des param`tres,
e
– le mapping vers des donn´es externes,
e
– etc.
Prenons par exemple les normes minimales pour l’estimation de la probabilit´ de d´faillance. Dans ce
e e
cas, la banque doit la calculer sur un an pour toutes ses cat´gories de notation interne. La probabilit´ de
e e
d´faillance doit ˆtre une mesure prudente de la probabilit´ de d´faillance moyenne ` long terme et une
e e e e a
mesure prospective. La longueur des s´ries historiques doit ˆtre d’au moins cinq ans. La fr´quence
e e e
des estimations est annuelle...
D’autres informations concernant la gestion du risque de cr´dit sont disponibles dans les documents
e
[1] et [2].
´
10.2. L’EXEMPLE DE LA METHODE IRB POUR LES ENTREPRISES 121](https://image.slidesharecdn.com/gestionrisques-130221132633-phpapp01/85/Gestion-risques-131-320.jpg)



![´
CHAPITRE 10. LA METHODE IRB
10.4.3 D´rivation du coefficient d’ajustement de granularit´
e e
Celle-ci est expliqu´e en d´tail dans l’article de Gordy [2001]. Une formalisation plus accessible est
e e
pr´sent´e dans Wilson [2001a,2001b]. Afin de bien comprendre comment l’ajustement est obtenu, nous
e e
reprenons les principaux points de ces articles.
10.4.3.1 La d´termination du coefficient β
e
Notons D la variable al´atoire de Bernoulli repr´sentant la d´faillance, LGD la perte (relative) en cas
e e e
de d´faillance et EAD l’exposition en cas de d´faillance. Consid´rons un portefeuille Πn compos´ de n
e e e e
lignes de cr´dit. La perte Ln du portefeuille Πn est donc
e
n
Ln = Di · LGDi · EADi (10.61)
i=1
Gordy [2001] d´finit Ln comme le ratio de la perte du portefeuille sur le total des expositions :
e
n
i=1 Di · LGDi · EADi
Ln = n (10.62)
i=1 EADi
Nous rappelons que pour un portefeuille infiniment granulaire ou asymptotique, la perte du portefeuille
Π∞ est la perte syst´matique
e
Pr {L∞ = E [L∞ ]} = 1 (10.63)
Afin de clarifier les notations, nous ´crivons la perte esp´r´e conditionnelle de la fa¸on suivante :
e ee c
E [Ln ] := E [Ln | X] (10.64)
avec X le facteur de risque syst´matique. Notons ψ (X; α) le quantile α de la variable al´atoire X.
e e
Michael Gordy donne une autre interpr´tation statistique de la notion de portefeuille infiniment granulaire
e
(Proposition 5 de Gordy [2001]) :
lim Pr {Ln ≤ E [Ln | ψ (X; α)]} = α (10.65)
n→∞
Cela veut dire que la valeur en risque d’un portefeuille infiniment granulaire VaR [L∞ ; α] est bien la perte
esp´r´e conditionnelle E [L∞ | ψ (X; α)] :
ee
VaR [L∞ ; α] := E [L∞ | ψ (X; α)]
ou qu’une charge en capital ´gale ` E [L∞ | ψ (X; α)] correspond bien ` une probabilit´ de solvabilit´
e a a e e
´gale ` α :
e a
[...] for an infinetely fine-grained portfolio, the proposed portfolio-invariant capital rule
provides a solvency probability of exactly α (Gordy [2001]).
Cela implique qu’une charge en capital ´gale ` E [Ln | ψ (X; α)] ne permet pas n´cessairement de couvrir
e a e
le risque au seuil de confiance α dans le cas non asymtotique :
VaR [Ln ; α] = E [Ln | ψ (X; α)] (10.66)
C’est pourquoi nous devons ajuster la perte esp´r´e conditionnelle afin d’obtenir le bon degr´ de couver-
ee e
ture :
VaR [Ln ; α] = E [Ln | ψ (X; α)] + ∆Ln (10.67)
L’ajustement de granularit´ correspond tout simplement ` ∆Ln .
e a
La question principale est alors de caract´riser cet ajustement ∆Ln . Pour cela, Gordy [2001] montre
e
la proposition suivante :
´
10.4. GRANULARITE DU PORTEFEUILLE 125](https://image.slidesharecdn.com/gestionrisques-130221132633-phpapp01/85/Gestion-risques-135-320.jpg)
![´
CHAPITRE 10. LA METHODE IRB
Proposition 1 (Gordy [2001, Proposition 6, p. 12]) If the portfolio is statistically homogeneous,
the function µ (x) := E [Ln | X = x] is continous, arbitrarily differentiable, and increasing, and the syste-
matic risk factor X is drawn from an arbitrary differentiable continuous distribution, then VaR converges
to its asymptotic limit at rate 1/n, that is,
VaR [Ln ; α] = µ (ψ (X; α)) + O n−1 (10.68)
L’interpr´tation de cette proposition est simple :
e
[...] it says that the difference between the VaR for a given homogeneous portfolio and
its asymtotic approximation E [Ln | ψ (X; α)] is proportional to 1/n. This suggests that the
accuracy of the asymptotic capital rule can be improved by introducing a “granularity add-on
charge” that is inversely proportional to the number of obligors in the portfolio. To calibrate
such add-on charge for a homogeneous portfolio, we need to find a constant of proportionality
β such that E [Ln | ψ (X; α)] + β/n is a good approximation to VaR [Ln ; α] (Gordy [2001]).
Nous en d´duisons que
e
∆Ln β/n (10.69)
Voyons maintenant comment d´terminer le coefficient β. Pour cela, nous utilisons les r´sultats de
e e
Wilson [2001b]. Michael Gordy d´rive l’ajustement (10.69) sous l’hypoth`se que le portefeuille est sta-
e e
tistiquement homog`ne. Cela veut dire que les lignes de cr´dit ont la mˆme exposition en cas de
e e e
d´faillance et la mˆme perte esp´r´e conditionnelle — ce qui implique la mˆme probabilit´ de d´faillance
e e ee e e e
non conditionnelle et la mˆme distribution de perte en cas de d´faillance. Les portfeuilles Πn de Gordy
e e
et ΠM de Wilson sont donc diff´rents, mais nous pouvons construire le portefeuille Πn ` partir du por-
e a
tefeuille ΠM . Pour cela, il suffit de poser I = 1 et M = n — voir le paragraphe 10.2.2. Reprenons les
notations de ce mˆme paragraphe. La perte du portfeuille (qui se r´duit ` la perte de la ligne de cr´dit
e e a e
puisque I est ´gal ` 1) est not´e L. Les deux premiers moments de la perte conditionnelle sont E [L | X]
e a e
et σ 2 [L | X] — dans le paragraphe 10.2.2, nous avions utilis´ l’´criture E [L] et σ 2 [L] puisque le condi-
e e
tionnement ´tait parfaitement explicite. Nous introduisons les fonctions µ (x) et υ (x) d´finies de la fa¸on
e e c
suivante :
µ (x) := E [L | X = x] (10.70)
et
υ (x) := σ 2 [L | X = x] (10.71)
Wilson [2001b] montre alors que4
1 d h (x) υ (x)
VaR [L; α] µ (ψ (X; α)) − (10.72)
2h (x) dx ∂x µ (x) x=ψ(X;α)
avec h la densit´ de X. Reprenons la construction du portefeuille infiniment granulaire de la page 115.
e
Nous avons
1 d h (x) υ (x)
VaR [LM ; α] µ (ψ (X; α)) − M (10.73)
2h (x) dx ∂x µ (x) x=ψ(X;α)
puisque E [LM | X = x] = E [L | X = x] et σ 2 [LM | X = x] = σ 2 [L | X = x] /M . Nous en d´duisons
e
que5
β
VaR [Ln ; α] VaR [L∞ ; α] + (10.74)
n
4 La d´monstration n’est pas tr`s technique, mais assez longue (pages 104 et 105 de Wilson [2001b]).
e e
5 puisque M = n et VaR [L∞ ; α] = E [L∞ | X = ψ (X; α)] = µ (ψ (X; α)).
INTRODUCTION A LA GESTION DES RISQUES 126](https://image.slidesharecdn.com/gestionrisques-130221132633-phpapp01/85/Gestion-risques-136-320.jpg)
![´
CHAPITRE 10. LA METHODE IRB
avec
1 d h (x) υ (x)
β = −
2h (x) dx ∂x µ (x) x=ψ(X;α)
2
1 ∂x µ (ψ (X; α)) ∂x ln h (ψ (X; α)) ∂x υ (ψ (X; α))
= υ (ψ (X; α)) 2 − υ (ψ (X; α)) −
2 [∂x µ (ψ (X; α))] ∂x µ (ψ (X; α)) ∂x µ (ψ (X; α))
(10.75)
Le Comit´ de Bˆle explique que la calibration du coefficient β a ´t´ faite ` partir du mod`le CreditRisk+ :
e a ee a e
Calibration of the β coefficient inevitably depends on the choice of model and its calibra-
tion. IRB benchmark risk-weights have been calibrated within a CreditMetrics style model. For
the purposes of designing a granularity adjustment, however, we use a generalised version of
the CreditRisk+ model. The advantage is that the functional form of CreditRisk+ risk-weights
allows the granularity adjustment to be assessed with minimal reporting and computational
burden. The obvious disadvantage is the greater potential for inconsistency with CreditMetrics-
based IRB exposure-level risk-weights. Fortunately, it is by now well-known that CreditRisk+
can be calibrated so that the tail of its loss distribution will align closely with the tail of
the CreditMetrics loss distribution. So long as care is exercised in calibration, the discrepancy
between our granularity adjustment and a full CreditMetrics-based estimate can be kept to a
minimum (§444 du document [3]).
Dans le cas du mod`le de type CreditMetrics (ou Merton), nous rappelons que la relation entre la proba-
e
bilit´ de d´faillance conditionnelle Pi et la probabilit´ de d´faillance non conditionnelle pi est
e e e e
√
Φ−1 (pi ) − ρX
Pi = Φ √ (10.76)
1−ρ
Dans le cas du mod`le de type CreditRisk+, nous avons6
e
Pi = pi (1 + i (X − 1)) (10.77)
avec i la pond´ration factorielle — i ∈ [0, 1] — et X le facteur syst´matique de distribution Γ (a, b)
e e
a−1
— h (x) = (x/b) exp (−x/b) / (bΓ (a)). Dans ce cas, les expressions (10.18) et (10.19) deviennent
µ (x) = E [L | X = x]
= E [LGD1 ] P1
= E1 p1 (1 + 1 (x − 1)) (10.78)
et
υ (x) = σ 2 [L | X = x]
= E2 [LGD1 ] P1 (1 − P1 ) + σ 2 [LGD1 ] P1
= E2 [LGD1 ] + σ 2 [LGD1 ] P1 − E2 [LGD1 ] P1
2
0
2 2
E [LGD1 ] + σ [LGD1 ] P1
= E1 + σ 2 [LGD1 ] p1 (1 +
2
1 (x − 1)) (10.79)
Le Comit´ de Bˆle fait l’hypoth`se suivante (§447 du document [3]) :
e a e
1
σ [LGD1 ] = E1 (1 − E1 ) (10.80)
2
6 voir Gordy [2000].
´
10.4. GRANULARITE DU PORTEFEUILLE 127](https://image.slidesharecdn.com/gestionrisques-130221132633-phpapp01/85/Gestion-risques-137-320.jpg)
![´
CHAPITRE 10. LA METHODE IRB
Nous en d´duisons que
e
1 3
υ (x) = E1 + E1 p1 (1 + 1 (x − 1)) (10.81)
4 4
2 1 3
Le calcul des d´riv´es donne ∂x µ (x) = E1 p1
e e 1, ∂x µ (x) = 0, ∂x υ (x) = E1 4 + 4 E1 p1 1 et ∂x ln h (ψ (X; α)) =
(a − 1) x−1 − b−1 . Nous avons donc
1 a−1 1 −1
β= (0.25 + 0.75E1 ) − − 1 + (x − 1) − 1 (10.82)
2 x b
Afin de maintenir une certaine coh´rence entre la formulation des pond´rations en risque et le facteur de
e e
granularit´, le Comit´ de Bˆle impose que les probabilit´s de d´faillance conditionnelles CreditMetrics et
e e a e e
CreditRisk+ co¨ ıncident :
√
Φ−1 (pi ) + ρΦ−1 (α)
Φ √ = pi (1 + i (x − 1)) (10.83)
1−ρ
Dans ce cas, la pond´ration factorielle
e i vaut
1 Fi
i = (10.84)
(x − 1) pi
avec
√
Φ−1 (pi ) + ρΦ−1 (α)
Fi = Φ √ − pi (10.85)
1−ρ
L’expression de β est donc
1 pi
β= (0.25 + 0.75E1 ) A − 1 + A (10.86)
2 Fi
avec
a−1 1
A=− − (x − 1) (10.87)
x b
Pour achever la calibration, le Comit´ de Bˆle indique que celle-ci a ´t´ faite sous l’hypoth`se que
e a ee e
E [X] = 1 et σ [X] = 2 (§445 du document [3]). Les param`tres de la distribution Gamma7 implicite sont
e
donc a = 0.25 et b = 4. Puisque α est ´gal ` 99.5%, le quantile correspondant de la distribution Gamma
e a
Γ (0.25, 4) est 12.007243 et la valeur prise par A est 3.4393485, ce qui donne
1 pi
β = (0.25 + 0.75E1 ) 2.4393485 + 3.4393485
2 Fi
pi
= (0.4 + 1.2E1 ) 0.76229640 + 1.0747964 (10.88)
Fi
Nous retrouvons (presque) la formule donn´e par le Comit´ de Bˆle (§456 du document [3]) :
e e a
PD
β = (0.4 + 1.2 × LGD) 0.76 + 1.10 × (10.89)
F
Pour retrouver exactement la formule du Comit´ de Bˆle, nous ne devons pas utiliser l’approxima-
e a
tion P12
4
3
0 pour calculer υ (x). Dans ce cas, nous avons υ (x) = E1 1 + 4 E1 p1 (1 + 1 (x − 1)) −
2 2 2 1 3 2 2
E1 p1 (1 + 1 (x − 1)) et ∂x υ (x) = E1 4 + 4 E1 p1 1 − 2E1 p1 1 (1 + 1 (x − 1)). Nous en d´duisons
e
que
1 a−1 1 −1
β = (0.25 + 0.75E1 ) − − 1 + (x − 1) − 1
2 x b
1 −1 a−1 1
+E1 p1 (1 + 1 (x − 1)) 1 + − (10.90)
2 1 x b
Terme de correction
7 Nous avons E [X] = ab et σ [X] = √ab.
INTRODUCTION A LA GESTION DES RISQUES 128](https://image.slidesharecdn.com/gestionrisques-130221132633-phpapp01/85/Gestion-risques-138-320.jpg)
![´
CHAPITRE 10. LA METHODE IRB
Dans le cas o` E1 varie de 5% ` 95%, PD de 0.10% ` 15% and ρ de 10% ` 30%, alors l’erreur relative
u a a a
entre la formule exacte (10.90) et la formule approch´e (10.89) n’exc`de pas 1%.
e e
A titre de remarque, il faut noter que le coefficient β est extrˆmement sensible aux valeurs des
e
param`tres : la perte en cas de d´faillance LGD, la probabilit´ de d´faillance PD, la corr´lation des actifs
e e e e e
ρ, le seuil de confiance α et la volatilit´ du facteur σ [X] — E [X] n’est pas un param`tre puisque nous
e e
avons l’´quivalence suivante E [Pi ] = pi ⇔ E [X] = 1. Le graphique 10.10 illustre cette sensibilit´.
e e
GRAPHIQUE 10.10. Impact des param`tres sur le coefficient β (valeurs par d´faut : LGD = 50%, α = 99.5%,
e e
ρ = 20% et σ [X] = 2)
10.4.3.2 Du coefficient β ` l’ajustement de granularit´ du Comit´ de Bˆle
a e e a
Nous devons dans un premier temps ‘transformer’ le coefficient β en actifs pond´r´s. De plus, le Comit´
ee e
de Bˆle indique qu’il a utilis´ un facteur d’´chelle c afin d’obtenir une pond´ration ´gale ` 100% pour
a e e e e a
une probabilit´ de d´faillance de 0.7%, une perte en cas de d´faillance de 50% et une maturit´ de 3 ans.
e e e e
(§457 du document [3]). Dans le paragraphe 10.2.2, nous l’avons d´j` calcul´ et obtenu c
ea e 1.5. Nous
avons donc
EAD ×β
∆ RWA = 1.5 × 8%
n
PD
= EAD × (0.6 + 1.8 × LGD) 9.5 + 13.75 × n (10.91)
F
Nous rappelons aussi que le coefficient β a ´t´ d´termin´ pour un portefeuille statistiquement homog`ne.
ee e e e
Dans la pratique, les portefeuilles Π d’engagement des banques ne sont pas homog`nes. Il faut donc
e
pouvoir trouver un portefeuille homog`ne ´quivalent ΠAG pour calculer l’ajustement de granularit´ G,
e e e
qui est exprim´ en terme d’actifs pond´r´s. Le Comit´ de Bˆle indique aussi que la calibration effectu´e
e ee e a e
est telle que 4% du capital couvre d´j` l’effet de granularit´. Nous avons donc
ea e
PDAG
G = EADAG × (0.6 + 1.8 × LGDAG ) 9.5 + 13.75 × nAG − 0.04 × RWANR (10.92)
FAG
´
10.4. GRANULARITE DU PORTEFEUILLE 129](https://image.slidesharecdn.com/gestionrisques-130221132633-phpapp01/85/Gestion-risques-139-320.jpg)
![´
CHAPITRE 10. LA METHODE IRB
En utilisant les notations du Comit´ de Bˆle, nous retrouvons la formule
e a
TNRE × GSF
G= − 0.04 × RWANR (10.93)
n
avec
PDAG
GSF = (0.6 + 1.8 × LGDAG ) 9.5 + 13.75 × (10.94)
FAG
Il nous reste maintenant ` justifier la construction du portefeuille homog`ne ´quivalent ΠAG . Celle-ci
a e e
est pr´sent´e dans la section 4 de Gordy [2001]. Nous reprenons les notations pr´c´dentes en introduisant
e e e e
les classes de risques C. Nous avons
L= Di · LGDi · EADi (10.95)
C i∈C
Nous notons pC la probabilit´ de d´faillance non conditionnelle de la classe de risque C et sC la part
e e
d’exposition au risque de la classe C dans le risque total :
i∈C EADi
sC = (10.96)
C i∈C EADi
Le but est alors de construire un portefeuille ‘´quivalent’ ΠAG au portefeuille Π de taille n et de
e
param`tres communs p , E , σ [LGD ], EAD , etc. (Gordy [2001]). Dans ce cas, l’expression de la
e
perte est
LAG = D · LGD · EAD (10.97)
L’id´e sous-jacente est d’ajuster diff´rents moments ou d’imposer des restrictions. Michael Gordy impose
e e
l’´galit´ des taux de d´faillance et des pertes esp´r´es (pond´r´s par les expositions). Nous avons donc
e e e ee ee
E [D · EAD ] = E Di · EADi (10.98)
C i∈C
Il est bien sˆr naturel de prendre EAD =
u C i∈C EADi (mˆme exposition dans le portefeuille ΠAG et
e
le portefeuille Π), ce qui implique
C i∈C pC · EADi
p =
C i∈C EADi
= sC · pC (10.99)
C
Nous avons aussi
E [D · LGD · EAD ] = E Ei · LGDi · EADi
C i∈C
p ·E · EADi = pC · Ei · EADi
C i∈C C i∈C
= pC Ei · EADi (10.100)
C i∈C
Introduisons la perte en cas de d´faillance moyenne par classe de risque EC d´finie par
e e
i∈C Ei · EADi
EC = (10.101)
i∈C EADi
INTRODUCTION A LA GESTION DES RISQUES 130](https://image.slidesharecdn.com/gestionrisques-130221132633-phpapp01/85/Gestion-risques-140-320.jpg)
![´
CHAPITRE 10. LA METHODE IRB
Nous en d´duisons que
e
p ·E · EADi = pC · EC · EADi (10.102)
C i∈C C i∈C
ou encore
pC i∈C EADi
E = · EC ·
p C i∈C EADi
C
sC · pC
= · EC (10.103)
C C sC · pC
Rappelons que la variance conditionnelle de la distribution de perte est
σ 2 [L | X] = EAD2 · Ei · Pi · (1 − Pi ) + σ 2 [LGDi ] · Pi
i
2
(10.104)
C i∈C
La variance non conditionnelle de la distribution de perte a donc pour expression8
σ 2 [L] = σ 2 [E [L | X]] + E σ 2 [L | X]
= σ2 Pi · Ei · EADi +E EAD2 · Ei · Pi · (1 − Pi ) + σ 2 [LGDi ] · Pi
i
2
C i∈C C i∈C
Contribution du risque syst´matique
e Contribution du risque idiosyncratique
= σ2 PC · EC · sC · EAD + pC · (1 − pC ) − σ 2 [PC ] · EAD2 ·Ei
i
2
C C i∈C
Contribution du risque syst´matique
e Contribution du risque de d´faut idiosyncratique
e
+ pC EAD2 ·σ 2 [LGDi ]
i (10.106)
C i∈C
Contribution du risque de recouvrement idiosyncratique
Pour le portefeuille ΠAG , nous avons
2
2 2 EAD 2
σ [LAG ] = σ [P · E · EAD ] + E · p · (1 − p ) − σ 2 [P ] + p · σ 2 [LGD ] (10.107)
n
Pour d´terminer n , nous allons calibrer les diff´rentes contributions avec un mod`le de type CreditRisk+ :
e e e
Pi = pi (1 + i (X − 1)) (10.108)
Nous avons d´j` utilis´ le fait que E [Pi ] = pi — ce qui implique que E [X] = 1. Pour la variance, nous
ea e
avons
σ 2 [Pi ] = p2
i
2 2
iσ [X] (10.109)
La calibration du risque syst´matique implique que la pond´ration factorielle
e e est
C pC C EC sC
=
p E
C pC C EC sC
= (10.110)
C sC pC EC
8 car nous avons
E [Pi · (1 − Pi )] = E [Pi ] − E Pi2
= E [Pi ] − σ2 P 2 − E2 [Pi ] (10.105)
´
10.4. GRANULARITE DU PORTEFEUILLE 131](https://image.slidesharecdn.com/gestionrisques-130221132633-phpapp01/85/Gestion-risques-141-320.jpg)
![´
CHAPITRE 10. LA METHODE IRB
Concernant la calibration du risque de d´faut idiosyncratique, nous avons
e
2 2
E p (1 − p ) − (p σ [X])
n = (10.111)
2 2 2 2
C EC pC (1 − pC ) − (pC C σ [X]) i∈C (EADi Ei ) (EAD EC )
Nous utilisons les ´galit´s suivantes
e e
2 2
i∈C (EADi Ei ) i∈C (EADi Ei )
2 = P 2
(EAD EC ) EAD i∈C Ei EADi
P
i∈C EADi
2 2
i∈C (EADi Ei ) i∈C EADi
= 2
i∈C Ei · EADi C i∈C EADi
= HC s 2
C
avec HC l’index d’Herfindahl d´fini par l’expression suivante
e
2
i∈C (EADi Ei )
HC = 2 (10.112)
i∈C Ei · EADi
Remarque 19 Nous n’obtenons pas exactement les mˆmes r´sultats que Gordy [2001], puisque celui-ci
e e
utilise l’expression suivante pour HC :
i∈C EAD2
i
HC = 2 (10.113)
i∈C EADi
Finalement, l’expression de n est
1
n = (10.114)
C Λc HC s2
C
avec
2 2
EC pC (1 − pC ) − (pC C σ [X])
Λc = (10.115)
2 2
E p (1 − p ) − (p σ [X])
Nous retrouvons l’expression de n du Comit´ de Bˆle (§445 du document [3]). Il existe n´anmoins une
e a e
diff´rence fondamentale entre l’analyse de Gordy [2001] et la formulation propos´e par le Comit´ de
e e e
Bˆle concernant Λc . Dans le document [3], la calibration de n ne se fait pas uniquement ` partir du
a a
risque de d´faut idiosyncratique, mais utilise aussi le risque de recouvrement idiosyncratique. Dans ce
e
cas, nous avons
2 2
EC pC (1 − pC ) − (pC C σ [X]) + pC σ 2 [LGDC ]
Λc = (10.116)
2 2
E p (1 − p ) − (p σ [X]) + p σ 2 [LGD ]
En reprenant les hypoth`ses du Comit´ de Bˆle, nous avons
e e a
2
2 σ [X]
(pi i σ [X]) = Fi (10.117)
(ψ (X; α) − 1)
et
1
σ [LGDi ] = Ei (1 − Ei ) (10.118)
2
Puisque X ∼ Γ (0.25, 4), ψ (X; 99.5%) et σ [X] prennent les valeurs 12.007243 et 2, et nous obtenons
2
(pi i σ [X]) = 0.033014360 × Fi2 (10.119)
INTRODUCTION A LA GESTION DES RISQUES 132](https://image.slidesharecdn.com/gestionrisques-130221132633-phpapp01/85/Gestion-risques-142-320.jpg)

![´
CHAPITRE 10. LA METHODE IRB
PD (en %) Janvier 2001 Novembre 2001
corporate retail corporate retail res. mortage
0.03 14.09 6.39 18.11 4.58 4.80
0.10 29.25 13.55 33.73 11.62 12.50
0.25 51.92 24.75 53.59 22.48 25.23
0.50 80.59 39.62 74.29 35.39 42.10
0.75 104.23 52.40 88.52 44.97 56.31
1.00 125.00 63.97 99.41 52.52 68.92
1.25 143.80 74.71 108.27 58.65 80.38
1.50 161.12 84.83 115.82 63.73 90.98
2.00 192.43 103.65 128.47 71.63 110.21
2.50 220.45 121.03 139.26 77.45 127.45
3.00 245.97 137.33 149.05 81.88 143.18
4.00 291.45 167.44 167.20 88.13 171.26
5.00 331.38 195.02 184.44 92.40 195.94
10.00 482.38 309.76 262.00 106.31 289.62
20.00 625.00 478.74 374.59 132.49 406.24
TABLE 10.10. Comparaison des pond´rations Janvier 2001 et Novembre 2001
e
3. Enfin, il n’y a plus de r´f´rence ` une calibration LGD = 50% et PD = 0.7%, ce qui explique la
ee a
disparition du facteur d’´chelle 976,5.
e
Remarque 20 L’ajustement de maturit´ existe toujours et n’a pas ´t´ modifi´. Il y a ici une certaine
e ee e
incoh´rence puisque celui-ci avait ´t´ calibr´ sur les probabilit´s conditionnelles de d´faillance ` 3 ans de
e ee e e e a
la forme
(3) 3
Pi = Φ 1.118 × Φ−1 1 − (1 − PD) + 1.288 (10.126)
Les hypoth`ses sous-jacentes ´taient alors un seuil de confiance de 99,5% et une corr´lation constante
e e e
de 20%.
Pour le risque retail, le Comit´ de Bˆle propose de distinguer les prˆts hypoth´caires (r´sidential
e a e e e
mortgage) des autres cr´dits. Dans le premier cas, la formule de pond´ration en risque est
e e
Φ−1 (PD) + ρ (PD)Φ−1 (99.9%)
RW = 12.50 × LGD ×Φ
1 − ρ (PD)
avec une corr´lation ρ (PD) constante et ´gale ` 15%. Pour les autres cr´dits, nous avons
e e a e
Φ−1 (PD) + ρ (PD)Φ−1 (99.9%)
RW = 12.50 × LGD × Φ − PD (10.127)
1 − ρ (PD)
avec
1 − e−25×PD 1 − 1 − e−25×PD
ρ (PD) = 0.04 × −50
+ 0.15 × (10.128)
1−e 1 − e−25
Outre les diff´rences mentionn´es plus haut, nous remarquons que le facteur d’ajustement de matu-
e e
rit´ disparaˆ
e ıt.
Afin de mesurer l’impact des nouvelles propositions, nous avons report´ dans la table 10.10 — voir
e
aussi les graphiques 10.11 et 10.12— les pond´rations Janvier 2001 et Novembre 2001 pour une perte en
e
cas de d´faillance de 50%. Globalement, nous observons une diminution de la valeur des actifs pond´r´s
e ee
pour les probabilit´s de d´faillance ´lev´es. Ceci s’explique par une corr´lation entre les valeurs des actifs
e e e e e
plus faible (voir le graphique 10.13).
Bibliographie
[1] Basel Committee on Banking Supervision, Best Practices for Credit Risk Disclosure, 74, September
2000
INTRODUCTION A LA GESTION DES RISQUES 134](https://image.slidesharecdn.com/gestionrisques-130221132633-phpapp01/85/Gestion-risques-144-320.jpg)
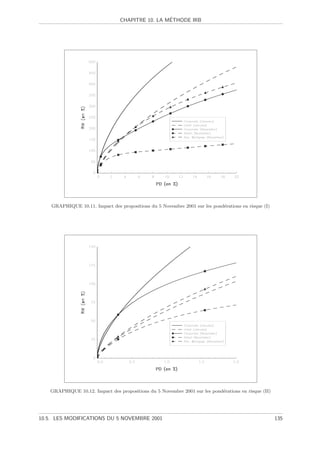
![GRAPHIQUE 10.13. Impact des propositions du 5 Novembre 2001 sur les corr´lations ρ (PD)
e
[2] Basel Committee on Banking Supervision, Principles for the Management of Credit Risk, 75, Sep-
tember 2000
[3] Basel Committee on Banking Supervision, The Internal Ratings-Based Approach — Consultative
Document, Supporting document to the New Basel Capital Accord, January 2001
[4] Basel Committee on Banking Supervision, Results of the Second Quantitative Impact Study, 5
November 2001
[5] Basel Committee on Banking Supervision, Potential Modifications to the Committee’s Proposals, 5
November 2001
[6] Koyluoglu, H.U. et A. Hickman [1998], Reconcilable differences, Risk Magazine, 11, October, 56-62
[7] Finger, C.C. [1999], Conditional approaches for CreditMetrics portfolio distributions, CreditMetrics
Monitor, April, 14-33
[8] Gordy, M.B. [2000], A comparative anatomy of credit risk models, Journal of Banking and Finance,
24, 119-149
[9] Gordy, M.B. [2001], A risk-factor model foundation for ratings-based bank capital rules, Board of
Governors of the Federal Reserve Systems, Working Paper
[10] Ieda, A., K. Marumo et T. Yoshiba [2000], A simplified method for calculating the credit risk of
lending portfolios, Institute for Monetary and Economic Studies, Bank of Japan, Discussion Paper,
2000-E-10
[11] Wilson, T. [2001a], IRB approach explained, Risk Magazine, 14, May, 87-90
[12] Wilson, T. [2001b], Probing granularity, Risk Magazine, 14, August, 103-106](https://image.slidesharecdn.com/gestionrisques-130221132633-phpapp01/85/Gestion-risques-146-320.jpg)




![12
Le mod`le de la firme
e
L’approche structurelle du risque de cr´dit est fond´e sur les m´thodes d’´valuation des options mises
e e e e
en place par Black et Scholes [1973] et Merton [1974]. Il s’agit d’une approche relativement intuitive
dans la mesure o` le risque de cr´dit encouru par le d´tenteur d’une obligation est directement reli´ ` la
u e e ea
r´alit´ ´conomique de la firme : le d´faut intervient d`s que la valeur de march´ de l’ensemble des actifs
e ee e e e
de la firme passe sous un certain seuil d´termin´ par le niveau global de la dette contract´e. Il s’agit d’une
e e e
vision optionnelle de la dette : l’´metteur re¸oit le droit de faire d´faut sur sa dette, droit qu’il exerce d`s
e c e e
que la valeur de ses actifs ne permet plus de la couvrir.
Merton est le premier ` proposer ce type de mod`le. Il l’applique ` la forme de dette la plus simple :
a e a
l’obligation z´ro coupon. Dans ce cadre, Merton obtient une formule ferm´e d’´valuation de la dette
e e e
faisant apparaˆ le spread de taux comme une prime li´e au risque de d´faut de la firme. D’un point de
ıtre e e
vue th´rorique, ce mod`le est tr`s s´duisant car il explicite directement les fondements ´conomiques du
e e e e e
risque obligataire :
– le taux sans risque ;
– la volatilit´ de la valeur de march´ des actifs de l’entreprise, c’est-`-dire l’incertitude pesant sur le
e e a
rendement de l’ensemble des actifs de la firme ;
– le levier, c’est-`-dire le rapport entre la valeur actualis´e au taux sans risque de la dette, et la valeur
a e
initiale des actifs : plus le levier est important (i.e. plus la part de la dette dans le total des actifs,
vu d’aujourd’hui, est importante) plus la dette est risqu´e. e
N´anmoins, d’un point de vue pratique, la prise en compte de variables ´conomiques propres ` chaque
e e a
entreprise limite le champ d’application du mod`le de Merton. De fa¸on g´n´rale, les mod`les structurels
e c e e e
s’av`rent difficiles ` mettre œuvre parce qu’ils requi`rent la connaissance de nombreux param`tres :
e a e e
1. la valeur des actifs, la structure financi`re de l’´metteur :
e e
Ces param`tres sont propres aux mod`les structurels. Si l’on souhaite ´valuer la dette d’un ´metteur
e e e e
de fa¸on pr´cise, il convient d’avoir une tr`s bonne connaissance de la valeur de march´ totale de ses
c e e e
actifs et de la fa¸on dont elle est susceptible d’´voluer au cours du temps. Cette valeur n’´tant pas
c e e
directement observable, il faut l’estimer le plus pr´cis´ment possible. Une telle d´marche n´cessite
e e e e
une base de donn´es particuli`rement riche portant sur la structure financi`re de l’entreprise et sa
e e e
valorisation boursi`re. L’exemple de Credit Monitor TM , outil de gestion du risque de cr´dit mis en
e e
place par K.M.V. (c.f. section 12.3), illustre la fa¸on dont ces donn´es peuvent ˆtre utilis´es pour
c e e e
estimer les probabilit´s de d´faut d’une entreprise. Cependant, d’un point de vue op´rationnel, il
e e e
est tr`s difficile d’acc´der ` ce type d’information, ce qui limite la port´e des mod`les structurels
e e a e e
pour la majorit´ des acteurs financiers engag´s sur les march´s obligataires. Notons de plus qu’on
e e e
ne peut contrˆler la structure capitalistique d’une entreprise en temps continu dans la mesure o`,
o u
la plupart du temps, les comptes sont publi´s une fois par an.
e](https://image.slidesharecdn.com/gestionrisques-130221132633-phpapp01/85/Gestion-risques-151-320.jpg)
![`
CHAPITRE 12. LE MODELE DE LA FIRME
2. les conditions d’´mission de la dette :
e
Il s’agit ici de prendre en compte les termes du contrat fixant entre autres la maturit´, les flux
e
vers´s, les ´ventuelles options de conversion, les ordres de priorit´ en cas de d´faut.
e e e e
3. La perte sachant le d´faut :
e
Une fois la faillite d´clar´e, une proc´dure de liquidation judicaire est mise en place. Un liquidateur
e e e
est alors nomm´, dont le rˆle est de r´aliser les actifs de la firme afin de rembourser les cr´anciers
e o e e
suivant leur ordre de priorit´. Notons que les modalit´s d’une telle proc´dure varient en fonction des
e e e
r´glementations propres ` chaque pays et que le montant total recouvr´ par les cr´anciers d´pend de
e a e e e
la mani`re dont est men´e la liquidation : par exemple, si la liquidation est rapide, les actifs risquent
e e
d’ˆtre brad´s. Dans les diff´rents mod`les structurels, la partie de la dette recouvr´e correspond `
e e e e e a
une fraction de la valeur de march´ de la firme ` l’instant de d´faut (Merton [1974], Leland
e a e
et Toft [1996]). Il peut ´galement s’agir d’une fonction de la valeur faciale de la dette, ou d’un
e
processus stochastique.
4. le processus du taux sans risque et la correlation entre ce processus et le prix des actifs :
Les spreads de taux peuvent difficilement ˆtre analys´s ind´pendemment de la structure des taux
e e e
sans risque. En effet, ce dernier d´pend fortement du cycle ´conomique, tout comme le risque de
e e
cr´dit. Par exemple, en p´riode de forte activit´, on peut s’attendre ` ce que d’une part, l’´cart
e e e a e
entre taux court et taux long s’acroisse, et d’autre part ` ce que la meilleure qualit´ du cr´dit
a e e
conduise ` une r´duction des spreads (l’´tude [4] men´e par Duffee en 1998 met en ´vidence ce type
a e e e e
de r´sultats). Pour pouvoir d´terminer le prix des instruments de cr´dit, il faut donc connaˆ le
e e e ıtre
lien entre la structure des taux sans risque et les probabilit´s de d´faut des entreprises.
e e
12.1 Le mod`le de Merton [1974]
e
Nous pr´sentons dans cette section les caract´ristiques du mod`le propos´ par Merton en 1974 et les
e e e e
principaux r´sultats qui en d´coulent. Les quatre points abord´s pr´c´demment sont sp´cifi´s de la fa¸on
e e e e e e e c
suivante :
1. Evolution de la valeur des actifs, Structure financi`re de l’´metteur :
e e
Merton utilise la dynamique suivante pour la valeur V (t) des actifs de la firme :
dV (t) = (αV (t) − C) dt + σV (t) dW (t) (12.1)
o` α repr´sente le taux de rendement instantan´ des actifs de la firme, C le montant des payouts (di-
u e e
videndes et int´rˆts) par unit´ de temps, et σ 2 la variance du processus de rendement. (W (t) , t ≥ 0)
ee e
est un mouvement brownien standard.
Les avoirs de la firme sont divis´s en deux classes : une classe unique et homog`ne de dette, le reste
e e
correpondant aux capitaux propres. De plus, la firme ne verse aucun dividende et ne peut proc´der e
a
` aucun remboursement partiel de sa dette avant la maturit´. e
2. Conditions d’´mission de la dette :
e
La firme promet de payer un montant B ` la maturit´ T . De plus, elle ne peut ni ´mettre de nouvelle
a e e
dette, ni rembourser une partie de sa dette avant la maturit´. Compte tenu de ces conditions
e
d’´mission et de la structure financi`re de la firme, le param`tre C de l’´quation (12.1) vaut 0 et la
e e e e
dynamique suivi par la valeur des actifs devient :
dV (t)
= α dt + σ dW (t) (12.2)
V (t)
3. Perte sachant le d´faut :
e
En cas de d´faut, le d´tenteur de la dette devient propri´taire de la firme. Merton suppose que la
e e e
firme fait d´faut si la valeur V (T ) ` la maturit´ T des actifs est inf´rieure ` B. En cas de d´faut, le
e a e e a e
d´tenteur de la dette re¸oit donc V (T ) , et il perd B − V (T ). Le payoff final peut d`s lors s’´crire
e c e e
D (T ) = B − max (B − V (T ) , 0) (12.3)
La d´tention d’une dette risqu´e s’interpr`te alors comme une strat´gie o` l’on aurait achet´ un z´ro-
e e e e u e e
coupon sans risque dont on aurait financ´ une partie du coˆt par la vente d’un put de sous-jacent
e u
V , de prix d’exercice B et de maturit´ T .
e
INTRODUCTION A LA GESTION DES RISQUES 142](https://image.slidesharecdn.com/gestionrisques-130221132633-phpapp01/85/Gestion-risques-152-320.jpg)
![`
CHAPITRE 12. LE MODELE DE LA FIRME
4. Processus de taux sans risque :
le taux d’int´rˆt sans risque demeure constant au cours du temps, ´gal ` r. Les probl`mes li´s ` la
ee e a e e a
dynamique des taux ne sont pas abord´s dans ce premier mod`le.
e e
La dette est valoris´e en supposant que les deux conditions suivantes sont v´rifi´es :
e e e
– il y a absence d’opportunit´ d’arbitrage : il est impossible de g´n´rer un profit presque sˆr ` partir
e e e u a
d’un investissement nul ;
– les march´s sont complets : il est possible de r´pliquer tout produit d´riv´ ` l’aide d’une strat´gie
e e e ea e
dynamique fond´e sur les actifs sous-jacents.
e
Ce sont deux hypoth`ses fortes qui, d’un point de vue pratique, assurent l’existence (absence d’opportunit´
e e
d’arbitrage) et l’unicit´ (compl´tude des march´s) des prix de march´. N´anmoins, contrairement aux
e e e e e
march´s d’actions, les march´s obligataires sont particuli`rement peu liquides. Supposer dans ce cas
e e e
pr´cis l’existence d’arbitrageurs qui contraignent les prix ` v´rifier certaines relations ne semble donc pas
e a e
tr`s r´aliste.
e e
Par contre, si on consid`re que ces hypoth`ses sont vraies sur le march´ des actions, la valorisation f
e e e
de la firme sur le march´ des actions (qui est connue) refl`te les anticipations du march´ concernant la
e e e
valeur de la firme ` la maturit´ et en utilisant l’identit´ vraie ` chaque instant
a e e a
F =V −f (12.4)
on obtient la valeur F aujourd’hui de la dette contract´e en fonction de f et de la valeur de march´ V
e e
des actifs de la firme. Notons que le param`tre V n’´tant pas accessible, il faut l’estimer. Comme nous
e e
le verrons ` la section 12.3, une telle estimation peut ˆtre r´lis´e ` partir de la valeur des actions f
a e e e a
et de la valeur comptable de la dette B. Les prix obtenus par une telle m´thode peuvent ˆtre qualifi´s
e e e
d’implicites : ce ne sont pas les prix observ´s sur le march´ mais les prix que l’on devrait observer compte
e e
tenu de la valorisation boursi`re de la firme.
e
Dans le cadre de ces hypoth`ses, la valeur de la dette correspond ` l’esp´rance des flux futurs actualis´s
e a e e
qu’elle g´n`re. Merton explicite alors le spread de taux par rapport au taux r du z´ro-coupon certain,
e e e
r´sultant du risque de d´faut :
e e
1 1
R (T ) − r = − ln Φ h2 d, σ 2 T + Φ h1 d, σ 2 T (12.5)
T d
o` Φ repr´sente la fonction de r´partition d’une loi normale centr´e r´duite et
u e e e e
B
d = V (0)erT
1
h (x, y) = −y − 2 1 y − ln x (12.6)
1 2
h (x, y) = −y − 2 1 y + ln x
1
2 2
Pour une maturit´ T donn´e, la prime de risque d´pend uniquement de la volatilit´ σ 2 de la valeur des
e e e e
actifs et du levier d. Merton montre que R (T ) − r est une fonction croissante de ces deux param`tres, ce
e
qui est conforme ` l’intuition :
a
– La volatilit´ de la valeur de march´ d’une firme refl`te l’incertitude des op´rateurs sur les rendements
e e e e
a
` venir de cette firme. Par cons´quent, plus la volatilit´ est ´lev´e, plus le risque encouru par le
e e e e
d´tenteur de la dette est important et plus la prime doit ˆtre cons´quente.
e e e
– L’effet de levier permet aux propri´taires d’une entreprise (les actionnaires) d’accroˆ
e ıtre le niveau
d’activit´ sans augmenter pour autant le montant de leurs engagements. Le risque suppl´mentaire
e e
li´ au surplus d’activit´ est alors support´ par les cr´anciers, ce qui se traduit par une meilleure
e e e e
r´mun´ration de leurs placements.
e e
Les graphiques suivants illustrent la fa¸on dont le levier influence la structure par terme des spreads
c
de taux :
`
12.1. LE MODELE DE MERTON [1974] 143](https://image.slidesharecdn.com/gestionrisques-130221132633-phpapp01/85/Gestion-risques-153-320.jpg)
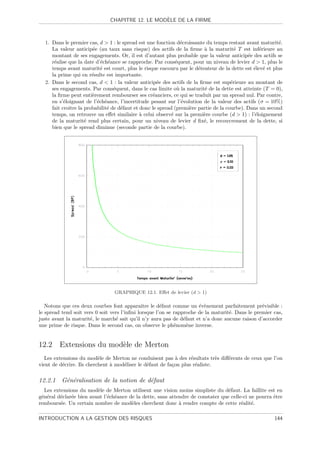
![`
CHAPITRE 12. LE MODELE DE LA FIRME
GRAPHIQUE 12.2. Effet de levier (d 1)
L’extension la plus directe du mod`le de Merton suppose que le d´faut peut se produire ` chaque date
e e a
de paiement du principal ou des int´rˆts (mod`le de Geske [1977]). Les actionnaires disposent d’une
ee e
option compos´e qu’ils peuvent exercer ` chaque date de versement.
e a
Un second type d’extension consiste ` appr´hender le d´faut non plus de fa¸on discr`te mais en temps
a e e c e
continu : la firme peut faire d´faut ` n’importe quelle date entre la date d’´mission et la maturit´, qu’il
e a e e
s’agisse ou non d’une date de paiement.
Black et Cox [1976] reprennent le cadre d’analyse de Merton en supposant de plus que la firme
peut-ˆtre mise en faillite d`s que la valeur de march´ V (t) passe sous un seuil critique K (t) tel que
e e e
K (t) = Ke−r(T −t) , 0K≤B (12.7)
¯
Black et Cox d´finissent ainsi un levier maximal d = B/K ≥ 1 que les actionnaires ne peuvent franchir
e
pour financer l’activit´ de leur entreprise. Notons que la barri`re K est fix´e de fa¸on exog`ne : elle doit
e e e c e
ˆtre d´finie de fa¸on explicite dans le contrat de dette.
e e c
12.2.2 Introduction de sauts dans le processus de valorisation des actifs
Comme nous l’avons d´j` remarqu´, le mod`le de Merton sp´cifie le d´faut comme un ph´nom`ne
ea e e e e e e
parfaitement pr´visible si bien que le spread tend vers zero ` mesure que l’on se rapproche de la maturit´.
e a e
Dans la pratique, on n’observe pas de tel ph´nom`ne : les spreads restent importants mˆme pour des
e e e
dates de maturit´ assez proches.
e
Zhou [1997] propose une solution ` ce probl`me tout en conservant un cadre d’analyse proche de
a e
celui de Merton : il int`gre un processus de sauts au processus de valorisation des actifs, si bien que les
e
trajectoires suivies par la valeur de march´ de la firme ne sont plus n´cessairement continues. Dans ce
e e
contexte, Zhou montre que les spreads demeurent significatifs mˆme pour une dette risqu´e proche de la
e e
maturit´ : les investisseurs demandent une prime permettant de s’assurer contre le risque suppl´mentaire
e e
engendr´ par les sauts.
e
`
12.2. EXTENSIONS DU MODELE DE MERTON 145](https://image.slidesharecdn.com/gestionrisques-130221132633-phpapp01/85/Gestion-risques-155-320.jpg)
![`
CHAPITRE 12. LE MODELE DE LA FIRME
12.3 M´thodologie mise en place par K.M.V. Corporation
e
En introduction de la section 8.1, nous avons pr´sent´ les trois composantes du risque de cr´dit : le risque
e e e
de d´faut, l’incertitude pesant sur le taux de recouvrement, et le risque de d´gradation de la qualit´ de la
e e e
contrepartie. Ce paragraphe constitue une illustration de la fa¸on dont le risque de d´faut est appr´hend´
c e e e
par K.M.V. Leur m´thodologie se fonde sur le mod`le de la firme : ` partir de la valeur comptable de la
e e a
dette d’une entreprise et de l’estimation de sa valeur de march´, K.M.V calcule la distance de la firme au
e
d´faut et en d´duit, pour un horizon donn´, sa probablit´ de d´faut, not´e EDFT M (Expected Default
e e e e e e
Frequency).
Cette section se fonde essentiellement sur le document [3] de P. Crosbie, publi´ par K.M.V., consultable
e
sur internet ` l’adresse suivante :
a
http ://www.kmv.com
12.3.1 Une mesure du risque de d´faut : la distance au d´faut
e e
Le mod`le de Merton laisse entendre qu’une mesure pertinente de la valeur nette d’une firme est sa
e
valeur de march´ moins la valeur comptable de sa dette, le d´faut intervenant d`s que la valeur nette
e e e
s’annule :
– La valeur de march´ des actifs rend compte de la rentabilit´ esp´r´e de l’activit´ de l’entreprise. Il
e e ee e
s’agit d’une mesure dynamique de sa valeur. Savoir si l’entreprise dispose du cash n´cessaire pour
e
faire face ` ses engagements n’est d`s lors pas fondamental. Si la valeur de march´ des actifs est
a e e
suffisante, l’entreprise peut toujours faire face au paiement de sa dette en vendant une partie de ses
actifs. Ce qui compte est donc davantage la valeur esp´r´e de l’entreprise reposant sur son activit´
ee e
future (valeur de march´), que la valeur de l’entreprise r´sultant de son activit´ pass´e (derni`re
e e e e e
ligne du bilan de l’entreprise).
– Il faut en revanche consid´rer la valeur comptable de la dette car elle correspond ` ce que la firme
e a
devra effectivement payer.
Dans la pratique, le d´faut peut se produire pour des valeurs nettes n´gatives. Ceci tient ` la nature des
e e a
engagements de l’entreprise, sa dette pouvant se d´composer en dette ` long terme et dette ` court terme.
e a a
La pr´sence d’une dette ` long terme dans le bilan de l’entreprise apporte donc une certaine flexibilit´.
e a e
Le point de d´faut se situe en g´n´ral entre le montant total de la dette et le montant de la dette de court
e e e
terme.
Pour ´valuer le risque de d´faut, la valeur nette ne peut ˆtre consid´r´e ind´pendamment du risque
e e e ee e
li´ ` l’activit´ de l’entreprise. En effet, il n’est int´ressant de connaˆ l’´cart entre la valeur de march´
ea e e ıtre e e
des actifs et le point de d´faut que si l’on sait dans quelle mesure il risque d’ˆtre combl´. La distance au
e e e
point de d´faut K d´finie par K.M.V normalise donc la valeur nette de l’entreprise en la comparant ` son
e e a
´cart-type :
e
VA − K
DD = (12.8)
σ A VA
DD correspond au nombre d’´carts-type s´parant la valeur de march´ des actifs du point de d´faut. On
e e e e
peut remarquer que cette mesure fait la synth`se des facteurs de risque mis en ´vidence par le mod`le de
e e e
Merton : elle int`gre ` la fois le levier et la volatilit´ des actifs. Notons de plus que la distance au d´faut
e a e e
prend en compte l’influence du secteur d’activit´, de la zone g´ographique et de la taille de l’entreprise
e e
par l’interm´diaire de la volatilit´ des actifs. Le graphique 12.3 publi´ par K.M.V met en ´vidence l’impact
e e e e
de deux de ces facteurs sur la volatilit´.e
– La volatilit´ des actifs est d’autant plus importante que la taille de l’entreprise est faible. Une grande
e
entreprise peut donc s’endetter davantage qu’une petite entreprise pour financer son activit´ sans e
que le risque de cr´dit associ´ soit pour autant sup´rieur.
e e e
– De fa¸on analogue, parmi les cinq secteurs d’activit´ pr´sent´s, le secteur bancaire est celui qui
c e e e
autorise les niveaux de levier les plus ´lev´s, le rendement des actifs y ´tant moins incertain.
e e e
La connaissance de la distance au d´faut et de la distribution de la valeur des actifs permet de calculer
e
directement les probabilit´s de d´faut.
e e
INTRODUCTION A LA GESTION DES RISQUES 146](https://image.slidesharecdn.com/gestionrisques-130221132633-phpapp01/85/Gestion-risques-156-320.jpg)

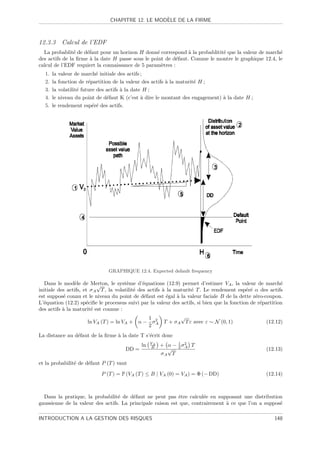
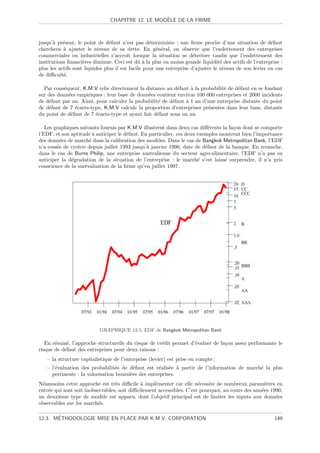
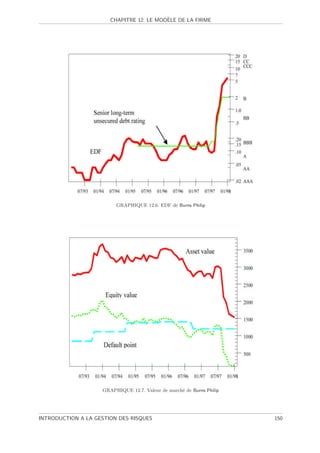
![12.4 Une application : le mod`le CreditMetrics
e
Le mod`le CreditMetrics sera d´velopp´ dans le cours “Gestion des Risques Multiples”.
e e e
Bibliographie
[1] Black, F. and M. Scholes [1973], The pricing of options and corporate liabilities, Journal of Political
Economy, 81, 637-659
[2] Black, F. and J. Cox [1976], Valuing corporate securities : some effects of bond indenture provisions,
Journal of Finance, 31, 351-367
[3] Crosbie, P. [1997], Modeling default risk, K.M.V., Working Paper
[4] Duffee, G.R. [1998], The relation between treasury yields and corporate bond yield spreads, Journal
of Finance, 53(6), 2225-2241
[5] Geske, R. [1977], The valuation of corporate liabilities as compound options, Journal of Financial
and Quantitative Analysis, 12(4), 541-552
[6] Leland, H. [1994], Corporate debt value, bond convenants, and optimal capital structure, Journal
of Finance, 49, 1213-1252
[7] Leland, H. and K. Toft [1996], Optimal capital structure, endogenous bankruptcy, and the term
structure of credit spreads, Journal of Finance, 51, 987-1019
[8] Merton, R.C. [1974], On the pricing of corporate debt : the risk structure of interest rates, Journal
of Finance, 29, 449-470
[9] Zhou, C. [1997], A jump-diffusion approach to modeling credit risk and valuing defaultable securities,
Federal Reserve Board, Working Paper](https://image.slidesharecdn.com/gestionrisques-130221132633-phpapp01/85/Gestion-risques-161-320.jpg)


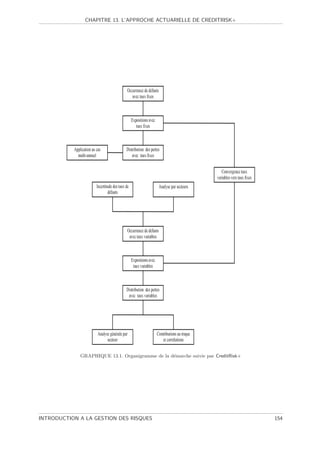






![On applique alors la relation de r´currence, apr`s avoir r´duit au mˆme d´nominateur la derni`re ex-
e e e e e e
pression. Evidemment, un choix judicieux de L, l’unit´ d’exposition, permettrait de r´duire le degr´ du
e e e
polynˆme B(z) de telle sorte que les calculs soient plus faciles ` traiter. On se retrouve alors en possession
o a
de la forme explicite de la distribution des pertes du portefeuille.
13.4 Conclusion
Tout d’abord, notons que cette approche peut ˆtre g´n´ralis´e en consid´rant l’´ventuelle appartenance
e e e e e e
d’un ´metteur ` plusieurs secteurs. On fait alors intervenir des coefficients θA,k qui pour chaque ´mission
e a e
A donne la proportion de l’influence de son taux de d´faut par la variable xk . En g´n´ralisant de la sorte,
e e e
on accorde ` tous les titres d’ˆtre d´pendants de plusieurs secteurs. Cette hypoth`se est trait´e dans
a e e e e
CreditRisk+, qui donne alors le processus et la nouvelle distribution des pertes encourus.
Remarquons, de plus, que la notion de corr´lation n’apparait pas explicitement dans le mod`le, mais
e e
est pris en compte indirectement dans les volatilit´s de chaque secteur et ´ventuellement dans le profil
e e
des coefficients θA,k . On peut toutefois calculer les contributions marginales de chacun des titres ainsi que
les corr´lations entre ces mˆmes titres a posteriori. Les ´tapes n´cessaires pour aboutir ` ces corr´lations
e e e e a e
et ` ces contributions ne sont pas pr´sent´es ici mais le sont dans CreditRisk+.
a e e
Le principal reproche adress´ ` CSFP r´side dans le fait que leur mod`le ignore la possibilit´ d’un
e a e e e
changement de spread des titres composant le portefeuille sans pour autant observer un quelconque
d´faut. Par analogie avec CreditMetrics, ce mod`le ne tient pas compte de la perte ou du gain de valeur
e e
du portefeuille provoqu´s par des changements de rating. Ce mod`le semble, en fait, s’adapter au cas de
e e
banques accordant des cr´dits, et cherchant ` se couvrir contre un certain niveau de risque dˆ au d´faut
e a u e
de paiement d’une contrepartie. Mais cet outil ne convient pas ` une gestion de portefeuille qui a pour
a
vocation d’ˆtre assez liquide et qui tire son rendement des spreads des titres qui le composent.
e
Bibliographie
[1] Credit Suisse Financial Products [1997], CreditRisk+ : A credit Risk Managment Framework, London](https://image.slidesharecdn.com/gestionrisques-130221132633-phpapp01/85/Gestion-risques-171-320.jpg)


![´ ´
CHAPITRE 14. L’APPROCHE INTENSITE : UNE APPROCHE SOUS FORME REDUITE
de liquidation judiciaire est mise en place : le montant recouvr´ d´pendra de la fa¸on dont la proc´dure
e e c e
se d´roulera.
e
L’instant avant d´faut est mod´lis´ par une variable al´atoire τ d´finie sur l’espace (Ω, G, P). On in-
e e e e e
troduit le processus de saut H associ´ ` τ : Ht = 1{τ ≤t}, ∀t ∈ R+ , et on d´finit H = (Ht )t∈R+ comme la
ea e
filtration engendr´e par ce processus : Ht = σ (Hu , u ≤ t) , ∀t ∈ R+ .
e
L’observation des donn´es de march´ montre qu’il est impossible de dire avec certitude si le d´faut
e e e
est survenu ou non uniquement ` partir de celles-ci. En effet, il se peut tr`s bien qu’` une date donn´e,
a e a e
deux obligations aient un prix identique alors mˆme que l’un des deux ´metteurs vient de faire d´faut.
e e e
Math´matiquement, cela signifie que Ft Ht : τ n’est pas un F−temps d’arrˆt.
e e
Si l’occurence du d´faut ne peut pas se lire dans les prix de march´, on peut n´anmoins supposer
e e e
que les op´rateurs financiers disposent de cette information par un autre biais. Autrement dit, ` une
e a
date t donn´e, l’information disponible peut ˆtre mod´lis´e par la tribu Gt = σ (Fu , Hu , u ≤ t). On note
e e e e
G = F ∨ H la filtration associ´e. Le temps de d´faut est alors un G−temps d’arrˆt.
e e e
A la date t, les op´rateurs financiers disposent de deux types d’information bien distincts :
e
– D’une part, ils savent si le d´faut est survenu ou non. Cette information est contenue dans la tribu
e
Ht .
– D’autre part, ils ont acc`s ` ce que l’on a appel´ dans un premier temps l’information de march´
e a e e
(provenant des prix). Cette information, mod´lis´e par Ft , permet de formuler des hypoth`ses sur la
e e e
qualit´ de l’´metteur de la dette. Il s’agit donc de l’information utile, si le d´faut ne s’est pas encore
e e e
produit, pour ´tablir le prix de la dette risqu´e ` la date t . D`s lors, Ft ne se r´duit pas forc´ment
e e a e e e
aux prix de march´, elle peut contenir toute information permettant une meilleure appr´ciation de
e e
la qualit´ de la contrepartie (notes de rating par exemple).
e
14.1.1 D´finition de l’intensit´ de survie
e e
La d´composition de G en deux sous-filtrations F et H permet d’isoler l’information pertinente pour
e
le calcul des probabilit´s de d´faut. En particulier, on peut construire le processus Ft = P (τ ≤ t | Ft ) ,
e e
∀t ∈ R+ : F est bien d´fini car τ n’est pas F−adapt´. Il s’agit d’une F−sous-martingale positive born´e,
e e e
que l’on peut par cons´quent supposer continue ` droite. Ft traduit les croyances du march´ ` la date t
e a ea
concernant la possible occurence du d´faut avant cette date. Notons que l’incertitude des march´s pesant
e e
sur l’apparition du d´faut se traduit par Ft 1 ∀t ∈ R+ . On peut d`s lors d´finir le processus de hazard
e e e
Γ associ´ au temps de d´faut τ : Γt = − ln (1 − Ft ) , ∀t ∈ R+ .
e e
A chaque instant, on sait si le d´faut s’est produit ou non. Par contre, s’il ne s’est pas produit, les
e
op´rateurs financiers formulent des hypoth`ses ` partir des donn´es de march´. Ceci se traduit de fa¸on
e e a e e c
math´matique par la relation suivante :
e
∀t s, P (τ s | Gt ) = 1{τ t} EP eΓt −Γs | Ft (14.1)
Dans l’hypoth`se o` Γ est un processus absolument continu, il existe un processus F−progressivement
e u
t
mesurable tel que Γt = 0 γ u du. La relation (14.1) peut donc se r´´crire
ee
Rs
∀t s, P (τ s | Gt ) = 1{τ t} EP e− t
γ u du
| Ft (14.2)
La signification intuitive de γ apparaˆ ici : il s’agit de l’intensit´ de survie (ou encore intensit´ de d´faut)
ıt e e e
sachant le flux d’information de march´ (Ft )t∈R+ .
e
Si de plus, on suppose que Γ est un processus croissant (i.e. γ 0), alors le processus m d´fini par
e
t∧τ
mt = Ht − γ u du, ∀t ∈ R+ (14.3)
0
est une G−martingale. Cette propri´t´ est particuli`rement importante car elle permet d’´tablir une
ee e e
nouvelle repr´sentation du prix de la dette risqu´e. De plus, historiquement, c’est ` partir de cette
e e a
propri´t´ que l’intensit´ de d´faut a ´t´ d´finie (cf. Duffie, Schroder et Skiadas [1996]).
ee e e ee e
INTRODUCTION A LA GESTION DES RISQUES 164](https://image.slidesharecdn.com/gestionrisques-130221132633-phpapp01/85/Gestion-risques-174-320.jpg)
![´ ´
CHAPITRE 14. L’APPROCHE INTENSITE : UNE APPROCHE SOUS FORME REDUITE
14.1.2 Une autre approche de l’intensit´ de d´faut
e e
La d´composition de la filtration G en deux sous-filtrations F et H a permis de mettre en ´vidence le
e e
processus γ. N´anmoins, si l’on raisonne sans prendre en compte cette d´composition, on peut montrer1
e e
qu’il existe un processus λ positif G−adapt´ tel que le processus M d´fini par
e e
t∧τ
Mt = Ht − λu du, ∀t ∈ R+ (14.4)
0
est une G−martingale.
En g´n´ral, l’intensit´ de d´faut est d´finie ` partir de ce processus λ. N´anmoins, l’interpr´tation de
e e e e e a e e
λ reste difficile. En particulier on ne peut rien dire de la relation existant entre λ et l’intensit´ de survie
e
γ. Il se peut par exemple que le processus λ soit d´fini sans que γ existe. De plus, la caract´risation du
e e
processus λ reste probl´matique dans la mesure o` il n’est d´fini de fa¸on unique que jusqu’` l’instant de
e u e c a
d´faut τ .
e
Compte tenu de ce que l’on a dit jusqu’ici, on sait que si Γ est un processus croissant absolument
continu, alors λt∧τ = γ t∧τ , ∀t ∈ R+ . L’int´rˆt de la d´composition de G en deux sous-filtrations F et
ee e
H apparaˆ ` nouveau ici : elle met en ´vidence de fa¸on assez intuitive la signification de l’intensit´ de
ıt a e c e
d´faut λ, λ ´tant l’objet math´matique g´n´ralement introduit dans les mod`les ` intensit´.
e e e e e e a e
Par la suite, nous d´finirons l’intensit´ de d´faut ` partir de ce processus λ. Pour de plus amples
e e e a
d´veloppements concernant les liens entre les processus λ et γ, on pourra se r´f´rer ` l’article [5] de
e ee a
Jeanblanc et Rutkowski.
14.2 Les diff´rentes repr´sentations du prix de la dette risqu´e
e e e
14.2.1 Premi`res repr´sentations
e e
Soit (X, Z, τ ) une dette risqu´e. Notons D le processus des “dividendes” associ´ :
e e
Dt = Zu dHu + X (1 − HT ) 1{t=T } (14.5)
]0,t]
A l’aide de ce processus, la valorisation rique-neutre de l’actif risqu´ ` la date t s’´crit :
ea e
−1
Vt = Bt EP Bu dDu | Gt (14.6)
]t,T ]
o` bien, de fa¸on ´quivalente :
u c e
−1 −1
Vt = Bt EP Bu Zu dHu + BT X1{T τ } | Gt (14.7)
]t,T ]
ce qui peut encore s’´crire :
e
−1 −1
Vt = Bt EP Bτ Zτ 1{tτ ≤T } + BT X1{T τ } | Gt (14.8)
En particulier, cette derni`re relation implique que la valeur de la dette ` la maturit´ est VT = X1{T τ } .
e a e
De plus on retrouve bien dans cette relation que la valeur de la dette apr`s l’instant de d´faut est nulle :
e e
on a suppos´ dans le mod`le que le porteur de l’actif risqu´ est ind´mnis´ ` hauteur de Z d`s que le
e e e e e a e
d´faut se produit.
e
En utilisant la relation (14.4) d´finissant le processus λ, on peut r´´crire (14.7) de la fa¸on suivante :
e ee c
−1 −1
Vt = Bt EP Bu Zu λu 1{u≤τ } du + BT X1{T τ } | Gt (14.9)
]t,T ]
1 La d´monstration repose sur l’existence du
e G−compensateur de H (d´composition de Doob-Meyer) et sur une hypoth`se
e e
d’absolue continuit´ de ce processus.
e
´ ´ ´
14.2. LES DIFFERENTES REPRESENTATIONS DU PRIX DE LA DETTE RISQUEE 165](https://image.slidesharecdn.com/gestionrisques-130221132633-phpapp01/85/Gestion-risques-175-320.jpg)
![´ ´
CHAPITRE 14. L’APPROCHE INTENSITE : UNE APPROCHE SOUS FORME REDUITE
14.2.2 Th´or`me de repr´sentation du prix de la dette risqu´e
e e e e
La repr´sentation suivante du prix de la dette risqu´e est le r´sultat le plus int´ressant, qui justifie
e e e e
le d´veloppement de l’approche ` intensit´. Il apparaˆ que le prix d’une dette risqu´e peut ˆtre calcul´
e a e ıt e e e
comme s’il s’agissait d’un actif sans risque de d´faut ` condition d’incorporer une prime de risque dans
e a
le facteur d’actualisation. Pour aboutir ` un tel r´sultat, il convient de formuler les deux hypoth`ses
a e e
suivantes :
– Il y a continuit´ de la valeur de march´ de la dette risqu´e ` l’instant de d´faut. Autrement dit, la
e e e a e
probabilit´ qu’un saut inattendu se produise ` l’instant de d´faut est nulle.
e a e
– Toute F−martingale est une G−martingale, ce qui peut ˆtre formul´ de fa¸on ´quivalente par la
e e c e
relation suivante :
P (τ ≤ u | Ft ) = P (τ ≤ u | F∞ ) ∀ 0 u ≤ t
Ainsi, si le d´faut s’est produit avant la date t, l’´volution des prix sur le march´ apr`s cette date
e e e e
ne s’enrichira pas d’information nouvelle ` ce sujet.
a
Compte tenu de ces deux hypoth`ses, la valeur Vt de la dette ` la date t peut s’´crit :
e a e
T
˜
Vt = 1{tτ } Bt EP ˜ −1 ˜ −1
Bu Zu λu du + BT X | Ft (14.10)
t
t
u ˜
o` Bt = exp 0
(ru + λu ) du .
Notons que le conditionnement n’est plus effectu´ par rapport ` la filtration G : seule l’information
e a
de march´ F est prise en compte. On s’est donc ramen´ au cadre classique o` la filtration consid´r´e est
e e u ee
la filtration brownienne des prix. Ceci permet d’int´grer les mod`les ` intensit´ dans une th´orie plus
e e a e e
g´n´rale (les mod`les d´riv´s de la th´orie de Black et Scholes ou bien encore les diff´rents mod`les de
e e e e e e e e
taux sont toujours sp´cifi´s en consid´rant la filtration des prix).
e e e
14.3 Un exemple d’application : le mod`le de Jarrow et Turnbull
e
[1995]
Le mod`le de Jarrow et Turnbull reprend l’ensemble des hypoth`ses formul´es pr´c´demment. Les
e e e e e
hypoth`ses sp´cifiques au mod`le sont les suivantes :
e e e
– L’´mission consid´r´e est une obligation z´ro-coupon de maturit´ T , donnant droit au versement
e ee e e
d’un dollar ` la date T .
a
– En cas de d´faut, l’entreprise ne versera qu’une fraction du paiement promis. Le taux de recouvre-
e
ment δ de la dette est suppos´ constant2 . Math´matiquement, cette hypoth`se s’´crit
e e e e
Bu
Zu = δ, ∀u ∈ [0, T ]
BT
– Le processus de d´faut (Ht ) associ´ ` l’instant de d´faut τ correspond ` un simple saut poissonien
e ea e a
entre deux ´tats. Autrement dit, l’intensit´ de d´faut λ est suppos´e constante au cours du temps3 .
e e e e
– Le processus du taux sans risque est suppos´ ind´pendant du processus de d´faut. Il s’agit ici d’une
e e e
hypoth`se simplificatrice et peu r´aliste, que l’on retrouve dans la plupart des mod`les ` intensit´.
e e e a e
2δ peut d´pendre du niveau de priorit´ de l’obligation risqu´e au sein de l’ensemble de la dette ´mise par l’entreprise.
e e e e
3 Notons que Jarrow, Lando et Turnbull [1997] proposent une extension de ce mod`le dans laquelle le processus de
e
d´faut est associ´ ` une chaˆ de Markov dont les diff´rents ´tats sont les classes de rating des agences de notation. A
e e a ıne e e
chaque classe de rating correspond alors une intensit´ de d´faut. Une telle mod´lisation permet de faire ´voluer la valeur
e e e e
de la dette risqu´e en fonction de la note qui lui est associ´e.
e e
INTRODUCTION A LA GESTION DES RISQUES 166](https://image.slidesharecdn.com/gestionrisques-130221132633-phpapp01/85/Gestion-risques-176-320.jpg)
![Compte tenu de ces quatre hypoth`ses suppl´mentaires, l’´quation (14.10) devient
e e e
Vt = 1{tτ } p (t, T ) δ 1 − e−λ(T −t) + e−λ(T −t) (14.11)
Bt
o` p (t, T ) = EP
u BT | Ft repr´sente le prix ` la date t d’un z´ro-coupon sans risque de maturit´ T .
e a e e
Cette derni`re formule est tr`s intuitive : le prix d’un z´ro-coupon risqu´ est ´gal au prix du z´ro-coupon
e e e e e e
sans risque multipli´ par l’esp´rance du payoff ` la maturit´ sous la probabilit´ risque-neutre.
e e a e e
Nous allons maintenant utiliser cette formule pour calculer le spread de taux entre le z´ro-coupon
e
∂
sans risque et la dette risqu´e. Notons F (t, T ) = − ∂T log Vt le taux forward d’un z´ro-coupon risqu´
e e e
et f (t, T ) le taux forward d’un z´ro-coupon sans risque. En utilisant l’´quation (14.11), on obtient la
e e
relation suivante :
(1 − δ) λe−λ(T −t)
F (t, T ) = f (t, T ) + (14.12)
δ 1 − e−λ(T −t) + e−λ(T −t)
En faisant tendre T vers t, on obtient la relation liant le taux spot risqu´ R au processus de taux sans
e
risque r :
R (t) = r (t) + (1 − δ) λ (14.13)
Ce r´sultat int´ressant montre que le spread de taux observ´ sur les march´s est dˆ au risque de cr´dit.
e e e e u e
En outre, il apparaˆ que ce spread d´pend tout autant du processus de d´faut que du processus de
ıt e e
recouvrement. On retrouve ici un r´sultat analogue ` celui obtenu par Duffie et Singleton de fa¸on plus
e a c
g´n´rale (cf. articles [1] et [3]).
e e
Bibliographie
[1] Duffie, D. et K. Singleton [1997], An econometric model of the term structure of interest rate
swap yields, Journal of Finance, 52, 1287-1321
[2] Duffie, D., M. Schroder et C. Skiadas [1996], Recursive valuation of defaultable securities and
the timing of resolution of uncertainty, Annals of Applied Prbability, 6, 1075-1090
[3] Duffie, D. et K. Singleton [1999], Modeling term structures of defaultable bonds, Review of Fi-
nancial Studies, 12-4, 687-720
[4] Jarrow], R., D. Lando et S. Turnbull [1997], A markov model for the term structure of credit
risk spreads, Review of Financial Studies, 10-2, 481-523
[5] Jeanblanc, M. et M. Rutkowski [1999], Modelling of default risk : an overview, Working Paper](https://image.slidesharecdn.com/gestionrisques-130221132633-phpapp01/85/Gestion-risques-177-320.jpg)



![15
La r´glementation prudentielle
e
Les documents consultatifs du Comit´ de Bˆle ouvrent la voie ` une prise en compte explicite des
e a a
risques op´rationnels dans le calcul des fonds propres r´glementaires bancaires, ` l’instar de ce qui existe
e e a
d´j` sur les risques de cr´dit et de march´. Toutefois, sur le plan m´thodologique, la mesure du risque
ea e e e
op´rationnel n’a pas encore la maturit´ qu’on constate sur les autres risques. En effet, sur ces derniers —
e e
risque de cr´dit et risque de march´ — les banques ont consacr´ des ressources importantes et ont ainsi
e e e
abouti ` des mod`les de type Value-At-Risk qui, mˆme s’ils sont loin d’ˆtre parfaits, ont atteint un degr´
a e e e e
de sophistication et de robustesse remarquable.
Ce manque de maturit´ intellectuelle sur les risques op´rationnels n’est ´videmment pas appel´ ` durer :
e e e ea
ce risque fera l’objet dans un avenir proche d’un traitement analogue aux autres, fond´ sur la construction
e
d’un mod`le interne et l’´valuation d’un capital ´conomique plus pr´cis qu’un calcul forfaitaire. Cette
e e e e
´volution est dans le sens de l’histoire r´glementaire. Elle r´sultera aussi d’une volont´ des banques de
e e e e
piloter en interne la cr´ation de valeur (Value-based management) et, en l’occurrence, de r´duire au
e e
minimum les destructions de valeur dues ` des d´fauts de proc´dure ou ` un manque de “best practices”
a e e a
que r´v`le la mat´rialisation des risques op´rationnels. R´aliser ce pilotage imposera tˆt ou tard de
e e e e e o
disposer de mesures des risques op´rationnels fond´es sur des calculs autres que des calculs forfaitaires.
e e
Il convient de nuancer tr`s fortement les r´flexions pr´c´dentes. Lors de la sortie du document consultatif
e e e e
du 16 janvier 2001, il semblait qu’effectivement les banques ´taient largement plus avanc´es sur la
e e
mod´lisation du risque de cr´dit que sur celle du risque op´rationnel. La mise en place de Groupes
e e e
de Travail (par exemple, WGOR — Working Group on Operational Risk — cr´´ par l’Institute ee
International Finance) a montr´ que certaines banques (mais le nombre est relativement faible) sont
e
tout ` fait capables de mesurer le risque op´rationnel avec un mod`le interne. Il est devenu
a e e
´vident aussi que le risque de cr´dit est beaucoup plus difficile ` mod´liser que le risque
e e a e
op´rationnel. Au mois de septembre 2001, la situation est donc la suivante :
e
– le Comit´ de Bˆle autorise l’utilisation d’un mod`le interne LDA pour mesurer les risques op´rationnels ;
e a e e
– pour l’instant, seulement une dizaine ( ?) de banques au monde sont capables de mettre en place la
m´thode LDA ;
e
– il n’est pas sˆr que ce nombre soit beaucoup plus important en 2005, lors de l’impl´mentation de
u e
l’Accord.
15.1 La d´finition du risque op´rationnel
e e
Rappelons que, selon le document consultatif [1] du comit´ de Bˆle, les risques op´rationnels se
e a e
d´finissent comme les risques de pertes directes ou indirectes r´sultant de l’inadaptation ou de la d´faillance
e e e](https://image.slidesharecdn.com/gestionrisques-130221132633-phpapp01/85/Gestion-risques-181-320.jpg)
![´
CHAPITRE 15. LA REGLEMENTATION PRUDENTIELLE
de proc´dures ou de personnes, de personnes ou de syst`mes ou r´sultant d’´v´nements ext´rieurs ( the
e e e e e e
risk of direct or indirect loss resulting from inadequate or failed internal processes, people and systems or
from external events ). Cette d´finition a ´t´ critiqu´e, car il est relativement difficile de calculer certaines
e ee e
pertes indirectes. Le 28 septembre 2001, le Comit´ de Bˆle a donc propos´ une seconde d´finition :
e a e e
Les risques op´rationnels se d´finissent comme le risque de pertes dues ` une inad´quation
e e a e
ou ` une d´faillance des proc´dures, personnels, syst`mes internes ou ` des ´v´nements
a e e e a e e
ext´rieurs (Thoraval [2001]).
e
Il est n´cessaire de pr´ciser les types de perte que comprend cette d´finition. Dans le document [1], le
e e e
Comit´ de Bˆle avait retenu 6 types de pertes :
e a
1. Write-Downs : direct reduction in value of assets due to theft, fraud, unauthorised activity or
market and credit losses arising as a result of operational events .
2. Loss of Recourse : payments or disbursements made to incorrect parties and not recovered .
3. Restitution : payments to clients of principal and/or interest by way of restitution, or the cost
of any other form of compensation paid to clients .
4. Legal Liability : judgements, settlements and other legal costs .
5. Regulatory and Compliance (incl. Taxation Penalties) : fines, or the direct cost of any other
penalties, such as license revocations .
6. Loss of or Damage to Assets : direct reduction in value of physical assets, including certificates,
due to some kind of accident (e.g. neglect, accident, fire, earthquake) .
Cette classification est relativement ´loign´e de celles qui avaient ´t´ mises en place par l’industrie ban-
e e ee
caire. Par exemple, la base de donn´es “Operational Risk Losses Database” de la BBA (British Bankers’
e
Association) consid´re 4 types de perte :
e
1. People
2. Process
3. Systems
4. External
Finalement, le Comit´ de Bˆle a adopt´ une nouvelle classification le 28 septembre 2001 :
e a e
1. Internal Fraud : losses due to acts of a type intended to defraud, misappropriate property or
circumvent regulations, the law or company policy, excluding diversity/discrimination events, which
involves at least one internal party .
2. External Fraud : losses due to acts of a type intended to defraud, misappropriate property or
circumvent the law, by a third party .
3. Employment Practices Workplace Safety : losses arising from acts inconsistent with
employment, health or safety laws or agreements, from payment of personal injury claims, or from
diversity/discrimination events .
4. Clients, Products Business Practices : losses arising from an unintentional or negligent
failure to meet a professional obligation to specific clients (including fiduciary and suitability requi-
rements), or from the nature or design of a product .
5. Damage to Physical Assets : losses arising from loss or damage to physical assets from natural
disaster or other events .
6. Business Disruption System Failures : losses arising from disruption of business or system
failures .
7. Execution, Delivery Process Management : losses from failed transaction processing or
process management, from relations with trade counterparties and vendors .
Nous remarquons donc que les risques strat´giques et r´putationnels sont exclus du p´rim`tre des risques
e e e e
op´rationnels.
e
INTRODUCTION A LA GESTION DES RISQUES 172](https://image.slidesharecdn.com/gestionrisques-130221132633-phpapp01/85/Gestion-risques-182-320.jpg)
![´
CHAPITRE 15. LA REGLEMENTATION PRUDENTIELLE
Le Comit´ de Bˆle consid´re un d´coupage matriciel de la banque. Celle-ci est donc divis´e en diff´rentes
e a e e e e
activit´s :
e
Business Units Business Lines
Investment Banking Corporate Finance
Trading Sales
Banking Retail Banking
Commercial Banking
Payment Settlement
Agency Services Custody
Others Asset Management
Retail Brokage
Toutefois, les typologies exactes des types de risque et des lignes de m´tier restent n´anmoins impr´cises.
e e e
Mˆme si le document consultatif donne beaucoup de pr´cisions, la banque doit faire un travail de mapping
e e
important. En outre, l’existence d’un “double-comptage” n’est pas exclu. En effet, le capital r´glementaire
e
allou´ au risque de cr´dit ou de march´ est d´j` cens´ couvrir une part du risque op´rationnel. Il y a donc
e e e ea e e
un risque d’allouer deux fois du capital pour le mˆme risque.
e
15.2 Les approches forfaitaires
A la lecture du document [1], il n’est pas encore clair de savoir si les fonds propres r´glementaires doivent
e
couvrir les seules pertes exceptionnelles (“unexepected loss”), ou en plus les pertes moyennes (“expected
loss”). En th´orie, les fonds propres ne couvrent que les seules pertes exceptionnelles et non les pertes
e
moyennes, ces derni`res ´tant cens´es ˆtre couvertes par des provisions ou imput´es sur le r´sultat courant.
e e e e e e
Toutefois, dans la mesure o` les normes comptables de provisionnement diff`rent d’un pays ` l’autre et
u e a
d’un type de risque ` un autre, les fonds propres au titre du risque op´rationnel pourraient ˆtre amen´s
a e e e
a
` jouer ce double rˆle. D’apr`s le document [2], la mesure du risque op´rationnel semble correspondre au
o e e
quantile, c’est-`-dire ` la somme de l’expected loss et de l’unexpected loss.
a a
S’agissant des m´thodologies propos´es par le document consultatif du Comit´ de Bˆle, elles s’inspirent
e e e a
fortement de celles que ce mˆme document envisage pour le risque de cr´dit. Il y a eu une volont´ assez
e e e
forte de mettre en parall`le le traitement de ces deux risques en proposant soit des m´thodes dites
e e
standards (c’est-`-dire forfaitaires) soit des m´thodes n´cessitant des ´l´ments rattach´s directement aux
a e e ee e
risques eux-mˆmes (probability of default/probability of event, Loss Given Default/Loss Given Event,
e
etc.). Le Comit´ de Bˆle utilisent le terme “Advanced Measurement Approaches” ou AMA pour
e a
d´finir ces approches non standards. Celles-ci seront expos´es dans le chapitre suivant.
e e
15.2.1 Basic Indicator Approach (BIA)
C’est une m´thode forfaitaire o` le calcul du capital se fait ` partir d’un indicateur d’exposition EI. Le
e u a
capital ´conomique associ´ au risque op´rationnel est donc reli´ aux r´sultats (par exemple, le PNB ou le
e e e e e
revenu) mais pas au risque op´rationnel r´el ni ` la qualit´ intrins`que de la banque en terme de maˆ
e e a e e ıtrise
de ces risques (qualit´ de l’audit interne par exemple). Ceci pose ´videmment probl`me en p´nalisant les
e e e e
banques profitables d’une part, et en n’incitant pas ` la maˆ
a ıtrise des risques d’autre part.
Le Comit´ de Bˆle propose de retenir le PNB — Gross Income — GI comme proxy. Les fonds propres
e a
FP se calcule alors tr`s facilement ` partir de la formule
e a
FP = α × GI (15.1)
o` α est un coefficient fix´ par les autorit´s r´glementaires. Dans le document [1], un premier calcul
u e e e
du Comit´ de Bˆle donnait α ´gal ` 30%. D’apr`s les r´sultats de QIS2, α est en fait proche de 20%.
e a e a e e
Notons que l’approche BIA sera calibrer afin d’obtenir une charge en capital pour la “Banque Mondiale
Moyenne” ´gale ` 20% de la charge totale en capital. Pour cette approche, aucun crit`re d’´ligibilt´ n’est
e a e e e
exig´.
e
15.2. LES APPROCHES FORFAITAIRES 173](https://image.slidesharecdn.com/gestionrisques-130221132633-phpapp01/85/Gestion-risques-183-320.jpg)
![´
CHAPITRE 15. LA REGLEMENTATION PRUDENTIELLE
15.2.2 Standardised Approach (SA)
C’est un prolongement plus fin de l’approche pr´c´dente en d´clinant ce type de calcul par type d’acti-
e e e
vit´. Selon l’activit´, l’indicateur retenu ne serait pas le mˆme. Ainsi, par exemple en gestion d’actifs, le
e e e
capital ´conomique pourrait ˆtre calcul´ sur la base du montant des fonds en gestion (voir document [1]).
e e e
N´anmoins, le document du 28 septembre 2001 utilise le PNB comme indicateurs des 8 lignes de m´tiers.
e e
Dans cette approche, les fonds propres de la banque pour le risque op´rationnel sont ´gaux ` la somme
e e a
des fonds propres de chaque ligne de m´tier. Nous avons
e
FP = FP (i) = β (i) × FI (i) (15.2)
i i
avec FI l’indicateur financier de la ligne de m´tier i.
e
Si l’indicateur financier est le PNB, les r´sultats de QIS2 sont les suivants :
e
Ligne de m´tier
e β (i) m´dian
e β (i) moyen
Financement d’entreprises 0.131 0.236
N´gociation et vente
e 0.171 0.241
Banque de d´tail
e 0.125 0.127
Banque commerciale 0.132 0.169
Paiements et r´glements
e 0.208 0.203
Services d’agence 0.174 0.232
Gestion d’actifs 0.133 0.185
Courtage de d´tail
e 0.113 0.149
Dans cette approche, le Comit´ de Bˆle indique que l’objectif de charge de capital est de 12% (et non
e a
de 20%). Les banques sont donc incit´es ` choisir cette m´thode plutˆt que celle de l’indicateur basique.
e a e o
N´anmoins, il y a des crit`res d’´ligibilit´ concernant la qualit´ du syst`me de gestion du risque et le suivi
e e e e e e
des donn´es de perte :
e
– Effective risk management and control
– The bank must have a well-documented, independent operational risk management and control
process, which includes firm-level policies and procedures concerning operational risk and
strategies for mitigating operational risk.
– The board of directors and senior management must be actively involved in the oversight of
the operational risk management process.
– There must be regular reporting of relevant operational risk data to business unit management,
senior management and the board of directors.
– Internal auditors must regularly review the operational risk management processes. This review
should include both the activities of the business units and the operational risk management
and control process.
– Measurement and validation
– The bank must have both appropriate risk reporting systems to generate data used in the
calculation of a capital charge and the ability to construct management reporting based on
the results.
– The bank must begin to systematically track relevant operational risk data, including internal
loss data, by business line.
– The bank must develop specific, documented criteria for mapping current business lines and
activities into the standardised framework. The criteria must be reviewed and adjusted for
new or changing business activities and risks as appropriate .
15.3 Annexe : composition du Risk Management Group (RMG) of the
Basel Committee on Banking Supervision
– Chairman : Roger Cole Federal – Reserve Board, Washington, D.C.
INTRODUCTION A LA GESTION DES RISQUES 174](https://image.slidesharecdn.com/gestionrisques-130221132633-phpapp01/85/Gestion-risques-184-320.jpg)
![– Banque Nationale de Belgique, Brussels : Dominique Gressens
– Commission Bancaire et Financi`re, Brussels : Jos Meuleman
e
– Office of the Superintendent of Financial Institutions, Ottawa : Jeff Miller
– Commission Bancaire, Paris Laurent Le Mou¨l
e
– Deutsche Bundesbank, Frankfurt am Main : Magdalene Heid et Karin Sagner
– Bundesaufsichtsamt f¨r das Kreditwesen, Bonn : J¨rgen Dreymann
u u
– Banca dItalia, Rome : Claudio Dauria et Sergio Sorrentino
– Bank of Japan, Tokyo : Eiji Harada
– Financial Services Agency, Tokyo : Hirokazu Matsushima
– Commission de Surveillance du Secteur Financier, Luxembourg : Davy Reinard
– De Nederlandsche Bank, Amsterdam : Klaas Knot
– Banco de Espa˜a, Madrid : Juan Serrano
n
– Finansinspektionen, Stockholm : Jan Hedquist
– Sveriges Riksbank, Stockholm : Camilla Ferenius
– Eidgen¨ssiche Bankenkommission, Bern : Daniel Sigrist et Martin Sprenger
o
– Financial Services Authority, London : Helmut Bauer et Victor Dowd
– Bank of England, London : Alison Emblow
– Federal Deposit Insurance Corporation, Washington, D.C. : Mark Schmidt
– Federal Reserve Bank of New York : Beverly Hirtle et Stefan Walter
– Federal Reserve Board, Washington, D.C. : Kirk Odegard
– Office of the Comptroller of the Currency, Washington, D.C. : Kevin Bailey et Tanya Smith
– European Central Bank, Frankfurt am Main : Panagiotis Strouzas
– European Commission, Brussels : Michel Martino et Melania Savino
– Secretariat of the Basel Committee on Banking Supervision, Bank for International Settlements :
Ralph Nash
Bibliographie
[1] Basel Committee on Banking Supervision, Operational Risk — Consultative Document, Supporting
document to the New Basel Capital Accord, January 2001
[2] Basel Committee on Banking Supervision, Working Paper on the Regulatory Treatment of Operational
Risk, september 2001
[3] Institute International Finance, Inc, Letter to Mr. Roger Cole, March 1, 2001
´
[4] Ceske, R. et J.V. Hernandez [1999], Where theory meets practice, Risk Magazine (Operational
Risk Report), 12, November, 17-20
´ ´
[5] Ceske, R., J.V. Hernandez et L.M. Sanchez [2000], Quantifying event risk : the next convergence,
The Journal of Risk Finance, 1(3), 9-23
[6] Lasry, J-M. [2001], Le calcul des fonds propres en face du risque op´rationnel, Club Banque,
e
F´d´ration des Banques Fran¸aises, 1er mars 2001
e e c](https://image.slidesharecdn.com/gestionrisques-130221132633-phpapp01/85/Gestion-risques-185-320.jpg)

![16
Les m´thodes AMA
e
Dans le document consultatif du 16 janvier 2001, le Comit´ de Bˆle proposait une troisi`me m´thode
e a e e
appel´e Internal Measurement Approach (IMA). Depuis le Comit´ de Bˆle a modifi´ sa position
e e a e
et propose de remplacer IMA par un “spectre” de m´thodes dites internes. En fait, cette d´cision a ´t´
e e ee
prise suite aux recommandations (et aux pressions) de l’organisation professionnelle IIF (Institute of
International Finance).
Pour pouvoir utiliser une m´thode AMA, la banque devra satisfaire de nombreux crit`res (voir l’annexe
e e
1 du document [2]). Notons aussi que la charge en capital calcul´e avec une m´thode AMA ne peut ˆtre
e e e
inf´rieure ` celle donn´e par la m´thode SA de plus de 25% :
e a e e
3
FPAMA ≥ FPSA
4
C’est la notion du Floor. Enfin, les assurances ne seront prises en compte que pour la m´thode LDA
e
uniquement.
16.1 L’approche IMA
La m´thode Internal Measurement Approach (IMA) fait l’objet du paragraphe VI de la section
e
B du document [1]. Nous notons UL la perte exceptionnelle. Celle-ci est calcul´e ` partir de la formule
e a
suivante :
UL = EL ×γ × RPI (16.1)
o` EL est la perte esp´r´e, γ le facteur d’´chelle et RPI l’indice de profil de risque. Cette charge en capital
u ee e
est calcul´e pour chaque business line et chaque type de risque :
e
Type de risque
business line 1 2 ··· j ··· Total
1 UL (1, 1) UL (1, 2) UL (1, ·)
2 UL (2, 1) UL (2, 2) UL (2, ·)
.
.
.
i UL (i, j) UL (i, ·)
.
.
.
Total UL (·, 1) UL (·, 2) UL (i, j)
i,j](https://image.slidesharecdn.com/gestionrisques-130221132633-phpapp01/85/Gestion-risques-187-320.jpg)
![´
CHAPITRE 16. LES METHODES AMA
Pour une business line i et un type de risque j, nous avons
UL (i, j) = EL (i, j) × γ (i, j) × RPI (i, j) (16.2)
La charge en capital au titre du risque op´rationnel est calcul´e en faisant la somme des diff´rentes charges
e e e
en capital UL (i, j).
Nous d´taillons maintenant les diff´rentes composantes de UL (i, j) :
e e
– EL (i, j) est la perte esp´r´e. Dans le document [1], le Comit´ de Bˆle propose qu’elle soit calcul´e
ee e a e
a
` partir de la formule suivante :
EL (i, j) = EI (i, j) × PE (i, j) × LGE (i, j) (16.3)
D´taillons ces diff´rents param`tres :
e e e
– EI (i, j) est l’indicateur d’exposition.
– PE (i, j) est la probabilit´ d’occurence d’une perte unitaire.
e
– LGE (i, j) est le montant de la perte unitaire.
– γ (i, j) est le facteur d’´chelle. La valeur de celui-ci est d´termin´e par les autorit´s r´glementaires.
e e e e e
C’est d’ailleurs le seul coefficient qui n’est pas propre ` l’´tablissement financier.
a e
– RPI (i, j) est l’indice de profil de risque. Pour l’instant, le Comit´ de Bˆle n’a propos´ aucune
e a e
formule pour le calculer. Le but de cet indice est de prendre en compte les propri´t´s leptokurtiques
ee
de la distribution r´elle des pertes de la banque. Il permet de convertir le facteur d’´chelle exog`ne
e e e
en un facteur d’´chelle propre ` la business line et au type de risque de la banque. Nous avons
e a
UL (i, j) = EL (i, j) × γ (i, j) × RPI (i, j)
Facteur d’´chelle r´glementaire
e e
= EL (i, j) × γ (i, j) (16.4)
Facteur d’´chelle “interne”
e
Il apparait clairement que γ (i, j) repr´sente la valeur du benchmark, c’est-`-dire la valeur pour la
e a
Banque Mondiale Moyenne (le comit´ de Bˆle emploie le terme de “scaling factor based on the
e a
industry wide loss distribution”) et RPI (i, j) sert ` prendre en compte les caract´ristiques de la
a e
banque par rapport ` la Banque Mondiale Moyenne.
a
Nous remarquons que ces param`tres (EI, PE, LGE, γ, RPI) sont diff´rents pour chaque business line
e e
et chaque type de risque. D’autres choix pourraient ˆtre possibles. Par exemple,
e
UL (i, j) = EI (i, j) × PE (i, j) × LGE (j) × γ (j) × RPI (i, j) (16.5)
Dans ce cas, les param`tres LGE et γ d´pendent uniquement du type de risque op´rationnel. Dans le
e e e
document [3], il ressort qu’en g´n´ral les membres du Groupe de Travail sur le Risque Op´rationnel
e e e
(WGOR) ont du mal ` distinguer l’indicateur d’exposition en fonction du type de risque. Dans ce cas,
a
nous avons
UL (i, j) = EI (i) × PE (i, j) × LGE (i, j) × γ (i, j) × RPI (i, j) (16.6)
Cela veut dire que l’indicateur d’exposition est propre ` la business line, et ne d´pend pas du type de
a e
risque.
Pour conclure, nous faisons deux remarques :
1. Dans le document [2], le Comit´ de Bˆle retient un d´coupage de la banque en 8 business lines. Avec
e a e
7 types de risque, nous obtenons donc un d´coupage matriciel de 56 cellules. Ce qui veut
e
dire aussi plus de 250 param`tres pour calculer la charge en capital. On peut penser
e
que des probl`mes de robustesse vont se poser. En particulier, on voit mal comment
e
les autorit´s r´glementaires vont ˆtre capables de calculer les 56 param`tres de facteur
e e e e
d’´chelle.
e
INTRODUCTION A LA GESTION DES RISQUES 178](https://image.slidesharecdn.com/gestionrisques-130221132633-phpapp01/85/Gestion-risques-188-320.jpg)
![´
CHAPITRE 16. LES METHODES AMA
2. Dans la pratique, le double indi¸age sera difficile ` mettre en place, par manque de donn´es. Des
c a e
approximations seront donc faites du type
LGE (i, j) = LGE (j) quelque que soit la business line
On le voit d’ailleurs avec l’´tude WGOR sur les indicateurs d’exposition qui sont presque toujours
e
les mˆmes. On risque finalement d’aboutir ` l’utilisation de tr`s peu d’indicateurs (moins d’une
e a e
dizaine). Il nous semble que la m´thode IMA devrait ˆtre simplifi´e :
e e e
– en r´duisant le double indi¸age ;
e c
– en r´duisant le nombre de variables ; Par exemple, pourquoi ne pas adopter une d´finition plus
e e
naturelle de la perte esp´r´e ` partir du nombre de pertes NE :
ee a
EL (i, j) = NE (i, j) × LGE (i, j) (16.7)
16.2 L’approche LDA
Cette approche est expos´e dans le document de travail de Frachot, Georges et Roncalli [2001].
e
C’est une approche actuarielle tr`s ancienne largement utilis´e en assurances (Klugman, Panjer et
e e
Willmot [1998]). Des trois m´thodes AMA, nous pouvons consid´rer que c’est v´ritablement la m´thode
e e e e
de r´f´rence pour le calcul de risque avec un mod`le interne. Nous donnons ici quelques ´l´ments, mais
ee e ee
l’expos´ oral du cours s’appuiera sur le document [8].
e
16.2.1 Pr´sentation de la m´thode statistique
e e
L’id´e g´n´rale est de mod´liser la perte li´e au risque op´rationnel pour une p´riode donn´e (par
e e e e e e e e
exemple, un an) et d’en d´duire la valeur en risque. La difficult´ provient du fait que cette perte ne
e e
correspond pas forc´ment ` une seule occurence. Pendant une ann´e, la perte totale est en fait le r´sultat
e a e e
de plusieurs pertes successives. La perte totale est donc une perte agr´g´e (aggregate loss distribution).
e e
Celle-ci se d´finit par
e
1. le nombre de pertes individuelles,
2. et le montant de chaque pertes individuelles.
Dans le cadre d’un mod`le probabiliste, le nombre de pertes est al´atoire. A priori, nous ne savons
e e
pas combien de fraudes “carte bleue” vont avoir lieu pour l’ann´e 2002. Nous allons donc mod´liser ce
e e
nombre de pertes par un processus de comptage, et la distribution de ce nombre de pertes est appel´e e
la distribution de la fr´quence des pertes (loss frequency distribution). Nous supposons alors que les
e
pertes individuelles sont ind´pendantes et identiquement distribu´es. La distribution du montant d’une
e e
perte individuelle est appel´e la distribution de la s´v´rit´ des pertes (loss severity distribution). Dans
e e e e
ce cas l`, la perte agr´g´e est la somme al´atoire des pertes individuelles. La distribution de la perte
a e e e
agr´g´e est donc une distribution compos´e (compound distribution).
e e e
La formulation math´matique est donc la suivante. Nous consid´rons diff´rentes lignes de m´tier (i =
e e e e
1, . . . , I) et diff´rents types de risque (j = 1, . . . , J). ζ (i, j) est la variable al´atoire repr´sentant le
e e e
montant d’une perte pour la ligne de m´tier i et le type de risque j. La distribution de la s´v´rit´ des
e e e e
pertes est not´e Fi,j . Nous supposons que le nombre d’occurences entre les dates t et t+τ est al´atoire. La
e e
variable al´atoire de comptage N (i, j) a une fonction de probabilit´ pi,j . La distribution de la fr´quences
e e e
n
des pertes Pi,j correspond alors ` Pi,j (n) = k=0 pi,j (k). La perte pour la ligne de m´tier i et le type
a e
N (i,j)
de risque j entre les dates t et t + τ est donc ϑ (i, j) = n=0 ζ n (i, j). Soit Gi,j la distribution de
probabilit´ de ϑ (i, j). Gi,j est la distribution compos´e suivante :
e e
∞
pi,j (n) Fn (x) x0
i,j
Gi,j (x) = n=1 (16.8)
p (0) x=0
i,j
Le graphique (16.1) pr´sente un exemple de calcul de la distribution de la perte agr´g´e. Dans de nom-
e e e
breux cas, il n’est pas possible d’obtenir une formulation analytique de Gi,j . Dans ce cas, nous pouvons
16.2. L’APPROCHE LDA 179](https://image.slidesharecdn.com/gestionrisques-130221132633-phpapp01/85/Gestion-risques-189-320.jpg)
![´
CHAPITRE 16. LES METHODES AMA
GRAPHIQUE 16.1. Distribution agr´g´e avec ζ (i, j) ∼ LN (8, 2.2) et N (i, j) ∼ P (50)
e e
approximer cette distribution en utilisant la m´thode de Monte Carlo ou d’autres m´thodes (la plus
e e
c´l`bre est l’algorithme de Panjer).
ee
La charge en capital pour la ligne de m´tier i et le type de risque j correspond alors au quantile α de
e
Gi,j :
CaR (i, j; α) = G−1 (α) = inf {x | Gi,j (x) ≥ α}
i,j (16.9)
La charge en capital pour la banque est alors la somme de toutes les charges en capital CaR (i, j; α) :
I J
CaR (α) = CaR (i, j; α) (16.10)
i=1 j=1
Cela implique une d´pendance positive parfaite des diff´rentes pertes ϑ (i, j). En janvier 2001, le Comit´
e e e
de Bˆle sugg´rait α ´gal ` 99.9%. Maintenant, α est fix´ ` 99%.
a e e a ea
16.2.2 Robustesse de l’approche LDA
Certaines banques ont l’intention de fonder leur mod`le interne sur la th´orie des extrˆmes et non
e e e
sur l’approche LDA. Suite ` l’attaque terroriste sur le World Trade Center, il semblerait (tout cela est
a
a
` prendre au conditionnel) que Roger Cole soit de plus en plus favorable ` la th´orie des extrˆmes. Je
a e e
pense que c’est une mauvaise vision des choses pour diff´rentes raisons :
e
– La th´orie des extrˆmes est math´matiquement s´duisante. En pratique, elle n´cessite une expertise
e e e e e
importante et un certain recul pour “lui faire dire quelque chose”.
– L’obstacle majeur ` la mise en place d’une m´thode bas´e sur la th´orie des extrˆmes est la dispo-
a e e e e
nibilit´ de donn´es.
e e
– Enfin, je crois qu’il y a confusion entre “th´orie des extrˆmes” et “mod´lisation des queues ´paisses”.
e e e e
Dans le document [8], nous pr´sentons diff´rents ´l´ments pour bien impl´menter la m´thode LDA. Le
e e ee e e
calcul des charges en capital par la m´thode LDA doit se faire en concertation avec le risk manager et son
e
INTRODUCTION A LA GESTION DES RISQUES 180](https://image.slidesharecdn.com/gestionrisques-130221132633-phpapp01/85/Gestion-risques-190-320.jpg)
![´
CHAPITRE 16. LES METHODES AMA
N τ 1 million 10 millions 100 millions 1 milliard 5 milliards
100 1 an 99.8 51.4 3.7 0.08 0.00
200 2 ans 99.9 76.4 7.2 0.17 0.00
300 3 ans 100.0 88.5 10.7 0.26 0.01
400 4 ans 100.0 94.4 14.0 0.35 0.01
500 5 ans 100.0 97.3 17.2 0.44 0.02
1000 10 ans 100.0 99.9 31.4 0.89 0.04
5000 50 ans 100.0 100.0 84.9 4.38 0.20
TABLE 16.1. µ = 10 and σ = 2.50
N τ 1 million 10 millions 100 millions 1 milliard 5 milliards
100 1 an 99.9 73.1 10.4 0.48 0.03
200 2 ans 100.0 92.7 19.7 0.95 0.07
300 3 ans 100.0 98.0 28.1 1.43 0.10
400 4 ans 100.0 99.4 35.5 1.91 0.14
500 5 ans 100.0 99.8 42.2 2.38 0.18
1000 10 ans 100.0 99.9 66.7 4.70 0.36
5000 50 ans 100.0 100.0 99.5 21.42 1.80
TABLE 16.2. µ = 10 and σ = 2.75
´quipe. Il est n´cessaire de comprendre les chiffres, de les interpr´ter et de les comparer. Le statisticien
e e e
apporte une aide technique, et doit proposer des outils pour aider le risk manager ` juger la pertinence
a
des r´sultats. Prenons un exemple. Nous pouvons calculer la fonction de survie du maximum de N pertes
e
de loi de probabilit´ Gi,j . Nous avons
e
N
pmax := Pr {max (ϑ1 (i, j) , . . . , ϑN (i, j)) ≥ x} = 1 − [Gi,j (x)] (16.11)
Cette probabilit´ a une interpr´tation tr`s intuitive. Supposons que N pertes surviennent. pmax est la
e e e
probabilit´ que la perte maximale soit sup´rieure au montant x. Le Risk Management a des id´es (ou des
e e e
benchmarks internes et externes) sur la perte maximale ` un an, deux ans, etc. Il peut donc confronter
a
ces propres croyances avec les r´sultats donn´s par le mod`le. Supposons que 100 pertes surviennent
e e e
en moyenne par an. Supposons aussi que la distribution de la s´v´rit´ est une distribution log-normale
e e e
LN (µ, σ). Une premi`re estimation ` partir des donn´es historiques donne µ = 10 et σ = 2, 50. Sur la
e a e
table 16.1, nous avons report´ les valeurs correspondantes de pmax pour diff´rentes valeurs de N et x.
e e
Par exemple, la probabilit´ que nous observons une perte maximale sur 5 ans sup´rieure ` 100 millions
e e a
est de 17, 2%. Si l’estimation a ´t´ faite avec un historique de 5 ans, et que nous observons dans la base
ee
de donn´es plusieurs pertes sup´rieures ` 100 millions, nous pouvons penser que cette distribution sous-
e e a
estime largement les pertes exceptionnelles. Si µ = 10 et σ = 2, 50, nous obtenons la table 16.2. Dans ce
cas, la probabilit´ est ´gale ` 42,2%. C’est ce genre d’outils que le statisticien doit fournir au risk
e e a
manager, car une mesure de risque ne veut rien dire en elle-mˆme, c’est sa compr´hension
e e
et son interpr´tation qui comptent.
e
16.3 Le mapping IMA/LDA
Je pr´senterai cette section en cours de fa¸on plus d´taill´e, car les travaux sur ce sujet ´voluent tr`s
e c e e e e
rapidement. Le mapping IMA/LDA consiste ` d´finir de fa¸on quantitative la m´thode IMA ` partir de la
a e c e a
m´thode LDA (Frachot, Georges et Roncalli [2001]). On peut penser en effet que l’IMA a ´t´ con¸ue
e ee c
comme une version simplifi´e, praticable et standardis´e d’une approche de type LDA plus compl`te et
e e e
plus satisfaisante mais plus compliqu´e ` mettre en œuvre. Au mois de septembre 2001, la situation sur
e a
le sujet est la suivante :
– Proposition d’une m´thodologie par Sakura Bank au mois de F´vrier 2001.
e e
– Prolongement de cette m´thodologie par l’I.I.F. Taskforce on “technical” I.M.A. issues.
e
16.3. LE MAPPING IMA/LDA 181](https://image.slidesharecdn.com/gestionrisques-130221132633-phpapp01/85/Gestion-risques-191-320.jpg)
![´
CHAPITRE 16. LES METHODES AMA
La derni`re proposition de l’I.I.F. est de d´finir l’indice de profil de risque par
e e
1
EIIndustry · PEIndustry 2
RPI =
EIBank · PEBank
On peut justifier cette formulation en utilisant une approximation du quantile α de la distribution com-
pos´e (Frachot, Georges et Roncalli [2001]).
e
16.4 L’approche Scorecard
Cette approche a ´t´ int´gr´e dans le dernier document de Bˆle. Comme il est difficile de comprendre
ee e e a
cette m´thode, voici la d´finition donn´e dans le document [2] :
e e e
In this approach, banks determine an initial level of operational risk capital at the firm or
business line level, and then modify these amounts over time on the basis of scorecards that
attempt to capture the underlying risk profile and risk control environment of the various
business lines. These scorecards are intended to bring a forward-looking component to the
capital calculations, that is, to reflect improvements in the risk control environment that will
reduce both the frequency and severity of future operational risk losses. The scorecards may
be based on actual measures of risk, but more usually identify a number of indicators as
proxies for particular risk types within business units/lines. The scorecard will normally be
completed by line personnel at regular intervals, often annually, and subject to review by a
central risk function.
In order to qualify for the AMA, a scorecard approach must have a sound quantitative basis,
with the overall size of the capital charge being based on a rigorous analysis of internal
and external loss data. In some cases, scorecard approaches are based on initial estimation
methods that are similar to those used in internal measurement or loss distribution approaches.
Where the scorecard approach differs from these approaches is that it relies less exclusively
on historical loss data in determining capital amounts. Instead, once the size of the capital
charge has been determined, its overall size and its allocation across business lines may be
modified on a qualitative basis. Nevertheless, historical loss data must be used to validate the
results of scorecards, with adjustments to capital size or allocation based upon such results.
At present, a range of scorecard approaches are in development with some banks already
operating a system of economic capital allocation based on such an approach. However, as
with the other approaches, no industry standards has emerged.
En fait, c’est sous la pression de certaines banques de l’IIF (notamment les banques anglaises) que
cette m´thode a ´t´ int´gr´e par le Comit´ de Bˆle. Pour mieux comprendre l’approche, voici la formule1
e ee e e e a
propos´e par l’IIF :
e
I J
CaR = EI (i, j) · ω (i, j) · RS (i, j) (16.12)
i=1 j=1
avec EI l’indicateur d’exposition (Exposure Indicator), RS le score de risque (Risk Score) et ω le
facteur d’´chelle.
e
Bibliographie
[1] Basel Committee on Banking Supervision, Operational Risk — Consultative Document, Supporting
document to the New Basel Capital Accord, January 2001
1 Dans la formule originale, c’est la racine car´e de l’indicateur d’exposition et non directement l’indicateur d’exposition
e
qui est utilis´e. A l’´poque, l’IIF travaillait sur la nature non-lin´aire du risque op´rationnel. Mais le Comit´ de Bˆle n’a
e e e e e a
pas suivi les recommandations de l’IIF sur ce sujet pour l’instant.
INTRODUCTION A LA GESTION DES RISQUES 182](https://image.slidesharecdn.com/gestionrisques-130221132633-phpapp01/85/Gestion-risques-192-320.jpg)
![[2] Basel Committee on Banking Supervision, Working Paper on the Regulatory Treatment of Operational
Risk, september 2001
[3] Institute International Finance, Inc, Letter to Mr. Roger Cole, March 1, 2001
[4] Institute International Finance, Inc, Report of the Working Group on Operational Risk, June 4 5,
2001 (Washington, D.C.)
[5] I.I.F. Taskforce on “technical” I.M.A. issues, March 2001
[6] Sakura Bank Ltd, Derivation of the IMA formula — RPI calculation, February 2001
[7] Mori, T. et E. Harada [2001], Internal Measurement Approach to operational risk capital charge,
Bank of Japan, Discussion Paper
[8] Frachot, A., P. Georges et T. Roncalli [2001], Loss Distribution Approach for operational risk,
Groupe de Recherche Op´rationnelle, Cr´dit Lyonnais, Working Paper
e e
[9] Klugman, S.A., H.H. Panjer et G.E. Willmot [1998], Loss Models : From Data to Decisions, Wiley
Series in Probability and Mathematical Statistics, John Wiley Sons, New York
[10] Thoraval, P-Y. [2001], Le risque op´rationnel, Club Banque, F´d´ration des Banques Fran¸aises,
e e e c
27 septembre 2001](https://image.slidesharecdn.com/gestionrisques-130221132633-phpapp01/85/Gestion-risques-193-320.jpg)

