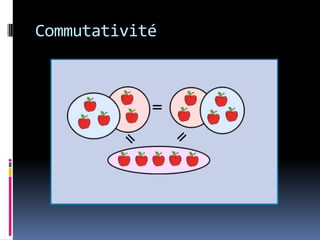
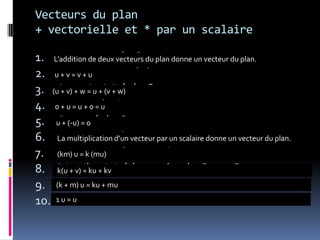
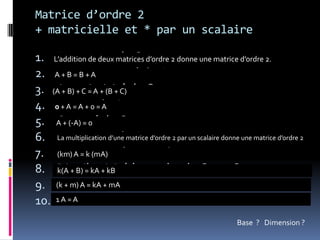
Le document traite des espaces vectoriels, en expliquant les concepts fondamentaux tels que les sous-espaces, les opérations internes et externes, ainsi que les propriétés associées. Il présente également les conditions nécessaires pour qu'un ensemble soit considéré comme un espace vectoriel, ainsi que des exemples d'addition et de multiplication de vecteurs et de matrices. Les notions de dimension et de base sont également abordées, ainsi que les sous-espaces vectoriels.

1. Espaces vectorielsSous-espaces et

3. EnsembleCollection d’objetsQuête de la théorie des ensemblesSymboles :Appartenance :   ∉Inclusion :   

4. ExemplesSoit l’ensemble A = { 1, 3, j , # ,• }1 __ Aj ____ A{ 1 } ____ A{ 1, 3} ____ A{ 1, 2, 3} ____ A

5. OpérationProcessus visant à obtenir un résultat à partir d’un ou de plusieurs objets appelés opérandes.Synonyme : Loi de composition

6. Opération interneProcessus impliquant uniquement un ou des éléments d’un ensemble.

7. PropriétéConstat fait sur tous les éléments d’un ensemble mis en relation à l’aide d’opérations.Exemples :CommutativitéAssociativitéFermeture

8. Commutativité

9. AssociativitéA (B   C ) = A   B   C = (A   B )   C

10. Fermeture∀(x ∈V , y∈V), x   y ∈ VCe qui se passe dans l’ensemble, reste dans l’ensemble !

11. Éléments remarquablesLe neutreLe symétrique

12. Opération externeProcessus impliquant un ou des éléments d’un ensemble avec un élément provenant d’un autre ensemble (corps).Par exemple : La multiplication de matrices par un scalaireLa multiplication de vecteurs par un scalaire

13. Propriété : Distributiviték ◊ ( A   B ) = (k ◊ A)   (k ◊ B )

14. Espace vectorielEnsemble VOpération interne : ⊕Opération externe : ⊗Qui répondent à 10 conditionsDans le cadre de ce cours, l’opération externe impliquera le corps des réels.

15. Conditions :Fermeture de Commutativité de Associativité de Neutre de Opposé de Fermeture de Associativité mixte de Distributivité à gauche de  sur Distributivité à droite de  sur Neutre de Page 405

16. DimensionTous les espaces vectoriels peuvent être engendrés par une base.Dimension = Nombre de vecteurs de la base

17. Exemples

18. Vecteurs du plan+ vectorielle et * par un scalaireFermeture de Commutativité de Associativité de Neutre de Opposé de Fermeture de Associativité mixte de Distributivité à gauche de  sur Distributivité à droite de  sur Neutre de L’addition de deux vecteurs du plan donne un vecteur du plan.u + v = v + u(u + v) + w = u + (v + w)0 + u = u + 0 = uu + (-u) = 0La multiplication d’un vecteur par un scalaire donne un vecteur du plan.(km) u = k (mu) k(u + v) = ku + kv (k + m) u = ku + mu 1 u = u

19. Matrice d’ordre 2+ matricielle et * par un scalaireFermeture de Commutativité de Associativité de Neutre de Opposé de Fermeture de Associativité mixte de Distributivité à gauche de  sur Distributivité à droite de  sur Neutre de L’addition de deux matrices d’ordre 2 donne une matrice d’ordre 2.A + B = B + A(A + B) + C = A + (B + C)0 + A = A + 0 = AA + (-A) = 0La multiplication d’une matrice d’ordre 2 par un scalaire donne une matrice d’ordre 2(km) A = k (mA) k(A + B) = kA + kB (k + m) A = kA + mA 1 A = ABase ? Dimension ?

20. Polynômes de degré 2+ fonctions et * par un scalaireFermeture de Commutativité de Associativité de Neutre de Opposé de Fermeture de Associativité mixte de Distributivité à gauche de  sur Distributivité à droite de  sur Neutre de NON

21. À quoi ça sert ???

22. Sous-espace vectoriel

23. Sous-espace vectorielEspace vectoriel inclus dans un espace vectoriel.

24. Soit <V ; ; > tel que :Fermeture de Commutativité de Associativité de Neutre de Opposé de Fermeture de Associativité mixte de Distributivité à gauche de  sur Distributivité à droite de  sur Neutre de 

25. Soit U ⊂ V… à voir :Fermeture de Commutativité de Associativité de Neutre de Opposé de Fermeture de Associativité mixte de Distributivité à gauche de  sur Distributivité à droite de  sur Neutre de 