Ce mémoire de master présente une étude sur la régularisation des réseaux de neurones convolutifs, appliquée à la classification des images. Il couvre divers aspects des réseaux de neurones, y compris leur fonctionnement, les méthodes de régularisation, et des applications pratiques en classification d'images. Le travail a été soutenu en juillet 2021 à la faculté des sciences de Dhar El Mahraz à Fès.

1. Année universitaire 2020-2021
Mémoire présenté à
La Faculté des Sciences Dhar El Mahraz Fès
Pour l’obtention du Diplôme de Master
Master Mathématiques Appliquées et Science des
Données (MASD)
Master en double diplomation avec l’Université Sorbonne
Paris Nord
Spécialité : EDPSD
Intitulé :
Régularisation des réseaux de neurones convolutifs :
application à la classification des images
Présenté par: Saloua Lagnaoui
Encadré par: Pr.Mounir Mekkour
Co-encadré par: Pr.Nour-eddine Joudar
Soutenu le 09/07/2021, devant le jury
Pr. TOUZANI Abdelfetah Président Etablissement FSDM
Pr. BENNANI MEZIANE Youness Examinateur Etablissement USPN
Pr. MATEI Basarab Examinateur Etablissement MCF-HDR
Pr. YAHYAOUI Ali Examinateur Etablissement FSDM
Pr. JOUDAR Nour-eddine Co-encadrant Etablissement ENSAMR
Pr. MEKKOUR Mounir Encadrant Etablissement FSDM

2. REMERCIEMENTS
Je tiens à remercier en tout premier lieu DIEU le tout puissant de m’avoir donné
la patience, la force et le courage, pour élaborer ce travail.
J’adresse mes plus vifs remerciements à tous les personnes de la FSDM , spécia-
lement les professeurs qui m’ont formé et encadré au cours de ces deux années de
Master.
Je remercie Monsieur Mounir Mekkour, professeur de FSDM et l’enseignant res-
ponsable de mon projet, et je remercie infiniment Monsieur Joudar Nour-eddine
pour sa direction, son amitié et ses conseils durant tout le travail, ainsi pour les
discussions qui me sont toujours intéressantes.
Que les membres du jury me trouvent ici Merci beaucoup d’avoir accepté le juge-
ment de mon travail.
Enfin, j’adresse également une pensée affectueuse à toute ma famille en particu-
lier mon père, ma mère, mes frères pour le soutien sans limite durant toutes mes
années d’étude.

3. TABLE DES MATIÈRES
Résumé 9
Introduction 11
1 Réseaux de neurones artificielles 13
1.1 Neurone biologique et neurone formel . . . . . . . . . . . . . . . . 13
1.1.1 Neurone biologique . . . . . . . . . . . . . . . . . . . . . . . 13
1.1.2 Neurone artificiel ou neurone formel . . . . . . . . . . . . . . 14
1.2 Fonctions d’activations . . . . . . . . . . . . . . . . . . . . . . . . . 15
1.3 Réseaux de neurones artificiels RNA . . . . . . . . . . . . . . . . . 18
1.3.1 Réseaux directs(Feedforward) . . . . . . . . . . . . . . . . . 20
1.3.2 Réseaux récurrents RNN . . . . . . . . . . . . . . . . . . . . 23
1.4 Apprentissage des réseaux de neurones artificiels . . . . . . . . . . . 24
1.4.1 Types d’apprentissage . . . . . . . . . . . . . . . . . . . . . 25
1.4.2 Règles d’apprentissage . . . . . . . . . . . . . . . . . . . . . 26
1.4.3 Fonction de perte (loss function) . . . . . . . . . . . . . . . 27
1.4.4 Méthodes d’optimisation pour l’apprentissage . . . . . . . . 28
1.5 Avantages et limites des RNAs . . . . . . . . . . . . . . . . . . . . 31
1.5.1 Avantages des RNAs . . . . . . . . . . . . . . . . . . . . . 31
1.5.2 Limites des RNAs . . . . . . . . . . . . . . . . . . . . . . . 31
1.6 Applications des RNAs . . . . . . . . . . . . . . . . . . . . . . . . 34
2 Régularisation des réseaux de neurones convolutifs 35
2.1 Régularisation des réseaux de neurones artificiels . . . . . . . . . . . 36
2.1.1 Principe de régularisation . . . . . . . . . . . . . . . . . . . 36
2.1.2 Méthodes de régularisation . . . . . . . . . . . . . . . . . . 37
3

4. 2.2 Réseaux de neurones convolutifs . . . . . . . . . . . . . . . . . . . . 43
2.2.1 Types de couches . . . . . . . . . . . . . . . . . . . . . . . . 44
2.2.2 Architecture d’un réseaux de neurones Convolutifs . . . . . 50
2.2.3 Paramétrage des couches . . . . . . . . . . . . . . . . . . . . 53
2.2.4 Régularisation des réseaux de neurones convolutifs . . . . . . 56
3 Classification des images par les réseaux de neurones convolutifs 60
3.1 Notion de base sur les images . . . . . . . . . . . . . . . . . . . . . 61
3.1.1 Types des images . . . . . . . . . . . . . . . . . . . . . . . . 61
3.1.2 Caractéristiques des images . . . . . . . . . . . . . . . . . . 62
3.2 Base de données (Dataset) . . . . . . . . . . . . . . . . . . . . . . . 63
3.3 Validation du modèle de classification . . . . . . . . . . . . . . . . . 65
3.3.1 Matrice de confusion . . . . . . . . . . . . . . . . . . . . . . 65
3.3.2 Courbe Roc . . . . . . . . . . . . . . . . . . . . . . . . . . . 66
3.4 Implémentation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 66
3.4.1 Outils et les librairies . . . . . . . . . . . . . . . . . . . . . . 67
3.4.2 Configuration de la machine . . . . . . . . . . . . . . . . . . 68
3.4.3 Architecture des modèles de CNNs : . . . . . . . . . . . . . 68
3.4.4 Résultats et discussions . . . . . . . . . . . . . . . . . . . . . 74
Conclusion 80
4

5. TABLE DES FIGURES
1.1 Neurone biologique . . . . . . . . . . . . . . . . . . . . . . . . . . . 14
1.2 Structure de neurone formel . . . . . . . . . . . . . . . . . . . . . . 15
1.3 Topologie des réseaux de neurones . . . . . . . . . . . . . . . . . . . 20
1.4 Exemple d’un perceptron monocouche . . . . . . . . . . . . . . . . 21
1.5 Exemple d’un perceptron multicouches . . . . . . . . . . . . . . . . 22
1.6 Réseaux à fonction radiale RBF . . . . . . . . . . . . . . . . . . . . 23
1.7 Exemple d’un RNN à trois entrée et quatre sorties. Les connexions
récurrentes sont notées en rouge. . . . . . . . . . . . . . . . . . . . 24
1.8 Modèle simple et modèle complexe . . . . . . . . . . . . . . . . . . 33
1.9 Variété de Bais-Variance en fonction de complexité du modèle . . . 33
2.1 Variation des erreurs en fonction de la complexité du modèle . . . . 37
2.2 Early stopping . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 39
2.3 Dropout appliqué à un MLP : neurone en noire est désactivé. . . . . 40
2.4 Schéma du parcours de la fenêtre de filtre sur l’image . . . . . . . . 44
2.5 Principe de retourné un filtre. . . . . . . . . . . . . . . . . . . . . . 45
2.6 Principe de calcule d’un produit de convolution. . . . . . . . . . . . 46
2.7 Exemple d’une matrice de taille 4 × 6 avec un pooling de taille 2. . 48
2.8 Exemple de Max-pooling pour une matrice de taille 4 × 6. . . . . . 49
2.9 Exemple de Average pooling pour une matrice de taille 4 × 6. . . . 49
2.10 Représentation graphique de la fonction ReLu . . . . . . . . . . . . 50
2.11 Architecture d’un réseau de neurones convolutif. . . . . . . . . . . . 51
2.12 Réseau de neurones convolutif LeNet. . . . . . . . . . . . . . . . . 52
2.13 Réseau de neurones convolutif AlexNet . . . . . . . . . . . . . . . . 52
2.14 Réseau de neurones convolutif ResNet . . . . . . . . . . . . . . . . 53
5

6. 2.15 Comparaison des régularisations de Tikhonov (L2 au carré) et L1 en
une dimension. Les courbes bleues représentent les régularisateurs
en fonction de α , et les courbes rouges sont les dérivés. . . . . . . . 56
2.16 Méthodes de régularisation : A Dropout et B DropConnect. . . . . 57
3.1 9 chiffres écrit à la main provenant du MNIST . . . . . . . . . . . 63
3.2 10 images aléatoires de chaque classes de CIFAR-10 . . . . . . . . . 64
3.3 16 images aléatoires de CIFAR-100 . . . . . . . . . . . . . . . . . . 64
3.4 Matrice de confusion dans le cas binaire . . . . . . . . . . . . . . . 65
3.5 Courbe Roc . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 66
3.6 À gauche : une unité au moment de l’entraı̂nement qui est présente
avec une probabilité p et est connectée aux unités de la couche
suivante avec des poids w. À droite : Au moment du test, l’unité
est toujours présente et les poids sont multipliés par p. La sortie au
moment du test est la même que la sortie attendue au moment de
l’entraı̂nement. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 69
3.7 Description numérique du premier modèle appliqué à MNIST. . . . 71
3.8 Description numérique du premier modèle appliqué à CIFAR-10
(CIFAR-100). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 71
3.9 Description numérique du deuxième modèle appliqué à MNIST. . . 72
3.10 Description numérique du deuxième modèle appliqué à CIFAR-10
(CIFAR-100). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 72
3.11 Description numérique du troisième modèle appliqué à MNIST. . . 73
3.12 Description numérique du troisième modèle appliqué à CIFAR-10
(CIFAR-100). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 73
3.13 Variation de l’erreur et d’accuracy par apport le nombre d’époque
(sans Dropout). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 74
3.14 Variation de l’erreur et d’accuracy par apport le nombre d’époque
(Dropout p = 0.2). . . . . . . . . . . . . . . . . . . . . . . . . . . . 74
3.15 Variation de l’erreur et d’accuracy par apport le nombre d’époque
(Dropout p = 0.5). . . . . . . . . . . . . . . . . . . . . . . . . . . . 75
3.16 Variation de l’erreur et d’accuracy par apport le nombre d’époque
(sans Dropout). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 75
3.17 Variation de l’erreur et d’accuracy par apport le nombre d’époque
(Dropout p = 0.2). . . . . . . . . . . . . . . . . . . . . . . . . . . . 76
3.18 Variation de l’erreur et d’accuracy par apport le nombre d’époque
(Dropout p = 0.5). . . . . . . . . . . . . . . . . . . . . . . . . . . . 76
6

7. 3.19 Variation de l’erreur et d’accuracy par apport le nombre d’époque
sans Dropout. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 77
3.20 Variation de l’erreur et d’accuracy par apport le nombre d’époque
(Dropout p = 0.2). . . . . . . . . . . . . . . . . . . . . . . . . . . . 77
3.21 Variation de l’erreur et d’accuracy par apport le nombre d’époque
(Dropout p = 0.5) . . . . . . . . . . . . . . . . . . . . . . . . . . . . 78
7

8. LISTE DES TABLEAUX
1.1 Exemple de fonction d’activation . . . . . . . . . . . . . . . . . . . 17
2.1 Les paramètres et les hyperparamètres d’un réseaux de neurones
convolutifs. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 54
3.1 Résultats du premier modèle implémenté sans Dropout. . . . . . . . 74
3.2 Résultats du premier modèle implémenté avec Dropout de probabi-
lité p = 0.2. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 74
3.3 Résultats du premier modèle implémenté avec Dropout de probabi-
lité p = 0.5. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 75
3.4 Résultats du deuxième modèle implémenté sans Dropout. . . . . . . 75
3.5 Résultats du deuxième modèle implémenté avec Dropout de proba-
bilité p = 0.2. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 76
3.6 Résultats du deuxième modèle implémenté avec Dropout de proba-
bilité p = 0.5. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 76
3.7 Résultats du troisième modèle implémenté sans Dropout. . . . . . . 77
3.8 Résultats du troisième modèle implémenté avec Dropout de proba-
bilité p = 0.2. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 77
3.9 Résultats du troisième modèle implémenté avec Dropout de proba-
bilité p = 0.5. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 78
8

9. RÉSUMÉ
Les réseaux de neurones artificiels sont des modèles mathématiques d’un réseau
de neurones biologiques, ils s’appliquent dans plusieurs domaines, ils se caracté-
risent par leur puissance et leur diversité de types. Pour le domaine de l’analyse des
images, les réseaux de neurones convolutifs donnent des meilleurs résultats pour
la classification des images, le but de ce travail est de décrire la régularisation de
ces modèles ainsi que leur applications à la classification des images. Pour ce faire,
nous nous intéressons à écrire un modèle de réseaux de neurones convolutifs, puis
nous appliquons ce modèle à des bases de données pour classer ces images, et nous
régulariserons pour éviter le sur-apprentissage et pour avoir une classification plus
efficace nous modifierons les hyperparamètres du modèle. Bref, l’effet de régulari-
sation pour ce type de réseau est très fructueux dans le domaine de la classification
des images.
Mots clés : Réseaux de neurone artificiels, Réseaux de neurones convolutifs,
Régularisation.
9

10. ABSTRACT
Artificial neural networks are mathematical models of a biological neural net-
work, they apply in several fields, they are characterized by their power and their
diversity of types. For the field of image analysis, convolutional neural networks
give better results for the classification of images, the aim of this work is to describe
the regularization of these models as well as their applications to the classification
of images. To do this, we are interested in writing a model of convolutional neural
networks, then we apply this model to databases to classify these images, and we
will regularize to avoid over-learning and to have a more efficient classification we
will modify hyperparameters of the model. In short, the regularization effect for
this type of network is very fruitful in the field of image classification.
Keywords : Artificial neural networks, Convolutional neural networks,
Regularization.
10

11. INTRODUCTION
Grâce aux résultats obtenus au cours des dernières décennies, les réseaux de neu-
rones artificiels (RNA) connaissent un succès croissant et ont prouvé leur efficacité
dans plusieurs domaines : analyse et compression des images classification, recon-
naissance de formes, analyse du signal.
Les réseaux de neurones artificiels ont été étudiés sur trois périodes. La première
apparition dans les années 1940 était due à McCullotch et Pitts qui ont proposé
un modèle de calcul paramétrique non linéaire simple d’un vrai neurone [1]. Le
deuxième développement s’est produit dans les années 1960 avec Rosenblatts qui
a proposé un réseau de neurones en couches composé de perceptrons et d’un al-
gorithme pour ajuster les paramètres d’une seule couche dans le but de mettre en
œuvre une tâche souhaitée [2]. Dans [3], Minsky et Paperts ont montré les limites
d’un simple perceptron. En conséquence, la la recherche en réseaux de neurones
artificiels a connu une accalmie qui a duré près de 20 ans. Depuis le début des
années 1980, Les ANN ont suscité un regain d’intérêt considérable. Les principaux
développements à l’origine de cette résurgence incluent les réseaux de neurones de
Hopfield [4] et l’algorithme de rétropropagation des perceptrons multicouches qui
est d’abord proposé par Webros [5], réinventé plusieurs fois, puis popularisé par
Remulhart et al en 1986 [6].
À la fin des années 1980, Yan le Cun a développé un type particulier de réseau
de neurones artificiels appelé réseau de neurones convolutifs [7], ces réseaux sont
une forme particulière de réseau de neurones multicouches dont l’architecture de
connexion est inspirée de celle du cortex visuel des mammifères. Par exemple,
chaque élément n’est connecté qu’à un petit nombre d’éléments voisins de la couche
précédente. En 1995, Yan le cun et deux autres ingénieurs ont développé un sys-
tème de lecture automatique de chèques qui a été largement déployé dans le monde.
Dans la fin des années 90, ce système lisait entre 10 et 20% de tous les chèques émis
11

12. aux États-Unis. Mais ces méthodes étaient assez difficiles à mettre en œuvre avec
les ordinateurs de l’époque, et malgré ce succès, les réseaux de neurones convolutifs
et plus généralement, les réseaux de neurones ont été délaissés par la communauté
des chercheurs entre 1997 et 2012.
Les réseaux de neurones convolutifs (CNN en anglais Convolutional Neural Net-
work), sont à ce jour parmi les modèles les plus efficaces pour classer les images.
Pour sûr que nos réseaux de neurones donnent de bons résultats en classification
d’images, et pour surmonter le problème de sur-apprentissage, nous allons décrire
les méthodes de régularisation.
Dans ce projet, nous allons décrire le fonctionnement intrinsèque des CNNs pour
la classification des images tout en expliquant le problème de sur apprentissage et
jusqu’à quel niveau les techniques de régularisation permettant d’en résoudre.
Ce travail s’articule autour de trois chapitres :
• Dans le premier chapitre, nous présenterons les réseaux de neurones artificiels,
ses différents types ainsi que ses modes et ses règles d’apprentissage.Nous ter-
minons ce chapitre par citer quelques difficultés et limites relatives à l’utili-
sation des RNA.
• Le deuxième chapitre est consacré à la description des méthodes de régulari-
sation des réseaux de neurones artificielles tout en précisant leurs avantages
et ses types, puis nous décrivons le fonctionnement de la technique Dropout
dans le cadre de la régularisation des réseaux convolutifs.
• Dans le troisième chapitre, nous appliquerons les réseaux de neurones convo-
lutifs au problème de la classification des images. En effet, nous allons montrer
l’intérêt de tels modèles dans cette application ainsi que l’impact de la régu-
larisation via Dropout pour surmonter le phénomène de sur-apprentissage.
Nous terminons ce travail par une conclusion générale.
12

13. CHAPITRE 1
RÉSEAUX DE NEURONES ARTIFICIELLES
Introduction
Les réseaux de neurones artificiels sont des modèles mathématiques et informa-
tiques, ils ont été présentés en 1943 par Mac Culloch et Pittis, ce sont des assem-
blages d’unités de calcul appelées neurones formels, et dont l’inspiration originale
était un modèle de la cellule nerveuse humaine [8].
Les réseaux de neurones artificiels ont été développés à des fins principales. D’une
part, la modélisation et la compréhension du fonctionnement du cerveau et d’autre
part la réalisation d’architectures ou d’algorithmes d’intelligence artificielle.
Dans ce chapitre, nous présentons d’abord des généralités sur les réseaux de neu-
rones artificiels, les concepts de base puis nous abordons le processus d’apprentis-
sage.
1.1 Neurone biologique et neurone formel
1.1.1 Neurone biologique
Cerveau humain est le meilleur modèle de la machine, polyvalent, incroyable-
ment rapide et surtout doté d’une incomparable capacité d’auto-organisation. Son
comportement est bien plus mystérieux que celui de ses cellules de base ; il est
constitué d’un grand nombre d’unités biologiques de base [9].
13

14. Définition 1.1.1 :
un neurone biologique est une cellule qui se caractérise par :
• Synapses, Points de connexion avec d’autres neurones, Fibres nerveuses.
• Dendrites, entrées de neurones.
• Axone, Sortie du neurone vers d’autres neurones ou fibres musculaires.
• Noyau qui active la sortie en fonction du stimulus d’entrée(Figure 1.1).
Figure 1.1 – Neurone biologique
1.1.2 Neurone artificiel ou neurone formel
Un neurone formel est un modèle mathématique du neurone biologique. Il cal-
cule la somme pondérée de ses entrées, suivie d’une non linéarité appelée fonction
d’activation ou fonction de transfert [10].
Définition 1.1.2 :
1. Neurone artificiel c’est un processeur élémentaire caractérisé par :
• Signaux d’entrée x = x0, x1, ..., xn
• Poids des connexions w = w0, w1, ..., wn
• Fonction d’activation f
• État de sortie y = f(x)
2. Neurone formel (artificiel) est une unité de traitement qui reçoit
des données en entrée, sous la forme d’un vecteur, et produit une sortie
réelle. Cette sortie est une fonction des entrées et des poids des
connexions.
14

15. Un neurone formel est une fonction non linéaire, paramétrée, à valeurs bornées, il
se caractérise par un état interne appartient à yj, des signaux d’entrée x1, ..., xn et
une fonction de transition (activation) d’état f comme suit (Figure 1.2) :
yj = f(w0 +
n
X
i=0
wijxi) (1.1)
Figure 1.2 – Structure de neurone formel
1.2 Fonctions d’activations
Une fonction d’activation est une fonction généralement présentée par une non-
linéarité aussi appelée fonction de transition ou fonction de transfert. Il permet de
définir l’état interne du neurone en fonction de son entrée totale [9].
Définition 1.2.1 :
Une fonction d’activation est une transformation linéaire ou non linéaire
d’une combinaison des signaux d’entrée.Cette combinaison est déterminée par
un vecteur de poids (w1j, ..., wnj) associé à chaque neurone et dont les valeurs
sont estimées dans la phase d’apprentissage, w0 étant appelé le biais du neurone,
il constitue la mémoire ou la connaissance répartie du réseau.
15

16. Parmi les modèles des réseaux de neurones artificiels :
• Modèle de Kohonen :
Réseau de Kohonen est un réseau de neurones dont la particularité est d’agir
comme un compresseur de données, en ne conservant que les informations
caractérisant l’objet présenté au réseau sans perte d’informations significative.
Le but est de présenter des données complexes et appartenant généralement
à un espace discret de grandes dimensions dont la topologie est limitée à une
ou deux dimensions.
• Modèle de Hopfield :
Réseau de Hopfield représentent une architecture plus historique que pratique.
Ils sont importants parce qu’ils sont apparus à un tournant de l’histoire du
connexionnisme. Ils sont considérés comme base de son redémarrage. Par
contre, ils ne sont plus guère utilisés dans leur version de base en raison de
leur coût en terme de temps de calcul et de leurs performances relativement
faibles.
• Modèle Adaline :
Réseau Adaline (ADAptive LINEar element) est le seul réseau de neurones
artificiels largement utilisé dans l’industrie, il a été présenté par B. Widrow
et M.E. Hoff au début des années 1960, ce circuit est utilisé dans les télécom-
munications pour améliorer le rapport signale sur bruit en tenant compte de
la variation de l’impédance des différentes lignes téléphoniques.
D’après cette variété des modèles de réseaux de neurones artificiels on distingue
plusieurs modèle de fonctions d’activation, on peut citer (Table 1.1) :
- Modèles linéaires et sigmoı̈daux : ces modèles sont très adaptés à l’appren-
tissage d’algorithmes comme celui de la rétropropagation du gradient car leur
fonction de transition (activation) est différentiable.
- Modèle à seuil : ce modèle est très proche et conforme à la réalité biologique
mais il pose des problèmes d’apprentissage.
- Modèle stochastique : ce modèle est utilisé pour des problèmes d’optimisation
globale de fonctions perturbées ou pour des analogies avec des systèmes de
particules.
16

17. Nom de la
fonction Relation entrée/sortie
Description de la
fonction Icône
Seuil y = f(x) =
y = 0 si x 0
y = 1 si x ≥ 0
(1.2)
Une entrée négative
ne franchit pas le
seuil. Une entrée
positive ou nulle
dépasse le seuil, et la
fonction renvoie 1
Seuil
symétrique
y = f(x) =
y = −1 si x 0
y = 1 si x ≥ 0
(1.3)
La fonction renvoie -1
si une entrée est
négatif et renvoie 1 si
une entrée est
positive ou nulle
Linéaire y = s (1.4) Affectation directe de
l’entrée à la sortie
Linéaire
saturée
y = f(x) =



y = 0 si x 0
y = x si 0 ≤ x ≥ 1
y = 1 si x 1
(1.5)
Une entrée négative
ne passe pas le seuil,
Une entrée nulle ou
supérieure ou égale au
seuil, la fonction
affecte directement
l’entrée à la sortie,
Une entrée
strictement supérieure
au seuil, la fonction
renvoie 1
Tangente
hyperbo-
lique
y =
ex
− e−x
ex + e−x
(1.6)
La fonction affecte
l’entrée à la sortie
dont les asymptotes
ont pour équation
y = −1 et y = 1
Sigmoı̈de y = f(x) =
1
1 + exp(−x)
(1.7)
Un arrangement entre
la fonction seuil et la
fonction linéaire
Table 1.1 – Exemple de fonction d’activation
17

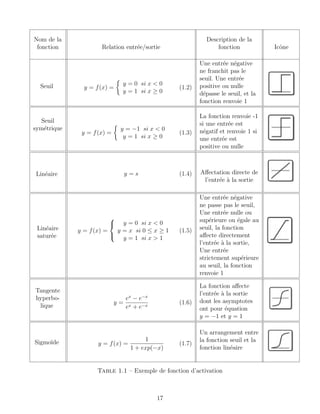
18. 1.3 Réseaux de neurones artificiels RNA
Les réseaux de neurones artificiels sont des modèles statistiques adaptatifs, basés
sur une analogie avec le cerveau humain. Leur adaptabilité vient du fait qu’ils
peuvent apprendre à estimer les paramètres d’un ensemble de données à l’aide
d’un certain nombre d’exemples. Dans sa structure de base, un réseau de neurones
artificiels est constitué d’un ensemble d’unités simples qui sont des neurones. Ceux-
ci sont inter-connectés à l’aide d’un ensemble de connexions pondérées [8].
Définition 1.3.1 :
Les réseaux de neurones artificiels sont des réseaux fortement connectés de
processeurs élémentaires fonctionnant en parallèle. Chaque processeur élémen-
taire calcule une sortie unique sur la base des informations qu’il reçoit. Toute
structure hiérarchique de réseaux est évidemment un réseau.
Remarque 1.3.2 :
Les Réseaux de neurones artificiels sont généralement organisés en couches :
• Première couche : est une couche d’entrée. Elle est responsable de la trans-
mission de l’information à analyser vers le réseau.
• Dernière couche : est une couche de sortie. Elle reçoit le résultat final qui
est la réponse du réseau.
• Les couches intermédiaires : sont des couches cachées, le nombre de ces
couches est défini selon le type du problème à résoudre. Elles relient les deux
couches d’entrée et de sortie
L’intérêt porté aujourd’hui aux réseaux de neurones se justifie par quelques pro-
priétés intéressantes qu’ils possèdent et qui devraient permettre de s’affranchir des
limitations. L’informatique traditionnelle, tant au niveau de la programmation
qu’au niveau de la machine.
Propriétés
• Parallélisme : Les réseaux de neurones artificiels sont constitués de neurones
simples, fortement inter-connectés, dont le but est la réalisation d’une fonc-
tion de type bien définie qui rend le traitement de l’information massivement
parallèle.
18

19. • Poids synaptiques : La pondération des liens synaptiques entre neurones in-
fluence l’efficacité et la fiabilité du réseau en termes de rapidité et de précision
des résultats fournis.
• Apprentissage : L’apprentissage est probablement la propriété la plus intéres-
sante des réseaux de neurones artificiels, il ne concerne cependant pas tous les
modèles mais le plus utilisé, son problème principal est de trouver un ensemble
de valeurs d’entrée des connexions afin d’atteindre les résultats souhaités.
• Capacité d’adaptation : Cela se manifeste par la capacité d’apprentissage
qui permet de prendre en compte de nouvelles contraintes ou de nouvelles
données du monde extérieur. Certains réseaux se caractérisent également par
leur capacité d’auto-organisation qui assure leur stabilité au fur et à mesure
des systèmes dynamiques capables de prendre en compte des situations encore
inconnues.
• Mémoire distribuée : Dans les réseaux de neurones, la mémoire correspond
à une carte d’activation neuronale. Cette carte est en quelque sorte un co-
dage du fait mémorisé qui donne à ces réseaux l’avantage de résister au bruit
(pannes) car la perte d’un élément ne correspond pas à la perte d’un fait
mémorisé.
Selon la topologie des réseaux de neurones, on peut distinguer deux types de
réseaux de neurones artificiels (Figure 1.3) :
- Réseaux en couches qui sont des réseaux de neurones dans lesquels les infor-
mations voyagent couche par couche sans revenir en arrière.
- Réseaux récurrents qui sont des réseaux de neurones dans lesquels il existe
un lien en amont. Les connexions de ces réseaux forment des boucles. Ainsi la
fonction d’activation peut circuler le long de ces boucles et affecter le réseau
pendant une durée arbitrairement longue.
19

20. Figure 1.3 – Topologie des réseaux de neurones
1.3.1 Réseaux directs(Feedforward)
Dans un réseau direct ou statistique, la sortie d’un neurone ne peut être in-
jectée ni directement à son entrée ni indirectement à travers d’autres neurones,
c’est-à-dire qu’une sortie actuelle n’a aucune influence sur les futures libérations.
Dans ce cas, la sortie du réseau est obtenue directement après l’application du
signal d’entrée, l’information circule dans un seul sens (c’est-à-dire non bouclé),
de l’entrée vers la sortie [10].
1.3.1.1 Perceptron simple (mono couche)
Fonctionnement : Les données sont présentées au réseau en activant la rétine.
L’activation se propage à la couche de sortie où la réponse du système peut être
notée. Cette réponse suit la formule suivante :
y = φ(w0 +
n
X
i=1
wixi) (1.8)
Où :
φ : La fonction d’activation utilisée.
wi : Les poids du neurone.
xi : Les entées.
w0 : Le seuil du neurone.
20

21. Exemple : le perceptron monocouche (Figure 1.4) se décompose en deux couches :
• Une couche d’entrée qui s’appelle la rétine et qui est une aire sensorielle.
• Une couche de sortie qui donne la réponse correspondante à la simulation
présentée à l’entrée .
Figure 1.4 – Exemple d’un perceptron monocouche
1.3.1.2 Perceptron multicouche MLP (Multi LayerPerceptron) :
Définition 1.3.3 :
Le Perceptron multicouche est un réseau dirigé de neurones artificiels en
couches, où l’information circule dans une seule direction, de la couche d’en-
trée à la couche de sortie.
Fonctionnement :
Le perceptron multicouches (Figure 1.5) est un modèle possédant une grande ca-
pacité de calcul. Sa structure est composée d’une couche d’entrée, une couche de
sortie, interprétée comme étant la réponse du réseau et d’une ou plusieurs couches
intermédiaires dites couches cachées. Un neurone d’une couche inférieure ne peut
être relié qu’à des neurones des couches suivantes. Il suit un apprentissage appris et
utilise la règle d’apprentissage de rétropropagation. En général, le fonctionnement
des neurones du perceptron multicouches est animé par une fonction d’activation
non linéaire au moins dans une des couches. Les choix classiques pour cette fonc-
tion sont :
• La fonction tangente hyperbolique.
• La fonction sigmoı̈de.
21

22. Figure 1.5 – Exemple d’un perceptron multicouches
1.3.1.3 Réseau de neurones convolutifs
Les réseaux de neurones convolutifs (convolutional neural network CNN) sont
des formes spéciales de réseaux de neurones multicouches caractérisée par leur
première couche convolutive (généralement une à trois). La couche convolutive
est basée sur le principe mathématique de la convolution et vise à reconnaı̂tre
l’existence de motifs (généralement dans des images ou des signaux). Les CNNs
ont de nombreuses applications dans la reconnaissance des images, de vidéos ou
dans le traitement du langage naturel. Nous apprendrons les détails de ce type de
réseau qui m’intéressent au chapitre 2.
1.3.1.4 Réseau de neurones à Fonction de base Radiale :
Les réseaux à fonction radiale RBF ont la même structure qu’un perceptron
multicouche sauf au niveau de la fonction d’activation. Dans ce type de réseaux,
la fonctions d’activation est de type gaussien.
Définition 1.3.4 :
Un RBF (Figure 1.6) est un type de réseaux de neurones artificiels qui utilise
souvent une règle d’apprentissage de correction d’erreur et une règle d’apprentis-
sage compétitif. L’apprentissage pour les RBFs combine à la fois l’apprentissage
supervisé et non supervisé, en même temps il est plus rapide et plus facile.
22

23. Fonctionnement :
• La fonction radiale est une classe de fonctions spéciales, leur réponse augmente
ou diminue de manière monotone par rapport à la distance d’un point central.
Le centre, la distance et la forme de l’entité à base radiale sont les paramètres
du modèle qui est linéaire s’ils sont fixes. Une caractéristique de base radiale
typique est de la forme :
g(x) = exp(−
(x − c2
)
r2
) (1.9)
• Une fonction à base radiale gaussienne diminue à mesure que la distance par
rapport au centre augmente. En revanche, une fonction de base radiale multi-
quadratique augmente la distance par rapport au centre augmente. Il a la
forme suivante :
g(x) =
p
(x − c2) + r2
r2
(1.10)
Figure 1.6 – Réseaux à fonction radiale RBF
1.3.2 Réseaux récurrents RNN
Ces réseaux sont des réseaux bouclés, appelés aussi réseaux dynamiques, sont
organisés de telle sorte que chaque neurone reçoit sur ses entrées une partie ou la
totalité de l’état du réseau (sortie des autres neurones) en plus des informations
externes (Figure 1.7). Pour les réseaux récurrents, l’influence entre les neurones
fonctionne dans les deux sens. L’état global du réseau dépend aussi de ses états
antérieurs [11].
23

24. Définition 1.3.5 :
• Les réseaux récurrents (Recurrent Neural Networks RNN) sont des réseaux
de neurones dans lesquels l’information peut se propager dans les deux sens,
y compris des couches profondes aux premières couches.
• les RNNs sont particulièrement adaptés aux applications au traitement des
séquences temporelles comme l’apprentissage et la génération de signaux,
c’est à dire quand les données forment une suite et ne sont pas
indépendantes les unes des autres.
Figure 1.7 – Exemple d’un RNN à trois entrée et quatre sorties. Les connexions récurrentes sont
notées en rouge.
1.4 Apprentissage des réseaux de neurones artificiels
On peut considérer les réseaux de neurones comme une boı̂te noire contenant les
informations qu’il doit apprendre et mémoriser. Mais au démarrage lorsque nous
choisissons notre réseau, la boı̂te noire est vide et ne contient aucune informa-
tion ou connaissance sur son sujet c’est pourquoi un apprentissage est nécessaire.
L’enseignement que doit subir le réseau de neurones est un apprentissage qui est
une phase de développement d’un réseau de neurones au cours de laquelle le com-
portement du réseau est modifié jusqu’à l’obtention du comportement souhaité.
L’apprentissage neuronal utilise une base de données formée par des exemples [12].
24

25. Définition 1.4.1 :
• L’apprentissage est une phase de développement d’un réseau de neurones
durant laquelle une modification du comportement du réseau se fait jusqu’à
l’obtention d’un comportement désiré.
• L’apprentissage est une action de mise à jour des poids des connexions dans
le but d’atteindre la sortie du réseau pour les exemples présentés en entrée.
1.4.1 Types d’apprentissage
• Apprentissage supervisé : ce mode est le plus courant, l’utilisateur a un com-
portement de référence précis qu’il souhaite que le réseau apprenne. Schéma-
tiquement, elle consiste à évaluer les poids synaptiques minimisant l’erreur
sur une base d’apprentissage, cette base comprend un ensemble d’observa-
tions pour lesquelles on connaı̂t à la fois les entrées et les sorties souhaitées.
L’apprentissage est dit supervisé, car il est nécessaire de connaı̂tre la sortie
attendue pour chaque ensemble d’entrées, le réseau de neurones ajustera ses
paramètres afin de minimiser l’erreur entre la sortie souhaitée et sa sortie
réelle.
• Apprentissage semi- supervisé : cet apprentissage est identique au précédent
dans la mesure où il repose sur la présence d’un concepteur, cependant la
valeur exacte de la sortie n’est pas disponible, en général la seule information
disponible est un signal d’échec ou de réussite.
• Apprentissage non supervisé : ce mode d’apprentissage est moins intuitif,
il correspond au cas où il n’y a pas de bases d’apprentissage, par exemple
lorsqu’on ne sait pas a priori déterminer ponctuellement si une sortie est valide
ou non. L’apprentissage est alors basé sur un critère interne de conformité du
comportement du réseau par rapport à des spécifications générales et non sur
des observations. Cet apprentissage consiste donc à détecter automatiquement
les régularités qui apparaissent dans les exemples présentés et à modifier les
poids des connexions pour que les exemples ayant les mêmes caractéristiques
de régularité provoquent la même sortie.
25

26. 1.4.2 Règles d’apprentissage
Son principe est de regrouper les données en catégories.
- Placés des neurones similaires dans la même classe en fonction des corrélations
de données et seront représentés par un seul neurone.
- Un formulaire est présenté à l’entrée du réseau. Il est ensuite projeté sur
chacun des neurones de la couche compétitive. Le neurone gagnant est celui
qui a un vecteur de poids le plus proche de la forme présentée en entrée.
Chaque neurone de sortie est connecté aux neurones de la couche d’entrée et
aux autres cellules de sortie cette connexion lorsqu’il appelle une connexion
inhibitrice ou à lui-même cette connexion lorsqu’il appelle une connexion ex-
citatrice. Les résultats obtenus dépendent alors de la compétition entre les
connexions inhibitrices et excitatrices.
• Règle de rétro-propagation : cette règle est utilisée pour ajuster les poids
de la couche d’entrée à la couche cachée, et peut également être considérée
comme une généralisation de la règle delta pour les fonctions d’activation non
linéaires et pour les réseaux multicouches. les neurones sont d’abord initialisés
avec des valeurs aléatoires. Nous considérons ensuite un ensemble de données
qui servira d’échantillon d’apprentissage. Chaque échantillon a ses valeurs
cibles qui sont celles que le réseau de neurones doit atteindre lorsqu’il est
présenté avec le même échantillon[13].
• Règle de Hebb : aider de modifier la valeur des poids synaptiques en fonction
de l’activité des unités qui les relient. Le but principal de cette règle si deux
unités s’activent en même temps, la connexion qui les lie est renforcée lors de
l’appel d’une connexion excitante sinon elle est affaiblie lors de l’appel d’une
connexion inhibitrice.
• Règle delta : permet de calculer la différence entre la valeur de sortie et la
valeur souhaitée pour ajuster les poids synaptiques. Pour cela, cette règle
utilise une fonction d’erreur, dite des moindres carrés moyens, basée sur les
différences utilisées pour l’ajustement des poids.
• Règle de corrélation en cascade : est une technique d’apprentissage qui ajoute
progressivement des neurones cachés au réseau jusqu’à ce que l’effet bénéfique
de ces nouveaux neurones ne soit plus perceptible. Il y a deux étapes pour
cette règle :
26

27. L’étape 1 : le système est entraı̂né par un apprentissage conventionnel
qui se déroule d’abord dans un petit réseau sans couche cachée.
L’étape 2 :on entraı̂ne ensuite un petit groupe de neurones supplémen-
taires qui doivent réduire l’erreur résiduelle du réseau. L’utilisation de la
règle d’apprentissage à pour but de modifie les poids de ces neurones. Le
neurone le plus performant est retenu et intégré au réseau. L’étape 1 est
redémarrée pour permettre au réseau de s’adapter à la nouvelle ressource.
• Règle de correction d’erreurs : cette règle contient trois étapes :
L’étape 1 : nous commençons par les valeurs des poids de connexion qui
sont prises au hasard.
L’étape 2 : nous introduisons un vecteur d’entrée de l’ensemble d’échan-
tillons pour l’apprentissage.
L’étape 3 : si la sortie ou la réponse n’est pas correcte, toutes les connexions
sont modifiées pour obtenir la réponse correcte.
1.4.3 Fonction de perte (loss function)
Nous avons besoin que nos systèmes d’apprentissage automatique fonctionnent
aussi bien que possible sur les nouvelles données, selon certaines mesures de per-
formance.
les mesures de performance les plus couramment rencontrées souvent ne sont pas
différentiables, une propriété qui est fortement souhaitable. Pour ces raisons, on op-
timisera souvent le système d’apprentissage automatique en terme d’une fonction
qu’on appelle fonction de perte ou d’erreur, liée aux performances recherchées.
1.4.3.1 Entropie croisée (Cross-entropy)
Maintenant dans le cadre de l’apprentissage supervisé. Nous avons un ensemble
d’apprentissage S d’exemples x associés aux étiquettes y et souhaitons former un
classificateur à fournir des étiquettes pour de nouveaux exemples non étiquetés x.
Nous allons entraı̂ner le classificateur à maximiser la probabilité p(yx) prédite par
le classificateur (ce qui équivaut à minimiser la probabilité log négative) [14]. En
désignant la fonction de perte par O(x, y), pour un seul exemple x avec l’étiquette
de vérité terrain associée y nous avons :
O(x, y) = −log(p(y x)) (1.11)
27

28. En supposant que les échantillons de données (x, y) sont indépendants, la fonction
de perte sur l’ensemble d’apprentissage O(S) devient la somme des fonctions de
perte sur chaque échantillon séparé (x, y) :
O(S) =
X
(x,y)∈S
[−log(p(y x))] (1.12)
Cette perte peut être minimisée grâce à une optimisation basée sur le gradient.
1.4.3.2 Erreur quadratique
Soit une base d’apprentissage composée de N vecteurs d’entrée {x(m)
}m=1,...,M
et d’un ensemble correspondant de vecteurs cibles {y(m)
}m=1,...,M . On définit une
fonction de perte classique qui est l’erreur quadratique moyenne :
L(W) =
1
2
M
X
m=1
kŷ(x(m)
, W) − y(m)
k2
. (1.13)
Cette fonction de perte quadratique apparait naturellement dans un problème de
régression si on suppose par exemple que les x(m)
sont des réalisations de variables
i.i.d, que chaque y(m)
suit une distribution gaussienne N(ŷ(x(m)
, W), σ2
) et que
l’on cherche les paramètres par maximum de vraisemblance. En effet, le maximum
de vraisemblance est calculé dans ce cas comme :
argminxW
M
Y
m=1
exp−ky(m)−ŷ(x(m),W )k2
2σ2
(1.14)
ce qui revient à minimiser L(W).
Remarque 1.4.2 :
La fonction de perte n’est pas une fonction convexe, elle peut donc être très
difficile à optimiser. En pratique, il est encore optimisé par descente du gradient,
agissant ainsi comme s’il était convexe.
1.4.4 Méthodes d’optimisation pour l’apprentissage
On explique dans cette section comment estimer les paramètres W du ré-
seau. Étant donnée une base d’apprentissage composée de N vecteurs d’entrée
{x(m)
}m=1,...,M et d’un ensemble correspondant de vecteurs cibles {y(m)
}m=1,...,M ,
on cherche les poids qui minimisent une fonction de perte (loss function) agrégeant
les erreurs de prédiction sur la base. On choisit une fonction de perte classique
comme une erreur quadratique moyenne [15].
28

29. 1.4.4.1 Descente du gradient
L’optimisation du réseau se fait par descente du gradient, avec les étapes sui-
vantes :
1. On commence par initialiser les poids W aléatoirement .
2. On calcule le gradient de la fonction de perte L par rapport à tous les poids
du réseau :
∇L =
(
∂L
∂W
[k]
ij
)
i,j,k
(1.15)
en utilisant la dérivation en chaine (backpropagation)
3. Pour un pas de descente α 0 donné, on met à jour les poids W .
W
[k]
ij ← W
[k]
ij − α
∂L
∂W
[k]
ij
(1.16)
et on retourne à l’étape 2, jusqu’à la convergence.
Remarque 1.4.3 :
On peut aussi utiliser un algorithme du gradient conjugué ou quasi-Newton
pour cette optimisation, ce qui permet de s’assurer que la fonction de perte
décroı̂t à chaque itération (ce n’est pas le cas avec une simple descente du gra-
dient). Comme la fonction L n’est pas convexe dans W, il peut être nécessaire
de relancer l’algorithme avec plusieurs initialisations différentes et de choisir le
résultat optimal. Le calcul de la pente de L, s’il peut être fait directement pour
les réseaux très simples, nécessite généralement un algorithme spécifique, appelé
Backpropagation.
1.4.4.2 Descente du gradient stochastique
Pour entrainer les réseaux de neurones avec des grandes bases de données, on
peut utiliser une méthode de descente du gradient séquentielle, aussi appelée des-
cente de gradient stochastique. Le principe est de décomposer la fonction d’erreur
sous la forme :
L(W) =
N
X
n=1
Ln(W) (1.17)
29

30. où l’indice n = 1, ..., N désigne différentes observations (ou groupes d’observations)
indépendantes (on parle aussi de groupe de données). Un pas de descente s’écrit :
Wk+1
= Wk
− α∇Ln(wk
) (1.18)
Cette mise à jour est répétée soit en choisissant n au hasard, soit dans un ordre
prédéfini. Nous parcourons les valeurs de n et recommençons lorsque les données
N ont toutes été utilisées. Chaque cycle sur l’ensemble de données est appelé une
époque .
On peut réinterpréter cette méthode comme une descente avec une version bruitée
du gradient à chaque étape. Si on suppose que ∇L(w) varie lentement, une époque
est quasiment équivalente à une descente dans la direction −∇L(w) avec le poids
α.
Ce type de méthode a la bonne propriété de pouvoir échapper aux minima locaux,
puisqu’un point stationnaire par rapport à L n’est généralement pas stationnaire
pour Ln. Elle s’adapte ainsi que l’apprentissage en ligne, pour lequel les données
ne sont pas toutes disponibles en même temps.
1.4.4.3 Principe de calcul du gradient par rétropropagation (Backpropagation)
Pour calculer efficacement le gradient ∇L, nous utilisons un algorithme dit la
rétropropagation. Cet algorithme part de l’erreur d’apprentissage et de la repro-
grammation en arrière dans le réseau vers les valeurs d’entrée pour calculer les
dérivées par rapport à chaque poids.
La rétropropagation repose sur le principe de dérivation en chaine. On rappelle
que si l’on a une fonction f de Rn
dans R et une fonction h de Rp
dans Rn
et que
l’on note L(x) = f ◦ h(x) (avec hj la cordonnée j de h), alors :
∂L
∂xi
=
n
X
j=1
∂f
∂hj
∂hj
∂xi
(1.19)
Notation : on écrira ∂L
∂hj
pour désigner le gradient ∂f
∂hj
. La dérivation en chaine
s’écrira donc :
∂L
∂xi
=
n
X
j=1
∂L
∂hj
∂hj
∂xi
(1.20)
où L est vue comme fonction de x dans la partie gauche de l’équation et comme
fonction de h dans la partie droite.
Notre but est de calculer, pour toutes les couches k du réseau, la dérivée de L par
30

31. rapport aux poids W
[k]
ij et aux offsets bk
j . On fait l’hypothèse pour l’instant que la
fonction de perte est quadratique .
L(W) =
1
2
M
X
m=1
kŷ(x(m)
, W) − y(m)
k2
. (1.21)
En dérivant, on a pour tout i,j, k :
∂L
∂W
[k]
ij
=
M
X
m=1
ŷ(x(m)
, W) − y(m)
,
∂ŷ
∂W
[k]
ij
(1.22)
1.5 Avantages et limites des RNAs
1.5.1 Avantages des RNAs
Nous avons plusieurs avantages des réseaux de neurones artificiels que nous ré-
duisons à quatre avantages :
Réutilisabilité : un réseau de neurones n’est pas programmé pour une application
mais pour une classe de problèmes .
Robustesse : Les couches cachées des réseaux de neurones forment une repré-
sentation abstraite des données, ce qui permet de savoir comment catégoriser les
données non traitées lors de l’apprentissage.
Parallélisme : l’architecture du réseau permet théoriquement de démarrer de ma-
nière concurrente un grand nombre d’éléments de calcul simples, ce qui facilite
l’obtention des résultats très rapide et facilite la mise en œuvre d’applications
ayant notamment des contraintes du temps réel.
Logique floue : les réseaux de neurones sont inspirés du fonctionnement du cer-
veau humain, ils savent utiliser des notions imprécises, modéliser des systèmes
dynamiques et non linéaires, le réseau lui-même établit ses connaissances, à partir
des exemples.
1.5.2 Limites des RNAs
Bien que les réseaux de neurones soient capables d’effectuer de nombreuses
tâches, ils souffrent néanmoins de certaines limitations, notamment :
Choix des attributs : pour pouvoir travailler avec des réseaux de neurones, il est
nécessaire de bien choisir la représentation des données. Les attributs ne peuvent
être que numériques.
Processus d’apprentissage : lorsque la durée d’apprentissage est très longue, la
31

32. possibilité de perdre la capacité de généralisation par les réseaux de neurones ar-
tificiels augmente, c’est-à-dire l’apparition du problème de sur-apprentissage.
Architecture du réseau : le nombre de nœuds dans les couches d’entrée et de sortie
sont généralement fixés par l’application, mais comment optimiser le nombre de
couches cachés et le nombre de nœuds dans ces couches ? Il n’existe pas des règles
claires dans ce sens.
Exploitabilité : il y a une grande difficulté à expliquer les résultats obtenus par
le réseau de neurones, car ce dernier fonctionne comme une boı̂te noire et peut
découvrir des règles et les exploiter pour résoudre des problèmes, mais il ne permet
pas la possibilité d’extraire des lois ou des formules à partir de ces règles.
Parmi toutes ces limites, la limite la plus dangereuse pour les réseaux de neu-
rones artificiels est le sur-apprentissage qui s’explique par plusieurs notions.
1.5.2.1 Sur-apprentissage(Over-fitting)
Si l’on considère un ensemble d’apprentissage et une fonction de coût quadra-
tique, il est toujours possible d’obtenir une fonction de coût aussi petite que l’on
veut sur l’ensemble d’apprentissage, à condition que suffisamment de neurones
soient cachés. Cependant, le but de l’apprentissage n’est pas d’apprendre exac-
tement la base d’apprentissage, mais le modèle sous-jacent qui a été utilisé pour
générer les données. Cependant, si la fonction apprise par le réseau de neurones
est trop finement ajustée aux données, il apprend les particularités de la base
d’apprentissage au détriment du modèle sous-jacent, le réseau de neurones est sur-
ajusté.
Notion de Bais et Variance :
Le sur-apprentissage s’explique souvent par les concepts de biais et de variance
introduits dans la communauté des réseaux de neurones artificiels. Si l’on consi-
dère plusieurs ensembles d’apprentissage, le biais explique la différence moyenne
entre les modèles et l’espérance mathématique. de la grandeur à modéliser. En
conclut que le biais est donc lié à la valeur du bruit du processus que l’on cherche
à modéliser. La variance rend compte des différences entre les modèles selon la
base d’apprentissage utilisée [16].
On parle souvent de compromis entre biais et variance. Si un modèle est trop
simple (Figure 1.8) par rapport au processus à modéliser, alors son biais est élevé,
mais sa variance est faible car peu influencée par les données. Si un modèle est
trop complexe (Figure 1.8), son biais est faible puisqu’il est capable de s’adapter
exactement à la base d’apprentissage, mais sa variance est élevée comme une nou-
32

33. velle base avec une réalisation différente du bruit peut aboutir à un modèle très
différent, c’est le cas du sur-apprentissage, donc la complexité du modèle doit être
ajustée pour trouver un compromis entre biais et variance (Figure 1.9). contrôler
la complexité du modèle et donc le sur-apprentissage en limitant le nombre de
neurones cachés.
Figure 1.8 – Modèle simple et modèle complexe
Figure 1.9 – Variété de Bais-Variance en fonction de complexité du modèle
Bref, le sur-apprentissage ne s’explique pas seulement par le compromis biais-
variance, surtout lorsque le nombre d’exemples est faible. En ce sens a été dé-
veloppés pour les problèmes de régression et ne provoquent pas simplement des
problèmes de classification.
33

34. 1.6 Applications des RNAs
Depuis leur importance et leur apparition, les réseaux de neurones ont été lar-
gement utilisés dans plusieurs domaines [17]
• Finance : prévision et modélisation du marché , sélection d’investissements,
attribution de crédits...
• Environnement : évaluation des risques, analyse chimique, prévisions et mo-
délisation météorologiques, gestion des ressources...
• Industrie : contrôle de qualité, diagnostic de panne, analyse de signature ou
d’écriture manuscrite, contrôle de procédés industriels...
• Télécommunications et informatique : analyse du signal, élimination du
bruit, reconnaissance de formes (bruits, images, paroles), compression de don-
nées...
• Militaire : guidage des missiles, Drones et avions sans pilotes,...
• Médical : diagnostique automatisé des maladies, et traitement automatique
des informations issues des imageries médicales...
Conclusion
Les réseaux de neurones artificiels sont des techniques de traitement des données
bien comprises et bien maı̂trisées. Ils sont connus pour leur pouvoir d’apprentis-
sage et de généralisation. En effet, ils assurent des fonctions d’identification, de
contrôle ou de filtrage, et étendent les techniques classiques d’automatisation non
linéaire pour aboutir à des solutions plus performantes et robustes. Dans ce cha-
pitre, un idée général est donné sur la notion de réseaux de neurones artificiels,
en passant par la définition, la structure et le fonctionnement et les types d’ap-
prentissage, Les différents types de réseaux sont également présentés avec quelques
domaines d’application. Et pour la suite on traitera au chapitre 2 la régularisation
des réseaux de neurones artificiels, dans le cadre de la résolution du problème de
sur-apprentissage.
34

35. CHAPITRE 2
RÉGULARISATION DES RÉSEAUX DE NEURONES
CONVOLUTIFS
La régularisation est souvent utilisée comme solution du problème de sur-
apprentissage dans le machine learning [18]. Les causes courantes de sur-ajustement
sont :
1. Lorsque le modèle est suffisamment complexe pour commencer à modéliser le
bruit dans les données d’entraı̂nement.
2. Lorsque les données d’apprentissage sont relativement petites et insuffisam-
ment représentables, la distribution sous-jacente échantillonnée à partir du
modèle ne parvient pas à apprendre un mappage généralisable.
La régularisation consiste en différentes techniques et méthodes utilisées pour ré-
soudre le problème du sur-ajustement en réduisant l’erreur de généralisation sans
trop affecter l’erreur d’apprentissage.
on peut classer les techniques de régularisation en trois catégories :
1. Modifier la fonction de perte
• Régularisation L1
• Régularisation L2
• Régularisation de l’entropie
2. Modifier la méthode d’échantillonnage
• Augmentation des données
• Validation croisée K-fold
35

36. 3. Modifier l’algorithme d’apprentissage
• Dropout
• Bruit d’injection
Dans ce chapitre, nous intéressons aux réseaux de neurones convolutifs. Nous com-
mençons d’abord par la régularisation du réseau de neurones artificiels, puis nous
définissons les réseaux de neurones convolutifs, et nous terminons ce chapitre par
la régularisation de ce modèle qui est lié à celui des réseaux de neurones artificiels.
2.1 Régularisation des réseaux de neurones artificiels
Le nombre d’entrées et de sorties dans un réseau est généralement déterminé
par les données d’apprentissage, mais le nombre total M de neurones des couches
intermédiaires et le nombre de ces couches est un hyperparamètre qui doit être
ajusté pour éviter à la fois le sur-ajustement (Over-fitting) et le sous-ajustement
(Under-fitting ). Si le nombre M est choisi très grand, le risque d’over-fitting l’est
aussi. Une manière d’éviter l’over-fitting est alors d’ajouter à la fonction de perte
un terme de régularisation sur les poids. Typiquement, on peut choisir une régu-
larisation quadratique ou L1 [19].
2.1.1 Principe de régularisation
Le but de l’apprentissage automatique est d’inférer un modèle à partir d’une
base d’apprentissage, de manière à ce que ce modèle soit également bien adapté
à de nouvelles données si elles suivent les mêmes lois que les données d’apprentis-
sage. Cette capacité, appelée capacité de généralisation, est mesurée par l’erreur
de généralisation de la méthode considérée.
Notations : Dtrain = {(x(m)
, y(m)
)}m=1,...,M et Dtest = {(x(m)
, y(m)
)}m=M+1,...,M2
deux bases d’entrainement et de test. Que supposées composées de réalisations in-
dépendantes de la même distribution p(x, y). Le réseau est entrainé pour minimiser
l’erreur d’entrainement .
Ltrain(W) =
1
M
M
X
m=1
L(ŷ(x(m)
, W), y(m)
) (2.1)
36

37. Avec ŷ(x, W) la sortie du réseau au point x pour les paramètres W.
On définit l’erreur de test par :
Ltest(W) =
1
M2 − M + 1
M2
X
m=M+1
L(ŷ(x(m)
, W), y(m)
) (2.2)
Le but est donc de choisir les paramètres W afin que Ltrain(W) soit petit et que
Ltest(W) soit du même ordre de grandeur
• Si Ltrain(W) est grand, on dit que le réseau est sous-ajusté (Figure 2.1),
insuffisamment complexe pour représenter les données .
• Si la différence kLtest(W) − Ltrain(W)k est grande, le réseau est sur-ajusté
(Figure 2.1), il colle trop aux données d’entrainement et peu généralisable.
Figure 2.1 – Variation des erreurs en fonction de la complexité du modèle
2.1.2 Méthodes de régularisation
La régularisation est introduite dans l’algorithme pour réduire l’erreur de géné-
ralisation sans perturber l’erreur d’apprentissage. Plusieurs types de régularisation
peuvent être envisagées :
• Pénalisation d’une norme des paramètres dans la fonction de perte Ltrain(W).
On pénalise seulement les poids W.
• Restriction de l’espace des paramètres : on peut par exemple imposer certaines
symétries sur W.
37

38. • Augmentation de données : consiste à augmenter la taille de la base d’ap-
prentissage en lui ajoutant des données obtenues par transformations (ajout
de bruit, transformations géométriques,...) des données de la base de départ.
Les méthodes de régularisation les plus puissantes et les plus utilisées et aussi
pratiques sont :
2.1.2.1 Early stopping
Consiste à entrainer le réseau en utilisant à la fois une base d’entrainement et
une base de test, et à stopper l’entrainement lorsque Ltest(W) (Figure 2.2) se met
à ré-augmenter [20].
Algorithm 1 Early stopping
Légende :
max epochs = nombre maximum d’époques pour s’entraı̂ner.
epoch = époque d’entraı̂nement actuelle .
max epochs no improvement = nombre maximum d’époques sans amélioration des performances
sur l’ensemble de validation pendant lesquelles la formation peut se poursuivre.
best epoque = époque à laquelle les meilleures performances de validation ont été obtenues.
while epoch max epochs do
mettre à jour les paramètres sur l’ensemble de l’entraı̂nement
mesurer les performances sur l’ensemble de validation
if meilleures performances sur l’ensemble de validation then
enregistrer les paramètres du système
best epoch = epoch
else {epoch − best epoch max epochs no improvement}
revenir aux paramètres du système enregistrés
end if
epoch = epoch + 1
end while
38

39. Figure 2.2 – Early stopping
2.1.2.2 Dropout
Consiste à désactiver certains neurones selon une distribution de probabilité à
chaque étape de descente du gradient (Figure 2.3), pour éviter le sur-apprentissage[21].
Algorithm 2 Dropout
Légende :
l= indice de couche.
xl
= entrée de la couche l.
yl
= sortie de la couche l.
bl
= biais.
p = probabilité de Dropout.
Équations sans Dropout pendant l’entraı̂nement :
yl
= Wl
∗ xl
+ bl
xl+1
= f(yl
)
Équations avec Dropout pendant l’entraı̂nement :
rl
∼ Bernoulli(p)
x̃l
= rl
· xl
yl
= Wl
∗ x̃l
+ bl
xl+1
= f(yl
)
Équations sans Dropout lors de la validation / test :
yl
= Wl
∗ xl
+ bl
xl+1
= f(yl
)
Équations avec Dropout lors de la validation / test :
yl
= p ∗ Wl
∗ xl
+ bl
xl+1
= f(yl
)
39

40. Figure 2.3 – Dropout appliqué à un MLP : neurone en noire est désactivé.
2.1.2.3 Régularisation quadratique des poids (Ridge Regression)
La régularisation L2 consiste à ajouter le terme kWk2
2 à la fonction de perte de
la manière suivant :
LR(W) = L(W) +
λ
2
kWk2
2 (2.3)
On va appliquer la descente de gradient sur LR(W), c’est-à-dire :
On a :
∇LR(W) = ∇L(W) + λW
donc la descente de gradient devient :
Wt+1 = Wt − α∇LR(Wt) = (1 − αλ)Wt − α∇L(Wt)
Si W∗
est un minimum local de L, on peut écrire au voisinage de W∗
L(W) ≈ L(W∗
) +
1
2
(W − W∗
)t
HL(W∗
)(W − W∗
)
avec HL la matrice hessienne de L. Ainsi, au voisinage de W∗
, le gradient ∇L est
bien approché par H(W − W∗
) et
∇LR(W) ≈ H(W − W∗
) + λW
donc le minimum local W∗
R correspondant devrait vérifier (en diagonalisant H =
QΛQt
avec Λ = diag(λ1, ..., λn))
W∗
R = (H + λId)−1
HW∗
= Q(Λ + λId)−1
Qt
W∗
En première approximation, le minimum local W∗
R est donc une version de W dans
laquelle on a réduit les coefficients dans la base Q par les quantités λi
λ+λi
.
40

41. 2.1.2.4 Régularisation L1 des poids
La régularisationL1 consiste à ajouter à la fonction de perte le terme pénalisant
kWk1. La fonction de perte devient :
LR(W) = L(W) + λkWk1 (2.4)
On va appliquer la descente de gradient sur LR(W), c’est-à-dire :
On a :
∇LR(W) = ∇L(W) + λsign(W)
donc la descente de gradient devient :
Wt+1 = Wt − α∇LR(Wt) = Wt − α∇L(Wt) − αλsign(Wt)
Si W∗
est un minimum local de L, on peut toujours écrire au voisinage de W∗
L(W) ≈ L(W∗
) +
1
2
(W − W∗
)t
HL(W∗
)(W − W∗
) + λkWk1
Pour donner un peu d’intuition à cette régularisation, on peut supposer (c’est
évidemment faux en général) que la hessienne HL(W∗
) est diagonale avec des
coefficients Hii sur la diagonale. On peut alors réécrire :
∇LR(W) = ∇L(W∗
) +
X
i
1
2
Hii(Wi − W∗
i )2
+ λ|Wi|
Ainsi, le minimum local W∗
R correspondant devrait vérifier :
(W∗
R)i =







max(W∗
i −
λ
Hii
, 0) si W∗
R 0
max(W∗
i +
λ
Hii
, 0) si W∗
R 0
La régularisation par une norme L1 revient donc dans ce cas à appliquer un
seuillage doux au coefficient de W∗
.
2.1.2.5 Comparaison des régularisations L1 et L2
La principale différence entre ces deux règlements est la durée de la pénalité.
mais La régulation L2 ajoute à la fonction d’erreur L(W) le carré de l’amplitude
des poids synaptiques comme terme de pénalité, la régularisation L1 ajoute à la
fonction d’erreur L(W) la valeur absolue de l’amplitude des poids synaptiques
41

42. comme terme de pénalité. Dans les deux cas de régularisation, si λ = 0, alors nous
avons la fonction de coût de base. Si λ est très grand, les poids synaptiques sont
trop augmentés et cela peut conduire à un sous-apprentissage. Choisir le meilleur
λ possible est donc très important.
Dans les deux cas de régularisation L1 et L2, le but est de pénaliser les grands poids
synaptiques. Mais la façon dont les poids diminuent est différente. Dans la régulari-
sation L1, les poids diminuent d’une valeur constante vers 0. Dans la régularisation
L2, ils diminuent de manière proportionnelle au poids. Et donc, lorsqu’un poids
particulier a une grande amplitude, la régularisation L1 réduit considérablement
le poids, contrairement à la régularisation L2. En revanche, quand le poids est
petit, la régularisation L1 réduit le poids beaucoup plus que la régularisation L2.
Le résultat final est que la régularisation L1 tend à concentrer les poids du réseau
sur un très petit nombre de connexions de haute importance, tandis que les autres
poids sont ramenés à zéro. Nous choisissons donc plutôt la régularisation L2 plu-
tôt que la régularisation L1 car en reconnaissance de motifs sur des images, cette
sparsité n’a pas vraiment de sens (le fait de mettre pas mal de poids à zéro). Donc
nous préférons la régularisation L2 qui apporte juste un effet de réduction. Autre-
ment dit la régularisation L2 est invariante. De plus, nous choisissons d’appliquer
une régularisation différenciée en fonction du module de l’architecture neuronal
profond bout-en-bout. Le réseau est en effet deux fois plus régularisé au niveau
du module convolutif (λ = 0, 02) qu’au niveau du module récurrent (λ = 0, 01) [22].
• Question : existe-t-il d’autres méthodes pour éviter le sur-apprentissage ?
La réponse est oui. Il existe deux familles de méthodes pour limiter le sur-apprentissage :
les méthodes passives et les méthodes actives. Les philosophies de ces deux familles
de méthodes sont différentes :
• Les méthodes passives tentent de détecter le sur-apprentissage a posteriori
pour éliminer les mauvais modèles. Parmi les méthodes les plus classiques
figurent l’utilisation d’une base validation au cours de l’apprentissage et me-
sures de critères d’information.
• Les méthodes actives interviennent lors de la phase d’apprentissage pour évi-
ter le sur-ajustement du modèle, par exemple les méthodes de régularisation
que nous avons bien détaillées dans ce chapitre.
42

43. 2.2 Réseaux de neurones convolutifs
Le réseau de neurones convolutifs est un type de réseau de neurones artificiels
qui utilise essentiellement des couches convolutives. Ce type de réseau, apparu
en 1989, est très utile pour le traitement des images. Elle s’inspire fortement du
constat que le filtrage des signaux par convolutions est devenu incontournable
dans le domaine du traitement numérique de l’image. Ce type de réseau présente
également l’avantage d’avoir un nombre très limité de paramètres à entraı̂ner par
rapport à une couche entièrement connectée, ce qui réduit considérablement la
probabilité d’avoir dû sur-entraı̂ner [23].
Un réseau de neurones à convolution est essentiellement composé de 4 parties :
• Convolution
• Non-linéarité (ReLu)
• Pooling
• Classification
Dans ce paragraphe, nous commençons par la description des réseaux de neurones
convolutifs, puis nous définissons les différents types des couches pour formant
ce modèle, et nous passons au paramétrage de ces couches, et nous terminons ce
paragraphe par la régularisation de ce modèle.
Définition 2.2.1 :
• On appelle réseau neuronal convolutif, ou réseau de neurones à convolu-
tion, (Convolutional Neural Network (CNN) un type de réseau de neurones
artificiels utilisé dans la reconnaissance et le traitement des images, et spé-
cialement conçu pour l’analyse des pixels[24].
• Un réseau de neurone à convolution est une forme particulière d’un ré-
seau neuronal multicouches dont l’architecture des connexions est inspirée
de celle du cortex visuel des mammifères.Plus précisément c’est un réseau
profond composé de multiples couches qui sont en générale organisées en
blocs.
43

44. 2.2.1 Types de couches
Un réseau de neurones convolutifs est composé de quatre couches décrire comme
suit [25] :
2.2.1.1 Couche de convolution
La couche convolutive est le composant clé des réseaux de neurones convolu-
tifs, elle constitue toujours au moins leur première couche. Son but est d’identifier
la présence d’un ensemble de caractéristiques dans les images reçues en entrée.
Pour cela, un filtrage par convolution est effectué, le principe est de ”faire glisser”
une fenêtre représentant la caractéristique sur l’image, et de calculer le produit
de convolution entre la caractéristique et chaque portion de l’image scannée (Fi-
gure 2.4). Une caractéristique est alors vue comme un filtre, les deux termes sont
équivalents dans ce contexte.
Figure 2.4 – Schéma du parcours de la fenêtre de filtre sur l’image
• Définition mathématique du produit de convolution
Soient f et g deux fonction réels . Le produit de convolution f ∗g est dont le terme
général est défini par [26] :
f ∗ g(x) =
Z +∞
−∞
f(x − t).g(t)dt =
Z +∞
−∞
f(t).g(x − t)dt (2.5)
aux terme des suites on a :
f ∗ g(n) =
+∞
X
k=−∞
f(n − k).g(k) (2.6)
44

45. • Produit de convolution et transformation de Fourier
La transformation de Fourier d’un produit de convolution s’obtient par multipli-
cation des transformation de Fourier des fonctions :
• Si f et g deux fonctions intégrables alors :
F(f ∗ g) = F(f)F(g) (2.7)
• Si f est intégrable et si g est de carré intégrable, on a aussi :
F(f ∗ g) = F(f)F(g) donc f ∗ g = F−1
(F(f)F(g)) (2.8)
• si f et g sont de carré intégrable alors :
f ∗ g = F−1
(F(f)F(g))f ∗ g = F−1
(F(f)F(g)) (2.9)
où F la transformation de Fourier et F−1
la transformation de Fourier inverse.
• Produit de convolution en deux dimension :
La convolution en deux dimensions notées A ∗ M est une opération qui calculé à
partir :
- d’une matrice d’entrée notée A
- d’une matrice d’un motif (filtre) noté M, qu’il faut nécessairement retourné
(Figure 2.5).
Figure 2.5 – Principe de retourné un filtre.
Ce produit A ∗ M est calculé de la manière suivante (Figure 2.6) :
45

46. • on centre le motif retourné sur la position du coefficient à calculer.
• on multiplie chaque coefficient de A par le coefficient du motif retourné en
face (quitte à ajouter des zéros virtuels sur les bords de A).
• la somme de ces produits donne un coefficient de A ∗ M.
Figure 2.6 – Principe de calcule d’un produit de convolution.
Exemple :
Calculons la convolution A ∗ M définie par :
On commence par retourner M. Pour calculer le premier coefficient de A ∗ M ,
on centre le motif sur le premier coefficient de A, puis on rajoute des zéros virtuels
à gauche et en haut. Ensuite on calcule les produits des coefficients de la matrice
M retournée avec les coefficients de A correspondants, et on les additionne :
0 × 3 + 0 × 0 + 0 × 1 + 0 × 0 + 2 × 1 + 1 × 2 + 0 × 2 + 1 × 0 + 1 × 1
Cette somme vaut 5, c’est le premier coefficient de A ∗ M.
46

47. On continue avec le second coefficient
Et ainsi de suite ,jusqu’à calculer entièrement la matrice A ∗ M
2.2.1.2 Couche de mise en commun (En anglais pooling)
Ce type de couche est souvent placé entre deux couches de convolution, il reçoit
en entrée plusieurs cartes caractéristiques, et s’applique à chacune des opérations
de Pooling [27].
• L’opération de mutualisation (ou sous-échantillonnage) consiste à réduire la
taille des images, tout en préservant leurs caractéristiques importantes. Pour
ce faire, nous découpons l’image en cellules régulières, puis nous gardons la
47

48. valeur maximale à l’intérieur de chaque cellule. En pratique, de petites cellules
carrées sont souvent utilisées pour ne pas perdre trop d’informations. Les
choix les plus courants sont des cellules adjacentes de taille 2 × 2 pixels qui
ne se chevauchent pas, ou des cellules de taille 3 × 3 pixels, séparées les unes
des autres par des pas de 2 pixels. On obtient en sortie le même nombre de
cartes caractéristiques qu’en entrée, mais celles-ci sont beaucoup plus petites.
• La couche de pooling réduit le nombre de paramètres et de calculs dans le
réseau. Cela améliore l’efficacité du réseau et évite le sur-apprentissage.
• la couche de mise en commun rend le réseau moins sensible à la position des
entités, donc qu’une entité soit un peu plus en haut ou en bas, ou même ait
une orientation légèrement différente ne devrait pas entraı̂ner de changement
drastique dans la classification de l’image.
Interprétation mathématique du Pooling
Le Pooling est consiste à transformer une matrice en une matrice plus petite tout
en essayant d’en garder les caractéristiques principales.
Un pooling de taille k transforme une matrice de taille n × p en une matrice de
taille k fois plus petite (Figure 2.7 ). Une sous-matrice de taille k ×k de la matrice
de départ produit un seul coefficient de la matrice d’arrivée [26].
Figure 2.7 – Exemple d’une matrice de taille 4 × 6 avec un pooling de taille 2.
Deux types de pooling sont les plus utilisés dans la littérature :
• Max-pooling de taille k consiste à retenir le maximum de chaque sous-matrice
de taille k × k (Figure 2.8) :
48

49. Figure 2.8 – Exemple de Max-pooling pour une matrice de taille 4 × 6.
• Pooling en moyenne de taille k (average pooling) consiste à retenir la moyenne
des termes de chaque sous-matrice de taille k × k (Figure 2.9) :
Figure 2.9 – Exemple de Average pooling pour une matrice de taille 4 × 6.
Remarque 2.2.2 :
Pour le type de Pooling le max-pooling, qui ne retient que la valeur la plus
élevée par sous-matrice, permet de détecter la présence d’une caractéristique (par
exemple un pixel blanc dans une image noire). De plus la mise en commun prend
en compte en moyenne tous les termes de chaque sous-matrice (par exemple avec
4 pixels d’une image de ciel, la couleur moyenne est retenue).
2.2.1.3 Couche de correction ReLU :
Cet couche permet d’améliorer l’efficacité du traitement en interposant entre
les couches de traitement une couche qui va opérer une fonction mathématique
(fonction d’activation) sur les signaux de sortie [28]. dans ce sens on trouve :
La fonction ReLU (Rectified Linear Units ) réelle non-linéaire définie par :
49

50. ReLU(x) = max(0, x).
Figure 2.10 – Représentation graphique de la fonction ReLu
Cette couche remplace donc toutes les valeurs négatives reçues en entrée par des
zéros (Figure 2.10). Il agit comme une fonction d’activation. Souvent la correction
Relu est préférable, mais il existe d’autres formes :
• La correction par tangente hyperbolique f(x) = tanh(x)
• La correction par la tangente hyperbolique saturante : f(x) = |tanh(x)|
• La correction par la fonction sigmoı̈de f(x) = (1 + e−x
)−1
.
2.2.1.4 Couche fully-connected
La couche entièrement connectée(fully-connected) est toujours la dernière couche
d’un réseau de neurones convolutifs, ce type de couche reçoit un vecteur en entrée
et produit un nouveau vecteur en sortie. Pour ce faire, il applique une combinai-
son linéaire puis éventuellement une fonction d’activation aux valeurs reçues en
entrée[29].
La couche entièrement connectée permet de classer l’image à l’entrée du réseau, elle
renvoie un vecteur de taille N, où N est le nombre de classes dans notre problème
de classification des images. Pour chaque élément du vecteur indique la probabilité
pour l’image d’entrée d’appartenir à une classe.
2.2.2 Architecture d’un réseaux de neurones Convolutifs
L’architecture d’un réseau de neurones convolutifs dépend du nombre de couches,
du nombre d’unités (neurones) par couche et les connexions entre les neurones et
50

51. entre les couches. Le nombre de couches et le nombre de neurones sont souvent
considérés comme des hyperparamètres. Un CNN peut constitue plusieurs étapes
de convolution, ReLu et Pooling. Un choix à respecter est que la fonction de ReLu
doit obligatoirement être appliquée après une étape de convolution afin d’avoir
une réponse non linéaire, mais le Pooling n n’est pas obligatoire [30].
Après avoir parcouru toutes les étapes de convolution, ReLu et Pooling, on peut
passer à la classification des images. Comme dernière étape qui consiste à envoyer
tous les pixels dans un réseau de neurones multicouches. Puisque nous avons pu
récupérer les parties les plus importantes d’une image que nous avons condensée,
la phase de classification sera beaucoup plus efficace que d’utiliser un réseau de
neurones artificiels sans convolution. En général, les réseaux de neurones convo-
lutifs se distinguent en deux parties, l’une est appelée partie de convolution et
l’autre est appelée partie de classification (Figure 2.11).
Figure 2.11 – Architecture d’un réseau de neurones convolutif.
Dans la littérature il existe plusieurs architectures de réseaux de neurones convo-
lutifs, qui ont été largement inversées dans plusieurs applications, parmi ces mo-
dèles nous citons [31] :
• LeNet :
Les premières architecture réussies des réseaux convolutionnels ont été déve-
loppées par Yann LeCun dans les années 1990. De plus, cette architecture est
les plus connu (Figure 2.12), utilisée pour lire les codes postaux, les chiffres,...
51

52. Figure 2.12 – Réseau de neurones convolutif LeNet.
• AlexNet :
AlexN à été développé par Alex Krizhevsky en 2012. Le réseau ayant une
architecture très similaire à celle de LeNet, mais il était plus profond, plus
grand et comportait des couches convolutives empilées les unes sur les autres.
Sont travail est comme suite :
• Diminution progressive de la taille des filtres.
• Diminution progressive de la taille de l’image.
• Augmentation progressive du nombre de filtres.
• Stride puis Max Pooling.
Figure 2.13 – Réseau de neurones convolutif AlexNet .
52

53. • ResNet :
Réseau résiduel développé par Kaiming He et al. en 2015. Il donne des connexions
spéciales et un usage intensif de la normalisation des lots. son architecture ne
contient pas de couches entièrement connectées à la fin du réseau. Res Nets
(Figure 2.14) sont actuellement des modèles de réseaux neuronaux convolu-
tifs de pointe et constituent le choix par défaut pour l’utilisation de ConvNets
dans la pratique.
Figure 2.14 – Réseau de neurones convolutif ResNet .
2.2.3 Paramétrage des couches
Un réseau de neurones convolutif se distingue l’un de l’autre par la façon dont
les couches sont empilées, mais également paramétrées (Table 2.1) [32].
Définition 2.2.3 :
- Paramètre : classiquement, on appelle ”paramètres ” les poids synaptiques.
La valeur des paramètres est déterminée par l’apprentissage. Ils sont donc
liés aux données présentées en entrée lors de l’apprentissage.
- Hyperparamètre : sont des paramètres dont la valeur est déterminée avant
la phase d’apprentissage. Ils sont indépendants des données présentées en
entrée. Ils influencent la façon dont se fera l’apprentissage.
Les paramètres et les hyperparamètres d’un réseaux de neurones à convolution
sont répartis comme suit :
53

54. Les paramètres Les hyperparamètres
Poids de connexions Nombre des couches
Nombre des neurones
Nombre des filtres
Taille des filtres
Pas s
Zero-padding P
Taille des cellules
Table 2.1 – Les paramètres et les hyperparamètres d’un réseaux de neurones convolutifs.
• Les couches de convolution et de pooling ont des hyperparamètres, c’est-à-dire
des paramètres dont vous devez d’abord définir la valeur.
• La taille des cartes de caractéristiques à la sortie des couches de convolution
et de regroupement dépend des hyperparamètres.
• Chaque image (ou feature map) a des dimensions W × H timesD, où W est
sa largeur en pixels, H sa hauteur en pixels et D le nombre de canaux (1 pour
une image en noir et blanc, 3 pour une image en couleur).
• La couche de convolution contient quatre hyperparamètres :
1. Le nombre de filtres K
2. La taille F des filtres : chaque filtre est de dimensions F × F × D pixels.
3. Le pas S avec lequel on fait glisser la fenêtre correspondant au filtre sur
l’image. Par exemple, un pas de 1 signifie qu’on déplace la fenêtre d’un
pixel à la fois
4. zero-padding : un contour noir d’épaisseur P pixels est ajouté à l’image
en entrée du calque. Sans ce contour, les dimensions de sortie sont plus
petites. Ainsi, plus les couches de convolution sont empilées avec
P = 0, plus l’image à l’entrée du réseau rétrécit. On perd donc beaucoup
d’informations rapidement, ce qui rend la tâche d’extraction de fonction-
nalités difficile.
• Pour chaque image de taille W × H × D en entrée, la couche de convolution
renvoie une matrice de dimensions WC × HC × DC, où
WC =
W − F + 2P
S
+ 1 , HC =
H − F + 2P
S
+ 1 et DC = K
54

55. • Le choix P =
F − 1
2
et S = 1 permet ainsi d’obtenir des feature maps de
même largeur et hauteur que celles reçues en entrée.
• La couche de pooling contient seulement deux hyperparamètres :
1. La taille F des cellules : l’image est découpée en cellules carrées de taille
F × F pixels .
2. Le pas S : les cellules sont séparées les unes des autres de S pixels .
• Pour chaque image de taille W ×H×D en entrée, la couche de pooling renvoie
une matrice de dimensions WP × HP × DP , où
WP =
W − F
S
+ 1, HP =
H − F
S
+ 1 et DP = D
• Le choix des hyperparamètres se fait selon un schéma classique
- Le choix pour la couche convolutive, les filtres sont petits et glissés sur
l’image un pixel à la fois. La valeur de remplissage à zéro est choisie
de sorte que la largeur et la hauteur du volume d’entrée ne soient pas
modifiées en sortie. En général, on prend alors F = 3, P = 1, S = 1 ou
F = 5, P = 2, S = 1
- Le choix pour la couche de pooling, F = 2 et S = 2 est un choix judicieux.
Cela permet d’éliminer 75 % des pixels en entrée. On peut également
trouver F = 3 et S = 2 , dans ce cas les cellules se chevauchent. Prendre
des cellules de plus grande taille provoque une perte trop importante
d’informations, et donne de moins bons résultats en pratique.
Remarque 2.2.4 :
Les caractéristiques de la couche de convolution et les poids de la couche
entièrement connectée ne sont pas des hyperparamètres, car ils sont appris par
le réseau de neurones lors de la phase d’apprentissage.
55

56. 2.2.4 Régularisation des réseaux de neurones convolutifs
Pour les réseaux de neurones convolutifs, nous avons deux types de méthodes
de régularisation, des méthodes empiriques qui sont des méthodes pratiques basées
sur l’effet des poids de connexion, et nous avons également des méthodes explicites
qui incluent la taille du réseau et la dégradation du réseau, qui contient les types
les plus importants de régularisation L1 et L2, la régularisation L1 son principe
est de réduire aléatoirement les poids des entrées faibles en ajoutant à la fonction
de perte la norme 1 des poids, le problème que ce genre rencontre est la non
différentiabilité au point zéro, mais pour la régularisation L2 on ajoute la norme
2 des poids à la fonction de perte qui est dérivable sans problème (Figure 2.15),
le but de cette régularisation est de réduire le poids des entrées fortes, ces deux
types de régularisations en termes pratiques ne sont pas encore développés [33].
Figure 2.15 – Comparaison des régularisations de Tikhonov (L2 au carré) et L1 en une dimension.
Les courbes bleues représentent les régularisateurs en fonction de α , et les courbes rouges sont les
dérivés.
2.2.4.1 Méthodes empiriques
• Dropout
Les couches Fully Connected (FC) occupent la majeure partie de la mémoire
de CNN. De plus, le concept de FC crée un problème de mémoire exponen-
tiel appelé sur-ajustement (sur-apprentissage) ralentissant le traitement de
l’information. Pour éviter cela, la méthode de décrochage est utilisée pour
désactiver les neurones de manière aléatoire (avec une probabilité prédéfinie,
56

57. souvent un neurone sur deux) ainsi que les neurones périphériques. Ainsi,
avec moins de neurones, le réseau est plus réactif et peut donc apprendre plus
rapidement. A la fin de la session d’apprentissage, les neurones éteints sont
rallumés (avec leurs poids d’origine). Plus la couche FC est proche de l’image
source, moins les neurones seront éteints.
L’objectif est d’éteindre et de rallumer des neurones au hasard (Figure 2.16),
dans le cadre d’entraı̂nements successifs. Une fois la série d’entraı̂nement ter-
minée, nous rallumons tous les neurones et utilisons le réseau comme d’habi-
tude. Cette technique a montré non seulement un gain en vitesse d’apprentis-
sage, mais en déconnectant les neurones, nous avons également limité les effets
marginaux, rendant le réseau plus robuste et capable de mieux généraliser les
concepts appris [34].
• DropConnect
DropConnect est une évolution du dropout, où l’on ne va plus éteindre un neu-
rone, mais une connexion (synapse), et toujours de manière aléatoire (Figure
2.16). Les résultats sont similaires (vitesse, capacité à généraliser l’appren-
tissage), mais montrent une différence en termes d’évolution des poids des
connexions. Une couche FC avec un DropConnect peut être comparée à une
couche de connexion diffuse [35].
Figure 2.16 – Méthodes de régularisation : A Dropout et B DropConnect.
• Comparaison de Dropout et DropConnect
Dropout consiste à remettre à zéro les sorties des neurones de la couche de
sortie avec une certaine probabilité (généralement 50 %), mais DropConnect
consiste à remettre à zéro les poids dans la couche de sortie avec une cer-
taine probabilité (généralement 50 %), La régularisation par Dropout donne
57

58. globalement de meilleurs résultats que DropConnect [36].
• Pooling stochastique
Le pooling stochastique utilise le même principe que le Max-pooling, mais la
sortie choisie sera prise au hasard, selon une distribution multinomiale définie
en fonction de l’activité de la zone adressée par le pool. En fait, ce système est
similaire à faire du Max-pooling avec un grand nombre de n images similaires,
qui ne varient que par des déformations localisées. On peut aussi considérer
cette méthode comme une adaptation aux déformations élastiques de l’image.
C’est pourquoi cette méthode est très efficace sur les images par exemples
MNIST (base de données des images représentant des chiffres manuscrits). La
force de la mise en commun stochastique est que ses performances augmentent
de façon exponentielle avec le nombre de couches du réseau [37].
2.2.4.2 Méthodes explicites
• Taille du réseau
Le moyen le plus simple de limiter le sur-apprentissage est de limiter le
nombre de couches dans le réseau et de libérer des paramètres réseau libres
(connexions). Cela réduit directement la puissance et le potentiel prédictif du
réseau. Cela équivaut à avoir une norme zéro.
• Dégradation du poids
Le concept est de considérer le vecteur des poids d’un neurone (liste des
poids associés aux signaux entrants), et d’y ajouter un vecteur d’erreur pro-
portionnel à la somme des poids (norme 1) ou au carré des poids (norme 2 ou
euclidienne). Ce vecteur d’erreur peut alors être multiplié par un coefficient
de proportionnalité qui sera augmenté pour pénaliser davantage les vecteurs
de poids élevé [33].
- La régularisation par norme 1 :la spécificité de cette régularisation est de
réduire le poids des entrées aléatoires et faibles et d’augmenter le poids
des entrées importantes. Le système obtenir moins sensible au bruit.
- La régularisation par norme 2 (norme euclidienne) : La spécificité de
cette régularisation est de réduire le poids des entrées fortes, et de forcer
le neurone à mieux prendre en compte les entrées faibles.
58

59. Conclusion
Dans ce chapitre, nous avons décrit les méthodes de régularisation des réseaux
de neurones artificiels notamment les réseaux de neurones convolutifs. Ces der-
niers sont capables d’extraire des caractéristiques des images présentées en entrée
et de classer ces caractéristiques. Ils reposent sur la notion de champs récepteurs,
ils mettent également en œuvre l’idée de partage de poids qui permet de réduire un
grand nombre de paramètres. libre de l’architecture. Ce partage de poids permet
également de réduire les temps de calcul et l’espace mémoire requis, et également
d’améliorer les capacités de généralisation du réseau.
Cependant, les réseaux de neurones convolutifs ont un certain nombre de limita-
tions, d’une part, les hyperparamètres de réseau sont difficiles à évaluer a priori.
En effet, le nombre de couches, le nombre de neurones par couche ou encore les dif-
férentes connexions entre couches sont des éléments cruciaux et essentiellement dé-
terminés par une bonne intuition ou par une succession de tests, de calcul d’erreurs.
Le nombre d’échantillons d’apprentissage est également un élément déterminant,
et il arrive souvent qu’il soit trop faible par rapport au nombre de paramètres
(poids) du réseau. Il existe des solutions comme augmenter artificiellement leur
nombre ou encore réduire le nombre de paramètres libres (en pré-apprenant les
premières couches par exemple).
Dans le chapitre suivant, nous proposerons un modèle CNN pour la classification
des images puis nous interpréterons les résultats obtenus dans la phase d’appren-
tissage et de test et nous discuterons.
59

60. CHAPITRE 3
CLASSIFICATION DES IMAGES PAR LES RÉSEAUX DE
NEURONES CONVOLUTIFS
Introduction
Les réseaux de neurones convolutifs CNN sont utilisés avec succès dans un grand
nombre d’applications. La tâche de reconnaissance de l’écriture manuscrite a été
l’une des premières applications de l’analyse des images de réseaux de neurones
convolutifs. En plus de fournir de bons résultats sur les tâches de détection d’ob-
jets et de classification des images, ils fonctionnent également bien lorsqu’ils sont
appliqués à la reconnaissance faciale, à l’analyse vidéo ou à la reconnaissance de
texte [38].
Dans ce chapitre, nous nous intéressons à l’application des réseaux de neurones
convolutifs à la classification des images, cette application donnant de bons résul-
tats dans le domaine de l’analyse des images grâce à la régularisation des réseaux
de neurones convolutifs.
Nous commencerons par des notions de base sur les images, puis nous définirons
les bases de données sur lesquelles nous allons appliquées des classifications, puis
nous décrirons le principe de validation d’un modèle de classifications, et enfin
nous allons généré des modèle CNNs et que nous allons appliqué sur trois bases
de données MNIST, CIFAR-10 et CIFAR-100.
60

61. 3.1 Notion de base sur les images
Définition 3.1.1 :
• Une image est une représentation plate d’une scène ou d’un objet qui est
généralement situé dans un espace tridimensionnel. C’est le résultat du
contact de la lumière de l’objet qui forme la scène avec un capteur (caméra,
scanner, radiographie, etc.). Il ne s’agit en fait que d’une représentation
spatiale de la lumière [39].
• L’image est considérée comme un ensemble de points auxquels est affec-
tée une grandeur physique (luminance, couleur). Ces grandeurs peuvent
être continues (image analogique) ou bien discrètes (images numériques).
Mathématiquement, l’image représente une fonction continue F, appelée
fonction image, de deux variables spatiales représentées par F(x, y) mesu-
rant la nuance du niveau de gris de l’image au coordonnées (x, y).
La fonction Image F peut se représenter sous la forme suivante :
F : R2
→ R
(x, y) → F(x, y).
Avec R l’ensemble des réelles et x,y deux variables réelles.
3.1.1 Types des images
Il existe trois types de format des images :
3.1.1.1 Image couleur RVB
L’œil humain analyse la couleur à l’aide de trois types de photocellules les cônes.
Ces cellules sont sensibles aux fréquences basses, moyennes ou hautes (rouge, vert,
bleu). Par conséquent, pour représenter la couleur du pixel, nous devons donner
trois nombres, qui correspondent aux doses des trois couleurs de base : rouge, vert
et bleu. Ainsi, une image couleur peut être représentée par trois matrices, chaque
matrice correspondant à une couleur primaire.
61

62. 3.1.1.2 Image d’intensités
C’est une matrice dans laquelle chaque élément est un nombre réel compris
entre 0 (noir) et 1 (blanc). On parle aussi d’images en niveaux de gris, car les
valeurs comprises entre 0 et 1 représentent différents niveaux de gris.
3.1.1.3 Image binaire
Une image binaire est une matrice rectangulaire dans l’élément valant 0 ou 1.
Lors de la visualisation d’une telle image, les 0 sont représentés par du noir et les
1 par du blanc.
3.1.2 Caractéristiques des images
Une image est un ensemble d’informations structurées, caractérisées par plu-
sieurs paramètres. Afin de classer par réseaux de neurones convolutifs, nous nous
intéressons à trois fonctionnalités :
3.1.2.1 Pixel
Le mot pixel vient de l’abréviation de l’expression britannique (picture element),
qui représente l’unité de base de l’image. Tous ces pixels sont contenus dans la
matrice bidimensionnelle qui constitue l’image finale. Chaque pixel est associé à
un niveau de gris ou niveau de couleur codé sur N bits, et représente la luminosité
ou le niveau de couleur de la zone correspondante dans la scène observée. Chaque
pixel est positionné par ses coordonnées x et y.
3.1.2.2 Dimension
C’est la taille de l’image. Il se présente sous la forme d’une matrice. Ses éléments
sont des valeurs numériques. Le nombre de lignes dans cette matrice est multiplié
par le nombre de colonnes pour nous donner le nombre total de pixels dans l’image.
3.1.2.3 Bruit
Le bruit est un phénomène parasite aléatoire (selon une distribution de proba-
bilité connue ou non), il correspond à des perturbations soit du dispositif d’acqui-
sition, soit de la scène observée elle-même [40].
62

63. Les sources de bruit dans une image sont nombreuses et diverses :
• bruits liés aux conditions de prise de vue (bougé, éclairage de la scène).
• bruits liés aux capteurs (appareil numérique de bas de gamme).
• bruits liés à l’échantillonnage.
• bruits liés à la nature de la scène (poussières, rayures).
3.2 Base de données (Dataset)
Dans le domaine de la classification des images par un réseau de neurones
convolutifs il existe plusieurs bases de données disponibles, les plus utilisées sont :
• MNIST :
MNIST (Mixed National Institute of Standards and Technology database)
est une base de données de chiffres manuscrits (Figure 3.1). la base de don-
nées a été téléchargée du site de Yan LeCun et comprend un ensemble d’en-
traı̂nement de 60000 observations et un ensemble test de 10000 observa-
tions.Chacune des images comprises dans le MNIST est de dimensions 28
pixels par 28 pixels et représente un chiffre écrit à la main de 0 à 9 [41].
Figure 3.1 – 9 chiffres écrit à la main provenant du MNIST
63

64. • CIFAR-10 :
La base des images de CIFAR−10 (Figure 3.2) est composée de 60000 images
couleur, chaque image à une taille de 32 × 32, ces images sont réparties en 10
classes, avec 6000 images par classe. Pour cette base on obtient 50000 images
d’apprentissage et 10000 images de test [42].
Figure 3.2 – 10 images aléatoires de chaque classes de CIFAR-10
• CIFAR-100 :
C’est une base d’image qui contient les mêmes caractéristiques que CIFAR−
10, sauf qu’elle possède 100 classes contenant 600 images pour chaque classe.
Il y a 500 images pour l’apprentissage et 100 images pour le test par classe (Fi-
gure 3.3). Les 100 classes du CIFAR−100 sont regroupées en 20 super-classes.
Chaque image est livrée avec une étiquette fine (la classe à laquelle elle appar-
tient) et une étiquette grossière (la super-classe à laquelle elle appartient)[43].
Figure 3.3 – 16 images aléatoires de CIFAR-100
64

65. 3.3 Validation du modèle de classification
Pour évaluer un modèle de classification et détecter le modèle le plus efficace,
nous avons deux manières pour le faire, soit de calculer la matrice de confusion
puis déduire la précision, le rappel et la F-mesure ou de tracer la courbe ROC [44].
3.3.1 Matrice de confusion
La première façon d’évaluer un classifieur consiste à comparer les valeurs ob-
servées de la variable dépendante Y avec les valeurs prédites Ŷ fournies par le
modèle. L’outil préféré est la matrice de confusion.
La matrice de confusion est un tableau de contingence comparant les classes obte-
nues (colonnes) et les classes souhaitées (lignes) pour l’échantillon. Sur la diagonale
principale on retrouve donc les valeurs bien classées, à l’exception de la diagonale
les éléments sont mal classés.
Figure 3.4 – Matrice de confusion dans le cas binaire
• V P sont les vrais positifs, c’est-à-dire les observations qui ont été classées
positives et qui sont réellement positives.
• FP sont les faux positifs, c’est-à-dire les individus classés positifs et qui sont
en réalité des négatifs.
• De la même manière, les FN sont les faux négatifs et V N sont les vrais
négatifs.
Cette matrice permet de déduire les paramètres suivants :
Précision : proportion d’éléments bien classés pour une classe donnée :
Precision =
V P
V P + FP
65

66. Rappel : proportion d’éléments bien classés par rapport au nombre d’éléments de
la classe à prédire :
Rappel =
V P
V P + FN
F-mesure : moyenne harmonique entre la précision et le rappel :
F − mesure =
2 × Precision × Rappel
Precision + Rappel
3.3.2 Courbe Roc
Roc Curve est un graphique qui montre les performances d’un modèle pour
tous les seuils. C’est le taux de vrais positifs versus celui de faux positifs. La
courbe ROC montre ces taux pour différents seuils et Plus cette courbe est éloignée
de la première bissectrice, plus le modèle a une forte capacité de discrimination.
L’indicateur synthétique associé à la courbe ROC est l’aire sous la courbe, c’est
AUC ( Aera under curve). Un modèle de classification fonctionne bien si l’AUC
est proche de 1. Inversement, un modèle de classification ne fait pas de distinction
si l’AUC est proche de 0, 5 [45].
Figure 3.5 – Courbe Roc
3.4 Implémentation
Dans cette section, nous présentons les utiles indispensables que nous allons
utiliser, ainsi que les modèles des réseaux de neurones convolutifs avec lesquels
nous allons classer les images tout en montrant l’importance de la régularisation
Dropout.
66

67. 3.4.1 Outils et les librairies
• TensorFlow
TensorFlow est une bibliothèque d’apprentissage automatique open source,
créée par l’équipe Google Brain en 2011, sous la forme d’un système proprié-
taire dédié aux réseaux de neurones d’apprentissage profond, est une biblio-
thèque logicielle open source pour le calcul numérique à l’aide de graphiques
de flux de données. Les nœuds des graphiques représentent des opérations
mathématiques, tandis que les bords des graphiques représentent les tableaux
multidimensionnels de données (tenseurs) qui circulent entre eux. Cette ar-
chitecture flexible vous permet de déployer des calculs sur un ou plusieurs
processeurs ou GPU sur un ordinateur de bureau, un serveur ou un appareil
mobile sans réécrire le code [46]. Cette bibliothèque permet notamment d’en-
traı̂ner et d’exécuter des réseaux de neurones pour la classification de chiffres
manuscrits, la reconnaissance des images, les inclusions de mots, les réseaux
de neurones récurrents, les modèles séquence à séquence pour la traduction
automatique, ou encore le traitement du langage naturel.
• Keras
Keras est une API de réseaux de neurones de haut niveau, écrite en Python et
capable de s’exécuter sur TensorFlow, CNTK ou Theano. Il a été développé
pour permettre une expérimentation rapide [47].
- Permet un prototypage simple et rapide (convivialité, modularité et ex-
tensibilité).
- Prend en charge les réseaux convolutionnels et les réseaux récurrents,
ainsi que les combinaisons des deux.
- Fonctionne de manière transparente sur CPU et GPU.
• Python
Python est un langage objet interprété de haut niveau, créé au début des
années 90 par Guido Van Rossum au Centrum voorWiskunde à Informatica,
Amsterdam. Python est un outile de programmation simple et puissante. Il
mise à disposition des structures de données puissantes et de haut niveau
et une approche simple mais réelle de la programmation orientée objet. La
syntaxe élégante et le typage dynamique de Python, ajoutés à sa nature in-
terprétée, le rendent idéal pour les scripts et pour le développement rapide
d’applications dans de nombreux domaines et sur la plupart des plates-formes
[48].
67

68. 3.4.2 Configuration de la machine
Dans ce travail, nous avons implémenter tout les codes sources avec un matériel
Configuré comme suit :
- Processeur i7 CPU 4.00 GHZ.
- RAM de taille 4 GO.
- Système d’exploitation Windows 10, 64 bit.
3.4.3 Architecture des modèles de CNNs :
Nous sommes intéressés à travailler sur des modèles de réseaux de neurones
convolutifs avec une régularisation Dropout.
3.4.3.1 L’importance de la régularisation Dropout
Les réseaux de neurones profonds contiennent plusieurs couches non linéaires
cachées, ce qui en fait des modèles très expressifs qui peuvent apprendre des re-
lations très compliquées entre leurs entrées et leurs sorties. La meilleure façon de
régulariser un modèle de taille fixe est de faire la moyenne des prédictions de tous
les réglages de paramètres possibles, en pondérant chaque réglage par sa probabi-
lité postérieure compte tenu des données d’apprentissage.
Dropout est une technique de régularisation. Il empêche le surapprentissage et
fournit un moyen de combiner de manière exponentielle de nombreux réseaux de
neurones différents avec différentes architectures de manière efficace. Le terme Dro-
pout fait référence à la suppression d’unités (cachées et visibles) dans un réseau
de neurones. En éliminant une unité, nous entendons la retirer temporairement du
réseau, ainsi que toutes ses connexions entrantes et sortantes. Le choix des unités
à supprimer est aléatoire. Dans le cas le plus simple, chaque unité est conservée
avec une probabilité fixe p indépendante des autres unités (Figure 3.6), où p peut
être choisi à l’aide d’un ensemble de validation ou peut être simplement fixé à
0.5, ce qui semble être proche de l’optimum pour une grande variété de réseaux
et tâches. Pour les unités d’entrée, cependant, la probabilité optimale de rétention
est généralement plus proche de 1 que de 0.5 [49].
68

69. Figure 3.6 – À gauche : une unité au moment de l’entraı̂nement qui est présente avec une
probabilité p et est connectée aux unités de la couche suivante avec des poids w.
À droite : Au moment du test, l’unité est toujours présente et les poids sont multipliés par p. La
sortie au moment du test est la même que la sortie attendue au moment de l’entraı̂nement.
L’application de Dropout à un réseau de neurones revient à échantillonner un
réseau affiné. Le réseau aminci se compose de toutes les unités qui ont survécu à
l’abandon Un réseau de neurones avec n unités peut être considéré comme une col-
lection de 2n
réseaux de neurones. Ces réseaux partagent tous des poids de sorte
que le nombre total de paramètres soit toujours O(n2
), ou moins. Pour chaque
présentation de chaque cas d’apprentissage, un nouveau réseau aminci est échan-
tillonné et entraı̂né. Ainsi, l’entraı̂nement d’un réseau de neurones avec Dropout
peut être considéré comme entraı̂nant une collection de réseaux éclaircis 2n
avec
un partage de poids étendu, où chaque réseau éclairci est entraı̂né très rarement.
Au moment du test, il n’est pas possible de faire explicitement la moyenne des
prédictions à partir d’un nombre exponentiel de modèles affinés. Cependant, une
méthode de moyenne approximative très simple fonctionne bien dans la pratique.
L’idée est d’utiliser un seul réseau neuronal au moment du test sans Dropout. Les
poids de ce réseau sont des versions réduites des poids entraı̂nés. Si une unité est
conservée avec une probabilité p pendant la formation, les poids sortants de cette
unité sont multipliés par p au moment du test. Cela garantit que pour toute unité
cachée, la sortie attendue (sous la distribution utilisée pour supprimer les unités
lors de la formation temps) est la même que la sortie réelle au moment du test. En
effectuant cette mise à l’échelle, 2n
réseaux avec des poids partagés peuvent être
combinés en un seul réseau de neurones à utiliser au moment du test.
Nous avons constaté que la formation d’un réseau avec Dropout et l’utilisation
de cette méthode de moyenne approximative au moment du test entraı̂nent une
erreur de généralisation significativement plus faible sur une grande variété de
69

70. problèmes de classification par rapport à la formation avec d’autres méthodes de
régularisation. L’idée de Dropout n’est pas limitée aux réseaux neuronaux de type
feed-forward. Elle peut être plus généralement appliquée à des modèles graphiques
tels que les machines de Boltzmann [50].
3.4.3.2 Les modèles proposés
• Premier modèle
Couche d’entrée : Base de données.
Couches cachées :
- Première couche cachées :
Couche de convolution avec 8 filtres de taille 3 × 3, suivie d’une non-
linéarité de type relu, puis d’une couche de Pooling max de taille 2 × 2,
et enfin d’un Dropout avec une probabilité 0.2.
- Deuxième couche cachées :
Couche de convolution avec 16 filtres de taille 3 × 3, suivie d’une non
linéarité de type relu, puis d’une couche de max Pooling de taille 2 × 2,et
en fin une Dropout avec une probabilité 0.2.
Couche de sortie : avant cette couche, on mettre à plat la sortie de la dernier
couche de convolution, puis une couches totalement connecté de taille 100
(nombre totale de neurones), et avec Dropout de probabilité 0.2, et on sortie
une couche de taille 10 avec une fonction d’activation de type Sofmax, pour
avoir notre classification des images.
• Deuxième modèle
On ajoute une troisième couche cachées au premier modèle. Donc ce modèle
est formé par une couche de convolution de 32 filtres de taille 3 × 3, et d’une
non linéarité de type relu, puis d’une couche de max Pooling de taille 2×2,et
finalement un Dropout avec une probabilité 0.2.
• Troisième modèle
Le modèle 3 est le même que le premier modèle avec 1000 neurones au lieu
de 100.
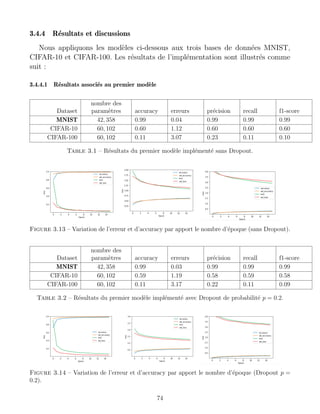
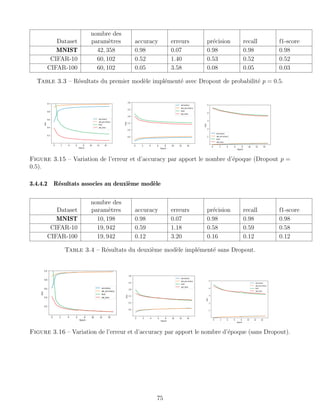
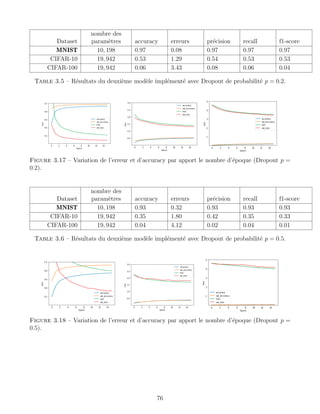
La génération de ces modèle sur python est décrite dans les Figures ( 3.7-3.12) :
70

71. Figure 3.7 – Description numérique du premier modèle appliqué à MNIST.
Figure 3.8 – Description numérique du premier modèle appliqué à CIFAR-10 (CIFAR-100).
71

72. Figure 3.9 – Description numérique du deuxième modèle appliqué à MNIST.
Figure 3.10 – Description numérique du deuxième modèle appliqué à CIFAR-10 (CIFAR-100).
72

73. Figure 3.11 – Description numérique du troisième modèle appliqué à MNIST.
Figure 3.12 – Description numérique du troisième modèle appliqué à CIFAR-10 (CIFAR-100).
73

74. 3.4.4 Résultats et discussions
Nous appliquons les modèles ci-dessous aux trois bases de données MNIST,
CIFAR-10 et CIFAR-100. Les résultats de l’implémentation sont illustrés comme
suit :
3.4.4.1 Résultats associés au premier modèle
Dataset
nombre des
paramètres accuracy erreurs précision recall f1-score
MNIST 42, 358 0.99 0.04 0.99 0.99 0.99
CIFAR-10 60, 102 0.60 1.12 0.60 0.60 0.60
CIFAR-100 60, 102 0.11 3.07 0.23 0.11 0.10
Table 3.1 – Résultats du premier modèle implémenté sans Dropout.
Figure 3.13 – Variation de l’erreur et d’accuracy par apport le nombre d’époque (sans Dropout).
Dataset
nombre des
paramètres accuracy erreurs précision recall f1-score
MNIST 42, 358 0.99 0.03 0.99 0.99 0.99
CIFAR-10 60, 102 0.59 1.19 0.58 0.59 0.58
CIFAR-100 60, 102 0.11 3.17 0.22 0.11 0.09
Table 3.2 – Résultats du premier modèle implémenté avec Dropout de probabilité p = 0.2.
Figure 3.14 – Variation de l’erreur et d’accuracy par apport le nombre d’époque (Dropout p =
0.2).
74

75. Dataset
nombre des
paramètres accuracy erreurs précision recall f1-score
MNIST 42, 358 0.98 0.07 0.98 0.98 0.98
CIFAR-10 60, 102 0.52 1.40 0.53 0.52 0.52
CIFAR-100 60, 102 0.05 3.58 0.08 0.05 0.03
Table 3.3 – Résultats du premier modèle implémenté avec Dropout de probabilité p = 0.5.
Figure 3.15 – Variation de l’erreur et d’accuracy par apport le nombre d’époque (Dropout p =
0.5).
3.4.4.2 Résultats associes au deuxième modèle
Dataset
nombre des
paramètres accuracy erreurs précision recall f1-score
MNIST 10, 198 0.98 0.07 0.98 0.98 0.98
CIFAR-10 19, 942 0.59 1.18 0.58 0.59 0.58
CIFAR-100 19, 942 0.12 3.20 0.16 0.12 0.12
Table 3.4 – Résultats du deuxième modèle implémenté sans Dropout.
Figure 3.16 – Variation de l’erreur et d’accuracy par apport le nombre d’époque (sans Dropout).
75

76. Dataset
nombre des
paramètres accuracy erreurs précision recall f1-score
MNIST 10, 198 0.97 0.08 0.97 0.97 0.97
CIFAR-10 19, 942 0.53 1.29 0.54 0.53 0.53
CIFAR-100 19, 942 0.06 3.43 0.08 0.06 0.04
Table 3.5 – Résultats du deuxième modèle implémenté avec Dropout de probabilité p = 0.2.
Figure 3.17 – Variation de l’erreur et d’accuracy par apport le nombre d’époque (Dropout p =
0.2).
Dataset
nombre des
paramètres accuracy erreurs précision recall f1-score
MNIST 10, 198 0.93 0.32 0.93 0.93 0.93
CIFAR-10 19, 942 0.35 1.80 0.42 0.35 0.33
CIFAR-100 19, 942 0.04 4.12 0.02 0.04 0.01
Table 3.6 – Résultats du deuxième modèle implémenté avec Dropout de probabilité p = 0.5.
Figure 3.18 – Variation de l’erreur et d’accuracy par apport le nombre d’époque (Dropout p =
0.5).
76

77. 3.4.4.3 Résultats associes au troisième modèle
Dataset
nombre des
paramètres accuracy erreurs précision recall f1-score
MNIST 412, 258 0.99 0.03 0.99 0.99 0.99
CIFAR-10 588, 402 0.65 1.00 0.66 0.65 0.65
CIFAR-100 588, 402 0.21 2.84 0.31 0.21 0.19
Table 3.7 – Résultats du troisième modèle implémenté sans Dropout.
Figure 3.19 – Variation de l’erreur et d’accuracy par apport le nombre d’époque sans Dropout.
Dataset
nombre des
paramètres accuracy erreurs précision recall f1-score
MNIST 412, 258 0.99 0.02 0.99 0.99 0.99
CIFAR-10 588, 402 0.66 0.99 0.65 0.66 0.65
CIFAR-100 588, 402 0.12 2.73 0.26 0.12 0.11
Table 3.8 – Résultats du troisième modèle implémenté avec Dropout de probabilité p = 0.2.
Figure 3.20 – Variation de l’erreur et d’accuracy par apport le nombre d’époque (Dropout p =
0.2).
77

78. Dataset
nombre des
paramètres accuracy erreurs précision recall f1-score
MNIST 412, 258 0.99 0.04 0.99 0.99 0.99
CIFAR-10 588, 402 0.54 1.28 0.57 0.54 0.53
CIFAR-100 588, 402 0.06 3.16 0.09 0.06 0.03
Table 3.9 – Résultats du troisième modèle implémenté avec Dropout de probabilité p = 0.5.
Figure 3.21 – Variation de l’erreur et d’accuracy par apport le nombre d’époque (Dropout p =
0.5)
3.4.4.4 Discussions
Remarque 3.4.1 :
On remarque en générale que l’erreur et la précision du classement avec Dro-
pout, plus d’erreur et moins de précision que le classement sans Dropout sauf
pour MNIST.
cette différence s’explique par l’effet de régularisation, plus le réseau est régularisé
cela fera moins de surapprentissage mais il aura plus de difficulté à modéliser
la bonne fonction de précision. Pour le Dataset MNIST il y a en effet un effet
de régularisation qui donne bien de meilleurs résultats de classification, on peut
conclure que le modèle de CNNs avec Dropout comme régularisation est bien
adapté aux données MNIST.
Remarque 3.4.2 :
noter que lorsque le nombre de couches augmente, le nombre des paramètres
de réseau diminue, de même pour l’erreur et la précision.
78

79. • La diminution du paramètre est due à la corrélation du nombre du paramètre
avec le nombre de couches et la taille de la filtres. le nombre du paramètre
pour une couche convolutive par exemple, et donne par la relation
suivante :
n.kx.ky + 1
Avec : n Nombre des couches, (kx, ky) Taille de filtres.
• La diminution de l’erreur et de la précision est due à la complexité du modèle,
l’ajout de couches cachées dans un réseau de neurones convolutifs signifie
généralement une augmentation de sa complexité.
Remarque 3.4.3 :
Le nombre de paramètres augmente en raison d’une augmentation du nombre
de neurones, nous remarquons que plus de neurones signifient plus de précision
et moins d’erreurs.
Nous expliquons cette remarque par, lorsque l’on ajoute le nombre de neurones,
cela signifie automatiquement une augmentation des poids de connexion, donc plus
de paramètres. De plus, ce résultat pour la régularisation est parfait.
Remarque 3.4.4 :
On remarque que pour le changement de probabilité de Dropout, plus de pro-
babilité, plus de régularité ce qui donne des résultats moins de sur-apprentissage
ce qui donnera directement moins de précision.
Conclusion
De toutes ces analyses que nous avons faites nous pouvons conclure que l’effet de
la régularisation est plus fructueux pour éviter le sur-apprentissage quel que soit le
type de régularisation et malgré toute ces confusion au niveau de la précision, reste
l’outil disponible pour le moment pour limiter le problème de sur-apprentissage
au domaine du machine learning, d’autre part, on peut aussi voir que le Dataset
qui répond positivement à son changement de paramètres et des hyperparamètres
du modèle de CNNs pour avoir la meilleure classification qui soit l’ensemble de
données MNIST avec une moyenne de précision égale à 97,7 %.
79

80. CONCLUSION
Les réseaux de neurones artificielles et notamment les réseaux de neurones
convolutifs sont devenus aujourd’hui l’alternative la plus privilégiée pour plusieurs
applications, en particulier celles relatives à la classification des images. Ces mo-
dèles, comme tous les modèles de machine learning, souffrent du problème de sur-
apprentissage qui reste jusqu’à nos jours l’un des grands défis des chercheurs dans
ce champs. Plusieurs techniques ont été utilisées pour surmonter cette probléma-
tique, les plus investies aux réseaux de neurones artificielles sont les régularisation
L1, L2 et la technique Dropout-Dropconnect pour les modèles convolutifs. Dans ce
rapport, nous avons commencé tout d’abord par décrire les réseaux de neurones
artificielles, leurs fonctionnement ainsi que leurs modes d’apprentissage tout en
expliquant le problème de sur-apprentissage. Ensuite, dans le deuxième chapitre,
nous avons décrit la méthode de régularisation ainsi que ses versions et notam-
ment celle de Dropout appliquée aux réseaux de neurones convolutifs. Finalement,
les CNNs ont été appliquées avec succès sur la classification des images et ceci
à travers plusieurs expérimentations numériques qui ont prouvé l’importance de
ces modèles en terme de la qualité de classification d’une part et la régularisation
d’autre part.
80

81. BIBLIOGRAPHIE
[1] McCulloch, W. S., Pitts, W. (1943). A logical calculus of the ideas immanent
in nervous activity. The bulletin of mathematical biophysics, 5(4), 115-133.
[2] Rosenblatt, F. (1962). Principles of neurodynamics.
[3] Minsky, M., Papert, S. A., Bottou, L. (2017). Perceptrons : An introduction to
computational geometry. MIT press.
[4] Hopfield, J. J. (1982). Neural networks and physical systems with emergent col-
lective computational abilities. Proceedings of the national academy of sciences,
79(8), 2554-2558.
[5] Werbos, P. (1974). Beyond regression : new fools for prediction and analysis in
the behavioral sciences. PhD thesis, Harvard University
[6] Rumelhart, D. E., McClelland, J. L., PDP Research Group. (1987). Parallel
distributed processing (Vol. 1, p. 184). Cambridge, MA : MIT press.
[7] Y. LeCun, B. Boser, J. S. Denker, D. Henderson, R. E. Howard, W. Hub-
bard, et al., ”Handwritten digit recognition with a back-propagation network”,
Advances in Neural Information Processing Systems 2 (NIPS’89), 1990.
[8] C. Touzet, Les Réseaux de Neurones Artificiels, 1992
[9] M.Rima, Apprentissage des réseaux de neurones MLP par une méthode hybride
à base d’une métaheuristique, Mémoire en électronique, Université OEB, 2019
[10] M.T. Khadir, Les Réseaux de Neurones Artificiels, 2005
[11] Yann MORERE, Les Réseaux de Neurones Récurrents , 1998
81

82. [12] H. Abdi,Neural Network,M. Lewis-Beck, A. Brymanet T. Futing
(Eds.),Encyclopedia of Social Sciences Research Methods, 2003
[13] M.Parizeau, Réseaux de neurones, 2004
[14] B.Cirstea, Contributions à la reconnaissance de l’écriture manuscrite en utili-
sant des réseaux de neurones profonds et le calcul quantique, Thèse de Doctorat
spécialité Signal et Image, 2018
[15] J.Delon,Introduction aux réseaux de neurones et à l’apprentissage, 2018
[16] https : //www.saagie.com/fr/blog/surapprentissage − vos − predictions −
sont − elles − correctes/
[17] M.Sila,Les Réseaux de neurones artificiels, Mémoire en Électronique, 2006
[18] Y.Bannani, Artificiel Neural Network, 2020
[19] Gallinari et Cibas,Practical complexity control in multilayer perceptrons, 1999
[20] Bogdan-Ionut Cirstea, Contributions to handwriting recognition using deep
neural networks and quantum computing, 2018
[21] Yoshua Bengio, Dropout : A Simple Way to Prevent Neural Networks from
Overfitting, 2014
[22] CAROLINE ETIENNE, Apprentissage profond appliqué à la reconnaissance
des émotions dans la voix, 2019
[23] A. Krizhevsky, I. Sutskever, and G. E. Hinton, Imagenet classification with
deep convolutional neural networks, in NIPS, 2012
[24] Jianxin Wu, Introduction to Convolutional Neural Networks, 2017
[25] F.BARREIRO LINDO,Interprétation des images basée sur la technologie des
réseaux de neurones, HEG-GE, 2018
[26] A.Bodin et F.Recher, Livre”Deep Math”
[27] Hossein Gholamalinezhad, Hossein Khosravi, Pooling Methods in Deep Neural
Networks, a Review, 2009
[28] https : //datasciencetoday.net/index.php/en − us/deep − learning/173 −
les − reseaux − de − neurones − convolutifs
82

83. [29] https : //www.oreilly.com/library/view/tensorflow − for −
deep/9781491980446/ch04.html
[30] Deshpande,Towards Unified Data and Lifecycle Management for Deep Lear-
ning, 2016
[31] https : //towardsdatascience.com/illustrated − 10 − cnn − architectures −
95d78ace614d
[32] B.Ghennam ,S.Smara, Les réseaux de neurone convolutionel (CNN) pour la
classification des images associées aux places de stationnement d’un parc de
véhicule, Mémoire en informatique ,2019
[33] Julien Mairal,Sparse coding for machine learning, image processing and com-
puter vision, 2011
[34] Jason Brownlee ,A Gentle Introduction to Dropout for Regularizing Deep Neu-
ral Networks, 2018
[35] Li Wan, Matthew, Sixin Zhang, Yann LeCun,Rob Fergus, Regularization of
Neural Networks using DropConnect, 2013
[36] Evgeny A. Smirnov*, Denis M. Timoshenko, Serge N. Andrianov, Comparison
of Regularization Methods for ImageNet Classification with Deep Convolutio-
nal Neural Networks, 2014
[37] Matthew D. Zeiler, Rob Fergus, Stochastic Pooling for Regularization of Deep
Convolutional Neural Networks, 2013
[38] Bishop - Pattern Recognition And Machine Learning - Springer 2006
[39] H.Naciri, N.Chaoui,Conception et Réalisation d’un système automatique
d’identification des empreintes digitales, Mémoire de PFE, Université de Tlem-
cen, 2003
[40] Rafael C.Gonzalez et Richard E.Woods ,Digital Image Processing, Pearson
Education Inc, 2008
[41] http ://yann.lecun.com/exdb/mnist/
[42] https ://www.cs.toronto.edu/ kriz/cifar.html
[43] https ://www.tensorflow.org/datasets/catalog/cifar100
83

84. [44] B.Ghennan, S.Smara, Les réseaux de neurone convolutionel (CNN) pour la
classification des images associées aux places de stationnement d’un parc de
véhicule, 2019
[45] Hoo, Z.H. orcid.org/0000-0002-7067-3783, Candlish, J. and Teare, M.D.
(2017) What is an ROC curve ? Emergency Medicine Journal. ISSN 1472-0205
[46] https ://www.tensorflow.org/overview/ ?hl=fr
[47] https ://keras.io/api/metrics/
[48] https ://www.python.org/
[49] Lei Jimmy Ba, Brendan Frey, Adaptive dropout for training deep neural net-
works, 2013
[50] Yoshua Bengio, Dropout : A Simple Way to Prevent Neural Networks from
Overfitting, 2014
84