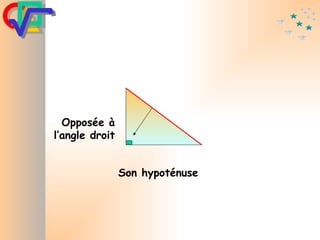
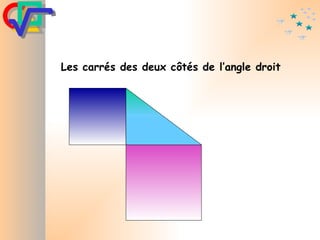
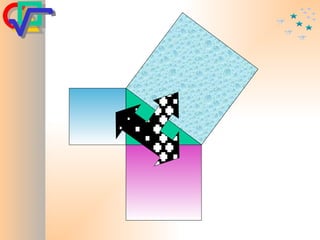
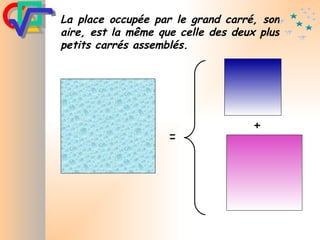
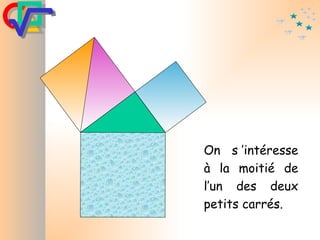
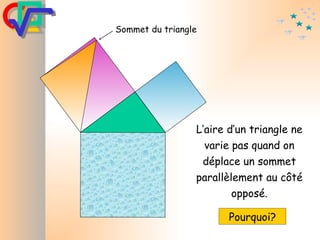
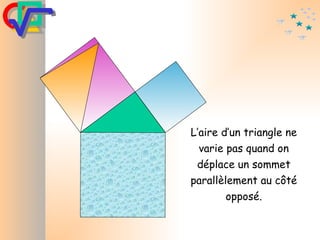
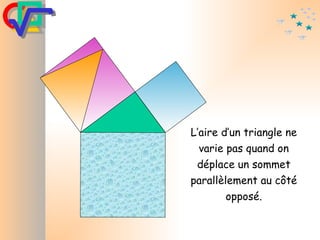
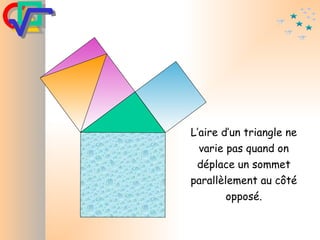
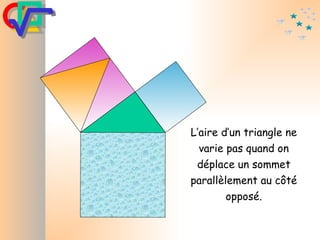
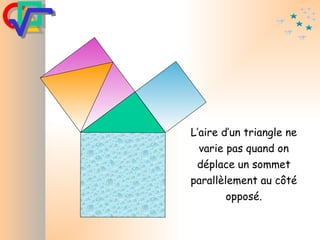
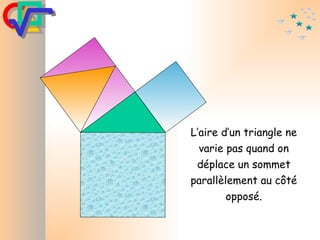
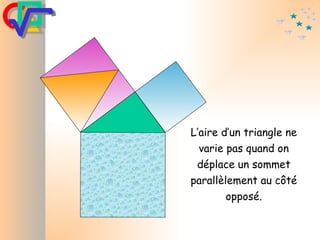
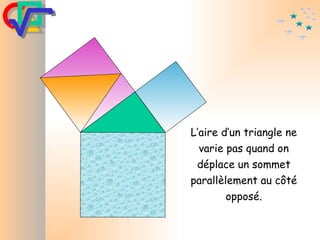
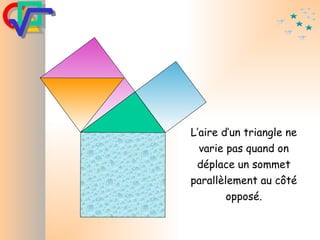
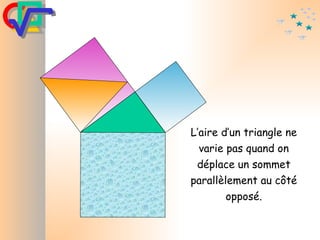
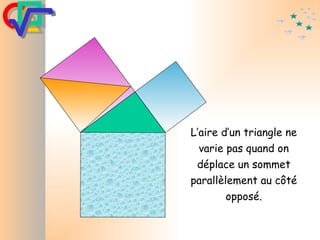
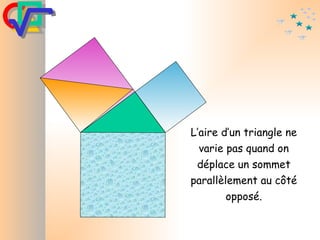
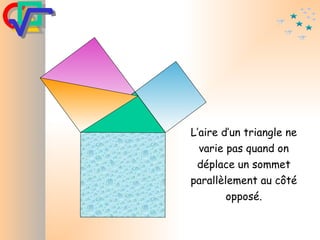
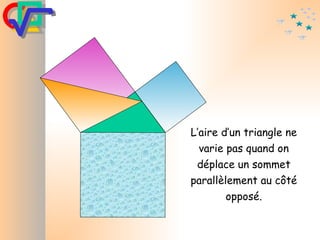
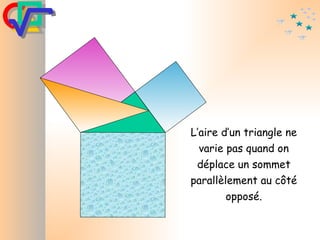
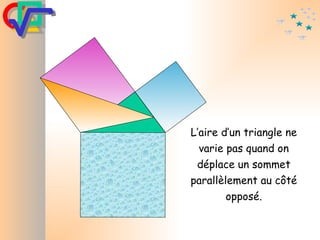
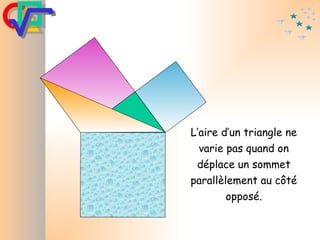
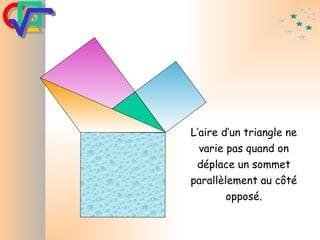
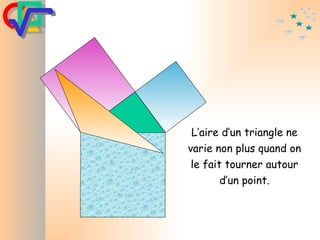
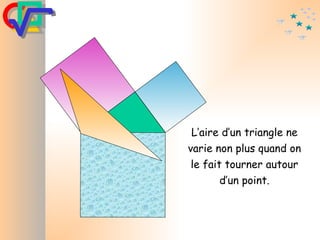
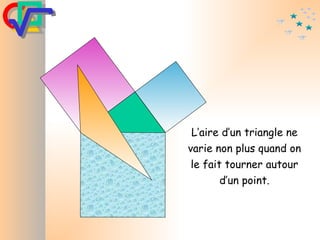
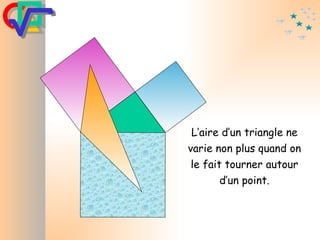
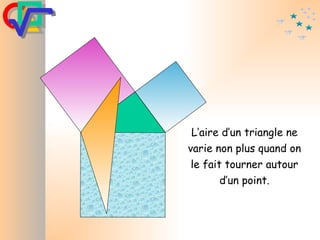
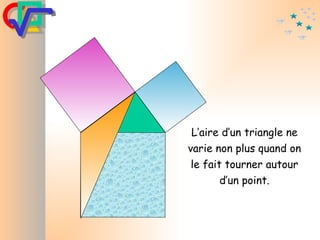
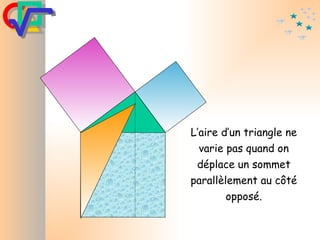
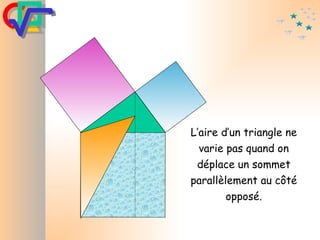
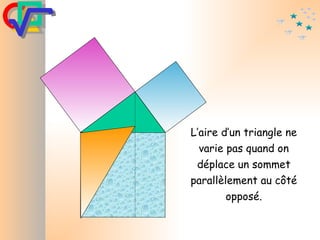
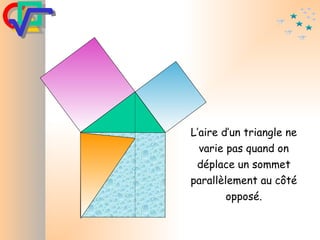
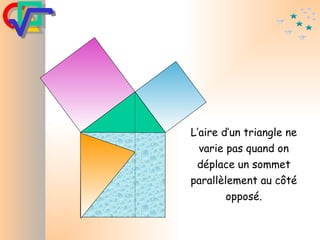
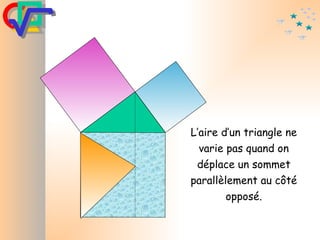
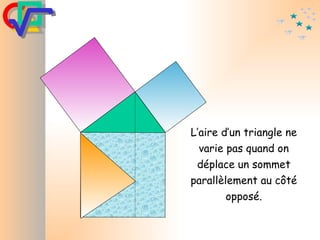
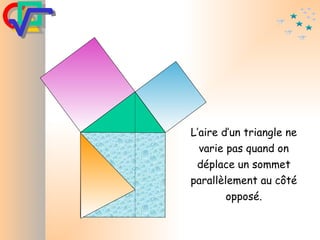
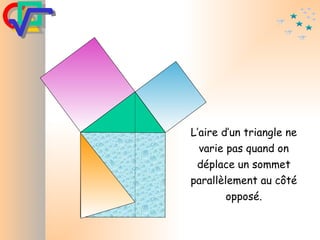
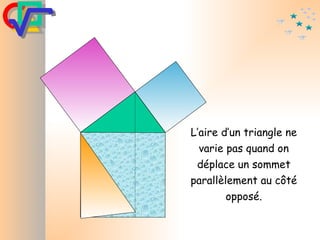
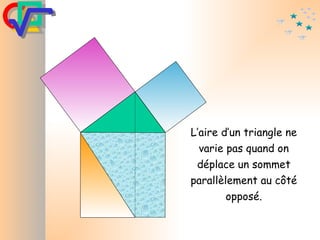
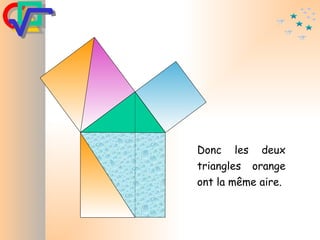
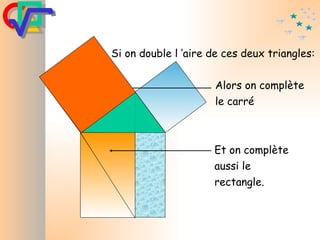
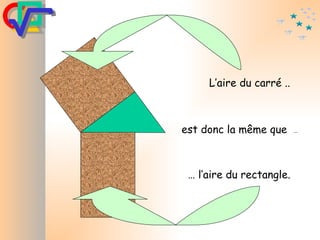
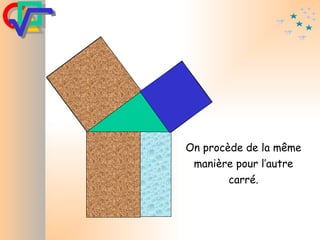
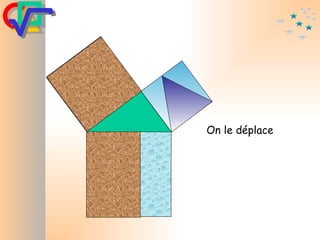
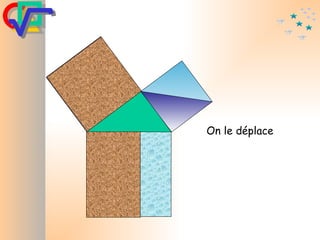
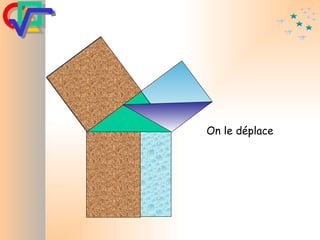
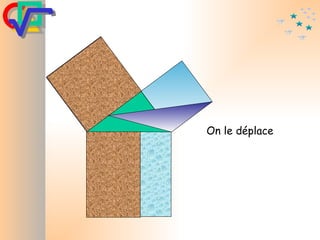
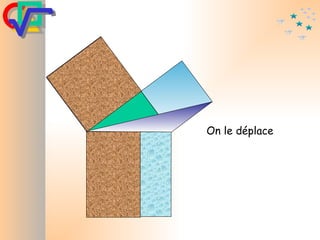
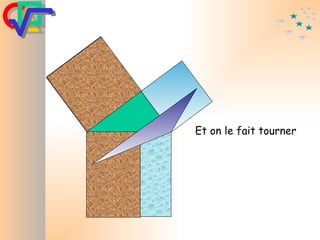
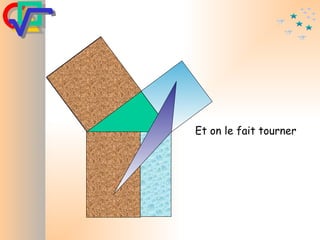
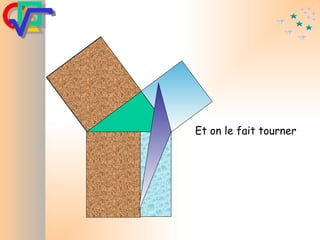
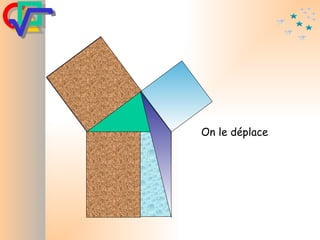
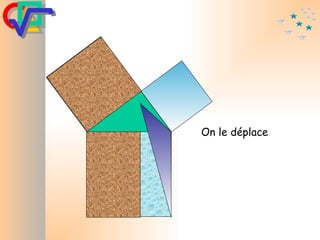
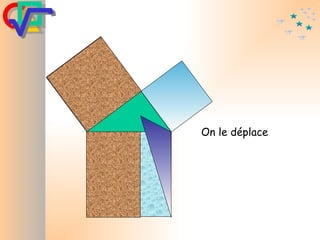
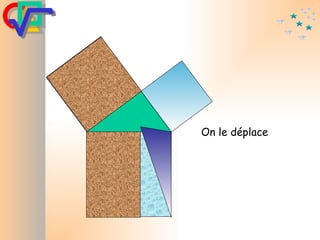
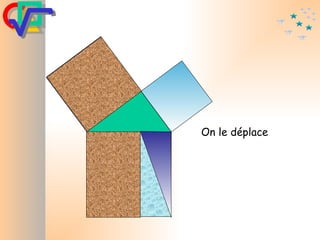
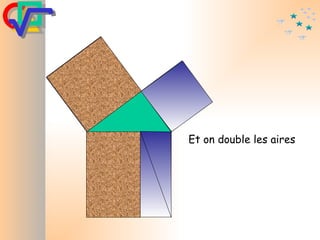
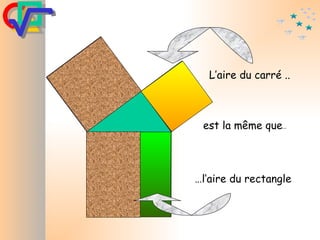
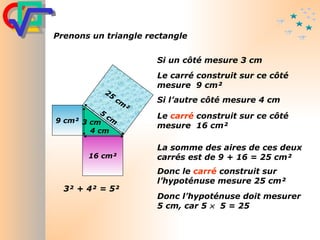
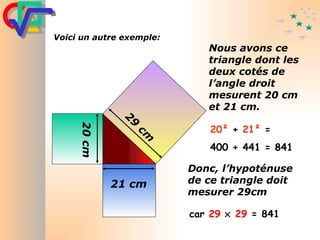
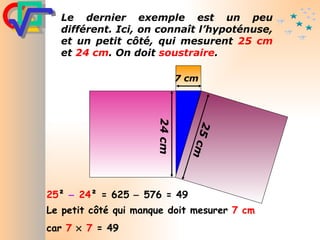
Le document traite du théorème de Pythagore, qui établit que dans un triangle rectangle, le carré de l'hypoténuse est égal à la somme des carrés des deux autres côtés. Il inclut des démonstrations visuelles et des exemples pratiques pour illustrer son application, ainsi qu'une brève histoire de sa découverte par Pythagore et d'autres civilisations antérieures. Enfin, il mentionne les triplets pythagoriciens, qui sont des ensembles de longueurs d'entiers pouvant former des triangles rectangles.

1. Le t h é o r è m e de P y t h a g o r e Francisca Bravo Lucas

2. Nous avons ici un triangle rectangle

3. Un triangle rectangle est un triangle qui contient un angle droit, c’est à dire, un angle qui mesure 90º. 90º

4. Son hypoténuse Opposée à l’angle droit

5. Si on trace deux côtés perpendiculaires Le triangle est formé Le troisième côté, l’hypoténuse, nous est imposé par la construction Donc, sa longueur dépend des longueurs choisies pour les deux premiers côtés. Mais de quelle manière? C’est le sujet que l’on va traiter aujourd’hui.

6. Le carré de l’hypoténuse est formé sur le côté de l'hypoténuse

7. Les carrés des deux côtés de l’angle droit

9. + La place occupée par le grand carré, son aire, est la même que celle des deux plus petits carrés assemblés. =

10. Théorème de Pythagore La place occupée par le grand carré, son aire, est la même que celle des deux plus petits carrés assemblés. En langage mathématique : Le carré de l ’hypoténuse est égal à la somme des carrés des deux autres côtés. X² + Y² = Z² x y z

11. Comment cette règle est-elle possible?

12. Voici la démonstration!

13. On s ’intéresse à la moitié de l’un des deux petits carrés.

14. L’aire d’un triangle ne varie pas quand on déplace un sommet parallèlement au côté opposé. Pourquoi? Sommet du triangle

15. L’aire d’un triangle ne varie pas quand on déplace un sommet parallèlement au côté opposé.

16. L’aire d’un triangle ne varie pas quand on déplace un sommet parallèlement au côté opposé.

17. L’aire d’un triangle ne varie pas quand on déplace un sommet parallèlement au côté opposé.

18. L’aire d’un triangle ne varie pas quand on déplace un sommet parallèlement au côté opposé.

19. L’aire d’un triangle ne varie pas quand on déplace un sommet parallèlement au côté opposé.

20. L’aire d’un triangle ne varie pas quand on déplace un sommet parallèlement au côté opposé.

21. L’aire d’un triangle ne varie pas quand on déplace un sommet parallèlement au côté opposé.

22. L’aire d’un triangle ne varie pas quand on déplace un sommet parallèlement au côté opposé.

23. L’aire d’un triangle ne varie pas quand on déplace un sommet parallèlement au côté opposé.

24. L’aire d’un triangle ne varie pas quand on déplace un sommet parallèlement au côté opposé.

25. L’aire d’un triangle ne varie pas quand on déplace un sommet parallèlement au côté opposé.

26. L’aire d’un triangle ne varie pas quand on déplace un sommet parallèlement au côté opposé.

27. L’aire d’un triangle ne varie pas quand on déplace un sommet parallèlement au côté opposé.

28. L’aire d’un triangle ne varie pas quand on déplace un sommet parallèlement au côté opposé.

29. L’aire d’un triangle ne varie pas quand on déplace un sommet parallèlement au côté opposé.

30. L’aire d’un triangle ne varie pas quand on déplace un sommet parallèlement au côté opposé.

31. L’aire d’un triangle ne varie pas quand on déplace un sommet parallèlement au côté opposé.

32. L’aire d’un triangle ne varie pas quand on déplace un sommet parallèlement au côté opposé.

33. L’aire d’un triangle ne varie non plus quand on le fait tourner autour d’un point.

34. L’aire d’un triangle ne varie non plus quand on le fait tourner autour d’un point.

35. L’aire d’un triangle ne varie non plus quand on le fait tourner autour d’un point.

36. L’aire d’un triangle ne varie non plus quand on le fait tourner autour d’un point.

37. L’aire d’un triangle ne varie non plus quand on le fait tourner autour d’un point.

38. L’aire d’un triangle ne varie non plus quand on le fait tourner autour d’un point.

39. L’aire d’un triangle ne varie pas quand on déplace un sommet parallèlement au côté opposé.

40. L’aire d’un triangle ne varie pas quand on déplace un sommet parallèlement au côté opposé.

41. L’aire d’un triangle ne varie pas quand on déplace un sommet parallèlement au côté opposé.

42. L’aire d’un triangle ne varie pas quand on déplace un sommet parallèlement au côté opposé.

43. L’aire d’un triangle ne varie pas quand on déplace un sommet parallèlement au côté opposé.

44. L’aire d’un triangle ne varie pas quand on déplace un sommet parallèlement au côté opposé.

45. L’aire d’un triangle ne varie pas quand on déplace un sommet parallèlement au côté opposé.

46. L’aire d’un triangle ne varie pas quand on déplace un sommet parallèlement au côté opposé.

47. L’aire d’un triangle ne varie pas quand on déplace un sommet parallèlement au côté opposé.

48. L’aire d’un triangle ne varie pas quand on déplace un sommet parallèlement au côté opposé.

49. L’aire d’un triangle ne varie pas quand on déplace un sommet parallèlement au côté opposé.

50. Donc les deux triangles orange ont la même aire.

51. Si on double l ’aire de ces deux triangles: Alors on complète le carré Et on complète aussi le rectangle.

52. L’aire du carré .. … l’aire du rectangle. est donc la même que …

53. On procède de la même manière pour l’autre carré.

54. On le déplace

55. On le déplace

56. On le déplace

57. On le déplace

58. On le déplace

59. Et on le fait tourner

60. Et on le fait tourner

61. Et on le fait tourner

62. On le déplace

63. On le déplace

64. On le déplace

65. On le déplace

66. On le déplace

67. Et on double les aires

68. L’aire du carré .. … l’aire du rectangle est la même que …

69. Donc, finalement, le grand carré est rempli par les deux petits, comme on voulait démontrer.

70. Quelques exemples d’utilisation de la propriété de Pythagore

71. Prenons un triangle rectangle 25 cm² Si un côté mesure 3 cm Le carré construit sur ce côté mesure 9 cm² 9 cm² Si l’autre côté mesure 4 cm Le carré construit sur ce côté mesure 16 cm² 16 cm² La somme des aires de ces deux carrés est de 9 + 16 = 25 cm² Donc le carré construit sur l’hypoténuse mesure 25 cm² Donc l’hypoténuse doit mesurer 5 cm, car 5  5 = 25 3² + 4² = 5² 3 cm 4 cm 5 cm 3 cm 4 cm

72. 20² + 21² = 400 + 441 = 841 car 29  29 = 841 Voici un autre exemple : Nous avons ce triangle dont les deux cotés de l’angle droit mesurent 20 cm et 21 cm. Donc, l’hypoténuse de ce triangle doit mesurer 29cm 21 cm 20 cm 29 cm

73. 25 ²  24 ² = 625  576 = 49 Le petit côté qui manque doit mesurer 7 cm car 7  7 = 49 Le dernier exemple est un peu différent. Ici, on connaît l’hypoténuse, et un petit côté, qui mesurent 25 cm et 24 cm . On doit soustraire . 24 cm 25 cm 7 cm

74. Ce sont des exemples de trois longueurs entières qui permettent de construire des triangles rectangles. On les appelle des triplets Pythagoriciens. (3, 4, 5) (20, 21, 29) (7, 24, 25) 3 cm 29 cm 4 cm 5 cm 21 cm 7 cm 25 cm 24 cm 20 cm

75. Qu’est-ce qu’une racine carrée? Dans un triangle rectangle dont les deux côtés de l’angle droit mesurent 4 cm et 7 cm On calcule la longueur de l’hypoténuse par la relation de Pythagore: h² = 4² + 7² = 16 + 49 = 65 Pour connaître la valeur de h, on cherche un nombre dont le carré est égal à 65. Il n ’existe pas de nombre entier qui réponde à cette situation. Par définition, on appelle «racine carrée» de 65 le nombre cherché. On le note 7 cm 4 cm h

76. UNE BRÈVE HISTOIRE DU THÉORÈME DE PYTHAGORE

77. Pythagore Le théorème de Pythagore doit son nom au mathématicien grec Pythagore, né à Samos (Grèce) vers -570 avant J.C . Toutefois, il n'existe aucun écrit de Pythagore. Il aurait vécu à Crotone au sud de l'actuelle Italie et y aurait fondé une école, l'école des pythagoriciens. De nombreux résultats élémentaires de géométrie leur sont attribués . Pythagore vu par Raphaël

78. LE THÉORÈME DE PYTHAGORE Le théorème de Pythagore n'est en fait pas une découverte de Pythagore , il était déjà connu sur des cas particuliers par les chinois et les babyloniens 1000 ans avant lui. La Columbia Institut conserve la célèbre tablette d’argile qui présente ce théorème. Elle est écrite en caractères cunéiformes et est baptisée Plimpton 322.

79. LE THÉORÈME DE PYTHAGORE Les Egyptiens connaissaient aussi le théorème. Ils utilisaient la corde à 13 nœuds (régulièrement répartis) qui une fois tendue formait le triangle rectangle 3 ; 4 ; 5 et permettait d’obtenir un angle droit entre deux «longueurs». Corde qui sera encore utilisée par les maçons du XXe siècle pour s’assurer de la perpendicularité des murs. Cependant, les pythagoriciens généralisent le théorème pour tout triangle rectangle. La première preuve écrite du théorème de Pythagore date du IV e siècle avant JC. C'est Euclide qui l'a donnée dans le livre I de ses Éléments : c'est une œuvre majeure dans l'histoire des mathématiques.

80. Fin Clique là bas